-
PDF
- Split View
-
Views
-
Cite
Cite
T. Borkovits, T. Hajdu, J. Sztakovics, S. Rappaport, A. Levine, I. B. Bíró, P. Klagyivik, A comprehensive study of the Kepler triples via eclipse timing, Monthly Notices of the Royal Astronomical Society, Volume 455, Issue 4, 01 February 2016, Pages 4136–4165, https://doi.org/10.1093/mnras/stv2530
Close - Share Icon Share
Abstract
We produce and analyse eclipse time variation (ETV) curves for some 2600 Kepler binaries. We find good to excellent evidence for a third body in 222 systems via either the light-travel-time (LTTE) or dynamical effect delays. Approximately half of these systems have been discussed in previous work, while the rest are newly reported here. Via detailed analysis of the ETV curves using high-level analytic approximations, we are able to extract system masses and information about the three-dimensional characteristics of the triple for 62 systems which exhibit both LTTE and dynamical delays; for the remaining 160 systems, we give improved LTTE solutions. New techniques of pre-processing the flux time series are applied to eliminate false positive triples and to enhance the ETV curves. The set of triples with outer orbital periods shorter than ∼2000 d is now sufficiently numerous for meaningful statistical analysis. We find that (i) there is a peak near im ≃ 40° in the distribution of the triple versus inner binary mutual inclination angles that provides strong confirmation of the operation of Kozai–Lidov cycles with tidal friction; (ii) the median eccentricity of the third-body orbits is e2 = 0.35; (iii) there is a deficit of triple systems with binary periods ≲1 d and outer periods between ∼50 and 200 d which might help guide the refinement of theories of the formation and evolution of close binaries; and (iv) the substantial fraction of Kepler binaries which have third-body companions is consistent with a very large fraction of all binaries being part of triples.
1 INTRODUCTION
The analysis of eclipse time variations (ETVs) via O−C (observed minus calculated) diagrams is a powerful tool for the investigation of period variations in eclipsing binary (EB) systems, and, therefore, has been used in many EB studies over more than a century. ETVs may arise from different causes that act on various time-scales with various amplitudes. It follows that O−C diagrams may show a wide range of variational forms. The causes may be either physical, i.e. connected to a real variation of the orbital period, or merely apparent.
Long-term physical ETVs mainly occur as a result of evolutionary effects such as mass exchange between the binary components, wind-driven mass-loss, magnetic braking, tidal dissipation, or even gravitational radiation. Often the characteristic time-scale of the phenomenon substantially exceeds the entire period of human EB observations. Generally in each such case, the ETVs are manifest as a slow, constant-rate variation of the orbital period which results in a quadratic O−C pattern (for the strict analytic forms of some of the listed effects on the ETV, see Nanouris et al. 2011, 2015). Shorter time-scale physical ETVs can arise, e.g., from magnetic activity (see, e.g., Hall 1989; Applegate 1992; Lanza & Rodonò 2002) or from the dynamical effects of a close companion star on a binary orbit (Söderhjelm 1975; Borkovits et al. 2015). These shorter time-scale effects tend to produce periodic or, at least, quasi-periodic ETV behaviour.
The two most well-known classes of apparent orbital period changes leading to ETVs are the light-travel time effect (LTTE), caused by the changing distance of a binary in a hierarchical multiple-star system, and the apsidal motion effect (AME) which may be seen in eccentric EBs. Apart from the extremely compact triples which were investigated by Borkovits et al. (2015), these two phenomena often result in quasi-sinusoidal monoperiodic O−C diagrams. In the case of AME, the O−C curve formed from the secondary minima anticorrelates with the curve formed from the primary minima, while in the case of LTTE the two kinds of minima must vary in the same manner. Additional apparent orbital period changes inducing ETVs may arise, in theory, from the precession of the orbital plane of the EB due to the perturbations induced by either a third-star companion revolving in an inclined orbit or the non-aligned rotation of each or both stars. Such ETVs are not yet known to have been observed.
In addition to the above effects, erratic variations have been observed as well. They may indicate physical effects such as variable mass transfer rates or currently unidentified apparent timing effects.
Finally, when a light curve is distorted by the effects of, e.g., stellar spots or pulsations, the measurement process tends to yield spurious ETVs that may include periodic or quasi-periodic components (see e.g. Kalimeris, Rovithis-Livaniou & Rovithis 2002; Tran et al. 2013; Balaji et al. 2015, for spots and Borkovits et al. 2014, for stellar oscillations).
The almost continuous 4-yr-long set of high-precision photometric observations from the Kepler mission (Borucki et al. 2010) offers an unprecedented opportunity to study ETVs in thousands of EBs and ellipsoidal variables (ELVs). Among a wide range of possibilities, these data are especially suited for searches for short-period third-star companions of these binaries. Third-star companions to binaries are interesting from several perspectives. Third stars may be particularly significant in the formation of close binaries; this has been discussed and investigated intensively over the past two decades (for a short summary, see Fabrycky & Tremaine 2007). The statistically significant lack of short (P2 < 1000 d) outer period ternaries amongst solar or lower mass binaries (Tokovinin 2014b) makes such investigations especially important.
The first, preliminary, systematic search of Kepler ETV data for hierarchical triples was carried out by Gies et al. (2012), who identified possible long-term ETVs in 14 of 41 EBs but did not find any evidence of short-period companions (P2 < 700 d). Later, Rappaport et al. (2013) surveyed the whole available Q0–Q13 data set for some 2100 EBs. They found 39 candidate triple systems in the short-outer-period domain (48 d <P2 < 960 d), for which they presented combined LTTE+dynamical effect solutions. This was the first systematic study of the dynamical effect in EBs using the Kepler data. Nearly contemporaneously, Conroy et al. (2014) determined eclipse times for all the short-period EBs, most of which are overcontact systems, and ELVs, and identified 236 systems for which the ETVs could be compatible with the LTTE. However, the majority of these were observed for less than one complete outer (third-body) orbital period. More recently, Borkovits et al. (2015) investigated 26 Kepler-field eccentric EBs which feature ETVs that are dominated by dynamical perturbations rather than LTTE. This work featured the simultaneous analysis of both the primary and secondary eclipses so as to break a number of degeneracies in the solutions. In a report published in 2015 June, during the preparation of the present paper, Zasche et al. (2015) published light-curve and ETV analyses of 10 detached or semi-detached Kepler-field EBs. For most of these 10 systems, the authors were able to extend the duration of the flux time series by including ground-based timing measurements. Finally, after the submission of the present paper, Gies et al. (2015) published an improved analysis on the same subset of 41 EBs which was previously investigated in their earlier work (Gies et al. 2012). They now provide third-body LTTE solutions for seven EBs. Additional studies of a possible third body affecting the ETVs of individual EBs in the Kepler field have also been reported in Steffen et al. (2011, for KOI-928 (=KIC 09140402)), Borkovits et al. (2013, for HD 181068 (=KIC 05952403)), Lee et al. (2013, for KIC 02856960), Lee et al. (2014, for V404 Lyr (=KIC 03228863)), and Lee, Hong & Hinse (2015, for KIC 05621294). Most recently, Baran et al. (2015) reported the detection of a planet-mass companion in the sdB+dM EB 2M1938+4603 (=KIC 09472174).
In the present paper, we regenerate and reanalyze the ETVs of all the previously investigated triple-body candidate EBs, with the exception of the 26 systems investigated in Borkovits et al. (2015), and we extend our analysis to longer period systems which were excluded from the study of Conroy et al. (2014). While the new study of the previously investigated systems is natural because of the significantly longer time span of the Q0–Q17 Kepler observations, there are additional reasons to further investigate the EBs listed in Conroy et al. (2014). First, our method for determination of times of minima gives results for semi-detached or detached systems, i.e. systems with relatively sharp and deep minima, that are significantly more accurate than the times for these systems used in Conroy et al. (2014). Secondly, for overcontact EBs and ELVs, we also analyse quadrature timing variations (QTV), i.e. O−C times of maxima. Thirdly, we checked the individual LTTE solutions in detail with particular attention to whether the inferred masses could be reliable, and, in the cases where further treatment was indicated, we modelled the effects of dynamical perturbations of the binaries. Finally, for the minority of the investigated EBs for which pre-Kepler ground-based times of minima were available, we also included these data in our analysis. In such a way, we were also able to improve the reliability of the LTTE solutions for previously investigated systems.
In what follows, in Section 2 we briefly describe the LTTE and dynamical perturbation effects. Then, in Section 3 we outline the method of calculating accurate times of eclipse and non-eclipse minima as well as our method for searching for ETV solutions. We introduce the idea of determining times of light-curve maxima, and utilize these so-called quadrature timing curves as diagnostics to weed out false positives. Section 4 discusses the use of supplementary ground-based timing data for extending the overall span of the observations for a small subset of our triples. Section 5 gives an overview of the 230 systems that we investigated. This includes a plot of each ETV curve with fitted solution as well as an extensive set of tables listing fitted system parameters. In Section 6, we discuss our findings from a number of different perspectives, and we draw some conclusions from this substantial statistical collection of triple-star systems. Finally, we summarize our work in Section 7.
2 EFFECTS OF A THIRD BODY ON THE ETV
The coefficients c0 and c1 were adjusted simultaneously with the physical terms in all analyses. The quadratic coefficient c2 was allowed to be non-zero only for originally parabolic ETVs or when the LTTE fitting yielded parabolic residuals; in these cases, the quadratic term was determined simultaneously with all other included terms. The coefficient of the cubic term was set to zero except in five cases wherein at least three full outer periods were observed; this yielded reduced-size O−C residuals without substantially altering the orbital parameters. The parameters of the LTTE-term (see below) were adjusted in all cases. Dynamical ETV contributions were considered for a subset of our sample where there was some indication that a pure LTTE solution would not be adequate. Finally, the apsidal motion contributions were also taken into account for a few eccentric EBs.
As will be discussed in Section 3, for systems with significant ellipsoidal light variations, we also measure and analyse the times of the ellipsoidal maxima. As most of the systems with well-measured ellipsoidal variations – being overcontact or semi-detached systems – revolve in circular orbits, the maximum brightnesses occur near quadrature phases (i.e. ϕ = 0.25 and 0.75) and, therefore, we refer to the O−C times of the maxima as QTV. The QTV curves for LTTE and quadratic variations must have the same form as given by equation (1). The dynamical contribution and the AME term would, however, be different for quadratures, but, practically speaking, these effects would have needed considerable extra care only for ‘heart-beat’ binaries (Thompson et al. 2012), of which only one, KIC 03766353, is covered in this paper. Note also that generalizing the natural convention that the epoch or cycle number (E) is integer for primary and half-integer for secondary minima, we calculate it as E + 0.25 for the first quadrature (at ϕ ∼ 0.25, i.e. after the primary minima) and E + 0.75 for the second quadrature.
The mathematical form and other properties of the different ETV contributions were discussed comprehensively in Borkovits et al. (2015). Here we discuss briefly, and from a bit different point of view, only the two main effects which were applied in this work.
2.1 The light-travel time effect
General criteria for the plausibility of an LTTE model of ETVs have been given by Frieboes-Conde & Herczeg (1973). The criteria may be summarized as follows. (1) The shape of the ETV curve must follow the analytical form of an LTTE solution. (2) The ETV of the secondary minima must be consistent in both phase and amplitude with the primary ETV. (3) The estimated mass or lower limit to the mass of the third component, derived from the amplitude of the hypothetical LTTE solution via the mass function – see below, must be in accord with photometric measurements or limits on third light in the system. (4) Variation of the system radial velocity should be in accord with the LTTE solution. While these criteria do not look very restrictive, none of their candidate systems fulfilled all of them. More than 50 years after the first mathematical description of the problem, there was only one system, Algol itself, where the LTTE was identified clearly via its ETV curve. Even over the ensuing decades, the number of confirmed LTTE cases has grown very slowly. The reason is as follows.
| Parameter . | Symbol . | Explanation . |
|---|---|---|
| Mass | ||
| EB members | mA, B | |
| Total mass of EB | mAB | mA + mB |
| Ternary's mass | mC | |
| Total mass | mABC | mA + mB + mC |
| Period | ||
| Sidereal/eclipsing | P1, 2 | |
| Anomalistic | Pa1, 2 | |
| Semi-major axis | ||
| Relative orbit | a1, 2 | |
| Absolute orbit of EB | aAB | mC/mABC · a2 |
| Eccentricity | e1, 2 | |
| Anomaly | ||
| True | v1, 2 | |
| Eccentric | E1, 2 | |$E=2\tan ^{-1}\left(\sqrt{\frac{1-e}{1+e}}\tan \frac{v}{2}\right)$| |
| Mean | l1, 2 | l = E − e sin E |
| Argument of periastron | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | ω1, 2 | |
| Dynamical | g1, 2 | |
| Inclination | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | i1, 2 | |
| Mutual (relative) | im | |
| Ascending node | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observational | Ω1, 2 | |
| ΔΩ | Ω2 − Ω1 | |
| Speed of light | c | |
| Gravity constant | G | |
| Times BJD | Barycentric Julian | Reduced Times |
| Times BJD | Date | BJD - 2400000.0 |
| Parameter . | Symbol . | Explanation . |
|---|---|---|
| Mass | ||
| EB members | mA, B | |
| Total mass of EB | mAB | mA + mB |
| Ternary's mass | mC | |
| Total mass | mABC | mA + mB + mC |
| Period | ||
| Sidereal/eclipsing | P1, 2 | |
| Anomalistic | Pa1, 2 | |
| Semi-major axis | ||
| Relative orbit | a1, 2 | |
| Absolute orbit of EB | aAB | mC/mABC · a2 |
| Eccentricity | e1, 2 | |
| Anomaly | ||
| True | v1, 2 | |
| Eccentric | E1, 2 | |$E=2\tan ^{-1}\left(\sqrt{\frac{1-e}{1+e}}\tan \frac{v}{2}\right)$| |
| Mean | l1, 2 | l = E − e sin E |
| Argument of periastron | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | ω1, 2 | |
| Dynamical | g1, 2 | |
| Inclination | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | i1, 2 | |
| Mutual (relative) | im | |
| Ascending node | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observational | Ω1, 2 | |
| ΔΩ | Ω2 − Ω1 | |
| Speed of light | c | |
| Gravity constant | G | |
| Times BJD | Barycentric Julian | Reduced Times |
| Times BJD | Date | BJD - 2400000.0 |
| Parameter . | Symbol . | Explanation . |
|---|---|---|
| Mass | ||
| EB members | mA, B | |
| Total mass of EB | mAB | mA + mB |
| Ternary's mass | mC | |
| Total mass | mABC | mA + mB + mC |
| Period | ||
| Sidereal/eclipsing | P1, 2 | |
| Anomalistic | Pa1, 2 | |
| Semi-major axis | ||
| Relative orbit | a1, 2 | |
| Absolute orbit of EB | aAB | mC/mABC · a2 |
| Eccentricity | e1, 2 | |
| Anomaly | ||
| True | v1, 2 | |
| Eccentric | E1, 2 | |$E=2\tan ^{-1}\left(\sqrt{\frac{1-e}{1+e}}\tan \frac{v}{2}\right)$| |
| Mean | l1, 2 | l = E − e sin E |
| Argument of periastron | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | ω1, 2 | |
| Dynamical | g1, 2 | |
| Inclination | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | i1, 2 | |
| Mutual (relative) | im | |
| Ascending node | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observational | Ω1, 2 | |
| ΔΩ | Ω2 − Ω1 | |
| Speed of light | c | |
| Gravity constant | G | |
| Times BJD | Barycentric Julian | Reduced Times |
| Times BJD | Date | BJD - 2400000.0 |
| Parameter . | Symbol . | Explanation . |
|---|---|---|
| Mass | ||
| EB members | mA, B | |
| Total mass of EB | mAB | mA + mB |
| Ternary's mass | mC | |
| Total mass | mABC | mA + mB + mC |
| Period | ||
| Sidereal/eclipsing | P1, 2 | |
| Anomalistic | Pa1, 2 | |
| Semi-major axis | ||
| Relative orbit | a1, 2 | |
| Absolute orbit of EB | aAB | mC/mABC · a2 |
| Eccentricity | e1, 2 | |
| Anomaly | ||
| True | v1, 2 | |
| Eccentric | E1, 2 | |$E=2\tan ^{-1}\left(\sqrt{\frac{1-e}{1+e}}\tan \frac{v}{2}\right)$| |
| Mean | l1, 2 | l = E − e sin E |
| Argument of periastron | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | ω1, 2 | |
| Dynamical | g1, 2 | |
| Inclination | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observable | i1, 2 | |
| Mutual (relative) | im | |
| Ascending node | see fig. 1 and appendix D of | |
| Borkovits et al. (2015) | ||
| Observational | Ω1, 2 | |
| ΔΩ | Ω2 − Ω1 | |
| Speed of light | c | |
| Gravity constant | G | |
| Times BJD | Barycentric Julian | Reduced Times |
| Times BJD | Date | BJD - 2400000.0 |
Over the last several decades, the advent of CCD detectors and other advances has led to the acquisition of much new and relatively accurate EB timing data that have, in turn, made it possible to tentatively or definitely detect LTTE in hundreds of EBs. Most of these LTTE solutions reveal companions with orbital periods longer than a decade. Third stars were found in shorter period orbits only for a very limited number of EBs. Before the era of the Kepler space mission, IU Aurigae was the only EB system in which there was a detection of LTTE due to a third-star companion with a period shorter than 1 yr (Mayer 1983). All the other tertiaries with periods less than 1 yr had been discovered spectroscopically in accord with the fact that spectroscopic detection is much more effective for short-period outer orbits (see, e.g., Mayer 1990; Tokovinin 2014a). However, spectroscopy requires much more light and, therefore, larger instruments as well as exposure time for a given system than photometry. Thus, the majority of the EBs are too faint to be suited for spectroscopic third-body detection.
In such a way, the Kepler mission offers an unprecedented opportunity for the discovery of short-period companions orbiting EBs, including also lower mass systems, such as, e.g., the majority of overcontact binaries, which are usually too faint for spectroscopic investigations. Furthermore, in contrast to the earlier, ground-based observations, which were inhomogeneous, and generally restricted to small portions of the EBs’ light curves around their eclipsing minima, Kepler observations provide almost continuous and highly homogeneous light curves over intervals as long as four years. As a consequence, we are now in a position to extend our timing investigations to the out-of-eclipse parts of the light curves. Accordingly, an additional criterion of reliable LTTE solution can be introduced, as (5) the times of the maxima of the ellipsoidal variations, at least in EBs that have circular orbits, should be in accord both in phase and amplitude with the ETVs.
Another never-seen-before feature is the presence, in a small number of Kepler light curves, of outer eclipses. For such systems, a further natural criterion for identifying the outer eclipsing body with the source of the observed LTTE is that (6) the LTTE should exhibit the same period as the extra eclipses, and the latter should occur around the extrema of the LTTE. In Sections 3 and 6.3, we illustrate the applications of these new criteria.
2.2 Dynamical perturbations of a third body on the ETV
If an EB has a more or less distant companion, its binary motion no longer remains purely Keplerian since time-dependent perturbations affect all six orbital elements. Naturally, the occurrence times of the eclipses are also affected. The perturbations of the ETVs were first studied in this context by Söderhjelm (1975) and Mayer (1990). Later, the third-body effects were elaborated in full in a series of papers by Borkovits et al. (2003, 2011, 2015), and, in the context of transit timing variations of exoplanets, by Agol et al. (2005).
Expressions for the dynamical perturbation ETVs for EBs with elliptical inner orbits (e1 > 0) are much more complicated (see Borkovits et al. 2011, 2015). In particular, the amplitude of the ETVs depends sensitively on the eccentricities of the binary and third-star orbits and on the mutual inclination of the two orbits. Therefore, even for a given mass and period ratio, the amplitude may take a value within a wide range, as was illustrated, e.g., in fig. 3 of Borkovits et al. (2011).
The analysis itself was carried out in the same manner and with the same code that was described in detail in Borkovits et al. (2015).
3 SYSTEM SELECTION AND DATA PREPARATION
We use the present version of the Kepler EB catalogue and light-curve files available at the Villanova website5 (Slawson et al. 2011; Matijevic et al. 2012; Conroy et al. 2014; LaCourse et al. 2015). All the light-curve files for the sources in the original Kepler field were downloaded, and, using the first (BJD), seventh (detrended relative flux), and eighth (uncertainty of the latter) columns of these files, O−C diagrams were formed in an automated way. For a significant portion of the systems to be investigated, some quarters of the observed data sets (Q4 and/or Q12–13) were not available at the Villanova site; in most of those cases, we downloaded the missing data directly from the MAST data base operated by the Space Telescope Science Institute,6 converted it into the proper format, and merged it with the Villanova-derived data set. We then selected those systems which either were mentioned in the context of having third components in previous literature or had interesting preliminary O−C curves. For the selected systems, we calculated more accurate eclipse times in a somewhat more sophisticated, semi-automated manner. Our method, which is based on forming folded, binned, and averaged light curves for the whole data set of each EB, then constructing polynomial templates for intervals around the minima of these averaged light curves, and finally using these templates for fitting individual minima, was described in detail in section 4 of Borkovits et al. (2015). Therefore, here we note only some subtleties and variations specific to the present work.
This procedure yielded some 400 ETVs for further analysis. The majority of these systems definitely show ellipsoidal variations, which makes it possible to calculate not only times of the eclipses, but also of the maxima in the light curves. The latter set of QTVs was produced in the same manner as the ETVs. We found that in the case of overcontact EBs and most of the ELV binaries, with the exception of a few eccentric ELVs, it was satisfactory to set the phase limits for building up minima and maxima templates to ϕp = [−0.15; 0.15], ϕs = [0.35; 0.65], for primary and secondary minima, and ϕq1 = [0.10; 0.40] and ϕq2 = [0.60; 0.90], for the first and second quadratures (maxima), respectively. For semi-detached and detached systems with definite and sharper eclipses, narrower phase limits were set for the minima. However, in so far as the out-of-eclipse section of a folded, binned light curve also exhibited ellipsoidal light variations, and the latter property of the averaged curve was not altered by any cycle-to-cycle variations (see below) on the original light curve, we again calculated quadrature (or maxima) templates, applying mostly the same phase constraints. (Note, however, that in the case of a few eccentric systems, we departed from the above-listed phase constraints in also calculating quadrature templates, in accordance with the properties of the given individual light curve.)
Then, having obtained templates, times of individual minima and maxima were determined in exactly the same manner as described in Borkovits et al. (2015). In such a way, we have obtained 1–2 ETV and 0–2 QTV curves for each system. In several cases, these curves are obviously distorted by the effects of stellar spots, pulsations, or oscillations. Fortunately, as was shown in Tran et al. (2013), stellar spots in general distort the primary and secondary ETVs in an anticorrelated way. Similarly, the distortions in the two QTVs due to stellar spots also anticorrelate with each other and, furthermore, they are shifted by |$\pm 90\deg$| in phase from the respective ETVs (see Fig. 1). Therefore, the effects of starspots can be significantly reduced by averaging the primary and secondary ETVs, and the two QTVs as well. Thus, we also calculated averaged ETVs and QTVs. This process was carried out by interpolating the times of the primary ETVs to the times of the corresponding secondary eclipses with the help of a cubic spline. The same was done for the QTV curves.
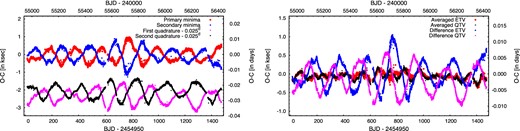
The highly anticorrelated, quasi-periodic ETV and QTV curves of the overcontact EB KIC 06431545. This type of ETV variations, which is likely attributable to large spotted areas on the stellar surface(s), was first reported in Tran et al. (2013), and was also investigated by Balaji et al. (2015). Left-hand panel: the individual primary (red circles) and secondary (blue boxes) ETV, and first quadrature (directly after the primary eclipses; magenta upward triangles) and second quadrature (black downward triangles) QTV curves. Right-hand panel: the averaged ETV (red) and QTV (black) curves show only some low-amplitude residuals, while the difference curves between the two ETVs (blue) and QTVs (magenta) exhibit a phase shift of one-fourth of a period between the two sets.
In our experience, this averaging process is most effective for overcontact EBs and low-eccentricity or circular orbit ELVs where the two minima, and also the two maxima, are comparable in both amplitude and duration. Therefore, on the one hand, the times of mid-minima and mid-maxima can be determined with approximately the same accuracy, while on the other hand, they are affected by the distortions more or less at the same level (see Fig. 2). Another benefit of forming averaged ETVs (and QTVs) is the reduced scatter in the O−C curves with respect to the original ones for several systems and, therefore, in these cases we used the averaged curves instead of the individual ETV curves for LTTE fitting.
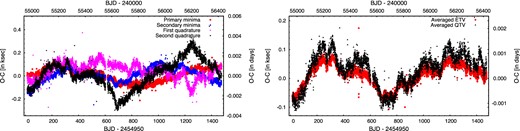
The highly irregular O−C curves of the low-amplitude, short-period, possibly overcontact EB KIC 02715417. Left-hand panel: the individual primary (red circles) and secondary (blue boxes) ETV, and first quadrature (directly after the primary eclipses; magenta upward triangles) and second quadrature (black downward triangles) QTV curves. Right-hand panel: the averaged ETV (red) and QTV (black) curves reveal some (quasi-)periodic variations similar both in magnitude and phase for the two curves; this indicates that the LTTE curve could be due a low-mass (or very low inclination) third companion.
Another method useful for reducing or eliminating the influences of intrinsic brightness variations on the times of minima is local smoothing of the light curves. This method was applied by fitting a low-order (typically fourth-order) polynomial to a portion of each light curve centred on each minimum but excluding the minimum itself, i.e. usually in the intervals [−0.25; ϕp, sleft − 0.02] and [ϕp, sright + 0.02; +0.25]. This polynomial was then subtracted from the entire interval ([−0.25; 0.25]; see the left-hand panels of Fig. 3). This method yielded excellent results for several systems affected by starspots and even for systems affected by stellar oscillations. Some examples are shown in the right-hand panels of Fig. 3. An additional example of the oscillating EB system KIC 08560861 can be found in fig. 1 of Borkovits et al. (2014). Local smoothing was found to be effective mainly for detached systems with definite and sharp eclipses, but we could also use it even for some semi-detached binaries. For overcontact EBs and ELVs, however, this algorithm cannot be used.
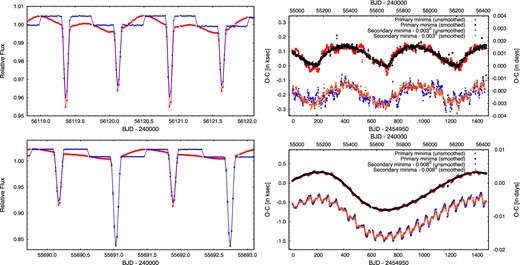
Two examples of the workings and efficiency of local smoothing with fourth-order polynomial fits. Both KIC 05216727 (upper row) and KIC 09711751 (bottom row) are Algol-type EBs, and exhibit likely rotational variations due to starspots. Left-hand panels show small segments of their detrended Kepler long-cadence light curves (red) and the corresponding locally smoothed curves (blue). Right-hand panels give the ETV curves obtained from both the original unsmoothed and the locally smoothed light curves. One can see that the method is more effective, and eliminates nearly perfectly the effects of the (rotational) distortions for the deeper primary minima. As to the shallower secondary minima, some residual distortions survive, but the magnitude has been substantially reduced. (For better visibility, the ETV curves for the secondary minima are shifted down from the primary ETV curves.)
The use of QTVs and the averaging and smoothing techniques made it possible not only to find and determine lower amplitude LTTE solutions, but also to apply more stringent criteria for filtering out false positive systems. An example is KIC 11247386, a possible overcontact EB (P1 = 0.394 d) with a remarkable O'Connell effect.7 Conroy et al. (2014) give an LTTE solution with a period P2 = 71.2 ± 0.1 d, which would be the shortest outer period in their sample. As one can see in the left-hand panel of Fig. 4, this periodicity is definitely present in the primary ETV and the second QTV with quite different amplitudes, is hardly visible in the first QTV, and is even weaker in the secondary ETV. Such amplitude ratios are not typical of LTTE induced by a third body. There are a few additional systems where the averaged QTVs behave similarly to the averaged ETVs, but there are minor discrepancies in the amplitudes. A typical example is shown in the right-hand panel of Fig. 4. In the latter cases, we accept the LTTE solution, and note the amplitude discrepancy in the tabulated results.
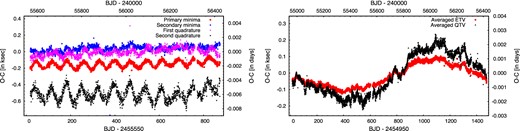
Examples of discrepant ETVs and QTVs. Left-hand panel: a clearly false positive case: the ETV and QTV curves of KIC 11247386. The P2 = 71.2 ± 0.1 d periodicity attributed to LTTE by Conroy et al. (2014) is readily visible. The different amplitudes for the different curves clearly show, however, that the origin of this feature cannot be LTTE due to a third body. Therefore, we categorized this system as a false positive in the sense that there is no evidence for this being a triple-star system. (Note that a careful inspection of the curves also reveals that some phase discrepancies also occur between the curves.) Right-hand panel: the case of a marginally acceptable LTTE solution: the averaged ETV and QTV curves of KIC 11246163. Although the amplitudes of the two curves differ slightly, we do not rule out a possible LTTE origin.
Another group of false positives comprises those objects where, although the ETV may suggest an LTTE solution, the Kepler target was erroneously classified as either an EB or as an ELV binary. For example, δ Scuti-type oscillating variables can easily be misclassified as ELVs or even low-amplitude overcontact EBs. This is quite likely especially in systems with P ≲ 0.15 d. In the absence of radial velocity measurements which would be able to confirm or reject the binary hypothesis for candidate ELV binaries (see, e.g., Tal-Or, Faigler & Mazeh 2015), we could make decisions on the nature of such systems based on temperature or colour information when available. Instead, our decisions are based on the characteristics of the folded, binned light curves and the ETV and QTV data.
There are light-curve-based checks that may reveal whether a target is actually a physical binary. For example, the light curve of an ELV binary is dominated by a sinusoidal component with a period that is half of the orbital period. The two sections of the folded and binned light curve in the phase ranges [0.0; 0.5] and [0.5; 1.0] typically differ noticeably from each other due to Doppler boosting (see, e.g., van Kerkwijk et al. 2010) and reflection effects (see, e.g., Zucker, Mazeh & Alexander 2007), not fully averaged-out spot effects, or even, in the case of detached ELVs, orbital eccentricity. On the other hand, if the variations originate in stellar oscillations or pulsations, the underlying oscillation period will be half of the inferred orbital period and the light curve will be more or less identical in the two phase intervals. Furthermore, in such cases the times of consecutive minima (or maxima) tend to consistently follow one ETV (or QTV) curve. By contrast, as was shown in Tran et al. (2013) and Balaji et al. (2015), in the case of ELVs and overcontact systems, especially those which are formed by spotted stars, consecutive minima and maxima timings may show different O−C patterns. Therefore, in accord with the suggestion of Tran et al. (2013), all the sources which produce significantly different pairs of ETVs (and/or pairs of QTVs) are not likely to be due to oscillations or pulsations. In summary, if the two sections of a light curve differ, the system may be a binary. If the two parts of the light curve happen to be identical, and ETVs and QTVs also look very similar, we take the source to be a false positive binary with a high likelihood. Examples of these checks may be found in Fig. 5.
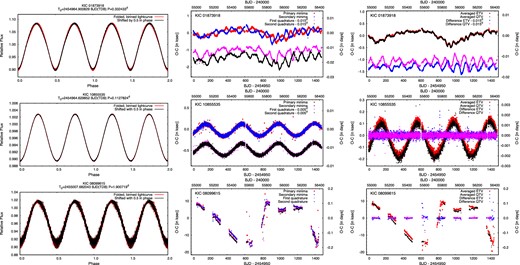
One verification and two rejections. Three systems where, at first, the classifications as binaries are ambiguous. Left-hand panels: the folded and binned long-cadence light curves and their 0.5 d phase-shifted versions (red and black, respectively). Middle panels show the individual O−C curves belonging to the purported primary and secondary ETVs as well as the first and second QTVs. Right-hand panels: the average and the difference of the two ETVs and QTVs are plotted. In the case of KIC 01873918, which has been flagged as a false positive in the Kepler EB catalogue (first row), the light curve shows alternating maxima and minima that are slightly different in amplitude, thereby indicating that this is not a sinusoidal pulsator. The quasi-anticorrelated behaviour in the ETV curves, and also in the QTV curves, adds confidence to this being a binary. Therefore, we conclude that this system is indeed a binary within a triple system. In the case of the ultrashort-period KIC 10855535 (middle row) and the longer period KIC 08099615 (bottom row), the alternating maxima and minima of the light curves look completely the same, suggesting another type of variability with half of the given period. Furthermore, the two ETVs and also the QTVs track each other, which further strengthens the false binary hypothesis. Independent of this fact, the presence of the LTTE effect in the ETV and QTV curves of KIC 10855535 seems very clear, and thus we may conclude that this system is actually a wide binary (instead of being a triple) with a period of PLTTE = 411.9 ± 0.2 d. For KIC 08099615, the large-amplitude, peculiar ETV (and QTV) might have a different origin.
After obtaining pre-processed ETV and QTV curves and weeding out likely false positives in the above manner, the next task was to decide whether a pure LTTE solution, or a combined dynamical and LTTE solution, for a given system should be sought. In most cases, the decision was evident as, on one hand, some of the ETVs had shown features typical of dynamical perturbations (for a detailed discussion, see Borkovits et al. 2015), or, on the other hand, a large P2/P1 ratio indicated that dynamical contributions would be negligible. Extra care was necessary, however, for systems with relatively sinusoidal ETVs and moderate P2/P1 ratios. Therefore, in all cases, when a pure LTTE solution was obtained, we also estimated the possible relative contribution of the dynamical perturbations. For this, the binary mass was approximated by 2 M⊙ and then by the use of the mass function f(mC) obtained from the LTTE solution, a minimum mass of the third body was calculated, as well as the minimum value of the dynamical amplitude (equation 12). Then, when the estimated ratio |$\mathcal {A}_\mathrm{dyn}/\mathcal {A}_\mathrm{LTTE}$| exceeded ∼25 per cent, we also calculated a combined LTTE+dynamical solution.
4 SUPPLEMENTAL GROUND-BASED ECLIPSE TIMING
Before giving an overview of our results, we briefly discuss the use of pre- or post-Kepler ground-based eclipse measurements which are available for a small number of our triples. As was discussed in Section 2, because of their limited accuracy, ground-based timing measurements of eclipses and light-curve minima are generally not suitable for third-body ETV studies in the period range of P2 ≲ 1–2 yr. Even for systems where the outer period is comparable to the length of the Kepler data set, supplementary ground-based times of minima collected over a somewhat wider time span may serve mainly to confirm or reject a possible solution rather than to quantitatively improve it.
Supplementary ground-based times of minima are most useful for those systems that were discovered as EBs well before the Kepler era when times of minima are available over a time span that is much longer even by order(s) of magnitude than the Kepler data train itself. However, our sample includes only seven EBs for which there are times of minima taken over a time span longer than a decade. Some dozens of our sample EBs, however, were observed a few years before the beginning of the original Kepler mission in the photometric surveys of ASAS (Pigulski et al. 2009), HATNET (Hartman et al. 2004), TRESS (Devor et al. 2008), and SuperWASP (Pollacco et al. 2006). Unfortunately, the times of minima obtained from these data bases often offer only lesser benefits because of the restricted extension of the data span and, in several cases, the sampling rate of the observations of each EB was so infrequent that the data do not yield times of individual eclipses with useful accuracy. For these reasons, we did not determine and utilize the times of minima from the observations of the above-listed surveys for all systems; we make use of the data only for those EBs for which the eclipse times were determined by Lee et al. (2014) and Zasche et al. (2015).
Ground-based times of minima obtained from targeted eclipse observations of individual binaries are particularly helpful. In most cases, these were collected from the Lichtenknecker-Database of the Bundesdeutsche Arbeitsgemeinschaft für Veränderliche Sterne e. V. (BAV),8 rather than from the journal literature. The sole exceptions are a few recently observed post-Kepler times of minima published in Zasche et al. (2015). Some of the oldest times of minima in the extended ground-based data sets are based on visual brightness estimations which have a highly limited accuracy of 5–10 min. Despite this, we decided to keep these observations (with the exception of the evident outliers) in the cases where they could substantially extend the overall span of the data.
Given the available data and the above considerations, we were able to extend our timing data sets with ground-based measurements for about a dozen systems. In some cases, however, the ground-based minima evidently contradict the Kepler observations. In the case of KIC 092883826 (=V2366 Cyg), we found two ground-based times of minimum which were obtained from observations during the Kepler era but were inconsistent with the Kepler times. In the case of KIC 09101279 (=V1580 Cyg), three ground-based times of minimum would have extended the data span by a factor of 3, but they did not match our ETV solution from the Kepler data and, therefore, were not considered further. In a case yielding an opposite conclusion, for KIC 010581918 (=WX Dra) we rejected the Kepler LTTE solution, and therefore deleted the EB from our sample because of the contradictory characteristics of the relatively numerous ground-based data.
In summary, we kept all or a part of the ground-based times of minima for eight EBs. In the 221 panels of Fig. 6, we plot the O−C curves of almost all of the investigated EBs (see Section 5). For the eight systems where ground-based minima were also incorporated for the third-body solution, these ground-based minima are plotted together with their uncertainties. As one can see, these uncertainties in some cases are larger than the full amplitude of the third-body ETV feature for these systems. In other cases, however, the extended data set was found to be suitable for confirming, or even improving, the third-body solutions as will be discussed in the next section.
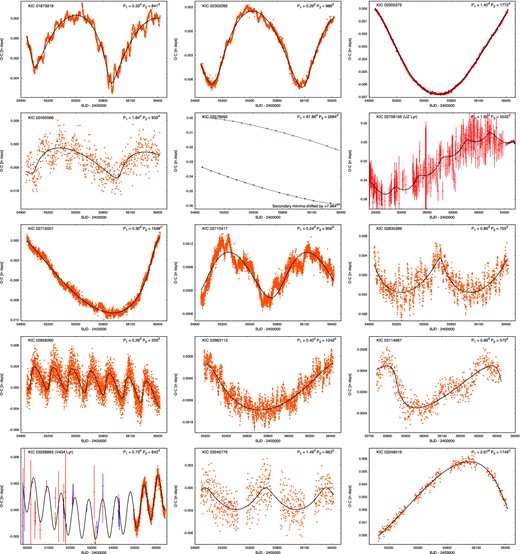
ETVs with third-body solutions. ETV curves calculated from Kepler observations of primary and secondary minima, and the average of the two, are denoted by red circles, blue boxes, and orange diamonds, respectively. We display and fit the ETV curves for both the primary and secondary eclipses only when the data quality warrants a joint analysis and the binary is eccentric. If the primary and secondary ETV curves are of comparable quality and the binary eccentricity is nearly zero, we display and fit only the average of the two ETV curves. If the quality of the primary ETV curve is significantly better than that of the secondary curve or if only primary eclipses are present, we present only the plot and the fit for the primary eclipses. Ground-based minima (taken from the literature, and available only for a few systems) are denoted by upward red triangles (primary) and downward blue triangles (secondary); their estimated uncertainties are also indicated. Pure LTTE solutions are plotted with black lines, while combined dynamical and LTTE solutions are drawn with grey lines. (Note that the use of quadratic or cubic terms is not indicated; for these and other details, see Table 2.) The complete figure covering 221 ETV curves is available in the online version of the journal.
5 OVERVIEW OF THE INVESTIGATED SYSTEMS
We give LTTE and/or dynamical solutions for 230 Kepler systems. Some parameters of these systems are given in Table 2, where the basic properties of the generated ETV and QTV curves, the types of our solutions, and relevant references are also listed.
Properties of the investigated systems. (1) E3 refers to tertiary eclipse(s) in the light curve. (2) In columns 2 and 3, we give the light-curve classifications according to both the classical eclipsing binary typology (see, e.g., Kallrath & Milone 2009) and the recently introduced morphology of Matijevic et al. (2012). (3) Sidereal period (P1) and epoch (T0) were used for plotting O−C curves. (4) Kepler magnitudes were taken from the Kepler Input Catalog (Batalha et al. 2010). (5) In column ETV/QTV, the numbers of calculated ETV and QTV curves are given. If both ETVs and/or QTVs were obtained, their average and (half-difference) curves were also determined. In the cases where we used local smoothing polynomials on the light curves, this is denoted by putting sn after the ETV number, where n gives the order of the smoothing polynomial. (6) Abbreviations in ‘Fitted curves’ column: ‘p’ – primary, ‘s’ – secondary, ‘a’ – averaged ETV curves, ‘e’ – ground-based times of minima were also included. (7) Abbreviations in ‘Fit type’ column: ‘l’ – LTTE, ‘a’ – AME (noted separately only for non-‘d’-type solutions), ‘d’ – dynamical, ‘q’ – quadratic, ‘c’ – cubic. Parentheses in this column indicate that two types of fits were performed; the unparenthesized terms were included in both fits while the term(s) in parentheses were included in only the less preferred fit. (8) Column ‘Tab’ is the location of the solution of the given system in one of Tables 3;5, 6–8, and 9 (‘L1’–‘L3’ for pure LTTE, ‘D1’–‘D3’ for combined LTTE and dynamical, and ‘F’ for false positive systems, respectively). References – 1: Gies et al. (2012); ; 2: Rappaport et al. (2013); 3: Conroy et al. (2014); 4: Borkovits et al. (2015); 5: Orosz (2015); 6: Zasche et al. (2015); 7: Tran et al. (2013); 8: Conroy et al. (2015); 9: Armstrong et al. (2012); 10: Lee et al. (2013); 11: Marsh, Armstrong & Carter (2014); 12: Lee et al. (2014); 13: Gaulme et al. (2013); 14: Lee et al. (2015); 15: Carter et al. (2011); 16: Borkovits et al. (2013); 17: Masuda, Uehara & Kawahara (2015); 18: Fabrycky et al. (in preparation); 19: Steffen et al. (2011); 20: Baran et al. (2015); 21: Liška (2014); 22: Csizmadia & Sándor (2001); 23: Gies et al. (2015).
| KIC No. . | Type . | Morph. . | T0 . | P1 . | Kp . | Data length . | |$\frac{\mathrm{ETV}}{\mathrm{QTV}}$| . | Fitted . | Fit . | Tab . | Refs. . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (BJD) . | (d) . | (mag) . | (d) . | . | curves . | type . | . | . |
| 1873918 | ELV(EW) | 0.86 | 54964.900829 | 0.332 433 | 13.7 | 1459 | 2/2 | a | l+q | L2-13 | 7 |
| 2302092 | EW | 0.89 | 54964.694441 | 0.294 673 | 14.4 | 1459 | 2/2 | a | l | L2-27 | 3 |
| 2305372 | EA | 0.58 | 54965.956227 | 1.404 6920 | 13.8 | 1458(4216) | 2s4/2 | p(+e) | l(+q) | L3-25 | 6, 23 |
| 2450566 | ELV | 0.98 | 55001.560102 | 1.844 5871 | 11.7 | 1468 | 2/2 | a | l | L2-24 | 3 |
| 2576692 | EA | 0.04 | 55027.103323 | 87.878 2329 | 12.7 | 1406 | 2/0 | p+s | l+d | D3-08 | |
| 2708156 | EA | 0.57 | 54954.336095 | 1.891 2671 | 10.7 | 33 912 | 2s8/0 | p+e | l+c | L1-38 | 1 |
| 2715007 | ELV | 0.87 | 54964.783119 | 0.297 1105 | 14.7 | 1459 | 2/2 | a | l | L3-17 | |
| 2715417 | ELV(EW) | 0.76 | 54964.667658 | 0.236 4399 | 14.1 | 1459 | 2/2 | a | l(+q) | L2-15 | |
| 2835289 | ELV+E3 | 0.92 | 55000.444609 | 0.857 762 | 13.0 | 1469 | 2/2 | a | l | L1-35 | 3, 8 |
| 2856960 | EA+E3 | 0.60 | 54964.661805 | 0.258 507 | 15.6 | 1458 | 2/0 | a | l+q | L1-03 | 3, 9, 10, 11 |
| 2983113 | EW | 0.89 | 55001.969640 | 0.395 1601 | 15.2 | 1238 | 2/2 | a | l | L3-04 | 3 |
| 3114667 | EA | 0.52 | 54999.758222 | 0.888 5832 | 17.4 | 683 | 2s4/0 | a | l | L2-02 | 3 |
| 3228863 | EB | 0.65 | 54954.26185 | 0.730 944 | 11.8 | 6636 | 2/2 | a+e | l+q | L1-29 | 2, 3, 12, 22 |
| 3245776 | ELV | 0.96 | 55001.663004 | 1.492 0589 | 14.4 | 1458 | 2/2 | a | l | L1-30 | 3 |
| 3248019 | EA | 0.37 | 55098.778000 | 2.668 2057 | 15.4 | 1329 | 2/0 | a | l | L3-24 | |
| 3335816 | EA | 0.16 | 54954.355631 | 7.422 0263 | 12.1 | 1462 | 2/0 | a | l | L3-38 | |
| 3338660 | EA | 0.60 | 55002.262623 | 1.873 3806 | 14.8 | 852 | 2s4/0 | p | l | L2-07 | |
| 3345675 | EA | 0.00 | 55083.146716 | 120.004 0103 | 15.6 | 1320 | 1/0 | p | l+d | D3-03 | |
| 3440230 | EA | 0.54 | 54967.238413 | 2.881 1010 | 13.6 | 1455 | 2s4/2 | p | l+q | L2-35 | 1, 6 |
| 3544694 | EA | 0.29 | 55740.65102 | 3.845 728 | 15.9 | 683 | 2s8/0 | p+s | l+d | D1-05 | |
| 3766353 | EA(HB) | −1.00 | 54966.722264 | 2.666 966 | 14.0 | 1456 | 2/2 | p | l | L3-12 | 3 |
| 3839964 | ELV(EW) | 0.78 | 54964.792432 | 0.256 1499 | 14.6 | 1459 | 2/2 | a | l+q | L3-40 | 3 |
| 3853259 | ELV(EW) | 0.98 | 54964.781808 | 0.276 6478 | 13.9 | 1459 | 2/2 | a | l+q | L1-10 | |
| 4037163 | EA | 0.58 | 55000.227976 | 0.635 4447 | 16.7 | 684 | 2/0 | a | l(+q) | L1-07 | 3 |
| 4055092 | EA | 0.01 | 54966.932772 | 76.464 989 | 15.3 | 1404 | 2/0 | p+s | l+d | D3-16 | |
| 4069063 | EA | 0.55 | 54964.906342 | 0.504 2953 | 13.3 | 1452 | 2s4/0 | a | l | L2-18 | 3 |
| 4074708 | EW | 0.73 | 54964.856673 | 0.302 1166 | 15.4 | 1459 | 2/2 | a | l | L2-37 | 3 |
| 4078157 | EA | 0.08 | 54960.300077 | 16.025 671 | 15.5 | 1202 | 2/0 | p+s | l+d | D3-02 | |
| 4079530 | EA | 0.07 | 54994.805374 | 17.727 1000 | 15.6 | 579 | 2/0 | p+s | l+d | D1-12 | |
| 4138301 | ELV | 0.90 | 54964.685221 | 0.253 379 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-14 | 3 |
| 4174507 | EA | 0.24 | 54966.041640 | 3.891 825 | 15.4 | 1456 | 2/0 | a | l(+d) | L3-31 | |
| 4244929 | EW | 0.91 | 54964.747256 | 0.341 403 | 15.1 | 1459 | 2/2 | a | l | L2-55 | 3 |
| 4451148 | EW | 0.82 | 54954.385233 | 0.735 9815 | 11.2 | 1470 | 2/2 | a | l | L2-06 | 3 |
| 4547308 | ELV | 0.88 | 54953.635293 | 0.576 9278 | 12.5 | 1470 | 2/2 | a | l | L2-17 | 3 |
| 4574310 | EA | 0.56 | 54954.662614 | 1.306 2201 | 13.2 | 1468 | 2s4/2 | p | l | L2-56 | 23 |
| 4647652 | EB | 0.68 | 54953.945894 | 1.064 824 95 | 11.8 | 1470 | 2/2 | p | l | L2-08 | 2, 3 |
| 4670267 | EA | 0.60 | 54966.375624 | 2.006 0974 | 15.1 | 1456 | 2s4/2 | a | l(+d) | L2-09 | 3 |
| 4681152 | EA | 0.55 | 54954.060778 | 1.835 930 | 13.1 | 1456 | 2s4/2 | p | l | L2-43 | 3 |
| 4753988 | EA | 0.16 | 54968.025737 | 7.304 476 | 15.0 | 1454 | 2/0 | p+s | l+d | D3-14 | |
| 4758368 | EA | 0.57 | 54958.206761 | 3.749 935 | 10.8 | 1468 | 2s4/2 | p+s | l+a | L3-45 | 3, 13 |
| 4762887 | ELV | 0.95 | 54964.771668 | 0.736 5737 | 14.4 | 1458 | 2/2 | a | l | L2-47 | 3 |
| 4769799 | EA | 0.12 | 54968.515532 | 21.928 614 | 10.9 | 1438 | 2/0 | p+s | l+d | D2-11 | 4, 5 |
| 4848423 | EA | 0.48 | 55000.595941 | 3.003 613 | 11.8 | 922 | 2/2 | a | l | L3-03 | 1, 23 |
| 4859432 | EW | 0.76 | 54949.996305 | 0.385 4799 | 15.5 | 1421 | 2/2 | a | l(+q) | L2-05 | 3 |
| 4909707 | EB | 0.72 | 54953.913193 | 2.302 3675 | 10.7 | 1470 | 2/2 | p+s | l+d | D1-28 | 2, 3 |
| 4937217 | EW | 0.82 | 54964.627330 | 0.429 3416 | 15.4 | 1459 | 2/2 | a | l+q | L3-42 | 3 |
| 4940201 | EA | 0.15 | 54967.276926 | 8.816 578 | 15.0 | 1455 | 2/0 | p+s | l+d | D1-23 | 2, 4, 5 |
| 4945857 | EW | 0.74 | 54964.830222 | 0.335 416 | 14.0 | 1459 | 2/2 | a | l | L2-59 | 3 |
| 4948863 | EA | 0.10 | 54972.831420 | 8.643 5903 | 15.4 | 1452 | 2/0 | p+s | l+d | D2-09 | |
| 5003117 | EA | 0.37 | 54986.095638 | 37.610 001 | 14.0 | 1429 | 2/0 | p+s | l+d | D3-06 | 4, 5 |
| 5039441 | EA | 0.39 | 54955.351360 | 2.151 383 | 12.9 | 1469 | 2s4/0 | p+s | l+a | L1-33 | 2 |
| 5080652 | EA | 0.30 | 54968.166959 | 4.144 357 | 15.1 | 1422 | 2/0 | p | l+d | D1-15 | |
| 5095269 | EA | 0.05 | 54966.865286 | 18.611 9616 | 13.5 | 1433 | 1/0 | p | l+d | D1-16 | 5 |
| 5128972 | EW | 0.74 | 54965.047601 | 0.505 323 | 13.2 | 1459 | 2/2 | a | l | L1-16 | 2, 3 |
| 5216727 | EA | 0.48 | 54964.929149 | 1.513 023 | 13.4 | 1459 | 2s4/2 | p | l | L1-22 | |
| 5255552 | EA+E3 | 0.17 | 54970.636491 | 32.458 635 | 15.2 | 1414 | 2/0 | p+s | l+d | D1-31 | 4, 5 |
| 5264818 | ELV | 0.92 | 54955.241047 | 1.905 050 | 8.9 | 1469 | 2/0 | a | l+d(+q) | D1-20 | 2, 3 |
| 5269407 | EA | 0.53 | 54965.651124 | 0.958 8631 | 14.2 | 1458 | 2s4/0 | a | l | L3-30 | 3 |
| 5307780 | EW | 0.88 | 54964.977524 | 0.308 851 | 14.9 | 1459 | 2/2 | a | l+q | L2-38 | |
| 5310387 | EW | 0.96 | 54953.664664 | 0.441 669 | 12.7 | 1470 | 2/2 | a | l+q | L1-04 | 2, 3 |
| 5353374 | EW | 0.78 | 54964.661848 | 0.393 3205 | 14.1 | 1459 | 2/2 | a | l | L3-11 | 3 |
| 5376552 | EW | 0.82 | 54954.083210 | 0.503 8188 | 12.9 | 1470 | 2/2 | a | l(+q) | L1-11 | 2, 3 |
| 5384802 | EA | 0.17 | 54966.988768 | 6.083 093 | 13.7 | 1454 | 2/0 | a | l+d | D1-19 | 2, 5 |
| 5459373 | ELV | 0.97 | 54964.670887 | 0.286 6088 | 15.1 | 1459 | 2/2 | a | l | L1-14 | 3 |
| 5478466 | EW | 0.97 | 54964.859645 | 0.482 5005 | 14.2 | 1459 | 2/2 | a | l | L2-04 | 3 |
| 5513861 | EA | 0.57 | 54954.995935 | 1.510 2117 | 11.6 | 3010 | 2/2 | a+e | l | L2-63 | 1, 3, 6, 23 |
| 5611561 | ELV(EW) | 0.74 | 55000.011420 | 0.258 694 65 | 14.0 | 1421 | 2/2 | a | l | L2-33 | 3 |
| 5621294 | EA | 0.60 | 54954.510518 | 0.938 905 | 13.6 | 1470 | 2s4/2 | p | l+q | L2-36 | 1, 6, 14 |
| 5653126 | EA | 0.09 | 54985.913152 | 38.493 382 | 13.2 | 1424 | 2/0 | p+s | l+d | D2-06 | 4, 5 |
| 5731312 | EA | 0.08 | 54968.093163 | 7.946 382 | 13.8 | 1456 | 2/0 | p+s | l+d | D2-05 | 4, 5 |
| 5771589 | EA | 0.12 | 54962.130765 | 10.738 342 | 11.8 | 1434 | 2/0 | p+s | l+d | D1-10 | 2, 4, 5 |
| 5897826 | EA+E3 | – | 55069.313 | 1.767 13 | 13.1 | – | – | – | – | D1-01 | 15 |
| 5903301 | EA | 0.41 | 55003.431007 | 2.320 302 | 15.1 | 1330 | 2/2 | a | l | L2-49 | |
| 5952403 | EA+E3 | 0.52 | 55051.237191 | 0.905 6774 | 7.0 | 1426 | 2s4/0 | a | l+d(+q) | D1-02 | 16 |
| 5956776 | EA | 0.61 | 55000.305505 | 0.569 1150 | 16.7 | 855 | 2s4/2 | p | l | L3-21 | |
| 5962716 | EA | 0.47 | 54965.398009 | 1.804 586 | 13.9 | 1458 | 2s4/0 | p | l | L3-32 | |
| 5975712 | ELV | 0.87 | 54953.924190 | 1.136 083 | 11.5 | 1469 | 2/2 | a | l(+q) | L3-39 | 3 |
| 6103049 | EA | 0.59 | 54964.888912 | 0.643 1712 | 15.1 | 1426 | 2s4/0 | a | l | L3-09 | |
| 6144827 | ELV | 0.79 | 54964.642040 | 0.234 650 | 15.0 | 1459 | 2/2 | a | l+q | L1-05 | 3 |
| 6233903 | EA | 0.36 | 55001.719115 | 5.990 8477 | 16.5 | 851 | 2s4/2 | p+s | l+a | L3-54 | |
| 6265720 | EW | 0.93 | 54964.729666 | 0.312 4277 | 14.8 | 1426 | 2/2 | a | l | L3-06 | 3 |
| 6281103 | ELV(EW) | 0.98 | 54964.870642 | 0.363 2811 | 14.9 | 1459 | 2/2 | a | l+q | L2-50 | 3 |
| 6287172 | FP? | 0.95 | 54953.651911 | 0.203 8732(/2) | 12.7 | 1469 | 2/2(1/1) | a | l | F-06 | |
| 6370665 | EW | 0.96 | 54965.405240 | 0.932 3155 | 14.0 | 1458 | 2/2 | a | l+q | L1-08 | 2, 3 |
| 6516874 | EA | 0.60 | 55001.4643225 | 0.916 3260 | 15.9 | 1237 | 2s4/0 | a | l | L2-20 | 3 |
| 6525196 | EA | 0.36 | 54954.353139 | 3.420 598 | 10.2 | 1467 | 2s4/0 | a | l+d | D1-26 | 2 |
| 6531485 | EA | 0.53 | 54964.801481 | 0.676 990 | 15.6 | 1459 | 2/0 | p+s | l+d | D1-03 | 2 |
| 6543674 | EA+E3 | 0.53 | 54965.303847 | 2.391 030 | 13.5 | 1456 | 2s4/2 | a | l | L1-36 | 3, 17 |
| 6545018 | EA | 0.42 | 54965.835642 | 3.991 460 | 13.7 | 1457 | 2/2 | p+s | l+d | D1-07 | 2, 4, 5 |
| 6546508 | EA | 0.20 | 55189.798579 | 6.107 057 | 15.7 | 1237 | 2/0 | p+s | l+d | D2-10 | |
| 6606282 | EA | 0.31 | 54965.433543 | 2.107 130 | 13.0 | 1456 | 2/0 | a | l | L3-22 | |
| 6615041 | EW | 0.75 | 54964.807732 | 0.340 0856 | 13.9 | 1459 | 2/2 | a | l(+q) | L3-49 | 3 |
| 6669809 | EB | 0.64 | 54953.997571 | 0.733 7388 | 10.8 | 1437 | 2s4/2 | p | l+c | L1-02 | |
| 6671698 | EW | 0.73 | 54954.077303 | 0.471 525 | 13.5 | 1437 | 2/2 | a | l+q | L2-52 | 3 |
| 6766325 | ELV(EW) | 0.92 | 54964.713835 | 0.439 9657 | 13.8 | 1459 | 2/2 | a | l | L3-26 | 3 |
| 6794131 | ELV? | 0.81 | 54954.298318 | 1.613 328 | 12.5 | 1455 | 2/2 | p | l(+q) | L3-52 | 3 |
| 6877673 | EA | 0.11 | 54989.092003 | 36.758 7372 | 13.7 | 1454 | 2/0 | p+s | l+d | D3-07 | |
| 6964043 | EA+E3 | 0.35 | 55190.170 | 10.725 518 | 15.6 | 1233 | 2/0 | p+s | l+d | D1-17 | 4 |
| 6965293 | EA | 0.18 | 54957.473848 | 5.077 746 | 12.8 | 1468 | 2/0 | p+s | l+a(+d) | L2-39 | |
| 7119757 | EA | 0.64 | 54965.304131 | 0.742 9217 | 15.6 | 1459 | 2s4/2 | a | l | L2-57 | 3 |
| 7177553 | EA | 0.06 | 54954.545842 | 17.996 467 | 11.5 | 1458 | 2/0 | p+s | l+d | D1-29 | |
| 7272739 | EW | 0.75 | 54964.853794 | 0.281 1644 | 13.0 | 1459 | 2/2 | a | l(+q) | L3-58 | 3 |
| 7289157 | EA+E3 | 0.37 | 54969.966600 | 5.266 525 | 12.9 | 1459 | 2/0 | p+s | l+d | D1-18 | 2, 4, 5 |
| 7339345 | EW | 0.74 | 54964.6478878 | 0.259 6643 | 15.2 | 1459 | 2/2 | a | l+q | L2-19 | 3 |
| 7362751 | ELV(EW) | 0.73 | 54964.744494 | 0.338 249 | 15.8 | 1459 | 2/2 | a | l+q | L1-25 | 3 |
| 7375612 | FP? | 0.98 | 54953.639904 | 0.160 0728(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-07 | 3 |
| 7385478 | EA | 0.54 | 54954.534784 | 1.655 478 | 11.5 | 1468 | 2s4/2 | p | l | L2-31 | 3 |
| 7440742 | EW(ELV) | 0.71 | 54949.930411 | 0.283 9922 | 11.8 | 1388 | 2/2 | a | l | L2-45 | |
| 7518816 | EB | 0.65 | 54953.692277 | 0.466 5805 | 12.8 | 1470 | 2s4/2 | a | l | L3-13 | 3 |
| 7552344 | EA | 0.24 | 54964.948438 | 2.001 491 | 15.4 | 1457 | 2/0 | a | l | L2-25 | |
| 7593110 | EA | 0.17 | 54999.192999 | 3.549 384 | 15.9 | 1235 | 2/0 | p | l+d | D1-22 | |
| 7630658 | EA | 0.47 | 55003.279035 | 2.151 155 | 13.9 | 1418 | 2s4/2 | a | l | L2-22 | 6 |
| 7668648 | EA+E3 | 0.08 | 54963.315401 | 27.825 590 | 15.3 | 1433 | 2/0 | p+s | l+d | D1-13 | 2, 4, 5 |
| 7670617 | EA | 0.07 | 54969.139216 | 24.703 160 | 15.5 | 1433 | 2/0 | p+s | l+d | D3-09 | 4, 5 |
| 7680593 | ELV(EW) | 0.97 | 54964.639100 | 0.276 3915 | 15.4 | 1459 | 2/2 | a | l+q | L2-32 | 3 |
| 7685689 | EW | 0.77 | 55001.994674 | 0.325 1596 | 15.5 | 1238 | 2/2 | a | l(+q) | L1-21 | 3 |
| 7690843 | EB | 0.69 | 54954.158345 | 0.786 260 | 11.1 | 1470 | 2s4/2 | a | l+d+c | D1-04 | 2, 3, 13 |
| 7811211 | EA | 0.49 | 54964.825947 | 0.902 4037 | 14.6 | 1458 | 2s4/0 | p | l(+q) | L1-19 | |
| 7812175 | EA | 0.06 | 55002.612666 | 17.793 925 | 16.3 | 658 | 2/0 | p+s | l+d | D2-01 | 4 |
| 7821010 | EA | 0.03 | 54969.615845 | 24.238 2426 | 10.8 | 1454 | 2/0 | p+s | l+d | D2-07 | 18 |
| 7837302 | EA | 0.06 | 54982.935571 | 23.837 136 | 13.7 | 1430 | 1/0 | p | l+d | D2-12 | 2 |
| 7877062 | EW | 0.81 | 54964.779743 | 0.303 6520 | 13.8 | 1459 | 2/2 | a | l | L2-54 | 3 |
| 7955301 | EA | 0.14 | 54967.950750 | 15.327 84 | 12.7 | 1448 | 2/0 | p+s | l+d | D1-14 | 2, 4, 5, 13 |
| 8016214 | EA | 0.53 | 54966.725645 | 3.174 9714 | 14.4 | 1454 | 2s4/2 | p | l(+q) | L3-57 | 3 |
| 8023317 | EA | 0.13 | 54979.733478 | 16.579 002 | 12.9 | 1465 | 2/2 | p+s | l+d | D1-30 | 2, 4 |
| 8043961 | EA | 0.63 | 54954.555903 | 1.559 2127 | 10.7 | 1469 | 2/2 | a | l(+d) | L1-20 | 2, 3 |
| 8045121 | FP? | 1.00 | 54953.761839 | 0.263 1774(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-02 | 3 |
| 8081389 | EA | 0.56 | 54965.003801 | 1.489 4435 | 14.0 | 1458 | 2s4/2 | p | l(+q) | L2-58 | |
| 8094140 | EA | 0.49 | 54965.145553 | 0.706 4292 | 15.2 | 1459 | 2s4/0 | a | l | L1-32 | |
| 8143170 | EA | 0.15 | 54970.113064 | 28.785 943 | 12.9 | 1455 | 2/0 | p+s | l+d | D3-04 | 4 |
| 8145477 | EW | 0.89 | 54965.076077 | 0.565 7843 | 14.8 | 497 | 2/2 | a | l | L2-01 | 3 |
| 8190491 | ELV | 0.95 | 54965.198125 | 0.777 8768 | 14.3 | 1459 | 2/2 | a | l(+q) | L1-27 | 3 |
| 8192840 | ELV(EW) | 0.95 | 54965.013933 | 0.433 549 25 | 13.5 | 1459 | 2/2 | a | l(+q) | L2-40 | 2, 3 |
| 8210721 | EA | 0.08 | 54971.157082 | 22.672 816 | 14.3 | 1451 | 2/0 | p+s | l+d | D2-03 | 4, 5 |
| 8242493 | EW | 0.73 | 54964.621844 | 0.283 2856 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-29 | 3 |
| 8265951 | EW | 0.81 | 54954.246763 | 0.779 9575 | 12.7 | 1469 | 2/2 | a | l | L3-48 | 3 |
| 8330092 | ELV(EW) | 0.79 | 54964.940576 | 0.321 723 55 | 13.5 | 1459 | 2/2 | a | l | L1-26 | 3 |
| 8386865 | ELV | 0.99 | 54953.942556 | 1.258 041 | 12.0 | 1466 | 2/2 | a | l(+d) | L1-09 | 2, 3 |
| 8394040 | ELV(EW) | 0.77 | 54964.878453 | 0.302 1262 | 14.5 | 1459 | 2/2 | a | l | L1-12 | 2, 3 |
| 8429450 | EA | 0.47 | 54954.217684 | 2.705 1516 | 13.1 | 1466 | 2/2 | a | l | L3-46 | 5 |
| 8444552 | EA | 0.49 | 54964.595346 | 1.178 090 | 13.6 | 1459 | 2s4/0 | a | l | L3-41 | |
| 8553788 | EA | 0.54 | 54954.997634 | 1.606 1632 | 12.7 | 2771 | 2s4/2 | p+e | l | L3-51 | 1, 5, 6, 23 |
| 8563964 | FP? | 1.00 | 54953.846748 | 0.338 436(/2) | 12.9 | 1470 | 2/2(1/1) | a | l | F-03 | 3 |
| 8690104 | EW | 0.77 | 54964.834110 | 0.408 7744 | 14.9 | 1459 | 2/2 | a | l | L3-27 | 3 |
| 8719897 | EA | 0.50 | 54955.237444 | 3.151 420 | 12.4 | 1469 | 2s4/0 | a | l+d | D1-21 | 2, 13 |
| 8739802 | ELV | 0.93 | 55001.999865 | 0.274 5129 | 14.9 | 1238 | 2/2 | a | l | L2-21 | 3 |
| 8758161a | EA | – | 54953.834107 | 1.996 4352 | 12.5 | 1467 | 2s4/2 | a | l | L3-43 | |
| 8868650 | EA | 0.62 | 54957.940589 | 4.447 430 | 11.9 | 1463 | 2s4/2 | p | l(+q) | L3-36 | |
| 8904448 | EW | 0.74 | 54965.059034 | 0.865 983 | 13.9 | 1458 | 2s2/2 | p | l+c | L1-23 | 2, 3 |
| 8938628 | EA | 0.14 | 54966.603088 | 6.862 216 | 13.7 | 1455 | 2/0 | p+s | l+d | D1-25 | 2, 4 |
| 8957887 | EW | 0.76 | 54964.884185 | 0.347 3543 | 15.4 | 1459 | 2/2 | a | l | L2-11 | 3 |
| 8982514 | EW | 0.83 | 54953.930563 | 0.414 4906 | 13.2 | 1470 | 2/2 | a | l | L3-28 | 3 |
| 9007918 | EA+E3 | 0.52 | 54954.748782 | 1.387 2066 | 11.7 | 1469 | 2s4/2 | p | l(+d) | L1-18 | 6 |
| 9028474 | EA | 0.00 | 55010.672516 | 124.936 5792 | 12.3 | 1374 | 2/0 | p+s | l+d | D3-11 | |
| 9075704 | EB | 0.68 | 54999.891435 | 0.513 1516 | 16.2 | 855 | 2/2 | a | l+q | L1-13 | 3 |
| 9083523 | EB | 0.65 | 54954.484907 | 0.918 4208 | 12.7 | 1470 | 2s4/2 | p | l | L3-16 | 3 |
| 9084778 | EA | 0.49 | 54964.654261 | 0.592 2444 | 15.7 | 1459 | 1/0 | p | l | L1-34 | |
| 9091810 | EB | 0.69 | 54953.600339 | 0.479 7214 | 12.8 | 1470 | 2s4/2 | a | l | L2-53 | 3 |
| 9101279 | EA | 0.58 | 54965.932213 | 1.811 4606 | 13.9 | 1456(4987) | 2s6/2 | p(+e) | l+q | L2-46 | 3 |
| 9110346 | EA | 0.43 | 55002.222003 | 1.790 5531 | 16.4 | 1330 | 2s4/2 | a | l | L3-47 | |
| 9140402 | EA | 0.27 | 54966.441095 | 4.988 3312 | 15.3 | 1457 | 2/0 | p+s | l+d | D1-11 | 19 |
| 9159301 | EA | 0.55 | 54956.304393 | 3.044 7712 | 12.1 | 1468 | 2s4/0 | p | l | L2-34 | 1 |
| 9181877 | EW | 0.74 | 54953.797919 | 0.321 0098 | 11.7 | 1470 | 2/2 | a | l | L3-55 | 3, 13 |
| 9272276 | EW | 0.78 | 54953.693247 | 0.280 615 | 13.2 | 1470 | 2/2 | a | l | L2-61 | 3 |
| 9283826 | EW | 0.84 | 54953.801153 | 0.356 5232 | 13.1 | 1470 | 2/2 | a(+e) | l | L3-08 | 3 |
| 9353234 | ELV | 0.86 | 54965.446983 | 1.486 5274 | 13.7 | 1458 | 2/2 | a | l | L2-28 | 3 |
| 9392702 | EA | 0.37 | 54964.893911 | 3.909 3245 | 14.6 | 868 | 2s4/0 | p | l | L3-02 | |
| 9402652b | EA | 0.65 | 54954.290416 | 1.073 106 | 11.8 | 2048(5723) | 2/2 | p+s+e | l | L2-62 | 1, 6, 23 |
| 9412114 | ELV | 0.85 | 55001.895873 | 0.250 2532 | 15.2 | 1147 | 2/2 | a | l(+q) | L3-56 | 3 |
| 9451096 | EA | 0.53 | 54954.729422 | 1.250 3906 | 12.6 | 1470 | 2s4/2 | p+s | l+d | D1-09 | 2, 3, 5 |
| 9472174a | oEA,sdB+dM | 0.78 | 54953.643197 | 0.125 765 28 | 12.3 | 1437 | 2/0 | p | l+c | L1-15 | 20 |
| 9532219 | EW | 0.74 | 55001.947386 | 0.198 1551 | 16.1 | 1330 | 2/2 | a | l | L3-50 | 3 |
| 9574614 | EA | 0.40 | 54965.687069 | 0.982 0954 | 15.9 | 1458 | 1/0 | p | l | L2-48 | |
| 9592145 | EB | 0.65 | 54965.015451 | 0.488 8674 | 14.0 | 1459 | 2/2 | p | l+q | L2-03 | 3 |
| 9596187 | EA | 0.47 | 54964.705879 | 0.953 2917 | 14.5 | 1459 | 2/0 | p | l | L3-18 | |
| 9612468 | FP? | 1.00 | 54953.604225 | 0.133 4715(/2) | 11.5 | 1470 | 2/2(1/1) | a | l | F-08 | 3 |
| 9664215 | EA | 0.27 | 54964.925032 | 3.319 4959 | 15.1 | 1459 | 2s4/0 | p+s | l+d | D2-04 | |
| 9665086 | EB | 0.67 | 55000.087903 | 0.296 536 | 13.9 | 1421 | 2/2 | a | l(+q) | L2-16 | 3 |
| 9706078 | EA | 0.56 | 54954.140288 | 0.613 5606 | 12.8 | 1470 | 2s4/0 | a | l | L3-20 | 3 |
| 9711751 | EA | 0.49 | 54965.352420 | 1.711 5283 | 13.8 | 1458 | 2s4/0 | p | l | L2-44 | |
| 9714358 | EA | 0.13 | 54967.395501 | 6.474 177 | 15.0 | 1454 | 2/0 | p+s | l+d | D1-08 | 2, 4, 5 |
| 9715925 | EA | 0.10 | 54998.920053 | 6.308 299 | 16.5 | 830 | 2/0 | p+s | l+d | D2-02 | 4 |
| 9722737 | EW | 0.78 | 54964.973629 | 0.418 5284 | 14.9 | 1459 | 2/2 | a | l | L1-17 | 2, 3 |
| 9777987 | EW | 0.74 | 55000.068578 | 0.258 5001 | 16.3 | 684 | 2/2 | a | l | L1-01 | |
| 9788457 | EA | 0.60 | 54965.186856 | 0.963 3378 | 13.0 | 1459 | 2s2/2 | p | l+q | L3-33 | 3 |
| 9821923 | EW | 0.95 | 54964.814614 | 0.349 5329 | 14.2 | 1459 | 2/2 | a | l | L3-10 | 3 |
| 9838047 | EW | 0.84 | 54953.713063 | 0.436 162 | 13.5 | 1470 | 2/2 | a | l | L2-41 | 3 |
| 9850387 | EA | 0.47 | 54956.416799 | 2.748 4986 | 13.5 | 1468 | 2s4/0 | a | l(+d) | L1-31 | |
| 9912977 | EA | 0.59 | 54966.709125 | 1.887 874 | 13.7 | 1457 | 2s4/2 | a | l | L2-10 | 2, 3 |
| 9963009 | EA | 0.06 | 54986.018248 | 40.069 657 | 14.5 | 1443 | 2/0 | p+s | l+d | D3-12 | 4 |
| 9994475 | EW | 0.76 | 54964.733082 | 0.318 4064 | 14.3 | 1459 | 2/2 | a | l+q | L1-28 | 3 |
| 10095469 | EA | 0.60 | 54999.865835 | 0.677 7625 | 14.7 | 855 | 2s4/0 | p | l | L3-01 | 3 |
| 10095512 | EA | 0.24 | 54953.888455 | 6.017 207 | 13.1 | 1468 | 2/0 | p+s | l+d | D1-27 | 2 |
| 10226388 | EW | 0.77 | 54954.120530 | 0.660 6583 | 10.8 | 1470 | 2/2 | a | l | L2-26 | 2, 3 |
| 10268809 | EA | 0.05 | 54971.999951 | 24.708 999 | 13.7 | 1450 | 2/0 | p+s | l+d | D3-15 | 4 |
| 10268903 | EA | 0.39 | 54999.901602 | 1.103 9788 | 17.4 | 683 | 2/0 | a | l | L3-05 | |
| 10275197 | EW | 0.79 | 54953.707304 | 0.390 8377 | 12.9 | 1470 | 2/2 | a | l | L3-37 | 3 |
| 10296163 | EA | 0.17 | 54959.387400 | 9.296 7444 | 13.2 | 1463 | 2/0 | p+s | l+d | D3-17 | |
| 10319590 | EA | 0.09 | 54965.716743 | 21.320 459 | 13.7 | 405 | 2/0 | p+s | l+d | D3-01 | 2, 4, 5 |
| 10383620 | EA | 0.64 | 54954.123817 | 0.734 5658 | 12.8 | 1470 | 2/2 | a | l | L3-14 | 3 |
| 10483644 | EA | 0.12 | 54966.314610 | 5.110 7711 | 14.0 | 1457 | 2/0 | p | l+d | D1-24 | |
| 10549576 | EA | 0.20 | 54972.078799 | 9.089 4658 | 13.0 | 1454 | 2/0 | p+s | l+d | D2-13 | |
| 10557008 | EW | 0.77 | 54964.639092 | 0.265 4186 | 14.7 | 1459 | 2/2 | a | l | L3-15 | |
| 10583181 | EA | 0.47 | 54955.206895 | 2.696 353 | 11.0 | 1467 | 2s4/2 | p | l | L2-42 | |
| 10613718 | EA | 0.39 | 54953.886226 | 1.175 878 | 12.7 | 1469 | 2s4/0 | a | l+d | D1-06 | 2 |
| 10686876 | EA | 0.45 | 54953.951815 | 2.618 4153 | 11.7 | 3820 | 2s4/2 | p+e | l | L3-53 | 6, 23 |
| 10724533 | EB | 0.75 | 54954.395189 | 0.745 0918 | 9.0 | 1470 | 2s4/2 | p | l | L3-35 | 3 |
| 10727655 | EW | 0.74 | 54953.910817 | 0.353 3652 | 13.4 | 4374 | 2/2 | a+e | l+q | L1-37 | 3 |
| 10848807 | EW | 0.74 | 54999.987867 | 0.346 2467 | 15.8 | 1421 | 2/2 | a | l | L2-12 | 3 |
| 10855535 | FP? | 0.99 | 54964.629852 | 0.112 7824(/2) | 13.9 | 1459 | 2/2(1/1) | a | l | F-01 | 3 |
| 10916675 | EW | 0.86 | 54953.700609 | 0.418 8675 | 13.4 | 1470 | 2/2 | a | l | L3-19 | 3 |
| 10934755 | EB | 0.68 | 54964.840450 | 0.786 486 | 14.4 | 1459 | 2/2 | p | l | L3-07 | 3 |
| 10979716 | EA | 0.10 | 54967.081259 | 10.684 056 | 15.8 | 1453 | 2/0 | p+s | l+d | D2-08 | 4 |
| 10991989 | EA | 0.54 | 54954.650910 | 0.974 4775 | 10.3 | 1470 | 2s4/0 | a | l | L1-24 | 2, 3, 13 |
| 11042923 | EW | 0.76 | 54964.970492 | 0.390 162 | 14.4 | 1459 | 2/2 | a | l | L2-30 | 2, 3 |
| 11234677 | EA | 0.42 | 54953.872607 | 1.587 425 | 13.3 | 1470 | 2s4/2 | p | l | L3-23 | |
| 11246163 | EW | 0.77 | 54964.565448 | 0.279 2271 | 14.5 | 1459 | 2/2 | a | l(+q) | L3-29 | 3 |
| 11502172 | EA | 0.05 | 54968.617081 | 25.431 9585 | 14.2 | 1435 | 2/0 | p+s | l+d | D3-10 | |
| 11519226 | EA | 0.03 | 54972.990000 | 22.161 715 | 13.0 | 1463 | 2/0 | p+s | l+d | D2-14 | 4 |
| 11558882 | EA | 0.01 | 54987.716793 | 73.914 770 | 15.4 | 1384 | 2/0 | p+s | l+d | D3-13 | |
| 11604958 | EW | 0.72 | 54964.653176 | 0.298 9297 | 13.9 | 1459 | 2/2 | a | l | L2-51 | 3 |
| 11825204 | FP? | 0.98 | 54964.751093 | 0.209 6356(/2) | 13.8 | 1458 | 2/2(1/1) | a | l+q | F-05 | 3 |
| 11968490 | EA | 0.49 | 54965.437249 | 1.078 890 | 13.7 | 1458 | 2s4/0 | a | l+q(+d) | L1-06 | 2 |
| 12019674 | EW | 0.76 | 53363.5350 | 0.354 4975 | 13.0 | 5188 | 2/2 | a+e | l | L2-64 | 3, 21 |
| 12055014 | EW | 0.85 | 54965.041294 | 0.499 9046 | 13.5 | 1459 | 2/2 | a | l | L3-34 | |
| 12055255 | ELV(EW) | 0.90 | 54964.528184 | 0.220 9404 | 15.9 | 1459 | 2/2 | a | l | L3-44 | 3 |
| 12071741 | ELV(EW) | 0.94 | 54964.820555 | 0.314 2642 | 14.8 | 1459 | 2/2 | a | l | L2-23 | 3 |
| 12356914 | EA | 0.03 | 54976.492322 | 27.308 455 | 15.5 | 1459 | 2/0 | p+s | l+d | D3-05 | 4 |
| 12508348 | FP? | 0.97 | 54951.682693 | 0.255 596(/2) | 13.4 | 1457 | 2/2(1/1) | a | l+q | F-04 | |
| 12554536 | EB | 0.63 | 54953.964623 | 0.684 4956 | 12.8 | 1470 | 2s4/2 | p | l | L2-60 | 3 |
| KIC No. . | Type . | Morph. . | T0 . | P1 . | Kp . | Data length . | |$\frac{\mathrm{ETV}}{\mathrm{QTV}}$| . | Fitted . | Fit . | Tab . | Refs. . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (BJD) . | (d) . | (mag) . | (d) . | . | curves . | type . | . | . |
| 1873918 | ELV(EW) | 0.86 | 54964.900829 | 0.332 433 | 13.7 | 1459 | 2/2 | a | l+q | L2-13 | 7 |
| 2302092 | EW | 0.89 | 54964.694441 | 0.294 673 | 14.4 | 1459 | 2/2 | a | l | L2-27 | 3 |
| 2305372 | EA | 0.58 | 54965.956227 | 1.404 6920 | 13.8 | 1458(4216) | 2s4/2 | p(+e) | l(+q) | L3-25 | 6, 23 |
| 2450566 | ELV | 0.98 | 55001.560102 | 1.844 5871 | 11.7 | 1468 | 2/2 | a | l | L2-24 | 3 |
| 2576692 | EA | 0.04 | 55027.103323 | 87.878 2329 | 12.7 | 1406 | 2/0 | p+s | l+d | D3-08 | |
| 2708156 | EA | 0.57 | 54954.336095 | 1.891 2671 | 10.7 | 33 912 | 2s8/0 | p+e | l+c | L1-38 | 1 |
| 2715007 | ELV | 0.87 | 54964.783119 | 0.297 1105 | 14.7 | 1459 | 2/2 | a | l | L3-17 | |
| 2715417 | ELV(EW) | 0.76 | 54964.667658 | 0.236 4399 | 14.1 | 1459 | 2/2 | a | l(+q) | L2-15 | |
| 2835289 | ELV+E3 | 0.92 | 55000.444609 | 0.857 762 | 13.0 | 1469 | 2/2 | a | l | L1-35 | 3, 8 |
| 2856960 | EA+E3 | 0.60 | 54964.661805 | 0.258 507 | 15.6 | 1458 | 2/0 | a | l+q | L1-03 | 3, 9, 10, 11 |
| 2983113 | EW | 0.89 | 55001.969640 | 0.395 1601 | 15.2 | 1238 | 2/2 | a | l | L3-04 | 3 |
| 3114667 | EA | 0.52 | 54999.758222 | 0.888 5832 | 17.4 | 683 | 2s4/0 | a | l | L2-02 | 3 |
| 3228863 | EB | 0.65 | 54954.26185 | 0.730 944 | 11.8 | 6636 | 2/2 | a+e | l+q | L1-29 | 2, 3, 12, 22 |
| 3245776 | ELV | 0.96 | 55001.663004 | 1.492 0589 | 14.4 | 1458 | 2/2 | a | l | L1-30 | 3 |
| 3248019 | EA | 0.37 | 55098.778000 | 2.668 2057 | 15.4 | 1329 | 2/0 | a | l | L3-24 | |
| 3335816 | EA | 0.16 | 54954.355631 | 7.422 0263 | 12.1 | 1462 | 2/0 | a | l | L3-38 | |
| 3338660 | EA | 0.60 | 55002.262623 | 1.873 3806 | 14.8 | 852 | 2s4/0 | p | l | L2-07 | |
| 3345675 | EA | 0.00 | 55083.146716 | 120.004 0103 | 15.6 | 1320 | 1/0 | p | l+d | D3-03 | |
| 3440230 | EA | 0.54 | 54967.238413 | 2.881 1010 | 13.6 | 1455 | 2s4/2 | p | l+q | L2-35 | 1, 6 |
| 3544694 | EA | 0.29 | 55740.65102 | 3.845 728 | 15.9 | 683 | 2s8/0 | p+s | l+d | D1-05 | |
| 3766353 | EA(HB) | −1.00 | 54966.722264 | 2.666 966 | 14.0 | 1456 | 2/2 | p | l | L3-12 | 3 |
| 3839964 | ELV(EW) | 0.78 | 54964.792432 | 0.256 1499 | 14.6 | 1459 | 2/2 | a | l+q | L3-40 | 3 |
| 3853259 | ELV(EW) | 0.98 | 54964.781808 | 0.276 6478 | 13.9 | 1459 | 2/2 | a | l+q | L1-10 | |
| 4037163 | EA | 0.58 | 55000.227976 | 0.635 4447 | 16.7 | 684 | 2/0 | a | l(+q) | L1-07 | 3 |
| 4055092 | EA | 0.01 | 54966.932772 | 76.464 989 | 15.3 | 1404 | 2/0 | p+s | l+d | D3-16 | |
| 4069063 | EA | 0.55 | 54964.906342 | 0.504 2953 | 13.3 | 1452 | 2s4/0 | a | l | L2-18 | 3 |
| 4074708 | EW | 0.73 | 54964.856673 | 0.302 1166 | 15.4 | 1459 | 2/2 | a | l | L2-37 | 3 |
| 4078157 | EA | 0.08 | 54960.300077 | 16.025 671 | 15.5 | 1202 | 2/0 | p+s | l+d | D3-02 | |
| 4079530 | EA | 0.07 | 54994.805374 | 17.727 1000 | 15.6 | 579 | 2/0 | p+s | l+d | D1-12 | |
| 4138301 | ELV | 0.90 | 54964.685221 | 0.253 379 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-14 | 3 |
| 4174507 | EA | 0.24 | 54966.041640 | 3.891 825 | 15.4 | 1456 | 2/0 | a | l(+d) | L3-31 | |
| 4244929 | EW | 0.91 | 54964.747256 | 0.341 403 | 15.1 | 1459 | 2/2 | a | l | L2-55 | 3 |
| 4451148 | EW | 0.82 | 54954.385233 | 0.735 9815 | 11.2 | 1470 | 2/2 | a | l | L2-06 | 3 |
| 4547308 | ELV | 0.88 | 54953.635293 | 0.576 9278 | 12.5 | 1470 | 2/2 | a | l | L2-17 | 3 |
| 4574310 | EA | 0.56 | 54954.662614 | 1.306 2201 | 13.2 | 1468 | 2s4/2 | p | l | L2-56 | 23 |
| 4647652 | EB | 0.68 | 54953.945894 | 1.064 824 95 | 11.8 | 1470 | 2/2 | p | l | L2-08 | 2, 3 |
| 4670267 | EA | 0.60 | 54966.375624 | 2.006 0974 | 15.1 | 1456 | 2s4/2 | a | l(+d) | L2-09 | 3 |
| 4681152 | EA | 0.55 | 54954.060778 | 1.835 930 | 13.1 | 1456 | 2s4/2 | p | l | L2-43 | 3 |
| 4753988 | EA | 0.16 | 54968.025737 | 7.304 476 | 15.0 | 1454 | 2/0 | p+s | l+d | D3-14 | |
| 4758368 | EA | 0.57 | 54958.206761 | 3.749 935 | 10.8 | 1468 | 2s4/2 | p+s | l+a | L3-45 | 3, 13 |
| 4762887 | ELV | 0.95 | 54964.771668 | 0.736 5737 | 14.4 | 1458 | 2/2 | a | l | L2-47 | 3 |
| 4769799 | EA | 0.12 | 54968.515532 | 21.928 614 | 10.9 | 1438 | 2/0 | p+s | l+d | D2-11 | 4, 5 |
| 4848423 | EA | 0.48 | 55000.595941 | 3.003 613 | 11.8 | 922 | 2/2 | a | l | L3-03 | 1, 23 |
| 4859432 | EW | 0.76 | 54949.996305 | 0.385 4799 | 15.5 | 1421 | 2/2 | a | l(+q) | L2-05 | 3 |
| 4909707 | EB | 0.72 | 54953.913193 | 2.302 3675 | 10.7 | 1470 | 2/2 | p+s | l+d | D1-28 | 2, 3 |
| 4937217 | EW | 0.82 | 54964.627330 | 0.429 3416 | 15.4 | 1459 | 2/2 | a | l+q | L3-42 | 3 |
| 4940201 | EA | 0.15 | 54967.276926 | 8.816 578 | 15.0 | 1455 | 2/0 | p+s | l+d | D1-23 | 2, 4, 5 |
| 4945857 | EW | 0.74 | 54964.830222 | 0.335 416 | 14.0 | 1459 | 2/2 | a | l | L2-59 | 3 |
| 4948863 | EA | 0.10 | 54972.831420 | 8.643 5903 | 15.4 | 1452 | 2/0 | p+s | l+d | D2-09 | |
| 5003117 | EA | 0.37 | 54986.095638 | 37.610 001 | 14.0 | 1429 | 2/0 | p+s | l+d | D3-06 | 4, 5 |
| 5039441 | EA | 0.39 | 54955.351360 | 2.151 383 | 12.9 | 1469 | 2s4/0 | p+s | l+a | L1-33 | 2 |
| 5080652 | EA | 0.30 | 54968.166959 | 4.144 357 | 15.1 | 1422 | 2/0 | p | l+d | D1-15 | |
| 5095269 | EA | 0.05 | 54966.865286 | 18.611 9616 | 13.5 | 1433 | 1/0 | p | l+d | D1-16 | 5 |
| 5128972 | EW | 0.74 | 54965.047601 | 0.505 323 | 13.2 | 1459 | 2/2 | a | l | L1-16 | 2, 3 |
| 5216727 | EA | 0.48 | 54964.929149 | 1.513 023 | 13.4 | 1459 | 2s4/2 | p | l | L1-22 | |
| 5255552 | EA+E3 | 0.17 | 54970.636491 | 32.458 635 | 15.2 | 1414 | 2/0 | p+s | l+d | D1-31 | 4, 5 |
| 5264818 | ELV | 0.92 | 54955.241047 | 1.905 050 | 8.9 | 1469 | 2/0 | a | l+d(+q) | D1-20 | 2, 3 |
| 5269407 | EA | 0.53 | 54965.651124 | 0.958 8631 | 14.2 | 1458 | 2s4/0 | a | l | L3-30 | 3 |
| 5307780 | EW | 0.88 | 54964.977524 | 0.308 851 | 14.9 | 1459 | 2/2 | a | l+q | L2-38 | |
| 5310387 | EW | 0.96 | 54953.664664 | 0.441 669 | 12.7 | 1470 | 2/2 | a | l+q | L1-04 | 2, 3 |
| 5353374 | EW | 0.78 | 54964.661848 | 0.393 3205 | 14.1 | 1459 | 2/2 | a | l | L3-11 | 3 |
| 5376552 | EW | 0.82 | 54954.083210 | 0.503 8188 | 12.9 | 1470 | 2/2 | a | l(+q) | L1-11 | 2, 3 |
| 5384802 | EA | 0.17 | 54966.988768 | 6.083 093 | 13.7 | 1454 | 2/0 | a | l+d | D1-19 | 2, 5 |
| 5459373 | ELV | 0.97 | 54964.670887 | 0.286 6088 | 15.1 | 1459 | 2/2 | a | l | L1-14 | 3 |
| 5478466 | EW | 0.97 | 54964.859645 | 0.482 5005 | 14.2 | 1459 | 2/2 | a | l | L2-04 | 3 |
| 5513861 | EA | 0.57 | 54954.995935 | 1.510 2117 | 11.6 | 3010 | 2/2 | a+e | l | L2-63 | 1, 3, 6, 23 |
| 5611561 | ELV(EW) | 0.74 | 55000.011420 | 0.258 694 65 | 14.0 | 1421 | 2/2 | a | l | L2-33 | 3 |
| 5621294 | EA | 0.60 | 54954.510518 | 0.938 905 | 13.6 | 1470 | 2s4/2 | p | l+q | L2-36 | 1, 6, 14 |
| 5653126 | EA | 0.09 | 54985.913152 | 38.493 382 | 13.2 | 1424 | 2/0 | p+s | l+d | D2-06 | 4, 5 |
| 5731312 | EA | 0.08 | 54968.093163 | 7.946 382 | 13.8 | 1456 | 2/0 | p+s | l+d | D2-05 | 4, 5 |
| 5771589 | EA | 0.12 | 54962.130765 | 10.738 342 | 11.8 | 1434 | 2/0 | p+s | l+d | D1-10 | 2, 4, 5 |
| 5897826 | EA+E3 | – | 55069.313 | 1.767 13 | 13.1 | – | – | – | – | D1-01 | 15 |
| 5903301 | EA | 0.41 | 55003.431007 | 2.320 302 | 15.1 | 1330 | 2/2 | a | l | L2-49 | |
| 5952403 | EA+E3 | 0.52 | 55051.237191 | 0.905 6774 | 7.0 | 1426 | 2s4/0 | a | l+d(+q) | D1-02 | 16 |
| 5956776 | EA | 0.61 | 55000.305505 | 0.569 1150 | 16.7 | 855 | 2s4/2 | p | l | L3-21 | |
| 5962716 | EA | 0.47 | 54965.398009 | 1.804 586 | 13.9 | 1458 | 2s4/0 | p | l | L3-32 | |
| 5975712 | ELV | 0.87 | 54953.924190 | 1.136 083 | 11.5 | 1469 | 2/2 | a | l(+q) | L3-39 | 3 |
| 6103049 | EA | 0.59 | 54964.888912 | 0.643 1712 | 15.1 | 1426 | 2s4/0 | a | l | L3-09 | |
| 6144827 | ELV | 0.79 | 54964.642040 | 0.234 650 | 15.0 | 1459 | 2/2 | a | l+q | L1-05 | 3 |
| 6233903 | EA | 0.36 | 55001.719115 | 5.990 8477 | 16.5 | 851 | 2s4/2 | p+s | l+a | L3-54 | |
| 6265720 | EW | 0.93 | 54964.729666 | 0.312 4277 | 14.8 | 1426 | 2/2 | a | l | L3-06 | 3 |
| 6281103 | ELV(EW) | 0.98 | 54964.870642 | 0.363 2811 | 14.9 | 1459 | 2/2 | a | l+q | L2-50 | 3 |
| 6287172 | FP? | 0.95 | 54953.651911 | 0.203 8732(/2) | 12.7 | 1469 | 2/2(1/1) | a | l | F-06 | |
| 6370665 | EW | 0.96 | 54965.405240 | 0.932 3155 | 14.0 | 1458 | 2/2 | a | l+q | L1-08 | 2, 3 |
| 6516874 | EA | 0.60 | 55001.4643225 | 0.916 3260 | 15.9 | 1237 | 2s4/0 | a | l | L2-20 | 3 |
| 6525196 | EA | 0.36 | 54954.353139 | 3.420 598 | 10.2 | 1467 | 2s4/0 | a | l+d | D1-26 | 2 |
| 6531485 | EA | 0.53 | 54964.801481 | 0.676 990 | 15.6 | 1459 | 2/0 | p+s | l+d | D1-03 | 2 |
| 6543674 | EA+E3 | 0.53 | 54965.303847 | 2.391 030 | 13.5 | 1456 | 2s4/2 | a | l | L1-36 | 3, 17 |
| 6545018 | EA | 0.42 | 54965.835642 | 3.991 460 | 13.7 | 1457 | 2/2 | p+s | l+d | D1-07 | 2, 4, 5 |
| 6546508 | EA | 0.20 | 55189.798579 | 6.107 057 | 15.7 | 1237 | 2/0 | p+s | l+d | D2-10 | |
| 6606282 | EA | 0.31 | 54965.433543 | 2.107 130 | 13.0 | 1456 | 2/0 | a | l | L3-22 | |
| 6615041 | EW | 0.75 | 54964.807732 | 0.340 0856 | 13.9 | 1459 | 2/2 | a | l(+q) | L3-49 | 3 |
| 6669809 | EB | 0.64 | 54953.997571 | 0.733 7388 | 10.8 | 1437 | 2s4/2 | p | l+c | L1-02 | |
| 6671698 | EW | 0.73 | 54954.077303 | 0.471 525 | 13.5 | 1437 | 2/2 | a | l+q | L2-52 | 3 |
| 6766325 | ELV(EW) | 0.92 | 54964.713835 | 0.439 9657 | 13.8 | 1459 | 2/2 | a | l | L3-26 | 3 |
| 6794131 | ELV? | 0.81 | 54954.298318 | 1.613 328 | 12.5 | 1455 | 2/2 | p | l(+q) | L3-52 | 3 |
| 6877673 | EA | 0.11 | 54989.092003 | 36.758 7372 | 13.7 | 1454 | 2/0 | p+s | l+d | D3-07 | |
| 6964043 | EA+E3 | 0.35 | 55190.170 | 10.725 518 | 15.6 | 1233 | 2/0 | p+s | l+d | D1-17 | 4 |
| 6965293 | EA | 0.18 | 54957.473848 | 5.077 746 | 12.8 | 1468 | 2/0 | p+s | l+a(+d) | L2-39 | |
| 7119757 | EA | 0.64 | 54965.304131 | 0.742 9217 | 15.6 | 1459 | 2s4/2 | a | l | L2-57 | 3 |
| 7177553 | EA | 0.06 | 54954.545842 | 17.996 467 | 11.5 | 1458 | 2/0 | p+s | l+d | D1-29 | |
| 7272739 | EW | 0.75 | 54964.853794 | 0.281 1644 | 13.0 | 1459 | 2/2 | a | l(+q) | L3-58 | 3 |
| 7289157 | EA+E3 | 0.37 | 54969.966600 | 5.266 525 | 12.9 | 1459 | 2/0 | p+s | l+d | D1-18 | 2, 4, 5 |
| 7339345 | EW | 0.74 | 54964.6478878 | 0.259 6643 | 15.2 | 1459 | 2/2 | a | l+q | L2-19 | 3 |
| 7362751 | ELV(EW) | 0.73 | 54964.744494 | 0.338 249 | 15.8 | 1459 | 2/2 | a | l+q | L1-25 | 3 |
| 7375612 | FP? | 0.98 | 54953.639904 | 0.160 0728(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-07 | 3 |
| 7385478 | EA | 0.54 | 54954.534784 | 1.655 478 | 11.5 | 1468 | 2s4/2 | p | l | L2-31 | 3 |
| 7440742 | EW(ELV) | 0.71 | 54949.930411 | 0.283 9922 | 11.8 | 1388 | 2/2 | a | l | L2-45 | |
| 7518816 | EB | 0.65 | 54953.692277 | 0.466 5805 | 12.8 | 1470 | 2s4/2 | a | l | L3-13 | 3 |
| 7552344 | EA | 0.24 | 54964.948438 | 2.001 491 | 15.4 | 1457 | 2/0 | a | l | L2-25 | |
| 7593110 | EA | 0.17 | 54999.192999 | 3.549 384 | 15.9 | 1235 | 2/0 | p | l+d | D1-22 | |
| 7630658 | EA | 0.47 | 55003.279035 | 2.151 155 | 13.9 | 1418 | 2s4/2 | a | l | L2-22 | 6 |
| 7668648 | EA+E3 | 0.08 | 54963.315401 | 27.825 590 | 15.3 | 1433 | 2/0 | p+s | l+d | D1-13 | 2, 4, 5 |
| 7670617 | EA | 0.07 | 54969.139216 | 24.703 160 | 15.5 | 1433 | 2/0 | p+s | l+d | D3-09 | 4, 5 |
| 7680593 | ELV(EW) | 0.97 | 54964.639100 | 0.276 3915 | 15.4 | 1459 | 2/2 | a | l+q | L2-32 | 3 |
| 7685689 | EW | 0.77 | 55001.994674 | 0.325 1596 | 15.5 | 1238 | 2/2 | a | l(+q) | L1-21 | 3 |
| 7690843 | EB | 0.69 | 54954.158345 | 0.786 260 | 11.1 | 1470 | 2s4/2 | a | l+d+c | D1-04 | 2, 3, 13 |
| 7811211 | EA | 0.49 | 54964.825947 | 0.902 4037 | 14.6 | 1458 | 2s4/0 | p | l(+q) | L1-19 | |
| 7812175 | EA | 0.06 | 55002.612666 | 17.793 925 | 16.3 | 658 | 2/0 | p+s | l+d | D2-01 | 4 |
| 7821010 | EA | 0.03 | 54969.615845 | 24.238 2426 | 10.8 | 1454 | 2/0 | p+s | l+d | D2-07 | 18 |
| 7837302 | EA | 0.06 | 54982.935571 | 23.837 136 | 13.7 | 1430 | 1/0 | p | l+d | D2-12 | 2 |
| 7877062 | EW | 0.81 | 54964.779743 | 0.303 6520 | 13.8 | 1459 | 2/2 | a | l | L2-54 | 3 |
| 7955301 | EA | 0.14 | 54967.950750 | 15.327 84 | 12.7 | 1448 | 2/0 | p+s | l+d | D1-14 | 2, 4, 5, 13 |
| 8016214 | EA | 0.53 | 54966.725645 | 3.174 9714 | 14.4 | 1454 | 2s4/2 | p | l(+q) | L3-57 | 3 |
| 8023317 | EA | 0.13 | 54979.733478 | 16.579 002 | 12.9 | 1465 | 2/2 | p+s | l+d | D1-30 | 2, 4 |
| 8043961 | EA | 0.63 | 54954.555903 | 1.559 2127 | 10.7 | 1469 | 2/2 | a | l(+d) | L1-20 | 2, 3 |
| 8045121 | FP? | 1.00 | 54953.761839 | 0.263 1774(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-02 | 3 |
| 8081389 | EA | 0.56 | 54965.003801 | 1.489 4435 | 14.0 | 1458 | 2s4/2 | p | l(+q) | L2-58 | |
| 8094140 | EA | 0.49 | 54965.145553 | 0.706 4292 | 15.2 | 1459 | 2s4/0 | a | l | L1-32 | |
| 8143170 | EA | 0.15 | 54970.113064 | 28.785 943 | 12.9 | 1455 | 2/0 | p+s | l+d | D3-04 | 4 |
| 8145477 | EW | 0.89 | 54965.076077 | 0.565 7843 | 14.8 | 497 | 2/2 | a | l | L2-01 | 3 |
| 8190491 | ELV | 0.95 | 54965.198125 | 0.777 8768 | 14.3 | 1459 | 2/2 | a | l(+q) | L1-27 | 3 |
| 8192840 | ELV(EW) | 0.95 | 54965.013933 | 0.433 549 25 | 13.5 | 1459 | 2/2 | a | l(+q) | L2-40 | 2, 3 |
| 8210721 | EA | 0.08 | 54971.157082 | 22.672 816 | 14.3 | 1451 | 2/0 | p+s | l+d | D2-03 | 4, 5 |
| 8242493 | EW | 0.73 | 54964.621844 | 0.283 2856 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-29 | 3 |
| 8265951 | EW | 0.81 | 54954.246763 | 0.779 9575 | 12.7 | 1469 | 2/2 | a | l | L3-48 | 3 |
| 8330092 | ELV(EW) | 0.79 | 54964.940576 | 0.321 723 55 | 13.5 | 1459 | 2/2 | a | l | L1-26 | 3 |
| 8386865 | ELV | 0.99 | 54953.942556 | 1.258 041 | 12.0 | 1466 | 2/2 | a | l(+d) | L1-09 | 2, 3 |
| 8394040 | ELV(EW) | 0.77 | 54964.878453 | 0.302 1262 | 14.5 | 1459 | 2/2 | a | l | L1-12 | 2, 3 |
| 8429450 | EA | 0.47 | 54954.217684 | 2.705 1516 | 13.1 | 1466 | 2/2 | a | l | L3-46 | 5 |
| 8444552 | EA | 0.49 | 54964.595346 | 1.178 090 | 13.6 | 1459 | 2s4/0 | a | l | L3-41 | |
| 8553788 | EA | 0.54 | 54954.997634 | 1.606 1632 | 12.7 | 2771 | 2s4/2 | p+e | l | L3-51 | 1, 5, 6, 23 |
| 8563964 | FP? | 1.00 | 54953.846748 | 0.338 436(/2) | 12.9 | 1470 | 2/2(1/1) | a | l | F-03 | 3 |
| 8690104 | EW | 0.77 | 54964.834110 | 0.408 7744 | 14.9 | 1459 | 2/2 | a | l | L3-27 | 3 |
| 8719897 | EA | 0.50 | 54955.237444 | 3.151 420 | 12.4 | 1469 | 2s4/0 | a | l+d | D1-21 | 2, 13 |
| 8739802 | ELV | 0.93 | 55001.999865 | 0.274 5129 | 14.9 | 1238 | 2/2 | a | l | L2-21 | 3 |
| 8758161a | EA | – | 54953.834107 | 1.996 4352 | 12.5 | 1467 | 2s4/2 | a | l | L3-43 | |
| 8868650 | EA | 0.62 | 54957.940589 | 4.447 430 | 11.9 | 1463 | 2s4/2 | p | l(+q) | L3-36 | |
| 8904448 | EW | 0.74 | 54965.059034 | 0.865 983 | 13.9 | 1458 | 2s2/2 | p | l+c | L1-23 | 2, 3 |
| 8938628 | EA | 0.14 | 54966.603088 | 6.862 216 | 13.7 | 1455 | 2/0 | p+s | l+d | D1-25 | 2, 4 |
| 8957887 | EW | 0.76 | 54964.884185 | 0.347 3543 | 15.4 | 1459 | 2/2 | a | l | L2-11 | 3 |
| 8982514 | EW | 0.83 | 54953.930563 | 0.414 4906 | 13.2 | 1470 | 2/2 | a | l | L3-28 | 3 |
| 9007918 | EA+E3 | 0.52 | 54954.748782 | 1.387 2066 | 11.7 | 1469 | 2s4/2 | p | l(+d) | L1-18 | 6 |
| 9028474 | EA | 0.00 | 55010.672516 | 124.936 5792 | 12.3 | 1374 | 2/0 | p+s | l+d | D3-11 | |
| 9075704 | EB | 0.68 | 54999.891435 | 0.513 1516 | 16.2 | 855 | 2/2 | a | l+q | L1-13 | 3 |
| 9083523 | EB | 0.65 | 54954.484907 | 0.918 4208 | 12.7 | 1470 | 2s4/2 | p | l | L3-16 | 3 |
| 9084778 | EA | 0.49 | 54964.654261 | 0.592 2444 | 15.7 | 1459 | 1/0 | p | l | L1-34 | |
| 9091810 | EB | 0.69 | 54953.600339 | 0.479 7214 | 12.8 | 1470 | 2s4/2 | a | l | L2-53 | 3 |
| 9101279 | EA | 0.58 | 54965.932213 | 1.811 4606 | 13.9 | 1456(4987) | 2s6/2 | p(+e) | l+q | L2-46 | 3 |
| 9110346 | EA | 0.43 | 55002.222003 | 1.790 5531 | 16.4 | 1330 | 2s4/2 | a | l | L3-47 | |
| 9140402 | EA | 0.27 | 54966.441095 | 4.988 3312 | 15.3 | 1457 | 2/0 | p+s | l+d | D1-11 | 19 |
| 9159301 | EA | 0.55 | 54956.304393 | 3.044 7712 | 12.1 | 1468 | 2s4/0 | p | l | L2-34 | 1 |
| 9181877 | EW | 0.74 | 54953.797919 | 0.321 0098 | 11.7 | 1470 | 2/2 | a | l | L3-55 | 3, 13 |
| 9272276 | EW | 0.78 | 54953.693247 | 0.280 615 | 13.2 | 1470 | 2/2 | a | l | L2-61 | 3 |
| 9283826 | EW | 0.84 | 54953.801153 | 0.356 5232 | 13.1 | 1470 | 2/2 | a(+e) | l | L3-08 | 3 |
| 9353234 | ELV | 0.86 | 54965.446983 | 1.486 5274 | 13.7 | 1458 | 2/2 | a | l | L2-28 | 3 |
| 9392702 | EA | 0.37 | 54964.893911 | 3.909 3245 | 14.6 | 868 | 2s4/0 | p | l | L3-02 | |
| 9402652b | EA | 0.65 | 54954.290416 | 1.073 106 | 11.8 | 2048(5723) | 2/2 | p+s+e | l | L2-62 | 1, 6, 23 |
| 9412114 | ELV | 0.85 | 55001.895873 | 0.250 2532 | 15.2 | 1147 | 2/2 | a | l(+q) | L3-56 | 3 |
| 9451096 | EA | 0.53 | 54954.729422 | 1.250 3906 | 12.6 | 1470 | 2s4/2 | p+s | l+d | D1-09 | 2, 3, 5 |
| 9472174a | oEA,sdB+dM | 0.78 | 54953.643197 | 0.125 765 28 | 12.3 | 1437 | 2/0 | p | l+c | L1-15 | 20 |
| 9532219 | EW | 0.74 | 55001.947386 | 0.198 1551 | 16.1 | 1330 | 2/2 | a | l | L3-50 | 3 |
| 9574614 | EA | 0.40 | 54965.687069 | 0.982 0954 | 15.9 | 1458 | 1/0 | p | l | L2-48 | |
| 9592145 | EB | 0.65 | 54965.015451 | 0.488 8674 | 14.0 | 1459 | 2/2 | p | l+q | L2-03 | 3 |
| 9596187 | EA | 0.47 | 54964.705879 | 0.953 2917 | 14.5 | 1459 | 2/0 | p | l | L3-18 | |
| 9612468 | FP? | 1.00 | 54953.604225 | 0.133 4715(/2) | 11.5 | 1470 | 2/2(1/1) | a | l | F-08 | 3 |
| 9664215 | EA | 0.27 | 54964.925032 | 3.319 4959 | 15.1 | 1459 | 2s4/0 | p+s | l+d | D2-04 | |
| 9665086 | EB | 0.67 | 55000.087903 | 0.296 536 | 13.9 | 1421 | 2/2 | a | l(+q) | L2-16 | 3 |
| 9706078 | EA | 0.56 | 54954.140288 | 0.613 5606 | 12.8 | 1470 | 2s4/0 | a | l | L3-20 | 3 |
| 9711751 | EA | 0.49 | 54965.352420 | 1.711 5283 | 13.8 | 1458 | 2s4/0 | p | l | L2-44 | |
| 9714358 | EA | 0.13 | 54967.395501 | 6.474 177 | 15.0 | 1454 | 2/0 | p+s | l+d | D1-08 | 2, 4, 5 |
| 9715925 | EA | 0.10 | 54998.920053 | 6.308 299 | 16.5 | 830 | 2/0 | p+s | l+d | D2-02 | 4 |
| 9722737 | EW | 0.78 | 54964.973629 | 0.418 5284 | 14.9 | 1459 | 2/2 | a | l | L1-17 | 2, 3 |
| 9777987 | EW | 0.74 | 55000.068578 | 0.258 5001 | 16.3 | 684 | 2/2 | a | l | L1-01 | |
| 9788457 | EA | 0.60 | 54965.186856 | 0.963 3378 | 13.0 | 1459 | 2s2/2 | p | l+q | L3-33 | 3 |
| 9821923 | EW | 0.95 | 54964.814614 | 0.349 5329 | 14.2 | 1459 | 2/2 | a | l | L3-10 | 3 |
| 9838047 | EW | 0.84 | 54953.713063 | 0.436 162 | 13.5 | 1470 | 2/2 | a | l | L2-41 | 3 |
| 9850387 | EA | 0.47 | 54956.416799 | 2.748 4986 | 13.5 | 1468 | 2s4/0 | a | l(+d) | L1-31 | |
| 9912977 | EA | 0.59 | 54966.709125 | 1.887 874 | 13.7 | 1457 | 2s4/2 | a | l | L2-10 | 2, 3 |
| 9963009 | EA | 0.06 | 54986.018248 | 40.069 657 | 14.5 | 1443 | 2/0 | p+s | l+d | D3-12 | 4 |
| 9994475 | EW | 0.76 | 54964.733082 | 0.318 4064 | 14.3 | 1459 | 2/2 | a | l+q | L1-28 | 3 |
| 10095469 | EA | 0.60 | 54999.865835 | 0.677 7625 | 14.7 | 855 | 2s4/0 | p | l | L3-01 | 3 |
| 10095512 | EA | 0.24 | 54953.888455 | 6.017 207 | 13.1 | 1468 | 2/0 | p+s | l+d | D1-27 | 2 |
| 10226388 | EW | 0.77 | 54954.120530 | 0.660 6583 | 10.8 | 1470 | 2/2 | a | l | L2-26 | 2, 3 |
| 10268809 | EA | 0.05 | 54971.999951 | 24.708 999 | 13.7 | 1450 | 2/0 | p+s | l+d | D3-15 | 4 |
| 10268903 | EA | 0.39 | 54999.901602 | 1.103 9788 | 17.4 | 683 | 2/0 | a | l | L3-05 | |
| 10275197 | EW | 0.79 | 54953.707304 | 0.390 8377 | 12.9 | 1470 | 2/2 | a | l | L3-37 | 3 |
| 10296163 | EA | 0.17 | 54959.387400 | 9.296 7444 | 13.2 | 1463 | 2/0 | p+s | l+d | D3-17 | |
| 10319590 | EA | 0.09 | 54965.716743 | 21.320 459 | 13.7 | 405 | 2/0 | p+s | l+d | D3-01 | 2, 4, 5 |
| 10383620 | EA | 0.64 | 54954.123817 | 0.734 5658 | 12.8 | 1470 | 2/2 | a | l | L3-14 | 3 |
| 10483644 | EA | 0.12 | 54966.314610 | 5.110 7711 | 14.0 | 1457 | 2/0 | p | l+d | D1-24 | |
| 10549576 | EA | 0.20 | 54972.078799 | 9.089 4658 | 13.0 | 1454 | 2/0 | p+s | l+d | D2-13 | |
| 10557008 | EW | 0.77 | 54964.639092 | 0.265 4186 | 14.7 | 1459 | 2/2 | a | l | L3-15 | |
| 10583181 | EA | 0.47 | 54955.206895 | 2.696 353 | 11.0 | 1467 | 2s4/2 | p | l | L2-42 | |
| 10613718 | EA | 0.39 | 54953.886226 | 1.175 878 | 12.7 | 1469 | 2s4/0 | a | l+d | D1-06 | 2 |
| 10686876 | EA | 0.45 | 54953.951815 | 2.618 4153 | 11.7 | 3820 | 2s4/2 | p+e | l | L3-53 | 6, 23 |
| 10724533 | EB | 0.75 | 54954.395189 | 0.745 0918 | 9.0 | 1470 | 2s4/2 | p | l | L3-35 | 3 |
| 10727655 | EW | 0.74 | 54953.910817 | 0.353 3652 | 13.4 | 4374 | 2/2 | a+e | l+q | L1-37 | 3 |
| 10848807 | EW | 0.74 | 54999.987867 | 0.346 2467 | 15.8 | 1421 | 2/2 | a | l | L2-12 | 3 |
| 10855535 | FP? | 0.99 | 54964.629852 | 0.112 7824(/2) | 13.9 | 1459 | 2/2(1/1) | a | l | F-01 | 3 |
| 10916675 | EW | 0.86 | 54953.700609 | 0.418 8675 | 13.4 | 1470 | 2/2 | a | l | L3-19 | 3 |
| 10934755 | EB | 0.68 | 54964.840450 | 0.786 486 | 14.4 | 1459 | 2/2 | p | l | L3-07 | 3 |
| 10979716 | EA | 0.10 | 54967.081259 | 10.684 056 | 15.8 | 1453 | 2/0 | p+s | l+d | D2-08 | 4 |
| 10991989 | EA | 0.54 | 54954.650910 | 0.974 4775 | 10.3 | 1470 | 2s4/0 | a | l | L1-24 | 2, 3, 13 |
| 11042923 | EW | 0.76 | 54964.970492 | 0.390 162 | 14.4 | 1459 | 2/2 | a | l | L2-30 | 2, 3 |
| 11234677 | EA | 0.42 | 54953.872607 | 1.587 425 | 13.3 | 1470 | 2s4/2 | p | l | L3-23 | |
| 11246163 | EW | 0.77 | 54964.565448 | 0.279 2271 | 14.5 | 1459 | 2/2 | a | l(+q) | L3-29 | 3 |
| 11502172 | EA | 0.05 | 54968.617081 | 25.431 9585 | 14.2 | 1435 | 2/0 | p+s | l+d | D3-10 | |
| 11519226 | EA | 0.03 | 54972.990000 | 22.161 715 | 13.0 | 1463 | 2/0 | p+s | l+d | D2-14 | 4 |
| 11558882 | EA | 0.01 | 54987.716793 | 73.914 770 | 15.4 | 1384 | 2/0 | p+s | l+d | D3-13 | |
| 11604958 | EW | 0.72 | 54964.653176 | 0.298 9297 | 13.9 | 1459 | 2/2 | a | l | L2-51 | 3 |
| 11825204 | FP? | 0.98 | 54964.751093 | 0.209 6356(/2) | 13.8 | 1458 | 2/2(1/1) | a | l+q | F-05 | 3 |
| 11968490 | EA | 0.49 | 54965.437249 | 1.078 890 | 13.7 | 1458 | 2s4/0 | a | l+q(+d) | L1-06 | 2 |
| 12019674 | EW | 0.76 | 53363.5350 | 0.354 4975 | 13.0 | 5188 | 2/2 | a+e | l | L2-64 | 3, 21 |
| 12055014 | EW | 0.85 | 54965.041294 | 0.499 9046 | 13.5 | 1459 | 2/2 | a | l | L3-34 | |
| 12055255 | ELV(EW) | 0.90 | 54964.528184 | 0.220 9404 | 15.9 | 1459 | 2/2 | a | l | L3-44 | 3 |
| 12071741 | ELV(EW) | 0.94 | 54964.820555 | 0.314 2642 | 14.8 | 1459 | 2/2 | a | l | L2-23 | 3 |
| 12356914 | EA | 0.03 | 54976.492322 | 27.308 455 | 15.5 | 1459 | 2/0 | p+s | l+d | D3-05 | 4 |
| 12508348 | FP? | 0.97 | 54951.682693 | 0.255 596(/2) | 13.4 | 1457 | 2/2(1/1) | a | l+q | F-04 | |
| 12554536 | EB | 0.63 | 54953.964623 | 0.684 4956 | 12.8 | 1470 | 2s4/2 | p | l | L2-60 | 3 |
aShort-cadence data only.
Notes.aTrue period is twice that given in the Villanova Catalog.
bHAT, ASAS, SWASP minima were omitted.
Properties of the investigated systems. (1) E3 refers to tertiary eclipse(s) in the light curve. (2) In columns 2 and 3, we give the light-curve classifications according to both the classical eclipsing binary typology (see, e.g., Kallrath & Milone 2009) and the recently introduced morphology of Matijevic et al. (2012). (3) Sidereal period (P1) and epoch (T0) were used for plotting O−C curves. (4) Kepler magnitudes were taken from the Kepler Input Catalog (Batalha et al. 2010). (5) In column ETV/QTV, the numbers of calculated ETV and QTV curves are given. If both ETVs and/or QTVs were obtained, their average and (half-difference) curves were also determined. In the cases where we used local smoothing polynomials on the light curves, this is denoted by putting sn after the ETV number, where n gives the order of the smoothing polynomial. (6) Abbreviations in ‘Fitted curves’ column: ‘p’ – primary, ‘s’ – secondary, ‘a’ – averaged ETV curves, ‘e’ – ground-based times of minima were also included. (7) Abbreviations in ‘Fit type’ column: ‘l’ – LTTE, ‘a’ – AME (noted separately only for non-‘d’-type solutions), ‘d’ – dynamical, ‘q’ – quadratic, ‘c’ – cubic. Parentheses in this column indicate that two types of fits were performed; the unparenthesized terms were included in both fits while the term(s) in parentheses were included in only the less preferred fit. (8) Column ‘Tab’ is the location of the solution of the given system in one of Tables 3;5, 6–8, and 9 (‘L1’–‘L3’ for pure LTTE, ‘D1’–‘D3’ for combined LTTE and dynamical, and ‘F’ for false positive systems, respectively). References – 1: Gies et al. (2012); ; 2: Rappaport et al. (2013); 3: Conroy et al. (2014); 4: Borkovits et al. (2015); 5: Orosz (2015); 6: Zasche et al. (2015); 7: Tran et al. (2013); 8: Conroy et al. (2015); 9: Armstrong et al. (2012); 10: Lee et al. (2013); 11: Marsh, Armstrong & Carter (2014); 12: Lee et al. (2014); 13: Gaulme et al. (2013); 14: Lee et al. (2015); 15: Carter et al. (2011); 16: Borkovits et al. (2013); 17: Masuda, Uehara & Kawahara (2015); 18: Fabrycky et al. (in preparation); 19: Steffen et al. (2011); 20: Baran et al. (2015); 21: Liška (2014); 22: Csizmadia & Sándor (2001); 23: Gies et al. (2015).
| KIC No. . | Type . | Morph. . | T0 . | P1 . | Kp . | Data length . | |$\frac{\mathrm{ETV}}{\mathrm{QTV}}$| . | Fitted . | Fit . | Tab . | Refs. . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (BJD) . | (d) . | (mag) . | (d) . | . | curves . | type . | . | . |
| 1873918 | ELV(EW) | 0.86 | 54964.900829 | 0.332 433 | 13.7 | 1459 | 2/2 | a | l+q | L2-13 | 7 |
| 2302092 | EW | 0.89 | 54964.694441 | 0.294 673 | 14.4 | 1459 | 2/2 | a | l | L2-27 | 3 |
| 2305372 | EA | 0.58 | 54965.956227 | 1.404 6920 | 13.8 | 1458(4216) | 2s4/2 | p(+e) | l(+q) | L3-25 | 6, 23 |
| 2450566 | ELV | 0.98 | 55001.560102 | 1.844 5871 | 11.7 | 1468 | 2/2 | a | l | L2-24 | 3 |
| 2576692 | EA | 0.04 | 55027.103323 | 87.878 2329 | 12.7 | 1406 | 2/0 | p+s | l+d | D3-08 | |
| 2708156 | EA | 0.57 | 54954.336095 | 1.891 2671 | 10.7 | 33 912 | 2s8/0 | p+e | l+c | L1-38 | 1 |
| 2715007 | ELV | 0.87 | 54964.783119 | 0.297 1105 | 14.7 | 1459 | 2/2 | a | l | L3-17 | |
| 2715417 | ELV(EW) | 0.76 | 54964.667658 | 0.236 4399 | 14.1 | 1459 | 2/2 | a | l(+q) | L2-15 | |
| 2835289 | ELV+E3 | 0.92 | 55000.444609 | 0.857 762 | 13.0 | 1469 | 2/2 | a | l | L1-35 | 3, 8 |
| 2856960 | EA+E3 | 0.60 | 54964.661805 | 0.258 507 | 15.6 | 1458 | 2/0 | a | l+q | L1-03 | 3, 9, 10, 11 |
| 2983113 | EW | 0.89 | 55001.969640 | 0.395 1601 | 15.2 | 1238 | 2/2 | a | l | L3-04 | 3 |
| 3114667 | EA | 0.52 | 54999.758222 | 0.888 5832 | 17.4 | 683 | 2s4/0 | a | l | L2-02 | 3 |
| 3228863 | EB | 0.65 | 54954.26185 | 0.730 944 | 11.8 | 6636 | 2/2 | a+e | l+q | L1-29 | 2, 3, 12, 22 |
| 3245776 | ELV | 0.96 | 55001.663004 | 1.492 0589 | 14.4 | 1458 | 2/2 | a | l | L1-30 | 3 |
| 3248019 | EA | 0.37 | 55098.778000 | 2.668 2057 | 15.4 | 1329 | 2/0 | a | l | L3-24 | |
| 3335816 | EA | 0.16 | 54954.355631 | 7.422 0263 | 12.1 | 1462 | 2/0 | a | l | L3-38 | |
| 3338660 | EA | 0.60 | 55002.262623 | 1.873 3806 | 14.8 | 852 | 2s4/0 | p | l | L2-07 | |
| 3345675 | EA | 0.00 | 55083.146716 | 120.004 0103 | 15.6 | 1320 | 1/0 | p | l+d | D3-03 | |
| 3440230 | EA | 0.54 | 54967.238413 | 2.881 1010 | 13.6 | 1455 | 2s4/2 | p | l+q | L2-35 | 1, 6 |
| 3544694 | EA | 0.29 | 55740.65102 | 3.845 728 | 15.9 | 683 | 2s8/0 | p+s | l+d | D1-05 | |
| 3766353 | EA(HB) | −1.00 | 54966.722264 | 2.666 966 | 14.0 | 1456 | 2/2 | p | l | L3-12 | 3 |
| 3839964 | ELV(EW) | 0.78 | 54964.792432 | 0.256 1499 | 14.6 | 1459 | 2/2 | a | l+q | L3-40 | 3 |
| 3853259 | ELV(EW) | 0.98 | 54964.781808 | 0.276 6478 | 13.9 | 1459 | 2/2 | a | l+q | L1-10 | |
| 4037163 | EA | 0.58 | 55000.227976 | 0.635 4447 | 16.7 | 684 | 2/0 | a | l(+q) | L1-07 | 3 |
| 4055092 | EA | 0.01 | 54966.932772 | 76.464 989 | 15.3 | 1404 | 2/0 | p+s | l+d | D3-16 | |
| 4069063 | EA | 0.55 | 54964.906342 | 0.504 2953 | 13.3 | 1452 | 2s4/0 | a | l | L2-18 | 3 |
| 4074708 | EW | 0.73 | 54964.856673 | 0.302 1166 | 15.4 | 1459 | 2/2 | a | l | L2-37 | 3 |
| 4078157 | EA | 0.08 | 54960.300077 | 16.025 671 | 15.5 | 1202 | 2/0 | p+s | l+d | D3-02 | |
| 4079530 | EA | 0.07 | 54994.805374 | 17.727 1000 | 15.6 | 579 | 2/0 | p+s | l+d | D1-12 | |
| 4138301 | ELV | 0.90 | 54964.685221 | 0.253 379 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-14 | 3 |
| 4174507 | EA | 0.24 | 54966.041640 | 3.891 825 | 15.4 | 1456 | 2/0 | a | l(+d) | L3-31 | |
| 4244929 | EW | 0.91 | 54964.747256 | 0.341 403 | 15.1 | 1459 | 2/2 | a | l | L2-55 | 3 |
| 4451148 | EW | 0.82 | 54954.385233 | 0.735 9815 | 11.2 | 1470 | 2/2 | a | l | L2-06 | 3 |
| 4547308 | ELV | 0.88 | 54953.635293 | 0.576 9278 | 12.5 | 1470 | 2/2 | a | l | L2-17 | 3 |
| 4574310 | EA | 0.56 | 54954.662614 | 1.306 2201 | 13.2 | 1468 | 2s4/2 | p | l | L2-56 | 23 |
| 4647652 | EB | 0.68 | 54953.945894 | 1.064 824 95 | 11.8 | 1470 | 2/2 | p | l | L2-08 | 2, 3 |
| 4670267 | EA | 0.60 | 54966.375624 | 2.006 0974 | 15.1 | 1456 | 2s4/2 | a | l(+d) | L2-09 | 3 |
| 4681152 | EA | 0.55 | 54954.060778 | 1.835 930 | 13.1 | 1456 | 2s4/2 | p | l | L2-43 | 3 |
| 4753988 | EA | 0.16 | 54968.025737 | 7.304 476 | 15.0 | 1454 | 2/0 | p+s | l+d | D3-14 | |
| 4758368 | EA | 0.57 | 54958.206761 | 3.749 935 | 10.8 | 1468 | 2s4/2 | p+s | l+a | L3-45 | 3, 13 |
| 4762887 | ELV | 0.95 | 54964.771668 | 0.736 5737 | 14.4 | 1458 | 2/2 | a | l | L2-47 | 3 |
| 4769799 | EA | 0.12 | 54968.515532 | 21.928 614 | 10.9 | 1438 | 2/0 | p+s | l+d | D2-11 | 4, 5 |
| 4848423 | EA | 0.48 | 55000.595941 | 3.003 613 | 11.8 | 922 | 2/2 | a | l | L3-03 | 1, 23 |
| 4859432 | EW | 0.76 | 54949.996305 | 0.385 4799 | 15.5 | 1421 | 2/2 | a | l(+q) | L2-05 | 3 |
| 4909707 | EB | 0.72 | 54953.913193 | 2.302 3675 | 10.7 | 1470 | 2/2 | p+s | l+d | D1-28 | 2, 3 |
| 4937217 | EW | 0.82 | 54964.627330 | 0.429 3416 | 15.4 | 1459 | 2/2 | a | l+q | L3-42 | 3 |
| 4940201 | EA | 0.15 | 54967.276926 | 8.816 578 | 15.0 | 1455 | 2/0 | p+s | l+d | D1-23 | 2, 4, 5 |
| 4945857 | EW | 0.74 | 54964.830222 | 0.335 416 | 14.0 | 1459 | 2/2 | a | l | L2-59 | 3 |
| 4948863 | EA | 0.10 | 54972.831420 | 8.643 5903 | 15.4 | 1452 | 2/0 | p+s | l+d | D2-09 | |
| 5003117 | EA | 0.37 | 54986.095638 | 37.610 001 | 14.0 | 1429 | 2/0 | p+s | l+d | D3-06 | 4, 5 |
| 5039441 | EA | 0.39 | 54955.351360 | 2.151 383 | 12.9 | 1469 | 2s4/0 | p+s | l+a | L1-33 | 2 |
| 5080652 | EA | 0.30 | 54968.166959 | 4.144 357 | 15.1 | 1422 | 2/0 | p | l+d | D1-15 | |
| 5095269 | EA | 0.05 | 54966.865286 | 18.611 9616 | 13.5 | 1433 | 1/0 | p | l+d | D1-16 | 5 |
| 5128972 | EW | 0.74 | 54965.047601 | 0.505 323 | 13.2 | 1459 | 2/2 | a | l | L1-16 | 2, 3 |
| 5216727 | EA | 0.48 | 54964.929149 | 1.513 023 | 13.4 | 1459 | 2s4/2 | p | l | L1-22 | |
| 5255552 | EA+E3 | 0.17 | 54970.636491 | 32.458 635 | 15.2 | 1414 | 2/0 | p+s | l+d | D1-31 | 4, 5 |
| 5264818 | ELV | 0.92 | 54955.241047 | 1.905 050 | 8.9 | 1469 | 2/0 | a | l+d(+q) | D1-20 | 2, 3 |
| 5269407 | EA | 0.53 | 54965.651124 | 0.958 8631 | 14.2 | 1458 | 2s4/0 | a | l | L3-30 | 3 |
| 5307780 | EW | 0.88 | 54964.977524 | 0.308 851 | 14.9 | 1459 | 2/2 | a | l+q | L2-38 | |
| 5310387 | EW | 0.96 | 54953.664664 | 0.441 669 | 12.7 | 1470 | 2/2 | a | l+q | L1-04 | 2, 3 |
| 5353374 | EW | 0.78 | 54964.661848 | 0.393 3205 | 14.1 | 1459 | 2/2 | a | l | L3-11 | 3 |
| 5376552 | EW | 0.82 | 54954.083210 | 0.503 8188 | 12.9 | 1470 | 2/2 | a | l(+q) | L1-11 | 2, 3 |
| 5384802 | EA | 0.17 | 54966.988768 | 6.083 093 | 13.7 | 1454 | 2/0 | a | l+d | D1-19 | 2, 5 |
| 5459373 | ELV | 0.97 | 54964.670887 | 0.286 6088 | 15.1 | 1459 | 2/2 | a | l | L1-14 | 3 |
| 5478466 | EW | 0.97 | 54964.859645 | 0.482 5005 | 14.2 | 1459 | 2/2 | a | l | L2-04 | 3 |
| 5513861 | EA | 0.57 | 54954.995935 | 1.510 2117 | 11.6 | 3010 | 2/2 | a+e | l | L2-63 | 1, 3, 6, 23 |
| 5611561 | ELV(EW) | 0.74 | 55000.011420 | 0.258 694 65 | 14.0 | 1421 | 2/2 | a | l | L2-33 | 3 |
| 5621294 | EA | 0.60 | 54954.510518 | 0.938 905 | 13.6 | 1470 | 2s4/2 | p | l+q | L2-36 | 1, 6, 14 |
| 5653126 | EA | 0.09 | 54985.913152 | 38.493 382 | 13.2 | 1424 | 2/0 | p+s | l+d | D2-06 | 4, 5 |
| 5731312 | EA | 0.08 | 54968.093163 | 7.946 382 | 13.8 | 1456 | 2/0 | p+s | l+d | D2-05 | 4, 5 |
| 5771589 | EA | 0.12 | 54962.130765 | 10.738 342 | 11.8 | 1434 | 2/0 | p+s | l+d | D1-10 | 2, 4, 5 |
| 5897826 | EA+E3 | – | 55069.313 | 1.767 13 | 13.1 | – | – | – | – | D1-01 | 15 |
| 5903301 | EA | 0.41 | 55003.431007 | 2.320 302 | 15.1 | 1330 | 2/2 | a | l | L2-49 | |
| 5952403 | EA+E3 | 0.52 | 55051.237191 | 0.905 6774 | 7.0 | 1426 | 2s4/0 | a | l+d(+q) | D1-02 | 16 |
| 5956776 | EA | 0.61 | 55000.305505 | 0.569 1150 | 16.7 | 855 | 2s4/2 | p | l | L3-21 | |
| 5962716 | EA | 0.47 | 54965.398009 | 1.804 586 | 13.9 | 1458 | 2s4/0 | p | l | L3-32 | |
| 5975712 | ELV | 0.87 | 54953.924190 | 1.136 083 | 11.5 | 1469 | 2/2 | a | l(+q) | L3-39 | 3 |
| 6103049 | EA | 0.59 | 54964.888912 | 0.643 1712 | 15.1 | 1426 | 2s4/0 | a | l | L3-09 | |
| 6144827 | ELV | 0.79 | 54964.642040 | 0.234 650 | 15.0 | 1459 | 2/2 | a | l+q | L1-05 | 3 |
| 6233903 | EA | 0.36 | 55001.719115 | 5.990 8477 | 16.5 | 851 | 2s4/2 | p+s | l+a | L3-54 | |
| 6265720 | EW | 0.93 | 54964.729666 | 0.312 4277 | 14.8 | 1426 | 2/2 | a | l | L3-06 | 3 |
| 6281103 | ELV(EW) | 0.98 | 54964.870642 | 0.363 2811 | 14.9 | 1459 | 2/2 | a | l+q | L2-50 | 3 |
| 6287172 | FP? | 0.95 | 54953.651911 | 0.203 8732(/2) | 12.7 | 1469 | 2/2(1/1) | a | l | F-06 | |
| 6370665 | EW | 0.96 | 54965.405240 | 0.932 3155 | 14.0 | 1458 | 2/2 | a | l+q | L1-08 | 2, 3 |
| 6516874 | EA | 0.60 | 55001.4643225 | 0.916 3260 | 15.9 | 1237 | 2s4/0 | a | l | L2-20 | 3 |
| 6525196 | EA | 0.36 | 54954.353139 | 3.420 598 | 10.2 | 1467 | 2s4/0 | a | l+d | D1-26 | 2 |
| 6531485 | EA | 0.53 | 54964.801481 | 0.676 990 | 15.6 | 1459 | 2/0 | p+s | l+d | D1-03 | 2 |
| 6543674 | EA+E3 | 0.53 | 54965.303847 | 2.391 030 | 13.5 | 1456 | 2s4/2 | a | l | L1-36 | 3, 17 |
| 6545018 | EA | 0.42 | 54965.835642 | 3.991 460 | 13.7 | 1457 | 2/2 | p+s | l+d | D1-07 | 2, 4, 5 |
| 6546508 | EA | 0.20 | 55189.798579 | 6.107 057 | 15.7 | 1237 | 2/0 | p+s | l+d | D2-10 | |
| 6606282 | EA | 0.31 | 54965.433543 | 2.107 130 | 13.0 | 1456 | 2/0 | a | l | L3-22 | |
| 6615041 | EW | 0.75 | 54964.807732 | 0.340 0856 | 13.9 | 1459 | 2/2 | a | l(+q) | L3-49 | 3 |
| 6669809 | EB | 0.64 | 54953.997571 | 0.733 7388 | 10.8 | 1437 | 2s4/2 | p | l+c | L1-02 | |
| 6671698 | EW | 0.73 | 54954.077303 | 0.471 525 | 13.5 | 1437 | 2/2 | a | l+q | L2-52 | 3 |
| 6766325 | ELV(EW) | 0.92 | 54964.713835 | 0.439 9657 | 13.8 | 1459 | 2/2 | a | l | L3-26 | 3 |
| 6794131 | ELV? | 0.81 | 54954.298318 | 1.613 328 | 12.5 | 1455 | 2/2 | p | l(+q) | L3-52 | 3 |
| 6877673 | EA | 0.11 | 54989.092003 | 36.758 7372 | 13.7 | 1454 | 2/0 | p+s | l+d | D3-07 | |
| 6964043 | EA+E3 | 0.35 | 55190.170 | 10.725 518 | 15.6 | 1233 | 2/0 | p+s | l+d | D1-17 | 4 |
| 6965293 | EA | 0.18 | 54957.473848 | 5.077 746 | 12.8 | 1468 | 2/0 | p+s | l+a(+d) | L2-39 | |
| 7119757 | EA | 0.64 | 54965.304131 | 0.742 9217 | 15.6 | 1459 | 2s4/2 | a | l | L2-57 | 3 |
| 7177553 | EA | 0.06 | 54954.545842 | 17.996 467 | 11.5 | 1458 | 2/0 | p+s | l+d | D1-29 | |
| 7272739 | EW | 0.75 | 54964.853794 | 0.281 1644 | 13.0 | 1459 | 2/2 | a | l(+q) | L3-58 | 3 |
| 7289157 | EA+E3 | 0.37 | 54969.966600 | 5.266 525 | 12.9 | 1459 | 2/0 | p+s | l+d | D1-18 | 2, 4, 5 |
| 7339345 | EW | 0.74 | 54964.6478878 | 0.259 6643 | 15.2 | 1459 | 2/2 | a | l+q | L2-19 | 3 |
| 7362751 | ELV(EW) | 0.73 | 54964.744494 | 0.338 249 | 15.8 | 1459 | 2/2 | a | l+q | L1-25 | 3 |
| 7375612 | FP? | 0.98 | 54953.639904 | 0.160 0728(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-07 | 3 |
| 7385478 | EA | 0.54 | 54954.534784 | 1.655 478 | 11.5 | 1468 | 2s4/2 | p | l | L2-31 | 3 |
| 7440742 | EW(ELV) | 0.71 | 54949.930411 | 0.283 9922 | 11.8 | 1388 | 2/2 | a | l | L2-45 | |
| 7518816 | EB | 0.65 | 54953.692277 | 0.466 5805 | 12.8 | 1470 | 2s4/2 | a | l | L3-13 | 3 |
| 7552344 | EA | 0.24 | 54964.948438 | 2.001 491 | 15.4 | 1457 | 2/0 | a | l | L2-25 | |
| 7593110 | EA | 0.17 | 54999.192999 | 3.549 384 | 15.9 | 1235 | 2/0 | p | l+d | D1-22 | |
| 7630658 | EA | 0.47 | 55003.279035 | 2.151 155 | 13.9 | 1418 | 2s4/2 | a | l | L2-22 | 6 |
| 7668648 | EA+E3 | 0.08 | 54963.315401 | 27.825 590 | 15.3 | 1433 | 2/0 | p+s | l+d | D1-13 | 2, 4, 5 |
| 7670617 | EA | 0.07 | 54969.139216 | 24.703 160 | 15.5 | 1433 | 2/0 | p+s | l+d | D3-09 | 4, 5 |
| 7680593 | ELV(EW) | 0.97 | 54964.639100 | 0.276 3915 | 15.4 | 1459 | 2/2 | a | l+q | L2-32 | 3 |
| 7685689 | EW | 0.77 | 55001.994674 | 0.325 1596 | 15.5 | 1238 | 2/2 | a | l(+q) | L1-21 | 3 |
| 7690843 | EB | 0.69 | 54954.158345 | 0.786 260 | 11.1 | 1470 | 2s4/2 | a | l+d+c | D1-04 | 2, 3, 13 |
| 7811211 | EA | 0.49 | 54964.825947 | 0.902 4037 | 14.6 | 1458 | 2s4/0 | p | l(+q) | L1-19 | |
| 7812175 | EA | 0.06 | 55002.612666 | 17.793 925 | 16.3 | 658 | 2/0 | p+s | l+d | D2-01 | 4 |
| 7821010 | EA | 0.03 | 54969.615845 | 24.238 2426 | 10.8 | 1454 | 2/0 | p+s | l+d | D2-07 | 18 |
| 7837302 | EA | 0.06 | 54982.935571 | 23.837 136 | 13.7 | 1430 | 1/0 | p | l+d | D2-12 | 2 |
| 7877062 | EW | 0.81 | 54964.779743 | 0.303 6520 | 13.8 | 1459 | 2/2 | a | l | L2-54 | 3 |
| 7955301 | EA | 0.14 | 54967.950750 | 15.327 84 | 12.7 | 1448 | 2/0 | p+s | l+d | D1-14 | 2, 4, 5, 13 |
| 8016214 | EA | 0.53 | 54966.725645 | 3.174 9714 | 14.4 | 1454 | 2s4/2 | p | l(+q) | L3-57 | 3 |
| 8023317 | EA | 0.13 | 54979.733478 | 16.579 002 | 12.9 | 1465 | 2/2 | p+s | l+d | D1-30 | 2, 4 |
| 8043961 | EA | 0.63 | 54954.555903 | 1.559 2127 | 10.7 | 1469 | 2/2 | a | l(+d) | L1-20 | 2, 3 |
| 8045121 | FP? | 1.00 | 54953.761839 | 0.263 1774(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-02 | 3 |
| 8081389 | EA | 0.56 | 54965.003801 | 1.489 4435 | 14.0 | 1458 | 2s4/2 | p | l(+q) | L2-58 | |
| 8094140 | EA | 0.49 | 54965.145553 | 0.706 4292 | 15.2 | 1459 | 2s4/0 | a | l | L1-32 | |
| 8143170 | EA | 0.15 | 54970.113064 | 28.785 943 | 12.9 | 1455 | 2/0 | p+s | l+d | D3-04 | 4 |
| 8145477 | EW | 0.89 | 54965.076077 | 0.565 7843 | 14.8 | 497 | 2/2 | a | l | L2-01 | 3 |
| 8190491 | ELV | 0.95 | 54965.198125 | 0.777 8768 | 14.3 | 1459 | 2/2 | a | l(+q) | L1-27 | 3 |
| 8192840 | ELV(EW) | 0.95 | 54965.013933 | 0.433 549 25 | 13.5 | 1459 | 2/2 | a | l(+q) | L2-40 | 2, 3 |
| 8210721 | EA | 0.08 | 54971.157082 | 22.672 816 | 14.3 | 1451 | 2/0 | p+s | l+d | D2-03 | 4, 5 |
| 8242493 | EW | 0.73 | 54964.621844 | 0.283 2856 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-29 | 3 |
| 8265951 | EW | 0.81 | 54954.246763 | 0.779 9575 | 12.7 | 1469 | 2/2 | a | l | L3-48 | 3 |
| 8330092 | ELV(EW) | 0.79 | 54964.940576 | 0.321 723 55 | 13.5 | 1459 | 2/2 | a | l | L1-26 | 3 |
| 8386865 | ELV | 0.99 | 54953.942556 | 1.258 041 | 12.0 | 1466 | 2/2 | a | l(+d) | L1-09 | 2, 3 |
| 8394040 | ELV(EW) | 0.77 | 54964.878453 | 0.302 1262 | 14.5 | 1459 | 2/2 | a | l | L1-12 | 2, 3 |
| 8429450 | EA | 0.47 | 54954.217684 | 2.705 1516 | 13.1 | 1466 | 2/2 | a | l | L3-46 | 5 |
| 8444552 | EA | 0.49 | 54964.595346 | 1.178 090 | 13.6 | 1459 | 2s4/0 | a | l | L3-41 | |
| 8553788 | EA | 0.54 | 54954.997634 | 1.606 1632 | 12.7 | 2771 | 2s4/2 | p+e | l | L3-51 | 1, 5, 6, 23 |
| 8563964 | FP? | 1.00 | 54953.846748 | 0.338 436(/2) | 12.9 | 1470 | 2/2(1/1) | a | l | F-03 | 3 |
| 8690104 | EW | 0.77 | 54964.834110 | 0.408 7744 | 14.9 | 1459 | 2/2 | a | l | L3-27 | 3 |
| 8719897 | EA | 0.50 | 54955.237444 | 3.151 420 | 12.4 | 1469 | 2s4/0 | a | l+d | D1-21 | 2, 13 |
| 8739802 | ELV | 0.93 | 55001.999865 | 0.274 5129 | 14.9 | 1238 | 2/2 | a | l | L2-21 | 3 |
| 8758161a | EA | – | 54953.834107 | 1.996 4352 | 12.5 | 1467 | 2s4/2 | a | l | L3-43 | |
| 8868650 | EA | 0.62 | 54957.940589 | 4.447 430 | 11.9 | 1463 | 2s4/2 | p | l(+q) | L3-36 | |
| 8904448 | EW | 0.74 | 54965.059034 | 0.865 983 | 13.9 | 1458 | 2s2/2 | p | l+c | L1-23 | 2, 3 |
| 8938628 | EA | 0.14 | 54966.603088 | 6.862 216 | 13.7 | 1455 | 2/0 | p+s | l+d | D1-25 | 2, 4 |
| 8957887 | EW | 0.76 | 54964.884185 | 0.347 3543 | 15.4 | 1459 | 2/2 | a | l | L2-11 | 3 |
| 8982514 | EW | 0.83 | 54953.930563 | 0.414 4906 | 13.2 | 1470 | 2/2 | a | l | L3-28 | 3 |
| 9007918 | EA+E3 | 0.52 | 54954.748782 | 1.387 2066 | 11.7 | 1469 | 2s4/2 | p | l(+d) | L1-18 | 6 |
| 9028474 | EA | 0.00 | 55010.672516 | 124.936 5792 | 12.3 | 1374 | 2/0 | p+s | l+d | D3-11 | |
| 9075704 | EB | 0.68 | 54999.891435 | 0.513 1516 | 16.2 | 855 | 2/2 | a | l+q | L1-13 | 3 |
| 9083523 | EB | 0.65 | 54954.484907 | 0.918 4208 | 12.7 | 1470 | 2s4/2 | p | l | L3-16 | 3 |
| 9084778 | EA | 0.49 | 54964.654261 | 0.592 2444 | 15.7 | 1459 | 1/0 | p | l | L1-34 | |
| 9091810 | EB | 0.69 | 54953.600339 | 0.479 7214 | 12.8 | 1470 | 2s4/2 | a | l | L2-53 | 3 |
| 9101279 | EA | 0.58 | 54965.932213 | 1.811 4606 | 13.9 | 1456(4987) | 2s6/2 | p(+e) | l+q | L2-46 | 3 |
| 9110346 | EA | 0.43 | 55002.222003 | 1.790 5531 | 16.4 | 1330 | 2s4/2 | a | l | L3-47 | |
| 9140402 | EA | 0.27 | 54966.441095 | 4.988 3312 | 15.3 | 1457 | 2/0 | p+s | l+d | D1-11 | 19 |
| 9159301 | EA | 0.55 | 54956.304393 | 3.044 7712 | 12.1 | 1468 | 2s4/0 | p | l | L2-34 | 1 |
| 9181877 | EW | 0.74 | 54953.797919 | 0.321 0098 | 11.7 | 1470 | 2/2 | a | l | L3-55 | 3, 13 |
| 9272276 | EW | 0.78 | 54953.693247 | 0.280 615 | 13.2 | 1470 | 2/2 | a | l | L2-61 | 3 |
| 9283826 | EW | 0.84 | 54953.801153 | 0.356 5232 | 13.1 | 1470 | 2/2 | a(+e) | l | L3-08 | 3 |
| 9353234 | ELV | 0.86 | 54965.446983 | 1.486 5274 | 13.7 | 1458 | 2/2 | a | l | L2-28 | 3 |
| 9392702 | EA | 0.37 | 54964.893911 | 3.909 3245 | 14.6 | 868 | 2s4/0 | p | l | L3-02 | |
| 9402652b | EA | 0.65 | 54954.290416 | 1.073 106 | 11.8 | 2048(5723) | 2/2 | p+s+e | l | L2-62 | 1, 6, 23 |
| 9412114 | ELV | 0.85 | 55001.895873 | 0.250 2532 | 15.2 | 1147 | 2/2 | a | l(+q) | L3-56 | 3 |
| 9451096 | EA | 0.53 | 54954.729422 | 1.250 3906 | 12.6 | 1470 | 2s4/2 | p+s | l+d | D1-09 | 2, 3, 5 |
| 9472174a | oEA,sdB+dM | 0.78 | 54953.643197 | 0.125 765 28 | 12.3 | 1437 | 2/0 | p | l+c | L1-15 | 20 |
| 9532219 | EW | 0.74 | 55001.947386 | 0.198 1551 | 16.1 | 1330 | 2/2 | a | l | L3-50 | 3 |
| 9574614 | EA | 0.40 | 54965.687069 | 0.982 0954 | 15.9 | 1458 | 1/0 | p | l | L2-48 | |
| 9592145 | EB | 0.65 | 54965.015451 | 0.488 8674 | 14.0 | 1459 | 2/2 | p | l+q | L2-03 | 3 |
| 9596187 | EA | 0.47 | 54964.705879 | 0.953 2917 | 14.5 | 1459 | 2/0 | p | l | L3-18 | |
| 9612468 | FP? | 1.00 | 54953.604225 | 0.133 4715(/2) | 11.5 | 1470 | 2/2(1/1) | a | l | F-08 | 3 |
| 9664215 | EA | 0.27 | 54964.925032 | 3.319 4959 | 15.1 | 1459 | 2s4/0 | p+s | l+d | D2-04 | |
| 9665086 | EB | 0.67 | 55000.087903 | 0.296 536 | 13.9 | 1421 | 2/2 | a | l(+q) | L2-16 | 3 |
| 9706078 | EA | 0.56 | 54954.140288 | 0.613 5606 | 12.8 | 1470 | 2s4/0 | a | l | L3-20 | 3 |
| 9711751 | EA | 0.49 | 54965.352420 | 1.711 5283 | 13.8 | 1458 | 2s4/0 | p | l | L2-44 | |
| 9714358 | EA | 0.13 | 54967.395501 | 6.474 177 | 15.0 | 1454 | 2/0 | p+s | l+d | D1-08 | 2, 4, 5 |
| 9715925 | EA | 0.10 | 54998.920053 | 6.308 299 | 16.5 | 830 | 2/0 | p+s | l+d | D2-02 | 4 |
| 9722737 | EW | 0.78 | 54964.973629 | 0.418 5284 | 14.9 | 1459 | 2/2 | a | l | L1-17 | 2, 3 |
| 9777987 | EW | 0.74 | 55000.068578 | 0.258 5001 | 16.3 | 684 | 2/2 | a | l | L1-01 | |
| 9788457 | EA | 0.60 | 54965.186856 | 0.963 3378 | 13.0 | 1459 | 2s2/2 | p | l+q | L3-33 | 3 |
| 9821923 | EW | 0.95 | 54964.814614 | 0.349 5329 | 14.2 | 1459 | 2/2 | a | l | L3-10 | 3 |
| 9838047 | EW | 0.84 | 54953.713063 | 0.436 162 | 13.5 | 1470 | 2/2 | a | l | L2-41 | 3 |
| 9850387 | EA | 0.47 | 54956.416799 | 2.748 4986 | 13.5 | 1468 | 2s4/0 | a | l(+d) | L1-31 | |
| 9912977 | EA | 0.59 | 54966.709125 | 1.887 874 | 13.7 | 1457 | 2s4/2 | a | l | L2-10 | 2, 3 |
| 9963009 | EA | 0.06 | 54986.018248 | 40.069 657 | 14.5 | 1443 | 2/0 | p+s | l+d | D3-12 | 4 |
| 9994475 | EW | 0.76 | 54964.733082 | 0.318 4064 | 14.3 | 1459 | 2/2 | a | l+q | L1-28 | 3 |
| 10095469 | EA | 0.60 | 54999.865835 | 0.677 7625 | 14.7 | 855 | 2s4/0 | p | l | L3-01 | 3 |
| 10095512 | EA | 0.24 | 54953.888455 | 6.017 207 | 13.1 | 1468 | 2/0 | p+s | l+d | D1-27 | 2 |
| 10226388 | EW | 0.77 | 54954.120530 | 0.660 6583 | 10.8 | 1470 | 2/2 | a | l | L2-26 | 2, 3 |
| 10268809 | EA | 0.05 | 54971.999951 | 24.708 999 | 13.7 | 1450 | 2/0 | p+s | l+d | D3-15 | 4 |
| 10268903 | EA | 0.39 | 54999.901602 | 1.103 9788 | 17.4 | 683 | 2/0 | a | l | L3-05 | |
| 10275197 | EW | 0.79 | 54953.707304 | 0.390 8377 | 12.9 | 1470 | 2/2 | a | l | L3-37 | 3 |
| 10296163 | EA | 0.17 | 54959.387400 | 9.296 7444 | 13.2 | 1463 | 2/0 | p+s | l+d | D3-17 | |
| 10319590 | EA | 0.09 | 54965.716743 | 21.320 459 | 13.7 | 405 | 2/0 | p+s | l+d | D3-01 | 2, 4, 5 |
| 10383620 | EA | 0.64 | 54954.123817 | 0.734 5658 | 12.8 | 1470 | 2/2 | a | l | L3-14 | 3 |
| 10483644 | EA | 0.12 | 54966.314610 | 5.110 7711 | 14.0 | 1457 | 2/0 | p | l+d | D1-24 | |
| 10549576 | EA | 0.20 | 54972.078799 | 9.089 4658 | 13.0 | 1454 | 2/0 | p+s | l+d | D2-13 | |
| 10557008 | EW | 0.77 | 54964.639092 | 0.265 4186 | 14.7 | 1459 | 2/2 | a | l | L3-15 | |
| 10583181 | EA | 0.47 | 54955.206895 | 2.696 353 | 11.0 | 1467 | 2s4/2 | p | l | L2-42 | |
| 10613718 | EA | 0.39 | 54953.886226 | 1.175 878 | 12.7 | 1469 | 2s4/0 | a | l+d | D1-06 | 2 |
| 10686876 | EA | 0.45 | 54953.951815 | 2.618 4153 | 11.7 | 3820 | 2s4/2 | p+e | l | L3-53 | 6, 23 |
| 10724533 | EB | 0.75 | 54954.395189 | 0.745 0918 | 9.0 | 1470 | 2s4/2 | p | l | L3-35 | 3 |
| 10727655 | EW | 0.74 | 54953.910817 | 0.353 3652 | 13.4 | 4374 | 2/2 | a+e | l+q | L1-37 | 3 |
| 10848807 | EW | 0.74 | 54999.987867 | 0.346 2467 | 15.8 | 1421 | 2/2 | a | l | L2-12 | 3 |
| 10855535 | FP? | 0.99 | 54964.629852 | 0.112 7824(/2) | 13.9 | 1459 | 2/2(1/1) | a | l | F-01 | 3 |
| 10916675 | EW | 0.86 | 54953.700609 | 0.418 8675 | 13.4 | 1470 | 2/2 | a | l | L3-19 | 3 |
| 10934755 | EB | 0.68 | 54964.840450 | 0.786 486 | 14.4 | 1459 | 2/2 | p | l | L3-07 | 3 |
| 10979716 | EA | 0.10 | 54967.081259 | 10.684 056 | 15.8 | 1453 | 2/0 | p+s | l+d | D2-08 | 4 |
| 10991989 | EA | 0.54 | 54954.650910 | 0.974 4775 | 10.3 | 1470 | 2s4/0 | a | l | L1-24 | 2, 3, 13 |
| 11042923 | EW | 0.76 | 54964.970492 | 0.390 162 | 14.4 | 1459 | 2/2 | a | l | L2-30 | 2, 3 |
| 11234677 | EA | 0.42 | 54953.872607 | 1.587 425 | 13.3 | 1470 | 2s4/2 | p | l | L3-23 | |
| 11246163 | EW | 0.77 | 54964.565448 | 0.279 2271 | 14.5 | 1459 | 2/2 | a | l(+q) | L3-29 | 3 |
| 11502172 | EA | 0.05 | 54968.617081 | 25.431 9585 | 14.2 | 1435 | 2/0 | p+s | l+d | D3-10 | |
| 11519226 | EA | 0.03 | 54972.990000 | 22.161 715 | 13.0 | 1463 | 2/0 | p+s | l+d | D2-14 | 4 |
| 11558882 | EA | 0.01 | 54987.716793 | 73.914 770 | 15.4 | 1384 | 2/0 | p+s | l+d | D3-13 | |
| 11604958 | EW | 0.72 | 54964.653176 | 0.298 9297 | 13.9 | 1459 | 2/2 | a | l | L2-51 | 3 |
| 11825204 | FP? | 0.98 | 54964.751093 | 0.209 6356(/2) | 13.8 | 1458 | 2/2(1/1) | a | l+q | F-05 | 3 |
| 11968490 | EA | 0.49 | 54965.437249 | 1.078 890 | 13.7 | 1458 | 2s4/0 | a | l+q(+d) | L1-06 | 2 |
| 12019674 | EW | 0.76 | 53363.5350 | 0.354 4975 | 13.0 | 5188 | 2/2 | a+e | l | L2-64 | 3, 21 |
| 12055014 | EW | 0.85 | 54965.041294 | 0.499 9046 | 13.5 | 1459 | 2/2 | a | l | L3-34 | |
| 12055255 | ELV(EW) | 0.90 | 54964.528184 | 0.220 9404 | 15.9 | 1459 | 2/2 | a | l | L3-44 | 3 |
| 12071741 | ELV(EW) | 0.94 | 54964.820555 | 0.314 2642 | 14.8 | 1459 | 2/2 | a | l | L2-23 | 3 |
| 12356914 | EA | 0.03 | 54976.492322 | 27.308 455 | 15.5 | 1459 | 2/0 | p+s | l+d | D3-05 | 4 |
| 12508348 | FP? | 0.97 | 54951.682693 | 0.255 596(/2) | 13.4 | 1457 | 2/2(1/1) | a | l+q | F-04 | |
| 12554536 | EB | 0.63 | 54953.964623 | 0.684 4956 | 12.8 | 1470 | 2s4/2 | p | l | L2-60 | 3 |
| KIC No. . | Type . | Morph. . | T0 . | P1 . | Kp . | Data length . | |$\frac{\mathrm{ETV}}{\mathrm{QTV}}$| . | Fitted . | Fit . | Tab . | Refs. . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | . | . | (BJD) . | (d) . | (mag) . | (d) . | . | curves . | type . | . | . |
| 1873918 | ELV(EW) | 0.86 | 54964.900829 | 0.332 433 | 13.7 | 1459 | 2/2 | a | l+q | L2-13 | 7 |
| 2302092 | EW | 0.89 | 54964.694441 | 0.294 673 | 14.4 | 1459 | 2/2 | a | l | L2-27 | 3 |
| 2305372 | EA | 0.58 | 54965.956227 | 1.404 6920 | 13.8 | 1458(4216) | 2s4/2 | p(+e) | l(+q) | L3-25 | 6, 23 |
| 2450566 | ELV | 0.98 | 55001.560102 | 1.844 5871 | 11.7 | 1468 | 2/2 | a | l | L2-24 | 3 |
| 2576692 | EA | 0.04 | 55027.103323 | 87.878 2329 | 12.7 | 1406 | 2/0 | p+s | l+d | D3-08 | |
| 2708156 | EA | 0.57 | 54954.336095 | 1.891 2671 | 10.7 | 33 912 | 2s8/0 | p+e | l+c | L1-38 | 1 |
| 2715007 | ELV | 0.87 | 54964.783119 | 0.297 1105 | 14.7 | 1459 | 2/2 | a | l | L3-17 | |
| 2715417 | ELV(EW) | 0.76 | 54964.667658 | 0.236 4399 | 14.1 | 1459 | 2/2 | a | l(+q) | L2-15 | |
| 2835289 | ELV+E3 | 0.92 | 55000.444609 | 0.857 762 | 13.0 | 1469 | 2/2 | a | l | L1-35 | 3, 8 |
| 2856960 | EA+E3 | 0.60 | 54964.661805 | 0.258 507 | 15.6 | 1458 | 2/0 | a | l+q | L1-03 | 3, 9, 10, 11 |
| 2983113 | EW | 0.89 | 55001.969640 | 0.395 1601 | 15.2 | 1238 | 2/2 | a | l | L3-04 | 3 |
| 3114667 | EA | 0.52 | 54999.758222 | 0.888 5832 | 17.4 | 683 | 2s4/0 | a | l | L2-02 | 3 |
| 3228863 | EB | 0.65 | 54954.26185 | 0.730 944 | 11.8 | 6636 | 2/2 | a+e | l+q | L1-29 | 2, 3, 12, 22 |
| 3245776 | ELV | 0.96 | 55001.663004 | 1.492 0589 | 14.4 | 1458 | 2/2 | a | l | L1-30 | 3 |
| 3248019 | EA | 0.37 | 55098.778000 | 2.668 2057 | 15.4 | 1329 | 2/0 | a | l | L3-24 | |
| 3335816 | EA | 0.16 | 54954.355631 | 7.422 0263 | 12.1 | 1462 | 2/0 | a | l | L3-38 | |
| 3338660 | EA | 0.60 | 55002.262623 | 1.873 3806 | 14.8 | 852 | 2s4/0 | p | l | L2-07 | |
| 3345675 | EA | 0.00 | 55083.146716 | 120.004 0103 | 15.6 | 1320 | 1/0 | p | l+d | D3-03 | |
| 3440230 | EA | 0.54 | 54967.238413 | 2.881 1010 | 13.6 | 1455 | 2s4/2 | p | l+q | L2-35 | 1, 6 |
| 3544694 | EA | 0.29 | 55740.65102 | 3.845 728 | 15.9 | 683 | 2s8/0 | p+s | l+d | D1-05 | |
| 3766353 | EA(HB) | −1.00 | 54966.722264 | 2.666 966 | 14.0 | 1456 | 2/2 | p | l | L3-12 | 3 |
| 3839964 | ELV(EW) | 0.78 | 54964.792432 | 0.256 1499 | 14.6 | 1459 | 2/2 | a | l+q | L3-40 | 3 |
| 3853259 | ELV(EW) | 0.98 | 54964.781808 | 0.276 6478 | 13.9 | 1459 | 2/2 | a | l+q | L1-10 | |
| 4037163 | EA | 0.58 | 55000.227976 | 0.635 4447 | 16.7 | 684 | 2/0 | a | l(+q) | L1-07 | 3 |
| 4055092 | EA | 0.01 | 54966.932772 | 76.464 989 | 15.3 | 1404 | 2/0 | p+s | l+d | D3-16 | |
| 4069063 | EA | 0.55 | 54964.906342 | 0.504 2953 | 13.3 | 1452 | 2s4/0 | a | l | L2-18 | 3 |
| 4074708 | EW | 0.73 | 54964.856673 | 0.302 1166 | 15.4 | 1459 | 2/2 | a | l | L2-37 | 3 |
| 4078157 | EA | 0.08 | 54960.300077 | 16.025 671 | 15.5 | 1202 | 2/0 | p+s | l+d | D3-02 | |
| 4079530 | EA | 0.07 | 54994.805374 | 17.727 1000 | 15.6 | 579 | 2/0 | p+s | l+d | D1-12 | |
| 4138301 | ELV | 0.90 | 54964.685221 | 0.253 379 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-14 | 3 |
| 4174507 | EA | 0.24 | 54966.041640 | 3.891 825 | 15.4 | 1456 | 2/0 | a | l(+d) | L3-31 | |
| 4244929 | EW | 0.91 | 54964.747256 | 0.341 403 | 15.1 | 1459 | 2/2 | a | l | L2-55 | 3 |
| 4451148 | EW | 0.82 | 54954.385233 | 0.735 9815 | 11.2 | 1470 | 2/2 | a | l | L2-06 | 3 |
| 4547308 | ELV | 0.88 | 54953.635293 | 0.576 9278 | 12.5 | 1470 | 2/2 | a | l | L2-17 | 3 |
| 4574310 | EA | 0.56 | 54954.662614 | 1.306 2201 | 13.2 | 1468 | 2s4/2 | p | l | L2-56 | 23 |
| 4647652 | EB | 0.68 | 54953.945894 | 1.064 824 95 | 11.8 | 1470 | 2/2 | p | l | L2-08 | 2, 3 |
| 4670267 | EA | 0.60 | 54966.375624 | 2.006 0974 | 15.1 | 1456 | 2s4/2 | a | l(+d) | L2-09 | 3 |
| 4681152 | EA | 0.55 | 54954.060778 | 1.835 930 | 13.1 | 1456 | 2s4/2 | p | l | L2-43 | 3 |
| 4753988 | EA | 0.16 | 54968.025737 | 7.304 476 | 15.0 | 1454 | 2/0 | p+s | l+d | D3-14 | |
| 4758368 | EA | 0.57 | 54958.206761 | 3.749 935 | 10.8 | 1468 | 2s4/2 | p+s | l+a | L3-45 | 3, 13 |
| 4762887 | ELV | 0.95 | 54964.771668 | 0.736 5737 | 14.4 | 1458 | 2/2 | a | l | L2-47 | 3 |
| 4769799 | EA | 0.12 | 54968.515532 | 21.928 614 | 10.9 | 1438 | 2/0 | p+s | l+d | D2-11 | 4, 5 |
| 4848423 | EA | 0.48 | 55000.595941 | 3.003 613 | 11.8 | 922 | 2/2 | a | l | L3-03 | 1, 23 |
| 4859432 | EW | 0.76 | 54949.996305 | 0.385 4799 | 15.5 | 1421 | 2/2 | a | l(+q) | L2-05 | 3 |
| 4909707 | EB | 0.72 | 54953.913193 | 2.302 3675 | 10.7 | 1470 | 2/2 | p+s | l+d | D1-28 | 2, 3 |
| 4937217 | EW | 0.82 | 54964.627330 | 0.429 3416 | 15.4 | 1459 | 2/2 | a | l+q | L3-42 | 3 |
| 4940201 | EA | 0.15 | 54967.276926 | 8.816 578 | 15.0 | 1455 | 2/0 | p+s | l+d | D1-23 | 2, 4, 5 |
| 4945857 | EW | 0.74 | 54964.830222 | 0.335 416 | 14.0 | 1459 | 2/2 | a | l | L2-59 | 3 |
| 4948863 | EA | 0.10 | 54972.831420 | 8.643 5903 | 15.4 | 1452 | 2/0 | p+s | l+d | D2-09 | |
| 5003117 | EA | 0.37 | 54986.095638 | 37.610 001 | 14.0 | 1429 | 2/0 | p+s | l+d | D3-06 | 4, 5 |
| 5039441 | EA | 0.39 | 54955.351360 | 2.151 383 | 12.9 | 1469 | 2s4/0 | p+s | l+a | L1-33 | 2 |
| 5080652 | EA | 0.30 | 54968.166959 | 4.144 357 | 15.1 | 1422 | 2/0 | p | l+d | D1-15 | |
| 5095269 | EA | 0.05 | 54966.865286 | 18.611 9616 | 13.5 | 1433 | 1/0 | p | l+d | D1-16 | 5 |
| 5128972 | EW | 0.74 | 54965.047601 | 0.505 323 | 13.2 | 1459 | 2/2 | a | l | L1-16 | 2, 3 |
| 5216727 | EA | 0.48 | 54964.929149 | 1.513 023 | 13.4 | 1459 | 2s4/2 | p | l | L1-22 | |
| 5255552 | EA+E3 | 0.17 | 54970.636491 | 32.458 635 | 15.2 | 1414 | 2/0 | p+s | l+d | D1-31 | 4, 5 |
| 5264818 | ELV | 0.92 | 54955.241047 | 1.905 050 | 8.9 | 1469 | 2/0 | a | l+d(+q) | D1-20 | 2, 3 |
| 5269407 | EA | 0.53 | 54965.651124 | 0.958 8631 | 14.2 | 1458 | 2s4/0 | a | l | L3-30 | 3 |
| 5307780 | EW | 0.88 | 54964.977524 | 0.308 851 | 14.9 | 1459 | 2/2 | a | l+q | L2-38 | |
| 5310387 | EW | 0.96 | 54953.664664 | 0.441 669 | 12.7 | 1470 | 2/2 | a | l+q | L1-04 | 2, 3 |
| 5353374 | EW | 0.78 | 54964.661848 | 0.393 3205 | 14.1 | 1459 | 2/2 | a | l | L3-11 | 3 |
| 5376552 | EW | 0.82 | 54954.083210 | 0.503 8188 | 12.9 | 1470 | 2/2 | a | l(+q) | L1-11 | 2, 3 |
| 5384802 | EA | 0.17 | 54966.988768 | 6.083 093 | 13.7 | 1454 | 2/0 | a | l+d | D1-19 | 2, 5 |
| 5459373 | ELV | 0.97 | 54964.670887 | 0.286 6088 | 15.1 | 1459 | 2/2 | a | l | L1-14 | 3 |
| 5478466 | EW | 0.97 | 54964.859645 | 0.482 5005 | 14.2 | 1459 | 2/2 | a | l | L2-04 | 3 |
| 5513861 | EA | 0.57 | 54954.995935 | 1.510 2117 | 11.6 | 3010 | 2/2 | a+e | l | L2-63 | 1, 3, 6, 23 |
| 5611561 | ELV(EW) | 0.74 | 55000.011420 | 0.258 694 65 | 14.0 | 1421 | 2/2 | a | l | L2-33 | 3 |
| 5621294 | EA | 0.60 | 54954.510518 | 0.938 905 | 13.6 | 1470 | 2s4/2 | p | l+q | L2-36 | 1, 6, 14 |
| 5653126 | EA | 0.09 | 54985.913152 | 38.493 382 | 13.2 | 1424 | 2/0 | p+s | l+d | D2-06 | 4, 5 |
| 5731312 | EA | 0.08 | 54968.093163 | 7.946 382 | 13.8 | 1456 | 2/0 | p+s | l+d | D2-05 | 4, 5 |
| 5771589 | EA | 0.12 | 54962.130765 | 10.738 342 | 11.8 | 1434 | 2/0 | p+s | l+d | D1-10 | 2, 4, 5 |
| 5897826 | EA+E3 | – | 55069.313 | 1.767 13 | 13.1 | – | – | – | – | D1-01 | 15 |
| 5903301 | EA | 0.41 | 55003.431007 | 2.320 302 | 15.1 | 1330 | 2/2 | a | l | L2-49 | |
| 5952403 | EA+E3 | 0.52 | 55051.237191 | 0.905 6774 | 7.0 | 1426 | 2s4/0 | a | l+d(+q) | D1-02 | 16 |
| 5956776 | EA | 0.61 | 55000.305505 | 0.569 1150 | 16.7 | 855 | 2s4/2 | p | l | L3-21 | |
| 5962716 | EA | 0.47 | 54965.398009 | 1.804 586 | 13.9 | 1458 | 2s4/0 | p | l | L3-32 | |
| 5975712 | ELV | 0.87 | 54953.924190 | 1.136 083 | 11.5 | 1469 | 2/2 | a | l(+q) | L3-39 | 3 |
| 6103049 | EA | 0.59 | 54964.888912 | 0.643 1712 | 15.1 | 1426 | 2s4/0 | a | l | L3-09 | |
| 6144827 | ELV | 0.79 | 54964.642040 | 0.234 650 | 15.0 | 1459 | 2/2 | a | l+q | L1-05 | 3 |
| 6233903 | EA | 0.36 | 55001.719115 | 5.990 8477 | 16.5 | 851 | 2s4/2 | p+s | l+a | L3-54 | |
| 6265720 | EW | 0.93 | 54964.729666 | 0.312 4277 | 14.8 | 1426 | 2/2 | a | l | L3-06 | 3 |
| 6281103 | ELV(EW) | 0.98 | 54964.870642 | 0.363 2811 | 14.9 | 1459 | 2/2 | a | l+q | L2-50 | 3 |
| 6287172 | FP? | 0.95 | 54953.651911 | 0.203 8732(/2) | 12.7 | 1469 | 2/2(1/1) | a | l | F-06 | |
| 6370665 | EW | 0.96 | 54965.405240 | 0.932 3155 | 14.0 | 1458 | 2/2 | a | l+q | L1-08 | 2, 3 |
| 6516874 | EA | 0.60 | 55001.4643225 | 0.916 3260 | 15.9 | 1237 | 2s4/0 | a | l | L2-20 | 3 |
| 6525196 | EA | 0.36 | 54954.353139 | 3.420 598 | 10.2 | 1467 | 2s4/0 | a | l+d | D1-26 | 2 |
| 6531485 | EA | 0.53 | 54964.801481 | 0.676 990 | 15.6 | 1459 | 2/0 | p+s | l+d | D1-03 | 2 |
| 6543674 | EA+E3 | 0.53 | 54965.303847 | 2.391 030 | 13.5 | 1456 | 2s4/2 | a | l | L1-36 | 3, 17 |
| 6545018 | EA | 0.42 | 54965.835642 | 3.991 460 | 13.7 | 1457 | 2/2 | p+s | l+d | D1-07 | 2, 4, 5 |
| 6546508 | EA | 0.20 | 55189.798579 | 6.107 057 | 15.7 | 1237 | 2/0 | p+s | l+d | D2-10 | |
| 6606282 | EA | 0.31 | 54965.433543 | 2.107 130 | 13.0 | 1456 | 2/0 | a | l | L3-22 | |
| 6615041 | EW | 0.75 | 54964.807732 | 0.340 0856 | 13.9 | 1459 | 2/2 | a | l(+q) | L3-49 | 3 |
| 6669809 | EB | 0.64 | 54953.997571 | 0.733 7388 | 10.8 | 1437 | 2s4/2 | p | l+c | L1-02 | |
| 6671698 | EW | 0.73 | 54954.077303 | 0.471 525 | 13.5 | 1437 | 2/2 | a | l+q | L2-52 | 3 |
| 6766325 | ELV(EW) | 0.92 | 54964.713835 | 0.439 9657 | 13.8 | 1459 | 2/2 | a | l | L3-26 | 3 |
| 6794131 | ELV? | 0.81 | 54954.298318 | 1.613 328 | 12.5 | 1455 | 2/2 | p | l(+q) | L3-52 | 3 |
| 6877673 | EA | 0.11 | 54989.092003 | 36.758 7372 | 13.7 | 1454 | 2/0 | p+s | l+d | D3-07 | |
| 6964043 | EA+E3 | 0.35 | 55190.170 | 10.725 518 | 15.6 | 1233 | 2/0 | p+s | l+d | D1-17 | 4 |
| 6965293 | EA | 0.18 | 54957.473848 | 5.077 746 | 12.8 | 1468 | 2/0 | p+s | l+a(+d) | L2-39 | |
| 7119757 | EA | 0.64 | 54965.304131 | 0.742 9217 | 15.6 | 1459 | 2s4/2 | a | l | L2-57 | 3 |
| 7177553 | EA | 0.06 | 54954.545842 | 17.996 467 | 11.5 | 1458 | 2/0 | p+s | l+d | D1-29 | |
| 7272739 | EW | 0.75 | 54964.853794 | 0.281 1644 | 13.0 | 1459 | 2/2 | a | l(+q) | L3-58 | 3 |
| 7289157 | EA+E3 | 0.37 | 54969.966600 | 5.266 525 | 12.9 | 1459 | 2/0 | p+s | l+d | D1-18 | 2, 4, 5 |
| 7339345 | EW | 0.74 | 54964.6478878 | 0.259 6643 | 15.2 | 1459 | 2/2 | a | l+q | L2-19 | 3 |
| 7362751 | ELV(EW) | 0.73 | 54964.744494 | 0.338 249 | 15.8 | 1459 | 2/2 | a | l+q | L1-25 | 3 |
| 7375612 | FP? | 0.98 | 54953.639904 | 0.160 0728(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-07 | 3 |
| 7385478 | EA | 0.54 | 54954.534784 | 1.655 478 | 11.5 | 1468 | 2s4/2 | p | l | L2-31 | 3 |
| 7440742 | EW(ELV) | 0.71 | 54949.930411 | 0.283 9922 | 11.8 | 1388 | 2/2 | a | l | L2-45 | |
| 7518816 | EB | 0.65 | 54953.692277 | 0.466 5805 | 12.8 | 1470 | 2s4/2 | a | l | L3-13 | 3 |
| 7552344 | EA | 0.24 | 54964.948438 | 2.001 491 | 15.4 | 1457 | 2/0 | a | l | L2-25 | |
| 7593110 | EA | 0.17 | 54999.192999 | 3.549 384 | 15.9 | 1235 | 2/0 | p | l+d | D1-22 | |
| 7630658 | EA | 0.47 | 55003.279035 | 2.151 155 | 13.9 | 1418 | 2s4/2 | a | l | L2-22 | 6 |
| 7668648 | EA+E3 | 0.08 | 54963.315401 | 27.825 590 | 15.3 | 1433 | 2/0 | p+s | l+d | D1-13 | 2, 4, 5 |
| 7670617 | EA | 0.07 | 54969.139216 | 24.703 160 | 15.5 | 1433 | 2/0 | p+s | l+d | D3-09 | 4, 5 |
| 7680593 | ELV(EW) | 0.97 | 54964.639100 | 0.276 3915 | 15.4 | 1459 | 2/2 | a | l+q | L2-32 | 3 |
| 7685689 | EW | 0.77 | 55001.994674 | 0.325 1596 | 15.5 | 1238 | 2/2 | a | l(+q) | L1-21 | 3 |
| 7690843 | EB | 0.69 | 54954.158345 | 0.786 260 | 11.1 | 1470 | 2s4/2 | a | l+d+c | D1-04 | 2, 3, 13 |
| 7811211 | EA | 0.49 | 54964.825947 | 0.902 4037 | 14.6 | 1458 | 2s4/0 | p | l(+q) | L1-19 | |
| 7812175 | EA | 0.06 | 55002.612666 | 17.793 925 | 16.3 | 658 | 2/0 | p+s | l+d | D2-01 | 4 |
| 7821010 | EA | 0.03 | 54969.615845 | 24.238 2426 | 10.8 | 1454 | 2/0 | p+s | l+d | D2-07 | 18 |
| 7837302 | EA | 0.06 | 54982.935571 | 23.837 136 | 13.7 | 1430 | 1/0 | p | l+d | D2-12 | 2 |
| 7877062 | EW | 0.81 | 54964.779743 | 0.303 6520 | 13.8 | 1459 | 2/2 | a | l | L2-54 | 3 |
| 7955301 | EA | 0.14 | 54967.950750 | 15.327 84 | 12.7 | 1448 | 2/0 | p+s | l+d | D1-14 | 2, 4, 5, 13 |
| 8016214 | EA | 0.53 | 54966.725645 | 3.174 9714 | 14.4 | 1454 | 2s4/2 | p | l(+q) | L3-57 | 3 |
| 8023317 | EA | 0.13 | 54979.733478 | 16.579 002 | 12.9 | 1465 | 2/2 | p+s | l+d | D1-30 | 2, 4 |
| 8043961 | EA | 0.63 | 54954.555903 | 1.559 2127 | 10.7 | 1469 | 2/2 | a | l(+d) | L1-20 | 2, 3 |
| 8045121 | FP? | 1.00 | 54953.761839 | 0.263 1774(/2) | 12.0 | 1470 | 2/2(1/1) | a | l(+q) | F-02 | 3 |
| 8081389 | EA | 0.56 | 54965.003801 | 1.489 4435 | 14.0 | 1458 | 2s4/2 | p | l(+q) | L2-58 | |
| 8094140 | EA | 0.49 | 54965.145553 | 0.706 4292 | 15.2 | 1459 | 2s4/0 | a | l | L1-32 | |
| 8143170 | EA | 0.15 | 54970.113064 | 28.785 943 | 12.9 | 1455 | 2/0 | p+s | l+d | D3-04 | 4 |
| 8145477 | EW | 0.89 | 54965.076077 | 0.565 7843 | 14.8 | 497 | 2/2 | a | l | L2-01 | 3 |
| 8190491 | ELV | 0.95 | 54965.198125 | 0.777 8768 | 14.3 | 1459 | 2/2 | a | l(+q) | L1-27 | 3 |
| 8192840 | ELV(EW) | 0.95 | 54965.013933 | 0.433 549 25 | 13.5 | 1459 | 2/2 | a | l(+q) | L2-40 | 2, 3 |
| 8210721 | EA | 0.08 | 54971.157082 | 22.672 816 | 14.3 | 1451 | 2/0 | p+s | l+d | D2-03 | 4, 5 |
| 8242493 | EW | 0.73 | 54964.621844 | 0.283 2856 | 14.7 | 1459 | 2/2 | a | l(+q) | L2-29 | 3 |
| 8265951 | EW | 0.81 | 54954.246763 | 0.779 9575 | 12.7 | 1469 | 2/2 | a | l | L3-48 | 3 |
| 8330092 | ELV(EW) | 0.79 | 54964.940576 | 0.321 723 55 | 13.5 | 1459 | 2/2 | a | l | L1-26 | 3 |
| 8386865 | ELV | 0.99 | 54953.942556 | 1.258 041 | 12.0 | 1466 | 2/2 | a | l(+d) | L1-09 | 2, 3 |
| 8394040 | ELV(EW) | 0.77 | 54964.878453 | 0.302 1262 | 14.5 | 1459 | 2/2 | a | l | L1-12 | 2, 3 |
| 8429450 | EA | 0.47 | 54954.217684 | 2.705 1516 | 13.1 | 1466 | 2/2 | a | l | L3-46 | 5 |
| 8444552 | EA | 0.49 | 54964.595346 | 1.178 090 | 13.6 | 1459 | 2s4/0 | a | l | L3-41 | |
| 8553788 | EA | 0.54 | 54954.997634 | 1.606 1632 | 12.7 | 2771 | 2s4/2 | p+e | l | L3-51 | 1, 5, 6, 23 |
| 8563964 | FP? | 1.00 | 54953.846748 | 0.338 436(/2) | 12.9 | 1470 | 2/2(1/1) | a | l | F-03 | 3 |
| 8690104 | EW | 0.77 | 54964.834110 | 0.408 7744 | 14.9 | 1459 | 2/2 | a | l | L3-27 | 3 |
| 8719897 | EA | 0.50 | 54955.237444 | 3.151 420 | 12.4 | 1469 | 2s4/0 | a | l+d | D1-21 | 2, 13 |
| 8739802 | ELV | 0.93 | 55001.999865 | 0.274 5129 | 14.9 | 1238 | 2/2 | a | l | L2-21 | 3 |
| 8758161a | EA | – | 54953.834107 | 1.996 4352 | 12.5 | 1467 | 2s4/2 | a | l | L3-43 | |
| 8868650 | EA | 0.62 | 54957.940589 | 4.447 430 | 11.9 | 1463 | 2s4/2 | p | l(+q) | L3-36 | |
| 8904448 | EW | 0.74 | 54965.059034 | 0.865 983 | 13.9 | 1458 | 2s2/2 | p | l+c | L1-23 | 2, 3 |
| 8938628 | EA | 0.14 | 54966.603088 | 6.862 216 | 13.7 | 1455 | 2/0 | p+s | l+d | D1-25 | 2, 4 |
| 8957887 | EW | 0.76 | 54964.884185 | 0.347 3543 | 15.4 | 1459 | 2/2 | a | l | L2-11 | 3 |
| 8982514 | EW | 0.83 | 54953.930563 | 0.414 4906 | 13.2 | 1470 | 2/2 | a | l | L3-28 | 3 |
| 9007918 | EA+E3 | 0.52 | 54954.748782 | 1.387 2066 | 11.7 | 1469 | 2s4/2 | p | l(+d) | L1-18 | 6 |
| 9028474 | EA | 0.00 | 55010.672516 | 124.936 5792 | 12.3 | 1374 | 2/0 | p+s | l+d | D3-11 | |
| 9075704 | EB | 0.68 | 54999.891435 | 0.513 1516 | 16.2 | 855 | 2/2 | a | l+q | L1-13 | 3 |
| 9083523 | EB | 0.65 | 54954.484907 | 0.918 4208 | 12.7 | 1470 | 2s4/2 | p | l | L3-16 | 3 |
| 9084778 | EA | 0.49 | 54964.654261 | 0.592 2444 | 15.7 | 1459 | 1/0 | p | l | L1-34 | |
| 9091810 | EB | 0.69 | 54953.600339 | 0.479 7214 | 12.8 | 1470 | 2s4/2 | a | l | L2-53 | 3 |
| 9101279 | EA | 0.58 | 54965.932213 | 1.811 4606 | 13.9 | 1456(4987) | 2s6/2 | p(+e) | l+q | L2-46 | 3 |
| 9110346 | EA | 0.43 | 55002.222003 | 1.790 5531 | 16.4 | 1330 | 2s4/2 | a | l | L3-47 | |
| 9140402 | EA | 0.27 | 54966.441095 | 4.988 3312 | 15.3 | 1457 | 2/0 | p+s | l+d | D1-11 | 19 |
| 9159301 | EA | 0.55 | 54956.304393 | 3.044 7712 | 12.1 | 1468 | 2s4/0 | p | l | L2-34 | 1 |
| 9181877 | EW | 0.74 | 54953.797919 | 0.321 0098 | 11.7 | 1470 | 2/2 | a | l | L3-55 | 3, 13 |
| 9272276 | EW | 0.78 | 54953.693247 | 0.280 615 | 13.2 | 1470 | 2/2 | a | l | L2-61 | 3 |
| 9283826 | EW | 0.84 | 54953.801153 | 0.356 5232 | 13.1 | 1470 | 2/2 | a(+e) | l | L3-08 | 3 |
| 9353234 | ELV | 0.86 | 54965.446983 | 1.486 5274 | 13.7 | 1458 | 2/2 | a | l | L2-28 | 3 |
| 9392702 | EA | 0.37 | 54964.893911 | 3.909 3245 | 14.6 | 868 | 2s4/0 | p | l | L3-02 | |
| 9402652b | EA | 0.65 | 54954.290416 | 1.073 106 | 11.8 | 2048(5723) | 2/2 | p+s+e | l | L2-62 | 1, 6, 23 |
| 9412114 | ELV | 0.85 | 55001.895873 | 0.250 2532 | 15.2 | 1147 | 2/2 | a | l(+q) | L3-56 | 3 |
| 9451096 | EA | 0.53 | 54954.729422 | 1.250 3906 | 12.6 | 1470 | 2s4/2 | p+s | l+d | D1-09 | 2, 3, 5 |
| 9472174a | oEA,sdB+dM | 0.78 | 54953.643197 | 0.125 765 28 | 12.3 | 1437 | 2/0 | p | l+c | L1-15 | 20 |
| 9532219 | EW | 0.74 | 55001.947386 | 0.198 1551 | 16.1 | 1330 | 2/2 | a | l | L3-50 | 3 |
| 9574614 | EA | 0.40 | 54965.687069 | 0.982 0954 | 15.9 | 1458 | 1/0 | p | l | L2-48 | |
| 9592145 | EB | 0.65 | 54965.015451 | 0.488 8674 | 14.0 | 1459 | 2/2 | p | l+q | L2-03 | 3 |
| 9596187 | EA | 0.47 | 54964.705879 | 0.953 2917 | 14.5 | 1459 | 2/0 | p | l | L3-18 | |
| 9612468 | FP? | 1.00 | 54953.604225 | 0.133 4715(/2) | 11.5 | 1470 | 2/2(1/1) | a | l | F-08 | 3 |
| 9664215 | EA | 0.27 | 54964.925032 | 3.319 4959 | 15.1 | 1459 | 2s4/0 | p+s | l+d | D2-04 | |
| 9665086 | EB | 0.67 | 55000.087903 | 0.296 536 | 13.9 | 1421 | 2/2 | a | l(+q) | L2-16 | 3 |
| 9706078 | EA | 0.56 | 54954.140288 | 0.613 5606 | 12.8 | 1470 | 2s4/0 | a | l | L3-20 | 3 |
| 9711751 | EA | 0.49 | 54965.352420 | 1.711 5283 | 13.8 | 1458 | 2s4/0 | p | l | L2-44 | |
| 9714358 | EA | 0.13 | 54967.395501 | 6.474 177 | 15.0 | 1454 | 2/0 | p+s | l+d | D1-08 | 2, 4, 5 |
| 9715925 | EA | 0.10 | 54998.920053 | 6.308 299 | 16.5 | 830 | 2/0 | p+s | l+d | D2-02 | 4 |
| 9722737 | EW | 0.78 | 54964.973629 | 0.418 5284 | 14.9 | 1459 | 2/2 | a | l | L1-17 | 2, 3 |
| 9777987 | EW | 0.74 | 55000.068578 | 0.258 5001 | 16.3 | 684 | 2/2 | a | l | L1-01 | |
| 9788457 | EA | 0.60 | 54965.186856 | 0.963 3378 | 13.0 | 1459 | 2s2/2 | p | l+q | L3-33 | 3 |
| 9821923 | EW | 0.95 | 54964.814614 | 0.349 5329 | 14.2 | 1459 | 2/2 | a | l | L3-10 | 3 |
| 9838047 | EW | 0.84 | 54953.713063 | 0.436 162 | 13.5 | 1470 | 2/2 | a | l | L2-41 | 3 |
| 9850387 | EA | 0.47 | 54956.416799 | 2.748 4986 | 13.5 | 1468 | 2s4/0 | a | l(+d) | L1-31 | |
| 9912977 | EA | 0.59 | 54966.709125 | 1.887 874 | 13.7 | 1457 | 2s4/2 | a | l | L2-10 | 2, 3 |
| 9963009 | EA | 0.06 | 54986.018248 | 40.069 657 | 14.5 | 1443 | 2/0 | p+s | l+d | D3-12 | 4 |
| 9994475 | EW | 0.76 | 54964.733082 | 0.318 4064 | 14.3 | 1459 | 2/2 | a | l+q | L1-28 | 3 |
| 10095469 | EA | 0.60 | 54999.865835 | 0.677 7625 | 14.7 | 855 | 2s4/0 | p | l | L3-01 | 3 |
| 10095512 | EA | 0.24 | 54953.888455 | 6.017 207 | 13.1 | 1468 | 2/0 | p+s | l+d | D1-27 | 2 |
| 10226388 | EW | 0.77 | 54954.120530 | 0.660 6583 | 10.8 | 1470 | 2/2 | a | l | L2-26 | 2, 3 |
| 10268809 | EA | 0.05 | 54971.999951 | 24.708 999 | 13.7 | 1450 | 2/0 | p+s | l+d | D3-15 | 4 |
| 10268903 | EA | 0.39 | 54999.901602 | 1.103 9788 | 17.4 | 683 | 2/0 | a | l | L3-05 | |
| 10275197 | EW | 0.79 | 54953.707304 | 0.390 8377 | 12.9 | 1470 | 2/2 | a | l | L3-37 | 3 |
| 10296163 | EA | 0.17 | 54959.387400 | 9.296 7444 | 13.2 | 1463 | 2/0 | p+s | l+d | D3-17 | |
| 10319590 | EA | 0.09 | 54965.716743 | 21.320 459 | 13.7 | 405 | 2/0 | p+s | l+d | D3-01 | 2, 4, 5 |
| 10383620 | EA | 0.64 | 54954.123817 | 0.734 5658 | 12.8 | 1470 | 2/2 | a | l | L3-14 | 3 |
| 10483644 | EA | 0.12 | 54966.314610 | 5.110 7711 | 14.0 | 1457 | 2/0 | p | l+d | D1-24 | |
| 10549576 | EA | 0.20 | 54972.078799 | 9.089 4658 | 13.0 | 1454 | 2/0 | p+s | l+d | D2-13 | |
| 10557008 | EW | 0.77 | 54964.639092 | 0.265 4186 | 14.7 | 1459 | 2/2 | a | l | L3-15 | |
| 10583181 | EA | 0.47 | 54955.206895 | 2.696 353 | 11.0 | 1467 | 2s4/2 | p | l | L2-42 | |
| 10613718 | EA | 0.39 | 54953.886226 | 1.175 878 | 12.7 | 1469 | 2s4/0 | a | l+d | D1-06 | 2 |
| 10686876 | EA | 0.45 | 54953.951815 | 2.618 4153 | 11.7 | 3820 | 2s4/2 | p+e | l | L3-53 | 6, 23 |
| 10724533 | EB | 0.75 | 54954.395189 | 0.745 0918 | 9.0 | 1470 | 2s4/2 | p | l | L3-35 | 3 |
| 10727655 | EW | 0.74 | 54953.910817 | 0.353 3652 | 13.4 | 4374 | 2/2 | a+e | l+q | L1-37 | 3 |
| 10848807 | EW | 0.74 | 54999.987867 | 0.346 2467 | 15.8 | 1421 | 2/2 | a | l | L2-12 | 3 |
| 10855535 | FP? | 0.99 | 54964.629852 | 0.112 7824(/2) | 13.9 | 1459 | 2/2(1/1) | a | l | F-01 | 3 |
| 10916675 | EW | 0.86 | 54953.700609 | 0.418 8675 | 13.4 | 1470 | 2/2 | a | l | L3-19 | 3 |
| 10934755 | EB | 0.68 | 54964.840450 | 0.786 486 | 14.4 | 1459 | 2/2 | p | l | L3-07 | 3 |
| 10979716 | EA | 0.10 | 54967.081259 | 10.684 056 | 15.8 | 1453 | 2/0 | p+s | l+d | D2-08 | 4 |
| 10991989 | EA | 0.54 | 54954.650910 | 0.974 4775 | 10.3 | 1470 | 2s4/0 | a | l | L1-24 | 2, 3, 13 |
| 11042923 | EW | 0.76 | 54964.970492 | 0.390 162 | 14.4 | 1459 | 2/2 | a | l | L2-30 | 2, 3 |
| 11234677 | EA | 0.42 | 54953.872607 | 1.587 425 | 13.3 | 1470 | 2s4/2 | p | l | L3-23 | |
| 11246163 | EW | 0.77 | 54964.565448 | 0.279 2271 | 14.5 | 1459 | 2/2 | a | l(+q) | L3-29 | 3 |
| 11502172 | EA | 0.05 | 54968.617081 | 25.431 9585 | 14.2 | 1435 | 2/0 | p+s | l+d | D3-10 | |
| 11519226 | EA | 0.03 | 54972.990000 | 22.161 715 | 13.0 | 1463 | 2/0 | p+s | l+d | D2-14 | 4 |
| 11558882 | EA | 0.01 | 54987.716793 | 73.914 770 | 15.4 | 1384 | 2/0 | p+s | l+d | D3-13 | |
| 11604958 | EW | 0.72 | 54964.653176 | 0.298 9297 | 13.9 | 1459 | 2/2 | a | l | L2-51 | 3 |
| 11825204 | FP? | 0.98 | 54964.751093 | 0.209 6356(/2) | 13.8 | 1458 | 2/2(1/1) | a | l+q | F-05 | 3 |
| 11968490 | EA | 0.49 | 54965.437249 | 1.078 890 | 13.7 | 1458 | 2s4/0 | a | l+q(+d) | L1-06 | 2 |
| 12019674 | EW | 0.76 | 53363.5350 | 0.354 4975 | 13.0 | 5188 | 2/2 | a+e | l | L2-64 | 3, 21 |
| 12055014 | EW | 0.85 | 54965.041294 | 0.499 9046 | 13.5 | 1459 | 2/2 | a | l | L3-34 | |
| 12055255 | ELV(EW) | 0.90 | 54964.528184 | 0.220 9404 | 15.9 | 1459 | 2/2 | a | l | L3-44 | 3 |
| 12071741 | ELV(EW) | 0.94 | 54964.820555 | 0.314 2642 | 14.8 | 1459 | 2/2 | a | l | L2-23 | 3 |
| 12356914 | EA | 0.03 | 54976.492322 | 27.308 455 | 15.5 | 1459 | 2/0 | p+s | l+d | D3-05 | 4 |
| 12508348 | FP? | 0.97 | 54951.682693 | 0.255 596(/2) | 13.4 | 1457 | 2/2(1/1) | a | l+q | F-04 | |
| 12554536 | EB | 0.63 | 54953.964623 | 0.684 4956 | 12.8 | 1470 | 2s4/2 | p | l | L2-60 | 3 |
aShort-cadence data only.
Notes.aTrue period is twice that given in the Villanova Catalog.
bHAT, ASAS, SWASP minima were omitted.
Table 2 contains a column for the system type and a column for ‘morphology’. The correct classification of each binary as an ELV or as a one of the subtypes of real EBs (EA, EB, EW)9 generally is difficult except when the binary is well detached. It is particularly difficult to distinguish low-amplitude overcontact systems (EW) from ELVs, especially when there is a significant amount of third light due to either a bound third star in the system or an unresolved background or foreground light source. Among true EBs, it is difficult to distinguish EWs having low filling factors from tight semi-detached systems; AW UMa is a good example (Pribulla & Rucinski 2008). Similarly, among ELVs, it may be problematic to separate low-inclination overcontact systems from not-so-low-inclination, semi-detached binaries. Finally, the possible misidentification of some kinds of pulsating variables as ELVs or EBs was already noted above. The classifications given in the second column of Table 2 should be considered with these caveats in mind. The reader may compare our classification results with the automated light-curve morphology classifications of Matijevic et al. (2012) that are given in the third column of Table 2. The classifications in the two columns are more or less consistent at least apart from the ambiguities between ELVs and EWs which remain unresolvable by either method. Note also that our sample contains 10 EBs which exhibit extra eclipse event(s) which most probably can be attributed to third bodies which are the subject of our investigations. Amongst these systems, the triply eclipsing nature of KIC 09007918, according to our knowledge, is reported here for the first time. These systems are marked in the second column of Table 2 with an additional ‘E3’ sign, and will be discussed shortly in Section 6.3.
The fourth and fifth columns give the epochs and periods that were used for initial light-curve folding and binning, template calculations, determinations of times of minima, and for calculating the ETV and QTV O−C diagrams. As corrections of the epoch and period were always obtained during our fitting process via the polynomial coefficients c0 and c1, the final epoch and period values differ from the values in this table. The other columns of Table 2 are either self-explanatory or are explained in the table notes.
The results of our analyses are tabulated in Tables 3–10. Of our 230 EBs, pure LTTE ETV solutions, some of which are supplemented by quadratic or cubic terms, were calculated for 160 systems, while combined LTTE and dynamical solutions were obtained for another 62 EBs. The remaining eight ‘systems’ were found to be false positives in the sense that was previously discussed. Despite this, we give LTTE solutions for these cases as well (Table 9) but do not plot them in Fig. 6.
Orbital elements from LTTE solutions for systems, where more than two outer periods are covered, or/and triply eclipsing systems.
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 9777987 | 0.258 502 59(5) | −6.3(1) | 95.28(6) | 20.6(2) | 0.19(2) | 245(5) | 54979(2) | 0.0129(3) | 0.42 | 0.04 | 2: |
| 6669809a | 0.733 741 52(7) | −101(2) | 193.8(1) | 25.9(2) | 0.12(2) | 74(8) | 54958(4) | 0.0062(2) | 0.32 | 0.09 | 2: |
| 2856960 | 0.258 507 90(6) | −2.2(2) | 204.8(2) | 94(3) | 0.55(3) | 164(3) | 55007(2) | 0.27(2) | 1.48 | 0.02 | 2: |
| 5310387 | 0.441 668 66(1) | 2.80(4) | 214.0(1) | 13.5(1) | 0.23(1) | 210(4) | 55051(2) | 0.000 72(2) | 0.15 | 0.03 | 2: |
| 6144827 | 0.234 651 60(1) | −5.80(4) | 228.0(2) | 32.8(3) | 0.15(2) | 52(6) | 54921(4) | 0.0091(2) | 0.37 | 0.008 | 2: |
| 11968490 | 1.078 890 66(9) | −3(1) | 253.9(1) | 111.9(5) | 0.374(8) | 284(1) | 54862(1) | 0.291(4) | 1.54 | 0.13 | 2: |
| 4037163 | 0.635 444 61(3) | – | 268(2) | 20(2) | 0.66(7) | 356(4) | 54901(10) | 0.0015(4) | 0.19 | 0.12 | 2: |
| 6370665 | 0.932 314 31(7) | 14.8(8) | 286.4(5) | 27.7(4) | 0.08(3) | 354(19) | 55027(15) | 0.0035(1) | 0.26 | 0.08 | 2: |
| 8386865 | 1.258 041 69(7) | – | 294.0(5) | 84(2) | 0.49(3) | 314(4) | 55028(3) | 0.092(6) | 0.92 | 0.19 | 2: |
| 3853259: | 0.276 647 14(1) | 2.48(4) | 325.7(6) | 17.2(4) | 0.60(3) | 121(3) | 54900(3) | 0.000 64(4) | 0.01 | 0.14 | 2: |
| 5376552 | 0.503 818 78(1) | – | 334.8(1) | 41.9(2) | 0.349(6) | 355.2(9) | 54874(1) | 0.0088(1) | 0.37 | 0.02 | 2: |
| 8394040 | 0.302 126 24(1) | – | 388.9(1) | 124.6(4) | 0.520(5) | 295(1) | 54809(1) | 0.171(2) | 1.21 | 0.007 | 2: |
| 9075704 | 0.513 1488(1) | 15.2(7) | 402.0(5) | 63.4(3) | 0.160(9) | 252(3) | 55084(4) | 0.0212(3) | 0.51 | 0.01 | 2: |
| 5459373 | 0.286 608 72(1) | – | 412.7(2) | 98.6(3) | 0.361(6) | 271(1) | 55051(1) | 0.0754(7) | 0.85 | 0.004 | 2: |
| 9472174b | 0.125 765 28(1) | −0.063(4) | 418(2) | 0.63(2) | 0.38(4) | 124(6) | 55118(8) | 20(2)E−9 | 0.0019 | 0.000 | 0.60(3) |
| 5128972 | 0.505 323 38(1) | – | 442.1(2) | 114.6(3) | 0.285(5) | 285(1) | 54940(1) | 0.1032(9) | 0.97 | 0.01 | 2: |
| 9722737 | 0.418 528 37(1) | – | 444.2(1) | 103.4(2) | 0.174(4) | 223(1) | 54913(2) | 0.0750(5) | 0.85 | 0.007 | 2: |
| 9007918 | 1.387 206 55(1) | – | 470.9(6) | 17.7(2) | 0.68(2) | 271(1) | 54827(2) | 0.000 33(1) | 0.11 | 0.19 | 2: |
| 7811211 | 0.902 403 46(9) | – | 477(6) | 35(3) | 0.29(12) | 169(24) | 55168(33) | 0.0026(6) | 0.24 | 0.04 | 2: |
| 8043961 | 1.559 212 80(1) | – | 478.6(2) | 82.6(2) | 0.245(5) | 13(1) | 54817(2) | 0.0330(3) | 0.61 | 0.10 | 2: |
| 7685689 | 0.325 159 63(1) | – | 514.9(5) | 80.2(3) | 0.125(8) | 170(4) | 54774(5) | 0.0261(3) | 0.55 | 0.003 | 2: |
| 5216727 | 1.513 022 92(1) | – | 532.9(6) | 30.1(2) | 0.50(1) | 129(1) | 55158(2) | 0.001 29(3) | 0.18 | 0.11 | 2: |
| 8904448c | 0.865 9838(1) | −99(3) | 543.7(6) | 68.5(4) | 0.525(9) | 307.7(9) | 54796(2) | 0.0146(3) | 0.44 | 0.04 | 2: |
| 10991989 | 0.974 477 59(5) | – | 548(1) | 106(1) | 0.35(2) | 29(4) | 54960(6) | 0.053(2) | 0.73 | 0.03 | 2: |
| 7362751 | 0.338 250 80(4) | −9.2(2) | 552.0(6) | 120.1(6) | 0.256(9) | 107(2) | 54930(3) | 0.076(1) | 0.85 | 0.004 | 2: |
| 8330092 | 0.321 723 65(1) | – | 581(1) | 52.9(4) | 0.18(1) | 2(4) | 55134(7) | 0.0059(1) | 0.32 | 0.003 | 2: |
| 8190491 | 0.777 876 99(4) | – | 621(3) | 65(1) | 0.54(3) | 67(4) | 54789(7) | 0.0097(7) | 0.38 | 0.02 | 2: |
| 9994475 | 0.318 409 31(2) | −13.28(6) | 626.6(5) | 85.3(3) | 0.288(6) | 199(1) | 54779(2) | 0.0212(2) | 0.51 | 0.003 | 2: |
| 3228863 | 0.730 943 52(1) | 3.31(7) | 642.8(6) | 83.8(6) | 0.05(1) | 57(16) | 55052(28) | 0.0191(4) | 0.49 | 0.01 | 2: |
| 3245776 | 1.492 0589(2) | – | 663(9) | 54(3) | 0.45(12) | 263(16) | 55003(33) | 0.0048(9) | 0.29 | 0.07 | 2: |
| 9850387 | 2.748 4978(1) | – | 671(2) | 98(1) | 0.46(2) | 121(3) | 54683(6) | 0.028(1) | 0.57 | 0.22 | 2: |
| 8094140 | 0.706 428 57(1) | – | 676(1) | 56.3(4) | 0.35(1) | 171(2) | 54774(4) | 0.0052(1) | 0.30 | 0.01 | 2: |
| 5039441 | 2.151 382 94(6) | – | 678(1) | 87.2(7) | 0.25(1) | 163(3) | 55217(6) | 0.0194(5) | 0.49 | 0.10 | 2: |
| 9084778 | 0.592 243 75(8) | – | 680(9) | 69(3) | 0.20(9) | 176(25) | 55168(49) | 0.009(1) | 0.38 | 0.008 | 2: |
| 2835289 | 0.857 7610(1) | – | 755(5) | 138(7) | 0.74(6) | 294(4) | 54933(11) | 0.06(1) | 0.78 | 0.04 | 2: |
| 6543674 | 2.391 030 51(1) | – | 1101.4(4) | 115.2(1) | 0.617(2) | 267.1(1) | 55038(1) | 0.016 89(6) | 0.47 | 0.10 | 2: |
| 10727655 | 0.353 365 09(1) | 0.38(4) | 1138.1(6) | 141.8(2) | 0.247(2) | 36.4(5) | 55063(2) | 0.0295(1) | 0.58 | 0.001 | 2: |
| 2708156:d | 1.891 2615(2) | −29.4(7) | 5532(26) | 137(7) | 0.46(3) | 242(9) | 55955(153) | 0.0011(2) | 0.17 | 0.003 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 9777987 | 0.258 502 59(5) | −6.3(1) | 95.28(6) | 20.6(2) | 0.19(2) | 245(5) | 54979(2) | 0.0129(3) | 0.42 | 0.04 | 2: |
| 6669809a | 0.733 741 52(7) | −101(2) | 193.8(1) | 25.9(2) | 0.12(2) | 74(8) | 54958(4) | 0.0062(2) | 0.32 | 0.09 | 2: |
| 2856960 | 0.258 507 90(6) | −2.2(2) | 204.8(2) | 94(3) | 0.55(3) | 164(3) | 55007(2) | 0.27(2) | 1.48 | 0.02 | 2: |
| 5310387 | 0.441 668 66(1) | 2.80(4) | 214.0(1) | 13.5(1) | 0.23(1) | 210(4) | 55051(2) | 0.000 72(2) | 0.15 | 0.03 | 2: |
| 6144827 | 0.234 651 60(1) | −5.80(4) | 228.0(2) | 32.8(3) | 0.15(2) | 52(6) | 54921(4) | 0.0091(2) | 0.37 | 0.008 | 2: |
| 11968490 | 1.078 890 66(9) | −3(1) | 253.9(1) | 111.9(5) | 0.374(8) | 284(1) | 54862(1) | 0.291(4) | 1.54 | 0.13 | 2: |
| 4037163 | 0.635 444 61(3) | – | 268(2) | 20(2) | 0.66(7) | 356(4) | 54901(10) | 0.0015(4) | 0.19 | 0.12 | 2: |
| 6370665 | 0.932 314 31(7) | 14.8(8) | 286.4(5) | 27.7(4) | 0.08(3) | 354(19) | 55027(15) | 0.0035(1) | 0.26 | 0.08 | 2: |
| 8386865 | 1.258 041 69(7) | – | 294.0(5) | 84(2) | 0.49(3) | 314(4) | 55028(3) | 0.092(6) | 0.92 | 0.19 | 2: |
| 3853259: | 0.276 647 14(1) | 2.48(4) | 325.7(6) | 17.2(4) | 0.60(3) | 121(3) | 54900(3) | 0.000 64(4) | 0.01 | 0.14 | 2: |
| 5376552 | 0.503 818 78(1) | – | 334.8(1) | 41.9(2) | 0.349(6) | 355.2(9) | 54874(1) | 0.0088(1) | 0.37 | 0.02 | 2: |
| 8394040 | 0.302 126 24(1) | – | 388.9(1) | 124.6(4) | 0.520(5) | 295(1) | 54809(1) | 0.171(2) | 1.21 | 0.007 | 2: |
| 9075704 | 0.513 1488(1) | 15.2(7) | 402.0(5) | 63.4(3) | 0.160(9) | 252(3) | 55084(4) | 0.0212(3) | 0.51 | 0.01 | 2: |
| 5459373 | 0.286 608 72(1) | – | 412.7(2) | 98.6(3) | 0.361(6) | 271(1) | 55051(1) | 0.0754(7) | 0.85 | 0.004 | 2: |
| 9472174b | 0.125 765 28(1) | −0.063(4) | 418(2) | 0.63(2) | 0.38(4) | 124(6) | 55118(8) | 20(2)E−9 | 0.0019 | 0.000 | 0.60(3) |
| 5128972 | 0.505 323 38(1) | – | 442.1(2) | 114.6(3) | 0.285(5) | 285(1) | 54940(1) | 0.1032(9) | 0.97 | 0.01 | 2: |
| 9722737 | 0.418 528 37(1) | – | 444.2(1) | 103.4(2) | 0.174(4) | 223(1) | 54913(2) | 0.0750(5) | 0.85 | 0.007 | 2: |
| 9007918 | 1.387 206 55(1) | – | 470.9(6) | 17.7(2) | 0.68(2) | 271(1) | 54827(2) | 0.000 33(1) | 0.11 | 0.19 | 2: |
| 7811211 | 0.902 403 46(9) | – | 477(6) | 35(3) | 0.29(12) | 169(24) | 55168(33) | 0.0026(6) | 0.24 | 0.04 | 2: |
| 8043961 | 1.559 212 80(1) | – | 478.6(2) | 82.6(2) | 0.245(5) | 13(1) | 54817(2) | 0.0330(3) | 0.61 | 0.10 | 2: |
| 7685689 | 0.325 159 63(1) | – | 514.9(5) | 80.2(3) | 0.125(8) | 170(4) | 54774(5) | 0.0261(3) | 0.55 | 0.003 | 2: |
| 5216727 | 1.513 022 92(1) | – | 532.9(6) | 30.1(2) | 0.50(1) | 129(1) | 55158(2) | 0.001 29(3) | 0.18 | 0.11 | 2: |
| 8904448c | 0.865 9838(1) | −99(3) | 543.7(6) | 68.5(4) | 0.525(9) | 307.7(9) | 54796(2) | 0.0146(3) | 0.44 | 0.04 | 2: |
| 10991989 | 0.974 477 59(5) | – | 548(1) | 106(1) | 0.35(2) | 29(4) | 54960(6) | 0.053(2) | 0.73 | 0.03 | 2: |
| 7362751 | 0.338 250 80(4) | −9.2(2) | 552.0(6) | 120.1(6) | 0.256(9) | 107(2) | 54930(3) | 0.076(1) | 0.85 | 0.004 | 2: |
| 8330092 | 0.321 723 65(1) | – | 581(1) | 52.9(4) | 0.18(1) | 2(4) | 55134(7) | 0.0059(1) | 0.32 | 0.003 | 2: |
| 8190491 | 0.777 876 99(4) | – | 621(3) | 65(1) | 0.54(3) | 67(4) | 54789(7) | 0.0097(7) | 0.38 | 0.02 | 2: |
| 9994475 | 0.318 409 31(2) | −13.28(6) | 626.6(5) | 85.3(3) | 0.288(6) | 199(1) | 54779(2) | 0.0212(2) | 0.51 | 0.003 | 2: |
| 3228863 | 0.730 943 52(1) | 3.31(7) | 642.8(6) | 83.8(6) | 0.05(1) | 57(16) | 55052(28) | 0.0191(4) | 0.49 | 0.01 | 2: |
| 3245776 | 1.492 0589(2) | – | 663(9) | 54(3) | 0.45(12) | 263(16) | 55003(33) | 0.0048(9) | 0.29 | 0.07 | 2: |
| 9850387 | 2.748 4978(1) | – | 671(2) | 98(1) | 0.46(2) | 121(3) | 54683(6) | 0.028(1) | 0.57 | 0.22 | 2: |
| 8094140 | 0.706 428 57(1) | – | 676(1) | 56.3(4) | 0.35(1) | 171(2) | 54774(4) | 0.0052(1) | 0.30 | 0.01 | 2: |
| 5039441 | 2.151 382 94(6) | – | 678(1) | 87.2(7) | 0.25(1) | 163(3) | 55217(6) | 0.0194(5) | 0.49 | 0.10 | 2: |
| 9084778 | 0.592 243 75(8) | – | 680(9) | 69(3) | 0.20(9) | 176(25) | 55168(49) | 0.009(1) | 0.38 | 0.008 | 2: |
| 2835289 | 0.857 7610(1) | – | 755(5) | 138(7) | 0.74(6) | 294(4) | 54933(11) | 0.06(1) | 0.78 | 0.04 | 2: |
| 6543674 | 2.391 030 51(1) | – | 1101.4(4) | 115.2(1) | 0.617(2) | 267.1(1) | 55038(1) | 0.016 89(6) | 0.47 | 0.10 | 2: |
| 10727655 | 0.353 365 09(1) | 0.38(4) | 1138.1(6) | 141.8(2) | 0.247(2) | 36.4(5) | 55063(2) | 0.0295(1) | 0.58 | 0.001 | 2: |
| 2708156:d | 1.891 2615(2) | −29.4(7) | 5532(26) | 137(7) | 0.46(3) | 242(9) | 55955(153) | 0.0011(2) | 0.17 | 0.003 | 2: |
Notes.aCubic ephemeris – c3 = 1.84(3) × 10−12 d/c3.
bCubic ephemeris – c3 = 3 × 10−16 d/c3.
cCubic ephemeris – c3 = 2.57(6) × 10−12 d/c3.
dCubic ephemeris – c3 = −0.058(2) × 10−12 d/c3.
Orbital elements from LTTE solutions for systems, where more than two outer periods are covered, or/and triply eclipsing systems.
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 9777987 | 0.258 502 59(5) | −6.3(1) | 95.28(6) | 20.6(2) | 0.19(2) | 245(5) | 54979(2) | 0.0129(3) | 0.42 | 0.04 | 2: |
| 6669809a | 0.733 741 52(7) | −101(2) | 193.8(1) | 25.9(2) | 0.12(2) | 74(8) | 54958(4) | 0.0062(2) | 0.32 | 0.09 | 2: |
| 2856960 | 0.258 507 90(6) | −2.2(2) | 204.8(2) | 94(3) | 0.55(3) | 164(3) | 55007(2) | 0.27(2) | 1.48 | 0.02 | 2: |
| 5310387 | 0.441 668 66(1) | 2.80(4) | 214.0(1) | 13.5(1) | 0.23(1) | 210(4) | 55051(2) | 0.000 72(2) | 0.15 | 0.03 | 2: |
| 6144827 | 0.234 651 60(1) | −5.80(4) | 228.0(2) | 32.8(3) | 0.15(2) | 52(6) | 54921(4) | 0.0091(2) | 0.37 | 0.008 | 2: |
| 11968490 | 1.078 890 66(9) | −3(1) | 253.9(1) | 111.9(5) | 0.374(8) | 284(1) | 54862(1) | 0.291(4) | 1.54 | 0.13 | 2: |
| 4037163 | 0.635 444 61(3) | – | 268(2) | 20(2) | 0.66(7) | 356(4) | 54901(10) | 0.0015(4) | 0.19 | 0.12 | 2: |
| 6370665 | 0.932 314 31(7) | 14.8(8) | 286.4(5) | 27.7(4) | 0.08(3) | 354(19) | 55027(15) | 0.0035(1) | 0.26 | 0.08 | 2: |
| 8386865 | 1.258 041 69(7) | – | 294.0(5) | 84(2) | 0.49(3) | 314(4) | 55028(3) | 0.092(6) | 0.92 | 0.19 | 2: |
| 3853259: | 0.276 647 14(1) | 2.48(4) | 325.7(6) | 17.2(4) | 0.60(3) | 121(3) | 54900(3) | 0.000 64(4) | 0.01 | 0.14 | 2: |
| 5376552 | 0.503 818 78(1) | – | 334.8(1) | 41.9(2) | 0.349(6) | 355.2(9) | 54874(1) | 0.0088(1) | 0.37 | 0.02 | 2: |
| 8394040 | 0.302 126 24(1) | – | 388.9(1) | 124.6(4) | 0.520(5) | 295(1) | 54809(1) | 0.171(2) | 1.21 | 0.007 | 2: |
| 9075704 | 0.513 1488(1) | 15.2(7) | 402.0(5) | 63.4(3) | 0.160(9) | 252(3) | 55084(4) | 0.0212(3) | 0.51 | 0.01 | 2: |
| 5459373 | 0.286 608 72(1) | – | 412.7(2) | 98.6(3) | 0.361(6) | 271(1) | 55051(1) | 0.0754(7) | 0.85 | 0.004 | 2: |
| 9472174b | 0.125 765 28(1) | −0.063(4) | 418(2) | 0.63(2) | 0.38(4) | 124(6) | 55118(8) | 20(2)E−9 | 0.0019 | 0.000 | 0.60(3) |
| 5128972 | 0.505 323 38(1) | – | 442.1(2) | 114.6(3) | 0.285(5) | 285(1) | 54940(1) | 0.1032(9) | 0.97 | 0.01 | 2: |
| 9722737 | 0.418 528 37(1) | – | 444.2(1) | 103.4(2) | 0.174(4) | 223(1) | 54913(2) | 0.0750(5) | 0.85 | 0.007 | 2: |
| 9007918 | 1.387 206 55(1) | – | 470.9(6) | 17.7(2) | 0.68(2) | 271(1) | 54827(2) | 0.000 33(1) | 0.11 | 0.19 | 2: |
| 7811211 | 0.902 403 46(9) | – | 477(6) | 35(3) | 0.29(12) | 169(24) | 55168(33) | 0.0026(6) | 0.24 | 0.04 | 2: |
| 8043961 | 1.559 212 80(1) | – | 478.6(2) | 82.6(2) | 0.245(5) | 13(1) | 54817(2) | 0.0330(3) | 0.61 | 0.10 | 2: |
| 7685689 | 0.325 159 63(1) | – | 514.9(5) | 80.2(3) | 0.125(8) | 170(4) | 54774(5) | 0.0261(3) | 0.55 | 0.003 | 2: |
| 5216727 | 1.513 022 92(1) | – | 532.9(6) | 30.1(2) | 0.50(1) | 129(1) | 55158(2) | 0.001 29(3) | 0.18 | 0.11 | 2: |
| 8904448c | 0.865 9838(1) | −99(3) | 543.7(6) | 68.5(4) | 0.525(9) | 307.7(9) | 54796(2) | 0.0146(3) | 0.44 | 0.04 | 2: |
| 10991989 | 0.974 477 59(5) | – | 548(1) | 106(1) | 0.35(2) | 29(4) | 54960(6) | 0.053(2) | 0.73 | 0.03 | 2: |
| 7362751 | 0.338 250 80(4) | −9.2(2) | 552.0(6) | 120.1(6) | 0.256(9) | 107(2) | 54930(3) | 0.076(1) | 0.85 | 0.004 | 2: |
| 8330092 | 0.321 723 65(1) | – | 581(1) | 52.9(4) | 0.18(1) | 2(4) | 55134(7) | 0.0059(1) | 0.32 | 0.003 | 2: |
| 8190491 | 0.777 876 99(4) | – | 621(3) | 65(1) | 0.54(3) | 67(4) | 54789(7) | 0.0097(7) | 0.38 | 0.02 | 2: |
| 9994475 | 0.318 409 31(2) | −13.28(6) | 626.6(5) | 85.3(3) | 0.288(6) | 199(1) | 54779(2) | 0.0212(2) | 0.51 | 0.003 | 2: |
| 3228863 | 0.730 943 52(1) | 3.31(7) | 642.8(6) | 83.8(6) | 0.05(1) | 57(16) | 55052(28) | 0.0191(4) | 0.49 | 0.01 | 2: |
| 3245776 | 1.492 0589(2) | – | 663(9) | 54(3) | 0.45(12) | 263(16) | 55003(33) | 0.0048(9) | 0.29 | 0.07 | 2: |
| 9850387 | 2.748 4978(1) | – | 671(2) | 98(1) | 0.46(2) | 121(3) | 54683(6) | 0.028(1) | 0.57 | 0.22 | 2: |
| 8094140 | 0.706 428 57(1) | – | 676(1) | 56.3(4) | 0.35(1) | 171(2) | 54774(4) | 0.0052(1) | 0.30 | 0.01 | 2: |
| 5039441 | 2.151 382 94(6) | – | 678(1) | 87.2(7) | 0.25(1) | 163(3) | 55217(6) | 0.0194(5) | 0.49 | 0.10 | 2: |
| 9084778 | 0.592 243 75(8) | – | 680(9) | 69(3) | 0.20(9) | 176(25) | 55168(49) | 0.009(1) | 0.38 | 0.008 | 2: |
| 2835289 | 0.857 7610(1) | – | 755(5) | 138(7) | 0.74(6) | 294(4) | 54933(11) | 0.06(1) | 0.78 | 0.04 | 2: |
| 6543674 | 2.391 030 51(1) | – | 1101.4(4) | 115.2(1) | 0.617(2) | 267.1(1) | 55038(1) | 0.016 89(6) | 0.47 | 0.10 | 2: |
| 10727655 | 0.353 365 09(1) | 0.38(4) | 1138.1(6) | 141.8(2) | 0.247(2) | 36.4(5) | 55063(2) | 0.0295(1) | 0.58 | 0.001 | 2: |
| 2708156:d | 1.891 2615(2) | −29.4(7) | 5532(26) | 137(7) | 0.46(3) | 242(9) | 55955(153) | 0.0011(2) | 0.17 | 0.003 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 9777987 | 0.258 502 59(5) | −6.3(1) | 95.28(6) | 20.6(2) | 0.19(2) | 245(5) | 54979(2) | 0.0129(3) | 0.42 | 0.04 | 2: |
| 6669809a | 0.733 741 52(7) | −101(2) | 193.8(1) | 25.9(2) | 0.12(2) | 74(8) | 54958(4) | 0.0062(2) | 0.32 | 0.09 | 2: |
| 2856960 | 0.258 507 90(6) | −2.2(2) | 204.8(2) | 94(3) | 0.55(3) | 164(3) | 55007(2) | 0.27(2) | 1.48 | 0.02 | 2: |
| 5310387 | 0.441 668 66(1) | 2.80(4) | 214.0(1) | 13.5(1) | 0.23(1) | 210(4) | 55051(2) | 0.000 72(2) | 0.15 | 0.03 | 2: |
| 6144827 | 0.234 651 60(1) | −5.80(4) | 228.0(2) | 32.8(3) | 0.15(2) | 52(6) | 54921(4) | 0.0091(2) | 0.37 | 0.008 | 2: |
| 11968490 | 1.078 890 66(9) | −3(1) | 253.9(1) | 111.9(5) | 0.374(8) | 284(1) | 54862(1) | 0.291(4) | 1.54 | 0.13 | 2: |
| 4037163 | 0.635 444 61(3) | – | 268(2) | 20(2) | 0.66(7) | 356(4) | 54901(10) | 0.0015(4) | 0.19 | 0.12 | 2: |
| 6370665 | 0.932 314 31(7) | 14.8(8) | 286.4(5) | 27.7(4) | 0.08(3) | 354(19) | 55027(15) | 0.0035(1) | 0.26 | 0.08 | 2: |
| 8386865 | 1.258 041 69(7) | – | 294.0(5) | 84(2) | 0.49(3) | 314(4) | 55028(3) | 0.092(6) | 0.92 | 0.19 | 2: |
| 3853259: | 0.276 647 14(1) | 2.48(4) | 325.7(6) | 17.2(4) | 0.60(3) | 121(3) | 54900(3) | 0.000 64(4) | 0.01 | 0.14 | 2: |
| 5376552 | 0.503 818 78(1) | – | 334.8(1) | 41.9(2) | 0.349(6) | 355.2(9) | 54874(1) | 0.0088(1) | 0.37 | 0.02 | 2: |
| 8394040 | 0.302 126 24(1) | – | 388.9(1) | 124.6(4) | 0.520(5) | 295(1) | 54809(1) | 0.171(2) | 1.21 | 0.007 | 2: |
| 9075704 | 0.513 1488(1) | 15.2(7) | 402.0(5) | 63.4(3) | 0.160(9) | 252(3) | 55084(4) | 0.0212(3) | 0.51 | 0.01 | 2: |
| 5459373 | 0.286 608 72(1) | – | 412.7(2) | 98.6(3) | 0.361(6) | 271(1) | 55051(1) | 0.0754(7) | 0.85 | 0.004 | 2: |
| 9472174b | 0.125 765 28(1) | −0.063(4) | 418(2) | 0.63(2) | 0.38(4) | 124(6) | 55118(8) | 20(2)E−9 | 0.0019 | 0.000 | 0.60(3) |
| 5128972 | 0.505 323 38(1) | – | 442.1(2) | 114.6(3) | 0.285(5) | 285(1) | 54940(1) | 0.1032(9) | 0.97 | 0.01 | 2: |
| 9722737 | 0.418 528 37(1) | – | 444.2(1) | 103.4(2) | 0.174(4) | 223(1) | 54913(2) | 0.0750(5) | 0.85 | 0.007 | 2: |
| 9007918 | 1.387 206 55(1) | – | 470.9(6) | 17.7(2) | 0.68(2) | 271(1) | 54827(2) | 0.000 33(1) | 0.11 | 0.19 | 2: |
| 7811211 | 0.902 403 46(9) | – | 477(6) | 35(3) | 0.29(12) | 169(24) | 55168(33) | 0.0026(6) | 0.24 | 0.04 | 2: |
| 8043961 | 1.559 212 80(1) | – | 478.6(2) | 82.6(2) | 0.245(5) | 13(1) | 54817(2) | 0.0330(3) | 0.61 | 0.10 | 2: |
| 7685689 | 0.325 159 63(1) | – | 514.9(5) | 80.2(3) | 0.125(8) | 170(4) | 54774(5) | 0.0261(3) | 0.55 | 0.003 | 2: |
| 5216727 | 1.513 022 92(1) | – | 532.9(6) | 30.1(2) | 0.50(1) | 129(1) | 55158(2) | 0.001 29(3) | 0.18 | 0.11 | 2: |
| 8904448c | 0.865 9838(1) | −99(3) | 543.7(6) | 68.5(4) | 0.525(9) | 307.7(9) | 54796(2) | 0.0146(3) | 0.44 | 0.04 | 2: |
| 10991989 | 0.974 477 59(5) | – | 548(1) | 106(1) | 0.35(2) | 29(4) | 54960(6) | 0.053(2) | 0.73 | 0.03 | 2: |
| 7362751 | 0.338 250 80(4) | −9.2(2) | 552.0(6) | 120.1(6) | 0.256(9) | 107(2) | 54930(3) | 0.076(1) | 0.85 | 0.004 | 2: |
| 8330092 | 0.321 723 65(1) | – | 581(1) | 52.9(4) | 0.18(1) | 2(4) | 55134(7) | 0.0059(1) | 0.32 | 0.003 | 2: |
| 8190491 | 0.777 876 99(4) | – | 621(3) | 65(1) | 0.54(3) | 67(4) | 54789(7) | 0.0097(7) | 0.38 | 0.02 | 2: |
| 9994475 | 0.318 409 31(2) | −13.28(6) | 626.6(5) | 85.3(3) | 0.288(6) | 199(1) | 54779(2) | 0.0212(2) | 0.51 | 0.003 | 2: |
| 3228863 | 0.730 943 52(1) | 3.31(7) | 642.8(6) | 83.8(6) | 0.05(1) | 57(16) | 55052(28) | 0.0191(4) | 0.49 | 0.01 | 2: |
| 3245776 | 1.492 0589(2) | – | 663(9) | 54(3) | 0.45(12) | 263(16) | 55003(33) | 0.0048(9) | 0.29 | 0.07 | 2: |
| 9850387 | 2.748 4978(1) | – | 671(2) | 98(1) | 0.46(2) | 121(3) | 54683(6) | 0.028(1) | 0.57 | 0.22 | 2: |
| 8094140 | 0.706 428 57(1) | – | 676(1) | 56.3(4) | 0.35(1) | 171(2) | 54774(4) | 0.0052(1) | 0.30 | 0.01 | 2: |
| 5039441 | 2.151 382 94(6) | – | 678(1) | 87.2(7) | 0.25(1) | 163(3) | 55217(6) | 0.0194(5) | 0.49 | 0.10 | 2: |
| 9084778 | 0.592 243 75(8) | – | 680(9) | 69(3) | 0.20(9) | 176(25) | 55168(49) | 0.009(1) | 0.38 | 0.008 | 2: |
| 2835289 | 0.857 7610(1) | – | 755(5) | 138(7) | 0.74(6) | 294(4) | 54933(11) | 0.06(1) | 0.78 | 0.04 | 2: |
| 6543674 | 2.391 030 51(1) | – | 1101.4(4) | 115.2(1) | 0.617(2) | 267.1(1) | 55038(1) | 0.016 89(6) | 0.47 | 0.10 | 2: |
| 10727655 | 0.353 365 09(1) | 0.38(4) | 1138.1(6) | 141.8(2) | 0.247(2) | 36.4(5) | 55063(2) | 0.0295(1) | 0.58 | 0.001 | 2: |
| 2708156:d | 1.891 2615(2) | −29.4(7) | 5532(26) | 137(7) | 0.46(3) | 242(9) | 55955(153) | 0.0011(2) | 0.17 | 0.003 | 2: |
Notes.aCubic ephemeris – c3 = 1.84(3) × 10−12 d/c3.
bCubic ephemeris – c3 = 3 × 10−16 d/c3.
cCubic ephemeris – c3 = 2.57(6) × 10−12 d/c3.
dCubic ephemeris – c3 = −0.058(2) × 10−12 d/c3.
Orbital elements from LTTE solutions which cover more than one but less than two outer periods.
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 8145477 | 0.565 783 95(8) | – | 364(4) | 59.2(8) | 0.41(2) | 190(2) | 54911(4) | 0.021(1) | 0.51 | 0.03 | 2: |
| 3114667: | 0.888 583 02(3) | – | 573(4) | 21(1) | 0.73(4) | 347(2) | 55275(9) | 0.000 38(7) | 0.12 | 0.10 | 2: |
| 9592145: | 0.488 867 28(1) | 0.75(3) | 730(2) | 6.88(6) | 0.28(2) | 260(3) | 55041(7) | 82(2)E−7 | 0.03 | 0.005 | 2: |
| 5478466 | 0.482 500 55(1) | – | 739.2(9) | 91.2(8) | 0.505(9) | 17.6(9) | 54961(2) | 0.0186(5) | 0.49 | 0.007 | 2: |
| 4859432 | 0.385 479 90(1) | – | 747.3(8) | 67.3(3) | 0.565(8) | 270.0(8) | 54634(2) | 0.0073(1) | 0.34 | 0.005 | 2: |
| 4451148 | 0.735 981 74(1) | – | 749.7(6) | 139.6(5) | 0.288(6) | 44(1) | 55002(3) | 0.0649(7) | 0.80 | 0.01 | 2: |
| 3338660: | 1.873 3818(1) | – | 752(18) | 7.7(8) | 0.76(8) | 308(5) | 54821(30) | 0.000 011(3) | 0.04 | 0.26 | 2: |
| 4647652 | 1.064 824 97(1) | – | 754.7(3) | 106.2(2) | 0.291(3) | 30.7(5) | 54760(1) | 0.0282(1) | 0.57 | 0.02 | 2: |
| 4670267 | 2.006 097 28(2) | – | 755(2) | 29.4(4) | 0.56(2) | 63(2) | 55052(5) | 0.000 60(3) | 0.14 | 0.13 | 2: |
| 9912977 | 1.887 873 19(1) | – | 756.2(5) | 47.4(1) | 0.282(5) | 76(1) | 55168(2) | 0.002 50(2) | 0.23 | 0.07 | 2: |
| 8957887 | 0.347 354 18(1) | – | 774.2(4) | 186.1(4) | 0.468(3) | 151.2(4) | 55275(1) | 0.144(1) | 1.12 | 0.003 | 2: |
| 10848807: | 0.346 246 70(1) | – | 785(3) | 11.3(2) | 0.36(3) | 339(1) | 55013(11) | 0.000 031(2) | 0.05 | 0.003 | 2: |
| 1873918 | 0.332 431 83(3) | −3.6(1) | 840.9(9) | 124.4(7) | 0.663(7) | 64.5(7) | 55035(2) | 0.0364(7) | 0.63 | 0.004 | 2: |
| 4138301 | 0.253 379 19(1) | – | 844(1) | 122.8(7) | 0.423(8) | 221(1) | 55049(3) | 0.0348(6) | 0.62 | 0.001 | 2: |
| 2715417 | 0.236 439 93(1) | – | 856(2) | 21.9(2) | 0.22(1) | 124(3) | 54939(8) | 0.000 19(1) | 0.09 | 0.001 | 2: |
| 9665086 | 0.296 536 88(2) | – | 856(2) | 253(3) | 0.51(1) | 66(2) | 54659(4) | 0.297(9) | 1.55 | 0.002 | 2: |
| 4547308 | 0.576 927 98(1) | – | 871(4) | 105(4) | 0.90(2) | 54(2) | 55078(7) | 0.020(2) | 0.50 | 0.06 | 2: |
| 4069063 | 0.504 295 27(3) | – | 876(1) | 233(2) | 0.64(1) | 132(1) | 55013(3) | 0.220(7) | 1.35 | 0.007 | 2: |
| 7339345: | 0.259 661 51(1) | 10.01(2) | 892(2) | 15.3(1) | 0.40(1) | 286(2) | 55120(5) | 0.000 060(1) | 0.06 | 0.001 | 2: |
| 6516874 | 0.916 325 49(7) | – | 905(4) | 102.3(8) | 0.24(1) | 205(2) | 54663(9) | 0.0175(4) | 0.48 | 0.01 | 2: |
| 8739802 | 0.274 512 78(1) | – | 907(5) | 41.1(6) | 0.40(2) | 191(3) | 55357(9) | 0.001 13(5) | 0.17 | 0.001 | 2: |
| 7630658 | 2.151 155 67(2) | – | 921.6(3) | 179.8(5) | 0.673(2) | 326.2(2) | 55353(1) | 0.0917(7) | 0.92 | 0.16 | 2: |
| 12071741 | 0.314 264 38(1) | – | 927(2) | 176(2) | 0.64(1) | 149.5(8) | 54932(2) | 0.085(3) | 0.89 | 0.003 | 2: |
| 2450566 | 1.844 5840(7) | – | 935(11) | 236(19) | 0.72(8) | 142(6) | 55050(19) | 0.20(5) | 1.30 | 0.12 | 2: |
| 7552344 | 2.001 4910(9) | – | 952(14) | 237(9) | 0.26(8) | 261(17) | 55330(47) | 0.20(2) | 1.29 | 0.05 | 2: |
| 10226388 | 0.660 658 35(1) | – | 954.6(8) | 211.3(5) | 0.276(4) | 108(1) | 54716(3) | 0.139(1) | 1.10 | 0.005 | 2: |
| 2302092 | 0.294 672 88(1) | – | 986.1(7) | 175.2(4) | 0.442(4) | 109.9(5) | 55112(2) | 0.0741(5) | 0.84 | 0.001 | 2: |
| 9353234 | 1.486 5278(2) | – | 987(20) | 60(4) | 0.18(11) | 121(39) | 55240(108) | 0.0029(5) | 0.24 | 0.03 | 2: |
| 8242493 | 0.283 285 69(1) | – | 1013(2) | 27.4(1) | 0.182(7) | 1(2) | 55094(7) | 0.000 268(3) | 0.11 | 0.001 | 2: |
| 11042923 | 0.390 162 14(1) | – | 1041.7(8) | 120.6(2) | 0.274(2) | 167.6(5) | 54483(2) | 0.021 65(9) | 0.52 | 0.002 | 2: |
| 7385478: | 1.655 473(1) | – | 1049(9) | 67(1) | 0.47(4) | 119(4) | 55039(14) | 0.0037(2) | 0.27 | 0.04 | 2: |
| 7680593: | 0.276 398 26(5) | −25.7(2) | 1051(5) | 43.6(8) | 0.54(2) | 148(2) | 55315(6) | 0.001 01(6) | 0.17 | 0.001 | 2: |
| 5611561 | 0.258 694 69(1) | – | 1052(2) | 44.5(2) | 0.205(9) | 347(2) | 55362(7) | 0.001 06(2) | 0.17 | 0.001 | 2: |
| 9159301 | 3.044 7717(1) | – | 1072(23) | 12.6(3) | 0.40(4) | 263(7) | 54922(27) | 0.000 023(2) | 0.05 | 0.12 | 2: |
| 3440230 | 2.881 1326(2) | −1277(10) | 1082(8) | 17.6(5) | 0.56(3) | 178(3) | 55203(11) | 0.000 063(5) | 0.06 | 0.17 | 2: |
| 5621294: | 0.938 909 79(5) | −59.2(8) | 1083(15) | 6.8(2) | 0.43(5) | 323(7) | 55143(22) | 36(4)E−7 | 0.02 | 0.01 | 2: |
| 4074708 | 0.302 116 49(1) | – | 1110(3) | 28.1(1) | 0.09(1) | 42(6) | 54843(18) | 0.000 243(4) | 0.10 | 0.001 | 2: |
| 5307780 | 0.308 849 72(3) | 5.7(1) | 1115(2) | 48(2) | 0.86(1) | 15(1) | 55101(5) | 0.0012(1) | 0.18 | 0.01 | 2: |
| 6965293 | 5.077 7443(1) | – | 1119(2) | 197.4(6) | 0.204(7) | 312(2) | 54716(6) | 0.0823(9) | 0.88 | 0.23 | 2: |
| 8192840 | 0.433 549 28(1) | – | 1145(4) | 118.4(7) | 0.655(4) | 3.5(3) | 55486(3) | 0.0170(3) | 0.47 | 0.005 | 2: |
| 9838047 | 0.436 162 06(3) | – | 1154(2) | 221.1(8) | 0.267(6) | 174(1) | 55008(4) | 0.109(1) | 0.99 | 0.002 | 2: |
| 10583181 | 2.696 353 89(2) | – | 1169.2(9) | 154.0(1) | 0.060(2) | 99(2) | 54503(6) | 0.0358(1) | 0.63 | 0.06 | 2: |
| 4681152 | 1.835 9276(2) | – | 1177(21) | 36.3(9) | 0.22(3) | 155(7) | 54998(26) | 0.000 46(4) | 0.13 | 0.03 | 2: |
| 9711751 | 1.711 528 18(1) | – | 1186.1(7) | 218.1(2) | 0.259(1) | 351.0(4) | 55385(1) | 0.0989(3) | 0.95 | 0.02 | 2: |
| 7440742 | 0.283 992 18(1) | – | 1200(4) | 29.9(4) | 0.66(3) | 287(2) | 55048(8) | 0.000 249(9) | 0.10 | 0.002 | 2: |
| 9101279: | 1.811 460 57(5) | – | 1202(8) | 46.8(4) | 0.17(1) | 129(5) | 55342(16) | 0.000 95(3) | 0.16 | 0.03 | 2: |
| 4762887 | 0.736 573 44(4) | – | 1233(37) | 25(1) | 0.25(8) | 5(20) | 55288(72) | 0.000 13(2) | 0.08 | 0.005 | 2: |
| 9574614 | 0.982 095(1) | – | 1234(43) | 266(12) | 0.02(5) | 208(113) | 55093(387) | 0.17(2) | 1.19 | 0.007 | 2: |
| 5903301 | 2.320 3030(4) | – | 1255(32) | 153(3) | 0.43(4) | 22(6) | 54977(31) | 0.031(2) | 0.59 | 0.06 | 2: |
| 6281103 | 0.363 283 30(1) | −9.98(6) | 1254(3) | 76.9(4) | 0.024(9) | 239(23) | 55179(81) | 0.003 88(7) | 0.27 | 0.001 | 2: |
| 11604958 | 0.298 929 82(1) | – | 1256(8) | 22.7(3) | 0.50(1) | 36(1) | 55122(6) | 0.000 099(4) | 0.08 | 0.001 | 2: |
| 6671698 | 0.471 532(1) | −42(6) | 1261(47) | 129(9) | 0.316(5) | 131(1) | 54743(39) | 0.018(4) | 0.48 | 0.002 | 2: |
| 9091810 | 0.479 721 30(1) | – | 1298(33) | 17.1(3) | 0.25(4) | 257(8) | 54488(37) | 0.000 040(3) | 0.06 | 0.002 | 2: |
| 7877062 | 0.303 651 94(5) | – | 1321(34) | 52(2) | 0.128(9) | 89(9) | 54716(41) | 0.0011(1) | 0.17 | 0.001 | 2: |
| 4244929 | 0.341 4038(1) | – | 1342(23) | 129(4) | 0.28(1) | 235(2) | 55116(13) | 0.016(2) | 0.46 | 0.001 | 2: |
| 4574310 | 1.306 220 13(1) | – | 1347(20) | 14.9(2) | 0.56(2) | 154(1) | 54557(16) | 0.000 025(1) | 0.05 | 0.02 | 2: |
| 8081389 | 1.489 443 01(3) | – | 1383(15) | 13.8(2) | 0.27(1) | 217(2) | 55181(12) | 0.000 018(1) | 0.04 | 0.02 | 2: |
| 7119757 | 0.742 9197(2) | – | 1402(43) | 179(5) | 0.60(1) | 181.8(5) | 54451(32) | 0.039(4) | 0.65 | 0.008 | 2: |
| 4945857 | 0.335 417 78(4) | – | 1423(6) | 346(2) | 0.402(2) | 343.0(2) | 54286(5) | 0.273(4) | 1.49 | 0.001 | 2: |
| 12554536 | 0.684 496 43(1) | – | 1448(7) | 44.8(2) | 0.515(9) | 246.9(6) | 54914(5) | 0.000 574(9) | 0.14 | 0.004 | 2: |
| 9272276 | 0.280 614 16(2) | – | 1458(7) | 235(1) | 0.252(3) | 325.4(9) | 55291(5) | 0.082(1) | 0.88 | 0.001 | 2: |
| 9402652 | 1.073 106 92(2) | – | 1506(2) | 163.9(3) | 0.805(1) | 86.6(2) | 54838(2) | 0.0260(2) | 0.55 | 0.03 | 2: |
| 5513861 | 1.510 209 53(9) | – | 2140(6) | 306(2) | 0.140(6) | 208(4) | 54202(22) | 0.084(1) | 0.89 | 0.007 | 2: |
| 12019674 | 0.354 497 43(3) | – | 2800(13) | 408(2) | 0.216(5) | 145(1) | 52584(14) | 0.116(2) | 1.02 | 0.001 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 8145477 | 0.565 783 95(8) | – | 364(4) | 59.2(8) | 0.41(2) | 190(2) | 54911(4) | 0.021(1) | 0.51 | 0.03 | 2: |
| 3114667: | 0.888 583 02(3) | – | 573(4) | 21(1) | 0.73(4) | 347(2) | 55275(9) | 0.000 38(7) | 0.12 | 0.10 | 2: |
| 9592145: | 0.488 867 28(1) | 0.75(3) | 730(2) | 6.88(6) | 0.28(2) | 260(3) | 55041(7) | 82(2)E−7 | 0.03 | 0.005 | 2: |
| 5478466 | 0.482 500 55(1) | – | 739.2(9) | 91.2(8) | 0.505(9) | 17.6(9) | 54961(2) | 0.0186(5) | 0.49 | 0.007 | 2: |
| 4859432 | 0.385 479 90(1) | – | 747.3(8) | 67.3(3) | 0.565(8) | 270.0(8) | 54634(2) | 0.0073(1) | 0.34 | 0.005 | 2: |
| 4451148 | 0.735 981 74(1) | – | 749.7(6) | 139.6(5) | 0.288(6) | 44(1) | 55002(3) | 0.0649(7) | 0.80 | 0.01 | 2: |
| 3338660: | 1.873 3818(1) | – | 752(18) | 7.7(8) | 0.76(8) | 308(5) | 54821(30) | 0.000 011(3) | 0.04 | 0.26 | 2: |
| 4647652 | 1.064 824 97(1) | – | 754.7(3) | 106.2(2) | 0.291(3) | 30.7(5) | 54760(1) | 0.0282(1) | 0.57 | 0.02 | 2: |
| 4670267 | 2.006 097 28(2) | – | 755(2) | 29.4(4) | 0.56(2) | 63(2) | 55052(5) | 0.000 60(3) | 0.14 | 0.13 | 2: |
| 9912977 | 1.887 873 19(1) | – | 756.2(5) | 47.4(1) | 0.282(5) | 76(1) | 55168(2) | 0.002 50(2) | 0.23 | 0.07 | 2: |
| 8957887 | 0.347 354 18(1) | – | 774.2(4) | 186.1(4) | 0.468(3) | 151.2(4) | 55275(1) | 0.144(1) | 1.12 | 0.003 | 2: |
| 10848807: | 0.346 246 70(1) | – | 785(3) | 11.3(2) | 0.36(3) | 339(1) | 55013(11) | 0.000 031(2) | 0.05 | 0.003 | 2: |
| 1873918 | 0.332 431 83(3) | −3.6(1) | 840.9(9) | 124.4(7) | 0.663(7) | 64.5(7) | 55035(2) | 0.0364(7) | 0.63 | 0.004 | 2: |
| 4138301 | 0.253 379 19(1) | – | 844(1) | 122.8(7) | 0.423(8) | 221(1) | 55049(3) | 0.0348(6) | 0.62 | 0.001 | 2: |
| 2715417 | 0.236 439 93(1) | – | 856(2) | 21.9(2) | 0.22(1) | 124(3) | 54939(8) | 0.000 19(1) | 0.09 | 0.001 | 2: |
| 9665086 | 0.296 536 88(2) | – | 856(2) | 253(3) | 0.51(1) | 66(2) | 54659(4) | 0.297(9) | 1.55 | 0.002 | 2: |
| 4547308 | 0.576 927 98(1) | – | 871(4) | 105(4) | 0.90(2) | 54(2) | 55078(7) | 0.020(2) | 0.50 | 0.06 | 2: |
| 4069063 | 0.504 295 27(3) | – | 876(1) | 233(2) | 0.64(1) | 132(1) | 55013(3) | 0.220(7) | 1.35 | 0.007 | 2: |
| 7339345: | 0.259 661 51(1) | 10.01(2) | 892(2) | 15.3(1) | 0.40(1) | 286(2) | 55120(5) | 0.000 060(1) | 0.06 | 0.001 | 2: |
| 6516874 | 0.916 325 49(7) | – | 905(4) | 102.3(8) | 0.24(1) | 205(2) | 54663(9) | 0.0175(4) | 0.48 | 0.01 | 2: |
| 8739802 | 0.274 512 78(1) | – | 907(5) | 41.1(6) | 0.40(2) | 191(3) | 55357(9) | 0.001 13(5) | 0.17 | 0.001 | 2: |
| 7630658 | 2.151 155 67(2) | – | 921.6(3) | 179.8(5) | 0.673(2) | 326.2(2) | 55353(1) | 0.0917(7) | 0.92 | 0.16 | 2: |
| 12071741 | 0.314 264 38(1) | – | 927(2) | 176(2) | 0.64(1) | 149.5(8) | 54932(2) | 0.085(3) | 0.89 | 0.003 | 2: |
| 2450566 | 1.844 5840(7) | – | 935(11) | 236(19) | 0.72(8) | 142(6) | 55050(19) | 0.20(5) | 1.30 | 0.12 | 2: |
| 7552344 | 2.001 4910(9) | – | 952(14) | 237(9) | 0.26(8) | 261(17) | 55330(47) | 0.20(2) | 1.29 | 0.05 | 2: |
| 10226388 | 0.660 658 35(1) | – | 954.6(8) | 211.3(5) | 0.276(4) | 108(1) | 54716(3) | 0.139(1) | 1.10 | 0.005 | 2: |
| 2302092 | 0.294 672 88(1) | – | 986.1(7) | 175.2(4) | 0.442(4) | 109.9(5) | 55112(2) | 0.0741(5) | 0.84 | 0.001 | 2: |
| 9353234 | 1.486 5278(2) | – | 987(20) | 60(4) | 0.18(11) | 121(39) | 55240(108) | 0.0029(5) | 0.24 | 0.03 | 2: |
| 8242493 | 0.283 285 69(1) | – | 1013(2) | 27.4(1) | 0.182(7) | 1(2) | 55094(7) | 0.000 268(3) | 0.11 | 0.001 | 2: |
| 11042923 | 0.390 162 14(1) | – | 1041.7(8) | 120.6(2) | 0.274(2) | 167.6(5) | 54483(2) | 0.021 65(9) | 0.52 | 0.002 | 2: |
| 7385478: | 1.655 473(1) | – | 1049(9) | 67(1) | 0.47(4) | 119(4) | 55039(14) | 0.0037(2) | 0.27 | 0.04 | 2: |
| 7680593: | 0.276 398 26(5) | −25.7(2) | 1051(5) | 43.6(8) | 0.54(2) | 148(2) | 55315(6) | 0.001 01(6) | 0.17 | 0.001 | 2: |
| 5611561 | 0.258 694 69(1) | – | 1052(2) | 44.5(2) | 0.205(9) | 347(2) | 55362(7) | 0.001 06(2) | 0.17 | 0.001 | 2: |
| 9159301 | 3.044 7717(1) | – | 1072(23) | 12.6(3) | 0.40(4) | 263(7) | 54922(27) | 0.000 023(2) | 0.05 | 0.12 | 2: |
| 3440230 | 2.881 1326(2) | −1277(10) | 1082(8) | 17.6(5) | 0.56(3) | 178(3) | 55203(11) | 0.000 063(5) | 0.06 | 0.17 | 2: |
| 5621294: | 0.938 909 79(5) | −59.2(8) | 1083(15) | 6.8(2) | 0.43(5) | 323(7) | 55143(22) | 36(4)E−7 | 0.02 | 0.01 | 2: |
| 4074708 | 0.302 116 49(1) | – | 1110(3) | 28.1(1) | 0.09(1) | 42(6) | 54843(18) | 0.000 243(4) | 0.10 | 0.001 | 2: |
| 5307780 | 0.308 849 72(3) | 5.7(1) | 1115(2) | 48(2) | 0.86(1) | 15(1) | 55101(5) | 0.0012(1) | 0.18 | 0.01 | 2: |
| 6965293 | 5.077 7443(1) | – | 1119(2) | 197.4(6) | 0.204(7) | 312(2) | 54716(6) | 0.0823(9) | 0.88 | 0.23 | 2: |
| 8192840 | 0.433 549 28(1) | – | 1145(4) | 118.4(7) | 0.655(4) | 3.5(3) | 55486(3) | 0.0170(3) | 0.47 | 0.005 | 2: |
| 9838047 | 0.436 162 06(3) | – | 1154(2) | 221.1(8) | 0.267(6) | 174(1) | 55008(4) | 0.109(1) | 0.99 | 0.002 | 2: |
| 10583181 | 2.696 353 89(2) | – | 1169.2(9) | 154.0(1) | 0.060(2) | 99(2) | 54503(6) | 0.0358(1) | 0.63 | 0.06 | 2: |
| 4681152 | 1.835 9276(2) | – | 1177(21) | 36.3(9) | 0.22(3) | 155(7) | 54998(26) | 0.000 46(4) | 0.13 | 0.03 | 2: |
| 9711751 | 1.711 528 18(1) | – | 1186.1(7) | 218.1(2) | 0.259(1) | 351.0(4) | 55385(1) | 0.0989(3) | 0.95 | 0.02 | 2: |
| 7440742 | 0.283 992 18(1) | – | 1200(4) | 29.9(4) | 0.66(3) | 287(2) | 55048(8) | 0.000 249(9) | 0.10 | 0.002 | 2: |
| 9101279: | 1.811 460 57(5) | – | 1202(8) | 46.8(4) | 0.17(1) | 129(5) | 55342(16) | 0.000 95(3) | 0.16 | 0.03 | 2: |
| 4762887 | 0.736 573 44(4) | – | 1233(37) | 25(1) | 0.25(8) | 5(20) | 55288(72) | 0.000 13(2) | 0.08 | 0.005 | 2: |
| 9574614 | 0.982 095(1) | – | 1234(43) | 266(12) | 0.02(5) | 208(113) | 55093(387) | 0.17(2) | 1.19 | 0.007 | 2: |
| 5903301 | 2.320 3030(4) | – | 1255(32) | 153(3) | 0.43(4) | 22(6) | 54977(31) | 0.031(2) | 0.59 | 0.06 | 2: |
| 6281103 | 0.363 283 30(1) | −9.98(6) | 1254(3) | 76.9(4) | 0.024(9) | 239(23) | 55179(81) | 0.003 88(7) | 0.27 | 0.001 | 2: |
| 11604958 | 0.298 929 82(1) | – | 1256(8) | 22.7(3) | 0.50(1) | 36(1) | 55122(6) | 0.000 099(4) | 0.08 | 0.001 | 2: |
| 6671698 | 0.471 532(1) | −42(6) | 1261(47) | 129(9) | 0.316(5) | 131(1) | 54743(39) | 0.018(4) | 0.48 | 0.002 | 2: |
| 9091810 | 0.479 721 30(1) | – | 1298(33) | 17.1(3) | 0.25(4) | 257(8) | 54488(37) | 0.000 040(3) | 0.06 | 0.002 | 2: |
| 7877062 | 0.303 651 94(5) | – | 1321(34) | 52(2) | 0.128(9) | 89(9) | 54716(41) | 0.0011(1) | 0.17 | 0.001 | 2: |
| 4244929 | 0.341 4038(1) | – | 1342(23) | 129(4) | 0.28(1) | 235(2) | 55116(13) | 0.016(2) | 0.46 | 0.001 | 2: |
| 4574310 | 1.306 220 13(1) | – | 1347(20) | 14.9(2) | 0.56(2) | 154(1) | 54557(16) | 0.000 025(1) | 0.05 | 0.02 | 2: |
| 8081389 | 1.489 443 01(3) | – | 1383(15) | 13.8(2) | 0.27(1) | 217(2) | 55181(12) | 0.000 018(1) | 0.04 | 0.02 | 2: |
| 7119757 | 0.742 9197(2) | – | 1402(43) | 179(5) | 0.60(1) | 181.8(5) | 54451(32) | 0.039(4) | 0.65 | 0.008 | 2: |
| 4945857 | 0.335 417 78(4) | – | 1423(6) | 346(2) | 0.402(2) | 343.0(2) | 54286(5) | 0.273(4) | 1.49 | 0.001 | 2: |
| 12554536 | 0.684 496 43(1) | – | 1448(7) | 44.8(2) | 0.515(9) | 246.9(6) | 54914(5) | 0.000 574(9) | 0.14 | 0.004 | 2: |
| 9272276 | 0.280 614 16(2) | – | 1458(7) | 235(1) | 0.252(3) | 325.4(9) | 55291(5) | 0.082(1) | 0.88 | 0.001 | 2: |
| 9402652 | 1.073 106 92(2) | – | 1506(2) | 163.9(3) | 0.805(1) | 86.6(2) | 54838(2) | 0.0260(2) | 0.55 | 0.03 | 2: |
| 5513861 | 1.510 209 53(9) | – | 2140(6) | 306(2) | 0.140(6) | 208(4) | 54202(22) | 0.084(1) | 0.89 | 0.007 | 2: |
| 12019674 | 0.354 497 43(3) | – | 2800(13) | 408(2) | 0.216(5) | 145(1) | 52584(14) | 0.116(2) | 1.02 | 0.001 | 2: |
Orbital elements from LTTE solutions which cover more than one but less than two outer periods.
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 8145477 | 0.565 783 95(8) | – | 364(4) | 59.2(8) | 0.41(2) | 190(2) | 54911(4) | 0.021(1) | 0.51 | 0.03 | 2: |
| 3114667: | 0.888 583 02(3) | – | 573(4) | 21(1) | 0.73(4) | 347(2) | 55275(9) | 0.000 38(7) | 0.12 | 0.10 | 2: |
| 9592145: | 0.488 867 28(1) | 0.75(3) | 730(2) | 6.88(6) | 0.28(2) | 260(3) | 55041(7) | 82(2)E−7 | 0.03 | 0.005 | 2: |
| 5478466 | 0.482 500 55(1) | – | 739.2(9) | 91.2(8) | 0.505(9) | 17.6(9) | 54961(2) | 0.0186(5) | 0.49 | 0.007 | 2: |
| 4859432 | 0.385 479 90(1) | – | 747.3(8) | 67.3(3) | 0.565(8) | 270.0(8) | 54634(2) | 0.0073(1) | 0.34 | 0.005 | 2: |
| 4451148 | 0.735 981 74(1) | – | 749.7(6) | 139.6(5) | 0.288(6) | 44(1) | 55002(3) | 0.0649(7) | 0.80 | 0.01 | 2: |
| 3338660: | 1.873 3818(1) | – | 752(18) | 7.7(8) | 0.76(8) | 308(5) | 54821(30) | 0.000 011(3) | 0.04 | 0.26 | 2: |
| 4647652 | 1.064 824 97(1) | – | 754.7(3) | 106.2(2) | 0.291(3) | 30.7(5) | 54760(1) | 0.0282(1) | 0.57 | 0.02 | 2: |
| 4670267 | 2.006 097 28(2) | – | 755(2) | 29.4(4) | 0.56(2) | 63(2) | 55052(5) | 0.000 60(3) | 0.14 | 0.13 | 2: |
| 9912977 | 1.887 873 19(1) | – | 756.2(5) | 47.4(1) | 0.282(5) | 76(1) | 55168(2) | 0.002 50(2) | 0.23 | 0.07 | 2: |
| 8957887 | 0.347 354 18(1) | – | 774.2(4) | 186.1(4) | 0.468(3) | 151.2(4) | 55275(1) | 0.144(1) | 1.12 | 0.003 | 2: |
| 10848807: | 0.346 246 70(1) | – | 785(3) | 11.3(2) | 0.36(3) | 339(1) | 55013(11) | 0.000 031(2) | 0.05 | 0.003 | 2: |
| 1873918 | 0.332 431 83(3) | −3.6(1) | 840.9(9) | 124.4(7) | 0.663(7) | 64.5(7) | 55035(2) | 0.0364(7) | 0.63 | 0.004 | 2: |
| 4138301 | 0.253 379 19(1) | – | 844(1) | 122.8(7) | 0.423(8) | 221(1) | 55049(3) | 0.0348(6) | 0.62 | 0.001 | 2: |
| 2715417 | 0.236 439 93(1) | – | 856(2) | 21.9(2) | 0.22(1) | 124(3) | 54939(8) | 0.000 19(1) | 0.09 | 0.001 | 2: |
| 9665086 | 0.296 536 88(2) | – | 856(2) | 253(3) | 0.51(1) | 66(2) | 54659(4) | 0.297(9) | 1.55 | 0.002 | 2: |
| 4547308 | 0.576 927 98(1) | – | 871(4) | 105(4) | 0.90(2) | 54(2) | 55078(7) | 0.020(2) | 0.50 | 0.06 | 2: |
| 4069063 | 0.504 295 27(3) | – | 876(1) | 233(2) | 0.64(1) | 132(1) | 55013(3) | 0.220(7) | 1.35 | 0.007 | 2: |
| 7339345: | 0.259 661 51(1) | 10.01(2) | 892(2) | 15.3(1) | 0.40(1) | 286(2) | 55120(5) | 0.000 060(1) | 0.06 | 0.001 | 2: |
| 6516874 | 0.916 325 49(7) | – | 905(4) | 102.3(8) | 0.24(1) | 205(2) | 54663(9) | 0.0175(4) | 0.48 | 0.01 | 2: |
| 8739802 | 0.274 512 78(1) | – | 907(5) | 41.1(6) | 0.40(2) | 191(3) | 55357(9) | 0.001 13(5) | 0.17 | 0.001 | 2: |
| 7630658 | 2.151 155 67(2) | – | 921.6(3) | 179.8(5) | 0.673(2) | 326.2(2) | 55353(1) | 0.0917(7) | 0.92 | 0.16 | 2: |
| 12071741 | 0.314 264 38(1) | – | 927(2) | 176(2) | 0.64(1) | 149.5(8) | 54932(2) | 0.085(3) | 0.89 | 0.003 | 2: |
| 2450566 | 1.844 5840(7) | – | 935(11) | 236(19) | 0.72(8) | 142(6) | 55050(19) | 0.20(5) | 1.30 | 0.12 | 2: |
| 7552344 | 2.001 4910(9) | – | 952(14) | 237(9) | 0.26(8) | 261(17) | 55330(47) | 0.20(2) | 1.29 | 0.05 | 2: |
| 10226388 | 0.660 658 35(1) | – | 954.6(8) | 211.3(5) | 0.276(4) | 108(1) | 54716(3) | 0.139(1) | 1.10 | 0.005 | 2: |
| 2302092 | 0.294 672 88(1) | – | 986.1(7) | 175.2(4) | 0.442(4) | 109.9(5) | 55112(2) | 0.0741(5) | 0.84 | 0.001 | 2: |
| 9353234 | 1.486 5278(2) | – | 987(20) | 60(4) | 0.18(11) | 121(39) | 55240(108) | 0.0029(5) | 0.24 | 0.03 | 2: |
| 8242493 | 0.283 285 69(1) | – | 1013(2) | 27.4(1) | 0.182(7) | 1(2) | 55094(7) | 0.000 268(3) | 0.11 | 0.001 | 2: |
| 11042923 | 0.390 162 14(1) | – | 1041.7(8) | 120.6(2) | 0.274(2) | 167.6(5) | 54483(2) | 0.021 65(9) | 0.52 | 0.002 | 2: |
| 7385478: | 1.655 473(1) | – | 1049(9) | 67(1) | 0.47(4) | 119(4) | 55039(14) | 0.0037(2) | 0.27 | 0.04 | 2: |
| 7680593: | 0.276 398 26(5) | −25.7(2) | 1051(5) | 43.6(8) | 0.54(2) | 148(2) | 55315(6) | 0.001 01(6) | 0.17 | 0.001 | 2: |
| 5611561 | 0.258 694 69(1) | – | 1052(2) | 44.5(2) | 0.205(9) | 347(2) | 55362(7) | 0.001 06(2) | 0.17 | 0.001 | 2: |
| 9159301 | 3.044 7717(1) | – | 1072(23) | 12.6(3) | 0.40(4) | 263(7) | 54922(27) | 0.000 023(2) | 0.05 | 0.12 | 2: |
| 3440230 | 2.881 1326(2) | −1277(10) | 1082(8) | 17.6(5) | 0.56(3) | 178(3) | 55203(11) | 0.000 063(5) | 0.06 | 0.17 | 2: |
| 5621294: | 0.938 909 79(5) | −59.2(8) | 1083(15) | 6.8(2) | 0.43(5) | 323(7) | 55143(22) | 36(4)E−7 | 0.02 | 0.01 | 2: |
| 4074708 | 0.302 116 49(1) | – | 1110(3) | 28.1(1) | 0.09(1) | 42(6) | 54843(18) | 0.000 243(4) | 0.10 | 0.001 | 2: |
| 5307780 | 0.308 849 72(3) | 5.7(1) | 1115(2) | 48(2) | 0.86(1) | 15(1) | 55101(5) | 0.0012(1) | 0.18 | 0.01 | 2: |
| 6965293 | 5.077 7443(1) | – | 1119(2) | 197.4(6) | 0.204(7) | 312(2) | 54716(6) | 0.0823(9) | 0.88 | 0.23 | 2: |
| 8192840 | 0.433 549 28(1) | – | 1145(4) | 118.4(7) | 0.655(4) | 3.5(3) | 55486(3) | 0.0170(3) | 0.47 | 0.005 | 2: |
| 9838047 | 0.436 162 06(3) | – | 1154(2) | 221.1(8) | 0.267(6) | 174(1) | 55008(4) | 0.109(1) | 0.99 | 0.002 | 2: |
| 10583181 | 2.696 353 89(2) | – | 1169.2(9) | 154.0(1) | 0.060(2) | 99(2) | 54503(6) | 0.0358(1) | 0.63 | 0.06 | 2: |
| 4681152 | 1.835 9276(2) | – | 1177(21) | 36.3(9) | 0.22(3) | 155(7) | 54998(26) | 0.000 46(4) | 0.13 | 0.03 | 2: |
| 9711751 | 1.711 528 18(1) | – | 1186.1(7) | 218.1(2) | 0.259(1) | 351.0(4) | 55385(1) | 0.0989(3) | 0.95 | 0.02 | 2: |
| 7440742 | 0.283 992 18(1) | – | 1200(4) | 29.9(4) | 0.66(3) | 287(2) | 55048(8) | 0.000 249(9) | 0.10 | 0.002 | 2: |
| 9101279: | 1.811 460 57(5) | – | 1202(8) | 46.8(4) | 0.17(1) | 129(5) | 55342(16) | 0.000 95(3) | 0.16 | 0.03 | 2: |
| 4762887 | 0.736 573 44(4) | – | 1233(37) | 25(1) | 0.25(8) | 5(20) | 55288(72) | 0.000 13(2) | 0.08 | 0.005 | 2: |
| 9574614 | 0.982 095(1) | – | 1234(43) | 266(12) | 0.02(5) | 208(113) | 55093(387) | 0.17(2) | 1.19 | 0.007 | 2: |
| 5903301 | 2.320 3030(4) | – | 1255(32) | 153(3) | 0.43(4) | 22(6) | 54977(31) | 0.031(2) | 0.59 | 0.06 | 2: |
| 6281103 | 0.363 283 30(1) | −9.98(6) | 1254(3) | 76.9(4) | 0.024(9) | 239(23) | 55179(81) | 0.003 88(7) | 0.27 | 0.001 | 2: |
| 11604958 | 0.298 929 82(1) | – | 1256(8) | 22.7(3) | 0.50(1) | 36(1) | 55122(6) | 0.000 099(4) | 0.08 | 0.001 | 2: |
| 6671698 | 0.471 532(1) | −42(6) | 1261(47) | 129(9) | 0.316(5) | 131(1) | 54743(39) | 0.018(4) | 0.48 | 0.002 | 2: |
| 9091810 | 0.479 721 30(1) | – | 1298(33) | 17.1(3) | 0.25(4) | 257(8) | 54488(37) | 0.000 040(3) | 0.06 | 0.002 | 2: |
| 7877062 | 0.303 651 94(5) | – | 1321(34) | 52(2) | 0.128(9) | 89(9) | 54716(41) | 0.0011(1) | 0.17 | 0.001 | 2: |
| 4244929 | 0.341 4038(1) | – | 1342(23) | 129(4) | 0.28(1) | 235(2) | 55116(13) | 0.016(2) | 0.46 | 0.001 | 2: |
| 4574310 | 1.306 220 13(1) | – | 1347(20) | 14.9(2) | 0.56(2) | 154(1) | 54557(16) | 0.000 025(1) | 0.05 | 0.02 | 2: |
| 8081389 | 1.489 443 01(3) | – | 1383(15) | 13.8(2) | 0.27(1) | 217(2) | 55181(12) | 0.000 018(1) | 0.04 | 0.02 | 2: |
| 7119757 | 0.742 9197(2) | – | 1402(43) | 179(5) | 0.60(1) | 181.8(5) | 54451(32) | 0.039(4) | 0.65 | 0.008 | 2: |
| 4945857 | 0.335 417 78(4) | – | 1423(6) | 346(2) | 0.402(2) | 343.0(2) | 54286(5) | 0.273(4) | 1.49 | 0.001 | 2: |
| 12554536 | 0.684 496 43(1) | – | 1448(7) | 44.8(2) | 0.515(9) | 246.9(6) | 54914(5) | 0.000 574(9) | 0.14 | 0.004 | 2: |
| 9272276 | 0.280 614 16(2) | – | 1458(7) | 235(1) | 0.252(3) | 325.4(9) | 55291(5) | 0.082(1) | 0.88 | 0.001 | 2: |
| 9402652 | 1.073 106 92(2) | – | 1506(2) | 163.9(3) | 0.805(1) | 86.6(2) | 54838(2) | 0.0260(2) | 0.55 | 0.03 | 2: |
| 5513861 | 1.510 209 53(9) | – | 2140(6) | 306(2) | 0.140(6) | 208(4) | 54202(22) | 0.084(1) | 0.89 | 0.007 | 2: |
| 12019674 | 0.354 497 43(3) | – | 2800(13) | 408(2) | 0.216(5) | 145(1) | 52584(14) | 0.116(2) | 1.02 | 0.001 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 8145477 | 0.565 783 95(8) | – | 364(4) | 59.2(8) | 0.41(2) | 190(2) | 54911(4) | 0.021(1) | 0.51 | 0.03 | 2: |
| 3114667: | 0.888 583 02(3) | – | 573(4) | 21(1) | 0.73(4) | 347(2) | 55275(9) | 0.000 38(7) | 0.12 | 0.10 | 2: |
| 9592145: | 0.488 867 28(1) | 0.75(3) | 730(2) | 6.88(6) | 0.28(2) | 260(3) | 55041(7) | 82(2)E−7 | 0.03 | 0.005 | 2: |
| 5478466 | 0.482 500 55(1) | – | 739.2(9) | 91.2(8) | 0.505(9) | 17.6(9) | 54961(2) | 0.0186(5) | 0.49 | 0.007 | 2: |
| 4859432 | 0.385 479 90(1) | – | 747.3(8) | 67.3(3) | 0.565(8) | 270.0(8) | 54634(2) | 0.0073(1) | 0.34 | 0.005 | 2: |
| 4451148 | 0.735 981 74(1) | – | 749.7(6) | 139.6(5) | 0.288(6) | 44(1) | 55002(3) | 0.0649(7) | 0.80 | 0.01 | 2: |
| 3338660: | 1.873 3818(1) | – | 752(18) | 7.7(8) | 0.76(8) | 308(5) | 54821(30) | 0.000 011(3) | 0.04 | 0.26 | 2: |
| 4647652 | 1.064 824 97(1) | – | 754.7(3) | 106.2(2) | 0.291(3) | 30.7(5) | 54760(1) | 0.0282(1) | 0.57 | 0.02 | 2: |
| 4670267 | 2.006 097 28(2) | – | 755(2) | 29.4(4) | 0.56(2) | 63(2) | 55052(5) | 0.000 60(3) | 0.14 | 0.13 | 2: |
| 9912977 | 1.887 873 19(1) | – | 756.2(5) | 47.4(1) | 0.282(5) | 76(1) | 55168(2) | 0.002 50(2) | 0.23 | 0.07 | 2: |
| 8957887 | 0.347 354 18(1) | – | 774.2(4) | 186.1(4) | 0.468(3) | 151.2(4) | 55275(1) | 0.144(1) | 1.12 | 0.003 | 2: |
| 10848807: | 0.346 246 70(1) | – | 785(3) | 11.3(2) | 0.36(3) | 339(1) | 55013(11) | 0.000 031(2) | 0.05 | 0.003 | 2: |
| 1873918 | 0.332 431 83(3) | −3.6(1) | 840.9(9) | 124.4(7) | 0.663(7) | 64.5(7) | 55035(2) | 0.0364(7) | 0.63 | 0.004 | 2: |
| 4138301 | 0.253 379 19(1) | – | 844(1) | 122.8(7) | 0.423(8) | 221(1) | 55049(3) | 0.0348(6) | 0.62 | 0.001 | 2: |
| 2715417 | 0.236 439 93(1) | – | 856(2) | 21.9(2) | 0.22(1) | 124(3) | 54939(8) | 0.000 19(1) | 0.09 | 0.001 | 2: |
| 9665086 | 0.296 536 88(2) | – | 856(2) | 253(3) | 0.51(1) | 66(2) | 54659(4) | 0.297(9) | 1.55 | 0.002 | 2: |
| 4547308 | 0.576 927 98(1) | – | 871(4) | 105(4) | 0.90(2) | 54(2) | 55078(7) | 0.020(2) | 0.50 | 0.06 | 2: |
| 4069063 | 0.504 295 27(3) | – | 876(1) | 233(2) | 0.64(1) | 132(1) | 55013(3) | 0.220(7) | 1.35 | 0.007 | 2: |
| 7339345: | 0.259 661 51(1) | 10.01(2) | 892(2) | 15.3(1) | 0.40(1) | 286(2) | 55120(5) | 0.000 060(1) | 0.06 | 0.001 | 2: |
| 6516874 | 0.916 325 49(7) | – | 905(4) | 102.3(8) | 0.24(1) | 205(2) | 54663(9) | 0.0175(4) | 0.48 | 0.01 | 2: |
| 8739802 | 0.274 512 78(1) | – | 907(5) | 41.1(6) | 0.40(2) | 191(3) | 55357(9) | 0.001 13(5) | 0.17 | 0.001 | 2: |
| 7630658 | 2.151 155 67(2) | – | 921.6(3) | 179.8(5) | 0.673(2) | 326.2(2) | 55353(1) | 0.0917(7) | 0.92 | 0.16 | 2: |
| 12071741 | 0.314 264 38(1) | – | 927(2) | 176(2) | 0.64(1) | 149.5(8) | 54932(2) | 0.085(3) | 0.89 | 0.003 | 2: |
| 2450566 | 1.844 5840(7) | – | 935(11) | 236(19) | 0.72(8) | 142(6) | 55050(19) | 0.20(5) | 1.30 | 0.12 | 2: |
| 7552344 | 2.001 4910(9) | – | 952(14) | 237(9) | 0.26(8) | 261(17) | 55330(47) | 0.20(2) | 1.29 | 0.05 | 2: |
| 10226388 | 0.660 658 35(1) | – | 954.6(8) | 211.3(5) | 0.276(4) | 108(1) | 54716(3) | 0.139(1) | 1.10 | 0.005 | 2: |
| 2302092 | 0.294 672 88(1) | – | 986.1(7) | 175.2(4) | 0.442(4) | 109.9(5) | 55112(2) | 0.0741(5) | 0.84 | 0.001 | 2: |
| 9353234 | 1.486 5278(2) | – | 987(20) | 60(4) | 0.18(11) | 121(39) | 55240(108) | 0.0029(5) | 0.24 | 0.03 | 2: |
| 8242493 | 0.283 285 69(1) | – | 1013(2) | 27.4(1) | 0.182(7) | 1(2) | 55094(7) | 0.000 268(3) | 0.11 | 0.001 | 2: |
| 11042923 | 0.390 162 14(1) | – | 1041.7(8) | 120.6(2) | 0.274(2) | 167.6(5) | 54483(2) | 0.021 65(9) | 0.52 | 0.002 | 2: |
| 7385478: | 1.655 473(1) | – | 1049(9) | 67(1) | 0.47(4) | 119(4) | 55039(14) | 0.0037(2) | 0.27 | 0.04 | 2: |
| 7680593: | 0.276 398 26(5) | −25.7(2) | 1051(5) | 43.6(8) | 0.54(2) | 148(2) | 55315(6) | 0.001 01(6) | 0.17 | 0.001 | 2: |
| 5611561 | 0.258 694 69(1) | – | 1052(2) | 44.5(2) | 0.205(9) | 347(2) | 55362(7) | 0.001 06(2) | 0.17 | 0.001 | 2: |
| 9159301 | 3.044 7717(1) | – | 1072(23) | 12.6(3) | 0.40(4) | 263(7) | 54922(27) | 0.000 023(2) | 0.05 | 0.12 | 2: |
| 3440230 | 2.881 1326(2) | −1277(10) | 1082(8) | 17.6(5) | 0.56(3) | 178(3) | 55203(11) | 0.000 063(5) | 0.06 | 0.17 | 2: |
| 5621294: | 0.938 909 79(5) | −59.2(8) | 1083(15) | 6.8(2) | 0.43(5) | 323(7) | 55143(22) | 36(4)E−7 | 0.02 | 0.01 | 2: |
| 4074708 | 0.302 116 49(1) | – | 1110(3) | 28.1(1) | 0.09(1) | 42(6) | 54843(18) | 0.000 243(4) | 0.10 | 0.001 | 2: |
| 5307780 | 0.308 849 72(3) | 5.7(1) | 1115(2) | 48(2) | 0.86(1) | 15(1) | 55101(5) | 0.0012(1) | 0.18 | 0.01 | 2: |
| 6965293 | 5.077 7443(1) | – | 1119(2) | 197.4(6) | 0.204(7) | 312(2) | 54716(6) | 0.0823(9) | 0.88 | 0.23 | 2: |
| 8192840 | 0.433 549 28(1) | – | 1145(4) | 118.4(7) | 0.655(4) | 3.5(3) | 55486(3) | 0.0170(3) | 0.47 | 0.005 | 2: |
| 9838047 | 0.436 162 06(3) | – | 1154(2) | 221.1(8) | 0.267(6) | 174(1) | 55008(4) | 0.109(1) | 0.99 | 0.002 | 2: |
| 10583181 | 2.696 353 89(2) | – | 1169.2(9) | 154.0(1) | 0.060(2) | 99(2) | 54503(6) | 0.0358(1) | 0.63 | 0.06 | 2: |
| 4681152 | 1.835 9276(2) | – | 1177(21) | 36.3(9) | 0.22(3) | 155(7) | 54998(26) | 0.000 46(4) | 0.13 | 0.03 | 2: |
| 9711751 | 1.711 528 18(1) | – | 1186.1(7) | 218.1(2) | 0.259(1) | 351.0(4) | 55385(1) | 0.0989(3) | 0.95 | 0.02 | 2: |
| 7440742 | 0.283 992 18(1) | – | 1200(4) | 29.9(4) | 0.66(3) | 287(2) | 55048(8) | 0.000 249(9) | 0.10 | 0.002 | 2: |
| 9101279: | 1.811 460 57(5) | – | 1202(8) | 46.8(4) | 0.17(1) | 129(5) | 55342(16) | 0.000 95(3) | 0.16 | 0.03 | 2: |
| 4762887 | 0.736 573 44(4) | – | 1233(37) | 25(1) | 0.25(8) | 5(20) | 55288(72) | 0.000 13(2) | 0.08 | 0.005 | 2: |
| 9574614 | 0.982 095(1) | – | 1234(43) | 266(12) | 0.02(5) | 208(113) | 55093(387) | 0.17(2) | 1.19 | 0.007 | 2: |
| 5903301 | 2.320 3030(4) | – | 1255(32) | 153(3) | 0.43(4) | 22(6) | 54977(31) | 0.031(2) | 0.59 | 0.06 | 2: |
| 6281103 | 0.363 283 30(1) | −9.98(6) | 1254(3) | 76.9(4) | 0.024(9) | 239(23) | 55179(81) | 0.003 88(7) | 0.27 | 0.001 | 2: |
| 11604958 | 0.298 929 82(1) | – | 1256(8) | 22.7(3) | 0.50(1) | 36(1) | 55122(6) | 0.000 099(4) | 0.08 | 0.001 | 2: |
| 6671698 | 0.471 532(1) | −42(6) | 1261(47) | 129(9) | 0.316(5) | 131(1) | 54743(39) | 0.018(4) | 0.48 | 0.002 | 2: |
| 9091810 | 0.479 721 30(1) | – | 1298(33) | 17.1(3) | 0.25(4) | 257(8) | 54488(37) | 0.000 040(3) | 0.06 | 0.002 | 2: |
| 7877062 | 0.303 651 94(5) | – | 1321(34) | 52(2) | 0.128(9) | 89(9) | 54716(41) | 0.0011(1) | 0.17 | 0.001 | 2: |
| 4244929 | 0.341 4038(1) | – | 1342(23) | 129(4) | 0.28(1) | 235(2) | 55116(13) | 0.016(2) | 0.46 | 0.001 | 2: |
| 4574310 | 1.306 220 13(1) | – | 1347(20) | 14.9(2) | 0.56(2) | 154(1) | 54557(16) | 0.000 025(1) | 0.05 | 0.02 | 2: |
| 8081389 | 1.489 443 01(3) | – | 1383(15) | 13.8(2) | 0.27(1) | 217(2) | 55181(12) | 0.000 018(1) | 0.04 | 0.02 | 2: |
| 7119757 | 0.742 9197(2) | – | 1402(43) | 179(5) | 0.60(1) | 181.8(5) | 54451(32) | 0.039(4) | 0.65 | 0.008 | 2: |
| 4945857 | 0.335 417 78(4) | – | 1423(6) | 346(2) | 0.402(2) | 343.0(2) | 54286(5) | 0.273(4) | 1.49 | 0.001 | 2: |
| 12554536 | 0.684 496 43(1) | – | 1448(7) | 44.8(2) | 0.515(9) | 246.9(6) | 54914(5) | 0.000 574(9) | 0.14 | 0.004 | 2: |
| 9272276 | 0.280 614 16(2) | – | 1458(7) | 235(1) | 0.252(3) | 325.4(9) | 55291(5) | 0.082(1) | 0.88 | 0.001 | 2: |
| 9402652 | 1.073 106 92(2) | – | 1506(2) | 163.9(3) | 0.805(1) | 86.6(2) | 54838(2) | 0.0260(2) | 0.55 | 0.03 | 2: |
| 5513861 | 1.510 209 53(9) | – | 2140(6) | 306(2) | 0.140(6) | 208(4) | 54202(22) | 0.084(1) | 0.89 | 0.007 | 2: |
| 12019674 | 0.354 497 43(3) | – | 2800(13) | 408(2) | 0.216(5) | 145(1) | 52584(14) | 0.116(2) | 1.02 | 0.001 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10095469 | 0.677 762 45(2) | – | 932(15) | 40.9(4) | 0.19(2) | 67(4) | 54958(19) | 0.001 06(5) | 0.17 | 0.006 | 2: |
| 9392702 | 3.909 33(1) | – | 976(170) | 103(29) | 0.29(3) | 281(14) | 55044(56) | 0.02(1) | 0.45 | 0.19 | 2: |
| 4848423 | 3.003 612(6) | – | 1190(68) | 227(22) | 0.14(3) | 358(7) | 55450(68) | 0.11(4) | 1.00 | 0.07 | 2: |
| 2983113 | 0.395 159 98(2) | – | 1249(36) | 36.9(9) | 0.49(4) | 303(3) | 55246(22) | 0.000 43(4) | 0.12 | 0.002 | 2: |
| 10268903 | 1.103 978(1) | – | 1286(318) | 211(33) | 0.66(8) | 130(4) | 54904(293) | 0.08(5) | 0.85 | 0.02 | 2: |
| 6265720 | 0.312 427 62(2) | – | 1447(15) | 220(2) | 0.652(7) | 192.4(6) | 55345(6) | 0.068(2) | 0.82 | 0.002 | 2: |
| 10934755 | 0.786 485 49(8) | – | 1466(32) | 51(1) | 0.26(1) | 47(3) | 54354(24) | 0.000 83(7) | 0.16 | 0.004 | 2: |
| 9283826 | 0.356 523 21(5) | – | 1475(27) | 98(2) | 0.31(3) | 30(3) | 54850(19) | 0.0057(4) | 0.31 | 0.001 | 2: |
| 6103049 | 0.643 1713(2) | – | 1482(62) | 59(5) | 0.49(4) | 243(2) | 54945(20) | 0.0013(3) | 0.18 | 0.004 | 2: |
| 9821923 | 0.349 5323(2) | – | 1493(63) | 110(7) | 0.48(2) | 293(12) | 54786(52) | 0.008(2) | 0.35 | 0.001 | 2: |
| 5353374 | 0.393 320 61(1) | – | 1494(33) | 29.1(5) | 0.13(3) | 268(8) | 55009(35) | 0.000 15(1) | 0.09 | 0.001 | 2: |
| 3766353 | 2.666 9672(8) | – | 1522(84) | 152(5) | 0.24(4) | 196(17) | 55267(84) | 0.020(3) | 0.50 | 0.04 | 2: |
| 7518816 | 0.466 580 65(6) | – | 1523(35) | 49(2) | 0.27(2) | 171(3) | 55022(22) | 0.000 67(8) | 0.15 | 0.001 | 2: |
| 10383620 | 0.734 5688(1) | – | 1541(12) | 277(3) | 0.219(4) | 0.9(3) | 54250(9) | 0.120(4) | 1.03 | 0.003 | 2: |
| 10557008 | 0.265 418 72(1) | – | 1545(15) | 79.2(5) | 0.343(5) | 188(2) | 55243(11) | 0.002 79(7) | 0.24 | 0.001 | 2: |
| 9083523 | 0.918 4227(3) | – | 1573(77) | 59(5) | 0.39(1) | 97(2) | 54664(53) | 0.0011(3) | 0.17 | 0.006 | 2: |
| 2715007 | 0.297 111 40(4) | – | 1598(21) | 256(3) | 0.623(6) | 213.3(7) | 54766(16) | 0.088(4) | 0.90 | 0.001 | 2: |
| 9596187 | 0.953 283(3) | – | 1599(97) | 508(52) | 0.18(4) | 41(7) | 54892(46) | 0.69(22) | 2.35 | 0.004 | 2: |
| 10916675 | 0.418 867 53(4) | – | 1626(77) | 20(1) | 0.31(3) | 36(7) | 55133(47) | 0.000 04(1) | 0.06 | 0.001 | 2: |
| 9706078: | 0.613 561(2) | – | 1632(287) | 109(54) | 0.49(11) | 73(10) | 54973(60) | 0.007(10) | 0.33 | 0.003 | 2: |
| 5956776 | 0.569 1161(6) | – | 1655(1122) | 33(19) | 0.57(20) | 16(5) | 54222(788) | 0.0002(4) | 0.09 | 0.003 | 2: |
| 6606282 | 2.107 135(1) | – | 1681(61) | 317(9) | 0.32(3) | 134(3) | 55781(45) | 0.15(2) | 1.14 | 0.02 | 2: |
| 11234677 | 1.587 418(2) | – | 1738(171) | 135(18) | 0.20(4) | 156(6) | 55586(99) | 0.011(5) | 0.40 | 0.01 | 2: |
| 3248019 | 2.668 200(5) | – | 1749(331) | 130(48) | 0.44(7) | 19(12) | 54706(162) | 0.010(11) | 0.38 | 0.04 | 2: |
| 2305372 | 1.404 691 57(8) | – | 1772(25) | 140(2) | 0.206(9) | 305(2) | 54966(14) | 0.0117(6) | 0.41 | 0.009 | 2: |
| 6766325: | 0.439 9650(4) | – | 1801(202) | 78(17) | 0.41(3) | 231(4) | 54460(149) | 0.002(1) | 0.21 | 0.001 | 2: |
| 8690104: | 0.408 7740(2) | – | 1835(222) | 46(9) | 0.24(6) | 287(7) | 54704(133) | 0.0004(2) | 0.12 | 0.001 | 2: |
| 8982514: | 0.414 490 27(4) | – | 1901(150) | 63(2) | 0.12(1) | 299(9) | 54288(70) | 0.0009(1) | 0.16 | 0.001 | 2: |
| 11246163 | 0.279 226 79(9) | – | 1902(149) | 56(5) | 0.36(3) | 210(3) | 55840(94) | 0.0006(2) | 0.14 | 0.001 | 2: |
| 5269407 | 0.958 860(2) | – | 1905(172) | 268(31) | 0.53(2) | 82(6) | 55206(61) | 0.07(3) | 0.83 | 0.005 | 2: |
| 4174507 | 3.891 79(1) | – | 1922(333) | 647(87) | 0.82(3) | 202(3) | 55730(181) | 0.98(52) | 2.85 | 0.34 | 2: |
| 5962716 | 1.804 5827(2) | – | 1935(29) | 208(2) | 0.507(8) | 253.4(9) | 55804(17) | 0.032(1) | 0.60 | 0.02 | 2: |
| 9788457: | 0.963 338 79(1) | – | 1960(425) | 27.9(2) | 0.46(1) | 17(1) | 55737(167) | 0.000 07(3) | 0.07 | 0.005 | 2: |
| 12055014 | 0.499 9043(1) | – | 1961(175) | 31(5) | 0.32(4) | 29(5) | 54568(72) | 0.000 10(6) | 0.08 | 0.001 | 2: |
| 10724533 | 0.745 0940(4) | – | 2028(198) | 70(10) | 0.499(9) | 77(3) | 54178(131) | 0.0011(5) | 0.17 | 0.003 | 2: |
| 8868650 | 4.447 4056(9) | – | 2040(88) | 367(9) | 0.62(2) | 234(2) | 55374(32) | 0.16(2) | 1.17 | 0.13 | 2: |
| 10275197 | 0.390 846(1) | – | 2127(82) | 612(72) | 0.268(4) | 210.7(9) | 54851(25) | 0.68(24) | 2.34 | 0.001 | 2: |
| 3335816 | 7.422 028(5) | – | 2250(1234) | 66(42) | 0.16(24) | 233(69) | 54351(703) | 0.001(2) | 0.15 | 0.16 | 2: |
| 5975712 | 1.136 080(1) | – | 2308(118) | 347(21) | 0.43(1) | 115(4) | 55530(59) | 0.11(2) | 0.98 | 0.004 | 2: |
| 3839964 | 0.256 1427(4) | 29(1) | 2404(371) | 311(22) | 0.17(1) | 4(5) | 53795(184) | 0.07(3) | 0.82 | 0.002 | 2: |
| 8444552 | 1.178 0785(7) | – | 2441(73) | 376(13) | 0.492(6) | 104(1) | 55301(22) | 0.12(1) | 1.03 | 0.005 | 2: |
| 4937217 | 0.429 3407(2) | 3.8(6) | 2468(1187) | 24(12) | 0.49(14) | 176(8) | 55622(453) | 0.000 03(5) | 0.05 | 0.001 | 2: |
| 8758161 | 1.996 4243(2) | – | 2501(276) | 133(2) | 0.196(7) | 103(1) | 55375(47) | 0.005(1) | 0.30 | 0.01 | 2: |
| 12055255 | 0.220 9449(6) | – | 2530(166) | 544(57) | 0.416(8) | 280(2) | 55142(33) | 0.34(12) | 1.65 | 0.001 | 2: |
| 4758368 | 3.749 98(1) | – | 2876(1289) | 357(127) | 0.7(1) | 313(10) | 55556(429) | 0.07(10) | 0.84 | 0.08 | 2: |
| 8429450 | 2.705 145(7) | – | 3088(1698) | 128(75) | 0.38(17) | 185(11) | 56136(894) | 0.003(6) | 0.24 | 0.02 | 2: |
| 9110346 | 1.790 580(3) | – | 3645(695) | 350(59) | 0.74(2) | 307(3) | 55406(129) | 0.04(3) | 0.68 | 0.01 | 2: |
| 8265951 | 0.779 9554(2) | – | 3721(247) | 423(19) | 0.76(1) | 215.9(5) | 55390(41) | 0.07(1) | 0.84 | 0.003 | 2: |
| 6615041 | 0.340 086 60(2) | – | 3951(1200) | 105(1) | 0.616(7) | 30.3(8) | 55747(238) | 0.0010(6) | 0.17 | 0.001 | 2: |
| 9532219 | 0.198 153 67(5) | – | 4401(900) | 217(7) | 0.38(1) | 205(2) | 55770(159) | 0.007(3) | 0.34 | 0.001 | 2: |
| 8553788 | 1.606 184(2) | – | 4579(552) | 473(66) | 0.75(1) | 56.2(7) | 56474(249) | 0.07(3) | 0.81 | 0.008 | 2: |
| 6794131 | 1.613 324(2) | – | 4743(2105) | 446(141) | 0.87(5) | 150(2) | 55889(604) | 0.05(7) | 0.73 | 0.03 | 2: |
| 10686876 | 2.618 397(8) | – | 5280(1590) | 400(147) | 0.33(10) | 174(3) | 54912(51) | 0.03(4) | 0.59 | 0.006 | 2: |
| 6233903 | 5.990 90(3) | – | 5359(2135) | 642(223) | 0.69(8) | 2(2) | 56036(582) | 0.12(16) | 1.05 | 0.08 | 2: |
| 9181877 | 0.321 019(5) | – | 5497(2957) | 963(711) | 0.35(15) | 332(12) | 55078(263) | 0.40(97) | 1.78 | 0.001 | 2: |
| 9412114 | 0.250 2592(2) | – | 5596(353) | 922(48) | 0.70(1) | 1(1) | 55540(53) | 0.34(7) | 1.65 | 0.001 | 2: |
| 8016214 | 3.174 930(5) | – | 7350(2008) | 484(113) | 0.71(5) | 173(3) | 55328(162) | 0.03(2) | 0.57 | 0.02 | 2: |
| 7272739 | 0.281 163 04(6) | – | 9256(910) | 218(17) | 0.75(2) | 184(1) | 55988(144) | 0.0016(5) | 0.20 | 0.001 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10095469 | 0.677 762 45(2) | – | 932(15) | 40.9(4) | 0.19(2) | 67(4) | 54958(19) | 0.001 06(5) | 0.17 | 0.006 | 2: |
| 9392702 | 3.909 33(1) | – | 976(170) | 103(29) | 0.29(3) | 281(14) | 55044(56) | 0.02(1) | 0.45 | 0.19 | 2: |
| 4848423 | 3.003 612(6) | – | 1190(68) | 227(22) | 0.14(3) | 358(7) | 55450(68) | 0.11(4) | 1.00 | 0.07 | 2: |
| 2983113 | 0.395 159 98(2) | – | 1249(36) | 36.9(9) | 0.49(4) | 303(3) | 55246(22) | 0.000 43(4) | 0.12 | 0.002 | 2: |
| 10268903 | 1.103 978(1) | – | 1286(318) | 211(33) | 0.66(8) | 130(4) | 54904(293) | 0.08(5) | 0.85 | 0.02 | 2: |
| 6265720 | 0.312 427 62(2) | – | 1447(15) | 220(2) | 0.652(7) | 192.4(6) | 55345(6) | 0.068(2) | 0.82 | 0.002 | 2: |
| 10934755 | 0.786 485 49(8) | – | 1466(32) | 51(1) | 0.26(1) | 47(3) | 54354(24) | 0.000 83(7) | 0.16 | 0.004 | 2: |
| 9283826 | 0.356 523 21(5) | – | 1475(27) | 98(2) | 0.31(3) | 30(3) | 54850(19) | 0.0057(4) | 0.31 | 0.001 | 2: |
| 6103049 | 0.643 1713(2) | – | 1482(62) | 59(5) | 0.49(4) | 243(2) | 54945(20) | 0.0013(3) | 0.18 | 0.004 | 2: |
| 9821923 | 0.349 5323(2) | – | 1493(63) | 110(7) | 0.48(2) | 293(12) | 54786(52) | 0.008(2) | 0.35 | 0.001 | 2: |
| 5353374 | 0.393 320 61(1) | – | 1494(33) | 29.1(5) | 0.13(3) | 268(8) | 55009(35) | 0.000 15(1) | 0.09 | 0.001 | 2: |
| 3766353 | 2.666 9672(8) | – | 1522(84) | 152(5) | 0.24(4) | 196(17) | 55267(84) | 0.020(3) | 0.50 | 0.04 | 2: |
| 7518816 | 0.466 580 65(6) | – | 1523(35) | 49(2) | 0.27(2) | 171(3) | 55022(22) | 0.000 67(8) | 0.15 | 0.001 | 2: |
| 10383620 | 0.734 5688(1) | – | 1541(12) | 277(3) | 0.219(4) | 0.9(3) | 54250(9) | 0.120(4) | 1.03 | 0.003 | 2: |
| 10557008 | 0.265 418 72(1) | – | 1545(15) | 79.2(5) | 0.343(5) | 188(2) | 55243(11) | 0.002 79(7) | 0.24 | 0.001 | 2: |
| 9083523 | 0.918 4227(3) | – | 1573(77) | 59(5) | 0.39(1) | 97(2) | 54664(53) | 0.0011(3) | 0.17 | 0.006 | 2: |
| 2715007 | 0.297 111 40(4) | – | 1598(21) | 256(3) | 0.623(6) | 213.3(7) | 54766(16) | 0.088(4) | 0.90 | 0.001 | 2: |
| 9596187 | 0.953 283(3) | – | 1599(97) | 508(52) | 0.18(4) | 41(7) | 54892(46) | 0.69(22) | 2.35 | 0.004 | 2: |
| 10916675 | 0.418 867 53(4) | – | 1626(77) | 20(1) | 0.31(3) | 36(7) | 55133(47) | 0.000 04(1) | 0.06 | 0.001 | 2: |
| 9706078: | 0.613 561(2) | – | 1632(287) | 109(54) | 0.49(11) | 73(10) | 54973(60) | 0.007(10) | 0.33 | 0.003 | 2: |
| 5956776 | 0.569 1161(6) | – | 1655(1122) | 33(19) | 0.57(20) | 16(5) | 54222(788) | 0.0002(4) | 0.09 | 0.003 | 2: |
| 6606282 | 2.107 135(1) | – | 1681(61) | 317(9) | 0.32(3) | 134(3) | 55781(45) | 0.15(2) | 1.14 | 0.02 | 2: |
| 11234677 | 1.587 418(2) | – | 1738(171) | 135(18) | 0.20(4) | 156(6) | 55586(99) | 0.011(5) | 0.40 | 0.01 | 2: |
| 3248019 | 2.668 200(5) | – | 1749(331) | 130(48) | 0.44(7) | 19(12) | 54706(162) | 0.010(11) | 0.38 | 0.04 | 2: |
| 2305372 | 1.404 691 57(8) | – | 1772(25) | 140(2) | 0.206(9) | 305(2) | 54966(14) | 0.0117(6) | 0.41 | 0.009 | 2: |
| 6766325: | 0.439 9650(4) | – | 1801(202) | 78(17) | 0.41(3) | 231(4) | 54460(149) | 0.002(1) | 0.21 | 0.001 | 2: |
| 8690104: | 0.408 7740(2) | – | 1835(222) | 46(9) | 0.24(6) | 287(7) | 54704(133) | 0.0004(2) | 0.12 | 0.001 | 2: |
| 8982514: | 0.414 490 27(4) | – | 1901(150) | 63(2) | 0.12(1) | 299(9) | 54288(70) | 0.0009(1) | 0.16 | 0.001 | 2: |
| 11246163 | 0.279 226 79(9) | – | 1902(149) | 56(5) | 0.36(3) | 210(3) | 55840(94) | 0.0006(2) | 0.14 | 0.001 | 2: |
| 5269407 | 0.958 860(2) | – | 1905(172) | 268(31) | 0.53(2) | 82(6) | 55206(61) | 0.07(3) | 0.83 | 0.005 | 2: |
| 4174507 | 3.891 79(1) | – | 1922(333) | 647(87) | 0.82(3) | 202(3) | 55730(181) | 0.98(52) | 2.85 | 0.34 | 2: |
| 5962716 | 1.804 5827(2) | – | 1935(29) | 208(2) | 0.507(8) | 253.4(9) | 55804(17) | 0.032(1) | 0.60 | 0.02 | 2: |
| 9788457: | 0.963 338 79(1) | – | 1960(425) | 27.9(2) | 0.46(1) | 17(1) | 55737(167) | 0.000 07(3) | 0.07 | 0.005 | 2: |
| 12055014 | 0.499 9043(1) | – | 1961(175) | 31(5) | 0.32(4) | 29(5) | 54568(72) | 0.000 10(6) | 0.08 | 0.001 | 2: |
| 10724533 | 0.745 0940(4) | – | 2028(198) | 70(10) | 0.499(9) | 77(3) | 54178(131) | 0.0011(5) | 0.17 | 0.003 | 2: |
| 8868650 | 4.447 4056(9) | – | 2040(88) | 367(9) | 0.62(2) | 234(2) | 55374(32) | 0.16(2) | 1.17 | 0.13 | 2: |
| 10275197 | 0.390 846(1) | – | 2127(82) | 612(72) | 0.268(4) | 210.7(9) | 54851(25) | 0.68(24) | 2.34 | 0.001 | 2: |
| 3335816 | 7.422 028(5) | – | 2250(1234) | 66(42) | 0.16(24) | 233(69) | 54351(703) | 0.001(2) | 0.15 | 0.16 | 2: |
| 5975712 | 1.136 080(1) | – | 2308(118) | 347(21) | 0.43(1) | 115(4) | 55530(59) | 0.11(2) | 0.98 | 0.004 | 2: |
| 3839964 | 0.256 1427(4) | 29(1) | 2404(371) | 311(22) | 0.17(1) | 4(5) | 53795(184) | 0.07(3) | 0.82 | 0.002 | 2: |
| 8444552 | 1.178 0785(7) | – | 2441(73) | 376(13) | 0.492(6) | 104(1) | 55301(22) | 0.12(1) | 1.03 | 0.005 | 2: |
| 4937217 | 0.429 3407(2) | 3.8(6) | 2468(1187) | 24(12) | 0.49(14) | 176(8) | 55622(453) | 0.000 03(5) | 0.05 | 0.001 | 2: |
| 8758161 | 1.996 4243(2) | – | 2501(276) | 133(2) | 0.196(7) | 103(1) | 55375(47) | 0.005(1) | 0.30 | 0.01 | 2: |
| 12055255 | 0.220 9449(6) | – | 2530(166) | 544(57) | 0.416(8) | 280(2) | 55142(33) | 0.34(12) | 1.65 | 0.001 | 2: |
| 4758368 | 3.749 98(1) | – | 2876(1289) | 357(127) | 0.7(1) | 313(10) | 55556(429) | 0.07(10) | 0.84 | 0.08 | 2: |
| 8429450 | 2.705 145(7) | – | 3088(1698) | 128(75) | 0.38(17) | 185(11) | 56136(894) | 0.003(6) | 0.24 | 0.02 | 2: |
| 9110346 | 1.790 580(3) | – | 3645(695) | 350(59) | 0.74(2) | 307(3) | 55406(129) | 0.04(3) | 0.68 | 0.01 | 2: |
| 8265951 | 0.779 9554(2) | – | 3721(247) | 423(19) | 0.76(1) | 215.9(5) | 55390(41) | 0.07(1) | 0.84 | 0.003 | 2: |
| 6615041 | 0.340 086 60(2) | – | 3951(1200) | 105(1) | 0.616(7) | 30.3(8) | 55747(238) | 0.0010(6) | 0.17 | 0.001 | 2: |
| 9532219 | 0.198 153 67(5) | – | 4401(900) | 217(7) | 0.38(1) | 205(2) | 55770(159) | 0.007(3) | 0.34 | 0.001 | 2: |
| 8553788 | 1.606 184(2) | – | 4579(552) | 473(66) | 0.75(1) | 56.2(7) | 56474(249) | 0.07(3) | 0.81 | 0.008 | 2: |
| 6794131 | 1.613 324(2) | – | 4743(2105) | 446(141) | 0.87(5) | 150(2) | 55889(604) | 0.05(7) | 0.73 | 0.03 | 2: |
| 10686876 | 2.618 397(8) | – | 5280(1590) | 400(147) | 0.33(10) | 174(3) | 54912(51) | 0.03(4) | 0.59 | 0.006 | 2: |
| 6233903 | 5.990 90(3) | – | 5359(2135) | 642(223) | 0.69(8) | 2(2) | 56036(582) | 0.12(16) | 1.05 | 0.08 | 2: |
| 9181877 | 0.321 019(5) | – | 5497(2957) | 963(711) | 0.35(15) | 332(12) | 55078(263) | 0.40(97) | 1.78 | 0.001 | 2: |
| 9412114 | 0.250 2592(2) | – | 5596(353) | 922(48) | 0.70(1) | 1(1) | 55540(53) | 0.34(7) | 1.65 | 0.001 | 2: |
| 8016214 | 3.174 930(5) | – | 7350(2008) | 484(113) | 0.71(5) | 173(3) | 55328(162) | 0.03(2) | 0.57 | 0.02 | 2: |
| 7272739 | 0.281 163 04(6) | – | 9256(910) | 218(17) | 0.75(2) | 184(1) | 55988(144) | 0.0016(5) | 0.20 | 0.001 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10095469 | 0.677 762 45(2) | – | 932(15) | 40.9(4) | 0.19(2) | 67(4) | 54958(19) | 0.001 06(5) | 0.17 | 0.006 | 2: |
| 9392702 | 3.909 33(1) | – | 976(170) | 103(29) | 0.29(3) | 281(14) | 55044(56) | 0.02(1) | 0.45 | 0.19 | 2: |
| 4848423 | 3.003 612(6) | – | 1190(68) | 227(22) | 0.14(3) | 358(7) | 55450(68) | 0.11(4) | 1.00 | 0.07 | 2: |
| 2983113 | 0.395 159 98(2) | – | 1249(36) | 36.9(9) | 0.49(4) | 303(3) | 55246(22) | 0.000 43(4) | 0.12 | 0.002 | 2: |
| 10268903 | 1.103 978(1) | – | 1286(318) | 211(33) | 0.66(8) | 130(4) | 54904(293) | 0.08(5) | 0.85 | 0.02 | 2: |
| 6265720 | 0.312 427 62(2) | – | 1447(15) | 220(2) | 0.652(7) | 192.4(6) | 55345(6) | 0.068(2) | 0.82 | 0.002 | 2: |
| 10934755 | 0.786 485 49(8) | – | 1466(32) | 51(1) | 0.26(1) | 47(3) | 54354(24) | 0.000 83(7) | 0.16 | 0.004 | 2: |
| 9283826 | 0.356 523 21(5) | – | 1475(27) | 98(2) | 0.31(3) | 30(3) | 54850(19) | 0.0057(4) | 0.31 | 0.001 | 2: |
| 6103049 | 0.643 1713(2) | – | 1482(62) | 59(5) | 0.49(4) | 243(2) | 54945(20) | 0.0013(3) | 0.18 | 0.004 | 2: |
| 9821923 | 0.349 5323(2) | – | 1493(63) | 110(7) | 0.48(2) | 293(12) | 54786(52) | 0.008(2) | 0.35 | 0.001 | 2: |
| 5353374 | 0.393 320 61(1) | – | 1494(33) | 29.1(5) | 0.13(3) | 268(8) | 55009(35) | 0.000 15(1) | 0.09 | 0.001 | 2: |
| 3766353 | 2.666 9672(8) | – | 1522(84) | 152(5) | 0.24(4) | 196(17) | 55267(84) | 0.020(3) | 0.50 | 0.04 | 2: |
| 7518816 | 0.466 580 65(6) | – | 1523(35) | 49(2) | 0.27(2) | 171(3) | 55022(22) | 0.000 67(8) | 0.15 | 0.001 | 2: |
| 10383620 | 0.734 5688(1) | – | 1541(12) | 277(3) | 0.219(4) | 0.9(3) | 54250(9) | 0.120(4) | 1.03 | 0.003 | 2: |
| 10557008 | 0.265 418 72(1) | – | 1545(15) | 79.2(5) | 0.343(5) | 188(2) | 55243(11) | 0.002 79(7) | 0.24 | 0.001 | 2: |
| 9083523 | 0.918 4227(3) | – | 1573(77) | 59(5) | 0.39(1) | 97(2) | 54664(53) | 0.0011(3) | 0.17 | 0.006 | 2: |
| 2715007 | 0.297 111 40(4) | – | 1598(21) | 256(3) | 0.623(6) | 213.3(7) | 54766(16) | 0.088(4) | 0.90 | 0.001 | 2: |
| 9596187 | 0.953 283(3) | – | 1599(97) | 508(52) | 0.18(4) | 41(7) | 54892(46) | 0.69(22) | 2.35 | 0.004 | 2: |
| 10916675 | 0.418 867 53(4) | – | 1626(77) | 20(1) | 0.31(3) | 36(7) | 55133(47) | 0.000 04(1) | 0.06 | 0.001 | 2: |
| 9706078: | 0.613 561(2) | – | 1632(287) | 109(54) | 0.49(11) | 73(10) | 54973(60) | 0.007(10) | 0.33 | 0.003 | 2: |
| 5956776 | 0.569 1161(6) | – | 1655(1122) | 33(19) | 0.57(20) | 16(5) | 54222(788) | 0.0002(4) | 0.09 | 0.003 | 2: |
| 6606282 | 2.107 135(1) | – | 1681(61) | 317(9) | 0.32(3) | 134(3) | 55781(45) | 0.15(2) | 1.14 | 0.02 | 2: |
| 11234677 | 1.587 418(2) | – | 1738(171) | 135(18) | 0.20(4) | 156(6) | 55586(99) | 0.011(5) | 0.40 | 0.01 | 2: |
| 3248019 | 2.668 200(5) | – | 1749(331) | 130(48) | 0.44(7) | 19(12) | 54706(162) | 0.010(11) | 0.38 | 0.04 | 2: |
| 2305372 | 1.404 691 57(8) | – | 1772(25) | 140(2) | 0.206(9) | 305(2) | 54966(14) | 0.0117(6) | 0.41 | 0.009 | 2: |
| 6766325: | 0.439 9650(4) | – | 1801(202) | 78(17) | 0.41(3) | 231(4) | 54460(149) | 0.002(1) | 0.21 | 0.001 | 2: |
| 8690104: | 0.408 7740(2) | – | 1835(222) | 46(9) | 0.24(6) | 287(7) | 54704(133) | 0.0004(2) | 0.12 | 0.001 | 2: |
| 8982514: | 0.414 490 27(4) | – | 1901(150) | 63(2) | 0.12(1) | 299(9) | 54288(70) | 0.0009(1) | 0.16 | 0.001 | 2: |
| 11246163 | 0.279 226 79(9) | – | 1902(149) | 56(5) | 0.36(3) | 210(3) | 55840(94) | 0.0006(2) | 0.14 | 0.001 | 2: |
| 5269407 | 0.958 860(2) | – | 1905(172) | 268(31) | 0.53(2) | 82(6) | 55206(61) | 0.07(3) | 0.83 | 0.005 | 2: |
| 4174507 | 3.891 79(1) | – | 1922(333) | 647(87) | 0.82(3) | 202(3) | 55730(181) | 0.98(52) | 2.85 | 0.34 | 2: |
| 5962716 | 1.804 5827(2) | – | 1935(29) | 208(2) | 0.507(8) | 253.4(9) | 55804(17) | 0.032(1) | 0.60 | 0.02 | 2: |
| 9788457: | 0.963 338 79(1) | – | 1960(425) | 27.9(2) | 0.46(1) | 17(1) | 55737(167) | 0.000 07(3) | 0.07 | 0.005 | 2: |
| 12055014 | 0.499 9043(1) | – | 1961(175) | 31(5) | 0.32(4) | 29(5) | 54568(72) | 0.000 10(6) | 0.08 | 0.001 | 2: |
| 10724533 | 0.745 0940(4) | – | 2028(198) | 70(10) | 0.499(9) | 77(3) | 54178(131) | 0.0011(5) | 0.17 | 0.003 | 2: |
| 8868650 | 4.447 4056(9) | – | 2040(88) | 367(9) | 0.62(2) | 234(2) | 55374(32) | 0.16(2) | 1.17 | 0.13 | 2: |
| 10275197 | 0.390 846(1) | – | 2127(82) | 612(72) | 0.268(4) | 210.7(9) | 54851(25) | 0.68(24) | 2.34 | 0.001 | 2: |
| 3335816 | 7.422 028(5) | – | 2250(1234) | 66(42) | 0.16(24) | 233(69) | 54351(703) | 0.001(2) | 0.15 | 0.16 | 2: |
| 5975712 | 1.136 080(1) | – | 2308(118) | 347(21) | 0.43(1) | 115(4) | 55530(59) | 0.11(2) | 0.98 | 0.004 | 2: |
| 3839964 | 0.256 1427(4) | 29(1) | 2404(371) | 311(22) | 0.17(1) | 4(5) | 53795(184) | 0.07(3) | 0.82 | 0.002 | 2: |
| 8444552 | 1.178 0785(7) | – | 2441(73) | 376(13) | 0.492(6) | 104(1) | 55301(22) | 0.12(1) | 1.03 | 0.005 | 2: |
| 4937217 | 0.429 3407(2) | 3.8(6) | 2468(1187) | 24(12) | 0.49(14) | 176(8) | 55622(453) | 0.000 03(5) | 0.05 | 0.001 | 2: |
| 8758161 | 1.996 4243(2) | – | 2501(276) | 133(2) | 0.196(7) | 103(1) | 55375(47) | 0.005(1) | 0.30 | 0.01 | 2: |
| 12055255 | 0.220 9449(6) | – | 2530(166) | 544(57) | 0.416(8) | 280(2) | 55142(33) | 0.34(12) | 1.65 | 0.001 | 2: |
| 4758368 | 3.749 98(1) | – | 2876(1289) | 357(127) | 0.7(1) | 313(10) | 55556(429) | 0.07(10) | 0.84 | 0.08 | 2: |
| 8429450 | 2.705 145(7) | – | 3088(1698) | 128(75) | 0.38(17) | 185(11) | 56136(894) | 0.003(6) | 0.24 | 0.02 | 2: |
| 9110346 | 1.790 580(3) | – | 3645(695) | 350(59) | 0.74(2) | 307(3) | 55406(129) | 0.04(3) | 0.68 | 0.01 | 2: |
| 8265951 | 0.779 9554(2) | – | 3721(247) | 423(19) | 0.76(1) | 215.9(5) | 55390(41) | 0.07(1) | 0.84 | 0.003 | 2: |
| 6615041 | 0.340 086 60(2) | – | 3951(1200) | 105(1) | 0.616(7) | 30.3(8) | 55747(238) | 0.0010(6) | 0.17 | 0.001 | 2: |
| 9532219 | 0.198 153 67(5) | – | 4401(900) | 217(7) | 0.38(1) | 205(2) | 55770(159) | 0.007(3) | 0.34 | 0.001 | 2: |
| 8553788 | 1.606 184(2) | – | 4579(552) | 473(66) | 0.75(1) | 56.2(7) | 56474(249) | 0.07(3) | 0.81 | 0.008 | 2: |
| 6794131 | 1.613 324(2) | – | 4743(2105) | 446(141) | 0.87(5) | 150(2) | 55889(604) | 0.05(7) | 0.73 | 0.03 | 2: |
| 10686876 | 2.618 397(8) | – | 5280(1590) | 400(147) | 0.33(10) | 174(3) | 54912(51) | 0.03(4) | 0.59 | 0.006 | 2: |
| 6233903 | 5.990 90(3) | – | 5359(2135) | 642(223) | 0.69(8) | 2(2) | 56036(582) | 0.12(16) | 1.05 | 0.08 | 2: |
| 9181877 | 0.321 019(5) | – | 5497(2957) | 963(711) | 0.35(15) | 332(12) | 55078(263) | 0.40(97) | 1.78 | 0.001 | 2: |
| 9412114 | 0.250 2592(2) | – | 5596(353) | 922(48) | 0.70(1) | 1(1) | 55540(53) | 0.34(7) | 1.65 | 0.001 | 2: |
| 8016214 | 3.174 930(5) | – | 7350(2008) | 484(113) | 0.71(5) | 173(3) | 55328(162) | 0.03(2) | 0.57 | 0.02 | 2: |
| 7272739 | 0.281 163 04(6) | – | 9256(910) | 218(17) | 0.75(2) | 184(1) | 55988(144) | 0.0016(5) | 0.20 | 0.001 | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10095469 | 0.677 762 45(2) | – | 932(15) | 40.9(4) | 0.19(2) | 67(4) | 54958(19) | 0.001 06(5) | 0.17 | 0.006 | 2: |
| 9392702 | 3.909 33(1) | – | 976(170) | 103(29) | 0.29(3) | 281(14) | 55044(56) | 0.02(1) | 0.45 | 0.19 | 2: |
| 4848423 | 3.003 612(6) | – | 1190(68) | 227(22) | 0.14(3) | 358(7) | 55450(68) | 0.11(4) | 1.00 | 0.07 | 2: |
| 2983113 | 0.395 159 98(2) | – | 1249(36) | 36.9(9) | 0.49(4) | 303(3) | 55246(22) | 0.000 43(4) | 0.12 | 0.002 | 2: |
| 10268903 | 1.103 978(1) | – | 1286(318) | 211(33) | 0.66(8) | 130(4) | 54904(293) | 0.08(5) | 0.85 | 0.02 | 2: |
| 6265720 | 0.312 427 62(2) | – | 1447(15) | 220(2) | 0.652(7) | 192.4(6) | 55345(6) | 0.068(2) | 0.82 | 0.002 | 2: |
| 10934755 | 0.786 485 49(8) | – | 1466(32) | 51(1) | 0.26(1) | 47(3) | 54354(24) | 0.000 83(7) | 0.16 | 0.004 | 2: |
| 9283826 | 0.356 523 21(5) | – | 1475(27) | 98(2) | 0.31(3) | 30(3) | 54850(19) | 0.0057(4) | 0.31 | 0.001 | 2: |
| 6103049 | 0.643 1713(2) | – | 1482(62) | 59(5) | 0.49(4) | 243(2) | 54945(20) | 0.0013(3) | 0.18 | 0.004 | 2: |
| 9821923 | 0.349 5323(2) | – | 1493(63) | 110(7) | 0.48(2) | 293(12) | 54786(52) | 0.008(2) | 0.35 | 0.001 | 2: |
| 5353374 | 0.393 320 61(1) | – | 1494(33) | 29.1(5) | 0.13(3) | 268(8) | 55009(35) | 0.000 15(1) | 0.09 | 0.001 | 2: |
| 3766353 | 2.666 9672(8) | – | 1522(84) | 152(5) | 0.24(4) | 196(17) | 55267(84) | 0.020(3) | 0.50 | 0.04 | 2: |
| 7518816 | 0.466 580 65(6) | – | 1523(35) | 49(2) | 0.27(2) | 171(3) | 55022(22) | 0.000 67(8) | 0.15 | 0.001 | 2: |
| 10383620 | 0.734 5688(1) | – | 1541(12) | 277(3) | 0.219(4) | 0.9(3) | 54250(9) | 0.120(4) | 1.03 | 0.003 | 2: |
| 10557008 | 0.265 418 72(1) | – | 1545(15) | 79.2(5) | 0.343(5) | 188(2) | 55243(11) | 0.002 79(7) | 0.24 | 0.001 | 2: |
| 9083523 | 0.918 4227(3) | – | 1573(77) | 59(5) | 0.39(1) | 97(2) | 54664(53) | 0.0011(3) | 0.17 | 0.006 | 2: |
| 2715007 | 0.297 111 40(4) | – | 1598(21) | 256(3) | 0.623(6) | 213.3(7) | 54766(16) | 0.088(4) | 0.90 | 0.001 | 2: |
| 9596187 | 0.953 283(3) | – | 1599(97) | 508(52) | 0.18(4) | 41(7) | 54892(46) | 0.69(22) | 2.35 | 0.004 | 2: |
| 10916675 | 0.418 867 53(4) | – | 1626(77) | 20(1) | 0.31(3) | 36(7) | 55133(47) | 0.000 04(1) | 0.06 | 0.001 | 2: |
| 9706078: | 0.613 561(2) | – | 1632(287) | 109(54) | 0.49(11) | 73(10) | 54973(60) | 0.007(10) | 0.33 | 0.003 | 2: |
| 5956776 | 0.569 1161(6) | – | 1655(1122) | 33(19) | 0.57(20) | 16(5) | 54222(788) | 0.0002(4) | 0.09 | 0.003 | 2: |
| 6606282 | 2.107 135(1) | – | 1681(61) | 317(9) | 0.32(3) | 134(3) | 55781(45) | 0.15(2) | 1.14 | 0.02 | 2: |
| 11234677 | 1.587 418(2) | – | 1738(171) | 135(18) | 0.20(4) | 156(6) | 55586(99) | 0.011(5) | 0.40 | 0.01 | 2: |
| 3248019 | 2.668 200(5) | – | 1749(331) | 130(48) | 0.44(7) | 19(12) | 54706(162) | 0.010(11) | 0.38 | 0.04 | 2: |
| 2305372 | 1.404 691 57(8) | – | 1772(25) | 140(2) | 0.206(9) | 305(2) | 54966(14) | 0.0117(6) | 0.41 | 0.009 | 2: |
| 6766325: | 0.439 9650(4) | – | 1801(202) | 78(17) | 0.41(3) | 231(4) | 54460(149) | 0.002(1) | 0.21 | 0.001 | 2: |
| 8690104: | 0.408 7740(2) | – | 1835(222) | 46(9) | 0.24(6) | 287(7) | 54704(133) | 0.0004(2) | 0.12 | 0.001 | 2: |
| 8982514: | 0.414 490 27(4) | – | 1901(150) | 63(2) | 0.12(1) | 299(9) | 54288(70) | 0.0009(1) | 0.16 | 0.001 | 2: |
| 11246163 | 0.279 226 79(9) | – | 1902(149) | 56(5) | 0.36(3) | 210(3) | 55840(94) | 0.0006(2) | 0.14 | 0.001 | 2: |
| 5269407 | 0.958 860(2) | – | 1905(172) | 268(31) | 0.53(2) | 82(6) | 55206(61) | 0.07(3) | 0.83 | 0.005 | 2: |
| 4174507 | 3.891 79(1) | – | 1922(333) | 647(87) | 0.82(3) | 202(3) | 55730(181) | 0.98(52) | 2.85 | 0.34 | 2: |
| 5962716 | 1.804 5827(2) | – | 1935(29) | 208(2) | 0.507(8) | 253.4(9) | 55804(17) | 0.032(1) | 0.60 | 0.02 | 2: |
| 9788457: | 0.963 338 79(1) | – | 1960(425) | 27.9(2) | 0.46(1) | 17(1) | 55737(167) | 0.000 07(3) | 0.07 | 0.005 | 2: |
| 12055014 | 0.499 9043(1) | – | 1961(175) | 31(5) | 0.32(4) | 29(5) | 54568(72) | 0.000 10(6) | 0.08 | 0.001 | 2: |
| 10724533 | 0.745 0940(4) | – | 2028(198) | 70(10) | 0.499(9) | 77(3) | 54178(131) | 0.0011(5) | 0.17 | 0.003 | 2: |
| 8868650 | 4.447 4056(9) | – | 2040(88) | 367(9) | 0.62(2) | 234(2) | 55374(32) | 0.16(2) | 1.17 | 0.13 | 2: |
| 10275197 | 0.390 846(1) | – | 2127(82) | 612(72) | 0.268(4) | 210.7(9) | 54851(25) | 0.68(24) | 2.34 | 0.001 | 2: |
| 3335816 | 7.422 028(5) | – | 2250(1234) | 66(42) | 0.16(24) | 233(69) | 54351(703) | 0.001(2) | 0.15 | 0.16 | 2: |
| 5975712 | 1.136 080(1) | – | 2308(118) | 347(21) | 0.43(1) | 115(4) | 55530(59) | 0.11(2) | 0.98 | 0.004 | 2: |
| 3839964 | 0.256 1427(4) | 29(1) | 2404(371) | 311(22) | 0.17(1) | 4(5) | 53795(184) | 0.07(3) | 0.82 | 0.002 | 2: |
| 8444552 | 1.178 0785(7) | – | 2441(73) | 376(13) | 0.492(6) | 104(1) | 55301(22) | 0.12(1) | 1.03 | 0.005 | 2: |
| 4937217 | 0.429 3407(2) | 3.8(6) | 2468(1187) | 24(12) | 0.49(14) | 176(8) | 55622(453) | 0.000 03(5) | 0.05 | 0.001 | 2: |
| 8758161 | 1.996 4243(2) | – | 2501(276) | 133(2) | 0.196(7) | 103(1) | 55375(47) | 0.005(1) | 0.30 | 0.01 | 2: |
| 12055255 | 0.220 9449(6) | – | 2530(166) | 544(57) | 0.416(8) | 280(2) | 55142(33) | 0.34(12) | 1.65 | 0.001 | 2: |
| 4758368 | 3.749 98(1) | – | 2876(1289) | 357(127) | 0.7(1) | 313(10) | 55556(429) | 0.07(10) | 0.84 | 0.08 | 2: |
| 8429450 | 2.705 145(7) | – | 3088(1698) | 128(75) | 0.38(17) | 185(11) | 56136(894) | 0.003(6) | 0.24 | 0.02 | 2: |
| 9110346 | 1.790 580(3) | – | 3645(695) | 350(59) | 0.74(2) | 307(3) | 55406(129) | 0.04(3) | 0.68 | 0.01 | 2: |
| 8265951 | 0.779 9554(2) | – | 3721(247) | 423(19) | 0.76(1) | 215.9(5) | 55390(41) | 0.07(1) | 0.84 | 0.003 | 2: |
| 6615041 | 0.340 086 60(2) | – | 3951(1200) | 105(1) | 0.616(7) | 30.3(8) | 55747(238) | 0.0010(6) | 0.17 | 0.001 | 2: |
| 9532219 | 0.198 153 67(5) | – | 4401(900) | 217(7) | 0.38(1) | 205(2) | 55770(159) | 0.007(3) | 0.34 | 0.001 | 2: |
| 8553788 | 1.606 184(2) | – | 4579(552) | 473(66) | 0.75(1) | 56.2(7) | 56474(249) | 0.07(3) | 0.81 | 0.008 | 2: |
| 6794131 | 1.613 324(2) | – | 4743(2105) | 446(141) | 0.87(5) | 150(2) | 55889(604) | 0.05(7) | 0.73 | 0.03 | 2: |
| 10686876 | 2.618 397(8) | – | 5280(1590) | 400(147) | 0.33(10) | 174(3) | 54912(51) | 0.03(4) | 0.59 | 0.006 | 2: |
| 6233903 | 5.990 90(3) | – | 5359(2135) | 642(223) | 0.69(8) | 2(2) | 56036(582) | 0.12(16) | 1.05 | 0.08 | 2: |
| 9181877 | 0.321 019(5) | – | 5497(2957) | 963(711) | 0.35(15) | 332(12) | 55078(263) | 0.40(97) | 1.78 | 0.001 | 2: |
| 9412114 | 0.250 2592(2) | – | 5596(353) | 922(48) | 0.70(1) | 1(1) | 55540(53) | 0.34(7) | 1.65 | 0.001 | 2: |
| 8016214 | 3.174 930(5) | – | 7350(2008) | 484(113) | 0.71(5) | 173(3) | 55328(162) | 0.03(2) | 0.57 | 0.02 | 2: |
| 7272739 | 0.281 163 04(6) | – | 9256(910) | 218(17) | 0.75(2) | 184(1) | 55988(144) | 0.0016(5) | 0.20 | 0.001 | 2: |
Orbital elements from combined dynamical and LTTE solutions for systems, where more than two outer periods are covered, or/and triply eclipsing systems.
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 5897826a | 1.767 13(19) | 33.921(1) | 53.6(4) | 0.304(2) | 52.9(3) | 55168.63(3) | 0.754(1) | 0.748(1) | 0.454(4) | 1.35(3) | 10.67 |
| 5952403 | 0.905 678 28(5) | 45.47(2) | 90.3(7) | 0.0 | – | – | 1.19(1) | 0.63(1) | 1.79(4) | 3.0(1) | 0.00 |
| 6531485 | 0.676 990 50(2) | 48.267(6) | 73(4) | 0.57(1) | 22(2) | 54983(1) | 0.198(9) | 0.45(2) | 1.3(2) | 1.0(2) | 2.89 |
| 7690843c | 0.786 2597(1) | 74.25(3) | 123(13) | 0.369(2) | 4(2) | 54919(1) | 1.25(5) | 0.66(7) | 1.6(6) | 3.0(1.0) | 0.60 |
| 3544694 | 3.845 7246(6) | 80.99(9) | 120(7) | 0.109(6) | 334(2) | 55724(7) | 0.11(2) | 0.32(3) | 2.4(4) | 1.1(2) | 3.17 |
| 10613718 | 1.175 877 88(3) | 88.20(4) | 93(10) | 0.10(3) | 49(12) | 54994(3) | 0.21(5) | 0.53(3) | 0.7(2) | 0.7(2) | 0.31 |
| 6545018 | 3.991 456 88(7) | 90.586(5) | 118(3) | 0.225(4) | 236(1) | 54971(1) | 0.044(9) | 0.25(2) | 2.0(2) | 0.7(1) | 6.68 |
| 9714358 | 6.474 2247(8) | 103.77(2) | 113(12) | 0.29(1) | 120(2) | 54977(1) | 0.010(3) | 0.178(8) | 1.5(5) | 0.3(1) | 23.98 |
| 9451096 | 1.250 390 69(1) | 106.89(1) | 121(12) | 0.093(2) | 159(2) | 54993(1) | 0.045(1) | 0.28(3) | 1.5(5) | 0.6(2) | 0.21 |
| 5771589 | 10.738 233(3) | 112.97(2) | 152(5) | 0.1294(8) | 290.8(5) | 54978(1) | 0.44(9) | 0.50(4) | 1.9(2) | 1.9(2) | 21.88 |
| 9140402 | 4.988 351(6) | 117.0(2) | 112(9) | 0.24(1) | 300(32) | 55022(15) | 0.48(14) | 0.71(9) | 0.41(2) | 1.0(3) | 8.89 |
| 4079530: | 17.727 14(2) | 144(1) | 134(106) | 0.06(5) | 89(90) | 54967(51) | 20(1)E−6 | 0.02(2) | 1.5(3.6) | 0.04(9) | 18.15 |
| 7668648 | 27.8256(2) | 204.8(4) | 179(17) | 0.33(2) | 341(5) | 54917(4) | 0.006(1) | 0.15(1) | 1.6(5) | 0.27(8) | 11.05 |
| 7955301 | 15.327 75(1) | 209.1(1) | 229(26) | 0.310(7) | 309(1) | 54879(1) | 0.22(7) | 0.40(1) | 2.2(8) | 1.5(5) | 33.26 |
| 5080652: | 4.144 3558(2) | 220.9(8) | 187(44) | 0.13(3) | 18(4) | 54966(8) | 0.16(10) | 0.45(5) | 1.0(7) | 0.8(6) | 0.99 |
| 5095269 | 18.611 868(5) | 236.26(8) | 204(28) | 0.071(3) | 324(3) | 55004(2) | 13(5)E−7 | 0.0090(5) | 2.0(8) | 0.018(8) | 30.50 |
| 6964043 | 10.725 53(2) | 239.1(2) | 248(25) | 0.52(1) | 311(2) | 55110(2) | 0.27(8) | 0.42(2) | 2.1(6) | 1.5(5) | 30.59 |
| 7289157 | 5.266 5478(4) | 243.36(8) | 215(6) | 0.309(3) | 156.5(7) | 54942(1) | 0.14(2) | 0.39(3) | 1.4(1) | 0.9(1) | 4.41 |
| 5384802 | 6.083 0921(3) | 255.23(5) | 244(11) | 0.357(5) | 11(2) | 55000(2) | 0.24(3) | 0.44(3) | 1.7(2) | 1.3(2) | 5.06 |
| 5264818 | 1.905 0517(1) | 299.4(6) | 296(40) | 0.44(3) | 214(6) | 54948(6) | 0.029(8) | 0.34(5) | 2.6(1.1) | 1.3(6) | 0.44 |
| 8719897 | 3.151 419 94(9) | 333.1(2) | 264(12) | 0.265(7) | 128(2) | 54997(2) | 0.12(2) | 0.38(3) | 1.4(2) | 0.9(1) | 0.62 |
| 7593110 | 3.549 3857(3) | 353(1) | 267(140) | 0.10(6) | 144(29) | 54997(29) | 0.0248(2) | 0.24(12) | 1.6(2.5) | 0.5(8) | 0.24 |
| 4940201 | 8.816 559(1) | 364.9(3) | 278(24) | 0.24(2) | 247(5) | 54864(7) | 0.0618(1) | 0.31(3) | 1.5(4) | 0.7(2) | 3.62 |
| 10483644 | 5.110 7702(2) | 371(2) | 287(131) | 0.17(4) | 343(5) | 54929(12) | 0.04(2) | 0.25(10) | 1.7(2.4) | 0.6(8) | 0.77 |
| 8938628 | 6.862 2000(2) | 388.6(2) | 308(27) | 0.21(1) | 63(2) | 54824(4) | 0.17(6) | 0.41(6) | 1.5(4) | 1.1(3) | 1.46 |
| 6525196 | 3.420 597 33(4) | 418.2(1) | 334(27) | 0.295(5) | 94(2) | 55070(3) | 0.066(10) | 0.29(3) | 2.0(5) | 0.8(2) | 0.51 |
| 10095512 | 6.017 2059(1) | 473.4(2) | 324(76) | 0.19(1) | 329(4) | 54865(8) | 0.17(4) | 0.44(10) | 1.1(8) | 0.9(7) | 0.81 |
| 4909707 | 2.302 3671(2) | 514.8(6) | 406(14) | 0.60(1) | 176(1) | 54848(2) | 0.276 | 0.43(2) | 1.9(2) | 1.5(2) | 0.65 |
| 7177553 | 17.996 28(6) | 529(2) | 339(50) | 0.46(2) | 201(5) | 54701(9) | 41(1)E−9 | 0.0028(3) | 1.9(8) | 0.005(2) | 47.93 |
| 8023317 | 16.579 07(1) | 610.6(5) | 342(11) | 0.249(4) | 164(1) | 55014(3) | 0.0015(7) | 0.10(2) | 1.3(1) | 0.15(3) | 7.86 |
| 5255552 | 32.465 339(2) | 862.1(2) | 510(17) | 0.4342(7) | 37.3(1) | 54875(1) | 0.0609(1) | 0.29(1) | 1.7(2) | 0.7(1) | 17.21 |
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 5897826a | 1.767 13(19) | 33.921(1) | 53.6(4) | 0.304(2) | 52.9(3) | 55168.63(3) | 0.754(1) | 0.748(1) | 0.454(4) | 1.35(3) | 10.67 |
| 5952403 | 0.905 678 28(5) | 45.47(2) | 90.3(7) | 0.0 | – | – | 1.19(1) | 0.63(1) | 1.79(4) | 3.0(1) | 0.00 |
| 6531485 | 0.676 990 50(2) | 48.267(6) | 73(4) | 0.57(1) | 22(2) | 54983(1) | 0.198(9) | 0.45(2) | 1.3(2) | 1.0(2) | 2.89 |
| 7690843c | 0.786 2597(1) | 74.25(3) | 123(13) | 0.369(2) | 4(2) | 54919(1) | 1.25(5) | 0.66(7) | 1.6(6) | 3.0(1.0) | 0.60 |
| 3544694 | 3.845 7246(6) | 80.99(9) | 120(7) | 0.109(6) | 334(2) | 55724(7) | 0.11(2) | 0.32(3) | 2.4(4) | 1.1(2) | 3.17 |
| 10613718 | 1.175 877 88(3) | 88.20(4) | 93(10) | 0.10(3) | 49(12) | 54994(3) | 0.21(5) | 0.53(3) | 0.7(2) | 0.7(2) | 0.31 |
| 6545018 | 3.991 456 88(7) | 90.586(5) | 118(3) | 0.225(4) | 236(1) | 54971(1) | 0.044(9) | 0.25(2) | 2.0(2) | 0.7(1) | 6.68 |
| 9714358 | 6.474 2247(8) | 103.77(2) | 113(12) | 0.29(1) | 120(2) | 54977(1) | 0.010(3) | 0.178(8) | 1.5(5) | 0.3(1) | 23.98 |
| 9451096 | 1.250 390 69(1) | 106.89(1) | 121(12) | 0.093(2) | 159(2) | 54993(1) | 0.045(1) | 0.28(3) | 1.5(5) | 0.6(2) | 0.21 |
| 5771589 | 10.738 233(3) | 112.97(2) | 152(5) | 0.1294(8) | 290.8(5) | 54978(1) | 0.44(9) | 0.50(4) | 1.9(2) | 1.9(2) | 21.88 |
| 9140402 | 4.988 351(6) | 117.0(2) | 112(9) | 0.24(1) | 300(32) | 55022(15) | 0.48(14) | 0.71(9) | 0.41(2) | 1.0(3) | 8.89 |
| 4079530: | 17.727 14(2) | 144(1) | 134(106) | 0.06(5) | 89(90) | 54967(51) | 20(1)E−6 | 0.02(2) | 1.5(3.6) | 0.04(9) | 18.15 |
| 7668648 | 27.8256(2) | 204.8(4) | 179(17) | 0.33(2) | 341(5) | 54917(4) | 0.006(1) | 0.15(1) | 1.6(5) | 0.27(8) | 11.05 |
| 7955301 | 15.327 75(1) | 209.1(1) | 229(26) | 0.310(7) | 309(1) | 54879(1) | 0.22(7) | 0.40(1) | 2.2(8) | 1.5(5) | 33.26 |
| 5080652: | 4.144 3558(2) | 220.9(8) | 187(44) | 0.13(3) | 18(4) | 54966(8) | 0.16(10) | 0.45(5) | 1.0(7) | 0.8(6) | 0.99 |
| 5095269 | 18.611 868(5) | 236.26(8) | 204(28) | 0.071(3) | 324(3) | 55004(2) | 13(5)E−7 | 0.0090(5) | 2.0(8) | 0.018(8) | 30.50 |
| 6964043 | 10.725 53(2) | 239.1(2) | 248(25) | 0.52(1) | 311(2) | 55110(2) | 0.27(8) | 0.42(2) | 2.1(6) | 1.5(5) | 30.59 |
| 7289157 | 5.266 5478(4) | 243.36(8) | 215(6) | 0.309(3) | 156.5(7) | 54942(1) | 0.14(2) | 0.39(3) | 1.4(1) | 0.9(1) | 4.41 |
| 5384802 | 6.083 0921(3) | 255.23(5) | 244(11) | 0.357(5) | 11(2) | 55000(2) | 0.24(3) | 0.44(3) | 1.7(2) | 1.3(2) | 5.06 |
| 5264818 | 1.905 0517(1) | 299.4(6) | 296(40) | 0.44(3) | 214(6) | 54948(6) | 0.029(8) | 0.34(5) | 2.6(1.1) | 1.3(6) | 0.44 |
| 8719897 | 3.151 419 94(9) | 333.1(2) | 264(12) | 0.265(7) | 128(2) | 54997(2) | 0.12(2) | 0.38(3) | 1.4(2) | 0.9(1) | 0.62 |
| 7593110 | 3.549 3857(3) | 353(1) | 267(140) | 0.10(6) | 144(29) | 54997(29) | 0.0248(2) | 0.24(12) | 1.6(2.5) | 0.5(8) | 0.24 |
| 4940201 | 8.816 559(1) | 364.9(3) | 278(24) | 0.24(2) | 247(5) | 54864(7) | 0.0618(1) | 0.31(3) | 1.5(4) | 0.7(2) | 3.62 |
| 10483644 | 5.110 7702(2) | 371(2) | 287(131) | 0.17(4) | 343(5) | 54929(12) | 0.04(2) | 0.25(10) | 1.7(2.4) | 0.6(8) | 0.77 |
| 8938628 | 6.862 2000(2) | 388.6(2) | 308(27) | 0.21(1) | 63(2) | 54824(4) | 0.17(6) | 0.41(6) | 1.5(4) | 1.1(3) | 1.46 |
| 6525196 | 3.420 597 33(4) | 418.2(1) | 334(27) | 0.295(5) | 94(2) | 55070(3) | 0.066(10) | 0.29(3) | 2.0(5) | 0.8(2) | 0.51 |
| 10095512 | 6.017 2059(1) | 473.4(2) | 324(76) | 0.19(1) | 329(4) | 54865(8) | 0.17(4) | 0.44(10) | 1.1(8) | 0.9(7) | 0.81 |
| 4909707 | 2.302 3671(2) | 514.8(6) | 406(14) | 0.60(1) | 176(1) | 54848(2) | 0.276 | 0.43(2) | 1.9(2) | 1.5(2) | 0.65 |
| 7177553 | 17.996 28(6) | 529(2) | 339(50) | 0.46(2) | 201(5) | 54701(9) | 41(1)E−9 | 0.0028(3) | 1.9(8) | 0.005(2) | 47.93 |
| 8023317 | 16.579 07(1) | 610.6(5) | 342(11) | 0.249(4) | 164(1) | 55014(3) | 0.0015(7) | 0.10(2) | 1.3(1) | 0.15(3) | 7.86 |
| 5255552 | 32.465 339(2) | 862.1(2) | 510(17) | 0.4342(7) | 37.3(1) | 54875(1) | 0.0609(1) | 0.29(1) | 1.7(2) | 0.7(1) | 17.21 |
Orbital elements from combined dynamical and LTTE solutions for systems, where more than two outer periods are covered, or/and triply eclipsing systems.
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 5897826a | 1.767 13(19) | 33.921(1) | 53.6(4) | 0.304(2) | 52.9(3) | 55168.63(3) | 0.754(1) | 0.748(1) | 0.454(4) | 1.35(3) | 10.67 |
| 5952403 | 0.905 678 28(5) | 45.47(2) | 90.3(7) | 0.0 | – | – | 1.19(1) | 0.63(1) | 1.79(4) | 3.0(1) | 0.00 |
| 6531485 | 0.676 990 50(2) | 48.267(6) | 73(4) | 0.57(1) | 22(2) | 54983(1) | 0.198(9) | 0.45(2) | 1.3(2) | 1.0(2) | 2.89 |
| 7690843c | 0.786 2597(1) | 74.25(3) | 123(13) | 0.369(2) | 4(2) | 54919(1) | 1.25(5) | 0.66(7) | 1.6(6) | 3.0(1.0) | 0.60 |
| 3544694 | 3.845 7246(6) | 80.99(9) | 120(7) | 0.109(6) | 334(2) | 55724(7) | 0.11(2) | 0.32(3) | 2.4(4) | 1.1(2) | 3.17 |
| 10613718 | 1.175 877 88(3) | 88.20(4) | 93(10) | 0.10(3) | 49(12) | 54994(3) | 0.21(5) | 0.53(3) | 0.7(2) | 0.7(2) | 0.31 |
| 6545018 | 3.991 456 88(7) | 90.586(5) | 118(3) | 0.225(4) | 236(1) | 54971(1) | 0.044(9) | 0.25(2) | 2.0(2) | 0.7(1) | 6.68 |
| 9714358 | 6.474 2247(8) | 103.77(2) | 113(12) | 0.29(1) | 120(2) | 54977(1) | 0.010(3) | 0.178(8) | 1.5(5) | 0.3(1) | 23.98 |
| 9451096 | 1.250 390 69(1) | 106.89(1) | 121(12) | 0.093(2) | 159(2) | 54993(1) | 0.045(1) | 0.28(3) | 1.5(5) | 0.6(2) | 0.21 |
| 5771589 | 10.738 233(3) | 112.97(2) | 152(5) | 0.1294(8) | 290.8(5) | 54978(1) | 0.44(9) | 0.50(4) | 1.9(2) | 1.9(2) | 21.88 |
| 9140402 | 4.988 351(6) | 117.0(2) | 112(9) | 0.24(1) | 300(32) | 55022(15) | 0.48(14) | 0.71(9) | 0.41(2) | 1.0(3) | 8.89 |
| 4079530: | 17.727 14(2) | 144(1) | 134(106) | 0.06(5) | 89(90) | 54967(51) | 20(1)E−6 | 0.02(2) | 1.5(3.6) | 0.04(9) | 18.15 |
| 7668648 | 27.8256(2) | 204.8(4) | 179(17) | 0.33(2) | 341(5) | 54917(4) | 0.006(1) | 0.15(1) | 1.6(5) | 0.27(8) | 11.05 |
| 7955301 | 15.327 75(1) | 209.1(1) | 229(26) | 0.310(7) | 309(1) | 54879(1) | 0.22(7) | 0.40(1) | 2.2(8) | 1.5(5) | 33.26 |
| 5080652: | 4.144 3558(2) | 220.9(8) | 187(44) | 0.13(3) | 18(4) | 54966(8) | 0.16(10) | 0.45(5) | 1.0(7) | 0.8(6) | 0.99 |
| 5095269 | 18.611 868(5) | 236.26(8) | 204(28) | 0.071(3) | 324(3) | 55004(2) | 13(5)E−7 | 0.0090(5) | 2.0(8) | 0.018(8) | 30.50 |
| 6964043 | 10.725 53(2) | 239.1(2) | 248(25) | 0.52(1) | 311(2) | 55110(2) | 0.27(8) | 0.42(2) | 2.1(6) | 1.5(5) | 30.59 |
| 7289157 | 5.266 5478(4) | 243.36(8) | 215(6) | 0.309(3) | 156.5(7) | 54942(1) | 0.14(2) | 0.39(3) | 1.4(1) | 0.9(1) | 4.41 |
| 5384802 | 6.083 0921(3) | 255.23(5) | 244(11) | 0.357(5) | 11(2) | 55000(2) | 0.24(3) | 0.44(3) | 1.7(2) | 1.3(2) | 5.06 |
| 5264818 | 1.905 0517(1) | 299.4(6) | 296(40) | 0.44(3) | 214(6) | 54948(6) | 0.029(8) | 0.34(5) | 2.6(1.1) | 1.3(6) | 0.44 |
| 8719897 | 3.151 419 94(9) | 333.1(2) | 264(12) | 0.265(7) | 128(2) | 54997(2) | 0.12(2) | 0.38(3) | 1.4(2) | 0.9(1) | 0.62 |
| 7593110 | 3.549 3857(3) | 353(1) | 267(140) | 0.10(6) | 144(29) | 54997(29) | 0.0248(2) | 0.24(12) | 1.6(2.5) | 0.5(8) | 0.24 |
| 4940201 | 8.816 559(1) | 364.9(3) | 278(24) | 0.24(2) | 247(5) | 54864(7) | 0.0618(1) | 0.31(3) | 1.5(4) | 0.7(2) | 3.62 |
| 10483644 | 5.110 7702(2) | 371(2) | 287(131) | 0.17(4) | 343(5) | 54929(12) | 0.04(2) | 0.25(10) | 1.7(2.4) | 0.6(8) | 0.77 |
| 8938628 | 6.862 2000(2) | 388.6(2) | 308(27) | 0.21(1) | 63(2) | 54824(4) | 0.17(6) | 0.41(6) | 1.5(4) | 1.1(3) | 1.46 |
| 6525196 | 3.420 597 33(4) | 418.2(1) | 334(27) | 0.295(5) | 94(2) | 55070(3) | 0.066(10) | 0.29(3) | 2.0(5) | 0.8(2) | 0.51 |
| 10095512 | 6.017 2059(1) | 473.4(2) | 324(76) | 0.19(1) | 329(4) | 54865(8) | 0.17(4) | 0.44(10) | 1.1(8) | 0.9(7) | 0.81 |
| 4909707 | 2.302 3671(2) | 514.8(6) | 406(14) | 0.60(1) | 176(1) | 54848(2) | 0.276 | 0.43(2) | 1.9(2) | 1.5(2) | 0.65 |
| 7177553 | 17.996 28(6) | 529(2) | 339(50) | 0.46(2) | 201(5) | 54701(9) | 41(1)E−9 | 0.0028(3) | 1.9(8) | 0.005(2) | 47.93 |
| 8023317 | 16.579 07(1) | 610.6(5) | 342(11) | 0.249(4) | 164(1) | 55014(3) | 0.0015(7) | 0.10(2) | 1.3(1) | 0.15(3) | 7.86 |
| 5255552 | 32.465 339(2) | 862.1(2) | 510(17) | 0.4342(7) | 37.3(1) | 54875(1) | 0.0609(1) | 0.29(1) | 1.7(2) | 0.7(1) | 17.21 |
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 5897826a | 1.767 13(19) | 33.921(1) | 53.6(4) | 0.304(2) | 52.9(3) | 55168.63(3) | 0.754(1) | 0.748(1) | 0.454(4) | 1.35(3) | 10.67 |
| 5952403 | 0.905 678 28(5) | 45.47(2) | 90.3(7) | 0.0 | – | – | 1.19(1) | 0.63(1) | 1.79(4) | 3.0(1) | 0.00 |
| 6531485 | 0.676 990 50(2) | 48.267(6) | 73(4) | 0.57(1) | 22(2) | 54983(1) | 0.198(9) | 0.45(2) | 1.3(2) | 1.0(2) | 2.89 |
| 7690843c | 0.786 2597(1) | 74.25(3) | 123(13) | 0.369(2) | 4(2) | 54919(1) | 1.25(5) | 0.66(7) | 1.6(6) | 3.0(1.0) | 0.60 |
| 3544694 | 3.845 7246(6) | 80.99(9) | 120(7) | 0.109(6) | 334(2) | 55724(7) | 0.11(2) | 0.32(3) | 2.4(4) | 1.1(2) | 3.17 |
| 10613718 | 1.175 877 88(3) | 88.20(4) | 93(10) | 0.10(3) | 49(12) | 54994(3) | 0.21(5) | 0.53(3) | 0.7(2) | 0.7(2) | 0.31 |
| 6545018 | 3.991 456 88(7) | 90.586(5) | 118(3) | 0.225(4) | 236(1) | 54971(1) | 0.044(9) | 0.25(2) | 2.0(2) | 0.7(1) | 6.68 |
| 9714358 | 6.474 2247(8) | 103.77(2) | 113(12) | 0.29(1) | 120(2) | 54977(1) | 0.010(3) | 0.178(8) | 1.5(5) | 0.3(1) | 23.98 |
| 9451096 | 1.250 390 69(1) | 106.89(1) | 121(12) | 0.093(2) | 159(2) | 54993(1) | 0.045(1) | 0.28(3) | 1.5(5) | 0.6(2) | 0.21 |
| 5771589 | 10.738 233(3) | 112.97(2) | 152(5) | 0.1294(8) | 290.8(5) | 54978(1) | 0.44(9) | 0.50(4) | 1.9(2) | 1.9(2) | 21.88 |
| 9140402 | 4.988 351(6) | 117.0(2) | 112(9) | 0.24(1) | 300(32) | 55022(15) | 0.48(14) | 0.71(9) | 0.41(2) | 1.0(3) | 8.89 |
| 4079530: | 17.727 14(2) | 144(1) | 134(106) | 0.06(5) | 89(90) | 54967(51) | 20(1)E−6 | 0.02(2) | 1.5(3.6) | 0.04(9) | 18.15 |
| 7668648 | 27.8256(2) | 204.8(4) | 179(17) | 0.33(2) | 341(5) | 54917(4) | 0.006(1) | 0.15(1) | 1.6(5) | 0.27(8) | 11.05 |
| 7955301 | 15.327 75(1) | 209.1(1) | 229(26) | 0.310(7) | 309(1) | 54879(1) | 0.22(7) | 0.40(1) | 2.2(8) | 1.5(5) | 33.26 |
| 5080652: | 4.144 3558(2) | 220.9(8) | 187(44) | 0.13(3) | 18(4) | 54966(8) | 0.16(10) | 0.45(5) | 1.0(7) | 0.8(6) | 0.99 |
| 5095269 | 18.611 868(5) | 236.26(8) | 204(28) | 0.071(3) | 324(3) | 55004(2) | 13(5)E−7 | 0.0090(5) | 2.0(8) | 0.018(8) | 30.50 |
| 6964043 | 10.725 53(2) | 239.1(2) | 248(25) | 0.52(1) | 311(2) | 55110(2) | 0.27(8) | 0.42(2) | 2.1(6) | 1.5(5) | 30.59 |
| 7289157 | 5.266 5478(4) | 243.36(8) | 215(6) | 0.309(3) | 156.5(7) | 54942(1) | 0.14(2) | 0.39(3) | 1.4(1) | 0.9(1) | 4.41 |
| 5384802 | 6.083 0921(3) | 255.23(5) | 244(11) | 0.357(5) | 11(2) | 55000(2) | 0.24(3) | 0.44(3) | 1.7(2) | 1.3(2) | 5.06 |
| 5264818 | 1.905 0517(1) | 299.4(6) | 296(40) | 0.44(3) | 214(6) | 54948(6) | 0.029(8) | 0.34(5) | 2.6(1.1) | 1.3(6) | 0.44 |
| 8719897 | 3.151 419 94(9) | 333.1(2) | 264(12) | 0.265(7) | 128(2) | 54997(2) | 0.12(2) | 0.38(3) | 1.4(2) | 0.9(1) | 0.62 |
| 7593110 | 3.549 3857(3) | 353(1) | 267(140) | 0.10(6) | 144(29) | 54997(29) | 0.0248(2) | 0.24(12) | 1.6(2.5) | 0.5(8) | 0.24 |
| 4940201 | 8.816 559(1) | 364.9(3) | 278(24) | 0.24(2) | 247(5) | 54864(7) | 0.0618(1) | 0.31(3) | 1.5(4) | 0.7(2) | 3.62 |
| 10483644 | 5.110 7702(2) | 371(2) | 287(131) | 0.17(4) | 343(5) | 54929(12) | 0.04(2) | 0.25(10) | 1.7(2.4) | 0.6(8) | 0.77 |
| 8938628 | 6.862 2000(2) | 388.6(2) | 308(27) | 0.21(1) | 63(2) | 54824(4) | 0.17(6) | 0.41(6) | 1.5(4) | 1.1(3) | 1.46 |
| 6525196 | 3.420 597 33(4) | 418.2(1) | 334(27) | 0.295(5) | 94(2) | 55070(3) | 0.066(10) | 0.29(3) | 2.0(5) | 0.8(2) | 0.51 |
| 10095512 | 6.017 2059(1) | 473.4(2) | 324(76) | 0.19(1) | 329(4) | 54865(8) | 0.17(4) | 0.44(10) | 1.1(8) | 0.9(7) | 0.81 |
| 4909707 | 2.302 3671(2) | 514.8(6) | 406(14) | 0.60(1) | 176(1) | 54848(2) | 0.276 | 0.43(2) | 1.9(2) | 1.5(2) | 0.65 |
| 7177553 | 17.996 28(6) | 529(2) | 339(50) | 0.46(2) | 201(5) | 54701(9) | 41(1)E−9 | 0.0028(3) | 1.9(8) | 0.005(2) | 47.93 |
| 8023317 | 16.579 07(1) | 610.6(5) | 342(11) | 0.249(4) | 164(1) | 55014(3) | 0.0015(7) | 0.10(2) | 1.3(1) | 0.15(3) | 7.86 |
| 5255552 | 32.465 339(2) | 862.1(2) | 510(17) | 0.4342(7) | 37.3(1) | 54875(1) | 0.0609(1) | 0.29(1) | 1.7(2) | 0.7(1) | 17.21 |
Orbital elements from combined dynamical and LTTE solutions which cover more than one but less than two outer periods.
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 7812175 | 17.793 59(2) | 583(2) | 389(50) | 0.030(4) | 207(6) | 54783(11) | 0.07(3) | 0.31(7) | 1.6(6) | 0.7(3) | 5.88 |
| 9715925 | 6.308 265(3) | 736(36) | 325(56) | 0.38(2) | 136(7) | 55083(42) | 0.007(2) | 0.21(4) | 0.7(4) | 0.2(1) | 1.23 |
| 8210721 | 22.673 18(4) | 789.7(4) | 492(19) | 0.259(2) | 212(1) | 54628(4) | 0.10(3) | 0.34(3) | 1.7(2) | 0.9(1) | 9.74 |
| 9664215 | 3.319 5345(8) | 910(7) | 539(68) | 0.536(8) | 190(2) | 54861(7) | 0.161(6) | 0.40(5) | 1.5(6) | 1.0(4) | 0.42 |
| 5731312 | 7.946 4246(2) | 911(3) | 423(42) | 0.584(2) | 25.9(4) | 54837(3) | 0.0015(5) | 0.11(2) | 1.1(3) | 0.13(4) | 4.96 |
| 5653126 | 38.492 33(5) | 968(2) | 586(31) | 0.189(4) | 326(1) | 55469(4) | 0.15(2) | 0.38(1) | 1.8(3) | 1.1(2) | 26.91 |
| 7821010 | 24.238 2191(1) | 991(3) | 551(23) | 0.372(9) | 126(2) | 55124(6) | 3(1)E−9 | 0.001 11(4) | 2.3(3) | 0.0025(3) | 32.60 |
| 10979716 | 10.684 099(2) | 1047(4) | 530(6) | 0.445(5) | 60.3(5) | 54518(4) | 0.099(2) | 0.389(5) | 1.12(4) | 0.71(3) | 2.57 |
| 4948863 | 8.643 5529(9) | 1060(11) | 80(2) | 0.11(2) | 124(7) | 55107(24) | 0.0060(5) | 0.15(3) | 1.7(9) | 0.3(2) | 0.28 |
| 6546508 | 6.107 118(6) | 1154(31) | 523(77) | 0.34(3) | 321(3) | 55123(19) | 0.26(2) | 0.56(8) | 0.6(3) | 0.8(4) | 0.47 |
| 4769799 | 21.9284(1) | 1231(8) | 653(74) | 0.191(8) | 233(9) | 55542(40) | 0.04(1) | 0.26(4) | 1.8(6) | 0.6(2) | 3.29 |
| 7837302 | 23.836 79(6) | 1382(2) | 213(238) | 0.260(4) | 3(5) | 54974(26) | 0.07(23) | 0.31(38) | 1.6(2.7) | 0.7(1.4) | 5.06 |
| 10549576 | 9.089 46(3) | 1411(52) | 821(461) | 0.54(7) | 139(6) | 55015(52) | 0.05(3) | 0.24(13) | 2.8(4.8) | 0.9(1.6) | 1.31 |
| 11519226 | 22.161 767(7) | 1437(1) | 745(8) | 0.332(2) | 321.7(5) | 55010(2) | 0.27(1) | 0.463(8) | 1.44(5) | 1.25(4) | 5.21 |
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 7812175 | 17.793 59(2) | 583(2) | 389(50) | 0.030(4) | 207(6) | 54783(11) | 0.07(3) | 0.31(7) | 1.6(6) | 0.7(3) | 5.88 |
| 9715925 | 6.308 265(3) | 736(36) | 325(56) | 0.38(2) | 136(7) | 55083(42) | 0.007(2) | 0.21(4) | 0.7(4) | 0.2(1) | 1.23 |
| 8210721 | 22.673 18(4) | 789.7(4) | 492(19) | 0.259(2) | 212(1) | 54628(4) | 0.10(3) | 0.34(3) | 1.7(2) | 0.9(1) | 9.74 |
| 9664215 | 3.319 5345(8) | 910(7) | 539(68) | 0.536(8) | 190(2) | 54861(7) | 0.161(6) | 0.40(5) | 1.5(6) | 1.0(4) | 0.42 |
| 5731312 | 7.946 4246(2) | 911(3) | 423(42) | 0.584(2) | 25.9(4) | 54837(3) | 0.0015(5) | 0.11(2) | 1.1(3) | 0.13(4) | 4.96 |
| 5653126 | 38.492 33(5) | 968(2) | 586(31) | 0.189(4) | 326(1) | 55469(4) | 0.15(2) | 0.38(1) | 1.8(3) | 1.1(2) | 26.91 |
| 7821010 | 24.238 2191(1) | 991(3) | 551(23) | 0.372(9) | 126(2) | 55124(6) | 3(1)E−9 | 0.001 11(4) | 2.3(3) | 0.0025(3) | 32.60 |
| 10979716 | 10.684 099(2) | 1047(4) | 530(6) | 0.445(5) | 60.3(5) | 54518(4) | 0.099(2) | 0.389(5) | 1.12(4) | 0.71(3) | 2.57 |
| 4948863 | 8.643 5529(9) | 1060(11) | 80(2) | 0.11(2) | 124(7) | 55107(24) | 0.0060(5) | 0.15(3) | 1.7(9) | 0.3(2) | 0.28 |
| 6546508 | 6.107 118(6) | 1154(31) | 523(77) | 0.34(3) | 321(3) | 55123(19) | 0.26(2) | 0.56(8) | 0.6(3) | 0.8(4) | 0.47 |
| 4769799 | 21.9284(1) | 1231(8) | 653(74) | 0.191(8) | 233(9) | 55542(40) | 0.04(1) | 0.26(4) | 1.8(6) | 0.6(2) | 3.29 |
| 7837302 | 23.836 79(6) | 1382(2) | 213(238) | 0.260(4) | 3(5) | 54974(26) | 0.07(23) | 0.31(38) | 1.6(2.7) | 0.7(1.4) | 5.06 |
| 10549576 | 9.089 46(3) | 1411(52) | 821(461) | 0.54(7) | 139(6) | 55015(52) | 0.05(3) | 0.24(13) | 2.8(4.8) | 0.9(1.6) | 1.31 |
| 11519226 | 22.161 767(7) | 1437(1) | 745(8) | 0.332(2) | 321.7(5) | 55010(2) | 0.27(1) | 0.463(8) | 1.44(5) | 1.25(4) | 5.21 |
Orbital elements from combined dynamical and LTTE solutions which cover more than one but less than two outer periods.
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 7812175 | 17.793 59(2) | 583(2) | 389(50) | 0.030(4) | 207(6) | 54783(11) | 0.07(3) | 0.31(7) | 1.6(6) | 0.7(3) | 5.88 |
| 9715925 | 6.308 265(3) | 736(36) | 325(56) | 0.38(2) | 136(7) | 55083(42) | 0.007(2) | 0.21(4) | 0.7(4) | 0.2(1) | 1.23 |
| 8210721 | 22.673 18(4) | 789.7(4) | 492(19) | 0.259(2) | 212(1) | 54628(4) | 0.10(3) | 0.34(3) | 1.7(2) | 0.9(1) | 9.74 |
| 9664215 | 3.319 5345(8) | 910(7) | 539(68) | 0.536(8) | 190(2) | 54861(7) | 0.161(6) | 0.40(5) | 1.5(6) | 1.0(4) | 0.42 |
| 5731312 | 7.946 4246(2) | 911(3) | 423(42) | 0.584(2) | 25.9(4) | 54837(3) | 0.0015(5) | 0.11(2) | 1.1(3) | 0.13(4) | 4.96 |
| 5653126 | 38.492 33(5) | 968(2) | 586(31) | 0.189(4) | 326(1) | 55469(4) | 0.15(2) | 0.38(1) | 1.8(3) | 1.1(2) | 26.91 |
| 7821010 | 24.238 2191(1) | 991(3) | 551(23) | 0.372(9) | 126(2) | 55124(6) | 3(1)E−9 | 0.001 11(4) | 2.3(3) | 0.0025(3) | 32.60 |
| 10979716 | 10.684 099(2) | 1047(4) | 530(6) | 0.445(5) | 60.3(5) | 54518(4) | 0.099(2) | 0.389(5) | 1.12(4) | 0.71(3) | 2.57 |
| 4948863 | 8.643 5529(9) | 1060(11) | 80(2) | 0.11(2) | 124(7) | 55107(24) | 0.0060(5) | 0.15(3) | 1.7(9) | 0.3(2) | 0.28 |
| 6546508 | 6.107 118(6) | 1154(31) | 523(77) | 0.34(3) | 321(3) | 55123(19) | 0.26(2) | 0.56(8) | 0.6(3) | 0.8(4) | 0.47 |
| 4769799 | 21.9284(1) | 1231(8) | 653(74) | 0.191(8) | 233(9) | 55542(40) | 0.04(1) | 0.26(4) | 1.8(6) | 0.6(2) | 3.29 |
| 7837302 | 23.836 79(6) | 1382(2) | 213(238) | 0.260(4) | 3(5) | 54974(26) | 0.07(23) | 0.31(38) | 1.6(2.7) | 0.7(1.4) | 5.06 |
| 10549576 | 9.089 46(3) | 1411(52) | 821(461) | 0.54(7) | 139(6) | 55015(52) | 0.05(3) | 0.24(13) | 2.8(4.8) | 0.9(1.6) | 1.31 |
| 11519226 | 22.161 767(7) | 1437(1) | 745(8) | 0.332(2) | 321.7(5) | 55010(2) | 0.27(1) | 0.463(8) | 1.44(5) | 1.25(4) | 5.21 |
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 7812175 | 17.793 59(2) | 583(2) | 389(50) | 0.030(4) | 207(6) | 54783(11) | 0.07(3) | 0.31(7) | 1.6(6) | 0.7(3) | 5.88 |
| 9715925 | 6.308 265(3) | 736(36) | 325(56) | 0.38(2) | 136(7) | 55083(42) | 0.007(2) | 0.21(4) | 0.7(4) | 0.2(1) | 1.23 |
| 8210721 | 22.673 18(4) | 789.7(4) | 492(19) | 0.259(2) | 212(1) | 54628(4) | 0.10(3) | 0.34(3) | 1.7(2) | 0.9(1) | 9.74 |
| 9664215 | 3.319 5345(8) | 910(7) | 539(68) | 0.536(8) | 190(2) | 54861(7) | 0.161(6) | 0.40(5) | 1.5(6) | 1.0(4) | 0.42 |
| 5731312 | 7.946 4246(2) | 911(3) | 423(42) | 0.584(2) | 25.9(4) | 54837(3) | 0.0015(5) | 0.11(2) | 1.1(3) | 0.13(4) | 4.96 |
| 5653126 | 38.492 33(5) | 968(2) | 586(31) | 0.189(4) | 326(1) | 55469(4) | 0.15(2) | 0.38(1) | 1.8(3) | 1.1(2) | 26.91 |
| 7821010 | 24.238 2191(1) | 991(3) | 551(23) | 0.372(9) | 126(2) | 55124(6) | 3(1)E−9 | 0.001 11(4) | 2.3(3) | 0.0025(3) | 32.60 |
| 10979716 | 10.684 099(2) | 1047(4) | 530(6) | 0.445(5) | 60.3(5) | 54518(4) | 0.099(2) | 0.389(5) | 1.12(4) | 0.71(3) | 2.57 |
| 4948863 | 8.643 5529(9) | 1060(11) | 80(2) | 0.11(2) | 124(7) | 55107(24) | 0.0060(5) | 0.15(3) | 1.7(9) | 0.3(2) | 0.28 |
| 6546508 | 6.107 118(6) | 1154(31) | 523(77) | 0.34(3) | 321(3) | 55123(19) | 0.26(2) | 0.56(8) | 0.6(3) | 0.8(4) | 0.47 |
| 4769799 | 21.9284(1) | 1231(8) | 653(74) | 0.191(8) | 233(9) | 55542(40) | 0.04(1) | 0.26(4) | 1.8(6) | 0.6(2) | 3.29 |
| 7837302 | 23.836 79(6) | 1382(2) | 213(238) | 0.260(4) | 3(5) | 54974(26) | 0.07(23) | 0.31(38) | 1.6(2.7) | 0.7(1.4) | 5.06 |
| 10549576 | 9.089 46(3) | 1411(52) | 821(461) | 0.54(7) | 139(6) | 55015(52) | 0.05(3) | 0.24(13) | 2.8(4.8) | 0.9(1.6) | 1.31 |
| 11519226 | 22.161 767(7) | 1437(1) | 745(8) | 0.332(2) | 321.7(5) | 55010(2) | 0.27(1) | 0.463(8) | 1.44(5) | 1.25(4) | 5.21 |
Orbital elements from combined dynamical and LTTE solutions which cover less than a full outer period.
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 10319590 | 21.321 16(6) | 452(2) | 330(11) | 0.146(4) | 316(2) | 54857(3) | 0.10(3) | 0.35(3) | 1.5(2) | 0.8(1) | 10.02 |
| 4078157 | 16.025 54(2) | 1377(26) | 736(66) | 0.480(8) | 70(3) | 54630(24) | 0.100 | 0.34(3) | 1.9(5) | 1.0(3) | 5.09 |
| 3345675: | 120.033(2) | 1662(94) | 671(336) | 0.39(2) | 95(65) | 54894(428) | 0.001 | 0.10(5) | 1.3(2.0) | 0.1(2) | 117.39 |
| 8143170 | 28.786 80 | 1710(35) | 864(21) | 0.704(6) | 108.7(9) | 54411(26) | 0.005(1) | 0.13(1) | 2.6(2) | 0.37(5) | 25.48 |
| 12356914 | 27.308 3183(3) | 1804(1) | 807(43) | 0.385(1) | 36.5(1) | 55860(1) | 0.0096(1) | 0.19(1) | 1.8(3) | 0.41(7) | 7.03 |
| 5003117 | 37.6094(2) | 2128(50) | 892(145) | 0.26(1) | 191(6) | 54750(49) | 0.06(1) | 0.33(6) | 1.4(7) | 0.7(4) | 6.32 |
| 6877673: | 36.759 691(6) | 2870(11) | 1112(254) | 0.468(2) | 155.5(5) | 54286(11) | 0.03(2) | 0.27(3) | 1.6(1.1) | 0.6(4) | 7.81 |
| 2576692 | 87.8797(1) | 2884(173) | 936(216) | 0.56(3) | 161(15) | 54277(213) | 0.000 04(2) | 0.032(5) | 1.3(9) | 0.04(3) | 33.85 |
| 7670617 | 24.703 17(4) | 3304(108) | 1054(30) | 0.707(7) | 86.4(9) | 55642(35) | 0.082(9) | 0.38(2) | 0.9(1) | 0.55(6) | 7.81 |
| 11502172: | 25.431 831(7) | 3313(58) | 1081(140) | 0.17(1) | 86(4) | 54359(47) | 0.020(3) | 0.25(3) | 1.2(5) | 0.4(2) | 0.83 |
| 9028474 | 124.935 73(1) | 3378(94) | 1258(421) | 0.09(2) | 242(8) | 54286(78) | 10(5)E−6 | 0.0163(4) | 2.3(1.2) | 0.04(2) | 44.23 |
| 9963009 | 40.0716(1) | 3770(10) | 1447(46) | 0.24(6) | 189(6) | 54074(79) | 0.111(7) | 0.41(1) | 1.7(2) | 1.2(1) | 2.98 |
| 11558882: | 73.9135(2) | 4050(50) | 1417(301) | 0.30(2) | 105(5) | 54919(80) | 0.016(7) | 0.19(3) | 1.9(1.2) | 0.4(3) | 7.16 |
| 4753988: | 7.304 51(1) | 5567(2325) | 1597(577) | 0.67(8) | 349(3) | 55359(238) | 0.007(9) | 0.20(3) | 1.4(1.9) | 0.4(5) | 0.13 |
| 10268809 | 24.708 43(1) | 7000(1000) | 2208(60) | 0.737(1) | 292.6(6) | 56147(169) | 0.32(10) | 0.48(2) | 1.5(5) | 1.4(4) | 2.66 |
| 4055092 | 76.464 532(9) | 11 548(88) | 2353(39) | 0.533(2) | 276.2(4) | 56487(21) | 0.242(2) | 0.65(1) | 0.5(1) | 0.9(1) | 3.08 |
| 10296163 | 9.296 847(4) | 15 271(760) | 3172(286) | 0.73(1) | 355(3) | 55918(132) | 0.016(4) | 0.26(1) | 1.4(4) | 0.5(1) | 0.13 |
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 10319590 | 21.321 16(6) | 452(2) | 330(11) | 0.146(4) | 316(2) | 54857(3) | 0.10(3) | 0.35(3) | 1.5(2) | 0.8(1) | 10.02 |
| 4078157 | 16.025 54(2) | 1377(26) | 736(66) | 0.480(8) | 70(3) | 54630(24) | 0.100 | 0.34(3) | 1.9(5) | 1.0(3) | 5.09 |
| 3345675: | 120.033(2) | 1662(94) | 671(336) | 0.39(2) | 95(65) | 54894(428) | 0.001 | 0.10(5) | 1.3(2.0) | 0.1(2) | 117.39 |
| 8143170 | 28.786 80 | 1710(35) | 864(21) | 0.704(6) | 108.7(9) | 54411(26) | 0.005(1) | 0.13(1) | 2.6(2) | 0.37(5) | 25.48 |
| 12356914 | 27.308 3183(3) | 1804(1) | 807(43) | 0.385(1) | 36.5(1) | 55860(1) | 0.0096(1) | 0.19(1) | 1.8(3) | 0.41(7) | 7.03 |
| 5003117 | 37.6094(2) | 2128(50) | 892(145) | 0.26(1) | 191(6) | 54750(49) | 0.06(1) | 0.33(6) | 1.4(7) | 0.7(4) | 6.32 |
| 6877673: | 36.759 691(6) | 2870(11) | 1112(254) | 0.468(2) | 155.5(5) | 54286(11) | 0.03(2) | 0.27(3) | 1.6(1.1) | 0.6(4) | 7.81 |
| 2576692 | 87.8797(1) | 2884(173) | 936(216) | 0.56(3) | 161(15) | 54277(213) | 0.000 04(2) | 0.032(5) | 1.3(9) | 0.04(3) | 33.85 |
| 7670617 | 24.703 17(4) | 3304(108) | 1054(30) | 0.707(7) | 86.4(9) | 55642(35) | 0.082(9) | 0.38(2) | 0.9(1) | 0.55(6) | 7.81 |
| 11502172: | 25.431 831(7) | 3313(58) | 1081(140) | 0.17(1) | 86(4) | 54359(47) | 0.020(3) | 0.25(3) | 1.2(5) | 0.4(2) | 0.83 |
| 9028474 | 124.935 73(1) | 3378(94) | 1258(421) | 0.09(2) | 242(8) | 54286(78) | 10(5)E−6 | 0.0163(4) | 2.3(1.2) | 0.04(2) | 44.23 |
| 9963009 | 40.0716(1) | 3770(10) | 1447(46) | 0.24(6) | 189(6) | 54074(79) | 0.111(7) | 0.41(1) | 1.7(2) | 1.2(1) | 2.98 |
| 11558882: | 73.9135(2) | 4050(50) | 1417(301) | 0.30(2) | 105(5) | 54919(80) | 0.016(7) | 0.19(3) | 1.9(1.2) | 0.4(3) | 7.16 |
| 4753988: | 7.304 51(1) | 5567(2325) | 1597(577) | 0.67(8) | 349(3) | 55359(238) | 0.007(9) | 0.20(3) | 1.4(1.9) | 0.4(5) | 0.13 |
| 10268809 | 24.708 43(1) | 7000(1000) | 2208(60) | 0.737(1) | 292.6(6) | 56147(169) | 0.32(10) | 0.48(2) | 1.5(5) | 1.4(4) | 2.66 |
| 4055092 | 76.464 532(9) | 11 548(88) | 2353(39) | 0.533(2) | 276.2(4) | 56487(21) | 0.242(2) | 0.65(1) | 0.5(1) | 0.9(1) | 3.08 |
| 10296163 | 9.296 847(4) | 15 271(760) | 3172(286) | 0.73(1) | 355(3) | 55918(132) | 0.016(4) | 0.26(1) | 1.4(4) | 0.5(1) | 0.13 |
Orbital elements from combined dynamical and LTTE solutions which cover less than a full outer period.
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 10319590 | 21.321 16(6) | 452(2) | 330(11) | 0.146(4) | 316(2) | 54857(3) | 0.10(3) | 0.35(3) | 1.5(2) | 0.8(1) | 10.02 |
| 4078157 | 16.025 54(2) | 1377(26) | 736(66) | 0.480(8) | 70(3) | 54630(24) | 0.100 | 0.34(3) | 1.9(5) | 1.0(3) | 5.09 |
| 3345675: | 120.033(2) | 1662(94) | 671(336) | 0.39(2) | 95(65) | 54894(428) | 0.001 | 0.10(5) | 1.3(2.0) | 0.1(2) | 117.39 |
| 8143170 | 28.786 80 | 1710(35) | 864(21) | 0.704(6) | 108.7(9) | 54411(26) | 0.005(1) | 0.13(1) | 2.6(2) | 0.37(5) | 25.48 |
| 12356914 | 27.308 3183(3) | 1804(1) | 807(43) | 0.385(1) | 36.5(1) | 55860(1) | 0.0096(1) | 0.19(1) | 1.8(3) | 0.41(7) | 7.03 |
| 5003117 | 37.6094(2) | 2128(50) | 892(145) | 0.26(1) | 191(6) | 54750(49) | 0.06(1) | 0.33(6) | 1.4(7) | 0.7(4) | 6.32 |
| 6877673: | 36.759 691(6) | 2870(11) | 1112(254) | 0.468(2) | 155.5(5) | 54286(11) | 0.03(2) | 0.27(3) | 1.6(1.1) | 0.6(4) | 7.81 |
| 2576692 | 87.8797(1) | 2884(173) | 936(216) | 0.56(3) | 161(15) | 54277(213) | 0.000 04(2) | 0.032(5) | 1.3(9) | 0.04(3) | 33.85 |
| 7670617 | 24.703 17(4) | 3304(108) | 1054(30) | 0.707(7) | 86.4(9) | 55642(35) | 0.082(9) | 0.38(2) | 0.9(1) | 0.55(6) | 7.81 |
| 11502172: | 25.431 831(7) | 3313(58) | 1081(140) | 0.17(1) | 86(4) | 54359(47) | 0.020(3) | 0.25(3) | 1.2(5) | 0.4(2) | 0.83 |
| 9028474 | 124.935 73(1) | 3378(94) | 1258(421) | 0.09(2) | 242(8) | 54286(78) | 10(5)E−6 | 0.0163(4) | 2.3(1.2) | 0.04(2) | 44.23 |
| 9963009 | 40.0716(1) | 3770(10) | 1447(46) | 0.24(6) | 189(6) | 54074(79) | 0.111(7) | 0.41(1) | 1.7(2) | 1.2(1) | 2.98 |
| 11558882: | 73.9135(2) | 4050(50) | 1417(301) | 0.30(2) | 105(5) | 54919(80) | 0.016(7) | 0.19(3) | 1.9(1.2) | 0.4(3) | 7.16 |
| 4753988: | 7.304 51(1) | 5567(2325) | 1597(577) | 0.67(8) | 349(3) | 55359(238) | 0.007(9) | 0.20(3) | 1.4(1.9) | 0.4(5) | 0.13 |
| 10268809 | 24.708 43(1) | 7000(1000) | 2208(60) | 0.737(1) | 292.6(6) | 56147(169) | 0.32(10) | 0.48(2) | 1.5(5) | 1.4(4) | 2.66 |
| 4055092 | 76.464 532(9) | 11 548(88) | 2353(39) | 0.533(2) | 276.2(4) | 56487(21) | 0.242(2) | 0.65(1) | 0.5(1) | 0.9(1) | 3.08 |
| 10296163 | 9.296 847(4) | 15 271(760) | 3172(286) | 0.73(1) | 355(3) | 55918(132) | 0.016(4) | 0.26(1) | 1.4(4) | 0.5(1) | 0.13 |
| KIC No. . | P1 . | P2 . | a2 . | e2 . | ω2 . | τ2 . | f(mC) . | |$\frac{m_\mathrm{C}}{m_\mathrm{ABC}}$| . | mAB . | mC . | |$\frac{{\cal {A}}^\mathrm{meas}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | (M⊙) . | . | . |
| 10319590 | 21.321 16(6) | 452(2) | 330(11) | 0.146(4) | 316(2) | 54857(3) | 0.10(3) | 0.35(3) | 1.5(2) | 0.8(1) | 10.02 |
| 4078157 | 16.025 54(2) | 1377(26) | 736(66) | 0.480(8) | 70(3) | 54630(24) | 0.100 | 0.34(3) | 1.9(5) | 1.0(3) | 5.09 |
| 3345675: | 120.033(2) | 1662(94) | 671(336) | 0.39(2) | 95(65) | 54894(428) | 0.001 | 0.10(5) | 1.3(2.0) | 0.1(2) | 117.39 |
| 8143170 | 28.786 80 | 1710(35) | 864(21) | 0.704(6) | 108.7(9) | 54411(26) | 0.005(1) | 0.13(1) | 2.6(2) | 0.37(5) | 25.48 |
| 12356914 | 27.308 3183(3) | 1804(1) | 807(43) | 0.385(1) | 36.5(1) | 55860(1) | 0.0096(1) | 0.19(1) | 1.8(3) | 0.41(7) | 7.03 |
| 5003117 | 37.6094(2) | 2128(50) | 892(145) | 0.26(1) | 191(6) | 54750(49) | 0.06(1) | 0.33(6) | 1.4(7) | 0.7(4) | 6.32 |
| 6877673: | 36.759 691(6) | 2870(11) | 1112(254) | 0.468(2) | 155.5(5) | 54286(11) | 0.03(2) | 0.27(3) | 1.6(1.1) | 0.6(4) | 7.81 |
| 2576692 | 87.8797(1) | 2884(173) | 936(216) | 0.56(3) | 161(15) | 54277(213) | 0.000 04(2) | 0.032(5) | 1.3(9) | 0.04(3) | 33.85 |
| 7670617 | 24.703 17(4) | 3304(108) | 1054(30) | 0.707(7) | 86.4(9) | 55642(35) | 0.082(9) | 0.38(2) | 0.9(1) | 0.55(6) | 7.81 |
| 11502172: | 25.431 831(7) | 3313(58) | 1081(140) | 0.17(1) | 86(4) | 54359(47) | 0.020(3) | 0.25(3) | 1.2(5) | 0.4(2) | 0.83 |
| 9028474 | 124.935 73(1) | 3378(94) | 1258(421) | 0.09(2) | 242(8) | 54286(78) | 10(5)E−6 | 0.0163(4) | 2.3(1.2) | 0.04(2) | 44.23 |
| 9963009 | 40.0716(1) | 3770(10) | 1447(46) | 0.24(6) | 189(6) | 54074(79) | 0.111(7) | 0.41(1) | 1.7(2) | 1.2(1) | 2.98 |
| 11558882: | 73.9135(2) | 4050(50) | 1417(301) | 0.30(2) | 105(5) | 54919(80) | 0.016(7) | 0.19(3) | 1.9(1.2) | 0.4(3) | 7.16 |
| 4753988: | 7.304 51(1) | 5567(2325) | 1597(577) | 0.67(8) | 349(3) | 55359(238) | 0.007(9) | 0.20(3) | 1.4(1.9) | 0.4(5) | 0.13 |
| 10268809 | 24.708 43(1) | 7000(1000) | 2208(60) | 0.737(1) | 292.6(6) | 56147(169) | 0.32(10) | 0.48(2) | 1.5(5) | 1.4(4) | 2.66 |
| 4055092 | 76.464 532(9) | 11 548(88) | 2353(39) | 0.533(2) | 276.2(4) | 56487(21) | 0.242(2) | 0.65(1) | 0.5(1) | 0.9(1) | 3.08 |
| 10296163 | 9.296 847(4) | 15 271(760) | 3172(286) | 0.73(1) | 355(3) | 55918(132) | 0.016(4) | 0.26(1) | 1.4(4) | 0.5(1) | 0.13 |
Orbital elements from LTTE solutions for systems which probably are oscillating variables instead of binaries (i.e. false positive EBs).
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10855535 | 0.112 782 41(1) | – | 411.9(2) | 61.4(2) | 0.096(5) | 296(3) | 55135(3) | 0.0183(1) | 0.48 | 0.006 | 2: |
| 0.056 391 21(1) | – | 411.9(2) | 60.6(2) | 0.106(8) | 292(4) | 55131(5) | 0.0176(2) | 0.48 | – | 2: | |
| 8045121 | 0.263 177 82(1) | – | 896(2) | 139(1) | 0.37(1) | 342(2) | 55237(6) | 0.045(1) | 0.69 | 0.001 | 2: |
| 0.131 588 91(1) | – | 896(3) | 140(2) | 0.37(2) | 342(3) | 55238(7) | 0.045(2) | 0.69 | – | 2: | |
| 8563964 | 0.338 435 76(2) | – | 1183(6) | 98.7(7) | 0.199(9) | 345(2) | 55035(7) | 0.0092(2) | 0.37 | 0.001 | 2: |
| 0.169 217 88(1) | – | 1184(6) | 98.7(7) | 0.196(9) | 345(2) | 55034(8) | 0.0092(2) | 0.37 | – | 2: | |
| 12508348 | 0.255 619(6) | −86(12) | 1839(472) | 789(235) | 0.36(9) | 218(3) | 55770(298) | 1.95(2.01) | 4.23 | 0.001 | 2: |
| 0.127 810(4) | −22(4) | 1814(618) | 754(319) | 0.30(13) | 213(5) | 55754(391) | 1.75(2.51) | 3.96 | – | 2: | |
| 11825204 | 0.209 6193(1) | 46.8(4) | 2230(236) | 107(9) | 0.75(3) | 297(2) | 55894(140) | 0.003(1) | 0.26 | 0.001 | 2: |
| 0.104 8096(2) | 11.8(2) | 2588(966) | 112(22) | 0.79(5) | 294(2) | 55887(488) | 0.003(3) | 0.24 | – | 2: | |
| 6287172 | 0.203 8728(2) | – | 3583(1875) | 365(159) | 0.95(3) | 170(2) | 56053(822) | 0.05(9) | 0.72 | 0.005 | 2: |
| 0.101 936 41(9) | – | 3320(1216) | 345(109) | 0.95(2) | 170(1) | 56052(575) | 0.05(6) | 0.72 | – | 2: | |
| 7375612 | 0.160 073 08(6) | – | 4417(835) | 287(46) | 0.41(7) | 306(4) | 55957(259) | 0.016(10) | 0.46 | 0.001 | 2: |
| 0.080 036 57(5) | – | 5859(2075) | 365(106) | 0.49(11) | 302(4) | 55938(478) | 0.019(21) | 0.49 | – | 2: | |
| 9612468 | 0.133 471 01(9) | – | 5307(1624) | 162(38) | 0.76(5) | 193(4) | 55450(225) | 0.002(2) | 0.22 | 0.001 | 2: |
| 0.066 735 54(5) | – | 4888(1842) | 133(38) | 0.75(7) | 192(5) | 55455(274) | 0.001(1) | 0.18 | – | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10855535 | 0.112 782 41(1) | – | 411.9(2) | 61.4(2) | 0.096(5) | 296(3) | 55135(3) | 0.0183(1) | 0.48 | 0.006 | 2: |
| 0.056 391 21(1) | – | 411.9(2) | 60.6(2) | 0.106(8) | 292(4) | 55131(5) | 0.0176(2) | 0.48 | – | 2: | |
| 8045121 | 0.263 177 82(1) | – | 896(2) | 139(1) | 0.37(1) | 342(2) | 55237(6) | 0.045(1) | 0.69 | 0.001 | 2: |
| 0.131 588 91(1) | – | 896(3) | 140(2) | 0.37(2) | 342(3) | 55238(7) | 0.045(2) | 0.69 | – | 2: | |
| 8563964 | 0.338 435 76(2) | – | 1183(6) | 98.7(7) | 0.199(9) | 345(2) | 55035(7) | 0.0092(2) | 0.37 | 0.001 | 2: |
| 0.169 217 88(1) | – | 1184(6) | 98.7(7) | 0.196(9) | 345(2) | 55034(8) | 0.0092(2) | 0.37 | – | 2: | |
| 12508348 | 0.255 619(6) | −86(12) | 1839(472) | 789(235) | 0.36(9) | 218(3) | 55770(298) | 1.95(2.01) | 4.23 | 0.001 | 2: |
| 0.127 810(4) | −22(4) | 1814(618) | 754(319) | 0.30(13) | 213(5) | 55754(391) | 1.75(2.51) | 3.96 | – | 2: | |
| 11825204 | 0.209 6193(1) | 46.8(4) | 2230(236) | 107(9) | 0.75(3) | 297(2) | 55894(140) | 0.003(1) | 0.26 | 0.001 | 2: |
| 0.104 8096(2) | 11.8(2) | 2588(966) | 112(22) | 0.79(5) | 294(2) | 55887(488) | 0.003(3) | 0.24 | – | 2: | |
| 6287172 | 0.203 8728(2) | – | 3583(1875) | 365(159) | 0.95(3) | 170(2) | 56053(822) | 0.05(9) | 0.72 | 0.005 | 2: |
| 0.101 936 41(9) | – | 3320(1216) | 345(109) | 0.95(2) | 170(1) | 56052(575) | 0.05(6) | 0.72 | – | 2: | |
| 7375612 | 0.160 073 08(6) | – | 4417(835) | 287(46) | 0.41(7) | 306(4) | 55957(259) | 0.016(10) | 0.46 | 0.001 | 2: |
| 0.080 036 57(5) | – | 5859(2075) | 365(106) | 0.49(11) | 302(4) | 55938(478) | 0.019(21) | 0.49 | – | 2: | |
| 9612468 | 0.133 471 01(9) | – | 5307(1624) | 162(38) | 0.76(5) | 193(4) | 55450(225) | 0.002(2) | 0.22 | 0.001 | 2: |
| 0.066 735 54(5) | – | 4888(1842) | 133(38) | 0.75(7) | 192(5) | 55455(274) | 0.001(1) | 0.18 | – | 2: |
Orbital elements from LTTE solutions for systems which probably are oscillating variables instead of binaries (i.e. false positive EBs).
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10855535 | 0.112 782 41(1) | – | 411.9(2) | 61.4(2) | 0.096(5) | 296(3) | 55135(3) | 0.0183(1) | 0.48 | 0.006 | 2: |
| 0.056 391 21(1) | – | 411.9(2) | 60.6(2) | 0.106(8) | 292(4) | 55131(5) | 0.0176(2) | 0.48 | – | 2: | |
| 8045121 | 0.263 177 82(1) | – | 896(2) | 139(1) | 0.37(1) | 342(2) | 55237(6) | 0.045(1) | 0.69 | 0.001 | 2: |
| 0.131 588 91(1) | – | 896(3) | 140(2) | 0.37(2) | 342(3) | 55238(7) | 0.045(2) | 0.69 | – | 2: | |
| 8563964 | 0.338 435 76(2) | – | 1183(6) | 98.7(7) | 0.199(9) | 345(2) | 55035(7) | 0.0092(2) | 0.37 | 0.001 | 2: |
| 0.169 217 88(1) | – | 1184(6) | 98.7(7) | 0.196(9) | 345(2) | 55034(8) | 0.0092(2) | 0.37 | – | 2: | |
| 12508348 | 0.255 619(6) | −86(12) | 1839(472) | 789(235) | 0.36(9) | 218(3) | 55770(298) | 1.95(2.01) | 4.23 | 0.001 | 2: |
| 0.127 810(4) | −22(4) | 1814(618) | 754(319) | 0.30(13) | 213(5) | 55754(391) | 1.75(2.51) | 3.96 | – | 2: | |
| 11825204 | 0.209 6193(1) | 46.8(4) | 2230(236) | 107(9) | 0.75(3) | 297(2) | 55894(140) | 0.003(1) | 0.26 | 0.001 | 2: |
| 0.104 8096(2) | 11.8(2) | 2588(966) | 112(22) | 0.79(5) | 294(2) | 55887(488) | 0.003(3) | 0.24 | – | 2: | |
| 6287172 | 0.203 8728(2) | – | 3583(1875) | 365(159) | 0.95(3) | 170(2) | 56053(822) | 0.05(9) | 0.72 | 0.005 | 2: |
| 0.101 936 41(9) | – | 3320(1216) | 345(109) | 0.95(2) | 170(1) | 56052(575) | 0.05(6) | 0.72 | – | 2: | |
| 7375612 | 0.160 073 08(6) | – | 4417(835) | 287(46) | 0.41(7) | 306(4) | 55957(259) | 0.016(10) | 0.46 | 0.001 | 2: |
| 0.080 036 57(5) | – | 5859(2075) | 365(106) | 0.49(11) | 302(4) | 55938(478) | 0.019(21) | 0.49 | – | 2: | |
| 9612468 | 0.133 471 01(9) | – | 5307(1624) | 162(38) | 0.76(5) | 193(4) | 55450(225) | 0.002(2) | 0.22 | 0.001 | 2: |
| 0.066 735 54(5) | – | 4888(1842) | 133(38) | 0.75(7) | 192(5) | 55455(274) | 0.001(1) | 0.18 | – | 2: |
| KIC No. . | P1 . | ΔP1 . | P2 . | aAB sin i2 . | e2 . | ω2 . | τ2 . | f(mC) . | (mC)min . | |$\frac{{\cal {A}}_\mathrm{dyn}}{{\cal {A}}_\mathrm{LTTE}}$| . | mAB . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | × 10−10 (d/c) . | (d) . | (R⊙) . | . | (deg) . | (BJD) . | (M⊙) . | (M⊙) . | . | (M⊙) . |
| 10855535 | 0.112 782 41(1) | – | 411.9(2) | 61.4(2) | 0.096(5) | 296(3) | 55135(3) | 0.0183(1) | 0.48 | 0.006 | 2: |
| 0.056 391 21(1) | – | 411.9(2) | 60.6(2) | 0.106(8) | 292(4) | 55131(5) | 0.0176(2) | 0.48 | – | 2: | |
| 8045121 | 0.263 177 82(1) | – | 896(2) | 139(1) | 0.37(1) | 342(2) | 55237(6) | 0.045(1) | 0.69 | 0.001 | 2: |
| 0.131 588 91(1) | – | 896(3) | 140(2) | 0.37(2) | 342(3) | 55238(7) | 0.045(2) | 0.69 | – | 2: | |
| 8563964 | 0.338 435 76(2) | – | 1183(6) | 98.7(7) | 0.199(9) | 345(2) | 55035(7) | 0.0092(2) | 0.37 | 0.001 | 2: |
| 0.169 217 88(1) | – | 1184(6) | 98.7(7) | 0.196(9) | 345(2) | 55034(8) | 0.0092(2) | 0.37 | – | 2: | |
| 12508348 | 0.255 619(6) | −86(12) | 1839(472) | 789(235) | 0.36(9) | 218(3) | 55770(298) | 1.95(2.01) | 4.23 | 0.001 | 2: |
| 0.127 810(4) | −22(4) | 1814(618) | 754(319) | 0.30(13) | 213(5) | 55754(391) | 1.75(2.51) | 3.96 | – | 2: | |
| 11825204 | 0.209 6193(1) | 46.8(4) | 2230(236) | 107(9) | 0.75(3) | 297(2) | 55894(140) | 0.003(1) | 0.26 | 0.001 | 2: |
| 0.104 8096(2) | 11.8(2) | 2588(966) | 112(22) | 0.79(5) | 294(2) | 55887(488) | 0.003(3) | 0.24 | – | 2: | |
| 6287172 | 0.203 8728(2) | – | 3583(1875) | 365(159) | 0.95(3) | 170(2) | 56053(822) | 0.05(9) | 0.72 | 0.005 | 2: |
| 0.101 936 41(9) | – | 3320(1216) | 345(109) | 0.95(2) | 170(1) | 56052(575) | 0.05(6) | 0.72 | – | 2: | |
| 7375612 | 0.160 073 08(6) | – | 4417(835) | 287(46) | 0.41(7) | 306(4) | 55957(259) | 0.016(10) | 0.46 | 0.001 | 2: |
| 0.080 036 57(5) | – | 5859(2075) | 365(106) | 0.49(11) | 302(4) | 55938(478) | 0.019(21) | 0.49 | – | 2: | |
| 9612468 | 0.133 471 01(9) | – | 5307(1624) | 162(38) | 0.76(5) | 193(4) | 55450(225) | 0.002(2) | 0.22 | 0.001 | 2: |
| 0.066 735 54(5) | – | 4888(1842) | 133(38) | 0.75(7) | 192(5) | 55455(274) | 0.001(1) | 0.18 | – | 2: |
| KIC No. . | Panom . | a1 . | e1 . | ω1 . | τ1 . | Papse . | im . | i1 . | i2 . | ΔΩ . | Pnode . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (R⊙) . | . | (deg) . | (MJD) . | (yr) . | (deg) . | (deg) . | (deg) . | (deg) . | (yr) . |
| 4758368 | 3.750(1) | – | 0.0043(5) | 4(69) | 54959.2(7) | 123(527) | |||||
| 5039441 | 2.151 385(8) | – | 0.01(4) | 283(42) | 54955.4(2) | 5286(18 159) | |||||
| 6233903 | 5.9910(2) | – | 0.006(15) | 290(48) | 55002.1(8) | 1690(4648) | |||||
| 6965293 | 5.077 754(6) | – | 0.020(7) | 239(12) | 54957.1(2) | 7095(4286) | |||||
| 2576692 | 87.8770(1) | 90(21) | 0.15(2) | 338(19) | 55040(4) | −7924 | 42(2) | 88 | 102 | 40(5) | 2118 |
| 3345675 | 120.054(2) | 112(57) | 0.11(4) | 279(97) | 55086(26) | 1820 | 24(19) | 86 | 62 | −1(27) | 348 |
| 3544694 | 3.847 8379(6) | 13.8(8) | 0.001 35(4) | 329(6) | 55741.28(6) | 19 | 0 | 84 | 84 | 0 | – |
| 4055092 | 76.460 808(9) | 58.5(1.1) | 0.345 15(7) | 309.53(1) | 54970.961(1) | −4298 | 54(1) | 88 | 119 | 46(1) | 6297 |
| 4078157 | 16.026 31(2) | 32.9(3.0) | 0.198(6) | 205(4) | 54958.3(1) | 913 | 10(3) | 84 | 75 | 5(14) | 697 |
| 4079530 | 17.727 46(8) | 33(26) | 0.2985(5) | 315(10) | 54996.0(3) | 2642(648) | 0 | 88 | 88 | 0 | – |
| 4753988 | 7.304 51(2) | 17.8(8.1) | 0.020(3) | 75(2) | 54971.35(6) | 21 051(37 135) | 47(7) | 84 | 53 | 38(7) | 40 986 |
| 4769799 | 21.9300(1) | 40.3(4.6) | 0.10(2) | 330(21) | 54972(1) | 805 | 22(2) | 86 | 69 | 14(10) | 826 |
| 4909707 | 2.302 3959(2) | 9.1(3) | 0.013(3) | 241(6) | 54953.74(4) | 503 | 6(1) | 88 | 87 | −6(1) | 471 |
| 4940201 | 8.817 798(1) | 20.6(1.8) | 0.0014(1) | 194(16) | 54965.4(4) | 172 | 6(2) | 85 | 86 | −6(2) | 139 |
| 4948863 | 8.643 6174(9) | 21.0(3.7) | 0.018 10(9) | 255 | 54972.5(3) | 3172 | 0 | 82 | 82 | 0 | – |
| 5003117 | 37.6141(2) | 53.0(8.8) | 0.14(3) | 309(10) | 54989.2(8) | 826 | 43(1) | 89 | 66 | 38(4) | 1484 |
| 5080652 | 4.1436 823(2) | 10.8(2.6) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 5095269 | 18.612 758(5) | 37.3(5.2) | 0.05(5) | 270(10) | 54966.9(5) | 1066 | 40(1) | 86 | 73 | 39(1) | 136 |
| 5255552 | 32.478 076(2) | 51.0(1.8) | 0.306 68(6) | 105.27(1) | 54956.79(1) | 227 | 6.4(1) | 83.8 | 89.5 | −2.8(1) | 140 |
| 5264818 | 1.905 0371(1) | 8.8(2.0) | 0 | – | – | – | 39(3) | 70(3) | 35 | 23(4) | 433 |
| 5384802 | 6.081 2488(3) | 16.7(8) | 0 | – | – | – | 5(3) | 83 | 78 | −0.8(7) | 65 |
| 5653126 | 38.508 48(5) | 58.1(3.1) | 0.247(6) | 313(1) | 54988.65(8) | 251 | 10(1) | 87 | 78 | −5(3) | 157 |
| 5731312 | 7.946 3939(2) | 17.2(1.7) | 0.4196(1) | 183.9(3) | 54967.198(5) | −5622 | 37.8(4) | 88.5 | 77.3 | 36.4(4) | 1013 |
| 5771589 | 10.7866(1) | 25.3(1.1) | 0.012 85(8) | 237.7(3) | 54961.139(9) | 6.53(2) | 7.9(8) | 86 | 82 | −6.9(8) | 7.5 |
| 5897826 | 1.7671(2) | 4.72(2) | 0.0223(4) | 269.5(4) | 55168.754(2) | 8 | 92.1 | 96.9 | 8.01(4) | ||
| 5952403 | 0.905 6768(2) | 4.78(4) | 0 | – | – | – | 0 | 87.5 | 87.5 | 0 | – |
| 6525196 | 3.420 5160(1) | 12.1(1.0) | 0 | – | – | – | 0a | 80 | 80 | 0 | – |
| 6531485 | 0.677 0720(1) | 3.5(2) | 0.0014(1) | 46(3) | 54965.056(6) | 15 | 0 | 80 | 80 | 0 | – |
| 6545018 | 3.991 4569(1) | 13.3(4) | 0.002 94(1) | 176.0(4) | 54964.796(4) | 27 | 0 | 86 | 86 | 0 | – |
| 6546508 | 6.107 205(6) | 12.0(1.9) | 0.002(2) | 65(27) | 55192.4(5) | 1172 | 0 | 86 | 86 | 0 | – |
| 6877673 | 36.759 92(4) | 54.8(12.6) | 0.180 38(3) | 57.196(6) | 55002.8378(9) | 16 411(2783) | 35(1) | 88 | 56 | 16(1) | 1998 |
| 6964043 | 10.737 21(2) | 26.0(2.7) | 0.0548(8) | 77.0(2) | 55195.103(6) | 27 | 19(1) | 91.2 | 89.5 | 19(1) | 26 |
| 7177553 | 17.9970(4) | 35.5(5.2) | 0.394 12(1) | 179.7(4) | 54952.23(1) | 1173(676) | 26(3) | 84 | 81 | 26(3) | 293 |
| 7289157 | 5.267 3864(4) | 14.1(4) | 0.0828(2) | 65.43(4) | 54972.1908(8) | 91 | 4.3(3) | 85.8 | 89.5 | 2.2(7) | 80 |
| 7593110 | 3.549 3317(3) | 11.4(6.0) | 0 | – | – | – | 30(13) | 82 | 77 | 30(13) | 536 |
| 7668648 | 27.865(5) | 45.0(4.4) | 0.08(1) | 85.7(8) | 54976.85(7) | 54(6) | 42(1) | 84 | 93 | −41(2) | 25 |
| 7670617 | 24.7049(1) | 34.3(1.3) | 0.249(5) | 135(1) | 54961.5(1) | 965(64) | 147.4(4) | 86 | 89 | −147.8(4) | −1678 |
| 7690843 | 0.786 1873(1) | 4.1(5) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 7812175 | 17.796 38(2) | 33.5(4.4) | 0.169(4) | 321(2) | 55004.44(7) | 311 | 17(2) | 85 | 79 | −16(2) | 176 |
| 7821010 | 24.238 246(2) | 46.4(2.0) | 0.6791b | 239.234(1) | 54969.3138(1) | 60 500(5000) | 25(1) | 88 | 105 | −19(2) | 618 |
| 7837302 | 23.838 59(6) | 40.9(22.7) | 0.15(5) | 314(6) | 54985.1(4) | 865 | 0 | 86 | 86 | 0 | – |
| 7955301 | 15.3713(6) | 33.8(3.9) | 0.028 86(8) | 115.5(7) | 54961.45(3) | 14.8(2) | 18.4(8) | 80 | 79 | −18.7(8) | 72(34) |
| 8023317 | 16.577 80(1) | 29.8(1.0) | 0.2511(2) | 177.7(9) | 54976.81(4) | −595 | 49.5(6) | 88 | 93 | −49.3(6) | 588 |
| 8143170 | 28.789 24(2) | 54.3(1.6) | 0.146(4) | 291.3(5) | 54971.38(3) | 929 | 38.5(3) | 89 | 114 | −30.5(3) | 890 |
| 8210721 | 22.677 27(4) | 40.2(1.7) | 0.140(1) | 158(1) | 54965.04(8) | 344 | 14(1) | 89.5 | 81.6 | −11(2) | 235 |
| 8719897 | 3.151 2989(1) | 10.1(5) | 0 | – | – | – | 0b | 80 | 80 | 0 | – |
| 8938628 | 6.862 8468(2) | 17.5(1.6) | 0.002 71(3) | 345(3) | 54968.04(6) | 199 | 14(1) | 87 | 80 | 12(1) | 170 |
| 9028474 | 124.934 03(2) | 139(24) | 0.805 75(5) | 2.2(3) | 55013.96(2) | −25 145 | 50.6(9) | 88 | 87 | −50.7(9) | 1557 |
| 9140402 | 4.981 371(6) | 91.(1.1) | 0 | – | – | – | 0 | 85 | 85 | 0 | – |
| 9451096 | 1.250 4286(1) | 5.6(6) | 0.000 67(1) | 181(8) | 54954.42(3) | 113 | 7(1) | 86 | 79 | −1(1) | 102 |
| 9664215 | 3.319 5565(8) | 10.8(1.4) | 0.02(1) | 96(3) | 54963.33(3) | 1371 | 0 | 86 | 86 | 0 | – |
| 9714358 | 6.474 2247(8) | 16.6(1.8) | 0.015 18(4) | 142.1(4) | 54965.109(7) | 30 | 0 | 83 | 83 | 0 | – |
| 9715925 | 6.308 231(3) | 12.6(2.2) | 0.201(8) | 355(18) | 55000.0(3) | −3182 | 37(2) | 83 | 76 | −37(2) | 1163 |
| 9963009 | 40.0714(1) | 58.7(1.9) | 0.22(10) | 258(5) | 54985.2(4) | −18 152 | 34(3) | 89.5 | 55.7 | 0(2) | 2703 |
| 10095512 | 6.017 5433(1) | 14.6(3.5) | 0.001 14(5) | 195(9) | 54952.6(1) | 294 | 0 | 83 | 83 | 0 | – |
| 10268809 | 24.709 35(5) | 41.3(4.1) | 0.314(2) | 143.1(3) | 54965.57(3) | 1830(99) | 23.7(4) | 84 | 94 | 21.6(4) | 3333 |
| 10296163 | 9.296 861(7) | 20.7(2.0) | 0.354(5) | 45.7(9) | 54962.00(4) | 16 784(7355) | 55(5) | 86 | 127 | −40(3) | 12 1561 |
| 10319590 | 21.339 46(6) | 37.3(1.4) | 0.0256(5) | 247.7(4) | 54964.45(2) | 68 | 40.2(4) | 88 | 102 | 38.0(5) | 110 |
| 10483644 | 5.110 517(2) | 15.0(6.9) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10549576 | 9.089 58(3) | 26.0(14.7) | 0.004 19(7) | 355(5) | 54974.2(1) | 1985 | 0 | 89 | 89 | 0 | – |
| 10613718 | 1.175 7655(1) | 4.1(4) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10979716 | 10.684 099(2) | 21.2(3) | 0.0753(8) | 106.0(2) | 54962.300(6) | 755 | 9(1) | 86 | 77 | 0(1) | 616 |
| 11502172 | 25.431 970(7) | 38.2(5.0) | 0.100 74(2) | 334(10) | 54972.4(6) | 12 746 | 26(1) | 88 | 110 | 15(2) | 5700 |
| 11519226 | 22.163 175(7) | 37.5(4) | 0.187 18(4) | 358.4(9) | 54977.11(5) | 955 | 17.0(4) | 88 | 89 | 17.0(4) | 510 |
| 11558882 | 73.9103(2) | 91.6(19.5) | 0.365(4) | 169(3) | 54975.8(6) | −4653 | 43(3) | 88 | 84 | −43(3) | 2702 |
| 12356914 | 27.308 12(2) | 46.0(2.4) | 0.325(1) | 113.2(9) | 54966.0(1) | −10 309(1210) | 40.2(1) | 88 | 60 | −30.4(1) | 1329 |
| KIC No. . | Panom . | a1 . | e1 . | ω1 . | τ1 . | Papse . | im . | i1 . | i2 . | ΔΩ . | Pnode . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (R⊙) . | . | (deg) . | (MJD) . | (yr) . | (deg) . | (deg) . | (deg) . | (deg) . | (yr) . |
| 4758368 | 3.750(1) | – | 0.0043(5) | 4(69) | 54959.2(7) | 123(527) | |||||
| 5039441 | 2.151 385(8) | – | 0.01(4) | 283(42) | 54955.4(2) | 5286(18 159) | |||||
| 6233903 | 5.9910(2) | – | 0.006(15) | 290(48) | 55002.1(8) | 1690(4648) | |||||
| 6965293 | 5.077 754(6) | – | 0.020(7) | 239(12) | 54957.1(2) | 7095(4286) | |||||
| 2576692 | 87.8770(1) | 90(21) | 0.15(2) | 338(19) | 55040(4) | −7924 | 42(2) | 88 | 102 | 40(5) | 2118 |
| 3345675 | 120.054(2) | 112(57) | 0.11(4) | 279(97) | 55086(26) | 1820 | 24(19) | 86 | 62 | −1(27) | 348 |
| 3544694 | 3.847 8379(6) | 13.8(8) | 0.001 35(4) | 329(6) | 55741.28(6) | 19 | 0 | 84 | 84 | 0 | – |
| 4055092 | 76.460 808(9) | 58.5(1.1) | 0.345 15(7) | 309.53(1) | 54970.961(1) | −4298 | 54(1) | 88 | 119 | 46(1) | 6297 |
| 4078157 | 16.026 31(2) | 32.9(3.0) | 0.198(6) | 205(4) | 54958.3(1) | 913 | 10(3) | 84 | 75 | 5(14) | 697 |
| 4079530 | 17.727 46(8) | 33(26) | 0.2985(5) | 315(10) | 54996.0(3) | 2642(648) | 0 | 88 | 88 | 0 | – |
| 4753988 | 7.304 51(2) | 17.8(8.1) | 0.020(3) | 75(2) | 54971.35(6) | 21 051(37 135) | 47(7) | 84 | 53 | 38(7) | 40 986 |
| 4769799 | 21.9300(1) | 40.3(4.6) | 0.10(2) | 330(21) | 54972(1) | 805 | 22(2) | 86 | 69 | 14(10) | 826 |
| 4909707 | 2.302 3959(2) | 9.1(3) | 0.013(3) | 241(6) | 54953.74(4) | 503 | 6(1) | 88 | 87 | −6(1) | 471 |
| 4940201 | 8.817 798(1) | 20.6(1.8) | 0.0014(1) | 194(16) | 54965.4(4) | 172 | 6(2) | 85 | 86 | −6(2) | 139 |
| 4948863 | 8.643 6174(9) | 21.0(3.7) | 0.018 10(9) | 255 | 54972.5(3) | 3172 | 0 | 82 | 82 | 0 | – |
| 5003117 | 37.6141(2) | 53.0(8.8) | 0.14(3) | 309(10) | 54989.2(8) | 826 | 43(1) | 89 | 66 | 38(4) | 1484 |
| 5080652 | 4.1436 823(2) | 10.8(2.6) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 5095269 | 18.612 758(5) | 37.3(5.2) | 0.05(5) | 270(10) | 54966.9(5) | 1066 | 40(1) | 86 | 73 | 39(1) | 136 |
| 5255552 | 32.478 076(2) | 51.0(1.8) | 0.306 68(6) | 105.27(1) | 54956.79(1) | 227 | 6.4(1) | 83.8 | 89.5 | −2.8(1) | 140 |
| 5264818 | 1.905 0371(1) | 8.8(2.0) | 0 | – | – | – | 39(3) | 70(3) | 35 | 23(4) | 433 |
| 5384802 | 6.081 2488(3) | 16.7(8) | 0 | – | – | – | 5(3) | 83 | 78 | −0.8(7) | 65 |
| 5653126 | 38.508 48(5) | 58.1(3.1) | 0.247(6) | 313(1) | 54988.65(8) | 251 | 10(1) | 87 | 78 | −5(3) | 157 |
| 5731312 | 7.946 3939(2) | 17.2(1.7) | 0.4196(1) | 183.9(3) | 54967.198(5) | −5622 | 37.8(4) | 88.5 | 77.3 | 36.4(4) | 1013 |
| 5771589 | 10.7866(1) | 25.3(1.1) | 0.012 85(8) | 237.7(3) | 54961.139(9) | 6.53(2) | 7.9(8) | 86 | 82 | −6.9(8) | 7.5 |
| 5897826 | 1.7671(2) | 4.72(2) | 0.0223(4) | 269.5(4) | 55168.754(2) | 8 | 92.1 | 96.9 | 8.01(4) | ||
| 5952403 | 0.905 6768(2) | 4.78(4) | 0 | – | – | – | 0 | 87.5 | 87.5 | 0 | – |
| 6525196 | 3.420 5160(1) | 12.1(1.0) | 0 | – | – | – | 0a | 80 | 80 | 0 | – |
| 6531485 | 0.677 0720(1) | 3.5(2) | 0.0014(1) | 46(3) | 54965.056(6) | 15 | 0 | 80 | 80 | 0 | – |
| 6545018 | 3.991 4569(1) | 13.3(4) | 0.002 94(1) | 176.0(4) | 54964.796(4) | 27 | 0 | 86 | 86 | 0 | – |
| 6546508 | 6.107 205(6) | 12.0(1.9) | 0.002(2) | 65(27) | 55192.4(5) | 1172 | 0 | 86 | 86 | 0 | – |
| 6877673 | 36.759 92(4) | 54.8(12.6) | 0.180 38(3) | 57.196(6) | 55002.8378(9) | 16 411(2783) | 35(1) | 88 | 56 | 16(1) | 1998 |
| 6964043 | 10.737 21(2) | 26.0(2.7) | 0.0548(8) | 77.0(2) | 55195.103(6) | 27 | 19(1) | 91.2 | 89.5 | 19(1) | 26 |
| 7177553 | 17.9970(4) | 35.5(5.2) | 0.394 12(1) | 179.7(4) | 54952.23(1) | 1173(676) | 26(3) | 84 | 81 | 26(3) | 293 |
| 7289157 | 5.267 3864(4) | 14.1(4) | 0.0828(2) | 65.43(4) | 54972.1908(8) | 91 | 4.3(3) | 85.8 | 89.5 | 2.2(7) | 80 |
| 7593110 | 3.549 3317(3) | 11.4(6.0) | 0 | – | – | – | 30(13) | 82 | 77 | 30(13) | 536 |
| 7668648 | 27.865(5) | 45.0(4.4) | 0.08(1) | 85.7(8) | 54976.85(7) | 54(6) | 42(1) | 84 | 93 | −41(2) | 25 |
| 7670617 | 24.7049(1) | 34.3(1.3) | 0.249(5) | 135(1) | 54961.5(1) | 965(64) | 147.4(4) | 86 | 89 | −147.8(4) | −1678 |
| 7690843 | 0.786 1873(1) | 4.1(5) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 7812175 | 17.796 38(2) | 33.5(4.4) | 0.169(4) | 321(2) | 55004.44(7) | 311 | 17(2) | 85 | 79 | −16(2) | 176 |
| 7821010 | 24.238 246(2) | 46.4(2.0) | 0.6791b | 239.234(1) | 54969.3138(1) | 60 500(5000) | 25(1) | 88 | 105 | −19(2) | 618 |
| 7837302 | 23.838 59(6) | 40.9(22.7) | 0.15(5) | 314(6) | 54985.1(4) | 865 | 0 | 86 | 86 | 0 | – |
| 7955301 | 15.3713(6) | 33.8(3.9) | 0.028 86(8) | 115.5(7) | 54961.45(3) | 14.8(2) | 18.4(8) | 80 | 79 | −18.7(8) | 72(34) |
| 8023317 | 16.577 80(1) | 29.8(1.0) | 0.2511(2) | 177.7(9) | 54976.81(4) | −595 | 49.5(6) | 88 | 93 | −49.3(6) | 588 |
| 8143170 | 28.789 24(2) | 54.3(1.6) | 0.146(4) | 291.3(5) | 54971.38(3) | 929 | 38.5(3) | 89 | 114 | −30.5(3) | 890 |
| 8210721 | 22.677 27(4) | 40.2(1.7) | 0.140(1) | 158(1) | 54965.04(8) | 344 | 14(1) | 89.5 | 81.6 | −11(2) | 235 |
| 8719897 | 3.151 2989(1) | 10.1(5) | 0 | – | – | – | 0b | 80 | 80 | 0 | – |
| 8938628 | 6.862 8468(2) | 17.5(1.6) | 0.002 71(3) | 345(3) | 54968.04(6) | 199 | 14(1) | 87 | 80 | 12(1) | 170 |
| 9028474 | 124.934 03(2) | 139(24) | 0.805 75(5) | 2.2(3) | 55013.96(2) | −25 145 | 50.6(9) | 88 | 87 | −50.7(9) | 1557 |
| 9140402 | 4.981 371(6) | 91.(1.1) | 0 | – | – | – | 0 | 85 | 85 | 0 | – |
| 9451096 | 1.250 4286(1) | 5.6(6) | 0.000 67(1) | 181(8) | 54954.42(3) | 113 | 7(1) | 86 | 79 | −1(1) | 102 |
| 9664215 | 3.319 5565(8) | 10.8(1.4) | 0.02(1) | 96(3) | 54963.33(3) | 1371 | 0 | 86 | 86 | 0 | – |
| 9714358 | 6.474 2247(8) | 16.6(1.8) | 0.015 18(4) | 142.1(4) | 54965.109(7) | 30 | 0 | 83 | 83 | 0 | – |
| 9715925 | 6.308 231(3) | 12.6(2.2) | 0.201(8) | 355(18) | 55000.0(3) | −3182 | 37(2) | 83 | 76 | −37(2) | 1163 |
| 9963009 | 40.0714(1) | 58.7(1.9) | 0.22(10) | 258(5) | 54985.2(4) | −18 152 | 34(3) | 89.5 | 55.7 | 0(2) | 2703 |
| 10095512 | 6.017 5433(1) | 14.6(3.5) | 0.001 14(5) | 195(9) | 54952.6(1) | 294 | 0 | 83 | 83 | 0 | – |
| 10268809 | 24.709 35(5) | 41.3(4.1) | 0.314(2) | 143.1(3) | 54965.57(3) | 1830(99) | 23.7(4) | 84 | 94 | 21.6(4) | 3333 |
| 10296163 | 9.296 861(7) | 20.7(2.0) | 0.354(5) | 45.7(9) | 54962.00(4) | 16 784(7355) | 55(5) | 86 | 127 | −40(3) | 12 1561 |
| 10319590 | 21.339 46(6) | 37.3(1.4) | 0.0256(5) | 247.7(4) | 54964.45(2) | 68 | 40.2(4) | 88 | 102 | 38.0(5) | 110 |
| 10483644 | 5.110 517(2) | 15.0(6.9) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10549576 | 9.089 58(3) | 26.0(14.7) | 0.004 19(7) | 355(5) | 54974.2(1) | 1985 | 0 | 89 | 89 | 0 | – |
| 10613718 | 1.175 7655(1) | 4.1(4) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10979716 | 10.684 099(2) | 21.2(3) | 0.0753(8) | 106.0(2) | 54962.300(6) | 755 | 9(1) | 86 | 77 | 0(1) | 616 |
| 11502172 | 25.431 970(7) | 38.2(5.0) | 0.100 74(2) | 334(10) | 54972.4(6) | 12 746 | 26(1) | 88 | 110 | 15(2) | 5700 |
| 11519226 | 22.163 175(7) | 37.5(4) | 0.187 18(4) | 358.4(9) | 54977.11(5) | 955 | 17.0(4) | 88 | 89 | 17.0(4) | 510 |
| 11558882 | 73.9103(2) | 91.6(19.5) | 0.365(4) | 169(3) | 54975.8(6) | −4653 | 43(3) | 88 | 84 | −43(3) | 2702 |
| 12356914 | 27.308 12(2) | 46.0(2.4) | 0.325(1) | 113.2(9) | 54966.0(1) | −10 309(1210) | 40.2(1) | 88 | 60 | −30.4(1) | 1329 |
Notes.aAdjusted mutual inclination resulted in |$i_\mathrm{m}=25\deg \pm 2\deg$| which would lead to |$\Delta i_1\sim 1\deg$| during Kepler observations and consequently, significant eclipse depth variations which is not the case.
be1 was kept fixed on the radial velocity solution result of Fabrycky et al. (in preparation).
cAdjusted mutual inclination resulted in |$i_\mathrm{m}=23\deg \pm 2\deg$| which would lead to Δi1 ∼ 1| $_{.}^{\circ}$|7 during Kepler observations and consequently, significant eclipse depth variations which is not the case.
| KIC No. . | Panom . | a1 . | e1 . | ω1 . | τ1 . | Papse . | im . | i1 . | i2 . | ΔΩ . | Pnode . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (R⊙) . | . | (deg) . | (MJD) . | (yr) . | (deg) . | (deg) . | (deg) . | (deg) . | (yr) . |
| 4758368 | 3.750(1) | – | 0.0043(5) | 4(69) | 54959.2(7) | 123(527) | |||||
| 5039441 | 2.151 385(8) | – | 0.01(4) | 283(42) | 54955.4(2) | 5286(18 159) | |||||
| 6233903 | 5.9910(2) | – | 0.006(15) | 290(48) | 55002.1(8) | 1690(4648) | |||||
| 6965293 | 5.077 754(6) | – | 0.020(7) | 239(12) | 54957.1(2) | 7095(4286) | |||||
| 2576692 | 87.8770(1) | 90(21) | 0.15(2) | 338(19) | 55040(4) | −7924 | 42(2) | 88 | 102 | 40(5) | 2118 |
| 3345675 | 120.054(2) | 112(57) | 0.11(4) | 279(97) | 55086(26) | 1820 | 24(19) | 86 | 62 | −1(27) | 348 |
| 3544694 | 3.847 8379(6) | 13.8(8) | 0.001 35(4) | 329(6) | 55741.28(6) | 19 | 0 | 84 | 84 | 0 | – |
| 4055092 | 76.460 808(9) | 58.5(1.1) | 0.345 15(7) | 309.53(1) | 54970.961(1) | −4298 | 54(1) | 88 | 119 | 46(1) | 6297 |
| 4078157 | 16.026 31(2) | 32.9(3.0) | 0.198(6) | 205(4) | 54958.3(1) | 913 | 10(3) | 84 | 75 | 5(14) | 697 |
| 4079530 | 17.727 46(8) | 33(26) | 0.2985(5) | 315(10) | 54996.0(3) | 2642(648) | 0 | 88 | 88 | 0 | – |
| 4753988 | 7.304 51(2) | 17.8(8.1) | 0.020(3) | 75(2) | 54971.35(6) | 21 051(37 135) | 47(7) | 84 | 53 | 38(7) | 40 986 |
| 4769799 | 21.9300(1) | 40.3(4.6) | 0.10(2) | 330(21) | 54972(1) | 805 | 22(2) | 86 | 69 | 14(10) | 826 |
| 4909707 | 2.302 3959(2) | 9.1(3) | 0.013(3) | 241(6) | 54953.74(4) | 503 | 6(1) | 88 | 87 | −6(1) | 471 |
| 4940201 | 8.817 798(1) | 20.6(1.8) | 0.0014(1) | 194(16) | 54965.4(4) | 172 | 6(2) | 85 | 86 | −6(2) | 139 |
| 4948863 | 8.643 6174(9) | 21.0(3.7) | 0.018 10(9) | 255 | 54972.5(3) | 3172 | 0 | 82 | 82 | 0 | – |
| 5003117 | 37.6141(2) | 53.0(8.8) | 0.14(3) | 309(10) | 54989.2(8) | 826 | 43(1) | 89 | 66 | 38(4) | 1484 |
| 5080652 | 4.1436 823(2) | 10.8(2.6) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 5095269 | 18.612 758(5) | 37.3(5.2) | 0.05(5) | 270(10) | 54966.9(5) | 1066 | 40(1) | 86 | 73 | 39(1) | 136 |
| 5255552 | 32.478 076(2) | 51.0(1.8) | 0.306 68(6) | 105.27(1) | 54956.79(1) | 227 | 6.4(1) | 83.8 | 89.5 | −2.8(1) | 140 |
| 5264818 | 1.905 0371(1) | 8.8(2.0) | 0 | – | – | – | 39(3) | 70(3) | 35 | 23(4) | 433 |
| 5384802 | 6.081 2488(3) | 16.7(8) | 0 | – | – | – | 5(3) | 83 | 78 | −0.8(7) | 65 |
| 5653126 | 38.508 48(5) | 58.1(3.1) | 0.247(6) | 313(1) | 54988.65(8) | 251 | 10(1) | 87 | 78 | −5(3) | 157 |
| 5731312 | 7.946 3939(2) | 17.2(1.7) | 0.4196(1) | 183.9(3) | 54967.198(5) | −5622 | 37.8(4) | 88.5 | 77.3 | 36.4(4) | 1013 |
| 5771589 | 10.7866(1) | 25.3(1.1) | 0.012 85(8) | 237.7(3) | 54961.139(9) | 6.53(2) | 7.9(8) | 86 | 82 | −6.9(8) | 7.5 |
| 5897826 | 1.7671(2) | 4.72(2) | 0.0223(4) | 269.5(4) | 55168.754(2) | 8 | 92.1 | 96.9 | 8.01(4) | ||
| 5952403 | 0.905 6768(2) | 4.78(4) | 0 | – | – | – | 0 | 87.5 | 87.5 | 0 | – |
| 6525196 | 3.420 5160(1) | 12.1(1.0) | 0 | – | – | – | 0a | 80 | 80 | 0 | – |
| 6531485 | 0.677 0720(1) | 3.5(2) | 0.0014(1) | 46(3) | 54965.056(6) | 15 | 0 | 80 | 80 | 0 | – |
| 6545018 | 3.991 4569(1) | 13.3(4) | 0.002 94(1) | 176.0(4) | 54964.796(4) | 27 | 0 | 86 | 86 | 0 | – |
| 6546508 | 6.107 205(6) | 12.0(1.9) | 0.002(2) | 65(27) | 55192.4(5) | 1172 | 0 | 86 | 86 | 0 | – |
| 6877673 | 36.759 92(4) | 54.8(12.6) | 0.180 38(3) | 57.196(6) | 55002.8378(9) | 16 411(2783) | 35(1) | 88 | 56 | 16(1) | 1998 |
| 6964043 | 10.737 21(2) | 26.0(2.7) | 0.0548(8) | 77.0(2) | 55195.103(6) | 27 | 19(1) | 91.2 | 89.5 | 19(1) | 26 |
| 7177553 | 17.9970(4) | 35.5(5.2) | 0.394 12(1) | 179.7(4) | 54952.23(1) | 1173(676) | 26(3) | 84 | 81 | 26(3) | 293 |
| 7289157 | 5.267 3864(4) | 14.1(4) | 0.0828(2) | 65.43(4) | 54972.1908(8) | 91 | 4.3(3) | 85.8 | 89.5 | 2.2(7) | 80 |
| 7593110 | 3.549 3317(3) | 11.4(6.0) | 0 | – | – | – | 30(13) | 82 | 77 | 30(13) | 536 |
| 7668648 | 27.865(5) | 45.0(4.4) | 0.08(1) | 85.7(8) | 54976.85(7) | 54(6) | 42(1) | 84 | 93 | −41(2) | 25 |
| 7670617 | 24.7049(1) | 34.3(1.3) | 0.249(5) | 135(1) | 54961.5(1) | 965(64) | 147.4(4) | 86 | 89 | −147.8(4) | −1678 |
| 7690843 | 0.786 1873(1) | 4.1(5) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 7812175 | 17.796 38(2) | 33.5(4.4) | 0.169(4) | 321(2) | 55004.44(7) | 311 | 17(2) | 85 | 79 | −16(2) | 176 |
| 7821010 | 24.238 246(2) | 46.4(2.0) | 0.6791b | 239.234(1) | 54969.3138(1) | 60 500(5000) | 25(1) | 88 | 105 | −19(2) | 618 |
| 7837302 | 23.838 59(6) | 40.9(22.7) | 0.15(5) | 314(6) | 54985.1(4) | 865 | 0 | 86 | 86 | 0 | – |
| 7955301 | 15.3713(6) | 33.8(3.9) | 0.028 86(8) | 115.5(7) | 54961.45(3) | 14.8(2) | 18.4(8) | 80 | 79 | −18.7(8) | 72(34) |
| 8023317 | 16.577 80(1) | 29.8(1.0) | 0.2511(2) | 177.7(9) | 54976.81(4) | −595 | 49.5(6) | 88 | 93 | −49.3(6) | 588 |
| 8143170 | 28.789 24(2) | 54.3(1.6) | 0.146(4) | 291.3(5) | 54971.38(3) | 929 | 38.5(3) | 89 | 114 | −30.5(3) | 890 |
| 8210721 | 22.677 27(4) | 40.2(1.7) | 0.140(1) | 158(1) | 54965.04(8) | 344 | 14(1) | 89.5 | 81.6 | −11(2) | 235 |
| 8719897 | 3.151 2989(1) | 10.1(5) | 0 | – | – | – | 0b | 80 | 80 | 0 | – |
| 8938628 | 6.862 8468(2) | 17.5(1.6) | 0.002 71(3) | 345(3) | 54968.04(6) | 199 | 14(1) | 87 | 80 | 12(1) | 170 |
| 9028474 | 124.934 03(2) | 139(24) | 0.805 75(5) | 2.2(3) | 55013.96(2) | −25 145 | 50.6(9) | 88 | 87 | −50.7(9) | 1557 |
| 9140402 | 4.981 371(6) | 91.(1.1) | 0 | – | – | – | 0 | 85 | 85 | 0 | – |
| 9451096 | 1.250 4286(1) | 5.6(6) | 0.000 67(1) | 181(8) | 54954.42(3) | 113 | 7(1) | 86 | 79 | −1(1) | 102 |
| 9664215 | 3.319 5565(8) | 10.8(1.4) | 0.02(1) | 96(3) | 54963.33(3) | 1371 | 0 | 86 | 86 | 0 | – |
| 9714358 | 6.474 2247(8) | 16.6(1.8) | 0.015 18(4) | 142.1(4) | 54965.109(7) | 30 | 0 | 83 | 83 | 0 | – |
| 9715925 | 6.308 231(3) | 12.6(2.2) | 0.201(8) | 355(18) | 55000.0(3) | −3182 | 37(2) | 83 | 76 | −37(2) | 1163 |
| 9963009 | 40.0714(1) | 58.7(1.9) | 0.22(10) | 258(5) | 54985.2(4) | −18 152 | 34(3) | 89.5 | 55.7 | 0(2) | 2703 |
| 10095512 | 6.017 5433(1) | 14.6(3.5) | 0.001 14(5) | 195(9) | 54952.6(1) | 294 | 0 | 83 | 83 | 0 | – |
| 10268809 | 24.709 35(5) | 41.3(4.1) | 0.314(2) | 143.1(3) | 54965.57(3) | 1830(99) | 23.7(4) | 84 | 94 | 21.6(4) | 3333 |
| 10296163 | 9.296 861(7) | 20.7(2.0) | 0.354(5) | 45.7(9) | 54962.00(4) | 16 784(7355) | 55(5) | 86 | 127 | −40(3) | 12 1561 |
| 10319590 | 21.339 46(6) | 37.3(1.4) | 0.0256(5) | 247.7(4) | 54964.45(2) | 68 | 40.2(4) | 88 | 102 | 38.0(5) | 110 |
| 10483644 | 5.110 517(2) | 15.0(6.9) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10549576 | 9.089 58(3) | 26.0(14.7) | 0.004 19(7) | 355(5) | 54974.2(1) | 1985 | 0 | 89 | 89 | 0 | – |
| 10613718 | 1.175 7655(1) | 4.1(4) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10979716 | 10.684 099(2) | 21.2(3) | 0.0753(8) | 106.0(2) | 54962.300(6) | 755 | 9(1) | 86 | 77 | 0(1) | 616 |
| 11502172 | 25.431 970(7) | 38.2(5.0) | 0.100 74(2) | 334(10) | 54972.4(6) | 12 746 | 26(1) | 88 | 110 | 15(2) | 5700 |
| 11519226 | 22.163 175(7) | 37.5(4) | 0.187 18(4) | 358.4(9) | 54977.11(5) | 955 | 17.0(4) | 88 | 89 | 17.0(4) | 510 |
| 11558882 | 73.9103(2) | 91.6(19.5) | 0.365(4) | 169(3) | 54975.8(6) | −4653 | 43(3) | 88 | 84 | −43(3) | 2702 |
| 12356914 | 27.308 12(2) | 46.0(2.4) | 0.325(1) | 113.2(9) | 54966.0(1) | −10 309(1210) | 40.2(1) | 88 | 60 | −30.4(1) | 1329 |
| KIC No. . | Panom . | a1 . | e1 . | ω1 . | τ1 . | Papse . | im . | i1 . | i2 . | ΔΩ . | Pnode . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| . | (d) . | (R⊙) . | . | (deg) . | (MJD) . | (yr) . | (deg) . | (deg) . | (deg) . | (deg) . | (yr) . |
| 4758368 | 3.750(1) | – | 0.0043(5) | 4(69) | 54959.2(7) | 123(527) | |||||
| 5039441 | 2.151 385(8) | – | 0.01(4) | 283(42) | 54955.4(2) | 5286(18 159) | |||||
| 6233903 | 5.9910(2) | – | 0.006(15) | 290(48) | 55002.1(8) | 1690(4648) | |||||
| 6965293 | 5.077 754(6) | – | 0.020(7) | 239(12) | 54957.1(2) | 7095(4286) | |||||
| 2576692 | 87.8770(1) | 90(21) | 0.15(2) | 338(19) | 55040(4) | −7924 | 42(2) | 88 | 102 | 40(5) | 2118 |
| 3345675 | 120.054(2) | 112(57) | 0.11(4) | 279(97) | 55086(26) | 1820 | 24(19) | 86 | 62 | −1(27) | 348 |
| 3544694 | 3.847 8379(6) | 13.8(8) | 0.001 35(4) | 329(6) | 55741.28(6) | 19 | 0 | 84 | 84 | 0 | – |
| 4055092 | 76.460 808(9) | 58.5(1.1) | 0.345 15(7) | 309.53(1) | 54970.961(1) | −4298 | 54(1) | 88 | 119 | 46(1) | 6297 |
| 4078157 | 16.026 31(2) | 32.9(3.0) | 0.198(6) | 205(4) | 54958.3(1) | 913 | 10(3) | 84 | 75 | 5(14) | 697 |
| 4079530 | 17.727 46(8) | 33(26) | 0.2985(5) | 315(10) | 54996.0(3) | 2642(648) | 0 | 88 | 88 | 0 | – |
| 4753988 | 7.304 51(2) | 17.8(8.1) | 0.020(3) | 75(2) | 54971.35(6) | 21 051(37 135) | 47(7) | 84 | 53 | 38(7) | 40 986 |
| 4769799 | 21.9300(1) | 40.3(4.6) | 0.10(2) | 330(21) | 54972(1) | 805 | 22(2) | 86 | 69 | 14(10) | 826 |
| 4909707 | 2.302 3959(2) | 9.1(3) | 0.013(3) | 241(6) | 54953.74(4) | 503 | 6(1) | 88 | 87 | −6(1) | 471 |
| 4940201 | 8.817 798(1) | 20.6(1.8) | 0.0014(1) | 194(16) | 54965.4(4) | 172 | 6(2) | 85 | 86 | −6(2) | 139 |
| 4948863 | 8.643 6174(9) | 21.0(3.7) | 0.018 10(9) | 255 | 54972.5(3) | 3172 | 0 | 82 | 82 | 0 | – |
| 5003117 | 37.6141(2) | 53.0(8.8) | 0.14(3) | 309(10) | 54989.2(8) | 826 | 43(1) | 89 | 66 | 38(4) | 1484 |
| 5080652 | 4.1436 823(2) | 10.8(2.6) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 5095269 | 18.612 758(5) | 37.3(5.2) | 0.05(5) | 270(10) | 54966.9(5) | 1066 | 40(1) | 86 | 73 | 39(1) | 136 |
| 5255552 | 32.478 076(2) | 51.0(1.8) | 0.306 68(6) | 105.27(1) | 54956.79(1) | 227 | 6.4(1) | 83.8 | 89.5 | −2.8(1) | 140 |
| 5264818 | 1.905 0371(1) | 8.8(2.0) | 0 | – | – | – | 39(3) | 70(3) | 35 | 23(4) | 433 |
| 5384802 | 6.081 2488(3) | 16.7(8) | 0 | – | – | – | 5(3) | 83 | 78 | −0.8(7) | 65 |
| 5653126 | 38.508 48(5) | 58.1(3.1) | 0.247(6) | 313(1) | 54988.65(8) | 251 | 10(1) | 87 | 78 | −5(3) | 157 |
| 5731312 | 7.946 3939(2) | 17.2(1.7) | 0.4196(1) | 183.9(3) | 54967.198(5) | −5622 | 37.8(4) | 88.5 | 77.3 | 36.4(4) | 1013 |
| 5771589 | 10.7866(1) | 25.3(1.1) | 0.012 85(8) | 237.7(3) | 54961.139(9) | 6.53(2) | 7.9(8) | 86 | 82 | −6.9(8) | 7.5 |
| 5897826 | 1.7671(2) | 4.72(2) | 0.0223(4) | 269.5(4) | 55168.754(2) | 8 | 92.1 | 96.9 | 8.01(4) | ||
| 5952403 | 0.905 6768(2) | 4.78(4) | 0 | – | – | – | 0 | 87.5 | 87.5 | 0 | – |
| 6525196 | 3.420 5160(1) | 12.1(1.0) | 0 | – | – | – | 0a | 80 | 80 | 0 | – |
| 6531485 | 0.677 0720(1) | 3.5(2) | 0.0014(1) | 46(3) | 54965.056(6) | 15 | 0 | 80 | 80 | 0 | – |
| 6545018 | 3.991 4569(1) | 13.3(4) | 0.002 94(1) | 176.0(4) | 54964.796(4) | 27 | 0 | 86 | 86 | 0 | – |
| 6546508 | 6.107 205(6) | 12.0(1.9) | 0.002(2) | 65(27) | 55192.4(5) | 1172 | 0 | 86 | 86 | 0 | – |
| 6877673 | 36.759 92(4) | 54.8(12.6) | 0.180 38(3) | 57.196(6) | 55002.8378(9) | 16 411(2783) | 35(1) | 88 | 56 | 16(1) | 1998 |
| 6964043 | 10.737 21(2) | 26.0(2.7) | 0.0548(8) | 77.0(2) | 55195.103(6) | 27 | 19(1) | 91.2 | 89.5 | 19(1) | 26 |
| 7177553 | 17.9970(4) | 35.5(5.2) | 0.394 12(1) | 179.7(4) | 54952.23(1) | 1173(676) | 26(3) | 84 | 81 | 26(3) | 293 |
| 7289157 | 5.267 3864(4) | 14.1(4) | 0.0828(2) | 65.43(4) | 54972.1908(8) | 91 | 4.3(3) | 85.8 | 89.5 | 2.2(7) | 80 |
| 7593110 | 3.549 3317(3) | 11.4(6.0) | 0 | – | – | – | 30(13) | 82 | 77 | 30(13) | 536 |
| 7668648 | 27.865(5) | 45.0(4.4) | 0.08(1) | 85.7(8) | 54976.85(7) | 54(6) | 42(1) | 84 | 93 | −41(2) | 25 |
| 7670617 | 24.7049(1) | 34.3(1.3) | 0.249(5) | 135(1) | 54961.5(1) | 965(64) | 147.4(4) | 86 | 89 | −147.8(4) | −1678 |
| 7690843 | 0.786 1873(1) | 4.1(5) | 0 | – | – | – | 0 | 80 | 80 | 0 | – |
| 7812175 | 17.796 38(2) | 33.5(4.4) | 0.169(4) | 321(2) | 55004.44(7) | 311 | 17(2) | 85 | 79 | −16(2) | 176 |
| 7821010 | 24.238 246(2) | 46.4(2.0) | 0.6791b | 239.234(1) | 54969.3138(1) | 60 500(5000) | 25(1) | 88 | 105 | −19(2) | 618 |
| 7837302 | 23.838 59(6) | 40.9(22.7) | 0.15(5) | 314(6) | 54985.1(4) | 865 | 0 | 86 | 86 | 0 | – |
| 7955301 | 15.3713(6) | 33.8(3.9) | 0.028 86(8) | 115.5(7) | 54961.45(3) | 14.8(2) | 18.4(8) | 80 | 79 | −18.7(8) | 72(34) |
| 8023317 | 16.577 80(1) | 29.8(1.0) | 0.2511(2) | 177.7(9) | 54976.81(4) | −595 | 49.5(6) | 88 | 93 | −49.3(6) | 588 |
| 8143170 | 28.789 24(2) | 54.3(1.6) | 0.146(4) | 291.3(5) | 54971.38(3) | 929 | 38.5(3) | 89 | 114 | −30.5(3) | 890 |
| 8210721 | 22.677 27(4) | 40.2(1.7) | 0.140(1) | 158(1) | 54965.04(8) | 344 | 14(1) | 89.5 | 81.6 | −11(2) | 235 |
| 8719897 | 3.151 2989(1) | 10.1(5) | 0 | – | – | – | 0b | 80 | 80 | 0 | – |
| 8938628 | 6.862 8468(2) | 17.5(1.6) | 0.002 71(3) | 345(3) | 54968.04(6) | 199 | 14(1) | 87 | 80 | 12(1) | 170 |
| 9028474 | 124.934 03(2) | 139(24) | 0.805 75(5) | 2.2(3) | 55013.96(2) | −25 145 | 50.6(9) | 88 | 87 | −50.7(9) | 1557 |
| 9140402 | 4.981 371(6) | 91.(1.1) | 0 | – | – | – | 0 | 85 | 85 | 0 | – |
| 9451096 | 1.250 4286(1) | 5.6(6) | 0.000 67(1) | 181(8) | 54954.42(3) | 113 | 7(1) | 86 | 79 | −1(1) | 102 |
| 9664215 | 3.319 5565(8) | 10.8(1.4) | 0.02(1) | 96(3) | 54963.33(3) | 1371 | 0 | 86 | 86 | 0 | – |
| 9714358 | 6.474 2247(8) | 16.6(1.8) | 0.015 18(4) | 142.1(4) | 54965.109(7) | 30 | 0 | 83 | 83 | 0 | – |
| 9715925 | 6.308 231(3) | 12.6(2.2) | 0.201(8) | 355(18) | 55000.0(3) | −3182 | 37(2) | 83 | 76 | −37(2) | 1163 |
| 9963009 | 40.0714(1) | 58.7(1.9) | 0.22(10) | 258(5) | 54985.2(4) | −18 152 | 34(3) | 89.5 | 55.7 | 0(2) | 2703 |
| 10095512 | 6.017 5433(1) | 14.6(3.5) | 0.001 14(5) | 195(9) | 54952.6(1) | 294 | 0 | 83 | 83 | 0 | – |
| 10268809 | 24.709 35(5) | 41.3(4.1) | 0.314(2) | 143.1(3) | 54965.57(3) | 1830(99) | 23.7(4) | 84 | 94 | 21.6(4) | 3333 |
| 10296163 | 9.296 861(7) | 20.7(2.0) | 0.354(5) | 45.7(9) | 54962.00(4) | 16 784(7355) | 55(5) | 86 | 127 | −40(3) | 12 1561 |
| 10319590 | 21.339 46(6) | 37.3(1.4) | 0.0256(5) | 247.7(4) | 54964.45(2) | 68 | 40.2(4) | 88 | 102 | 38.0(5) | 110 |
| 10483644 | 5.110 517(2) | 15.0(6.9) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10549576 | 9.089 58(3) | 26.0(14.7) | 0.004 19(7) | 355(5) | 54974.2(1) | 1985 | 0 | 89 | 89 | 0 | – |
| 10613718 | 1.175 7655(1) | 4.1(4) | 0 | – | – | – | 0 | 86 | 86 | 0 | – |
| 10979716 | 10.684 099(2) | 21.2(3) | 0.0753(8) | 106.0(2) | 54962.300(6) | 755 | 9(1) | 86 | 77 | 0(1) | 616 |
| 11502172 | 25.431 970(7) | 38.2(5.0) | 0.100 74(2) | 334(10) | 54972.4(6) | 12 746 | 26(1) | 88 | 110 | 15(2) | 5700 |
| 11519226 | 22.163 175(7) | 37.5(4) | 0.187 18(4) | 358.4(9) | 54977.11(5) | 955 | 17.0(4) | 88 | 89 | 17.0(4) | 510 |
| 11558882 | 73.9103(2) | 91.6(19.5) | 0.365(4) | 169(3) | 54975.8(6) | −4653 | 43(3) | 88 | 84 | −43(3) | 2702 |
| 12356914 | 27.308 12(2) | 46.0(2.4) | 0.325(1) | 113.2(9) | 54966.0(1) | −10 309(1210) | 40.2(1) | 88 | 60 | −30.4(1) | 1329 |
Notes.aAdjusted mutual inclination resulted in |$i_\mathrm{m}=25\deg \pm 2\deg$| which would lead to |$\Delta i_1\sim 1\deg$| during Kepler observations and consequently, significant eclipse depth variations which is not the case.
be1 was kept fixed on the radial velocity solution result of Fabrycky et al. (in preparation).
cAdjusted mutual inclination resulted in |$i_\mathrm{m}=23\deg \pm 2\deg$| which would lead to Δi1 ∼ 1| $_{.}^{\circ}$|7 during Kepler observations and consequently, significant eclipse depth variations which is not the case.
5.1 EBs with LTTE solution
In this section, we consider the systems with pure LTTE solutions. We divide them into three groups approximately following Conroy et al. (2014). Broadly speaking, for groups one, two, and three, the data span more than two, more than one, and less than one outer orbital periods. The motivation for this grouping is that the more outer orbital periods that are covered, the more secure are the solutions. In what follows, we give more specifics on the systems included in each group.
The first group consists of 38 EBs, with outer periods of 95 d ≲ P2 ≲ 5532 d. Generally, our data on each of these cover more than two outer orbital cycles. The only exception is KIC 06543674 where even though the Kepler observations cover only ∼1.32 outer orbits, outer eclipses at the expected times evidently verify the third-body solution. For KIC 10727655 (=V2280 Cyg) and KIC 02708156 (=UZ Lyr), ground-based observations extend the observing interval sufficiently to justify their inclusion. The second group, the most numerous subgroup with its 64 members, contains EBs whose outer periods are shorter than the length of the time series, i.e. at least one full outer orbital cycle was observed. The period range is 364 d ≲ P2 ≲ 2800 d. KIC 05513861, KIC 09402652 (=V2281 Cyg), and KIC 12019674 (=V2294 Cyg) are included in this group on the basis of both Kepler and ground-based observations. Finally, 58 triples are included in the third group wherein each system was observed over less than one complete outer orbit. The outer period domain for this group is 932 d ≲ P2 ≲ 9256 d.
For these three groups, the orbital elements and their uncertainties are given in Tables 3–5. In each table, the systems are ordered by increasing outer orbital period (P2). As is well-known, similar to single-line radial velocity observations, the LTTE solution does not allow either the inclination (i2) of the wide orbit or the mass of the third companion (mC) to be uniquely deduced. Nevertheless, a crude estimate can readily be found for mC by use of the reasonable approximation that the mass of the EB is likely to be about 2 M⊙. Then, solving equation (7) which is third order in mC, the mass of the third object can be estimated for different i2 inclinations. We list these approximate minimum values of mC, i.e. for |$i_2=90\deg$|, in our tables. Naturally, if the inner binary mass, mAB, of any of our investigated systems is more accurately known, a better estimate for (mC)min can be obtained. In most cases, our rough estimate is likely to be fairly satisfactory for judging the nature of the third object, and can also be used to forecast the expected amount of third light either for any future photometric light-curve solutions or spectroscopic follow-up observations. We use the same approximation to estimate the ratio of the amplitudes of the dynamical and LTTE contributions (|${\cal {A}}_\mathrm{dyn}/{\cal {A}}_\mathrm{LTTE}$|) of the ETVs.
5.2 EBs with combined dynamical and LTTE solution
We list 62 triples with combined dynamical and LTTE solutions. With the exception of the two shortest outer period systems discussed below, our fitting process was practically identical in great detail with that described in Borkovits et al. (2015). These systems allow, in principle, the determination of all the system masses, though in principle, there are some degeneracies in the parameters (Rappaport et al. 2013) unless the inner binary is eccentric and the ETV curves for both the primary and secondary eclipses can be measured and fitted simultaneously (Borkovits et al. 2015).
The two exceptional systems in this group are KIC 05897826 and KIC 05952403. The inner binary in KIC 05897826 is just barely an EB; the two stars do actually eclipse each other at favourable phases of the rapid precession of the binary orbital plane. Consequently, we cannot find an ETV solution for this triple. Therefore, we borrow the orbital elements and masses from the photodynamical solution of Carter et al. (2011). KIC 05952403 (HD 181068) is a triply eclipsing system where the inner and outer orbits are both circular and coplanar. Hence, the usually dominant quadrupole dynamical term disappears. In our analysis, we have obtained a pure LTTE solution for this triple, and the other parameters, which can usually be deduced from the dynamical part of the combined solution, were taken from Borkovits et al. (2013). This is also a prime example for emphasizing that the theoretical ratio |${\cal {A}}_\mathrm{dyn}/{\cal {A}}_\mathrm{LTTE}$| is merely a rough estimate (for this system |${\cal {A}}_\mathrm{dyn}/{\cal {A}}_\mathrm{LTTE}=1.22$|).
As noted above, a combined solution offers several parameters which cannot be obtained from a pure LTTE solution. Therefore, Tables 6–8 contain information somewhat different from that in Tables 3–5. The masses of the two components of the wide binary, mAB and mC, are calculated from the mass function, f(mC), and the outer mass ratio, mC/mABC, which are direct outputs of the combined solution. All four of these quantities are listed in the present tables. We are also able to give the full semimajor axis of the outer orbit (a2) instead of the projected semimajor axis of the LTTE orbit of the binary (aAB sin i2). Lastly, instead of the theoretically calculated ratio |${\cal {A}}_\mathrm{dyn}/{\cal {A}}_\mathrm{LTTE}$|, we give the actual ‘measured’ value. In regard to the latter point, we note that in the case of an eccentric EB, the true amplitude of the dynamical term may differ by as much as a factor of 2 for the primary and secondary minima of a given system. In all cases, we tabulate the larger of the two dynamical amplitudes. See Borkovits et al. (2011) for a discussion, and, as examples, the ETV curves of KICs 05255512, 07670617, 08143170, and 10258809 in the appropriate panels of Fig. 6.
Additional parameters, none of which can be obtained from a pure LTTE solution, are tabulated in Table 10. These refer to the orbital elements of the inner binary orbit and spatial orientations. The mutual inclination (im) has extraordinary importance in connection to the dynamical evolution of a triple system. Its determination, and more generally the complete three-dimensional orientation of a triple, was discussed in great detail in Borkovits et al. (2015, especially in appendix D), but some additional remarks are in order here.
During the first step in our analysis, the mutual inclination, im, and one of the additional node-like angles were taken as adjustable parameters. For many of the systems, the result is a low, but definitely non-zero mutual inclination (typically |$i_\mathrm{m}<10\deg$|). For such low values of im, the EB's orbital plane should precess very rapidly with a low amplitude. KIC 05897826, discussed above, is a good example of this. Orbital inclination (i1) variations should then be visible as eclipse depth variations. In most cases, variation of the eclipse depths is not seen. In these cases, we fixed im at |$0\deg$| manually, and then reran our parameter solver. We believe that this is reasonable because the lack of variation of the eclipse depths rules out a small non-zero misalignment of the orbits, and, because the ETV solution fundamentally rules out the possibility of a larger mutual inclination, which would result in a larger amplitude, substantially slower precession. Furthermore, from a dynamical and/or evolutionary point of view, there is no fundamental difference between strictly and nearly coplanar configurations; therefore, we believe that it is justified to use these systems with |$i_\mathrm{m}=0\deg$| in our statistical studies.
As was done for the LTTE systems, we divided the set of 62 triples into three subgroups according to coverage of their outer orbits. The first group contains 31 members with outer periods 34 d ≲ P2 ≲ 862 d. The middle group has 14 triples in the period range 583 d ≲ P2 ≲ 1437 d, while the systems for which less than one outer cycle was observed include 17 potential triples with 452 d ≲ P2 ≲ 15271 d.
6 RESULTS
6.1 The reliability of the results
In the following subsections, we provide a general statistical analysis of our sample, and then discuss the specific properties of selected subsets of our triples. Before this, however, it is crucial to establish the reliability of our third-body solutions. Two questions naturally arise. First, do our third-body model and solution really demonstrate the presence of a third body in a given system? Secondly, if the third component does exist, how reliable are the parameters we have obtained? The answers to these questions are somewhat different for the systems with pure LTTE solutions and those with combined LTTE and dynamical solutions, and even for the three different subgroups of each of these two overall categories. For the 10 triply eclipsing systems in our sample, the eclipses involving the third star validate not only the existence of the third object, but also the orbital parameters of the wide orbits as well. For the remaining 212 EBs, we can expect that a larger number of complete outer orbits covered generally yield a solution with higher reliability. However, there may be other effects which can mimic short-period periodic or quasi-periodic LTTE-like ETVs, as was discussed previously in Section 3. Although, by introducing the QTV analysis and using smoothing polynomials, we are able to filter out the majority of such false positives, we cannot completely eliminate the possibility that a few false positives might remain in our sample. On the other hand, for the subgroup with the shortest outer periods, we can say that if an LTTE model turns out to be real, the estimated orbital parameters and mass ratio that are obtained are expected to be reliable and accurate enough for statistical analyses. With regard to the well-covered systems with combined LTTE and dynamical solutions, there is only a slight chance of misidentifying a non-dynamical ETV curve as having a dynamical third-body origin. This is due to the fact that in most cases the dynamically perturbed ETVs have very characteristic shapes.
For the systems where less than two but more than one outer periods are covered, the differences between pure LTTE and dynamical systems become even more clear. Because of the specific features of the dynamical ETVs, we are convinced that all the systems listed in Tables 6–8 are triples or higher order multiples, though the reliability of the outer periods and orbital elements depends as usual on the length of the orbital coverage. For pure LTTE systems, we cannot offer general rules. When fitting LTTE solutions to systems in the second and third subgroups, we generally tried to avoid incorporating quadratic functions because, in the absence of well-defined and separable short-period ETV modulations, quadratic terms can easily produce spurious LTTE solutions. For example, Borkovits et al. (2005) illustrated that artificial ETVs consisting of two constant period sections with an abrupt period jump between them were nicely fitted with the combination of a quadratic polynomial and an LTTE orbit. However, there were a few cases, e.g. KICs 03440230, 05621294, 07339345, and 07680593, where we were only able to obtain an LTTE solution with the combination of a quadratic fit and an LTTE orbit. In these instances, we generally obtained a very low mass third-star companion with a period of about 1000 d. In our opinion, such types of solutions should be considered with considerable caution. Regarding those LTTE solutions where the inferred outer period exceeds the length of the observed data train, the only thing we can say is that, in most cases, the ETVs really signify the presence of a third companion. However, the parameters obtained in most cases are necessarily uncertain and are less suited for statistical analysis.
6.2 Distributions and statistics
Since this is the largest collection of triple systems with known outer orbital periods, P2 ≲ few years, it makes sense to examine distributions of several of the system parameters and other statistics. Certain of these parameters, including P1, P2, e2, ω2, and |$f(m_{\rm C})=m_\mathrm{C}^3 \sin ^3 i/m_{\rm ABC}^2$|, can be determined using only the LTTE delays. Hence, these parameters are available for 222 systems (see Tables 3–8).
For many of the 62 LTTE-dynamical combined-solution systems listed in Tables 6–8 and 10, there is also information about parameters associated with the three-dimensional structure of the triple, including the mutual orbital inclination angle, im, and with the system masses, i.e. f(mC), mC/mABC, mC, and mAB.
In Fig. 7, we show the outer orbital period distribution, f(P2), for some 200 triple systems. This distribution is flat, at least within the limits of Poisson fluctuations, out to P2 ≃ 1600 d, a value comparable to the ∼1400 d duration of the Kepler mission. For longer periods, the distribution declines rapidly. This may be wholly or partially due to observational selection effects, since longer period ETV curves are more difficult to definitively identify. At the same time, it also suggests a possible |$f(P_2) \propto P_2^{-1}$| decrease with increasing P2. Let us define F(P2) and f(P2) as the orbital period distributions per logarithmic and per linear period intervals, respectively. In that case, F(P2) ≡ P2 f(P2). The possible functional forms of F(P2) include uniform per logarithmic interval, lognormal with a peak at about 180 yr which was found to fit the period distribution of a large sample of binary stars (Abt & Levy 1978; Duquennoy & Mayor 1991), or even a form with a peak near ∼3000 yr which was obtained both from observations (Tokovinin 2008) and numerical simulations (Naoz & Fabrycky 2014) for triples with close binaries. For any of these three possibilities, f(P2) would vary roughly like |$P_2^{-1}$| in the period range of Fig. 7.
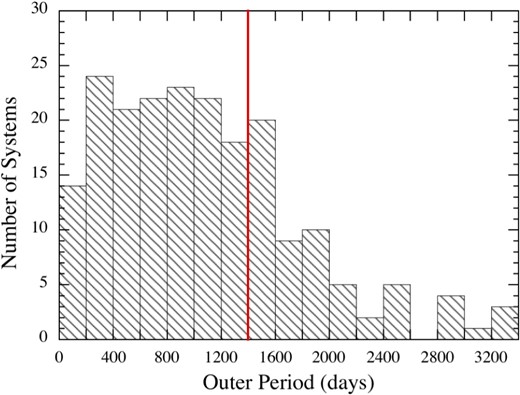
Distribution of the outer orbital periods, P2, for 222 triple systems found in the Kepler field. The vertical red line denotes the duration of the Kepler mission.
As for the lower end of the outer period distribution, the question arises as to whether the limit is set by observational selection effects or results from actual dynamical effects. Fig. 8, which shows a correlation plot of P2 versus P1 for all 222 systems, provides an answer. In this figure, the blue lines denote the limits of the regions where the |$\mathcal {A}_\mathrm{LTTE}$| and the |$\mathcal {A}_\mathrm{dyn}$| amplitudes are likely to exceed 50 s, a value which roughly approximates the threshold for likely detection of an ETV. The shaded cyan region indicates the period ranges where the dynamical delays are still detectable even though the LTTE delays might not be. There is only one system in this region, which is KIC 05897826 (=KOI-126). This system, however, was discovered via its triply eclipsing nature rather than via an ETV analysis. The region shaded in yellow indicates part of the lower outer period range where systems should nominally be detectable via the LTTE delays even though the dynamical delays might be undetectable. The fact that there are almost no systems in this region, where detection of the LTTE delays should be straightforward, proves that our sample of triples at the lower edge of the outer period distribution has most probably been shaped by dynamical or evolutionary processes rather than by observational selection effects. For the cyan region, one might argue that the combination of tightest binaries and tightest ternary orbits would lead to two circular or, at least low-eccentricity, nearly aligned orbits due to tidal effects or other interactions; in that case, |$\mathcal {A}_\mathrm{dyn}$| is rather small. For the yellow region, however, the ETV amplitude is dominated by |$\mathcal {A}_\mathrm{LTTE}$| rather than by |$\mathcal {A}_\mathrm{dyn}$|, so this objection is not relevant. Therefore, we can surely conclude that the tightest EBs, and especially the contact binaries, do not have very close ternary companions. This result might imply some additional differences between the dynamical processes which lead to the formation of the tightest close binaries, e.g. those with P1 ≲ 1/2 d, and the processes which lead to the formation of binaries with longer P1.
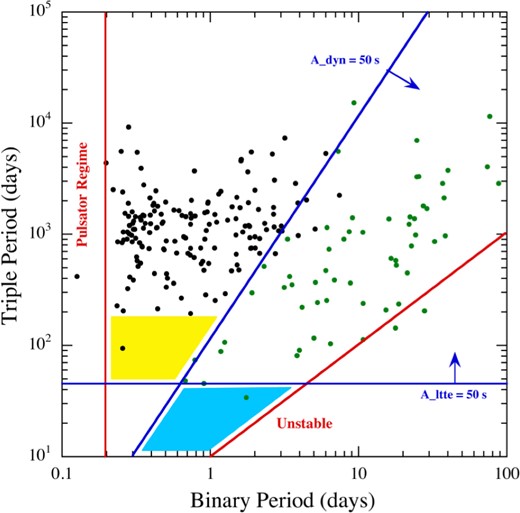
Outer triple orbital period, P2, versus the inner binary period, P1, for 222 triple systems found in the Kepler field. The vertical red line denotes the typical minimum orbital period of contact binaries, while the sloped red line roughly separates regions of stability and instability. The horizontal and sloped blue lines are boundaries that roughly separate detectable ETVs from undetectable ETVs assuming that the ETVs must be ∼50 s or greater in amplitude to be detectable. These amplitudes were calculated using mA = mB = mC = 1 M⊙, e2 = 0.35, |$i_2=60\deg$|, and |$\omega _2=90\deg$|. The arrows indicate the direction of greater detectability as long as P2 ≲ 2000 d. The shaded cyan region indicates the period ranges where the dynamical delays are still detectable even though the LTTE delays might not be. There is only one known system in this region (see the text for a discussion). The region shaded in yellow indicates the period ranges where systems should nominally be detectable via the LTTE delays even though the dynamical delays might be undetectable. The fact that there are almost no systems in this region may have interesting physical implications (see the text).
In Fig. 8, the sloped red line approximately separates dynamically stable systems from unstable systems. The position of the line is based on an expression for dynamical stability in hierarchical triples in Mardling & Aarseth (2001; see equation 27 of Borkovits et al. 2015). In applying this expression, we assumed that the outer orbital eccentricity e2 is equal to the median value of 0.35 computed from the eccentricity distribution in Fig. 9. The vertical line in this figure indicates a value of P2 ≃ 0.2 d, approximately the shortest orbital period of ordinary contact binaries. All but 3 of the 222 systems lie between these two limiting curves, and, given the approximate nature of both constraints, this seems entirely satisfactory.
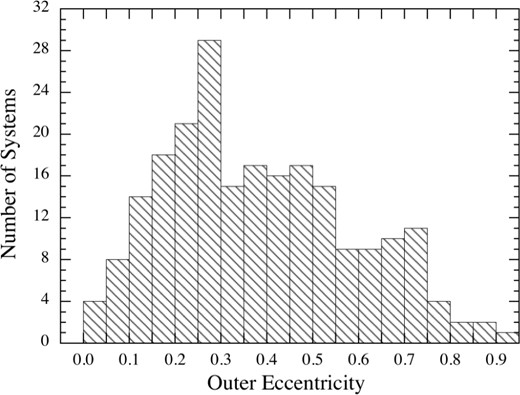
Distribution of the eccentricities, e2, of the outer orbits for 222 triple systems found in the Kepler field.
The outer orbit eccentricities have a wide range of values (Fig. 9). The distribution is characterized by a broad peak together with a narrow peak near e2 ≃ 0.28. We have no immediate explanation for either feature. In any event, the distribution is clearly inconsistent with a ‘thermal’ distribution of eccentricities such as that originally posited by Jeans (1919) which would be linearly rising with e2. In contrast, our finding is in good accord with the eccentricity distributions of different populations of field binaries obtained from recent surveys. This may be seen by comparison of the cumulative distribution of the outer eccentricities of our complete sample (Fig. 10) with the distributions shown in fig. 3 of Duchêne & Kraus (2013) for homogeneous subgroups of binaries with periods in the regime of 100 ≤ P ≤ 10 000 d. (Note that here we are treating the triple systems as binaries composed of the outer body and the inner binary.) For further comparison, we also plot the cumulative distributions expected for a uniformly distributed set of eccentricities and for an eccentricity distribution that increases linearly with e2. As is the case for the binaries in Duchêne & Kraus (2013), neither comparison curve is a good match to the observed distribution, which results from the eccentricities tending to peak near ∼0.3.
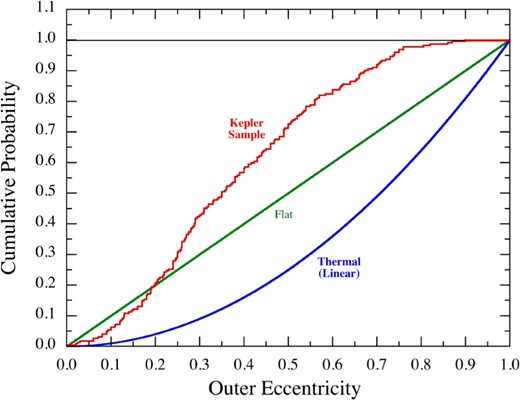
Cumulative distribution of the outer eccentricity (e2) for all 222 Kepler triples in our sample. The green curve, shown for comparison, represents the cumulative distribution expected for a uniformly distributed set of eccentricities between zero and 1. The blue curve is for an eccentricity distribution that increases linearly with e2. Neither comparison curve is a good match to the observed distribution, which results from the eccentricities tending to peak near ∼0.3. For comparison to the eccentricities of unperturbed wide-field binaries in the same period regime, see Duchêne & Kraus (2013).
The relation between the outer orbital period and outer orbital eccentricity is shown in Fig. 11. The red curve shows the result of a fit to a linear relation; the correlation coefficient is 0.34. For a sample of 222 systems, this is significant with a false-alarm probability of only 10−6. In spite of this, the correlation is clearly not particularly striking. Jeans (1919) showed that for a population of binaries in ‘thermal equilibrium’, the eccentricity would be uncorrelated with the period; this does not appear to be the case for the currently observed population of binaries (Duchêne & Kraus 2013).
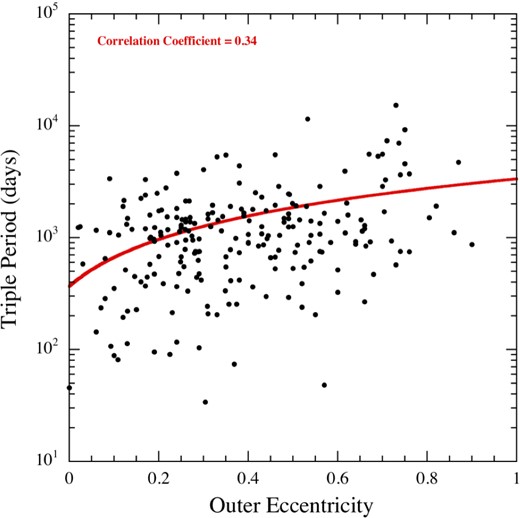
Triple period, P2, versus eccentricity, e2, for 222 triple systems found in the Kepler field. The red curve is the best linear fit which has a correlation coefficient of 0.34.
Fig. 12 presents the distribution of the tertiary masses. For 62 triples in which both the LTTE and dynamical effects are measured, there is sufficient information to determine reasonably accurate masses mC for the third star. For the remaining 160 systems, we estimate mC from the mass function, f(mC) after adopting the reasonable assumption/approximation that mAB ≃ 2 M⊙. We see from this figure that, overall, the mass distribution is well populated out to mC ≃ 1 M⊙ and then falls off steeply towards higher masses. We also note that the vast bulk of the systems have mC ≲ 1.8 M⊙. This is likely a selection effect since Kepler targets included relatively few (≲1/2 per cent) stars with masses greater than this. The masses of the tertiaries in the LTTE systems tend to be low, at least relative to the tertiary masses for the systems with combined solutions. This is likely a natural consequence of the fact that the LTTE mass values only represent lower limits. Therefore, for triples with small outer inclinations, i2, the true tertiary masses may be substantially larger. Despite this, however, the modestly enhanced peak at masses between 0.1 and 0.2 M⊙ suggests that caution should be used before accepting the LTTE interpretations of the lowest amplitude ETVs. Here we mention again those systems where the combination of low amplitude, 2–3 yr periodicities plus quadratic terms might have been misinterpreted as LTTE orbits.
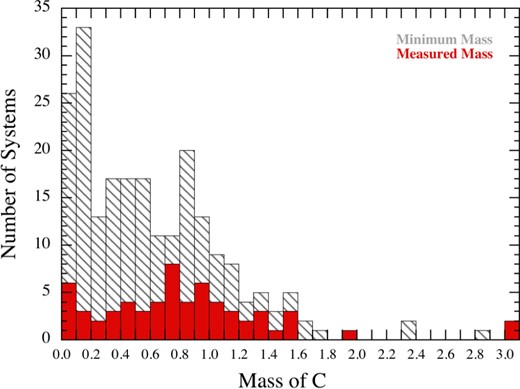
Distribution of the tertiary masses, mC (in M⊙), for 222 triple systems found in the Kepler field. The 62 systems marked in red are the ones for which there is sufficient information in the ETV curves from both dynamical and LTTE effects so that both the tertiary mass and the inner binary mass, mC and mAB, respectively, can be determined. The other tertiary masses are based on the LTTE solutions, and make the assumption that mAB ≃ 2 M⊙.
Fig. 13 shows the correlation between mC and mAB for the 62 combined-solution systems. The straight line with the smaller slope indicates what would be expected for the special case of mA = mB = mC, while the line with the larger slope illustrates the locus of points where mC = mAB. Roughly half the systems lie between these two lines, while a nearly equal number lie below the lower line. Only a few systems lie above the higher line. Broadly speaking, the tertiary masses range from rivaling that of the binary to being quite low. The systems with very low tertiary masses (near the very bottom of the plot) are discussed below in Section 6.4.
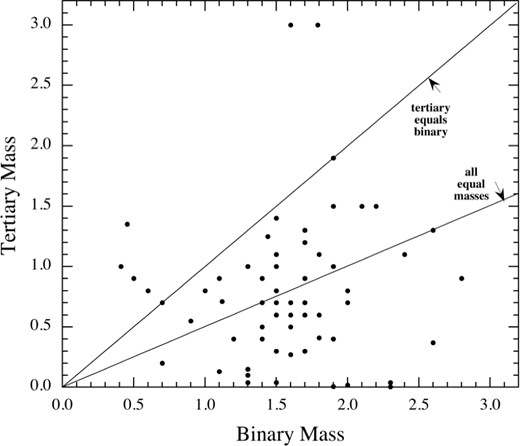
Relation between the tertiary mass, mC (in M⊙), and the inner binary mass, mAB, for the 62 for which the ETV curves yield combined dynamical and LTTE solutions.
In Fig. 14, we plot the ratio of the dynamical to LTTE amplitude versus the ratio of periods P1/P2. For the 62 systems shown in red symbols, the ratio |$\mathcal {A}_{\rm dyn}/\mathcal {A}_{\rm LTTE}$| is directly measured from the fits to the ETV curves. For the remaining systems where the ETV curve is dominated by the LTTE effect, |$\mathcal {A}_{\rm dyn}/\mathcal {A}_{\rm LTTE}$| is estimated using the measured periods and outer eccentricity and is also based on the assumption that mAB ≃ 2 M⊙. The quite strong correlation can be understood with the help of the theoretical ratio of the two amplitudes, as was discussed in Section 5.1. It was shown there that, aside from dependences on masses and eccentricities, the ratio is proportional to |$P_1^2/P_2^{5/3}$|. This would give a slope of ∼2 in a log –log plot, i.e. a value close to the slope exhibited in the figure.
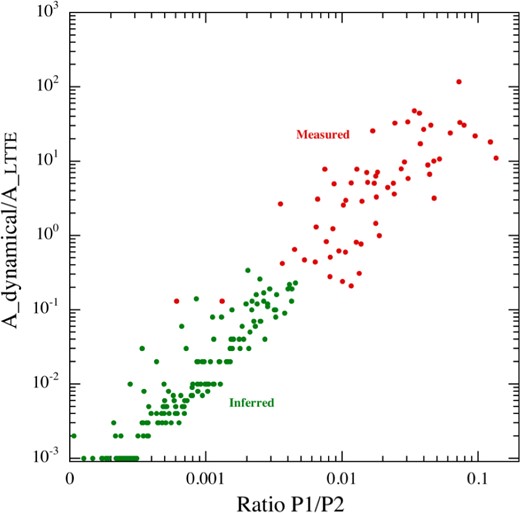
The relation between the dynamical and LTTE amplitudes, |$\mathcal {A}_{\rm dyn}/\mathcal {A}_{\rm LTTE}$|, and the ratio of inner to outer periods, P1/P2. The systems marked in red are directly measured from the dynamical plus LTTE solutions to the ETV curves. By contrast, the green points are estimates based on the assumption that mAB ≃ 2 M⊙.
In Fig. 15, we show the distribution of mutual inclination angles, im, for the combined-solution systems. Some 32 per cent of the systems are contained in a peak centred at im ≃ 40°. For systems where the primordial value of im lies in the range 39| $_{.}^{\circ}$|2 ≲ im ≲ 140| $_{.}^{\circ}$|8, it has been shown that the tertiary star drives Kozai–Lidov cycles with tidal friction (hereafter KCTF; see, e.g., Kozai 1962; Lidov 1962; Kiseleva, Eggleton & Mikkola 1998; Fabrycky & Tremaine 2007) that may involve large-amplitude oscillations of the eccentricity and inclination of the inner binary. The large eccentricities thereby induced in the binary ultimately lead via tidal friction to shrinkage and circularization of the orbit – with im ‘frozen out’ near |$i_\mathrm{m}\simeq \sin ^{-1}(\sqrt{2/5)}$|. This explains the peak in the im distribution near 40°. In that regard, our results may be taken as confirmation of the KCTF model. On the other hand, however, some caution is necessary because the inner period–mutual inclination relation (Fig. 16) does not confirm the expected final period distribution of Fabrycky & Tremaine (2007) which predicts an enhancement of 3 ≲ P1 ≲ 10 d short-period binaries amongst the |$i_\mathrm{m}\sim 40\deg$| mutual inclination triples. Finally, we note that many of the lower mutual inclination systems in our sample are likely to have been originally formed with mutual inclination angles less than 39| $_{.}^{\circ}$|2.
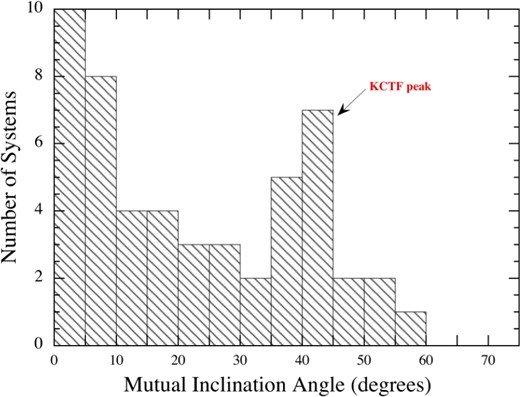
Distribution of the mutual orbital inclination angle, im, for 62 systems where there was sufficient information in the ETV curves to allow for its determination. Note the peak centred around im ≃ 40° which we associate with Kozai cycles with tidal friction in systems with initial values of 39° ≲ im ≲ 141° (see the text for a discussion and references). The peak between |$i_\mathrm{m}=0\deg$| and |$5\deg$| actually contains 21 systems, but goes off the top of the plot.
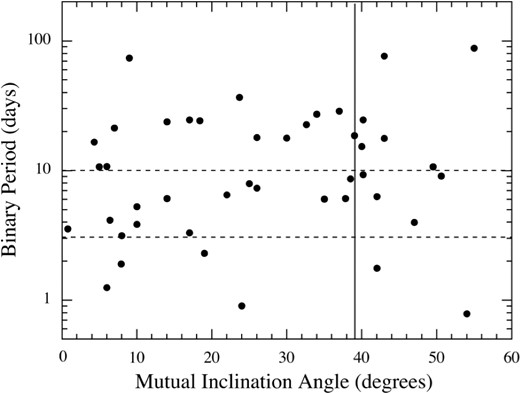
The relation between the mutual orbital inclination angle, im, and the inner binary period (P1) for 44 systems where there was sufficient information in the ETV curves to allow for their determination (see the text). Only systems with non-zero im are shown for clarity. The two dashed horizontal lines indicate the expected range of P1 values near im ∼ 39° (vertical line) from the Fabrycky & Tremaine (2007) model.
Apsidal motion time-scales, such as those shown in Fig. 17, are discussed extensively in Borkovits et al. (2015). As noted there, in the presence of a close ternary, the dynamically forced apsidal motion of an eccentric EB can substantially exceed, even by several orders of magnitudes, the classical and the relativistic apsidal motion contributions. In such a way, the apsidal advance rate in these EBs is fully constrained by the dynamical ETV solution and vice versa, and these constraints are built into our ETV solution procedures.10 As a consequence, the dynamical apsidal motion time-scale is a derived output of our combined ETV solution. These Papse time-scales, which are shown in Fig. 17, are distributed widely from ∼10–104 years, with more than half of them above 500 years.
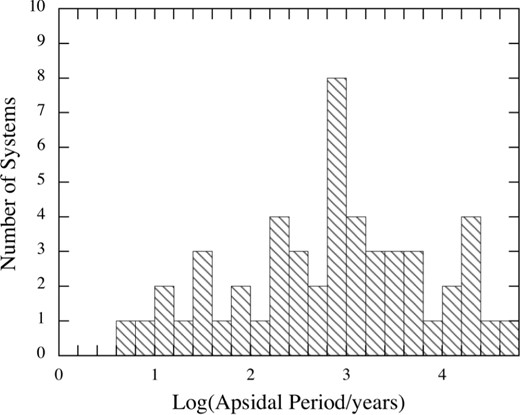
Distribution of the apsidal period in the inner eccentric binary driven by the tertiary star. There was sufficient information in the ETV curves of 45 systems to derive Papse.
We conclude this section by noting that our collection of 222 Kepler triples constitutes nearly 10 per cent of the entire Kepler catalogue of ∼2600 binaries. The outer periods range from approximately 30 to more than 2000 d; the sample is rather incomplete for outer periods longer than 2000 d. Thus, our sample covers only 1.8 dex out of the possible total range of approximately 6–7 dex. If the outer periods of triples are roughly uniformly spaced logarithmically, this immediately implies that at least 30 per cent of all binaries are located in triples or higher order multiples. Furthermore, we may have missed some substantial fraction of the triples in the Kepler data set due to a variety of causes. We conclude that a very substantial fraction, perhaps approaching unity, of the binaries are likely bound together with third bodies or more.
6.3 Systems with extra eclipse events
As mentioned before, 10 EBs among our sample exhibit anomalous extra eclipsing events which we have attributed to the same third bodies identified as the sources of the ETVs. Nine of these ten systems were recognized earlier. They are KIC 05897826 (=KOI-126; Carter et al. 2011), KIC 05952403 (=HD 181068; Derekas et al. 2011), KICs 06543674, 07289157 (Slawson et al. 2011), KIC 02856960 (Armstrong et al. 2012), KIC 02835289 (Conroy et al. 2014), and KICs 05255552, 06964043, 07668648 (Borkovits et al. 2015). The 10th triply eclipsing EB is KIC 09007918 which shows one extra eclipsing event around day 56236.2 and has not been reported previously (see Fig. 18). In most cases, these extra eclipses have a variety of shapes and large depths. In a minority of cases, these extra events are manifest only as barely discernible short disturbances or shallow transit-like fadings which might even be aperiodic, and their real nature can only be verified with the help of an LTTE or combined ETV solution. Such events are seen in the light curves of KIC 06543674, KIC 07668648, and, most notably, KIC 09007918.
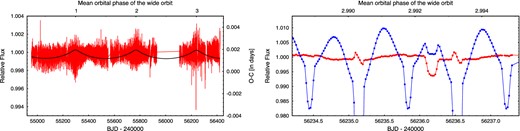
The identification of an extra eclipse event in the Kepler light curve of KIC 09007918. Left-hand panel: after subtraction of the folded, binned, averaged light curve from the detrended full time series, a definite fading event can be seen around day 56236.2 in the residual light curve (red) which coincides with one of the sharply peaked maxima of the ETV curve and, therefore, the LTTE solution (black curve) as well. Right-hand panel: a close-up of this fading shows a transit-like extra eclipse event, which can nicely be identified not only on the residual light curve (red), but also on the original, detrended light curve (blue). The event occurred very close to the time of the maximum Roemer delay of the EB, which in this triple happens almost at the same moment as periastron passage of the wide orbit. In such a scenario, the physical (i.e. spatial) and the projected distances of the EB and the ternary reach their minimum values at the same time, which increases the likelihood of the outer eclipses. The regular, transit-like shape of the fading, and the fact that it happened during the second quadrature of the EB, i.e. when the projected distance of the two binary members is maximal, makes it most likely that only one of the binary members was eclipsed by the ternary.
The modelling of eclipses involving a third body brings great sensitivity to the determination of the complete configuration of a system and of its dynamical properties. On the other hand, this great sensitivity implies that it may be extremely difficult to obtain a model that accurately predicts the extra eclipse times and other characteristics. For example, even if the outer orbit is wide enough to nearly eliminate any dynamical perturbations, the same cannot be done for the light-curve solution, i.e. a model of all light-curve details in addition to eclipse times, because the characteristics of the light curve around each outer eclipse will be strongly affected when the two orbits are not perfectly coplanar and there is precession of the orbital planes, or when either of the two orbits is eccentric and undergoes apsidal motion. In practice, the accurate interpretation of such a system can be carried out only by simultaneous modelling of its photometric and dynamical properties, as was done for KIC 05897826 (=KOI-126) by Carter et al. (2011).
Two additional triply eclipsing systems for which light-curve solutions are available in the literature are KIC 05952403 (=HD 181068; Borkovits et al. 2013) and KIC 06543674 (Masuda et al. 2015). For neither of them is there a complete photodynamical solution. In the case of KIC 05952403, this can be understood from the fact that this is the only system in our sample which consists of two nearly perfectly coplanar circular orbits and, therefore, cannot show significant perturbations to the orbits such as orbital plane precession or apsidal motion. In the case of KIC 06543674, only one set of outer eclipse events has been observed. It is therefore unfit for a complete photodynamical analysis. Note also that the outer period of P2 = 1101.4 ± 0.4 d of this system is the longest period known for any triply eclipsing system. The outer orbit thus represents the ‘EB’ with the longest period in the entire Kepler EB sample.
There are other systems in the Kepler EB sample which have light curves that exhibit extra eclipsing events or other complex features, but do not turn out to be hierarchical triples or do not show ETVs. They are not included in our sample.
Amongst these systems, KIC 07670485 shows only one extra fading event around day 55665 (Orosz 2015). The primary and secondary O−C curves of this EB, however, do not show any ETVs, but only some scatter with an amplitude of ∼3 × 10−4 d.
For KICs 04247791 and 07622486, the strict periodicity and unaltered shapes of the extra eclipses make it evident that what is seen in these two light curves are the blends of two EBs. In the case of KIC 04247791, it has already been reported by Lehmann et al. (2012) that this source consists of two double-lined (SB2) binaries. The question that naturally arises for these blended EBs is whether these form 2+2 hierarchical quadruple systems or not. In order to investigate this question, we proceeded to disentangle the light curve of each of the two targets in the following manner. First, we folded, binned, and averaged the complete Kepler light curve independently according to each of the two periods. Each folded light curve allowed the determination of the average phases of the first and last contacts of each eclipse. The folding, binning, and averaging procedures were then repeated for each of the two binaries, but this time excluding those light-curve sections containing eclipses of the other binary. Then, these folded, binned, and averaged light curves were subtracted from the original time series with a three-point local Lagrangian polynomial interpolation. In such a manner, we obtained two residual light curves, each of which primarily contained only the eclipsing structure of the other binary of the blended source. In a final stage, the times of minima were determined from these residual light curves in the same way as was done for all the other systems in this study.
For KIC 04247791, the four O−C curves (two primary and two secondary, respectively) do not exhibit any significant curvature; therefore, we have not observed non-linear behaviour in the ETVs of these two blended EBs. This result does not eliminate the possibility that the two EBs could be gravitationally bound, but we can conclude that the period of the possible wide (quadruple) orbit most probably exceeds a few decades.
The situation in KIC 07622486 is a bit complicated. This source consists of a long-period (P1A = 40.25 d) eccentric EB with a sharp and relatively deep primary eclipse. A secondary eclipse is not observed (but the disentangled average light curve reveals a low-amplitude, asymmetric, heartbeat-like feature around the edges of the primary eclipse). The other binary is most probably a semi-detached system (P1B = 2.28 d) with shallow transit-like dips in flux as primary eclipses, and with nearly invisible secondary occultations. Therefore, we used only the O−C diagrams of the primary events for our ETV analysis. According to this analysis, the longer period binary does not exhibit any interesting ETVs (with an accuracy of 3–4 × 10−4 d). By contrast, the primary minima of the shorter period binary show a cyclic feature with a period of P ≃ 231 ± 4 d. More in-depth analysis indicates that this periodicity is the consequence of stellar oscillations in the short-period range of some tenths to hundredths of a day; these alter the times of the shallow primary transits in a quasi-periodic manner. Therefore, we conclude that there is neither a periodic signal nor any curvature in the ETVs of the two blended binaries in KIC 07622486. Thus, our assessment of this system is the same as that for KIC 04247791.
Perhaps the most complex EB light curve ever observed is that of KIC 04150611. It exhibits eclipses with three different periods, of which the longest period eclipses exhibit very complex and variable features. Therefore, the multiple nature of this system is beyond question. Instead of the comprehensive analysis of the ETVs, we determined O−C diagrams only for those eclipses which belong to the ∼8.65 d eccentric binary component. We were able to obtain its disentangled light curve with only a little effort (by the use the above-described technique). Neither the primary nor the secondary O−C curves exhibit any curvature or periodicity; therefore, due to the lack of interesting and informative ETVs, we have not included this intriguing system in our sample.
6.4 Non-transiting circumbinary planet candidates
Our ETV analysis has identified three triples where the third body is most probably a planetary-mass object. These systems are KICs 07177553, 07821010, and 09472174.
KIC 09472174 contains the only short-period, low-mass sdB+dM binary in our sample. The periodic ETVs have already been interpreted as being due to the LTTE effect by Baran et al. (2015). Because our analysis yielded results similar to those of this previous study, we simply report the analysed ETV curve and the corresponding orbital solution. We also note that if we accept mAB = 0.60 ± 0.03 M⊙ for the total mass of the EB (Ostensen et al. 2010), then we obtain (mC)min = 2.0 MJ. This implies that the third body would exceed the lower mass limit of a brown dwarf only for |$i_2 \lesssim 15\deg$|. If the periodic signal really arises from the LTTE effect, the third object may well have a mass in the planetary range.
10 transiting circumbinary planets have been previously reported (Doyle et al. 2011; Orosz et al. 2012a,b; Welsh et al. 2012, 2015; Kostov et al. 2013, 2014; Schwamb et al. 2013). Candidate circumbinary exoplanets may also be found in KIC 07177553 and KIC 07821010. These two candidates revolve around relatively wide eccentric binaries (P1 = 18.00 and 24.24 d; e1 = 0.39 and 0.68 for KICs 07177553 and 07821010, respectively), with periods of P2 = 529 ± 2 and 991 ± 3 d. In both cases, the ETVs are dominated by dynamical effects (|${\cal {A}}_\mathrm{dyn}/{\cal {A}}_\mathrm{LTTE}\sim 48$| and 33). The possible non-transiting circumbinary planet in the KIC 07177553 system is reported here for the first time, while the circumbinary planet candidate in KIC 07821010 has been recently investigated by D. Fabrycky and his collaborators (Fabrycky et al., in preparation). Their preliminary results have been presented at a conference by W. Welsh.11 Considering our own finding for KIC 07177553, because of the very low contribution of the LTTE term to the ETV solution, instead of the individual masses, our ETV solution yields only the ratio mC/mABC with satisfactory accuracy. Therefore, strictly speaking, we can say only that if the total mass of the EB mAB is less than ∼3 M⊙, then the potential third body is in the mass range of a giant planet instead of a brown dwarf. Spectroscopic follow-up to confirm or reject this result is in progress.
6.5 Comparison with previous surveys
Here we compare our results with those of previous systematic ETV surveys of the Kepler EB sample. As mentioned in the introduction, apart from the pioneering investigations of Gies et al. (2012), which due to its very preliminary nature does not allow for quantitative comparisons, third-body solutions via ETV analyses for Kepler EBs were first published by Rappaport et al. (2013). The latter reported combined LTTE and dynamical ETV solutions constrained by the circular-inner-orbit approximation for a sample of 39 EBs. 20 of these 39 triples, i.e. those where the dynamical terms had yielded a negligible contribution, were also considered in Conroy et al. (2014). The remaining 10 eccentric EBs out of the 39 systems of Rappaport et al. (2013) were reinvestigated by Borkovits et al. (2015) with the first application of an improved, much more sophisticated approximation for the dynamical contribution of the ETVs. The present sample includes the 39 EBs of Rappaport et al. (2013). For 38 of 39 triples, the present solutions differ only slightly in terms of numerical values, which is in accord with our statement in Section 6.1 that, for well- and multiply-covered outer orbits, the ETV solutions yield robust and reliable orbital parameters. The one exception of the 39 systems is KIC 07837302 for which, due to insufficient data length, the ETV behaviour was misinterpreted. For this triple, by the use of the entire, 4-yr-long Kepler data set, we give a completely different dynamically dominated solution. The latter solution, however, should also be considered with caution, since the outer period we obtain is shorter than the data length only by a small amount.
The largest sample of triple-star candidates amongst Kepler EBs was published by Conroy et al. (2014). They produced and investigated the O−C diagrams of all the short-period Kepler EBs and ELVs and identified 236 systems for which they found that the ETV might be compatible with the presence of a third companion. Our compilation contains only 115 of their 236 triple system candidates, mainly as a result of our more stringent selection criteria.
To be specific, our criteria filtered out seven of the first group of Conroy et al. (2014), the most likely of their triple candidates, which consists of 35 systems. Amongst these are KICs 05560831 and 10014830 where the smoothing polynomial killed the cyclic ETV pattern, while in the cases of KICs 03641446, 07657914, 08211618, and 11247386, we found highly discrepant and/or anticorrelated ETV and QTV curves (see the left-hand panel of Fig. 4). The seventh rejected system, KIC 06302592, has a morphological classification (Matijevic et al. 2012) value of 0.93, indicating that this system is an ELV binary, although the folded, averaged light curve reveals clear, very low amplitude grazing eclipses. For this system, we were unable to find a third-body solution for the distorted quasi-periodic primary ETV curve. One of the remaining 28 of the 35 first-group systems in Conroy et al. (2014), KIC 010855535, proved to be a false positive in the sense that although the ETV signal is quite possibly due to the LTTE effect induced by a third star, the modulations in the Kepler light curve are most probably due to the pulsations of single star instead of an EB or ELV (Fig. 5). We dropped 10 of the 80 members of the middle group of Conroy et al. (2014) for similar reasons used in rejecting the seven systems of the first group, and an additional four of the 80 were found to be false positive EBs. Most of the systems we eliminated belonged to the third group of Conroy et al. (2014). These are EBs where no complete LTTE solutions were given, but only a possible outer period was listed. In most cases, we confirm the claim of Conroy et al. (2014) that these ETVs might arise from long-period LTTEs. Due to insufficient length of the available data, however, we were unable to obtain reasonable LTTE solutions for most of these ETVs and, therefore, they are not included in our sample.
All of the 26 eccentric EBs with strongly dynamically dominated ETVs which were investigated by (Borkovits et al. 2015) are naturally included in the present survey. We repeated the analysis only for those systems for which additional Kepler light-curve data are now available relative to that used in the previous study. Our results on these do not depart significantly from those which were given in Borkovits et al. (2015). The only remarkable difference is that, while in the previous work there was an ambiguity regarding the mutual inclination of KIC 12356914, being either prograde or retrograde, our new solution clearly prefers a prograde configuration.
During the preparation of this work, an additional study was published by Zasche et al. (2015). These authors give third-body LTTE solutions for 10 Kepler EBs for which they used both ground-based and Kepler observations of eclipse times, thereby extending the length of the available data sets. We confirm the solutions of seven of the ten targets. We attempted to find a solution for KIC 10581918 (=WX Dra), but were not able to obtain a reliable solution which covered the ground-based eclipse times. The two other exceptions are KIC 05621294 and KIC 03440230. The very questionable nature of the combined quadratic and low-amplitude LTTE solution given for KIC 05621294 was discussed above in Section 6.1. In addition, for KIC 05621294, after the application of the smoothing polynomials, the ETVs were found to be very low in amplitude and even significantly smaller than those of the low-amplitude solutions of both Zasche et al. (2015) and Lee et al. (2015). For KIC 03440230, our smoothed O−C curves, especially for the primary eclipse (see Fig. 6), do not show the periodic pattern which is visible in fig. 3 of Zasche et al. (2015). Therefore, unfortunately, we are not able to confirm their findings of a low-mass third body in a 1 yr orbit. We also note that if the 1 yr periodic feature happens to be real, this system most probably would require a combined LTTE plus dynamical solution. We give instead a parabolic plus low-amplitude LTTE solution. The reliability of the latter LTTE solution is, however, questionable.
In summary, we find that our work (i) is in reasonable agreement with earlier studies, (ii) effectively doubles the sample of well-diagnosed Kepler triples, (iii) substantially improves on many of the earlier solutions, and (iv) adds a significant degree of rigour in selecting valid triples.
6.6 Additional interesting ETVs
There are hundreds of other EBs in the Kepler sample for which O−C diagrams show a wide variety of ETVs. Unfortunately, however, these cannot be interpreted either qualitatively or quantitatively because of the short length of the data train with respect to the probable time-scale(s) of these features. Not counting the simply diverging or converging primary and secondary ETV curves, which are clear markers of the classical and/or relativistic apsidal motions of eccentric EBs, i.e. apsidal motions not due to third-body forced perturbations, the most typical examples of these ETVs are more or less parabolically shaped. Because of the large numbers of such systems, we do not list them individually in this work. There are a few other systems, however, where the features of the O−C diagrams make it very probable that they indicate the presence of third-body perturbed dynamical ETVs. We list those systems in Table 11.
| KIC No. . | P1 . | ETV characteristics . |
|---|---|---|
| 05393558 | 10.22 | Displaced secondary eclipses |
| with different curvature | ||
| 05553624 | 25.76 | Displaced secondary eclipses |
| with different curvature | ||
| 06146838a | 27.47 | Periastron passage event of an eccentric, |
| inclined tertiary? (only primary eclipses) | ||
| 09032900 | 67.42 | Sine-like curve with enormous amplitude |
| 10666242 | 87.24 | Section of a large amplitude sine? |
| (eclipse depth decreases, no sec. eclipses) |
| KIC No. . | P1 . | ETV characteristics . |
|---|---|---|
| 05393558 | 10.22 | Displaced secondary eclipses |
| with different curvature | ||
| 05553624 | 25.76 | Displaced secondary eclipses |
| with different curvature | ||
| 06146838a | 27.47 | Periastron passage event of an eccentric, |
| inclined tertiary? (only primary eclipses) | ||
| 09032900 | 67.42 | Sine-like curve with enormous amplitude |
| 10666242 | 87.24 | Section of a large amplitude sine? |
| (eclipse depth decreases, no sec. eclipses) |
Note.aSee also: http://www.exoplanet-science.com/koi-6668.html
| KIC No. . | P1 . | ETV characteristics . |
|---|---|---|
| 05393558 | 10.22 | Displaced secondary eclipses |
| with different curvature | ||
| 05553624 | 25.76 | Displaced secondary eclipses |
| with different curvature | ||
| 06146838a | 27.47 | Periastron passage event of an eccentric, |
| inclined tertiary? (only primary eclipses) | ||
| 09032900 | 67.42 | Sine-like curve with enormous amplitude |
| 10666242 | 87.24 | Section of a large amplitude sine? |
| (eclipse depth decreases, no sec. eclipses) |
| KIC No. . | P1 . | ETV characteristics . |
|---|---|---|
| 05393558 | 10.22 | Displaced secondary eclipses |
| with different curvature | ||
| 05553624 | 25.76 | Displaced secondary eclipses |
| with different curvature | ||
| 06146838a | 27.47 | Periastron passage event of an eccentric, |
| inclined tertiary? (only primary eclipses) | ||
| 09032900 | 67.42 | Sine-like curve with enormous amplitude |
| 10666242 | 87.24 | Section of a large amplitude sine? |
| (eclipse depth decreases, no sec. eclipses) |
Note.aSee also: http://www.exoplanet-science.com/koi-6668.html
7 SUMMARY AND CONCLUSIONS
We have carried out ETV analyses for the complete EB sample of the original Kepler mission. Our precise determinations of times of light-curve extrema were enhanced by the use of refinements such as averaging primary and secondary ETVs, and fitting and subtracting smoothing polynomials over intervals of the light curves around individual eclipses. For the first time, we extended our analyses to include the portions of the light curves around the quadrature-phase brightness maxima of the tidally distorted EBs, most of which are contact systems and ELV binaries, and in such a way produced ‘QTV curves’. We have thereby obtained ETVs for all and QTVs for many of more than 2500 binary systems. We then selected systems for further analysis where the ETV curves most probably indicate LTTE delays and/or dynamical perturbations caused by a third body in the system. We selected 230 systems, ∼9 per cent of the entire Kepler sample, that appear to harbour third-body companions. According to the results of our investigations, we have classified these 230 EBs into three main groups, as follows.
Group I. These are EBs for which the ETVs are dominated by the LTTE delays and the dynamical contributions to the ETVs are likely to be negligible. With 160 systems, this is the most highly populated group. The outer periods fall in the range 95 ≲ P2 ≲ 9256 d. In 25 cases, an additional quadratic term was fitted simultaneously to the ETV curve, while a cubic polynomial was required for four of the EBs. Furthermore, for 4 of these 160 EBs, the AME was also considered.
Group II. This group contains 62 EBs that exhibit remarkable dynamical perturbations. Therefore, in each of these cases, we fit for a combined LTTE plus dynamical ETV solution including apsidal motion terms for the eccentric EBs. The fits yield several system parameters beyond those which can be obtained from a pure LTTE solution. The most important such parameters are the masses of the EB (mAB) and the ternary component (mC), as well as the mutual inclination angle (im) between the inner and outer orbits. In most cases, the masses can be obtained only with a limited accuracy not appropriate for deeper astrophysical considerations. In addition, a cubic polynomial was also fitted for one system. The outer period range for the Group II systems is 34 ≲ P2 ≲ 15 271 d.
Group III. Each of the remaining eight systems was categorized as a false positive in the sense that, although the observable ETVs most probably arise from LTTE delays due to a companion body, the modulations of the Kepler light curve are likely due to intrinsic variability of the target star rather than to a binary orbit. For these systems, we also give LTTE solutions that are naturally excluded from our statistical analyses.
Groups I and II were also divided into subgroups according to the lengths of the ETV data sets relative to the outer periods. Those systems for which the observational data, in some cases extended with ground-based eclipse timing observations, cover more than two orbital periods were selected to be in the first subgroup. These can generally be considered as the most reliable candidates and those for which we can expect the most accurate parameters. We also placed into this first subgroup all the triply eclipsing systems, irrespective of their outer period/data length ratio, as long as the locations of the outer eclipse(s) were in accord with the corresponding ETV solutions. This subgroup contains a total of 69 triple candidates, 38 and 31 for pure LTTE and combined ETV solutions, respectively. The second subgroup comprises 78 triples, 64 LTTE and 14 combined-solution systems, that have outer periods shorter than the length of the available data, but longer than half the length of the data train. For the remaining 75 EBs, 58 LTTE and 17 combined-solution systems, less than one outer period was observed and, therefore, the solutions are generally the least certain.
Among our candidates, there are 10 systems which exhibit triple eclipses which are consistent with the third-body ETV solutions. From this set, the occurrence of an outer eclipse in KIC 09007918 is reported here for the first time. In the case of four additional EBs, where the light curves also reveal extra eclipse event(s), we were not able to confirm the multiplicity via our ETV analysis. This does not refute the possible multiple nature of these systems, but rather provides restrictions on the period(s) of the outer orbit(s).
There are three EBs in our sample where our analysis revealed companions that are probably of planetary mass. These non-transiting circumbinary planet candidates are found in KICs 07177553, 7821010, and 94721714; that in KIC 07177553 is reported here for the first time. For the other two planet candidates, our solutions are in accord with earlier reported findings.
In Section 6.2, we have presented a statistical analysis of the system parameters obtained for our sample of 222 triple candidates. Here we highlight three interesting results. The first concerns the distribution of mutual inclination angles obtained for 51 favourable cases among the systems with combined LTTE and dynamical effect solutions. Two peaks are seen in the distribution. The larger of the two peaks is at small values that indicate coplanar or nearly coplanar configurations. A significant portion (some 38 per cent) of the systems are contained in a second peak centred at |$i_\mathrm{m}\simeq 40\deg$|. The centroid of this peak is in good agreement with the predictions of the KCTF models. Secondly, our collection, which contains 104 triple candidates with outer period P2 < 1000 d and 155 triples with P2 < 1500 d, is the richest sample to date of short-outer-period triples. We find that the outer period distribution is more or less flat in the range 200 ≲ P2 ≲ 1600 d. For longer periods, the distribution decreases rapidly. Thirdly, we note the almost complete absence of ternaries with P2 ≲ 200 d among the short-period mostly overcontact binaries. This cannot be an observational selection effect since we expect to be able to detect the majority of the shortest outer period companions of the closest EBs down to the limit of P2 ≳ 40–50 d. This result is in agreement with the findings of Conroy et al. (2014) and might offer additional guidelines for the refinement of theories of the formation and evolution of close binaries.
Finally, we stress the importance of future follow-up observations of the systems investigated here. In the cases where ternary eclipses and dynamical perturbations are absent, spectroscopic observations could yield definitive confirmations of the presence of the third stars. Such confirmations would be of special importance for the shorter outer period systems, because of their significance in the statistics, formation, dynamics, and evolution of hierarchical triples. Furthermore, it is also possible that in some cases spectroscopy may reveal that the third body is also a binary even though this was not apparent in our ETV solution.
Extension of the eclipse time data sets via new photometric observations is also highly desirable. Many of the Kepler EBs offer ideal targets even for proficient amateur astronomers. While the amplitudes of the LTTE and/or the dynamical effects in the shorter outer period systems remain below the realistically available accuracy of ground-based observations, the long-term follow-up of these systems would still be useful for detecting longer time-scale variations in the ETV curves. For EBs with longer outer periods, and therefore, larger amplitude ETVs, the ground-based follow-up may even be critical for the confirmation or rejection of the triple system hypothesis, not to mention the quantitative refinement of orbital parameters. A significant fraction of Kepler EBs and of our sample have eclipses that are too shallow or too long to be good targets for ground-based eclipse monitoring. Nonetheless, we are convinced that, for many of the wider Kepler triple candidates, the triplicity can be confirmed within a few years with the help of ground-based observations.
This project has been supported by the Hungarian OTKA Grant K113117. This research has made use of data collected by the Kepler mission, which is funded by the NASA Science Mission Directorate. Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX13AC07G and by other grants and contracts. TB would like to thank the City of Szombathely for support under agreement no. S-11-1027. PK acknowledges support by grant AYA2012-39346-C02-02 of the Spanish Secretary of State for R&D&i (MINECO).
Here we define ΔP1 in terms of the quadratic coefficient as ΔP1 = 2c2 which is the change in binary orbital period per orbital cycle (units of [d/c]). The usual orbital period derivative is given by |$\dot{P}_1 \simeq 2 c_2/P_1$|. Similarly, c3 is related to |$\ddot{P}_1$| as |${\approx } 6 c_3/P_1^2$|.
In his seminal work, Irwin (1952) shifts the reference plane of the light-time orbit from the centre of mass of the triple, i.e. the focal point of the ellipse, to the centre of the orbit, and this is the origin of the extra term aABe2 sin ω2 sin i2/c in his equation (compare his equations 1 and 2). This extra term has been also given in many of the recent papers dealing with LTTE. Note, however, that this was done by the author only for practical reasons, as his graphical solution had a more comfortable form with this formalism, but there are no reasons to use this form in the era of the numeric fitting procedures. An additional caution is also necessary, as this step can be justified only as far as the orbital elements of the light-time orbit remain constant. Being the situation different, this extra term would no longer remain constant and would lead to error. Therefore, we recommend to omit the usage of this additional e2 sin ω2 term in the future studies.
In Borkovits et al. (2015), an analogous dynamical amplitude was defined as |${\cal {A}}_\mathrm{dyn}=\frac{15}{16\pi }\frac{m_\mathrm{C}}{m_\mathrm{ABC}}\frac{P_1^2}{P_2}(1-e_2^2)^{-3/2}$|; here, however, we have chosen a different definition, because most of the presently investigated systems have low or zero inner eccentricity (e1) in which case the present definition is more realistic.
For the definitions of these light-curve morphology classes, see e.g. Kallrath & Milone (2009).
Two different approximations which are used by our code for determining the constrained apsidal motion parameters and, furthermore, the difference between the dynamical and the apparent (geometrical) apsidal advance rate are explained in appendix C of Borkovits et al. (2015).
REFERENCES
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
Figure 6. ETVs with third-body solutions.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the paper.



