-
PDF
- Split View
-
Views
-
Cite
Cite
Nicolas Tejos, J. Xavier Prochaska, Neil H. M. Crighton, Simon L. Morris, Jessica K. Werk, Tom Theuns, Nelson Padilla, Rich M. Bielby, Charles W. Finn, Towards the statistical detection of the warm–hot intergalactic medium in intercluster filaments of the cosmic web, Monthly Notices of the Royal Astronomical Society, Volume 455, Issue 3, 21 January 2016, Pages 2662–2697, https://doi.org/10.1093/mnras/stv2376
Close - Share Icon Share
Abstract
Modern analyses of structure formation predict a universe tangled in a ‘cosmic web’ of dark matter and diffuse baryons. These theories further predict that at low z, a significant fraction of the baryons will be shock-heated to T ∼ 105–107 K yielding a warm–hot intergalactic medium (WHIM), but whose actual existence has eluded a firm observational confirmation. We present a novel experiment to detect the WHIM, by targeting the putative filaments connecting galaxy clusters. We use HST/COS to observe a remarkable quasi-stellar object (QSO) sightline that passes within Δd = 3 Mpc from the seven intercluster axes connecting seven independent cluster pairs at redshifts 0.1 ≤ z ≤ 0.5. We find tentative excesses of total H i, narrow H i (NLA; Doppler parameters b < 50 km s−1), broad H i (BLA; b ≥ 50 km s−1) and O vi absorption lines within rest-frame velocities of Δv ≲ 1000 km s−1 from the cluster-pairs redshifts, corresponding to ∼2, ∼1.7, ∼6 and ∼4 times their field expectations, respectively. Although the excess of O vi likely comes from gas close to individual galaxies, we conclude that most of the excesses of NLAs and BLAs are truly intergalactic. We find the covering fractions, fc, of BLAs close to cluster pairs are ∼4–7 times higher than the random expectation (at the ∼2σ c.l.), whereas the fc of NLAs and O vi are not significantly enhanced. We argue that a larger relative excess of BLAs compared to those of NLAs close to cluster pairs may be a signature of the WHIM in intercluster filaments. By extending this analysis to tens of sightlines, our experiment offers a promising route to detect the WHIM.
1 INTRODUCTION
Perhaps the most distinctive feature of the cosmic web is its intricate pattern of filamentary structures. Cosmological simulations in a Λ cold dark matter (ΛCDM) paradigm predict that these filaments account for ∼40 per cent of all mass in the Universe at z = 0 and occupy roughly ∼10 per cent of the volume (e.g. Aragón-Calvo, van de Weygaert & Jones 2010). When gas and hydrodynamical effects are included in these simulations, a remarkable conclusion is reached: ∼30–50 per cent of baryons at low z should reside in dense filaments, primarily in the form of a diffuse plasma phase with temperatures T ∼ 105–107 K, which would be very difficult to detect (e.g. Cen & Ostriker 1999; Davé et al. 2001). This material is usually referred to as the warm–hot intergalactic medium (WHIM), and indeed is currently the best candidate to host a significant fraction of the so-called missing baryons at z < 1 (Persic & Salucci 1992; Fukugita, Hogan & Peebles 1998; Bregman 2007; Prochaska & Tumlinson 2009; Shull, Smith & Danforth 2012, and references therein). According to these models, the physical origin of the WHIM is through gravitational shocks from the collapse of matter into the large-scale structure (LSS) of the Universe.
One well-studied example of gravitational shock-heating is the so-called intracluster medium (ICM) of galaxy clusters, where the virial temperatures typically reach T ∼ 107–108 K. A plasma at these temperatures mostly cools through Bremsstrahlung (a.k.a. free–free) thermal radiation, emitting X-rays at ∼ keV energies that may be observed with modern satellites (e.g. Kravtsov & Borgani 2012, and references therein). X-ray spectroscopy has also revealed the presence of high-ionization state metal emission lines in the ICM, consistent with these large temperatures (e.g. Sanders et al. 2008). Thereby one constrains the density, chemical abundances and morphology of the ICM. Several decades of research have revealed a highly enriched medium (∼1/3 solar) with a total mass consistent with the cosmic ratio of baryons to dark matter (e.g. Allen et al. 2008).
In the ΛCDM paradigm, galaxy clusters correspond to the nodes of the cosmic web, i.e. they mark the intersection of several filamentary threads. These models further predict that matter flows through the filamentary structures, driving the growth of the galaxy clusters. Ideally, one would image these filaments in a similar manner to the ICM to reveal their structure and physical properties as tests of the cosmic web paradigm. Unfortunately, once at the outskirts of galaxy clusters, the densities and temperatures are too low for viable X-ray detection in emission (e.g. Bremsstrahlung radiation is proportional to the density squared of the emitting gas). To study this dominant component of the cosmic web and its putative relationship to a WHIM, one must pursue alternate strategies.
In principle, one may scour the volumes surrounding galaxy clusters for signatures of cosmic filaments. A random search, however, would be compromised by the fact that their volume filling factor is predicted to be low, even in this environment. To raise the probability of isolating a cosmic filament, researchers have turned to pairs of neighbouring clusters on the expectation that these massive structures will be preferentially connected. Indeed, cosmological dark matter simulations find high probabilities of having a coherent filamentary structure between close (<20 Mpc) and massive (>1014 M⊙) galaxy clusters (e.g. Colberg, Krughoff & Connolly 2005, Aragón-Calvo et al. 2010; Gonzalez 2010). This probability is mostly a function of the galaxy cluster masses and the separation between them: the larger the masses and the shorter the separation, the higher the probability. Therefore, the volume between close pairs of galaxy clusters is a natural place to search for signatures of filaments and an associated WHIM.
Intercluster filaments (i.e. filaments between galaxy cluster pairs) have been inferred from galaxy distributions, either individually from spectroscopic galaxy surveys (e.g. Pimbblet, Drinkwater & Hawkrigg 2004), or by stacking analysis from photometric galaxy surveys (e.g. Zhang et al. 2013). While these studies confirm the strategy to focus on cluster pairs, they provide limited information into the nature of cosmic filaments; these luminous systems represent ≲ 10 per cent of the baryonic matter, their distribution and motions need not trace the majority of the gas, and they offer no insight into the presence of a WHIM.
Promising results from stacking multiple intercluster regions have found an excess of X-ray counts in such regions with respect to the background (Fraser-McKelvie, Pimbblet & Lazendic 2011). In contrast to galaxies, one would be truly observing the bulk of baryonic matter. Unfortunately, the geometry of the emission and the actual origin of the detected photons was not well constrained by this original work. Remarkable detection of individual intercluster filaments have also been reported from gravitational weak lensing signal (Dietrich et al. 2012),1 and X-ray emission (Kull & Böhringer 1999; Werner et al. 2008). Despite their indisputable potential for characterizing cosmological filaments, these techniques are currently limited to the most massive systems with geometries maximizing the observed surface densities, i.e. filaments almost aligned with the line of sight (LOS).
To complement these and other relevant studies to address the ‘missing baryons’ problem (e.g. Hernández-Monteagudo et al. 2015; Nevalainen et al. 2015; Planck Collaboration XXXVII 2015), we have designed a program to detect the putative filaments connecting cluster pairs in absorption. This technique has several advantages over attempts to detect the gas in emission. Firstly, absorption-line spectroscopy is linearly proportional to the density of the absorbing gas, offering much greater sensitivity to a diffuse medium. Secondly, the absorption lines encode the kinematic characteristics of the gas, including constraints on the temperature, turbulence, and line-of-sight (LOS) velocity. Thirdly, one may assess the chemical enrichment and ionization state of the gas through the analysis of multiple ions. The obvious drawback to this technique is that one requires the fortuitous alignment of a bright background source with these rare cluster pairs, to probe a greatly reduced spatial volume: in essence a single pinprick through a given filament. However, with a large enough survey one may also statistically map the geometry/morphology of the filaments.
Here we focus on far ultra-violet (FUV) spectroscopy leveraging the unprecedented sensitivity of the Cosmic Origins Spectrograph (COS) onboard the Hubble Space Telescope (HST), to greatly increase the sample of intercluster filaments probed.2 With such UV capabilities we can directly access H i Ly α– the strongest and most common transition for probing the intergalactic medium (IGM). Having direct coverage of H i independent of the presence of metals is of great value for detecting the WHIM (e.g. Richter et al. 2006; Danforth, Stocke & Shull 2010), because this medium may remain metal poor. Neutral hydrogen generally traces cool and photoionized gas, but it may also trace collisionally ionized gas in the WHIM through broad (Doppler parameters b ≳ 50 km s−1) lines (e.g. Tepper-García et al. 2012). Although the circumgalactic medium (CGM) surrounding galaxies is responsible for producing H i absorption lines (especially at column densities ≳1015 cm−2; e.g. Tumlinson et al. 2013), the majority of them must arise in the diffuse IGM (e.g. Prochaska et al. 2011; Tejos et al. 2012, 2014). FUV spectroscopy also allows the detection of the O vi doublet, a common highly ionized species. The physical origin of O vi absorption lines is controversial, including scenarios of photoionized and/or collisionally ionized gas in the CGM of individual galaxies and/or galaxy groups (e.g. Thom & Chen 2008; Tripp et al. 2008; Wakker & Savage 2009; Savage et al. 2014; Stocke et al. 2014). Thus, a collisionally ionized component could well be present, some of which may come from a WHIM (although see Oppenheimer & Davé 2009; Tepper-García et al. 2011).
In a more general context, H i and O vi offer an optimal approach to study filamentary gas in absorption. As mentioned, this pair of diagnostics correspond to the most common transitions observed in the low-z Universe (e.g. Danforth & Shull 2008; Tripp et al. 2008; Danforth et al. 2014), allowing a good characterization of the background signal against which one may search for signatures of WHIM in filamentary gas. Such signatures could include an elevated/suppressed incidence, covering fractions, and/or unique distributions in the strengths or widths of the absorption features. In contrast to studies where absorption systems could be associated with filaments on an individual basis (e.g. Aracil et al. 2006; Narayanan et al. 2010),3 our methodology is statistical in nature and a large sample of independent structures must be collected.
The current advent of big extragalactic surveys makes our approach feasible. For instance, the SDSS (Ahn et al. 2014) provides large samples of large scale structure (LSS) traced by galaxies and known QSOs in the same volume. In particular, by using the galaxy cluster catalogue of Rykoff et al. (2014) we have constructed a cluster-pair sample and found that, on average, a random sightline extending between 0.1 ≤ z ≤ 0.5 intersects 1 ± 1 independent cluster pairs with projected separations of ≤3 Mpc to the intercluster axis (defined as the line segment joining the centres of the two galaxy clusters of a pair; see Fig. 1 for an illustration, and Section 3 for further details), with a very skewed distribution towards zero (see Section 3.4). In order to enhance the efficiency however, we have cross-matched such cluster-pair sample with known FUV luminous QSOs from the Schneider et al. (2010) catalogue, and identified particular sightlines intersecting more than one of these structures. Our approach is highly complementary to that of Wakker et al. (2015), where a single galaxy filament is targeted with multiple QSO sightlines.
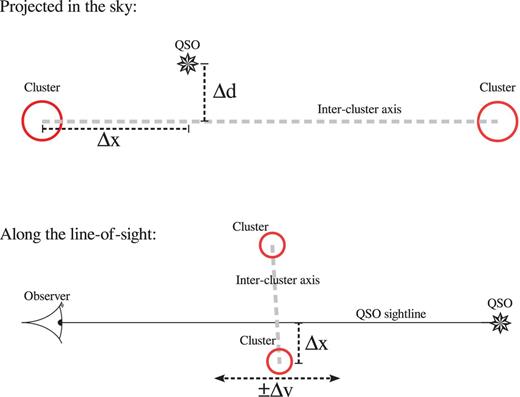
Schematic representation of our survey geometry projected in the sky (top) and along the LOS (bottom), for a single cluster pair. Galaxy clusters are represented by red circles, while the intercluster axis is represented by the grey dashed lines. The QSO itself is represented by an eight-pointed star. The impact parameter between the QSO sightline and the intercluster axis is defined as Δd, while the distance to the closest cluster of the pair along the projected intercluster axis is defined as Δx. A rest-frame velocity window around the position of the cluster pair is defined as ±Δv.
In this paper, we present HST/COS FUV observations of a single bright QSO at z ≈ 0.8 (namely SDSS J141038.39+230447.1, hereafter referred to as Q1410; see Table 1), whose unique sightline intersects seven independent cluster pairs within 3 Mpc from their intercluster axes. This sightline is highly exceptional; the random expectation of finding such a number of cluster pairs is ≲0.01 per cent (see Section 3.4). With this one data set, we offer a first statistical assessment of the presence of diffuse gas close to cluster pairs. Although we are only reporting tentative results (∼1–2σ c.l.), the primary focus of this manuscript is to establish the experimental design and methodology. Future work will extend this study to tens of sightlines, eventually leading towards the statistical detection of the WHIM in intercluster filaments of the cosmic web.
Our paper is structured as follows. In Section 2, we present both the galaxy cluster catalogue used to create our cluster-pair sample and our HST/COS observations of Q1410. In Section 3, we characterize the volume around the Q1410 sightline in terms of known clusters and cluster pairs, quantifying how unusual the Q1410 field is. In Section 4, we provide a full characterization of the Q1410 HST/COS FUV spectrum in terms of absorption line systems, regardless of the presence of known intervening structures. In Section 5, we present our methodology to cross-match the information provided by the cluster-pair sample and absorption line systems, while in Section 6 we present our observational results for the Q1410 field. A discussion of these results is presented in Section 7, and a summary of the paper is presented in Section 8. Supplementary material is presented in the appendix. All distances are in comoving coordinates assuming H0 = 67.3 km s−1 Mpc−1, Ωm = 0.315, ΩΛ = 0.685, k = 0 (unless otherwise stated), where H0, Ωm, ΩΛ and k are the Hubble constant, mass energy density, ‘dark energy’ density and spatial curvature of the Universe, respectively (Planck Collaboration XVI 2014).
2 DATA
2.1 Galaxy clusters
In this section, we briefly describe the cluster catalogue used in this paper. We used red-sequence Matched-filter Probabilistic Percolation (redMaPPer; Rykoff et al. 2014) applied to the SDSS (DR8; Aihara et al. 2011). This is one of the largest galaxy cluster catalogues currently available, containing ∼25 000 rich galaxy clusters (>20 galaxies having luminosities L ≥ 0.2L*)4 at 0.08 ≤ z ≤ 0.55.
The redMaPPer catalogue is very well suited for statistical analysis; it defines clusters properties in terms of probabilities (e.g. position, richness, redshift, galaxy members), with a well-understood selection function; it adopts an optimal mass–richness relationship (Rykoff et al. 2012); and it has high completeness and purity levels compared to others cluster catalogues (Rozo & Rykoff 2014; Rozo et al. 2015; Rykoff et al. 2014).
We note that because we are only using these clusters as tracers of high-density regions in the cosmic web, the exact mass of the clusters will not be particularly relevant, making potential systematic uncertainties in the mass–richness calibration and its extrapolation to lower values not a critical issue. Moreover, low-richness cluster samples suffer more from impurity and incompleteness (Rykoff et al. 2014), but such issues should not create a fake signal in differentiating the properties of absorption line systems in environments traced by these cluster pairs with respect to the field, in the presence of real intercluster filaments. On the contrary, our approach is conservative in the sense that impurity and incompleteness would dilute such a signal, if present.
For the purposes of this paper, we also required the clusters to lie between 0.1 ≤ z ≤ 0.5, yielding a total of 162 144 clusters (see Section 3.1 and Appendix A for further details).
Although the redMaPPer catalogue is mostly based on photometry, the spectroscopic redshift of the most likely centre is also given when available (typically from its brightest cluster galaxy (BCG)).6 This is advantageous for our experiment; a high precision in the cluster redshifts is needed for a reliable association with the gas observed in absorption with intercluster filaments (if any). About 44 per cent (71 701/162 144) of the redMaPPer clusters have spectroscopic redshifts, yielding velocity precision of ≈30 km s−1 in those clusters’ rest frames. We note that for the subsample of clusters most relevant to our paper (i.e. within 20 Mpc of the Q1410), such fraction increases to ∼70 per cent (40/57; see Section 3.1 for further details).
2.2 Q1410 absorption lines
2.2.1 Specific selection of Q1410
In this section, we describe in detail the selection criteria of our targeted QSO, Q1410. We emphasize that the original selection of Q1410 was done using the galaxy cluster catalogue published by Hao et al. (2010) instead of the redMaPPer catalogue (Rykoff et al. 2014) used here.
The Gaussian Mixture Brightest Cluster Galaxy (GMBCG) catalogue (Hao et al. 2010) is based on data from the Seventh Data Release (DR7) of the SDSS (Abazajian et al. 2009), and similar to redMaPPer, it is mainly based on photometry. From the GMBCG catalogue we searched for cluster pairs where at least one member has a spectroscopic redshift and where the redshift difference between them is less than 3× the combined redshift uncertainty, and over clusters having GMBCG richness >15. We then measured the transverse comoving separation between clusters at the redshift of the cluster with spectroscopic identification (if both clusters had spectroscopic redshifts we used the average redshift), and kept the ones separated by <25 Mpc.
We selected our target from the QSO catalogue published by Schneider et al. (2010), which is also based on SDSS DR7 data. This catalogue comprises ≳100 000 QSOs with well-known magnitudes and spectroscopic redshifts. We looked for QSOs having redshifts greater than individual cluster pairs and located inside their sky-projected cylinder areas as defined above. We imposed a magnitude limit of r < 17.5 mag to select relatively bright QSOs. We gave priority to QSOs z > 0.3, ensuring large redshift path coverage. We also searched in the Galaxy Evolution Explorer (GALEX) (Martin et al. 2005) data base and prioritized those QSOs with high FUV fluxes to ensure no higher-z Lyman Limit Systems (LLS) were present,7 enabling a signal-to-noise ratio (S/N) ∼10 spectra to be observed in a relatively short exposure time (no larger than 15 orbits). For each of these QSOs we counted the number of independent cluster pairs (defined as those which were separated by more than 1000 km s−1 from another, and by more than 5000 km s−1 from the background QSO in rest-frame velocity space) at impact parameters Δd ≤ 2 Mpc from the QSO sightline (see Fig. 1 for an illustration). We note that in this paper we adopted a larger limit of 3 Mpc as the fiducial minimum impact parameter (see Section 3), motivated by the results obtained in Section 6. We finally selected the sightline that maximized the number of independent cluster-pair structures, for the minimum observing time. Table 1 presents a summary of the properties of the targeted QSO, Q1410.
| QSO name . | R.A. . | Dec. . | zQSO . | Magnitudes . | ||
|---|---|---|---|---|---|---|
| . | (hms) . | (° ″ ″) . | . | r . | NUV . | FUV . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J141038.39+230447.1 | 14 10 38.39 | +23 04 47.18 | 0.7958 | 17.0 | 17.4 | 18.7 |
| QSO name . | R.A. . | Dec. . | zQSO . | Magnitudes . | ||
|---|---|---|---|---|---|---|
| . | (hms) . | (° ″ ″) . | . | r . | NUV . | FUV . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J141038.39+230447.1 | 14 10 38.39 | +23 04 47.18 | 0.7958 | 17.0 | 17.4 | 18.7 |
Notes. (1) Name of the QSO. (2) Right ascension (J2000). (3) Declination (J2000). (4) Redshift of the QSO. (5) Apparent r (visual) magnitude from Sloan Digital Sky Survey (SDSS). (6) Apparent near-ultra-violet (UV) magnitude from GALEX. (7) Apparent far-UV magnitude from GALEX.
| QSO name . | R.A. . | Dec. . | zQSO . | Magnitudes . | ||
|---|---|---|---|---|---|---|
| . | (hms) . | (° ″ ″) . | . | r . | NUV . | FUV . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J141038.39+230447.1 | 14 10 38.39 | +23 04 47.18 | 0.7958 | 17.0 | 17.4 | 18.7 |
| QSO name . | R.A. . | Dec. . | zQSO . | Magnitudes . | ||
|---|---|---|---|---|---|---|
| . | (hms) . | (° ″ ″) . | . | r . | NUV . | FUV . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . |
| SDSS J141038.39+230447.1 | 14 10 38.39 | +23 04 47.18 | 0.7958 | 17.0 | 17.4 | 18.7 |
Notes. (1) Name of the QSO. (2) Right ascension (J2000). (3) Declination (J2000). (4) Redshift of the QSO. (5) Apparent r (visual) magnitude from Sloan Digital Sky Survey (SDSS). (6) Apparent near-ultra-violet (UV) magnitude from GALEX. (7) Apparent far-UV magnitude from GALEX.
2.2.2 HST/COS observations and data reduction of Q1410
In this paper, we present FUV spectroscopic data of Q1410 (see Table 1 for a summary of its main properties) from HST/COS (Green et al. 2012) taken under program General Observer (GO) 12958 (PI Tejos).
The QSO Q1410 was observed in 2013 August using both G130M and G160M gratings centred at 1318 and 1611 Å, respectively, using the four fixed-pattern noise positions (FP-POSs) available for each configuration. These settings provided medium resolution (|$R \equiv \frac{\lambda }{\Delta \lambda } \sim 16\,000\hbox{--}21\,000$| or FWHM ∼ 0.07–0.09 Å) over the FUV wavelength range of ∼1160–1790 Å, but having two ∼20 Å gaps around each central wavelength. We chose this approach rather than a continuous wavelength coverage to increase the S/N at spectral regions where we expected to find H i absorption line systems associated with intercluster filaments. Having multiple FP-POS (as in our observations) is crucial, however, to minimize the effect of fixed-pattern noise present in COS (see Osterman et al. 2011; Green et al. 2012, for more details on the technical aspects of COS).
Data reduction was performed in the same fashion as presented in Finn et al. (2014) and Tejos et al. (2014), for the G130M and G160M COS gratings. In summary, we used the calcos v2.18.5 pipeline with extraction windows of 25 and 20 pixels for the G130M and G160M gratings, respectively. We applied a customized background estimation smoothing (boxcar) over 1000 and 500 pixels for the FUVA and FUVB stripes, respectively, while masking out and linearly interpolating over regions close to geocoronal emission lines and pixels flagged as having bad quality. The uncertainty was calculated in the same manner as in calcos but using our customized background. The co-alignment was performed using strong Galactic interstellar medium (ISM) features as reference. We finally binned the original spectra having dispersions of ∼0.010 and ∼0.012 Å pixel−1 for the G130M and G160M gratings, respectively, into a single linear wavelength scale of 0.0395 Å pixel−1 (roughly corresponding to two pixels per resolution element). Due to the difficulties in assessing the degree of geocoronal contamination in the final reduced Q1410 spectrum, we opted to mask out the spectral regions close to rest-frame N i, H i Ly α and O i (namely 1300.0–1307.5, 1198.5–1201.0 and 1213.5–1217.8 Å, respectively).
Our pseudo-continuum8 fit was modelled as in Tejos et al. (2014), but also introducing the presence of three partial LLS breaks at ≈1232, 1401 and 1637 Å. Fig. E1 shows the reduced Q1410 spectrum (black line), its corresponding uncertainty (green lines) and our adopted pseudo-continuum fit (blue dotted line).
3 CHARACTERIZATION OF LSSs AROUND THE Q1410 SIGHTLINE
3.1 Galaxy clusters
From the redMaPPer catalogue described in Section 2.1, we define a subsample of clusters according to the following criteria:
the redshift has to lie between 0.1 ≤ z ≤ 0.5; and,
the impact parameter to the Q1410 sightline has to be no larger than 20 Mpc.
There are a total of 57 clusters from the redMaPPer catalogue satisfying the aforementioned criteria, whose relevant information is presented in Table 2. We also show their distribution around the Q1410 sightline in Fig. 2 (coloured circles).
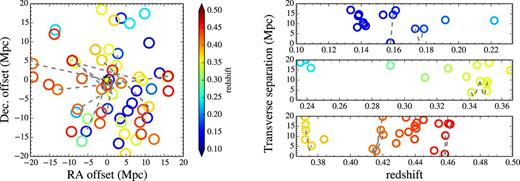
Representation of the LSSs within 20 Mpc around the Q1410 sightline at redshifts 0.1 ≤ z ≤ 0.5, as traced by the 57 galaxy clusters from the redMaPPer catalogue (see Section 3 and Table 2). Galaxy clusters are represented by coloured circles according to redshift, as given by the colour bar scale. Cluster pairs at impact parameters Δd ≤ 3 Mpc of the Q1410 sightline are represented by dashed grey lines. The left-hand panel shows to the projected in the sky distributions in comoving Mpc, where the Q1410 sightline is represented by the yellow star at the origin. The right-hand panel shows the distribution along the LOS in terms of total transverse separation (in comoving Mpc) as a function of redshift (note that intercluster axes appear as hyperbolas in these coordinates). See Section 3 for further details.
Properties of the redMaPPer clusters at 0.1 ≤ z ≤ 0.5 and within 20 Mpc from the Q1410 sightline.
| Cluster ID . | R.A. . | Dec. . | zspec . | zphoto . | Richness . | Mass . | R200 . | Impact parameter . | ||
|---|---|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | . | . | . | (1014 M⊙) . | (Mpc) . | (°) . | (Mpc) . | (R200) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| 1 | 212.994 666 | 21.418 861 | 0.1335 | 0.150 ± 0.006 | 11.0 | 0.92 | 0.9 | 1.6895 | 16.9 | 18.5 |
| 2 | 213.481 691 | 22.808 351 | 0.1376 | 0.147 ± 0.005 | 20.4 | 1.80 | 1.1 | 0.8039 | 8.3 | 7.3 |
| 3 | 214.114 059 | 23.256 258 | 0.1381 | 0.138 ± 0.005 | 33.0 | 3.03 | 1.4 | 1.3484 | 13.9 | 10.3 |
| 4 | 213.817 562 | 24.020 988 | 0.1386 | 0.152 ± 0.006 | 16.5 | 1.43 | 1.1 | 1.4184 | 14.7 | 13.9 |
| 5 | 213.014 763 | 22.125 043 | 0.1413 | 0.141 ± 0.006 | 18.3 | 1.60 | 1.1 | 1.0093 | 10.6 | 9.7 |
| 6 | 213.223 623 | 22.319 874 | 0.1417 | 0.150 ± 0.005 | 20.3 | 1.79 | 1.1 | 0.9208 | 9.7 | 8.6 |
| 7 | 213.330 826 | 22.510 559 | – | 0.143 ± 0.005 | 17.9 | 1.56 | 1.1 | 0.8405 | 9.0 | 8.3 |
| 8 | 213.664 909 | 22.216 942 | 0.1535 | 0.171 ± 0.007 | 10.9 | 0.91 | 0.9 | 1.2667 | 14.5 | 16.0 |
| 9 | 212.712 357 | 23.086 999 | 0.1580 | 0.157 ± 0.006 | 13.0 | 1.11 | 1.0 | 0.0487 | 0.6 | 0.6 |
| 10 | 212.162 442 | 21.946 327 | 0.1596 | 0.145 ± 0.006 | 11.3 | 0.95 | 0.9 | 1.2231 | 14.5 | 15.9 |
| 11 | 212.999 309 | 24.435 343 | 0.1612 | 0.171 ± 0.006 | 16.1 | 1.39 | 1.0 | 1.3907 | 16.6 | 16.1 |
| 12 | 212.674 015 | 22.495 683 | 0.1733 | 0.179 ± 0.006 | 23.0 | 2.05 | 1.2 | 0.5842 | 7.5 | 6.4 |
| 13 | 212.895 979 | 23.605 206 | 0.1787 | 0.167 ± 0.007 | 11.4 | 0.96 | 0.9 | 0.5684 | 7.5 | 8.3 |
| 14 | 213.557 346 | 22.914 918 | 0.1918 | 0.195 ± 0.007 | 12.4 | 1.05 | 0.9 | 0.8423 | 11.9 | 12.8 |
| 15 | 212.123 899 | 22.560 692 | 0.2220 | 0.241 ± 0.012 | 11.2 | 0.94 | 0.9 | 0.7167 | 11.6 | 13.1 |
| 16 | 211.805 856 | 23.845 513 | 0.2359 | 0.233 ± 0.008 | 21.4 | 1.90 | 1.1 | 1.0955 | 18.8 | 16.8 |
| 17 | 213.277 561 | 24.079 481 | 0.2392 | 0.234 ± 0.012 | 10.6 | 0.89 | 0.9 | 1.1488 | 20.0 | 23.1 |
| 18 | 213.029 395 | 23.923 686 | 0.2424 | 0.254 ± 0.010 | 24.9 | 2.23 | 1.2 | 0.9094 | 16.0 | 13.6 |
| 19 | 212.319 446 | 22.314 272 | 0.2914 | 0.482 ± 0.021 | 11.4 | 0.96 | 0.9 | 0.8275 | 17.3 | 19.8 |
| 20 | 212.415 280 | 22.627 699 | 0.3127 | 0.306 ± 0.020 | 11.4 | 0.96 | 0.9 | 0.5052 | 11.3 | 13.0 |
| 21 | 213.395 595 | 23.114 057 | – | 0.327 ± 0.020 | 12.2 | 1.03 | 0.9 | 0.6775 | 15.8 | 17.9 |
| 22 | 212.831 535 | 22.621 344 | 0.3382 | 0.368 ± 0.017 | 30.0 | 2.73 | 1.2 | 0.4849 | 11.6 | 9.6 |
| 23 | 212.723 980 | 22.929 555 | 0.3412 | 0.357 ± 0.017 | 28.1 | 2.54 | 1.2 | 0.1614 | 3.9 | 3.3 |
| 24 | 213.000 928 | 22.437 411 | – | 0.345 ± 0.018 | 23.6 | 2.10 | 1.1 | 0.7152 | 17.5 | 15.7 |
| 25 | 212.293 470 | 23.265 859 | 0.3465 | 0.349 ± 0.019 | 21.2 | 1.88 | 1.1 | 0.3849 | 9.4 | 8.8 |
| 26 | 212.684 410 | 23.402 739 | 0.3506 | 0.358 ± 0.024 | 11.4 | 0.96 | 0.9 | 0.3237 | 8.0 | 9.4 |
| 27 | 212.770 942 | 23.232 412 | 0.3508 | 0.357 ± 0.022 | 10.4 | 0.87 | 0.8 | 0.1836 | 4.6 | 5.5 |
| 28 | 213.066 601 | 23.075 991 | 0.3511 | 0.378 ± 0.021 | 20.6 | 1.82 | 1.1 | 0.3741 | 9.3 | 8.8 |
| 29 | 212.600 828 | 23.822 434 | 0.3520 | 0.358 ± 0.020 | 15.0 | 1.29 | 0.9 | 0.7446 | 18.5 | 19.7 |
| 30 | 212.854 438 | 22.531 418 | – | 0.365 ± 0.021 | 13.5 | 1.15 | 0.9 | 0.5769 | 14.8 | 16.5 |
| 31 | 212.861 147 | 22.341 353 | 0.3718 | 0.385 ± 0.016 | 22.8 | 2.03 | 1.1 | 0.7614 | 19.9 | 18.3 |
| 32 | 213.011 303 | 23.110 255 | 0.3722 | 0.395 ± 0.019 | 13.6 | 1.16 | 0.9 | 0.3246 | 8.5 | 9.4 |
| 33 | 212.737 954 | 23.677 308 | 0.3725 | 0.379 ± 0.017 | 18.4 | 1.61 | 1.0 | 0.6018 | 15.8 | 15.7 |
| 34 | 213.115 594 | 22.812 719 | 0.3725 | 0.400 ± 0.022 | 16.9 | 1.46 | 1.0 | 0.4973 | 13.0 | 13.4 |
| 35 | 212.604 626 | 23.277 634 | – | 0.376 ± 0.018 | 22.2 | 1.98 | 1.1 | 0.2043 | 5.4 | 5.0 |
| 36 | 212.538 462 | 23.376 505 | – | 0.384 ± 0.019 | 17.6 | 1.53 | 1.0 | 0.3170 | 8.5 | 8.7 |
| 37 | 212.800 638 | 23.052 477 | 0.4138 | 0.426 ± 0.015 | 20.0 | 1.76 | 1.0 | 0.1323 | 3.8 | 3.7 |
| 38 | 212.609 281 | 22.997 888 | 0.4159 | 0.425 ± 0.015 | 10.6 | 0.89 | 0.8 | 0.0942 | 2.7 | 3.4 |
| 39 | 212.177 450 | 22.994 366 | 0.4188 | 0.424 ± 0.015 | 25.4 | 2.28 | 1.1 | 0.4522 | 13.1 | 11.9 |
| 40 | 213.120 494 | 22.548 543 | – | 0.420 ± 0.014 | 38.4 | 3.57 | 1.3 | 0.6800 | 19.8 | 15.4 |
| 41 | 211.935 365 | 23.227 769 | 0.4199 | 0.416 ± 0.019 | 10.7 | 0.90 | 0.8 | 0.6825 | 19.9 | 24.5 |
| 42 | 212.374 306 | 22.818 205 | – | 0.420 ± 0.019 | 17.3 | 1.50 | 1.0 | 0.3710 | 10.8 | 11.2 |
| 43 | 212.420 269 | 23.093 511 | – | 0.428 ± 0.018 | 14.5 | 1.24 | 0.9 | 0.2209 | 6.6 | 7.3 |
| 44 | 212.593 164 | 22.699 892 | – | 0.430 ± 0.017 | 12.1 | 1.02 | 0.8 | 0.3848 | 11.5 | 13.6 |
| 45 | 211.957 129 | 23.106 715 | – | 0.434 ± 0.014 | 28.6 | 2.59 | 1.1 | 0.6471 | 19.4 | 16.9 |
| 46 | 212.999 005 | 22.821 469 | 0.4358 | 0.443 ± 0.019 | 12.5 | 1.06 | 0.9 | 0.4052 | 12.2 | 14.3 |
| 47 | 212.607 221 | 22.800 250 | – | 0.440 ± 0.018 | 13.0 | 1.10 | 0.9 | 0.2837 | 8.6 | 10.0 |
| 48 | 212.115 194 | 23.041 513 | 0.4397 | 0.442 ± 0.016 | 11.1 | 0.94 | 0.8 | 0.5027 | 15.3 | 18.7 |
| 49 | 212.968 630 | 22.717 594 | – | 0.441 ± 0.021 | 11.0 | 0.92 | 0.8 | 0.4604 | 14.0 | 17.3 |
| 50 | 212.980 494 | 22.615 241 | – | 0.441 ± 0.018 | 15.6 | 1.34 | 0.9 | 0.5505 | 16.7 | 18.2 |
| 51 | 212.172 529 | 23.471 857 | – | 0.445 ± 0.018 | 15.6 | 1.35 | 0.9 | 0.5952 | 18.3 | 19.8 |
| 52 | 212.710 891 | 23.162 554 | – | 0.452 ± 0.017 | 11.4 | 0.96 | 0.8 | 0.0951 | 3.0 | 3.6 |
| 53 | 212.336 805 | 22.647 284 | – | 0.454 ± 0.019 | 15.5 | 1.34 | 0.9 | 0.5251 | 16.4 | 18.0 |
| 54 | 212.658 634 | 23.039 911 | 0.4582 | 0.437 ± 0.014 | 37.2 | 3.44 | 1.3 | 0.0399 | 1.3 | 1.0 |
| 55 | 212.346 270 | 23.242 090 | 0.4585 | 0.449 ± 0.016 | 15.6 | 1.35 | 0.9 | 0.3310 | 10.4 | 11.4 |
| 56 | 213.213 654 | 22.988 852 | 0.4603 | 0.477 ± 0.013 | 47.9 | 4.52 | 1.4 | 0.5176 | 16.4 | 11.9 |
| 57 | 213.210 168 | 23.112 030 | 0.4615 | 0.469 ± 0.013 | 48.9 | 4.62 | 1.4 | 0.5071 | 16.1 | 11.7 |
| Cluster ID . | R.A. . | Dec. . | zspec . | zphoto . | Richness . | Mass . | R200 . | Impact parameter . | ||
|---|---|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | . | . | . | (1014 M⊙) . | (Mpc) . | (°) . | (Mpc) . | (R200) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| 1 | 212.994 666 | 21.418 861 | 0.1335 | 0.150 ± 0.006 | 11.0 | 0.92 | 0.9 | 1.6895 | 16.9 | 18.5 |
| 2 | 213.481 691 | 22.808 351 | 0.1376 | 0.147 ± 0.005 | 20.4 | 1.80 | 1.1 | 0.8039 | 8.3 | 7.3 |
| 3 | 214.114 059 | 23.256 258 | 0.1381 | 0.138 ± 0.005 | 33.0 | 3.03 | 1.4 | 1.3484 | 13.9 | 10.3 |
| 4 | 213.817 562 | 24.020 988 | 0.1386 | 0.152 ± 0.006 | 16.5 | 1.43 | 1.1 | 1.4184 | 14.7 | 13.9 |
| 5 | 213.014 763 | 22.125 043 | 0.1413 | 0.141 ± 0.006 | 18.3 | 1.60 | 1.1 | 1.0093 | 10.6 | 9.7 |
| 6 | 213.223 623 | 22.319 874 | 0.1417 | 0.150 ± 0.005 | 20.3 | 1.79 | 1.1 | 0.9208 | 9.7 | 8.6 |
| 7 | 213.330 826 | 22.510 559 | – | 0.143 ± 0.005 | 17.9 | 1.56 | 1.1 | 0.8405 | 9.0 | 8.3 |
| 8 | 213.664 909 | 22.216 942 | 0.1535 | 0.171 ± 0.007 | 10.9 | 0.91 | 0.9 | 1.2667 | 14.5 | 16.0 |
| 9 | 212.712 357 | 23.086 999 | 0.1580 | 0.157 ± 0.006 | 13.0 | 1.11 | 1.0 | 0.0487 | 0.6 | 0.6 |
| 10 | 212.162 442 | 21.946 327 | 0.1596 | 0.145 ± 0.006 | 11.3 | 0.95 | 0.9 | 1.2231 | 14.5 | 15.9 |
| 11 | 212.999 309 | 24.435 343 | 0.1612 | 0.171 ± 0.006 | 16.1 | 1.39 | 1.0 | 1.3907 | 16.6 | 16.1 |
| 12 | 212.674 015 | 22.495 683 | 0.1733 | 0.179 ± 0.006 | 23.0 | 2.05 | 1.2 | 0.5842 | 7.5 | 6.4 |
| 13 | 212.895 979 | 23.605 206 | 0.1787 | 0.167 ± 0.007 | 11.4 | 0.96 | 0.9 | 0.5684 | 7.5 | 8.3 |
| 14 | 213.557 346 | 22.914 918 | 0.1918 | 0.195 ± 0.007 | 12.4 | 1.05 | 0.9 | 0.8423 | 11.9 | 12.8 |
| 15 | 212.123 899 | 22.560 692 | 0.2220 | 0.241 ± 0.012 | 11.2 | 0.94 | 0.9 | 0.7167 | 11.6 | 13.1 |
| 16 | 211.805 856 | 23.845 513 | 0.2359 | 0.233 ± 0.008 | 21.4 | 1.90 | 1.1 | 1.0955 | 18.8 | 16.8 |
| 17 | 213.277 561 | 24.079 481 | 0.2392 | 0.234 ± 0.012 | 10.6 | 0.89 | 0.9 | 1.1488 | 20.0 | 23.1 |
| 18 | 213.029 395 | 23.923 686 | 0.2424 | 0.254 ± 0.010 | 24.9 | 2.23 | 1.2 | 0.9094 | 16.0 | 13.6 |
| 19 | 212.319 446 | 22.314 272 | 0.2914 | 0.482 ± 0.021 | 11.4 | 0.96 | 0.9 | 0.8275 | 17.3 | 19.8 |
| 20 | 212.415 280 | 22.627 699 | 0.3127 | 0.306 ± 0.020 | 11.4 | 0.96 | 0.9 | 0.5052 | 11.3 | 13.0 |
| 21 | 213.395 595 | 23.114 057 | – | 0.327 ± 0.020 | 12.2 | 1.03 | 0.9 | 0.6775 | 15.8 | 17.9 |
| 22 | 212.831 535 | 22.621 344 | 0.3382 | 0.368 ± 0.017 | 30.0 | 2.73 | 1.2 | 0.4849 | 11.6 | 9.6 |
| 23 | 212.723 980 | 22.929 555 | 0.3412 | 0.357 ± 0.017 | 28.1 | 2.54 | 1.2 | 0.1614 | 3.9 | 3.3 |
| 24 | 213.000 928 | 22.437 411 | – | 0.345 ± 0.018 | 23.6 | 2.10 | 1.1 | 0.7152 | 17.5 | 15.7 |
| 25 | 212.293 470 | 23.265 859 | 0.3465 | 0.349 ± 0.019 | 21.2 | 1.88 | 1.1 | 0.3849 | 9.4 | 8.8 |
| 26 | 212.684 410 | 23.402 739 | 0.3506 | 0.358 ± 0.024 | 11.4 | 0.96 | 0.9 | 0.3237 | 8.0 | 9.4 |
| 27 | 212.770 942 | 23.232 412 | 0.3508 | 0.357 ± 0.022 | 10.4 | 0.87 | 0.8 | 0.1836 | 4.6 | 5.5 |
| 28 | 213.066 601 | 23.075 991 | 0.3511 | 0.378 ± 0.021 | 20.6 | 1.82 | 1.1 | 0.3741 | 9.3 | 8.8 |
| 29 | 212.600 828 | 23.822 434 | 0.3520 | 0.358 ± 0.020 | 15.0 | 1.29 | 0.9 | 0.7446 | 18.5 | 19.7 |
| 30 | 212.854 438 | 22.531 418 | – | 0.365 ± 0.021 | 13.5 | 1.15 | 0.9 | 0.5769 | 14.8 | 16.5 |
| 31 | 212.861 147 | 22.341 353 | 0.3718 | 0.385 ± 0.016 | 22.8 | 2.03 | 1.1 | 0.7614 | 19.9 | 18.3 |
| 32 | 213.011 303 | 23.110 255 | 0.3722 | 0.395 ± 0.019 | 13.6 | 1.16 | 0.9 | 0.3246 | 8.5 | 9.4 |
| 33 | 212.737 954 | 23.677 308 | 0.3725 | 0.379 ± 0.017 | 18.4 | 1.61 | 1.0 | 0.6018 | 15.8 | 15.7 |
| 34 | 213.115 594 | 22.812 719 | 0.3725 | 0.400 ± 0.022 | 16.9 | 1.46 | 1.0 | 0.4973 | 13.0 | 13.4 |
| 35 | 212.604 626 | 23.277 634 | – | 0.376 ± 0.018 | 22.2 | 1.98 | 1.1 | 0.2043 | 5.4 | 5.0 |
| 36 | 212.538 462 | 23.376 505 | – | 0.384 ± 0.019 | 17.6 | 1.53 | 1.0 | 0.3170 | 8.5 | 8.7 |
| 37 | 212.800 638 | 23.052 477 | 0.4138 | 0.426 ± 0.015 | 20.0 | 1.76 | 1.0 | 0.1323 | 3.8 | 3.7 |
| 38 | 212.609 281 | 22.997 888 | 0.4159 | 0.425 ± 0.015 | 10.6 | 0.89 | 0.8 | 0.0942 | 2.7 | 3.4 |
| 39 | 212.177 450 | 22.994 366 | 0.4188 | 0.424 ± 0.015 | 25.4 | 2.28 | 1.1 | 0.4522 | 13.1 | 11.9 |
| 40 | 213.120 494 | 22.548 543 | – | 0.420 ± 0.014 | 38.4 | 3.57 | 1.3 | 0.6800 | 19.8 | 15.4 |
| 41 | 211.935 365 | 23.227 769 | 0.4199 | 0.416 ± 0.019 | 10.7 | 0.90 | 0.8 | 0.6825 | 19.9 | 24.5 |
| 42 | 212.374 306 | 22.818 205 | – | 0.420 ± 0.019 | 17.3 | 1.50 | 1.0 | 0.3710 | 10.8 | 11.2 |
| 43 | 212.420 269 | 23.093 511 | – | 0.428 ± 0.018 | 14.5 | 1.24 | 0.9 | 0.2209 | 6.6 | 7.3 |
| 44 | 212.593 164 | 22.699 892 | – | 0.430 ± 0.017 | 12.1 | 1.02 | 0.8 | 0.3848 | 11.5 | 13.6 |
| 45 | 211.957 129 | 23.106 715 | – | 0.434 ± 0.014 | 28.6 | 2.59 | 1.1 | 0.6471 | 19.4 | 16.9 |
| 46 | 212.999 005 | 22.821 469 | 0.4358 | 0.443 ± 0.019 | 12.5 | 1.06 | 0.9 | 0.4052 | 12.2 | 14.3 |
| 47 | 212.607 221 | 22.800 250 | – | 0.440 ± 0.018 | 13.0 | 1.10 | 0.9 | 0.2837 | 8.6 | 10.0 |
| 48 | 212.115 194 | 23.041 513 | 0.4397 | 0.442 ± 0.016 | 11.1 | 0.94 | 0.8 | 0.5027 | 15.3 | 18.7 |
| 49 | 212.968 630 | 22.717 594 | – | 0.441 ± 0.021 | 11.0 | 0.92 | 0.8 | 0.4604 | 14.0 | 17.3 |
| 50 | 212.980 494 | 22.615 241 | – | 0.441 ± 0.018 | 15.6 | 1.34 | 0.9 | 0.5505 | 16.7 | 18.2 |
| 51 | 212.172 529 | 23.471 857 | – | 0.445 ± 0.018 | 15.6 | 1.35 | 0.9 | 0.5952 | 18.3 | 19.8 |
| 52 | 212.710 891 | 23.162 554 | – | 0.452 ± 0.017 | 11.4 | 0.96 | 0.8 | 0.0951 | 3.0 | 3.6 |
| 53 | 212.336 805 | 22.647 284 | – | 0.454 ± 0.019 | 15.5 | 1.34 | 0.9 | 0.5251 | 16.4 | 18.0 |
| 54 | 212.658 634 | 23.039 911 | 0.4582 | 0.437 ± 0.014 | 37.2 | 3.44 | 1.3 | 0.0399 | 1.3 | 1.0 |
| 55 | 212.346 270 | 23.242 090 | 0.4585 | 0.449 ± 0.016 | 15.6 | 1.35 | 0.9 | 0.3310 | 10.4 | 11.4 |
| 56 | 213.213 654 | 22.988 852 | 0.4603 | 0.477 ± 0.013 | 47.9 | 4.52 | 1.4 | 0.5176 | 16.4 | 11.9 |
| 57 | 213.210 168 | 23.112 030 | 0.4615 | 0.469 ± 0.013 | 48.9 | 4.62 | 1.4 | 0.5071 | 16.1 | 11.7 |
Notes. (1) Cluster ID. (2) Right ascension (J2000). (3) Declination (J2000). (4) Spectroscopic redshift. (5) Photometric redshift. (6) Richness of galaxies having L ≥ 0.2L*, corrected for incompleteness (hence non-integer). (7) Inferred mass using equation (1); typical scatter of ∼0.25 in ln (M) (Rykoff et al. 2012). (8) Inferred virial radii of the cluster using equation (2). (9) Projected separation to the Q1410 sightline in degrees. (10) Projected separation to the Q1410 sightline in Mpc. (11) Projected separation to the Q1410 sightline in units of our R200 estimation.
Properties of the redMaPPer clusters at 0.1 ≤ z ≤ 0.5 and within 20 Mpc from the Q1410 sightline.
| Cluster ID . | R.A. . | Dec. . | zspec . | zphoto . | Richness . | Mass . | R200 . | Impact parameter . | ||
|---|---|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | . | . | . | (1014 M⊙) . | (Mpc) . | (°) . | (Mpc) . | (R200) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| 1 | 212.994 666 | 21.418 861 | 0.1335 | 0.150 ± 0.006 | 11.0 | 0.92 | 0.9 | 1.6895 | 16.9 | 18.5 |
| 2 | 213.481 691 | 22.808 351 | 0.1376 | 0.147 ± 0.005 | 20.4 | 1.80 | 1.1 | 0.8039 | 8.3 | 7.3 |
| 3 | 214.114 059 | 23.256 258 | 0.1381 | 0.138 ± 0.005 | 33.0 | 3.03 | 1.4 | 1.3484 | 13.9 | 10.3 |
| 4 | 213.817 562 | 24.020 988 | 0.1386 | 0.152 ± 0.006 | 16.5 | 1.43 | 1.1 | 1.4184 | 14.7 | 13.9 |
| 5 | 213.014 763 | 22.125 043 | 0.1413 | 0.141 ± 0.006 | 18.3 | 1.60 | 1.1 | 1.0093 | 10.6 | 9.7 |
| 6 | 213.223 623 | 22.319 874 | 0.1417 | 0.150 ± 0.005 | 20.3 | 1.79 | 1.1 | 0.9208 | 9.7 | 8.6 |
| 7 | 213.330 826 | 22.510 559 | – | 0.143 ± 0.005 | 17.9 | 1.56 | 1.1 | 0.8405 | 9.0 | 8.3 |
| 8 | 213.664 909 | 22.216 942 | 0.1535 | 0.171 ± 0.007 | 10.9 | 0.91 | 0.9 | 1.2667 | 14.5 | 16.0 |
| 9 | 212.712 357 | 23.086 999 | 0.1580 | 0.157 ± 0.006 | 13.0 | 1.11 | 1.0 | 0.0487 | 0.6 | 0.6 |
| 10 | 212.162 442 | 21.946 327 | 0.1596 | 0.145 ± 0.006 | 11.3 | 0.95 | 0.9 | 1.2231 | 14.5 | 15.9 |
| 11 | 212.999 309 | 24.435 343 | 0.1612 | 0.171 ± 0.006 | 16.1 | 1.39 | 1.0 | 1.3907 | 16.6 | 16.1 |
| 12 | 212.674 015 | 22.495 683 | 0.1733 | 0.179 ± 0.006 | 23.0 | 2.05 | 1.2 | 0.5842 | 7.5 | 6.4 |
| 13 | 212.895 979 | 23.605 206 | 0.1787 | 0.167 ± 0.007 | 11.4 | 0.96 | 0.9 | 0.5684 | 7.5 | 8.3 |
| 14 | 213.557 346 | 22.914 918 | 0.1918 | 0.195 ± 0.007 | 12.4 | 1.05 | 0.9 | 0.8423 | 11.9 | 12.8 |
| 15 | 212.123 899 | 22.560 692 | 0.2220 | 0.241 ± 0.012 | 11.2 | 0.94 | 0.9 | 0.7167 | 11.6 | 13.1 |
| 16 | 211.805 856 | 23.845 513 | 0.2359 | 0.233 ± 0.008 | 21.4 | 1.90 | 1.1 | 1.0955 | 18.8 | 16.8 |
| 17 | 213.277 561 | 24.079 481 | 0.2392 | 0.234 ± 0.012 | 10.6 | 0.89 | 0.9 | 1.1488 | 20.0 | 23.1 |
| 18 | 213.029 395 | 23.923 686 | 0.2424 | 0.254 ± 0.010 | 24.9 | 2.23 | 1.2 | 0.9094 | 16.0 | 13.6 |
| 19 | 212.319 446 | 22.314 272 | 0.2914 | 0.482 ± 0.021 | 11.4 | 0.96 | 0.9 | 0.8275 | 17.3 | 19.8 |
| 20 | 212.415 280 | 22.627 699 | 0.3127 | 0.306 ± 0.020 | 11.4 | 0.96 | 0.9 | 0.5052 | 11.3 | 13.0 |
| 21 | 213.395 595 | 23.114 057 | – | 0.327 ± 0.020 | 12.2 | 1.03 | 0.9 | 0.6775 | 15.8 | 17.9 |
| 22 | 212.831 535 | 22.621 344 | 0.3382 | 0.368 ± 0.017 | 30.0 | 2.73 | 1.2 | 0.4849 | 11.6 | 9.6 |
| 23 | 212.723 980 | 22.929 555 | 0.3412 | 0.357 ± 0.017 | 28.1 | 2.54 | 1.2 | 0.1614 | 3.9 | 3.3 |
| 24 | 213.000 928 | 22.437 411 | – | 0.345 ± 0.018 | 23.6 | 2.10 | 1.1 | 0.7152 | 17.5 | 15.7 |
| 25 | 212.293 470 | 23.265 859 | 0.3465 | 0.349 ± 0.019 | 21.2 | 1.88 | 1.1 | 0.3849 | 9.4 | 8.8 |
| 26 | 212.684 410 | 23.402 739 | 0.3506 | 0.358 ± 0.024 | 11.4 | 0.96 | 0.9 | 0.3237 | 8.0 | 9.4 |
| 27 | 212.770 942 | 23.232 412 | 0.3508 | 0.357 ± 0.022 | 10.4 | 0.87 | 0.8 | 0.1836 | 4.6 | 5.5 |
| 28 | 213.066 601 | 23.075 991 | 0.3511 | 0.378 ± 0.021 | 20.6 | 1.82 | 1.1 | 0.3741 | 9.3 | 8.8 |
| 29 | 212.600 828 | 23.822 434 | 0.3520 | 0.358 ± 0.020 | 15.0 | 1.29 | 0.9 | 0.7446 | 18.5 | 19.7 |
| 30 | 212.854 438 | 22.531 418 | – | 0.365 ± 0.021 | 13.5 | 1.15 | 0.9 | 0.5769 | 14.8 | 16.5 |
| 31 | 212.861 147 | 22.341 353 | 0.3718 | 0.385 ± 0.016 | 22.8 | 2.03 | 1.1 | 0.7614 | 19.9 | 18.3 |
| 32 | 213.011 303 | 23.110 255 | 0.3722 | 0.395 ± 0.019 | 13.6 | 1.16 | 0.9 | 0.3246 | 8.5 | 9.4 |
| 33 | 212.737 954 | 23.677 308 | 0.3725 | 0.379 ± 0.017 | 18.4 | 1.61 | 1.0 | 0.6018 | 15.8 | 15.7 |
| 34 | 213.115 594 | 22.812 719 | 0.3725 | 0.400 ± 0.022 | 16.9 | 1.46 | 1.0 | 0.4973 | 13.0 | 13.4 |
| 35 | 212.604 626 | 23.277 634 | – | 0.376 ± 0.018 | 22.2 | 1.98 | 1.1 | 0.2043 | 5.4 | 5.0 |
| 36 | 212.538 462 | 23.376 505 | – | 0.384 ± 0.019 | 17.6 | 1.53 | 1.0 | 0.3170 | 8.5 | 8.7 |
| 37 | 212.800 638 | 23.052 477 | 0.4138 | 0.426 ± 0.015 | 20.0 | 1.76 | 1.0 | 0.1323 | 3.8 | 3.7 |
| 38 | 212.609 281 | 22.997 888 | 0.4159 | 0.425 ± 0.015 | 10.6 | 0.89 | 0.8 | 0.0942 | 2.7 | 3.4 |
| 39 | 212.177 450 | 22.994 366 | 0.4188 | 0.424 ± 0.015 | 25.4 | 2.28 | 1.1 | 0.4522 | 13.1 | 11.9 |
| 40 | 213.120 494 | 22.548 543 | – | 0.420 ± 0.014 | 38.4 | 3.57 | 1.3 | 0.6800 | 19.8 | 15.4 |
| 41 | 211.935 365 | 23.227 769 | 0.4199 | 0.416 ± 0.019 | 10.7 | 0.90 | 0.8 | 0.6825 | 19.9 | 24.5 |
| 42 | 212.374 306 | 22.818 205 | – | 0.420 ± 0.019 | 17.3 | 1.50 | 1.0 | 0.3710 | 10.8 | 11.2 |
| 43 | 212.420 269 | 23.093 511 | – | 0.428 ± 0.018 | 14.5 | 1.24 | 0.9 | 0.2209 | 6.6 | 7.3 |
| 44 | 212.593 164 | 22.699 892 | – | 0.430 ± 0.017 | 12.1 | 1.02 | 0.8 | 0.3848 | 11.5 | 13.6 |
| 45 | 211.957 129 | 23.106 715 | – | 0.434 ± 0.014 | 28.6 | 2.59 | 1.1 | 0.6471 | 19.4 | 16.9 |
| 46 | 212.999 005 | 22.821 469 | 0.4358 | 0.443 ± 0.019 | 12.5 | 1.06 | 0.9 | 0.4052 | 12.2 | 14.3 |
| 47 | 212.607 221 | 22.800 250 | – | 0.440 ± 0.018 | 13.0 | 1.10 | 0.9 | 0.2837 | 8.6 | 10.0 |
| 48 | 212.115 194 | 23.041 513 | 0.4397 | 0.442 ± 0.016 | 11.1 | 0.94 | 0.8 | 0.5027 | 15.3 | 18.7 |
| 49 | 212.968 630 | 22.717 594 | – | 0.441 ± 0.021 | 11.0 | 0.92 | 0.8 | 0.4604 | 14.0 | 17.3 |
| 50 | 212.980 494 | 22.615 241 | – | 0.441 ± 0.018 | 15.6 | 1.34 | 0.9 | 0.5505 | 16.7 | 18.2 |
| 51 | 212.172 529 | 23.471 857 | – | 0.445 ± 0.018 | 15.6 | 1.35 | 0.9 | 0.5952 | 18.3 | 19.8 |
| 52 | 212.710 891 | 23.162 554 | – | 0.452 ± 0.017 | 11.4 | 0.96 | 0.8 | 0.0951 | 3.0 | 3.6 |
| 53 | 212.336 805 | 22.647 284 | – | 0.454 ± 0.019 | 15.5 | 1.34 | 0.9 | 0.5251 | 16.4 | 18.0 |
| 54 | 212.658 634 | 23.039 911 | 0.4582 | 0.437 ± 0.014 | 37.2 | 3.44 | 1.3 | 0.0399 | 1.3 | 1.0 |
| 55 | 212.346 270 | 23.242 090 | 0.4585 | 0.449 ± 0.016 | 15.6 | 1.35 | 0.9 | 0.3310 | 10.4 | 11.4 |
| 56 | 213.213 654 | 22.988 852 | 0.4603 | 0.477 ± 0.013 | 47.9 | 4.52 | 1.4 | 0.5176 | 16.4 | 11.9 |
| 57 | 213.210 168 | 23.112 030 | 0.4615 | 0.469 ± 0.013 | 48.9 | 4.62 | 1.4 | 0.5071 | 16.1 | 11.7 |
| Cluster ID . | R.A. . | Dec. . | zspec . | zphoto . | Richness . | Mass . | R200 . | Impact parameter . | ||
|---|---|---|---|---|---|---|---|---|---|---|
| . | (°) . | (°) . | . | . | . | (1014 M⊙) . | (Mpc) . | (°) . | (Mpc) . | (R200) . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . |
| 1 | 212.994 666 | 21.418 861 | 0.1335 | 0.150 ± 0.006 | 11.0 | 0.92 | 0.9 | 1.6895 | 16.9 | 18.5 |
| 2 | 213.481 691 | 22.808 351 | 0.1376 | 0.147 ± 0.005 | 20.4 | 1.80 | 1.1 | 0.8039 | 8.3 | 7.3 |
| 3 | 214.114 059 | 23.256 258 | 0.1381 | 0.138 ± 0.005 | 33.0 | 3.03 | 1.4 | 1.3484 | 13.9 | 10.3 |
| 4 | 213.817 562 | 24.020 988 | 0.1386 | 0.152 ± 0.006 | 16.5 | 1.43 | 1.1 | 1.4184 | 14.7 | 13.9 |
| 5 | 213.014 763 | 22.125 043 | 0.1413 | 0.141 ± 0.006 | 18.3 | 1.60 | 1.1 | 1.0093 | 10.6 | 9.7 |
| 6 | 213.223 623 | 22.319 874 | 0.1417 | 0.150 ± 0.005 | 20.3 | 1.79 | 1.1 | 0.9208 | 9.7 | 8.6 |
| 7 | 213.330 826 | 22.510 559 | – | 0.143 ± 0.005 | 17.9 | 1.56 | 1.1 | 0.8405 | 9.0 | 8.3 |
| 8 | 213.664 909 | 22.216 942 | 0.1535 | 0.171 ± 0.007 | 10.9 | 0.91 | 0.9 | 1.2667 | 14.5 | 16.0 |
| 9 | 212.712 357 | 23.086 999 | 0.1580 | 0.157 ± 0.006 | 13.0 | 1.11 | 1.0 | 0.0487 | 0.6 | 0.6 |
| 10 | 212.162 442 | 21.946 327 | 0.1596 | 0.145 ± 0.006 | 11.3 | 0.95 | 0.9 | 1.2231 | 14.5 | 15.9 |
| 11 | 212.999 309 | 24.435 343 | 0.1612 | 0.171 ± 0.006 | 16.1 | 1.39 | 1.0 | 1.3907 | 16.6 | 16.1 |
| 12 | 212.674 015 | 22.495 683 | 0.1733 | 0.179 ± 0.006 | 23.0 | 2.05 | 1.2 | 0.5842 | 7.5 | 6.4 |
| 13 | 212.895 979 | 23.605 206 | 0.1787 | 0.167 ± 0.007 | 11.4 | 0.96 | 0.9 | 0.5684 | 7.5 | 8.3 |
| 14 | 213.557 346 | 22.914 918 | 0.1918 | 0.195 ± 0.007 | 12.4 | 1.05 | 0.9 | 0.8423 | 11.9 | 12.8 |
| 15 | 212.123 899 | 22.560 692 | 0.2220 | 0.241 ± 0.012 | 11.2 | 0.94 | 0.9 | 0.7167 | 11.6 | 13.1 |
| 16 | 211.805 856 | 23.845 513 | 0.2359 | 0.233 ± 0.008 | 21.4 | 1.90 | 1.1 | 1.0955 | 18.8 | 16.8 |
| 17 | 213.277 561 | 24.079 481 | 0.2392 | 0.234 ± 0.012 | 10.6 | 0.89 | 0.9 | 1.1488 | 20.0 | 23.1 |
| 18 | 213.029 395 | 23.923 686 | 0.2424 | 0.254 ± 0.010 | 24.9 | 2.23 | 1.2 | 0.9094 | 16.0 | 13.6 |
| 19 | 212.319 446 | 22.314 272 | 0.2914 | 0.482 ± 0.021 | 11.4 | 0.96 | 0.9 | 0.8275 | 17.3 | 19.8 |
| 20 | 212.415 280 | 22.627 699 | 0.3127 | 0.306 ± 0.020 | 11.4 | 0.96 | 0.9 | 0.5052 | 11.3 | 13.0 |
| 21 | 213.395 595 | 23.114 057 | – | 0.327 ± 0.020 | 12.2 | 1.03 | 0.9 | 0.6775 | 15.8 | 17.9 |
| 22 | 212.831 535 | 22.621 344 | 0.3382 | 0.368 ± 0.017 | 30.0 | 2.73 | 1.2 | 0.4849 | 11.6 | 9.6 |
| 23 | 212.723 980 | 22.929 555 | 0.3412 | 0.357 ± 0.017 | 28.1 | 2.54 | 1.2 | 0.1614 | 3.9 | 3.3 |
| 24 | 213.000 928 | 22.437 411 | – | 0.345 ± 0.018 | 23.6 | 2.10 | 1.1 | 0.7152 | 17.5 | 15.7 |
| 25 | 212.293 470 | 23.265 859 | 0.3465 | 0.349 ± 0.019 | 21.2 | 1.88 | 1.1 | 0.3849 | 9.4 | 8.8 |
| 26 | 212.684 410 | 23.402 739 | 0.3506 | 0.358 ± 0.024 | 11.4 | 0.96 | 0.9 | 0.3237 | 8.0 | 9.4 |
| 27 | 212.770 942 | 23.232 412 | 0.3508 | 0.357 ± 0.022 | 10.4 | 0.87 | 0.8 | 0.1836 | 4.6 | 5.5 |
| 28 | 213.066 601 | 23.075 991 | 0.3511 | 0.378 ± 0.021 | 20.6 | 1.82 | 1.1 | 0.3741 | 9.3 | 8.8 |
| 29 | 212.600 828 | 23.822 434 | 0.3520 | 0.358 ± 0.020 | 15.0 | 1.29 | 0.9 | 0.7446 | 18.5 | 19.7 |
| 30 | 212.854 438 | 22.531 418 | – | 0.365 ± 0.021 | 13.5 | 1.15 | 0.9 | 0.5769 | 14.8 | 16.5 |
| 31 | 212.861 147 | 22.341 353 | 0.3718 | 0.385 ± 0.016 | 22.8 | 2.03 | 1.1 | 0.7614 | 19.9 | 18.3 |
| 32 | 213.011 303 | 23.110 255 | 0.3722 | 0.395 ± 0.019 | 13.6 | 1.16 | 0.9 | 0.3246 | 8.5 | 9.4 |
| 33 | 212.737 954 | 23.677 308 | 0.3725 | 0.379 ± 0.017 | 18.4 | 1.61 | 1.0 | 0.6018 | 15.8 | 15.7 |
| 34 | 213.115 594 | 22.812 719 | 0.3725 | 0.400 ± 0.022 | 16.9 | 1.46 | 1.0 | 0.4973 | 13.0 | 13.4 |
| 35 | 212.604 626 | 23.277 634 | – | 0.376 ± 0.018 | 22.2 | 1.98 | 1.1 | 0.2043 | 5.4 | 5.0 |
| 36 | 212.538 462 | 23.376 505 | – | 0.384 ± 0.019 | 17.6 | 1.53 | 1.0 | 0.3170 | 8.5 | 8.7 |
| 37 | 212.800 638 | 23.052 477 | 0.4138 | 0.426 ± 0.015 | 20.0 | 1.76 | 1.0 | 0.1323 | 3.8 | 3.7 |
| 38 | 212.609 281 | 22.997 888 | 0.4159 | 0.425 ± 0.015 | 10.6 | 0.89 | 0.8 | 0.0942 | 2.7 | 3.4 |
| 39 | 212.177 450 | 22.994 366 | 0.4188 | 0.424 ± 0.015 | 25.4 | 2.28 | 1.1 | 0.4522 | 13.1 | 11.9 |
| 40 | 213.120 494 | 22.548 543 | – | 0.420 ± 0.014 | 38.4 | 3.57 | 1.3 | 0.6800 | 19.8 | 15.4 |
| 41 | 211.935 365 | 23.227 769 | 0.4199 | 0.416 ± 0.019 | 10.7 | 0.90 | 0.8 | 0.6825 | 19.9 | 24.5 |
| 42 | 212.374 306 | 22.818 205 | – | 0.420 ± 0.019 | 17.3 | 1.50 | 1.0 | 0.3710 | 10.8 | 11.2 |
| 43 | 212.420 269 | 23.093 511 | – | 0.428 ± 0.018 | 14.5 | 1.24 | 0.9 | 0.2209 | 6.6 | 7.3 |
| 44 | 212.593 164 | 22.699 892 | – | 0.430 ± 0.017 | 12.1 | 1.02 | 0.8 | 0.3848 | 11.5 | 13.6 |
| 45 | 211.957 129 | 23.106 715 | – | 0.434 ± 0.014 | 28.6 | 2.59 | 1.1 | 0.6471 | 19.4 | 16.9 |
| 46 | 212.999 005 | 22.821 469 | 0.4358 | 0.443 ± 0.019 | 12.5 | 1.06 | 0.9 | 0.4052 | 12.2 | 14.3 |
| 47 | 212.607 221 | 22.800 250 | – | 0.440 ± 0.018 | 13.0 | 1.10 | 0.9 | 0.2837 | 8.6 | 10.0 |
| 48 | 212.115 194 | 23.041 513 | 0.4397 | 0.442 ± 0.016 | 11.1 | 0.94 | 0.8 | 0.5027 | 15.3 | 18.7 |
| 49 | 212.968 630 | 22.717 594 | – | 0.441 ± 0.021 | 11.0 | 0.92 | 0.8 | 0.4604 | 14.0 | 17.3 |
| 50 | 212.980 494 | 22.615 241 | – | 0.441 ± 0.018 | 15.6 | 1.34 | 0.9 | 0.5505 | 16.7 | 18.2 |
| 51 | 212.172 529 | 23.471 857 | – | 0.445 ± 0.018 | 15.6 | 1.35 | 0.9 | 0.5952 | 18.3 | 19.8 |
| 52 | 212.710 891 | 23.162 554 | – | 0.452 ± 0.017 | 11.4 | 0.96 | 0.8 | 0.0951 | 3.0 | 3.6 |
| 53 | 212.336 805 | 22.647 284 | – | 0.454 ± 0.019 | 15.5 | 1.34 | 0.9 | 0.5251 | 16.4 | 18.0 |
| 54 | 212.658 634 | 23.039 911 | 0.4582 | 0.437 ± 0.014 | 37.2 | 3.44 | 1.3 | 0.0399 | 1.3 | 1.0 |
| 55 | 212.346 270 | 23.242 090 | 0.4585 | 0.449 ± 0.016 | 15.6 | 1.35 | 0.9 | 0.3310 | 10.4 | 11.4 |
| 56 | 213.213 654 | 22.988 852 | 0.4603 | 0.477 ± 0.013 | 47.9 | 4.52 | 1.4 | 0.5176 | 16.4 | 11.9 |
| 57 | 213.210 168 | 23.112 030 | 0.4615 | 0.469 ± 0.013 | 48.9 | 4.62 | 1.4 | 0.5071 | 16.1 | 11.7 |
Notes. (1) Cluster ID. (2) Right ascension (J2000). (3) Declination (J2000). (4) Spectroscopic redshift. (5) Photometric redshift. (6) Richness of galaxies having L ≥ 0.2L*, corrected for incompleteness (hence non-integer). (7) Inferred mass using equation (1); typical scatter of ∼0.25 in ln (M) (Rykoff et al. 2012). (8) Inferred virial radii of the cluster using equation (2). (9) Projected separation to the Q1410 sightline in degrees. (10) Projected separation to the Q1410 sightline in Mpc. (11) Projected separation to the Q1410 sightline in units of our R200 estimation.
The redshift range of 0.1 ≤ z ≤ 0.5 was chosen to ensure simultaneous coverage of both H i and O vi transitions from our COS data, while the impact parameter of 20 Mpc (arbitrary) was chosen to cover scales expected to be relevant for intercluster filaments (e.g. Colberg et al. 2005; González & Padilla 2010).
In Appendix A we show how our subsample of clusters compares to appropriate control samples drawn from the full redMaPPer catalogue. We found no statistically significant differences for the mass (richness) and redshift distributions between our subsample and the control samples, implying that no noticeable bias is present in the subsample close to the Q1410 sightline.
3.2 Cluster pairs
From the subsample of clusters around the Q1410 sightline presented in Table 2, we define a sample of cluster pairs according to the following criteria:
the rest-frame velocity difference between the clusters redshifts has to be <2000 km s−1;
at least one of the two members has to have a spectroscopic redshift determination (typically from a BCG), and the other has to have a redshift uncertainty no larger than 0.05.9
the transverse separation between the cluster centres has to be no larger than 25 Mpc; and,
the impact parameter between the intercluster axis and the Q1410 sightline has to be Δd ≤ 3 Mpc.
When these criteria are satisfied, we assign the cluster-pair redshift to be the average between the two cluster members. There are a total of 11 cluster pairs satisfying these criteria around the Q1410 sightline (see the grey dashed lines in Fig. 2), and whose relevant information is presented in Table 3.
| Pair ID . | Cluster IDs . | z . | Separation between clusters . | Δd . | Δx . | Both spec-z? . | Grouped ID . | |
|---|---|---|---|---|---|---|---|---|
| . | . | . | Transverse (Mpc) . | LOS (km s−1) . | (Mpc) . | (Mpc) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | 9,10 | 0.1588 | 14.7 | 419 | 0.48 | 0.31 | y | 1 |
| 2 | 12,13 | 0.1760 | 14.7 | 1378 | 1.54 | 7.33 | y | 2 |
| 3 | 23,25 | 0.3439 | 12.7 | 1189 | 1.85 | 3.43 | y | 3 |
| 4 | 25,28 | 0.3488 | 18.1 | 1021 | 2.29 | 9.00 | y | 4 |
| 5 | 34,35 | 0.3726 | 17.3 | 771 | 2.76 | 4.63 | n | 5 |
| 6 | 37,42 | 0.4139 | 13.2 | 1365 | 2.59 | 2.79 | n | 6 |
| 7 | 37,38 | 0.4149 | |$\phantom{2}$|5.3 | 435 | 1.86 | 1.99 | y | 6 |
| 8 | 37,39 | 0.4163 | 16.7 | 1043 | 1.16 | 3.62 | y | 6 |
| 9 | 37,41 | 0.4169 | 23.6 | 1284 | 0.03 | 3.80 | y | 6 |
| 10 | 54,55 | 0.4584 | 11.1 | 68 | 1.05 | 0.69 | y | 7 |
| 11 | 54,57 | 0.4599 | 16.2 | 682 | 1.24 | 0.21 | y | 7 |
| Pair ID . | Cluster IDs . | z . | Separation between clusters . | Δd . | Δx . | Both spec-z? . | Grouped ID . | |
|---|---|---|---|---|---|---|---|---|
| . | . | . | Transverse (Mpc) . | LOS (km s−1) . | (Mpc) . | (Mpc) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | 9,10 | 0.1588 | 14.7 | 419 | 0.48 | 0.31 | y | 1 |
| 2 | 12,13 | 0.1760 | 14.7 | 1378 | 1.54 | 7.33 | y | 2 |
| 3 | 23,25 | 0.3439 | 12.7 | 1189 | 1.85 | 3.43 | y | 3 |
| 4 | 25,28 | 0.3488 | 18.1 | 1021 | 2.29 | 9.00 | y | 4 |
| 5 | 34,35 | 0.3726 | 17.3 | 771 | 2.76 | 4.63 | n | 5 |
| 6 | 37,42 | 0.4139 | 13.2 | 1365 | 2.59 | 2.79 | n | 6 |
| 7 | 37,38 | 0.4149 | |$\phantom{2}$|5.3 | 435 | 1.86 | 1.99 | y | 6 |
| 8 | 37,39 | 0.4163 | 16.7 | 1043 | 1.16 | 3.62 | y | 6 |
| 9 | 37,41 | 0.4169 | 23.6 | 1284 | 0.03 | 3.80 | y | 6 |
| 10 | 54,55 | 0.4584 | 11.1 | 68 | 1.05 | 0.69 | y | 7 |
| 11 | 54,57 | 0.4599 | 16.2 | 682 | 1.24 | 0.21 | y | 7 |
Notes. (1) Cluster pair ID. (2) IDs of clusters defining the cluster pair as given in Table 2. (3) Redshift of the cluster pair. (4) Transverse separation between clusters in Mpc. (5) Along the LOS separation between the clusters in restframe km s−1. (6) Impact parameter to the Q1410 sightline. (7) Projected on the sky distance to the closest cluster of the pair, along the intercluster axis. (8) Whether both clusters have spectroscopic redshifts. (9) Grouped ID for independent cluster pairs.
| Pair ID . | Cluster IDs . | z . | Separation between clusters . | Δd . | Δx . | Both spec-z? . | Grouped ID . | |
|---|---|---|---|---|---|---|---|---|
| . | . | . | Transverse (Mpc) . | LOS (km s−1) . | (Mpc) . | (Mpc) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | 9,10 | 0.1588 | 14.7 | 419 | 0.48 | 0.31 | y | 1 |
| 2 | 12,13 | 0.1760 | 14.7 | 1378 | 1.54 | 7.33 | y | 2 |
| 3 | 23,25 | 0.3439 | 12.7 | 1189 | 1.85 | 3.43 | y | 3 |
| 4 | 25,28 | 0.3488 | 18.1 | 1021 | 2.29 | 9.00 | y | 4 |
| 5 | 34,35 | 0.3726 | 17.3 | 771 | 2.76 | 4.63 | n | 5 |
| 6 | 37,42 | 0.4139 | 13.2 | 1365 | 2.59 | 2.79 | n | 6 |
| 7 | 37,38 | 0.4149 | |$\phantom{2}$|5.3 | 435 | 1.86 | 1.99 | y | 6 |
| 8 | 37,39 | 0.4163 | 16.7 | 1043 | 1.16 | 3.62 | y | 6 |
| 9 | 37,41 | 0.4169 | 23.6 | 1284 | 0.03 | 3.80 | y | 6 |
| 10 | 54,55 | 0.4584 | 11.1 | 68 | 1.05 | 0.69 | y | 7 |
| 11 | 54,57 | 0.4599 | 16.2 | 682 | 1.24 | 0.21 | y | 7 |
| Pair ID . | Cluster IDs . | z . | Separation between clusters . | Δd . | Δx . | Both spec-z? . | Grouped ID . | |
|---|---|---|---|---|---|---|---|---|
| . | . | . | Transverse (Mpc) . | LOS (km s−1) . | (Mpc) . | (Mpc) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | 9,10 | 0.1588 | 14.7 | 419 | 0.48 | 0.31 | y | 1 |
| 2 | 12,13 | 0.1760 | 14.7 | 1378 | 1.54 | 7.33 | y | 2 |
| 3 | 23,25 | 0.3439 | 12.7 | 1189 | 1.85 | 3.43 | y | 3 |
| 4 | 25,28 | 0.3488 | 18.1 | 1021 | 2.29 | 9.00 | y | 4 |
| 5 | 34,35 | 0.3726 | 17.3 | 771 | 2.76 | 4.63 | n | 5 |
| 6 | 37,42 | 0.4139 | 13.2 | 1365 | 2.59 | 2.79 | n | 6 |
| 7 | 37,38 | 0.4149 | |$\phantom{2}$|5.3 | 435 | 1.86 | 1.99 | y | 6 |
| 8 | 37,39 | 0.4163 | 16.7 | 1043 | 1.16 | 3.62 | y | 6 |
| 9 | 37,41 | 0.4169 | 23.6 | 1284 | 0.03 | 3.80 | y | 6 |
| 10 | 54,55 | 0.4584 | 11.1 | 68 | 1.05 | 0.69 | y | 7 |
| 11 | 54,57 | 0.4599 | 16.2 | 682 | 1.24 | 0.21 | y | 7 |
Notes. (1) Cluster pair ID. (2) IDs of clusters defining the cluster pair as given in Table 2. (3) Redshift of the cluster pair. (4) Transverse separation between clusters in Mpc. (5) Along the LOS separation between the clusters in restframe km s−1. (6) Impact parameter to the Q1410 sightline. (7) Projected on the sky distance to the closest cluster of the pair, along the intercluster axis. (8) Whether both clusters have spectroscopic redshifts. (9) Grouped ID for independent cluster pairs.
We chose 2000 km s−1 (arbitrary) for the rest-frame velocity difference limit for the clusters in a cluster pair, in order to account for the typical velocity dispersion of galaxy clusters (∼600 km s−1) and a contribution from a cosmological redshift difference. We note however that the majority of the clusters in a given cluster pair have rest-frame velocity differences <1000 km s−1 and that all of them have <1400 km s−1 (see the fifth column of Table 3). The need for relatively small redshift uncertainties for the clusters is necessary to minimize the dilution of a real signal due to unconstrained positions for the cluster pairs along the LOS. The 25 Mpc (arbitrary) maximum separation between clusters in a cluster pair was motivated by theoretical results from N-body simulations in ΛCDM universes. These studies indicate that at <25 Mpc there is relatively high probability of having coherent filamentary structures between galaxy clusters (e.g. Colberg et al. 2005; González & Padilla 2010). We stress that the majority of cluster pairs in our sample have projected separations ∼10–15 Mpc (see the fourth column of Table 3). The choice for the maximum impact parameter between the cluster-pair intercluster axis and the Q1410 sightline of Δd = 3 Mpc was directly motivated by one of our observational results (see Section 6), and is in good agreement with the typical scales for the radii of intercluster filaments inferred from N-body simulations (e.g. Colberg et al. 2005; González & Padilla 2010; Aragón-Calvo et al. 2010).
3.3 Independent cluster pairs
As expected from the clustering of galaxy clusters, many cluster pairs are grouped together and hence might not be tracing independent structures. We therefore have grouped cluster pairs if they are within 1000 km s−1 from one another and we treat them as independent. There are a total of seven independent cluster pairs; a unique identifier is given for each of these in the last column of Table 3. We can clearly see these structures in the right-hand panel of Fig. 2 at z ∼ 0.16, 0.18, 0.34, 0.35, 0.37, 0.41 and 0.46.
Again, this velocity limit of 1000 km s−1 is arbitrary and chosen to account for the typical velocity dispersion of galaxy clusters and a contribution from a cosmological redshift difference. As reference, if 3000 km s−1 is used instead, then there are six independent structures rather than seven (i.e. the structures at z ∼ 0.34–0.35 are joined together). We note however that in our subsequent analysis of associating IGM absorption lines with cluster pairs, we will only use the impact parameter to the closest cluster pair independently of the group it belongs to (see Section 6). Therefore, the velocity limit for grouping cluster pairs is irrelevant for the main results of this paper. Still, this definition allows us to quantify how many independent cluster pairs the Q1410 sightline is probing, making sure that our results are not dominated by a single coherent structure spanning a large redshift range.
3.4 How unusual is the Q1410 field?
As explained in Section 2.2.1, the field around Q1410 was selected to maximize the presence of cluster pairs close to the QSO sightline. Therefore, it is by no means a randomly selected sightline. To quantify how unusual the sightline is, we have performed the same search for clusters, cluster pairs and independent cluster pairs in 1000 randomly selected sightlines having coordinates R.A. ∈ [140, 222]° and Dec. ∈ [4, 56]° (i.e. well within the SDSS footprint), using the same set of criteria used to characterize the Q1410 field (see Sections 3.1, 3.2 and 3.3).
In Fig. 3 we compare our observed (dashed black vertical lines) number of redMaPPer clusters (left-hand panel), cluster pairs (middle panel) and independent cluster pairs (right-hand panel), to the distributions from our control samples (solid red histograms). There are a total of 57 clusters at redshifts 0.1 ≤ z ≤ 0.5 satisfying the condition of being at impact parameter of <20 Mpc from the Q1410 sightline, whereas the average random expectation is 32 ± 10 with median of 32. Likewise, the actual number of cluster pairs and independent cluster pair within our constraints are 11 and 7 respectively, whereas the average random expectations are 1.6 ± 2.2 and 1 ± 1, with medians of 1 and 1, respectively. These last two distributions are very skewed towards zero.
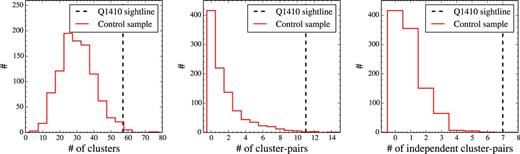
Comparison between our observed (dashed black vertical lines) number of redMaPPer clusters (left-hand panel), cluster pairs (middle panel) and independent cluster pairs (right-hand panel) in the Q1410 sightline satisfying our criteria (see Sections 3.1, 3.2 and 3.3, respectively), and the distributions from control samples (solid red histograms; see Section 3.4). The Q1410 sightline is highly exceptional in terms of number of LSS traced by galaxy clusters close to it.
Although the number of clusters around Q1410 exceeds that from the random expectation at only the 2σ–3σ confidence level (c.l.), the excesses of total and independent cluster pairs are highly significant (>5σ), making Q1410 a very exceptional sightline. We take this fact into account when comparing the incidences of absorption line systems close to cluster pairs and the field as estimated from the Q1410 sightline itself (see Section 5.2).
4 CHARACTERIZATION OF ABSORPTION LINES IN THE Q1410 SPECTRUM
We performed a full characterization of absorption lines in the HST/COS FUV spectrum of Q1410. This approach is more time consuming than just restricting ourselves to spectral regions associated with the redshifts where known structures exist (e.g. clusters, cluster pairs; see Section 3), but is necessary to avoid potential biases and systematic effects. In particular, our approach allows us to: (i) identify absorption lines independently of the presence of known structures; (ii) quantify how the rest of the redshift path unassociated with these known structures compares to the field expectation in terms of absorption features (see Section 5.2); and (iii) assess the extent of contamination by blended unassociated lines in a given redshift. This last point is crucial to minimize misidentification of lines, but some ambiguous cases are unavoidable. In this section, we present our methodology for the identification and characterization of absorption lines in the Q1410 spectrum, and how we handled ambiguity.
4.1 Absorption line identification
We searched for individual absorption line components10 in the continuum normalized QSO spectrum manually (i.e. eyeballing), based on an iterative algorithm described as follows.
Identify all possible absorption components (H i and metals) within ±500 km s−1 from redshift z = 0, and assign them to the ‘reliable’ category (label ‘a’; see Section 4.5).
Identify all possible absorption components (H i and metals) within ±500 km s−1 from redshift z = zQSO, and assign them to the ‘reliable’ category.
Identify H i absorption components, showing at least two transitions (e.g. Ly α and Ly β or Ly β and Ly γ, and so on; i.e. strong H i)11, starting at z = zQSO until z = 0, and assign them to the ‘reliable’ category. This identification includes the whole Lyman series covered by the spectrum in a given component.
Identify all possible metal absorption components within ±200 km s−1 from each H i redshift found in the previous step, and assign them to the ‘reliable’ category. When the wavelength coverage allows the detection of multiple transitions of a single ion, we require the relative positions of these to coincide; in the case of multiple adjacent components blending with each other, we require them to have similar kinematic structure across the multiple transitions of the same ion.
Identify high-ionization transitions (namely: Ne viii, O vi, N v, C iv, Si iv) showing in at least two transitions, independently of the presence of H i, starting at z = zQSO until z = 0, and assign them to the ‘reliable’ category.
Identify low-ionization transitions (namely: C ii, C iii, N ii, N iii, O i, O ii, Si ii, Si iii, Fe ii, Fe iii and Al ii), showing at least two transitions, independently of the presence of H i, starting at z = zQSO until z = 0, and assign them to the ‘reliable’ category.12
Assume all the unidentified absorption features to be H i Ly α and repeat step (iv). If metals satisfying the criteria in step (iv) exist, assign the component to the ‘reliable’ category; otherwise assign the component to the ‘possible’ category (label ‘b’; see Section 4.5).
For complex blended systems we allowed for the presence of extra heavily blended (hidden) ions, preferentially H i Ly α unless a metal ion showing at least one unblended transition exist, and update the identification accordingly. In cases where the metal ion shows at least two unblended transitions, assign them to the ‘reliable’ category. In the rest of the cases (including H i Ly α only) assign them to the ‘possible’ category.
We note that we will then degrade some of the components in the ‘possible’ category to the ‘uncertain’ category (‘c’), based on an equivalent width significance criterium in Section 4.5.
For all the identified components, we set initial guesses for their redshifts, column densities (N), and Doppler parameters (b), which are used as the inputs of our automatic Voigt profile fitting process described in the Section 4.2. We based these guesses on the intensities and widths of the spectral features, keeping the number of individual components to the minimum: we only added a component when there is a clear presence of multiple adjacent local minima or asymmetries. In the case of symmetric and intense H i Ly α absorption lines showing no corresponding H i Ly β absorption (when the spectral coverage and the S/N would have allowed it), this last condition would require the components to have relatively large b-values (typically ≳40–50 km s−1). We warn the reader that this is a potential source of bias, especially for the broad Ly α systems (≥50 km s−1) expected to trace portions of the WHIM (but see Section 7.5).
4.2 Voigt profile fitting
We fit Voigt profiles to the identified absorption line components using vpfit13. We accounted for the non-Gaussian COS line spread function (LSF), by interpolating between the closest COS LSF tabulated values provided by the Space Telescope Science Institute (STScI)14 at a given wavelength. We used the guesses provided by the absorption line search (see Section 4.1) as the initial input of vpfit, and modified them when needed to reach converged solutions with low reduced χ2.15
When dealing with H i absorption lines, we used at least two spectral regions associated with their Lyman series transitions when the spectral coverage allowed it. This means that for those showing only the Ly α transition, we also included their associated Ly β regions (even though they do not show evident absorption) when available. This last condition provides reliable upper limits to the column density of these components. For strong H i components, we used regions associated with as many Lyman series transitions as possible, but excluding those heavily blended or in spectral regions of poor S/N (≲1 per pixel). For metal transitions we used all spectral regions available.
We fitted absorption line systems starting from z = zQSO until z = 0. When a given system at redshift 0 < z ≤ zQSO showed strong blends from lower redshifts, we fitted them all simultaneously in a given vpfit iteration (i.e. including all spectral regions associated with them). When a given system at redshift 0 < z < zQSO showed weak blending from higher redshifts, we allowed vpfit to modify the ‘effective’ continuum by adding the previously found absorption line solutions to it. This last condition accounts for the blending of weak lines (especially from higher order Lyman series) – whose solutions are already well determined – in a more efficient manner than fitting all regions involved simultaneously. In the whole process, we allowed vpfit to add lines automatically when the χ2 and the Kolmogorov–Smirnov test (K–S) test probabilities were below 0.01 (see vpfit manual for details).
Table 4 shows our final list of identified absorption line components, and their corresponding fits. Unique component IDs are given in the first column to components for each ion (second column). The observed wavelength associated with the strongest transition of an ion is shown in the third column (but note that some ions can show up in multiple wavelengths when having multiple transitions). The fitted redshifts, column densities and Doppler parameters are given in the fourth, fifth and sixth columns, respectively. Our final reduced χ2 have an average (and median) of 1.1. In Fig. E1 we show how these fits (red line) compare to the observed spectrum (black line), by means of their residuals (grey dots) defined as the difference between the two (i.e. in the same units as the spectrum). We see how these residuals are mostly distributed within the spectrum uncertainty level (green line).
| Component ID . | Ion . | Obs. wavelength . | z . | log (N/cm−2) . | b . | Wr . | 〈S/N〉res . | Label . |
|---|---|---|---|---|---|---|---|---|
| . | . | (Å) . | . | . | (km s−1) . | (Å) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | C iv | 1547.8 | −0.000 24 ± 0.000 13 | 13.98 ± 0.82 | 18 ± 35 | 0.205 ± 0.383 | 14 ± 1 | a |
| 2 | Si iv | 1393.4 | −0.000 24 ± 0.000 03 | 13.38 ± 0.82 | 15 ± 22 | 0.134 ± 0.231 | 12 ± 1 | a |
| 3 | Al ii | 1670.5 | −0.000 18 ± 0.001 00 | 14.13 ± 40.72 | 11 ± 131 | 0.268 ± 2.683 | 11 ± 1 | a |
| 4 | N v | 1238.6 | −0.000 18 ± 0.000 11 | 13.55 ± 0.53 | 23 ± 55 | 0.064 ± 0.105 | 15 ± 1 | a |
| 5 | Si iv | 1393.6 | −0.000 14 ± 0.000 08 | 13.73 ± 0.38 | 35 ± 14 | 0.304 ± 0.203 | 12 ± 1 | a |
| 6 | Si iii | 1206.4 | −0.000 12 ± 0.000 03 | 16.24 ± 1.53 | 16 ± 10 | 0.534 ± 1.077 | 14 ± 1 | a |
| 7 | C iv | 1548.0 | −0.000 11 ± 0.000 11 | 14.09 ± 0.66 | 18 ± 29 | 0.227 ± 0.340 | 15 ± 1 | a |
| 8 | Si ii | 1260.3 | −0.000 10 ± 0.000 01 | 16.58 ± 0.08 | 17 ± 1 | 0.700 ± 0.057 | 16 ± 1 | a |
| 9 | C ii | 1334.4 | −0.000 10 ± 0.000 03 | 18.32 ± 1.65 | 23 ± 9 | 0.824 ± 1.500 | 11 ± 1 | a |
| 10 | Al ii | 1670.7 | −0.000 06 ± 0.001 07 | 14.07 ± 66.61 | 9 ± 204 | 0.222 ± 2.217 | 11 ± 1 | a |
| 11 | C ii* | 1335.6 | −0.000 06 ± 0.000 07 | 14.11 ± 0.38 | 24 ± 32 | 0.164 ± 0.188 | 12 ± 1 | a |
| 12 | Si iii | 1206.7 | 0.000 19 ± 0.000 04 | 13.28 ± 3.99 | 11 ± 41 | 0.121 ± 0.894 | 14 ± 1 | a |
| 13 | Si iii | 1207.2 | 0.000 56 ± 0.000 16 | 12.37 ± 0.92 | 17 ± 88 | 0.043 ± 0.169 | 13 ± 1 | a |
| 14 | H i | 1222.7 | 0.005 79 ± 0.000 03 | 12.86 ± 0.17 | 19 ± 17 | 0.036 ± 0.019 | 13 ± 1 | c |
| 15 | H i | 1224.7 | 0.007 44 ± 0.000 02 | 12.90 ± 0.12 | 12 ± 11 | 0.037 ± 0.020 | 14 ± 1 | c |
| 16 | H i | 1225.0 | 0.007 71 ± 0.000 02 | 12.92 ± 0.30 | 7 ± 14 | 0.034 ± 0.032 | 14 ± 1 | c |
| 17 | H i | 1250.5 | 0.028 65 ± 0.000 01 | 13.49 ± 0.06 | 18 ± 5 | 0.115 ± 0.022 | 16 ± 1 | b |
| 18 | H i | 1250.9 | 0.028 94 ± 0.000 01 | 13.57 ± 0.05 | 32 ± 7 | 0.155 ± 0.023 | 16 ± 1 | b |
| 19 | H i | 1259.4 | 0.035 94 ± 0.000 01 | 13.74 ± 0.05 | 27 ± 4 | 0.197 ± 0.025 | 16 ± 1 | b |
| 20 | H i | 1268.9 | 0.043 75 ± 0.000 01 | 13.49 ± 9.56 | 4 ± 26 | 0.044 ± 0.441 | 15 ± 1 | c |
| 21 | H i | 1269.4 | 0.044 18 ± 0.000 04 | 12.93 ± 0.16 | 30 ± 19 | 0.043 ± 0.017 | 15 ± 1 | c |
| 22 | H i | 1292.0 | 0.062 77 ± 0.000 01 | 13.32 ± 0.08 | 21 ± 7 | 0.089 ± 0.019 | 14 ± 1 | b |
| 23 | H i | 1295.9 | 0.065 99 ± 0.000 04 | 12.86 ± 0.17 | 21 ± 16 | 0.036 ± 0.017 | 14 ± 1 | c |
| 24 | H i | 1298.3 | 0.068 00 ± 0.000 77 | 14.32 ± 6.43 | 25 ± 76 | 0.300 ± 3.003 | 14 ± 1 | c |
| 25 | H i | 1324.8 | 0.089 81 ± 0.000 02 | 13.29 ± 0.10 | 22 ± 10 | 0.087 ± 0.025 | 10 ± 1 | b |
| 26 | H i | 1372.7 | 0.129 20 ± 0.000 02 | 13.55 ± 0.06 | 44 ± 8 | 0.159 ± 0.023 | 12 ± 1 | b |
| 27 | H i | 1410.9 | 0.160 58 ± 0.000 05 | 13.40 ± 0.11 | 59 ± 22 | 0.123 ± 0.033 | 14 ± 1 | b |
| 28 | H i | 1416.4 | 0.165 15 ± 0.000 06 | 12.80 ± 0.28 | 23 ± 26 | 0.032 ± 0.026 | 14 ± 1 | c |
| 29 | H i | 1419.3 | 0.167 48 ± 0.000 05 | 12.76 ± 0.17 | 30 ± 19 | 0.030 ± 0.013 | 16 ± 2 | c |
| 30 | H i | 1424.7 | 0.171 92 ± 0.000 04 | 12.88 ± 0.13 | 34 ± 16 | 0.039 ± 0.013 | 19 ± 2 | b |
| 31 | H i | 1429.4 | 0.175 80 ± 0.000 04 | 12.86 ± 0.15 | 31 ± 17 | 0.037 ± 0.014 | 22 ± 2 | c |
| 32 | H i | 1433.2 | 0.178 94 ± 0.000 02 | 13.07 ± 0.09 | 23 ± 8 | 0.057 ± 0.013 | 21 ± 4 | b |
| 33 | H i | 1441.1 | 0.185 43 ± 0.000 02 | 13.00 ± 0.07 | 22 ± 6 | 0.048 ± 0.009 | 24 ± 1 | b |
| 34 | H i | 1444.1 | 0.187 94 ± 0.000 07 | 13.41 ± 0.08 | 112 ± 28 | 0.133 ± 0.026 | 23 ± 2 | b |
| 35 | H i | 1449.9 | 0.192 67 ± 0.000 02 | 12.91 ± 0.09 | 24 ± 9 | 0.041 ± 0.009 | 23 ± 2 | b |
| 36 | C ii | 1613.5 | 0.209 04 ± 0.000 01 | 14.53 ± 1.73 | 6 ± 6 | 0.096 ± 0.135 | 8 ± 2 | a |
| 37 | Si ii | 1523.9 | 0.209 05 ± 0.000 02 | 12.54 ± 0.10 | 11 ± 8 | 0.046 ± 0.016 | 16 ± 1 | a |
| 38 | H i | 1469.8 | 0.209 08 ± 0.000 01 | 16.15 ± 1.03 | 11 ± 3 | 0.257 ± 0.155 | 18 ± 1 | a |
| 39 | Si iii | 1458.8 | 0.209 09 ± 0.000 01 | 12.63 ± 0.06 | 13 ± 4 | 0.066 ± 0.011 | 20 ± 1 | a |
| 40 | C iii | 1181.4 | 0.209 15 ± 0.000 01 | 14.60 ± 13.57 | 8 ± 35 | 0.113 ± 1.134 | 12 ± 1 | a |
| 41 | N iii | 1196.8 | 0.209 16 ± 0.000 02 | 13.84 ± 0.10 | 19 ± 10 | 0.060 ± 0.017 | 13 ± 1 | a |
| 42 | H i | 1470.0 | 0.209 20 ± 0.000 30 | 13.37 ± 2.72 | 14 ± 47 | 0.088 ± 0.571 | 18 ± 1 | a |
| 43 | Si ii | 1524.5 | 0.209 55 ± 0.00001 | 13.05 ± 0.15 | 13 ± 5 | 0.109 ± 0.043 | 15 ± 2 | a |
| 44 | C ii | 1614.2 | 0.209 55 ± 0.000 01 | 14.96 ± 1.42 | 10 ± 7 | 0.174 ± 0.184 | 8 ± 2 | a |
| 45 | Si iv | 1685.8 | 0.209 56 ± 0.000 01 | 13.67 ± 0.08 | 14 ± 3 | 0.170 ± 0.033 | 10 ± 1 | a |
| 46 | H i | 1470.5 | 0.209 58 ± 0.000 15 | 16.29 ± 3.61 | 14 ± 7 | 0.330 ± 3.272 | 18 ± 1 | a |
| 47 | N iii | 1197.3 | 0.209 62 ± 0.000 01 | 14.94 ± 1.48 | 14 ± 12 | 0.151 ± 0.192 | 13 ± 1 | a |
| 48 | Si iii | 1459.4 | 0.209 62 ± 0.000 01 | 13.56 ± 0.07 | 23 ± 3 | 0.256 ± 0.032 | 20 ± 1 | a |
| 49 | C iii | 1181.8 | 0.209 64 ± 0.002 36 | 15.03 ± 59.37 | 13 ± 98 | 0.188 ± 1.884 | 12 ± 1 | a |
| 50 | N v | 1498.5 | 0.209 64 ± 0.000 03 | 13.57 ± 0.09 | 31 ± 10 | 0.071 ± 0.015 | 17 ± 1 | a |
| 51 | O vi | 1248.3 | 0.209 67 ± 0.000 05 | 14.31 ± 0.21 | 26 ± 10 | 0.164 ± 0.073 | 16 ± 1 | a |
| 52 | Si ii | 1524.8 | 0.209 73 ± 0.000 05 | 13.06 ± 0.16 | 34 ± 13 | 0.150 ± 0.058 | 15 ± 2 | a |
| 53 | C ii | 1614.5 | 0.209 76 ± 0.000 01 | 14.48 ± 0.04 | 20 ± 3 | 0.233 ± 0.029 | 8 ± 2 | a |
| 54 | H i | 1470.7 | 0.209 80 ± 0.000 24 | 15.93 ± 2.00 | 27 ± 15 | 0.534 ± 0.567 | 18 ± 1 | a |
| 55 | Si iv | 1686.2 | 0.209 81 ± 0.000 02 | 13.27 ± 0.07 | 26 ± 7 | 0.128 ± 0.025 | 10 ± 1 | a |
| 56 | Si iii | 1459.7 | 0.209 86 ± 0.000 01 | 13.17 ± 0.05 | 21 ± 4 | 0.178 ± 0.025 | 20 ± 1 | a |
| 57 | C iii | 1182.1 | 0.209 86 ± 0.000 21 | 17.15 ± 0.78 | 14 ± 18 | 0.488 ± 0.515 | 12 ± 1 | a |
| 58 | O vi | 1248.5 | 0.209 87 ± 0.000 06 | 14.16 ± 0.31 | 26 ± 16 | 0.129 ± 0.095 | 16 ± 1 | a |
| 59 | N iii | 1197.5 | 0.209 87 ± 0.000 03 | 14.09 ± 0.11 | 25 ± 12 | 0.100 ± 0.031 | 13 ± 1 | a |
| 60 | H i | 1471.3 | 0.210 28 ± 0.000 01 | 13.70 ± 0.05 | 19 ± 3 | 0.157 ± 0.020 | 18 ± 1 | a |
| 61 | O vi | 1248.9 | 0.210 28 ± 0.000 01 | 14.50 ± 0.03 | 50 ± 6 | 0.270 ± 0.022 | 16 ± 1 | a |
| 62 | N v | 1499.3 | 0.210 29 ± 0.000 06 | 13.53 ± 0.15 | 50 ± 24 | 0.068 ± 0.024 | 16 ± 1 | a |
| 63 | C iii | 1182.5 | 0.210 33 ± 0.000 02 | 13.09 ± 0.18 | 11 ± 11 | 0.055 ± 0.040 | 12 ± 1 | a |
| 64 | H i | 1478.4 | 0.216 15 ± 0.000 02 | 13.30 ± 0.05 | 42 ± 7 | 0.096 ± 0.012 | 17 ± 1 | b |
| 65 | H i | 1481.9 | 0.219 00 ± 0.000 02 | 13.10 ± 0.07 | 36 ± 9 | 0.063 ± 0.011 | 17 ± 1 | b |
| 66 | H i | 1486.8 | 0.223 00 ± 0.000 02 | 13.32 ± 0.05 | 52 ± 8 | 0.104 ± 0.012 | 17 ± 1 | b |
| 67 | H i | 1497.1 | 0.231 50 ± 0.000 01 | 13.45 ± 0.04 | 32 ± 4 | 0.125 ± 0.012 | 17 ± 1 | b |
| 68 | O vi | 1274.5 | 0.235 08 ± 0.000 01 | 14.08 ± 0.05 | 24 ± 4 | 0.111 ± 0.014 | 15 ± 1 | a |
| 69 | H i | 1501.5 | 0.235 11 ± 0.000 01 | 14.48 ± 0.04 | 32 ± 1 | 0.395 ± 0.021 | 17 ± 1 | a |
| 70 | H i | 1509.0 | 0.241 26 ± 0.000 03 | 13.29 ± 0.06 | 54 ± 10 | 0.097 ± 0.014 | 16 ± 1 | b |
| 71 | H i | 1538.8 | 0.265 84 ± 0.000 05 | 14.91 ± 0.41 | 28 ± 4 | 0.419 ± 0.111 | 15 ± 1 | a |
| 72 | C iii | 1236.8 | 0.265 87 ± 0.000 01 | 13.70 ± 40.19 | 3 ± 66 | 0.041 ± 0.406 | 15 ± 1 | a |
| 73 | H i | 1539.0 | 0.265 93 ± 0.000 01 | 15.88 ± 0.06 | 16 ± 2 | 0.328 ± 0.041 | 15 ± 1 | a |
| 74 | H i | 1541.8 | 0.268 27 ± 0.000 10 | 12.78 ± 0.22 | 50 ± 37 | 0.032 ± 0.017 | 15 ± 1 | c |
| 75 | H i | 1545.5 | 0.271 32 ± 0.000 04 | 12.98 ± 0.12 | 36 ± 16 | 0.049 ± 0.015 | 14 ± 2 | b |
| 76 | H i | 1550.9 | 0.275 74 ± 0.000 04 | 13.87 ± 0.32 | 21 ± 17 | 0.200 ± 0.166 | 14 ± 1 | c |
| 77 | H i | 1566.7 | 0.288 74 ± 0.000 07 | 13.06 ± 0.15 | 49 ± 25 | 0.059 ± 0.022 | 13 ± 1 | c |
| 78 | H ia | 1573.8 | 0.294 59 ± 0.000 17 | 13.58 ± 0.13 | 157 ± 57 | 0.193 ± 0.058 | 14 ± 1 | b |
| 79 | H i | 1576.7 | 0.296 96 ± 0.000 10 | 12.75 ± 0.23 | 45 ± 37 | 0.030 ± 0.017 | 13 ± 1 | c |
| 80 | H i | 1578.8 | 0.298 74 ± 0.000 01 | 13.68 ± 0.03 | 36 ± 4 | 0.191 ± 0.015 | 13 ± 1 | b |
| 81 | H i | 1582.7 | 0.301 88 ± 0.000 02 | 13.25 ± 0.07 | 32 ± 8 | 0.084 ± 0.014 | 13 ± 1 | b |
| 82 | H i | 1584.2 | 0.303 14 ± 0.000 03 | 13.32 ± 0.07 | 47 ± 11 | 0.102 ± 0.017 | 13 ± 1 | b |
| 83 | H i | 1613.9 | 0.327 56 ± 0.000 03 | 13.24 ± 0.11 | 24 ± 11 | 0.079 ± 0.024 | 8 ± 2 | b |
| 84 | H i | 1617.4 | 0.330 44 ± 0.000 04 | 13.38 ± 0.09 | 45 ± 13 | 0.113 ± 0.024 | 10 ± 1 | b |
| 85 | H i | 1631.6 | 0.342 17 ± 0.000 06 | 13.75 ± 0.05 | 153 ± 19 | 0.276 ± 0.030 | 10 ± 1 | b |
| 86 | O vi | 1392.6 | 0.349 54 ± 0.000 02 | 13.77 ± 0.09 | 21 ± 8 | 0.061 ± 0.015 | 11 ± 1 | a |
| 87 | Si iii | 1628.6 | 0.349 86 ± 0.000 01 | 13.50 ± 0.03 | 45 ± 4 | 0.378 ± 0.032 | 10 ± 1 | a |
| 88 | H i | 1641.0 | 0.349 86 ± 0.000 01 | 15.88 ± 0.03 | 17 ± 1 | 0.344 ± 0.015 | 11 ± 1 | a |
| 89 | O vi | 1393.0 | 0.349 89 ± 0.000 01 | 14.07 ± 0.06 | 19 ± 5 | 0.101 ± 0.018 | 11 ± 1 | a |
| 90 | C ii | 1801.5 | 0.349 89 ± 0.000 01 | 13.31 ± 0.36 | 5 ± 5 | 0.030 ± 0.028 | 11 ± 1 | a |
| 91 | N iii | 1336.2 | 0.349 98 ± 0.000 06 | 14.04 ± 0.11 | 50 ± 20 | 0.102 ± 0.028 | 12 ± 1 | a |
| 92 | H i | 1641.4 | 0.350 20 ± 0.000 04 | 14.29 ± 0.09 | 97 ± 10 | 0.701 ± 0.116 | 11 ± 1 | b |
| 93 | O vi | 1393.4 | 0.350 29 ± 0.000 01 | 14.48 ± 0.05 | 35 ± 5 | 0.233 ± 0.029 | 12 ± 1 | a |
| 94 | H i | 1641.6 | 0.350 35 ± 0.000 01 | 14.57 ± 0.06 | 26 ± 3 | 0.346 ± 0.047 | 11 ± 1 | a |
| 95 | H i | 1642.4 | 0.351 06 ± 0.000 01 | 15.43 ± 0.03 | 25 ± 1 | 0.440 ± 0.015 | 11 ± 1 | a |
| 96 | H i | 1652.3 | 0.359 18 ± 0.000 02 | 13.61 ± 0.05 | 31 ± 5 | 0.163 ± 0.022 | 11 ± 1 | b |
| 97 | H i | 1658.1 | 0.363 97 ± 0.000 03 | 13.52 ± 0.06 | 58 ± 10 | 0.156 ± 0.021 | 11 ± 1 | b |
| 98 | H i | 1664.1 | 0.368 86 ± 0.000 05 | 13.25 ± 0.11 | 50 ± 18 | 0.089 ± 0.023 | 11 ± 1 | b |
| 99 | H i | 1666.8 | 0.371 06 ± 0.000 01 | 14.06 ± 0.03 | 36 ± 2 | 0.329 ± 0.022 | 11 ± 1 | a |
| 100 | H i | 1667.6 | 0.371 76 ± 0.000 03 | 13.24 ± 0.08 | 29 ± 9 | 0.081 ± 0.016 | 11 ± 1 | a |
| 101 | H i | 1673.8 | 0.376 86 ± 0.000 01 | 13.59 ± 0.04 | 31 ± 4 | 0.159 ± 0.018 | 11 ± 1 | a |
| 102 | O vi | 1426.5 | 0.382 38 ± 0.000 02 | 13.43 ± 0.14 | 7 ± 12 | 0.026 ± 0.016 | 21 ± 2 | c |
| 103 | H i | 1680.6 | 0.382 42 ± 0.000 05 | 12.91 ± 0.16 | 27 ± 17 | 0.041 ± 0.017 | 10 ± 1 | c |
| 104 | H i | 1683.8 | 0.385 08 ± 0.000 01 | 14.25 ± 0.03 | 32 ± 2 | 0.345 ± 0.019 | 11 ± 1 | a |
| 105 | H i | 1691.0 | 0.390 97 ± 0.000 07 | 13.19 ± 0.14 | 53 ± 25 | 0.078 ± 0.027 | 10 ± 1 | c |
| 106 | H i | 1704.6 | 0.402 19 ± 0.000 12 | 13.28 ± 0.20 | 79 ± 49 | 0.097 ± 0.048 | 10 ± 1 | c |
| 107 | H i | 1704.7 | 0.402 24 ± 0.000 03 | 13.07 ± 0.30 | 15 ± 14 | 0.053 ± 0.046 | 10 ± 1 | c |
| 108 | H i | 1716.3 | 0.411 82 ± 0.000 05 | 13.47 ± 0.09 | 62 ± 18 | 0.142 ± 0.031 | 9 ± 1 | b |
| 109 | H i | 1723.3 | 0.417 58 ± 0.000 01 | 14.38 ± 0.03 | 19 ± 1 | 0.254 ± 0.014 | 9 ± 1 | a |
| 110 | H i | 1726.5 | 0.420 22 ± 0.000 06 | 13.25 ± 0.12 | 56 ± 20 | 0.090 ± 0.025 | 10 ± 1 | b |
| 111 | H i | 1737.3 | 0.429 11 ± 0.000 08 | 13.08 ± 0.15 | 55 ± 27 | 0.062 ± 0.023 | 9 ± 1 | c |
| 112 | H i | 1740.4 | 0.431 67 ± 0.000 05 | 13.73 ± 0.83 | 23 ± 14 | 0.179 ± 0.213 | 10 ± 1 | a |
| 113 | H i | 1740.6 | 0.431 83 ± 0.000 83 | 13.21 ± 2.74 | 37 ± 102 | 0.079 ± 0.793 | 9 ± 1 | c |
| 114 | H i | 1768.4 | 0.454 66 ± 0.000 06 | 13.46 ± 0.08 | 81 ± 18 | 0.143 ± 0.026 | 9 ± 1 | b |
| 115 | H i | 1775.9 | 0.460 85 ± 0.000 35 | 13.55 ± 0.25 | 192 ± 141 | 0.185 ± 0.115 | 9 ± 1 | c |
| 116 | H i | 1777.7 | 0.462 35 ± 0.000 02 | 13.77 ± 0.07 | 26 ± 5 | 0.199 ± 0.037 | 9 ± 1 | a |
| 117 | O ii | 1281.0 | 0.535 09 ± 0.000 01 | 13.85 ± 0.25 | 10 ± 10 | 0.041 ± 0.033 | 15 ± 1 | a |
| 118 | H i | 1574.6 | 0.535 10 ± 0.000 01 | 16.52 ± 0.02 | 16 ± 1 | 0.274 ± 0.010 | 14 ± 1 | a |
| 119 | C ii | 2048.6 | 0.535 10 ± 0.000 01 | 13.30 ± 0.56 | 10 ± 10 | 0.034 ± 0.051 | 14 ± 1 | a |
| 120 | O iii | 1078.2 | 0.535 12 ± 0.000 01 | 14.51 ± 0.25 | 13 ± 5 | 0.078 ± 0.036 | 14 ± 1 | a |
| 121 | C iii | 1499.9 | 0.535 20 ± 0.000 01 | 13.98 ± 0.25 | 19 ± 4 | 0.177 ± 0.054 | 16 ± 1 | a |
| 122 | O iv | 1209.3 | 0.535 24 ± 0.000 03 | 14.22 ± 0.11 | 23 ± 10 | 0.076 ± 0.023 | 13 ± 1 | a |
| 123 | H i | 1574.8 | 0.535 31 ± 0.000 03 | 14.99 ± 0.15 | 17 ± 4 | 0.180 ± 0.050 | 14 ± 1 | a |
| 124 | H i | 1717.1 | 0.674 02 ± 0.000 01 | 14.80 ± 0.04 | 31 ± 3 | 0.238 ± 0.024 | 9 ± 1 | a |
| 125 | C iii | 1752.5 | 0.793 72 ± 0.000 03 | 14.84 ± 7.41 | 4 ± 9 | 0.065 ± 0.653 | 9 ± 1 | a |
| 126 | O iv | 1412.9 | 0.793 73 ± 0.000 02 | 14.68 ± 0.09 | 20 ± 5 | 0.128 ± 0.032 | 14 ± 1 | a |
| 127 | O iii | 1259.8 | 0.793 76 ± 0.000 01 | 14.41 ± 14.69 | 3 ± 22 | 0.023 ± 0.234 | 16 ± 1 | a |
| 128 | H i | 1839.9 | 0.793 78 ± 0.000 05 | 15.55 ± 0.10 | 37 ± 6 | 0.426 ± 0.077 | 16 ± 1 | a |
| 129 | C iii | 1752.7 | 0.793 96 ± 0.000 02 | 15.14 ± 8.93 | 10 ± 22 | 0.151 ± 1.514 | 9 ± 1 | a |
| 130 | O iv | 1413.2 | 0.794 01 ± 0.000 02 | 15.51 ± 4.99 | 9 ± 15 | 0.097 ± 0.831 | 14 ± 1 | a |
| 131 | O iii | 1260.0 | 0.794 04 ± 0.000 01 | 14.59 ± 0.20 | 12 ± 3 | 0.077 ± 0.024 | 16 ± 1 | a |
| 132 | H i | 1840.2 | 0.794 04 ± 0.000 05 | 14.91 ± 0.42 | 18 ± 10 | 0.176 ± 0.115 | 16 ± 1 | a |
| Component ID . | Ion . | Obs. wavelength . | z . | log (N/cm−2) . | b . | Wr . | 〈S/N〉res . | Label . |
|---|---|---|---|---|---|---|---|---|
| . | . | (Å) . | . | . | (km s−1) . | (Å) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | C iv | 1547.8 | −0.000 24 ± 0.000 13 | 13.98 ± 0.82 | 18 ± 35 | 0.205 ± 0.383 | 14 ± 1 | a |
| 2 | Si iv | 1393.4 | −0.000 24 ± 0.000 03 | 13.38 ± 0.82 | 15 ± 22 | 0.134 ± 0.231 | 12 ± 1 | a |
| 3 | Al ii | 1670.5 | −0.000 18 ± 0.001 00 | 14.13 ± 40.72 | 11 ± 131 | 0.268 ± 2.683 | 11 ± 1 | a |
| 4 | N v | 1238.6 | −0.000 18 ± 0.000 11 | 13.55 ± 0.53 | 23 ± 55 | 0.064 ± 0.105 | 15 ± 1 | a |
| 5 | Si iv | 1393.6 | −0.000 14 ± 0.000 08 | 13.73 ± 0.38 | 35 ± 14 | 0.304 ± 0.203 | 12 ± 1 | a |
| 6 | Si iii | 1206.4 | −0.000 12 ± 0.000 03 | 16.24 ± 1.53 | 16 ± 10 | 0.534 ± 1.077 | 14 ± 1 | a |
| 7 | C iv | 1548.0 | −0.000 11 ± 0.000 11 | 14.09 ± 0.66 | 18 ± 29 | 0.227 ± 0.340 | 15 ± 1 | a |
| 8 | Si ii | 1260.3 | −0.000 10 ± 0.000 01 | 16.58 ± 0.08 | 17 ± 1 | 0.700 ± 0.057 | 16 ± 1 | a |
| 9 | C ii | 1334.4 | −0.000 10 ± 0.000 03 | 18.32 ± 1.65 | 23 ± 9 | 0.824 ± 1.500 | 11 ± 1 | a |
| 10 | Al ii | 1670.7 | −0.000 06 ± 0.001 07 | 14.07 ± 66.61 | 9 ± 204 | 0.222 ± 2.217 | 11 ± 1 | a |
| 11 | C ii* | 1335.6 | −0.000 06 ± 0.000 07 | 14.11 ± 0.38 | 24 ± 32 | 0.164 ± 0.188 | 12 ± 1 | a |
| 12 | Si iii | 1206.7 | 0.000 19 ± 0.000 04 | 13.28 ± 3.99 | 11 ± 41 | 0.121 ± 0.894 | 14 ± 1 | a |
| 13 | Si iii | 1207.2 | 0.000 56 ± 0.000 16 | 12.37 ± 0.92 | 17 ± 88 | 0.043 ± 0.169 | 13 ± 1 | a |
| 14 | H i | 1222.7 | 0.005 79 ± 0.000 03 | 12.86 ± 0.17 | 19 ± 17 | 0.036 ± 0.019 | 13 ± 1 | c |
| 15 | H i | 1224.7 | 0.007 44 ± 0.000 02 | 12.90 ± 0.12 | 12 ± 11 | 0.037 ± 0.020 | 14 ± 1 | c |
| 16 | H i | 1225.0 | 0.007 71 ± 0.000 02 | 12.92 ± 0.30 | 7 ± 14 | 0.034 ± 0.032 | 14 ± 1 | c |
| 17 | H i | 1250.5 | 0.028 65 ± 0.000 01 | 13.49 ± 0.06 | 18 ± 5 | 0.115 ± 0.022 | 16 ± 1 | b |
| 18 | H i | 1250.9 | 0.028 94 ± 0.000 01 | 13.57 ± 0.05 | 32 ± 7 | 0.155 ± 0.023 | 16 ± 1 | b |
| 19 | H i | 1259.4 | 0.035 94 ± 0.000 01 | 13.74 ± 0.05 | 27 ± 4 | 0.197 ± 0.025 | 16 ± 1 | b |
| 20 | H i | 1268.9 | 0.043 75 ± 0.000 01 | 13.49 ± 9.56 | 4 ± 26 | 0.044 ± 0.441 | 15 ± 1 | c |
| 21 | H i | 1269.4 | 0.044 18 ± 0.000 04 | 12.93 ± 0.16 | 30 ± 19 | 0.043 ± 0.017 | 15 ± 1 | c |
| 22 | H i | 1292.0 | 0.062 77 ± 0.000 01 | 13.32 ± 0.08 | 21 ± 7 | 0.089 ± 0.019 | 14 ± 1 | b |
| 23 | H i | 1295.9 | 0.065 99 ± 0.000 04 | 12.86 ± 0.17 | 21 ± 16 | 0.036 ± 0.017 | 14 ± 1 | c |
| 24 | H i | 1298.3 | 0.068 00 ± 0.000 77 | 14.32 ± 6.43 | 25 ± 76 | 0.300 ± 3.003 | 14 ± 1 | c |
| 25 | H i | 1324.8 | 0.089 81 ± 0.000 02 | 13.29 ± 0.10 | 22 ± 10 | 0.087 ± 0.025 | 10 ± 1 | b |
| 26 | H i | 1372.7 | 0.129 20 ± 0.000 02 | 13.55 ± 0.06 | 44 ± 8 | 0.159 ± 0.023 | 12 ± 1 | b |
| 27 | H i | 1410.9 | 0.160 58 ± 0.000 05 | 13.40 ± 0.11 | 59 ± 22 | 0.123 ± 0.033 | 14 ± 1 | b |
| 28 | H i | 1416.4 | 0.165 15 ± 0.000 06 | 12.80 ± 0.28 | 23 ± 26 | 0.032 ± 0.026 | 14 ± 1 | c |
| 29 | H i | 1419.3 | 0.167 48 ± 0.000 05 | 12.76 ± 0.17 | 30 ± 19 | 0.030 ± 0.013 | 16 ± 2 | c |
| 30 | H i | 1424.7 | 0.171 92 ± 0.000 04 | 12.88 ± 0.13 | 34 ± 16 | 0.039 ± 0.013 | 19 ± 2 | b |
| 31 | H i | 1429.4 | 0.175 80 ± 0.000 04 | 12.86 ± 0.15 | 31 ± 17 | 0.037 ± 0.014 | 22 ± 2 | c |
| 32 | H i | 1433.2 | 0.178 94 ± 0.000 02 | 13.07 ± 0.09 | 23 ± 8 | 0.057 ± 0.013 | 21 ± 4 | b |
| 33 | H i | 1441.1 | 0.185 43 ± 0.000 02 | 13.00 ± 0.07 | 22 ± 6 | 0.048 ± 0.009 | 24 ± 1 | b |
| 34 | H i | 1444.1 | 0.187 94 ± 0.000 07 | 13.41 ± 0.08 | 112 ± 28 | 0.133 ± 0.026 | 23 ± 2 | b |
| 35 | H i | 1449.9 | 0.192 67 ± 0.000 02 | 12.91 ± 0.09 | 24 ± 9 | 0.041 ± 0.009 | 23 ± 2 | b |
| 36 | C ii | 1613.5 | 0.209 04 ± 0.000 01 | 14.53 ± 1.73 | 6 ± 6 | 0.096 ± 0.135 | 8 ± 2 | a |
| 37 | Si ii | 1523.9 | 0.209 05 ± 0.000 02 | 12.54 ± 0.10 | 11 ± 8 | 0.046 ± 0.016 | 16 ± 1 | a |
| 38 | H i | 1469.8 | 0.209 08 ± 0.000 01 | 16.15 ± 1.03 | 11 ± 3 | 0.257 ± 0.155 | 18 ± 1 | a |
| 39 | Si iii | 1458.8 | 0.209 09 ± 0.000 01 | 12.63 ± 0.06 | 13 ± 4 | 0.066 ± 0.011 | 20 ± 1 | a |
| 40 | C iii | 1181.4 | 0.209 15 ± 0.000 01 | 14.60 ± 13.57 | 8 ± 35 | 0.113 ± 1.134 | 12 ± 1 | a |
| 41 | N iii | 1196.8 | 0.209 16 ± 0.000 02 | 13.84 ± 0.10 | 19 ± 10 | 0.060 ± 0.017 | 13 ± 1 | a |
| 42 | H i | 1470.0 | 0.209 20 ± 0.000 30 | 13.37 ± 2.72 | 14 ± 47 | 0.088 ± 0.571 | 18 ± 1 | a |
| 43 | Si ii | 1524.5 | 0.209 55 ± 0.00001 | 13.05 ± 0.15 | 13 ± 5 | 0.109 ± 0.043 | 15 ± 2 | a |
| 44 | C ii | 1614.2 | 0.209 55 ± 0.000 01 | 14.96 ± 1.42 | 10 ± 7 | 0.174 ± 0.184 | 8 ± 2 | a |
| 45 | Si iv | 1685.8 | 0.209 56 ± 0.000 01 | 13.67 ± 0.08 | 14 ± 3 | 0.170 ± 0.033 | 10 ± 1 | a |
| 46 | H i | 1470.5 | 0.209 58 ± 0.000 15 | 16.29 ± 3.61 | 14 ± 7 | 0.330 ± 3.272 | 18 ± 1 | a |
| 47 | N iii | 1197.3 | 0.209 62 ± 0.000 01 | 14.94 ± 1.48 | 14 ± 12 | 0.151 ± 0.192 | 13 ± 1 | a |
| 48 | Si iii | 1459.4 | 0.209 62 ± 0.000 01 | 13.56 ± 0.07 | 23 ± 3 | 0.256 ± 0.032 | 20 ± 1 | a |
| 49 | C iii | 1181.8 | 0.209 64 ± 0.002 36 | 15.03 ± 59.37 | 13 ± 98 | 0.188 ± 1.884 | 12 ± 1 | a |
| 50 | N v | 1498.5 | 0.209 64 ± 0.000 03 | 13.57 ± 0.09 | 31 ± 10 | 0.071 ± 0.015 | 17 ± 1 | a |
| 51 | O vi | 1248.3 | 0.209 67 ± 0.000 05 | 14.31 ± 0.21 | 26 ± 10 | 0.164 ± 0.073 | 16 ± 1 | a |
| 52 | Si ii | 1524.8 | 0.209 73 ± 0.000 05 | 13.06 ± 0.16 | 34 ± 13 | 0.150 ± 0.058 | 15 ± 2 | a |
| 53 | C ii | 1614.5 | 0.209 76 ± 0.000 01 | 14.48 ± 0.04 | 20 ± 3 | 0.233 ± 0.029 | 8 ± 2 | a |
| 54 | H i | 1470.7 | 0.209 80 ± 0.000 24 | 15.93 ± 2.00 | 27 ± 15 | 0.534 ± 0.567 | 18 ± 1 | a |
| 55 | Si iv | 1686.2 | 0.209 81 ± 0.000 02 | 13.27 ± 0.07 | 26 ± 7 | 0.128 ± 0.025 | 10 ± 1 | a |
| 56 | Si iii | 1459.7 | 0.209 86 ± 0.000 01 | 13.17 ± 0.05 | 21 ± 4 | 0.178 ± 0.025 | 20 ± 1 | a |
| 57 | C iii | 1182.1 | 0.209 86 ± 0.000 21 | 17.15 ± 0.78 | 14 ± 18 | 0.488 ± 0.515 | 12 ± 1 | a |
| 58 | O vi | 1248.5 | 0.209 87 ± 0.000 06 | 14.16 ± 0.31 | 26 ± 16 | 0.129 ± 0.095 | 16 ± 1 | a |
| 59 | N iii | 1197.5 | 0.209 87 ± 0.000 03 | 14.09 ± 0.11 | 25 ± 12 | 0.100 ± 0.031 | 13 ± 1 | a |
| 60 | H i | 1471.3 | 0.210 28 ± 0.000 01 | 13.70 ± 0.05 | 19 ± 3 | 0.157 ± 0.020 | 18 ± 1 | a |
| 61 | O vi | 1248.9 | 0.210 28 ± 0.000 01 | 14.50 ± 0.03 | 50 ± 6 | 0.270 ± 0.022 | 16 ± 1 | a |
| 62 | N v | 1499.3 | 0.210 29 ± 0.000 06 | 13.53 ± 0.15 | 50 ± 24 | 0.068 ± 0.024 | 16 ± 1 | a |
| 63 | C iii | 1182.5 | 0.210 33 ± 0.000 02 | 13.09 ± 0.18 | 11 ± 11 | 0.055 ± 0.040 | 12 ± 1 | a |
| 64 | H i | 1478.4 | 0.216 15 ± 0.000 02 | 13.30 ± 0.05 | 42 ± 7 | 0.096 ± 0.012 | 17 ± 1 | b |
| 65 | H i | 1481.9 | 0.219 00 ± 0.000 02 | 13.10 ± 0.07 | 36 ± 9 | 0.063 ± 0.011 | 17 ± 1 | b |
| 66 | H i | 1486.8 | 0.223 00 ± 0.000 02 | 13.32 ± 0.05 | 52 ± 8 | 0.104 ± 0.012 | 17 ± 1 | b |
| 67 | H i | 1497.1 | 0.231 50 ± 0.000 01 | 13.45 ± 0.04 | 32 ± 4 | 0.125 ± 0.012 | 17 ± 1 | b |
| 68 | O vi | 1274.5 | 0.235 08 ± 0.000 01 | 14.08 ± 0.05 | 24 ± 4 | 0.111 ± 0.014 | 15 ± 1 | a |
| 69 | H i | 1501.5 | 0.235 11 ± 0.000 01 | 14.48 ± 0.04 | 32 ± 1 | 0.395 ± 0.021 | 17 ± 1 | a |
| 70 | H i | 1509.0 | 0.241 26 ± 0.000 03 | 13.29 ± 0.06 | 54 ± 10 | 0.097 ± 0.014 | 16 ± 1 | b |
| 71 | H i | 1538.8 | 0.265 84 ± 0.000 05 | 14.91 ± 0.41 | 28 ± 4 | 0.419 ± 0.111 | 15 ± 1 | a |
| 72 | C iii | 1236.8 | 0.265 87 ± 0.000 01 | 13.70 ± 40.19 | 3 ± 66 | 0.041 ± 0.406 | 15 ± 1 | a |
| 73 | H i | 1539.0 | 0.265 93 ± 0.000 01 | 15.88 ± 0.06 | 16 ± 2 | 0.328 ± 0.041 | 15 ± 1 | a |
| 74 | H i | 1541.8 | 0.268 27 ± 0.000 10 | 12.78 ± 0.22 | 50 ± 37 | 0.032 ± 0.017 | 15 ± 1 | c |
| 75 | H i | 1545.5 | 0.271 32 ± 0.000 04 | 12.98 ± 0.12 | 36 ± 16 | 0.049 ± 0.015 | 14 ± 2 | b |
| 76 | H i | 1550.9 | 0.275 74 ± 0.000 04 | 13.87 ± 0.32 | 21 ± 17 | 0.200 ± 0.166 | 14 ± 1 | c |
| 77 | H i | 1566.7 | 0.288 74 ± 0.000 07 | 13.06 ± 0.15 | 49 ± 25 | 0.059 ± 0.022 | 13 ± 1 | c |
| 78 | H ia | 1573.8 | 0.294 59 ± 0.000 17 | 13.58 ± 0.13 | 157 ± 57 | 0.193 ± 0.058 | 14 ± 1 | b |
| 79 | H i | 1576.7 | 0.296 96 ± 0.000 10 | 12.75 ± 0.23 | 45 ± 37 | 0.030 ± 0.017 | 13 ± 1 | c |
| 80 | H i | 1578.8 | 0.298 74 ± 0.000 01 | 13.68 ± 0.03 | 36 ± 4 | 0.191 ± 0.015 | 13 ± 1 | b |
| 81 | H i | 1582.7 | 0.301 88 ± 0.000 02 | 13.25 ± 0.07 | 32 ± 8 | 0.084 ± 0.014 | 13 ± 1 | b |
| 82 | H i | 1584.2 | 0.303 14 ± 0.000 03 | 13.32 ± 0.07 | 47 ± 11 | 0.102 ± 0.017 | 13 ± 1 | b |
| 83 | H i | 1613.9 | 0.327 56 ± 0.000 03 | 13.24 ± 0.11 | 24 ± 11 | 0.079 ± 0.024 | 8 ± 2 | b |
| 84 | H i | 1617.4 | 0.330 44 ± 0.000 04 | 13.38 ± 0.09 | 45 ± 13 | 0.113 ± 0.024 | 10 ± 1 | b |
| 85 | H i | 1631.6 | 0.342 17 ± 0.000 06 | 13.75 ± 0.05 | 153 ± 19 | 0.276 ± 0.030 | 10 ± 1 | b |
| 86 | O vi | 1392.6 | 0.349 54 ± 0.000 02 | 13.77 ± 0.09 | 21 ± 8 | 0.061 ± 0.015 | 11 ± 1 | a |
| 87 | Si iii | 1628.6 | 0.349 86 ± 0.000 01 | 13.50 ± 0.03 | 45 ± 4 | 0.378 ± 0.032 | 10 ± 1 | a |
| 88 | H i | 1641.0 | 0.349 86 ± 0.000 01 | 15.88 ± 0.03 | 17 ± 1 | 0.344 ± 0.015 | 11 ± 1 | a |
| 89 | O vi | 1393.0 | 0.349 89 ± 0.000 01 | 14.07 ± 0.06 | 19 ± 5 | 0.101 ± 0.018 | 11 ± 1 | a |
| 90 | C ii | 1801.5 | 0.349 89 ± 0.000 01 | 13.31 ± 0.36 | 5 ± 5 | 0.030 ± 0.028 | 11 ± 1 | a |
| 91 | N iii | 1336.2 | 0.349 98 ± 0.000 06 | 14.04 ± 0.11 | 50 ± 20 | 0.102 ± 0.028 | 12 ± 1 | a |
| 92 | H i | 1641.4 | 0.350 20 ± 0.000 04 | 14.29 ± 0.09 | 97 ± 10 | 0.701 ± 0.116 | 11 ± 1 | b |
| 93 | O vi | 1393.4 | 0.350 29 ± 0.000 01 | 14.48 ± 0.05 | 35 ± 5 | 0.233 ± 0.029 | 12 ± 1 | a |
| 94 | H i | 1641.6 | 0.350 35 ± 0.000 01 | 14.57 ± 0.06 | 26 ± 3 | 0.346 ± 0.047 | 11 ± 1 | a |
| 95 | H i | 1642.4 | 0.351 06 ± 0.000 01 | 15.43 ± 0.03 | 25 ± 1 | 0.440 ± 0.015 | 11 ± 1 | a |
| 96 | H i | 1652.3 | 0.359 18 ± 0.000 02 | 13.61 ± 0.05 | 31 ± 5 | 0.163 ± 0.022 | 11 ± 1 | b |
| 97 | H i | 1658.1 | 0.363 97 ± 0.000 03 | 13.52 ± 0.06 | 58 ± 10 | 0.156 ± 0.021 | 11 ± 1 | b |
| 98 | H i | 1664.1 | 0.368 86 ± 0.000 05 | 13.25 ± 0.11 | 50 ± 18 | 0.089 ± 0.023 | 11 ± 1 | b |
| 99 | H i | 1666.8 | 0.371 06 ± 0.000 01 | 14.06 ± 0.03 | 36 ± 2 | 0.329 ± 0.022 | 11 ± 1 | a |
| 100 | H i | 1667.6 | 0.371 76 ± 0.000 03 | 13.24 ± 0.08 | 29 ± 9 | 0.081 ± 0.016 | 11 ± 1 | a |
| 101 | H i | 1673.8 | 0.376 86 ± 0.000 01 | 13.59 ± 0.04 | 31 ± 4 | 0.159 ± 0.018 | 11 ± 1 | a |
| 102 | O vi | 1426.5 | 0.382 38 ± 0.000 02 | 13.43 ± 0.14 | 7 ± 12 | 0.026 ± 0.016 | 21 ± 2 | c |
| 103 | H i | 1680.6 | 0.382 42 ± 0.000 05 | 12.91 ± 0.16 | 27 ± 17 | 0.041 ± 0.017 | 10 ± 1 | c |
| 104 | H i | 1683.8 | 0.385 08 ± 0.000 01 | 14.25 ± 0.03 | 32 ± 2 | 0.345 ± 0.019 | 11 ± 1 | a |
| 105 | H i | 1691.0 | 0.390 97 ± 0.000 07 | 13.19 ± 0.14 | 53 ± 25 | 0.078 ± 0.027 | 10 ± 1 | c |
| 106 | H i | 1704.6 | 0.402 19 ± 0.000 12 | 13.28 ± 0.20 | 79 ± 49 | 0.097 ± 0.048 | 10 ± 1 | c |
| 107 | H i | 1704.7 | 0.402 24 ± 0.000 03 | 13.07 ± 0.30 | 15 ± 14 | 0.053 ± 0.046 | 10 ± 1 | c |
| 108 | H i | 1716.3 | 0.411 82 ± 0.000 05 | 13.47 ± 0.09 | 62 ± 18 | 0.142 ± 0.031 | 9 ± 1 | b |
| 109 | H i | 1723.3 | 0.417 58 ± 0.000 01 | 14.38 ± 0.03 | 19 ± 1 | 0.254 ± 0.014 | 9 ± 1 | a |
| 110 | H i | 1726.5 | 0.420 22 ± 0.000 06 | 13.25 ± 0.12 | 56 ± 20 | 0.090 ± 0.025 | 10 ± 1 | b |
| 111 | H i | 1737.3 | 0.429 11 ± 0.000 08 | 13.08 ± 0.15 | 55 ± 27 | 0.062 ± 0.023 | 9 ± 1 | c |
| 112 | H i | 1740.4 | 0.431 67 ± 0.000 05 | 13.73 ± 0.83 | 23 ± 14 | 0.179 ± 0.213 | 10 ± 1 | a |
| 113 | H i | 1740.6 | 0.431 83 ± 0.000 83 | 13.21 ± 2.74 | 37 ± 102 | 0.079 ± 0.793 | 9 ± 1 | c |
| 114 | H i | 1768.4 | 0.454 66 ± 0.000 06 | 13.46 ± 0.08 | 81 ± 18 | 0.143 ± 0.026 | 9 ± 1 | b |
| 115 | H i | 1775.9 | 0.460 85 ± 0.000 35 | 13.55 ± 0.25 | 192 ± 141 | 0.185 ± 0.115 | 9 ± 1 | c |
| 116 | H i | 1777.7 | 0.462 35 ± 0.000 02 | 13.77 ± 0.07 | 26 ± 5 | 0.199 ± 0.037 | 9 ± 1 | a |
| 117 | O ii | 1281.0 | 0.535 09 ± 0.000 01 | 13.85 ± 0.25 | 10 ± 10 | 0.041 ± 0.033 | 15 ± 1 | a |
| 118 | H i | 1574.6 | 0.535 10 ± 0.000 01 | 16.52 ± 0.02 | 16 ± 1 | 0.274 ± 0.010 | 14 ± 1 | a |
| 119 | C ii | 2048.6 | 0.535 10 ± 0.000 01 | 13.30 ± 0.56 | 10 ± 10 | 0.034 ± 0.051 | 14 ± 1 | a |
| 120 | O iii | 1078.2 | 0.535 12 ± 0.000 01 | 14.51 ± 0.25 | 13 ± 5 | 0.078 ± 0.036 | 14 ± 1 | a |
| 121 | C iii | 1499.9 | 0.535 20 ± 0.000 01 | 13.98 ± 0.25 | 19 ± 4 | 0.177 ± 0.054 | 16 ± 1 | a |
| 122 | O iv | 1209.3 | 0.535 24 ± 0.000 03 | 14.22 ± 0.11 | 23 ± 10 | 0.076 ± 0.023 | 13 ± 1 | a |
| 123 | H i | 1574.8 | 0.535 31 ± 0.000 03 | 14.99 ± 0.15 | 17 ± 4 | 0.180 ± 0.050 | 14 ± 1 | a |
| 124 | H i | 1717.1 | 0.674 02 ± 0.000 01 | 14.80 ± 0.04 | 31 ± 3 | 0.238 ± 0.024 | 9 ± 1 | a |
| 125 | C iii | 1752.5 | 0.793 72 ± 0.000 03 | 14.84 ± 7.41 | 4 ± 9 | 0.065 ± 0.653 | 9 ± 1 | a |
| 126 | O iv | 1412.9 | 0.793 73 ± 0.000 02 | 14.68 ± 0.09 | 20 ± 5 | 0.128 ± 0.032 | 14 ± 1 | a |
| 127 | O iii | 1259.8 | 0.793 76 ± 0.000 01 | 14.41 ± 14.69 | 3 ± 22 | 0.023 ± 0.234 | 16 ± 1 | a |
| 128 | H i | 1839.9 | 0.793 78 ± 0.000 05 | 15.55 ± 0.10 | 37 ± 6 | 0.426 ± 0.077 | 16 ± 1 | a |
| 129 | C iii | 1752.7 | 0.793 96 ± 0.000 02 | 15.14 ± 8.93 | 10 ± 22 | 0.151 ± 1.514 | 9 ± 1 | a |
| 130 | O iv | 1413.2 | 0.794 01 ± 0.000 02 | 15.51 ± 4.99 | 9 ± 15 | 0.097 ± 0.831 | 14 ± 1 | a |
| 131 | O iii | 1260.0 | 0.794 04 ± 0.000 01 | 14.59 ± 0.20 | 12 ± 3 | 0.077 ± 0.024 | 16 ± 1 | a |
| 132 | H i | 1840.2 | 0.794 04 ± 0.000 05 | 14.91 ± 0.42 | 18 ± 10 | 0.176 ± 0.115 | 16 ± 1 | a |
Notes. (1) Absorption component ID. (2) Ion (see Section 4.1 for details on the line identification process). (3) Observed wavelength of the strongest transition of the ion in the HST/COS spectrum. (4) Redshift from the Voigt profile fitting (see Section 4.2). (5) Column density from the Voigt profile fitting (see Section 4.2). (6) Doppler parameter from the Voigt profile fitting (see Section 4.2). (7) Inferred rest-frame equivalent width from fitted values (note that uncertainties are greatly overestimated for saturated lines or unconstrained fits; see Section 4.3). (8) Averaged local S/N (see Section 4.4). (9) Line reliability flag (‘a’ secure, ‘b’ possible and ‘c’ uncertain; see Section 4.4).
aCould be a very broad H i Ly β at redshift z = 0.535 31 instead, but we cannot confirm it with our current data.
| Component ID . | Ion . | Obs. wavelength . | z . | log (N/cm−2) . | b . | Wr . | 〈S/N〉res . | Label . |
|---|---|---|---|---|---|---|---|---|
| . | . | (Å) . | . | . | (km s−1) . | (Å) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | C iv | 1547.8 | −0.000 24 ± 0.000 13 | 13.98 ± 0.82 | 18 ± 35 | 0.205 ± 0.383 | 14 ± 1 | a |
| 2 | Si iv | 1393.4 | −0.000 24 ± 0.000 03 | 13.38 ± 0.82 | 15 ± 22 | 0.134 ± 0.231 | 12 ± 1 | a |
| 3 | Al ii | 1670.5 | −0.000 18 ± 0.001 00 | 14.13 ± 40.72 | 11 ± 131 | 0.268 ± 2.683 | 11 ± 1 | a |
| 4 | N v | 1238.6 | −0.000 18 ± 0.000 11 | 13.55 ± 0.53 | 23 ± 55 | 0.064 ± 0.105 | 15 ± 1 | a |
| 5 | Si iv | 1393.6 | −0.000 14 ± 0.000 08 | 13.73 ± 0.38 | 35 ± 14 | 0.304 ± 0.203 | 12 ± 1 | a |
| 6 | Si iii | 1206.4 | −0.000 12 ± 0.000 03 | 16.24 ± 1.53 | 16 ± 10 | 0.534 ± 1.077 | 14 ± 1 | a |
| 7 | C iv | 1548.0 | −0.000 11 ± 0.000 11 | 14.09 ± 0.66 | 18 ± 29 | 0.227 ± 0.340 | 15 ± 1 | a |
| 8 | Si ii | 1260.3 | −0.000 10 ± 0.000 01 | 16.58 ± 0.08 | 17 ± 1 | 0.700 ± 0.057 | 16 ± 1 | a |
| 9 | C ii | 1334.4 | −0.000 10 ± 0.000 03 | 18.32 ± 1.65 | 23 ± 9 | 0.824 ± 1.500 | 11 ± 1 | a |
| 10 | Al ii | 1670.7 | −0.000 06 ± 0.001 07 | 14.07 ± 66.61 | 9 ± 204 | 0.222 ± 2.217 | 11 ± 1 | a |
| 11 | C ii* | 1335.6 | −0.000 06 ± 0.000 07 | 14.11 ± 0.38 | 24 ± 32 | 0.164 ± 0.188 | 12 ± 1 | a |
| 12 | Si iii | 1206.7 | 0.000 19 ± 0.000 04 | 13.28 ± 3.99 | 11 ± 41 | 0.121 ± 0.894 | 14 ± 1 | a |
| 13 | Si iii | 1207.2 | 0.000 56 ± 0.000 16 | 12.37 ± 0.92 | 17 ± 88 | 0.043 ± 0.169 | 13 ± 1 | a |
| 14 | H i | 1222.7 | 0.005 79 ± 0.000 03 | 12.86 ± 0.17 | 19 ± 17 | 0.036 ± 0.019 | 13 ± 1 | c |
| 15 | H i | 1224.7 | 0.007 44 ± 0.000 02 | 12.90 ± 0.12 | 12 ± 11 | 0.037 ± 0.020 | 14 ± 1 | c |
| 16 | H i | 1225.0 | 0.007 71 ± 0.000 02 | 12.92 ± 0.30 | 7 ± 14 | 0.034 ± 0.032 | 14 ± 1 | c |
| 17 | H i | 1250.5 | 0.028 65 ± 0.000 01 | 13.49 ± 0.06 | 18 ± 5 | 0.115 ± 0.022 | 16 ± 1 | b |
| 18 | H i | 1250.9 | 0.028 94 ± 0.000 01 | 13.57 ± 0.05 | 32 ± 7 | 0.155 ± 0.023 | 16 ± 1 | b |
| 19 | H i | 1259.4 | 0.035 94 ± 0.000 01 | 13.74 ± 0.05 | 27 ± 4 | 0.197 ± 0.025 | 16 ± 1 | b |
| 20 | H i | 1268.9 | 0.043 75 ± 0.000 01 | 13.49 ± 9.56 | 4 ± 26 | 0.044 ± 0.441 | 15 ± 1 | c |
| 21 | H i | 1269.4 | 0.044 18 ± 0.000 04 | 12.93 ± 0.16 | 30 ± 19 | 0.043 ± 0.017 | 15 ± 1 | c |
| 22 | H i | 1292.0 | 0.062 77 ± 0.000 01 | 13.32 ± 0.08 | 21 ± 7 | 0.089 ± 0.019 | 14 ± 1 | b |
| 23 | H i | 1295.9 | 0.065 99 ± 0.000 04 | 12.86 ± 0.17 | 21 ± 16 | 0.036 ± 0.017 | 14 ± 1 | c |
| 24 | H i | 1298.3 | 0.068 00 ± 0.000 77 | 14.32 ± 6.43 | 25 ± 76 | 0.300 ± 3.003 | 14 ± 1 | c |
| 25 | H i | 1324.8 | 0.089 81 ± 0.000 02 | 13.29 ± 0.10 | 22 ± 10 | 0.087 ± 0.025 | 10 ± 1 | b |
| 26 | H i | 1372.7 | 0.129 20 ± 0.000 02 | 13.55 ± 0.06 | 44 ± 8 | 0.159 ± 0.023 | 12 ± 1 | b |
| 27 | H i | 1410.9 | 0.160 58 ± 0.000 05 | 13.40 ± 0.11 | 59 ± 22 | 0.123 ± 0.033 | 14 ± 1 | b |
| 28 | H i | 1416.4 | 0.165 15 ± 0.000 06 | 12.80 ± 0.28 | 23 ± 26 | 0.032 ± 0.026 | 14 ± 1 | c |
| 29 | H i | 1419.3 | 0.167 48 ± 0.000 05 | 12.76 ± 0.17 | 30 ± 19 | 0.030 ± 0.013 | 16 ± 2 | c |
| 30 | H i | 1424.7 | 0.171 92 ± 0.000 04 | 12.88 ± 0.13 | 34 ± 16 | 0.039 ± 0.013 | 19 ± 2 | b |
| 31 | H i | 1429.4 | 0.175 80 ± 0.000 04 | 12.86 ± 0.15 | 31 ± 17 | 0.037 ± 0.014 | 22 ± 2 | c |
| 32 | H i | 1433.2 | 0.178 94 ± 0.000 02 | 13.07 ± 0.09 | 23 ± 8 | 0.057 ± 0.013 | 21 ± 4 | b |
| 33 | H i | 1441.1 | 0.185 43 ± 0.000 02 | 13.00 ± 0.07 | 22 ± 6 | 0.048 ± 0.009 | 24 ± 1 | b |
| 34 | H i | 1444.1 | 0.187 94 ± 0.000 07 | 13.41 ± 0.08 | 112 ± 28 | 0.133 ± 0.026 | 23 ± 2 | b |
| 35 | H i | 1449.9 | 0.192 67 ± 0.000 02 | 12.91 ± 0.09 | 24 ± 9 | 0.041 ± 0.009 | 23 ± 2 | b |
| 36 | C ii | 1613.5 | 0.209 04 ± 0.000 01 | 14.53 ± 1.73 | 6 ± 6 | 0.096 ± 0.135 | 8 ± 2 | a |
| 37 | Si ii | 1523.9 | 0.209 05 ± 0.000 02 | 12.54 ± 0.10 | 11 ± 8 | 0.046 ± 0.016 | 16 ± 1 | a |
| 38 | H i | 1469.8 | 0.209 08 ± 0.000 01 | 16.15 ± 1.03 | 11 ± 3 | 0.257 ± 0.155 | 18 ± 1 | a |
| 39 | Si iii | 1458.8 | 0.209 09 ± 0.000 01 | 12.63 ± 0.06 | 13 ± 4 | 0.066 ± 0.011 | 20 ± 1 | a |
| 40 | C iii | 1181.4 | 0.209 15 ± 0.000 01 | 14.60 ± 13.57 | 8 ± 35 | 0.113 ± 1.134 | 12 ± 1 | a |
| 41 | N iii | 1196.8 | 0.209 16 ± 0.000 02 | 13.84 ± 0.10 | 19 ± 10 | 0.060 ± 0.017 | 13 ± 1 | a |
| 42 | H i | 1470.0 | 0.209 20 ± 0.000 30 | 13.37 ± 2.72 | 14 ± 47 | 0.088 ± 0.571 | 18 ± 1 | a |
| 43 | Si ii | 1524.5 | 0.209 55 ± 0.00001 | 13.05 ± 0.15 | 13 ± 5 | 0.109 ± 0.043 | 15 ± 2 | a |
| 44 | C ii | 1614.2 | 0.209 55 ± 0.000 01 | 14.96 ± 1.42 | 10 ± 7 | 0.174 ± 0.184 | 8 ± 2 | a |
| 45 | Si iv | 1685.8 | 0.209 56 ± 0.000 01 | 13.67 ± 0.08 | 14 ± 3 | 0.170 ± 0.033 | 10 ± 1 | a |
| 46 | H i | 1470.5 | 0.209 58 ± 0.000 15 | 16.29 ± 3.61 | 14 ± 7 | 0.330 ± 3.272 | 18 ± 1 | a |
| 47 | N iii | 1197.3 | 0.209 62 ± 0.000 01 | 14.94 ± 1.48 | 14 ± 12 | 0.151 ± 0.192 | 13 ± 1 | a |
| 48 | Si iii | 1459.4 | 0.209 62 ± 0.000 01 | 13.56 ± 0.07 | 23 ± 3 | 0.256 ± 0.032 | 20 ± 1 | a |
| 49 | C iii | 1181.8 | 0.209 64 ± 0.002 36 | 15.03 ± 59.37 | 13 ± 98 | 0.188 ± 1.884 | 12 ± 1 | a |
| 50 | N v | 1498.5 | 0.209 64 ± 0.000 03 | 13.57 ± 0.09 | 31 ± 10 | 0.071 ± 0.015 | 17 ± 1 | a |
| 51 | O vi | 1248.3 | 0.209 67 ± 0.000 05 | 14.31 ± 0.21 | 26 ± 10 | 0.164 ± 0.073 | 16 ± 1 | a |
| 52 | Si ii | 1524.8 | 0.209 73 ± 0.000 05 | 13.06 ± 0.16 | 34 ± 13 | 0.150 ± 0.058 | 15 ± 2 | a |
| 53 | C ii | 1614.5 | 0.209 76 ± 0.000 01 | 14.48 ± 0.04 | 20 ± 3 | 0.233 ± 0.029 | 8 ± 2 | a |
| 54 | H i | 1470.7 | 0.209 80 ± 0.000 24 | 15.93 ± 2.00 | 27 ± 15 | 0.534 ± 0.567 | 18 ± 1 | a |
| 55 | Si iv | 1686.2 | 0.209 81 ± 0.000 02 | 13.27 ± 0.07 | 26 ± 7 | 0.128 ± 0.025 | 10 ± 1 | a |
| 56 | Si iii | 1459.7 | 0.209 86 ± 0.000 01 | 13.17 ± 0.05 | 21 ± 4 | 0.178 ± 0.025 | 20 ± 1 | a |
| 57 | C iii | 1182.1 | 0.209 86 ± 0.000 21 | 17.15 ± 0.78 | 14 ± 18 | 0.488 ± 0.515 | 12 ± 1 | a |
| 58 | O vi | 1248.5 | 0.209 87 ± 0.000 06 | 14.16 ± 0.31 | 26 ± 16 | 0.129 ± 0.095 | 16 ± 1 | a |
| 59 | N iii | 1197.5 | 0.209 87 ± 0.000 03 | 14.09 ± 0.11 | 25 ± 12 | 0.100 ± 0.031 | 13 ± 1 | a |
| 60 | H i | 1471.3 | 0.210 28 ± 0.000 01 | 13.70 ± 0.05 | 19 ± 3 | 0.157 ± 0.020 | 18 ± 1 | a |
| 61 | O vi | 1248.9 | 0.210 28 ± 0.000 01 | 14.50 ± 0.03 | 50 ± 6 | 0.270 ± 0.022 | 16 ± 1 | a |
| 62 | N v | 1499.3 | 0.210 29 ± 0.000 06 | 13.53 ± 0.15 | 50 ± 24 | 0.068 ± 0.024 | 16 ± 1 | a |
| 63 | C iii | 1182.5 | 0.210 33 ± 0.000 02 | 13.09 ± 0.18 | 11 ± 11 | 0.055 ± 0.040 | 12 ± 1 | a |
| 64 | H i | 1478.4 | 0.216 15 ± 0.000 02 | 13.30 ± 0.05 | 42 ± 7 | 0.096 ± 0.012 | 17 ± 1 | b |
| 65 | H i | 1481.9 | 0.219 00 ± 0.000 02 | 13.10 ± 0.07 | 36 ± 9 | 0.063 ± 0.011 | 17 ± 1 | b |
| 66 | H i | 1486.8 | 0.223 00 ± 0.000 02 | 13.32 ± 0.05 | 52 ± 8 | 0.104 ± 0.012 | 17 ± 1 | b |
| 67 | H i | 1497.1 | 0.231 50 ± 0.000 01 | 13.45 ± 0.04 | 32 ± 4 | 0.125 ± 0.012 | 17 ± 1 | b |
| 68 | O vi | 1274.5 | 0.235 08 ± 0.000 01 | 14.08 ± 0.05 | 24 ± 4 | 0.111 ± 0.014 | 15 ± 1 | a |
| 69 | H i | 1501.5 | 0.235 11 ± 0.000 01 | 14.48 ± 0.04 | 32 ± 1 | 0.395 ± 0.021 | 17 ± 1 | a |
| 70 | H i | 1509.0 | 0.241 26 ± 0.000 03 | 13.29 ± 0.06 | 54 ± 10 | 0.097 ± 0.014 | 16 ± 1 | b |
| 71 | H i | 1538.8 | 0.265 84 ± 0.000 05 | 14.91 ± 0.41 | 28 ± 4 | 0.419 ± 0.111 | 15 ± 1 | a |
| 72 | C iii | 1236.8 | 0.265 87 ± 0.000 01 | 13.70 ± 40.19 | 3 ± 66 | 0.041 ± 0.406 | 15 ± 1 | a |
| 73 | H i | 1539.0 | 0.265 93 ± 0.000 01 | 15.88 ± 0.06 | 16 ± 2 | 0.328 ± 0.041 | 15 ± 1 | a |
| 74 | H i | 1541.8 | 0.268 27 ± 0.000 10 | 12.78 ± 0.22 | 50 ± 37 | 0.032 ± 0.017 | 15 ± 1 | c |
| 75 | H i | 1545.5 | 0.271 32 ± 0.000 04 | 12.98 ± 0.12 | 36 ± 16 | 0.049 ± 0.015 | 14 ± 2 | b |
| 76 | H i | 1550.9 | 0.275 74 ± 0.000 04 | 13.87 ± 0.32 | 21 ± 17 | 0.200 ± 0.166 | 14 ± 1 | c |
| 77 | H i | 1566.7 | 0.288 74 ± 0.000 07 | 13.06 ± 0.15 | 49 ± 25 | 0.059 ± 0.022 | 13 ± 1 | c |
| 78 | H ia | 1573.8 | 0.294 59 ± 0.000 17 | 13.58 ± 0.13 | 157 ± 57 | 0.193 ± 0.058 | 14 ± 1 | b |
| 79 | H i | 1576.7 | 0.296 96 ± 0.000 10 | 12.75 ± 0.23 | 45 ± 37 | 0.030 ± 0.017 | 13 ± 1 | c |
| 80 | H i | 1578.8 | 0.298 74 ± 0.000 01 | 13.68 ± 0.03 | 36 ± 4 | 0.191 ± 0.015 | 13 ± 1 | b |
| 81 | H i | 1582.7 | 0.301 88 ± 0.000 02 | 13.25 ± 0.07 | 32 ± 8 | 0.084 ± 0.014 | 13 ± 1 | b |
| 82 | H i | 1584.2 | 0.303 14 ± 0.000 03 | 13.32 ± 0.07 | 47 ± 11 | 0.102 ± 0.017 | 13 ± 1 | b |
| 83 | H i | 1613.9 | 0.327 56 ± 0.000 03 | 13.24 ± 0.11 | 24 ± 11 | 0.079 ± 0.024 | 8 ± 2 | b |
| 84 | H i | 1617.4 | 0.330 44 ± 0.000 04 | 13.38 ± 0.09 | 45 ± 13 | 0.113 ± 0.024 | 10 ± 1 | b |
| 85 | H i | 1631.6 | 0.342 17 ± 0.000 06 | 13.75 ± 0.05 | 153 ± 19 | 0.276 ± 0.030 | 10 ± 1 | b |
| 86 | O vi | 1392.6 | 0.349 54 ± 0.000 02 | 13.77 ± 0.09 | 21 ± 8 | 0.061 ± 0.015 | 11 ± 1 | a |
| 87 | Si iii | 1628.6 | 0.349 86 ± 0.000 01 | 13.50 ± 0.03 | 45 ± 4 | 0.378 ± 0.032 | 10 ± 1 | a |
| 88 | H i | 1641.0 | 0.349 86 ± 0.000 01 | 15.88 ± 0.03 | 17 ± 1 | 0.344 ± 0.015 | 11 ± 1 | a |
| 89 | O vi | 1393.0 | 0.349 89 ± 0.000 01 | 14.07 ± 0.06 | 19 ± 5 | 0.101 ± 0.018 | 11 ± 1 | a |
| 90 | C ii | 1801.5 | 0.349 89 ± 0.000 01 | 13.31 ± 0.36 | 5 ± 5 | 0.030 ± 0.028 | 11 ± 1 | a |
| 91 | N iii | 1336.2 | 0.349 98 ± 0.000 06 | 14.04 ± 0.11 | 50 ± 20 | 0.102 ± 0.028 | 12 ± 1 | a |
| 92 | H i | 1641.4 | 0.350 20 ± 0.000 04 | 14.29 ± 0.09 | 97 ± 10 | 0.701 ± 0.116 | 11 ± 1 | b |
| 93 | O vi | 1393.4 | 0.350 29 ± 0.000 01 | 14.48 ± 0.05 | 35 ± 5 | 0.233 ± 0.029 | 12 ± 1 | a |
| 94 | H i | 1641.6 | 0.350 35 ± 0.000 01 | 14.57 ± 0.06 | 26 ± 3 | 0.346 ± 0.047 | 11 ± 1 | a |
| 95 | H i | 1642.4 | 0.351 06 ± 0.000 01 | 15.43 ± 0.03 | 25 ± 1 | 0.440 ± 0.015 | 11 ± 1 | a |
| 96 | H i | 1652.3 | 0.359 18 ± 0.000 02 | 13.61 ± 0.05 | 31 ± 5 | 0.163 ± 0.022 | 11 ± 1 | b |
| 97 | H i | 1658.1 | 0.363 97 ± 0.000 03 | 13.52 ± 0.06 | 58 ± 10 | 0.156 ± 0.021 | 11 ± 1 | b |
| 98 | H i | 1664.1 | 0.368 86 ± 0.000 05 | 13.25 ± 0.11 | 50 ± 18 | 0.089 ± 0.023 | 11 ± 1 | b |
| 99 | H i | 1666.8 | 0.371 06 ± 0.000 01 | 14.06 ± 0.03 | 36 ± 2 | 0.329 ± 0.022 | 11 ± 1 | a |
| 100 | H i | 1667.6 | 0.371 76 ± 0.000 03 | 13.24 ± 0.08 | 29 ± 9 | 0.081 ± 0.016 | 11 ± 1 | a |
| 101 | H i | 1673.8 | 0.376 86 ± 0.000 01 | 13.59 ± 0.04 | 31 ± 4 | 0.159 ± 0.018 | 11 ± 1 | a |
| 102 | O vi | 1426.5 | 0.382 38 ± 0.000 02 | 13.43 ± 0.14 | 7 ± 12 | 0.026 ± 0.016 | 21 ± 2 | c |
| 103 | H i | 1680.6 | 0.382 42 ± 0.000 05 | 12.91 ± 0.16 | 27 ± 17 | 0.041 ± 0.017 | 10 ± 1 | c |
| 104 | H i | 1683.8 | 0.385 08 ± 0.000 01 | 14.25 ± 0.03 | 32 ± 2 | 0.345 ± 0.019 | 11 ± 1 | a |
| 105 | H i | 1691.0 | 0.390 97 ± 0.000 07 | 13.19 ± 0.14 | 53 ± 25 | 0.078 ± 0.027 | 10 ± 1 | c |
| 106 | H i | 1704.6 | 0.402 19 ± 0.000 12 | 13.28 ± 0.20 | 79 ± 49 | 0.097 ± 0.048 | 10 ± 1 | c |
| 107 | H i | 1704.7 | 0.402 24 ± 0.000 03 | 13.07 ± 0.30 | 15 ± 14 | 0.053 ± 0.046 | 10 ± 1 | c |
| 108 | H i | 1716.3 | 0.411 82 ± 0.000 05 | 13.47 ± 0.09 | 62 ± 18 | 0.142 ± 0.031 | 9 ± 1 | b |
| 109 | H i | 1723.3 | 0.417 58 ± 0.000 01 | 14.38 ± 0.03 | 19 ± 1 | 0.254 ± 0.014 | 9 ± 1 | a |
| 110 | H i | 1726.5 | 0.420 22 ± 0.000 06 | 13.25 ± 0.12 | 56 ± 20 | 0.090 ± 0.025 | 10 ± 1 | b |
| 111 | H i | 1737.3 | 0.429 11 ± 0.000 08 | 13.08 ± 0.15 | 55 ± 27 | 0.062 ± 0.023 | 9 ± 1 | c |
| 112 | H i | 1740.4 | 0.431 67 ± 0.000 05 | 13.73 ± 0.83 | 23 ± 14 | 0.179 ± 0.213 | 10 ± 1 | a |
| 113 | H i | 1740.6 | 0.431 83 ± 0.000 83 | 13.21 ± 2.74 | 37 ± 102 | 0.079 ± 0.793 | 9 ± 1 | c |
| 114 | H i | 1768.4 | 0.454 66 ± 0.000 06 | 13.46 ± 0.08 | 81 ± 18 | 0.143 ± 0.026 | 9 ± 1 | b |
| 115 | H i | 1775.9 | 0.460 85 ± 0.000 35 | 13.55 ± 0.25 | 192 ± 141 | 0.185 ± 0.115 | 9 ± 1 | c |
| 116 | H i | 1777.7 | 0.462 35 ± 0.000 02 | 13.77 ± 0.07 | 26 ± 5 | 0.199 ± 0.037 | 9 ± 1 | a |
| 117 | O ii | 1281.0 | 0.535 09 ± 0.000 01 | 13.85 ± 0.25 | 10 ± 10 | 0.041 ± 0.033 | 15 ± 1 | a |
| 118 | H i | 1574.6 | 0.535 10 ± 0.000 01 | 16.52 ± 0.02 | 16 ± 1 | 0.274 ± 0.010 | 14 ± 1 | a |
| 119 | C ii | 2048.6 | 0.535 10 ± 0.000 01 | 13.30 ± 0.56 | 10 ± 10 | 0.034 ± 0.051 | 14 ± 1 | a |
| 120 | O iii | 1078.2 | 0.535 12 ± 0.000 01 | 14.51 ± 0.25 | 13 ± 5 | 0.078 ± 0.036 | 14 ± 1 | a |
| 121 | C iii | 1499.9 | 0.535 20 ± 0.000 01 | 13.98 ± 0.25 | 19 ± 4 | 0.177 ± 0.054 | 16 ± 1 | a |
| 122 | O iv | 1209.3 | 0.535 24 ± 0.000 03 | 14.22 ± 0.11 | 23 ± 10 | 0.076 ± 0.023 | 13 ± 1 | a |
| 123 | H i | 1574.8 | 0.535 31 ± 0.000 03 | 14.99 ± 0.15 | 17 ± 4 | 0.180 ± 0.050 | 14 ± 1 | a |
| 124 | H i | 1717.1 | 0.674 02 ± 0.000 01 | 14.80 ± 0.04 | 31 ± 3 | 0.238 ± 0.024 | 9 ± 1 | a |
| 125 | C iii | 1752.5 | 0.793 72 ± 0.000 03 | 14.84 ± 7.41 | 4 ± 9 | 0.065 ± 0.653 | 9 ± 1 | a |
| 126 | O iv | 1412.9 | 0.793 73 ± 0.000 02 | 14.68 ± 0.09 | 20 ± 5 | 0.128 ± 0.032 | 14 ± 1 | a |
| 127 | O iii | 1259.8 | 0.793 76 ± 0.000 01 | 14.41 ± 14.69 | 3 ± 22 | 0.023 ± 0.234 | 16 ± 1 | a |
| 128 | H i | 1839.9 | 0.793 78 ± 0.000 05 | 15.55 ± 0.10 | 37 ± 6 | 0.426 ± 0.077 | 16 ± 1 | a |
| 129 | C iii | 1752.7 | 0.793 96 ± 0.000 02 | 15.14 ± 8.93 | 10 ± 22 | 0.151 ± 1.514 | 9 ± 1 | a |
| 130 | O iv | 1413.2 | 0.794 01 ± 0.000 02 | 15.51 ± 4.99 | 9 ± 15 | 0.097 ± 0.831 | 14 ± 1 | a |
| 131 | O iii | 1260.0 | 0.794 04 ± 0.000 01 | 14.59 ± 0.20 | 12 ± 3 | 0.077 ± 0.024 | 16 ± 1 | a |
| 132 | H i | 1840.2 | 0.794 04 ± 0.000 05 | 14.91 ± 0.42 | 18 ± 10 | 0.176 ± 0.115 | 16 ± 1 | a |
| Component ID . | Ion . | Obs. wavelength . | z . | log (N/cm−2) . | b . | Wr . | 〈S/N〉res . | Label . |
|---|---|---|---|---|---|---|---|---|
| . | . | (Å) . | . | . | (km s−1) . | (Å) . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . |
| 1 | C iv | 1547.8 | −0.000 24 ± 0.000 13 | 13.98 ± 0.82 | 18 ± 35 | 0.205 ± 0.383 | 14 ± 1 | a |
| 2 | Si iv | 1393.4 | −0.000 24 ± 0.000 03 | 13.38 ± 0.82 | 15 ± 22 | 0.134 ± 0.231 | 12 ± 1 | a |
| 3 | Al ii | 1670.5 | −0.000 18 ± 0.001 00 | 14.13 ± 40.72 | 11 ± 131 | 0.268 ± 2.683 | 11 ± 1 | a |
| 4 | N v | 1238.6 | −0.000 18 ± 0.000 11 | 13.55 ± 0.53 | 23 ± 55 | 0.064 ± 0.105 | 15 ± 1 | a |
| 5 | Si iv | 1393.6 | −0.000 14 ± 0.000 08 | 13.73 ± 0.38 | 35 ± 14 | 0.304 ± 0.203 | 12 ± 1 | a |
| 6 | Si iii | 1206.4 | −0.000 12 ± 0.000 03 | 16.24 ± 1.53 | 16 ± 10 | 0.534 ± 1.077 | 14 ± 1 | a |
| 7 | C iv | 1548.0 | −0.000 11 ± 0.000 11 | 14.09 ± 0.66 | 18 ± 29 | 0.227 ± 0.340 | 15 ± 1 | a |
| 8 | Si ii | 1260.3 | −0.000 10 ± 0.000 01 | 16.58 ± 0.08 | 17 ± 1 | 0.700 ± 0.057 | 16 ± 1 | a |
| 9 | C ii | 1334.4 | −0.000 10 ± 0.000 03 | 18.32 ± 1.65 | 23 ± 9 | 0.824 ± 1.500 | 11 ± 1 | a |
| 10 | Al ii | 1670.7 | −0.000 06 ± 0.001 07 | 14.07 ± 66.61 | 9 ± 204 | 0.222 ± 2.217 | 11 ± 1 | a |
| 11 | C ii* | 1335.6 | −0.000 06 ± 0.000 07 | 14.11 ± 0.38 | 24 ± 32 | 0.164 ± 0.188 | 12 ± 1 | a |
| 12 | Si iii | 1206.7 | 0.000 19 ± 0.000 04 | 13.28 ± 3.99 | 11 ± 41 | 0.121 ± 0.894 | 14 ± 1 | a |
| 13 | Si iii | 1207.2 | 0.000 56 ± 0.000 16 | 12.37 ± 0.92 | 17 ± 88 | 0.043 ± 0.169 | 13 ± 1 | a |
| 14 | H i | 1222.7 | 0.005 79 ± 0.000 03 | 12.86 ± 0.17 | 19 ± 17 | 0.036 ± 0.019 | 13 ± 1 | c |
| 15 | H i | 1224.7 | 0.007 44 ± 0.000 02 | 12.90 ± 0.12 | 12 ± 11 | 0.037 ± 0.020 | 14 ± 1 | c |
| 16 | H i | 1225.0 | 0.007 71 ± 0.000 02 | 12.92 ± 0.30 | 7 ± 14 | 0.034 ± 0.032 | 14 ± 1 | c |
| 17 | H i | 1250.5 | 0.028 65 ± 0.000 01 | 13.49 ± 0.06 | 18 ± 5 | 0.115 ± 0.022 | 16 ± 1 | b |
| 18 | H i | 1250.9 | 0.028 94 ± 0.000 01 | 13.57 ± 0.05 | 32 ± 7 | 0.155 ± 0.023 | 16 ± 1 | b |
| 19 | H i | 1259.4 | 0.035 94 ± 0.000 01 | 13.74 ± 0.05 | 27 ± 4 | 0.197 ± 0.025 | 16 ± 1 | b |
| 20 | H i | 1268.9 | 0.043 75 ± 0.000 01 | 13.49 ± 9.56 | 4 ± 26 | 0.044 ± 0.441 | 15 ± 1 | c |
| 21 | H i | 1269.4 | 0.044 18 ± 0.000 04 | 12.93 ± 0.16 | 30 ± 19 | 0.043 ± 0.017 | 15 ± 1 | c |
| 22 | H i | 1292.0 | 0.062 77 ± 0.000 01 | 13.32 ± 0.08 | 21 ± 7 | 0.089 ± 0.019 | 14 ± 1 | b |
| 23 | H i | 1295.9 | 0.065 99 ± 0.000 04 | 12.86 ± 0.17 | 21 ± 16 | 0.036 ± 0.017 | 14 ± 1 | c |
| 24 | H i | 1298.3 | 0.068 00 ± 0.000 77 | 14.32 ± 6.43 | 25 ± 76 | 0.300 ± 3.003 | 14 ± 1 | c |
| 25 | H i | 1324.8 | 0.089 81 ± 0.000 02 | 13.29 ± 0.10 | 22 ± 10 | 0.087 ± 0.025 | 10 ± 1 | b |
| 26 | H i | 1372.7 | 0.129 20 ± 0.000 02 | 13.55 ± 0.06 | 44 ± 8 | 0.159 ± 0.023 | 12 ± 1 | b |
| 27 | H i | 1410.9 | 0.160 58 ± 0.000 05 | 13.40 ± 0.11 | 59 ± 22 | 0.123 ± 0.033 | 14 ± 1 | b |
| 28 | H i | 1416.4 | 0.165 15 ± 0.000 06 | 12.80 ± 0.28 | 23 ± 26 | 0.032 ± 0.026 | 14 ± 1 | c |
| 29 | H i | 1419.3 | 0.167 48 ± 0.000 05 | 12.76 ± 0.17 | 30 ± 19 | 0.030 ± 0.013 | 16 ± 2 | c |
| 30 | H i | 1424.7 | 0.171 92 ± 0.000 04 | 12.88 ± 0.13 | 34 ± 16 | 0.039 ± 0.013 | 19 ± 2 | b |
| 31 | H i | 1429.4 | 0.175 80 ± 0.000 04 | 12.86 ± 0.15 | 31 ± 17 | 0.037 ± 0.014 | 22 ± 2 | c |
| 32 | H i | 1433.2 | 0.178 94 ± 0.000 02 | 13.07 ± 0.09 | 23 ± 8 | 0.057 ± 0.013 | 21 ± 4 | b |
| 33 | H i | 1441.1 | 0.185 43 ± 0.000 02 | 13.00 ± 0.07 | 22 ± 6 | 0.048 ± 0.009 | 24 ± 1 | b |
| 34 | H i | 1444.1 | 0.187 94 ± 0.000 07 | 13.41 ± 0.08 | 112 ± 28 | 0.133 ± 0.026 | 23 ± 2 | b |
| 35 | H i | 1449.9 | 0.192 67 ± 0.000 02 | 12.91 ± 0.09 | 24 ± 9 | 0.041 ± 0.009 | 23 ± 2 | b |
| 36 | C ii | 1613.5 | 0.209 04 ± 0.000 01 | 14.53 ± 1.73 | 6 ± 6 | 0.096 ± 0.135 | 8 ± 2 | a |
| 37 | Si ii | 1523.9 | 0.209 05 ± 0.000 02 | 12.54 ± 0.10 | 11 ± 8 | 0.046 ± 0.016 | 16 ± 1 | a |
| 38 | H i | 1469.8 | 0.209 08 ± 0.000 01 | 16.15 ± 1.03 | 11 ± 3 | 0.257 ± 0.155 | 18 ± 1 | a |
| 39 | Si iii | 1458.8 | 0.209 09 ± 0.000 01 | 12.63 ± 0.06 | 13 ± 4 | 0.066 ± 0.011 | 20 ± 1 | a |
| 40 | C iii | 1181.4 | 0.209 15 ± 0.000 01 | 14.60 ± 13.57 | 8 ± 35 | 0.113 ± 1.134 | 12 ± 1 | a |
| 41 | N iii | 1196.8 | 0.209 16 ± 0.000 02 | 13.84 ± 0.10 | 19 ± 10 | 0.060 ± 0.017 | 13 ± 1 | a |
| 42 | H i | 1470.0 | 0.209 20 ± 0.000 30 | 13.37 ± 2.72 | 14 ± 47 | 0.088 ± 0.571 | 18 ± 1 | a |
| 43 | Si ii | 1524.5 | 0.209 55 ± 0.00001 | 13.05 ± 0.15 | 13 ± 5 | 0.109 ± 0.043 | 15 ± 2 | a |
| 44 | C ii | 1614.2 | 0.209 55 ± 0.000 01 | 14.96 ± 1.42 | 10 ± 7 | 0.174 ± 0.184 | 8 ± 2 | a |
| 45 | Si iv | 1685.8 | 0.209 56 ± 0.000 01 | 13.67 ± 0.08 | 14 ± 3 | 0.170 ± 0.033 | 10 ± 1 | a |
| 46 | H i | 1470.5 | 0.209 58 ± 0.000 15 | 16.29 ± 3.61 | 14 ± 7 | 0.330 ± 3.272 | 18 ± 1 | a |
| 47 | N iii | 1197.3 | 0.209 62 ± 0.000 01 | 14.94 ± 1.48 | 14 ± 12 | 0.151 ± 0.192 | 13 ± 1 | a |
| 48 | Si iii | 1459.4 | 0.209 62 ± 0.000 01 | 13.56 ± 0.07 | 23 ± 3 | 0.256 ± 0.032 | 20 ± 1 | a |
| 49 | C iii | 1181.8 | 0.209 64 ± 0.002 36 | 15.03 ± 59.37 | 13 ± 98 | 0.188 ± 1.884 | 12 ± 1 | a |
| 50 | N v | 1498.5 | 0.209 64 ± 0.000 03 | 13.57 ± 0.09 | 31 ± 10 | 0.071 ± 0.015 | 17 ± 1 | a |
| 51 | O vi | 1248.3 | 0.209 67 ± 0.000 05 | 14.31 ± 0.21 | 26 ± 10 | 0.164 ± 0.073 | 16 ± 1 | a |
| 52 | Si ii | 1524.8 | 0.209 73 ± 0.000 05 | 13.06 ± 0.16 | 34 ± 13 | 0.150 ± 0.058 | 15 ± 2 | a |
| 53 | C ii | 1614.5 | 0.209 76 ± 0.000 01 | 14.48 ± 0.04 | 20 ± 3 | 0.233 ± 0.029 | 8 ± 2 | a |
| 54 | H i | 1470.7 | 0.209 80 ± 0.000 24 | 15.93 ± 2.00 | 27 ± 15 | 0.534 ± 0.567 | 18 ± 1 | a |
| 55 | Si iv | 1686.2 | 0.209 81 ± 0.000 02 | 13.27 ± 0.07 | 26 ± 7 | 0.128 ± 0.025 | 10 ± 1 | a |
| 56 | Si iii | 1459.7 | 0.209 86 ± 0.000 01 | 13.17 ± 0.05 | 21 ± 4 | 0.178 ± 0.025 | 20 ± 1 | a |
| 57 | C iii | 1182.1 | 0.209 86 ± 0.000 21 | 17.15 ± 0.78 | 14 ± 18 | 0.488 ± 0.515 | 12 ± 1 | a |
| 58 | O vi | 1248.5 | 0.209 87 ± 0.000 06 | 14.16 ± 0.31 | 26 ± 16 | 0.129 ± 0.095 | 16 ± 1 | a |
| 59 | N iii | 1197.5 | 0.209 87 ± 0.000 03 | 14.09 ± 0.11 | 25 ± 12 | 0.100 ± 0.031 | 13 ± 1 | a |
| 60 | H i | 1471.3 | 0.210 28 ± 0.000 01 | 13.70 ± 0.05 | 19 ± 3 | 0.157 ± 0.020 | 18 ± 1 | a |
| 61 | O vi | 1248.9 | 0.210 28 ± 0.000 01 | 14.50 ± 0.03 | 50 ± 6 | 0.270 ± 0.022 | 16 ± 1 | a |
| 62 | N v | 1499.3 | 0.210 29 ± 0.000 06 | 13.53 ± 0.15 | 50 ± 24 | 0.068 ± 0.024 | 16 ± 1 | a |
| 63 | C iii | 1182.5 | 0.210 33 ± 0.000 02 | 13.09 ± 0.18 | 11 ± 11 | 0.055 ± 0.040 | 12 ± 1 | a |
| 64 | H i | 1478.4 | 0.216 15 ± 0.000 02 | 13.30 ± 0.05 | 42 ± 7 | 0.096 ± 0.012 | 17 ± 1 | b |
| 65 | H i | 1481.9 | 0.219 00 ± 0.000 02 | 13.10 ± 0.07 | 36 ± 9 | 0.063 ± 0.011 | 17 ± 1 | b |
| 66 | H i | 1486.8 | 0.223 00 ± 0.000 02 | 13.32 ± 0.05 | 52 ± 8 | 0.104 ± 0.012 | 17 ± 1 | b |
| 67 | H i | 1497.1 | 0.231 50 ± 0.000 01 | 13.45 ± 0.04 | 32 ± 4 | 0.125 ± 0.012 | 17 ± 1 | b |
| 68 | O vi | 1274.5 | 0.235 08 ± 0.000 01 | 14.08 ± 0.05 | 24 ± 4 | 0.111 ± 0.014 | 15 ± 1 | a |
| 69 | H i | 1501.5 | 0.235 11 ± 0.000 01 | 14.48 ± 0.04 | 32 ± 1 | 0.395 ± 0.021 | 17 ± 1 | a |
| 70 | H i | 1509.0 | 0.241 26 ± 0.000 03 | 13.29 ± 0.06 | 54 ± 10 | 0.097 ± 0.014 | 16 ± 1 | b |
| 71 | H i | 1538.8 | 0.265 84 ± 0.000 05 | 14.91 ± 0.41 | 28 ± 4 | 0.419 ± 0.111 | 15 ± 1 | a |
| 72 | C iii | 1236.8 | 0.265 87 ± 0.000 01 | 13.70 ± 40.19 | 3 ± 66 | 0.041 ± 0.406 | 15 ± 1 | a |
| 73 | H i | 1539.0 | 0.265 93 ± 0.000 01 | 15.88 ± 0.06 | 16 ± 2 | 0.328 ± 0.041 | 15 ± 1 | a |
| 74 | H i | 1541.8 | 0.268 27 ± 0.000 10 | 12.78 ± 0.22 | 50 ± 37 | 0.032 ± 0.017 | 15 ± 1 | c |
| 75 | H i | 1545.5 | 0.271 32 ± 0.000 04 | 12.98 ± 0.12 | 36 ± 16 | 0.049 ± 0.015 | 14 ± 2 | b |
| 76 | H i | 1550.9 | 0.275 74 ± 0.000 04 | 13.87 ± 0.32 | 21 ± 17 | 0.200 ± 0.166 | 14 ± 1 | c |
| 77 | H i | 1566.7 | 0.288 74 ± 0.000 07 | 13.06 ± 0.15 | 49 ± 25 | 0.059 ± 0.022 | 13 ± 1 | c |
| 78 | H ia | 1573.8 | 0.294 59 ± 0.000 17 | 13.58 ± 0.13 | 157 ± 57 | 0.193 ± 0.058 | 14 ± 1 | b |
| 79 | H i | 1576.7 | 0.296 96 ± 0.000 10 | 12.75 ± 0.23 | 45 ± 37 | 0.030 ± 0.017 | 13 ± 1 | c |
| 80 | H i | 1578.8 | 0.298 74 ± 0.000 01 | 13.68 ± 0.03 | 36 ± 4 | 0.191 ± 0.015 | 13 ± 1 | b |
| 81 | H i | 1582.7 | 0.301 88 ± 0.000 02 | 13.25 ± 0.07 | 32 ± 8 | 0.084 ± 0.014 | 13 ± 1 | b |
| 82 | H i | 1584.2 | 0.303 14 ± 0.000 03 | 13.32 ± 0.07 | 47 ± 11 | 0.102 ± 0.017 | 13 ± 1 | b |
| 83 | H i | 1613.9 | 0.327 56 ± 0.000 03 | 13.24 ± 0.11 | 24 ± 11 | 0.079 ± 0.024 | 8 ± 2 | b |
| 84 | H i | 1617.4 | 0.330 44 ± 0.000 04 | 13.38 ± 0.09 | 45 ± 13 | 0.113 ± 0.024 | 10 ± 1 | b |
| 85 | H i | 1631.6 | 0.342 17 ± 0.000 06 | 13.75 ± 0.05 | 153 ± 19 | 0.276 ± 0.030 | 10 ± 1 | b |
| 86 | O vi | 1392.6 | 0.349 54 ± 0.000 02 | 13.77 ± 0.09 | 21 ± 8 | 0.061 ± 0.015 | 11 ± 1 | a |
| 87 | Si iii | 1628.6 | 0.349 86 ± 0.000 01 | 13.50 ± 0.03 | 45 ± 4 | 0.378 ± 0.032 | 10 ± 1 | a |
| 88 | H i | 1641.0 | 0.349 86 ± 0.000 01 | 15.88 ± 0.03 | 17 ± 1 | 0.344 ± 0.015 | 11 ± 1 | a |
| 89 | O vi | 1393.0 | 0.349 89 ± 0.000 01 | 14.07 ± 0.06 | 19 ± 5 | 0.101 ± 0.018 | 11 ± 1 | a |
| 90 | C ii | 1801.5 | 0.349 89 ± 0.000 01 | 13.31 ± 0.36 | 5 ± 5 | 0.030 ± 0.028 | 11 ± 1 | a |
| 91 | N iii | 1336.2 | 0.349 98 ± 0.000 06 | 14.04 ± 0.11 | 50 ± 20 | 0.102 ± 0.028 | 12 ± 1 | a |
| 92 | H i | 1641.4 | 0.350 20 ± 0.000 04 | 14.29 ± 0.09 | 97 ± 10 | 0.701 ± 0.116 | 11 ± 1 | b |
| 93 | O vi | 1393.4 | 0.350 29 ± 0.000 01 | 14.48 ± 0.05 | 35 ± 5 | 0.233 ± 0.029 | 12 ± 1 | a |
| 94 | H i | 1641.6 | 0.350 35 ± 0.000 01 | 14.57 ± 0.06 | 26 ± 3 | 0.346 ± 0.047 | 11 ± 1 | a |
| 95 | H i | 1642.4 | 0.351 06 ± 0.000 01 | 15.43 ± 0.03 | 25 ± 1 | 0.440 ± 0.015 | 11 ± 1 | a |
| 96 | H i | 1652.3 | 0.359 18 ± 0.000 02 | 13.61 ± 0.05 | 31 ± 5 | 0.163 ± 0.022 | 11 ± 1 | b |
| 97 | H i | 1658.1 | 0.363 97 ± 0.000 03 | 13.52 ± 0.06 | 58 ± 10 | 0.156 ± 0.021 | 11 ± 1 | b |
| 98 | H i | 1664.1 | 0.368 86 ± 0.000 05 | 13.25 ± 0.11 | 50 ± 18 | 0.089 ± 0.023 | 11 ± 1 | b |
| 99 | H i | 1666.8 | 0.371 06 ± 0.000 01 | 14.06 ± 0.03 | 36 ± 2 | 0.329 ± 0.022 | 11 ± 1 | a |
| 100 | H i | 1667.6 | 0.371 76 ± 0.000 03 | 13.24 ± 0.08 | 29 ± 9 | 0.081 ± 0.016 | 11 ± 1 | a |
| 101 | H i | 1673.8 | 0.376 86 ± 0.000 01 | 13.59 ± 0.04 | 31 ± 4 | 0.159 ± 0.018 | 11 ± 1 | a |
| 102 | O vi | 1426.5 | 0.382 38 ± 0.000 02 | 13.43 ± 0.14 | 7 ± 12 | 0.026 ± 0.016 | 21 ± 2 | c |
| 103 | H i | 1680.6 | 0.382 42 ± 0.000 05 | 12.91 ± 0.16 | 27 ± 17 | 0.041 ± 0.017 | 10 ± 1 | c |
| 104 | H i | 1683.8 | 0.385 08 ± 0.000 01 | 14.25 ± 0.03 | 32 ± 2 | 0.345 ± 0.019 | 11 ± 1 | a |
| 105 | H i | 1691.0 | 0.390 97 ± 0.000 07 | 13.19 ± 0.14 | 53 ± 25 | 0.078 ± 0.027 | 10 ± 1 | c |
| 106 | H i | 1704.6 | 0.402 19 ± 0.000 12 | 13.28 ± 0.20 | 79 ± 49 | 0.097 ± 0.048 | 10 ± 1 | c |
| 107 | H i | 1704.7 | 0.402 24 ± 0.000 03 | 13.07 ± 0.30 | 15 ± 14 | 0.053 ± 0.046 | 10 ± 1 | c |
| 108 | H i | 1716.3 | 0.411 82 ± 0.000 05 | 13.47 ± 0.09 | 62 ± 18 | 0.142 ± 0.031 | 9 ± 1 | b |
| 109 | H i | 1723.3 | 0.417 58 ± 0.000 01 | 14.38 ± 0.03 | 19 ± 1 | 0.254 ± 0.014 | 9 ± 1 | a |
| 110 | H i | 1726.5 | 0.420 22 ± 0.000 06 | 13.25 ± 0.12 | 56 ± 20 | 0.090 ± 0.025 | 10 ± 1 | b |
| 111 | H i | 1737.3 | 0.429 11 ± 0.000 08 | 13.08 ± 0.15 | 55 ± 27 | 0.062 ± 0.023 | 9 ± 1 | c |
| 112 | H i | 1740.4 | 0.431 67 ± 0.000 05 | 13.73 ± 0.83 | 23 ± 14 | 0.179 ± 0.213 | 10 ± 1 | a |
| 113 | H i | 1740.6 | 0.431 83 ± 0.000 83 | 13.21 ± 2.74 | 37 ± 102 | 0.079 ± 0.793 | 9 ± 1 | c |
| 114 | H i | 1768.4 | 0.454 66 ± 0.000 06 | 13.46 ± 0.08 | 81 ± 18 | 0.143 ± 0.026 | 9 ± 1 | b |
| 115 | H i | 1775.9 | 0.460 85 ± 0.000 35 | 13.55 ± 0.25 | 192 ± 141 | 0.185 ± 0.115 | 9 ± 1 | c |
| 116 | H i | 1777.7 | 0.462 35 ± 0.000 02 | 13.77 ± 0.07 | 26 ± 5 | 0.199 ± 0.037 | 9 ± 1 | a |
| 117 | O ii | 1281.0 | 0.535 09 ± 0.000 01 | 13.85 ± 0.25 | 10 ± 10 | 0.041 ± 0.033 | 15 ± 1 | a |
| 118 | H i | 1574.6 | 0.535 10 ± 0.000 01 | 16.52 ± 0.02 | 16 ± 1 | 0.274 ± 0.010 | 14 ± 1 | a |
| 119 | C ii | 2048.6 | 0.535 10 ± 0.000 01 | 13.30 ± 0.56 | 10 ± 10 | 0.034 ± 0.051 | 14 ± 1 | a |
| 120 | O iii | 1078.2 | 0.535 12 ± 0.000 01 | 14.51 ± 0.25 | 13 ± 5 | 0.078 ± 0.036 | 14 ± 1 | a |
| 121 | C iii | 1499.9 | 0.535 20 ± 0.000 01 | 13.98 ± 0.25 | 19 ± 4 | 0.177 ± 0.054 | 16 ± 1 | a |
| 122 | O iv | 1209.3 | 0.535 24 ± 0.000 03 | 14.22 ± 0.11 | 23 ± 10 | 0.076 ± 0.023 | 13 ± 1 | a |
| 123 | H i | 1574.8 | 0.535 31 ± 0.000 03 | 14.99 ± 0.15 | 17 ± 4 | 0.180 ± 0.050 | 14 ± 1 | a |
| 124 | H i | 1717.1 | 0.674 02 ± 0.000 01 | 14.80 ± 0.04 | 31 ± 3 | 0.238 ± 0.024 | 9 ± 1 | a |
| 125 | C iii | 1752.5 | 0.793 72 ± 0.000 03 | 14.84 ± 7.41 | 4 ± 9 | 0.065 ± 0.653 | 9 ± 1 | a |
| 126 | O iv | 1412.9 | 0.793 73 ± 0.000 02 | 14.68 ± 0.09 | 20 ± 5 | 0.128 ± 0.032 | 14 ± 1 | a |
| 127 | O iii | 1259.8 | 0.793 76 ± 0.000 01 | 14.41 ± 14.69 | 3 ± 22 | 0.023 ± 0.234 | 16 ± 1 | a |
| 128 | H i | 1839.9 | 0.793 78 ± 0.000 05 | 15.55 ± 0.10 | 37 ± 6 | 0.426 ± 0.077 | 16 ± 1 | a |
| 129 | C iii | 1752.7 | 0.793 96 ± 0.000 02 | 15.14 ± 8.93 | 10 ± 22 | 0.151 ± 1.514 | 9 ± 1 | a |
| 130 | O iv | 1413.2 | 0.794 01 ± 0.000 02 | 15.51 ± 4.99 | 9 ± 15 | 0.097 ± 0.831 | 14 ± 1 | a |
| 131 | O iii | 1260.0 | 0.794 04 ± 0.000 01 | 14.59 ± 0.20 | 12 ± 3 | 0.077 ± 0.024 | 16 ± 1 | a |
| 132 | H i | 1840.2 | 0.794 04 ± 0.000 05 | 14.91 ± 0.42 | 18 ± 10 | 0.176 ± 0.115 | 16 ± 1 | a |
Notes. (1) Absorption component ID. (2) Ion (see Section 4.1 for details on the line identification process). (3) Observed wavelength of the strongest transition of the ion in the HST/COS spectrum. (4) Redshift from the Voigt profile fitting (see Section 4.2). (5) Column density from the Voigt profile fitting (see Section 4.2). (6) Doppler parameter from the Voigt profile fitting (see Section 4.2). (7) Inferred rest-frame equivalent width from fitted values (note that uncertainties are greatly overestimated for saturated lines or unconstrained fits; see Section 4.3). (8) Averaged local S/N (see Section 4.4). (9) Line reliability flag (‘a’ secure, ‘b’ possible and ‘c’ uncertain; see Section 4.4).
aCould be a very broad H i Ly β at redshift z = 0.535 31 instead, but we cannot confirm it with our current data.
4.3 Rest-frame equivalent widths
For each component we estimate the rest-frame equivalent width of the strongest transition, Wr, using the approximation given by Draine (2011, see his equation 9.27), based on their fitted N and b values. The resulting values are given in the seventh column of Table 4. We chose this approach in order to avoid complications when dealing with blended components. We emphasize that passing from Wr → (N, b) is not always robust when on of the flat part of the curve of growth, but passing from (N, b) → Wr is robust. We compared the results in Wr from our adopted approach and that from a direct pixel integration, in a subsample of 10 unblended and unsaturated lines, and obtained consistent results within the uncertainties.
The rest-frame equivalent width uncertainty, δWr, was estimated as follows. We first calculated the maximum/minimum equivalent width, |$W_{\rm r}^{\rm max/min}$|, still consistent within 1σ from the N and b fitted values, i.e. using the aforementioned approximation for |$(N \pm \delta N,b \pm \delta b) \rightarrow W_{\rm r}^{\rm max/min}$|, where δN and δb are the column density and Doppler parameter uncertainties, respectively, as given by vpfit. We then took |$\delta W_{\rm r} \equiv (1/2)(W_{\rm r}^{\rm max} - W_{\rm r}^{\rm min})$|. In catastrophic cases where the fits are unconstrained (i.e. δWr ≫ Wr), we arbitrarily imposed δWr = 10 × Wr, ensuring a very low significance level.
By using the actual fitted parameters and their corresponding errors, our δWr uncertainty estimation takes into account the non-Gaussian shape of the COS LSF (particularly important for broad absorption lines). For saturated lines, our method will give unrealistically large δWr uncertainties due to a poor constraint in N, which is a conservative choice.
4.4 Local S/N estimation
For each component we estimated the average local spectral S/N per pixel, 〈S/N〉pixel, over the 50 closest pixels around its strongest transition, without considering those with flux values below 90 per cent of the continuum. We then estimated the local S/N per resolution element 〈S/N〉res as |$\sqrt{2}\langle \text{S/N} \rangle _{\rm pixel}$|. The resulting values are given in the eight column of Table 4.
4.5 Absorption line reliability
To deal with ambiguity and significance of the absorption lines we have introduced a reliability flag scheme as follows.
Reliable (‘a’): absorption line components showing at least two transitions or showing up in at least two ions, independently of the significance of its corresponding Wr.
Probable (‘b’): absorption line components showing only one transition, showing up in only one ion, and having Wr/δWr ≥ 3.
Uncertain (‘c’): absorption line components showing only one transition, showing up in only one ion, and having Wr/δWr < 3. Components in this category will be excluded from the main scientific analysis presented in this paper.
This reliability scheme applied to our absorption line list is shown in the ninth column of Table 4. We also show these flags together with the ion component ID given (first column of Table 4) in Fig. E1 as vertical labels.
We note that previous studies on Broad Ly α (BLA) lines have suggested one to quantifying the completeness level of these broad lines by means of 〈S/N〉res × N/b (Richter et al. 2006). The motivation of this criterion is that the BLA is sensitive to both S/N and the optical depth at the line centres, τ0 ∝ N/b. Therefore, it is not appropriate to use the commonly adopted formalism based on a minimum equivalent width threshold for unresolved lines (these broad lines are usually resolved). In Appendix B, we compare the proposed approach by Richter et al. (2006) to ours, and show that imposing a minimum Wr/δWr value (as defined here) is roughly consistent with imposing a minimum 〈S/N〉res × N/b value for broad lines16, but is more conservative when applied to narrow lines. Moreover, our approach has the advantage of being straightforwardly applicable to any absorption line irrespective of its Doppler parameter and ionic transition, hence more appropriate for an homogeneous analysis.
Fig. 4 shows the distribution Doppler parameters b as a function of column densities N, for our sample of H i (black circles) and O vi (green squares) between 0.1 ≤ z ≤ 0.5 and excluding those in the ‘c’ category (i.e. uncertain). White stars mark components that lie within Δv ≤ 1000 km s−1 and within impact parameters of Δd ≤ 3 Mpc from cluster pairs, our fiducial values for associating absorption lines with cluster pairs (see Section 5).
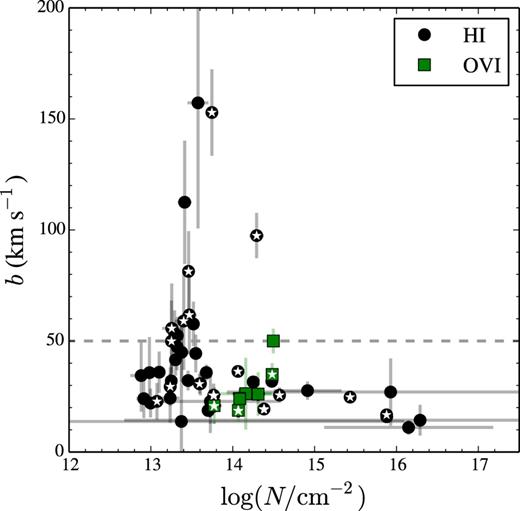
Distribution of Doppler parameters (b) as a function of column density (N) for H i (black circles) and O vi (green squares) absorption lines found in the HST/COS FUV spectrum between 0.1 ≤ z ≤ 0.5 and excluding those in category ‘c’ (uncertain; see Section 4.5). White stars mark absorbers associated with cluster pairs (see Section 5). The horizontal dashed grey line corresponds to a Doppler parameter of b = 50 km s−1, our adopted limit to split H i lines into broad and narrow.
5 Redshift number density of absorption line systems around cluster pairs
After having characterized LSS traced by galaxy cluster pairs around the Q1410 sightline (Section 3) and intervening absorption lines (Section 4), we can now provide a cross-match between the two. Because the completeness level of the redMaPPer clusters with richness <20 (<40) at z ∼ 0.1–0.4 (z ∼ 0.4–0.5) is lower than ∼50 per cent (see top panel of fig. 22 of Rykoff et al. 2014), in this paper we will only match absorption lines close to the position of known cluster pairs rather than the other way around (or both). We also note that the purity of redMaPPer clusters is fairly constant with richness and redshift (some trends are present though), but with values above 95 per cent in all the cases (see bottom panel of fig. 22 of Rykoff et al. 2014); still, the presence of fake clusters will only dilute any real signal when associating absorption lines to intercluster filaments traced by cluster pairs.
In this paper, we use the redshift number density of absorption lines, dN/dz, as a function of cluster-pair separation, as the relevant statistical quantity to characterize intercluster filaments (if any). We have chosen dN/dz as opposed to the number of systems per absorption distance, dN/dX, (or both), only for simplicity. Still, in Appendix G we provide tables with relevant quantities and results for both dN/dz and dN/dX. We note that our conclusions are independent of this choice.
At this point, it is also important to emphasize that we do not know a priori that cluster pairs in our sample are tracing true intercluster filaments, and that even if they do, we do not know if these could produce a signal in the observed incidences of H i and O vi absorption lines at the S/N level obtained in our Q1410 HST/COS spectrum. Although cosmological hydrodynamical simulations suggest that this may be the case, this paper aims to provide a direct test of such an hypothesis. Therefore, we will explore the behaviour of dN/dz over a wide range of scales around cluster pairs both along and transverse to the Q1410 LOS. This means that in the following, we will allow the maximum impact parameter for clusters and cluster-pair intercluster axes to the Q1410 sightline to be larger than the fiducial values adopted in Sections 3.1 and 3.2 (i.e. larger than 20 and 3 Mpc, respectively).
5.1 Measuring the redshift number density of absorption lines around cluster pairs
Fig. 5 shows the redshift path, Δz, along the Q1410 sightline as a function of minimum rest-frame equivalent width,|$W_{\rm r}^{\rm min}$|, for our survey of H i (black solid line and circles) and O vi ( green dashed line and squares) absorption lines. The left-hand panel shows the corresponding redshift path associated with regions of our Q1410 HST/COS spectrum within rest-frame velocity differences Δv = 1000 km s−1 from cluster pairs at impact parameters smaller than Δd = 3 Mpc, while the right-hand panel shows the total corresponding redshift path for the full Q1410 HST/COS spectrum between 0.1 ≤ z ≤ 0.5. We see that the completeness level is very similar between the portions of the spectrum close to cluster pairs and that of the full spectrum. We checked that this is also the case for multiple choices of Δv and Δd values, increasing from our fiducial values to cover the full spectrum (not shown). The vertical lines in Fig. 5 show the minimum rest-frame equivalent width for our H i (black solid; |$W_{\rm r}^{\rm min}=0.039$| Å) and O vi (dashed green; |$W_{\rm r}^{\rm min}=0.061$| Å) absorption line samples, excluding those labelled as ‘uncertain’ (category ‘c’; see Section 4.5). We see that these values correspond to high completeness levels and are therefore adopted as the minimum equivalent widths in the forthcoming analysis (but note that we could have detected O vi down to Wr ∼ 0.03 Å with a similar completeness).
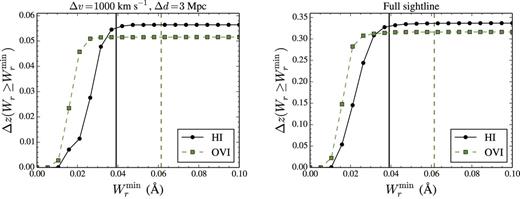
Redshift path, Δz, as a function of minimum rest-frame equivalent width, |$W_{\rm r}^{\rm min}$|, for our survey of H i (black solid line and circles) and O vi (green dashed line and squares) absorption lines. The left-hand panel shows the corresponding redshift path associated with regions of our Q1410 HST/COS spectrum within rest-frame velocity differences Δv = 1000 km s−1 from cluster pairs at impact parameters smaller than Δd = 3 Mpc. The right-hand panel shows the total corresponding redshift path for the full Q1410 HST/COS spectrum between 0.1 ≤ z ≤ 0.5. Vertical lines show the minimum rest-frame equivalent width for our detected H i (solid black; Wr = 0.039Å) and O vi (dashed green; Wr = 0.061Å) absorption line samples, excluding those in the category ‘c’ (uncertain; see Section 4.5). See Section 5.1 for further details.
5.2 Estimating the field redshift number density from the Q1410 sightline
In this paper, we have introduced slightly different ways to count and assess the statistical significance of absorption lines compared with has been done in previous published works. This is so because we opted to do a uniform analysis for H i (either total, broad or narrow) and O vi absorption lines, while previous works have usually focused on one type at a time. Therefore, we estimate the field redshift number density of a given species using our own methodology using the Q1410 sightline data alone. This is justified by the fact that cluster-pair filaments (if any) should only influence specific portions of the spectrum (in our case about ∼1/6 of it), while the rest should match the field expectation (i.e. that from a randomly selected sightline).
This methodology assumes (i) that there is an excess of absorption lines in the data compared to the field expectation, and (ii) that this excess is purely confined within Δv = 1000 km s−1 and Δd = 3 Mpc from the known cluster pairs. If assumption (i) is incorrect, then our field expectation estimation will be underestimated. If assumption (i) is correct, but assumption (ii) is incorrect, then our field expectation estimation will be overestimated. In Section 6, we show that our field estimations based on Q1410 alone matches those of comparable previously published blind surveys, making our assumptions reasonable.
5.3 Statistical uncertainty estimations
The statistical uncertainty in our calculations is dominated by the uncertainty in N(Δd, Δv), which we assume is Poissonian and estimate from the analytical approximation given by Gehrels (1986): |$\sigma ^{+}_N \approx \sqrt{N+3/4} + 1$| and |$\sigma ^{-}_N \approx \sqrt{N -1/4}$|. The statistical uncertainty in our estimation of Nfield is taken from the contributions of both the Poissonian uncertainty of Ntot, and the statistical uncertainty of |$n_{\rm cpair}^{\rm field}$|, which we propagate assuming independence between these two quantities. Given that the statistical uncertainties in Δz(Δd, Δv) and ΔX(Δd, Δv) are much smaller, we neglect them.
6 RESULTS
In this section, we report our results on dN/dz, for our different samples of H i (total, narrow and broad) and O vi absorption lines observed in the Q1410 sightline (see Section 4) applying the methodology described in Section 5 to associate them with cluster pairs (see Section 3). For simplicity, and in order to reduce the ‘shot noise’ of the measurements, the following results are obtained by varying Δv and Δd for fixed values of Δd and Δv, respectively (as opposed to varying both values at the same time).
A summary of all the results presented in this section (and those of dN/dX, not described here), are given in Tables G1–G4.
6.1 Redshift number densities
Fig. 6 shows the dN/dz of total H i (top panels; brown circles) and O vi (bottom panels; green squares) absorption components as a function of maximum velocity window (Δv; left-hand panels) and maximum impact parameter (Δd; right-hand panels) for a fixed Δd = 3 Mpc and Δv = 1000 km s−1, respectively. The expected field values following our approach described in Section 5.2 are shown by the horizontal dashed line with its ±1σ uncertainty represented by the grey region. We also show the ±1σ field values from the Danforth & Shull (2008) survey as the darker grey hashed regions, which is consistent with ours.
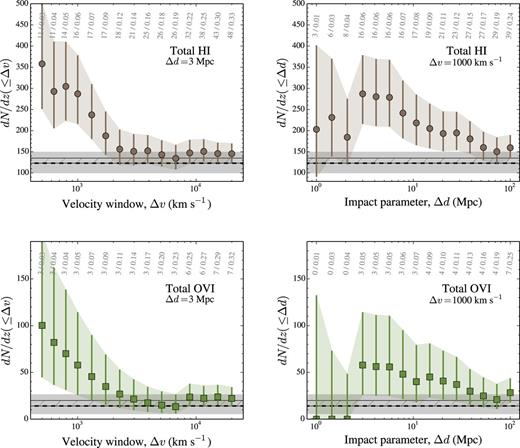
Redshift number density of total H i (brown circles; top panels) and O vi (green squares; bottom panels) absorption components as a function of rest-frame velocity window (Δv; left-hand panels) and maximum impact parameter to the closest cluster-pair axis (Δd; right-hand panels) for a fixed Δd = 3 Mpc and Δv = 1000 km s−1, respectively. Note that bins are not independent from each other, as emphasized by the coloured areas. The total number of lines and redshift paths per bin are given in grey numbers on top of the data points. The expected field value estimated from our Q1410 sightline is represented by the horizontal dashed line with its ±1σ uncertainty represented by the darker grey region. The darkest grey hashed regions represents the ±1σ field values from the Danforth & Shull (2008) survey. See Section 6.1 for further details.
When we fix Δd = 3 Mpc (left-hand panels), we observe a clear overall increase in the redshift number density of H i and O vi absorption lines with decreasing Δv. Similarly, when we fix Δv = 1000 km s−1 (right-hand panels), we observe an overall increase in the redshift number density of H i and O vi absorption lines with decreasing Δd, but only down to Δd ∼ 3 Mpc; at Δd ≲ 3 Mpc a flattening (or even decrease) trend is observed, which we believe is mostly due to our small sample in such bins.20 This change of behaviour motivated our adopted fiducial value of 3 Mpc for the maximum transverse separation between cluster-pair axis and the Q1410 sightline (see Section 3.2).
To test whether kinematic trends are present in the H i data, we repeated the dN/dz measurements for both NLA (b < 50 km s−1) and BLA (b ≥ 50 km s−1) lines. Although the canonical value for BLAs tracing the WHIM is 40 km s−1, this limit assumes that the broadening is purely thermal. Following more recent work (Richter et al. 2006; Danforth et al. 2010), it is acknowledged that non-thermal broadening mechanisms are likely to be present in absorption line samples. Thus, our adopted value of b ≥ 50 km s−1 is more conservative (see also Section 7.4).
Fig. 7 is equivalent to Fig. 6 but for NLA (top panels) and BLA (bottom panels) absorption line samples. The hashed darker grey area in the bottom panels represents the field value obtained by Danforth et al. (2010) for BLAs.
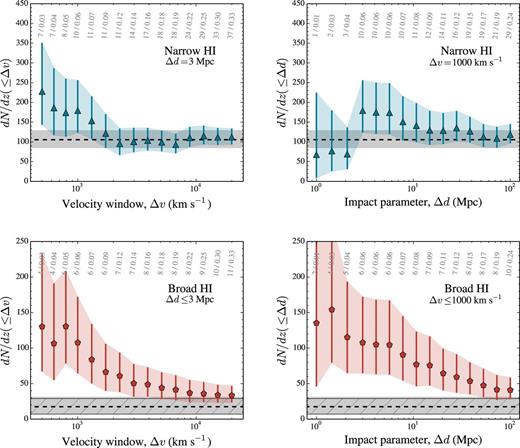
When we fix Δd = 3 Mpc (left-hand panels), we observe a clear overall increase in the redshift number density of both narrow and broad H i absorption lines with decreasing Δv. When we fix Δv = 1000 km s−1 (right-hand panels), we also observe an overall increase down to Δd ∼ 3 Mpc; below this scale a decreasing trend may be present for narrow H i lines, while for broad H i lines the increasing trend persists.
We also note that our estimation of the field expectations are fully consistent with those from previous blind surveys (Danforth & Shull 2008; Danforth et al. 2010).21 This implies that our characterization of absorption lines (see Section 4) and our methodology for estimating the field expectation from our Q1410 data alone (see Section 5.2) are reasonable. Therefore, we can conclude that the vast majority (if not all) of the observed excesses come from scales within Δv = 1000 km s−1 and Δd = 3 Mpc (see Section 7 for further discussion).
6.2 Relative excesses with respect to the field
Fig. 8 shows the relative excesses of redshift number densities of our absorption line samples compared to their respective field expectations, defined as |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$|, as a function of rest-frame velocity window (Δv; left-hand panels) and maximum impact parameter to the closest cluster-pair axis (Δd; right-hand panels), for fixed Δd = 3 Mpc, Δv = 1000 km s−1, respectively. The top panels show the results for our total H i (brown circles, solid line) and O vi (green squares, dashed line) samples, while the bottom panels show the results for our NLA (blue triangles, solid line) and BLA (red pentagons, dashed line) samples. Coloured light shaded areas represent the ±1σ statistical uncertainties.
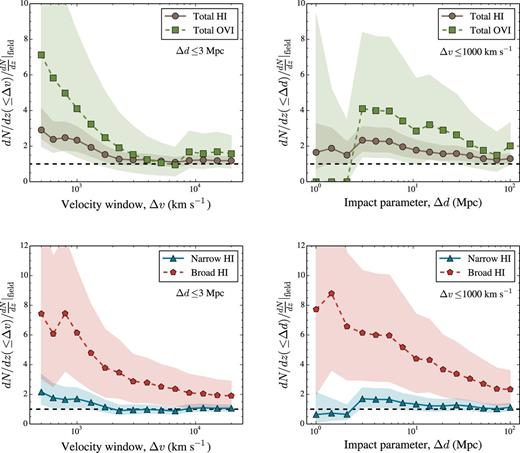
Relative excesses of redshift number densities compared to the field expectation, as a function of rest-frame velocity window (Δv; left-hand panels) and maximum impact parameter to the closest cluster-pair axis (Δd; right-hand panels), for fixed Δd = 3 Mpc and Δv = 1000 km s−1 values respectively. The top panels show those for total H i (brown circles, solid lines) and O vi (green squares, dashed lines) absorption line samples. The bottom panels show those for narrow (NLA; b < 50 km s−1; blue triangles, solid lines) and broad (BLAs; b ≥ 50 km s−1; red pentagons, dashed lines) H i absorption line samples. Coloured light shaded areas represent ±1σ statistical uncertainties. See Section 6.2 for further details.
Although subject to large statistical uncertainties, the relative excess for BLAs tends to be the highest of all, reaching a value of ∼6 times its field expectation at Δd = 3 Mpc and Δv = 1000 km s−1. On the other hand, the excess of NLAs tends to be the smallest of all, reaching a value of only ∼1.5 times its field expectation at the same scales. The relative excess of total H i tends to lie in between that of NLAs and BLAs, but is closer to that of NLAs because these type of absorbers dominate the neutral hydrogen sample. The sample of O vi has the largest statistical uncertainties (it is indeed the smallest sample), which makes its relative excess to be consistent with all others even at the 1σ c.l. Strictly, within ∼2σ c.l. all the reported excesses are consistent with each other across different samples, and are also consistent with their respective field expectations. Therefore, it is important to test these trends with larger data sets.
6.3 Equivalent widths distributions
In Appendix D, we provide a comparison between equivalent widths distributions for our different samples. We did not find statistically significant differences between systems close to cluster pairs and the field expectation in terms of equivalent widths, at least from our limited sample sizes.
7 DISCUSSION
7.1 Filamentary structure
Here, we argue that our results are roughly consistent with a filamentary structure for the absorbing gas close to cluster pairs. This is so because when we restrict the analysis to a fixed Δv = 1000 km s−1, the excess is maximized at impact parameters of Δd ∼ 3 Mpc (or even Δd ≲ 3 Mpc for broad H i), while the typical separation between clusters in our cluster pairs are of the order of ≳ 10–15 Mpc (see sixth and seventh column of Table 3). Moreover, we have also found that when we consider scales far outside our fiducial values, we fully recover the field expectation (see reasoning presented in Section 5.2). From the cumulative results presented in Section 6, we can directly calculate dN/dz in independent intervals instead by subtracting both the reported number of absorption lines and redshift path in a given bin (i.e. Nbin and Δzbin) of a smaller scale, to those at the scale of interest. For instance, if we focus on the total H i sample and consider scales between 3 and 100 Mpc as those of interest, we can estimate dN/dz as |$\frac{{\rm d}N}{{\rm d}z} \sim \frac{(38-16)}{(0.25-0.06)} \sim \frac{22}{0.19} \sim 116 \pm 25$| (see top panel of Fig. 6 and Table G1). This number is fully consistent with the field expectation (e.g. Danforth & Shull 2008), and therefore we conclude the vast majority (if not all) of the observed excesses come from scales within Δv = 1000 km s−1 and Δd = 3 Mpc. However, because we did not impose a minimum distance between the QSO sightline and the closest cluster of a cluster pair, there is also the possibility that our survey geometry does not represent that of a filamentary structure. If those separations are all ≲3 Mpc for instance, our survey could be probing a more spherical (or disc) geometry instead.
Fig. 9 shows a geometrical representation of our survey. We observe that the distances probed by our survey cover scales between Δx ∼ 0–10 Mpc along the intercluster axes, roughly uniformly. Therefore, we conclude that the geometry of our survey is indeed consistent with that of a filamentary structure, but we also stress that a larger sample must be analysed in order to better constrain the geometry.
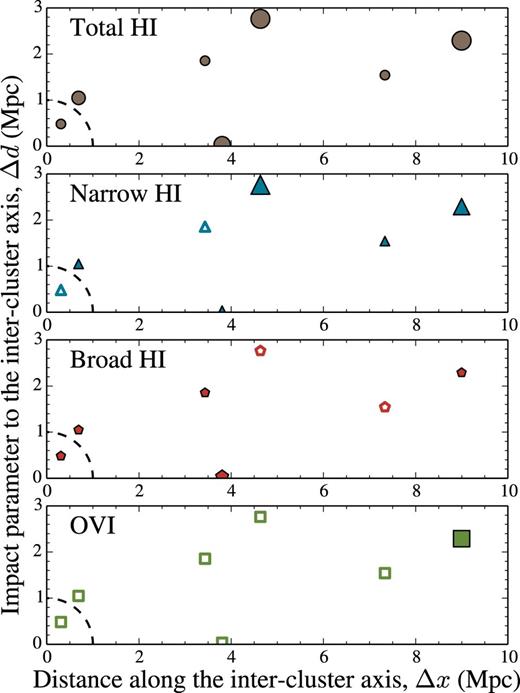
Representation of the position of the Q1410 sightline with respect to different independent cluster pairs in our sample. The y-axes correspond to the impact parameter to a given cluster pair, Δd, while the x-axes correspond to the distance to the closest galaxy cluster in a given cluster pair, along the cluster-pair axis, Δx, (see Fig. 1 for a schematic diagram). The four panels correspond to different absorption line samples, from top to bottom: total H i, narrow H i (NLAs; b < 50 km s−1), broad H i (BLAs; b ≥ 50 km s−1), and total O vi. Filled symbols correspond to portions of the sightline showing absorption lines within Δv = 1000 km s−1 from the redshifts of a given cluster pair, where the sizes of the symbols are proportional to the number of absorption lines. Empty symbols correspond to portions of the sightline showing no absorption. When multiple cluster pairs lie at similar redshifts (i.e. from grouped ones), the absorption lines are associated with the one having the smallest impact parameter value and the rest of the cluster pairs are obviated. We also show the typical virial radii of our sample of clusters with a quarter dashed circumference of radii 1 Mpc centred at the origin. See Section 7.1 for further details.
7.2 Covering fractions of absorbing gas close to cluster pairs
Here we provide a first estimation of the covering fractions, |$f_{\rm c}^{\rm flmnt}$|, of the absorbing gas close to cluster pairs and compare them with the random expectation, |$f_{\rm c}^{\rm rand}$|. Our adopted fiducial Δv = ±1000 km s−1 corresponds to ∼±16 Mpc along the LOS (if cosmological). This is a larger scale compared to our fiducial filament radius of ∼3 Mpc. Therefore, the excesses do not necessarily come from single intercluster filaments. Although our reported dN/dz signals tend to keep increasing at smaller rest-frame velocity differences, the samples also get smaller, which makes the statistical uncertainties larger too (see Figs 6 and 7). By comparing the observed covering fractions to random expectations, we can shed light into the origin of the reported excesses in relation to the cluster pairs themselves.
From Fig. 9, we observe that 7/7 sightlines close to cluster pairs did show at least 1 H i absorber, which implies a covering fraction of |$f_{\rm c}^{\rm flmt}({\rm HI}) \sim 1.00^{+0.00}_{-0.23}$|.22 Similarly, NLAs and BLAs were both found in 5/7 of the sightlines probing them (although different subsamples; see second and third panel of Fig. 9), implying |$f_{\rm c}^{\rm flmt}({\rm NLA}) \approx f_{\rm c}^{\rm flmt}({\rm BLA}) \approx 0.71^{+0.18}_{-0.26}$|. In contrast, O vi absorbers were found in 1/7 of the sightlines probing them, implying a smaller covering fraction of |$f_{\rm c}^{\rm flmt}({\rm OVI}) \approx 0.14^{+0.26}_{-0.12}$|. These results are summarized in Table 5 (upper half) and shown in Fig. 10 (filled symbols), using the same symbol/colour convention as in previous figures.
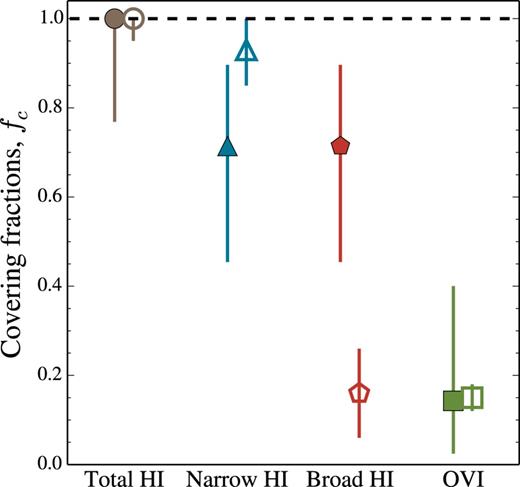
Estimated covering fractions of gas close to cluster pairs (|$f_{\rm c}^{\rm flmnt}$|; filled symbols) and in the random expectation (|$f_{\rm c}^{\rm rand}$|; open symbols), for our different samples of absorption lines using the same symbol/colour convention as in previous figures. We observe that broad H i absorbers (b ≥ 50 km s−1) have about approximately four times a larger covering fraction close to cluster pairs than from the random expectation. See Section 7.2 for further details.
| Sample . | nhits . | ntrials . | |$f_{\rm c}^{\rm flmnt}$| . | |$f_{\rm c}^{\rm rand}$| . | Excess . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| Δv = ±1000 km s−1 and Δd = 3 Mpc | |||||
| H i | 7 | 7 | |$1.00^{+0.00}_{-0.23}$| | |$1.00^{+0.00}_{-0.05}$| | ∼1 |
| NLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.93^{+0.07}_{-0.08}$| | ∼1 |
| BLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.16^{+0.10}_{-0.10}$| | ∼4 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.15^{+0.03}_{-0.03}$| | ∼1 |
| Δv = ±500 km s−1 and Δd = 3 Mpc | |||||
| H i | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.58^{+0.03}_{-0.03}$| | ∼1 |
| NLA | 3 | 7 | |$0.43^{+0.25}_{-0.22}$| | |$0.47^{+0.04}_{-0.04}$| | ∼1 |
| BLA | 4 | 7 | |$0.57^{+0.22}_{-0.25}$| | |$0.08^{+0.05}_{-0.05}$| | ∼7 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.08^{+0.02}_{-0.02}$| | ∼1 |
| Sample . | nhits . | ntrials . | |$f_{\rm c}^{\rm flmnt}$| . | |$f_{\rm c}^{\rm rand}$| . | Excess . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| Δv = ±1000 km s−1 and Δd = 3 Mpc | |||||
| H i | 7 | 7 | |$1.00^{+0.00}_{-0.23}$| | |$1.00^{+0.00}_{-0.05}$| | ∼1 |
| NLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.93^{+0.07}_{-0.08}$| | ∼1 |
| BLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.16^{+0.10}_{-0.10}$| | ∼4 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.15^{+0.03}_{-0.03}$| | ∼1 |
| Δv = ±500 km s−1 and Δd = 3 Mpc | |||||
| H i | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.58^{+0.03}_{-0.03}$| | ∼1 |
| NLA | 3 | 7 | |$0.43^{+0.25}_{-0.22}$| | |$0.47^{+0.04}_{-0.04}$| | ∼1 |
| BLA | 4 | 7 | |$0.57^{+0.22}_{-0.25}$| | |$0.08^{+0.05}_{-0.05}$| | ∼7 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.08^{+0.02}_{-0.02}$| | ∼1 |
Notes. (1) Sample of absorbing gas. (2) Number of ‘hits’ defined as sightlines showing absorption in a given sample, within Δv = {±1000, ±500} km s−1 and within Δd = 3 Mpc. (3) Number of ‘trials’ defined as the total number of sightlines to look for absorption. (4) Covering fraction close to cluster pairs estimated as nhits/ntrials (uncertainties correspond to those of a binomial 1σ c.l.). (5) Covering fraction in a random sightline for a given Δv = {±1000, ±500} km s−1. (6) Excess covering fraction defined as |$f_{{\rm c}}^{\rm flmnt}/f_{{\rm c}}^{\rm rand}$|.
| Sample . | nhits . | ntrials . | |$f_{\rm c}^{\rm flmnt}$| . | |$f_{\rm c}^{\rm rand}$| . | Excess . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| Δv = ±1000 km s−1 and Δd = 3 Mpc | |||||
| H i | 7 | 7 | |$1.00^{+0.00}_{-0.23}$| | |$1.00^{+0.00}_{-0.05}$| | ∼1 |
| NLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.93^{+0.07}_{-0.08}$| | ∼1 |
| BLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.16^{+0.10}_{-0.10}$| | ∼4 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.15^{+0.03}_{-0.03}$| | ∼1 |
| Δv = ±500 km s−1 and Δd = 3 Mpc | |||||
| H i | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.58^{+0.03}_{-0.03}$| | ∼1 |
| NLA | 3 | 7 | |$0.43^{+0.25}_{-0.22}$| | |$0.47^{+0.04}_{-0.04}$| | ∼1 |
| BLA | 4 | 7 | |$0.57^{+0.22}_{-0.25}$| | |$0.08^{+0.05}_{-0.05}$| | ∼7 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.08^{+0.02}_{-0.02}$| | ∼1 |
| Sample . | nhits . | ntrials . | |$f_{\rm c}^{\rm flmnt}$| . | |$f_{\rm c}^{\rm rand}$| . | Excess . |
|---|---|---|---|---|---|
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . |
| Δv = ±1000 km s−1 and Δd = 3 Mpc | |||||
| H i | 7 | 7 | |$1.00^{+0.00}_{-0.23}$| | |$1.00^{+0.00}_{-0.05}$| | ∼1 |
| NLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.93^{+0.07}_{-0.08}$| | ∼1 |
| BLA | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.16^{+0.10}_{-0.10}$| | ∼4 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.15^{+0.03}_{-0.03}$| | ∼1 |
| Δv = ±500 km s−1 and Δd = 3 Mpc | |||||
| H i | 5 | 7 | |$0.71^{+0.18}_{-0.26}$| | |$0.58^{+0.03}_{-0.03}$| | ∼1 |
| NLA | 3 | 7 | |$0.43^{+0.25}_{-0.22}$| | |$0.47^{+0.04}_{-0.04}$| | ∼1 |
| BLA | 4 | 7 | |$0.57^{+0.22}_{-0.25}$| | |$0.08^{+0.05}_{-0.05}$| | ∼7 |
| O vi | 1 | 7 | |$0.14^{+0.26}_{-0.12}$| | |$0.08^{+0.02}_{-0.02}$| | ∼1 |
Notes. (1) Sample of absorbing gas. (2) Number of ‘hits’ defined as sightlines showing absorption in a given sample, within Δv = {±1000, ±500} km s−1 and within Δd = 3 Mpc. (3) Number of ‘trials’ defined as the total number of sightlines to look for absorption. (4) Covering fraction close to cluster pairs estimated as nhits/ntrials (uncertainties correspond to those of a binomial 1σ c.l.). (5) Covering fraction in a random sightline for a given Δv = {±1000, ±500} km s−1. (6) Excess covering fraction defined as |$f_{{\rm c}}^{\rm flmnt}/f_{{\rm c}}^{\rm rand}$|.
7.3 Could the observed excesses of gas be due to galaxy clusters/groups or individual galaxy haloes?
Regarding massive structures, we can see from Fig. 9 that the vast majority of sightlines are probing regions far away from the virial radii of known galaxy clusters (see also the left-hand panels of Fig. F1). However, because of the limited completeness level of the redMaPPer catalogue, there could still be unknown clusters or groups in such regions. In order to directly address this question, one must survey the Q1410 field for individual galaxies and LSS close to the Q1410 LOS, which we leave for future work (see Section 7.6). Still, in the following we provide an assessment of the plausible incidence of gas associated with individual haloes from two indirect but independent arguments.
7.3.1 Redshift number density of galaxies
Based on the reasoning presented by Prochaska et al. (2011), one can estimate the redshift number density of galaxies of luminosity L ≥ Lmin, dN/dz|gals, intersecting a given LOS by assuming a given cross-section for them. For galaxies with L ≥ 0.01–0.001L* and assuming cross-sections given by the virial radius of galaxies with unity covering fractions,24 Prochaska et al. (2011) find that dN/dz|gals ≈ 10–20 (see their fig. 8). This estimate is valid for the field and so we need to correct for the fact that cluster pairs generally probe LSS overdensities. We use the excess of narrow H i lines to estimate the overall overdensity in our cluster-pair sample, as ∼1–2 times the mean density of the Universe (note that these values are consistent with the expected overdensities traced by cluster pairs from cosmological simulations). Therefore, we estimate |${\rm d}N/{\rm d}z|^{\rm flmnt}_{\rm gals} \approx 10\hbox{--}40$|. This number is lower than the typical dN/dz ∼ 60–300 observed for our samples of H i (either narrow or broad), but is comparable to the dN/dz ∼ 30–100 observed for O vi. Therefore, it seems unlikely that most of the excess observed for narrow and broad H i gas close to cluster pairs is driven by galaxy haloes of individual galaxies. On the other hand, our reported excess of O vi gas might well be produced (at least partly) by individual galaxy haloes (see also below).
7.3.2 Metal absorption lines
One can also infer the presence of galaxy halo material by means of metal absorption lines, in particular from low-ionization species (e.g. Werk et al. 2014). There is only one absorption system in our cluster-pair sample showing metal absorption lines: the one at z ≈ 0.35 from which all the three observed O vi components come from (see the fourth panel in Fig. F1). This system has strong H i absorption with column densities N > 1014 cm−2 and shows a complex kinematic structure (four components in total, three narrow and one broad). The second narrow component also shows the presence of C ii, Si iii and N iii (see Table 4). Therefore, although it seems very likely that an important fraction of the absorbing gas in this system comes from an individual galaxy halo or its immediate surroundings, this system only accounts for 3/10 ∼ 30 per cent of NLAs and 1/6 ∼ 16 per cent of BLAs in our sample. Again, from this independent reasoning we reached the same conclusion as before, i.e. individual galaxy haloes could account for the observed excess in O vi lines (although not a requirement), but not for the majority of H i gas.
7.4 Statistical evidence of the WHIM
Here, we consider whether the observed trends could also be consistent with the presence of a WHIM. Ideally, one would require a full characterization of the physical conditions of individual absorbers using multiple species and comparing them with the expectations of different models of ionization. However, because our sample is dominated by absorption systems having no other species than H i, this approach is not feasible. Even when other species are present in individual systems (e.g. H i and O vi) this approach requires the uncertain assumption that the majority of the gas comes from a single phase, which is controversial at the very least (e.g. Werk et al., in preparation). In view of this intrinsic limitation for an individual characterization, here we opted for a purely statistical approach.
The WHIM is usually defined as gas at temperatures in the range of T ∼ 105–107 K, implying a minimum Doppler parameter of b = 40 km s−1 for H i (i.e. assuming the broadening is purely thermal). Therefore, H i lines with b < 40 km s−1 cannot be caused by a WHIM. Non-thermal processes can also broaden absorption line profiles, including turbulence, Hubble broadening and unresolved blends (e.g. Garzilli, Theuns & Schaye 2015, and references therein). In overdense environments, we expect turbulence to be the dominant source of non-thermal physical broadening (but see Section 7.5 for a discussion regarding unresolved blends). Assuming that the turbulence contribution is higher for hotter gas, we should have bturb ≈ αbT, and hydrodynamical simulations suggest 0 ≤ α ≤ 1 (e.g. Tepper-García et al. 2012). Assuming the most extreme case of α = 1, we have that the observed Doppler parameter would be |$b = \sqrt{2} b_{\rm T}$|, making a limit |$b > 40 \sqrt{2}\approx 57$| km s−1 extremely conservative in ensuring to trace H i gas at T > 105 K. However, there could still be genuine WHIM H i absorption lines in the |$40 < b_{\rm lim}<40 \sqrt{2}$| km s−1 range (i.e. when thermal broadening does dominate).
In this paper, we used a limiting Doppler parameter value of blim = 50 km s−1 instead, which is in between |$40<b_{\rm lim} < 40 \sqrt{2}$| km s−1. This limit was partly chosen for allowing a direct comparison to previous published work (e.g. Danforth et al. 2010), but also because it minimizes potential misidentification of lines that are supposed to trace warm–hot gas but trace cool gas instead, and viceversa (i.e. genuine warm–hot absorbers having b < blim, and genuine cool absorbers having b ≥ blim).25 Indeed, using blim = 50 km s−1, there is only 1 (1) line in the range 40 < b < 50 km s−1 (|$50 < b < 40\sqrt{2}$| km s−1) in our NLA (BLA) sample associated with cluster pairs (e.g. see points with white stars in Fig. 4). A limit of blim = 50 km s−1 also corresponds to a α = 0.75, and therefore is still quite conservative in ensuring that BLAs trace gas at T ≥ 105 K, even with a substantial turbulence contribution. Regardless of these considerations, we also note that about half of the BLAs associated with cluster pairs in our sample are actually very broad, with Doppler parameters b ∼ 80–150 km s−1 (e.g. see Fig. 4), which should make them more likely to trace gas at WHIM temperatures (but see Section 7.5).
One of our proposed diagnostics is to compare the excesses in the incidence of narrow and broad H i absorbers (and eventually O vi when larger samples are gathered) found close to cluster pairs with respect to their field expectations (see Fig. 8). Because intercluster filaments correspond to overdense regions in the Universe, an excess of gas is generally expected to occur, and indeed we have shown that this is the case (see Section 6). Under the null hypothesis that BLAs and NLAs probe gas in similar physical conditions (i.e. similar physical entities), then we expect both these excesses to behave in a consistent manner. On the other hand, if BLAs and NLAs are not probing similar physical conditions, a different behaviour for the excesses is expected instead. A WHIM signature associated with intercluster filaments may include the relative excess of BLAs to be higher than that of NLAs, which is exactly what we observed (although only at the ∼1σ c.l.; see Fig. 8, bottom panels). By increasing the sample sizes we may test for any statistically significant difference between them.
Another proposed diagnostic is to constrain the overall geometry for the excess of gas, in terms of both BLAs and NLAs (and O vi when larger samples are gathered). A WHIM signature in this context would require an increase in the covering fractions of BLAs towards the intercluster axes compared to the random expectations, which is also what we have observed (again, only at the ∼2σ c.l.; see Section 7.2). Moreover, one can also look for trends in the Doppler parameters of H i absorption lines with respect to impact parameter to the intercluster axes, as a proxy of temperature. Assuming simple models for the ionization of the gas (e.g. purely collisional), one can even use the inferred temperatures to estimate a total hydrogen column density from the observed H i one. A WHIM signature should produce, on average, higher hydrogen column densities for higher temperatures.
Although all our tentative results (∼1–2σ c.l.) may be consistent with the presence of a WHIM in intercluster filaments, we emphasize that a larger sample must be analysed before reaching a definite conclusion.
7.5 Caveat
Probably the most important source of concern in our experimental design, is our limited ability to disentangle blends, which is key to detect broad and shallow absorption features expected to arise in the WHIM. The importance of this systematic uncertainty depends on the S/N, as the higher the S/N, the easier it is to assess the kinematic structure of the absorption feature (e.g. Richter et al. 2006; Danforth et al. 2010). We emphasize that this is an intrinsic limitation of the absorption-line technique, meaning that all these kind of observational samples are, to some extent, affected by this issue. As described in Section 4, we attempted to avoid this bias by fitting asymmetric lines with at least two components. Although not impossible, we believe that the likelihood of having misidentified multiple narrower blended components as a single broader and symmetric one in a large fraction of our H i sample is low (see Fig. F1 for individual examples close to cluster pairs). Given that we are comparing the relative incidences of lines between different samples drawn from spectra of similar S/N (see Section 6), our statistical approach seems adequate for minimizing this potential source of uncertainty (as opposed to attempting a full physical characterization of individual systems).
7.6 Future prospects
Despite our promising results, the existence of the WHIM in intercluster filaments still needs to be observationally confirmed; our pilot survey was not design to draw statistically significant results, but primarily to show that such a goal is currently possible with existing instrumentation. In this section, we enumerate remaining work for providing a firm detection of the elusive WHIM in the context of our methodology.
7.6.1 Increase the sample sizes
Increasing the sample sizes is a key requirement. In this respect, we are actively working on two fronts: (i) pursuing new HST/COS observations of targeted QSO sightlines intersecting multiple cluster pairs; and (ii) searching in the HST archive for already observed QSOs whose sightline intersects single or multiple cluster pairs. We estimate that the HST/COS archive will allow us to extend this work to tens of sightlines, but approach (i) will still be necessary for efficient follow up observations (e.g. galaxy surveys; see Section 7.6.2).
7.6.2 Survey for galaxies around the QSO sightline
As discussed in Section 7.3, we need to survey galaxies around our QSO sightline in order to directly rule out the potential association of BLAs with the haloes of individual galaxies. To this end, spectroscopic redshifts are needed (current galaxy photometric redshift uncertainties are too large for meaningful associations with absorption lines). We are currently pursuing multi-object spectroscopy (MOS) and integral field units (IFU) observations around the Q1410 field. We will use MOS surveys to assess the distribution of galaxies over 0.3–10 Mpc scales. This will be important not only for determining whether galaxy groups or clusters are responsible of our observed excesses of absorbing gas, but also to determine the actual geometry of the LSSs intersected by the Q1410 sightline, including: (i) assess whether these putative intercluster filaments are straight or bent; and (ii) refine the cosmological redshift of the structures at the position of the Q1410 sightline. The IFU observations will primarily focus on mapping galaxies on scales within ≲100–300 kpc to the QSO sightline (the typical CGM scales) at a very high completeness level, including faint star-forming galaxies with no detectable continuum but having bright enough emission lines.
7.6.3 Comparison to hydrodynamical simulations
Another key aspect of this project, is the comparison of our observational results to those obtained from cosmological simulations. Our experimental design offers a unique opportunity to test the prediction of the ΛCDM paradigm in the largest and densest filaments of the cosmic web, while also constraining current galaxy evolution models. As we have shown, H i dominates the gaseous content found in intercluster filaments (see Section 6), and is very likely that they originate far away from individual galaxy haloes (see Section 7.3). This makes a direct comparison to simulations straightforward because we expect this gas to be unaffected by the uncertain baryonic processes occurring in galaxies (e.g. SNe/AGN feedback). On the other hand, the subsample of absorption systems showing metal absorption (e.g. those with O vi) can put constraints on these uncertain ‘sub-grid physic’ models for galaxy formation. However, the need for a full treatment of shocks in the gas limits the approach to being hydrodynamical. If the predictions of WHIM signatures in intercluster filaments match our observational results, they will provide yet another piece of evidence supporting the existence of this elusive medium.
8 SUMMARY
The warm–hot intergalactic medium (WHIM) has been predicted to account for a significant fraction of the baryons at low z, but its actual existence has eluded a firm observational confirmation. In this paper, we have presented a novel approach for detecting the WHIM, by targeting regions of the cosmic web where its presence is predicted to be ubiquitous: the putative filaments connecting galaxy clusters. As a proof of concept, we selected a single bright QSO (namely Q1410), whose exceptional sightline passes within Δd = 3 Mpc from the seven intercluster axes connecting seven independent cluster pairs at redshifts 0.1 ≤ z ≤ 0.5, and observed it with HST/COS. We performed a full characterization of absorption features in the FUV spectrum of Q1410, independently of the presence of known LSS traced by the galaxy cluster pairs. From this data set, we conducted a survey of diffuse gas along the QSO sightline with special focus on H i and O vi absorption lines. This survey allowed us to provide, for the first time, a systematic and statistical measurement of the incidence, dN/dz, of intervening H i and O vi absorption lines close to cluster pairs. We split the sample of H i Ly α into broad (BLA) and narrow (NLA) using a Doppler parameter limit of blim = 50 km s−1, which ensures BLAs to be mostly from gas at temperatures T ≥ 105 K, even when accounting for turbulence. We quantified the incidence of H i, NLAs, BLAs and O vi absorption lines close to cluster pairs by varying the minimum rest-frame velocity window, Δv, and the minimum impact parameter to the intercluster axes, Δd, and found that the incidence of diffuse gas is maximized at Δv ≲ 1000 km s−1 and Δd ≲ 3 Mpc. At these scales we report:
|${\rm d}N/{\rm d}z({\rm HI})|_{\rm flmnt} = 287^{+91}_{-71}$|, which corresponds to |$2.3^{+0.8}_{-0.6}$| times the field expectation;
|${\rm d}N/{\rm d}z({\rm NLA})|_{\rm flmnt} = 179^{+77}_{-56}$| which corresponds to |$1.7^{+0.7}_{-0.6}$| times the field expectation;
|${\rm d}N/{\rm d}z({\rm BLA})|_{\rm flmnt} = 108^{+65}_{-43}$| which corresponds to |$6.1^{+4.2}_{-3.2}$| times the field expectation; and,
|${\rm d}N/{\rm d}z({\rm OVI})|_{\rm flmnt} = 58^{+57}_{-32}$| which corresponds to |$4.1^{+4.3}_{-2.7}$| times the field expectation.
Although individually these excesses are only at the ∼1–2σ c.l., in concert they suggest a physical overdensity close to cluster pairs. Our results are also roughly consistent with a filamentary geometry for the absorbing gas connecting cluster pairs, with covering fractions of: |$f_{\rm c}({\rm HI})|_{\rm flmnt} = 1.0^{+0.0}_{-0.2}$|; |$f_{\rm c}({\rm NLA})|_{\rm flmnt} = 0.7^{+0.2}_{-0.3}$|; |$f_{\rm c}({\rm BLA})|_{\rm flmnt} = 0.7^{+0.2}_{-0.3}$|; and |$f_{\rm c}({\rm OVI})|_{\rm flmnt} = 0.14^{+0.3}_{-0.1}$|. Our reported covering fractions of total H i, NLAs and O vi are all consistent with their random expectations. In contrast, the reported covering fraction of BLAs is a factor of ∼4 larger than the random expectation. Because a rest-frame velocity window of Δv ≈ ±1000 km s−1 corresponds to a rather large comoving distance along the LOS (i.e ∼± 16 Mpc), having consistency with the random expectation is not surprising, and suggests that most of the excesses of NLAs and O vi absorption come from the overall LSS overdensities around massive structures traced by galaxy cluster pairs. On the other hand, a higher covering fraction of BLAs close to cluster pairs compared to the random expectation, suggests that the excess of BLAs is physically associated with the cluster pairs themselves. Indeed, we also reported covering fractions using a Δv ≈ ±500 km s−1 and reached the same conclusion.
Based on statistical arguments, we also concluded that most of the reported excesses of NLAs and BLAs cannot be attributed to individual galaxy haloes but rather to truly intergalactic material. In contrast, the reported excess of O vi most likely comes from gas associated with individual galaxy haloes or their immediate surroundings.
We argued that a behaviour in which BLAs show larger relative excesses compared to that of NLAs (as tentatively reported here), may be a direct signature of the WHIM, especially if identified in the regions close to cluster pairs. With a larger sample of QSOs and a careful accounting of systematic effects, the technique we have presented here should therefore enable a firm detection of the WHIM in intercluster filaments.
We thank the anonymous referee for their constructive criticism that improved the paper. We thank E. Rozo and E. Rykoff for providing us with the extended version of their redMaPPer catalogue used in this work. We thank Ryan Cooke, Kathy Cooksey, Joe Hennawi, Akio Inoue, John O'Meara, Philipp Richter, John Stocke and Todd Tripp for helpful discussions. NT acknowledges support from the IMPS Fellowship26 that allowed him to conduct independent research in the areas of intergalactic or interstellar media at University of California, Santa Cruz. NT is partially funded by NASA grant HST-GO-134491.008-A and JXP is partially funded by NSF AST-1412981.
We thank contributors to scipy27, matplotlib28, astropy29, the python programming language30, and the free and open-source community.
This work was mainly based on observations made with the NASA/ESA Hubble Space Telescope under programme GO 12958, obtained at the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS 5-26555.
This research has made use of: the NASA/IPAC Extragalactic Database (NED)31, the NASA's Astrophysics Data System (ADS)32, and data products from the SDSS, SDSS-II33 and SDSS-III34.
See also Jauzac et al. (2012) for a weak lensing signal of a filament connecting to a single galaxy cluster.
We note that X-ray spectroscopy could also be used to trace the WHIM in absorption, mostly through O vii absorption lines (e.g. Nicastro et al. 2005; Fang et al. 2010; Nicastro et al. 2010; Zappacosta et al. 2010). However, the poor sensitivities of current X-ray spectrographs considerably limits the sample sizes for these studies. Furthermore, such poor sensitivities and poor spectral resolutions make the interpretation of signals particularly challenging (e.g. Yao et al. 2012).
We note that even in individual cases where such absorption does coincide with known structures traced by galaxies, it is still unclear whether the gas is actually produced by a WHIM or individual galaxy haloes (e.g. Stocke et al. 2006; Prochaska et al. 2011; Tumlinson et al. 2011; Williams, Mulchaey & Kollmeier 2013).
Kindly provided by E. Rykoff and E. Rozo (private communication).
We note that the typical photometric redshift uncertainties for the redMaPPer clusters are of the order of δz ∼ 0.006.
We believe that biasing against LLS is unimportant for this study.
i.e, including intrinsic broad emission lines and the Galaxy's damped Ly α system wings.
Although a photometric uncertainty of δz = 0.05 corresponds to a very large δv ≈ 15 000/(1 + z) km s−1, we note that in most of our cluster-pair sample both clusters have spectroscopic redshifts (see Table 3).
In this paper, a ‘component’ is defined as an individual absorption line in a given ion; and a ‘system’ is defined as the union of components lying within a given velocity window (usually arbitrary) from a given redshift.
Note that this condition allow us to identify strong H i components at redshifts greater than z > 0.477 by means of higher order Lyman series transitions.
No low-ionization transition was found without having associated H i, so this step was redundant.
Our final reduced χ2 have in average (and median) values of 1.1. See also residuals in Fig. E1.
We note that Danforth et al. (2010) reached a similar conclusion although using the commonly adopted formalism based on a minimum equivalent width threshold for unresolved lines.
In our analysis, we will also impose the line to be detected at Wr/δWr ≥ 3 (see Section 6), but this is not a requirement of the methodology.
This redshift range condition is not a requirement of the methodology in the most general case.
We note that a consistent correction factor of Nfield = Ntot − (0.85 ± 0.2) Ncpairs is found when considering the total number of cluster pairs instead of independent ones, i.e. |$n_{\rm cpair}^{\rm Q1410}=11$| and |$n_{\rm cpair}^{\rm field}=1.6 \pm 2.2$|.
But note that with this limited sample, we cannot rule out that a real decreasing signal is present either.
Note that in the case of BLAs, both field values have similar uncertainty. This is because Danforth et al. (2010) included a systematic contribution to the error, whereas ours is purely statistical.
The uncertainty is estimated assuming a binomial distribution for the number of ‘hits’ given the 7 independent ‘trials’, using the Bayesian formalism described by Cameron (2011) with a flat prior.
For |$f_{\rm c}^{\rm flmt}$| obtained from non-independent structures (e.g. a single well-mapped filament), a meaningful estimation of |$f_{\rm c}^{\rm rand}$| must take clustering into account. At first order, there will be two opposing effects (when clustering is positive): clustering along the LOS will tend to decrease |$f_{\rm c}^{\rm rand}$|, while the clustering transverse to the LOS will tend to increase it. Moreover, higher order correlations must also be considered to account for the joint probability of having multiple ‘hits’ in such large single non-independent volume.
This is not the same as choosing the limit that maximizes the difference between observed incidences though (which we did not try).
http://www.astropy.org (Astropy Collaboration et al. 2013)
We note that the expected number of clusters per random sightline is ∼32 (see Section 3.4), and so 162 144/32 ≈ 5000 should cover a significant fraction of the cluster catalogue in our chosen redMaPPer subvolumes.
Based partly on observations made with the NASA/ESA Hubble Space Telescope under program GO 12958.
REFERENCES
APPENDIX A: PROPERTIES OF CLUSTERS CLOSE TO Q1410 COMPARED TO A CONTROL SAMPLE
In this section, we investigate whether our subsample of clusters close to the Q1410 sightline is a fair representation of the cluster population in the whole redMaPPer catalogue. To do so, we will compare the mass (estimated from equation 1) and redshift distributions of our sample to appropriate control samples drawn from the redMaPPer catalogue.
The left-hand panel of Fig. A1 shows the mass distribution for our subsample of 57 clusters within 20 Mpc of Q1410, having richness values >10 and lying between 0.1 ≤ z ≤ 0.5 (thick black line), and the normalized mass distribution from a control sample satisfying only the richness and redshift range criteria (162 144 clusters in total; thin red line). We see no apparent difference between these two distributions, and no statistically significant differences are detected either: the K–S test over the full unbinned samples gives a ≈60 per cent probability of both being drawn from the same parent distribution.
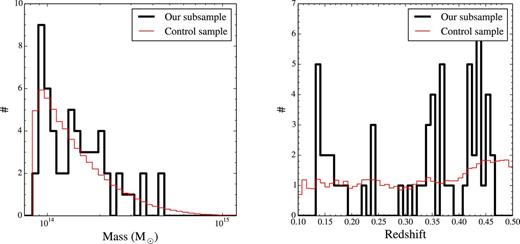
Comparison between mass (left-hand panel) and redshift (right-hand panel) distributions between our subsample of 57 redMaPPer clusters within 20 Mpc from the Q1410 sightline, having richness values ≥10 and lying between 0.1 ≤ z ≤ 0.5 (thick black line), and normalized control samples satisfying only the richness and redshift range criteria (thin red line; see Section A for details). A K–S test to the unbinned distributions give no statistically significant differences between the samples.
In the case of the redshift distribution, we cannot directly compare that of the 162 144 clusters satisfying only the richness and redshift range criteria, to our subsample. This is so because our subsample of clusters are defined by a cylinder (i.e. constant volume as a function of redshift), rather than fixed solid angle (increasing volume as a function of redshift). In order to provide an appropriate control sample, we looked at the redshift distribution of redMaPPer clusters having richness values >10 and lying between 0.1 ≤ z ≤ 0.5, in 5000 cylinders of radius 20 Mpc, selected at random positions between R.A. ∈ [140, 222]° and Dec. ∈ [4, 56]° (i.e. well within the SDSS footprint).35 The right-hand panel of Fig. A1 shows the redshift distribution for our subsample of 57 clusters (thick black line), and the normalized redshift distribution from our aforementioned control sample (thin red line). Again, no statistically significant difference is detected: the K–S test over the full unbinned samples gives a ≈20 per cent probability of both being drawn from the same parent distribution.
From these comparisons, we conclude that no strong bias is present in our subsample of clusters close to the Q1410 sightline.
APPENDIX B: COMPARISON BETWEEN ABSORPTION LINE SIGNIFICANCE ESTIMATION METHODS
Here, we compare two methods for estimating the significance level of absorption features, namely our Wr/δWr criterion (see Sec-tion 4.3) and 〈S/N〉res × N/b proposed by Richter et al. (2006) for broad H i absorption systems. The motivation for the later being that what matters to confidently detect a broad absorption line is both S/N and the optical depth at the line centres, τ0 ∝ N/b, and so it will not be appropriate to use the commonly adopted formalism based on a minimum equivalent width threshold for unresolved lines.
Fig. B1 shows a comparison between these two quantities 〈S/N〉res × N/b in the x-axis and Wr/δWr in the y-axis), for our sample of H i absorption lines. Blue triangles correspond to H i absorption components with b < 50 km s−1 (narrow), while red pentagons correspond to H i absorption components with b ≥ 50 km s−1 (broad) over the full Q1410 spectrum. White crosses mark components having multiple transitions, which we always account as reliable (label ‘a’; see Section 4.5). The grey shaded area corresponds to values Wr/δWr < 3.
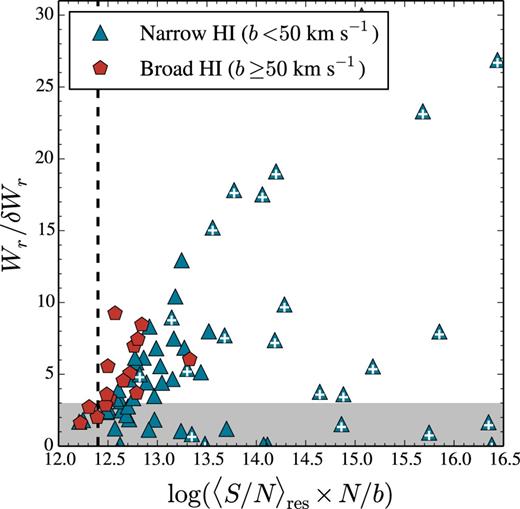
Comparison between two different methods for estimating the significance level of absorption line features. The x-axis corresponds to the log (〈S/N〉res × N/b) values proposed by Richter et al. (2006) (at least for broad H i lines) where N is in units of cm−2 and b in km s−1, while the y-axis corresponds to our Wr/δWr (see Section 4.3). Blue triangles correspond to narrow H i absorption components (b < 50 km s−1), while red pentagons correspond to broad H i absorption components (b ≥ 50 km s−1), both found across the full Q1410 spectrum. White crosses mark components having multiple transitions, hence reliable (label ‘a’; see Section 4.5). The grey shaded area correspond to values Wr/δWr < 3, while the vertical dashed line correspond to a value of 〈S/N〉res × N/b = 2.5 × 1012 cm−2 (km s−1)−1. See Appendix B for further details.
Restricting ourselves to broad H i lines (red pentagons in Fig. B1), we see a clear correlation between these two criteria. The dashed vertical line in Fig. B1 corresponds to a value of 〈S/N〉res × N/b ≥ 2.5 × 1012 cm−2 (km s−1)−1 for our COS data, which is needed to make both approaches roughly consistent with each other for broad H i lines. Such a value is similar to the one reported by Richter et al. (2006), 〈S/N〉res × N/b ≥ 3 × 1012 cm−2 (km s−1)−1 in their STIS data.
For narrow H i lines (blue triangles in Fig. B1) however, no clear correlation is present between these two methods, where several components having Wr/δWr < 3, can still have large values of 〈S/N〉res × N/b. We note that many of the large 〈S/N〉res × N/b components are reliable (white crosses in Fig. B1), but many others at the lower end are not. In terms of Wr/δWr, we see that some reliable lines fall below the limit of Wr/δWr < 3. This is due to the fact that our adopted conservative method for estimating Wr (see Section 4.3) will give unrealistically large uncertainties, δWr, for unconstrained or saturated components. Indeed the vast majority of reliable components with Wr/δWr < 3 are saturated lines for which the column densities are not well determined.
Our proposed significance estimation based on Wr/δWr (and the presence of multiple transitions in a given component; see Section 4.5) can be straightforwardly applicable to any absorption line irrespective of its Doppler parameter and ionic transition. Therefore it has the advantage of allowing an homogeneous analysis.
APPENDIX C: ESTIMATION OF REDSHIFT PATHS AND ABSORPTION DISTANCES
APPENDIX D: EQUIVALENT WIDTHS DISTRIBUTIONS
In this section, we explore how do the equivalent widths distributions from our sample of lines associated with cluster pairs (i.e. adopting our fiducial values of Δd = 3 Mpc and Δv = 1000 km s−1), compare to those of the field expectation.
Fig. D1 shows the redshift number density, dN/dz, of our different samples of absorption lines as a function of minimum rest-frame equivalent width, |$W_{\rm r}^{\rm min}$|, associated with our cluster pairs: total H i (top-left panel; brown circles), O vi (top-right panel; green squares), narrow H i (bottom-left panel; blue triangles) and broad H i (bottom-right panel; red pentagons). The field distributions estimated from our Q1410 sightline are represented by the dashed line with its ±1σ uncertainty represented by the darker grey region. Such field estimation comes from lines not being in the sample associated with cluster pairs, and its redshift path is estimated by excluding that of cluster pairs too.
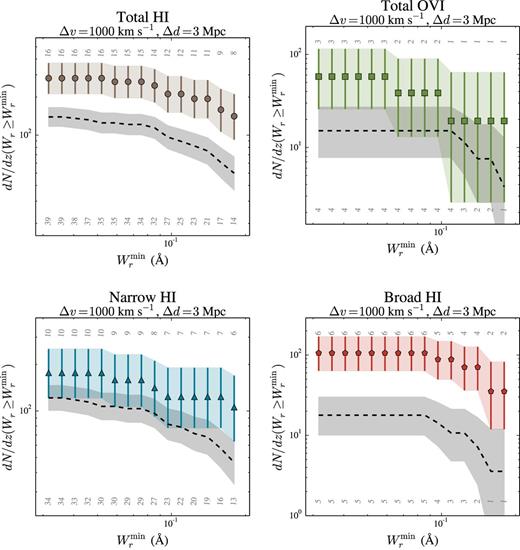
Redshift number density of our different samples of absorption lines associated with our cluster pairs (i.e. using our fiducial values of Δd = 3 Mpc and Δv = 1000 km s−1), as a function of minimum rest-frame equivalent width |$W_{\rm r}^{\rm min}$|. The top panels show the results for our total H i (left-hand panel) and O vi (right-hand panel), while the bottom panels show the results for narrow (NLA; b < 50 km s−1) and broad (BLA; b ≥ 50 km s−1) H i, using the same colour/symbol convention as in Figs 6–10. Note that bins are not independent from each other, as emphasized by the light coloured areas. The field distributions estimated from our Q1410 sightline are represented by the dashed line with its ±1σ uncertainty represented by the darker grey region. The total number of lines per bin are given in grey numbers on top and bottom of each panel, for our cluster pairs and field samples respectively. See Section D for further details.
We observe that the equivalent widths distributions are not remarkably different between lines associated with cluster pairs and the field expectation, and hence the relative excess in dN/dz seems to remain somewhat constant as a function of |$W_{\rm r}^{\rm min}$|. The K–S test for the unbinned Wr distributions between our cluster pair and field samples give no statistically significant differences between them, but we note any possible real difference would be hard to detect because the samples are quite small (≲10).
We conclude that, in terms of equivalent widths, our cluster-pair absorption line samples and the field expectations are not significantly different, at least from what can be obtained in our limited sample.
APPENDIX E: Q1410 HST/COS spectrum
Fig. E1 shows the reduced Q1410 spectrum (black line), its corresponding uncertainty (green lines) and our adopted pseudo-continuum fit (blue dotted line). The figure also shows our Voigt profile fit solutions and residuals (red lines and grey dots respectively; see Section 4.2), and their corresponding IDs and reliability labels (see Section 4.5 and Table 4).
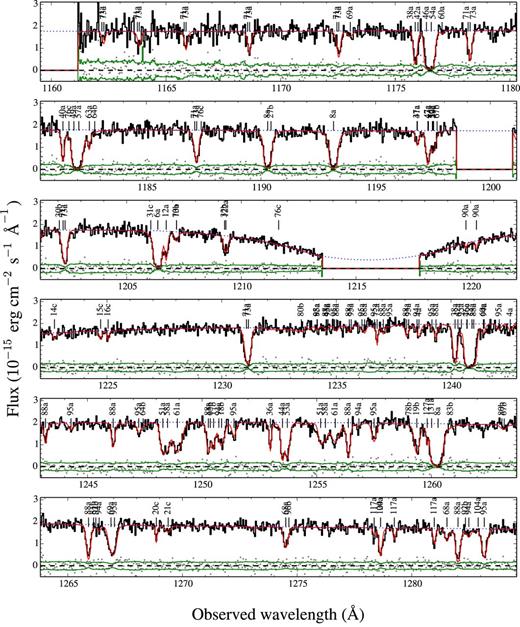
Observed HST/COS FUV spectrum of QSO Q1410 (black line), and its respective uncertainty (green lines). The red line correspond to our fit of the spectrum (see Section 4.2), while the blue dotted line corresponds to the assumed unabsorbed pseudo-continuum (i.e. including broad emission lines and the Milky Way's DLA; see Section 2.2). Vertical tick lines indicate individual absorption lines, where the numbers correspond to the IDs given in Table 4 and the letters indicate their reliability (see Section 4.5). Grey points show the difference between our model and the observed data. We see that distribution of these residuals are consistent with the uncertainty of the data.
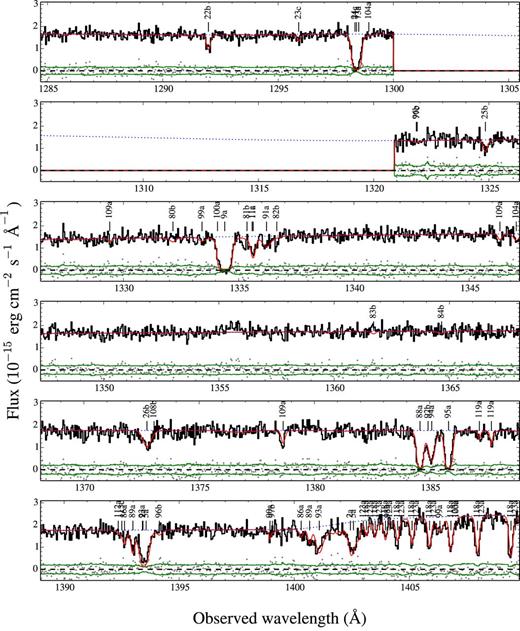
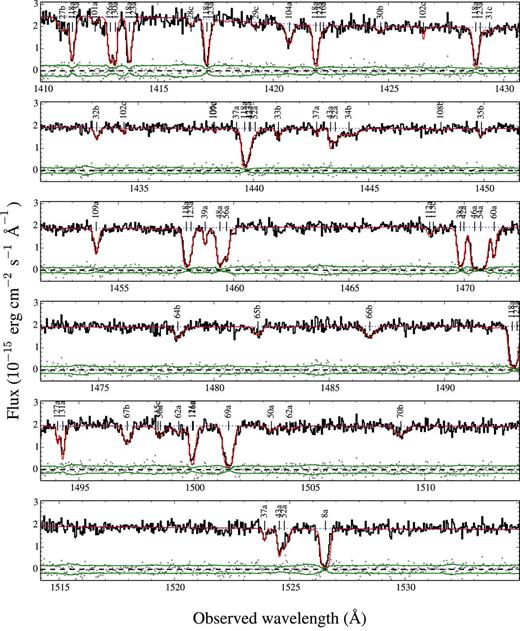
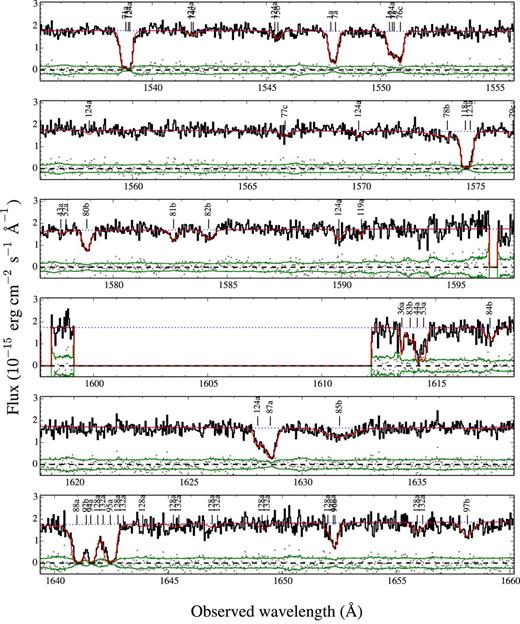
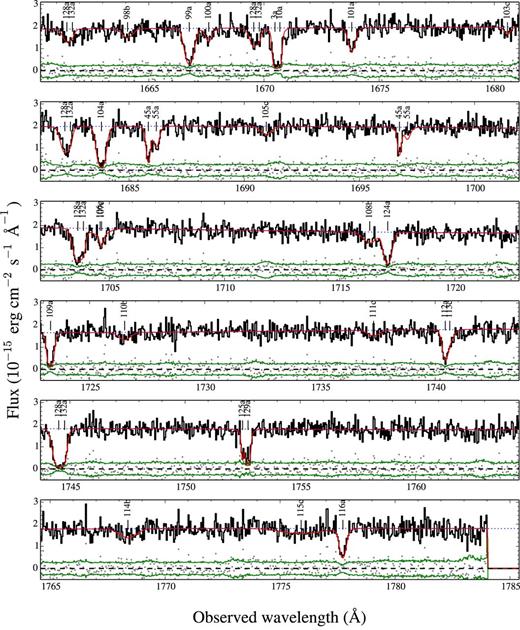
APPENDIX F: VISUAL ASSOCIATION OF ABSORPTION LINE SYSTEMS WITH cluster pairS
Fig. F1 shows an schematic view of the association between H i and O vi absorption line systems and our known cluster pairs obtained from the redMaPPer catalogue (see Section 3). These plots are for illustrative purposes only; in cases with multiple grouped cluster pairs (see Section 3.3) the chosen redshifts for defining rest frames are arbitrary, but such choice is not used in our scientific analyses.

Schematic view of the clusters and cluster pairs around the Q1410 sightline at different given redshifts (see top label in subpanels). The left-hand panels correspond to the projected in the sky distribution of clusters (circles) and cluster pairs (dashed lines) around the Q1410 sightline (yellow star) in comoving Mpc. Numbers close to the circles correspond to the cluster IDs as given in Table 2. The colour of the circles correspond to the rest-frame velocity difference of each cluster with respect to the given redshift, according to the colour bar scale on the right of the panel. The right-hand panels correspond to portions of the normalized Q1410 HST/COS spectrum within a rest-frame velocity window of ±1000 km s−1 from the given redshift, for the H i Ly α transition (top) and the O vi λλ1032, 1038 Å transitions (middle and bottom, respectively). The spectrum itself is represented by the black lines and the uncertainty is represented by the green line. Our fits to associated absorption line systems are represented by the thick coloured lines according to the colour bar scale on the left of the panel, while the fits for unassociated absorption line systems (i.e. at different redshifts) are represented by the red lines. Absorption line ID and reliability flags are given for associated absorption line systems.
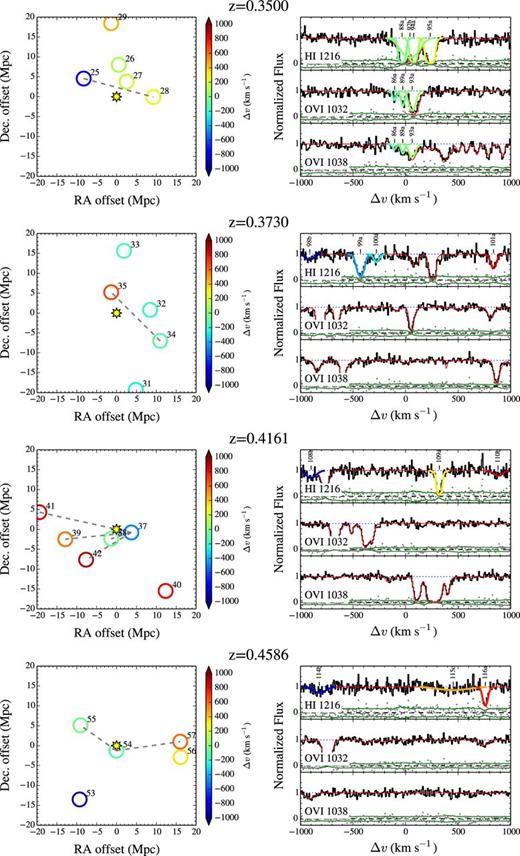
APPENDIX G: SUMMARY TABLES FOR OUR INCIDENCE MEASUREMENTS
Tables G1 –G4 show a summary of our main dN/dz and dN/dX calculations for our different samples of absorption lines.
Summary of relevant quantities for our sample of total H i absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Mpc) . | (km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 11 | |$358^{+144}_{-107}$| | |$238^{+96}_{-71}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.9^{+1.2}_{-0.9}$| | |$2.7^{+1.1}_{-0.9}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 11 | |$293^{+118}_{-87}$| | |$195^{+78}_{-58}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.4^{+1.0}_{-0.7}$| | |$2.2^{+0.9}_{-0.7}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 14 | |$305^{+105}_{-81}$| | |$203^{+70}_{-54}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.5^{+0.9}_{-0.7}$| | |$2.3^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 17 | |$237^{+73}_{-57}$| | |$159^{+49}_{-38}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+0.6}_{-0.5}$| | |$1.8^{+0.6}_{-0.5}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 17 | |$188^{+58}_{-45}$| | |$126^{+39}_{-30}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.5}_{-0.4}$| | |$1.5^{+0.5}_{-0.4}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 18 | |$156^{+46}_{-37}$| | |$105^{+31}_{-25}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 21 | |$151^{+41}_{-33}$| | |$101^{+27}_{-22}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 25 | |$152^{+37}_{-30}$| | |$102^{+25}_{-20}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 26 | |$143^{+34}_{-28}$| | |$97^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 26 | |$134^{+32}_{-26}$| | |$91^{+22}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 32 | |$147^{+31}_{-26}$| | |$101^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 38 | |$151^{+29}_{-24}$| | |$105^{+20}_{-17}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 43 | |$146^{+26}_{-22}$| | |$103^{+18}_{-16}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 48 | |$145^{+24}_{-21}$| | |$103^{+17}_{-15}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 3 | |$203^{+199}_{-112}$| | |$140^{+137}_{-77}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+1.6}_{-0.9}$| | |$1.6^{+1.6}_{-0.9}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 6 | |$231^{+139}_{-92}$| | |$150^{+90}_{-60}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+1.1}_{-0.8}$| | |$1.7^{+1.1}_{-0.7}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 8 | |$184^{+91}_{-64}$| | |$124^{+61}_{-43}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.8}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$280^{+89}_{-69}$| | |$187^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$279^{+89}_{-69}$| | |$186^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.1^{+0.7}_{-0.6}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 16 | |$242^{+77}_{-60}$| | |$164^{+52}_{-41}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.0^{+0.7}_{-0.5}$| | |$1.9^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 17 | |$218^{+67}_{-53}$| | |$147^{+45}_{-35}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.8^{+0.6}_{-0.5}$| | |$1.7^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 19 | |$205^{+59}_{-47}$| | |$140^{+40}_{-32}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.7^{+0.5}_{-0.4}$| | |$1.6^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 21 | |$193^{+52}_{-42}$| | |$132^{+36}_{-29}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.5}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 23 | |$195^{+50}_{-40}$| | |$133^{+34}_{-28}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.4}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 27 | |$180^{+42}_{-35}$| | |$124^{+29}_{-24}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.4}_{-0.3}$| | |$1.4^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 27 | |$160^{+37}_{-31}$| | |$111^{+26}_{-21}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.3}$| | |$1.3^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 29 | |$150^{+33}_{-28}$| | |$105^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 39 | |$160^{+30}_{-25}$| | |$113^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.2}$| | |$1.3^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$136^{+26}_{-22}$| | |$97^{+18}_{-16}$| | |$2.1^{+0.8}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$132^{+26}_{-22}$| | |$94^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.3^{+0.8}_{-0.7}$| | |$2.1^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 14 | |$247^{+85}_{-65}$| | |$165^{+57}_{-44}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$2.2^{+0.9}_{-0.7}$| | |$2.0^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$2.2^{+1.0}_{-0.8}$| | |$2.0^{+0.9}_{-0.7}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$89^{+22}_{-18}$| | |$64^{+15}_{-13}$| | |$2.4^{+1.0}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$2.4^{+1.1}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$75^{+20}_{-16}$| | |$54^{+14}_{-12}$| | |$2.6^{+1.2}_{-1.0}$| | |$2.4^{+1.1}_{-0.9}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$61^{+19}_{-15}$| | |$43^{+13}_{-10}$| | |$2.6^{+1.4}_{-1.1}$| | |$2.4^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$50^{+17}_{-13}$| | |$36^{+12}_{-9}$| | |$2.8^{+1.6}_{-1.3}$| | |$2.6^{+1.5}_{-1.2}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Mpc) . | (km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 11 | |$358^{+144}_{-107}$| | |$238^{+96}_{-71}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.9^{+1.2}_{-0.9}$| | |$2.7^{+1.1}_{-0.9}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 11 | |$293^{+118}_{-87}$| | |$195^{+78}_{-58}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.4^{+1.0}_{-0.7}$| | |$2.2^{+0.9}_{-0.7}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 14 | |$305^{+105}_{-81}$| | |$203^{+70}_{-54}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.5^{+0.9}_{-0.7}$| | |$2.3^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 17 | |$237^{+73}_{-57}$| | |$159^{+49}_{-38}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+0.6}_{-0.5}$| | |$1.8^{+0.6}_{-0.5}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 17 | |$188^{+58}_{-45}$| | |$126^{+39}_{-30}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.5}_{-0.4}$| | |$1.5^{+0.5}_{-0.4}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 18 | |$156^{+46}_{-37}$| | |$105^{+31}_{-25}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 21 | |$151^{+41}_{-33}$| | |$101^{+27}_{-22}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 25 | |$152^{+37}_{-30}$| | |$102^{+25}_{-20}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 26 | |$143^{+34}_{-28}$| | |$97^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 26 | |$134^{+32}_{-26}$| | |$91^{+22}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 32 | |$147^{+31}_{-26}$| | |$101^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 38 | |$151^{+29}_{-24}$| | |$105^{+20}_{-17}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 43 | |$146^{+26}_{-22}$| | |$103^{+18}_{-16}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 48 | |$145^{+24}_{-21}$| | |$103^{+17}_{-15}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 3 | |$203^{+199}_{-112}$| | |$140^{+137}_{-77}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+1.6}_{-0.9}$| | |$1.6^{+1.6}_{-0.9}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 6 | |$231^{+139}_{-92}$| | |$150^{+90}_{-60}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+1.1}_{-0.8}$| | |$1.7^{+1.1}_{-0.7}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 8 | |$184^{+91}_{-64}$| | |$124^{+61}_{-43}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.8}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$280^{+89}_{-69}$| | |$187^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$279^{+89}_{-69}$| | |$186^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.1^{+0.7}_{-0.6}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 16 | |$242^{+77}_{-60}$| | |$164^{+52}_{-41}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.0^{+0.7}_{-0.5}$| | |$1.9^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 17 | |$218^{+67}_{-53}$| | |$147^{+45}_{-35}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.8^{+0.6}_{-0.5}$| | |$1.7^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 19 | |$205^{+59}_{-47}$| | |$140^{+40}_{-32}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.7^{+0.5}_{-0.4}$| | |$1.6^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 21 | |$193^{+52}_{-42}$| | |$132^{+36}_{-29}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.5}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 23 | |$195^{+50}_{-40}$| | |$133^{+34}_{-28}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.4}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 27 | |$180^{+42}_{-35}$| | |$124^{+29}_{-24}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.4}_{-0.3}$| | |$1.4^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 27 | |$160^{+37}_{-31}$| | |$111^{+26}_{-21}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.3}$| | |$1.3^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 29 | |$150^{+33}_{-28}$| | |$105^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 39 | |$160^{+30}_{-25}$| | |$113^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.2}$| | |$1.3^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$136^{+26}_{-22}$| | |$97^{+18}_{-16}$| | |$2.1^{+0.8}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$132^{+26}_{-22}$| | |$94^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.3^{+0.8}_{-0.7}$| | |$2.1^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 14 | |$247^{+85}_{-65}$| | |$165^{+57}_{-44}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$2.2^{+0.9}_{-0.7}$| | |$2.0^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$2.2^{+1.0}_{-0.8}$| | |$2.0^{+0.9}_{-0.7}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$89^{+22}_{-18}$| | |$64^{+15}_{-13}$| | |$2.4^{+1.0}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$2.4^{+1.1}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$75^{+20}_{-16}$| | |$54^{+14}_{-12}$| | |$2.6^{+1.2}_{-1.0}$| | |$2.4^{+1.1}_{-0.9}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$61^{+19}_{-15}$| | |$43^{+13}_{-10}$| | |$2.6^{+1.4}_{-1.1}$| | |$2.4^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$50^{+17}_{-13}$| | |$36^{+12}_{-9}$| | |$2.8^{+1.6}_{-1.3}$| | |$2.6^{+1.5}_{-1.2}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated with absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C). (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).
Summary of relevant quantities for our sample of total H i absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Mpc) . | (km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 11 | |$358^{+144}_{-107}$| | |$238^{+96}_{-71}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.9^{+1.2}_{-0.9}$| | |$2.7^{+1.1}_{-0.9}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 11 | |$293^{+118}_{-87}$| | |$195^{+78}_{-58}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.4^{+1.0}_{-0.7}$| | |$2.2^{+0.9}_{-0.7}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 14 | |$305^{+105}_{-81}$| | |$203^{+70}_{-54}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.5^{+0.9}_{-0.7}$| | |$2.3^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 17 | |$237^{+73}_{-57}$| | |$159^{+49}_{-38}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+0.6}_{-0.5}$| | |$1.8^{+0.6}_{-0.5}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 17 | |$188^{+58}_{-45}$| | |$126^{+39}_{-30}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.5}_{-0.4}$| | |$1.5^{+0.5}_{-0.4}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 18 | |$156^{+46}_{-37}$| | |$105^{+31}_{-25}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 21 | |$151^{+41}_{-33}$| | |$101^{+27}_{-22}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 25 | |$152^{+37}_{-30}$| | |$102^{+25}_{-20}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 26 | |$143^{+34}_{-28}$| | |$97^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 26 | |$134^{+32}_{-26}$| | |$91^{+22}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 32 | |$147^{+31}_{-26}$| | |$101^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 38 | |$151^{+29}_{-24}$| | |$105^{+20}_{-17}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 43 | |$146^{+26}_{-22}$| | |$103^{+18}_{-16}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 48 | |$145^{+24}_{-21}$| | |$103^{+17}_{-15}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 3 | |$203^{+199}_{-112}$| | |$140^{+137}_{-77}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+1.6}_{-0.9}$| | |$1.6^{+1.6}_{-0.9}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 6 | |$231^{+139}_{-92}$| | |$150^{+90}_{-60}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+1.1}_{-0.8}$| | |$1.7^{+1.1}_{-0.7}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 8 | |$184^{+91}_{-64}$| | |$124^{+61}_{-43}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.8}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$280^{+89}_{-69}$| | |$187^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$279^{+89}_{-69}$| | |$186^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.1^{+0.7}_{-0.6}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 16 | |$242^{+77}_{-60}$| | |$164^{+52}_{-41}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.0^{+0.7}_{-0.5}$| | |$1.9^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 17 | |$218^{+67}_{-53}$| | |$147^{+45}_{-35}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.8^{+0.6}_{-0.5}$| | |$1.7^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 19 | |$205^{+59}_{-47}$| | |$140^{+40}_{-32}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.7^{+0.5}_{-0.4}$| | |$1.6^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 21 | |$193^{+52}_{-42}$| | |$132^{+36}_{-29}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.5}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 23 | |$195^{+50}_{-40}$| | |$133^{+34}_{-28}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.4}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 27 | |$180^{+42}_{-35}$| | |$124^{+29}_{-24}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.4}_{-0.3}$| | |$1.4^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 27 | |$160^{+37}_{-31}$| | |$111^{+26}_{-21}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.3}$| | |$1.3^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 29 | |$150^{+33}_{-28}$| | |$105^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 39 | |$160^{+30}_{-25}$| | |$113^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.2}$| | |$1.3^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$136^{+26}_{-22}$| | |$97^{+18}_{-16}$| | |$2.1^{+0.8}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$132^{+26}_{-22}$| | |$94^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.3^{+0.8}_{-0.7}$| | |$2.1^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 14 | |$247^{+85}_{-65}$| | |$165^{+57}_{-44}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$2.2^{+0.9}_{-0.7}$| | |$2.0^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$2.2^{+1.0}_{-0.8}$| | |$2.0^{+0.9}_{-0.7}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$89^{+22}_{-18}$| | |$64^{+15}_{-13}$| | |$2.4^{+1.0}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$2.4^{+1.1}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$75^{+20}_{-16}$| | |$54^{+14}_{-12}$| | |$2.6^{+1.2}_{-1.0}$| | |$2.4^{+1.1}_{-0.9}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$61^{+19}_{-15}$| | |$43^{+13}_{-10}$| | |$2.6^{+1.4}_{-1.1}$| | |$2.4^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$50^{+17}_{-13}$| | |$36^{+12}_{-9}$| | |$2.8^{+1.6}_{-1.3}$| | |$2.6^{+1.5}_{-1.2}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| (Mpc) . | (km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 11 | |$358^{+144}_{-107}$| | |$238^{+96}_{-71}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.9^{+1.2}_{-0.9}$| | |$2.7^{+1.1}_{-0.9}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 11 | |$293^{+118}_{-87}$| | |$195^{+78}_{-58}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.4^{+1.0}_{-0.7}$| | |$2.2^{+0.9}_{-0.7}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 14 | |$305^{+105}_{-81}$| | |$203^{+70}_{-54}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.5^{+0.9}_{-0.7}$| | |$2.3^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 17 | |$237^{+73}_{-57}$| | |$159^{+49}_{-38}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+0.6}_{-0.5}$| | |$1.8^{+0.6}_{-0.5}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 17 | |$188^{+58}_{-45}$| | |$126^{+39}_{-30}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.5}_{-0.4}$| | |$1.5^{+0.5}_{-0.4}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 18 | |$156^{+46}_{-37}$| | |$105^{+31}_{-25}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 21 | |$151^{+41}_{-33}$| | |$101^{+27}_{-22}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 25 | |$152^{+37}_{-30}$| | |$102^{+25}_{-20}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 26 | |$143^{+34}_{-28}$| | |$97^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 26 | |$134^{+32}_{-26}$| | |$91^{+22}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 32 | |$147^{+31}_{-26}$| | |$101^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 38 | |$151^{+29}_{-24}$| | |$105^{+20}_{-17}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.2}$| | |$1.2^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 43 | |$146^{+26}_{-22}$| | |$103^{+18}_{-16}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 48 | |$145^{+24}_{-21}$| | |$103^{+17}_{-15}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.2}_{-0.2}$| | |$1.2^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 3 | |$203^{+199}_{-112}$| | |$140^{+137}_{-77}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+1.6}_{-0.9}$| | |$1.6^{+1.6}_{-0.9}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 6 | |$231^{+139}_{-92}$| | |$150^{+90}_{-60}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.9^{+1.1}_{-0.8}$| | |$1.7^{+1.1}_{-0.7}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 8 | |$184^{+91}_{-64}$| | |$124^{+61}_{-43}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.8}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 16 | |$287^{+91}_{-71}$| | |$191^{+61}_{-47}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$280^{+89}_{-69}$| | |$187^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.2^{+0.7}_{-0.6}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$279^{+89}_{-69}$| | |$186^{+59}_{-46}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.3^{+0.8}_{-0.6}$| | |$2.1^{+0.7}_{-0.6}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 16 | |$242^{+77}_{-60}$| | |$164^{+52}_{-41}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$2.0^{+0.7}_{-0.5}$| | |$1.9^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 17 | |$218^{+67}_{-53}$| | |$147^{+45}_{-35}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.8^{+0.6}_{-0.5}$| | |$1.7^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 19 | |$205^{+59}_{-47}$| | |$140^{+40}_{-32}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.7^{+0.5}_{-0.4}$| | |$1.6^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 21 | |$193^{+52}_{-42}$| | |$132^{+36}_{-29}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.5}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 23 | |$195^{+50}_{-40}$| | |$133^{+34}_{-28}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.6^{+0.4}_{-0.4}$| | |$1.5^{+0.4}_{-0.4}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 27 | |$180^{+42}_{-35}$| | |$124^{+29}_{-24}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.5^{+0.4}_{-0.3}$| | |$1.4^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 27 | |$160^{+37}_{-31}$| | |$111^{+26}_{-21}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.3}$| | |$1.3^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 29 | |$150^{+33}_{-28}$| | |$105^{+23}_{-19}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.2^{+0.3}_{-0.3}$| | |$1.2^{+0.3}_{-0.3}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 39 | |$160^{+30}_{-25}$| | |$113^{+21}_{-18}$| | |$123^{+26}_{-23}$| | |$87^{+18}_{-16}$| | |$1.3^{+0.3}_{-0.2}$| | |$1.3^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$139^{+26}_{-22}$| | |$100^{+19}_{-16}$| | |$2.0^{+0.7}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$136^{+26}_{-22}$| | |$97^{+18}_{-16}$| | |$2.1^{+0.8}_{-0.6}$| | |$1.9^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$132^{+26}_{-22}$| | |$94^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 16 | |$282^{+90}_{-70}$| | |$188^{+60}_{-47}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.3^{+0.8}_{-0.7}$| | |$2.1^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$125^{+25}_{-21}$| | |$89^{+18}_{-15}$| | |$2.1^{+0.8}_{-0.7}$| | |$2.0^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 15 | |$265^{+88}_{-68}$| | |$176^{+58}_{-45}$| | |$121^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$2.2^{+0.8}_{-0.7}$| | |$2.0^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 14 | |$247^{+85}_{-65}$| | |$165^{+57}_{-44}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$2.2^{+0.9}_{-0.7}$| | |$2.0^{+0.8}_{-0.7}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$2.2^{+1.0}_{-0.8}$| | |$2.0^{+0.9}_{-0.7}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 12 | |$212^{+81}_{-60}$| | |$141^{+54}_{-40}$| | |$89^{+22}_{-18}$| | |$64^{+15}_{-13}$| | |$2.4^{+1.0}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$2.4^{+1.1}_{-0.9}$| | |$2.2^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 11 | |$194^{+78}_{-58}$| | |$129^{+52}_{-39}$| | |$75^{+20}_{-16}$| | |$54^{+14}_{-12}$| | |$2.6^{+1.2}_{-1.0}$| | |$2.4^{+1.1}_{-0.9}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$61^{+19}_{-15}$| | |$43^{+13}_{-10}$| | |$2.6^{+1.4}_{-1.1}$| | |$2.4^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$50^{+17}_{-13}$| | |$36^{+12}_{-9}$| | |$2.8^{+1.6}_{-1.3}$| | |$2.6^{+1.5}_{-1.2}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated with absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C). (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).
Summary of relevant quantities for our sample of total O vi absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.06 | 0.03 | 0.05 | 3 | |$100^{+98}_{-55}$| | |$66^{+64}_{-36}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$7.1^{+7.4}_{-4.7}$| | |$6.9^{+7.2}_{-4.5}$| |
| 3.0 | 630 | 0.06 | 0.04 | 0.06 | 3 | |$82^{+80}_{-45}$| | |$54^{+53}_{-30}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.8^{+6.1}_{-3.8}$| | |$5.6^{+5.9}_{-3.7}$| |
| 3.0 | 794 | 0.06 | 0.04 | 0.07 | 3 | |$70^{+69}_{-39}$| | |$46^{+45}_{-26}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.0^{+5.2}_{-3.3}$| | |$4.8^{+5.0}_{-3.2}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 3.0 | 1313 | 0.06 | 0.07 | 0.10 | 3 | |$45^{+45}_{-25}$| | |$30^{+29}_{-17}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+3.4}_{-2.1}$| | |$3.1^{+3.3}_{-2.1}$| |
| 3.0 | 1724 | 0.06 | 0.09 | 0.13 | 3 | |$35^{+34}_{-19}$| | |$23^{+23}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.5^{+2.6}_{-1.6}$| | |$2.4^{+2.5}_{-1.6}$| |
| 3.0 | 2264 | 0.06 | 0.11 | 0.17 | 3 | |$27^{+26}_{-15}$| | |$18^{+17}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.9^{+2.0}_{-1.3}$| | |$1.9^{+1.9}_{-1.2}$| |
| 3.0 | 2972 | 0.06 | 0.14 | 0.21 | 3 | |$22^{+21}_{-12}$| | |$14^{+14}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.6}_{-1.0}$| | |$1.5^{+1.6}_{-1.0}$| |
| 3.0 | 3903 | 0.06 | 0.17 | 0.26 | 3 | |$17^{+17}_{-10}$| | |$12^{+11}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.2^{+1.3}_{-0.8}$| | |$1.2^{+1.3}_{-0.8}$| |
| 3.0 | 5125 | 0.06 | 0.20 | 0.30 | 3 | |$15^{+15}_{-8}$| | |$10^{+10}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.1^{+1.1}_{-0.7}$| | |$1.0^{+1.1}_{-0.7}$| |
| 3.0 | 6729 | 0.06 | 0.23 | 0.34 | 3 | |$13^{+13}_{-7}$| | |$9^{+9}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.9^{+1.0}_{-0.6}$| | |$0.9^{+1.0}_{-0.6}$| |
| 3.0 | 8835 | 0.06 | 0.25 | 0.38 | 6 | |$24^{+14}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.2}_{-0.9}$| | |$1.7^{+1.2}_{-0.9}$| |
| 3.0 | 11601 | 0.06 | 0.27 | 0.40 | 6 | |$22^{+13}_{-9}$| | |$15^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.1}_{-0.9}$| | |$1.6^{+1.1}_{-0.8}$| |
| 3.0 | 15232 | 0.06 | 0.29 | 0.44 | 7 | |$24^{+13}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.1}_{-0.9}$| | |$1.7^{+1.1}_{-0.9}$| |
| 3.0 | 20000 | 0.06 | 0.32 | 0.46 | 7 | |$22^{+12}_{-8}$| | |$15^{+8}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.8}$| |
| 1.0 | 1000 | 0.06 | 0.01 | 0.02 | 0 | |$0^{+132}_{-0}$| | |$0^{+91}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+9.4}_{-0.0}$| | |$0.0^{+9.5}_{-0.0}$| |
| 1.4 | 1000 | 0.06 | 0.03 | 0.04 | 0 | |$0^{+73}_{-0}$| | |$0^{+47}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+5.2}_{-0.0}$| | |$0.0^{+4.9}_{-0.0}$| |
| 2.1 | 1000 | 0.06 | 0.04 | 0.06 | 0 | |$0^{+48}_{-0}$| | |$0^{+32}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+3.4}_{-0.0}$| | |$0.0^{+3.3}_{-0.0}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 4.1 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.2}_{-2.6}$| | |$3.9^{+4.0}_{-2.6}$| |
| 5.7 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.1}_{-2.6}$| | |$3.8^{+4.0}_{-2.5}$| |
| 7.8 | 1000 | 0.06 | 0.06 | 0.09 | 3 | |$48^{+47}_{-27}$| | |$32^{+32}_{-18}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.4^{+3.6}_{-2.3}$| | |$3.4^{+3.5}_{-2.2}$| |
| 10.7 | 1000 | 0.06 | 0.07 | 0.11 | 3 | |$40^{+39}_{-22}$| | |$27^{+26}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.8^{+3.0}_{-1.9}$| | |$2.8^{+2.9}_{-1.8}$| |
| 14.8 | 1000 | 0.06 | 0.09 | 0.13 | 4 | |$45^{+36}_{-22}$| | |$31^{+24}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+2.8}_{-1.9}$| | |$3.2^{+2.8}_{-1.9}$| |
| 20.3 | 1000 | 0.06 | 0.10 | 0.15 | 4 | |$41^{+32}_{-20}$| | |$28^{+22}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.9^{+2.5}_{-1.8}$| | |$2.9^{+2.5}_{-1.7}$| |
| 27.9 | 1000 | 0.06 | 0.11 | 0.16 | 4 | |$37^{+29}_{-18}$| | |$25^{+20}_{-12}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.6^{+2.3}_{-1.6}$| | |$2.6^{+2.3}_{-1.6}$| |
| 38.4 | 1000 | 0.06 | 0.13 | 0.20 | 4 | |$30^{+24}_{-14}$| | |$20^{+16}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.1^{+1.9}_{-1.3}$| | |$2.1^{+1.8}_{-1.3}$| |
| 52.9 | 1000 | 0.06 | 0.16 | 0.24 | 4 | |$25^{+20}_{-12}$| | |$17^{+13}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.8^{+1.5}_{-1.1}$| | |$1.7^{+1.5}_{-1.1}$| |
| 72.7 | 1000 | 0.06 | 0.19 | 0.28 | 4 | |$21^{+17}_{-10}$| | |$14^{+11}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.3}_{-0.9}$| | |$1.5^{+1.3}_{-0.9}$| |
| 100.0 | 1000 | 0.06 | 0.25 | 0.37 | 7 | |$28^{+15}_{-11}$| | |$19^{+10}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.0^{+1.3}_{-1.0}$| | |$2.0^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.03 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.07 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.08 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.09 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.10 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.11 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$1.3^{+3.1}_{-1.3}$| | |$1.2^{+3.0}_{-1.2}$| |
| 3.0 | 1000 | 0.12 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$11^{+11}_{-6}$| | |$8^{+8}_{-4}$| | |$1.7^{+4.2}_{-1.7}$| | |$1.6^{+4.0}_{-1.6}$| |
| 3.0 | 1000 | 0.14 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.16 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.18 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$4^{+9}_{-3}$| | |$3^{+6}_{-2}$| | |$5.1^{+14.3}_{-5.1}$| | |$4.9^{+13.8}_{-4.9}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.06 | 0.03 | 0.05 | 3 | |$100^{+98}_{-55}$| | |$66^{+64}_{-36}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$7.1^{+7.4}_{-4.7}$| | |$6.9^{+7.2}_{-4.5}$| |
| 3.0 | 630 | 0.06 | 0.04 | 0.06 | 3 | |$82^{+80}_{-45}$| | |$54^{+53}_{-30}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.8^{+6.1}_{-3.8}$| | |$5.6^{+5.9}_{-3.7}$| |
| 3.0 | 794 | 0.06 | 0.04 | 0.07 | 3 | |$70^{+69}_{-39}$| | |$46^{+45}_{-26}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.0^{+5.2}_{-3.3}$| | |$4.8^{+5.0}_{-3.2}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 3.0 | 1313 | 0.06 | 0.07 | 0.10 | 3 | |$45^{+45}_{-25}$| | |$30^{+29}_{-17}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+3.4}_{-2.1}$| | |$3.1^{+3.3}_{-2.1}$| |
| 3.0 | 1724 | 0.06 | 0.09 | 0.13 | 3 | |$35^{+34}_{-19}$| | |$23^{+23}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.5^{+2.6}_{-1.6}$| | |$2.4^{+2.5}_{-1.6}$| |
| 3.0 | 2264 | 0.06 | 0.11 | 0.17 | 3 | |$27^{+26}_{-15}$| | |$18^{+17}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.9^{+2.0}_{-1.3}$| | |$1.9^{+1.9}_{-1.2}$| |
| 3.0 | 2972 | 0.06 | 0.14 | 0.21 | 3 | |$22^{+21}_{-12}$| | |$14^{+14}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.6}_{-1.0}$| | |$1.5^{+1.6}_{-1.0}$| |
| 3.0 | 3903 | 0.06 | 0.17 | 0.26 | 3 | |$17^{+17}_{-10}$| | |$12^{+11}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.2^{+1.3}_{-0.8}$| | |$1.2^{+1.3}_{-0.8}$| |
| 3.0 | 5125 | 0.06 | 0.20 | 0.30 | 3 | |$15^{+15}_{-8}$| | |$10^{+10}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.1^{+1.1}_{-0.7}$| | |$1.0^{+1.1}_{-0.7}$| |
| 3.0 | 6729 | 0.06 | 0.23 | 0.34 | 3 | |$13^{+13}_{-7}$| | |$9^{+9}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.9^{+1.0}_{-0.6}$| | |$0.9^{+1.0}_{-0.6}$| |
| 3.0 | 8835 | 0.06 | 0.25 | 0.38 | 6 | |$24^{+14}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.2}_{-0.9}$| | |$1.7^{+1.2}_{-0.9}$| |
| 3.0 | 11601 | 0.06 | 0.27 | 0.40 | 6 | |$22^{+13}_{-9}$| | |$15^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.1}_{-0.9}$| | |$1.6^{+1.1}_{-0.8}$| |
| 3.0 | 15232 | 0.06 | 0.29 | 0.44 | 7 | |$24^{+13}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.1}_{-0.9}$| | |$1.7^{+1.1}_{-0.9}$| |
| 3.0 | 20000 | 0.06 | 0.32 | 0.46 | 7 | |$22^{+12}_{-8}$| | |$15^{+8}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.8}$| |
| 1.0 | 1000 | 0.06 | 0.01 | 0.02 | 0 | |$0^{+132}_{-0}$| | |$0^{+91}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+9.4}_{-0.0}$| | |$0.0^{+9.5}_{-0.0}$| |
| 1.4 | 1000 | 0.06 | 0.03 | 0.04 | 0 | |$0^{+73}_{-0}$| | |$0^{+47}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+5.2}_{-0.0}$| | |$0.0^{+4.9}_{-0.0}$| |
| 2.1 | 1000 | 0.06 | 0.04 | 0.06 | 0 | |$0^{+48}_{-0}$| | |$0^{+32}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+3.4}_{-0.0}$| | |$0.0^{+3.3}_{-0.0}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 4.1 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.2}_{-2.6}$| | |$3.9^{+4.0}_{-2.6}$| |
| 5.7 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.1}_{-2.6}$| | |$3.8^{+4.0}_{-2.5}$| |
| 7.8 | 1000 | 0.06 | 0.06 | 0.09 | 3 | |$48^{+47}_{-27}$| | |$32^{+32}_{-18}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.4^{+3.6}_{-2.3}$| | |$3.4^{+3.5}_{-2.2}$| |
| 10.7 | 1000 | 0.06 | 0.07 | 0.11 | 3 | |$40^{+39}_{-22}$| | |$27^{+26}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.8^{+3.0}_{-1.9}$| | |$2.8^{+2.9}_{-1.8}$| |
| 14.8 | 1000 | 0.06 | 0.09 | 0.13 | 4 | |$45^{+36}_{-22}$| | |$31^{+24}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+2.8}_{-1.9}$| | |$3.2^{+2.8}_{-1.9}$| |
| 20.3 | 1000 | 0.06 | 0.10 | 0.15 | 4 | |$41^{+32}_{-20}$| | |$28^{+22}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.9^{+2.5}_{-1.8}$| | |$2.9^{+2.5}_{-1.7}$| |
| 27.9 | 1000 | 0.06 | 0.11 | 0.16 | 4 | |$37^{+29}_{-18}$| | |$25^{+20}_{-12}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.6^{+2.3}_{-1.6}$| | |$2.6^{+2.3}_{-1.6}$| |
| 38.4 | 1000 | 0.06 | 0.13 | 0.20 | 4 | |$30^{+24}_{-14}$| | |$20^{+16}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.1^{+1.9}_{-1.3}$| | |$2.1^{+1.8}_{-1.3}$| |
| 52.9 | 1000 | 0.06 | 0.16 | 0.24 | 4 | |$25^{+20}_{-12}$| | |$17^{+13}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.8^{+1.5}_{-1.1}$| | |$1.7^{+1.5}_{-1.1}$| |
| 72.7 | 1000 | 0.06 | 0.19 | 0.28 | 4 | |$21^{+17}_{-10}$| | |$14^{+11}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.3}_{-0.9}$| | |$1.5^{+1.3}_{-0.9}$| |
| 100.0 | 1000 | 0.06 | 0.25 | 0.37 | 7 | |$28^{+15}_{-11}$| | |$19^{+10}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.0^{+1.3}_{-1.0}$| | |$2.0^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.03 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.07 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.08 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.09 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.10 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.11 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$1.3^{+3.1}_{-1.3}$| | |$1.2^{+3.0}_{-1.2}$| |
| 3.0 | 1000 | 0.12 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$11^{+11}_{-6}$| | |$8^{+8}_{-4}$| | |$1.7^{+4.2}_{-1.7}$| | |$1.6^{+4.0}_{-1.6}$| |
| 3.0 | 1000 | 0.14 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.16 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.18 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$4^{+9}_{-3}$| | |$3^{+6}_{-2}$| | |$5.1^{+14.3}_{-5.1}$| | |$4.9^{+13.8}_{-4.9}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated with absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C) (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).
Summary of relevant quantities for our sample of total O vi absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.06 | 0.03 | 0.05 | 3 | |$100^{+98}_{-55}$| | |$66^{+64}_{-36}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$7.1^{+7.4}_{-4.7}$| | |$6.9^{+7.2}_{-4.5}$| |
| 3.0 | 630 | 0.06 | 0.04 | 0.06 | 3 | |$82^{+80}_{-45}$| | |$54^{+53}_{-30}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.8^{+6.1}_{-3.8}$| | |$5.6^{+5.9}_{-3.7}$| |
| 3.0 | 794 | 0.06 | 0.04 | 0.07 | 3 | |$70^{+69}_{-39}$| | |$46^{+45}_{-26}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.0^{+5.2}_{-3.3}$| | |$4.8^{+5.0}_{-3.2}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 3.0 | 1313 | 0.06 | 0.07 | 0.10 | 3 | |$45^{+45}_{-25}$| | |$30^{+29}_{-17}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+3.4}_{-2.1}$| | |$3.1^{+3.3}_{-2.1}$| |
| 3.0 | 1724 | 0.06 | 0.09 | 0.13 | 3 | |$35^{+34}_{-19}$| | |$23^{+23}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.5^{+2.6}_{-1.6}$| | |$2.4^{+2.5}_{-1.6}$| |
| 3.0 | 2264 | 0.06 | 0.11 | 0.17 | 3 | |$27^{+26}_{-15}$| | |$18^{+17}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.9^{+2.0}_{-1.3}$| | |$1.9^{+1.9}_{-1.2}$| |
| 3.0 | 2972 | 0.06 | 0.14 | 0.21 | 3 | |$22^{+21}_{-12}$| | |$14^{+14}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.6}_{-1.0}$| | |$1.5^{+1.6}_{-1.0}$| |
| 3.0 | 3903 | 0.06 | 0.17 | 0.26 | 3 | |$17^{+17}_{-10}$| | |$12^{+11}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.2^{+1.3}_{-0.8}$| | |$1.2^{+1.3}_{-0.8}$| |
| 3.0 | 5125 | 0.06 | 0.20 | 0.30 | 3 | |$15^{+15}_{-8}$| | |$10^{+10}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.1^{+1.1}_{-0.7}$| | |$1.0^{+1.1}_{-0.7}$| |
| 3.0 | 6729 | 0.06 | 0.23 | 0.34 | 3 | |$13^{+13}_{-7}$| | |$9^{+9}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.9^{+1.0}_{-0.6}$| | |$0.9^{+1.0}_{-0.6}$| |
| 3.0 | 8835 | 0.06 | 0.25 | 0.38 | 6 | |$24^{+14}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.2}_{-0.9}$| | |$1.7^{+1.2}_{-0.9}$| |
| 3.0 | 11601 | 0.06 | 0.27 | 0.40 | 6 | |$22^{+13}_{-9}$| | |$15^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.1}_{-0.9}$| | |$1.6^{+1.1}_{-0.8}$| |
| 3.0 | 15232 | 0.06 | 0.29 | 0.44 | 7 | |$24^{+13}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.1}_{-0.9}$| | |$1.7^{+1.1}_{-0.9}$| |
| 3.0 | 20000 | 0.06 | 0.32 | 0.46 | 7 | |$22^{+12}_{-8}$| | |$15^{+8}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.8}$| |
| 1.0 | 1000 | 0.06 | 0.01 | 0.02 | 0 | |$0^{+132}_{-0}$| | |$0^{+91}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+9.4}_{-0.0}$| | |$0.0^{+9.5}_{-0.0}$| |
| 1.4 | 1000 | 0.06 | 0.03 | 0.04 | 0 | |$0^{+73}_{-0}$| | |$0^{+47}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+5.2}_{-0.0}$| | |$0.0^{+4.9}_{-0.0}$| |
| 2.1 | 1000 | 0.06 | 0.04 | 0.06 | 0 | |$0^{+48}_{-0}$| | |$0^{+32}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+3.4}_{-0.0}$| | |$0.0^{+3.3}_{-0.0}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 4.1 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.2}_{-2.6}$| | |$3.9^{+4.0}_{-2.6}$| |
| 5.7 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.1}_{-2.6}$| | |$3.8^{+4.0}_{-2.5}$| |
| 7.8 | 1000 | 0.06 | 0.06 | 0.09 | 3 | |$48^{+47}_{-27}$| | |$32^{+32}_{-18}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.4^{+3.6}_{-2.3}$| | |$3.4^{+3.5}_{-2.2}$| |
| 10.7 | 1000 | 0.06 | 0.07 | 0.11 | 3 | |$40^{+39}_{-22}$| | |$27^{+26}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.8^{+3.0}_{-1.9}$| | |$2.8^{+2.9}_{-1.8}$| |
| 14.8 | 1000 | 0.06 | 0.09 | 0.13 | 4 | |$45^{+36}_{-22}$| | |$31^{+24}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+2.8}_{-1.9}$| | |$3.2^{+2.8}_{-1.9}$| |
| 20.3 | 1000 | 0.06 | 0.10 | 0.15 | 4 | |$41^{+32}_{-20}$| | |$28^{+22}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.9^{+2.5}_{-1.8}$| | |$2.9^{+2.5}_{-1.7}$| |
| 27.9 | 1000 | 0.06 | 0.11 | 0.16 | 4 | |$37^{+29}_{-18}$| | |$25^{+20}_{-12}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.6^{+2.3}_{-1.6}$| | |$2.6^{+2.3}_{-1.6}$| |
| 38.4 | 1000 | 0.06 | 0.13 | 0.20 | 4 | |$30^{+24}_{-14}$| | |$20^{+16}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.1^{+1.9}_{-1.3}$| | |$2.1^{+1.8}_{-1.3}$| |
| 52.9 | 1000 | 0.06 | 0.16 | 0.24 | 4 | |$25^{+20}_{-12}$| | |$17^{+13}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.8^{+1.5}_{-1.1}$| | |$1.7^{+1.5}_{-1.1}$| |
| 72.7 | 1000 | 0.06 | 0.19 | 0.28 | 4 | |$21^{+17}_{-10}$| | |$14^{+11}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.3}_{-0.9}$| | |$1.5^{+1.3}_{-0.9}$| |
| 100.0 | 1000 | 0.06 | 0.25 | 0.37 | 7 | |$28^{+15}_{-11}$| | |$19^{+10}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.0^{+1.3}_{-1.0}$| | |$2.0^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.03 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.07 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.08 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.09 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.10 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.11 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$1.3^{+3.1}_{-1.3}$| | |$1.2^{+3.0}_{-1.2}$| |
| 3.0 | 1000 | 0.12 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$11^{+11}_{-6}$| | |$8^{+8}_{-4}$| | |$1.7^{+4.2}_{-1.7}$| | |$1.6^{+4.0}_{-1.6}$| |
| 3.0 | 1000 | 0.14 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.16 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.18 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$4^{+9}_{-3}$| | |$3^{+6}_{-2}$| | |$5.1^{+14.3}_{-5.1}$| | |$4.9^{+13.8}_{-4.9}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.06 | 0.03 | 0.05 | 3 | |$100^{+98}_{-55}$| | |$66^{+64}_{-36}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$7.1^{+7.4}_{-4.7}$| | |$6.9^{+7.2}_{-4.5}$| |
| 3.0 | 630 | 0.06 | 0.04 | 0.06 | 3 | |$82^{+80}_{-45}$| | |$54^{+53}_{-30}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.8^{+6.1}_{-3.8}$| | |$5.6^{+5.9}_{-3.7}$| |
| 3.0 | 794 | 0.06 | 0.04 | 0.07 | 3 | |$70^{+69}_{-39}$| | |$46^{+45}_{-26}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$5.0^{+5.2}_{-3.3}$| | |$4.8^{+5.0}_{-3.2}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 3.0 | 1313 | 0.06 | 0.07 | 0.10 | 3 | |$45^{+45}_{-25}$| | |$30^{+29}_{-17}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+3.4}_{-2.1}$| | |$3.1^{+3.3}_{-2.1}$| |
| 3.0 | 1724 | 0.06 | 0.09 | 0.13 | 3 | |$35^{+34}_{-19}$| | |$23^{+23}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.5^{+2.6}_{-1.6}$| | |$2.4^{+2.5}_{-1.6}$| |
| 3.0 | 2264 | 0.06 | 0.11 | 0.17 | 3 | |$27^{+26}_{-15}$| | |$18^{+17}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.9^{+2.0}_{-1.3}$| | |$1.9^{+1.9}_{-1.2}$| |
| 3.0 | 2972 | 0.06 | 0.14 | 0.21 | 3 | |$22^{+21}_{-12}$| | |$14^{+14}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.6}_{-1.0}$| | |$1.5^{+1.6}_{-1.0}$| |
| 3.0 | 3903 | 0.06 | 0.17 | 0.26 | 3 | |$17^{+17}_{-10}$| | |$12^{+11}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.2^{+1.3}_{-0.8}$| | |$1.2^{+1.3}_{-0.8}$| |
| 3.0 | 5125 | 0.06 | 0.20 | 0.30 | 3 | |$15^{+15}_{-8}$| | |$10^{+10}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.1^{+1.1}_{-0.7}$| | |$1.0^{+1.1}_{-0.7}$| |
| 3.0 | 6729 | 0.06 | 0.23 | 0.34 | 3 | |$13^{+13}_{-7}$| | |$9^{+9}_{-5}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.9^{+1.0}_{-0.6}$| | |$0.9^{+1.0}_{-0.6}$| |
| 3.0 | 8835 | 0.06 | 0.25 | 0.38 | 6 | |$24^{+14}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.2}_{-0.9}$| | |$1.7^{+1.2}_{-0.9}$| |
| 3.0 | 11601 | 0.06 | 0.27 | 0.40 | 6 | |$22^{+13}_{-9}$| | |$15^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.1}_{-0.9}$| | |$1.6^{+1.1}_{-0.8}$| |
| 3.0 | 15232 | 0.06 | 0.29 | 0.44 | 7 | |$24^{+13}_{-9}$| | |$16^{+9}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.7^{+1.1}_{-0.9}$| | |$1.7^{+1.1}_{-0.9}$| |
| 3.0 | 20000 | 0.06 | 0.32 | 0.46 | 7 | |$22^{+12}_{-8}$| | |$15^{+8}_{-6}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.6^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.8}$| |
| 1.0 | 1000 | 0.06 | 0.01 | 0.02 | 0 | |$0^{+132}_{-0}$| | |$0^{+91}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+9.4}_{-0.0}$| | |$0.0^{+9.5}_{-0.0}$| |
| 1.4 | 1000 | 0.06 | 0.03 | 0.04 | 0 | |$0^{+73}_{-0}$| | |$0^{+47}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+5.2}_{-0.0}$| | |$0.0^{+4.9}_{-0.0}$| |
| 2.1 | 1000 | 0.06 | 0.04 | 0.06 | 0 | |$0^{+48}_{-0}$| | |$0^{+32}_{-0}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$0.0^{+3.4}_{-0.0}$| | |$0.0^{+3.3}_{-0.0}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.1^{+4.3}_{-2.7}$| | |$4.0^{+4.2}_{-2.6}$| |
| 4.1 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.2}_{-2.6}$| | |$3.9^{+4.0}_{-2.6}$| |
| 5.7 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$56^{+55}_{-31}$| | |$37^{+36}_{-20}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$4.0^{+4.1}_{-2.6}$| | |$3.8^{+4.0}_{-2.5}$| |
| 7.8 | 1000 | 0.06 | 0.06 | 0.09 | 3 | |$48^{+47}_{-27}$| | |$32^{+32}_{-18}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.4^{+3.6}_{-2.3}$| | |$3.4^{+3.5}_{-2.2}$| |
| 10.7 | 1000 | 0.06 | 0.07 | 0.11 | 3 | |$40^{+39}_{-22}$| | |$27^{+26}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.8^{+3.0}_{-1.9}$| | |$2.8^{+2.9}_{-1.8}$| |
| 14.8 | 1000 | 0.06 | 0.09 | 0.13 | 4 | |$45^{+36}_{-22}$| | |$31^{+24}_{-15}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$3.2^{+2.8}_{-1.9}$| | |$3.2^{+2.8}_{-1.9}$| |
| 20.3 | 1000 | 0.06 | 0.10 | 0.15 | 4 | |$41^{+32}_{-20}$| | |$28^{+22}_{-13}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.9^{+2.5}_{-1.8}$| | |$2.9^{+2.5}_{-1.7}$| |
| 27.9 | 1000 | 0.06 | 0.11 | 0.16 | 4 | |$37^{+29}_{-18}$| | |$25^{+20}_{-12}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.6^{+2.3}_{-1.6}$| | |$2.6^{+2.3}_{-1.6}$| |
| 38.4 | 1000 | 0.06 | 0.13 | 0.20 | 4 | |$30^{+24}_{-14}$| | |$20^{+16}_{-10}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.1^{+1.9}_{-1.3}$| | |$2.1^{+1.8}_{-1.3}$| |
| 52.9 | 1000 | 0.06 | 0.16 | 0.24 | 4 | |$25^{+20}_{-12}$| | |$17^{+13}_{-8}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.8^{+1.5}_{-1.1}$| | |$1.7^{+1.5}_{-1.1}$| |
| 72.7 | 1000 | 0.06 | 0.19 | 0.28 | 4 | |$21^{+17}_{-10}$| | |$14^{+11}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$1.5^{+1.3}_{-0.9}$| | |$1.5^{+1.3}_{-0.9}$| |
| 100.0 | 1000 | 0.06 | 0.25 | 0.37 | 7 | |$28^{+15}_{-11}$| | |$19^{+10}_{-7}$| | |$14^{+12}_{-8}$| | |$10^{+8}_{-6}$| | |$2.0^{+1.3}_{-1.0}$| | |$2.0^{+1.3}_{-1.0}$| |
| 3.0 | 1000 | 0.03 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.04 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.05 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.06 | 0.05 | 0.08 | 3 | |$58^{+57}_{-32}$| | |$38^{+37}_{-21}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$3.8^{+4.5}_{-3.2}$| | |$3.7^{+4.3}_{-3.1}$| |
| 3.0 | 1000 | 0.07 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.08 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.09 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.10 | 0.05 | 0.08 | 2 | |$39^{+51}_{-25}$| | |$25^{+34}_{-17}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$2.5^{+3.8}_{-2.3}$| | |$2.5^{+3.6}_{-2.3}$| |
| 3.0 | 1000 | 0.11 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$15^{+12}_{-7}$| | |$10^{+8}_{-5}$| | |$1.3^{+3.1}_{-1.3}$| | |$1.2^{+3.0}_{-1.2}$| |
| 3.0 | 1000 | 0.12 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$11^{+11}_{-6}$| | |$8^{+8}_{-4}$| | |$1.7^{+4.2}_{-1.7}$| | |$1.6^{+4.0}_{-1.6}$| |
| 3.0 | 1000 | 0.14 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.16 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$8^{+10}_{-5}$| | |$5^{+7}_{-3}$| | |$2.5^{+6.4}_{-2.5}$| | |$2.5^{+6.2}_{-2.5}$| |
| 3.0 | 1000 | 0.18 | 0.05 | 0.08 | 1 | |$19^{+45}_{-17}$| | |$13^{+29}_{-11}$| | |$4^{+9}_{-3}$| | |$3^{+6}_{-2}$| | |$5.1^{+14.3}_{-5.1}$| | |$4.9^{+13.8}_{-4.9}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated with absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C) (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).
Summary of relevant quantities for our sample of narrow H i (b < 50 km s−1) absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 7 | |$228^{+123}_{-85}$| | |$151^{+82}_{-56}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$2.2^{+1.2}_{-0.8}$| | |$2.0^{+1.1}_{-0.8}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 7 | |$186^{+101}_{-69}$| | |$124^{+67}_{-46}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.8^{+1.0}_{-0.7}$| | |$1.7^{+0.9}_{-0.6}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 8 | |$174^{+86}_{-61}$| | |$116^{+57}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.6^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 11 | |$154^{+62}_{-46}$| | |$103^{+41}_{-31}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.5^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 11 | |$121^{+49}_{-36}$| | |$82^{+33}_{-24}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.1^{+0.5}_{-0.3}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 11 | |$95^{+38}_{-28}$| | |$64^{+26}_{-19}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.4}_{-0.3}$| | |$0.9^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 14 | |$101^{+35}_{-27}$| | |$68^{+23}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 17 | |$104^{+32}_{-25}$| | |$70^{+21}_{-17}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 18 | |$99^{+29}_{-23}$| | |$67^{+20}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 18 | |$93^{+28}_{-22}$| | |$63^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.8^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 24 | |$110^{+27}_{-22}$| | |$76^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 29 | |$115^{+26}_{-21}$| | |$80^{+18}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 33 | |$112^{+23}_{-19}$| | |$79^{+16}_{-14}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 37 | |$112^{+22}_{-18}$| | |$79^{+15}_{-13}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 1 | |$68^{+157}_{-59}$| | |$47^{+108}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.6^{+1.5}_{-0.6}$| | |$0.6^{+1.5}_{-0.5}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 2 | |$77^{+102}_{-51}$| | |$50^{+67}_{-33}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+1.0}_{-0.5}$| | |$0.7^{+0.9}_{-0.4}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 3 | |$69^{+68}_{-38}$| | |$46^{+45}_{-26}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+0.6}_{-0.4}$| | |$0.6^{+0.6}_{-0.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$175^{+75}_{-55}$| | |$117^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$174^{+74}_{-54}$| | |$116^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 10 | |$151^{+65}_{-47}$| | |$103^{+44}_{-32}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.4^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 11 | |$141^{+57}_{-42}$| | |$95^{+38}_{-28}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.6}_{-0.4}$| | |$1.3^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 12 | |$129^{+49}_{-37}$| | |$88^{+34}_{-25}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.2^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 14 | |$129^{+45}_{-34}$| | |$88^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 16 | |$135^{+43}_{-34}$| | |$93^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 19 | |$127^{+36}_{-29}$| | |$87^{+25}_{-20}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 19 | |$113^{+32}_{-26}$| | |$78^{+22}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 21 | |$109^{+29}_{-24}$| | |$76^{+21}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 29 | |$119^{+26}_{-22}$| | |$84^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$118^{+24}_{-20}$| | |$84^{+17}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.5^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$1.5^{+0.9}_{-0.7}$| | |$1.4^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$79^{+21}_{-17}$| | |$56^{+15}_{-12}$| | |$1.6^{+0.9}_{-0.7}$| | |$1.5^{+0.9}_{-0.6}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$71^{+20}_{-16}$| | |$51^{+14}_{-11}$| | |$1.7^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.7}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$68^{+19}_{-15}$| | |$48^{+14}_{-11}$| | |$1.8^{+1.1}_{-0.8}$| | |$1.7^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$57^{+18}_{-14}$| | |$41^{+13}_{-10}$| | |$2.2^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-0.9}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$46^{+17}_{-13}$| | |$33^{+12}_{-9}$| | |$2.3^{+1.5}_{-1.2}$| | |$2.1^{+1.4}_{-1.1}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 7 | |$228^{+123}_{-85}$| | |$151^{+82}_{-56}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$2.2^{+1.2}_{-0.8}$| | |$2.0^{+1.1}_{-0.8}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 7 | |$186^{+101}_{-69}$| | |$124^{+67}_{-46}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.8^{+1.0}_{-0.7}$| | |$1.7^{+0.9}_{-0.6}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 8 | |$174^{+86}_{-61}$| | |$116^{+57}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.6^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 11 | |$154^{+62}_{-46}$| | |$103^{+41}_{-31}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.5^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 11 | |$121^{+49}_{-36}$| | |$82^{+33}_{-24}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.1^{+0.5}_{-0.3}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 11 | |$95^{+38}_{-28}$| | |$64^{+26}_{-19}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.4}_{-0.3}$| | |$0.9^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 14 | |$101^{+35}_{-27}$| | |$68^{+23}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 17 | |$104^{+32}_{-25}$| | |$70^{+21}_{-17}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 18 | |$99^{+29}_{-23}$| | |$67^{+20}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 18 | |$93^{+28}_{-22}$| | |$63^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.8^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 24 | |$110^{+27}_{-22}$| | |$76^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 29 | |$115^{+26}_{-21}$| | |$80^{+18}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 33 | |$112^{+23}_{-19}$| | |$79^{+16}_{-14}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 37 | |$112^{+22}_{-18}$| | |$79^{+15}_{-13}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 1 | |$68^{+157}_{-59}$| | |$47^{+108}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.6^{+1.5}_{-0.6}$| | |$0.6^{+1.5}_{-0.5}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 2 | |$77^{+102}_{-51}$| | |$50^{+67}_{-33}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+1.0}_{-0.5}$| | |$0.7^{+0.9}_{-0.4}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 3 | |$69^{+68}_{-38}$| | |$46^{+45}_{-26}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+0.6}_{-0.4}$| | |$0.6^{+0.6}_{-0.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$175^{+75}_{-55}$| | |$117^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$174^{+74}_{-54}$| | |$116^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 10 | |$151^{+65}_{-47}$| | |$103^{+44}_{-32}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.4^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 11 | |$141^{+57}_{-42}$| | |$95^{+38}_{-28}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.6}_{-0.4}$| | |$1.3^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 12 | |$129^{+49}_{-37}$| | |$88^{+34}_{-25}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.2^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 14 | |$129^{+45}_{-34}$| | |$88^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 16 | |$135^{+43}_{-34}$| | |$93^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 19 | |$127^{+36}_{-29}$| | |$87^{+25}_{-20}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 19 | |$113^{+32}_{-26}$| | |$78^{+22}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 21 | |$109^{+29}_{-24}$| | |$76^{+21}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 29 | |$119^{+26}_{-22}$| | |$84^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$118^{+24}_{-20}$| | |$84^{+17}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.5^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$1.5^{+0.9}_{-0.7}$| | |$1.4^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$79^{+21}_{-17}$| | |$56^{+15}_{-12}$| | |$1.6^{+0.9}_{-0.7}$| | |$1.5^{+0.9}_{-0.6}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$71^{+20}_{-16}$| | |$51^{+14}_{-11}$| | |$1.7^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.7}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$68^{+19}_{-15}$| | |$48^{+14}_{-11}$| | |$1.8^{+1.1}_{-0.8}$| | |$1.7^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$57^{+18}_{-14}$| | |$41^{+13}_{-10}$| | |$2.2^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-0.9}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$46^{+17}_{-13}$| | |$33^{+12}_{-9}$| | |$2.3^{+1.5}_{-1.2}$| | |$2.1^{+1.4}_{-1.1}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{\rm r}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C). (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).
Summary of relevant quantities for our sample of narrow H i (b < 50 km s−1) absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 7 | |$228^{+123}_{-85}$| | |$151^{+82}_{-56}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$2.2^{+1.2}_{-0.8}$| | |$2.0^{+1.1}_{-0.8}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 7 | |$186^{+101}_{-69}$| | |$124^{+67}_{-46}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.8^{+1.0}_{-0.7}$| | |$1.7^{+0.9}_{-0.6}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 8 | |$174^{+86}_{-61}$| | |$116^{+57}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.6^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 11 | |$154^{+62}_{-46}$| | |$103^{+41}_{-31}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.5^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 11 | |$121^{+49}_{-36}$| | |$82^{+33}_{-24}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.1^{+0.5}_{-0.3}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 11 | |$95^{+38}_{-28}$| | |$64^{+26}_{-19}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.4}_{-0.3}$| | |$0.9^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 14 | |$101^{+35}_{-27}$| | |$68^{+23}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 17 | |$104^{+32}_{-25}$| | |$70^{+21}_{-17}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 18 | |$99^{+29}_{-23}$| | |$67^{+20}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 18 | |$93^{+28}_{-22}$| | |$63^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.8^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 24 | |$110^{+27}_{-22}$| | |$76^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 29 | |$115^{+26}_{-21}$| | |$80^{+18}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 33 | |$112^{+23}_{-19}$| | |$79^{+16}_{-14}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 37 | |$112^{+22}_{-18}$| | |$79^{+15}_{-13}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 1 | |$68^{+157}_{-59}$| | |$47^{+108}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.6^{+1.5}_{-0.6}$| | |$0.6^{+1.5}_{-0.5}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 2 | |$77^{+102}_{-51}$| | |$50^{+67}_{-33}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+1.0}_{-0.5}$| | |$0.7^{+0.9}_{-0.4}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 3 | |$69^{+68}_{-38}$| | |$46^{+45}_{-26}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+0.6}_{-0.4}$| | |$0.6^{+0.6}_{-0.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$175^{+75}_{-55}$| | |$117^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$174^{+74}_{-54}$| | |$116^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 10 | |$151^{+65}_{-47}$| | |$103^{+44}_{-32}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.4^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 11 | |$141^{+57}_{-42}$| | |$95^{+38}_{-28}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.6}_{-0.4}$| | |$1.3^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 12 | |$129^{+49}_{-37}$| | |$88^{+34}_{-25}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.2^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 14 | |$129^{+45}_{-34}$| | |$88^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 16 | |$135^{+43}_{-34}$| | |$93^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 19 | |$127^{+36}_{-29}$| | |$87^{+25}_{-20}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 19 | |$113^{+32}_{-26}$| | |$78^{+22}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 21 | |$109^{+29}_{-24}$| | |$76^{+21}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 29 | |$119^{+26}_{-22}$| | |$84^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$118^{+24}_{-20}$| | |$84^{+17}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.5^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$1.5^{+0.9}_{-0.7}$| | |$1.4^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$79^{+21}_{-17}$| | |$56^{+15}_{-12}$| | |$1.6^{+0.9}_{-0.7}$| | |$1.5^{+0.9}_{-0.6}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$71^{+20}_{-16}$| | |$51^{+14}_{-11}$| | |$1.7^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.7}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$68^{+19}_{-15}$| | |$48^{+14}_{-11}$| | |$1.8^{+1.1}_{-0.8}$| | |$1.7^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$57^{+18}_{-14}$| | |$41^{+13}_{-10}$| | |$2.2^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-0.9}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$46^{+17}_{-13}$| | |$33^{+12}_{-9}$| | |$2.3^{+1.5}_{-1.2}$| | |$2.1^{+1.4}_{-1.1}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 7 | |$228^{+123}_{-85}$| | |$151^{+82}_{-56}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$2.2^{+1.2}_{-0.8}$| | |$2.0^{+1.1}_{-0.8}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 7 | |$186^{+101}_{-69}$| | |$124^{+67}_{-46}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.8^{+1.0}_{-0.7}$| | |$1.7^{+0.9}_{-0.6}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 8 | |$174^{+86}_{-61}$| | |$116^{+57}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.6^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 11 | |$154^{+62}_{-46}$| | |$103^{+41}_{-31}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.5^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 11 | |$121^{+49}_{-36}$| | |$82^{+33}_{-24}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.1^{+0.5}_{-0.3}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 11 | |$95^{+38}_{-28}$| | |$64^{+26}_{-19}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.4}_{-0.3}$| | |$0.9^{+0.4}_{-0.3}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 14 | |$101^{+35}_{-27}$| | |$68^{+23}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.3}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 17 | |$104^{+32}_{-25}$| | |$70^{+21}_{-17}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.3}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 18 | |$99^{+29}_{-23}$| | |$67^{+20}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.9^{+0.3}_{-0.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 18 | |$93^{+28}_{-22}$| | |$63^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.9^{+0.3}_{-0.2}$| | |$0.8^{+0.3}_{-0.2}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 24 | |$110^{+27}_{-22}$| | |$76^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 29 | |$115^{+26}_{-21}$| | |$80^{+18}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 33 | |$112^{+23}_{-19}$| | |$79^{+16}_{-14}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 37 | |$112^{+22}_{-18}$| | |$79^{+15}_{-13}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.2}_{-0.2}$| | |$1.1^{+0.2}_{-0.2}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 1 | |$68^{+157}_{-59}$| | |$47^{+108}_{-40}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.6^{+1.5}_{-0.6}$| | |$0.6^{+1.5}_{-0.5}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 2 | |$77^{+102}_{-51}$| | |$50^{+67}_{-33}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+1.0}_{-0.5}$| | |$0.7^{+0.9}_{-0.4}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 3 | |$69^{+68}_{-38}$| | |$46^{+45}_{-26}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$0.7^{+0.6}_{-0.4}$| | |$0.6^{+0.6}_{-0.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 10 | |$179^{+77}_{-56}$| | |$120^{+51}_{-37}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.6}$| | |$1.6^{+0.7}_{-0.5}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$175^{+75}_{-55}$| | |$117^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.7^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$174^{+74}_{-54}$| | |$116^{+50}_{-36}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.6^{+0.7}_{-0.5}$| | |$1.6^{+0.7}_{-0.5}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 10 | |$151^{+65}_{-47}$| | |$103^{+44}_{-32}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.4^{+0.6}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 11 | |$141^{+57}_{-42}$| | |$95^{+38}_{-28}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.6}_{-0.4}$| | |$1.3^{+0.5}_{-0.4}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 12 | |$129^{+49}_{-37}$| | |$88^{+34}_{-25}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.5}_{-0.4}$| | |$1.2^{+0.5}_{-0.4}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 14 | |$129^{+45}_{-34}$| | |$88^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 16 | |$135^{+43}_{-34}$| | |$93^{+30}_{-23}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.3^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 19 | |$127^{+36}_{-29}$| | |$87^{+25}_{-20}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.2^{+0.4}_{-0.3}$| | |$1.2^{+0.4}_{-0.3}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 19 | |$113^{+32}_{-26}$| | |$78^{+22}_{-18}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.3}$| | |$1.1^{+0.3}_{-0.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 21 | |$109^{+29}_{-24}$| | |$76^{+21}_{-16}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.0^{+0.3}_{-0.2}$| | |$1.0^{+0.3}_{-0.2}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 29 | |$119^{+26}_{-22}$| | |$84^{+19}_{-15}$| | |$106^{+23}_{-20}$| | |$75^{+16}_{-14}$| | |$1.1^{+0.3}_{-0.2}$| | |$1.1^{+0.3}_{-0.2}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$122^{+25}_{-21}$| | |$87^{+18}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.6}_{-0.5}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$118^{+24}_{-20}$| | |$84^{+17}_{-15}$| | |$1.5^{+0.7}_{-0.5}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$114^{+24}_{-20}$| | |$82^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 10 | |$176^{+75}_{-55}$| | |$118^{+50}_{-37}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.6^{+0.8}_{-0.6}$| | |$1.5^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$107^{+23}_{-19}$| | |$77^{+17}_{-14}$| | |$1.5^{+0.7}_{-0.6}$| | |$1.4^{+0.7}_{-0.5}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 9 | |$159^{+73}_{-52}$| | |$106^{+48}_{-35}$| | |$104^{+23}_{-19}$| | |$74^{+16}_{-14}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 8 | |$141^{+70}_{-49}$| | |$94^{+47}_{-33}$| | |$96^{+22}_{-18}$| | |$69^{+16}_{-13}$| | |$1.5^{+0.8}_{-0.6}$| | |$1.4^{+0.7}_{-0.6}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$82^{+21}_{-17}$| | |$59^{+15}_{-12}$| | |$1.5^{+0.9}_{-0.7}$| | |$1.4^{+0.8}_{-0.6}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$79^{+21}_{-17}$| | |$56^{+15}_{-12}$| | |$1.6^{+0.9}_{-0.7}$| | |$1.5^{+0.9}_{-0.6}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$71^{+20}_{-16}$| | |$51^{+14}_{-11}$| | |$1.7^{+1.0}_{-0.8}$| | |$1.6^{+1.0}_{-0.7}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$68^{+19}_{-15}$| | |$48^{+14}_{-11}$| | |$1.8^{+1.1}_{-0.8}$| | |$1.7^{+1.0}_{-0.8}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 7 | |$123^{+67}_{-46}$| | |$82^{+44}_{-31}$| | |$57^{+18}_{-14}$| | |$41^{+13}_{-10}$| | |$2.2^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-0.9}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$46^{+17}_{-13}$| | |$33^{+12}_{-9}$| | |$2.3^{+1.5}_{-1.2}$| | |$2.1^{+1.4}_{-1.1}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{\rm r}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C). (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).
Summary of relevant quantities for our sample of broad H i (b ≥ 50 km s−1) absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 4 | |$130^{+103}_{-63}$| | |$86^{+69}_{-42}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.4^{+6.4}_{-4.4}$| | |$7.0^{+6.0}_{-4.1}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 4 | |$106^{+85}_{-52}$| | |$71^{+56}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+5.2}_{-3.6}$| | |$5.7^{+4.9}_{-3.4}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 6 | |$131^{+78}_{-52}$| | |$87^{+52}_{-35}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.5^{+5.1}_{-3.9}$| | |$7.0^{+4.8}_{-3.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 6 | |$84^{+50}_{-33}$| | |$56^{+34}_{-22}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.8^{+3.3}_{-2.5}$| | |$4.5^{+3.1}_{-2.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 6 | |$66^{+40}_{-26}$| | |$44^{+27}_{-18}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.8^{+2.6}_{-2.0}$| | |$3.6^{+2.5}_{-1.9}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 7 | |$61^{+33}_{-23}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.5^{+2.2}_{-1.7}$| | |$3.3^{+2.1}_{-1.7}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 7 | |$50^{+27}_{-19}$| | |$34^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.9^{+1.8}_{-1.4}$| | |$2.7^{+1.7}_{-1.4}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 8 | |$49^{+24}_{-17}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.8^{+1.7}_{-1.3}$| | |$2.6^{+1.6}_{-1.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 8 | |$44^{+22}_{-15}$| | |$30^{+15}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.5^{+1.5}_{-1.2}$| | |$2.4^{+1.4}_{-1.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+20}_{-14}$| | |$28^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 8 | |$37^{+18}_{-13}$| | |$25^{+13}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.1^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-1.0}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 9 | |$36^{+16}_{-12}$| | |$25^{+11}_{-8}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.0^{+1.2}_{-1.0}$| | |$2.0^{+1.1}_{-0.9}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 10 | |$34^{+14}_{-11}$| | |$24^{+10}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.1}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 11 | |$33^{+13}_{-10}$| | |$24^{+9}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.0}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 2 | |$135^{+180}_{-89}$| | |$93^{+124}_{-62}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.7^{+10.6}_{-5.7}$| | |$7.5^{+10.3}_{-5.6}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 4 | |$154^{+122}_{-75}$| | |$100^{+80}_{-48}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$8.8^{+7.6}_{-5.2}$| | |$8.1^{+7.0}_{-4.8}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 5 | |$115^{+78}_{-50}$| | |$77^{+53}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.6^{+5.0}_{-3.6}$| | |$6.3^{+4.7}_{-3.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$105^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.7^{+3.9}_{-3.0}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$104^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.6^{+3.9}_{-2.9}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 6 | |$91^{+54}_{-36}$| | |$62^{+37}_{-25}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$5.2^{+3.6}_{-2.7}$| | |$5.0^{+3.4}_{-2.6}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 6 | |$77^{+46}_{-31}$| | |$52^{+31}_{-21}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.4^{+3.0}_{-2.3}$| | |$4.2^{+2.9}_{-2.2}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 7 | |$76^{+41}_{-28}$| | |$52^{+28}_{-19}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.3^{+2.7}_{-2.2}$| | |$4.2^{+2.7}_{-2.1}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 7 | |$64^{+35}_{-24}$| | |$44^{+24}_{-16}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.7^{+2.3}_{-1.8}$| | |$3.6^{+2.3}_{-1.8}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 7 | |$59^{+32}_{-22}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.4^{+2.1}_{-1.7}$| | |$3.3^{+2.1}_{-1.6}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 8 | |$53^{+26}_{-19}$| | |$37^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.1^{+1.8}_{-1.5}$| | |$3.0^{+1.8}_{-1.4}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 8 | |$47^{+23}_{-16}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.7^{+1.6}_{-1.3}$| | |$2.7^{+1.6}_{-1.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+21}_{-14}$| | |$29^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 10 | |$41^{+18}_{-13}$| | |$29^{+12}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.3^{+1.3}_{-1.1}$| | |$2.3^{+1.3}_{-1.1}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$14^{+11}_{-7}$| | |$10^{+8}_{-5}$| | |$6.2^{+5.8}_{-4.8}$| | |$5.8^{+5.4}_{-4.5}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$8.2^{+8.4}_{-7.3}$| | |$7.7^{+7.9}_{-6.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$6.6^{+7.3}_{-6.0}$| | |$6.1^{+6.8}_{-5.6}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$7^{+9}_{-5}$| | |$5^{+7}_{-3}$| | |$9.9^{+12.6}_{-9.9}$| | |$9.2^{+11.7}_{-9.2}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 4 | |$130^{+103}_{-63}$| | |$86^{+69}_{-42}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.4^{+6.4}_{-4.4}$| | |$7.0^{+6.0}_{-4.1}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 4 | |$106^{+85}_{-52}$| | |$71^{+56}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+5.2}_{-3.6}$| | |$5.7^{+4.9}_{-3.4}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 6 | |$131^{+78}_{-52}$| | |$87^{+52}_{-35}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.5^{+5.1}_{-3.9}$| | |$7.0^{+4.8}_{-3.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 6 | |$84^{+50}_{-33}$| | |$56^{+34}_{-22}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.8^{+3.3}_{-2.5}$| | |$4.5^{+3.1}_{-2.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 6 | |$66^{+40}_{-26}$| | |$44^{+27}_{-18}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.8^{+2.6}_{-2.0}$| | |$3.6^{+2.5}_{-1.9}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 7 | |$61^{+33}_{-23}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.5^{+2.2}_{-1.7}$| | |$3.3^{+2.1}_{-1.7}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 7 | |$50^{+27}_{-19}$| | |$34^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.9^{+1.8}_{-1.4}$| | |$2.7^{+1.7}_{-1.4}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 8 | |$49^{+24}_{-17}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.8^{+1.7}_{-1.3}$| | |$2.6^{+1.6}_{-1.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 8 | |$44^{+22}_{-15}$| | |$30^{+15}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.5^{+1.5}_{-1.2}$| | |$2.4^{+1.4}_{-1.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+20}_{-14}$| | |$28^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 8 | |$37^{+18}_{-13}$| | |$25^{+13}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.1^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-1.0}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 9 | |$36^{+16}_{-12}$| | |$25^{+11}_{-8}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.0^{+1.2}_{-1.0}$| | |$2.0^{+1.1}_{-0.9}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 10 | |$34^{+14}_{-11}$| | |$24^{+10}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.1}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 11 | |$33^{+13}_{-10}$| | |$24^{+9}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.0}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 2 | |$135^{+180}_{-89}$| | |$93^{+124}_{-62}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.7^{+10.6}_{-5.7}$| | |$7.5^{+10.3}_{-5.6}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 4 | |$154^{+122}_{-75}$| | |$100^{+80}_{-48}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$8.8^{+7.6}_{-5.2}$| | |$8.1^{+7.0}_{-4.8}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 5 | |$115^{+78}_{-50}$| | |$77^{+53}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.6^{+5.0}_{-3.6}$| | |$6.3^{+4.7}_{-3.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$105^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.7^{+3.9}_{-3.0}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$104^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.6^{+3.9}_{-2.9}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 6 | |$91^{+54}_{-36}$| | |$62^{+37}_{-25}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$5.2^{+3.6}_{-2.7}$| | |$5.0^{+3.4}_{-2.6}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 6 | |$77^{+46}_{-31}$| | |$52^{+31}_{-21}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.4^{+3.0}_{-2.3}$| | |$4.2^{+2.9}_{-2.2}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 7 | |$76^{+41}_{-28}$| | |$52^{+28}_{-19}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.3^{+2.7}_{-2.2}$| | |$4.2^{+2.7}_{-2.1}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 7 | |$64^{+35}_{-24}$| | |$44^{+24}_{-16}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.7^{+2.3}_{-1.8}$| | |$3.6^{+2.3}_{-1.8}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 7 | |$59^{+32}_{-22}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.4^{+2.1}_{-1.7}$| | |$3.3^{+2.1}_{-1.6}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 8 | |$53^{+26}_{-19}$| | |$37^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.1^{+1.8}_{-1.5}$| | |$3.0^{+1.8}_{-1.4}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 8 | |$47^{+23}_{-16}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.7^{+1.6}_{-1.3}$| | |$2.7^{+1.6}_{-1.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+21}_{-14}$| | |$29^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 10 | |$41^{+18}_{-13}$| | |$29^{+12}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.3^{+1.3}_{-1.1}$| | |$2.3^{+1.3}_{-1.1}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$14^{+11}_{-7}$| | |$10^{+8}_{-5}$| | |$6.2^{+5.8}_{-4.8}$| | |$5.8^{+5.4}_{-4.5}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$8.2^{+8.4}_{-7.3}$| | |$7.7^{+7.9}_{-6.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$6.6^{+7.3}_{-6.0}$| | |$6.1^{+6.8}_{-5.6}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$7^{+9}_{-5}$| | |$5^{+7}_{-3}$| | |$9.9^{+12.6}_{-9.9}$| | |$9.2^{+11.7}_{-9.2}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated with absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C). (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).
Summary of relevant quantities for our sample of broad H i (b ≥ 50 km s−1) absorption lines.
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 4 | |$130^{+103}_{-63}$| | |$86^{+69}_{-42}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.4^{+6.4}_{-4.4}$| | |$7.0^{+6.0}_{-4.1}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 4 | |$106^{+85}_{-52}$| | |$71^{+56}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+5.2}_{-3.6}$| | |$5.7^{+4.9}_{-3.4}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 6 | |$131^{+78}_{-52}$| | |$87^{+52}_{-35}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.5^{+5.1}_{-3.9}$| | |$7.0^{+4.8}_{-3.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 6 | |$84^{+50}_{-33}$| | |$56^{+34}_{-22}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.8^{+3.3}_{-2.5}$| | |$4.5^{+3.1}_{-2.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 6 | |$66^{+40}_{-26}$| | |$44^{+27}_{-18}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.8^{+2.6}_{-2.0}$| | |$3.6^{+2.5}_{-1.9}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 7 | |$61^{+33}_{-23}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.5^{+2.2}_{-1.7}$| | |$3.3^{+2.1}_{-1.7}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 7 | |$50^{+27}_{-19}$| | |$34^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.9^{+1.8}_{-1.4}$| | |$2.7^{+1.7}_{-1.4}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 8 | |$49^{+24}_{-17}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.8^{+1.7}_{-1.3}$| | |$2.6^{+1.6}_{-1.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 8 | |$44^{+22}_{-15}$| | |$30^{+15}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.5^{+1.5}_{-1.2}$| | |$2.4^{+1.4}_{-1.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+20}_{-14}$| | |$28^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 8 | |$37^{+18}_{-13}$| | |$25^{+13}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.1^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-1.0}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 9 | |$36^{+16}_{-12}$| | |$25^{+11}_{-8}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.0^{+1.2}_{-1.0}$| | |$2.0^{+1.1}_{-0.9}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 10 | |$34^{+14}_{-11}$| | |$24^{+10}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.1}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 11 | |$33^{+13}_{-10}$| | |$24^{+9}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.0}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 2 | |$135^{+180}_{-89}$| | |$93^{+124}_{-62}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.7^{+10.6}_{-5.7}$| | |$7.5^{+10.3}_{-5.6}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 4 | |$154^{+122}_{-75}$| | |$100^{+80}_{-48}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$8.8^{+7.6}_{-5.2}$| | |$8.1^{+7.0}_{-4.8}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 5 | |$115^{+78}_{-50}$| | |$77^{+53}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.6^{+5.0}_{-3.6}$| | |$6.3^{+4.7}_{-3.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$105^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.7^{+3.9}_{-3.0}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$104^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.6^{+3.9}_{-2.9}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 6 | |$91^{+54}_{-36}$| | |$62^{+37}_{-25}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$5.2^{+3.6}_{-2.7}$| | |$5.0^{+3.4}_{-2.6}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 6 | |$77^{+46}_{-31}$| | |$52^{+31}_{-21}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.4^{+3.0}_{-2.3}$| | |$4.2^{+2.9}_{-2.2}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 7 | |$76^{+41}_{-28}$| | |$52^{+28}_{-19}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.3^{+2.7}_{-2.2}$| | |$4.2^{+2.7}_{-2.1}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 7 | |$64^{+35}_{-24}$| | |$44^{+24}_{-16}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.7^{+2.3}_{-1.8}$| | |$3.6^{+2.3}_{-1.8}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 7 | |$59^{+32}_{-22}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.4^{+2.1}_{-1.7}$| | |$3.3^{+2.1}_{-1.6}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 8 | |$53^{+26}_{-19}$| | |$37^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.1^{+1.8}_{-1.5}$| | |$3.0^{+1.8}_{-1.4}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 8 | |$47^{+23}_{-16}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.7^{+1.6}_{-1.3}$| | |$2.7^{+1.6}_{-1.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+21}_{-14}$| | |$29^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 10 | |$41^{+18}_{-13}$| | |$29^{+12}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.3^{+1.3}_{-1.1}$| | |$2.3^{+1.3}_{-1.1}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$14^{+11}_{-7}$| | |$10^{+8}_{-5}$| | |$6.2^{+5.8}_{-4.8}$| | |$5.8^{+5.4}_{-4.5}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$8.2^{+8.4}_{-7.3}$| | |$7.7^{+7.9}_{-6.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$6.6^{+7.3}_{-6.0}$| | |$6.1^{+6.8}_{-5.6}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$7^{+9}_{-5}$| | |$5^{+7}_{-3}$| | |$9.9^{+12.6}_{-9.9}$| | |$9.2^{+11.7}_{-9.2}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
| Δd . | Δv . | |$W_{\rm r}^{\rm min}$| . | Δz . | ΔX . | N . | |$\frac{{\rm d}N}{{\rm d}z}$| . | |$\frac{{\rm d}N}{{\rm d}X}$| . | |$\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}z}/\frac{{\rm d}N}{{\rm d}z}|_{\rm field}$| . | |$\frac{{\rm d}N}{{\rm d}X}/\frac{{\rm d}N}{{\rm d}X}|_{\rm field}$| . |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ( Mpc) . | ( km s−1) . | (Å) . | . | . | . | . | . | . | . | . | . |
| (1) . | (2) . | (3) . | (4) . | (5) . | (6) . | (7) . | (8) . | (9) . | (10) . | (11) . | (12) . |
| 3.0 | 500 | 0.04 | 0.03 | 0.05 | 4 | |$130^{+103}_{-63}$| | |$86^{+69}_{-42}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.4^{+6.4}_{-4.4}$| | |$7.0^{+6.0}_{-4.1}$| |
| 3.0 | 630 | 0.04 | 0.04 | 0.06 | 4 | |$106^{+85}_{-52}$| | |$71^{+56}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+5.2}_{-3.6}$| | |$5.7^{+4.9}_{-3.4}$| |
| 3.0 | 794 | 0.04 | 0.05 | 0.07 | 6 | |$131^{+78}_{-52}$| | |$87^{+52}_{-35}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.5^{+5.1}_{-3.9}$| | |$7.0^{+4.8}_{-3.7}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 3.0 | 1313 | 0.04 | 0.07 | 0.11 | 6 | |$84^{+50}_{-33}$| | |$56^{+34}_{-22}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.8^{+3.3}_{-2.5}$| | |$4.5^{+3.1}_{-2.4}$| |
| 3.0 | 1724 | 0.04 | 0.09 | 0.13 | 6 | |$66^{+40}_{-26}$| | |$44^{+27}_{-18}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.8^{+2.6}_{-2.0}$| | |$3.6^{+2.5}_{-1.9}$| |
| 3.0 | 2264 | 0.04 | 0.12 | 0.17 | 7 | |$61^{+33}_{-23}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.5^{+2.2}_{-1.7}$| | |$3.3^{+2.1}_{-1.7}$| |
| 3.0 | 2972 | 0.04 | 0.14 | 0.21 | 7 | |$50^{+27}_{-19}$| | |$34^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.9^{+1.8}_{-1.4}$| | |$2.7^{+1.7}_{-1.4}$| |
| 3.0 | 3903 | 0.04 | 0.16 | 0.24 | 8 | |$49^{+24}_{-17}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.8^{+1.7}_{-1.3}$| | |$2.6^{+1.6}_{-1.3}$| |
| 3.0 | 5125 | 0.04 | 0.18 | 0.27 | 8 | |$44^{+22}_{-15}$| | |$30^{+15}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.5^{+1.5}_{-1.2}$| | |$2.4^{+1.4}_{-1.2}$| |
| 3.0 | 6729 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+20}_{-14}$| | |$28^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 3.0 | 8835 | 0.04 | 0.22 | 0.32 | 8 | |$37^{+18}_{-13}$| | |$25^{+13}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.1^{+1.3}_{-1.0}$| | |$2.0^{+1.2}_{-1.0}$| |
| 3.0 | 11601 | 0.04 | 0.25 | 0.36 | 9 | |$36^{+16}_{-12}$| | |$25^{+11}_{-8}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.0^{+1.2}_{-1.0}$| | |$2.0^{+1.1}_{-0.9}$| |
| 3.0 | 15232 | 0.04 | 0.30 | 0.42 | 10 | |$34^{+14}_{-11}$| | |$24^{+10}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.1}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 3.0 | 20000 | 0.04 | 0.33 | 0.47 | 11 | |$33^{+13}_{-10}$| | |$24^{+9}_{-7}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$1.9^{+1.0}_{-0.9}$| | |$1.9^{+1.0}_{-0.9}$| |
| 1.0 | 1000 | 0.04 | 0.01 | 0.02 | 2 | |$135^{+180}_{-89}$| | |$93^{+124}_{-62}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$7.7^{+10.6}_{-5.7}$| | |$7.5^{+10.3}_{-5.6}$| |
| 1.4 | 1000 | 0.04 | 0.03 | 0.04 | 4 | |$154^{+122}_{-75}$| | |$100^{+80}_{-48}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$8.8^{+7.6}_{-5.2}$| | |$8.1^{+7.0}_{-4.8}$| |
| 2.1 | 1000 | 0.04 | 0.04 | 0.06 | 5 | |$115^{+78}_{-50}$| | |$77^{+53}_{-34}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.6^{+5.0}_{-3.6}$| | |$6.3^{+4.7}_{-3.4}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.08 | 6 | |$108^{+65}_{-43}$| | |$72^{+43}_{-29}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.1^{+4.2}_{-3.2}$| | |$5.8^{+4.0}_{-3.0}$| |
| 4.1 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$105^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.7^{+3.9}_{-3.0}$| |
| 5.7 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$104^{+63}_{-42}$| | |$70^{+42}_{-28}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$6.0^{+4.1}_{-3.1}$| | |$5.6^{+3.9}_{-2.9}$| |
| 7.8 | 1000 | 0.04 | 0.07 | 0.10 | 6 | |$91^{+54}_{-36}$| | |$62^{+37}_{-25}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$5.2^{+3.6}_{-2.7}$| | |$5.0^{+3.4}_{-2.6}$| |
| 10.7 | 1000 | 0.04 | 0.08 | 0.12 | 6 | |$77^{+46}_{-31}$| | |$52^{+31}_{-21}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.4^{+3.0}_{-2.3}$| | |$4.2^{+2.9}_{-2.2}$| |
| 14.8 | 1000 | 0.04 | 0.09 | 0.14 | 7 | |$76^{+41}_{-28}$| | |$52^{+28}_{-19}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$4.3^{+2.7}_{-2.2}$| | |$4.2^{+2.7}_{-2.1}$| |
| 20.3 | 1000 | 0.04 | 0.11 | 0.16 | 7 | |$64^{+35}_{-24}$| | |$44^{+24}_{-16}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.7^{+2.3}_{-1.8}$| | |$3.6^{+2.3}_{-1.8}$| |
| 27.9 | 1000 | 0.04 | 0.12 | 0.17 | 7 | |$59^{+32}_{-22}$| | |$41^{+22}_{-15}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.4^{+2.1}_{-1.7}$| | |$3.3^{+2.1}_{-1.6}$| |
| 38.4 | 1000 | 0.04 | 0.15 | 0.22 | 8 | |$53^{+26}_{-19}$| | |$37^{+18}_{-13}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$3.1^{+1.8}_{-1.5}$| | |$3.0^{+1.8}_{-1.4}$| |
| 52.9 | 1000 | 0.04 | 0.17 | 0.24 | 8 | |$47^{+23}_{-16}$| | |$33^{+16}_{-11}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.7^{+1.6}_{-1.3}$| | |$2.7^{+1.6}_{-1.3}$| |
| 72.7 | 1000 | 0.04 | 0.19 | 0.28 | 8 | |$41^{+21}_{-14}$| | |$29^{+14}_{-10}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.4^{+1.4}_{-1.1}$| | |$2.3^{+1.4}_{-1.1}$| |
| 100.0 | 1000 | 0.04 | 0.24 | 0.35 | 10 | |$41^{+18}_{-13}$| | |$29^{+12}_{-9}$| | |$18^{+13}_{-10}$| | |$12^{+9}_{-7}$| | |$2.3^{+1.3}_{-1.1}$| | |$2.3^{+1.3}_{-1.1}$| |
| 3.0 | 1000 | 0.03 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.04 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.05 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.06 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.07 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.08 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.09 | 0.06 | 0.09 | 6 | |$106^{+63}_{-42}$| | |$71^{+42}_{-28}$| | |$18^{+12}_{-8}$| | |$13^{+9}_{-6}$| | |$5.9^{+4.9}_{-4.1}$| | |$5.5^{+4.5}_{-3.8}$| |
| 3.0 | 1000 | 0.10 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$14^{+11}_{-7}$| | |$10^{+8}_{-5}$| | |$6.2^{+5.8}_{-4.8}$| | |$5.8^{+5.4}_{-4.5}$| |
| 3.0 | 1000 | 0.11 | 0.06 | 0.09 | 5 | |$88^{+60}_{-38}$| | |$59^{+40}_{-26}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$8.2^{+8.4}_{-7.3}$| | |$7.7^{+7.9}_{-6.8}$| |
| 3.0 | 1000 | 0.12 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$11^{+10}_{-6}$| | |$8^{+7}_{-4}$| | |$6.6^{+7.3}_{-6.0}$| | |$6.1^{+6.8}_{-5.6}$| |
| 3.0 | 1000 | 0.14 | 0.06 | 0.09 | 4 | |$71^{+56}_{-34}$| | |$47^{+37}_{-23}$| | |$7^{+9}_{-5}$| | |$5^{+7}_{-3}$| | |$9.9^{+12.6}_{-9.9}$| | |$9.2^{+11.7}_{-9.2}$| |
| 3.0 | 1000 | 0.16 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
| 3.0 | 1000 | 0.18 | 0.06 | 0.09 | 2 | |$35^{+47}_{-23}$| | |$24^{+31}_{-16}$| | |$4^{+8}_{-3}$| | |$3^{+6}_{-2}$| | |$9.9^{+20.5}_{-9.9}$| | |$9.2^{+19.1}_{-9.2}$| |
Notes. (1) Maximum transverse separation between cluster-pair axes and the Q1410 sightline (see Section 5.1). (2) Maximum velocity difference to any cluster pair within Δd from the Q1410 sightline (see Section 5.1). (3) Minimum rest-frame equivalent width (see Section 5.1). (4) Redshift path (see Section 5.1 and Appendix C). (5) Absorption distance (see Appendix C). (6) Total number of absorption components having |$W_{\rm r} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (7) Redshift number density associated with absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (see Section 5.1). (8) Absorption distance number density to absorption components having |$W_{{\rm r}} \ge W^{\rm min}_{{\rm r}}$| within Δd and Δv from cluster pairs (analogous to dN/dz but see also Appendix C). (9) Field expectation for the redshift number density (see Section 5.2). (10) Field expectation for the absorption distance number density (see Section 5.2). (11) Excess of the measured redshift number density compared to the field expectation (see Section 6.2). (12) Excess of the measured absorption distance number density compared to the field expectation (see Section 6.2).



