Stable, levitating, optically thin atmospheres of Eddington-luminosity neutron stars

Wielgus, M.; Kluźniak, W.; Sa̧dowski, A.; Narayan, R.; Abramowicz, M.

doi:10.1093/mnras/stv2191

Abstract

In general relativity, static gaseous atmospheres may be in hydrostatic balance in the absence of a supporting stellar surface, provided that the luminosity is close to the Eddington value. We construct analytic models of optically thin, spherically symmetric shells supported by the radiation pressure of a luminous central body in the Schwarzschild metric. Opacity is assumed to be dominated by Thomson scattering. The inner parts of the atmospheres, where the luminosity locally has supercritical values, are characterized by a density and pressure inversion. The atmospheres are convectively and Rayleigh–Taylor stable, and there is no outflow of gas.

gravitation, relativistic processes, stars: atmospheres, stars: neutron

INTRODUCTION

Several systems with super-Eddington luminosity have been reported (e.g. McClintock & Remillard 2006), the ‘LMC transient’ A0535-668 (Bradt & McClintock 1983) being oft discussed. Recently, interest in very luminous neutron stars has been revived with the discovery of a clear example of a neutron star with super-Eddington flux in the guise of the ultraluminous 1.37 s pulsar NuSTAR J095551+6940.8 in the nearby galaxy M82 (Bachetti et al. 2014). It is clear that for some accreting neutron stars, radiation pressure may exceed the pull of gravity close to their surface (at least in a certain solid angle if the radiation is beamed).

In this paper, we report the presence of a new type of atmospheric solutions in general relativity (GR) for neutron stars radiating at nearly Eddington luminosities. These solutions are qualitatively different from the ones obtained in Newtonian physics. In the classical solutions, the atmospheric density increases monotonically as the stellar surface is approached, and this remains true in previously obtained atmospheric solutions in GR (e.g. Paczynski & Anderson 1986), where the atmospheres in question have always been supported at their base by the stellar surface. Here, we report solutions in which the atmosphere has the form of a shell suspended above the stellar surface. The maximum of pressure is attained on a surface enclosing a volume in which the star is contained (together with some space around it), and the atmospheric density and pressure drop precipitously on both sides of that surface, i.e. in the radial direction away from the star (as is usually the case), but also in the radial direction towards the star.

This paper discusses the simplest case of optically thin, spherically symmetric atmospheres in the Schwarzschild metric, which admit of analytic solutions. Optically thick atmospheres require numerical treatment of radiative transfer, and these will be reported elsewhere (Wielgus et al., in preparation).

We consider atmospheres consisting of pure ionized hydrogen. All the results are given for the Schwarzschild space–time. The luminosity of the star will be parametrized by the ratio of the luminosity observed at infinity to the Eddington luminosity,

\begin{equation} \lambda =L_\infty /L_{\text{Edd}}, \end{equation}

(1)

with the standard expression for the latter, |$L_{\text{Edd}} = {4 \pi GM m_{\rm p}c }/{\sigma _{\text{T}}}$|⁠. The stellar radius will be denoted by R_*, it is taken to correspond to a canonical neutron star, e.g. R_* ≈ 5 GM/c², with M ≈ 1.4 M_⊙ being the stellar mass.

BALANCE BETWEEN GRAVITY AND RADIATION PRESSURE

In the Schwarzschild metric, the stellar luminosity (which we take to be constant in time), as measured by a local observer at radius r, declines with the radial coordinate distance r as

\begin{equation} L(r)=L_\infty \left(1-\frac{2GM}{rc^2}\right)^{-1}, \end{equation}

(2)

and a static balance between gravity and radiation pressure owing to Thomson scattering can only be achieved at one radius, at which

\begin{equation} L(r)=L_{\text{Edd}}(1- R_{\text{S}}/r)^{-1/2}, \end{equation}

(3)

where R_S = 2GM/c² is the Schwarzschild radius (e.g. Phinney 1987; Stahl et al. 2013). That radius can be written as

\begin{equation} r= R_{\text{S}}/\left(1-\lambda ^2\right) \equiv R_{\text{ECS}}. \end{equation}

(4)

The sphere at R_ECS has been called the Eddington capture sphere (ECS) by Stahl et al. (2012). These results have been derived rigorously within the mathematical formalism of Einstein's GR, and they can be intuitively understood in terms of the different dependence on redshift of the luminosity and of the ‘gravitational’ acceleration. Equation (2) reflects the dependence of luminosity at infinity on two redshift factors (1 + z)⁻¹, one for the energy of the photons, and one for the rate of their arrival. However, the acceleration of a static observer in the Schwarzschild metric scales with only one factor of (1 + z), where the redshift is defined by

\begin{equation} 1+ z(r) =(1- R_{\text{S}}/r)^{-1/2}. \end{equation}

(5)

Hence, the condition for local balance between acceleration and the momentum flux of photons (multiplied by the Thomson opacity) is given by equation (3), and contains one factor of (1 + z), which introduces into the balance condition a dependence on the radial coordinate. This is in contrast with Newtonian gravity (which can formally be recovered in the limit R_S → 0, or z → 0), where the balance condition has no radial dependence, and therefore is either satisfied, or not satisfied, equally at all distances from the source.

Numerous authors have shown that test particles initially orbiting the star (at various radii) may settle on the spherical surface at r = R_ECS > R_*, provided that

\begin{equation} (1- R_{\text{S}}/R_*)^{1/2}<\lambda <1, \end{equation}

(6)

their angular momentum having been removed by radiation drag (Bini, Jantzen & Stella 2009; Sok Oh, Kim & Mok Lee 2011; Stahl et al. 2012; Mishra & Kluźniak 2014). In fact, any point on the ECS is a position of stable equilibrium in the radial direction (Abramowicz, Ellis & Lanza 1990), and neutral equilibrium in directions tangent to the ECS surface (Stahl et al. 2012). Note that the redshift z(r) attains the following value on the ECS,

\begin{equation} z_{\text{ECS}}\equiv z(R_{\text{ECS}})=1/\lambda -1. \end{equation}

(7)

We now take the step of replacing test particles on the ECS with a fluid. For simplicity, let us assume¹ that the fluid is optically thin. This will allow us to decouple the temperature of the fluid from the radiation field and to find analytic solutions of the atmospheric structure. It is clear that the condition of hydrostatic equilibrium will be achieved if the pressure gradient is in the radial direction and its magnitude compensates the imbalance between radiation pressure and gravity. In particular, the pressure must reach a maximum value at r = R_ECS, and must decrease in both directions, towards and away from the star, as the distance to the ECS grows and so does with it the imbalance between radiation pressure and gravity.

For atmospheric temperatures of no more than a few keV, we can safely assume that the energy density of the fluid is given by its baryon rest mass energy density ρc². In other words, one can neglect the contribution of pressure p and the internal energy ϵ to the energy density, ρc² ≫ p + ϵ. The equation of hydrostatic equilibrium then becomes

\begin{equation} \frac{1}{\rho } \frac{\text{d} p}{\text{d} r} = - \frac{GM}{r^2\left(1-{R_{\text{S}}}/{r}\right)} \left[1 - {\lambda }{\left(1-\frac{R_{\text{S}}}{r}\right)^{-1/2}}\right] \ \text{,} \end{equation}

(8)

where the last term reflects the radiation force owing to Thomson scattering, with the luminosity of the star scaled by the Eddington luminosity per equation (1). In the limit R_S/r → 0 one recovers the classical Eddington balance at λ = 1, while in general the pressure gradient vanishes for r = R_ECS, cf. equation (4).

Equation (8) is readily solved for a polytropic or an isothermal atmosphere, as it can be integrated over the redshift to yield

\begin{equation} \int \frac{\text{d} p}{\rho c^2} = \ln (1 + z) - \lambda z. \end{equation}

(9)

For an ideal gas equation of state, p = ρk_BT/(μm_p) with k_B the Boltzmann constant, m_p the proton mass, and μ = 1/2 the mean molecular weight, we obtain the following analytic solutions.

ISOTHERMAL ATMOSPHERE

For an isothermal atmosphere at temperature T, the integral in equation (9) yields

\begin{equation} \frac{k_{\rm B}T}{\mu m_{\rm p}c^2} \ln \left(\frac{\rho }{\rho _0}\right) =\ln (1 + z) - \lambda z. \end{equation}

(10)

with z defined in equation (5). In the GR case, the maximum value of density is attained at the ECS, assuming a luminosity in the range given by equation (6), and the density can be taken to be proportional to this maximum value ρ_max = ρ(z_ECS),

\begin{eqnarray} \rho (z) &=& \rho _{\max}\times [\lambda (1 + z)]^{(\mu m_{\rm p}c^2)/(k_{\rm B}T)}\nonumber \\ && \times \exp \left\lbrace [ 1- \lambda (1 + z)]{(\mu m_{\rm p}c^2)/(k_{\rm B}T)}\right\rbrace . \end{eqnarray}

(11)

Thus, as expected, the density decreases in both directions away from the ECS, giving the atmosphere a shell-like form. The same result, given as a function of the radius, is

\begin{eqnarray} \rho (r) &=& \rho _{\max}\times [\lambda (1-R_{{\rm S}}/r)^{-1/2}]^{(\mu m_{\rm p}c^2)/(k_{\rm B}T)} \nonumber \\ &&\times \exp \left\lbrace [ 1- \lambda (1-R_{{\rm S}}/r)^{-1/2}]{(\mu m_{\rm p}c^2)/(k_{\rm B}T)}\right\rbrace . \end{eqnarray}

(12)

However, far from the star this solution is unphysical, as the mass in an isothermal atmosphere would be infinite—note that at z = 0, i.e. as r → ∞, the density tends to a finite value, |$\rho \rightarrow \rho _\infty \equiv \rho _{\max}\times [\lambda \exp {(1- \lambda )}]^{(\mu m_{\rm p}c^2)/(k_{\rm B}T)}$|⁠.

The Newtonian Eddington limit is recovered with a different normalization from the one in equations (11)–(12). To first order in z, from any of the three equations (10)–(12) one gets, ρ(r) = ρ_∞ × exp [μm_pGM(1 − λ)/(k_BTr)]. The classical Eddington limit, dp/dr = 0, or ρ = const for an isothermal atmosphere, is now obtained for λ = 1, while the Newtonian limit of an exponentially decaying atmosphere holds for |r − r₀| ≪ r₀

\begin{equation} \rho (r) \approx \rho _0 \exp \left[-\frac{\mu m_{\rm p}}{k_{\rm B}T}\frac{GM(1-\lambda )}{r_0^2}(r-r_0)\right], \end{equation}

(13)

with arbitrary constants ρ₀ and r₀ of dimension density and length, respectively.

Although we have assumed Thomson scattering, this is not strictly necessary. In fact, all the above considerations in Section 3, as well as equation (4), remain valid if we replace the Thomson value, σ_T, of the photon electron scattering cross-section by a more general cross-section σ(T), e.g. the Klein–Nishina formula, provided that we make the substitution λ → λ₁ = λa₁, with a₁ = σ(T)/σ_T.

We stress once again that unlike the decaying atmosphere of the Newtonian limit in equation (13), the GR solution in equations (10)–(12) is not monotonically decreasing with radius everywhere, but instead is monotonically increasing for r < R_ECS up to the maximum on the ECS, and is only monotonically decreasing for r > R_ECS, as illustrated in Fig. 1.

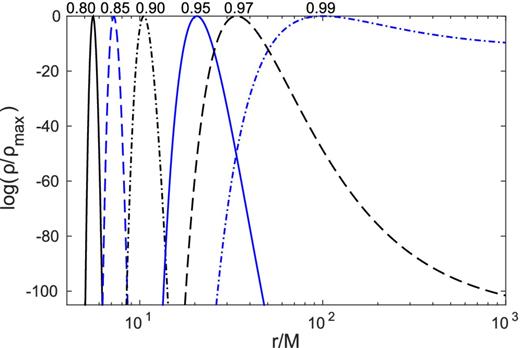
Density profiles for the isothermal solutions with T = 107 K. Each curve corresponds to a different value of the luminosity parameter: λ = 0.8, 0.85, 0.9, 0.95, 0.97, 0.99 from left- to right-hand (as labelled at the maxima).

Figure 1.

Density profiles for the isothermal solutions with T = 10⁷ K. Each curve corresponds to a different value of the luminosity parameter: λ = 0.8, 0.85, 0.9, 0.95, 0.97, 0.99 from left- to right-hand (as labelled at the maxima).

Open in new tab Download slide

POLYTROPIC ATMOSPHERE

For a polytrope, |$p=K\rho ^\Gamma$|⁠, the specific enthalpy w = (p/ρ)Γ/(Γ − 1) following from equation (8) or equation (9) is

\begin{equation} w(z)=w_{{\rm ECS}} + c^2\left\lbrace \ln \left[\lambda (1 + z) \right] - \lambda (1 + z) +1\right\rbrace \end{equation}

(14)

and it attains its maximum value, w_ECS = w(z_ECS), at r = R_ECS, see equation (7).

Making use of the ideal gas equation of state we obtain a corresponding solution for the temperature

\begin{eqnarray} T(r) - T_{\max} &=& - \left(\frac{\Gamma -1}{\Gamma }\frac{\mu m_{\rm p}c^2}{k_{\rm B}}\right) \bigg\lbrace \frac{\lambda }{(1-{R_{{\rm S}}}/{r})^{1/2}} \nonumber\\ & & - \ln \left[ \frac{\lambda }{(1-R_{{\rm S}}/r)^{1/2}} \right] - 1 \bigg\rbrace , \end{eqnarray}

(15)

also attaining its maximum value on the ECS. Note that for any given value of the luminosity, λ, the temperature falls of on both sides of the ECS in a universal way (Fig. 2) independently of the value of the maximum temperature T_max, which is just an additive constant in equation (15). Of course the temperature cannot go to negative values, so the plot must be cut off at T − T_max = −T_max. Fig. 2 corresponds to T_max = 10⁹ K, i.e. a hot ∼100 keV corona.

Figure 2.

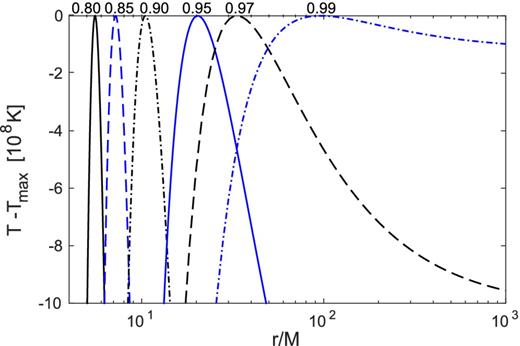
Temperature profiles for the polytropic solutions. Each curve corresponds to a different value of the luminosity parameter: λ = 0.8, 0.85, 0.9, 0.95, 0.97, 0.99 from left- to right-hand. Note that the temperature difference on the y-axis is in units of 10⁸ K.

Open in new tab Download slide

The density scales with its arbitrary value at the ECS, ρ_max ≡ ρ(R_ECS), which is proportional to the total mass of the atmosphere:

\begin{equation} \rho (r) = \rho _0\left[\ln (1-R_{{\rm S}}/r)^{-1/2} -\lambda (1-R_{{\rm S}}/r)^{-1/2} +\lambda \right]^\frac{1}{\Gamma -1}, \end{equation}

(16)

with ρ(R_ECS) = ρ₀[λ − ln λ − 1]^1/(Γ−1).

This being a polytrope, the atmosphere has a sharp edge, the enthalpy, temperature and density vanishing at the top of the atmosphere. In fact, when the condition of equation (6) is satisfied, there are two ‘tops’ of the atmosphere (Figs 3 and 4), one at r₊ > R_ECS, with z₊ ≡ z(r₊) < z_ECS, and one at r₋ < R_ECS, with z₋ ≡ z(r₋) > z_ECS. The redshift at the top of the atmosphere is given by the condition

\begin{equation} \left\lbrace \ln \left[\lambda (1 + z_\pm ) \right] - \lambda (1 + z_\pm ) +1\right\rbrace =-w_{{\rm ECS}}/ c^2. \end{equation}

(17)

For maximum temperatures not much larger than a few keV, the atmospheric profile is quite symmetric with respect to the sign of r − R_ECS (Figs 3 and 4), and the height of the atmosphere is proportional to the speed of sound at its ‘base’, |$c_{\rm s}=\sqrt{(\Gamma -1)w_{{\rm ECS}}}$|⁠.

Figure 3.

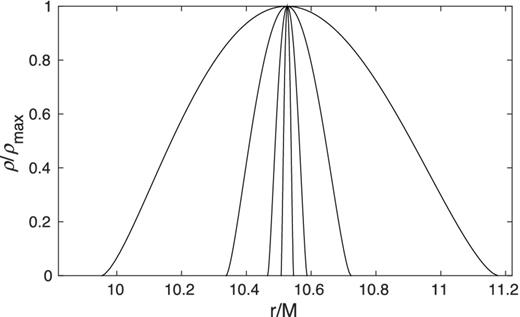
Density profiles of polytropic Thomson-scattering atmospheres for λ = 0.9. For a luminosity this large, the atmosphere is well separated from the neutron star surface (at R_*/M ≈ 5). Temperatures from outside in (more extended atmospheres to less extended atmospheres) are T_max = 5 × 10⁷ K, 5 × 10⁶ K, 5 × 10⁵ K, 5 × 10⁴ K, respectively, with μ = 1/2 and Γ = 5/3 in all cases. The density maxima are at R_ECS = 10.5 GM/c².

Open in new tab Download slide

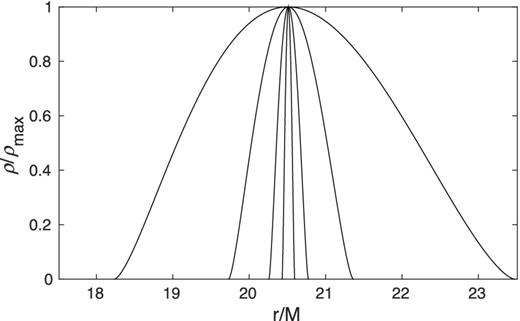
Same as Fig. 3, but for λ = 0.95. The density maxima are at RECS = 20.5 GM/c2.

Figure 4.

Same as Fig. 3, but for λ = 0.95. The density maxima are at R_ECS = 20.5 GM/c².

Open in new tab Download slide

Indeed, for H ≡ |r_± − R_ECS| ≪ R_ECS,

\begin{equation} \frac{H}{R_{{\rm ECS}}}={\frac{\sqrt{2}\lambda ^2}{\sqrt{\Gamma -1}}} \frac{c_{\rm s}c}{v_{{\rm K}}^2}, \end{equation}

(18)

where |$v_{{\rm K}}=\sqrt{GM/R_{{\rm ECS}}}$| is the Keplerian orbital velocity at the ECS. This is reminiscent of the result for accretion discs, where H/r ≈ c_s/v_K (Shakura & Sunyaev 1973); however, the ECS atmospheres are more extended, H here being enhanced by a factor of c/v_K. In terms of the temperature at the base of the atmospheric shell, this reads

\begin{equation} \frac{H}{R_{{\rm ECS}}}= \frac{2\lambda ^2}{1-\lambda ^2}\left({\frac{2\Gamma }{\Gamma -1}}\right)^{1/2} \left(\frac{k_BT_{\max}}{\mu m_{\rm p}c^2}\right)^{1/2}. \end{equation}

(19)

For k_BT_max = 2 keV, and L_∞ ≈ L_Edd the shell thickness works out to be H ≈ 2 × 10⁻³(1 − λ)⁻²R_S. For a neutron star this gives H ≈ 10(1 − λ)⁻² m, i.e. H = 1 km for λ = 0.9, and H = 4 km for λ = 0.95. One can see that as the luminosity increases, the thickness of the levitating atmospheric shell increases more quickly than the radius of the ECS.

DISCUSSION

We have shown that luminous compact stars (e.g. neutron stars) in Einstein's GR may have atmospheres which are detached from the surface. This may have applications to astrophysical phenomena of those compact objects in which the luminosity is close to its Eddington value, either on a quasi-permanent basis or in a transient state. The former case includes highly luminous neutron stars accreting matter from low-mass stellar companions, such as the Z-sources (which include the brightest X-ray source in the sky, Sco X-1). One would expect quasi-spherical coronae in such sources to be described by our solutions with implications for the hard X-ray spectra in these sources, and possibly also for their quasi-periodic modulations. The latter include X-ray bursts, some of which exhibit the phenomenon of radius expansion (e.g. Strohmayer & Bildsten 2006). However, here we have only considered optically thin atmospheric shells, whereas the atmospheres of X-ray bursters are optically thick. For this reason, we are postponing a detailed discussion of bursters to another paper, where optically thick solutions will be reported (Wielgus et al., in preparation).

The atmospheres presented here can be thought of as an (extreme) example of density and pressure inversion. Atmospheric density inversion owing to variations of opacity has been discussed previously in various contexts. In stellar structure theory discussion of density inversion goes back to Chandrasekhar (1936), see also Sen (1941). In contemporary papers, such layers are often invoked in the context of wind loss² and stellar pulsations (e.g. Townsend & MacDonald 2006).

The possibility of gas pressure inversion was pointed out by Erika Böhm-Vitense, and explained as a result of a change of sign in the effective gravitational acceleration, g_eff, with g_eff being the difference between the true acceleration of gravity and the acceleration owing to radiative forces, which are proportional to the product of opacity and the radiative flux (Böhm-Vitense 1958). This is indeed the cause of the pressure inversion in the atmospheres presented in our paper. However, there are several important differences between the results obtained previously and those reported in this work.

First, the inversion layers familiar from stellar structure theory are caused by variations of opacity, while our results are of a different origin – the (Thomson) opacity in our solutions is uniform, and the density (and pressure) inversion arises solely owing to effects of GR. More generally, its presence is related to purely geometrical effects that allow the radiative flux to have a different functional dependence on the distance from the source than the acceleration of gravity.

Secondly, we are presenting optically thin atmospheres, whereas the stellar discussion occurred for optical depths greater than unity.

Thirdly, in the optically thick case considered by Joss, Salpeter & Ostriker (1973) density inversion occurs in regions where the luminosity is near-Eddington (although still subcritical), the pressure is dominated by radiation, and the temperature gradient is superadiabatic. While the atmospheres discussed in our paper do require near-Eddington luminosities, none of the other conditions is met. Density inversion occurs only in the region of supercritical luminosity, the radiation pressure is zero, as the radiation freely streams through the optically thin gas, and the temperature gradient is subadiabatic for the isothermal atmosphere, of course, as well as for polytropic atmospheres with Γ < 5/3. Gas-pressure inversion occurs at supercritical luminosities. The region of pressure inversion coincides with that of density inversion in the optically thin atmospheres presented here.

Fourthly, Joss et al. (1973), in their discussion of optically thick inversion layers in hydrostatic equilibrium, referring to the work of Lucy & Solomon (1970) observe that their own ‘results do not alter the well-known conclusion that mass-outflow from the surface must result if |$L>L^{\rm s}_{\rm crit}$|⁠, where L and |$L^{\rm s}_{\rm crit}$| are the photospheric values’ of luminosity and its critical value. We note that our atmospheric solutions do ‘alter the well-known conclusion’, as the levitating atmospheric shell is in hydrostatic equilibrium even though L > L_Edd in (a part of) the optically thin shell, i.e. the luminosity is supercritical above the photosphere of the underlying luminous star. This is possible because Lucy & Solomon (1970) used Newtonian gravity while our solutions are valid in GR.

We conclude with a brief discussion of stability. The atmospheres presented in this paper are convectively stable, as shown by the appropriate Schwarzschild criterion, in the isothermal case and for polytropes with Γ < 5/3. This result can be intuitively understood by realizing that by the law of Archimedes a hot parcel of gas is initially accelerated in the direction opposite to the gradient of pressure, hence the pressure-inversion layer is as stable as the layer of radially decreasing pressure. A polytropic atmosphere with Γ = 5/3 is marginally stable to convection. The atmospheres are also Rayleigh–Taylor stable as the denser layers are always ‘below’ (in the sense of the direction of effective gravity) the less-dense layers. Investigation of the normal modes of the atmospheres will be presented elsewhere. Here, we only note that (as shown by Abarca & Kluźniak 2015) the radiation drag efficiently damps oscillatory motion in a class of fundamental modes, just as it does the radial and azimuthal motion of test particles (Stahl et al. 2012).

It is a pleasure to thank Lars Bildsten for a discussion on density inversion. We thank the anonymous referee for the very helpful comments. This research was supported in part by the Polish NCN grant UMO-2013/08/A/ST9/00795.

1

The optically thick case will be treated in a separate paper (Wielgus et al., in preparation).

2

In LBV and hypergiant stars ‘the most striking propert[y] is the strong density inversion in the outer layers, where a thin gaseous layer floats upon a radiatively supported zone. This is due to the peak in the opacity which forces supra-Eddington luminosities in some layers.’ (Chiosi 1998)

REFERENCES

Abramowicz

M. A.

Ellis

G. F. R.

Lanza

A.

1990

ApJ

361

470

Crossref

Search ADS

Bachetti

M.

et al.

2014

Nature

514

202

Crossref

Search ADS

PubMed

Bini

D.

Jantzen

R. T.

Stella

L.

2009

Class. Quantum Gravity

26

055009

Crossref

Search ADS

Böhm-Vitense

E.

1958

Z. Astrophys.

46

108

Bradt

H. V. D.

McClintock

J. E.

1983

ARA&A

21

13

Crossref

Search ADS

Chandrasekhar

S.

1936

MNRAS

97

132

Crossref

Search ADS

Chiosi

C.

1998

Aparicio

A.

Herrero

A.

Sánchez

F.

Stellar Astrophysics for the Local Group – VIII – Canary Islands Winter School of Astrophysics

Cambridge Univ. Press

Cambridge

1

Google Scholar

Joss

P. C.

Salpeter

E. E.

Ostriker

J. P.

1973

ApJ

181

429

Crossref

Search ADS

Lucy

L. B.

Solomon

P. M.

1970

ApJ

159

879

Crossref

Search ADS

McClintock

J. E.

Remillard

R. A.

2006

Lewin

W. H. G.

van der Klis

M.

Compact stellar X-ray sources

Cambridge Univ. Press

Cambridge

157

Google Scholar

Mishra

B.

Kluźniak

W.

2014

A&A

566

A62

Crossref

Search ADS

Paczynski

B.

Anderson

N.

1986

ApJ

302

1

Crossref

Search ADS

Phinney

E. S.

1987

Zensus

J. A.

Pearson

T. J.

Superluminal Radio Sources

Cambridge Univ. Press

Cambridge

301

Google Scholar

Sen

N.

1941

Natl. Acad. Sci. India

7

183

Shakura

N. I.

Sunyaev

R. A.

1973

A&A

24

337

Sok

Oh J.

Kim

H.

Mok Lee

H.

2011

New Astron.

16

183

Crossref

Search ADS

Stahl

A.

Wielgus

M.

Abramowicz

M.

Kluźniak

W.

Yu

W.

2012

A&A

546

A54

Crossref

Search ADS

Stahl

A.

Kluźniak

W.

Wielgus

M.

Abramowicz

M.

2013

A&A

555

A114

Crossref

Search ADS

Strohmayer

T.

Bildsten

L.

2006

Lewin

W. H. G.

van der Klis

M.

Compact stellar X-ray sources

Cambridge Univ. Press

Cambridge

113

Google Scholar

Townsend

R. H. D.

MacDonald

J.

2006

MNRAS

368

L57

Crossref

Search ADS

Download all slides

Month:	Total Views:
January 2017	2
February 2017	3
March 2017	3
April 2017	1
May 2017	7
June 2017	4
August 2017	2
October 2017	2
November 2017	3
February 2018	5
March 2018	2
April 2018	2
May 2018	2
June 2018	2
July 2018	2
August 2018	2
September 2018	1
October 2018	2
December 2018	3
January 2019	3
February 2019	6
March 2019	11
April 2019	9
May 2019	5
June 2019	7
July 2019	10
August 2019	2
October 2019	8
November 2019	10
December 2019	8
January 2020	5
February 2020	3
March 2020	3
April 2020	8
May 2020	2
June 2020	6
July 2020	6
August 2020	10
September 2020	4
November 2020	2
December 2020	3
January 2021	4
February 2021	1
March 2021	6
April 2021	5
May 2021	1
June 2021	1
July 2021	6
August 2021	6
September 2021	10
October 2021	3
November 2021	5
December 2021	2
January 2022	1
February 2022	1
March 2022	4
April 2022	3
May 2022	2
June 2022	2
July 2022	6
August 2022	10
September 2022	4
October 2022	2
November 2022	1
December 2022	2
January 2023	3
February 2023	4
March 2023	1
April 2023	2
May 2023	1
June 2023	2
July 2023	3
August 2023	3
September 2023	1
October 2023	1
November 2023	2
December 2023	8
January 2024	6
February 2024	4
March 2024	4
April 2024	5
May 2024	5
June 2024	8
July 2024	8
August 2024	4
September 2024	7
October 2024	7
November 2024	2
December 2024	1
January 2025	10
February 2025	4
March 2025	10
April 2025	15
May 2025	2

Article Contents

Stable, levitating, optically thin atmospheres of Eddington-luminosity neutron stars

Abstract

INTRODUCTION

BALANCE BETWEEN GRAVITY AND RADIATION PRESSURE

ISOTHERMAL ATMOSPHERE

POLYTROPIC ATMOSPHERE

DISCUSSION

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Stable, levitating, optically thin atmospheres of Eddington-luminosity neutron stars

Abstract

INTRODUCTION

BALANCE BETWEEN GRAVITY AND RADIATION PRESSURE

ISOTHERMAL ATMOSPHERE

POLYTROPIC ATMOSPHERE

DISCUSSION

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only