On the magnetic fields of Be/X-ray pulsars in the Small Magellanic Cloud

Ikhsanov, N. R.; Mereghetti, S.

doi:10.1093/mnras/stv2108

Abstract

We explore the possibility of explaining the properties of the Be/X-ray pulsars observed in the Small Magellanic Cloud (SMC) within the magnetic levitation accretion scenario. This implies that their X-ray emission is powered by a wind-fed accretion on to a neutron star (NS) which captures matter from a magnetized stellar wind. The NS in this case is accreting matter from a non-Keplerian magnetically levitating disc which is surrounding its magnetosphere. This allows us to explain the observed periods of the pulsars in terms of spin equilibrium without the need of invoking dipole magnetic fields outside the usual range ∼10¹¹–10¹³ G inferred from cyclotron features of Galactic high-mass X-ray binaries. We find that the equilibrium period of a NS, under certain conditions, depends strongly on the magnetization of the stellar wind of its massive companion and, correspondingly, on the magnetic field of the massive companion itself. This may help to explain why similar NSs in binaries with similar properties rotate with different periods yielding a large scatter of periods of the accretion-powered pulsar observed in SMC and our galaxy.

accretion, accretion discs, pulsars: general, stars: winds, outflows, X-rays: binaries

INTRODUCTION

The Small Magellanic Cloud (SMC) contains a large number of accreting pulsars in high-mass X-ray binaries (HMXBs). These sources, being at a well-known, virtually uniform distance and with small interstellar absorption, constitute an ideal sample for population studies of neutron star (NS) binaries (Haberl & Pietsch 2004; Shtykovskiy & Gilfanov 2005; Laycock et al. 2010).

Klus et al. (2014) have recently reported parameters of 42 Be/X-ray binaries in the SMC observed with the Rossi X-ray Timing Explorer (RXTE) satellite over a time span of 14 yr. These systems, most of which are transients, contain pulsars in which the X-ray emission is powered by wind-fed accretion on to a magnetized NS. The average spin periods of these pulsars are in the range P_s ∼ 2.37–1323 s and change at an average rate |$|\dot{P}| \sim (0.02 {\rm -} 620) \times 10^{-2}\,{\rm s\,yr^{-1}}$|⁠. Their orbital periods range from about 4 to 500 d.

Klus et al. (2014) estimated the magnetic fields of these NSs considering the situation in which they accrete matter from a Keplerian disc and rotate close to their equilibrium spin period. In this case, the estimated fields of the majority of the stars (including all those with P_s > 100 s) turn out to be over the quantum critical value |$B_{\rm cr} = m_{\rm e}^2 c^3/e \hbar \simeq 4.4 \times 10^{13}$| G. Here m_e and e are the mass and electric charge of an electron, c is the speed of light, and ℏ is the reduced Planck constant. Alternatively, if these NSs are not close to spin equilibrium, their inferred magnetic fields are smaller than ∼10¹⁰ G. Such results are rather unexpected since the majority of NSs in our Galaxy, including accretion-powered pulsars in HMXBs in which the magnetic field is measured from the cyclotron resonance scattered features, have magnetic fields between 10¹¹ and 10¹³ G (see e.g. Revnivtsev & Mereghetti 2015). An attempt to invoke currently used quasi-spherical accretion scenarios did not help much to improve the situation either, leading to estimated magnetic fields in excess of 10¹³ G.

It is not unusual that the magnetic fields evaluated from the spin parameters of NSs in Galactic HMXBs significantly exceed those measured through observations of their cyclotron resonance features. As recently indicated by Ikhsanov et al. (2014), this inconsistency may reflect an oversimplification of currently used wind-fed accretion scenarios, in which the magnetic field of the matter captured by the NS from its environment is neglected. The incorporation of the fossil magnetic field of the accreting matter into the model leads, under certain conditions, to a different accretion regime which is referred to as magnetic levitation accretion. In this scenario, which is briefly outlined in the next section, accretion occurs through a non-Keplerian magnetically levitating disc (ML-disc) and the maximum possible torque exerted on the NS significantly exceeds that previously evaluated in traditional non-magnetic scenarios. This leads to a new expression for the equilibrium period (see Section 3), which allows us to explain the observed values of the spin and orbital periods of the SMC pulsars without invoking magnetic fields outside the canonical range of 10¹¹–10¹³ G (Section 4).

MAGNETIC LEVITATION ACCRETION

We consider an HMXB, with orbital period P_orb, composed of a magnetized NS rotating with spin period P_s and a massive early-type star, which underfills its Roche lobe and loses matter through a stellar wind. The X-ray emission of the system is powered by wind-fed accretion on to the NS. This implies that the NS captures matter from the wind at a rate |$\dot{\mathfrak {M}}\le \dot{\mathfrak {M}}_{\rm c} = \pi r_{\!_{\rm G}}^2 \rho _0 v_{\rm rel}$|⁠, where |$r_{\!_{\rm G}} = 2 GM_{\rm ns}/v_{\rm rel}^2$| is the Bondi radius, M_ns is the NS mass, v_rel is its velocity in the frame of the wind, and |$\rho _0 = \rho (r_{\!_{\rm G}})$| is the density of matter in the region of interaction. The captured matter moves towards the NS forming an accretion flow, which interacts with the stellar magnetic field and confines the magnetosphere within the radius r_m, where the flow pressure is balanced by the pressure of the NS magnetic field. The accreting matter penetrates into the field at the magnetospheric boundary and, finally, falls on to the stellar surface at the magnetic pole regions by moving along the magnetic field lines.

The analysis of this accretion scenario reported by Ikhsanov & Finger (2012) indicates that the structure of the accretion flow, as well as the appearance of the accretion-powered source, strongly depends on the physical conditions of the matter captured at the Bondi radius, which, in general, possesses some angular momentum and magnetic field. Under these conditions, the structure of the accretion flow beyond the magnetosphere can be treated in the following basic approximations: (i) a spherically symmetrical or quasi-spherical flow, (ii) a Keplerian disc, and (iii) an ML-disc. A key parameter which allows us to determine which of these situations applies is the relative velocity of the NS with respect to surrounding matter, v_rel.

The spherically symmetrical accretion occurs if the gas surrounding the NS does not possess angular momentum and is non-magnetized. The captured matter in this case moves towards the NS in the radial direction with the free-fall velocity, v_ff(r) = (2GM_ns/r)^1/2 in a spherically symmetrical fashion. Its density scales with the radius as |$\rho (r) = \dot{\mathfrak {M}}/\left(4 \pi r^2 v_{\rm ff}\right)$| and the ram pressure is

\begin{equation} \scr {E}_{\rm ram}(r) = \rho (r) v_{\rm ff}^2(r) \propto r^{-5/2}. \end{equation}

(1)

The minimum distance to which the spherical flow can approach a NS with dipole magnetic moment μ is |$r \ge r_{\!_{\rm A}}$| (Arons & Lea 1976; Elsner & Lamb 1977), where

\begin{equation} r_{\!_{\rm A}} = \left(\frac{\mu ^2}{\dot{\mathfrak {M}}(2GM_{\rm ns})^{1/2}}\right)^{2/7} \end{equation}

(2)

is the Alfvén radius which is defined by equating the ram pressure of the free-falling gas, with the magnetic pressure due to dipole magnetic field of the NS, p_m = μ²/(2πr⁶)∝r^{− 6}.

The structure of a non-magnetized accretion flow deviates from spherically symmetrical if the captured matter possesses angular momentum. The process of mass accretion in this case is accompanied by the accretion of angular momentum, which in a binary system with the orbital angular velocity Ω_orb = 2π/P_orb occurs at the rate |$\dot{J} = \xi \,\Omega _{\rm orb}\,r_{\!_{\rm G}}^2\,\dot{\mathfrak {M}}$| (Illarionov & Sunyaev 1975). Here ξ is the parameter accounting for dissipation of angular momentum due to density and velocity gradients in the accreting non-magnetized gas (see e.g. Ruffert 1999, and references therein). The angular velocity of matter in this so called quasi-spherical accretion flow scales with the radius as

\begin{equation} \Omega _{\rm f}(r) = \xi \,\Omega _{\rm orb}\, \left(\frac{r_{\!_{\rm G}}}{r} \right)^2, \end{equation}

(3)

and the azimuthal component of the dynamical pressure of the flow,

\begin{equation} \scr {E}_{\phi }(r) = \xi \,\rho _0\,\Omega _{\rm orb}\,r_{\!_{\rm G}}^2\, \left(\frac{r_{\!_{\rm G}}}{r}\right)^{7/2}\ \propto r^{-7/2}, \end{equation}

(4)

increases more rapidly than the ram pressure. The accretion proceeds in a quasi-spherical fashion up to the circularization radius

\begin{equation} r_{\rm circ} = \frac{\xi ^2\,\Omega _{\rm orb}^2\,r_{\!_{\rm G}}^4}{GM_{\rm ns}}, \end{equation}

(5)

at which condition |$\scr {E}_{\phi }(r) = \scr {E}_{\rm ram}(r)$| is satisfied. The angular velocity of the accreting matter, Ω_f(r), at this radius reaches the Keplerian angular velocity, Ω_k = (r³/2GM_ns)^1/2, and the accretion flow switches into a Keplerian accretion disc (Pringle & Rees 1972; Shakura & Sunyaev 1973).

The accretion picture may differ from that presented above if the matter captured by the NS at the Bondi radius is magnetized. As long as the Alfvén velocity, v_a(r) = B_f(r)/[4πρ(r)]^1/2, in the accreting matter is smaller than the free-fall velocity, the magnetic field of the accreting gas, B_f, does not influence significantly the flow structure. Therefore, the captured matter initially follows ballistic trajectories forming a quasi-spherical accretion flow in which the angular momentum and magnetic flux are almost conserved. However, the magnetic pressure in the free-falling gas increases rapidly,

\begin{equation} \scr {E}_{\rm m}(r) = \frac{B_{\rm f}^2(r)}{8 \pi } \propto r^{-4}, \end{equation}

(6)

and reaches the ram pressure at the Shvartsman radius (Shvartsman 1971)

\begin{equation} R_{\rm sh} = \beta _0^{-2/3}\ r_{\!_{\rm G}}\ \left(\frac{c_{\rm so}}{v_{\rm rel}}\right)^{4/3}, \end{equation}

(7)

which is defined by equating the magnetic to ram pressure. Here |$\beta _0 = \beta (r_{\!_{\rm G}}) = 8 \pi \rho _0 c_{\rm so}^2/B_{\rm f0}^2$| is the ratio of thermal to magnetic pressure in the captured matter at the Bondi radius, |$c_{\rm so} = c_{\rm s}(r_{\!_{\rm G}})$| is the sound speed and |$B_{\rm f0} = B_{\rm f}(r_{\!_{\rm G}})$| is the magnetic field in the accreting matter. The flow at this radius is converted into a non-Keplerian ML-disc in which the accreting matter is confined by its own magnetic field (for discussion see Bisnovatyi-Kogan & Ruzmaikin 1976; Igumenshchev, Narayan, & Abramowicz 2003). The accretion inside the ML-disc proceeds on the time-scale of the magnetic flux dissipation and, in the general case, can be treated in a diffusion approximation. The value of the effective diffusion coefficient strongly depends on the configuration of the magnetic field in the disc and its stability. It ranges from the Bohm diffusion coefficient, if the magnetic field annihilation in the disc is governed by dissipative instabilities and magnetic reconnections, up to much larger values if the field configuration is interchange unstable (for discussion see Igumenshchev 2009; Tchekhovskoy, Narayan and McKinney 2011; Dexter et al. 2014, and references therein).

Thus, a quasi-spherical accretion on to a NS in a wind-fed HMXB occurs if the Alfvén radius is larger than both the circularization and the Shvartsman radii. The angular momentum and magnetic field of the accreting material in this case are too small to significantly influence the flow structure before the ballistic trajectories of the accreting matter are truncated by the magnetic field of the NS. Solving the inequality |$r_{\!_{\rm A}} \ge \max \lbrace r_{\rm circ}, R_{\rm sh}\rbrace$| for v_rel one finds

\begin{equation} v_{\rm rel} \ge \left\lbrace \begin{array}{lc}v_{\rm cr}, \hspace{-2.84526pt}& {\rm for} \hspace{2.84526pt} R_{\rm sh}<r_{\rm circ}, \\ v_{\rm ma}, \hspace{-2.84526pt}& {\rm for} \hspace{2.84526pt} R_{\rm sh} > r_{\rm circ}, \end{array} \right. \end{equation}

(8)

where (Ikhsanov 2007)

\begin{equation} v_{\rm cr} \simeq 160\,{\rm km\,s^{-1}} \xi _{0.2}^{1/4} \mu _{30}^{-1/14} m^{11/28} \dot{\mathfrak {M}}_{15}^{1/28} P_{50}^{-1/4}, \end{equation}

(9)

and (Ikhsanov & Beskrovnaya 2012; Ikhsanov & Finger 2012)

\begin{eqnarray} v_{\rm ma} \simeq 460\,{\rm km\,s^{-1}}\ \times \ \beta _0^{-1/5}\ \mu _{30}^{-6/35}\ m^{12/35}\ \dot{\mathfrak {M}}_{15}^{3/35}\ \left(\frac{c_{\rm so}}{10\,{\rm km\,s^{-1}}}\right)^{2/5}\!\!.\!\!\!\nonumber\\ \end{eqnarray}

(10)

Here μ₃₀ = μ/(10³⁰ G cm³) is the dipole magnetic moment (⁠|$\mu = (1/2) B_{\rm ns} R_{\rm ns}^3$|⁠) of a NS with surface magnetic field B_ns and radius R_ns, m = M_ms/1.4 M_⊙, |$\dot{\mathfrak {M}}_{15} = \dot{\mathfrak {M}}/\left(10^{15}\,{\rm g\,s^{-1}}\right)$|⁠, P₅₀ = P_orb/50 d, and the parameter ξ_0.2 = ξ/0.2 is normalized according to Ruffert (1999). The radius of the magnetosphere, within this scenario, is comparable or slightly exceeds the Alfvén radius (Arons & Lea 1976; Elsner & Lamb 1977), and accretion beyond the magnetospheric boundary proceeds in the form of a free-falling gas or a hot turbulent spherical envelope (Lamb et al. 1977; Ikhsanov 2001, 2003).

A Keplerian accretion disc in a wind-fed HMXB can form if the circularization radius exceeds both the Alfvén and Shvartsman radii. Solving inequality |$r_{\rm circ} \ge \max \lbrace r_{\!_{\rm A}}, R_{\rm sh}\rbrace$| for v_rel one finds

\begin{equation} v_{\rm rel} \le \left\lbrace \begin{array}{lc}v_{\rm cr}, \hspace{-2.84526pt}& {\rm for} \hspace{2.84526pt} R_{\rm sh}<r_{\!_{\rm A}}, \\ v_{\rm ca}, \hspace{-2.84526pt}& {\rm for} \hspace{2.84526pt} R_{\rm sh} > r_{\!_{\rm A}}, \end{array} \right. \end{equation}

(11)

where (Ikhsanov, Kim & Beskrovnaya 2015)

\begin{equation} v_{\rm ca} \simeq 80\,{\rm km\,s^{-1}} \xi _{0.2}^{3/7}\,\beta _0^{1/7}\,m^{3/7}\,P_{50}^{-3/7} \left(\frac{c_{\rm so}}{10\,{\rm km\,s^{-1}}}\right)^{-2/7}. \end{equation}

(12)

Finally, a non-Keplerian ML-disc can form in a wind-fed HMXB if the Shvartsman radius is larger than both, the Alfvén and circularization radii. Solving inequality |$R_{\rm sh} \ge \max \lbrace r_{\!_{\rm A}}, r_{\rm circ}\rbrace$| for v_rel yields

\begin{equation} v_{\rm ca}<v_{\rm rel}<v_{\rm ma}. \end{equation}

(13)

The inequality v_ca < v_ma is satisfied if β₀ < β_max, where

\begin{equation} \beta _{\rm max} \simeq 164\ \xi _{0.2}^{-5/4}\ m^{-1/4}\ P_{50}^{5/4}\ \mu _{30}^{-1/2}\ \dot{\mathfrak {M}}_{15}^{1/4} \left(\frac{c_{\rm so}}{10\,{\rm km\,s^{-1}}}\right)^2. \end{equation}

(14)

This indicates that the magnetic levitation accretion scenario occurs if the fossil magnetic field in the matter captured by the NS is |$B_{\rm f}(r_{\!_{\rm G}}) \ge B_{\rm min}$|⁠, where

\begin{eqnarray} B_{\rm min} & = & \left(\frac{2\,\dot{\mathfrak {M}}\,v_{\rm rel}^3\,c_{\rm so}^2}{(GM_{\rm ns})^2\,\beta _{\rm max}}\right)^{1/2} \simeq 5 \times 10^{-4}\,{\rm G}\ \times \nonumber\\ && \times\, \xi _{0.2}^{5/8}\ \mu _{30}^{1/4} m^{-7/8}\ P_{50}^{-5/8}\ \dot{\mathfrak{M}}_{15}^{3/8}\left(\frac{v_{\rm rel}}{100\,{\rm km\,s^{-1}}}\right)^{3/2}. \end{eqnarray}

(15)

The matter in an ML-disc approaches the NS until the radius

\begin{equation} r_{\rm ma} = \left(\frac{c\,m_{\rm p}^2}{16\,\sqrt{2}\,e\,k_{\rm B}}\right)^{2/13} \frac{\alpha _{\rm B}^{2/13} \mu ^{6/13} (GM_{\rm ns})^{1/13}}{T_0^{2/13} \dot{\mathfrak {M}}^{4/13}}, \end{equation}

(16)

where the pressure exerted by the disc on to the stellar magnetosphere is equal to the magnetic pressure due to the NS dipole field and the rate of diffusion of the accreting matter into the stellar field is equal to the mass capture rate by the star from its environment (for discussion see Ikhsanov 2012; Ikhsanov et al. 2014). Here m_p is the proton mass, k_B is the Boltzmann constant, and T₀ is the temperature of the matter at the inner radius of the disc. The parameter |$\alpha _{\!_{\rm B}} = D_{\rm eff}/D_{\rm B}$| is the ratio of the effective coefficient of diffusion of the accreting matter into the stellar field at the magnetospheric boundary, D_eff, to the Bohm diffusion coefficient, which in the considered case can be expressed as |$D_{\rm B} = c k_{\rm B} T_0 r_{\rm ma}^3/(32 e \mu )$|⁠. Numerical simulations of the diffusion process and measurements of the rate at which the solar wind penetrates into the magnetosphere of the Earth suggest that |$\alpha _{\!_{\rm B}} \sim 0.01 {\rm -} 1$| (Gosling et al. 1991). The matter being diffused into the stellar field flows along the magnetospheric field lines and reaches the NS surface at the magnetic pole regions.

The possibility of explaining the parameters of the SMC Be/X-ray pulsars within the quasi-spherical and the Keplerian disc accretion scenarios has been already discussed by Klus et al. (2014). Here we explore the possibility that these pulsars accrete matter from an ML-disc. In the next section we evaluate the equilibrium period of an NS in this scenario and present the expected Corbet (P_s versus P_orb) diagram in Section 4.

EQUILIBRIUM PERIOD

The equation governing the spin evolution of an NS accreting matter from an ML-disc reads

\begin{equation} 2 \pi I \dot{\nu } = K_{\rm a} + K_{\rm b} + K_{\rm c}, \end{equation}

(17)

where I is the moment of inertia and ν = 1/P_s = ω_s/2π is the spin frequency of the NS. The first term in the right-hand side of this equation,

\begin{equation} K_{\rm a} = \dot{\mathfrak {M}}\ \ell (r_{\rm ma}) \simeq \dot{\mathfrak {M}}\,\omega _{\rm s}\,r_{\rm ma}^2, \end{equation}

(18)

is the rate at which angular momentum is transferred to the NS by the matter flowing inside the magnetosphere. Here ℓ(r_ma) ≃ r_ma × (r_maω_s) is the specific angular momentum of matter in the magnetopause at the rotational equator. This matter, which penetrates into the stellar field at the magnetospheric boundary, corotates with the NS and flows towards its surface along the field lines. K_a has a positive sign and represents the minimum possible spin-up torque exerted on to a star which is surrounded by a magnetosphere of radius r_ma and accretes matter on to its surface at a rate |$\dot{\mathfrak {M}}$|⁠.

The second term (Ikhsanov 2012; Ikhsanov et al. 2014),

\begin{equation} K_{\rm b} = \frac{k_{\rm t}\,\mu ^2}{\left(r_{\rm ma}\,r_{\rm cor}\right)^{3/2}}\ \left(\frac{\Omega _{\rm f}(r_{\rm ma})}{\omega _{\rm s}} - 1\right), \end{equation}

(19)

accounts for the angular momentum exchanged between the star and the disc at the magnetospheric boundary (here k_t is a dimensionless parameter of order unity). The sign of this term depends on the ratio between the angular velocity of matter at the inner radius of the disc, Ω_f(r_ma), and the angular velocity of the NS.

The last term, K_c, accounts for the angular momentum exchanged between the NS and the disc at radii r > r_ma. Under the conditions of interest (dΩ_f/dr ≤ 0), this term is smaller than K_b at least by a factor ∼(r/r_ma)^3/2. Therefore, its contribution is relatively small and we neglect it in the following.

The equilibrium period, P_eq, is defined by equating the total torque exerted on the NS (right-hand side of equation 17) to zero, which, using equations (18) and (19), yields

\begin{equation} P_{\rm eq} \simeq P_{\rm f}(r_{\rm ma}) \left[1 - \frac{1}{\sqrt{2}k_{\rm t}} \left(\frac{r_{\rm ma}}{r_{\!_{\rm A}}}\right)^{7/2}\right], \end{equation}

(20)

where P_f(r_ma) = 2π/Ω_f(r_ma).

This equation suggests that the angular velocity of the NS in spin equilibrium exceeds the angular velocity of the matter at the inner radius of the disc by a factor of |$[1 - (1/\sqrt{2}k_{\rm t}) (r_{\rm ma}/r_{\!_{\rm A}})^{7/2}]$|⁠. The torque K_b in this case has a negative sign and tends to spin-down the star. It, however, is compensated by the spin-up torque K_a and thus, the total torque exerted on the NS is zero.

Evaluating the ratio

\begin{equation} \left(\frac{r_{\rm ma}}{r_{\!_{\rm A}}}\right)^{7/2} \sim 10^{-3}\ \alpha _{\rm B}^{7/13}\ \mu _{30}^{-5/13}\ m^{10/13}\ \dot{\mathfrak {M}}_{15}^{-1/13} T_6^{-7/13}, \end{equation}

(21)

one finds that the expression in the brackets in the conditions of interest (10⁻³ ≪ k_t ≤ 1) is close to unity (here T₆ = T₀/10⁶ K is normalized to the temperature of optically thick gas irradiated by the pulsar emission; see e.g. Hickox, Narayan and Kallman 2004). This indicates that the angular velocity of the NS in spin equilibrium is close to the angular velocity of the matter at the inner radius of the disc. This allows us for simplicity to approximate the equilibrium period of the NS by P_f(r_ma).

The analysis of the transport of angular momentum across the ML-disc is rather complicated and beyond the scope of this paper. The angular momentum extracted from the NS can be stored in the disc (Sunyaev & Shakura 1977; D'Angelo & Spruit 2012) or/and transferred out from the disc by Alfvén waves. Here we simply assume that the angular velocity of the matter in the disc scales with the radius as Ω_f(r) ∝ (R_sh/r)^γ, where γ is a free parameter, which in the general case is limited to¹ γ ≤ 2. The angular velocity of matter at the inner radius of the disc can be expressed as

\begin{equation} \Omega _{\rm f}(r_{\rm ma}) = \Omega _{\rm f}(R_{\rm sh}) \left(\frac{R_{\rm sh}}{r_{\rm ma}}\right)^{\gamma }, \end{equation}

(22)

where

\begin{equation} \Omega _{\rm f}(R_{\rm sh}) \simeq \xi \,\Omega _{\rm orb} \left(\frac{r_{\!_{\rm G}}}{R_{\rm sh}}\right)^2 \end{equation}

(23)

is the angular velocity of matter at the Shvartsman radius. This is derived by taking into account that the magnetic field of the accreting matter does not significantly influence the flow structure beyond the Shvartsman radius and the matter in the region |$R_{\rm sh}<r\le r_{\!_{\rm G}}$| moves towards the NS quasi-spherically.

Putting equations (7), (16), and (23) into equation (22) and taking into account that the relative velocity in the considered case is v_rel = ζv_ma, with ζ < 1, one finds

\begin{equation} P_{\rm f}(r_{\rm ma}) = 0.5 \left(\frac{1.3^{10\gamma/3}}{2^{\gamma}}\right)A_{\rm m} P_{\rm orb}, \end{equation}

(24)

where

\begin{eqnarray} A_{\rm m} = \xi ^{-1} \beta _0^{-4/5} c_{\rm so}^{8/5} \mu ^{a_1} \dot{\mathfrak {M}}^{-a_2} \zeta ^{a_3} (GM_{\rm ns})^{a_4} \left(\frac{c\,m_{\rm p}^2 \alpha _{\!_{\rm B}}}{16 \sqrt{2} e k_{\rm B} T_0} \right)^{2\gamma /13}\nonumber\\ \end{eqnarray}

(25)

and

\begin{equation*} a_1 = (208 - 50\,\gamma )/455, \end{equation*}

\begin{equation*} a_2 = (10\,\gamma +104)/455, \end{equation*}

\begin{equation*} a_3 = (10\,\gamma - 8)/3, \end{equation*}

\begin{equation*} a_4 = (100\,\gamma - 416)/455. \end{equation*}

Finally, the value of the dimensionless parameter ζ in the general case lies in the interval ζ_min < ζ < 1, where

\begin{equation} \zeta _{\rm min} = \left\lbrace \begin{array}{lc}v_{\rm ns}/v_{\rm ma}, \hspace{2.84526pt}& {\rm for} \hspace{14.22636pt} v_{\rm ns} > v_{\rm ca}, \\ v_{\rm ca}/v_{\rm ma}, \hspace{2.84526pt}& {\rm for} \hspace{14.22636pt} v_{\rm ns}<v_{\rm ca}, \end{array} \right. \end{equation}

(26)

and v_ns is the orbital velocity of the NS.

APPLICATION TO THE SMC PULSARS

In this section we explore the possibility of explaining the spin properties of the SMC Be/X-ray pulsars in terms of the magnetic levitation accretion scenario described above. We assume that the NSs in these systems rotate close to the equilibrium period P_eq ≃ P_f(r_ma) given by equation (24) and accrete matter from an ML-disc. This implies that the relative velocity of the NSs in the frame of stellar wind of their companions meets the condition v_cr ≤ v_rel ≤ v_ma and β₀ < β_max expressed by equation (14). Since the accretion process in an ML-disc is fully controlled by the magnetic field of the accreting matter itself, we consider the case of rigid rotation of the disc by setting γ = 0.

The minimum possible value of the equilibrium period, P_min, which an NS can acquire within the magnetic levitation accretion scenario can be derived from equation (24), by setting β₀ = β_max and, correspondingly, ζ = 1. This yields

\begin{equation} P_{\rm min}^{\rm eq} \simeq 14\,{\rm s} \times \mu _{30}^{0.86}\ \dot{\mathfrak {M}}_{15}^{-0.43}\ m^{-0.71}, \end{equation}

(27)

where |$\dot{\mathfrak {M}}_{15}$| is the average mass accretion rate normalized to 10¹⁵ g s⁻¹.

In Fig. 1 the values of |$P_{\rm min}^{\rm eq}$| are compared to the observed values of P_s and P_orb for representative values of μ (10³⁰ G cm³ solid lines; 10²⁹ G cm³ dashed lines) and |$\dot{\mathfrak {M}}$| (10¹⁴ and 10¹⁵ g s⁻¹). The corresponding lines indicate the minimum possible equilibrium period of a NS which captures matter from a relatively slow, moderately magnetized stellar wind in the magnetic levitation accretion scenario.

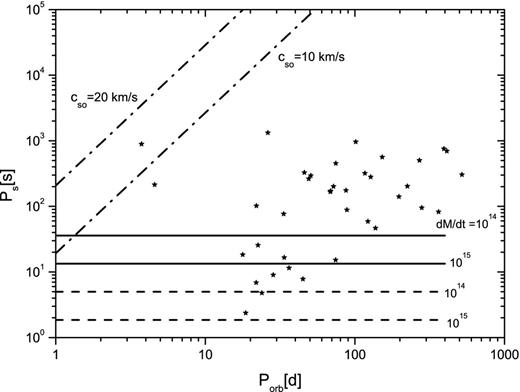
$Corbet diagram of the Be/NS pulsars in the SMC, with lines of maximum and minimum equilibrium period in the ML-disc accretion hypothesis. The solid lines are the minimum equilibrium period for μ = 1030 G cm3 and $\dot{\mathfrak {M}}=10^{14}$ and 1015 g s−1. The dashed lines are the minimum equilibrium period for μ = 1029 G cm3 and $\dot{\mathfrak {M}}=10^{14}$ and 1015 g s−1. The dash–dotted line indicates the maximum equilibrium period (independent of μ and $\dot{\mathfrak {M}}$).$

Figure 1.

Corbet diagram of the Be/NS pulsars in the SMC, with lines of maximum and minimum equilibrium period in the ML-disc accretion hypothesis. The solid lines are the minimum equilibrium period for μ = 10³⁰ G cm³ and |$\dot{\mathfrak {M}}=10^{14}$| and 10¹⁵ g s⁻¹. The dashed lines are the minimum equilibrium period for μ = 10²⁹ G cm³ and |$\dot{\mathfrak {M}}=10^{14}$| and 10¹⁵ g s⁻¹. The dash–dotted line indicates the maximum equilibrium period (independent of μ and |$\dot{\mathfrak {M}}$|⁠).

Open in new tab Download slide

The maximum possible equilibrium period, P_max, can be evaluated from equation (24) by setting β₀ = 1 and ζ = ζ_min, which for the case v_ns < v_ca is (see equation 26)

\begin{equation} \zeta _{\rm min} \simeq 0.17\ \beta _0^{12/35}\ \mu _{30}^{6/35}\ \dot{\mathfrak {M}}_{15}^{-3/35}\ \xi _{0.2}^{3/7}\ m^{3/35}\ c_6^{-24/35}\ P_{50}^{-3/7}. \end{equation}

(28)

Putting this value into equation (24) one finds

\begin{equation} P_{\rm max}^{\rm eq} \simeq 20\,{\rm s} \times P_{\rm orb(d)}^{15/7}\ \xi _{0.2}^{-15/7}\ \beta _0^{-1.71}\ c_6^{3.43}\ m^{-1.14}. \end{equation}

(29)

The function |$P_{\rm max}^{\rm eq} = P_{\rm max}^{\rm eq}(P_{\rm orb})$| is shown by the dot–dashed line in Fig. 1. The maximum equilibrium period of an NS which accretes from a magnetized slow wind does not depend on the magnetic field of the NS itself and on the X-ray luminosity of the pulsar. However, it is a strong function of the sound speed in the surrounding matter and, therefore, it can exceed the value given by equation (29) if the temperature of the stellar wind exceeds 10⁴ K.

Fig. 1 shows that practically all the pulsars reported by Klus et al. (2014) have spin-period values smaller than P_max = P_max(P_orb) and lying above the lines of P_min corresponding to μ ∼ 10^29–30 G cm³ and accretion rates consistent with the long-term average luminosities of these sources. This suggests that the observed spin periods can be explained within the magnetic levitation accretion scenario with surface magnetic fields of the NSs in the canonical interval B_ns ∼ 10¹¹–10¹³ G.

DISCUSSION

We find that the observed spin periods of the SMC Be/X-ray pulsars are in a range consistent with the values expected for the equilibrium periods of NSs with magnetic fields of B ∼ 10^11–13 G and accreting from an ML-disc. The assumption that the NSs in these systems are spinning close to an equilibrium value is supported by the fact that they show alternate episodes of spin-up and spin-down, which do not change P_s significantly on the long term. We believe that the equilibrium period is set by the average accretion rate experienced by these NS during the long time intervals of quiescence (or low X-ray luminosity) between their bright outbursts. In fact these sources spend most of the time in such low-|$\dot{\mathfrak {M}}$| conditions, resulting in X-ray luminosities well below the RXTE sensitivity limit of ∼10³⁶ erg s⁻¹. For this reason we have adopted in Fig. 1 values of |$\dot{\mathfrak {M}}$| corresponding to luminosities of ∼10^{34 − 35} erg s⁻¹.

The equilibrium period of an NS which accretes from a ML-disc tends to increase with the orbital period of a binary system (see equation 24). This, in particular, can be a reason for a lack of pulsars in the lower-right part of the Corbet plot. On the other hand, P_eq also depends on several other parameters, such as the magnetic field and relative velocity of a NS, the mass accretion rate, and physical conditions in the stellar wind with which the NS interacts. The great diversity of possible combinations of these parameters is responsible for the large scatter of the observed spin periods in the Corbet plot. In this accretion regime, the magnetic field of the massive star plays an important role, with stronger fields leading to longer equilibrium periods of the pulsar.

Spectropolarimetric observations of O/B-type stars give evidence for a relatively strong magnetization of these objects (see e.g. Walder, Folini & Meynet 2012, and references therein). The strength of the large-scale field at the surface of several of these objects has been measured in the range ∼500–5000 G, and in some cases beyond 10 kG (Hubrig et al. 2006; Martins et al. 2010; Oksala et al. 2010). Some of the early-type stars are surrounded by X-ray coronae which indicate the magnetic activity of these objects (Schulz et al. 2003). As most of these stars rotate relatively fast (see e.g. Rosen, Krumholz & Ramirez-Ruiz 2012, and references therein), the magnetic field in the wind is dominated by the toroidal component which scales with the radius ∝ r⁻¹.

A similar situation is realized in the solar wind in which the magnetic field at a distance of 1 au is B_sw ∼ 10⁻⁵ G and the parameter β is close to the equipartition value, β ∼ 1 (Mullan & Smith 2006). Following this similarity one can suggest that the surface large-scale magnetic field of massive stars in the considered systems is a factor of B_min/B_sw ∼ 50 larger than the surface large-scale magnetic field of the Sun and can be as large as a few hundred Gauss. A smaller magnetization of these stars cannot be also excluded if the dynamo action applies in their outflowing discs. The fact that periods of the considered pulsars are much shorter than the maximum possible period predicted by our model may indicate that the average value of β₀ exceeds unity and hence, the stellar wind of early spectral type stars is less magnetized than the solar wind. The observed range of periods of the pulsars (∼1–1000 s) in this case can be explained in terms of variation of β₀ parameter from system to system within an order of magnitude.

Our study confirms the conclusion of Klus et al. (2014) that all of the considered pulsars are situated in a relatively slow wind. This is consistent with current views on the mass outflow process of Be stars, in which the stellar wind at the equatorial plane is dominated by a dense outflowing disc. The radial velocity of matter in the disc is comparable or even smaller than the orbital velocity of the NS (Okazaki & Negueruela 2001).

We finally note that our results apply also to the Be/X-ray pulsars in our Galaxy, which show a distribution in the P_orb–P_s similar to that of the SMC sources. This supports the view that the properties and evolution of HMXBs in the SMC and in our Galaxy share a common nature and are governed by similar physical processes.

We would like to thank anonymous referee for very useful and stimulating comments. NRI thanks INAF at Milano for kind hospitality and acknowledges support of the Russian Scientific Foundation under the grant no. 14-50-00043. This work has been partially supported through financial contribution from the agreement ASI/INAF I/037/12/0 and from PRIN INAF 2014.

1

The value γ = 2 corresponds to conservation of angular momentum, γ = 1.5 to Keplerian rotation, γ = 1 to rotation with constant linear velocity, and γ = 0 to solid body rotation.

REFERENCES

Arons

J.

Lea

S. M.

1976

ApJ

207

914

Month:	Total Views:
January 2017	3
February 2017	2
May 2017	1
June 2017	1
July 2017	2
August 2017	1
September 2017	2
December 2017	1
January 2018	1
March 2018	1
August 2018	4
November 2018	1
December 2018	3
January 2019	5
February 2019	1
March 2019	8
April 2019	9
May 2019	4
July 2019	4
August 2019	2
September 2019	1
October 2019	4
November 2019	8
December 2019	6
January 2020	4
February 2020	5
March 2020	3
April 2020	1
June 2020	2
July 2020	2
August 2020	3
September 2020	2
October 2020	1
November 2020	6
December 2020	2
January 2021	2
February 2021	2
March 2021	6
April 2021	4
May 2021	2

Article Contents

On the magnetic fields of Be/X-ray pulsars in the Small Magellanic Cloud

Abstract

INTRODUCTION

MAGNETIC LEVITATION ACCRETION

EQUILIBRIUM PERIOD

APPLICATION TO THE SMC PULSARS

DISCUSSION

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only