-
PDF
- Split View
-
Views
-
Cite
Cite
Mark R. Lovell, Gianfranco Bertone, Alexey Boyarsky, Adrian Jenkins, Oleg Ruchayskiy, Decaying dark matter: the case for a deep X-ray observation of Draco, Monthly Notices of the Royal Astronomical Society, Volume 451, Issue 2, 01 August 2015, Pages 1573–1585, https://doi.org/10.1093/mnras/stv963
Close - Share Icon Share
Abstract
Recent studies of M31, the Galactic Centre (GC), and galaxy clusters have made tentative detections of an X-ray line at ∼3.5 keV that could be produced by decaying dark matter. We use high-resolution simulations of the Aquarius project to predict the likely amplitude of the X-ray decay flux observed in the GC relative to that observed in M31, and also of the GC relative to other parts of the Milky Way halo and to dwarf spheroidal galaxies. We show that the reported detections from M31 and the GC are compatible with each other, and with upper limits arising from high galactic latitude observations, and imply a decay time τ ∼ 1028 s. We argue that this interpretation can be tested with deep observations of dwarf spheroidal galaxies: in 95 per cent of our mock observations, a 1.3 Ms pointed observation of Draco with XMM–Newton will enable us to discover or rule out at the 3σ level an X-ray feature from dark matter decay at 3.5 keV, for decay times τ < 0.8 × 1028 s.
1 INTRODUCTION
One of the most pressing and interesting questions in fundamental physics and cosmology today is the identity of the dark matter (DM; see e.g. Bertone 2010, and references therein). The properties of hypothetical DM particles remain largely unknown and there are many attempts to find phenomenological constraints on particular models from astronomical observations. For example, if DM particles were born relativistic, deep in the radiation-dominated epoch (so called ‘warm dark matter’, or WDM) they would affect the way structures were formed at small scales, leaving their imprints in the Lyman α forest (e.g. Viel et al. 2005; Boyarsky et al. 2009a; Viel et al. 2013) and satellite galaxy abundances and structure (Polisensky & Ricotti 2011; Kennedy et al. 2014; Lovell et al. 2014). Satellite structure may also provide limits on DM self-interactions (Vogelsberger, Zavala & Loeb 2012; Zavala, Vogelsberger & Walker 2013). One further constraint is the detection of electromagnetic radiation originating from the decay or annihilation of DM particles. Many studies to date have centred on attempts to detect the annihilation of weakly interacting massive particles (WIMPs; see e.g. Bertone, Hooper & Silk 2005; Feng 2010, for a review). This generic class of particles is attractive as a DM candidate due to their stability, their potential relation to electroweak symmetry breaking, and the possibility that they may be detected in laboratory experiments (see e.g. Cerdeño & Green 2010, and references therein). WIMPs cannot decay, but are predicted to annihilate with one another in regions of high DM density, and could be detected via their annihilation products.
Currently, the most interesting candidate WIMP signal is an excess of GeV photons from the centre of the Galaxy (Hooper & Goodenough 2011; Daylan et al. 2014; Calore, Cholis & Weniger 2015), but further evidence is needed to rule out a possible astrophysical origin of the signal (Boyarsky, Malyshev & Ruchayskiy 2011).
The interaction strength of WIMPs limits their mass to the few GeV–few TeV range (in order to give the correct primordial abundance). Once the assumption about the interaction strength is relaxed, particle physics theories predict the existence of DM of different masses. If the particle mass is at the keV scale, and its lifetime longer than the age of the Universe, it may in principle be detectable indirectly, through the observation of X-ray photons produced by its decay (see e.g. Abazajian, Fuller & Tucker 2001; Dolgov & Hansen 2002; Boyarsky et al. 2006; Abazajian 2009; den Herder et al. 2009). An X-ray line signal consistent with such a decay has been identified at an energy of ∼3.5 keV in galaxy clusters, in the Milky Way centre (or Galactic Centre, GC) and in M31 by several studies (Boyarsky et al. 2014a,c; Bulbul et al. 2014a).1 although others have reported non-detections (Anderson, Churazov & Bregman 2014; Malyshev, Neronov & Eckert 2014) or reported detections but attributed them to have astrophysical origins (Riemer-Sorensen 2014; Jeltema & Profumo 2015 but see also Boyarsky et al. 2014b; Bulbul et al. 2014b). These two classes of systems – clusters and L* galaxies – are separated in mass by three orders of magnitude, therefore the correlation of the measured signal with expected projected DM mass is compelling evidence for DM decay as the origin of the signal.
These studies have based their estimates of the DM distribution in their targets on dark halo mass models that do not take into account fully the triaxiality of the halo, the presence of substructure, or the effects of baryons. Some of these issues have been examined in Bernal et al. (2014), who used a low-resolution cosmological simulation containing ∼105 Milky Way halo analogues to motivate better triaxial halo mass models. We instead make use of a series of high-resolution simulations of Milky Way-analogue DM haloes, some of which were run with a full hydrodynamical treatment of the baryonic component, to estimate the X-ray decay signal from these targets and compare the results to the reported detections.
Targets such as the Milky Way and M31 are attractive due to their large projected mass densities; however, their analysis is complicated by the presence of X-ray emission lines from the interstellar medium. Therefore, the nature of the line – DM or astrophysical – may be better ascertained by performing observations of objects with much cleaner backgrounds. One particularly promising class of candidates is that of the Milky Way's dwarf spheroidal satellites (Boyarsky et al. 2006). These galaxies have very high mass-to-light ratios (Walker et al. 2009, 2010; Wolf et al. 2010), and very low gas fractions (Gallagher et al. 2003, and references therein). Their X-ray emitting gas fractions will be lower still due to their small gas fractions. Any detection from these galaxies would thus have a very low probability of an astrophysical origin and therefore dwarf spheroidal satellites have previously been targets of decaying DM searches in X-rays (Boyarsky et al. 2006, 2007; Loewenstein, Kusenko & Biermann 2009; Riemer-Sorensen & Hansen 2009; Loewenstein & Kusenko 2010; Mirabal 2010; Loewenstein & Kusenko 2012; Malyshev et al. 2014). With our set of simulations, we can also set out to calculate the flux from dwarf spheroidals in their full cosmological context, including the contribution from the host halo.
In this work, we use the high-resolution simulations of the Aquarius project (Springel et al. 2008) to predict the likely amplitude of the X-ray decay flux observed in the GC relative to that observed in M31, and also of the GC relative to other parts of the Milky Way halo and to dwarf spheroidal galaxies. As we shall see, a sufficiently deep observation of the Draco dwarf galaxy would allow us to test the DM interpretation of the observed X-ray line signal in a very large region of the parameter space.
This paper is organized as follows. In Section 2, we present the simulations used in this paper. We discuss our methods for calculating the X-ray flux from the simulations in Section 3. In Section 4, we present our results for the expected fluxes of the GC, M31, and two dwarf spheroidal galaxies, and draw conclusions in Section 5. In the appendices, we test the convergence of the simulations as function of resolution and number of sightlines (Appendix A), and consider the effects of cosmology, baryonic physics, and DM power spectrum (Appendix B). We present observational analysis and predictions for signal from Draco in Appendix C.
2 SIMULATIONS
Each of the simulations used in this study is either taken directly from or derived from the Aquarius project. This is a set of Milky Way halo-analogue DM-only simulations run with the p-gadget3 code (Springel et al. 2008), and uses the cosmological parameters consistent with the one-year data of the Wilkinson Microwave Anisotropy Probe (WMAP1): H0 = 100 h = 73 km s−1 Mpc−1, Ωm = 0.25, ΩΛ = 0.75, σ8 = 0.9, and ns = 1 (Spergel et al. 2003). The six haloes are labelled Aq-A through to Aq-F. Aq-F was found to experience a major merger at redshift 0.4–0.5, and has been shown to be likely to host an S0 galaxy rather than a disc galaxy at redshift zero (Cooper et al. 2011): we therefore do not consider it in this study. The remaining five haloes span a range of masses and concentrations, and thus enable us to examine the effect of these parameters for different possible values of Milky Way and M31 mass and concentration.
The Aq-A halo has been rerun at five different simulation resolution levels for the purpose of checking that results are converged and not influenced by simulation resolution. These levels are labelled from 1 (highest resolution, particle mass ∼103 M⊙) to 5 (lowest resolution, particle mass ∼3 × 106 M⊙). The precise particle masses are reproduced in Table 1. Aq-A5 is very poorly resolved for the purposes of this experiment and is therefore not used here.
Parameters of the simulations. We include the simulation DM particle mass mp, the smoothing length ϵ, the mass of the central halo encompassing a region of 200 times the critical density of the Universe, M200, the halo concentration c, and the WDM particle mass, mWDM, where applicable. Concentration is determined by fitting NFW profiles to each halo at radii between 1 kpc and 100 kpc.
| Simulation . | mp (M⊙) . | ϵ (pc) . | M200 (M⊙) . | c . | mWDM(keV) . |
|---|---|---|---|---|---|
| Aq-A1 | 1.712 × 103 | 20.5 | 1.839 × 1012 | 18.6 | – |
| Aq-A2 | 1.370 × 104 | 65.8 | 1.842 × 1012 | 18.5 | – |
| Aq-A3 | 4.911 × 104 | 120.5 | 1.836 × 1012 | 18.5 | – |
| Aq-A4 | 3.929 × 105 | 342.5 | 1.838 × 1012 | 18.6 | – |
| Aq-A2(W7) | 1.545 × 104 | 68.2 | 1.938 × 1012 | 16.1 | – |
| Aq-A2–m1.5(W7) | 1.545 × 104 | 68.2 | 1.797 × 1012 | 15.9 | 1.456 |
| Aq-A2–m1.6(W7) | 1.545 × 104 | 68.2 | 1.802 × 1012 | 16.2 | 1.637 |
| Aq-A2–m2.0(W7) | 1.545 × 104 | 68.2 | 1.843 × 1012 | 16.0 | 2.001 |
| Aq-A2–m2.3(W7) | 1.545 × 104 | 68.2 | 1.875 × 1012 | 16.1 | 2.322 |
| Aq-A4-S-NoWinds | 3.222 × 105 | 342.5 | 1.709 × 1012 | 25.1 | – |
| Aq-A4-S-Winds | 3.222 × 105 | 342.5 | 1.590 × 1012 | 27.5 | – |
| Aq-B2 | 6.447 × 103 | 65.8 | 8.194 × 1011 | 11.7 | – |
| Aq-C2 | 1.399 × 104 | 65.8 | 1.774 × 1012 | 18.4 | – |
| Aq-D2 | 1.397 × 104 | 65.8 | 1.774 × 1012 | 12.4 | – |
| Aq-E2 | 9.593 × 103 | 65.8 | 1.185 × 1012 | 15.3 | – |
| Simulation . | mp (M⊙) . | ϵ (pc) . | M200 (M⊙) . | c . | mWDM(keV) . |
|---|---|---|---|---|---|
| Aq-A1 | 1.712 × 103 | 20.5 | 1.839 × 1012 | 18.6 | – |
| Aq-A2 | 1.370 × 104 | 65.8 | 1.842 × 1012 | 18.5 | – |
| Aq-A3 | 4.911 × 104 | 120.5 | 1.836 × 1012 | 18.5 | – |
| Aq-A4 | 3.929 × 105 | 342.5 | 1.838 × 1012 | 18.6 | – |
| Aq-A2(W7) | 1.545 × 104 | 68.2 | 1.938 × 1012 | 16.1 | – |
| Aq-A2–m1.5(W7) | 1.545 × 104 | 68.2 | 1.797 × 1012 | 15.9 | 1.456 |
| Aq-A2–m1.6(W7) | 1.545 × 104 | 68.2 | 1.802 × 1012 | 16.2 | 1.637 |
| Aq-A2–m2.0(W7) | 1.545 × 104 | 68.2 | 1.843 × 1012 | 16.0 | 2.001 |
| Aq-A2–m2.3(W7) | 1.545 × 104 | 68.2 | 1.875 × 1012 | 16.1 | 2.322 |
| Aq-A4-S-NoWinds | 3.222 × 105 | 342.5 | 1.709 × 1012 | 25.1 | – |
| Aq-A4-S-Winds | 3.222 × 105 | 342.5 | 1.590 × 1012 | 27.5 | – |
| Aq-B2 | 6.447 × 103 | 65.8 | 8.194 × 1011 | 11.7 | – |
| Aq-C2 | 1.399 × 104 | 65.8 | 1.774 × 1012 | 18.4 | – |
| Aq-D2 | 1.397 × 104 | 65.8 | 1.774 × 1012 | 12.4 | – |
| Aq-E2 | 9.593 × 103 | 65.8 | 1.185 × 1012 | 15.3 | – |
Parameters of the simulations. We include the simulation DM particle mass mp, the smoothing length ϵ, the mass of the central halo encompassing a region of 200 times the critical density of the Universe, M200, the halo concentration c, and the WDM particle mass, mWDM, where applicable. Concentration is determined by fitting NFW profiles to each halo at radii between 1 kpc and 100 kpc.
| Simulation . | mp (M⊙) . | ϵ (pc) . | M200 (M⊙) . | c . | mWDM(keV) . |
|---|---|---|---|---|---|
| Aq-A1 | 1.712 × 103 | 20.5 | 1.839 × 1012 | 18.6 | – |
| Aq-A2 | 1.370 × 104 | 65.8 | 1.842 × 1012 | 18.5 | – |
| Aq-A3 | 4.911 × 104 | 120.5 | 1.836 × 1012 | 18.5 | – |
| Aq-A4 | 3.929 × 105 | 342.5 | 1.838 × 1012 | 18.6 | – |
| Aq-A2(W7) | 1.545 × 104 | 68.2 | 1.938 × 1012 | 16.1 | – |
| Aq-A2–m1.5(W7) | 1.545 × 104 | 68.2 | 1.797 × 1012 | 15.9 | 1.456 |
| Aq-A2–m1.6(W7) | 1.545 × 104 | 68.2 | 1.802 × 1012 | 16.2 | 1.637 |
| Aq-A2–m2.0(W7) | 1.545 × 104 | 68.2 | 1.843 × 1012 | 16.0 | 2.001 |
| Aq-A2–m2.3(W7) | 1.545 × 104 | 68.2 | 1.875 × 1012 | 16.1 | 2.322 |
| Aq-A4-S-NoWinds | 3.222 × 105 | 342.5 | 1.709 × 1012 | 25.1 | – |
| Aq-A4-S-Winds | 3.222 × 105 | 342.5 | 1.590 × 1012 | 27.5 | – |
| Aq-B2 | 6.447 × 103 | 65.8 | 8.194 × 1011 | 11.7 | – |
| Aq-C2 | 1.399 × 104 | 65.8 | 1.774 × 1012 | 18.4 | – |
| Aq-D2 | 1.397 × 104 | 65.8 | 1.774 × 1012 | 12.4 | – |
| Aq-E2 | 9.593 × 103 | 65.8 | 1.185 × 1012 | 15.3 | – |
| Simulation . | mp (M⊙) . | ϵ (pc) . | M200 (M⊙) . | c . | mWDM(keV) . |
|---|---|---|---|---|---|
| Aq-A1 | 1.712 × 103 | 20.5 | 1.839 × 1012 | 18.6 | – |
| Aq-A2 | 1.370 × 104 | 65.8 | 1.842 × 1012 | 18.5 | – |
| Aq-A3 | 4.911 × 104 | 120.5 | 1.836 × 1012 | 18.5 | – |
| Aq-A4 | 3.929 × 105 | 342.5 | 1.838 × 1012 | 18.6 | – |
| Aq-A2(W7) | 1.545 × 104 | 68.2 | 1.938 × 1012 | 16.1 | – |
| Aq-A2–m1.5(W7) | 1.545 × 104 | 68.2 | 1.797 × 1012 | 15.9 | 1.456 |
| Aq-A2–m1.6(W7) | 1.545 × 104 | 68.2 | 1.802 × 1012 | 16.2 | 1.637 |
| Aq-A2–m2.0(W7) | 1.545 × 104 | 68.2 | 1.843 × 1012 | 16.0 | 2.001 |
| Aq-A2–m2.3(W7) | 1.545 × 104 | 68.2 | 1.875 × 1012 | 16.1 | 2.322 |
| Aq-A4-S-NoWinds | 3.222 × 105 | 342.5 | 1.709 × 1012 | 25.1 | – |
| Aq-A4-S-Winds | 3.222 × 105 | 342.5 | 1.590 × 1012 | 27.5 | – |
| Aq-B2 | 6.447 × 103 | 65.8 | 8.194 × 1011 | 11.7 | – |
| Aq-C2 | 1.399 × 104 | 65.8 | 1.774 × 1012 | 18.4 | – |
| Aq-D2 | 1.397 × 104 | 65.8 | 1.774 × 1012 | 12.4 | – |
| Aq-E2 | 9.593 × 103 | 65.8 | 1.185 × 1012 | 15.3 | – |
We determine the properties of DM structures using the subfind algorithm (Springel et al. 2001), which identifies bound overdensities as haloes and subhaloes. The largest subfind halo in each of the simulations is referred to as the ‘main halo’, and we take the Milky Way/M31 halo centre to be that of the main halo's centre-of-potential. The positions of dwarf spheroidal candidates are likewise the centres-of-potential of DM subhaloes.
The original Aquarius runs are DM-only simulations; however, it is likely that baryonic physics will have an impact on the distribution of DM in the Galaxy. We therefore make use of two gas physics resimulations of Aq-A4. Both have been run with the p-gadget3 code (Springel et al. 2008) and adopt the gas physics and star formation prescriptions of Springel & Hernquist (2003). The two runs differ only in that one has the galactic winds model of Springel & Hernquist (2003) enabled whereas the other does not. The inclusion of winds inhibits further star formation such that the stellar mass of the central galaxy is reduced from 1.45 × 1011 M⊙ in the no-winds case to 9.19 × 1010 M⊙ when winds are included. Both of these values are higher than the Milky Way stellar mass inferred by McMillan (2011, 6.43 ± 0.63 × 1010 M⊙), so care should be taken when comparing these models to the Milky Way, especially the model that does not make use of the winds physics.
To check for the likely effect of our choice of cosmological parameters, we have also performed a resimulation of Aq-A2 that instead uses the WMAP7 year values: H0 = 100 h = 70.4 km s−1 Mpc−1, Ωm = 0.272, ΩΛ = 0.728, σ8 = 0.81, and ns = 0.967 (Komatsu et al. 2011). Since one candidate for producing the decay line is a 7.1 keV sterile neutrino, which has the kinematic properties of WDM, we make use of four WDM simulations of Aq-A2 in the WMAP7 cosmology. These are identical to the Aq-A2-WMAP7 run except that the initial conditions wave amplitudes are rescaled with thermal relic WDM power spectra (Bode, Ostriker & Turok 2001; Viel et al. 2005). The WDM models used have thermal relic particle masses 1.5, 1.6, 2.0, and 2.3 keV. The 2.0 keV model is a good approximation to a sterile neutrino produced in the presence of both very low and very high lepton asymmetries (Abazajian 2014, Lovell et al., in preparation), and the other three enable us to examine the effect of larger and smaller effective particle masses. Further details about these simulations and the definition of WDM particle mass may be found in Lovell et al. (2014). Important properties for each of the simulations are given in Table 1.
3 MODELLING THE X-RAY SIGNAL
We make use of two methods for calculating the flux from our chosen targets: sightlines for particular observer positions, and the spherically averaged flux for an observer at a given distance from the target. Both of these are discussed in detail below.
3.1 Sightlines
In this method, we treat each simulation particle as a point source of X-ray photons. We randomly select positions on the surface of a sphere of some radius (8 kpc for the GC, 780 kpc for M31) around the centre of the largest subfind halo, and place our observers at these positions. We then define a cone with an opening angle of the XMM–Newton MOS field-of-view (FoV; 14 arcmin radius) and central axis connecting the observer to the halo centre, and calculate the total flux of all simulation particles found within that cone: this is our ‘sightline’ measurement. For the measurements in which we observe the GC or M31 (‘on-centre’ measurements), the cone is directed towards the halo centre as described above; the procedures for ‘off-centre’ and dwarf spheroidal observations are described in Section 4.
All of our runs are zoom simulations, in which the halo of interest resides within a region of diameter ∼2 Mpc populated with high-resolution particles; the remainder of the box contains more massive, low-resolution particles to provide the correct large-scale forces. We use only the high-resolution particles for our study. We find that our results are insensitive to any edge effects where the high-resolution region ends, and we can truncate the region of particles sampled down to 50 kpc from the halo centre without affecting any of our results: we therefore do not impose any truncation. Background DM sources beyond the high-resolution region will make a negligible contribution due to the redshifting of the emission, and are thus not included in the analysis (Boyarsky et al. 2006). In all cases, we take the centre of the Milky Way (Sagittarius A*) to be at the simulated halo centre-of-potential as determined by our halo finder. We discuss briefly the number of sightlines required for our results to be robust in Section A.
3.2 Spherically averaged flux calculation
In this method, we smear out each simulation particle into a spherical shell around the halo centre. We then calculate the flux from the shell surface area that intersects the line-of-sight cone as described above. This approach is equivalent to using an infinite number of sightlines. The numerical noise is reduced relative to the sightline method, with the penalty that we wash out anisotropies due to halo triaxiality and substructure.
4 RESULTS
We now consider the effect of comparing different observations: on-centre versus off-centre observations of the GC, on-centre GC versus on-centre M31, and on-centre GC versus two dwarf spheroidal galaxies. All observers are placed at randomly selected positions around the centre of the target halo as described in subsection 3.1.
4.1 On-centre versus off-centre observations
To begin, we generate 5000 ‘on-centre’ observations of the Aq-A1 halo as discussed in subsection 3.1, at a distance of 8 kpc from the halo centre. In order to generate off-centre observations, we retain the positions used for the on-centre observers and target our sightlines in a random direction of some angular separation from the halo centre for 5000 sightlines; we do not attempt to identify or exclude sightlines that contain large substructures. We perform this procedure for a series of angular separations between 10° and 100° in the Aq-A1 data set. We take the ratio of each observer's off-centre flux measurement and on-centre measurements and plot the results as a function of the offset angle, ϕ, in Fig. 1.
![The ratio of off-centre flux to on-centre flux of the Aq-A1 halo as a function of angular separation from the halo centre. The crosses mark the median sightline flux for each distribution. The 95 per cent distributions are shown as solid lines and continued to 99 per cent as dashed lines. The dotted curve is fit to the median data and has the form bn[ϕ + b]−n, where b = 4 $_{.}^{\circ}$3 and n = 1.1.](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/451/2/10.1093/mnras/stv963/3/m_stv963fig1.jpeg?Expires=1750302516&Signature=FaZZyYQnbaq7z5Ye1j9uTp5meqNO7C5WAHXxYD8EZrxa2hu74b6ni1Bq7puuKNstJBgzHoSq~uaQ9XK7PktExRXi1eIRC5EyUkbglZuUA4wMcCMm9F0oddfwp0305vLl0plwHu~GozjE9oSPmA5nBCVl9D3dr1sKz-iOCGlFJ34myc~jR2TSoELcjELeMnX68qI7IXWVAoGhZYmDUNBa1rBP7RaTa~uL~GIDBmz-dLOaguizcIOSaFn1GcRSiEU75OOl8ztBtYak69n9zJVkA2HV77-Z0RQnLviC1IU01zLbWkDsZSgSYbqk4t1GPwjxa~Z84fevXP9BEp3zDE96hw__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
The ratio of off-centre flux to on-centre flux of the Aq-A1 halo as a function of angular separation from the halo centre. The crosses mark the median sightline flux for each distribution. The 95 per cent distributions are shown as solid lines and continued to 99 per cent as dashed lines. The dotted curve is fit to the median data and has the form bn[ϕ + b]−n, where b = 4| $_{.}^{\circ}$|3 and n = 1.1.
The flux ratios taper off with offset angle in a way that can be approximated by a power law. We impose a functional form of bn[ϕ + b]−n to the data, thus ensuring that the function has a value of 1 at 0°. Our best fit for the median data is b = 4| $_{.}^{\circ}$|3 and n = 0.94. We repeated the fitting procedure for the 95 per cent upper and lower bounds and found that the best-fitting parameters when using the same function were b = 4| $_{.}^{\circ}$|5, n = 0.71 and b = 4| $_{.}^{\circ}$|1, n = 1.1, respectively.
4.2 Blank sky observations
One particular application of off-centre measurements is the ability to obtain a blank sky data set. Boyarsky et al. (2014c) used a stack of observations taken at several offset angles, for simplicity we use 100°. In the same way as for Fig. 1, we calculate the ratio of the 100° offset and on-centre measurements. We then bin up these ratios and plot the results in Fig. 2 for Aq-A1, Aq-A2, and Aq-B2. We retrieve a broad distribution centred around 0.05 and obtain a very small probability density either below 0.02 or above 0.13. The 95 per cent lower bound of the ratio, as shown in the figure, is 0.025. Boyarsky et al. (2014c) obtained a 2σ upper limit on the blank sky data set flux of 0.7 × 10−6 cts s−1 cm−2; we would therefore expect the flux of the GC to be no higher than ∼3.6 × 10−5 cts s−1 cm−2 since it can be shown that the highest possible value of the GC flux would be the lowest value of this ratio multiplied by the 2σ error on the blank sky flux. The Aq-A2 curve differs somewhat from that of Aq-A1, which shows that we have not achieved good convergence at least for Aq-A2. We also include the result for Aq-B2, as this is the lightest halo and therefore perhaps the best GC candidate (albeit with a low concentration). When we combine the 2σ exclusion limit from Boyarsky et al. (2014c) with the reported detection in the GC (|$2.9^{+0.5}_{-0.5}\times 10^{-5}\,{\rm cts\,s^{-1}\,cm}^{-2}$|; Boyarsky et al. 2014a), we obtain the shaded region shown in Fig. 2. We also show the plot for observers in the plane of the inner halo minor axis, since this is the most likely orientation of the stellar disc with respect to the DM halo (Bailin et al. 2005; Aumer & White 2013, see appendix subsection B5). The distribution becomes skewed towards lower ratio values, however the lower limit to the distribution remains remarkably similar. There is some tension between the simulation result and the observational constraint. However, it should be noted that we do not attempt to identify sightlines that would be the most appropriate matches to blank sky targets such as the Lockman hole. Such sightlines may well have a lower projected mass density than that the unbiased selection offered here: actively selecting underdense light cones could well alleviate this tension.
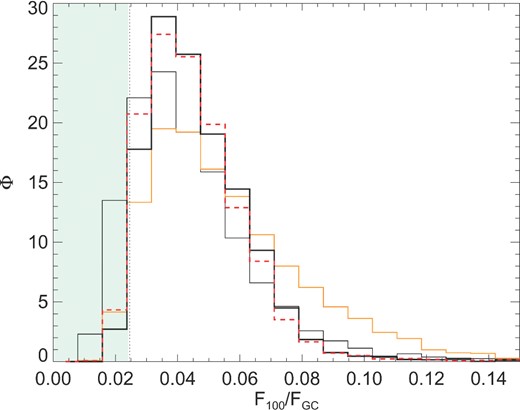
Histogram of the flux ratios for the 100° Milky Way halo offset angle (black lines, Aq-A1 thick, Aq-A2 thin). We also plot the same result for Aq-B2 (orange), and again for Aq-A1 when observers are constrained to the plane normal to the minor axis vector (red dashed line). The vertical dotted line marks the 95 per cent lower bound on the flux distribution. The combined allowed region from the 2σ limit on the Boyarsky et al. (2014a) GC detection and the Boyarsky et al. (2014c) blank sky non-detection is given by the shaded green region.
4.3 M31 versus GC observations
We now determine the likely ratio of the GC and M31 flux measurements. We assume initially that each of the five level two haloes used in our study (Aq-A to Aq-E) are all equally likely host haloes for the Milky Way and M31. We combine the lists of GC sightlines for each of the five haloes into one large catalogue, and likewise for the M31 sightlines. The simulations we use are resolution level 2; we multiply the flux of each GC sightline by a factor of 1.2 to compensate for resolution suppression as derived in Appendix A. We then extract one million randomly selected (with replacement, such that we can pick the same sightlines to be part of more than one pair) M31/GC sightline pairs in order to build a probability distribution function as the ratio of M31/GC observed flux. We plot the results for the combined list of sightlines in Fig. 3.
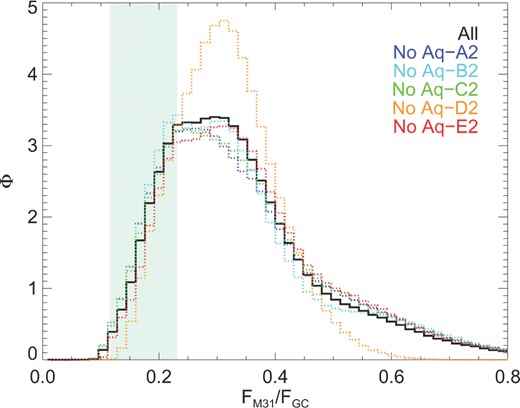
The probability distribution function for the M31/GC flux ratio. The result returned when all haloes are included is shown as the solid black line. The dotted lines correspond to cases where the data from one halo is omitted from the sample: Aq-A (blue), Aq-B (cyan), Aq-C (green), Aq-D (orange), and Aq-E(red). The shaded region corresponds to the 1σ uncertainty on the ratio of the detections of M31 Boyarsky et al. (2014c) and the GC Boyarsky et al. (2014a).
We find that the distribution peaks at FM31/FGC = 0.3. The distribution as a whole is very broad: 95 per cent of the data is in the range [0.15,0.72]. To test how sensitive the result is to the properties of individual haloes, in the same figure we also plot the same quantity whilst removing one halo at a time from the sample (as both a GC and M31 candidate). The position of the peak changes very little as a result of this procedure. However, the omission of the Aq-D halo from the sample is seen to remove much of the probability distribution at the high- and low-value tails: the 95 per cent bounds then tighten to [0.18,0.52]. The effect of removing any of the other four haloes is much smaller by comparison. The position of the peak varies between 0.23 and 0.33.
Boyarsky et al. (2014a,c) claim a detection from M31 of a line with flux |$4.9^{+1.6}_{-1.3}\times 10^{-6}\,{\rm cts\,s^{-1}\,cm}^{-2}$|, and in the GC of |$2.9^{+0.5}_{-0.5}\times 10^{-5}\,{\rm cts\,s^{-1}\,cm}^{-2}$|. Combining these two results and their associated errors, we obtain the shaded region shown in Fig. 3. It is in broad agreement with all combinations of our haloes.
We now consider other variables that may affect the distribution of M31/GC flux ratios. In Fig. 4, we plot three additional versions of the flux ratio histogram. The first is for GC observers constrained to reside in the inner-halo minor axis plane. The requirement that the observers reside in the minor axis plane has very little effect on the result. The second and third consider the case in which M31 is much more massive than the Milky Way (Peñarrubia et al. 2014). We take Aq-B2 – our smallest halo – to be our Milky Way candidate and Aq-C2 and Aq-D2 to be M31 halo candidates. Despite having the same mass to four significant figures, the flux histograms for the two combinations of GC and M31 (Aq-B2 – Aq-C2 versus Aq-B2 – Aq-D2) are displaced by a factor of 1.6; the large difference in concentration (18.4 for Aq-C2, 12.4 for Aq-D2) plays an important role in the result.
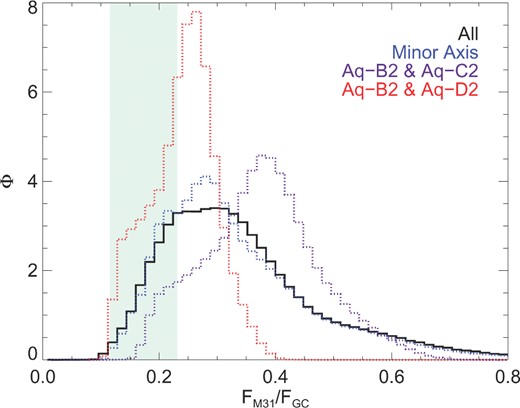
The probability distribution function for the M31/GC flux ratio is reproduced in black (all haloes). We also include data for observers in the plane of the minor axis (blue dotted line). The other two lines are obtained when our GC target is Aq-B2 and the M31 halo analogue is taken to be Aq-C2 (purple) and Aq-D2 (red). We reproduce the observational constraints as the shaded green region.
4.4 Dwarf spheroidal galaxies
Additionally, one can hope to detect the signal in still more targets. Dwarf spheroidal galaxies are exceptionally good objects for further study (Boyarsky et al. 2006; Riemer-Sorensen & Hansen 2009; Malyshev et al. 2014): they have very high mass-to-light ratios (e.g. Wolf et al. 2010), they represent a different mass regime to clusters and L* galaxies, and also contain very little if any interstellar gas (see Gallagher et al. 2003, and references therein). They therefore offer a set of circumstances in which the ratio of the predicted DM emission to the astrophysical background is very high.
The mass enclosed in the half-mass radius has been estimated by several studies (Walker et al. 2009, 2010; Wolf et al. 2010). Two of the satellites measured to have the highest central densities are Draco and Sculptor (Geringer-Sameth, Koushiappas & Walker 2015). We will select Draco and Sculptor candidates from our simulations and use these to make predictions for the likely amplitude of X-ray decay fluxes from these two satellites. We reproduce the observational data published in Wolf et al. (2010) in Table 2.
Selected parameters of the Draco and Sculptor dwarf spheroidals as reproduced from Wolf et al. (2010): distance, d, luminosity, L, de-projected 3D half-light radius, r1/2, and half-light mass, M1/2.
| . | Draco . | Sculptor . |
|---|---|---|
| d (kpc) | 76 ± 5 | 86 ± 5 |
| L (L⊙, V) | |$2.2^{+0.7}_{-0.6}\times 10^{5}$| | |$2.5^{+0.9}_{-0.7}\times 10^{6}$| |
| r1/2 (pc) | 291 ± 14 | 375 ± 54 |
| M1/2 (M⊙) | |$2.11^{+0.31}_{-0.31}\times 10^{7}$| | |$2.25^{+0.16}_{-0.15}\times 10^{7}$| |
| . | Draco . | Sculptor . |
|---|---|---|
| d (kpc) | 76 ± 5 | 86 ± 5 |
| L (L⊙, V) | |$2.2^{+0.7}_{-0.6}\times 10^{5}$| | |$2.5^{+0.9}_{-0.7}\times 10^{6}$| |
| r1/2 (pc) | 291 ± 14 | 375 ± 54 |
| M1/2 (M⊙) | |$2.11^{+0.31}_{-0.31}\times 10^{7}$| | |$2.25^{+0.16}_{-0.15}\times 10^{7}$| |
Selected parameters of the Draco and Sculptor dwarf spheroidals as reproduced from Wolf et al. (2010): distance, d, luminosity, L, de-projected 3D half-light radius, r1/2, and half-light mass, M1/2.
| . | Draco . | Sculptor . |
|---|---|---|
| d (kpc) | 76 ± 5 | 86 ± 5 |
| L (L⊙, V) | |$2.2^{+0.7}_{-0.6}\times 10^{5}$| | |$2.5^{+0.9}_{-0.7}\times 10^{6}$| |
| r1/2 (pc) | 291 ± 14 | 375 ± 54 |
| M1/2 (M⊙) | |$2.11^{+0.31}_{-0.31}\times 10^{7}$| | |$2.25^{+0.16}_{-0.15}\times 10^{7}$| |
| . | Draco . | Sculptor . |
|---|---|---|
| d (kpc) | 76 ± 5 | 86 ± 5 |
| L (L⊙, V) | |$2.2^{+0.7}_{-0.6}\times 10^{5}$| | |$2.5^{+0.9}_{-0.7}\times 10^{6}$| |
| r1/2 (pc) | 291 ± 14 | 375 ± 54 |
| M1/2 (M⊙) | |$2.11^{+0.31}_{-0.31}\times 10^{7}$| | |$2.25^{+0.16}_{-0.15}\times 10^{7}$| |
We select Draco and Sculptor candidate subhaloes as follows. For each of our level 2 simulations, we identify subhaloes that are between 88 and 148 kpc from the main halo centre. These values are chosen to increase our sample size beyond what is possible at the true distance of these satellites, such that the observer will be at a distance of 80–140kpc from the satellite. We then draw a sphere of radius equal to the Draco/Sculptor half-light radii around the subhalo centre. If the mass enclosed within that radius falls within the published uncertainty on the ‘half-light mass’ of the satellite galaxy in question then it is added to our sample. In this way, we obtain 19 candidates for Draco and 33 for Sculptor. The shapes of the density profiles of these simulated subhaloes is quite different to that inferred for dwarf spheroidals by some studies (cf. Springel et al. 2008; Walker & Peñarrubia 2011 but see also Strigari, Frenk & White 2014); however; our study is sensitive to the total subhalo mass within the satellite half-light radius alone, and not the density profile.
We place 5000 observers at random within the ring defined such that the observer-main halo distance is 8 kpc and the observer-target subhalo distance is either 80, 90, 100, 110, 120, 130, or 140 kpc from the centre as permitted by the main halo–subhalo separation. For subhalo positions such that more than one of these observer-target separations are possible, we select the smallest available. We then calculate the flux from the target at the position of the observers in the same way as for the GC and M31. By this method, we obtain the combined flux from the subhalo and the outskirts of the main halo. The results for both Draco and Sculptor are presented in Fig. 5.
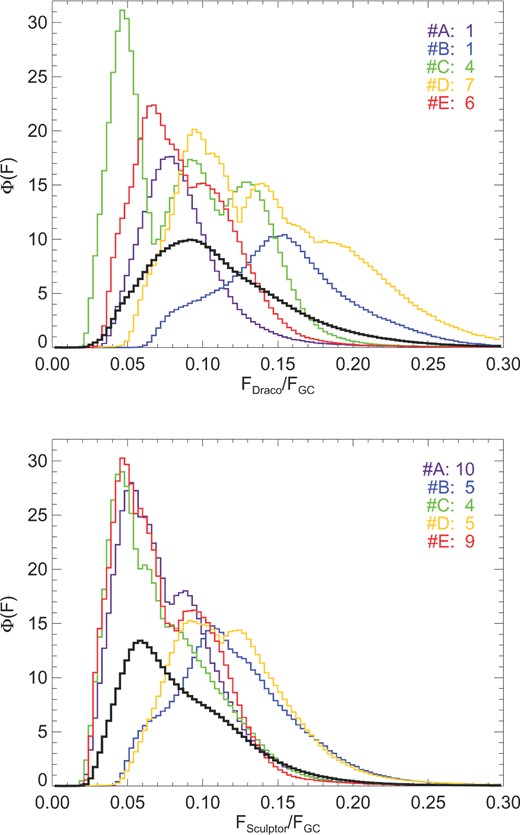
The probability distribution function envelopes for the flux ratios of Draco/GC (top panel) and Sculptor/GC (bottom panel). We calculate the normalized histogram for each individual satellite/GC pair and then, for each central halo, plot the curve that envelopes all of the curves associated with that central. The new histogram is not renormalized. The histograms for central haloes Aq-A2, Aq-B2, Aq-C2, Aq-D2, and Aq-E2 are shown in purple, blue, green, orange, and red, respectively. The black line is the distribution obtained when all the distributions in each panel are merged.
There is a great deal of variation between different dwarf spheroidal candidates. For Draco the peak in the probability distribution may be as much as 20 per cent of the GC or as little as 5 per cent; for Sculptor the range in peaks is smaller. It is possible to see the effects of central halo concentration and mass: the Aq-D2 results are all clustered towards more modest ratios, as are those of Aq-B2.
4.5 Compatibility of X-ray line claims and limits in different targets
We now bring the results from each of these targets together to examine the likelihood that each (non-)detection is consistent with being generated by a DM particle of the same decay lifetime. In Fig. 6, we plot the flux distributions for each of our targets as a function of projected mass for a series of different decay lifetimes τ27 = τ/(1027s). We take Aq-B2 to be our Milky Way candidate due to its low mass (Deason et al. 2012; Peñarrubia et al. 2014), and Aq-D2 to be our M31 analogue because of its relatively low concentration(Corbelli et al. 2010). We also include the 1σ allowed regions for the detections of the GC and M31, and also 2σ upper bounds for the blank sky data set and Draco.
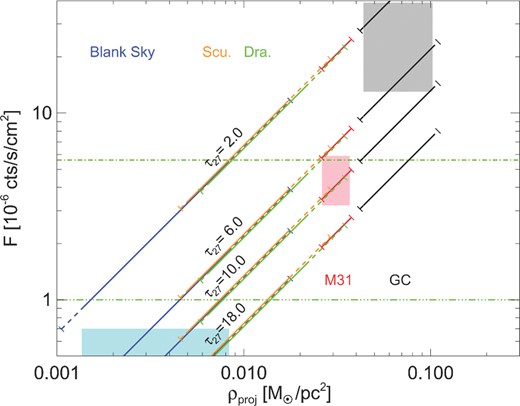
The distribution of fluxes from each of our targets as a function of the projected mass density for a series of four decay lifetimes (τ27 = 2, 6, 10, 18). The GC (Aq-B2), M31 (Aq-D2), Draco (all candidates), Sculptor (all candidates) and Milky Way 100° offset (Aq-B2) are denoted by the black, red, green, orange, and blue lines, respectively. Lines are solid for the 95 per cent region and extended to 99 per cent with dashed lines. The grey shaded region denotes the 1σ allowed region from the GC detection of Boyarsky et al. (2014a), the red shaded region that of the M31 detection (Boyarsky et al. 2014c), and the blue shaded region the 2σ upper bound from the Boyarsky et al. (2014c) blank sky data set. The dot–dashed green line represents the current 2σ upper bound on the flux from Draco (107.1 ks of XMM-MOS1 and XMM-MOS2 data; 40.4 ks XMM-PN data) and the triple dot–dashed green line the 3σ limit that would be expected for ∼1.3 Ms of XMM data. Good agreement between the simulation predictions and the observations is achieved when the lines overlap with their associated shaded regions for a single value of τ27.
We find that the best agreement between the corresponding simulation predictions and the observational constraints is approximately in the range τ27 = (6–10). This lifetime agrees within 1σ range with the results of Bulbul et al. (2014a) and Boyarsky et al. (2014a,c), and is consistent with non-observation of the line from stacked observations of dSphs (Malyshev et al. 2014) where the limit τ27 > 7.3 (3σ upper bound) was established. There is more tension with the limits from Anderson et al. (2014), who claim to rule out the line as found by (Bulbul et al. 2014a) at as much as 11.8σ, however their applications of scaling relations and their stacking procedure may have consequences for the error estimates. These estimates are based on our haloes that are the best candidate matches for the Milky Way and GC. The projected mass will increase if the expected mass or concentration of either target were higher will cause the projected mass to change slightly. A proper implementation of baryon physics in particular will likely increases the projected mass densities (see Appendix B).
In addition to the published upper bound from the blank sky observations and also the published detections in the GC and M31, we include in Fig. 6 the upper limit from the non-detection of Draco, as well as an estimate of the sensitivity of XMM–Newton with future observations. Based on archival data from the XMM–Newton observatory (∼107 ks of MOS1+MOS2 instruments, and 40.4 ks with PN) the 2σ upper bound is 5.6 × 10−6 cts s−1 cm−2. Simulations using the xspec's (Arnaud 1996) fakeit command find that a Draco flux of ∼1 × 10−6 cts s−1 cm−2 would be detected at 3σ with an XMM–Newton exposure of 1.34 Ms. For values of τ27 ∼ 8, 95 per cent of our realizations lead to an X-ray flux from Draco consistent with existing upper limits, and within the 3σ reach of XMM–Newton with an exposure of 1.34 Ms.
5 CONCLUSIONS
The identity of the DM remains unknown. The detection of a series of unexplained lines in the X-ray spectra of a number of different astrophysical targets are suggested to be consistent with the decay of light DM particles. We have expanded on these studies by estimating the likely distribution of X-ray fluxes from these targets.
To this end, we have used simulations of Milky Way-analogue DM haloes to ascertain the likely signal of the decay of DM into X-ray photons from the GC, M31, and two dwarf spheroidal galaxies. We placed 5000 observers at a distance of 8 kpc around the simulated main halo centre and calculated the flux measured within the FoV of radius 14 arcmin, treating each simulation DM particle as a point source of X-ray photons. This procedure were also performed with observers 780 kpc from the halo centre to simulate the likely M31 flux.
We then calculated the likely signal from other parts of the Milky Way halo. We performed an off-centre analysis in which we take a series of 5000 sightlines 100° away from the main halo centre. We obtain a flux distribution that is slightly in tension with the 95 per cent exclusion limit from the Boyarsky et al. (2014c) blank sky data set.
Pairs of GC and M31 measurements were compared to the ratio of fluxes found by Boyarsky et al. (2014a,c), and were found to be in good agreement for a wide range of sampling procedures.
Finally, we repeated the procedure for the Draco and Sculptor dwarf spheroidal satellite galaxies. We find a wide range of possible probability curves, with the central halo density as a very important parameter. Our results in this regime are consistent with a non-detection reported using ∼100 ks of archival XMM–Newton data, and future pointings of Draco will have the ability to rule out a DM decay signal from this object for values of τ27 < 8 at 95 per cent confidence.
We would like to thank Dima Iakubovskyi and Jeroen Franse for reading the manuscript and for collaboration on X-ray data analysis and on estimates of sensitivity of future observations. We would also like to thank Christoph Weniger for useful comments, and the anonymous referee for a careful reading of the text and helpful suggestions. This work used the DiRAC Data Centric system at Durham University, operated by the Institute for Computational Cosmology on behalf of the STFC DiRAC HPC Facility (www.dirac.ac.uk). This equipment was funded by BIS National E-infrastructure capital grant ST/K00042X/1, STFC capital grant ST/H008519/1, and STFC DiRAC Operations grant ST/K003267/1 and Durham University. DiRAC is part of the National E-Infrastructure. This work is part of the D-ITP consortium, a programme of the Netherlands Organization for Scientific Research (NWO) that is funded by the Dutch Ministry of Education, Culture and Science (OCW). GB acknowledges support from the European Research Council through the ERC Starting Grant WIMPs Kairos.
Both the Milky Way (Riemer-Sorensen, Hansen & Pedersen 2006; Abazajian et al. 2007; Boyarsky, Nevalainen & Ruchayskiy 2007) and M31 (Watson et al. 2006; Boyarsky et al. 2008, 2010; Watson, Li & Polley 2012; Horiuchi et al. 2014) have been extensively studied in this aspect. However, each of the data sets used in previous decaying DM searches has poorer statistics than used in Boyarsky et al. (2014a,c), Jeltema & Profumo (2015) and Riemer-Sorensen (2014). The non-detection of any signal in these works does not contradict current results.
REFERENCES
APPENDIX A: RESOLUTION AND SIGHTLINE TESTS
We discuss here the convergence with numerical resolution of our simulations. In Fig. A1, we plot surface density flux as a function of radius for a generic decaying DM particle of decay lifetime τ = 1028 s, and are not interested in the mass of the DM particle. At the distance of M31, the separation between all four simulations is minimal and therefore we can consider even our level 4 simulation to resolve the system accurately. At smaller radii, the curves start to diverge systematically with resolution. The flux amplitude at the GC distance is suppressed by 70 per cent in Aq-A4 relative to Aq-A1, compared to a difference in particle mass between the two runs of over two orders of magnitude. We also plot the expected flux for an Navarro–Frenk–White profile (NFW; Navarro, Frenk & White 1996, 1997) with the same M200 and c as our Aq-A1 halo (M200 = 1.839 × 1012 M⊙ and c = 18.6) for distances between 7 and 500 kpc. It predicts approximately 22 per cent more flux than our Aq-A1 halo. However, Navarro et al. (2010) found that the Aquarius haloes were better described by an Einasto profile (Einasto 1965) than by an NFW. The Einasto profile has a shallower central slope compared to the NFW, so the NFW curve may be interpreted as an upper limit on the ‘true’ flux. Therefore it is unlikely that a simulation of infinite resolution would return an GC flux more than ∼20 per cent higher than that found in Aq-A1.
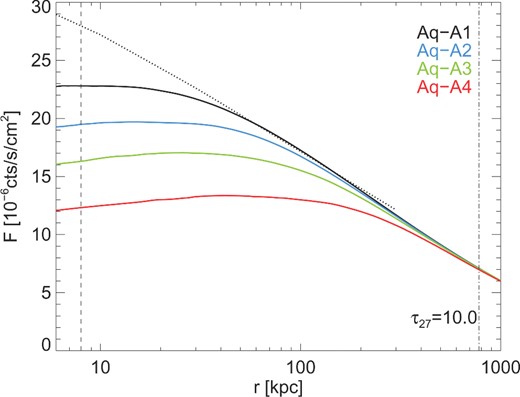
The expected X-ray flux from a Milky Way-analogue DM halo (Aq-A) as a function of distance from the halo centre. Each curve represents a different resolution simulation: Aq-A1 (black), Aq-A2 (blue), Aq-A3 (green), and Aq-A4 (red). The dotted line at 780 kpc marks the distance to M31, and the dashed line at 8 kpc the distance to the GC. We also include an NFW profile with the same M200 and c as the Aq-A1 halo (dotted line); it is normalized to the Aq-A1 curve at 50 kpc.
A more demanding criterion for convergence is that our sightline measurements converge. In Fig. A2, we plot the distribution of fluxes for the GC and M31 for different resolution simulations of the Aq-A halo. The peak in the GC distribution moves to higher fluxes with increasing resolution, since the addition of more particles to the simulation increases the mass contained within the FoV on small scales. The distribution of the second highest resolution – Aq-A2 – is suppressed relative to that of the highest by 20 per cent, which is comparable to the suppression between these two simulations in Fig. A1. Interestingly, the shape and width of the distribution changes very little between runs Aq-A2 and Aq-A1, which suggests that our derived bounds relative to the distribution peak for the fluxes will not be affected by resolution as much as the amplitude.
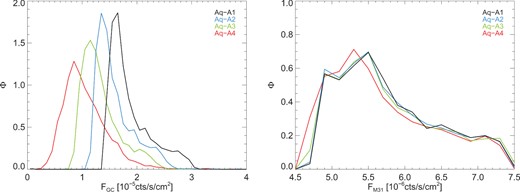
The flux distributions, Φ, for the GC (left) and M31 (right) when different resolution simulations of the Aq-A halo are used as the target halo. Each distribution is normalized such that the area under the curve is equal to 1. The fluxes for Aq-A1, Aq-A2, Aq-A3, and Aq-A4 are shown in black, blue, green, and red, respectively.
As was the case for the spherically averaged method, the convergence of the M31 measurement is much better. The Aq-A1, Aq-A2, and Aq-A3 distributions all peak at the same flux and have very similar shapes. This is due to the physical radius of the FoV at the target in configuration space (740pc) being much larger than the spatial resolution of the simulation, unlike the GC case (only 8pc).
Finally, we checked that 5000 sightlines measurements are sufficient for the convergence of the flux distribution functions and adopt this number throughout.
APPENDIX B: INFLUENCE OF COSMOLOGY, BARYON PHYSICS, AND HALO PROPERTIES
In this section, we examine the impact of various factors on our estimations of the fluxes from the GC and M31, including the possible effects of our choice of cosmological parameters, WDM power spectra, baryons, and halo mass and concentration.
B1 Cosmological parameters
First we consider the effect of cosmology. The halo properties will be sensitive to parameters such as the age of the Universe and at what redshift the halo centres form. In Fig. B1, we plot the cumulative flux functions of the WMAP1 and WMAP7 versions of Aq-A2. In the GC and M31 regimes the WMAP7 flux distribution is suppressed relative to WMAP1 by up to 10 per cent. This occurs despite the increase in M200 from WMAP1 to WMAP7; instead the halo becomes less concentrated. σ8 has a lower value in WMAP7 compared to WMAP1 (see Table 1), and this change delays the halo formation time to an epoch when the Universe is less dense (Lovell et al. 2014; Polisensky & Ricotti 2014). Any such discrepancy may be magnified artificially by resolution issues since the WMAP7 run particle mass is slightly higher. In conclusion, it is likely that the choice of cosmological parameters will have an impact on the M31 and GC fluxes of not more than a few per cent.
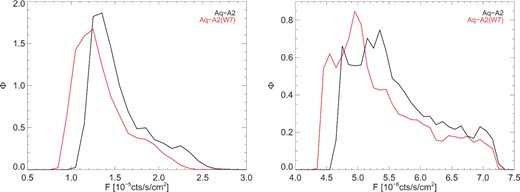
The flux distributions for Aq-A2 (black) and Aq-A2(W7) (red) for the GC (left) and M31 (right).
B2 Warm dark matter
We now address the effect of changing the primordial matter power spectrum. One well-motivated candidate for decaying DM is a resonantly-produced sterile neutrino (Shi & Fuller 1999; Laine & Shaposhnikov 2008; Boyarsky, Ruchayskiy & Shaposhnikov 2009b). A sterile neutrino with a mass of 7 keV has a non-negligible free-streaming length that erases small-scale power in the early Universe. The resulting matter power spectrum therefore possesses a cutoff similar to that of WDM. The position and slope of the cutoff is not uniquely determined by the sterile neutrino mass, as the sterile neutrino momentum distribution is modified in the presence of a lepton asymmetry, which is a relatively unconstrained parameter. The family of spectra for a sterile neutrino mass of 7 keV and an unconstrained lepton asymmetry has cutoffs in the range between those of a 2.0 and 3.3 keV thermal WDM candidate (Abazajian 2014, Lovell et al., in preparation). WDM models of this type have a considerable effect on the structure of dwarf galaxies (Lovell et al. 2012; Macciò et al. 2012, 2013; Shao et al. 2013; Schneider et al. 2014), and perhaps to a much smaller extent, on that of Milky Way-analogue haloes. In Fig. B2, we plot the M31 sightlines measurement and the surface density flux as a function of radius for our WMAP7 version of Aq-A2 (CDM) and four WDM models (see figure caption).
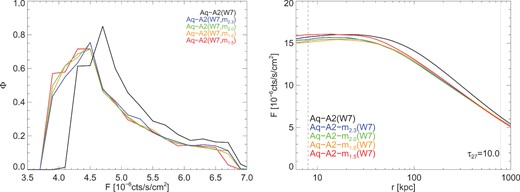
Impact of WDM. Left: the M31 flux distributions for Aq-A2(W7) as simulated with CDM (black) and WDM models of thermal relic particle masses 1.5 kev (red), 1.6 keV (orange), 2.0 keV (green), and 2.3 keV(blue). Right: the flux surface density as a function of radius for these five models.
The WDM flux distributions are suppressed relative to cold dark matter (CDM) for the M31 measurement by the order of a few per cent. The variation between WDM models is by comparison very small. The 1.5 keV model is further suppressed than the 2.3 keV, suggesting that flux correlates inversely with the free-streaming length, albeit weakly for this range of models. The discrepancy between CDM and the WDM models is reflected in the flux surface density profile, where CDM has a notably higher flux amplitude for observer distances greater than 40 kpc. At the distance of M31 this again amounts to a few per cent. At the GC observer distance the separation is much smaller and no longer correlates consistently with DM free-streaming length. This result is reflected in the sightlines distribution for the GC (not shown). The 7keV sterile neutrinos will likely have a cooler power spectrum than that of even the 2.3 keV thermal relic, therefore we do not consider further the effect of the DM free-streaming length on the flux distribution.
B3 Baryonic physics
One crucial component of the cosmological model that is missing from the simulations presented so far is baryonic physics. Through the action of feedback and adiabatic contraction it is possible for baryons to alter considerably the distribution of DM and hence the expected X-ray flux (Blumenthal et al. 1986). We have run realizations of Aq-A4 (WMAP1) with two baryonic models. Both make use of the star formation and gas physics prescriptions introduced in Springel & Hernquist (2003); one includes galactic winds and the other does not. With these simulations, we are also able to relax the assumption that DM and baryons have the same spatial distribution. The M31 flux distribution functions for these simulations along with that of DM-only Aq-A4 are plotted in Fig. B3.
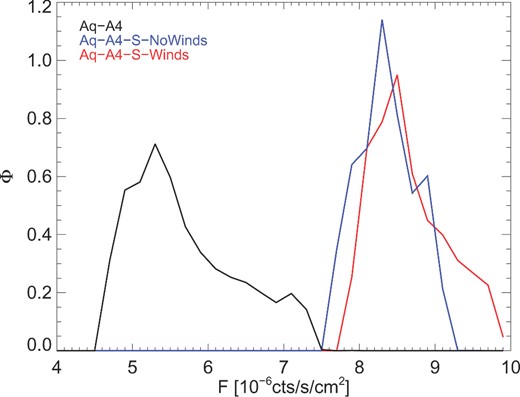
Impact of baryons. Left: the flux distributions from M31 for Aq-A4 as simulated with just DM (black), and two gas-hydro models: red includes winds and blue does not.
The variation in flux distributions is substantial. Both baryon model simulations exhibit M31-distance flux distributions that are ∼50 per cent higher than that of the DM-only run. Alternative gas/star formation physics and subgrid recipes may produce different results (e.g. Schaller et al. 2014; Mollitor, Nezri & Teyssier 2015): here we simply state that the precise effect of gas physics is uncertain and likely to affect the outcome of our measurement for M31. Due to the poor resolution of the GC measurement in Aq-A4, we do not attempt to draw conclusions about the likely effect of baryons on the GC results. For the same reason, we also do not attempt to use the baryonic simulations for the dwarf spheroidals; the precise effect of baryonic physics on dwarf galaxy mass distribution has been highly debated in the literature (cf. Di Cintio et al. 2012; Garrison-Kimmel et al. 2013; Brooks & Zolotov 2014).
B4 Halo sample variance
The measured flux will be very sensitive to the concentration of both the MW and M31 haloes, which decreases with halo mass albeit with considerable scatter (Gao et al. 2004; Neto et al. 2007). Also, individual haloes will have very stochastic formation histories, and so will likely have very different structures. We therefore use four further Aquarius haloes (B-E) to examine the scatter in flux measurements that is likely to result from these variations in halo properties. In Fig. B4, we plot the GC and M31 flux distributions for Aq-A2 plus these extra four haloes, also simulated at resolution level 2.
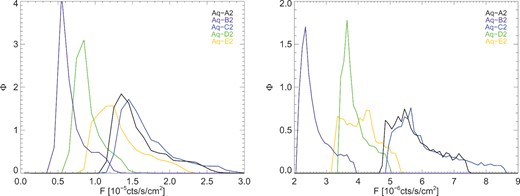
The flux distributions for Aq-A2 (black), Aq-B2 (purple), Aq-C2, (blue), Aq-D2 (green), and Aq-E2 (orange). The left-hand panel is for the GC, the right for M31.
The GC flux distribution of the Aq-C2 halo is enhanced by over a factor of 2 relative to Aq-B2 (the least massive halo). It is also a factor of 2 larger than is the case for Aq-D2, which is remarkable in that the Aq-D2 and Aq-C2 haloes have the same mass to at least three significant figures. The underlying difference is halo concentration: the value of the concentration parameter c is 18.4 for Aq-C2 and 12.4 for Aq-D2. The difference between haloes is even larger for the M31 case: therefore, the variation in halo concentration between our haloes will be very important for our results.
B5 Position of observer
The final effect that we consider is that of the position of the observer within the Milky Way halo. It has been shown that the stellar disc is at its most stable when aligned with the inner DM halo's minor axis (Bailin et al. 2005; Aumer & White 2013), and that the orientation of these vectors is constant from the inner resolution limit to 0.1 × r200 (Vera-Ciro et al. 2011). We therefore calculate the inertia tensor of all the DM particles within the sphere of radius 0.1r200, extract the minor axis vector for the corresponding ellipsoid, and then randomly distribute observers in rings of radius 8 kpc with the minor axis as the normal vector. We plot the distribution functions in Fig. B5; for completeness we also include the results when the intermediate and major axes are used as the normal vector. The simulation used is Aq-A1.

Flux distributions for the GC (Aq-A1) when the observer is constrained to lie in the plane normal to the minor (orange), intermediate (green), and major (cyan) axes; the spherically uniform sample is reproduced in black.
The different axes have a noticeable effect on the distribution of fluxes. The shapes of the constrained-observer curves have quite different shapes to the spherical-sampling case. For the major axis measurement the distribution at low fluxes is remarkably similar to the spherical case, but is then skewed heavily towards higher fluxes. The minor axis has consistently higher fluxes than does spherical sampling, by up to a few tens of per cent. Given that the effect is non-negligible, we will therefore build the possibility that our observer is biased towards the minor plane axis into our final results.
APPENDIX C: ANALYSIS OF XMM–Newton/EPIC OBSERVATIONS OF DRACO DWARF SPHEROIDAL GALAXY
In this section, we describe the details of our analysis of the Draco dwarf spheroidal galaxy (dSph) as observed with the European Photon Imaging Camera (EPIC) on-board the XMM–Newton space mission. Based on these observations, we fail to detect any significant line at ∼3.5 keV, thus placing an upper bound on its strength. Finally, we estimated the exposure of Draco observations by XMM–Newton necessary to confirm the DM origin of the ∼3.5 keV line. The results of this section have also been used for XMM–Newton proposal #076480, which was accepted in XMM–Newton 14th Announcement of Opportunity (AO-14); see http://xmm.esac.esa.int/external/xmm_news/otac_results/ao14_results for details.
C1 Data reduction
In this paper, we use data from the publicly available XMM–Newton observations of the Draco dSph (ObsIDs 0603190101, 0603190201, 0603190301, 0603190401 and 0603190501). Initial data files from the MOS and PN cameras of XMM–Newton/EPIC are pre-processed with the emproc and epproc procedures of the standard XMM–Newton software sas v.13.5.0. We detect data patterns with significant spatial (bright point sources) and temporal (proton flares) variabilities using the standard sas procedures espfilt and edetect_chain, remove these patterns from the subsequent analysis, and extract source spectra from 14 arcmin radius circle centred on Draco dSph centre (RA =17:20:12.4, DEC = +57:54:55.3) using sas procedure evselect. Redistribution matrix files and ancillary response files are created with the standard sas procedures rmfgen and arfgen, respectively. Finally, we group the obtained source spectra and response files, co-add them channel-by-channel using ftools procedure addspec, and rebin the obtained spectra by 60 eV (∼2–3 times smaller than the instrument's energy resolution) to make the energy bins roughly statistically independent. The total cleaned exposure of the obtained spectra is 107.1 ks for MOS (either MOS1 or MOS2) cameras and 40.4 ks for PN.
C2 Spectral modelling
We model the obtained Draco spectra in the 0.8–10.0 keV range using the X-ray spectral fitting package xspec v.12.8.1g. Because previous studies of dwarf spheroidal galaxies have not revealed the presence of any X-ray emitting gas, our model is a sum of instrumental and astrophysical background components. No signature of residual soft protons has been found according to the procedure of De Luca & Molendi (2004), so we have not added the residual soft proton component. The instrumental background (mostly caused by cosmic MeV protons penetrating inside XMM–Newton satellite) is modelled by an unfolded power law model and the sum of several narrow Gaussians representing bright fluorescence lines. The astrophysical background was modelled by a sum of the cosmic X-ray background (a folded power law) and the Galactic X-ray background (two apec models), in full accordance with Malyshev et al. (2014). The resulting fit quality is good, with χ2 = 221.64 for 223 d.o.f. Then, by adding further narrow Gaussian lines, we looked for line-like residuals in our region of interest near 3.5 keV. No statistically significant residuals were found. This produces a 2σ upper bound of 5.6 × 10−6 cts s−1 cm−2 on extra line flux in the 3.45–3.58 keV range.
C3 Calculation of sensitivity with respect to narrow line at ∼3.5 keV
To determine the exposure of Draco observation necessary to check the decaying DM hypothesis of the ∼3.5 keV line, we first calculate the expected line strength. According to Fig. 5, the best-fitting ratio FDraco/FGC = 0.09 with the scatter ranging from 0.04 to 0.2 (95 per cent range). Taking the results of Boyarsky et al. (2014a), where the line was detected from the GC with the highest significance, the best-fitting line flux of 26 × 10−6 cts s−1 cm−2 leads us to the conclusion that the range of fluxes expected from the Draco dSph is (1.0–5.2) × 10−6 cts s−1 cm−2 with the most plausible value being 2.3 × 10−6 cts s−1 cm−2. We take the value FDraco, min = 1.0 × 10−6cts s−1 cm−2 as a conservative lower bound on the expected DM signal in Draco.
The existing observations of Draco (Fig. C1, left-hand panel) allow us to determine the count rate at the energies of interest. It shows that one expects Nbg = 5.79 × 104 cts (two MOS cameras combined) or Nbg = 8.36 × 104 cts (PN camera) from a 1.34 Ms observation in a 180 eV energy interval (corresponding to the broadening of a narrow line due to the spectral resolution of XMM). Using the same exposure and the expected DM line flux of 1.02 × 10−6cts s−1 cm−2 we find |$N_{\scriptscriptstyle \rm DM}= 528$| cts for the MOS cameras (combined MOS1 and MOS2) and |$N_{\scriptscriptstyle \rm DM}= 600$| cts for the PN camera. Therefore the expected significance of the signal against this background is |$N_{\scriptscriptstyle \rm DM}/\sqrt{N_{\rm bg}}= (528+600)/\sqrt{(5.79+8.36)\times 10^4} \approx 3.0$|.
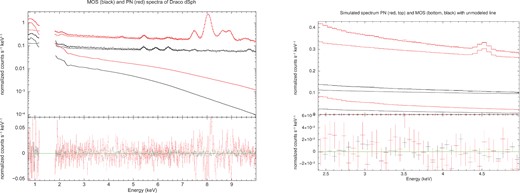
Left: combined spectrum of existing Draco dSph observations modelled as a combination of folded components (absorbed thermal low energy Galactic emission), an extragalactic power law (sharply falling component), and an instrumental component (unfolded power law plus instrumental Gaussians). The quality of fit: χ2 = 221.64 per 223 d.o.f. Right: simulated spectrum of 1.34 Ms of Draco dSph. The line with the flux FDraco, min is detected in two cameras with combined Δχ2 = 13.0.
To make this conclusion more robust we performed simulations of long-exposure observations. First, using the fakeit command of xspec, we simulated realizations of the Draco dSph spectrum with the line added at the 10−6 cts s−1 cm−2 level and with a XMM–Newton exposure 1.34 Ms: we recovered the line at a more than 3σ level. An example of the simulated spectrum with a positive line-like residual at ∼3.5 keV is show in Fig. C1, right-hand panel.
We also generate 250 realizations of spectra of a 1 Ms observation of the Draco dSph (based on the model of the existing Draco data, see Fig. C1). The simulated spectra do not contain a line at E ≈ 3.5 keV. We then try to detect a line at this energy and find that only in 12 simulations (i.e. in 4.8 per cent of cases) were we able to detect a line-like residual at a level of 10−6 cts s−1 cm−2 or above. This supports our estimate that a 1 Ms observation will either confirm the existence of the line or will instead rule it out at least at the 95 per cent confidence level.
In addition we have simulated 100 realizations of the Draco dSph spectrum with the line added at the 10−6 cts s−1 cm−2 level. In 68 per cent of the realizations the line was recovered with a flux in the range (0.71–1.45) × 10−6 cts s−1 cm−2, consistent with the Gaussian scatter around the simulated value.



