-
PDF
- Split View
-
Views
-
Cite
Cite
M. A. Muñoz-Gutiérrez, M. Reyes-Ruiz, B. Pichardo, Chaotic dynamics of Comet 1P/Halley: Lyapunov exponent and survival time expectancy, Monthly Notices of the Royal Astronomical Society, Volume 447, Issue 4, 11 March 2015, Pages 3775–3784, https://doi.org/10.1093/mnras/stu2639
Close - Share Icon Share
Abstract
The orbital elements of Comet Halley are known to a very high precision, suggesting that the calculation of its future dynamical evolution is straightforward. In this paper we seek to characterize the chaotic nature of the present day orbit of Comet Halley and to quantify the time-scale over which its motion can be predicted confidently. In addition, we attempt to determine the time-scale over which its present day orbit will remain stable. Numerical simulations of the dynamics of test particles in orbits similar to that of Comet Halley are carried out with the mercury 6.2 code. On the basis of these we construct survival time maps to assess the absolute stability of Halley's orbit, frequency analysis maps to study the variability of the orbit, and we calculate the Lyapunov exponent for the orbit for variations in initial conditions at the level of the present day uncertainties in our knowledge of its orbital parameters. On the basis of our calculations of the Lyapunov exponent for Comet Halley, the chaotic nature of its motion is demonstrated. The e-folding time-scale for the divergence of initially very similar orbits is approximately 70 yr. The sensitivity of the dynamics on initial conditions is also evident in the self-similarity character of the survival time and frequency analysis maps in the vicinity of Halley's orbit, which indicates that, on average, it is unstable on a time-scale of hundreds of thousands of years. The chaotic nature of Halley's present day orbit implies that a precise determination of its motion, at the level of the present-day observational uncertainty, is difficult to predict on a time-scale of approximately 100 yr. Furthermore, we also find that the ejection of Halley from the Solar system or its collision with another body could occur on a time-scale as short as 10 000 yr.
1 INTRODUCTION
Halley's Comet is probably one of the most studied and therefore best-known minor bodies in the Solar system to date. Historical records of Comet Halley start in the year 240 bc (Kiang 1972), but it is until its last perihelion passage, in 1986 February, when it became visible to modern telescopes and even physically accessible to spacecrafts, that the amount of available data has hugely grown. In particular, the parameters of its retrograde orbit, semi-major axis, a, and eccentricity, e, are since then determined with a precision of the order of 10−6 (σq = 771 × 10−9 and σe = 91 × 10−8, respectively, where σ is standard deviation and q the perihelion distance, according to Landgraf 1986).
The origin of Halley's Comet has been a matter of discussion for decades. One of the likely sources of Halley-type comets (i.e. short-period comets with Tisserand parameters T < 2 with respect to Jupiter, periods 20 < P < 200 yr and semi-major axis less than 40 au, as defined by Levison 1996) seems to be the Oort cloud (Fernandez 1980). Indeed, since giant planet perturbations of trans-Neptunian objects in the vicinity of the Kuiper Belt, will not generally drive comets to the observed inclinations on Halley-type comets, so the origin of their orbits must be different. In their computations, Fernandez (1980), Duncan, Quinn & Tremaine (1988) and Quinn, Tremaine & Duncan (1990) show that the dynamical evolution of comets from the Oort cloud towards the inner Solar system is a probable origin of the random inclination of Halley-type comets, since they tend to preserve their random orbital inclinations. On the other hand, Levison, Dones & Duncan (2001) noticed that the inclination distribution of Halley-type comets is not isotropic, meaning that they could not be readily explained as originating from a rather isotropic source as the Oort cloud, but from a flattened component or inner disc-like portion of the Oort cloud. Earlier, Duncan & Levison (1997) had investigated a viable origin of Jupiter family comets coming from the already known flattened scattered disc (Luu et al. 1997). They found that approximately 1 per cent of their scattered disc objects survived the full 4 Gyr simulation, where some of these reach semi-major axis of thousands of au. In a more recent paper, Levison et al. (2006) show that these objects, once they reach a semi-major axis of the order of 104 au, are rapidly reduced in their perihelia due to Galactic tides. If just 0.01 per cent of these comets then evolve, due to giant planet interactions, on to Halley-type orbits, the resultant statistical orbital distribution is consistent with observations.
The physical properties of Comet Halley are also known as never before (for a review see Mumma & Charnley 2011). A'Hearn et al. (1995) have shown that Halley-type comets differ from Jupiter Family comets on their average coma carbon abundances, suggesting a different origin for both families. Comet Halley seems to lose mass at an approximate rate of 0.5 per cent every perihelion passage (Whipple 1951; Kresak & Kresakova 1987). At this rate, the comet might be severely diminished or even vanished in about 15 000 yr. Halley's Comet has been spreading particles that settle down on the known Orionid stream for thousands of years (Sekhar & Asher 2014).
From the dynamical point of view the evolution of this comet has also been profusely studied through numerical integrations (Yeomans & Kiang 1981; Dvorak & Kribbel 1990; Levison & Duncan 1994; Bailey & Emel'Yanenko 1996; van der Helm & Jeffers 2012; Sekhar & Asher 2014). Detailed calculations show for example that Halley's Comet has been trapped in the past by resonances with Jupiter and secular perturbations, such as the Kozai resonance and other secular resonances (Quinn et al. 1990; Bailey & Emel'Yanenko 1996; Thomas & Morbidelli 1996) affecting considerably its long-term dynamical evolution (Sekhar & Asher 2014). From numerical simulations under various approximations, Halley's Comet and other Halley-type comets seem to be intrinsically chaotic (Petrosky 1986; Froeschle & Gonczi 1988; Chirikov & Vecheslavov 1989).
In the pioneering work of Chirikov & Vecheslavov (1989), they used a simple analytical model based on the results of integrations by Yeomans & Kiang (1981) which resembles the perihelion passage over the past ∼3000 yr, in order to obtain a measure of the chaotic behaviour of the Halley's Comet. They found that Jupiter plays the major role in driving the local instabilities of the motion while Saturn contributes an order of magnitude less in the random changes suffered by the comet. Apart from these early work, not many attempts have been made to obtain a reliable quantification of the chaotic behaviour of Halley's Comet with modern numerical integration tools. This means that a standard Lyapunov exponent or Lyapunov time has not been established with confidence for Halley by means of direct numerical integrations.
In this work, we explore numerically the evolution of test particles in the surrounding phase space of Halley's Comet in order to determine the chaoticity of this region quantified through frequency analysis maps and a simple auxiliary visual tool that we have called ‘survival time maps’. Additionally we compute, for the first time directly from numerical integration, the Lyapunov exponent for Halley's Comet in its current orbit considering its observational uncertainty. By finding a positive exponent, we have determined that current known orbit is actually chaotic. We also estimated the e-folding time-scale for the separation of neighbouring orbits. Finally we provide an estimation of sojourn time in the Solar system for the comet in a qualitative similar manner to that used by Chirikov & Vecheslavov (1989) finding a median value almost an order of magnitude smaller than theirs.
The outline of this paper is as follows: in Section 2, we describe the three different analysis techniques to determine the chaotic nature of the dynamics of Halley's Comet and the corresponding numerical simulations done for this purpose. In Section 3, we show results of the numerical simulations while discussing these results in Section 4. Finally we give our conclusions in Section 5.
2 METHODS AND SIMULATIONS
We have used three different analysis methods to determine the chaotic nature of Halley's Comet dynamics. We describe these in the next subsections.
2.1 Survival time maps
Survival time maps (STMs hereafter) are an auxiliary tool to visualize the absolute stability, against ejection from the system or collision with other bodies in orbits of a given phase space region, corresponding in our case to the plane of semi-major axis, a, versus eccentricity, e, surrounding Halley's current position in this plane. In the STM a colour code indicates the total survival time in the simulation according to the particle's initial condition given by its position in the phase space plane. In order to explore this we have used the mercury integrator package developed by Chambers (1999) to integrate the orbits of clones of Comet Halley as test particles in a Solar system N-body simulation. The clones were generated in such a way that their initial conditions cover a region on the a–e plane with different zoom levels.
We performed three different simulations to construct STMs corresponding to different ranges of a and e. In the first simulation (a) semi-major axis, a, ranges from 15 to 20 au and e ranges from 0 to 1 with both intervals divided uniformly in 100 values each, giving a total of 104 particles. In the second simulation (b) a ranges from 17.385 to 18.385 au divided uniformly in 100 values and e ranges from 0 to 1 for a total of 3300 particles (33 values in e). Although the small e space comprises a very different dynamical region than that for Comet Halley, we explore it to put into perspective the importance of giant planets influence zones and to get a glimpse into the possible behaviour of other Halley-type comets that may be explored in a future work. In the third simulation (c) the domain of a–e space covers the observational error according to Landgraf (1986) both in a (σa ∼ 10−6 au) and e (σe ∼ 10−6) sampled with 104 total particles. In all cases the angular elements, argument of pericentre, ω, longitude of the ascending node, Ω, mean anomaly, M, and inclination, i, were set the same as that of Halley's Comet as given by the Horizons website1 at the beginning date of the simulations 2012 October 1 in heliocentric coordinates. A final simulation (d) was performed varying semi-major axis and inclination and letting the four remaining orbital parameters, including eccentricity, be the same as for Comet Halley on the same date, and covering the observational error in a–i phase space (with σi ∼ 10−5 deg, according to Landgraf 1986). We divide both ranges in 100 uniformly spaced values for a total of 104 particles.
For (a) and (b) simulations, the radau integrator from Everhart (1985) as implemented in the mercury package was selected for the integrations with a tolerated accuracy parameter of 10−10 and an initial time step of 20 d. Simulations (c) and (d) were carried on using the optimized Bulirsch–Stöer integrator implemented in the mercury package (BS2) with a tolerated accuracy parameter of 10−12 and an initial time step of 1 d, in order to be confident in the integration of small perihelion, high-eccentricity orbits. All simulations spanned over 106 yr and include as N-bodies the planets except Mercury in order to avoid incorporating relativistic effects. We also include five Dwarf Planets (all but Sedna which orbits far beyond the 100 au sojourn limit imposed in the simulation) and five of the greatest minor bodies (Orcus, Quaoar, Varuna, Ixion and 2002 AW197) not yet classified as dwarf planets but likely to be in the near future.
According to the sojourn criterion for STM, the particle is still part of the simulation at the end of the 1 × 106 yr of it, regardless the changes in orbital parameters of each particle. So a particle is lost when its a becomes greater than 100 au, collides with the Sun or with another planet.
2.2 Frequency analysis map
We then performed one 5 × 105 yr simulation using the radau integrator from the mercury package with a toleration accuracy parameter of 10−10 and an initial time step of 20 d. We cover a semi-major axis span of just 1 au from 17.385 to 18.385 au, this is ±0.5 au from the current semi-major axis of Comet Halley, and from 0 to 1 in e. We have used 100 uniformly spaced particles in a and 33 particles to uniformly cover e, in order to save computational time as we are bounded to record an extensive output cadence of parameters evolution.
2.3 Lyapunov exponent
We have calculated the Lyapunov exponent for six neighbouring orbits around the current orbit for Comet Halley separated by the present-day observational uncertainty. The six orbits are the result of varying initial position by ±10−6 au in each Cartesian axis X, Y, Z in a heliocentric reference frame, while maintaining the velocity at the same value of the fiducial orbit. This means that each one of the six orbits differs initially from the fiducial one by a distance of 10−6 au distance, δ(0).
In this context, we have used the Bulirsch–Stöer integrator from the mercury package in order to perform a set of 30 simulations, extending over 100 yr each in succession, of Halley's fiducial orbit plus six orbits around it. The total simulated time is 3000 yr, starting from 2012 October 1 in order to avoid the first close encounter of the fiducial Halley with Jupiter expected to occur at about ∼3400 yr into the future. These close encounters produce random variations in the orbit that are capable of modifying the separation of the orbits by several au on a very short time-scale (see Fig. 6 for details). The initial time step was chosen to be 3 d with an accuracy parameter of 10−12 in order to obtain high enough precision to calculate a real separation of the orbits, resulting from dynamical effects, and not a computational artefact. In this manner, we have calculated the Lyapunov exponent for each one of the six orbits previously defined using the iterative process just as described, and a maximum Lyapunov exponent for the full set of orbits.
3 RESULTS
In order to assess the stability of the orbit of Comet Halley (and possibly other Halley-type comets), and to characterize its dynamics, we have carried out numerical simulations as previously described. The results of these studies are presented in this section.
3.1 Survival time maps
Fig. 1 shows the STM for orbits with initial semi-major axis extending from 15 to 20 au and eccentricity less than 1. The test particles sampling these orbits all have the same inclination, corresponding to the present day inclination of Comet Halley, 162.180 42 |$\deg$| according to the Horizons website for the beginning date of our simulations. For comparison, we also show in the figure the nominal orbit of Comet Halley (black dot).
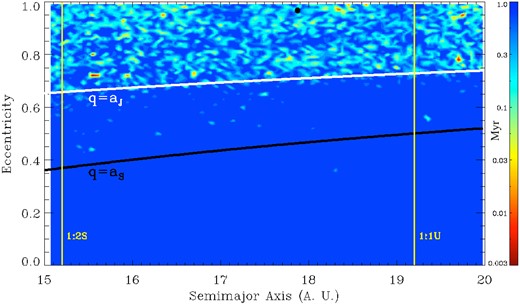
Survival time map for orbits with semi-major axis up to a few au from Comet Halley's orbit, all with the same inclination. The colour scale indicates the survival time as a function of initial semi-major axis and eccentricity of the orbit. Halley's present day orbit is indicated by the black circle. The thick black and white lines correspond to particles crossing the orbit of Saturn and Jupiter, respectively. Also shown with vertical yellow lines are the strongest mean-motion resonances (MMR) in the region, 1:2 with Saturn and 1:1 with Uranus (Gallardo 2006).
Evident in Fig. 1 is the fact that a wide range of orbits crossing that of Jupiter are strongly unstable, with a median lifetime, for such orbits, of 5.6 × 105 yr. Note that this lifetime is a lower limit for the expected lifetime of small bodies in this region of a–e phase space, as the survival time of stable orbits may be much greater than the 1 Myr time-scale considered in our simulations. This result is also seen in Fig. 2 which shows the STM zooming-in on the semi-major axis to a range extending within 0.5 au of Halley's orbit. In this case, the median survival time is 5.1 × 105 yr which is consistent with the result from the previous map, considering the use of less particles on a broader range in eccentricity.
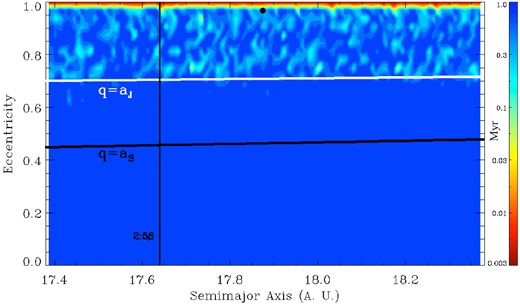
Same as Fig. 1 but zooming-in on the orbits with semi-major axis within 0.5 au of Halley's Comet orbit. The stronger MMR in this region, the 2:5 resonance with Saturn, is indicated by the vertical black line.
An important feature steaming from the comparison of the sequence of increasing zoom Figs 1, 2 and 3, the last one corresponding to a semi-major axis and eccentricity range covered by the observational uncertainty for Comet Halley (Landgraf 1986) is the fact that the ‘structure’ of the stable/unstable zones is apparently self-similar likely fractal in nature. The determination of the fractal dimension for these structures is beyond the scope of the present study. This result is already suggestive of strongly chaotic dynamics for small bodies in the region, as orbits within a very small neighbourhood in a–e space can have extremely different behaviour regarding their stability properties.
A similar result is found in the structure of the stable/unstable zones, where we plot them as a function of orbit inclination of the test particles. Fig. 4 shows the STM for orbits with the present day eccentricity of Comet Halley, 0.967 623, again according to the Horizons website, but different inclinations spanning over the |$10^{-5}\deg$| observational uncertainty in this parameter (Landgraf 1986).
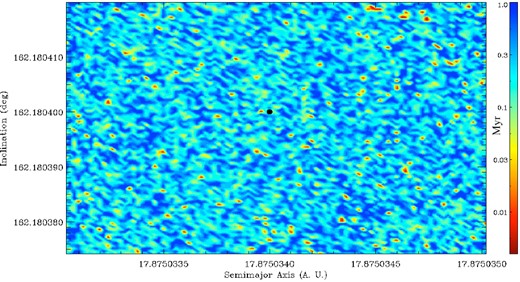
STM for orbits with semi-major axis and inclination within the observational uncertainty of Comet Halley (Landgraf 1986). The eccentricity in all cases is taken at the nominal value.
In both a–e and a–i phase space stability maps extending over the observational uncertainty (Figs 3 and 4), the median survival time for particles in the region is found to be 3.2 × 105 yr. This value is then a reliable estimate of the stability time for the current known orbit of Comet Halley in the Solar system.
3.2 Frequency analysis maps
A more detailed analysis of the stability of orbits within 0.5 au of Halley's orbit (with its nominal inclination) is shown in Fig. 5, where contours of the rate of change in the mean motion of particles initially on a given orbit, over the extent of a 5 × 105 yr simulation, are plotted. Red and orange coloured areas in this figure denote regions of phase space where orbital parameters, particularly the mean motion, change by more than 5 per cent over this time-scale. While these orbits are not unstable in the sense of the results presented in the STMs of Section 3.1, they do change significantly and may lead to a different dynamical evolution of particles on these zones.
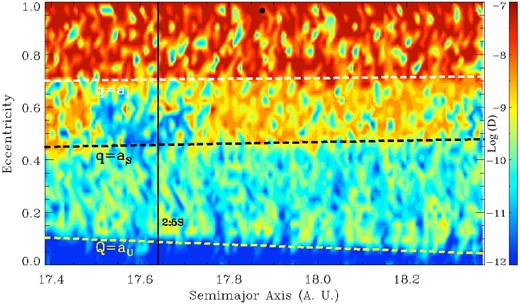
Frequency analysis map for orbits with Comet Halley's inclination but differing in semi-major axis (by up to 0.5 au) and eccentricity. Red coloured regions correspond to the most unstable orbits. Horizontal lines indicate orbits with perihelia crossing Jupiter's orbit (white dashed), Saturn's orbit (black dashed) and with aphelia crossing the orbit of Uranus (yellow dashed). The black vertical line indicates the position of the 2:5 MMR with Saturn, the stronger one in the region (Gallardo 2006).
As in the STM corresponding to the same zoom level (Fig. 2), a region of strong orbital variation is shown in Fig. 5 for orbits with perihelia that cross the orbit of Jupiter, indicated by the (nearly) horizontal, dashed white line. A large proportion of orbits above this line exhibit significant variation over the length of the simulation. In addition, a pair of families of unstable orbits are also found, corresponding to those particles that cross the orbit of Saturn and do not cross that of Jupiter, and to those particles with aphelia large enough to cross the orbit of Uranus but not to cross Saturn's orbit. These features are not found on the basis of the STMs previously presented, as they do not correspond to strictly unstable orbits. A mean value for the D parameter in each region is found to be as follows: D ∼ 10−7.8 for particles crossing Jupiter's orbit, D ∼ 10−9.2 for particles crossing Saturn's orbit but not Jupiter's, and D ∼ 10−10.1 for particles that reach the orbit of Uranus but not Saturn's.
A simple numerical estimation of the time-scale for orbits to evolve significantly according to the D parameter, τD, can be found from the definition of diffusion parameter given in equation (1), from which it is clear that τD ∼ n/D ∼ 1/PD years, where P is the orbital period. As P ∼ 75 yr across this whole region of phase space, the corresponding time-scale in the three regions mentioned above is ∼8 × 105, ∼2 × 107 and ∼2 × 108 yr, respectively. The time-scale τD can be understood as the time required for the particle to suffer major changes in its orbit. The instability time obtained from STM and Laskar frequency analysis is roughly consistent for particles crossing Jupiter's orbit. In addition, these estimations are also consistent with the fact that particles not crossing Jupiter's orbit can survive the whole 1 Myr simulation, as found from the STMs.
Islands of stability/instability (blue/red zones) exist throughout the region mapped in Fig. 5, where no relation with major resonances or other bodies in the Solar system are easily identified. Although we have not carried out simulations to accomplish the Laskar frequency analysis at different zoom levels, the rapidly changing structure of the stable/unstable regions of phase space suggests a strong dependence on the initial conditions for the dynamical evolution of small bodies in the region.
3.3 Lyapunov exponent
The strong sensitivity on initial conditions depicted by our results in connection to the STMs and the Laskar stability analysis, is further illustrated in Fig. 6 which shows the separation distance between two orbits and the nominal solution for Comet Halley. One of the orbits considered (red line in Fig. 6) is for a particle starting from initial coordinates with the X component of its position greater than the nominal solution by an amount δ0 = 10−6 au, the reported observational error for the ephemerides of Comet Halley. The other orbit differs initially from Halley's nominal solution in the same amount but in the Y coordinate (blue line in Fig. 6). Both orbits rapidly diverge from the nominal solution.
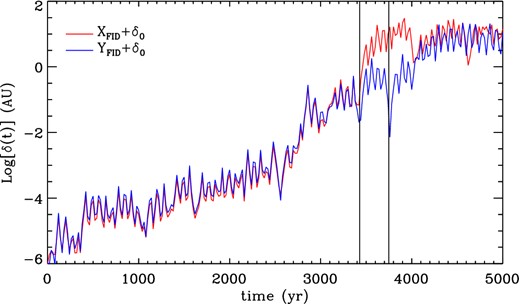
Evolution of the separation distance between modified orbits and Halley's fiducial orbit. Curves correspond to initial conditions in which the X coordinate (red line) and the Y coordinate (blue line) are varied by δ0 from the fiducial coordinate for Halley's Comet. Vertical black lines indicate times of close encounters between the comet on the fiducial orbit and Jupiter.
As illustrated in Fig. 6, there are two processes leading to an increase in the separation of neighbouring orbits. A gradual increase, as that occurring up to 3400 yr during which the separation increases by approximately five orders of magnitude due to the effect of distant encounters with other bodies in the system. And a phase of abrupt change in orbital parameters due to a close encounter of the particle with Jupiter. During this phase, the dynamical evolution is particularly sensitive to the initial conditions, as can be seen from the widely different separation for the orbits considered following the close encounters. These events, during which the particle approaches the planet to within three Hill radii (RH = (Mp/3 M⊙)1/3), are marked by black vertical lines in Fig. 6, a bit after 3400 yr and at slightly less than 3800 yr.
The formal definition of the term chaos is matter of debate. In this paper we follow Strogatz et al. (1994) who proposes a working definition of chaotic behaviour as ‘aperiodic long-term behaviour in a deterministic system that exhibits sensitive dependence on initial conditions’. Our system is clearly deterministic and the sensitive dependence on initial conditions is usually measured in terms of the Lyapunov exponents which quantify the exponential rates at which neighbouring orbits diverge (or converge) as the system evolves in time. If such system exhibits at least one positive Lyapunov exponent, then it is said that the dynamics of the system is chaotic.
To formally assess the chaotic behaviour of Comet Halley we have computed the maximum Lyapunov exponent for particles on Halley's nominal orbit, with respect to variations in the orbital parameters at the level of their current observational uncertainty. The resulting Lyapunov exponent is shown in Fig. 7. The corresponding Lyapunov time-scale is approximately 70 yr. It is important to point out that this time-scale corresponds to the time-scale for orbits to diverge by 1 part in 106, which is approximately the observational uncertainty.
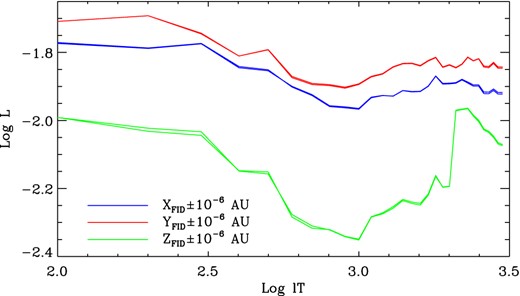
Lyapunov exponents for the six orbits after 3000 yr integrations. The maximum Lyapunov exponent which results from variations in the Y Cartesian axis (red curves) implies a Lyapunov time of ∼70 yr.
4 DISCUSSION
In this section, we discuss in more detail some of the implications of our results and analyse the effect of some of the assumptions and methodology used in our study.
4.1 Predictability of Halley's orbit
One of the important consequences of the chaotic nature of Halley's orbit is the possibility of making long-term predictions of its motion. On one hand, we can interpret our results of Section 3.3 in terms of the so-called Lyapunov time-scale, |$\tau _{\mathcal {L}}$|, defined as the inverse of |$\mathcal {L}$|, corresponding to the e-folding time-scale of the separation of initially neighbouring orbits. The fact that |$\tau _{\mathcal {L}}\approx 70$| yr, is an indication that over such time-scale two orbits initially separated in semi-major axis, eccentricity or inclination by 1 part in 106, diverge from one another by a factor of e in separation. This precludes the possibility of making high-precision predictions, at a level similar to that of the present-day observational uncertainty in its orbital parameters, the ‘short’ term, ∼70 yr, evolution of the orbit of Comet Halley, i.e. from one perihelion passage to the next.
On the other hand, the fact that the contours in the STMs, which reflect the structure of regions of dynamical stability in a–e phase space, have an apparently self-similar or fractal nature (commonly found in chaotic dynamical systems) as can be seen from comparing Figs 1, 2 and 3 corresponding to STMs at different ‘zoom’ levels around Halley's orbit, also suggests that the survival time of the comet cannot be accurately determined. As evident in Fig. 3, closely neighbouring orbits (within the observational uncertainty) can have widely different stability properties. The time over which Halley remains stable can range from 104 to 106 yr (or more), with the median value in a domain ranging over the observational uncertainty of a and e being approximately 3.2 × 105 yr, at the zoom level shown in Fig. 3. Furthermore, this result implies that an orbit, such as Halley's nominal solution, apparently located in a stability island on a given ‘zoom’ level, may turn out to be much more unstable as we zoom-in around it. A similar conclusion is reached from the distribution of values for the Laskar D index which measures the change in the orbit and has also an apparent ‘fractal’ structure as shown in Fig. 5.
Another illustration of the strong dependence of Halley's motion on its initial position and velocity and of the difficulty in predicting its future motion is given in Fig. 8, which shows the evolution of the orbital parameters a, e, i and the Tisserand parameter with respect to Jupiter, TJ, for seven particles located at extreme values of these parameters, within the box defined by the observational uncertainty for Halley's orbit. Over a time-scale of 105 yr or more, even orbits starting out with a difference in orbital parameters of less than the observational uncertainty can have widely different outcomes.
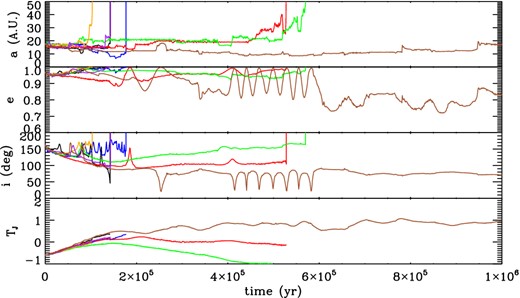
Temporal evolution of the main orbital parameters of seven particles with initial conditions within the present-day observational uncertainties in Comet Halley's orbit. Particles 1 and 2 correspond to initial conditions deviating in ±10−6 au in the X coordinate from the centre of the a–e box defined in Fig. 3, similarly, particles 3, 4, 5 and 6 correspond to initial conditions within ±10−6 au in the Y and Z coordinate, respectively. Particle 7 starts out from initial conditions corresponding to the centre of the box.
4.2 On the fate of Halley's orbit
Halley-type comets as a class (HTCs hereafter) are characterized by orbital periods less than 200 yr and Tisserand parameter with respect to Jupiter smaller than 2. In the present study, we have assumed that Comet Halley is already on its present day orbit and followed its subsequent evolution, not much can be said about the origin of its orbit.
Nevertheless, the results presented in Section 3.1 indicate that the survival time for objects in Halley-type orbits ranges from 104 to 106 yr, implying that a body in a Halley-like orbit can remain on it, or on one very similar to it, for no more than approximately 1 Myr. This, together with the fact that Halley is still an active comet, which suggests that it has probably been in its present, short period and small perihelion orbit, less than 104 yr, implies that Halley will probably remain on it for at least a similar time-scale.
In order to estimate the probability that Comet Halley remains in a stable orbit similar to the one it has in the present day, we have computed the fraction of particles remaining in the simulations as a function of time. Fig. 9 shows the number of particles colliding with the Sun or ejected from the Solar system, for a collection of 10 000 particles started from initial conditions within a domain in a–e phase space defined by the observational uncertainties in these parameters, as we did in the construction of the STM of Fig. 3. The initial sharp increase in the number of ejected particles is related with the first close encounter of all particles with Jupiter after ∼3400 yr of the beginning of the simulation. It is worth to mention that although all particles suffer this close encounter, as a result of it just a few of them are ejected from the system. This due likely to the chaotic nature of its motion. We find that 105 yr after the start of the simulation, 2 per cent of all particles have collided with the Sun and approximately 10 per cent have been ejected from the system. Hence, we could estimate that Comet Halley has approximately a 90 per cent chance of surviving at least 105 yr in the Solar system. However, in a similar manner we can estimate that by 106 yr, there is a 28 per cent chance that it will collide with the Sun and a 50 per cent chance that it will be ejected from the system.
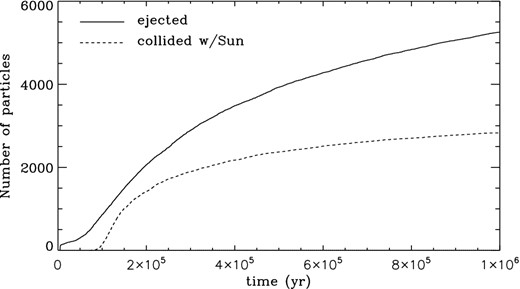
Temporal evolution of the number of particles ejected from the Solar system and that collide with the Sun out of the 104 particles originally present in the simulation. All particles are started from a set of orbits consistent with the present day orbit of Comet Halley, i.e. with a and e values within the observational uncertainties. Additionally, from the whole set of particles, six collided with one of the planets.
One final piece of interesting information to be gathered from our results is that the orbits consistent with Comet Halley (within the observational uncertainty) that are not lost from the system due to ejection or collision with the Sun, have a tendency to evolve conserving a Tisserand parameter with respect to Jupiter, as seen in Fig. 10, which shows the evolution of a, e, i and TJ for 200 randomly chosen particles in our simulations. Again, the initial orbit of all these particles is consistent with Halley's present day orbit, and most of the particles in the ensemble are seen to evolve as follows.
A rapid increase, on a time-scale of a few thousand years, in the spread of a, e and i representing the diversity of possible orbits to be followed by Halley if it survives.
A large fraction of orbits evolve into periods greater than 200 yr, i.e. they are no longer short period comets.
The average eccentricity of the ensemble increases slightly on a time-scale of 105 yr.
The inclination of most possible orbits consistent with Halley's current orbit tends to evolve into lower inclination, almost polar orbits.
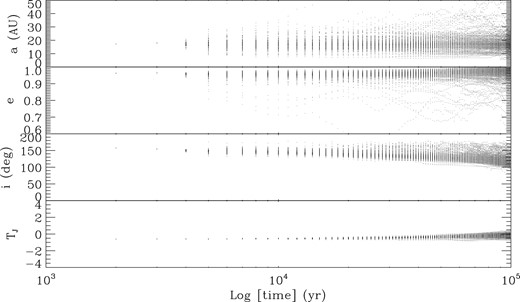
Temporal evolution of the main orbital parameters of 200 randomly chosen particles with initial conditions within the present-day observational uncertainties in Comet Halley's orbit. All particles have initial conditions corresponding to orbits consistent with the present day orbit of Comet Halley. Each point represent the instantaneous value of the parameters for a particular solution at a given time.
Although there is a wide spread in possible outcomes for Comet Halley as we have discussed in previous sections, it seems likely that, if it survives for more than 105 yr, its orbit will evolve into a more eccentric and less inclined orbit.
4.3 Origin of chaos
It is generally believed that chaotic dynamics of small bodies in the Solar system, such as asteroids in the Main Belt or comets in the Kuiper Belt, results from the overlapping of mean-motion and secular resonances with the major bodies in the Solar system (for a review of the topic see Malhotra 1998, an references therein).
Comet Halley, however, is not trapped in any of the known strong resonances with the outer planets, and this is not expected due to the comet's high eccentricity and inclination. So the origin of the chaotic character of its orbit is not straightforward to identify. Furthermore, it appears that the chaotic motion we have identified is not directly related to the close encounters of the comet with the giant planets, particularly with Jupiter. This is a well-known source of strong chaos in the system which however develops on a greater time-scale of many orbital periods. This is illustrated in Fig. 6, where the first close encounters of the comets with Jupiter are shown to occur after approximately 50 orbital periods.
The weak chaotic behaviour we have characterized by the Lyapunov exponent analysis of Section 3.3 is not directly related to these close encounters, as it develops long before the first close encounter occurs. One possible explanation for the origin of the chaotic motion of Halley's Comet is the overlap of p: 1 mean-motion resonances, where p is an integer, with the binary conformed by the Sun and Jupiter (Shevchenko 2014). In a previous work Shevchenko (2007) performs an analytical estimation of the Lyapunov time for the Halley's Comet obtaining a lower limit for this of ∼34 yr, which is consistent with our numerical estimation. We intend to analyse this issues in more detail in a future work.
4.4 Neglected dynamical effects
In the present study, we have neglected the effect of non-gravitational forces known to affect the dynamics of active comets near perihelion (Marsden 1968). The effect on Comet Halley is particularly well known, but along with this is the fact that the estimated time in which the gaseous jet forces are actively present in comets is just a few hundred perihelion passages, which corresponds to a few thousand years of the dynamical lifetime of Halley-type comets. As we are interested in the long-term dynamical evolution of Halley's Comet, we decided to neglect this effect in the simulations presented in this work.
To test the previous assumption, we carried out a simulation of the long-term evolution of Halley's Comet including non-gravitational forces as prescribed in the Horizons website,2 to construct an STM for the conditions studied in Fig. 1. In doing that we are highly overestimating the importance of this effect because we implicitly assume that the comet is active for the whole 1 Myr simulation. Nevertheless, even in this extreme scenario, the results as far as survival expectancies are statistically equivalent to the one without non-gravitational forces presented in the previous sections.
Finally, it is worth mentioning that the results we have obtained are strictly related with the gravitational interaction of test particles with the major Solar system bodies, except for Mercury. The mass of Mercury could be added to that of the sun, but this adds just ∼1.6 × 10−7 M⊙ to the total mass of the Sun, therefore, in the long term, there is not a measurable difference for Halley's Comet fate. To correctly account for the influence of Mercury in a simulation of the Solar system, it would require a relativistic treatment of the equations of motion, but given the chaotic nature of the problem and the short time-scale of the simulations, compared to the Solar system lifetime, we considered this a second-order effect in our analysis to be considered in future studies.
5 CONCLUSIONS
We have carried out a series of numerical simulations aimed to assessing the dynamical stability of Halley's Comet. Three types of analysis are carried out to demonstrate and characterize the chaotic behaviour of the Halley's orbit on the basis of STMs, frequency analysis maps and a direct calculation of the Lyapunov exponent.
From our analysis of STMs we conclude that it is common for Halley-like orbits to be unstable up to the point of being ejected from the system, or colliding with another Solar system body. We also find that the long-term evolution of Comet Halley, even with the high precision of its observed orbital parameters, is difficult to predict on account of the strong dependence on the initial conditions. The time-scale for particles in orbits differing in less than today's observational uncertainties in a or e can range by at least two orders of magnitude, from 104 to 106 yr approximately. The median time-scale for the survival of particles in a range of a and e within the observational constraints is 3.2 × 105 yr.
Based on the Laskar stability analysis in a neighbourhood of Halley's Comet, we conclude that even stable orbits, in which the particles are not ejected or collide with a Solar system body, can change significantly on a time-scale of millions of years. Again, the precise determination of what will be the fate of Comet Halley is hindered by the strong dependence on the initial conditions, even within today's observational uncertainties at the level of 1 part in 106. On time-scales of more than 105 yr, it seems likely that the Halley, if it does not collide with the Sun or is ejected from the Solar system, will evolve into a higher eccentricity, lower inclination orbit.
Finally, we have computed the Lyapunov exponent for the present-day Halley's orbit and a series of other orbits differing in a and e by an amount equivalent to the observational uncertainty. We have found that |${\mathcal {L}}$| is greater than zero with a value of approximately 10−2, indicating that the orbit is indeed chaotic. The corresponding time-scale for the prediction of Halley's orbit to within present-day observational constraints is less than 100 yr, suggesting that the orbit of Halley's Comet cannot be accurately predicted for time-scales much greater than this. An important finding in our work is that the chaotic behaviour is not related to close encounters of Halley with any of the planets in the Solar system, nor to the overlap of any known system of resonances. The origin of the chaos in such eccentric orbits is a subject to be explored in more detail in future studies.
We acknowledge Carlos Chávez for his help in the implementation of the routines for the frequency analysis maps. We are also very grateful to the anonymous referee for comments that improved the quality of this paper. We also acknowledge support from DGAPA-UNAM PAPIIT grants nos. IN115109 and IN114114. MAM is thankful to CONACYT-Mexico for a scholarship to conduct graduate studies.




