-
PDF
- Split View
-
Views
-
Cite
Cite
R. Smolec, I. Soszyński, A. Udalski, M. K. Szymański, P. Pietrukowicz, J. Skowron, S. Kozłowski, R. Poleski, D. Skowron, G. Pietrzyński, Ł. Wyrzykowski, K. Ulaczyk, P. Mróz, Blazhko-type modulation in the double-mode RR Lyrae stars of the OGLE Galactic bulge collection, Monthly Notices of the Royal Astronomical Society, Volume 447, Issue 4, 11 March 2015, Pages 3756–3774, https://doi.org/10.1093/mnras/stu2684
Close - Share Icon Share
Abstract
We present the analysis of Blazhko-type modulation in double-mode RR Lyrae (RRd) stars found in the Optical Gravitational Lensing Experiment (OGLE) photometry of the Galactic bulge. Modulation is detected in 15 stars. Most of them have non-typical period ratio of the radial modes. In the Petersen diagram, at a given period of the fundamental mode, they are located significantly below or above the sequence formed by the majority of RRd stars. Multiperiodic modulation is very frequent; two or three modulation periods are detected in eight stars. Modulation periods vary from ∼20 to more than 300 d. Radial mode amplitudes can be modulated by a few to nearly 100 per cent. Both radial modes may be modulated with the same period. More commonly however, dominant modulation for the fundamental mode has different period than dominant modulation for the first overtone. Quite often modulation of only one mode is detected in the data. We find a clear feedback between pulsation amplitude of the dominant mode and mean stellar brightness: the lower the pulsation amplitude, the brighter the star. At phases of low pulsation amplitude, the mode periods are prone to fast changes. All the stars share the common feature: their pulsation properties are non-stationary. Amplitudes and phases of the radial modes vary irregularly on a long time-scale of a few hundred or thousand days. The short-term modulations are also irregular. One of the stars has switched the pulsation mode recently: from single-mode fundamental mode pulsation to RRd state. In other star the non-radial mode with characteristic ∼0.61 period ratio to the first overtone is detected. This non-radial mode is likely modulated with the same period as the radial modes.
1 INTRODUCTION
RR Lyrae stars are classical pulsators oscillating in the radial modes. A majority of these stars are single-mode pulsators pulsating either in the fundamental mode (F-mode, RRab stars) or in the first overtone mode (1O-mode, RRc stars). Less frequent is pulsation in the two modes simultaneously (RRd stars). RR Lyrae stars play an important role in distance determination and in the studies of Galactic structure and evolution. RRd stars, or multiperiodic pulsators in general, are important for the determination of basic stellar parameters, in particular of stellar masses (see e.g. Petersen 1978; Popielski, Dziembowski & Cassisi 2000).
RR Lyrae stars are relatively simple pulsators, nevertheless they are not well understood. The most stubborn problem is the origin of the Blazhko effect – a long-term quasi-periodic modulation of pulsation amplitude and phase (Blazhko 1907). The other unsolved problem is mode selection mechanism. We do not know why some stars pulsate in two modes simultaneously and what is the mechanism behind (for a review see Smolec 2014). In the recent years our knowledge about RR Lyrae stars significantly increased. The progress is not only thanks to space photometry revolution, caused by space telescopes Convection, Rotation and planetary Transits (CoRoT) and Kepler, but also thanks to long-term ground-based photometric sky surveys, like the Optical Gravitational Lensing Experiment (OGLE).
The ultraprecise photometry of space telescopes allows to investigate a relatively small sample of stars, but with unprecedented accuracy and detail. As a result our knowledge about the Blazhko effect significantly increased. Space photometry indicates that nearly 50 per cent of RRab stars are affected by the Blazhko effect (Benkő et al. 2010, 2014). The most important discoveries are detection of period doubling effect in about half of the modulated stars observed from space (Szabó et al. 2010; Szabó 2014), detection of additional radial modes in the Blazhko variables in the mmag regime (mainly of the second overtone; Benkő et al. 2010, 2014; Molnár, Kolláth & Szabó 2012), multiple modulation periods and clear demonstration of irregular nature of the modulation (e.g. Guggenberger et al. 2012; Benkő et al. 2014).
Although new models behind the Blazhko modulation were proposed (e.g. Buchler & Kolláth 2011) we are still far from the solution of the Blazhko puzzle (for a review see Szabó 2014).
Space photometry allowed clearly establishing a new group of double-mode pulsators, pulsating in the first overtone and in a yet not identified non-radial mode, with characteristic period ratio of the two modes in a narrow range around Px/P1 ≈ 0.61. Such period ratios were also detected in RRd stars. First such stars were discovered in the Microvariability and Oscillations of Stars (MOST) photometry and in the ground-based photometry of ω Centauri (Gruberbauer et al. 2007; Olech & Moskalik 2009). Analysis of space observations of RRc and RRd stars indicates that this form of pulsation must be common (e.g. Chadid 2012; Szabó, Benkő & Paparó 2014; Moskalik et al. 2015 and references therein). Nearly all RRc/RRd stars observed from space show the additional non-radial mode. A similar form of pulsation was detected in the first overtone Cepheids, mostly in the OGLE data (Moskalik & Kołaczkowski 2009; Soszyński et al. 2010a). We do not understand this form of pulsation (see however Dziembowski 2012).
Many interesting discoveries come from analysis of data collected by the long-term ground-based photometric campaigns, of which the OGLE is the longest and of highest photometric quality (e.g. Udalski et al. 2008). The large area of sky monitored by the OGLE project allowed identification of several hundred thousands of pulsating stars only during the first three phases of the experiment. More than 38 000 of RR Lyrae stars were identified in the OGLE-III and OGLE-IV photometry of the Galactic bulge (Soszyński et al. 2014b). Such a large collection of RR Lyrae stars must contain unique objects. Indeed, a few mode switching stars were reported (Soszyński et al. 2014a,b), a gravitationally lensed RRc star was observed (Soszyński et al. 2014b) and new type of pulsator mimicking RR Lyrae variability, binary evolution pulsator (BEP), was discovered (Pietrzyński et al. 2012; Smolec et al. 2013). The OGLE data are also perfect for search and study of non-radial modes of low amplitude. The study of Galactic bulge OGLE-III data by Netzel, Smolec & Moskalik (2015) increased a sample of known radial–non-radial double-mode pulsators by a factor of 6. Yet another application is study of the Blazhko effect (e.g. Mizerski 2003; Moskalik & Poretti 2003).
In this paper we present the analysis of the Blazhko-type modulation detected in several RRd stars from the OGLE-III and OGLE-IV photometry of the Galactic bulge (Soszyński et al. 2011, 2014b). These are the first objects of this type, in which modulation is observed on top of the genuine double-mode pulsation. The properties of the stars are studied in detail. We note that after Soszyński et al. (2014b) announced the discovery of the first modulated RRd stars, Jurcsik et al. (2014) also reported the modulated RRd stars in their photometry of M3 (see also Section 5.3).
Structure of the paper is the following. In Section 2 we present the data and the adopted analysis methods. The general overview of the data with basic properties of double-mode pulsation and properties of modulation are presented in Section 3. In Section 4 we discuss the analysis of individual stars in detail. Discussion of the emerging picture of the modulation in RRd stars is in Section 5. Summary closes the paper.
2 OBSERVATIONS AND DATA ANALYSIS
The I-band light curves we analyse in this paper were collected during the third and fourth phases of the OGLE. The OGLE-III project was conducted from 2001 to 2009. The number of data points in the OGLE-III light curves varies strongly from field to field: from 335 to 2933. OGLE-IV is an ongoing survey started in 2010 March. In this study we have used the data obtained up to 2014 September, so the time span of the OGLE-IV observations reaches 4.5 yr, with the total number of the observational points from about 1000 to 10 000. The accuracy of the individual photometric measurements is better than 10 mmag for most of the stars in our sample. The reader is referred to Udalski et al. (2008) and Soszyński et al. (2014b) for description of the instrument set-up and photometry reduction procedures. The photometry is publicly available and may be downloaded from the OGLE ftp archive (http://ftp://ftp.astrouw.edu.pl/ogle/ogle4/OCVS/blg/rrlyr/; for the description see Soszyński et al. 2014b).
For all analysed stars we first find full light-curve solution: in the frequency spectrum of the residuals we do not detect any significant signal, or, what is more common, we can detect only unresolved power at the pre-whitened frequencies, and possibly a signal at low frequencies – a signature of slow trends. At this phase the data are 6σ clipped, the trend is removed from the original data with polynomial of chosen order, and again light-curve solution is updated and outliers at a lower 5σ level are removed. All further analysis is conducted on the resulting detrended time series with severe outliers removed.
In a majority of the cases, frequencies included in the full light-curve solution are frequencies of the fundamental mode and of the first overtone, f0 and f1, respectively, their linear combinations, kf0 ± lf1, and modulation components arising from the detected Blazhko effect. These frequencies appear as equally spaced multiplet structures at f0, f1 and their combinations, or as close doublets (incomplete triplets, see next section for more details). The separation between the multiplet (doublet) components defines the modulation (Blazhko) frequency, fB, and modulation period, PB = 1/fB. If the modulation period is longer than T/2, or pulsation mode (its amplitude and/or phase) vary on a long time-scale, unresolved power will remain in the frequency spectrum at f0 and/or at f1 after pre-whitening. In the case of OGLE-IV data T ≈ 1600 d and the longest possible modulation we can detect is ≈800 d. In the combined OGLE-III and OGLE-IV data this limit is longer, up to ≈3000 d (depending on the time span of OGLE-III observations).
By default the analysis is based on OGLE-IV data which are more densely sampled. When we suspect long-term modulation/variation of the radial modes, and OGLE-III data are available, we also analyse the merged data. We note that there are systematic differences in the zero-points in OGLE-III and OGLE-IV data, which may be as high as 0.2 mag in extreme cases (Soszyński et al. 2014b). To correctly merge the data we first find the full light-curve solution for OGLE-III and for OGLE-IV data independently, as described above. The mean brightness difference, Δm0, between OGLE-III and OGLE-IV data is then taken into account when merging the data.
The side peaks at the radial mode frequencies can also be non-coherent, i.e. they cannot be pre-whitened with a single sine wave with constant amplitude and phase. After pre-whitening, residual, unresolved power remains in the spectrum. The presence of such signals is not a surprise – they may originate from the non-periodic nature of the light variation, which is expected. The Blazhko effect in single periodic RR Lyrae stars is a quasi-periodic effect. The results of space missions leave no doubt: consecutive Blazhko cycles differ, modulation periods and amplitudes sometimes change in an irregular fashion (e.g. Guggenberger et al. 2012; Benkő et al. 2014).
If variation occurs on a long time-scale (of order of data length) and is irregular it produces unresolved power in the frequency spectrum at f0 and/or at f1, which increases the noise level in the Fourier transform and may hide e.g. the signs of modulation on the shorter time-scale. To get rid of these unwanted signals we follow the time-dependent Fourier analysis by the time-dependent pre-whitening (Moskalik et al. 2015). The residuals from the just described sine series fits, separate for each of the subsets, are merged. In a resulting time series the long-term variability is filtered out, while short-term modulation remains. Of course f0, f1 and their combinations are also pre-whitened and should not appear in the frequency spectrum, provided they do not vary significantly on a time-scale shorter than Δt.
All analysis described in this paper was conducted using the software written by one of us (RS).
3 OVERVIEW OF THE DATA
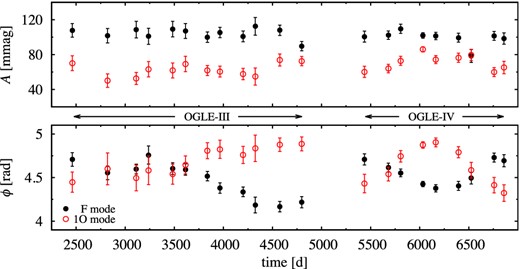
In this study we analyse RRd stars suspected of long-term modulation of radial modes, the Blazhko effect. The sample was first pre-selected by (i) visual inspection – see Fig. 1 for obvious signature of modulation and (ii) automatic analysis of frequency spectra of all RRd stars. In the latter case, the stars showing additional close side peaks at the fundamental and/or at the first overtone frequency were marked as suspected of long-term modulation. For details on the automatic analysis of frequency spectrum, see Soszyński et al. (2014b). The selected sample contained 16 stars (primary targets). Our analysis showed that nearly all of these RRd stars that show the modulation, have non-typical period ratios (see Fig. 2). Therefore, the sample was extended with 11 other stars (secondary targets) having non-typical period ratios, of which in two we detected modulation. Altogether 27 stars were analysed in detail (marked with large symbols in Fig. 2) and in 15 (marked with diamonds/pentagon) we found modulation of at least one radial mode.
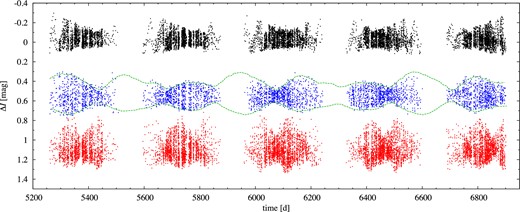
OGLE-IV data for the three modulated RRd stars; from top to bottom: OGLE-BLG-RRLYR-06283, -07393 and -05762 (arbitrarily shifted in the vertical direction). The dashed line plotted for OGLE-BLG-RRLYR-07393 corresponds to the envelope of the full light-curve solution (see Section 4.3). Here and in this paper time is expressed as t = HJD – 245 0000.

The Petersen diagram for 173 RRd stars of the OGLE Galactic bulge sample (Soszyński et al. 2014b). Stars that show the Blazhko-type modulation are marked with diamonds/pentagon. Location of two stars overlap at a clump corresponding to suspected members of the tidal stream crossing the bulge. In stars marked with circles we do not find close secondary peaks. In stars marked with squares a long-term variation of first overtone is present. Triangle marks the triple-mode RR Lyrae star (Smolec et al. 2015) and pentagon marks the star that recently switched the pulsation mode (and is also modulated).
All of the investigated stars pulsate simultaneously in the fundamental and in the first overtone modes (RRd). In all cases we detect combination frequencies of f0 and f1 – no doubt the two frequencies originate from the same star. In all but two cases the period ratios P1/P0 are rather far from that typical for a majority of the Galactic bulge RRd stars – see the Petersen diagram in Fig. 2. The two stars that fit the main progression are also not typical – they are located at nearly the same place, at a clump of 28 stars – the likely members of a tidal stream crossing the Galactic bulge, as analysed by Soszyński et al. (2014b). We will comment the non-typical location of modulated stars in the Petersen diagram in the Discussion (Section 5.2). In Table 1 we collect periods, period ratio and amplitudes of the fundamental and first overtone modes. These values come from the full light-curve solution of OGLE-IV data, only, and are mean values (see tables in the Appendix in the on-line version of the journal). The solutions include frequencies of both modes, their combinations and all additional close side peaks we could detect in the data. If the peak at f0 or at f1 is non-coherent, its amplitude is marked with asterisk in Table 1. The period of the dominant, higher amplitude mode is written with bold fonts. In eight stars pulsation in the first overtone dominates (≈53 per cent). In the full OGLE RRd sample (173 stars)1 the dominant pulsation in the first overtone is significantly more frequent and occurs in 82.1 per cent of the sample. We comment on this more in the Discussion.
Basic properties of RRd stars derived from the analysis of the OGLE-IV photometry. Period of the dominant mode is written with bold font. Asterisk at mode amplitude indicates that unresolved signal remains at f0 or at f1 in the frequency spectrum of the data pre-whitened with the full light-curve solution.
| Star . | P0 (d) . | P1 (d) . | P1/P0 . | A0 (mmag) . | A1 (mmag) . | Remarks . |
|---|---|---|---|---|---|---|
| OGLE-BLG-RRLYR-00951 | 0.5446346(6) | 0.3976183(3) | 0.7301 | *73.4 | *58.0 | |
| OGLE-BLG-RRLYR-02530 | 0.463563(1) | 0.3406466(7) | 0.7348 | 95.6 | *67.3 | |
| OGLE-BLG-RRLYR-02862 | 0.459812(1) | 0.3354003(6) | 0.7294 | *50.7 | 81.4 | |
| OGLE-BLG-RRLYR-04598 | 0.4622854(6) | 0.3467316(4) | 0.7500 | 64.9 | *71.0 | P1: P0 = 3: 4 |
| OGLE-BLG-RRLYR-05762 | 0.4662964(1) | 0.3472844(2) | 0.7448 | 94.5 | *51.5 | |
| OGLE-BLG-RRLYR-06283 | 0.5051447(4) | 0.3734973(2) | 0.7394 | 52.4 | *62.5 | |
| OGLE-BLG-RRLYR-07393 | 0.4626906(6) | 0.3448963(3) | 0.7454 | 44.7 | *56.9 | Px/P1 = 0.6163 |
| OGLE-BLG-RRLYR-09284 | 0.4367995(4) | 0.3229961(1) | 0.7395 | *25.5 | 60.1 | Tidal stream |
| OGLE-BLG-RRLYR-10728 | 0.4816758(3) | 0.3553088(5) | 0.7377 | *179.9 | *54.2 | |
| OGLE-BLG-RRLYR-11311 | 0.468425(1) | 0.3453771(4) | 0.7373 | *50.3 | *91.5 | |
| OGLE-BLG-RRLYR-13442 | 0.486091(1) | 0.354019(1) | 0.7283 | *115.3 | *44.3 | Mode switch |
| OGLE-BLG-RRLYR-14915 | 0.4333758(2) | 0.3170019(2) | 0.7315 | *99.7 | *64.1 | |
| OGLE-BLG-RRLYR-22356 | 0.4426324(4) | 0.323662(1) | 0.7312 | *147.5 | 21.9 | |
| OGLE-BLG-RRLYR-30986 | 0.494275(1) | 0.3630309(8) | 0.7345 | 63.8 | 73.6 | |
| OGLE-BLG-RRLYR-32462 | 0.4357845(7) | 0.3222565(3) | 0.7395 | *67.6 | *82.7 | Tidal stream |
| Star . | P0 (d) . | P1 (d) . | P1/P0 . | A0 (mmag) . | A1 (mmag) . | Remarks . |
|---|---|---|---|---|---|---|
| OGLE-BLG-RRLYR-00951 | 0.5446346(6) | 0.3976183(3) | 0.7301 | *73.4 | *58.0 | |
| OGLE-BLG-RRLYR-02530 | 0.463563(1) | 0.3406466(7) | 0.7348 | 95.6 | *67.3 | |
| OGLE-BLG-RRLYR-02862 | 0.459812(1) | 0.3354003(6) | 0.7294 | *50.7 | 81.4 | |
| OGLE-BLG-RRLYR-04598 | 0.4622854(6) | 0.3467316(4) | 0.7500 | 64.9 | *71.0 | P1: P0 = 3: 4 |
| OGLE-BLG-RRLYR-05762 | 0.4662964(1) | 0.3472844(2) | 0.7448 | 94.5 | *51.5 | |
| OGLE-BLG-RRLYR-06283 | 0.5051447(4) | 0.3734973(2) | 0.7394 | 52.4 | *62.5 | |
| OGLE-BLG-RRLYR-07393 | 0.4626906(6) | 0.3448963(3) | 0.7454 | 44.7 | *56.9 | Px/P1 = 0.6163 |
| OGLE-BLG-RRLYR-09284 | 0.4367995(4) | 0.3229961(1) | 0.7395 | *25.5 | 60.1 | Tidal stream |
| OGLE-BLG-RRLYR-10728 | 0.4816758(3) | 0.3553088(5) | 0.7377 | *179.9 | *54.2 | |
| OGLE-BLG-RRLYR-11311 | 0.468425(1) | 0.3453771(4) | 0.7373 | *50.3 | *91.5 | |
| OGLE-BLG-RRLYR-13442 | 0.486091(1) | 0.354019(1) | 0.7283 | *115.3 | *44.3 | Mode switch |
| OGLE-BLG-RRLYR-14915 | 0.4333758(2) | 0.3170019(2) | 0.7315 | *99.7 | *64.1 | |
| OGLE-BLG-RRLYR-22356 | 0.4426324(4) | 0.323662(1) | 0.7312 | *147.5 | 21.9 | |
| OGLE-BLG-RRLYR-30986 | 0.494275(1) | 0.3630309(8) | 0.7345 | 63.8 | 73.6 | |
| OGLE-BLG-RRLYR-32462 | 0.4357845(7) | 0.3222565(3) | 0.7395 | *67.6 | *82.7 | Tidal stream |
Basic properties of RRd stars derived from the analysis of the OGLE-IV photometry. Period of the dominant mode is written with bold font. Asterisk at mode amplitude indicates that unresolved signal remains at f0 or at f1 in the frequency spectrum of the data pre-whitened with the full light-curve solution.
| Star . | P0 (d) . | P1 (d) . | P1/P0 . | A0 (mmag) . | A1 (mmag) . | Remarks . |
|---|---|---|---|---|---|---|
| OGLE-BLG-RRLYR-00951 | 0.5446346(6) | 0.3976183(3) | 0.7301 | *73.4 | *58.0 | |
| OGLE-BLG-RRLYR-02530 | 0.463563(1) | 0.3406466(7) | 0.7348 | 95.6 | *67.3 | |
| OGLE-BLG-RRLYR-02862 | 0.459812(1) | 0.3354003(6) | 0.7294 | *50.7 | 81.4 | |
| OGLE-BLG-RRLYR-04598 | 0.4622854(6) | 0.3467316(4) | 0.7500 | 64.9 | *71.0 | P1: P0 = 3: 4 |
| OGLE-BLG-RRLYR-05762 | 0.4662964(1) | 0.3472844(2) | 0.7448 | 94.5 | *51.5 | |
| OGLE-BLG-RRLYR-06283 | 0.5051447(4) | 0.3734973(2) | 0.7394 | 52.4 | *62.5 | |
| OGLE-BLG-RRLYR-07393 | 0.4626906(6) | 0.3448963(3) | 0.7454 | 44.7 | *56.9 | Px/P1 = 0.6163 |
| OGLE-BLG-RRLYR-09284 | 0.4367995(4) | 0.3229961(1) | 0.7395 | *25.5 | 60.1 | Tidal stream |
| OGLE-BLG-RRLYR-10728 | 0.4816758(3) | 0.3553088(5) | 0.7377 | *179.9 | *54.2 | |
| OGLE-BLG-RRLYR-11311 | 0.468425(1) | 0.3453771(4) | 0.7373 | *50.3 | *91.5 | |
| OGLE-BLG-RRLYR-13442 | 0.486091(1) | 0.354019(1) | 0.7283 | *115.3 | *44.3 | Mode switch |
| OGLE-BLG-RRLYR-14915 | 0.4333758(2) | 0.3170019(2) | 0.7315 | *99.7 | *64.1 | |
| OGLE-BLG-RRLYR-22356 | 0.4426324(4) | 0.323662(1) | 0.7312 | *147.5 | 21.9 | |
| OGLE-BLG-RRLYR-30986 | 0.494275(1) | 0.3630309(8) | 0.7345 | 63.8 | 73.6 | |
| OGLE-BLG-RRLYR-32462 | 0.4357845(7) | 0.3222565(3) | 0.7395 | *67.6 | *82.7 | Tidal stream |
| Star . | P0 (d) . | P1 (d) . | P1/P0 . | A0 (mmag) . | A1 (mmag) . | Remarks . |
|---|---|---|---|---|---|---|
| OGLE-BLG-RRLYR-00951 | 0.5446346(6) | 0.3976183(3) | 0.7301 | *73.4 | *58.0 | |
| OGLE-BLG-RRLYR-02530 | 0.463563(1) | 0.3406466(7) | 0.7348 | 95.6 | *67.3 | |
| OGLE-BLG-RRLYR-02862 | 0.459812(1) | 0.3354003(6) | 0.7294 | *50.7 | 81.4 | |
| OGLE-BLG-RRLYR-04598 | 0.4622854(6) | 0.3467316(4) | 0.7500 | 64.9 | *71.0 | P1: P0 = 3: 4 |
| OGLE-BLG-RRLYR-05762 | 0.4662964(1) | 0.3472844(2) | 0.7448 | 94.5 | *51.5 | |
| OGLE-BLG-RRLYR-06283 | 0.5051447(4) | 0.3734973(2) | 0.7394 | 52.4 | *62.5 | |
| OGLE-BLG-RRLYR-07393 | 0.4626906(6) | 0.3448963(3) | 0.7454 | 44.7 | *56.9 | Px/P1 = 0.6163 |
| OGLE-BLG-RRLYR-09284 | 0.4367995(4) | 0.3229961(1) | 0.7395 | *25.5 | 60.1 | Tidal stream |
| OGLE-BLG-RRLYR-10728 | 0.4816758(3) | 0.3553088(5) | 0.7377 | *179.9 | *54.2 | |
| OGLE-BLG-RRLYR-11311 | 0.468425(1) | 0.3453771(4) | 0.7373 | *50.3 | *91.5 | |
| OGLE-BLG-RRLYR-13442 | 0.486091(1) | 0.354019(1) | 0.7283 | *115.3 | *44.3 | Mode switch |
| OGLE-BLG-RRLYR-14915 | 0.4333758(2) | 0.3170019(2) | 0.7315 | *99.7 | *64.1 | |
| OGLE-BLG-RRLYR-22356 | 0.4426324(4) | 0.323662(1) | 0.7312 | *147.5 | 21.9 | |
| OGLE-BLG-RRLYR-30986 | 0.494275(1) | 0.3630309(8) | 0.7345 | 63.8 | 73.6 | |
| OGLE-BLG-RRLYR-32462 | 0.4357845(7) | 0.3222565(3) | 0.7395 | *67.6 | *82.7 | Tidal stream |
In a few RRd stars Blazhko-type modulation is apparent already from the investigation of the time series alone. Three examples are presented in Fig. 1. Large modulation on a long time-scale is well visible.
Periodic modulation of a pulsation mode manifests in the frequency spectrum as equally spaced multiplets around main frequency and its harmonics. The inverse of frequency separation between multiplet components corresponds to modulation period. Multiplets (i.e. quintuplets, septuplets, etc.) are detected in the space observations of the Blazhko RRab stars (e.g. Chadid et al. 2010; Guggenberger et al. 2012) and in the top-quality ground-based observations dedicated to study of the Blazhko phenomenon (e.g. Jurcsik et al. 2008). In a typical ground-based data from massive sky surveys, such as OGLE or MACHO, modulation manifests as equally spaced triplets or as close doublets (e.g. Alcock et al. 2003; Moskalik & Poretti 2003). Following Alcock et al. (2003) we denote these two frequency patterns as BL2 (triplets) and BL1 (doublets). Triplets are obvious signature of modulation. They are detected in four stars only (see Table 2). In the case of doublets, only one side peak is detected at kf0. To interpret a close peak (doublet) as arising from modulation of a radial mode we require that it is detected not only at the primary frequency, but also at its harmonics or combination frequencies with other mode, with the same separation [and, like for all signals, its detection must be significant, with signal-to-noise ratio (S/N) > 4, and its frequency must be well resolved with frequency of the radial mode and other frequencies detected earlier in the analysis]. In principle, doublets at kf0 may correspond to a close non-radial mode and its combination frequencies with radial modes. The Blazhko (modulation) period, as defined above, is then a beating period. The more likely explanation, however, is that doublets are incomplete triplets with one component of low amplitude, hidden in the noise. Because of noise present in the data, the equally spaced but strongly asymmetric triplet may appear as doublet. Indeed, the triplets we detect in four stars may be strongly asymmetric. To quantify the asymmetry we use Q parameter as defined by Alcock et al. (2003), Q = (A+ − A−)/(A+ + A−), where A+/ − refers to the amplitude of the higher/lower frequency triplet component. For the five triplet structures reported in Table 2 (two triplets are detected in OGLE-BLG-RRLYR-07393) we find the following values of asymmetry parameter: −0.36 (OGLE-BLG-RRLYR-05762), −0.83 and 0.32 (OGLE-BLG-RRLYR-07393, modulation with PB1 and PB2), −0.1 (OGLE-BLG-RRLYR-00951) and −0.57 (OGLE-BLG-RRLYR-02862). Strong asymmetry is not an exception. We also note that for Blazhko RRab stars Alcock et al. (2003) analysed the distribution of side peaks’ amplitudes and showed that there seems to be a continuous transition between the stars with equidistant triplet in the frequency spectrum and those showing only doublet. In a few cases the data are good enough to directly show the modulation of radial modes, their amplitudes and periods and of mean stellar brightness, with time-dependent Fourier analysis, both for BL2 and BL1 stars.
Modulation properties of the investigated RRd stars. In the consecutive columns we provide the modulation period, the frequency of the highest modulation peak, its amplitude and structure of the modulation spectrum, for the fundamental and then for the first overtone modes. Asterisk at amplitude value indicates that corresponding peak is non-coherent. Remarks: ‘a’ – side peaks are also detected at frequency combinations of radial modes, kf0 ± lf1; ‘b’ – a peak at f = fBi is detected at low frequencies; ‘s’ – subharmonic of the modulation frequency, i.e. a peak at f0/1 ± 0.5fBi is detected.
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | PB (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-00951 | 142.7(3) | f1 − fB1 | 5.5 | BL2 | a | |||
| OGLE-BLG-RRLYR-02530 | 469(3) | f0 + fB1 | 22.9 | BL1+ | f1 + fB1 | 18.7 | BL1+ | a |
| OGLE-BLG-RRLYR-02862 | 173.6(5) | f0 − fB1 | 28.6 | BL2 | f1 − fB1 | 10.3 | BL1− | a |
| OGLE-BLG-RRLYR-04598 | 281(1) | f0 − fB1 | 12.9 | BL1− | a | |||
| 85.6(2) | f0 − fB2 | 10.8 | BL1− | a | ||||
| OGLE-BLG-RRLYR-05762 | 97.95(2) | f0 − fB1 | *53.0 | BL2 | f1 − fB1 | 5.6 | BL1− | a, b |
| 23.000(4) | f0 + fB2 | 7.1 | BL1+ | a, b | ||||
| 81.12(8) | f1 − fB3 | 7.3 | BL1− | a | ||||
| OGLE-BLG-RRLYR-06283 | 332.8(3) | f0 − fB1 | *37.0 | BL1− | a, b | |||
| OGLE-BLG-RRLYR-07393 | 209.8(2) | f0 + fB1 | 3.8 | BL1+ | f1 − fB1 | 50.8 | BL2 | a, b |
| 322.9(4) | f0 + fB2 | *34.4 | BL1+ | f1 + fB2 | 21.5 | BL2 | a | |
| OGLE-BLG-RRLYR-09284 | 41.78(2) | f0 + fB1 | *6.4 | BL1+ | a | |||
| 40.76(3) | f0 − fB2 | 3.8 | BL1− | a | ||||
| 47.69(5) | f0 + fB3 | *2.8 | BL1+ | a | ||||
| OGLE-BLG-RRLYR-10728 | 98.71(8) | f0 + fB1 | 26.7 | BL1+ | f1 − fB1 | 8.6 | BL1− | a, b |
| 313(1) | f0 − fB2 | 8.9 | BL1− | a | ||||
| OGLE-BLG-RRLYR-11311 | 49.13(2) | f1 − fB1 | *32.4 | BL1− | a | |||
| 87.1(2) | f0 + fB2 | 13.8 | BL1+ | s | ||||
| OGLE-BLG-RRLYR-13442 | 179.1(9) | f0 + fB1 | *14.0 | BL1+ | ||||
| OGLE-BLG-RRLYR-14915 | 62.89(2) | f1 − fB1 | *41.2 | BL1− | a, b, s | |||
| OGLE-BLG-RRLYR-22356 | 255.5(5) | f0 − fB1 | 40.1 | BL1− | a, b | |||
| 51.59(6) | f1 + fB2 | *15.0 | BL1+ | a | ||||
| 32.46(4) | f0 − fB3 | 7.4 | BL1− | |||||
| OGLE-BLG-RRLYR-30986 | 111.4(1) | f0 − fB1 | 51.0 | BL1− | f1 − fB1 | 14.4 | BL1− | a |
| OGLE-BLG-RRLYR-32462 | 190.1(3) | f1 + fB1 | *31.4 | BL1+ | a | |||
| 125.6(2) | f0 + fB2 | 23.5 | BL1+ | f1 − fB2 | 8.8 | BL1− | a | |
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | PB (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-00951 | 142.7(3) | f1 − fB1 | 5.5 | BL2 | a | |||
| OGLE-BLG-RRLYR-02530 | 469(3) | f0 + fB1 | 22.9 | BL1+ | f1 + fB1 | 18.7 | BL1+ | a |
| OGLE-BLG-RRLYR-02862 | 173.6(5) | f0 − fB1 | 28.6 | BL2 | f1 − fB1 | 10.3 | BL1− | a |
| OGLE-BLG-RRLYR-04598 | 281(1) | f0 − fB1 | 12.9 | BL1− | a | |||
| 85.6(2) | f0 − fB2 | 10.8 | BL1− | a | ||||
| OGLE-BLG-RRLYR-05762 | 97.95(2) | f0 − fB1 | *53.0 | BL2 | f1 − fB1 | 5.6 | BL1− | a, b |
| 23.000(4) | f0 + fB2 | 7.1 | BL1+ | a, b | ||||
| 81.12(8) | f1 − fB3 | 7.3 | BL1− | a | ||||
| OGLE-BLG-RRLYR-06283 | 332.8(3) | f0 − fB1 | *37.0 | BL1− | a, b | |||
| OGLE-BLG-RRLYR-07393 | 209.8(2) | f0 + fB1 | 3.8 | BL1+ | f1 − fB1 | 50.8 | BL2 | a, b |
| 322.9(4) | f0 + fB2 | *34.4 | BL1+ | f1 + fB2 | 21.5 | BL2 | a | |
| OGLE-BLG-RRLYR-09284 | 41.78(2) | f0 + fB1 | *6.4 | BL1+ | a | |||
| 40.76(3) | f0 − fB2 | 3.8 | BL1− | a | ||||
| 47.69(5) | f0 + fB3 | *2.8 | BL1+ | a | ||||
| OGLE-BLG-RRLYR-10728 | 98.71(8) | f0 + fB1 | 26.7 | BL1+ | f1 − fB1 | 8.6 | BL1− | a, b |
| 313(1) | f0 − fB2 | 8.9 | BL1− | a | ||||
| OGLE-BLG-RRLYR-11311 | 49.13(2) | f1 − fB1 | *32.4 | BL1− | a | |||
| 87.1(2) | f0 + fB2 | 13.8 | BL1+ | s | ||||
| OGLE-BLG-RRLYR-13442 | 179.1(9) | f0 + fB1 | *14.0 | BL1+ | ||||
| OGLE-BLG-RRLYR-14915 | 62.89(2) | f1 − fB1 | *41.2 | BL1− | a, b, s | |||
| OGLE-BLG-RRLYR-22356 | 255.5(5) | f0 − fB1 | 40.1 | BL1− | a, b | |||
| 51.59(6) | f1 + fB2 | *15.0 | BL1+ | a | ||||
| 32.46(4) | f0 − fB3 | 7.4 | BL1− | |||||
| OGLE-BLG-RRLYR-30986 | 111.4(1) | f0 − fB1 | 51.0 | BL1− | f1 − fB1 | 14.4 | BL1− | a |
| OGLE-BLG-RRLYR-32462 | 190.1(3) | f1 + fB1 | *31.4 | BL1+ | a | |||
| 125.6(2) | f0 + fB2 | 23.5 | BL1+ | f1 − fB2 | 8.8 | BL1− | a | |
Modulation properties of the investigated RRd stars. In the consecutive columns we provide the modulation period, the frequency of the highest modulation peak, its amplitude and structure of the modulation spectrum, for the fundamental and then for the first overtone modes. Asterisk at amplitude value indicates that corresponding peak is non-coherent. Remarks: ‘a’ – side peaks are also detected at frequency combinations of radial modes, kf0 ± lf1; ‘b’ – a peak at f = fBi is detected at low frequencies; ‘s’ – subharmonic of the modulation frequency, i.e. a peak at f0/1 ± 0.5fBi is detected.
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | PB (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-00951 | 142.7(3) | f1 − fB1 | 5.5 | BL2 | a | |||
| OGLE-BLG-RRLYR-02530 | 469(3) | f0 + fB1 | 22.9 | BL1+ | f1 + fB1 | 18.7 | BL1+ | a |
| OGLE-BLG-RRLYR-02862 | 173.6(5) | f0 − fB1 | 28.6 | BL2 | f1 − fB1 | 10.3 | BL1− | a |
| OGLE-BLG-RRLYR-04598 | 281(1) | f0 − fB1 | 12.9 | BL1− | a | |||
| 85.6(2) | f0 − fB2 | 10.8 | BL1− | a | ||||
| OGLE-BLG-RRLYR-05762 | 97.95(2) | f0 − fB1 | *53.0 | BL2 | f1 − fB1 | 5.6 | BL1− | a, b |
| 23.000(4) | f0 + fB2 | 7.1 | BL1+ | a, b | ||||
| 81.12(8) | f1 − fB3 | 7.3 | BL1− | a | ||||
| OGLE-BLG-RRLYR-06283 | 332.8(3) | f0 − fB1 | *37.0 | BL1− | a, b | |||
| OGLE-BLG-RRLYR-07393 | 209.8(2) | f0 + fB1 | 3.8 | BL1+ | f1 − fB1 | 50.8 | BL2 | a, b |
| 322.9(4) | f0 + fB2 | *34.4 | BL1+ | f1 + fB2 | 21.5 | BL2 | a | |
| OGLE-BLG-RRLYR-09284 | 41.78(2) | f0 + fB1 | *6.4 | BL1+ | a | |||
| 40.76(3) | f0 − fB2 | 3.8 | BL1− | a | ||||
| 47.69(5) | f0 + fB3 | *2.8 | BL1+ | a | ||||
| OGLE-BLG-RRLYR-10728 | 98.71(8) | f0 + fB1 | 26.7 | BL1+ | f1 − fB1 | 8.6 | BL1− | a, b |
| 313(1) | f0 − fB2 | 8.9 | BL1− | a | ||||
| OGLE-BLG-RRLYR-11311 | 49.13(2) | f1 − fB1 | *32.4 | BL1− | a | |||
| 87.1(2) | f0 + fB2 | 13.8 | BL1+ | s | ||||
| OGLE-BLG-RRLYR-13442 | 179.1(9) | f0 + fB1 | *14.0 | BL1+ | ||||
| OGLE-BLG-RRLYR-14915 | 62.89(2) | f1 − fB1 | *41.2 | BL1− | a, b, s | |||
| OGLE-BLG-RRLYR-22356 | 255.5(5) | f0 − fB1 | 40.1 | BL1− | a, b | |||
| 51.59(6) | f1 + fB2 | *15.0 | BL1+ | a | ||||
| 32.46(4) | f0 − fB3 | 7.4 | BL1− | |||||
| OGLE-BLG-RRLYR-30986 | 111.4(1) | f0 − fB1 | 51.0 | BL1− | f1 − fB1 | 14.4 | BL1− | a |
| OGLE-BLG-RRLYR-32462 | 190.1(3) | f1 + fB1 | *31.4 | BL1+ | a | |||
| 125.6(2) | f0 + fB2 | 23.5 | BL1+ | f1 − fB2 | 8.8 | BL1− | a | |
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | PB (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-00951 | 142.7(3) | f1 − fB1 | 5.5 | BL2 | a | |||
| OGLE-BLG-RRLYR-02530 | 469(3) | f0 + fB1 | 22.9 | BL1+ | f1 + fB1 | 18.7 | BL1+ | a |
| OGLE-BLG-RRLYR-02862 | 173.6(5) | f0 − fB1 | 28.6 | BL2 | f1 − fB1 | 10.3 | BL1− | a |
| OGLE-BLG-RRLYR-04598 | 281(1) | f0 − fB1 | 12.9 | BL1− | a | |||
| 85.6(2) | f0 − fB2 | 10.8 | BL1− | a | ||||
| OGLE-BLG-RRLYR-05762 | 97.95(2) | f0 − fB1 | *53.0 | BL2 | f1 − fB1 | 5.6 | BL1− | a, b |
| 23.000(4) | f0 + fB2 | 7.1 | BL1+ | a, b | ||||
| 81.12(8) | f1 − fB3 | 7.3 | BL1− | a | ||||
| OGLE-BLG-RRLYR-06283 | 332.8(3) | f0 − fB1 | *37.0 | BL1− | a, b | |||
| OGLE-BLG-RRLYR-07393 | 209.8(2) | f0 + fB1 | 3.8 | BL1+ | f1 − fB1 | 50.8 | BL2 | a, b |
| 322.9(4) | f0 + fB2 | *34.4 | BL1+ | f1 + fB2 | 21.5 | BL2 | a | |
| OGLE-BLG-RRLYR-09284 | 41.78(2) | f0 + fB1 | *6.4 | BL1+ | a | |||
| 40.76(3) | f0 − fB2 | 3.8 | BL1− | a | ||||
| 47.69(5) | f0 + fB3 | *2.8 | BL1+ | a | ||||
| OGLE-BLG-RRLYR-10728 | 98.71(8) | f0 + fB1 | 26.7 | BL1+ | f1 − fB1 | 8.6 | BL1− | a, b |
| 313(1) | f0 − fB2 | 8.9 | BL1− | a | ||||
| OGLE-BLG-RRLYR-11311 | 49.13(2) | f1 − fB1 | *32.4 | BL1− | a | |||
| 87.1(2) | f0 + fB2 | 13.8 | BL1+ | s | ||||
| OGLE-BLG-RRLYR-13442 | 179.1(9) | f0 + fB1 | *14.0 | BL1+ | ||||
| OGLE-BLG-RRLYR-14915 | 62.89(2) | f1 − fB1 | *41.2 | BL1− | a, b, s | |||
| OGLE-BLG-RRLYR-22356 | 255.5(5) | f0 − fB1 | 40.1 | BL1− | a, b | |||
| 51.59(6) | f1 + fB2 | *15.0 | BL1+ | a | ||||
| 32.46(4) | f0 − fB3 | 7.4 | BL1− | |||||
| OGLE-BLG-RRLYR-30986 | 111.4(1) | f0 − fB1 | 51.0 | BL1− | f1 − fB1 | 14.4 | BL1− | a |
| OGLE-BLG-RRLYR-32462 | 190.1(3) | f1 + fB1 | *31.4 | BL1+ | a | |||
| 125.6(2) | f0 + fB2 | 23.5 | BL1+ | f1 − fB2 | 8.8 | BL1− | a | |
Sample table with light-curve solution for OGLE-BLG-RRLYR-00951. Full table and tables for all analysed stars are in the on-line only Appendix.
| Freq. id . | f (d−1) . | A (mmag) . | σ . | ϕ (rad) . | σ . | Remarks . |
|---|---|---|---|---|---|---|
| fB1 | 0.007010(15) | bl | ||||
| f1 − f0 − fB1 | 0.6718715 | 4.3 | 0.4 | 2.57 | 0.59 | |
| f1 − f0 | 0.6788813 | 6.0 | 0.4 | 2.18 | 0.13 | |
| f0 | 1.8360933(18) | *73.4 | 0.4 | 5.64 | 0.07 | |
| f1 − fB1 | 2.5079647 | 5.5 | 0.4 | 3.23 | 0.59 | |
| f1 | 2.5149745(21) | *58.0 | 0.4 | 1.11 | 0.08 | |
| … | … | … | … | … | … |
| Freq. id . | f (d−1) . | A (mmag) . | σ . | ϕ (rad) . | σ . | Remarks . |
|---|---|---|---|---|---|---|
| fB1 | 0.007010(15) | bl | ||||
| f1 − f0 − fB1 | 0.6718715 | 4.3 | 0.4 | 2.57 | 0.59 | |
| f1 − f0 | 0.6788813 | 6.0 | 0.4 | 2.18 | 0.13 | |
| f0 | 1.8360933(18) | *73.4 | 0.4 | 5.64 | 0.07 | |
| f1 − fB1 | 2.5079647 | 5.5 | 0.4 | 3.23 | 0.59 | |
| f1 | 2.5149745(21) | *58.0 | 0.4 | 1.11 | 0.08 | |
| … | … | … | … | … | … |
Sample table with light-curve solution for OGLE-BLG-RRLYR-00951. Full table and tables for all analysed stars are in the on-line only Appendix.
| Freq. id . | f (d−1) . | A (mmag) . | σ . | ϕ (rad) . | σ . | Remarks . |
|---|---|---|---|---|---|---|
| fB1 | 0.007010(15) | bl | ||||
| f1 − f0 − fB1 | 0.6718715 | 4.3 | 0.4 | 2.57 | 0.59 | |
| f1 − f0 | 0.6788813 | 6.0 | 0.4 | 2.18 | 0.13 | |
| f0 | 1.8360933(18) | *73.4 | 0.4 | 5.64 | 0.07 | |
| f1 − fB1 | 2.5079647 | 5.5 | 0.4 | 3.23 | 0.59 | |
| f1 | 2.5149745(21) | *58.0 | 0.4 | 1.11 | 0.08 | |
| … | … | … | … | … | … |
| Freq. id . | f (d−1) . | A (mmag) . | σ . | ϕ (rad) . | σ . | Remarks . |
|---|---|---|---|---|---|---|
| fB1 | 0.007010(15) | bl | ||||
| f1 − f0 − fB1 | 0.6718715 | 4.3 | 0.4 | 2.57 | 0.59 | |
| f1 − f0 | 0.6788813 | 6.0 | 0.4 | 2.18 | 0.13 | |
| f0 | 1.8360933(18) | *73.4 | 0.4 | 5.64 | 0.07 | |
| f1 − fB1 | 2.5079647 | 5.5 | 0.4 | 3.23 | 0.59 | |
| f1 | 2.5149745(21) | *58.0 | 0.4 | 1.11 | 0.08 | |
| … | … | … | … | … | … |
In the following, doublets detected in the frequency spectrum are interpreted as arising from modulation (see also Discussion in Section 5.1).
In Table 2 we collected information about properties of the modulation detected in the analysed stars. In the following, modulation frequencies are denoted as fBi, and corresponding modulation periods as PBi = 1/fBi. In each row of Table 2 data for one modulation period are presented. In Table 2 we provide the amplitude and frequency of the highest side peak at respective radial mode frequency and the associated frequency pattern (‘BL2’ for triplets or ‘BL1+’/‘BL1−’ for side peak on higher/lower frequency side of the radial mode). In the remarks section we provide some additional information on the frequency spectrum: ‘a’ indicates that modulation peaks appear also at radial mode combination frequencies, i.e. at kf0 ± lf1 ± fBi; ‘b’ indicates that peak is detected in the low frequency range, at f = fBi; ‘s’ indicates that subharmonic of the modulation frequency, i.e. a peak at f0/1 ± 0.5fBi was detected.
From one up to three modulation periods are present in each star. In seven stars we detected a single modulation period. Both modes may be modulated with the same period, but in a few cases each of the modes is modulated with its own period.
In the following subsections each of the stars is analysed in detail. In Section 5 the emerging picture of the Blazhko modulation in RRd stars is discussed in detail.
4 ANALYSIS OF INDIVIDUAL STARS
Stars are discussed in a somewhat arbitrary order. First the most interesting cases are presented, for which data allow the detailed analysis. For all discussed stars light-curve solutions of OGLE-IV data are collected in tables in the Appendix available in the on-line version of the paper. Tables contain frequency identification, frequency value, amplitude and phase, all with standard errors. For a sample, see Table 3.
4.1 OGLE-BLG-RRLYR-05762
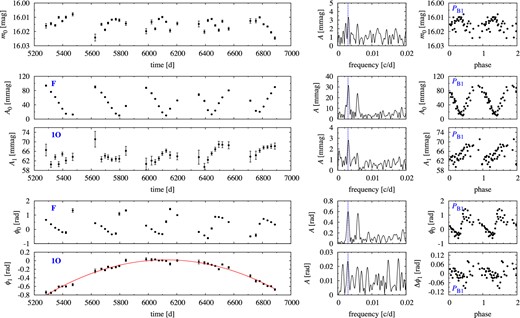
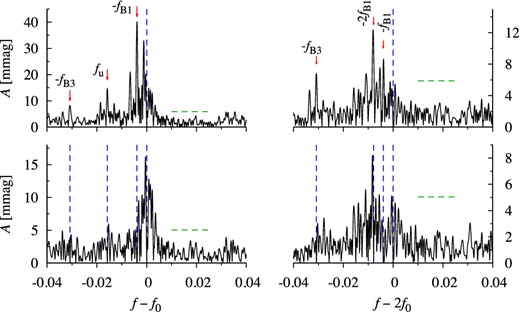
This is one of the stars for which data are most numerous and densely sampled (10 359 data points, ρ = 814 in OGLE-IV). Pulsation in the fundamental mode dominates (Table 1). The frequency spectrum is very rich. We identify three modulation periods (see Table 2). The strongest modulation has period of nearly PB1 ≈ 98 d and affects mostly the fundamental mode (53 mmag at f0 − fB1). A family of triplets is well visible at all harmonics till 5f0 (Fig. 3). In addition, a quintuplet component of lower frequency is present at 2f0. A strong peak at f = fB1 is also detected (6.7 mmag). First overtone is also affected by this modulation, very weakly, however. We only detect one significant (S/N = 8.9) side peak at f1 − fB1 and its amplitude is 10 times smaller than in the case of the fundamental mode (5.6 mmag). In addition to the triplets with fB1 separation we find two families of doublets with fB2 and fB3 separations. The side peaks with fB2 separation (PB2 = 23 d) appear on the higher frequency side of f0, i.e. at kf0 + fB2 and are detected at all harmonics up to 7f0 (Fig. 3). The amplitude of the highest side peak (at 2f0 + fB2) is 8.3 mmag. Combination frequencies are also accompanied by fB2 but we do not detect such peaks at the first overtone frequency and at its harmonics (kf1). The side peaks with fB3 separation (PB3 = 81.1 d) are detected on lower frequency side of f1, 2f1 and at combination frequencies with f0, but not at kf0. In Fig. 3 we show all detected peaks at kf0 and at combination frequencies kf0 + f1 in the form of echelle diagram, i.e. frequency is plotted versus f − f0 (Guggenberger et al. 2012).
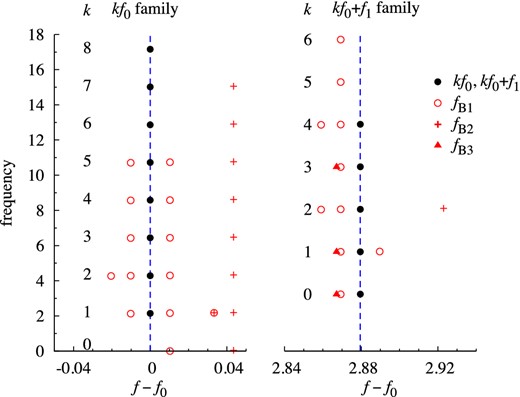
Echelle diagram of peaks detected at kf0 and kf0 + f1 for OGLE-BLG-RRLYR-05762. Side peaks with different separations are marked with different symbols.
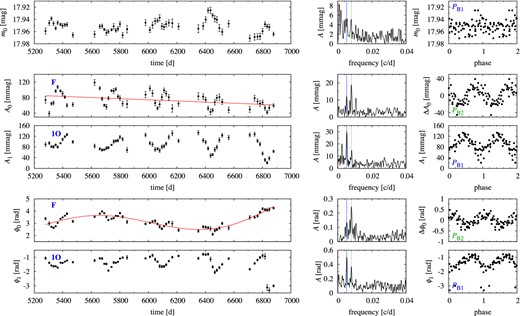
As data sampling is very dense we conducted the time-dependent Fourier analysis (Δt ≈ 5 d) which confirms the picture emerging from the frequency analysis. Results are collected in Fig. 4. The left-hand panels show, from top to bottom, time variation of the mean stellar brightness, m0, variation of the amplitude of the fundamental and of the first overtone modes (A0 and A1) and variation of their phases (ϕ0 and ϕ1). Middle panels show the Fourier transform of the time series presented in the left-hand panels, and rightmost panels are phased modulation curves. We note that in the top left-hand panel (mean stellar brightness) a possible season-to-season differences in the photometric zero-point will also be revealed, but we believe these are small.
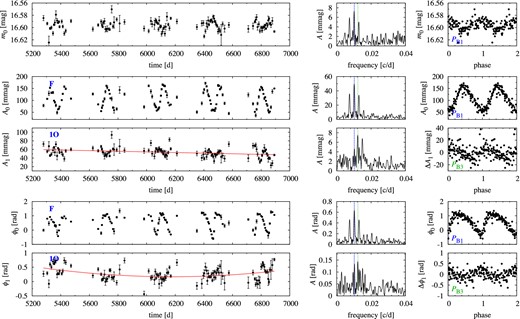
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-05762. Leftmost panels show the time variation of the mean stellar brightness, radial mode amplitudes and phases. Panels in the middle column show the frequency spectrum of the data displayed in the left-hand column. The dashed and dotted lines in the frequency spectra mark fB1 and fB3, respectively. In the rightmost panels (phased modulation curves) data were phased either with PB1(A0, F-mode data) or with PB3 (1O-mode data), resulting from frequency analysis. For clarity, error bars are not plotted in the phase plots (rightmost panels).
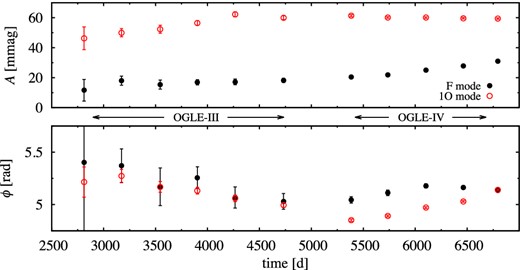
Modulation of the fundamental mode with PB1, both amplitude and phase modulation, is obvious. Suspected modulation of the fundamental mode with PB2 is masked by a much larger modulation with PB1. PB2 is also too short to be well resolved in the time-dependent Fourier analysis. In the case of first overtone, modulation with PB3 is dominant. We observe the following correlations. (i) The mean stellar brightness is modulated with PB1 and is anticorrelated with the amplitude of the fundamental mode: the lower the pulsation amplitude, the brighter the star. (ii) Both amplitude and phase of the fundamental mode are modulated with PB1. (iii) The lowest amplitude of the fundamental mode corresponds to the longest value of its period; the following period decrease is faster than the increase of pulsation amplitude (see equation 2). (iv) First overtone varies on a long time-scale: its mean amplitude decreases, so is its period (at an estimated rate of 1.4 × 10−5 d per 1000 d). These long-term trends (solid lines in the leftmost panels of Fig. 4) are removed before analysing short-term modulation. (v) Both amplitude and phase of the first overtone are modulated with PB3. (vi) Because of low modulation amplitude, the phase relation between amplitude and phase modulation for the first overtone is not as clearly marked as in the case of the fundamental mode.
OGLE-III data for OGLE-BLG-RRLYR-05762 exist but the observation cadence is much lower (ρ = 115). Only four significant side peaks are detected in the frequency spectrum, to be compared with 43 detected in OGLE-IV data. One of the side peaks appears nearly exactly at f0 + fB2 just as in the case of OGLE-IV data. Other side peaks appear on lower frequency side of f0 and of f1. The inverse of frequency separation corresponds to modulation period of 91 d – in between PB1 and PB3 detected in OGLE-IV data. We note a significant power excess in large frequency range around both f0 and f1 – OGLE-III data are not good enough to analyse the short-term modulation in detail, but indicate that it occurs. It is possible however to analyse long-term variation of radial modes. In Fig. 5 we present the results of time-dependent Fourier analysis with Δt ≈ 150 d, which effectively averages the shorter period modulations. Both modes are non-stationary on a long time-scale. We note a very low amplitude of the first overtone at the first seasons of OGLE-III observations and pronounced phase (period, equation 2) change of both modes. At 2500 < t < 4500 d the amplitudes of both modes are anticorrelated.
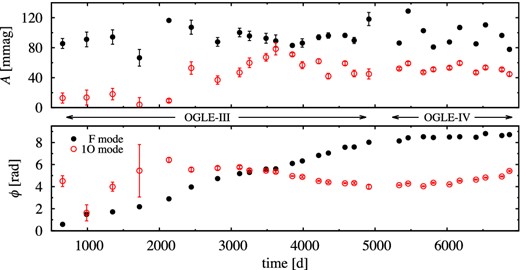
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-05762 (Δt ≈ 150 d).
4.2 OGLE-BLG-RRLYR-06283
It is the second star in the analysed sample with the largest number of points (10 310 data points, ρ = 810 in OGLE-IV). Pulsation in the first overtone is dominant (Table 1). Its frequency spectrum is rather simple. Except f0, f1 and their combinations we see side peaks on the lower frequency side of f0, 2f0 and 3f0, and at detected combination frequencies with f1 (doublets). The highest side peak at f0 − fB1 has an amplitude of 37 mmag and is non-coherent. After pre-whitening a noticeable power excess is detected at f0. One of the peaks closet to f0 may correspond to the high frequency triplet component, but it is weak and non-coherent.
The low frequency signal at f = fB1 is firmly (S/N = 6.5) detected. The signal at kf1 is non-coherent and cannot be removed with a single sine wave. We detect bunches of closely spaced peaks at kf1. Such structure is a signature of strong period and/or amplitude change of the first overtone which may hide the possible modulation structure. This is confirmed with the time-dependent Fourier analysis (Δt ≈ 25 d), results of which are presented in Fig. 6. We observe the following. (i) A weak signature of modulation of mean stellar brightness with PB1. The mean stellar brightness is anticorrelated with amplitude of the fundamental mode: the lower the pulsation amplitude, the brighter the star. (ii) Both amplitude and phase of the fundamental mode are modulated with PB1; amplitude modulation is more symmetric than phase modulation. (iii) At the phase slightly preceding the minimum pulsation amplitude of the fundamental mode its period is longest. The following period decrease is very fast, lasts roughly 1/3 of the modulation cycle, and occurs at a phase of small amplitude of the fundamental mode. (iv) Period of the first overtone varies on a long time-scale. It increases at an estimated rate of 5 × 10−5 d per 1000 d. The parabolic trend was removed from phase variation before we searched for short-term modulation of the first overtone. (v) We find a weak signature of the modulation of the first overtone with PB1. The amplitude modulation is best visible, but weak (2.8 mmag as determined from the frequency spectrum). Phase modulation may be masked by the use of approximate model for long-term variation (parabolic trend). (vi) Phase relation between modulation of the fundamental and first overtone modes is not clear: first, the phase of maximum amplitude of the fundamental mode is weakly sampled; second, modulation of the first overtone is weak and clearly non-stationary (left-hand panel of Fig. 6).
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-06283. The dashed lines in the frequency spectra mark fB1. In the rightmost panels all data were phased with PB1 resulting from frequency analysis. For clarity, error bars are not plotted in the phase plots (rightmost panels).
OGLE-III data for the star are insufficient for detailed frequency analysis (ρ = 118). Only one significant side peak is detected in the frequency spectrum. The merged data set allows us to study the long-term variation of radial modes. This analysis confirms a fast and linear change of the first overtone period. The phase of the fundamental mode is stable. We only note a ∼20 per cent lower mean amplitude of the fundamental mode within OGLE-III data.
4.3 OGLE-BLG-RRLYR-07393
In this star pulsation in the first overtone dominates (Table 1). We clearly detect modulation with two periods, PB1 = 209.8 d and PB2 = 322.9 d (Table 2). Both modes are affected by these two modulations but to a different extent. The modulation is strongest for the first overtone – two equidistant triplets, one with fB1 separation, the other with fB2 separation, are detected at f1. The highest side peak, at f1 − fB1, has an amplitude of 50.8 mmag and the highest side peak connected with PB2 has an amplitude of 21.5 mmag (at f1 + fB2). In the case of fundamental mode, modulation with PB2 is dominant (34.4 mmag at f0 + fB2), while modulation with PB1 is very weak (3.8 mmag at f0 + fB1). We note that PB1/PB2 ≈ 2: 3. The beat frequency is fbeat = fB1 − fB2 ≈ 0.00167 d−1 which corresponds to beat period of ≈600 d. Nearly three beat periods are covered in the OGLE-IV data. The beating is well visible in the envelope of the full light-curve solution which we schematically plotted with the dashed line in Fig. 1.
Strong modulation of the first overtone is reflected in rich modulation pattern at f1. We detect triplet f1 ± fB1, incomplete quintuplet, i.e. peaks at f1 ± fB2 and at f1 − 2fB2, and triplet with beat frequency, i.e. f1 ± fbeat. Exactly the same modulation pattern is detected at combination frequency, f0 + f1. After pre-whitening with these frequencies, an excess power is still detected at f1. The highest peak is at location unresolved with f1 (S/N = 7.9). The second highest peak is located close, but not exactly at f1 − fB1 − fB2. Pre-whitening with this frequency does not remove the signal. The excess power at f1 is a signature of non-stationary nature of the first overtone and its modulation.
In the low frequency range we clearly (S/N = 11) detect a peak at f = fB1. In addition there is a peak at 2fB2 (S/N = 4.8) and likely at fB2 (S/N = 5.2) but the latter detection is uncertain. At even lower frequency there is a peak of slightly higher amplitude, which may be a signature of weak long-term trend. These two peaks are 1-yr aliases of each other.
After pre-whitening the data with f0, f1, their combinations and modulation components, additional signal remains in the data. We detect four significant peaks located at frequencies corresponding to the inverse of sidereal day and its three consecutive harmonics. We treat this signal as of instrumental origin. In addition we find a significant (S/N = 4.8) peak at fx ≈ 4.705 d−1 (Ax = 2.9 mmag). The period ratio Px/P1 = 0.6163 indicates that Px cannot correspond to a radial mode. This untypical period ratio is not new for RR Lyrae stars however. It is found in both RRc and RRd stars. It corresponds to the new class of radial–non-radial RR Lyrae stars (see Introduction; Netzel et al. 2015; Moskalik et al. 2015). In particular, Px/P1 perfectly fits the sequence of more than 100 such stars detected in the OGLE-III data of the Galactic bulge (see Petersen diagram in fig. 7 of Netzel et al. 2015). We also find a signature of modulation of non-radial mode. At fx − fB2 we detect a weak (S/N = 4.1, 2.5 mmag) peak, which indicates that non-radial mode is modulated with the same period as the two radial modes.
In Fig. 7 we present the results of the time-dependent Fourier analysis (Δt ≈ 11 d), which confirms the picture emerging from the frequency analysis. In the case of the fundamental mode, modulation with PB2 is apparent and dominant. The phased modulation curve is sharp, with little scatter, as modulation amplitude with PB1 is 10 times smaller. This is not the case for the first overtone. The modulation of the first overtone with PB1 is well visible. The phased modulation curve has large scatter however, as modulation with both periods is strong (Table 2). The behaviour of stellar mean brightness is clearly anticorrelated with the amplitude of the first overtone mode. When amplitude of the first overtone drops, the mean brightness of the star increases. In the phased modulation curve (top right-hand panel in Fig. 7) the same scatter as in the case of first overtone is observed. As modulations dominant for the fundamental mode and for the first overtone have different periods, there is no obvious correlation between the amplitudes of the two modes. Sometimes they vary in phase, sometimes the amplitudes are anticorrelated – a pattern that repeats with a beat period.
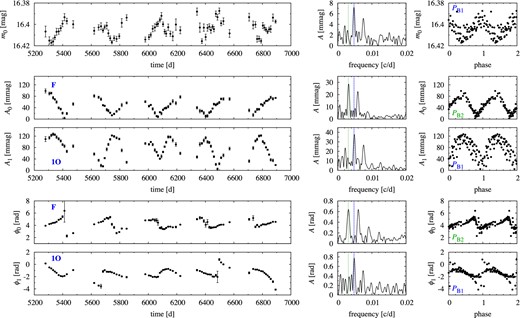
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-07393. The dashed and dotted lines in the frequency spectra mark fB1 and fB2, respectively. In the rightmost panels data were phased either with PB1(A0, 1O-mode data) or with PB2 (F-mode data), resulting from the frequency analysis. For clarity, error bars are not plotted in the phase plots (rightmost panels).
Of particular interest is behaviour of mode phases and their correlation with mode amplitudes. Phases (pulsation periods) are modulated with the period dominant for a given mode (PB1 for the first overtone, PB2 for the fundamental mode). We recall that in the case of OGLE-BLG-RRLYR-05762 and OGLE-BLG-RRLYR-06283 this modulation was smooth and continuous. This is not the case for OGLE-BLG-RRLYR-07393, however. We observe phase jumps when the corresponding mode amplitude is lowest (leftmost panels in Fig. 7). Unlike in the two mentioned stars the amplitudes of the fundamental and of the first overtone modes are very low (nearly vanish) from time to time. The apparent discontinuity in the pulsation phase is then detected (see also Discussion in Section 5.1).
The sampling of OGLE-III data for this star is lower than in OGLE-IV (ρ = 66 versus ρ = 322 in OGLE-IV). Their independent analysis yields a somewhat different frequency spectrum. The resulting modulation properties are summarized in Table 4. Two modulation periods are apparent, which we denote with ‘′’. PB2′ ≈ PB2, but PB1′ = 180 d and is significantly shorter than PB1 (Table 2). We observe triplet structures at the fundamental mode frequency rather than at the first overtone frequency. In the case of the first overtone and PB2′ a triplet is also likely, but higher frequency component overlaps with 1-yr alias of unresolved signal at f1. For both modes modulation with PB2′ ≈ PB2 is dominant within OGLE-III. This is visible in the time-dependent Fourier analysis for the merged data, results of which are presented in Fig. 8. The last three seasons of OGLE-III data, 3750 < t < 4750 d, are densely sampled and allow to see the modulation. Phase plots provide the most clear view. It is visible that the dominant period of modulation of the first overtone's phase is PB2′ = PB2 at the end of OGLE-III observations, and a shorter period (PB1) during OGLE-IV observations (see also Fig. 7). Modulation of the fundamental mode is always dominated by PB2. Its mean amplitude vary on a long time-scale with the event of significantly larger amplitudes at 3750 < t < 4500 d.
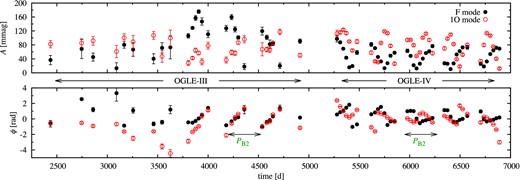
Time-dependent Fourier analysis for OGLE-III and OGLE-IV data for OGLE-BLG-RRLYR-07393.
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | |$P_{\rm B}^{\prime }$| (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-07393 | 180.4(4) | f0 + fB1′ | *23.2 | BL2 | f1 − fB1′ | *18.3 | BL1− | |
| 322.4(1.1) | f0 − fB2′ | *39.5 | BL2 | f1 − fB2′ | *38.8 | BL1− | b | |
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | |$P_{\rm B}^{\prime }$| (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-07393 | 180.4(4) | f0 + fB1′ | *23.2 | BL2 | f1 − fB1′ | *18.3 | BL1− | |
| 322.4(1.1) | f0 − fB2′ | *39.5 | BL2 | f1 − fB2′ | *38.8 | BL1− | b | |
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | |$P_{\rm B}^{\prime }$| (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-07393 | 180.4(4) | f0 + fB1′ | *23.2 | BL2 | f1 − fB1′ | *18.3 | BL1− | |
| 322.4(1.1) | f0 − fB2′ | *39.5 | BL2 | f1 − fB2′ | *38.8 | BL1− | b | |
| . | . | F-mode . | 1O-mode . | . | ||||
|---|---|---|---|---|---|---|---|---|
| Star . | |$P_{\rm B}^{\prime }$| (d) . | Freq. . | A (mmag) . | Struct. . | Freq. . | A (mmag) . | Struct. . | Remarks . |
| OGLE-BLG-RRLYR-07393 | 180.4(4) | f0 + fB1′ | *23.2 | BL2 | f1 − fB1′ | *18.3 | BL1− | |
| 322.4(1.1) | f0 − fB2′ | *39.5 | BL2 | f1 − fB2′ | *38.8 | BL1− | b | |
Based on the data we have we cannot judge what has happened with the shorter modulation period. We lack the crucial data in between OGLE-III and OGLE-IV, also lower cadence of OGLE-III observations data does not help to resolve the issue. We also note that all modulation side peaks are non-coherent (Table 4). The modulation with the shorter period, as well as both fundamental and first overtone modes, is non-stationary on a longer time-scales.
4.4 OGLE-BLG-RRLYR-14915
For this star fundamental mode pulsation dominates (Table 1). The highest side peak, with amplitude of 41.2 mmag, is detected at the first overtone frequency (f1 − fB1; PB1 = 62.89 d). A side peak with the same separation also appears at 2f1 and at all detected combination frequencies involving f0 and f1 (doublets). A low frequency peak at f = fB1 is well visible (S/N = 3.7). At f1 we also detect a side peak exactly at f1 − fB1/2. We postpone discussion of its origin till the end of this subsection.
Interestingly, side peak with different separation, fB2 (PB2 = 140.2 d), is detected only at the combination frequencies: f0 + f1 + fB2, 2f0 + f1 + fB2, 2f0 + 2f1 + fB2 and at f1 − f0 − fB1 − fB2, but not directly at f0 or at f1. These peaks (at combination frequencies) have low amplitudes. The highest, at f0 + f1 + fB2, has an amplitude of 5.7 mmag (S/N = 6.0). As no side peak with fB2 separation is detected directly at f0 or at f1, we cannot claim the modulation of these modes with PB2 and therefore no information is provided in Table 2. We note that other interpretation of these peaks is possible, namely, the highest peak at f0 + f1 + fB2 can correspond to the fourth radial overtone, f4. Other peaks involving fB2 are then linear combinations of f0, f1, f4 and fB1. Indeed, P4/P1 = 0.577 which is close to the expected period ratio of the radial modes – see e.g. fig. 4 in Netzel et al. (2015). The best match with the models is obtained assuming low metallicity, but then we cannot match the P1/P0 ratio, which requires high metallicity (see the Discussion in Section 5.2 and Smolec et al. 2015, for similar considerations for other star). Therefore, such explanation also faces a difficulty.
In the frequency spectrum of residual data we observe unresolved power at both f0 and f1 which may increase the noise level in the transform and hide the modulation peaks. It indicates that both modes undergo period and/or amplitude change on a long time-scale. To investigate it we merged OGLE-III and OGLE-IV data and conducted a time-dependent Fourier analysis (Δt ≈ 120 d), to search for a possible long-term modulation (for this star data are insufficient to investigate short-term modulation with PB1 or PB2; ρ = 39/87 in OGLE-III/OGLE-IV). Results are presented in Fig. 9. Phases of the fundamental and of the first overtone modes vary on a long time-scale and are anticorrelated. The variation is not single periodic, however; based on the data we have we cannot judge whether it is multiperiodic or irregular. The amplitudes also vary on the same time-scale and for most of the time are also anticorrelated but the effect is not as strong as in the case of pulsation phases. In the Fourier transform of the combined OGLE-III and OGLE-IV data we observe weakly resolved, and non-coherent peaks at both f0 and f1 in agreement with the just described picture.
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-14915 (Δt ≈ 120 d).
Since the variation presented in Fig. 9 occurs on a long time-scale, and associated unresolved power at f0 and f1 increases the noise level in the transform, we decided to filter out this long-term variation using time-dependent pre-whitening. With Δt ≈ 300 d most of the long-term variation should be filtered out, while leaving the short-term variation (associated with PB1 and PB2) unchanged. Main pulsation frequencies (and their combinations) should also be removed provided the associated phase/amplitude variation is small within a ≈300 d data chunk. This is not the case however, and small residual power at f0, f1, 2f1 and f1 − f0 remains. The secondary side peaks dominate the Fourier spectrum; all detected in the original, combined OGLE-III and OGLE-IV data are recovered, however, no new significant detections are made.
We recall that in OGLE-IV data, but also in OGLE-III and in the merged data we detect a peak exactly (within frequency resolution) at f1 − fB1/2. This is a significant (S/N = 5.2 in OGLE-IV, S/N = 6.5 in the merged data) detection with peak amplitude of 4.8 mmag in the OGLE-IV data set. Three interpretations are possible. (i) fB1/2 corresponds to basic modulation frequency and fB1 is its harmonic. This is unlikely however, as peak at f1 − fB1/2 is weak (4.8 mmag to be compared with 41.2 mmag at f1 − fB1 in the OGLE-IV) and is not detected at 2f1 or at combination frequencies where doublet with fB1 separation is present. (ii) fB1/2 may correspond to the independent modulation period for first overtone mode. (iii) fB1/2 is subharmonic of modulation frequency and thus full modulation cycle lasts 2PB1 with alternating modulation cycles. This, in our opinion, is the most likely explanation. In other star, OGLE-BLG-RRLYR-11311, we find a similar frequency pattern.
4.5 OGLE-BLG-RRLYR-09284
The star is a likely member of a tidal stream crossing the Galactic bulge (Soszyński et al. 2014b). Pulsation in the first overtone is dominant (Table 1). We detect three side peaks at fundamental mode frequency, all with low amplitudes, below 7 mmag. The two highest side peaks appear on either side of f0 and at first glance resemble equally spaced triplet. This is not the case, however. The separations correspond to slightly different modulation periods: PB1 = 41.78 d (f0 + fB1, 6.4 mmag) and PB2 = 40.76 d (f0 − fB2, 3.8 mmag). Analysis of the merged OGLE-III and OGLE-IV data confirms the asymmetry. The two frequencies fB1 and fB2 are well resolved in a merged data set. In addition, on the higher frequency side of f0 we find additional side peak at f0 + fB3 (PB3 = 47.7 d). The doublets are also found at combination frequencies with the first overtone mode and at 2f0 (2f0 + fB1). A significant unresolved power remains at f0 after pre-whitening (and also at the side peaks).
At first overtone frequency we detect a bunch of close (weakly resolved) peaks which may correspond to long-term variability of the first overtone. They are present only at f1 and not at frequency combinations with f0 and have small amplitudes (all below 1.5 mmag). As such they are not convincing signature of modulation. There is a significant single peak on the higher frequency side of f1, at fu (separation with f1 is ≈0.075 d−1, S/N = 5.6), but we do not find any combination frequency involving fu in the spectrum. In addition we find weak peaks at f1 + fB1 and f1 − fB1 (S/N equal to 3.4 for both peaks). They likely correspond to the modulation present for the fundamental mode, but the detections are marginal, and hence not reported in Table 2.
For this star the data have relatively good sampling (ρ = 320) but suspected modulation is of low amplitude. Nevertheless we attempted the time-dependent Fourier analysis with short Δt ≈ 7 d to capture the modulation of the fundamental mode. Only in the case of the fundamental mode's phase we find a weak evidence of its modulation with the three reported periods. In the Fourier transform of fundamental mode phases, Fig. 10, we first detect a signal at fB1, and after pre-whitening also with fB2 and fB3.
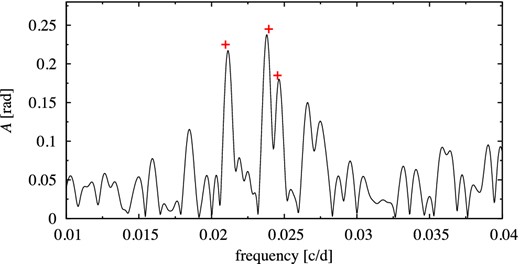
Frequency spectrum for fundamental mode phases extracted with time-dependent Fourier analysis for OGLE-BLG-RRLYR-09284. ‘+’ signs mark the location of modulation frequencies derived from the analysis of OGLE-IV data (Table 2).
For the first overtone signatures of modulation (only with PB1) are very weak, if any. They may be masked however by long-term variation of the first overtone mode. We also expect such long-term variation for fundamental mode as at f0 we detect unresolved residual power. To investigate the nature of long-term variability of the first overtone and of the fundamental mode we conducted time-dependent Fourier analysis of the merged data (Δt ≈ 300 d). Results are presented in Fig. 11. Long-term variability of both modes is well visible. The phases seem to be correlated and vary on a long time-scale. Interestingly, a significant and steady increase of the fundamental mode amplitude is well visible within the OGLE-IV data. First overtone amplitude is roughly constant then. Reverse is true during early seasons of the OGLE-III observations, but the trends are less significant, also due to larger errors caused by sparse sampling within OGLE-III (ρ = 40).
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-09284 (Δt ≈ 300 d). For better visibility the phase of first overtone was shifted vertically by 1 rad.
The described long-term variability was subtracted from the data using the time-dependent pre-whitening. We recover all modulation components detected in the analysis of OGLE-IV data, however, do not find any additional, significant side peak.
4.6 OGLE-BLG-RRLYR-32462
For this star data were collected only during the OGLE-IV phase. The star is a likely member of a tidal stream crossing the Galactic bulge (Soszyński et al. 2014b). Pulsation in the first overtone is dominant and so is its modulation with PB1 = 190.1 d (doublets on higher frequency side, the highest peak at f1 + fB1 has an amplitude of 31.4 mmag). A side peak with fB1 separation is not detected at f0. We only detect a very weak signals at 2f0 + 2fB1 and 2f0 + fB1 (S/N equal to 3.4 and 3.2, respectively), which may indicate that also fundamental mode is modulated with PB1 but firm evidence is missing. No doubt fundamental mode is modulated with a shorter period, PB2 = 125.6 d (23.5 mmag at f0 + fB2). The same modulation affects the first overtone (8.8 mmag at f1 − fB2). The fundamental mode is clearly non-stationary (unresolved power at f0 with S/N = 15.3). Unresolved power also remains at f1 (S/N = 7.1) but the signal is lower than non-coherent signal at f1 + fB1 (S/N = 9.5).
Although in the frequency spectrum we find doublets only, we conclude that both modes are modulated with the two periods. Modulation is well visible in the time-dependent Fourier analysis (Δt ≈ 15 d; Fig. 12). We observe the following. (i) Fundamental mode, both amplitude and phase, is modulated with PB2. The amplitude of the fundamental mode steadily decreases, its phase underwent a large and long-term variation which we modelled with fifth-degree polynomial. As a result of this long-term variation the peak at f0 in the frequency spectrum of original data is non-coherent as described above. (ii) First overtone, both amplitude and phase, is modulated with PB1. The amplitude of modulation clearly increases. As a result a peak at f1 + fB1 is non-coherent as pointed above. (iii) When amplitude of first overtone is significantly reduced (around t = 6800 d) a glitch in its phase variation is observed. (iv) No clear modulation of the mean stellar brightness is detected in the Fourier spectrum and in the phased data for analysed subsets. However, the correlation between m0 and A1 is clearly visible in the leftmost panels of Fig. 12, in particular during the fourth and fifth observing seasons: mean brightness increases when amplitude of first overtone decreases and vice versa. The effect is not as clear in the earlier observing seasons as modulation amplitude of the first overtone is smaller.
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-32462. The dashed and dotted lines in the frequency spectra mark fB1 and fB2, respectively. In the rightmost panels data were phased either with PB1(A0, 1O-mode data) or with PB2 (F-mode data), resulting from the frequency analysis.
Time-dependent pre-whitening does not provide additional insight into modulation properties of the star. Modulation periods are rather long, and hence it is difficult to pick Δt such that long-term variation is eliminated, while periodic modulation remains unaffected.
4.7 OGLE-BLG-RRLYR-22356
For this star data were collected only during the OGLE-IV phase. Pulsation in the fundamental mode dominates. On the lower frequency side of f0 we detect three significant close peaks. Side peaks at f0 − fB1 and at f0 − fB3 have amplitudes of 40.1 and 7.4 mmag, respectively (periods corresponding to the doublet separations are 255.5 and 32.46 d, respectively; see Table 2). Side peaks with the same separation are present also at the only detected harmonic, 2f0, where in addition 2f0 − 2fB1 is present. The pre-whitening sequence at f0 and at 2f0 is illustrated in Fig. 13 (left- and right-hand panels, respectively). One additional significant peak appears on the lower frequency side of f0; its frequency is denoted with fu in Fig. 13. It is significant (S/N = 10, 13.1 mmag), however no significant close peaks with f0 − fu separation or significant combination frequencies involving fu are detected in the spectrum (see also below).
Pre-whitening of the side peaks at f0 and 2f0 for OGLE-BLG-RRLYR-22356. The short horizontal line segments are placed at four times the noise level in the frequency spectrum. Arrows in the top panels indicate the significant frequencies. f0 and 2f0 are pre-whitened in all panels (the rightmost dashed lines).
Side peaks with fB1 separation also appear at combination frequencies with the first overtone, but not at f1. Here, we only detect one side peak on higher frequency side, at f1 + fB2, with amplitude of 15.0 mmag (PB2 = 51.59 d). We note that amplitude of the first overtone itself is lower than amplitude of the highest side peak at f0. We note that fB2 ≈ 5fB1 (strictly fB2/fB1 = 4.95). Also, fu ≈ f0 − fB2 + fB1. In fact, fu and f0 − fB2 + fB1 are not resolved within the OGLE-IV data. Based on the data we have, we cannot determine whether fu is an independent frequency corresponding to modulation, or it corresponds to the above combination of other modulation frequencies.
Fig. 13 indicates that the fundamental mode is non-stationary. We have investigated the temporal variation of the fundamental and first overtone modes with the time-dependent Fourier analysis, first with large Δt ≈ 100 d. In Fig. 14 we plot the mode amplitudes and mean stellar brightness. The fundamental mode is dominant and vary on a time-scale of ∼1000 d. Its amplitude is strongly correlated with the mean stellar brightness. The lower the amplitude of the fundamental mode, the brighter the star. A long-term variation on a time-scale of ∼1000 d is also visible for the first overtone mode.
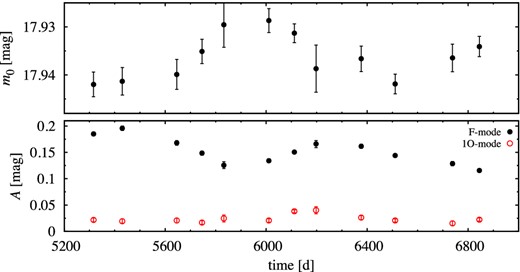
Mean stellar brightness (top) and mode amplitudes (bottom) for OGLE-BLG-RRLYR-22356 extracted with the time-dependent Fourier analysis (Δt ≈ 100 d).
We next investigated the suspected short-term modulations revealed in the frequency spectrum using lower Δt ≈ 10 d. Results are rather noisy as data for this star are not too dense (ρ ≈ 310) and the chosen Δt is the lowest possible. Nevertheless, in the frequency spectra of the resulting 83-point time series and in the phase plots we confirm the modulation of the first overtone with PB2 and of the fundamental mode with PB1. We cannot confirm modulation with PB3 – this requires a lower value of Δt, which is not possible with the data we have. The pulsation amplitude of the fundamental mode slowly decreases during the observations, which is also visible in Fig. 14.
4.8 OGLE-BLG-RRLYR-00951
In this star pulsation in the fundamental mode dominates, however, no sign of its modulation is detected (Tables 1 and 2). A clear, equally spaced triplet is visible at the first overtone frequency. Modulation period is PB1 = 142.7 d and modulation amplitude is very low, of order of 5 mmag. The triplet is also detected at f0 + f1, while at f1 − f0 a higher frequency component is missing. No other modulation components are detected.
We note that signals at f0 and at f1 are non-coherent and dominate the pre-whitened frequency spectrum (S/N = 20.4 and 7.6, respectively). It is a consequence of the long-term variation of fundamental and first overtone modes, clearly revealed in the time-dependent Fourier analysis – Fig. 15. Here we joined OGLE-III and OGLE-IV data, however, we note that data sampling in OGLE-III is poor (ρ = 33). Reasonable data are available only for four seasons. The gap between OGLE-III and OGLE-IV data is nearly 1600 d. No modulation is detected in OGLE-III data alone. The long-term variation of both modes is obvious and significant.
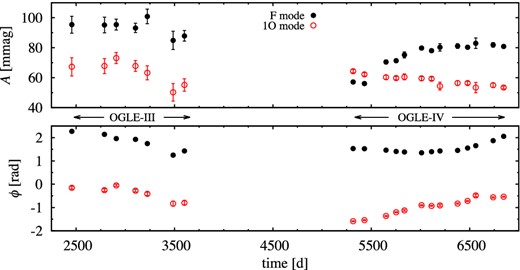
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-00951 (Δt ≈ 100 d).
To get rid of non-coherent signal at f0 and f1 we conducted time-dependent pre-whitening (Δt ≈ 140 d) using OGLE-IV data only. Non-stationary signals at f0 and f1 were removed. We recovered all modulation components detected in the earlier analysis, but no new significant signal appeared. Because of low modulation amplitude time-dependent Fourier analysis cannot be used to study modulation with PB1. With sufficiently low Δt, necessary for this analysis, errors of mode amplitudes are larger than the expected modulation amplitude.
4.9 OGLE-BLG-RRLYR-11311
Pulsation in the first overtone is dominant (Table 1). Both at f0 and at f1 we detect doublets, with different separations, however: one side peak is located at f1 − fB1 (32.4 mmag, PB1 = 49.13 d) and the other at f0 + fB2 (13.8 mmag, PB2 = 87.1 d). The side peaks with fB1 separation are also detected at the combination frequencies, while side peak with fB2 separation is detected only at f0 and 2f0. Interestingly, we also find a significant (S/N = 5.9) peak at f0 + fB2/2 with amplitude of 6.7 mmag. As in the case of OGLE-BLG-RRLYR-14915 (see comments in Section 4.4) we interpret this signal as corresponding to subharmonic frequency.
The frequency spectrum of residual data is dominated by strong non-coherent signals at f0 and at f1 (S/N = 14.1 and 6.8, respectively). Using the time-dependent Fourier analysis we confirm that both modes vary on a long time-scale – Fig. 16. It seems that long-term modulation of both modes, their amplitudes and phases, on a time-scale of ∼2000 d occurs. More data are necessary to resolve the suspected modulation.
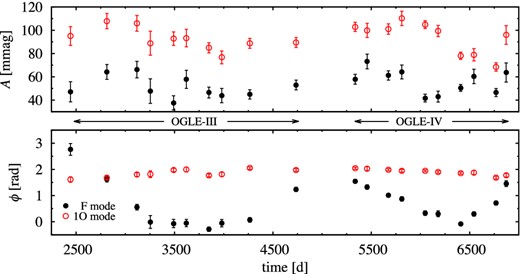
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-11311 (Δt ≈ 150 d).
To get rid of the non-coherent signals at f0 and at f1 we conducted the time-dependent pre-whitening (Δt ≈ 100 d) using the OGLE-IV data only. Non-stationary signal at f1 was removed and at f0 was strongly reduced. We recovered all side peaks detected in the earlier analysis, but no new significant signal appeared. Because of low cadence of observations (ρ = 43/99 in OGLE-III/IV) the data are insufficient to reveal radial mode modulations with PB1 or PB2 using time-dependent Fourier analysis. At the required Δt, errors of the determined amplitudes become larger than expected amplitude of modulation.
4.10 OGLE-BLG-RRLYR-10728
In this star fundamental mode dominates – its mean amplitude is the highest in our sample. Two doublets with different separations are detected at f0. The highest peak is located at f0 + fB1 (26.7 mmag, PB1 = 98.7 d). The highest peak on the lower frequency side of f0 (8.9 mmag at f0 − fB2) corresponds to modulation with period of PB2 = 313 d. We cannot exclude that equidistant triplet with fB2 separation is present – unfortunately, f0 + fB2 falls exactly at location of 1-yr alias of unresolved signal at f0. Also a triplet with fB1 separation is possible, the peak at f0 − fB1 is well visible, but weak (S/N = 3.4).
Side peak with fB1 separation is also detected at first overtone frequency (at f1 − fB1, 8.6 mmag). No side peaks with fB2 separation are detected at kf1. The modulation spectrum is rich for this star. In addition to side peaks with fB1 and fB2 separation also side peaks with fB1 + fB2 separation appear at 2f0 and 3f0 (on the higher frequency side; also at 4f0 and f1 − f0, but these peaks have S/N < 4) and also at f0, f0 + f1 and 2f0 + f1, but on the lower frequency side. Amplitudes of these peaks are all below 6 mmag. In the pre-whitened spectrum we find a weak residual power at f0 (S/N = 5.5) and at f1 (S/N = 5). The time-dependent Fourier analysis indicates that both amplitude and phase of the radial modes slowly vary within the OGLE-IV data.
The OGLE-III data for this star are scarce: only for four weakly sampled seasons (ρ = 30) reasonable data are available, separated from OGLE-IV observations by a large gap of nearly 1600 d. Independent analysis of this data reveals that likely a sudden change in the pulsation properties of the star occurred in between OGLE-III and OGLE-IV observations. The pulsation periods as derived from OGLE-III data are P0 = 0.481690(4) d and P1 = 0.358121(3) d (cf. Table 1). Hence, period of the first overtone decreased by nearly 0.003 d, i.e. by 0.8 per cent. Period of the fundamental mode decreased only slightly (0.003 per cent). As a result period ratio decreased from 0.7435 (OGLE-III) to 0.7377 (OGLE-IV). The phase of fast change of first overtone period had to occur before OGLE-IV data, as within OGLE-IV the phase/amplitude changes are slow. In the OGLE-III data we detect only one side peak on the higher frequency side of f0 with separation corresponding to modulation period of 92.3 d (to be compared with PB1 = 98.7 d detected in the OGLE-IV data). The nature of these intriguing changes will remain obscure as we lack the crucial observations in between OGLE-III and OGLE-IV.
4.11 OGLE-BLG-RRLYR-04598
This star has the highest period ratio in our sample. In addition P1/P0 is almost exactly 0.75 indicating that 3: 4 resonance may play a role in this star. Pulsation in the first overtone dominates. At the location of the fundamental mode we detect two lower frequency side peaks, at f0 − fB1 and at f0 − fB2, with amplitudes 12.9 and 10.8 mmag, respectively (PB1 = 281 d, PB2 = 85.6 d). Side peaks at the same separations are also detected near combination frequency f0 + f1, the one at f0 + f1 − fB2 is very weak, however (S/N = 4.0). No side peak is detected directly at first overtone frequency, we note, however, that unresolved peak remains close to f1 after pre-whitening (S/N = 9.5). Location of its 1-yr alias is unresolved with f1 − fB1. There is also a weak detection at f = 2f1 − fB1 (S/N = 4). Since there is no firm evidence of modulation of the first overtone the relevant part of Table 2 is not filled.
In OGLE-III data we also find two side peaks on lower frequency side of f0, one of them at roughly the same separation (fB2), the other farther away, the inverse of separation corresponds to 258 d, to be compared with PB1 = 281 d. This indicates that possible modulation with PB1 is non-stationary on a longer time-scale.
In Fig. 17 we present a long-term variation of radial mode amplitudes and phases extracted with the time-dependent Fourier analysis (Δt ≈ 130 d). Both modes vary on a long time-scale in an irregular fashion. Phase variation is more pronounced. The periods of both modes increase on average. A faster, ∼few hundred days irregular phase variation is also well visible. A slow trend of increasing amplitude of the fundamental mode and decreasing amplitude of the first overtone is apparent.
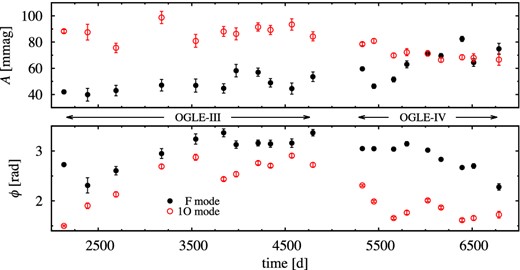
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-04598 (Δt ≈ 130 d).
Although the data are relatively dense (ρ = 146/375 in OGLE-III/IV), the amplitude of suspected modulation is low. In addition, the irregular variability we see in Fig. 17 is of higher amplitude. Therefore, we cannot detect modulation using the time-dependent Fourier analysis with low Δt.
4.12 OGLE-BLG-RRLYR-13442
OGLE-BLG-RRLYR-13442 (marked with pentagon in Fig. 2) is a special star. As reported by Soszyński et al. (2014b) the star switched pulsation mode between single-mode fundamental mode pulsation (RRab star, OGLE-III) to double-mode RRd pulsation (OGLE-IV). In the OGLE-IV data we detect three significant close peaks on the higher frequency side of f0. The highest, located at fu1 ≈ f0 + 0.028 has an amplitude of 29.4 mmag (S/N = 13.4), but no other significant peak with the same separation is detected. Only a weak (S/N = 3.3) peak is present on higher frequency side of f0 + f1. Similarly, at fu2 ≈ f0 + 0.032 we find a much weaker peak (S/N = 5.1), but again, no combination frequencies involving fu2 are detected in the spectrum. The other side peak, which we associate with modulation, is located at f0 + fB1 (14.0 mmag, PB1 = 179.1 d). A side peak with the same separation is detected also at 2f0. We find no significant side peak at the frequency of the ‘just born’ first overtone. The frequency spectrum of residual data is dominated by strong unresolved signals at f0 (S/N = 15.3) and also at f1 (S/N = 4.6).
Interestingly, side peak with fB1′ ≈ fB1 (PB1′ = 171.3 d, equal to PB1 within data resolution) separation and a peak at |$f_{\rm u}^{\prime }=f_{\rm u}$| are also detected in the OGLE-III data, in which we find no evidence for the presence of the first overtone. The side peak at f0 + fB1′ has an amplitude of 29.0 mmag. Despite a rather dramatic change of pulsation state – the star switched pulsation mode from RRab to RRd – the side peaks at the fundamental mode, their location and height, changed little.
Pulsation of this interesting star is clearly non-stationary. A lot of unresolved power remains in the frequency spectrum after pre-whitening with significant frequencies. In Fig. 18 we plot a merged OGLE-III and OGLE-IV data (top) with season-to-season amplitudes and phases of the fundamental and first overtone modes extracted with the time-dependent Fourier analysis. The figure suggests that pulsation may be modulated on a long time-scale of ∼1000 d. Data are insufficient to reveal possible short-term modulation (with PB1/PB2) with the time-dependent Fourier analysis.
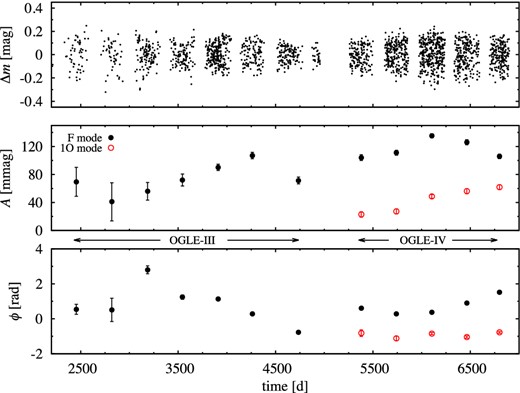
Data (top) and time-dependent Fourier analysis (middle and bottom) for OGLE-BLG-RRLYR-13442 (each point corresponds to one observing season).
4.13 OGLE-BLG-RRLYR-30986
For this star the data were collected only during the OGLE-IV phase. First overtone pulsation is dominant. Both at f0 and at f1, on their lower frequency side, we detect side peaks at equal separation, fB1 (Table 2). In addition at f1 there is a peak at f1 − 2fB1. We interpret these side peaks as due to modulation of both modes with a common period of PB1 = 111.4 d. Modulation of the fundamental mode is stronger (51 mmag at f0 − fB1 to be compared with 14.4 mmag at f1 − fB1). Side peaks appear also at combination frequencies at the same separation. In the frequency spectrum of residual data a weak (S/N = 4.1) signal at 2f0 remains. The data for this star are too sparse (ρ ≈ 98) to apply the time-dependent Fourier analysis in order to investigate the modulation in more detail.
4.14 OGLE-BLG-RRLYR-02530
We note a significant difference in the first overtone period given in the OGLE-III and in the OGLE-IV catalogues. In Fig. 19 we explain the origin of the difference. There are three significant peaks in the OGLE-III data in the frequency range of interest. The highest, marked with arrow in the top panel (fu), was interpreted as corresponding to the first overtone. In OGLE-IV and in the merged OGLE-III and OGLE-IV data other, lower frequency peak is the highest. Following Soszyński et al. (2014b) we interpret this peak as corresponding to the first overtone. In fact, the peak interpreted as corresponding to the first overtone mode in the OGLE-III data is weak in OGLE-IV, and we do not find any combination frequencies involving fu. Therefore, we do not have a proof that this frequency originates from OGLE-BLG-RRLYR-02530.
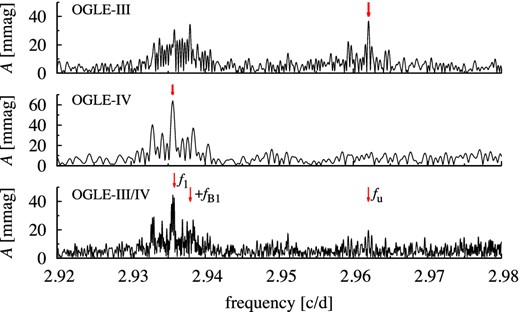
Fourier spectrum for OGLE-BLG-RRLYR-02530 in the frequency range around the first overtone frequency. Top panel for OGLE-III, middle panel for OGLE-IV and bottom panel for the merged data. Arrows mark the location of the first overtone frequency adopted in the respective catalogues. In the bottom panel we mark the first overtone frequency as adopted in this analysis and the location of modulation peak (visible in the OGLE-III data, top panel, and also in the OGLE-IV data, but only after pre-whitening).
We detect a family of modulation peaks with the same separation (fB1, PB1 = 469 d) at both radial modes and their combination frequencies, on their higher frequency sides. The highest side peak is located at f0 + fB1 and has an amplitude of 22.9 mmag. The highest peak at the first overtone frequency (f1 + fB1) has an amplitude of 18.7 mmag. Interestingly at f0 + f1 and 2f0 we also detect the quintuplet components, i.e. peaks with separations +fB1 and +2fB1. Data are too scarce to reveal the discussed modulation in the time-dependent Fourier analysis (ρ = 30/43 in OGLE-III/IV).
Fig. 19 indicates that pulsation of the star is certainly non-stationary. In Fig. 20 we show the season-to-season variation of the radial modes. Both modes, their amplitudes and phases, strongly vary on a long time-scale.
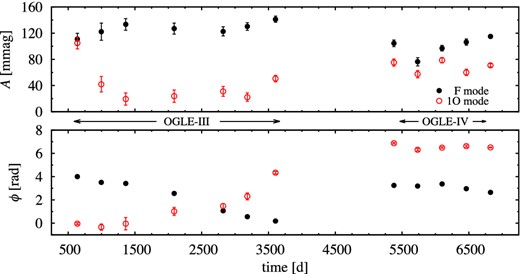
Time-dependent Fourier analysis for OGLE-BLG-RRLYR-02530 (each point corresponds to one observing season).
4.15 OGLE-BLG-RRLYR-02862
We find side peaks with the same separation, fB1 (PB1 = 173.6 d), at f0 (equidistant triplet) and on the lower frequency side of f1, f0 + f1 and of 2f1 (weak). The triplet is asymmetric, the higher component at f0 − fB1 has an amplitude of 28.6 mmag, while the other component at f0 + fB1 has an amplitude of only 7.9 mmag (S/N = 4.3). There are two additional, significant peaks in the frequency spectrum, one on the higher frequency side of f0 (separation ≈0.038 d−1), the other on its lower frequency side (separation ≈0.0072 d−1), but we do not detect any other side peaks with these separations. Data for this star are insufficient to conduct more detailed analysis (ρ ≈ 34 both in OGLE-III and in OGLE-IV). On a long time-scale variation of both radial modes is apparent and irregular. In particular during the OGLE-III the fundamental mode pulsation was dominant, while the first overtone dominates during the OGLE-IV observations.
4.16 Other analysed stars
In OGLE-BLG-RRLYR-02985, −12660, −33181, −13804, −13302 and −31786 (marked with circles in Fig. 2) we do not find additional significant signals beyond f0, f1 and their combinations. We note that first four stars are located relatively close to the main progression formed by the majority of RRd stars in the Petersen diagram. Data for all these stars are rather sparse and presence of additional signal cannot be excluded.
In frequency spectra of OGLE-BLG-RRLYR-05475, −09965, −14031, −15012 and −19451 (marked with squares in Fig. 2), after pre-whitening with radial mode frequencies and their combinations, we detect signal at first overtone frequency, unresolved with f1 – a signature of long-term variation of this mode. OGLE-BLG-RRLYR-05475 and OGLE-BLG-RRLYR-14031 are located within the main group of RRd stars (they were selected as primary targets).
OGLE-BLG-RRLYR-24137 (marked with triangle in Fig. 2) turned out to be very unusual and interesting. It is likely a triple-mode RR Lyrae star. Except fundamental and first overtone modes we detect a third mode, which is either the third radial overtone or a non-radial mode. Interestingly, the period doubling of the third mode is clearly detected. We discuss this star in detail in a separate publication (Smolec et al. 2015).
5 DISCUSSION
5.1 Modulation properties of the stars
Modulation properties of the analysed stars are collected in Table 2. In six stars the modulation is well established: either triplets are detected in the frequency spectrum or modulation is directly visible in the time-dependent Fourier analysis. In the latter case, doublets in the frequency spectrum are not an exception (e.g. in OGLE-BLG-RRLYR-05762, -06283, -7393 and -32462). Therefore, we assume that doublets detected in nine other stars are also due to modulation (see also Section 3 and Alcock et al. 2003). The other explanation that additional close side peaks correspond to non-radial modes and their combinations with radial mode frequencies cannot be excluded, but in our opinion is less probable.
In the adopted modulation picture, doublets are in fact triplets with highly asymmetric components. As pointed in Section 3 the detected triplets can indeed be highly asymmetric. To generate highly asymmetric triplets both amplitude and phase modulation of comparable strength is needed, as analysed by Benkő, Szabó & Paparó (2011). This is indeed the case for the stars in which time-dependent Fourier analysis of modulation was possible (Figs 4, 6, 7 and 12). The other factor necessary to generate the highly asymmetric triplet is a close to ± π/2 phase-lag between the amplitude and phase modulations. If the offset is 0 or π a triplet should be symmetric. Unfortunately, the phased modulation curves we get for some stars are characterized by large scatter due to irregularities in the modulation and presence of other modulation periods. The lag between the amplitude and phase modulation cannot be determined accurately. Nevertheless we note that in the best case of OGLE-BLG-RRLYR-05762 and modulation of fundamental mode with PB1 (Fig. 4) the lag is certainly very small. A triplet with comparable height of the modulation components (53 and 25 mmag) is detected in its frequency spectrum. This is a rare case and, as analysed above, modulation we see in some stars and suspect in the others must be both amplitude and phase modulation, with a significant, close to ± π/2, lag between the two modulations.
In seven stars we detect a single modulation period, in five stars we detect two modulation periods and in three stars three modulation periods are detected. Altogether in 15 stars 26 modulation periods are found, of which 20 are connected with the fundamental mode, 14 are connected with the first overtone and eight with both of the modes simultaneously. In six out of seven stars in which both modes are modulated, modulation of the fundamental mode is stronger (has higher amplitude). Modulation periods vary from few tenths to few hundred days, radial mode amplitudes may be modulated by a few to nearly 100 per cent. We do not find any significant correlations between e.g. the modulation periods and modulation amplitudes. We note, however, that any statistics and description of modulation properties in our sample must be biased: the sample is small and not homogeneous. Data for different stars are of very different quality. Only in few densely sampled cases very detailed analysis of modulation was possible. Below we describe the most interesting phenomena found in the data.
Feedback effect between star brightness and pulsation mode amplitudes. Because of radial mode modulation, the kinetic energy of pulsation varies in time. It is transferred to the thermal energy of the star and vice versa. The star adjusts its structure to the instantaneous mode amplitudes, which we observe through mean brightness variation. Since modulation we observe in analysed stars is typically dominant for one of the modes, the feedback effect we observe is the following: the larger the amplitude of the dominant mode, the smaller the mean stellar brightness. Then kinetic energy of pulsation drops, the mean brightness increases. The effect is best visible for OGLE-BLG-RRLYR-05762 (A0 − m0, Fig. 4), OGLE-BLG-RRLYR-06283 (A0 − m0, Fig. 6), OGLE-BLG-RRLYR-07393 (A1 − m0, Fig. 7) and OGLE-BLG-RRLYR-22356 (A0 − m0, Fig. 14).
Properties of one radial mode are coupled with properties of the other mode. Both modes compete for the same driving mechanism and their amplitudes and phases are coupled through the cross-saturation effects. Therefore, modulation of one radial mode should be accompanied by modulation of the other mode with the same period. Some of the analysed stars seem to contradict the above statement, as modulation of only one mode is detected in the data (e.g. OGLE-BLG-RRLYR-09284, -04598) or the other mode is modulated, but with different period (e.g. OGLE-BLG-RRLYR-11311). We note, however, that modulation amplitudes for each of the modes can differ significantly. In stars in which we find common modulation period for both modes, the modulation amplitudes can strongly differ (e.g. modulation with PB1 in OGLE-BLG-RRLYR-05762, -07393 and -02862, Table 2) and rarely are of comparable strength. Because of the relatively high noise, inherent to ground-based observations, we will miss all modulations with amplitude below ≈3 mmag (the exact limit depends on data quality for particular star). Moreover, modulation side peaks may be hidden in the bumps of excess power which we often find in the pre-whitened spectra around radial mode frequencies. This excess power results from long-term irregular variations commonly present in the analysed stars (see below).
In principle, when both modes are modulated simultaneously with the same period, the increase of one mode's amplitude should be accompanied by the decrease of other mode's amplitude. This is the case for the modulated double-overtone Cepheids analysed by Moskalik & Kołaczkowski (2009). In these stars amplitudes of both modes are always modulated with a common (and long, >700 d) period and are anticorrelated (see table 7 and figs 15 and 16 in Moskalik & Kołaczkowski 2009). We do not find a clear evidence of such behaviour in our stars. When only one, common modulation period is detected, the data are insufficient to conduct the detailed analysis (our modulation periods are significantly shorter than in the case of the double-overtone Cepheids). When data are good enough, at least two modulation periods are detected and each of them is dominant for different radial mode: one for the fundamental, the other for the first overtone mode. One other factor that hinders the analysis of radial modes’ amplitude correlations is non-stationary nature of the pulsation and of the modulation, which we discuss in more detail below.
The origin and mechanism of the detected modulations are unknown. We still lack the explanation for the single-periodic Blazhko effect in single-periodic RR Lyrae stars, despite the great progress made recently thanks to Kepler and CoRoT observations (see Szabó 2014, for a review). One of the crucial discoveries was detection of period doubling of the fundamental mode in the modulated RRab stars (Szabó et al. 2010), which motivated a new resonant model proposed by Buchler & Kolláth (2011) to explain the Blazhko effect. We do not find period doubling of any of the radial modes in our stars, but its detection may be difficult in the ground-based data.
Long-term stability of the pulsations. All of the investigated stars share a common feature: their pulsation properties are non-stationary. Amplitudes and phases of the radial modes vary irregularly on a long time-scales of few hundred, or thousands days. The long-term variations are clearly revealed in stars for which OGLE-III data are available. There are many examples in the paper, see e.g. Figs 5, 8, 11, 14–17 and 20. Both amplitude and periods of both radial modes vary on a long time-scale. This variation is most likely irregular, at least no obvious long-period modulation is clear in the discussed cases. These long-term irregular changes are reflected in the pre-whitened frequency spectrum as close, but unresolved peaks at the location of radial modes.
The short-term modulations reported in Table 2 are also not strictly periodic. The modulation side peaks are non-coherent. Irregularities are also visible in the modulations revealed with the time-dependent Fourier analysis. In some cases the short-term modulation differs significantly in the OGLE-III and OGLE-IV data for the same star. Although OGLE-III data are less suitable for the study of short-term modulation, in some cases differences are obvious and significant. Example includes OGLE-BLG-RRLYR-07393 (see Table 4 and Fig. 8).
Period changes. Long-term phase variations are common to all analysed stars as pointed above. In the case of OGLE-BLG-RRLYR-05762, -06283, -07393 and -32462 we could analyse the radial mode's phase (period, equation 2) variation in more detail (Figs 4, 6, 7 and 12, respectively). We note that phases of low amplitude of the radial mode are accompanied by fast phase change. In other words, mode of low amplitude is prone to fast period change. In particular, when amplitude of the mode drops to very small value a glitch in the phase variation is observed (OGLE-BLG-RRLYR-07393, Fig. 7; OGLE-BLG-RRLYR-32462, Fig. 12). The apparent phase discontinuity is an effect of our coarse sampling of the modulation properties (large Δt). We note that the correlation: the lower the amplitude, the faster the phase change is also apparent in RRc stars observed from space by Kepler Space Telescope. In the case of these stars the phase variation can be traced continuously. The described effect is well visible in fig. 6 of Moskalik et al. (2015). When amplitude of the mode drops, phase variation is rapid but continuous.
In two cases we find an evidence for fast and linear change of first overtone period (OGLE-BLG-RRLYR-06283, Fig. 6; OGLE-BLG-RRLYR-05762, Fig. 4) on a time-scale shorter than expected as due to evolutionary changes. In other star, OGLE-BLG-RRLYR-10728, we find an evidence for an abrupt change of the first overtone period.
5.2 Peculiarities of the analysed stars; the Petersen diagram
A glimpse at the Petersen diagram, presented in Fig. 2, reveals that nearly all stars showing modulation are located off the main progression formed by the majority of RRd stars. At a given period of the fundamental mode their period ratios are either significantly smaller or significantly higher than in the majority of RRd stars. Two stars have typical period ratios, but are unusual for other reason – they are likely members of a tidal stream crossing the Galactic bulge (Soszyński et al. 2014b).
We admit that we have not analysed all 173 RRd stars from the OGLE Galactic bulge collection. We only analysed those stars for which automatic pre-whitening revealed close or unresolved signal at f0 or at f1 (see Section 2). Later, then it was clear that all such stars have non-typical location in the Petersen diagram, we analysed all deviating stars and found additional two stars with modulation. We note that the OGLE-III data for all 92 RRd stars present in the OGLE-III catalogue of variable stars were analysed while searching for non-radial modes (Netzel et al. 2015). Some close side peaks or unresolved frequencies at f0 and/or at f1 were detected in a few stars. All of them are included in our sample and their period ratios are not typical. We cannot exclude that there are more stars which show modulation among the typical RRd stars, but we conclude that the fraction of stars showing modulation must be significantly lower there. Analysis of all 173 RRd stars using both OGLE-III and OGLE-IV data is ongoing. The present analysis indicates that at least ∼8.7 per cent of RRd stars from the OGLE Galactic bulge collection are modulated, but their period ratios are not typical.
We note that location of these stars in the Petersen diagram presents a difficulty for stellar pulsation theory. Metallicity is the dominant parameter that affects the location of a star in the Petersen diagram. In particular the short period–low period ratio tail, well visible in Fig. 2 and absent in the Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC) populations (Soszyński et al. 2009, 2010b), is explained by larger metallicity spread in the Galactic bulge population and higher metallicity of these stars – see fig. 4 in Soszyński et al. (2011) and fig. 2 in Soszyński et al. (2014a). Explanation for stars off the main progression is missing. Their period ratios can also be matched with higher metallicity models (see Smolec et al. 2015), but the reason why they deviate from the main progression in the Petersen diagram is unknown.
Not only period ratios are not typical in our sample. We note that in seven stars (∼47 per cent) the fundamental mode dominates. If we consider only the stars located off the main progression in the Petersen diagram, the fraction is even higher (∼54 per cent). To the contrary, in the full sample of 173 Galactic bulge RRd stars the first overtone pulsation strongly dominates (82.1 per cent). Interestingly, one of the analysed stars, with the dominant fundamental mode pulsation, OGLE-BLG-RRLYR-13442, has switched the pulsation mode recently: from RRab to RRd pulsation. It is marked with a pentagon in Fig. 2 and its period ratio is also not typical. Its pulsation state is clearly non-stationary (like in other analysed stars). The same modulation side peaks were present both before the mode switch and after the mode switch. With the data we have, speculations about possible connection between non-typical period ratio, RRab→RRd mode switch, and non-stationary modulations are premature. We think, however, that the hypothesis that such connection exists is interesting and worth investigating. We plan a detailed analysis of long-term stability of radial mode properties in the full sample of RRd stars. Certainly, the stars that deviate from the main progression in the Petersen diagram require long-term monitoring. We note that there are two other Galactic bulge stars in OGLE data base that switched the pulsation mode but in a reverse direction: from RRd to RRab (OGLE-BLG-RRLYR-12245 and OGLE-BLG-RRLYR-07226; see Soszyński et al. 2014a,b). Before the mode switch, their period ratios were typical.
5.3 Modulation properties as compared to Blazhko effect reported in the literature
The Blazhko effect, amplitude and phase modulation of radial modes, is commonly detected in single-periodic RR Lyrae stars, both in RRab and in RRc stars. The effect is more frequent in RRab stars. Space photometry and analysis of top-quality ground-based data indicate that it may occur in up to 50 per cent of stars (Jurcsik et al. 2009; Benkő et al. 2010, 2014). The frequency is likely lower in the case of RRc stars, up to 10 per cent (e.g. Mizerski 2003; Nagy & Kovács 2006), but these stars are relatively little studied; in particular we lack space photometry for modulated RRc stars. We note that in the ground-based data, multiple modulation periods are rare. 20 such stars are listed in the Skarka (2013) catalogue of the Galactic field Blazhko stars (two modulation periods are commonly detected in the space photometry; see Benkő et al. 2014). The modulation observed in single-periodic stars is not strictly periodic. The consecutive modulation cycles can differ strongly, which is best visible in the space photometry for these stars (see e.g. Guggenberger et al. 2012; Benkő et al. 2014). In some stars the modulation is not stable on the long time-scale. The best studied example is RR Lyr, in which modulation nearly vanished recently. Whether it will reappear in a rhythm of a postulated 4-yr cycle is not clear at the moment (Le Borgne et al. 2014). We lack a thorough and detailed analysis of long-term stability of the Blazhko modulation. The coupled OGLE-III and OGLE-IV data seem best for this purpose.
Our results also indicate that the fundamental mode is more prone to modulation (Table 2 and discussion above). In our stars multiperiodic modulation is very frequent. Only in seven stars we detect a single modulation period. Modulation we detect in our stars is clearly irregular and non-stationary.
We also note that Blazhko effect was previously detected in double-mode 1O+2O Cepheids – see Moskalik & Kołaczkowski (2009) for detailed analysis. These stars have very different properties however, as pointed out above.
Just as we finished our analysis, the paper by Jurcsik et al. (2014) was published, in which they announce the discovery of the Blazhko effect in four RRd stars in M3 cluster. Their results are very similar to ours. Their stars have non-typical period ratios. In three of them the two radial modes are modulated with different periods (see fig. 3 and table 1 in Jurcsik et al. 2014).
6 SUMMARY
We have analysed the OGLE data for RRd stars of the Galactic bulge collection suspected of Blazhko-type modulation and selected by visual inspection of the data or by automatic analysis of the frequency spectrum. In the case of 13 stars we found a modulation of at least one radial mode (triplets or close doublets in the frequency spectrum). Since 11 of these stars are located off the main progression of RRd stars in the Petersen diagram, we decided to check all of the remaining deviating stars. Additional two stars with modulation of the radial modes were found and thus the full sample counts 15 stars. For all these stars we analysed long-term stability of pulsation and modulation properties using OGLE-IV and OGLE-III data, if available. Most important findings and conclusions of this study are the following.
RRd stars located off the main progression in the Petersen diagram are prone to modulation. 13 out of 23 deviating stars show the modulation.
The short-term modulation is typically multiperiodic, with modulation periods between few tenths to few hundred days; modulation is not strictly periodic.
In most of the stars we detect a long-term, irregular variation of radial mode amplitudes and periods on top of the short-term modulation.
In several stars we find a feedback between the amplitude of the dominant radial mode and mean stellar brightness: the lower the pulsation amplitude, the brighter the star.
Two stars deserve a special mention.
In OGLE-BLG-RRLYR-07393 we find additional non-radial mode excited, with characteristic period ratio to first overtone, around ∼0.61. It is a member of new class of radial–non-radial RR Lyrae stars revealed recently (Moskalik et al. 2015, and references therein). We find an evidence that the non-radial mode is modulated with the same period as the radial modes.
OGLE-BLG-RRLYR-13442 experienced a pulsation mode switch, from RRab to RRd pulsation, in between the third and fourth phases of the OGLE project. Its suspected modulation, manifesting through close doublets in the frequency spectrum, was not affected significantly by the mode switching event.
What is the mechanism behind modulation in RRd stars? Is it the same mechanism as in the case of the Blazhko effect in single-periodic stars? What is the mechanism behind the multiperiodic modulation? These are all open questions. The data presented in this paper will help to verify the theories to come. As (i) the majority of the discussed stars are located off the main progression of RRd stars in the Petersen diagram, (ii) one of them experienced an RRab→RRd mode switch, (iii) in a large fraction of these stars pulsation in the fundamental mode dominate (in contrast to the stars with the typical period ratios) and (iv) pulsation properties of these stars are non-stationary we form a loose hypothesis: the investigated stars are in a transient pulsation state that possibly follows the RRab→ RRd mode switching. To test the hypothesis detailed analysis of all RRd stars is necessary and ongoing. More importantly, long-term monitoring of the discussed stars is needed to shed more light on their intriguing nature.
We are grateful to Paweł Moskalik for stimulating discussions, reading the manuscript and detailed comments. Fruitful conversation with Wojtek Dziembowski is also acknowledged.
This research is supported by the Polish National Science Centre through grant DEC-2012/05/B/ST9/03932 and by the Polish Ministry of Science and Higher Education through the program ‘Ideas Plus’ award no. IdP2012 000162. The OGLE project has received funding from the European Research Council under the European Community's Seventh Framework Programme (FP7/2007-2013)/ERC grant agreement no. 246678 to AU.
Soszyński et al. (2014b) list 174 RRd stars. During this study we have found that one of these stars is not RRd pulsator; the daily alias of non-coherent signal at the suspected fundamental mode frequency was misinterpreted as the first overtone.
REFERENCES
APPENDIX A: ON-LINE ONLY TABLES WITH LIGHT-CURVE SOLUTIONS
In this appendix we present the full light-curve solutions of OGLE-IV data for all analysed stars. Tables, available in the on-line version of the journal, contain frequency identification, frequency value, amplitude and phase, all with standard errors. For a sample see Table 3.
SUPPORTING INFORMATION
Additional Supporting Information may be found in the online version of this article:
Appendix A. on-line only tables with light-curve solutions (Supplementary Data).
Please note: Oxford University Press are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.



