Asymptotic solutions for the case of SIE lens models and application to the quadruply imaged quasar Q2237+0305

Wertz, O.; Surdej, J.

doi:10.1093/mnras/stu866

Abstract

Considering a small misalignment between a point-like source, a singular isothermal ellipsoid deflector and an observer, we derive to first order simple relations between the model parameters and the lensed image positions, and an expression for the time delay between pairs of opposed images which is analogue to the one previously derived for the case of ε − γ models. Combined with the first-order astrometric relations, we retrieve a simple expression for the time delays, in agreement with Witt, Mao & Keeton, which solely depends on the lensed image positions. The real advantage of using the first-order equations when dealing with symmetric gravitational lens systems is to directly test the validity of the adopted lens model without having to perform any accurate numerical fit. In this paper, we present in detail the calculations which lead to those relations between the singular isothermal ellipsoid lens model parameters and the lensed image positions. In addition, we model the well-known Einstein cross Q2237+0305 with three families of models: ε − γ, singular isothermal ellipsoid and non-singular isothermal ellipsoid plus shear, using a genetic algorithm from the Qubist Optimization Toolbox. We conclude that although the non-singular isothermal ellipsoid plus shear model shows the best agreement between the calculated and the observed image positions (〈Δx〉 = 0.0026 arcsec), the more simple singular isothermal ellipsoid also leads to quite satisfactory and acceptable results (〈Δx〉 = 0.0059 arcsec).

gravitational lensing: strong, cosmological parameters

1 INTRODUCTION

According to Refsdal (1964a,b), the gravitational lens phenomenon provides a powerful tool to derive the values of several cosmological parameters, i.e. H₀, Ω_Λ, as well as to deduce the absolute mass of the lensing object, independently on the distance ladder. Unfortunately, such a determination turns out to be model dependent. However, for the case of a small misalignment between the source, the deflector and the observer, Wertz, Pelgrims & Surdej (2012) have recently shown that a first-order perturbative approach applied to the lensed image positions may lead to the determination of the Hubble parameter using observable quantities only (Wertz et al. 2012). Let us note that a similar kind of approach has been developed by Alard (2007) but his singular perturbative method proves to be more restrictive.

The main idea of this paper is to investigate for the case of the singular isothermal ellipsoid (SIE) model whether we can derive first-order equations linking the model parameters to the lensed image positions only. These equations are then used in order to derive model-independent expressions for the time delays between lensed images and the Hubble parameter. Let us note that the derived expressions of H₀ are consistent with the ones already presented by Witt, Mao & Keeton (2000).

The outline of this paper is as follows. In Section 2, we recall the basic gravitational lens and astrometric equations for the case of the SIE. We also assume that the lensed images are not resolved individually. Assuming a very small misalignment between the source, the deflector and the observer, we then derive, in Section 3, first-order expressions which link the image positions to the model parameters, as well as the possibility to infer from only observable quantities the value of the Hubble parameter from the linearized astrometric and time delay expressions. Afterwards, we discuss the apparent problem of the degeneracy in determining the value of the parameter ϖ which represents the a priori unknown orientation of the elliptic-shape isodensity contours, and we propose to test the validity range of the astrometric equations. In Section 4, we test the first-order equations for the case of the well-known quadruply imaged quasar: Q2237+0305. We compare the first-order model parameters obtained with those determined numerically using a sophisticated genetic algorithm, called Ferret, which is a component of the Qubist Global Optimization Toolbox (Fiege 2010). Some general conclusions form the last section.

2 THE SINGULAR ISOTHERMAL ELLIPSOID MODEL

The SIE represents a particular case of more general models with elliptical mass distributions (Bourassa, Kantowski & Norton 1973; Bourassa & Kantowski 1975, corrected by Bray 1984; Kormann, Schneider & Bartelmann 1994; Keeton & Kochanek 1998). It can be described by its normalized surface mass density κ(ρ) defined as

\begin{eqnarray} \kappa (\rho ) = \frac{\sqrt{f}}{2 \rho }, \end{eqnarray}

(1)

where f represents the axis ratio and |$\rho = \sqrt{x_{1}^{2}+f^{2}x_{2}^{2}}$| with x_i the normalized Cartesian coordinates of the impact parameter |$\boldsymbol {x}$|⁠. The associated normalized deflection angle |$\hat{\boldsymbol {\alpha }}(\boldsymbol {x})$| is given by

\begin{eqnarray} \hat{\boldsymbol {\alpha }}(\boldsymbol {x})= - \frac{\sqrt{f}}{f^{\prime}} \left[\!{\rm arcsinh}\left(\!\frac{f^{\prime}}{f} \cos \left(\varphi \right)\!\right)\ \boldsymbol {e}_1 + {\rm arcsin}(f^{\prime} \sin(\varphi ) )\ \boldsymbol {e}_2\! \right]\!,\!\!\!\!\!\! \nonumber\\ \end{eqnarray}

(2)

where |$\boldsymbol {e}_i$| represents the unit vector along the direction x_i, φ the angular coordinate of the impact parameter, and |$f^{\prime } = \sqrt{1-f^{2}}$|⁠. Accounting for the notation defined by Kormann, Schneider & Bartelmann (1994), the |$\boldsymbol {e}_1$| direction corresponds to the semiminor axis direction of the isodensity contours. Therefore, the coordinate system adopted in that paper is not arbitrarily oriented. Considering now an arbitrarily oriented coordinate system for which the abscissa axis form an angle ϖ with the semiminor axis (see Fig. 1), the expression of the two components of the lens equation can be expressed as

\begin{eqnarray} y \cos \left(\theta + \varpi \right) &=& r^{(i)} \cos \left(\varphi ^{(i)}+ \varpi \right) \nonumber\\&& -\, \frac{\sqrt{f}}{f^{\prime}}\ {\rm arcsinh} \left(\frac{f^{\prime}}{f} \cos \left(\varphi ^{(i)}+ \varpi \right)\right), \end{eqnarray}

(3)

\begin{eqnarray} \nonumber\\ y \sin(\theta + \varpi ) &=& r^{(i)} \sin(\varphi ^{(i)}+ \varpi ) \nonumber\\ && -\, \frac{\sqrt{f}}{f^{\prime}}\ {\rm arcsin} (f^{\prime} \sin(\varphi ^{(i)}+ \varpi ) )\,, \end{eqnarray}

(4)

where (r⁽ⁱ⁾, φ⁽ⁱ⁾) represent the normalized polar coordinates of the position of the image i, (y, θ), the normalized polar coordinates of the point-like source and where θ and φ⁽ⁱ⁾ are now measured from the arbitrarily oriented coordinate system.

Figure 1.

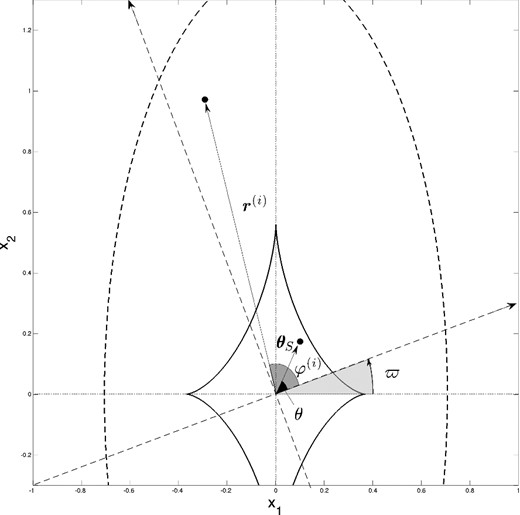
Illustration of the arbitrarily oriented coordinate system which abscissa axis form an angle ϖ with the semiminor axis of the isodensity elliptic contours. The azimuthal angles θ and φ⁽ⁱ⁾ are, respectively, associated with the source and the ith image positions. Both are measured from the arbitrarily oriented coordinate system.

Open in new tab Download slide

3 FIRST-ORDER EQUATIONS AND SOLUTIONS

3.1 Small deviations from the perfect alignment

For the case of a perfect alignment between the source, the deflector and the observer, i.e. y = 0, we may deduce from equations (3) and (4) the exact positions |$(r^{(i)}_0 ; \varphi ^{(i)}_0 )$| of the lensed images. On one hand, equation (3) × sin(φ⁽ⁱ⁾ + ϖ) − equation (4) × cos(φ⁽ⁱ⁾ + ϖ) leads to

\begin{eqnarray} &&{y \sin (\varphi ^{(i)}- \theta )}\nonumber \\ &&\qquad =\, \frac{\sqrt{f}}{f^{\prime}} \left[ {\rm arcsin} \left(f^{\prime}\sin \left(\varphi ^{(i)}+ \varpi \right) \right) \cos \left(\varphi ^{(i)}+ \varpi \right)\right. \nonumber\\ &&\left.\qquad\quad\ -\, {\rm arcsinh} \left(f^{\prime}\cos \left(\varphi ^{(i)}+ \varpi \right) /f\right) \sin \left(\varphi ^{(i)}+ \varpi \right)\right], \end{eqnarray}

(5)

and from the latter equation and for y = 0, the exact image angular coordinates are expressed as

\begin{eqnarray} \varphi ^{(i)}_0 = \frac{i\pi }{2} - \varpi , \end{eqnarray}

(6)

where i ∈ [0, 1, 2, 3] indicates that there are up to four lensed images. On the other hand, equation (3) × cos(φ⁽ⁱ⁾ + ϖ) + equation (4) × sin(φ⁽ⁱ⁾ + ϖ) leads to

\begin{eqnarray} y \cos (\varphi ^{(i)}- \theta ) = r^{(i)}- \frac{1}{r^{(i)}} \hat{\psi }( r^{(i)}, \varphi ^{(i)}+ \varpi ), \end{eqnarray}

(7)

where |$\hat{\psi } (r,\varphi )$| represents the normalized deflection potential defined by

\begin{eqnarray} \hat{\psi} (r,\varphi) &=& \frac{\sqrt{f}}{f^{\prime}} r \left[\vphantom{\frac{f^{\prime}}{f}}\sin(\varphi )\ {\rm arcsin}(f^{\prime} \sin(\varphi ) ) \right.\nonumber \\ &&\left.+\, \cos (\varphi )\ {\rm arcsinh}\left(\frac{f^{\prime}}{f} \cos (\varphi )\right) \right] \,. \end{eqnarray}

(8)

From equation (7) and for y = 0, the exact image radial coordinates are expressed as

\begin{eqnarray} r_0^{(0)} = r_0^{(2)} = \frac{\sqrt{f}}{f^{\prime}}\ {\rm arcsinh}\left(\frac{f^{\prime}}{f}\right), \end{eqnarray}

(9)

and

\begin{eqnarray} r_0^{(1)} = r_0^{(3)} = \frac{\sqrt{f}}{f^{\prime}}\ {\rm arcsin}(f^{\prime} ). \end{eqnarray}

(10)

When considering a small misalignment between the source, the lens and the observer, the resulting image positions only slightly deviate from the perfect alignment case. Thus, the ith image position (r⁽ⁱ⁾; φ⁽ⁱ⁾) can be expressed as

\begin{eqnarray} r^{(i)}= r^{(i)}_0 + \Delta r^{(i)}, \end{eqnarray}

(11)

and

\begin{eqnarray} \varphi ^{(i)}= \varphi ^{(i)}_0 + \Delta \varphi ^{(i)}, \end{eqnarray}

(12)

where Δr⁽ⁱ⁾ and Δφ⁽ⁱ⁾ represent small variations of the image polar coordinates, i.e. |Δr⁽ⁱ⁾| ≪ 1 and |Δφ⁽ⁱ⁾| ≪ 1. To first order, and after substituting equations (11) and (12) into equation (5), the latter becomes

\begin{eqnarray} && {y\ \left[ \sin\left(\frac{{i}\pi}{2} - \theta - \varpi \right) + \cos \left(\frac{{i}\pi }{2} - \theta - \varpi \right)\ \Delta \varphi ^{(i)}\right]} \nonumber \\ &&\quad = - \frac{\sqrt{f}}{f^{\prime}} \left[ {\rm arcsinh}\left(\frac{f^{\prime}}{f} \mathcal {S}^{(i)}\right) \mathcal {C}^{(i)} - {\rm arcsin}\left(f^{\prime}\mathcal {C}^{(i)} \right) \mathcal {S}^{(i)}\right], \nonumber\\ \end{eqnarray}

(13)

where |$\mathcal {S}^{(i)} = \cos ({i}\pi /2) - \sin({i}\pi /2)\ \Delta \varphi ^{(i)}$| and |$\mathcal {C}^{(i)} = \sin({i}\pi /2) + \cos ({i}\pi /2)\ \Delta \varphi ^{(i)}$|⁠. To first order, we find that arcsin(( − 1)^i/2f′Δφ⁽ⁱ⁾) ≃ ( − 1)^i/2f′Δφ⁽ⁱ⁾ for i ∈ {0, 2} and arcsinh(( − 1)^{(3 − i)/2}f′Δφ⁽ⁱ⁾/f) ≃ ( − 1)^{(3 − i)/2}f′Δφ⁽ⁱ⁾/f for i ∈ {1, 3}. As a result, for i ∈ [0, 1, 2, 3], equation (13) takes the form

\begin{eqnarray} \Delta \varphi ^{(0)} = -\Delta \varphi ^{(2)} = \frac{y \sin\left(\theta + \varpi \right)}{\sqrt{f} \left[ \frac{1}{f^{\prime}}\ {\rm arcsinh}\left(\frac{f^{\prime}}{f}\right) - 1 \right]}, \end{eqnarray}

(14)

and

\begin{eqnarray} \Delta \varphi ^{(1)} = - \Delta \varphi ^{(3)} = \frac{y \cos \left(\theta + \varpi \right)}{\sqrt{f} \left[ \frac{1}{f} - \frac{1}{f^{\prime}} {\rm arcsin}(f^{\prime} ) \right]}. \end{eqnarray}

(15)

To first order, and after substituting equations (11) and (12) into equation (7), the latter becomes

\begin{eqnarray} &&{y \left[ \cos \left(\theta + \varpi - \frac{{i}\pi }{2}\right) + \sin\left(\theta + \varpi - \frac{{i}\pi }{2}\right) \Delta \varphi ^{(i)}\right]} \nonumber \\ && = r^{(i)}_0 \,{+}\, \Delta r^{(i)} \,{-}\, \frac{\sqrt{f}}{f^{\prime}} \!\left[ {\rm arcsinh}\left(\!\frac{f^{\prime}}{f} \mathcal {S}^{(i)}\!\right) \mathcal {S}^{(i)} \,{+}\, {\rm arcsin}\,(f^{\prime}\mathcal {C}^{(i)} ) \mathcal {C}^{(i)} \right]\!. \!\!\!\nonumber\\ \end{eqnarray}

(16)

As a result, from equations (9), (10) and for i ∈ [0, 1, 2, 3], equation (16) reduces to

\begin{eqnarray} \Delta r^{(0)} = - \Delta r^{(2)} = y \cos \left(\theta + \varpi \right), \end{eqnarray}

(17)

and

\begin{eqnarray} \Delta r^{(1)} = - \Delta r^{(3)} = y \sin\left(\theta + \varpi \right). \end{eqnarray}

(18)

We note that the small azimuthal and radial variations of the lensed image polar coordinates only depend on the source position compared to the semiminor axis direction of the isodensity contours.

3.2 The SIE lens model parameters

In this section, we will recover all lens model parameters from equations (6), (9), (10), (14), (15), (17) and (18). First of all, we need to be careful with the handling of the measured image angular coordinates φ⁽ⁱ⁾. As a reminder, these coordinates are measured from the arbitrarily oriented coordinate system, which implies that φ⁽ⁱ⁾ ∈ [0, 2π]. However, according to the value of ϖ and θ, we may have |$\varphi ^{(i)}_{0} + \Delta \varphi ^{(i)} = {i}\pi /2 - \varpi + \Delta \varphi ^{(i)} < 0$| with i ∈ {0, 1, 2, 3}. Therefore, for (θ + ϖ) ∈ [0, π] and ϖ ∈ [0, Δφ⁽⁰⁾[, we have, to first order, φ⁽ⁱ⁾ = iπ/2 − ϖ + Δφ⁽ⁱ⁾; but for (θ + ϖ) ∈ [0, 2π] and |$\varpi \in [\tilde{\varphi }^{(i)}, \tilde{\varphi }^{(i+1)}]$| with |$\tilde{\varphi }$| representing the image angular coordinate measured from the semiminor axis direction of the isodensity contours, we have φ^(k) = kπ/2 − ϖ + Δφ^(k) with k ∈ {i + 1, …, 3} and φ^(l) ≠ iπ/2 − ϖ + Δφ^(l) with l ∈ {0, …, i}. In the latter equation, since the angular quantities are cyclic, the two members are equivalent but not equal. In fact, we have φ^(l) = iπ/2 − ϖ + Δφ^(l)mod 2π, where mod represents the modulo operation. In the remainder of this section, we will take into account these properties, in particular for the determination of the parameter ϖ.

From equations (14) and (15), we note that Δφ⁽⁰⁾ + Δφ⁽¹⁾ + Δφ⁽²⁾ + Δφ⁽³⁾ = 0. Therefore, we have

\begin{eqnarray} \sum _{j = 0}^{3} \left(\varphi ^{(j)}_0 + \Delta \varphi ^{(j)}\right) = 3\pi - 4 \varpi . \end{eqnarray}

(19)

As a consequence, from the latter equation, the expression of ϖ can be retrieved:

\begin{eqnarray} \varpi = \frac{1}{4}\left(3\pi - \sum _{j = 0}^{3} \varphi ^{(j)} \right) + \frac{l\pi }{2} \equiv \varpi _{0} + \frac{l\pi }{2}\,, \end{eqnarray}

(20)

where l ∈ {0, 1, 2, 3, 4} such as |$\varpi \in [\tilde{\varphi }^{(l-1)}, \tilde{\varphi }^{(l)}]$| with |$\tilde{\varphi }^{(-1)} = 0$| and |$\tilde{\varphi }^{(4)} = \tilde{\varphi }^{(0)}$|⁠. Although we are not able to determine l unequivocally from the lensed image positions, we can reduce the degeneracy to only two values: ϖ_real and ϖ_real + π, which lead to two equivalent SIE models. The latter property is shown in the next section.

From equations (9)–(11), (17) and (18), we note that r⁽⁰⁾ − r⁽²⁾ = Δr⁽⁰⁾ − Δr⁽²⁾ = 2 y cos(θ + ϖ), and r⁽¹⁾ − r⁽³⁾ = Δr⁽¹⁾ − Δr⁽³⁾ = 2 y sin(θ + ϖ). Therefore, we have

\begin{eqnarray} \theta ^{(0)} - \theta ^{(2)} = 2\ \theta _{{\mathrm{S}}} \cos \left(\theta + \varpi \right), \end{eqnarray}

(21)

and

\begin{eqnarray} \theta ^{(1)} - \theta ^{(3)} = 2\ \theta _{{\mathrm{S}}} \sin\left(\theta + \varpi \right). \end{eqnarray}

(22)

Dividing equation (22) by equation (21), the relative angular coordinate θ of the point-like source can be deduced from

\begin{eqnarray} {\rm tan}\left(\theta + \varpi \right) = \frac{\theta ^{(1)} - \theta ^{(3)}}{\theta ^{(0)} - \theta ^{(2)}}. \end{eqnarray}

(23)

Since the determination of θ depends on the value of ϖ, the latter parameter seems to be also degenerated. In fact, we show in the next section that the value of θ can be derived unequivocally.

From equations (21) and (22), the relative radial coordinate θ_S of the point-like source can be expressed as

\begin{eqnarray} \theta _{{\mathrm{S}}}=\frac{1}{2} \sqrt{(\theta ^{(0)} - \theta ^{(2)})^2 + (\theta ^{(1)} - \theta ^{(3)})^2}. \end{eqnarray}

(24)

From equation (17), we note that |$r^{(0)} + r^{(2)} = 2\ r_0^{(0)}$|⁠. In addition, from equation (18), we note that |$r^{(1)} + r^{(3)} = 2\ r_0^{(1)}$|⁠. Therefore, we have

\begin{eqnarray} \theta ^{(0)} + \theta ^{(2)} = 2\ \theta _{{\mathrm{E}}}\frac{\sqrt{f}}{f^{\prime}} {\rm arcsinh}\left(\frac{f^{\prime}}{f}\right), \end{eqnarray}

(25)

and

\begin{eqnarray} \theta^{(1)} + \theta ^{(3)} = 2\ \theta _{{\mathrm{E}}}\frac{\sqrt{f}}{f^{\prime}} {\rm arcsin}(f^{\prime} ). \end{eqnarray}

(26)

Dividing equation (25) by equation (26), the axis ratio f is found to be

\begin{eqnarray} \frac{{\rm arcsinh}(f^{\prime}/f)}{{\rm arcsin}(f^{\prime} )} = \frac{\theta ^{(0)} + \theta ^{(2)}}{\theta ^{(1)} + \theta ^{(3)}}, \end{eqnarray}

(27)

the latter equation consisting of an implicit definition of f. From equations (25) and (26), the value of the Einstein ring angular radius is given by

\begin{eqnarray} \theta _{{\mathrm{E}}}= \frac{f^{\prime}}{2 \sqrt{f}} \frac{\theta ^{(0)} + \theta ^{(2)}}{{\rm arcsinh}(f^{\prime}/f)} = \frac{f^{\prime}}{2 \sqrt{f}} \frac{\theta ^{(1)} + \theta ^{(3)}}{{\rm arcsin}(f^{\prime} )}, \end{eqnarray}

(28)

where the axis ratio f is retrieved from equation (27).

As a result, we have thus determined the values of f, θ_S, θ, ϖ and θ_E from the only astrometric positions of the lensed images. In addition, we note that the index of the lensed images i = {0, 1, 2, 3} is in principle unknown. However, only four possible combinations remain since the index values have to be consecutive. Furthermore, due to the symmetries in the relations between all model parameters and the lensed image positions (see equations 20, 23, 24, 27 and 28), we note that the inversion between the index of two opposed lensed images does not have any impact on their determination: 0↔2 and 1↔3. In order to differentiate the two remaining combinations |$( 02 \stackrel{?}{\leftrightarrow } 13)$|⁠, we only need to calculate the value of f from equation (27). Indeed, one combination leads to f < 1 while the other one to f > 1, which points towards a non-physical situation of having the minor axis larger than the major one.

3.3 The degeneracy affecting the value of ϖ

As shown in the previous section, the parameter ϖ can only take four possible values in accordance with the relation ϖ_l = ϖ₀ + lπ/2 for l ∈ {0, 1, 2, 3}. Furthermore, from equation (23) and after substituting the different values of ϖ, the different possible angular coordinates θ of the source can be expressed as

\begin{eqnarray} \theta _{lk} = \mbox{atan}\left(\frac{\theta ^{(1)} - \theta ^{(3)}}{\theta ^{(0)} - \theta ^{(2)}} \right) - \left(\varpi _{0}+ \frac{l\pi }{2}\right) + k \,, \end{eqnarray}

(29)

with k ∈ {0, 1}. From the latter equation, we may deduce eight different combinations for the pair of parameters (ϖ_l, θ_lk).

For each pair of these parameters and the already determined values of f, θ_S and θ_E, we derive eight sets of four lensed image positions. By comparison with the real lensed image positions, there only remain two pairs of parameters: the real one (ϖ_real, θ_real) and another one which leads to the same lensed image positions. Due to the symmetry of the SIE lens models which leads to a diamond-shaped tangential caustic curve, and for fixed values of f, θ_S and θ_E, the two pairs of parameters (ϖ, θ) and (ϖ +, θ) rigorously lead to the same lensed image positions. As a consequence, among the eight different remaining combinations of parameter pairs (ϖ_l, θ_lk), the only valid ones are (ϖ_real, θ_real) and (ϖ_real +, θ_real). We thus find that the parameter θ_real is unequivocally determined.

3.4 Time delays and the Hubble parameter

Let us now consider the determination of the value of the Hubble parameter H₀ from the measurement of the time delay Δt between two lensed image light curves for the case of the SIE lens model. The time-delay function |$t(\boldsymbol {x})$| for the ith image is given by (Narayan & Bartelmann 1996)

\begin{eqnarray} t(\boldsymbol {x}^{(i)}) = \left(\frac{1+z_{\rm l}}{c}\right) \left(\frac{D_{{\mathrm{OL}}}D_{{\mathrm{OS}}}}{D_{{\mathrm{LS}}}}\right)\ \theta _{{\mathrm{E}}}^2 \left[ \frac{1}{2} \left( \boldsymbol {x} - \boldsymbol {y} \right)^2 - \hat{\psi }_{{\rm tot}}(\boldsymbol {x}) \right], \nonumber\\ \end{eqnarray}

(30)

where z_l represents the redshift of the lens, D_OL, D_OS and D_LS represent the usual angular-diameter distances between the observer, lens and source, c the speed of light in vacuum and |$\hat{\psi }_{{\rm tot}}$| the total lensing potential, which gradient corresponds to the general deflection angle, apart from an irrelevant constant

\begin{eqnarray} \boldsymbol {\hat{\alpha }}_{{\mathrm{gen}}}(\boldsymbol {x}) = - \nabla _{\boldsymbol {x}}\hat{\psi }_{{\rm tot}}. \end{eqnarray}

(31)

For the case of the SIE lens model, the time delay between the lensed images i and j is therefore given by

\begin{eqnarray} \Delta t_{i,j} &=& \left(\frac{1 + z_{\rm l}}{c} \right) \left(\frac{D_{{\mathrm{OL}}}D_{{\mathrm{OS}}}}{D_{{\mathrm{LS}}}}\right)\ \theta _{{\mathrm{E}}}^2\ \bigg [ \frac{1}{2}\left( \boldsymbol {x}^{(j)} - \boldsymbol {y} \right)^2 \nonumber \\ &&- \,\frac{1}{2}( \boldsymbol {x}^{(i)} - \boldsymbol {y} )^2 - \hat{\psi }_{{\rm SIE}}(r^{(j)} ; \varphi ^{(j)} ) + \hat{\psi }_{{\rm SIE}}(r^{(i)} ; \varphi ^{(i)} ) \bigg ], \nonumber\\ \end{eqnarray}

(32)

where |$\hat{\psi }_{{\rm SIE}}$| is defined by equation (8). To first order, the expression of the lensing potential can be simplified as follows. Considering the image i, from equations (11) and (12) we have, respectively, |$r^{(i)} = r^{(i)}_0 + \Delta r^{(i)}$| and φ⁽ⁱ⁾ = iπ/2 + Δφ⁽ⁱ⁾ − ϖ. After substituting the latter results into equation (8), the expression of the deflection potential for the lensed image i reduces, to first order, to

\begin{eqnarray} \hat{\psi }_{{\rm SIE}}( r^{(i)} ; \varphi ^{(i)} ) = r^{(i)}_0 ( r^{(i)}_0 + \Delta r^{(i)} ), \end{eqnarray}

(33)

where |$r^{(i)}_0$| is defined by equations (9) and (10), and Δr⁽ⁱ⁾ by equations (17) and (18). Therefore, from equations (32) and (33), the time delay between the lensed images i and j can be expressed as

\begin{eqnarray} \Delta t_{i,j} &=& \left(\frac{1 + z_{\rm l}}{c} \right) \left(\frac{D_{{\mathrm{OL}}}D_{{\mathrm{OS}}}}{D_{{\mathrm{LS}}}}\right)\ \Big [ \frac{1}{2} \left(\left(\theta _{0}^{(i)}\right)^{2} - \left(\theta _{0}^{(j)}\right)^{2} \right) \nonumber \\ &&-\,\theta _{{\mathrm{S}}}\left[\theta ^{(j)} \cos \left(\varphi ^{(j)}_{0}-\theta \right) - \theta ^{(i)} \cos \left(\varphi ^{(i)}_{0}-\theta \right) \right. \nonumber \\ &&\left. - \,\theta _{0}^{(j)} \Delta \varphi ^{(j)}\sin\left(\varphi ^{(j)}_{0}-\theta \right)+ \theta _{0}^{(i)} \Delta \varphi ^{(i)}\sin\left(\varphi ^{(i)}_{0}-\theta \right) \right] \Big ].\nonumber\\ \end{eqnarray}

(34)

Since there are three independent time delays for a four-lensed gravitational lens system, we only specify Δt_{i, i + 1} and Δt_{i, i + 2}. The expression Δt_{i, i + 1} reduces to

\begin{eqnarray} \Delta t_{i,i+1} &=& \left(\frac{1 + z_{\rm l}}{c} \right) \left(\frac{D_{{\mathrm{OL}}}D_{{\mathrm{OS}}}}{D_{{\mathrm{LS}}}}\right)\ \bigg [ \frac{1}{2} \left(\left(\theta _{0}^{(i)}\right)^{2} - \left(\theta _{0}^{(i+1)}\right)^{2} \right) \nonumber \\ &&+\, \theta _{{\mathrm{S}}}\left[ \cos \left(\frac{{\rm i}\pi}{2}-\varpi -\theta \right) \left(\theta ^{(i)} + \theta _{0}^{(i+1)} \Delta \varphi ^{(i+1)} \right) \right. \nonumber \\ &&\left. \left. +\, \sin\left(\frac{{\rm i}\pi}{2}-\varpi -\theta \right) \left(\theta ^{(i+1)} - \theta _{0}^{(i)} \Delta \varphi ^{(i)} \right)\right)\right]\bigg ], \end{eqnarray}

(35)

while Δt_{i, i + 2} simply reduces to

\begin{eqnarray} \Delta t_{i,i+2} &=&y \left(\frac{1 + z_{\rm l}}{c} \right) \left(\frac{D_{{\mathrm{OL}}}D_{{\mathrm{OS}}}}{D_{{\mathrm{LS}}}}\right)\ \theta _{{\mathrm{S}}}\ (\theta ^{(i)} + \theta ^{(i+2)})\nonumber\\ &&\times\, \cos (\varpi + \theta - { i}\pi/2). \end{eqnarray}

(36)

The latter equation is identical to the one already derived for a power-law axially symmetric lens model with an external large-scale gravitational field (the shear; see equation 92 in Wertz et al. 2012). In the latter paper, the authors had already demonstrated that these two families of models remain strictly distinct, even at the first order, except when the alignment between the source, the lens and the observer is perfect or when the SIE reduces to the SIS model without any shear. Furthermore, from equations (21) and (22), we easily deduce that

\begin{eqnarray} \theta _{{\mathrm{S}}} \cos \left(\varpi + \theta - {i}\pi /2\right) = \frac{1}{2} (\theta ^{(i)} - \theta ^{(i+2)} ) \,. \end{eqnarray}

(37)

After substituting equation (37) into equation (36), the time delay between two opposed lensed images i and i + 2 becomes

\begin{eqnarray} \Delta t_{i,i+2} = \left(\frac{1 + z_{\rm l}}{2 c} \right) \left(\frac{D_{{\mathrm{OL}}}D_{{\mathrm{OS}}}}{D_{{\mathrm{LS}}}}\right)\ ((\theta ^{(i)})^{2} - (\theta ^{(i+2)})^{2}) \,. \end{eqnarray}

(38)

So we have retrieved the same expression for the time delays between two lensed images as the one already derived by Witt et al. (2000). According to them, equation (38) remains valid irrespective of the degree of misalignment. This implies that equation (36) derived from the first-order astrometric equations is rigorously identical to the one derived without any approximation.

For completeness, we retrieve the expression of the Hubble parameter for the case of the SIE lens model. From equation (38), H₀ can be expressed as

\begin{eqnarray} H_{0} = \frac{1+z_{\rm l}}{2\ \Delta t_{i,i+2}} \left(\frac{z_{\rm l}\ z_{\rm s}}{z_{\rm s}-z_{\rm l}}\right) \left(\frac{F(z_{\rm l}) F(z_{\rm s})}{F(z_{\rm s}-z_{\rm l})}\right) [(\theta ^{(i)})^{2} - (\theta ^{(i+2)})^{2}], \!\!\! \nonumber\\ \end{eqnarray}

(39)

where F(z) is a function that depends on the redshift and on the cosmological parameters Ω_M and Ω_Λ. This function, which tends towards 1 for small values of z, can easily be calculated numerically.

3.5 Validity range of the first-order equations

We propose to test the validity range of the first-order equations (20), (23), (24), (27) and (28). It is clear that the accuracy of these latter equations is directly dependent on the accuracy of the two equations (11) and (12). Indeed, for the case of a perfect alignment between the source, the lens and the observer, the differences between the real SIE lensed image positions and those derived from the first-order equations should be equal to zero. As soon as the source is no longer perfectly aligned, the first-order determination of the lensed image positions loses some accuracy. Furthermore, these differences become larger as the point-like source gets closer to the tangential caustic curve. As a consequence, we can deduce a first estimation of the validity range of the first-order equations by illustrating the distribution of the mean error |$\overline{E}$| between the exact lensed image positions and the derived first order ones as a function of the smallest distance D between the point-like source and the tangential caustic curve (see Fig. 2)

\begin{eqnarray} \overline{E} = \frac{1}{4}\sum _{j=0}^{3} \sqrt{\left(x_{1}^{(j)} - \underline{x}_{1}^{(j)}\right)^{2} + \left(x_{2}^{(j)} - \underline{x}_{2}^{(j)}\right)^{2}} \,, \end{eqnarray}

(40)

where |$\underline{x}_{i}$| represents the first-order lensed image positions derived from the numerical inversion of the lens equation characterized by the model parameters deduced from equations (20), (23), (24), (27) and (28). The angular distance D is illustrated in Fig. 2. As shown in Fig. 3, from a set of 1000 model parameters randomly chosen, the mean error |$\overline{E}$| increases with the degree of misalignment between the source, the lens and the deflector, the latter being represented by small values of the angular distance D between the point-like source and the nearest point of the tangential caustic curve. We note that the radius of the Einstein ring has been fixed to θ_E = 1 arcsec. For any value of f, we notice that the condition D ≥ 0.1 is sufficient to obtain |$\overline{E} \le 0.05$| arcsec, but not necessarily. Indeed, we note that even for small values of D, we can have small mean error values of |$\overline{E}$|⁠. This occurs when the two following conditions are being fulfilled: the misalignment is very small and the intrinsic size of the tangential caustic curve is small, i.e. for large values of f ≤ 1. Thus, even if the source is intrinsically close to the tangential caustic curve, the quantities Δr⁽ⁱ⁾ and Δφ⁽ⁱ⁾ remain small compared to |$r^{(i)}_{0}$| and |$\varphi ^{(i)}_{0}$|⁠.

Figure 2.

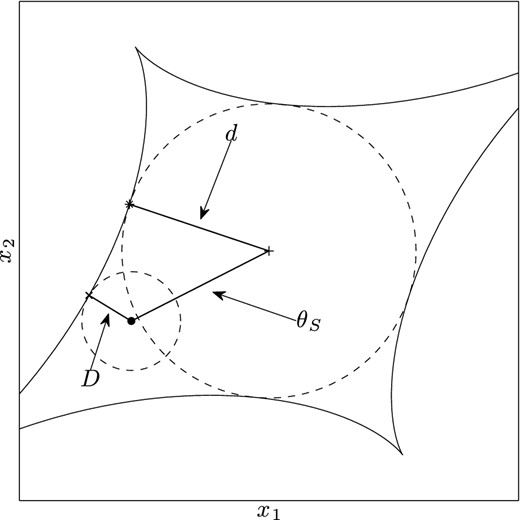
Illustration of the different angular distances involved in the test of the validity range of the first-order equations (see text).

Open in new tab Download slide

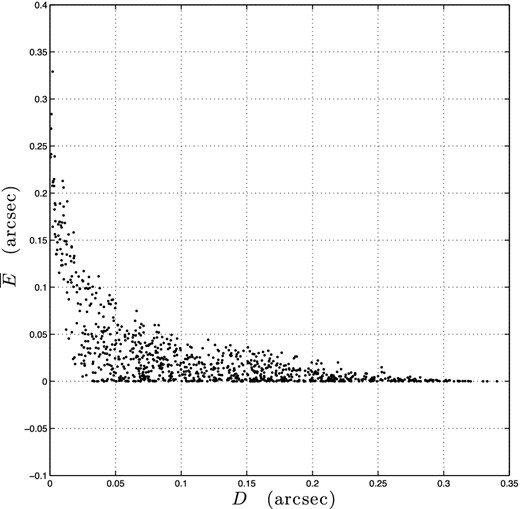
$For a set of 1000 model parameters randomly chosen and θE = 1 arcsec, we have represented the distribution of the mean error $\overline{E}$ between the exact lensed image positions and the derived first order ones as a function of the angular distance between the point-like source and the tangential caustic curve.$

Figure 3.

For a set of 1000 model parameters randomly chosen and θ_E = 1 arcsec, we have represented the distribution of the mean error |$\overline{E}$| between the exact lensed image positions and the derived first order ones as a function of the angular distance between the point-like source and the tangential caustic curve.

Open in new tab Download slide

In order to further investigate this, we have represented |$\overline{E}$| as a function of the distance D (or θ_S since these two quantities are correlated) divided by the smallest angular distance d between the tangential caustic curve and the centre of the lens (see Fig. 4). The angular distance d is illustrated in Fig. 2. As shown in Fig. 4, from the same set of the 1000 previous model parameters and for the case θ_E = 1 arcsec, a more precise condition on the alignment can be derived. For the case of a perfect alignment, i.e. D/d = 1 and θ_S/d = 0, the mean error |$\overline{E}$| equals zero, as expected. Furthermore, for θ_S/d < 0.13, the mean error is always such as |$\overline{E} < 0.003$| arcsec which typically corresponds to the error on the observed positions of the lensed images of Q2237+0305. Since the value of d is correlated with the value of f, the latter validity range takes the form θ_S < 0.13 d(f) where the analytical function d(f) has not yet been determined but could be numerically evaluated.

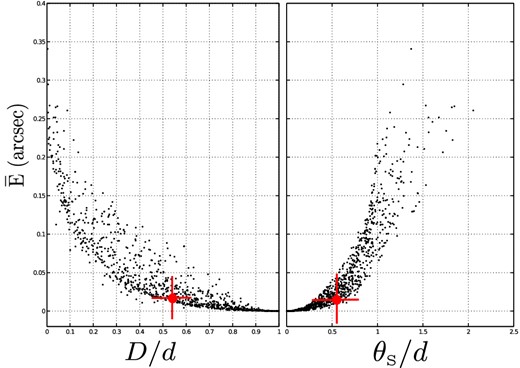
$For the same set of 1000 model parameters randomly chosen (see Fig. 3) and θE = 1 arcsec, we have represented the distribution of the mean error $\overline{E}$ between the exact lensed image positions and the derived first order ones as a function of the normalized distance D/d between the point-like source and the tangential caustic curve (left-hand panel) and as a function of the point-like source radial coordinate θS divided by the smallest distance between the tangential caustic curve and the centre of the lens (right-hand panel). The red crosses correspond to the case of the multiply imaged quasar Q2237+0305.$

Figure 4.

For the same set of 1000 model parameters randomly chosen (see Fig. 3) and θ_E = 1 arcsec, we have represented the distribution of the mean error |$\overline{E}$| between the exact lensed image positions and the derived first order ones as a function of the normalized distance D/d between the point-like source and the tangential caustic curve (left-hand panel) and as a function of the point-like source radial coordinate θ_S divided by the smallest distance between the tangential caustic curve and the centre of the lens (right-hand panel). The red crosses correspond to the case of the multiply imaged quasar Q2237+0305.

Open in new tab Download slide

Furthermore, we have represented, respectively, in Figs 5, 6 and 7 the lensed images, the point-like source, the tangential critical and caustic curves for 12 SIE models and their associated first order ones characterized by θ_S/d ∈ [0.0, 0.25], θ_S/d ∈ [0.25, 0.50] and θ_S/d ∈ [0.50, 1.25], respectively. The model parameters related to those SIE models are given in Tables 1 –3. We notice that as θ_S/d increases, the accuracy of the first-order SIE model decreases.

Figure 5.

Illustration of different lensed image configurations corresponding to the SIE lens model (open circles ○) and the SIE first order one (pluses +). The source positions associated with the SIE lens model (open square □) and the SIE first order one (cross ×) are also represented. The lens model parameters were randomly chosen such as θ_S/d(f) ∈ [0, 0.25]. The solid lines correspond to the tangential critical and caustic curves deduced from the SIE lens model, whereas the dashed lines correspond to the SIE first order ones.

Open in new tab Download slide

Figure 6.

Illustration of different lensed image configurations corresponding to the SIE lens model (open circles ○) and the SIE first order one (pluses +). The source positions associated with the SIE lens model (open square □) and the SIE first order one (cross ×) are also represented. The lens model parameters were randomly chosen such as θ_S/d(f) ∈ [0.25, 0.50]. The solid lines correspond to the tangential critical and caustic curves deduced from the SIE lens model, whereas the dashed lines correspond to the SIE first order ones.

Open in new tab Download slide

Figure 7.

Illustration of different lensed image configurations corresponding to the SIE lens model (open circles ○) and the SIE first order one (pluses +). The source positions associated with the SIE lens model (open square □) and the SIE first order one (cross ×) are also represented. The lens model parameters were randomly chosen such as θ_S/d(f) ∈ [0.50, 1.25]. The solid lines correspond to the tangential critical and caustic curves deduced from the SIE lens model, whereas the dashed lines correspond to the SIE first order ones.

Open in new tab Download slide

Figure 8.

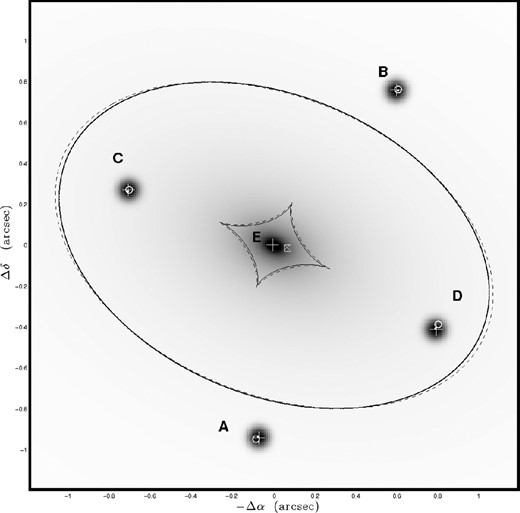
Illustration of the Q2237+0305 gravitational lens system. We have represented the corresponding surface mass density κ(ρ) characterized by the model parameters f and ϖ, as derived from the first-order equations. We have both represented the lensed image positions and the source position, all of them from the model derived by the numerical SIE fitting (see the dots), the NSIE + γ (see the pluses +) and the first-order equations (see the open circles ○). The diamond-shape and ellipse-shape solid lines represent the numerically derived tangential caustic and critical curves, respectively. The diamond-shape and ellipse-shape dashed lines represent the corresponding first-order tangential caustic and critical curves, respectively.

Open in new tab Download slide

Table 1.

Open in new tab

Real and first-order lens parameters for the 12 SIE models represented, respectively, in Fig. 5. For each lens model denoted by #i, we have reported the real model parameters (first line) and the retrieved first order ones (second line).

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0875	0	0.0871	0.0616	0.9807	0.1876
	0.0865	0.0006	0.0871	0.0610	0.9829
#2	0.6401	0.3307	0.0189	5.2981	0.8911	0.1459
	0.6386	0.3300	0.0189	5.2988	0.8912
#3	0.1806	0.6614	0.0661	5.7952	1.1218	0.1379
	0.1796	0.6621	0.0661	5.7944	1.1226
#4	0.0451	0.9921	0.0807	4.8440	1.1944	0.1459
	0.0447	0.9896	0.0806	4.8461	1.1982
#5	0.7232	1.3228	0.0111	0.2680	0.8120	0.1280
	0.7222	1.3228	0.0111	0.2680	0.8123
#6	0.3474	1.6535	0.0066	2.3762	1.0143	0.0206
	0.3474	1.6535	0.0066	2.3762	1.0143
#7	0.6606	1.9842	0.0204	4.4255	0.8348	0.1799
	0.6585	1.9845	0.0204	4.4249	0.8346
#8	0.3839	2.3149	0.0808	4.5837	1.1208	0.2490
	0.3786	2.3189	0.0805	4.5805	1.1228
#9	0.6273	2.6456	0.0161	1.4092	1.1957	0.0886
	0.6267	2.6459	0.0161	1.4092	1.1958
#10	0.0216	2.9762	0.0841	1.6905	0.8268	0.2428
	0.0201	2.9770	0.0841	1.6905	0.8561
#11	0.9106	3.3069	0.0032	4.2288	1.1758	0.0866
	0.9104	0.1653	0.0032	4.2290	1.1758
#12	0.8006	3.6376	0.0132	3.0002	0.8073	0.2216
	0.7985	0.4965	0.0132	2.9984	0.8071

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0875	0	0.0871	0.0616	0.9807	0.1876
	0.0865	0.0006	0.0871	0.0610	0.9829
#2	0.6401	0.3307	0.0189	5.2981	0.8911	0.1459
	0.6386	0.3300	0.0189	5.2988	0.8912
#3	0.1806	0.6614	0.0661	5.7952	1.1218	0.1379
	0.1796	0.6621	0.0661	5.7944	1.1226
#4	0.0451	0.9921	0.0807	4.8440	1.1944	0.1459
	0.0447	0.9896	0.0806	4.8461	1.1982
#5	0.7232	1.3228	0.0111	0.2680	0.8120	0.1280
	0.7222	1.3228	0.0111	0.2680	0.8123
#6	0.3474	1.6535	0.0066	2.3762	1.0143	0.0206
	0.3474	1.6535	0.0066	2.3762	1.0143
#7	0.6606	1.9842	0.0204	4.4255	0.8348	0.1799
	0.6585	1.9845	0.0204	4.4249	0.8346
#8	0.3839	2.3149	0.0808	4.5837	1.1208	0.2490
	0.3786	2.3189	0.0805	4.5805	1.1228
#9	0.6273	2.6456	0.0161	1.4092	1.1957	0.0886
	0.6267	2.6459	0.0161	1.4092	1.1958
#10	0.0216	2.9762	0.0841	1.6905	0.8268	0.2428
	0.0201	2.9770	0.0841	1.6905	0.8561
#11	0.9106	3.3069	0.0032	4.2288	1.1758	0.0866
	0.9104	0.1653	0.0032	4.2290	1.1758
#12	0.8006	3.6376	0.0132	3.0002	0.8073	0.2216
	0.7985	0.4965	0.0132	2.9984	0.8071

Table 1.

Open in new tab

Real and first-order lens parameters for the 12 SIE models represented, respectively, in Fig. 5. For each lens model denoted by #i, we have reported the real model parameters (first line) and the retrieved first order ones (second line).

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0875	0	0.0871	0.0616	0.9807	0.1876
	0.0865	0.0006	0.0871	0.0610	0.9829
#2	0.6401	0.3307	0.0189	5.2981	0.8911	0.1459
	0.6386	0.3300	0.0189	5.2988	0.8912
#3	0.1806	0.6614	0.0661	5.7952	1.1218	0.1379
	0.1796	0.6621	0.0661	5.7944	1.1226
#4	0.0451	0.9921	0.0807	4.8440	1.1944	0.1459
	0.0447	0.9896	0.0806	4.8461	1.1982
#5	0.7232	1.3228	0.0111	0.2680	0.8120	0.1280
	0.7222	1.3228	0.0111	0.2680	0.8123
#6	0.3474	1.6535	0.0066	2.3762	1.0143	0.0206
	0.3474	1.6535	0.0066	2.3762	1.0143
#7	0.6606	1.9842	0.0204	4.4255	0.8348	0.1799
	0.6585	1.9845	0.0204	4.4249	0.8346
#8	0.3839	2.3149	0.0808	4.5837	1.1208	0.2490
	0.3786	2.3189	0.0805	4.5805	1.1228
#9	0.6273	2.6456	0.0161	1.4092	1.1957	0.0886
	0.6267	2.6459	0.0161	1.4092	1.1958
#10	0.0216	2.9762	0.0841	1.6905	0.8268	0.2428
	0.0201	2.9770	0.0841	1.6905	0.8561
#11	0.9106	3.3069	0.0032	4.2288	1.1758	0.0866
	0.9104	0.1653	0.0032	4.2290	1.1758
#12	0.8006	3.6376	0.0132	3.0002	0.8073	0.2216
	0.7985	0.4965	0.0132	2.9984	0.8071

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0875	0	0.0871	0.0616	0.9807	0.1876
	0.0865	0.0006	0.0871	0.0610	0.9829
#2	0.6401	0.3307	0.0189	5.2981	0.8911	0.1459
	0.6386	0.3300	0.0189	5.2988	0.8912
#3	0.1806	0.6614	0.0661	5.7952	1.1218	0.1379
	0.1796	0.6621	0.0661	5.7944	1.1226
#4	0.0451	0.9921	0.0807	4.8440	1.1944	0.1459
	0.0447	0.9896	0.0806	4.8461	1.1982
#5	0.7232	1.3228	0.0111	0.2680	0.8120	0.1280
	0.7222	1.3228	0.0111	0.2680	0.8123
#6	0.3474	1.6535	0.0066	2.3762	1.0143	0.0206
	0.3474	1.6535	0.0066	2.3762	1.0143
#7	0.6606	1.9842	0.0204	4.4255	0.8348	0.1799
	0.6585	1.9845	0.0204	4.4249	0.8346
#8	0.3839	2.3149	0.0808	4.5837	1.1208	0.2490
	0.3786	2.3189	0.0805	4.5805	1.1228
#9	0.6273	2.6456	0.0161	1.4092	1.1957	0.0886
	0.6267	2.6459	0.0161	1.4092	1.1958
#10	0.0216	2.9762	0.0841	1.6905	0.8268	0.2428
	0.0201	2.9770	0.0841	1.6905	0.8561
#11	0.9106	3.3069	0.0032	4.2288	1.1758	0.0866
	0.9104	0.1653	0.0032	4.2290	1.1758
#12	0.8006	3.6376	0.0132	3.0002	0.8073	0.2216
	0.7985	0.4965	0.0132	2.9984	0.8071

Table 2.

Open in new tab

Real and first-order lens parameters for the 12 SIE models represented, respectively, in Fig. 6. For each lens model denoted by #i, we have reported the real model parameters (first line) and the retrieved first order ones (second line).

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0991	0	0.2414	5.5107	1.1990	0.4278
	0.0900	3.1177	0.2381	5.5227	1.2407
#2	0.4898	0.3307	0.1029	2.2189	1.1246	0.4061
	0.4760	0.3227	0.1019	2.2266	1.1272
#3	0.1932	0.6614	0.1655	2.8239	0.9943	0.3977
	0.1835	0.6723	0.1647	2.8129	1.0023
#4	0.8959	0.9921	0.0176	6.0540	1.1578	0.4151
	0.8916	0.9935	0.0174	6.0528	1.1579
#5	0.0991	1.3228	0.1054	0.2658	0.8550	0.2619
	0.0946	1.3225	0.1054	0.2658	0.8729
#6	0.0442	1.6535	0.1491	6.1133	0.9560	0.3372
	0.0397	1.6563	0.1491	6.1134	1.0058
#7	0.5573	1.9842	0.0798	1.1888	1.1709	0.3628
	0.5475	1.9846	0.0798	1.1881	1.1696
#8	0.7725	2.3149	0.0309	4.1916	1.1670	0.3102
	0.7679	2.3157	0.0309	4.1888	1.1663
#9	0.3119	2.6456	0.1569	3.6847	1.0854	0.4288
	0.2983	2.6470	0.1569	3.6828	1.0872
#10	0.1790	2.9762	0.2080	4.2419	1.0473	0.4640
	0.1630	2.9980	0.2052	4.2355	1.0807
#11	0.3390	3.3069	0.0958	2.2684	0.9373	0.3204
	0.3301	0.1577	0.0952	2.2732	0.9418
#12	0.2101	3.6376	0.2070	3.8973	1.1744	0.4328
	0.1940	0.5068	0.2061	3.8979	1.2098

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0991	0	0.2414	5.5107	1.1990	0.4278
	0.0900	3.1177	0.2381	5.5227	1.2407
#2	0.4898	0.3307	0.1029	2.2189	1.1246	0.4061
	0.4760	0.3227	0.1019	2.2266	1.1272
#3	0.1932	0.6614	0.1655	2.8239	0.9943	0.3977
	0.1835	0.6723	0.1647	2.8129	1.0023
#4	0.8959	0.9921	0.0176	6.0540	1.1578	0.4151
	0.8916	0.9935	0.0174	6.0528	1.1579
#5	0.0991	1.3228	0.1054	0.2658	0.8550	0.2619
	0.0946	1.3225	0.1054	0.2658	0.8729
#6	0.0442	1.6535	0.1491	6.1133	0.9560	0.3372
	0.0397	1.6563	0.1491	6.1134	1.0058
#7	0.5573	1.9842	0.0798	1.1888	1.1709	0.3628
	0.5475	1.9846	0.0798	1.1881	1.1696
#8	0.7725	2.3149	0.0309	4.1916	1.1670	0.3102
	0.7679	2.3157	0.0309	4.1888	1.1663
#9	0.3119	2.6456	0.1569	3.6847	1.0854	0.4288
	0.2983	2.6470	0.1569	3.6828	1.0872
#10	0.1790	2.9762	0.2080	4.2419	1.0473	0.4640
	0.1630	2.9980	0.2052	4.2355	1.0807
#11	0.3390	3.3069	0.0958	2.2684	0.9373	0.3204
	0.3301	0.1577	0.0952	2.2732	0.9418
#12	0.2101	3.6376	0.2070	3.8973	1.1744	0.4328
	0.1940	0.5068	0.2061	3.8979	1.2098

Table 2.

Open in new tab

Real and first-order lens parameters for the 12 SIE models represented, respectively, in Fig. 6. For each lens model denoted by #i, we have reported the real model parameters (first line) and the retrieved first order ones (second line).

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0991	0	0.2414	5.5107	1.1990	0.4278
	0.0900	3.1177	0.2381	5.5227	1.2407
#2	0.4898	0.3307	0.1029	2.2189	1.1246	0.4061
	0.4760	0.3227	0.1019	2.2266	1.1272
#3	0.1932	0.6614	0.1655	2.8239	0.9943	0.3977
	0.1835	0.6723	0.1647	2.8129	1.0023
#4	0.8959	0.9921	0.0176	6.0540	1.1578	0.4151
	0.8916	0.9935	0.0174	6.0528	1.1579
#5	0.0991	1.3228	0.1054	0.2658	0.8550	0.2619
	0.0946	1.3225	0.1054	0.2658	0.8729
#6	0.0442	1.6535	0.1491	6.1133	0.9560	0.3372
	0.0397	1.6563	0.1491	6.1134	1.0058
#7	0.5573	1.9842	0.0798	1.1888	1.1709	0.3628
	0.5475	1.9846	0.0798	1.1881	1.1696
#8	0.7725	2.3149	0.0309	4.1916	1.1670	0.3102
	0.7679	2.3157	0.0309	4.1888	1.1663
#9	0.3119	2.6456	0.1569	3.6847	1.0854	0.4288
	0.2983	2.6470	0.1569	3.6828	1.0872
#10	0.1790	2.9762	0.2080	4.2419	1.0473	0.4640
	0.1630	2.9980	0.2052	4.2355	1.0807
#11	0.3390	3.3069	0.0958	2.2684	0.9373	0.3204
	0.3301	0.1577	0.0952	2.2732	0.9418
#12	0.2101	3.6376	0.2070	3.8973	1.1744	0.4328
	0.1940	0.5068	0.2061	3.8979	1.2098

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.0991	0	0.2414	5.5107	1.1990	0.4278
	0.0900	3.1177	0.2381	5.5227	1.2407
#2	0.4898	0.3307	0.1029	2.2189	1.1246	0.4061
	0.4760	0.3227	0.1019	2.2266	1.1272
#3	0.1932	0.6614	0.1655	2.8239	0.9943	0.3977
	0.1835	0.6723	0.1647	2.8129	1.0023
#4	0.8959	0.9921	0.0176	6.0540	1.1578	0.4151
	0.8916	0.9935	0.0174	6.0528	1.1579
#5	0.0991	1.3228	0.1054	0.2658	0.8550	0.2619
	0.0946	1.3225	0.1054	0.2658	0.8729
#6	0.0442	1.6535	0.1491	6.1133	0.9560	0.3372
	0.0397	1.6563	0.1491	6.1134	1.0058
#7	0.5573	1.9842	0.0798	1.1888	1.1709	0.3628
	0.5475	1.9846	0.0798	1.1881	1.1696
#8	0.7725	2.3149	0.0309	4.1916	1.1670	0.3102
	0.7679	2.3157	0.0309	4.1888	1.1663
#9	0.3119	2.6456	0.1569	3.6847	1.0854	0.4288
	0.2983	2.6470	0.1569	3.6828	1.0872
#10	0.1790	2.9762	0.2080	4.2419	1.0473	0.4640
	0.1630	2.9980	0.2052	4.2355	1.0807
#11	0.3390	3.3069	0.0958	2.2684	0.9373	0.3204
	0.3301	0.1577	0.0952	2.2732	0.9418
#12	0.2101	3.6376	0.2070	3.8973	1.1744	0.4328
	0.1940	0.5068	0.2061	3.8979	1.2098

Table 3.

Open in new tab

Real and first-order lens parameters for the 12 SIE models represented, respectively, in Fig. 7. For each lens model denoted by #i, we have reported the real model parameters (first line) and the retrieved first order ones (second line).

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.2578	0.3307	0.3797	5.0953	1.0881	0.9326
	0.1858	0.2560	0.3560	5.1187	1.1923
#2	0.3317	0.6614	0.1831	3.0445	1.0887	0.5194
	0.3090	0.6805	0.1803	3.0279	1.0997
#3	0.1522	0.9921	0.4275	4.7548	1.1511	0.8349
	0.1102	0.9129	0.4068	4.8169	1.2520
#4	0.3480	1.3228	0.3183	2.6204	1.0330	0.9847
	0.2588	1.3930	0.2941	2.5930	1.1025
#5	0.1217	1.6535	0.3406	6.1059	0.8283	0.8909
	0.0780	1.6678	0.3401	6.1076	1.0078
#6	0.8842	1.9842	0.0373	6.2076	1.1691	0.7792
	0.8672	1.9807	0.0367	6.1899	1.1725
#7	0.9300	2.6456	0.0248	2.4434	0.9144	1.1221
	0.9066	2.6410	0.0236	2.3989	0.9173
#8	0.3424	3.6376	0.3250	4.9287	1.0863	0.9449
	0.2614	0.4324	0.3040	4.9469	1.1578
#9	0.7360	3.9683	0.1326	5.5470	1.1356	1.1544
	0.6634	0.8327	0.1321	5.5258	1.1241
#10	0.5449	4.6297	0.1924	3.5078	0.9882	1.0013
	0.4648	1.4665	0.1888	3.4897	1.0290
#11	0.6862	4.9604	0.0829	3.7628	1.0243	0.6551
	0.6577	1.8069	0.0805	3.7732	1.0266
#12	0.8936	5.2911	0.0337	0.9354	0.9076	0.9904
	0.8692	2.1485	0.0337	0.9435	0.9040

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.2578	0.3307	0.3797	5.0953	1.0881	0.9326
	0.1858	0.2560	0.3560	5.1187	1.1923
#2	0.3317	0.6614	0.1831	3.0445	1.0887	0.5194
	0.3090	0.6805	0.1803	3.0279	1.0997
#3	0.1522	0.9921	0.4275	4.7548	1.1511	0.8349
	0.1102	0.9129	0.4068	4.8169	1.2520
#4	0.3480	1.3228	0.3183	2.6204	1.0330	0.9847
	0.2588	1.3930	0.2941	2.5930	1.1025
#5	0.1217	1.6535	0.3406	6.1059	0.8283	0.8909
	0.0780	1.6678	0.3401	6.1076	1.0078
#6	0.8842	1.9842	0.0373	6.2076	1.1691	0.7792
	0.8672	1.9807	0.0367	6.1899	1.1725
#7	0.9300	2.6456	0.0248	2.4434	0.9144	1.1221
	0.9066	2.6410	0.0236	2.3989	0.9173
#8	0.3424	3.6376	0.3250	4.9287	1.0863	0.9449
	0.2614	0.4324	0.3040	4.9469	1.1578
#9	0.7360	3.9683	0.1326	5.5470	1.1356	1.1544
	0.6634	0.8327	0.1321	5.5258	1.1241
#10	0.5449	4.6297	0.1924	3.5078	0.9882	1.0013
	0.4648	1.4665	0.1888	3.4897	1.0290
#11	0.6862	4.9604	0.0829	3.7628	1.0243	0.6551
	0.6577	1.8069	0.0805	3.7732	1.0266
#12	0.8936	5.2911	0.0337	0.9354	0.9076	0.9904
	0.8692	2.1485	0.0337	0.9435	0.9040

Table 3.

Open in new tab

Real and first-order lens parameters for the 12 SIE models represented, respectively, in Fig. 7. For each lens model denoted by #i, we have reported the real model parameters (first line) and the retrieved first order ones (second line).

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.2578	0.3307	0.3797	5.0953	1.0881	0.9326
	0.1858	0.2560	0.3560	5.1187	1.1923
#2	0.3317	0.6614	0.1831	3.0445	1.0887	0.5194
	0.3090	0.6805	0.1803	3.0279	1.0997
#3	0.1522	0.9921	0.4275	4.7548	1.1511	0.8349
	0.1102	0.9129	0.4068	4.8169	1.2520
#4	0.3480	1.3228	0.3183	2.6204	1.0330	0.9847
	0.2588	1.3930	0.2941	2.5930	1.1025
#5	0.1217	1.6535	0.3406	6.1059	0.8283	0.8909
	0.0780	1.6678	0.3401	6.1076	1.0078
#6	0.8842	1.9842	0.0373	6.2076	1.1691	0.7792
	0.8672	1.9807	0.0367	6.1899	1.1725
#7	0.9300	2.6456	0.0248	2.4434	0.9144	1.1221
	0.9066	2.6410	0.0236	2.3989	0.9173
#8	0.3424	3.6376	0.3250	4.9287	1.0863	0.9449
	0.2614	0.4324	0.3040	4.9469	1.1578
#9	0.7360	3.9683	0.1326	5.5470	1.1356	1.1544
	0.6634	0.8327	0.1321	5.5258	1.1241
#10	0.5449	4.6297	0.1924	3.5078	0.9882	1.0013
	0.4648	1.4665	0.1888	3.4897	1.0290
#11	0.6862	4.9604	0.0829	3.7628	1.0243	0.6551
	0.6577	1.8069	0.0805	3.7732	1.0266
#12	0.8936	5.2911	0.0337	0.9354	0.9076	0.9904
	0.8692	2.1485	0.0337	0.9435	0.9040

Real	f	ϖ	θ_S	θ	θ_E	θ_S/d
first order
#1	0.2578	0.3307	0.3797	5.0953	1.0881	0.9326
	0.1858	0.2560	0.3560	5.1187	1.1923
#2	0.3317	0.6614	0.1831	3.0445	1.0887	0.5194
	0.3090	0.6805	0.1803	3.0279	1.0997
#3	0.1522	0.9921	0.4275	4.7548	1.1511	0.8349
	0.1102	0.9129	0.4068	4.8169	1.2520
#4	0.3480	1.3228	0.3183	2.6204	1.0330	0.9847
	0.2588	1.3930	0.2941	2.5930	1.1025
#5	0.1217	1.6535	0.3406	6.1059	0.8283	0.8909
	0.0780	1.6678	0.3401	6.1076	1.0078
#6	0.8842	1.9842	0.0373	6.2076	1.1691	0.7792
	0.8672	1.9807	0.0367	6.1899	1.1725
#7	0.9300	2.6456	0.0248	2.4434	0.9144	1.1221
	0.9066	2.6410	0.0236	2.3989	0.9173
#8	0.3424	3.6376	0.3250	4.9287	1.0863	0.9449
	0.2614	0.4324	0.3040	4.9469	1.1578
#9	0.7360	3.9683	0.1326	5.5470	1.1356	1.1544
	0.6634	0.8327	0.1321	5.5258	1.1241
#10	0.5449	4.6297	0.1924	3.5078	0.9882	1.0013
	0.4648	1.4665	0.1888	3.4897	1.0290
#11	0.6862	4.9604	0.0829	3.7628	1.0243	0.6551
	0.6577	1.8069	0.0805	3.7732	1.0266
#12	0.8936	5.2911	0.0337	0.9354	0.9076	0.9904
	0.8692	2.1485	0.0337	0.9435	0.9040

Finally, we have determined exact and first-order time delays, between pairs of lensed images for the first eight simulated models represented in Figs 5–7. For this purpose, we have assumed a spatially flat Λ cold dark matter cosmology with a value H₀ = 67.3 ± 1.2 km s⁻¹ Mpc⁻¹ for the Hubble parameter and the matter density parameter Ω_m = 0.315 ± 0.017 (Planck Collaboration 2013). We have fixed the redshifts of the simulated sources and lenses according to realistic cases of expected multiply imaged quasars as in Finet (2013). From the normalized redshift distribution of the sources that are detected as multiply imaged, we have selected the most likely redshift of the sources for Ω_m = 0.315, i.e. z_s = 2.350. For this source redshift, we have calculated the differential contribution to the lensing optical depth as a function of the deflector redshift. We have then selected the most likely deflector redshift corresponding to the maximum of this distribution, i.e. z_s = 0.66, as well as those corresponding to the two halves of its maximum, i.e. z_s = 0.263 and z_s = 1.294. Added to this, we have also considered the source and lens redshifts of the gravitational lens system Q2237+0305. The values of the corresponding time delays are summarized in Tables 4 –6. As expected, we note that the first-order time delays for a pair of opposed lensed images are identical to the exact time delays.

Table 4.

Open in new tab

Comparison between the values of the time delays derived from the first-order equations and the real SIE lens model ones. The corresponding lensed image configurations are represented in Fig. 5. The time delays are expressed in days.

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.95	1.97
			Δt₀₂	0.76	0.76
			Δt₀₃	1.97	1.99
#2	1.695	0.217	Δt₀₁	3.44	3.47
			Δt₀₂	0.70	0.70
			Δt₀₃	2.98	3.01
#3	1.695	0.54	Δt₀₁	29.47	29.68
			Δt₀₂	8.59	8.59
			Δt₀₃	30.34	30.55
#4	1.695	0.97	Δt₀₁	47.91	48.32
			Δt₀₂	14.14	14.14
			Δt₀₃	45.19	45.60
#5	2.350	0.039	Δt₀₁	0.29	0.30
			Δt₀₂	−0.002	−0.002
			Δt₀₃	0.37	0.38
#6	2.350	0.263	Δt₀₁	8.37	8.37
			Δt₀₂	−0.25	−0.25
			Δt₀₃	8.15	8.15
#7	2.350	0.66	Δt₀₁	6.32	6.40
			Δt₀₂	2.04	2.04
			Δt₀₃	6.55	6.63
#8	2.350	1.294	Δt₀₁	35.11	36.03
			Δt₀₂	14.47	14.47
			Δt₀₃	42.55	43.47

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.95	1.97
			Δt₀₂	0.76	0.76
			Δt₀₃	1.97	1.99
#2	1.695	0.217	Δt₀₁	3.44	3.47
			Δt₀₂	0.70	0.70
			Δt₀₃	2.98	3.01
#3	1.695	0.54	Δt₀₁	29.47	29.68
			Δt₀₂	8.59	8.59
			Δt₀₃	30.34	30.55
#4	1.695	0.97	Δt₀₁	47.91	48.32
			Δt₀₂	14.14	14.14
			Δt₀₃	45.19	45.60
#5	2.350	0.039	Δt₀₁	0.29	0.30
			Δt₀₂	−0.002	−0.002
			Δt₀₃	0.37	0.38
#6	2.350	0.263	Δt₀₁	8.37	8.37
			Δt₀₂	−0.25	−0.25
			Δt₀₃	8.15	8.15
#7	2.350	0.66	Δt₀₁	6.32	6.40
			Δt₀₂	2.04	2.04
			Δt₀₃	6.55	6.63
#8	2.350	1.294	Δt₀₁	35.11	36.03
			Δt₀₂	14.47	14.47
			Δt₀₃	42.55	43.47

Table 4.

Open in new tab

Comparison between the values of the time delays derived from the first-order equations and the real SIE lens model ones. The corresponding lensed image configurations are represented in Fig. 5. The time delays are expressed in days.

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.95	1.97
			Δt₀₂	0.76	0.76
			Δt₀₃	1.97	1.99
#2	1.695	0.217	Δt₀₁	3.44	3.47
			Δt₀₂	0.70	0.70
			Δt₀₃	2.98	3.01
#3	1.695	0.54	Δt₀₁	29.47	29.68
			Δt₀₂	8.59	8.59
			Δt₀₃	30.34	30.55
#4	1.695	0.97	Δt₀₁	47.91	48.32
			Δt₀₂	14.14	14.14
			Δt₀₃	45.19	45.60
#5	2.350	0.039	Δt₀₁	0.29	0.30
			Δt₀₂	−0.002	−0.002
			Δt₀₃	0.37	0.38
#6	2.350	0.263	Δt₀₁	8.37	8.37
			Δt₀₂	−0.25	−0.25
			Δt₀₃	8.15	8.15
#7	2.350	0.66	Δt₀₁	6.32	6.40
			Δt₀₂	2.04	2.04
			Δt₀₃	6.55	6.63
#8	2.350	1.294	Δt₀₁	35.11	36.03
			Δt₀₂	14.47	14.47
			Δt₀₃	42.55	43.47

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.95	1.97
			Δt₀₂	0.76	0.76
			Δt₀₃	1.97	1.99
#2	1.695	0.217	Δt₀₁	3.44	3.47
			Δt₀₂	0.70	0.70
			Δt₀₃	2.98	3.01
#3	1.695	0.54	Δt₀₁	29.47	29.68
			Δt₀₂	8.59	8.59
			Δt₀₃	30.34	30.55
#4	1.695	0.97	Δt₀₁	47.91	48.32
			Δt₀₂	14.14	14.14
			Δt₀₃	45.19	45.60
#5	2.350	0.039	Δt₀₁	0.29	0.30
			Δt₀₂	−0.002	−0.002
			Δt₀₃	0.37	0.38
#6	2.350	0.263	Δt₀₁	8.37	8.37
			Δt₀₂	−0.25	−0.25
			Δt₀₃	8.15	8.15
#7	2.350	0.66	Δt₀₁	6.32	6.40
			Δt₀₂	2.04	2.04
			Δt₀₃	6.55	6.63
#8	2.350	1.294	Δt₀₁	35.11	36.03
			Δt₀₂	14.47	14.47
			Δt₀₃	42.55	43.47

Table 5.

Open in new tab

Comparison between the values of the time delays derived from the first-order equations and the real SIE lens model ones. The corresponding lensed image configurations are represented in Fig. 6. The time delays are expressed in days.

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.11	1.33
			Δt₀₂	−1.89	−1.89
			Δt₀₃	2.00	2.23
#2	1.695	0.217	Δt₀₁	3.27	3.79
			Δt₀₂	−5.12	−5.12
			Δt₀₃	5.96	6.48
#3	1.695	0.54	Δt₀₁	13.63	15.00
			Δt₀₂	−18.32	−18.32
			Δt₀₃	9.81	11.18
#4	1.695	0.97	Δt₀₁	5.28	5.68
			Δt₀₂	2.99	2.99
			Δt₀₃	8.03	8.43
#5	2.350	0.039	Δt₀₁	1.00	1.06
			Δt₀₂	−0.01	−0.01
			Δt₀₃	1.40	1.46
#6	2.350	0.263	Δt₀₁	6.02	6.54
			Δt₀₂	0.55	0.55
			Δt₀₃	8.57	9.09
#7	2.350	0.66	Δt₀₁	9.40	10.26
			Δt₀₂	−11.46	−11.46
			Δt₀₃	9.11	9.97
#8	2.350	1.294	Δt₀₁	13.39	13.87
			Δt₀₂	6.62	6.62
			Δt₀₃	14.75	15.23

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.11	1.33
			Δt₀₂	−1.89	−1.89
			Δt₀₃	2.00	2.23
#2	1.695	0.217	Δt₀₁	3.27	3.79
			Δt₀₂	−5.12	−5.12
			Δt₀₃	5.96	6.48
#3	1.695	0.54	Δt₀₁	13.63	15.00
			Δt₀₂	−18.32	−18.32
			Δt₀₃	9.81	11.18
#4	1.695	0.97	Δt₀₁	5.28	5.68
			Δt₀₂	2.99	2.99
			Δt₀₃	8.03	8.43
#5	2.350	0.039	Δt₀₁	1.00	1.06
			Δt₀₂	−0.01	−0.01
			Δt₀₃	1.40	1.46
#6	2.350	0.263	Δt₀₁	6.02	6.54
			Δt₀₂	0.55	0.55
			Δt₀₃	8.57	9.09
#7	2.350	0.66	Δt₀₁	9.40	10.26
			Δt₀₂	−11.46	−11.46
			Δt₀₃	9.11	9.97
#8	2.350	1.294	Δt₀₁	13.39	13.87
			Δt₀₂	6.62	6.62
			Δt₀₃	14.75	15.23

Table 5.

Open in new tab

Comparison between the values of the time delays derived from the first-order equations and the real SIE lens model ones. The corresponding lensed image configurations are represented in Fig. 6. The time delays are expressed in days.

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.11	1.33
			Δt₀₂	−1.89	−1.89
			Δt₀₃	2.00	2.23
#2	1.695	0.217	Δt₀₁	3.27	3.79
			Δt₀₂	−5.12	−5.12
			Δt₀₃	5.96	6.48
#3	1.695	0.54	Δt₀₁	13.63	15.00
			Δt₀₂	−18.32	−18.32
			Δt₀₃	9.81	11.18
#4	1.695	0.97	Δt₀₁	5.28	5.68
			Δt₀₂	2.99	2.99
			Δt₀₃	8.03	8.43
#5	2.350	0.039	Δt₀₁	1.00	1.06
			Δt₀₂	−0.01	−0.01
			Δt₀₃	1.40	1.46
#6	2.350	0.263	Δt₀₁	6.02	6.54
			Δt₀₂	0.55	0.55
			Δt₀₃	8.57	9.09
#7	2.350	0.66	Δt₀₁	9.40	10.26
			Δt₀₂	−11.46	−11.46
			Δt₀₃	9.11	9.97
#8	2.350	1.294	Δt₀₁	13.39	13.87
			Δt₀₂	6.62	6.62
			Δt₀₃	14.75	15.23

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	1.11	1.33
			Δt₀₂	−1.89	−1.89
			Δt₀₃	2.00	2.23
#2	1.695	0.217	Δt₀₁	3.27	3.79
			Δt₀₂	−5.12	−5.12
			Δt₀₃	5.96	6.48
#3	1.695	0.54	Δt₀₁	13.63	15.00
			Δt₀₂	−18.32	−18.32
			Δt₀₃	9.81	11.18
#4	1.695	0.97	Δt₀₁	5.28	5.68
			Δt₀₂	2.99	2.99
			Δt₀₃	8.03	8.43
#5	2.350	0.039	Δt₀₁	1.00	1.06
			Δt₀₂	−0.01	−0.01
			Δt₀₃	1.40	1.46
#6	2.350	0.263	Δt₀₁	6.02	6.54
			Δt₀₂	0.55	0.55
			Δt₀₃	8.57	9.09
#7	2.350	0.66	Δt₀₁	9.40	10.26
			Δt₀₂	−11.46	−11.46
			Δt₀₃	9.11	9.97
#8	2.350	1.294	Δt₀₁	13.39	13.87
			Δt₀₂	6.62	6.62
			Δt₀₃	14.75	15.23

Table 6.

Open in new tab

Comparison between the values of time delays derived from the first-order equations and the real SIE lens model ones. The corresponding lensed image configurations are represented in Fig. 7. The time delays are expressed in days.

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	4.66	5.32
			Δt₀₂	2.62	2.62
			Δt₀₃	2.69	3.35
#2	1.695	0.217	Δt₀₁	6.99	8.04
			Δt₀₂	−8.98	−8.98
			Δt₀₃	3.09	4.14
#3	1.695	0.54	Δt₀₁	64.40	71.77
			Δt₀₂	47.63	47.63
			Δt₀₃	49.56	56.93
#4	1.695	0.97	Δt₀₁	33.93	44.81
			Δt₀₂	−46.41	−46.41
			Δt₀₃	0.21	11.09
#5	2.350	0.039	Δt₀₁	0.74	1.26
			Δt₀₂	0.23	0.23
			Δt₀₃	2.11	2.63
#6	2.350	0.263	Δt₀₁	0.31	0.71
			Δt₀₂	−0.77	−0.77
			Δt₀₃	2.54	2.94
#7	2.350	0.66	Δt₀₁	3.13	3.62
			Δt₀₂	0.81	0.81
			Δt₀₃	0.82	1.31
#8	2.350	1.294	Δt₀₁	77.74	88.43
			Δt₀₂	42.18	42.18
			Δt₀₃	43.04	53.73

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	4.66	5.32
			Δt₀₂	2.62	2.62
			Δt₀₃	2.69	3.35
#2	1.695	0.217	Δt₀₁	6.99	8.04
			Δt₀₂	−8.98	−8.98
			Δt₀₃	3.09	4.14
#3	1.695	0.54	Δt₀₁	64.40	71.77
			Δt₀₂	47.63	47.63
			Δt₀₃	49.56	56.93
#4	1.695	0.97	Δt₀₁	33.93	44.81
			Δt₀₂	−46.41	−46.41
			Δt₀₃	0.21	11.09
#5	2.350	0.039	Δt₀₁	0.74	1.26
			Δt₀₂	0.23	0.23
			Δt₀₃	2.11	2.63
#6	2.350	0.263	Δt₀₁	0.31	0.71
			Δt₀₂	−0.77	−0.77
			Δt₀₃	2.54	2.94
#7	2.350	0.66	Δt₀₁	3.13	3.62
			Δt₀₂	0.81	0.81
			Δt₀₃	0.82	1.31
#8	2.350	1.294	Δt₀₁	77.74	88.43
			Δt₀₂	42.18	42.18
			Δt₀₃	43.04	53.73

Table 6.

Open in new tab

Comparison between the values of time delays derived from the first-order equations and the real SIE lens model ones. The corresponding lensed image configurations are represented in Fig. 7. The time delays are expressed in days.

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	4.66	5.32
			Δt₀₂	2.62	2.62
			Δt₀₃	2.69	3.35
#2	1.695	0.217	Δt₀₁	6.99	8.04
			Δt₀₂	−8.98	−8.98
			Δt₀₃	3.09	4.14
#3	1.695	0.54	Δt₀₁	64.40	71.77
			Δt₀₂	47.63	47.63
			Δt₀₃	49.56	56.93
#4	1.695	0.97	Δt₀₁	33.93	44.81
			Δt₀₂	−46.41	−46.41
			Δt₀₃	0.21	11.09
#5	2.350	0.039	Δt₀₁	0.74	1.26
			Δt₀₂	0.23	0.23
			Δt₀₃	2.11	2.63
#6	2.350	0.263	Δt₀₁	0.31	0.71
			Δt₀₂	−0.77	−0.77
			Δt₀₃	2.54	2.94
#7	2.350	0.66	Δt₀₁	3.13	3.62
			Δt₀₂	0.81	0.81
			Δt₀₃	0.82	1.31
#8	2.350	1.294	Δt₀₁	77.74	88.43
			Δt₀₂	42.18	42.18
			Δt₀₃	43.04	53.73

Model				Time delays	Time delays
index	z_s	z_l		(real)	(to first order)
#1	1.695	0.039	Δt₀₁	4.66	5.32
			Δt₀₂	2.62	2.62
			Δt₀₃	2.69	3.35
#2	1.695	0.217	Δt₀₁	6.99	8.04
			Δt₀₂	−8.98	−8.98
			Δt₀₃	3.09	4.14
#3	1.695	0.54	Δt₀₁	64.40	71.77
			Δt₀₂	47.63	47.63
			Δt₀₃	49.56	56.93
#4	1.695	0.97	Δt₀₁	33.93	44.81
			Δt₀₂	−46.41	−46.41
			Δt₀₃	0.21	11.09
#5	2.350	0.039	Δt₀₁	0.74	1.26
			Δt₀₂	0.23	0.23
			Δt₀₃	2.11	2.63
#6	2.350	0.263	Δt₀₁	0.31	0.71
			Δt₀₂	−0.77	−0.77
			Δt₀₃	2.54	2.94
#7	2.350	0.66	Δt₀₁	3.13	3.62
			Δt₀₂	0.81	0.81
			Δt₀₃	0.82	1.31
#8	2.350	1.294	Δt₀₁	77.74	88.43
			Δt₀₂	42.18	42.18
			Δt₀₃	43.04	53.73

4 APPLICATION TO A REAL CASE: Q2237+0305

The gravitational lens Q2237+0305 consists of a quadruply imaged QSO at z = 1.695, discovered by Huchra et al. (1985) in the CfA Redshift Survey of Galaxies. The deflector which leads to the formation of the lensed images is a nearby 15 mag face-on spiral galaxy, at z = 0.0394 (e.g. Schmidt, Webster & Lewis Geraint 1998). Due to its proximity, the lensing galaxy has already been explored in detail. Different approaches have been applied to model this system, e.g. a constant mass-to-light ratio (Schneider et al. 1988; Rix, Schneider & Bahcall 1992; Chae, Khersonsky & Turnshek 1998; Keeton & Kochanek 1998) or multiparametric models (e.g. a de Vaucouleurs law and King profile, Kent & Falco 1988; singular isothermal sphere and point mass along with external shear, Kochanek 1991; a singular power-law axially symmetric deflector with an external shear, Wambsganss & Paczyński 1994; a non-singular power-law density for the distribution of mass, Chae et al. 1998). The astrometric positions of the four lensed images of Q2237+0305, which come from the CASTLES¹ survey, are listed in Table 7.

Table 7.

Open in new tab

The lensed image positions for the Q2237+0305 system from the CASTLES^a survey.

	−Δα	Δδ
	(arcsec)	(arcsec)
A	0.0	0.0
B	0.673 ± 0.003	1.697 ± 0.003
C	−0.635 ± 0.003	1.210 ± 0.003
D	0.866 ± 0.003	0.528 ± 0.003
G	0.075 ± 0.004	0.939 ± 0.003

	−Δα	Δδ
	(arcsec)	(arcsec)
A	0.0	0.0
B	0.673 ± 0.003	1.697 ± 0.003
C	−0.635 ± 0.003	1.210 ± 0.003
D	0.866 ± 0.003	0.528 ± 0.003
G	0.075 ± 0.004	0.939 ± 0.003

^ahttp://cfa-www.harvard.edu/castles/.

Table 7.

Open in new tab

The lensed image positions for the Q2237+0305 system from the CASTLES^a survey.

	−Δα	Δδ
	(arcsec)	(arcsec)
A	0.0	0.0
B	0.673 ± 0.003	1.697 ± 0.003
C	−0.635 ± 0.003	1.210 ± 0.003
D	0.866 ± 0.003	0.528 ± 0.003
G	0.075 ± 0.004	0.939 ± 0.003

	−Δα	Δδ
	(arcsec)	(arcsec)
A	0.0	0.0
B	0.673 ± 0.003	1.697 ± 0.003
C	−0.635 ± 0.003	1.210 ± 0.003
D	0.866 ± 0.003	0.528 ± 0.003
G	0.075 ± 0.004	0.939 ± 0.003

^ahttp://cfa-www.harvard.edu/castles/.

For the case of a singular power-law axially symmetric model with external shear, the so-called ε − γ model, Wertz et al. (2012) have already derived first-order equations which link the lensed image positions to the model parameters. As a consequence, we may determine which set of first-order equations, between SIE and ε − γ, leads to the best agreement with the observed lensed images. Furthermore, we have performed numerical modelling in order to independently determine the lens model parameters, for both the ε-γ and SIE lens models. In addition, we have performed another numerical modelling for the case of the non-singular isothermal ellipsoid with external shear (NSIE + γ) which constitutes a much more detailed model for the deflector. For this purpose, the function of merit to be minimized is the following

\begin{eqnarray} \chi ^2_r = \frac{1}{N}\sum _{j=0}^{3}\left( \frac{x_{1}^{(j)} - \underline{x}_{1}^{(j)} }{\sigma _{1}^{(j)}}\right)^{2} + \frac{1}{N} \sum _{j=0}^{3} \left( \frac{x_{2}^{(j)} - \underline{x}_{2}^{(j)}}{\sigma _{2}^{(j)}}\right)^{2} \,, \end{eqnarray}

(41)

where N represents the number of degrees of freedom, |$\sigma _{1}^{(j)}$|(resp. |$\sigma _{2}^{(j)}$|⁠) the measured uncertainties affecting the observed positions |$x_{1}^{(j)}$| (resp. |$x_{2}^{(j)}$|⁠), and |$\underline{x}_{i}^{(j)}$| the image positions derived from the numerical inversion of the lens equation characterized by the deduced model parameters. For the case of the SIE (resp. ε − γ and NSIE + γ) model, the number of independent parameters equals 3 (resp. 4 and 6). Therefore, the corresponding number of degrees of freedom is N_SIE = 5 (resp. N_{ε − γ} = 4 and N_{NSIE + γ} = 2). The global optimization has been performed using a sophisticated genetic algorithm, called ferret, which is a component of the Qubist Global Optimization Toolbox (Fiege 2010). The best sets of parameters for both the SIE and ε − γ models, as well as first-order lens parameters are summarized in Table 8.

Table 8.

Open in new tab

Optimal SIE and ε − γ lens parameters for the Q2237+0305 system, derived by the ferret sophisticated genetic algorithm which is a component of the Qubist Global Optimization Toolbox.

	SIE	SIE	ε − γ	ε − γ	NSIE + γ
		first order		first order
\|$\chi ^{2}_{r}$\|	1.5466	12.204	18.165	–	0.7319
f	\|$0.6649_{-0.0094}^{+0.0100}$\|	\|$0.6479_{-0.0097}^{+0.0097}$\|	–	–	\|$0.6634_{-0.0096}^{+0.0110}$\|
ϖ	\|$1.9720_{-0.0029}^{+0.0028}$\|	\|$1.9686_{-0.0024}^{+0.0024}$\|	–	–	\|$2.0111_{-0.0023}^{+0.0023}$\|
ε	–	–	\|$0.6653_{-0.0094}^{+0.0100}$\|	1.5949	–
γ	–	–	\|$0.1047_{-0.0094}^{+0.0100}$\|	-0.0292	\|$0.0138_{-0.00012}^{+0.00012}$\|
ω	–	–	\|$2.7437_{-0.0094}^{+0.0100}$\|	1.1729	\|$2.7107_{-0.0010}^{+0.0010}$\|
θ_S	\|$0.0652_{-0.0021}^{+0.0021}$\|	\|$0.0669_{-0.0035}^{+0.0035}$\|	\|$0.0595_{-0.0094}^{+0.0100}$\|	-0.0166	\|$0.0632_{-0.0011}^{+0.0012}$\|
θ	\|$6.1261_{-0.0146}^{+0.0150}$\|	\|$6.0629_{-0.0408}^{+0.0408}$\|	\|$6.0589_{-0.0094}^{+0.0100}$\|	6.0524	\|$6.1236_{-0.0118}^{+0.0119}$\|
θ_E	\|$0.8974_{-0.0023}^{+0.0023}$\|	\|$0.9024_{-0.0021}^{+0.0021}$\|	\|$0.8812_{-0.0094}^{+0.0100}$\|	0.8865	\|$0.9396_{-0.0019}^{+0.0019}$\|
ρ_c	–	–	–	–	\|$0.0332_{-0.0013}^{+0.0013}$\|
Δx_A	0.0031	0.0163	0.0064	–	0.0028
Δx_B	0.0087	0.0097	0.0082	–	0.0020
Δx_C	0.0082	0.0006	0.0210	–	0.0030
Δx_D	0.0036	0.0268	0.0335	–	0.0027

	SIE	SIE	ε − γ	ε − γ	NSIE + γ
		first order		first order
\|$\chi ^{2}_{r}$\|	1.5466	12.204	18.165	–	0.7319
f	\|$0.6649_{-0.0094}^{+0.0100}$\|	\|$0.6479_{-0.0097}^{+0.0097}$\|	–	–	\|$0.6634_{-0.0096}^{+0.0110}$\|
ϖ	\|$1.9720_{-0.0029}^{+0.0028}$\|	\|$1.9686_{-0.0024}^{+0.0024}$\|	–	–	\|$2.0111_{-0.0023}^{+0.0023}$\|
ε	–	–	\|$0.6653_{-0.0094}^{+0.0100}$\|	1.5949	–
γ	–	–	\|$0.1047_{-0.0094}^{+0.0100}$\|	-0.0292	\|$0.0138_{-0.00012}^{+0.00012}$\|
ω	–	–	\|$2.7437_{-0.0094}^{+0.0100}$\|	1.1729	\|$2.7107_{-0.0010}^{+0.0010}$\|
θ_S	\|$0.0652_{-0.0021}^{+0.0021}$\|	\|$0.0669_{-0.0035}^{+0.0035}$\|	\|$0.0595_{-0.0094}^{+0.0100}$\|	-0.0166	\|$0.0632_{-0.0011}^{+0.0012}$\|
θ	\|$6.1261_{-0.0146}^{+0.0150}$\|	\|$6.0629_{-0.0408}^{+0.0408}$\|	\|$6.0589_{-0.0094}^{+0.0100}$\|	6.0524	\|$6.1236_{-0.0118}^{+0.0119}$\|
θ_E	\|$0.8974_{-0.0023}^{+0.0023}$\|	\|$0.9024_{-0.0021}^{+0.0021}$\|	\|$0.8812_{-0.0094}^{+0.0100}$\|	0.8865	\|$0.9396_{-0.0019}^{+0.0019}$\|
ρ_c	–	–	–	–	\|$0.0332_{-0.0013}^{+0.0013}$\|
Δx_A	0.0031	0.0163	0.0064	–	0.0028
Δx_B	0.0087	0.0097	0.0082	–	0.0020
Δx_C	0.0082	0.0006	0.0210	–	0.0030
Δx_D	0.0036	0.0268	0.0335	–	0.0027

Notes. The parameters ε represents the slope of the power-law mass distribution, γ the magnitude of the external shear, ω the orientation of the external shear and ρ_c the size of the core radius in arcsec. The lower and upper limits correspond to the range of the lens parameters used by the genetic algorithm routine. The distances between the lensed images and the modelled images are represented by Δx.

Table 8.

Open in new tab

Optimal SIE and ε − γ lens parameters for the Q2237+0305 system, derived by the ferret sophisticated genetic algorithm which is a component of the Qubist Global Optimization Toolbox.

	SIE	SIE	ε − γ	ε − γ	NSIE + γ
		first order		first order
\|$\chi ^{2}_{r}$\|	1.5466	12.204	18.165	–	0.7319
f	\|$0.6649_{-0.0094}^{+0.0100}$\|	\|$0.6479_{-0.0097}^{+0.0097}$\|	–	–	\|$0.6634_{-0.0096}^{+0.0110}$\|
ϖ	\|$1.9720_{-0.0029}^{+0.0028}$\|	\|$1.9686_{-0.0024}^{+0.0024}$\|	–	–	\|$2.0111_{-0.0023}^{+0.0023}$\|
ε	–	–	\|$0.6653_{-0.0094}^{+0.0100}$\|	1.5949	–
γ	–	–	\|$0.1047_{-0.0094}^{+0.0100}$\|	-0.0292	\|$0.0138_{-0.00012}^{+0.00012}$\|
ω	–	–	\|$2.7437_{-0.0094}^{+0.0100}$\|	1.1729	\|$2.7107_{-0.0010}^{+0.0010}$\|
θ_S	\|$0.0652_{-0.0021}^{+0.0021}$\|	\|$0.0669_{-0.0035}^{+0.0035}$\|	\|$0.0595_{-0.0094}^{+0.0100}$\|	-0.0166	\|$0.0632_{-0.0011}^{+0.0012}$\|
θ	\|$6.1261_{-0.0146}^{+0.0150}$\|	\|$6.0629_{-0.0408}^{+0.0408}$\|	\|$6.0589_{-0.0094}^{+0.0100}$\|	6.0524	\|$6.1236_{-0.0118}^{+0.0119}$\|
θ_E	\|$0.8974_{-0.0023}^{+0.0023}$\|	\|$0.9024_{-0.0021}^{+0.0021}$\|	\|$0.8812_{-0.0094}^{+0.0100}$\|	0.8865	\|$0.9396_{-0.0019}^{+0.0019}$\|
ρ_c	–	–	–	–	\|$0.0332_{-0.0013}^{+0.0013}$\|
Δx_A	0.0031	0.0163	0.0064	–	0.0028
Δx_B	0.0087	0.0097	0.0082	–	0.0020
Δx_C	0.0082	0.0006	0.0210	–	0.0030
Δx_D	0.0036	0.0268	0.0335	–	0.0027

	SIE	SIE	ε − γ	ε − γ	NSIE + γ
		first order		first order
\|$\chi ^{2}_{r}$\|	1.5466	12.204	18.165	–	0.7319
f	\|$0.6649_{-0.0094}^{+0.0100}$\|	\|$0.6479_{-0.0097}^{+0.0097}$\|	–	–	\|$0.6634_{-0.0096}^{+0.0110}$\|
ϖ	\|$1.9720_{-0.0029}^{+0.0028}$\|	\|$1.9686_{-0.0024}^{+0.0024}$\|	–	–	\|$2.0111_{-0.0023}^{+0.0023}$\|
ε	–	–	\|$0.6653_{-0.0094}^{+0.0100}$\|	1.5949	–
γ	–	–	\|$0.1047_{-0.0094}^{+0.0100}$\|	-0.0292	\|$0.0138_{-0.00012}^{+0.00012}$\|
ω	–	–	\|$2.7437_{-0.0094}^{+0.0100}$\|	1.1729	\|$2.7107_{-0.0010}^{+0.0010}$\|
θ_S	\|$0.0652_{-0.0021}^{+0.0021}$\|	\|$0.0669_{-0.0035}^{+0.0035}$\|	\|$0.0595_{-0.0094}^{+0.0100}$\|	-0.0166	\|$0.0632_{-0.0011}^{+0.0012}$\|
θ	\|$6.1261_{-0.0146}^{+0.0150}$\|	\|$6.0629_{-0.0408}^{+0.0408}$\|	\|$6.0589_{-0.0094}^{+0.0100}$\|	6.0524	\|$6.1236_{-0.0118}^{+0.0119}$\|
θ_E	\|$0.8974_{-0.0023}^{+0.0023}$\|	\|$0.9024_{-0.0021}^{+0.0021}$\|	\|$0.8812_{-0.0094}^{+0.0100}$\|	0.8865	\|$0.9396_{-0.0019}^{+0.0019}$\|
ρ_c	–	–	–	–	\|$0.0332_{-0.0013}^{+0.0013}$\|
Δx_A	0.0031	0.0163	0.0064	–	0.0028
Δx_B	0.0087	0.0097	0.0082	–	0.0020
Δx_C	0.0082	0.0006	0.0210	–	0.0030
Δx_D	0.0036	0.0268	0.0335	–	0.0027

Notes. The parameters ε represents the slope of the power-law mass distribution, γ the magnitude of the external shear, ω the orientation of the external shear and ρ_c the size of the core radius in arcsec. The lower and upper limits correspond to the range of the lens parameters used by the genetic algorithm routine. The distances between the lensed images and the modelled images are represented by Δx.

We have assumed that the errors are described by a normal distribution and are uncorrelated. Therefore, the probability that the error of a single measurement lies in the interval [−a, a] is given by |$p = \mbox{erf}(a/(\sigma \sqrt{2}))$|⁠, where erf(.) represents the error function. As a consequence, the corresponding inverse of the χ² cumulative distribution function with the number of degrees of freedom specified by N_SIE = 5 is given by χ_cutoff² = F^{− 1}(p|N_SIE) = {χ_cutoff²: F(χ_cutoff²|N_SIE) = p}, where

\begin{eqnarray} F(\chi _{{\mathrm{cutoff}}}^{2}|N_{{\mathrm{SIE}}}) = \int \limits _{0}^{\chi _{{\mathrm{cutoff}}}^{2}} \frac{t^{(N_{{\mathrm{SIE}}}-2)}\ \mbox{e}^{-t/2}}{2^{N_{{\mathrm{SIE}}}/2}\ \Gamma (N_{{\mathrm{SIE}}}/2)}\ \mbox{d}t \,. \end{eqnarray}

(42)

For a 1σ error calculation, we have found χ_cutoff² = 5.8876 which leads to the reduced value χ_{r, cutoff}² = 1.1775. Finally, we have separately constructed 1D paraboloid-like curves of best |$\chi _{r}^{2}$| as a function of each lens model parameter. The χ_{r, cutoff}² associated with these curves gives the value of the error bars (see Table 8, columns 1 and 3). Concerning the uncertainties of the first-order lens parameters, we have derived them by means of the Monte Carlo method.

The SIE lens model shows the best agreement with the observed image positions in comparison with the ε − γ model: <Δx_SIE > = 0.0059 arcsec whereas <Δx_ε−γ > ≃0.0173 arcsec. Therefore, this is what convinces us to use the SIE first-order equations instead of the ε − γ ones. Furthermore, for the case of the ε − γ model, the first-order values of γ and θ_S appear to be non-physical. However, we note that the determined value of θ_E is similar for both lens models which seems to indicate that the determination of the Einstein angular radius very slightly depends on the choice of the deflector's family of models. We notice that both sets of lens parameters (SIE and first-order SIE) are quite similar, which leads to the conclusion that the use of the first-order astrometric equations is justified here. For both SIE and first-order SIE models, we have derived the value of θ_S/d and D/d from the parameters found in Table 8. For the case of SIE, one finds θ_S/d = 0.5438, D/d = 0.5649, and for the case of first-order SIE, θ_S/d = 0.5231 and D/d = 0.6054.

The NSIE + γ model shows the best agreement with the observed lensed image positions in comparison with the SIE model: < Δx_{NSIE + γ} > ≃0.0026 arcsec, which is smaller than the precision of the observed image positions (see Table 7). The large number of independent parameters (N_{NSIE + γ} = 6) and the very high precision on the modelled image positions explain why we have found |$\chi ^{2}_{r} < 1$|⁠. We note that the parameters f, ϖ, θ_S and θ between the SIE and NSIE + γ models are very similar, which seems to indicate that the NSIE + γ derived numerical solution is the best for this model, i.e. not a local minimum. The addition of a core leads to the appearance of a fifth lensed image, denoted by E, located very close to the gravity centre of the deflector: −Δα = −0.0069 arcsec and Δδ = 0.0018 arcsec. The observational existence of a fifth lensed image has first been reported by Racine (1991), but it has never been independently confirmed. For the case of the SIE, the first-order SIE and the NSIE + γ models, we have illustrated the corresponding lensed image positions in Fig. 8. Furthermore, we have derived the values of the time delays (in hours) and amplification ratio between the lensed image A and the other ones. We have summarized all the information in Table 9. As expected, the comparison between the values of the time delay Δt_AB (resp. Δt_CD) for the case of the SIE and the first-order SIE models are extremely close. Indeed, we have shown that the first-order time delay expression (equation 38) is identical to the one derived by Witt et al. (2000). Since equation (38) remains valid without any approximation for any pairs of lensed images, equation (35) seems to be useless. However, the SIE (resp. ε − γ) first-order equations (20), (23), (24), (27) and (28) have the advantage to test straightforwardly, and without any numerical simulations, to what extent the SIE (resp. ε − γ) family of models constitutes a good choice and therefore whether the derived values for the time delays and amplification ratios are trustworthy. Without using these first-order equations, equation (38) could still be applied to any symmetric quadruply imaged quasar but without the immediate confidence that the SIE family of models constitutes a good approximation to represent the mass distribution. For Q2237+0305, we have shown that the ε − γ family of models did not properly fit the lensed image positions while the SIE family of models does.

Table 9.

Open in new tab

Comparison between the values of the time delays (in hours) and amplification ratios between pairs of lensed images derived from the first-order equations and the real SIE and NSIE + γ models for Q2237+0305.

	SIE	SIE	NSIE + γ
		first order
Δt_AD/h	−5.3821 ± 0.6841	−7.2966 ± 0.5278	−5.4112 ± 0.4291
Δt_AB/h	2.5992 ± 0.7172	2.5983 ± 0.6152	2.5080 ± 0.5192
Δt_AC/h	−17.969 ± 0.6969	−19.877 ± 0.7448	−18.009 ± 0.6192
Δt_CD/h	12.587 ± 0.6849	12.580 ± 0.6541	12.597 ± 0.5812
μ_B/μ_A	0.797 172	–	0.84483
μ_C/μ_A	−0.184 621	–	−0.294 92
μ_D/μ_A	−0.305 474	–	−0.490 83
μ_E/μ_A	–	–	0.001 2186

	SIE	SIE	NSIE + γ
		first order
Δt_AD/h	−5.3821 ± 0.6841	−7.2966 ± 0.5278	−5.4112 ± 0.4291
Δt_AB/h	2.5992 ± 0.7172	2.5983 ± 0.6152	2.5080 ± 0.5192
Δt_AC/h	−17.969 ± 0.6969	−19.877 ± 0.7448	−18.009 ± 0.6192
Δt_CD/h	12.587 ± 0.6849	12.580 ± 0.6541	12.597 ± 0.5812
μ_B/μ_A	0.797 172	–	0.84483
μ_C/μ_A	−0.184 621	–	−0.294 92
μ_D/μ_A	−0.305 474	–	−0.490 83
μ_E/μ_A	–	–	0.001 2186

Notes. We have fixed the value of the Hubble parameter to 67.3 ± 1.2 km s⁻¹Mpc⁻¹ and the matter density parameter Ω_m = 0.315 ± 0.017 (Planck Collaboration 2013).

Table 9.

Open in new tab

Comparison between the values of the time delays (in hours) and amplification ratios between pairs of lensed images derived from the first-order equations and the real SIE and NSIE + γ models for Q2237+0305.

	SIE	SIE	NSIE + γ
		first order
Δt_AD/h	−5.3821 ± 0.6841	−7.2966 ± 0.5278	−5.4112 ± 0.4291
Δt_AB/h	2.5992 ± 0.7172	2.5983 ± 0.6152	2.5080 ± 0.5192
Δt_AC/h	−17.969 ± 0.6969	−19.877 ± 0.7448	−18.009 ± 0.6192
Δt_CD/h	12.587 ± 0.6849	12.580 ± 0.6541	12.597 ± 0.5812
μ_B/μ_A	0.797 172	–	0.84483
μ_C/μ_A	−0.184 621	–	−0.294 92
μ_D/μ_A	−0.305 474	–	−0.490 83
μ_E/μ_A	–	–	0.001 2186

	SIE	SIE	NSIE + γ
		first order
Δt_AD/h	−5.3821 ± 0.6841	−7.2966 ± 0.5278	−5.4112 ± 0.4291
Δt_AB/h	2.5992 ± 0.7172	2.5983 ± 0.6152	2.5080 ± 0.5192
Δt_AC/h	−17.969 ± 0.6969	−19.877 ± 0.7448	−18.009 ± 0.6192
Δt_CD/h	12.587 ± 0.6849	12.580 ± 0.6541	12.597 ± 0.5812
μ_B/μ_A	0.797 172	–	0.84483
μ_C/μ_A	−0.184 621	–	−0.294 92
μ_D/μ_A	−0.305 474	–	−0.490 83
μ_E/μ_A	–	–	0.001 2186

Notes. We have fixed the value of the Hubble parameter to 67.3 ± 1.2 km s⁻¹Mpc⁻¹ and the matter density parameter Ω_m = 0.315 ± 0.017 (Planck Collaboration 2013).

The values of the estimated time delay listed in Table 9 can be compared with those in Table 10 which constitutes a summary of the model predictions for Q2237+0305. A description of the corresponding lens models may be found in Vakulik et al. (2006). We note that the determination of the time delays depends on the considered models. Unfortunately, the possibility of measuring very accurate time delays between two lensed images from their light curves seems to be very difficult. Different attempts have already been performed (see e.g. Koptelova, Oknyanskij & Shimanovskaya 2006; Vakulik et al. 2006) but none of them allows the authors to definitely conclude. The uncertainties obtained, which correspond to a 95 per cent confidence level, exceed 100 per cent. Therefore, we are not able to compare the measured and the predicted time delays. In order to estimate the value of the Hubble parameter with, at least, the same precision as the Planck Collaboration (2013), we have calculated that the uncertainties on Δt_AB and Δt_CD should be, respectively, smaller than σ_AB ≤ 0.0465 h (i.e. 2.8 min) and σ_CD ≤ 0.225 h (i.e. 13.5 min).

Table 10.

Open in new tab

Model predictions for the time delays (in hours) Δt_AB, Δt_AC and Δt_AD for Q2237+0305.

Reference	Lens model	Δt_AB/h	Δt_AC/h	Δt_AD/h
Schneider et al.	Constant	2.4	29.5	26.6
(1988)	mass-to-light ratio
	Best fit	0.54	−6.48	−6.12
	Model 1	−2.1	−11	−7.1
Rix et al. (1992)	Model 2	−1.5	−10.1	−6.1
	Model 2a	1.7	−9.8	−3.7
	Best fit	1.3	−7.4	−2.8
Wambsganss	Point lens	2.97	−17.41	−4.87
& Paczyński	SIS	1.51	−8.91	−2.46
(1994)	Best fit	0.44	−2.54	−0.7
Schmidt et al.	Bar accounted	2.0	−16.2	−4.9
(1998)
Chae et al.	Triaxial model	[0.13,3.4]	[−16.6,−0.77]	[−5.5,−0.22]
(1998)

Reference	Lens model	Δt_AB/h	Δt_AC/h	Δt_AD/h
Schneider et al.	Constant	2.4	29.5	26.6
(1988)	mass-to-light ratio
	Best fit	0.54	−6.48	−6.12
	Model 1	−2.1	−11	−7.1
Rix et al. (1992)	Model 2	−1.5	−10.1	−6.1
	Model 2a	1.7	−9.8	−3.7
	Best fit	1.3	−7.4	−2.8
Wambsganss	Point lens	2.97	−17.41	−4.87
& Paczyński	SIS	1.51	−8.91	−2.46
(1994)	Best fit	0.44	−2.54	−0.7
Schmidt et al.	Bar accounted	2.0	−16.2	−4.9
(1998)
Chae et al.	Triaxial model	[0.13,3.4]	[−16.6,−0.77]	[−5.5,−0.22]
(1998)

Notes. The model 1 by Rix et al. (1992) refers to an R^1/4 profile, model 2, R^1/4 with unresolved nucleus and model 2a is identical to model 2 with only image positions fitted. The model in Schmidt et al. (1998) takes into account the central galaxy bar.

Table 10.

Open in new tab

Model predictions for the time delays (in hours) Δt_AB, Δt_AC and Δt_AD for Q2237+0305.

Reference	Lens model	Δt_AB/h	Δt_AC/h	Δt_AD/h
Schneider et al.	Constant	2.4	29.5	26.6
(1988)	mass-to-light ratio
	Best fit	0.54	−6.48	−6.12
	Model 1	−2.1	−11	−7.1
Rix et al. (1992)	Model 2	−1.5	−10.1	−6.1
	Model 2a	1.7	−9.8	−3.7
	Best fit	1.3	−7.4	−2.8
Wambsganss	Point lens	2.97	−17.41	−4.87
& Paczyński	SIS	1.51	−8.91	−2.46
(1994)	Best fit	0.44	−2.54	−0.7
Schmidt et al.	Bar accounted	2.0	−16.2	−4.9
(1998)
Chae et al.	Triaxial model	[0.13,3.4]	[−16.6,−0.77]	[−5.5,−0.22]
(1998)

Reference	Lens model	Δt_AB/h	Δt_AC/h	Δt_AD/h
Schneider et al.	Constant	2.4	29.5	26.6
(1988)	mass-to-light ratio
	Best fit	0.54	−6.48	−6.12
	Model 1	−2.1	−11	−7.1
Rix et al. (1992)	Model 2	−1.5	−10.1	−6.1
	Model 2a	1.7	−9.8	−3.7
	Best fit	1.3	−7.4	−2.8
Wambsganss	Point lens	2.97	−17.41	−4.87
& Paczyński	SIS	1.51	−8.91	−2.46
(1994)	Best fit	0.44	−2.54	−0.7
Schmidt et al.	Bar accounted	2.0	−16.2	−4.9
(1998)
Chae et al.	Triaxial model	[0.13,3.4]	[−16.6,−0.77]	[−5.5,−0.22]
(1998)

Notes. The model 1 by Rix et al. (1992) refers to an R^1/4 profile, model 2, R^1/4 with unresolved nucleus and model 2a is identical to model 2 with only image positions fitted. The model in Schmidt et al. (1998) takes into account the central galaxy bar.

5 CONCLUSIONS

Use of the first-order equations leads to a straightforward method of determining whether the deflector's mass distribution can be modelled with the SIE or ε − γ family of models, without the need of any precise model fitting. We have retrieved the same expression for the time delays between pairs of opposite lensed images as already published by Witt et al. (2000). However, combined with the first-order equations, we could easily estimate the validity of these time delay estimates and the relevance of the use of such a family of models. In order to obtain a mean astrometric error ≤0.003 arcsec, the validity range of the first-order equations has been estimated to be θ_S < 0.13 d(f) which is similar to the one already deduced for the ε − γ family of models (see Wertz et al. 2012).

Application to the quadruply imaged quasar Q2237+0305 constitutes a very interesting way of comparing the results of accurate SIE modelling with those derived from the first-order equations. We have noticed that the model parameters deduced from the first-order equations and the numerical fit are very closed. This leads to the conclusion that the numerical fit, besides being time consuming, does not bring any significant improvement in this case. The degree of misalignment has been evaluated to θ_S/d = 0.5438 > 0.13. This latter value allows us to understand why the mean astrometric error <Δx_1er order > = 0.0134 arcsec is larger than the 0.003 arcsec which corresponds to the error on the observed positions.

Unfortunately, the uncertainties obtained for the observed time delays between the light curves of pairs of lensed images make any comparison very risky. However, we have shown that in order to derive the Hubble parameter with a high precision requires very accurate values for the time delays. Therefore, we suggest that monitoring the gravitational lens system Q2237+0305 with a very high time sampling should constitute a promising way of determining accurate values of the time delays and a precise determination of the Hubble parameter based upon gravitational lensing.

We thank J. Fiege for gratefully providing his very performing Qubist Global Optimization Toolbox. OW thanks the Belgian National Fund for Scientific Research (FNRS). JS and OW acknowledge support from the Communauté française de Belgique - Actions de recherche concertées - Académie universitaire Wallonie-Europe, from the ESA PRODEX Programme ‘GAIA’, and from the Belgian Federal Science Policy Office.

1

http://cfa-www.harvard.edu/castles/

REFERENCES

Alard

C.

,

MNRAS

,

2007

, vol.

382

pg.

L58

Crossref

Search ADS

Bourassa

R. R.

Kantowski

R.

,

ApJ

,

1975

, vol.

195

pg.

13

Crossref

Search ADS

Bourassa

R. R.

Kantowski

R.

Norton

T. D.

,

ApJ

,

1973

, vol.

185

pg.

747

Crossref

Search ADS

Bray

I.

,

MNRAS

,

1984

, vol.

208

pg.

511

Chae

K.-H.

Khersonsky

V.

Turnshek

D.

,

AJ

,

1998

, vol.

506

pg.

80

Crossref

Search ADS

Fiege

J.

,

Qubist Users Guide: Optimization, Data Modeling, and Visualization with the Qubist Optimization Toolbox for MATLAB

,

2010

Winnipeg, Canada

nQube Technical Computing

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Finet

F.

,

PhD thesis

,

2013

Univ. Liège

(http://hdl.handle.net/2268/146860)

Huchra

J.

Gorenstein

M.

Kent

S.

Shapiro

I.

Smith

G.

Horine

E.

Perley

R.

,

AJ

,

1985

, vol.

90

pg.

691

Crossref

Search ADS

Keeton

C. R.

Kochanek

C. S.

,

ApJ

,

1998

, vol.

495

pg.

157

Crossref

Search ADS

Kent

S. M.

Falco

E. E.

,

AJ

,

1988

, vol.

96

pg.

1570

Crossref

Search ADS

Kochanek

C. S.

,

ApJ

,

1991

, vol.

373

pg.

354

Crossref

Search ADS

Koptelova

E.

Oknyanskij

V.

Shimanovskaya

E.

,

A&A

,

2006

, vol.

452

pg.

37

Crossref

Search ADS

Kormann

R.

Schneider

P.

Bartelmann

M.

,

A&A

,

1994

, vol.

284

pg.

285

Narayan

R.

Bartelmann

M.

,

1996

preprint (arXiv:astro-ph/9606001)

Planck Collaboration

. ,

2013

preprint (arXiv:1303.5076)

Racine

R.

,

AJ

,

1991

, vol.

102

pg.

454

Crossref

Search ADS

Refsdal

S.

,

MNRAS

,

1964a

, vol.

128

pg.

295

Crossref

Search ADS

Refsdal

S.

,

MNRAS

,

1964b

, vol.

128

pg.

307

Crossref

Search ADS

Rix

H. W.

Schneider

D. P.

Bahcall

J. N.

,

AJ

,

1992

, vol.

104

pg.

959

Crossref

Search ADS

Schmidt

R.

Webster

R.

Lewis Geraint

F.

,

MNRAS

,

1998

, vol.

295

pg.

488

Crossref

Search ADS

Schneider

D. P.

Turner

E. L.

Gunn

J. E.

Hewitt

J. N.

Schmidt

M.

Lawrence

C. R.

,

AJ, 95, 1619; Erratum, 1988, AJ

,

1988

, vol.

96

pg.

1755

Vakulik

V.

Schild

R.

Dudinov

V.

Nuritdinov

S.

Tsvetkova

V.

Burkhonov

O.

Akhunov

T.

,

A&A

,

2006

, vol.

447

pg.

905

Crossref

Search ADS

Wambsganss

J.

Paczyński

B.

,

AJ

,

1994

, vol.

108

pg.

1156

Crossref

Search ADS

Wertz

O.

Pelgrims

V.

Surdej

J.

,

MNRAS

,

2012

, vol.

424

pg.

1543

Crossref

Search ADS

Witt

H.

Mao

S.

Keeton

C.

,

AJ

,

2000

, vol.

544

pg.

98

Crossref

Search ADS

Author notes

†

E-mail: [email protected]

‡

Also Directeur de Recherche honoraire du F.R.S. -FNRS.

Download all slides

Month:	Total Views:
February 2017	2
March 2017	2
April 2017	2
May 2017	1
August 2017	2
September 2017	1
October 2017	4
November 2017	1
December 2017	6
January 2018	5
February 2018	3
March 2018	14
April 2018	3
May 2018	1
June 2018	6
July 2018	10
August 2018	6
September 2018	8
October 2018	4
November 2018	7
December 2018	6
January 2019	2
February 2019	9
March 2019	10
April 2019	7
May 2019	13
June 2019	7
July 2019	4
August 2019	3
September 2019	3
October 2019	3
November 2019	6
December 2019	2
January 2020	5
February 2020	1
March 2020	2
April 2020	3
May 2020	2
June 2020	3
July 2020	7
August 2020	2
September 2020	2
October 2020	6
November 2020	1
December 2020	4
February 2021	4
March 2021	9
April 2021	3
May 2021	2
June 2021	6
July 2021	11
August 2021	3
September 2021	3
October 2021	11
November 2021	3
December 2021	4
January 2022	7
February 2022	1
March 2022	7
April 2022	10
May 2022	4
July 2022	13
August 2022	30
September 2022	8
October 2022	4
November 2022	16
December 2022	6
January 2023	8
February 2023	8
March 2023	18
April 2023	11
May 2023	5
June 2023	4
July 2023	6
August 2023	44
September 2023	13
October 2023	4
November 2023	20
December 2023	22
January 2024	10
February 2024	45
March 2024	26
April 2024	13
May 2024	10
June 2024	6
July 2024	16
August 2024	9
September 2024	25
October 2024	31
November 2024	21
December 2024	6
January 2025	15
February 2025	10
March 2025	32
April 2025	10
May 2025	3

Article Contents

Asymptotic solutions for the case of SIE lens models and application to the quadruply imaged quasar Q2237+0305

Abstract

1 INTRODUCTION

2 THE SINGULAR ISOTHERMAL ELLIPSOID MODEL

3 FIRST-ORDER EQUATIONS AND SOLUTIONS

3.1 Small deviations from the perfect alignment

3.2 The SIE lens model parameters

3.3 The degeneracy affecting the value of ϖ

3.4 Time delays and the Hubble parameter

3.5 Validity range of the first-order equations

4 APPLICATION TO A REAL CASE: Q2237+0305

5 CONCLUSIONS

REFERENCES

Author notes

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Asymptotic solutions for the case of SIE lens models and application to the quadruply imaged quasar Q2237+0305

Abstract

1 INTRODUCTION

2 THE SINGULAR ISOTHERMAL ELLIPSOID MODEL

3 FIRST-ORDER EQUATIONS AND SOLUTIONS

3.1 Small deviations from the perfect alignment

3.2 The SIE lens model parameters

3.3 The degeneracy affecting the value of ϖ

3.4 Time delays and the Hubble parameter

3.5 Validity range of the first-order equations

4 APPLICATION TO A REAL CASE: Q2237+0305

5 CONCLUSIONS

REFERENCES

Author notes

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only