On the effect of the ionizing background on the Lyα forest autocorrelation function

Gontcho A Gontcho, Satya; Miralda-Escudé, Jordi; Busca, Nicolás G.

doi:10.1093/mnras/stu860

Abstract

An analytical framework is presented to understand the effects of a fluctuating intensity of the cosmic ionizing background on the correlations of the Lyα forest transmission fraction measured in quasar spectra. In the absence of intensity fluctuations, the Lyα power spectrum should have the expected cold dark matter power spectrum with redshift distortions in the linear regime, with a bias factor b_δ and a redshift distortion parameter β that depend on redshift but are independent of scale. The intensity fluctuations introduce a scale dependence in both b_δ and β, but keeping their product b_δβ fixed. Observations of the Lyα correlations and cross-correlations with radiation sources like those being done at present in the Baryon Oscillation Spectroscopic Survey of Sloan Digital Sky Survey third generation have the potential to measure this scale dependence, which reflects the biasing properties of the sources and absorbers of the ionizing background. We also compute a second term affecting the Lyα spectrum, due to shot noise in the sources of radiation. This term is very large if luminous quasars are assumed to produce the ionizing background and to emit isotropically with a constant luminosity, but should be reduced by a contribution from galaxies, and by the finite lifetime and anisotropic emission of quasars.

intergalactic medium, quasars: absorption lines, diffuse radiation, large-scale structure of Universe

1 INTRODUCTION

The Lyα forest absorption measured in spectra of high-redshift quasars has now been established as a powerful tracer of large-scale structure. Assuming that the intrinsic continuum spectrum of the observed quasar can be accurately modelled, then the observed flux divided by the fitted continuum yields the transmitted fraction, F = e^{− τ} (where τ is the optical depth), at every wavelength pixel. This one-dimensional map that is obtained from the spectrum of every observed source is related (neglecting the contamination by metal lines) to the gas density, temperature and peculiar velocity of the hydrogen gas in the intergalactic medium that is intercepted by the line of sight.

After the initial measurements of the Lyα power spectrum along the line of sight from individual spectra (Croft et al. 1998, 1999, 2002; McDonald et al. 2000, 2006), the first determination of the power spectrum of the Lyα forest in three-dimensional redshift space came with the Baryon Oscillation Spectroscopic Survey (BOSS) of Sloan Digital Sky Survey third generation (SDSS-III; Eisenstein et al. 2011; Dawson et al. 2013). Analysis of the first 14 000 quasars led to the detection of redshift space distortions (Slosar et al. 2011), as expected in a simple biased linear theory where the Lyα power spectrum follows that of the dark matter with two bias parameters, reflecting the large-scale variation of the mean Lyα transmission with the fluctuation in the mean mass density and peculiar velocity gradient.

However, large-scale fluctuations in the Lyα forest can also be affected by variations in the intensity of the ionizing background radiation, as well as the imprint that reionization may have left on the gas temperature distribution as a function of gas density. These effects have been studied and discussed by several authors in the past. Analytic models of randomly distributed sources were considered by Zuo (1992), and numerical realizations of random sources to compute the fluctuation properties of the ionizing background were used in several subsequent papers (Croft et al. 1999; Croft 2004; Meiksin & White 2004; McDonald et al. 2005; Slosar et al. 2009; White et al. 2010). The impacts of these ionizing background fluctuations on the Lyα forest were found to be generally small compared to the intrinsic Lyα forest fluctuations due to the large-scale structure of the mass distribution. However, as pointed out in the early work of Croft et al. (1999), the long mean free path of ionizing radiation in the intergalactic medium at z ∼ 3 implies that the fluctuations induced by the ionizing background can become relatively more important in the limit of very large scales. These large scales are now becoming highly relevant with the recent detections of the baryon acoustic oscillation (BAO) peak in the Lyα forest (Busca et al. 2013; Slosar et al. 2013; Delubac et al. 2014; Font-Ribera et al. 2014).

In this paper, we reanalyse with an analytic method the impact of large-scale fluctuations in the ionizing radiation intensity and the gas temperature–density relation on the observable redshift space Lyα power spectrum. There are two independent effects on the power spectrum. The first arises from the clustering of sources and absorbers of radiation, which are assumed to trace the large-scale mass density fluctuations, each with their own bias factor. This clustering term is independent of the luminosity function, variability and anisotropic emission of the sources, as well as the size or other geometric properties of the absorbers: it depends only on how the density of sources and absorbers follow the underlying large-scale structure. The second effect is due to the fluctuations in the radiation intensity that arises from shot noise in the number of sources. This second term is independent of the source clustering, but depends on other source characteristics like the luminosity function. An analytical framework to treat these contributions to the Lyα power spectrum is described in Section 2, and results for simple illustrating models are presented in Section 3, with a discussion and conclusions in Section 4. We use a cold dark matter cosmological model with parameter values that are consistent with Ade, Efstathiou, Planck Collaboration (2014): H₀ = 67.3 km s⁻¹ Mpc⁻¹, baryon density Ω_b h² = 0.022 05, Ω_m = 0.315, n_s = 0.96 and σ₈ = 0.856.

As this paper was being finalized, we became aware of the work by Pontzen (2014), presenting very similar ideas as here. We mention in Section 4 the similarities and differences between the two papers.

2 ANALYTIC FORMALISM

The use of the Lyα forest as a tracer of large-scale structure lies on the principle that, when averaged over a large scale, the mean value of the transmission fluctuation through the Lyα forest, |$\delta _\alpha =F/\bar{F}(z)-1$| (where F is equal to the observed flux divided by a model quasar continuum, and |$\bar{F}$| is the mean value of F over all the Universe at redshift z), has a linear relation to the local deformation tensor of large-scale structure when smoothed in the same way over a large scale. On small scales, the distribution of δ_α and its correlations have a complex dependence on the physics of non-linear collapse of the intergalactic gas into filaments and haloes, and the shock-heating, ionization and cooling of the gas. However, on large scales, all these effects are absorbed into a first-order dependence of δ_α on the local deformation tensor in the linear regime (e.g. Kaiser 1987),

\begin{equation} {1\over H(z)}{\rm{\partial} v_i\over \rm{\partial} x_j} , \end{equation}

(1)

where |${\boldsymbol v}$| is the peculiar velocity smoothed over a large scale in the same way as F, x is the comoving coordinate and H(z) is the Hubble constant at redshift z. For an observer measuring F along a direction specified by a unit vector |${\boldsymbol n}$|⁠, there are two first-order scalars that can be obtained from the deformation tensor: its trace, H^{− 1}∂v_i/∂x_i = f(Ω_m)δ, where f(Ω_m) = dlog D(a)/dlog a is the logarithmic derivative of the growth factor D(a), and the peculiar velocity gradient along the line of sight, η = n_in_j(∂v_i/∂x_j)/H. Therefore, the fluctuation in the Lyα transmission must be given to first order by a linear combination of δ and η, with two bias factors, b_δ = ∂δ_α/∂δ and b_η = ∂δ_α/∂η, with numerical values that depend on redshift and on the small-scale physics of the intergalactic gas (McDonald et al. 2000; McDonald 2003; Slosar et al. 2009, 2011). Whereas galaxy surveys require only one bias factor to relate galaxy density to mass density fluctuations, the Lyα forest requires two of them because of the non-linear transformation from the Lyα optical depth to the observed transmission fraction, which alters the dependence on the direction vector of the observation |${\boldsymbol n}$|⁠.

This dependence on δ and η is only valid, however, if one assumes that no other independent physical quantities that are correlated on large scales can affect the value of δ_α; in particular, a homogeneous ionizing background intensity is assumed. The quantity that matters for determining the Lyα transmission is the photoionization rate, |$\Gamma ({\boldsymbol x})$|⁠, obtained from the integration over frequency of the background intensity times the cross-section. Its fluctuation is |$\delta _\Gamma ({\boldsymbol x})= \Gamma ({\boldsymbol x})/\bar{\Gamma }- 1$|⁠. Including these large-scale variations of the photoionization rate, the total Lyα transmission fluctuation smoothed over a large scale is

\begin{equation} \delta _{\alpha }({\boldsymbol x})=b_{\delta }\delta ({\boldsymbol x}) + b_{\eta }\eta ({\boldsymbol x})+b_{\Gamma }\delta _{\Gamma }({\boldsymbol x}), \end{equation}

(2)

where |$b_\Gamma$| is now a third bias factor for the photoionization rate. Therefore, the total Lyα correlation depends now not only on the correlations of δ and η (which are related to the primordial linear power spectrum with redshift distortions) but also on the correlation of |$\delta _\Gamma$| with itself, δ and η. We now compute these correlations, and we will do this taking into account two different effects: the fact that sources are clustered and trace the mass fluctuations, and the shot noise due to the random distribution of discrete sources.

2.1 Source clustering

We assume that the sources of the ionizing background have a spatial distribution tracing the mass density field, with a bias factor b_s, so the mean large-scale overdensity of sources is δ_s = b_sδ. In addition, the ionizing radiation is being absorbed by a population of absorbers, which are Lyman limit systems as well as absorption systems with Lyman continuum optical depths below unity that have a comparable contribution to the overall absorption. This population of absorbers has a large-scale distribution that is affected by both the underlying mass density fluctuations and the radiation intensity fluctuations. So, the absorber density fluctuation can be written as |$\delta _{\rm a} = b_{\rm a}\delta + b_{\rm a}^{\prime }\delta _{\Gamma }$|⁠. We expect these absorbers to increase in high-density regions and decrease in response to an increased ionizing intensity, so b_a should be positive and |$b_{\rm a}^{\prime }$| should be negative.

Even though the opacity to ionizing photons depends on frequency, and a detailed treatment has to include the intensity spectrum and the combined effect of absorption and redshift modifying the background spectrum compared to that emitted by the sources, here we shall treat the opacity as a single quantity, neglecting the effect of redshift. The opacity due to absorbers with density fluctuation δ_a is |$\kappa ({\boldsymbol x}) = \kappa _0[1+\delta _{\rm a}({\boldsymbol x})]$|⁠, where the average mean free path for an ionizing photon is |$\lambda _0 = \kappa _0^{-1}$|⁠. The radiation intensity fluctuation at a point |$\boldsymbol x$| due to the combination of all sources at any position |$\boldsymbol x$|+|${\boldsymbol r}$| is

\begin{equation} \delta _{\Gamma }({\boldsymbol x}) = \int {\rm d}^3r\, \kappa _0 \frac{[1+\delta _{\rm s}({\boldsymbol x}+{\boldsymbol r})]{\rm e}^{-\tau ({\boldsymbol x},{\boldsymbol r})} - {\rm e}^{-\kappa _0 r}}{4\pi r^2}, \end{equation}

(3)

where r is the modulus of the vector |${\boldsymbol r}$|⁠. Defining also |${\boldsymbol u}_r$| to be the unit vector in the direction |${\boldsymbol r}$|⁠, the optical depth from |${\boldsymbol x}$| to |$\boldsymbol x$|+|${\boldsymbol r}$| is

\begin{eqnarray} \tau ({\boldsymbol x},{\boldsymbol r})&=& \int ^r_0 \rm{d}y\, \kappa _0 [1+\delta _{\rm a}({\boldsymbol x}+y{\boldsymbol u}_r)]\nonumber \\ &=&\kappa _0 r \left[1+\int ^r_0\frac{{\rm d}y}{r}\delta _{\rm a}({\boldsymbol x}+y{\boldsymbol u}_r)\right] . \end{eqnarray}

(4)

Neglecting second-order terms in δ_s and δ_a, equation (3) is simplified to

\begin{eqnarray} \delta _{\Gamma }({\boldsymbol x})& =&\int \frac{{\rm d}{\boldsymbol u}_r}{4\pi } \int ^{\infty }_0\rm{d}r \kappa _0\, {\rm e}^{-\kappa _0 r} \nonumber \\ && \times \left[\delta _{\rm s}({\boldsymbol x}+r{\boldsymbol u}_r) - \kappa _0 \int ^r_0 \rm{d}y \, \delta _{\rm a}({\boldsymbol x}+y{\boldsymbol u}_r)\right] . \end{eqnarray}

(5)

For the second term involving the absorbers, the order of the integrals over r and y can be inverted, and we find

\begin{eqnarray} &&\!\!\!\int ^{\infty }_0 \rm{d}r \kappa _0^2 {\rm e}^{-\kappa _0 r} \int ^{r}_0{\rm d}y\delta _{\rm a}({\boldsymbol x}+y{\boldsymbol u}_r) \nonumber \\ &&\quad=\int ^{\infty }_0 \rm{d}y\, \kappa _0^2\delta _{\rm a}({\boldsymbol x}+y{\boldsymbol u}_r) \int ^{\infty }_y \rm{d}r {\rm e}^{-\kappa _0 r}\nonumber \\ &&\quad=\int ^{\infty }_0 \rm{d}y\, \kappa _0 {\rm e}^{-\kappa _0 y} \delta _{\rm a}({\boldsymbol x}+y{\boldsymbol u}_r) , \end{eqnarray}

(6)

and so finally, changing the name of the dummy variable y back to r, and re-expressing the integral in terms of the variable |${\boldsymbol x}^{\prime }={\boldsymbol x}+{\boldsymbol r}$|⁠, we get

\begin{equation} \delta _{\Gamma }({\boldsymbol x})=\int \frac{{\rm d} {\boldsymbol x^{\prime }}}{4\pi r^2} [\delta _{\rm s}({\boldsymbol x^{\prime }})-\delta _{\rm a}(({\boldsymbol x^{\prime }})]\kappa _0 {\rm e}^{-\kappa _0 r} . \end{equation}

(7)

This result is easy to understand, because an absorber actually acts in the same way as a negative source in this linear regime.

We now replace |$\delta _{\Gamma }({\boldsymbol x})$| and |$\delta _{\rm s}({\boldsymbol x^{\prime }})$|⁠, |$\delta _{\rm a}({\boldsymbol x^{\prime }})$| in equation (7) by their Fourier transforms, invert the order of the integrals over |${\boldsymbol k}$| and |${\boldsymbol x}^{\prime }$|⁠, and do the integral over |${\boldsymbol x}^{\prime }$|⁠, to find that the Fourier transforms are related by

\begin{eqnarray} \delta _{\Gamma }({\boldsymbol k}) &=& [\delta _{\rm s}({\boldsymbol k})-\delta _{\rm a}({\boldsymbol k})]\, W{\left(\frac{k}{\kappa _0}\right)}\nonumber \\ &=& [(b_{\rm s}-b_{\rm a})\delta ({\boldsymbol k}) - b^{\prime }_{\rm a}\delta _{\Gamma }({\boldsymbol k})]\, W{\left(\frac{k}{\kappa _0}\right)} , \end{eqnarray}

(8)

where

\begin{equation} W(s)=\int ^{\infty }_0 \rm{d}x\, \frac{{\rm e}^{-x}\sin {(sx)}}{sx} = \frac{{\rm arctan}(s)}{s} . \end{equation}

(9)

Writing now equation (2) in Fourier space, and suppressing dependences on k for brevity, the correlation of the Fourier modes of the Lyα transmission fluctuation is

\begin{eqnarray} \langle \delta _{\alpha }\delta _{\alpha }\rangle & = &b^2_{\delta }\langle \delta \delta \rangle + b^2_{\eta }\langle \eta \eta \rangle + b^2_{\Gamma }\langle \delta _{\Gamma }\delta _{\Gamma }\rangle \nonumber \\ && +\, 2b_{\delta } b_{\eta }\langle \delta \eta \rangle + 2b_{\delta }b_{\Gamma }\langle \delta \delta _{\Gamma }\rangle + 2b_{\eta }b_{\Gamma }\langle \eta \delta _{\Gamma }\rangle . \end{eqnarray}

(10)

Using the linear redshift distortion theory of Kaiser (1987), the Fourier modes of δ and η are related by |$\eta =f(\Omega _{\rm m})\mu _k^2\delta$|⁠, where |$\mu _k\equiv {\boldsymbol n}\cdot {\boldsymbol k}/k$|⁠, and the power spectrum without including the radiation term |$\delta _\Gamma$| can be written as usual in the form |$b_\delta ^2(1+\beta \mu _k^2)^2$|⁠, where the redshift distortion parameter is β = f(Ω_m)b_η/b_δ. When the radiation term is included and expressed as a function of δ using equation (8), we find that the total Lyα power spectrum is given by

\begin{equation} P_{\alpha }(k,\mu _k) = P_{\rm L}(k)\, b_{\delta }^{^{\prime }2}(k) \left[1+\beta ^{\prime }(k)\mu _k^2\right]^2 , \end{equation}

(11)

where

\begin{equation} b_{\delta }^{\prime }(k)= b_{\delta } + b_{\Gamma } \frac{(b_{\rm s}-b_{\rm a})W(k/\kappa _0)}{1+ b^{\prime }_{\rm a}W(k/\kappa _0)} \end{equation}

(12)

and |$\beta ^{\prime }(k)= b_\delta \beta /b_\delta ^{\prime }(k)= b_\eta f(\Omega _{\rm m})/b_\delta ^{\prime }(k)$|⁠.

Therefore, the effect of the photoionization rate fluctuations that is induced by the clustering of sources and absorbers is to modify the bias factor and redshift distortion parameter in the power spectrum, replacing them with the effective values |$b_\delta ^{\prime }$| and β′ that are scale dependent, while their product |$b_\delta ^{\prime }\beta ^{\prime }=b_\delta \beta$| remains fixed. At small scales, W is very small and the bias factor has its usual value |$b^{\prime }_{\delta }=b_{\delta }$|⁠. But in the limit of large scales, W approaches unity and |$b_{\delta }^{\prime }$| reaches the asymptotic value of |$b_{\delta }+b_{\Gamma }(b_{\rm s}-b_{\rm a})/(1+b_{\rm a}^{\prime })$|⁠.

We now interpret physically the variation of the effective bias |$b_\delta ^{\prime }$| with the Fourier scale k. We mention first that any realistic model for the absorbers needs to have |$0 > b_{\rm a}^{\prime } > -1$|⁠: the density of absorbers (which we identify with the observed population of Lyman limit systems, as well as lower column density systems that also contribute to the global absorption of ionizing photons) needs to decrease with |$\delta _\Gamma$| as the increased photoionization reduces the size of the absorbing regions, but the relative fluctuation in absorbers cannot be reduced faster than that in the ionizing intensity because this would imply a runaway unstable process where any slight increase in emission leads to an arbitrarily large increase in the mean free path and the ionizing intensity as the absorbers are completely ionized. Moreover, the sign of b_δ is negative while that of b_Γ is positive, so if b_s > b_a, the effective bias factor |$b_{\delta }^{\prime }$| decreases in absolute value with scale. The simple interpretation is that on scales larger as compared to the mean free path of ionizing photons, denser regions also have a greater ionizing intensity, and so the corresponding increase of Lyα absorption that is caused by the higher density is reduced. If |$b_\Gamma (b_{\rm s}-b_{\rm a})/(1+b_{\rm a}^{\prime })$| is larger than −b_δ, then the value of |$b_\delta ^{\prime }$| is actually positive in the limit of large scales. Ignoring for now the effect of the peculiar velocity gradient (we return to this in Section 3), this means that the effect of the higher ionizing intensity overwhelms that of the higher mass density, causing denser regions to have an increased Lyα transmission (or reduced absorption), opposite to the behaviour on small scales. In this case, there needs to be a critical scale k_r where |$b_\delta ^{\prime }$| has a root, and the only surviving term for the power spectrum in equation (11) is |$P_\alpha (k_r)= P_{\rm L}(k_r) (b_\delta \beta \mu _k^2)^2$|⁠. In practice, the power spectrum near μ_k = 0 can never quite go down to zero owing to the shot noise from individual sources of radiation, as discussed below, as well as non-linear effects from small scales which we are not including here, but a change of sign of |$b_\delta ^{\prime }$| as a function of scale still implies the presence of a dip in the power spectrum at small μ_k which should be measurable in the observations.

2.2 Shot noise from individual sources

Our treatment so far includes only the correlation of sources and absorbers with the matter density fluctuations. Next, we consider the term that is added to the correlation function because of the shot noise from individual sources. We assume that all the ionizing sources emit their radiation isotropically at a constant luminosity. As we shall discuss below, this assumption is crucial for our computation of the shot noise term, even though it does not affect the source clustering term calculated above. We start defining the source luminosity function, per unit of volume, as Φ(L). The mean emissivity of the ionizing sources is

\begin{equation} \epsilon _{\rm q} = \int _0^\infty \rm{d}L\Phi (L)L . \end{equation}

(13)

If all the sources have the same luminosity, the power spectrum of the relative emissivity fluctuations is simply equal to the inverse of the source density, 1/n_s = L/ϵ_q. With a distribution of luminosities, the fraction of the emissivity provided by sources of luminosity L is LΦ(L) dL/ϵ_q, and therefore the overall power spectrum is equal to the constant

\begin{equation} 4\pi C=\int _0^\infty \rm{d}L\, \frac{\Phi (L)L^2}{\epsilon _{\rm q}^2} , \end{equation}

(14)

where we have introduced the factor 4π in the definition of C for later convenience. The intensity correlation can now be obtained by multiplying by the kernel in equation (9), and applying the Fourier transform. It is also instructive, however, to directly compute the correlation function by considering the correlated intensity at two spatial positions separated by a distance x caused by the flux that arrives at the two points from the same individual sources.

We choose one of the two spatial positions to be at the origin of coordinates, |${\boldsymbol r}=0$|⁠, and the other one to lie on the x-axis at a distance x. The ionizing intensity fluctuation at the origin is

\begin{equation} \delta _{\Gamma }(\boldsymbol {r}=0)=\sum _i\frac{L_i}{4\pi r^2_i} \frac{\kappa _0{\rm e}^{-\kappa _0 r_i}}{\epsilon _{\rm q}}-1 , \end{equation}

(15)

where the sum is over each source i located at a distance r_i from the origin. The intensity fluctuation at |${\boldsymbol x}$| is similarly expressed, replacing r_i by |$| {\boldsymbol r}_i - {\boldsymbol x} |$|⁠. Using the fact that the probability per unit of volume to find a source of luminosity L within dL at any point |${\boldsymbol r}_i$| is Φ(L) dL, the correlation function of |$\delta _\Gamma$| is then obtained as

\begin{eqnarray} \xi _{\Gamma }(x) &= & \langle \delta _{\Gamma }(\boldsymbol {r}=0)\delta _{\Gamma }(\boldsymbol {x})\rangle = \nonumber \\ && {C\over 4\pi } \int \rm{d}^3r \frac{\kappa _0^2 {\rm e}^{-\kappa _0(r+|\boldsymbol {r}-\boldsymbol {x}|)}}{r^2|\boldsymbol {r}-\boldsymbol {x}|^2} . \end{eqnarray}

(16)

We compute this integral by transforming |$\boldsymbol r$| to spherical coordinates. Defining |$\mu = {\boldsymbol r\cdot u}_x/r$|⁠, where |${\boldsymbol u}_x$| is the unit vector along the x-axis, and changing r to the variable s = r/x, the result is

\begin{eqnarray} \xi _{\Gamma }(x) &=& C \kappa _0^2 \int ^\infty _0 \frac{{\rm d}s}{x} \nonumber \\ &&\times \, \int ^1_{-1} \rm{d}\mu \, { \exp \left[-\kappa _0 x \left( s+\sqrt{1+s^2-2s\mu } \right)\right] \over 1+s^2-2s\mu } . \end{eqnarray}

(17)

This can be further re-expressed in terms of the exponential integral function, |$E_i(x)=-\int _{-x}^{\infty } {\rm d}t\, {\rm e}^{-t}/t$|⁠. The final expression for the intensity correlation function is

\begin{equation} \xi _{\Gamma }(x)= \frac{C\kappa _0^2}{x}A(\kappa _0 x) , \end{equation}

(18)

where the dimensionless function A is (replacing κ₀x = τ and κ₀r = ρ)

\begin{eqnarray} A(\tau )&=& \int _0^{\infty }{\rm d}\rho \, \frac{{\rm e}^{-\rho }}{\rho } \nonumber \\ &&\times \left[ E_i\left(- \rho \sqrt{1+\frac{\tau ^2}{\rho ^2}}\right) - E_i\left(- \rho \left|1-\frac{\tau }{\rho }\right|\right)\right] . \end{eqnarray}

(19)

The function A is plotted in Fig. 1.

Figure 1.

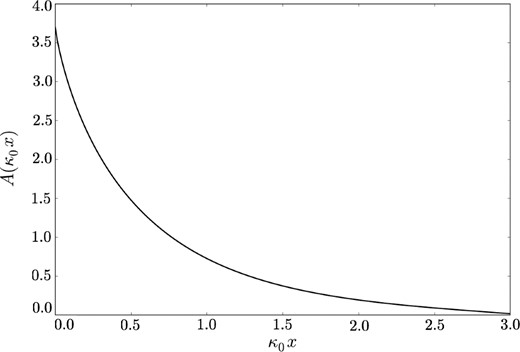
The dimensionless function A defined in equation (19), giving the shape of the intensity correlation function due to a set of randomly distributed, isotropic and constant sources of radiation.

Open in new tab Download slide

The sources that dominate the fluctuations in the ionizing radiation intensity are the most luminous ones, which are well known from observations of the quasar luminosity function. We now estimate the constant C from recent measurements of the quasar luminosity function by Ross et al. (2013), who used the BOSS survey of the SDSS-III Data Release 9 (see Eisenstein et al. 2011; Ahn et al. 2012; Dawson et al. 2013). The quasar luminosity function was fitted to a double power law of the form

\begin{equation} \Phi _{\rm q}(L)\,{\rm d}L=\frac{\Phi _{*}/L_*}{(L/L_*)^{-\alpha } + (L/L_*)^{-\gamma }}\, {\rm d}L . \end{equation}

(20)

The values of the fitted parameters obtained by Ross et al. (2013) are α = 1.52, γ = 3.10 and |$\Phi ^{(R)}_{*}=10^{-6.37}\, {\rm Mpc}^{-3}\,{\rm mag}^{-1}$|⁠, where they defined |$\Phi ^{(R)}_{*}$| to be a number density of quasars per unit of absolute magnitude. We convert their value |$\Phi ^{(R)}_{*}$| to our cosmological model, at z = 2.25 (the model used by Ross et al. 2013 had Ω_m = 0.30 and H₀ = 70 km s⁻¹ Mpc⁻¹) and to our units, finding Φ_* = 1.42 × 10⁻⁶( h⁻¹ Mpc)⁻³. With these numbers, we compute the quantity C_q for quasars using equation (14), and we find C_q = 9.5 × 10⁴( h^{− 1} Mpc)³. Note that the value of C_q is independent of L_*, and depends only on Φ_* and the shape of the luminosity function. The value of C_q diverges as γ approaches 3, so the fitted value of γ = 3.1 from Ross et al. (2013) implies a large uncertainty of C_q depending on the exact shape of the luminosity function at the high-luminosity end.

The intensity of the ionizing background is likely to have a contribution from galaxies, in addition to quasars. Assuming that all galaxies are much less luminous than the quasars that contribute appreciably to the constant C_q, then the faint galactic sources can increase the mean intensity, but can be neglected for the fluctuations, i.e. their contribution to the integral ∫dL Φ(L)L² is negligible. In that case, equation (14) implies that the emissivity power spectrum amplitude is determined by the constant

\begin{equation} C=\frac{\epsilon _{\rm q}^2 C_{\rm q}}{(\epsilon _{\rm g} + \epsilon _{\rm q})^2} , \end{equation}

(21)

where ϵ_g and ϵ_q are the emissivities of galaxies and quasars. The correlation due to shot noise is therefore reduced as the contribution from galaxies to the ionizing intensity is increased.

Apart from the effect of galaxies, the amplitude of the intensity correlation function contributed by shot noise from the observed quasars that is obtained from equation (18) ought to be considered as an upper limit only. The reason is that real quasars are likely to emit anisotropically and to be highly variable in their luminosity on the light-crossing time of the cosmological scales at which the correlations are being measured. The effects of the variability and anisotropy of the emission from individual quasars can be highly complex and difficult to model, but an order-of-magnitude estimate can be made by assuming the opposite limit in which quasars emit in very narrow cones and short bursts. If |$f_\Omega$| is the fraction of the solid angle over which the light of a quasar is emitted, f_t is the fraction of time during which a quasar is shining and we assume that the quasar luminosity is zero outside of this fraction of solid angle and time, then the correlation function |$\xi _\Gamma$| in equation (18) is reduced by a factor |$f_\Omega f_{\rm t}$|⁠, because assuming that a source is being observed at a point |${\boldsymbol r}=0$|⁠, the probability that it is also observed at a point |${\boldsymbol x}$| with the same luminosity is only |$f_\Omega f_{\rm t}$|⁠.

The total correlation function of the Lyα transmission is equal to the sum of the term due to source clustering, from equation (11), and the shot noise term in equation (18) multiplied by |$b_\Gamma ^2$|⁠.

2.3 Values of the bias parameters

We now discuss how the values of the various bias parameters that have appeared in our derivation of the radiation effects in the Lyα correlation function can be estimated. All the bias factors should generally depend on redshift, and our discussion here will be focused at z = 2.25, the redshift near which the observations of Lyα correlations have so far been done with the BOSS survey.

We start with the bias factor that relates the ionizing intensity fluctuations to the Lyα transmission fluctuations. As described in (Font-Ribera et al. 2013, see their equation 5.4), this bias factor can easily be calculated from its definition as |$b_\Gamma = \rm{\partial} \delta _\alpha / \rm{\partial} \delta \Gamma$|⁠, where the values δ_α and |$\delta _\Gamma$| are smoothed over sufficiently large, linear scales, if the true, unsmoothed distribution of the Lyα transmission is known, and under two additional assumptions: photoionization equilibrium in a highly ionized medium (neglecting any contribution from collisional ionization), and that any changes of temperature and hydrodynamic evolution of the intergalactic gas with the ionizing background intensity can be neglected (in a more detailed treatment, small temperature variations would likely be induced by changes in the spectral shape of the ionizing background rather than its intensity). In this case, the effect of the ionizing intensity fluctuations is simply to divide the Lyα optical depth by a factor |$1+\delta _\Gamma$| at every pixel in the spectrum. If P(F) is the unsmoothed probability distribution of F, one obtains

\begin{equation} b_\Gamma = - {1\over \bar{F}} \int _0^1 \rm{d}F\, P(F)\, F\, \log (F) . \end{equation}

(22)

At z = 2.25, the distribution of the Lyα optical depth, τ = −log F, can be approximated as a lognormal function, constrained to produce a mean transmission |$\bar{F}=0.8$| and a dispersion in the transmission σ_F = 0.124. This distribution yields a value |$b_\Gamma \simeq 0.13$|⁠.

The values of b_δ and b_η have to be measured observationally. They are related to the redshift distortion parameter by β = f(Ω_m)b_η/b_δ (Kaiser 1987). Measurements from the Lyα forest correlation in the scale range 10-60 h^{− 1} Mpc in Slosar et al. (2011) resulted in a good measurement of b_δ(1 + β) = −0.336 ± 0.012 at z = 2.25, with a more poorly constrained β ∼ 1. We shall assume β = 1, which is also favoured by the measurement of cross-correlations (see Font-Ribera et al. 2012b, 2013), and b_δ = −0.17 (so b_η = βb_δ/f(Ω_m) ≃ −0.17; note that the negative sign of b_δ and b_η results from the convention that δ_α is a transmission fluctuation, which is therefore negative when the mass density perturbation is positive). These observational results may change in the future since they were obtained by neglecting the radiation effects that are examined here, and they are subject to other possible systematic errors (e.g. Font-Ribera & Miralda-Escudé 2012a).

For the bias of the sources, quasars have had their bias factor measured from their autocorrelation (White et al. 2012, and references therein) and cross-correlation with the Lyα forest (Font-Ribera et al. 2013), resulting in values in the range 3.5–4. The actual bias of the sources, however, depends also on the contribution that galaxies make to the ionizing background intensity and on the bias factor of these galaxies. If the bias factors of quasars and galaxies are b_q and b_g, then b_s = (ϵ_qb_q + ϵ_gb_g)/(ϵ_q + ϵ_g). Galaxies are on average associated with lower mass haloes than quasars, so their bias factor should be smaller and therefore b_s should be lower than b_q.

The population of absorbers determining the mean free path of the ionizing radiation is dominated by systems that have an optical depth of order unity at the Lyman limit, with column densities ∼ 1.6 × 10¹⁷ cm^{− 2}. Note that only systems with column densities above this value are usually referred to as Lyman limit systems, but absorbers of lower column density are about equally important (e.g. Miralda-Escudé & Ostriker 1990; Haardt & Madau 1996). The bias factor has only been measured for systems of higher column densities, the damped Lyα systems (Font-Ribera et al. 2012b), and a value b_a ≃ 2 was obtained. Lyman limit systems are of lower column density than the damped systems but they should have a similar bias factor if haloes of all masses give rise to the same distribution of hydrogen column densities, depending on the impact parameter. However, a population of low-mass haloes might exist in which the self-shielded gas does not reach as high column densities as in high-mass haloes, which would then reduce the mean bias factor of the Lyman limit systems. Both b_s and b_a are therefore rather uncertain. The effective Lyα forest bias depends only on the difference b_s − b_a (see equation 12), for which we shall assume a fiducial value b_s − b_a = 1.

Finally, the bias factor controlling the response of the absorbers to changes in the ionizing intensity can be related to the column density distribution of Lyman limit systems, which we model as a power law, |$f(N_{{\rm H\,{\small i}}}) \, {\rm d}N_{{\rm H\,{\small i}}}\propto N_{{\rm H\,{\small i}}}^{-a}\, {\rm d}N_{{\rm H\,{\small i}}}$|⁠. This implies a radial profile of the column density in spherical haloes |$N_{{\rm H\,{\small i}}}\propto r^{2/(1-a)}$|⁠. In photoionization equilibrium, the column density at a fixed radius r outside the region where the gas starts to self-shield will vary in proportion to the inverse of the photoionization rate. The self-shielding radius r_s occurs at a fixed column density, and will therefore change as r_s∝Γ^{(1 − a)/2} in response to a change of the external ionizing intensity. The cross-section to produce a Lyman limit system scales as |$r_{\rm s}^2$|⁠, so the number of absorbers that are intercepted per unit length should scale as Γ^1 − a. For small changes in Γ, this implies a bias factor |$b_{\rm a}^{\prime }=1-a$|⁠. We shall use here a = 5/3 (the value corresponding to a gas density profile ρ_g∝r^{− 2}, and |$N_{_{{\rm H\,{\small i}}}}\propto r^{-3}$|⁠), and therefore |$b_{\rm a}^{\prime }=-2/3$|⁠.

With the values we adopt here for the fiducial model, the value of |$b_\delta ^{\prime }(k)$| in equation (12) is plotted in the left-hand panel of Fig. 2 as the solid line. Here and in the rest of the paper, we use a mean free path λ₀ = 300 h⁻¹ Mpc as our fiducial value. Observational estimates of the mean free path of an ionizing photon for being absorbed by hydrogen in the intergalactic medium or Lyman limit systems give a value λ₀ ≃ 350 h⁻¹ Mpc (Rudie et al. 2013). Our approximate treatment in Section 2.2 neglects the redshift of the photons, which effectively acts in the same way as an additional source of opacity with a comoving mean free path of the order of the horizon, c(1 + z)/H(z) ≃ 3000 h⁻¹ Mpc. The effective overall mean free path is therefore close to our fiducial value of 300 h⁻¹ Mpc.

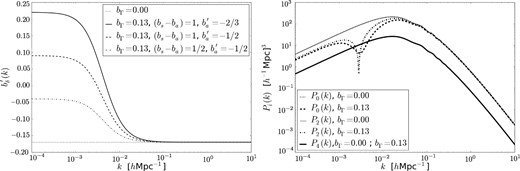
$Effective bias (left) and power spectrum (right) of the Lyα forest, for several values of the bias parameters regulating the clustering strength of sources minus absorbers (bs − ba) and the response of the absorbers to the ionizing intensity ($b_{\rm a}^{\prime }$). The dotted line is for no radiation effects, and the solid line in the left-hand panel is for our fiducial radiation model. The mean free path is fixed to λ0 = 300 h−1 Mpc. The right-hand panel shows the monopole, quadrupole and hexadecapole of the power spectrum, for the cases of no radiation fluctuations and for our fiducial radiation model.$

Figure 2.

Effective bias (left) and power spectrum (right) of the Lyα forest, for several values of the bias parameters regulating the clustering strength of sources minus absorbers (b_s − b_a) and the response of the absorbers to the ionizing intensity (⁠|$b_{\rm a}^{\prime }$|⁠). The dotted line is for no radiation effects, and the solid line in the left-hand panel is for our fiducial radiation model. The mean free path is fixed to λ₀ = 300 h⁻¹ Mpc. The right-hand panel shows the monopole, quadrupole and hexadecapole of the power spectrum, for the cases of no radiation fluctuations and for our fiducial radiation model.

Open in new tab Download slide

The two other curves in Fig. 2 are for variations of the bias values that will be used in Section 3. For our fiducial model, |$b_\delta ^{\prime }(k)$| is positive in the limit of large scales and negative at small scales, and therefore changes sign at a critical scale k_r. Depending on the uncertain values of all the bias factors we have discussed, this critical scale can have very different values, and is likely to vary substantially with redshift.

2.4 Fluctuations due to helium reionization

In addition to the intensity of the ionizing background, the intergalactic medium may be affected by other physical elements that are correlated over large scales. Here, we consider as another possibility the imprint that may have been left by helium reionization in the temperature of the intergalactic gas. At the mean baryonic density of the universe, the recombination time at z = 2.25 is much longer than the age of the universe, and so is the cooling time of photoionized gas. As helium is doubly ionized for the first time, probably by luminous quasars at z ≃ 3 (Worseck et al. 2011, and references therein), the gas is heated to a spatially variable temperature depending on the spectrum and luminosity of the sources producing the ionization fronts that eventually overlap when reionization ends (e.g. Miralda-Escudé & Rees 1994; McQuinn et al. 2009). The long cooling time then implies that the gas temperature at every spatial location may keep a memory of the time at which helium reionization occurred, or the spectral shape of the sources, or other characteristics that were imprinted at the reionization time. If the temperature fluctuates according to δ_T = b_Tδ_Γe, where δ_Γe is an intensity fluctuation of the He ii-ionizing radiation that was present at the reionization time arising from sources that may long have been dead, then the observed Lyα transmission in hydrogen would vary as δ_α = b_eδ_Γe owing to the dependence of the recombination coefficient on temperature, which follows the approximate relation α_rec(T)∝T^{− 0.7}. Using similar arguments as in Section 2.3 for deriving b_Γ, we can infer that |$b_{\rm e} = 0.7 b_\Gamma b_T$|⁠.

If the helium-ionizing radiation intensity follows the same behaviour as the radiation that ionized hydrogen, with a different mean opacity κ_0e, a similar derivation as in Section 2.1 shows that the total power spectrum that includes also the clustering term for the sources inducing the helium-reionization perturbations is the same as in equation (11), with the new bias factor

\begin{eqnarray} b_{\delta }^{\prime }(k) &=& b_{\delta } + b_{\Gamma } \frac{(b_{\rm s}-b_{\rm a})W(k/\kappa _0)}{1+ b^{\prime }_{\rm a}W(k/\kappa _0)} \nonumber \\ &&+\, b_{\rm e} \frac{(b_{{\rm s}{\rm e}}-b_{{\rm ae}})W(k/\kappa _{0{\rm e}})}{1+ b^{\prime }_{{\rm ae}}W(k/\kappa _{0{\rm e}})} , \end{eqnarray}

(23)

where the bias factors with the additional subscript e are the analogous ones for helium to those that were described for hydrogen in Section 2.1.

3 RESULTS

The correlation function of δ_α is obtained from the Fourier transform of the power spectrum in equation (11), which includes the source clustering term. To include the shot noise term, the correlation |$\xi _\Gamma$| from equation (18) multiplied by |$b_\Gamma ^2$| must be added. Following the formalism and notation of Kirkby et al. (2013, see their section 2.2), the multipole terms of the power spectrum of equation (11) have their usual form with the new scale-dependent bias factor |$b_\delta ^{\prime }(k)$| and redshift distortion parameter β′(k) (Kaiser 1987; Hamilton 1992):

\begin{equation} P_{\ell ,\alpha }(k)=P_{\rm L}(k)\, b_{\delta }^{\prime 2}(k)\, C_{\ell }[\beta ^{\prime }(k)] , \end{equation}

(24)

where

\begin{eqnarray} C_0 &=& 1+{2\over 3} \beta ^{\prime }(k) + {1\over 5} \beta ^{\prime 2}(k) , \nonumber \\ C_2 &=& {4\over 3} \beta ^{\prime }(k) + {4\over 7} \beta ^{\prime 2}(k) , \nonumber \\ C_4 &=& {8\over 35} \beta ^{\prime 2}(k) . \end{eqnarray}

(25)

The multipoles of the real space Lyα correlation function are

\begin{equation} \xi _{\ell } = \frac{i^{\ell }}{2\pi ^2}\int _0^{\infty } \rm{d}k\, k^2j_{\ell }(kr)\, P_{\ell ,\alpha }(k) , \end{equation}

(26)

where j_ℓ are the spherical Bessel functions. Note that these correlation multipoles are no longer given by the equations in Hamilton (1992) because of the scale dependence of |$b_\delta ^{\prime }$| and β′, except for the hexadecapole which does not change because |$b_\delta ^{\prime } \beta ^{\prime } = b_\delta \beta$|⁠. We have used a fast Fourier transform method to calculate these multipoles numerically.

As shown in the left-hand panel of Fig. 2, the bias factor |$b_\delta ^{\prime }(k)$| in our fiducial radiation model changes sign at a critical scale k_r ≃ 0.005 h Mpc⁻¹. The monopole, quadrupole and hexadecapole of the power spectrum are well defined and non-zero at k = k_r because |$b_\delta ^{\prime } \beta ^{\prime }$| is constant. At k < k_r, the redshift distortion parameter β′(k) is negative. While the monopole is always positive for any value of β′, the quadrupole is zero when β′(k) = −7/3, and becomes negative at small k, when −7/3 < β′ < 0. This is seen in the right-hand panel of Fig. 2, where the monopole, quadrupole and hexadecapole of the power spectrum are shown for the no radiation case, and the case that includes the source clustering effect for our fiducial values of the radiation bias parameters (the power spectrum is computed for the cold dark matter model with the parameters mentioned in the Introduction; all results for power spectra and correlation functions in this paper are shown at z = 2.25). The monopole has a dip near k = k_r, and the quadrupole has a root at the slightly smaller value of k where β′ = −7/3. The reason for this behaviour is that when |$b_\delta ^{\prime }$| is negative on large scales, high-density regions produce reduced absorption owing to the larger ionizing intensity that overwhelms the gas density effect, but the gradient of peculiar velocity counteracts that, resulting in a negative quadrupole for the power spectrum.

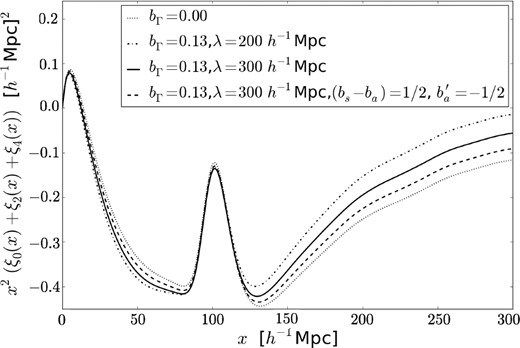
The monopole and quadrupole terms in the Lyα correlation for our fiducial case of the values of the bias parameters discussed in Section 2.3 are shown in the two panels of Fig. 3, multiplied for convenience by x². The dotted line is for a uniform ionizing background. The well-known BAO peak appears at its characteristic scale of ∼100 h⁻¹ Mpc. The dashed, solid and dash–dotted lines include the source clustering effect, with no shot noise, for three different values of the comoving mean free path: 200, 300 and 400 h⁻¹ Mpc (our fiducial value used in all other figures is λ₀ = 300 h⁻¹ Mpc). This mean free path decreases rapidly with redshift, which should change the way that intensity fluctuations modify the correlation function as the redshift increases.

Figure 3.

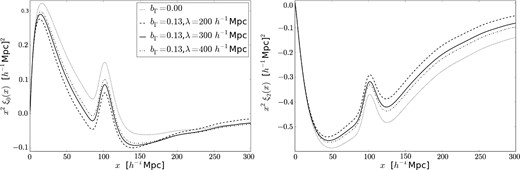
Monopole (ℓ = 0, left) and quadrupole (ℓ = 2, right) of the Lyα autocorrelation function. The dotted line is with no radiation effects, and the other three lines include them with our fiducial value of the bias factors in Section 2.3 and three different values of the mean free path.

Open in new tab Download slide

The radiation from clustered sources adds a broad-band term that is negative in the monopole and positive in the quadrupole. This is because the absolute value of the bias |$b_\delta ^{\prime }$| in equation (12) is reduced at scales smaller as compared to λ₀, as long as b_s > b_a. The shorter the mean free path, the larger the radiation effects. On scales larger than the mean free path, the impact of the radiation on the monopole becomes positive. The effects are predicted to be relatively large, and they should be measurable as long as the broad-band shape can be retrieved from the data without substantial systematic errors caused by the quasar continuum fitting operation. In the observations reported so far, broad-band terms were marginalized (Busca et al. 2013; Slosar et al. 2013; Font-Ribera et al. 2014) and therefore the effect of the ionizing intensity fluctuations would not have been detected. Note that the position of the BAO peak is practically not affected; even if the peak shifts by a small amount owing to the addition of the radiation effects, any such shift should be further reduced when fitting with a parametrized broad-band term.

Fig. 4 shows how the radiation effects vary with some of the bias parameters (again, with the monopole on the left-hand panel and the quadrupole on the right-hand panel). The dotted line (no radiation effects) and the solid line (for the fiducial values of the bias parameters in Section 2.3) are the same as in Fig. 3. The dashed line shows that the radiation effect is very insensitive to |$b_{\rm a}^{\prime }$| on scales smaller as compared to λ₀. The dash–dotted line has a reduced value of b_s − b_a, and shows that the radiation effect is basically proportional to this bias difference between sources and absorbers.

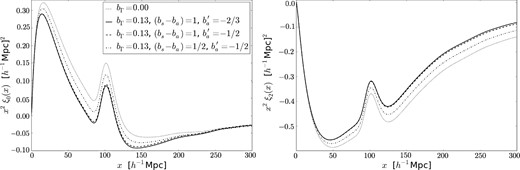
$Monopole (left) and quadrupole (right) of the Lyα autocorrelation function, for different values of the bias parameters regulating the clustering strength of sources minus absorbers (bs − ba) and the response of the absorbers to the ionizing intensity ($b_{\rm a}^{\prime }$). The dotted line is with no radiation effects. The mean free is fixed to λ0 = 300 h−1 Mpc.$

Figure 4.

Monopole (left) and quadrupole (right) of the Lyα autocorrelation function, for different values of the bias parameters regulating the clustering strength of sources minus absorbers (b_s − b_a) and the response of the absorbers to the ionizing intensity (⁠|$b_{\rm a}^{\prime }$|⁠). The dotted line is with no radiation effects. The mean free is fixed to λ₀ = 300 h⁻¹ Mpc.

Open in new tab Download slide

Observations of the correlation function (or one-dimensional power spectrum) can also be done exclusively on the line of sight (McDonald et al. 2006; Palanque-Delabrouille et al. 2013). The correlation function along the line of sight is equal to the sum of all the multipoles. The result is shown in Fig. 5 for some of the same models shown in Figs 3 and 4. This figure shows that the correlation along the line of sight on scales smaller as compared to the mean free path is much less affected by the radiation fluctuations than the three-dimensional correlation.

Figure 5.

The sum of the monopole, quadrupole and hexadecapole of the Lyα autocorrelation function. The dotted and solid lines are as in Figs 2 and 3. The dash–dotted line changes the mean free path to 200 h⁻¹ Mpc, and the dashed line shows the effect of changing the bias parameters from our fiducial model to the values indicated in the legend.

Open in new tab Download slide

A simple model for the possible helium effect on the monopole of the correlation function, computed as explained in Section 2.4, has been included in the dashed line in Fig. 6. We have assumed a mean free path for the helium reionization influence on the gas temperature of |$\lambda _{0{\rm e}}= \kappa _{0{\rm e}}^{-1}=30 \, h^{-1}\, {\rm Mpc}$|⁠, and a relation between the gas temperature fluctuation and helium-ionizing intensity fluctuation of b_T = 0.1, implying b_e = 0.0084 (see Section 2.4). The small value that we estimate for this bias factor means that the effect from the imprint on the gas temperature that may be left from double helium reionization is very small, even with a much smaller mean free path than for the case of hydrogen. However, the effects might be more substantial if different spectra of the ionizing sources in regions of different density gave rise to a larger variation of gas temperature than our assumed value b_T = 0.1.

Figure 6.

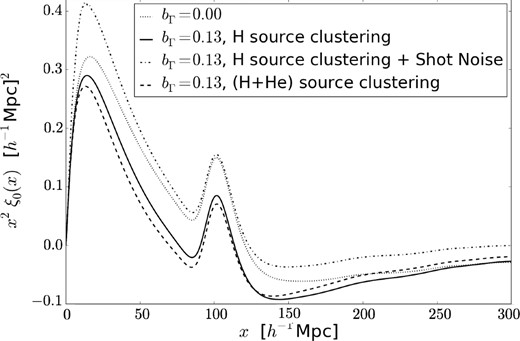
Monopole of the Lyα autocorrelation function. The dotted and solid lines are the same as in Figs 2 and 3. The dashed line includes the effect of helium reionization, assuming an influence on the gas temperature with an effective mean free path λ_0e = 30 h^{− 1} Mpc. The dash–dotted line shows the effect of adding the shot noise from individual sources, multiplied by a reduction factor as explained in the text.

Open in new tab Download slide

The effect of shot noise is also analysed in Fig. 6. The dotted and solid lines are again like in Figs 3 and 4 (only the monopole is shown here), and the dashed line adds to the solid one the shot noise term from equation (18), multiplied by |$b_\Gamma ^2$|⁠, and multiplied also by a reduction factor that we now describe. If quasars are the sources of the ionizing background with the luminosity function used in Section 2.2, and they are isotropic and constant, the shot noise is an extremely large effect which brings the value of the correlation function near the BAO peak, at x ≃ 100 h⁻¹ Mpc, to x²ξ₀(x) ≃ 2( h⁻¹ Mpc)², well above the upper bound of the axis in Fig. 6. However, as discussed at the end of Section 2.2, the shot noise term is likely to be reduced by the contribution from galaxies to the ionizing background (by the factor C/C_q in equation 21), the fraction of solid angle over which quasars emit their radiation, and the fraction of the time over which an individual quasar is emitting. For the purpose of visualization, we multiply the shot noise by the overall factor

\begin{equation} {C\over C_{\rm q}} f_\Omega f_{\rm t} = {1\over 4} {10 \, h^{-1}\, {\rm Mpc}\over {\rm max}(x, 10\, h^{-1}\, {\rm Mpc}) } . \end{equation}

(27)

The effect of variability in reducing the shot noise may reasonably be expected to scale as x⁻¹, because two points in the Lyα forest are affected by the same luminosity of a certain quasar only if they are both within the paraboloid of constant retarded time for the light emitted by the quasar that ionizes the gas producing the observed Lyα absorption, and this paraboloid has a fixed width determined by the duration of the quasar luminous phase. We stress, however, that the effects of anisotropy and variability are complicated and that here we multiply the shot noise by this simple reduction factor for display purposes.

The result in Fig. 6 shows that the shot noise can be a large and highly significant effect. Clearly, the case of constant and isotropic quasars was already ruled out by the observations of Slosar et al. (2011), which showed that the correlation function was well fitted by the linear approximation that generalizes the redshift distortion effects (Kaiser 1987) to the Lyα forest. Even with a large reduction of the shot noise term, the effects are likely to be comparable to the source and absorber clustering term, and this will make the interpretation of any observed differences from linear theory to be complicated. One can hope, nevertheless, that by combining a detailed observation of the monopole and quadrupole terms, and using joint constraints from cross-correlations of the Lyα forest with quasars and other objects in addition to the Lyα autocorrelation, the impact of the biasing of sources and absorbers and the shot noise from a complex population of ionizing sources can be disentangled in the future.

4 DISCUSSION AND CONCLUSIONS

The first observational determination of the large-scale Lyα power spectrum in redshift space by Slosar et al. (2011) showed remarkably good agreement with the simple linear theory of redshift space distortions with the cold dark matter power spectrum. The same conclusion was reached from measurements of the cross-correlations with damped Lyα systems and quasars (Font-Ribera et al. 2012b, 2013). However, the ionizing intensity fluctuations should have an impact on these correlations. We have presented an analytical framework in this paper to model these effects in the Lyα autocorrelation, which can also be easily generalized to the cross-correlation with quasars or other objects, assuming they contribute as sources of the ionizing background. Our conclusion from the results obtained in a few illustrating cases is that both the clustering term that measures how sources and absorbers of the ionizing background trace the mass density fluctuations, and the shot noise term that depends on the luminosity function and other properties of the sources, have an important and measurable effect on the monopole and quadrupole of the Lyα autocorrelation. A substantial broad-band term is added as a contamination to this autocorrelation, which is being marginalized over in present studies that are focused on inferring the scale of the BAO peak (Busca et al. 2013; Slosar et al. 2013). As the modelling of the spectral calibration and quasar continua and the accuracy of the Lyα correlation measurements in BOSS and upcoming surveys improve in the future, we can look forward to a detection of the broad-band terms induced by radiation fluctuations discussed in this paper.

There are several parameters that are important in determining how the Lyα correlation is modified by intensity fluctuations. These are the quantities appearing in equation (12) for the effective Lyα bias factor, and the mean free path of ionizing photons. The additional shot noise term is also dependent on many characteristics of the sources: the luminosity function, luminosity history and emission anisotropy. Disentangling all these effects from a detailed measurement and model fit to the redshift space autocorrelations and cross-correlations will probably be a difficult challenge. However, if the emission properties and typical luminosity histories of quasars can be well understood from an accurate determination of the quasar–Lyα cross-correlation, it should be possible to model the shot noise contribution to the autocorrelation and to infer from the observations some constraints on the biasing terms that affect the source clustering term. It is also worth noting that in the Lyα power spectrum, the term proportional to |$\mu _k^4$| is affected by neither the source clustering nor shot noise effects, and the other two terms proportional to |$\mu _k^2$| and independent of μ_k can in principle be used to separate the influence of the source clustering and shot noise effects (the term proportional to |$\mu _k^2$| is not affected by shot noise for constant and isotropic sources, but would acquire a contribution for anisotropic and variable sources). The three-dimensional Lyα power spectrum therefore provides a way of separating the radiation influences by separating the multipole terms, which are predicted to have the specific features near the scale of the mean free path shown in Fig. 2 and can then be compared to constraints obtained from cross-correlations.

The conclusions of our work are in agreement with those of Pontzen (2014), who has presented very similar ideas with a somewhat different mathematical treatment. There are a few differences in the way that absorbers are treated, and our incorporation of the redshift distortion effects allows us to predict the different behaviour of the monopole and quadrupole terms in the Lyα power spectrum, but the basic conclusions of the two papers are similar.

While the radiation intensity fluctuations make the large-scale Lyα forest correlations substantially more difficult to interpret as a tracer of the primordial fluctuations in the universe, these complications practically do not affect the measurement of the BAO scale, and they should constitute a new motivation for studying the evolution of the source and absorber population of the ionizing background.

SGG thanks the APC, especially the ‘Cosmology & Gravitation’ group, for their hospitality during part of the time when this work was being carried out. We also thank David Kirkby, Pat McDonald and Andrew Pontzen for stimulating discussions and for sharing their work on this subject. This work is supported in part by Spanish grant AYA-2012-33938.

REFERENCES

Ade

P.

Efstathiou

G.

Planck Collaboration

. ,

A&A

,

2014

doi:10.1051/0004-6361/201321591

Ahn

C. P.

et al. ,

ApJS

,

2012

, vol.

203

pg.

21

Crossref

Search ADS

Busca

N. G.

et al. ,

A&A

,

2013

, vol.

552

pg.

A96

Crossref

Search ADS

Croft

R. A. C.

,

ApJ

,

2004

, vol.

610

pg.

642

Crossref

Search ADS

Croft

R. A. C.

Weinberg

D. H.

Katz

N.

Hernquist

L.

,

ApJ

,

1998

, vol.

495

pg.

44

Crossref

Search ADS

Croft

R. A. C.

Weinberg

D. H.

Pettini

M.

Hernquist

L.

Katz

N.

,

ApJ

,

1999

, vol.

520

pg.

1

Crossref

Search ADS

Croft

R. A. C.

Weinberg

D. H.

Bolte

M.

Burles

S.

Hernquist

L.

Katz

N.

Kirkman

D.

Tytler

D.

,

ApJ

,

2002

, vol.

581

pg.

20

Crossref

Search ADS

Dawson

K. S.

et al. ,

AJ

,

2013

, vol.

145

pg.

10

Crossref

Search ADS

Delubac

T.

et al. ,

A&A

,

2014

preprint (arXiv:1404.1801)

Eisenstein

D. J.

et al. ,

AJ

,

2011

, vol.

142

pg.

72

Crossref

Search ADS

Font-Ribera

A.

Miralda-Escudé

J.

,

J. Cosmol. Astropart. Phys.

,

2012a

, vol.

7

pg.

28

Crossref

Search ADS

Font-Ribera

A.

et al. ,

J. Cosmol. Astropart. Phys.

,

2012b

, vol.

11

pg.

59

Crossref

Search ADS

Font-Ribera

A.

et al. ,

J. Cosmol. Astropart. Phys.

,

2013

, vol.

5

pg.

18

Crossref

Search ADS

Font-Ribera

A.

et al. ,

J. Cosmol. Astropart. Phys.

,

2014

preprint (arXiv:1311.1767)

Haardt

F.

Madau

P.

,

ApJ

,

1996

, vol.

461

pg.

20

Crossref

Search ADS

Hamilton

A. J. S.

,

ApJ

,

1992

, vol.

385

pg.

L5

Crossref

Search ADS

Kaiser

N.

,

MNRAS

,

1987

, vol.

227

pg.

1

Crossref

Search ADS

Kirkby

D.

et al. ,

J. Cosmol. Astropart. Phys.

,

2013

, vol.

3

pg.

24

Crossref

Search ADS

McDonald

P.

,

ApJ

,

2003

, vol.

585

pg.

34

Crossref

Search ADS

McDonald

P.

et al. ,

ApJ

,

2000

, vol.

543

pg.

1

Crossref

Search ADS

McDonald

P.

Seljak

U.

Cen

R.

Bode

P.

Ostriker

J. P.

,

MNRAS

,

2005

, vol.

360

pg.

1471

Crossref

Search ADS

McDonald

P.

et al. ,

ApJS

,

2006

, vol.

163

pg.

80

Crossref

Search ADS

McQuinn

M.

Lidz

A.

Zaldarriaga

M.

Hernquist

L.

Hopkins

P. F.

Dutta

S.

Faucher-Giguère

C.-A.

,

ApJ

,

2009

, vol.

694

pg.

842

Crossref

Search ADS

Meiksin

A.

White

M.

,

MNRAS

,

2004

, vol.

350

pg.

1107

Crossref

Search ADS

Miralda-Escudé

J.

Ostriker

J. P.

,

ApJ

,

1990

, vol.

350

pg.

1

Crossref

Search ADS

Miralda-Escudé

J.

Rees

M. J.

,

MNRAS

,

1994

, vol.

266

pg.

343

Crossref

Search ADS

Palanque-Delabrouille

N.

et al. ,

A&A

,

2013

, vol.

559

pg.

85

Crossref

Search ADS

Pontzen

A.

,

Phys. Rev. D

,

2014

, vol.

89

pg.

083010

Crossref

Search ADS

Ross

N. P.

et al. ,

ApJ

,

2013

, vol.

773

pg.

14

Crossref

Search ADS

Rudie

G. C.

Steidel

C. C.

Shapley

A. E.

Pettini

M.

,

ApJ

,

2013

, vol.

769

pg.

146

Crossref

Search ADS

Slosar

A.

Ho

S.

White

M.

Louis

T.

,

J. Cosmol. Astropart. Phys.

,

2009

, vol.

910

pg.

19

Crossref

Search ADS

Slosar

A.

et al. ,

J. Cosmol. Astropart. Phys.

,

2011

, vol.

9

pg.

1

Crossref

Search ADS

Slosar

A.

et al. ,

J. Cosmol. Astropart. Phys.

,

2013

, vol.

4

pg.

26

Crossref

Search ADS

White

M.

Pope

A.

Carlson

J.

Heitmann

K.

Habib

S.

Fasel

P.

Daniel

D.

Lukic

Z.

,

ApJ

,

2010

, vol.

713

pg.

383

Crossref

Search ADS

White

M.

et al. ,

MNRAS

,

2012

, vol.

424

pg.

933

Crossref

Search ADS

Worseck

G.

et al. ,

ApJ

,

2011

, vol.

733

pg.

L24

Crossref

Search ADS

Zuo

L.

,

MNRAS

,

1992

, vol.

258

pg.

36

Crossref

Search ADS

Download all slides

Month:	Total Views:
February 2017	2
March 2017	2
April 2017	6
May 2017	4
June 2017	7
July 2017	1
August 2017	3
September 2017	3
October 2017	7
November 2017	6
December 2017	10
January 2018	7
February 2018	4
March 2018	13
April 2018	8
May 2018	9
June 2018	13
July 2018	13
August 2018	10
September 2018	4
October 2018	4
November 2018	2
December 2018	5
January 2019	8
February 2019	9
March 2019	6
April 2019	11
May 2019	14
June 2019	7
July 2019	10
August 2019	20
September 2019	4
October 2019	7
November 2019	13
December 2019	8
January 2020	7
February 2020	7
March 2020	8
April 2020	2
May 2020	2
June 2020	5
July 2020	4
August 2020	5
September 2020	7
October 2020	2
November 2020	4
December 2020	2
January 2021	4
February 2021	1
March 2021	10
April 2021	3
May 2021	8
June 2021	2
July 2021	3
September 2021	7
October 2021	6
November 2021	3
December 2021	4
January 2022	8
February 2022	9
March 2022	5
April 2022	4
May 2022	3
June 2022	10
July 2022	8
August 2022	19
September 2022	18
October 2022	27
November 2022	16
January 2023	3
February 2023	2
March 2023	8
April 2023	19
May 2023	3
June 2023	4
July 2023	3
August 2023	6
September 2023	2
October 2023	3
November 2023	1
December 2023	5
January 2024	8
February 2024	6
March 2024	7
April 2024	5
May 2024	5
June 2024	9
July 2024	5
August 2024	4
September 2024	3
October 2024	3
November 2024	14
December 2024	6
January 2025	13
February 2025	6
March 2025	18
April 2025	16
May 2025	2

Article Contents

On the effect of the ionizing background on the Lyα forest autocorrelation function

Abstract

1 INTRODUCTION

2 ANALYTIC FORMALISM

2.1 Source clustering

2.2 Shot noise from individual sources

2.3 Values of the bias parameters

2.4 Fluctuations due to helium reionization

3 RESULTS

4 DISCUSSION AND CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

On the effect of the ionizing background on the Lyα forest autocorrelation function

Abstract

1 INTRODUCTION

2 ANALYTIC FORMALISM

2.1 Source clustering

2.2 Shot noise from individual sources

2.3 Values of the bias parameters

2.4 Fluctuations due to helium reionization

3 RESULTS

4 DISCUSSION AND CONCLUSIONS

REFERENCES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only