Delayed outflows from black hole accretion tori following neutron star binary coalescence

Fernández, Rodrigo; Metzger, Brian D.

doi:10.1093/mnras/stt1312

Abstract

Expulsion of neutron-rich matter following the merger of neutron star binaries is crucial to the radioactively powered electromagnetic counterparts of these events and to their relevance as sources of r-process nucleosynthesis. Here we explore the long-term (viscous) evolution of remnant black hole accretion discs formed in such mergers by means of two-dimensional, time-dependent hydrodynamical simulations. The evolution of the electron fraction due to charged-current weak interactions is included, and neutrino self-irradiation is modelled as a lightbulb that accounts for the disc geometry and moderate optical depth effects. Over several viscous times (∼1 s), a fraction of ∼10 per cent of the initial disc mass is ejected as a moderately neutron-rich wind (Y_e ∼ 0.2) powered by viscous heating and nuclear recombination, with neutrino self-irradiation playing a sub-dominant role. Although the properties of the outflow vary in time and direction, their mean values in the heavy-element production region are relatively robust to variations in the initial conditions of the disc and the magnitude of its viscosity. The outflow is sufficiently neutron-rich that most of the ejecta forms heavy r-process elements with mass number A ≳ 130, thus representing a new astrophysical source of r-process nucleosynthesis, distinct from that produced in the dynamical ejecta. Due to its moderately high entropy, disc outflows contain a small residual fraction ∼1 per cent of helium, which could produce a unique spectroscopic signature.

accretion, accretion discs, dense matter, gravitational waves, hydrodynamics, neutrinos, nuclear reactions, nucleosynthesis, abundances

1 INTRODUCTION

Coalescing neutron star (NS) and stellar mass black hole (BH) binaries are among the most promising sources for detection with networks of ground-based gravitational wave (GW) observatories, including Advanced LIGO and Virgo (Abramovici et al. 1992; Acernese et al. 2009; Caron et al. 1999; Abadie et al. 2010, 2012). The GW signal provides information on the properties of the merging binary (e.g. Ajith et al. 2007; van der Sluys et al. 2008), a potential probe of the equation of state (EOS) of dense matter (e.g. Faber et al. 2002; Shibata 2005; Read et al. 2009; Bauswein et al. 2012) and even a test of General Relativity itself (e.g. Cornish et al. 2011).

To maximize the scientific benefit of a GW detection, it is important to identify a coincident electromagnetic counterpart (e.g. Bloom et al. 2009; Metzger & Berger 2012; Bartos, Brady & Marka 2013; Nissanke, Kasliwal & Georgieva 2013). The sky localization provided by initial Advanced LIGO/Virgo will be tens to hundreds of square degrees (e.g. Fairhurst 2009; Wen & Chen 2010; Nissanke et al. 2011), but a coincident X-ray, optical or radio signal could provide a much more accurate position, such that the host galaxy and redshift of the merger could be identified. Electromagnetic emission also indirectly probes the (magneto-)hydrodynamics of the merger and its aftermath.

The BH created from a NS–NS merger, following a metastable hypermassive NS phase, is typically surrounded by a thick torus of mass ∼10⁻³–0.1 M_⊙ (Ruffert & Janka 1999; Uryū, Shibata & Eriguchi 2000; Rosswog & Liebendörfer 2003; Oechslin & Janka 2006; Chawla et al. 2010; Rezzolla et al. 2010; Hotokezaka et al. 2011). A torus also forms following a BH–NS merger if the binary mass ratio is sufficiently low that the NS is tidally disrupted outside the BH instead of being swallowed whole (e.g. Faber et al. 2006; Duez et al. 2010; Foucart et al. 2011; Stephens, East & Pretorius 2011; Foucart et al. 2012; East, Pretorius & Stephens 2012). The short accretion time-scale t_visc ≲ 1 s, and large accretion rates |$\dot{M} \gtrsim \,\mathrm{M}_{{\odot }}$| s⁻¹, of such remnant tori motivates the current paradigm that NS–NS/NS–BH mergers are the central engines powering short duration gamma-ray bursts (SGRBs) (Paczynski 1986; Eichler et al. 1989).

Despite being well-studied, SGRBs do not necessarily represent an ideal counterpart for most GW-detected mergers because SGRBs are difficult to localize on the sky and their observed rate is relatively low (≲1 yr⁻¹) within the sensitivity range of Advanced LIGO/Virgo (Chen & Holz 2012; Metzger & Berger 2012). These drawbacks have motivated the study of more isotropic merger counterparts, such as supernova-like optical transients powered by the decay of radioactive elements synthesized in the merger ejecta (‘kilonovae’, Li & Paczyński 1998; Kulkarni 2005; Metzger et al. 2010b). Merger simulations show that a modest quantity of highly neutron-rich material (electron fraction Y_e ≲ 0.1) is ejected by tidal forces during the merger (Lattimer & Schramm 1974; Rosswog et al. 1999; Rosswog 2005, 2013; Chawla et al. 2010; Stephens et al. 2011; East et al. 2012; Rosswog, Piran & Nakar 2013; Bauswein, Goriely & Janka 2013), and recent nuclear reaction network calculations largely agree on the amount of radioactive heating provided by such decaying r-process elements (Metzger et al. 2010b; Goriely, Bauswein & Janka 2011; Roberts et al. 2011).

One large uncertainty, however, is the opacity of the ejecta, because current kilonova models predict a composition dominated by heavy r-process nuclei (atomic mass number A ≳ 130). Recent atomic structure calculations show that the opacity of material containing even a small quantity of Lathanide elements (A ∼ 139–175) could be orders of magnitude higher than that of Fe (Kasen, Badnell & Barnes 2013). This implies that the predicted transient peaks on longer time-scales – up to ∼ a week – and at a lower luminosity and frequency – in the near-infrared rather than optical (Barnes & Kasen 2013; Tanaka & Hotokezaka 2013) – than in original models that assumed opacity similar to Fe (e.g. Metzger et al. 2010b; Piran, Nakar & Rosswog 2013). Given the sensitive dependence of the signal on the Lathanide fraction, it is thus crucial to identify any diversity in the nucleosynthetic composition of the ejecta.

Another uncertainty is the mass of the ejecta M_ej. Although the quantity of matter expelled in dynamical ‘tidal tails’ from the merger can be large (≳10⁻² M_⊙) in some cases (e.g. eccentric mergers; East et al. 2012), it is often found to be significantly smaller (∼10⁻⁴–10⁻³ M_⊙; Hotokezaka et al. 2013).

Dynamical expulsion is not the only source of ejecta, however. Mass loss also occurs in outflows from the accretion disc over longer, viscous time-scales. Initially, neutrinos radiated from the disc – or from the central hypermassive NS prior to its collapse – can heat and drive an outflow from the surface of the disc (a ‘neutrino-driven’ wind; e.g. McLaughlin & Surman 2005; Metzger, Thompson & Quataert 2008b; Surman et al. 2008; Dessart et al. 2009; Kizivat et al. 2010; Wanajo & Janka 2012). A potentially even larger quantity of mass is lost from the disc at later times due to powerful outflows driven by viscous heating and recombination of free nuclei into α-particles (Lee & Ramirez-Ruiz 2007; Beloborodov 2008; Metzger, Piro & Quataert 2008a; Lee, Ramirez-Ruiz & López-Cámara 2009; Metzger, Piro & Quataert 2009a, hereafter MPQ09).

MPQ09 constructed a height-integrated, time-dependent model of the viscous spreading of accretion discs formed from NS–NS/NS–BH mergers, including the evolution of the midplane electron fraction Y_e due to weak interactions. MPQ09 find that as the disc spreads due to angular momentum transport and the temperature decreases, e⁻/e⁺ captures become slow compared to the viscous evolution time-scale. Since these captures both cool the disc and affect its composition, the disc becomes geometrically thick and Y_e freezes out. Soon after freeze-out, free neutrons and protons recombine into α-particles, starting near the outer edge of the disc and moving inwards with time. MPQ09 estimated that ∼20–50 per cent of the initial disc mass is unbound by this energy deposition, with a range of electron fractions Y_e ∼ 0.1 to 0.4 resulting from varying local conditions during freeze-out (see also Lee & Ramirez-Ruiz 2007; Beloborodov 2008).

Lee et al. (2009) performed axisymmetric (2D) global simulations of long-term disc evolution, which confirmed this process of He ‘evaporation’ explicitly. However, since they assumed β-equilibrium instead of explicitly following the weak interactions, they could not accurately determine the energy released by α-recombination or the electron fraction of the final ejecta. The electron fraction of disc outflows is critically important because it controls whether the heavy elements synthesized in the outflow are dominated by second/third peak r-process elements (if Y_e ≲ 0.3–0.4), lighter neutron-rich elements (if 0.3–0.4 ≲ Y_e ≲ 0.495) or significant quantities of ⁵⁶Ni (Y_e ≳ 0.495) (e.g. Hoffman, Woosley & Qian 1997). Given the potentially large difference in the optical opacity of Fe-group and r-process elements, and the different geometry of tidal tails and disc winds, the resulting kilonova light curve, including contributions from both sources of ejecta, could in principle be much more complex than previously anticipated (Barnes & Kasen 2013; Tanaka & Hotokezaka 2013).

Beyond their implication for electromagnetic emission, disc outflows from binary NS mergers also represent an essentially unexplored astrophysical site for heavy-element synthesis. This issue is particularly important because the astrophysical origin of r-process nuclei remains a mystery (Qian & Wasserburg 2007), and binary NS mergers could be an important – and possibly dominant – source (Lattimer & Schramm 1974; Freiburghaus, Rosswog & Thielemann 1999; Korobkin et al. 2012). Nevertheless, with the exception of neutrino-driven disc outflows (e.g. Surman et al. 2008; Wanajo & Janka 2012), to date most studies of the r-process in such environments focus on the dynamical ejecta.

In this series of papers, we explore the long-term evolution of the accretion discs formed by NS–NS/NS–BH mergers by means of axisymmetric (2D) time-dependent hydrodynamic simulations. In Paper I (this work) we explore the dynamics of the disc evolution and the properties of the resulting disc outflows. In separate works, our results for the disc outflows will be used to make predictions for the resulting transient electromagnetic signature and nucleosynthetic yields.

Our models employ a finite-volume hydrodynamic method, a realistic EOS, and a complete implementation of charged-current weak interactions in the optically thin regime. Approximations are made in order to capture the key physical processes at a low computational cost: (1) the effects of general relativity on the disc dynamics are approximated via a pseudo-Newtonian potential; (2) neutrino self-irradiation is modelled as a ‘lightbulb’ that accounts for the basic disc geometry and includes corrections for moderate optical depth effects and (3) angular momentum transport is approximated by an anomalous shear-stress tensor with an α-viscosity. These approximations enable us to evolve accretion discs for a large number of orbits (∼1000) and thus perform a parameter space study on the outflow properties which can guide future, more detailed calculations.

The paper is organized as follows. In Section 2 we briefly summarize the properties of the initial accretion disc. The numerical implementation is described in Section 3. Results are presented in Section 4, followed by a discussion in Section 5. Our conclusions are summarized in Section 6. The Appendices provide additional information on the neutrino treatment as well as general information on accretion regimes and nucleosynthesis in NS merger discs.

2 disc PROPERTIES

The mass of the torus formed during a NS–NS merger can vary considerably, M_t ∼ 10⁻³ − 0.1 M_⊙, depending on the binary mass ratio, the assumed EOS, the eccentricity of the initial orbit and whether the system undergoes a long-lived hypermassive NS phase prior to BH formation (see Faber & Rasio 2012 for a recent review). The disc mass in a NS–BH merger also depends on the spin of the BH, since spin controls the location of the innermost circular orbit. If the NS is tidally disrupted outside the BH horizon, then the torus mass is relatively large M_t ∼ 0.1 M_⊙; otherwise, the NS is swallowed whole and little or no torus forms (e.g. Foucart 2012). Merger simulations find that the initial torus is distributed across a wide range of radii, with most of the mass and angular momentum concentrated on a radial scale R₀ ∼ 20–100 km.

The (Newtonian) orbital time at this radial scale is

\begin{equation} t_{\rm orb} = 3.5\times 10^{-3}\left(\frac{R_0}{50\,{\rm km}}\right)^{3/2} \left( \frac{M_{\rm BH}}{3\,\mathrm{M}_{\odot }}\right)^{-1/2}{\rm s}, \end{equation}

(1)

where M_BH is the BH mass. The characteristic time-scale for matter to accrete may be estimated by the viscous time

\begin{eqnarray} t_{\rm visc}& \simeq & \alpha ^{-1}\left(\frac{R_{0}^{3}}{GM_{\rm BH}}\right)^{1/2}\left(\frac{H_{0}}{R_{0}}\right)^{-2}\nonumber \\ & \sim & 1{\rm \,s} \left(\frac{0.03}{\alpha }\right)\left(\frac{R_{0}}{50{\,\rm km}}\right)^{3/2} \left(\frac{3\,\mathrm{M}_{\odot }}{M_{\rm BH}}\right)^{1/2} \left(\frac{H_0}{3R_{0}}\right)^2, \end{eqnarray}

(2)

where H₀ is the vertical scaleheight and α parametrizes the disc viscosity (Section 3.3), resulting in a characteristic accretion rate

\begin{eqnarray} \dot{M}_{0} & \sim& \frac{M_{\rm t}}{t_{\rm visc}} \sim 10^{-2}\,\mathrm{M}_{\odot }{\,\rm s^{-1}}\left(\frac{\alpha }{0.03}\right) \left(\frac{M_{\rm t}}{10^{-2}\,\mathrm{M}_{\odot }}\right)\left(\frac{R_{0}}{50{\,\rm km}}\right)^{-3/2}\nonumber\\ && \times \,\left(\frac{M_{\rm BH}}{3\,\mathrm{M}_{\odot }}\right)^{1/2} \left(\frac{3H_0}{R_{0}}\right)^{2}. \end{eqnarray}

(3)

Due to the high densities and rapid evolution of the disc, photons are not an important source of cooling on time-scales of relevance. However, the temperature is sufficiently high that neutrinos are relevant, especially in the earliest phases of the disc evolution (e.g. Popham, Woosley & Fryer 1999; Narayan, Piran & Kumar 2001; Di Matteo, Perna & Narayan 2002; Chen & Beloborodov 2007, hereafter CB07). A straightforward calculation shows that a thin neutrino-cooled disc (H ∼ 0.1–0.3R₀) obtains when the accretion rate at radius R₀ exceeds a critical value |$\dot{M}_{\nu }$| given by (see Metzger et al. 2008b, their equation 11)

\begin{eqnarray} \dot{M}_{\nu } \approx 1.3\times 10^{-2}\,\mathrm{M}_{{\odot }}{\rm s^{-1}}\left(\frac{R_{0}}{50\,{\rm km}}\right)^{5/6}\left(\frac{\alpha }{0.03}\right)^{5/3}\left(\frac{M_{\rm BH}}{3\,\mathrm{M}_{{\odot }}}\right)^{1/2},\nonumber\\ \end{eqnarray}

(4)

where the dominant source of cooling is assumed to be charged-current weak interactions, and general-relativistic corrections have been neglected. Unlike photon-cooled discs, such as those in X-ray binaries or active galactic nuclei, neutrino-cooled discs are the most radiatively efficient at small radii.

By equating R₀ in equation (4) with the radius R_isco of the innermost stable circular orbit of the BH, one obtains a critical accretion rate |$\dot{M}_{\rm ign}$| (the ‘ignition’ rate) above which the disc is thin near its innermost radii:

\begin{eqnarray} \dot{M}_{\rm ign} \approx 6\times 10^{-2}[2\times 10^{-2}]\left(\frac{\alpha }{0.03}\right)^{5/3}\left(\frac{M_{\rm BH}}{3\,\mathrm{M}_{{\odot }}}\right)^{4/3}\,\mathrm{M}_{{\odot }}{\rm s^{-1}},\nonumber\\ \end{eqnarray}

(5)

where the prefactor was calculated by CB07 for a 3 M_⊙ BH of spin a = 0[a = 0.95] using a steady-state accretion model in a Kerr metric.

When the disc is neutrino-cooled (⁠|$\dot{M} > \dot{M}_{\nu }$|⁠) its internal energy e_int is dominated by non-degenerate nucleons (CB07). The characteristic temperature of the torus midplane, which is attained on a cooling time-scale t_cool ∼ t_visc(H/R₀)², is thus approximately given by

\begin{equation} T_{\rm vir} \simeq 7.6(1+Y_{\rm e})\left(\frac{M_{\rm BH}}{3\,\mathrm{M}_{\odot }}\right)\left(\frac{3H_{0}}{R_{0}}\right)^{2}\left(\frac{50\,{\rm km}}{R_0}\right){\rm MeV}, \end{equation}

(6)

where Y_e = n_p/(n_n + n_p) is the electron fraction and n_p(n_n) are the number densities of protons(neutrons), respectively. The initial temperature of the disc is sufficiently high that all nuclei are dissociated into free nucleons. Alpha particles and heavier nuclei form only once the disc temperature decreases to ≲1 MeV.

3 NUMERICAL SETUP

3.1 Equations solved and numerical method

We solve the equations of mass, momentum, energy and lepton number conservation on an axisymmetric spherical polar grid (r, θ), with source terms due to gravity, shear viscosity and optically thin weak interactions

\begin{eqnarray} \frac{\mathrm{\partial} \rho }{\mathrm{\partial} t} + \nabla \cdot (\rho \boldsymbol {v}_{\rm p}) & = & 0 \end{eqnarray}

(7)

\begin{eqnarray} \frac{{\mathrm{d}}\boldsymbol {v}_{\rm p}}{{\mathrm{d}}t} & = & \boldsymbol {f}_{\rm c}-\frac{1}{\rho }\nabla p -\nabla \Phi \end{eqnarray}

(8)

\begin{eqnarray} \rho \frac{{\mathrm{d}}\ell _z}{{\mathrm{d}}t} & = & r\,\sin \theta \,(\nabla \cdot \mathbb {T})_\phi \end{eqnarray}

(9)

\begin{eqnarray} \rho \frac{{\mathrm{d}}e_{\rm int}}{{\mathrm{d}}t} + p\nabla \cdot \boldsymbol {v}_{\rm p} & = & \frac{1}{\rho \nu }\mathbb {T}:\mathbb {T} + \rho \dot{Q}_{\rm net} \end{eqnarray}

(10)

\begin{eqnarray} \frac{{\mathrm{d}}Y_{\rm e}}{{\mathrm{d}}t} & = & \Gamma _{\rm net}. \end{eqnarray}

(11)

Here ρ, p, |$\boldsymbol {v}_{\rm p}=v_r\hat{r} + v_\theta \hat{\theta }$|⁠, and e_int denote the fluid density, pressure, poloidal velocity and internal energy, respectively. The Lagrangian differential operator is |${\mathrm{d}}/{\mathrm{d}}t\equiv \mathrm{\partial} /\mathrm{\partial} t + \boldsymbol {v}_{\rm p}\cdot \nabla$|⁠. The specific angular momentum along the symmetry axis is given by ℓ_z = rsin θv_ϕ, with v_ϕ the azimuthal velocity, and |$\boldsymbol {f}_{\rm c}$| is the centrifugal force in the poloidal direction.

The pseudo-Newtonian gravitational potential of Paczyńsky & Wiita (1980) is employed, Φ = −GM_BH/(r − R_S), with R_S = 2GM_BH/c² the Schwarzschild radius, as applicable to a BH of moderate spin.¹ The BH mass is kept constant in the simulation. The neutrino source terms are |$\dot{Q}_{\rm net}$| and Γ_net (see Section 3.2), and the viscous stress tensor is denoted by |$\mathbb {T}$| (see Section 3.3).

The Helmholtz EOS (Timmes & Swesty 2000) is used to relate internal energy and pressure. The ion component is an ideal gas of neutrons, protons and alpha particles, with relative abundances that satisfy nuclear statistical equilibrium (NSE). Heavier nuclei are not included, since the energy release in their formation is much smaller in comparison, and hence should have little impact on the outflow dynamics.² An additional (inert) hydrogen gas is used to populate the ambient medium that initially surrounds the torus. The zero-point of energy is taken to be the pure nucleon state, with the internal energy becoming

\begin{equation} e_{\rm int} = e_{\rm int,0} - \frac{Q_\alpha }{m_\alpha }\,X_\alpha , \end{equation}

(12)

where e_{int, 0} is the specific internal energy provided by the Helmholtz EOS, X_α is the mass fraction of alpha particles, m_α is the mass of an alpha particle and Q_α ≃ 28.3 MeV is the nuclear binding energy of an alpha particle (e.g. Audi, Wapstra & Thibault 2003). In addition, the thermodynamic derivatives of the pressure, internal energy and entropy of the ions acquire terms that originate in the dependence of the ion abundances on temperature and density. If the temperature falls below 5 × 10⁹ K, or if the mass fraction of inert hydrogen exceeds 1 per cent, the abundances are frozen. Any hydrogen mixed with torus material is added to the proton mass fraction if the temperature is higher than 5 × 10⁹ K.

We use flash3.2 (Dubey et al. 2009) to evolve the system of equations (7)–(11) with the dimensionally split version of the Piecewise Parabolic Method (PPM; Colella & Woodward 1984). The public version of the code has been modified to allow for a non-uniformly spaced grid in spherical polar coordinates, as described in Fernández (2012).

The computational grid is logarithmically spaced in radius, covering the range 2R_S to 2 × 10³R_S in most models. In the polar direction, the cell spacing is uniform in cos θ, covering the interval [0, π]. We adopt this grid structure because we intend to cover a large dynamic range in radius, and to concentrate the resolution near the midplane, given the quasi-spherical character of the outflows. Our standard resolution uses 64 cells per decade in radius and 56 cells in the polar direction, yielding approximately square cells at the midplane (Δr/r ≃ Δθ ≃ 2°). The coarsest angular cell next to the polar axis is 10.8°. One model is evolved at double the resolution in both radius and in angle, to quantify convergence.

The boundary conditions at the polar axis are reflecting in all variables. At the inner and outer radial boundaries, we impose a zero-gradient boundary condition for all variables. In addition, the radial velocity in the ghost cells of the radial boundaries is set to zero if its value in the first active cell next to the boundary would imply mass entering the domain.

All energy and viscous source terms are set to zero when the density falls below a fiducial value of 10 g cm⁻³. This value is sufficiently low as to not impact the outflows from the torus, yet sufficiently high to avoid requiring too small of a time-step due to angular momentum transport in (unimportant) low-density regions.

To prevent numerical problems in the funnel that develops around the rotation axis, we impose a floor of density equal to 1 g cm⁻³, and a floor of temperature at 10⁵ K.

3.2 Neutrino treatment

The inner regions of the disc become opaque to neutrinos above an accretion rate (Appendix A)

\begin{eqnarray} \dot{M}_{\rm opaque} \simeq 0.15\,\mathrm{M}_{{\odot }}{\rm \,s^{-1}}\,\left(\frac{\alpha }{0.03}\right)^{4/5} \left(\frac{M}{3\,\mathrm{M}_{{\odot }}}\right)^{7/10}\left(\frac{R_{\rm isco}}{6R_{\rm g}}\right)^{9/5}.\nonumber\\ \end{eqnarray}

(13)

The condition |$\dot{M}_{\rm opaque} \gtrsim \dot{M}_{0}$| (equation 3) sets the minimum disc mass for optical thickness. For slowly spinning BHs, this mass is ∼0.1 M_⊙.

Most of the discs we explore (M_t ≲ 0.1 M_⊙) are thus only marginally optically thick to neutrinos at early times. Since the disc density decreases as accretion proceeds, full neutrino transparency is always achieved. The models we explore undergo this transition before weak freezout occurs, as quantified by the magnitude of the optical depth, and hence we adopt an optically thin treatment of energy exchange with matter and regulation of the electron fraction in all cases. Finite optical depth corrections are included to prevent excessive heating at early times in the few massive tori we evolve.

Charged-current weak interactions are included as formulated by Bruenn (1985) and implemented by Fernández (2012). These reactions control the evolution of the electron fraction, and provide the dominant energy exchange channel between neutrinos and matter. The relevant source terms are the net rate of change of the electron fraction

\begin{equation} \Gamma _{\rm net} = \Gamma _{\rm e-} - \Gamma _{\rm e+}, \end{equation}

(14)

where Γ_e- and Γ_{e +} are the rates of electron and positron creation per baryon, respectively, and the net specific heating rate of the gas

\begin{equation} \dot{Q}_{\rm net} = \mathcal {H}_{\nu _{\rm e}} + \mathcal {H}_{\bar{\nu }_{\rm e}} - \mathcal {C}_{\nu _{\rm e}} - \mathcal {C}_{\bar{\nu }_{\rm e}} - \mathcal {C}_{\rm pairs}, \end{equation}

(15)

where |$\mathcal {H}_{\nu _{\rm e}}$| and |$\mathcal {H}_{\bar{\nu }_{\rm e}}$| are the heating by absorption of neutrinos and antineutrinos on nucleons, respectively, and |$\mathcal {C}_{\nu _{\rm e}}$| and |$\mathcal {C}_{\bar{\nu }_{\rm e}}$| are the cooling rates from electron and positron capture, respectively. Explicit forms for these terms are provided in Appendix B. Additional neutrino energy losses from pair creation (⁠|$\mathcal {C}_{\rm pairs}$|⁠) are included via the Itoh et al. (1996) parametrization.³ Source terms are included via explicit operator split in the equations for energy and lepton number conservation.

Self-irradiation of the disc is implemented via a lightbulb-type prescription that accounts for the disc geometry (Appendix B). All of the neutrino emission is assumed to come from a ring of material on the midplane, with a radius R_em chosen to be an average value weighted by the neutrino emissivity,

\begin{equation} R_{\rm em} = \frac{\int \sin \theta \,{\mathrm{d}}\theta \,{\mathrm{d}}r\, r^3\rho (\mathcal {C}_{\nu _{\rm e}} + \mathcal {C}_{\bar{\nu }_{\rm e}})}{\int \sin \theta \,{\mathrm{d}}\theta \,{\mathrm{d}}r\, r^2\rho (\mathcal {C}_{\nu _{\rm e}} + \mathcal {C}_{\bar{\nu }_{\rm e}})}. \end{equation}

(16)

This approximation is justified by the highly peaked form of this emissivity (Appendix B), and the low optical depth of most of the disc masses considered. The neutrino luminosities of electron-type neutrinos |$L_{\nu _{\rm e}}$| and antineutrinos |$L_{\bar{\nu }_{\rm e}}$| used in this self-irradiation treatment are calculated at the end of the previous time-step by integrating the corresponding emissivities over the whole torus. Spectra are assumed to follow a Fermi-Dirac distribution with zero chemical potential, with a temperature equal to the gas temperature in an angle-averaged radial shell (10 per cent spread) around the emission radius R_em. Self-irradiation is included to explore its influence on the ejecta composition and its relative energetic contribution to the total mass loss. Results are not expected to be very sensitive to the particular choices of luminosities and spectra, because the process is energetically subdominant (e.g. Ruffert & Janka 1999; MPQ09).

To explore more massive tori, finite optical depth effects are approximated by a modified version of the Lee, Ramirez-Ruiz & Page (2004) treatment. At each time-step, four optical depth functions for each neutrino species are computed from the neutrino emission peak,

\begin{eqnarray} \tau _{\rm i}^{\rm up}(\theta ) = \int _0^{\theta } \kappa _{\rm i}\, R_{\rm em}{\mathrm{d}}\theta ^\prime , \quad \theta \in [0,\pi /2]{\rm , }r=R_{\rm em } \end{eqnarray}

(17)

\begin{eqnarray} \tau _{\rm i}^{\rm dn}(\theta ) = \int _\theta ^{\pi} \kappa _{\rm i}\, R_{\rm em}{\mathrm{d}}\theta ^\prime , \quad \theta \in [\pi /2,\pi ]{\rm , }r=R_{\rm em} \end{eqnarray}

(18)

\begin{eqnarray} \tau _{\rm i}^{\rm out}(r) = \int _{r}^{r_{\rm out}} \kappa _{\rm i}\,{\mathrm{d}}r^\prime , \quad r\in [R_{\rm em},r_{\rm out}]{\rm , }\theta =\frac{\pi }{2} \end{eqnarray}

(19)

\begin{eqnarray} \tau _{\rm i}^{\rm in}(r) = \int _{r_{\rm in}}^{r} \kappa _{\rm i}\, {\mathrm{d}}r^\prime , \quad r\in [r_{\rm in},R_{\rm em}]{\rm , }\theta =\frac{\pi }{2}, \end{eqnarray}

(20)

corresponding to the four coordinate directions. Given that most of the torus mass lies within ∼45° of the equator, we use angular integration to estimate the vertical optical depth. For fast computation, the absorption coefficients for this optical depth functions⁴ are approximated as in Janka (2001)

\begin{eqnarray} \kappa _{\nu _{\rm e}} & \simeq & 2.2\times 10^{-7}\,\rho _{10}T^2_{\nu _{\rm e},4}\,\sqrt{X_{\rm p}(2X_{\rm n}+X_{\rm p})}{\rm cm}^{-1}, \end{eqnarray}

(21)

\begin{eqnarray} \kappa _{\bar{\nu }_{\rm e}} & \simeq & 2.2\times 10^{-7}\,\rho _{10}T^2_{\nu _{\rm e},4}\,\sqrt{X_{\rm p}(2X_{\rm p}+X_{\rm n})}{\rm cm}^{-1}. \end{eqnarray}

(22)

The neutrino emissivities |$\mathcal {C}_{\nu _{\rm e}}$| and |$\mathcal {C}_{\bar{\nu }_{\rm e}}$| are then suppressed everywhere by a factor exp ( − τ_{i, peak}), where

\begin{equation} \tau _{i,\rm peak} = \min \left[\tau _{\rm i}^{\rm up}({\pi }/2), \tau _{\rm i}^{\rm dn}(\pi /2),\tau _{\rm i}^{\rm out}(R_{\rm em}), \tau _{\rm i}^{\rm in}(R_{\rm em})\right]. \end{equation}

(23)

This prescription accounts for the fact that most neutrinos will escape along the path with the least optical depth, which in most cases is the vertical direction. In contrast to Lee et al. (2004), we ignore the neutrino pressure contribution, which is a small correction (our tori are not radiation-dominated while optically thick).

The neutrino luminosity used for self-irradiation, first computed from the attenuated emissivities, is further suppressed by a local factor exp ( − τ_{i, irr}), where

\begin{eqnarray} \tau _{i,\rm irr}(r,\theta ) = \left[\tau _{\rm i}^{x}(R_{\rm em})-\tau _{\rm i}^{x}(r)\right]+ \frac{\tau _{\rm i}^x(r)}{\tau _{\rm i}^x(R_{\rm em})}\left[\tau _{\rm i}^{y}(\pi /2)-\tau _{\rm i}^{y}(\theta )\right].\nonumber\\ \end{eqnarray}

(24)

The superscripts x and y are the radial and angular optical depths for the appropriate quadrant, respectively (equations 17–20). This prescription attempts to capture the attenuation of the neutrino flux in regions far from the emission peak, and smoothly approaches the semi-transparent lightbulb limit for decreasing torus density. It is a coarse approximation, however, since it does not account for attenuation along lateral directions, and assumes that the vertical density and abundance dependence differ only by a constant scaling factor at different radii.

In optically thick discs, the rate of change of the electron fraction (equation 14) is affected indirectly via the suppression of the self-irradiation luminosities. The portion due to the local neutrino emissivities is not modified, however, since its contribution will still vanish in beta equilibrium.

3.3 Angular momentum transport

Angular momentum transport is mediated by a viscous stress tensor |$\mathbb {T}$| for which only the azimuthal components are non-zero (e.g. Stone, Pringle & Begelman 1999),

\begin{eqnarray} T_{r\phi } = \rho \nu \,\frac{r}{\sin \theta }\frac{\mathrm{\partial} }{\mathrm{\partial} r}\left(\frac{\ell _z}{r^2} \right) \end{eqnarray}

(25)

\begin{eqnarray} T_{\theta \phi } = \rho \nu \,\frac{\sin \theta }{r^2}\frac{\mathrm{\partial} }{\mathrm{\partial} \theta }\left(\frac{\ell _z}{\sin ^2\theta } \right). \end{eqnarray}

(26)

Including all components of the stress would suppress convection in the poloidal direction (e.g. Igumenshchev & Abramowicz 1999). Our simulations mimic turbulent angular momentum transport via thermally driven convection. Given the low mass of the torus relative to that of the central BH, and its relatively thick scaleheight, we consider our neglect of self gravity as a good approximation.

To connect with previous calculations, we employ a Shakura & Sunyaev (1973) parametrization of the kinematic viscosity coefficient

\begin{eqnarray} \nu _\alpha = \alpha \frac{c_{\rm i}^2}{\Omega _{\rm K}} =\alpha \left( \frac{c_{\rm i}^2}{GM_{\rm BH}/r}\right) \sqrt{GM_{\rm BH}R_0} \left(1-\frac{R_{\rm S}}{r} \right)\left( \frac{r}{R_0}\right)^{1/2} \nonumber\\ \end{eqnarray}

(27)

where Ω_K is the Keplerian frequency of the Paczyńsky & Wiita (1980) potential and |$c_{\rm i}^2 = p /\rho$| is the isothermal sound speed.

The implementation of angular momentum evolution in flash is described in Fernández & Metzger (2013). Viscous heating is handled as an explicit source term in the energy equation, while the diffusive momentum flux is added to the advective fluxes obtained during the Riemann solver step. Tests of this implementation are provided in Fernández & Metzger (2013).

3.4 Initial conditions

The initial condition is an equilibrium torus with constant entropy, angular momentum and electron fraction (e.g. Papaloizou & Pringle 1984; Hawley 2000). The initial solution is obtained by first finding the local density given the entropy, electron fraction and position in the disc,

\begin{eqnarray} w(\rho ,r,\theta )\,\big |_{{\rm s},Y_{\rm e}} &=& \frac{GM_{\rm BH}}{R_0}\Big[\frac{R_0}{r-R_{\rm S}} -\frac{1}{2}\frac{R_0^2}{(r\sin \theta )^2}\nonumber\\ && \times\,\left(\frac{R_0}{r-R_{\rm S}}\right)^2- \frac{1}{2d}\Big], \end{eqnarray}

(28)

where w = e_int + p/ρ is the specific enthalpy of the fluid, and d is the torus distortion parameter. The resulting density distribution is then integrated to obtain the disc mass. The procedure is repeated, changing the entropy, until the desired torus mass is obtained. The distortion parameter d controls the thermal content of the solution; for fixed mass and electron fraction, it is uniquely determined by demanding a given entropy or a value of H/R = c_i/(rΩ_K) at the point of maximum density.

Evolving this equilibrium torus against a low-density background results in the emergence of a shock from the edges of the disc due to strong gradients. To avoid confusing this initial transient with the viscously driven outflow we are interested in, we evolve the initial torus for 100 orbital times at r = R₀ without angular momentum transport or energy source terms. At this time a power-law density profile has been established at large radii, and the total mass in torus material has decreased by a small amount (<1 per cent), due to the spread to larger radii. The mass accretion rate at the ISCO due to numerical viscosity is ∼10⁻⁵ M_⊙ s⁻¹. We then reset all positive radial velocities to zero and take this as the initial condition for the simulations.

A realistic merger will produce a torus with a more general radial distribution of mass, angular momentum and thermal energy, than we have assumed. However, we do not expect our results to be overly sensitive to the initial thermal distribution of the torus, since the temperature profile will equilibrate on a thermal time-scale t_cool ∼ t_visc(H/R)² ∼ 0.1t_visc.

The torus is surrounded by an ambient medium of constant density with a value ∼20 per cent higher than the floor of density (Section 3.1), and pressure distribution p_amb = −Φρ_amb (Stone et al. 1999). The magnitude of the ambient density is chosen as the lowest value that does not cause numerical problems in the inner regions of the polar funnel.

3.5 Models evolved

We evolve a number of models that explore the effect of (1) varying fundamental parameters in the system, and (2) artificially removing critical processes for outflow generation. All models are shown in Table 1.

Table 1.

Open in new tab

Models evolved and outflow properties. Columns from left to right are: initial torus mass, BH mass, initial torus radius (equation 28), initial electron fraction, initial entropy, viscosity coefficient (equation 27), spatial resolution (std=standard, hi=high; Section 3.1), inclusion of recombination energy (equation 12), inclusion of self-irradiation (Section 3.2), mass-flux-weighted values of the electron fraction, entropy, and expansion time |$t_{\rm } = r/\bar{v}_r$| at a radius where |$\bar{T}\sim 5\times 10^9$| K and within ±60° of the midplane (equation 31), ratio of the total mass with positive energy ejected beyond r = 10⁹ cm to the total mass accreted through the ISCO radius, each in units of the initial torus mass, and mass-flux-weighted density (in units of 100 g cm⁻³) and velocity (in units of 10 000 km s⁻¹) at r = 10⁹ cm and within ±60° of the midplane.

Model	M_t0	M_BH	R₀	Y_e0	s₀	α	Res.	Rec.	Irr.	\|$\bar{Y}_{\rm e}$\|	\|$\bar{s}$\|	t_exp	M_ej/M_acc	\|$\bar{\rho }_2$\|	\|$\bar{v}_{r,9}$\|
	( M_⊙)		(km)		(k_B/b)						(k_B/b)	(ms)	(M_t0/M_t0)
S-def	0.03	3	50	0.10	8	0.03	std	Yes	Yes	0.16	16	95	0.10/0.90	1.6	2.2
S-m0.01	0.01	3	50	0.10	8	0.03	std	Yes	Yes	0.15	18	68	0.10/0.90	0.5	2.2
S-m0.10	0.10									0.17	17	119	0.11/0.89	6.3	2.3
S-r75	0.03	3	75							0.16	16	126	0.22/0.78	3.6	2.2
S-M10		10	150							0.18	17	77	0.04/0.92	0.8	1.8
S-y0.05		3	50	0.05						0.15	16	93	0.10/0.90	1.5	2.2
S-y0.15				0.15						0.17	16	92	0.10/0.90	1.6	2.3
S-s6				0.10	6					0.14	17	86	0.08/0.91	1.2	1.9
S-s10					10					0.19	16	87	0.12/0.88	1.9	2.6
S-v0.01					8	0.01				0.20	18	193	0.11/0.89	1.5	2.5
S-v0.10						0.10				0.14	19	38	0.13/0.87	2.2	2.4
S-hr						0.03	hi			0.15	16	94	0.10/0.90	1.5	2.2
P-rec	0.03	3	50	0.10	8	0.03	std	No	Yes	0.18	17	43	0.03/0.93	0.8	0.9
P-irr								Yes	No	0.15	16	90	0.10/0.90	1.4	2.2
P-rec-irr								No	No	0.17	17	47	0.03/0.93	0.9	0.6
P-tau								Yes	Yes	0.21	17	76	0.13/0.87	2.1	2.7

Model	M_t0	M_BH	R₀	Y_e0	s₀	α	Res.	Rec.	Irr.	\|$\bar{Y}_{\rm e}$\|	\|$\bar{s}$\|	t_exp	M_ej/M_acc	\|$\bar{\rho }_2$\|	\|$\bar{v}_{r,9}$\|
	( M_⊙)		(km)		(k_B/b)						(k_B/b)	(ms)	(M_t0/M_t0)
S-def	0.03	3	50	0.10	8	0.03	std	Yes	Yes	0.16	16	95	0.10/0.90	1.6	2.2
S-m0.01	0.01	3	50	0.10	8	0.03	std	Yes	Yes	0.15	18	68	0.10/0.90	0.5	2.2
S-m0.10	0.10									0.17	17	119	0.11/0.89	6.3	2.3
S-r75	0.03	3	75							0.16	16	126	0.22/0.78	3.6	2.2
S-M10		10	150							0.18	17	77	0.04/0.92	0.8	1.8
S-y0.05		3	50	0.05						0.15	16	93	0.10/0.90	1.5	2.2
S-y0.15				0.15						0.17	16	92	0.10/0.90	1.6	2.3
S-s6				0.10	6					0.14	17	86	0.08/0.91	1.2	1.9
S-s10					10					0.19	16	87	0.12/0.88	1.9	2.6
S-v0.01					8	0.01				0.20	18	193	0.11/0.89	1.5	2.5
S-v0.10						0.10				0.14	19	38	0.13/0.87	2.2	2.4
S-hr						0.03	hi			0.15	16	94	0.10/0.90	1.5	2.2
P-rec	0.03	3	50	0.10	8	0.03	std	No	Yes	0.18	17	43	0.03/0.93	0.8	0.9
P-irr								Yes	No	0.15	16	90	0.10/0.90	1.4	2.2
P-rec-irr								No	No	0.17	17	47	0.03/0.93	0.9	0.6
P-tau								Yes	Yes	0.21	17	76	0.13/0.87	2.1	2.7

Table 1.

Open in new tab

Models evolved and outflow properties. Columns from left to right are: initial torus mass, BH mass, initial torus radius (equation 28), initial electron fraction, initial entropy, viscosity coefficient (equation 27), spatial resolution (std=standard, hi=high; Section 3.1), inclusion of recombination energy (equation 12), inclusion of self-irradiation (Section 3.2), mass-flux-weighted values of the electron fraction, entropy, and expansion time |$t_{\rm } = r/\bar{v}_r$| at a radius where |$\bar{T}\sim 5\times 10^9$| K and within ±60° of the midplane (equation 31), ratio of the total mass with positive energy ejected beyond r = 10⁹ cm to the total mass accreted through the ISCO radius, each in units of the initial torus mass, and mass-flux-weighted density (in units of 100 g cm⁻³) and velocity (in units of 10 000 km s⁻¹) at r = 10⁹ cm and within ±60° of the midplane.

Model	M_t0	M_BH	R₀	Y_e0	s₀	α	Res.	Rec.	Irr.	\|$\bar{Y}_{\rm e}$\|	\|$\bar{s}$\|	t_exp	M_ej/M_acc	\|$\bar{\rho }_2$\|	\|$\bar{v}_{r,9}$\|
	( M_⊙)		(km)		(k_B/b)						(k_B/b)	(ms)	(M_t0/M_t0)
S-def	0.03	3	50	0.10	8	0.03	std	Yes	Yes	0.16	16	95	0.10/0.90	1.6	2.2
S-m0.01	0.01	3	50	0.10	8	0.03	std	Yes	Yes	0.15	18	68	0.10/0.90	0.5	2.2
S-m0.10	0.10									0.17	17	119	0.11/0.89	6.3	2.3
S-r75	0.03	3	75							0.16	16	126	0.22/0.78	3.6	2.2
S-M10		10	150							0.18	17	77	0.04/0.92	0.8	1.8
S-y0.05		3	50	0.05						0.15	16	93	0.10/0.90	1.5	2.2
S-y0.15				0.15						0.17	16	92	0.10/0.90	1.6	2.3
S-s6				0.10	6					0.14	17	86	0.08/0.91	1.2	1.9
S-s10					10					0.19	16	87	0.12/0.88	1.9	2.6
S-v0.01					8	0.01				0.20	18	193	0.11/0.89	1.5	2.5
S-v0.10						0.10				0.14	19	38	0.13/0.87	2.2	2.4
S-hr						0.03	hi			0.15	16	94	0.10/0.90	1.5	2.2
P-rec	0.03	3	50	0.10	8	0.03	std	No	Yes	0.18	17	43	0.03/0.93	0.8	0.9
P-irr								Yes	No	0.15	16	90	0.10/0.90	1.4	2.2
P-rec-irr								No	No	0.17	17	47	0.03/0.93	0.9	0.6
P-tau								Yes	Yes	0.21	17	76	0.13/0.87	2.1	2.7

Model	M_t0	M_BH	R₀	Y_e0	s₀	α	Res.	Rec.	Irr.	\|$\bar{Y}_{\rm e}$\|	\|$\bar{s}$\|	t_exp	M_ej/M_acc	\|$\bar{\rho }_2$\|	\|$\bar{v}_{r,9}$\|
	( M_⊙)		(km)		(k_B/b)						(k_B/b)	(ms)	(M_t0/M_t0)
S-def	0.03	3	50	0.10	8	0.03	std	Yes	Yes	0.16	16	95	0.10/0.90	1.6	2.2
S-m0.01	0.01	3	50	0.10	8	0.03	std	Yes	Yes	0.15	18	68	0.10/0.90	0.5	2.2
S-m0.10	0.10									0.17	17	119	0.11/0.89	6.3	2.3
S-r75	0.03	3	75							0.16	16	126	0.22/0.78	3.6	2.2
S-M10		10	150							0.18	17	77	0.04/0.92	0.8	1.8
S-y0.05		3	50	0.05						0.15	16	93	0.10/0.90	1.5	2.2
S-y0.15				0.15						0.17	16	92	0.10/0.90	1.6	2.3
S-s6				0.10	6					0.14	17	86	0.08/0.91	1.2	1.9
S-s10					10					0.19	16	87	0.12/0.88	1.9	2.6
S-v0.01					8	0.01				0.20	18	193	0.11/0.89	1.5	2.5
S-v0.10						0.10				0.14	19	38	0.13/0.87	2.2	2.4
S-hr						0.03	hi			0.15	16	94	0.10/0.90	1.5	2.2
P-rec	0.03	3	50	0.10	8	0.03	std	No	Yes	0.18	17	43	0.03/0.93	0.8	0.9
P-irr								Yes	No	0.15	16	90	0.10/0.90	1.4	2.2
P-rec-irr								No	No	0.17	17	47	0.03/0.93	0.9	0.6
P-tau								Yes	Yes	0.21	17	76	0.13/0.87	2.1	2.7

The S-series of models include all the physics, and vary parameters around a fiducial model with M_BH = 3 M_⊙, α = 0.03, M_t = 0.03 M_⊙, Y_e = 0.1 and s = 8k_B per baryon, with standard resolution (Section 3.1). We call this model S-def, and it is intended to roughly match the parameters of model B10 PaWi of Ruffert & Janka (1999, cf. their fig. 14). This model is also marginally optically thick to neutrinos at early times, becoming transparent [as measured by the minimum optical depth τ_peak (equation 23)] after five orbits at r = R₀. Models in this series explore the effect on the outflows of varying the torus mass (S-m0.01, S-m0.10), torus radius (S-r75), BH mass (S-M10), initial electron fraction (S-y0.05 and S-y0.150), initial entropy (S-s6 and S-s10), magnitude of the viscous stress tensor (S-v0.01 and S-0.10) and resolution (S-hr). Models in this series are evolved for 1000 orbits at r = R₀, except S-def, which is evolved for 3000 orbits at the same location.

The P-series explores the effect of suppressing physical processes relative to model S-def, to study the effect on the outflow generation. In model P-rec, we remove the binding energy of alpha particles by setting Q_α = 0 in equation (12) in both the initial condition and the subsequent evolution. The series also explores the effect of shutting down self-irradiation (P-irr), as well as the effect of suppressing both recombination and self-irradiation simultaneously (P-rec-irr). We also test the effect of the optical depth corrections to self-irradiation, by setting τ_{i, irr} = 0 (equation 24) in model P-tau (the global suppression of neutrino emission by τ_peak equation 23 is still included). All models in this series are evolved for 3000 orbits at r = R₀.

4 RESULTS

4.1 Outflow generation

All tori undergo the same basic evolutionary stages. The disc spreads in radius due to angular momentum transport, and the internal energy is modified by viscous heating, nuclear recombination and neutrino source terms. The accretion rate at the ISCO reaches a peak magnitude at time ∼0.1/α orbits at r = R₀, later decaying as a power law in time after ∼1/α orbits at the same location (Fig. 1).

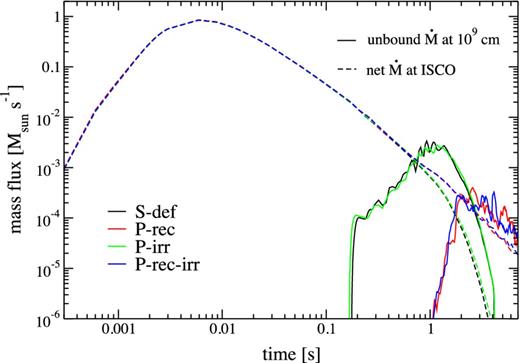
Angle-integrated mass outflow rate in unbound material at r = 109 cm (solid lines) and net mass accretion rate at the ISCO (dashed lines) as a function of time for model S_def (black). Also shown are models that suppress the nuclear binding energy of alpha particles (P-rec, red), self-irradiation (P-irr, green), or both (P-rec-irr, blue). The orbital time at r = R0 is 2.9 ms.

Figure 1.

Angle-integrated mass outflow rate in unbound material at r = 10⁹ cm (solid lines) and net mass accretion rate at the ISCO (dashed lines) as a function of time for model S_def (black). Also shown are models that suppress the nuclear binding energy of alpha particles (P-rec, red), self-irradiation (P-irr, green), or both (P-rec-irr, blue). The orbital time at r = R₀ is 2.9 ms.

Open in new tab Download slide

The inner regions of the disc are initially sufficiently hot for neutrino cooling to balance viscous heating. In contrast, the outer regions are colder, and viscous heating dominates over neutrino cooling (e.g. MPQ09). This net heating, combined with the transport of angular momentum to larger radii, causes an expansion in the outer regions of the disc as shown in Fig. 2 for model S-def. The outermost regions achieve positive specific energy

\begin{equation} e_{\rm tot} = \frac{1}{2}\boldsymbol {v}_{\rm p}^2 + \frac{1}{2}\frac{\ell _z^2}{(r\sin \theta )^2} + e_{\rm int} + \Phi \end{equation}

(29)

and are therefore unbound from the central BH.

Figure 2.

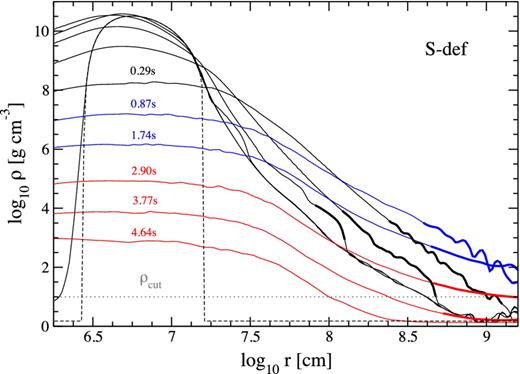
Evolution of the angle-averaged density in model S_def, illustrating the generation of the outflow. Curves correspond to times chosen in multiples of the orbital time at r = R₀ (2.9 ms), showing 0, 3, 10, 30, 100, 300, 600, 1000, 1300, 1600 orbits, as labelled. The bold curve segments correspond to material that has positive energy (equation 29). The horizontal dotted line marks the density at which source terms are suppressed for numerical reasons, and the dashed line shows the equilibrium torus before relaxation for the initial condition (Section 3.4).

Open in new tab Download slide

The mass outflow rate in unbound material at r = 10⁹ cm for model S-def is shown in Fig. 1. It rises from low values to a peak at ∼1 s or (∼ 400 orbits at r = R₀) that exceeds the magnitude of the mass loss at the ISCO. This outflow is much denser than that generated by the initial expansion of the equilibrium torus in the low-density ambient medium, and which generates the background power-law density profile (Fig. 2).

The relative contribution of viscous heating, nuclear recombination and self-irradiation to the outflow generation is examined in Fig. 1. The mass accretion rate and outflow rate of the default model S-def is compared with those from models that suppress the nuclear recombination energy (P-rec), self-irradiation (P-irr), and both nuclear energy and self-irradiation simultaneously (P-rec-irr). The recombination of alpha particles has the strongest effect on the disc evolution, by (1) causing a more energetic and massive outflow to arise earlier, and (2) by strongly suppressing the mass accretion rate at the ISCO. This drop in the accretion rate at late times is consistent with the results of Lee et al. (2009).

Self-irradiation has only a minor effect on the energetics of the system. In model S-def, neutrino heating is always smaller than viscous heating by at least a factor of several. This sub-dominance of self-irradiation can be traced to a few causes: (1) the neutrino luminosities are high only for a limited period of time, because both the mass and the temperature of the torus decrease with time, as shown in Fig. 3 for model S-def; (2) self-irradiation is the strongest at the time where the torus becomes optically thin, and affects mostly vertical, low-density regions of the inner disc; and (3) the temperature in the emission region decreases with time (Fig. 3), resulting in lower mean energies of the neutrinos and thus a decreasing energy deposition rate. For illustration, a snapshot of the ratio of neutrino heating to viscous heating in model S-def-hr is shown in Fig. 4. The effect is not entirely negligible however, as turning off optical depth corrections leads to ∼20 per cent changes in the electron fraction and the asymptotic velocity (Section 4.2).

Figure 3.

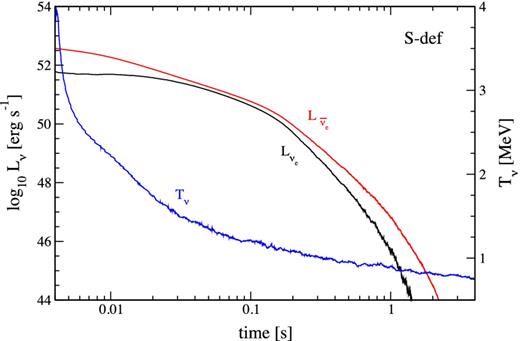
Time evolution of the neutrino and antineutrino luminosities (black and red, respectively) and neutrino temperature (blue) for model S-def.

Open in new tab Download slide

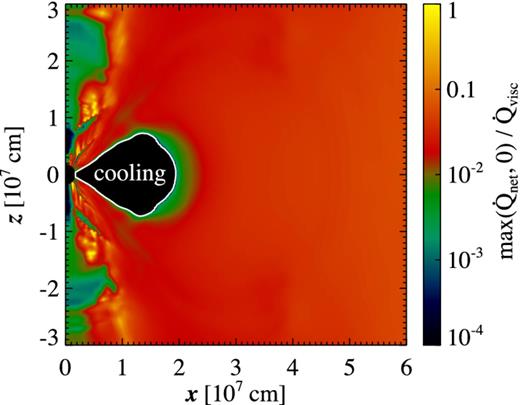
$Ratio of neutrino heating to viscous heating $\dot{Q}_{\rm visc} = \mathbb {T}:\mathbb {T}/(\nu \rho ^2)$ (equation 10) in model S-def-hr at time 0.058 s (orbit 20 at r = R0). The white contour shows the surface $\dot{Q}_{\rm net} = 0$, inside which neutrino cooling dominates.$

Figure 4.

Ratio of neutrino heating to viscous heating |$\dot{Q}_{\rm visc} = \mathbb {T}:\mathbb {T}/(\nu \rho ^2)$| (equation 10) in model S-def-hr at time 0.058 s (orbit 20 at r = R₀). The white contour shows the surface |$\dot{Q}_{\rm net} = 0$|⁠, inside which neutrino cooling dominates.

Open in new tab Download slide

The total mass accreted through the ISCO radius and the mass with e_tot > 0 ejected beyond a radius of 10⁹ cm are given in Table 1 as fractions of the initial torus mass. In most models, approximately 10 per cent of the torus mass is ejected, with the rest accreting on to the BH. One exception is the model S-r75 with a larger initial torus radius, which ejects twice as much mass as the default model. Another exception is model S-M10, which while having a large disc radius also has a higher BH mass, which leads to smaller mass ejection by ∼50 per cent. The other two outliers are the models that suppress nuclear recombination (P-rec and P-rec-irr), for which ∼3 per cent of the mass is ejected (cf. Fig. 1). Doubling the resolution in each coordinate direction leads to insignificant quantitative differences, so we consider our results converged. Given the range of disc masses explored, the ejecta mass from delayed outflows can thus range from 10⁻³ to 10⁻² M_⊙.

The morphology of the ejecta is quasi-spherical, with most of the material being ejected within ∼60° of the disc midplane, as shown in Fig. 5. The bulk of the disc has moderate entropy (∼20), particularly in regions relevant for nucleosynthesis (Section 4.2). At large radii (∼10⁹ cm), the outflowing material develops shocks that raise its entropy. Large-scale instabilities are also seeded by convection in the disc, which cannot cool efficiently once its accretion rate falls below |$\dot{M}_{\rm ign}$| (equation 5). The funnel within a few tens of degrees from the polar axis has different properties; we do not study them here given our very approximate treatment of general relativity, and our omission of energy deposition by neutrino pair annihilation.

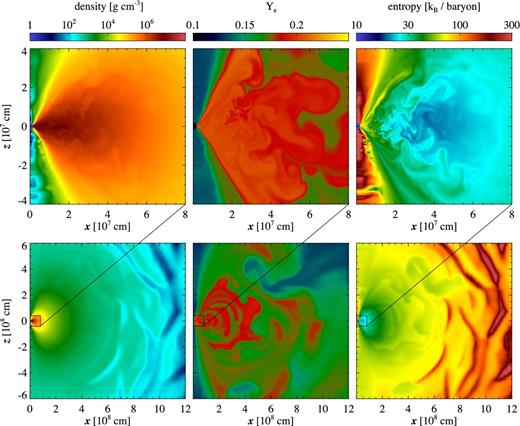
$Colour maps of density (left), electron fraction (middle) and entropy (right) in model S-def-hr at time 1.16 s (orbit 400 at r = R0), illustrating the wind morphology. Upper panels show zoomed in regions of the panels directly below, as indicated by the boxes. An animated version of this figure is available in the online journal.$

Figure 5.

Colour maps of density (left), electron fraction (middle) and entropy (right) in model S-def-hr at time 1.16 s (orbit 400 at r = R₀), illustrating the wind morphology. Upper panels show zoomed in regions of the panels directly below, as indicated by the boxes. An animated version of this figure is available in the online journal.

Open in new tab Download slide

4.2 Outflow properties

At early times and in the innermost regions of the disc (r ≲ 100 km), weak interactions are faster than the viscous time, and the electron fraction reaches its equilibrium value given the local density and temperature (e.g. Beloborodov 2003). As the disc evolves, the temperature and density decrease to the point that weak interactions operate slower than the viscous time and the electron fraction freezes out, becoming an advected quantity only (MPQ09). This process is illustrated for our fiducial model in Fig. 6.

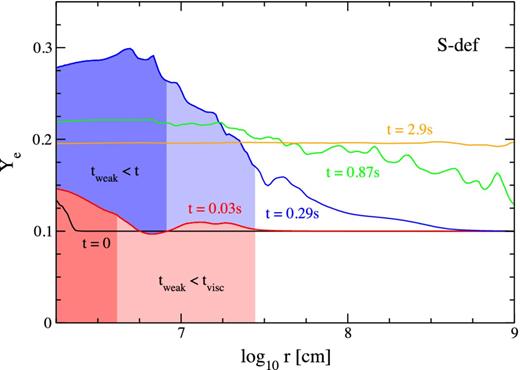
$Angle-averaged, mass-weighted electron fraction at selected times for model S-def, as labelled. The dark-filled region corresponds to the weak equilibration time tweak = Ye/|Γnet| being smaller than the curve time, while the light-filled region is such that tweak is shorter than the viscous time tvisc.$

Figure 6.

Angle-averaged, mass-weighted electron fraction at selected times for model S-def, as labelled. The dark-filled region corresponds to the weak equilibration time t_weak = Y_e/|Γ_net| being smaller than the curve time, while the light-filled region is such that t_weak is shorter than the viscous time t_visc.

Open in new tab Download slide

In the inner regions of the disc, the equilibrium electron fraction is initially small because electrons are more abundant than positrons when the disc is degenerate. However, with time Y_e rises to a maximum value ∼0.3 because the disc becomes less degenerate as the density decreases. Most of this high-Y_e material is accreted on to the BH, however. The outer parts of the disc that eventually become unbound never achieve such high electron fractions and are instead ejected with Y_e ≲ 0.2.

At a given radius, the wind material is not homogeneous in composition, but instead shows some variation around mean values. Fig. 7 shows mass-flux-weighted quantities crossing a spherical surface at the fixed radius R_out = 10⁹ cm in the models S-def and P-irr. Quantities are computed according to

\begin{equation} \langle A(R_{\rm out},t) \rangle = \frac{\int _{\theta _{\rm min}}^{\theta _{\rm max}}\sin \theta {\mathrm{d}}\theta \,R_{\rm out}^2\rho v_r A(R_{\rm out},\theta ,t)}{ \int _{\theta _{\rm min}}^{\theta _{\rm max}}\sin \theta {\mathrm{d}}\theta \,R_{\rm out}^2\rho v_r}, \end{equation}

(30)

where A(R_out, θ , t) is a generic scalar quantity, and [θ_min, θ_max] is the angular range of the meridional integral, chosen as a wedge within 60° of the midplane (cf. Fig. 5). The bulk of the ejected material has Y_e ∼ 0.2 and velocities v_r ∼ 20 000 km s⁻¹.

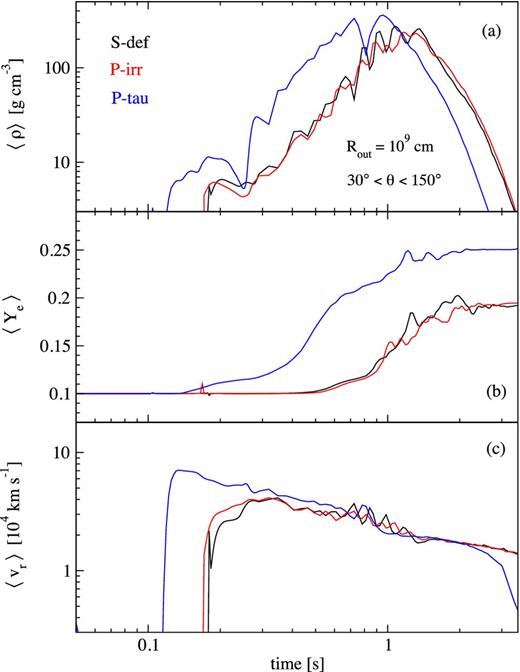
$Instantaneous mass-flux-weighted quantities at a radius Rout = 109 cm for models S-def, P-irr (no self-irradiation) and P-tau (no optical depth suppression). Shown are the density ρ (a), electron fraction Ye (b) and velocity vr (c). The average is conducted over polar angles within 60° of the equator.$

Figure 7.

Instantaneous mass-flux-weighted quantities at a radius R_out = 10⁹ cm for models S-def, P-irr (no self-irradiation) and P-tau (no optical depth suppression). Shown are the density ρ (a), electron fraction Y_e (b) and velocity v_r (c). The average is conducted over polar angles within 60° of the equator.

Open in new tab Download slide

Heavy nuclei generation occurs in regions where T ∼ 5 × 10⁹ K (Hoffman et al. 1997). In the fiducial model S-def, this corresponds to a range of radii 200–400 km on the midplane depending on the phase in the disc evolution. To quantify the thermodynamic properties relevant for nucleosynthesis in the disc, we compute time- and angle-integrated mass-weighted mean values

\begin{equation} \bar{A}(R_{\rm nuc}) = \frac{\int {\mathrm{d}}t\int \sin \theta {\mathrm{d}}\theta \, R_{\rm nuc}^2\rho v_r\, A(R_{\rm nuc},\theta ,t)}{ \int {\mathrm{d}}t\int \sin \theta {\mathrm{d}}\theta \, R_{\rm nuc}^2\rho v_r}, \end{equation}

(31)

where the radius R_nuc is chosen so that |$\bar{T} \simeq 5\times 10^9$| K. The resulting mean values of the electron fraction, entropy and expansion time at R_nuc (within 60° of the midplane) are shown for all models in Table 1.

The composition is largely insensitive to variations in the model parameters, with typical mean values |$\bar{Y}_{\rm e} \sim 0.2$|⁠, |$\bar{S}\sim 20k_{\rm B}$| per baryon, and expansion time-scales |$t_{\rm exp} = R_{\rm nuc}/\bar{v}_r \sim 0.1$| s. The magnitude of the spread from the mean value is illustrated in Fig. 8, which breaks up the mean values of Y_e, entropy and expansion time for model S-def.

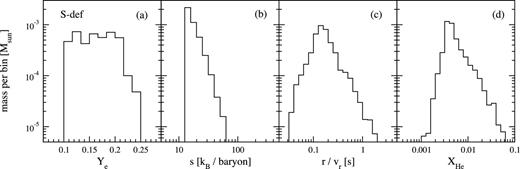
$Thermodynamic properties of disc material for model S-def at a radius Rnuc = 400 km, where $\bar{T}\simeq 5\times 10^9$ K. The histograms are constructed by considering all material that crosses this radius, within 60° of the midplane, over the entire disc evolution. Shown are the electron fraction Ye (a), entropy S (b), expansion time texp = r/vr (c) and final helium mass fraction (d) computed from equation (C1).$

Figure 8.

Thermodynamic properties of disc material for model S-def at a radius R_nuc = 400 km, where |$\bar{T}\simeq 5\times 10^9$| K. The histograms are constructed by considering all material that crosses this radius, within 60° of the midplane, over the entire disc evolution. Shown are the electron fraction Y_e (a), entropy S (b), expansion time t_exp = r/v_r (c) and final helium mass fraction (d) computed from equation (C1).

Open in new tab Download slide

The value of |$\bar{Y}_{\rm e}$| is relatively insensitive to the initial electron fraction because most of the disc mass achieves weak equilibrium, erasing its initial composition. The largest difference in |$\bar{Y}_{\rm e}$| occurs due to changes in the initial entropy of the disc and the magnitude of the viscosity. The entropy of the torus is related to the level of degeneracy, which in turn determines the value of the equilibrium electron fraction (e.g. Beloborodov 2003). The magnitude of the viscosity determines the ratio of the weak equilibration time t_weak to the viscous times t_visc. A smaller viscosity implies that these two time-scales become equal at a large radius, which increases the amount of processed Y_e that enters the outflow. This modest dependence of Y_e on α is, however, mitigated by two facts: (1) the disc is regulated by neutrino cooling to moderate degeneracy (CB07), independent of the magnitude of viscous heating; (2) the disc becomes radiatively inefficient (and hence thicker and less degenerate) on the same time-scale that Y_e freezes out. This coincidence in time-scales results from the fact that e⁻/e⁺ captures both cool the disc and change Y_e (MPQ09).

The effects of self-irradiation on the ejecta composition are illustrated by Fig. 7, which compares the polar mass-flux-weighted composition for model S-def, P-irr (which suppresses self-irradiation) and P-tau (which turns off optical depth corrections to self-irradiation). Including self-irradiation with optical depth correction leads to a nearly identical outcome than suppressing irradiation altogether. As with the small energetic relevance of neutrino heating, changes in the composition due to neutrino irradiation are important only around the time when the disc becomes transparent to neutrinos and its luminosity is still high. This time-scale of peak irradiation is somewhat shorter than that required to significantly change the composition by weak interactions. The largest possible effect of neutrino heating on the outflow is probed by model P-tau, which completely suppresses optical depth corrections to the self-irradiation luminosity (while still globally suppressing the cooling rates). The outflow begins earlier, achieves asymptotic velocities that are ∼20 per cent larger, and has a mean Y_e that is 0.05 larger than the default model. Such moderate changes given an unrealistically large neutrino absorption rate reaffirms our conclusion that self-irradiation is only a small correction to the overall dynamics for low-mass discs.

The expansion velocity at larger radii is remarkably constant, sensitive only to the inclusion of the nuclear binding energy of alpha particles. Note, however, that these values likely underestimate the true expansion velocities by a factor of ∼ 1.4–1.7 since we do not include the additional energy of ∼ a few MeV nucleon⁻¹ released in forming seed particles and (on somewhat longer time-scales ∼1 s) heavy r-process nuclei.

5 DISCUSSION

5.1 Nucleosynthesis in disc outflows

Appendix C reviews the conditions for heavy-element nucleosynthesis in hot outflows, such as those from NS merger accretion discs, and provides analytic formulae for the fraction of the ejected mass synthesized into heavy r-process nuclei X_h and the fraction X_α = 1 − X_h that remains in α-particles (equation C1). Given the low electron fraction Y_e ≲ 0.2 of the disc outflows found in our calculations, we conclude that most of the ejecta will go into second and third peak r-process elements with mass number A ∼ 130–200 (X_h ≃ 1). A much smaller fraction, X_He ∼ 10⁻², will remain in ⁴He, which may have implications for the spectroscopic signatures of these events (Section 5.2).

The average Galactic production rate of r-process nuclei due to accretion disc outflows from binary NS mergers is given by

\begin{eqnarray} \dot{M}_{\rm r} &=& \mathcal {R}_{\rm NS^{2}}f_{\rm ej}\bar{M}_{\rm t} \nonumber \\ &=& 10^{-7}\,\mathrm{M}_{{\odot }}{\rm yr^{-1}}\left(\frac{\mathcal {R}_{\rm NS^{2}}}{10^{-4}{\rm yr^{-1}}}\right)\left(\frac{f_{\rm ej}}{0.1}\right)\left(\frac{\bar{M}_{\rm t}}{10^{-2}\,\mathrm{M}_{{\odot }}}\right), \end{eqnarray}

(32)

where |$\mathcal {R}_{\rm NS^{2}}$| is the rate of NS–NS mergers scaled to its estimated value in the Milky Way (uncertain by at least an order of magnitude; Kalogera et al. 2004), |$\bar{M}_{\rm t}$| is the average mass of the initial accretion torus and f_ej ∼ 0.1 is the fraction of M_t ejected in outflows, scaled to the characteristic value derived from our numerical simulations. Equation (32) should be compared with the ‘observed’ rate |$\dot{M}_{\rm r}^{\rm obs} \sim 5\times 10^{-7}\,\mathrm{M}_{{\odot }}$| yr⁻¹ required to explain the abundances of heavy A ≳ 130 r-process elements produced over the age of the Galaxy (Qian 2000). This shows that NS merger disc outflows constitute a potentially significant r-process source.

Although the idea that NS mergers are a promising r-process source is not new (Lattimer & Schramm 1974), previous studies have focused almost exclusively on nucleosynthesis of the dynamical ejecta.

Our simulations show no clear evidence for outflows powered primarily by neutrino heating. Such a wind was previously anticipated to dominate mass loss from small radii in the disc (e.g. Metzger et al. 2008a; Surman et al. 2008; Wanajo & Janka 2012). Because neutrinos and antineutrinos from the disc have similar luminosities and mean energies, neutrino absorption is expected to drive Y_e to a value ∼0.5. Although our simulations do show unbound polar outflows, the electron fraction of this material is increased only slightly by neutrino irradiation (Fig. 7), since viscous heating dominates the unbinding of matter from the disc (Fig. 4). This hierarchy is contingent upon our assumption of an α-viscosity, which may not reflect the true vertical distribution of turbulent dissipation in the disc. Our approximate treatment of neutrino physics prevents us from definitively ruling out a strong role of self-irradiation. However, if an even larger fraction of the dissipation occurs in the disc corona in more realistic magnetized discs (e.g. Hirose, Krolik & Stone 2006), then the dominance of ‘viscous’-driven (low Y_e) polar outflows may turn out to be a robust feature of the launching mechanism. Regardless of the composition of the [possibly neutrino-driven] winds from small radii in the disc, the late outflows powered by α recombination and viscous heating almost certainly dominate the total (time-integrated) mass loss.

5.2 Radioactively powered emission

Radioactive decay of r-process elements synthesized in the disc outflows gives rise to an electromagnetic transient similar to a dim supernova (e.g. Li & Paczyński 1998). Although the disc outflows are mildly anisotropic (Fig. 5), the ejecta will become increasingly spherical as it expands homologously with a characteristic velocity |$\bar{v}_r \simeq 0.1c$| (Table 1). Most of the energy released by the r-process occurs on a time-scale ∼ seconds, but this heating is lost to adiabatic expansion since the outflow is highly optically thick at this early stage. Nevertheless, radioactive decay continues to add energy to the ejecta, at an approximately constant rate per logarithmic time (e.g. Metzger et al. 2010b). Electromagnetic emission peaks only once the time-scale for photons to diffuse through the ejecta t_d ∝ κM_ej/cr becomes shorter than the expansion time-scale |$t_{\rm exp} = r/\bar{v}_r$|⁠. This occurs on a time-scale (Metzger et al. 2010b, equations 3 and 4)

\begin{equation} t_{\rm p} \approx 7{\rm d}\left(\frac{\bar{v}_r}{0.1c}\right)^{1/2}\left(\frac{M_{\rm ej}}{10^{-2}\,\mathrm{M}_{{\odot }}}\right)^{1/2} \left(\frac{\kappa }{10{\rm \,cm^{2}g^{-1}}}\right)^{1/2} \end{equation}

(33)

resulting in emission with a characteristic peak luminosity

\begin{eqnarray} L_{\rm p} & \simeq& 2.4\times 10^{40}{\rm erg\,s^{-1}}\left(\frac{\bar{v}_r}{0.1c}\right)^{-1/2} \nonumber \\ && \times \left(\frac{M_{\rm ej}}{10^{-2}\,\mathrm{M}_{{\odot }}}\right)^{1/2}\left(\frac{\kappa }{10{\rm \,cm^{2}g^{-1}}}\right)^{-1/2}, \end{eqnarray}

(34)

where κ is the opacity, scaled to a value characteristic of the line opacities of Lanthanide elements, given their expected abundance in the r-process ejecta (Kasen et al. 2013).

Because the composition of the disc outflows (predominantly heavy r-process nuclei) is similar to that of the dynamically ejected tidal tails, it may be observationally challenging to distinguish their contribution to the transient emission. One unique feature of the disc outflows, however, is the presence of a modest amount of helium (X_He ∼ 10⁻²), which is not present in the dynamical ejecta due to its much lower entropy S ≲ k_b baryon⁻¹ (since X_He ∝ S^3/2; equation C1).

Even a small quantity of He may be detectable if emission/absorption lines (e.g. He I 1.083 μm and He i 2.058 μm) are produced as the result of non-thermal excitation, induced by energetic γ-rays, β-decay electrons and fission products from decaying r-process elements. This is in analogy to the mechanism responsible for producing He lines in core-collapse SNe as the result of mixing radioactive ⁵⁶Ni into the outer layers of the ejecta (e.g. Lucy 1991; Dessart et al. 2012). Though a potentially promising diagnostic of conditions close to the merger site, future work is required to quantify the strength of He emission lines in kilonovae.

5.3 Effects of a long-lived hypermassive NS

In the case of NS–NS mergers, our calculations implicitly assume that a BH forms within a few dynamical times after coalescence. If, however, the collapse is significantly delayed due to, e.g., thermal pressure and/or differential rotational support (Morrison, Baumgarte & Shapiro 2004; O'Connor & Ott 2011; Lehner et al. 2012; Paschalidis, Etienne & Shapiro 2012), then the effects of neutrino irradiation from the hyper-massive NS (HMNS) could qualitatively alter the properties of the disc evolution and its outflows.

To significantly alter the disc dynamics, neutrino emission from the HMNS would need to maintain both a high flux level and a high mean neutrino energy, for a time-scale longer than both (1) the time required to achieve neutrino transparency; and (2) the thermal time of the disc, such that the internal energy is raised sufficiently to unbind the disc. Such neutrino-driven outflows necessarily occur via thermal evaporation (e.g. McLaughlin & Surman 2005; Metzger et al. 2008a; Surman et al. 2008; Dessart et al. 2009), as in the case of proto-NS winds, since momentum transfer from neutrinos is negligible.⁵

Even if neutrino irradiation from the HMNS is insufficient to alter the dynamics of the disc, it may still alter its composition, especially in outer parts of the disc where the rate of electron/positron captures is slow. To the extent that the HMNSs formed in binary NS merger are similar to the proto-NSs formed in core-collapse supernovae, the neutrino and antineutrino luminosities and temperatures are expected to be similar. The net effect of HMNS irradiation on the disc would thus be to raise Y_e in both the disc midplane and in subsequent outflows (Dessart et al. 2009; see Metzger, Piro & Quataert 2009b and Darbha et al. 2010 for an analogous scenario following the accretion-induced collapse of a white dwarf). Spectroscopic or photometric signatures of elements synthesized exclusively in proton-rich ejecta of kilonovae (e.g. Fe or ⁵⁶Ni) could thus be taken as evidence for a long-lived HMNS. One significant difference between an r-process-rich and an Fe-rich outflow is the opacity of the ejecta, which drastically changes the rise time and peak luminosity of the light curve (Barnes & Kasen 2013; Tanaka & Hotokezaka 2013). Future work is necessary to quantify how long such a HMNS must survive in order to appreciably alter the outflow properties from the purely BH accretion scenario studied in this paper.

5.4 Comparison with previous work

Ruffert & Janka (1999) first studied the evolution of discs formed after NS coalescence in 3D using a realistic EOS, a finite volume hydrodynamic method, Newtonian and pseudo-Newtonian potentials, and a neutrino leakage scheme (Ruffert, Janka & Schaefer 1996). Follow up work by Setiawan, Ruffert & Janka (2004) and Setiawan, Ruffert & Janka (2006) explored the effect of including an α viscosity over a wide range of disc masses, finding that neutrino emission is sensitive to the magnitude of α. Our results cannot be directly compared to theirs, however, because their models were evolved only up to 70 ms. Also, due to the EOS used, their density floor was set at 10⁸ g cm⁻³, which would make it hard to develop any viscously driven outflow (cf. Fig. 2).

The interplay between magnetohydrodynamic and general-relativistic effects was explored by Shibata, Sekiguchi & Takahashi (2007), finding that if poloidal fields and differential rotation are present, the magnetorotational instability drives turbulence that transports angular momentum and heats the disc. Due to the MHD algorithm employed, these models also require a floor of density ∼10⁶ g cm⁻³, which again prevents the development of viscously driven winds out to large radius. The effect of grey radiation transport has been investigated by Shibata & Sekiguchi (2012), and general-relativistic simulations of tori formed in BH–NS mergers have recently been reported by Deaton et al. (2013).

Lee, Ramirez-Ruiz & Page (2005) evolved tori over time-scales up to a few 100 ms, using initial conditions from a merger simulation. They used a smoothed particle hydrodynamics method, and included a realistic EOS, neutrino optical depth corrections, and the effect of nuclear recombination in the energetics of the disc. In contrast to our models, they assumed that the electron fraction satisfies beta equilibrium, parametrized the NSE abundances by the analytic relation of Qian & Woosley (1996), included all components of the viscous stress tensor and focused on relatively massive tori. Lee et al. (2009) extended the evolution to a few seconds, considered a pseudo-Newtonian potential, and explored a wide range of tori masses and viscosity parameters. They found that the accretion rate drops sharply at late times as a consequence of including the recombination energy of alpha particles, an effect that we reproduce in our models (cf. Fig. 1).

The properties of the disc evolution and outflows found here are in qualitative agreement with the 1D model of MPQ09. MPQ09 predicted a somewhat larger mass of unbound material, and a distribution of electron fraction extending to higher values Y_e ≳ 0.3. In hindsight, this discrepancy can be understood by the fact that MPQ09 counted all mass in the disc outside the point of Y_e freeze-out as eventually becoming unbound, whereas our calculations show that only the outer edge of the disc (where Y_e is lowest) achieves sufficiently high energy to become unbound. The temperature and density of the disc midplane in our simulations are also somewhat lower than in the 1D α-disc models of MPQ09 (they find an inner disc temperature of ∼10 MeV), resulting in less effective neutrino cooling. This discrepancy can partially be understood by the fact that α-disc models assume that viscous heating exactly balances cooling, which is not everywhere achieved in our models, leading the 1D models to overestimate the midplane density. Since radiation pressure is moderately important, lower density implies a lower temperature in vertical hydrostatic balance.

6 CONCLUSIONS

We have explored the properties of outflows generated on the viscous time by accretion discs formed in NS–NS and NS–BH mergers, with an eye on detectable electromagnetic counterparts of the GW emission and r-process nucleosynthesis. Two-dimensional, time-dependent hydrodynamic simulations with a realistic EOS, weak interactions, self-irradiation in moderately optically thick environments and angular momentum transport via an α-viscosity are used to characterize the driving, composition and parameter dependencies of these outflows. Our main findings are as follows:

Discs eject ∼10 per cent of their mass in an unbound outflow. The composition is neutron rich, with typical electron fractions Y_e ∼ 0.2. This value arises because the ejected material comes from the outer part of the disc, which is never processed to a high equilibrium electron fraction by weak interactions. The high-Y_e material in the inner disc regions is accreted on to the BH (Fig. 6). Neutron-rich freeze-out is robust because (a) neutrino cooling regulates the disc to be mildly degenerate, which in turn regulates the equilibrium Y_e prior to the freeze-out; (b) outflows begin once the disc becomes advective and α-particles form, both of which occur nearly simultaneous with freeze-out.
The outflow composition is relatively robust relative to initial disc parameters (Table 1). In regions where heavy elements form (T ∼ 5 × 10⁹ K), we obtain characteristic entropies ∼20 k_b baryon⁻¹ and expansion times ∼0.1 s. The composition is not homogeneous, with spatial as well as temporal variations around the mean value (Figs 5 and 8). The expected nucleosynthetic output consists in second/third peak r-process elements (A ≳ 130), with a small trace of He (∼1 per cent by mass, but ≳10 per cent by number), which may generate a spectroscopic signature.
Small variations ∼10 per cent in the electron fraction are introduced by changes in the initial torus entropy and the magnitude of the viscosity. The entropy of the outflow is moderately sensitive to the initial torus mass and its initial entropy. The amount of mass ejected is sensitive only to the radius at which the torus mass resides initially. The outflow velocity is remarkably robust, with a characteristic value of ∼20 000 km s⁻¹ at 10⁹ cm.
In addition to viscous heating, nuclear recombination is a fundamental component in the generation of the outflow (Fig. 1). Its exclusion results in much lower ejected masses and asymptotic velocities. We also witness the drop in the accretion rate at late times first seen by Lee et al. (2009).
Self-irradiation appears to be both energetically and compositionally sub-dominant. This stems in part from the fact that irradiation is maximal around the time when the disc becomes transparent to neutrinos, which for most of our low-mass discs corresponds to early times in the disc evolution. The subsequent drop in disc temperatures and densities lowers both the amount of neutrinos emitted and their mean energies (Fig. 3), diminishing the relative importance of neutrino energy deposition as time passes. The effects of self-irradiation become noticeable only when completely removing optical depth corrections (Fig. 7). Even then, changes in global quantities are only of the order of 10 per cent.

There are many possible improvements to the model. Self-consistent angular momentum transport by magnetohydrodynamic turbulence, magnetocentrifugal winds and/or self-gravity (for more massive discs) would yield a first principles estimate on the spatial distribution of angular momentum and heating in the disc. A full general-relativistic code would help address whether the properties of the inner disc are important, particularly regarding neutrino self-irradiation with rapidly spinning BHs. More realistic initial conditions would shed light on whether the initial angular momentum distribution is of consequence for the timing and asymptotic properties of the ejecta. The possible effects of late ‘fall-back’ accretion of tidal tail material (e.g. Metzger et al. 2010a) on the disc evolution and outflows should also be explored. More accurate neutrino physics and three-dimensional modelling would be needed if precise predictions for the outflow properties are necessary.

A more detailed analysis of the nucleosynthesis products and electromagnetic signal generated by these outflows will be carried out in subsequent work.

We thank Stephan Rosswog, Thomas Janka, Almudena Arcones, Gabriel Martínez, Will East, Andrei Beloborodov, Tony Piro, Eliot Quatert, Dan Kasen and Luke Roberts for stimulating discussions and/or comments on the manuscript. We also thank the anonymous referee for helpful comments that improved the manuscript. RF is supported by NSF grant number AST-0807444. BDM acknowledges support from Columbia University. The software used in this work was in part developed by the DOE NNSA-ASC OASCR Flash Center at the University of Chicago. Computations were performed at the IAS Aurora cluster.

1

BHs formed from NS–NS mergers have typical spin parameter a ∼ 0.7–0.8 (e.g. Rezzolla et al. 2010).

2

The formation of heavy nuclei would indeed occur at radii within our simulation grid; however, see Section 5.1.

3

http://cococubed.asu.edu/code_pages/codes.shtml

4

Not to be confused with the absorption coefficients used in the actual neutrino absorption rates (Appendix B).

5

Even a neutrino luminosity as large as L_ν ∼ 10⁵³ erg s⁻¹ is sub-Eddington.

REFERENCES

Abadie

J.

et al. ,

Classical Quantum Gravity

,

2010

, vol.

27

pg.

173001

Crossref

Search ADS

Abadie

J.

et al. ,

Phys. Rev. D

,

2012

, vol.

85

pg.

122007

Crossref

Search ADS

Abramovici

A.

et al. ,

Sci

,

1992

, vol.

256

pg.

325

Crossref

Search ADS

Acernese

F.

et al. ,

Classical Quantum Gravity

,

2009

, vol.

26

pg.

085009

Crossref

Search ADS

Ajith

P.

et al. ,

Classical Quantum Gravity

,

2007

, vol.

24

pg.

689

Crossref

Search ADS

Audi

G.

Wapstra

A. H.

Thibault

C.

,

Nucl. Phys. A

,

2003

, vol.

729

pg.

337

Crossref

Search ADS

Barnes

J.

Kasen

D.

,

ApJ

,

2013

preprint (arXiv:1303.5787)

Bartos

I.

Brady

P.

Marka

S.

,

Classical Quantum Gravity

,

2013

, vol.

30

pg.

123001

Crossref

Search ADS

Bauswein

A.

Janka

H.-T.

Hebeler

K.

Schwenk

A.

,

Phys. Rev. D

,

2012

, vol.

86

pg.

063001

Crossref

Search ADS

Bauswein

A.

Goriely

S.

Janka

H.-T.

,

ApJ

,

2013

in press (arXiv:1302.6530)

Beloborodov

A. M.

,

ApJ

,

2003

, vol.

588

pg.

931

Crossref

Search ADS

Beloborodov

A. M.

Axelsson

M.

,

AIP Conf. Ser. Vol. 1054, Hyper-accreting Black Holes

,

2008

New York

Am. Inst. Phys.

pg.

51

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Bloom

J. S.

et al. ,

astro2010: The Astronomy and Astrophysics Decadal Survey

,

2009

preprint (arXiv:0902.1527)

Bruenn

S. W.

,

ApJS

,

1985

, vol.

58

pg.

771

Crossref

Search ADS

Caron

B.

et al. ,

Astropart. Phys.

,

1999

, vol.

10

pg.

369

Crossref

Search ADS

Chawla

S.

Anderson

M.

Besselman

M.

Lehner

L.

Liebling

S. L.

Motl

P. M.

Neilsen

D.

,

Phys. Rev. Lett.

,

2010

, vol.

105

pg.

111101

Crossref

Search ADS

PubMed

Chen

H.-Y.

Holz

D. E.

,

2012

preprint (arXiv:1206.0703)

Chen

W.-X.

Beloborodov

A. M.

,

ApJ

,

2007

, vol.

657

pg.

383

(CB07)

Crossref

Search ADS

Colella

P.

Woodward

P. R.

,

J Comput. Phys.

,

1984

, vol.

54

pg.

174

Crossref

Search ADS

Cornish

N.

Sampson

L.

Yunes

N.

Pretorius

F.

,

Phys. Rev. D

,

2011

, vol.

84

pg.

062003

Crossref

Search ADS

Darbha

S.

Metzger

B. D.

Quataert

E.

Kasen

D.

Nugent

P.

Thomas

R.

,

MNRAS

,

2010

, vol.

409

pg.

846

Crossref

Search ADS

Deaton

M. B.

et al. ,

2013

preprint (arXiv:1304.3384)

Dessart

L.

Ott

C. D.

Burrows

A.

Rosswog

S.

Livne

E.

,

ApJ

,

2009

, vol.

690

pg.

1681

Crossref

Search ADS

Dessart

L.

Hillier

D. J.

Li

C.

Woosley

S.

,

MNRAS

,

2012

, vol.

424

pg.

2139

Crossref

Search ADS

Di Matteo

T.

Perna

R.

Narayan

R.

,

ApJ

,

2002

, vol.

579

pg.

706

Crossref

Search ADS

Dubey

A.

Antypas

K.

Ganapathy

M. K.

Reid

L. B.

Riley

K.

Sheeler

D.

Siegel

A.

Weide

K.

,

J. Par. Comp.

,

2009

, vol.

35

pg.

512

Crossref

Search ADS

Duez

M. D.

Foucart

F.

Kidder

L. E.

Ott

C. D.

Teukolsky

S. A.

,

Classical Quantum Gravity

,

2010

, vol.

27

pg.

114106

Crossref

Search ADS

East

W. E.

Pretorius

F.

Stephens

B. C.

,

Phys. Rev. D

,

2012

, vol.

85

pg.

124009

Crossref

Search ADS

Eichler

D.

Livio

M.

Piran

T.

Schramm

D. N.

,

Nat

,

1989

, vol.

340

pg.

126

Crossref

Search ADS

Faber

J. A.

Rasio

F. A.

,

Living Rev. Relativ.

,

2012

, vol.

15

pg.

8

Crossref

Search ADS

PubMed

Faber

J. A.

Grandclément

P.

Rasio

F. A.

Taniguchi

K.

,

Phys. Rev. Lett.

,

2002

, vol.

89

pg.

231102

Crossref

Search ADS

PubMed

Faber

J. A.

Baumgarte

T. W.

Shapiro

S. L.

Taniguchi

K.

Rasio

F. A.

,

Phys. Rev. D

,

2006

, vol.

73

pg.

024012

Crossref

Search ADS

Fairhurst

S.

,

New J. Phys.

,

2009

, vol.

11

pg.

123006

Crossref

Search ADS

Fernández

R.

,

ApJ

,

2012

, vol.

749

pg.

142

Crossref

Search ADS

Fernández

R.

Metzger

B. D.

,

ApJ

,

2013

, vol.

763

pg.

108

Crossref

Search ADS

Foucart

F.

,

Phys. Rev. D

,

2012

, vol.

86

pg.

124007

Crossref

Search ADS

Foucart

F.

Duez

M. D.

Kidder

L. E.

Teukolsky

S. A.

,

Phys. Rev. D

,

2011

, vol.

83

pg.

024005

Crossref

Search ADS

Foucart

F.

Duez

M. D.

Kidder

L. E.

Scheel

M. A.

Szilagyi

B.

Teukolsky

S. A.

,

Phys. Rev. D

,

2012

, vol.

85

pg.

044015

Crossref

Search ADS

Freiburghaus

C.

Rosswog

S.

Thielemann

F.

,

ApJ

,

1999

, vol.

525

pg.

L121

Crossref

Search ADS

Goriely

S.

Bauswein

A.

Janka

H.-T.

,

ApJ

,

2011

, vol.

738

pg.

L32

Crossref

Search ADS

Hawley

J. F.

,

ApJ

,

2000

, vol.

528

pg.

462

Crossref

Search ADS

Hirose

S.

Krolik

J. H.

Stone

J. M.

,

ApJ

,

2006

, vol.

640

pg.

901

Crossref

Search ADS

Hoffman

R. D.

Woosley

S. E.

Qian

Y.-Z.

,

ApJ

,

1997

, vol.

482

pg.

951

Crossref

Search ADS

Hotokezaka

K.

Kyutoku

K.

Okawa

H.

Shibata

M.

Kiuchi

K.

,

Phys. Rev. D

,

2011

, vol.

83

pg.

124008

Crossref

Search ADS

Hotokezaka

K.

Kiuchi

K.

Kyutoku

K.

Okawa

H.

Sekiguchi

Y.-i.

Shibata

M.

Taniguchi

K.

,

Phys. Rev. D

,

2013

, vol.

87

pg.

024001

Crossref

Search ADS

Igumenshchev

I. V.

Abramowicz

M. A.

,

MNRAS

,

1999

, vol.

303

pg.

309

Crossref

Search ADS

Itoh

N.

Hayashi

H.

Nishikawa

A.

Kohyama

Y.

,

ApJS

,

1996

, vol.

102

pg.

411

Crossref

Search ADS

Janka

H.-T.

,

A&A

,

2001

, vol.

368

pg.

527

Crossref

Search ADS

Kalogera

V.

et al. ,

ApJ

,

2004

, vol.

614

pg.

L137

Crossref

Search ADS

Kasen

D.

Badnell

N. R.

Barnes

J.

,

ApJ

,

2013

preprint (arXiv:1303.5788)

Kizivat

L.-T.

Martínez-Pinedo

G.

Langanke

K.

Surman

R.

McLaughlin

G. C.

,

Phys. Rev. C

,

2010

, vol.

81

pg.

025802

Crossref

Search ADS

Korobkin

O.

Rosswog

S.

Arcones

A.

Winteler

C.

,

MNRAS

,

2012

, vol.

426

pg.

1940

Crossref

Search ADS

Kulkarni

S. R.

,

2005

preprint (astro-ph/0510256)

Lattimer

J. M.

Schramm

D. N.

,

ApJ

,

1974

, vol.

192

pg.

L145

Crossref

Search ADS

Lee

W. H.

Ramirez-Ruiz

E.

,

New J. Phys.

,

2007

, vol.

9

pg.

17

Crossref

Search ADS

Lee

W. H.

Ramirez-Ruiz

E.

López-Cámara

D.

,

ApJ

,

2009

, vol.

699

pg.

L93

Crossref

Search ADS

Lee

W. H.

Ramirez-Ruiz

E.

Page

D.

,

ApJ

,

2004

, vol.

608

pg.

L5

Crossref

Search ADS

Lee

W. H.

Ramirez-Ruiz

E.

Page

D.

,

ApJ

,

2005

, vol.

632

pg.

421

Crossref

Search ADS

Lehner

L.

Palenzuela

C.

Liebling

S. L.

Thompson

C.

Hanna

C.

,

Phys. Rev. D

,

2012

, vol.

86

pg.

104035

Crossref

Search ADS

Li

L.

Paczyński

B.

,

ApJ

,

1998

, vol.

507

pg.

L59

Crossref

Search ADS

Lucy

L. B.

,

ApJ

,

1991

, vol.

383

pg.

308

Crossref

Search ADS

McLaughlin

G. C.

Surman

R.

,

Nucl. Phys. A

,

2005

, vol.

758

pg.

189

Crossref

Search ADS

Metzger

B. D.

Berger

E.

,

ApJ

,

2012

, vol.

746

pg.

48

Crossref

Search ADS

Metzger

B. D.

Piro

A. L.

Quataert

E.

,

MNRAS

,

2008a

, vol.

390

pg.

781

Metzger

B. D.

Thompson

T. A.

Quataert

E.

,

ApJ

,

2008b

, vol.

676

pg.

1130

Crossref

Search ADS

Metzger

B. D.

Piro

A. L.

Quataert

E.

,

MNRAS

,

2009a

, vol.

396

pg.

304

(MPQ09)

Crossref

Search ADS

Metzger

B. D.

Piro

A. L.

Quataert

E.

,

MNRAS

,

2009b

, vol.

396

pg.

1659

Crossref

Search ADS

Metzger

B. D.

Arcones

A.

Quataert

E.

Martínez-Pinedo

G.

,

MNRAS

,

2010a

, vol.

402

pg.

2771

Crossref

Search ADS

Metzger

B. D.

et al. ,

MNRAS

,

2010b

, vol.

406

pg.

2650

Crossref

Search ADS

Morrison

I. A.

Baumgarte

T. W.

Shapiro

S. L.

,

ApJ

,

2004

, vol.

610

pg.

941

Crossref

Search ADS

Narayan

R.

Piran

T.

Kumar

P.

,

ApJ

,

2001

, vol.

557

pg.

949

Crossref

Search ADS

Nissanke

S.

Sievers

J.

Dalal

N.

Holz

D.

,

ApJ

,

2011

, vol.

739

pg.

99

Crossref

Search ADS

Nissanke

S.

Kasliwal

M.

Georgieva

A.

,

ApJ

,

2013

, vol.

767

pg.

124

Crossref

Search ADS

O'Connor

E.

Ott

C. D.

,

ApJ

,

2011

, vol.

730

pg.

70

Crossref

Search ADS

Oechslin

R.

Janka

H.-T.

,

MNRAS

,

2006

, vol.

368

pg.

1489

Crossref

Search ADS

Paczynski

B.

,

ApJ

,

1986

, vol.

308

pg.

L43

Crossref

Search ADS

Paczyńsky

B.

Wiita

P. J.

,

A&A

,

1980

, vol.

88

pg.

23

Papaloizou

J. C. B.

Pringle

J. E.

,

MNRAS

,

1984

, vol.

208

pg.

721

Crossref

Search ADS

Paschalidis

V.

Etienne

Z. B.

Shapiro

S. L.

,

Phys. Rev. D

,

2012

, vol.

86

pg.

064032

Crossref

Search ADS

Piran

T.

Nakar

E.

Rosswog

S.

,

MNRAS

,

2013

, vol.

430

pg.

2121

Crossref

Search ADS

Popham

R.

Woosley

S. E.

Fryer

C.

,

ApJ

,

1999

, vol.

518

pg.

356

Crossref

Search ADS

Qian

Y.-Z.

,

ApJ

,

2000

, vol.

534

pg.

L67

Crossref

Search ADS

Qian

Y.-Z.

Wasserburg

G. J.

,

Phys Rep.

,

2007

, vol.

442

pg.

237

Crossref

Search ADS

Qian

Y.-Z.

Woosley

S. E.

,

ApJ

,

1996

, vol.

471

pg.

331

Crossref

Search ADS

Read

J. S.

Markakis

C.

Shibata

M.

Uryū

K.

Creighton

J. D. E.

Friedman

J. L.

,

Phys. Rev. D

,

2009

, vol.

79

pg.

124033

Crossref

Search ADS

Rezzolla

L.

Baiotti

L.

Giacomazzo

B.

Link

D.

Font

J. A.

,

Classical Quantum Gravity

,

2010

, vol.

27

pg.

114105

Crossref

Search ADS

Roberts

L. F.

Kasen

D.

Lee

W. H.

Ramirez-Ruiz

E.

,

ApJ

,

2011

, vol.

736

pg.

L21

Crossref

Search ADS

Rosswog

S.

,

ApJ

,

2005

, vol.

634

pg.

1202

Crossref

Search ADS

Rosswog

S.

,

Phil. Trans. A

,

2013

, vol.

371

pg.

20120272

Crossref

Search ADS

Rosswog

S.

Liebendörfer

M.

,

MNRAS

,

2003

, vol.

342

pg.

673

Crossref

Search ADS

Rosswog

S.

Liebendörfer

M.

Thielemann

F.

Davies

M. B.

Benz

W.

Piran

T.

,

A&A

,

1999

, vol.

341

pg.

499

Rosswog

S.

Piran

T.

Nakar

E.

,

MNRAS

,

2013

, vol.

430

pg.

2585

Crossref

Search ADS

Ruffert

M.

Janka

H.-T.

,

A&A

,

1999

, vol.

344

pg.

573

Ruffert

M.

Janka

H.-T.

Schaefer

G.

,

A&A

,

1996

, vol.

311

pg.

532

Setiawan

S.

Ruffert

M.

Janka

H.-T.

,

MNRAS

,

2004

, vol.

352

pg.

753

Crossref

Search ADS

Setiawan

S.

Ruffert

M.

Janka

H.-T.

,

A&A

,

2006

, vol.

458

pg.

553

Crossref

Search ADS

Shakura

N. I.

Sunyaev

R. A.

,

A&A

,

1973

, vol.

24

pg.

337

Shibata

M.

,

Phys. Rev. Lett.

,

2005

, vol.

94

pg.

201101

Crossref

Search ADS

PubMed

Shibata

M.

Sekiguchi

Y.

,

Progress Theor. Phys.

,

2012

, vol.

127

pg.

535

Crossref

Search ADS

Shibata

M.

Sekiguchi

Y.-I.

Takahashi

R.

,

Progress Theor. Phys.

,

2007

, vol.

118

pg.

257

Crossref

Search ADS

Stephens

B. C.

East

W. E.

Pretorius

F.

,

ApJ

,

2011

, vol.

737

pg.

L5

Crossref

Search ADS

Stone

J. M.

Pringle

J. E.

Begelman

M. C.

,

MNRAS

,

1999

, vol.

310

pg.

1002

Crossref

Search ADS

Surman

R.

McLaughlin

G. C.

Ruffert

M.

Janka

H.-T.

Hix

W. R.

,

ApJ

,

2008

, vol.

679

pg.

L117

Crossref

Search ADS

Tanaka

M.

Hotokezaka

K.

,

ApJ

,

2013

in press (arXiv:1306.3742)

Timmes

F. X.

Swesty

F. D.

,

ApJS

,

2000

, vol.

126

pg.

501

Crossref

Search ADS

Uryū

K. ō.

Shibata

M.

Eriguchi

Y.

,

Phys. Rev. D

,

2000

, vol.

62

pg.

104015

Crossref

Search ADS

van der Sluys

M.

Raymond

V.

Mandel

I.

Röver

C.

Christensen

N.

Kalogera

V.

Meyer

R.

Vecchio

A.

,

Classical Quantum Gravity

,

2008

, vol.

25

pg.

184011

Crossref

Search ADS

Wanajo

S.

Janka

H.-T.

,

ApJ

,

2012

, vol.

746

pg.

180

Crossref

Search ADS

Wen

L.

Chen

Y.

,

Phys. Rev. D

,

2010

, vol.

81

pg.

082001

Crossref

Search ADS

Woosley

S. E.

Hoffman

R. D.

,

ApJ

,

1992

, vol.

395

pg.

202

Crossref

Search ADS

APPENDIX A: ACCRETION RATE FOR OPAQUENESS TO NEUTRINOS

Here we provide an analytic derivation of the critical accretion rate |$\dot{M}_{\rm opaque}$| above which the inner disc becomes opaque to neutrinos. A steady-state disc is optically thick at radii interior to the point at which the vertical optical depth to neutrino absorption obeys

\begin{equation} \tau _{\nu } \equiv \Sigma \kappa _{\nu }/2 > 1, \end{equation}

(A1)

where Σ is the disc surface density and κ_ν is the mean opacity. For an accretion disc in steady state, the accretion rate and surface density are related by |$\dot{M} = 3\pi \nu \Sigma$| at radii much greater than the inner boundary, where ν = αc_sH is the kinematic viscosity, c_s is the sound speed, H = c_s/Ω_K is the disc scaleheight and Ω_K = (GM_BH/r³)^1/2 is the Keplerian orbital frequency. At accretion rates |$\dot{M} \gtrsim \dot{M}_{\rm ign}$|⁠, the inner disc is neutrino-cooled, such that the midplane is sufficiently dense that gas pressure exceeds radiation pressure, and the opacity is dominated by the absorption of neutrinos on free nuclei (CB07). In this case c_s ≃ (4k_BT/3m_p)^1/2 and κ_ν ≃ κ₀T² (where κ₀ ≃ 4.5 × 10⁻³⁹ K⁻²cm²g⁻¹; e.g. Di Matteo et al. 2002). Equation (A1) can thus be expressed as a condition on the accretion rate

\begin{equation} \dot{M} > \frac{8\pi \alpha k_{B}}{\kappa _0 m_{\rm p} \Omega _{\rm K} T} \end{equation}

(A2)

Now, for an optically thin disc, the midplane temperature is determined by the balance between viscous heating |$\dot{q}_{\rm visc} = (9/4)\nu \Omega _{\rm K}^{2}$| and neutrino cooling |$\dot{q}_{\nu } \simeq \dot{q}_{\nu ,0}T^{6}$| (due to e⁻/e⁺ captures on free nuclei, where |$\dot{q}_{\nu ,0} \simeq 8\times 10^{-43}$|T⁶ erg s⁻¹g⁻¹K⁻⁶), viz.

\begin{eqnarray} T & \simeq & 1.25(\alpha k_{B}/m_{\rm p})^{1/5}\Omega _{\rm K}^{1/5}\dot{q}_{\nu ,0}^{-1/5} \end{eqnarray}

(A3)

\begin{eqnarray} & \approx & 5.9\times 10^{10}{\rm \,K}\left(\frac{\alpha }{0.03}\right)^{1/5}\left(\frac{M_{\rm BH}}{3\,\mathrm{M}_{{\odot }}}\right)^{-1/5}\left(\frac{r}{R_{\rm g}}\right)^{-3/10}, \end{eqnarray}

(A4)

where we have now expressed radius in terms of gravitational radii R_g = GM_BH/c². Substituting equation (A4) into equation (A2), we find

\begin{eqnarray} \dot{M} > 2\times 10^{-3}\,\mathrm{M}_{{\odot }}{\rm \,s^{-1}}\,\left(\frac{\alpha }{0.03}\right)^{4/5}\left(\frac{M_{\rm BH}}{3\,\mathrm{M}_{{\odot }}}\right)^{7/10}\left(\frac{r}{R_{\rm g}}\right)^{9/5}. \nonumber\\ \end{eqnarray}

(A5)

Now, since most of the total neutrino luminosity is released from radii just outside the innermost stable circular orbit R_isco, we can evaluate equation (A5) at r ≈ 2R_isco to define a critical accretion rate

\begin{eqnarray} \dot{M}_{\rm opaque} \simeq 0.15\,\mathrm{M}_{{\odot }}{\rm \,s^{-1}}\,\left(\frac{\alpha }{0.03}\right)^{4/5}\left(\frac{M_{\rm BH}}{3\,\mathrm{M}_{{\odot }}}\right)^{7/10}\left(\frac{R_{\rm isco}}{6R_{\rm g}}\right)^{9/5} \nonumber\\ \end{eqnarray}

(A6)

above which the majority of the radiated energy will originate from an optically thick environment. This expression agrees reasonably well with CB07, who find that for α = 0.1, |$\dot{M}_{\rm opaque} = 0.7\,\mathrm{M}_{{\odot }}$| s⁻¹ and 0.06 M_⊙ s⁻¹ for a BH of spin a = 0(R_isco = 6R_g) and a = 0.95(R_isco ≃ 1.5R_g), respectively, although the dependence on α that they find, |$\dot{M}_{\rm opaque} \propto \alpha$|⁠, is slightly different than that of the ∝α^4/5 dependence that we find in equation (A6).

APPENDIX B: SELF-IRRADIATION AND WEAK INTERACTIONS

The implementation of charged-current weak interaction and self-irradiation follows closely that of Fernández (2012) in the context of core-collapse supernovae, with suitable modifications to account for the disc geometry. We consider only electron-type neutrinos and antineutrinos, with emission and absorption rates following Bruenn (1985).

Our prescription for self-irradiation assumes that neutrinos are emitted from a ring of material at a radius R_em. This approximation is motivated by the fact that the neutrino emissivity displays a single peak inside the disc, where most of the emission is generated. Fig. B1 illustrates the shape of the function for model S-def. We choose the emission radius to be an average weighted by the neutrino emissivity (equation 16). This location coincides within ∼10 per cent with the radius inside which 50 per cent of the neutrino emission is generated.

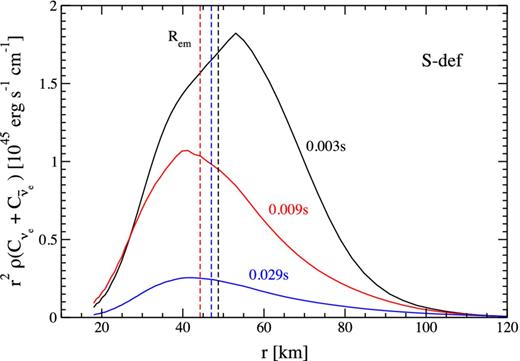
Snapshots of the angle-integrated neutrino emissivity for model S-def. Times shown correspond to orbits 1 (black), 3 (red) and 10 (blue) at r = R0. The vertical dashed line shows the location of Rem (equation 16) in each of the models.

Figure B1.

Snapshots of the angle-integrated neutrino emissivity for model S-def. Times shown correspond to orbits 1 (black), 3 (red) and 10 (blue) at r = R₀. The vertical dashed line shows the location of R_em (equation 16) in each of the models.

Open in new tab Download slide

Each fluid element on the ring is assumed to emit isotropically, with a total luminosity equal to the instantaneous volume integral of the emissivities, and with an energy spectrum following a Fermi-Dirac distribution with zero chemical potential. The number density of neutrino species i per unit energy ϵ, propagation direction |$\hat{k}$| and angular position on the ring ϕ^′ is

\begin{eqnarray} \frac{\mathrm{\partial} ^3 n_{\nu _{\rm i}}}{\mathrm{\partial} \phi ^\prime \,\mathrm{\partial} \cos \theta _k\,\mathrm{\partial} \epsilon } & = & \frac{2\pi }{(hc)^3}\,f_{\nu _{\rm i}}(\epsilon ,T_{\nu _{\rm i}},L_{\nu _{\rm i}};r,\theta )\qquad \qquad \nonumber \\ & = & \frac{2\pi }{(hc)^3}\, \frac{L_{\nu _{\rm i}}/2\pi }{(7/16)4\pi \mathcal {R}^2\sigma _{\rm SB}T_{\nu _{\rm i}}^4}\,\nonumber \\ && \times F_{\rm FD}(\epsilon ,T_{\nu _{\rm i}},0)\,\Theta (\cos \theta _k - \cos \theta _{k,\rm min}) \end{eqnarray}

(B1)

where θ_k is the angle between the propagation vector and the radial direction, and Θ is the step function. The intensity is assumed to be azimuthally symmetric around the propagation direction. The Fermi-Dirac function is given by

\begin{equation} F_{\rm FD}(\epsilon ,T,\mu ) = \frac{1}{e^{(\epsilon -\mu )/kT} + 1}, \end{equation}

(B2)

and the minimum angle between |$\boldsymbol k$| and the radial direction is

\begin{equation} \cos \theta _{k,\rm min} \simeq 1 - \frac{1}{2}\left(\frac{\mathcal {R}}{D} \right)^2 \end{equation}

(B3)

to lowest order in |$\mathcal {R}/D$|⁠, where |$\mathcal {R}$| is the radius of a spherical emitting element in the ring, and

\begin{eqnarray} D(r,\theta ,R_{\rm em},\phi ^\prime ) = r\left[1 + \left(\frac{R_{\rm em}}{r}\right)^2 -2\frac{R_{\rm em}}{r}\,\sin \theta \,\cos \phi ^\prime \right]^{1/2}\nonumber \\ \phantom{A = B} \end{eqnarray}

(B4)

is the distance to a point in the disc with coordinates (r, θ) from the emitting blob in the ring, as depicted in Fig. B2. Keeping the lowest order terms arising from equation (B3) ensures that |$\mathcal {R}$| scales out of the problem. By using equation (B4) to capture the global geometry of the problem, we are ignoring light bending and Doppler effects.

Figure B2.

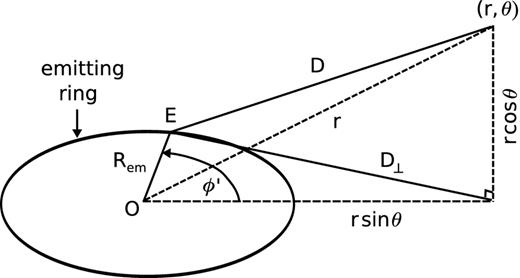
Geometry for self-irradiation. All of the neutrino luminosity is assumed to originate in a ring on the midplane with radius R_em. A point in the disc with coordinates (r, θ) lies at a distance D from an emitting element E with azimuthal angle ϕ^′. The total emission received by the point in the disc is a sum over the emission from each ring element, leading to an angular dependence I_ang (equation B15, Fig. B3).

Open in new tab Download slide

The rates per baryon of production and destruction of electrons and positrons that enter equation (14) are given respectively by

\begin{eqnarray} \Gamma _{\rm e-} & = & \frac{2\pi m_{\rm n} c}{(hc)^3\rho } \left[\int {\mathrm{d}}\phi ^\prime \int {\mathrm{d}}\cos \theta _k \int \epsilon ^2 {\mathrm{d}}\epsilon \,\left(\kappa _{\nu _{\rm e}}+j_{\nu _{\rm e}}\right)\, f_{\nu _{\rm e}}\right.\nonumber \\ && \left.- \int {\mathrm{d}}\cos \theta _k\int \epsilon ^2 {\mathrm{d}}\epsilon j_{\nu _{\rm e}}\right] \end{eqnarray}

(B5)

\begin{eqnarray} \Gamma _{\rm e+} & = & \frac{2\pi m_{\rm n} c}{(hc)^3\rho } \left[\int {\mathrm{d}}\phi ^\prime \int {\mathrm{d}}\cos \theta _k \int \epsilon ^2 {\mathrm{d}}\epsilon \,\left(\kappa _{\bar{\nu }_{\rm e}} + j_{\bar{\nu }_{\rm e}} \right)\,f_{\bar{\nu }_{\rm e}}\right.\nonumber \\ && \left. - \int {\mathrm{d}}\cos \theta _k \int \epsilon ^2 {\mathrm{d}}\epsilon j_{\bar{\nu }_{\rm e}}\right] \end{eqnarray}

(B6)

where |$j_{\nu _{\rm i}}$| and |$\kappa _{\nu _{\rm i}}$| are the emissivity and absorption coefficient, respectively, associated with electron-type neutrinos or antineutrinos (as subscripted). The coefficients are given by (Bruenn 1985)

\begin{eqnarray} j_{\nu _{\rm e}}(\epsilon ,T,\mu _{\rm e},n_{\rm p}) & = & \frac{\tilde{G}_{\rm F}^2}{\pi }\left(g_{\rm V}^2 + 3g_{\rm A}^2\right)\, n_{\rm p} F_{\rm FD}(\epsilon ,T,\mu _{\rm e})\nonumber \\ && \times \left[\epsilon + \Delta _m \right]^2 \left[1 - \frac{m_{\rm e}^2 c^4}{(\epsilon + \Delta _m)^2}\right]^{1/2} \end{eqnarray}

(B7)

\begin{eqnarray} j_{\bar{\nu _{\rm e}}}(\epsilon ,T,\mu _{\rm e},n_{\rm p}) & = & \frac{\tilde{G}_{\rm F}^2}{\pi }\left(g_{\rm V}^2 + 3g_{\rm A}^2\right)\, n_{\rm n}\nonumber \\ && \times F_{\rm FD}(\epsilon -\Delta _m,T,-\mu _{\rm e})\nonumber \\ && \times \left[\epsilon - \Delta _m \right]^2 \left[1 - \frac{m_{\rm e}^2 c^4}{(\epsilon - \Delta _m)^2}\right]^{1/2}\nonumber \\ && \times \Theta (\epsilon -\Delta _m - m_{\rm e} c^2) \end{eqnarray}

(B8)

\begin{eqnarray} \kappa _{\nu _{\rm e}}(\epsilon ,T,\mu _{\rm e},n_{\rm p}) & = & \frac{\tilde{G}_{\rm F}^2}{\pi }\left(g_{\rm V}^2 + 3g_{\rm A}^2\right)\, n_{\rm n} \left[1-F_{\rm FD}(\epsilon ,T,\mu _{\rm e})\right]\nonumber \\ && \times \left[\epsilon + \Delta _m \right]^2 \left[1 - \frac{m_{\rm e}^2 c^4}{(\epsilon + \Delta _m)^2}\right]^{1/2} \end{eqnarray}

(B9)

\begin{eqnarray} \kappa _{\bar{\nu _{\rm e}}}(\epsilon ,T,\mu _{\rm e},n_{\rm p}) & = & \frac{\tilde{G}_{\rm F}^2}{\pi }\left(g_{\rm V}^2 + 3g_{\rm A}^2\right)\, n_{\rm p}\nonumber \\ && \times \left[1-F_{\rm FD}(\epsilon -\Delta _m,T,-\mu _{\rm e})\right]\nonumber \\ && \times \left[\epsilon - \Delta _m \right]^2 \left[1 - \frac{m_{\rm e}^2 c^4}{(\epsilon - \Delta _m)^2}\right]^{1/2}\nonumber \\ && \times \Theta (\epsilon -\Delta _m - m_{\rm e} c^2), \end{eqnarray}

(B10)

where μ_e is the chemical potential of electrons, n_n and n_p the number density of free neutrons and protons, respectively, |$\tilde{G}_{\rm F} = G_F/(\hbar c)^3$| the Fermi constant, g_V and g_A the vector and axial coupling constants, respectively, and Δ_m = (m_n − m_p)c² the difference between the rest mass energy of neutrons and protons.

The energy source terms that enter equation (15) are

\begin{eqnarray} \mathcal {H}_{\nu _{\rm e}} & = & \frac{2\pi m_{\rm n} c}{(hc)^3\rho }\int {\mathrm{d}}\phi ^\prime \, \int {\mathrm{d}}\,\cos \theta _k \int \epsilon ^3 {\mathrm{d}}\,\epsilon \left[ j_{\nu _{\rm e}} + \kappa _{\nu _{\rm e}}\right]f_{\nu _{\rm e}} \end{eqnarray}

(B11)

\begin{eqnarray} \mathcal {H}_{\bar{\nu }_{\rm e}} & = & \frac{2\pi m_{\rm n} c}{(hc)^3\rho }\int {\mathrm{d}}\phi ^\prime \int {\mathrm{d}}\,\cos \theta _k \int \epsilon ^3 {\mathrm{d}}\,\epsilon \left[ j_{\bar{\nu }_{\rm e}} + \kappa _{\bar{\nu }_{\rm e}}\right]f_{\bar{\nu }_{\rm e}} \end{eqnarray}

(B12)

\begin{eqnarray} \mathcal {C}_{\nu _{\rm e}} & = & \frac{4\pi m_{\rm n} c}{(hc)^3\rho }\int \epsilon ^3 {\mathrm{d}}\,\epsilon \, j_{\nu _{\rm e}} \end{eqnarray}

(B13)

\begin{eqnarray} \mathcal {C}_{\bar{\nu }_{\rm e}} & = & \frac{4\pi m_{\rm n} c}{(hc)^3\rho }\int \epsilon ^3 {\mathrm{d}}\,\epsilon \, j_{\bar{\nu }_{\rm e}}. \end{eqnarray}

(B14)

The anisotropy of the global radiation field decouples from the energy integrals, and enters through a dimensionless prefactor

\begin{eqnarray} I_{\rm ang} & = & \frac{1}{2\pi } \left(\frac{R_{\rm em}}{r} \right)^2 \int _0^{2\pi }\frac{{\mathrm{d}}\phi ^\prime }{2\left[D(r,\theta ,R_{\rm em},\phi ^\prime )/r \right]^2} \end{eqnarray}

(B15)

\begin{eqnarray} & \simeq & \frac{1}{2}\left(\frac{R_{\rm em}}{r} \right)^2\left[1 -\left(\frac{R_{\rm em}}{r}\right)^2\right] + \frac{1}{2\pi }\left(\frac{R_{\rm em}}{r} \right)^4\sin ^2\theta \end{eqnarray}

(B16)

in all terms containing an |$f_{\nu _{\rm i}}$| factor (D is given by equation B4). The spatial dependence of I_ang is shown in Fig. B3. In the inner regions of the disc, this function varies by factors of the order of unity following the annular geometry of the emission region. It becomes increasingly spherical for larger radii. Quantitatively, this can be seen from equation (B16), which is a series expansion in R_em/r. Due to the azimuthal averaging, the leading error term scales like the fourth power of this ratio. The integral diverges when r = R_em. To avoid excessive heating by artificial concentration of the emission at this radius, and given that the spatial distribution of the emission has a finite width (Fig. B1), we impose I_ang ≤ 1. The effect of this upper limit can also be seen in Fig. B3.

Figure B3.

Angular dependence of the radiation field (equation B15). The angular factor approaches a pure inverse square law at large distances from the origin (equation B16).

Open in new tab Download slide

All terms containing a |$f_{\nu _{\rm i}}$| factor are also multiplied by a normalization constant |$N_{\nu _{\rm i}}$|

\begin{equation} N_{\nu _{\rm i}} = \frac{L_{\nu _{\rm i}}}{(7/16)4\pi R_{\rm em}^2 \sigma _{\rm SB}T_{\nu }^4}, \end{equation}

(B17)

which ensures that the incident flux is consistent with the total neutrino luminosity |$L_{\nu _{\rm i}}$| emitted by the disc. The denominator normalizes the assumed Fermi-Dirac spectrum in |$f_{\nu _{\rm i}}$|⁠. The neutrino temperature used is the same for both neutrino species, and is equal to the average, mass-weighted gas temperature in an (angle integrated) annular region centred on R_em, with a radial width of 10 per cent. This averaging is performed to smooth over stochastic fluctuations in localized disc regions.

Weak rates are tabulated as a function of the gas temperature T, electron degeneracy parameter including rest mass μ_e/(k_BT), and neutrino temperature T_ν. The angular function I_ang is also tabulated in cylindrical coordinates, covering the range (r/R_em) ∈ [0, 10]. Outside of this range, the asymptotic expansion in equation (B16) is used.

APPENDIX C: HEAVY-ELEMENT NUCLEOSYNTHESIS

Here we review the conditions for nucleosynthesis of heavy elements in hot outflows, such as those from binary NS merger accretion discs. Free nuclei recombine into α-particles once the temperature decreases to T ≲ 10¹⁰ K, the energy from which plays a key role in powering the disc outflows explored in this paper. Heavier elements start to form once the temperature decreases further, T ≲ 5 × 10⁹ K, such that the reaction ⁴He(αn,γ)⁹Be(α,n)¹²C occurs (at higher temperatures, the abundance of ⁹Be is limited by photodisintegration).

Immediately after ¹²C forms, multiple additional α-captures produce heavy ‘seed’ nuclei with characteristic mass |$\bar{A} \simeq$| 90–120 and charge |$\bar{Z}\simeq 35$| (the ‘α-process’; Woosley & Hoffman 1992). Whether nucleosynthesis proceeds to even heavier r-process nuclei depends primarily on the ratio of free neutrons to seed nuclei once the α-process completes. Since the formation of ¹²C is the rate limiting step in forming seeds, the quantity and distribution of r-nuclei synthesized depends on the entropy S, electron fraction Y_e, and expansion time-scale t_exp at the radius where T ≃ 5 × 10⁹ K.

If the electron fraction of the outflow is less than that of the seed nuclei themselves, i.e. |$Y_{\rm e} \lesssim \frac{\bar{Z}}{\bar{A}} \simeq 0.3$|⁠, then the ⁴He(αn,γ)⁹Be(α,n)¹²C reaction is ultimately limited by the total number of α-particles (the neutron abundance can be considered fixed for purposes of calculating the ¹²C reaction yield). In this case the final mass fraction of alpha particles is approximately given by (Hoffman et al. 1997)

\begin{equation} X_{\rm He} = \left[(2Y_{\rm e})^{-2} + \mathcal {F}\right]^{-1/2}, \end{equation}

(C1)

where

\begin{eqnarray} \mathcal {F} =1.8\times 10^{4}(1-2Y_{\rm e})\left(\frac{\bar{Z}}{36}\right)\left(\frac{t_{\rm exp}}{\rm 0.1\,s}\right)\left(\frac{S}{\rm 20\, k_b\,nuc^{-1}}\right)^{-3}, \nonumber\\ \end{eqnarray}

(C2)

where |$\mathcal {F}$| is proportional to the reaction rate for ⁴He → ¹²C integrated over the time-scale available for burning ∼t_exp. The reaction rate depends on S⁻³ since ρ ∝ 1/S at fixed temperature, and since ⁴He(αn,γ)⁹Be(α,n)¹²C is an effective four-body reaction. Any mass not trapped in α-particles ends up in r-process nuclei with mass fraction

\begin{equation} X_{\rm r} = 1-X_{\rm He}, \end{equation}

(C3)

and mass number greater than

\begin{equation} A = \bar{A}\left(1 - \frac{1-2Y_{\rm e}}{X_r}\right)^{-1}. \end{equation}

(C4)

If |$\mathcal {F} \ll 1$| then very little ¹²C forms (‘He-rich freeze-out’), in which case helium achieves its maximum abundance X_He = 2Y_e, unchanged from its value just after α recombination. Since most of the available protons are trapped in ⁴He, the r-process nuclei produced in this case are very massive, easily reaching beyond the third peak A ≳ 195 (and likely undergoing fission). Even if |$\mathcal {F} = \infty$| (X_r = 1), however, nucleosynthesis will still reach the Lanthanide elements (A ≳ 139 = A_La) if the outflow is sufficiently neutron-rich: |$Y_{\rm e} \lesssim \frac{\bar{A}}{2A_{\rm La}} \approx$| 0.30–0.40. Thus, given the low electron fraction of the disc outflows that we find in Section 4.2 (⁠|$\bar{Y}_{\rm e} \approx 0.2$|⁠), we expect Lathanides to easily form, resulting in a high optical opacity (Kasen et al. 2013).

SUPPORTING INFORMATION

Additional Supporting Information may be found in the online version of this article:

Figure 5. Colour maps of density (left), electron fraction (middle) and entropy (right) in model S-def-hr at time 1.16 s (orbit 400 at r = R₀), illustrating the wind morphology. Upper panels show zoomed in regions of the panels directly below, as indicated by the boxes (Supplementary Data)..

Please note: Oxford University Press are not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the article.

Download all slides

Month:	Total Views:
January 2017	1
February 2017	5
March 2017	1
April 2017	8
May 2017	11
June 2017	2
July 2017	8
August 2017	8
September 2017	7
October 2017	12
November 2017	9
December 2017	21
January 2018	50
February 2018	17
March 2018	18
April 2018	15
May 2018	30
June 2018	16
July 2018	19
August 2018	16
September 2018	13
October 2018	13
November 2018	22
December 2018	32
January 2019	28
February 2019	28
March 2019	19
April 2019	23
May 2019	18
June 2019	24
July 2019	35
August 2019	47
September 2019	16
October 2019	14
November 2019	19
December 2019	27
January 2020	21
February 2020	12
March 2020	23
April 2020	11
May 2020	83
June 2020	41
July 2020	12
August 2020	10
September 2020	12
October 2020	4
November 2020	19
December 2020	15
January 2021	10
February 2021	22
March 2021	20
April 2021	15
May 2021	26
June 2021	26
July 2021	14
August 2021	7
September 2021	14
October 2021	10
November 2021	11
December 2021	7
January 2022	18
February 2022	7
March 2022	18
April 2022	11
May 2022	16
June 2022	23
July 2022	21
August 2022	27
September 2022	23
October 2022	27
November 2022	20
December 2022	20
January 2023	33
February 2023	15
March 2023	28
April 2023	29
May 2023	19
June 2023	14
July 2023	23
August 2023	24
September 2023	18
October 2023	20
November 2023	29
December 2023	27
January 2024	30
February 2024	23
March 2024	24
April 2024	40
May 2024	24
June 2024	6
July 2024	21
August 2024	22
September 2024	28
October 2024	18
November 2024	20
December 2024	15
January 2025	15
February 2025	9
March 2025	14
April 2025	10
May 2025	9

Article Contents

Delayed outflows from black hole accretion tori following neutron star binary coalescence

Abstract

1 INTRODUCTION

2 disc PROPERTIES

3 NUMERICAL SETUP

3.1 Equations solved and numerical method

3.2 Neutrino treatment

3.3 Angular momentum transport

3.4 Initial conditions

3.5 Models evolved

4 RESULTS

4.1 Outflow generation

4.2 Outflow properties

5 DISCUSSION

5.1 Nucleosynthesis in disc outflows

5.2 Radioactively powered emission

5.3 Effects of a long-lived hypermassive NS

5.4 Comparison with previous work

6 CONCLUSIONS

REFERENCES

APPENDIX A: ACCRETION RATE FOR OPAQUENESS TO NEUTRINOS

APPENDIX B: SELF-IRRADIATION AND WEAK INTERACTIONS

APPENDIX C: HEAVY-ELEMENT NUCLEOSYNTHESIS

SUPPORTING INFORMATION

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Delayed outflows from black hole accretion tori following neutron star binary coalescence Free

Abstract

1 INTRODUCTION

2 disc PROPERTIES

3 NUMERICAL SETUP

3.1 Equations solved and numerical method

3.2 Neutrino treatment

3.3 Angular momentum transport

3.4 Initial conditions

3.5 Models evolved

4 RESULTS

4.1 Outflow generation

4.2 Outflow properties

5 DISCUSSION

5.1 Nucleosynthesis in disc outflows

5.2 Radioactively powered emission

5.3 Effects of a long-lived hypermassive NS

5.4 Comparison with previous work

6 CONCLUSIONS

REFERENCES

APPENDIX A: ACCRETION RATE FOR OPAQUENESS TO NEUTRINOS

APPENDIX B: SELF-IRRADIATION AND WEAK INTERACTIONS

APPENDIX C: HEAVY-ELEMENT NUCLEOSYNTHESIS

SUPPORTING INFORMATION

Supplementary data

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Delayed outflows from black hole accretion tori following neutron star binary coalescence