Dynamics of prolate spheroidal mass distributions with varying eccentricity

Rathulnath, R.; Jog, Chanda J.

doi:10.1093/mnras/stt759

Abstract

In this paper we calculate the potential for a prolate spheroidal distribution as in a dark matter halo with a radially varying eccentricity. This is obtained by summing up the shell-by-shell contributions of isodensity surfaces, which are taken to be concentric and with a common polar axis and with an axis ratio that varies with radius. Interestingly, the constancy of potential inside a shell is shown to be a good approximation even when the isodensity contours are dissimilar spheroids, as long as the radial variation in eccentricity is small as seen in realistic systems. We consider three cases where the isodensity contours are more prolate at large radii, or are less prolate or have a constant eccentricity. Other relevant physical quantities like the rotation velocity, the net orbital and vertical frequency due to the halo and an exponential disc of finite thickness embedded in it are obtained. We apply this to the kinematical origin of Galactic warp, and show that a prolate-shaped halo is not conducive to making long-lived warps – contrary to what has been proposed in the literature. The results for a prolate mass distribution with a variable axis ratio obtained are general, and can be applied to other astrophysical systems, such as prolate bars, for a more realistic treatment.

methods: analytical, Galaxy: structure, galaxies: haloes, galaxies: kinematics and dynamics, galaxies: structure

INTRODUCTION

A galactic disc is believed to be embedded in a dark matter halo, but the actual shape of the dark matter halo is not yet well understood. Usually, the halo is taken to be spherical for simplicity, or oblate. When a deviation from sphericity is considered at all, typically an oblate shape is used (e.g. Sackett & Sparke 1990). A prolate halo has been used in a few cases, e.g. to study warps in galaxies (Sparke 1984; Ideta et al. 2000), and to explain the tidal streaming in the Galaxy (Helmi 2004). In these the axis ratio is taken to be constant, again for simplicity.

Recently, it was shown that the dark matter halo in the Milky Way is prolate with the vertical-to-planar axis ratio monotonically increasing to 2.0 at 24 kpc (Banerjee & Jog 2011). This was obtained by modelling the observed steeply flaring atomic hydrogen gas layer in the outer Galaxy, where the gas is supported by pressure against the net gravitational field of the disc and the halo. It is then natural to ask what would be the dynamical consequences of such a progressively prolate halo. This is the motivation for the present paper.

N-body simulations of galaxies show that the dark matter halo is triaxial. Along the Cartesian cuts (X–Y or X–Z), the haloes show a range of value from oblate to prolate with a preference for a prolate shape (Bailin & Steinmetz 2005; Bett et al. 2007; Vera-Ciro et al. 2011). Further the axis ratio varies with radius. Indeed, there is no simple physical reason why the shape should be constant with radius. Thus a radially variable axis ratio for an ellipsoidal mass distribution is not just of academic interest but of practical use for a study of dark matter haloes, and in other astrophysical systems as well.

To study the dynamics of a prolate halo, we need to first calculate its potential and other physical quantities. Mathematically this reduces to the problem of inversion of Poisson equation for a given density distribution. This is a rich and an old subject, which had attracted the attention of mighty mathematicians like MacLaurin, Lagrange, Jacobi, Gauss to name a few (e.g. Rohlfs 1977), also see Chandrasekhar (1969) for details. Yet, interestingly, the calculation for a prolate case with varying eccentricity has to our knowledge not been studied in the literature so far.

Motivated by this, in this paper we study prolate ellipsoidal mass distributions with an eccentricity that varies with radius. The ellipsoids are taken to be concentric and coaxial or coplanar. We show that the constancy of potential within a shell as in homoeoids is a good approximation even when the shell is bounded by dissimilar ellipsoids, for small variation in the eccentricity as seen in realistic systems. This is an important general result from this paper.

We calculate the potential for a general density distribution by adding the shell-by-shell contributions from isodensity surfaces from shells internal and external to a point, and from this obtain the radial and planar force equations and frequencies. Next, these results are applied to the specific case of pseudo-isothermal density distribution for the dark matter halo, and an exponential disc of finite thickness, to study the longevity of the Galactic warp for a disc in a prolate halo. We show that the prolate halo does not result in a long-lived warp, contrary to the literature where a prolate halo (Ideta et al. 2000) or a halo with a radially variable shape (Binney & Tremaine 1987) have been suggested to explain long-lived warps.

The calculation of the potential and related physical quantities is given in Section 2. In Section 3 this is applied to toy mass models so as to study the properties of a prolate spheroidal system. In Section 4 we apply this to the Milky Way and study the effect of the prolate halo on the warp and show that the halo does not yield long-lived warps. Section 5 summarizes our conclusions.

The reader who is mainly interested in the application of a prolate halo to the study of warps, may wish to skip the technical material involving potential theory in Sections 2 and 3, and go directly to Section 4.

POTENTIAL OF A PROLATE ELLIPSOID WITH VARYING ECCENTRICITY

The dark matter halo is usually modelled as a spherical or oblate distribution of constant ratio, for simplicity (e.g. Sackett & Sparke 1990). In a rare case, an oblate mass distribution with radially varying axis ratio has been studied (Ryden 1990) in the quadrupolar limit, and extended for the prolate case by Buote & Canizares (1996) in the same limit. The general case of a prolate spheroidal mass distribution, in particular with a varying axis ratio, has not been studied in the literature so far. The potential for a general triaxial case (with constant axis ratios) is stated in Binney & Tremaine (1987) without derivation, and has been derived in Chandrasekhar (1969), and by de Zeeuw & Pfenniger (1988). From this one can derive the potential for a prolate spheroid of constant axis ratio, as for example was done by Das & Jog (1995) for modelling bars in a study of heating due bars.

In this paper, we give the analytical calculation of the potential and other relevant physical quantities of a body for which the isodensity surfaces are prolate in shape with radially varying eccentricity. In this way of formulation of the problem, the case of a constant axis ratio comes out naturally as a simple case of the general calculation, as shown later in this section. First the potential due to a prolate spheroidal surface is calculated, following the approach developed for an oblate spheroidal surface by Binney & Tremaine (1987). Then by summing over the contribution by the various shells, the net potential is obtained.

Potential of a prolate spheroidal surface

To calculate the potential of a prolate spheroidal surface, it is appropriate to use the prolate spheroidal coordinate system (u, v, ϕ). However, the galactic disc is usually represented in cylindrical coordinates. The prolate spheroidal coordinates (u, v) and the cylindrical coordinates (R, z) are related by

\begin{eqnarray} &&\!\!\!\!R=\Delta \,\sinh \,u\,\sin \,v, \nonumber \\ &&\!\!\!\!z=\Delta \,\cosh \,u\,\cos \,v, \end{eqnarray}

(1)

where Δ is a constant (see e.g. Arfken 1970).

The Laplacian of the potential can be expressed in prolate spheroidal coordinates as

\begin{eqnarray} \nabla ^2{\Phi }&=&\frac{1}{h_{u}h_{v}h_{\phi }}\left[\frac{\mathrm{\partial} }{\mathrm{\partial} u}\left(\frac{h_vh_{\phi }}{h_u}\frac{\mathrm{\partial} {\Phi }}{\mathrm{\partial} u}\right)+ \frac{\mathrm{\partial} }{\mathrm{\partial} v}\left(\frac{h_uh_{\phi }}{h_v}\frac{\mathrm{\partial} {\Phi }}{\mathrm{\partial} v}\right)\right. \nonumber \\ &&\quad\left. +\frac{\mathrm{\partial} }{\mathrm{\partial} {\phi }}\left(\frac{h_vh_u}{h_{\phi }}\frac{\mathrm{\partial} {\Phi }}{\mathrm{\partial} \phi }\right) \right], \end{eqnarray}

(2)

where the scale factors are

\begin{eqnarray} h_u&=&\Delta (\sinh ^2u+\sin ^2v)^{1/2}, \nonumber \\ h_v&=&\Delta (\sinh ^2u+\sin ^2v)^{1/2}, \nonumber \\ h_{\phi }&=&\Delta \cosh \,u \sin \,v. \end{eqnarray}

(3)

Here the density is a function of u only, so we expect the potential Φ(u) to be a function of only the coordinate u. For potentials of this class, after substituting the scale factors in the equation (2), ∇²Φ = 0 reduces to

\begin{equation} \frac{{\rm d}}{{\rm d}u}\left(\sinh \,u\,\frac{{\rm d}\Phi }{{\rm d}u}\right)=0. \end{equation}

(4)

Hence either

\begin{equation} \Phi =\Phi _0, \end{equation}

(5)

which is a constant, or

\begin{equation} \left(\mathrm{d}\Phi /\mathrm{d}u\right)=A\,{\rm csch} \, u, \end{equation}

(6)

where A is a constant. On integrating this equation we find

\begin{equation} \Phi =-A/2 \left[\ln \left(\frac{1+\mathrm{sech}\,u}{1-\mathrm{sech}\,u}\right)+\ln \psi _0\right]. \end{equation}

(7)

For large u, sech u → 0, and sech u = Δ/r so a potential of the form (equation 7) varies as

\begin{equation} \Phi \simeq \,(-A/ 2) \left(2\,\mathrm{sech}\,u + \ln \psi _0\right)\,\simeq \,-A\left(\frac{\Delta }{r}-\frac{1}{2}\ln \psi _0\right), \end{equation}

(8)

where r is the usual spherical radius.

Hence, if we set ln ψ₀ = 0, and A = GM/(Δ), the potential given by equation (8) tends to zero at infinity like the gravitational potential of mass M, as expected, here M is the mass of the surface. Thus we are led to consider

\begin{equation} \Phi = \left\lbrace \begin{array}{ll}\displaystyle-\frac{GM}{2\ \Delta }\,\ln \left(\frac{1+\mathrm{sech}\,u_0}{1-\mathrm{sech}\,u_0}\right) &\quad \mbox{when}\ u<u_0, \nonumber\\ \displaystyle -\frac{GM}{2\, \Delta }\,\ln \left(\frac{1+\mathrm{sech}\,u}{1-\mathrm{sech}\,u}\right) &\quad \mbox{when}\ u\ge u_0. \end{array} \right. \end{equation}

(9)

This potential is discontinuous on the spheroid u = u₀. Hence it is the gravitational potential of a shell of material on the surface u = u₀. This shell has principal semimajor and semiminor axis of lengths c₀ ≡ Δ cosh u₀ and a₀ ≡ Δ sinh u₀, respectively. Hence eccentricity of the shell, e = sech u₀, thus the constant Δ = c₀e. We may rewrite equation (9) as

\begin{equation} \Phi = \left\lbrace \begin{array}{ll}\displaystyle-\frac{GM}{2\,c_0\,e}\, \ln \left(\frac{1+e}{1-e}\right) &\quad \mbox{when}\ u<u_0,\nonumber\\ \displaystyle -\frac{GM}{2\,c_0\,e}\, \ln \left(\frac{1+\mathrm{sech}\,u}{1-\mathrm{sech}\,u}\right) &\quad \mbox{when}\ u\ge u_0. \end{array} \right. \end{equation}

(10)

On applying Gauss's theorem to the potential across this surface, its surface density (following the approach in Binney & Tremaine 1987, see equations 2–68) is derived, to be

\begin{equation} \Sigma =\frac{\hat{n}_u\cdot \nabla \Phi }{4\pi G}, \end{equation}

(11)

where, |$\hat{n}_u$| is a unit vector normal to the surface, and ∇Φ is the gradient of the potential:

\begin{equation} \nabla \Phi =\frac{1}{\Delta ({\sinh ^2u+\sin ^2v})^{1/2}}\: \frac{{\rm d}\Phi }{{\rm d}u}|_{u=u_0}. \end{equation}

(12)

Hence,

\begin{equation} \Sigma =\frac{M}{4\pi a^2 q ({1-e^2\cos ^2v})^{1/2}}. \end{equation}

(13)

Potential of prolate mass distribution

The potential due to a prolate spheroidal surface is obtained above (equation 10). A prolate spheroidal mass distribution can be considered as the combination of such surfaces, with the condition that the isodensity surfaces should not intersect each other. This is so that the function is not unphysical or double-valued. Then we can calculate the potential of such distributions using equation (10).

Define a quantity

\begin{equation} \sigma \left(a\right)=\frac{a}{q}\,\frac{{\rm d}q}{{\rm d}a}, \end{equation}

(14)

where a is the semiminor axis. The constraint that the shells do not cross is equivalent to stating that the semimajor axis of the outer shell must not be shorter than the semimajor axis of the inner shell, this requires that σ(a) ≥ − 1.

Consider a thin shell of matter whose inner surface is a prolate spheroid with a semiminor axis a and semimajor to semiminor axis ratio q, and outer surface is a prolate spheroid with a semiminor axis a + δa and an axis ratio q + δq. The mass of this prolate spheroidal shell, when δa ≪ a, can be shown to be

\begin{equation} \delta M=4\pi \,a^2\,q\,\rho \left(a\right)\left[1+\frac{\sigma \left(a\right)}{3}\right]\,\delta a. \end{equation}

(15)

We next calculate |$\bar{\Sigma }$|⁠, the surface density of a prolate spheroidal shell with dissimilar surfaces following the procedure in Binney & Tremaine (1987, see their equations 2– 71) as

\begin{equation} \bar{\Sigma }=\frac{\rho (a) \delta a}{|\nabla a|}, \end{equation}

(16)

\begin{equation} \bar{\Sigma }=\frac{\rho (a) \delta a}{\left(R^2+\frac{z^2}{q^4}\right)^{1/2}} \left(a+\frac{z^2}{q^3}\frac{{\rm d}q}{{\rm d}a}\right), \end{equation}

(17)

where R and z are the cylindrical coordinates. On using equation (1), and the discussion following equation (9), these reduce to

\begin{eqnarray} R=a\,\sin v, \end{eqnarray}

(18)

\begin{eqnarray} z=aq\,\cos v. \end{eqnarray}

(19)

Hence, the surface density of the shell is given as

\begin{equation} \bar{\Sigma }=\frac{\rho \delta a}{a \left(1-e^2\cos ^2v\right)^{1/2} }\left[1+\sigma \cos ^2v\right]. \end{equation}

(20)

Using equation (15) for the mass of the shell, equation (20) reduces to

\begin{equation} \bar{\Sigma }=\frac{\delta M}{4\pi a^2 q \left(1-e^2\cos ^2v\right)^{1/2} }\left[\frac{1+\sigma \,\cos ^2v}{1+ (\sigma /3)}\right]. \end{equation}

(21)

Note that for similar surfaces, σ = 0 (equation 14), hence the surface density of a shell within two similar surfaces obtained by taking a projection of the mass on the inner surface of the shell (equations 16 and 21) is identically equal to that obtained using the Gauss's theorem approach (equation 13). Hence the potential inside a shell bounded by similar surfaces can be taken to be constant (Newton's theorem), or there is no force at an internal point due to such a shell. This is the standard homoeoidal theory of ellipsoids (e.g. Chandrasekhar 1969).

It is not clear a priori that the results from the homoeoidal potential theory are applicable for a shell bounded by dissimilar surfaces considered here. In fact, in this case, the surface density obtained by taking the projection (equation 21) differs from that obtained earlier by the Gauss's theorem approach (equation 13) by a dimensionless scale factor S, defined as

\begin{equation} S = \left[\frac{1+\sigma \,\cos ^2v}{1+ (\sigma /3)}\right]. \end{equation}

(22)

This scale factor denotes the deviation from the case of constant internal potential. We show in Appendix A that the values of S are small for the small variation in eccentricity with radius considered here. Thus, interestingly the homoeoidal potential theory though not rigorously valid, is still a good approximation. Hence the potential within a shell (u < u₀, see equation 10) can be assumed to be constant even for the case of a shell bounded by dissimilar spheroids. In analogy with a homoeoid which is a shell bounded by two similar spheroids, we define a heteroid to be a shell bounded by two dissimilar spheroids. In this paper we study the gravitational potential and force due to a heteroid.

Hence, for a field point lying inside the spheroid of semiminor axis a (with a prolate coordinate u_a), the contribution of potential at that point due to this shell (from equations 9 and 15) is given as

\begin{equation} \delta \Phi _{{\rm int}}=-2\pi G\frac{a}{e}\left[1+\frac{\sigma \left(a\right)}{3}\right]\ln \left(\frac{1+{\rm sech}\,u_a}{1-{\rm sech}\,u_a}\right)\rho \left(a\right)\delta a. \end{equation}

(23)

From equation (23) onwards, e ≡ sech u_a.

Similarly if the point lies outside the shell, then

\begin{equation} \delta \Phi _{\rm ext}=-2\pi G\frac{a}{e}\left[1+\frac{\sigma \left(a\right)}{3}\right]\ln \left(\frac{1+\mathrm{sech}\,u_a^{\prime \prime }}{1-\mathrm{sech}\,u_a^{\prime \prime }}\right)\rho \left(a\right)\delta a, \end{equation}

(24)

where |$u_a^{\prime \prime }$| is the label of the spheroid that is confocal with the spheroid with semiminor axis a and lies outside of it.

The potential of the entire body is the sum of contributions from all the shells which make up the body. The contribution from the outer shells at a point (R, z) is

\begin{eqnarray} \sum _{a>a^{\prime }}\delta \Phi _{\rm int}&=&-2\pi G\int _{a^{\prime }}^\infty \frac{a}{e}\left[1+\frac{\sigma (a)}{3}\right]\nonumber \\ && \times \ln \left(\frac{1+\mathrm{sech}\,u_a}{1-\mathrm{sech}\,u_a}\right)\rho (a)\,\mathrm{d}a. \end{eqnarray}

(25)

The contribution from the inner shells to the potential at the point (R, z) is

\begin{eqnarray} \sum _{a<a^{\prime }}\delta \Phi _{\rm ext}&=&-2\pi G\int _{0}^{a^{\prime }}\frac{a}{e} \left[1+\frac{\sigma (a)}{3}\right]\nonumber \\ &&\times \ln \left(\frac{1+\mathrm{sech}\,u_a^{\prime \prime }}{1-\mathrm{sech}\,u_a^{\prime \prime }}\right)\rho (a)\,{\rm d}a, \end{eqnarray}

(26)

where a^′ is given by

\begin{equation} {a^{\prime }}^2=R^2+\frac{z^2}{q^2\left(a^{\prime }\right)}. \end{equation}

(27)

The total potential, Φ, is given by the summation of equations (15) and (16) as

\begin{equation} \Phi =\sum _{a>a^{\prime }}\delta \Phi _{\rm int}\,+\,\sum _{a<a^{\prime }}\delta \Phi _{\rm ext}. \end{equation}

(28)

In the limit of a constant axis ratio, σ = 0, hence the above expression simplifies to the result for the prolate spheroidal mass distribution of a constant shape.

Related physical quantities

Using the above expression for the potential, we next obtain other relevant physical quantities such as the force components along R and z, and the angular and vertical frequencies at the mid-plane for a particle in this potential. These are applied to the particular problem of warps in Section 4.

Angular frequency, Ω_h

By taking the gradient of equation (28), we can calculate the force in horizontal and vertical directions. Then force in the radial direction is

\begin{eqnarray} F_R\left(R,z\right)&=&2\pi G\frac{\mathrm{\partial} }{\mathrm{\partial} R}\int _{0}^{a^{\prime }}\frac{a}{e}\left[1+\frac{\sigma (a)}{3}\right]\nonumber \\ &&\times \ln \left(\frac{1+\mathrm{sech}\,u_a^{\prime \prime }}{1-\mathrm{sech}\,u_a^{\prime \prime }}\right)\rho (a)\,\mathrm{d}a. \end{eqnarray}

(29)

The contribution of force from the outer shells is zero since the potential is constant inside such shells. To take the gradient in the cylindrical coordinate system, we rewrite |$\mathrm{sech}\,u_a^{\prime \prime }$| in terms of R and z, by using the relation

\begin{equation} \left({a\,q\,e}\right)^2=\frac{R^2{\mathrm{sech}^2u_a^{\prime \prime }}}{1-\mathrm{sech}^2u_a^{\prime \prime }}+z^2{\mathrm{sech}^2u_a^{\prime \prime }}. \end{equation}

(30)

At the galactic mid-plane (z = 0), equation (30) reduces to

\begin{equation} \mathrm{sech}\,u_a^{\prime \prime }=\frac{a\,q\,e}{(R^2+a^2(q^2-1))^{1/2}}. \end{equation}

(31)

Substituting equation (31) in equation (29), and taking the derivative in the radial direction, gives

\begin{eqnarray} F_R\left(R\right)=\frac{4\pi G}{R}\int _{0}^{R}a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{[R^2+a^2(q^2-1)]^{1/2}}\,\mathrm{d}a. \nonumber\\ \end{eqnarray}

(32)

Notice that at the galactic plane, a^′ = R.

Then the square of the rotation velocity (⁠|$V^2_{\rm c}=F_R R$|⁠) is

\begin{eqnarray} V^2_{\rm c}\left(R\right)=4\pi G\int _{0}^{R}a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{[R^2+a^2(q^2-1)]^{1/2}}\,\mathrm{d}a. \nonumber\\ \end{eqnarray}

(33)

The square of the angular frequency, (Ω² = F_R/R), is

\begin{eqnarray} \Omega _{\rm h}^2\left(R\right)=\frac{4\pi G}{R^2}\int _{0}^{R}a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{[R^2+a^2(q^2-1)]^{1/2}}\,\mathrm{d}a, \nonumber\\ \end{eqnarray}

(34)

where the subscript ‘h’ denotes the halo.

Vertical frequency, ν_h

The force in the vertical direction is obtained by taking a gradient of equation (18) along z:

\begin{eqnarray} F_z\left(R,z\right)&=&2\pi G\frac{\mathrm{\partial} }{\mathrm{\partial} z}\int _{0}^{a^{\prime }}\frac{a}{e}\left[1+\frac{\sigma (a)}{3}\right] \nonumber \\ &&\times \ln \left(\frac{1+\mathrm{sech}\,u_a^{\prime \prime }}{1-\mathrm{sech}\,u_a^{\prime \prime }}\right)\rho (a)\,\mathrm{d}a. \end{eqnarray}

(35)

On simplifying,

\begin{equation} \frac{\mathrm{\partial} }{\mathrm{\partial} z} \ln \frac{1+\mathrm{sech}\,u_a^{\prime \prime }}{1-\mathrm{sech}\,u_a^{\prime \prime }}=2\,\frac{\frac{\mathrm{\partial} \mathrm{sech}\,u_a^{\prime \prime }}{\mathrm{\partial} z}}{1-\mathrm{sech}^2u_a^{\prime \prime }}. \end{equation}

(36)

On taking the derivative of equation (30) in the vertical direction, we get

\begin{equation} \frac{\mathrm{\partial} \mathrm{sech}\,u_a^{\prime \prime }}{\mathrm{\partial} z} =\,\frac{z\,\left(\mathrm{sech}\,u_a^{\prime \prime }-\mathrm{sech}^3u_a^{\prime \prime }\right)}{2z^2\,\mathrm{sech}^2u_a^{\prime \prime }-(z^2+R^2+a^2(q^2-1))}. \end{equation}

(37)

Substituting equations (36) and (37) into equation (35) and taking the limit z → 0 gives

\begin{eqnarray} F_z(R,z)=4\pi Gz\int _{0}^{R}a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{(R^2+a^2(q^2-1)) ^{3/2}}\,\mathrm{d}a. \nonumber\\ \end{eqnarray}

(38)

Then the square of the vertical frequency, ν² = F_z/z, is

\begin{eqnarray} \nu _{\rm h}^2\left(R\right)=4\pi G\int _{0}^{R}a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{(R^2+a^2(q^2-1))^{3/2}}\,\mathrm{d}a. \nonumber\\ \end{eqnarray}

(39)

For the sake of completeness, in Appendix B a similar calculation is given for an oblate spheroid with varying eccentricity.

APPLICATION FOR VARIOUS MODEL MASS DISTRIBUTIONS

In Section 2, we derived the expressions of potential, forces, angular frequency and vertical frequency of prolate shaped mass distributions. In order to get an idea of how these quantities vary with radius, we now apply those equations to some simple toy models of mass distributions. We will consider that the density distribution varies isothermally as

\begin{equation} \rho (a)=\frac{\rho _0}{1+\frac{a^2}{a_{\rm c}^2}}, \end{equation}

(40)

where ρ₀ and a_c are the core density and core radius, respectively (Binney & Tremaine 1987).

The isodensity surfaces are taken to be aligned prolate spheroids whose axis ratio has the value

\begin{equation} q(a^{\prime })=\beta \left(1+\frac{a}{a_{\rm c}}\right)^\alpha , \end{equation}

(41)

where a/a_c is the dimensionless semiminor axis and α and β are constants. Within the constraint σ(a/a_c) ≥ −1 (equation 14), we use the values of α = −0.1, 0 and 0.1 and value of β = 1.5. Fig. 1 shows the isodensity contours of these mass distributions. For α = 0 we get isodensity contours of constant axis ratio (q = 1.5) for all radii (Fig. 1a). For α = 0.1, the spheroids become more prolate at larger radii (from q = 1.5 to 1.9) (Fig. 1b), and for α = −0.1 the isodensity surfaces become less prolate (from q = 1.5 to 1.2) (Fig. 1c).

Figure 1.

Isodensity contours in a plane containing the polar axis for a prolate spheroidal mass distribution with an axis ratio that is (a) constant, (b) increasing and (c) decreasing with radius.

Open in new tab Download slide

We next obtain the rotation curves for the three cases considered. For a density profile with a constant axis ratio, the expression for the square of the rotation velocity V_c² can be obtained analytically by integrating equation (33) as

\begin{eqnarray} V_{\rm c}^2=\frac{4{\pi }G\rho _0a_{\rm c}^2}{e}\left[\frac{1}{2}\ln \left(\frac{1+e}{1-e}\right)- \Big(\frac{c}{b}\Big)^{\!\!{1/2}}\arctan { \: e\Big(\frac{b}{c}\Big)^{\!\!{1/2}}}\right]. \nonumber\\ \end{eqnarray}

(42)

At large radii, this is independent of radius, and in the limit of R → ∞, the constant terminal velocity square is given by

\begin{equation} V_{\rm H}^2=\frac{2{\pi }G\rho _0a_{\rm c}^2q}{({q^2-1})^{1/2}} \ln \left(\frac{1+e}{1-e}\right), \end{equation}

(43)

where c and b are defined as

\begin{eqnarray} c &=& a_{\rm c}^2(q^2-1), \nonumber \\ b &=& R^2-a_{\rm c}^2(q^2-1). \end{eqnarray}

(44)

For the case of varying axis ratio, rotation velocity is calculated numerically. Fig. 2 shows the rotation velocity curve for α = 0, + 0.1 and −0.1. The per cent differences in resulting velocities at large radii for the various values of α are not very large. In Section 4, we will apply these results to study the pattern speed and winding of the Galactic warp. Here we calculate the pattern speed of warp due to dark matter halo alone. In the kinematical picture of warps, the pattern speed for the slow mode is given by Ω − ν, where Ω and ν represent the angular speed and the vertical frequency, respectively (e.g. Binney & Tremaine 1987). This is obtained by treating the warp as a small perturbation and keeping only the slow mode since the fast mode will wind up faster. The pattern speed of a galactic warp due to dark matter halo alone, ((Ω_p)_h), is defined by

\begin{equation} (\Omega _{\rm p})_{\rm h}=\Omega _{\rm h}-\nu _{\rm h}, \end{equation}

(45)

where the subscript ‘h’ represents the halo contribution. Using the density profile and the axis ratio of the dark matter halo, as a function of the semiminor axis from equations (40) and (41), and substituting these in equations (34) and (39), gives the square of the angular and vertical frequencies. For the case of a constant axis ratio, Ω_h² = V_c²/R², where V_c² is as given by equation (42), and the vertical frequency square is given by integrating equation (39) to be

\begin{equation} \nu _{\rm h}^2=\frac{4{\pi }G\rho _0a_{\rm c}^2}{b\,e}\left[ e-{\Big(\frac{c}{b}\Big)^{\!\!{1/2}}}\arctan { e \Big({\frac{b}{c}}\Big)^{\!\!{1/2}}}\right], \end{equation}

(46)

where b and c are defined in equation (44).

Figure 2.

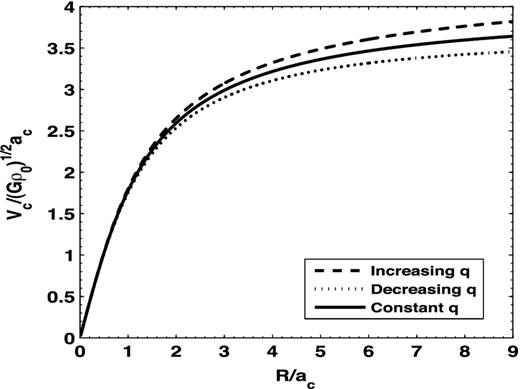
The rotation velocity for a pseudo-isothermal prolate-shaped halo density distribution with an axis ratio that is constant (q = 1.5), increasing (q = 1.5–1.9) and decreasing (q = 1.5–1.2) with radius.

Open in new tab Download slide

For density profiles with a varying axis ratio, Ω_h and ν_h are calculated numerically. Fig. 3 shows the pattern speed curves of different distributions: the pattern speed decreases at different rates with radius and approaches zero at large radii. For each axis ratio considered, the mass distribution near the mid-plane is different which mainly determines the rate of fall of the pattern speed curves. The important result to note from Fig. 3 is that for a prolate halo the pattern speed is >0, that is, Ω_h > ν_h. In contrast, for a flattened disc or an oblate halo, the reverse is true (e.g. Binney & Tremaine 1987). The net value of the pattern speed is determined by taking account of the contribution from the galactic disc also, as will be discussed in Section 4.

Figure 3.

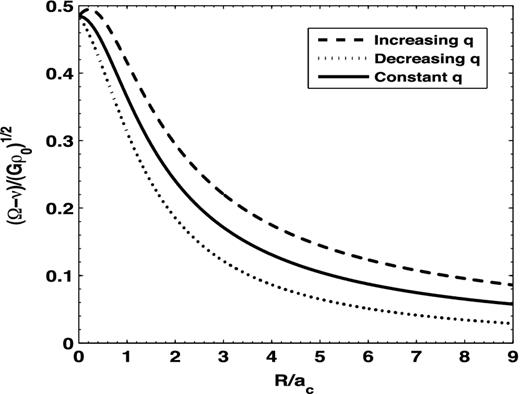
The pattern speed for the halo-alone case, for a prolate-shaped halo density distribution with an axis ratio that is constant (q = 1.5), increasing (q = 1.5–1.9) and decreasing (q = 1.5–1.2) with radius.

Open in new tab Download slide

APPLICATION TO WARP IN THE GALAXY

Here we apply the results obtained in Section 2 to the particular case of the Milky Way to study the pattern speed and winding in the Galactic warp. The aim is to see what effect a progressively prolate halo has on the winding time of a warp.

In the past it has been suggested that a prolate halo (Ideta et al. 2000) or an oblate halo with an eccentricity that changes with radius (Binney & Tremaine 1987) can help in making warps long-lived. The severity of the winding problem depends on the differential precession rate or on how rapidly the pattern speed changes with radius. In the kinematical picture of warps, the pattern speed for the slow mode is given by Ω − ν (Section 3). We need to calculate the contribution to this both from the disc and the halo. In a disc, the pattern speed is negative since ν > Ω for a gravitating disc, while for a spherical halo the two are equal, and for a prolate halo the reverse is true, namely, ν < Ω. Thus it can be seen that adding a prolate halo may help sustain a warp. Qualitatively this was the motivation for trying a prolate halo in the present paper.

Vertical and angular frequencies due to Galactic disc

For most dynamical studies, the Galactic disc is considered to be infinitesimally thin for simplicity. However, the vertical force is then discontinuous at the galactic plane, hence it is not possible to approximate small displacements in the vertical direction perturbatively as a simple harmonic motion. Hence we have to use a three-dimensional density distribution. Here we use the simple double exponential density distribution for the Galactic disc which is given by

\begin{equation} \rho \left(R,z\right)=\rho \left(0,0\right)\exp \left({-\frac{R}{R_{\rm d}}}\right)\exp \left({-\frac{z}{z_{\rm d}}}\right), \end{equation}

(47)

where ρ(0, 0) is the central density; R_d and z_d are the radial and vertical disc scale lengths, respectively.

The corresponding potential at a point (R, z) is given by Kuijken & Gilmore (1989), also see Sackett & Sparke (1990) and Cuddeford (1993):

\begin{eqnarray} \Phi _{\rm d}\left(R,z\right)&=&-4{\pi }G\rho \left(0,0\right) R_{\rm d}^2 z_{\rm d} \nonumber \\ &&\times \int _0^{\infty }\frac{J_0\left(kR\right)}{\left(1+\left(kR_{\rm d}\right)^2\right)^{3/2}} \frac{[k z_{\rm d} \exp ^{{- \vert z \vert }/ z_{\rm d}} - \exp ^{- k \vert z \vert ]}}{k^2 z_{\rm d}^2 - 1}\,\mathrm{d}k, \nonumber\\ \end{eqnarray}

(48)

where J₀(x) is the first-order Bessel function of order zero.

The radial force F_R(R, z) is given by − ∂Φ_d/∂R, and then taking the limit as z → 0, we get its value at mid-plane to be (also see Kuijken & Gilmore 1989)

\begin{eqnarray} F_R(R,0)&=&4{\pi }G\rho (0,0)R_{\rm d}^2z_{\rm d} \nonumber \\ &&\times \,\int _0^{\infty }\frac{kJ_1\left(kR\right)}{\left(1+kz_{\rm d}\right)\left(1+\left(kR_{\rm d}\right)^2\right)^{3/2}}\,\mathrm{d}k. \end{eqnarray}

(49)

Similarly, for the force along the vertical direction at the mid-plane, we obtain F_z(R, z) = −∂Φ_d/∂z and take its limit at z = 0 to get

\begin{eqnarray} F_z(R, z\rightarrow 0)&=&4{\pi }G\rho \left(0,0\right)R_{\rm d}^2z \nonumber \\ &&\times \int _0^{\infty }\frac{kJ_0\left(kR\right)}{\left(1+kz_{\rm d}\right)\left(1+\left(kR_{\rm d}\right)^2\right)^{3/2}}\,{\rm d}k. \end{eqnarray}

(50)

From these equations of force (equations 49 and 50), the angular and vertical frequencies are given by the expressions

\begin{equation} {\Omega _{\rm d}} ^2 = {F_R (R,0)}/{R} \end{equation}

(51)

and

\begin{equation} {\nu _{\rm d}} ^2 = {F_z (R, z \rightarrow 0)}/{z}. \end{equation}

(52)

Disc and halo parameters for the Galaxy

For the Galaxy, the radial disc scale length R_d = 3.2 kpc (Mera et al. 1998) and z_d = 0.35 kpc (Binney & Tremaine 1987) are used for calculating the force components and the frequencies given above. The mid-plane volume density of the stellar disc at the solar neighbourhood is observed to be 0.07 M_⊙ pc⁻³ (Binney & Tremaine 1987). Substituting the values of R_d, z_d and ρ at solar neighbourhood in equation (47), we get the value of the central density, ρ(0, 0) ≈ 0.99 M_⊙ pc⁻³.

Three types of halo distributions are considered.

A pseudo-isothermal spherical distribution as in equation (40), obtained in the Galactic mass model by Mera et al. (1998), where ρ₀ = 0.035 M_⊙ pc⁻³ and a_c = 5 kpc.
A prolate spheroidal distribution with an increasing axis ratio, that is obtained by modelling the steep flaring of H i in the outer Galaxy (Banerjee & Jog 2011); where axis ratio q and the halo density ρ(a) are given, respectively, by
\begin{equation} q = 1+\alpha _1\,(a-9)+\alpha _2\,(a-9)^2\ \mbox{when}\ 9 \le a\le 24\,\mathrm{kpc} \end{equation}
(53)
and
\begin{equation} \rho (a)=\frac{ {{\rho _0}/\left[{1+{(\frac{a}{a_{\rm c}})}^2}\right]}}{q}, \end{equation}
(54)
where q = 1 when a ≤ 9 kpc, and the constants α₁ = 0.020 and α₂ = 0.003, and ρ₀ = 0.035 M_⊙ pc⁻³ and a_c = 5 kpc.
A prolate shape with a constant axis ratio, q = 1.9: we change the shape of the dark matter halo from a sphere to a prolate spheroid by keeping the semiminor axis fixed such that the total mass inside does not change. Thus equating the mass inside both spheroids, one can find out the value of the core radius a_c for the prolate spheroid. The mass enclosed by the prolate spheroid of semiminor axis a is
\begin{equation} M({<}a)=4{\pi }G\rho _0a_{\rm c}^2q\left(a-a_{\rm c}\arctan \left(\frac{a}{a_{\rm c}}\right)\right). \end{equation}
(55)
Equating this with the mass inside a sphere (i.e. M(q = 1)) of radius a_c, gives the value of a_c as a function of q:
\begin{equation} \frac{a_{\rm c}(q)}{a_{\rm c}(1)}\arctan \frac{a_{\rm c}(1)}{a_{\rm c}(q)}=1-\frac{4-{\pi }}{4 (q^2-1)^{1/2}}\,\frac{1}{2} \ln \left(\frac{1+e}{1-e}\right). \end{equation}
(56)
Equating the terminal velocities of the prolate spheroid (equation 43) and of the sphere gives the value of ρ₀(q):
\begin{equation} \frac{\rho _0(q)}{\rho _0(1)}=\frac{a_{\rm c}^2(1)}{a_{\rm c}^2(q)}\,\frac{({1-q^2})^{1/2}}{q}\,\frac{1}{\frac{1}{2} \ln \left(\frac{1+e}{1-e}\right)}, \end{equation}
(57)
where a_c(1) = 5 kpc and ρ₀(1) = 0.035 M_⊙ pc⁻³ for the spherical case (q = 1) (Mera et al. 1998). For q = 1.9, this gives a_c = 5.98 kpc and ρ₀ = 0.016 M_⊙ pc⁻³. For another typical value, q = 1.5, we get a_c = 5.57 kpc and ρ₀ = 0.021 M_⊙ pc⁻³.

Pattern speed for warp

The pattern speed for a galactic disc embedded in a dark matter halo is set by adding in quadrature the contributions from both, and is defined to be

\begin{equation} \Omega _{\rm p}= \left[{\left(\Omega _{\rm h}^2\,+\,\Omega _{\rm d}^2\right)\,-\,\left(\nu _{\rm h}^2\,+\,\nu _{\rm d}^2\right)}\right]^{1/2} \end{equation}

(58)

Using the values of the disc and the three cases of halo parameters as discussed above, the resulting pattern speed curves are shown in Fig. 4. The disc determines the main behaviour of the pattern speed, hence the latter is <0. Surprisingly, the presence of dark matter halo makes little difference to the pattern speed curve. This is in contradiction to the expectation from the literature that halo would affect the pattern speed significantly (Section 4.5).

Figure 4.

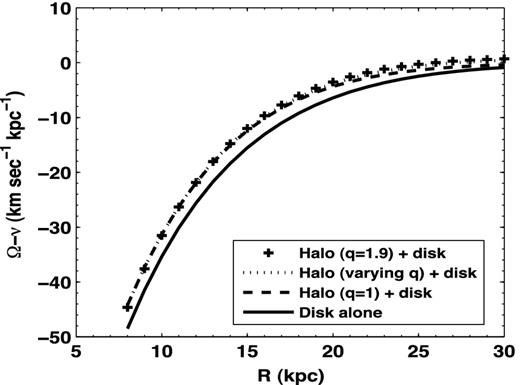
The pattern speed of warp in the Galaxy consisting of an exponential disc of finite height and dark matter halo of different shapes and distributions. Clearly, the halo contribution to the pattern speed is negligible.

Open in new tab Download slide

Winding time

The winding time of a warp between the radii R₁ and R₂ is defined in terms of the pattern speeds at these two radii as

\begin{equation} t_{{\rm winding}} = \pi / [ \Omega _{\rm p} (R_1) -\Omega _{\rm p} (R_2) ]. \end{equation}

(59)

In order to quantify how rapidly warp gets wound up, we need to calculate the winding time using equation (59). If the Milky Way were to contain only the galactic disc, then the winding time of the warp that extends from 3R_d to 8R_d is obtained to be ∼9.2 × 10⁷ yr. That is, the warp will be wound up within the age of the Galaxy (≈10¹⁰ yr). If the galactic disc is embedded either in a pseudo-isothermal spherical halo or in a prolate spheroidal halo, the winding time is almost the same (to within a few per cent). This shows that the dark matter halo with parameters as chosen here does not make any difference in the winding time. Hence, if the warp is considered as a bending wave in the galactic disc, the gravitational field of the dark matter halo does not solve the winding problem of the Galactic warp.

Comparison with previous work

In the past, it has been claimed (Binney & Tremaine 1987; Ideta et al. 2000) that the dark matter halo could increase the winding time of kinematic bending wave for a particular choice of halo parameters. In these, the galactic disc was taken to be infinitesimally thin, with a surface density that falls exponentially with radius:

\begin{equation} \Sigma (R)=\Sigma _0\, {\rm e}^{-{R}/{R_{\rm d}}}, \end{equation}

(60)

where R_d is the disc scale length (the same as in equation 47) and Σ₀ is the central surface density.

For such a disc, at radii much larger than the outer edge of the disc, the potential can be approximated as a sum of a monopole and a quadrupole term as shown by Binney & Tremaine (1987) to be

\begin{equation} \Phi _{\rm d}=-\frac{GM_{\rm d}}{r}\left[1+\frac{3R_{\rm d}^2(R^2-2z^2)}{2r^4}\right], \end{equation}

(61)

where r is the radius in spherical coordinate system, and M_d is the total mass of the disc (M_d = 2πΣ₀R_d²). The horizontal and vertical frequencies are given by

\begin{equation} \Omega _{\rm d}^2=\frac{GM_{\rm d}}{R^3}\left[1+\frac{9R_{\rm d}^2}{2R^2}\right] ;\ \nu _{\rm d}^2=\frac{GM_{\rm d}}{R^3}\left[1+\frac{27R_{\rm d}^2}{2R^2}\right]. \end{equation}

(62)

We caution that these are strictly valid only at large radii (≫ the size of the disc), whereas in the above references, these were incorrectly applied to lower radii within the disc ∼10 kpc where the warp begins (see Binney & Tremaine 1987, figs 6–30; Ideta et al. 2000, fig. 8). Both these references use a logarithmic potential for the halo while we have derived a rigorous expression for the halo potential. Fig. 5 shows the results obtained using this approximation (dashed line), and that obtained in this paper (equations 51 and 52) for a disc of finite thickness (solid line). Here we used R_d = 3.2 kpc (see Section 4.2) and Σ₀ = 640 M_⊙ pc⁻² (Binney & Tremaine 1987) for plotting the curves.

Figure 5.

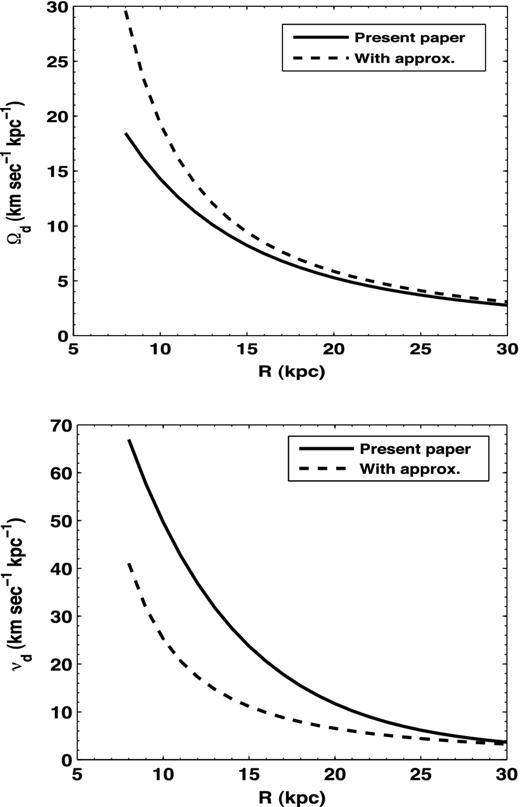
Ω_d and ν_d versus R for a particle in the Galactic disc using the correct treatment as in this paper (solid line), and using the approximation of an infinitesimally thin disc and potential valid at large radii as in Binney & Tremaine (1987) (dashed line).

Open in new tab Download slide

In this approximation, ν and Ω have comparable values – we note that this result is incorrect, since it is well known that within a self-gravitating disc ν > Ω. Check that the correct treatment for a finite height disc in the present paper does satisfy this criterion (see Fig. 4 which shows Ω − ν < 0), which results in a pattern speed that varies rapidly with radius and is dominated by the disc contribution (Fig. 4).

Fig. 6 shows results for the pattern speed of warp at the galactic plane for a prolate halo of q = 1.9 and the correct treatment for the disc as in this paper (the solid line), and it also shows the erroneous results obtained using the approximation for the disc (equation 62) either by itself, or with a spherical halo, and the logarithmic halo as in Ideta et al. (2000). The last three cases, in particular the one with the prolate halo, show an almost constant pattern speed throughout the range of radii of interest where the warp is seen. This led Ideta et al. (2000) to the conclusion that a prolate halo results in a Galactic warp that can be sustained for more than the Hubble time. To summarize, they arrived at this wrong conclusion due to the use of an approximate expression for the potential for an infinitesimally thin disc as applied to a low radial range where it is not valid.

Figure 6.

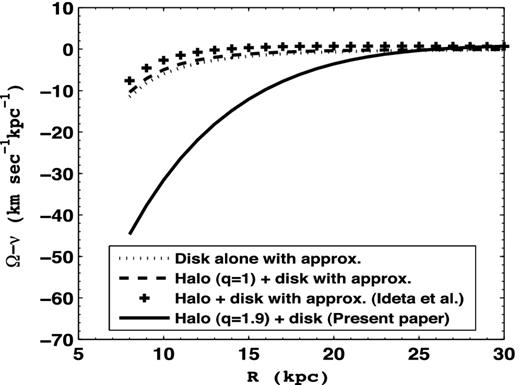
The pattern speed of warp in the Galaxy consisting of a disc of finite thickness and a prolate halo (q = 1.9) from the present paper (solid line), and that using the approximation of an infinitesimally thin disc and potential valid only at large radii (as in Binney & Tremaine 1987; Ideta et al. 2000) and different halo shapes.

Open in new tab Download slide

The correct treatment for the disc in the present paper shows that the disc contribution to the pattern speed is dominant (solid line, Fig. 6, also see Fig. 4), and that the prolate dark matter halo, indeed halo of any shape, has very little effect on the pattern speed of the Galactic warp. The normalized differential force due to the heteroid shells considered is negligible (<1 per cent, see Appendix A), hence that too cannot affect the above result. In retrospect, this is not surprising, since the previous work on the origin of warps by non-axisymmetric response showed that the radius of onset of warps in a galactic disc depends weakly on whether or not an oblate halo is included or on its shape, as shown for a disc with an exponential vertical distribution (Saha & Jog 2006) or a general z distribution (Pranav & Jog 2010).

We caution that we have only considered a simple kinematical model of warp, as an application of the potential obtained for prolate ellipsoids of varying eccentricity. The latter was the main aim of this paper. A complete treatment of the dynamics and origin of warps would be much more complex and could involve a responsive and triaxial halo (e.g. Binney, Jiang & Dutta 1998; Dubinski & Chakrabarti 2009) and is beyond the scope of this paper.

CONCLUSIONS

In this paper, we have given the analytical calculation for the potential of a prolate ellipsoidal mass distribution with radially varying eccentricity. This is obtained by summing up the shell-by-shell contributions of isodensity surfaces. We define a heteroid to be a shell that is bounded by two dissimilar surfaces. An important result from this paper is that the potential within a heteroid is shown to be approximately constant as long as the radial variation and the range of values of eccentricity spanned are small as in realistic systems. The normalized differential force across such a shell is non-zero but small and does not affect the dynamical stability of such figures on a Hubble time.

The motivation for this work was to see if the progressively prolate halo for the Galaxy (as in Banerjee & Jog 2011) could help sustain long-term warps. We apply the above calculation to the case of Galactic warp, and on using the correct treatment for the disc, find that the disc mainly determines the warp pattern speed. Thus, the dark matter halo has only a marginal effect on the pattern speed, and it does not lead to long-lived warps.

The results for the potential and force components obtained here are general and could be applied for a more realistic treatment of other astrophysical systems such as prolate bars with a varying shape. We also give a similar exact calculation for the oblate case for the sake of completeness. This can be applied to oblate spheroidal systems with varying eccentricity.

We thank the anonymous referee for raising the very important issue about the applicability of the homoeoid potential theory for the case of spheroids of varying eccentricity studied in our paper.

REFERENCES

Arfken

G. B.

,

Mathematical Methods for Physicists

,

1970

New York

Academic Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Bailin

J.

Steinmetz

M.

,

ApJ

,

2005

, vol.

627

pg.

647

Crossref

Search ADS

Banerjee

A.

Jog

C. J.

,

ApJ

,

2011

, vol.

732

pg.

L8

Crossref

Search ADS

Bett

P.

Eke

V.

Frenk

C. S.

Jenkins

A.

Helly

J.

Navarro

J.

,

MNRAS

,

2007

, vol.

376

pg.

215

Crossref

Search ADS

Binney

J.

Tremaine

S.

,

Galactic Dynamics

,

1987

Princeton, NJ

Princeton Univ. Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Binney

J.

Jiang

I.-G.

Dutta

S.

,

MNRAS

,

1998

, vol.

297

pg.

1237

Crossref

Search ADS

Buote

D. A.

Canizares

C. R.

,

ApJ

,

1996

, vol.

457

pg.

565

Crossref

Search ADS

Chandrasekhar

S.

,

Ellipsoidal Figures of Equilibrium

,

1969

New Haven

Dover Press

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Cuddeford

P.

,

MNRAS

,

1993

, vol.

262

pg.

1076

Crossref

Search ADS

Das

M.

Jog

C. J.

,

ApJ

,

1995

, vol.

451

pg.

167

Crossref

Search ADS

de Zeeuw

T.

Pfenniger

D.

,

MNRAS

,

1988

, vol.

235

pg.

949

Crossref

Search ADS

Dubinski

J.

Chakrabarti

D.

,

ApJ

,

2009

, vol.

703

pg.

2068

Crossref

Search ADS

Helmi

A.

,

ApJ

,

2004

, vol.

610

pg.

L97

Crossref

Search ADS

Ideta

M.

Hozumi

S.

Tsuchiya

T.

Takizawa

M.

,

MNRAS

,

2000

, vol.

311

pg.

733

Crossref

Search ADS

Jing

Y. P.

Suto

Y.

,

ApJ

,

2002

, vol.

574

pg.

538

Crossref

Search ADS

Kuijken

K.

Gilmore

G.

,

MNRAS

,

1989

, vol.

239

pg.

571

Crossref

Search ADS

Mera

D.

Chabrier

G.

Schaeffer

R.

,

A&A

,

1998

, vol.

330

pg.

953

Pranav

P.

Jog

C. J.

,

MNRAS

,

2010

, vol.

406

pg.

576

Crossref

Search ADS

Rohlfs

K.

,

Lectures on Density Wave Theory

,

1977

Berlin

Springer-Verlag

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Ryden

B. S.

,

MNRAS

,

1990

, vol.

244

pg.

341

Sackett

P. D.

Sparke

L. S.

,

ApJ

,

1990

, vol.

361

pg.

408

Crossref

Search ADS

Saha

K.

Jog

C. J.

,

MNRAS

,

2006

, vol.

367

pg.

1297

Crossref

Search ADS

Sparke

L. S.

,

ApJ

,

1984

, vol.

280

pg.

117

Crossref

Search ADS

Vera-Ciro

C. A.

Sales

L. V.

Helmi

A.

Frenk

C. S.

Navarro

J. F.

Springel

V.

Vogelsberger

M.

White

S. D. M.

,

MNRAS

,

2011

, vol.

416

pg.

1377

Crossref

Search ADS

APPENDIX A: POTENTIAL AND FORCE INSIDE A PROLATE SHELL WITHIN DISSIMILAR SURFACES

In this paper we treat spheroids of radially varying eccentricity. In analogy with a homoeoid which is a shell bounded by two similar spheroids, we define a heteroid to be a shell bounded by two dissimilar spheroids (Section 2.2). We show next that the results from the standard homoeoid potential theory, namely the constancy of potential inside a shell and no net force within it, are good approximations even for the case of a shell with dissimilar surfaces – when the radial variation in eccentricity is small as seen in realistic systems. This is an important general result and to our knowledge the heteroid case has not been studied systematically in the past.

Potential inside a shell within dissimilar spheroids. Recall from Section 2.2 that for the dissimilar prolate surfaces with the variation in eccentricity, the dimensionless scale factor S (see equation 21) denotes the deviation from the case of constant internal potential:

\begin{equation} S = \left[\frac{1+\sigma \,\cos ^2v}{1+ (\sigma /3)}\right], \end{equation}

(A1)

where σ denotes the dimensionless change in the eccentricity with radius.

In Fig. A1, we plot the values of this scale factor versus the semiminor axis a/a_c normalized with respect to the core radius, for decreasing q (as given by equation 41) with α = −0.1 for the prolate coordinate v = 0 and v = π/2 and similarly for increasing prolateness with q increasing (as given by equation 41) with α = 0.1. This figure clearly shows that the scale factor values are small (<a few per cent). Hence the deviation from the case of similar shells treated in homoeoidal theory is non-zero but small. Thus, interestingly, we find that for the small variation in eccentricity with radius and for the range of q values as considered in this paper – the assumption of a constant potential within a shell is a good approximation even for the case of a shell bounded by dissimilar surfaces.

Figure A1.

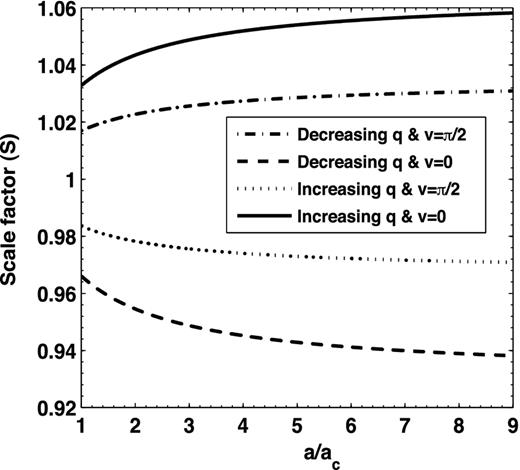
The values of the dimensionless scale factor, S, that denote the deviation of the surface density within dissimilar surfaces compared to the case of similar surfaces versus the dimensionless semiminor axis, for increasing and decreasing prolateness, and for different values of the prolate coordinate v. Note that the deviation from the similar shells corresponding to the usual homoeoidal case is small <a few per cent.

Open in new tab Download slide

Force inside a shell within dissimilar spheroids. From the homoeoidal theorem we know that the force inside a shell bounded by similar spheroids is zero (e.g. Chandrasekhar 1969; Binney & Tremaine 1987). Here we find out the force due to a shell bounded by two dissimilar spheroids (a heteroid). The expression of the internal potential of homogenous spheroid is (Binney & Tremaine 1987, equation 2–87)

\begin{equation} \Phi (R,z) = -\pi G \rho (I a^2 -A_1 R^2-A_3 z^2), \end{equation}

(A2)

where I, A₁ and A₃ are defined for the prolate case as follows (see Binney & Tremaine 1987, tables 2-1 and 2-2):

\begin{equation} I = \frac{1}{qe} \ln \left( \frac{1+e}{1-e}\right), \end{equation}

(A3)

\begin{equation} A_1 = \frac{1-e^2}{e^2}\left[ \frac{1}{1-e^2}-\frac{1}{2e}\ln \left( \frac{1+e}{1-e}\right)\right], \end{equation}

(A4)

\begin{equation} A_3 = 2 \frac{1-e^2}{e^2}\left[ \frac{1}{2e} \ln \left(\frac{1+e}{1-e}\right)-1 \right]. \end{equation}

(A5)

Hence the radial component of the gravitational field generated by a homogenous spheroid at an internal point (R, z) is

\begin{equation} F_R = - 2 \pi G \rho A_1 R. \end{equation}

(A6)

The vertical force component is

\begin{equation} F_z = - 2 \pi G \rho A_3 z. \end{equation}

(A7)

We can think of the force at an internal point of a heteroid shell as being obtained by the subtraction of force due to the outer spheroid and that due to the inner spheroid. Thus, the differential radial force due to the shell is

\begin{equation} F_R = -2 \pi G \rho R (A_1^{\rm o}-A_1^{\rm i}), \end{equation}

(A8)

where the superscripts o and i denote the outer and inner spheroids, respectively, and where ρ is the density of the shell. Similarly the vertical force is

\begin{equation} F_z = - 2 \pi G \rho z \left(A_3^{\rm o}-A_3^{\rm i}\right). \end{equation}

(A9)

First, check that the force inside of such a shell would be identically equal to zero if the surfaces are similar (homoeoids). Next, we can find out the total differential force at a point (R, z) due to outer dissimilar shells by adding the contributions of each shell. The magnitude of the differential force depends on the eccentricities of ellipsoids which surround the shell. The total differential force at a point is obtained for the density distribution (equation 40) and the eccentricities (equation 41) used in our work, and this is normalized with the force due to a homogenous spheroid which has the surface that is passing through the point (R, z) and has that value of constant density. For normalization, a constant density ellipsoid is assumed for simplicity. The increasing q (more prolate at larger radii) corresponds to α = 0.1 while decreasing q (less prolate at smaller radii) has α = −0.1 (see Section 3). These correspond to a variation in the prolate axis ratio, q = 1.5–1.9 and 1.5–1.2, respectively (Section 3). The increasing case covers the range of values of q similar to the range deduced from flaring of H i data in the outer Milky Way (Banerjee & Jog 2011, also see Section 4.2).

The values for different semiminor axis are given in Table A1. Clearly, the differential force is very small (with magnitudes ≤1 per cent) for the range of semiminor axis values that we are interested in. As expected, the differential force magnitudes are highest at inner radii but still small ∼1 per cent. The typical value of a_c, the core radius, is 5 kpc in our Galaxy (Section 4), thus the ratio a/a_c = 1–8 corresponds to about 5–40 kpc. Therefore, we can take the internal force due to the spheroids of varying eccentricity to be zero for our calculation. This further confirms that Newton's theorem is a good assumption even for the case of dissimilar ellipsoids considered here. This is an important, general result and can be applied to other realistic cases. For example, this is also applicable for studies of dark matter haloes in simulations which show an even smaller variation in the prolate or oblate axes ratio (e.g. Jing & Suto 2002; Vera-Ciro et al. 2011).

Table A1.

Open in new tab

Normalized differential force magnitudes due to a shell within dissimilar surfaces.

a/a_c	F_R	F_z
Increasing q
1	0.0120	0.0018
3	0.0098	0.0072
8	0.0023	0.0085
Decreasing q
1	0.0141	0.0020
3	0.0128	0.0071
8	0.0033	0.0072

Table A1.

Open in new tab

Normalized differential force magnitudes due to a shell within dissimilar surfaces.

a/a_c	F_R	F_z
Increasing q
1	0.0120	0.0018
3	0.0098	0.0072
8	0.0023	0.0085
Decreasing q
1	0.0141	0.0020
3	0.0128	0.0071
8	0.0033	0.0072

Since the typical dynamical time-scale in a homogenous spheroid with a surface at say 3a_c = 15 kpc is ∼a few ×10⁸ yr, hence the differential force of <1 per cent of the force due to the inner spheroid is not likely to affect the stability of such a distribution over 100 times the dynamical time-scales or over a Hubble time.

APPENDIX B: OBLATE SPHEROIDAL MASS DISTRIBUTION WITH RADIALLY VARYING ECCENTRICITY

In this appendix, we give the oblate case with varying eccentricity for the sake of completeness, with an approach similar to that developed in this paper for the prolate case. This problem has been looked at earlier by Ryden (1990), who however used the method of multipoles limiting to the quadrupole approximations. Thus Ryden's results are approximate and in particular not rigorous for inner regions, as we check by comparing with the exact calculations below. Hence we give the exact calculation below. This could be of use not just for dark matter halo but also for other systems of varying eccentricity such as bulges.

The method of derivation of physical quantities for the case of oblate spheroidal mass distribution is similar to the method that is described for the prolate spheroidal mass distributions. So the resulting equations of potential, forces, vertical and horizontal frequencies are given here without detailed derivations. The density profile, axis ratio and σ are used as the functions of semimajor axis a. (Remember that in the case of prolate distribution, a is the semiminor axis.) Here the axis ratio is always less than 1.

The potential of the oblate spheroidal shell on the surface u = u₀ in oblate spheroidal coordinate system is given in Binney & Tremaine (1987), to be

\begin{equation} \Phi = -\frac{GM}{a_0\,e} \left\lbrace \begin{array}{ll}\,\mathrm{arcsin}\left(e\right) &\quad \mbox{when}\quad u<u_0, \\ \,\mathrm{arcsin}\left(\mathrm{sech}\,u\right) &\quad \mbox{when}\quad u\ge u_0, \end{array} \right. \end{equation}

(B1)

where u is defined in cylindrical coordinates as

\begin{equation} R = \Delta \,\cosh u\,\sin v ;\: \: z = \Delta \,\sinh u\,\cos v, \end{equation}

(B2)

where Δ = a₀e is a constant, a₀ ≡ cosh u₀, e = sech u₀ and M is the mass on the surface u = u₀.

When the axis ratio varies with radius, the constraint that the shells do not cross is again given by σ(a) ≥ −1, where σ(a) is defined by equation (14), except that a is now the semimajor axis.

We next obtain the scale factor for oblate mass distribution with varying eccentricity similar to the prolate case (equation 22) to check the validity of the homoeoidal theory. From above equation (equation B1), we can calculate the surface density of an oblate spheroidal surface using Gauss's theorem, as obtained in Binney & Tremaine (1987, see equation 2.68):

\begin{equation} \Sigma = \frac{M}{4\pi a^2(1-e^2\sin ^2v)^{1/2}}. \end{equation}

(B3)

Using the equation of spheroid we can find out the expression of surface density of a shell bounded by two dissimilar oblate spheroidal surfaces by taking the projection of the mass on the inner surface of the shell to be

\begin{equation} \bar{\Sigma } = \frac{\rho \delta a}{\left(R^2+\frac{z^2}{q^4}\right)^{1/2}} \left(a+\frac{z^2}{q^3}\frac{\mathrm{d}q}{\mathrm{d}a}\right). \end{equation}

(B4)

By replacing the cylindrical coordinates by spheroidal coordinates, we get

\begin{equation} \bar{\Sigma } = \frac{ q \rho \delta a}{(1-e^2\sin ^2v)^{1/2} }[1+\sigma \cos ^2v]. \end{equation}

(B5)

Using the equation (15), we rewrite the above equation as

\begin{equation} \bar{\Sigma } = \frac{\delta M \,S}{4\pi a^2 (1-e^2\sin ^2v)^{1/2}}. \end{equation}

(B6)

Check that the function S defined here is exactly the scale factor as obtained for the prolate case (equation 22). On comparing equations (B3) and (B6), it can be seen that the case of dissimilar spheroids deviates from the similar spheroids by this scale factor. In this case also, the values of the scale factor S would be small. Hence as discussed in the case of prolate mass distribution, we can still apply the homoeoidal potential theory. That is, we can substitute the expression of mass of the shell (equation 15) in equation (B1) to calculate the potential due to a shell which is bounded by two dissimilar oblate spheroidal surfaces.

It can then be shown that the contribution of the potential at a point (R, z) from outer shells is (this is analogous to equation 25)

\begin{equation} \sum _{a>a^{\prime }}\delta \Phi _{\rm int} = -4\pi G\int _{a^{\prime }}^\infty \frac{aq}{e}\left[1+\frac{\sigma (a)}{3}\right]\arcsin (e)\rho (a)\,{\rm d}a. \end{equation}

(B7)

From equation (B7) onwards, e ≡ sech u_a.

The contribution from inner shells is (this is analogous to equation 26)

\begin{eqnarray} \sum _{a<a^{\prime }}\delta \Phi _{\rm ext} = -4\pi G\int _{0}^{a^{\prime }}\frac{aq}{e}\left[1+\frac{\sigma (a)}{3}\right] \arcsin (\mathrm{sech}\,u_a^{\prime \prime })\rho (a)\,\mathrm{d}a, \nonumber\\ \end{eqnarray}

(B8)

where |$u_a^{\prime \prime }$| is the label of the spheroid that is confocal with the spheroid with semiminor axis a. We can replace |$\mathrm{sech}\,u_a^{\prime \prime }$| in terms of the cylindrical coordinates (R, z) using the relation

\begin{equation} \left({ae}\right)^2 = \frac{z^2{\mathrm{sech}^2u_a^{\prime \prime }}}{1-\mathrm{sech}^2u_a^{\prime \prime }}+R^2{\mathrm{sech}^2u_a^{\prime \prime }}. \end{equation}

(B9)

The potential at (R, z) is

\begin{equation} \Phi \left(R,z\right) = \sum _{a>a^{\prime }}\delta \Phi _{\rm int}\,+\,\sum _{a<a^{\prime }}\delta \Phi _{\rm ext}. \end{equation}

(B10)

The force in the radial direction is

\begin{equation} F_R = 4\pi G\frac{\mathrm{\partial} }{\mathrm{\partial} R}\!\int _{0}^{a^{\prime }}\!\frac{aq}{e}\left[1+\frac{\sigma (a)}{3}\right]\arcsin (\mathrm{sech}\,u_a^{\prime \prime })\rho (a)\,\mathrm{d}a. \end{equation}

(B11)

At the galactic plane, equation (B9) reduces to

\begin{equation} \mathrm{sech}\,u_a^{\prime \prime } = \frac{a\,e}{R}, \end{equation}

(B12)

and a^′ becomes R. Substituting equation (B12) into equation (B11) and taking the derivative gives

\begin{equation} F_R = \frac{4\pi G}{R}\!\int _{0}^{R}\!a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{(R^2+a^2(q^2-1))^{1/2} }\,\mathrm{d}a. \end{equation}

(B13)

Then the square of the rotation velocity is

\begin{equation} V^2_{\rm c} = 4\pi G\!\int _{0}^{R}\!a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{(R^2+a^2(q^2-1))^{1/2}}\,\mathrm{d}a. \end{equation}

(B14)

Check that for the special case of a pseudo-isothermal density distribution (equation 40), and for a constant axis ratio so that q(a) = q, the above equation reduces to

\begin{eqnarray} V^2_{\rm c} &=& 4 \pi G \rho _0 a^2_{\rm c} q \left[\frac{1}{(1-q^2)^{1/2}} \arcsin (1-q^2)^{1/2} \right.\nonumber \\ && -\left. \frac{a_{\rm c}}{[R^2 + a^2_{\rm c} (q^2 - 1)]^{1/2}} \arctan \frac{[R^2 + a^2_{\rm c} (q^2 - 1)]^{1/2}}{a_{\rm c} q} \right]. \nonumber\\ \end{eqnarray}

(B15)

Hence, in the limit R → ∞, the terminal velocity V_c is

\begin{equation} V^2_{\rm c} (R \rightarrow \infty ) = \frac{4 \pi G \rho _0 a^2_{\rm c} q}{(1-q^2)^{1/2}} \arcsin (1-q^2)^{1/2}. \end{equation}

(B16)

Note that this agrees with the expression obtained by Sackett & Sparke (1990) for an oblate spheroid of constant shape, as expected.

The square of the angular frequency, |$\Omega _{\rm h}^2 = {F_R}/{R}$| is

\begin{equation} \Omega _{\rm h}^2 = \frac{4\pi G}{R^2}\!\int _{0}^{R}\!a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{(R^2+a^2(q^2-1))^{1/2}}\,\mathrm{d}a. \end{equation}

(B17)

The force in the vertical direction is

\begin{eqnarray} F_z = 4\pi G\frac{\mathrm{\partial} }{\mathrm{\partial} z}\int _{0}^{a^{\prime }}\frac{aq}{e}\left[1+\frac{\sigma \left(a\right)}{3}\right]\arcsin \left(\mathrm{sech}\,u_a^{\prime \prime }\right)\rho (a)\,\mathrm{d}a. \nonumber\\ \end{eqnarray}

(B18)

Using equation (B5), we get

\begin{equation} \lim _{z\rightarrow 0}\frac{\mathrm{\partial} \,\mathrm{sech}\,u_a^{\prime \prime }}{\mathrm{\partial} z} = \frac{zae}{R(R^2+a^2(q^2-1))}. \end{equation}

(B19)

Taking the derivative in the vertical direction and using equation (B19), equation (B18) reduces to

\begin{eqnarray} F_z = 4\pi Gz\int _{0}^{R}\,a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{(R^2+a^2(q^2-1))^ {3/2}}\,\mathrm{d}a.\nonumber\\ \end{eqnarray}

(B20)

Then the square of the vertical frequency, |$\nu _{\rm h}^2 = {F_z}/{z}$| is

\begin{equation} \nu _{\rm h}^2 = 4\pi G\int _{0}^{R}a^2q\left[1+\frac{\sigma (a)}{3}\right]\frac{\rho (a)}{(R^2+a^2(q^2-1))^{3/2}}\,\mathrm{d}a. \end{equation}

(B21)

The expressions for F_R, F_z, V_c, Ω_h and ν_h are the same as those in the case of prolate spheroidal mass distributions. The difference lies in the fact that a is semimajor axis and the axis ratio q is always <1. In the prolate case, a is semiminor axis and the axis ratio is always >1.

Download all slides

Month:	Total Views:
February 2017	2
March 2017	4
April 2017	1
May 2017	6
August 2017	1
September 2017	1
October 2017	2
November 2017	1
December 2017	4
January 2018	3
February 2018	6
March 2018	3
April 2018	11
May 2018	17
June 2018	8
July 2018	11
August 2018	9
September 2018	7
October 2018	5
November 2018	4
December 2018	4
January 2019	6
February 2019	4
March 2019	6
April 2019	12
May 2019	7
June 2019	2
July 2019	8
August 2019	12
September 2019	2
October 2019	6
November 2019	7
December 2019	9
January 2020	8
February 2020	7
March 2020	10
April 2020	17
May 2020	2
June 2020	4
July 2020	5
August 2020	6
September 2020	12
October 2020	9
November 2020	4
December 2020	9
January 2021	6
February 2021	7
March 2021	17
April 2021	13
May 2021	11
June 2021	8
July 2021	7
August 2021	2
September 2021	9
October 2021	11
November 2021	3
December 2021	1
January 2022	3
February 2022	10
March 2022	13
April 2022	7
May 2022	4
June 2022	7
July 2022	9
August 2022	12
September 2022	4
October 2022	9
November 2022	7
December 2022	5
January 2023	9
February 2023	5
March 2023	4
April 2023	4
May 2023	7
June 2023	2
July 2023	7
August 2023	15
September 2023	4
October 2023	12
November 2023	4
December 2023	15
January 2024	8
February 2024	9
March 2024	6
April 2024	14
May 2024	3
June 2024	5
July 2024	12
August 2024	8
September 2024	5
October 2024	8
November 2024	9
December 2024	2
January 2025	7
February 2025	15
March 2025	9
April 2025	11
May 2025	7

Article Contents

Dynamics of prolate spheroidal mass distributions with varying eccentricity

Abstract

INTRODUCTION

POTENTIAL OF A PROLATE ELLIPSOID WITH VARYING ECCENTRICITY

Potential of a prolate spheroidal surface

Potential of prolate mass distribution

Related physical quantities

Angular frequency, Ω_h

Vertical frequency, ν_h

APPLICATION FOR VARIOUS MODEL MASS DISTRIBUTIONS

APPLICATION TO WARP IN THE GALAXY

Vertical and angular frequencies due to Galactic disc

Disc and halo parameters for the Galaxy

Pattern speed for warp

Winding time

Comparison with previous work

CONCLUSIONS

REFERENCES

APPENDIX A: POTENTIAL AND FORCE INSIDE A PROLATE SHELL WITHIN DISSIMILAR SURFACES

APPENDIX B: OBLATE SPHEROIDAL MASS DISTRIBUTION WITH RADIALLY VARYING ECCENTRICITY

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Dynamics of prolate spheroidal mass distributions with varying eccentricity Free

Abstract

INTRODUCTION

POTENTIAL OF A PROLATE ELLIPSOID WITH VARYING ECCENTRICITY

Potential of a prolate spheroidal surface

Potential of prolate mass distribution

Related physical quantities

Angular frequency, Ωh

Vertical frequency, νh

APPLICATION FOR VARIOUS MODEL MASS DISTRIBUTIONS

APPLICATION TO WARP IN THE GALAXY

Vertical and angular frequencies due to Galactic disc

Disc and halo parameters for the Galaxy

Pattern speed for warp

Winding time

Comparison with previous work

CONCLUSIONS

REFERENCES

APPENDIX A: POTENTIAL AND FORCE INSIDE A PROLATE SHELL WITHIN DISSIMILAR SURFACES

APPENDIX B: OBLATE SPHEROIDAL MASS DISTRIBUTION WITH RADIALLY VARYING ECCENTRICITY

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Dynamics of prolate spheroidal mass distributions with varying eccentricity

Angular frequency, Ω_h

Vertical frequency, ν_h