-
PDF
- Split View
-
Views
-
Cite
Cite
Bence Kocsis, Zoltán Haiman, Abraham Loeb, Gas pile-up, gap overflow and Type 1.5 migration in circumbinary discs: application to supermassive black hole binaries, Monthly Notices of the Royal Astronomical Society, Volume 427, Issue 3, December 2012, Pages 2680–2700, https://doi.org/10.1111/j.1365-2966.2012.22118.x
Close - Share Icon Share
Abstract
We study the interaction of a supermassive black hole (SMBH) binary and a standard radiatively efficient thin accretion disc. We examine steady-state configurations of the disc and migrating SMBH system, self-consistently accounting for tidal and viscous torques and heating, radiative diffusion limited cooling, gas and radiation pressure, and the decay of the binary's orbit. We obtain a ‘phase diagram’ of the system as a function of binary parameters, showing regimes in which both the disc structure and migration have a different character. Although massive binaries can create a central gap in the disc at large radii, the tidal barrier of the secondary causes a significant pile-up of gas outside of its orbit, which can lead to the closing of the gap. We find that this spillover occurs at an orbital separation as large as  gravitational radii, where M• = 107M7 M⊙ is the total binary mass. If the secondary is less massive than ∼106 M⊙, then the gap is closed before gravitational waves (GWs) start dominating the orbital decay. In this regime, the disc is still strongly perturbed, but the piled-up gas continuously overflows as in a porous dam, and crosses inside the secondary's orbit. The corresponding migration rate, which we label Type 1.5, is slower than the usual limiting cases known as Type I and II migration. Compared to an unperturbed disc, the steady-state disc in the overflowing regime is up to several hundred times brighter in the optical bands. Surveys such as PanSTARRS or LSST may discover the periodic variability of this population of binaries. Our results imply that the circumbinary discs around SMBHs can extend to small radii during the last stages of their merger, when they are detectable by LISA, and may produce coincident electromagnetic emission similar to active galactic nuclei.
gravitational radii, where M• = 107M7 M⊙ is the total binary mass. If the secondary is less massive than ∼106 M⊙, then the gap is closed before gravitational waves (GWs) start dominating the orbital decay. In this regime, the disc is still strongly perturbed, but the piled-up gas continuously overflows as in a porous dam, and crosses inside the secondary's orbit. The corresponding migration rate, which we label Type 1.5, is slower than the usual limiting cases known as Type I and II migration. Compared to an unperturbed disc, the steady-state disc in the overflowing regime is up to several hundred times brighter in the optical bands. Surveys such as PanSTARRS or LSST may discover the periodic variability of this population of binaries. Our results imply that the circumbinary discs around SMBHs can extend to small radii during the last stages of their merger, when they are detectable by LISA, and may produce coincident electromagnetic emission similar to active galactic nuclei.
1 Introduction
1.1 Overview
Understanding the coevolution of binaries and the accretion discs in which they are embedded is critical in several fields of astrophysics, including planet formation and migration (Goldreich & Tremaine 1980; Ward 1997), patterns in planetary rings (Goldreich & Tremaine 1982), stellar binaries (Shu, Adams & Lizano 1987; McKee & Ostriker 2007), the final parsec phase of black hole binaries (Begelman, Blandford & Rees 1980; Escala et al. 2005; Lodato et al. 2009), stars and black holes (BHs) in active galactic nuclei (AGN) (Goodman & Tan 2004; Miralda-Escudé & Kollmeier 2005; Levin 2007), and electromagnetic (EM) counterparts to gravitational wave (GW) events (Kocsis, Haiman & Menou 2008; Haiman et al. 2009a; Schnittman 2011). These systems may also provide observational probes to test models of the anomalous viscosity in accretion discs (Kocsis, Yunes & Loeb 2011; Yunes et al. 2011).
Despite the long history of the subject, there are very few self-consistent analytic models for the coevolution of binaries and accretion discs, incorporating the fundamental physical effects over the long time-scales on which the binary separation evolves. The standard α-model of radiatively efficient turbulent thin accretion discs (Shakura & Sunyaev 1973) relates the effective kinematic viscosity of the disc to the pressure ν ∝ αp. The viscous evolution of the disc, however, is often modelled without considering the pressure dependence of the viscosity (Lynden-Bell & Pringle 1974). Similarly, models of the gravitational interaction between the disc, which describe the launching of spiral density waves in the disc that remove angular momentum from the binary, also do not account for the tidal heating of the disc and the corresponding feedback on the torques (Goldreich & Tremaine 1980).
In an accompanying paper (Kocsis, Haiman & Loeb 2012, hereafter Paper I) we derive an analytic steady-state model for the coevolution of the disc and the orbital migration of the secondary, in which we combine a Shakura & Sunyaev (1973) disc with the theory of the binary--disc interaction by Goldreich & Tremaine (1980) self-consistently. In particular, we adopt the viscosity prescription for standard thin α- or β-discs, calculate the sound speed and vertical balance including both gas and radiation pressure (pgas and prad), adopt a simple analytic approximation to the angular momentum exchange between the binary and the disc of Armitage & Natarajan (2002), consider the viscous and tidal heating of the disc (Lodato et al. 2009), and self-consistently account for the feedback on the pressure, viscosity, scaleheight, and the torque cutoff near the secondary's orbit, as well as on the migration rate of the secondary. We derive azimuthally averaged analytic disc models which recover the Goodman & Tan (2004) solution for arbitrary β = pgas/(pgas + prad) in the limit that the secondary mass ms approaches zero. The solution is then generalized for larger ms, i.e. to the case when the disc structure is significantly modified by the secondary, over multiple accretion time-scales.
In this paper, we explore the implications of the new binary+disc evolution solutions, found in Paper I, for supermassive black hole (SMBH) binary systems. By varying the binary parameters systematically, we explore possible distinct behaviours of the disc-secondary system. We recover the two limiting cases known previously, and identify a new intermediate phase. Low-mass objects perturb the disc only weakly, and the linear density perturbations lead to the extensively studied Type I migration of the secondary (Goldreich & Tremaine 1980). For very massive objects, the tidal torque clears a gap in the disc, and the viscous radial inflow of the gas pushes the object inwards (known as Type II migration). A particular subclass of the latter is the so-called secondary-dominated Type II migration, in which the secondary's mass exceeds the nearby gas mass, causing the migration to slow down, and the surface density outside of the gap to build up, before it is able to efficiently push the object inwards (Syer & Clarke 1995). This assumes that the pile-up is 100 per cent efficient and no gas can cross the secondary's orbit. We identify a separate, intermediate class of migration, Type 1.5, in which the gas piles up significantly outside of the perturber's orbit, but the viscosity increases to the point that in steady state, the gas enters the non-linear gravitational field of the secondary (i.e. its Hill sphere), and is able to flow across its orbit. Not surprisingly, the corresponding migration rate is significantly different from both the Type I and II cases.1
In most previous investigations, the gap opening conditions were based on the comparison of viscous and tidal torques in a weakly perturbed disc (Crida, Morbidelli & Masset 2006; Armitage 2007; Kocsis et al. 2011). The orbital decay of the binary and the evolution of the disc density profile are then coupled; this coupled evolution has not been followed on the long time-scales on which the orbit evolves. Although a cavity may indeed be opened at large radii, in accretion discs where the gas build-up outside the cavity is significant, the cavity may close after several accretion time-scales. Our solutions allow us to derive the long-term gap opening and closing criteria.
There are many possible observational implications of our findings for BH binaries, and perhaps also for planetary dynamics. Here we restrict our attention to the former context. First, gap-closing makes it more likely that GW inspiral events are accompanied by EM emission, since the binary is embedded in a gaseous disc, with no central cavity, even at the last stages of the merger. Previously, Liu, Wu & Cao (2003) and Milosavljević & Phinney (2005) have argued that as the GW inspiral accelerates beyond the rate at which the gas at the edge of the cavity can viscously follow the binary, the binary decouples from the disc. Consequently, they argued that luminous AGN or radio emission from jets is expected only after the gas has had time to accrete on to the remnant. The post-merger delay is between years and decades for binaries in the mass range 105–106 M⊙ expected to be detectable by eLISA/NGO2 (Amaro-Seoane et al. 2012; see also Tanaka, Haiman & Menou 2010; Tanaka & Menou 2010; Shapiro 2010). However, if the central cavity refills before the GW emission becomes significant (which we find is the case in the above mass range, in particular), then the gas can accrete on to the primary and shine much like a normal bright AGN, even during the last stages of the merger, producing coincident EM counterparts or precursors to LISA sources.
Second, gas accumulation outside of the secondary leads to a greatly enhanced surface brightness (Lodato et al. 2009). This may help in searches for EM counterparts to more massive (108–109 M⊙) SMBH binaries at larger separations, still in the gas-driven stage, emitting GWs in the pulsar timing array (PTA) frequency bands (Sesana et al. 2012; Tanaka, Menou & Haiman 2012). The EM spectrum of the disc missing the emission at high frequencies if the disc has a gap (Syer & Clarke 1995), and the bright gap edge has a characteristic ultraviolet–optical–infrared profile (Lodato et al. 2009). We investigate the brightening as a function of component masses and separations. If these sources produce correspondingly bright periodic EM variability on the orbital time-scale, they can be identified in future time-domain optical/IR surveys. The statistics of many such sources can observationally test the migration and GW inspiral rates (Haiman, Kocsis & Menou 2009b). Combining the predictions for the variability time-scale, disc brightness and spectrum offers new independent tests of the physical models of the accretion physics, disc–satellite interactions and GW emission.
Goodman & Tan (2004) and McKernan et al. (2012) pointed out that supermassive stars or intermediate mass black holes (IMBHs) in the range 102–105 M⊙ may form in AGN discs. These objects would perturb the accretion disc, causing a pile up and gap overflow as described here. Our studies imply a slow-down of migration for these objects, making these systems longer-lived, and thus increasing the likelihood of their detection.
1.2 Relation to previous works
Without the aim of completeness, we highlight here the similarities and main differences between our study and some related papers in the recent literature.
Based on the solutions of Zel'dovich & Raizer (1967) and Pringle (1991), Ivanov, Papaloizou & Polnarev (1999) showed that the circumbinary disc with a binary evolves in a self-similar way on scales much larger than the binary, assuming that the initial and outer boundary conditions represent an unperturbed stationary α-disc with a fixed  , and assuming that a gap is always present which truncates the disc within the secondary and causes the radial gas velocity to be effectively zero near the secondary (see also Rafikov 2012). Here, we examine the opposite limiting case in which the radial gas velocity is non-negligible near the secondary due to gap overflow and the disc is approximately in a steady state.
, and assuming that a gap is always present which truncates the disc within the secondary and causes the radial gas velocity to be effectively zero near the secondary (see also Rafikov 2012). Here, we examine the opposite limiting case in which the radial gas velocity is non-negligible near the secondary due to gap overflow and the disc is approximately in a steady state.
Chang et al. (2010) examined the coevolution of the disc and the secondary, and found that the former may exhibit a rapid brightening in the GW-driven regime as the binary shepherds gas inward before merger (however, see Baruteau, Ramirez-Ruiz & Masset 2012). They included almost the same physics as this study and solved the time-dependent equations in one dimension numerically for a binary with 107 and 106 M⊙ mass components. Their initial conditions were that of an unperturbed disc and focused on the final GW-driven regime. In this case, they found no gas overflow across the gap.
Liu & Shapiro (2010) constructed an analytic steady-state model, and showed that the disc may brighten significantly when an object is placed in the disc (locally by a factor of 104 for a mass ratio q = 0.1). However, they have considered a constant H/r (here H is the disc scaleheight and r is the radius) and a viscosity profile corresponding to an unperturbed disc, and neglected the changes in these quantities due to the secondary.
Lodato et al. (2009) considered a disc model whose local physics is very similar to ours, but solved the time evolution numerically in one dimension for a very different choice of initial and boundary conditions. In particular, they focused on the specific case where the SMBH binary is very massive, and has a ‘one-time’ disc that is much less massive, compact (spreading over at most a factor of 10 in radii) and not replenished by accreting new material from large radii. They found gas pileup outside the secondary, leading to a brightening of the outer disc, and a modified spectrum. Their numerical results provide a useful independent reference to qualitatively verify our steady-state radial disc surface density and scaleheight profiles. For the particular binaries they have considered, the migration rate was greatly reduced, such that the binary is not transported to the GW-driven regime within a Hubble time, and they showed that this poses an obstacle against solving the final parsec problem (Begelman et al. 1980). In our paper, we examine the steady-state configuration, under the assumption of a constant accretion rate in the disc (set by the Eddington limit near the primary). This assumes a constant mass supply from larger radii, and is therefore very different from the ‘one-time’ disc in Lodato et al. (2009). As a result, we reach essentially the opposite conclusions: we find a stronger pileup, which increases radiation pressure in the disc and stabilizes it against gravitational fragmentation, and yields a much faster migration (well within the Hubble time). Another practical difference in our study is that we consider a broad range of binary masses, mass ratios and semimajor axes, including the radiation pressure-dominated regime, and we map out the distinct phases for disc structure and migration.
Most studies on planetary migration neglect the tidal heating effect and radiation pressure, and are therefore inapplicable for our purposes. We investigate AGN accretion discs where radiation effects are more significant. Interestingly, we find that the disc becomes strongly radiation pressure-dominated outside the secondary, even in regions far from the primary, which, in the absence of the secondary, would be gas pressure dominated. Therefore, this requires treating the fluid as comprising both gas and radiation. The use of a single of state parameter, as in most papers in planetary dynamics, becomes invalid in this regime. We note that D'Angelo, Henning & Kley (2003) did account for tidal heating and temperature variations in a two-dimensional simulation, but neglected the effects of radiation pressure. Paardekooper & Mellema (2006, 2008) and Kley & Crida (2008) presented results from numerical simulations with radiation, showing that tidal heating and radiation pressure have a significant effect on the migration of planets.
Criteria for gap opening and closing have been investigated extensively for protoplanetary discs (Lin & Papaloizou 1986; Artymowicz & Lubow 1994; Ward 1997; Crida et al. 2006). Previous numerical studies typically neglected the effects of gas build-up outside the gap, and did not consider self-consistently the effects of the excess viscous and tidal heating of the gas, and neglected both radiation pressure and the migration of the secondary. However, two- and three-dimensional simulations have shown that even if the gap opening conditions are satisfied, gas can periodically flow in along non-axisymmetric steams into the gap and accrete on to the primary and the planet, particularly if the ratio of the distance to the gap edge to the Hill radius is of the order of unity (Artymowicz & Lubow 1996; Lubow, Seibert & Artymowicz 1999; Lubow & D'Angelo 2006; Hayasaki, Mineshige & Sudou 2007; MacFadyen & Milosavljević 2008; Cuadra et al. 2009). In this paper, we revisit the standard gap opening/closing conditions in circumbinary accretion discs, including the effects of radiation pressure (Kocsis et al. 2011), as well as gas build-up, tidal heating and migration. For simplicity, we neglect a possible non-axisymmetric inflow if the gap is larger than the Roche lobe and also neglect accretion on to the secondary. We also do not model the magneto-rotational instability (MRI), which may influence the conditions for gap opening (Winters, Balbus & Hawley 2003; Farris et al. 2012; Noble et al. 2012; Shi et al. 2012). These effects are likely to be important, and should be investigated in the future in two- or three-dimensional simulations.
1.3 Outline and conventions
This paper is organized as follows. In Section 2, we briefly lay out the physical model that we adopt. In Section 3, we present numerical and analytic solutions to the disc and identify its distinct physical phases. In Section 4, we elaborate on the gap opening and closing conditions in steady state. In Section 5, we discuss the migration of the secondary, comparing the new Type 1.5 solution in a continuously overflowing disc with the Type I and Type II cases. In Section 6, we discuss observable implications, including the lightcurve, spectrum, the abundance of AGN with periodic variability, as well as GW observations with LISA/NGO and PTAs (Hobbs et al. 2010). We summarize our main conclusions in Section 7. The interested reader can find details of analytic derivations in Paper I.
Our basic notation for the disc and secondary parameters is depicted in Fig. 1. We denote the primary and secondary mass with M• and ms, and the mass ratio with q ≡ ms/M•. We use geometrical units G = c = 1 and suppress factors of G/c2 and G/c3 in conversions between mass, length and time units. We use  to label the radius in gravitational radii. A subscript ‘
to label the radius in gravitational radii. A subscript ‘ ’ refers to quantities describing the secondary, while the subscript ‘0’ refers to quantities in the unperturbed disc around a single compact object.
’ refers to quantities describing the secondary, while the subscript ‘0’ refers to quantities in the unperturbed disc around a single compact object.
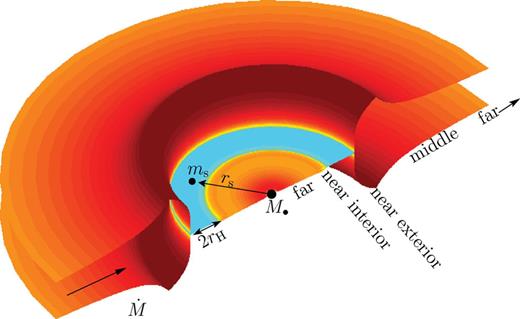
Gas pile-up and overflow in a circumbinary accretion disc with component masses M• and ms, binary separation rs, and accretion rate  . We distinguish five distinct radial zones in the disc: an inner and an outer far zone where the effects of the secondary are negligible, an interior and an exterior near zone, where the tidal effects are significant, and an extended middle zone, where the disc is still significantly perturbed. Our model breaks down inside the secondary's Hill radius, denoted by rH.
. We distinguish five distinct radial zones in the disc: an inner and an outer far zone where the effects of the secondary are negligible, an interior and an exterior near zone, where the tidal effects are significant, and an extended middle zone, where the disc is still significantly perturbed. Our model breaks down inside the secondary's Hill radius, denoted by rH.
2 Thermo-Hydrodynamical Interaction Between A Disc and A Secondary
We examine the evolution of the secondary and an azimuthally and vertically averaged Shakura–Sunyaev disc (i.e. axisymmetric one-zone disc) in local thermal equilibrium. The equations are laid out in detail, and solved both numerically and under various approximations, analytically in Paper I. Here we only briefly summarize the basic conceptual framework and the features of the solutions; we refer the reader to Paper I for the complete set of equations and a detailed description.
2.1 Equations governing the evolution of the disc structure and the binary's orbit
We denote the azimuthally averaged surface density profile of the disc by Σ(r), and the radial (bulk) velocity of the gas in the disc by  , which is negative as gas accretes towards the primary at r = 0 with an accretion rate
, which is negative as gas accretes towards the primary at r = 0 with an accretion rate  . We assume a nearly Keplerian disc and denote the angular velocity with Ω.
. We assume a nearly Keplerian disc and denote the angular velocity with Ω.
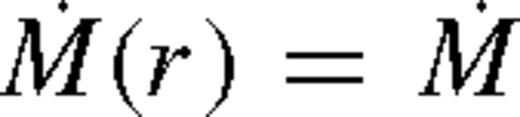 is a constant. The angular momentum flow in the disc is driven by the viscous torques (Tν) and the tidal torque exerted by the secondary (Td), while the angular momentum loss of the secondary is due to the backreaction of the tidal torque and GW losses
is a constant. The angular momentum flow in the disc is driven by the viscous torques (Tν) and the tidal torque exerted by the secondary (Td), while the angular momentum loss of the secondary is due to the backreaction of the tidal torque and GW losses 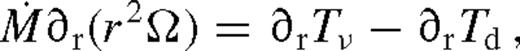
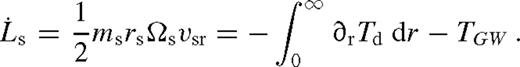
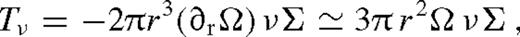
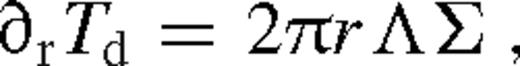
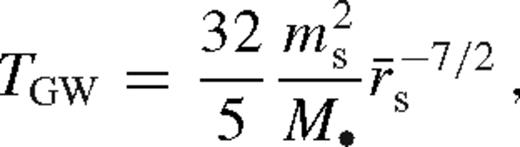

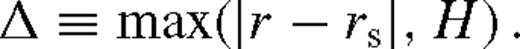
Given the viscosity ν(r) and the scaleheight H(r), equation (1) can be integrated to find the surface density of the disc, Σ(r), for any location of the secondary, and equation (2) gives the inward migration velocity of the secondary (Liu & Shapiro 2010). However ν(r) and H(r) are not known a priori, since they depend on Σ(r) and the mid-plane temperature Tc(r). With the standard Shakura–Sunyaev ansatz ν(r) = αcs(r)H(r) for viscosity or its variant where the viscosity is assumed to scale with the gas (rather than the total) pressure, ν(r) = αcs(r)H(r)β(r), where β(r) ≡ pgas(r)/p(r) (also known as a ‘β-disc’). Since α-discs are thought to suffer from a thermal instability (but see Hirose, Krolik & Blaes 2009), in the solutions discussed in this paper, we follow earlier work and focus on the latter case (also known as a ‘β-disc’). We derive the temperature profile assuming thermal equilibrium between gas and radiation, radiative cooling which balances the heating associated with viscous dissipation tidal heating. These provide a non-linear closed set of equations for the steady-state disc profile. In practice, we note that all of the equations are non-linear local algebraic equations at each radius with the exception of the angular momentum flux equation (1) which is a first-order ordinary differential equation for Tν(r). We solve these equations for specific boundary conditions given below, for a fixed value of the secondary orbital radius. Once the disc profile has been obtained, equation (2) gives the migration velocity of the secondary.
2.2 Boundary conditions
We look for steady-state disc solutions with a constant  , assuming that the radial profile of the disc relaxes on a time-scale shorter than the migration time-scale of the secondary. We find the corresponding equilibrium steady-state configuration of the disc for each orbital radius of the secondary, and then assume that the disc proceeds through a sequence of such steady-state configurations as the secondary migrates inwards.
, assuming that the radial profile of the disc relaxes on a time-scale shorter than the migration time-scale of the secondary. We find the corresponding equilibrium steady-state configuration of the disc for each orbital radius of the secondary, and then assume that the disc proceeds through a sequence of such steady-state configurations as the secondary migrates inwards.
We distinguish two types of inner boundary conditions, corresponding to whether or not a gap is assumed to be present in the steady-state configuration.
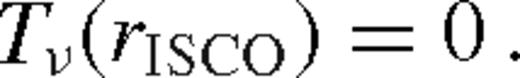
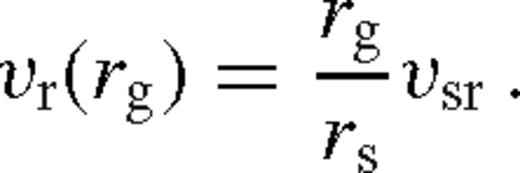
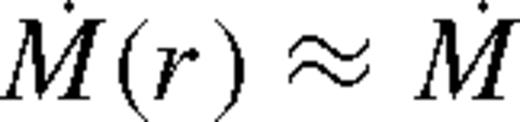 at r > rg (see discussion below).
at r > rg (see discussion below).By construction, only one of the above two boundary conditions will lead to a self-consistent solution. We speculate that a real time-dependent binary would evolve through the sequence of steady-steady solutions we obtain below – switching between the case with and without a gap around the transition radii that follows from the above.
We emphasize that the solutions with a gap are somewhat similar to those obtained in previous works (Syer & Clarke 1995), and also that our solutions in this regime still suffer from a few possible inconsistencies, as will be discussed below. However, the main new result in this paper is the independent overflowing solution, corresponding to the first of the two boundary conditions. As we will argue below, the assumptions leading to this regime are relatively more robust. The uncertainties about the behaviour of the disc with a gap could affect only our results for when the gap closes (as argued below, we took a conservative approach, in the sense that the ‘overflow’ regime may be present for a wider range of radii than in our fiducial models).
3 Disc Structure
3.1 Numerical solutions
In Fig. 2, we present the most relevant physical parameters in our steady-state disc as a function of radius (we neglected TGW for clarity in this figure) for several choices of parameters. For details on how these solutions were obtained in practice, the reader is again referred to Paper I. As the figure shows, the secondary acts as a hydro dam and causes gas to pile-up (second row) and heat up (third row) relative to the unperturbed solution. Interestingly, the disc brightens not only in the near zone of the secondary, where the tidal effects dominate, but even much farther away (see the panels in the fourth row showing the disc brightness relative to the tidal heating rate). This is not surprising, since viscosity needs to balance the tidal torque at the boundary in equilibrium, and pushing the gas past this obstacle requires a greatly accumulated local gas mass, even far from this region. Our results are in qualitative agreement with the radial profiles presented in Lodato et al. (2009).
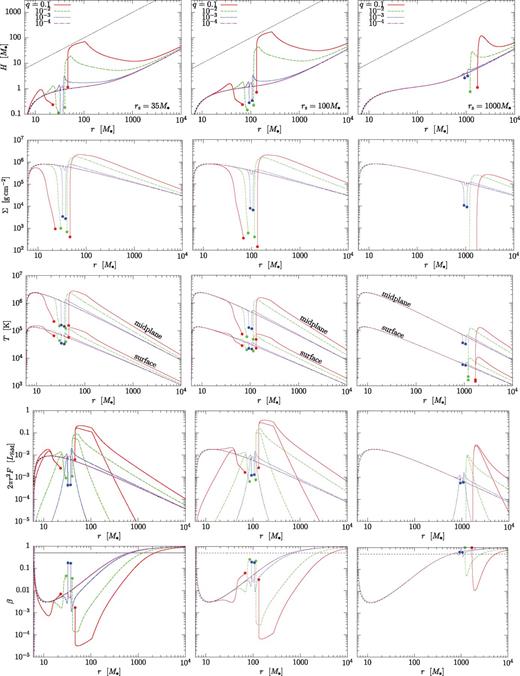
Steady-state tidally heated discs with the secondary located at rs = {35, 100, 1000}M• (left-, centre, right-hand panels) for various mass ratios q = ms/M• = 10−n with n ∈ {1, 2, 3, 4} (red, green, blue, magenta curves) for M• = 107 M⊙. The five different rows from top to bottom show the local scaleheight, surface density, surface and midplane temperature, surface brightness and tidal heating, and the gas to total pressure ratio. The magenta curve with q = 10−4 is similar to a solitary disc without a secondary. An inner cavity forms in the disc for q = 0.1 and 0.01 for r = 1000 M• on the right-hand panels. The gas continuously overflows for the other cases shown in the figure, but the surface density can still drop significantly near the secondary's Hill sphere (marked by filled circles). (For clarity, the curves are not connected within the Hill sphere, where our model becomes invalid.)
Of the 12 cases shown in Fig. 2 with rs = (35, 100, 1000)M• and q = (10−1, 10−2, 10−3, 10−4), a gap forms only in the two cases with the largest binary separations and mass ratios: rs = 1000M• with q = 0.1 and 0.01 (red and green curves on the right-hand panels). In these cases, there is no inner disc within the secondary's orbit in the steady-state configuration (if there was it would accrete on to the SMBH without being replenished from the outside). All other cases do not have a gap.5 To avoid confusion, we note that the profiles are not shown within the Hill sphere of the secondary in Fig. 2. Although our working assumptions break down, the parameters are expected to transition continuously across this region.
One may identify visually distinct zones in the radial profiles of the physical parameters in Fig. 2. At very large radii, which we call the far zone, the disc asymptotes to the unperturbed state. Interior to a certain radius, in the exterior middle zone, the scaleheight starts to deviate initially gradually then quite rapidly as the radiation pressure becomes significant relative to the gas pressure. Note that the transition to a radiation pressure-dominated disc (i.e. β < 0.5) is around 600M• without a secondary. However, the disc can become radiation pressure dominated outside a secondary much farther out as shown by the fifth row (cf. dotted black line showing β = 0.5). In the near zone of the satellite, the tidal effects become significant. For relatively massive binaries, the sharp knee in the tidal heating rate, as seen in the fourth row, corresponds to the torque cutoff where the midplane pressure gradient shifts the tidal effects out of resonance (H ∼ |r − rs|).6 After crossing the radius of the secondary's orbit, the accretion velocity is more rapid than for an unperturbed disc by many orders of magnitude (see Fig. 5). The disc profile asymptotes to the unperturbed disc profile near the inner boundary close to the SMBH. Note, however, that the tangential velocity [vt ∼ (r/M•)−1/2c] and sound speed [cs ∼ (H/r)vt] are much larger than the radial velocity even in this region.
We will discuss migration rates in detail in Section 5, but let us mention already which of the 12 cases shown in Fig. 2 correspond to the well-known Type I and II cases. The two cases rs = 1000 M• with q = 0.1 or 0.01 have a gap, and thus imply Type II migration. The case with q = 10−4 and rs = 35M• corresponds to Type I migration, where the disc structure lies close to the unperturbed case. The seven cases with q ≥ 10−3 without a gap have a significantly perturbed overflowing disc, which corresponds to the distinct new class of Type 1.5 migration. The remaining two cases with q = 10−4 and with rs = (100, 1000)M• are between Type I and 1.5. However, comparing the disc-driven migration speed with the GW inspiral rate, we find that GW emission is significant for many of these binaries, so that the steady-state assumption is violated (see Fig. 4 for the conditions under which this occurs).
3.2 Analytic solutions
To generalize the numerical solutions given above for arbitrary parameters, we derived in Paper I approximate analytic formulae. These solutions exist in different regions where either the tidal, the viscous torques, or the angular momentum flux is negligible relative to the other two terms in equation (1). In particular, we identify the two far zones, well outside and far inside the secondary's orbit, where the effects of the secondary are negligible, a single middle zone outside the secondary's orbit, where the disc structure is greatly modified but where the tidal torque and heating are negligible, and two near zones just inside and outside rs, where the tidal effects dominate. We distinguish two possible cases for the middle zone, depending on whether the disc has a gap or if the disc is overflowing. In the external near zone, we likewise have two possible behaviours, depending on whether the tidal torque is unsaturated or saturated [i.e. whether the torque cutoff is in play: Δ = |r − rs| or H in equation (6), respectively]. We refer the reader to Paper I for detailed derivations of the analytic solution for the disc structure in each zone; here we provide only the most important results, and discuss their implications for SMBH binaries.
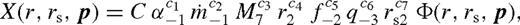
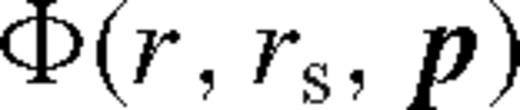 denotes an extra function of the parameters which is different in different zones. The constant parameters C and ci and Φ are given explicitly in Paper I (see table 1 therein). Here we only discuss the structure of the solution.
denotes an extra function of the parameters which is different in different zones. The constant parameters C and ci and Φ are given explicitly in Paper I (see table 1 therein). Here we only discuss the structure of the solution.The steady-state viscous torque density Tν in different regions constitutes the backbone of the analytic solution. Every physical quantity in the disc follows directly from Tν by simple arithmetic relations. To verify the analytic model with the numerical solutions of Section 3.1, it is sufficient to examine Tν in the various regions. We do this by generating the numerical solution for randomly chosen constant model parameters  , and compare these to the analytic solution. We find a good agreement between the two solutions to within 20 per cent for a wide range of parameters for which Tν is substantially modified exterior to the rs. We do not develop analytic approximations in the opposite, weakly perturbed case, because in that regime other physical processes which have been neglected may be more significant (see Type I migration in Section 5.1).
, and compare these to the analytic solution. We find a good agreement between the two solutions to within 20 per cent for a wide range of parameters for which Tν is substantially modified exterior to the rs. We do not develop analytic approximations in the opposite, weakly perturbed case, because in that regime other physical processes which have been neglected may be more significant (see Type I migration in Section 5.1).
The analytic solution is self-consistent in the strongly perturbed case if Tν matches continuously in the different zones outside the Hill sphere. In practice, note that Tν increases in the external near zone quite rapidly with radius, both in the tidal torque-saturated and in unsaturated regimes. At larger radii, the tidal effects vanish (middle zone) and Tν is approximately constant. If Tν in the middle zone without a gap is lower than with a gap, then this represents the correct overflowing solution; otherwise a gap forms. Since for a steady-state disc, the migration rate is simply proportional to Tν in the middle zone (see equation 30 in Paper I), this definition is equivalent to that based on the velocities (equation (9)). If so, the secondary and the gas propagate inwards with similar velocities to maintain this configuration, while in the former case, the secondary moves slower than the inflow speed of the gas. We elaborate on these issues related to gap opening and migration in Sections 4 and 5.
We emphasize that the disc parameters can differ dramatically from the unperturbed (or far zone) values not only in the near zone, where the tidal effects dominate, but also in the middle zone, where tidal effects are already negligible. This is analogous to how the water level is raised in a dam not just in the immediate vicinity of the dam wall but also far away from the boundary, regions in which the local hydrodynamics is explicitly independent of the wall. The tidal effects of the secondary are also short range, but the corresponding effect is communicated to distant regions by setting an effective boundary condition. The middle region subtends a large radial range, and is representative of the strongly perturbed disc. Here, the viscous torque  (in all three cases: with a gap, or overflowing with saturated or unsaturated torques; see the corresponding solutions
(in all three cases: with a gap, or overflowing with saturated or unsaturated torques; see the corresponding solutions  ,
,  and
and  in table 1 of Paper I) is approximately constant with radius as in a decretion disc (Pringle 1991). It is remarkable that the perturbation to the disc can be represented by a single number in the middle zone. Here, the radial profile of the disc is independent of the details of the tidal torque up to this constant factor.
in table 1 of Paper I) is approximately constant with radius as in a decretion disc (Pringle 1991). It is remarkable that the perturbation to the disc can be represented by a single number in the middle zone. Here, the radial profile of the disc is independent of the details of the tidal torque up to this constant factor.
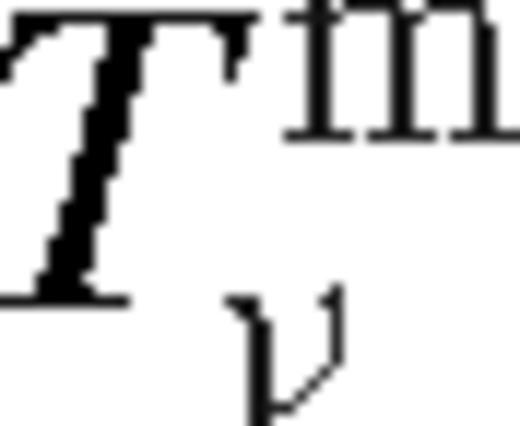 , we introduce a more physically revealing quantity,
, we introduce a more physically revealing quantity, 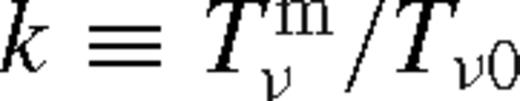 , representing the fractional change of the viscous torque relative to its unperturbed value (
, representing the fractional change of the viscous torque relative to its unperturbed value (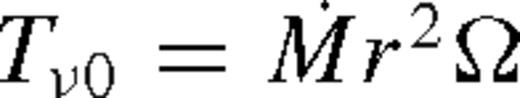 ) in the middle zone. This parameter, which we refer to as the dimensionless angular momentum flux or brightening factor, sets the relative brightening of the disc and the increase in the scaleheight in the middle zone, as well as the migration rate. It can take one of three values, depending on whether a gap is open, or whether the gas overflows in the saturated torque cutoff regime or in the unsaturated regime:7
) in the middle zone. This parameter, which we refer to as the dimensionless angular momentum flux or brightening factor, sets the relative brightening of the disc and the increase in the scaleheight in the middle zone, as well as the migration rate. It can take one of three values, depending on whether a gap is open, or whether the gas overflows in the saturated torque cutoff regime or in the unsaturated regime:7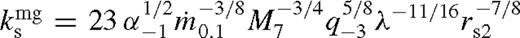
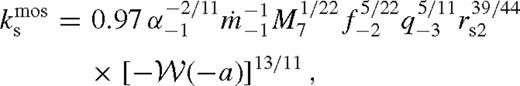
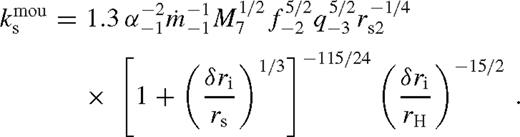
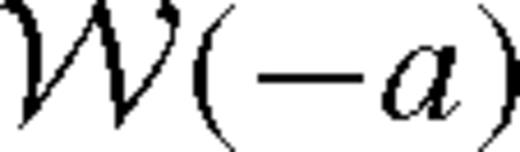 is the Lambert W-function defined for a > 1/e = 0.368 approximately as
is the Lambert W-function defined for a > 1/e = 0.368 approximately as 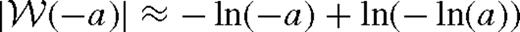
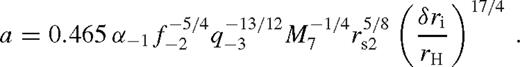
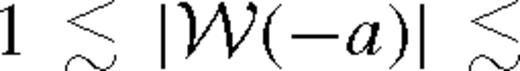 for a wide range of parameters. In the above equations, δri is the radial distance from rs at which the torque model breaks down near the secondary, for which we assume δri ∼ rH. Further, λrs is the characteristic radius in the near zone outside the gap where most of the tidal torque is exerted. In practice, λ is of the order of unity given by equation (41).
for a wide range of parameters. In the above equations, δri is the radial distance from rs at which the torque model breaks down near the secondary, for which we assume δri ∼ rH. Further, λrs is the characteristic radius in the near zone outside the gap where most of the tidal torque is exerted. In practice, λ is of the order of unity given by equation (41).The smallest of the three,  , sets the state of the disc in the middle zone if greater than one.8 Note that
, sets the state of the disc in the middle zone if greater than one.8 Note that  increases quickly with decreasing binary separation, rs, but interior to some radius the gap closes and the dimensionless angular momentum flux or brightening factor is limited by the near-zone torque cutoff,
increases quickly with decreasing binary separation, rs, but interior to some radius the gap closes and the dimensionless angular momentum flux or brightening factor is limited by the near-zone torque cutoff,  . The brightening factor is largest at the gap-closing boundary for comparable mass ratios. The torque cutoff does not impose a limitation if q is sufficiently small, but the gap can still close by shrinking to within the Hill radius (in this case
. The brightening factor is largest at the gap-closing boundary for comparable mass ratios. The torque cutoff does not impose a limitation if q is sufficiently small, but the gap can still close by shrinking to within the Hill radius (in this case  sets the brightening factor).
sets the brightening factor).
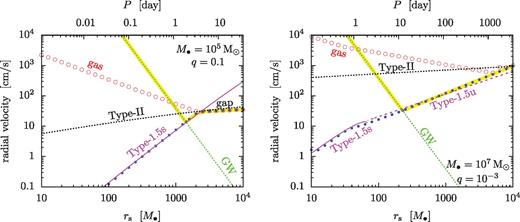
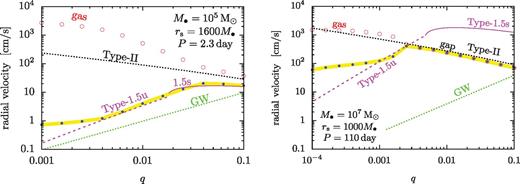
Fig. 3 shows the phase diagram of the disc for different rs and q, set by equations (11)–(13) for M• = 105, 107 and 109 M⊙. Colours indicate the brightening factor, ks. The figure shows large deviations from a solitary disc in many cases. The disc brightens in the middle zone by a factor of up to 500 or 100 for a binary with M• = 105 or 107 M⊙, respectively, which we discuss in Section 6. The brightening is less significant for binaries with 109 M⊙. Note that GW emission is neglected here; this modifies the picture at small radii significantly, especially for M• = 109 M⊙ (see Fig. 4).
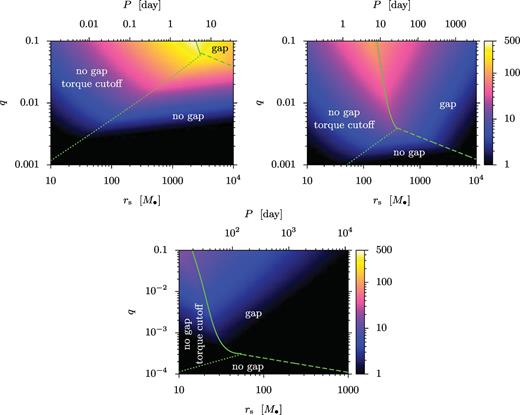
The phase diagram of the disc for M• = 105 M⊙ (top left), 107 M⊙ (top right) and 109 M⊙ (bottom) and for different binary semimajor axes, orbital periods and mass ratios. Colours show the relative brightening of the disc outside the secondary relative to the same region of a solitary disc. Three zones can be distinguished as marked: ‘gap’ in which the tidal torque can support a gap against viscosity even in steady state, ‘no gap’ in which the gap overflows in steady state with the tidal torque in the linear regime all the way to the Hill sphere or ‘no gap with torque cutoff’ in which the torques are saturated outside the Hill sphere. We do not show comparable mass ratios (q > 0.1) where the adopted perturbative tidal torque formula and the axisymmetric steady-state approximations are strongly violated.
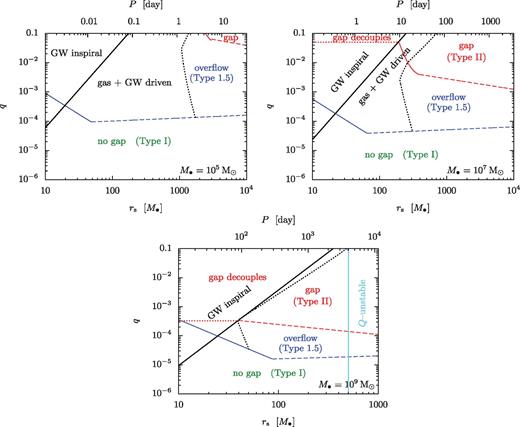
Ranges of binary separation rs and mass ratio q for which: (i) a gap can remain open in the disc; (ii) the gap refills after gas pileup (labelled as ‘overflow’) and (iii) a gap cannot open. Different panels show different primary masses (105, 107 and 109 M⊙) as labelled. The type of migration is shown in each region, including the region where GW losses start to become relevant (dotted line) and where they dominate (solid black line). Solid and dashed coloured lines show the boundary where the tidal torque becomes saturated outside the Hill sphere (viscous filling, Δ = H) and where the gas enters the Hill sphere without becoming saturated (gravitational filling, Δ = rH), respectively, based on standard criteria using unperturbed discs. The gap (if present) decouples in the GW inspiral regime as shown. The disc is gravitationally unstable at large radii as marked.

The accretion speed for the discs shown in Fig. 2 and the migration speed of the secondary neglecting GW emission.
 is fixed at the outer boundary (Syer & Clarke 1995, see however discussion in Section 5.2). In contrast, steady state is possible in the overflowing case because there ks decreases as the secondary moves inwards. A global steady state is possible if ks ≲ kmax where
is fixed at the outer boundary (Syer & Clarke 1995, see however discussion in Section 5.2). In contrast, steady state is possible in the overflowing case because there ks decreases as the secondary moves inwards. A global steady state is possible if ks ≲ kmax where 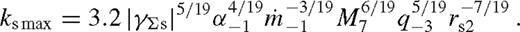
 may still hold locally in the inner regions of the middle zone, but in this case, the outer parts of the middle zone within
may still hold locally in the inner regions of the middle zone, but in this case, the outer parts of the middle zone within 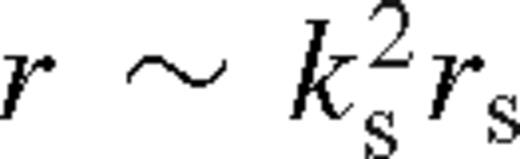 cannot respond to the inward migration of the secondary and the steady-state disc model becomes inaccurate there (see further discussion in Section 5.2).
cannot respond to the inward migration of the secondary and the steady-state disc model becomes inaccurate there (see further discussion in Section 5.2).We finally comment on the stability of the accretion disc in the middle zone. Although the surface density increases as gas accumulates outside the secondary as k3/5, the radiation pressure grows even more rapidly as prad ∝ k in that region (see equations 40– (41) in Paper I). The net effect is to increase the Toomre-Q parameter as Q ∝ cs/Σ ∝ prad/Σ ∝ k2/5. Therefore, the enhanced radiation pressure dominates over the increase in surface density, and makes the disc more stable against axisymmetric fragmentation relative to an unperturbed disc without a secondary (Tanaka et al. 2012). Although gravitationally stable, the disc may become dynamically unstable against global non-axisymmetric perturbations if the disc develops a steep pressure gradient in the near zone around a high-mass secondary (Papaloizou & Pringle 1985; Goldreich, Goodman & Narayan 1986). A proper stability analysis, and exploring its implications, is left to future work.
4 Gap Opening
Next we elaborate on the gap opening and closing conditions in more detail. Gap opening is traditionally examined by comparing the tidal and viscous torques in an initially unperturbed steady-state thin disc. However, after a sufficient amount of gas has built up outside the gap, the enhanced viscous torque may close the gap. We discuss these points in turn.
Gap opening also affects the migration rate of the secondary and has several potentially observable signatures which we discuss in Sections 5 and 6.
4.1 Initial gap-opening
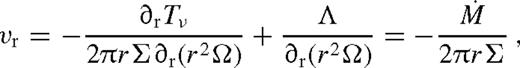
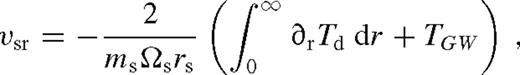
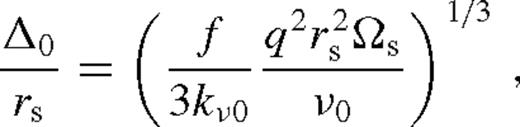
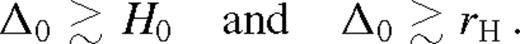
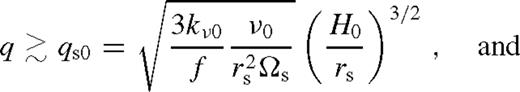
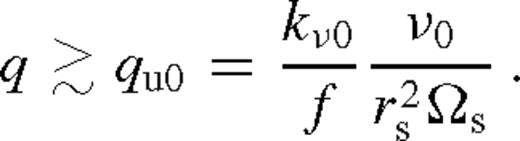
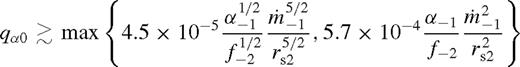
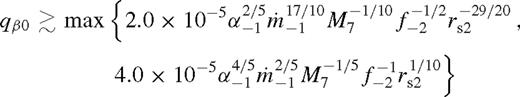
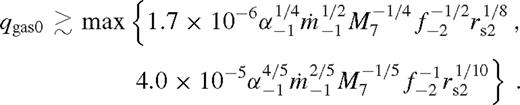
Fig. 4 shows the gap opening criteria for β-discs with our standard parameters as a function of mass ratio and binary separation for M• = 105, 7, 9 M⊙. The blue solid and the dashed curves represent qs0 and qu0, respectively. For smaller mass ratios, the disc is practically unperturbed.
4.2 Steady-state gap-closing
In the regime where a gap never opens (i.e. weakly perturbed discs, q < qcrit0), our solutions do not change the picture. However, in the regime when a gap initially opens, the accumulation of gas outside the binary changes Σ, H, ν and kν in the gap-opening conditions (equations (19)–(20)). Let us now examine whether the gap can stay open on longer time-scales once the disc and binary have reached steady state.
As the binary migrates inwards the local pressure and viscosity change even in an unperturbed disc, which may lead to gap opening for mass ratios of order q ∼ 10−4 within separations rs ∼ 103M• (see blue lines in Fig. 4). However, the usual gap opening conditions (equations (21)–(22)) (Lin & Papaloizou 1986; Syer & Clarke 1995) may fail in the long run and lead to gap-closing for a much wider range of masses and radii, if either the scaleheight, the viscosity, or the steepness of the radial profile increases during the pile-up. Note that if only H increased by a factor x while ν and kν were kept constant, then the mass ratio for gap opening would increase by x3/2 relative to the first terms in equations (23)–(25). Furthermore, if ν or kν changed by a factor y, then the critical mass ratio for gap opening would further increase by an extra factor of  and y in the first and second terms in equations (23)–(25), respectively. Thus, the combination of these effects shifts the solid and dashed blue lines in Fig. 4 upwards by a factor x3/2y1/2 and y, respectively. We determine the actual value of x and y in the self-consistent steady-state model to derive the necessary conditions for gap opening next.
and y in the first and second terms in equations (23)–(25), respectively. Thus, the combination of these effects shifts the solid and dashed blue lines in Fig. 4 upwards by a factor x3/2y1/2 and y, respectively. We determine the actual value of x and y in the self-consistent steady-state model to derive the necessary conditions for gap opening next.
In a self-consistent description, gas accumulation outside the gap leads to the following effects. First, the gravitational torque of a denser disc drives the migration of the secondary faster, increasing |vsr| (see equations (4) and (18)). For a fixed accretion rate,  , the increase of Σ leads to the decrease of |vr|, analogous to the slowdown of the flow velocity in a river upstream a dam. The pressure and kinematic viscosity increase due to the pile-up, and lead to a smaller gap. The tidal heating in the gas outside the disc increases the pressure and scaleheight further which can quench the tidal torque (see torque cutoff in equation (6)). Ultimately, the combination of these effects can have several outcomes.
, the increase of Σ leads to the decrease of |vr|, analogous to the slowdown of the flow velocity in a river upstream a dam. The pressure and kinematic viscosity increase due to the pile-up, and lead to a smaller gap. The tidal heating in the gas outside the disc increases the pressure and scaleheight further which can quench the tidal torque (see torque cutoff in equation (6)). Ultimately, the combination of these effects can have several outcomes.
- (i)
If the mass of the secondary is very small, the disc is weakly perturbed (no gap is present in particular) and the object exhibits Type I migration as usual (see Section 5).
- (ii)
The other extreme limit is Type II migration, where |vsr| = |vr(λrs)|/λ is reached so that the disc and the secondary spiral inward in a self-similar way (see equation (9)). Here the relative gap size, λ = rg/rs, is somewhat decreased after the gas has accumulated outside the gap, but it is still much larger than the Hill radius.
- (iii)
An intermediate possibility is that the gap size shrinks over time to within the secondary's Hill sphere as gas accumulates outside the gap, and eventually closes. The equilibrium steady-state configuration in this continuously overflowing case has an increased density and pressure exterior to the secondary's orbit (see disc profiles in Fig. 2 for q ≳ 10−3).
- (iv)
Finally, it is also possible that the disc becomes geometrically so thick (H > r) and/or luminous (L > LEdd) to drive a wind or a three dimensional inflow across the orbit of the secondary.
 and calculate whether these conditions are satisfied. In practice, we calculate the corresponding range of q and rs by requiring that the viscous torque at the outer boundary of the near zone be equal to that at the inner edge of the middle zone with a gap assuming unsaturated and saturated tidal torques, respectively (see Paper I for details). This is equivalent to finding q or rs for gap opening at which the dimensionless angular momentum flux of an overflowing solution becomes first equal to that of the model with a gap. At the gap opening/closing transition kmg = min {kmos, kmos} in equations (11)–(13). Assuming radiation pressure-dominated β-discs and negligible GW losses, we find that a truncated disc with an inner cavity forms if
and calculate whether these conditions are satisfied. In practice, we calculate the corresponding range of q and rs by requiring that the viscous torque at the outer boundary of the near zone be equal to that at the inner edge of the middle zone with a gap assuming unsaturated and saturated tidal torques, respectively (see Paper I for details). This is equivalent to finding q or rs for gap opening at which the dimensionless angular momentum flux of an overflowing solution becomes first equal to that of the model with a gap. At the gap opening/closing transition kmg = min {kmos, kmos} in equations (11)–(13). Assuming radiation pressure-dominated β-discs and negligible GW losses, we find that a truncated disc with an inner cavity forms if 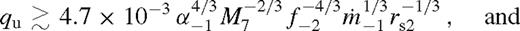
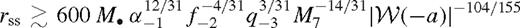
 and a). Here, the first and second conditions are analogous to Δ ≳ rH (or equation (22)) and Δ ≳ H (or equation (21)), respectively, but account for the self-consistent steady-state radial variations in H, Σ and ν when calculating the viscous and integrated tidal torques for a β-disc. Note that equation (27) is defined only for a > 1/e = 0.368, otherwise the tidal torque is in the unsaturated state. Since a depends on qs and rs, equation (27) is a non-linear equation for rs for a fixed qs. However, the dependence is logarithmically weak, typically the last factor in equation (27) is between 0.3 and 0.8, making the saturated gap-closing radius vary between (200 and 400)M7M• for all q for the fiducial disc parameters.
and a). Here, the first and second conditions are analogous to Δ ≳ rH (or equation (22)) and Δ ≳ H (or equation (21)), respectively, but account for the self-consistent steady-state radial variations in H, Σ and ν when calculating the viscous and integrated tidal torques for a β-disc. Note that equation (27) is defined only for a > 1/e = 0.368, otherwise the tidal torque is in the unsaturated state. Since a depends on qs and rs, equation (27) is a non-linear equation for rs for a fixed qs. However, the dependence is logarithmically weak, typically the last factor in equation (27) is between 0.3 and 0.8, making the saturated gap-closing radius vary between (200 and 400)M7M• for all q for the fiducial disc parameters.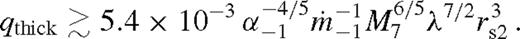
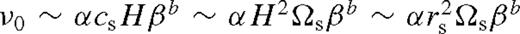 in the simple gap opening conditions, equations (21)–(22), which implies qthick ≳ (3kν0/f)1/2α1/2βb/2. Since the constant of proportionality 3kν0/f is of the order of 40–50 in the non-linear regime (Lin & Papaloizou 1986; Crida et al. 2006), there is no secondary mass that satisfies this condition for α > 0.025 for an α-disc with b = 0. We note that Rafikov (2012) arrived at the opposite conclusion using the same argument but setting 3kν0/f ∼ 1, claiming that the disc typically becomes thick and would drive an outflow before the gap may close due to overflow. Furthermore, note that the tidal dissipation effects and the steepening of the angular momentum flux profile kν > kν0 help further to make the disc prone to overflow before the disc becomes very thick.
in the simple gap opening conditions, equations (21)–(22), which implies qthick ≳ (3kν0/f)1/2α1/2βb/2. Since the constant of proportionality 3kν0/f is of the order of 40–50 in the non-linear regime (Lin & Papaloizou 1986; Crida et al. 2006), there is no secondary mass that satisfies this condition for α > 0.025 for an α-disc with b = 0. We note that Rafikov (2012) arrived at the opposite conclusion using the same argument but setting 3kν0/f ∼ 1, claiming that the disc typically becomes thick and would drive an outflow before the gap may close due to overflow. Furthermore, note that the tidal dissipation effects and the steepening of the angular momentum flux profile kν > kν0 help further to make the disc prone to overflow before the disc becomes very thick.The red line in Fig. 4 shows the boundary where the gap remains open in steady state and where the disc overflows. Remarkably, the gas overflows in steady state and closes the gap for q ≳ 10−4 for all binary separations below 1000 M•, and gaps remain open only for much larger secondary masses.
The gap-closing criteria derived above are independent of the initial conditions of the disc assuming that the disc is strongly perturbed and relaxes to steady state. However, in equation (16) we have shown that this condition does not always hold near the gap-closing boundary and a time-dependent study is necessary for a more accurate description of gap-closing. Furthermore, GW emission becomes more and more efficient for decreasing binary separations. Fig. 4 shows regions where GW emission starts to become relevant and where it dominates. In the region marked ‘gas+GW driven’, the GW inspiral is slower than the unperturbed viscous accretion speed but faster than the steady-state gas overflow. We did not consider this regime in detail, but Paper I indicates that there may still be a build-up of gas mass, and possibly overflow here, albeit at a slower rate than if GW emission was neglected. In the region marked as ‘GW inspiral’ in Fig. 4, steady-state overflow is prevented by the faster GW inspiral. In this region, the actual state of the disc depends on the initial condition. If a gap is open when the binary crosses the critical radius where GW-emission becomes dominant, then the gap decouples from the binary and remains empty until the merger. Fig. 4 shows that this occurs if the secondary mass is larger than approximately ms ≳ 4 × 105 M⊙. For these masses, an X-ray afterglow is activated once the gas refills the gap on the viscous time-scale, typically many years after a GW event (Milosavljević & Phinney 2005; Tanaka et al. 2010; Liu & Shapiro 2010; Tanaka & Menou 2010; Shapiro 2010). However, for smaller secondary masses, Fig. 4 shows that the gap overflows and closes before entering the GW inspiral phase. We conclude that a gap may not be present, and significant X-ray emission accompanies the GW-emitting stage for these LISA/NGO sources. The EM counterpart may be modulated by the GW-driven binary (Armitage & Natarajan 2002; Chang et al. 2010; Bogdanović et al. 2011; Farris, Liu & Shapiro 2011; Bode et al. 2012; Baruteau et al. 2012; Farris et al. 2012; Giacomazzo et al. 2012; Noble et al. 2012), but future work is necessary to explore this possibility in more detail with initial conditions consistent with the overflowing solution.
5 Migration
 is given in terms of Σ and H using equations (4)–(6) for which we use the steady-state solution derived above. The result can be expressed in terms of the dimensionless angular momentum flux ks in equations (11)–(13) as
is given in terms of Σ and H using equations (4)–(6) for which we use the steady-state solution derived above. The result can be expressed in terms of the dimensionless angular momentum flux ks in equations (11)–(13) as 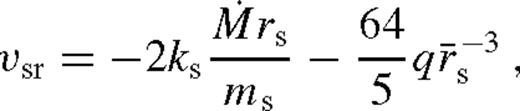
Fig. 5 shows the gas velocity as a function of radius, and the migration rate of the secondary for the numerical solutions corresponding to Fig. 2. The disc has a gap for q = 0.1 and 0.01 when rs = 103M•, where the nearby gas mass and the secondary move radially at a similar speed. In this case, the secondary and the disc move inwards to maintain a ratio vr(λrs)/vsr = λ, where λrs is the characteristic radius where the tidal torque is exerted. The increase of the gas velocity near the gap edge is due to the fact that the steady-state assumption is strongly violated there (see further discussion in Section 5.2). At smaller binary separations, the gas can flow across the barrier represented by the secondary, the disc is no longer truncated and the migration rate is much slower than the gas velocity.
The gas–secondary interaction has a different character when the mass of the secondary is so small that it does not perturb the surface density and scaleheight profile significantly (Type I), and when it is so large that a gap opens (Type II). We first discuss these two limiting cases below, and then turn to the intermediate state with a steady-state overflowing disc with a pile-up (which we label ‘Type 1.5’).
5.1 Type I migration
Let us first consider a secondary with a mass so small that it makes only a small change in the surface density and scaleheight profile Σ0 and H0 and the azimuthal density perturbations are in the linear regime (i.e. rH < H). Here we estimate the corresponding Type I migration rate using the adopted simple tidal torque model (equation (6)).10 For this estimate we extrapolate the torque to within the Hill sphere.
These estimates are included for completeness here, but we emphasize that they are very sensitive to the approximations used in the tidal torque and the disc physics. The true Type I migration rate (even the sign!) can be significantly different for many reasons including: thermal effects (Paardekooper & Mellema 2006; Paardekooper & Papaloizou 2008), heat diffusion (Paardekooper, Baruteau & Kley 2011), inclination (Bitsch & Kley 2011), turbulence and MHD effects (Nelson & Papaloizou 2004; Laughlin, Steinacker & Adams 2004), non-linearities (Dong, Rafikov & Stone 2011), resonance overlaps (Rafikov & Petrovich 2012), and gas in horseshoe orbits (Type III migration) (Paardekooper et al. 2010). 3D effects for relatively thin discs are less significant (Tanaka, Takeuchi & Ward 2002).
We assume that near rs,  and
and  , where the exponents γΣ and γH may be slightly different inside and outside the secondary's orbit due to the tidal effects,
, where the exponents γΣ and γH may be slightly different inside and outside the secondary's orbit due to the tidal effects,  and
and  , respectively. For unperturbed discs, γH ≈ 0 and γΣ ≈ 3/2 and γΣ ≈ −3/5 for α- and β-discs, respectively, in the radiation pressure-dominated case, while in the gas pressure-dominated case γH ≈ 21/20 and γΣ ≈ −3/5 [see table 1 in Paper I and equation (5) in Haiman et al. 2009b]. Note that the scaleheight gradient can be expressed in terms of the midplane temperature gradient
, respectively. For unperturbed discs, γH ≈ 0 and γΣ ≈ 3/2 and γΣ ≈ −3/5 for α- and β-discs, respectively, in the radiation pressure-dominated case, while in the gas pressure-dominated case γH ≈ 21/20 and γΣ ≈ −3/5 [see table 1 in Paper I and equation (5) in Haiman et al. 2009b]. Note that the scaleheight gradient can be expressed in terms of the midplane temperature gradient  as γH = 3 − γΣ + 4γT for β ≪ 1 and
as γH = 3 − γΣ + 4γT for β ≪ 1 and  for β ∼ 1.
for β ∼ 1.
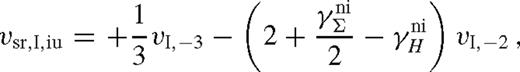
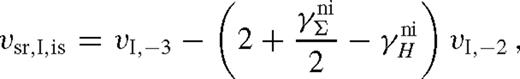
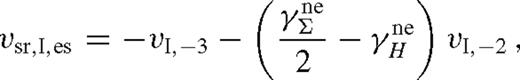
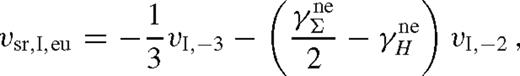
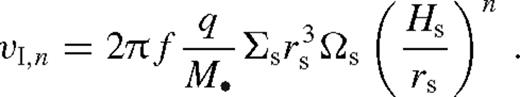
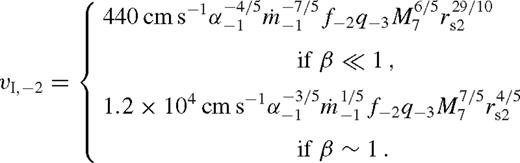
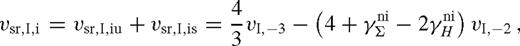
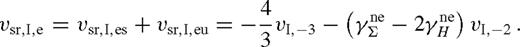
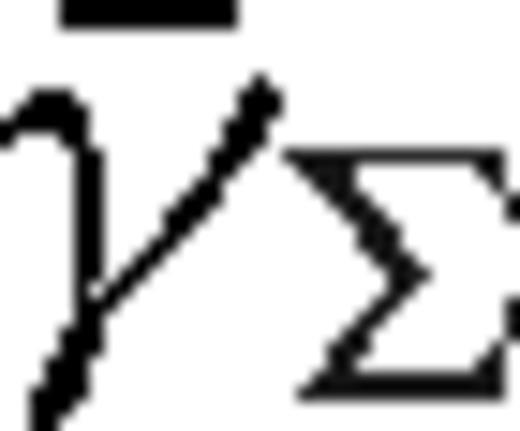 and
and 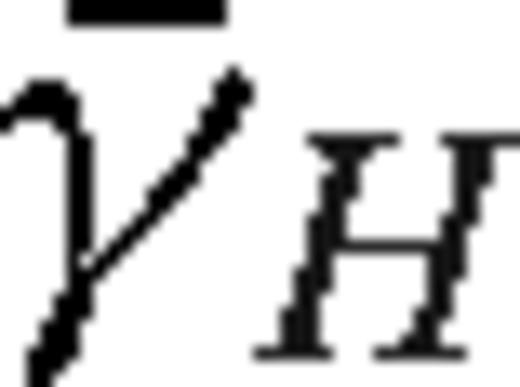 ,
, 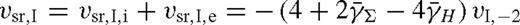
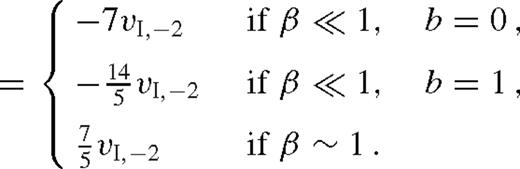
Equation equation (38) can be understood as follows. The migration rate is a consequence of the opposing repulsive tidal effects of the inner and the outer discs. Since the local disc mass is proportional to  , the migration rate is directed inwards for a constant thickness disc (γH = 0), if and only if the local disc mass increases outwards. However, the scaleheight sets the scale at which the torque is suppressed, and acts to reduce the effect. For gas pressure-dominated discs, these estimates match the magnitude of the Type I migration rate of more accurate local torque and hydrodynamical models of Tanaka et al. (2002) and Paardekooper et al. (2010) if f ∼ 0.3 in equation (6) and (34). A different overall offset, mostly due to co-rotation torques and pressure gradient effects, directs the migration inwards in those models for a gas-pressure-dominated disc. However, recent numerical simulations of non-isothermal optically thick discs with tidal heating find outward migration (Paardekooper & Mellema 2006), and for MHD turbulent discs the sign of the migration oscillates stochastically (Nelson & Papaloizou 2004). This highlights the extreme sensitivity of Type I migration to subtleties in the disc physics for low-mass secondaries.
, the migration rate is directed inwards for a constant thickness disc (γH = 0), if and only if the local disc mass increases outwards. However, the scaleheight sets the scale at which the torque is suppressed, and acts to reduce the effect. For gas pressure-dominated discs, these estimates match the magnitude of the Type I migration rate of more accurate local torque and hydrodynamical models of Tanaka et al. (2002) and Paardekooper et al. (2010) if f ∼ 0.3 in equation (6) and (34). A different overall offset, mostly due to co-rotation torques and pressure gradient effects, directs the migration inwards in those models for a gas-pressure-dominated disc. However, recent numerical simulations of non-isothermal optically thick discs with tidal heating find outward migration (Paardekooper & Mellema 2006), and for MHD turbulent discs the sign of the migration oscillates stochastically (Nelson & Papaloizou 2004). This highlights the extreme sensitivity of Type I migration to subtleties in the disc physics for low-mass secondaries.
5.2 Type II migration
Next let us consider the limit that the mass ratio is sufficiently large (i.e. more comparable masses), the tidal torque clears a gap such that the nearby gas accretion velocity matches the migration rate of the secondary. If the mass of the secondary is larger than the local disc mass then gas builds up outside the gap, reducing the accretion velocity and increasing the migration rate until the two match. The resulting secondary-dominated Type II migration is much slower than the accretion velocity of an unperturbed disc.
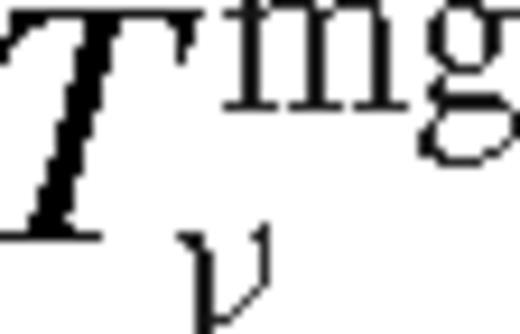 from Paper I in equation (18) we get
from Paper I in equation (18) we get 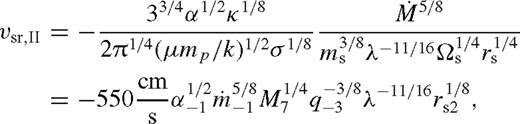
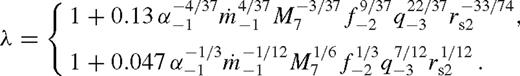
Migration rate of the secondary (small blue bullets), radial velocity of the gas (red circles) from the numerical solution neglecting GW emission for (M•, q) = (105 M⊙, 0.1) (left-hand panel) and (107 M⊙, 0.001) (right-hand panel). Analytic migration rates are also shown as labelled (Type II, 1.5, GW) as a function of orbital radius. The magenta line shows the saturated and unsaturated Type 1.5 migration rates, and the black dotted line is the Type II rate. A gap is present when the blue bullets and red circles overlap. The green dotted line shows the GW inspiral rate. The numerical result tracks the analytic Type 1.5 rate when there is no gap. The actual evolutionary sequence of the binary is highlighted with a thick yellow line.
Our result for steady-state Type II migration, equation (40), is consistent with the secondary-dominated Type II migration rate of Syer & Clarke (1995), suppressed by a factor λ−11/16 ≲ 2. Note that other than  and this weak λ dependence, the Type II migration rate is insensitive to the details of the disc physics and the disc–satellite interaction whenever a gap exists. [In particular to the f coefficient in the tidal torque (equation (6)), the pressure gradient, the thermal state of the disc and the torque cutoff.] The Type II migration rate is set by the accretion rate, which is set by the boundary condition, which we assume is a fixed fraction of the Eddington value of the primary.
and this weak λ dependence, the Type II migration rate is insensitive to the details of the disc physics and the disc–satellite interaction whenever a gap exists. [In particular to the f coefficient in the tidal torque (equation (6)), the pressure gradient, the thermal state of the disc and the torque cutoff.] The Type II migration rate is set by the accretion rate, which is set by the boundary condition, which we assume is a fixed fraction of the Eddington value of the primary.
Further modifications are possible if the disc is not in steady state. The self-similar solution of Ivanov et al. (1999) (see also Rafikov 2012) leads to a slower migration rate (by another factor of ∼2 relative to equation (40)). There, the steady-state accretion rate is assumed to hold in the far zone outside the gap and equal to the rate  corresponding to the Eddington limit near the primary, but the accretion rate is reduced in the middle zone relative to the steady-state solution, as a fraction of
corresponding to the Eddington limit near the primary, but the accretion rate is reduced in the middle zone relative to the steady-state solution, as a fraction of  is continuously used to gradually build-up the gas mass outside the gap, which never fully reaches the steady-state level. While these models may be more realistic, however, there is no strong reason to believe that the far zone accretion rate is related to the Eddington limit of the primary, in a scenario with a gap where the gas is not present in the vicinity of the primary. If one were to assume that
is continuously used to gradually build-up the gas mass outside the gap, which never fully reaches the steady-state level. While these models may be more realistic, however, there is no strong reason to believe that the far zone accretion rate is related to the Eddington limit of the primary, in a scenario with a gap where the gas is not present in the vicinity of the primary. If one were to assume that  is set by the inner boundary condition in the middle zone to a given fraction of
is set by the inner boundary condition in the middle zone to a given fraction of  (implying that this may require a correspondingly somewhat larger
(implying that this may require a correspondingly somewhat larger  in the far-zone), this would have led to the original, quasi-steady-state Syer & Clarke (1995) migration rate.
in the far-zone), this would have led to the original, quasi-steady-state Syer & Clarke (1995) migration rate.
Another possibility was considered in Lodato et al. (2009), in which the total amount of gas mass is limited to be less than the secondary mass, so that the steady state with  cannot be reached. They argued that the migration is much slower in this case, and the disc cannot deliver the secondary efficiently to separations where GW emission is sufficient to lead to merger in a Hubble time (final parsec problem; see Section 5.4).
cannot be reached. They argued that the migration is much slower in this case, and the disc cannot deliver the secondary efficiently to separations where GW emission is sufficient to lead to merger in a Hubble time (final parsec problem; see Section 5.4).
5.3 Type 1.5 migration
In the previous description, Type I migration requires azimuthally linear perturbations, which is applicable if rH ≲ H, implying that q ≲ 3 (H/r)3. In contrast Type II migration assumes a truncated disc with negligible overflow which is valid if the gap does not close as discussed in Section 4. Let us now consider the intermediate Type 1.5 case, when the secondary mass is large enough that its tidal torques cause a significant gas build-up exterior to the secondary orbit but without completely truncating the disc.
The transition between Type I and II migration as a function of secondary mass was previously investigated analytically by Hourigan & Ward (1984) and Ward & Hourigan (1989) (see also Ward 1997), numerically by Bate et al. (2003), and in both ways by Crida & Morbidelli (2007), assuming a constant sound speed and viscosity, in cases where the gas pile-up outside the secondary is small. Here, we discuss Type 1.5 migration assuming a quasi-steady state derived in Paper I in the limit of a large pile-up, self-consistently accounting for variations caused by tidal heating, which changes the temperature, scaleheight, viscosity in the disc.
The migration rate is generally proportional to the dimensionless angular momentum flux in the gas-driven regime (equation (29)). This is sensitive to the nearby gas density and the characteristic radius at which the torque is exerted, vsr ∝ k ∝ ΣΔ−3, where Δ ∼ max (rH, H). If a wide gap forms, Δ is set such that vsr matches the gas inflow rate  (Type II). However, in the overflowing case, the migration rate becomes slower than Type II as the pile-up is limited by gap overflow, decreasing Σ and H compared to the case with a gap. Relative to an unperturbed disc, although Σ is decreased close to the secondary, it is strongly increased due to pile-up outside of Δ. However, more importantly, the pile-up also increases the viscous stress and H, which affects the migration rate greatly as vsr ∝ H−3 if H > rH. Accounting for the change in H is essential to correctly estimate the migration rate. The competition of these effects determines the Type 1.5 migration rate in the overflowing regime.
(Type II). However, in the overflowing case, the migration rate becomes slower than Type II as the pile-up is limited by gap overflow, decreasing Σ and H compared to the case with a gap. Relative to an unperturbed disc, although Σ is decreased close to the secondary, it is strongly increased due to pile-up outside of Δ. However, more importantly, the pile-up also increases the viscous stress and H, which affects the migration rate greatly as vsr ∝ H−3 if H > rH. Accounting for the change in H is essential to correctly estimate the migration rate. The competition of these effects determines the Type 1.5 migration rate in the overflowing regime.
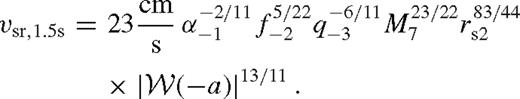
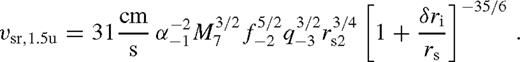
The migration rate is not always Type 1.5 for other choices of q and rs as shown in Figs 6 and 7. However, the migration rate is approximated to within 20 per cent by Type 1.5, equations (42)–(43), for q ≳ 10−3 and rs ≫ rISCO whenever a gap is not present and GW emission is negligible, provided that the disc is in a quasi-steady state and the torque model is given by (6). These formulae capture the (q, rs) parameter dependence remarkably well in this range, where the Type I and II rates are inapplicable. Note, however, that since our results, equations (42)–(43), correspond to the case of a large pile-up, this is insufficient to investigate very small mass ratios where the transition between the Type I and 1.5 regimes takes place.
Figs 6 and 7 show that Type 1.5 migration is generally slower than the other velocity scales in the problem. Increasing the secondary mass at a fixed orbital radius generally increases the amount of gas mass accumulated outside the secondary, which causes the gas velocity to be reduced for a fixed accretion rate. However, since there is no gap in the disc, gas still flows in faster than the migration rate of the object. Type 1.5 migration is slower than the secondary-dominated Type II migration rate, since the gas pileup in these overflowing solutions just outside the orbit is less pronounced compared to the case with a gap. Finally, it is also slower than the Type I rate if the tidal torques decrease the gas density close to the secondary or if the scaleheight is increased.
5.4 GW-driven inspiral
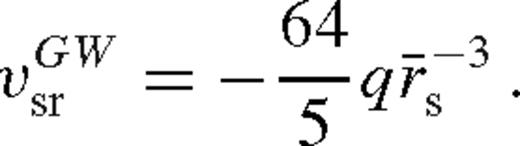
5.5 Summary of migration rates
We can now summarize and interpret the trends seen for different mass ratios and radii in Figs 6 and 7. At sufficiently large radii, a gap opens for comparable mass ratio binaries. As gas accumulates outside the gap, the radial gas velocity is slowed down to match the migration rate of the secondary, according to Type II migration. For smaller secondary masses in this regime, the amount of accumulated gas is less and the corresponding gas accretion velocity becomes higher and the migration rate faster. At sufficiently small secondary mass and binary separation, the tidal torque cannot keep the gas outside the Hill sphere and the gap closes. The gas accretion velocity in this regime is still far slower than the unperturbed value, and the pressure and gas density are significantly enhanced outside the orbit. The migration here is well approximated by the Type 1.5 rate given by equations (42)–(43). The secondary tends to decrease the surface density and pressure within the Hill sphere relative to the unperturbed value. The migration rate approaches the Type I rate from below for very small q. Along the inward migration of the binary, the amount of local gas mass torquing the binary decreases. This implies that the migration rate decreases with decreasing radius for all three cases (Type I, 1.5 and II). GW emission dominates over gas-driven migration in the final stages before merger.11
6 Observational Implications
6.1 Bolometric luminosity
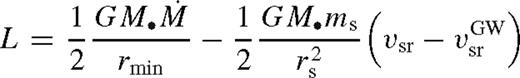
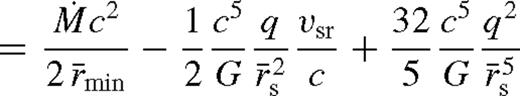
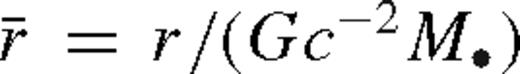 and vsr is the migration rate due to gas and GW losses (vsr < 0 for inward motion), and
and vsr is the migration rate due to gas and GW losses (vsr < 0 for inward motion), and  is the GW inspiral rate neglecting torques from the gas. The first term is due to accretion, the second and third terms together are due to tidal heating, labelled Lacc and ΔLheat, respectively.
is the GW inspiral rate neglecting torques from the gas. The first term is due to accretion, the second and third terms together are due to tidal heating, labelled Lacc and ΔLheat, respectively.Fig. 8 shows the two components of the luminosity Lacc and ΔLheat relative to  as a function of the binary orbital time when neglecting GW emission. Here, we assume that
as a function of the binary orbital time when neglecting GW emission. Here, we assume that  where M7 = M/107 M⊙. The point and line styles are the same as in Figs 6 and 7 in the various regimes of migration. The figure shows that the secondary can greatly modify the luminosity of the disc. The accretion luminosity is greatly decreased if a gap forms, but the excess brightness of the outer disc, ΔLheat, can overcompensate for the decrease of Lacc.
where M7 = M/107 M⊙. The point and line styles are the same as in Figs 6 and 7 in the various regimes of migration. The figure shows that the secondary can greatly modify the luminosity of the disc. The accretion luminosity is greatly decreased if a gap forms, but the excess brightness of the outer disc, ΔLheat, can overcompensate for the decrease of Lacc.
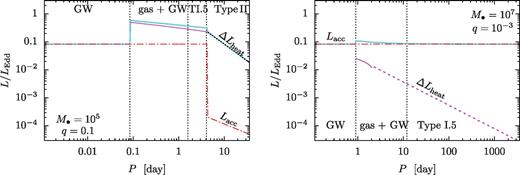
The bolometric luminosity corresponding to accretion and tidal heating as a function of the orbital period of the secondary for (M•, q) = (105 M⊙, 0.1) and (107 M⊙, 10−3) in the various evolutionary stages. The line styles for ΔLheat are the same as in Fig. 6: black dotted for Type II migration, and solid and dashed magenta for saturated and unsaturated Type 1.5 migration. The cyan line shows the total bolometric luminosity Lacc + ΔLheat. Note that our calculations for ΔLheat neglect GW emission; it breaks down in the GW inspiral regime. Lacc is quenched when a gap opens.
The analytic results for the migration rates in Section 5 can be used to understand the features shown in Fig. 8. If a gap is opened and the secondary exhibits Type II migration, then the luminosity associated with accretion scales with the orbital period P as Lacc, II ∝ 1/rs ∝ P−2/3 and the secondary causes an excess  . In the GW-driven regime before gap decoupling, the accretion luminosity is the same but the excess tidal heating rate is negligible. At smaller separations the accretion luminosity increases, and reaches
. In the GW-driven regime before gap decoupling, the accretion luminosity is the same but the excess tidal heating rate is negligible. At smaller separations the accretion luminosity increases, and reaches  as the gap closes. As the binary becomes GW driven at smaller separations the gas build-up is decreased outside of the secondary and the excess heating is suppressed. This transition happens in the region marked as gas+GW driven in Fig. 4: at orbital periods
as the gap closes. As the binary becomes GW driven at smaller separations the gas build-up is decreased outside of the secondary and the excess heating is suppressed. This transition happens in the region marked as gas+GW driven in Fig. 4: at orbital periods  for q = (0.1, 0.01, 0.001), respectively, for M• = 107 M⊙ in particular. Once the gap closes, rmin is associated with the ISCO, and the accretion luminosity is constant. The tidal heating in the overflowing state is ΔLheat, 1.5 = q2vsr, 1.5/r2 ∝ q7/2r−5/4 ∝ q7/2P−5/6 in the unsaturated Type 1.5 state, and
for q = (0.1, 0.01, 0.001), respectively, for M• = 107 M⊙ in particular. Once the gap closes, rmin is associated with the ISCO, and the accretion luminosity is constant. The tidal heating in the overflowing state is ΔLheat, 1.5 = q2vsr, 1.5/r2 ∝ q7/2r−5/4 ∝ q7/2P−5/6 in the unsaturated Type 1.5 state, and  in the saturated case. For weakly perturbed discs where the secondary undergoes Type I migration,
in the saturated case. For weakly perturbed discs where the secondary undergoes Type I migration,  in the radiation pressure-dominated regime and q3r−6/5 = q3P−12/15 in the gas pressure-dominated regime.
in the radiation pressure-dominated regime and q3r−6/5 = q3P−12/15 in the gas pressure-dominated regime.
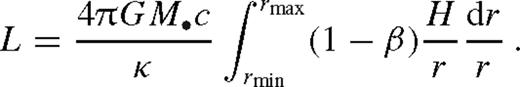
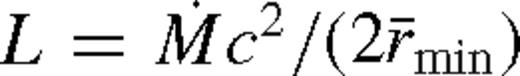 . More generally,
. More generally, 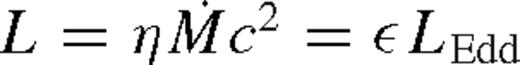 . In Fig. 8, we conservatively chose
. In Fig. 8, we conservatively chose 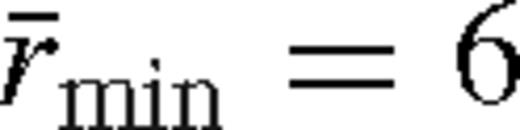 corresponding to a non-spinning BH, and ε = η consistent with AGN observations showing that ε ∼ 10–25 per cent for bright AGNs (Kollmeier et al. 2006; Trump et al. 2009). The luminosity increase due the secondary is significant if H/r is larger near the secondary than near the ISCO and if the disc is radiation pressure dominated. Indeed, Fig. 2 has shown that H/r can increase dramatically for q > 10−3. Equation equation (47) shows that a thick, radiation pressure-dominated accretion disc can exceed the hydrostatic Eddington limit by a logarithmic factor, ln (rmax /rmin ). This is due to the velocity shear and vorticity in the disc, which are neglected in the hydrostatic Eddington limit (Abramowicz et al. 1980; Abramowicz 2004).
corresponding to a non-spinning BH, and ε = η consistent with AGN observations showing that ε ∼ 10–25 per cent for bright AGNs (Kollmeier et al. 2006; Trump et al. 2009). The luminosity increase due the secondary is significant if H/r is larger near the secondary than near the ISCO and if the disc is radiation pressure dominated. Indeed, Fig. 2 has shown that H/r can increase dramatically for q > 10−3. Equation equation (47) shows that a thick, radiation pressure-dominated accretion disc can exceed the hydrostatic Eddington limit by a logarithmic factor, ln (rmax /rmin ). This is due to the velocity shear and vorticity in the disc, which are neglected in the hydrostatic Eddington limit (Abramowicz et al. 1980; Abramowicz 2004).We conclude that the disc luminosity may be modified significantly by the orbiting object. Whenever a gap forms, the disc becomes either fainter due to the loss of accretion on to the primary or brighter due to the accumulated gas mass outside the secondary heated by tidal dissipation (with the latter effect dominating near the end of the Type II migration phase in many cases). The competition of these effects generates a unique lightcurve which is sensitive to the type of migration as well as to GW losses. These conclusions assume axisymmetry; an obvious caveat is that non-axisymmetric accretion streams could generate significant luminosity (Hayasaki, Mineshige & Ho 2008; Roedig et al. 2011, 2012).
6.2 Disc spectrum
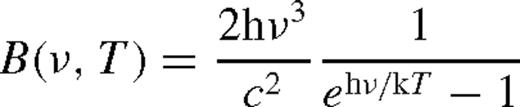
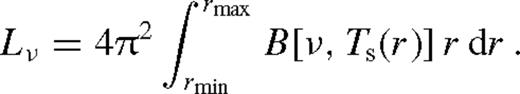
 (however, see discussion below).
(however, see discussion below).The outer parts of the accretion disc have a much lower temperature than the inner parts. Therefore, the brightening caused by a secondary affects the spectrum more prominently at shorter wavelengths. The disc spectrum can be used to disentangle the effects of a secondary from the properties of the inner disc.
Fig. 9 shows the disc spectra in two representative cases when the orbital period is P = 3 or 110 d for M• = 105 and 107 M⊙, respectively. Different curves show different mass ratios. The spectrum is truncated at high frequencies when a gap forms, as the hottest central regions are removed from the disc. Relative to an accretion disc with no secondary, the disc is much brighter in the ultraviolet, optical and infrared bands for large secondary masses, both in the gap forming and in the overflowing cases. The extra energy originates from the orbital energy of the binary which heats the disc through the gravitational torques on top of the viscous heating. For other binary masses and separations assuming the binary are in the gas-driven regime, the dimensionless angular momentum flux or brightening factor is shown in Fig. 3. For smaller binary separations when the GW inspiral overtakes the accretion rate, the optical and infrared enhancement associated with the exterior gas pileup goes away.
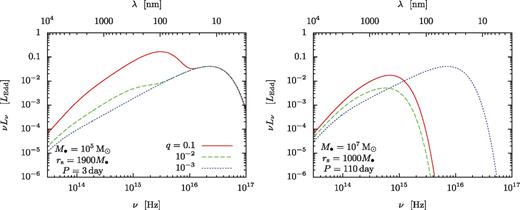
Disc spectra in units of LEdd ∼ 1043 and  for M• = 105 and 107M• binaries with periods as marked. Different curves correspond to different mass ratios as labelled. The dotted curve (q = 10−3) represents the asymptotic spectrum of a solitary disc. The spectrum on the right-hand panel is truncated for q = 0.1 and 0.01 when a gap forms. The optical enhancement at lower frequencies is due to the outer disc.
for M• = 105 and 107M• binaries with periods as marked. Different curves correspond to different mass ratios as labelled. The dotted curve (q = 10−3) represents the asymptotic spectrum of a solitary disc. The spectrum on the right-hand panel is truncated for q = 0.1 and 0.01 when a gap forms. The optical enhancement at lower frequencies is due to the outer disc.
Note that our estimates neglect accretion on to the secondary which can generate an additional spectral peak in X-rays (Sesana et al. 2012; Tanaka et al. 2012). We also neglected relativistic corrections to the disc spectrum, and other features such as spectral lines and the high-frequency tail associated with the corona. Since the orbital velocity of the secondary on a circular orbit is  , the offset and broadening of spectral lines can be quite significant for SMBH binaries (Haiman et al. 2009b; Shen & Loeb 2010; Dotti, Sesana & Decarli 2012; McKernan et al. 2012). Thus, the actual AGN binary spectra shown in Fig. 9 may also exhibit relativistically broadened and/or offset spectral lines by 6900 and 9500 km s−1 in the left- and right-hand panels, respectively. The lightcurve is expected to be periodically modulated on the binary orbital period (3 and 110 d, respectively, in the two panels; see also discussion below), with harmonics appearing at ∼3 and 0.5 times the orbital period for mass ratios q ≳ 0.05 (D'Orazio, Haiman & MacFadyen 2012). These signatures together can help future observational efforts to identify SMBH binaries in the overflowing regime.
, the offset and broadening of spectral lines can be quite significant for SMBH binaries (Haiman et al. 2009b; Shen & Loeb 2010; Dotti, Sesana & Decarli 2012; McKernan et al. 2012). Thus, the actual AGN binary spectra shown in Fig. 9 may also exhibit relativistically broadened and/or offset spectral lines by 6900 and 9500 km s−1 in the left- and right-hand panels, respectively. The lightcurve is expected to be periodically modulated on the binary orbital period (3 and 110 d, respectively, in the two panels; see also discussion below), with harmonics appearing at ∼3 and 0.5 times the orbital period for mass ratios q ≳ 0.05 (D'Orazio, Haiman & MacFadyen 2012). These signatures together can help future observational efforts to identify SMBH binaries in the overflowing regime.
6.3 Transient and periodic variability statistics
We have calculated the rate at which the binary evolves towards merger and have shown that the state of the disc changes during this process. From this one can predict the residence time tres ≡ r/vsr the binary resides in the various states. Assuming that the luminosity of the accretion disc is modulated periodically on the orbital time-scale (Hayasaki et al. 2007; MacFadyen & Milosavljević 2008; Cuadra et al. 2009), it is possible to predict the relative fraction of binaries that exhibit variability as a function of orbital period (Haiman et al. 2009b). One may expect to see EM transients when the binary is surrounded by gas, and a different distinct population of dimmer or softer sources decoupled from the disc assuming that the GW inspiral dominates the evolution inside of a gap in the disc. The predictions can be observationally tested using large deep variability surveys, such as the Panoramic Survey Telescope and Rapid Response System (PanSTARRS) or the Large Synoptic Survey Telescope (LSST).
Previously, Haiman et al. (2009b) have carried out this exercise assuming a GW inspiral at short periods and Type II migration for long periods. These predictions have to be revised in two respects. First, many of the binaries may be in the Type 1.5 regime which has a longer residence time. Secondly, we predict that tidal torques cannot sustain a gap once a sufficient amount of gas has accumulated, which may cause gap-refilling, before the binary can ‘run away’ from the gap edge in the GW-driven inspiral regime. Without gap-refilling or an inner disc around the primary and secondary, periodic variability is not expected in the GW-driven regime with a decoupled outer disc (see however Farris et al. 2011; Bode et al. 2012; Farris et al. 2012; Noble et al. 2012). Future studies should investigate the expected variability in circumbinary or overflowing discs, where the secondary is in the GW-driven regime.
Fig. 10 shows the residence time the binary spends at various orbital periods for different masses and mass ratios. Different line styles show the type of migration. The residence time increases with period very quickly ( ) in the GW-driven regime, but not so rapidly in the gas-driven regime. The dependence is flatter for Type II, and even more so for Type 1.5, where it can even decrease with period in the torque-cutoff state (at P ∼ 1 d for 105 M⊙ in the right-hand panel). This shows that the efficiency at which gas can deliver objects to the GW-driven regime is deteriorated by gas overflow. The transitions to GW-driven inspiral occur at longer periods for the Type 1.5 than for Type II migration (see Fig. 6). The fraction of binaries at orbital periods between a few days and years is larger if Type 1.5 migration operates, relative to the Type II rate. As a rule of thumb, we find this to be the case if one of the BHs is less massive than 105 M⊙. Conversely, the residence time follows the Type II rate all the way to the GW inspiral regime if both objects are more massive than 105 M⊙.
) in the GW-driven regime, but not so rapidly in the gas-driven regime. The dependence is flatter for Type II, and even more so for Type 1.5, where it can even decrease with period in the torque-cutoff state (at P ∼ 1 d for 105 M⊙ in the right-hand panel). This shows that the efficiency at which gas can deliver objects to the GW-driven regime is deteriorated by gas overflow. The transitions to GW-driven inspiral occur at longer periods for the Type 1.5 than for Type II migration (see Fig. 6). The fraction of binaries at orbital periods between a few days and years is larger if Type 1.5 migration operates, relative to the Type II rate. As a rule of thumb, we find this to be the case if one of the BHs is less massive than 105 M⊙. Conversely, the residence time follows the Type II rate all the way to the GW inspiral regime if both objects are more massive than 105 M⊙.
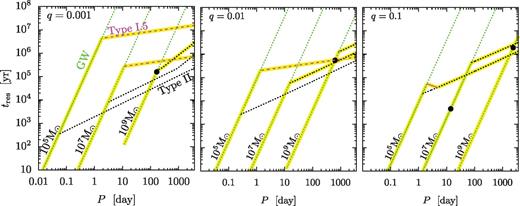
The amount of time the binary spends at various orbital periods during its evolution towards merger. The three panels show different mass ratios, and in each panel the three sets of curves show different total masses as marked. For each mass, different line styles correspond to different types of migration, GW inspiral (green), saturated and unsaturated Type 1.5 (magenta dashed and solid), and Type II (black dotted). The evolutionary tracks are highlighted with a thick yellow line. Big black dots mark gap decoupling; for much smaller periods, the tidal torques may not generate EM variability.
Gap refilling may be witnessed through the increase in the bolometric luminosity and spectral X-ray hardening of the source (Milosavljević & Phinney 2005; Tanaka et al. 2010). Our results show that this may occur already before merger, particularly for 105 M⊙ SMBH masses in the LISA/NGO range (Sesana et al. 2005), generating bright EM sources coincident with GWs. Gap refilling may occur more rapidly compared to the viscous time without the pile-up, due to the enhanced gas mass and stress outside the gap and the presence of the secondary, implying a larger population of birthing quasars for all-sky optical (e.g. LSST) or soft X-ray surveys. However, since this occurs at larger radii where the viscous time is longer, it is unclear whether this yields a larger or smaller population of birthing quasars with significant brightening during the mission lifetime of all-sky optical (e.g. LSST) or soft X-ray surveys.
The significant excess flux in the gas-driven regime may increase the prospects for identifying SMBH binary sources. Future surveys for these sources can provide observational evidence for SMBH mergers in the NGO mass range or IMBHs orbiting around SMBHs.
6.4 Gravitational wave measurements
Gap refilling and Type 1.5 migration has implications for GW measurements in several ways. First, we have shown that the gap closes much earlier than previously thought. This implies that the LISA/NGO binaries may be embedded in gas even for nearly comparable mass ratios. This helps the prospects of identifying coincident EM counterparts to LISA sources. Secondly, the effects of gas may be identified directly from the GW signal itself. The GWs emitted by SMBH binaries are in the frequency bands detectable by PTAs if the orbital period is between a few days and a few years, and in the planned LISA range if it is between a few seconds and an ∼half day. Fig. 10 shows that the corresponding mass range is below 106 M⊙ for LISA and above 107 M⊙ for PTAs. Here we describe how the accretion disc affects the GW signal for LISA and PTAs, and discuss the implications of gas overflow and Type 1.5 migration.
6.4.1 PTAs
The nHz GW background, measurable by PTAs, is generated by SMBH binaries (Sesana, Vecchio & Colacino 2008; Sesana, Vecchio & Volonteri 2009), which emit a stationary signal with angular frequency 2Ω for circular sources and many distinct upper harmonics for eccentric sources. The background is affected by the disc in two ways: (i) by changing the relative fraction of binaries at particular orbital radii according to the residence time (Kocsis & Sesana 2011), and (ii) by changing the eccentricity distribution of sources if a gap is opened (Artymowicz 1992; Armitage & Natarajan 2005; Cuadra et al. 2009; Roedig et al. 2011, 2012).
Kocsis & Sesana (2011) calculated the GW background for a population of binaries that undergo Type II migration in steady-state α- or β-discs, or the self-similar migration according to the quasi-stationary model in Ivanov et al. (1999). They found that the unresolved GW background is typically not reduced significantly in the PTA frequency band if the sources undergo secondary-dominated Type II migration.13 This is due to the fact that the background is dominated by comparable mass binaries for which (1) the slowdown of Type II migration in the secondary-dominated regime is more significant and (2) many of these sources transition to a GW-dominated evolution at large orbital periods outside the PTA range. Regarding the individually resolvable GW sources with PTAs, they are typically the most massive q ∼ 1, ∼109 M⊙ binaries, which are not affected by gas in any case at these frequencies. Fig. 10 shows that Type 1.5 migration in β-discs is not relevant for PTA measurements since it does not affect the binaries with masses larger than 106 M⊙. Since gaps are expected not to close for these masses for β-discs, these sources are expected to exhibit GW spectra characteristic of eccentric sources. Further studies should examine whether gap overflow may occur for PTA sources embedded in α-discs, and the implications for eccentricity.
6.4.2 LISA/NGO
As mentioned above, the frequency range of LISA/NGO corresponds to binary orbital periods shorter than a day; the sensitivity is best for P ∼ 10 min . In this regime, the binaries are typically already in the GW inspiral regime. Nevertheless, the effects of gas are imprinted on the frequency and phase evolution of the signal as the orbital period shrinks during the measurement. In Kocsis et al. (2011) and Yunes et al. (2011), we have shown that the corresponding GW phase perturbation is very significant (∼1000 rad yr−1) relative to the LISA measurement accuracy (∼1 rad yr−1) if the gaseous torque corresponds to secondary-dominated Type II migration (particularly for M• = 106 M⊙), and less pronounced (∼10 rad yr−1) but still significant if it corresponds to Type I migration. Here, we have not examined the gaseous torques in the GW-driven regime. In that case, since the viscous inflow is slower than the GW inspiral, the gas does not bank-up outside of the secondary.14 Therefore, we conclude that gas effects are expected to be reduced compared to the Type II case in Yunes et al. (2011), but future studies should examine whether the corresponding phase shift is still measurable with the LISA accuracy.
The GW spectrum may also be affected by the binary eccentricity, reminiscent of gas (Armitage & Natarajan 2002). We have shown that the disc overflows for typical LISA binaries. Further studies should investigate whether the eccentricity is excited in the overflowing state, and whether this remains significant in the GW inspiral regime when the binary enters the LISA frequency range.
7 Conclusions
We have examined the self-consistent steady-state structure of accretion discs around SMBH binaries, conditions of gap-closing, and migration rates of the binaries. Our main conclusions can be summarized as follows.
- (i)
Gap-closing – The secondary represents a strong tidal barrier in the accretion disc, which causes a significant accumulation of gas in an extended range outside of the secondary. Still, the tidal torque cannot counteract the enhanced viscous torque in steady state for a large range of binary masses, particularly for ≲ 105 M⊙, and the disc does not form a gap. The steady state exhibits continuous overflow across the orbit.
- (ii)
Phase diagram – The disc is described by separate formulae in the two main regions in the binary parameter space when GW emission is negligible: a gap is present for sufficiently large separations and masses (Fig. 3) but typically refills before GW-driven decoupling. We identify further sub-regions in this ‘phase space’ depending on whether the tidal torques are saturated.
- (iii)
Type 1.5 migration – The gas-driven migration rate is Type I for weakly perturbed discs, Type II where the gap can remain open and Type 1.5 in the intermediate strongly perturbed inflowing state. We have derived analytic formulae for the Type 1.5 rates and have found these to be slow compared to both Type I and II rates.
- (iv)
Optical and infrared excess – The disc flux is increased by a factor of up to 100–500 due to gas pileup outside the orbit of the secondary for binaries with M• = 105–107 M⊙ in the Type 1.5 and Type II migration regimes, enhancing the ultraviolet, optical and near-infrared brightness of the disc. The enhancement is more pronounced for lower M•. The disc can become moderately super-Eddington at these frequencies. The excess brightness is mitigated by gas overflow and further suppressed for binaries for which GW-emission is significant. This can be used to indirectly indicate the presence of GWs.
- (v)
Periodically variable AGN – The orbital period is between 1 d and 10 years for binaries in the Type 1.5 migration regime. Periodic variability surveys of AGNs can discover these sources and test the predicted spectral signatures. The statistics of the relative abundance of many such sources with different periods can be used to observationally test the migration and GW inspiral rate, and to estimate the expected LISA merger rate.
- (vi)
EM counterparts for LISA – The masses most affected by gap overflow and Type 1.5 migration are in the LISA range (near ∼105 M⊙). The gap closes even for comparable mass ratios before GW emission dominates, implying that normal AGN-like activity may be coincident with LISA sources (Kocsis et al. 2006).
- (vii)
PTA sources – The gap can remain open for the massive 108–109 M⊙ binaries, implying that the GW background is not affected by Type 1.5 migration for PTAs. The presence of gas can be inferred either from EM surveys or indirectly from the GW spectrum, since the gas increases the binary eccentricity if a gap is open, which adds orbital harmonics to the spectrum. The eccentricity is expected to be much smaller for systems devoid of gas (Sesana 2010; Preto et al. 2011; Madigan & Levin 2012).
- (viii)
Star formation and final parsec problem – Previously, Lodato et al. (2009) argued that the migration rate is greatly reduced by star formation feedback if the disc is unstable to gravitational fragmentation and the disc mass is smaller than the secondary mass. However, for the low-mass, but continuously replenished discs considered here we find that the disc is stabilized against gravitational fragmentation. This is because viscous heating increases the sound speed over a large range of radii outside the secondary's orbit, and this effect is more important than the increase of surface density in the same region.
We note that all of these findings correspond to a disc model in which the effective viscosity is proportional to the gas pressure in the disc (so-called β-discs). Future studies should investigate alternative models in which the viscosity is proportional to the total gas+radiation pressure. We also assumed steady-state models, where the accretion rate is constant, and set by the Eddington limit of the primary. While we expect these assumptions to be justified in the overflowing regime, where the gas inflow rate is much higher than the migration rate of the secondary, the steady-state Eddington accretion assumption is suspect for circumbinary discs with gaps (Ivanov et al. 1999; Lodato et al. 2009; Rafikov 2012). Future studies should address comparable mass binaries where the disc may be significantly non-axisymmetric (MacFadyen & Milosavljević 2008; Cuadra et al. 2009) and where the accretion of the secondary is non-negligible (Lubow et al. 1999), and examine whether binary eccentricity is excited in the overflowing steady state (Artymowicz 1992; Armitage & Natarajan 2005; Hayasaki 2009; Roedig et al. 2011, 2012).
Acknowledgments
We thank Re'em Sari, Taka Tanaka, Roman Rafikov and Alberto Sesana for useful discussions. BK acknowledges support from NASA through Einstein Postdoctoral Fellowship Award Number PF9-00063 issued by the Chandra X-ray Observatory Center, which is operated by the Smithsonian Astrophysical Observatory for and on behalf of the National Aeronautics Space Administration under contract NAS8-03060. This work was supported in part by NSF grant AST-0907890 and NASA grants NNX08AL43G and NNA09DB30A (to AL) and NASA grant NNX11AE05G (to ZH).
References
The non-axisymmetric part of the perturbations may be either linear or non-linear depending on the magnitude of pile-up. In both cases, we adopt the tidal torque model of Armitage & Natarajan (2002), reminiscent of Type I migration, which we use with the azimuthally averaged self-consistent disc profile (see Paper I).
That is, the viscous torque is greatly reduced (increased) in the near zone interior (exterior) to the secondary's orbit relative to the solitary disc without a secondary.
In our numerical solutions we define rg as the radius where the tidal torque density drops to 10 per cent of its peak value, although our results are insensitive to this precise choice.
Here by ‘gap’ we mean regions in which Σ(r) = 0 (i.e. r < r0 where r0 > rs + rH falls outside the Hill radius; see above). Regardless, note that Σ(r) can be greatly decreased in the overflowing solutions near the secondary.
Note that the changes seem deceptively abrupt on a logarithmic scale. To see this, consider y = (x − 1)2, a smooth function, that exhibits a similar feature on a log–log plot near x = 1.
The brightening factor has a simple radial dependence in the middle zone k ∝ r−1/2. We extrapolate the brightening factor in the middle zone to the location of the secondary, typically a conservative estimate of the true brightening of the disc outside the secondary's orbit as this neglects the excess brightening due to tidal heating in the near zone (see Paper I).
We do not consider the cases where either  ,
,  or
or  is less than one. In this case, the analytic solutions need further modifications (see Paper I).
is less than one. In this case, the analytic solutions need further modifications (see Paper I).
The gap opening conditions are sometimes written as Δ0 ≳ rH ≳ H0, where rH ≳ H0 is the condition for the azimuthal perturbations to become non-linear (Korycansky & Papaloizou 1996; Ward 1997). We shall not require rH ≳ H0 here over the two conditions in equation (20).
The tidal torque coefficient in equation (6) is f = 0.80 in this case [see Goldreich & Tremaine (1980) and Paper I].
A separate class of migration for low-mass planets, which we did not consider here, is Type III migration associated with torques exerted by the gas on horseshoe orbits around the secondary (Masset & Papaloizou 2003). This is significant if the gas mass is considerable relative to the secondary mass. Although the secondary mass dominates over the local disc mass for BH binaries embedded in accretion discs of interest here, future studies should investigate the effects of the gas crossing the secondary orbit (see the recent study by Roedig et al. 2012 for the importance of torques due to gas streams in the central cavity around a SMBH binary).
We include factors of G and c in this section.
The background could be reduced only if Type II migration occurs on the viscous time-scale with no accumulation of gas.
Gas may bank up interior to the orbit in the GW-driven regime (Chang et al. 2010) [see however Baruteau et al. (2012) and Section 1.2].
Author notes
Einstein Fellow.



