Abstract
Cross-sections and rate coefficients have been calculated for the rovibrational excitation of CO by ortho- and para-H2 and by He. We adopted the quantal coupled channels method of solving the scattering equations, including CO rotational levels in the v = 0, 1 and 2 vibrational manifolds. Comparison is made with the results of previous calculations, which employed different interaction potentials and less accurate approximations to the collision dynamics. We consider that the present calculations yield reliable values of the rate coefficients for rovibrational excitation of CO at kinetic temperatures T ≈ 103 K.
Introduction
Rotational transitions within the v = 0 vibrational ground state of the CO molecule and its isotopic variants, 13CO, C17O and C18O, have been observed extensively in the interstellar medium. Such transitions have provided important diagnostics of conditions in regions of star formation and in stellar envelopes. Because of its relatively high abundance and ease of observation by radio telescopes on the ground, CO has been used as a surrogate for the H2 molecule when mapping the distribution of molecular gas in our own and in other galaxies. CO is also an important coolant of interstellar molecular gas, particularly at temperatures 
K at which the rotational excitation of H2 is less effective, owing to its rotational energy level spacings being much larger than in the more massive CO molecule.
At kinetic temperatures T ≳103 K, excited vibrational states of CO become energetically accessible. Consequently, rovibrational transitions of CO, particularly v = 0 → 1, can be excited by collisions in regions that have been heated by the passage of a shock wave, such as the outflows associated with star formation, and in circumstellar envelopes. There have been many detections at 4.6
m of the v = 1 → 0 fundamental transition and at 2.3
m of the v = 2 → 0 first overtone transition of CO in circumstellar discs and envelopes (see e.g. Wheelwright et al. ; Herczeg et al. ). To be able to interpret such observations, the rate coefficients for rovibrational excitation of CO by the principal perturbers, H2 and He, are required; these data are also necessary to determine the contribution of rovibrational excitation of CO to the cooling of the medium.
In order to evaluate cross-sections for vibrationally inelastic transitions, it is necessary to determine the energy of interaction between CO and the perturber as a function not only of their separation and relative orientation but also as a function of the CO internuclear distance. Vibrational relaxation in collisions of CO with H2 was investigated by Bacić et al. (), who used the CO–H2 interaction potential computed by Schinke et al. () and considered transitions induced by both ortho- and para-H2; comparison was made with measurements of the v = 1 → 0 vibrational relaxation rate coefficient for kinetic temperatures T ≤ 300 K. The CO–He system was investigated by Wickham-Jones et al. (), who made a multiparameter fit to the CO–He interaction potential, previously computed by Thomas et al. () and Schinke & Diercksen (), and hence determined cross-sections for the vibrational relaxation v = 1 → 0 of 12C16O and 13C18O by 4He and 3He. They computed the corresponding rate coefficients, which they compared with experimental measurements of the rate coefficients for vibrational relaxation at temperatures up to T = 2326 K, in the case of 12C16O–4He. In subsequent work, Reid et al. () used the same potential fit but a more accurate treatment of the collision dynamics to recalculate the rate coefficients and compare them with new experimental measurements of the vibrational relaxation of CO by 4He and 3He at temperatures T ≤ 295 K.
More recently, Kobayashi et al. () have redetermined the CO–He interaction potential and computed also the corresponding CO–H2 potential. Using their results, we have calculated the cross-sections and rate coefficients for the rovibrational excitation of CO by helium and also by ortho- and para-H2, which are the principal exciting species in the molecular gas of the interstellar medium. Peterson & McBane () undertook a new and detailed study of the CO–He interaction potential, from which they computed rovibrationally inelastic cross-sections and the v = 1 → 0 relaxation rate coefficient for T ≤ 1500 K. Their calculations, and the experimental measurements, provide a means of gauging the reliability of the present calculations for the CO–He system and, by inference, for the astrophysically more important CO–H2 system, which is the primary concern of the present study.
In Section , we summarize the methods that we have used to perform the calculations. In Section , we present our results and make comparisons with previous studies of the CO–H2 and CO–He collision processes. Our concluding remarks are made in Section .
Method
We present first the approach that we adopted for the simpler CO–He system and then proceed to consider CO–H2.
CO-He
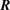and the internuclear vector, 
, of the molecule, in the range of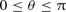 
; and for three values of the internuclear separation, r = 1.898 a0, 2.132 a0 and 2.234 a0, where r = 2.132 a0 is the CO equilibrium bond length. Their results, for each value of r, may be fitted to an expansion in terms of Legendre polynomials, Pλ(cos θ), of the form: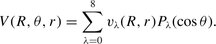 
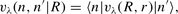
When evaluating the collisional rate coefficients, we used a basis of CO eigenstates that comprised rotational states 0 ≤ j ≤ 14 in each of the three vibrational manifolds n = 0, 1 and 2. The molcol collision code (Flower et al. ) was used in the production calculations, with the Johnson–Manolopoulos method of integrating the coupled differential equations (Manolopoulos ). Both the CO basis set and the numerical method for solving the scattering equations were varied in order to establish the precision of the numerical results. We found no significant dependence on the numerical method; but cross-sections for transitions involving levels at the periphery of the rotational basis were susceptible to change as the basis was extended.
In addition to the potential of Kobayashi et al. (), we employed the multiparameter fit, by Wickham-Jones et al. (; subject to the minor corrections given by Reid et al. ), to the CO–He interaction potential computed by Thomas et al. () and Schinke & Diercksen (). Using this fit, the interaction potential could be generated on a finer grid of values of the atom–molecule separation, R. Furthermore, the potential could be extended to R > 9 a0, which was the limit of the calculations by Kobayashi et al. () and beyond which we had assumed a rapid (exponential) decrease of the interaction towards zero. In practice, we used a grid in the range of 2.6 ≤ R ≤ 20 a0, in steps of 0.2 a0.
CO–H2
, between the H2 internuclear vector, r2, and the vector, R, joining the centres of mass of the two molecules; the relative angle of rotation, ϕ = ϕ2 − ϕ1, of the CO and H2 internuclear axes about the intermolecular vector R; and the H2 internuclear separation, r2. As in the case of CO–He, Kobayashi et al. () computed the CO–H2 interaction potential, V, for nine values of R in the range of 4 ≤ R ≤ 9 a0, for nine values of θ1 in the range of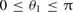 
, and for three values of the CO internuclear separation, r1 = 1.898 a0, 2.132 a0 and 2.234 a0; the H2 internuclear separation was fixed at its equilibrium value, r2 = 1.4 a0, and the potential was given for ϕ = 0 only, in view of the weak dependence of the interaction energy on the value of this relative angle that they had found. Using their data for θ2 = 0 and π/2, the interaction potential may be fitted to the functional form required by the molcol program, namely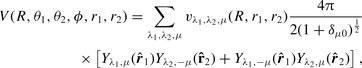 
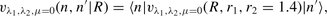
When evaluating the cross-sections, a basis of CO rotational eigenstates 0 ≤ j1 ≤ 14 in each of the three vibrational manifolds n = 0, 1 and 2 was used for collisions with para-H2 (j2 = 0). For collisions with ortho-H2 (j2 = 1), a smaller CO rotational basis, 0 ≤ j1 ≤ 9, was employed. The Johnson–Manolopoulos option was adopted in the molcol molecular scattering code. The cross-sections, σ(E), were computed on a grid of collision energies in the range of 200 ≤ E/kB ≤ 20 000 K for para-H2 and 200 ≤ E/kB ≤ 16 500 K for ortho-H2. At the highest energies, several hundred partial waves were necessary to converge the rotationally inelastic, but vibrationally elastic, cross-sections: pure rotational transitions can be induced at relatively long range. Far fewer partial waves are required to converge only the vibrationally inelastic cross-sections.
is the mean relative collision velocity, T is the kinetic temperature and 
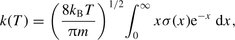
is the reduced mass of the CO–H2 system. The rate coefficients could be evaluated reliably up to temperatures T ≈ 2000 K by this means. The rate coefficients for excitation, k′(T), were obtained from the detailed balance relation: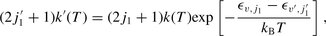 
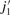are the rotational quantum numbers of the upper and lower CO rovibrational states, respectively, and 
, 
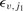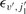are their corresponding energies, relative to the v = 0 = j1 ground state.RESULTS AND DISCUSSION
From the viewpoint of the dynamics of rovibrationally inelastic collisions, the main limitation of the potential energy calculations by Kobayashi et al. () is the sparseness of the grid of values of R, the CO–H2 (He) separation, and of the grid of values of r1, the CO internuclear distance. Kobayashi et al. tabulated results for only nine values of R and three values of r1. We have varied other parameters which intervene in the scattering calculations, notably the size of the CO rovibrational basis set and the numerical method used to integrate the coupled differential equations, and found no significant variations in the magnitude of the CO vibrational relaxation cross-sections, considered below. Fortunately, the uncertainties associated with the sparseness of the grids are most pronounced at low (near threshold) energies, where the cross-sections become very small. At higher energies, the values of the rovibrationally inelastic cross-sections should be more reliable; and it is at higher energies, where the cross-sections are larger, that this process is significant. Furthermore, the cross-sections for rotationally inelastic, but vibrationally elastic, transitions were found to be less sensitive to the sparseness of the potential grids.
Collisions with He
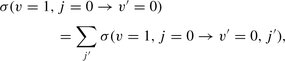
The cross-section for the vibrational relaxation, v = 1, j = 0 → v′ = 0, of CO in collisions with He; results obtained with the potential of Kobayashi et al. (2000) and with the potential fit adopted by Reid et al. (1995) are compared. The cross-section is plotted as a function of the collision energy, expressed relative to the upper v = 1, j = 0 level. The molscat computations of Reid et al. (1995) were in the coupled states (CS) approximation; the present molcol computations employ the full coupled channels (CC) method.
It may be seen from Fig. 1 that the values of the vibrational relaxation cross-section that we calculate, using the two different potentials, are in satisfactory agreement, differing by less than a factor of 2 over the entire energy range. On the other hand, our results exceed those of Reid et al. (), by a factor of approximately 3 at the highest energy (E1, 0 = 3657 cm−1) that they considered and by about an order of magnitude at E1, 0 ≈ 1000 cm−1. Reid et al. used an angular momentum decoupling approximation – the ‘coupled states’ (CS) approximation – in their calculations of the cross-section. In the present ‘coupled channels’ (CC) calculations, this approximation is no longer made; but the discrepancies with the results of Reid et al. are larger than would arise from their use of the decoupling approximation alone. In addition, test calculations have shown that the differences in the CO rovibrational basis sets that were employed are not responsible for the discrepancies.
At lower collision energies, the relaxation cross-section computed by Reid et al. decreases to values of the order of 10−25 cm2, whereas our results fall to ‘only’ 10−21 cm2. Such cross-sections are extremely small: 10−24 cm2 (1 barn) is the natural unit for nuclear reactions, as compared with 10−16 cm2 for atomic and molecular scattering processes. The decrease in the cross-section towards threshold occurs because of the increasing disparity in the values of the de Broglie wavelength in the initial and final scattering channels, which leads to cancellation when calculating the corresponding potential matrix element. Our technique, which involves cubic spline interpolation of the potential expansion coefficients on a grid values of R, appears to fail to yield the vibrationally inelastic matrix elements accurately in the region close to threshold, where they become extremely small. Test calculations with molcol, in which we adopted the illustrative atom-vibrating rotor potential2 provided as part of the documentation of the molscat code3, confirmed this to be the case. However, by the same token, the region near threshold is not material to determinations of the rate coefficients for vibrationally inelastic transitions at temperatures that are sufficiently high for this process to be significant in the interstellar medium.
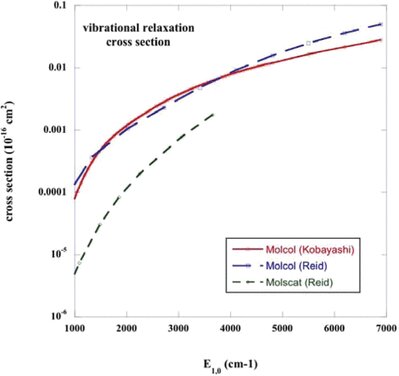
The rate coefficient for CO v = 1, j = 0 → v′ = 0 vibrational relaxation is plotted in Fig. 2; results are shown for collisions not only with He but also with ortho- and para-H2, considered below. In interstellar molecular clouds, collisions with H2 will dominate this process, owing to its larger rate coefficients and higher number density [n(H2)/n(He) ≈ 5]. Also plotted in Fig. 2 are the experimental measurements of the rate coefficient for vibrational relaxation of CO in He, reported by Wickham-Jones et al. () and the results of the CS calculations by Peterson & McBane (2005).
The rate coefficient, k1 − 0, for the vibrational relaxation, v = 1, j = 0 → v′ = 0, of CO in collisions with He and with ortho- and para-H2; the results were obtained with the potentials of Kobayashi et al. (2000). The experimental measurements of Chenery (1984) for CO–He, reported by Wickham-Jones et al. (1987), are shown as the vertical crosses and the results of the computations by Peterson & McBane (2005) are shown by the diagonal crosses, connected by the broken curve. The rate coefficient is plotted as a function of the kinetic temperature.
Peterson & McBane () computed a much larger number of ab initio points on the CO–He potential energy surface than was available to Wickham-Jones et al. (). They interpolated their ab initio energies using a procedure developed by Ho & Rabitz (), which differs from that employed earlier by Wickham-Jones et al. () and appears to be better adapted to interpolation at long than at short range. Peterson & McBane were able to use a higher order expansion in terms of both r, the CO intramolecular distance, and θ, the relative CO–He orientation angle, when calculating the collision cross-sections. In addition, they determined the rovibrational eigenstates numerically for each of the CO energy levels, which represents an improvement on the adoption of harmonic oscillator eigenstates. Combined with the use of large rovibrational basis sets in the CS calculations, these improvements make their study of rovibrational scattering of CO on He the most sophisticated and almost certainly the most accurate to date.
The vibrational relaxation rate coefficient computed by Peterson & McBane () is in good agreement with the measurements up to the highest temperature (T = 1500 K) for which they tabulate its values. It may be seen from Fig. 2 that, whilst the present calculations exceed the experimental measurements and the results of Peterson & McBane () at the lower temperatures, they are in satisfactory agreement with the measurements by T ≈ 2000 K; this agreement confirms the validity of our results at temperatures that are sufficiently high for the process of vibrational excitation to assume importance.
Collisions with H2
The most recent calculations of pure rotationally inelastic scattering of CO on H2 were performed by Yang et al. (), who used the CO–H2 interaction potential computed by Jankowski & Szalewicz (). In an earlier study of the rotational excitation of CO by H2, Flower () used a previous determination of the interaction potential by these same authors (Jankowski & Szalewicz ). The rate coefficients calculated by Yang et al. () are generally in good agreement with the determinations of Flower (), for transitions between rotational states that are common to the two studies. Such an outcome is unsurprising, given that the interaction potentials have the same pedigree. It is instructive to compare these rate coefficients with those obtained with the CO–H2 potential of Kobayashi et al. (), which was calculated independently, using different techniques.
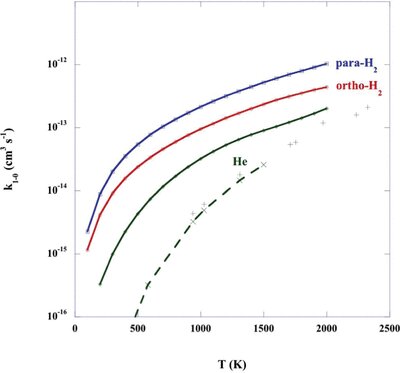
In Figs 3 and 4, we compare the temperature dependence of the rate coefficients for the CO rotational transitions j1 = 2 → 1 and j1 = 2 → 0, induced by collisions with ortho- and para-H2, respectively; the present results and those of Yang et al. () and Flower () are displayed in these figures. Towards low temperatures, 
K, the present values of the rate coefficients, which were obtained with the potential of Kobayashi et al. (), fall away rapidly; this behaviour is a consequence of the (non-physical) exponential decrease that was imposed on the potential beyond the largest value of the intermolecular distance (R = 9 a0) for which Kobayashi et al. tabulated their results. On the other hand, for T ≳100 K all three determinations of both rate coefficients, k2 → 1 and k2 → 0, agree well. The discrepancies in k2 → 0 are somewhat larger for collisions with ortho-H2 (j2 = 1) than para-H2 (j2 = 0); but this outcome is unsurprising, given the higher dimensionality of the potential coupling in the case of j2 > 0.
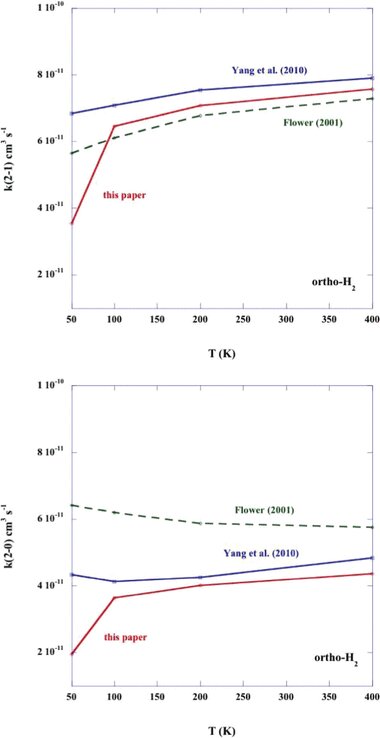
Rate coefficients for the rotational de-excitation of CO (v = 0; j = 2 → 1 and j = 2 → 0) by ortho-H2. The results of the present calculations are compared with those of Yang et al. (2010) and Flower (2001).
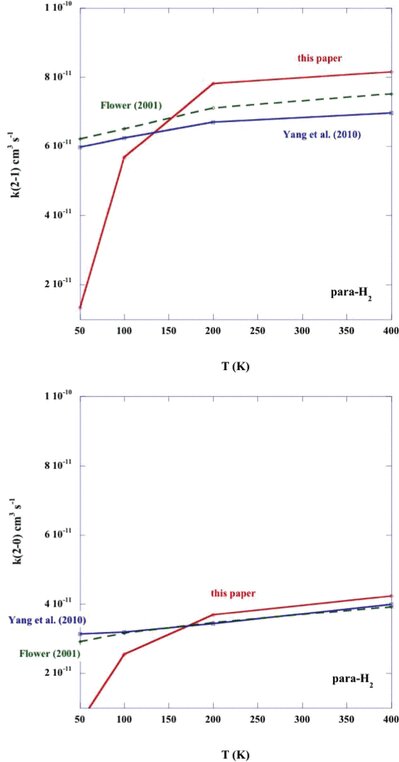
Rate coefficients for the rotational de-excitation of CO (v = 0; j = 2 → 1 and j = 2 → 0) by para-H2. The results of the present calculations are compared with those of Yang et al. (2010) and Flower (2001).
For a few collision energies, we recomputed the cross-sections for rotationally inelastic transitions in CO, induced by collisions with H2, using the same CO bases (0 ≤ j1 ≤ 29 for collisions with para-H2; 0 ≤ j1 ≤ 20 for collisions with ortho-H2) as Flower (); the potential of Kobayashi et al. () was employed. In Fig. 5, the cross-sections for transitions j1 → j1 − 1 are compared at two illustrative collision energies, E = 2000 and 20 000 K, for collisions with para-H2 (j2 = 0). At the lower collision energy, channels only up to j1 = 26 are open, i.e. levels j1 > 26 have excitation energies 
K. The energy defects of the transitions, 
, increase approximately linearly with the rotational quantum number, j1; BCO = 2.8 K is the CO rotational constant. As may be seen from Fig. 5, the cross-sections, σ(j1 → j1 − 1), computed with the two independent interaction potentials, agree reasonably well, except for j1 ≳15 at the lower collision energy, E = 2000 K. However, the values of the cross-sections decrease rapidly beyond j1 ≈ 15, owing to the increasing energy defects of the transitions, and so the largest discrepancies are for the smallest cross-sections.
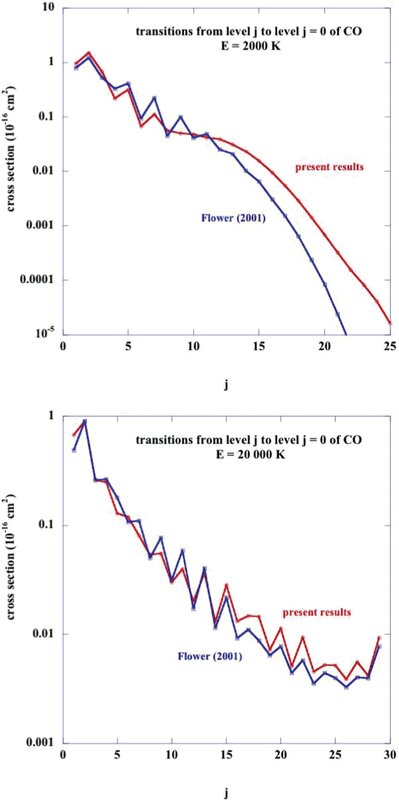
Cross sections for rotational transitions j → j − 1 within the v = 0 vibrational ground state of CO, at two illustrative collision energies, E = 2000 K and E = 20000 K; the collision partner is para-H2. Cross-sections calculated by Flower (2001), using the potential of Jankowski & Szalewicz (1998), are compared with the present results, obtained with the potential of Kobayashi et al. (2000); the same CO rotational basis (0 ≤ j ≤ 29) was used in both of these calculations.
Bacić et al. () computed cross-sections for the vibrational relaxation v = 1, j = 0 → v′ = 0 of CO by both para- and ortho-H2. They employed their own determination of the CO–H2 interaction potential (Schinke et al. ) and studied collision energies 
K in the CS approximation, extending to E ≈ 2800 K in the ‘infinite-order sudden’ (IOS) approximation to the rotational motion of the CO molecule. In the range of collision energies up to E ≈ 1000 K, cross-sections deriving from these two approximations agreed to within a factor of 2, in the case of collisions with para-H2, treated as a structureless perturber. The vibrational relaxation rate coefficients at low temperatures (
K) were found to be in satisfactory agreement with experimental measurements for CO–para-H2 but not for CO–ortho-H2: the calculated rate coefficients were found to be similar in magnitude for both ortho- and para-H2.
In Fig. 6, we compare the results of Bacić et al. (), for collisions with para-H2 (j2 = 0), with our own determination of the v = 1, j = 0 → v′ = 0 vibrational relaxation cross-section, obtained in the CC approximation, using the potential of Kobayashi et al. (). The values of the relaxation cross-section that we obtain may be seen to exceed those computed by Bacić et al., increasingly so as threshold is approached. In this respect, the comparison is reminiscent of that for collisions with He, shown in Fig. 1. We believe that the discrepancies in the cross-sections at low collision energies arise, once again, from our use of cubic spline interpolation of the R dependence of the potential expansion coefficients, 
(cf. equation ) on the sparse grid of values of R for which Kobayashi et al. () calculated the interaction energy. Although Bacić et al. used cubic spline interpolation on a similarly sparse R grid in their calculations, they interpolated not the energies themselves but their logarithms, with negative values being accommodated by the addition of sufficiently large constant energies: see Schinke et al. (). This approach is better adapted to the calculation of the vibrational coupling matrix elements, which depend on the behaviour of the potential at short range, where it varies exponentially. However, the same approach is less appropriate when calculating pure rotational coupling matrix elements, which are more dependent on the form of the potential in the region of its minimum.
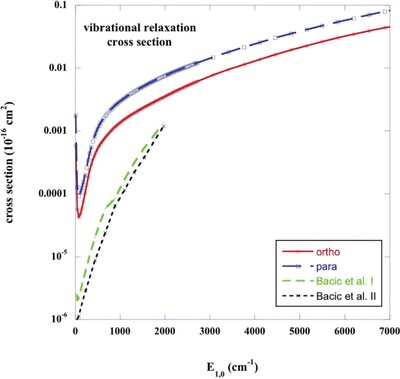
The cross-section for the vibrational relaxation, v = 1, j = 0 → v′ = 0, of CO in collisions with H2. The results displayed for para-H2 ( j2 = 0) and ortho-H2 ( j2 = 1) collisions were obtained with the potential of Kobayashi et al. (2000). Also shown are the calculations of Bacić et al. (1985a,b); labelled I and II, respectively) for para-H2 ( j2 = 0).
Test calculations have shown that these alternative methods of interpolation give rise to differences in the behaviour of the expansion coefficients, between the grid points, that are significant for calculations of the corresponding vibrational coupling matrix elements, as threshold is approached and cancellation becomes pronounced. These differences – in the ab initio determinations of the CO–H2 interaction potential and in the interpolation procedures – are sufficient in themselves to account for the discrepancies in the corresponding cross-sections at low collision energies.
Our computed values of the rate coefficients for the vibrational relaxation of CO in ortho- and para-H2 are plotted in Fig. 2. That the rate coefficients are smaller in the case of ortho-H2 is at least partly attributable to the reduced CO rotational basis (j1 ≤ 9) that was used in this case, which restricts the summation over j′ in equation . However, we note that the measurements of the rate coefficients at temperatures T ≤ 300 K, with which Bacić et al. (, fig. 3) compared, show the values for para-H2 to exceed those for ortho-H2.
Concluding remarks
We have computed cross-sections and rate coefficients for the rovibrational excitation of CO by ortho- and para-H2 and by He; the H2 molecules were constrained to their rotational ground states. The cross-sections for the pure rotational excitation of CO were found to agree well with previous calculations. The cross-sections for vibrational relaxation of the first vibrationally excited level are overestimated near threshold, where they exceed previous determinations, but agreement improves with increasing collision energy. Because the cross-sections for vibrationally inelastic transitions become extremely small as threshold is approached, the values of the rate coefficients for excitation of the vibrationally excited states from the vibrational ground state should not be affected significantly by these discrepancies, at the kinetic temperatures for which vibrational excitation assumes significance. The complete sets of rate coefficients are available as Supporting Information with the online version of the article: Tables 1– 3 for transitions induced by He, ortho-H2 and para-H2, respectively.
Acknowledgment
I thank Jeremy Hutson for information relating to the molscat code of Hutson & Green () and the referee for drawing my attention to the work of Peterson & McBane ().
References
1 cm−1 ≡ 1.4388 K
