-
PDF
- Split View
-
Views
-
Cite
Cite
A. C. Becker, D. Homrighausen, A. J. Connolly, C. R. Genovese, R. Owen, S. J. Bickerton, R. H. Lupton, Regularization techniques for PSF-matching kernels - I. Choice of kernel basis, Monthly Notices of the Royal Astronomical Society, Volume 425, Issue 2, September 2012, Pages 1341–1349, https://doi.org/10.1111/j.1365-2966.2012.21542.x
Close - Share Icon Share
Abstract
We review current methods for building point spread function (PSF)-matching kernels for the purposes of image subtraction or co-addition. Such methods use a linear decomposition of the kernel on a series of basis functions. The correct choice of these basis functions is fundamental to the efficiency and effectiveness of the matching – the chosen bases should represent the underlying signal using a reasonably small number of shapes, and/or have a minimum number of user-adjustable tuning parameters. We examine methods whose bases comprise multiple Gauss–Hermite polynomials, as well as a form-free basis composed of delta-functions. Kernels derived from delta-functions are unsurprisingly shown to be more expressive; they are able to take more general shapes and perform better in situations where sum-of-Gaussian methods are known to fail. However, due to its many degrees of freedom (the maximum number allowed by the kernel size) this basis tends to overfit the problem and yields noisy kernels having large variance. We introduce a new technique to regularize these delta-function kernel solutions, which bridges the gap between the generality of delta-function kernels and the compactness of sum-of-Gaussian kernels. Through this regularization we are able to create general kernel solutions that represent the intrinsic shape of the PSF-matching kernel with only one degree of freedom, the strength of the regularization λ. The role of λ is effectively to exchange variance in the resulting difference image with variance in the kernel itself. We examine considerations in choosing the value of λ, including statistical risk estimators and the ability of the solution to predict solutions for adjacent areas. Both of these suggest moderate strengths of λ between 0.1 and 1.0, although this optimization is likely data set dependent. This model allows for flexible representations of the convolution kernel that have significant predictive ability and will prove useful in implementing robust image subtraction pipelines that must address hundreds to thousands of images per night.
Introduction
Studies of variability in astronomy typically use image subtraction techniques in order to characterize the magnitude and type of the variability. This practice involves subtracting a prior-epoch [generally high signal-to-noise (S/N)] template image from a recent science image; any flux remaining in their difference may be attributed to phenomena that have varied in the interim. This technique is sensitive to both photometric and astrometric variability and can uncover variability of both point sources (such as stars or supernovae; e.g. Sako et al. ; Udalski et al. ) and extended sources (such as comets or light echoes; e.g. Newman & Rest ). Successful application of this technique shows that it is sensitive to variability at the Poisson noise limit in a variety of astrophysical conditions (Alard & Lupton ; Alard ; Bramich ; Kerins et al. ) and in this regard may be considered optimal.
There are several reasons for preferring such an approach over catalogue-based searches. First, many types of variability are found in confused regions of the sky, and it may be difficult to deblend the time-variable signal from the non-temporally-variable surrounding area. This is particularly true for supernovae and active galactic nuclei, which are typically blended with light from their host galaxies. However, such confusion is not limited to stationary objects. Moving Solar system bodies may serendipitously yield false brightness enhancements in the measurement of a background object if the impact parameter is small compared to the image's point spread function (PSF). For this reason, removal of non-variable objects is preferred before attempting to characterize variable sources in images.
Image subtraction is also an efficient technique as the vast majority of pixels in an image do not contain signatures of astrophysical variability. Any pixel-level analysis of a difference image will, therefore, be restricted to those sources that are temporally variable (as opposed to analysing all sources within an image). While many variants of this technique have been published (Tomaney & Crotts ; Alard & Lupton ; Bramich ; Albrow et al. ) and many versions implemented in automated variability-detection pipelines (Bond et al. ; Rest et al. ; Darnley et al. ; Miller, Pennypacker & White ; Udalski et al. ), there does remain room for improvement in the robustness of the image subtraction and in the reduction of subtraction artefacts. We refer the reader to Wozniak () for an in-depth summary on the practical application of these image subtraction techniques.
Image subtraction
In image subtraction we assume that we have two images of the same portion of the sky, taken at different epochs, but in the same filter. We will call the image that contains the variability of interest the ‘science’ image and the template image to be subtracted the ‘reference’ image. The images will, in general, be astrometrically misaligned, but this can be resolved by using sinc-based image registration methods that preserve the noise properties of the original image. In practice, windowed sinc functions are used that do introduce covariance between the pixels; there is a direct trade-off between the size of the warping kernel and the degree of correlation after registration (the correlation trends to zero as the window becomes infinite in extent). After astrometric alignment, a given astrophysical object will be represented in the reference image as a sub-array of pixels R(x, y) and in the science image as S(x, y), with the same span in x and y. Each image will, however, have a different PSF, which is the spatial response of a point source due to the atmosphere, telescope optics and instrumental signatures. PSF matching of the images is required before we can subtract one image from the other and is the essence of the image subtraction technique.
PSF MATCHING
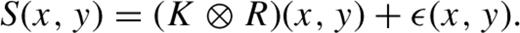
Linear modelling of K(u, v)
As inputs to the PSF-matching technique, we assume that images are astrometrically registered and background subtracted (while the latter constraint is not a necessity, it does enable us to restrict our analysis here to the respective shapes of the PSFs). To proceed, we make the assumption that K(u, v) may be modelled as a linear combination of basis functions Ki(u, v), such that K(u, v) = ∑iaiKi (u, v) (Alard & Lupton ). The basis components do not have to be orthonormal, nor does the basis need to be complete (indeed, it may be overcomplete). However, it is desirable to choose a shape set that compactly describes K(u, v), such that the number of required terms is small.

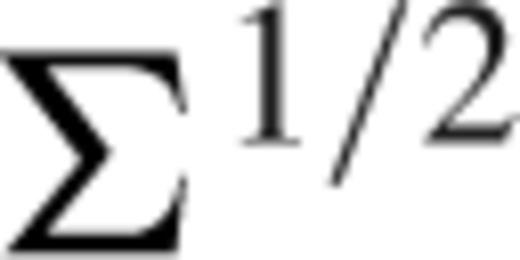 (which must exist as covariance matrices are positive definite and hence invertible) we obtain the modified equation
(which must exist as covariance matrices are positive definite and hence invertible) we obtain the modified equation 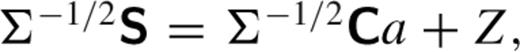
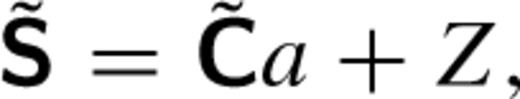
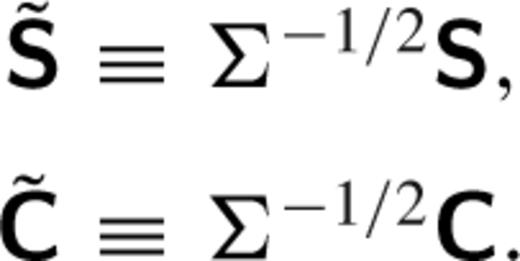
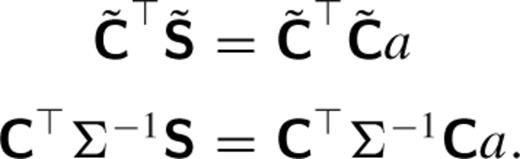
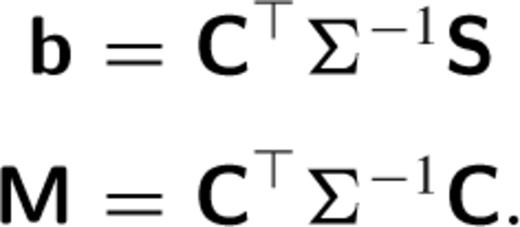
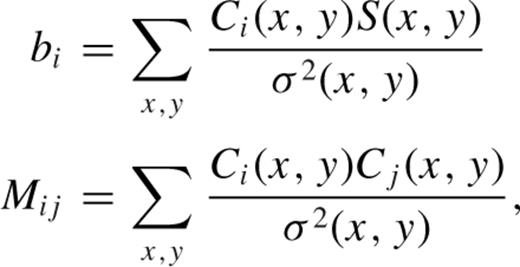
The least-squares estimate for a is  . A difference image is then constructed as
. A difference image is then constructed as  . Because the estimate of
. Because the estimate of  is explicitly dependent on both S(x, y) and R(x, y), the residuals in the difference image may not necessarily follow a normal
is explicitly dependent on both S(x, y) and R(x, y), the residuals in the difference image may not necessarily follow a normal  distribution1, with σ2 ≠ 1 due to this covariance. The residuals should however have a flat power spectral density.
distribution1, with σ2 ≠ 1 due to this covariance. The residuals should however have a flat power spectral density.
Invertability of ![graphic]()
When a large set of basis functions is used, the matrix  may be ill-conditioned or even singular. This can be quantified by the ‘condition number’ of M, which we define as the ratio of the largest to the smallest eigenvalues. When the condition number is large, inversion of M will be numerically unstable or infeasible.
may be ill-conditioned or even singular. This can be quantified by the ‘condition number’ of M, which we define as the ratio of the largest to the smallest eigenvalues. When the condition number is large, inversion of M will be numerically unstable or infeasible.
A common approach when trying to invert an ill-conditioned matrix is to compute instead a pseudo-inverse, or an approximation to one in which eigenvalues that are numerically small are zeroed out. As M is symmetric, we can decompose it as  with V an orthogonal matrix and
with V an orthogonal matrix and  with eigenvalues d1 ≥ d2 ≥ ⋅⋅⋅ ≥ dn ≥ 0. We define
with eigenvalues d1 ≥ d2 ≥ ⋅⋅⋅ ≥ dn ≥ 0. We define  to be a truncation of D where d1/di + 1 becomes too large. Then, we define the pseudo-inverse of Di as
to be a truncation of D where d1/di + 1 becomes too large. Then, we define the pseudo-inverse of Di as  . Note that this allows for the definition of a pseudo-inverse of M as
. Note that this allows for the definition of a pseudo-inverse of M as  . Analogous to Di, define ssVi to be the same as the matrix Vi in the first i columns and zero elsewhere. Typically this truncation threshold is defined by the machine precision of the computation (e.g. for double-valued calculations,
. Analogous to Di, define ssVi to be the same as the matrix Vi in the first i columns and zero elsewhere. Typically this truncation threshold is defined by the machine precision of the computation (e.g. for double-valued calculations,  ). However, significantly larger limits for dmin may be used to avoid underconstrained parameters, such as in Section .
). However, significantly larger limits for dmin may be used to avoid underconstrained parameters, such as in Section .
SUM-OF-GAUSSIAN BASES
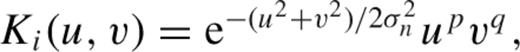
The number N and width σn of the Gaussians, as well as spatial order of the polynomials On, are configurable but are not fitted parameters in the linear least-squares minimization. Therefore these are tuning parameters of the model. Typically, a priori information such as the widths of the image PSFs is used to choose these values (e.g. Israel, Hessman & Schuh ). In a representative implementation (Smith et al. ), three Gaussians are used, with the narrowest Gaussian expanded out to order 6, the middle to order 4 and the widest to order 2. This leads to a total of 49 basis functions used in the kernel expansion.
The practical application of this algorithm has been very successful, and it has been used by various time-domain surveys such as MACHO (Alcock et al. ), OGLE (Wozniak ; Udalski et al. ), MOA (Bond et al. ), SuperMACHO (Smith et al. ; Rest et al. ), the Deep Lens Survey (Becker et al. ), ESSENCE (Miknaitis et al. ), the SDSS-II Supernova Survey (Sako et al. ) and most recently analysis of commissioning data from Pan-STARRS (Botticella et al. ).
The top row of Fig. 1 shows an instance of successful PSF matching using this sum-of-Gaussians basis. The first column represents a high-S/N image of a star R(x, y) generated from an image co-addition process applied to data from the Canada–France–Hawaii Telescope (CFHT). The second column shows this same star, aligned with the template image to sub-pixel accuracy, in a single science image S(x, y). The star is obviously asymmetric, potentially due to optical distortions such as focus or astigmatism, or due to tracking problems during acquisition of the image. The PSF-matching kernel thus will need to take the symmetric R(x, y) and elongate it along a vector oriented approximately 135° from horizontal. The first row, third column shows the best-fit PSF-matching kernel using N = 3 Gaussians with σn = [0.75, 1.5, 3.0] pixels and each modified by Hermite polynomials of the order of On = [4, 3, 2], respectively. The total number of terms in the expansion is 31. The first row, right column shows the resulting difference image D(x, y). The subtraction is obviously very good, with the remaining pixels described by a  distribution.
distribution.
![Difference imaging results when using a sum-of-Gaussian basis. The first column shows the reference image to be convolved R(x, y), the second shows the science image S(x, y) the reference is matched to, the third column shows the best-fit 19 × 19 pixel PSF-matching kernel K(u, v) and the fourth column shows the resulting difference image D(x, y). Row 1: results when using a basis set with σn = [0.75, 1.5, 3.0] pixels, On = [4, 3, 2]. Row 2: results when the images are misregistered by 3 pixels in both coordinates, requiring significant off-centre power in the kernel. Row 3: results when the basis Gaussians are too large compared to the actual PSF-matching kernel (σn = [3.0, 5.0] pixels, On = [3, 2]). Row 4: results when the polynomial expansion is not carried to high enough order (σn = [0.75, 1.5, 3.0] pixels, On = [1, 1, 1]).](https://oup.silverchair-cdn.com/oup/backfile/Content_public/Journal/mnras/425/2/10.1111/j.1365-2966.2012.21542.x/2/m_425-2-1341-fig001.jpeg?Expires=1750554497&Signature=MAAFnb83RNVoBlHBK9Qey1scIVbToL3ZRRPBQTxvWClqZurP-6V8yTAru3MykEgfPZna1TXutAxmPZ35PE0ofFD9QsKWCGRh~OpRtMF0YYB83dqYoiSgzuUuGv0N83OrFePnkrpIMkcljy-xN9oVzVZlt7PnNG1SxqKEQEs1EQCN8sq6ooMGdb52L2ecJfkD1hLwgNTnMhx3jUCkS~t6QVwvM-gxOvOIM6ZHFlqFNl02Nqfu~L7ENZ9vjZ2cyuh56YLuw2x8f1czDxx8IBwn2YNyb6sz3efG2yuMlKiIRMIemVpmpGbKSeBed85YgGSAuzhwl-eRA6higFceX6DKAQ__&Key-Pair-Id=APKAIE5G5CRDK6RD3PGA)
Difference imaging results when using a sum-of-Gaussian basis. The first column shows the reference image to be convolved R(x, y), the second shows the science image S(x, y) the reference is matched to, the third column shows the best-fit 19 × 19 pixel PSF-matching kernel K(u, v) and the fourth column shows the resulting difference image D(x, y). Row 1: results when using a basis set with σn = [0.75, 1.5, 3.0] pixels, On = [4, 3, 2]. Row 2: results when the images are misregistered by 3 pixels in both coordinates, requiring significant off-centre power in the kernel. Row 3: results when the basis Gaussians are too large compared to the actual PSF-matching kernel (σn = [3.0, 5.0] pixels, On = [3, 2]). Row 4: results when the polynomial expansion is not carried to high enough order (σn = [0.75, 1.5, 3.0] pixels, On = [1, 1, 1]).
Limitations of the model
The intrinsic symmetries of Hermite polynomials (symmetric for even order, anti-symmetric for odd order) mean that the Gauss–Hermite bases possess a high degree of symmetry about the central pixel. This makes it difficult to concentrate the kernel power off-centre when using an incomplete basis expansion. Such functionality is necessary when the flux needs to be redistributed on the scale of the kernel size, such as when there are astrometric misalignments. While it is possible to compensate for misalignment using kernels derived from this basis, this requires concentrating the kernel strength in the high-order terms. There are practical limitations to the efficacy of this including the scale and orientation of the required shift and the number of basis terms used.
As a concrete example, the second row in Fig. 1 shows the best-fit kernel derived when there is a 3-pixel shift in both the x and y directions. The kernel needs to have power in the first quadrant (upper-right) at the scale of 3 pixels. The image of the kernel (third column) shows that while it is obviously able to do so, the matching suffers in the third quadrant, as the difference image shows obvious residuals. These pixels result in an unacceptable  distribution; recall that we were able to yield σ2 = 1.01 for well-registered images (top row).
distribution; recall that we were able to yield σ2 = 1.01 for well-registered images (top row).
Another limitation of the model is that there are a variety of tuning parameters. This includes the number of Gaussians in the basis, their widths and their spatial orders. These parameters are typically chosen using a set of heuristics. If there is a mismatch compared to the true underlying kernel, this process will fail. The third row of Fig. 1 shows PSF-matching results when the basis Gaussians are too big and are unable to reproduce the small-scale differences in the PSFs. This yields obvious residuals in the difference image, which follow a  distribution. The fourth row of Fig. 1 shows results when the Gauss–Hermite polynomials are not allowed to vary to high enough order, also yielding unacceptable
distribution. The fourth row of Fig. 1 shows results when the Gauss–Hermite polynomials are not allowed to vary to high enough order, also yielding unacceptable  residuals in the difference image.
residuals in the difference image.
Clearly the results of this process are sensitive to the choice of several tuning parameters, which makes this difficult to implement robustly. In a statistical sense, selection of tuning parameters (which includes selecting the number of basis functions used) usually has a much larger effect on performance than does the choice of basis functions. A process that results in a reduction in the number of kernel tuning parameters, while maintaining the quality of the difference images, would greatly improve the effectiveness of this method.
DELTA-FUNCTION BASES
The most general technique for modelling K(u, v) is to use a ‘shape-free’ basis, which consists of a delta-function at each kernel pixel index: Kij(u, v) = δ(u − i)δ(v − j). A kernel of size 19 × 19 will then have 361 orthonormal, single-pixel bases. In this situation there are no tuning parameters, which is an obvious benefit. However, in any choice of basis there is a trade-off between flexibility in the forms the fitted function can take and variability in the resulting fit (the so-called ‘bias-variance’ trade-off). The delta-function basis provides complete flexibility, and as such can account for features such as arbitrary off-centre power required to compensate for astrometric misregistration (e.g. Bramich ). But to avoid gross overfitting, that flexibility needs to be tempered to keep the variance in check.
Fig. 2 shows the results of PSF matching using such a basis, using the same objects as in Fig. 1. The top row demonstrates the results for exactly aligned images, while the bottom row demonstrates the results for images misaligned by 3 pixels in both x and y. The difference images are qualitatively similar. However, the best-fit solutions obviously yield large variations within the kernels themselves, and do not match expectations of what the actual kernel should look like. The reason for this can be found in the distribution of pixels residuals in the difference image. Both images follow a  distribution. This indicates that the residuals have lower variance than Gaussian statistics would suggest. Indeed, in Fig. 2, column 4, the residuals appear smoother than random noise. This is impossible unless we have overestimated the variance in our images, or unless the kernels themselves are removing some fraction of the noise.
distribution. This indicates that the residuals have lower variance than Gaussian statistics would suggest. Indeed, in Fig. 2, column 4, the residuals appear smoother than random noise. This is impossible unless we have overestimated the variance in our images, or unless the kernels themselves are removing some fraction of the noise.

Difference imaging results when using a delta-function basis. Columns are the same as in Fig. 1. Row 1: results when using an unregularized delta-function basis. Row 2: results when the images are misregistered by 3 pixels in both coordinates.
The large numbers of basis shapes (361 degrees of freedom versus 31 for the sum-of-Gaussians) make it highly likely that we are overfitting the problem. The kernel thus has the ability to match both the underlying signal and the associated noise in the two images. So while this technique is optimal for matching pixels in two images – where those pixels are a combination of signal and noise – it is not necessarily optimal for uncovering the true PSF-matching kernel.
Current codes that use digital kernels (Bramich ; Albrow et al. ) are able to achieve relatively noise-free representations of the matching kernel by using all pixels in the image as constraints on K(u, v). Importantly, this technique has been generalized to allow construction of a spatial model of the kernel K(u, v, x, y), which must vary across an image due to spatial variation in the underlying PSF fields (e.g. Quinn, Clocchiatti & Hamuy ). In practice, these spatial models enable interpolation of the matching kernel at all locations in an image, using fitted kernels at particular locations as constraints on the global model.
In this context, one consequence of the overfitting is that the PSF-matching kernel derived for any given object may not be directly applied to neighbouring objects, since the solution is significantly driven by the local noise properties. These types of high variance estimators are particularly poor as inputs to interpolation routines, or as constraints on the spatial model of the kernel K(u, v, x, y). Below, we explore how introducing a certain amount of bias into this estimator can improve its performance.
DELTA-FUNCTION BASES WITH REGULARIZATION
The delta-function basis can flexibly fit a kernel of any form, but as we have shown, this flexibility is both its strength and weakness. As is, the method significantly overfits, absorbing substantial noise fluctuations into the fit and thus giving estimated kernels with excessive variance. A solution is to introduce some amount of bias into the fit to reduce the solution variance by a much larger factor [if ‘bias’ sounds pejorative, note that this is just a kind of smoothing; we note that digital kernel codes of Bramich () and Albrow et al. () achieve a degree of smoothing by using binned pixels in the outer portions of the kernels]. When fitting a smooth function such as K(u, v, x, y), we prefer fitted kernels for which nearby solutions do not vary too greatly. This bias will enable such a fit with vastly reduced mean-squared error.
Among the various approaches to dealing with overfitting, the most common are through linear regularization techniques (e.g. section 18.5; Press et al. ). Using these, we may penalize undesirable features of the fit, usually by adding a penalty term to our optimization criterion. For instance, when fitting a smooth function, we want to penalize fits f that are too rough or irregular. One way to do this is to add to the least-squares objective a term penalizing the second derivative, λ · ∫|f′′(x)|2dx. Here, the scaling factor λ is a tuning parameter that determines the balance between fidelity to the data and the desired smoothness. In the case of kernel matching, we may extend this idea with a two-dimensional penalty that approximates λ · ∫∫|∇f(x, y)|2 dx dy.

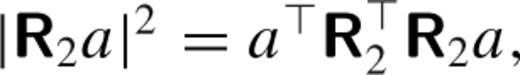
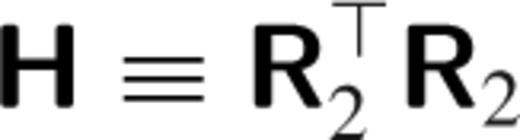 , which makes the second derivative penalty
, which makes the second derivative penalty  . This matrix is used to regularize the normal equations (equation ) with strength λ,
. This matrix is used to regularize the normal equations (equation ) with strength λ, 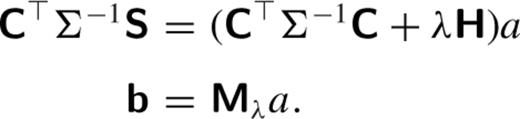
 . Here λ represents the strength of the regularization penalty, and is the sole tuning parameter in this model.
. Here λ represents the strength of the regularization penalty, and is the sole tuning parameter in this model.Fig. 3 shows results for the same set of objects displayed in Figs 1 and 2, but using regularization of the delta-function basis set. The top row shows the results for aligned images, and λ = 1. Note that the kernel looks very much as anticipated, being compact and having a shape aligned approximately 135° from horizontal. Residuals in the difference image follow a  distribution. The second row shows the results when the images are misaligned by 3 pixels in x and y. The kernel merely appears shifted by the same amount compared to the aligned images, and the difference image follows a quantitatively similar
distribution. The second row shows the results when the images are misaligned by 3 pixels in x and y. The kernel merely appears shifted by the same amount compared to the aligned images, and the difference image follows a quantitatively similar  distribution. This effectively demonstrates that this method can reproduce kernels with off-centre power. The third row shows the results with λ = 0.01; the shape of the PSF-matching component of the kernel is just barely discernible above its noise, suggesting that the regularization is too weak. The difference image is, however, acceptable [
distribution. This effectively demonstrates that this method can reproduce kernels with off-centre power. The third row shows the results with λ = 0.01; the shape of the PSF-matching component of the kernel is just barely discernible above its noise, suggesting that the regularization is too weak. The difference image is, however, acceptable [ ]. The fourth row shows the results with λ = 100. The kernel is far smoother than in previous runs. However, this appears to be at the expense of residuals in the difference image, which follow a
]. The fourth row shows the results with λ = 100. The kernel is far smoother than in previous runs. However, this appears to be at the expense of residuals in the difference image, which follow a  distribution. This suggests that too much weight has been given the smoothness of the kernel compared to the residuals in the difference image, indicating that the regularization is too strong. The general trend is that with increasing lambda, the variance in the difference image increases. The noise properties of the difference image evolve from being too smooth, to approximately white in spectrum, to having residual features at a similar scale as the kernel.
distribution. This suggests that too much weight has been given the smoothness of the kernel compared to the residuals in the difference image, indicating that the regularization is too strong. The general trend is that with increasing lambda, the variance in the difference image increases. The noise properties of the difference image evolve from being too smooth, to approximately white in spectrum, to having residual features at a similar scale as the kernel.

Difference imaging results when using a regularized delta-function basis. Columns are the same as in Fig. 1. Row 1: results when using a regularized delta-function basis with λ = 1.0. Row 2: results when the images are misregistered by 3 pixels in both coordinates, λ = 1.0. Row 3: results using ‘weak’ regularization of the kernel, with λ = 0.01. Row 4: results using ‘strong’ regularization of the kernel, with λ = 100.
Overall, this technique appears very effective. We are able to create general, compact kernels that represent the underlying shape of the PSF-matching kernel with only one tuning parameter, the strength of the regularization λ. The role of λ is effectively to exchange variance in the resulting difference image with variance in the kernel itself. By increasing the value of λ, we are able to smooth the kernel while increasing the variance in the difference image. We explore various methods to establish the optimal value of λ below.
Choice of tuning parameter »
Choosing a good tuning parameter is essential for good performance of a regularization method. If λ is too high, the fit will be too smooth (high bias, low variance); if λ is too low, the fit will be too rough (low bias, high variance). The goal of data-driven methods for choosing tuning parameters is to find the sweet spot in the bias-variance trade-off. While choosing a good value for λ is a hard statistical problem, there are a variety of methods that have proven successful in practice. These methods construct a statistical estimate of mean-squared error and choose λ to minimize it. For instance in cross-validation (reviewed in Kohavi ), the data set is broken into pieces, and each piece is left out in turn during the fit. The (prediction) mean-squared error is derived from the average-squared error of the fits in predicting the part of the data that was left out. Another approach, called empirical risk estimation (Stein ), uses the data themselves to compute an (unbiased) estimate of original fit's mean-squared error and chooses λ to minimize it. The theoretical justification for these methods is that, when properly done and with sufficiently large data sets, the chosen λ is close to the value that minimizes the corresponding mean-squared error function.
A second tuning consideration is that frequently a set of fitted kernels will be used to constrain a spatial model K(u, v, x, y) that will be applied to all pixels in an image. Therefore we must give a large weight to our ability to interpolate between the ensemble of kernel realizations used to constrain K(u, v, x, y). One metric for this is to examine the predictive power of a kernel derived from one object, and applied to a neighbouring object. At small separations, the quality of each difference image should be similar, indicating that the initial solution was not significantly driven by the local noise properties.
We explore the practical application of these ideas below using several sets of CCD images from the CFHT plus Megacam imager, calibrated using the ELIXIR pipeline of Magnier & Cuillandre (). The template image used is the median of several images into a single high-S/N representation of the field. The variance per pixel is determined from the image pixel values divided by the gain.
Empirical risk estimation
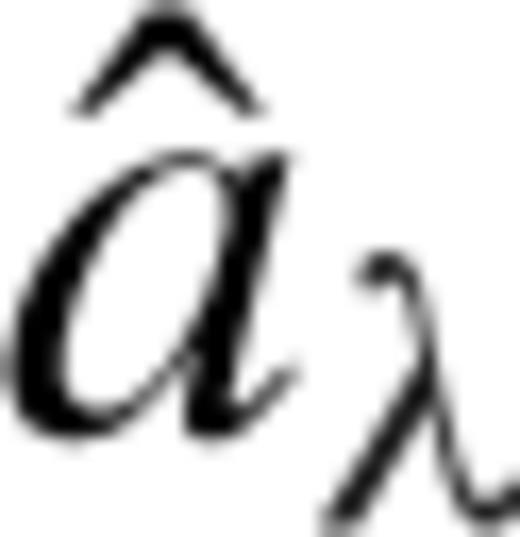 , which is our estimate of the kernel coefficients when the tuning parameter is set to the value λ:
, which is our estimate of the kernel coefficients when the tuning parameter is set to the value λ: 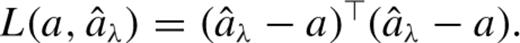
 is the statistical risk we will minimize through our choice of λ3. When M is well conditioned, we can construct an unbiased estimator of the true risk
is the statistical risk we will minimize through our choice of λ3. When M is well conditioned, we can construct an unbiased estimator of the true risk  as (section 2, Stein )
as (section 2, Stein ) 
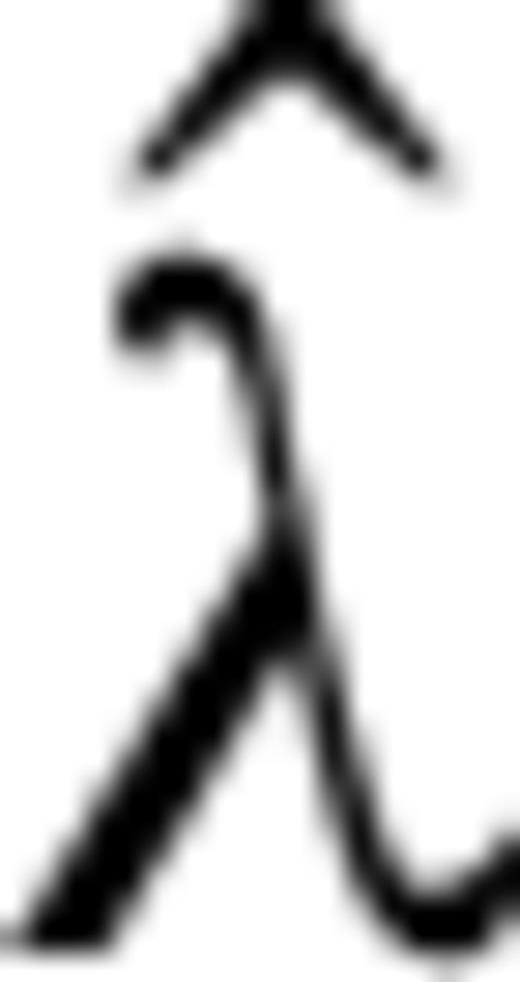 be the minimizer of R, then we choose
be the minimizer of R, then we choose 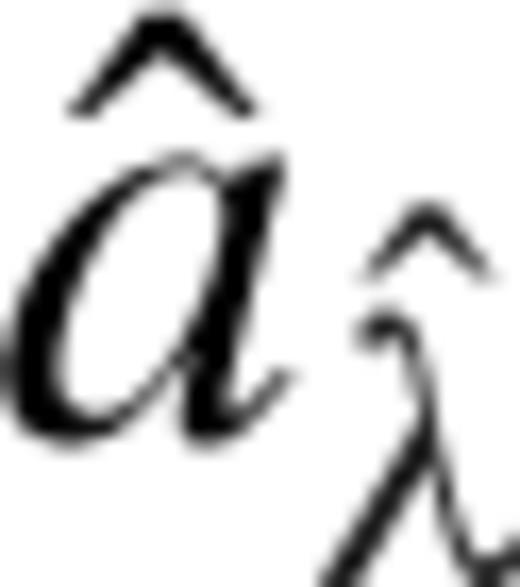 as the estimate of a.
as the estimate of a.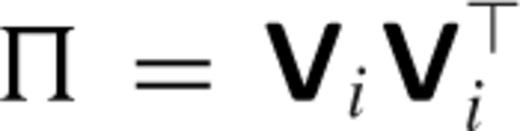 . This corresponds to
. This corresponds to 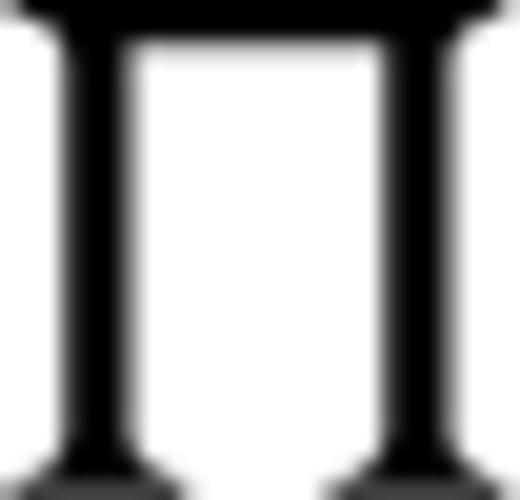 being a projection matrix on to the space of the eigenvectors of M that correspond to its i largest eigenvalues. Note that i is now an additional tuning parameter, corresponding to the choice of condition number (denoted by symbol Λ) for matrix M (Section ). A biased estimate of the statistical risk is then
being a projection matrix on to the space of the eigenvectors of M that correspond to its i largest eigenvalues. Note that i is now an additional tuning parameter, corresponding to the choice of condition number (denoted by symbol Λ) for matrix M (Section ). A biased estimate of the statistical risk is then 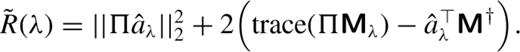
For each object detected in the CFHT images, and for given values of the condition number Λ in the range 4 ≤ log (Λ) < 6, we evaluate R(λ) at values of −2 ≤ log (λ) < 2. Fig. 4 shows a typical outcome of this analysis for a single object. Along the y-axis we show the associated value of the conditioning parameter Λ, and along the x-axis the value of λ at which R(λ) is evaluated. The solid line shows the minimum value of R(λ) for each Λ.
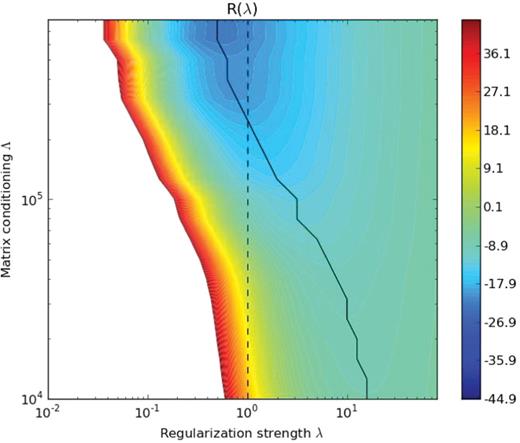
Values of the empirical risk R(λ), as defined in equation (14), for different values of the matrix conditioning parameter Λ, and the regularization strength λ. At all Λ, we determine the minimum values of R(λ), which are connected by the solid black line. The dotted vertical line represents the fiducial value of λ = 1. The global minimum of R(λ) is realized with minimal matrix conditioning and at a value of λ = 0.5.
We note that as we decrease the acceptable matrix condition number, thereby truncating more eigenvalues from the matrix pseudoinverse, the optimum value of λ increases. For matrices with effectively no conditioning (large Λ), the optimal value of λ is near λ = 0.5. This is in fact the global minimum of the risk. A similar result is obtained by looking at all objects within an image and summing their cumulative risk surfaces. We regard λ = 0.5 as the value preferred by the empirical risk estimation technique, with a range of nearly-equivalent risk in the range 0.3 < λ < 1.0.
Predictive ability
In most PSF-matching implementations, several dozen objects across a pair of registered images are used to create individual K(u, v); ideally these should evenly sample the spatial extent of the images. Due to spatial variation in the PSFs of the images, caused by optical aberrations or bulk atmospheric effects, the single kernel that PSF-matches all objects in an image must itself vary spatially. In this case each of the kernels K(u, v) is used to build the spatially varying PSF-matching kernel K(u, v, x, y). This is typically implemented as a spatial variation on the kernel coefficients K(u, v, x, y) = ∑iai(x, y)Ki(u, v). This assumption of a slowly varying underlying kernel suggests a new metric for consideration: the quality of the subtraction for data that were not used in the kernel fit. This predictive ability is quantified below by comparing the subtractions of neighbouring stars with each other's kernels.
In all CFHT images, we identify object pairs separated by more than 5 pixels but less than 50, a range of separations where we expect the intrinsic spatial variation of the underlying kernel to be minimal. The kernel derived for each object in a pair is applied to its complement, and the quality of each difference image assessed. For components A and B of each object pair, this yields difference image DAA which is the difference image of object A with kernel A, DAB which is the difference image of object A with kernel B and analogous images DBA and DBB. We assess the quality of each difference image using the width of the pixel distribution normalized by the noise, defined as e.g. σAA, within the central 7 × 7 pixels of the difference image. While we do not expect this distribution to have a width of exactly 1.0 due to the covariance between the solution and the input images, we do desire that the quality of DAB and DBA should not be significantly worse than that of DAA and DBB.
We aggregate the ‘even’ statistics σAA and σBB into distribution ΣE and the ‘odd’ statistics (σAB, σBA) into ΣO. We further examine the distribution of  , which is created from all measurements of
, which is created from all measurements of  and
and  . This statistic reflects the deterioration in an object's difference image when using a counterpart's kernel, compared to the optimal kernel derived for that object.
. This statistic reflects the deterioration in an object's difference image when using a counterpart's kernel, compared to the optimal kernel derived for that object.
We plot the distributions of these values in Fig. 5. The top panel provides the median values of these distributions for the sum-of-Gaussian (AL) basis (left), for the unregularized delta function basis (λ = 0; centre) and for delta-function regularization strengths of −2 < log (λ) < 2 (right). The bottom panel plots the effective standard deviation of the distribution, defined as 74 per cent of the interquartile range.
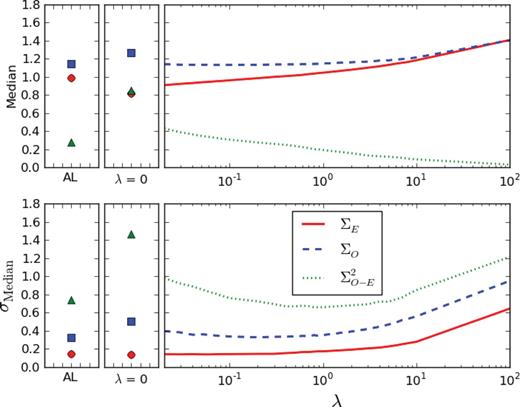
Median statistics assessing the predictive ability of different kernel bases. The top panel shows the median values of statistics ΣE (red circle and solid line), ΣO (blue square and dashed line) and Σ2O-E (green triangle and dotted line) for ‘Alard–Lupton’ (AL) bases, for delta-function bases with λ = 0 and then for a range of −2 < log (λ) < 2. All statistics are defined in Section 5.1.2. The bottom panel shows the standard deviation of the distribution, defined as 74 per cent of the interquartile range.
The lowest median residual variance ΣE comes from difference images made using an unregularized λ = 0 basis, the reasons for which we have examined in detail in Section . However, as expected the predictive ability of this basis is by far the worst, having the highest median  , as well as large variance within this distribution. As we ramp up the regularization strength, the predictive ability of the kernels increases (low
, as well as large variance within this distribution. As we ramp up the regularization strength, the predictive ability of the kernels increases (low  ), but at the expense of the quality of the difference image itself (large ΣE).
), but at the expense of the quality of the difference image itself (large ΣE).
To find an acceptable medium between these two considerations, we will use the results from the sum-of-Gaussian (AL) basis as a benchmark, since it has been shown to produce effective spatial models (Section ). For the AL basis, the median values of ΣE, ΣO and  are 0.99, 1.14 and 0.28, respectively. Similar results are obtained with delta-function regularization strengths of λ ≈ 0.2, 0.7 and 0.2. For AL the σmedian values of ΣE, ΣO and
are 0.99, 1.14 and 0.28, respectively. Similar results are obtained with delta-function regularization strengths of λ ≈ 0.2, 0.7 and 0.2. For AL the σmedian values of ΣE, ΣO and  are 0.14, 0.33 and 0.74, respectively. These are matched (or bested) in the regularized basis for λ ≤ 0.2, λ = 0.2 and 0.2 ≤ λ ≤ 6, respectively.
are 0.14, 0.33 and 0.74, respectively. These are matched (or bested) in the regularized basis for λ ≤ 0.2, λ = 0.2 and 0.2 ≤ λ ≤ 6, respectively.
In summary, using delta-function regularization strengths of λ ≈ 0.2, we are able to achieve difference images with a similar quality to those yielded by the sum-of-Gaussian AL basis (using ΣE as our metric). These models have similar predictive ability when applied to neighbouring objects (quantified using ΣO and  ), making them useful for full-image spatial modelling. Finally, they are seen to be generally applicable, having a small variance in the above statistics when evaluated over several hundreds of object pairs.
), making them useful for full-image spatial modelling. Finally, they are seen to be generally applicable, having a small variance in the above statistics when evaluated over several hundreds of object pairs.
Conclusions
We have examined here the choice of basis set on the quality of PSF-matching kernels and their resulting difference images. These include the traditional sum-of-Gaussian (AL) basis and a digital basis based upon delta-functions. We find that while the delta-function kernels are the most expressive, they are also the least compact in terms of localization of power within the kernel. Having one basis component per pixel in the kernel, they tend to overfit the data and are more sensitive to the noise in the images instead of the intrinsic PSF-matching signal.
We introduce a new technique of linear regularization to impose smoothness on these delta-function kernels, at the expense of slightly higher noise in the difference images. These regularized shapes are shown to be flexible and yield solutions with sufficient predictive power to prove useful for spatial interpolation. We outline two methods to determine the strength of this regularization that minimize the statistical risk of the kernel estimate and examine the predictive ability of the derived kernels. Both methods suggest values of λ that are between 0.1 and 1.0.
Given the large range of image qualities used in image subtraction pipelines compared to the small number of images used in the analysis here, we caution that these estimates may not be applicable under all conditions and should really be estimated on a data set-by-data set basis. The optimal value of λ will be a function of the S/N in the template and science images, which should affect the level of kernel smoothing needed and of the respective seeings in the input images, which may impact the suitability of our finite-difference smoothness approximation.
While this implementation appears successful and practical, there are various improvements we might consider in our regularization efforts. This includes changing the scale over which the regularization stencil is calculated based upon the seeing in the images; currently this is being done in pixel-based coordinates, and not adjusted depending on the full width at half-maximum of the input PSFs. We also plan to examine additional metrics to determine the optimal value of λ, including the power spectrum of noise in the resulting difference image, which should be flat. Ultimately, the overall quality of the entire difference image is the optimal metric to use in assessing choice of basis; we will be expanding our analysis to include full-image metrics and spatial modelling of the kernel.
Finally, the wealth of statistical techniques to efficiently choose basis shapes has not been exhausted. Other potential methods include the use of overcomplete bases, where the choice of the correct subset of components to use is made though through basis pursuit (Chen et al. ), as well as the process of ‘basis shrinkage’ through the use of multi-scale wavelets (Donoho & Johnstone , ). In all considerations, it is an advantage to yield solutions that, as an ensemble, have a low dimensionality so that spatial modelling is efficient and spatial degrees of freedom are not being used to compensate for an inefficient choice of basis. However, for any given basis set the choice of regularization (none at all or using a fixed set of functions) is likely to be the proper place for optimization.
Acknowledgment
This material is based, in part, upon work supported by the National Science Foundation under Grant Number AST-0709394.
References
We use the mean and variance, not mean and standard deviation, as the two parameters of Normal distributions.
The absolute value of the kernel's border pixels may also be penalized through the addition of a row at both the top and bottom of R1.
It should be noted that other risk estimators may be constructed, e.g. ones that maximize the quality of the full difference image.



