Abstract
Little attention has so far been paid to the division of the observed population between pulsars of the two spin directions that are possible. Almost all pulsars with positive corotational charge density at the polar caps are expected to satisfy space-charge-limited flow boundary conditions. Charge separation by blackbody photoelectric transitions in moving ions limits the acceleration potential, analogously with the more usually considered pair creation. However, the limitation is more severe so that proton and ion energies can be relativistic but not ultrarelativistic, and these allow the growth of Langmuir-mode-induced turbulence that couples directly with the radiation field, as shown by Asseo, Pelletier & Sol. The consequences of this, and of the several possible physical states of the polar cap, are described, qualitatively, as possible explanations for the complex phenomena of nulls, subpulse drift and mode switching observed in subsets of pulsars.
1 Introduction
The past 20 years have seen a number of developments that are likely to be relevant to pulsar radio and X-ray emission. Apart from the many improvements in the quality and scope of observations, there has been the recognition of the role of the Lense–Thirring effect in acceleration at the polar cap (Muslimov & Tsygan 1992) and of the significance of plasma turbulence (see the review of Melrose 2000). Most of the very many theoretical papers published have assumed a relative orientation of rotation spin 
and polar-cap magnetic flux density B such that 
with Goldreich–Julian charge density ρGJ < 0 and electron acceleration. In this case, there can be no doubt that the electron work function is so small that the space-charge-limited flow (SCLF) boundary condition on the corotating-frame electric field, 
, is satisfied on the polar-cap surface at all instants of time. (The subscripts ∥ and ⊥ refer to directions locally parallel with and perpendicular to B.) There appears to be no reason why neutron stars with 
and ρGJ > 0 should not be present in the pulsar population, but in this case, the best existing calculations of ion separation energies (see Medin & Lai 2006) combined with estimates of the polar-cap temperatures can be used to obtain values of the minimum magnetic field for which the boundary condition 
is possible. These are typically of the order of 1014 G (Jones 2011) and are indirect evidence that all except possibly a very small number of pulsars with spin direction such that 
satisfy the SCLF boundary condition rather than the 
condition assumed in the classic polar-cap model of Ruderman & Sutherland (1975).
The concept of localized regions of electron–positron pair production, referred to as sparks, moving over the neutron-star surface within the polar cap in an organized way, has been adapted from the Ruderman–Sutherland model and the 
boundary condition, but is now widely used phenomenologically, with no reference to boundary conditions or to the sign of 
, in describing observations such as nulls and subpulse drift. In the 
case, with SCLF, no physical basis for such a phenomenological description has so far been published, the reason being that electrons are the only possible negatively charged particles for outward acceleration and the SCLF boundary condition 
can be satisfied at any conceivable polar-cap surface temperature. The state of the accelerated plasma is then simply a problem in electromagnetism with defined boundary conditions. However, for 
, it has been shown that subpulse formation and movement, either organized or disorganized, over the polar-cap surface are quite natural and should be observable in most radio pulsars with this spin direction (Jones 2010a, hereafter Paper I; Jones 2011, hereafter Paper II). The basis for this conclusion is an examination of the physical processes occurring in electromagnetic showers formed at the polar-cap surface by photoelectrons accelerated inwards. The problem of finding the state of the accelerated plasma is not restricted to electromagnetism but also depends on proton production by the formation and decay of the giant dipole resonance in the electromagnetic showers.
Subpulse modulation (the wide variations of intensity at a fixed longitude in a sequence of observed pulses) has been recognized as an almost universal property of pulsars ever since their discovery. Weltevrede, Edwards & Stappers (2006a) found it present in 170 out of a sample of 187 pulsars selected only by signal-to-noise ratio, evidence that its presence is very likely to be independent of the sign of 
. Strong plasma turbulence is now viewed as the most probable source of radio emission (see Melrose 2000). Its development from a quasi-longitudinal Langmuir mode and the possible formation of a random array of stable Langmuir solitons have been investigated by Asseo, Pelletier & Sol (1990) and by Asseo & Porzio (2006). It has been shown recently (Jones 2012, hereafter Paper III) that the formation of this mode is also possible in a two-component beam consisting of protons and relativistic but not ultrarelativistic ions that can be formed as a consequence of the reverse flow of photoelectrons to the polar cap. Thus it is not surprising that subpulse modulation is almost universal. That a secondary low-energy electron–positron plasma is not the only possible source of plasma turbulence is also consistent with the fact that common characteristics of coherent radio emission are observed in the pulsar population even though the inferred polar-cap magnetic flux densities vary by five orders of magnitude. Pulsars with either sign of 
are therefore expected to produce individual pulses of similar form, although if there is no pair production, there may be differences that are difficult to detect such as in the distributions of spectral index caused by the different plasma frequencies and Lorentz factors in the two cases. However, this paper (see also Paper II) proposes that phenomena such as nulls, mode changes and organized subpulse motion are restricted to the 
case. These involve time-scales that have no obvious explanation in the 
direction of spin.
Existing observations show that subpulse drift is a frequent though not universal phenomenon. Weltevrede, Edwards & Stappers found that 68 of their sample of 187 pulsars show observable subpulse drift. There appears to be no published survey either of nulls or of mode changes based on a carefully defined sample as in the above work. However, the most recent and largest tabulation of data (Wang, Manchester & Johnston 2007) shows that nulls must be a moderately frequent phenomenon. Systematic information about mode changing is much more sparse (see Kramer et al. 2006).
Models of subpulse formation and drift recently developed (see e.g. Gil & Sendyk 2000) are based on the classic paper of Ruderman & Sutherland (1975) and assume the 
case with the polar-cap surface boundary condition 
. These have all the attributes of a good physical model, particularly simplicity and predictive capability in that it is possible to write down an expression for the 
subpulse drift velocity. However, the boundary condition requires surface magnetic flux densities approximately two orders of magnitude larger than the dipole fields inferred from the spin-down rates. Although the presence of highly complex field geometries formed from higher multipole components cannot be excluded, it would be strange if they were present with the frequency indicated by the survey of Weltevrede, Edwards & Stappers. Consequently, Papers I and II investigated physical processes at the polar-cap surface and have shown that the composition of the plasma accelerated under the SCLF boundary condition is usually neither time-independent nor uniform over its whole area. Localized areas in which the accelerated plasma is suitable for the growth of the quasi-longitudinal Langmuir mode exist naturally and can move in either an organized or disorganized way, thus acting as sources for subpulses with the same properties. Thus plasma systems analogous with Ruderman–Sutherland sparks are present under the 
boundary condition. However, we emphasize that their motion is unrelated with 
drift but is determined by the time τp in which electromagnetic shower protons diffuse to the surface.
This paper attempts to present a description of the early stages of the coherent emission mechanism that is very different from the canonical. In particular, the unexpected conclusion of Paper III that relatively low energy ion and proton beams can be formed means that it is necessary to reassess the model of subpulse drift discussed in Paper II. Polar caps of pulsars with spin 
are seen to be very complex systems compared with those of the electron acceleration 
case. However, we must presume that both are present in the neutron-star population and so it is worth examining how the properties of the observed pulsar population may be related with spin direction.
Before proceeding further, it must be admitted that the work has at least one drawback. Processes of the kind considered in Papers I and II, occurring at a continuously changing real condensed-matter surface, are not necessarily susceptible to the formulation of simple physical theories. The behaviour of such systems can be varied and complex. However, this is not inconsistent with the observed properties of many individual pulsars.
Section 2 summarizes the assumptions about the properties of the open region of the magnetosphere that we are obliged to make in both qualitative and quantitative works. Strong plasma turbulence is possible only for limited intervals of particle energy at altitudes z above the polar-cap surface smaller than z∼ 10R, where R is the neutron-star radius. This is described in more detail in Section 3. Section 4 draws on the work of Paper III to obtain values of the parameter K, which is the number of protons produced by photoelectrons per unit nuclear charge accelerated. We then give in Section 5 a description of the polar cap showing how subpulses are formed and that either chaotic or organized motion is possible. An attempt is made to show that this model of the polar cap provides a physical basis for phenomena such as nulls, subpulse drift and mode changes.
2 The open magnetosphere at the polar cap
At the base of the magnetosphere there is an atmosphere of ions, assumed to be in local thermodynamic equilibrium (LTE), having a scale height of the order of 10−1 cm. Its total mass is temperature-dependent but is broadly equivalent to 10−1 to 101 radiation lengths. Thus it contains only the earlier part of the electromagnetic showers formed by the reverse-electron flux. There is fractionation of the ionic charge to mass ratio. Ions with the highest value are concentrated at the top of the atmosphere and so preferentially enter the acceleration region. The proton number density is many orders of magnitude smaller than that of the ions and consequently has no effect on the structure of the atmosphere. Protons are not in static equilibrium within the LTE ion atmosphere but are subject to an outward-directed net gravitational and electrostatic force. Their motion is therefore a combination of diffusion and drift with a characteristic time τp elapsing between formation and arrival at the top of the atmosphere. If the rate of formation is such that the Goldreich–Julian flux would be exceeded, the excess protons form a thin atmosphere in equilibrium at the top of the LTE ion atmosphere. We refer to Sections 2, 3 and 5 of Paper II for a more complete account of these topics. Values of τp∼ 10−1–100 s are estimated.
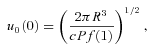
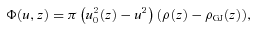
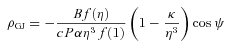
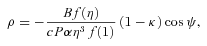
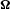and B. Equation (4) also assumes that particle velocities, including those of protons and ions, differ negligibly from the velocity of light. The function f(η)/αf(1) including the red-shift factor α is a slowly varying function of η and is approximately unity at low altitudes. Thus ρGJ(0) = (1 −κ)ρGJ(∞), where ρGJ(∞) is the flat space–time Goldreich–Julian charge density. Equations (3) and (4) exclude terms that can become significant at higher altitudes for which our geometrical model also fails, but nevertheless equation (2) is adequate for the estimation of proton and ion energies and of photoelectric transition rates. It is convenient to use the energy units of particle physics for polar-cap processes and therefore we define a potential energy difference 
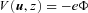. It has the value Vmax(u, z) on a flux line with polar-cap coordinate u for the undisturbed SCLF charge density of equation (4). It is also useful to have a simple expression for Vmax on the magnetic axis,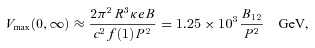 
The above statement is subject to a serious qualification concerning the definition of the open magnetosphere. If many secondary low-energy electron–positron pairs were created per primary particle accelerated, there would be no difficulty in assuming the unconstrained outward flow of primary particles and secondary pairs on any magnetic flux line intersecting the light cylinder. The separate velocity distributions of secondary electrons and positrons would have the capacity to adjust so as to maintain the condition 
at all points in the open region. However, there must be serious doubts about the universal existence, in the pulsar population, of the necessary density of secondary-pair plasma. Apart from 
pulsars in which there may be no pair creation, calculations of the secondary pair density produced by the inverse-Compton scattering (ICS) of polar-cap photons by outward accelerated electrons in the 
case (Hibschman & Arons 2001; Harding & Muslimov 2002) predict in many pulsars pair densities that are small compared with unity, per primary electron. It is true that more complex field geometries, such as the offset dipole, are possible and may enhance pair production (see Harding & Muslimov 2011), but there remain at least some hints of a problem in the pair density. In the absence of a pair plasma with the required properties, motion in the magnetosphere beyond the η∼ 10 region depends on the sense of curvature of the open flux line: there is further acceleration if |cos ψ| increases, but deceleration in the opposite case which is capable of cancelling the acceleration at lower altitudes. A section of the polar cap is then a dead zone from which there is no outward particle flux. Whilst the change in active polar-cap shape is not very significant, the potential given by equation (2) is reduced, very roughly, in proportion to the decrease in area. The component 
in the dead volume is very small and is that required to maintain a charge-separated equilibrium with gravity and the centrifugal force.
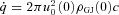whose compensation is likely to be easy if there is strong secondary pair creation, but is otherwise obscure. An order of magnitude estimate of the relevant time-scale can be found by dividing a typical light-cylinder field strength by the rate of change of the light-cylinder radial electric field given by 
. This is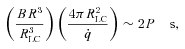 
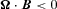pulsars is in the atomic number of matter at the neutron-star surface. If this were small (Z∼ 6), there would be a negligible reverse-electron flux and, as we shall see in Section 3, no coherent radio emission unless curvature radiation (CR) electron–positron pair production is possible. There is some indirect observational evidence for Z= 6 (Ho & Heinke 2009; see also Bogdanov & Grindlay 2009; Zhu et al. 2009; Yakovlev et al. 2011), but it does not appear strong. Theoretical work does indicate the possibility of atomic numbers other than the canonical Z= 26. Calculations by Hoffman & Heyl (2009) for isolated neutron stars (INSs) with no mass accretion show the presence of Z= 14, though with small total mass, but Pearson, Goriely & Chamel (2011) find a range of values Z > 26. The mass per unit area removed by a Goldreich–Julian current density of nuclei with mass number A in an 
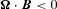pulsar in a lifetime t is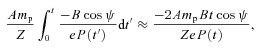 
The uncertainty in the atomic number of polar-cap surface nuclei has an obvious effect on photoelectric transitions, and therefore on the reverse-electron flux and the acceleration potential difference for particles moving on any given magnetic flux line. The dependence of Φ on ρ(z) in equation (2) means that the production of oppositely charged particles in a charge-separated region at altitude z under the SCLF boundary condition tends to cancel the local electric field 
. This is well known in the case of electron–positron pairs but is, of course, also true for photoelectrons (see Paper III).
Equation (2) is not valid at low altitudes z∼u0(0). Near the polar-cap surface, z≪u0(0), 
is the inertial acceleration field first described by Michel (1974). The problem of finding the electric field is 1D in z and the inertial 
is not large. Its contribution to particle acceleration is small compared with that of the Muslimov–Tsygan effect. We refer to Paper III for an approximate model for this region.
The polar-cap and whole-surface neutron-star temperatures are treated as distinct in Paper III and in the present work. Calculated photoelectric transition rates for polar-cap blackbody photons are negligibly small above an altitude z=h≈ 4u0(0), principally because the photon momentum component perpendicular to B becomes small at higher altitudes. This is unfavourable both for the Lorentz transformation to the rest frame of the accelerated ion and for the cross-section to the lowest Landau state of the emitted electron (see Paper III).
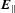and of photoelectric transitions in this interval. However, the boundary conditions also limit the extent to which ρ(z) can change if the condition E∥ > 0 is to be satisfied. Thus the difference between the mean ion charges Zh at z=h and 
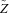in the assumed LTE of the atmosphere at z= 0 cannot be large. Adjustments in ρ(z) and in 
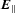maintain this state by limiting ion Lorentz factors and hence photoelectric transition rates. The ratio,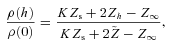 
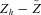is small, it is undoubtedly finite, and the associated reverse-electron flux gives a modest energy input, εh, to the polar-cap surface even in the absence of any whole-surface contribution to photoionization at z > h. We refer to Paper III for its approximate size, εh∼ 20 GeV.For a relatively small fraction of pulsars, pair creation by the conversion of CR photons is possible. However, for most 
pulsars, it is believed that the source of pairs is the conversion of outward-directed ICS polar-cap photons (see Hibschman & Arons 2001; Harding & Muslimov 2002). However, in the case of the 
pulsars considered here, there is an essential difference in that the electron–photon momentum in the frame of the rotating neutron star is directed inwards. There is likely to be some pair creation at low values of z from γ-rays emitted by the capture of shower-generated neutrons at the polar-cap surface, but the rate is difficult to estimate. Thus pair creation rates in most 
pulsars are likely to be one or two orders of magnitude smaller than for those with spin direction 
. However, even for the latter spin direction, the number of ICS pairs formed per primary electron can be much smaller than unity (see Harding & Muslimov 2002; also fig. 8 of Hibschman & Arons). Thus for the 
spin direction, there is a very real problem in understanding how a density of low-energy secondary electron–positron pairs adequate for coherent radio emission can be formed.
3 Conditions for strong turbulence
There is now a consensus that, in almost all observable radio pulsars, the source of the coherent emission lies within radii η∼ 101–102 and its energy is derived from particle acceleration at the polar cap. There is also a growing consensus that the formation of strong plasma turbulence is involved (Melrose 2000). The unstable mode that develops into strong plasma turbulence and transfers energy from particle beams to the electromagnetic field must therefore have a high growth rate. This severely constrains the energy of the beam particles. The equations of motion for the system are the Maxwell equations and those for a relativistic particle fluid. In a strong magnetic field, the mass-to-charge ratio present in the equations is 
for particles of species i, where qi is the charge and γi the Lorentz factor. The longitudinal effective mass is 
and this factor necessarily determines the growth rate of any unstable mode.
We consider in this paper, specifically, the growth of a quasi-longitudinal Langmuir mode (Asseo et al. 1990) from which a random array of stable Langmuir solitons may develop (Asseo & Porzio 2006). A different longitudinal mode has been studied by Weatherall (1997, 1998) and may be the source of the nanosecond pulses observed in certain pulsars (Hankins et al. 2003; Soglasnov et al. 2004). (We refer to the paper of Asseo & Porzio for an account of the history of plasma turbulence in relation to pulsar physics.) The Langmuir mode and solitons have components 
, 
and Bt perpendicular to 
and so can transfer energy to the radiation field directly (see Asseo et al. 1990). Hence the direct transfer of energy to the radiation field is determined only by the longitudinal effective mass and by the departure of the mode wavevector from the purely longitudinal state. Examination of growth rates shows at once that primary electrons or positrons of ∼103 GeV energy have longitudinal effective masses so large that they are unable to participate in the mode. The beams that interact in 
pulsars can be only secondary electrons and positrons whose velocity distributions satisfy the relativistic Penrose condition (Buschauer & Benford 1977). However, ion and proton beams that have longitudinal effective masses of the same order as secondary electrons and positrons can be produced in 
neutron stars. Thus it is anticipated that pulsars of both directions exist and produce very similar coherent emission.
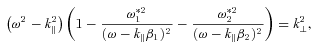
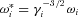in which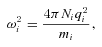 
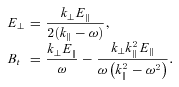
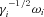and so, following Asseo et al., a natural wavenumber for which to seek a solution is defined in terms of the slower moving component, and is 
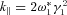. With the definition of a new variable s such that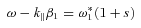 
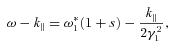
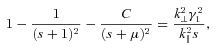
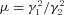and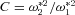 
. In the limit k⊥→ 0, equation (13) is a quartic with two real and two complex roots, whose properties were investigated in Paper III. The amplitude growth rate was found to be of the order of 
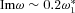and is a slowly varying function of the ratio γ1/γ2 and, for ions, the proton–ion number density ratio. However, we have to consider the quasi-longitudinal case of k⊥≠ 0 in which the transverse field components are non-zero. Equation (13) is then less transparent, being a quintic with three real and two complex roots, but we can use perturbation theory to estimate the extent to which a non-zero k⊥ changes a given complex root. Let s=s0+δs, where s0 is a root of the quartic. Then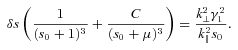 
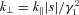. Then for typical values of C, μ and s0, we have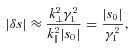 
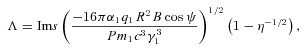
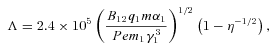
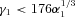for electrons or 
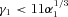for ion beams at η= 2 increasing to 
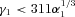and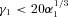 
, respectively, at η= 10. Development of turbulence or of stable solitons is then possible for either electrons or ions, although for electrons the cold beam hypothesis is clearly unrealistic and the distributions of electron and positron velocities must satisfy the Penrose condition.
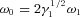. The actual maximum in the intensity distribution presumably depends on the extent to which developed turbulence moves energy towards higher wavenumbers. This is unknown except that some examples of soliton formation considered by Asseo & Porzio have maxima at ω≈ 1.5ω0. As functions of η and for cos ψ=−1, the frequencies 
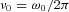are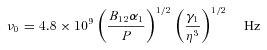 
There have been many calculations of pair formation densities above polar caps, but of particular interest is the paper of Harding & Muslimov (2011) who have studied the effect of a specific type of field, that of an offset dipole. Pair formation densities, assuming outward moving ICS photons to be the source, are rapidly increasing functions of the degree of offset. The most extreme case in which pair formation might be thought doubtful is that of PSR J2144−3933 which has a period P= 8.51 s and whose observers (Young, Manchester & Johnston 1999) commented specifically on the problem. The value of its parameter BP−2= 2.87 × 1010 G s−2 is almost an order of magnitude smaller than the apparent cut-off value of 2.2 × 1011 G s−2 in the distribution of that quantity obtained from the ATNF pulsar catalogue (Manchester et al. 2005) representing a death-line in the P–
distribution below which pair creation is not possible. It is old (2.7 × 108 yr) with a relatively low mean flux density at 400 MHz, and may be observable only as a consequence of close proximity (170 pc). Although the maximum acceleration potential given by equation (5) is very small, Vmax= 36 GeV, ICS pair formation is possible in principle although a very high degree of offset would be required (see figs 7–9 of Harding & Muslimov 2011). However, given a spin direction 
, accelerated ions would have Lorentz factors appropriate for growth of the quasi-longitudinal mode for any field geometry. However, the value of ν0 given by equations (18) is rather small in this case, even assuming that the radiation field is largely decoupled from the magnetosphere at quite low altitudes η∼ 2. (For this spin direction, the pair multiplicities produced by ICS photons would probably be one or two orders of magnitude smaller than for 
because the momentum of the electron–photon system is inward directed.) However, more extensive observations at low frequencies may reveal whether or not J2144−3933 is unique or merely a nearby example of an otherwise unobserved population.
4 Instability and proton production
Owing to our late recognition that photoelectric transitions have a very significant effect on particle acceleration under SCLF boundary conditions, it is necessary to revise the estimates of the reverse-electron energy flux that were used in Papers I and II. Photoelectric transitions and the consequent reverse-electron flux produce changes in mean nuclear and ion charge that we can summarize here as follows. The initial nuclear charge is Z (canonical value Z= 26), but formation and decay of the giant dipole state in electromagnetic showers reduce it to Zs at the top of the neutron-star atmosphere. We assume LTE in this region with ion charge 
. Then ions with charge Zh are injected into the main acceleration region at z=h. Typically, 
owing to interaction with polar-cap blackbody photons. Then further acceleration produces more extensive ionization to Z∞≤Zs by the whole-surface blackbody field with Z(z) as the altitude-dependent ion charge during this process.
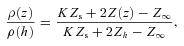
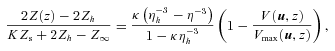
Photoelectric transition rates are rapidly increasing functions of the ion Lorentz factor γ. The reverse-electron flux they produce leads to a charge density that increases with altitude, thus reducing the potential given by equation (2). Thus we might expect a self-consistent set of functions V(z, u), 
and 
that are time-independent. In order to investigate this possibility, it is necessary to calculate the reverse-electron energy flux taking into account the fact that photoelectric transitions reduce the potential energy V=−eΦ derived from equation (2) to levels below Vmax. Broadly, we expect that γ(z) will increase from its initial value γh but that 
, and our initial attempt to model this is to assume that V(u, z) =Vmax(u, z) until a cut-off Vc is reached.
With the procedures and assumptions of Paper III, we calculate the mean reverse-electron energy εs per ion resulting from interaction with whole-surface blackbody photons, and the mean ion charge Z∞. Transition rates are obtained to an altitude zmax= 3R, beyond which they become small and equation (2) predicts negligible further acceleration. The polar-cap temperature is treated as distinct from the general surface temperature of the star and its value is equal to that generated by the reverse-electron flux which produces protons at the Goldreich–Julian current density. A flux exceeding this produces an accumulation of protons at the top of the neutron-star atmosphere which, until exhausted, reduces the ion component of the current density to zero. We adopt equation (33) of Paper I, with cos ψ=−1 and rotation period P= 1 s, and a typical proton production rate per unit shower energy of 
, i.e. one proton per 2.5 GeV shower energy. This quantity is a slowly varying function of B and Z and has been estimated in Papers I and II. Then (εh+εs)Wp=KZs, with εh∼ 20 GeV being the contribution of polar-cap blackbody photons. The temperatures are 
, 0.82 × 106 and 1.10 × 106 K, respectively, for B= 1.0 × 1012, 3.0 × 1012 and 1013 G. These have negligible effect on the acceleration but determine the initial ion charge 
. Actual values of Zs are unknown ab initio but are given by 
, where 
is the time-average of K at a specific position u on the polar cap and Z is the pre-shower nuclear charge. Hence we assume arbitrary values Zs= 10 or 20 with mass numbers A= 20 or 40 and note that ions with very small Zs tend to be completely ionized by the polar-cap or whole-surface temperature at the start of acceleration and so produce no reverse-electron flux. The initial ion Lorentz factor is fixed as γh= 5 at an altitude z=h= 0.05R. The initial ion charges at z=h are the following: for Zs= 10, Zh= 8, 6 or 5 and for Zs= 20, Zh= 15, 12 or 9, respectively, at B= 1.0 × 1012, 3.0 × 1012 or 1013 G.
Values of εs and Z∞ obtained on this basis are given in Table 1. With the approximations and methods of Paper III in mind, it is obvious that the absolute values of εs do not have the accuracy that the number of figures given might indicate. However, comparison of columns for different values of Ts shows that whole-surface photons can generate very high transition rates not only at large Vc for Ts= 105 K, but also at progressively lower Vc as whole-surface temperature increases. By combining the results of Table 1, which are estimates of εs(V) and Z∞(V), with equation (19) it should be possible, given Zh, to solve for 
. It can be seen by inspection of the equation, with reference to values of K(V) found from the Table, that there is always a solution, the value of V depending principally on Ts and to a lesser extent on B. Values V≪Vmax occur at high Ts and small B.
Values of the mean reverse-electron energy per ion (εs) at the polar-cap surface in units of GeV, and of the mean ion charge at the end of photoionization (Z∞) have been calculated. The magnetic flux density is in units of 1012 G and the acceleration potential cut-off Vc is in units of GeV. Arbitrary values Zs= 10 or 20 have been assumed for the mean surface nuclear charge. We refer to Section 4 for discussion of Zs and other parameters on which the calculated values are dependent. The final three pairs of columns give the values of εs and Z∞ for whole-surface temperatures Ts= 105, 2 × 105 and 4 × 105 K. The rotation period is P= 1 s. Blank spaces denote energies that are negligibly small.
| B12 | Zs | Vc (GeV) | εs | Z∞ (Ts= 105 K) | εs | Z∞ ( K) | εs | Z∞ ( K) |
| 1.0 | 10 | 1000 | 1389 | 9.9 | 650 | 10.0 | 255 | 10.0 |
| 500 | 253 | 8.5 | 650 | 10.0 | 255 | 10.0 | ||
| 250 | 4 | 8.0 | 392 | 9.6 | 255 | 10.0 | ||
| 125 | 38 | 8.3 | 228 | 10.0 | ||||
| 80 | 12 | 8.1 | 128 | 9.6 | ||||
| 50 | 2 | 8.0 | 67 | 9.2 | ||||
| 20 | 1000 | 2196 | 18.0 | 2044 | 20.0 | 803 | 20.0 | |
| 500 | 328 | 15.7 | 1783 | 19.7 | 803 | 20.0 | ||
| 250 | 5 | 15.0 | 640 | 17.5 | 802 | 20.0 | ||
| 125 | 56 | 15.4 | 395 | 18.4 | ||||
| 80 | 14 | 15.2 | 241 | 17.9 | ||||
| 50 | 2 | 15.0 | 136 | 17.3 | ||||
| 3.0 | 10 | 2000 | 6438 | 9.3 | 4264 | 10.0 | 1607 | 10.0 |
| 1000 | 138 | 6.1 | 3767 | 10.0 | 1607 | 10.0 | ||
| 500 | 36 | 6.1 | 581 | 7.2 | 1524 | 10.0 | ||
| 250 | 7 | 6.0 | 244 | 7.0 | 734 | 9.3 | ||
| 125 | 64 | 6.5 | 373 | 8.9 | ||||
| 80 | 16 | 6.2 | 225 | 8.5 | ||||
| 50 | 2 | 6.0 | 119 | 7.9 | ||||
| 20 | 2000 | 10 580 | 17.4 | 9196 | 20.0 | 3760 | 20.0 | |
| 1000 | 104 | 12.1 | 6677 | 18.9 | 3760 | 20.0 | ||
| 500 | 27 | 12.1 | 647 | 13.3 | 3346 | 19.8 | ||
| 250 | 3 | 12.0 | 225 | 12.9 | 1348 | 17.7 | ||
| 125 | 35 | 12.3 | 604 | 16.5 | ||||
| 80 | 5 | 12.1 | 319 | 15.4 | ||||
| 50 | 124 | 14.0 | ||||||
| 10.0 | 10 | 2000 | 85 | 5.0 | 3114 | 6.6 | 8521 | 10.0 |
| 1000 | 47 | 5.0 | 631 | 5.7 | 3578 | 8.9 | ||
| 500 | 12 | 5.0 | 345 | 5.7 | 1724 | 8.6 | ||
| 250 | 1 | 5.0 | 98 | 5.4 | 814 | 8.1 | ||
| 125 | 10 | 5.1 | 314 | 7.3 | ||||
| 80 | 1 | 5.0 | 144 | 6.5 | ||||
| 50 | 47 | 5.7 | ||||||
| 20 | 2000 | 137 | 9.1 | 3061 | 10.6 | 19 778 | 20.0 | |
| 1000 | 58 | 9.1 | 1055 | 10.1 | 6523 | 16.1 | ||
| 500 | 10 | 9.0 | 456 | 9.9 | 3269 | 15.6 | ||
| 250 | 1 | 9.0 | 90 | 9.3 | 1388 | 14.3 | ||
| 125 | 5 | 9.0 | 440 | 12.1 | ||||
| 80 | 155 | 10.6 | ||||||
| 50 | 31 | 9.5 |
| B12 | Zs | Vc (GeV) | εs | Z∞ (Ts= 105 K) | εs | Z∞ ( K) | εs | Z∞ ( K) |
| 1.0 | 10 | 1000 | 1389 | 9.9 | 650 | 10.0 | 255 | 10.0 |
| 500 | 253 | 8.5 | 650 | 10.0 | 255 | 10.0 | ||
| 250 | 4 | 8.0 | 392 | 9.6 | 255 | 10.0 | ||
| 125 | 38 | 8.3 | 228 | 10.0 | ||||
| 80 | 12 | 8.1 | 128 | 9.6 | ||||
| 50 | 2 | 8.0 | 67 | 9.2 | ||||
| 20 | 1000 | 2196 | 18.0 | 2044 | 20.0 | 803 | 20.0 | |
| 500 | 328 | 15.7 | 1783 | 19.7 | 803 | 20.0 | ||
| 250 | 5 | 15.0 | 640 | 17.5 | 802 | 20.0 | ||
| 125 | 56 | 15.4 | 395 | 18.4 | ||||
| 80 | 14 | 15.2 | 241 | 17.9 | ||||
| 50 | 2 | 15.0 | 136 | 17.3 | ||||
| 3.0 | 10 | 2000 | 6438 | 9.3 | 4264 | 10.0 | 1607 | 10.0 |
| 1000 | 138 | 6.1 | 3767 | 10.0 | 1607 | 10.0 | ||
| 500 | 36 | 6.1 | 581 | 7.2 | 1524 | 10.0 | ||
| 250 | 7 | 6.0 | 244 | 7.0 | 734 | 9.3 | ||
| 125 | 64 | 6.5 | 373 | 8.9 | ||||
| 80 | 16 | 6.2 | 225 | 8.5 | ||||
| 50 | 2 | 6.0 | 119 | 7.9 | ||||
| 20 | 2000 | 10 580 | 17.4 | 9196 | 20.0 | 3760 | 20.0 | |
| 1000 | 104 | 12.1 | 6677 | 18.9 | 3760 | 20.0 | ||
| 500 | 27 | 12.1 | 647 | 13.3 | 3346 | 19.8 | ||
| 250 | 3 | 12.0 | 225 | 12.9 | 1348 | 17.7 | ||
| 125 | 35 | 12.3 | 604 | 16.5 | ||||
| 80 | 5 | 12.1 | 319 | 15.4 | ||||
| 50 | 124 | 14.0 | ||||||
| 10.0 | 10 | 2000 | 85 | 5.0 | 3114 | 6.6 | 8521 | 10.0 |
| 1000 | 47 | 5.0 | 631 | 5.7 | 3578 | 8.9 | ||
| 500 | 12 | 5.0 | 345 | 5.7 | 1724 | 8.6 | ||
| 250 | 1 | 5.0 | 98 | 5.4 | 814 | 8.1 | ||
| 125 | 10 | 5.1 | 314 | 7.3 | ||||
| 80 | 1 | 5.0 | 144 | 6.5 | ||||
| 50 | 47 | 5.7 | ||||||
| 20 | 2000 | 137 | 9.1 | 3061 | 10.6 | 19 778 | 20.0 | |
| 1000 | 58 | 9.1 | 1055 | 10.1 | 6523 | 16.1 | ||
| 500 | 10 | 9.0 | 456 | 9.9 | 3269 | 15.6 | ||
| 250 | 1 | 9.0 | 90 | 9.3 | 1388 | 14.3 | ||
| 125 | 5 | 9.0 | 440 | 12.1 | ||||
| 80 | 155 | 10.6 | ||||||
| 50 | 31 | 9.5 |
Values of the mean reverse-electron energy per ion (εs) at the polar-cap surface in units of GeV, and of the mean ion charge at the end of photoionization (Z∞) have been calculated. The magnetic flux density is in units of 1012 G and the acceleration potential cut-off Vc is in units of GeV. Arbitrary values Zs= 10 or 20 have been assumed for the mean surface nuclear charge. We refer to Section 4 for discussion of Zs and other parameters on which the calculated values are dependent. The final three pairs of columns give the values of εs and Z∞ for whole-surface temperatures Ts= 105, 2 × 105 and 4 × 105 K. The rotation period is P= 1 s. Blank spaces denote energies that are negligibly small.
| B12 | Zs | Vc (GeV) | εs | Z∞ (Ts= 105 K) | εs | Z∞ ( K) | εs | Z∞ ( K) |
| 1.0 | 10 | 1000 | 1389 | 9.9 | 650 | 10.0 | 255 | 10.0 |
| 500 | 253 | 8.5 | 650 | 10.0 | 255 | 10.0 | ||
| 250 | 4 | 8.0 | 392 | 9.6 | 255 | 10.0 | ||
| 125 | 38 | 8.3 | 228 | 10.0 | ||||
| 80 | 12 | 8.1 | 128 | 9.6 | ||||
| 50 | 2 | 8.0 | 67 | 9.2 | ||||
| 20 | 1000 | 2196 | 18.0 | 2044 | 20.0 | 803 | 20.0 | |
| 500 | 328 | 15.7 | 1783 | 19.7 | 803 | 20.0 | ||
| 250 | 5 | 15.0 | 640 | 17.5 | 802 | 20.0 | ||
| 125 | 56 | 15.4 | 395 | 18.4 | ||||
| 80 | 14 | 15.2 | 241 | 17.9 | ||||
| 50 | 2 | 15.0 | 136 | 17.3 | ||||
| 3.0 | 10 | 2000 | 6438 | 9.3 | 4264 | 10.0 | 1607 | 10.0 |
| 1000 | 138 | 6.1 | 3767 | 10.0 | 1607 | 10.0 | ||
| 500 | 36 | 6.1 | 581 | 7.2 | 1524 | 10.0 | ||
| 250 | 7 | 6.0 | 244 | 7.0 | 734 | 9.3 | ||
| 125 | 64 | 6.5 | 373 | 8.9 | ||||
| 80 | 16 | 6.2 | 225 | 8.5 | ||||
| 50 | 2 | 6.0 | 119 | 7.9 | ||||
| 20 | 2000 | 10 580 | 17.4 | 9196 | 20.0 | 3760 | 20.0 | |
| 1000 | 104 | 12.1 | 6677 | 18.9 | 3760 | 20.0 | ||
| 500 | 27 | 12.1 | 647 | 13.3 | 3346 | 19.8 | ||
| 250 | 3 | 12.0 | 225 | 12.9 | 1348 | 17.7 | ||
| 125 | 35 | 12.3 | 604 | 16.5 | ||||
| 80 | 5 | 12.1 | 319 | 15.4 | ||||
| 50 | 124 | 14.0 | ||||||
| 10.0 | 10 | 2000 | 85 | 5.0 | 3114 | 6.6 | 8521 | 10.0 |
| 1000 | 47 | 5.0 | 631 | 5.7 | 3578 | 8.9 | ||
| 500 | 12 | 5.0 | 345 | 5.7 | 1724 | 8.6 | ||
| 250 | 1 | 5.0 | 98 | 5.4 | 814 | 8.1 | ||
| 125 | 10 | 5.1 | 314 | 7.3 | ||||
| 80 | 1 | 5.0 | 144 | 6.5 | ||||
| 50 | 47 | 5.7 | ||||||
| 20 | 2000 | 137 | 9.1 | 3061 | 10.6 | 19 778 | 20.0 | |
| 1000 | 58 | 9.1 | 1055 | 10.1 | 6523 | 16.1 | ||
| 500 | 10 | 9.0 | 456 | 9.9 | 3269 | 15.6 | ||
| 250 | 1 | 9.0 | 90 | 9.3 | 1388 | 14.3 | ||
| 125 | 5 | 9.0 | 440 | 12.1 | ||||
| 80 | 155 | 10.6 | ||||||
| 50 | 31 | 9.5 |
| B12 | Zs | Vc (GeV) | εs | Z∞ (Ts= 105 K) | εs | Z∞ ( K) | εs | Z∞ ( K) |
| 1.0 | 10 | 1000 | 1389 | 9.9 | 650 | 10.0 | 255 | 10.0 |
| 500 | 253 | 8.5 | 650 | 10.0 | 255 | 10.0 | ||
| 250 | 4 | 8.0 | 392 | 9.6 | 255 | 10.0 | ||
| 125 | 38 | 8.3 | 228 | 10.0 | ||||
| 80 | 12 | 8.1 | 128 | 9.6 | ||||
| 50 | 2 | 8.0 | 67 | 9.2 | ||||
| 20 | 1000 | 2196 | 18.0 | 2044 | 20.0 | 803 | 20.0 | |
| 500 | 328 | 15.7 | 1783 | 19.7 | 803 | 20.0 | ||
| 250 | 5 | 15.0 | 640 | 17.5 | 802 | 20.0 | ||
| 125 | 56 | 15.4 | 395 | 18.4 | ||||
| 80 | 14 | 15.2 | 241 | 17.9 | ||||
| 50 | 2 | 15.0 | 136 | 17.3 | ||||
| 3.0 | 10 | 2000 | 6438 | 9.3 | 4264 | 10.0 | 1607 | 10.0 |
| 1000 | 138 | 6.1 | 3767 | 10.0 | 1607 | 10.0 | ||
| 500 | 36 | 6.1 | 581 | 7.2 | 1524 | 10.0 | ||
| 250 | 7 | 6.0 | 244 | 7.0 | 734 | 9.3 | ||
| 125 | 64 | 6.5 | 373 | 8.9 | ||||
| 80 | 16 | 6.2 | 225 | 8.5 | ||||
| 50 | 2 | 6.0 | 119 | 7.9 | ||||
| 20 | 2000 | 10 580 | 17.4 | 9196 | 20.0 | 3760 | 20.0 | |
| 1000 | 104 | 12.1 | 6677 | 18.9 | 3760 | 20.0 | ||
| 500 | 27 | 12.1 | 647 | 13.3 | 3346 | 19.8 | ||
| 250 | 3 | 12.0 | 225 | 12.9 | 1348 | 17.7 | ||
| 125 | 35 | 12.3 | 604 | 16.5 | ||||
| 80 | 5 | 12.1 | 319 | 15.4 | ||||
| 50 | 124 | 14.0 | ||||||
| 10.0 | 10 | 2000 | 85 | 5.0 | 3114 | 6.6 | 8521 | 10.0 |
| 1000 | 47 | 5.0 | 631 | 5.7 | 3578 | 8.9 | ||
| 500 | 12 | 5.0 | 345 | 5.7 | 1724 | 8.6 | ||
| 250 | 1 | 5.0 | 98 | 5.4 | 814 | 8.1 | ||
| 125 | 10 | 5.1 | 314 | 7.3 | ||||
| 80 | 1 | 5.0 | 144 | 6.5 | ||||
| 50 | 47 | 5.7 | ||||||
| 20 | 2000 | 137 | 9.1 | 3061 | 10.6 | 19 778 | 20.0 | |
| 1000 | 58 | 9.1 | 1055 | 10.1 | 6523 | 16.1 | ||
| 500 | 10 | 9.0 | 456 | 9.9 | 3269 | 15.6 | ||
| 250 | 1 | 9.0 | 90 | 9.3 | 1388 | 14.3 | ||
| 125 | 5 | 9.0 | 440 | 12.1 | ||||
| 80 | 155 | 10.6 | ||||||
| 50 | 31 | 9.5 |
Basically, incomplete ionization at z=h means that there will be further ionization at z > h unless Ts or Vmax, or both, are too small for it to be possible. In this latter case, relevant for old pulsars, there remains the polar-cap contribution εh giving a small factor K < 1 and a solution V(u, z) =Vmax(u, z). Such a solution would be time-independent and of uniform ρ over the polar cap, with both ion and proton components. However, it would not lead to radio emission unless Vmax were small enough to give an adequate growth rate for the Langmuir mode, as described in Section 3. The general cut-off BP−2= 2.2 × 1011 G s−2 obtained from the ATNF pulsar catalogue gives 
GeV. Ion Lorentz factors γ∼ 20 and proton energies ∼60 GeV are possible on flux lines originating near the edge of the polar cap. However, in the more general case, large values of εs in the uniform time-independent model lead to K≫ 1 and hence to instability, as shown in section 4.3 of Paper I. The actual state of the polar-cap surface is therefore time-dependent.
5 Qualitative modelling of the polar cap
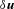of surface at any instant is a function only of its past time distribution of reverse-electron energy flux. The flux of accelerated protons Jp (u, t) is given by 
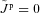within intervals for which Jp does not exceed the Goldreich–Julian current density ρGJ(0)c. Most protons are produced in the vicinity of the shower maximum whose depth is only a slowly varying function of the primary electron energy. Their motion towards the surface is better described by a drift velocity, rather than diffusion, in most of the LTE atmosphere so that the distribution of arrival times can be modelled as fp(t−t′) =δ(t−t′−τp). We refer to Section 5 of Paper II for further details. Following Paper III, equation (20) recognizes that K is a function of u and t owing to its V-dependence, and can vary on time-scales of the order of τp. The protons are preferentially accelerated, but if Jp reaches the Goldreich–Julian flux, as can be the case if K≫ 1, a thin proton atmosphere forms at the top of the ion atmosphere at a rate given by 
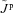, and the local ion flux falls to zero until it is exhausted.As a first approximation, equation (20) shows that the condition of an element of polar-cap area can be represented by two possible states: ion emission with duration τp or proton emission of duration 
, where 
is the time average over the interval τp. Values 
ensure that proton production is so large that an atmosphere of protons forms at the top of the LTE atmosphere of ions. Then the ion phase ends and the proton phase is maintained until the proton component of the atmosphere is exhausted. Areas in the ion phase necessarily move with time and so can be seen as moving subpulses within the time-averaged radio pulse profile. The motion could be chaotic or, as proposed in Paper II, organized so as to give regular subpulse drift.
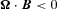case with SCLF boundary conditions. Self-sustaining pair creation requires adequate conversion probabilities for both outward- and inward-directed CR photons at z < zmax. Thus pair creation is not uniform over the whole cross-sectional area 
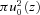of the open flux tube, but depends on a combination of V and flux-line curvature. For the suitable values of u, the equation analogous to (19), obtained by comparison of current densities at z= 0 and z=zmax, can be most compactly expressed in terms of the particle flux φ on the relevant flux lines: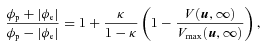 
Quantitative model construction is not attempted here. Owing to the uncertainties in significant parameters that are listed in Section 6, quantitative testing of a model against observed data does not appear immediately profitable. The purpose of this paper is less ambitious. It is an attempt to show that the condition of the polar-cap surface provides a physical basis for nulls, mode switches and subpulse drift. To do this, we describe qualitatively some of the possible polar-cap states.
Assume, initially, that CR pair production as described above is possible over some limited area of the polar cap. Its boundary can be defined as that within which proton production by the reverse electrons of CR pairs exceeds the Goldreich–Julian rate so that a proton atmosphere forms and grows in density. Between this boundary and u0 there is an annular strip within which ion acceleration can occur and proton formation is governed by equation (20). (Any contribution from CR reverse electrons is neglected here.) Solutions of equation (20) then exist in which zones of ion phase circulate around the CR region. Equation (20) is local in u and so cannot itself determine the circulation sense or velocity. Suppose that there are n ion zones. Then in the usual notation by which subpulse drift is described, the circulation time is 
, where P3 is the band separation and in the model is given by P3=τgap+τp= (K+ 1)τp. Association with subpulse drift would require either secondary pair creation on the ion phase flux lines or the presence of proton and ion components in the current density near to u0 so that energies are low enough for Langmuir-mode growth. A further consideration is that excess proton production within the CR area must be accompanied by lateral diffusion on the polar-cap surface, perpendicular to B. We have chosen the example of a clearly defined annular region, but there is no reason why organized motion of this kind should not occur more generally and in the absence of a CR component.
A further possibility is that the active CR region could be switched off by changes in the potential inside it which is also dependent on the state of the remaining parts of the polar cap. In general, in a less organized state, there is no reason why either the whole polar cap or large parts of it should not be in the proton phase for intervals of time of the order of τgap and, in the absence of CR pair production, there would be no possibility of Langmuir mode growth. Thus nulls are a natural phenomenon within the model. Obviously, there are many possible polar-cap states, their relevance to widely observed phenomena being limited only by the requirement that they should not be too dependent on neutron-star parameters having critical or particular values.
Mode changes have been studied extensively in a small number of pulsars, some of which also exhibit subpulse drift. Bartel et al. (1982) summarizes the main characteristics of this phenomenon. These authors emphasize that the spectral and polarization changes that occur on mode switching are consistent with a change in the optical depth of the source region within the magnetosphere and that the sources of the two or more modes would be on different sets of flux lines. (They also suggest that the explanation of mode switching lies in the polar-cap surface, though in the context of the Ruderman & Sutherland model.) Switching of emission between different sets of flux lines occurs naturally in our qualitative model which is sufficiently diverse to accommodate the characteristics of mode switching that are observed, including changes in subpulse drift rates.
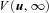with no possibility of Langmuir-mode growth if CR pair creation is not possible. A broad measure of the time-scale for this instability is provided by the time in which a depth of surface nuclei equivalent to one radiation length is removed from the polar cap at the Goldreich–Julian current density. From equations (4) and (5) of Paper I, this is given by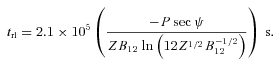 
6 Conclusions and uncertainties
Both neutron-star spin directions, defined by the sign 
at the polar caps, presumably exist, and it is one of the purposes of this paper to question how, if at all, each sign contributes to the observed radio pulsar population. Previous papers (Papers I–III) have been directed towards the 
case because it has positive polar-cap corotational charge density so that the flux of accelerated particles can have ionic, proton and positron components. There appears to have been some reluctance in the published literature to consider in any detail the physics of the polar cap for this spin direction. However, Papers I–III have attempted to show that such considerations are essential and that the radio emission characteristics are not solely determined by electrodynamics, as may be so for 
.
Weltevrede et al. (2006a) detected subpulse drift in almost one-half of a sample of 187 pulsars selected only by signal-to-noise ratio. Nulls and mode changes are less frequently observed. We propose that results obtained in Papers I–III and in this paper lead to the idea that these phenomena are all related to the physics of the polar cap in 
pulsars and that the opposite spin direction, with only electrons as primary accelerated particles, is then observed as the population showing subpulse modulation, perhaps as a consequence of plasma turbulence, but none of the above phenomena. The problem with polar-cap physics is that a real condensed-matter system can be extremely complex and, as we noted in Section 1, does not always lend itself to the construction of simple models (see also Section 2 of Paper II). A further difficulty is that some of the parameters concerned are either unknown, such as the atomic number of surface nuclei, or can vary over several orders of magnitude.
Calculated values in Table 1 are limited to B= 1012–1013 G which is representative of pulsars in the nulls tabulation of Wang et al. (2007) and, for example, of those pulsars with drifting subpulses investigated by Gil et al. (2008). Photoelectric cross-sections obtained in Paper III are not valid at B < 1012 G in which region interpolation between zero-field cross-sections and those at 1012 G would be necessary. At higher fields, B > Bc= 4.41 × 1013 G, approximate cross-sections for bremsstrahlung and pair creation have been found (Jones 2010b) and electromagnetic shower development investigated. It was confirmed that the value of the proton production parameter Wp decreases only slowly at B > Bc, but also that the Landau–Pomeranchuk–Migdal effect, known to exist in zero field, is significant in the neutron-star atmosphere, and has the effect of reducing high-energy bremsstrahlung and pair creation cross-sections and therefore of increasing shower depth and hence the proton diffusion-drift time τp.
The whole-surface temperature Ts is a further important parameter that is not well known. Paper III did not incorporate general relativistic corrections that should strictly have been made in transforming the blackbody radiation field to the ion rest frame. However, for most transitions, the radiation field is better approximated by that of the neutron-star surface proper frame rather than by 
, the temperature inferred by a distant observer. Since 
for the neutron-star mass and radius assumed here in Section 2, the temperatures used in Table 1 are well below those that can presently be observed. Yakovlev & Pethick (2004) list only a small number of young pulsars whose blackbody temperatures have been measured. These are 
K. All model predictions reviewed by these authors show 
decreasing very rapidly at age >106 yr. However, on the other hand, temperatures below Ts= 105 K, the lowest used in Table 1, could be maintained by a very small and obscure level of dissipation within the star. INSs certainly have higher temperatures 
K (see e.g. Kaplan & van Kerkwijk 2009). However, they are few in number and their radio beams (if they exist) would be narrow compared with the 
observability of unpulsed blackbody radiation. Given this uncertainty, we do not regard them as part of the population considered here.
The energy of the coherent radio emission must presumably be transferred from particle beams in high magnetic field regions near the polar caps. Whatever the coherent emission mechanism is eventually established to be, provided it is not CR, the criteria in Section 3 for growth of Langmuir modes must be relevant. This paper does not attempt to judge whether low-energy secondary electrons or small Lorentz factor ions form the particle beams producing radio emission in any particular group, but asserts that both possibilities exist for 
pulsars. It follows that evolution of a pulsar to old age may include long intervals, perhaps of the order of 106 yr, in which pair creation is not possible because Vmax is too small, but ion Lorentz factors remain too large to give adequate Langmuir-mode growth rates. Because 
, at least approximately, the highest growth rates will be on flux lines with u near u0. This is entirely consistent with the conal pattern of emission in the pulsar morphology developed by Rankin (1983).
Pulsars exhibit nulls with mean duration as short as several rotation periods or, for those described as intermittent pulsars, times of the order of 10 d. PSR 1931+24 is an example of the latter (Kramer et al. 2006), but long-duration nulls have now also been observed in J1832+0029 (see Lyne 2009) and in J1841−0500 (Camilo et al. 2012). Such null durations allow separate measurement of the spin-down rate in both on and off states of emission. In each case, the off-state spin-down rate is about half that of the on state, indicating some substantial difference in the condition of the magnetosphere. Obviously, it is not known if this is also true for short-duration nulls, but for 
pulsars in our model of the polar cap, it occurs naturally owing to the change in the extent to which the electromagnetic fields near and beyond the light cylinder are loaded and the total momentum density modified by particle emission. If the whole polar cap were in the proton phase, as discussed in Section 5, there would be no significant pair creation (assuming no CR pair production) and, of course, no possibility of Langmuir-mode growth. However, if creation of low-energy secondary pairs were possible, the flux of particles to be accelerated at or beyond the light cylinder could greatly exceed the Goldreich–Julian value. Even though we lack a comprehensive understanding of acceleration at RLC and beyond, it is entirely plausible that the changes in particle number density inherent in our model would lead to the observed changes in spin-down torque.
Interesting reviews of pulsars with large nulling fractions and of the rotating radio transients (RRAT) have been given recently by Burke-Spolaor & Bailes (2010), Keane et al. (2011) and Keane & McLaughlin (2011). In particular, pulsars are shown in the g–P plane, where g is the fraction of periods in which a pulse is detected. The distribution appears roughly uniform in log g within the interval 10−4 < g < 10−1. The existence of these objects is not inconsistent with the complexity of possible polar-cap states of the 
pulsars described here given the time-scale trl defined by equation (22). But Keane & McLaughlin note that there is a scarcity of objects whose behaviour is governed by time-scales that are longer than the above but shorter than the very long time-scales (∼106–107 s) associated with the intermittent pulsars such as PSR 1931+24. Very long time-scales much exceeding those given by equation (22) still remain a problem whose explanation may be more subtle than those attempted in this paper or may lie in quite different considerations.
A simple explanation for the RRAT has been proposed by Weltevrede et al. (2006b). These authors compared RRAT pulses with the infrequent very large amplitude pulses seen in PSR 0656+14. They note that if 0656+14 were as distant in the Galaxy as most of the RRAT, its observed emission would appear to be that of the typical RRAT. However, this may be inconsistent with the periodicities in individual RRAT pulse arrival times found recently by Palliyaguru et al. (2011). These are mostly of the order of 104 s, but a minority are much longer, of the order of 106–107 s. If these complex sets of periodicities are established and are not loose quasi-periodicities, they represent a very real problem for the model of the polar cap described here. It is difficult to see how they can be present in a truly INS, with either spin direction, not interacting with any other periodic system. Quasi-periodicities might be understandable in terms of natural phenomena at the condensed-matter surface, possibly connected with the diffusion of low-Zs nuclei perpendicular to B in the vicinity of the polar cap or with the two sections of the open magnetosphere described in Section 2. However, well-defined periodicities would remain a problem.
REFERENCES
