Abstract
We analyse the role of bars in the build-up of central mass concentrations in massive, disc galaxies. Our parent sample consists of 3757 face-on disc galaxies with redshifts between 0.01 and 0.05, selected from the seventh Data Release of the Sloan Digital Sky Survey. 1555 galaxies with bars are identified using the position angle and ellipticity profiles of the i-band light. We compare the ratio of the specific star formation rate measured in the 1–3 kpc central region of the galaxy to that measured for the whole galaxy. Galaxies with strong bars have centrally enhanced star formation; the degree of enhancement depends primarily on the ellipticity of the bar and not on the size of the bar or on the mass or structure of the host galaxy. The fraction of galaxies with strong bars is highest at stellar masses greater than 3 × 1010 M⊙, stellar surface densities less than 3 × 108 M⊙ and concentration indices less than 2.5. In this region of parameter space, galaxies with strong bars either have enhanced central star formation rates, or star formation that is suppressed compared to the mean. This suggests that bars may play a role in the eventual quenching of star formation in galaxies. Only 50 per cent of galaxies with strongly concentrated star formation have strong bars, indicating that other processes such as galaxy interactions also induce central starbursts. We also find that the ratio of the size of the bar to that of the disc depends mainly on the colour of the galaxy, suggesting that the growth and destruction of bars are regulated by gas accretion, as suggested by simulations.
1 INTRODUCTION
It has long been conjectured that spiral galaxies evolve along the Hubble sequence from ‘late-type’ disc-dominated systems to ‘early-type’ galaxies with very massive bulges. This scenario is supported by the fact that the comoving number density of massive bulge-dominated galaxies increases from high redshifts to the present day, while the number density of lower mass star-forming disc galaxies evolves comparatively little with redshift (Couch et al. 1998; Fasano et al. 2000; Kovač et al. 2010). It is believed that major merger events build classical bulges with light profiles that follow an r1/4 law (Toomre 1977; Barnes & Hernquist 1992), while pseudo-bulges with light profiles that are close to exponential are formed from the disc itself (see reviews by Wyse, Gilmore & Franx 1997; Kormendy & Kennicutt 2004). Pseudo-bulges are common in disc-dominated galaxies at low redshift (Balcells et al. 2003; Laurikainen et al. 2007; Weinzirl et al. 2009).
There are many mechanisms that may cause discs to become unstable and gas to flow towards the centre of the galaxy, eventually forming a bulge. Tidal forces exerted by an interacting companion cause gas to lose angular momentum and to flow into the central region of the galaxy where it forms stars at an elevated rate (a so-called starburst) (Mihos & Hernquist 1996; di Matteo et al. 2007; Cox et al. 2008). More than half of the galaxies with the highest central specific star formation rates (sSFR) in the local Universe are interacting with a close companion (Li et al. 2008). Alternatively, asymmetric structures in the disc including bars and spiral arms exert torques that drive gas inwards (see the review by Kormendy & Kennicutt 2004).
The mechanisms by which bars influence the flow of gas in galaxies have been studied in considerable detail using simulations. Bars induce gravitational torques that drive the gas towards the leading end of the bar where it is compressed and shocked, and where it loses energy by radiative processes, causing it to flow to the centre of the galaxy (Athanassoula 1992; Piner et al. 1995; Knapen, Shlosman & Peletier 2000; Sheth et al. 2002; Regan & Teuben 2004; Zurita & Pérez 2008). Galaxies with thick bars tend to form nuclear rings (Piner et al. 1995; Regan & Teuben 2003; Schinnerer, Böker & Meier 2003). Some of the gas will reach the centre and produce a disc-like bulge (Athanassoula 1992, 2005). Bars are robust if the galaxy remains undisturbed (Athanassoula, Lambert & Dehnen 2005).
Observational evidence that this basic picture is correct have come from highly resolved maps of the ionized, atomic and molecular gas in individual barred galaxies (e.g. Quillen et al. 1995; Sheth et al. 2000; Schinnerer et al. 2002), which allow one to track the motion of the gas in detail. In addition, there have been studies of samples of barred and unbarred galaxies that have revealed higher gas concentrations (Sakamoto et al. 1999; Jogee, Scoville & Kenney 2005; Sheth et al. 2005), higher central SFR and flatter chemical abundance gradients (de Jong et al. 1984; Hawarden et al. 1986; Devereux 1987; Puxley, Hawarden & Mountain 1988; Martin & Roy 1994; Zaritsky, Kennicutt & Huchra 1994; Ho & Filippenko 1997) in the barred galaxies. On average, these differences are most pronounced in galaxies with the strongest bars (Martin & Roy 1994; Martin 1995; Ho & Filippenko 1997). Recent observations suggest that most disc galaxies at high redshift are extremely gas rich and hence dynamically unstable, and will likely form bulges on a short time-scale (Genzel et al. 2006, 2008).
It would be valuable to quantify the role that bars have played in the formation of the present-day bulge and pseudo-bulge population. There has been a controversy about whether bars are found more frequently in early-type or in late-type disc galaxies (Barazza, Jogee & Marinova 2008; Sheth et al. 2008; Marinova et al. 2009). Enhanced central SFR are more likely to be found in early-type galaxies with bars than in late-type galaxies with bars (Devereux 1987; Ho & Filippenko 1997). These results are somewhat difficult to interpret because the Hubble type is a complex function of both bulge-to-disc ratio and SFR.
In semi-analytic models of galaxy formation, discs form when gas cools and settles at the centre of a dark matter halo, while conserving angular momentum. In recent years, simple prescriptions for bulge growth through disc instabilities have been included in these models (Parry, Eke & Frenk 2009; Benson & Devereux 2010; De Lucia et al. 2011), but these have only been tested against observations in a rudimentary way. Ideally, these models should be able to account for the fraction of disc galaxies with pseudo-bulges as a function of both halo mass and stellar mass, and the size of the disc.
In this paper, we study the effect of bars in building the central mass concentrations in galaxies as a function of parameters such as stellar mass, stellar mass surface density and concentration. We make use of imaging data from the Sloan Digital Sky Survey (SDSS; York et al. 2000). The SDSS images have a pixel scale of 0.396 arcsec and a mean point spread function (PSF) of 1.4 arcsec (full width at half-maximum, FWHM). In this study, we identify bars from the images of ∼ 4000 disc galaxies with redshifts in the range 0.01–0.05 drawn from the seventh data release (DR7) of the SDSS. We first investigate the bar strength needed to cause enhancement in the central SFR of the galaxy. We then divide our galaxies into a four-dimensional parameter space of stellar mass, concentration, stellar mass surface density and colour, and quantify the fraction of galaxies that are undergoing bar-driven central mass growth at the present day.
In Section 2, we describe our sample and the methods used to identify bars and to quantify their strength. In Section 3.1, we examine how strongly star formation is concentrated towards the centres of barred galaxies compared to the control samples of non-barred galaxies matched in stellar mass, stellar mass surface density and colour. In this analysis, we parametrize bar strength using the ellipticity of the bar, ebar. In Section 3.2, we examine the colours of bars, showing that the strongest bars have the bluest colours. In Section 3.3, we show how the fraction of barred galaxies varies according to the location of the galaxy in the four-dimensional parameter space of stellar mass, stellar mass surface density, concentration and colour. In Section 3.4, we investigate which galaxy properties correlate most strongly with bar strength and size. Finally, in Section 4, we summarize and discuss our results.
2 DATA
2.1 The sample
We select galaxies with M* > 1010 M⊙ in the redshift range 0.01 < z < 0.05 from the Max-Planck-Institut für Astrophysik/Johns Hopkins University (MPA
JHU) spectroscopic catalogue (http://www.mpa-garching.mpg.de/SDSS/DR7/), which is drawn from the DR7 of the SDSS (Abazajian et al. 2009). This yields a sample of 16 573 galaxies. Our aim is to assess the role of bars in building bulges in present-day disc-dominated systems, so we also select systems with R90/R50 < 2.6, where R90 and R50 are the radii of the circular apertures enclosing 90 and 50 per cent of the total r-band light from the galaxy. We further limit the sample to galaxies with ellipticity 1 −b/a < 0.25 (or an inclination of less than 41°.4), where a and b are the major and minor axes of an ellipsoidal fit in the r band to each galaxy. We employ this criterion to select relatively face-on galaxies, because it is difficult to identify bars in more inclined galaxies (Laurikainen & Salo 2002). These cuts yield a sample of 3890 galaxies, which we will use to characterize bars.
In this paper, we describe global SFR by fitting the observed FUV-, NUV-, u-, g-, r-, i- and z-band fluxes of the galaxy with a library of model spectral energy distributions (Saintonge et al. 2011; Wang et al. 2011). The model SED library is generated using stellar population synthesis models (Bruzual & Charlot 2003) and includes model ‘galaxies’ spanning a range in metallicity, age, star formation history and dust attenuation strength. The probability that the observed SED can be described by each model SED is calculated, and the SFR of the galaxy is then given as the probability-weighted SFR averaged over the whole model library. We also use the Av (attenuation in the V band) derived using this method to correct the global colours of galaxies for internal reddening.
We also make use of SFR estimated directly from the SDSS spectra, which are obtained through 3 arcsec diameter fibres. These SFR, which are taken directly from the MPA/JHU catalogue, are obtained by fitting the measured emission line fluxes to a set of photoionization and stellar population synthesis models (Brinchmann et al. 2004).
Finally, we derive morphological parameters, such as an asymmetry index for all the galaxies (see Wang et al. 2011, for more details).
2.2 Bar identification
We use the position angle and ellipticity profiles to identify bars in galaxies. Similar methods have been employed in many past papers (e.g. Wozniak et al. 1995; Knapen, Pérez-Ramírez & Laine 2002; Laine et al. 2002; Whyte et al. 2002; Sheth et al. 2003; Jogee et al. 2004; Menéndez-Delmestre et al. 2007; Barazza et al. 2008).
We first use SExtractor to estimate galaxy sizes (Petrosian radii, R50 and R90), ellipticities and disc position angles. We mask neighbouring sources in the vicinity of the main galaxy. We then run the irafellipse task twice on the SDSS r-band images over a range of radii extending from twice the Petrosian radius down to a radius of 0.8 arcsec from the centre of the galaxy.
The sampling radius in the fit increases exponentially with a step of 1.1, and the centre of each ellipse is allowed to vary. During the first run of the ellipse task, we set R90 as the starting radius. During the second run, we set the starting radius to maximum (R50, 1.5 arcsec). During both runs, the initial values of ellipticity and position angle are set equal to the values measured by SExtractor for the whole galaxy. The two profiles are then merged and bad points are discarded. Bad points are defined as the points where the ellipse task fails to find a solution, the error on the ellipticity measurement is larger than 0.05, or the error on the position angle is larger than 5.
The fit is said to have been successful if the merged profile covers the radius ranging from 1.4 arcsec to R90, and if it covers more than 60 per cent of the original range in radii that served as input for the irafellipse task. We also visually examined all the fits and found that our procedure was successful in almost all cases. Failures occurred for 133 galaxies (less than ∼3.5 per cent of the sample), mainly because the galaxies were strongly disturbed or had extended low surface brightness discs. We note that Barazza et al. (2008) and Jogee et al. (2004) obtained a similar failure rate in their own analysis of bars in galaxies in the SDSS. The remaining 3757 galaxies are well fitted with ellipses throughout the entire disc, and our analysis of bars will be confined to these systems from now on. We do not deproject the images or the profiles before classifying a galaxy as barred or unbarred. Such deprojections are subject to considerable uncertainty, particularly for more bulge-dominated galaxies. Errors introduced by projection effects will be discussed later.
The criteria we use to classify a galaxy as ‘barred’ are similar to those adopted by Jogee et al. (2004), hereafter J04, with a few changes that are detailed below. J04 required that (1) within the bar, the ellipticity should rise to a maximum value greater than 0.25, and that the position angle within the bar should remain constant to within 20°; (2) at the end of the bar, the ellipticity should drop by more than 0.1 and the position angle should change by more than 10°. Fig. 1 illustrates the ellipticity and position angle profiles of a galaxy that is classified as barred according to these criteria.
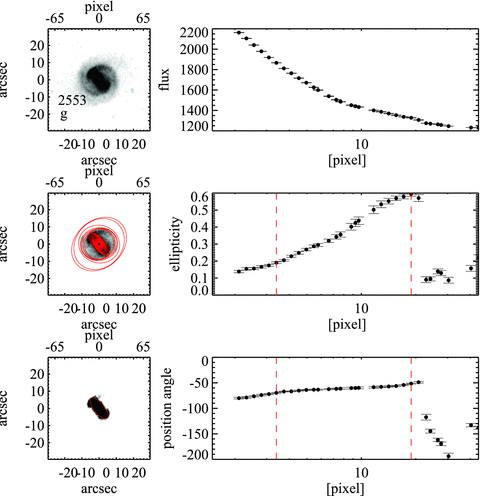
An example of a galaxy identified as barred. In the left-hand column, the top panel shows the image of the galaxy, the middle panel shows the fitted ellipses superimposed on the galaxy image, while the bottom panel shows the same image with the barred region highlighted. From top to bottom, the right-hand column shows the surface brightness, ellipticity and position angle profiles of the galaxy.
We imposed the following additional requirements after visually inspecting all the fits. (1) the inner radius of the bar should be less than 0.5 times the outer radius of the bar, and ellipticity should increase monotonically as a function of radius from 0.33Router to the end of the bar. This requirement improves the ability of the algorithm to identify bars in galaxies with prominent bulges; Martin (1995) showed that the size of the bulge is on average about half the size of the bar. It also prevents complicated spiral structures and inner rings from being mistakenly identified as bars. (2) The outer radius of the bar should be less than 0.8 times the semimajor axis of the outermost fitted ellipse. This requirement ensures that edge-on, disc-dominated galaxies, where the inclination has been incorrectly measured, do not enter our sample of barred galaxies. (3) if criterion 1 adopted by J04 is satisfied, and the ellipticity drops by more than 0.25 at the end of the bar, but the position angle does not change by more than 10°, we still classify the galaxy as barred.
The final requirement ensures that we do not exclude galaxies which have a long bar surrounded by an aligned ring. Examples of such systems are given in Gadotti & de Souza (2003). We also note that Menéndez-Delmestre et al. (2007) estimated that the position angle criterion of J04 could introduce incompleteness at the 10 per cent level. Criterion 3 resolves this problem for bars which have high ellipticity (ebar >0.5), which is the focus of our study.
As well as classifying galaxies into barred and non-barred systems, we compute two quantitative parameters: (1) the bar ellipticity ebar, defined as the value of the ellipticity at the end of the bar, and (2) the relative bar size Dbar/Ddisc, where Dbar is the diameter of the bar and Ddisc is the diameter of the 25 mag arcsec−2 isophote measured in the g band. The median value of ebar is 0.47 and the median value of Dbar/Ddisc is 0.3 for the galaxies in this study.
The most distant galaxies in our sample are at z∼ 0.05, where 2.5 times the FWHM of the SDSS PSF (∼ 3.5 arcsec) corresponds to a physical scale of 3.8 kpc. Note that a 3.8 kpc bar aligned along the minor axis of an inclined galaxy with 1 −b/a= 0.25 has a deprojected physical size of 5 kpc, so our sample is complete for bars larger than 5 kpc.
To demonstrate that our 5 kpc cut produces an unbiased sample of barred galaxies, we plot the fraction of barred systems as a function of redshift and galaxy size in the left-hand panel of Fig. 2. If the barred galaxy sample suffers from incompleteness because we miss bars with smaller angular sizes, we might expect the bar fraction to drop at higher redshifts, particularly in small galaxies. We see, however, that bar fractions do not vary with redshift at fixed physical size. The right-hand panel of Fig. 2 shows the fraction of barred galaxies as a function of galaxy size and ellipticity. As can be seen, the bar fraction does not vary with the ellipticity, so there is no clear inclination-dependent bias in our estimates of bar fraction, at least for the values of edisc less than 0.25. We will refer to the sample of galaxies with bars larger than 5 kpc as bar sample A.
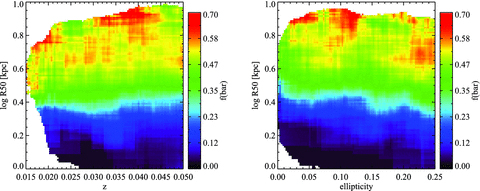
The distribution of galaxies in our sample is plotted in the plane of physical size versus redshift (left) and physical size versus ellipticity (right). The coloured contours denote the fraction of bars as a function of position in this plane. Only sample A barred galaxies are plotted.
One might worry, however, that by adopting a fixed cut in the physical diameter of the bar, one would be able to identify a larger proportion of the bars present in large galaxies compared to smaller ones. Another possibility is to adopt a fixed cut on Dbar/Ddisc. We have examined the distribution of the diameters D25 of the galaxies in our sample. We find a lower limit of D25 of around 16 kpc, corresponding to the diameter of the most compact galaxies with stellar masses of 1010 M⊙. We have therefore constructed a second sample of barred galaxies with Dbar/Ddisc >0.3, which we will refer to as bar sample B.
In total, we identify 1555 barred galaxies with Dbar > 5 kpc (41.4 per cent of the original sample of 3757 galaxies), of which 827 (22 per cent) have ebar > 0.5. We note that a similar fraction were found by Marinova & Jogee (2007) and J04 when a similar cut in bar size and bar ellipticity was applied. Bar sample B contains 506 galaxies, and 363 of them have ebar > 0.5. In general, bar sample B is most robust for investigating how the fraction of bars depends on galaxy structural parameters, such as stellar mass surface density or concentration. Bar sample A is most useful for investigating the fraction of central starbursts that are triggered by bar-induced inflows.
Another issue that may potentially bias our results is that if the galaxy has a bulge, it may be more difficult to measure the shape of the bar by means of the ellipse-fitting technique. The bulge will make the surface brightness contours of the galaxy rounder, causing ebar to be underestimated. As a result, some barred galaxies will then be missing from our sample. One way by which we can quantify this effect is simulations, which are described in detail in Appendix A. The main conclusion of this study is that the identification of ‘strong bars’ with ebar > 0.5 is reasonably robust to the presence of a bulge. The interested reader is referred to Appendix A for more details. In the rest of the paper, our conclusions will be based on the analysis of bars with ebar > 0.5.
2.3 Control samples
There have been many papers that have found that barred spiral galaxies have higher central SFR than unbarred spirals (de Jong et al. 1984; Hawarden et al. 1986; Devereux 1987; Puxley et al. 1988; Martin & Roy 1994; Zaritsky et al. 1994; Ho & Filippenko 1997). The enhancement is more pronounced for strongly barred galaxies than for weakly barred galaxies (Martin & Roy 1994; Martin 1995; Ho & Filippenko 1997).
It should be noted that the SFR in both barred and un-barred galaxies vary strongly as a function of their structural parameters, such as concentration and stellar mass surface density. If we wish to quantify the enhancement in the central SFR accurately, we need to create control samples that are closely matched with the barred galaxy sample in these parameters.
For each barred galaxy from sample A, we search the parent sample for a matching galaxy (selected without regard to whether or not it has a bar) with stellar mass difference Δlog M* less than 0.15, stellar mass surface density difference Δlog μ* less than 0.1 and g−i colour difference Δ(g−i) less than 0.1.
2.4 Photometry of bars and pseudo-rings
As described in Section 2.2, the outer end of a bar is defined as the point where the ellipticity profile reaches its maximum. From now on, we will refer to the region within the ellipse enclosing the end of the bar as the ‘barred region’ of the galaxy. According to the simulations of Athanassoula (1992), the gas will flow from the end of the bar towards the centre of the galaxy, following a curved path which is determined by the strength of the bar and the central mass density of the galaxy. The region of the galaxy that we define to be barred will cover the path of the inflowing gas until it condenses into a ring at the inner Lindblad resonance (see Fig. 3).
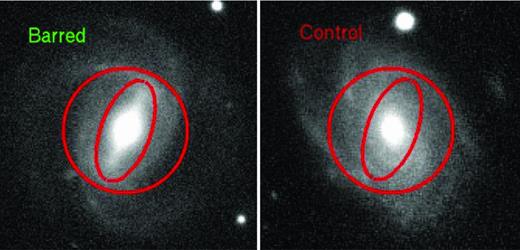
An example of a barred galaxy (left) and its matched control galaxy (right). In the left-hand panel, the inner ellipse encloses the ‘barred’ region of the galaxy (see the text). The area between the inner and outer ellipses is referred to as the pseudo-ring region. In the right-hand panel, the same inner and outer ellipses are plotted on the image of the control galaxy.
We also define an outer ellipse with ellipticity equal to that of the disc measured at its 25 mag arcsec−2 isophote in the r band and with major axis equal to 1.2Dbar. The ‘pseudo-ring’ region of the galaxy is defined as the region between the ellipse enclosing the barred region of the galaxy and this outer ellipse. The motivation for defining such a ring is that an ultraharmonic resonance ring in disc galaxies is often found at the end of the bar (Regan et al. 2002; Regan & Teuben 2003; Athanassoula, Romero-Gómez & Masdemont 2009a; Athanassoula et al. 2009b, 2010). The gas will tend to accumulate in this ring and if the density reaches high enough values, stars will form. These outer resonance rings are usually aligned parallel to the bar and may extend out to the corotation radius of the disc (Schwarz 1981; Buta et al. 2010). The ‘pseudo-ring’ region defined in this study is thus designed to cover the location of potential resonance rings in our galaxies.
For each barred galaxy in our sample, we measure the SDSS g−i colour within the barred region and within the ‘pseudo-ring’ region. We also measure colours within the same regions in the corresponding control galaxy, even though these systems often do not have bars (see the right-hand panel of Fig. 3). [Note that when we define the corresponding barred and pseudo-ring regions of the control galaxy, we scale the major and minor axes of both regions by the ratio D25 (control galaxy)/D25 (barred galaxy), so that the outer radii of the two systems match exactly.]1 We will compare the colours between the barred galaxies and control galaxies in Section 3.2.
All the colours in the barred and ‘pseudo-ring’ regions are corrected for dust attenuation using the average of the central attenuation and the global attenuation. The central attenuation is derived from the Balmer decrement measured from the SDSS fibre spectrum. We have assumed a Calzetti et al. (2000) extinction curve and the line-to-continuum attenuation ratio from Wild et al. (2011). We apply a dust correction when both the Hα and Hβ fluxes have signal-to-noise ratio > 3. If the emission lines are too weak to measure the Balmer decrement, we adopt 
from the measurements of the attenuation of the stellar continuum of the galaxy provided in the MPA
JHU catalogue (tauv_cont). This parameter is obtained by fitting Bruzual & Charlot (2003) population synthesis models to the stellar continuum; the reddening may then be estimated by determining the extra ‘tilt’ that must be applied to the models in order to fit the shape of the observed spectrum. The global attenuation is derived using SED-fitting techniques.
3 RESULTS
3.1 Establishing a link between strong bars and enhanced central star formation in galaxies
As discussed in Section 2.3, we have constructed a control sample with the same stellar masses, structural properties and global colours as the barred galaxies. By examining whether the central SFR are enhanced in the barred galaxy sample when compared to the controls, we can test whether there is a causal link between bars and central starbursts. By binning the barred galaxy sample and the control sample according to stellar mass, stellar surface density and morphological type, we ascertain to what extent the degree of central star formation enhancement is influenced by global galaxy properties.
In this paper, we use the quantity sSFRfib/sSFRtot, which we will denote by C(SF) as a measure of how concentrated the star formation is in a galaxy: sSFRfib is the specific SFR measured within the 3 arcsec SDSS fibre, and sSFRtot is the global specific SFR of the galaxy.
In Fig. 4, we compare the distribution of log C(SF) for our barred galaxies (shown as black histograms on the plot) and control galaxies (red-dashed histograms). The two columns on the left show results for galaxies with weak bars (ebar < 0.5), while the columns on the right are for strong bars (ebar > 0.5). Each row in the figure shows results for galaxies split according to a set of global galaxy properties that include stellar mass, stellar mass surface density, concentration parameter, g−i colour, galaxy asymmetry index A and ratio of the diameter of the bar to that of the disc (Dbar/Ddisc). In each case, the split is made at the median value of the parameter under investigation. The difference in the average log C(SF) and Kolmogorov–Smirnov probability for the barred and control galaxies for each subsample in each plot are summarized in Table 1.
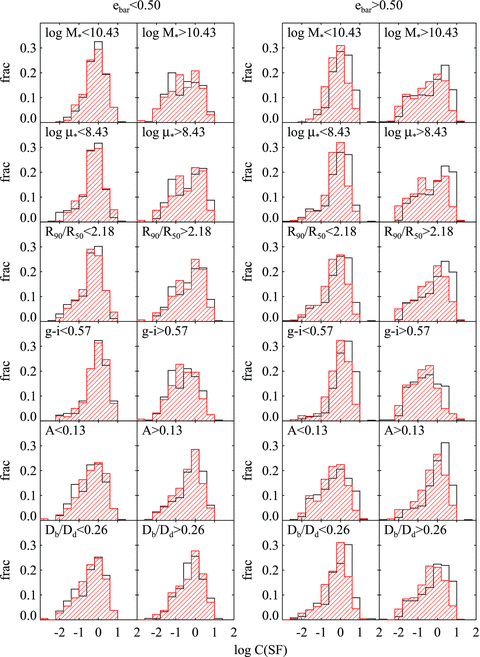
Histograms of the ratio of SSFR evaluated within the SDSS fibre to SSFR for the galaxy as a whole (log C(SF)) are shown for the barred galaxy sample (open histograms), and for the control sample matched in stellar mass, stellar mass surface density and g−i colour (red hatched histograms). The plots on the left show results for galaxies with weak bars (ebar < 0.5), while the plots on the right are for galaxies with strong bars (ebar > 0.5). The samples are further divided by stellar mass (log M*, M* is in units of M⊙), stellar mass surface density (log μ*, μ* is in units of M⊙ kpc−2), concentration (R90/R50), g−i colour, asymmetry index (A) and relative bar size (Dbar/Ddisc) at the median value of each parameter as denoted in each plot. Only bar sample A galaxies are plotted.
The difference of C(SF) between the barred and control galaxies (see Fig. 4). 
is the average value of log C(SF, barred) −log C(SF, control). KS prob is the Kolmogorov–Smirnov probability that the two distributions [C(SF) for the barred and control galaxies] are drawn from an identical parent population. The columns on the left show results for galaxies with weak bars (ebar < 0.5), while the columns on the right are for galaxies with strong bars (ebar > 0.5). The samples are further divided by the stellar mass (log M*, M* is in units of M⊙), stellar mass surface density (log μ*, μ* is in units of M⊙ kpc−2), concentration (R90/R50), g−i colour, asymmetry index (A) and relative bar size (Dbar/Ddisc) at the median value of each parameter, as denoted in the second row of the table. Only bar sample A galaxies are calculated.
| X | ebar < 0.5 | ebar > 0.5 | ||||||
| X< median (X) | X> median(X) | X< median (X) | X> median (X) | |||||
 | KS prob |  | KS prob |  | KS prob |  | KS prob | |
| M* | 0.03 | 0.14 | −0.01 | 0.34 | 0.23 | 0.00 | 0.19 | 0.00 |
| μ* | −0.04 | 0.75 | 0.07 | 0.32 | 0.11 | 0.00 | 0.32 | 0.00 |
| R90/R50 | −0.03 | 0.84 | 0.05 | 0.41 | 0.19 | 0.00 | 0.23 | 0.00 |
| g−i | −0.00 | 0.93 | 0.03 | 0.46 | 0.26 | 0.00 | 0.12 | 0.09 |
| A | −0.03 | 0.47 | 0.08 | 0.06 | 0.11 | 0.02 | 0.29 | 0.00 |
| Dbar/Ddisc | −0.01 | 0.40 | 0.06 | 0.82 | 0.17 | 0.00 | 0.23 | 0.00 |
| X | ebar < 0.5 | ebar > 0.5 | ||||||
| X< median (X) | X> median(X) | X< median (X) | X> median (X) | |||||
| KS prob | | KS prob | | KS prob | | KS prob | |
| M* | 0.03 | 0.14 | −0.01 | 0.34 | 0.23 | 0.00 | 0.19 | 0.00 |
| μ* | −0.04 | 0.75 | 0.07 | 0.32 | 0.11 | 0.00 | 0.32 | 0.00 |
| R90/R50 | −0.03 | 0.84 | 0.05 | 0.41 | 0.19 | 0.00 | 0.23 | 0.00 |
| g−i | −0.00 | 0.93 | 0.03 | 0.46 | 0.26 | 0.00 | 0.12 | 0.09 |
| A | −0.03 | 0.47 | 0.08 | 0.06 | 0.11 | 0.02 | 0.29 | 0.00 |
| Dbar/Ddisc | −0.01 | 0.40 | 0.06 | 0.82 | 0.17 | 0.00 | 0.23 | 0.00 |
The difference of C(SF) between the barred and control galaxies (see Fig. 4). is the average value of log C(SF, barred) −log C(SF, control). KS prob is the Kolmogorov–Smirnov probability that the two distributions [C(SF) for the barred and control galaxies] are drawn from an identical parent population. The columns on the left show results for galaxies with weak bars (ebar < 0.5), while the columns on the right are for galaxies with strong bars (ebar > 0.5). The samples are further divided by the stellar mass (log M*, M* is in units of M⊙), stellar mass surface density (log μ*, μ* is in units of M⊙ kpc−2), concentration (R90/R50), g−i colour, asymmetry index (A) and relative bar size (Dbar/Ddisc) at the median value of each parameter, as denoted in the second row of the table. Only bar sample A galaxies are calculated.
| X | ebar < 0.5 | ebar > 0.5 | ||||||
| X< median (X) | X> median(X) | X< median (X) | X> median (X) | |||||
| KS prob | | KS prob | | KS prob | | KS prob | |
| M* | 0.03 | 0.14 | −0.01 | 0.34 | 0.23 | 0.00 | 0.19 | 0.00 |
| μ* | −0.04 | 0.75 | 0.07 | 0.32 | 0.11 | 0.00 | 0.32 | 0.00 |
| R90/R50 | −0.03 | 0.84 | 0.05 | 0.41 | 0.19 | 0.00 | 0.23 | 0.00 |
| g−i | −0.00 | 0.93 | 0.03 | 0.46 | 0.26 | 0.00 | 0.12 | 0.09 |
| A | −0.03 | 0.47 | 0.08 | 0.06 | 0.11 | 0.02 | 0.29 | 0.00 |
| Dbar/Ddisc | −0.01 | 0.40 | 0.06 | 0.82 | 0.17 | 0.00 | 0.23 | 0.00 |
| X | ebar < 0.5 | ebar > 0.5 | ||||||
| X< median (X) | X> median(X) | X< median (X) | X> median (X) | |||||
| KS prob | | KS prob | | KS prob | | KS prob | |
| M* | 0.03 | 0.14 | −0.01 | 0.34 | 0.23 | 0.00 | 0.19 | 0.00 |
| μ* | −0.04 | 0.75 | 0.07 | 0.32 | 0.11 | 0.00 | 0.32 | 0.00 |
| R90/R50 | −0.03 | 0.84 | 0.05 | 0.41 | 0.19 | 0.00 | 0.23 | 0.00 |
| g−i | −0.00 | 0.93 | 0.03 | 0.46 | 0.26 | 0.00 | 0.12 | 0.09 |
| A | −0.03 | 0.47 | 0.08 | 0.06 | 0.11 | 0.02 | 0.29 | 0.00 |
| Dbar/Ddisc | −0.01 | 0.40 | 0.06 | 0.82 | 0.17 | 0.00 | 0.23 | 0.00 |
Our conclusion is very simple. For each of the parameters shown in the two left-hand panels (ebar < 0.5), there is no significant difference between the black and red histograms, i.e. there are no significant differences between the barred and the control samples. For each of the parameters shown in the two right-hand panels (ebar > 0.5), the differences are very significant. This shows that only strong bars are capable of inducing enhanced central star formation in galaxies. In the two right-hand panels, the offset between the black and red histograms is roughly the same for each parameter. This shows that the global galaxy properties considered here do not play a significant role in determining the degree of central star formation enhancement caused by bar-driven inflows.
In the left-hand panel of Fig. 5, we show how the degree of central star formation enhancement depends on both ebar and the concentration index of the galaxy (note that the concentration index is a simple measure of the bulge-to-disc ratio). We plot the contours of 
C(SF) in the plane of ebar versus R90/R50, where 
C(SF) is the difference in log [sSFRfib/sSFRtot] for the barred galaxies and the controls. We see that when ebar > 0.5, 
C(SF) is positive, indicating that star formation is more concentrated in the barred galaxies. When ebar < 0.5, star formation in barred galaxies and control galaxies is similarly concentrated.
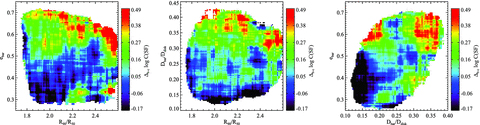
The distribution of C(SF) of barred galaxies minus C(SF) of control sample galaxies is plotted in the plane of the bar ellipticity parameter ebar versus concentration (left), bar relative size parameter Dbar/Ddisc versus concentration (middle) and ebar versus bar relative size parameter (right). The coloured contours indicate the average value of C(SF, barred)−C(SF, control) as a function of position in this plane. Note that the control galaxies are assigned the values of ebar and Dbar of their corresponding barred galaxies when making the plots. Only bar sample A galaxies are considered.
We note that there is an apparent deficit of galaxies with large concentrations and with high values of ebar in Fig. 5. As discussed in Appendix A, one possible reason for this is that ebar will be systematically underestimated in galaxies with larger bulge-to-disc ratios. In Fig. A2, we see that ebar is underestimated by about 0.1–0.15 when R90/R50 > 2.5, which agrees well with the observed deficit. After taking this bias into account, we conclude that there is no clear evidence that strong bars are less efficient at channelling gas to the central regions of galaxies if a bulge component is already present. On the other hand, Fig. 5 shows that the degree of central star formation enhancement appears to be smaller in strongly barred galaxies with low central mass concentration (C < 1.9), in agreement with simulation results from Athanassoula (1992) and Sheth et al. (2000).
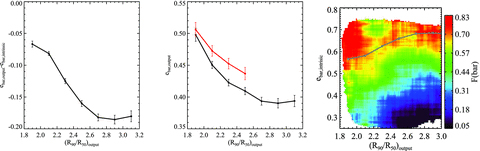
In the left-hand panel, (ebar, output−ebar, intrinsic) is plotted as a function of R90/R50. The line shows the average value, with the error bars calculated using bootstrapping. In the middle panel, ebar, output (black line) and ebar, obs (red line) from real galaxies are plotted as a function of R90/R50. In the right-hand panel, the distribution of simulated galaxies is plotted in the two-dimensional plane of the output concentration R90/R50 versus input ebar, intrinsic. The coloured contours denote the bar verification rate (F(bar)) as a function of position in the plane. The grey curve shows the average input ebar, intrinsic that corresponds to an ebar, outout value of 0.5 as a function of R90/R50.
In the middle panel of Fig. 5, we investigate whether the degree of central star formation enhancement exhibits any dependence on the length of the bar relative to that of the disc. We plot 
C(SF) in the plane of Dbar/Ddisc versus concentration index. We see that 
C(SF) is somewhat higher when Dbar/Ddisc >0.3. We note, however, that this effect is mainly due to the fact that the size of the bar is correlated with its ellipticity. This is clearly demonstrated in the right-hand panel of this figure, which shows the contours of 
C(SF) in the Dbar/Ddisc versus ebar plane. The main dependence of C(SF) is on ebar and not on Dbar/Ddisc.
In summary, we find that the central star formation enhancement depends mainly on the ellipticity of the bar and not on the size of the bar or on the mass or structure of the host galaxy.
3.2 Bar and pseudo-ring colours
In this section, we compare the colours of the barred and pseudo-ring regions in the barred and control galaxy samples. As shown in the previous section, the degree of central star formation depends primarily on ellipticity, so we simply split the sample at ebar= 0.5. The left-hand panels of Fig. 6 show that the colours in the barred and pseudo-ring regions do not differ significantly from those measured in the control samples when ebar < 0.5. Much stronger differences are found when ebar > 0.5. These results imply that the enhanced central star formation extends well beyond the central region of the galaxy when the bar is strong. Enhanced star formation is found in regions where gas is likely to flow inwards, as well as in the outer regions of the galaxy, where gas is compressed by the resonance.
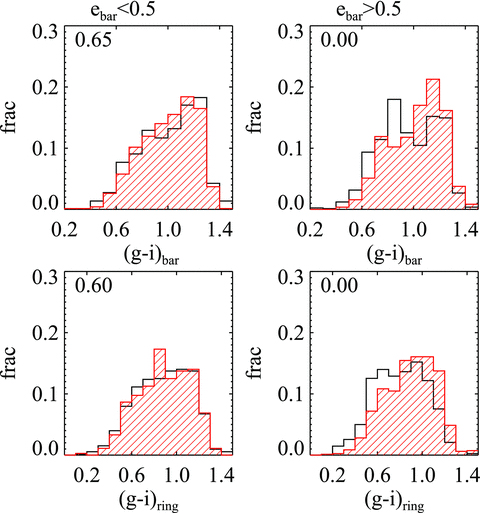
The top panels show a comparison of the distribution of g−i colours measured for the ‘barred regions’ of the galaxies classified as barred (black histograms) with the distribution of g−i colours measured for the same regions in the sample of control galaxies (red dashed histograms). Results are shown for weak bars (left) and for strong bars (right). The bottom panels show a comparison of g−i colours measured for the ‘pseudo-ring’ regions of the barred and control galaxy samples. Only bar sample A galaxies are plotted.
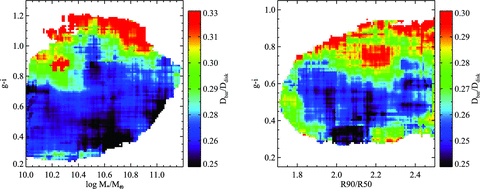
Finally, in the left-hand panel of Fig. 7, we examine how the average ellipticity of the bar varies as a function of location in the plane of bar colour versus global galaxy colour. As can be seen, if the barred region of the galaxy is blue, then a strong bar is generally located within it (note that the ‘noise’ in the plot probably arises because the barred region only traces the gas inflow region in an approximate way). On the other hand, there is no obvious effect seen as a function of the global colour of the galaxy. In the right-hand panel, we examine how Dbar/Ddisc varies as a function of the same two parameters. In contrast to the results obtained for ebar, the size of the bar (scaled to that of the disc) does not correlate with the colour of the bar, but scales strongly as a function of the global colour of the galaxy. The reddest galaxies host the longest bars. We will discuss possible explanations for this result in Section 4.
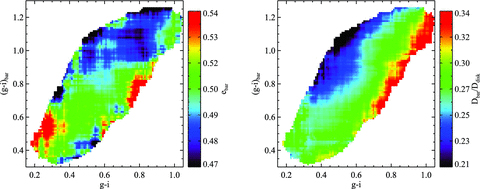
The barred galaxy sample is plotted in the two-dimensional plane of bar colour versus global galaxy colours. In the left-hand panel, the coloured contours denote the average ebar as a function of position in the plane. In the right-hand panel, the contours indicate the average value of Dbar/Ddisc. Only bar sample A galaxies are plotted.
3.3 Fraction of galaxies with strong bars
In this section, we examine how the fraction of disc galaxies with strong bars (i.e. galaxies having ebar > 0.5) varies as a function of the stellar mass, stellar mass surface density and concentration. We show results for bar samples A and B. Sample A, which includes all galaxies with bars larger than a physical size of 5 kpc, is useful for deriving a stronger lower limit to the fraction of galaxies with strong bars. Sample B, which includes only those galaxies with Dbar/Ddisc >0.3, should yield unbiased trends in strong bar fraction as a function of parameters such as stellar mass surface density, which scale with the size of the galaxy.
In the top row of Fig. 8, we plot the contours of strong bar fraction from bar sample A in the plane of stellar mass versus stellar mass surface density (left) and stellar mass versus concentration index (right). The fraction of galaxies with strong bars exceeds 0.5 for galaxies with log M*/M⊙ > 10.6 with low stellar mass surface densities (
) and low concentrations (C < 2.5). For lower mass galaxies, the strong bar fraction is a factor of 2 smaller, but also peaks at low stellar surface densities and concentrations.
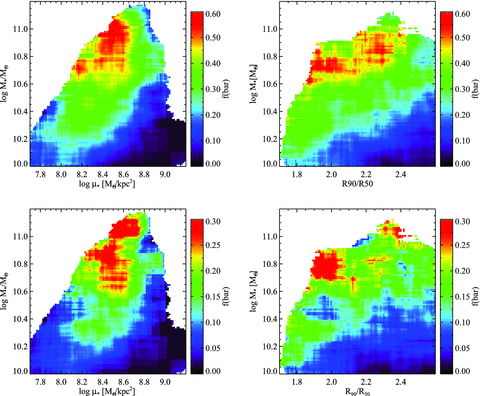
The distribution of galaxies from bar sample A (top row) and bar sample B (bottom row) is plotted in the two-dimensional plane of stellar mass versus mass surface density and stellar mass versus concentration. The coloured contours denote the strong bar fraction as a function of position in the plane.
In the bottom row of Fig. 8, we show results for sample B. The strong bar fractions are lower and the plots are noisier, but the same qualitative trends are apparent. We conclude, therefore, that the bar-driven mode of bulge formation appears to be most ubiquitous in massive, disc-dominated galaxies at the present day.
Finally, in Fig. 9 we plot the contours of strong bar fraction in the plane of C(SF) versus stellar mass, stellar mass surface density and concentration parameter. This plot should not only tell us whether strong bars are a sufficient condition for enhanced central star formation in galaxies, but also whether they are a necessary condition. Note that in this plot, Δ(log C(SF)) is defined as log C(SF) minus the average value for all galaxies with similar stellar mass surface density and concentration from the ‘parent sample’: positive values indicate that star formation is more concentrated than the average and negative values that it is less concentrated.
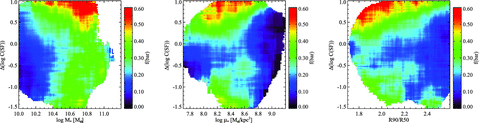
The distribution of galaxies from bar sample A is plotted in the two-dimensional plane of ΔC(SF) versus stellar mass, ΔC(SF) versus mass surface density and ΔC(SF) versus concentration. The coloured contours denote the strong bar fraction as a function of position in the plane.
We see from Fig. 9 that the strong bar fraction peaks in galaxies with the most concentrated star formation and with stellar masses greater than ∼3 × 1010 M⊙, stellar surface densities less than ∼3 × 108 M⊙ kpc−2 and concentration parameters less than ∼2.4. The peak strong bar fraction is around 0.5. This implies that although bar-driven inflows constitute a major channel for inducing enhanced central star formation in disc-dominated galaxies, they are not the only process at work. As shown by Li et al. (2008) and Reichard et al. (2009), galaxies with close companions and lopsided galaxies also have enhanced SFR. We note that in the highest surface density galaxies, bars appear to play no role at all in inducing enhanced central star formation.
Very interestingly, there appears to be a secondary peak in the fraction of strong bars in galaxies with the same stellar masses, stellar surface densities and concentrations, but with central SFR that are significantly below average. In other words, there also appears to be a population of quenched galaxies with strong bars. This is consistent with the finding in Sheth et al. (2005) that some barred spirals have nuclear regions that are deficient in gas.
This result raises the question as to whether central starbursts produced by bar-driven inflows play any role in shutting down star formation in some galaxies, either by using up the available gas more quickly or by generating winds/outflows that expel the gas from the central regions of these systems. We find no enhancement of optical or radio active galactic nucleus fraction in this population, which suggests that starburst-driven processes may be at work. Another possible explanation is that the gas has simply been consumed and that the galaxies are in a temporarily quiescent state. This will be the subject of a future investigation.
Finally, we note that for the low-density, low-concentration galaxy population (μ* < 3 × 108 M⊙ kpc−2, C < 2.5), the strong bar fraction is smallest when there is no enhancement in the central SFR. This is consistent with the idea that in the absence of any dynamical perturbations, the SFR in present-day disc galaxies are regulated by accretion from the surrounding halo (e.g. Kauffmann et al. 1993). Bar-driven inflows then play a key role in regulating the rate at which the accreted gas in consumed into stars.
3.4 The relation between bar properties and global galaxy properties
In Figs 10 and 11, we examine how ebar and Dbar/Ddisc depend on global galaxy properties such as stellar mass, concentration index and g−i colour.
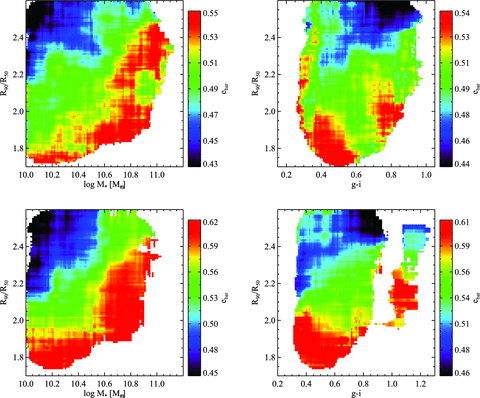
Galaxies from bar sample A (top row) and bar sample B (bottom row) are plotted in the two-dimensional plane of concentration versus stellar mass and concentration versus g−i colour. The coloured contours denote the average value of ebar as a function of position in the plane.
Galaxies from bar sample A are plotted in the two-dimensional plane of stellar mass and concentration versus g−i colour. The coloured contours denote the average value of Dbar/Ddisc as a function of position in the plane.
The left-hand panels of Fig. 10 show that more massive and less concentrated galaxies tend to have stronger bars. This is in agreement with the results discussed previously, showing that the fraction of galaxies with strong bars peaks for massive, disc-dominated galaxies (see Appendix A for a discussion about bulge contamination). The right-hand panel shows that at a fixed concentration, there does not appear to be any direct connection between ebar and global g−i colour. Once again, the results for bar samples A and B are qualitatively very similar.
In Fig. 11, we again see that Dbar/Ddisc is strongly correlated with global g−i colour. At a fixed stellar mass or concentration, redder galaxies have higher bar-to-disc size ratios. In some extreme cases, the whole galaxy consists of a long bar and a surrounding ring. These galaxies are almost all red. Fig. 12 shows a compendium of the SDSS images of such galaxies. It is interesting to note that at a fixed colour, Dbar/Ddisc does not vary as a function of the concentration or stellar mass.
A gallery of images of galaxies with long bars.
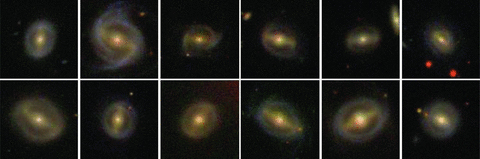
In summary, ebar is correlated with both stellar mass and structural parameters such as concentration, but not with global colour. Dbar/Ddisc is very strongly correlated with global colour, and only weakly correlated with mass and structural parameters.
4 SUMMARY AND DISCUSSION
We have identified 1555 galaxies with bars longer than 5 kpc in a sample of 3757 face-on disc galaxies with stellar masses greater than 1010 M⊙ and redshifts in the range 0.01 < z < 0.05 drawn from the DR7 of the SDSS. We have measured the ellipticity, length and g−i colour of the bars and have explored the relationship between global galaxy properties, bar properties and enhanced central star formation in galaxies.
Our main conclusions may be summarized as follows.
Only strong bars with ellipticity greater than 0.5 result in enhanced central star formation in galaxies. This result holds for all galaxies regardless of their stellar mass, stellar mass surface density or bulge-to-disc ratio (Section 3.1, Fig. 4).
Strong bars tend to have blue colours and are surrounded by a blue outer ring. This indicates that the enhanced star formation is occurring on the scale of the bar itself (Section 3.2, Fig. 6).
The incidence of strong bars is highest for massive galaxies with low mass surface densities and concentrations, reaching values as high as 60 per cent for galaxies with stellar masses greater than 3 × 1010 M⊙, stellar surface densities less than 3 × 108 M⊙ kpc−2 and concentration indices less than ∼2.5 (Section 3.3, Fig. 8).
Within this population, the incidence of strong bars appears to be bimodal. The fraction of bars is highest for galaxies with central SFR that are higher than the average by a factor of 2–3. There is a secondary peak in strong bar fraction for galaxies with central SFR that are lower than the average by more than a factor of 10 (Section 3.3, Fig. 9).
There is no correlation between the ellipticity (or strength) of the bar and the global colour of the galaxy. There is a strong correlation between the size of the bar and the global colour of the galaxy.
4.1 Relation of this work to other recent studies of bars in large galaxy samples
There have been a number of studies focusing on how the fraction and properties of bars vary as a function of the Hubble type, or the parameters such as stellar mass. Because most of the galaxy properties are strongly correlated, it is difficult to identify which is the primary parameter in many of these correlations. Our approach for analysing the properties of bars in the two-dimensional projections of different galaxy parameters helps us differentiate primary from secondary correlations.
Marinova et al. (2009, hereafter M09) found an increasing bar fraction as a function of the galaxy luminosity and stellar mass consistent with our results. Barazza et al. (2008, hereafter B08) found the opposite trend. However, our trends in bar fraction as a function of the concentration index are consistent with B08, but at odds with M09. The main reasons for these discrepancies are the very different sample definitions (see the discussion in Nair & Abraham 2010). We note that the analysis in this paper has been carried out for a volume-limited sample of galaxies with stellar masses greater than 1010 M⊙, so the statistics presented in this paper should not suffer from any sample selection biases.
Laurikainen et al. (2007) found that ebar does not vary as a function of the Hubble type; Whyte et al. (2002) and Aguerri, Méndez-Abreu & Corsini (2009) found a tendency for late-type galaxies to have higher ebar, while Martin (1995) found a tendency for early-type galaxies to have higher ebar. Our result show a possible explanation for these discrepancies from different studies: early-type galaxies are both more massive and more concentrated than late-type galaxies, while we show that the trend of ebar varying with stellar mass is contrary to the trend with concentration. We have chosen to bypass the Hubble type altogether, focusing instead on concentration index and stellar surface densities as parameters that have a simpler physical interpretation.
There have been many attempts to link the length of the bar length with the global structure of galaxies. Longer bars were found to correlate with more prominent bulges in early-type galaxies (Athanassoula & Martinet 1980; Martin 1995; Athanassoula 2003; Erwin 2005; Aguerri et al. 2009). Hoyle et al. (2011) were the first to find that galaxies hosting longer bars also tend to be redder. Our results show that Dbar/Ddisc has the tightest correlation with colour, and at a fixed colour Dbar/Ddisc does not vary with stellar mass or concentration.
There have also been numerous studies of the relation between bars, gas concentration, central SFR and metallicity gradients in galaxies, supporting the picture that bars induce gas inflows in galaxies (de Jong et al. 1984; Martin & Roy 1994; Zaritsky et al. 1994; Martin 1995; Sakamoto et al. 1999; Jogee et al. 2005; Sheth et al. 2005). Recently, Ellison et al. (2011) used a large, visually classified sample to show that barred galaxies with stellar M* > 1010 M⊙ have centrally enhanced SFR. This is consistent with our results. No dependence of central star formation enhancement on bar ellipticity was found in Ellison et al. (2011). One possible reason for this discrepancy is that their control sample was only matched in stellar mass, while our control sample was matched in stellar mass, mass surface density and colour. Because the central SFR of galaxies depend on all these parameters (and on colour in particular), Ellison et al. (2011) might not have had the sensitivity to isolate the ellipticity dependence.
Finally, we note that our results are inconsistent with some past findings (Devereux 1987; Ho & Filippenko 1997) that late-type galaxies do not have significantly enhanced central star formation. One possible reason for this discrepancy is that these studies did not distinguish strongly barred galaxies from weakly barred galaxies. As we have seen, the fraction of galaxies with strong bars peaks at higher stellar masses, so the late-type samples investigated in these older studies may have only contained galaxies with weak bars. We also caution that bar classifications in bulge-dominated galaxies are subject to strong biases. Two-dimensional image decomposition techniques that allow the bulge component to be properly subtracted are one obvious way forward (for example, Gadotti 2009; Weinzirl et al. 2009), but this lies well beyond the scope of this study.
4.2 Comments on the results in this paper
4.2.1 Only bars with ebar > 0.5 induce enhanced central star formation in galaxies
We found that only bars with ebar > 0.5 were able to induce enhanced levels of star formation in the central and bar-dominated regions of the galaxies in our sample. In addition, star formation in the circular region surrounding the bar was also found to be enhanced.
These results are qualitatively consistent with simulations that show that gas inflows are stronger in galaxies with strong bars, because such bars induce stronger torques that pull the gas off their initially circular orbits, causing it to flow towards the centre of the galaxy. Some of the inflowing gas will stop outside the corotation radius and form a ring (Athanassoula 1992; Friedli & Benz 1993).
Theoretically, the torques induced by the bar are proportional to the mass and elongation of the bar, but inversely proportional to the central axisymmetric mass (Combes & Sanders 1981). Observationally, these three factors correspond to the mass of the bar relative to that of the disc, the bar ellipticity and the bulge-to-disc ratio of the galaxy. In order to determine the mass of the bar, we would need to subtract a model for the bulge and the disc of the galaxy, which is beyond the scope of this work. In this study, ellipticity has been used as our measure of bar strength, because it is the more easily accessible observational parameter (Block et al. 2001; Laurikainen, Salo & Rautiainen 2002; Martinez-Valpuesta, Shlosman & Heller 2006).
As the bulge-to-disc ratio increases, the effect of the bar will become weaker (Whyte et al. 2002; Laurikainen et al. 2007). Parametrizing bar strength in terms of ebar for all galaxies, independent of their bulge-to-disc ratio, does not take this effect into account. However, as we have discussed, ebar will be underestimated by our ellipse-fitting method in bulge-dominated galaxies. These two effects may somehow conspire to make ebar an excellent predictor of central star formation enhancement, but we admit that further simulation studies are required to make a more detailed interpretation of our results.
4.2.2 The fraction of strong bars in galaxies with central starbursts is peaked at a value of 0.5–0.6
Tidal interactions are another obvious mechanism for inducing enhanced central star formation in galaxies (Bournaud, Jog & Combes 2007; Cox et al. 2008). Li et al. (2008) found that >∼40 per cent of SDSS galaxies with the highest central SSFR estimated have a close companion within a projected radius of 100 kpc. Li et al. (2009) showed that barred galaxies do not have an excess of close companions (similar results were also found by Marinova et al. 2009 and Barazza et al. 2009). In our study, we have excluded interacting and merging galaxies from the ‘parent sample’ in order to ensure that the ellipse-fitting procedure delivers robust results.
In summary, our main conclusion seems to be that bars and galaxy–galaxy interactions are independent phenomena that together could explain most of the central starbursts in galaxies in the local Universe.
4.2.3 The size of the bar is strongly correlated with the global colour of the host galaxy
Simulation results indicate that once a bar is formed, it will rapidly slow down and grow longer as angular momentum is transferred to the bulge and to the halo. On the other hand, if gas continues to accrete on to the galaxy, the gas may transfer angular momentum to the bar, thereby reaccelerating it. This suppresses the growth of the bar and can even cause it to become shorter (Weinberg 1985; Friedli & Benz 1993; Debattista & Sellwood 2000; Athanassoula 2002, 2003; Berentzen et al. 2007; Curirs, Mazzei & Murante 2007; Villa-Vargas, Shlosman & Heller 2010). Given that there is a tight correlation between colour and H i gas fraction in galaxies (Catinella et al. 2010), our results suggest that the observation effect may come about because the size growth of the bar is being regulated by gas accretion in galaxies. Red galaxies have not had a gas accretion event for many Gyr, so their bars have been able to grow. The fact that the colour of the bar and the size of the bar do not correlate may imply that the size of the bar depends on the gas accretion rate integrated over the past history of the galaxy, whereas the colour of the bar depends on the current gas inflow rate.
4.2.4 The incidence of bars peaks in disc-dominated galaxies with high masses and low stellar surface densities
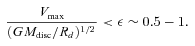
We find that f (bar) peaks when M* is high, in agreement with the De Lucia et al. (2011) results. However, at fixed stellar mass f(bar) increases at lower stellar surface densities. When μ > 108.5 M⊙ kpc−2 or R90/R50 > 2.6, f(bar) quickly drops to values near 0. This is not easily understood in the context of the formula given above. Athanassoula (2008) has criticized the Efstathiou et al. (1982) criterion, pointing out that it is not of general applicability and should not be used in semi-analytic models. In particular, stellar discs containing gas would be expected to be significantly more unstable than predicted.
Studies have shown that μ*∼ 108.5 M⊙ kpc−2 is a special transition point for galaxies in the local Universe. At surface densities lower than this value, galaxies contain significant amount of gas, but at higher surface densities, the atomic and molecular gas fraction in galaxies drop suddenly in many galaxies (Catinella et al. 2010; Saintonge et al. 2011). A similar transition is seen at R90/R50∼ 2.6. In contrast, the correlation between gas content and stellar mass is not as pronounced. It is thus reasonable to suppose that the fraction of bars may peak at stellar surface densities below 108.5 M⊙ kpc−2 in the local Universe, because this currently represents some special instability point for galactic discs. What we are not able to say from these observations is what role bars have played over the whole history of the Universe in shaping this instability point. In any case, our results do suggest that gas accretion, disc instabilities, structural changes and quenching of gas and star formation may happen coherently in galaxies. In the present-day Universe, bars are clearly an important regulatory mechanism in the ‘transition regime’ between the blue and the red populations.
We thank A. Cooper, T. Heckman, S. Jogee and S. White et al. for useful discussions.
XK is supported by the National Natural Science Foundation of China (NSFC, Nos. 10633020 and 10873012), the Knowledge Innovation Program of the Chinese Academy of Sciences (No. KJCX2-YW-T05) and National Basic Research Program of China (973 Programme; No. 2007CB815404).
GALEX (Galaxy Evolution Explorer) is a NASA Small Explorer, launched in 2003 April, developed in cooperation with the Centre National d’Etudes Spatiales of France and the Korean Ministry of Science and Technology.
Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society and the Higher Education Funding Council for England. The SDSS website is http://www.sdss.org/.
Footnotes
We test two ways of measuring colour from a ‘barred region’ (defined by the barred galaxy) in the control galaxy. In the first way, we do not change the orientation of a ‘barred region’ and in the second way, we orientate the ‘barred region’ so that its major axis points to the same direction as the major axis of the disc. These two types of colour measurements yield very similar results. In what follows, we present results using the first set of colour measurements.
REFERENCES
Appendix
APPENDIX A: TESTS OF OUR BAR IDENTIFICATION PROCEDURE
In Section 2.2, we discussed that the existence of prominent bulges will make the elliptical isophotes of galactic bars rounder, causing us to miss bars in bulge-dominated galaxies and underestimate the bar ellipticity. Here, we quantify the effect of bulge contamination on our estimates of ellipticity and bar fraction by simulating the effect of the bulge of our measurements.
First, we select the galaxies with R90/R50 < 2.2 from the original barred sample. According to the formula from Gadotti (2009), R90/R50 < 2.2 corresponds to a bulge mass fraction of less than 14 per cent. We use the images of these galaxies as ‘inputs’, and we then add idealized bulge components on to them as described below. From now on, the bar parameters related to the original images will be referred to as intrinsic, and the parameters related to the simulated images will be referred to as the output.
A pseudo-bulge is more compact than the classical bulge (Gadotti 2009), and is thus more likely to distort the inner isophote of galaxies, so to be conservative, we only simulate pseudo-bulges in this test. We set the stellar mass of the pseudo-bulges to range from 0.03 to 1.8 times the stellar mass of the original galaxies. This range is chosen to produce the R90/R50 range of the galaxies in our ‘parent sample’.
From fig. 13 of Gadotti (2009), we estimate 
, where re and M* are the effective radius and stellar mass of the pseudo-bulge. We describe the surface brightness of a pseudo-bulge by a Sérsic profile with index 1.4, 
, where I(r) is the surface brightness at radius r and I0 is the central surface brightness (Kormendy & Kennicutt 2004). We assume that the i-band flux is linearly proportional to the stellar mass (Bell et al. 2003). Integrating the surface brightness profile to obtain the total flux, I0 is estimated as 
.
We produce 2000 simulated galaxy images by adding the simulated pseudo-bulge components to the real i-band images of the disc-dominated galaxies. The distribution of concentration indices (R90/R50) of the simulated galaxies is shown in Fig. A1. We can see that the simulated R90/R50 ranges from 1.8 to ∼ 3 and follows the same relation with the bulge-to-total mass ratio of the galaxy shown in Gadotti (2009).
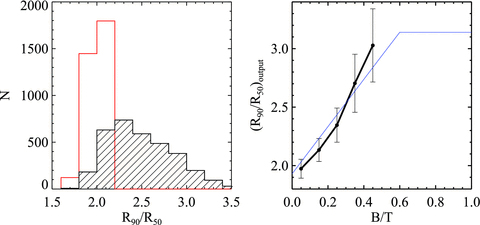
The left-hand panel plots the distribution of input (red histogram) and output (black- hatched histogram) R90/R50 values. In the right-hand panel, the black line shows the correlation between the output concentration and the bulge-to-disc ratio. The blue lines show the relation between the concentration and the bulge-to-disc ratio from the two-dimensional decompositions of Gadotti (2009).
We then use the ellipse-fitting method described in Section 2.2 to identify and measure bars from the simulated images. We refer to the fraction of bars identified from the simulated images as the output bar fraction (Foutput(bar)) and the correspondingly measured bar ellipticity as ebar, output.
In the left-hand panel of Fig. A2, we show how the intrinsic ellipticity of the bar (ebar, intrinsic) is underestimated as the concentration increases. We see that when R90/R50= 1.8, 2.4 and 2.8, ebar, intrinsic is underestimated by 0.065, 0.15 and 0.18. When R90/R50 > 2.7, the error flattens at a value of ∼ 0.18.
In the middle panel of Fig. A2, we show how the ebar, output from simulation and the ebar, obs measured from real galaxies vary as a function of the concentration R90/R50. The relation between ebar, output and R90/R50 (black line) shows the pure bulge contamination effect. We can see that the bulge contamination could be responsible for all the decreasing trend of ebar as a function of R90/R50. Thus it is unclear whether there is an intrinsic trend that when R90/R50 is lower, ebar, intrinsic is higher.
In the right-hand panel of Fig. A2, we show the bar verification rate (F(bar)) from the simulated images in the plane of output concentration R90/R50 versus input ebar, intrinsic. We can see that at a fixed R90/R50, F(bar) is strongly correlated with input ebar, intrinsic. At R90/R50∼ 2.6, when ebar, intrinsic∼ 0.3, only ∼20 per cent of the barred galaxies are identified. This is expected because we require ebar, output > 0.25 for a galaxy to be classified as barred. When ebar, intrinsic∼ 0.5, ∼50 per cent of the barred galaxies are identified. When ebar, intinsic > 0.6, F(bar) flattens at a value of about 0.7. Bulge contamination thus results in the loss of bars with low values of ebar.
In this study, we focus on galaxies which have ebar, obs∼ 0.5. This corresponds to an input ebar, intrinsic that is a weakly rising function of R90/R50, as shown by the grey curve in the right-hand panel of Fig. A2). We see that most of the region above the ebar, obs∼ 0.5 curve corresponds to F(bar) values greater than 70 per cent. In the region enclosed by the curve and ebar, intrinsic∼ 0.5, F(bar) can vary from values of around 70 per cent for the less concentrated galaxies to values of around 50 per cent for the more concentrated galaxies. We conclude, therefore, that we are likely correctly identifying between 2/3 and 3/4 of the barred galaxies with intrinsic ellipticities greater than 0.5.
