Separable triaxial potential–density pairs in modified Newtonian dynamics

Abstract

1 INTRODUCTION

Milgrom (1983) proposed that the failure of galactic rotation curves to decline in Keplerian fashion outside the galaxies’ luminous body arises not because galaxies are embedded in massive dark haloes obeying Newtonian gravity, but because Newton’s law of gravity has to be modified for fields that generate accelerations smaller than some characteristic value a₀≃ 1.2 × 10⁻⁸ cm s⁻². Subsequently, in order to solve basic problems presented by this phenomenological formulation of the theory (now known as modified Newtonian dynamics or MOND), such as conservation of linear momentum (e.g. Felten 1984), Bekenstein & Milgrom (1984) substituted the heuristic model with the MOND non-relativistic field equation:

1

where ‖⋅⋅⋅‖ is the standard Euclidean norm, μ is a scalar function, φ is the gravitational potential produced by the density distribution ρ and

2

is the MOND gravitational field experienced by a test particle. For an isolated system of finite mass, equation (1) is supplemented with the natural boundary condition ∇φ→ 0 for ⁠. Equation (1) is obtained from a variational principle applied to a Lagrangian with all the required symmetries, so the standard conservation laws are obeyed.1 In the regime of intermediate accelerations the function μ is not fully constrained by theory or observations, while asymptotically

3

A common choice is

4

(see also Famaey & Binney 2005; Zhao & Famaey 2006).

From equation (3) it follows that equation (1) reduces to the Poisson equation when ‖∇φ‖≫a₀, while the limit equation,

5

describes systems for which (or regions of space where) ‖∇φ‖≪a₀, i.e. systems for which the MOND predictions differ most from the Newtonian ones. Equation (5), characterizing the so-called ‘deep-MOND regime’ (hereafter dMOND), is then of particular relevance in MOND investigations, as this is the regime where one hopes to find the most significant differences with the predictions of Newtonian gravity. From the mathematical point of view, the left-hand side (lhs) of equation (5) is a special case of the so-called p-Laplace operator ∇(‖∇φ‖^{p− 2}∇φ). The dMOND case corresponds to p= 3, the so-called critical case for ℜ³. A large body of mathematical literature is dedicated to the p-Laplacian, but due to its non-linearity it is not surprising that several important questions are still open (e.g. see Lindqvist & Manfredi 2008). We anticipate that the general results in the present paper are independent of the specific form of μ, because they just follow from the fact that μ is a function of ‖∇φ‖, or they are obtained for the dMOND regime.

A considerable body of observational data seems to support MOND well beyond its originally intended field of application (see e.g. Milgrom 2002; Sanders & McGaugh 2002; Famaey & McGaugh 2011), but potential problems of the theory have been pointed out by many authors (see e.g. The & White 1988; Buote et al. 2002; Sanders 2003; Ciotti & Binney 2004; Knebe & Gibson 2004; Zhao et al. 2006; Galianni et al. 2011; Ibata et al. 2011). At present, the situation is in general considered unsettled. It is thus natural to study in detail MOND predictions, in particular focusing on dMOND systems, i.e. systems that in Newtonian gravity would be dark matter dominated. Unfortunately, MOND investigations, especially on the theory side, have been considerably slowed down by the almost complete lack of aspherical density–potential pairs, needed to test the predictions in cases more realistic than those described by spherical symmetry. In MOND, the main difficulty to obtain exact aspherical density–potential pairs originates from the fact that a simple relation between the Newtonian and the MOND gravity fields, produced by an assigned density distribution, in general does not exist. In fact, the Newtonian potential φ_N obeys the Poisson equation:

6

so that μ(‖∇φ‖/a₀)∇φ and ∇φ_N differ, for assigned ρ, by a solenoidal field S= curl h. In turn, the potential vector h depends on ρ, and so it is a priori unknown. The only exception is provided by density distributions in which the modulus g_N=‖g_N‖ of the Newtonian field g_N=−∇φ_N is stratified on surfaces of constant φ_N (particularly simple cases are those of spherically and cylindrically symmetric densities, or densities stratified on homogeneous planes; see also Brada & Milgrom 1995; Shan et al. 2008). In such cases S vanishes, and

7

Equation (7) coincides with the original MOND formulation of Milgrom (1983) and can be solved algebraically for g in terms of g_N, just by taking its norm.

A general method to build aspherical and exact MOND density potential pairs is presented in Ciotti et al. (2006) where, by extending the homeoidal expansion technique introduced in Ciotti & Bertin (2005) for Newtonian gravity, it is shown how a ‘seed’ spherical potential can be deformed to an axisymmetric or triaxial shape, leading to analytical density–potential pairs satisfying the MOND equation. Unfortunately, the resulting density distributions are not fully under control in the case of major departures from spherical symmetry, and regions of unphysical negative density may result.

For these reasons here we explore a different approach, i.e. we focus on the possibility to extend to MOND some of the remarkable results obtained in Newtonian gravity for potentials separable in ellipsoidal coordinates. This not only to better understand the properties of MOND systems but also to develop a new method to generate exact solutions deviating from spherical symmetry for the p-Laplace operator. While we refer to other papers for the full account of separability in ellipsoidal coordinates (de Zeeuw 1985b, hereafter Z85; de Zeeuw & Lynden-Bell 1985, hereafter ZLB85), here we just summarize the properties of Newtonian separable potentials in ellipsoidal coordinates relevant to the present investigation. Some of these properties are indeed shared by similar but non-separable families described in de Zeeuw & Pfenniger (1988, hereafter ZP88). Specifically, in Newtonian separable systems the following properties hold.

1. The potential along the long axis of the coordinate ellipsoids (the z-axis in the standard convention) is related to the density profile along this axis by a linear second-order ordinary differential equation (ODE). This is the Kuzmin property.

2. For assigned density profile along the z-axis, the ODE can be integrated completely. Once the parameters of the ellipsoidal coordinate systems are fixed, the solution determines uniquely the potential (and so the density) over the whole space. The density elsewhere is related to that on the z-axis by the so-called Kuzmin formula. Usually, the z-axis is the short axis of the density distribution.

3. The Kuzmin formula shows that the density is everywhere non-negative if this holds along the short axis. This is the Kuzmin theorem.

4. The Kuzmin formula also shows that density profiles that fall off along the z-axis faster than z⁻³ lead to finite mass. Density profiles that fall off less steep than z⁻⁴ become spherical at large radii, while for ρ(z) ∝z⁻⁴ or steeper the models have finite flattening at large radii. In particular, density profiles that fall off faster than z⁻⁴ lead to density distributions that in all other directions falls off as r⁻⁴, so that such models are quasi-toroidal (de Zeeuw, Peletier & Franx 1986; ZP88).

Of course, separable potentials are a special – albeit very important – class of potentials expressed in ellipsoidal coordinates. The interest in separable potentials is that, once a supporting positive density can be found, then their orbital classification can be done exactly, and equally well in MOND or in Newtonian gravity. In addition, as we will briefly discuss in the Conclusions, separable potentials may allow for a constructive approach towards the assembly of self-consistent MOND modes, i.e. collisionless systems supported by a positive phase-space distribution function obeying the Jeans theorem (e.g. Lynden-Bell 1962; Binney & Tremaine 2008). However, when considering the more general problem of obtaining a flexible approach to the construction of triaxial MOND potential–density pairs, different classes of (non-separable) potentials still obeying the Kuzmin property are worth to be explored, such as those described in ZP88. These models are not separable, but their simpler algebraical structure leads to simpler equations that might be solved (numerically) more easily than in the separable case.

The paper is organized as follows. In Section 2 we derive the ODE along the z-axis for separable models in the dMOND regime, and then we extend the result to the full MOND case, thus showing that the Kuzmin property holds in MOND. In Section 3 we derive the general asymptotic behaviour at the centre and at large radii of the density distributions generated by MOND regular separable potentials. Some explicit examples of everywhere positive densities associated with separable potentials are then presented in Section 4. A discussion of a special family of non-separable triaxial potentials (the V₁ family of ZP88) is carried out in Section 5, where among other findings it is shown that the Kuzmin property holds also for V₁ systems. The main conclusions are summarized in Section 6. In the appendix we list technical details together with a brief discussion of the separable axisymmetric power-law models by Sridhar & Touma (1997) in the context of MOND.

2 THE KUZMIN PROPERTY FOR SEPARABLE MOND SYSTEMS

We consider mass models that correspond to (triaxial) MOND potentials for which the Hamilton–Jacobi equation separates in ellipsoidal coordinates (λ, μ, ν), and investigate whether a Kuzmin formula holds for them. This is not obvious, as the MOND field equation is non-linear and considerably more complicated than the Poisson equation. We recall that the most general form of a separable potential in ellipsoidal coordinates can be written as

8

where F(τ) is an arbitrary2 function (Z85; ZLB85); the relevant properties of ellipsoidal coordinates needed in the following discussion are summarized in Appendix A.

It turns out that we can obtain information on the full MOND case just by restricting to the simpler case of dMOND systems, i.e. by focusing on the properties of the p-Laplacian. First, we rewrite equation (5) in the more convenient form

9

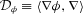where the explicit expression for the linear differential operator in terms of ellipsoidal coordinates is given in equation (A8). The advantage of working with equation (9) instead of equation (5) is that one avoids the computation of the derivatives of a norm, with the involved square root.

In principle, by inserting equation (8) in equation (9), and using the formulae reported in the appendix, some heavy algebra will give the expression for the density distribution over the whole space as a function of F, and its first- and second-order derivative, F′ and F″. Not unexpectedly, the resulting formula is quite formidable, and of little use. In practice, given F(τ), the explicit computation can be performed by using one of the many available computer algebra packages, and some cases will be discussed in Section 4.

Here instead we are interested in a more general property, i.e. if the Kuzmin formula (or even the Kuzmin theorem) holds also for MOND separable systems. From equation (A2) it follows that the density profile along the whole z-axis of a generic density distribution ρ(λ, μ, ν) is given by the function

10

where in the three intervals z²=τ+γ. In analogy with Z85 (see also Kuzmin 1956 for the oblate axisymmetric case), we now show that the right-hand side (rhs) of equation (9), evaluated on the z-axis, reduces in the three intervals of τ to the same second-order ODE for the unknown function F(τ), thus proving that also in dMOND the function ψ(τ) determines F(τ), and so the density field everywhere. In other words, the Kuzmin property (and so a Kuzmin-like formula) holds also for separable dMOND systems.

Let us consider the restriction of equation (9) to the z-axis. The Laplace operator satisfies the Kuzmin property, so there is nothing to prove, and its expression along the z-axis is given in equation (27) of Z85. An explicit computation then shows that the restriction to the z-axis of ||∇φ||² is given by the unique expression,

11

in the three intervals spanned by τ, where

12

Remarkably, we note that, with the exception of the factor ⁠, no irrationalities are involved in the expression of ||∇φ||_z. Of course, care is needed in the evaluation of this latter quantity, as it contains the absolute value ⁠. Finally, some algebra shows that the restriction of 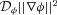to the z-axis also admits the unique representation:

13

where

14

Combining the previous results, we obtain the following second-order ODE relating, for separable dMOND systems, the density profile along the whole z-axis to F(τ):

15

Thus, the preliminary result is that the Kuzmin property holds in dMOND (i.e. for the p-Laplacian). Furthermore, with the aid of the previous results it follows immediately, by restriction of to the z-axis, that the Kuzmin property (and in principle a Kuzmin formula) also holds for the full MOND field equation, as the μ function in depends on ‖∇φ‖. Unfortunately, the non-linearity of the problem seems to prevent the construction of the explicit Kuzmin formula even in dMOND, so that the successive analysis of positivity of the density as in Newtonian gravity (Z85) cannot be performed, and the Kuzmin theorem remains unproven.

We conclude this general section by noticing that, as pointed out by the referee, a more general result on Kuzmin property can in fact be obtained, encompassing the present results and those in Section 5. In practice, with some analytical work, it can be shown that the Kuzmin property certainly hold in Newtonian gravity and in MOND for any potential that can be written as a symmetric function of ellipsoidal coordinates, i.e. by a function invariant for the transformation λ→μ→ν.

3 ASYMPTOTIC BEHAVIOURS

In the previous section we proved that MOND systems with separable potentials in ellipsoidal coordinates obey the Kuzmin property, and so in principle a Kuzmin formula holds for them. Before embarking on the study of the density distributions associated with specific separable potentials, we focus on the more general question of the asymptotic behaviour of the density, both at the centre and at large radii (for systems with finite total mass).

3.1 Behaviour at the centre

For a (regular) function F(τ) we begin by considering its second-order Taylor expansion near the centre, i.e.

16

In the expansion above we limit to second order, but the present analysis can be carried out (with increasing algebraically complexity) to any desired order.3 Before embarking on the following discussion, it is important to recall that the function F allows for a linear gauge, i.e. two functions differing for aτ+b, with a and b constants, lead to the same function φ in equation (8), as can be easily verified by direct substitution. With the aid of this gauge it is possible to assign two prescribed values to F at two arbitrary points, for example to impose that F(−α) =F(−γ) = 0, so that for regular F one can write F(τ) = (τ+α)(τ+γ)G(τ). This form has been proved very useful in several investigations (e.g. de Zeeuw 1985a,b; Hunter & de Zeeuw 1992; Arnold, de Zeeuw & Hunter 1994; van de Ven et al. 2003). Here we refrain from using the factorized form, and all the formulae are given in full generality: of course, more compact (but less symmetric) expressions in terms of the function G can be immediately found from those reported here, by simple algebraical substitution.

We focus first on the dMOND regime, recalling that near the centre λ+α∼x², and analogous relations hold for the μ and ν coordinates (see equation A3). We consider the behaviour of the different operators at the rhs of equation (9), beginning with the Laplacian. As is well known, the application of the Laplace operator to a regular separable potential leads to a finite central value:

17

where

18

(Z85, equation 27). Therefore, barring the special case of null derivatives of F at τ=−α,−β and −γ (or the more general case discussed later), according to equation (6) the value of the central density is non-zero in separable Newtonian systems.

We now move to the term ||∇φ||, noticing that it appears in the denominator of equation (9), and so the convergence of the density near the origin may be not guaranteed in the case of a vanishing gradient left unbalanced by the behaviour of the term ⁠. Indeed, the vanishing of ||∇φ|| at the centre of a regular triaxial potential is expected from geometrical considerations, and in fact, by using equation (16) we find that near the origin

19

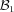where the three constants ⁠, and 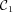depend on α, β and γ, and their explicit expression is given in equations (A11) and (A12). Note that the expression above is positive, because the expanded function is positive definite, and the higher order terms cannot affect the sign for sufficiently small displacements from the origin. In particular, as the three ellipsoidal coordinates are independent, the three coefficients must be positive, and in fact they are perfect squares. More generally, a similar positivity argument holds for the leading term in the expansion of ||∇φ||² independently of the order, i.e. the first non-zero term in the expansion is necessarily positive near the origin, as we will show in the following.

We now focus on the last term in equation (9). After some computation, it is found that near the origin

20

where the three coefficients are the same as in equation (19).

Finally, by combining the previous results, a simple calculation shows that in general near the origin

21

A change to spherical coordinates then proves that the central density of dMOND separable systems vanishes, linearly with the spherical radius r.

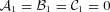A natural question arises, i.e. can we say something about ρ in the special circumstance of ? It could be that the order balance between the numerator and the denominator in equation (9) breaks down when the leading term of ||∇φ||² near the origin is of higher order. The obtained results are indeed quite interesting. First of all, by inspection of equations (A11) and (A12), it follows that the condition 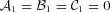is equivalent to the requirement that F′(−α), F′(−β) and F′(−γ) are well defined functions of α, β, γ, and of F(−α), F(−β), F(−γ). Accordingly, we consider the potential in equation (16), with the values of F′ fixed by the special case just described (and increasing the adopted order of expansion of F to the third one). The leading terms of the expansions now read

22

where the explicit form of the coefficients is given in equations (A13) and (A14). Note that in this case also the Laplace operator vanishes at the origin, and a simple calculation shows that the density near the centre vanishes as r⁵.

We finally repeat the argument above, with the additional request that also ⁠, thus fixing the values of F″(−α), F″(−β) and F″(−γ) from equations (A13) and (A14). By using equation (16) with F(τ) expanded up to the fourth order inclusive, we now find

23

where the coefficients are given in equations (A15): now the density at the centre vanishes as r⁹. By repeating this exploration to higher and higher orders, we find that the order of vanishing of the density, as a function of radius r, increases by 4 for each additional order of regularity imposed on ‖∇φ‖ near the origin. 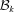We also found that, from the third order upward, the first non-zero coefficients ⁠, and 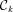of the leading terms near the origin depend only on the derivatives F^(k)(τ) evaluated at −α, −β and −γ, so that high-order regularity at the centre can be expressed directly as the vanishing of the corresponding derivatives of F at the origin.

Therefore, the previous analysis shows that a generic dMOND system associated with a regular triaxial separable potential has – at variance with Newtonian gravity – a zero density at the centre. This fact leads to some non-trivial consequences. The first is that this result remains true even when using the full MOND equation, as can be verified with a formal expansion. A simple argument is as follows. If we use the full MOND equation, and the central regions are not in dMOND regime, then they are described by Newtonian gravity. However, the Newtonian force in triaxial regular separable potentials vanishes, so all MOND separable systems at the centre are actually in dMOND regime, with the consequent vanishing central density. Of course, the vanishing of the central density in MOND may well occur also for other families of non-separable potentials (e.g. for potentials with a sufficient degree of reflection symmetries along the coordinate axes).

The second consequence follows from a further argument. Suppose MOND holds, and consider a separable system of baryonic density ρ, so that from the previous result ρ= 0 at the origin. We now focus on the total density ρ_N of the so-called equivalent Newtonian system associated with the baryonic density ρ, i.e. the mass distribution needed in Newtonian gravity to produce the same gravity field of MOND. Of course, ρ_N is obtained by application of the Laplace operator to the MOND potential, so that in the Newtonian framework the baryonic density ρ results ‘immersed’ in a dark matter halo of density ρ_h≡ρ_N−ρ, and from equation (17) the halo density at the centre will be different from zero. Provided ρ_h≥ 0 everywhere (a non-trivial request), we are lead to conclude that a separable MOND system would appear, when interpreted in the context of Newtonian gravity, fully dark matter dominated at the centre, with an arbitrarily large (formally infinite) mass-to-light ratio near the origin. Note that this property may be expected also in other families of MOND potentials, not necessarily separable. In fact, it can be easily proved that a regular potential with reflection symmetries –φ=φ(x², y², z²) – leads to a density with an expansion near the centre identical to equation (21), independently of separability. However, at higher orders the special form of equations (22) and (23) is not obtained, showing that separability removes the cross-terms and leaves diagonalized quartics, sextics and so on.

We conclude by noting that the addition of a central black hole would change the central force field from dMOND to Newtonian, in principle opening the possibility to have systems with a non-zero central density. Unfortunately, the addition of a central mass breaks down separability of triaxial potentials (excluding exceptional axisymmetric cases, such that discussed in Appendix B).

3.2 Behaviour at large radii

The other place where the asymptotic analysis can be carried out in generality is at infinity. In particular, from equations (A1) and (A2), it follows that λ∼r² for r→∞, with r being the radius in spherical coordinates. In order to better illustrate the MOND case, we begin by recalling the idea behind the computation in Newtonian gravity. For a system of finite total mass M, Newtonian gravity dictates that φ∼−GM/r for r→∞. If we ask also for separability, then it is easy to show that the required asymptotic trend is matched in equation (8) if and only if

24

Note that in the expression above we fixed GM= 1: it is simple to restore this dimensional factor in the obtained density distribution after the application of the Laplace operator. From now on we refer to h(τ) as to the shape function: its relevance in determining the mass profile at large radii will be discussed in detail in the dMOND context.

By evaluating the Laplace operator, one recovers the well-known result of Newtonian gravity (e.g. de Zeeuw et al. 1986) that regular separable potentials in ellipsoidal coordinates, associated with finite total mass and finite flattening at large radii, lead to density distributions that share the asymptotic radial behaviour (in general modulated by angular dependence):

25

with additional properties listed in point (4) in the Introduction.

We now use a similar approach in MOND. For a finite mass system, the leading monopole term of the MOND potential follows from equation (7), with ⁠, due to the r⁻¹ decline of the MOND acceleration at large distances (where the field is weak, and so the system is actually dMOND). Therefore, if we ask for separability we are now forced to assume

26

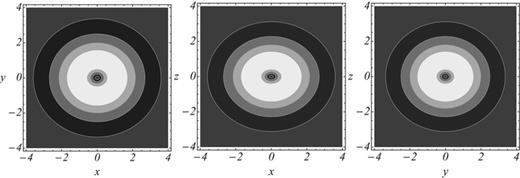
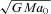where the coefficient 1/2 takes into account the relation λ∼r². Again, the dimensional coefficient is set equal to 1: in the density profile obtained by the application of the MOND operator, due to its non-linearity, the resulting coefficient is GMa₀.

As in the Newtonian case, the detailed behaviour at infinity of the shape function h(τ) determines the radial profile of the density distribution (note that this is not quite the same as the three-dimensional shape, which is also a function of the angular coordinates). In fact, also the first and second derivatives of h are involved in the computation of ρ and, as is well known, asymptotic properties of functions in general are not shared by their derivatives.4 In particular, an arbitrary choice of h can lead to a system with negative densities or infinite total mass, in contrast with the hypothesis behind equation (26). For this reason, the convergence of the total mass must be checked for any specific choice of h(τ). In order to carry out a sufficiently general analysis (encompassing a large fraction of the cases arising in practical situations), here we restrict to shape functions h with a Frobenius expansion for τ→∞, i.e. we assume

27

with ε≥ 0. Note that equation (26) imposes A= 0 for ε= 0, while for ε integer we are actually dealing with a regular function at infinity.

We begin with the regular case ε= 1. The computation of the dMOND operator does not pose special difficulties in the regular case, and for λ→∞ one finds

28

so that, after restoring the dimensional factor, we obtain, for λ→∞,

29

A few important points should be noted. First, only the leading coefficient A appears, while all the higher order coefficients do not affect the leading term of the density expansion: at infinity, systems with A= 0 are indistinguishable from systems with constant h= 1. Secondly, the density distribution at large radii is not spherically symmetric, a consequence of the exact cancellation of the leading terms in equation (28) when combined in equation (9). Thirdly, at large radii the density is nowhere negative for A≥ (2α+ 3β+ 3γ)/4: this positivity result is not expected a priori, especially when considering the non-linear nature of the p-Laplacian. Finally, the radial behaviour of the density at large radii is proportional to ln (r)/r⁵. Curiously, the light distribution of elliptical galaxies in their external regions seems to be described better by the 1/r⁴ profile (e.g. see Jaffe 1983; Bertin & Stiavelli 1984; Hernquist 1990; Dehnen 1993; Tremaine et al. 1994, see also Bertin & Stiavelli 1989), characteristic of the regular Newtonian separable case.

The discussion above concludes the case of an h function with a regular expansion at infinity. Moving to the case of non-integer ε, with some additional work it can be shown that for ε > 1 equation (29) still holds with A= 0, thus extending to the irregular cases the result on the effect of higher order terms obtained for a regular function h. Therefore, we are left with the irregular case 0 < ε < 1, i.e. when the shape function h(τ) admits a genuine Frobenius expansion at ∞.

Lengthy algebra and a careful order balance show that the following rigorous formulae, extending the validity of those in equation (28), hold:

30

where

31

For ε= 1 we recover the results in equation (28). Combining the expansions above in equation (9), and expanding the norm at the denominator, some additional work finally shows that

32

and again for ε= 1 the regular case in equation (29) is recovered. The density profile at large radii consists of the Frobenius contribution dependent on A, ε and λ, and in the regular part, independent of ε. The first component becomes spherical at large radii, at variance with the regular component, dependent also on the μ and ν coordinates. In addition, the spherical component is dominant for 0 < ε < 1, being asymptotic to 4Aε²ln (λ)/λ^{3/2 +ε}. Therefore, when 0 < ε < 1 the density at large radii is spherical and positive for A > 0, while for ε≥ 1 it is non-spherical: it is always positive for ε > 1, and for ε= 1 positivity is assured for A greater than some negative value. We conclude by noticing that the choice of the potential (26) implicitly assumes a finite total mass, and in fact this is found in the solution, as ρ∝ ln (r)/r^{3 + 2ε} for 0 < ε < 1 and ρ∝ ln (r)/r⁵ for 1 ≤ε.

4 EXPLICIT CASES

From the general analysis in Section 3 we found that the central density of MOND models vanishes for regular potentials separable in ellipsoidal coordinates. We also found that at large radii the positivity is assured, provided a certain coefficient in the series expansion of the shape function at infinity is larger than a threshold value (0 in a genuine Frobenius expansion, and negative in the regular case, with the specific value given by a linear combination of the three axial coefficients α, β and γ defining the ellipsoidal coordinate system). Therefore, we have at least indications that everywhere positive triaxial densities with separable potentials may exist in MOND.

Unfortunately, without the explicit Kuzmin formula, in general the positivity of the density associated with an assigned F(τ) can be checked only numerically. We now show that such cases in fact can be found routinely. For illustrative purposes, we start with a representative dMOND positive separable model, then we illustrate with a few examples how the shape function h affects the resulting densities. For simplicity, all the examples presented in this section are considered in the dMOND regime. The use of the full MOND equation would introduce a dependence on total mass, leading to a more complicated discussion, without adding new information to the present discussion.

The reference model is perhaps the simplest possible, and it is obtained by using F(τ) =−τ²ln (τ)/2 in equation (8), i.e. we just fix h= 1 in equation (26). We also assume α=−3, β=−2 and γ=−1, but we stress that global positivity has been found for all the explored values of the three parameters, even in the cases characterized by very different values of the axial parameters. The relations between ellipsoidal and Cartesian coordinates needed for the plots of the isodensity contours in the three coordinate planes are reported in Appendix A3.

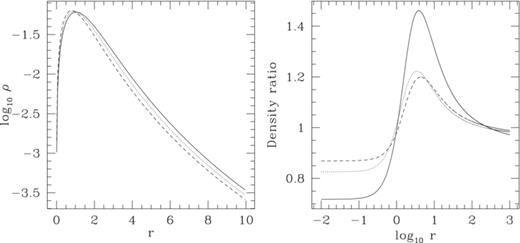
In the left-hand panel of Fig. 1 we show the density profiles ρ(x, 0, 0), ρ(0, y, 0) and ρ(0, 0, z) of the reference model, where it is intended that now the density is expressed in Cartesian coordinates, and x=y=z=r, where r is the radial distance from the origin. It is apparent how the density vanishes at the centre, then reaches a peak and finally declines again, in accordance with the previous asymptotic analysis. The model is not spherical, as can be seen from Fig. 2, where we present the density cross-sections (in the central regions) in the three Cartesian coordinate planes: dark greys correspond to low-density values, while light greys are the density peaks. All the main features of Fig. 1 can be easily recognized, and in particular the density depression in the inner regions: overall the density of the reference model is characterized by a very nice ellipsoidal shape. In practice, the resulting density distribution looks similar to a heterogeneous ellipsoid with a non-monotonic density stratification. The radial trend of the density shape is quantified, on a much larger radial interval, in the right-hand panel of Fig. 1, where the density ratios ρ(x, 0, 0)/ρ(0, 0, z), ρ(0, y, 0)/ρ(0, 0, z) and ρ(x, 0, 0)/ρ(0, y, 0) are represented by the solid, dotted and dashed lines, respectively, for x=y=z=r. Note that in general the density ratios ρ(r, 0, 0)/ρ(0, 0, r), and ρ(0, r, 0)/ρ(0, 0, r), for a density distribution flattened along the z direction, are ≥1 (≤1) if the density is decreasing (increasing) with r. A visual inspection of Fig. 2 then explains the behaviour of the density ratios up to r≈ 100: in these regions the z-axis (the long axis of the coordinate ellipsoids) corresponds to the ‘short’ axis of the density distribution, thus confirming that this property usually holds not only in Newtonian separable systems, but also in MOND. We also note the interesting occurrence of a double switch between the intermediate and the long axis. However, for large r, the density ratios drop again below 1, i.e. the density distribution in these regions (not shown in Fig. 2) becomes elongated along the z-axis: it has been verified that this non-sphericity is in perfect agreement with equation (29) evaluated for A= 0. Therefore, this model represents a counterexample (in MOND) for the Eddington (1915) conjecture, fully discussed in by de Zeeuw et al. (1986, Section 4 therein).

Figure 1

Left-hand panel: density profiles (normalized to M/4π, where M is the total mass of the model) along the Cartesian coordinate axes, at radial distance r from the centre (x: solid; y: dotted; z: dashed) for a separable model with F(τ) =−τ²ln (τ)/2 and α=−3, β=−2 and γ=−1. Note how the density vanishes at the centre. Right-hand panel: density ratios ρ(x, 0, 0)/ρ(0, 0, z), ρ(0, y, 0)/ρ(0, 0, z) and ρ(x, 0, 0)/ρ(0, y, 0) as a function of distance from the origin, i.e. x=y=z=r, where ρ is intended expressed in Cartesian coordinates. Lines are, in order, solid, dotted and dashed, respectively.

Open in new tabDownload slide

Figure 2

Isodensity contours in the three Cartesian coordinate planes for the reference model, given by F(τ) =−τ²ln (τ)/2 (see Fig. 1). Darker grey corresponds to lower values of the density. From the figure it is apparent how the density decreases near the centre and at large radii, so that the model presents an ellipsoidal corona of higher density. Note also how the z-axis corresponds to the shortest axis of the density distribution in the radial interval shown.

Open in new tabDownload slide

We stress that the remarkable ellipsoid-like density distribution of the reference model (preserved also for significantly different values of the axial parameters α, β and γ) is not a general property of MOND models with separable potentials. In models where we allow for a non-constant shape function, the resulting (positive) densities are quite peculiar, in some cases with high-density, detached lobes along the z-axis or, in other cases, by the presence of curious low-density regions. Of course, in accordance with the asymptotic analysis, the central density of all these models still vanishes. In Fig. 3 we show a suite of such densities obtained for different choices of the function h, listed in the caption, and for the same values α=−3, β=−2 and γ=−1 of the reference model in Fig. 2. In particular, moving from the top to the bottom rows the coefficient A in equation (27) decreases, and the corresponding densities become more and more complicated. This is not surprising, because the coefficient A approaches the positivity limit for the density at large radii discussed after equation (29). Finally, the comparison of the model in the last row with the reference model in Fig. 2 shows how higher order terms in the expansion of h may affect the density, as A= 0 in both cases.

Figure 3

Isodensity contours in the coordinate planes for different choices of the shape function h in equation (26), and for α=−3, β=−2 and γ=−1. From top to bottom: h(τ) = 1 + 4/τ+ 11/τ², 1 + 3/τ, 1 + 2/τ+ 1/2τ⁵ and ⁠. Dark greys correspond to lower density values.

Open in new tabDownload slide

5 THE V₁ FAMILY OF DE Zeeuw & Pfenniger (1988)

As discussed in the Introduction, this paper focuses on MOND triaxial models with the potential separable in ellipsoidal coordinates. Separable models are a very special subset of triaxial models, and so it is of some interest to see what properties of separable models are in fact shared by more general triaxial models, and what are the main properties of the density distributions associated with some MOND (non-separable) potentials in ellipsoidal coordinates. Here we restrict for sake of simplicity to the important V₁ family,

33

introduced and fully discussed in ZP88. V₁ potentials are relevant here because in Newtonian gravity they obey the Kuzmin theorem; in addition, although non-separable, they are algebraically simpler than separable potentials (which comprise the family V₂ and can be derived from V₁ by application of a linear operator; ZP88). Based on the results obtained for separable models, it is reasonable to expect that also V₁ potentials in MOND satisfy the Kuzmin property.

In fact, we now show that the restriction to the z-axis of the rhs of equation (9) with the potential (33), reduces in the three intervals of τ in equation (10) to the same second-order ODE. This proves that the Kuzmin property holds also for V₁ potentials in dMOND regime (i.e. for the p-Laplacian). The Laplace operator satisfies the Kuzmin property, so there is nothing to prove, and its expression along the z-axis is given in section 3.1 of ZP88. An explicit computation then shows that over the whole z-axis

34

and

35

The following second-order ODE along the z-axis for dMOND V₁ systems is finally obtained:

36

Again, in analogy with the separable case, it is not difficult to show that the Kuzmin property (and in principle a Kuzmin formula) also holds for V₁ potentials in the full MOND regime.

As expected, equation (36) is considerably simpler than the corresponding equation (15), and some additional classification and elaboration can be carried out. In fact, albeit equation (36) is still second order, non-homogeneous and non-linear, the function F(τ) is missing, so that for general V₁ systems in dMOND, the z-axis ODE can be reduced to a non-linear first-order equation, solving for F′. In particular, in each τ interval where the sign of F′ is constant, the ODE belongs to the important family of Abel differential equations of the second kind:

37

(e.g. Kamke 1948; Zwillinger 1997),5 a generalization of the Riccati equations (Ince 1964). Clearly, the problem is complicated by the fact that the sign of F′ is not known a priori: in the following discussion we assume, for simplicity, that F′ does not change sign for τ≥−γ, and so we set F′(τ) =±H(τ), with H(τ) ≥ 0. Under this assumption, equation (36) can be rewritten as

38

so that in our case we have an Abel equation with g₀=f₃= 0, g₁= 1, and

39

The choice of the sign in front of f₀ determines (if they exist) two solutions H_±(τ) ≥ 0, so that the problem is finally solved for F′(τ) =±H_±(τ). Unfortunately, the general solution of Abel ODEs (first and second kind) is not known, but several remarkable transformations have been found (e.g. Polyanin & Zaitsev 2003). For example, by setting H=g(τ)p(τ) it is possible to determine p(τ) so that equation (38) can be written in the reduced (but not yet canonical) form

40

in our case

41

The canonical form would be then obtained by requiring R(τ) = 1, through the definition of the new independent variable ξ=∫R dτ. Unfortunately, in the triaxial case the evaluation of the integral requires Appell functions, so that the inversion τ=τ(ξ) is impossible in closed form. In the prolate case (β=γ) the integral reduces to a standard hypergeometric function, and inversion is again impossible, but in the oblate case (β=α),

42

and so the reduction to the canonical form is possible by using circular and hyperbolic functions. However, the resulting Abel equation is still unsolvable.

As the general problem is not solvable, we elaborate on the possibility to solve a restricted problem, searching for special solutions with H(−α) =H(−β) = 0, i.e. with f₁= 0 in equation (38). This is done by writing, in full generality,

43

where l and m are integer numbers ≥1, and k is a regular function at τ=−α and τ=−β. The parity of the exponents forces k to be positive for τ≥−γ, consistently with the non-negativity of H, and equation (38) reduces to a linear ODE for k²(τ), so that only solutions everywhere positive are acceptable. Some algebra shows that the exact solution is

44

where k₀ is the free parameter. Note that the integral under square root is monotonic increasing (f₀≥ 0), so that positivity is assured when k₀≥ 0 and the sign ‘+’ is adopted. If the integral is convergent for τ→∞, then the sign ‘−’ can be adopted, provided k₀ is larger than the value of the integral at infinity. In all cases, the square root cannot vanish for τ=τ₀ > −γ, as monotonicity of the integral then would produce negative values of k² for τ > τ₀. It follows that H diverges at τ=−α and −β as p(τ) (independently of the value of l and m), against the assumption, and reduced solutions with f₁ do not exist. A simple argument shows that this negative it is to be expected. In fact, if one is allowed to fix H(−α) =H(−β) = 0 in equation (38), then the resulting non-homogeneous ODE becomes first-order linear for H², and so it can solved in closed form. However, as the reduced equation is first order, its solution depends on a single parameter, and so in general only one of the two values H(−α) and H(−β) can be set equal to zero. The arguments above show that the z-axis ODE for V₁ potentials in dMOND is a genuine Abel equation of the second kind, to be solved numerically for assigned density profile.

Concerning the asymptotic behaviour of the density, following the same treatment done for separable models in Section 3.1, it can be shown that also regular V₁ models are characterized by a vanishing density at the centre. The asymptotic analysis at infinity reveals some interesting difference with the cases in Section 3.2. In fact, let us consider the V₁ family,

45

similar to the family of finite mass systems discussed in Section 3.2. We note that the parallel is only formal: while in the separable models the potential at large radii becomes spherical, in this case it remains ellipsoidal. This means that, at variance with the separable case, V₁ models in the family above are characterized by infinite mass (or, in the case of finite mass, by space sectors with negative density), because the potential of finite mass systems is dominated by the monopole term at large radii.

We note that in Newtonian gravity equation (45) with h= 1 corresponds to the Binney (1981) triaxial logarithmic potential, ln (1 +x²/a²+y²/b²+z²/c²) ∝ ln (λμν), fully discussed in ZP88 (sections 3.1 and 6.1 therein). Here we found that the Binney potential in dMOND leads to a non-spherical density distribution of infinite mass, with a radial r⁻³ profile at large radii, with a negative density along the z-axis for sufficiently large τ, independently of the values of a, b, c. In Cartesian coordinates,

46

What happens if we allow for a more general h function in equation (45)? For simplicity we do not repeat the analysis done in Section 3.2 for separable potentials, but we just report a few results. First, we found that the negative densities at large radii along the z-axis can be removed by appropriate choices of A and ε in equation (27), but we were unable to construct everywhere positive mass models in the family (45). Secondly, at variance with the separable case, at large radii ρ∝ 1/r³ (modulated by an angular part) independently of ε, so that finite mass dMOND systems in the V₁ family (45) do not exist.

Obviously, other choices of F in equation (33) are possible and worth of investigation. For example, ZP88 (equation 2.13) show that the Newtonian potential of the density distribution,

47

belongs to the V₁, and that the gradient of the potential can be written in terms of Carlson’s (1979) symmetrized version of incomplete elliptic integrals. These functions are a closed family under differentiation, and therefore the dMOND density distribution associated with this family can be written explicitly by using functions no more complicated than elliptic integrals. Here, we do not study these models.

6 SUMMARY AND CONCLUSIONS

In this paper we studied the properties of density distributions obtained from MOND potentials separable in ellipsoidal coordinates. The investigation, besides the astrophysical context, is also interesting because the MOND operator, in the weak field limit (the so-called dMOND regime), reduces to the non-linear p-Laplace operator ∇(‖∇φ‖^{p− 2}∇φ) with p= 3, the critical case in ℜ³.

The main results obtained can be summarized as follows.

1. We proved that, as in the case of Newtonian gravity, also for MOND systems with separable potentials in ellipsoidal coordinates, the density profile along the z-axis (the long axis of the ellipsoidal λ-surfaces) determines the potential and so the density everywhere. The second-order ODE is however highly non-linear, and probably unsolvable in closed form, even in dMOND, in the limit of small flattenings and/or at large distances from the origin. Therefore, while we formally proved that the Kuzmin property holds in MOND, the associated Kuzmin formula is not known, and the Kuzmin Theorem remains unproven.

2. However, we obtained rigorous asymptotic formulae for the density near the origin and at infinity, in the case of regular separable potentials. We showed that, at variance with the case of Newtonian separable systems, the density at the centre vanishes, and we studied the order of vanishing as a function of the order of regularity of the potential. From this result it follows that MOND separable systems with regular potentials are necessarily in the dMOND regime at their centre, so that they would appear as centrally dark matter dominated (formally, with an infinite value for the mass-to-light ratio) when interpreted in the context of Newtonian gravity. Of course, this property may be shared by other sufficiently regular non-separable potentials in MOND.

3. The analysis at large radii was performed under the assumptions of finite total mass system and a separable potential sufficiently regular to allow for a Frobenius expansion at infinity. In the regular case (i.e. when the expansion of the shape function h in equation 27 reduces to a Taylor series in terms of integer powers of 1/τ), the density at large radii is positive, provided a certain coefficient in the expansion is greater than a negative value (determined by the axial parameters of the ellipsoidal coordinates). The density shape is not spherically symmetric, and the radial decline is proportional to ln (r)/r⁵, at variance with the Newtonian case of finite mass and finite flattening, when ρ∝ 1/r⁴. In the case of a genuine Frobenius expansion with exponent 0 < ε < 1, the total mass is still finite, but the density profile at large radii is instead spherically symmetric, with a milder radial decline ρ∝ ln (r)/r^{3 + 2ε}, and positive provided the constant mentioned above is positive. This resembles the Newtonian case of finite mass when the density profile along the symmetry axis is steeper than 1/z³ but shallower than 1/z⁴.

4. We constructed some triaxial separable MOND models, everywhere positive for all the explored axial ratios. The shapes range from almost perfectly ellipsoidal systems to curious systems with density depressions or overdensities (some of them similar to the models constructed in Ciotti et al. 2006), depending on the specific choice for the shape function h: these last models are unlikely to be useful for the description of real stellar systems.

5. We briefly addressed the properties of the class of V₁ potentials introduced in ZP88: these potentials, albeit non-separable, are simpler than the separable case, and they are known to obey the Kuzmin theorem in Newtonian gravity. We showed that they obey the Kuzmin property also in MOND, and we derived the ODE relating the potential to the density profile along the z-axis. This equation is considerably simpler than in the separable case, and in fact can be transformed in an Abel equation of second kind. Unfortunately, the general solution of this class of ODEs is not known, so the Kuzmin theorem cannot be proved. As an example of V₁ systems, we studied the case of the MOND analogue of the Binney (1981) logarithmic potential, and we showed that the density profile becomes negative along the z-axis, while the radial profile declines as 1/r³. Some variants of this potential however admits positive densities (at large radii) for some function h, but still declining as 1/r³, and so being characterized by infinite total mass.

6. Finally, we showed (Appendix B) that power-law axisymmetric potentials separable in parabolic coordinates, associated with a central (weak) cusp can be constructed in MOND, in analogy with the family discovered by Sridhar & Touma (1997), albeit for a more restricted range of central slopes. If a central black hole is added, the central regions are still cuspy, but the cusp is Newtonian.

We conclude by noting a few points that are relevant for successive investigations. The first is related to the phase-space distribution function. Presently our understanding of the phase-space distribution function of MOND non-spherical systems still rely mostly on the numerical Schwarzschild method (Wang, Wu & Zhao 2008; Wu et al. 2009; Wu, Zhao & Famaey 2010) or N-body simulations (Nipoti, Londrillo & Ciotti 2007a,b; Nipoti, Ciotti & Londrillo 2011), and the resulting systems are expected to be non-separable. Here we can derive some firm conclusion on MOND separable models. In fact, the vanishing central density of triaxial regular models forces the associated distribution functions to vanish for the values of the three integral of motions allowing for orbits that cross the centre. Now, the orbit classification for the Newtonian case assumes that the third derivative of F(τ) is negative everywhere (e.g. Kuzmin 1973; Hunter & de Zeeuw 1992). This is the case for the reference model with F(τ) =−τ²ln (τ)/2, leading to a third derivative which is in fact −1/τ so indeed negative as we choose τ≥−γ≥ 0. Moreover, in the case of a Frobenius h function, it is easy to prove that the expansion coefficients can be chosen so that negativity is assured (leaving true the positivity of the density). In all these case, the models are supported by the four major orbit families. This indicates that these MOND models have the same orbit structure as Newtonian separable systems. If the condition is violated, then there are other/more orbit families possible. Restricting to the first cases, it makes plausible that self-consistent models with vanishing central density might well exist by populating the tube orbits only, leaving the box orbits out, as these would be contributing positive density in the centre. The machinery to construct such models with thin tubes only (zero radial action) is available from Hunter & de Zeeuw (1992): by leaving the boxes out, this avoids having to compute the box orbit distribution function by numerically solving a large set of linear equations. The thin tube distribution functions are given in closed form, once F(τ) is chosen and the density is known.

The second point is that the obtained results would change if the μ function in equation (3) has a non-zero lower bound, i.e. μ(t) →μ₀ for t→ 0. In fact, the deepest gravity regimes observationally probed in isolated galaxies are ≈0.01a₀ (e.g. see Famaey et al. 2007; Zhao 2007; Wu et al. 2008). If such a lower limit for μ exists, then the dynamics would be Newtonian at very large radii and at very small radii, opening the possibility of MOND Stäckel models with finite total mass and non-zero central density.

We thank the referee, Jin H. An, for very useful comments. HZ and LC enjoyed the Oxford Problematik 2010 meeting, where aspects of this work were discussed with S. Sridhar. LC was supported by the MIUR grant PRIN2008; the warm hospitality of IPMU (Tokyo University) and of Princeton University, where some part of this work was done, is also acknowledged.

Footnotes

REFERENCES

Appendices

APPENDIX A: ELLIPSOIDAL COORDINATES

We report here the main properties of ellipsoidal coordinates relevant for the present work; for a full discussion and further references on the subject, see Z85 and ZLB85.

A1 Definitions

Ellipsoidal coordinates (λ, μ, ν) are curvilinear orthogonal coordinates defined as the three real roots for τ of the cubic equation:

(A1)

where without loss of generality we assume α < β < γ < 0, so that 0 < −γ≤ν≤−β≤μ≤−α≤λ. Surfaces of constant λ are ellipsoids, surfaces of constant μ are hyperboloids of one sheet and surfaces of constant ν are hyperboloids of two sheets.6 For very large values of λ, the ellipsoidal surfaces become more and more similar to spheres of radius ⁠. The relations between (λ, μ, ν) and the Cartesian coordinates (x, y, z) of a given point are

(A2)

so that the origin corresponds to λ=−α, μ=−β and ν=−γ. A series expansion shows that near the origin Cartesian and ellipsoidal coordinates are related by the (first order) asymptotic relations:

(A3)

The metric coefficients are

(A4)

where

(A5)

note that a_λ > 0, a_ν > 0, but a_μ < 0, consistent with the positivity of the metric coefficients. The gradient operator reads

(A6)

where (e_λ, e_μ, e_ν) are the local basis of mutually orthogonal unitary vectors (e.g. Arfken & Weber 2005). Therefore, the squared norm of the gravitational field becomes

(A7)

while the differential operator in equation (9) is

(A8)

Finally, the Laplace operator can be written as

(A9)

where

(A10)

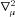and and 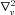follow from the equation above by the rotation λ→μ→ν→λ, applied once and twice, respectively.

A2 The leading terms of density expansion at the centre

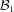With heavy but straightforward computation it can be shown that the coefficients ⁠, and 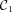appearing in equations (19) and (20), needed in the density expansion near the centre of generic separable dMOND system, are

(A11)

where ▵ is defined in equation (18), and

(A12)

 In the special case ⁠, the values of F′ at the centre are fixed by the vanishing of the system above. The coefficients of the resulting expansions reported in equation (22) are

(A13)

where now

(A14)

 The additional request of regularity, i.e. ⁠, fixes the values of F″ at the centre from the vanishing of the system above. The coefficients of the resulting expansions reported in equation (23) are

(A15)

A3 Cartesian planes in ellipsoidal coordinates

In the study of the shape and density distribution of triaxial mass models expressed in ellipsoidal coordinates it may be helpful to have the expression for the coordinate planes (x, y, 0), (x, 0, z) and (0, y, z) in terms of the ellipsoidal coordinates. The following formulae can be easily deduced by simple geometrical arguments (see also de Zeeuw et al. 1986).

The (x, y) plane is obtained by requiring that z= 0 in equation (A2). This request leads to fix ν=−γ, and solve for assigned x² and y² the resulting system for L≡λ+α≥ 0 and M≡μ+β≥ 0. Therefore,

(A16)

where the density at the lhs is intended to be expressed in Cartesian coordinates,

(A17)

and M=R²−L, R²=x²+y².

The situation is slightly more complicated for the other two planes. In fact, the (x, z) plane is fully covered by the union of the region,

(A18)

obtained by fixing μ=−β in equation (A2), with the complementary region S_ν≡ℜ²/S_μ, obtained for ν=−β. Solving the resulting systems and asking for positivity of the functions L≡λ+α and N≡ν+γ (in S_μ), or M≡μ+γ (in S_ν), one gets

(A19)

where L is again given by equation (A17) but now R²=x²+z², δ=γ−α≥ 0 and M=N=R²−L.

Finally, a similar analysis shows that the (y, z) plane is also separated in two regions,

(A20)

obtained by fixing λ=−α in equation (A2), and the complementary region S_μ≡ℜ²/S_λ, obtained for μ=−α. Solving the resulting systems and asking for positivity of the functions N≡ν+γ and M≡μ+β (in S_λ), or L≡λ+β (in S_μ), we now get

(A21)

where

(A22)

R²=y²+z² and N=R²−M.

APPENDIX B: THE POWER-LAW AXISYMMETRIC SEPARABLE MODEL

A property common to all triaxial systems with a Newtonian potential separable in ellipsoidal coordinates is a constant density core. In the axisymmetric case, Sridhar & Touma (1997) were able to construct separable potentials supporting a central density cusp. The question is whether such property carries on in MOND as well. We show that this is in fact the case. We start from the separable potential:

(B1)

where the parabolic coordinates r₊ and r₋ are related to the standard spherical coordinates by the identities

(B2)

Sridhar & Touma (1997) show that the density distribution associated with the potential above, via the Laplace operator, is

(B3)

and discuss its properties as a function of k. In particular, for 0 < k < 1 the density is cusped at the origin and positive everywhere, and so they conclude that cuspy systems (of infinite mass) with separable potential exist, at least in the axisymmetric case. In the critical case, k= 1, the density is cuspy, but it vanishes on the z-axis, being ρ∝ sin ²θ/r.

We do not embark on the interesting but long discussion of the density related to the potential (B1) in MOND, but we note the following results. First, it is easy to show that the force depends on radius as r^{1 −k}, and does not vanish along any direction (as the radial component of ∇φ never vanishes). It follows that for k > 1 the MOND system will be similar – near the origin – to the Newtonian case, when however the density is unphysical (Sridhar & Touma 1997). For 0 < k < 1 the system is in the dMOND regime near the origin (and Newtonian at infinity), while in the critical k= 1 case the force is independent of r, and so the system can be constructed in the dMOND regime everywhere. An application of the 3-Laplace operator to the family of power-law potential with 0 < k≤ 1 easily shows that the density near the centre (or everywhere, in the k= 1 case), can be written as

(B4)

where the explicit function f_k is easily calculated but is not reported here. Remarkably, in the range 0 < k≤ 1 the function f_k is nowhere negative. From equation (B4) it follows that the density vanishes at the centre for 0 < k < 1/2, is independent of r for k= 1/2 (but with different values along different directions) and it is cusped for 1/2 < k≤ 1. Moreover, f₁∝ sin ²θ, as in the Newtonian case. Therefore, separable potentials with a central (weak) cusp can be constructed also in MOND, but only in the restricted range 1/2 < k < 1. However, the resulting densities, albeit positive, are still characterized by an infinite total mass, and their shapes are quite unnatural, as can be seen from Fig. A1, where some examples are presented. Sridhar & Touma (1997) also showed that a black hole can be added at the centre of these models, leaving separability unaffected. This remains true in MOND, as the gravitational field of the black hole switches the field near the centre from dMOND to Newtonian, so that the system will be cuspy also for 0 < k≤ 1/2; however, this is not a ‘genuine’ MOND cusp.

Figure A1

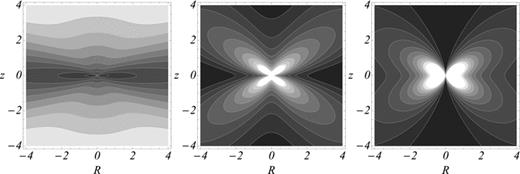
Isodensity contours of the dMOND analogues of the Sridhar & Touma (1997) power-law axisymmetric cuspy models with separable potential in parabolic coordinates. From left to right: k= 1/3, 2/3 and 1. As explained in the test, the density diverges at the origin for 1/2 < k≤ 1, while it vanishes for 0 < k < 1/2. For k= 1/2 the density (not shown) is independent of r, i.e. it is constant on cones with the common vertex on the origin.

Open in new tabDownload slide

We finally note that the superposition of potentials of the family (B1) with different values of k is still a separable potential. Of course, the dMOND operator is non-linear, so that the associated densities are not the sum of the separate components. However, we performed some numerical experiments, and we found that the resulting densities (for 0 < k≤ 1) are still positive. This could open the way to the construction of new families of axisymmetric MOND systems with separable potentials and more general density distributions than pure power laws.