The rotational structure of methanol and its excitation by helium Free

Abstract

1 INTRODUCTION

Methanol (CH₃OH) is a slightly asymmetric top in which the methyl (CH₃) group performs internal torsional motion around the molecular symmetry axis, relative to the hydroxyl (OH) radical. The torsional motion is a form of vibration, where the corresponding degree of freedom is an angle, rather than an internuclear separation. CH₃OH has a large dipole moment and a rich spectrum, notably in the mm and submm domains. Methanol has been observed extensively in the interstellar medium. As the emission occurs under conditions which are far removed from thermodynamic equilibrium, the interpretation of its spectrum requires a knowledge of the rate coefficients for collisional excitation by, principally, H₂ and He, which are the most abundant perturbers in the molecular gas in which CH₃OH is detected. Both anomalous emission, owing to population inversion (Martín-Pintado et al. 1999), and anomalous absorption, of the cosmic background radiation field (Walmsley et al. 1988), have been observed from methanol in the interstellar medium.

Inelastic collisions of He atoms with interstellar molecules, particularly those which are observable from the ground at radio and infrared wavelengths, have long been a subject of study (see Flower 2007). Atomic helium is the second most abundant species in the interstellar molecular gas, where it is five times less abundant than H₂ but much more abundant than any other constituent. Consequently, helium plays a role in transferring population between the energy levels of CH₃OH by means of collisions. Being a rare gas, helium is chemically inert and behaves as a structureless perturber when interacting with methanol and other interstellar molecules. Furthermore, He has often been considered to be a surrogate for the H₂ molecule – at least for para-H₂ in its rotational ground state (j= 0)– although there are examples of this hypothesis proving subsequently to be unfounded; see, for example, the recent study of ortho-H₂O by Dubernet et al. (2009).

In previous work on the CH₃OH–He and CH₃OH–para-H₂ systems (Pottage, Flower & Davis 2001, 2002, 2004a,b), we performed calculations of cross-sections and rate coefficients for the rotational excitation of methanol in its ground and first excited torsional states. The rate coefficients that were obtained were restricted to low kinetic temperatures (T≤ 200 K). Furthermore, the rotational basis set was complete only up to approximately 110 K, which is the energy of the lowest level with rotational quantum number j= 9 (the largest value of j considered). These calculations have been used to interpret radio observations of methanol in the interstellar medium (e.g. Leurini et al. 2004; Cragg, Sobolev & Godfrey 2005; Maret et al. 2005).

We are now undertaking a new set of computations, with a view to complementing and extending our earlier studies. One of our objectives is to improve the treatment of the structure of the methanol molecule, in such a way as to be able to extend readily the rotational basis, whilst maintaining the accuracy of the computed eigenenergies and eigenfunctions. In this first paper, we present cross-sections for the rotational excitation of methanol by helium atoms. Section 2 contains the relevant aspects of the theory. Our numerical results are discussed in Section 3, and concluding remarks are made in Section 4. Subsequent work will concentrate on collisions with H₂, both para-H₂, in rotational state j= 0, and ortho-H₂, in rotational state j= 1, for which no previous calculations are available.

2 THEORY

2.1 Molecular structure

In previous work (Pottage et al. 2001, 2002), the method of continued fractions was used to calculate the modifications to the matrix elements of the Hamiltonian of an asymmetric top molecule that are required, in order to take into account the internal torsional motion of the methanol molecule (see Lin & Swalen 1959). Whilst this approach proved to be acceptable, in terms of the accuracy of the eigenvalues that was ultimately obtained, it is unwieldy to use when extending the rotational basis set, which is one of our current objectives. Accordingly, we have adopted a more direct method of solving the Schrödinger equation for the methanol molecule, which involves diagonalizing the Hamiltonian,

1

expressed on a basis of rotational–torsional states

2

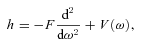
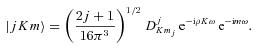
In these equations, 0 ≤ω≤ 2π is the torsion angle, defined as the angle of internal rotation of the CH₃ group, relative to the OH radical, and V(ω) is the torsional potential, defined in equation (6). F is the torsional constant, whose numerical value is given below. In equation (2), is a rotation matrix element, which is a function of the Euler angles specifying the orientation of the methanol molecule, relative to a space-fixed (laboratory) coordinate system, j is the rotational angular momentum quantum number, m_j is the projection of the rotational angular momentum on the space–fixed z-axis and K is its projection on the symmetry axis of the molecule. ρ= 0.8097 is the fraction contributed by the CH₃ group to the rotational angular momentum of the molecule about its symmetry axis (Davis 1992).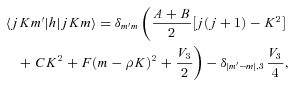

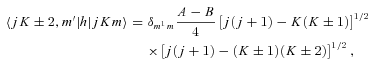
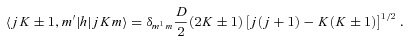
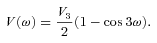
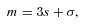
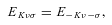
For a given value of j, the non-vanishing matrix elements of the methanol Hamiltonian, expressed in the basis (2), are

3

4

5

In these equations, A= 0.823 cm⁻¹, B= 0.793 cm⁻¹ and C= 4.257 cm⁻¹ are the rotational constants of the molecule, and V₃= 373.1 cm⁻¹ is the depth of the three-fold symmetric torsional potential

6

The constants F= 27.633 cm⁻¹ and D= 0.0026 cm⁻¹ arise from the kinetic energy associated with the torsional motion (Lin & Swalen 1959); the numerical values of the spectroscopic constants are from Pei, Zeng & Gou (1988).

Diagonalization of the methanol Hamiltonian, whose non-zero elements are given by equations (3)–(5), yields the eigenenergies and eigenfunctions of A-, E₁- and E₂-type methanol simultaneously, for a given j. The torsional angular momentum quantum number, m, satisfies the relation

where s is any integer and σ= 0 for A-type, σ=+1 for E₁-type and σ=−1 for E₂-type methanol. E₁ and E₂ are degenerate, in that

where ν= 0, 1, 2, … is the torsional quantum number.

The distinction between A- and E-type methanol relates to the total spin (I) state of the hydrogen nuclei in the CH₃ group. Because protons are identical fermions, their total spin functions have to be either symmetric (I= 3/2; A type) or asymmetric (I= 1/2; E type) under exchange, and these spin functions must be associated with asymmetric and symmetric, respectively, rotational eigenfunctions. The same requirement gives rise to the analogous distinction between ortho- and para-NH₃ (Townes & Schawlow 1955). Because the value of I can change only in proton-exchanging (reactive) collisions with hydrogen-bearing perturbers – a process not considered here – the collisions of He with A- and E-type methanol may be treated completely independently.

2.1.1 A type

As in the case of ortho-ammonia, the eigenfunctions of the Hamiltonian of A-type methanol are also eigenfunctions of the parity operator (inversion of the coordinates of all particles in the origin). These basis functions are

7

which have inversion parity

where ε=±1 and m= 3s (s is any integer). For a given j, states for which (−1)^Kε=±1 are denoted A^±. The energies of states A^± of given j and K tend rapidly towards being degenerate as |K| increases.

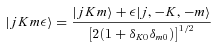
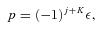
The total parity of the CH₃OH–He system is (−1)^j+K+lε, where l is the orbital angular momentum of the He atom, relative to the centre of mass of the methanol molecule. Since the total parity is conserved, there is no coupling between the positive and negative parity blocks.

2.1.2 E type

As mentioned above, E₁- and E₂-type methanol are degenerate. Furthermore, the corresponding eigenstates are not simultaneous eigenstates of the parity operator. However, such eigenstates can readily be formed as linear combinations of the degenerate E₁ and E₂ functions, as explained by Lees (1973). The appropriate linear combinations are given by equation (7), where the state |jKm〉 is E₁ and the state |j, −K, −m〉 is E₂; m= 3s± 1. These symmetrized eigenstates have the same inversion parity, (−1)^j+Kε, as the A-type eigenfunctions and are better adapted to use in the collision calculations, where the total parity (−1)^j+K+lε is, once again, a good quantum number. We note that this symmetrization of the E-type eigenfunctions was not performed in previous studies of CH₃OH scattering from He and para-H₂ (Pottage et al. 2001, 2002, 2004a,b).

The energy level structure and rotational eigenfunctions of E-type methanol depart from the forms appropriate to a rigid, nearly symmetric top more than is the case for A type. As a consequence, it is possible to label the E-type levels by j and K.

2.2 CH₃OH–He collisions

2.2.1 The interaction potential

The potential of interaction between CH₃OH and He may be expressed as

8

where Y_λμ is normalized spherical harmonic, and (R, θ, φ) are the spherical polar coordinates of the helium atom relative to a coordinate system fixed in the molecule, in which z points along the symmetry axis, from the CH₃ radical to the centre of mass of the molecule. The x–z plane, which contains the COH group, is the symmetry plane of the molecule. The coordinate origin is located at the centre of mass, with all the atoms assumed to occupy their equilibrium positions (see Davis & Entley 1992). When the internuclear distances are treated as being fixed, the molecule reduces to a rigid rotor. We note that the z-axis of the molecule-fixed coordinate system is parallel to, but slightly displaced from, the symmetry axis of the CH₃ group.

The potential (8) is three-fold symmetric about the z-axis, and n is an integral multiple of 3. The torsion angle, ω, measures the rotation of the CH₃ group about its symmetry axis, and ω= 0 (the so-called staggered conformation) is the angle for which the potential energy, given by equation (6), is a minimum. If the CH₃ group is assumed to remain fixed at this minimum energy position, the interaction potential (8) reduces to

9

where

The potential (9) has the form required to describe the interaction between an atom and an asymmetric top (cf. Garrison et al. 1976), which is consonant with the fact that, when ω is constant, the methanol molecule is assimilated to a rigid asymmetric top.

When the dependence of the interaction potential (8) on the torsion angle, ω, is known, a ‘torsionally averaged’ potential may be determined (Pottage et al. 2001). Expanding the eigenfunction of the torsional Hamiltonian, equation (1), as

10

where a_Kνm is an expansion coefficient, the torsionally averaged potential may be written as

11

where

and

We recall that n is an integral multiple of 3. The torsionally averaged potential (11) depends on K, K′ (the projection of the rotational angular momentum of the molecule on the z-axis) and on ν, ν′ (the torsional quantum number); it depends also on the symmetry type (A or E) of the methanol molecule. The torsionally averaged potential is analogous to the vibrationally averaged potential that is often used to study pure rotational scattering in collisions involving diatomic molecules. Then, its use is justified provided that the vibrational energy spacing is much larger than the rotational spacing. However, in the case of methanol, the energetic separation of the torsional states is an order of magnitude smaller than the vibrational spacing in a typical diatomic molecule, and consequently the validity of torsional averaging is more questionable. In the calculations reported below, we used the potential (9) for the staggered conformation. In any case, when we consider methanol–para-H₂ collisions, in future publications (in which comparisons with methanol–He will be made), the corresponding interaction potential is available only for the staggered conformation.

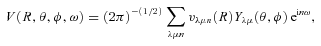
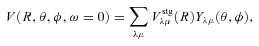
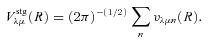
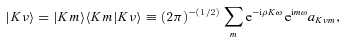
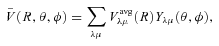
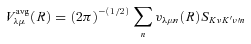
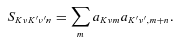
The ab initio MP2 potential was computed (by Steven L. Davis) at fixed values of R, extending from R= 4a₀ to 12a₀. The molscat collision code can automatically extend the potential to smaller and larger values of R. In the former case, use is made of the exponential behaviour of the potential, and in the latter case, it is fitted by inverse powers of R. However, the long-range form of the interaction may also be derived directly from the expressions for the induction and dispersion interactions, in terms of the molecular and atomic properties (multipole moments and polarizabilities; see Davis & Entley 1992). Accordingly, we used cubic–spline interpolation of the MP2 potential for 4 ≤R≤ 12a₀ and the automatic molscat extension to R < 4a₀. For R > 12a₀, we generated the expansion coefficients V^stg_λμ (R) of the interaction potential (9) on a fine grid of equally spaced R values, using the inverse power (R⁻⁶ and R⁻⁷) induction and dispersion interactions from Davis & Entley (1992).

2.2.2 The collision

The quantum mechanical [coupled channels(CC)] approach to CH₃OH–He scattering has been presented by Pottage et al. (2004a) and will not be repeated here. The present calculations are formally analogous with some technical differences. We express the CH₃OH eigenfunctions as expansions of the rotational–torsional states (2) above. On the other hand, Pottage et al. determined first the eigenfunctions of the torsional Hamiltonian and then used the corresponding linear combinations (equation 10) of the basis states,

when deriving the rotational–torsional wavefunctions of the molecule. The present approach is more direct and is better adapted to investigations of the convergence of the cross-sections with increasing size of the molecular rotational–torsional basis.

3 RESULTS

3.1 Calculations of the eigenenergies and eigenfunctions

Using the expressions for the matrix elements of the methanol Hamiltonian (equations 3–5), the eigenenergies and eigenfunctions may be obtained by matrix diagonalization. For a given value of the rotational angular momentum, j, the dimension of the Hamiltonian matrix, (2j+ 1)(2m_max+ 1), depends on the maximum value, m_max, of the torsional angular momentum quantum number, m, that is retained. We found that m_max= 16 was sufficient to yield eigenenergies in agreement with the empirical values (http://ftp.monash.edu.au/pub/chem/1998a/energy.d; see Cragg et al. 2005) to better than 0.1 per cent, except for large values of j, i.e. as the limit of the rotational basis is approached, where the accuracy degrades to several 10th of a per cent. This level of accuracy is not as high as that of the spectroscopic data but is quite sufficient to enable the energy levels to be assigned unambiguously in the collision calculations, considered below.

In Figs 1 and 2 are presented the computed energy levels for E- and A type, respectively, up to 430 K and 420 K (1 cm⁻¹≡ 1.4388 K), for the ground torsional state, ν= 0. Methanol is a near-symmetric top, and the dependence of its eigenenergies on both the rotational quantum number, j, and its projection on the symmetry axis, K, results in an eigenvalue spectrum in which levels with large differences in j can have similar energies. On the other hand, in molecular scattering calculations, the limit of the basis is determined by the maximum value of j that is considered, with all (2K+ 1) values of K for a given j being included in the calculations. These considerations explain the large size of the collision calculations that must be envisaged. In order to use a basis that is complete to 420 K, rotational states j≤ 18 would have to be included. Allowing for the coupling between the rotational and relative CH₃OH–He angular momenta, and the K dependence of the CH₃OH eigenstates, there are potentially thousands of coupled second-order differential equations to be integrated in order to derive the S matrix and hence the cross-sections. Such a computational task is challenging, even with access to multiprocessor supercomputers.

Figure 1

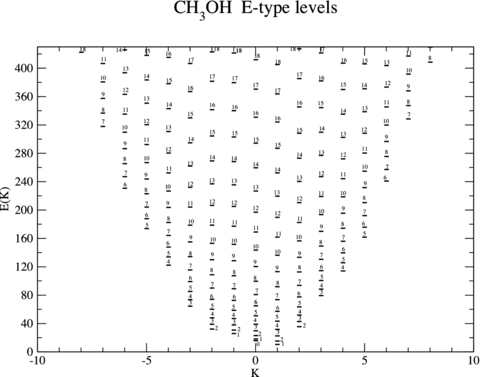
The computed values of the eigenenergies (expressed in Kelvin) of E-type methanol; see text, Section 3.1. The levels are labelled by the value of the rotational quantum number, j. The projection quantum number, K, is given along the abscissa.

Open in new tabDownload slide

Figure 2

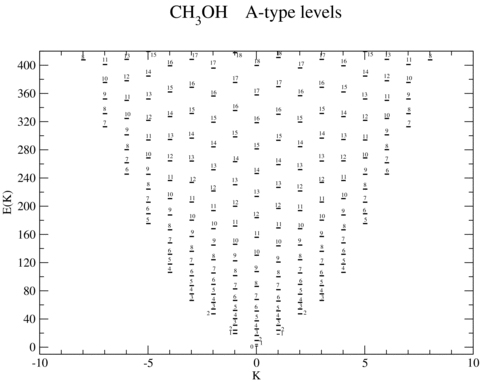
The computed values of the eigenenergies (expressed in Kelvin) of A-type methanol; see text, Section 3.1. The levels are labelled by the value of the rotational quantum number, j. The magnitude of the projection quantum number, K, is given along the abscissa. For the purpose of presentation, negative values of K are taken to correspond to A⁻ levels, and positive values of K to A⁺ levels.

Open in new tabDownload slide

Illustrative numerical values of the computed energies, for states j≤ 3 of A-type methanol, are listed in Table 1, where they are compared with the empirical values and with the calculations of Pottage et al. (2004a). In both A- and E type, the lowest energy level of the first excited torsional state, ν= 1, lies approximately 200 cm⁻¹ above the respective rotational– torsional ground state, ν= 0 and j, K= 0, 0 (A⁺) or j, K= 1, −1 (E-type). In order that the rotational basis should be complete up to this energy, it is necessary to include rotational states through j= 15. However, for the reasons given above, cross-sections for transitions to states with values of j close to this upper limit are not fully converged. Test calculations for E-type methanol at a collision energy E= 200 cm⁻¹, in which the rotational basis was extended to j≤ 17, showed mean and median deviations of the cross-sections obtained with j≤ 15 of 4.2 and 1.5 per cent, respectively, but a maximum deviation of 63.5 per cent for a transition to the level with j= 15.

3.2 Calculations of cross-sections

All the calculations of cross-sections reported below were performed with a version of the molscat code of Hutson & Green (1995) that has been modified to allow for the torsional motion of the methanol molecule.

A-type methanol (Fig. 2) has an energy level structure in which the A⁺ and A⁻ states of given j≥ |K| > 0 are split slightly, owing to the asymmetry of the molecule. For a given value of j, as |K| increases in magnitude, the states come closer to being degenerate. This description applies equally well to a rigid, nearly symmetric top, in which there is no torsional motion. Given that the interaction potential (9) for the staggered conformation of methanol assumes the torsional angle to be fixed (ω= 0), it seems pertinent to establish the extent to which collisions of A-type methanol with He atoms might be simulated adequately as atom–asymmetric top scattering events.

In Table 2 we compared cross-sections, for A-type methanol, with values obtained using an asymmetric top approximation. The asymmetric top wavefunctions were calculated with the rotational constants, A, B and C, specified in Section 2.1, but empirical values were adopted for the eigenenergies. Cross-sections are given for two collision energies, E= 25 and 50 cm⁻¹, relative to the j, K= 0, 0 A⁺ ground state.

As may be seen from the results in Table 2, the cross-sections obtained using asymmetric top eigenfunctions agree reasonably well with the ‘exact’ CC values. The rms deviation between the present calculations and those of Pottage et al., for inelastic transitions, decreases with collision energy and is 0.25 × 10⁻¹⁶ cm² at a collision energy E= 50 cm⁻¹.

Tables 3 and 4 provide a comparison between the present calculations for E-type methanol, in which both the ‘exact’ (CC) method and the coupled states (CS) approximation were used, and the results of Pottage et al. (2004a). Transitions involving the lowest energy state, j, K= 1, −1, are considered, for the purposes of illustration. It may be seen that the propensities of the collisional process are the same in all three calculations. There are quantitative differences, for certain transitions, both between the present CC and the previous results and between the present CC and CS approximations. Comparing the sets of data, at E= 50 cm⁻¹, we find that the cross-sections of Pottage et al. (2004a) are, on the average, about 94 per cent of the current CC values, although discrepancies can be much larger for individual transitions. The current CC and CS results agree generally to better than a factor of 2. Note that the cross-section for the j, K= 1, −1 → 0, 0 transition is identically zero in the CS (but not the CC) approximation; this is a consequence of the implementation the CS approximation, as will now be shown.

As discussed in Section 2, the parity of the E-type eigenfunctions, following symmetrization of the degenerate pairs of E₁ and E₂ rotational eigenfunctions, is p= (−1)^j+Kε, where ε=±1. The total parity of the CH₃OH–He system is then (−1)^j+K+lε, where l is the relative angular momentum quantum number. We have verified that, in both the CC and the CS calculations, identical cross-sections are obtained when setting ε=+1 or ε=−1, as is expected. For a given value of ε, conservation of the total parity, p, requires that

where the primed and unprimed quantum numbers refer to the initial and final states of the transition.

Consider now transitions involving the state j, K= 0, 0 of E-type methanol. The potential coupling matrix elements (Pottage et al. 2004a, equation 21) are proportional to a product of two 3j coefficients:

where λ and μ are the indices of the expansion of the interaction potential in equation (9). When j=K= 0, the second of the 3j coefficients implies that λ=j′, in which case the first 3j coefficient vanishes unless l+l′+j′ is even. It may be seen that parity conservation then requires that K′ is even for non-vanishing, direct potential coupling. In the CS approximation, we have found that this condition applies strictly and accounts for the CS cross-sections being identically zero (and absent from Tables 3 and 4) for certain transitions, whereas the CC cross-sections for these same transitions are non-zero. This qualitative difference in the CS and CC results arises from the implementation of the CS method – which derives from the work of McGuire & Kouri (1974) on atom–diatom scattering – in the atom–asymmetric top mode of operation of the molscat code.

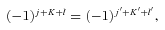
Some of the differences between the present results and those of Pottage et al. (2004a) are attributable to the improvements that we have made in the representation of the methanol eigenfunctions; see Section 2. We tried to ensure that the interaction potential used in the current calculations was consistent with that used previously; but it is possible that differences, for example, in the procedure that has been adopted to interpolate the interaction potential on a fine grid of atom–molecule separations, R, may be responsible for some of the discrepancies.

We have recomputed the cross-sections for transitions in both A- and E-type methanol on a collision energy grid (steps of 5 up to 1000 cm⁻¹ above ground, and then steps of 50 up to 2000 cm⁻¹) that is adapted to evaluating the rate coefficients for transitions between states j≤ 15 up to approximately 200 K. This limiting value of j ensures that the methanol bases are complete up to the opening of the threshold of the first excited torsional state, at about 200 cm⁻¹ above ground. The data of Pottage et al. (2004a) were obtained with a smaller basis, j≤ 9, which is complete only to approximately 100 cm⁻¹ above ground, as may be seen from Figs 1 and 2. The new rate coefficients are available as http://massey.dur.ac.uk/drf/methanol_He/A0-type_rates.out and http://massey.dur.ac.uk/drf/methanol_He/E0-type_rates.out.1

Rate coefficients are available also for rotational transitions within the first and the second excited torsional states, ν= 1 and 2 (A1-type_rates.out, A2-type_rates.out, E1-type_rates.out, E2-type_rates.out). The energies of the torsionally excited rotational levels were generated following the matrix-diagonalization procedure described in Section 2.1, which yields eigenvalues and eigenvectors not only for the ground but also for excited torsional states. We note that the interaction potential used to calculate rotationally inelastic cross-sections within the excited torsional states was identical to that used for the ground torsional state, i.e. the potential for the staggered conformation of methanol. We find that the propensity towards transitions in which ΔK= 0 increases as ν increases and hence the internal rigidity of the methanol molecule decreases.

A limited study of torsionally inelastic scattering was made by Pottage et al. (2004a), who found that the cross-sections for this process are typically two orders of magnitude smaller than for torsionally elastic scattering. Calculations that include the torsional degree of freedom become rapidly intractable, even at the CS level of approximation. At the present time, it would be necessary to degrade further the treatment of the rotational degrees of freedom, e.g. to the IoS level of approximation, in order to be able to calculate the torsionally inelastic cross-sections on an energy grid that is adequate for the evaluation of the corresponding rate coefficients.

4 CONCLUDING REMARKS

We have revisited the problem of the torsional excitation of the methanol molecule by helium atoms. The method of solving for the eigenvalues and the eigenvectors of the molecule has been revised, with a view to both improving their accuracy and simplifying the process of extending the rotational basis set. In the case of E-type methanol, the degenerate E₁ and E₂ eigenfunctions of the Hamiltonian operator were symmetrized in order to form simultaneous eigenfunctions of the parity operator. The methanol basis has been increased, from rotational quantum numbers j≤ 9, used in previous work, to j≤ 15. Following this extension, the basis is now complete up to the threshold of the first torsionally excited state of the molecule.

Comparisons with earlier calculations (Pottage et al. 2001, 2002, 2004a) exhibit better agreement for A-type than for E-type methanol. The spectrum of the former resembles more closely that of a nearly symmetric top, and cross-sections calculated in this limit show reasonable agreement with the values obtained when allowance is made for the torsional degree of freedom. Production calculations are under way that will enable thermal rate coefficients to be computed for transitions between rotational states j≤ 15.

In future work, our attention will turn to the excitation of methanol by H₂. In the interstellar medium, H₂ is the dominant molecular perturber and is present in both its para and ortho forms. Pottage et al. (2004b) studied collisions of methanol j≤ 9 with para-H₂ in its rotational ground state, j= 0. Our intention is to extend this study to rotational states of methanol j > 9 and rotational states of H₂j > 0– in particular, to ortho-H₂j= 1.

This work was supported by a research grant from the STFC (UK). We thank an anonymous referee for a number of constructive suggestions for the improvement of our paper.

REFERENCES