A resonance model with magnetic connection for 3:2 HFQPO pairs in black hole binaries Free

Abstract

1 INTRODUCTION

As is well known, the high-frequency quasi-periodic oscillations (HFQPOs) have been observed in several X-ray binaries. As argued by van der Klis (2000, 2006), HFQPOs in X-ray binaries probably originate from the inner edge of an accretion disc around a black hole (BH) of stellar mass, since millisecond is the natural time-scale for accretion process in these regions. Although a number of models have been proposed to explain the HFQPOs in X-ray binaries, no consensus has been reached on their physical origin (see a review by McClintock & Remillard 2006, hereafter MR06). The 3:2 HFQPO pairs have been observed in a few BH binaries, i.e. GRO J1655−40 (450, 300 Hz; Remillard et al. 1999; Strohmayer 2001; Remillard et al. 2002), XTE J1550−564 (276, 184 Hz; Miller et al. 2001; Remillard et al. 2002) and GRS 1915+105 (168, 113 Hz; MR06; Remillard & McClintock 2006, hereafter RM06).

It has been pointed out that HFQPOs are generally associated with the steep power-law (SPL) state in BH X-ray binaries. Although the 3:2 HFQPO pairs could be interpreted in some epicyclic resonance models (Abramowicz & Kluźniak 2001; Abramowicz et al. 2003; Kluźniak, Abramowicz & Lee 2004; Török et al. 2005), there remain serious uncertainties as to whether epicyclic resonance could overcome the severe damping forces and emit X-rays with sufficient amplitude and coherence to produce the HFQPOs (e.g. see a review in MR06).

Very recently, Gan, Wang & Lei (2009, hereafter G09) proposed a model of magnetically induced disc-corona to interpret the spectrum states in some BH binaries, in which the magnetic connection (MC) of a BH with its surrounding accretion disc can be produced naturally based on several minimal assumptions. It is found that the spectrum states in the BH binaries depend on accretion rate and BH spin, and henceforth this model is referred to as the MC model.

In this paper, we intend to combine the resonance model with the MC model to fit the association of the 3:2 HFQPO pairs with the SPL state in the BH binaries. This paper is organized as follows. In Section 2, we discuss the association of HFQPOs with the SPL state based on the MC model. In Section 3, we discuss the input of the electromagnetic energy on to the resonance modes to overcome the severe damping by transferring energy from the BH to the inner disc via the MC process. Finally, in Section 4 we discuss some issues related to our model. Throughout this paper, the geometric units G=c= 1 are used.

2 ASSOCIATION OF HFQPOS WITH SPL STATES

G09 resolved the dynamic equations of standard thin disc model, combining the MC effects in a typical disc-corona scenario, and the main points are summarized as follows. The interior viscous stress is assumed to be proportional to gas pressure, which is comparable to magnetic pressure. The interior viscous process is dominantly governed by tangled small-scale magnetic fields. A fraction of the viscously dissipated energy is released in the disc, emitting eventually as blackbody radiation and supplying seed photons for Comptonization of corona, and the rest viscously dissipated energy is converted into energy in the corona, heating corona and maintaining its relativistic temperature. It is assumed that the large-scale magnetic field is generated from the small-scale magnetic field, between which the relation is given as follows (Livio, Ogilvie & Pringle 1999):

1

In equation (1), B_p is the poloidal component of the large-scale magnetic field anchored on the disc and h is the half height of the disc. The rotational energy of a BH can be extracted via the MC process, which contributes to the energy dissipation of the disc-corona system, and the mapping relation between the BH horizon and the inner disc can be determined based on the conservation of magnetic flux as follows:

2

where the left- and right-hand sides represent the magnetic fluxes threading the disc and the BH horizon, respectively. The quantities M, r_H and B_H are the BH mass, the horizon radius and the magnetic field at the horizon, respectively, and θ is the angular coordinate of the horizon. The quantities A and D in equation (2) are relativistic correction factors in Kerr metric, and they read

3

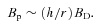
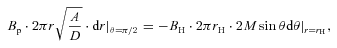
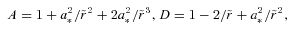
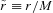where a_*≡J/M² is the BH spin defined in terms of the BH mass M and BH angular momentum J, and is dimensionless disc radius.

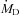In our model, we assume that the magnetic field is uniform at the horizon, and it is related to accretion rate based on the equilibrium between magnetic pressure and the ram pressure given by Moderski, Sikora & Lasota (1997):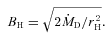

4

As argued in G09, the energy dissipation in the MC process can be derived by resolving relativistic conservation equations of energy and angular momentum for a disc with the MC. The X-ray spectra of the BH binaries can be simulated by resolving the magnetic disc-corona system with Monte Carlo method.

According to the epicyclic resonance model (Aschenbach 2004; Török et al. 2005), the 3:2 HFQPO pairs are fitted by the radial and vertical resonance frequencies as follows:

5

6

7

where

8

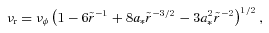
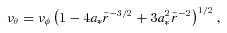
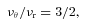
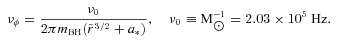
In equations (5)–(8), ν_φ is the Keplerian frequency, ν_r and ν_θ are respectively the radial and vertical resonance frequencies of the general relativistic disc and m_BH is the BH mass in terms of the solar mass.

By using equations (5)–(8), we obtain the resonance radii and the BH spins of the three BH binaries for the given BH mass in fitting the 3:2 HFQPO pairs. In addition, we can fit the SPL states of these sources by combining the resonance model with the MC model given in G09, and the concerned observational quantities and the fitting parameters are listed in Tables 1 and 2, respectively.

Table 2

Open in new tab

The parameters in fitting the SPL state of the BH binaries with the 3:2 HFQPO pairs.

Source	mBH	a*	r32/rms			α	Photon index	LX(LEdd)	Fdisc/Ftotal	FPL/Ftotal
GRS 1915+105	10	0.685	1.931	14.255	0.250	0.300	2.875	0.460	0.274	0.722
	18	0.994	2.895	18.046	0.088	0.390	2.466	0.927	0.383	0.612
XTE J1550−564	8.4	0.888	2.114	19.670	0.130	0.300	2.348	0.442	0.234	0.757
	10.8	0.990	2.741	16.913	0.100	0.391	2.615	0.897	0.420	0.576
GRO J1655−40	6.0	0.955	2.332	19.463	0.110	0.300	2.585	0.549	0.347	0.646
	6.6	0.989	2.712	19.380	0.090	0.335	2.592	0.754	0.400	0.593

Source	mBH	a*	r32/rms			α	Photon index	LX(LEdd)	Fdisc/Ftotal	FPL/Ftotal
GRS 1915+105	10	0.685	1.931	14.255	0.250	0.300	2.875	0.460	0.274	0.722
	18	0.994	2.895	18.046	0.088	0.390	2.466	0.927	0.383	0.612
XTE J1550−564	8.4	0.888	2.114	19.670	0.130	0.300	2.348	0.442	0.234	0.757
	10.8	0.990	2.741	16.913	0.100	0.391	2.615	0.897	0.420	0.576
GRO J1655−40	6.0	0.955	2.332	19.463	0.110	0.300	2.585	0.549	0.347	0.646
	6.6	0.989	2.712	19.380	0.090	0.335	2.592	0.754	0.400	0.593

Table 2

Open in new tab

The parameters in fitting the SPL state of the BH binaries with the 3:2 HFQPO pairs.

Source	mBH	a*	r32/rms			α	Photon index	LX(LEdd)	Fdisc/Ftotal	FPL/Ftotal
GRS 1915+105	10	0.685	1.931	14.255	0.250	0.300	2.875	0.460	0.274	0.722
	18	0.994	2.895	18.046	0.088	0.390	2.466	0.927	0.383	0.612
XTE J1550−564	8.4	0.888	2.114	19.670	0.130	0.300	2.348	0.442	0.234	0.757
	10.8	0.990	2.741	16.913	0.100	0.391	2.615	0.897	0.420	0.576
GRO J1655−40	6.0	0.955	2.332	19.463	0.110	0.300	2.585	0.549	0.347	0.646
	6.6	0.989	2.712	19.380	0.090	0.335	2.592	0.754	0.400	0.593

Source	mBH	a*	r32/rms			α	Photon index	LX(LEdd)	Fdisc/Ftotal	FPL/Ftotal
GRS 1915+105	10	0.685	1.931	14.255	0.250	0.300	2.875	0.460	0.274	0.722
	18	0.994	2.895	18.046	0.088	0.390	2.466	0.927	0.383	0.612
XTE J1550−564	8.4	0.888	2.114	19.670	0.130	0.300	2.348	0.442	0.234	0.757
	10.8	0.990	2.741	16.913	0.100	0.391	2.615	0.897	0.420	0.576
GRO J1655−40	6.0	0.955	2.332	19.463	0.110	0.300	2.585	0.549	0.347	0.646
	6.6	0.989	2.712	19.380	0.090	0.335	2.592	0.754	0.400	0.593

The quantities m_BH, D and i in Table 1 are the BH mass in terms of the solar mass, the distance estimated for each source and the orbital inclination angle, respectively. The values of r₃₂/r_ms in Table 2 are the resonance radii in terms of the radius of the innermost stable circular orbit (ISCO), being obtained by invoking ν_θ/ν_r= 3/2. The parameters and α are the accretion rate in terms of the Eddington accretion rate and the viscous efficiency, respectively.

Inspecting Table 2, we find that the values of the concerned parameters are in accordance with the definition of the SPL state given in RM06, and some issues in the fittings are given as follows.

• As shown in Table 2, the resonance radius r₃₂ is less than the radius r_out, i.e. r₃₂ is located in disc region covered by corona, and the radiation from the resonance mode is influenced directly by the corona.

• We take the upper limit to the BH mass with the lower limit to the distance from the observers to fit the spectra of the three sources, since the bigger BH mass and the less distance give rise to the stronger photon flux in the fittings based on the MC model.

• As shown in Table 2, the power-law component dominates significantly over the disc component for each source. The adjustable parameters are only accretion rate and viscous coefficient α for the given 3:2 HFQPO pairs. It is found that the soft (< ∼10 keV) and hard (> ∼10 keV) parts of the power-law component in the radiation increase and decrease with the increasing accretion rate, respectively, while the corresponding fractions increase and decrease with the decreasing viscous coefficient α. Thus, as shown in Table 2, we fit the bigger photon index in the SPL state by invoking greater accretion rate. The high values of α given in Table 2 arise probably from the differential rotation strengthened due to the transfer of angular momentum from the spinning BH to the inner disc in the MC process.

• The higher BH spins are required in fitting the 3:2 HFQPO pairs based on equations (5)–(8). On the other hand, according to the MC model, the higher spin corresponds to the lower hardness of the power-law component in the radiation, giving rise to the steeper photon index. Thus, we have the association of the 3:2 HFQPO pairs with the SPL state in these BH binaries.

Based on the MC model, we have the emerged spectra of SPL states of the three sources as shown in Fig. 1.

Figure 1

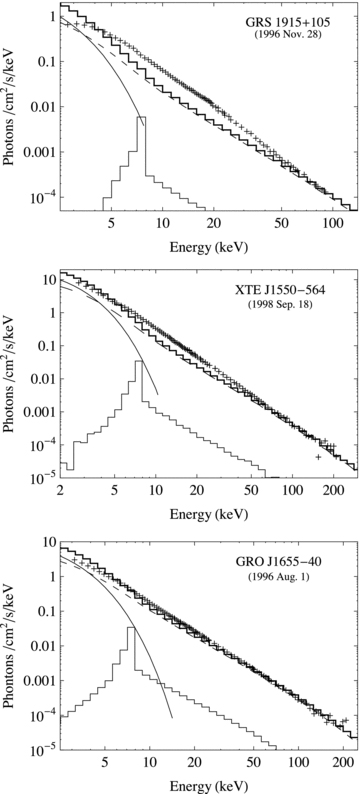
Emerged spectra of the three sources in the SPL state: (a) GRS 1915+105 (1996 Nov. 28) fitted with and α= 0.39 in the upper panel; (b) XTE J1550−564 (1998 Sep. 18) fitted with and α= 0.391 in the middle panel and (c) GRO J1655−40 (1996 Aug. 1) fitted with in the bottom panel. The total emissive spectrum and its thermal, Comptonized and reflective components are plotted in thick-zigzag, thin-solid, dashed and thin-zigzag lines, respectively. The observation data (without error bars) of GRS 1915+105 are taken from fig. 4.13 of MR06, and those of GRO J1655−40 and XTE J1550−564 taken respectively from figs 1 and 2 of Remillard (2004).

Open in new tabDownload slide

3 ENERGY INPUT ONTO RESONANCE MODES

In order to understand the input of the electromagnetic energy onto the resonance modes, we have an analogy of the BH magnetosphere to an electric circuit as shown in Fig. 2. In both cases, we find that the electromagnetic energy is transported to the load as the Poynting flux. As argued by Wang et al. (2003), the energy is extracted magnetically from a fast-spinning BH, and transferred to the inner disc via the closed field lines in the MC process as shown in the upper panel of Fig. 2. This scenario is very similar to the energy transfer from a battery to the resistive load in a circuit as shown in the lower panel of Fig. 2. In the circuit, electrons are accelerated by the electric field, resulting in the dissipation of the kinetic energy in Joule heating. In the MC process, the electromagnetic energy transferred into the inner disc could be converted into the kinetic energy of electrons by the induced electric field due to the magnetic reconnection. In this way, the severe damping in resonance modes could be avoided.

Figure 2

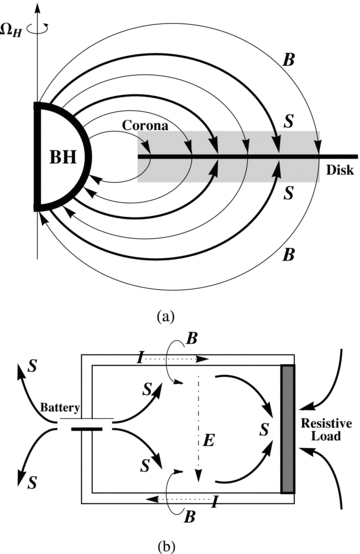
(a) A magnetosphere with closed field lines connecting a spinning BH with its surrounding disc is shown in the upper panel, where the thin and thick arrows represent the closed magnetic field and the Poynting energy flux, respectively. (b) A steady circuit is shown in the lower panel, where the thin and dot–dashed arrows represent magnetic and electric fields, respectively. The thick solid and thin dotted arrows represent the Poynting energy flux and the current in the circuit, respectively.

Open in new tabDownload slide

On the other hand, the magnetic reconnection is more likely to occur due to the resonance of the plasmoids in the accretion flow, and the electrons in the corona could be accelerated to upscatter soft photons to hard photons in inverse-Compton radiation. This scenario is helpful to understand the association of the HFQPO with non-thermal radiation observed in the SPL state of the BH binaries. A rough comparison of the two processes of transporting electromagnetic energy is given in Table 3.

4 DISCUSSION

In this paper, we combine the epicyclic resonances in a relativistic accretion disc with the MC to interpret the 3:2 HFQPOs pairs in the BH X-ray binaries. It turns out that the 3:2 HFQPO pairs are associated with the SPL state, and the severe damping can be overcome by transferring energy from a spinning BH to the inner disc via the MC process. Some issues related to this scenario are discussed as follows.

4.1 Weak Magnetic Field Assumption

Li (2002) discussed the condition of quasi-steady state in the MC of a spinning BH with an accretion disc, and he assumed that the magnetic field is weak so that its influence on the dynamics of particles in a thin Keplerian disc can be negligible. The ‘weak magnetic field assumption’ is given by

9

where ρ is the mass density of the disc and g is the gravitational acceleration produced by the BH.

It is easy to check that the assumption given by equation (9) is valid in our scenario for the 3:2 HFQPO pairs, so that the epicyclic resonance radii can be determined in the context of general relativity. Replacing the gravitational acceleration g in equation (9) by Ω²r, we have

10

where Ω= 2πν_φ is the Keplerian angular velocity. Based on equation (10) and the values of the parameters given in Table 1, we have the ratios versus disc radius as shown in Fig. 3, from which we find that the ratios are much less than unity for these sources. Thus, the ‘weak magnetic field assumption’ remains effective in our model.

Figure 3

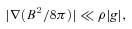
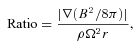
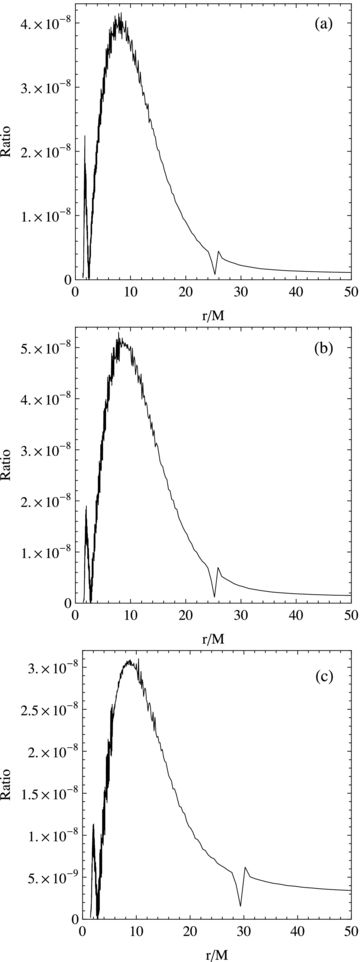
The ratio of |∇(B²/8π)| to ρΩ²r versus the disc radius in the scenario for the 3:2 HFQPO pairs. (a) GRS 1915+105 with and α= 0.39; (b) XTE J1550−564 with and α= 0.391 and (c) GRO J1655−40 with ⁠.

Open in new tabDownload slide

4.2 Estimating the BH Mass of H1743−322 based on 3:2 HFQPO pair

Since HFQPOs are probably produced in the inner disc region very close to ISCO, they might offer the most reliable measurement of BH spins (MR06; RM06). Compared with other methods for measuring spin, such as fitting the spectrum of the X-ray continuum, HFQPO method is much more simple, being independent of disc inclination relative to the BH's spin axis. Furthermore, the 3:2 HFQPO pairs provide a very strict constraint to the BH spin, provided the BH mass is estimated.

A very narrow range of the BH spin, 0.989 < a_* < 0.994, can be found in Table 2, which corresponds to the upper limit to the BH mass for fitting the 3:2 HFQPO pairs associated with the SPL states observed in the three BH binaries. Combining this narrow range of the BH spin with equations (5)–(7), we obtain a very simple relation between BH mass and the upper frequency of the 3:2 HFQPO pairs as follows:

11

where the upper frequency ν_up=ν_θ is equal to the vertical resonance frequency given in equation (6). It is noted that m_BH in equation (11) is the upper limit to the BH mass. Replacing ν_up in equation (11) by 3ν₀, we have almost the same relation ν₀(Hz) = 931m⁻¹_BH given in MR06.

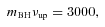
The 3:2 HFQPO pair has been observed in the bright X-ray transient H1743−322. Although the mass of its BH primary has not been measured, its behaviour resembles the BH binaries XTE J1550−564 and GRO J1655−40 in many ways (Remillard et al. 2002; Homan et al. 2005; Kalemci et al. 2006; Remillard et al. 2006). Very recently, McClintock et al. (2009) pointed out that H1743−322 does contain a BH primary based on a detailed analysis of its strong similarities to XTE J1550−564. As a simple analysis, we have the upper limit to the BH mass of H1743−322, m_BH < 12.5, by substituting ν_up= 240 Hz in equation (11). We expect that this upper limit can be checked by future observations on H1743−322.

This work is supported by the National Natural Science Foundation of China under grant 10873005, the Research Fund for the Doctoral Program of Higher Education under grant 200804870050 and National Basic Research Program of China under grant 2009CB824800. We are very grateful to the anonymous referee for his (her) helpful suggestion for improving our work.

REFERENCES