-
PDF
- Split View
-
Views
-
Cite
Cite
Lidia Pieri, Massimiliano Lattanzi, Joseph Silk, Constraining the dark matter annihilation cross-section with Cherenkov telescope observations of dwarf galaxies, Monthly Notices of the Royal Astronomical Society, Volume 399, Issue 4, November 2009, Pages 2033–2040, https://doi.org/10.1111/j.1365-2966.2009.15388.x
Close - Share Icon Share
Abstract
The presence of dark matter in the halo of our Galaxy could be revealed through indirect detection of its annihilation products. Dark matter annihilation is one possible interpretation of the recently measured excesses in positron and electron fluxes, provided that boost factors of the order of 103 or more are taken into account. Such boost factors are actually achievable through the velocity-dependent Sommerfeld enhancement of the annihilation cross-section. Here, we study the expected γ-ray flux from two local dwarf galaxies for which Cherenkov telescope measurements are available, namely Draco and Sagittarius. We use recent stellar kinematical measurements to model the dark matter haloes of the dwarfs and the results of numerical simulations to model the presence of an associated population of subhaloes. We incorporate the Sommerfeld enhancement of the annihilation cross-section. We compare our predictions with the observations of Draco and Sagittarius performed by MAGIC and HESS, respectively, and derive exclusion limits on the effective annihilation cross-section. We also study the sensitivities of Fermi and of the future Cherenkov telescope array to cross-section enhancements. We find that the boost factor due to the Sommerfeld enhancement is already constrained by the MAGIC and HESS data, with enhancements greater than ∼104 being excluded.
1 INTRODUCTION
Detection of a rise in the high-energy cosmic ray e+ fraction by the PAMELA satellite experiment (Adriani et al. 2009) and of a possible peak in the e++ e− flux by the ATIC balloon experiment (Chang et al. 2008) has stimulated considerable recent theoretical activity in indirect detection signatures of particle dark matter (DM) via annihilations of the lightest supersymmetric particle and other massive particle candidates (Bergström, Bringmann & Edsjö 2008; Cirelli & Strumia 2008; Cholis et al. 2008; Grajek et al. 2008; Hooper, Stebbins & Zurek 2009; Liu, Yin & Zhu 2009; de Boer 2009; Donato et al. 2009; Hooper & Zurek 2009). Several hurdles must be surmounted if these signals are to be associated with DM annihilations. First, a high boost factor (103–104) is needed within a kiloparsec of the solar circle (Cirelli, Franceschini & Strumia 2008). Secondly, the boost factor must be suppressed in the inner galaxy to avoid excessive γ-ray and synchrotron radio emission (Bertone et al. 2009). Thirdly, the annihilation channels must be largely lepton-dominated to avoid  production (Cirelli et al. 2009). Finally, account must be taken of the FERMI/HESS observations of electron/positron fluxes that do not reproduce part of the ATIC data (Abdo et al. 2009; Aharonian et al. 2009).
production (Cirelli et al. 2009). Finally, account must be taken of the FERMI/HESS observations of electron/positron fluxes that do not reproduce part of the ATIC data (Abdo et al. 2009; Aharonian et al. 2009).
The third of these requirements is addressed in various particle physics models for the DM candidate (Cirelli et al. 2009). Here, we explore the implications of the first two requirements and comment on the implications of the newest data on particle fluxes. The higher annihilation cross-section needed for the interpretation of the positron excess in terms of DM annihilations can be obtained via the Sommerfeld effect (Arkani-Hamed et al. 2009; Lattanzi & Silk 2009). This effect occurs only at low relative velocities of the annihilating particles and does not change the thermal cross-section required by cosmological measurements. Robertson & Zentner (2009) examined possible signatures of the Sommerfeld enhancement arising from the non-trivial dependence of the DM velocity distribution upon position within a DM halo. Here, we consider the Sommerfeld enhancement in the substructures of our Galaxy, where the velocity dispersion is as low as 10 km s−1 in the dwarf galaxies and becomes even lower for smaller subhalo masses. The boost, which is inversely proportional to the particle velocity, is especially relevant on the smallest scales that are unresolved by numerical simulations (Springel et al. 2008a). Throughout this paper, we will not consider the full velocity distribution function but will take the central values as a reference for computing the boost.
The second requirement can be understood because the unresolved substructures that dominate the local boost are likely to be tidally disrupted in the inner Galaxy (Lattanzi & Silk 2009). The predictions for signals coming from the Galactic Centre (GC) are also reduced by adopting a shallower DM profile. We note that these effects also lower the local  contribution.
contribution.
In this paper, we focus on the γ-ray signal coming from the Draco dwarf galaxy. We choose Draco because its DM density profile is determined in detail (Walker et al. 2009) and because it has been observed by the MAGIC Cherenkov telescope (Albert et al. 2008). Our aim is to constrain the Sommerfeld enhancement through such a measurement. We will show how the constraints depend sensitively on the astrophysical uncertainties due to both numerical simulations and astronomical measurements. Moreover, we will show how the result is mainly dominated by the smooth DM halo of the dwarf galaxy, so that it is almost independent of the subsubstructure model used. We also derive exclusion plots for the effective annihilation cross-section obtained with the available measurements, as well as for the sensitivities achievable with future detectors. We apply our results to the case of the Sagittarius dwarf galaxy, which has also been observed with the HESS Cherenkov telescope (Aharonian et al. 2008). This galaxy, much closer to us than Draco, would give a higher γ-ray flux, and thus sets the greatest constraint. Unfortunately, the tidal stripping of Sagittarius because of its proximity to the GC makes it difficult to model the DM profile. In this paper, we will assume that its mass profile can be modelled in the same way as Draco, by adopting the universality of mass profiles in the dwarf galaxies found in Walker et al. (2009). Since neither MAGIC nor HESS has observed any signal along the direction of the targets, we therefore set 95 per cent confidence limit (CL) upper limits on the γ-ray coming from these sources.
The paper is organized as follows. In Section 2, we model the particle physics scenarios where the Sommerfeld enhancement is largest, as well as the astrophysical uncertainties in the determination of the γ-ray flux. In Section 3, we derive the constraints on the effective cross-section set with the available Cherenkov telescope measurements, and give exclusion plots achievable with the next generation of experiments that make use of Cherenkov telescope technology, namely the proposed Cherenkov telescope array (CTA). We give our conclusions in Section 4.
2 γ-RAY FLUX FROM DM ANNIHILATION IN DRACO AND SAGITTARIUS
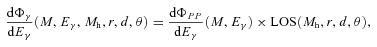

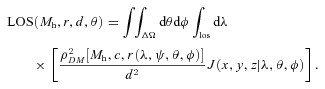
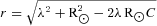 , where R⊙ is the distance of the Sun from the GC (R⊙= 8.5 kpc) and C= cos (θ) cos (ψ) − cos (φ) sin (θ) sin (ψ); finally, inside the cone, d=λ and J(x, y, z|λ, θ, φ) is the Jacobian determinant from cartesian to polar coordinates. The presence of the Sommerfeld effect is reflected by setting σ v=S[β(Mh, r), M] (σv)0. The Sommerfeld enhancement S now enters the LOS integral of equation (3).
, where R⊙ is the distance of the Sun from the GC (R⊙= 8.5 kpc) and C= cos (θ) cos (ψ) − cos (φ) sin (θ) sin (ψ); finally, inside the cone, d=λ and J(x, y, z|λ, θ, φ) is the Jacobian determinant from cartesian to polar coordinates. The presence of the Sommerfeld effect is reflected by setting σ v=S[β(Mh, r), M] (σv)0. The Sommerfeld enhancement S now enters the LOS integral of equation (3).2.1 The particle physics sector
The DM annihilation cross-section can be enhanced, with respect to its primordial value, in the presence of the so-called Sommerfeld effect. This is a (non-relativistic) quantum effect occurring when the slow-moving annihilating particles interact through a potential (Sommerfeld 1931). The idea that the γ-ray flux from DM annihilations can be enhanced in this way was first proposed in a pioneering paper by Hisano et al. (2004) (see also Hisano et al. 2005). Recently, the possibility of explaining the large boost factor required by PAMELA using this mechanism has stimulated several studies of this effect (see for example Cirelli, Strumia & Tamburini 2007; March-Russell et al. 2008; Arkani-Hamed et al. 2009; Lattanzi & Silk 2009; March-Russell & West 2009; Pospelov & Ritz 2009).
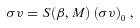
The enhancement is effective in the low-velocity regime and disappears (S= 1) in the limit β→ 1. In general, one can distinguish two distinct behaviours, resonant and non-resonant, depending on the value of the annihilating particle mass. In the non-resonant case, the cross-section grows like 1/β before saturation occurs at a certain value Smax of the enhancement. In the resonant case, occurring for particular values of M, the cross-section first grows like 1/β (as in the non-resonant case), then at some point it grows like 1/β2 before saturating. The Sommerfeld boost can reach very large values. In both the resonant and non-resonant cases, the values of β and S for which the saturation occurs depend, other than on the particle mass, on the parameters of the interaction potential, namely the coupling constant α and the mass of the exchange boson mV.
In this paper, we will consider two different particle physics scenarios. In the first, we consider a weakly interacting massive particle (WIMP) DM candidate. In this case, the Sommerfeld effect is caused by the standard model weak interaction, mediated by W and Z bosons, so that mV= 90 GeV and α= 1/30. If the DM is a Majorana particle, such as the supersymmetric neutralino, its annihilation into a fermionic final state f is helicity-suppressed by a factor (mf/M)2. For a DM particle in the 1–10 TeV range, this is a factor of 10−2/10−4 even for the heaviest possible final state, i.e. the top quark. Thus, we are naturally led to consider a candidate that annihilates mainly to weak gauge bosons. However, for completeness we have also considered the heavy quark and lepton annihilation channels. The differential photon spectra per annihilation dNfγ/dEγ for the various final states have been computed using pythia (Sjöstrand et al. 2001), including also the contribution from final state radiation.
We consider the following values for the mass of the particle: M= (4.3, 4.45, 4.5, 4.55 TeV). These values are chosen because, in the case of a weak interaction potential, a resonance in the Sommerfeld-enhanced cross-section occurs for M≃ 4.5 TeV (Lattanzi & Silk 2009). Being so close to the resonance, even a relatively small change in the mass of the particle can produce order of magnitude changes in the Sommerfeld boost. In fact, the maximum achievable boost goes from S≃ 1.5 × 103 for M= 4.3 TeV to S≃ 4 × 105 for M= 4.55 TeV.
The second scenario we consider has been introduced by Arkani-Hamed et al. (2009) [hereafter AH]. In this model, a new force with a coupling constant α∼ 10−2 is introduced in the dark sector, mediated by a boson φ having a mass mV=mφ≲ 1 GeV. It is this new force that is responsible for the Sommerfeld enhancement. In this case, it is found that the large boosts required to explain the PAMELA and ATIC data can be obtained for a DM particle of mass M≃ 700 GeV. In AH models, the DM annihilates mainly to φ bosons, that in turn decay into electrons or muons (depending on the mass of the φ). The γ-rays are produced in the decay of the φ as final state radiation (Bergström et al. 2009). We consider two particular realizations of this scenario: we take the DM mass to be M= 700 GeV in both, and mφ equal to either 100 MeV or 1 GeV. We note that the DM interaction cross-section in the first case is only one order of magnitude away from the upper bound coming from observations of the mass distribution inside clusters of galaxies (Miralda-Escudé 2002).
The enhancement as a function of velocity in the models considered is depicted in Fig. 1. The main properties of the enhancement, i.e. the maximum value Smax and the saturation velocity  , are summarized in Table 1 for the different models, together with the parameters of the interaction potential that is responsible for the Sommerfeld boost. We point out that, in the case of dwarf galaxies and their subhaloes, the dispersion velocity is of the order of 10 km s−1, which means that we are always in the saturation regime, and the enhancement is always maximum and equal to Smax. As we show in the next sections, these large boost factors can be tested through Cherenkov telescope observations of dwarf galaxies.
, are summarized in Table 1 for the different models, together with the parameters of the interaction potential that is responsible for the Sommerfeld boost. We point out that, in the case of dwarf galaxies and their subhaloes, the dispersion velocity is of the order of 10 km s−1, which means that we are always in the saturation regime, and the enhancement is always maximum and equal to Smax. As we show in the next sections, these large boost factors can be tested through Cherenkov telescope observations of dwarf galaxies.
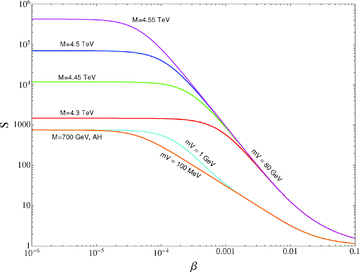
Sommerfeld enhancement S as a function of the particle velocity β for different values of the DM mass close to the resonance in our model with α= 1/30 and mV= 80 GeV, as well as for a model with α= 10−2 and mV= 1 GeV and 100 MeV (labelled AH).
Values of the maximum possible boost Smax and of the saturation velocity  , for different DM models. Each model is defined by the value of the DM particle mass M, and by the parameters of the Yukawa potential responsible for the enhancement, namely the mass mV of the exchange boson and the coupling constant α.
, for different DM models. Each model is defined by the value of the DM particle mass M, and by the parameters of the Yukawa potential responsible for the enhancement, namely the mass mV of the exchange boson and the coupling constant α.
| Mass (TeV) | mV (GeV) | α | Smax |  |
| 4.3 | 80 | 1/30 | 1.5 × 103 | 8.0 × 10−4 |
| 4.45 | 80 | 1/30 | 1.2 × 104 | 2.8 × 10−4 |
| 4.5 | 80 | 1/30 | 7.0 × 104 | 1.1 × 10−4 |
| 4.55 | 80 | 1/30 | 4.2 × 105 | 4.7 × 10−5 |
| 0.7 | 1 | 10−2 | 750 | 2.4 × 10−5 |
| 0.7 | 0.1 | 10−2 | 750 | 8.5 × 10−6 |
| Mass (TeV) | mV (GeV) | α | Smax |  |
| 4.3 | 80 | 1/30 | 1.5 × 103 | 8.0 × 10−4 |
| 4.45 | 80 | 1/30 | 1.2 × 104 | 2.8 × 10−4 |
| 4.5 | 80 | 1/30 | 7.0 × 104 | 1.1 × 10−4 |
| 4.55 | 80 | 1/30 | 4.2 × 105 | 4.7 × 10−5 |
| 0.7 | 1 | 10−2 | 750 | 2.4 × 10−5 |
| 0.7 | 0.1 | 10−2 | 750 | 8.5 × 10−6 |
Values of the maximum possible boost Smax and of the saturation velocity  , for different DM models. Each model is defined by the value of the DM particle mass M, and by the parameters of the Yukawa potential responsible for the enhancement, namely the mass mV of the exchange boson and the coupling constant α.
, for different DM models. Each model is defined by the value of the DM particle mass M, and by the parameters of the Yukawa potential responsible for the enhancement, namely the mass mV of the exchange boson and the coupling constant α.
| Mass (TeV) | mV (GeV) | α | Smax |  |
| 4.3 | 80 | 1/30 | 1.5 × 103 | 8.0 × 10−4 |
| 4.45 | 80 | 1/30 | 1.2 × 104 | 2.8 × 10−4 |
| 4.5 | 80 | 1/30 | 7.0 × 104 | 1.1 × 10−4 |
| 4.55 | 80 | 1/30 | 4.2 × 105 | 4.7 × 10−5 |
| 0.7 | 1 | 10−2 | 750 | 2.4 × 10−5 |
| 0.7 | 0.1 | 10−2 | 750 | 8.5 × 10−6 |
| Mass (TeV) | mV (GeV) | α | Smax |  |
| 4.3 | 80 | 1/30 | 1.5 × 103 | 8.0 × 10−4 |
| 4.45 | 80 | 1/30 | 1.2 × 104 | 2.8 × 10−4 |
| 4.5 | 80 | 1/30 | 7.0 × 104 | 1.1 × 10−4 |
| 4.55 | 80 | 1/30 | 4.2 × 105 | 4.7 × 10−5 |
| 0.7 | 1 | 10−2 | 750 | 2.4 × 10−5 |
| 0.7 | 0.1 | 10−2 | 750 | 8.5 × 10−6 |
2.2 The astrophysical sector: smooth DM halo
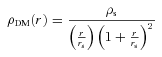
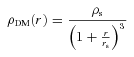
| Draco fit | rs(kpc) |  |  |
| NFW | 0.795 | 1.05 × 10−3 | 4.43 × 10−3 |
| NFW +2σ | 3.0 | 7.85 × 10−4 | 2.8 × 10−3 |
| NFW −2σ | 0.3 | 1.91 × 10−3 | 9.8 × 10−3 |
| Core | 0.15 | 7.5 × 10−4 | 2.17 × 10−3 |
| Core +2σ | 0.3 | 5.2 × 10−4 | 9.4 × 10−4 |
| Core −2σ | 0.085 | 1.54 × 10−3 | 6.9 × 10−3 |
| Draco fit | rs(kpc) |  |  |
| NFW | 0.795 | 1.05 × 10−3 | 4.43 × 10−3 |
| NFW +2σ | 3.0 | 7.85 × 10−4 | 2.8 × 10−3 |
| NFW −2σ | 0.3 | 1.91 × 10−3 | 9.8 × 10−3 |
| Core | 0.15 | 7.5 × 10−4 | 2.17 × 10−3 |
| Core +2σ | 0.3 | 5.2 × 10−4 | 9.4 × 10−4 |
| Core −2σ | 0.085 | 1.54 × 10−3 | 6.9 × 10−3 |
Note. First column: models reflecting the astronomical uncertainties from a fit to the Draco stellar velocity dispersion. Second column: scale radius for each model. Third column: values for the LOS integral towards the centre of Draco. Fourth column: values for the LOS integral towards the centre of Sagittarius.
| Draco fit | rs(kpc) |  |  |
| NFW | 0.795 | 1.05 × 10−3 | 4.43 × 10−3 |
| NFW +2σ | 3.0 | 7.85 × 10−4 | 2.8 × 10−3 |
| NFW −2σ | 0.3 | 1.91 × 10−3 | 9.8 × 10−3 |
| Core | 0.15 | 7.5 × 10−4 | 2.17 × 10−3 |
| Core +2σ | 0.3 | 5.2 × 10−4 | 9.4 × 10−4 |
| Core −2σ | 0.085 | 1.54 × 10−3 | 6.9 × 10−3 |
| Draco fit | rs(kpc) |  |  |
| NFW | 0.795 | 1.05 × 10−3 | 4.43 × 10−3 |
| NFW +2σ | 3.0 | 7.85 × 10−4 | 2.8 × 10−3 |
| NFW −2σ | 0.3 | 1.91 × 10−3 | 9.8 × 10−3 |
| Core | 0.15 | 7.5 × 10−4 | 2.17 × 10−3 |
| Core +2σ | 0.3 | 5.2 × 10−4 | 9.4 × 10−4 |
| Core −2σ | 0.085 | 1.54 × 10−3 | 6.9 × 10−3 |
Note. First column: models reflecting the astronomical uncertainties from a fit to the Draco stellar velocity dispersion. Second column: scale radius for each model. Third column: values for the LOS integral towards the centre of Draco. Fourth column: values for the LOS integral towards the centre of Sagittarius.
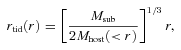
In our case, the host halo is the MW, which we model after the recent high-resolution N-body simulations Aquarius (Springel et al. 2008a,b) and Via Lactea II (Diemand et al. 2008): while the latter describes the MW with an NFW profile (Mh∼ 1.9 × 1012 M⊙, rs= 21 kpc, ρs= 8.09 × 106 M⊙ kpc−3), the former finds a shallower profile in the inner regions. We have checked that the difference between the two profiles is irrelevant for our analysis.
At the distance of Draco, we find rtid= 11.2 kpc. We note that the condition rtid > rs holds, which guarantees that the binding energy is negative, and the system is not dispersed by tides. The value of rtid found making use of the Roche criterion is indeed an upper limit since it has been computed in the point-like approximation.
The LOS integral for the Draco galaxy is computed by numerically integrating equation (3), assuming that the integral is different from zero only in the interval [d−rtid, d+rtid].
In the case of the dwarf galaxies, their mass and therefore the masses of the subsubhaloes lie in the region at low β where the Sommerfeld enhancement saturates. This is true for every DM mass except for the one which lies closest to the resonance (in our model, M= 4.55 TeV). In this case, however, the radial dependence of the enhancement produces a variation of a few per cent, so that as a good approximation, the Sommerfeld enhancement S can be considered constant and taken out of the LOS integral. The result of the computation of the LOS integral (S= 1) according to equation (3) in the case of Draco is depicted in Fig. 2 as a function of the angle of view ψ with respect to the centre of Draco. Only the LOS relative to the central value for the NFW fit to the data is shown.
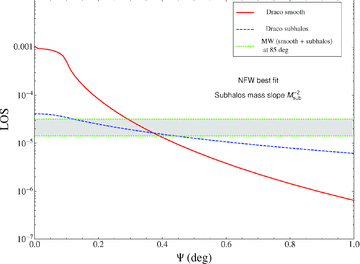
Φcosmo as a function of the angle of view ψ from the centre of halo, computed in the case of Draco, for the smooth halo and from the subhalo population. The shaded region represents the uncertainty due to the numerical simulations in the value of Φcosmo computed for the MW, including its substructures, at the position of Draco.
In view of the DM profile universality, we model the inner regions of the closer Sagittarius galaxy using the same profile parameters as in the case of Draco (see also Evans, Ferrer & Sarkar 2004 for a comparison between the Draco and Sagittarius inner DM profiles), although there is no direct evidence of the shape of its DM halo. The Sagittarius dwarf galaxy is located at a distance of about 24 kpc from us, at low latitudes ψS= 15°. Its vicinity to the GC causes significant tidal stripping due to the interaction with the gravitational potential of the MW. Yet, the surviving stellar component suggests that its inner DM halo also survives. Moreover, the observations show that Sagittarius is indeed DM-dominated with a central stellar velocity dispersion of about 10 km s−1 (Ibata et al. 1997), similar to the one observed in Draco. At the distance of Sagittarius, the tidal radius is rtid= 4 kpc, still larger than the scale radius.
The results of the LOS integral towards the centre of each dwarf galaxy are shown in Table 2, for the central value and the 95 per cent CL values of both the best fit NFW and the cored profile obtained by Walker et al. (2009).
In Table 3, we list the values of the LOS computed for the smooth component of the MW in the direction of the dwarf galaxies, which will provide a foreground for the detection of the dwarfs themselves. We do not describe in this paper the details of these computations, which are studied extensively in Pato, Pieri & Bertone (2009) and Pieri et al. (2009b). We observe that, both for Draco and for Sagittarius, the dwarf centre is brighter in γ-ray than the MW foreground.
LOS integral for the smooth component of the MW integrated along a direction pointing towards the centre of the dwarf galaxies.
| MW model |  |  |
| VL2 | 1.18 × 10−5 | 2.73 × 10−4 |
| Aquarius | 1.13 × 10−5 | 4 × 10−4 |
| MW model |  |  |
| VL2 | 1.18 × 10−5 | 2.73 × 10−4 |
| Aquarius | 1.13 × 10−5 | 4 × 10−4 |
Note. First column: MW model from numerical simulation. Second column: LOS integral towards the centre of Draco. Third column: LOS integral towards the centre of Sagittarius.
LOS integral for the smooth component of the MW integrated along a direction pointing towards the centre of the dwarf galaxies.
| MW model |  |  |
| VL2 | 1.18 × 10−5 | 2.73 × 10−4 |
| Aquarius | 1.13 × 10−5 | 4 × 10−4 |
| MW model |  |  |
| VL2 | 1.18 × 10−5 | 2.73 × 10−4 |
| Aquarius | 1.13 × 10−5 | 4 × 10−4 |
Note. First column: MW model from numerical simulation. Second column: LOS integral towards the centre of Draco. Third column: LOS integral towards the centre of Sagittarius.
2.3 The astrophysical sector: substructures
The recent Aquarius and the Via Lactea II simulations have succeeded in determining the properties of the subhaloes and subsubhaloes such as spatial and mass distribution, density profiles and spatial dependence of the concentration parameter. We therefore study the effects on the expected γ-ray flux of a population of subsubhaloes inside the dwarfs according to the recent findings of numerical simulations, although we do not expect a significant impact on the expected flux towards the centre of the dwarf, where the smooth halo flux is larger (Giocoli, Pieri & Tormen 2008; Giocoli et al. 2009). We populate Draco with subsubhaloes with masses as small as 10−6 M⊙, corresponding to the damping scale of a typical DM candidate with M= 100 GeV (Hofmann, Schwarz & Stoecker 2001; Green, Hofmann & Schwarz 2004, 2005; Loeb & Zaldarriaga 2005). It should, however, be noted that such a minimum mass may vary between 10−12 and 10−4 M⊙ depending on the particle physics model considered (Profumo & Sigurdson 2006).

As a second step, we remove all of the subhaloes which lie beyond rtid. This is indeed an upper value for the number of surviving subsubhaloes, since we are not considering here the 50 per cent of the subhaloes that exit the virial radius of the parent halo during their first orbit (Tormen, Moscardini & Yoshida 2004) and are therefore dispersed into the halo of the MW.
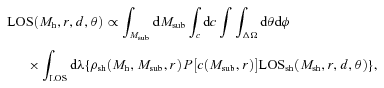
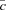 :
: 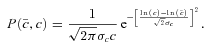
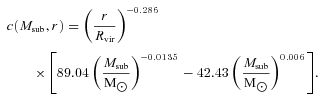
We repeat the same analysis for Sagittarius, assuming its subsubhalo population is modelled in the same way as the Draco's one, yet with a smaller todal radius. The result of the integration of equation (9) along a direction pointing towards the centre of the dwarfs is listed in Table 4. Although the values in the case of Sagittarius are slightly larger than for Draco, due to its proximity to us, the relative strength of the smooth to clumpy component is larger in Draco, making the presence of subsubhaloes in Sagittarius almost irrelevant with respect to the smooth component.
| Draco fit | Mass slope |  |  |
| NFW | −2 | 4.13 × 10−5 | 5.40 × 10−5 |
| NFW | −1.9 | 1.03 × 10−5 | 1.34 × 10−5 |
| NFW +2σ | −2 | 3.85 × 10−6 | 4.25 × 10−6 |
| NFW +2σ | −1.9 | 9.5 × 10−7 | 1.05 × 10−6 |
| NFW −2σ | −2 | 1.98 × 10−4 | 3.10 × 10−4 |
| NFW −2σ | −1.9 | 4.94 × 10−5 | 7.71 × 10−5 |
| Draco fit | Mass slope |  |  |
| NFW | −2 | 4.13 × 10−5 | 5.40 × 10−5 |
| NFW | −1.9 | 1.03 × 10−5 | 1.34 × 10−5 |
| NFW +2σ | −2 | 3.85 × 10−6 | 4.25 × 10−6 |
| NFW +2σ | −1.9 | 9.5 × 10−7 | 1.05 × 10−6 |
| NFW −2σ | −2 | 1.98 × 10−4 | 3.10 × 10−4 |
| NFW −2σ | −1.9 | 4.94 × 10−5 | 7.71 × 10−5 |
Note. First column: models reflecting the astronomical uncertainties from a fit to the Draco stellar velocity dispersion. Second column: subhalo mass slope. Third column: values for the LOS integral towards the centre of Draco. Fourth column: values for the LOS integral towards the centre of Sagittarius.
| Draco fit | Mass slope |  |  |
| NFW | −2 | 4.13 × 10−5 | 5.40 × 10−5 |
| NFW | −1.9 | 1.03 × 10−5 | 1.34 × 10−5 |
| NFW +2σ | −2 | 3.85 × 10−6 | 4.25 × 10−6 |
| NFW +2σ | −1.9 | 9.5 × 10−7 | 1.05 × 10−6 |
| NFW −2σ | −2 | 1.98 × 10−4 | 3.10 × 10−4 |
| NFW −2σ | −1.9 | 4.94 × 10−5 | 7.71 × 10−5 |
| Draco fit | Mass slope |  |  |
| NFW | −2 | 4.13 × 10−5 | 5.40 × 10−5 |
| NFW | −1.9 | 1.03 × 10−5 | 1.34 × 10−5 |
| NFW +2σ | −2 | 3.85 × 10−6 | 4.25 × 10−6 |
| NFW +2σ | −1.9 | 9.5 × 10−7 | 1.05 × 10−6 |
| NFW −2σ | −2 | 1.98 × 10−4 | 3.10 × 10−4 |
| NFW −2σ | −1.9 | 4.94 × 10−5 | 7.71 × 10−5 |
Note. First column: models reflecting the astronomical uncertainties from a fit to the Draco stellar velocity dispersion. Second column: subhalo mass slope. Third column: values for the LOS integral towards the centre of Draco. Fourth column: values for the LOS integral towards the centre of Sagittarius.
In Table 5, we compute the values of the LOS flux computed for the clumpy component of the MW in the direction of the dwarf galaxies. We observe that, both for Draco and for Sagittarius, the dwarf centre is brighter in γ-rays than the MW clumpy foreground. We do not describe in this paper the details of these computations, which can be found in Pato et al. (2009) and Pieri et al. (2009b). The MW foreground contribution to Draco, computed including its smooth and clumpy component, is shown in Fig. 2. The band of values accounts for the different simulations as well as for the different subhalo mass slopes. The MW foreground begins hiding Draco at around  from the Draco centre. We have checked that the same happens in the case of Sagittarius.
from the Draco centre. We have checked that the same happens in the case of Sagittarius.
LOS integral for the clumpy component of the MW integrated along a direction pointing towards the centre of the dwarf galaxies.
| Subhalo mass slope |  |  |
| −2 | 2 × 10−5 | 5.5 × 10−5 |
| −1.9 | 2.5 × 10−6 | 6.5 × 10−6 |
| Subhalo mass slope |  |  |
| −2 | 2 × 10−5 | 5.5 × 10−5 |
| −1.9 | 2.5 × 10−6 | 6.5 × 10−6 |
Note. First column: subhalo mass slope. Second column: LOS integral towards the centre of Draco. Third column: LOS integral towards the centre of Sagittarius.
LOS integral for the clumpy component of the MW integrated along a direction pointing towards the centre of the dwarf galaxies.
| Subhalo mass slope |  |  |
| −2 | 2 × 10−5 | 5.5 × 10−5 |
| −1.9 | 2.5 × 10−6 | 6.5 × 10−6 |
| Subhalo mass slope |  |  |
| −2 | 2 × 10−5 | 5.5 × 10−5 |
| −1.9 | 2.5 × 10−6 | 6.5 × 10−6 |
Note. First column: subhalo mass slope. Second column: LOS integral towards the centre of Draco. Third column: LOS integral towards the centre of Sagittarius.
The mass modelling of the dwarf galaxies at large distances from their centres is just an educated guess; as a check of consistency of our results, we repeated our calculations in the case when the DM halo extends only up to 600 pc, that is to say to the King radius (we remind that the mass within the King radius is directly measured through stellar kinematics). The differences between the computations extending to Rvir and the ones extending to the 600 pc amount to 5 per cent at most.
In the following section, we will compare our predictions with the available data and expected sensitivities from the atmospheric Cherenkov telescopes (ACTs). To compare with the data, we will consider the sum of the four contributions to the photon flux: (1) annihilations in the smooth halo of the dwarf galaxy; (2) annihilations in the subhaloes of the dwarf galaxy; (3) annihilations in the smooth halo of the MW and (4) annihilations in the subhaloes of the MW, computed along the direction which corresponds to the position of the dwarf galaxy in the sky. The relative importance of the four terms depends on the angle of view from the centre of the dwarf galaxy, as well as on the particle physics model. The contribution due to the annihilation in the smooth halo of the dwarf galaxy is always predominant when looking at the dwarf centre.
3 COMPARISON WITH THE EXPERIMENTAL DATA
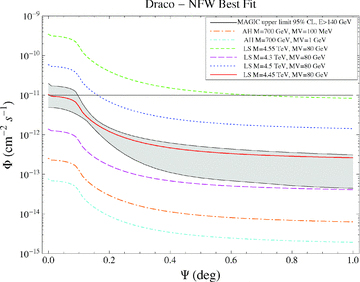
The MAGIC and HESS ACTs have put 95 per cent upper limits on the γ-ray fluxes from Draco and Sagittarius, respectively. The upper limit for Draco integrated over energies above 140 GeV is 10−11 ph cm−2 s−1. In the case of Sagittarius, this limit is 3.6 × 10−12 ph cm−2 s−1, integrated above 250 GeV.
In Figs 3 and 4, we compare these values with the prediction of the γ-ray flux from DM annihilations. We compute the flux for the particle DM models described in Section 2. We show the result in the case of the central value for the scale radius in the NFW best fit to the kinematic data, as derived in Walker et al. (2009). Indeed, in the case of M= 4.45 TeV, the shaded area shows the astrophysical uncertainty, computed taking into account NFW and cored fits, for central and 95 per cent CL values of the scale radius.
Expected γ-ray flux above 140 GeV as a function of the angle of view ψ from the centre of Draco. The shaded area represents the astrophysical uncertainties.
Expected γ-ray flux above 250 GeV as a function of the angle of view ψ from the centre of Sagittarius. The shaded area represents the astrophysical uncertainties.
We note that our dwarfs actually appear as point sources for an angular resolution of  .
.
The data from both MAGIC and HESS already exclude the highest Sommerfeld-enhanced cross-sections.
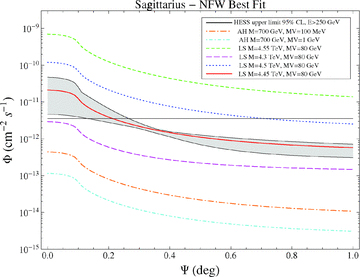
Since the main contribution to the γ-ray flux at the centre of the dwarf comes from haloes which are in saturation with respect to the velocity-dependent enhancement, we can present the previous results in terms of an exclusion plot on the effective Sommerfeld-enhanced cross-section. In Fig. 5, we show the exclusion limit on the effective annihilation cross-section imposed by the MAGIC upper limit on Draco, in the case when the DM particle annihilates in gauge bosons. The band of values reflects the astrophysical uncertainties due to astronomical data and numerical simulations. For comparison, we also show the exclusion plot obtained by the observation of the GC with the HESS telescope. HESS has extensively observed the GCsource, measuring an integrated flux above 160 GeV of Φ (>160 TeV) = 1.87 × 10−11 ph cm−2 s−1 in 2003 and 2004 (Aharonian et al. 2006).
Exclusion plot (MAGIC and HESS GC) and expected sensitivity (CTA and Fermi) for the effective annihilation cross-section, in the case of γ-ray observations of the Draco galaxy and for DM particles annihilating into W+W−. The band represents the astrophysical uncertainty.
In order to compute the Sommerfeld enhancement of the MW halo towards the GC, it is necessary to convolve the information on the rotation curve of our Galaxy with the β-dependence of the effect, and including the presence of the black hole at the centre of the Galaxy. This computation has been done in Pato et al. (2009) and brings enhancements of the order of 103 to 104 for the Lattanzi & Silk models, and of the order of 102 for the Arkani-Hamed model. In Fig. 5, we report the exclusion limit with respect to a constant effective Sommerfeld-enhanced annihilation cross-section. The band of values for each experiment reflects the astrophysical uncertainty due to the inner profile. We have used the spiky NFW profiles obtained by Via Lactea II and a cored isothermal profile with scale radius rs= 5 kpc normalized to the same local value for the DM density as found in Via Lactea II (i.e. ∼ 0.4 GeV cm−3). Since simulations do not include baryons which may play an important role at the GC, the large uncertainty on the inner profile prevents this measurement to put strong limits. As an exercise, we computed the sensitivity to Draco to the space-based telescope Fermi and the future CTA.1 The CTA is a proposed experiment which will make use of Cherenkov telescope technology on a large scale, in order to lower the threshold energy down to ∼50 GeV. The instrument is being designed. The tens of telescopes in the array could either look at different portions of the sky, thus reaching up to ∼ 1 sr of the field of view, or focus on the same source, thus dramatically increasing the single telescope sensitivity. We take a sample sensitivity from the CTA home page, according to which the CTA will be able to detect Φ (>50 GeV) = 7 × 10−12 ph cm−2 s−1 and Φ (>1 TeV) = 2.9 × 10−14 ph cm−2 s−1. Such a sensitivity to a single source could improve if more telescopes could point at the same source. In the case of Fermi, we took the sensitivity to point sources from Baltz et al. (2008), that is to say, Φ (>3 GeV) = 10−10 ph cm−2 s−1. We show the sensitivity bands for Fermi and the CTA in Fig. 5. The uncertainty always derives from astrophysics. Although a boost to the thermal annihilation cross-section is always required to observe Draco (see also Pieri et al. 2009a), the limits will improve significantly with the future data.
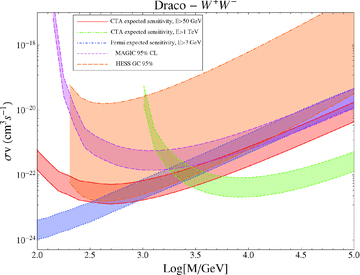
In Fig. 6, we show the same kind of exclusion limits and expected bands of sensitivities as in Fig. 5, yet computed for a DM particle annihilating into e+e− and producing photons as a final state radiation. The limits and sensitivities at high DM masses are in this case poorly restrictive.
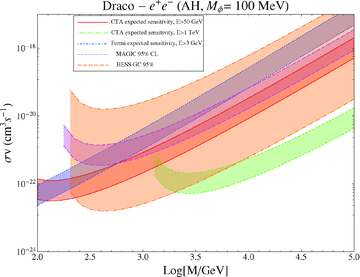
Exclusion plot (MAGIC and HESS GC) and expected sensitivity (CTA and Fermi) for the effective annihilation cross-section, in the case of γ-ray observations of the Draco galaxy and for DM particles annihilating into e+e− in the AH case with MV= 100 MeV. The band represents the astrophysical uncertainty.
Finally, in Fig. 7 we show the sensitivity to Sagittarius with Fermi and the CTA, under the assumption that we have used all throughout the paper, namely that the inner DM halo of Sagittarius is modelled as the one of Draco. We superimpose the effective cross-section as a function of the DM particle mass in the case of a Sommerfeld effect mediated by a 80 GeV boson, for different values of β. For TeV DM masses close to the resonance, with a boost of a factor ∼103, the CTA would be the only instrument able to detect the signal.
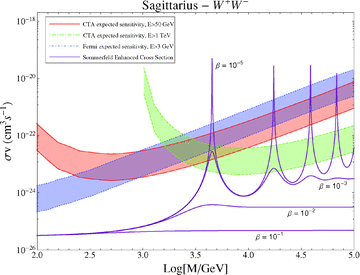
Expected sensitivity for the effective annihilation cross-section, in the case of γ-ray observations of the Sagittarius galaxy and for DM particles annihilating into WW. The band represents the astrophysical uncertainty.
In general, the constraints will depend, among other things, on the final states for annihilation. In the case of the WIMP scenario, the results discussed so far have been obtained considering a DM particle of mass M≃ 4.5 TeV annihilating exclusively into gauge bosons. Considering instead annihilation into heavy quarks or leptons as possible final states changes the predicted fluxes by factors of order unity, thus leaving our conclusions basically unchanged. In particular, a particle that annihilates only to heavy quarks would produce a flux 1.6–1.7 times larger than that shown in the figures, for all experiments. The limits on the Sommerfeld boost would then be proportionally tighter. In the case of a particle annihilating to τ leptons, the change in the flux depends on the energy threshold: for MAGIC, HESS and CTA it is, respectively, 0.5, 0.8 and 3.8 times the flux from the gauge boson channel. Ligther leptonic and quark final states are strongly disfavoured due to the helicity suppression; however, they could become important if the helicity suppression is lifted in some way. In the case of the AH scenario, the final spectrum is instead naturally driven to light leptons (electrons and muons) since heavier states are kinematically forbidden.
4 CONCLUSIONS
The excess in cosmic ray positrons and electrons has motivated a wealth of theoretical efforts in order to be explained in terms of DM. In particular, the annihilation mechanism has been revised in the light of the Sommerfeld enhancement, a velocity-dependent effect. Such an effect is maximal in the dwarf galaxies and in their substructures. The enhancement actually saturates for DM halo masses smaller than the dwarf scale. Several studies (see e.g. Bertone et al. 2009; Cirelli & Panci 2009; Galli et al. 2009; Pato et al. 2009) have recently constrained the Sommerfeld enhancement and thus the interpretation of the PAMELA excess in terms of DM. However, the DM halo of the dwarf galaxies can now be modelled making use of kinematic stellar data with a precision which is far better than the uncertainties on the MW DM profile or on the subhalo population or on the propagation parameters which affect the limits set by antimatter, radio and γ-ray signals. We have computed the expected γ-ray flux from the Draco and the Sagittarius dwarf galaxies, for which upper limits are available from the ACTs. We have computed the flux within the astrophysical uncertainties, and find that the measurements of MAGIC and HESS are able to constrain the enhancement and set an upper limit of ∼104. We have shown that the future CTA experiment should be able to test the boost relative to the thermal annihilation cross-sections up to values of a few hundred.
CTA homepage: http://www.cta-observatory.org/.
We acknowledge useful discussions with Gianfranco Bertone.
REFERENCES



