Estimating and improving dynamic treatment regimes with a time-varying instrumental variable

Chen, Shuxiao; Zhang, Bo

doi:10.1093/jrsssb/qkad011

Abstract

Estimating dynamic treatment regimes (DTRs) from retrospective observational data is challenging as some degree of unmeasured confounding is often expected. In this work, we develop a framework of estimating properly defined ‘optimal’ DTRs with a time-varying instrumental variable (IV) when unmeasured covariates confound the treatment and outcome, rendering the potential outcome distributions only partially identified. We derive a novel Bellman equation under partial identification, use it to define a generic class of estimands (termed IV-optimal DTRs) and study the associated estimation problem. We then extend the IV-optimality framework to tackle the policy improvement problem, delivering IV-improved DTRs that are guaranteed to perform no worse and potentially better than a prespecified baseline DTR. Importantly, this IV-improvement framework opens up the possibility of strictly improving upon DTRs that are optimal under the no unmeasured confounding assumption (NUCA). We demonstrate via extensive simulations the superior performance of IV-optimal and IV-improved DTRs over the DTRs that are optimal only under the NUCA. In a real data example, we embed retrospective observational registry data into a natural, two-stage experiment with noncompliance using a differential-distance-based, time-varying IV and estimate useful IV-optimal DTRs that assign mothers to a high-level or low-level neonatal intensive care unit based on their prognostic variables.

causal inference, dynamic treatment regime, instrumental variable, offline reinforcement learning, partial identification

1 Introduction

1.1 Dynamic treatment regime and instrumental variable

Estimating single-stage individualized treatment rules (ITRs) and the more general multiple-stage dynamic treatment regimes (DTRs) has attracted a lot of interest from diverse disciplines. Many estimation strategies have been proposed in the literature for data derived from randomized controlled trials or observational databases. Two main strands of work are Q-learning based on positing regression models for the outcome of interest at each stage based on study participants’ information and A-learning based on modelling the contrasts among treatments. Both methods can further be combined with classification tools to yield more robust and interpretable decision rules. Important examples of these methodologies include Murphy et al. (2001), Murphy (2003), Robins (2004), Chakraborty et al. (2010), Rubin and van der Laan (2012), Zhao et al. (2012), Zhao et al. (2015), Laber and Zhao (2015), Zhou et al. (2017), Tao et al. (2018), Zhang et al. (2018), Zhang and Zhang (2018), and Athey and Wager (2020), among many others. For a more comprehensive review of various methods, see, e.g., Moodie et al. (2007), Chakraborty and Murphy (2014), and Schulte et al. (2014).

Estimating optimal policies (ITRs or DTRs) can be challenging when data comes from observational databases (e.g., Medicare and Medicaid claims database, disease registry, etc) where some degree of unmeasured confounding is always expected. In these scenarios, an instrumental variable (IV) is a useful tool to infer the treatment effect (Angrist et al., 1996). An instrumental variable is valid if it is associated with the treatment (IV relevance), affects the outcome only through its association with the treatment (exclusion restriction) and is independent of the unobserved treatment-outcome confounding variables, possibly conditional on a rich set of observed covariates (IV unconfoundedness). We will rigorously define these IV identification assumptions in Section 2.

One subtlety in IV-based analyses is that even a valid IV cannot always identify the mean potential outcomes; rather, a valid IV along with appropriate, application-specific identification assumptions places certain restrictions on the potential outcome distributions, and this line of research is known as partial identification of probability distributions (Manski, 2003). This subtlety is inherited by the policy estimation problem using an IV. In particular, when the conditional average treatment effect (CATE) is not point identified from data, the optimal policy that maximizes the value function cannot be identified either, necessitating researchers to target alternative optimality criteria. While such criteria have been proposed in the single-stage setting from different perspectives (Cui & Tchetgen Tchetgen, 2020, 2021; Pu & Zhang, 2021), literature on the more general, multiple-stage setting is scarce.

Our first contribution in this article is to generalize the optimality criteria in the single-stage setting and develop a framework that is tailored to general sequential decision-making problems and incorporates rich information contained in a time-varying IV. This optimality criterion, termed IV-optimality, is based on a carefully weighted version of the partially identified Q-function and value function subject to the distributional constraints imposed by the IV. This criterion is distinct from the framework of Han (2019) that endows the collection of partially identified DTRs with a partial order and characterizes the set of maximal elements (see Zhang et al., 2020 for similar ideas). It is also distinct from Liao et al. (2021) that models the transition dynamics and assumes that the unmeasured treatment-outcome confounder is additive and not an effect modifier itself at any stage, or Shi et al. (2022) that utilizes Pearl’s (2009) ‘front-door criterion’ to aid point identification of optimal DTR in the presence of unmeasured treatment-outcome confounding. In the current work, we do not impose, a priori, assumptions that induce point identification. Importantly, our proposed set of optimality criteria collapse to that targeted by Liao et al. (2021) if the time-varying IV point identifies the treatment effect under an additional ‘additive unmeasured confounding’ assumption studied in Liao et al. (2021) and more general point-identification assumptions proposed and reviewed in Frangakis and Rubin (1999), Hernán and Robins (2006), Wang and Tchetgen Tchetgen (2018), and Swanson et al. (2018, Section 5). We take a hybrid approach of Q-learning (Schulte et al., 2014; Watkins & Dayan, 1992) and weighted classification (Zhang et al., 2012; Zhao et al., 2012) to target this optimality criterion and establish nonasymptotic rate of convergence of the proposed estimators.

The IV-optimality framework also motivates a conceptually simple yet informative variant framework that allows researchers to leverage a time-varying IV to improve upon a baseline DTR. The policy improvement problem was first considered in a series of papers by Kallus et al. (2019) and Kallus and Zhou (2020a, 2020b) under a ‘Rosenbaum-bounds-type’ sensitivity analysis model (Rosenbaum, 2002b). Despite its novelty and usefulness in a range of application scenarios, a sensitivity-analysis-based policy improvement framework does have a few limitations. In particular, each improved policy is indexed by a sensitivity parameter Γ that controls the degree of unmeasured confounding. Since the sensitivity parameter is not identified from the observed data, it is often unclear which improved policy best serves the purpose. Moreover, ‘Rosenbaum-bounds-type’ sensitivity analysis model does not fully take into account unmeasured confounding heterogeneity (Bonvini & Kennedy, 2021; Heng & Small, 2020). On the contrary, an IV-based policy improvement framework outputs data-driven partial identification intervals that are not indexed by sensitivity parameters. Additional information contained in the IV also opens up the possibility of strictly improving upon a policy that is optimal under the no unmeasured confounding assumption (NUCA) (Robins, 1992; Rosenbaum & Rubin, 1983), when the NUCA is in fact violated.

Our proposed method has two important applications. First, it is applicable when empirical researchers want to estimate useful DTRs from noisy observational data and have access to a time-varying IV at each stage, e.g., daily precipitation, differential distance, etc. Second, the framework described here is central to many sequential multiple assignment randomized trial (SMART) designs (Murphy, 2005) where interest lies in comparing adaptive interventions, and patients assigned to a particular treatment at each stage may not adhere to it. Noncompliance makes the treatment assigned at every stage a valid time-varying IV, and our proposed method provides a principled way to account for systematic noncompliance in SMART designs.

The rest of the article is organized as follows. We describe a real data application in Section 1.2. Section 2 reviews optimality criteria in the single-stage setting and provides a general IV-optimality framework that is amenable to being extended to the multiple-stage setting. Section 3 considers improving upon a baseline ITR with an IV. Building upon Sections 2 and 3, we describe an IV-optimality framework for policy estimation in the multiple-stage setting and extend this framework to tackle the policy improvement problem in Section 4. Section 5 studies the theoretical properties of the proposed methods. We report simulation results in Section 6 and revisit the application in Section 7. Section 8 concludes with a brief discussion. For brevity, all proofs are deferred to the Online Supplemental Materials S2 and S3.

1.2 Application: a natural, two-stage experiment derived from registry data

Lorch et al. (2012) conducted a retrospective cohort study to investigate the effect of delivery hospital on premature babies (gestational age between 23 and 37 weeks) and found a significant benefit to neonatal outcomes when premature babies were delivered at hospitals with high-level neonatal intensive care units (NICUs) compared to those without high-level NICUs. Lorch et al. (2012) used the differential travel time to the nearest high-level versus low-level NICU as an IV so that the outcome analysis is less confounded by mothers’ self-selection into hospitals with high-level NICUs. In their original study design, Lorch et al. (2012) further controlled for mothers’ neighbourhood characteristics, as well as their demographic information and variables related to delivery, in their matching-based study design so that the differential travel time was more likely to be a valid IV conditional on these variables. Put another way, the differential travel time created a natural experiment with noncompliance: Similar mothers who lived relatively close to a hospital with high-level NICUs were encouraged (but not forced) to deliver at a high-level NICU. More recently, Michael et al. (2020) considered mothers who delivered exactly two babies from 1996 to 2005 in Pennsylvania and investigated the cumulative effect of delivering at a high-level NICU on neonatal survival probability using the same differential travel time IV.

Currently, there is still limited capacity at high-level NICUs, so it is not practical to direct all mothers to these high-technology, high-volume hospitals. Understanding which mothers would most significantly benefit from delivering at a high-level NICU helps design optimal perinatal regionalization systems that designate hospitals by the scope of perinatal service provided and designate where infants are born or transferred according to the level of care they need at birth (Kroelinger et al., 2018; Lasswell et al., 2010). Indeed, previous studies seemed to suggest that although high-level NICUs significantly reduced deaths for babies of small gestational age, they made little difference for almost mature babies like 37 weeks (Yang et al., 2014).

Mothers who happened to relocate during two consecutive deliveries of babies constitute a natural two-stage, two-arm randomized controlled trial with noncompliance and present a unique opportunity to investigate an optimal DTR. See Figure 1 for the directed acyclic graph (DAG) illustrating this application. We will revisit the application after developing a methodology precisely suited for this purpose.

Figure 1.

A DAG illustrating the NICU application. Observed baseline covariates like mothers’ demographics, neighbourhood characteristics, etc., are omitted for clearer presentation.

Open in new tab Download slide

2 Estimating individualized treatment rules with an instrumental variable

2.1 Optimal and NUCA-optimal ITRs

We first define the estimand of interest, an optimal ITR, under the potential outcome framework (Neyman, 1923; Rubin, 1974) and briefly review how to estimate the optimal ITR under the NUCA.

Consider a single-stage decision problem where one observes the covariates $X = x \in X \subseteq R^{d}$ ⁠, takes a binary action $A = a \in {\pm 1}$ and receives the response $Y (a) \in Y \subseteq R$ ⁠. Here, $Y (a)$ denotes the potential outcome under action a. This decision-making process is formalized by an individualized treatment rule (or a single-stage policy), which is a map π from prognostic variables $x$ to a treatment decision $a = π (x)$ ⁠. Denote by $p_{a}^{*} (\cdot | x)$ the conditional law of $Y (a)$ given the realization of $X = x$ ⁠. The quality of π is quantified by its value:

V^{π} = E [Y (π (X))] = E_{X} E_{Y \sim p_{π (X)}^{*} (\cdot | X)} [Y],

(1)

where the outer expectation is taken with respect to the law of $X$ and the inner expectation the potential outcome distribution $p_{a}^{*} (\cdot | X)$ with action a set to $π (X)$ ⁠. Intuitively, $V^{π}$ measures the expected value of the response if the population were to follow π. Let $V^{*} = max_{π \in Π} V^{π}$ denote the maximal value of an ITR when restricted to a policy class Π. An ITR is said to be optimal with respect to Π if it achieves $V^{*}$ ⁠.

A well-known result of Zhang et al. (2012) (see also Zhao et al., 2012) asserts the duality between value maximization and risk minimization, in the sense that any optimal ITR that maximizes the value $V^{π}$ also minimizes the following risk (and vice versa):

R^{π} = E_{X} [| C^{*} (X) | \cdot 1 {π (X) \neq sgn (C^{*} (X))}],

(2)

where $C^{*} (x) = E_{Y \sim p_{+ 1}^{*} (\cdot | x)} [Y] - E_{Y \sim p_{- 1}^{*} (\cdot | x)} [Y]$ is the CATE. It is not hard to show that the sign of the CATE, $sgn (C^{*} (x))$ ⁠, is the Bayes ITR (i.e., the optimal ITR when Π consists of all Boolean functions), and therefore the risk $R^{π}$ admits a natural interpretation as a weighted misclassification error.

Suppose we have a dataset consisting of independent and identically distributed (i.i.d.) samples from the law of the triplet $(X^{o b s}, A^{o b s}, Y^{o b s})$ ⁠. In parallel to the potential outcome distribution $p_{a}^{*} (\cdot | x)$ ⁠, let $p_{a}^{o b s} (\cdot | x)$ denote the conditional law of ${Y^{o b s} | A^{o b s} = a, X^{o b s} = x}$ ⁠. One can then define counterparts of the value and the risk as in (1) and (2), but with $p_{a}^{*} (\cdot | x)$ replaced by $p_{a}^{o b s} (\cdot | x)$ ⁠. We define

R^{o b s, π} = E_{X} [| C^{o b s} (X) | \cdot 1 {π (X) \neq sgn (C^{o b s} (X))}],

(3)

where $C^{o b s} (x) = E_{Y \sim p_{+ 1}^{o b s} (\cdot | x)} [Y] - E_{Y \sim p_{- 1}^{o b s} (\cdot | x)} [Y]$ ⁠. The distribution $p_{a}^{o b s} (\cdot | x)$ and hence $R^{o b s, π}$ are always identified from the observed data, thus rendering it feasible to minimize $R^{o b s, π}$ using the observed data. Under a version of the no unmeasured confounding assumption, the two distributions $p_{a}^{*} (\cdot | X)$ and $p_{a}^{o b s} (\cdot | X)$ agree, and hence a minimizer of $R^{o b s, π}$ also minimizes $R^{π}$ and is an optimal ITR. To make the distinction clear, we refer to any minimizer of $R^{o b s, π}$ as a NUCA-optimal ITR (i.e., only optimal in the conventional sense under the NUCA) and denote it as $π_{N U C A}$ ⁠.

2.2 Instrumental variables and IV-optimal ITRs

The NUCA is often a heroic assumption for observational data. In the classical causal inference literature, an instrumental variable is a widely used tool to infer the causal effect from noisy observational data (Angrist et al., 1996; Hernán & Robins, 2006; Imbens, 2004; Rosenbaum, 2002a). Let $Z_{i} \in {- 1, 1}$ denote a binary IV of unit i, $A_{i} (Z_{i})$ the potential treatment received under IV assignment $Z_{i}$ ⁠, and $Y_{i} (A_{i} (Z_{i}), Z_{i})$ the potential outcome under IV assignment $Z_{i}$ and treatment $A_{i}$ ⁠. This definition implicitly assumes the Stable Unit Treatment Value Assumption, which states that a unit’s potential treatment status depends on its own IV assignment, the potential outcome status depends on its own IV and treatment assignments, and there are not multiple versions of the same IV or treatment. Other core IV assumptions include IV relevance: $P (A = 1 ∣ Z = 1, X) > P (A = 1 ∣ Z = - 1, X)$ ⁠, exclusion restriction: $Y_{i} (z, a) = Y_{i} (a)$ for all $z, a$ and i, and IV unconfoundedness (possibly conditional on $X$ ⁠): $Z ⨿ A (z), Y (z, a) ∣ X$ for $z = \pm 1$ and $a = \pm 1$ ⁠. A variable Z is said to be a valid IV if it satisfies these core IV assumptions (Angrist et al., 1996; Baiocchi et al., 2014). There are many versions of core IV assumptions; in particular, the IV unconfoundedness assumption may be relaxed and replaced by (marginal, partial joint, or full joint) exchangeability assumptions (Swanson et al., 2018, Section 2). A valid IV satisfying core IV assumptions cannot point identify the mean conditional potential outcomes $E [Y (\pm 1) | X = x]$ or CATE $C^{*} (x)$ (Manski, 2003; Robins & Greenland, 1996; Swanson et al., 2018); hence, neither the value nor the risk of an ITR is point identified even with a valid IV.

Although a valid IV may not point identify the causal effects, it may still be useful because even under minimal identification assumptions, a valid IV can yield meaningful partial identification intervals or bounds for the CATE. That is, one can construct two functions $L (x)$ and $U (x)$ ⁠, both of which are functionals of the observed data distribution (and thus estimable from the data), such that the CATE satisfies $C^{*} (x) \in [L (x), U (x)]$ almost surely. Important examples include the natural bounds (Manski, 1990; Robins, 1989), Balke-Pearl bounds (Balke & Pearl, 1997), and Manski-Pepper bounds (Manski & Pepper, 2000). More recently, Finkelstein and Shpitser (2020) and Duarte et al. (2021) further developed optimization-based algorithms that output sharp partial identification bounds for IV models with observed covariates.

Given the partial identification interval $[L (x), U (x)]$ ⁠, the risk of an ITR π defined in (2) is bounded between

{\underline{R}}^{π} = E_{X} [inf_{C (X) \in [L (X), U (X)]} | C (X) | \cdot 1 {π (X) \neq sgn (C (X))}]

and

{\bar{R}}^{π} = E_{X} [sup_{C (X) \in [L (X), U (X)]} | C (X) | \cdot 1 {π (X) \neq sgn (C (X))}] .

(4)

Pu and Zhang (2021) argued that a sensible criterion is to minimize the expected worst-case risk ${\bar{R}}^{π}$ ⁠, and the resulting minimizer is termed an IV-optimal ITR, as this ITR is ‘worst-case risk-optimal’ with respect to the partial identification interval induced by an IV and its associated identification assumptions; see also (Ben-Michael et al., 2021). Note that an IV-optimal ITR is not an optimal ITR without further assumptions.

Cui and Tchetgen Tchetgen (2021) proposed an alternative set of optimality criteria from the perspective of the partially identified value function. Instead of constructing two functions $L (x), U (x)$ that bound the CATE, one may alternatively construct functions $\underline{Q} (x, a)$ ⁠, $\bar{Q} (x, a)$ that sandwich the conditional mean potential outcome $E [Y (a) | X = x]$ ⁠, and the value defined in (1) satisfies $E [\underline{Q} (X, π (X))] \leq V^{π} \leq E [\bar{Q} (X, π (X))]$ ⁠. Cui and Tchetgen Tchetgen (2021) advocated maximizing some carefully chosen middle ground between the lower and upper bounds of the value:

V_{λ}^{π} = E_{X} [λ (X, π (X)) \cdot \underline{Q} (X, π (X)) + [1 - λ (X, π (X))] \cdot \bar{Q} (X, π (X))],

(5)

where $λ (x, a)$ is a prespecified function that captures a second-level individualism, i.e., how optimistic/pessimistic individuals with covariates $X = x$ are.

Cui and Tchetgen Tchetgen (2021) pointed out that minimizing the maximum risk ${\bar{R}}^{π}$ is not equivalent to maximizing the minimum value $V_{λ = 0}^{π}$ ⁠, even when the bounds of the CATE are obtained via bounds on the Q-functions, i.e., $L (x) = \bar{Q} (x, + 1) - \underline{Q} (x, - 1)$ and $U (x) = \underline{Q} (x, + 1) - \bar{Q} (x, - 1)$ ⁠. Rather, minimizing ${\bar{R}}^{π}$ is equivalent to maximizing the midpoint of the minimum and maximum values, namely $V_{λ = 1 / 2}^{π}$ ⁠.

2.3 A general IV-optimality framework

Conceptually, a valid IV and the associated identification assumptions impose distributional constraints on potential outcome distributions $p_{a}^{*} (\cdot | x)$ ⁠. Under assumptions in Cui and Tchetgen Tchetgen (2020) and Qiu et al. (2020), $p_{a}^{*} (\cdot | x)$ can be expressed as functionals of the observed data distribution. Alternatively, if weaker assumptions are imposed and preclude point identification, the partial identification results assert that $p_{a}^{*} (\cdot | x)$ is ‘weakly bounded’ in the sense that for a sufficiently regular function f, we can find two functions $\underline{Q} (x, a; f)$ and $\bar{Q} (x, a; f)$ such that

\underline{Q} (x, a; f) \leq \int f (y) p_{a}^{*} (d y | x) \leq \bar{Q} (x, a; f) .

(6)

If f is the identity function, then the above display is precisely the partial identification intervals of the mean conditional potential outcome $E [Y (a) | X = x]$ in (5). In both cases, a valid IV with identification assumptions specifies a collection of distributions $P_{x, a}$ such that $p_{a}^{*} (\cdot | x) \in P_{x, a}$ ⁠. In the point-identification case, the set $P_{x, a}$ is a singleton consisting only of the ground truth potential outcome distribution $p_{a}^{*} (\cdot | x)$ ⁠; in the partial identification case, $P_{x, a}$ consists of all distributions that are weakly bounded in the sense of (6). In other words, $P_{x, a}$ is the collection of all possible potential outcome distributions $p_{a}^{*} (\cdot | x)$ that are compatible with the putative IV and associated IV identification assumptions, and we refer to it as an IV-constrained set. We may further equip an IV-constrained set $P_{x, a}$ with a prior distribution $P_{x, a}$ ⁠. Here, $P_{x, a}$ is a probability distribution on $P_{x, a}$ ⁠, the latter of which is itself a collection of probability distributions. To have a fully rigorous treatment, we equip $P_{x, a}$ with a metric (e.g., Wasserstein metric) and work with the induced Borel sigma algebra (Parthasarathy, 2005).

Given the prior distributions ${P_{x, a} : x \in X, a = \pm 1}$ ⁠, we can define the IV-constrained value of a policy π as

V_{P}^{π} = E_{X} E_{p_{π (X)} \sim P_{X, π (X)}} E_{Y \sim p_{π (X)}} [Y],

(7)

where we write $p_{π (x)} = p_{π (x)} (\cdot | x)$ for notational simplicity. From now on, we will refer to the collection of criteria given by maximizing $V_{P}^{π}$ as IV-optimality. An ITR is said to be IV-optimal with respect to the prior distributions ${P_{x, a} : x \in X, a = \pm 1}$ and a policy class Π if it maximizes $V_{P}^{π}$ among all $π \in Π$ ⁠. The flow chart in Figure 2 summarizes this conceptual framework.

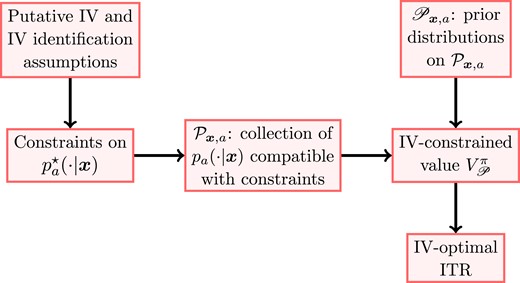
A schematic plot of IV-optimality. Prior distributions {Px,a:x∈Rd,a=±1} imposed on the IV-constrained sets {Px,a:x∈Rd,a=±1} give rise to the IV-constrained value VPπ. An IV-optimal ITR maximizes VPπ over a policy class Π.

Figure 2.

A schematic plot of IV-optimality. Prior distributions ${P_{x, a} : x \in R^{d}, a = \pm 1}$ imposed on the IV-constrained sets ${P_{x, a} : x \in R^{d}, a = \pm 1}$ give rise to the IV-constrained value $V_{P}^{π}$ ⁠. An IV-optimal ITR maximizes $V_{P}^{π}$ over a policy class Π.

Open in new tab Download slide

The formulation in (5) can be recovered by carefully choosing the prior distributions. In particular, let ${\underline{p}}_{a} (\cdot | x)$ and ${\bar{p}}_{a} (\cdot | x)$ be distributions that witness the partial identification bounds $\underline{Q} (x, a)$ and $\bar{Q} (x, a)$ ⁠, respectively:

\underline{Q} (x, a) = \int y {\underline{p}}_{a} (d y | x), \underline{Q} (x, a) = \int y {\bar{p}}_{a} (d y | x) .

(8)

Then, criterion (5) is recovered by considering the following two-point priors:

P_{x, a}^{t w o - p o i n t} = λ (x, a) \cdot δ_{{\underline{p}}_{a} (\cdot | x)} + [1 - λ (x, a)] \cdot δ_{{\bar{p}}_{a} (\cdot | x)},

where $δ_{p}$ is a point mass at p. As discussed near the end of Section 2.2, setting $λ (x, a)$ uniformly equal to $1 / 2$ recovers the original IV-optimality criterion considered in Pu and Zhang (2021) that minimizes the worst-case risk (4). In fact, under certain regularity conditions, one can show that the reverse is also true: the formulation (7) for a specified collection prior distributions can also be recovered from (5) by a careful choice of λ. In view of such an equivalence, criterion (7) should not be regarded as a generalization of (5). Rather, it is a convenient tool amenable to being generalized to the multiple-stage setting. A proof of this equivalence statement will appear in Section 4.

3 Improving individualized treatment rules with an instrumental variable

Compared to estimating an optimal ITR, a less ambitious goal is to improve upon a baseline ITR $π^{b}$ ⁠, so that the improved ITR is no worse and potentially better than $π^{b}$ ⁠. In this section, we show how to achieve this goal with an IV in the single-stage setup.

The goal of ‘never being worse’ is reminiscent of the min-max risk criterion in (4), and it is natural to consider minimizing the maximum excess risk with respect to the baseline ITR $π^{b}$ ⁠, subject to the IV-informed partial identification constraints. Definition 1 summarizes this strategy.

Risk-based IV-improved ITR

Definition 1

Let $π^{b}$ denote a baseline ITR, Π a policy class, and $[L (x), U (x)]$ an IV-informed partial identification interval of the CATE $C^{*} (x)$ ⁠. A risk-based IV-improved ITR is any solution to the optimization problem below:

min_{π \in Π} E_{X} [sup_{C (X) \in [L (X), U (X)]} | C (X) | \cdot (1 {π (X) \neq sgn (C (X))} - 1 {π^{b} (X) \neq sgn (C (X))})] .

(9)

When Π consists of all Boolean functions, (9) admits the following explicit solution.

Formula for risk-based IV-improved ITR

Proposition 1

Define

π^{R} (x) = 1 {L (x) > 0} - 1 {U (x) < 0} + 1 {L (x) \leq 0 \leq U (x)} \cdot π^{b} (x) .

(10)

Then, $π^{R}$ is a risk-based IV-improved ITR when Π consists of all Boolean functions.

The ITR in (10) admits an intuitive explanation: it takes action $+ 1$ when the partial identification interval is positive (i.e., $0 < L (x) \leq U (x)$ ⁠), takes action $- 1$ when the interval is negative (i.e., $L (x) \leq U (x) < 0$ ⁠), and otherwise follows the baseline ITR $π^{b}$ ⁠.

A second criterion closely related to that in Definition 1 maximizes the minimum excess value with respect to $π^{b}$ ⁠, subject to the distributional constraints imposed by the putative IV and its associated identification assumptions.

Value-based IV-improved ITR

Definition 2

Let $π^{b}$ denote a baseline ITR, Π a policy class, and ${P_{x, a} : x \in R^{d}, a \pm 1}$ a collection of IV-constrained sets. A value-based IV-improved ITR is any solution to the following optimization problem:

max_{π \in Π} E_{X} [inf_{\begin{matrix} p_{π (X)} \in P_{X, π (X)} \\ p_{π^{b} (X)} \in P_{X, π^{b} (X)} \end{matrix}} {E_{\begin{matrix} Y \sim p_{π (X)}, Y^{'} \sim p_{π^{b} (X)} \end{matrix}} [Y - Y^{'}]}] .

(11)

The above formulation is referred to as distributionally robust optimization in the optimization literature (Delage & Ye, 2010). When the IV-constrained sets are derived from partial identification intervals $[\underline{Q} (x, a), \bar{Q} (x, a)]$ and Π consists of all Boolean functions, the optimization problem (11) admits the explicit solution below, analogous to the one given in Proposition 1.

Formula for value-based IV-improved ITR

Proposition 2

Assume ${\underline{p}}_{a} (\cdot | x)$ and ${\bar{p}}_{a} (\cdot | x)$ ⁠, the two distributions defined in (8) that witness the partial identification bounds $\underline{Q} (x, a)$ ⁠, $\bar{Q} (x, a)$ ⁠, are both inside $P_{x, a}$ ⁠. Define

π^{V} (x) = 1 {L^{V} (x) > 0} - 1 {U^{V} (x) < 0} + 1 {L^{V} (x) \leq 0 \leq U^{V} (x)} \cdot π^{b} (x),

(12)

where $L^{V} (x) = \underline{Q} (x, + 1) - \bar{Q} (x, - 1)$ and $U^{V} (x) = \bar{Q} (x, + 1) - \underline{Q} (x, - 1)$ ⁠. Then, $π^{V}$ is a value-based IV-improved policy when Π consists of all Boolean functions.

Propositions 1 and 2 together reveal an interesting duality between worst-case excess risk minimization and worst-case excess value maximization. When the partial identification interval for the CATE is derived directly from the partial identification intervals for the mean conditional potential outcomes, so that $L^{V} = L$ and $U^{V} = U$ ⁠, then the two ITRs defined in (10) and (12) agree, and they simultaneously satisfy the two IV-improvement criteria presented in Definitions 1 and 2. Hence, we will not distinguish between two types of IV-improved ITRs henceforth.

Recall that a similar duality exists in the classical policy estimation problem under the NUCA, but disappears when extended to the partial identification settings. It is thus curious to see such a duality restored in the policy improvement problem.

4 Estimating dynamic treatment regimes with an instrumental variable

4.1 Optimal and SRA-optimal DTRs

We now consider a general K-stage decision-making problem (Murphy, 2003; Schulte et al., 2014). At the first stage $k = 1$ ⁠, we are given baseline covariates $X_{1} = x_{1} \in X$ ⁠, make a decision $a_{1} = π_{1} (x_{1})$ ⁠, and observe a reward $R_{1} (a_{1}) = r_{1}$ ⁠. At stage $k = 2, \dots, K$ ⁠, let ${\vec{a}}_{k - 1} = (a_{1}, \dots, a_{k - 1})$ denote treatment decisions from stage 1 up to $k - 1$ ⁠, and ${\vec{R}}_{k - 1} ({\vec{a}}_{k - 1}) = (R_{1} (a_{1}), R_{2} ({\vec{a}}_{2}), \dots, R_{k - 1} ({\vec{a}}_{k - 1}))$ the rewards from stage 1 to $k - 1$ ⁠. Meanwhile, denote by $X_{k} ({\vec{a}}_{k - 1})$ new covariate information (e.g., time-varying covariates, auxiliary outcomes, etc.) that would arise after stage $k - 1$ but before stage k had the participant followed the treatment decisions ${\vec{a}}_{k - 1}$ ⁠, and ${\vec{X}}_{k} ({\vec{a}}_{k - 1}) = (X_{1}, X_{2} (a_{1}), \dots, X_{k} ({\vec{a}}_{k - 1}))$ the entire covariate history up to stage k. Given ${\vec{R}}_{r - 1} = {\vec{r}}_{k - 1}, {\vec{X}}_{k} = {\vec{x}}_{k}$ ⁠, a data-driven decision $a_{k} = π_{k} ({\vec{a}}_{k - 1}, {\vec{r}}_{k - 1}, {\vec{x}}_{k})$ is then made and we observe reward $R_{k} ({\vec{a}}_{k}) = r_{k}$ ⁠. Our goal is to estimate a DTR $π = {π_{k}}_{k = 1}^{K}$ ⁠, such that the expected value of cumulative rewards $\sum_{k = 1}^{K} r_{k}$ is maximized if the population were to follow π.

To simplify the notations, the historical information available for making the decision at stage k is denoted by ${\vec{H}}_{1} = X_{1}$ for $k = 1$ and ${\vec{H}}_{k} = ({\vec{a}}_{k - 1}, {\vec{R}}_{k - 1} ({\vec{a}}_{k - 1}), {\vec{X}}_{k} ({\vec{a}}_{k - 1}))$ for any $2 \leq k \leq K .$ The information ${\vec{H}}_{k}$ consists of ${\vec{H}}_{k - 1}$ and $H_{k}$ ⁠: ${\vec{H}}_{k - 1}$ is the information available at the previous stage and $H_{k} = (a_{k - 1}, R_{k - 1} ({\vec{a}}_{k - 1}), X_{k} ({\vec{a}}_{k - 1}))$ is the new information generated after decision $a_{k - 1}$ is made. Let $p_{a_{K}}^{*} (\cdot | {\vec{h}}_{K})$ be the conditional law of $R ({\vec{a}}_{K})$ given a specific realization of the historical information ${\vec{H}}_{K} = {\vec{h}}_{k}$ ⁠. We define the following action-value function (or Q-function) at stage K:

Q_{K} ({\vec{h}}_{K}, a_{K}) = E [R_{K} ({\vec{a}}_{K}) ∣ {\vec{H}}_{K} = {\vec{h}}_{k}] = E_{R_{K} \sim p_{a_{K}}^{*} (\cdot | {\vec{h}}_{K})} [R_{K}],

(13)

where we emphasize again that the expectation is taken over the potential outcome distribution $p_{a_{K}}^{*} (\cdot | {\vec{h}}_{K})$ ⁠. For a policy π, its value function at stage K is then defined as

V_{K}^{π} ({\vec{h}}_{K}) = Q_{K} ({\vec{h}}_{K}, π_{K} ({\vec{h}}_{K})),

and depends on π only through $π_{K}$ ⁠.

Next, we define Q-functions and value functions at a generic stage $k \in [K]$ recursively (denote $[K] = {1, \dots, K}$ ⁠). In particular, for $k = K - 1, \dots, 1$ ⁠, we let $p_{a_{k}}^{*} (\cdot, \cdot | {\vec{h}}_{k})$ denote the joint law of the reward $R_{k} ({\vec{a}}_{k})$ and new covariate information $X_{k + 1} ({\vec{a}}_{k})$ observed immediately after decision $a_{k}$ has been made conditional on ${\vec{H}}_{k} = {\vec{h}}_{k}$ ⁠. The Q-function of π at stage k is then defined as:

\begin{aligned} Q_{k}^{π} ({\vec{h}}_{k}, a_{k}) & = E [R_{k} ({\vec{a}}_{k}) + V_{k + 1}^{π} ({\vec{H}}_{k + 1}) ∣ {\vec{H}}_{k} = {\vec{h}}_{k}] \\ = E_{(R_{k}, X_{k + 1}) \sim p_{a_{k}}^{*} (\cdot, \cdot | {\vec{h}}_{k})} [R_{k} + V_{k + 1}^{π} ({\vec{H}}_{k + 1})], \end{aligned}

(14)

where ${\vec{H}}_{k + 1} = ({\vec{h}}_{k}, a_{k}, R_{k}, X_{k + 1})$ is a function of $R_{k}$ and $X_{k + 1}$ ⁠. The corresponding value function of π is taken to be $V_{k}^{π} ({\vec{h}}_{k}) = Q_{k}^{π} ({\vec{h}}_{k}, π_{k} ({\vec{h}}_{k})) .$ Similar to (13), the expectation is taken over the potential outcome distribution $p_{a_{k}}^{*} (\cdot, \cdot | {\vec{h}}_{k})$ ⁠. We interpret the Q-function $Q_{k}^{π} ({\vec{h}}_{k}, a_{k})$ as the cumulative rewards collected by executing $a_{k}$ at stage k and follow π from stage $k + 1$ and onwards, and the value function $V_{k}^{π} ({\vec{h}}_{k})$ the cumulative rewards collected by executing π from stage k and onwards. Therefore, $Q_{k}^{π}$ depends on π only via $π_{(k + 1) : K} = (π_{k + 1}, \dots, π_{K})$ and $V_{k}^{π}$ depends on π only via $π_{k : K} = (π_{k}, \dots, π_{K})$ ⁠. For notational simplicity, we interpret quantities whose subscripts do not make sense (e.g., $a_{0}, r_{0}$ ⁠, and $x_{K + 1}$ ⁠) as ‘null’ quantities and their occurrences in mathematical expressions will be disregarded.

With a slight abuse of notation, we let $Π = Π_{1} \times \dots Π_{K}$ be a policy class. A DTR is said to be optimal with respect to Π if it maximizes $V_{1}^{π} (x_{1})$ for all fixed $x_{1}$ (and hence $E [V_{1}^{π} (X_{1})]$ for an arbitrary covariate distribution) over the policy class Π.

Assume for now that Π consists of all DTRs (i.e., each $Π_{k}$ consists of all Boolean functions). A celebrated result from the control theory states that the dynamic programming approach below, also known as backward induction, yields an optimal DTR $π^{*}$ (Murphy, 2003; Sutton & Barto, 2018):

π_{K}^{*} ({\vec{h}}_{K}) = \underset{a_{K} \in {\pm 1}}{argmax} Q_{K} ({\vec{h}}_{K}, a_{K}), π_{k}^{*} ({\vec{h}}_{k}) = \underset{a_{k} \in {\pm 1}}{argmax} Q_{k}^{π^{*}} ({\vec{h}}_{k}, a_{k}), k = K - 1, \dots, 1.

(15)

In other words, $π^{*}$ satisfies $V_{k}^{π^{*}} ({\vec{h}}_{k}) = max_{π} V_{k}^{π} ({\vec{h}}_{k})$ for any $k \in [K]$ and historical information ${\vec{h}}_{k}$ ⁠, and is well defined as $Q_{k}^{π^{*}}$ depends on $π^{*}$ only through $π_{(k + 1) : K}^{*}$ ⁠.

The foregoing discussion is based on the potential outcome distributions. Suppose that we have collected i.i.d. data from the law of the random trajectory $(X_{k}^{o b s}, A_{k}^{o b s}, R_{k}^{o b s})_{k = 1}^{K}$ ⁠. Let ${p_{a_{k}}^{o b s} (\cdot, \cdot | {\vec{h}}_{k})}_{k = 1}^{K - 1}$ be the conditional laws of the observed rewards and new covariate information identified from the observed data:

\begin{aligned} (R_{K}^{o b s} ∣ {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}, A_{K}^{o b s} = a_{K}) \sim p_{a_{K}}^{o b s} (\cdot | {\vec{h}}_{K}), \\ (R_{k}^{o b s}, X_{k + 1}^{o b s} ∣ {\vec{H}}_{k}^{o b s} = {\vec{h}}_{k}, A_{k}^{o b s} = a_{k}) \sim p_{a_{k}}^{o b s} (\cdot, \cdot | {\vec{h}}_{k}), k = K - 1, \dots, 1. \end{aligned}

Here, ${\vec{H}}_{k}^{o b s}$ denotes the observed historical information up to stage k. Suppose that we obtain a DTR using the dynamic programming approach described in (15) with $p_{a_{k}}^{o b s}$ in place of $p_{a_{k}}^{*}$ ⁠. Under a version of the sequential randomization assumptions (Robins, 1998) and with additional assumptions of consistency and positivity, we have $p_{a_{k}}^{*} = p_{a_{k}}^{o b s},$ from which it follows that the DTR is optimal (Murphy, 2003; Schulte et al., 2014). We will refer to this policy as an SRA-optimal DTR and denote it as $π_{_{SRA}}$ ⁠.

4.2 Identification with a time-varying instrumental variable

Suppose that, in addition to $(X_{k}^{o b s}, A_{k}^{o b s}, R_{k}^{o b s})_{k = 1}^{K}$ ⁠, we also observe a binary, time-varying instrumental variable ${Z_{k}}_{k = 1}^{K}$ at each stage k and write ${\vec{Z}}_{k} = (Z_{1}, \dots, Z_{k})$ ⁠. The time-varying IV ${Z_{k}}_{k = 1}^{K}$ is said to be valid if it satisfies the longitudinal generalizations of core IV assumptions including IV relevance: $P (A_{k} = 1 ∣ Z_{k}, {\vec{H}}_{k}^{o b s}) > P (A_{k} = - 1 ∣ Z_{k}, {\vec{H}}_{k}^{o b s})$ for all k, exclusion restriction: $R_{k} ({\vec{a}}_{k}, {\vec{z}}_{k}) = R_{k} ({\vec{a}}_{k})$ for all k and ${\vec{a}}_{k}$ ⁠, and IV unconfoundedness: $Z_{k} ∣ {\vec{a}}_{K} ({\vec{z}}_{K}), {\vec{R}}_{K} ({\vec{a}}_{K}, {\vec{z}}_{K})$ ⁠. The IV unconfoundedness assumption holds by design in sequential randomized trials and is more likely to hold conditional on historical information ${\vec{H}}_{k}^{o b s}$ for IV studies using observational data. The IV unconfoundedness assumption may also be replaced by weaker exchangeability assumptions discussed in Swanson et al. (2018, Section 2).

It is essential to have a time-varying IV (e.g., daily precipitation) rather than a time-independent IV (e.g., genetic variant like the sickle cell trait) in this setting. To illustrate this point, Figure 3 exhibits a causal direct acyclic graph (DAG) for $K = 2$ ⁠: $Z_{1}$ and $Z_{2}$ are time-varying IVs, $A_{1}$ and $A_{2}$ treatment received, $R_{1}$ and $R_{2}$ outcomes, and $U_{1}$ ⁠, $U_{2}$ ⁠, and U unmeasured confounders. We omit any observed covariates for clearer presentation. Figure 3 explicitly differentiates between two types of unmeasured confounding in the DAG: $U_{1}$ and $U_{2}$ represent unmeasured confounding specific to the first and second stages, and U represents unmeasured confounding shared between both stages. When studying the effect of $A_{2}$ on $R_{2}$ ⁠, $Z_{2}$ is a valid IV for $A_{2}$ ⁠; on the contrary, $Z_{1}$ is not a valid IV for $A_{2}$ ⁠, because conditioning on $A_{1}$ induces association between $Z_{1}$ and U (represented by the dashed line in the DAG), thus violating the IV unconfoundedness assumption (Hernán et al., 2004), and not conditioning on $A_{1}$ (i.e., marginalizing over $A_{1}$ ⁠) violates the exclusion restriction assumption; see, e.g., Verma and Pearl (2022).

Figure 3.

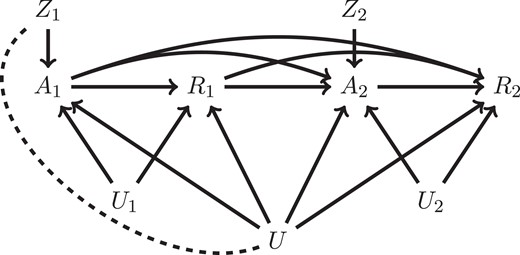
Direct acyclic graph (DAG) when $K = 2$ with time-varying IVs. $U_{1}$ (and $U_{2}$ ⁠) represents stage $k = 1$ (and stage $k = 2$ ⁠) unmeasured confounding, and U shared unmeasured confounding. $Z_{1}$ is an IV for $A_{1}$ and $Z_{2}$ an IV for $A_{2}$ ⁠. $Z_{1}$ is not a valid IV for $A_{2}$ because conditioning on $A_{1}$ induces association between $Z_{1}$ and U, and not conditioning on $A_{1}$ violates exclusion restriction.

Open in new tab Download slide

Point identification of $A_{k}$ ’s effect on $R_{k}$ conditional on historical information ${\vec{H}}_{k}^{o b s}$ is possible under some version of homogeneity or no-interaction assumption. Michael et al. (2020, Section 3) describe sufficient conditions for point identification under a latent variable formulation of an IV model. Their conditions extend those in Wang and Tchetgen Tchetgen (2018) from static to longitudinal settings and generalize the ‘additive unmeasured confounder’ assumption studied in Liao et al. (2021). Michael et al.’s (2020) proposed point identification assumptions essentially entail further restriction that $Z_{k}$ cannot have an additive interaction with any component of unmeasured confounding in affecting the actual treatment received. For instance, in Figure 3, $Z_{2}$ cannot interact with $U_{2}$ or U and have an additive effect on $A_{2}$ conditional on ${\vec{H}}_{k}^{o b s}$ ⁠, so that all systematic difference in a person’s compliance type at each stage k is completely accounted for by historical information up to stage k.

In the rest of article, we focus on developing a framework that accommodates both point and partial identification. In the context of estimating an ITR, Zhang and Pu (2020) and Pu and Zhang (2021) discussed some desirable features of a partial identification strategy in IV studies. Partial identification allows an IV-optimal ITR be well defined under minimal IV identification assumptions and amenable to different choices of an IV in empirical studies. Moreover, the quality of the estimated IV-optimal ITR adapts to the quality of the selected IV (Pu & Zhang, 2021, Remarks 5 and 6). These considerations remain relevant in estimating a DTR. In a multiple-stage, IV-assisted decision problem, point identification requires posting no-interaction-type assumptions at each stage k. It is likely that the no-interaction-type assumption is deemed reasonable towards later stages after having collected rich covariate history data, but not at initial stages, further necessitating a comprehensive framework covering both modes of identification.

4.3 IV-optimality for DTRs and dynamic programming under partial identification

Similar to the single-stage setting in Section 2.3, the IV at each stage, along with its associated identification assumptions, imposes distributional constraints on the potential outcome distributions $p_{a_{k}}^{*} (\cdot, \cdot | {\vec{h}}_{k})$ ⁠. That is, we can specify, for each action $a_{k}$ and historical information ${\vec{h}}_{k}$ at stage k, an IV-constrained set $P_{{\vec{h}}_{k}, a_{k}}$ that contains the ground truth potential outcome distribution $p_{a_{k}}^{*} (\cdot, \cdot | {\vec{h}}_{k})$ ⁠. We treat $P_{{\vec{h}}_{k}, a_{k}}$ as a generic set of distributions compatible with the IV and identification assumptions for now; concrete examples will be given when we formally describe estimation procedures in Section 4.5.

Given the IV-constrained set $P_{{\vec{h}}_{k}, a_{k}}$ ⁠, we impose a prior distribution $P_{{\vec{h}}_{k}, a_{k}}$ on it. This notion generalizes the single-stage setting in Section 2.3. We use $p_{a_{k}} (\cdot, \cdot | {\vec{h}}_{k}) \sim P_{{\vec{h}}_{k}, a_{k}}$ to denote sampling a distribution $p_{a_{k}} (\cdot, \cdot | {\vec{h}}_{k}) \in P_{{\vec{h}}_{k}, a_{k}}$ from $P_{{\vec{h}}_{k}, a_{k}}$ ⁠. We will use the shorthand $p_{a_{k}}$ for $p_{a_{k}} (\cdot, \cdot | {\vec{h}}_{k})$ where there is no ambiguity.

Under these notations, we introduce IV-constrained counterparts of the conventional Q- and value functions defined in (13) and (14).

IV-constrained Q- and value function

Definition 3

For each stage $k \in [K]$ ⁠, each action $a_{k} \in {\pm 1}$ ⁠, and each configuration of the historical information ${\vec{H}}_{k} = {\vec{h}}_{k}$ ⁠, let $P_{{\vec{h}}_{k}, a_{k}}$ be a prior distribution on the IV-constrained set $P_{{\vec{h}}_{k}, a_{k}}$ ⁠. The IV-constrained Q-function and the corresponding value function of a DTR π with respect to the collection of prior distributions ${P_{{\vec{h}}_{k}, a_{k}}}$ at stage K are

\begin{aligned} Q_{P, K} ({\vec{h}}_{K}, a_{K}) & = E_{p_{a_{K}} \sim P_{{\vec{h}}_{K}, a_{K}}} E_{R_{K} \sim p_{a_{K}}} [R_{K}], \\ and V_{P, K}^{π} ({\vec{h}}_{K}) & = Q_{P, K} ({\vec{h}}_{K}, π_{K} ({\vec{h}}_{K})), \end{aligned}

respectively. Recursively, at stage $k = K - 1, \dots, 1$ ⁠, the IV-constrained Q-function and the corresponding value function are

\begin{aligned} Q_{P, k}^{π} ({\vec{h}}_{k}, a_{k}) & = E_{p_{a_{k}} \sim P_{{\vec{h}}_{k}, a_{k}}} E_{(R_{k}, X_{k + 1}) \sim p_{a_{k}}} [R_{k} + V_{P, k + 1}^{π} ({\vec{H}}_{k + 1})], \\ and V_{P, k}^{π} ({\vec{h}}_{k}) & = Q_{P, k}^{π} ({\vec{h}}_{k}, π_{k} ({\vec{h}}_{k})), \end{aligned}

respectively, where ${\vec{H}}_{k + 1} = ({\vec{h}}_{k}, a_{k}, R_{k}, X_{k + 1})$ is a function of $R_{k}$ and $X_{k + 1}$ ⁠.

Similar to the conventional Q- and value functions, the IV-constrained Q-function $Q_{P, k}^{π}$ depends on π only through $π_{(k + 1) : K}$ and the IV-constrained value function $V_{P, k}^{π}$ depends on π only through $π_{k : K}$ ⁠.

Definition 4 follows from Definition 3 and defines IV-optimality for DTRs.

IV-optimal DTR

Definition 4

A DTR $π^{*}$ is said to be IV-optimal with respect to the collection of prior distributions ${P_{{\vec{h}}_{k}, a_{k}}}$ and a policy class Π if it satisfies

π^{*} \in \underset{π \in Π}{argmax} V_{P, 1}^{π} (x_{1})

(16)

for every fixed $h_{1} = x_{1} \in X$ ⁠.

Theorem 1 proves that an IV-optimal policy $π^{*}$ that maximizes the IV-constrained value function for every $x_{1}$ exists and can be obtained via a modified dynamic programming algorithm when Π consists of all policies.

Dynamic programming for the IV-optimal DTR

Theorem 1

Let $π^{*}$ be recursively defined as follows:

π_{K}^{*} ({\vec{h}}_{K}) = \underset{a_{K} \in {\pm 1}}{argmax} Q_{P, K} ({\vec{h}}_{K}, a_{K}), π_{k}^{*} ({\vec{h}}_{k}) = \underset{a_{k} \in {\pm 1}}{argmax} Q_{P, k}^{π^{*}} ({\vec{h}}_{k}, a_{k}), k \leq K - 1.

Then, the DTR $π^{*}$ satisfies

V_{P, k}^{π^{*}} ({\vec{h}}_{k}) = max_{π} V_{P, k}^{π} ({\vec{h}}_{k})

(17)

for any stage k and any configuration of the historical information ${\vec{h}}_{k}$ ⁠, where the maximization is taken over all DTRs.

Theorem 1 generalizes the classical dynamic programming algorithm under a partial identification scheme. The policy $π^{*}$ in Theorem 1 is always well-defined as $Q_{P_{k}}^{π^{*}}$ depends on $π^{*}$ only through $π_{(k + 1) : K}^{*}$ ⁠.

4.4 An alternative characterization of IV-optimal DTRs

Estimation of an IV-optimal DTR based on Theorem 1 is difficult, as the definitions of the IV-constrained Q- and value functions involve integration over the prior distributions ${P_{{\vec{h}}_{k}, a_{k}}}$ ⁠, which may be difficult to specify. Recall that in the single-stage setting, there is an equivalence between the IV-constrained value (7) and the convex combination of the lower and upper bounds of value (5). The convex combination is easier to compute provided that the weights are specified. We now extend this equivalence relationship to the multiple-stage setting to get rid of the intractable integration over prior distributions and facilitate a practical estimation strategy.

We start by defining the worst-case and best-case IV-constrained Q- and value functions as well as their weighted versions as follows.

Worst-case, best-case, and weighted Q- and value functions

Definition 5

Let the prior distributions ${P_{{\vec{h}}_{k}, a_{k}}}$ be specified and ${λ_{k} ({\vec{h}}_{k}, a_{k})}$ be a collection of weighting functions taking values in $[0, 1]$ ⁠. The worst-case, best-case, and weighted Q-functions at stage K with respect to ${P_{{\vec{h}}_{k}, a_{k}}}$ and ${λ_{k} ({\vec{h}}_{k}, a_{k})}$ are defined as

\begin{aligned} {\underline{Q}}_{K} ({\vec{h}}_{K}, a_{K}) = inf_{\begin{matrix} p_{a_{K}} \in P_{{\vec{h}}_{K}, a_{K}} \end{matrix}} E_{R_{K} \sim p_{a_{K}}} [R_{K}], \\ {\bar{Q}}_{K} ({\vec{h}}_{K}, a_{K}) = sup_{\begin{matrix} p_{a_{K}} \in P_{{\vec{h}}_{K}, a_{K}} \end{matrix}} E_{R_{K} \sim p_{a_{K}}} [R_{K}], \end{aligned}

(18)

\begin{aligned} Q_{\vec{λ}, K} ({\vec{h}}_{K}, a_{K}) = & λ_{K} ({\vec{h}}_{K}, a_{K}) \cdot {\underline{Q}}_{K} ({\vec{h}}_{K}, a_{K}) + (1 - λ_{K} ({\vec{h}}_{K}, a_{K})) \\ \cdot {\bar{Q}}_{K} ({\vec{h}}_{K}, a_{K}) . \end{aligned}

(19)

The corresponding worst-case, best-case, and weighted value functions, denoted as ${\underline{V}}_{K}^{π} ({\vec{h}}_{K})$ ⁠, ${\bar{V}}_{K}^{π} ({\vec{h}}_{K})$ ⁠, and $V_{\vec{λ}, K}^{π} ({\vec{h}}_{K})$ ⁠, respectively, are obtained by setting $a_{k} = π_{K} ({\vec{h}}_{K})$ in the above displays. Recursively, at stage $k = K - 1, \dots, 1$ ⁠, we define the worst-case, best-case, and weighted Q-functions as

\begin{aligned} {\underline{Q}}_{\vec{λ}, k}^{π} ({\vec{h}}_{k}, a_{k}) & = inf_{p_{a_{k}} \in P_{{\vec{h}}_{k}, a_{k}}} E_{(R_{k}, X_{k + 1}) \sim p_{a_{k}}} [R_{k} + V_{\vec{λ}, k + 1}^{π} ({\vec{H}}_{k + 1})], \\ {\bar{Q}}_{\vec{λ}, k}^{π} ({\vec{h}}_{k}, a_{k}) & = sup_{p_{a_{k}} \in P_{{\vec{h}}_{k}, a_{k}}} E_{(R_{k}, X_{k + 1}) \sim p_{a_{k}}} [R_{k} + V_{\vec{λ}, k + 1}^{π} ({\vec{H}}_{k + 1})], \end{aligned}

(20)

\begin{aligned} Q_{\vec{λ}, k}^{π} ({\vec{h}}_{k}, a_{k}) = λ_{k} ({\vec{h}}_{k}, a_{k}) \cdot {\underline{Q}}_{\vec{λ}, k}^{π} ({\vec{h}}_{k}, a_{k}) + (1 - λ_{k} ({\vec{h}}_{k}, a_{k})) \cdot {\bar{Q}}_{\vec{λ}, k}^{π} ({\vec{h}}_{k}, a_{k}), \end{aligned}

(21)

respectively. Again, replacing $a_{k}$ in the above Q-functions with $π_{k} ({\vec{h}}_{k})$ yields their corresponding value functions ${\underline{V}}_{\vec{λ}, k}^{π}, {\bar{V}}_{\vec{λ}, k}^{π}$ ⁠, and $V_{\vec{λ}, k}^{π}$ ⁠.

Definition 5 generalizes criterion (5). According to Definition 5, the worst-case and best-case Q-functions ${\underline{Q}}_{\vec{λ}, k}^{π}$ and ${\bar{Q}}_{\vec{λ}, k}^{π}$ depend on the weighting functions only through $λ_{t} ({\vec{h}}_{t}, a_{t})$ for $k + 1 \leq t \leq K$ ⁠, whereas the corresponding value functions depend on the weighting functions only through $λ_{t} ({\vec{h}}_{t}, a_{t})$ for $k \leq t \leq K$ ⁠. For notational simplicity, we will add superscript π and subscript $\vec{λ}$ in Q-functions at stage K (e.g., we write ${\underline{Q}}_{K} = Q_{\vec{λ}, K}^{π}$ ⁠), although they have no dependence on π or the weighting functions.

Proposition 3 establishes the equivalence between the weighted Q-functions (resp. value functions) and their IV-constrained counterparts in Definition 3.

Equivalence between weighted and IV-constrained Q- and value functions

Proposition 3

The following two statements hold:

Fix any collection of weighting functions ${λ_{k} ({\vec{h}}_{k}, a_{k})}$ ⁠. Assume that in Definition 5, the infimums and supremums when defining weighted Q- and value functions are all attained. Then, there exists a collection of prior distributions ${P_{{\vec{h}}_{k}, a_{k}}}$ such that
$Q_{\vec{λ}, k}^{π} = Q_{P, k}^{π}, V_{\vec{λ}, k}^{π} = V_{P, k}^{π}, \forall k \in [K] .$
Reversely, if any collection of prior distributions ${P_{{\vec{h}}_{k}, a_{k}}}$ is fixed, then there exists a collection of weighting functions ${λ_{k} ({\vec{h}}_{k}, a_{k})}$ such that the above display holds true.

Proposition 3 effectively translates the problem of specifying a collection of prior distributions to specifying a collection of weighting functions, thus allowing one to bypass integration over prior distributions. Combine Proposition 3 and Theorem 1 and we have the following alternative characterization of the IV-optimal DTR.

Alternative characterization of the IV-optimal DTR

Corollary 1

Under the setting in Part 1 of Proposition 3, if we recursively define $π^{*}$ as

\begin{aligned} π_{k}^{*} ({\vec{h}}_{k}) = sgn {C_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k})} = sgn {Q_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, + 1) - Q_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, - 1)}, \\ k = K, \dots, 1, \end{aligned}

(22)

where the two quantities

\begin{aligned} Q_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, + 1) & = λ_{k} ({\vec{h}}_{k}, + 1) \cdot {\underline{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, + 1) + (1 - λ_{k} ({\vec{h}}_{k}, + 1)) \cdot {\bar{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, + 1), \\ Q_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, - 1) & = λ_{k} ({\vec{h}}_{k}, - 1) \cdot {\underline{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, - 1) + (1 - λ_{k} ({\vec{h}}_{k}, - 1)) \cdot {\bar{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, - 1) \end{aligned}

depend on $π^{*}$ only through $π_{(k + 1) : K}^{*}$ and are hence well-defined, then $π^{*}$ satisfies (17) for any stage k and any configuration of the historical information ${\vec{h}}_{k}$ ⁠. In particular, $π^{*}$ is an IV-optimal DTR in the sense of Definition 4 when Π consists of all Boolean functions.

As an alternative to Theorem 1, Corollary 1 gives an analytic and constructive characterization of the IV-optimal DTR.

Example 1

Figure 4 illustrates the decision process when $K = 2$ ⁠. At the second stage, given ${\vec{h}}_{2}^{+} = (h_{1}, a_{1} = + 1, R_{1} (+ 1) = r_{1}^{+}, X_{2} (+ 1) = x_{2}^{+})$ and $λ_{2} ({\vec{h}}_{2}^{+}, \pm 1)$ ⁠, an IV-optimal action is made based on comparing two weighted Q-functions $Q_{\vec{λ}, 2} ({\vec{h}}_{2}^{+}, + 1) = 0.8$ and $Q_{\vec{λ}, 2} ({\vec{h}}_{2}^{+}, - 1) = 0.5$ ⁠, and we have $π_{2}^{*} ({\vec{h}}_{2}^{+}) = + 1$ ⁠. Analogously, we have $π_{2}^{*} ({\vec{h}}_{2}^{-}) = - 1$ ⁠.

Given the knowledge of $π_{2}^{*}$ ⁠, we can compute the weighted value function $V_{\vec{λ}, 2}^{π^{*}} (\cdot)$ of $π^{*}$ at the second stage. This allows us to construct a ‘pseudo-outcome’ at the first stage, denoted as $P O_{1} (r_{1}, x_{2} | h_{1}, a_{1}) = r_{1} + V_{2}^{π^{*}} (h_{1}, a_{1}, r_{1}, x_{2})$ ⁠. Importantly, $P O_{1}$ depends on $π_{2}^{*}$ ⁠, as it is the cumulative rewards if we observe $h_{1}$ at the first stage, take an immediate action $a_{1}$ ⁠, and then act according to the IV-optimal decision $π_{2}^{*}$ at the second stage.

The partial identification interval for the expected value of $P O_{1} (R_{1} (a_{1}), X_{2} (a_{1}) | h_{1}, a_{1})$ ⁠, where the expectation is taken over the potential outcome distribution of $R_{1} (a_{1})$ and $X_{2} (a_{1})$ ⁠, is precisely the worst-case and best-case Q-functions ${\underline{Q}}_{\vec{λ}, 1}^{π^{*}} (h_{1}, a_{1})$ and ${\bar{Q}}_{\vec{λ}, 1}^{π^{*}} (h_{1}, a_{1})$ ⁠. We can then compute the weighted Q-function $Q_{\vec{λ}, 1}^{π^{*}} (h_{1}, a_{1})$ given $λ_{1} (h_{1}, a_{1})$ ⁠, from which we can decide $π_{1}^{*}$ ⁠. Reading the numbers off Figure 4, we conclude that $π_{1}^{*} (h_{1}) = - 1$ ⁠.

An illustrative example of an IV-optimal DTR when K=2. According to the values of the weighted Q-functions at k=2, we have π2*(h→2+)=+1 and π2*(h→2−)=−1. Given π2*, the weighted Q-functions at k=1 can be computed, and the IV-optimal action is π1*(h1)=−1.

Figure 4.

An illustrative example of an IV-optimal DTR when $K = 2$ ⁠. According to the values of the weighted Q-functions at $k = 2$ ⁠, we have $π_{2}^{*} ({\vec{h}}_{2}^{+}) = + 1$ and $π_{2}^{*} ({\vec{h}}_{2}^{-}) = - 1$ ⁠. Given $π_{2}^{*}$ ⁠, the weighted Q-functions at $k = 1$ can be computed, and the IV-optimal action is $π_{1}^{*} (h_{1}) = - 1$ ⁠.

Open in new tab Download slide

Weighting functions

Remark 1

The specification of weighting functions reveals one’s level of optimism. Fix all future weighting functions ${λ_{t} : t \geq k + 1}$ ⁠. At stage k, if one adopts a worst-case perspective and would like to maximize the worst-case gain at this stage, then it suffices to compare the two worse-case Q-functions at stage k, namely ${\underline{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, + 1)$ and ${\underline{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, - 1)$ ⁠. This pessimistic action equals the sign of the difference of the two worst-case Q-functions and corresponds to taking $λ_{k} ({\vec{h}}_{k}, \pm 1) = 1$ (see Figure 5a). Alternatively, if one adopts a best-case perspective at stage k and would like to maximize the best-case gain at this stage, then one compares the two best-case Q-functions, namely ${\bar{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, + 1)$ and ${\bar{Q}}_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, - 1)$ ⁠. This optimistic action equals the sign of the difference between the two best-case Q-functions and corresponds to taking $λ_{k} ({\vec{h}}_{k}, \pm 1) = 0$ (see Figure 5b). Recall that in the single-stage setting, the min-max risk criterion (4) corresponds to maximizing the weighted value (5) with weights set to be $1 / 2$ ⁠. This criterion can be seamlessly generalized to the current multiple-stage setting by setting $λ_{k} ({\vec{h}}_{k}, \pm 1) = 1 / 2$ (see Figure 5c). Other choices of weighting functions can also be made to incorporate domain knowledge and reflect individual-level preference, as suggested by Cui and Tchetgen Tchetgen (2021).

Figure 5.

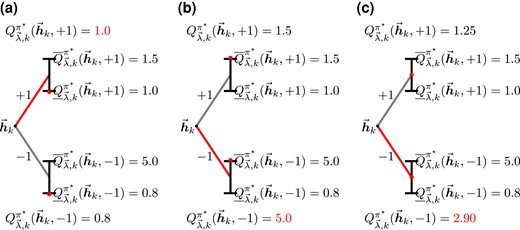
IV-optimal DTR at stage k with different choices of weighting functions. The weighted Q-functions are marked by red dots, and the corresponding IV-optimal action is coloured in red. (a–c) correspond to the worst-case, best-case, and the min-max perspectives, respectively. In each case, the IV-optimal action is $sgn {Q_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, + 1) - Q_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, - 1)}$ ⁠. (a) Worst: $λ_{k} ({\vec{h}}_{k}, \pm 1) = 1$ ⁠. (b) Best: $λ_{k} ({\vec{h}}_{k}, \pm 1) = 0$ ⁠. (c) Min-max: $λ_{k} ({\vec{h}}_{k}, \pm 1) = \frac{1}{2}$ ⁠.

Open in new tab Download slide

4.5 Estimating IV-optimal DTRs

According to Corollary 1, it suffices to estimate the weighted Q-functions ${Q_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}, \pm 1)}$ and hence contrast functions ${C_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k})}$ defined in (22) in order to estimate the IV-optimal DTR $π^{*}$ ⁠. We first consider a Q-learning approach to the estimation problem (Schulte et al., 2014; Watkins & Dayan, 1992). As a concrete example, we estimate the worst-case and best-case Q-functions using Manski and Pepper’s ‘minimal-assumptions’ bounds that depend only on core IV assumptions (Manski, 1997; Manski & Pepper, 2000). These core IV assumptions are automatically satisfied, for instance, in a SMART design with noncompliance. In the Online Supplementary Material S5, we review other useful partial identification bounds, including those depending on the monotone instrumental variable assumption, monotone treatment selection assumption (MTS), and monotone treatment response assumption (MTR).

At Stage K, define

\begin{aligned} ψ_{K} ({\vec{h}}_{K}, a_{k}, z_{k}; C) & = C \cdot P (A_{K}^{o b s} = - a_{k} ∣ Z_{K} = z_{k}, {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}) \\ + E [R_{K}^{o b s} ∣ {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}, Z_{K} = z_{k}, A_{K}^{o b s} = a_{k}] \cdot P (A_{K}^{o b s} = a_{k} ∣ {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}, Z_{K} = z) . \end{aligned}

(23)

Manski-Pepper bounds state that if $R_{K} \in [{\underline{C}}_{K}, {\bar{C}}_{K}]$ almost surely, then its conditional mean potential outcome $E_{R_{K} \sim p_{a_{K}}^{*} (\cdot | {\vec{h}}_{k})} [R_{K}]$ is lower bounded by

\begin{aligned} {LB}_{K} & : = P (Z_{K} = - 1 | {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}) \cdot ψ_{K} ({\vec{h}}_{K}, a_{K}, - 1; {\underline{C}}_{K}) \\ + P (Z_{K} = + 1 | {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}) \cdot ψ_{K} ({\vec{h}}_{K}, a_{K}, + 1; {\underline{C}}_{K}), \end{aligned}

and upper bounded by

\begin{aligned} {UB}_{K} & : = P (Z_{K} = - 1 | {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}) \cdot ψ_{K} ({\vec{h}}_{K}, a_{K}, - 1; {\bar{C}}_{K}) \\ + P (Z_{K} = + 1 | {\vec{H}}_{K}^{o b s} = {\vec{h}}_{k}) \cdot ψ_{K} ({\vec{h}}_{K}, a_{K}, + 1; {\bar{C}}_{K}) . \end{aligned}

Hence, we set ${\underline{Q}}_{K} ({\vec{h}}_{K}, a_{K}) = {LB}_{K}$ ⁠, ${\bar{Q}}_{K} ({\vec{h}}_{K}, a_{K}) = {UB}_{K}$ ⁠, and construct the stage-K weighted Q-function $Q_{\vec{λ}, K} ({\vec{h}}_{k}, a_{K})$ provided values of $λ_{K} ({\vec{h}}_{k}, a_{K})$ ⁠. In practice, we may estimate all relevant quantities from the observed data by fitting parametric models (e.g., linear models) or flexible machine learning models (e.g., regression trees and random forests) and then invoke the plug-in principle.

Given an estimate ${\hat{Q}}_{\vec{λ}, K}^{*}$ of $Q_{\vec{λ}, K}$ ⁠, we can then estimate the contrast function $C_{\vec{λ}, K} ({\vec{h}}_{k})$ by ${\hat{C}}_{\vec{λ}, K}^{*} ({\vec{h}}_{k}) = {\hat{Q}}_{\vec{λ}, K}^{*} ({\vec{h}}_{k}, + 1) - {\hat{Q}}_{\vec{λ}, K}^{*} ({\vec{h}}_{k}, - 1)$ ⁠, and the stage-K IV-optimal DTR $π_{K}^{*} ({\vec{h}}_{k})$ can be estimated by ${\hat{π}}_{K}^{Q} ({\vec{h}}_{k}) = sgn {{\hat{C}}_{\vec{λ}, K} ({\vec{h}}_{k})}$ according to Corollary 1. Moreover, the weighted value function of $π^{*}$ at stage K, $V_{\vec{λ}, K}^{π^{*}} ({\vec{h}}_{k})$ ⁠, can be estimated by ${\hat{V}}_{\vec{λ}, K}^{*} = {\hat{Q}}_{\vec{λ}, K}^{*} ({\vec{h}}_{k}, {\hat{π}}_{K}^{Q} ({\vec{h}}_{k}))$ ⁠.

Now, assume for any stage $t \geq k + 1$ ⁠, the stage-t weighted value function $V_{\vec{λ}, t}^{π^{*}} ({\vec{h}}_{t})$ has been estimated by ${\hat{V}}_{\vec{λ}, t}^{*} ({\vec{h}}_{t})$ ⁠, and that $R_{t} \in [{\underline{C}}_{t}, {\bar{C}}_{t}]$ almost surely. At stage k, define the pseudo-outcome $P O_{k} (r_{k}, x_{k + 1} | {\vec{h}}_{k}, a_{k}) = r_{k} + V_{\vec{λ}, k + 1}^{π^{*}} ({\vec{h}}_{k}, a_{k}, r_{k}, x_{k + 1})$ ⁠. By construction, we have $P O_{k} (R_{k}, X_{k + 1} | {\vec{h}}_{k}, a_{k}) \in [\sum_{t \geq k} {\underline{C}}_{t}, \sum_{t \geq k} {\bar{C}}_{t}]$ almost surely for $(R_{k}, X_{k + 1}) \sim p_{a_{k}}^{*} (\cdot, \cdot | {\vec{h}}_{k})$ ⁠. Thus, we can apply Manski-Pepper bounds (or other partial identification bounds) one more time to bound the expected value of $P O_{k} (R_{k}, X_{k + 1} | {\vec{h}}_{k}, a_{k})$ ⁠. Alternatively, two terms involved in the pseudo-outcome may be bounded separately using some stylized bounds based on firm domain knowledge; see Online Supplementary Material S5 for details. In this way, we obtain an estimate ${\hat{Q}}_{\vec{λ}, k}^{*}$ of the weighted Q-function of $π^{*}$ at stage k; see Online Supplemental Material S4 for detailed expressions. One nuance is that the pseudo-outcome $P O_{k} (r_{k}, x_{k + 1} | {\vec{h}}_{k}, a_{k})$ depends on the unknown quantity $V_{\vec{λ}, k + 1}^{π^{*}}$ ⁠. At stage k, we have already obtained an estimate ${\hat{V}}_{\vec{λ}, k + 1}^{*}$ of $V_{\vec{λ}, k + 1}^{π^{*}}$ ⁠. Thus, the pseudo-outcome can be estimated by ${\hat{P O}}_{k} (r_{k}, x_{k + 1} | {\vec{h}}_{k}, a_{k}) = r_{k} + {\hat{V}}_{\vec{λ}, k + 1}^{*} ({\vec{h}}_{k}, a_{k}, r_{k}, x_{k + 1})$ ⁠.

Finally, the contrast function $C_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k})$ is estimated by ${\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}) = {\hat{Q}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}, + 1) - {\hat{Q}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}, - 1)$ ⁠, the stage-k IV-optimal DTR by ${\hat{π}}_{k}^{Q} ({\vec{h}}_{k}) = sgn {{\hat{C}}_{\vec{λ}, k} ({\vec{h}}_{k})}$ ⁠, and the stage-k weighted value function by ${\hat{V}}_{\vec{λ}, k}^{*} = {\hat{Q}}_{\vec{λ}, k} ({\vec{h}}_{k}, {\hat{π}}_{k}^{Q} ({\vec{h}}_{k}))$ ⁠. In this way, we recursively estimate all contrast functions and obtain an estimated IV-optimal DTR ${\hat{π}}^{Q}$ ⁠.

Algorithm 1:

Open in new tab

Estimation of the IV-Optimal DTR

Input: Trajectories and instrument variables

{(x_{k, i}, a_{k, i}, r_{k, i}, z_{k, i}) : k \in [K], i \in [n]}

⁠, weighting functions

{λ ({\vec{h}}_{k}, a_{k})}

⁠, policy class Π, forms of partial identification intervals.

Output: Estimated IV-optimal DTR

{\hat{π}}^{*}

⁠.

# Step I: Q-learning

Obtain an estimate

{\hat{Q}}_{\vec{λ}, K}^{*}

of

Q_{\vec{λ}, K}

using

({\vec{h}}_{K, i}, r_{K, i}, z_{K, i})_{i = 1}^{n}

⁠;

Estimate

C_{\vec{λ}, K}

by

{\hat{C}}_{\vec{λ}, K}^{*} ({\vec{h}}_{K}) = {\hat{Q}}_{\vec{λ}, K}^{*} ({\vec{h}}_{K}, + 1) - {\hat{Q}}_{\vec{λ}, K}^{*} ({\vec{h}}_{K}, - 1)

⁠;

Set

{\hat{π}}_{K}^{Q} ({\vec{h}}_{K}) = sgn ({\hat{C}}_{\vec{λ}, K}^{*} ({\vec{h}}_{K}))

and

{\hat{V}}_{\vec{λ}, k}^{*} ({\vec{h}}_{K}) = {\hat{Q}}_{\vec{λ}, K}^{*} ({\vec{h}}_{K}, {\hat{π}}_{K}^{Q} ({\vec{h}}_{K}))

⁠;

for

k = K - 1, \dots, 1

do

For each

i \in [n]

⁠, construct

{\hat{P O}}_{k, i} = r_{k, i} + {\hat{V}}_{\vec{λ}, k + 1}^{*} ({\vec{h}}_{k + 1, i})

⁠;

Obtain an estimate

{\hat{Q}}_{\vec{λ}, k}^{*}

of

Q_{\vec{λ}, k}^{π^{*}}

using using

({\vec{h}}_{k, i}, {\hat{P O}}_{k, i}, z_{k, i})_{i = 1}^{n}

⁠;

Estimate

C_{\vec{λ}, k}^{π^{*}}

by

{\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}) = {\hat{Q}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}, + 1) - {\hat{Q}}_{\vec{λ}, K}^{*} ({\vec{h}}_{k}, - 1)

⁠;

Set

{\hat{π}}_{k}^{Q} ({\vec{h}}_{k}) = sgn ({\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}))

and

{\hat{V}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}) = {\hat{Q}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}, {\hat{π}}_{k}^{Q} ({\vec{h}}_{k}))

end

# Step II: Weighted classification

for

k = K, \dots, 1

do

Solve the weighted classification problem in (24) to obtain

{\hat{π}}_{k}^{*}

⁠;

end

return

{\hat{π}}^{*}

In many applications, it may be desirable to obtain parsimonious and interpretable DTRs inside some prespecified function class $Π = Π_{1} \times \dots \times Π_{K}$ ⁠. To achieve this, we may ‘project’ ${\hat{π}}^{Q}$ ⁠, the DTR obtained by Q-learning and is thus not necessarily inside Π, onto the function class Π. With some algebra, one readily checks that $π^{*}$ is a solution to the following weighted classification problem:

π_{k}^{*} ({\vec{h}}_{k}) \in \underset{a_{k} \in {\pm 1}}{argmin} | C_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k}) | \cdot 1 {sgn (C_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k})) \neq a_{k}} .

(24)

This representation illuminates a rich class of strategies to search for a DTR π within a desired, possibly parsimonious function class Π, via sequentially solving the following weighted classification problem:

{\hat{π}}_{k}^{*} ({\vec{h}}_{k}) \in \underset{π_{k} \in Π_{k}}{argmin} \frac{1}{n} \sum_{i = 1}^{n} | {\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k, i}) | \cdot 1 {sgn ({\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k, i})) \neq π_{k} ({\vec{h}}_{k, i})},

where we recall that ${\hat{C}}_{\vec{λ}, k}^{*}$ is an estimate of ${\hat{C}}_{\vec{λ}, k}^{π^{*}}$ obtained via Q-learning, and ${{\vec{h}}_{k, i}}_{i = 1}^{n}$ is the historical information at stage k in our dataset. This strategy is similar to the proposal in Zhao et al. (2015). Algorithm 1 summarizes the procedure.

4.6 Improving dynamic treatment regimes with an instrumental variable

The IV-optimality framework developed in Sections 4.3–4.5 can be modified to tackle the policy improvement problem under the multiple-stage setup. Let $π^{b}$ be a baseline DTR to be improved. Some most important baseline DTRs include the standard-of-care DTR (i.e., ${π^{b}}_{k} = - 1$ for any k) and the SRA-optimal DTR defined in Section 4.1. The goal of policy improvement, as discussed in Section 3, is to obtain a DTR $π^{↑}$ such that $π^{↑}$ is no worse and potentially better than $π^{b}$ ⁠.

Similar to the materials in Sections 4.3–4.5, one can leverage additional information encoded in the collection of IV-constrained sets ${P_{{\vec{h}}_{k}, a_{k}}}$ ⁠. Briefly speaking, instead of starting from the usual value function, one now starts from the ‘relative’ value function, which characterizes the excess value collected by a certain policy compared to the baseline policy $π^{b}$ ⁠. One can then define the notion of IV-improved DTRs using similar constructions as those appeared in Sections 4.3–4.5. We refer the readers to Online Supplemental Material S1 for a detailed exposition.

5 Theoretical properties

In this section, we prove nonasymptotic bounds on the deviance between the estimated IV-optimal DTR to its population counterpart. The theoretical guarantees for IV-improved DTR are deferred to Online Supplementary Material S1.2.

We need several standard assumptions, which we detail below. First of all, we need a proper control on the complexity of the policy class $Π = Π_{1} \times \dots Π_{K}$ ⁠. Note that any $π_{k} \in Π_{k}$ is a Boolean function that sends a specific configuration of the historical information ${\vec{h}}_{k}$ to a binary decision $π_{k} ({\vec{h}}_{k})$ ⁠. Let $H_{k}$ be the collection of all possible ${\vec{h}}_{k}$ s. A canonical measure of complexity of Boolean functions is the Vapnik–Chervonenkis (VC) dimension (Vapnik & Chervonenkis, 1968). The VC dimension of $Π_{k}$ ⁠, denoted as $v c (Π_{k})$ ⁠, is the largest positive integer d such that there exists a set of d points ${{\vec{h}}_{k}^{(1)}, \dots, {\vec{h}}_{k}^{(d)}} \subseteq H_{k}$ shattered by $Π_{k}$ ⁠, in the sense that for any binary vector $v \in {\pm 1}^{d}$ ⁠, there exists $π_{k}^{(v)} \in Π_{k}$ such that $π_{k}^{(v)} ({\vec{h}}_{k}^{(j)}) = v_{j}$ for $j \in [d]$ ⁠. If no such d exists, then $v c (Π_{k}) = \infty$ ⁠.

In practice, a DTR is most useful when it is parsimonious. For this reason, the class of linear decision rules and the class of decision trees with a fixed depth are popular in various application fields (Speth et al., 2020; Tao et al., 2018). It is well known that when the domain is a subset of $R^{d}$ ⁠, the VC dimension of the class of linear decision rules is at most $d + 1$ [see, e.g., Example 4.21 of Wainwright (2019)] and the VC dimension of the class of decision tree with L leaves is $O (L \log (L d))$ (Leboeuf et al., 2020).

Note that a DTR $π_{1 : (k - 1)}$ ⁠, along with the distributions ${p_{a_{t}} (\cdot, \cdot | {\vec{h}}_{t}) : a_{t} \in {\pm 1}, {\vec{h}}_{t} \in H_{t}}_{t = 1}^{k - 1}$ ⁠, induces a probability distribution on $H_{k}$ ⁠, the set of stage-k historical information. Let $H_{k}$ denote the set of all such probability distributions when we vary $π_{1 : (k - 1)} \in Π_{1 : (k - 1)}$ and $p_{a_{t}} (\cdot, \cdot | {\vec{h}}_{t}) \in P_{{\vec{h}}_{t}, a_{t}}$ for $t \in [k - 1]$ ⁠. An element in $H_{k}$ will be denoted as $q_{k}$ ⁠, and the law of ${\vec{H}}_{k}^{o b s}$ will be denoted as $q_{k}^{o b s}$ ⁠. The next assumption concerns how much information on $q_{k}^{o b s}$ can be generalized to the information on a specific $q_{k} \in H_{k}$ ⁠.

Bounded concentration coefficients

Assumption 1

Suppose there exist positive constants ${c_{k}}_{k = 1}^{K}$ such that

sup_{q_{k} \in H_{k}} sup_{{\vec{h}}_{k} \in H_{k}} \frac{d q_{k}}{d q_{k}^{o b s}} ({\vec{h}}_{k}) \leq c_{k} .

Assumption 1 is often made in the reinforcement learning literature (see, e.g., Chen & Jiang, 2019; Munos, 2003; Szepesvári & Munos, 2005) and is closely related to the ‘overlap’ assumption in causal inference. A sufficient condition for the above assumption to hold is that the probability of seeing any historical information (according to the observed data distribution or any distribution in $H_{k}$ ⁠) is strictly bounded away from 0 and 1.

Recall that our proposed algorithm for estimating an IV-optimal DTR is a two-step procedure, where in Step I, the contrast functions are estimated via Q-learning, and in Step II, a parsimonious DTR is obtained via weighted classification. As mentioned in Section 4.5, in the first step, there is a lot of flexibility in choosing the specific models and algorithms for estimating the contrast functions, and a fine-grained understanding of this step would require a case-by-case analysis. In order not to over-complicate the discussion, we assume the existence of a ‘contrast estimation oracle’.

Existence of the contrast estimation oracle

Assumption 2

Suppose in Q-learning, we use an algorithm that takes n i.i.d. samples and outputs ${{\hat{C}}_{\vec{λ}, k}^{*}}_{k = 1}^{K}$ that satisfy

P (E | {\hat{C}}_{\vec{λ}, k}^{*} ({\vec{H}}_{k}^{o b s}) - C_{\vec{λ}, k}^{π^{*}} ({\vec{H}}_{k}^{o b s}) | \geq C_{k, δ} \cdot n^{- α_{k}}) \leq δ

(25)

for any $k \in [K], δ > 0$ ⁠, where the probability is taken over the randomness in the n samples and the expectation is taken over the randomness in a fresh trajectory ${\vec{H}}_{k}^{o b s} \sim q_{k}^{o b s}$ ⁠.

Assumption 2 is usually a relatively mild assumption. The ground truth contrast functions $C_{\vec{λ}, k}^{π^{*}}$ are superimpositions of several conditional expectations of the observed data distribution, and it is reasonable to assume that they can be estimated at a vanishing rate as the sample size tends to infinity. While this assumption simplifies the analysis by bypassing the case-by-case analyses of Q-learning, the analysis of the weighted classification remains nontrivial.

To proceed further, we adopt a form of sample splitting procedure called cross-fitting (Athey & Wager, 2020; Chernozhukov et al., 2018). Specifically, we split the n samples into m equally-sized batches: $[n] = \cup_{j \in [m]} B_{j}$ ⁠, where $m \geq 2$ and $m ≍ 1$ (i.e., of constant order). Each batch has size $| B_{j} | = n_{j} ≍ n / m ≍ n$ ⁠. For each $i \in [n]$ ⁠, let $j_{i} \in [m]$ be the index of its batch, so that $i \in B_{j_{i}}$ ⁠. For the ith sample, we apply the contrast estimation oracle in Assumption 2 on the out-of-batch samples $B_{- j_{i}} = [n] ∖ B_{j_{i}}$ to obtain either an estimate ${\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k}; B_{- j_{i}})$ of $C_{\vec{λ}, k}^{π^{*}} ({\vec{h}}_{k})$ ⁠. We then solve the following optimization problem:

min_{π_{k} \in Π_{k}} \frac{1}{n} \sum_{i = 1}^{n} | {\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k, i}; B_{- j_{i}}) | \cdot 1 {sgn ({\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k, i}; B_{- j_{i}})) \neq π_{k} ({\vec{h}}_{k, i})} .

(26)

We emphasize that cross-fitting is mostly for theoretical convenience. The performance of our algorithm with and without cross-fitting is similar.

In practice, given a limited computational budget, we may only solve the optimization problem (26) up to a certain precision. Our analysis will be conducted for the approximate minimizer ${\hat{π}}_{k}^{*}$ that satisfies

\frac{1}{n} \sum_{i = 1}^{n} | {\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k, i}; B_{- j_{i}}) | \cdot 1 {sgn ({\hat{C}}_{\vec{λ}, k}^{*} ({\vec{h}}_{k, i}; B_{- j_{i}})) \neq {\hat{π}}_{k}^{*} ({\vec{h}}_{k, i})} \leq (26) + ε_{k}^{o p t},

(27)

respectively, where $ε_{k}^{o p t}$ is the optimization error when solving (26).

To quantify the loss of information from restriction to the policy class Π, we define

{\tilde{π}}_{k}^{*} \in \underset{π_{k} \in Π_{k}}{argmin} E [| C_{\vec{λ}, k}^{π^{*}} ({\vec{H}}_{k}^{o b s}) | \cdot 1 {sgn (C_{\vec{λ}, k}^{π^{*}} ({\vec{H}}_{k}^{o b s}) \neq π_{k} ({\vec{H}}_{k}^{o b s})}] .

Note that according to Corollaries 1, when $Π_{k}$ is the set of all Boolean functions, we have ${\tilde{π}}_{k}^{*} = π_{k}^{*}$ ⁠. Otherwise, the difference between ${\tilde{π}}_{k}^{*}$ and $π_{k}^{*}$ measures the approximation error when we restrict ourselves to $Π_{k}$ instead of the set of all Boolean functions in the policy estimation (resp. policy improvement) problem.

We are now ready to present the main result of this section.

Performance of the estimated IV-optimal DTR

Theorem 2

Let Assumptions 1 and 2 hold. Fix any $δ \in (0, 1)$ ⁠. Let the optimization error be $E_{_{opt}} = \sum_{k = 1}^{K} c_{k} \cdot ε_{k}^{o p t}$ ⁠. Let the approximation error be

E_{a p p r o x} = \sum_{k = 1}^{K} c_{k} \cdot E [V_{\vec{λ}, k}^{π_{k : K}^{*}} ({\vec{H}}_{k}^{o b s}) - V_{\vec{λ}, k}^{{\tilde{π}}_{k}^{*} π_{(k + 1) : K}^{*}} ({\vec{H}}_{k}^{o b s})],

where $π_{k} π'_{(k + 1) : K}$ denotes the DTR that acts according to $π_{k}$ at stage k and follows $π'$ from stage $k + 1$ to K. Finally, define the generalization error

E_{g e n} = \sum_{k = 1}^{K} c_{k} \cdot (C_{k, \frac{δ}{4 m K}} \cdot n^{- α_{k}} + (K - k + 1) \cdot \sqrt{\frac{v c (Π_{k}) + \log (K / δ)}{n}}) .

Then, there exists an absolute constant $C > 0$ such that with probability $1 - δ$ ⁠, we have

E [V_{\vec{λ}, 1}^{π^{*}} (X_{1}^{o b s}) - V_{\vec{λ}, 1}^{{\hat{π}}^{*}} (X_{1}^{o b s})] \leq E_{o p t} + E_{a p p r o x} + C \cdot E_{g e n} .

(28)

In the above display, the expectations are taken over a fresh sample of the observed first stage covariates $X_{1}^{o b s}$ ⁠.

Theorem 2 shows that the weighted value function of ${\hat{π}}^{*}$ at the first stage converges to that of the IV-optimal DTR up to three sources of errors: the optimization error that stems from approximately solving the weighted classification problem, the approximation error that results from the restriction to a parsimonious policy class Π, and a vanishing generalization error. We defer the proof to Online Supplemental Material S3.

6 Simulation studies

6.1 Comparing IV and non-IV approaches

We considered a data-generating process with two time-independent covariates $X_{1}$ ⁠, $X_{2} \sim Bernoulli (1 / 2)$ ⁠. At stage one, there exist an unmeasured confounder $U_{1} \sim Rademacher (1 / 2)$ ⁠, an instrumental variable $Z_{1} \sim Rademacher (1 / 2)$ ⁠, a treatment assignment $A_{1}$ that is Rademacher with probability $expit {- 3 + C (1 + Z_{1}) / 2 + ξ (1 + U_{1}) / 2}$ ⁠, and a reward $R_{1}$ that is Bernoulli with probability $expit {0.2 X_{1} + 0.05 X_{2} (1 + A_{1}) - ξ (1 + U_{1}) / 2}$ ⁠, where $expit {x} = 1 / (1 + e^{- x})$ ⁠. According to this data-generating process, treatment $A_{1}$ has no causal effect on $R_{1}$ for those with $X_{2} = 0$ but a modest effect for those with $X_{2} = 1$ ⁠. The unmeasured confounder $U_{1}$ represents some unmeasured disease severity, so that patients with $U_{1} = 1$ are more likely to receive treatment and have a smaller reward $R_{1}$ ⁠. This mimics the NICU application where sicker mothers are more likely to deliver in high-level NICUs and these sicker mothers and their newborns are at higher risk. Because of the unmeasured confounder $U_{1}$ ⁠, a naive non-IV analysis based on the observed data $(X_{1}, X_{2}, A_{1}, R_{1})$ underestimates the treatment effect of $A_{1}$ on $R_{1}$ ⁠. At the second stage, there exist a second unmeasured confounder $U_{2} \sim Rademacher (1 / 2)$ ⁠, a second instrumental variable $Z_{2} \sim Rademacher (1 / 2)$ ⁠, a second treatment assignment $A_{2}$ that is Rademacher with probability $expit {- 3 + C (1 + Z_{2}) / 2 + ξ (1 + U_{2}) / 2}$ ⁠, and a second reward $R_{2}$ that is Bernoulli with probability $expit {0.2 X_{1} + 0.1 R_{1} (1 + A_{2}) / 2 - ξ (1 + U_{2}) / 2}$ ⁠. Similar to $U_{1}$ ⁠, $U_{2}$ represents unmeasured risk factors and a naive, non-IV analysis ignoring $U_{2}$ underestimates the treatment effect of $A_{2}$ on $R_{2}$ ⁠. Parameters C in the above data-generating process controls the strength of IV-treatment association and $ξ$ controls the level of unmeasured confounding. Both parameters C and $ξ$ will be varied later.

An ‘SRA-optimal’ DTR $π_{S R A}$ does not leverage the IV data and is based solely on the observed data $D_{obs} = {(X_{1}, X_{2}, A_{1}, R_{1}, A_{2}, R_{2}), i = 1, \dots, n}$ and falsely assumes the SRA. To estimate $π_{_{SRA}}$ ⁠, we estimated the CATE using a robust stabilized augmented inverse probability weighting estimator (SAIPW) and then applied a weighted classification routine. This is known as C-learning in the literature (Zhang & Zhang, 2018), and it can also be viewed as a variant of the backward outcome weighted learning procedure (Zhao et al., 2015). We then estimated the IV-optimal DTR $π_{I V, 1 / 2}$ corresponding to $λ_{k} ({\vec{h}}_{k}, \pm 1) = 0.5$ for $k = 1, 2$ ⁠. When constructing the IV-optimal DTRs, we used ‘minimal-assumptions’ bounds (Balke-Pearl bounds for a binary outcome and Manski-Pepper bounds otherwise). All classification problems involved in estimating $π_{S R A}$ and $π_{I V, 1 / 2}$ were implemented using a classification tree with a maximum depth of 2, which is meant to replicate the real data application where parsimonious rules are more useful and may deliver most insight (Laber & Zhao, 2015; Speth et al., 2020). Finally, we evaluated each estimated regime by generating $1, 000, 000$ fresh samples of $(X_{1}, X_{2})$ and integrating out the unmeasured confounders $U_{1}$ and $U_{2}$ ⁠.

Figure 6 summarizes the cumulative distribution functions of the value of estimated SRA-optimal policy $π_{_{SRA}}$ and IV-optimal policy $π_{I V, 1 / 2}$ when $C = 4$ and for assorted training sample sizes n and levels of confounding $ξ$ ⁠. It is transparent that the IV-based approach has superior performance compared to the non-IV approach in all of these cases; moreover, the improvement becomes more conspicuous as the sample size increases. Table 1 further puts the percentage of improvement in the context of maximal possible improvement (comparing an optimal policy to a baseline policy that treats no one). For instance, when $n = 5, 000$ and $ξ = 0.5$ ⁠, the IV-based DTR $π_{I V, 1 / 2}$ attained a median of $77.7 %$ of maximal possible improvement, while the non-IV approach only attained a median of $13.4 %$ of maximal possible improvement. What explained the performance gap between IV and non-IV methods? The SAIPW estimates obtained from a naive non-IV approach tended to underestimate the treatment effect and indicate a spurious, negative treatment effect at either stage as a result of omitting the unmeasured confounders. Therefore, the estimated $π_{S R A}$ often recommended withholding the treatment even when the treatment was in fact beneficial. On the other hand, the IV-based interval estimates of the CATEs more faithfully tracked the genuine treatment effect. This difference in estimating the CATE then translated into the performance gap between IV and non-IV DTRs. In Online Supplementary Material S6, we further report simulation results corresponding to different levels of IV-treatment association as controlled by the parameter C. We found two consistent trends. First, $π_{I V, 1 / 2}$ achieved better performance when the IV-treatment association increases (that is, when C grows holding $ξ$ fixed). Second, IV-optimal DTR $π_{I V, 1 / 2}$ consistently outperformed $π_{_{SRA}}$ in these simulation settings though the degree of improvement depends on the specifics of the data-generating processes.

Figure 6.

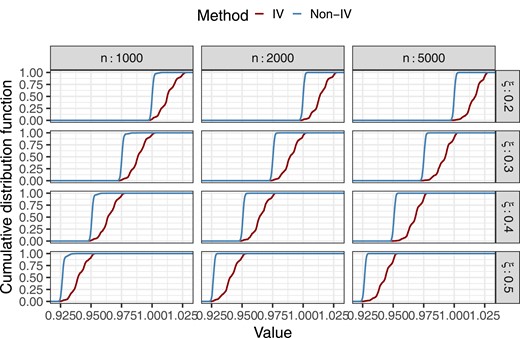
Cumulative distribution functions of the value of the estimated SRA-optimal policy $π_{_{SRA}}$ and IV-optimal policy $π_{I V, 1 / 2}$ (min-max) for various n and $ξ$ values and $C = 4$ ⁠.

Open in new tab Download slide

Table 1.

Open in new tab

Performance of IV and non-IV approaches for various training sample sizes n and levels of unmeasured confounding $ξ$ when $C = 4$

	Non-IV method: $π_{_{SRA}}$				IV method: $π_{I V, 1 / 2}$
	% Improvement		% Correct		% Improvement		% Correct
$ξ$	Median	IQR	Stage I	Stage II	Median	IQR	Stage I	Stage II
n = 1000
0.2	12.4	[10.2, 14.9]	0.0	0.9	51.0	[35.9, 68.3]	45.0	58.9
0.3	14.5	[11.8, 17.2]	0.1	1.4	58.9	[45.9, 76.1]	47.6	61.7
0.4	12.8	[10.3, 15.3]	0.1	1.8	58.3	[46.4, 76.9]	51.0	62.4
0.5	13.6	[10.3, 16.5]	0.2	3.1	61.5	[50.4, 81.6]	51.2	63.5
n = 2000
0.2	12.3	[10.1, 14.6]	0.0	0.0	54.2	[45.5, 70.1]	49.0	64.4
0.3	14.6	[11.8, 17.2]	0.0	0.1	62.3	[51.2, 79.0]	51.1	67.0
0.4	12.6	[10.1, 15.0]	0.0	0.1	59.8	[49.9, 76.5]	50.6	67.2
0.5	13.1	[10.3, 16.1]	0.0	0.1	64.6	[53.5, 82.5]	53.5	66.7
n = 5000
0.2	12.4	[10.1, 14.6]	0.0	0.0	65.7	[50.1, 74.5]	57.0	74.4
0.3	14.3	[11.6, 17.1]	0.0	0.0	74.0	[55.2, 83.3]	60.0	73.7
0.4	12.7	[10.0, 15.5]	0.0	0.0	73.4	[55.8, 86.2]	62.8	76.8
0.5	13.4	[10.4, 16.2]	0.0	0.0	77.7	[58.1, 92.6]	60.1	77.9

	Non-IV method: $π_{_{SRA}}$				IV method: $π_{I V, 1 / 2}$
	% Improvement		% Correct		% Improvement		% Correct
$ξ$	Median	IQR	Stage I	Stage II	Median	IQR	Stage I	Stage II
n = 1000
0.2	12.4	[10.2, 14.9]	0.0	0.9	51.0	[35.9, 68.3]	45.0	58.9
0.3	14.5	[11.8, 17.2]	0.1	1.4	58.9	[45.9, 76.1]	47.6	61.7
0.4	12.8	[10.3, 15.3]	0.1	1.8	58.3	[46.4, 76.9]	51.0	62.4
0.5	13.6	[10.3, 16.5]	0.2	3.1	61.5	[50.4, 81.6]	51.2	63.5
n = 2000
0.2	12.3	[10.1, 14.6]	0.0	0.0	54.2	[45.5, 70.1]	49.0	64.4
0.3	14.6	[11.8, 17.2]	0.0	0.1	62.3	[51.2, 79.0]	51.1	67.0
0.4	12.6	[10.1, 15.0]	0.0	0.1	59.8	[49.9, 76.5]	50.6	67.2
0.5	13.1	[10.3, 16.1]	0.0	0.1	64.6	[53.5, 82.5]	53.5	66.7
n = 5000
0.2	12.4	[10.1, 14.6]	0.0	0.0	65.7	[50.1, 74.5]	57.0	74.4
0.3	14.3	[11.6, 17.1]	0.0	0.0	74.0	[55.2, 83.3]	60.0	73.7
0.4	12.7	[10.0, 15.5]	0.0	0.0	73.4	[55.8, 86.2]	62.8	76.8
0.5	13.4	[10.4, 16.2]	0.0	0.0	77.7	[58.1, 92.6]	60.1	77.9

Note. The metric % Improvement is defined as the improvement in the value as a fraction of the maximal possible improvement (comparing an optimal policy to a baseline policy that treats no one). The metric % Correct at Stage II is defined as the percentage of subjects with $R_{1} = 1$ who are assigned $A_{2} = 1$ by the estimated DTR. The metric % Correct at Stage I is defined as the percentage of subjects with $X_{2} = 1$ who are assigned $A_{1} = 1$ by the estimated DTR.

Table 1.

Open in new tab

Performance of IV and non-IV approaches for various training sample sizes n and levels of unmeasured confounding $ξ$ when $C = 4$

	Non-IV method: $π_{_{SRA}}$				IV method: $π_{I V, 1 / 2}$
	% Improvement		% Correct		% Improvement		% Correct
$ξ$	Median	IQR	Stage I	Stage II	Median	IQR	Stage I	Stage II
n = 1000
0.2	12.4	[10.2, 14.9]	0.0	0.9	51.0	[35.9, 68.3]	45.0	58.9
0.3	14.5	[11.8, 17.2]	0.1	1.4	58.9	[45.9, 76.1]	47.6	61.7
0.4	12.8	[10.3, 15.3]	0.1	1.8	58.3	[46.4, 76.9]	51.0	62.4
0.5	13.6	[10.3, 16.5]	0.2	3.1	61.5	[50.4, 81.6]	51.2	63.5
n = 2000
0.2	12.3	[10.1, 14.6]	0.0	0.0	54.2	[45.5, 70.1]	49.0	64.4
0.3	14.6	[11.8, 17.2]	0.0	0.1	62.3	[51.2, 79.0]	51.1	67.0
0.4	12.6	[10.1, 15.0]	0.0	0.1	59.8	[49.9, 76.5]	50.6	67.2
0.5	13.1	[10.3, 16.1]	0.0	0.1	64.6	[53.5, 82.5]	53.5	66.7
n = 5000
0.2	12.4	[10.1, 14.6]	0.0	0.0	65.7	[50.1, 74.5]	57.0	74.4
0.3	14.3	[11.6, 17.1]	0.0	0.0	74.0	[55.2, 83.3]	60.0	73.7
0.4	12.7	[10.0, 15.5]	0.0	0.0	73.4	[55.8, 86.2]	62.8	76.8
0.5	13.4	[10.4, 16.2]	0.0	0.0	77.7	[58.1, 92.6]	60.1	77.9

	Non-IV method: $π_{_{SRA}}$				IV method: $π_{I V, 1 / 2}$
	% Improvement		% Correct		% Improvement		% Correct
$ξ$	Median	IQR	Stage I	Stage II	Median	IQR	Stage I	Stage II
n = 1000
0.2	12.4	[10.2, 14.9]	0.0	0.9	51.0	[35.9, 68.3]	45.0	58.9
0.3	14.5	[11.8, 17.2]	0.1	1.4	58.9	[45.9, 76.1]	47.6	61.7
0.4	12.8	[10.3, 15.3]	0.1	1.8	58.3	[46.4, 76.9]	51.0	62.4
0.5	13.6	[10.3, 16.5]	0.2	3.1	61.5	[50.4, 81.6]	51.2	63.5
n = 2000
0.2	12.3	[10.1, 14.6]	0.0	0.0	54.2	[45.5, 70.1]	49.0	64.4
0.3	14.6	[11.8, 17.2]	0.0	0.1	62.3	[51.2, 79.0]	51.1	67.0
0.4	12.6	[10.1, 15.0]	0.0	0.1	59.8	[49.9, 76.5]	50.6	67.2
0.5	13.1	[10.3, 16.1]	0.0	0.1	64.6	[53.5, 82.5]	53.5	66.7
n = 5000
0.2	12.4	[10.1, 14.6]	0.0	0.0	65.7	[50.1, 74.5]	57.0	74.4
0.3	14.3	[11.6, 17.1]	0.0	0.0	74.0	[55.2, 83.3]	60.0	73.7
0.4	12.7	[10.0, 15.5]	0.0	0.0	73.4	[55.8, 86.2]	62.8	76.8
0.5	13.4	[10.4, 16.2]	0.0	0.0	77.7	[58.1, 92.6]	60.1	77.9

Note. The metric % Improvement is defined as the improvement in the value as a fraction of the maximal possible improvement (comparing an optimal policy to a baseline policy that treats no one). The metric % Correct at Stage II is defined as the percentage of subjects with $R_{1} = 1$ who are assigned $A_{2} = 1$ by the estimated DTR. The metric % Correct at Stage I is defined as the percentage of subjects with $X_{2} = 1$ who are assigned $A_{1} = 1$ by the estimated DTR.

6.2 Additional simulation results

In Online Supplementary Material S7, we verified that IV-improved DTRs had superior performance compared to their corresponding baseline DTRs, including an SRA-optimal DTR. In Online Supplementary Material S8.1, we discussed the primary difference between two IV-based approaches: a Wald-estimator-based, point-identification approach $π_{I V, W a l d}$ and the more generic, partial identification approach. Without additional identification assumptions, a conditional Wald estimator identifies the conditional local average treatment effect, which is the average treatment effect among a latent subgroup known as compliers conditional on observed covariates. When there is treatment heterogeneity among different latent subgroups, e.g., when the treatment effect among compliers and that among the rest of the population are different, then a Wald-estimator-based approach may mistakenly assign study participants to treatment even when they are hurt by the treatment assignment on average conditional on covariate history. Simulation results that confirm this can be found in Online Supplementary Material S8.2 and S8.3.

7 Application

We considered a total of $183, 487$ mothers who delivered exactly two births during 1995 and 2009 in the Commonwealth of Pennsylvania and relocated at their second deliveries so that their ‘excess-travel-time’ IVs at two deliveries were different. We followed the study design in Baiocchi et al. (2010) and Lorch et al. (2012) and controlled for covariates that measured mothers’ neighbourhood circumstances including poverty rate, median income, etc., mothers’ demographic information including race (white or not), age, years of education, etc., and variables related to delivery including gestational age in weeks and length of prenatal care in months, and eight congenital diseases; see Online Supplemental Material S9 for details. The ‘excess-travel-time’ IVs in both stages were then dichotomized: 1 if above the median and 0 otherwise. Mothers’ treatment choice and their babies’ mortality status at the first delivery were included as covariates for studying the second delivery. We used the multiple imputation by chained equations method (Buuren & Groothuis-Oudshoorn, 2010) implemented in the R package MICE to impute missing covariate data and repeated the analysis on five imputed datasets.

We assume that high-level NICUs do no harm compared to low-level NICUs; therefore, all partial identification intervals in this application were estimated under the MTR assumption (Manski, 2003, Chp. 8). We considered estimating an IV-optimal DTR minimizing the maximum risk at each delivery (see Section 4.4) and explored the trade-off between minimizing the maximum risk and the cost/capacity constraint by adding a generic penalty to the value function. We performed weighted classification using a classification tree with maximum depth equal to 3 so that the resulting DTR is interpretable. Figure 7 plots three estimated DTRs corresponding to no penalty attached, a moderate penalty, and a large penalty attached to attending a high-level NICU. When there is no penalty attached, all mothers are assigned to a high-level NICU. As we increase the penalty, fewer mothers (albeit mothers who benefit most from attending a high-level NICU) are assigned to a high-level NICU. For instance, Figure 7b corresponds to sending $68 %$ mothers to a high-level NICU at their first deliveries and $59.9 %$ at their second deliveries. Mothers assigned to a high-level NICU according to this DTR either belong to racial and ethnic minority groups or are older and have premature gestational age. Similarly, Figure 7c plots a regime where less than $10 %$ of mothers are assigned to a high-level NICU. Mothers who are assigned to a high-level NICU according to this DTR belong to racial and ethnicity minority groups and have premature births. Our analysis here seems to suggest that, in general, race and ethnicity, mother’s age, and gestational age are the most promising effect modifiers. Gestational age has long been hypothesized as an effect modifier; see Lorch et al. (2012), Yang et al. (2014), and Michael et al. (2020); more recently, Yannekis et al. (2020) found a differential effect between different races and ethnic groups. On the other hand, mother’s age as an effect modifier appears to be a new discovery that is worth looking into. Overall, our method both complemented previous published results and generated new insights.

Figure 7.

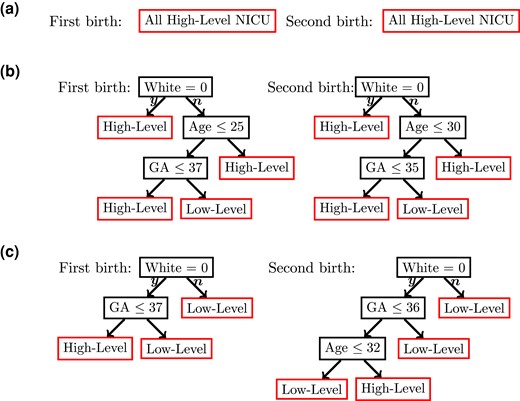
Estimated IV-optimal DTRs using the NICU data. GA is gestational age. (a) No penalty for attending a high-level NICU. All mothers are assigned to high-level NICUs. (b) Moderate penalty for attending a high-level NICU. $68.3 %$ and $59.9 %$ of all mothers are assigned to high-level NICUs for their first and second deliveries, respectively. (c) Large penalty for attending a high-level NICU. $4.53 %$ and $8.56 %$ of all mothers are assigned to high-level NICUs for their first and second deliveries, respectively.

Open in new tab Download slide

8 Discussion

We systematically studied the problem of estimating a DTR from retrospective observational data using a time-varying instrumental variable. We formulated the problem under a generic partial identification framework, derived a counterpart of the classical Q-learning and Bellman equation under partial identification and used it as the basis for generalizing a notion of IV-optimality to the DTRs. One important variant of the developed framework is a strategy to improve upon a baseline DTR. As demonstrated via extensive simulations, IV-improved DTRs indeed have favourable performance compared to the baseline DTRs, including baseline DTRs that are optimal under the NUCA.

With the increasing availability of administrative databases that keep track of clinical data, it is tempting to estimate some useful, real-world-evidence-based DTRs from such retrospective data. To make any causal/treatment effect statements from non-RCT data, an instrumental variable analysis is often better received by clinicians. Fortunately, many reasonably good instrumental variables are available, e.g., daily precipitation, geographic distances, service providers’ preference, etc. Many of these IVs are intrinsically time-varying and could be leveraged to estimate a DTR using the framework proposed in this article. In practice, to deliver the most useful policy intervention, it is important to take into account various practical constraints, e.g., those arising from limited facility capacity or increased cost. Our framework can be readily extended to incorporating various constraints.

To make the theoretical analyses versatile, we have assumed Assumptions 1 and 2 as well as the finiteness of VC dimension of policy classes in the current analysis. An alternative route that could potentially yield sharper bounds would be to assume margin-type conditions so that the Q-function has a separation between the optimal and nonoptimal treatments. See, e.g., Qian and Murphy (2011) for applying this strategy to the single-stage setting, and Luedtke and Van Der Laan (2016) and Shi et al. (2020) for extending this strategy to a multiple-stage, non-IV setting.

Acknowledgments

The authors would like to thank Dr. Zongming Ma, Dr. Dylan S. Small, three reviewers and editors for constructive feedback and comments. The authors would like to acknowledge Dr. Scott A. Lorch for the use of the data from the NICU study.

Data availability

The participants of this study did not give written consent for their data to be shared publicly, so due to the sensitive nature of the research supporting data is not available. The authors received no financial support for the research, authorship, and publication of this article.

Supplementary material

Supplementary material are available at Journal of the Royal Statistical Society: Series B online.

References

Angrist

J. D.

,

Imbens

G. W.

, &

Rubin

D. B.

(

1996

).

Identification of causal effects using instrumental variables

.

Journal of the American Statistical Association

,

91

(

434

),

444

–

455

. https://doi.org/10.1080/01621459.1996.10476902

Google Scholar

Crossref

WorldCat

Athey

,

S.

, &

Wager

,

S.

(

2020

).

Policy learning with observational data

.

Econometrica

,

89

(

1

),

133

–

161

.

Google Scholar

Crossref

WorldCat

Baiocchi

M.

,

Cheng

J.

, &

Small

D. S.

(

2014

).

Instrumental variable methods for causal inference

.

Statistics in Medicine

,

33

(

13

),

2297

–

2340

. https://doi.org/10.1002/sim.6128

Baiocchi

M.

,

Small

D. S.

,

Lorch

S.

, &

Rosenbaum

P. R.

(

2010

).

Building a stronger instrument in an observational study of perinatal care for premature infants

.

Journal of the American Statistical Association

,

105

(

492

),

1285

–

1296

. https://doi.org/10.1198/jasa.2010.ap09490

Google Scholar

Crossref

WorldCat

Balke

A.

, &

Pearl

J.

(

1997

).

Bounds on treatment effects from studies with imperfect compliance

.

Journal of the American Statistical Association

,

92

(

439

),

1171

–

1176

. https://doi.org/10.1080/01621459.1997.10474074

Google Scholar

Crossref

WorldCat

Ben-Michael

E.

,

Greiner

D. J.

,

Imai

K.

, &

Jiang

Z.

(

2021

).

‘Safe policy learning through extrapolation: Application to pre-trial risk assessment’, arXiv, arXiv:2109.11679, preprint: not peer reviewed

.

Bonvini

,

M.

, &

Kennedy

,

E. H.

(

2022). Sensitivity analysis via the proportion of unmeasured confounding

.

Journal of the American Statistical Association

,

117

(

539

),

1540

–

1550

. https://doi.org/10.1080/01621459.2020.1864382

Crossref

WorldCat

Chakraborty

B.

,

Murphy

S.

, &

Strecher

V.

(

2010

).

Inference for non-regular parameters in optimal dynamic treatment regimes

.

Statistical Methods in Medical Research

,

19

(

3

),

317

–

343

. https://doi.org/10.1177/0962280209105013

Chakraborty

B.

, &

Murphy

S. A.

(

2014

).

Dynamic treatment regimes

.

Annual Review of Statistics and Its Application

,

1

(

1

),

447

–

464

. https://doi.org/10.1146/annurev-statistics-022513-115553

Chen

J.

, &

Jiang

N.

(

2019

).

Information-theoretic considerations in batch reinforcement learning. In International conference on machine learning (pp. 1042–1051). PMLR

.

Chernozhukov

V.

,

Chetverikov

D.

,

Demirer

M.

,

Duflo

E.

,

Hansen

C.

,

Newey

W.

, &

Robins

J.

(

2018

).

Double/debiased machine learning for treatment and structural parameters

.

The Econometrics Journal

,

21

(

1

),

C1

–

C68

. https://doi.org/10.1111/ectj.12097

Google Scholar

Crossref

WorldCat

Cui

,

Y.

, &

Tchetgen Tchetgen

,

E.

(

2020

).

A semiparametric instrumental variable approach to optimal treatment regimes under endogeneity

.

Journal of the American Statistical Association

,

116

(

533

),

162

–

173

. https://doi.org/10.1080/01621459.2020.1783272

Cui

Y.

, &

Tchetgen Tchetgen

E.

(

2021

).

Machine intelligence for individualized decision making under a counterfactual world: A rejoinder

.

Journal of the American Statistical Association

,

116

(

533

),

200

–

206

. https://doi.org/10.1080/01621459.2021.1872580

Delage

E.

, &

Ye

Y.

(

2010

).

Distributionally robust optimization under moment uncertainty with application to data-driven problems

.

Operations Research

,

58

(

3

),

595

–

612

. https://doi.org/10.1287/opre.1090.0741

Google Scholar

Crossref

WorldCat

Duarte

G.

,

Finkelstein

N.

,

Knox

D.

,

Mummolo

J.

, &

Shpitser

I.

(

2021

).

‘An automated approach to causal inference in discrete settings’, arXiv, arXiv:2109.13471, preprint: not peer reviewed

.

Finkelstein

N.

, &

Shpitser

I.

(

2020

).

Deriving bounds and inequality constraints using logical relations among counterfactuals. In Conference on uncertainty in artificial intelligence (pp. 1348–1357). PMLR

.

Frangakis

C. E.

, &

Rubin

D. B.

(

1999

).

Addressing complications of intention-to-treat analysis in the combined presence of all-or-none treatment-noncompliance and subsequent missing outcomes

.

Biometrika

,

86

(

2

),

365

–

379

. https://doi.org/10.1093/biomet/86.2.365

Google Scholar

Crossref

WorldCat

Han

S.

(

2019

).

‘Optimal dynamic treatment regimes and partial welfare ordering’, arXiv, arXiv:1912.10014, preprint: not peer reviewed

.

Heng

,

S.

, &

Small

,

D. S.

(

2021

).

Sharpening the Rosenbaum sensitivity bounds to address concerns about interactions between observed and unobserved covariates

.

Statistica Sinica

,

31

,

2331

–

2353

. https://doi.org/10.5705/ss.202020.0395

Google Scholar

OpenURL Placeholder Text

WorldCat

Hernán

,

M. A.

,

Hernández-Díaz

,

S.

, &

Robins

,

J. M.

(

2004

).

A structural approach to selection bias

.

Epidemiology

,

15

(

5

),

615

–

625

. https://doi.org/10.1097/01.ede.0000135174.63482.43

Hernán

,

M. A.

, &

Robins

,

J. M.

(

2006

).

Instruments for causal inference: An epidemiologist’s dream?

Epidemiology

,

17

(

4

),

360

–

372

. https://doi.org/10.1097/01.ede.0000222409.00878.37

Imbens

G. W.

(

2004

).

Nonparametric estimation of average treatment effects under exogeneity: A review

.

Review of Economics and Statistics

,

86

(

1

),

4

–

29

. https://doi.org/10.1162/003465304323023651

Google Scholar

Crossref

WorldCat

Kallus

,

N.

,

Mao

,

X.

, &

Zhou

,

A.

(

2019

).

Interval estimation of individual-level causal effects under unobserved confounding. In The 22nd international conference on artificial intelligence and statistics (pp. 2281–2290)

. PMLR.

Kallus

,

N.

, &

Zhou

,

A.

(

2020a

).

Confounding-robust policy evaluation in infinite-horizon reinforcement learning.

In Advances in neural information processing systems

(Vol. 33, pp. 22293–22304).

Kallus

,

N.

, &

Zhou

,

A.

(

2020b

).

Minimax-optimal policy learning under unobserved confounding

.

Management Science

,

67

(

5)

,

2870

–

2890

. https://doi.org/10.1287/mnsc.2020.3699

Google Scholar

OpenURL Placeholder Text

WorldCat

Kroelinger

C. D.

,

Okoroh

E. M.

,

Goodman

D. A.

,

Lasswell

S. M.

, &

Barfield

W. D.

(

2018

).

Comparison of state risk-appropriate neonatal care policies with the 2012 AAP policy statement

.

Journal of Perinatology

,

38

(

4

),

411

–

420

. https://doi.org/10.1038/s41372-017-0006-6

Laber

E. B.

, &

Zhao

Y. -Q.

(

2015

).

Tree-based methods for individualized treatment regimes

.

Biometrika

,

102

(

3

),

501

–

514

. https://doi.org/10.1093/biomet/asv028

Lasswell

S. M.

,

Barfield

W. D.

,

Rochat

R. W.

, &

Blackmon

L.

(

2010

).

Perinatal regionalization for very low-birth-weight and very preterm infants: A meta-analysis

.

JAMA

,

304

(

9

),

992

–

1000

. https://doi.org/10.1001/jama.2010.1226

Leboeuf

,

J.-S.

,

LeBlanc

,

F.

, &

Marchand

,

M.

(

2020

).

Decision trees as partitioning machines to characterize their generalization properties. In

Advances in neural information processing systems

(Vol. 33, pp. 18135–18145).

Liao

L.

,

Fu

Z.

,

Yang

Z.

,

Kolar

M.

, &

Wang

Z.

(

2021

).

‘Instrumental variable value iteration for causal offline reinforcement learning’, arXiv, arXiv:2102.09907, preprint: not peer reviewed

.

Lorch

S. A.

,

Baiocchi

M.

,

Ahlberg

C. E.

, &

Small

D. S.

(

2012

).

The differential impact of delivery hospital on the outcomes of premature infants

.

Pediatrics

,

130

(

2

),

270

–

278

. https://doi.org/10.1542/peds.2011-2820

Luedtke

A. R.

, &

Van Der Laan

M. J.

(

2016

).

Statistical inference for the mean outcome under a possibly non-unique optimal treatment strategy

.

Annals of Statistics

,

44

(

2

),

713

. https://doi.org/10.1214/15-AOS1384

Manski

,

C. F.

(

1990

).

Nonparametric bounds on treatment effects

.

The American Economic Review

,

80

,

319

–

323

. https://www.jstor.org/stable/2006592

Google Scholar

OpenURL Placeholder Text

WorldCat

Manski

C. F.

(

1997

).

Monotone treatment response

.

Econometrica: Journal of the Econometric Society

,

65

(

6

),

1311

–

1334

. https://doi.org/10.2307/2171738

Google Scholar

Crossref

WorldCat

Manski

C. F.

(

2003

).

Partial identification of probability distributions

.

Springer Science & Business Media

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Manski

C. F.

, &

Pepper

J. V.

(

2000

).

Monotone instrumental variables: With an application to the returns to schooling

.

Econometrica

,

68

(

4

),

997

–

1010

. https://doi.org/10.1111/1468-0262.00144

Google Scholar

Crossref

WorldCat

Michael

,

H.

,

Cui

,

Y.

,

Lorch

,

S.

, &

Tchetgen

,

E. T.

(

202

3).

Instrumental variable estimation of marginal structural mean models for time-varying treatment

.

Journal of the American Statistical Association (just accepted)

. https://doi.org/10.1080/01621459.2023.2183131

Google Scholar

OpenURL Placeholder Text

WorldCat

Moodie

E. E.

,

Richardson

T. S.

, &

Stephens

D. A.

(

2007

).

Demystifying optimal dynamic treatment regimes

.

Biometrics

,

63

(

2

),

447

–

455

. https://doi.org/10.1111/j.1541-0420.2006.00686.x

Munos

,

R.

(

2003

) Error bounds for approximate policy iteration. In International conference on machine learning (Vol. 3, pp. 560–567)

.

Murphy

S. A.

(

2003

).

Optimal dynamic treatment regimes

.

Journal of the Royal Statistical Society: Series B (Statistical Methodology)

,

65

(

2

),

331

–

355

. https://doi.org/10.1111/1467-9868.00389

Google Scholar

Crossref

WorldCat

Murphy

S. A.

(

2005

).

An experimental design for the development of adaptive treatment strategies

.

Statistics in Medicine

,

24

(

10

),

1455

–

1481

. https://doi.org/10.1002/sim.2022

Murphy

S. A.

,

van der Laan

M. J.

,

Robins

J. M.

, & Conduct Problems Prevention Research Group (

2001

).

Marginal mean models for dynamic regimes

.

Journal of the American Statistical Association

,

96

(

456

),

1410

–

1423

. https://doi.org/10.1198/016214501753382327

Neyman

J. S.

(

1923

).

On the application of probability theory to agricultural experiments. Essay on principles. Section 9 (Translated and edited by D.M. Dabrowska and T.P. Speed, Statistical Science (1990), 5, 465–480)

.

Annals of Agricultural Sciences

,

10

,

1

–

51

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Parthasarathy

K. R.

(

2005

).

Probability measures on metric spaces

(Vol.

352

).

American Mathematical Society

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Pearl

J.

(

2009

).

Causality

.

Cambridge University Press

.

Pu

H.

, &

Zhang

B.

(

2021

).

Estimating optimal treatment rules with an instrumental variable: A partial identification learning approach

.

Journal of the Royal Statistical Society: Series B (Statistical Methodology)

,

83

(

2

),

318

–

345

. https://doi.org/10.1111/rssb.12413

Google Scholar

Crossref

WorldCat

Qian

M.

, &

Murphy

S. A.

(

2011

).

Performance guarantees for individualized treatment rules

.

The Annals of Statistics

,

39

(

2

),

1180

. https://doi.org/10.1214/10-AOS864

Qiu

H.

,

Carone

M.

,

Sadikova

E.

,

Petukhova

M.

,

Kessler

R. C.

, &

Luedtke

A.

(

2020

).

Optimal individualized decision rules using instrumental variable methods

.

Journal of the American Statistical Association

,

1

–

46

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Robins

J. M.

(

1989

).

The analysis of randomized and non-randomized aids treatment trials using a new approach to causal inference in longitudinal studies

.

Health Service Research Methodology: A focus on AIDS

,

113

–

159

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Robins

J. M.

(

1992

).

Estimation of the time-dependent accelerated failure time model in the presence of confounding factors

.

Biometrika

,

79

(

2

),

321

–

334

. https://doi.org/10.1093/biomet/79.2.321

Google Scholar

Crossref

WorldCat

Robins

J. M.

(

1998

).

Marginal structural models. In 1997 Proceedings of the section on Bayesian Statistical Science (pp. 1–10). American Statistical Association

.

Robins

J. M.

(

2004

).

Optimal structural nested models for optimal sequential decisions. In Proceedings of the second Seattle symposium in biostatistics (pp. 189–326). Springer

.

Robins

J. M.

, &

Greenland

S.

(

1996

).

Identification of causal effects using instrumental variables: Comment

.

Journal of the American Statistical Association

,

91

,

456

–

458

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Rosenbaum

P. R.

(

2002a

).

Covariance adjustment in randomized experiments and observational studies

.

Statistical Science

,

17

(

3

),

286

–

327

. https://doi.org/10.1214/ss/1042727942

Google Scholar

Crossref

WorldCat

Rosenbaum

P. R.

(

2002b

).

Observational studies

.

Springer

.

Rosenbaum

P. R.

, &

Rubin

D. B.

(

1983

).

The central role of the propensity score in observational studies for causal effects

.

Biometrika

,

70

(

1

),

41

–

55

. https://doi.org/10.1093/biomet/70.1.41

Google Scholar

Crossref

WorldCat

Rubin

D. B.

(

1974

).

Estimating causal effects of treatments in randomized and nonrandomized studies

.

Journal of Educational Psychology

,

66

(

5

),

688

–

701

. https://doi.org/10.1037/h0037350

Google Scholar

Crossref

WorldCat

Rubin

D. B.

, &

van der Laan

M. J.

(

2012

).

Statistical issues and limitations in personalized medicine research with clinical trials

.

The International Journal of Biostatistics

,

8

(

1

),

18

. https://doi.org/10.1515/1557-4679.1423

Schulte

P. J.

,

Tsiatis

A. A.

,

Laber

E. B.

, &

Davidian

M.

(

2014

).

Q-and a-learning methods for estimating optimal dynamic treatment regimes

.

Statistical Science: A Review Journal of the Institute of Mathematical Statistics

,

29

(

4

),

640

. https://doi.org/10.1214/13-STS450

Shi

,

C.

,

Lu

,

W.

, &

Song

,

R.

(

2020

).

Breaking the curse of nonregularity with subagging: Inference of the mean outcome under optimal treatment regimes

.

Journal of Machine Learning Research

,

21

(

176

),

1

–

67

. http://jmlr.org/papers/v21/20-066.html

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

Shi

,

C.

,

Zhu

,

J.

,

Ye

,

S.

,

Luo

,

S.

,

Zhu

,

H.

, &

Song

,

R.

(

2022

).

Off-policy confidence interval estimation with confounded Markov decision process

.

Journal of the American Statistical Association (just accepted)

. https://doi.org/10.1080/01621459.2022.2110878

Google Scholar

OpenURL Placeholder Text

WorldCat

Speth

K. A.

,

Yoon

A. P.

,

Wang

L.

, &

Chung

K. C.

(

2020

).

Assessment of tree-based statistical learning to estimate optimal personalized treatment decision rules for traumatic finger amputations

.

JAMA Network Open

,

3

(

2

),

e1921626

–

e1921626

. https://doi.org/10.1001/jamanetworkopen.2019.21626

Sutton

R. S.

, &

Barto

A. G.

(

2018

).

Reinforcement learning: An introduction

.

MIT Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Swanson

S. A.

,

Hernán

M. A.

,

Miller

M.

,

Robins

J. M.

, &

Richardson

T. S.

(

2018

).

Partial identification of the average treatment effect using instrumental variables: Review of methods for binary instruments, treatments, and outcomes

.

Journal of the American Statistical Association

,

113

(

522

),

933

–

947

. https://doi.org/10.1080/01621459.2018.1434530

Szepesvári

C.

, &

Munos

R.

(

2005

).

Finite time bounds for sampling based fitted value iteration. In Proceedings of the 22nd international conference on machine learning (pp. 880–887)

.

Tao

Y.

,

Wang

L.

, &

Almirall

D.

(

2018

).

Tree-based reinforcement learning for estimating optimal dynamic treatment regimes

.

The Annals of Applied Statistics

,

12

(

3

),

1914

. https://doi.org/10.1214/18-AOAS1137

Van Buuren

,

S.

, &

Groothuis-Oudshoorn

,

K.

(

2010

).

Mice: Multivariate imputation by chained equations in R

.

Journal of Statistical Software

,

45

(

3

),

1

–

67

. https://doi.org/10.18637/jss.v045.i03

Google Scholar

OpenURL Placeholder Text

WorldCat

Vapnik

V. N.

, &

Chervonenkis

A. Y.

(

1968

).

The uniform convergence of frequencies of the appearance of events to their probabilities. In Doklady Akademii Nauk (Vol. 181, pp. 781–783). Russian Academy of Sciences

.

Verma

,

T. S.

, &

Pearl

,

J.

(

2022

) Equivalence and synthesis of causal models. In Probabilistic and causal inference: The works of Judea Pearl.

Association for Computing Machinery

.

Wainwright

M. J.

(

2019

).

High-dimensional statistics: A non-asymptotic viewpoint

(Vol.

48

).

Cambridge University Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Wang

L.

, &

Tchetgen Tchetgen

E.

(

2018

).

Bounded, efficient and multiply robust estimation of average treatment effects using instrumental variables

.

Journal of the Royal Statistical Society: Series B (Statistical Methodology)

,

80

(

3

),

531

–

550

. https://doi.org/10.1111/rssb.12262

Watkins

,

C. J.

, &

Dayan

,

P.

(

1992

).

Q-learning

.

Machine Learning

,

8

,

279

–

292

. https://doi.org/10.1007/BF00992698

Google Scholar

OpenURL Placeholder Text

WorldCat

Yang

F.

,

Lorch

S. A.

, &

Small

D. S.

(

2014

).

Estimation of causal effects using instrumental variables with nonignorable missing covariates: Application to effect of type of delivery NICU on premature infants

.

Annals of Applied Statistics

,

8

(

1

),

48

–

73

. https://doi.org/10.1214/13-AOAS699

Google Scholar

Crossref

WorldCat

Yannekis

G.

,

Passarella

M.

, &

Lorch

S.

(

2020

).

Differential effects of delivery hospital on mortality and morbidity in minority premature and low birth weight neonates

.

Journal of Perinatology

,

40

(

3

),

404

–

411

. https://doi.org/10.1038/s41372-019-0423-9

Zhang

,

B.

, &

Pu

,

H.

(

2020

).

Discussion of Cui and Tchetgen Tchetgen (2020) and Qiu et al. (2020)

.

Journal of the American Statistical Association

,

116

(

533

),

196

–

199

. https://doi.org/10.1080/01621459.2020.1832500

Google Scholar

Crossref

WorldCat

Zhang

B.

,

Tsiatis

A. A.

,

Davidian

M.

,

Zhang

M.

, &

Laber

E.

(

2012

).

Estimating optimal treatment regimes from a classification perspective

.

Stat

,

1

(

1

),

103

–

114

. https://doi.org/10.1002/sta.411

Zhang

,

B.

,

Weiss

,

J.

,

Small

,

D. S.

, &

Zhao

,

Q.

(

2020

).

Selecting and ranking individualized treatment rules with unmeasured confounding

.

Journal of the American Statistical Association

,

116

(

533

),

295

–

308

. https://doi.org/10.1080/01621459.2020.1736083

Google Scholar

Crossref

WorldCat

Zhang

B.

, &

Zhang

M.

(

2018

).

C-learning: A new classification framework to estimate optimal dynamic treatment regimes

.

Biometrics

,

74

(

3

),

891

–

899

. https://doi.org/10.1111/biom.12836

Zhang

Y.

,

Laber

E. B.

,

Davidian

M.

, &

Tsiatis

A. A.

(

2018

).

Interpretable dynamic treatment regimes

.

Journal of the American Statistical Association

,

113

(

524

),

1541

–

1549

. https://doi.org/10.1080/01621459.2017.1345743

Zhao

Y.

,

Zeng

D.

,

Rush

A. J.

, &

Kosorok

M. R.

(

2012

).

Estimating individualized treatment rules using outcome weighted learning

.

Journal of the American Statistical Association

,

107

(

499

),

1106

–

1118

. https://doi.org/10.1080/01621459.2012.695674

Zhao

Y.-Q.

,

Zeng

D.

,

Laber

E. B.

, &

Kosorok

M. R.

(

2015

).

New statistical learning methods for estimating optimal dynamic treatment regimes

.

Journal of the American Statistical Association

,

110

(

510

),

583

–

598

. https://doi.org/10.1080/01621459.2014.937488

Zhou

X.

,

Mayer-Hamblett

N.

,

Khan

U.

, &

Kosorok

M. R.

(

2017

).

Residual weighted learning for estimating individualized treatment rules

.

Journal of the American Statistical Association

,

112

(

517

),

169

–

187

. https://doi.org/10.1080/01621459.2015.1093947

Author notes

Conflict of interest None declared.

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/pages/standard-publication-reuse-rights)

Download all slides

Month:	Total Views:
March 2023	111
April 2023	73
May 2023	47
June 2023	33
July 2023	26
August 2023	12
September 2023	30
October 2023	57
November 2023	46
December 2023	23
January 2024	28
February 2024	18
March 2024	26
April 2024	120
May 2024	60
June 2024	52
July 2024	68
August 2024	54
September 2024	40
October 2024	28
November 2024	73
December 2024	56
January 2025	67
February 2025	46
March 2025	82
April 2025	54
May 2025	33

Article Contents

Estimating and improving dynamic treatment regimes with a time-varying instrumental variable Free

Abstract

1 Introduction

1.1 Dynamic treatment regime and instrumental variable

1.2 Application: a natural, two-stage experiment derived from registry data

2 Estimating individualized treatment rules with an instrumental variable

2.1 Optimal and NUCA-optimal ITRs

2.2 Instrumental variables and IV-optimal ITRs

2.3 A general IV-optimality framework

3 Improving individualized treatment rules with an instrumental variable

Risk-based IV-improved ITR

Formula for risk-based IV-improved ITR

Value-based IV-improved ITR

Formula for value-based IV-improved ITR

4 Estimating dynamic treatment regimes with an instrumental variable

4.1 Optimal and SRA-optimal DTRs

4.2 Identification with a time-varying instrumental variable

4.3 IV-optimality for DTRs and dynamic programming under partial identification

IV-constrained Q- and value function

IV-optimal DTR

Dynamic programming for the IV-optimal DTR

4.4 An alternative characterization of IV-optimal DTRs

Worst-case, best-case, and weighted Q- and value functions

Equivalence between weighted and IV-constrained Q- and value functions

Alternative characterization of the IV-optimal DTR

Weighting functions

4.5 Estimating IV-optimal DTRs

4.6 Improving dynamic treatment regimes with an instrumental variable

5 Theoretical properties

Bounded concentration coefficients

Existence of the contrast estimation oracle

Performance of the estimated IV-optimal DTR

6 Simulation studies

6.1 Comparing IV and non-IV approaches

6.2 Additional simulation results

7 Application

8 Discussion

Acknowledgments

Data availability

Supplementary material

References

Author notes

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Estimating and improving dynamic treatment regimes with a time-varying instrumental variable