-
PDF
- Split View
-
Views
-
Cite
Cite
Clement Minaudier, The Value of Confidential Policy Information: Persuasion, Transparency, and Influence, The Journal of Law, Economics, and Organization, Volume 38, Issue 2, July 2022, Pages 570–612, https://doi.org/10.1093/jleo/ewab020
Close - Share Icon Share
Abstract
Transparency of the lobbying process is hailed as an effective means to limit the influence of special interest groups, but should transparency also apply to the information obtained by policy makers (PMs)? This article extends theories of informational lobbying by explicitly modeling the choice of PMs to obtain information before interacting with lobbyists. This approach reveals a new channel for the value of confidentiality: extracting evidence from special interest groups. It shows that, counter-intuitively, the influence of special interest groups can increase as PMs become more expert. These results shed light on the relationship between confidentiality, good governance, and influence.
1. Introduction
Transparent policy making is often considered a defining feature of democracy. When the information available to policy makers (PMs) is easily accessible, the public can scrutinize policy decisions and hold elected representatives accountable.
While governments have started disclosing the identity of external sources of information and the interests they represent, through bills such as the Lobbying Disclosure Act in the USA in 1995 or the Transparency of Lobbying Act in the UK in 2014, there is an ongoing debate about whether their internal sources should remain confidential. For example, the Congressional Research Service (CRS) has defended the confidentiality of its research for many years until eventually agreeing to make its reports publicly available in 2018 (DeBonis 2017; Hayden 2018).1 One of the arguments advanced by the CRS to defend the confidentiality of its reports is the risk of influence by outsiders: “Widespread public dissemination will almost certainly increase partisan and special interest pressure […]. Such pressure from the public […] could subtly affect the way CRS authors write their reports. Congress may ultimately benefit less from the information in CRS Reports.”2 In parallel, a debate arose about how much influence legislators should have on the way this research is carried out. According to a former CRS researcher, following pressure from members of congress “CRS analysts were told not to end their reports with a section titled ‘conclusion.’ That sounded far too definitive and authoritative.” (Kosar 2015).3
In this article, I evaluate the effect of keeping internal information confidential on the influence that special interest groups exert on policies. I extend theories of informational lobbying—the influence of interest groups through the provision of information, rather than through monetary contributions—by explicitly considering PMs’ control over their internal information. This approach reveals a novel channel through which confidentiality can be beneficial: by keeping their own information confidential, PMs can induce special interest groups to provide more evidence. The value of confidentiality to PMs is not driven by reputational concerns or bargaining considerations, and hence can be socially beneficial. Therefore, while preventing the release of CRS reports might have been driven by more prosaic considerations such as the cost of disseminating them or legal protection for its authors, this confidentiality might have had positive effects on the quality of policies. I characterize the PMs’ strategic choices of internal information and show that they can benefit from limiting the precision of their information. To the extent that avoiding authoritative conclusions reduces the precision of the information available, legislators’ suggestions to CRS researchers may have led to better policy decisions.
The relationship between PMs’ choices of internal information and the provision of information by special interest groups is driven by a simple intuition. When interest groups can observe the information already available to PMs, they can produce evidence that is just sufficiently accurate to tilt the policy decision in their favor. When the information available to the government is not publicly available, interest groups form beliefs about the information PMs are most likely to have. These beliefs determine whether interest groups want to offer more or less information: if they believe that PMs are likely to be skeptical about their preferred policy, then they need to offer more evidence. Therefore, PMs should shape their preliminary investigations to let lobbyists believe that they are sufficiently skeptical and that more evidence is needed.
I formalize this intuition to address the following questions. First, when is confidentiality valuable to PMs, and therefore most likely to be used by governments? Second, how does the government’s control over internal investigations affect the influence that special interest groups exert on policy making?
To answer these questions, I consider a model with a single PM and a lobbyist. The PM has to decide whether to enact a new policy that is supported by the lobbyist, but faces uncertainty. In the first stage, the PM chooses the precision of a signal about an unknown state of nature that she receives confidentially. She would like to choose the welfare-maximizing policy given the state, but her limited expertise constrains the precision of her signal. The lobbyist also acquires some independent signals to share with the PM. His expertise is not limited and he can perfectly adjust the precision of his information to persuade the PM to choose his preferred policy.
I show that confidentiality is valuable as it forces the lobbyist to choose an investigation that reveals more evidence than necessary to persuade the PM. By keeping her own signal realizations confidential, the PM strategically creates a situation of asymmetric information which allows her to extract informational rent. This occurs even when her preliminary information would have no effect on her policy choice, in the absence of lobbying.
The value of confidentiality has limits, however. I show that the PM may need to distort her own information in order to induce the lobbyist to provide more evidence than he would like to. These distortions involve reducing the precision of certain conclusions of the investigation, and hence reduce its overall informativeness. There is thus a tradeoff between obtaining information internally and extracting it from external sources.
This tradeoff generates results relevant to two commonly studied policy questions. First, the value of confidentiality is non-monotonic in the PM’s expertise. When government expertise is low, the value of confidentiality increases in expertise, as more expertise allows the PM to extract more evidence from the lobbyist. However, when expertise is high, that value eventually declines as the additional gains from inducing the lobbyist to provide more information are relatively less important, compared to the costs of distorting internal information. In addition, the value of confidentiality is higher for PMs who are initially opposed to the lobbyist’s policy than for allies of the lobbyist.
Second, the influence of the lobbyist on policy can sometimes increase with the government’s expertise. This arises because more expertise can make the PM more likely to choose the lobbyist’s least-preferred policy and therefore makes the lobbyist’s presence even more important to overturn that choice. This occurs despite the fact that expertise improves policy choice and makes the PM better-off. The influence of the lobbyist is also higher on PMs who initially agree with them than on those who initially disagree with them, because the former is easier to re-convince, should they temporarily change their mind after acquiring their own information. These results have both positive implications for evaluating the influence of interest groups, and normative consequences for the optimal design of institutions.
Consider the fact that the resources spent on lobbying in the USA have significantly increased in real terms over the last 15 years, while the budget of the CRS has remained relatively constant (Figure 1). This could suggest that information generation is increasingly being outsourced to external groups whose influence is increasing. An alternative explanation is that even with limited resources, PMs can force lobbyists to provide additional information, and therefore expend more resources, so these changes in fact reflect a loss of influence. Which of these two explanations is correct depends on how these sources of information interact with one another. More generally, whether returns to lobbying expenditures can be interpreted as influence depends on the information available to PMs in a counterfactual world without lobbying. This article offers a framework to think about this counterfactual scenario.
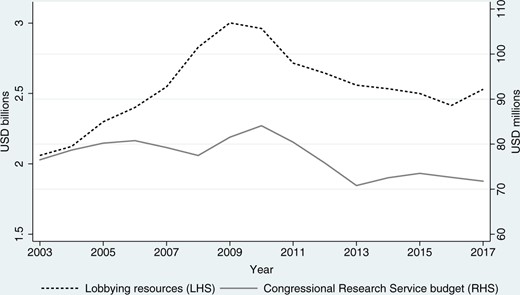
Lobbying Resources (excluding campaign donations) (LHS) and CRS Budget (RHS), Inflation-Adjusted.
Sources: CRS annual report and Center for Responsive Politics.
The results also explain why preferences over confidentiality can vary over time and across policy areas as the policy agenda evolves or as more technocratic PMs get elected. These strategic preferences for confidentiality can be positively correlated with the quality of policy making even in the absence of a causal relationship between the two variables. This is consistent with empirical evidence that higher levels of transparency are associated with better governance (e.g., Islam 2006) but suggests that there can be other factors, such as government expertise, moving both of these variables. In fact, the model shows that shining too much light on the policy process can reduce the quality of policy making.
Finally, the article offers a new rationale for the observation that lobbyists often target friendly legislators who already support their policies.4 Lobbyists may want to provide information to PMs who already support their proposal because there is a risk that the PMs change their policy choice after acquiring their own information. Since these PMs are easier to re-convince, lobbyists have more to gain from targeting them.
1.1 Related Literature
This article relates to two strands of literature: models of informational lobbying and studies of transparency in political institutions. It shows that these two questions are linked: transparency determines how information flows between PMs and lobbyists which, in turn, affects the information that lobbyists provide.
A large literature has looked at how information is transmitted to legislators by lobbyists (e.g., Potters and van Winden 1992, Austen-Smith and Wright 1992, Rasmusen 1993, Austen-Smith 1993, and Lagerlof 1997). The most closely related papers study how informational lobbying is affected by information already held by PMs. Felgenhauer (2013) shows that expert politicians are not always better than non-experts in the presence of lobbyists. In his model, the expertise of the politician only has an effect when two lobbies compete. By allowing the information to be concealed, I show that even a single lobby can be induced to provide more information as the politician’s expertise increases. Cotton and Dellis (2016) show that informational lobbying can be detrimental if more information provided by lobbyists shifts the focus of a PM toward less important issues and thus reduces the information she collects. This substitution across the two sources of information relies on the existence of multiple policies and the limited capacity of the PM to act on these policies. Substitution arises in my model even with one policy dimension because information can be confidential, so that the PM’s choice of information affects the beliefs of lobbyists and the evidence they provide. Finally, in Ellis and Groll (2020), the tradeoff between acquiring costly information in-house or relying on that provided by lobbyists comes from the difference in their resource constraints. Information is costless in my model and the interaction between the two types of information depends on whether that information is made public or not.5
Another closely related paper, Cotton and Li (2018), studies the effect of internal information on monetary lobbying. They show that because a better-informed politician might be harder to sway through contributions, politicians might prefer to reduce the informativeness of their signals. Because they focus on the effect of internal information on monetary rather than informational lobbying, this article is complementary to theirs. In particular, I show that additional internal information can be detrimental even with a benevolent politician rather than one who maximizes contributions.
In the transparency literature, Felgenhauer (2010) and Gailmard and Patty (2019) study the effect of making PMs’ information public.6Felgenhauer (2010) finds that confidentiality can be socially beneficial as it can reduce monetary contributions from lobbyists and result in better policies. More internal information is unambiguously valuable as it reduces lobbyists’ influence. Instead, I show that with informational lobbying, more precise information can be detrimental. Gailmard and Patty (2019) find that transparency of the PM’s information can reduce the amount of information transmitted from a bureaucrat. Their focus on bureaucracies, rather than interest groups’ influence, leads them to study optimal delegation rules rather than distortions in the PM’s information.
From a technical perspective, this article builds on the persuasion literature with privately informed receivers, such as Kolotilin (2018) and Guo and Shmaya (2019). These papers show that the receiver’s payoff can be decreasing in the precision of her private information. This article extends their analysis in a simpler setting by showing that the receiver would indeed prefer to keep her information private as long as its precision is limited, and by characterizing the optimal investigation of the receiver. This article mainly differs in its objective, however: to propose a simple model of the relationship between PMs’ information choices and the influence of lobbyists, rather than to add to the theory of persuasion.
The rest of the article is organized as follows. Section 2 introduces the model. Section 3 characterizes the lobbyist’s and the PM’s choice of information and shows that the PM can gain from confidentiality. Section 4 shows that both confidentiality and interest group influence vary non-monotonically in the PM’s expertise and compares these outcomes between allied and opposed PMs. Section 5 discusses some empirical implications of these results and some extensions. Section 6 concludes. All proofs are presented in Appendix.
2. Model
The lobbyist can credibly commit to this strategy and to revealing s to the PM. I denote the posterior belief of the PM following realizations r and s by .
This bound implies that the PM cannot learn the state of the world perfectly: the posterior beliefs μr must belong to an interval . The lowest and highest posterior beliefs that she can induce are: and . The parameter B captures the difference in expertise between the PM and the lobbyist and is public knowledge. The lobbyist’s advantage stems from facing no expertise bound as, in effect, B = + ∞ for him.
I refer to the investigation p such that as the most informative investigation available to the PM and denote it . This investigation induces interim beliefs and .
I consider three possible regimes. Under transparency, the lobbyist observes both the PM’s choice of investigation p and its outcome r. Under partial confidentiality, the lobbyist observes the choice of p but not its outcome r. Finally, under full confidentiality, the lobbyist observes neither p nor r.
Under partial confidentiality, the timing is as follows:
the PM publicly chooses a preliminary investigation p;
is realized but only observed by the PM;
the lobbyist chooses a persuasion strategy π after observing p;
is publicly realized; and
the PM updates her beliefs and chooses .
Under transparency, the timing is the same, but the lobbyist can observe the realized r and therefore condition π on both p and r. The full confidentiality case is equivalent to both players choosing π and p simultaneously, before observing both realizations r and s.
The equilibrium concept is weak perfect Bayesian equilibrium: the players’ strategies are sequentially rational given their beliefs, and beliefs are updated according to Bayes rule whenever possible.8 I focus on pure strategy equilibria within this class.9
2.1 Discussion of Assumptions
The assumption that the lobbyist can commit to disclosing his information makes the model more tractable and allows me to focus on the type of evidence that both parties generate, and the influence this information has on policies. While there are some lobbying situations that satisfy this assumption,10 not all interactions between lobbyists and PMs necessarily involve truthful communication. In the Supplementary Appendix (Section A), I consider an extension of the model in which the lobbyist can lie about his information.11 I show that the main results continue to hold: the PM can benefit from confidential information but the benefits from confidentiality disappear as her information becomes more precise, she can gain from reducing the precision of internal information, and an increase in her expertise can both force the lobbyist to spend more resources and decrease his influence. In the Supplementary Appendix (Section C), I also show that it is not necessary for the PM to commit to keeping that information confidential: if she had the possibility to disclose it, she would never choose to do so in equilibrium.
2.2 Policy Choice
These expected utilities are illustrated in Figure 2.
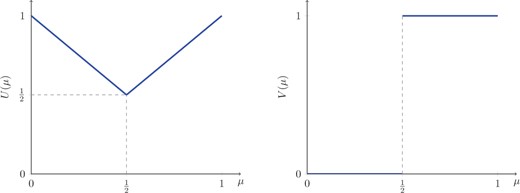
When the PM’s prior belief μ0 is below 1/2, she needs to be persuaded to take action x = 1. When , the PM does not need to be persuaded absent any preliminary information. However, the information she acquires can push her belief below 1/2 and induce the lobbyist to provide additional information. In line with the literature on friendly lobbying (see e.g., Cotton and Dellis 2016; Schnakenberg 2017; Awad 2020), I refer to the PM in the first case as an enemy and in the second case as an ally. In both cases, I say that the PM becomes more sympathetic after receiving some preliminary information if her belief increases toward 1 and becomes more skeptical if her belief decreases.
3. The Role of Confidential Policy Information
In this section, I explain how the PM can extract information from the lobbyist. I first describe the players’ strategies under transparency. I then show how the lobbyist adapts his strategy to confidentiality and how the PM maximizes the benefits from her investigation.
3.1 Transparency
Suppose first that the PM’s information is not confidential. Following realization r from the PM’s investigation, both players share the belief μr.
3.1.1 Lobbyist’s Persuasion Strategy
The lobbyist’s strategy, π, induces a lottery over the PM’s posterior beliefs: with probability , the PM observes s0 and updates her belief to , while with probability she updates her belief to , where . The lobbyist only gains when the PM chooses x = 1, which requires her belief to be above 1/2. If the PM already chooses the lobbyist’s preferred policy given her own information (), the lobbyist does not need to provide any evidence.
If , a posterior belief above can only occur following realization s1. The lobbyist’s problem is therefore to maximize the probability that s1 occurs, while ensuring that the PM chooses policy x = 1 after observing that realization. As shown in Kamenica and Gentzkow (2011), this can be achieved with a persuasion strategy π such that the PM is just sufficiently persuaded following favorable evidence (), and such that unfavorable evidence is as precise as possible ().
As μr increases, persuasion becomes easier ( increases), and the lobbyist needs to provide less information (the “noise” from his persuasion strategy, , increases).
3.1.2 PM’s Preliminary Investigation
The PM chooses her investigation to maximize the total information that she receives. If the PM is an enemy and her expertise is limited (so that μr is always below ), the lobbyist will optimally adjust his persuasion strategy to the PM’s belief. The PM cannot gain from her own information and is therefore indifferent between any investigation. If her expertise is sufficiently high (), the lobbyist provides no valuable information following r1 if . The PM faces a sharp tradeoff: if she chooses the most informative investigation herself, and obtains some belief , the lobbyist stops providing information. This tradeoff is resolved in favor of obtaining more preliminary information: by choosing the most informative investigation (and inducing ), she can become more confident in her policy decision than she would ever be with the lobbyist’s information. If the PM is an ally and her expertise is sufficiently high (), she can trigger the lobbyist to provide information following r0 if , so choosing the most informative investigation is beneficial. An allied PM with limited expertise () never obtains information from the lobbyist and is indifferent between any investigation.
In any of these cases, the PM does not gain from the lobbyist’s information, and it is optimal for her to obtain as much preliminary information as possible.12
Under transparency, the most informative investigation () is an equilibrium strategy for the PM.
3.2 Partial Confidentiality
Suppose now that the PM’s information is confidential. The lobbyist observes the investigation commissioned by the PM (p), but not the conclusions of this investigation (r). This corresponds to situations where PMs can run pilot projects, or commission reports in visible ways without having to publicize the results. Each realization r of the investigation defines a type of the PM.
3.2.1 Lobbyist’s Persuasion Strategy
When the PM is an ally and her expertise is limited (), the lobbyist is indifferent between any persuasion strategy that keeps posterior beliefs above for any possible realization of r. Therefore, providing no information is an optimal strategy.
When the PM is an enemy and her expertise is limited, her interim beliefs (μr) are always below , so one realization of the lobbyist’s strategy (s0) will not persuade any type. The lobbyist needs to choose between generating favorable evidence (s1) that persuades both the skeptical type r0 and the sympathetic type r1 and favorable evidence that only persuades the sympathetic type r1.
When the PM’s expertise is sufficiently high, her own information is sometimes persuasive () and sometimes not (). This can happen both for allies and enemies. In this case, the favorable realization (s1) should always persuade both types but the lobbyist chooses whether the unfavorable realization (s0) should fully reveal the state to be ω = 0, or be sufficiently imprecise that the sympathetic type (r1) still prefers policy x = 1, that is, .
In equilibrium, the lobbyist will choose one of two persuasion strategies. In particular, restricting the lobbyist’s persuasion strategy to binary signals is without loss of generality. This is illustrated in Figure 3 for the case where . If the lobbyist’s favorable evidence is not very informative, and only induces a belief at point A, it only persuades the sympathetic type (), and generates a payoff less than 1. If it is more informative, and induces a belief at B, it can persuade both types and generates a payoff of 1. The optimal persuasion strategy can be determined by the concavification of this step function.13
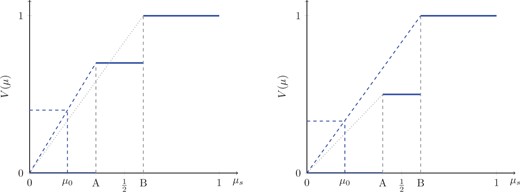
In Equilibrium, the Lobbyist Only Chooses One of Two Strategies with Binary Signals.
I refer to the optimal persuasion strategy which targets the sympathetic type r1 as the targeted persuasion strategy (πT). If the sympathetic type is not already persuaded (), this persuasion strategy should be designed as if the lobbyist knew that the PM had observed r1, that is , as defined in Lemma 1.
When the sympathetic type is already persuaded (), favorable evidence (s1) should persuade the skeptical type () and unfavorable evidence (s0) should leave the sympathetic type just persuaded to choose policy x = 1 ().
I call the optimal persuasion strategy which persuades both types a general persuasion strategy (πG). This strategy should be designed as if the lobbyist knew that the PM had observed r0: , as defined in Lemma 1.
These conditions can be expressed in terms of interim beliefs and . As the skeptical type’s belief becomes more skeptical ( decreases), the PM becomes more likely to be sympathetic (r = r1), and a targeted strategy πT becomes more attractive. The lobbyist, therefore, chooses the targeted strategy πT if the skeptical type is sufficiently skeptical and the general strategy otherwise.
Under confidentiality, there is a threshold such that the lobbyist chooses a general persuasion strategy πG if the belief is above , and chooses a targeted strategy πT otherwise.
I refer to the condition as the incentive constraint. The expertise constraint refers to the bounds imposed on and by the PM’s expertise: and . These constraints are illustrated in Figure 4.
Intuitively, there are two reasons why the lobbyist prefers a targeted persuasion strategy πT if the interim belief of the skeptical type r0 is too low. First, the more skeptical the PM is, the more evidence a general persuasion strategy requires. Second, the lower the skeptical belief an investigation generates, the more likely that investigation is to make the PM sympathetic (r = r1). Conversely, as the belief of the sympathetic PM increases, the probability of r1 decreases, which makes the general persuasion strategy πG more valuable to the lobbyist. The threshold , therefore, decreases as the sympathetic type becomes more sympathetic ( increases).
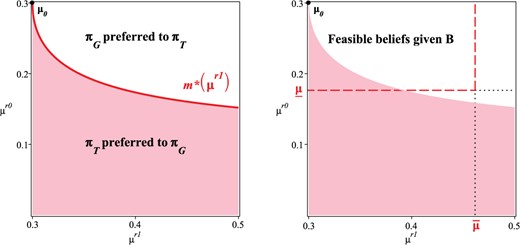
Incentive Constraint (Solid, Left) and Expertise Constraint (Dashed, Right).
3.2.2 PM’s Preliminary Investigation
I first show under what conditions the PM strictly benefits from confidential information, and then show that these benefits are limited by the incentive constraint. I focus on the case where the PM is either an enemy, or an ally with sufficient expertise to generate some interim beliefs below . An ally with insufficient expertise never receives any information from the lobbyist and is indifferent between any investigation.
3.2.3 Gains from Confidentiality
Where, as before, , is determined by the pair of interim beliefs and the Bayes plausibility constraint: .
The PM’s gain from confidential information arises when the lobbyist chooses a general persuasion strategy: πG is designed to persuade the skeptical type r0 who requires more evidence to be persuaded. This additional evidence is valuable to the sympathetic type r1 who gains some informational rent. Had the lobbyist known that the PM was sympathetic, he would have provided less evidence.
The rent obtained from confidential information is captured by the distance between the belief that the lobbyist would like to induce the following favorable evidence (), and the belief the sympathetic type actually has (). When the latter is strictly above , the PM is more confident that choosing policy x = 1 is the correct thing to do: she is better off because her uncertainty is reduced. This intuition is illustrated in Figure 5.

Distribution of Posterior Beliefs When the PM’s Information is Public (Left) and When it is Confidential and the Lobbyist Chooses πG (Right).
When the lobbyist chooses a targeted strategy πT, the PM gains no informational rent since the beliefs induced by the lobbyist never make her strictly prefer policy x = 1. A targeted persuasion strategy πT, therefore, yields the same payoff as public information.15 These results are formalized in Proposition 2.
For any pair of interim beliefs the PM strictly gains from confidentiality, , if and only if satisfies the incentive constraint: .
For low expertise, the incentive constraint is satisfied even under the most informative investigation , so the PM strictly gains from confidentiality. Interestingly, if , the PM would not change her decision based on her own information and her information would have no value in the absence of lobbying. The PM, therefore, does not gain from her own information because that information helps her decision directly, or because she uses this information to audit the information provided by the lobbyist.16 Instead, the PM gains from her information indirectly, by inducing the lobbyist to provide additional evidence. While it is natural to expect the PM to gain from having a second source of information, this mechanism allows her to gain even if that second source of information is redundant from a policy choice perspective.17
3.2.4 Limits of Confidentiality and Optimal Investigation
Given a general persuasion strategy, the PM prefers to be as skeptical as possible as this forces the lobbyist to provide more evidence. This is illustrated in Figure 6: the lower the skeptical belief , the more evidence the lobbyist needs to produce under a general strategy πG to ensure that the skeptical PM chooses policy x = 1. The PM’s expected utility given πG is therefore decreasing in .18
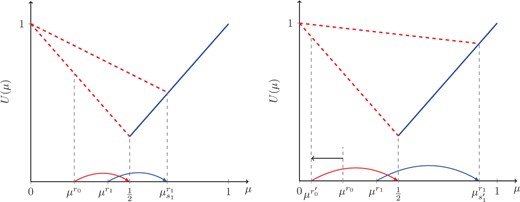
Reducing to Forces the Lobbyist to Provide more Evidence to Induce . This increases and the PM’s expected utility.
However, to induce the lobbyist to choose that strategy, the PM may need to distort her information. When expertise B is high, making full use of expertise (choosing ) induces beliefs that violate the incentive constraint (). The lobbyist, therefore, chooses a targeted strategy πT (Lemma 2) which provides less evidence than a general strategy πG.
The PM, therefore, faces a tradeoff: to extract more information from the lobbyist, she needs to distort the preliminary information she obtains. The distortion needs to ensure that the skeptical type is sufficiently likely and not too hard to persuade, so the PM chooses an investigation that makes her skeptical type not too skeptical (). This limits the value of confidential information.
These observations lead to the following characterization of the PM’s optimal strategy.
Under partial confidentiality, there exist thresholds and such that:
The PM chooses the most informative investigation if either or
She imposes distortions on her investigation if and sets
The precision of the PM’s investigation relative to her expertise B is therefore non-linear in expertise: at low expertise, the PM chooses the most informative investigation, at intermediate expertise she restricts her information to induce the lobbyist to choose a general persuasion strategy, and at higher expertise she chooses the most informative investigation. This is illustrated in Figure 7. The solid line represents the skeptical type’s belief induced by the PM’s equilibrium investigation. The dashed line represents the lowest possible belief and the dash–dot line the incentive constraint , both as functions of B.
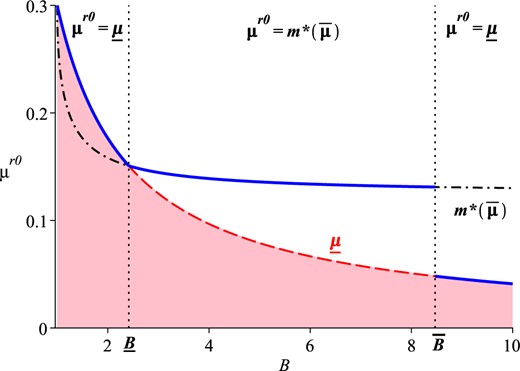
Skeptical Belief Induced in Equilibrium as a Function of Expertise B.
When expertise (B) is low, the expertise constraint () binds before the incentive constraint (). The PM does not need to distort her information to induce the lobbyist to choose πG and generates the lowest possible skeptical belief: .19 The solid line (equilibrium ) coincides with the dashed line (lowest possible belief ).
When expertise (B) is intermediate, the incentive constraint binds so the PM faces a tradeoff between obtaining more preliminary information (setting ) and inducing the lobbyist to provide more evidence (choosing πG). The loss in expected utility from distorting her information (setting ) is small relative to the gain from extracting information from the lobbyist (inducing πG instead of πT). Conditional on inducing the lobbyist to play a general persuasion strategy πG, she chooses her investigation to induce the lowest possible skeptical belief: . As the constraint is decreasing in the sympathetic type’s belief , it is optimal to induce . The solid line, therefore, coincides with the dash–dot line (incentive constraint ).
As expertise (B) becomes sufficiently large, the PM is willing to give up inducing a general persuasion strategy πG if the gains from making full use of her expertise ( and ) are sufficiently large. The solid line (equilibrium ) coincides again with the dashed line (lowest possible belief ). Intuitively, in the limit (as B becomes very large), the PM can learn the state almost perfectly and the lobbyist’s signal becomes negligible.
The interval is nonempty as long as μ0 is not too large,20 so this characterization applies to any enemy and to an ally who faces sufficient uncertainty. An ally who is sufficiently certain that the state is 1 would always choose the most informative investigation, because the lowest belief which satisfies the incentive constraint, , is never far enough below for a general strategy to be beneficial.
3.3 Full Confidentiality
Another possible regime is full confidentiality. Under this regime, neither the PM’s investigation p nor the results r are observable. This transforms the problem into a simultaneous move game.
3.3.1 Lobbyist’s Persuasion Strategy
In this modified game, the lobbyist best responds to the investigation that he expects the PM to choose in equilibrium. His best-response to a given equilibrium investigation p, inducing interim beliefs is determined exactly as in Lemma 2. If are such that , then the lobbyist chooses a general strategy, and if he chooses a targeted strategy.
3.3.2 PM’s Preliminary Investigation
The PM’s payoff in equilibrium (i.e., when the lobbyist has the correct beliefs about the PM’s choice of investigation) is the same as under the partial confidentiality case. However, her payoff following a deviation is now different: because the lobbyist cannot observe that deviation, deviating to a different investigation does not affect the choice of persuasion strategy. However, the posterior beliefs induced by the lobbyist’s strategy are now different than what the lobbyist intended.
As a result, starting from any candidate equilibrium investigation that induces beliefs and , the PM prefers to deviate to a more informative investigation. In particular, the PM would deviate from an investigation inducing to one inducing . She can therefore no longer manipulate the beliefs of the lobbyist. Intuitively, the only reason the PM would deliberately limit the informativeness of her investigation is to induce the lobbyist to choose a general strategy. However, given that the lobbyist chooses such as a strategy, the PM would prefer to deviate and obtain more information. The lobbyist anticipates this behavior and chooses the optimal persuasion strategy corresponding to the PM’s most informative investigation.
Choosing the most informative investigation does constitute an equilibrium. Indeed, given this preliminary investigation, the lobbyist optimally chooses a targeted strategy (πT) if expertise is high (), and the PM would get a lower payoff by deviating to a less informative investigation. If expertise is low (), the lobbyist would choose a general strategy and it is indeed optimal for the PM to choose the most informative investigation .21
The PM only gains from concealing r when the lobbyist plays a general persuasion strategy. If expertise is sufficiently low (), the lobbyist chooses a general persuasion strategy (πG) in equilibrium. But if expertise is too high (), the lobbyist plays a targeted persuasion strategy in any equilibrium. We, therefore, obtain the following result.
Under full confidentiality, there exists an equilibrium such that the PM chooses the most informative investigation, and every equilibrium yields the same payoff for the PM. The PM strictly gains from confidentiality if and only if her expertise is sufficiently low: .
Under full confidentiality, the PM still gains from concealing information. However, she only gains when her expertise B is not too large, and she can no longer manipulate the beliefs of the lobbyist by simply choosing a different investigation. Instead, extracting additional information would require more drastic steps such as reducing the expertise available.
It is worth noting that the same equilibrium would arise if the order of move were reversed.22 If the lobbyist first chooses his strategy and the PM moves second, the PM always prefers to choose the most informative investigation. Anticipating this, the lobbyist designs his optimal persuasion strategy based on his expectation of the distribution of signals that the PM will receive under the most informative investigation. This corresponds to the general strategy when expertise is low enough and the targeted strategy otherwise.
4. The Value of Confidentiality and Its Effect on Influence
In this section, I show that confidentiality improves the quality of policy making most when government expertise is intermediate and that the lobbyist’s influence (how often his preferred policy is passed) can increase in the PM’s expertise. I also show that an allied PM values confidentiality less than an enemy, and that a lobbyist has more influence on an allied PM than an enemy, but only if the PM’s expertise is sufficiently large. The discussion below focuses on the case of partial confidentiality, which provides richer results, but the main observations also apply to full confidentiality.23
4.1 Value of Confidentiality
Expertise affects the equilibrium choice of investigation p and persuasion strategy π, as well as the probability of error given some strategies. For example, increasing expertise (B) can decrease the probability of error under transparency, but also make the lobbyist switch from a general persuasion strategy to a targeted one.
The first result is that the value of confidentiality varies nonmonotonically in expertise (B) for both enemies and allies as illustrated in Figure 8.
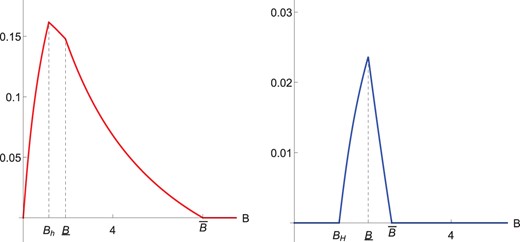
Value of Confidentiality to an Enemy (Left, ) and to an Ally (Right, ).
The value of confidentiality satisfies the following properties:
It is weakly increasing in expertise (B) at low levels and weakly decreasing at higher levels. For sufficiently high expertise, the PM is indifferent between transparency and confidentiality.
Holding the distance between μ0 and constant, that value is higher for an enemy than an ally.
The nonmonotonicity in expertise is always strict for an enemy or an ally with sufficiently low prior μ0. For an ally with prior close to 1, the value of confidentiality is always zero.
Intuitively, as the expertise of the PM increases, two opposite effects arise. The PM can extract more information from the lobbyist when keeping her information confidential: she can make her skeptical belief () more skeptical and force the lobbyist to produce more evidence. This increases the probability of choosing the right policy. On the other hand, expertise increases the value of information under transparency, which decreases the value of confidentiality. The second effect does not arise when expertise is low, so the value of confidentiality initially increases in expertise. When expertise is high, the probability of making the right policy choice increases under both transparency and confidentiality. However, the increase under confidentiality dampens as the PM needs to distort her information. As a result, the value of confidentiality decreases in expertise.
When expertise is very large, the PM prefers to make full use of her expertise (Proposition 3). The lobbyist uses a targeted strategy which induces the same probability of choosing the correct policy as in the transparency regime (Proposition 2). In this case, confidentiality does not improve policy making. In fact, the PM receives strictly less information under confidentiality than under transparency.25
The second part of the proposition suggests that an ally would be more open to sharing information with lobbyists than an enemy. Intuitively, if expertise is low, an ally cannot extract additional information under confidentiality, while an enemy can, so an enemy benefits more. If expertise is high, both can extract information and the amount of information extracted is inversely proportional to the PM’s skeptical belief (), this belief is higher for an ally than an enemy, so the enemy benefits more.
Proposition 5 reveals that the effect of transparent institutions on the quality of policy making depends on both the policy environment and the political environment. Transparent institutions should be more prevalent in areas where the government is either not very competent, or on the contrary, very good at obtaining precise policy-relevant information. This depends on the policy’s complexity, on whether the government is composed of technocrats, or on the attractiveness of the civil service relative to the private sector for competent researchers. Transparency is also relatively more valuable when legislators are sufficiently aligned with lobbyists and cannot extract much information from them.
Even though the results presented here are for partial confidentiality, it is easy to see that partial confidentiality is weakly preferred to full confidentiality. When expertise is low, the incentive constraint does not bind and the equilibrium outcomes are the same in both confidentiality regimes. When expertise is intermediate, the PM can only extract additional information under partial confidentiality, when the lobbyist is aware of the type of investigation run by the PM. When expertise is high, the equilibrium outcomes are again the same in both regimes. If she can, the PM would therefore prefer to inform the lobbyist about the design of her investigation (but to withhold the results of that investigation).26
4.2 Effect of Confidential Information on Influence
In this section, I analyze how the PM’s control over her investigation affects the lobbyist’s influence. In line with the existing literature (e.g., Cotton and Dellis 2016; Ellis and Groll 2020), I view influence as the change in policy choice that results from the presence of the lobbyist.27 One might expect that the better informed a PM is, the less likely she is to be influenced by a lobbyist. I show that under certain conditions, an increase in government expertise can both increase the lobbyist’s influence and the probability of choosing the right policy. This result cautions against the popular view that external influence always has a negative impact on policy making.
Influence is a different metric than the lobbyist’s payoff because it accounts for the policy that the PM would choose in the absence of lobbying. Explicitly modeling the PM’s choice of information highlights that her equilibrium strategy in the counterfactual (in the absence of lobbyist) may be different.28
In the absence of lobbying, the PM weakly prefers the most informative investigation. If her expertise is too low to ever change her choice ( or ), the probability of choosing policy x = 1 is 0 for an enemy and 1 for an ally. Otherwise, it is equal to the probability of observing signal r1.
In the presence of lobbying, the lobbyist chooses a general persuasion strategy πG in equilibrium whenever the PM strictly prefers information to be confidential (). The probability of inducing policy x = 1 is therefore the probability of producing a signal s = s1. When the PM prefers information to be public (), the probability that the policy is x = 1 is also the probability that s = s1, unless the PM is already persuaded (r = r1 and ).
As government expertise increases, the PM is better equipped to defend herself. She can make the lobbyist believe that she is very skeptical and force him to produce more evidence. Therefore, as expertise B increases, influence initially decreases.
However, influence can also increase in expertise. If the PM is an enemy (), ω = 0 is more likely than ω = 1. An increase in expertise makes the PM’s signal more precise, and her investigation is more likely to indicate that the state is ω = 0. In the absence of lobbying, the PM, therefore, becomes more likely to choose policy x = 0. In contrast, the presence of a lobbyist leads to a relatively high probability that the policy chosen is x = 1. As a result, influence increases in the PM’s expertise B. The co-movement of influence and the probability of making the correct decision is illustrated in Figure 9.29
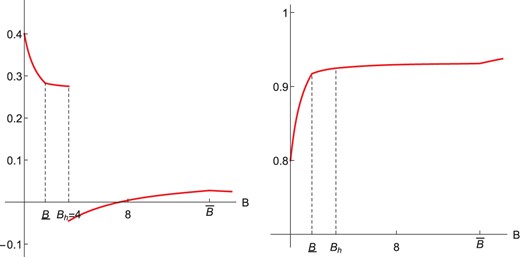
Influence and Probability of Correct Policy for an Enemy ().
There exists a range such that both influence and the probability of making the correct decision increase in B when .
Since the lobbyist always provides information that would not otherwise be available to the PM, lobbying is valuable in this setup, and the PM’s interests and those of the lobbyist may be aligned. However, the presence of lobbying implies that policy x = 1 is chosen more often than it would in its absence. Proposition 6 shows that this is not always against the interest of the PM, or detrimental to social welfare. More influence can be associated with better policy making. Although increasing expertise can also increase influence, this effect should not stop the acquisition of expertise as more expertise always makes the PM better-off.
A second interesting result is that whenever the lobbyist has some influence on the decision of an ally, that influence is higher than on an enemy, holding uncertainty constant i.e., comparing an enemy with prior and an ally with prior ). This occurs only if the ally has sufficient expertise to sometimes choose the lobbyist’s less preferred policy.30 We, therefore, obtain the following result, illustrated in Figure 10.
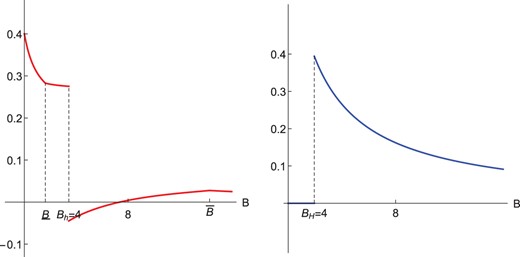
As long as the lobbyist’s influence on an ally is positive, the lobbyist’s influence is higher on an ally than on an enemy.
This result can rationalize the existence of “friendly lobbying”. Lobbyists engage in friendly lobbying because there is a possibility that an ally changes her policy choice after carrying out her own investigation. They are more likely to target allies because it is easier to influence them. This complements recent theoretical explanations for the empirical observation that lobbyists prefer to work with friendly legislators (Cotton and Dellis 2016; Schnakenberg 2017; Awad 2020; Ellis and Groll 2020). However, the results also highlight that this preference depends on the expertise of legislators: it is only valuable to target an ally if that ally can sometimes change her decision based on her own information.
Finally, it is worth noting that influence may be negative, as shown in Figure 10. The probability of enacting the lobbyist’s preferred policy can be higher without the lobbyist than with him. Without a lobbyist, the PM would choose the most informative investigation whereas she distorts her information when facing a lobbyist. This distortion decreases the probability that she chooses the lobbyist’s preferred policy x = 1, even following the lobbyist’s persuasion attempt. The lobbyist would therefore like to commit not to intervene in the policy process for some levels of expertise and alignment. By distorting her information, the PM forces the lobbyist to intervene and provide information.
Corollary 1. Confidentiality can force the lobbyist to provide information when he would prefer not to intervene ex ante.
5. Discussion
5.1 Evolution of Institutions
The results from Section 4 provide a rationale for the development of information-gathering institutions and contribute to a more general literature on the role and development of legislative institutions (e.g., Krehbiel 1991, Bimber 1991, Krehbiel 2004). The diversity of sources of information within governments (agencies, legislative research services, public consultations, legislative hearings, etc.) raises a number of questions: why might legislators obtain redundant information from both internal and external sources? What explains transitions from confidentiality to transparency, such as congressional hearings in the USA in the 1970s and congressional research memos more recently?
The model shows that internal information is valuable to the PM even when that information would not impact policy in the absence of lobbying (Proposition 2). This can account for the puzzling observation that the government may choose to obtain information even if that information is redundant. Clark (2016) quotes an Appropriations Committee aide describing the CRS research as “quick and dirty analysis that is sometimes not perfect.” This suggests that the evidence obtained internally may not be precise enough to determine policy choices. The model shows that “quick and dirty analysis” can result in significant policy improvements in the presence of lobbyists, as the two sources can be strategic complements.
Proposition 5 also shows that, for a large enough level of expertise, confidentiality is no longer valuable to the PM. As a result, increases in expertise within the government can lead to more transparency of government information. This can arise independently of the role of transparency for accountability (as in Argenziano and Weeds 2019). In addition, since expertise varies across policy areas (Howlett 2015), it is possible for transparent institutions (such as hearings) to be used in certain domains, and confidential ones (such as agency memos) in others.
Finally, since the value of confidentiality decreases with expertise when expertise is high (Proposition 5), we should observe empirically a positive correlation between expertise and transparency. This is consistent with the findings of Islam (2006) that transparency (measured by the timeliness of governments in releasing economic information and the presence of freedom of information laws) is correlated with the quality of governance. However, it would be incorrect to conclude that transparency necessarily causes improvements in governance. In particular, Proposition 5 indicates that, at low levels of expertise, transparency would lead to worse policy making.
5.2 Risk of Leaks Under Partial Confidentiality
Under partial confidentiality, lobbyists are aware that the PM is obtaining some information. Publicizing the design of this investigation can expose the PM to risk of leaks, as lobbyists could request to obtain the results of that investigation under freedom of information requests. Under full confidentiality, this is less likely as lobbyists do not know for sure that the PM has investigated. In the Supplementary Appendix (Section B), I analyze a model where the outcome of the investigation r can leak with some positive probability under partial confidentiality but not under full confidentiality. In this case, the PM continues to prefer distorting her preliminary investigation when her expertise is intermediate, but only if the risk of leaks is not too high. Since the gains from distortions only arise when the investigation’s outcome remains confidential, distorting information becomes less valuable when the risk of leaks increase. In the presence of leaks, the PM would now strictly prefer the full confidentiality regime when expertise is low () since both regimes induce the same behavior from the lobbyist, but full confidentiality avoids the risk of damaging leaks. She would still prefer partial confidentiality otherwise. If the risk of leaks differs across policies areas, we should also expect differences in institutional design. For instance, exempting some policy areas from having to publish public notice or fulfilling freedom of information requests on national security grounds reduces the ability of legislators to share both the design and the results of their investigation. These exemptions can be valuable when the risks of leaks are high.31
5.3 Costly Investigations
The analysis conducted so far assumed that investigations were costless, to highlight that the PM might want to restrict her investigation even in the absence of costs. Introducing costs can lead to further distortions. Suppose, for example, that the players face a fixed cost to generate information, independent of the precision of the investigation, but that the PM’s investigation has limited precision as in the existing model.
If the fixed costs are sufficiently low for both players, then the results presented so far would not change.32 If the lobbyist’s costs are large enough, the PM might prefer to restrict her information in order to induce the lobbyist to generate information. By restricting her information, she makes persuasion easier and sufficiently valuable for the lobbyist to justify the fixed cost. As long as the distortions are not too important, this strictly benefits the PM. If not, the PM might give up on extracting information from the lobbyist and choose the most informative investigation. The PM only gains from these restrictions under partial confidentiality. Under transparency, she never strictly benefits from the lobbyist’s information and therefore does not want to incentivize the lobbyist to generate information. Under full confidentiality, she cannot credibly commit to these distortions. If introducing costs forces the PM to restrict her investigation beyond the restrictions already identified, then the more costly the lobbyist’s investigation is, the less valuable confidentiality is to the PM. In the Supplementary Appendix (Section F), I show that there always exists costs low enough that the results above are unchanged, and provide an example where costs force the PM to reduce the precision of her investigation.33
6. Conclusion
This article examined the effect of a PM’s internal information on the provision of information by special interest groups. When PMs can control their preliminary investigations, they can extract additional evidence from special interest groups by distorting these investigations. Internal information becomes valuable even when it is limited, as long as it is confidential. This makes confidentiality valuable to PMs even in the absence of reputational concerns and explains why internal research is kept secret in many governments.
Governments can use confidential information to force special interest groups to adjust how they influence policy. This article, therefore, highlights that influence cannot be simply measured based on whether policy changed or not. The definition of influence should consider what policy would have been chosen in the absence of lobbying. Given this definition, it is possible that influence and welfare increase at the same time, when government expertise or ideological alignment change. When the CRS opens its research to the public, as is currently planned, it will increase the influence that interest groups exert on policy making. But if this move toward transparency is driven by an increase in expertise, then this increase in influence could be accompanied by an increase in welfare.
Understanding the control of governments over the production of internal information is therefore critical not only to the study of special interest groups but also to the relationship between transparency and the quality of government.
Footnotes
Memos to individual congress members remain confidential and can be made public only at the discretion of members.
This is also suggested in the UK Parliament’s Parliamentary Research Handbook: “On subjects that are controversial and for which there is not good evidence, be particularly careful about giving conclusions.” (House of Commons Library 2017: 44)
See Kollman (1997), Hojnacki and Kimball (1998), Hall and Miler (2008), and Beyers and Hanegraaff (2017) for evidence and for example, Cotton and Dellis (2016), Schnakenberg (2017), and Awad (2020) for existing theoretical explanations.
Other papers also study how political institutions affect the influence of informational lobbying. Bennedsen and Feldmann (2002a) look at the effect of the vote of confidence procedure, Bennedsen and Feldmann (2002b) at party cohesion, Dellis and Oak (2020) at the legislature’s subpoena power, while Dahm and Porteiro (2008) and Wolton (2021) look at the interaction between informational lobbying and other forms of pressure.
A large literature has shown how transparency of an agent’s actions can be damaging in a number of institutions, including decision making in committees of experts (Levy 2007, Meade and Stasavage 2008, Seidmann 2011, Swank and Visser 2013, Hansen et al. 2017, Fehrler and Hughes 2018, Gradwohl and Feddersen 2018) or more general principal–agent relationships (Prat (2005) and Fox (2007)). This article focuses instead on transparency of information.
The main insights continue to hold if the PM has access to a more complex investigation generating more than two signals. See Supplementary Appendix (Section D) for details.
Players cannot signal any private information through their actions so there is no need to refine beliefs following off-equilibrium actions.
In equilibrium, the PM never mixes across policy choices. If she did, the lobbyist would deviate to break the PM’s indifference and increase the probability of getting his preferred policy. Mixing across persuasion strategies leads to another distribution over posterior beliefs which could be replicated with a pure strategy.
For instance, special interest groups may fund and help design scientific studies. Once the results of these studies are released in peer-reviewed publications, special interest groups can no longer control their disclosure (e.g., see White and Bero 2010, Kearns et al. 2016, and Nestle 2016). Pharmaceutical companies have also funded patient advocacy groups to send patients to testify in Congress (Kopp et al. 2018). The companies can influence what patients are likely to reveal, but do not have control over the final testimony, so this type of influence strategy is akin to running an uncertain experiment and committing to disclosing the results. Other existing models of informational lobbying (e.g., Austen–Smith 1998 and Cotton and Dellis 2016) also make this assumption.
I extend the present model to three possible states and allow partial alignment between the players so that some (but not necessary all) information can potentially be credibly transmitted.
The PM does not gain from the lobbyist’s information because it never makes her change her policy choice. She either continues to prefer policy x = 0 or is indifferent between the two policies.
Kolotilin (2018) shows that the problem faced by the lobbyist allocating probabilities across different possible realizations is a linear programming problem. The relative marginal gains and marginal costs associated with each realization can be ranked and one of the two possible persuasive realization will dominate the other. The lobbyist therefore always prefers either the persuasion strategy that exactly persuades the favorable type r1 or the one that persuades both, but never a combination of these strategies.
A similar intuition applies when the PM’s own preliminary information is sometimes persuasive ().
When information is public, the lobbyist perfectly targets each of the PM’s types. The targeted strategy is designed to persuade the sympathetic PM, so a skeptical PM obtains little information. By revealing herself to be skeptical, the PM would force the lobbyist to provide additional evidence to persuade her. However, that additional information would never be sufficient to make her strictly prefer a different policy, so she does not gain from it.
As for instance in Dellis and Oak (2020).
The information is redundant in the sense that the lobbyist’s strategy will reveal at least as much information as the PM’s investigation. Alonso and Camara (2018) also show that strategic uses of redundant information can arise when the sender (rather than the receiver) is privately informed.
The PM’s expected utility is independent of because the increase in utility due to a higher posterior belief is exactly offset by the lower probability of that belief occurring. However, when the incentive constraint binds , it is still preferable to choose the highest sympathetic belief since this loosens the constraint: , for any .
Since her payoff is independent of , she can choose any such that induces πG. In particular, choosing the most informative investigation is an equilibrium.
In particular, we need .
However, multiple equilibria can arise under full confidentiality. In particular, in an equilibrium where the lobbyist chooses πG, the PM’s utility is independent of , so any investigation that induces and some is an equilibrium. Similarly, when the lobbyist chooses πT, any investigation that induces is an equilibrium.
Many government agencies can only make policies after a case is brought to their attention and information is provided by the petitioners. This is the case for consumer protection agencies (Consumer Product Safety Commission, FDA), or agencies in charge of permits or licenses (see Carpenter and Ting 2004). I am grateful to anonymous referees for suggesting this extension and these examples.
See Supplementary Appendix (Section E).
This also corresponds to the difference in the PM’s equilibrium expected utility when information is confidential (UC from Equation (2)) and when information is public (UP from Equation (1)).
The probability of choosing the correct policy under both regimes is the same because the additional information available under transparency has no effect on the PM’s policy choice. If one also cared about the total amount of information received, the transparency regime would be strictly more valuable than partial confidentiality.
Partial confidentiality might have unintended consequences, such as generating interest from the lobbyist in that investigation and increasing the risk of leaks. I discuss this possibility in the next section.
This effect does not necessarily result from unfair or unethical lobbying strategies (such as misrepresenting evidence or exchanging policies for donations), or be detrimental to policy choice.
For a similar argument based on the role of outside lobbying, see Wolton (2021).
Note that this co-movement can also occur with an ally but for a different reason. When expertise is low, influence is 0 as the PM chooses the lobbyist’s preferred policy with or without the lobbyist. However, when expertise increases the PM would sometimes choose policy x = 0, so the lobbyist’s influence becomes positive.
Otherwise, the ally chooses x = 1 with or without the lobbyist, and the lobbyist has no influence.
Exemptions from the Administrative Procedure Act for example can be requested for “Good cause” if the agency shows that following notice-and-comment rules is “impracticable, unnecessary, or contrary to the public interest.” Garvey (2017).
With the caveat that the players would now strictly prefer not investigating whenever they are indifferent between all investigations.
An alternative way to model costly investigations is to assume that costs are proportional to the precision of the information obtained. In such a situation, both players would increase the precision of their information until the marginal costs of doing so outweigh the marginal benefits, given the strategy of the other player. The results are therefore unchanged as long as the lobbyist finds it relatively more valuable to increase the precision of his information than the PM, and the PM finds it unprofitable to fully learn the state by herself. The PM might then want to distort her information for two reasons: either because the gains from extracting more information are too low relative to the costs, or because it induces the lobbyist to stop providing as much information.
Additional details available in the Supplementary Appendix.
Further details on how the expected utilities are derived are available in the Supplementary Appendix.
Further details available in the Supplementary Appendix.
Further details on derivatives and inequalities are available in the Supplementary Appendix.
Appendix
Let be the posterior induced by from signal , starting from interim , and the posterior belief induced by from signal , starting from the prior μ0.
This defines a set of pairs of beliefs , denoted
The lobbyist, therefore, prefers πG only if . It is easy to verify that for any and , we have .
Finally, the highest root is always greater than μ0, so condition (Equation A2) is satisfied for all . As a result, for any is positive if and only if , so the lobbyist prefers πG if and only if .
The left-hand side of the first inequality in condition (Equation A2) is increasing in while the right-hand side is decreasing in . As increases, the right-hand side shifts down. The value of that makes the two sides equal is therefore decreasing in , so is decreasing in .
2. Lobbyist only needs to persuade lower type:
The left-hand side of this inequality is from Equation (A3). The rest of the proof, therefore, follows the same logic as in the previous case.
I first show that the PM’s expected utility is always strictly higher when the lobbyist chooses πG than when her information is public for a given pair of interim beliefs (“if” statement). I then show that the PM’s expected utility is the same when the lobbyist chooses πT as when her information is public (“only if” statement).35
2. If the incentive constraint is not satisfied, confidentiality is not strictly preferred:
Therefore, for any , we have
When , the incentive constraint does not bind () and the optimal investigation induces . The PM is indifferent between any , so any can be in the support of an equilibrium investigation. Therefore, when , choosing is an equilibrium strategy for the PM.
When , the constraint binds () and the optimal investigation induces . Since is decreasing in and is independent of , it is optimal to induce . Therefore, when , the only equilibrium is for the PM to choose an investigation that induces and .
2. Lobbyist only needs to persuade lower type:
Suppose now that . Note that is unchanged in this case. I show that the PM now sometimes prefers to induce πT.
Claim 3: If the lobbyist were to choose πT, the PM would choose .
Proof: Taking derivatives of (Equation (A5)) for the case shows that is increasing in and decreasing in . Therefore, the optimal investigation given πT induces interim beliefs .
Claim 4: If , the PM strictly prefers .
Proof: As shown above, if , the PM induces the lobbyist to choose πG even when using . From the proof of Proposition 2, we know that
Finally, from claim 2, we have . Therefore if the incentive constraint does not bind (), the PM prefers .
Claim 5: If , there exists such that the PM prefers an investigation such that and to induce the lobbyist to choose πG if , and prefers an investigation such that and to induce the lobbyist to choose πT if .
Proof: If , the incentive constraint binds so the optimal investigation that induces πG generates interim beliefs and (claim 2). Given claim 3, if the PM’s investigation induces πT, it is optimal to generate interim beliefs and . To show the existence and uniqueness of , I proceed in three steps.
Step 1: At so by claim 4.
Step 3: As .
Therefore, and the PM eventually prefers to give up trying to induce πG.
Combining steps 1–3, and the intermediate value theorem implies that there exists a unique that satisfies Claim 5.
Claim 6: If , then the PM always prefers an investigation such that and to induce the lobbyist to choose πT.
Proof: Let such that . Note that if and only if , since for any B whenever . Let such that . If , then , so it is always possible to generate whenever it is possible to generate some , and the logic of Claim 5 applies. If , then .
For , the PM receives no information if she induces . Therefore inducing the lobbyist to generate some information requires breaking the incentive constraint, and the optimal investigation is the most informative investigation, which induces the lobbyist to choose a targeted strategy.
And since by step 2 of Claim 5, we know that is decreasing in B, we can conclude that it is never optimal for the PM to restrict her belief to to induce πG. We can define to prove the statement in Proposition 3.
Finally, for any for any B since whenever . In this case, it is always optimal to choose since any belief that would satisfy the incentive constraint is above and would therefore induce the lobbyist to produce no information. Setting again proves the statement in Proposition 3. Note that in these last two cases, the interval is empty and the PM always chooses .
1. Lobbyist does not need to persuade any type: Suppose that for any feasible pair of beliefs, : in this case, the lobbyist provides no information for any choice of investigation of the PM. The PM is therefore indifferent between any preliminary investigation, so choosing is an equilibrium. Setting proves Proposition 3 for this case.
Claims 1–6 then imply that the PM makes full use of her expertise if either or and otherwise distorts her investigation such that . □
First note that for any equilibrium investigation p, the lobbyist’s best response is determined by Lemma 2. Deviating to a different strategy would not affect the choice of investigation by the PM (since she moves first), but would lower the probability of persuading her. I next characterize features that any equilibrium must satisfy, and then show that there is always an equilibrium in which the PM chooses . Finally, I show that every other equilibrium yields the same payoff as this one.
Lemma 3.
If , there exists a set of equilibria in which the lobbyist chooses and the PM chooses a preliminary investigation which must induce but can induce any . In particular, is an equilibrium strategy for the PM.
Such equilibria exist only if .
Every equilibrium in this set yields the same payoff to the PM.
Proof. The proof proceeds in three steps.
Claim 1: If an equilibrium exists where is played, then .
A deviation to does not affect the strategy of the lobbyist, but changes (1) the relative likelihood of the two types of the PM and (2) the expected payoff conditional on r0 and s1, which now becomes instead of . The derivative of this expected utility function with respect to is negative and therefore it is always profitable to deviate to some .
Claim 2: In any strategy profile such that the PM chooses an investigation p that induces interim beliefs and the lobbyist chooses a persuasion strategy πG, the PM has no incentives to deviate to such that .
Proof: Such a deviation yields . Deviating to changes the expected payoff conditional on r0 and s1, which becomes instead of . The indirect expected utility is linear in this region, so the deviation payoff is independent of and there can be no gain.
Claim 3: In any strategy profile such that the PM chooses an investigation p that induces interim beliefs and the lobbyist chooses a persuasion strategy πG, the PM has no incentives to deviate to such that .
Proof: Such a deviation gives . Deviating to changes the expected payoff conditional on r1 and s1, which now becomes , but such that (since ). Because the indirect expected utility is linear in this region, the deviation payoff is independent of and there can be no gain.
Combining Claims 2 and 3 implies that the PM does not deviate from any investigation-inducing beliefs given that the lobbyist chooses πG. Given Lemma 2, if , that is, if (and not too small), the lobbyist does want to play πG so this is an equilibrium. This proves the “if” part of the existence statement.
In addition, since this holds for any such that , it holds in particular for , so is an equilibrium. And by Claim 3, the expected utility of the PM is the same for any , so it is the same across all equilibria.
If , then for any , so Lemma 2 implies that the lobbyist chooses πT if the PM’s strategy is such that . Suppose that the PM chose an investigation such that , then the lobbyist would choose strategy πG, but Claim 1 implies that the PM would then prefer to deviate to some . Therefore if there does not exist an equilibrium in which πG is played. This proves the “only if” part of the existence statement. □
Lemma 4.
If , there exists a set of equilibria in which the lobbyist chooses and the PM chooses an investigation which must induce and some . In particular, is an equilibrium strategy for the PM.
Such equilibria exist only if .
Every equilibrium in this set yields the same payoff to the PM, which is the same utility as if information was public.
Proof.
If , Lemma 3 implies that the only possible equilibrium involves πT.
Claim 1: If (), in any equilibrium where πT is played.
Proof: By contradiction, suppose there was an equilibrium where . In such an equilibrium, the PM would get utility because her posterior beliefs are always on the same linear portion of her expected utility function. If she deviates to inducing such that , then her posterior belief following s1 will be such that . This is therefore a profitable deviation.
Claim 2: If () the PM does not deviate from any investigation inducing , and any such that .
Proof: The PM’s expected utility in equilibrium is as defined in Equation (A5). When , this is equal to . Deviating to gives the same expected utility , independently of , so the PM would not deviate. Deviating to gives expected utility of . This is also the same as the equilibrium utility, independently of , so the PM would not deviate.
Claim 3: If () an investigation inducing and , and a persuasion strategy πT is the only equilibrium strategy profile.
Proof: The PM’s expected utility in equilibrium is as defined in Equation (A5). Deviating to an investigation that induces a pair of interim beliefs such that and gives: . Which is the same as when and , so the PM does not deviate to any and . This is the only equilibrium. Suppose there was an equilibrium such that interim beliefs were such that and with at least one inequality strict. The derivatives of each payoff function when deviating show that: (1) If , the PM would deviate to inducing , and (2) If , the PM would deviate to inducing .
Claims 1 and 2 imply that there exists a set of equilibria in which πT is played when , that all these equilibria yield the same payoff to the PM and that in one of these equilibria, the PM chooses . Claim 3 implies that when , there exists a unique equilibrium in which the lobbyist chooses πT and the PM chooses .
Finally, since the PM’s expected utility is the same under confidentiality with πT and transparency (Proposition 2), the two regimes yield the same utility whenever , so there are no gains from confidentiality in this case. □
Lemmas 3 and 4 imply Proposition 4: (a) If , then and πG is an equilibrium, all equilibria yield the same payoff to the PM as this one, and the PM’s utility is strictly greater than under transparency. (b) If , then and πT is an equilibrium, and when multiple equilibria exist, they all yield the same payoff to the PM as this one and the same payoff as under transparency. □
If and , then .
If and .
If and or if and if and only if .
If , as and .
If , .
Finally, when (or ), the PM uses the most informative investigation, the lobbyist either chooses a targeted strategy or provides no information, and the probability of error is the same under transparency and confidentiality. Therefore, the value of confidentiality is in all these cases.
To prove the second part of the proposition, let be the prior of an enemy, and be the symmetric prior for an ally. I show that in each case, .
If , then for an ally , while for an enemy .
If and , then .
If and , then . Note that is not possible as is decreasing in μ0 (see Claim 5 in proof of Proposition 3).
If and (note that since ), then which is strictly decreasing in μ0 (see Claim 5 in proof of Proposition 3), so .
If and , then which is strictly decreasing in μ0 (see Supplementary Appendix for details), so . Note that is not possible when .
Finally, when and .
If .
If , since (see Supplementary Appendix for details).
If , then we need to show that . Since in this case, is increasing in μ0 and is decreasing in μ0 (increasing in ), we just need to show that at for any . At simplifies to: , so if and only if . This is equivalent to , which always holds for any B.
If .
Suppose , since , there are two cases:
If as in case 3.
If .
Supplementary Material
Supplementary material is available at Journal of Law, Economics, & Organization online.
Funding
This work was supported by the Economic and Social Research Council grant number ES/J500070/1.
Conflict of interest statement. None declared.
I am deeply grateful to my supervisor Gilat Levy for invaluable guidance and to Ricardo Alonso and Stephane Wolton for precious advice. I would like to thank the editor and three anonymous referees for insightful suggestions, Simon Franklin, Andy Guess, Yingni Guo, Niall Hughes, Federica Izzo, Ronny Razin, Herschel Thomas, and Chris Tyson for helpful comments as well as seminar and conference participants at the LSE PSPE and Microeconomic Theory seminars, RES Junior Symposium 2018, MPSA Annual Conference 2018, LSE-Oxford Political Economy Conference, Queen Mary Economics and Finance Workshop, Max Plank Institute Political Economy workshop, and POLECON UK Conference 2019.


