Simple sequent systems for the modal logics K,D,T, and S4

Abstract

1 Introduction

Modal logics pose a long-standing challenge to proof theorists.¹ While their model theoretic accounts—in terms of various constraints on accessibility relations in Kripke models—are neat and transparent, there do not appear to be correspondingly elegant proof-theoretic accounts. The problem is how to formulate proof systems where, as for the non-modal connectives, the rules governing modal operators can be said to define their meanings. To be sure, axiomatic systems for modal logics are easy to formulate, but as is known, such systems are inadequate for meaning-theoretical purposes. Many natural deduction systems and sequent calculi of modal logics face analogous problems. Still other systems—notably, hypersequent and display calculi—are highly abstract, and so it is questionable whether they are fit for meaning-theoretical purposes, as they abstract away from our actual inferential practice.

Drawing on the recent literature on metainferences, I develop in the present paper a novel approach to this challenge, in the form of sequent calculi augmented with natural deduction-like rules for assuming and discharging sequents. Based on this approach, I introduce an elegant calculus for the modal logic |$S4$|⁠. Various discharging conditions on assumptions are shown to yield the weaker logics |$K,D$|⁠, and |$T$|⁠. The question of whether we can provide similar accounts of other systems such as |$B$| and |$S5$| will be left open, as a task for future research.

I proceed as follows. Section 2 sets the stage by introducing the model-theoretic accounts of |$K,D,T,$| and |$S4$|⁠, as well as their axiomatic proof systems. In Section 3, I introduce the basic sequent system that is going to be analyzed here, and prove that it is sound and complete with respect to |$S_{4}$|-Kripke models. In Section 4, I introduce various discharging conditions on assumptions that weaken the proof system of |$S4$|⁠, thereby yielding proof systems for |$K,D,$| and |$T$|⁠; I also establish soundness and completeness results for the latter systems, each with respect to its relevant class of models. I conclude with directions for future research.

2 The existing approaches

I work here with a propositional language |$\mathscr{L}$| that includes, besides the connectives |$\wedge ,\vee ,\neg $|⁠, and |$\supset $|⁠, the modal operator |$\square $|⁠. Let us recall that a Kripke Frame |$\mathscr{F}=<W_{\mathscr{F}},R_{\mathscr{F}}>$| is an ordered pair of a non-empty set of possible worlds (points of evaluation) |$W_{\mathscr{F}}$|⁠, and a binary accessibility relation |$R_{\mathscr{F}}\subseteq W_{\mathscr{F}}\times W_{\mathscr{F}}$|⁠. We denote by |$\mathbb{K}$| the class of all frames, by |$\mathbb{D}$| the class of all such frames in which the accessibility relation is directed, by |$\mathbb{T}$| the the class of all such frames in which the accessibility relation is reflexive, and by |$\mathbb{S}4$| the the class of all such frames in which the accessibility relation is both reflexive and transitive. A Kripke model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| is an ordered pair of a Kripke frame |$\mathscr{F}$| and |$\models _{M_{\mathscr{F}}}\subseteq W_{\mathscr{F}}\times \mathscr{L}$| (or simply |$\models $|⁠, where the relevant model is known) is a satisfaction relation. The semantic clauses for the connectives are regular, and for |$\square $| we have:

(1) |$w\models \square A$| iff for all |$w^{\prime}$| such that |$wRw^{\prime}$|⁠: |$w^{\prime}\models A$|⁠.

We say that a sentence |$A$| is valid with respect to some frame |$\mathbb{F}$| if there is no model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| (where |$\mathscr{F\in \mathbb{F}}$|⁠) such that, for some |$w\in W_{\mathscr{F}}$|  |$w\nvDash _{M_{\mathscr{F}}}A$|⁠; we say that a sequent |$\varGamma \Rightarrow \varDelta $| is valid with respect to some frame |$\mathbb{F}$| if there is no model |$M_{\mathscr{F}}$| (where |$\mathscr{F\in \mathbb{F}}$|⁠) such that, for some |$w\in W_{\mathscr{F}}$|⁠, |$w\models _{M_{\mathscr{F}}}\gamma $| for all |$\gamma \in \varGamma $| but |$w\nvDash _{M_{\mathscr{F}}}\delta $| for all |$\delta \in \varDelta $|⁠.

Let |$CL$| be some Hilbert-style proof system for classical logic.² We add to |$CL$| the rule of necessitation (⁠|$Nec$|⁠): |${\frac{A}{\square A}}$| (where the derivation of |$A$| does not involve any non-axiom premise). To generate axiomatic (Hilbert-style) proof systems for |$K,D,T,$| and |$S4$|⁠, we need the following axioms:

|$K$|⁠: |$\square (A\supset B)\supset (\square A\supset \square B)$|

|$D$|⁠: |$\square A\supset \neg \square \neg A$|

|$T$|⁠: |$\square A\supset A$|

|$S4$|⁠: |$\square A\supset \square \square A$|

To generate the system |$K$|⁠, we add the axiom |$K$| to |$CL+Nec$|⁠; to generate the system |$D$|⁠, we add the axiom |$D$| to the system |$K$|⁠; to generate the system |$T$|⁠, we add the axiom |$T$| to the system |$K$|⁠; and to generate the system |$S4$|⁠, we add the axiom |$S4$| to the system |$T$|⁠. It is known that |$S4$| is stronger than |$T$|⁠, which is stronger than |$D$|⁠, which is stronger than |$K$|⁠.

Now, the apparent problem with these axioms—and with the systems generated by these axioms—is that they are inadequate for meaning-theoretical purposes. Namely, the axioms do not reveal much about the meaning of the modal vocabulary—that is, of “necessarily,” or |$\square $|—that is at stake here. This problem is particularly important to those interested in proof-theoretic semantics. Thus, attempts were made to develop more transparent proof systems for these logics. Unfortunately, regular natural deduction systems and sequent calculi seem to face the same predicament (see, e.g. [2, 7, 8, 14, 18–20, 28, 30, 32]). For one thing, consider the list of “regular” sequent rules in Table 1, discussed in the literature. A sequent calculus for classical logic along with the rule |$K$| yields a sequent system for the modal logic |$K$| [30]; such a calculus along with |$K$| and |$D$| yields a sequent system for |$D$| [32]; such a calculus along with |$K$| and |$T$| yields a sequent system for |$T$| [20]; and such a calculus along with |$K$|⁠, |$T$|⁠, and |$S_{4}$| yields a sequent system for |$S4$| (ibid).

Table 1.

Open in new tab

Sequent rules for modal logics

Table 1.

Open in new tab

Sequent rules for modal logics

However, these rules—and thereby the resultant systems—lack what many authors take to be sine qua non properties in proof-theoretic semantics. Let me be more explicit here. The following is a (partial) list of such properties, along with explanations as to why the above rules violate them:³

1. Explicitness: A rule for an expression |$e$| is explicit if there is only one essential occurrence of |$e$| in the conclusion. This property guarantees that the rule defines only one status of a sentence at a time. Regarding the above rules, only |$T$| is explicit, and so none of the above systems enjoys explicitness as they all contain the |$K$| rule.

2. Symmetry: A set of rules for an expression |$e$| is symmetrical if each rule introduces |$e$| either on the left-hand side or on the right-hand side, and there is at least one rule for each side. This property guarantees that the rules specify |$e$|’s premisory and conclusory roles separately. None of the above systems enjoys that property, as they all contain the |$K$| rule that introduces |$\square $| on both sides (and the same goes for the |$S4$| rule.)

3. Non-Circularity: A set of rules for an expression |$e$| is non-circular if there is no essential occurrence of |$e$| in the premises of each rule. This property guarantees that the rules define |$e$| in a non-circular way. In this sense, |$S4$| is clearly circular.

All in all, it seems unclear whether we can provide simple and intuitive sequent systems (or natural-deduction systems, for that matter) for these logics that enjoy properties 1-3.

It is worth mentioning other kinds of systems that are discussed in the literature. First, there are approaches that enrich the object language with model-theoretic notions like relations between worlds (see, e.g. [18]); the problem with such systems is that there is something ad hoc about them, as they sneak in (to the syntax) model-theoretic notions. Second, there are abstract systems such as hypersequent and display calculi (see, e.g. [1, 15, 21, 23, 24, 26, 27, 35]); however, the notion of inference—with which sequents are naturally associated—is replaced in such systems by more abstract notions such as hypersequents. It is thus questionable whether such systems are fit for meaning-theoretical purposes, as they abstract away from our actual inferential practice.⁴

The present paper develops a novel technical approach to the challenge of accounting for modal logics proof-theoretically: regular sequent systems augmented with natural deduction-like rules for assuming and discharging sequents. As opposed to the sequent rules described above, the rules in my systems are all explicit, symmetrical, and non-circular; moreover, they enjoy the subformula property. I now turn to discuss the first (and main) system, which is a calculus for |$S4$|⁠.

3 A sequent system for |$S4$|

3.1 Proof theory

The underlying proof system for classical logic that will be in use throughout this paper is the sequent calculus in Table 2, known as |$G3cp$| [17, pp. 49–60].

Table 2.

Open in new tab

The |$G3cp$| sequent rules

Table 2.

Open in new tab

The |$G3cp$| sequent rules

The contexts are read here as sets rather than multisets, and so Contraction and Permutation are built-in properties. Here are some properties of this system: (i) even though the axioms are restricted to atomic formulas, one can prove by structural induction that for every formula |$A$| and sets of formulas |$\varGamma ,\varDelta $|⁠, the sequent |$\varGamma ,A\Rightarrow A,\varDelta $| is derivable; (ii) the operational rules of |$G3cp$| are all invertible; and (iii) weakening and cut are both admissible in |$G3cp$| (ibid).

Now, my goal in this paper is to add to |$G3cp$| rules for the modal expression |$\square $|⁠. Ideally, there should be left and right rules for |$\square $|⁠, allowing us to derive sequents like |$\varGamma ,\square A\Rightarrow \varDelta $| and |$\varGamma \Rightarrow \square A,\varDelta $|⁠, respectively, where (i) the contexts |$\varGamma ,\varDelta $| are arbitrary, (ii) |$A$| occurs unembedded (at least once) in the premises of each rule, and (iii) |$\square A$| does not occur (unembedded or otherwise) in any such premise.

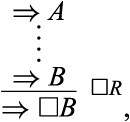
As for the right rule, a natural candidate suggests itself: the |$Nec$| rule from the axiomatic systems. Articulated in a sequent calculus setting, this rule takes the form: |$ {\frac{\Rightarrow \square A}{\Rightarrow A}{\square\textrm{R}}}$|⁠.⁵ Moreover, |$\square R$| gives us a proof-theoretic indication of the meaning of the expression |$\square A$|⁠. For there is a long-standing tradition in proof-theoretic semantics according to which the introduction/right rules of a given expression specify the meaning of that expression (see, e.g. [6, 25]). According to this tradition, then, the meaning of |$\square A$| amounts to the claim that |$A$| is a theorem, i.e. derivable from no premises.⁶

How should we understand the sequent |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, given the above account of the meaning of |$\square A$|? Simply put, this sequent amounts to the claim that |$\varDelta $| follows from the set of assumptions |$\varGamma $| together with the assumption that |$A$| is a theorem. Notice that by this account, |$A$| is merely assumed to be a theorem—this is just one of our assumptions—but it need not be a theorem as a matter of fact. That is to say, |$\varGamma ,\square A\Rightarrow \varDelta $| may be derivable even in cases where |$A$| is not a theorem.⁷

How do we express such an assumption? I would like to rely here on recent literature that suggests augmenting sequent calculi with natural deduction-like rules for assuming and discharging sequents [10–12]. In essence, these papers suggest integrating into our calculus “assumed sequents” that need not be derivable. Thus, we may assume |$\Rightarrow A$|—and thereby assume that |$A$| is a theorem—regardless of whether |$A$| is actually a theorem. Whenever such an assumption gives us what we need—i.e. a proof of |$\varDelta $| from |$\varGamma $|—we may discharge it and derive the sequent |$\varGamma ,\square A\Rightarrow \varDelta $|⁠. In this way, we arrive at the following rule:

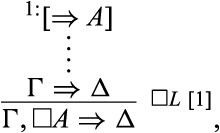
where the assumption |$\Rightarrow A$| is presented within square brackets and the superscript |$1$| is not part of the syntax, but rather is meant to keep track of our assumptions that need to be discharged. Assumption |$1$| is discharged in the last step of the derivation, and the derivation marked by the four dots—namely, the derivation of |$\varGamma \Rightarrow \varDelta $| from |$\Rightarrow A$|—may involve more than one leaf (and so more than one assumption).⁸ At this point, we do not impose any special constraints on the derivation of |$\varGamma \Rightarrow \varDelta $| from |$\Rightarrow A$|⁠; we will do so later, in order to generate various modal logics. Here is a formal definition of derivability in |$G3cp+\square R+\square L$|⁠:

Notice that |$\square L$| and |$\square R$| are explicit, symmetric, and non-circular: there is only one essential occurrence of |$\square $| in the conclusion of each rule, there is no essential occurrence of |$\square $| in the premise of each rule, and |$\square L,\square R$| are in the form of left/right rules, respectively. Moreover, these rules enjoy the subformula property. For |$\square R$|⁠, this is obvious. For |$\square L$|⁠, we first need to extend the property to cases where sequents are assumed and discharged. The following is a natural such extension: |$\Rightarrow A$| and |$\varGamma \Rightarrow \varDelta $| contain only formulas that are subformulas of formulas in |$\varGamma ,\square A\Rightarrow \varDelta $|⁠.⁹

Now, the following lemma will prove useful:

Proof.

As usual, the proof proceeds by induction on the structure of |$A$|⁠. The only special case that we need to consider here is where |$A$| is of the form |$\square B$|⁠. In that case, we reason as follows:

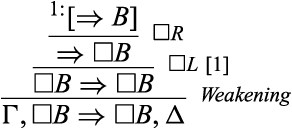
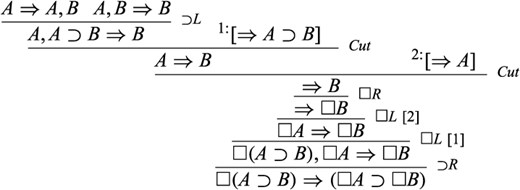
Next, I would like to point out that |$\square R$| and |$\square L$| fit together productively: axioms |$K,D,T$|⁠, and |$S_{4}$| can all be derived in |$G3cp+\square R+\square L$|⁠.¹⁰ The derivation of |$K$| goes as follows:

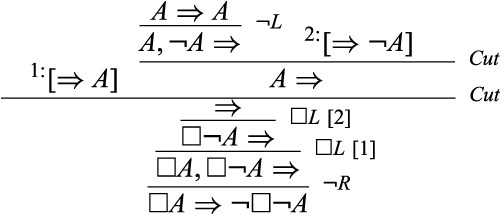
The derivation of |$D$| goes as follows:

The derivation of |$T$| is much simpler, as it involves only one assumption, which is discharged at once:

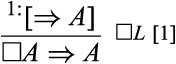
and the derivation of |$S4$| is somewhat similar:

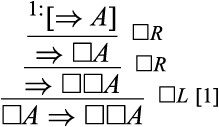
Let me stress what has been achieved so far: not only do |$\square R$| and |$\square L$| have attractive proof-theoretic properties—as opposed to the rules discussed in Section 2—but we can also derive from |$\square R$| and |$\square L$| no less than four different axioms that are characteristic of central modal systems! Thus, I claim, |$\square R$| and |$\square L$| together form an elegant set of rules, and the method of assuming and discharging sequents has proven itself quite valuable.

We may add possibility rules that parallel the necessity ones to the above system, by flipping the sides. Thus, the left possibility rule will be of the form |$ {\frac{\lozenge A\Rightarrow }{A\Rightarrow } {}^{_{\lozenge L}}}$|⁠, and the right possibility rule will be of the form:

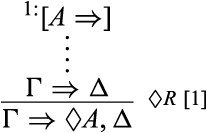
Having added these rules, one can show that the resultant system allows for the (cut-free) derivation of the interdefinability of possibility and necessity. Namely, the following sequents are cut-free derivable: |$\neg \square \neg A\Rightarrow \lozenge A$|⁠, |$\lozenge A\Rightarrow \neg \square \neg A$|⁠, |$\neg \lozenge \neg A\Rightarrow \square A$|⁠, and |$\square A\Rightarrow \neg \lozenge \neg A$|⁠. For the sake of simplicity, though, the possibility rules will not be discussed here any further.

I conclude the proof-theoretic presentation of |$G3cp+\square R+\square L$| with some comments on the eliminability of Cut in it. To begin with, notice that Cut is not entirely eliminable in this system, as can be seen, e.g. in the above derivation of axiom |$D$|⁠. The problem is that, even though the applications of Cut can all be “pushed” up a given proof tree, there is no way to push these applications beyond assumptions or applications of |$\square L$|⁠; and, as opposed to a cut on axioms, a cut on assumptions and sequents of the form |$\varGamma ,\square A\Rightarrow \varDelta $| that are derived by |$\square L$| cannot always be dispensed with.

In response, I would like to make two points. First, for many logicians, cut-elimination is a virtue because it guarantees conservativity (see, e.g. [6, pp. 217–220, 250]). But |$\square R$| and |$\square L$| form a conservative extension of |$G3cp$| anyway, as guaranteed by the |$S4$| soundness theorem result below (Corollary 3.8). That is to say, if a sequent |$\varGamma \Rightarrow \varDelta $| whose expressions are taken from the fragment of the language that does not contain the |$\square $| operator is derivable in |$G3cp+\square R+\square L$|⁠, then it is already derivable solely with the |$G3cp$| rules. Otherwise, there would be a Boolean valuation function |$v$| that poses a counterexample to |$\varGamma \Rightarrow \varDelta $|⁠; it is then a simple exercise to construct an |$S4$|-Kripke model that poses a counterexample to |$\varGamma \Rightarrow \varDelta $|⁠, contradicting Corollary 3.8.¹¹

Secondly, it is worth mentioning that we can push all such applications of Cut as far up the proof tree as possible. One way of putting this accurately is to say that Cut is semi-eliminable in this system: if |$\varGamma \Rightarrow \varDelta $| is derivable in |$G3cp+\square R+\square L$|⁠, then it is derivable by a proof tree in which each application of Cut is immediately preceded either by an application of |$\square L$|⁠, or by an assumption.

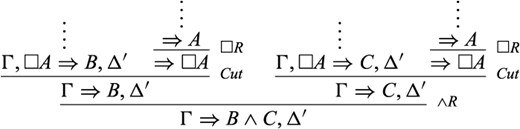
The proofs of the other operational rules are analogous.

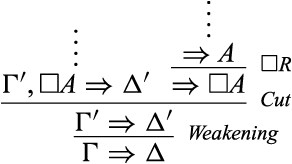
2.2. |$\varGamma ,\square A\Rightarrow \varDelta $| is derived by Weakening. If we weaken with |$\square A$| (and perhaps other formulas in |$\varGamma \cup \varDelta $|⁠), then |$\varGamma ,\square A\Rightarrow \varDelta $| is derived from |$\varGamma ^{\prime}\Rightarrow \varDelta ^{\prime}$|⁠, where |$\varGamma ^{\prime}\subseteq \varGamma ,\varDelta ^{\prime}\subseteq \varDelta $|⁠. Hence, we may immediately derive |$\varGamma \Rightarrow \varDelta $| by Weakening, thereby eliminating the cut application altogether. Otherwise, |$\varGamma ,\square A\Rightarrow \varDelta $| is derived from |$\varGamma ^{\prime},\square A\Rightarrow \varDelta ^{\prime}$|⁠, where |$\varGamma ^{\prime}\subseteq \varGamma ,\varDelta ^{\prime}\subseteq \varDelta $|⁠. We may then “push” the application of Cut upward in the following way:

3. The cut-formula is principal in the derivation of |$\varGamma ,\square A\Rightarrow \varDelta $| but not in the derivation of |$\varSigma \Rightarrow \square A,\varPi $|⁠. Therefore, |$\varGamma ,\square A\Rightarrow \varDelta $| is derived by |$\square L$|⁠, and so there is a derivation of |$\varGamma \Rightarrow \varDelta $| from |$\Rightarrow A$|⁠. Notice that for Cut to be semi-eliminable, we only need to prove that its application can be pushed up the branch of |$\varSigma \Rightarrow \square A,\varPi $|⁠. There are three general subcases:

3.1. |$\varSigma \Rightarrow \square A,\varPi $| is derived by Weakening. If we weaken with |$\square A$|⁠, then |$\varSigma \Rightarrow \square A,\varPi $| is derived from |$\varSigma ^{\prime}\Rightarrow \varPi ^{\prime}$| where |$\varSigma ^{\prime}\subseteq \varSigma ,\varPi ^{\prime}\subseteq \varPi $|⁠. Hence, one application of Weakening gives us:

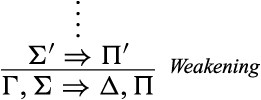
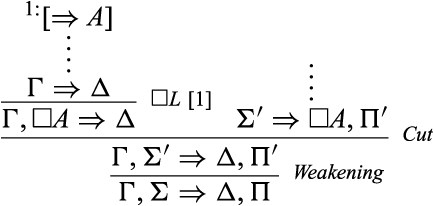
and so we can completely dispense with the cut application in this case. Otherwise, |$\varSigma \Rightarrow \square A,\varPi $| is derived from |$\varSigma ^{\prime}\Rightarrow \square A,\varPi ^{\prime}$|⁠, where |$\varSigma ^{\prime}\subseteq \varSigma ,\varPi ^{\prime}\subseteq \varPi $|⁠. We may then “push” the application of Cut upward as follows:

3.2. |$\varSigma \Rightarrow \square A,\varPi $| is derived by an operational rule of |$G3cp$|⁠, with one or two premise-sequent(s) of the form |$\varSigma ^{\prime}_{i}\Rightarrow \square A,\varPi ^{\prime}_{i}$| (⁠|$i=1,2$|⁠). The general strategy here is to cut on the premise-sequents before applying the operational rule. For example, suppose that |$\varSigma \Rightarrow \square A,\varPi $| is of the form |$\varSigma ^{\prime},B\vee C\Rightarrow \square A,\varPi $| (where |$\varSigma ^{\prime}=\varSigma \backslash \{B\vee C\}$|⁠), and that it is derived by |$\vee L$| from |$\varSigma ^{\prime},B\Rightarrow \square A,\varPi $| and |$\varSigma ^{\prime},C\Rightarrow \square A,\varPi $|⁠. We then reason as follows:

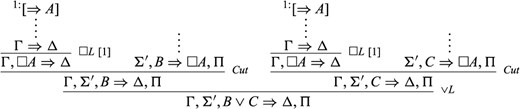
The proofs of the other operational rules are analogous.

3.3. |$\varSigma \Rightarrow \square A,\varPi $| is derived by |$\square L$|⁠, in which case there is nothing to prove for semi-eliminability.

4. The cut-formula is not principal in the derivation of either sequent. It follows that the last step in the derivation of each sequent involves only the |$G3cp$| rules, and so the proof proceeds as in Negri and von Plato.

3.2 Model theory

We now turn to the task of proving that |$G3cp+\square R+\square L$| is sound and complete with respect to models of |$\mathbb{S}4$| frames, starting with soundness. To begin with, since this system involves a rule that allows us to assume and discharge sequents, we have to deal with the question of what it even means for such a rule to be “sound.” To answer this question, observe that a move like that of inferring |$\varGamma \Rightarrow \varDelta $| from |$\Rightarrow A$|—i.e. an inference between inferences—is sometimes being called a “metainference” in the literature.¹² The sequent |$\Rightarrow A$| plays the role of a premise-inference in that metainference, whereas the sequent |$\varGamma \Rightarrow \varDelta $| plays the role of a conclusion-inference in it. Needless to say, such metainferences may also be of the form —i.e. involve more than one premise-inference—in case we apply |$\square L$| several times in the proof tree.

Now, one can find in the literature (e.g. [3, 9, 13]) two criteria for assessing metainferences model-theoretically, known as the global and the local notions of metainferential validity:

1. According to the global notion, metainferential validity is a matter of validity preservation. That is, a metainference is globally valid if, given that its premiss-inferences are all valid, its conclusion-inference is valid too.

2. According to the local notion, metainferential validity is a matter of satisfaction preservation. That is, a metainference is locally valid if there is no model that satisfies its premiss-inferences, but does not satisfy its conclusion-inference.¹³

The debate over which of these two criteria is better is an ongoing issue in the philosophy of logic (ibid), but we need not engage with it here. For, the global notion is clearly unfit for the purpose of the present paper, i.e. for assessing metainferences with a premise-inference of the form |$\Rightarrow A$|⁠.¹⁴ To see this, notice that assessing |$\Rightarrow A$| globally necessarily results in one of the following scenarios:

(i) |$A$| is a theorem, and so the mechanism of assuming and discharging sequents does not make any contribution to |$G3cp+\square R$| : if |$A$| is a theorem then we may derive |$\varGamma \Rightarrow \varDelta $| without any assumption, and |$\varGamma ,\square A\Rightarrow \varDelta $| then follows by one application of Weakening.

(ii) |$A$| is not a theorem, and so the metainference is globally valid vacuously, no matter what |$\varGamma ,\varDelta $| are. In that case, |$\square L$| is unsound. For example, if |$p$| and |$q$| are atoms then the metainference |$ {\frac{\Rightarrow p} {\Rightarrow q}}$| is globally valid vacuously, because there are some models that do not satisfy |$p$|⁠. Thus, in the global reading, the following application of |$\square L$|⁠:

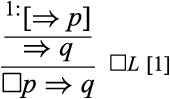
has a valid premise (i.e. the metainference |$ {\frac{\Rightarrow p}{\Rightarrow q}}$|⁠), but an invalid conclusion (i.e. the sequent |$\square p\Rightarrow q$|⁠). In sum, in the global reading the applications of |$\square L$| are trivial in some cases and unsound in others.

By contrast, the local reading requires that we focus exclusively on those Kripke models that satisfy |$\Rightarrow A$|⁠, and then check whether some such models do not satisfy |$\varGamma \Rightarrow \varDelta $|⁠. On the face of it, then, the local reading seems a more promising criterion for assessing whether metainferences of the form are valid. Let us therefore adopt this criterion, and see what follows.

Before we do so, however, we need to say more about what it means for a model to satisfy a sequent. After all, the local criterion draws on satisfaction preservation rather than validity preservation. Let |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| be some Kripke model. What does it mean to say that |$M_{\mathscr{F}}$| satisfies sequents like |$\Rightarrow A$| and |$\varGamma \Rightarrow \varDelta $|? At first glance, one may be tempted to assess such satisfaction in terms of not posing a counterexample. Thus, |$M_{\mathscr{F}}$| will be said to satisfy a given sequent |$\varGamma \Rightarrow \varDelta $| if it does not pose a counterexample to that sequent: either |$M_{\mathscr{F}}\nvDash _{M_{\mathscr{F}}}\gamma $| for some |$\gamma \in \varGamma $|⁠, or |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\delta $| for some |$\delta \in \varDelta $|⁠; indeed, satisfaction is often cashed out in such terms in the literature on metainferences (ibid). Notice that this idea seems to rely on associating each such sequent with a corresponding sentence. Thus, a sequent of the form |$\varGamma \Rightarrow \varDelta $| is naturally associated with the sentence |$\bigwedge \varGamma \supset \bigvee \varDelta $|⁠.

Now, for my purposes here a slightly different notion of satisfaction is required, which can be motivated along the following lines. As opposed to extensional languages, I work in this paper with an intensional language that contains the |$\square $| operator. In this context, there is at least some plausibility in associating a sequent of the form |$\varGamma \Rightarrow \varDelta $| with the sentence |$\square (\bigwedge \varGamma \supset \bigvee \varDelta )$|⁠. After all, such a sequent expresses a claim of a modal nature; it tells us that necessarily one of the following is the case: either some |$\gamma \in \varGamma $| does not hold, or some |$\delta \in \varDelta $| holds.¹⁵ Adopting this latter notion, we will say that a Kripke model |$M$| satisfies a sequent |$\varGamma \Rightarrow \varDelta $| iff |$M\models \square (\bigwedge \varGamma \supset \bigvee \varDelta )$|⁠. Hence, we arrive at the following definitions:

Based on Definition 4, we finally get our local criterion for assessing metainferences in |$G3cp+\square R+\square L$| model-theoretically:

1. The derivation of |$T$| is the easiest. Assume that |$\varGamma ,A\Rightarrow \varDelta $| is derivable. We reason as follows:

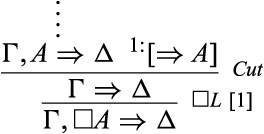
2. We derive the instances of |$K$| by induction on the cardinality of |$\varGamma $|⁠. If |$\varGamma =\emptyset $| then we assume that |$\Rightarrow A$| is derivable, and so one instance of |$\square R$| does the job. If |$\varGamma =\{\gamma \}$| (a singleton) then we assume that |$\gamma \Rightarrow A$| is derivable. We then reason as follows:

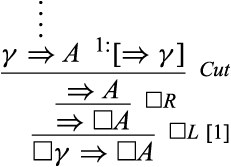
Assume now that |$\varGamma =\{\gamma _{1},...,\gamma _{n+1}\}$|⁠. We then assume that |$\gamma _{1},...,\gamma _{n},\gamma _{n+1}\Rightarrow A$| is derivable. We reason as follows:

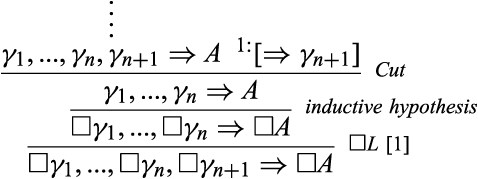
3. Likewise, we derive the instances of |$S4$| by induction on the cardinality of |$\varGamma $|⁠. If |$\varGamma =\emptyset $| then we assume that |$\Rightarrow A$| is derivable, and so one instance of |$\square R$| does the job. If |$\varGamma =\{\gamma \}$| (a singleton) then we assume that |$\square \gamma \Rightarrow A$| is derivable. We then reason as follows:

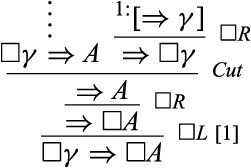
Assume now that |$\varGamma =\{\gamma _{1},...,\gamma _{n+1}\}$|⁠, and that |$\square \gamma _{1},...,\square \gamma _{n},\square \gamma _{n+1}\Rightarrow A$| is derivable. We then reason as follows:

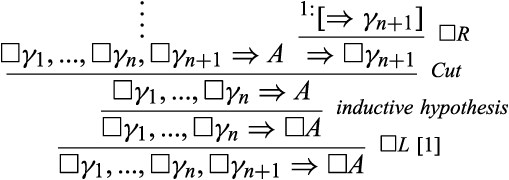
4 |$K,D$|⁠, and |$T$|

|$G3cp+\square R+\square L$| is a proof system for |$S4$|⁠, which is stronger than |$K,D$|⁠, and |$T$|⁠. Therefore, to generate proof systems for |$K,D$|⁠, and |$T$| we have to somehow weaken |$G3cp+\square R+\square L$|⁠. In particular, we have to weaken |$\square L$|⁠, since all the other rules and axioms are derivable in these systems. To be specific, notice that |$\square L$| lets us assume and discharge sequents unrestrictedly. Therefore, to weaken this rule, we shall impose restrictions on reasoning within the scope of assumptions; those restrictions will actually serve as discharging conditions on assumptions.

Now, the restrictions presented below are somewhat complicated. As of yet, I have not found a way to explain them intuitively. The rationale behind those restrictions, however, is explainable: each restriction is meant to block some of the above derivations of the axioms. Bearing Lemma 3.6 in mind, one may understand why they model-theoretically work the way they do. The reader may also notice that the restrictions below are modular, in the sense that each one is independent of the others. Thus, there is no problem getting other subsystems of S4 by combining these restrictions in various ways (see footnote 17 for an example).

At any rate, the systems below are all sub-systems of the above |$S4$| calculus; as such, they can be looked upon as (admittedly cumbersome) ways of recovering |$K,D$|⁠, and |$T$| within the intuitive framework laid out above. I now turn to introduce the appropriate restrictions for each system.

4.1 A sequent system for |$K$|

Model-theoretically, the intuition behind |$\square _{K}L$| relies on part (ii) of Lemma 3.6, namely, that for every world |$w\in W_{\mathscr{F}}$|⁠: |$w\models _{M_{\mathscr{F}}}\Rightarrow A$| iff |$w\models _{M_{\mathscr{F}}}\square A$|⁠. Consequently, the assumption |$\Rightarrow A$| amounts to exclusively focusing on models in which |$\square A$| is true. Hence, the need to make use of |$\square R$| at least once: a model does not pose a counterexample to whatever is derived from this assumption unless |$\square A$| is false in it. To be more concrete, suppose that we derive |$\varGamma \Rightarrow \varDelta $| from |$\Rightarrow A$|⁠, then part (ii) of Lemma 3.6 guarantees that for every model, either |$\square A$| is false (in which case we focus on the wrong model), or the model does not pose a counterexample to |$\varGamma \Rightarrow \varDelta $|⁠. However, |$\square R$| cannot be used more than once because that would entail that |$w\models _{M_{\mathscr{F}}}\Rightarrow A$| guarantees |$w\models _{M_{\mathscr{F}}}\square \square A$|⁠, which is true (according to Lemma 3.6) only of |$S4$| models.

Now, the following theorem will be useful for establishing soundness:

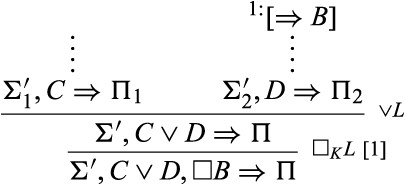
We can then “push” the application of |$\square _{K}L$| above the application of |$\vee L$| in the following way:

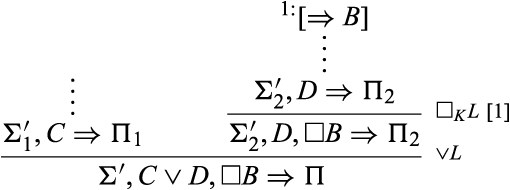
As I said, the other cases are all proved analogously.

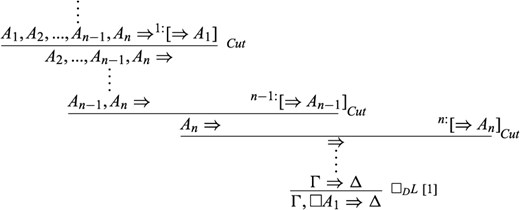
where the derivation of |$\Rightarrow B$| from |$\Rightarrow A$| involves only |$G3cp$| rules.

Now, if |$M_{\mathscr{F}}\nvDash _{M_{\mathscr{F}}}\Rightarrow A$|⁠, then part (ii) of Lemma 3.6 gives us |$M\nvDash _{M_{\mathscr{F}}}\square A$|⁠, and so |$M_{\mathscr{F}}$| does not pose a counterexample to |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, as required. Otherwise, |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\Rightarrow A$|⁠. Since the derivation of |$\Rightarrow B$| from |$\Rightarrow A$| involves only |$G3cp$| rules, and part (i) of Lemma 3.6 guarantees that if |$M_{\mathscr{F}}$| satisfies the premise-sequent(s) of some |$G3cp$| rule it satisfies its conclusion-sequent, it follows by induction on proof height that |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\Rightarrow B$|⁠. By part (ii) of Lemma 3.6 we then get |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\square B$|⁠, and so |$M_{\mathscr{F}}$| does not pose a counterexample to |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, which is |$\square A\Rightarrow \square B$|⁠, as required.

It remains to deal with the case where the derivation of |$\varGamma ,\square A\Rightarrow \varDelta $| makes use not only of the assumption |$\Rightarrow A$|⁠, but of other assumptions, say, |$\Rightarrow C_{1},...,\Rightarrow C_{n}$|⁠. Once again we assume, based on Theorem 4.2, that |$\varGamma ,\square A\Rightarrow \varDelta $| is derivable with a proof tree in which each assumption is discharged immediately below the application of |$\square R$| in its branch, and work with that tree. Thus, |$\varGamma ,\square A\Rightarrow \varDelta $| is the bottom sequent of that tree, and it is derived by an application |$\square _{K}L$| immediately after the application of |$\square R$| in the branch, possibly with some other applications of |$\square _{K}L$| in-between, but with no application of other rules in-between. It follows in particular that no two-premise rule is applied in this branch below the application of |$\square R$|⁠. That is to say, any other branch in the tree must be combined with the branch of the assumption |$\Rightarrow A$| above the application of |$\square R$| in the latter branch. Which is to say, the application of |$\square R$| in the branch of |$\Rightarrow A$| is common to all the other branches in the tree, and so it is the only application of |$\square R$| in the tree. In this case, the situation must be as follows: |$\varGamma =\square C_{1},...,\square C_{n}$|⁠, and |$\varDelta =\{\square B\}$| and the tree looks like this:

Now, if |$M_{\mathscr{F}}\nvDash _{M_{\mathscr{F}}}\Rightarrow C_{i}$| for some |$1\leq i\leq n$| then, by part (ii) of Lemma 3.6, |$M\nvDash _{M_{\mathscr{F}}}\square C_{i}$|⁠, and so |$M_{\mathscr{F}}$| does not pose a counterexample to |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, which is |$\square C_{1},...,\square C_{n},\square A\Rightarrow \square B$|⁠, as required. For the same reason, if |$M_{\mathscr{F}}\nvDash _{M_{\mathscr{F}}}\Rightarrow A$| then |$M_{\mathscr{F}}$| does not pose a counterexample to |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, as required. Otherwise, |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\Rightarrow C_{i}$| for all |$1\leq i\leq n$| and |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\Rightarrow A$|⁠. As before, we then get by induction on proof height that |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\Rightarrow B$|⁠; after all, above the application of |$\square R$| there are only |$G3cp$| rules, and part (i) of Lemma 3.6 guarantees that if |$M_{\mathscr{F}}$| satisfies the premise-sequent(s) of some |$G3cp$| rule, it satisfies its conclusion-sequent. By part (ii) of Lemma 3.6, we then get |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\square B$|⁠, and so |$M_{\mathscr{F}}$| does not pose a counterexample to |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, which is |$\square C_{1},...,\square C_{n},\square A\Rightarrow \square B$|⁠, as required.¹⁷

4.2 A sequent system for |$D$|

Proof.

For completeness, notice that the derivation of the sequent rule |$K$| in Theorem 3.9 meets the |$\square _{D}L$| requirement. It thus remains to prove that the |$D$| rule is derivable in |$G3cp+\square R+\square _{D}L$| since |$G3cp+K+D$| is complete with respect to |$D$|-Kripke models [32]. Assume that |$\varGamma =\{\gamma _{1},...,\gamma _{n}\}$|⁠, and that |$\varGamma \Rightarrow $| is derivable. We then reason as follows:

For soundness, we have to show in particular that |$\square _{D}L$| is sound.¹⁸ Suppose that we derive |$\varGamma ,\square A\Rightarrow \varDelta $| by |$\square _{D}L$|⁠, and that the derivation of |$\varGamma \Rightarrow \varDelta $| from |$\Rightarrow A$| involves |$n$| assumptions |$\Rightarrow A_{1},...,\Rightarrow A_{n}$|⁠, where |$A=A_{1}$|⁠. Since Theorem 4.3 establishes the soundness of |$\square _{K}L$| with respect to all Kripke models (regardless of classes of frames), and since every |$D$|-Kripke model is a |$K$|-Kripke model, we only need to prove the case where each assumption is discharged by the empty sequent in its branch. Thus, we may safely assume that no application of |$\square R$| occurs in the proof tree of |$\varGamma ,\square A\Rightarrow \varDelta $| and so only the |$G3cp$| rules and |$\square _{D}L$| are used in that derivation. We now argue as follows, in five steps:

1. All the rules of |$G3cp+\square R+\square _{D}L$| except for Cut enjoy the subformula property, and so each derivation of the empty sequent in the tree is achieved by an application of Cut. We now carry out the following procedure:

1.1. Following Theorem 3.3, we “push” all the applications of Cut up the proof tree so that each such application is immediately preceded either by an application of |$\square _{D}L$| or by an assumption.

1.2. Following Lemma 4.5, we “push” all the applications of |$\square _{D}L$| up the proof tree so that each such application is immediately preceded by an application of Cut.

We carry out steps 1.1 and 1.2 repeatedly for as long as possible. The result is a proof tree of |$\varGamma ,\square A\Rightarrow \varDelta $| in which each application of Cut is not preceded by any |$G3cp$| rule. Thus, each assumption is being cut immediately after it is introduced.

2. There aren’t many such proof trees. One option is the following proof tree:

(1)

where the sequent |$A_{1},...,A_{n}\Rightarrow $| is derivable. In other options the applications of Cut are made in different orderings, e.g.

(2)

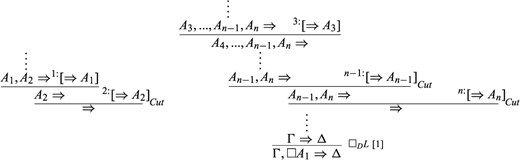
where both |$A_{1},A_{2}\Rightarrow $| and |$A_{3},...,A_{n-1},A_{n}\Rightarrow $| are derivable.

Now, notice that we can easily transform derivation (2) into derivation (1) because if |$A_{1},A_{2}\Rightarrow $| is derivable, then one application of Weakening gives us |$A_{1},...,A_{n}\Rightarrow $|⁠, which is the starting point of derivation (1). For the same reason, one can easily convince oneself that each and every other proof tree—in which each assumption is cut immediately after it is introduced—can be transformed into derivation (1). Thus, we may safely assume that we are working here with the proof tree of derivation (1).

3. Given that there are no applications of |$\square R$| in the tree, we may safely assume by Lemma 4.5 that we are working with a proof tree in which the assumptions are all discharged successively, immediately below the derivation of the empty sequent. That is, we may safely assume that we are working here with the following proof tree:

(3)

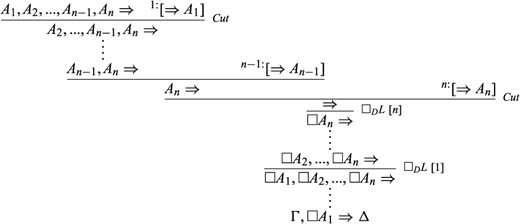
4. Now, |$A_{1},...,A_{n}\Rightarrow $| is derivable. By the inductive hypothesis, there is no frame |$\mathscr{F}\in \mathbb{D}$| and model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| such that |$M_{\mathscr{F}}$| poses a counterexample to |$A_{1},...,A_{n}\Rightarrow $|⁠. That is to say, there is no frame |$\mathscr{F}\in \mathbb{D}$| and model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| such that |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}A_{i}$| for all |$1\leq i\leq n$|⁠. Since the accessibility relation in such models is directed, it follows that there is no frame |$\mathscr{F}\in \mathbb{D}$| and model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| such that |$M_{\mathscr{F}}\models _{M_{\mathscr{F}}}\square A_{i}$| for all |$1\leq i\leq n$|⁠. Therefore, there is no frame |$\mathscr{F}\in \mathbb{D}$| and model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| such that |$M_{\mathscr{F}}$| poses a counterexample to |$\square A_{1},...,\square A_{n}\Rightarrow $|⁠.

5. Notice that the derivation of |$\varGamma ,\square A\Rightarrow \varDelta $| from |$\square A_{1},...,\square A_{n}\Rightarrow $| (in derivation (3)) does not include any application of |$\square _{D}L$|⁠, since all the assumptions have already been discharged above the derivation of |$\square A_{1},...,\square A_{n}\Rightarrow $| in the proof tree. By the inductive hypothesis of the soundness proof—namely, that all the rules except for |$\square _{D}L$| are sound—we get that there is no frame |$\mathscr{F}\in \mathbb{D}$| and model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| such that |$M_{\mathscr{F}}$| poses a counterexample to |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, which is what we wanted to prove.

4.3 A sequent system for |$T$|

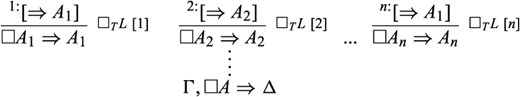
Now, it is clear that there is no frame |$\mathscr{F}\in \mathbb{T}$| and model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| such that |$M_{\mathscr{F}}$| poses a counterexample to some instance of the (sequent version of the) |$T$| axiom that occurs in this tree. Moreover, below those instances only |$G3cp$| rules are applied. It thus follows by the inductive assumption of the soundness proof—namely, that all the other rules are sound—that there is no frame |$\mathscr{F}\in \mathbb{T}$| and model |$M_{\mathscr{F}}=<\mathscr{F},\models _{M_{\mathscr{F}}}>$| such that |$M_{\mathscr{F}}$| poses a counterexample to |$\varGamma ,\square A\Rightarrow \varDelta $|⁠, as required.

5 Conclusion

Drawing on the recent literature on metainferences, I have presented a novel proof-theoretic approach to modal logics: regular sequent systems augmented with natural deduction-like rules for assuming and discharging sequents. Based on this approach, I have introduced remarkably simple calculi for the modal logics |$K,D,T,$| and |$S4$|⁠. The only differences between these calculi lie in the discharging conditions on assumptions. The rules in the resultant systems have attractive properties: they are explicit, symmetrical, and non-circular, and they enjoy the subformula property.

To conclude, I would like to point out one issue, namely, the question of whether my approach is applicable to other modal logics. It seems particularly interesting to inquire whether the modal logics |$B$| and |$S5$| can be accounted for in similar terms. As of now, I don’t have an answer to this question, and so I leave it as an open question for future research.

Acknowledgements

I would like to thank Robert Brandom, Ulf Hlobil, Ryan Simonelli, and Shuhei Shimamura for fruitful discussions.

Footnotes

11

In addition, there are reasons to develop a more nuanced criterion of harmony for such a system. Needless to say, a full discussion of this point goes beyond the scope of the paper. Let me nevertheless point out that the |$\square $| rule do meet something like a levelling of local peaks criterion for a sequent setting. For, suppose that |$\square A$| is introduced and eliminated at once. In a sequent system, this amounts to a cut on |$\square A$| immediately after it is derived on both sides by the |$\square $| rules, namely,

In this case, |$\Rightarrow A$| is derivable, and there is also a derivation of |$\varGamma \Rightarrow \varDelta $| from |$\Rightarrow A$|⁠, which means that the latter sequent is derivable too. Namely, we can derive |$\varGamma \Rightarrow \varDelta $| directly from |$\Rightarrow A$|⁠, without the detour of the |$\square $| rules.

References