-
PDF
- Split View
-
Views
-
Cite
Cite
Ivan Chajda, Helmut Länger, Algebraic structures formalizing the logic with unsharp implication and negation, Logic Journal of the IGPL, Volume 33, Issue 1, February 2025, Pages 36–48, https://doi.org/10.1093/jigpal/jzad023
Close - Share Icon Share
Abstract
It is well-known that intuitionistic logics can be formalized by means of Heyting algebras, i.e. relatively pseudocomplemented semilattices. Within such algebras the logical connectives implication and conjunction are formalized as the relative pseudocomplement and the semilattice operation meet, respectively. If the Heyting algebra has a bottom element |$0$|, then the relative pseudocomplement with respect to |$0$| is called the pseudocomplement and it is considered as the connective negation in this logic. Our idea is to consider an arbitrary meet-semilattice with |$0$| satisfying only the Ascending Chain Condition (these assumptions are trivially satisfied in finite meet-semilattices) and introduce the operators formalizing the connectives negation |$x^{0}$| and implication |$x\rightarrow y$| as the set of all maximal elements |$z$| satisfying |$x\wedge z=0$| and as the set of all maximal elements |$z$| satisfying |$x\wedge z\leq y$|, respectively. Such a negation and implication is ‘unsharp’ since it assigns to one entry |$x$| or to two entries |$x$| and |$y$| belonging to the semilattice, respectively, a subset instead of an element of the semilattice. Surprisingly, this kind of negation and implication still shares a number of properties of these connectives in intuitionistic logic, in particular the derivation rule Modus Ponens. Moreover, unsharp negation and unsharp implication can be characterized by means of five, respectively seven simple axioms. We present several examples. The concepts of a deductive system and of a filter are introduced as well as the congruence determined by such a filter. We finally describe certain relationships between these concepts.
1 Introduction
Intuitionistic logic is usually algebraically formalized by means of Heyting algebras, i.e. semilattices |$(S,\wedge ,*)$| where * denotes relative pseudocomplementation, which is considered as a formalization of the connective implication, see [1], [2], [12], [15] and [16]. If |$(S,\wedge ,*)$| has a |$0$|, then |$x*0$| is the pseudocomplement of |$x$| usually denoted by |$x^{*}$| and considered as negation of |$x$| in this logic. Heyting algebras were introduced by L. E. J. Brouwer [1] and A. Heyting, see [14] and [17]. For posets, the authors extended and studied the concept of pseudocomplementation in [4] and [5].
It is well-known that every Heyting algebra is distributive. The concept of relative pseudocomplementation was extended by the first author to non-distributive lattices under the name sectional pseudocomplementation, see [3] and [9]. Hence, a kind of non-distributive intuitionistic logic can be created on sectionally pseudocomplemented lattices.
In their previous papers [6] and [8], the authors showed that some important logics can also be based on posets that need not be lattices. An example of such a logic is the logic of quantum mechanics based on orthomodular posets, see e.g. [6], [10], [11] and [18]. It is evident that in this case, some logical connectives such as disjunction or conjunction may be only partial operations or, as pointed out by the authors in [7] and [8], they may be considered in an ‘unsharp version’, i.e. their result need not be a single element but may be a subset of the poset in question. Thus also the connective implication is created in this way as ‘unsharp’ (for ‘unsharpness’ see also [13]). This motivated us to study algebraic structures based on lattices, which need neither be relatively pseudocomplemented nor even sectionally pseudocomplemented, but can be used for a formalization of a variant of intuitionistic logic whose connective implication is unsharp.
2 Preliminaries
In the following, we identify singletons with their unique element, i.e. we will write |$x$| instead of |$\{x\}$|. Moreover, all posets considered in the sequel are assumed to satisfy the Ascending Chain Condition, which we will abbreviate by ACC. This condition says that within the considered poset there do not exist infinite ascending chains. This implies that every element lies under a maximal one. Of course, every finite poset satisfies the ACC. Let |$(P,\leq )$| be a poset and |$A,B\subseteq P$|. By |$\operatorname {Max} A$|, we will denote the set of all maximal elements of |$A$|. We define
The relations |$\leq _{1}$| and |$\approx _{1}$| are a quasiorder relation on |$2^{P}$| and an equivalence relation on |$2^{P}$|, respectively. It is easy to see that |$A\leq _{1}\operatorname {Max} B$| provided |$A\subseteq B$| and that |$A\leq _{1}b$| is equivalent to |$A\leq b \ (b\in P)$|.
Let |$\mathbf S=(S,\wedge )$| be an arbitrary meet-semilattice and |$A,B\subseteq S$|. We define
For the sake of simplicity, throughout the paper, we will use terms ‘negation’ and ‘implication’ for algebraic operators formalizing these logical connectives without explicitly establishing the corresponding logic.
3 Unsharp negation
Let |$(S,\wedge ,0)$| be a meet-semilattice with |$0$| satisfying the ACC, |$a\in S$| and |$A$| a non-empty subset of |$S$|. We define
Hence, |$^{0}$| is a unary operator on the meet-semilattice |$(S,\wedge ,0)$| with |$0$| satisfying the ACC, which assigns to every element |$x\in S$| the non-void subset |$x^{0}\subseteq S$|. The element |$a$| is called sharp if |$a^{00}=a$|. Moreover, we define
We are going to prove the following properties of the operator |$^{0}$|.
Let |$\mathbf S=(S,\wedge ,0)$| be a meet-semilattice with |$0$| satisfying the ACC, |$a,b\in S$| and |$A$| and |$B$| non-empty subsets of |$S$|. Then the following holds:
- (i)
|$A^{0}$| is an antichain,
- (ii)
|$A\leq _{1}A^{00}$|,
- (iii)
|$A\leq _{1}B$| implies |$B^{0}\leq _{1}A^{0}$|,
- (iv)
|$A^{000}=A^{0}$|,
- (v)
|$0^{0}=\operatorname {Max} S$|,
- (vi)
|$a\wedge a^{0}=0$|,
- (vii)
if |$\mathbf S$| is bounded, then |$0^{0}=1$| and |$1^{0}=0$|,
- (viii)
|$a\wedge 0^{0}\approx _{1}a$|,
- (ix)
|$a\wedge (a\wedge b)^{0}\approx _{1}a\wedge b^{0}$|.
- (i)
This is clear.
- (ii)
We have |$A\subseteq \{x\in S\mid A^{0}\wedge x=0\}$|.
- (iii)
If |$A\leq _{1}B$|, then |$\{x\in S\mid B\wedge x=0\}\subseteq \{x\in S\mid A\wedge x=0\}$|.
- (iv)
From (ii) and (iii), we conclude |$A^{000}\approx _{1}A^{0}$|. Now assume |$a\in A^{000}$|. Because of |$A^{000}\leq _{1}A^{0}$|, there exists some |$b\in A^{0}$| with |$a\leq b$|, and because of |$A^{0}\leq _{1}A^{000}$|, there exists some |$c\in A^{000}$| with |$b\leq c$|. Together, we obtain |$a\leq b\leq c$| and hence |$a\leq c$|. Since both |$a$| and |$c$| belong to the antichain |$A^{000}$|, we conclude |$a=c$| and hence |$a=b\in A^{0}$|. This shows |$A^{000}\subseteq A^{0}$|. Interchanging the roles of |$A^{000}$| and |$A^{0}$| gives |$A^{0}\subseteq A^{000}$|. Together, we obtain |$A^{000}=A^{0}$|.
- (v)
and (vi) follow directly from the definition of |$a^{0}$|.
- (vii)If |$\mathbf S$| is bounded, then according to (v)$$ \begin{align*} 0^{0} & =\operatorname{Max} S=1, \\ 1^{0} & =\operatorname{Max}\{x\in S\mid1\wedge x=0\}=\operatorname{Max}\{0\}=0. \end{align*}$$
- (viii)
According to (v), we have |$a\leq _{1}\operatorname {Max} S=0^{0}$| and hence |$a\leq _{1}a\wedge 0^{0}\leq a$|.
- (ix)Any of the following statements implies the next one:From |$a\wedge b\leq b$|, we conclude |$b^{0}\leq _{1}(a\wedge b)^{0}$| according to (iii) and hence |$a\wedge b^{0}\leq _{1}a\wedge (a\wedge b)^{0}$|.$$ \begin{align*} (a\wedge b)\wedge(a\wedge b)^{0} & =0, \\ b\wedge\big(a\wedge(a\wedge b)^{0}\big) & =0, \\ a\wedge(a\wedge b)^{0} & \leq_{1}b^{0}, \\ a\wedge(a\wedge b)^{0} & \leq_{1}a\wedge b^{0}. \end{align*}$$
From (iii) of Theorem 3.1, we immediately obtain |$A^{0}\wedge B^{0}\leq _{1}(A\wedge B)^{0}$|.
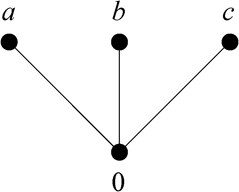
Consider the meet-semilattice visualized in Figure 1:
Consider the modular lattice |$\mathbf L$| depicted in Figure 2:
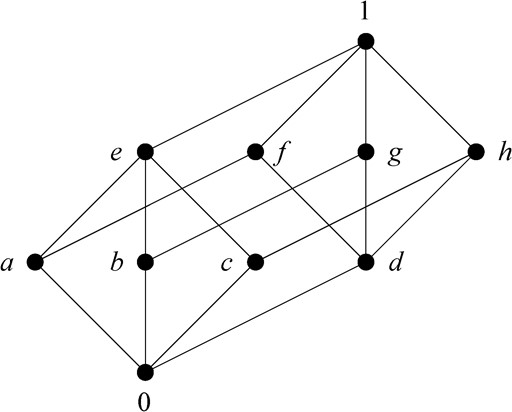
If |$a^{0}$| is a singleton, it need not be a complement of |$a$|, even if the semilattice in question is a lattice. For instance, consider the four-element lattice with atoms |$a$| and |$b$| and with an additional greatest element |$1$|. Then |$a^{0}=b$|, but |$a\vee b\neq 1$|, therefore |$a^{0}$| is not a complement of |$a$|.
For every cardinal number |$n$|, let |$\mathbf M_{n}=(M_{n},\vee ,\wedge )$| denote the bounded modular lattice of length |$2$| having |$n$| atoms.
The situation from Figure 2 can be generalized as follows.
Every element of a direct product of a Boolean algebra and an arbitrary number of lattices of the form |$\mathbf M_{n}$| (possibly different |$n$|) is sharp.
This follows immediately from the fact that every element of a Boolean algebra or lattice of the form |$\mathbf M_{n}$| is sharp.
However, if the lattice |$\mathbf L$| is not a direct product of two-element lattices and various lattices of the form |$\mathbf M_{n}$|, then the assertion of Remark 3.2 need not hold, see the following example.
Consider the lattice visualized in Figure 3:

We are going to show that the operator |$^{0}$| can be characterized by means of four simple conditions.
Let |$(S,\wedge ,0)$| be a meet-semilattice with |$0$| satisfying the ACC and |$^{0}$| a mapping from |$S$| to |$2^{S}$|. Then the following are equivalent:
- (i)
|$x^{0}=\operatorname {Max}\{y\in S\mid x\wedge y=0\}$| for all |$x\in S$|,
- (ii)
the operator |$^{0}:2^{S}\rightarrow 2^{S}$| (restricted to |$S$|) satisfies the following conditions:
- (P1)
|$x^{0}$| is an antichain,
- (P2)
|$x\wedge 0^{0}\approx _{1}x$|,
- (P3)
|$x\wedge x^{0} = 0$|,
- (P4)
|$x\wedge (x\wedge y)^{0}\approx _{1}x\wedge y^{0}$|.
- (P1)
4 Unsharp implication
In the sequel, we extend the operation of relative pseudocomplementation to arbitrary meet-semilattices with |$0$| satisfying the ACC as follows: let |$\mathbf S=(S,\wedge ,0)$| be a meet-semilattice with |$0$| satisfying the ACC, |$a,b\in S$| and |$A,B\subseteq S$|. We define
Thus, |$\rightarrow $| is a binary operator on |$S$| assigning to every pair |$(x,y)\in S^{2}$| the non-void subset |$x\rightarrow y\subseteq S$|. It is evident that
Moreover, we define
Now we prove some properties of the binary operator |$\rightarrow $|. Let us remark that if |$(P,\leq )$| is a poset satisfying the ACC and |$A$| a non-empty subset of |$P$| then |$\operatorname {Max} A\neq \emptyset $|.
Let |$\mathbf S=(S,\wedge ,0)$| be a meet-semilattice with |$0$| satisfying the ACC and |$a,b,c\in S$|. Then the following holds:
- (i)
|$a\rightarrow b$| is an antichain,
- (ii)
|$a\leq b$| implies |$a\rightarrow b=\operatorname {Max} S$|,
- (iii)
|$b\in \operatorname {Max} S$| implies |$b\in a\rightarrow b$|,
- (iv)
|$b\leq _{1}a\rightarrow b$|,
- (v)
|$a\leq _{1}(a\rightarrow b)\rightarrow b$|,
- (vi)
|$a\leq b$| implies |$c\rightarrow a\leq _{1}c\rightarrow b$| and |$b\rightarrow c\leq _{1}a\rightarrow c$|.
- (vii)
|$a\wedge (a\rightarrow b)\approx _{1}a\wedge b$|,
- (viii)
|$a\rightarrow (b\wedge c)\approx _{1}(a\rightarrow b)\wedge (a\rightarrow c)$|,
- (ix)
|$(a\rightarrow b)\wedge b\approx _{1}b$|,
- (x)
if |$\mathbf S$| is bounded, then |$1\rightarrow b=b$|,
- (xi)
|$a\wedge (b\rightarrow b)\approx _{1}a$|,
- (xii)
if |$\mathbf S$| is bounded, then |$a\rightarrow b=1$| if and only if |$a\leq b$|,
- (xiii)
|$b\leq _{1}a\rightarrow (a\wedge b)$|.
- (i)
This is clear.
- (ii)
, (iv), (x), (xii) and (xiii) follow immediately from the definition of |$\rightarrow $|.
- (iii)
If |$b\in \operatorname {Max} S$|, then because of |$a\wedge b\leq b$|, we have |$b\in \operatorname {Max}\{x\in S\mid a\wedge x\leq b\}=a\rightarrow b$|.
- (v)
Because |$a\wedge x\leq b$| for all |$x\in a\rightarrow b$|, we obtain |$a\wedge (a\rightarrow b)\leq b$|, i.e. |$(a\rightarrow b)\wedge a\leq b$|.
- (vi)If |$a\leq b$|, then$$ \begin{align*} \{x\in S\mid c\wedge x\leq a\} & \subseteq\{x\in S\mid c\wedge x\leq b\}, \\ \{x\in S\mid b\wedge x\leq c\} & \subseteq\{x\in S\mid a\wedge x\leq c\}. \end{align*}$$
- (vii)
We have |$a\wedge x\leq b$| and hence |$a\wedge x\leq a\wedge b$| for all |$x\in a\rightarrow b$| and therefore |$a\wedge b\leq _{1}a\wedge (a\rightarrow b)\leq a\wedge b$| by (iv).
- (viii)
According to (vii), we have |$a\rightarrow (b\wedge c)\leq _{1}(a\rightarrow b)\wedge (a\rightarrow c)$|. Conversely, assume |$d\in a\rightarrow b$| and |$e\in a\rightarrow c$|. Then |$a\wedge d\leq b$| and |$a\wedge e\leq c$| and hence |$a\wedge (d\wedge e)\leq b\wedge c$|, which implies |$d\wedge e\leq _{1}a\rightarrow (b\wedge c)$|. This shows |$(a\rightarrow b)\wedge (a\rightarrow c)\leq _{1}a\rightarrow (b\wedge c)$|.
- (ix)
We have |$b\leq _{1}a\rightarrow b$| by (iv) and hence |$b\leq _{1}(a\rightarrow b)\wedge b\leq b$|.
- (xi)
According to (ii), we have |$a\leq _{1}\operatorname {Max} S=b\rightarrow b$| and hence |$a\leq _{1}a\wedge (b\rightarrow b)\leq a$|.
From Theorem 4.1, it becomes evident that the binary operator |$\rightarrow $| shares properties of the logical connective implication in intuitionistic logic despite the fact that it is unsharp, which means that for |$x,y\in S$| the result of |$x\rightarrow y$| need not be a singleton. This extends the intuitionistic logic based on a Heyting algebra |$(L,\vee ,\wedge ,*,0)$| where |$\vee $|, |$\wedge $|, |$\rightarrow $| and |$^{0}$| formalize disjunction, conjunction, unsharp implication and unsharp negation, respectively. Note that |$x\rightarrow 0 = x^{0}$| as remarked at the beginning of Section 4.
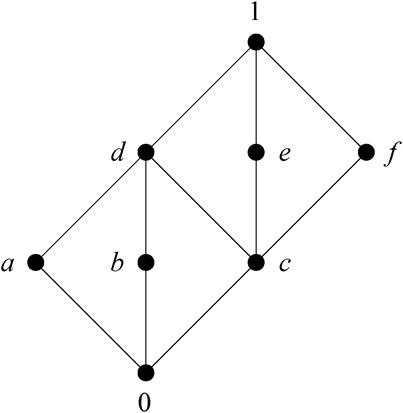
Consider the modular lattice visualized in Figure 4:
Similarly as for the unary operator |$^{0}$|, we can characterize the binary operator |$\rightarrow $| on a meet-semilattice with |$0$| satisfying the ACC as follows.
Let |$(S,\wedge ,0)$| be a meet-semilattice with |$0$| satisfying the ACC and |$\rightarrow $| a binary operator on |$S$|. Then the following are equivalent:
- (i)
|$x\rightarrow y=\operatorname {Max}\{z\in S\mid x\wedge z\leq y\}$| for all |$x,y\in S$|,
- (ii)
The operator |$\rightarrow $| satisfies the following conditions:
- (R1)
|$x\rightarrow y$| is an antichain,
- (R2)
|$x\wedge (x\rightarrow y)\approx _{1}x\wedge y$|,
- (R3)
|$(x\rightarrow y)\wedge y\approx _{1}y$|,
- (R4)
|$x\rightarrow (y\wedge z)\approx _{1}(x\rightarrow y)\wedge (x\rightarrow z)$|,
- (R5)
|$x\wedge (y\rightarrow y)\approx _{1}x$|,
- (R6)
|$y\leq z$| implies |$x\rightarrow y\leq _{1}x\rightarrow z$|.
- (R1)
5 Deductive systems
It is well-known that the connective implication in intuitionistic logic is closely related to the so-called deductive systems in the corresponding Heyting algebra. Let us show that a certain modification of the concept of a deductive system plays a similar role for logics with unsharp implication. We define
A deductive system of a meet-semilattice |$\mathbf S=(S,\wedge ,0)$| with |$0$| satisfying the ACC is a subset |$D$| of |$S$| satisfying the following conditions for |$x,y\in S$|:
- (D1)
|$(\operatorname {Max} S)\cap D\neq \emptyset $|,
- (D2)
|$x\in D$| and |$(x\rightarrow y)\cap D\neq \emptyset $| imply |$y\in D$|.
In a Heyting algebra, there are everywhere defined operations |$\vee $| and |$\wedge $| since it is a lattice and hence the definition of a deductive system is different as follows: if |$x\in D$| and |$x\rightarrow y\in D$|, then |$y\in D$|.
Recall that a filter of a meet-semilattice |$\mathbf S=(S,\wedge )$| is a non-empty subset |$F$| of |$S$| satisfying the following conditions for |$x,y\in S$|:
- (F1)
|$x,y\in F$| implies |$x\wedge y\in F$|,
- (F2)
|$x\in F$| and |$x\leq y$| imply |$y\in F$|.
It is clear that if |$S$| is finite then all filters of |$\mathbf S$| are given by the sets |$[x):=\{y\in S\mid x\leq y\}$|, |$x\in S$|, and hence the poset of all filters of |$\mathbf S$| is dually isomorphic to |$\mathbf S$| and therefore a join-semilattice where |$[x)\vee [y)=[x\wedge y)$| for all |$x,y\in S$|.
For every non-empty subset |$A$| of the universe of a meet-semilattice |$(S,\wedge )$|, we define a binary relation |$\varTheta (A)$| on |$S$| as follows:
Although the following result is known, for the reader’s convenience, we present a proof.
Let |$\mathbf S=(S,\wedge ,1)$| be a meet-semilattice with |$1$| and |$\varPhi \in \operatorname {Con}\mathbf S$|. Then the following holds:
- (i)
|$[1]\varPhi $| is an filter of |$\mathbf S$|,
- (ii)
|$\varTheta ([1]\varPhi )\subseteq \varPhi $|.
- (i)
- (F1)
If |$a,b\in [1]\varPhi $|, then |$a\wedge b\in [1\wedge 1]\varPhi =[1]\varPhi $|.
- (F2)
If |$a\in [1]\varPhi $|, |$b\in S$| and |$a\leq b$|, then |$b=1\wedge b\in [a\wedge b]\varPhi =[a]\varPhi =[1]\varPhi $|.
- (F1)
- (ii)If |$(a,b)\in \varTheta ([1]\varPhi )$|, then there exists some |$c\in [1]\varPhi $| with |$a\wedge c=b\wedge c$| whencewhich shows |$(a,b)\in \varPhi $|.$$ \begin{align*} & a=a\wedge1\mathrel\varPhi a\wedge c=b\wedge c\mathrel\varPhi b\wedge1=b, \end{align*}$$
Although our definition of a deductive system differs from that one known for relatively pseudocomplemented semilattices, we are still able to prove the following relationships between the concepts mentioned before.
Let |$\mathbf S=(S,\wedge ,0,1)$| be a bounded meet-semilattice satisfying the ACC and |$D$| a non-empty subset of |$S$|. Then the following are equivalent:
- (i)
|$D$| is a deductive system of |$\mathbf S$|,
- (ii)
|$D$| is an filter of |$\mathbf S$|,
- (iii)
|$\varTheta (D)\in \operatorname {Con}\mathbf S$| and |$D=[1]\big (\varTheta (D)\big )$|.
- (F2)
Assume |$a\in D$|, |$b\in S$| and |$a\leq b$|. Then |$a\rightarrow b=\operatorname {Max} S$| because of (ii) of Theorem 4.1. According to (D1) we have |$(a\rightarrow b)\cap D=\operatorname {Max} S\cap D\neq \emptyset $| and hence |$b\in D$| by (D2).
- (F1)
Let |$a,b\in D$|. Then by (xiii) of Theorem 4.1, we obtain |$b\leq _{1}a\rightarrow (a\wedge b)$|. Hence, there exists some |$c\in a\rightarrow (a\wedge b)$| with |$b\leq c$|. Axiom (F2) implies |$c\in D$| and therefore |$\big (a\rightarrow (a\wedge b)\big )\cap D\neq \emptyset $| from which we conclude |$a\wedge b\in D$| by (D2).
- (D1)If |$a\in D$| then, since |$\mathbf S$| satisfies the ACC, there exists some |$b\in \operatorname {Max} S$| with |$a\leq b$| and hence$$ \begin{align*} & b=1\wedge b\in[a\wedge b]\big(\varTheta(D)\big)=[a]\big(\varTheta(D)\big)=[1]\big(\varTheta(D)\big)=D. \end{align*}$$
- (D2)If |$a\in D$|, |$b\in S$| and |$(a\rightarrow b)\cap D\neq \emptyset $|, then there exists some |$c\in D$| with |$c\in a\rightarrow b$| and hence |$a\wedge c\leq b$| whence$$ \begin{align*} & b=1\wedge1\wedge b\in[a\wedge c\wedge b]\big(\varTheta(D)\big)=[a\wedge c]\big(\varTheta(D)\big)=[1\wedge1]\big(\varTheta(D)\big)=[1]\big(\varTheta(D)\big)=D. \end{align*}$$
It is well known that for a filter |$F$| of a relatively pseudocomplemented semilattice, we have |$(a,b)\in \varTheta (F)$| if and only if both |$a\rightarrow b\in F$| and |$b\rightarrow a\in F$|. However, we can also modify this result for an arbitrary meet-semilattice with |$0$| satisfying the ACC provided our unsharp implication is considered.
Let |$\mathbf S=(S,\wedge ,0)$| be a meet-semilattice with |$0$| satisfying the ACC, |$F$| a filter of |$\mathbf S$| and |$a,b\in S$|. Then the following are equivalent:
- (i)
|$(a,b)\in \varTheta (F)$|,
- (ii)
|$(a\rightarrow b)\cap F\neq \emptyset $| and |$(b\rightarrow a)\cap F\neq \emptyset $|.
Conclusion
Although the operator used for a formalization of implication based on the structure |$(S,\wedge ,0,\rightarrow )$| is unsharp, i.e. |$x\rightarrow y$| may be a subset |$I$| of |$S$|, which need not be a singleton, it has some logical meaning. Namely, we ask that |$x\rightarrow y$| consists of the maximal elements |$c$| of |$S$| satisfying |$x\wedge c\leq y$| (here |$\wedge $| denotes conjunction). Moreover, the elements of |$I$| are mutually incomparable. Thus, there is no need to prefer one of them with respect to others. However, the expression
is nothing else than the derivation rule Modus Ponens (both in classical as well as in non-classical logic) since it properly says that the truth value of |$y$| cannot be less than the truth value of the conjunction |$x\wedge (x\rightarrow y)$| of |$x$| and the implication |$x\rightarrow y$|. Hence, despite of the fact of unsharpness, such a logic based on our algebraic structure is sound although it is derived from an arbitrary meet-semilattice with |$0$| satisfying the ACC.
Acknowledgements
The authors are grateful to the anonymous referees whose valuable remarks helped to increase the quality of the paper. Support of the research of the authors by the Austrian Science Fund (FWF), project I 4579-N, and the Czech Science Foundation (GAČR), project 20-09869L, entitled ‘The many facets of orthomodularity’, is gratefully acknowledged.
References


