Calculation and application of elastic modulus of mineral components in tight sandstone based on an adaptive method

Rock-frame models.

Rock-frame model	Bulk modulus	Shear modulus	Parameterization
Pride model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + 1.5 c ϕ})$	Coefficient of consolidation, c
Lee model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$\begin{matrix} μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + γ c ϕ}) \\ γ = \frac{1 + 2 c}{1 + c} \end{matrix}$	γ factor

Rock-frame model	Bulk modulus	Shear modulus	Parameterization
Pride model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + 1.5 c ϕ})$	Coefficient of consolidation, c
Lee model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$\begin{matrix} μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + γ c ϕ}) \\ γ = \frac{1 + 2 c}{1 + c} \end{matrix}$	γ factor

Table 1.

Rock-frame models.

Rock-frame model	Bulk modulus	Shear modulus	Parameterization
Pride model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + 1.5 c ϕ})$	Coefficient of consolidation, c
Lee model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$\begin{matrix} μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + γ c ϕ}) \\ γ = \frac{1 + 2 c}{1 + c} \end{matrix}$	γ factor

Rock-frame model	Bulk modulus	Shear modulus	Parameterization
Pride model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + 1.5 c ϕ})$	Coefficient of consolidation, c
Lee model	$K_{d r y} = K_{m} (\frac{1 - ϕ}{1 + c ϕ})$	$\begin{matrix} μ_{d r y} = μ_{m} (\frac{1 - ϕ}{1 + γ c ϕ}) \\ γ = \frac{1 + 2 c}{1 + c} \end{matrix}$	γ factor

First, the shear modulus of the tight sandstone matrix was calculated. The result is unaffected by pore fluids at low frequencies and can be expressed as

\begin{array}{r} μ_{s} = μ_{d r y}, \end{array}

(5)

where the shear modulus of the dry frame is represented by $μ_{d r y}$ ⁠.

The tight sandstone shear modulus matrix can be obtained using the Lee model:

\begin{array}{r} μ_{m} = μ_{s} \frac{1 + γ c φ}{1 - φ}, \end{array}

(6)

\begin{array}{r} γ = \frac{1 + 2 c}{1 + c}, \end{array}

(7)

where $μ_{m}$ and $φ$ stand for the shear modulus and porosity of tight sandstone matrix, respectively; c is the coefficient of consolidation, which is assumed to be four based on the actual conditions of the study area; and $γ$ is an expression related to c.

To determine the bulk modulus of the tight sandstone matrix, the Lee model was substituted into the Gassmann equation (Equations 8 and 9). The incorporation of the Lee model transforms the Gassmann equation into a quadratic equation (Equation 10), which depends only on the bulk modulus of rock matrix. In Equation (10), $K_{f}$ is obtained from the Brie model. Solving Equation (10), discarding the negative value, yields the bulk modulus of the tight sandstone matrix. The equations are expressed as follows:

\begin{array}{r} K_{d r y} = K_{m} (\frac{1 - φ}{1 + c φ}), \end{array}

(8)

\begin{array}{r} K_{s} = K_{d r y} + \frac{{(1 - \frac{K_{d r y}}{K_{m}})}^{2}}{\frac{φ}{K_{f}} + \frac{1 - φ}{K_{m}} - \frac{K_{d r y}}{K_{m}^{2}}}, \end{array}

(9)

\begin{array}{r} \frac{1 - φ}{1 + c φ} φ K_{m}^{2} + [K_{f} - K_{f} \frac{1 - φ}{1 + c φ} - K_{f} \frac{1 - φ}{1 + c φ} φ - K_{s} φ] K_{m} - (1 - φ - \frac{1 - φ}{1 + c φ}) K_{s} K_{f} = 0, \end{array}

(10)

where $K_{f}$ is the bulk modulus of the pore fluid and $K_{m}$ is the bulk modulus of the rock matrix.

2.2. Random-walk algorithm for determining the equivalent elasticity modulus of the mineral components

The VRH model provides a wider range of equivalent elasticity modulus than the Hashin–Shtrikman limits (Fig. 1). This wide range creates a large space for search and optimization by the random-walk algorithm, which is beneficial for the optimization process. Therefore, the VRH model was used to compute the range of equivalent elasticity modulus of the mineral components of tight sandstone.

Figure 1.

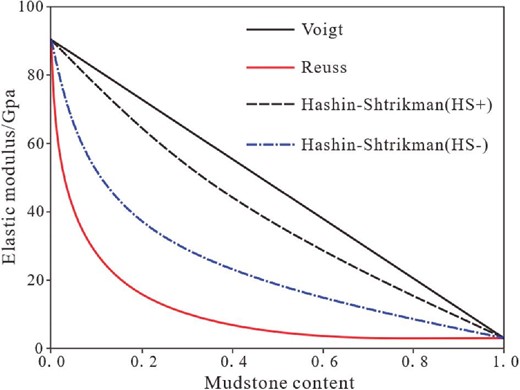
Limits of the VRH model and H–S bounds.

Initially, the Voigt model was employed to conduct correlation calculations on the upper limit of the equivalent elasticity modulus of the sandstone and mudstone. To achieve this, the Voigt model was reformulated as linear relations between mudstone content and the equivalent elasticity modulus of the matrix, as illustrated here:

\begin{array}{r} K_{m} = (K_{s h}^{V} - K_{s a n d}^{V}) \times V_{s h} + K_{s a n d}^{V}, \end{array}

(11)

\begin{array}{r} a_{1}^{V} = K_{s h}^{V} - K_{s a n d}^{V}, \end{array}

(12)

\begin{array}{r} b_{1}^{V} = K_{s a n d}^{V}, \end{array}

(13)

\begin{array}{r} μ_{m} = (μ_{s h}^{V} - μ_{s a n d}^{V}) \times V_{s h} + μ_{s a n d}^{V}, \end{array}

(14)

\begin{array}{r} a_{2}^{V} = μ_{s h}^{V} - μ_{s a n d}^{V}, \end{array}

(15)

\begin{array}{r} b_{2}^{V} = μ_{s a n d}^{V}, \end{array}

(16)

where a and b are the gradient and intercept of the linear equation, respectively; the bulk moduli of the mudstone and sandstone are denoted by $K_{s h}$ and $K_{s a n d}$ ⁠, respectively; the shear moduli of the sandstone and mudstone are $μ_{s a n d}$ and $μ_{s h}$ ⁠, respectively; $V_{s h}$ is the volumetric percentage of the mudstone component; and the superscript V indicates the elastic modulus derived from the Voigt model.

Next, the correlation between the mudstone and sandstone lower limit of the equivalent elasticity modulus was determined using the Reuss model. The Reuss model can be reformulated as follows:

\begin{array}{r} \frac{1}{K_{m}} = (\frac{1}{K_{s h}^{R}} - \frac{1}{K_{s a n d}^{R}}) \times V_{s h} + \frac{1}{K_{s a n d}^{R}}, \end{array}

(17)

\begin{array}{r} a_{1}^{R} = \frac{1}{K_{s h}^{R}} - \frac{1}{K_{s a n d}^{R}}, \end{array}

(18)

\begin{array}{r} b_{1}^{R} = \frac{1}{K_{s a n d}^{R}}, \end{array}

(19)

\begin{array}{r} \frac{1}{μ_{m}} = (\frac{1}{μ_{s h}^{R}} - \frac{1}{μ_{s a n d}^{R}}) \times V_{s h} + \frac{1}{μ_{s a n d}^{R}}, \end{array}

(20)

\begin{array}{r} a_{2}^{R} = \frac{1}{μ_{s h}^{R}} - \frac{1}{μ_{s a n d}^{R}}, \end{array}

(21)

\begin{array}{r} b_{2}^{R} = \frac{1}{μ_{s a n d}^{R}}, \end{array}

(22)

where the superscript R represents the elastic modulus derived from the Reuss model.

This method can determine the range of elastic modulus of the sandstone and mudstone components in tight sandstone. However, in practice, the relation between the mudstone content and the elastic modulus of the tight sandstone matrix is unlikely to be perfectly linear. Therefore, it is necessary to perform linear fitting on the obtained data. This paper employs the least-squares method for linear fitting. The least-squares method is a mathematical optimization technique that seeks the best function fit to data by minimizing the sum of the squares of the errors. This method can obtain the optimal value of the objective function, and can also be used for curve fitting to solve the regression problem. The formula is expressed as follows:

\begin{array}{r} S = \sum_{i = 1}^{n} {[y_{i} - y (x_{i})]}^{2} = \sum_{i = 1}^{n} {[y_{i} - (a x_{i} + b)]}^{2}, \end{array}

(23)

where S represents the sum of squared errors, y_i represents the measured data, and y(x_i) represents the function to be determined.

After obtaining the range of equivalent elasticity modulus of the mineral components, the random-walk algorithm was used to compute their exact equivalent elasticity modulus (Fig. 2). This algorithm works as follows: first, the algorithm gives a starting position, and then gets a new position after a random jump of a certain step length. The fitness of the new position is assessed by comparing the function values of the old and new ones, with the position having the smaller function value being chosen as the new position. Based on the new position, the function value is compared again after the random jump of the same step length. When a certain position still maintains the best fitness after reaching the specified number of iterations, the position is considered the optimal solution under this step length. Next, the step size is shortened and the calculation is repeated until the step size is reduced to the given control accuracy, so the obtained position can be considered the global optimal solution. The reliability of the optimal solution depends on the number of iterations and step length of the algorithm (Liu et al. 2017), and it has been shown that step length is more important than the number of iterations through many trials (Luo & Zhao 2006). Therefore, considering the computational cost, the usual method is to vary the step length to improve the predictive accuracy.

Figure 2.

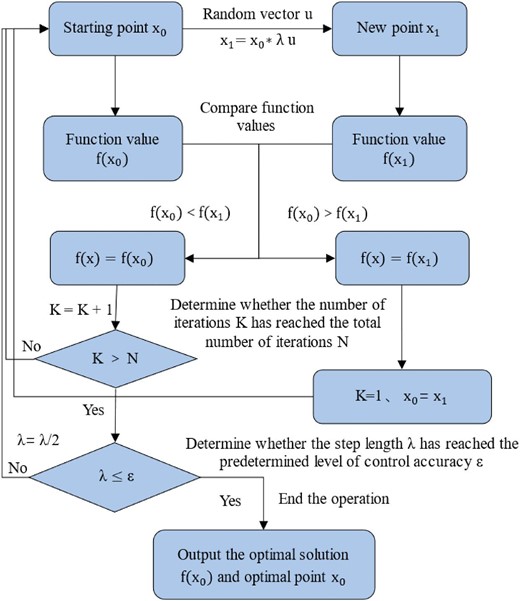
Flow of the random-walk algorithm.

Taking the process of determining the shear modulus for sandstone and mudstone as an example, the specific solution method is as follows: during the calculation process, the S-wave velocity is used as an effective parameter. The square of the difference between the S-wave velocities calculated from the shear modulus of sandstone and mudstone and the actual S-wave velocities is defined as the objective function (Equation 25), which is then optimized to find the solution. By this transformation, the calculation of the shear modulus of sandstone and mudstone is transformed into a global optimal problem of finding the minimum value of the objective function in a certain range:

\begin{array}{r} V_{s}^{'} = \sqrt{\frac{[(1 - V_{s h}) μ_{s a n d} + V_{s h} μ_{s h} + μ_{s a n d} μ_{s h} / ((1 - V_{s h}) μ_{s h} + V_{s h} μ_{s a n d})] (1 - ϕ / 0.4)}{2 ρ}}, \end{array}

(24)

\begin{array}{r} f = {(V_{s} - V_{s}^{'})}^{2}, \end{array}

(25)

where $V_{s}$ and $V_{s}^{'}$ are the true and calculated S-wave velocities.

2.3. Petrophysics model for tight sandstone

Based on the previous sections, we use the obtained density sandstone mineral component equivalent elastic modulus to build rock physical models. The modeling process is shown in Fig. 3, and the entire modeling work is based on the Xu–White model framework. The key links are shown next.

Figure 3.

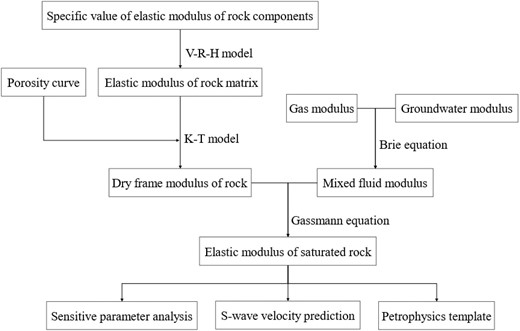
Petrophysical model process.

2.3.1. Calculating the equivalent elasticity modulus of the dry frame

The KT model, which is based on the first-order wave scattering approximation, establishes a relation between pore structure and rock elasticity parameters (Kuster & Toksöz 1974; Toksöz et al. 1976). After studying the mechanical properties of different pores, Berryman (1995) divided pores into sphere-, needle-, disk-, and coin-shaped, based on geometry and representing different stress states of rocks. Berryman, thus, obtained an improved KT model whose equations are as follows:

\begin{array}{r} (K_{k t}^{*} - K_{m}) \frac{(K_{m} + \frac{4}{3} μ_{m})}{(K_{k t}^{*} + \frac{4}{3} μ_{m})} = \sum_{i = 1}^{N} c_{i} (K_{i} - K_{m}) P^{m i}, \end{array}

(26)

\begin{array}{r} (μ_{k t}^{*} - μ_{m}) \frac{(μ_{m} + \frac{4}{3} ξ_{m})}{(μ_{k t}^{*} + \frac{4}{3} ξ_{m})} = \sum_{i = 1}^{N} c_{i} (μ_{i} - μ_{m}) Q^{m i}, \end{array}

(27)

\begin{array}{r} ξ_{m} = \frac{μ_{m}}{6} \frac{9 K_{m} + 8 μ_{m}}{K_{m} + 2 μ_{m}}, \end{array}

(28)

where $K_{k t}^{*}$ and $μ_{k t}^{*}$ are the bulk and shear modulus of saturated rock, respectively; for pore fluid in the ith kind of pore, $K_{i}$ and $μ_{i}$ represent the bulk and shear modulus, respectively; $P^{m i}$ and $Q^{m i}$ are coefficients associated with adding the ith kind of pore into the mineral matrix; $ξ_{m}$ is the compression coefficient of minerals in the rock; and $c_{i}$ is the volumetric percentage of the ith kind of pore. If $K_{i}$ = 0 and $μ_{i}$ = 0, the bulk and shear modulus of the dry-frame rock can be determined using the aforementioned formulas.

2.3.2. Calculating the equivalent elasticity modulus of mixed pore fluids

Based on experimental data, Brie et al. (1995) established relations between water saturation and the elastic modulus of the liquid and gaseous phases and introduced a water content exponent, e, which depends on the mixing between liquid and gas. The introduction of e improves the accuracy of the equivalent elasticity modulus (for mixed fluids) calculated by the Brie equation. The Brie equation can be written as follows:

\begin{array}{r} K_{f} = (K_{w} - K_{g}) S_{w}^{e} + K_{g}, \end{array}

(29)

where the gas and liquid bulk modulus are denoted by $K_{g}$ and $K_{w}$ ⁠, respectively; $S_{w}$ represents the level of water saturation; and e is the water content exponent, which is assumed to be 3.

By substituting this equivalent elasticity modulus into the Gassmann equations, the equivalent elasticity modulus of saturated tight sandstone can be obtained, thus completing the construction of the petrophysics model for tight sandstone.

3. Case study

3.1. Geological background of the research area

The study area is close to Jinxi flexural fold belt on the Yishan Slope of the Ordos Basin. The target stratum is the Shanxi Formation, which is composed of tight sandstone, coals, and mudstones. The tight sandstones consist of medium- and coarse-grained sandstones with diverse mineral components, which makes it difficult to ascertain the elastic modulus of their sandstone and mudstone components.

3.2. Calculating the equivalent elasticity modulus of the mineral components of the tight sandstone

Petrophysics analysis was performed via X-ray diffraction spectrometry on nine core samples from the study area to characterize the mineral components of tight sandstone in the target stratum. The results of whole-rock analysis are shown in Table 2.

Table 2.

Mineral components of the rock cores.

		Percentage content (%)
Core no.	Type of rock	Quartz (Q)	Potassium feldspar (KF)	Calcite (Ca)	Dolomite (D)	Pyrite (P)	Siderite (L)	Ankerite (Ank)	Clay minerals (Clay)
1	Sandstone	33	26	2	0	1	11	3	24
2	Sandstone	36	13	18	3	0	12	5	13
3	Sandstone	28	13	4	0	1	19	4	31
4	Sandstone	35	15	7	4	0	12	0	27
5	Sandstone	63	2	14	0	0	8	7	6
6	Sandstone	83	1	0	0	0	6	6	4
7	Sandstone	83	0	0	0	0	9	6	2
8	Sandstone	78	1	0	0	0	13	5	3
9	Sandstone	55	0	0	0	0	37	4	4

		Percentage content (%)
Core no.	Type of rock	Quartz (Q)	Potassium feldspar (KF)	Calcite (Ca)	Dolomite (D)	Pyrite (P)	Siderite (L)	Ankerite (Ank)	Clay minerals (Clay)
1	Sandstone	33	26	2	0	1	11	3	24
2	Sandstone	36	13	18	3	0	12	5	13
3	Sandstone	28	13	4	0	1	19	4	31
4	Sandstone	35	15	7	4	0	12	0	27
5	Sandstone	63	2	14	0	0	8	7	6
6	Sandstone	83	1	0	0	0	6	6	4
7	Sandstone	83	0	0	0	0	9	6	2
8	Sandstone	78	1	0	0	0	13	5	3
9	Sandstone	55	0	0	0	0	37	4	4

Table 2.

Mineral components of the rock cores.

		Percentage content (%)
Core no.	Type of rock	Quartz (Q)	Potassium feldspar (KF)	Calcite (Ca)	Dolomite (D)	Pyrite (P)	Siderite (L)	Ankerite (Ank)	Clay minerals (Clay)
1	Sandstone	33	26	2	0	1	11	3	24
2	Sandstone	36	13	18	3	0	12	5	13
3	Sandstone	28	13	4	0	1	19	4	31
4	Sandstone	35	15	7	4	0	12	0	27
5	Sandstone	63	2	14	0	0	8	7	6
6	Sandstone	83	1	0	0	0	6	6	4
7	Sandstone	83	0	0	0	0	9	6	2
8	Sandstone	78	1	0	0	0	13	5	3
9	Sandstone	55	0	0	0	0	37	4	4

		Percentage content (%)
Core no.	Type of rock	Quartz (Q)	Potassium feldspar (KF)	Calcite (Ca)	Dolomite (D)	Pyrite (P)	Siderite (L)	Ankerite (Ank)	Clay minerals (Clay)
1	Sandstone	33	26	2	0	1	11	3	24
2	Sandstone	36	13	18	3	0	12	5	13
3	Sandstone	28	13	4	0	1	19	4	31
4	Sandstone	35	15	7	4	0	12	0	27
5	Sandstone	63	2	14	0	0	8	7	6
6	Sandstone	83	1	0	0	0	6	6	4
7	Sandstone	83	0	0	0	0	9	6	2
8	Sandstone	78	1	0	0	0	13	5	3
9	Sandstone	55	0	0	0	0	37	4	4

Table 2 shows that the quartz and clay contents vary substantially in the nine core samples. For example, Core 3 has a quartz content of 28%, whereas Cores 6 and 7 have quartz contents as high as 83%. Likewise, Core 7 has a clay content of only 2% (the lowest of the nine), whereas Core 3 has a clay content of 31%. Furthermore, some cores have higher percentages of minerals such as potassium feldspar, calcite, and siderite than the other cores. In a few cores, the sum of these minerals may exceed those of quartz or clay. Therefore, treating the sandstone and mudstone components as pure quartz and clay will result in substantial errors in elastic modulus calculations.

To improve the accuracy of the calculations, we initially employed the Gassmann relations and Lee model to determine the equivalent elasticity modulus of the matrix. We then extracted the upper and lower elasticity modulus limits of the sandstone and mudstone components from the mudstone content curve using the least-squares method and the VRH model. Figures 4 and 5 show the fitting graphs for the bulk and shear modulus of sandstones and mudstones under the Voigt model and Reuss model.

Figure 4.

Fitting of bulk modulus using the Voigt and Reuss models. (a) Bulk modulus fitting of Voigt model. (b) Bulk modulus fitting of Reuss model.

Figure 5.

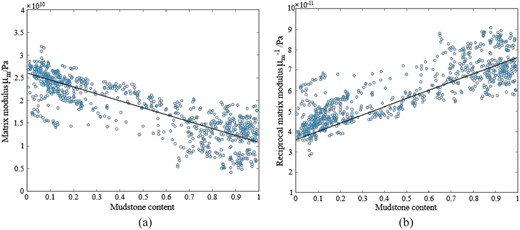
Fitting of shear modulus using the Voigt and Reuss models. (a) Shear modulus fitting of Voigt model. (b) Shear modulus fitting of Reuss model.

As seen in Figs. 4 and 5, using the least-squares method to fit the data can achieve a good fitting effect. From the VRH model, it may be inferred that the fitting process provides a linear relation between certain coefficients and the equivalent elasticity modulus of the sandstone and mudstone components. Therefore, calculating the gradient (a) and intercept (b) of the linear relation provides the upper and lower limits for the equivalent elasticity modulus of the sandstone and mudstone components, respectively (Table 3).

Table 3.

Upper and lower limits for the equivalent elasticity modulus of the sandstone and mudstone components.

	Sandstone		Mudstone
Equivalent elastic modulus	Upper limits	Lower limits	Upper limits	Lower limits
Bulk modulus (GPa)	36.2	35.1	32.1	29.9
Shear modulus (GPa)	26.5	25.8	13.4	10.9

	Sandstone		Mudstone
Equivalent elastic modulus	Upper limits	Lower limits	Upper limits	Lower limits
Bulk modulus (GPa)	36.2	35.1	32.1	29.9
Shear modulus (GPa)	26.5	25.8	13.4	10.9

Table 3.

Upper and lower limits for the equivalent elasticity modulus of the sandstone and mudstone components.

	Sandstone		Mudstone
Equivalent elastic modulus	Upper limits	Lower limits	Upper limits	Lower limits
Bulk modulus (GPa)	36.2	35.1	32.1	29.9
Shear modulus (GPa)	26.5	25.8	13.4	10.9

	Sandstone		Mudstone
Equivalent elastic modulus	Upper limits	Lower limits	Upper limits	Lower limits
Bulk modulus (GPa)	36.2	35.1	32.1	29.9
Shear modulus (GPa)	26.5	25.8	13.4	10.9

The equivalent elasticity modulus of the sandstone and mudstone components were subsequently accurately calculated using the acoustic-log curve and the random-walk algorithm. Table 4 contains the calculation's outcomes.

Table 4.

Calculated equivalent elasticity modulus of the sandstone and mudstone components.

equivalent elasticity modulus	Sandstone	Mudstone
Bulk modulus (GPa)	36.7	32.4
Shear modulus (GPa)	26.9	13.0

Table 4.

Calculated equivalent elasticity modulus of the sandstone and mudstone components.

equivalent elasticity modulus	Sandstone	Mudstone
Bulk modulus (GPa)	36.7	32.4
Shear modulus (GPa)	26.9	13.0

Then, the equivalent elastic modulus of sandstone and mudstone was used to calculate the equivalent elastic modulus of the matrix, and it was compared with the actual measured values and the results calculated by the conventional model, as shown in Table 5.

Table 5.

Error analysis on the predicted equivalent elasticity modulus of the rock matrix.

Core no.	Type of rock	Measured matrix modulus of the rock core (GPa)	Matrix modulus predicted by the conventional model (GPa)	Relative error (%)	Matrix modulus predicted by the proposed model (GPa)	Relative error (%)
1	Sandstone	19.2	21.5	12.9	17.6	8.5
2	Sandstone	18.0	21.3	17.8	17.2	4.5
3	Sandstone	15.1	19.4	28.4	14.9	1.2
4	Sandstone	23.9	26.3	10.0	24.7	3.2
5	Sandstone	24.5	27.0	10.2	22.7	7.1
6	Sandstone	25.0	22.1	11.8	24.5	2.0
7	Sandstone	25.1	22.4	10.9	24.7	1.6

Core no.	Type of rock	Measured matrix modulus of the rock core (GPa)	Matrix modulus predicted by the conventional model (GPa)	Relative error (%)	Matrix modulus predicted by the proposed model (GPa)	Relative error (%)
1	Sandstone	19.2	21.5	12.9	17.6	8.5
2	Sandstone	18.0	21.3	17.8	17.2	4.5
3	Sandstone	15.1	19.4	28.4	14.9	1.2
4	Sandstone	23.9	26.3	10.0	24.7	3.2
5	Sandstone	24.5	27.0	10.2	22.7	7.1
6	Sandstone	25.0	22.1	11.8	24.5	2.0
7	Sandstone	25.1	22.4	10.9	24.7	1.6

Table 5.

Error analysis on the predicted equivalent elasticity modulus of the rock matrix.

Core no.	Type of rock	Measured matrix modulus of the rock core (GPa)	Matrix modulus predicted by the conventional model (GPa)	Relative error (%)	Matrix modulus predicted by the proposed model (GPa)	Relative error (%)
1	Sandstone	19.2	21.5	12.9	17.6	8.5
2	Sandstone	18.0	21.3	17.8	17.2	4.5
3	Sandstone	15.1	19.4	28.4	14.9	1.2
4	Sandstone	23.9	26.3	10.0	24.7	3.2
5	Sandstone	24.5	27.0	10.2	22.7	7.1
6	Sandstone	25.0	22.1	11.8	24.5	2.0
7	Sandstone	25.1	22.4	10.9	24.7	1.6

Core no.	Type of rock	Measured matrix modulus of the rock core (GPa)	Matrix modulus predicted by the conventional model (GPa)	Relative error (%)	Matrix modulus predicted by the proposed model (GPa)	Relative error (%)
1	Sandstone	19.2	21.5	12.9	17.6	8.5
2	Sandstone	18.0	21.3	17.8	17.2	4.5
3	Sandstone	15.1	19.4	28.4	14.9	1.2
4	Sandstone	23.9	26.3	10.0	24.7	3.2
5	Sandstone	24.5	27.0	10.2	22.7	7.1
6	Sandstone	25.0	22.1	11.8	24.5	2.0
7	Sandstone	25.1	22.4	10.9	24.7	1.6

Considering actual measurements, the conventional model has an average error of 14.57%, whereas our improved model has an average error of 4.01% (Table 5). As our model predictions are much closer to the actual values, the model can be used to accurately predict the equivalent elasticity modulus of the tight sandstone matrix in the study area.

3.3. Application of the petrophysics model

3.3.1. Prediction of S-wave velocities using the petrophysics model

After obtaining the accurate equivalent elastic modulus of the tight sandstone matrix, a rock physics model was constructed based on the modeling approach described earlier. Figure 6 presents a comparative analysis of the S-wave velocities predictions between the improved model proposed in this study and conventional models.

Comparative analysis of S-wave velocities prediction with different models. (a) Well M1, (b) Well M2, (c) Well M3, and (d) Well M4.

Figure 6.

Comparative analysis of S-wave velocities prediction with different models. (a) Well M1, (b) Well M2, (c) Well M3, and (d) Well M4.

The red and blue curves, respectively, represent the expected and measured S-wave velocity curves. The green curve indicates the relative error between the predictions and measurements. By analyzing Fig. 6, it can be found that the S-wave velocity curve predicted by conventional models generally has large errors, while the petrophysical model constructed in this paper is more consistent with the actual measurement results in terms of S-wave velocity prediction, and the relative error of the overall prediction curve is controlled within 15%. This demonstrates that the aforementioned model method not only accurately reflects the true rock physical characteristics of the target layer in the study area but also effectively corrects inaccuracies in shear wave velocity caused by wellbore collapse. Further, the data obtained using this method can be used for cross-plot analysis and the construction of petrophysics templates.

3.3.2. Sensitivity analysis of parameters

The selection of optimally sensitive parameters increases the accuracy and efficiency of reservoir prediction. Therefore, finding the rock elasticity parameters, which are sensitive to the presence of reservoirs, is an important part of rock physics model. By performing a cross-plot analysis between the available data and the petrophysics model, the elastic parameter that are sensitive to reservoirs can be identified. In this study, cross-plot analysis was performed using the V_p/V_s, S-wave acoustic impedance, and P-wave acoustic impedance. The results are shown in Figs. 7 and 8.

Figure 7.

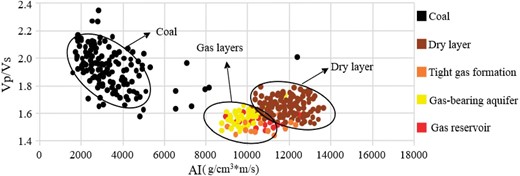
Cross-plot analysis between the V_p/V_s and P-wave acoustic impedance.

Figure 8.

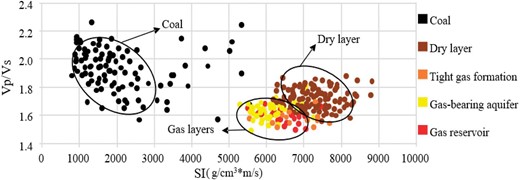
Cross-plot analysis between the V_p/V_s and S-wave acoustic impedance.

The cross-plot analyses on elasticity parameters obtained using our improved model can be used to differentiate reservoir strata (Figs. 7 and 8). For example, the coal in the figure as a whole is characterized by a high V_p/V_s values and low P-wave acoustic impedance and S-wave acoustic impedance, whereas sandstone strata have low V_p/V_s values and high P-wave acoustic impedance and S-wave acoustic impedance. Additionally, the dry layer of the sandstone exhibits higher V_p/V_s values than gas layers. Therefore, the V_p/V_s can serve as a sensitive elastic parameter for identifying gas reservoirs.

3.3.3. Construction of a petrophysics template

Based on the improved petrophysics model, we constructed a petrophysics template and obtained relations between P-wave acoustic impedance and V_p/V_s and porosity, mudstone content, and water saturation (Fig. 9).

Figure 9.

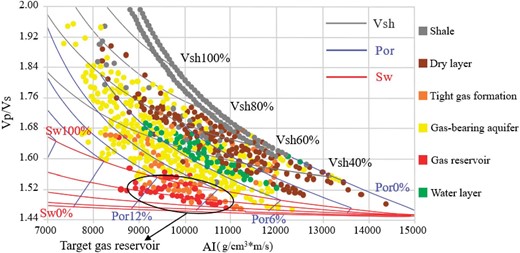
Petrophysics template for V_p/V_s and P-wave acoustic impedance.

The red, blue, and gray lines represent water saturation, porosity, and mudstone content, respectively. The division of reservoir range can be realized through the analysis of petrophysics template (Table 6). The target gas reservoir in the study area is primarily distributed within the following ranges: P-wave acoustic impedance of 8500 to 11 500 g/cm³·m/s, V_p/V_s ratio of 1.48 to 1.56, mudstone content of 3% to 35%, porosity of 6% to 12%, and water saturation of 40% to 65%. Using this range can provide a basis for reservoir prediction in the subsequent inversion process.

Table 6.

Elasticity parameter zones for reservoir strata.

Reservoir type	P-wave acoustic impedance (g/cm³ m/s)	V_p/V_s	Water saturation (%)	Porosity (%)	Mudstone content (%)
Class I reservoir (gas strata)	8500–11 100	1.48–1.56	40–50	8–12	3–10
Class II reservoir (tight gas formation)	9000–11 500	1.48–1.58	50–65	7–12	3–35
Class III reservoir (gas-bearing aquifer and dry layer)	8000–13 500	1.48–1.84	>60	1–12	4–60

Reservoir type	P-wave acoustic impedance (g/cm³ m/s)	V_p/V_s	Water saturation (%)	Porosity (%)	Mudstone content (%)
Class I reservoir (gas strata)	8500–11 100	1.48–1.56	40–50	8–12	3–10
Class II reservoir (tight gas formation)	9000–11 500	1.48–1.58	50–65	7–12	3–35
Class III reservoir (gas-bearing aquifer and dry layer)	8000–13 500	1.48–1.84	>60	1–12	4–60

Table 6.

Elasticity parameter zones for reservoir strata.

Reservoir type	P-wave acoustic impedance (g/cm³ m/s)	V_p/V_s	Water saturation (%)	Porosity (%)	Mudstone content (%)
Class I reservoir (gas strata)	8500–11 100	1.48–1.56	40–50	8–12	3–10
Class II reservoir (tight gas formation)	9000–11 500	1.48–1.58	50–65	7–12	3–35
Class III reservoir (gas-bearing aquifer and dry layer)	8000–13 500	1.48–1.84	>60	1–12	4–60

Reservoir type	P-wave acoustic impedance (g/cm³ m/s)	V_p/V_s	Water saturation (%)	Porosity (%)	Mudstone content (%)
Class I reservoir (gas strata)	8500–11 100	1.48–1.56	40–50	8–12	3–10
Class II reservoir (tight gas formation)	9000–11 500	1.48–1.58	50–65	7–12	3–35
Class III reservoir (gas-bearing aquifer and dry layer)	8000–13 500	1.48–1.84	>60	1–12	4–60

3.3.4. Prediction of sweet spots

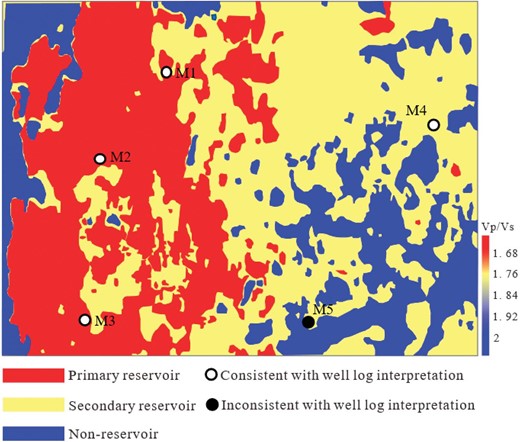
Eight wells in the study area were used for sweet spot prediction, whereas five wells were used to validate the predictions. Figure 10 shows the sweet spot area of the target layer predicted by using the preferred reservoir-sensitive parameters. In the figure, the red area indicates the area with gas layer development (primary reservoir), the yellow area indicates the area with poor gas layer development (secondary reservoir), and the blue area indicates that there is no gas layer development (non-reservoir) in the area. The gas-bearing properties of the predicted area are verified by using the existing logging data. The results indicate that the gas-bearing properties of M1, M2, M3, and M4 wells are consistent with the well-log interpretation. The predictions were 80% consistent with the actual values, which shows a great predictive performance.

Figure 10.

Sweet spot prediction in the target stratum.

4. Conclusion

Using the elastic modulus of sandstone and mudstone derived from the random-walk algorithm to calculate the elastic modulus of the rock matrix, the results reveal an average error of 4.01% compared to actual measurements. This relatively small error indicates that the calculated values are closer to the observed data. This method can effectively improve the calculation accuracy of elastic modulus of tight sandstone matrix in the study area.
Research results indicate that the improved rock physics model provides a good fit for the actual rock physics characteristics of the study area. Through cross-plot analysis and the construction of rock physics templates, V_p/V_s was identified as the elastic parameter most sensitive to gas layers. Additionally, the distribution range of elastic parameters for the main gas-bearing layers in the study area was determined.
When the sensitive parameters were used to predict sweet spots in the target stratum, the agreement between the ground truth and predictions was 80% (validation via well-log data). Therefore, the suggested approach can direct the investigation of tight gas reservoirs in the research region.

Conflict of interest statement

None declared.

Funding

This work was supported by fundamental research funds for the National Natural Science Foundation of China (grant no. 42474186), the central universities (grant no. 2023JCCXLX01) and Open Fund of State Key Laboratory of ‘Coal Resources and Safe Mining’ (grant no. SKLCRSM20KFA13).

Data availability

The data that support the findings of this study are available from the corresponding author, Suzhen Shi, upon reasonable request.

References

Avseth

Johansen

Bakhorji

Mustafa

HM.

2014

Rock-physics modeling guided by depositional and burial history in low-to-intermediate-porosity sandstones

Geophysics

D115

–

10.1190/geo2013-0226.1

10.1016/j.petrol.2020.107864

Azadpour

Saberi

Javaherian

Shabani

2020

Rock physics model-based prediction of shear wave velocity utilizing machine learning technique for a carbonate reservoir, southwest Iran

J Pet Sci Eng

195

107864

10.1016/j.petrol.2011.06.004

Tan

Müller

TM.

2021

Brittle mineral prediction based on rock-physics modelling for tight oil reservoir rocks

J Geophys Eng

970

–

Berryman

JG.

1995

Mixture theories for rock properties

. In:

Ahrens

(ed.),

Rock Physics and Phase Relations: A Handbook of Physical Constants

205

–

AGU Publications

10.1029/rf003p0205

Bosch

Carvajal

Rodrigues

Torres

Aldana

Sierra

2009

Petrophysical seismic inversion conditioned to well-log data: methods and application to a gas reservoir

Geophysics

–

O15

Brie

Pampuri

Marsala

Meazza

1995

Shear sonic interpretation in gas-bearing sands

SPE Annual Technical Conference and Exhibition

701

–

10.2118/30595-MS

Desbois

Urai

Kukla

Konstanty

Claudia

2011

High-resolution 3D fabric and porosity model in a tight gas sandstone reservoir: a new approach to investigate microstructures from mm-to nm-scale combining argon beam cross-sectioning and SEM imaging

J Pet Sci Eng

243

–

10.19509/j.cnki.dzkq.2022.0155

Liu

Bai

Zhang

Lin

Shi

SZ.

2022

Prediction of tight sandstone reservoirs based on waveform indication simulation

Bull Geol Sci Technol

–

100

(in Chinese)

OpenURL Placeholder Text

10.1007/s11600-023-01069-6

Durrani

MZA

Rahman

Talib

Sarosh

2023

Discrimination of lithofacies in tight gas reservoir using field-specific rock physics modeling scheme. A case study from a mature field of middle Indus Basin, Pakistan

Acta Geophys

2763

–

Goodway

Perez

Varsek

Abaco

2010

Seismic petrophysics and isotropic-anisotropic AVO methods for unconventional gas exploration

Leading Edge

1500

–

10.1190/1.3525367

Guo

Xie

Zou

Ding

YJ.

2016

Numerical simulation of multi-dimensional NMR response in tight sandstone

J Geophys Eng

285

–

10.1088/1742-2132/13/3/285

10.11897/SP.J.1016.2017.01275

Xiao

Liu

XF.

2023

Construction of multi-mineral digital rocks for upscaling the numerical simulation of tight rock physical properties

Adv Geo-Energ Res

–

10.46690/ager.2023.07.07

Kuster

Toksöz

MN.

1974

Velocity and attenuation of seismic waves in two-phase media: part I. Theoretical formulations

Geophysics

587

–

606

Lee

MW.

2005

Proposed moduli of dry rock and their application to predicting elastic velocities of sandstones

United States Department of the Interior, United States Geological Survey, Reston, VA

10.3133/sir20055119

Liu

Han

Jiang

Liu

Geng

2017

Two-tier random walk based relational inference algorithm

Chinese J Comput

1275

–

(in Chinese)

OpenURL Placeholder Text

10.1016/j.energy.2013.01.048

Luo

Zhao

LW.

2006

Manifold learning algorithms based on spectral graph theory

J Comput Res Dev

1173

–

(in Chinese)

McGlade

Speirs

Sorrell

2013

Unconventional gas–a review of regional and global resource estimates

Energy

571

–

10.1088/1742-2132/13/4/526

Nur

Mavko

Dvorkin

Galmudi

1998

Critical porosity: a key to relating physical properties to porosity in rocks

Leading Edge

357

–

Ruiz

Azizov

2011a

Tight shale elastic properties using the soft-porosity and single aspect ratio models

SEG Technical Program Expanded Abstracts

Houston, Texas, USA

Society of Exploration Geophysicists

2241

–

Ruiz

Azizov

2011b

Fluid substitution in tight shale using the soft-porosity model

SEG Technical Program Expanded Abstracts

Houston, Texas, USA

Society of Exploration Geophysicists

2272

–

Ruiz

Cheng

2010

A rock physics model for tight gas sand

Leading Edge

1484

–

10.1190/1.3525364

Smith

Sayers

Sondergeld

CH.

2009

Rock properties in low-porosity/low-permeability sandstones

Leading Edge

–

Sun

Wei

Chen

XL.

2016

Fluid identification in tight sandstone reservoirs based on a new rock physics model

J Geophys Eng

526

–

10.1016/j.petrol.2021.109607

Szabó

Remeczki

Jobbik

Kiss

Dobróka

2022

Interval inversion based well log analysis assisted by petrophysical laboratory measurements for evaluating tight gas formations in Derecske through, Pannonian Basin, east Hungary

J Pet Sci Eng

208

109607

10.1007/s10712-022-09712-5

Toksöz

Cheng

Timur

1976

Velocities of seismic waves in porous rocks

Geophysics

621

–

Wang

Cui

Liu

JX.

2022

Fluid discrimination based on inclusion-based method for tight sandstone reservoirs

Surv Geophys

1469

–

10.3969/j.issn.1673-5005.2016.02.006

Wang

GC.

2015

The rock physics modeling for tight reservoir based on the self-consistent approximation

Progr Geophys

2233

–

(in Chinese)

10.6038/pg20150533

Yang

Wang

2018

Shear wave velocity prediction with optimized Xu-White model constrained by varying aspect ratios in tight sandstone reservoir

International Geophysical Conference, Beijing, China, 24-27 April

2018

;

514

–

10.1190/IGC2018-126

Yin

Liu

2016

Anisotropic rock physics modeling of tight sandstone and applications

J China Univ Petrol (Edition of Natural Science)

–

(in Chinese)

OpenURL Placeholder Text

10.1016/j.jappgeo.2024.105318

Zhang

Yin

Zhou

YQ.

2024

Sandstone reservoir rock physics modeling and time-lapse seismic analysis

J Appl Geophys

222

105318

Zhao

Jia

Song

Hou

Jiang

2023

Dynamic mechanisms of tight gas accumulation and numerical simulation methods: narrowing the gap between theory and field application

Adv Geo-Energy Res

146

–

10.46690/ager.2023.06.02