Fractionized based rheological features of transient motion of Walter’s B fluid in a rectangular oscillatory duct with cosine and sine oscillations

heat transfer, rectangular oscillatory duct, Caputo fractional derivative, Walter’s B fluid, double finite Fourier transform

Highlights

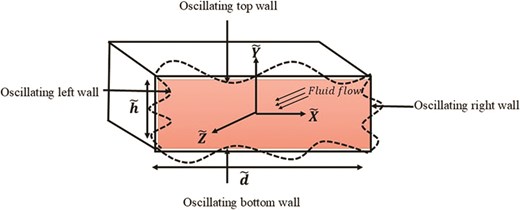
Oscillatory rectangular duct with porous medium is taken to scrutinize fractionalized based flow problem.
Flow properties of non-Newtonian Walter’s B fluid with fractional approach are examined.
Caputo fractional operator is implemented subject to sine and cosine oscillations.
Laplace transform and double finite Fourier transform are utilized to acquire solution of velocity.
Graphical illustration of velocity field is manifested for pertinent parameters.

Nomenclature

|${\boldsymbol{S}}$|
Cauchy stress tensor

|${t}^*$|
Time |$( s )$|

|$\bar{\omega }$|
Frequency parameter

|${d}^*$|
Width of channel |$( m )$|

|$p$|
Pressure |$(N/{m}^2)$|

|${\boldsymbol{I}}$|
Identity tensor

|$\rho $|
Density |$( {\frac{{kg}}{{{m}^3}}} )$|

|${k}^*$|
Elastic parameter

|${K}^*$|
Porosity parameter

|$\vartheta $|
Kinematics viscosity |$( {\frac{{{m}^2}}{s}} )$|

|${B}_0$|
Magnetic field strength |$( {{\rm{{kg}} \!\mathord{/ {\vphantom {{kg} {{s}^2}}}} \!\rm{{{s}^2}}}} )$|

|${h}^*$|
Height of channel |$( m )$|

|${K}_1$|
Porous medium permeability

|$({x}^*,{y}^*,{z}^*)$|
Cartesian coordinates |$( m )$|

|${\mu }_0$|
Dynamic viscosity |$( {Pas} )$|

|$\sigma $|
Electrical conductivity |${( {\Omega m} )}^{ - 1}$|

|${\omega }^*$|
Frequency of oscillations

|$( {{u}^*,\ {w}^*} )$|
Velocity elements |$( {\frac{m}{s}} )$|

|$M$|
Magnetic parameter

|${\boldsymbol{V}}$|
Velocity field

|$\gamma $|
Fluid parameter

|${\boldsymbol{T}}$|
Extra stress tensor

|${U}_0$|
Positive constants

|$\delta $|
Fractional parameter

|${\varrho }_1$|
Porosity

|${\boldsymbol{A}}$|
Strain rate tensor

1. Introduction

Fractional calculus focuses on the brief investigation of integration and differentiation of fractional or noninteger order. In casual differentiation and integration, only integer order-based calculations are involved but in the case of fractional calculus, the noninteger or fractional order-based calculations are involved. Fractional calculus has a significant range of implementations in various disciplines due to the involvement of fractional ordered differentiation. The practices of fractional operators include the fields of bioengineering, population growth, signal processing, image and video processing, chaos and nonlinear dynamics, etc. The theory of fractional calculus incorporates different kinds of fractional derivatives. The Riemann-Liouville (Liouville, 1832) and Caputo derivatives (Caputo, 1967) are among the most frequently used types of fractional derivatives. Caputo derivative is one of the significant fractional derivatives in which initially ordinary derivative of the desired function is calculated and then implemented the interpretation of Riemann-Liouville fractional integral. Caputo fractional operator has considerable advantage over other fractional derivatives in the sense that it incorporates the initial and boundary conditions similarly to usual derivatives. Various researchers study the fractional derivatives for different physical systems. Qi et al. (2017) experimentally investigated the fluid flow by incorporating the fractional approach. With the consideration of a vertical medium, the investigation of Maxwell fluid with magnetized fractional flow was deliberated by Abro et al. (2018). Sun et al. (2018) discussed fractional field in the context of real-life implementations. Li et al. (2024) demonstrated the application of fractional operator to the characteristics of a differential equation. Kumar et al. (2020) analytically explored fractionalized flow equations by taking into account two different methodologies. More recent developments in the study of fractional derivatives are included in Kumam et al. (2022), Nadeem et al. (2023), and Bani-Fwaz et al. (2024, 2024).

Non-Newtonian fluids are very complicated in their nature and cannot be well deliberated by taking into account an individual equation. The perplexing attributes of non-Newtonian fluids can be briefly analyzed via different fluid models. Walter’s B fluid model falls under the viscoelastic category of non-Newtonian fluid models. This fluid model yields a variety of utilizations in different disciplines including food processing, geophysical flows, polymer extrusion, oil and gas industry, etc. Walter’s B fluid flows have been briefly studied by numerous researchers corresponding to the different physical conditions. An analytical description of Walter’s B fluid flow nature in the context of fractional operator was addressed by Al-Mdallal et al. (2018). The radiative thermal analysis of Walter’s B fluid in the context of a porous medium was inspected by Mahabaleshwar et al. (2018). The authors discussed two distinct thermal constraints for the flow phenomenon. The dynamical flow properties of Walter’s B fluid corresponding to physical constraints was addressed by Qaiser et al. (2021). The haphazard movement of Walter’s B fluid by taking into account various physical impacts was demonstrated by Wakif et al. (2021). The work of Awasthi et al. (2022) was to discuss the stability analysis of Walter’s B fluid. The implementation of fractional approach on the one-dimensional flow behavior of Walter’s B fluid was manifested by Ishtiaq et al. (2023). The authors discussed the flow characteristics in the context of two different time periods. The flow characteristics of Walter’s B fluids with more developments are depicted in Upreti et al. (2020), Yasir and Khan (2023), Yasir et al. (2023), and Sultan et al. (2024).

The branch of magnetohydrodynamic (MHD) communicates with the brief study of electrically conducting fluids. The discipline of MHD involves many utilizations such as metal processing, geophysics, electric power generation, plasma control, etc. Many researchers have briefly discussed the behavior of electrically conducting fluids in the presence of a magnetic field. Wang et al. (2020) conducted experiments to investigate the flow features of fluid by taking into account the consequences of a magnetic field. Within a cavity with U shaped, the convective based magnetized flow analysis of a nanofluid was performed by Ali et al. (2020). Abo-Eldahab et al. (2021) discussed the nanofluid with its magnetized dynamical behavior. On the surface of a slendering plate, the non-Newtonian fluid motion in three dimensions with the participation of a magnetic field was manifested by Nadeem et al. (2022). The dynamics of a ferrofluid within a twisted tube corresponding to the significance of magnetic field was disclosed by Sun et al. (2023).

Upon reviewing the previously discussed studies, it becomes clear that the two-dimensional fractional flow analysis of Walter’s B fluid with a rectangular oscillatory duct has not been examined until now. The current study is novel and includes the Caputo fractional derivative based study of a non-Newtonian type Walter’s B fluid. The two-dimensional transient motion of Walter’s B fluid is contemplated within the region of an oscillatory rectangular duct. The significance of magnetic field and porosity are also interpolated through the study. To identify the exact solution of the fractional derivative based fluid flow, two efficient analytical techniques of Laplace transform, and finite double Fourier transform are taken into account. After determining the exact outcomes of the flow phenomenon, the graphical scrutinization of velocity distribution is manifested by taking distinct magnitude of the pertinent parameters.

2. Development of Problem

Let us assume the two-dimensional time-dependent flow phenomenon of Walter’s B non-Newtonian fluid within the region of a rectangular duct. The rectangular duct is taken to be oscillatory. For physical interpretation, Figure. 1 is sketched in which rectangular duct is placed in Cartesian coordinates system. Along |$\tilde{X}$|-axis, the width of the duct is chosen and along |$\tilde{Y}$|-axis, height of the duct is taken. The length of the duct is considered to be towards |$\tilde{Z}$|-axis. Primarily, the considered fluid and duct are supposed to be in stationary position at time |$\tilde{t} = 0$|⁠. After the passage of time, the cosine and sine oscillations of rectangular duct occurs towards the direction of |$\tilde{Z}$|-axis. The movement of the fluid is also taken along |$\tilde{Z}$|-axis. With the oscillations of the duct, the flow properties of the considered fluid vary along both |$\tilde{X}$|-axis and |$\tilde{Y}$|-axis with time but remain constant corresponding to the |$\tilde{Z}$|-axis.

Figure 1:

Geometry of oscillatory duct.

2.1. Walter’s B fluid analysis

Walter’s B fluid has the following general form of constitutive equation:

$$\begin{eqnarray} {\boldsymbol{S}} = {\boldsymbol{T}} - {\boldsymbol{I}}p. \end{eqnarray}$$

(1)

The extra stress tensor in Equation 1 is denoted by |${\boldsymbol{T}}$|⁠. This tensor is elucidated according to the following equation for Walter’s B fluid (Akbar, 2016):

$$\begin{eqnarray} {\boldsymbol{T}} = 2{\mu }_0{\boldsymbol{A}} - 2{k}^*\frac{{D{\boldsymbol{A}}}}{{Dt}}. \end{eqnarray}$$

(2)

In Equation 2, the first Rivlin Ericksen tensor |${\boldsymbol{A}}$| and the converted differentiation |$\frac{{D{\boldsymbol{A}}}}{{Dt}}$| of a tensor are depicted in the following way (Akbar, 2016; Al-Mdallal et al., 2018):

$$\begin{eqnarray} \begin{array}{@{}*{1}{c}@{}} {{\boldsymbol{A}} = (\nabla {\boldsymbol{V}}) + {{(\nabla {\boldsymbol{V}})}}^T}\\ {\frac{{D{\boldsymbol{A}}}}{{Dt}} = \frac{{\partial {\boldsymbol{A}}}}{{\partial t}} + ({\boldsymbol{V}}.\nabla ){\boldsymbol{A}} - {\boldsymbol{A}}(\nabla {\boldsymbol{V}}) - {{(\nabla {\boldsymbol{V}})}}^T{\boldsymbol{A}}} \end{array} \end{eqnarray}$$

(3)

In relation to the fluid movement, the fluid velocity is taken in the following form:

$$\begin{eqnarray} \begin{array}{@{}*{1}{c}@{}} {\boldsymbol{V = }}\left\{ {0,0,\tilde{W}\left( {\tilde{X},\tilde{Y},\tilde{t}} \right)} \right\},\\ {\boldsymbol{V}} = \tilde{U}\left( {\tilde{X},\tilde{Y},\tilde{t}} \right). \end{array} \end{eqnarray}$$

(4)

The utilization of Equations 3 and 4 to Equation 2, the following components of extra stress are acquired:

$$\begin{eqnarray} && {{T}_{\tilde{X}\tilde{X}} = {k}^*{{\left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{X}}}} \right)}}^2,\quad {T}_{\tilde{Y}\tilde{Y}} = {k}^*{{\left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{Y}}}} \right)}}^2,\quad {T}_{\tilde{Z}\tilde{Z}} = 0,}\\ && \quad {\ {T}_{\tilde{X}\tilde{Y}} = {T}_{\tilde{Y}\tilde{X}} = {k}^*\left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{X}}}} \right)\left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{Y}}}} \right),\quad {T}_{\tilde{X}\tilde{Z}} = {T}_{\tilde{Z}\tilde{X}} = {\mu }_0\left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{X}}}} \right) - {k}^*\left( {\frac{{{\partial }^2\tilde{U}}}{{\partial \tilde{X}\tilde{t}}}} \right)},\\ && \quad {\ {T}_{\tilde{Y}\tilde{Z}} = {T}_{\tilde{Z}\tilde{Y}} = {\mu }_0\left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{Y}}}} \right) - {k}^*\left( {\frac{{{\partial }^2\tilde{U}}}{{\partial \tilde{Y}\tilde{t}}}} \right)}, \end{eqnarray}$$

(5)

In Equation 5, |${k}^*$| identify as elastic parameter of Walter’s-B fluid. As the Walter’s-B fluid is a viscoelastic fluid so |${\mu }_0$| presents its viscosity property and |${k}^*$| manifest the elasticity property. The presence of |${k}^*$| in Equation 5 demonstrates the fluid’s capability to exhibit elastic behavior in response to deformation.

The momentum equation that governs the fluid behavior corresponding to the fluid movement is manifested as follows:

$$\begin{eqnarray} \rho \left[ {\frac{{\partial \tilde{U}}}{{\partial \tilde{t}}}} \right] = \frac{\partial }{{\partial \tilde{X}}}\left[ {{T}_{\tilde{Z}\tilde{X}}} \right] + \frac{\partial }{{\partial \tilde{Y}}}\left[ {{T}_{\tilde{Z}\tilde{Y}}} \right] + \frac{\partial }{{\partial \tilde{Z}}}\left[ {{T}_{\tilde{Z}\tilde{Z}}} \right], \end{eqnarray}$$

(6)

Equations 5 and 6 yield the following constitutive equation of the flow phenomenon:

$$\begin{eqnarray} \rho \left[ {\frac{{\partial \tilde{U}}}{{\partial \tilde{t}}}} \right] = \left[ {{\mu }_0 - {k}^* -\!\!\!\!D _{\tilde{t}}^\delta } \right]\left[ {\frac{{{\partial }^2\tilde{U}}}{{\partial {{\tilde{X}}}^2}} + \frac{{{\partial }^2\tilde{U}}}{{\partial {{\tilde{Y}}}^2}}} \right] - \frac{{{\varrho }_1}}{{{K}_1}}\left[ {{\mu }_0 - {k}^* -\!\!\!\!D _{\tilde{t}}^\delta } \right]\tilde{U} - \sigma B_0^2\tilde{U}, \end{eqnarray}$$

(7)

The above equation is related to the following suitable initial and boundary conditions, which correspond to the duct’s cosine and sine oscillations (Nadeem et al., 2024):

$$\begin{eqnarray} \tilde{U}\left( {\tilde{X},\tilde{Y},0} \right) &=& 0,\\ \tilde{U}\left( {0,\tilde{Y},\tilde{t}} \right) &=& {U}_0Cos\left\{ {\tilde{\omega }\tilde{t}} \right\},\\ \tilde{U}\left( {\tilde{X},0,\tilde{t}} \right) &=& {U}_0Cos\left\{ {\tilde{\omega }\tilde{t}} \right\},\\ \tilde{U}\left( {\tilde{d},\tilde{Y},\tilde{t}} \right) &=& {U}_0Cos\left\{ {\tilde{\omega }\tilde{t}} \right\},\\ \tilde{U}\left( {\tilde{X},\tilde{h},\tilde{t}} \right) &=& {U}_0Cos\left\{ {\tilde{\omega }\tilde{t}} \right\}, \end{eqnarray}$$

(8)

$$\begin{eqnarray} \tilde{U}\left( {\tilde{X},\tilde{Y},0} \right) &=& 0,\\ \tilde{U}\left( {0,\tilde{Y},\tilde{t}} \right) &=& {U}_0Sin\left\{ {\tilde{\omega }\tilde{t}} \right\},\\ \tilde{U}\left( {\tilde{X},0,\tilde{t}} \right) &=& {U}_0Sin\left\{ {\tilde{\omega }\tilde{t}} \right\},\\ \tilde{U}\left( {\tilde{d},\tilde{Y},\tilde{t}} \right) &=& {U}_0Sin\left\{ {\tilde{\omega }\tilde{t}} \right\},\\ \tilde{U}\left( {\tilde{X},\tilde{h},\tilde{t}} \right) &=& {U}_0Sin\left\{ {\tilde{\omega }\tilde{t}} \right\}. \end{eqnarray}$$

(9)

In Equation 7, |${\rm{ -\!\!\!\!D }}_{\tilde{t}}^\delta $| indicates the Caputo fractional derivative of order |$\delta $|⁠.

2.2. Fractal dimension of porous medium

It is examined that fractal dimension is a key factor in different mechanisms as mostly mechanical properties of a medium strongly rely on fractal dimensions. For an instant, the volume can be relate to the measured size as |$\bar{V} \propto {\bar{r}}^3$|⁠. Likewise in the case of a porous medium, the volume is manifested as |$\bar{V} \propto {\bar{r}}^n$| and |$n$| identify as the fractal dimensions. Now the task is to find out the fractal dimensions |$n$| for a porous medium. Numerous researchers introduced different formulas to find out |$n$| according to their problem. Among them, one of the best way to identify fractal dimensions was introduced by He and Liu (2023). They calculate the area of a porous medium by implementing two scale fractal dimensions with two scales |$\bar{C}$| and |$\bar{L}$|⁠. As the present problem’s geometry is a porous rectangular duct so we can implement two-scale fractal dimensions approach (He & Liu, 2023). The length of the duct is taken here as |$\tilde{d}$| and any pores in the considered medium with sizes less than |$\tilde{d}$| are neglected, when we utilize the |$\tilde{d}$| scale. So, the area is taken as |${\tilde{d}}^2$|⁠. In the case of |$\bar{C}$| scale, the area is calculated as |${\tilde{d}}^2 - {\tilde{C}}^2$|⁠. The two-scale fractal dimensions approach yields the following expressions (He & Liu, 2023):

$$\begin{eqnarray} 2\left\{ {\frac{1}{n}} \right\} = \left\{ {{{\tilde{d}}}^2} \right\}\left\{ {\frac{1}{{{{\tilde{d}}}^2 - {{\tilde{C}}}^2}}} \right\} \end{eqnarray}$$

(10)

$$\begin{eqnarray} \left\{ n \right\} = 2\left\{ {{{\tilde{d}}}^2 - {{\tilde{C}}}^2} \right\}\left\{ {\frac{1}{{{{\tilde{d}}}^2}}} \right\}. \end{eqnarray}$$

(11)

The relation between volume of a porous medium and two-scale fractal dimensions is expressed as follow:

$$\begin{eqnarray} n\left\{ {\frac{1}{3}} \right\} = \left\{ {\bar{V} - {{\bar{V}}}_{\rm{pore}}} \right\}\left\{ {\frac{1}{{\bar{V}}}} \right\}. \end{eqnarray}$$

(12)

In Equation 12, |${\bar{V}}_{\textit{pore}}$| presents the pores’ total volume. Moreover, the porosity is deliberated as follow:

$$\begin{eqnarray} \Phi = \left\{ {{{\bar{V}}}_{\rm{pore}}} \right\}\left\{ {\frac{1}{{\bar{V}}}} \right\}, \end{eqnarray}$$

(13)

Thus, for a porous medium, the two-scale fractal dimensions is manifested in the following way:

$$\begin{eqnarray} n = 3\left\{ { - \Phi + 1} \right\}. \end{eqnarray}$$

(14)

Similarly, the two-scale fractal dimensions in the context of a porous space in a medium is deliberated as follow:

$$\begin{eqnarray} {n}_{\textit{Pore}} = 3\left\{ {\Phi} \right\} = \left\{ {3 - n} \right\}. \end{eqnarray}$$

(15)

2.3. Caputo fractional derivative

To explore the current flow problem in the context of fractional derivative, the fractional approach of Caputo (Caputo, 1967) with order |$\delta $| is implemented. The Caputo fractional operator has primarily the advantage of utilizing the boundary and initial conditions in the same manner as used in usual derivatives. Further, in Caputo fractional approach, the value of |$\delta = 1$| provides the same outcomes as the usual derivatives provide and by taking |$\delta = 0$|⁠, the original function is acquired. The following equation illustrates the form of the Caputo fractional derivative having |$\delta $| order (Caputo, 1967):

$$\begin{eqnarray} {\rm{ -\!\!\!\!D }}_{\tilde{t}}^\delta \left[ {g\left( {\tilde{t}} \right)} \right] = \left[ {{{1} \!\mathord{\left/ {\vphantom {1 {\Gamma \left( {1 - \delta } \right)}}}\right.} \!\rm{{\Gamma \left( {1 - \delta } \right)}}}} \right]\mathop \int \nolimits_{\xi = 0}^{\xi = \tilde{t}} \left( {\frac{{g^{\prime}\left( \xi \right)}}{{{{\left( {\tilde{t} - \xi } \right)}}^\delta }}} \right){\rm d}\xi ,\quad 0 < \delta < 1. \end{eqnarray}$$

(16)

In Equation 16, |$\Gamma $| presents the gamma function.

Now, to acquire the dimensionless form of Equations 7–9, the appropriate similarity variables are expressed in the following equation (Ali et al., 2017; Nadeem et al., 2024):

$$\begin{eqnarray} \begin{array}{@{}*{1}{c}@{}} {\bar{Y} = \left( {\displaystyle\frac{{\tilde{Y}{U}_0}}{\vartheta }} \right),\ \bar{t} = \left( {\displaystyle\frac{{\tilde{t}U_0^2}}{\vartheta }} \right),\ \bar{D} = \left( {\displaystyle\frac{{\tilde{d}}}{L}} \right),\ \gamma = \left( {\displaystyle\frac{{{k}^*U_0^2}}{{{\vartheta }^2\rho }}} \right),\ \bar{X} = \left( {\displaystyle\frac{{\tilde{X}{U}_0}}{\vartheta }} \right),}\\ {\bar{U} = \left( {\displaystyle\frac{{\tilde{U}}}{{{U}_0}}} \right),\ M = \left( {\displaystyle\frac{{\sigma \vartheta B_0^2}}{{U_0^2\rho }}} \right),\ \bar{H} = \left( {\displaystyle\frac{{\tilde{h}}}{L}} \right),\ {K}^* = \left( {\displaystyle\frac{{{K}_1U_0^2}}{{{\varrho }_1{\vartheta }^2}}} \right),\ \bar{\omega } = \left( {\displaystyle\frac{{\tilde{\omega }\vartheta }}{{U_0^2}}} \right)} .\end{array} \end{eqnarray}$$

(17)

Implementation of Equation 17 to Equation 7, the governing equation in dimensionless form is given in the following equation:

$$\begin{eqnarray} \left[ {\frac{{\partial \bar{U}}}{{\partial \bar{t}}}} \right] = \left[ {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right]\left[ {\frac{{{\partial }^2\bar{U}}}{{\partial {{\bar{X}}}^2}} + \frac{{{\partial }^2\bar{U}}}{{\partial {{\bar{Y}}}^2}}} \right] - \frac{1}{{{K}^*}}\left[ {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right]\bar{U} - M\bar{U}, \end{eqnarray}$$

(18)

Equations 8, 9, and 17 yield the following equations:

$$\begin{eqnarray} \begin{array}{@{}*{1}{l}@{}} {\bar{U}\left( {\bar{X},\bar{Y},\ 0} \right) = 0,}\\ {\bar{U}\left( {0,\ \bar{Y},\ \bar{t}} \right) = \cos \left( {\bar{\omega }\bar{t}} \right) = Re\big[ {{e}^{i\bar{\omega }\bar{t}}} \big],}\\ {\bar{U}\left( {\bar{X},\ 0,\ \bar{t}} \right) = \cos \left( {\bar{\omega }\bar{t}} \right) = Re\big[ {{e}^{i\bar{\omega }\bar{t}}} \big],\ }\\ { {bar {U}} \left( {\bar{D},\ \bar{Y},\ \bar{t}} \right) = \cos \left( {\bar{\omega }\bar{t}} \right) = Re\big[ {{e}^{i\bar{\omega }\bar{t}}} \big],\ }\\ {{\bar{U}}\left( {\bar{X},\ \bar{H},\ \bar{t}} \right) = \cos \left( {\bar{\omega }\bar{t}} \right) = Re\big[ {{e}^{i\bar{\omega }\bar{t}}} \big],\ } \end{array} \end{eqnarray}$$

(19)

$$\begin{eqnarray} \begin{array}{@{}*{1}{l}@{}} {\bar{U}\left( {\bar{X},\bar{Y},0} \right) = 0,}\\ {\bar{U}\left( {0,\ \bar{Y},\ \bar{t}} \right) = \sin \left( {\bar{\omega }\bar{t}} \right) = Im\big[ {{e}^{i\bar{\omega }\bar{t}}} \big],}\\ {\bar{U}\left( {\bar{X},\ 0,\ \bar{t}} \right) = \sin \left( {\bar{\omega }\bar{t}} \right) = Im\big[ {{e}^{i\bar{\omega }\bar{t}}} \big],}\\ {\bar{U}\left( {\bar{D},\ \bar{Y},\ \bar{t}} \right) = \sin \left( {\bar{\omega }\bar{t}} \right) = Im\big[ {{e}^{i\bar{\omega }\bar{t}}} \big],}\\ {\bar{U}\left( {\bar{X},\ \bar{H},\ \bar{t}} \right) = \sin \left( {\bar{\omega }\bar{t}} \right) = Im\big[ {{e}^{i\bar{\omega }\bar{t}}} \big].} \end{array} \end{eqnarray}$$

(20)

3. Exact Solution

After implementing the application of Caputo fractional operator on governing equations of problem, the next aim is to find out the exact solution of the dimensionless equation. Two efficient techniques are utilized to acquire the exact solution of the velocity field for the current flow problem. For duct’s sine oscillation and cosine oscillation, the exact outcomes are obtained through Laplace transform technique and finite Fourier double sine transform (Nadeem et al., 2024). Firstly, the technique of finite Fourier double sine transform is executed to Equations 18–20. After that, the Laplace transform method is implemented to the resulting equations. After applying the inverse double finite Fourier sine transform and inverse Laplace transform, the final outcomes of the velocity field corresponding to sine oscillation and cosine oscillation are acquired. To start this novel procedure, let us denote the solution of Equation 18 relative to Equation 19 by |${F}_c( {\bar{X},\bar{Y},\ \bar{t}} )$| for cosine oscillation and solution of Equation 8 relative to Equation 20 by |${F}_s( {\bar{X},\bar{Y},\ \bar{t}} )$| for sine oscillation. For both solutions in the context of different solutions, the combined velocity field is expressed as follows:

$$\begin{eqnarray} F\left( {\bar{X},\bar{Y},\ \bar{t}} \right) = {F}_c\left( {\bar{X},\bar{Y},\ \bar{t}} \right) + i{F}_s\left( {\bar{X},\bar{Y},\ \bar{t}} \right), \end{eqnarray}$$

(21)

For Equation 21, the momentum equation with conditions corresponding to both oscillations is given as follows:

$$\begin{eqnarray} \left[ {\frac{{\partial F}}{{\partial \bar{t}}}} \right] = \left[ {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right]\left[ {\frac{{{\partial }^2F}}{{\partial {{\bar{X}}}^2}} + \frac{{{\partial }^2F}}{{\partial {{\bar{Y}}}^2}}} \right] - \frac{1}{{{K}^*}}\left[ {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right]F - MF, \end{eqnarray}$$

(22)

$$\begin{eqnarray} F\left( {\bar{X},\bar{Y},\ 0} \right) = 0, \end{eqnarray}$$

(23a)

$$\begin{eqnarray} \begin{array}{@{}l@{}} F\left( {0,\ \bar{Y},\ \bar{t}} \right) = {e}^{i\bar{\omega }\bar{t}},\\ F\left( {\bar{D},\ \bar{Y},\ \bar{t}} \right) = {e}^{i\bar{\omega }\bar{t}},\\ F\left( {\bar{X},\ 0,\ \bar{t}} \right) = {e}^{i\bar{\omega }\bar{t}},\\ F\left( {\bar{X},\ \bar{H},\ \bar{t}} \right) = {e}^{i\bar{\omega }\bar{t}}. \end{array} \end{eqnarray}$$

(23b)

To acquire the exact outcomes of above equations, the velocity field |$F( {\bar{X},\bar{Y},\ \bar{t}} )$| with its double finite Fourier transform is deliberated as follows (Nadeem et al., 2024):

$$\begin{eqnarray} {F}_{\rm rs}\left( {\bar{t}} \right) = \mathop \int \nolimits_0^{\bar{D}} \mathop \int \nolimits_0^{\bar{H}} F\left( {\bar{X},\bar{Y},\ \bar{t}} \right){\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\rm d}\bar{X}{\rm d}\ \bar{Y},\quad r = s = 1,2,3,\cdots \end{eqnarray}$$

(24)

After applying a double finite Fourier sine transform on both sides of Equation 22 and considering Equation 23b, the following outcomes are obtained:

$$\begin{eqnarray} && {\frac{{\partial {F}_{\rm rs}}}{{\partial \bar{t}}} + \left\{ {{\lambda }_{\rm rs}\left( {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right) + M + \frac{1}{{{K}^*}}\left( {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right)} \right\}{F}_{rs}}\\ && \quad { = \left( {1 - \gamma i\bar{\omega }} \right)\frac{{{\lambda }_{\rm rs}}}{{{\lambda }_r{\lambda }_s}}{e}^{i\bar{\omega }\bar{t}}\left\{ {\left( {1 - {{\left( { - 1} \right)}}^r} \right)\left( {1 - {{\left( { - 1} \right)}}^s} \right)} \right\}}, \end{eqnarray}$$

(25)

where

$$\begin{eqnarray} {\lambda }_s = \left( {{\raise0.7ex\hbox{${s\pi }$} \!\mathord{\left/ {\vphantom {{s\pi } {\bar{H}}}}\right.} \!\lower0.7ex\hbox{${\bar{H}}$}}} \right),\ {\lambda }_{rs} = {\lambda }_r^2 + {\lambda }_s^2 = {\left( {{\raise0.7ex\hbox{${r\pi }$} \!\mathord{\left/ {\vphantom {{r\pi } {\bar{D}}}}\right.} \!\lower0.7ex\hbox{${\bar{D}}$}}} \right)}^2 + {\left( {{\raise0.7ex\hbox{${s\pi }$} \!\mathord{\left/ {\vphantom {{s\pi } {\bar{H}}}}\right.} \!\lower0.7ex\hbox{${\bar{H}}$}}} \right)}^2,\ {\lambda }_r = \left( {{\raise0.7ex\hbox{${r\pi }$} \!\mathord{\left/ {\vphantom {{r\pi } {\bar{D}}}}\right.} \!\lower0.7ex\hbox{${\bar{D}}$}}} \right). \end{eqnarray}$$

(26)

After applying Equation 24, Equation 23a provides the following equation:

$$\begin{eqnarray} {F}_{rs}\left( {\ \bar{t}} \right) = 0,\quad {\rm{at\quad }}\bar{t} = 0, \end{eqnarray}$$

(27)

Now, after performing the Laplace transform to both sides of Equation 25 and utilizing Equation 27, the following equation is acquired:

$$\begin{eqnarray} {\bar{F}}_{rs}\left( q \right) = \frac{{{\lambda }_{rs}}}{{{\lambda }_r{\lambda }_s}}\frac{{\left( {1 - \gamma i\bar{\omega }} \right)}}{{\left( {q - i\bar{\omega }} \right)}}\left( {\frac{{\left\{ {\left( {1 - {{\left( { - 1} \right)}}^r} \right)\left( {1 - {{\left( { - 1} \right)}}^s} \right)} \right\}}}{{\left( {q + {\lambda }_{rs}\left( {1 - \gamma {q}^\delta } \right) + \frac{{\left( {1 - \gamma {q}^\delta } \right)}}{{{K}^*}} + M} \right)}}} \right), \end{eqnarray}$$

(28)

where the Laplace transform of |$ -\!\!\!\!D _{\ \bar{t}}^\delta $| is defined as follows (Sene, 2022):

$$\begin{eqnarray} \mathcal{L}\left[ { -\!\!\!\!D _{\ \bar{t}}^\delta \left\{ {{F}_{rs}\left( {\ \bar{t}} \right)} \right\}} \right] = {q}^\delta {\bar{F}}_{rs}\left( q \right) - {q}^{\delta - 1}{F}_{rs}\left( 0 \right). \end{eqnarray}$$

(29)

In Equation 29, |$q$| denotes the Laplace transform variable.

Equation 28 can be rewritten as follow:

$$\begin{eqnarray} {\bar{F}}_{rs}\left( q \right) = \frac{{{\lambda }_{rs}\left( {1 - \gamma i\bar{\omega }} \right)}}{{\left( {q - i\bar{\omega }} \right)}}\left( {\frac{{{\varepsilon }_{rs}}}{{\left( {q + {\lambda }_{rs}\left( {1 - \gamma {q}^\delta } \right) + \frac{{\left( {1 - \gamma {q}^\delta } \right)}}{{{K}^*}} + M} \right)}}} \right) \end{eqnarray}$$

(30)

$$\begin{eqnarray} {\bar{F}}_{rs}\left( q \right) = \frac{{{\varepsilon }_{rs}}}{{\left( {q - i\bar{\omega }} \right)}} - \frac{{{\varepsilon }_{rs}}}{{\left( {q - i\bar{\omega }} \right)}}\left( {1 - \frac{{{\lambda }_{rs}\left( {1 - \gamma i\bar{\omega }} \right)}}{{\left( {q + {\lambda }_{rs}\left( {1 - \gamma {q}^\delta } \right) + \frac{{\left( {1 - \gamma {q}^\delta } \right)}}{{{K}^*}} + M} \right)}}} \right), \end{eqnarray}$$

(31)

where

$$\begin{eqnarray} {\varepsilon }_{\rm rs} = \frac{{\left\{ {\left( {1 - {{\left( { - 1} \right)}}^r} \right)\left( {1 - {{\left( { - 1} \right)}}^s} \right)} \right\}}}{{{\lambda }_r{\lambda }_s}}. \end{eqnarray}$$

(32)

Let |${G}_{rs}( q ) = ( {1 - \frac{{{\lambda }_{rs}( {1 - \gamma i\bar{\omega }} )}}{{( {q + {\lambda }_{rs}( {1 - \gamma {q}^\delta } ) + \frac{{( {1 - \gamma {q}^\delta } )}}{{{K}^*}} + M} )}}} )$|⁠, which can be define in the form of series in the following way:

$$\begin{eqnarray} \begin{array}{@{}*{1}{l}@{}} {{G}_{rs}\left( q \right) = \displaystyle\sum\limits_{\zeta _1^* = 0}^{inf} {\displaystyle\sum\limits_{\zeta _2^* = 0}^{inf} {\displaystyle\sum\limits_{\zeta _3^* = 0}^{inf} {\displaystyle\sum\limits_{\zeta _4^* = 0}^{inf} {\Gamma \left[\kern-0.15em\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\kern-0.15em\right]{{\left( {{\lambda }_{rs}} \right)}}^{\left\{ { + \zeta _1^*} \right\}}} } } } \left\{ {\displaystyle\frac{1}{{\Gamma \left[\kern-0.15em\left[ {9 + \zeta _4^* - 8} \right]\kern-0.15em\right]}}} \right\}\left\{ {\displaystyle\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - \zeta _3^*} \right\}}}}} \right\}\left\{ {\displaystyle\frac{1}{{{{\left( q \right)}}^{\left\{ { + \zeta _4^*} \right\}}}}} \right\}\left\{ {\displaystyle\frac{1}{{\zeta _1^*\left\{ {\zeta _1^* - 1} \right\}\left\{ {\zeta _1^* - 2} \right\}\left\{ {\zeta _1^* - 3} \right\} \ldots 4.3.2.1}}} \right\}}\\ {{{\left( { - 5 - \gamma i\bar{\omega } + 6} \right)}}^{\left\{ { + \zeta _1^*} \right\}}\left\{ {\displaystyle\frac{1}{{\Gamma \left[\kern-0.15em\left[ {11 + \zeta _3^* - 10} \right]\kern-0.15em\right]}}} \right\}{{\left( q \right)}}^{\left\{ { - 1} \right\}}\left\{ {\displaystyle\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 2 - \zeta _1^* + 4} \right]\kern-0.15em\right]}}} \right\}\left\{ {\displaystyle\frac{1}{{{{\left( q \right)}}^{\left\{ {1 + \zeta _2^* - 1} \right\}}}}} \right\}}\\ {\Gamma \left[\kern-0.15em\left[ {\zeta _2^* + 1} \right]\kern-0.15em\right]{{\left( {\displaystyle\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}}^{\left\{ { - 4 + \zeta _2^* + 4} \right\}}\left\{ {\displaystyle\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - 7 - \zeta _1^* + 7} \right\}}}}} \right\}\left\{ {\displaystyle\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - \zeta _3^* + 9 + \zeta _2^* - 8} \right]\kern-0.15em\right]}}} \right\}\left\{ {\displaystyle\frac{1}{{\zeta _2^*\left\{ {\zeta _2^* - 1} \right\} \ldots 3.\ 2.1}}} \right\}}\\ {\Gamma \left[\kern-0.15em\left[ 2 \right]\kern-0.15em\right]{{\left( { - 1} \right)}}^{\left\{ { + \zeta _4^*} \right\}}\left\{ {{q}^{\left\{ { + \zeta _3^*} \right\}\left\{ { + \delta } \right\}}} \right\}\left\{ {\displaystyle\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\zeta _3^*} \right\}}}}} \right\}\left\{ {\displaystyle\frac{1}{{\Gamma \left[\kern-0.15em\left[ {\zeta _1^*} \right]\kern-0.15em\right]}}} \right\}\left\{ {{q}^1} \right\}{{\left( M \right)}}^{\left\{ { + \zeta _4^*} \right\}}\left\{ {{q}^{ - \left\{ {\zeta _1^*} \right\}}} \right\}{{\left( { - 1} \right)}}^{\left\{ { - 1 + \zeta _2^* + 1} \right\}}} .\end{array} \end{eqnarray}$$

(:33)

Now perform the inverse double finite Fourier sine transform on Equation 31, we have

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},q} \right) = \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\bar{F}}_{rs}\left( q \right). \end{eqnarray}$$

(34)

The execution of Equation 31 to Equation 34, we have

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},q} \right) &=& \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right)\frac{{{\varepsilon }_{rs}}}{{\left( {q - i\bar{\omega }} \right)}}\\ && - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right)\frac{{{\varepsilon }_{rs}}}{{\left( {q - i\bar{\omega }} \right)}}{G}_{rs}\left( q \right). \end{eqnarray}$$

(35)

After the execution of Equation 33 to Equation 35, the following equation is acquired:

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},q} \right) &=& \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\sum\limits_{r = 1,s = 1}^{\rm inf} {{\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right)\frac{{{\varepsilon }_{\rm rs}}}{{\left( {q - i\bar{\omega }} \right)}} - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\sum\limits_{r = 1,s = 1}^{inf} {{\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right)} }\\ && {\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right)\frac{{{\varepsilon }_{\rm rs}}}{{\left( {q - i\bar{\omega }} \right)}}\mathop \sum \limits_{\zeta _1^* = 0,\zeta _2^* = 0,\zeta _3^* = 0,\zeta _4^* = 0}^{\rm inf} \Gamma \left[\kern-0.15em\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\kern-0.15em\right]\left\{ {{q}^{ - \left\{ {\zeta _4^*} \right\}}} \right\}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{\rm rs}} \right)}^{\left\{ { - 11 + \zeta _2^* + 11} \right\}}\\ && \left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 6 + \zeta _4^* + 7} \right]\kern-0.15em\right]}}} \right\}{\left( {{\lambda }_{\rm rs}} \right)}^{\left\{ { - 16 + \zeta _1^* + 16} \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {11 - \zeta _3^* - 10 + \zeta _2^*} \right]\kern-0.15em\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ { - 46 + \zeta _2^* + 46} \right\}}\Gamma \left[\kern-0.15em\left[ {4 + \zeta _2^* - 3} \right]\kern-0.15em\right]\\ && {\left( {15 - \gamma i\bar{\omega } - 12 - 14 + 12} \right)}^{\left\{ { - 30 + \zeta _1^* + 30} \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {9 + \zeta _1^* - 9} \right]\kern-0.15em\right]}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 12 + \zeta _3^* + 14 + 13 - 14} \right]\kern-0.15em\right]}}} \right\}\\ && \left\{ {{q}^{\left( { - 1} \right)}} \right\}\left\{ {\frac{1}{{\left\{ { - 4 + \zeta _2^* - 1 + 3 + 1} \right\}\left\{ {\zeta _2^*} \right\} \ldots 3.\ 2.1}}} \right\}{\left( { - 1} \right)}^{\left\{ {3 + \zeta _1^* - 2 - 1} \right\}}\left\{ {{q}^{ - \left\{ { - 1 + \zeta _1^* + 1} \right\}}} \right\}\Gamma \left[\kern-0.15em\left[ {14 - 12} \right]\kern-0.15em\right]\\ && \left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {11 - \zeta _1^* - 8 - 9 + 8} \right]\kern-0.15em\right]}}} \right\}{\left( M \right)}^{\left\{ { - 10 + \zeta _4^* + 10} \right\}}{\left( { - 1} \right)}^{\left\{ {\hat{d}} \right\}}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { + 17 - \zeta _2^* - 17} \right\}}}}} \right\}\left\{ {{q}^{ - \left\{ {12 + \zeta _2^* - 12} \right\}}} \right\}\left\{ {{{\left( \gamma \right)}}^{\left\{ { - 16 + \zeta _3^* + 16} \right\}}} \right\}\\ && \left\{ {{q}^{\left( {12 - 11} \right)}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 15 + \zeta _1^* + 16} \right]\kern-0.15em\right]}}} \right\}\left\{ {{q}^{\left\{ { + 12 + \zeta _3^* - 12} \right\}\left\{ \delta \right\}}} \right\}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - 37 - \zeta _3^* + 37} \right\}}}}} \right\}. \end{eqnarray}$$

(36)

Equation 36 can be rewritten as follows:

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},q} \right) &=& \frac{1}{{\left( {q - i\bar{\omega }} \right)}} - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\sum\limits_{r = 1}^\infty {\sum\limits_{s = 1}^\infty {{\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right)\frac{{{\varepsilon }_{\rm rs}}}{{\left( {q - i\bar{\omega }} \right)}}} } \\ && \sum\limits_{\zeta _1^* = 0}^{\rm inf} {\sum\limits_{\zeta _2^* = 0}^{\rm inf} {\sum\limits_{\zeta _3^* = 0}^{\rm inf} {\sum\limits_{\zeta _4^* = 0}^{\rm inf} {\Gamma \left[\kern-0.15em\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\kern-0.15em\right]} } } } {\left( {\frac{1}{{{K}^*}} + {\lambda }_{\rm rs}} \right)}^{\left\{ { - 20 + \zeta _2^* - 1 + 20 + 1} \right\}}\left\{ {\frac{1}{{\left\{ {{q}^{\left\{ { - 5 + \zeta _4^* + 5} \right\}}} \right\}}}} \right\} \\ && {\left( M \right)}^{\left\{ { + 16 - 1 + \zeta _4^* + 1 - 16} \right\}}\left\{ {\frac{1}{{\left\{ {\zeta _4^* - 1} \right\}\zeta _4^*\left\{ {\zeta _4^* - 2} \right\} \ldots 2.1}}} \right\}\left\{ {{q}^{\left( { - 1} \right)}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {\zeta _2^* + 11 - 2 - \zeta _3^* - 10 + 2} \right]\kern-0.15em\right]}}} \right\} \\ && {\left( { - 12 - \gamma i\bar{\omega } + 13} \right)}^{\left\{ {\zeta _1^* - 50 + 50} \right\}}\left\{ {\frac{1}{{{{\left( \gamma \right)}}^{\left\{ { - 12 + 2 - \zeta _3^* - 2 + 12} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 2 + 4 - \zeta _1^*} \right]\kern-0.15em\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _2^*} \right\}}{\left( {{\lambda }_{rs}} \right)}^{\left\{ {\zeta _1^*} \right\}} \\ && \left\{ {{q}^{ - \left\{ {\zeta _2^*} \right\}}} \right\}\Gamma \left[\kern-0.15em\left[ {\zeta _2^* + 1} \right]\kern-0.15em\right]{\left( { - 1} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 2 + 1 + \zeta _1^* + 2 - 1} \right]\kern-0.15em\right]}}} \right\}\Gamma \left[\kern-0.15em\left[ 2 \right]\kern-0.15em\right]\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - 21 - \zeta _3^* + 21 - 2 + 2} \right\}}}}} \right\} \\ && \left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {1 + 13 + \zeta _3^* - 1 - 12} \right]\kern-0.15em\right]}}} \right\}\left\{ {{q}^{\left\{ {\zeta _3^* - 43 + 43} \right\}\left\{ \delta \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 6 + \zeta _2^* + 7} \right]\kern-0.15em\right]}}} \right\}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 20 + \zeta _1^* + 21} \right]\kern-0.15em\right]}}} \right\} \\ && \left\{ {{q}^{ - \left\{ {\zeta _1^*} \right\} + 21 - 2 - 21 + 2}} \right\}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - \zeta _4^* + 19 - 19} \right\}}}}} \right\}, \end{eqnarray}$$

(37)

where |$( {\frac{4}{{\bar{D}\bar{H}}}} )\mathop \sum \nolimits_{r = 1}^\infty \mathop \sum \nolimits_{s = 1}^\infty {\varepsilon }_{rs}{\rm Sin}( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} ){\rm Sin}( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} ) = 1$|⁠.

Equation 37 can be reformulated in a more convenient form as follows:

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},q} \right) &=& \frac{1}{{\left( {q - i\bar{\omega }} \right)}}\ - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{rs}\left( {1 + \frac{{i\bar{\omega }}}{{\left( {q - i\bar{\omega }} \right)}}} \right)\\ && \mathop \sum \limits_{\zeta _1^* = 0,\zeta _2^* = 0,\zeta _3^* = 0,\zeta _4^* = 0}^{inf} \Gamma \left[\kern-0.15em\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\kern-0.15em\right]\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {\zeta _1^* + 15 - 1 - 14 + 1} \right]\kern-0.15em\right]}}} \right\}\left\{ {\frac{1}{{{q}^{\left\{ {\zeta _1^*} \right\} - 14 + 14}}}} \right\}{\left( { - 1} \right)}^{\left\{ { + 23 + \zeta _2^* - 23} \right\}}\\ && {\left( {20 - \gamma i\bar{\omega } - 19} \right)}^{\left\{ { - 4 - 1 + \zeta _1^* + 1 + 4} \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {2 - 21 + \zeta _3^* + 22 - 2} \right]\kern-0.15em\right]}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {1 + \zeta _2^* - \zeta _3^*} \right]\kern-0.15em\right]}}} \right\}\Gamma \left[\kern-0.15em\left[ 2 \right]\kern-0.15em\right]\\ && \left\{ {{q}^{ - \left\{ {\zeta _4^*} \right\}}} \right\}\left\{ {\frac{1}{{\left\{ {\zeta _4^* - 2} \right\}\zeta _4^*\left\{ {\zeta _4^* - 1} \right\} \ldots 2.1}}} \right\}\left\{ {{q}^{\left\{ { - 1 + 2 + \zeta _3^* - 2 + 1} \right\}\left\{ \delta \right\}}} \right\}{\left( {1 - \gamma i\bar{\omega }} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ {10 - \zeta _4^* - 10} \right\}}}}} \right\}\\ && \left\{ {{q}^{ - \left\{ {\zeta _2^*} \right\}}} \right\}\Gamma \left[\kern-0.15em\left[ {\zeta _2^* + 1} \right]\kern-0.15em\right]{\left( { - 1} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 2 + 4 - \zeta _1^*} \right]\kern-0.15em\right]}}} \right\}\left\{ {{q}^{ - \left\{ { - 4 + 1 + \zeta _4^* + 4 - 1} \right\}}} \right\}{\left( { - 1} \right)}^{\left\{ { - 11 + \zeta _3^* + 11} \right\}}\left\{ {{q}^{\left\{ {18 - \zeta _1^* - 18} \right\}}} \right\}\\ && {\left( {\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}^{\left\{ { - 1 + \zeta _2^* + 1} \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {29 + \zeta _2^* - 28} \right]\kern-0.15em\right]}}} \right\}\left\{ {{q}^{\left( { - 1} \right)}} \right\}{\left( {{\lambda }_{\rm rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\zeta _3^*} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {\zeta _1^*} \right]\kern-0.15em\right]}}} \right\}{\left( M \right)}^{\left\{ {\zeta _4^*} \right\}}, \end{eqnarray}$$

(38)

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},q} \right) &=& \frac{1}{{\left( {q - i\bar{\omega }} \right)}}\ - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{rs}\\ && \sum\limits_{\zeta _1^* = 0}^{\rm inf} \sum\limits_{\zeta _2^* = 0}^{\rm inf} \sum\limits_{\zeta _3^* = 0}^{\rm inf} \sum\limits_{\zeta _4^* = 0}^{\rm inf} \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right] \left\{\frac{1}{\left( M \right)^{\lbrace- \zeta _4^* - 9 + 8 + 9 - 8 \rbrace}}\right\}\left\{ \frac{1}{\Gamma \left[\left[23 - 1 + \zeta _3^* - 21\right]\right]}\right\}\\ && \left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ {4 - \zeta _2^* - 4} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 12 + \zeta _1^* + 14 - 1} \right]\right]}}} \right\}\left\{ {\frac{1}{{\left\{ {{q}^{\left( 1 \right)}} \right\}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {1 + \zeta _2^* - \zeta _3^*} \right]\right]}}} \right\}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ {3 - 9 - \zeta _4^* + 6} \right\}}}}} \right\}\\ && \left\{ {{q}^{ - \left\{ {\zeta _4^*} \right\}}} \right\}\left\{ {\frac{1}{{\left\{ {\zeta _4^* - 1} \right\}\zeta _4^*\left\{ {\zeta _4^* - 2} \right\} \ldots 6.5.4.32.1}}} \right\}{\left( { - 1} \right)}^{\left\{ { - 9 + \zeta _1^* + 8 + 1} \right\}}\left\{ {\frac{1}{{{{\left( {1 - \gamma i\bar{\omega }} \right)}}^{ - \left\{ {\zeta _1^*} \right\}}}}} \right\}\left\{ {{{\left( \gamma \right)}}^{\left\{ { - 1 + \zeta _3^* + 1} \right\}}} \right\}\\ && \Gamma \left[\left[ {\zeta _2^* + 1} \right]\right]\left\{ {\frac{1}{{\Gamma \left[\left[ { - 2 + 4 - \zeta _1^*} \right]\right]}}} \right\}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{\rm rs}} \right)}^{\left\{ {\zeta _2^*} \right\}}\left\{ {\frac{1}{{\left\{ {{q}^{\left\{ {7 + \zeta _2^* - 6 - 1} \right\}}} \right\}}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}\left\{ {{q}^{ - \left\{ {\zeta _1^*} \right\}}} \right\}{\left( {{\lambda }_{rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}\\ && \left\{ {\frac{1}{{\left\{ {\zeta _2^* - 1} \right\}\left\{ {\zeta _2^*} \right\} \ldots 3.\ 2.1}}} \right\}\Gamma \left[\left[ 2 \right]\right]\left\{ {{q}^{\left\{ { - 9 + \zeta _3^* + 3 + 6} \right\}\left\{ \delta \right\}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {\hat{a}} \right]\right]}}} \right\} - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^{inf} \mathop \sum \limits_{s = 1}^{inf} {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right)\\ && {\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{\rm rs}\frac{{i\bar{\omega }}}{{\left( {q - i\bar{\omega }} \right)}}\mathop \sum \limits_{\zeta _1^* = 0,\zeta _2^* = 0,\zeta _3^* = 0,\zeta _4^* = 0}^{inf} \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right]\left\{ {\frac{1}{{{{\left( M \right)}}^{\left\{ { - \zeta _4^* - 10 + 9 + 1} \right\}}}}} \right\}\\ && \left\{ {\frac{1}{{\zeta _4^*\left\{ {\zeta _4^* - 1} \right\}\left\{ {\zeta _4^* - 2} \right\} \ldots 2.1}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 2 + 4 - \zeta _1^*} \right]\right]}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 7 + 1 + \zeta _1^* + 6} \right]\right]}}} \right\}\left\{ {{q}^{ - \left\{ {\zeta _2^*} \right\}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}\\ && \left\{ {{q}^{\left\{ {\zeta _3^* - 2 + 3 - 1} \right\}\left\{ \delta \right\}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 12 + \zeta _3^* + 11 + 13 - 11} \right]\right]}}} \right\}\left\{ {{q}^{\left\{ {4 - 6 - \zeta _4^* + 2} \right\}}} \right\}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - \zeta _4^* - 9 + 8 + 1} \right\}}}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _2^*} \right\}} \end{eqnarray}$$

(39)

$$\begin{eqnarray} \qquad \qquad \quad && \left\{ {\frac{1}{{\Gamma \left[\left[ { - \zeta _3^* + \zeta _2^* - 5 + 6} \right]\right]}}} \right\}\left\{ {{q}^{\left\{ {11 - 12 - \zeta _1^* + 1} \right\}}} \right\}{\left( {{\lambda }_{rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ {11 - 10 + \zeta _1^*} \right]\right]}}} \right\}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - \zeta _1^* - 11 + 12 - 1} \right\}}}}} \right\}\\ \qquad \qquad \quad && \left\{ {\frac{1}{{\zeta _2^*\left( {\zeta _2^* - 1} \right) \ldots 3.\ 2.1}}} \right\}\Gamma \left[\left[ 2 \right]\right]\left\{ {\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\hat{c}} \right\}}}}} \right\}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}^{\left\{ {\zeta _2^*} \right\}}\Gamma \left[\left[ {\zeta _2^* + 1} \right]\right]\left\{ {{q}^{\left( { - 7 + 6} \right)}} \right\}\left\{ {\frac{1}{{{{\left( {1 - \gamma i\bar{\omega }} \right)}}^{ - \left\{ {\zeta _1^*} \right\}}}}} \right\}. \end{eqnarray}$$

The following equation is accomplished after applying the inverse Laplace transform to Equation 39:

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},\bar{t}} \right) &=& {e}^{i\bar{\omega }\bar{t}}\ - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{\rm rs}{\left( {\bar{t}} \right)}^{\left\{ {\zeta _2^* - \delta \zeta _3^* + \zeta _4^* + \zeta _1^*} \right\}}\\ && \sum\limits_{\zeta _1^* = 0}^{\rm inf} {\sum\limits_{\zeta _2^* = 0}^{\rm inf} {\sum\limits_{\zeta _3^* = 0}^{\rm inf} {\sum\limits_{\zeta _4^* = 0}^{\rm inf} {} } } } \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right]\left\{ {\frac{1}{{\Gamma \left[\left[ {4 - 3 + \zeta _3^* + 3 - 3} \right]\right]}}} \right\}\{ \frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - \zeta _2^*} \right\}}}}\}\\ && \left\{ {\frac{1}{{\Gamma \left[\left[ {12 - 11 + \zeta _4^*} \right]\right]}}} \right\}\left\{ {{{\left( \gamma \right)}}^{4 - 3 + \left\{ {\zeta _3^*} \right\} - 1}} \right\}{\left( {15 - \gamma i\bar{\omega } - 14} \right)}^{\left\{ {9 - 7 + \zeta _1^* - 2} \right\}}{\left( { - 1} \right)}^{\left\{ { - 4 - 1 + \zeta _4^* + 5} \right\}}\\ && \Gamma \left[\left[ {\zeta _2^* + 1} \right]\right]{\left( { - 1} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ {22 + 1 - \zeta _1^* - 21} \right]\right]}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 1 - 2 + \zeta _1^* + 5 - 2} \right]\right]}}} \right\}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}^{\left\{ {\zeta _2^*} \right\}}\\ && \left\{ {\frac{1}{{\Gamma \left[\left[ {\zeta _2^* + 4 - 5 - \zeta _3^* + 2} \right]\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}{\left( {{\lambda }_{rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ {\zeta _1^* + 5 - 9 + 5} \right]\right]}}} \right\}{\left( M \right)}^{\left\{ {5 - 4 + \zeta _4^* - 1} \right\}}\\ && \left\{ {\frac{1}{{\zeta _2^*\left\{ {\zeta _2^* - 1} \right\} \ldots 3.\ 2.1}}} \right\}\Gamma \left[\left[ 2 \right]\right]\left\{ {\frac{1}{{\Gamma \left[\left[ {\zeta _4^* - \delta \zeta _3^* + 1 + \zeta _2^* + \zeta _1^*} \right]\right]}}} \right\} - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\\ && \mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{rs}i\bar{\omega }\left[ {{e}^{i\bar{\omega }\bar{t}}*{{\left( {\bar{t}} \right)}}^{\left\{ {\zeta _1^* + \zeta _4^* + \zeta _2^* - \delta \zeta _3^*} \right\}}} \right]\mathop \sum \limits_{\zeta _1^* = 0,\zeta _2^* = 0,\zeta _3^* = 0,\zeta _4^* = 0}^{\rm inf} \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right]\\ && \left\{ {\frac{1}{{\Gamma \left[\left[ {\zeta _4^* - \delta \zeta _3^* + 1 + \zeta _2^* + \zeta _1^*} \right]\right]}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {4 - 5 + \zeta _3^* + 2} \right]\right]}}} \right\}\Gamma \left[\left[ {4 - 2 + \zeta _2^* - 1} \right]\right]{\left( { - 1} \right)}^{\left\{ {\zeta _2^*} \right\}}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}^{\left\{ {\zeta _2^*} \right\}} \end{eqnarray}$$

(40)

$$\begin{eqnarray} \qquad \qquad \qquad \qquad && \left\{ {\frac{1}{{\Gamma \left[\left[ {1 - 8 + \zeta _1^* + 8} \right]\right]}}} \right\}\Gamma \left[\left[ 2 \right]\right]{\left( {1 - \gamma i\bar{\omega }} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\zeta _3^*} \right\}}}}} \right\},\left\{ {\frac{1}{{\Gamma \left[\left[ {1 - 7 + \zeta _4^* + 7} \right]\right]}}} \right\}{\left( {{\lambda }_{rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}{\left( M \right)}^{\left\{ {\zeta _4^*} \right\}}\\ \qquad \qquad \qquad \qquad && {\left( { - 1} \right)}^{\left\{ {4 - 5 + \zeta _1^* + 1} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ {9 - 9 - \zeta _1^* - 7 + 9} \right]\right]}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {1 + \zeta _2^* - \zeta _3^*} \right]\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ {\zeta _1^*} \right]\right]}}} \right\}\left\{ {\frac{1}{{\left\{ {4 - 3 + \zeta _2^*} \right\}}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _4^*} \right\}}. \end{eqnarray}$$

In Equation 40, the convolution product is denoted by “|$*$|” which is described in the following way:

$$\begin{eqnarray} {e}^{i\bar{\omega }\bar{t}}*{\left( {\bar{t}} \right)}^{\left\{ {\zeta _1^* + \zeta _4^* + \zeta _2^* - \delta \zeta _3^*} \right\}} &=& \mathop \int \nolimits_0^{\bar{t}} {e}^{i\bar{\omega }\left( {\bar{t} - \bar{\tau }} \right)}{(\bar{\tau })}^{\left\{ {\zeta _1^* + \zeta _4^* + \zeta _2^* - \delta \zeta _3^*} \right\}}d\bar{\tau },\\ {e}^{i\bar{\omega }\bar{t}}*{\left( {\bar{t}} \right)}^{\left\{ {\zeta _1^* + \zeta _4^* + \zeta _2^* - \delta \zeta _3^*} \right\}} &=& \left\{ {{{\left( {\bar{t}} \right)}}^{\left\{ {3 + \zeta _1^* - 2 + \zeta _4^* + 1 - \zeta _3^*\delta - 1 + \zeta _2^*} \right\}}} \right\}\left\{ {{{\left( {i\bar{\omega }\bar{t}} \right)}}^{\left\{ {\delta \zeta _3^* - 4 - \zeta _1^* - 1 + 3 - \zeta _2^* - \zeta _4^* + 1} \right\}}} \right\}\\ && \left\{ { - \Gamma \left[\kern-0.15em\left[ {\zeta _2^* - \delta \zeta _3^* + \zeta _4^* + 1 + \zeta _1^*,i\bar{t}\bar{\omega }} \right]\kern-0.15em\right] + \Gamma \left[\kern-0.15em\left[ {\zeta _4^* + 1 + \zeta _2^* - \delta \zeta _3^* + \zeta _1^*} \right]\kern-0.15em\right]} \right\}\left\{ {{e}^{i\bar{\omega }\bar{t}}} \right\}. \end{eqnarray}$$

(41)

Implementation of Equation 41 to Equation 40 yield the following results:

$$\begin{eqnarray} \bar{F}\left( {\bar{X},\bar{Y},\bar{t}} \right) &=& {e}^{i\bar{\omega }\bar{t}}\ - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{\rm rs}{\left( {\bar{t}} \right)}^{\left\{ {\zeta _2^* - \delta \zeta _3^* + \zeta _4^* + \zeta _1^*} \right\}}\\ && \mathop \sum \limits_{\zeta _1^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _2^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _3^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _4^* = 0}^{\rm inf} \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right]\left\{ {{{\left( \gamma \right)}}^{\left\{ { - 7 + 8 + \zeta _3^* - 4 + 3} \right\}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - \zeta _3^* - 4 + \zeta _2^* + 5} \right]\right]}}} \right\}\\ && \left\{ {\frac{1}{{\zeta _4^*!}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 8 + 7 + \zeta _1^* + 2 - 1} \right]\right]}}} \right\}\left\{ {\frac{1}{{{{\left( { - 1} \right)}}^{\left\{ { - 3 + 4 - \zeta _2^* - 9 + 8} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 9 + 11 + \zeta _3^* - 1} \right]\right]}}} \right\}{\left( M \right)}^{\left\{ {\zeta _4^*} \right\}}{\left( {{\lambda }_{\rm rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}\\ && \Gamma \left[\left[ {12 - 10} \right]\right]\left\{ {\frac{1}{{{{\left( {5 - 3 - \gamma i\bar{\omega } - 1} \right)}}^{\left\{ { - 4 + 3 - \zeta _1^* + 1} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {7 - 3 + \zeta _1^* - 3} \right]\right]}}} \right\}{\left( { - 4 + 3} \right)}^{\left\{ { - 11 + 12 + \zeta _4^* - 4 + 3} \right\}}\\ && \Gamma \left[\left[ {\{ \zeta _2^* + 1} \right]\right]\left\{ {\frac{1}{{\{ \zeta _2^*\} !}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {\zeta _4^* - \delta \zeta _3^* + 1 + \zeta _2^* + \zeta _1^*} \right]\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 2 + 4 - \zeta _1^*} \right]\right]}}} \right\}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}^{\left\{ {\hat{b}} \right\}}\\ && {\left( { - 1} \right)}^{\left\{ { - 2 + \zeta _3^* + 2} \right\}} - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{rs}i\bar{\omega }\mathop \sum \limits_{\zeta _1^* = 0,\zeta _2^* = 0,\zeta _3^* = 0,\zeta _4^* = 0}^{inf} \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right]\\ && \left\{ {\left\{ {{{\left( {\bar{t}} \right)}}^{3 + \zeta _2^* + 4 - \zeta _3^*\delta - 4 + \zeta _1^* - 2 + \zeta _4^*}} \right\}} \right.\left. {\left\{ {{e}^{i\bar{\omega }\bar{t}}} \right\}\left\{ {{{\left( {i\bar{\omega }\bar{t}} \right)}}^{\left\{ { - \zeta _2^* - 1 - \zeta _4^* - \zeta _1^* + \delta \zeta _3^*} \right\}}} \right\}} \right\}\left\{ { - \Gamma \left[\left[ {\zeta _1^* + 1 + \zeta _2^* - \delta \zeta _3^* + \zeta _4^*,i\bar{t}\bar{\omega }} \right]\right]} \right.\\ && \left. {\left. { + \Gamma \left[\left[ { - 3 + \zeta _2^* + 5 + \zeta _4^* - 2 - \delta \zeta _3^* + 1 + \zeta _1^*} \right]\right]} \right\}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 19 + \zeta _2^* + 20 + \left\{ { - \zeta _3^*} \right\}} \right]\right]}}} \right\}\left\{ {\frac{1}{{{{\left( { - 5 + 4} \right)}}^{\left\{ { - \zeta _2^*} \right\}}}}} \right\} \end{eqnarray}$$

(42)

$$\begin{eqnarray} \qquad \qquad \quad && \left\{ {\frac{1}{{\left\{ {\zeta _2^* - 1} \right\}\left\{ {\zeta _2^*} \right\} \ldots 2!}}} \right\}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}^{\left\{ {\zeta _2^*} \right\}}\left\{ {\frac{1}{{{{\left( { - 20 + 19} \right)}}^{\left\{ { - 11 + 10 - \zeta _1^* + 2 - 1} \right\}}}}} \right\}\left\{ {\frac{1}{{\zeta _4^*\left\{ {\zeta _4^* - 1} \right\}\left\{ {\zeta _4^* - 2} \right\} \ldots 2.1}}} \right\}\\ \qquad \qquad \quad && \left\{ {\frac{1}{{\hat{d}\left\{ {\hat{d} - 1} \right\}\left\{ {\hat{d} - 2} \right\} \ldots 2.1}}} \right\}\left\{ {\frac{1}{{{{\left( {1 - \gamma i\bar{\omega }} \right)}}^{ - \left\{ {\hat{a}} \right\}}}}} \right\}\Gamma \left[\left[ {\hat{b} + 1} \right]\right]{\left( M \right)}^{\left\{ {\zeta _4^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 2 + 4 - \hat{a}} \right]\right]}}} \right\}\left\{ {\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\zeta _3^*} \right\}}}}} \right\}\\ \qquad \qquad \quad && \left\{ {\frac{1}{{\left\{ {\zeta _3^*} \right\}!}}} \right\}{\left( { - 1} \right)}^{\left\{ { - 11 + 2 + \zeta _4^* + 9} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 2 + 7 + \zeta _1^* - 4 - 1} \right]\right]}}} \right\}\left\{ {\frac{1}{{{{\left( { - 32 + 31} \right)}}^{\left\{ { - 2 + 1 + \zeta _3^* + 3 - 2} \right\}}}}} \right\}\left\{ {\frac{1}{{\left\{ {\zeta _1^*} \right\}!}}} \right\}\\ \qquad \qquad \quad && \Gamma \left[\left[ 2 \right]\right]\left\{ {\frac{1}{{\Gamma \left[\left[ { - 3 + \zeta _1^* + 4 - \delta \zeta _3^* + 5 + \zeta _2^* - 5 + \zeta _4^*} \right]\right]}}} \right\}. \end{eqnarray}$$

The final exact solution of velocity field corresponding to the cosine oscillation is obtained by taking real part of above Equation 42 as follows:

$$\begin{eqnarray} {F}_c\left( {\bar{X},\bar{Y},\bar{t}} \right) &=& Re[{e}^{i\bar{\omega }\bar{t}}\ - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{\rm rs}{\left( {\bar{t}} \right)}^{\zeta _2^* - \delta \zeta _3^* + \zeta _4^* + \zeta _1^*}\\ && \mathop \sum \limits_{\zeta _1^* = 0,\zeta _2^* = 0,\zeta _3^* = 0,\zeta _4^* = 0}^{\rm inf} \Gamma \left[\kern-0.15em\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\kern-0.15em\right]{\left( M \right)}^{\left\{ {\zeta _4^*} \right\}}\Gamma \left[\kern-0.15em\left[ {5 + 4 + \zeta _2^* - 8} \right]\kern-0.15em\right]\Gamma \left[\kern-0.15em\left[ 2 \right]\kern-0.15em\right]{\left( { - 1} \right)}^{\left\{ {\zeta _4^*} \right\}}\left\{ {\frac{1}{{\left\{ {\zeta _4^*} \right\}!}}} \right\}\\ && \left\{ {\frac{1}{{{{\left\{ { - \gamma i\bar{\omega } - 5 + 6} \right\}}}^{\left\{ { - 2 + 3 + \zeta _1^* - 1} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {\zeta _4^* - \delta \zeta _3^* + 1 + \zeta _2^* + \zeta _1^*} \right]\kern-0.15em\right]}}} \right\}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{\rm rs}} \right)}^{\left\{ {\zeta _2^*} \right\}}\left\{ {\frac{1}{{\left\{ {\zeta _3^*} \right\} \ldots 3!}}} \right\}\\ && \left\{ {\frac{1}{{{{\left( {21 - 22} \right)}}^{\left\{ {11 + 12 - \zeta _3^* - 23} \right\}}}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}{\left( {{\lambda }_{\rm rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 2 + 4 - \zeta _1^*} \right]\kern-0.15em\right]}}} \right\}\Gamma \left[\kern-0.15em\left[ {\zeta _2^* + 1} \right]\kern-0.15em\right]\left\{ {\frac{1}{{\left\{ {\zeta _1^*} \right\}!}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _1^*} \right\}}\\ && \left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {\left\{ { - \zeta _3^*} \right\} + 4 - 6 + \left\{ { + \zeta _1^*} \right\} + 3} \right]\kern-0.15em\right]}}} \right\}\left\{ {\frac{1}{{{{\left( {24 - 25} \right)}}^{\left\{ {25 - \zeta _2^* - 24 - 1} \right\}}}}} \right\}\left\{ {\frac{1}{{\zeta _2^*\left\{ {\zeta _2^* - 1} \right\} \ldots 3.\ 2.1}}} \right\}\left\{ {\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\zeta _3^*} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {\zeta _1^*} \right]\kern-0.15em\right]}}} \right\}\\ \end{eqnarray}$$

(43)

$$\begin{eqnarray} && - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right)Sin\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{\rm rs}i\bar{\omega }\mathop \sum \limits_{\zeta _1^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _2^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _3^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _4^* = 0}^{\rm inf} \Gamma \left[\kern-0.15em\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\kern-0.15em\right]\\ && \left\{ {\left\{ { - \Gamma \left[\kern-0.15em\left[ {\zeta _2^* - \delta \zeta _3^* + \zeta _4^* + 1 + \zeta _1^*,i\bar{t}\bar{\omega }} \right]\kern-0.15em\right] + \Gamma \left[\kern-0.15em\left[ {\zeta _4^* + 1 + \zeta _2^* - \delta \zeta _3^* + \zeta _1^*} \right]\kern-0.15em\right]} \right\}\left\{ {{e}^{i\bar{\omega }\bar{t}}} \right\}} \right.\\ && \left\{ {{{\left( {i\bar{\omega }\bar{t}} \right)}}^{\left\{ { - 5 + \delta \zeta _3^* - 4 - \zeta _1^* + 4 - \zeta _2^* + 4 - \zeta _4^*} \right\}}} \right\}\left. {\left\{ {{{\left( {\bar{t}} \right)}}^{4 + \zeta _1^* + 5 + \zeta _4^* - 3 - \zeta _3^*\delta - 5 + \zeta _2^*}} \right\}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _2^*} \right\}}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{\rm rs}} \right)}^{\left\{ {\zeta _2^*} \right\}}\\ && \left\{ {\frac{1}{{\left\{ {\zeta _1^*} \right\}!}}} \right\}\left\{ {\frac{1}{{{{\left( {31 - 32} \right)}}^{\left\{ {3 - 2 - \zeta _4^* - 1} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {12 + \zeta _1^* - 11 + \zeta _4^* - 1 + \zeta _2^* + 1 - \delta \zeta _3^*} \right]\kern-0.15em\right]}}} \right\}\left\{ {\frac{1}{{\zeta _2^*\left\{ {\zeta _2^* - 1} \right\} \ldots 3.1}}} \right\}\\ && \Gamma \left[\kern-0.15em\left[ {34 - 32} \right]\kern-0.15em\right]\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {1 - 5 + \left\{ {\zeta _1^*} \right\} + 3 + 1} \right]\kern-0.15em\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}{\left( M \right)}^{\left\{ {\zeta _4^*} \right\}}\left\{ {\frac{1}{{\left\{ {\left\{ {\zeta _3^*} \right\} - 1} \right\}\left\{ {\zeta _3^*} \right\} \ldots \ 1}}} \right\}\\ && \frac{1}{{{{\left( { - 21 + 20} \right)}}^{\left\{ { - 4 + 3 + \zeta _1^* + 1} \right\}}}}\left\{ {\frac{1}{{\zeta _4^*\left\{ {\zeta _4^* - 1} \right\}\left\{ {\zeta _4^* - 2} \right\} \ldots 2.1}}} \right\}\left\{ {{{\left( \gamma \right)}}^{\left\{ { - 1 - 2 + \zeta _3^* - 3 + 6} \right\}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ { - 11 + \left\{ { - \zeta _1^*} \right\} + 13} \right]\kern-0.15em\right]}}} \right\}\\ && \left\{ {\frac{1}{{{{\left( {1 - \gamma i\bar{\omega }} \right)}}^{ - \left\{ {\zeta _1^*} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\kern-0.15em\left[ {4 + \left\{ { - \zeta _3^*} \right\} - 2 + 2 - 3 + \zeta _2^*} \right]\kern-0.15em\right]}}} \right\}\Gamma \left[\kern-0.15em\left[ {13 - 15 + \left\{ {\zeta _3^*} \right\} + 3} \right]\kern-0.15em\right] . \end{eqnarray}$$

The final exact solution of velocity field corresponding to the sine oscillation is obtained by taking imaginary part of Equation 42 as follows:

$$\begin{eqnarray} {F}_s\left( {\bar{X},\bar{Y},\bar{t}} \right) &=& Im[{e}^{i\bar{\omega }\bar{t}}\ - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty {\rm Sin}\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right){\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{rs}{\left( {\bar{t}} \right)}^{\zeta _2^* - \delta \zeta _3^* + \zeta _4^* + \zeta _1^*}\\ && \mathop \sum \limits_{\zeta _1^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _2^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _3^* = 0}^{\rm inf} \mathop \sum \limits_{\zeta _4^* = 0}^{\rm inf} \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right]\left\{ {\frac{1}{{\left\{ {\zeta _3^*} \right\}!}}} \right\}\Gamma \left[\left[ {13 + 12 - \left\{ { - \zeta _2^*} \right\} - 24} \right]\right]{\left( M \right)}^{\left\{ {\zeta _4^*} \right\}}\\ && \left\{ {\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\hat{c}} \right\}}}}} \right\}\left\{ {\frac{1}{{\left\{ {\zeta _4^* - 1} \right\}\left\{ {\zeta _4^*} \right\}\left\{ {\zeta _4^* - 2} \right\} \ldots 2!}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {\hat{a}} \right]\right]}}} \right\}\left\{ {\frac{1}{{\left\{ {\zeta _1^*} \right\}\left\{ ! \right\}}}} \right\}\left\{ {\frac{1}{{{{\left( { - \gamma i\bar{\omega } - 19 + 20} \right)}}^{ - \left\{ { - 4 + 2 + \zeta _1^* + 2} \right\}}}}} \right\}\\ && \left\{ {\frac{1}{{\Gamma \left[\left[ {12 - \left\{ { - \zeta _2^*} \right\} - 13 + \left\{ { - \zeta _3^*} \right\} + 2} \right]\right]}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 2 + 4 - \left\{ {\zeta _1^*} \right\}} \right]\right]}}} \right\}{\left( { - 20 + 18 + 1} \right)}^{\left\{ { - 14 + 12 + \zeta _2^* + 1 + 1} \right\}}\\ && \left\{ {\frac{1}{{\Gamma \left[\left[ {\left\{ {\zeta _4^*} \right\} - \delta \left\{ {\zeta _3^*} \right\} + 1 + \left\{ {\zeta _2^*} \right\} + \left\{ {\zeta _1^*} \right\}} \right]\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ {12 - 2 + \zeta _1^* + 2 - 12} \right\}}{\left( {{{\left\{ {{K}^*} \right\}}}^{ - 2 + 1} + {\lambda }_{rs}} \right)}^{\left\{ { - 4 - 2 + \zeta _2^* + 4 + 2} \right\}}\\ && {\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}{\left( {{\lambda }_{rs}} \right)}^{\left\{ {\zeta _1^*} \right\}}\left\{ {\frac{1}{{\zeta _2^*\left\{ {\zeta _2^* - 1} \right\} \ldots 3.\ 2.1}}} \right\}\Gamma \left[\left[ 2 \right]\right]{\left( { - 1} \right)}^{\left\{ {\zeta _4^*} \right\}} - \left( {\frac{4}{{\bar{D}\bar{H}}}} \right)\mathop \sum \limits_{r = 1}^\infty \mathop \sum \limits_{s = 1}^\infty Sin\left( {\frac{{r\pi \bar{X}}}{{\bar{D}}}} \right)\\ && {\rm Sin}\left( {\frac{{s\pi \bar{Y}}}{{\bar{H}}}} \right){\varepsilon }_{\rm rs}i\bar{\omega }\mathop \sum \limits_{\zeta _1^* = 0,\zeta _2^* = 0,\zeta _3^* = 0,\zeta _4^* = 0}^{\rm inf} \Gamma \left[\left[ {\zeta _4^* + \zeta _1^* + \zeta _2^*} \right]\right]{\left( { - 1} \right)}^{\left\{ {\zeta _2^*} \right\}}{\left( {\frac{1}{{{K}^*}} + {\lambda }_{rs}} \right)}^{\left\{ {\zeta _2^*} \right\}}\\ && \left\{ {\left\{ {{e}^{i\bar{\omega }\bar{t}}} \right\}\left\{ {{{\left( {i\bar{\omega }\bar{t}} \right)}}^{\left\{ { - \zeta _1^* - 1 - \zeta _4^* - \zeta _2^* + \delta \zeta _3^*} \right\}}} \right\}} \right.\left\{ {{{\left( {\bar{t}} \right)}}^{14 + \zeta _1^* - 15 + \left\{ { - \zeta _3^*\delta } \right\} + 1 + \zeta _4^* + 1 + \zeta _2^*}} \right\}\left\{ { - \Gamma \left[\left[ {\zeta _2^* - \delta \zeta _3^* + \zeta _4^* + 1 + \zeta _1^*,i\bar{t}\bar{\omega }} \right]\right]\left. {\Gamma \left. {\left[\left[ {\zeta _4^* + 1 + \zeta _2^* - \delta \zeta _3^* + \zeta _1^*} \right]\right]} \right\}} \right\}} \right.\\ && \left\{ {\frac{1}{{\zeta _4^*\left\{ {\zeta _4^* - 1} \right\}\left\{ {\zeta _4^* - 2} \right\} \ldots 2.1}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {\left\{ {\zeta _1^*} \right\}} \right]\right]}}} \right\} \end{eqnarray}$$

(44)

$$\begin{eqnarray} \qquad \qquad \quad && \left\{ {\frac{1}{{\left\{ {\zeta _1^*} \right\}!}}} \right\}\Gamma \left[\left[ { - 15 + 25 - \left\{ { - \zeta _2^*} \right\} - 9} \right]\right]\left\{ {\frac{1}{{{{\left( {31 - 32} \right)}}^{\left\{ {12 - 2 - \zeta _4^* - 10} \right\}}}}} \right\}\left\{ {\frac{1}{{ - \{ - \zeta _2^*\} !}}} \right\}\left\{ {\frac{1}{{{{\left( \gamma \right)}}^{ - \left\{ {\zeta _3^*} \right\}}}}} \right\}\\ \qquad \qquad \quad && \left\{ {\frac{1}{{{{\left( {1 - \gamma i\bar{\omega }} \right)}}^{ - \left\{ {\hat{a}} \right\}}}}} \right\}\left\{ {\frac{1}{{\Gamma \left[\left[ {\left\{ { - \zeta _3^*} \right\} + 15 - \left\{ { - \zeta _2^*} \right\} - 14} \right]\right]}}} \right\}{\left( { - 1} \right)}^{\left\{ {\hat{a}} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ { - 2 + 4 - \hat{a}} \right]\right]}}} \right\}\\ \qquad \qquad \quad && {\left( { - 1} \right)}^{\left\{ {\zeta _3^*} \right\}}{\left( M \right)}^{\left\{ {\left\{ {\zeta _4^*} \right\}} \right\}}\left\{ {\frac{1}{{\Gamma \left[\left[ {9 + \zeta _2^* + 2 + \zeta _4^* - 9 - \delta \zeta _3^* - 1 + \zeta _1^*} \right]\right]}}} \right\}\Gamma \left[\left[ 2 \right]\right]\left\{ {\frac{1}{{ - \{ - \zeta _3^*\} !}}} \right\}. \end{eqnarray}$$

4. Finite Difference Method

To confirm the validation of current flow problem which is solved through two efficient techniques (Laplace transform and double finite Fourier transform), we apply two-dimensional finite difference numerical method and compare the outcomes. To implement this method to the present problem, the following approximations are used for spaces |$\bar{X}$| and |$\bar{Y}\ $| and time |$\bar{t}$| derivatives.

$$\begin{eqnarray} \frac{{\partial \bar{U}}}{{\partial \bar{t}}} & \approx & \left\{ {\frac{1}{{\nabla \bar{t}}}} \right\}\left\{ {\check{u}_{i,j}^{n + 1} - \check{u}_{i,j}^n} \right\},\\ \frac{{\partial \bar{U}}}{{\partial \bar{X}}} & \approx & \left\{ {\frac{1}{{2\nabla \bar{X}}}} \right\}\left\{ {{{\check{u}}}_{i + 1,j} - {{\check{u}}}_{i - 1,j}} \right\},\\ \frac{{\partial \bar{U}}}{{\partial \bar{Y}}} & \approx & \left\{ {\frac{1}{{2\nabla \bar{Y}}}} \right\}\left\{ {{{\check{u} }}_{i,j + 1} - {{\check{u} }}_{i,j - 1}} \right\},\\ \frac{{{\partial}^2\bar{U}}}{{\partial {{\bar{X}}}^2}} & \approx & \left\{{\frac{1}{{\nabla {{\bar{X}}}^2}}} \right\},\left\{\check{u}_{i-1,j} +\check{u}_{i+1,j}-2\check{u}_{i,j} \right\}\\ \frac{{{\partial }^2\bar{U}}}{{\partial {{\bar{Y}}}^2}} & \approx & \left\{ {\frac{1}{{\nabla {{\bar{Y}}}^2}}} \right\}\left\{ {{{\check{u}}}_{i,j - 1} + {{\check{u} }}_{i,j + 1} - 2{{\check{u} }}_{i,j}} \right\}. \end{eqnarray}$$

(45)

Now the execution of the above Equation 45 to Equation 18, the following equation is acquired:

$$\begin{eqnarray} \begin{array}{@{}l@{}} \left[ {\left\{ {\displaystyle\frac{1}{{\Delta \bar{t}}}} \right\}\left\{ {\check{u}_{i,j}^{n + 1} - \check{u}_{i,j}^n} \right\}} \right]\\ = \left[ {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right]\left[ {\left\{ {\displaystyle\frac{1}{{\Delta {{\bar{X}}}^2}}} \right\}\left\{ {{{\check{u}}}_{i - 1,j} + {{\check{u}}}_{i + 1,j} - 2{{\check{u}}}_{i,j}} \right\} + \left\{ {\displaystyle\frac{1}{{\Delta {{\bar{Y}}}^2}}} \right\}\left\{ {{{\check{u}}}_{i,j - 1} + {{\check{u}}}_{i,j + 1} - 2{{\check{u}}}_{i,j}} \right\}} \right]\\ - \displaystyle\frac{1}{{{K}^*}}\left[ {1 - \gamma -\!\!\!\!D _{\ \bar{t}}^\delta } \right]\bar{U} - M\bar{U}. \end{array} \end{eqnarray}$$

(46)

To find the consistency of Caputo fractional derivative to the current flow problem, the local truncation error is determined by using approximations in finite difference method. In this numerical method, the following approximation for Caputo fractional derivative is implemented:

$$\begin{eqnarray} {\rm{ -\!\!\!\!D }}_{\tilde{t}}^\delta \left[ {\bar{U}\left( {{{\tilde{t}}}_n} \right)} \right] \approx \left[ {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\Gamma \left( {1 - \delta } \right)}}}\right.} \!\lower0.7ex\hbox{${\Gamma \left( {1 - \delta } \right)}$}}} \right]\mathop \sum \limits_{N = 0}^n {\tilde{W}}_N^\delta \bar{U}\left( {{{\tilde{t}}}_{n - N}} \right). \end{eqnarray}$$

(47)

Here, |${\tilde{W}}_N^\delta $| identify as weights which can be deliberated as follows:

$$\begin{eqnarray} \begin{array}{@{}l@{}} {{\tilde{W}}}_N^\delta = \left( {\begin{array}{@{}*{1}{c}@{}} \delta \\ N \end{array}} \right){\left( { - 1} \right)}^N,\\ \left( {\begin{array}{@{}*{1}{c}@{}} \delta \\ N \end{array}} \right) = \text{Gamma}\left\{ {1 + \delta } \right\}\left\{ {\displaystyle\frac{1}{{\text{Gamma}\left\{ {\delta - N + 1} \right\}\text{Gamma}\left\{ {N + 1} \right\}}}} \right\}. \end{array} \end{eqnarray}$$

(48)

With this approximation, the local truncation error is |$O[ {\Delta {{\tilde{t}}}^{1 - \delta }} ]$|⁠. So, the method is consistent with order {|$1 - \delta $|}.

5. Zuo’s Fractal Rheological Model

Zuo’s fractal rheological model is another fractional operator which efficiently analyze the complex rheological features of different fluid models. Zuo (2021) developed this fractal rheological model by working on the viscosity of 3D print paste. Based on the two-scale fractal theory, Zuo examined the following differential equation for viscosity determination:

$$\begin{eqnarray} \begin{array}{@{}*{1}{l}@{}} {\displaystyle\frac{{{\rm d}\bar{\eta }}}{{{\rm d}{{\left( {\mathop {\rm{\omega }}\limits^{\prime} } \right)}}^{\bar{y}}}} + \bar{\eta }\bar{\varepsilon } = 0,}\\ {\bar{\eta }(0) = {{\bar{\eta }}}_0.} \end{array} \end{eqnarray}$$

(49)

In Equation 49, |$\bar{\gamma }$| identify as the fractal derivative order. The fractal derivative involved in Equation 49 is expressed in the following way (Zuo, 2021):

$$\begin{eqnarray} \frac{{{\rm d}\bar{\eta }}}{{{\rm d}{{\left( {\mathop {\rm{\omega }}\limits^{\prime} } \right)}}^{\bar{\gamma }}}}\left( {{{\mathop {\rm{\omega }}\limits^{\prime} }}_0} \right) = \text{Gamma}\left\{ {1 + \bar{\gamma }} \right\}{\rm li{m}}_{\begin{array}{@{}*{1}{c}@{}} {\left( {\mathop {\rm{\omega }}\limits^{\prime} } \right) - \left( {{{\mathop {\rm{\omega }}\limits^{\prime} }}_0} \right) \to \Delta \left( {\mathop {\rm{\omega }}\limits^{\prime} } \right)}\\ {\Delta \left( {\mathop {\rm{\omega }}\limits^{\prime} } \right) \ne 0} \end{array}}\left\{ {\frac{{\bar{\eta } - {{\bar{\eta }}}_0}}{{{{\left\{ {\left( {\mathop {\rm{\omega }}\limits^{\prime} } \right) - \left( {{{\mathop {\rm{\omega }}\limits^{\prime} }}_0} \right)} \right\}}}^{\bar{\gamma }}}}} \right\}. \end{eqnarray}$$

(50)

Moreover, He and Liu (2022) also used Zuo’s fractal model to briefly observe the fluidity of a cement mortar. This efficient fractal rheological model can be implemented to the present transient flow problem of Walter’s B fluid to observe its complicated flow characteristics in a more significant way. According to Zuo’s fractal model, the governing equation for the considered fluid can be expressed as follows:

$$\begin{eqnarray} \rho \left[ {\frac{{\partial \tilde{U}}}{{\partial {{\tilde{t}}}^{\bar{\gamma }}}}} \right] = \left[ {{\mu }_0 - {k}^*\frac{\partial }{{\partial {{\tilde{t}}}^{\bar{\gamma }}}}} \right]\left[ {\frac{{{\partial }^2\tilde{U}}}{{\partial {{\tilde{X}}}^2}} + \frac{{{\partial }^2\tilde{U}}}{{\partial {{\tilde{Y}}}^2}}} \right] - \frac{{{\varrho }_1}}{{{K}_1}}\left[ {{\mu }_0 - {k}^*\frac{\partial }{{\partial {{\tilde{t}}}^{\bar{\gamma }}}}} \right]\tilde{U} - \sigma B_0^2\tilde{U}. \end{eqnarray}$$

(51)

In Equation 51, Zuo’s fractal operator is defined as follows (He & Liu, 2022; Zuo, 2021):

$$\begin{eqnarray} \frac{{\partial \tilde{U}}}{{\partial {{\tilde{t}}}^{\bar{\gamma }}}}\left( {{{\tilde{t}}}_0} \right) = \text{Gamma}\left\{ {1 + \bar{\gamma }} \right\}{\rm li{m}}_{\begin{array}{@{}*{1}{c}@{}} {\left( {\tilde{t}} \right) - \left( {{{\tilde{t}}}_0} \right) \to \Delta \left( {\tilde{t}} \right)}\\ {\Delta\left( {\tilde{t}} \right) \ne 0} \end{array}}\left\{ {\frac{{\tilde{U} - {{\tilde{U}}}_0}}{{{{\left\{ {\left( {\tilde{t}} \right) - \left( {{{\tilde{t}}}_0} \right)} \right\}}}^{\bar{\gamma }}}}} \right\}. \end{eqnarray}$$

(52)

After executing Equation 52 to Equation 51 and using conditions given in Equations 19–20, the outcomes of the velocity field regarding Zuo’s fractal model can be acquired.

6. Results and Explanation

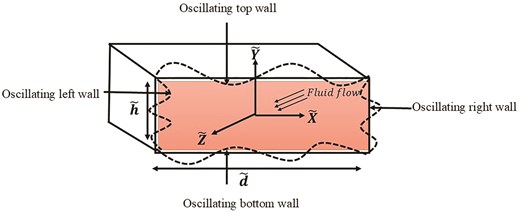
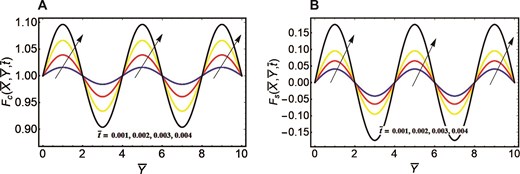
An exploration of Walter’s B fluid with its transient characteristics inside a rectangular oscillatory duct is conducted, considering the application of fractional derivatives. The desirable exact outcomes are achieved in the context of both types of duct’s oscillation. Two efficient techniques of Laplace transform, and Fourier sine finite double transform are taken into account to acquire the exact outcomes of the velocity field. To validate and confirm the existence of exact results, a numerical finite difference method is implemented to the current flow problem. After analyzing the present flow problem in the context of finite difference method, the numerical outcomes of the velocity field are compared with exact outcomes in Table 1. This table portrays that the exact and numerical values of the velocity field are in good agreement regarding distinct parameters. This strong agreement confirms the validation of the exact results of the velocity field. Moreover, to compare our results with the previous results in literature, Table 2 is prepared. In this table, the values of the velocity field are calculated by finite difference method and compared with previous published study. The present values are in good agreement with the previous findings that validate and confirm the present problem. After calculating the exact results, the velocity distribution is graphically visualized corresponding to both case of different oscillations with pertinent parameters. Figure 2A is created to analyze the behavior of the flow field in relation to the cosine oscillation with the improved time interval. With the passage of time, an increase flow pattern is developed in the velocity curve. Similarly, the velocity field with accelerating curve for improved time period is manifested in Figure. 2B relative to sine oscillation. The reason behind the enhanced nature of the velocity field for both types of oscillation is that the fractional derivative provides memory effects in the flow system. These effects become more significant with the enhancement of time intervals. Consequently, an augmentation in the velocity field is noted with an extended period of time. The significance of fluid parameter with its escalating values on the fluid movement for cosine oscillation is portrayed in Figure. 3A. The fluid motion in the context of cosine oscillation demonstrates an augmenting pattern with the improved fluid parameter. For the case of sine oscillation, the flow pattern of velocity is elucidated in Figure. 3B influenced by fluid parameter. This graphic depicts that the velocity field yields rising behavior in the context of improved fluid parameter. The enhancement of the velocity distribution relative to both types of oscillation is due to the existence of an inverse connection with fluid parameter and viscosity. The fluid viscosity becomes lower with the escalation of the fluid parameter. A fluid encounters lower resistance to its movement with reduced viscosity and accordingly depicts an escalating flow pattern. The velocity curve in relation to both types of cosine oscillation and sine oscillation with the improved fractional parameter is portrayed in Figure. 4A and B. In the context of both oscillations, the improved fractional parameter also strengthens the flow field. The involvement of Caputo fractional derivative manifest that the flow system has memory effects. This means that the present state of the system depends on the past state, or the flow system also incorporates the effects that were encountered in the past. The contribution of the previous effects to the present flow behavior is determined via fractional parameter. The increment of the fractional parameter results in a less contribution of the previous impacts to the present flow system. As a result, the memory impacts become less significant within the flow system corresponding to the improved fractional parameter and system provides quicker result to the present effects. Consequently, there is an escalating development in the flow field for both oscillations. An inclination in the velocity field for both oscillations is observed in Figure. 5A and B in the context of improved porosity parameter. The enlargement of the porosity parameter yields an inclination in the flow pattern. The viscosity property of the considered fluid reduces with the improved porosity parameter and fluid experience lower resistance in its movement. Accordingly, fluid shows enhancing nature in the context of both oscillations. Figure. 6A and B are sketched to discuss the significance of improved frequency parameter in the context of cosine and sine oscillations for velocity distribution. The velocity field relative to cosine oscillation depicts an accelerating behavior and exhibits the same increasing pattern for sine oscillation. The improved magnetic field deteriorates the velocity pattern relative to cosine and sine oscillations, as depicted in Figure. 7A and B. An obstructive Lorentz force within the flow system is developed due to the collaboration of an electrically conducting fluid and magnetic field. This force opposes the movement of the fluid by acting in the reverse direction of the flow. Consequently, the flow velocity experiences a reduction relative to both types of oscillations.

Figure 2:

Velocity curves correspond to different oscillations. (A) Cosine oscillation and time period. (B) Sine oscillation and time period.

Figure 3:

Velocity curves correspond to different oscillations. (A) Cosine oscillation and fluid parameter. (B) Sine oscillation and fluid parameter.

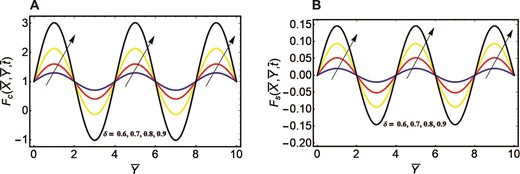
$Velocity curves correspond to different oscillations. (A) Cosine oscillation and fractional parameter. (B) Sine oscillation and fractional parameter.$

Figure 4:

Velocity curves correspond to different oscillations. (A) Cosine oscillation and fractional parameter. (B) Sine oscillation and fractional parameter.

Figure 5:

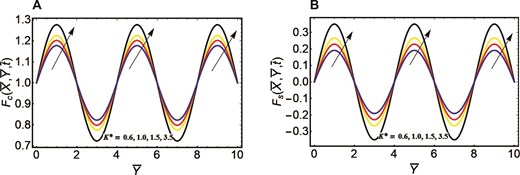
Velocity curves correspond to different oscillations. (A) Cosine oscillation and porosity parameter. (B) Sine oscillation and porosity parameter.

Figure 6:

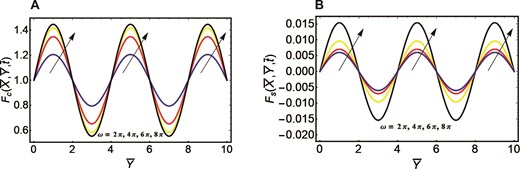
Velocity curves correspond to different oscillations. (A) Cosine oscillation and frequency parameter. (B) Sine oscillation and frequency parameter.

Figure 7:

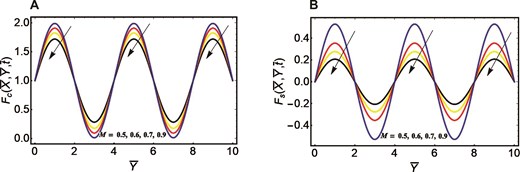
Velocity curves correspond to different oscillations. (A) Cosine oscillation and magnetic parameter. (B) Sine oscillation and magnetic parameter.

Table 1:

Values of velocity field regarding finite difference method and current method.

\|$\gamma $\|	\|${K}^*$\|	\|$M$\|	Current method	Finite difference method
0.2	0.8	0.5	0.28 740	0.28 667
0.4			0.29 764	0.29 735
0.6			0.30 871	0.30 765
	0.8		0.23 876	0.23 786
	0.9		0.27 653	0.27 643
	1.0		0.30 452	0.30 432
		0.6	0.12 876	0.12 755
		0.8	0.13 543	0.12 498
		1.2	0.14 896	0.14 765

\|$\gamma $\|	\|${K}^*$\|	\|$M$\|	Current method	Finite difference method
0.2	0.8	0.5	0.28 740	0.28 667
0.4			0.29 764	0.29 735
0.6			0.30 871	0.30 765
	0.8		0.23 876	0.23 786
	0.9		0.27 653	0.27 643
	1.0		0.30 452	0.30 432
		0.6	0.12 876	0.12 755
		0.8	0.13 543	0.12 498
		1.2	0.14 896	0.14 765

Table 1:

Values of velocity field regarding finite difference method and current method.

\|$\gamma $\|	\|${K}^*$\|	\|$M$\|	Current method	Finite difference method
0.2	0.8	0.5	0.28 740	0.28 667
0.4			0.29 764	0.29 735
0.6			0.30 871	0.30 765
	0.8		0.23 876	0.23 786
	0.9		0.27 653	0.27 643
	1.0		0.30 452	0.30 432
		0.6	0.12 876	0.12 755
		0.8	0.13 543	0.12 498
		1.2	0.14 896	0.14 765

\|$\gamma $\|	\|${K}^*$\|	\|$M$\|	Current method	Finite difference method
0.2	0.8	0.5	0.28 740	0.28 667
0.4			0.29 764	0.29 735
0.6			0.30 871	0.30 765
	0.8		0.23 876	0.23 786
	0.9		0.27 653	0.27 643
	1.0		0.30 452	0.30 432
		0.6	0.12 876	0.12 755
		0.8	0.13 543	0.12 498
		1.2	0.14 896	0.14 765

Table 2:

Comparative values of velocity regarding finite difference method and different magnetic parameter values.

\|$M$\|	Present result	(Raslan & Ali, 2020)
0	0.287 654	0.294 107
2	0.245 987	0.258 625
5	0.165 429	0.171 475
8	0.113 972	0.118 782

Table 2:

10.1016/j.cmpb.2016.04.022

Comparative values of velocity regarding finite difference method and different magnetic parameter values.

\|$M$\|	Present result	(Raslan & Ali, 2020)
0	0.287 654	0.294 107
2	0.245 987	0.258 625
5	0.165 429	0.171 475
8	0.113 972	0.118 782

7. Conclusions

In this study, a powerful tool of fractional derivative is implemented on the transient flow phenomenon of Walter’s B fluid in a porous medium. A rectangular duct with sine and cosine oscillations is taken to explore the magnetized flow pattern in two dimensions. By applying two efficient techniques, the exact solution of the velocity field corresponding to both oscillations is deliberated by including the definition of Caputo fractional derivative. The following key findings are acquired from this study:

The profile of velocity provides augmented behavior in the context of fractional parameter.
The improved fractional parameter and time period demonstrate more prominent memory impacts within the flow system and enhance the field of the velocity.
With the improved frequency parameter and augmented number of cosine and sine oscillations, there exists an inclination in the flow behavior of fluid.
For both oscillations, the velocity distribution portrays deteriorating nature in response to ameliorated magnetic field.
The fluid parameter with increasing magnitude strengthens the flow field corresponding to both oscillations.
The present flow problem can be further analyzed for different non-Newtonian fluid models with complex nature and Caputo fractional derivative. Moreover, this present fractional problem can be examined with heat transfer mechanism by taking different physical impacts. Such fractional derivative-based models will provide applications in oil and gas recovery processes, filtration processes, industrial lubricants, climate modeling, and paper industries.

Conflicts of Interest

The authors declare no conflict of interest.

Author Contributions

Muhammad Yasir: Conceptualization, Investigation, Methodology, Writing—original draft. A. Ahmed: Methodology, Software. F. M. Aldosari: Writing—original draft, Visualization. Walid Abdelfattah: Validation, Writing—review & editing, Investigation. Haifaa F. Alrihieli: Supervision, Software, Writing—original draft. Ibrahim E. Elseesy: Writing—review & editing.

Data Availability

The data underlying this article will be shared on reasonable request to the corresponding author.

Acknowledgments

The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through Large Research Project under grant number RGP2/177/46.

References

Abo-Eldahab

E. M.

Adel

Mobarak

H. M.

Abdelhakem

(

2021

The effects of magnetic field on boundary layer nano-fluid flow over stretching sheet

Applied Mathematics & Information Sciences

731

–

741

Abro

K. A.

Khan

Tassaddiq

(

2018

Application of Atangana-Baleanu fractional derivative to convection flow of MHD Maxwell fluid in a porous medium over a vertical plate

Mathematical Modelling of Natural Phenomena

Akbar

N. S.

(

2016

Blood flow suspension in tapered stenosed arteries for Walter’s B fluid model

Computer Methods and Programs in Biomedicine

132

–

Ali

Saqib

Khan

Sheikh

N. A.

Jan

S. A. A.

(

2017

Exact analysis of MHD flow of a Walter’s-B fluid over an isothermal oscillating plate embedded in a porous medium

The European Physical Journal Plus

132

–

10.1140/epjp/i2017-11404-2

10.1016/j.ijmecsci.2020.105887

Ali

F. H.

Hamzah

H. K.

Egab

Arıcı

Shahsavar

(

2020

Non-Newtonian nanofluid natural convection in a U-shaped cavity under magnetic field

International Journal of Mechanical Sciences

186

105887

10.1177/09544062221101831

Al-Mdallal

Abro

K. A.

Khan

(

2018

Analytical solutions of fractional Walter’s B fluid with applications

Complexity

2018

8131329

Awasthi

M. K.

Dharamendra

Yadav

(

2022

Stability characteristics of Walter’s B viscoelastic fluid in a cylindrical configuration with heat transfer

Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science

236

10370

–

10377

10.1111/j.1365-246x.1967.tb02303.x

Bani-Fwaz

M. Z.

Mahmood

Bilal

Ei-Zahhar

A. A.

Khan

Niazai

(

2024

Computational investigation of thermal process in radiated nanofluid modulation influenced by nanoparticles (Al2O3) and molecular (H2O) diameters

Journal of Computational Design and Engineering

–

Caputo

(

1967

Linear models of dissipation whose Q is almost frequency independent—II

Geophysical Journal International

529

–

539

C. H.

Liu

(

2022

Fractal approach to the fluidity of a cement mortar

Nonlinear Engineering

–

10.1515/nleng-2022-0001

C. H.

Liu

(

2023

Fractal dimensions of a porous concrete and its effect on the concrete's strength

Facta Universitatis, Series: Mechanical Engineering

137

–

150

10.22190/fume221215005h

10.1016/j.matcom.2021.02.005

Ishtiaq

Nadeem

Alzabut

(

2023

Thermal analysis of magnetized Walter's-B fluid with the application of Prabhakar fractional derivative over an exponentially moving inclined plate

Physics of Fluids

123115

Kumam

Tassaddiq

Watthayu

Shah

Anwar

(

2022

Modeling and simulation based investigation of unsteady MHD radiative flow of rate type fluid; a comparative fractional analysis

Mathematics and Computers in Simulation

201

486

–

507

10.1016/j.aej.2024.03.021

Kumar

Odibat

Aldhaifallah

Nisar

K. S.

(

2020

A comparison study of two modified analytical approach for the solution of nonlinear fractional shallow water equations in fluid flow

AIMS Mathematics

3035

–

3055

ur Rahman

Naz

Gómez-Aguilar

J. F.

(

2024

Modeling of implicit multi term fractional delay differential equation: Application in pollutant dispersion problem

Alexandria Engineering Journal

–

10.1016/j.ijheatmasstransfer.2018.02.084

Liouville

(

1832

Memoir on Some Questions of Geometry and Mechanics, and on a New Type of Calculation to Solve These Questions

Journal of the École Polytechnique

–

Mahabaleshwar

U. S.

Sarris

I. E.

Lorenzini

(

2018

Effect of radiation and Navier slip boundary of Walters’ liquid B flow over a stretching sheet in a porous media

International Journal of Heat and Mass Transfer

127

1327

–

1337

10.1016/j.csite.2023.103077

Nadeem

Ishtiaq

Alzabut

Eldin

S. M.

(

2023

Three parametric Prabhakar fractional derivative-based thermal analysis of Brinkman hybrid nanofluid flow over exponentially heated plate

Case Studies in Thermal Engineering

103077

10.1142/s0219887824400310

Nadeem

Ishtiaq

Saleem

Alzabut

(

2024

Exact exploration of time fractional-based magnetized flow of a generalized second grade fluid through an oscillating rectangular duct

International Journal of Geometric Methods in Modern Physics

2440031

OpenURL Placeholder Text

10.1080/17455030.2022.2143928

Nadeem

Tumreen

Ishtiaq

Abbas

(

2022

Three-dimensional second-grade nanofluid flow with MHD effects through a slandering stretching sheet: A numerical solution

Waves in Random and Complex Media

–

OpenURL Placeholder Text

10.1016/j.tsep.2020.100801

Qaiser

Zheng

Khan

M. R.

(

2021

Numerical assessment of mixed convection flow of Walters-B nanofluid over a stretching surface with newtonian heating and mass transfer

Thermal Science and Engineering Progress

100801

10.1016/j.ijmultiphaseflow.2017.03.016

Luo

Wang

Liu

Zhou

Yan

Zhang

(

2017

Mechanical study of the effect of fractional-wettability on multiphase fluid flow

International Journal of Multiphase Flow

205

–

212

10.53391/mmnsa.2022.01.002

Raslan

K. R.

Ali

K. K.

(

2020

Numerical study of MHD-duct flow using the two-dimensional finite difference method

Applied Mathematics & Information Sciences

693

–

697

Sene

(

2022

Second-grade fluid with newtonian heating under Caputo fractional derivative: Analytical investigations via Laplace transforms

Mathematical Modelling and Numerical Simulation with Applications

–

10.1016/j.jmmm.2023.171128

Sultan

H. S.

Mohammed

H. I.

Biswas

Togun

Ibrahem

R. K.

Mahdi

J. M.

Yaïci

Keshmiri

Talebizadehsardari

(

2024

Revolutionizing the latent heat storage: Boosting discharge performance with innovative undulated phase change material containers in a vertical shell-and-tube system

Journal of Computational Design and Engineering

122

–

145

Sun

Geng

Glowacz

Sulowicz

Siarry

Gupta

M. K.

(

2023

The heat transfer and fluid flow characteristics of water/Fe3O4 ferrofluid flow in a tube with V-cut twisted tape turbulator under the magnetic field effect

Journal of Magnetism and Magnetic Materials

586

171128

10.1016/j.cnsns.2018.04.019

Sun

Zhang

Baleanu

Chen

(

2018

A new collection of real world applications of fractional calculus in science and engineering

Communications in Nonlinear Science and Numerical Simulation

213

–

231

Upreti

Pandey

A. K.

Kumar

(

2020

Thermophoresis and suction/injection roles on free convective MHD flow of Ag–kerosene oil nanofluid

Journal of Computational Design and Engineering

386

–

396

Wakif

Animasaun

I. L.

Khan

Shah

N. A.

Thumma

(

2021

Dynamics of radiative-reactive Walters-b fluid due to mixed convection conveying gyrotactic microorganisms, tiny particles experience haphazard motion, thermo-migration, and Lorentz force

Physica Scripta

125239

10.1088/1402-4896/ac2b4b

10.1016/j.jmapro.2020.06.006

Wang

Chen

Gao

(

2020

Experimental measurement of fluid flow in high-speed GMAW assisted by transverse magnetic field

Journal of Manufacturing Processes

1193

–

1200

10.1016/j.aej.2023.05.065

Yasir

Khan

(

2023

Dynamics of unsteady axisymmetric of Oldroyd-B material with homogeneous-heterogeneous reactions subject to Cattaneo-Christov heat transfer

Alexandria Engineering Journal

665

–

674

10.1016/j.icheatmasstransfer.2022.106577

Yasir

Khan

Malik

Z. U.

(

2023

Analysis of thermophoretic particle deposition with Soret-Dufour in a flow of fluid exhibit relaxation/retardation times effect

International Communications in Heat and Mass Transfer

141

106577

Zuo

(

2021

Effect of SiC particles on viscosity of 3-D print paste: A fractal rheological model and experimental verification

Thermal Science

(3 Part B)

2405

–

2409

10.2298/tsci200710131z