-
PDF
- Split View
-
Views
-
Cite
Cite
Zafar Hayat Khan, Mohammad Hamid, Waqar Ahmed Khan, Rashid Ahmad, Liu Jie, Effects of sinusoidal wall temperature on thermal dynamics and irreversibility around an inclined plate embedded in a square cavity, Journal of Computational Design and Engineering, Volume 11, Issue 5, October 2024, Pages 355–368, https://doi.org/10.1093/jcde/qwae076
Close - Share Icon Share
Abstract
Effective thermal and flow control within complex geometries is essential for engineering applications. In this study, an in-depth examination of flow dynamics, entropy, and thermal regulation is undertaken within a square cavity featuring sinusoidal wall temperature. To introduce complexity, an inclined plate obstacle is strategically positioned within the cavity with an inclination angle of 45°, and the investigation spans three distinct scenarios: adiabatic, cold, and hot conditions. The initial physical model is developed by formulating a system of partial differential equations, which are then transformed into a dimensionless representation using relevant variables. Subsequently, the Galerkin method is employed for approximated analysis of the simplified fluid flow model, and the computational code is verified in tabular format. The embedded physical parameters are constrained to specific numerical values to ensure the convergence of the physical model in each scenario. The physical characteristics of isotherms, streamlines, Nusselt numbers, entropy, and Bejan numbers are investigated. Notably, the results demonstrate that the introduction of a cold inclined plate leads to peak values in generating the entropy and average heat transfer rates. When comparing the cold inclined plate to the heated inclined plate, an increase of approximately 20% in the average heat transfer rate and a 15% rise in the entropy generation rate was found for the cold inclined plate. Furthermore, the Bejan number showed a 10% decrease for the cold inclined plate compared to the heated inclined plate. Additionally, increasing the amplitude and wavenumber led to a rise in average heat transfer and entropy generation rates, with 25% and 30% increases, respectively.
Effective thermal and flow control are crucial across engineering domains.
In-depth study reveals flow dynamics, entropy and thermal regulation.
Investigation spans adiabatic, cold, and hot conditions.
Cold inclined plate leads to peak entropy generation.
Nomenclature
- Be
Bejan number
- B0
Magnetic field strength
- cp
Specific heat capacity, [J kg−1 K−1]
- g
Gravity force acceleration, [m s−2]
- E
Kinetic energy, [m2 s−2]
- L
Cavity size, [m]
- k
Thermal conductivity, [W/mK]
- Nu
Nusselt number
- p
Pressure, [Pa]
- P
Non-dimensional pressure
- Pr
Prandtl number
- Ra
Rayleigh number
- |${\dot S^{\prime\prime\prime}_{gen}}$|
Entropy generation rate per unit volume, [W/m−3 K−1]
- T
Temperature, [K]
- Tc
Cooled wall temperature, [K]
- Th
Heated wall temperature, [K]
- u, v
Velocities for x- and y-coordinates, [m s−1]
- U, V
Dimensionless velocities
- x, y
Cartesian coordinates, [m]
- X, Y
Non-dimensional Cartesian coordinates
- α
Thermal diffusivity, α = k/ρcp, [m2 s−1]
- β
Thermal expansion coefficient, [K−1]
- θ
Non-dimensional temperature
- μ
Dynamic viscosity, [Pa s]
- ν
Kinematic viscosity, v/ ρ, [m2 s−1]
- ρ
Density, m/V, [kg m−3]
- σ
Electrical conductivity
- |$\psi $|
Dimensional stream function, [m2 s−1]
- Ψ
Non-dimensional stream function
- c
Cold
- h
Hot
1. Introduction
Control of thermal processes and analysis of fluid flow within enclosures hold significant importance across diverse engineering applications. These applications span various sectors, including avionics, automotive, building climate control systems, furnaces, food production, electronic equipment, containers with hot/cold water, phase change materials, ovens, petrochemicals, and textiles. Over the past few decades, numerous studies have explored these phenomena through experimental methods or mathematical modelling, often governed by non-linear equations. Mathematical techniques are pragmatic and cost-effective, saving time, resources, and experimental equipment. While modelling for enclosures of various shapes has been previously conducted, square-shaped cavities are particularly prevalent in real-world applications and have garnered attention from various scholars. Bendaraa et al. (2019) studied the impact of free convection in a differentially heated square enclosure enhanced with fins and nanofluids. Their findings unveiled a decrease in the mean Nusselt number when fins were integrated on the heated surface, whereas an augmentation was noticed for the cool and insulated surfaces, ultimately augmenting thermal efficiency. The hydrothermal behaviour and entropy of magnetically driven buoyancy-induced Al2O3–TiO2–water hybrid nanofluids in a semi-circular chamber with a triangular heater fitted to the bottom wall were investigated by Acharya & Öztop (2023). In their study, the curved periphery was cooled, while the remaining triangular parts and bottom walls were heated and insulated, correspondingly. The Galerkin finite element discretization procedure was used to execute the numerical simulation. In analysis, both approximated and experimental studies were conducted to compare the accuracy of the results. Kumar & Subudhi (2023) numerically investigated an magnetohydrodynamic (MHD) nanofluid using a two-step experimental method wherein, the properties of nanofluid were subsequently determined. The numerical simulations utilized experimentally measured thermophysical parameters to investigate the influence of the material of two thick fins on the natural convection of Fe3O4–water nanofluid.
Employing an unbalanced framework amidst Lorentz forces, Sheikholeslami & Rokni (2018) delved into the augmentation of the average heat transfer rate of the nanofluid within a permeable enclosure. Their findings suggested that convective flux diminishes with escalating heat transfer parameters, but it intensifies with increasing Rayleigh numbers. The correlation between temperature gradient and permeability exhibited an inverse relationship. In a computational study conducted by Kefayati (2019) two-dimensional dual disseminative under the usual convection in a porous enclosure containing visco-plastic fluids was scrutinized. The investigation underscored that a higher Lewis number enhances mass transfer for different Bingham numbers at both elevated and diminished buoyancy ratios. Subsequently, Kefayati (2020) introduced the boundary-lattice Boltzmann methodology, applied to tackle diverse thermal and thermal-solutal obstacles involving fluids having both Newtonian and non-Newtonian behaviour. The effectiveness of the approach was illustrated both in simulating dual diffusing mixed convection of a Bingham fluid and dual diffusing convection of a Carreau fluid in configurations with curved boundaries. Sheremet et al. (2018) computationally explored the natural convection of the nanofluid containing Alumina nanoparticles with water as the base fluid inside a square enclosure subjected to time dependent sinusoidal temperature fluctuations. Their analysis investigated the impact of frequency oscillation, Rayleigh number, angle of inclination, and volume fraction of the nano-particles both on the fluid flow and heat transfer characteristics. Especially, an escalation in the frequency of boundary temperature fluctuations correlated with an increase in the average amplitude of heat transfer coefficient oscillations and a decrease in the oscillation period. The investigation highlighted that the boundary temperature oscillation frequency acts as an efficacious control parameter for enhancing convective flux and heat transfer coefficients. Utilizing a rotating deformable disc, Khan et al. (2018) probed viscous fluid flow, heat generation or absorption alongside non-linear thermal radiation with variable characteristics. Their exploration divulged that both the Reynolds number and magnetic constraints led to a reduction in the entropy generation rate. Furthermore, assorted heat transfer phenomena were observed for various radiative and slip variable estimations.
Kardgar (2021) explored the combined average Nusselt number mechanisms involving entropy generation and natural convection in a square enclosure tilted at an angle, affected by an external magnetic field. Their study revealed that increasing the concentration of nanoparticles in the nanofluids ranging from 0.0 to 0.08 resulted in a noticeable 9% rise in the average heat transfer coefficient. This improvement is attributed to the formation of two smaller vortices with opposing rotation patterns, leading to a more concentrated alignment of isotherm lines in the vertical direction. The Nusselt number showed an upward trend with increasing tilted angle up to 40°, followed by a sudden decrease at 90°. Several investigations have explored the thermal and fluid dynamics within a square chamber featuring sinusoidal wall temperature. Alsabery et al. (2016a) utilized the finite difference method to analyse conjugate spontaneous heat transfer in a square enclosure filled with nanofluid containing four different types of nanoparticles and subjected to sinusoidal wall temperature. Their research uncovered a significantly enhanced heat transfer rate by increasing the thickness of the solid wall, with diverse thermal conductivity ratio measurements demonstrating a range of improvements in heat transfer. Ghalambaz et al. (2020) employed the finite-element approach to investigate a square enclosure with differential heating, where a sinusoidal temperature variation was applied to both the right and left vertical walls. In another model presented by Pordanjani et al. (2018), the impacts of spontaneous heat transfer and magnetic influence within a square chamber were examined, where the wall temperature varied sinusoidally, and isothermal obstacles were strategically positioned. Biswas et al. (2021) documented enhanced heat transfer within a square porous enclosure using hybrid nanofluids, encouraging readers to explore the referenced literature (Mullick et al. 2020; Alsabery et al. 2022; Ullah et al. 2022) for more recent findings.
Numerous inquiries have focused on entropy examination within square enclosures. Shuja et al. (2010) presented an entropy evaluation within a square-shaped chamber, emphasizing the influence of spatial arrangements of porous blocks. Sahin (2020) numerically investigated thermal transfer and entropy within a square container featuring a cold vertical wall opposite a vertically heated one. Rabbi et al. (2020) carried out a computational investigation of MHD flow inside a square reservoir containing nanofluid, employing the model of artificial neural network as a cutting-edge forecasting tool. Sheremet et al. (2017) probed entropy generation within a rectangular enclosure containing nanoscopic fluid, with a variable temperature assigned to the left vertical wall. They observed that higher wave number values and increasing temperature distribution amplitudes along the left wall amplify the average entropy generation. In a separate inquiry by Tayebi & Chamkha (2020), explored the fluid-solid thermal conductivity ratio, entropy generation and natural convection in a square enclosure housing a hybrid nanofluid and a conductive wavy-shaped solid structure. Chamkha et al. (2017) delved into the impacts of thermal emitter and entropy generation on MHD mixed convection flow and thermal transfer within a lid-driven permeable square container incorporating a copper-water nanofluid. They observed that the presence of nanoparticle suspension hampers the average Nusselt number across all thermal input/output values within the permeable chamber. The findings concerning the impact of the applied magnetic field reveal a notable decrease in the rate of thermal energy transfer.
Roslan et al. (2014) investigated the natural convection phenomenon in an inclined enclosure consisting of a sinusoidally heated cylindrical source wherein, the unsteady natural convection driven by a temperature difference between a cold outer enclosure and a hot inner circular cylinder was studied. They also found the maximum heat transfer augmentation for frequency between 25π and 30π in case of a large amplitude and a moderate source radius. Alsabery et al. (2016b) numerically examined the unsteady free convective heat transfer in a nano-liquid-saturated porous square cavity with a sinusoidal boundary condition. Their findings indicate that overall heat transfer rate enhanced with relatively non-uniform heating. Saleh et al. (2022) investigated the free convection of a nanofluid, specifically nano-encapsulated phase-change material suspended in water (H2O), with temperature variation between a cold enclosure and a hot cylinder. The empty area of the enclosure was filled with hybrid nanofluids. It was demonstrated that suspending 1% of hybrid particles might enhance the heat transfer rate by 10%. Dogonchi et al. (2019) numerically examined the MHD natural convection of a nanofluid in a wavy cavity considering Brownian motion by implementing the control volume finite element method. It was observed that the strength of the convective flow has a direct relationship with the Rayleigh number, while an inverse relationship exists with the wavy contraction ratio. Hashemi-Tilehnoee et al. (2020) examined MHD natural convection and entropy generation analyses inside an incinerator-shaped porous cavity filled with Al2O3–H2O nanofluid, influenced by a magnetic field, with a rectangular wavy heater block positioned at the cavity wall bottom. It was demonstrated that in the laminar regime, the Nusselt number and entropy generation rate increase with higher Rayleigh and Darcy numbers, while an upsurge with increasing Hartmann number. In the turbulent regime, the average Nusselt number reduces as the Darcy number increases.
Saeid & Pop (2005) undertook a computational exploration of steady free convection within a square container permeated with a porous material. They investigated the influence of inertial factors on the average Nusselt number and fluid motion within the porous enclosure across various Rayleigh numbers. Their results revealed a decline in the average Nusselt number at constant Rayleigh numbers with increasing inertial factors, resulting in a slowdown of spontaneous flow patterns inside the container. Bilgen & Muftuoglu (2008) examined heat transfer through natural convection in an aperture-exposed cavity with uniform heat flux. Their research revealed that the volume flow rate and heat transfer rates increased with the Rayleigh-number, decreased with the number of apertures, and increased with the aperture ratio. Notably, there existed an optimal aperture ratio for high Rayleigh numbers. Mahmoudi et al. (2010) conducted a numerical investigation into the spontaneous convection-based cooling of a heat emitter positioned horizontally against the left vertical wall of a chamber filled with a copper-water nanofluid. Their findings emphasized the significant influence of heat source size on flow pattern and temperature distribution, with the average heat transfer rate decreasing as the heater elongated. Additionally, observed a linear rise in the average heat transfer rate with an increase in the solid volume fraction of the nanofluid for a given Rayleigh number and a specified heat source shape. Recently, the natural convection linking sinusoidal temperature dispersal of a heat source within an enclosed square cavity was studied by Zeng et al. (2024). The lattice Boltzmann technique was employed to simulate the thermal features of heat sources with sinusoidal temperature distribution within a square cavity. Several conditions were considered, including different amplitudes, phase angles and angular velocities. Jain & Bhargava (2023) examined the natural convection flow in a bent wavy vertical enclosure occupied with power-law nanofluid by implementing the Element Free Galerkin method (EFGM). Their study investigated the heat transfer characteristics of a power-law nanofluid in a bent vertical wavy wall enclosure. The EFGM was used to solve the differential equations. Their results demonstrated significant insights into heat transfer processes rate at the hot wall, isotherms and streamlines under the influence of certain embedding parameters. The natural convection thermal characteristics of sinusoidal cavities filled with nanofluids were investigated by Tian et al. (2022). New sinusoidal cavities were established to improve the heat transfer process of free convection in the field of photothermal conversion and electronic component cooling.
The motivation for the current analysis lies in understanding the complex dynamics of flow, entropy, and thermal management within a square cavity subjected to sinusoidal wall temperature, with an inclined plate inside the cavity. This investigation holds significance in various engineering contexts, such as electronics cooling systems, Heating, Ventilating and Air Conditioning (HVAC) systems, solar collectors, or environmental chambers, where precise control of temperature distribution is critical. By formulating the governing physical model as partial differential equations and subsequently non-dimensionalising it, the study aims to uncover fundamental principles governing the interplay relationship between thermal exchange and fluid motion in the proposed geometry. The numerical examination using the finite element method allows for a practical simulation of these physical processes. The detailed evaluation of the model, presented through graphs and tabular comparisons, offers a visual and quantitative understanding of how sinusoidal wall temperature influences flow patterns, entropy production rate, and heat efficiency within the square cavity. The outcomes of this analysis have practical implications for designing efficient thermal control systems in various engineering applications.
2. Model Formulation
This study investigates two-dimensional free convection phenomena inside a square container, as presented in Fig. 1, featuring a prominently inclined plate as a distinctive element. The length of the square cavity is L, whereas the length of the inclined plate is 0.25L and the width is 0.05L with an inclination angle of 45°. The presumed flow characteristics are steady and incompressible. The enclosure's horizontal walls are considered to be thermally isolated, while the temperature of the right vertical wall remains constant. Notably, the vertical wall on the left undergoes a dynamic thermal profile defined by a sinusoidal temperature distribution, precisely expressed as follows:
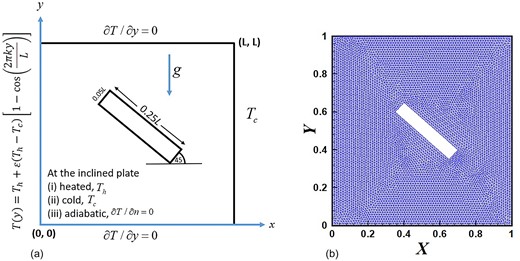
(a) Schematic design and (b) mesh layout of the proposed cavity.
In the provided equation |${T_h} > {T_c}$|, |$\varepsilon $|signifies the magnitude, while k denotes the wavenumber linked with the temperature fluctuation along the hot wall. The dynamics of fluid flow within the system are shaped by the buoyancy force arising from the distinct heating of surfaces. In this context, the gravitational force operates vertically downward, playing a pivotal role in influencing the overall fluid behaviour.
2.1 Mathematical model
By applying the Boussinesq approximation and neglecting both viscous dissipation and compressibility effects, the dimensional governing equations for two-dimensional laminar incompressible flows can be written as follows (Sheremet et al. 2018; Bendaraa et al. 2019):
where |$\vec V$| signifies the velocity vector, ρ denotes density, β denotes the thermal expansion, g is gravity, p denotes the pressure, e stands for the unit vector aligned with the buoyancy direction, α denotes thermal diffusivity, and T represents the temperature.
To cast Equations (2)–(4) into a dimensionless framework, we define the subsequent array of non-dimensional parameters as
Equations (2) through (4) simplify to the subsequent non-dimensional representation
where |$\Pr = \frac{v}{\alpha },\ Ra = \frac{{\beta g( {{T_h} - {T_c}} ){L^3}}}{{v\alpha }}$| are the Prandtl (Pr = 7 for water in this study) and Rayleigh numbers, respectively. The non-dimensional boundary conditions for the problem under consideration can be written as
The local and average heat transfer rates along the sinusoidally heated left vertical wall can be expressed as:
2.2 Entropy generation rate
In the system being studied, irreversible phenomena occur due to both heat transfer and viscous dissipation. The assessment of these irreversible effects is conducted via entropy-production analysis. The expression of entropy-production is succinctly stated as follows:
where |${T_0} = {{( {{T_h} - {T_c}} )} \mathord{/ {\vphantom {{( {{T_h} - {T_c}} )} 2}}} 2}$|. The initial expression to the right indicates the localized entropy-production due to thermal effects, whereas the subsequent expression in the equation denotes the localized entropy generation stemming from shear energy indulgence. The non-dimensional rate of entropy-production, represented as |${N_S}$|, is established as the ratio of the local volumetric entropy-generation rate |${\dot S^{\prime\prime\prime}_0}$| to a representative entropy-generation rate is |${\dot S^{\prime\prime\prime}_{gen,0}} = {{T_0^2{L^2}} \mathord{/ {\vphantom {{T_0^2{L^2}} {{k_f}\Delta {T^2}}}}} {{k_f}\Delta {T^2}}}$|. The dimensionless representation of the local entropy generation rate is
where |$\phi $| is the entropy-production or irreversibility factor. The entropy generation rate can be determined by aggregating the local entropy-generation rate (13) across the entire volume of the enclosure as
where the Ω denotes the entirety of the computational space. The local irreversibility Φ is defined as a ratio between the local entropy generation rate due to fluid friction to the local entropy generation rate due to heat transfer NS, h. The traditional local Bejan-number is characterized as the proportion of the local entropy-production rate attributed to heat transfer to the overall entropy-generation rate. This correlation is expressed mathematically as
The local Bejan number serves as a critical parameter in analysing the thermal irreversibility inside a framework, and it is confined to the inclusive interval [0, 1]. The significance of thermal inefficiency is maximized when Be > 1/2, indicating a predominant influence of heat transfer processes. Bejan coefficient of 1/2 indicates a condition of balance where the rates of thermal transfer, fluid resistance, and generation of entropy from solute interactions are equally significant, offsetting the factors of irreversibility within the system. The average Bejan number is determined by numerically integrating the local Bejan number (15) across the entire cavity volume, and it is expressed as follows:
3. Computational Methodology and Verification
This section covers the methodology related to the proposed mathematical model, which is further broken down into two subsections: the numerical method implemented and the validation of the code.
3.1 Finite element method approach
The collection of governing Equations (6)–(9) and associated boundary conditions (10) have been systematically addressed using the Galerkin technique. The solution is achieved through the utilization of the penalty-finite element method (penalty- FEM; Khanafer et al. 2003; Haq et al. 2019), where the penalty parameter ‘H’ is strategically employed to enforce the elimination of pressure in the following manner:
It is noteworthy that assigning a significant value to the penalty parameter ‘H’ automatically satisfies the continuity equation. Utilizing Equation (17), the momentum equation can be reformulated as follows:
Application of the well-established Galerkin finite element method is employed to solve Equations (18)–(19) along with the specified boundary conditions. The solutions for velocities (U, V) and temperature are determined utilizing the selected basis set |$\{ {{\Upsilon _n}} \}_{n = 1}^N$|as
Upon substituting these solutions into Equations (18)–(19), a system of non-linear residual equations is formulated for all nodes within the internal domain of the square cavity. The resolution of these non-linear algebraic equations is accomplished through a reduced integration method coupled with the Newton–Raphson approach.
3.2 Grid dependency test and code verification
The reliability of the proposed approximated scheme is evaluated through a test for grid dependence, which encompasses five trials conducted on uniform grids of various dimensions: 50 × 50, 100 × 100, 150 × 150, 200 × 200, and 300 × 300 points. The findings, summarized in Table 1, illustrate the impact of various grid resolutions on the average physical quantities for the inclined plate at a cold temperature. Based on this scrutiny, a grid with different points were selected for the present study. To further affirm the robustness of the approximated technique employed in this study, a comparative analysis is undertaken by comparing the present results with existing literature. This comparison is conducted in a specific case involving a square cavity without the inclined plate, and the findings are summarized in Table 2. The congruence observed in this comparison underscores the consistency and reliability of the adopted numerical method in the current study.
Sensitivity of average quantities to grid resolution with Ra = 105, k = 1, and ϵ = 1.
| Uniform grid . | |$N{u_{avg}}$| . | |$N{s_{avg}}$| . | |$B{e_{avg}}$| . |
|---|---|---|---|
| 50 × 50 | 18.84 610 | 108.9021 | 0.32 806 |
| 100 × 100 | 18.77 609 | 108.84 701 | 0.30 954 |
| 150 × 150 | 18.60 905 | 108.59 701 | 0.299 821 |
| 200 × 200 | 18.60 025 | 108.56 690 | 0.299 708 |
| Uniform grid . | |$N{u_{avg}}$| . | |$N{s_{avg}}$| . | |$B{e_{avg}}$| . |
|---|---|---|---|
| 50 × 50 | 18.84 610 | 108.9021 | 0.32 806 |
| 100 × 100 | 18.77 609 | 108.84 701 | 0.30 954 |
| 150 × 150 | 18.60 905 | 108.59 701 | 0.299 821 |
| 200 × 200 | 18.60 025 | 108.56 690 | 0.299 708 |
Sensitivity of average quantities to grid resolution with Ra = 105, k = 1, and ϵ = 1.
| Uniform grid . | |$N{u_{avg}}$| . | |$N{s_{avg}}$| . | |$B{e_{avg}}$| . |
|---|---|---|---|
| 50 × 50 | 18.84 610 | 108.9021 | 0.32 806 |
| 100 × 100 | 18.77 609 | 108.84 701 | 0.30 954 |
| 150 × 150 | 18.60 905 | 108.59 701 | 0.299 821 |
| 200 × 200 | 18.60 025 | 108.56 690 | 0.299 708 |
| Uniform grid . | |$N{u_{avg}}$| . | |$N{s_{avg}}$| . | |$B{e_{avg}}$| . |
|---|---|---|---|
| 50 × 50 | 18.84 610 | 108.9021 | 0.32 806 |
| 100 × 100 | 18.77 609 | 108.84 701 | 0.30 954 |
| 150 × 150 | 18.60 905 | 108.59 701 | 0.299 821 |
| 200 × 200 | 18.60 025 | 108.56 690 | 0.299 708 |
Comparative analysis of the average nusselt number from the current study with existing literature in a square cavity scenario, without the inclusion of an inclined plate.
Comparative analysis of the average nusselt number from the current study with existing literature in a square cavity scenario, without the inclusion of an inclined plate.
The convergence behaviour of the FEM for the proposed model and for different Rayleigh numbers is shown in Fig. 2. The plot displays the L2-norm of the residuals against the number of iterations, highlighting the error reduction during the numerical solution process. Initially, for all Rayleigh numbers 104, 105, and 106, the residuals start at 100 and rapidly decrease up to around 200 iterations, indicating an efficient capture of the dominant flow features early in the iteration process. Beyond 200 iterations, the reduction rate slows, reflecting the increased difficulty in further refining the solution. By approximately 400 iterations, all curves converge to a residual norm between 10−10 and 10−12, demonstrating that the method achieves high accuracy regardless of the Rayleigh number. The graph also implies that the CPU time required for convergence would correlate with the number of iterations, with each case taking around 2–3 hours to reach a highly accurate solution. This behaviour confirms the robustness of FEM for different convective intensities, with practical implications for its suitability in simulating fluid flow driven by thermal convection in a square cavity.
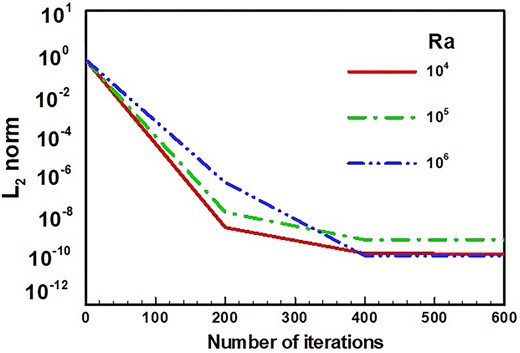
L2 norm vs number of iterations with fixed values of governing parameters such as ϵ = 1, k = 2, and Pr = 7.
4. Outcomes and Analysis
This investigation centres on simulating the flow, thermal transfer, and entropy-production rate in the context of free convection within a square cavity featuring an inclined plate. Depending upon engineering applications, three thermal conditions are applied on the inclined plate, including hot, cold, and adiabatic conditions. Initially, the simulations are performed for all these three conditions, and then, based on the results, the cold plate is selected for further investigations. The default values of the governing parameters are |${10^3} \le Ra \le {10^5},0 \le k \le 3,$| Pr = 7, |$0 \le \varepsilon \le 1,\phi = 0.0001$| until and unless specified.
Figure 3a–c depict the variations in streamlines, isotherms, and total entropy generation rate within the cavity, focusing on conditions specific to the inclined plate. As the Rayleigh number increases, convection heat transfer becomes more pronounced in the cavity. This is because higher Rayleigh numbers correspond to stronger buoyancy-driven flows, where heated fluid rises and cooler fluid sinks, enhancing heat transfer through convection. In the case of a heated inclined plate [Fig. 3a(i)], two distinct convective cells form on either side of the plate. The larger convective cell on the left heated wall is attributed to greater thermal buoyancy effects and the formation of a stronger thermal gradient along that surface. This gradient intensifies the upward flow of heated fluid, creating a more significant convective cell compared to the right side. Conversely, for the cold and adiabatic plate scenarios, only one convective cell is observed near the left heated wall [Fig. 3a(ii) and a(iii), respectively]. The absence of significant thermal gradients on the plate surface limits buoyancy-driven flow, resulting in a weaker convective cell formation. The influence of the cold wall specifically weakens the strength of the convective cell on the right side by reducing the temperature differential that drives fluid movement. The stream function, which represents the flow velocity components, shows maximum values for the cold inclined plate and minimum values for the heated inclined plate. This difference arises because colder fluid tends to sink and accumulate near the bottom of the cavity, enhancing fluid movement and hence increasing the stream function, whereas warmer fluid rises, resulting in lower stream function values.

Assessment of (a) streamlines, (b) isotherms, and (c) total entropy generation rate for various temperatures on inclined plate with fixed values of other parameters such as ϵ = 1, k = 3, Pr = 7, and Ra = 105.
The temperature distribution depicted in Fig. 3b(i)–(iii) shows three local maximum points along the left wall due to the parameter k = 3 in the selected plate conditions. This parameter refers to the amplitude of the sinusoidal temperature variation imposed on the left wall. A higher value of k increases the amplitude of temperature oscillations, leading to more pronounced peaks and valleys in the temperature profile along the wall. An enhanced Rayleigh number signifies stronger buoyancy-driven convection near the left heated wall, which influences the distribution of isotherms within the cavity. As the Rayleigh number increases, convection becomes more dominant, causing warmer fluid to rise along the left wall and cooler fluid to descend along the right wall. This results in a lower region of isotherm distribution in the cavity, reflecting the vertical movement of heat through the fluid due to buoyancy effects. In Fig. 3c(i)–(iii), the local entropy generation rate pattern highlights three distinct hot regions along the left wall due to substantial heat transfer occurring in those areas. Entropy generation rate is closely related to irreversible processes such as fluid friction and heat transfer inefficiencies. The presence of hot regions indicates higher levels of entropy generation rate due to increased thermal gradients and fluid motion, which contribute to entropy production rate. Interestingly, the cold inclined plate scenario yields maximum entropy generation rate, primarily attributed to steeper temperature gradients induced by the colder surface. Larger temperature differentials between the plate and the surrounding fluid intensify heat transfer rates and fluid motion, thereby increasing entropy generation rate.
Figure 4a–c provide insights into the variations of local heat transfer rate, dimensionless entropy generation rate, and Bejan number under specific conditions and parameters. In Fig. 4a, the depiction of three maxima in the local Nusselt number along the left hot wall, corresponding to k = 3, can be attributed to the higher amplitude of the sinusoidal temperature variation applied to the left wall. This parameter k influences the temperature gradient and thus the heat transfer rate, with larger k values leading to enhanced heat transfer near the peaks of temperature oscillations. Interestingly, the cold inclined plate scenario exhibits the maximum heat transfer, which can be explained by the steeper temperature gradient between the cold plate and the surrounding fluid. This steep gradient promotes more vigorous convective currents, resulting in increased heat transfer rates compared to scenarios with less pronounced temperature differentials. In Fig. 4b, the distribution of local entropy generation rate along the X-axis at Y = 0.5 highlights peaks at the corners of the cold inclined plate under all conditions. This phenomenon occurs due to the sharper temperature gradients near the plate edges, leading to higher entropy generation rate associated with increased heat transfer and fluid motion in those localized regions. Simultaneously, the Bejan number, depicted in Fig. 4c at corresponding positions on the inclined plate and under various parameters, peaks due to the higher heat transfer rates observed at the left hot wall and the edges of the inclined plane. The Bejan number reflects the ratio of heat transfer irreversibility to fluid friction irreversibility, thus emphasizing locations where heat transfer is most intense, such as near sharp temperature gradients and high convective heat transfer rates.
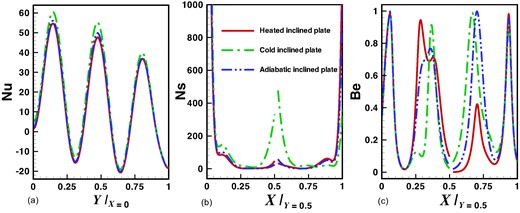
Assessment of local quantities (a) heat transfer rate, (b) local entropy generation rate, and (c) Bejan number for several temperature on inclined plate with fixed values of other parameters such as ϵ = 1, k = 3, Pr = 7, and Ra = 105.
Figure 5a and b illustrate the effects of the Rayleigh number on isotherms and local entropy generation rate, respectively, while maintaining constant governing parameters. Increasing the Rayleigh number leads to expanded isotherms along the left heated wall [Fig. 5a(i)–(iii)], where higher Rayleigh numbers amplify buoyancy-driven convection. At lower Rayleigh numbers, efficient heat conduction prevails due to less pronounced buoyancy effects, resulting in reduced entropy generation rate within the cavity [Fig. 5b(i)]. As the Rayleigh number escalates, the dominance of convection intensifies, leading to higher heat transfer rates and consequently, an increase in entropy generation rate [Fig. 5a(ii) and a(iii)].
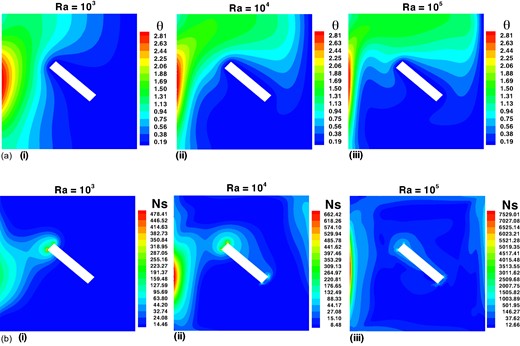
Effect of Rayleigh number on (a) isotherms, and (b) total entropy generation rate with such as ϵ = 1, Pr = 7, and k = 2.
In Fig. 6a–c, the influence of the Rayleigh number on the local Nusselt number, entropy generation rate, and Bejan number is examined. The local Nusselt number increases along the heated wall with rising Rayleigh numbers due to enhanced convective heat transfer, Fig. 6a. At a Rayleigh number of 103, where conduction prevails, the fluid distribution remains symmetrical, resulting in lower overall heat transfer rates across the cavity (see Fig. 6a). As Rayleigh numbers increase, convective heat transfer intensifies, reaching maximum rates at Y = 0.5 and minimum rates at the cold wall across all scenarios (Fig. 6a). Consequently, the entropy generation rate is minimal at the lowest Rayleigh number (see Fig. 6b) but increases along the hot wall as Rayleigh numbers rise, reflecting higher heat transfer rates and fluid movement (see Fig. 6b). For the cold inclined plate, the entropy generation rate peaks at the plate's centre and rises near the cold wall due to significant temperature gradients influencing fluid dynamics (see Fig. 6b). The Bejan number variation with the Rayleigh number for the cold inclined plate (see Fig. 6c) shows peaks at the walls and edges, indicating regions with pronounced temperature and velocity gradients that contribute significantly to irreversibility in heat transfer processes.
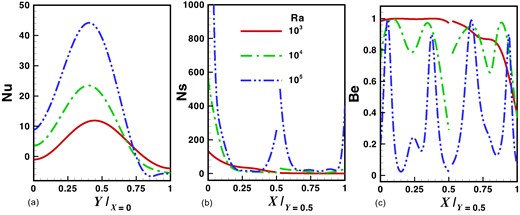
Effect of Rayleigh numbers on local quantities (a) heat transfer rate, (b) entropy generation rate, and (c) Bejan number with fixed parameters such as ϵ = 1, Pr = 7, and k = 2.
The impact of the wave number k on streamlines, isotherms, and total entropy generation rate is explored in Fig. 7, focusing particularly on the scenario with a cold inclined plate. In the absence of waviness [see Fig. 7a(i)], the plane wall exhibits a uniform dimensionless temperature along the left wall because there are no variations introduced by a sinusoidal pattern. However, as the wave number k increases [see Fig. 7a(ii)–(iii)] the dimensionless temperature along the left wall begins to vary due to the sinusoidal temperature distribution. The lower region of the cavity shows a minimum temperature due to the cooling effect of the inclined cold plate, which results in reduced overall temperature gradients within the cavity. In the absence of waviness, lower total entropy generation rate is observed because of the uniform temperature distribution along the left wall [see Fig. 7b(i)]. Conversely, for k = 1 and k = 2, higher entropy generation rate values are recorded due to larger temperature gradients induced by sinusoidal variations along the left wall [see Fig. 7b(ii)–(iii)]. The introduction of waviness alters temperature patterns significantly, thereby influencing entropy generation rates within the cavity.
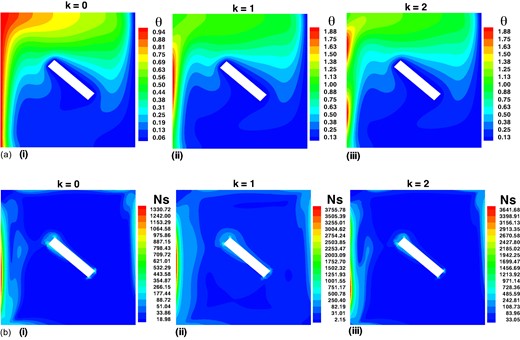
Impact of k on (a) streamlines, (b) isotherms, and (c) total entropy generation rate while maintaining constant values for other parameters such as ϵ = 1, Pr = 7 and Ra = 105.
The influence of identical wavenumbers on local physical quantities for the cold inclined plate is demonstrated in Fig. 8a–c through two-dimensional plots at various positions within the cavity. For k = 0, representing a plane wall scenario, Fig. 8a shows a uniformly decreasing local Nusselt number from the left to the right wall due to the constant hot temperature along the left wall. This results in consistent heat transfer rates across the cavity from the heat source to the cooler boundary. As waviness increases (see Fig. 8a), temperature oscillations along the left wall induce an oscillatory decline in the local Nusselt number from the hot to the cold wall. This variation occurs because the sinusoidal temperature profile alters thermal gradients, affecting convective heat transfer rates along the cavity's walls. In Fig. 8b, the local entropy generation rate exhibits minor variations with different wavenumbers, particularly at positions where the oscillatory changes in the local Nusselt number are less pronounced. The presence of the inclined cold plate at the cavity's centre plays a crucial role in moderating these variations by influencing temperature gradients and fluid dynamics. Figure 8c illustrates the fluctuation of the Bejan number for different wavenumbers, oscillating between 0 and 1. This variation indicates the contributions of entropy generation rate due to fluid friction and heat transfer inefficiencies across the cavity.
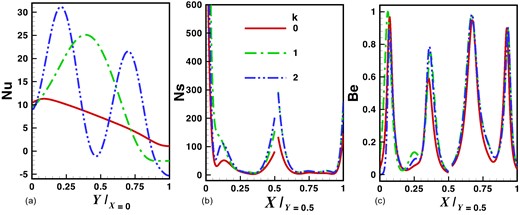
Impact of k on local quantities (a) heat transfer rate, (b) entropy generation rate and (c) Bejan number while maintaining constant values for other parameters such as ϵ = 1, Pr = 7, and Ra = 105.
The influence of varying the amplitude of the hot-wall temperature on isotherms and the total entropy generation rate is depicted in Fig. 9a–b, with constant governing parameters. Increasing the amplitude of the hot-wall temperature results in higher dimensionless temperatures across the cavity [see Fig. 9a(i)–(iii)] because larger amplitudes create more significant temperature differentials along the left wall. This pronounced heating occurs due to the elevated temperature maintained on the left wall, driving increased heat transfer rates throughout the cavity. Consequently, the total entropy generation rate increases as higher temperature gradients along the left sidewall intensify irreversible processes such as fluid friction and heat transfer [see Fig. 9b(i)–(iii)]. Moreover, an increased wave amplitude expands the effective surface area exposed to temperature variations, further enhancing irreversibility and contributing to higher entropy generation rates.
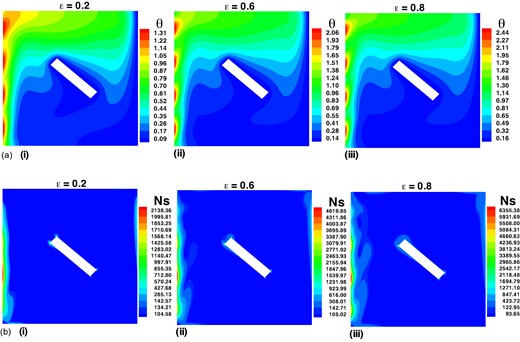
Impact of ϵ on (a) isotherms and (b) total entropy generation number while maintaining constant values for other parameters such as k = 1, Pr = 7, and Ra = 105.
Figure 10a–c illustrate how the local Nusselt number, entropy generation rate, and Bejan number change with increasing amplitude of the variable hot-wall temperature, particularly focusing on the cold inclined plate scenario. Figure 10a shows a rising trend in the maximum local Nusselt number along the vertical wall as the sinusoidal wall temperature amplitude increases. This trend occurs because larger amplitude variations induce greater temperature differentials, enhancing convective heat transfer rates along the wall. As the wave amplitude grows, Fig. 10a also demonstrates a sinusoidal decrease in the local Nusselt number along the Y-axis, indicating how temperature oscillations affect heat transfer efficiency at different points on the vertical wall. In Fig. 10b, the variation in total entropy generation rate with wall temperature amplitude is depicted at Y = 0.5 along the X-axis. It shows higher total entropy generation rates on the left wall due to significant temperature gradients present in that region. The increasing amplitude of the hot-wall temperature leads to more substantial temperature differentials, intensifying irreversibility through increased fluid friction and heat transfer inefficiencies, thus contributing to higher total entropy generation rates overall. The same phenomena can be observed for local Bejan number in Fig. 10c.
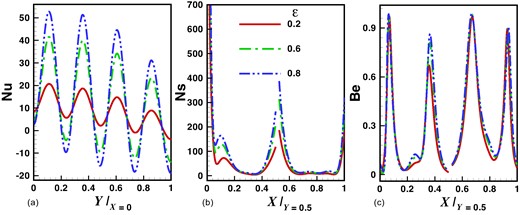
Effects of amplitude on local physical quantities (a) Nusselt number (b) entropy generation rate, and (c) Bejan number with fixed values of other parameters such as k = 1, Pr = 7, and Ra = 105.
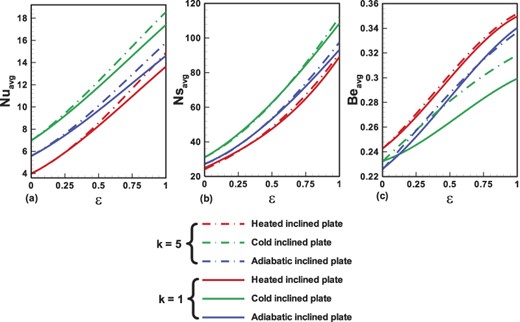
In Fig. 11a–c, variations in physical parameters such as average heat transfer and entropy generation rates are detailed for three selected scenarios. Across all cases, these parameters consistently increase with higher amplitudes and wavenumbers due to the expanded heated surface area within the cavity, facilitating greater heat transfer and entropy generation rate. Specifically, average heat transfer and entropy generation rates are lower for the heated inclined plate compared to the adiabatic and cold inclined plates, indicating less heat-related irreversibility. The higher average Bejan number for the heated inclined plate underscores increased entropy generation rate due to heat, emphasizing heat-related irreversibility in this configuration. Notably, smaller amplitudes show no discernible effect of thermal conditions on observed parameters, but as amplitude increases, the influence of thermal conditions becomes more pronounced, highlighting the importance of amplitude and wavenumber in comprehensive thermal analyses. In summary, these findings offer valuable insights into the complex interaction of amplitude, wavenumber, and key physical parameters, providing a deeper understanding of thermal behaviours within the cavity.
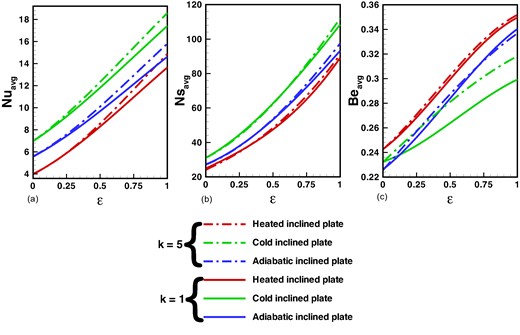
Effects of wave number and amplitude on average physical quantities (a) Nusselt number (b) entropy generation rate, and (c) Bejan number with fixed values of other parameters such as Pr = 7 and Ra = 105.
5. Conclusions
This investigation explores the impact of different thermal conditions applied to the inclined plate within a square cavity, yielding the following key findings:
The cold inclined plate exhibits the highest average heat transfer and entropy generation rates.
Average heat transfer, entropy generation rates, and the Bejan number demonstrate an upward trend with increasing amplitude and wavenumber of the variable hot temperature.
The average Bejan number attains its lowest value for the cold inclined plate.
An elevation in Rayleigh’s number correlates with increased entropy generation along the hot walls.
The cold inclined plate registers the highest values for the local Nusselt number, entropy generation rate, and Bejan number.
Variations in wall temperature directly influence the Rayleigh number (Ra), indicating their impact on thermal dynamics and reversibility. These variations illustrate how thermal conditions affect the physical field within the square cavity, enhancing applicability and broadening generalization.
Based on the present study, it is essential to explore refined thermal management strategies utilizing advanced computational techniques and experimental validations. This includes refining numerical models to incorporate multi-physics interactions, such as magnetic fields or chemical reactions, to comprehensively analyse their impact on fluid dynamics and heat transfer. Additionally, investigating dynamic flow control mechanisms through active and passive strategies promises to enhance efficiency further. Exploring the integration of nanofluids and advanced materials within cavity configurations could yield breakthroughs in maximizing heat transfer rates while minimizing entropy generation.
Funding
This work was supported by the Guangxi Natural Science Foundation (Grant No. 2024GXNSFAA010481) and Guangxi Science Technology Base and Special Talents (Grant No. AD20238065 and Grant No. AD23023003).
Conflicts of interest statement
None declared.
Author Contributions
Z.H.K.: Conceptualization, methodology, formal analysis, and software. M.H.: Project administration, methodology, and data curation. W.A.K.: Writing (original draft), visualization, and supervision. R.A.: Writing (original draft) and software. L.J.: Writing (original draft), resources, project administration, and funding acquisition.
Acknowledgement
This work is supported by the Guangxi Natural Science Foundation (Grant No. 2024GXNSFAA010481) and National Natural Science Foundation of China> (Grant No. 12250410244). The first author acknowkedge is finincial support by Guangxi Science Technology Base and Special Talents (Grant No. AD20238065 and Grant No. AD23023003). This work is supported by the Jiangsu Funding Program for Excellent Postdoctoral Talent (2023ZB884). The author (M. Hamid) acknowledges the support of the Ministry of Science and Technology China through Foreign Expert Project funding (Grant No. WGXZ2023017L), Shuang Chuang (SC) Doctor Program of Jiangsu Province and Longshan Scholar Program of NUIST.).
Data availability
Data sets generated during the current study are available from the corresponding author on reasonable request.


