Lévy trajectories of Peruvian purse-seiners as an indicator of the spatial distribution of anchovy (Engraulis ringens) Open Access

Abstract

Introduction

Fishers are predators, so we can hypothesize that part of their spatial behaviour reflects the spatial distribution of fish. However, predator–prey relationships are composed of interactions across different scales (Steele, 1989; Levin, 1992). For instance, the spatial aggregation of small pelagic fish is characterized by a nested hierarchical organization (Kotliar and Wiens, 1990; Wu and Loucks, 1995; Fauchald, 1999): the school, the cluster of schools, the cluster of clusters, and ultimately the population (Fréon and Misund, 1999; Petitgas et al., 2001). This hierarchy leads to two major inferences: (i) from a functional perspective, fishers have to develop a spatial strategy for dealing with the multi-scale aggregation pattern (Russel et al., 1992); (ii) from a methodological perspective, studying the process of interaction between fish and fishers implies use of metrics that allow multiple scales of potential interactions to be taken into account.

Several studies have focused on spatial predator–prey relationships in a multi-scale, hierarchical patch dynamic framework, using various metrics (Rose and Leggett, 1990; Fauchald et al., 2000; Davoren et al., 2002; Fauchald and Erikstad, 2002; Bertrand et al., 2004a). Frontier (1987) conjectured that if the search for prey is the main determinant for the distribution of organisms, there should be a type of “behavioural cascade” in space. Choosing the fractal dimension as a natural and simple method for describing objects across a range of scales (Kotliar and Wiens, 1990; Sugihara and May, 1990; Halley et al., 2004), Russel et al. (1992) argued, and to some extent showed, that under the “behavioural cascade” hypothesis, the fractal dimensions of predator and prey distributions are correlated.

During the past decade, vessel monitoring systems (VMS) have been increasingly implemented in fisheries. In Peru for instance, the entire industrial fleet is equipped with satellite transmitters that record vessel positions. This system produces real-time data with high spatial resolution, which has largely been used for law enforcement purposes. However, the information has great potential for monitoring exploited marine resources, and may be applied in an ecosystem context. In parallel, the Peruvian marine institute (IMARPE) usually performs between one and four acoustic surveys per year to assess biomass and spatial distribution of pelagic resources.

Based on these spatially explicit data and within the conceptual framework of interacting hierarchical multi-scale processes, our purpose here is to investigate whether fishing vessel trajectories can be used as an indicator of pelagic fish distribution. To test this hypothesis, we (i) characterize fishing vessel trajectories, (ii) characterize anchovy spatial distribution, and (iii) investigate if there is a relation between the spatial behaviour of fish and fishers.

Material and methods

Vessel monitoring system data

Since 1999, a VMS (SISESAT: SIstema de SEguimiento SATelital) has been operational for the entire Peruvian industrial fishing fleet (about 800 vessels). Each vessel is equipped with an Argos satellite transmitter (CLS Argos, Toulouse, France) furnished with its own Global Positioning System (GPS) receiver. In principle, each transmitter sends its time-referenced position with an accuracy of 100 m on an hourly basis. When a GPS position (marked as class G) is not available, Argos provides a position with a lower level of accuracy (labeled class 1, 2, or 3).

The data considered cover the period November 1999–March 2003. SISESAT transmits continuously, providing vessel positions without any distinction between positions at sea or in port. A first algorithm for pre-processing data aimed to identify positions at sea by excluding consecutive emissions located within a 2-nautical-mile radius of any port. Trips were defined as series of emissions originating at sea, bounded by emissions at port. We chose to work only with “accurate” data, retaining only trips for which all positions belonged to the G class and whose duration between consecutive emissions was ≤2 h. A second algorithm aimed to identify those trips that were most likely intended for fishing. Fishing trips usually last between 24 and 48 h, and cannot last much longer because the purse-seiners do not have freezing systems aboard. Therefore, we arbitrarily set maximum trip duration to 120 h, and rejected longer trips. Moreover, because fishing sets impose speeds <3 knots, we discarded trips for which speed was always greater. A third algorithm split the trajectory of each remaining “fishing trip” into elementary moves, moves being defined (Turchin, 1998) as the sum of consecutive positions of a vessel in the same direction. Instantaneous direction at sea is liable to be highly variable, so we arbitrarily defined a change of direction as when the angular difference between two consecutive pairs of positions exceeded 10°. Move lengths were calculated as orthodromic distances.

A common method used to characterize animal trajectories (Turchin, 1998) is to describe the statistical distribution of move lengths between successive changes of direction. The probability density functions of these distributions can be formulated in a generalized form as an inverse power-law distribution (Viswanathan et al., 1996):

(1)

where P(l) is the probability for a move length equal to l. Values of μ are related to different types of redistribution kernel (Mandelbrot, 1977; Viswanathan et al., 1999): μ ≥ 3 corresponds to a Gaussian distribution or Brownian motion; μ ≤ 1 corresponds to probability distributions that cannot be normalized, but as μ tends towards 1, the fraction of short moves becomes negligible and the forager moves along straight lines (i.e. close to a ballistic motion); 1 < μ < 3 defines the domain of long-tailed distributions named “Lévy flights”. This last type of motion has a high probability of large moves, and the variance (and even the mean) of the move-length distribution diverges with increasing number of moves, indicating that there is no characteristic scale for the observed distribution (scale invariance). The Lévy flight type of spatial behaviour has been documented for a variety of foraging natural predators: Drosophila (Cole, 1995), albatross (Viswanathan et al., 1996), reindeer (Mårell et al., 2002), jackal (Atkinson et al., 2002), and seals (Austin et al., 2004).

To estimate μ from VMS observations, first we built the histogram of the move-length frequency distribution of the fishing trips for each vessel and month (Figure 1a). Histogram shape, and any fitting procedure, is sensitive to the bin size. The most commonly applied rule for selecting the number of classes in constructing a histogram is that proposed by Sturges (1926). However, two problems arise with this method: (i) data are supposed to have a normal distribution, and (ii) the method tends to oversmooth the histogram. To overcome these limitations, histograms were constructed with Scott's (1979) rule for estimating bin width (h):

(2)

where s is the standard deviation of the sample and n is total sample size. Finally, a least-squares linear regression was fitted through the tail (Viswanathan et al., 1999) of the log-log plot of the move-length frequency distribution (Figure 1b), the slope being an estimate of the inverse power-law exponent (μ).

Figure 1

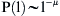
(a) A fishing trip trajectory (black dots correspond to VMS positions), and (b) a move-length frequency distribution of the same vessel in April 2000 (histogram for 9 trips corresponding to 113 moves), with inset a log-log scale plot plus fitted regression line (μ = 2.01, r² = 0.96, p < 0.001).

Open in new tabDownload slide

Acoustic survey data

IMARPE research vessels conducted 13 pelagic acoustic surveys between December 1999 and March 2003. Acoustic data were collected with a scientific echosounder system (38 and 120 kHz split-beam SIMRAD EK500, Kongsberg SIMRAD AS, Norway), calibrated using standard procedures (Foote et al., 1987). The water column was sampled to depths of 250 and 500 m, for 120 and 38 kHz, respectively. Standard survey design consisted of parallel transects running from 3.7 km from the coast to about 185 km offshore, with inter-transect distance varying between 26 and 30 km. Acoustic backscattered energy by surface unit (s_A) was recorded in each elementary sampling distance unit (ESDU) of 1852 m. Species composition was identified through trawling, echo-trace characteristics, and abiotic conditions. Data corresponding to anchovy were selected, and s_A was considered to represent an index of anchovy local abundance.

For each survey, anchovy spatial distribution was characterized by three metrics: (i) IMARPE routinely produces an estimate of the total surface occupied by anchovy (S in km²); (ii) an index of spatial concentration (Ss; Petitgas, 1998; Bertrand et al., 2004b) was calculated as the difference between the experimental concentration profile of s_A and a theoretical homogeneous spatial distribution; (iii) the fractal dimension of anchovy distribution was estimated using the method proposed by Bruno and Raspa (1989) and Halley et al. (2004). These authors showed that fractal dimension (D) is linearly related to the slope at the origin (α) of the log-transformed semi-variogram (Matheron, 1965) for a pattern on a two-dimensional landscape:

(3)

For each survey, we computed the Napierian log-log semi-variogram on presence–absence data for anchovy (Figure 2), and α was estimated by least-squares regression. The number of points included in the linear regression was chosen so as to maximize r².

Figure 2

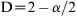
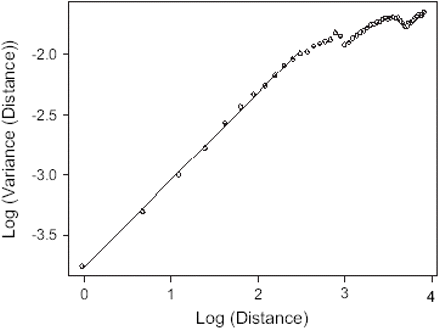
Napierian log-log transformation of the semi-variogram of the anchovy distribution for the survey October/November 2000 (x-axis corresponds to the distance between pairs of points for which variance is computed; slope-derived D = 1.639, r² > 0.999).

Open in new tabDownload slide

Results

Raw data consisted of 41 months, 809 vessels, and 14 106 533 emissions, corresponding to 210 530 trips. Pre-processing of the data identified 68 025 fishing trips (1 266 712 moves) performed by 756 vessels during the 41 months studied. Mean μ values among vessels by month ranged between 1.13 and 2.09 (Figure 3). Consequently, fishing trip trajectories are in the domain of Lévy flights motion. Months exhibiting particularly high variability of μ correspond to the austral winter, when relatively few fishing trips were identified (Table 1). At that time of year, fishing closures are frequent, and the aberrant values may correspond to exploratory trips, or other atypical behaviour.

Figure 3

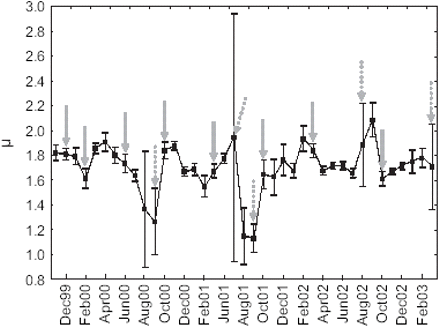
Time-series of estimated μ by month (black squares: means; vertical bars: 0.95 confidence intervals; grey arrows indicate acoustic survey dates, dashed when corresponding to a period of fishing closure).

Open in new tabDownload slide

Over the period studied, the total distribution area of anchovy (S) ranged between 23 911 and 80 955 km², spatial concentration (Ss) varied by a ratio of 13%, and fractal dimension (D) by a ratio of 4.7% (Table 1). Among the 13 surveys carried out, the five potentially coinciding with periods of fishing closure (threshold set at 100 fishing trips) were excluded. Therefore, only eight surveys could be used to compare vessels' trajectories and anchovy distribution metrics (Figure 4). Only the correlation between D and μ was significant (Table 2).

Figure 4

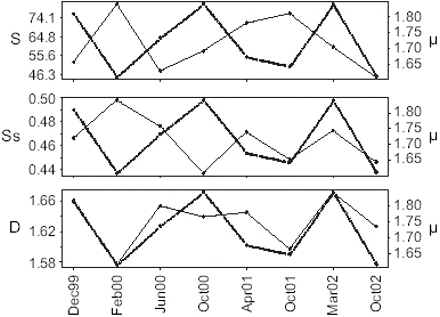
Time-series comparisons between the sinuosity of vessel trajectories (μ, dashed line) and (a) anchovy spatial extent (S), (b) spatial concentration (Ss), and (c) fractal dimension (D).

Open in new tabDownload slide

Discussion

The three metrics used to describe the spatial distribution of the fish were chosen as satisfying a trade-off between available data and the need to describe the system over a continuum of scales. While spatial extent (S) has a direct interpretation, spatial concentration (Ss) and fractal dimension (D) have no intuitive interpretation. Ss can be taken as a measure of the way by which a given fish biomass “fills” the available space (Bertrand et al., 2004b), but it provides no information on the relative location of aggregations. Geometrically speaking, D can be seen as the degree of occupation of the physical space by a contorted or fragmented surface (Mandelbrot, 1977; Frontier, 1987), or as the degree of spatial irregularity of the analysed spatial function. Ecologically speaking, D is usually interpreted in terms of degree of patchiness or clustering of aggregations (Frontier, 1987).

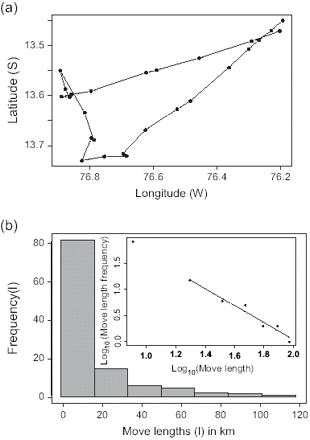
Results revealed that trajectories of fishers can be described as Lévy flights, but what does this mean? As μ decreases, long moves are made longer, and short moves are made shorter (Mandelbrot, 1977). This has two related consequences: from a Lagrangian perspective, as μ decreases, sinuosity of the trajectories decreases, whereas from an Eulerian perspective, as μ decreases, diffusion of the individuals increases, so the area explored increases (Berkolaiko et al., 1996). Lévy flights are also characterized by their scale invariance (Mandelbrot, 1977). Following this idea, the spatial distribution of the points visited by a Lévy flyer (corresponding to the points of changing direction) has been shown to form a fractal with dimension D = μ − 1 (Viswanathan et al., 1996; Atkinson et al., 2002). Mandelbrot (1977) indicated that as this fractal dimension (or μ) decreases, clusters of visited points by the Lévy flyer become increasingly tightly packed, and thus increasingly separate from neighbouring clusters, and the number of apparent hierarchical levels seems to increase. In other words, μ indicates the degree of clustering of the visited points.

The significant correlation between D and μ confirms the hypothesis that fishers' spatial behaviour reflects to some degree the spatial distribution of fish. The absence of correlation between μ and either S or Ss for the study period suggests that fishers' spatial searching behaviour is mainly determined by the degree of clustering of fish. This, it is thought, is due to the process of information acquisition by fishers, and to their perception of the environment. Although significant, the correlation between D and μ may appear weak. This may be explained by three factors: (i) the range of variation of D for the study period is about 4.7%, so although the linear regressions for estimating D had very high r² (>0.99), the estimated value is sensitive to the regression used; (ii) variability in behaviour among vessels may weaken the relationship; (iii) the pelagic ecosystem is characterized by strong interannual variability owing to El Niño events, which affect patchiness and connectivity of highly productive zones (Sugihara and May, 1990). Because there were no strong El Niño events during the period investigated, we do not think that we have seen the entire range of variability of the system. This would argue in favour of analysing longer time-series with this approach.

We conclude that the μ statistic of fishing vessel trajectories constitutes a good candidate as an ecosystem indicator because: (i) Lévy flights are intuitively and statistically appropriate for describing the spatial behaviour of fishers; (ii) they can easily be related to fractal geometry, and are appropriate for describing multi-scale processes; (iii) μ is easy to compute and its interpretation is straightforward; (iv) the method can be applied in any ecosystem where VMS data are being collected; (v) owing to the ongoing development of VMS, its application should be cost-effective. If analysis of a longer time-series confirms the observed trend between μ and D, μ may be a promising indicator of the degree of clustering of fish aggregations that could contribute to real-time monitoring of ecosystems.

We thank IMARPE for providing the VMS and acoustic survey data, Arnaud Bertrand for his active participation during the study, and Pierrick Penven and François Colas for fruitful conversations about Lévy flights. This work is a contribution of IRD's Research Unit ACTIVE UR061 and the Interdepartemental Thematic Action “Humboldt Current System” (ATI “SCH”) funded by IRD.

References