-
PDF
- Split View
-
Views
-
Cite
Cite
C DeMets, S Merkouriev, High-resolution reconstructions of South America plate motion relative to Africa, Antarctica and North America: 34 Ma to present, Geophysical Journal International, Volume 217, Issue 3, June 2019, Pages 1821–1853, https://doi.org/10.1093/gji/ggz087
Close - Share Icon Share
SUMMARY
From an inversion of ≈7000 crossings of 37 magnetic reversals between chrons C1n (0.78 Ma) and C13 (33.7 Ma) and numerous crossings of 43 transform faults and fracture zones in the central and southern Atlantic basin, we estimate finite rotations and stage angular velocities that describe South America plate motion relative to Africa (Nubia), and via plate circuit closures relative to the Antarctic and North America plates. Our newly estimated Nubia–South America rotations, which are spaced at ≈1-Myr intervals, reveal for the first time a transition from steady motion before 24–22 Ma to continuously slowing motion since 20 Ma, including a previously unknown, sudden spreading rate slowdown at 7–6 Ma, when similar declines in seafloor spreading rates also occurred in the northern Atlantic and Arctic basins and along the Southwest Indian Ridge. Geodetic measurements from Nubia and South America, which record the instantaneous plate motion, corroborate the slowdown and indicate it has continued to the present. Our newly determined North America–South America rotations and angular velocities indicate that the pole for this plate pair was stationary from 20 to 12 Ma, but has migrated steadily southward since ≈12 Ma, causing the plate motion direction to change by up to 90° anticlockwise along parts of the diffuse oceanic plate boundary. Since ≈14 Ma, the plate motion rates have averaged 3±0.5 mm yr−1 of N–S to NW–SE-directed divergence near the Mid-Atlantic Ridge and 1–2 mm yr−1 of obliquely convergent motion near the Lesser Antilles Trench, consistent with geodetic estimates. Our new Antarctic–South America rotations and angular velocities predict that American–Antarctic Ridge seafloor spreading rates and plate slip directions have slowed gradually by 60 per cent and rotated 5–7° clockwise since 20 Ma in response to the post-20 Ma slowdown in Nubia–South America seafloor spreading rates. Fracture zone flow lines that are predicted with the new Antarctic–South America rotations agree well with the trends of fracture zone valleys and ridges that flank the American–Antarctic Ridge, offering independent evidence for the accuracy of our new rotations. The Antarctic–South America rotations for chrons C5n.2 (11.1 Ma) and C6no (19.7 Ma) predict that 15–40 km less seafloor has accreted since these times than is indicated by identifications of these two reversals along the American–Antarctic Ridge. Slow westwards movement of the previously postulated Sur microplate with respect to the South America plate may explain the discrepancy—a strong test of this hypothesis awaits better magnetic anomaly data from this remote seafloor spreading centre.
1 INTRODUCTION
Comparisons of geodetic estimates of instantaneous plate motions to conventional estimates that span geological timescales reveal that the largest differences between the two are typically associated with the India, Nazca and South America plates (Sella & Dixon 2002; Argus et al.2010; DeMets et al.2010). The discrepancies associated with the South America and Nazca plates are arguably the most intriguing given compelling plate kinematic evidence for a slowdown in Nazca–South America convergence rates during the Neogene and Quaternary (Norabuena et al.1999; Somoza & Ghidella 2012) and a possible cause-and-effect relationship between the growth of the Andean mountain belt and the convergence slowdown (Iaffaldano et al. 2006; Iaffaldano & Bunge 2008, 2009; Colli et al.2014). Geodynamic modelling also predicts that the long-term growth of the Andes may have caused seafloor spreading rates to decrease in the southern Atlantic basin (Iaffaldano & Bunge 2009), which if true illustrates the potential of geodynamic modelling for explaining the cause(s) of changes in plate motions both locally and in the far field.
The central goal of this paper is to estimate new high-resolution rotations that quantify the movement of the South America plate relative to the adjacent Nubia, Antarctic and North America plates (Fig. 1). Our work has three primary motivations. First, we wish to resolve whether seafloor spreading rates in the southern Atlantic have slowed down since 20 Ma, as is predicted by geodynamic models that link growth of the Andes to the Neogene/Quaternary slowdown in the rate of Nazca plate subduction beneath western South America (Iaffaldano & Bunge 2009; Colli et al.2014). Second, high-resolution rotations for the Nubia–South America plate pair are the starting point for reliable reconstructions of the motions of the South America plate relative to the Nazca and Scotia plates. Such reconstructions are broadly useful for studies of the evolution of the Peru–Chile subduction zone and Andean mountain belt (e.g. Iaffaldano & Bunge 2008; O’Driscoll et al.2012; Iaffaldano et al.2014; Schepers et al.2017) and the opening history of the Drake Passage between South America and Antarctica, which has paleoclimatic implications (Eagles et al.2005; Livermore et al.2005). Finally, this study is part of our long-term effort to quantify at high temporal resolution the Neogene/Quaternary opening histories of all the major seafloor spreading centres, which we believe are critical for ongoing efforts to develop a unified description of how plate motions and plate driving and resisting forces have evolved during the past ≈200 Myr.
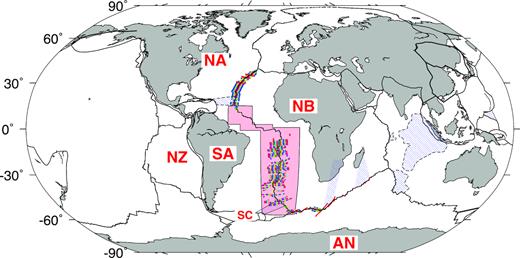
Southern Atlantic Ocean basin study area (pink region) displayed in subsequent figures. Coloured circles along the spreading centres that separate the Nubia plate from Antarctica and North and South America show the locations of ∼19 000 identifications of magnetic reversals 1n (0.78 Ma) through 13no (33.7 Ma) used in this study for high-resolution reconstructions of motions between the Nubia, South America, Antarctica and North America plates. Plate name abbreviations are as follows: AN - Antarctic; NA - North America; NB - Nubia; NZ - Nazca; SA - South America; SC - Scotia.
Our efforts are preceded by those of numerous authors, beginning with Wegener’s (1920) and Bullard, Everett & Smith’s (1965) early efforts to reconstruct the pre-Atlantic configuration of Africa and South America from correlative geologic and physiographic features along their continental margins. Early plate tectonic efforts to reconstruct Nubia (western Africa) plate motion relative to South America were hampered by the sparse magnetic and bathymetric observations that were then available (e.g. Dickson et al.1968; Le Pichon 1968; Morgan 1968). By the 1980s, satellite altimetric mapping of the numerous Atlantic basin fracture zones and improved coverage of magnetic anomalies in the southern Atlantic significantly improved our knowledge of Nubia–South America plate motion (e.g. Shaw 1987; Cande et al.1988, Gibert et al.1989; Shaw & Cande 1990; Nurnberg & Muller 1991; Weiland et al.1995; Nankivell 1997; Muller et al.1999; Torsviket al.2009; Seton et al.2012; Perez-Diaz & Eagles 2014; Granot & Dyment 2015). Geodetic measurements at sites on the Africa and South America plates now provide an independent check on the accuracy of conventional plate motion estimates (Norabuena et al.1999; Sella et al.2002; DeMets et al.2010).
During the past 34 Myr (Chron 13), the period covered by this study, southern Atlantic spreading-rate histories that have been estimated by previous authors sometimes differ substantially, which complicates efforts to test and refine geodynamic models that relate the relative plate motion to the forces that have acted on the two plates (e.g. Iaffaldano & Bunge 2009; Colli et al.2014). For example, Weiland et al. (1995) report no significant change in southern Atlantic basin seafloor spreading rates during the past 6 Myr, whereas Cande et al. (1988) and Cande & Kent (1992) estimate a 20 –30 per cent slowdown during the same period. In addition, seafloor spreading rates that are estimated by different authors for common time intervals sometimes differ by up to 50 per cent. These disagreements are caused by a variety of factors that include differences in the magnetic data, spreading-rate averaging intervals and magnetic reversal timescales that were used by previous authors.
In an effort to overcome all these issues, we estimate Nubia–South America plate motion since Chron 13 using methods that have proved successful in our previous efforts to estimate high-resolution rotation sequences and uncertainties for other plate pairs (e.g. Merkouriev & DeMets 2014a). Our analysis is based on our own compilation of magnetic and bathymetric data from this plate boundary, including Russian shipboard data not previously used for this kind of study. From ≈7000 identifications of 37 magnetic reversals between chron C1n (0.78 Ma) and C13 (33.7 Ma) and nearly 30 000 crossings of 43 transform faults and fracture zones along the central and southern Mid-Atlantic Ridge, we estimate best-fitting finite rotations at ≈1-Myr intervals since 33.7 Ma, constituting the most detailed kinematic description to date for this plate pair. Using a Bayesian algorithm that is tailored to mitigate noise in sequences of closely spaced rotations (Iaffaldano et al.2014), we estimate noise-reduced rotations and demonstrate that they fit the underlying data nearly as well as the best-fitting rotations, thereby giving a simpler, preferable description of the plate motion. Finally, we use angular velocities from the GEODVEL geodetic study (Argus et al.2010) to extend our plate kinematic estimates to the present and evaluate the accuracy of our youngest rotations.
In the latter half of this study, we determine the first ever high-resolution rotation sequences for the North America–South America and Antarctic–South America plate pairs by combining our newly determined Nubia–South America rotations with published high-resolution rotation sequences for the Nubia–North America and Nubia–Antarctic plate pairs (Merkouriev & DeMets 2014a; DeMets et al. 2015a; DeMets et al. 2015b). We use the North America–South America rotation sequence to quantify the deformation since 20 Ma along the diffuse oceanic boundary between these two plates, with emphasis on the deformation history across the extensional Royal Trough and Researcher Ridge and a previously unknown extensional feature near the Royal Trough that may accommodate some plate motion near the Mid-Atlantic Ridge. Along the American–Antarctic Ridge, we use the newly estimated Antarctic–South America rotations to better understand the evolution of the fracture-zone-dominated seafloor fabric that flanks the ridge, to evaluate whether the Nubia–Antarctic–South America plate circuit has satisfied closure over the past 20 Myr and to approximate the long-term movement of the proposed Sur microplate (DeMets et al.2010).
2 DATA
The Nubia–South America plate boundary is defined by the Mid-Atlantic Ridge between the Fifteen-Twenty transform fault at 15.28°N and the Bouvet triple junction at 54.7°S. The plate boundary extends 14 340 km between these features, of which seafloor spreading segments comprise 8300 km and transform faults or higher-order ridge–axis discontinuities the remaining 6040 km. The magnetic reversal, fracture zone and transform fault crossings that are the basis for our newly estimated rotations are derived from our compilation and interpretation of marine magnetic data and GeoMapApp bathymetric grids (Carbotte et al. 2004 and www.marine-geo.org) from the entire plate boundary.
Maps S1–S9 in the Supporting Information, which are suitable for viewing the data at large scale, display all the along-track magnetic anomaly data and our magnetic reversal identifications on GeoMapApp seafloor bathymetry.
2.1 Magnetic data and magnetic reversal identifications
The magnetic data we compiled for our analysis are from the following sources: (1) A U.S. Naval Research Laboratory low-altitude aeromagnetic survey centred on the Mid-Atlantic Ridge between 8°S and 18°S (Brozena 1986). These survey data, which are indicated by the red tracks in Fig. 2, consist of 62 east–west profiles that are spaced every 18 km along-strike and sample seafloor out to ages of ≈15 Myr on both sides of the ridge. (2) The ‘Sevmorgeologiya’ and ‘Yuzhmorgeologiya’ Russian cruises from 1979 to 1987 (Pogrebitsky et al.1990), which to our knowledge have not been used for previous reconstructions. The 9–17°S area surveyed by these cruises (green track lines in Fig. 2) largely overlaps that covered by the aeromagnetic survey described above, but extends to significantly older seafloor. We also use several track lines from the Zarya non-magnetic schooner (Batkova et al.2007), which have not been used for previous reconstructions. (3) An Italian/Russian survey of ridge segments in the vicinity of the Bouvet triple junction (Ligi et al.1999; shown by the green track lines near 55°S in Fig. 2). (4) Other cruise and aeromagnetic data from the National Geophysical Data Center, including Project Magnet aeromagnetic data (black tracks in Fig. 2).
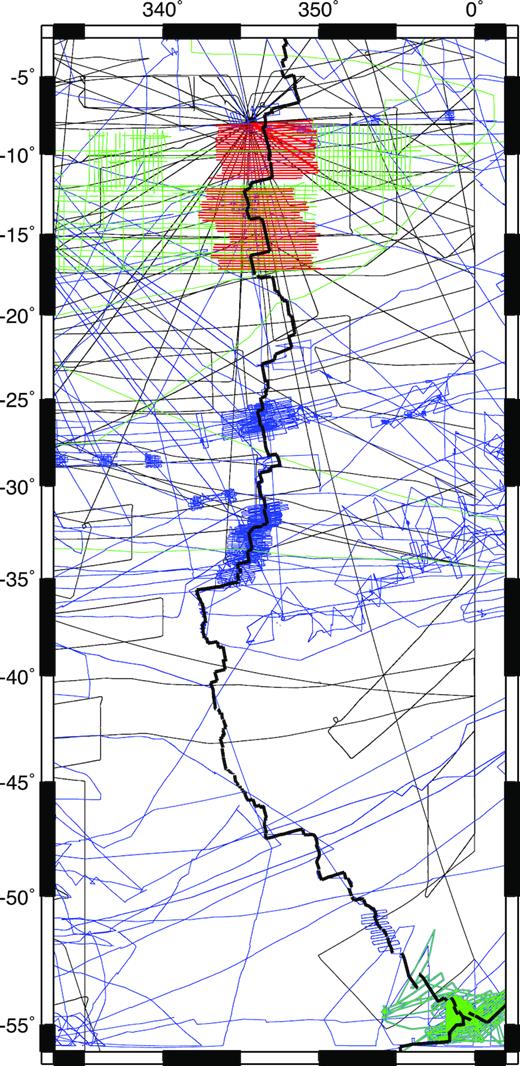
Ship and airplane tracks for all cruises and flights used for the analysis. The red lines are aeromagnetic flight tracks described by Brozena (1986); the green lines are tracks from Russian sources; the black lines are Project Magnetic aeromagnetic flight tracks and the blue lines are tracks for cruises available from the National Geophysical Data Center.
Via comparisons of the along-track magnetic anomaly profiles to synthetic magnetic profiles appropriate for our study area, we identified 37 magnetic reversals between chron C1n (0.78 Ma) and the old edge of chron C13 (33.7 Ma). Identifiers and ages for all 37 magnetic reversals are shown in Fig. 3 and listed in Table S1 (Supporting Information). All the reversal ages are adopted from the astronomically tuned GTS12 timescale (Hilgen et al.2012; Ogg 2012).
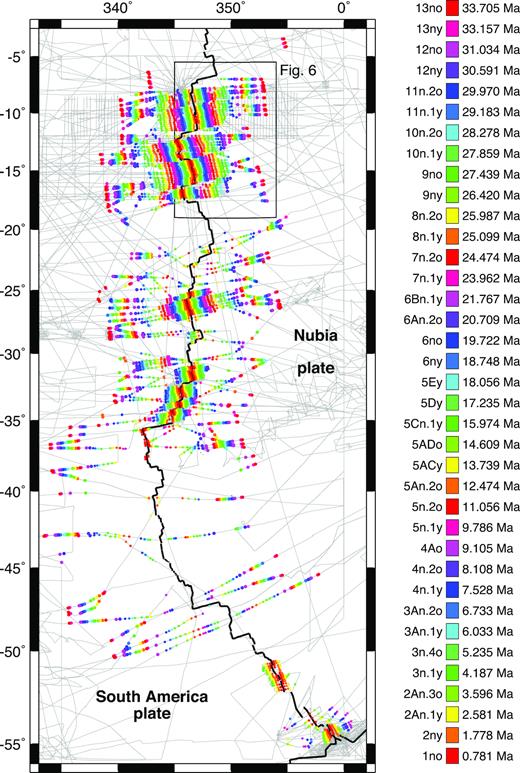
Magnetic reversal identifications used for the analysis consisting of 6952 crossings of chrons C1n (0.781 Ma) to C13 (33.73 Ma). The grey lines show the ship and airplane tracks from Fig. 2. The rectangle delineates the region shown in Fig. 6. The letters ‘o’ and ‘y’ that are appended to the magnetic reversal identifiers, respectively, indicate the reversal’s old or young edge (also see Table S1 of the Supporting Information).
Between 7°S and 36°S, where the magnetic survey coverage is superb (Fig. 3), magnetic reversals between chrons C1n and C13 were identified with high confidence. South of 36°S, where the survey coverage consists mostly of transit tracks, the sparsely mapped reversals were often difficult to identify. Consequently, most (88 per cent) of the reversal crossings used for our reconstructions come from the seafloor north of 36°S. We also compiled and interpreted magnetic data between the equator and 15°N (Map 1, Supporting Information). Due to the low quality of many of these data, we only identified crossings of chrons C1n to C3n.4 with enough confidence to use for our analysis. No reversals were identified between ≈10°S and ≈12°N due to the proximity to the magnetic equator.
2.2 Transform fault and fracture zone crossings
The numerous transform faults and fracture zones that offset the central and southern Mid-Atlantic Ridge are well surveyed by satellite altimetric measurements and conventional and multibeam shipboard surveys (Fig. 4). Based on the bathymetry displayed in Maps S1–S9 and Figs S4–S8 of the Supporting Information, we digitized the traces of 37 transform faults between the Bouvet Triple Junction and Marathon transform fault at 13°N (blue lines in Fig. 3). The transform faults, which describe small circles about the present rotation pole, are used to help constrain the location of the pole for chron C1n, the youngest in our rotation sequence. Uncertainties that we assigned to the transform fault crossings range from 0.5 to 2.5 km, with the smallest uncertainties reserved for transform faults with full or partial multibeam sonar survey coverage.
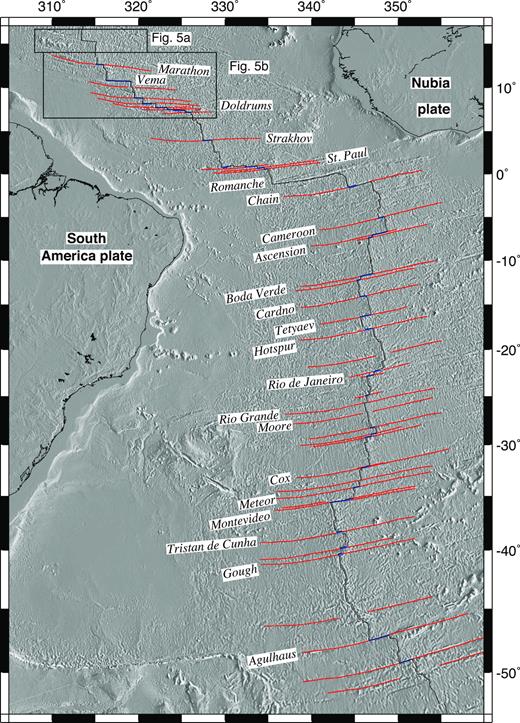
Fracture zone flow lines (red) and transform faults (blue) used for the analysis. The fracture zone crossings, which we digitized from GeoMappApp bathymetry (Carbotte et al.2004), are overlaid on seafloor bathymetry extracted from Version 17.1 of a global seafloor grid (Smith & Sandwell 1997). Fracture zones south of and including the Marathon fracture zone at 12.6°N were used to estimate the Nubia–South America rotations (see the text). The long-offset Vema and Romanche fracture zones were excluded from the analysis. Fracture zone names are adopted from a variety of sources and follow the GEBCO convention where available.
Following previous authors (e.g. Shaw & Cande 1990), we use central and southern Atlantic fracture zones as flow lines to constrain the stage poles that describe past slip directions in Nubia and South America frames of reference. We digitized the traces of 43 well-defined fracture zones (red lines in Fig. 4) between the Bouvet triple junction and Fifteen-Twenty FZ. In areas where fracture zone traces were constrained mostly or only by the 1-arcmin satellite altimetry embedded in the GeoMapApp bathymetric grid, we sampled the fracture zone traces at an along-strike spacing of ≈1–2 km, the approximate resolution of the grid. In areas mapped with multibeam or dense conventional bathymetry, we sampled the fracture zone traces more densely, reflecting the higher resolution of those data. The fracture zone crossing uncertainties vary along strike depending on the width of the fracture zone valley. Four fracture zone valleys, all west of the Mid-Atlantic Ridge (Figs S6a,b and S8b, Supporting Information), have partial-to-complete multibeam sonar coverage that unambiguously identifies the locus of paleo-slip within those four valleys. We therefore assigned small uncertainties to the well-mapped portions of these four fracture zones.
In order to reduce possible biases that large age-offset fracture zones might introduce into our rotations, we excluded the 850-km-offset Romanche FZ (Fig. 4) from our analysis. We also excluded the 310-km-offset Vema FZ (Fig. 4), whose trace we could not reconcile with Nubia–North America or Nubia–South America plate motions. The 43 fracture zones used in our inversions offset the present ridge axis by distances of 21 to 303 km. Their maximum corresponding age offsets range from 0.7 to 10 Myr for a full spreading rate of ∼30 km Myr−1.
3 METHODS
3.1 Best-fitting rotations, data-fitting functions and uncertainties
Merkouriev & DeMets (2014a) describe in detail the methods and fitting functions that we use herein to find best-fitting rotations and their uncertainties. Briefly, crossings of magnetic reversals, transform faults and fracture zones are fit using great-circle, small-circle and flow-line fitting functions, respectively. All the data are inverted simultaneously to find the sequence of finite rotations that minimizes the cumulative weighted least-squares misfit. A priori corrections are applied to each rotation to compensate for outward displacement (Section 4.2), which is primarily an important source of systematic error in estimates of the chron C1n rotation (DeMets & Wilson 2008).
Covariances are estimated for all 37 best-fitting finite rotations via bootstrap resampling of the conjugate spreading segments, fracture zone flow lines and transform faults that comprise our data (Merkouriev & DeMets 2014a). Specifically, each conjugate spreading segment, fracture zone flow line and transform fault is assigned a unique integer code. Random sampling of the segment integer codes is then used to create 1000 alternative data samples, each consisting of the same number of fracture zones, transform faults and spreading segments as the original data. Due to the random sampling, the integer codes (and hence data) for some spreading segments, fracture zones or transform faults may be sampled two or more times for a given bootstrap sample, whereas data from other segments may be omitted entirely. The 1000 bootstrap data sets thus implicitly sample a wide range of relative data weightings (grouped by their segments).
Based on the unique integer codes that comprise a single bootstrap data sample, all of the magnetic reversal, fracture zone and transform fault crossings from the segments represented in that sample are gathered and inverted to find the sample’s best-fitting rotation sequence. Covariances for all 37 best-fitting rotations were estimated from the scatter in the 1000 bootstrap rotation sequences. Unlike the formal rotation covariances, which vary depending on which of the two reconstructed plates is assigned to be stationary in the inversion (e.g. Chang 1988), the bootstrap covariances are the same no matter which of the two reconstructed plates is fixed. They may thus be combined with finite rotation covariances for other plate pairs (e.g. via eq. 2 below) without concern for which plate was fixed when the covariances were estimated.
The uncertainties in the reconstructed positions of points on the Nubia and/or South America plates that are propagated from our Nubia–South America bootstrap rotation covariances are three to five times larger for all 37 rotations than are the uncertainties propagated from covariances estimated using methods described by Chang (1988) and Royer & Chang (1991), which depend on the geographic distribution of the reconstructed data and their assigned uncertainties. The bootstrap covariances used herein are thus a conservative approximation of the underlying uncertainties.
3.2 Mitigation of rotation noise and timing of plate motion changes
Differentiating a sequence of finite rotations that are closely spaced in time can give rise to stage rotations that predict implausibly large short-term variations in stage velocities (Iaffaldano et al.2012). To mitigate these variations, which are almost surely attributable to noise in the finite rotations, we apply REDBACK software (Iaffaldano et al.2014) to our best-fitting sequence of Nubia–South America rotations. REDBACK uses a trans-dimensional, hierarchical Bayesian algorithm to identify optimal, less-noisy sequences of finite rotations and stage angular velocities that are consistent with the original rotations within their estimated covariances. REDBACK also estimates when discrete changes in plate motion are most likely to have occurred.
Like the bootstrap-derived covariances, the finite rotation covariances estimated by REDBACK are invariant with respect to whichever of the two plates is assumed to be stationary.
3.3 Combining plate rotations and their uncertainties
Operations related to (2) were carried out with the ADDROT algorithm (Royer & Chang 1991).
3.4 Best-fitting and noise-reduced stage angular velocities
Stage rotations and their corresponding angular velocities, which are used throughout to quantify how seafloor spreading rates and directions evolve through time, were determined using the standard method. Given two finite rotations |$\skew{6}\hat{A}_{t_2}$| and |$\skew{6}\hat{A}_{t_1}$| that reconstruct Plate B onto Plate A for times |$t\, _2$| and |$t\, _1$|, the stage rotation |$\skew{6}\hat{A}_{{t_2}{\rightarrow }{t_1}}$| that describes the movement of Plate B relative to Plate A from t2 to t1 is given by |$\skew{6}\hat{A}_{t_1} {\skew{6}\hat{A}_{t_2}}^T$|. The |$\skew{6}\hat{A}_{{t_2}{\rightarrow }{t_1}}$| stage rotation covariances are the sum of the covariances for |$\skew{6}\hat{A}_{t_1}$| and |$\skew{6}\hat{A}_{t_2}$| and require both sets of covariances to be in a common frame of reference. Angular velocities were estimated by normalizing each stage rotation by its corresponding time interval.
The noise-reduced angular velocities estimated by REDBACK are determined from each successive pair of the noise-reduced finite rotations and thus maximize the temporal resolution of our rotation sequence. The noise-reduced angular velocities span intervals of 0.42–2.20 Myr, averaging ≈1 Myr. The covariances for the noise-reduced stage angular velocities are estimated separately from the covariances for the noise-reduced finite rotations by REDBACK—the REDBACK stage rotation covariances thus cannot be derived from the finite rotation covariances using the methodology that is described in the previous paragraph. We therefore explicitly tabulate the noise-reduced angular velocities and their covariances in the tables below and our Supporting Information.
For comparative purposes, we also determine stage rotations from the noisier best-fitting finite rotations. The best-fitting stage rotations purposely span periods of ≈2 Myr in order to reduce their otherwise-large uncertainties. Although stage rotations that span intervals longer than the maximum temporal resolution of their finite rotations may not accurately depict the true plate motion (Iaffaldano et al.2014), we find that stage rotations that span 2-Myr time intervals adequately approximate the velocity history determined from the maximum-resolution noise-reduced rotations. Best-fitting stage rotations and their covariances are easily derived from the best-fitting finite rotations and covariances via the methods described above and are thus not tabulated.
4 ASSUMPTIONS
4.1 Spreading symmetry and fracture zone flow lines
The synthetic fracture zone flow lines used in our inversions are created using half-angle stage rotations derived from our finite rotations. Our analysis thus implicitly assumes that seafloor spreading is symmetric. Widespread asymmetries in seafloor spreading could thus cause a misalignment between the synthetic and observed fracture zone flow lines that could result in mistiming the ages of any fracture zone bends.
We evaluated the magnitude and extent of possible asymmetric spreading along the southern Mid-Atlantic Ridge by comparing the distances between the present ridge axis and chrons C5n.2 (11.06 Ma) and C6no (19.7 Ma) on both sides of the ridge. For seven spreading segments where chron C5n.2 is well surveyed on both sides of the ridge, the seven segment-specific spreading asymmetries range from 3.4 per cent more accretion on the Nubia plate to 1.4 per cent more on the South America plate. Averaged for all seven segments, the spreading asymmetry is a mere 0.9 per cent and favours the Nubia plate. Given that ≈400 km of new seafloor has been created since chron C5n.2, the average 0.9 per cent spreading asymmetry implies only a 3.6 km misalignment of the synthetic and observed fracture zones. This small misalignment is equivalent to an error of only 0.1 Myr in the ages estimated for any bends in the fracture zones for an average full spreading rate of 40 km Myr−1 since 10 Ma.
The asymmetries for four spreading segments where chron C6no is well surveyed range from 2.1 per cent favouring the Nubia plate to 1.3 per cent favouring the South America plate, with a four-segment average of only 0.6 per cent. For ≈800 km of total seafloor accretion since chron C6no, the average asymmetry implies a misalignment of only 5 km between the synthetic and observed fracture zones, also equivalent to a mistiming of 0.1 Myr or less in the ages of the fracture zone bends.
We conclude that the effect of asymmetric seafloor spreading on our estimates of the timing of any changes in fracture zone directions are no more than ≈0.1 Myr, too small to affect any of the results or conclusions presented below.
4.2 Outward displacement of magnetic reversals
In-situ surveys of magnetic reversal polarity transition zones (e.g. Macdonald et al.1983; Sempere et al.1987) and detailed kinematic studies of young seafloor spreading lineations (e.g. DeMets & Wilson 2008) independently confirm that magnetic reversals are displaced 1–5 km outwards from their idealized locations during the accretion of new seafloor and acquisition of its magnetization. For this analysis, we correct all finite rotations for assumed outward displacement of 2 km, equal to the global average reported by DeMets & Wilson (2008). A later comparison between the GEODVEL geodetic estimate of instantaneous Nubia–South America seafloor spreading rates and our new estimate of opening rates since 0.78 Ma suggests that outward displacement in the southern Atlantic is unlikely to differ by more than ±1 km from the 2-km correction that we apply.
4.3 North America–South America boundary location
We assume that the Fifteen-Twenty fracture zone marks the primary transition from seafloor spreading between the Nubia and North America plates to spreading between Nubia and South America. Over time periods back to 34 Myr (chron C13), Cande et al. (1988) and Muller & Smith (1993) find that the Mid-Atlantic Ridge fracture zones located south of the Fifteen-Twenty fracture zone are consistent with Nubia–South America flow lines, but are poorly matched by Nubia–North America flow lines. Synthetic fracture zone flow lines that we created from the high-resolution Nubia–North America rotations of Merkouriev & DeMets (2014a) also systematically misfit the traces of fracture zones south of and including the Fifteen-Twenty fracture zone (Fig. 5), consistent with previously reported results.
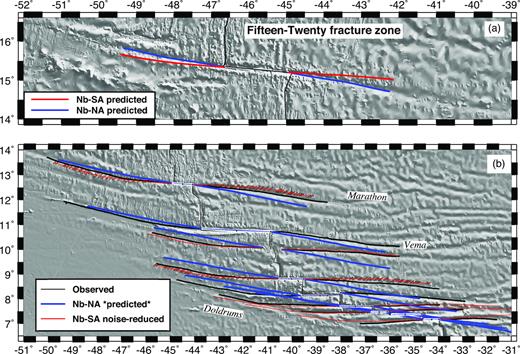
Reconstructed Nubia–North America (blue lines) and Nubia–South America fracture zone flow lines (red lines) on GeoMapApp bathymetry, 6.5°N–16.6°N. Where shown, the black lines are the digitized fracture zone traces. (a) and (b) The synthetic flow lines are created with Nubia–South America half-angle noise-reduced stage rotations from this study (red lines) and Nubia–North America half-angle stage rotations from DeMets et al. (2015a; blue lines). The red-shaded ellipses for selected flow lines show the 1-sigma uncertainties that are propagated from the noise-reduced rotation covariances.
For more recent times, DeMets et al. (2010) report discontinuities of 2 mm yr−1 and 7° in 3.16-Myr-average seafloor spreading rates and plate slip directions at the Fifteen-Twenty transform fault. Our own analysis and the GEODVEL geodetic study also indicate similar discontinuities in the opening rates and slip directions at this location (Section 5.2.1).
5 RESULTS
5.1 Nubia–South America rotations, fits and kinematic history
Table S2 of the Supporting Information lists the 37 rotations and covariances that we derived from inversions of 1000 bootstrap samples of the data, which include 6952 crossings of magnetic reversals C1n to C13n, 2480 crossings of 37 transform faults and 26 410 distinct crossings of 43 fracture zone flow lines. The number of reversal crossings that constrain the individual rotations ranges from 76 to 475 (Table S1, Supporting Information). The numerous identifications of chrons C1n to C3n.4 span nearly 80 arc-degrees (Fig. 3) and thus strongly constrain the rotations for those reversals. Crossings of chrons C3An.1 through C13, though less numerous, nonetheless span nearly 50 arc-degrees and thus also strongly constrain their respective finite rotations. All the magnetic reversal, transform fault and fracture zone crossings used to estimate the rotations described herein are archived at http://www.soest.hawaii.edu/PT/GSFML/ML/index.html (Seton et al.2014).
Although we inverted ≈4 times more fracture zone crossings than crossings of magnetic reversals, the two data types contributed nearly equally to our solution because the fracture zone crossings were assigned larger overall uncertainties. For simplicity, all the reversal crossings were assigned the same uncertainty in our inversions because the segment-based bootstrap methodology that we used to estimate the best-fitting rotations and covariances (Section 3.1) is relatively insensitive to the uncertainties that are assigned to the individual data.
The Nubia–South America noise-reduced rotations (Table 1) and their corresponding angular velocities (Table 2), which are our preferred estimates of Nubia–South America plate motion for reasons that are described below, were determined via a REDBACK analysis of the best-fitting rotations and covariances from Table S2 (Supporting Information). Noise-reduced angular velocities and covariances in reference frames fixed to the Nubia and South America plates are, respectively, tabulated in Table 2 and Table S3 (Supporting Information).
| Chron . | Lat. . | Long. . | Ω . | REDBACK covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 60.35 | 321.26 | 0.221 | 307.9 | −245.9 | 313.5 | 198.4 | −254.0 | 325.7 |
| 2n | 60.60 | 320.99 | 0.507 | 319.1 | −233.2 | 284.0 | 195.7 | −253.4 | 335.9 |
| 2An.1 | 60.77 | 320.80 | 0.741 | 382.8 | −232.2 | 251.2 | 206.9 | −273.3 | 386.4 |
| 2An.3 | 60.94 | 320.60 | 1.046 | 480.2 | −213.7 | 167.6 | 211.0 | −288.5 | 453.4 |
| 3n.1 | 61.01 | 320.52 | 1.227 | 529.0 | −186.9 | 92.1 | 201.2 | −282.6 | 479.0 |
| 3n.4 | 61.09 | 320.41 | 1.550 | 641.7 | −152.2 | −32.1 | 195.1 | −287.2 | 548.7 |
| 3An.1 | 61.14 | 320.35 | 1.798 | 833.5 | −191.8 | −58.4 | 249.9 | −368.8 | 714.8 |
| 3An.2 | 61.17 | 320.31 | 2.030 | 1007.6 | −196.8 | −142.6 | 277.1 | −416.4 | 847.6 |
| 4n.1 | 61.19 | 320.28 | 2.312 | 1244.7 | −169.4 | −325.0 | 288.7 | −451.7 | 1011.2 |
| 4n.2 | 61.20 | 320.26 | 2.521 | 1539.4 | −201.8 | −427.9 | 348.8 | −547.1 | 1248.7 |
| 4A | 61.21 | 320.26 | 2.881 | 2299.6 | −351.4 | −577.2 | 548.6 | −842.6 | 1897.1 |
| 5n.1 | 61.21 | 320.27 | 3.131 | 2964.0 | −481.4 | −718.8 | 719.2 | −1093.1 | 2459.8 |
| 5n.2 | 61.16 | 320.35 | 3.621 | 4382.4 | −698.3 | −1167.1 | 1031.9 | −1562.5 | 3635.0 |
| 5An.2 | 61.05 | 320.52 | 4.221 | 5607.5 | −645.6 | −2072.4 | 1112.9 | −1744.3 | 4557.0 |
| 5AC | 60.89 | 320.74 | 4.773 | 5782.1 | −339.4 | −2835.9 | 886.3 | −1489.9 | 4563.2 |
| 5AD | 60.76 | 320.92 | 5.154 | 5713.9 | −232.8 | −3037.7 | 795.4 | −1378.5 | 4491.9 |
| 5Cn.1 | 60.57 | 321.19 | 5.752 | 5887.5 | −259.5 | −3165.1 | 828.4 | −1424.2 | 4699.2 |
| 5D | 60.39 | 321.44 | 6.313 | 6213.4 | −359.3 | −3254.9 | 932.4 | −1560.1 | 5062.7 |
| 5E | 60.28 | 321.60 | 6.692 | 6432.6 | −299.8 | −3571.2 | 899.8 | −1535.7 | 5257.9 |
| 6ny | 60.17 | 321.74 | 7.019 | 6708.5 | −207.7 | −3989.2 | 843.9 | −1489.3 | 5482.6 |
| 6no | 60.02 | 321.96 | 7.485 | 7381.1 | −157.4 | −4631.8 | 842.1 | −1522.4 | 6045.3 |
| 6An.2 | 59.82 | 322.20 | 7.960 | 8320.8 | −374.6 | −4957.4 | 1063.6 | −1809.0 | 6904.4 |
| 6Bn.1 | 59.54 | 322.52 | 8.463 | 8992.2 | −777.1 | −4751.2 | 1407.7 | −2203.4 | 7612.4 |
| 7n.1 | 58.79 | 323.29 | 9.432 | 6906.6 | −664.4 | −3640.2 | 1131.5 | −1741.7 | 6020.6 |
| 7n.2 | 58.60 | 323.48 | 9.649 | 6272.3 | −571.0 | −3393.1 | 1001.8 | −1554.3 | 5493.1 |
| 8n.1 | 58.38 | 323.71 | 9.913 | 5729.3 | −478.6 | −3212.5 | 879.4 | −1381.2 | 5044.6 |
| 8n.2 | 58.07 | 324.02 | 10.287 | 5273.3 | −351.7 | −3171.6 | 738.4 | −1197.0 | 4684.6 |
| 9ny | 57.93 | 324.17 | 10.469 | 5161.3 | −292.0 | −3226.8 | 681.7 | −1129.9 | 4608.3 |
| 9no | 57.64 | 324.49 | 10.897 | 4995.0 | −172.0 | −3385.7 | 573.6 | −1006.7 | 4518.7 |
| 10n.1 | 57.55 | 324.61 | 11.073 | 4880.9 | −145.9 | −3371.0 | 542.4 | −964.9 | 4440.3 |
| 10n.2 | 57.47 | 324.71 | 11.249 | 4749.6 | −134.1 | −3314.4 | 520.3 | −930.6 | 4344.8 |
| 11n.1 | 57.35 | 324.90 | 11.629 | 4296.3 | −167.7 | −2945.5 | 501.3 | −868.4 | 3975.1 |
| 11n.2 | 57.28 | 325.03 | 11.959 | 3772.0 | −258.6 | −2399.0 | 517.5 | −831.8 | 3512.1 |
| 12ny | 57.23 | 325.14 | 12.220 | 3349.5 | −349.4 | −1917.3 | 544.9 | −815.9 | 3128.3 |
| 12no | 57.20 | 325.21 | 12.407 | 3062.7 | −399.0 | −1612.2 | 555.3 | −797.8 | 2867.1 |
| 13ny | 57.06 | 325.53 | 13.317 | 2257.0 | −195.4 | −1464.2 | 313.4 | −474.2 | 2169.0 |
| 13no | 57.02 | 325.62 | 13.551 | 2620.2 | −135.5 | −1908.1 | 288.8 | −474.0 | 2554.4 |
| Chron . | Lat. . | Long. . | Ω . | REDBACK covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 60.35 | 321.26 | 0.221 | 307.9 | −245.9 | 313.5 | 198.4 | −254.0 | 325.7 |
| 2n | 60.60 | 320.99 | 0.507 | 319.1 | −233.2 | 284.0 | 195.7 | −253.4 | 335.9 |
| 2An.1 | 60.77 | 320.80 | 0.741 | 382.8 | −232.2 | 251.2 | 206.9 | −273.3 | 386.4 |
| 2An.3 | 60.94 | 320.60 | 1.046 | 480.2 | −213.7 | 167.6 | 211.0 | −288.5 | 453.4 |
| 3n.1 | 61.01 | 320.52 | 1.227 | 529.0 | −186.9 | 92.1 | 201.2 | −282.6 | 479.0 |
| 3n.4 | 61.09 | 320.41 | 1.550 | 641.7 | −152.2 | −32.1 | 195.1 | −287.2 | 548.7 |
| 3An.1 | 61.14 | 320.35 | 1.798 | 833.5 | −191.8 | −58.4 | 249.9 | −368.8 | 714.8 |
| 3An.2 | 61.17 | 320.31 | 2.030 | 1007.6 | −196.8 | −142.6 | 277.1 | −416.4 | 847.6 |
| 4n.1 | 61.19 | 320.28 | 2.312 | 1244.7 | −169.4 | −325.0 | 288.7 | −451.7 | 1011.2 |
| 4n.2 | 61.20 | 320.26 | 2.521 | 1539.4 | −201.8 | −427.9 | 348.8 | −547.1 | 1248.7 |
| 4A | 61.21 | 320.26 | 2.881 | 2299.6 | −351.4 | −577.2 | 548.6 | −842.6 | 1897.1 |
| 5n.1 | 61.21 | 320.27 | 3.131 | 2964.0 | −481.4 | −718.8 | 719.2 | −1093.1 | 2459.8 |
| 5n.2 | 61.16 | 320.35 | 3.621 | 4382.4 | −698.3 | −1167.1 | 1031.9 | −1562.5 | 3635.0 |
| 5An.2 | 61.05 | 320.52 | 4.221 | 5607.5 | −645.6 | −2072.4 | 1112.9 | −1744.3 | 4557.0 |
| 5AC | 60.89 | 320.74 | 4.773 | 5782.1 | −339.4 | −2835.9 | 886.3 | −1489.9 | 4563.2 |
| 5AD | 60.76 | 320.92 | 5.154 | 5713.9 | −232.8 | −3037.7 | 795.4 | −1378.5 | 4491.9 |
| 5Cn.1 | 60.57 | 321.19 | 5.752 | 5887.5 | −259.5 | −3165.1 | 828.4 | −1424.2 | 4699.2 |
| 5D | 60.39 | 321.44 | 6.313 | 6213.4 | −359.3 | −3254.9 | 932.4 | −1560.1 | 5062.7 |
| 5E | 60.28 | 321.60 | 6.692 | 6432.6 | −299.8 | −3571.2 | 899.8 | −1535.7 | 5257.9 |
| 6ny | 60.17 | 321.74 | 7.019 | 6708.5 | −207.7 | −3989.2 | 843.9 | −1489.3 | 5482.6 |
| 6no | 60.02 | 321.96 | 7.485 | 7381.1 | −157.4 | −4631.8 | 842.1 | −1522.4 | 6045.3 |
| 6An.2 | 59.82 | 322.20 | 7.960 | 8320.8 | −374.6 | −4957.4 | 1063.6 | −1809.0 | 6904.4 |
| 6Bn.1 | 59.54 | 322.52 | 8.463 | 8992.2 | −777.1 | −4751.2 | 1407.7 | −2203.4 | 7612.4 |
| 7n.1 | 58.79 | 323.29 | 9.432 | 6906.6 | −664.4 | −3640.2 | 1131.5 | −1741.7 | 6020.6 |
| 7n.2 | 58.60 | 323.48 | 9.649 | 6272.3 | −571.0 | −3393.1 | 1001.8 | −1554.3 | 5493.1 |
| 8n.1 | 58.38 | 323.71 | 9.913 | 5729.3 | −478.6 | −3212.5 | 879.4 | −1381.2 | 5044.6 |
| 8n.2 | 58.07 | 324.02 | 10.287 | 5273.3 | −351.7 | −3171.6 | 738.4 | −1197.0 | 4684.6 |
| 9ny | 57.93 | 324.17 | 10.469 | 5161.3 | −292.0 | −3226.8 | 681.7 | −1129.9 | 4608.3 |
| 9no | 57.64 | 324.49 | 10.897 | 4995.0 | −172.0 | −3385.7 | 573.6 | −1006.7 | 4518.7 |
| 10n.1 | 57.55 | 324.61 | 11.073 | 4880.9 | −145.9 | −3371.0 | 542.4 | −964.9 | 4440.3 |
| 10n.2 | 57.47 | 324.71 | 11.249 | 4749.6 | −134.1 | −3314.4 | 520.3 | −930.6 | 4344.8 |
| 11n.1 | 57.35 | 324.90 | 11.629 | 4296.3 | −167.7 | −2945.5 | 501.3 | −868.4 | 3975.1 |
| 11n.2 | 57.28 | 325.03 | 11.959 | 3772.0 | −258.6 | −2399.0 | 517.5 | −831.8 | 3512.1 |
| 12ny | 57.23 | 325.14 | 12.220 | 3349.5 | −349.4 | −1917.3 | 544.9 | −815.9 | 3128.3 |
| 12no | 57.20 | 325.21 | 12.407 | 3062.7 | −399.0 | −1612.2 | 555.3 | −797.8 | 2867.1 |
| 13ny | 57.06 | 325.53 | 13.317 | 2257.0 | −195.4 | −1464.2 | 313.4 | −474.2 | 2169.0 |
| 13no | 57.02 | 325.62 | 13.551 | 2620.2 | −135.5 | −1908.1 | 288.8 | −474.0 | 2554.4 |
The noise-reduced finite rotations, which reconstruct the South America plate onto the Nubia plate, were derived via a REDBACK analysis of the best-fitting rotations in Table S2 (Supporting Information). The rotation angles Ω are positive CCW. The Cartesian finite rotation covariances have units of 10−10 radians2 and specify the 2-D position uncertainty when rotating points from the Nubia onto the South America plate or vice versa. Elements a, d and f are the variances of the (0°N, 0°E), (0°N, 90°E) and 90°N components of the rotation. The covariance matrices are reconstructed as follows: 
| Chron . | Lat. . | Long. . | Ω . | REDBACK covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 60.35 | 321.26 | 0.221 | 307.9 | −245.9 | 313.5 | 198.4 | −254.0 | 325.7 |
| 2n | 60.60 | 320.99 | 0.507 | 319.1 | −233.2 | 284.0 | 195.7 | −253.4 | 335.9 |
| 2An.1 | 60.77 | 320.80 | 0.741 | 382.8 | −232.2 | 251.2 | 206.9 | −273.3 | 386.4 |
| 2An.3 | 60.94 | 320.60 | 1.046 | 480.2 | −213.7 | 167.6 | 211.0 | −288.5 | 453.4 |
| 3n.1 | 61.01 | 320.52 | 1.227 | 529.0 | −186.9 | 92.1 | 201.2 | −282.6 | 479.0 |
| 3n.4 | 61.09 | 320.41 | 1.550 | 641.7 | −152.2 | −32.1 | 195.1 | −287.2 | 548.7 |
| 3An.1 | 61.14 | 320.35 | 1.798 | 833.5 | −191.8 | −58.4 | 249.9 | −368.8 | 714.8 |
| 3An.2 | 61.17 | 320.31 | 2.030 | 1007.6 | −196.8 | −142.6 | 277.1 | −416.4 | 847.6 |
| 4n.1 | 61.19 | 320.28 | 2.312 | 1244.7 | −169.4 | −325.0 | 288.7 | −451.7 | 1011.2 |
| 4n.2 | 61.20 | 320.26 | 2.521 | 1539.4 | −201.8 | −427.9 | 348.8 | −547.1 | 1248.7 |
| 4A | 61.21 | 320.26 | 2.881 | 2299.6 | −351.4 | −577.2 | 548.6 | −842.6 | 1897.1 |
| 5n.1 | 61.21 | 320.27 | 3.131 | 2964.0 | −481.4 | −718.8 | 719.2 | −1093.1 | 2459.8 |
| 5n.2 | 61.16 | 320.35 | 3.621 | 4382.4 | −698.3 | −1167.1 | 1031.9 | −1562.5 | 3635.0 |
| 5An.2 | 61.05 | 320.52 | 4.221 | 5607.5 | −645.6 | −2072.4 | 1112.9 | −1744.3 | 4557.0 |
| 5AC | 60.89 | 320.74 | 4.773 | 5782.1 | −339.4 | −2835.9 | 886.3 | −1489.9 | 4563.2 |
| 5AD | 60.76 | 320.92 | 5.154 | 5713.9 | −232.8 | −3037.7 | 795.4 | −1378.5 | 4491.9 |
| 5Cn.1 | 60.57 | 321.19 | 5.752 | 5887.5 | −259.5 | −3165.1 | 828.4 | −1424.2 | 4699.2 |
| 5D | 60.39 | 321.44 | 6.313 | 6213.4 | −359.3 | −3254.9 | 932.4 | −1560.1 | 5062.7 |
| 5E | 60.28 | 321.60 | 6.692 | 6432.6 | −299.8 | −3571.2 | 899.8 | −1535.7 | 5257.9 |
| 6ny | 60.17 | 321.74 | 7.019 | 6708.5 | −207.7 | −3989.2 | 843.9 | −1489.3 | 5482.6 |
| 6no | 60.02 | 321.96 | 7.485 | 7381.1 | −157.4 | −4631.8 | 842.1 | −1522.4 | 6045.3 |
| 6An.2 | 59.82 | 322.20 | 7.960 | 8320.8 | −374.6 | −4957.4 | 1063.6 | −1809.0 | 6904.4 |
| 6Bn.1 | 59.54 | 322.52 | 8.463 | 8992.2 | −777.1 | −4751.2 | 1407.7 | −2203.4 | 7612.4 |
| 7n.1 | 58.79 | 323.29 | 9.432 | 6906.6 | −664.4 | −3640.2 | 1131.5 | −1741.7 | 6020.6 |
| 7n.2 | 58.60 | 323.48 | 9.649 | 6272.3 | −571.0 | −3393.1 | 1001.8 | −1554.3 | 5493.1 |
| 8n.1 | 58.38 | 323.71 | 9.913 | 5729.3 | −478.6 | −3212.5 | 879.4 | −1381.2 | 5044.6 |
| 8n.2 | 58.07 | 324.02 | 10.287 | 5273.3 | −351.7 | −3171.6 | 738.4 | −1197.0 | 4684.6 |
| 9ny | 57.93 | 324.17 | 10.469 | 5161.3 | −292.0 | −3226.8 | 681.7 | −1129.9 | 4608.3 |
| 9no | 57.64 | 324.49 | 10.897 | 4995.0 | −172.0 | −3385.7 | 573.6 | −1006.7 | 4518.7 |
| 10n.1 | 57.55 | 324.61 | 11.073 | 4880.9 | −145.9 | −3371.0 | 542.4 | −964.9 | 4440.3 |
| 10n.2 | 57.47 | 324.71 | 11.249 | 4749.6 | −134.1 | −3314.4 | 520.3 | −930.6 | 4344.8 |
| 11n.1 | 57.35 | 324.90 | 11.629 | 4296.3 | −167.7 | −2945.5 | 501.3 | −868.4 | 3975.1 |
| 11n.2 | 57.28 | 325.03 | 11.959 | 3772.0 | −258.6 | −2399.0 | 517.5 | −831.8 | 3512.1 |
| 12ny | 57.23 | 325.14 | 12.220 | 3349.5 | −349.4 | −1917.3 | 544.9 | −815.9 | 3128.3 |
| 12no | 57.20 | 325.21 | 12.407 | 3062.7 | −399.0 | −1612.2 | 555.3 | −797.8 | 2867.1 |
| 13ny | 57.06 | 325.53 | 13.317 | 2257.0 | −195.4 | −1464.2 | 313.4 | −474.2 | 2169.0 |
| 13no | 57.02 | 325.62 | 13.551 | 2620.2 | −135.5 | −1908.1 | 288.8 | −474.0 | 2554.4 |
| Chron . | Lat. . | Long. . | Ω . | REDBACK covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 60.35 | 321.26 | 0.221 | 307.9 | −245.9 | 313.5 | 198.4 | −254.0 | 325.7 |
| 2n | 60.60 | 320.99 | 0.507 | 319.1 | −233.2 | 284.0 | 195.7 | −253.4 | 335.9 |
| 2An.1 | 60.77 | 320.80 | 0.741 | 382.8 | −232.2 | 251.2 | 206.9 | −273.3 | 386.4 |
| 2An.3 | 60.94 | 320.60 | 1.046 | 480.2 | −213.7 | 167.6 | 211.0 | −288.5 | 453.4 |
| 3n.1 | 61.01 | 320.52 | 1.227 | 529.0 | −186.9 | 92.1 | 201.2 | −282.6 | 479.0 |
| 3n.4 | 61.09 | 320.41 | 1.550 | 641.7 | −152.2 | −32.1 | 195.1 | −287.2 | 548.7 |
| 3An.1 | 61.14 | 320.35 | 1.798 | 833.5 | −191.8 | −58.4 | 249.9 | −368.8 | 714.8 |
| 3An.2 | 61.17 | 320.31 | 2.030 | 1007.6 | −196.8 | −142.6 | 277.1 | −416.4 | 847.6 |
| 4n.1 | 61.19 | 320.28 | 2.312 | 1244.7 | −169.4 | −325.0 | 288.7 | −451.7 | 1011.2 |
| 4n.2 | 61.20 | 320.26 | 2.521 | 1539.4 | −201.8 | −427.9 | 348.8 | −547.1 | 1248.7 |
| 4A | 61.21 | 320.26 | 2.881 | 2299.6 | −351.4 | −577.2 | 548.6 | −842.6 | 1897.1 |
| 5n.1 | 61.21 | 320.27 | 3.131 | 2964.0 | −481.4 | −718.8 | 719.2 | −1093.1 | 2459.8 |
| 5n.2 | 61.16 | 320.35 | 3.621 | 4382.4 | −698.3 | −1167.1 | 1031.9 | −1562.5 | 3635.0 |
| 5An.2 | 61.05 | 320.52 | 4.221 | 5607.5 | −645.6 | −2072.4 | 1112.9 | −1744.3 | 4557.0 |
| 5AC | 60.89 | 320.74 | 4.773 | 5782.1 | −339.4 | −2835.9 | 886.3 | −1489.9 | 4563.2 |
| 5AD | 60.76 | 320.92 | 5.154 | 5713.9 | −232.8 | −3037.7 | 795.4 | −1378.5 | 4491.9 |
| 5Cn.1 | 60.57 | 321.19 | 5.752 | 5887.5 | −259.5 | −3165.1 | 828.4 | −1424.2 | 4699.2 |
| 5D | 60.39 | 321.44 | 6.313 | 6213.4 | −359.3 | −3254.9 | 932.4 | −1560.1 | 5062.7 |
| 5E | 60.28 | 321.60 | 6.692 | 6432.6 | −299.8 | −3571.2 | 899.8 | −1535.7 | 5257.9 |
| 6ny | 60.17 | 321.74 | 7.019 | 6708.5 | −207.7 | −3989.2 | 843.9 | −1489.3 | 5482.6 |
| 6no | 60.02 | 321.96 | 7.485 | 7381.1 | −157.4 | −4631.8 | 842.1 | −1522.4 | 6045.3 |
| 6An.2 | 59.82 | 322.20 | 7.960 | 8320.8 | −374.6 | −4957.4 | 1063.6 | −1809.0 | 6904.4 |
| 6Bn.1 | 59.54 | 322.52 | 8.463 | 8992.2 | −777.1 | −4751.2 | 1407.7 | −2203.4 | 7612.4 |
| 7n.1 | 58.79 | 323.29 | 9.432 | 6906.6 | −664.4 | −3640.2 | 1131.5 | −1741.7 | 6020.6 |
| 7n.2 | 58.60 | 323.48 | 9.649 | 6272.3 | −571.0 | −3393.1 | 1001.8 | −1554.3 | 5493.1 |
| 8n.1 | 58.38 | 323.71 | 9.913 | 5729.3 | −478.6 | −3212.5 | 879.4 | −1381.2 | 5044.6 |
| 8n.2 | 58.07 | 324.02 | 10.287 | 5273.3 | −351.7 | −3171.6 | 738.4 | −1197.0 | 4684.6 |
| 9ny | 57.93 | 324.17 | 10.469 | 5161.3 | −292.0 | −3226.8 | 681.7 | −1129.9 | 4608.3 |
| 9no | 57.64 | 324.49 | 10.897 | 4995.0 | −172.0 | −3385.7 | 573.6 | −1006.7 | 4518.7 |
| 10n.1 | 57.55 | 324.61 | 11.073 | 4880.9 | −145.9 | −3371.0 | 542.4 | −964.9 | 4440.3 |
| 10n.2 | 57.47 | 324.71 | 11.249 | 4749.6 | −134.1 | −3314.4 | 520.3 | −930.6 | 4344.8 |
| 11n.1 | 57.35 | 324.90 | 11.629 | 4296.3 | −167.7 | −2945.5 | 501.3 | −868.4 | 3975.1 |
| 11n.2 | 57.28 | 325.03 | 11.959 | 3772.0 | −258.6 | −2399.0 | 517.5 | −831.8 | 3512.1 |
| 12ny | 57.23 | 325.14 | 12.220 | 3349.5 | −349.4 | −1917.3 | 544.9 | −815.9 | 3128.3 |
| 12no | 57.20 | 325.21 | 12.407 | 3062.7 | −399.0 | −1612.2 | 555.3 | −797.8 | 2867.1 |
| 13ny | 57.06 | 325.53 | 13.317 | 2257.0 | −195.4 | −1464.2 | 313.4 | −474.2 | 2169.0 |
| 13no | 57.02 | 325.62 | 13.551 | 2620.2 | −135.5 | −1908.1 | 288.8 | −474.0 | 2554.4 |
The noise-reduced finite rotations, which reconstruct the South America plate onto the Nubia plate, were derived via a REDBACK analysis of the best-fitting rotations in Table S2 (Supporting Information). The rotation angles Ω are positive CCW. The Cartesian finite rotation covariances have units of 10−10 radians2 and specify the 2-D position uncertainty when rotating points from the Nubia onto the South America plate or vice versa. Elements a, d and f are the variances of the (0°N, 0°E), (0°N, 90°E) and 90°N components of the rotation. The covariance matrices are reconstructed as follows: 
| Age (y) . | Age (o) . | Lat. . | Long. . | |$\dot{\Omega }$| . | Covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ma . | Ma . | (°N) . | (°E) . | ° Myr−1 . | a . | b . | c . | d . | e . | f . |
| 0.000 | 0.781 | 60.35 | 321.26 | −0.284 | 3.96 | −3.15 | 8.67 | 2.54 | −6.95 | 19.65 |
| 0.781 | 1.778 | 60.79 | 320.79 | −0.287 | 1.16 | −0.79 | 1.83 | 0.67 | −1.53 | 4.59 |
| 1.778 | 2.581 | 61.15 | 320.36 | −0.292 | 1.31 | −0.75 | 1.41 | 0.66 | −1.27 | 4.07 |
| 2.581 | 3.596 | 61.34 | 320.11 | −0.300 | 1.21 | −0.65 | 1.13 | 0.58 | −1.06 | 3.51 |
| 3.596 | 4.187 | 61.40 | 320.01 | −0.306 | 1.28 | −0.69 | 1.16 | 0.65 | −1.09 | 3.68 |
| 4.187 | 5.235 | 61.41 | 319.98 | −0.308 | 1.23 | −0.67 | 1.25 | 0.62 | −1.16 | 3.77 |
| 5.235 | 6.033 | 61.42 | 319.95 | −0.310 | 1.61 | −0.88 | 1.70 | 0.79 | −1.58 | 5.05 |
| 6.033 | 6.733 | 61.39 | 319.99 | −0.331 | 2.37 | −1.36 | 2.85 | 1.20 | −2.60 | 8.12 |
| 6.733 | 7.528 | 61.34 | 320.06 | −0.356 | 2.66 | −1.30 | 2.16 | 1.13 | −2.17 | 7.23 |
| 7.528 | 8.108 | 61.35 | 320.09 | −0.359 | 2.88 | −1.26 | 1.90 | 1.14 | −2.03 | 6.90 |
| 8.108 | 9.105 | 61.28 | 320.22 | −0.361 | 2.97 | −1.18 | 1.58 | 1.05 | −1.84 | 6.38 |
| 9.105 | 9.786 | 61.14 | 320.46 | −0.366 | 4.25 | −1.88 | 3.01 | 1.65 | −3.15 | 10.50 |
| 9.786 | 11.056 | 60.89 | 320.85 | −0.386 | 5.22 | −2.47 | 4.53 | 2.12 | −4.51 | 14.40 |
| 11.056 | 12.474 | 60.38 | 321.56 | −0.423 | 4.13 | −1.68 | 2.36 | 1.50 | −2.66 | 9.15 |
| 12.474 | 13.739 | 59.66 | 322.50 | −0.437 | 3.38 | −1.33 | 1.04 | 1.22 | −1.45 | 5.99 |
| 13.739 | 14.609 | 59.15 | 323.18 | −0.438 | 7.36 | −2.08 | −1.03 | 1.66 | −0.91 | 7.00 |
| 14.609 | 15.974 | 58.99 | 323.52 | −0.439 | 3.74 | −1.45 | 0.68 | 1.24 | −1.26 | 5.92 |
| 15.974 | 17.235 | 58.62 | 324.05 | −0.445 | 4.40 | −1.62 | 0.66 | 1.33 | −1.38 | 6.56 |
| 17.235 | 18.056 | 58.40 | 324.39 | −0.462 | 6.46 | −2.53 | 1.76 | 2.04 | −2.60 | 11.01 |
| 18.056 | 18.748 | 58.19 | 324.68 | −0.473 | 8.31 | −3.11 | 1.63 | 2.49 | −2.85 | 12.70 |
| 18.748 | 19.722 | 57.75 | 325.19 | −0.479 | 9.70 | −3.49 | 1.65 | 2.85 | −3.06 | 13.91 |
| 19.722 | 20.709 | 56.79 | 326.10 | −0.482 | 11.76 | −4.26 | 2.41 | 3.56 | −3.94 | 17.45 |
| 20.709 | 21.767 | 55.21 | 327.45 | −0.477 | 13.23 | −4.26 | −0.07 | 3.58 | −2.55 | 15.32 |
| 21.767 | 23.962 | 52.36 | 329.76 | −0.445 | 12.32 | −3.35 | −2.85 | 2.36 | −0.67 | 9.49 |
| 23.962 | 24.474 | 50.75 | 331.12 | −0.430 | 23.41 | −5.36 | −9.15 | 3.57 | 0.83 | 13.02 |
| 24.474 | 25.099 | 50.40 | 331.50 | −0.428 | 22.33 | −4.51 | −9.90 | 2.98 | 1.29 | 10.80 |
| 25.099 | 25.987 | 50.13 | 331.90 | −0.427 | 19.49 | −3.55 | −9.34 | 2.56 | 1.42 | 8.76 |
| 25.987 | 26.420 | 50.13 | 332.14 | −0.426 | 21.83 | −3.59 | −10.85 | 3.00 | 1.76 | 9.37 |
| 26.420 | 27.439 | 50.78 | 332.02 | −0.424 | 17.08 | −2.44 | −8.29 | 2.37 | 1.11 | 7.40 |
| 27.439 | 27.859 | 52.10 | 331.48 | −0.423 | 20.79 | −2.41 | −10.20 | 2.87 | 1.24 | 8.61 |
| 27.859 | 28.278 | 52.84 | 331.13 | −0.422 | 19.26 | −2.12 | −9.29 | 2.65 | 1.00 | 8.10 |
| 28.278 | 29.183 | 53.98 | 330.53 | −0.421 | 12.20 | −1.45 | −5.29 | 1.85 | 0.29 | 5.96 |
| 29.183 | 29.970 | 54.84 | 330.08 | −0.420 | 10.36 | −1.53 | −3.76 | 1.96 | −0.03 | 6.17 |
| 29.970 | 30.591 | 55.15 | 329.96 | −0.421 | 10.20 | −1.79 | −3.09 | 2.24 | −0.28 | 7.00 |
| 30.591 | 31.034 | 55.27 | 329.96 | −0.423 | 19.26 | −7.99 | 13.53 | 6.72 | −11.96 | 39.30 |
| 31.034 | 33.157 | 55.33 | 330.12 | −0.429 | 12.68 | −3.00 | −1.29 | 3.45 | −1.67 | 12.24 |
| 33.157 | 33.705 | 55.17 | 330.57 | −0.429 | 28.69 | −6.69 | 2.94 | 9.13 | −7.22 | 34.17 |
| Age (y) . | Age (o) . | Lat. . | Long. . | |$\dot{\Omega }$| . | Covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ma . | Ma . | (°N) . | (°E) . | ° Myr−1 . | a . | b . | c . | d . | e . | f . |
| 0.000 | 0.781 | 60.35 | 321.26 | −0.284 | 3.96 | −3.15 | 8.67 | 2.54 | −6.95 | 19.65 |
| 0.781 | 1.778 | 60.79 | 320.79 | −0.287 | 1.16 | −0.79 | 1.83 | 0.67 | −1.53 | 4.59 |
| 1.778 | 2.581 | 61.15 | 320.36 | −0.292 | 1.31 | −0.75 | 1.41 | 0.66 | −1.27 | 4.07 |
| 2.581 | 3.596 | 61.34 | 320.11 | −0.300 | 1.21 | −0.65 | 1.13 | 0.58 | −1.06 | 3.51 |
| 3.596 | 4.187 | 61.40 | 320.01 | −0.306 | 1.28 | −0.69 | 1.16 | 0.65 | −1.09 | 3.68 |
| 4.187 | 5.235 | 61.41 | 319.98 | −0.308 | 1.23 | −0.67 | 1.25 | 0.62 | −1.16 | 3.77 |
| 5.235 | 6.033 | 61.42 | 319.95 | −0.310 | 1.61 | −0.88 | 1.70 | 0.79 | −1.58 | 5.05 |
| 6.033 | 6.733 | 61.39 | 319.99 | −0.331 | 2.37 | −1.36 | 2.85 | 1.20 | −2.60 | 8.12 |
| 6.733 | 7.528 | 61.34 | 320.06 | −0.356 | 2.66 | −1.30 | 2.16 | 1.13 | −2.17 | 7.23 |
| 7.528 | 8.108 | 61.35 | 320.09 | −0.359 | 2.88 | −1.26 | 1.90 | 1.14 | −2.03 | 6.90 |
| 8.108 | 9.105 | 61.28 | 320.22 | −0.361 | 2.97 | −1.18 | 1.58 | 1.05 | −1.84 | 6.38 |
| 9.105 | 9.786 | 61.14 | 320.46 | −0.366 | 4.25 | −1.88 | 3.01 | 1.65 | −3.15 | 10.50 |
| 9.786 | 11.056 | 60.89 | 320.85 | −0.386 | 5.22 | −2.47 | 4.53 | 2.12 | −4.51 | 14.40 |
| 11.056 | 12.474 | 60.38 | 321.56 | −0.423 | 4.13 | −1.68 | 2.36 | 1.50 | −2.66 | 9.15 |
| 12.474 | 13.739 | 59.66 | 322.50 | −0.437 | 3.38 | −1.33 | 1.04 | 1.22 | −1.45 | 5.99 |
| 13.739 | 14.609 | 59.15 | 323.18 | −0.438 | 7.36 | −2.08 | −1.03 | 1.66 | −0.91 | 7.00 |
| 14.609 | 15.974 | 58.99 | 323.52 | −0.439 | 3.74 | −1.45 | 0.68 | 1.24 | −1.26 | 5.92 |
| 15.974 | 17.235 | 58.62 | 324.05 | −0.445 | 4.40 | −1.62 | 0.66 | 1.33 | −1.38 | 6.56 |
| 17.235 | 18.056 | 58.40 | 324.39 | −0.462 | 6.46 | −2.53 | 1.76 | 2.04 | −2.60 | 11.01 |
| 18.056 | 18.748 | 58.19 | 324.68 | −0.473 | 8.31 | −3.11 | 1.63 | 2.49 | −2.85 | 12.70 |
| 18.748 | 19.722 | 57.75 | 325.19 | −0.479 | 9.70 | −3.49 | 1.65 | 2.85 | −3.06 | 13.91 |
| 19.722 | 20.709 | 56.79 | 326.10 | −0.482 | 11.76 | −4.26 | 2.41 | 3.56 | −3.94 | 17.45 |
| 20.709 | 21.767 | 55.21 | 327.45 | −0.477 | 13.23 | −4.26 | −0.07 | 3.58 | −2.55 | 15.32 |
| 21.767 | 23.962 | 52.36 | 329.76 | −0.445 | 12.32 | −3.35 | −2.85 | 2.36 | −0.67 | 9.49 |
| 23.962 | 24.474 | 50.75 | 331.12 | −0.430 | 23.41 | −5.36 | −9.15 | 3.57 | 0.83 | 13.02 |
| 24.474 | 25.099 | 50.40 | 331.50 | −0.428 | 22.33 | −4.51 | −9.90 | 2.98 | 1.29 | 10.80 |
| 25.099 | 25.987 | 50.13 | 331.90 | −0.427 | 19.49 | −3.55 | −9.34 | 2.56 | 1.42 | 8.76 |
| 25.987 | 26.420 | 50.13 | 332.14 | −0.426 | 21.83 | −3.59 | −10.85 | 3.00 | 1.76 | 9.37 |
| 26.420 | 27.439 | 50.78 | 332.02 | −0.424 | 17.08 | −2.44 | −8.29 | 2.37 | 1.11 | 7.40 |
| 27.439 | 27.859 | 52.10 | 331.48 | −0.423 | 20.79 | −2.41 | −10.20 | 2.87 | 1.24 | 8.61 |
| 27.859 | 28.278 | 52.84 | 331.13 | −0.422 | 19.26 | −2.12 | −9.29 | 2.65 | 1.00 | 8.10 |
| 28.278 | 29.183 | 53.98 | 330.53 | −0.421 | 12.20 | −1.45 | −5.29 | 1.85 | 0.29 | 5.96 |
| 29.183 | 29.970 | 54.84 | 330.08 | −0.420 | 10.36 | −1.53 | −3.76 | 1.96 | −0.03 | 6.17 |
| 29.970 | 30.591 | 55.15 | 329.96 | −0.421 | 10.20 | −1.79 | −3.09 | 2.24 | −0.28 | 7.00 |
| 30.591 | 31.034 | 55.27 | 329.96 | −0.423 | 19.26 | −7.99 | 13.53 | 6.72 | −11.96 | 39.30 |
| 31.034 | 33.157 | 55.33 | 330.12 | −0.429 | 12.68 | −3.00 | −1.29 | 3.45 | −1.67 | 12.24 |
| 33.157 | 33.705 | 55.17 | 330.57 | −0.429 | 28.69 | −6.69 | 2.94 | 9.13 | −7.22 | 34.17 |
These noise-reduced angular velocities specify South America plate motion in a Nubia plate frame of reference for time intervals given in the first two columns. The angular velocities and covariances, which are outputs of the REDBACK software (Iaffaldano et al.2014), were determined from a REDBACK analysis of the finite rotations in Table S2 (Supporting Information). The angular rotation rates |$\dot{\omega }$| are positive anticlockwise. The Cartesian angular velocity covariances are calculated in a Nubia-fixed reference frame and have units of 10−8 radians2 Myr−2 (see Table 1 for instructions on constructing the covariance matrix from elements a–f in the table).
| Age (y) . | Age (o) . | Lat. . | Long. . | |$\dot{\Omega }$| . | Covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ma . | Ma . | (°N) . | (°E) . | ° Myr−1 . | a . | b . | c . | d . | e . | f . |
| 0.000 | 0.781 | 60.35 | 321.26 | −0.284 | 3.96 | −3.15 | 8.67 | 2.54 | −6.95 | 19.65 |
| 0.781 | 1.778 | 60.79 | 320.79 | −0.287 | 1.16 | −0.79 | 1.83 | 0.67 | −1.53 | 4.59 |
| 1.778 | 2.581 | 61.15 | 320.36 | −0.292 | 1.31 | −0.75 | 1.41 | 0.66 | −1.27 | 4.07 |
| 2.581 | 3.596 | 61.34 | 320.11 | −0.300 | 1.21 | −0.65 | 1.13 | 0.58 | −1.06 | 3.51 |
| 3.596 | 4.187 | 61.40 | 320.01 | −0.306 | 1.28 | −0.69 | 1.16 | 0.65 | −1.09 | 3.68 |
| 4.187 | 5.235 | 61.41 | 319.98 | −0.308 | 1.23 | −0.67 | 1.25 | 0.62 | −1.16 | 3.77 |
| 5.235 | 6.033 | 61.42 | 319.95 | −0.310 | 1.61 | −0.88 | 1.70 | 0.79 | −1.58 | 5.05 |
| 6.033 | 6.733 | 61.39 | 319.99 | −0.331 | 2.37 | −1.36 | 2.85 | 1.20 | −2.60 | 8.12 |
| 6.733 | 7.528 | 61.34 | 320.06 | −0.356 | 2.66 | −1.30 | 2.16 | 1.13 | −2.17 | 7.23 |
| 7.528 | 8.108 | 61.35 | 320.09 | −0.359 | 2.88 | −1.26 | 1.90 | 1.14 | −2.03 | 6.90 |
| 8.108 | 9.105 | 61.28 | 320.22 | −0.361 | 2.97 | −1.18 | 1.58 | 1.05 | −1.84 | 6.38 |
| 9.105 | 9.786 | 61.14 | 320.46 | −0.366 | 4.25 | −1.88 | 3.01 | 1.65 | −3.15 | 10.50 |
| 9.786 | 11.056 | 60.89 | 320.85 | −0.386 | 5.22 | −2.47 | 4.53 | 2.12 | −4.51 | 14.40 |
| 11.056 | 12.474 | 60.38 | 321.56 | −0.423 | 4.13 | −1.68 | 2.36 | 1.50 | −2.66 | 9.15 |
| 12.474 | 13.739 | 59.66 | 322.50 | −0.437 | 3.38 | −1.33 | 1.04 | 1.22 | −1.45 | 5.99 |
| 13.739 | 14.609 | 59.15 | 323.18 | −0.438 | 7.36 | −2.08 | −1.03 | 1.66 | −0.91 | 7.00 |
| 14.609 | 15.974 | 58.99 | 323.52 | −0.439 | 3.74 | −1.45 | 0.68 | 1.24 | −1.26 | 5.92 |
| 15.974 | 17.235 | 58.62 | 324.05 | −0.445 | 4.40 | −1.62 | 0.66 | 1.33 | −1.38 | 6.56 |
| 17.235 | 18.056 | 58.40 | 324.39 | −0.462 | 6.46 | −2.53 | 1.76 | 2.04 | −2.60 | 11.01 |
| 18.056 | 18.748 | 58.19 | 324.68 | −0.473 | 8.31 | −3.11 | 1.63 | 2.49 | −2.85 | 12.70 |
| 18.748 | 19.722 | 57.75 | 325.19 | −0.479 | 9.70 | −3.49 | 1.65 | 2.85 | −3.06 | 13.91 |
| 19.722 | 20.709 | 56.79 | 326.10 | −0.482 | 11.76 | −4.26 | 2.41 | 3.56 | −3.94 | 17.45 |
| 20.709 | 21.767 | 55.21 | 327.45 | −0.477 | 13.23 | −4.26 | −0.07 | 3.58 | −2.55 | 15.32 |
| 21.767 | 23.962 | 52.36 | 329.76 | −0.445 | 12.32 | −3.35 | −2.85 | 2.36 | −0.67 | 9.49 |
| 23.962 | 24.474 | 50.75 | 331.12 | −0.430 | 23.41 | −5.36 | −9.15 | 3.57 | 0.83 | 13.02 |
| 24.474 | 25.099 | 50.40 | 331.50 | −0.428 | 22.33 | −4.51 | −9.90 | 2.98 | 1.29 | 10.80 |
| 25.099 | 25.987 | 50.13 | 331.90 | −0.427 | 19.49 | −3.55 | −9.34 | 2.56 | 1.42 | 8.76 |
| 25.987 | 26.420 | 50.13 | 332.14 | −0.426 | 21.83 | −3.59 | −10.85 | 3.00 | 1.76 | 9.37 |
| 26.420 | 27.439 | 50.78 | 332.02 | −0.424 | 17.08 | −2.44 | −8.29 | 2.37 | 1.11 | 7.40 |
| 27.439 | 27.859 | 52.10 | 331.48 | −0.423 | 20.79 | −2.41 | −10.20 | 2.87 | 1.24 | 8.61 |
| 27.859 | 28.278 | 52.84 | 331.13 | −0.422 | 19.26 | −2.12 | −9.29 | 2.65 | 1.00 | 8.10 |
| 28.278 | 29.183 | 53.98 | 330.53 | −0.421 | 12.20 | −1.45 | −5.29 | 1.85 | 0.29 | 5.96 |
| 29.183 | 29.970 | 54.84 | 330.08 | −0.420 | 10.36 | −1.53 | −3.76 | 1.96 | −0.03 | 6.17 |
| 29.970 | 30.591 | 55.15 | 329.96 | −0.421 | 10.20 | −1.79 | −3.09 | 2.24 | −0.28 | 7.00 |
| 30.591 | 31.034 | 55.27 | 329.96 | −0.423 | 19.26 | −7.99 | 13.53 | 6.72 | −11.96 | 39.30 |
| 31.034 | 33.157 | 55.33 | 330.12 | −0.429 | 12.68 | −3.00 | −1.29 | 3.45 | −1.67 | 12.24 |
| 33.157 | 33.705 | 55.17 | 330.57 | −0.429 | 28.69 | −6.69 | 2.94 | 9.13 | −7.22 | 34.17 |
| Age (y) . | Age (o) . | Lat. . | Long. . | |$\dot{\Omega }$| . | Covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ma . | Ma . | (°N) . | (°E) . | ° Myr−1 . | a . | b . | c . | d . | e . | f . |
| 0.000 | 0.781 | 60.35 | 321.26 | −0.284 | 3.96 | −3.15 | 8.67 | 2.54 | −6.95 | 19.65 |
| 0.781 | 1.778 | 60.79 | 320.79 | −0.287 | 1.16 | −0.79 | 1.83 | 0.67 | −1.53 | 4.59 |
| 1.778 | 2.581 | 61.15 | 320.36 | −0.292 | 1.31 | −0.75 | 1.41 | 0.66 | −1.27 | 4.07 |
| 2.581 | 3.596 | 61.34 | 320.11 | −0.300 | 1.21 | −0.65 | 1.13 | 0.58 | −1.06 | 3.51 |
| 3.596 | 4.187 | 61.40 | 320.01 | −0.306 | 1.28 | −0.69 | 1.16 | 0.65 | −1.09 | 3.68 |
| 4.187 | 5.235 | 61.41 | 319.98 | −0.308 | 1.23 | −0.67 | 1.25 | 0.62 | −1.16 | 3.77 |
| 5.235 | 6.033 | 61.42 | 319.95 | −0.310 | 1.61 | −0.88 | 1.70 | 0.79 | −1.58 | 5.05 |
| 6.033 | 6.733 | 61.39 | 319.99 | −0.331 | 2.37 | −1.36 | 2.85 | 1.20 | −2.60 | 8.12 |
| 6.733 | 7.528 | 61.34 | 320.06 | −0.356 | 2.66 | −1.30 | 2.16 | 1.13 | −2.17 | 7.23 |
| 7.528 | 8.108 | 61.35 | 320.09 | −0.359 | 2.88 | −1.26 | 1.90 | 1.14 | −2.03 | 6.90 |
| 8.108 | 9.105 | 61.28 | 320.22 | −0.361 | 2.97 | −1.18 | 1.58 | 1.05 | −1.84 | 6.38 |
| 9.105 | 9.786 | 61.14 | 320.46 | −0.366 | 4.25 | −1.88 | 3.01 | 1.65 | −3.15 | 10.50 |
| 9.786 | 11.056 | 60.89 | 320.85 | −0.386 | 5.22 | −2.47 | 4.53 | 2.12 | −4.51 | 14.40 |
| 11.056 | 12.474 | 60.38 | 321.56 | −0.423 | 4.13 | −1.68 | 2.36 | 1.50 | −2.66 | 9.15 |
| 12.474 | 13.739 | 59.66 | 322.50 | −0.437 | 3.38 | −1.33 | 1.04 | 1.22 | −1.45 | 5.99 |
| 13.739 | 14.609 | 59.15 | 323.18 | −0.438 | 7.36 | −2.08 | −1.03 | 1.66 | −0.91 | 7.00 |
| 14.609 | 15.974 | 58.99 | 323.52 | −0.439 | 3.74 | −1.45 | 0.68 | 1.24 | −1.26 | 5.92 |
| 15.974 | 17.235 | 58.62 | 324.05 | −0.445 | 4.40 | −1.62 | 0.66 | 1.33 | −1.38 | 6.56 |
| 17.235 | 18.056 | 58.40 | 324.39 | −0.462 | 6.46 | −2.53 | 1.76 | 2.04 | −2.60 | 11.01 |
| 18.056 | 18.748 | 58.19 | 324.68 | −0.473 | 8.31 | −3.11 | 1.63 | 2.49 | −2.85 | 12.70 |
| 18.748 | 19.722 | 57.75 | 325.19 | −0.479 | 9.70 | −3.49 | 1.65 | 2.85 | −3.06 | 13.91 |
| 19.722 | 20.709 | 56.79 | 326.10 | −0.482 | 11.76 | −4.26 | 2.41 | 3.56 | −3.94 | 17.45 |
| 20.709 | 21.767 | 55.21 | 327.45 | −0.477 | 13.23 | −4.26 | −0.07 | 3.58 | −2.55 | 15.32 |
| 21.767 | 23.962 | 52.36 | 329.76 | −0.445 | 12.32 | −3.35 | −2.85 | 2.36 | −0.67 | 9.49 |
| 23.962 | 24.474 | 50.75 | 331.12 | −0.430 | 23.41 | −5.36 | −9.15 | 3.57 | 0.83 | 13.02 |
| 24.474 | 25.099 | 50.40 | 331.50 | −0.428 | 22.33 | −4.51 | −9.90 | 2.98 | 1.29 | 10.80 |
| 25.099 | 25.987 | 50.13 | 331.90 | −0.427 | 19.49 | −3.55 | −9.34 | 2.56 | 1.42 | 8.76 |
| 25.987 | 26.420 | 50.13 | 332.14 | −0.426 | 21.83 | −3.59 | −10.85 | 3.00 | 1.76 | 9.37 |
| 26.420 | 27.439 | 50.78 | 332.02 | −0.424 | 17.08 | −2.44 | −8.29 | 2.37 | 1.11 | 7.40 |
| 27.439 | 27.859 | 52.10 | 331.48 | −0.423 | 20.79 | −2.41 | −10.20 | 2.87 | 1.24 | 8.61 |
| 27.859 | 28.278 | 52.84 | 331.13 | −0.422 | 19.26 | −2.12 | −9.29 | 2.65 | 1.00 | 8.10 |
| 28.278 | 29.183 | 53.98 | 330.53 | −0.421 | 12.20 | −1.45 | −5.29 | 1.85 | 0.29 | 5.96 |
| 29.183 | 29.970 | 54.84 | 330.08 | −0.420 | 10.36 | −1.53 | −3.76 | 1.96 | −0.03 | 6.17 |
| 29.970 | 30.591 | 55.15 | 329.96 | −0.421 | 10.20 | −1.79 | −3.09 | 2.24 | −0.28 | 7.00 |
| 30.591 | 31.034 | 55.27 | 329.96 | −0.423 | 19.26 | −7.99 | 13.53 | 6.72 | −11.96 | 39.30 |
| 31.034 | 33.157 | 55.33 | 330.12 | −0.429 | 12.68 | −3.00 | −1.29 | 3.45 | −1.67 | 12.24 |
| 33.157 | 33.705 | 55.17 | 330.57 | −0.429 | 28.69 | −6.69 | 2.94 | 9.13 | −7.22 | 34.17 |
These noise-reduced angular velocities specify South America plate motion in a Nubia plate frame of reference for time intervals given in the first two columns. The angular velocities and covariances, which are outputs of the REDBACK software (Iaffaldano et al.2014), were determined from a REDBACK analysis of the finite rotations in Table S2 (Supporting Information). The angular rotation rates |$\dot{\omega }$| are positive anticlockwise. The Cartesian angular velocity covariances are calculated in a Nubia-fixed reference frame and have units of 10−8 radians2 Myr−2 (see Table 1 for instructions on constructing the covariance matrix from elements a–f in the table).
5.1.1 Magnetic reversal crossing reconstructions and fits
Fig. 6 shows best-fitting reconstructions of 19 of the 37 magnetic reversals that are included in the study for the well-mapped 6°S–19°S region. The small circles centred on the chron C1n pole show the best fits to the transform faults and synthetic flow lines created with half-angle stage rotations derived from the best-fitting rotation sequence (Table S2, Supporting Information) show the fits to the digitized fracture zone traces. Similar reconstructions for the rest of our study area are found in Maps S1–S9 of the Supporting Information and throughout our supplemental document.

Reconstructions of magnetic reversals and fracture zone flow lines, 6–19°S, limited for clarity to 19 of the 37 reversals selected for this study. The reversal crossings and fracture zone flow lines were all reconstructed using the best-fitting rotations in Table S2 (Supporting Information). The solid symbols show reversal crossings at their original locations. The open symbols show reversal crossings rotated onto the opposite plate. The solid black line marks the present Mid-Atlantic Ridge axis. Thin black lines are the best, reconstructed great circle segments. The open white circles show the digitized fracture zone crossings. Maps S1 to S9 in the Supporting Information show large-scale reconstructions of all 37 reversals overlaid on bathymetry.
Fig. 7 shows the weighted root-mean-square (WRMS) misfits of the 37 best-fitting rotations to the data (also see Table S1 in the Supporting Information). Misfits to the reversal crossings increase gradually from 1.1 km for chron C1n to 4–6 km for chrons C6Bn.1 to C13 (Fig. 7c). The factors responsible for the gradual increase in misfit with reversal age include sparser mapping of the older reversals, which increases the likelihood of their misidentification, and the greater difficulty in defining conjugate crossings for the older reversals, particularly south of 34°S where the magnetic survey coverage is poor (Maps S6 and S7, Supporting Information).
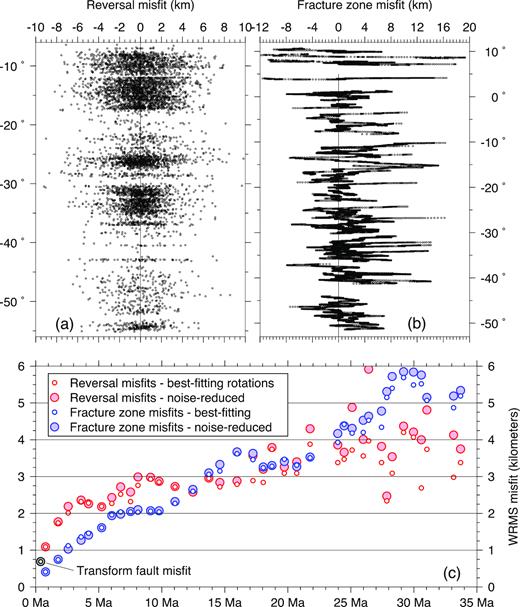
(a) Misfits of best-fitting rotations in Table S2 of the Supporting Information to 6952 crossings of chrons C1n through C13n versus plate boundary latitude. (b) Misfits by plate boundary latitude to 26 410 crossings of 43 fracture zones (also see Fig. 8 and Figs S1–S3 of the Supporting Information). (c) Weighted root-mean-square (WRMS) misfits by age for crossings of magnetic reversals (red circles), transform faults (black circle) and fracture zones (blue circles) for all 37 reversals reconstructed in this study. Ages of fracture zone crossings are approximated from the age of their nearest neighbouring flow-line point assuming symmetric seafloor spreading. Misfits are determined for best-fitting rotations in Table S2 of the Supporting Information and noise-reduced rotations in Table 1.
Fig. 7(c) also compares the WRMS misfits for the noise-reduced rotations in Table 1 to those for the best-fitting rotations. For chrons C1n through C5Cn.1, the noise-reduced misfits are insignificantly larger than for the best-fitting rotations, typically by no more than 0.1 km. For five of the twelve noise-reduced rotations older than 25 Ma (chrons C8n.1 to C13o), the noise-reduced misfits exceed their best-fitting misfits by 1–2 km (Fig. 7c). We attribute the larger misfits for these five reversals to a combination of errors in the GTS12 reversal ages that are used by REDBACK to calibrate the noise-reduced sequence of stage angular velocities and possible 1–2 km systematic mislocations of those magnetic reversals. Overall, the noise-reduced rotations fit the original data nearly as well as their best-fitting counterparts for 32 of the 37 reversals that are reconstructed herein, and modestly degrade the misfit for the other five reversals. For this reason, we adopt the noise-reduced rotations (Table 1) and their derivative stage rotations and angular velocities (Table 2 and Table S3 of the Supporting Information) as our preferred estimates.
5.1.2 Fracture zone flow line reconstructions and fits
Fig. 8 displays the fits of the best-fitting and noise-reduced rotations to 10 of the 43 fracture zone flow lines used for our analysis. Fits for the other 33 fracture zones are shown in Figs S1–S3 (Supporting Information). Overlays of all 43 observed and modelled flow lines on GeoMapApp bathymetry are shown in Fig. 5 and Figs S4–S8 (Supporting Information).
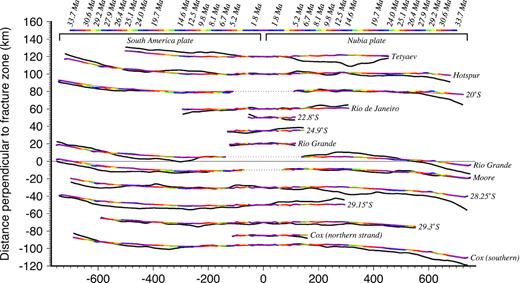
Modelled versus digitized fracture zone traces, 15–33°S. The black lines show the digitized traces, whereas the colour-coded and red lines show the flow line traces created with half-angle stage rotations that we determined, respectively, from the best-fitting and noise-reduced rotations in Tables S1 and S2 of the Supporting Information herein. The noise-reduced traces coincide closely with the best-fitting traces and are thus difficult to see. The horizontal and vertical axes, respectively, show linear distance measured along each fracture zone or orthogonal to each fracture zone. Vertical-axis distances are exaggerated by three times relative to horizontal distances to emphasize the misfits. Zero distance on the horizontal axis marks the ridge–transform intersection for fracture zones that extend to the ridge. Transform faults are omitted from this plot. Figs S1–S3 of the Supporting Information show similar comparisons for the other 33 fracture zone flow lines that were used for our analysis.
The youngest flow-line crossings, consisting of the 2480 transform fault crossings and 637 fracture zone crossings younger than chron C1n, are nearly always located within 1 km of the predicted small circles and flow lines and have respective WRMS misfits of 0.69 and 0.41 km (Fig. 7c). The WRMS misfits increase gradually with age to 5–6 km for ages of 30–35 Ma (Fig. 7c), with mismatches as large as 15–20 km between the synthetic and observed flow lines at the oldest ends of several flow lines. Likely causes of the age-related increase in the misfit include challenges in identifying the precise traces of fracture zones in older seafloor and deviations of the traces of some fracture zones from pure-slip flow lines as transform faults migrate in response to propagating rift tips.
Nearly every modeled fracture zone flow line is located within its bathymetrically-defined fracture zone valley (Figs S6–S10 and Maps 1–9, Supporting Information). Given the usual ambiguities in identifying the locus of paleo-slip within a given fracture zone valley (absent multibeam mapping), we interpret all predicted flow lines that fall within their associated fracture zone valley as evidence of an acceptable fit. Flow lines that fall outside their associated fracture zone valley may do so for multiple reasons. For example, diffuse deformation associated with the North America–South America triple junction likely explains the poor fit at the Fifteen-Twenty Fracture zone (Fig. 5a and Section 5.2) and may also explain the poor fit to the nearby Marathon fracture zone (Fig. 5b). The poor fit to the eastern Chain fracture zone (Fig. S4b, Supporting Information) may be due to fracture zone ‘wander’ in response to a migrating rift tip or a possible reconfiguration of the paleo-ridge-transform geometry, as suggested by the complex seafloor fabric south of the eastern Chain fracture zone. Finally, thermal seafloor contraction may contribute to some of the misfit at all the fracture zones (e.g. Mishra & Gordon 2016).
Whereas the flow lines that are created with the noisier best-fitting rotations exhibit occasional, short-duration changes in direction that are artefacts of changes in the balance of information that magnetic reversal and fracture zone crossings contribute to successive best-fitting rotations, the synthetic flow lines created from the noise-reduced rotations vary more smoothly (Fig. 8) and thus describe a simpler plate kinematic history. The WRMS misfits for the noise-reduced flow lines differ by no more than 0.2 km from the best-fitting WRMS flow-line misfits at all ages (compare the small and large blue circles in Fig. 7c). The fitting penalty for the noise-reduced rotations relative to their best-fitting counterparts is too small to affect any of our results. The noise-reduced rotations and angular velocities thus constitute our preferred estimates for Nubia–South America plate motion.
5.1.3 Kinematic history: poles and stage velocities
The best-fitting Nubia–South America rotation poles trace a ≈600-km-long arc near southern Greenland (Fig. 9), with poles for chrons C13 to C9 (33.7–27 Ma) clustered near 57°N, 326°E and poles for chron C6Bn.1 (21.8 Ma) to the present clustered near 60.5°N. The bimodal, age-related clustering of the poles is qualitatively consistent with two distinct stages of plate opening since 34 Ma, which is strongly supported by other results reported below.

Nubia–South America finite rotation poles, including our best-fitting and noise-reduced poles (open and filled circles, respectively), the GEODVEL space geodetic estimate (black triangle) of Argus et al. (2010) and the 3.16-Ma-average MORVEL estimate (red star) of DeMets et al. (2010). Pole confidence regions are omitted for clarity, but are displayed in Fig. 21 for selected poles. The poles for all 37 reversals are coded by colour and number, as indicated in the legend along the right-hand side of the map. The noise-reduced and best-fitting poles are from Table 1 and Table S2 of the Supporting Information, respectively.
The noise-reduced poles are also distributed bimodally, but are grouped even more tightly than are the best-fitting poles (Fig. 9). We conclude that the pole has been stationary since at least 20 Ma and possibly since 21.8 Ma (C6Bn.1) within the uncertainties.
Our poles for times since ≈5 Ma agree well with the independently derived 3.16-Myr-average MORVEL pole (DeMets et al.2010) and GEODVEL geodetic pole (Argus et al.2010; respectively located by the filled star and triangle in Fig. 9). The pole location for geologically recent times thus appears to be well described.
Fig. 10 shows best-fitting and noise-reduced stage seafloor spreading rates and directions for 33.7 Ma to the present along a flow line at 10.0°S, where the stage opening rates are strongly constrained by the well-mapped magnetic lineations. The stage rates estimated with angular velocities derived from the best-fitting rotations (i.e. the circles in Fig. 10a) reveal a clear slowdown in seafloor spreading rates from ≈20 Ma to the present. The best-fitting stage rates younger than 20 Ma generally agree to within ±0.5 mm yr−1 for adjacent time intervals, implying that their approximate 1σ uncertainties are on the order of ±0.5 mm yr−1. The larger ±2–3 mm yr−1 scatter in the best-fitting stage rates for times earlier than ≈20 Ma is likely due to a combination of factors such as larger errors in the GTS12 age estimates for magnetic reversals older than Chron 5C, larger uncertainties in our identifications of anomalies older than chron C6, decreasing data density for times before chron 6, and possible errors in identifying and matching conjugate reversal crossings across the ridge for older times. For these reasons, greater caution is warranted in interpreting the best-fitting seafloor spreading rates for times before ≈20 Ma.
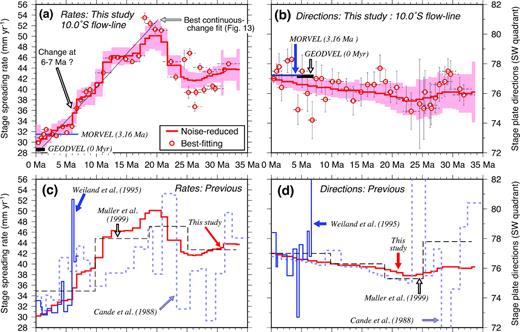
(a) and (b) Newly estimated South America plate stage velocities relative to Nubia along a Nubia plate flow line that originates at 10.0°S, 13.0°W on the Mid-Atlantic Ridge (Fig. 11a). The velocities and their 1σ uncertainties are determined from the best-fitting angular velocities and their covariances (see the text) and noise-reduced angular velocities and covariances in Table 2. Thin black line in (a) shows rates predicted by the best continuous fit model in Fig. 13 and described in the text. The black bars show instantaneous rates and directions predicted by the GEODVEL space geodetic angular velocity (Argus et al.2010). The blue lines show 3.2-Myr-average rates and directions estimated with the MORVEL angular velocity (DeMets et al.2010). Directions are degrees in the southwest quadrant, consistent with WSW-directed movement of South America relative to Nubia across the Mid-Atlantic Ridge. (c) and (d) Stage rates and directions estimated from rotations in three previous studies compared to our noise-reduced velocity estimates (red line) from (a) and (b).
The stage rates that are predicted by the noise-reduced angular velocities in Table 2 clearly reveal a 40–45 per cent slowdown from 21.8 Ma to the present (Fig. 10a), from a high of 50±2 mm yr−1 before 17 Ma to 30 mm yr±2 mm yr−1 since 0.78 Ma. Similar 40–45 per cent spreading rate slowdowns are predicted for the densely surveyed region from 25–33°S (Fig. 11c) and near the Bouvet triple junction (Fig. 11d). Spreading rates thus decreased significantly along the entire plate boundary.
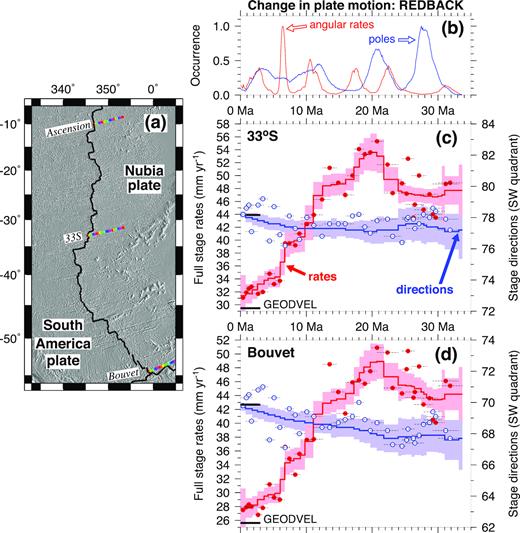
(a) Flow line locations for Fig. 10 and this figure. (b) Timing of changes in angular rotation rates (red) and poles (blue) estimated with REDBACK software. ‘Occurrence’ gives the relative probability through time of a change in the angular rate or pole, where the probability for each time is normalized to the most probable change. The most probable changes in the angular rate and pole location are at 6.4 Ma and 27.5 Ma, respectively. (c) and (d) Full spreading rates (red lines and symbols) and directions (blue lines and symbols) for South America plate relative to Nubia along reconstructed Nubia plate flow lines for 33°S and near the Bouvet triple junction in (a). The circles show velocities determined from the best-fitting stage angular velocities (uncertainties omitted for clarity). The lines show velocities estimated with the noise-reduced stage angular velocities from Table 4. Horizontal lines span the time interval for each best-fitting stage velocity. The black lines indicate rates and azimuths predicted by the Argus et al. (2010) GEODVEL geodetic angular velocity for the Nubia–South America plate pair.
The stage slip directions, which are strongly constrained by the numerous fracture zone crossings that are used to estimate our rotations, have been steady since 34 Ma, with no evidence for a directional change of more than 1.5° anywhere along the plate boundary (Figs 10b and 11c,d). Although the pole locations indicate that the plate motion can be divided into two distinct stages since 34 Ma (Fig. 9), the plate slip direction and hence fracture zone traces are geometrically insensitive to the observed migration of the pole along a great circle that is orthogonal to the southern Atlantic fracture zones.
To first order, our newly determined poles and stage velocities are consistent with a model in which the Nubia and South America plates have rotated about a stationary pole for the past 21.8 Myr, but at steadily decreasing angular rotation rates. Several higher-order variations in the well-determined stage velocity history may indicate that spreading rates decreased in a punctuated rather than continuous manner (Fig. 10a). In particular, the best-fitting and noise-reduced stage rate histories along the 10.0°S flow line both show evidence for rapidly declining seafloor spreading rates from 7–6 Ma and possibly 18–17 Ma, and more slowly declining spreading rates from 6 Ma to the present and possibly 17–12 Ma (Fig. 10a).
We tested the robustness of the possible higher-order spreading rate variations described above by determining their reproducibility from different subsets of our data, as follows: (1) We subdivided the numerous crossings of chrons C1n through C6An.2 (20.7 Ma) into geographically distinct subsets north and south of 20°S, consisting of 2914 and 2753 reversal crossings, respectively. (2) We separately inverted both subsets of reversal crossings with all of the transform fault and fracture zone crossings described in Section 2 to find their best-fitting rotation sequences and associated sequences of angular velocities. (3) We determined a spreading-rate history for the 10°S flow line from the stage angular velocities that fit the data north of 20°S and an independent spreading-rate history for the 33°S flow line from the angular velocities that fit the data south of 20°S.
Fig. 12 compares the independent spreading-rate histories for the areas north and south of 20°S. Both clearly show the 40–45 per cent spreading rate slowdown since 20 Ma. Both also indicate that spreading rates dropped suddenly at 7–6 Ma, including nearly identical 4.2 and 4.3 mm yr−1 decreases in the northern and southern areas, respectively. The evidence that a spreading-rate decrease occurred in both areas at 7–6 Ma is consistent with results from our REDBACK analysis of the best-fitting rotations, which indicates that the highest probability for a change in the angular rotation rate at any time since chron C13 was at 6.4 Ma (Fig. 11b). Highly significant spreading rate slowdowns at 7–6 Ma along the Nubia–North America and Eurasia–North America plate boundaries (Merkouriev & DeMets 2014a,b) and the Southwest Indian Ridge (DeMets et al.2015b) indirectly support the evidence for this previously unknown 7–6 Ma slowdown in Nubia–South America rates.
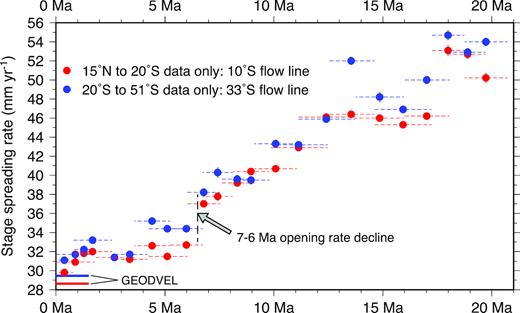
Nubia–South America stage opening rates determined from separate sequences of rotations and angular velocities that, respectively, best fit crossings of chrons C1n through C6An.2 from the northern (20°S–15°N) and southern (52°S–20°S) halves of the plate boundary and crossings of all 37 transform faults and 43 fracture zones used in the analysis. The red circles show best-fitting stage rates determined from the rotations that best fit the 2914 reversal crossings from 20°S to 15°N along the 10.0°S flow line shown in Fig. 11. The blue circles show the best-fitting stage rates derived from the rotations that best fit the 2753 reversal crossings from 52°S to 20°S along the 33°S flow line. The red and blue lines labelled ‘GEODVEL’ are instantaneous geodetic rates predicted by the GEODVEL geodetic model for the same flow lines (Argus et al.2010).
The evidence for a sudden drop in spreading rates at 18–17 Ma and period of steady motion from 17 to 12 Ma is less compelling. Whereas data from the northern region clearly define a 6–7 mm yr−1 drop in the spreading rate at 18–17 Ma, followed by a period of steady spreading from 17–12 Ma (red circles in Fig. 12), the noisier rates estimated from data south of 20°S instead support a steady decline in spreading rates from 20 to 7 Ma (blue circles in Fig. 12). Improved survey coverage of magnetic reversals older than chron C5 is needed south of ≈20°S for a stronger test of these possible variations in motion.
The spreading-rate histories for areas north and south of 20°S both indicate that seafloor spreading rates during the past 6.5 Myr have continued to decline, but by only 0.5 mm yr−1 per Myr, less than half the >1 mm yr−1 per Myr rate of decline between 20 and 7 Ma. Opening rates predicted by the GEODVEL angular velocity confirm that the slowdown has continued to the present (Figs 10a, 11c,d and 12). Interestingly, both of the spreading-rate histories and the GEODVEL rate prediction suggest that the rate of decline may have increased during the past 2.5 Myr. We hesitate to interpret this as significant because our 0.78-Myr-average rate could be up to 1.3 mm yr−1 faster or slower than is indicated in the figures if outward displacement along the plate boundary differs by ±1 km from the 2-km correction that we applied to all our rotations.
5.1.4 Has the plate motion changed continuously since 22 Ma?
Although our REDBACK analysis of the best-fitting rotation sequence suggests that the Nubia–South America angular rotation rate may have changed as many as four times since 21.8 Ma (Fig. 11b), we also tested a simple alternative model in which the two plates have rotated about a stationary pole since 21.8 Ma but at a continuously decreasing angular rotation rate. To undertake this test, we transformed all 37 best-fitting and noise-reduced Nubia–South America finite rotations onto an alternative set of axes (Wilson 1993) that decompose the rotation into orthogonal components that isolate the information about the total opening distance between the two plates (labelled |${\hat{\Omega }}^{\mathrm{ Open}}$| in Fig. 13a), the gradient in the opening distance along the spreading centre (labelled |$\hat{{\Omega }}^{\mathrm{ Grad}}$| in Fig. 13a) and the net opening direction (|$\hat{{\Omega }}^{fz}$| in Fig. 13a). |$\hat{{\Omega }}^{\mathrm{ Grad}}$| is defined to coincide with the geographic centroid of the seafloor spreading centre, whereas |$\hat{{\Omega }}^{\mathrm{ Open}}$| is located 90 arc-degrees from |$\hat{{\Omega }}^{\mathrm{ Grad}}$| in the direction of the rotation poles.
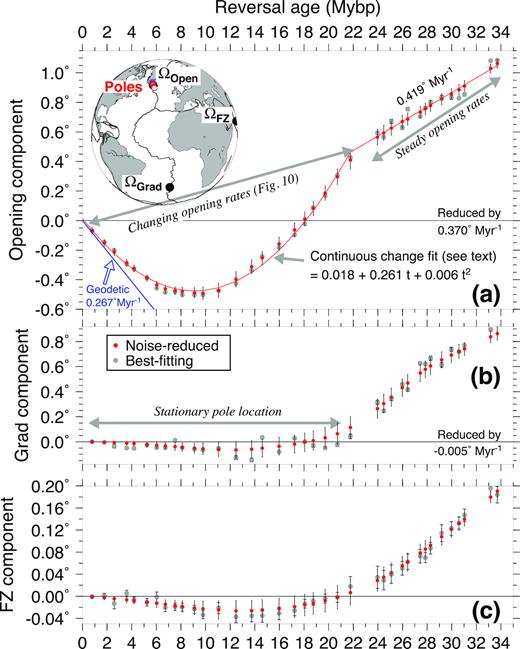
Orthogonal components of Nubia–South America chron C1n to C13 best-fitting rotations (grey circles and Table S2, Supporting Information) and noise-reduced rotations (red circles and Table 1) and their 1σ uncertainties projected onto the orthogonal ΩOpen (a), ΩGrad (b) and ΩFZ (c) axes located on the inset globe. Component angles in A and B are reduced by the listed slopes to emphasize changes in plate motion. The red curve in (a) best fits the noise-reduced angles using the intercept, slope and acceleration terms listed in the panel. The blue line in (a) shows ΩOpen component (0.267° Myr−1) of the GEODVEL geodetic angular velocity extrapolated back to 6 Ma for comparison to the angular rates for our continuous-change estimate (see the text for further discussion).
During periods of steady plate motion, the ΩOpen component angles increase linearly with time, reflecting the steady, uniform accretion of new seafloor everywhere along the plate boundary. Non-zero values for the ΩGrad rotation angles give rise to along-strike differences in the amount of seafloor that accretes along a spreading centre and hence along-strike fanning of the magnetic lineations. Small or zero values for the ΩFZ rotation angles are consistent with a steady opening direction, whereas slowly increasing or decreasing values for ΩFZ are evidence for boundary-wide changes in the direction of relative plate motion.
Fig. 13 shows the time-series for all three of the component angles for the best-fitting rotation sequence (Table S2, Supporting Information) and noise-reduced rotation sequence (Table 1), with the ΩOpen and ΩGrad angles reduced by arbitrary slopes in order to emphasize changes in those angles through time. All three sets of angles reveal evidence for two primary kinematic stages, one from 34 Ma to ≈24 Ma and a second from 21.8 Ma to the present. To first order, the ΩGrad and ΩFZ component angles change linearly during both periods, consistent with opening gradients and plate slip directions that remained the same or evolved only slowly during both periods. In particular, the changes in the ΩFZ component angles are only 20 percent or less of the changes in the other component angles, consistent with small-to-no changes in the stage slip directions along the plate boundary (Figs 10 and 11).
The ΩOpen component angles also change linearly before 22 Ma and are well fit by an angular rate of 0.419° Myr−1 (Fig. 13a). The evidence for linear or nearly linear changes in all three component angles for times from 34 to 24 Ma is consistent with a kinematic model in which the Nubia and South America plates rotated at a steady angular rate about a stationary pole during this period.
For times since 22 Ma, the ΩOpen component angles define a apparently parabolic curve, consistent with a continuously changing angular rotation rate (Fig. 13a). As a test, we inverted the ΩOpen(t) component angles and their associated ages t for a continuous-change model described by ΩOpen(t) = a + bt + ct2, where a, b and c are the intercept, slope and acceleration terms. This gave best-fitting values and 1σ uncertainties of a = 0.018 ± 0.016°, b = 0.261 ± 0.004° Myr−1 and c = 0.006 ± 0.0002 (° Myr−1)2. The derivative of this best-fitting continuous-change model, |$\dot{{\Omega }}^{\mathrm{ Open}}(t) =0.261^{\circ } +t \times 0.012^{\circ }$| Myr−1, indicates that seafloor spreading rates have decelerated by 0.012° per Myr or 1.4 mm yr−1 per Myr since 21.8 Ma .
Not only are the noise-reduced ΩOpen(t) component angles fit well by the above continuous-change model (see the red curve in Fig. 13a), but the slope that is defined by our continuous-change model for the past 2 Myr closely approximates the independently derived GEODVEL angular rate (blue line in Fig. 13a). Geodetic measurements are thus consistent with the continuous-change model, suggesting that it constitutes a useful first-order approximation of the underlying kinematics.
Fig. 10(a) (black line) compares the spreading-rate history that is predicted by the continuous-change model to the observed rates. The continuous-change model nicely captures the decline in the seafloor spreading rates, but departs from the observed stage rates during some periods, including the apparently robust sudden spreading-rate slowdown at 7.6 Ma (Section 5.1.3). We conclude that the observations from 21.8 Ma to the present are well described by a model that combines a continuous long-term decline in the southern Atlantic seafloor spreading rates with at least one period of more rapid slowing from 7 to 6 Ma.
5.2 North America–South America plate motion
Motion between the North and South America plates is accommodated along their ≈1400-km-long diffuse oceanic boundary between the Mid-Atlantic Ridge and Lesser Antilles trench (Fig. 14a). Roest & Collette (1986) interpret extension and volcanism within the Royal Trough and along the Researcher Ridge and Trough west of the Mid-Atlantic Ridge (Fig. 15c) as evidence that the plate motion near the Mid-Atlantic Ridge includes a divergent component. Shortening across the east–west-trending, uplifted Barracuda Ridge (Roest & Collette 1986; Muller & Smith 1993) and other structures within a ≈200-km-wide zone east of the Lesser Antille Trench (Patriat et al.2011) is interpreted by those authors as evidence for a convergent component of plate motion near the Lesser Antilles trench. Estimates of the relative plate motion based on reconstructions of Mid-Atlantic Ridge chron C2A (DeMets et al.2010), chrons C5, C6, C8 and C13 (Muller et al.1999) and geodetic data (Dixon & Mao 1997; Sella, Dixon & Mao 2002; Argus et al.2010) all indicate that the plate motion changes from obliquely divergent to obliquely convergent from east to west along the diffuse plate boundary, in accord with the evidence described above and with scattered earthquake focal mechanisms from this region (Fig. 14a).
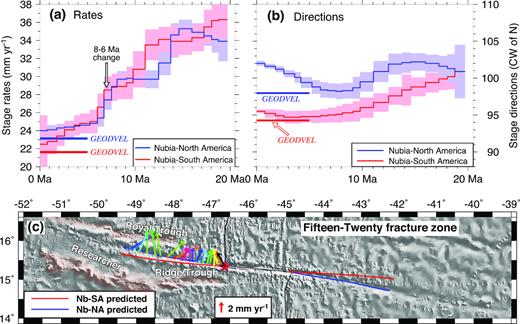
(a) Chron C1n (0.781 Ma) to C6no (19.7 Ma) North America–South America finite rotation poles and representative 95 per cent confidence regions from Table 3 (open coloured circles) and previous studies. Poles from Muller et al. (1999) from Mid-Atlantic Ridge reconstructions of chron C5n.1 (C5) and C6 (C6) are labelled ‘M99’. The GEODVEL space geodetic and 3.16-Ma-average MORVEL poles and their 95 per cent error ellipses are from Argus et al.2010) and DeMets et al. (2010), respectively. Ages in Myr are indicated adjacent to selected poles to illustrate the general pole migration path. Most pole ellipses are omitted for clarity. A clockwise rotation about each pole restores the North America plate to its past positions relative to South America; anticlockwise rotations around the same poles give the time-averaged forward motion of North America relative to South America. The open blue circle labelled RC86 shows the 7-Myr-to-present pole location estimated from seafloor morphology by Roest & Collette (1986). Focal mechanisms span the period 1964 to 2017 and are compiled from Bergman (1986) and global centroid–moment tensor solutions (Dziewonski et al.1981; Ekstrom et al.2012). Earthquake epicentres span 1920 to 1962 (Wysession et al.1995) and 1963 to 2017 (U.S.G.S.). Seafloor depths are extracted from Version 17 of a global 1-minute depth grid (Smith & Sandwell 1997). (b) Small circles around the GEODVEL geodetic and newly determined 0.78-Ma poles (black-dashed and red solid lines, respectively) and tensional axes for the earthquake focal mechanisms from (a).
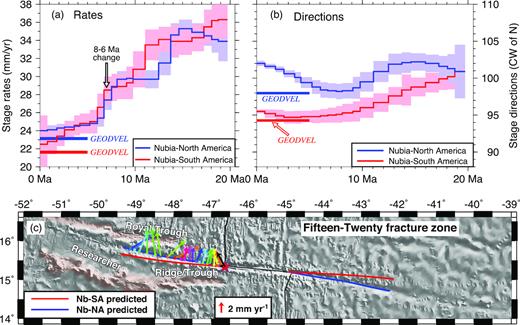
Nubia plate stage seafloor spreading rates (a) and directions (b) relative to the North America (blue) and South America (red) plates along the flow line (coloured circles in c) that reconstructs the location of the western end of the Fifteen-Twenty transform fault relative to the North America plate. Nubia–North America motion is predicted with chron C6n (19.7 Ma)-to-present noise-reduced angular velocities from DeMets et al. (2015a). Nubia–South America motion is estimated with noise-reduced angular velocities for chron C6 to the present. The bold lines labelled ‘GEODVEL’ mark instantaneous geodetic rates at the location of the red star in (c) predicted by Nubia–North America (blue line) and Nubia–South America (red line) angular velocities from Argus et al. (2010). (c) Reconstructed Nubia–North America (blue) and Nubia–South America (red) flow lines for the Fifteen-Twenty Fracture Zone overlaid on GeoMapApp bathymetry. The flow lines were predicted using noise-reduced half-angle finite rotations from Table 1 and DeMets et al. (2015a) . Coloured arrows show North America stage velocities relative to South America from angular velocities in Table 3.
5.2.1 Comparative seafloor spreading histories at the Fifteen-Twenty transform fault
We begin our analysis of movement between the North and South American plates since 20 Ma by comparing the seafloor spreading histories for the Nubia–North America and Nubia–South America plate pairs along a common flow line at the Fifteen-Twenty Fracture Zone (Fig. 15). The plate slip directions and fracture zone flow lines reconstructed for the two plate pairs (Figs 15b and c, respectively) indicate that the North America plate has consistently moved in a direction 3–8 degrees clockwise from the South America plate slip direction since 18.7 Ma (C6ny). By implication, movement between the North and South America plates has included a component of ridge-normal divergence at the location of the Fifteen-Twenty fracture zone since at least 19 Ma.
Seafloor spreading rates reconstructed for the two plate pairs also closely resemble each other for the past 20 Myr (Fig. 15a). To first order, the spreading rates for both plate pairs each decreased roughly one-third between ≈14 and 7 Ma, including rapid, ≈15 per cent slowdowns from 8–6 Ma that coincided with a 7–6 Ma ≈20 per cent slowdown in Eurasia–North America seafloor spreading rates (Merkouriev & DeMets 2008, 2014b). Between 6 and 3 Ma, the nearly identical spreading rates for the two plate pairs imply that the movement between North and South America was dominated by divergence orthogonal to the Fifteen-Twenty fracture zone. Since 2.6 Ma, the rate of seafloor spreading between Nubia and South America has decreased more rapidly than between Nubia and North America, such that the spreading rate immediately north of the Fifteen-Twenty fracture zone has been 1.5 mm yr−1 faster than to the south since 0.78 Ma (Fig. 15a). The GEODVEL angular velocities for the two plate pairs also predict a 1.5 mm yr−1 spreading rate difference at the Fifteen-Twenty transform fault (Fig. 15a). In addition, 3.16-Myr-average opening rates estimated from numerous magnetic profiles from the spreading segments immediately north and south of the Fifteen-Twenty transform fault also differ by 1.5–2 mm yr−1 (DeMets et al.2010). The difference in spreading rates, though small, thus appears to be significant.
5.2.2 North America–South America finite displacements and stage velocities
Using methods described in Section 3.3, we combined our noise-reduced Nubia–South America rotations (Table 1) with noise-reduced Nubia–North America rotations from DeMets et al. (2015a) to estimate finite rotations and covariances for the North America–South America plate pair (Table 3). Because the Nubia–South America and Nubia–North America rotation sequences sample the same 21 magnetic reversals, no interpolations were required to combine the two sets of rotations. Stage angular velocities that we derived from the newly estimated finite rotations and their corresponding reversal ages are given in Table S4 (Supporting Information).
| Chron . | Lat. . | Long. . | Ω . | Scaled covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 9.53 | −56.96 | −0.104 | 0.8 | −0.1 | 0.2 | 0.4 | −0.5 | 0.6 |
| 2n | 10.55 | −57.15 | −0.242 | 0.9 | 0.0 | 0.0 | 0.4 | −0.6 | 0.7 |
| 2An.1 | 11.35 | −57.21 | −0.357 | 1.0 | 0.0 | −0.1 | 0.5 | −0.7 | 0.9 |
| 2An.3 | 12.57 | −57.04 | −0.512 | 1.2 | 0.1 | −0.3 | 0.6 | −0.8 | 1.2 |
| 3n.1 | 13.21 | −56.87 | −0.606 | 1.4 | 0.2 | −0.5 | 0.7 | −0.9 | 1.4 |
| 3n.4 | 14.04 | −56.55 | −0.776 | 1.6 | 0.4 | −0.9 | 0.8 | −1.2 | 1.9 |
| 3An.1 | 14.48 | −56.30 | −0.907 | 2.0 | 0.5 | −1.0 | 1.0 | −1.5 | 2.5 |
| 3An.2 | 15.10 | −56.02 | −1.033 | 2.3 | 0.5 | −1.2 | 1.2 | −1.7 | 3.0 |
| 4n.1 | 15.49 | −55.75 | −1.186 | 2.7 | 0.5 | −1.2 | 1.1 | −1.7 | 3.3 |
| 4n.2 | 15.51 | −55.62 | −1.300 | 3.3 | 0.4 | −1.0 | 1.2 | −1.8 | 3.7 |
| 4A | 15.50 | −55.41 | −1.498 | 5.0 | 0.3 | −0.7 | 1.5 | −2.2 | 5.1 |
| 5n.1 | 15.55 | −55.27 | −1.637 | 6.8 | 0.3 | −0.3 | 1.9 | −2.7 | 6.7 |
| 5n.2 | 16.14 | −54.97 | −1.911 | 10.3 | 0.4 | −0.4 | 2.8 | −3.9 | 10.3 |
| 5An.2 | 17.47 | −54.72 | −2.246 | 13.9 | 1.0 | −1.2 | 3.6 | −5.4 | 14.3 |
| 5AC | 18.05 | −54.82 | −2.536 | 16.9 | 1.7 | −1.0 | 3.8 | −5.8 | 16.3 |
| 5AD | 17.75 | −55.15 | −2.712 | 19.7 | 1.5 | 1.2 | 3.6 | −5.3 | 16.3 |
| 5Cn.1 | 17.37 | −55.75 | −2.958 | 20.9 | −0.5 | 3.1 | 3.2 | −5.3 | 15.4 |
| 5D | 17.24 | −56.15 | −3.175 | 20.0 | −2.0 | 3.2 | 3.2 | −5.7 | 14.8 |
| 5E | 17.36 | −56.30 | −3.318 | 19.8 | −2.6 | 3.0 | 3.3 | −6.0 | 14.7 |
| 6ny | 17.57 | −56.36 | −3.438 | 21.9 | −3.5 | 4.1 | 3.8 | −6.9 | 16.5 |
| 6no | 17.98 | −56.42 | −3.582 | 25.4 | −6.5 | 6.4 | 6.9 | −11.1 | 21.9 |
| Chron . | Lat. . | Long. . | Ω . | Scaled covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 9.53 | −56.96 | −0.104 | 0.8 | −0.1 | 0.2 | 0.4 | −0.5 | 0.6 |
| 2n | 10.55 | −57.15 | −0.242 | 0.9 | 0.0 | 0.0 | 0.4 | −0.6 | 0.7 |
| 2An.1 | 11.35 | −57.21 | −0.357 | 1.0 | 0.0 | −0.1 | 0.5 | −0.7 | 0.9 |
| 2An.3 | 12.57 | −57.04 | −0.512 | 1.2 | 0.1 | −0.3 | 0.6 | −0.8 | 1.2 |
| 3n.1 | 13.21 | −56.87 | −0.606 | 1.4 | 0.2 | −0.5 | 0.7 | −0.9 | 1.4 |
| 3n.4 | 14.04 | −56.55 | −0.776 | 1.6 | 0.4 | −0.9 | 0.8 | −1.2 | 1.9 |
| 3An.1 | 14.48 | −56.30 | −0.907 | 2.0 | 0.5 | −1.0 | 1.0 | −1.5 | 2.5 |
| 3An.2 | 15.10 | −56.02 | −1.033 | 2.3 | 0.5 | −1.2 | 1.2 | −1.7 | 3.0 |
| 4n.1 | 15.49 | −55.75 | −1.186 | 2.7 | 0.5 | −1.2 | 1.1 | −1.7 | 3.3 |
| 4n.2 | 15.51 | −55.62 | −1.300 | 3.3 | 0.4 | −1.0 | 1.2 | −1.8 | 3.7 |
| 4A | 15.50 | −55.41 | −1.498 | 5.0 | 0.3 | −0.7 | 1.5 | −2.2 | 5.1 |
| 5n.1 | 15.55 | −55.27 | −1.637 | 6.8 | 0.3 | −0.3 | 1.9 | −2.7 | 6.7 |
| 5n.2 | 16.14 | −54.97 | −1.911 | 10.3 | 0.4 | −0.4 | 2.8 | −3.9 | 10.3 |
| 5An.2 | 17.47 | −54.72 | −2.246 | 13.9 | 1.0 | −1.2 | 3.6 | −5.4 | 14.3 |
| 5AC | 18.05 | −54.82 | −2.536 | 16.9 | 1.7 | −1.0 | 3.8 | −5.8 | 16.3 |
| 5AD | 17.75 | −55.15 | −2.712 | 19.7 | 1.5 | 1.2 | 3.6 | −5.3 | 16.3 |
| 5Cn.1 | 17.37 | −55.75 | −2.958 | 20.9 | −0.5 | 3.1 | 3.2 | −5.3 | 15.4 |
| 5D | 17.24 | −56.15 | −3.175 | 20.0 | −2.0 | 3.2 | 3.2 | −5.7 | 14.8 |
| 5E | 17.36 | −56.30 | −3.318 | 19.8 | −2.6 | 3.0 | 3.3 | −6.0 | 14.7 |
| 6ny | 17.57 | −56.36 | −3.438 | 21.9 | −3.5 | 4.1 | 3.8 | −6.9 | 16.5 |
| 6no | 17.98 | −56.42 | −3.582 | 25.4 | −6.5 | 6.4 | 6.9 | −11.1 | 21.9 |
These finite rotations, which reconstruct the North America plate onto the South America plate, were determined by combining North America–Nubia noise-reduced rotations from DeMets et al. (2015a) with Nubia–South America noise-reduced rotations from Table 1. Rotation angles Ω are positive anticlockwise. The Cartesian rotation covariances, which are tied to the North America plate, specify the 2-D uncertainty in the location of the North America plate upon its rotation onto the South America plate. The covariances, which have units of 10−8 radians2, have been reduced by a factor of 16 so as to approximate the scatter in results obtained from the best-fitting North America–South America rotations. Instructions for reconstructing the covariance matrix are found in the Table 1 footnotes.
| Chron . | Lat. . | Long. . | Ω . | Scaled covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 9.53 | −56.96 | −0.104 | 0.8 | −0.1 | 0.2 | 0.4 | −0.5 | 0.6 |
| 2n | 10.55 | −57.15 | −0.242 | 0.9 | 0.0 | 0.0 | 0.4 | −0.6 | 0.7 |
| 2An.1 | 11.35 | −57.21 | −0.357 | 1.0 | 0.0 | −0.1 | 0.5 | −0.7 | 0.9 |
| 2An.3 | 12.57 | −57.04 | −0.512 | 1.2 | 0.1 | −0.3 | 0.6 | −0.8 | 1.2 |
| 3n.1 | 13.21 | −56.87 | −0.606 | 1.4 | 0.2 | −0.5 | 0.7 | −0.9 | 1.4 |
| 3n.4 | 14.04 | −56.55 | −0.776 | 1.6 | 0.4 | −0.9 | 0.8 | −1.2 | 1.9 |
| 3An.1 | 14.48 | −56.30 | −0.907 | 2.0 | 0.5 | −1.0 | 1.0 | −1.5 | 2.5 |
| 3An.2 | 15.10 | −56.02 | −1.033 | 2.3 | 0.5 | −1.2 | 1.2 | −1.7 | 3.0 |
| 4n.1 | 15.49 | −55.75 | −1.186 | 2.7 | 0.5 | −1.2 | 1.1 | −1.7 | 3.3 |
| 4n.2 | 15.51 | −55.62 | −1.300 | 3.3 | 0.4 | −1.0 | 1.2 | −1.8 | 3.7 |
| 4A | 15.50 | −55.41 | −1.498 | 5.0 | 0.3 | −0.7 | 1.5 | −2.2 | 5.1 |
| 5n.1 | 15.55 | −55.27 | −1.637 | 6.8 | 0.3 | −0.3 | 1.9 | −2.7 | 6.7 |
| 5n.2 | 16.14 | −54.97 | −1.911 | 10.3 | 0.4 | −0.4 | 2.8 | −3.9 | 10.3 |
| 5An.2 | 17.47 | −54.72 | −2.246 | 13.9 | 1.0 | −1.2 | 3.6 | −5.4 | 14.3 |
| 5AC | 18.05 | −54.82 | −2.536 | 16.9 | 1.7 | −1.0 | 3.8 | −5.8 | 16.3 |
| 5AD | 17.75 | −55.15 | −2.712 | 19.7 | 1.5 | 1.2 | 3.6 | −5.3 | 16.3 |
| 5Cn.1 | 17.37 | −55.75 | −2.958 | 20.9 | −0.5 | 3.1 | 3.2 | −5.3 | 15.4 |
| 5D | 17.24 | −56.15 | −3.175 | 20.0 | −2.0 | 3.2 | 3.2 | −5.7 | 14.8 |
| 5E | 17.36 | −56.30 | −3.318 | 19.8 | −2.6 | 3.0 | 3.3 | −6.0 | 14.7 |
| 6ny | 17.57 | −56.36 | −3.438 | 21.9 | −3.5 | 4.1 | 3.8 | −6.9 | 16.5 |
| 6no | 17.98 | −56.42 | −3.582 | 25.4 | −6.5 | 6.4 | 6.9 | −11.1 | 21.9 |
| Chron . | Lat. . | Long. . | Ω . | Scaled covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| 1n | 9.53 | −56.96 | −0.104 | 0.8 | −0.1 | 0.2 | 0.4 | −0.5 | 0.6 |
| 2n | 10.55 | −57.15 | −0.242 | 0.9 | 0.0 | 0.0 | 0.4 | −0.6 | 0.7 |
| 2An.1 | 11.35 | −57.21 | −0.357 | 1.0 | 0.0 | −0.1 | 0.5 | −0.7 | 0.9 |
| 2An.3 | 12.57 | −57.04 | −0.512 | 1.2 | 0.1 | −0.3 | 0.6 | −0.8 | 1.2 |
| 3n.1 | 13.21 | −56.87 | −0.606 | 1.4 | 0.2 | −0.5 | 0.7 | −0.9 | 1.4 |
| 3n.4 | 14.04 | −56.55 | −0.776 | 1.6 | 0.4 | −0.9 | 0.8 | −1.2 | 1.9 |
| 3An.1 | 14.48 | −56.30 | −0.907 | 2.0 | 0.5 | −1.0 | 1.0 | −1.5 | 2.5 |
| 3An.2 | 15.10 | −56.02 | −1.033 | 2.3 | 0.5 | −1.2 | 1.2 | −1.7 | 3.0 |
| 4n.1 | 15.49 | −55.75 | −1.186 | 2.7 | 0.5 | −1.2 | 1.1 | −1.7 | 3.3 |
| 4n.2 | 15.51 | −55.62 | −1.300 | 3.3 | 0.4 | −1.0 | 1.2 | −1.8 | 3.7 |
| 4A | 15.50 | −55.41 | −1.498 | 5.0 | 0.3 | −0.7 | 1.5 | −2.2 | 5.1 |
| 5n.1 | 15.55 | −55.27 | −1.637 | 6.8 | 0.3 | −0.3 | 1.9 | −2.7 | 6.7 |
| 5n.2 | 16.14 | −54.97 | −1.911 | 10.3 | 0.4 | −0.4 | 2.8 | −3.9 | 10.3 |
| 5An.2 | 17.47 | −54.72 | −2.246 | 13.9 | 1.0 | −1.2 | 3.6 | −5.4 | 14.3 |
| 5AC | 18.05 | −54.82 | −2.536 | 16.9 | 1.7 | −1.0 | 3.8 | −5.8 | 16.3 |
| 5AD | 17.75 | −55.15 | −2.712 | 19.7 | 1.5 | 1.2 | 3.6 | −5.3 | 16.3 |
| 5Cn.1 | 17.37 | −55.75 | −2.958 | 20.9 | −0.5 | 3.1 | 3.2 | −5.3 | 15.4 |
| 5D | 17.24 | −56.15 | −3.175 | 20.0 | −2.0 | 3.2 | 3.2 | −5.7 | 14.8 |
| 5E | 17.36 | −56.30 | −3.318 | 19.8 | −2.6 | 3.0 | 3.3 | −6.0 | 14.7 |
| 6ny | 17.57 | −56.36 | −3.438 | 21.9 | −3.5 | 4.1 | 3.8 | −6.9 | 16.5 |
| 6no | 17.98 | −56.42 | −3.582 | 25.4 | −6.5 | 6.4 | 6.9 | −11.1 | 21.9 |
These finite rotations, which reconstruct the North America plate onto the South America plate, were determined by combining North America–Nubia noise-reduced rotations from DeMets et al. (2015a) with Nubia–South America noise-reduced rotations from Table 1. Rotation angles Ω are positive anticlockwise. The Cartesian rotation covariances, which are tied to the North America plate, specify the 2-D uncertainty in the location of the North America plate upon its rotation onto the South America plate. The covariances, which have units of 10−8 radians2, have been reduced by a factor of 16 so as to approximate the scatter in results obtained from the best-fitting North America–South America rotations. Instructions for reconstructing the covariance matrix are found in the Table 1 footnotes.
Between 19.7 and 12.5 Ma (C6no to C5An.2), North America–South America poles were tightly grouped ≈100 km northeast of the Barrucada Ridge (Fig. 14a). After 12.5 Ma, the poles migrated steadily southwards along an arc between the compressional Barracuda Ridge and extensional Researcher Ridge/Trough and Royal Trough (Fig. 14a). The poles and stage angular velocities predict that the plate motion at the longitudes of the Researcher Ridge/Trough and Royal Trough has included a component of divergence at all times since 19.7 Ma (Fig. 15c). The poles furthermore predict that the Barracuda Ridge and adjacent structures have accommodated a component of convergence since 13.7 Ma. The motions predicted by our newly estimated poles agree with those inferred by previous authors from seafloor morphology and seismicity (Roest & Collette 1986) and plate kinematic reconstructions (Muller & Smith 1993; Muller et al.1999; DeMets et al.2010).
At the location of the Royal Trough, which affects seafloor as young as 11.1 Myr (Fig. 16c), our chron C5n.2 finite rotation predicts that the North and South America plates have diverged by 24.8±1.8 km (1σ) towards N02°E-S02°W (±4°) since 11.06 Ma. The predicted displacement is nearly orthogonal to the N85-90°E-trending Royal Trough, but exceeds its measured 14-km width by 11 km. The Royal Trough is thus too narrow to account for all the plate divergence since 11 Ma. Some and perhaps most of the missing divergence may have been accommodated by the 12-km-wide, E-W-trending Researcher Trough, which is also orthogonal to the N02°E-S02°W-directed plate divergence (Fig. 15c). A discussion of how the young seafloor near the Mid-Atlantic Ridge accommodates extension between these two plates can be found in Section 6.3.

20 Ma to present stage rates (a) and directions (b) for the North America plate relative to South America along a flow line (coloured circles in Fig. 15c) that reconstructs the paleolocations of the western end of the Fifteen-Twenty fracture zone relative to the South America plate. The stage velocities predicted by noise-reduced angular velocities in Table S4 of the Supporting Information and by best-fitting angular velocities are shown by the bold red line and red circles, respectively. All angular velocities are in a South America plate frame of reference. Other stage velocities are determined from the Muller et al. (1999) reconstructions of chrons C5n.1 and C6 for the Mid-Atlantic Ridge (labelled M99), the GEODVEL space geodetic estimate of Argus et al. (2010) and the 3.16-Ma-average MORVEL estimate (DeMets et al.2010). The shaded areas and vertical bars show the 1σ uncertainties. (c) Half-displacement paths for North America and South America plates relative to Nubia for a flow line that originates at 15.75°N, 46.65°W for all 21 times since 19.72 Ma (chron C6) included in the study. Ages in Myr are shown for selected points on the flow paths. The differential movements between the North and South America plates for the same 21 times, which are shown by the bold red and black lines, can equivalently be derived from the noise-reduced rotations in Table 3. Bathymetry is extracted from GeoMapApp (www.marine-geo.org).
The chron C6no rotation (Table 3) predicts net divergence of 49±2.5 km towards N16°E±3° across the Royal Trough (Fig. 16c), roughly double the 26-km summed widths of the Royal and Researcher troughs. Our new rotations thus indicate that these two features cannot have accommodated all the plate motion since 20 Ma.
Along a flow line near the Fifteen-Twenty fracture zone, the newly determined angular velocities (Table S4, Supporting Information) predict that the motion between the North and South America plates has consistently averaged 2.5–3 mm yr−1 since 11.06 Ma (Figs 15c and 16a), but has rotated nearly 90° clockwise (Figs 15c and 16b). Encouragingly, a 9.7-Myr-average rate that we predicted using the C5n.1 rotation of Muller et al. (1999) agrees well with our new stage rates (compare the red and dashed black lines in Fig. 16a).
Across the Barracuda Ridge and uplifted and folded basement features and sediments immediately to its north and south (Patriat et al.2011), our new rotations predict that the convergence diminishes rapidly from west to east. For example, at the western end of the Barracuda Ridge (16.8°N, 58.8°W), shortening of 13.8±2.0 km towards N10°E-S10°W (±7°) is predicted by the chron C5n.2 finite rotation, nearly orthogonal to the N75°W-trending ridge. The predicted shortening diminishes by half (7.2±1.9 km, N06°E-S06°W) at the Barracuda Ridge midpoint (16.3°N, 57°W) and to insignificant levels at locations east of 56°W. Spanning the past 20 Myr, our chron C6no rotation predicts shortening of 17.8±2.2 km towards N28°W-S28°E at the western end of the ridge. Resolved onto the direction orthogonal to the Barracuda Ridge, the ridge-normal shortening since 19.7 Ma has been 13.1±2 km, insignificantly different from the shortening since 11.06 Ma (13.8±2 km). Most or possibly all of the shortening across the Barracuda Ridge and adjacent features thus may have occurred during the past 11 Myr. The earliest age that our rotations predict any shortening for the Barracuda Ridge and adjacent areas is ≈10 Ma, much older than the 3.6 Ma earliest uplift age estimated by Patriat et al. (2011) from their biostratigraphic analysis of Barracuda Ridge sediments.
5.2.3 Recent North America–South America plate motion and geodetic comparison
Our 0.78-Ma-average pole and the GEODVEL geodetic pole are both located hundreds of km south of the chron C5 and older poles estimated by ourselves and previous authors (Fig. 14a), suggesting that the rotation pole has migrated gradually southwards to a latitude that is presently near ≈10°N. The GEODVEL pole is located ≈500 km east of our 0.78-Ma-average pole, raising the question of whether one or possibly both estimates could be biased. From their modelling of the effects of post-glacial isostatic rebound on the motions of the tectonic plates, Klemann et al. (2008) conclude that angular velocities estimated from geodetic measurements in North America are more susceptible to biases from post-glacial rebound than for any other tectonic plate. The ≈5° difference in the longitudes of our 0.78-Ma pole and the GEODVEL pole may thus be a geodetic artefact.
Weak evidence for a possible bias in the GEODVEL pole emerges from a comparison of the tensional axes for all intraplate earthquakes located in the diffuse deforming region between the two plates to small-circle lines of pure slip around our 0.78-Ma-average pole and the GEODVEL pole (red and dashed lines in Fig. 14b). Although both poles correctly predict the orientations of the tensional axes for earthquakes near the Mid-Atlantic Ridge, the slip lines around the 0.78-Ma-average pole better match the T-axis orientations for earthquakes from locations farther west than do the GEODVEL slip lines. The 0.78-Ma-average pole is thus more predictive of the seismologically defined deformation than is the GEODVEL pole, with the caveat that the T-axis orientations are not necessarily parallel to plate slip directions in zones of distributed deformation.
5.3 Antarctic–South America plate motion
The 2000-km-long American–Antarctic Ridge, which connects the Bouvet triple junction to the southern end of the South Sandwich trench (Fig. 17b), transfers slow left-lateral movement between the (East) Antarctic and South America plates. (Note: References throughout this paper to the Antarctic plate refer to the traditionally defined Antarctic plate for times back to 11 Ma, but to the East Antarctic plate for times before 11 Ma, when kinematically distinct East and West Antarctic plates existed; Granot & Dyment 2018).
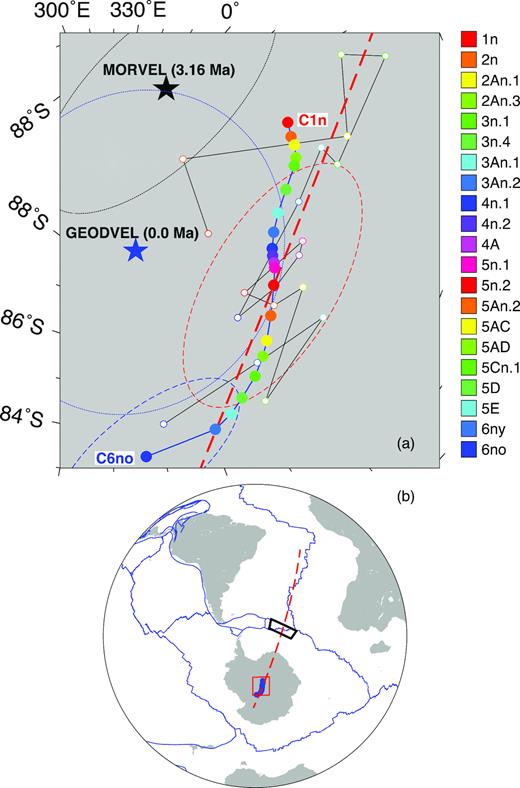
(a) Best-fitting and noise-reduced Antarctic-South America poles from Table 4 (open circles filled circles, respectively) and poles for the GEODVEL (Argus et al.2010) and MORVEL 3.16-Myr average angular velocities (DeMets et al.2010). Representative 2-D 95 per cent confidence regions are shown for the chron C5n.2 and 6no rotations and for the GEODVEL and MORVEL poles. The red dashed line in (a) and (b) shows the great circle that connects the chron C5n.2 pole to the geographic centroid of the plate boundary (see the text). (b) The red rectangle locates the area shown in (a). The black rectangle encompasses the American–Antarctic Ridge, including both of the areas that are shown in Fig. 18.
Despite sparse survey coverage of the geographically remote American–Antarctic Ridge and the generally low quality of its magnetic anomalies, several authors have used observations from this spreading centre to estimate rotations for its seafloor spreading history (Nankivell 1997; Livermore et al.2005; DeMets et al.2010; Eagles 2016). Given the dearth of the marine magnetic data that are available from the American–Antarctic Ridge, we instead estimate the motion between Antarctica and South America by summing high-resolution rotations for the better-mapped Nubia–South America and Nubia–Antarctic plate boundaries. In particular, we estimate best-fitting and noise-reduced Antarctic–South America finite rotations and covariances (both in Table 4) for 21 reversals between chrons C1n and C6 from the best-fitting and noise-reduced Nubia–South America rotations and best-fitting and noise-reduced Nubia–Antarctic rotations from DeMets et al. (2015b). Our newly estimated rotations are derived solely from closure of the Nubia–Antarctic–South America plate circuit and thus predict the plate motion independent of any data from the American–Antarctic Ridge.
Antarctic–South America closure-derived rotations: best-fitting and noise-reduced.
| Chron . | Lat. . | Long. . | Ω . | Rotation covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| Best-fitting | |||||||||
| 1n | −87.73 | 40.65 | 0.201 | 1.4 | −0.7 | −0.6 | 0.6 | −0.1 | 0.9 |
| 2n | −87.40 | 39.34 | 0.468 | 6.8 | 2.1 | −9.4 | 1.5 | −2.4 | 19.0 |
| 2An.1 | −84.21 | 39.84 | 0.740 | 14.5 | 3.5 | −8.8 | 2.4 | −0.8 | 14.8 |
| 2An.3 | −84.78 | 24.60 | 1.054 | 17.2 | 5.6 | −18.1 | 4.4 | −4.1 | 29.3 |
| 3n.1 | −84.12 | 29.80 | 1.236 | 21.4 | 7.0 | −23.9 | 5.2 | −4.8 | 42.7 |
| 3n.4 | −85.74 | 58.33 | 1.508 | 26.0 | 7.8 | −28.8 | 5.4 | −7.6 | 45.3 |
| 3An.1 | −86.68 | 59.57 | 1.679 | 23.0 | 4.4 | −25.2 | 5.1 | −3.6 | 41.1 |
| 3An.2 | −86.69 | 81.99 | 1.836 | 32.0 | 7.0 | −36.4 | 4.5 | −7.6 | 56.7 |
| 4n.1 | −85.54 | 97.44 | 2.125 | 39.7 | 9.9 | −44.8 | 6.7 | −12.9 | 66.3 |
| 4n.2 | −85.71 | 90.32 | 2.308 | 46.3 | 7.8 | −48.7 | 8.6 | −14.2 | 78.4 |
| 4A | −85.26 | 72.62 | 2.726 | 75.6 | 10.5 | −71.3 | 13.4 | −24.0 | 97.3 |
| 5n.1 | −85.35 | 72.60 | 2.894 | 93.1 | 31.5 | −95.0 | 18.4 | −39.2 | 121.6 |
| 5n.2 | −85.64 | 91.33 | 3.290 | 33.3 | 7.2 | −31.1 | 5.1 | −8.0 | 45.9 |
| 5An.2 | −85.10 | 86.78 | 3.858 | 40.0 | 8.8 | −40.2 | 7.4 | −13.6 | 60.5 |
| 5AC | −84.99 | 84.56 | 4.422 | 33.6 | 5.9 | −25.8 | 7.2 | −8.4 | 34.4 |
| 5AD | −83.58 | 107.44 | 4.733 | 42.3 | 8.6 | −37.3 | 9.4 | −10.6 | 50.1 |
| 5Cn.1 | −84.18 | 89.92 | 5.418 | 231.6 | 45.0 | −251.7 | 40.0 | −91.3 | 366.7 |
| 6ny | −84.10 | 104.34 | 6.456 | 502.5 | 23.7 | −321.5 | 31.6 | −28.1 | 271.9 |
| 6no | −83.65 | 133.85 | 6.405 | 75.5 | 27.6 | −46.0 | 46.8 | −14.8 | 73.4 |
| Noise-reduced | |||||||||
| 1n | −85.92 | 36.10 | 0.206 | 11.4 | −7.8 | 3.0 | 5.9 | −2.7 | 9.3 |
| 2n | −85.91 | 40.81 | 0.475 | 13.5 | −7.7 | 2.4 | 6.3 | −1.9 | 10.7 |
| 2An.1 | −85.86 | 43.53 | 0.700 | 16.9 | −7.7 | 2.1 | 7.2 | −1.3 | 13.2 |
| 2An.3 | −85.85 | 47.54 | 0.993 | 22.6 | −7.3 | 1.2 | 8.4 | 0.1 | 17.3 |
| 3n.1 | −85.89 | 50.12 | 1.164 | 26.2 | −6.9 | −0.1 | 9.1 | 1.5 | 19.6 |
| 3n.4 | −86.05 | 58.00 | 1.462 | 30.9 | −6.5 | −2.6 | 9.8 | 2.5 | 22.7 |
| 3An.1 | −86.11 | 66.12 | 1.685 | 39.7 | −9.5 | −5.5 | 12.6 | 3.0 | 28.9 |
| 3An.2 | −86.06 | 72.70 | 1.894 | 50.1 | −11.8 | −9.3 | 15.5 | 5.1 | 35.8 |
| 4n.1 | −85.93 | 77.70 | 2.151 | 57.3 | −10.6 | −11.8 | 16.6 | 5.5 | 41.1 |
| 4n.2 | −85.84 | 79.63 | 2.341 | 64.4 | −10.0 | −12.3 | 17.9 | 4.0 | 46.8 |
| 4A | −85.73 | 81.30 | 2.670 | 81.6 | −10.3 | −11.6 | 22.0 | −1.2 | 61.5 |
| 5n.1 | −85.66 | 82.52 | 2.895 | 96.7 | −11.1 | −12.3 | 25.5 | −5.7 | 74.0 |
| 5n.2 | −85.46 | 86.84 | 3.337 | 127.0 | −11.5 | −17.1 | 31.5 | −15.0 | 99.1 |
| 5An.2 | −85.06 | 93.79 | 3.885 | 153.9 | −4.9 | −29.6 | 33.9 | −18.7 | 119.9 |
| 5AC | −84.71 | 98.95 | 4.392 | 160.3 | 8.5 | −35.9 | 31.3 | −12.6 | 124.7 |
| 5AD | −84.49 | 102.09 | 4.743 | 168.7 | 16.2 | −31.3 | 33.3 | −5.4 | 132.6 |
| 5Cn.1 | −84.22 | 106.26 | 5.291 | 209.6 | 24.4 | −16.8 | 46.8 | 12.1 | 166.8 |
| 5D | −83.96 | 111.19 | 5.789 | 270.6 | 43.7 | 19.4 | 66.4 | 37.3 | 221.2 |
| 5E | −83.74 | 114.80 | 6.109 | 307.6 | 64.7 | 45.2 | 78.0 | 56.6 | 258.6 |
| 6ny | −83.56 | 119.01 | 6.343 | 332.9 | 83.5 | 63.4 | 84.3 | 68.8 | 285.6 |
| 6no | −83.32 | 133.62 | 6.622 | 322.3 | 69.2 | 30.5 | 67.4 | 42.3 | 267.7 |
| Chron . | Lat. . | Long. . | Ω . | Rotation covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| Best-fitting | |||||||||
| 1n | −87.73 | 40.65 | 0.201 | 1.4 | −0.7 | −0.6 | 0.6 | −0.1 | 0.9 |
| 2n | −87.40 | 39.34 | 0.468 | 6.8 | 2.1 | −9.4 | 1.5 | −2.4 | 19.0 |
| 2An.1 | −84.21 | 39.84 | 0.740 | 14.5 | 3.5 | −8.8 | 2.4 | −0.8 | 14.8 |
| 2An.3 | −84.78 | 24.60 | 1.054 | 17.2 | 5.6 | −18.1 | 4.4 | −4.1 | 29.3 |
| 3n.1 | −84.12 | 29.80 | 1.236 | 21.4 | 7.0 | −23.9 | 5.2 | −4.8 | 42.7 |
| 3n.4 | −85.74 | 58.33 | 1.508 | 26.0 | 7.8 | −28.8 | 5.4 | −7.6 | 45.3 |
| 3An.1 | −86.68 | 59.57 | 1.679 | 23.0 | 4.4 | −25.2 | 5.1 | −3.6 | 41.1 |
| 3An.2 | −86.69 | 81.99 | 1.836 | 32.0 | 7.0 | −36.4 | 4.5 | −7.6 | 56.7 |
| 4n.1 | −85.54 | 97.44 | 2.125 | 39.7 | 9.9 | −44.8 | 6.7 | −12.9 | 66.3 |
| 4n.2 | −85.71 | 90.32 | 2.308 | 46.3 | 7.8 | −48.7 | 8.6 | −14.2 | 78.4 |
| 4A | −85.26 | 72.62 | 2.726 | 75.6 | 10.5 | −71.3 | 13.4 | −24.0 | 97.3 |
| 5n.1 | −85.35 | 72.60 | 2.894 | 93.1 | 31.5 | −95.0 | 18.4 | −39.2 | 121.6 |
| 5n.2 | −85.64 | 91.33 | 3.290 | 33.3 | 7.2 | −31.1 | 5.1 | −8.0 | 45.9 |
| 5An.2 | −85.10 | 86.78 | 3.858 | 40.0 | 8.8 | −40.2 | 7.4 | −13.6 | 60.5 |
| 5AC | −84.99 | 84.56 | 4.422 | 33.6 | 5.9 | −25.8 | 7.2 | −8.4 | 34.4 |
| 5AD | −83.58 | 107.44 | 4.733 | 42.3 | 8.6 | −37.3 | 9.4 | −10.6 | 50.1 |
| 5Cn.1 | −84.18 | 89.92 | 5.418 | 231.6 | 45.0 | −251.7 | 40.0 | −91.3 | 366.7 |
| 6ny | −84.10 | 104.34 | 6.456 | 502.5 | 23.7 | −321.5 | 31.6 | −28.1 | 271.9 |
| 6no | −83.65 | 133.85 | 6.405 | 75.5 | 27.6 | −46.0 | 46.8 | −14.8 | 73.4 |
| Noise-reduced | |||||||||
| 1n | −85.92 | 36.10 | 0.206 | 11.4 | −7.8 | 3.0 | 5.9 | −2.7 | 9.3 |
| 2n | −85.91 | 40.81 | 0.475 | 13.5 | −7.7 | 2.4 | 6.3 | −1.9 | 10.7 |
| 2An.1 | −85.86 | 43.53 | 0.700 | 16.9 | −7.7 | 2.1 | 7.2 | −1.3 | 13.2 |
| 2An.3 | −85.85 | 47.54 | 0.993 | 22.6 | −7.3 | 1.2 | 8.4 | 0.1 | 17.3 |
| 3n.1 | −85.89 | 50.12 | 1.164 | 26.2 | −6.9 | −0.1 | 9.1 | 1.5 | 19.6 |
| 3n.4 | −86.05 | 58.00 | 1.462 | 30.9 | −6.5 | −2.6 | 9.8 | 2.5 | 22.7 |
| 3An.1 | −86.11 | 66.12 | 1.685 | 39.7 | −9.5 | −5.5 | 12.6 | 3.0 | 28.9 |
| 3An.2 | −86.06 | 72.70 | 1.894 | 50.1 | −11.8 | −9.3 | 15.5 | 5.1 | 35.8 |
| 4n.1 | −85.93 | 77.70 | 2.151 | 57.3 | −10.6 | −11.8 | 16.6 | 5.5 | 41.1 |
| 4n.2 | −85.84 | 79.63 | 2.341 | 64.4 | −10.0 | −12.3 | 17.9 | 4.0 | 46.8 |
| 4A | −85.73 | 81.30 | 2.670 | 81.6 | −10.3 | −11.6 | 22.0 | −1.2 | 61.5 |
| 5n.1 | −85.66 | 82.52 | 2.895 | 96.7 | −11.1 | −12.3 | 25.5 | −5.7 | 74.0 |
| 5n.2 | −85.46 | 86.84 | 3.337 | 127.0 | −11.5 | −17.1 | 31.5 | −15.0 | 99.1 |
| 5An.2 | −85.06 | 93.79 | 3.885 | 153.9 | −4.9 | −29.6 | 33.9 | −18.7 | 119.9 |
| 5AC | −84.71 | 98.95 | 4.392 | 160.3 | 8.5 | −35.9 | 31.3 | −12.6 | 124.7 |
| 5AD | −84.49 | 102.09 | 4.743 | 168.7 | 16.2 | −31.3 | 33.3 | −5.4 | 132.6 |
| 5Cn.1 | −84.22 | 106.26 | 5.291 | 209.6 | 24.4 | −16.8 | 46.8 | 12.1 | 166.8 |
| 5D | −83.96 | 111.19 | 5.789 | 270.6 | 43.7 | 19.4 | 66.4 | 37.3 | 221.2 |
| 5E | −83.74 | 114.80 | 6.109 | 307.6 | 64.7 | 45.2 | 78.0 | 56.6 | 258.6 |
| 6ny | −83.56 | 119.01 | 6.343 | 332.9 | 83.5 | 63.4 | 84.3 | 68.8 | 285.6 |
| 6no | −83.32 | 133.62 | 6.622 | 322.3 | 69.2 | 30.5 | 67.4 | 42.3 | 267.7 |
These finite rotations reconstruct the Antarctic plate relative to the South America plate. The rotations labelled ‘best-fitting’ are determined from the best-fitting Nubia–South America rotations in Table S2 of the Supporting Information and best-fitting Nubia–Antarctic rotations from Table 2 of DeMets et al. (2015b). Rotations for chrons C5D and C5E were not estimated due to insufficient shipboard coverage of these two magnetic anomalies along the western third of the Southwest Indian Ridge. The rotations labelled ‘noise-reduced’, our preferred estimates, are determined from noise-reduced Nubia–South America rotations in Table 1 and noise-reduced Nubia–Antarctic rotations from Table S1 of the Supporting Information of DeMets et al. (2015b). The rotation angles Ω are positive CCW. All the covariances are Cartesian and have units of 10 −8 radians2. Both sets of covariances are tied to the Antarctic plate and specify the uncertainty in the location of the Antarctic plate upon its rotation onto the South America plate. Instructions for reconstructing the covariance matrix are given in Table 1 footnotes.
Antarctic–South America closure-derived rotations: best-fitting and noise-reduced.
| Chron . | Lat. . | Long. . | Ω . | Rotation covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| Best-fitting | |||||||||
| 1n | −87.73 | 40.65 | 0.201 | 1.4 | −0.7 | −0.6 | 0.6 | −0.1 | 0.9 |
| 2n | −87.40 | 39.34 | 0.468 | 6.8 | 2.1 | −9.4 | 1.5 | −2.4 | 19.0 |
| 2An.1 | −84.21 | 39.84 | 0.740 | 14.5 | 3.5 | −8.8 | 2.4 | −0.8 | 14.8 |
| 2An.3 | −84.78 | 24.60 | 1.054 | 17.2 | 5.6 | −18.1 | 4.4 | −4.1 | 29.3 |
| 3n.1 | −84.12 | 29.80 | 1.236 | 21.4 | 7.0 | −23.9 | 5.2 | −4.8 | 42.7 |
| 3n.4 | −85.74 | 58.33 | 1.508 | 26.0 | 7.8 | −28.8 | 5.4 | −7.6 | 45.3 |
| 3An.1 | −86.68 | 59.57 | 1.679 | 23.0 | 4.4 | −25.2 | 5.1 | −3.6 | 41.1 |
| 3An.2 | −86.69 | 81.99 | 1.836 | 32.0 | 7.0 | −36.4 | 4.5 | −7.6 | 56.7 |
| 4n.1 | −85.54 | 97.44 | 2.125 | 39.7 | 9.9 | −44.8 | 6.7 | −12.9 | 66.3 |
| 4n.2 | −85.71 | 90.32 | 2.308 | 46.3 | 7.8 | −48.7 | 8.6 | −14.2 | 78.4 |
| 4A | −85.26 | 72.62 | 2.726 | 75.6 | 10.5 | −71.3 | 13.4 | −24.0 | 97.3 |
| 5n.1 | −85.35 | 72.60 | 2.894 | 93.1 | 31.5 | −95.0 | 18.4 | −39.2 | 121.6 |
| 5n.2 | −85.64 | 91.33 | 3.290 | 33.3 | 7.2 | −31.1 | 5.1 | −8.0 | 45.9 |
| 5An.2 | −85.10 | 86.78 | 3.858 | 40.0 | 8.8 | −40.2 | 7.4 | −13.6 | 60.5 |
| 5AC | −84.99 | 84.56 | 4.422 | 33.6 | 5.9 | −25.8 | 7.2 | −8.4 | 34.4 |
| 5AD | −83.58 | 107.44 | 4.733 | 42.3 | 8.6 | −37.3 | 9.4 | −10.6 | 50.1 |
| 5Cn.1 | −84.18 | 89.92 | 5.418 | 231.6 | 45.0 | −251.7 | 40.0 | −91.3 | 366.7 |
| 6ny | −84.10 | 104.34 | 6.456 | 502.5 | 23.7 | −321.5 | 31.6 | −28.1 | 271.9 |
| 6no | −83.65 | 133.85 | 6.405 | 75.5 | 27.6 | −46.0 | 46.8 | −14.8 | 73.4 |
| Noise-reduced | |||||||||
| 1n | −85.92 | 36.10 | 0.206 | 11.4 | −7.8 | 3.0 | 5.9 | −2.7 | 9.3 |
| 2n | −85.91 | 40.81 | 0.475 | 13.5 | −7.7 | 2.4 | 6.3 | −1.9 | 10.7 |
| 2An.1 | −85.86 | 43.53 | 0.700 | 16.9 | −7.7 | 2.1 | 7.2 | −1.3 | 13.2 |
| 2An.3 | −85.85 | 47.54 | 0.993 | 22.6 | −7.3 | 1.2 | 8.4 | 0.1 | 17.3 |
| 3n.1 | −85.89 | 50.12 | 1.164 | 26.2 | −6.9 | −0.1 | 9.1 | 1.5 | 19.6 |
| 3n.4 | −86.05 | 58.00 | 1.462 | 30.9 | −6.5 | −2.6 | 9.8 | 2.5 | 22.7 |
| 3An.1 | −86.11 | 66.12 | 1.685 | 39.7 | −9.5 | −5.5 | 12.6 | 3.0 | 28.9 |
| 3An.2 | −86.06 | 72.70 | 1.894 | 50.1 | −11.8 | −9.3 | 15.5 | 5.1 | 35.8 |
| 4n.1 | −85.93 | 77.70 | 2.151 | 57.3 | −10.6 | −11.8 | 16.6 | 5.5 | 41.1 |
| 4n.2 | −85.84 | 79.63 | 2.341 | 64.4 | −10.0 | −12.3 | 17.9 | 4.0 | 46.8 |
| 4A | −85.73 | 81.30 | 2.670 | 81.6 | −10.3 | −11.6 | 22.0 | −1.2 | 61.5 |
| 5n.1 | −85.66 | 82.52 | 2.895 | 96.7 | −11.1 | −12.3 | 25.5 | −5.7 | 74.0 |
| 5n.2 | −85.46 | 86.84 | 3.337 | 127.0 | −11.5 | −17.1 | 31.5 | −15.0 | 99.1 |
| 5An.2 | −85.06 | 93.79 | 3.885 | 153.9 | −4.9 | −29.6 | 33.9 | −18.7 | 119.9 |
| 5AC | −84.71 | 98.95 | 4.392 | 160.3 | 8.5 | −35.9 | 31.3 | −12.6 | 124.7 |
| 5AD | −84.49 | 102.09 | 4.743 | 168.7 | 16.2 | −31.3 | 33.3 | −5.4 | 132.6 |
| 5Cn.1 | −84.22 | 106.26 | 5.291 | 209.6 | 24.4 | −16.8 | 46.8 | 12.1 | 166.8 |
| 5D | −83.96 | 111.19 | 5.789 | 270.6 | 43.7 | 19.4 | 66.4 | 37.3 | 221.2 |
| 5E | −83.74 | 114.80 | 6.109 | 307.6 | 64.7 | 45.2 | 78.0 | 56.6 | 258.6 |
| 6ny | −83.56 | 119.01 | 6.343 | 332.9 | 83.5 | 63.4 | 84.3 | 68.8 | 285.6 |
| 6no | −83.32 | 133.62 | 6.622 | 322.3 | 69.2 | 30.5 | 67.4 | 42.3 | 267.7 |
| Chron . | Lat. . | Long. . | Ω . | Rotation covariances . | |||||
|---|---|---|---|---|---|---|---|---|---|
| . | (°N) . | (°E) . | (degrees) . | a . | b . | c . | d . | e . | f . |
| Best-fitting | |||||||||
| 1n | −87.73 | 40.65 | 0.201 | 1.4 | −0.7 | −0.6 | 0.6 | −0.1 | 0.9 |
| 2n | −87.40 | 39.34 | 0.468 | 6.8 | 2.1 | −9.4 | 1.5 | −2.4 | 19.0 |
| 2An.1 | −84.21 | 39.84 | 0.740 | 14.5 | 3.5 | −8.8 | 2.4 | −0.8 | 14.8 |
| 2An.3 | −84.78 | 24.60 | 1.054 | 17.2 | 5.6 | −18.1 | 4.4 | −4.1 | 29.3 |
| 3n.1 | −84.12 | 29.80 | 1.236 | 21.4 | 7.0 | −23.9 | 5.2 | −4.8 | 42.7 |
| 3n.4 | −85.74 | 58.33 | 1.508 | 26.0 | 7.8 | −28.8 | 5.4 | −7.6 | 45.3 |
| 3An.1 | −86.68 | 59.57 | 1.679 | 23.0 | 4.4 | −25.2 | 5.1 | −3.6 | 41.1 |
| 3An.2 | −86.69 | 81.99 | 1.836 | 32.0 | 7.0 | −36.4 | 4.5 | −7.6 | 56.7 |
| 4n.1 | −85.54 | 97.44 | 2.125 | 39.7 | 9.9 | −44.8 | 6.7 | −12.9 | 66.3 |
| 4n.2 | −85.71 | 90.32 | 2.308 | 46.3 | 7.8 | −48.7 | 8.6 | −14.2 | 78.4 |
| 4A | −85.26 | 72.62 | 2.726 | 75.6 | 10.5 | −71.3 | 13.4 | −24.0 | 97.3 |
| 5n.1 | −85.35 | 72.60 | 2.894 | 93.1 | 31.5 | −95.0 | 18.4 | −39.2 | 121.6 |
| 5n.2 | −85.64 | 91.33 | 3.290 | 33.3 | 7.2 | −31.1 | 5.1 | −8.0 | 45.9 |
| 5An.2 | −85.10 | 86.78 | 3.858 | 40.0 | 8.8 | −40.2 | 7.4 | −13.6 | 60.5 |
| 5AC | −84.99 | 84.56 | 4.422 | 33.6 | 5.9 | −25.8 | 7.2 | −8.4 | 34.4 |
| 5AD | −83.58 | 107.44 | 4.733 | 42.3 | 8.6 | −37.3 | 9.4 | −10.6 | 50.1 |
| 5Cn.1 | −84.18 | 89.92 | 5.418 | 231.6 | 45.0 | −251.7 | 40.0 | −91.3 | 366.7 |
| 6ny | −84.10 | 104.34 | 6.456 | 502.5 | 23.7 | −321.5 | 31.6 | −28.1 | 271.9 |
| 6no | −83.65 | 133.85 | 6.405 | 75.5 | 27.6 | −46.0 | 46.8 | −14.8 | 73.4 |
| Noise-reduced | |||||||||
| 1n | −85.92 | 36.10 | 0.206 | 11.4 | −7.8 | 3.0 | 5.9 | −2.7 | 9.3 |
| 2n | −85.91 | 40.81 | 0.475 | 13.5 | −7.7 | 2.4 | 6.3 | −1.9 | 10.7 |
| 2An.1 | −85.86 | 43.53 | 0.700 | 16.9 | −7.7 | 2.1 | 7.2 | −1.3 | 13.2 |
| 2An.3 | −85.85 | 47.54 | 0.993 | 22.6 | −7.3 | 1.2 | 8.4 | 0.1 | 17.3 |
| 3n.1 | −85.89 | 50.12 | 1.164 | 26.2 | −6.9 | −0.1 | 9.1 | 1.5 | 19.6 |
| 3n.4 | −86.05 | 58.00 | 1.462 | 30.9 | −6.5 | −2.6 | 9.8 | 2.5 | 22.7 |
| 3An.1 | −86.11 | 66.12 | 1.685 | 39.7 | −9.5 | −5.5 | 12.6 | 3.0 | 28.9 |
| 3An.2 | −86.06 | 72.70 | 1.894 | 50.1 | −11.8 | −9.3 | 15.5 | 5.1 | 35.8 |
| 4n.1 | −85.93 | 77.70 | 2.151 | 57.3 | −10.6 | −11.8 | 16.6 | 5.5 | 41.1 |
| 4n.2 | −85.84 | 79.63 | 2.341 | 64.4 | −10.0 | −12.3 | 17.9 | 4.0 | 46.8 |
| 4A | −85.73 | 81.30 | 2.670 | 81.6 | −10.3 | −11.6 | 22.0 | −1.2 | 61.5 |
| 5n.1 | −85.66 | 82.52 | 2.895 | 96.7 | −11.1 | −12.3 | 25.5 | −5.7 | 74.0 |
| 5n.2 | −85.46 | 86.84 | 3.337 | 127.0 | −11.5 | −17.1 | 31.5 | −15.0 | 99.1 |
| 5An.2 | −85.06 | 93.79 | 3.885 | 153.9 | −4.9 | −29.6 | 33.9 | −18.7 | 119.9 |
| 5AC | −84.71 | 98.95 | 4.392 | 160.3 | 8.5 | −35.9 | 31.3 | −12.6 | 124.7 |
| 5AD | −84.49 | 102.09 | 4.743 | 168.7 | 16.2 | −31.3 | 33.3 | −5.4 | 132.6 |
| 5Cn.1 | −84.22 | 106.26 | 5.291 | 209.6 | 24.4 | −16.8 | 46.8 | 12.1 | 166.8 |
| 5D | −83.96 | 111.19 | 5.789 | 270.6 | 43.7 | 19.4 | 66.4 | 37.3 | 221.2 |
| 5E | −83.74 | 114.80 | 6.109 | 307.6 | 64.7 | 45.2 | 78.0 | 56.6 | 258.6 |
| 6ny | −83.56 | 119.01 | 6.343 | 332.9 | 83.5 | 63.4 | 84.3 | 68.8 | 285.6 |
| 6no | −83.32 | 133.62 | 6.622 | 322.3 | 69.2 | 30.5 | 67.4 | 42.3 | 267.7 |
These finite rotations reconstruct the Antarctic plate relative to the South America plate. The rotations labelled ‘best-fitting’ are determined from the best-fitting Nubia–South America rotations in Table S2 of the Supporting Information and best-fitting Nubia–Antarctic rotations from Table 2 of DeMets et al. (2015b). Rotations for chrons C5D and C5E were not estimated due to insufficient shipboard coverage of these two magnetic anomalies along the western third of the Southwest Indian Ridge. The rotations labelled ‘noise-reduced’, our preferred estimates, are determined from noise-reduced Nubia–South America rotations in Table 1 and noise-reduced Nubia–Antarctic rotations from Table S1 of the Supporting Information of DeMets et al. (2015b). The rotation angles Ω are positive CCW. All the covariances are Cartesian and have units of 10 −8 radians2. Both sets of covariances are tied to the Antarctic plate and specify the uncertainty in the location of the Antarctic plate upon its rotation onto the South America plate. Instructions for reconstructing the covariance matrix are given in Table 1 footnotes.
5.3.1 Poles and rotation uncertainties
The newly estimated Antarctic–South America best-fitting and noise-reduced poles (Table 4) are located near the South Pole, ≈30 arc-degrees south of the American–Antarctic Ridge (Fig. 17). Both sets of poles are scattered along a great circle that connects the poles to the geographic centre of the plate boundary (Fig. 17). Both also have error ellipses that are elongated parallel to that great circle. Together, these indicate that the distance between the poles and plate boundary is only weakly constrained by the Nubia–South America and Nubia–Antarctic rotations. The 1σ prediction uncertainties in the Antarctic-South America opening distances, which approximate a lower threshold for detecting non-closures of this plate circuit, increase gradually from ±2–3 km for the younger reversals (chrons C1n to C3n.4) to ±11km for chron C6. The uncertainties in fracture zone flow lines that are reconstructed with our noise-reduced rotations are somewhat smaller, ranging from ±1 km for chron C1n to ±6 km for chron C6.
5.3.2 Flow line comparison to seafloor bathymetry
Because our Antarctic–South America rotations predict the plate motion independent of any constraints from data along the American–Antarctic Ridge, the seafloor fabric and magnetic lineations created by seafloor spreading along the ridge can be used as independent checks of our rotations. Encouragingly, all eight fracture zone flow lines that are reconstructed with our noise-reduced rotations closely match their corresponding ENE-WSW-trending fracture zone valleys (Fig. 18). In contrast, flow lines that we derived from the chron C3An.2, C5n.2, C5Cn.3 and C6no rotation sequence of Eagles (2016; blue lines in Fig. 18) crosscut several prominent fracture zone ridges from 59–59.5°S (Fig. 18b) and generally mismatch the ENE–WSW-dominated fracture zone fabric. The latter flow lines, which trend significantly clockwise from our flow lines, are all located outside the 2-D, 1σ confidence regions for our reconstructed flow line locations (red-shaded ellipses in Fig. 18). Our newly determined rotations thus appear to satisfy the best-determined, independent constraint on closure of the Nubia–Antarctica–South America plate circuit, namely the American–Antarctic Ridge fracture zone flow lines.
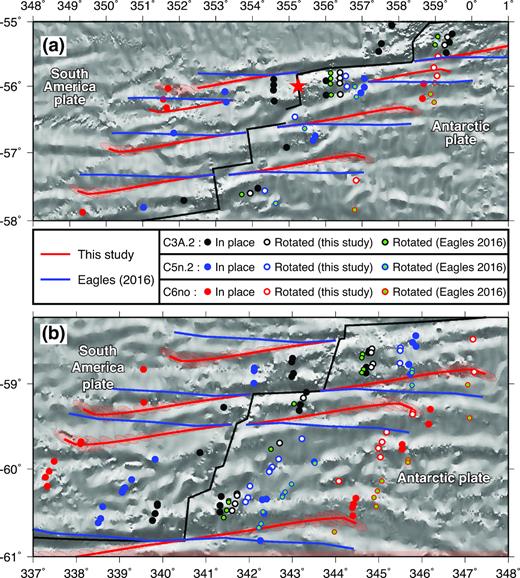
Fracture zone flow lines and chron C3An.2, C5n.2 and C6no reversal identifications on the Antarctic and South America plates reconstructed using noise-reduced rotations from Table 4 and from Eagles (2016; blue). The red-shaded areas along the reconstructed flow lines are the 1σ uncertainties propagated from the noise-reduced rotation covariances. The areas shown in (a) and (b) are included within the black rectangle identified in Fig. 17(b). All reversal identifications are from Eagles (2016).
5.3.3 Magnetic reversal reconstructions and evidence for a Sur microplate
We next evaluated the consistency of our rotations with constraints that are imposed by magnetic lineations C3An.2, 5n.2 and 6no that were identified Eagles (2016) along several American–Antarctic Ridge spreading segments and which are stored in the repository for marine magnetic identifications (Seton et al.2014). Using the noise-reduced rotations from Table 4, we rotated the crossings for all three of these magnetic reversals from their locations on the South America plate to their positions on the Antarctic plate (Fig. 18). We then compared their rotated locations to the in situ reversals on the Antarctic plate as identified by Eagles (2016).
Of the six spreading segments for which Eagles (2016) identified conjugate crossings of C3An.2 (solid black circles in Fig. 18), the reversal crossings from three of the spreading segments are more precisely reconstructed by our closure-derived C3An.2 rotation than by the best-fitting C3An.2 rotation estimated by Eagles (2016; Fig. 18). The Eagles (2016) rotation better reconstructs the conjugate reversal crossings for two other segments and the fits are equivalently good for the spreading segment located just north of 59°S (Fig. 18b). The good fits of our C3An.2 rotation for some of the conjugate segments are encouraging; however, the poor fit for the crossings from the conjugate segment at 56°S is troubling and leaves unanswered the question of whether circuit closure is fully satisfied for chron C3An.2.
Of the four spreading segments for which Eagles (2016) identified conjugate crossings of chron C5n.2, our closure-derived chron C5n.2 rotation under-rotates the reversal crossings for all four segments by 10–15 km (Fig. 18). Similarly, of the three spreading segments with conjugate crossings of C6no, our chron C6no rotation under-rotates the reversal crossings for all three segments by 30–45 km (Fig. 18). Both misfits equal or exceed the ±13 and ±22 km 95 per cent opening distance uncertainties that are propagated, respectively, from our C5n.2 and C6no rotation covariances.
Possible explanations for the systematic under-rotations of chrons C5n.2 and C6no include misidentifications of chrons C5n.2 and C6no along the American–Antarctic Ridge or deformation within one or more of the Nubia, Antarctic or South America plates. We consider it unlikely that previous authors have systematically misidentified chrons 5 and 6 everywhere along the American-Antarctic Ridge, but cannot categorically exclude this possibility without compiling and interpreting the original magnetic data, which is beyond the scope of this study. It also seems unlikely that deformation within the Nubia or Antarctic plates is responsible for the C5n.2 and C6no under-rotations. Deformation between west and east Antarctics before 11 Ma (Granot & Dyment 2018) cannot be the cause of the under-rotation since it did not affect areas of Antarctica relevant to the Nubia–South America–Antarctic plate circuit. More generally, if distributed deformation within either or both of the Nubia or Antarctic plates were biasing our Antarctic–South America rotations, it is unlikely that our Antarctic–South America rotations would predict flow lines that closely match the American–Antarctic Ridge fracture zone fabric (Fig. 18).
We instead suggest that the oceanic lithosphere subducting along the South Sandwich trench has detached from and moves more rapidly westwards (i.e. towards the subduction zone) than does the remainder of the South America plate, possibly as part of the postulated Sur microplate (DeMets et al.2010). Seismic evidence for left-lateral slip along reactivated fracture zones between the South Sandwich trench and American–Antarctic Ridge is consistent with more rapid subduction of the lithosphere between the ridge and trench (shown in fig. 18 of DeMets et al.2010). The 10–15 km and 30–45 km under-rotations of our chron C5n.2 and C6no Antarctic–South America rotations imply that seafloor accretion across the American–Antarctic Ridge has been ≈1–2 km Myr−1 faster than is predicted by our closure-derived rotations, which implicitly assume a rigid South America plate. The Sur-South America angular velocity estimated by DeMets et al. (2010) similarly predicts 1–2 km Myr−1 of SW-directed Sur plate motion relative to the South America plate during the past 3.16 Myr.
5.3.4 Stage velocities and kinematic implications
Fig. 19 shows Antarctic–South America stage velocities along a flow line near the midpoint of the American–Antarctic Ridge as estimated with angular velocities from Table S5 of the Supporting Information, which were derived from the noise-reduced finite rotations in Table 4. The new angular velocities predict an ≈60 per cent gradual slowdown in the seafloor spreading rates since 20 Ma (Fig. 19a). The instantaneous motion predicted at the same location by the GEODVEL Antarctic–South America angular velocity differs by only 0.6 mm yr−1 and 2.1° from our 0.78-Ma-average velocity (Fig. 19). Our youngest rotations thus appear to accurately describe the recent plate motion. Our velocity history corroborates evidence from lower-resolution models that the spreading rate decreased sometime during the past 20 Myr (Nankivell 1997; Eagles 2016; dashed lines in Fig. 19a), but reveals for the first time that the spreading-rate slowdown was gradual rather than abrupt.
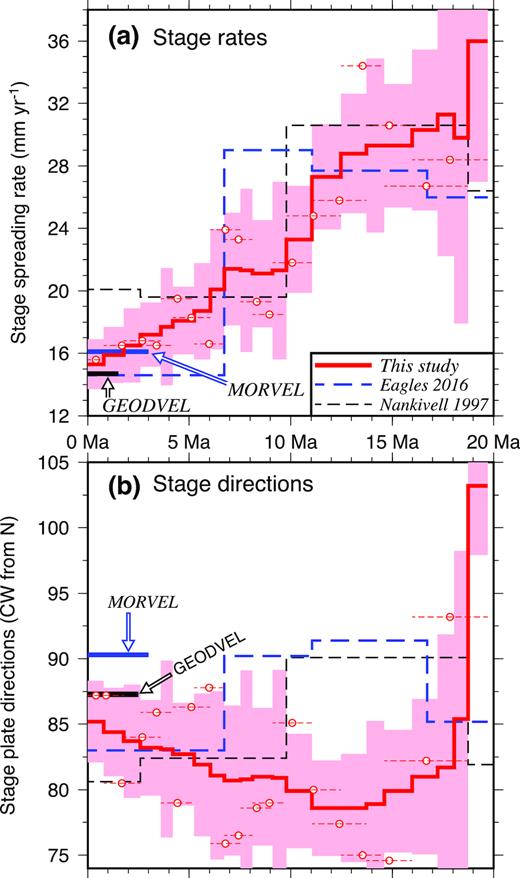
Antarctic–South America rates (a) and directions (b) along a South America plate flow line that originates at the location of the red star in Fig. 18(a). Interval rates are predicted using the noise-reduced stage angular velocities in Table S5 of the Supporting Information, the MORVEL (DeMets et al.2010) and GEODVEL (Argus et al.2010) angular velocities and angular velocities determined from chron C3An.2, C5n.2 and C6no finite rotations from Eagles (2016) and chrons C2An.1, C5n.1 and C6ny from Nankivell (1997).
Fig. 20 shows selected Nubia–Antarctic–South America velocity triangles at the Bouvet triple junction spanning the past 14 Myr. The evolution through time of the geometries of the velocity triangles illustrates how the well-defined gradual slowdown in Nubia–South America seafloor spreading rates combined with the steady Nubia–Antarctic velocities had to have been accompanied by a slowdown in Antarctic–South America rates in order to satisfy closure of this three-plate circuit. Fig. 20 illustrates another seemingly robust consequence of the southern Mid-Atlantic spreading rate slowdown, namely, a progressive clockwise rotation of Antarctic–South America slip directions and thus apparent anticlockwise changes in the orientations of progressively older portions of the fracture zone flow lines. The closure requirements that are imposed by the linear velocity triangles in Fig. 20 appear to preclude purely E–W slip directions at any point since 14 Ma or any anticlockwise rotation of the slip directions, contrary to the flow lines (Fig. 18) and stage slip directions (Fig. 19b) that are predicted by finite rotations estimated by Eagles (2016).
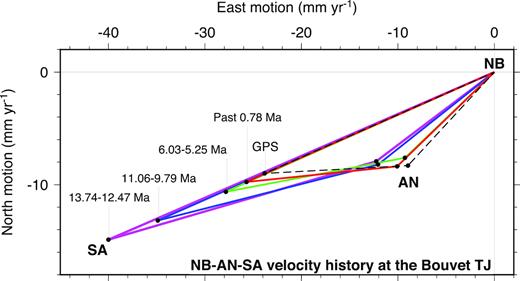
Velocity diagram for the Nubia–Antarctic–South America plate circuit at the Bouvet Triple Junction 54.8°S, 0.0°E, 14 Myr to the present, from Nubia–South America noise-reduced angular velocities (Table 2), Nubia–Antarctic noise-reduced angular velocities from DeMets et al. (2015b), the GEODVEL Nubia–South America angular velocity (Argus et al.2010) and a Nubia–Antarctica GPS-derived angular velocity from DeMets et al. (2017; both labelled GPS and indicated by the dashed black lines).
6 IMPLICATIONS
6.1 Geodynamic implications and limitations
A key goal of our analysis was to ascertain whether southern Atlantic seafloor spreading rates declined during the past 20 Ma, as predicted by geodynamic models that link the torques acting on western South America to a well-documented slowdown in Nazca–South America plate convergence rates (Iaffaldano & Bunge 2009; Colli et al.2014). Our analysis unequivocally demonstrates that southern Atlantic seafloor spreading rates have declined by 40–45 per cent since 24–20 Ma (e.g. Figs 10 and 11). Spreading-rate histories determined from Mid-Atlantic Ridge data south and north of 20°S independently confirm the existence and magnitude of the slowdown (Fig. 12), indicating that it is a robust outcome of our analysis.
The transition at 24–22 Ma from apparently steady Nubia–South America plate motion to continuously slowing motion (e.g. Fig. 13a) may be evidence for a significant change in the balance of the torques that were acting on one or both of the South America and Nubia plates before and after 24 –22 Ma. The 40–45 per cent slowdown in Nubia–South America seafloor spreading rates during this period, which coincided with a 50 per cent slowdown in Nazca–South America convergence rates since 25 Ma (Somoza & Ghidella 2012) and increasing paleoelevations in the Andes of western South America (Colli et al.2014) indirectly supports a linkage between a change in the torques that were acting on South America’s western boundary and the southern Atlantic spreading rate slowdown. Other notable tectonic events at 24–22 Ma that could have affected the balance of torques acting on the Nubia or South America plates include a factor-of-two spreading rate slowdown along the Southwest Indian Ridge between 30 and 20 Ma (Patriat & Sloan 2008) and the fission of the former Farallon plate into separate Cocos and Nazca plates at 23 Ma (Lonsdale 2005).
Although a continuous-change model nicely captures the first-order slowdown in Nubia–South America seafloor spreading rates since ≈20 Ma (Figs 10 a and 13a), other robust features of our new kinematic estimates include a rapid decline in spreading rates from 7–6 Ma and more slowly declining spreading rates during the past 6 Ma (Section 5.1.3 and Figs 10–12). High-resolution reconstructions of Neogene seafloor spreading along the Eurasia–North America, Nubia–North America, Nubia–Antarctic, Lwandle–Antarctic and Somalia–Antarctic plate boundaries reveal similar slowdowns at 7-6 Ma in seafloor spreading rates along all five plate boundaries (Merkouriev & DeMets 2014a,b; DeMets et al.2015a,b), but no evidence for widespread sustained slowdowns since 20 Ma. We thus speculate that the forces that were responsible for the widely observed seafloor spreading rate decrease at 7–6 Ma (e.g. Iaffaldano & DeMets 2016) were different from the forces that triggered and sustained the long-term slowdown in Nubia–South America motion during the past ≈20 Myr.
Given the larger scatter in our best-fitting Nubia–South America stage rates before 22 Ma (Figs 10a and 11b,c), it may be premature to use them for detailed geodynamic modelling. Most of the scatter may be attributable to larger likely errors in the GTS12 estimates of the ages of magnetic reversals older than chron C6. Since the publication of the GTS12 reversal age timescale, refined ages have been published for 14 of the 23 reversals that are used herein between chrons C13 and C5An.2 (33.7–12.5 Ma). Future reversal timescales that integrate these and other astronomically tuned reversal ages in a consistent manner can be easily applied to the Nubia–South America rotations in Table 1 to rederive noise-reduced rotations and, via circuit closures, all the other rotations and angular velocities that are described above.
6.2 Comparisons to previous plate motion estimates
Cande et al. (1988), Shaw & Cande (1990), Nankivell (1997) and Muller et al. (1999) estimated Nubia–South America rotations for chrons C5n.1, C6ny, C8n.1 and C13ny and are thus easily compared to our results for these four reversals. Encouragingly, all four of the previously published pole sequences migrate towards the NNW by several angular degrees between C13 and C5n.1, consistent with our own results (Figs 9 and 21). In detail, our newly estimated poles differ significantly from some of the earlier determinations. For example, our well-constrained C6ny pole and that of Nankivell (1997) differ by far more than their estimated 95 per cent pole uncertainties (Fig. 21). This strongly suggests that the uncertainties in the Nankivell (1997) and possibly our own pole are underestimated. Remarkably, the four most recently published estimates of the chron C13ny pole location, including our own, are located within 1.0 angular degree of each other (Fig. 21). We attribute the consistency of our new and previous estimates to the abundant fracture zone and magnetic reversal data from the southern Atlantic basin and their broad geographic distribution.
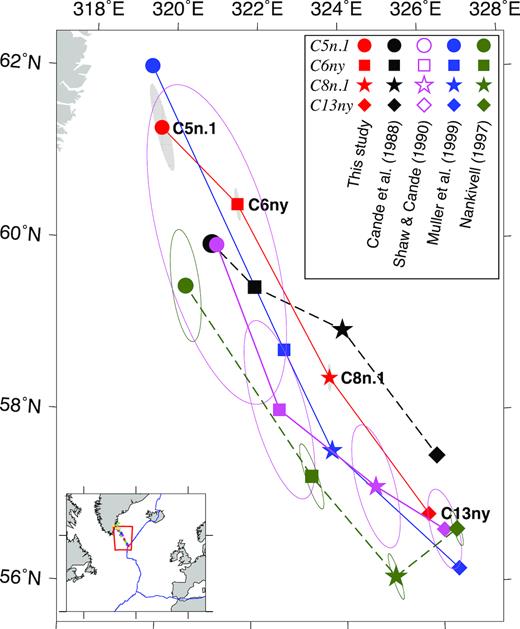
Comparison of Nubia–South America finite rotation poles for this study (Table 1) and previous studies. All ellipses show 2-D, 95 per cent pole confidence regions.
Figs 10(c) and (d) compare stage velocity histories estimated from our own finite rotations and rotations estimated by previous authors. The stage slip directions estimated with our own and previous rotations largely agree (Fig. 10d), which we attribute to the strong constraints that the southern Atlantic fracture zones impose on our own and previous estimates of Nubia–South America poles. The stage rates we determined from the Cande et al. (1988), Weiland et al. (1995) and Muller et al. (1999) rotations change more erratically than do the stage rates estimated with our noise-reduced and best-fitting angular velocities. Relative to the instantaneous opening rate that is predicted at 10°S by the GEODVEL angular velocity (Figs 10a,c), previously published estimates of recent Nubia–South America motion predict seafloor spreading rates that are 4–6 mm yr−1 (13–20 per cent) faster during the past few Myr. In contrast, our 0.78-Ma-average best-fitting and noise-reduced angular velocities predicted spreading rates that are only 1.5 mm yr−1 faster than predicted by GEODVEL (Fig. 10a).
6.3 Accommodation of North America–South America plate motion near the Mid-Atlantic Ridge
Although the Royal Trough does not extend into Mid-Atlantic Ridge seafloor any younger than 11 Myr old (Fig. 16c), the earthquakes and young volcanics associated with this enigmatic feature strongly suggest that it is an active, obliquely divergent structure associated with the North America–South America plate boundary (Roest & Collette 1986). Within the younger seafloor between the Mid-Atlantic Ridge and the eastern end of the Royal Trough, a transit multibeam track appears to cross a previously unrecognized, E–W trending fault that crosscuts at right angles the Mid-Atlantic Ridge abyssal hill fabric (labelled ‘Cross-cutting graben’ in Fig. 16c). We postulate that this feature and other as-yet undiscovered structures connect eastwards to the Mid-Atlantic Ridge and accommodate some of the plate motion. Structures close to the ridge axis may be difficult to locate given the small amount of ridge-normal extension that our rotations predict within the near-ridge seafloor (e.g. Fig. 16c). They may instead be easier to locate by their elevated seismic activity given that deformation rates between North and South America increase eastward towards the ridge (Fig. 14).
Other near-ridge structures almost surely also accommodate some motion between North and South America. For example, Escartin, Smith & Cannat (2003) report numerous earthquakes at 13.5–14°N, ≈250 km south of the Royal Trough and 70 km west of the Mid-Atlantic Ridge (also see Fig. 14). The tensional axes for these earthquakes are consistent with the predicted plate motion (Fig. 14b) and may thus identify structures that are part of a several-hundred-km-wide diffuse plate boundary.
7 CONCLUSIONS
High-resolution sequences of best-fitting and noise-reduced finite rotations and their associated stage angular velocities for the Nubia–South America plate pair are derived from ≈7000 crossings of 37 magnetic reversals spanning chrons C1n to 13no and ≈29 000 crossings of 43 transform faults and fracture zones in the central and southern Atlantic basin, including Russian shipboard magnetic data not previously used for this type of analysis. The newly estimated rotations and angular velocities reveal several important features of the recent kinematics of these two plates, as well as for the North America–South America and Antarctic–South America plate pairs, as follows:
Nubia–South America seafloor spreading rates decreased by 40–45 per cent everywhere in the central and southern Atlantic during the past ≈20 Myr (Figs 10a, 11 and Fig. 15a). To first order, seafloor spreading rates appear to have slowed continuously since ≈20 Ma (Fig. 13a), including more rapid slowing from 7–6 Ma (Fig. 10a), when abrupt slowdowns also occurred in the northern Atlantic and Arctic basins (Merkouriev & DeMets 2008; 2014a,b) and along the Southwest Indian Ridge (DeMets et al.2015b).
Newly derived, high-resolution rotation and angular velocity sequences for the North America–South America plate pair predict that their relative motion since 11 Ma has averaged 2.5–3 mm yr−1 at locations near the Mid-Atlantic Ridge, but has rotated anticlockwise by up to ≈90°. Our rotations predict that the relative motion across the extensional Royal Trough and Researcher Ridge has been divergent to obliquely divergent at all times since 20 Ma, with approximate net divergence of ≈50±5 km (95 per cent uncertainty). In contrast, obliquely convergent motion across the uplifted Barracuda Ridge and nearby structures near the Lesser Antilles trench is not predicted until after ≈14 Ma, when the pole of rotation migrated southwards to a location conducive to convergence across these structures.
New high-resolution sequences of rotations and angular velocities for the Antarctic–South America plate pair predict a gradual 60 per cent slowdown in seafloor spreading rates and gradual clockwise change in the plate slip direction since 20 Ma. Fracture zone flow lines that are predicted by our new rotations match the trends of fracture zone valleys and ridges along the American–Antarctic Ridge, suggesting that the closure-derived rotations are accurate. Our new rotations under-rotate conjugate crossings of chrons C5n.2 and C6no from the American–Antarctic Ridge by 10–15 km and 30–45 km, respectively. We interpret the under-rotations as evidence for slow (≈1 mm yr−1) westward movement of the postulated Sur microplate relative to the South America plate, in accord with elevated seismicity within the seafloor north and east of the South Sandwich trench.
SUPPORTING INFORMATION
Figure S1. Digitized fracture zone traces (black) compared to best-fitting (colour-coded lines) and noise-reduced (red lines) synthetic fracture zone traces, 2–15°N. The flow lines, which are created with the rotations in Tables S2 and Table 1 of the main document, assume symmetric seafloor spreading. The same fracture zones and flow lines are shown with bathymetry in Fig. 5 of the main document and Fig. S8a. Horizontal and vertical axes, respectively, show linear distance along or orthogonal to each fracture zone. Vertical-axis distances are exaggerated by three times relative to horizontal distances to emphasize the misfits. Zero distance on the horizontal axis marks the ridge-transform intersection for fracture zones that extend to the ridge . Transform faults are omitted from this plot.
Figure S2. Digitized fracture zone traces (black) compared to best-fitting (colour-coded lines) and noise-reduced (red lines) synthetic fracture zone traces, 2°N–15°S. The same fracture zones and flow lines are shown with bathymetry in Figs S4 and S5 (see the caption to Fig. S1 for further information).
Figure S3. Digitized fracture zone traces (black) compared to best-fitting (colour-coded lines) and noise-reduced (red lines) synthetic fracture zone traces, 33–50°S. The same fracture zones and flow lines are shown with bathymetry in Figs S7 and S8 (see the caption to Fig. S1 for further information).
Figure S4. Reconstructed (blue and red) and digitized (black) Nubia–South America fracture zone flow lines and transform faults and fracture zone crossings overlaid on GeoMapApp bathymetry, 2°N–8°S. The blue and red lines are best-fitting and noise-reduced flow lines, respectively. The solid circles are reversal identifications at their original locations. The open circles are reversal crossings rotated onto the opposite side of the ridge with the best-fitting rotations in Table S2. The red-shaded ellipses for selected flow lines show the 1 − σ uncertainties propagated from the noise-reduced rotation covariances. Reconstructions and the original magnetic data for the entire study area are shown at larger scale in Maps S1–S9.
Figure S5. Reconstructed (blue and red) and digitized (black) Nubia–South America fracture zone flow lines and transform faults and fracture zone crossings overlaid on GeoMapApp bathymetry, 10°S–19°S (see the caption to Fig. S4 for further information).
Figure S6. Reconstructed (blue and red) and digitized (black) Nubia–South America fracture zone flow lines and transform faults and fracture zone crossings overlaid on GeoMapApp bathymetry, 19°S–30°S (see the caption to Fig. S4 for further information).
Figure S7. Reconstructed (blue and red) and digitized (black) Nubia–South America fracture zone flow lines and transform faults and fracture zone crossings overlaid on GeoMapApp bathymetry, 30°S–42°S (see the caption to Fig. S4 for further information).
Figure S8. Reconstructed (blue and red) and digitized (black) Nubia–South America fracture zone flow lines and transform faults and fracture zone crossings overlaid on GeoMapApp bathymetry. Panel A shows the Strakhov flow line north of the equator and Panel B shows 44°S– 52°S fracture zones (see the caption to Fig. S4 for further information).
Figures S9 to S17 are large-scale maps that display the along-track magnetic anomaly data that were used for the study along with bathymetry and all of the in-place and reconstructed magnetic anomaly, fracture zone, and transform fault crossings for the Nubia-South America plate pair. Color-coded labels are included with each map to indicate which anomalies are displayed and reconstructed per map.
Table S1. Nubia–South America noise-reduced finite rotations.
Table S2. South America–Nubia noise-reduced stage angular velocities.
Table S3. South America–North America noise-reduced finite rotations.
Table S4. Antarctica–South America closure-derived rotations: best-fitting and noise-reduced.
Table S5. Antarctica–South America stage angular velocities.
Please note: Oxford University Press is not responsible for the content or functionality of any supporting materials supplied by the authors. Any queries (other than missing material) should be directed to the corresponding author for the paper.
ACKNOWLEDGEMENTS
We thank Roi Granot, Duncan Agnew and an anonymous reviewer for constructive reviews. This work was supported by grant 06-05-64297 from the Russian Foundation for Basic Research and U.S. National Science Foundation grant OCE-1433323. Figures were drafted using Generic Mapping Tools software (Wessel & Smith 1991).




