-
PDF
- Split View
-
Views
-
Cite
Cite
Huihong Cheng, Bei Zhang, Luyuan Huang, Huai Zhang, Yaolin Shi, Calculating coseismic deformation and stress changes in a heterogeneous ellipsoid earth model, Geophysical Journal International, Volume 216, Issue 2, February 2019, Pages 851–858, https://doi.org/10.1093/gji/ggy444
Close - Share Icon Share
SUMMARY
Coseismic deformation and stress change are important for geodetic interpretation and seismic hazard assessment. Most existing coseismic deformation models are based on the simplified geometry, such as the homogeneous half-space model or symmetric spherical earth model. In this work, taking the advantage of high-resolution parallel finite element methods, we construct a realistic full 3-D ellipsoidal earth model to properly account for the effects of topography, lateral heterogeneity, the curvature of the Earth and geometry variations at discontinuities (Moho/410 km/660 km) that are often ignored in the existing models. Our results show that, when calculating coseismic deformation and stress change induced by dislocations of large earthquakes, the relative error due to the Earth's curvature can be as high as 60 per cent, while the combined effects of topography and heterogeneity resulted in a 40 per cent discrepancy when the model is applied to, for example, the 2011 Tohoku Mw 9.0 earthquake, with the effect of the topography accounting for ∼10 per cent. The effect of the Earth's heterogeneity is more than 30 per cent in the case of the coseismic strain changes produced in northern China by the Tohoku earthquake. The effect of the Earth's ellipticity is relatively small, but should not be overlooked.
1 INTRODUCTION
A complete cycle of an earthquake includes nucleation, coseismic dislocation, energy release, relocking and potential recharge (Kanamori & Brodsky 2004; Sun et al.2014). Among them, the instantaneous coseismic deformation is the predominant process for ground deformation, stress redistribution and energy potential release following an earthquake. Dislocation theory is used to calculate coseismic deformation and stress change that are responsible for other important issues, for examples, dynamic fault propagation, the distribution or triggering of aftershocks and the evaluation of seismic hazard (Lay et al.2011; Lin et al.2002; Zhang et al.2015a; Tung & Masterlark 2016). Using fault rupture models based on inversion of seismic waves, one can quickly calculate the coseismic changes of the Coulomb Failure Stress (ΔCFS) on fault planes, which can help further evaluate the stability of earthquake affected faults (Steketee 1958; Hao et al.2009; Grandin et al.2015; Zhang et al.2015a; Xiong et al.2017). first introduced the dislocation theory into seismology. Others have developed several models to calculate the coseismic effects. Typical models include the half-space homogeneous medium model (Chinnery 1961; Press 1965; Okada 1985), the layered medium earth model (Okada 1992; Wang et al.2003), the homogeneous spherical model (Ben-Menahem & Singh 1968; McGinley 1969; Saito 1974; Sun 1992; Zhang et al.2015b; Dong et al.2016), and the heterogeneous spherical model (Rudle 1982; Sabadini et al.1995; Wang 1999; Fu & Sun 2007, 2008; Fu et al.2010). These models and related investigations promoted the awareness of coseismic effects and enhanced our understanding of earthquake rupture processes. In particular, the half-space homogeneous model developed by Okada (1985) is broadly used as the analytical expression of the dislocation theory. Wang et al. (2003, 2006), as well as other researchers, improved on it and developed the half-space layered elastic and viscoelastic medium models, which were capable of calculating the coseismic and post-seismic displacements, stress change and gravity field changes. The open source Fortran EDGRN/EDCMP programs are also widely shared. In recent years, the updated models developed by Okada (1992), Wang et al.(2003, 2006), Sun (1992), and Coulomb 3 Software package developed by USGS (https://earthquake.usgs.gov/research/software/coulomb/) are widely adopted to address the calculation of coseismic, post-seismic effects and the related issues.
These models involves varies simplifications that makes them inadequate for explaining high-resolution geodetic observations. For instance, half-space model is incapable of taking the role of the Earth's curvature into consideration. But many studies proved that, to some extent, systematic model errors should arise when the effect of the Earth's curvature was not considered (Ben-Menahem et al.1969; Ben-Menahem & Israel 1970; Amelung & Wolf 1994; Pollitz 1996; Antonioli et al.1998; Nostro et al.1999, 2001; Sun & Okubo 2002; Dong et al.2014). Moreover, using weight-free global homogeneous model, Ben-Menahem et al. (1969, 1970) concluded that the maximum error due to the influence of the Earth's curvature was even up to 30 per cent for an M8.5 earthquake. Pollitz (1996) proposed that the influence of the Earth's curvature could not be ignored while free-oscillation method is applied to calculate coseismic displacement, especially when the area of interest is more than 100 km away from the epicentre. Sun & Okubo (2002) and Dong et al.(2014, 2016) also discussed the effect of the Earth's curvature by homogeneous half-space and SNREI (Spherically Symmetric, Non-Rotating, Elasticand Isotropic) earth model (Dahlen 1968), respectively. They argued that the effects both of the Earth's curvature and stratification should be considered.
Some previous studies investigated the effect of the Earth's curvature, analysing it based on point dislocation or finite fault sources along the Equator or a great circle (Sun & Okubo 2002; Fu et al.2010; Dong et al.2014). Only a few models fully considered the effects of the realistic Earth's curvature, ellipticity, heterogeneity and topography. Cesca et al. (2000) found that stratification of the lithosphere and mantle had major impact on the results of co- and post-seismic deformations. Using a 2-D finite element model, Lin & Sun (2014) showed discrepancies up to 55 per cent between models with and without considering topographic effect for the 2011 Tohoku Mw 9.0 earthquake.
In this study, based on high-performance finite element method and equivalent body force technique (Zhang et al.2015b), we constructed a fully 3-D global ellipsoidal earth model that considers the Earth's curvature, topography, variations at discontinuities and lateral heterogeneity for coseismic deformation. In order to comprehensively examine the effects of these factors on the calculation of coseismic effects, we also established several comparison models. We present a case study of the 2011 Mw 9.0 Tohoku earthquake to quantitatively illustrate the importance of considering the Earth's heterogeneity and topography.
2 THE NEED FOR USING A SPHERICAL EARTH MODEL
Spherical earth models are need for two issues. One is the necessity of spherical coordinate system when large dimension or far field phenomena are studied; the other is the difference of strain/stress values by different ways of spherical surface projections during the visualization of the calculated results.
As noted previously, many researches (Pollitz 1996; Nostro et al.1999, 2001; Sun & Okubo 2002; Dong et al.2014) have shown that the effect of the Earth's curvature on the coseismic displacement should not be ignored. Because the coseismic strain and stress are the first derivatives of displacement, systematic errors are introduced when plane-space model is adopted without considering the spherical characteristics of the Earth (Shi & Zhu 2006). For example, the expressions of strain in the Cartesian coordinates differ from those in the spherical coordinates, in the latter the radial deformation contributes to both longitudinal and latitudinal strains. More naturally, when large-scale phenomena are considered, the spherical curvature cannot be ignored. As shown in Fig. 1(b), longitudinal deformation affects latitudinal strain, while latitudinal deformation generates shear strain too.
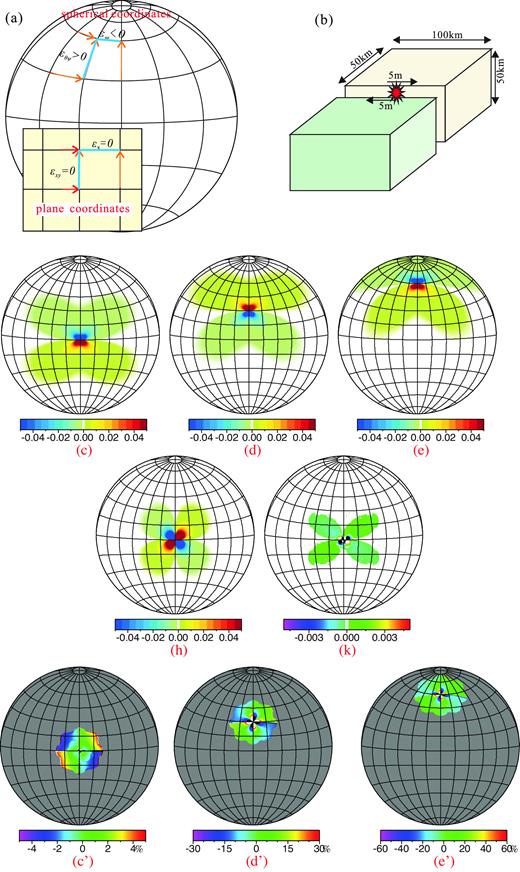
Difference of coseismic displacements between the half-space model and spherical model. (a) Sketch map of an hypothesized M 7.5 strike-slip earthquake; (b) Sketch map of the difference of coseismic displacement between half-space model and spherical model; (c–e) Surface coseismic displacements along the slip direction for the M7.5 strike–slip earthquake when projecting the results of half-space model on spherical coordinate system. Here, we adopt cylindrical projection. The hypocentres of the three models locate at the Equator, 30°N and 60°N, respectively; (h) Total horizontal plane coseismic strain changes along the latitude in spherical model; (k) Absolute errors (results of spherical model minus that of plane model) of the horizontal plane coseismic strain; (c’–e’) Relative errors of the horizontal plane coseismic strain when the earthquake occurring on the Equator, 30°N and 60°N, respectively. The relative error is equal to the ratio between the absolute errors and the results obtained with the spherical model.
Due to linearity of gradient operator, strain and stress are both linearly dependent on the first derivatives of displacement. When coseismic strain or stress is calculated, if only the Cartesian coordinate system, rather than the spherical coordinate system, is adopted, the system errors will be greater in the case of huge earthquakes. Under such case, the vast area on the Earth's surface is affected both horizontally and vertically deep in the crust. Compared to the gradient operator in spherical coordination system, although the system errors are not longitude/latitude dependent, their relative errors are identical because the results from Cartesian coordinate system neglect the effects of the radial direction.
Hence, to better reflect the effect of the Earth's curvature on coseismic strain or stress changes, we generated a global homogeneous spherical earth model with topography and ellipticity, based on high-performance parallel finite element method. This spherical model effectively avoids the uncertainties of the lateral boundary conditions. Adaptive mesh refinement technique is automatically adopted when the finite element mesh covering the fault zone, as devised by Zhang et al. (2015b). Our numerical procedures have been verified through benchmarking with EDGRN/EDCMP programs (Zhang et al.2015a,b). It proves that our spherical model is reliable, flexible and efficient. It is successfully applied to the coseismic displacement calculation of the 2015 Nepal M 8.1 earthquake (Zhang et al.2015a) and the 2016 Kaikoura Mw 7.8 earthquake (Cheng et al.2017).
Consider a model M 7.5 strike–slip earthquake. Assume the length of seismic fault is 500 km, its depth is 50 km and the average slip is 10 m, as shown in Fig. 1(a). We can get the coseismic displacements using the EDGRN/EDCMP programs, as shown in Fig. 1(c). The results should be the same regardless of where the earthquake occurs. However, this is not the case when Cartesian coordinate system is used, as shown in Figs 1(c)–(e).
Moreover, during the visualization of the calculated results, when projecting the results of the coseismic displacement obtained from models based on Cartesian coordinates on the spherical coordinates and without considering the topography and properties of crust, system errors inevitably appear due to the Earth's curvature, no matter what the projection method is applied. As shown in Figs 1(c’)–(e’), when projecting the results of the coseismic strain induced by the occurrence of an earthquake from Cartesian coordinates on the spherical coordinates, system errors occur with different project methods. Here, the total area is ∼9 × 106 km2.
3 EFFECTS OF THE EARTH'S ELLIPTICITY
The Earth is an approximate rotational ellipsoid with the flat rate around 1:298.257. Its diameter at the Equator is 43 km larger than the Pole-to-Pole diameter. Numerous investigations on the impact of the Earth's ellipticity have been undertaken in both astronomy and geodesy, especially with regards to the effects of the lunar tidal potential and tidal generation forces (Wilhelm 1983; Dahlen 1993; Roussel et al.2015; Chao 2017). However, the influence of Earth's ellipticity on the coseismic deformation calculation is poorly constrained. When the Earth's ellipticity is considered in analytical approach, it may greatly increase the complexity of solution and computation, or make a solution unreachable.
We again take the hypothesized M 7.5 strike-slip earthquake, as mentioned above, as an example to analyse the influence of the Earth's ellipticity and topography on the calculation of coseismic deformation. For comparison, we set up three groups of end-member models with finite seismogenic faults, that is, along the Equator, perpendicular to the Equator, and Pole-to-Pole, respectively. In order to obtain high-resolution results, the total number of finite elements is 1622 700. As shown in Fig. 2, the coseismic displacements differ between pure spherical model and ellipsoidal model when the epicentre is located on the Equator. The effect by the earth's ellipticity is less than 5 per cent. But the impact cannot be ignored if an earthquake occurs at high latitude. For example, as shown in Fig. 2, the absolute errors may reach up to 0.1 m with the relative error of more than 30 per cent when the epicentre is located at the North Pole.
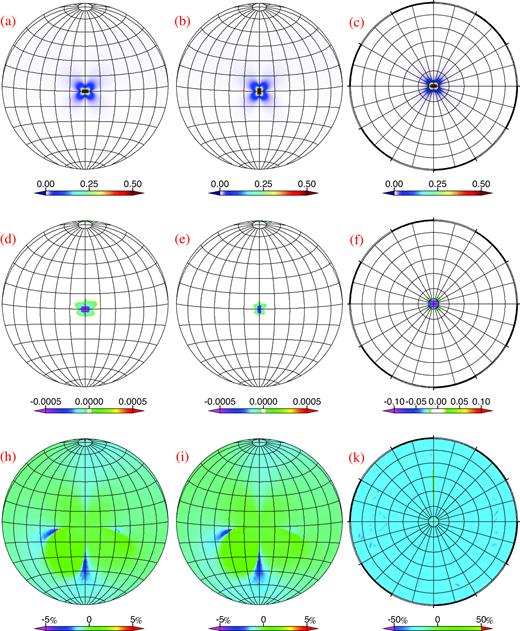
Effects of the Earth's ellipticity. (a–c) show calculated coseismic displacement along the different striking directions and locations; (d–f) exhibit the absolute errors when the ellipticity of the Earth is considered. The absolute error is the ratios of result obtained with the ellipsoid model and with the pure spherical model; (h–k) represent the relative errors. The relative error is equal to the ratio between absolute errors and the results obtained with the pure spherical model.
4 EFFECTS OF EARTH'S HETEROGENEITY AND TOPOGRAPHY
During the journey of complicated geological evolution, the Earth becomes tremendously heterogeneous with spectacularly varying topography. Modern geodetic technologies, seismic tomography, in situ borehole observation and other observational method have increasingly improved the constraints on the heterogeneous nature of the Earth. In recent years, considerable efforts have been devoted to examine the effects of the Earth's heterogeneity and topography on coseismic deformation. For example, Sun & Okubo (2002) found that the stratified Earth properties produced more than 25 per cent of variations of the computed coseismic displacement. Given the wide distribution over the shallow portion in the inversion of the coseismic slip distribution of the 2011 Mw 9.0 Tōhoku earthquake, Kyriakopoulos et al. (2013) proposed that the heterogeneous model could better fit the observations than the simple homogeneous model. In particular, Qu et al. (2016) found that more aftershocks occurred in those regions with a positive Coulomb Failure Stress Change (ΔCFS) when using a laterally heterogeneous model, and the maximum variations could reach 40 per cent due to the Earth's heterogeneity. Similarly, Lin et al. (2014) found that coseismic deformation could change as much as 55 per cent when the topographic effect was considered for the Tōhoku earthquake.
Neither the analytical solution of Okada (1992) nor the hierarchical model (Wang et al.2003) can account for the lateral heterogeneity. The 2-D model (Lin & Sun 2014) and the 3-D model based on perturbation theory (Fu & Sun 2007) cannot handle the realistic heterogeneity of the Earth either. In our 3-D model for coseismic deformation calculation, we address the heterogeneous and variable Moho discontinuities without distorting the mesh quality. Whereas, we interpolate the material parameters of the heterogeneity and discontinuity directly in association with the Gauss integration points during the numerical quadrature process. Therefore, finite element grids are not required to move when the finite element stiffness matrix and right-hand-side vector are formed. This offers higher accuracy of numerical quadrature during the element stiff matrix calculation than conventional mesh-based element stiff matrix calculation.
The heterogeneity parameters of our global 3-D heterogeneity model consists of two parts: the crustal parameters from CRUST 1.0 (Laske et al.2013), and the mantle parameters from GyPSuM (Simmons et al.2010). The new global CRUST 1.0 model (Laske et al.2013) is specified on a 1° × 1° grid resolution and consists of less than 40 crustal types. Each of the 1° × 1° cells has a unique 8-layer crustal profile. And, parameters VP, VS and density (rho) are given explicitly for these layers as well as the mantle below the Moho. The GuPSuM model (Simmons et al.2010) divides the earth into 22 layers from the earth's surface to the core–mantle boundary (CMB), and its resolution is also 1° × 1°. The maximum velocity variations of Pwave and Swave are 1.6 and 3.5 per cent, respectively, relative to the reference values.
The topography in our models are from ETOPO1 by NOAA National Center for Environmental Information (NCEI). Automatic adaptive mesh refinement is performed at regions with large displacement gradients to improve the numerical accuracy during the finite element calculation.
Boundary conditions are assigned as follows: Earth's surface is stress free, and the third-kind of boundary condition |${\rm{\sigma }} \cdot {\rm{n}} = - Ku + c$| at core-mantle boundary describing the buoyant force from the Earth's outer core, where K is selected as the Young's modulus of the lowermost mantle. The parameter c is a constant as the initial radial stress at the CMB, and is generally taken as 0 if no core-mantle coupling is considered. The global numerical model includes ∼6200 000 finite elements.
According to previous studies, it is clear that the influence of the Earth's heterogeneity and topography on coseismic effects varies with different regions on the Earth's surface. Considering that huge earthquakes often occur in subduction zones or collision zones, we can estimate the relative amplitudes of the effect of the Earth's heterogeneity and topography. Here we take the 2011 Tōhoku earthquake as an example to analyse the effects of the Earth's heterogeneity and topography on coseismic deformation calculation. This event caused unprecedented damages in Japan. Its coseismic displacement and stress change can be monitored in the farfield of the northeastern part of China (Wang et al.2011; Zhao et al.2012). The hypocentre is at a depth of 30 km located at (38.297°N, 142.372°E) (http://earthquake.usgs.gov/)(We want to modify it as Duputel et al. 2012 accroding to the https://earthquake.usgs.gov/earthquakes/eventpage/official20110311054624120_30/executive. The full details are 'Duputel Z., Rivera L., Kanamori H., Hayes G., 2012. W phase source inversion for moderate to large earthquakes (1990–2010), Geophys. J. Int., 189(2), 1125-1147. ), and the rupture area covers 400 × 200 km2 (Ozawa et al.2011; Zhou et al.2012; Dong et al.2014). During the calculation, we use the equivalent body force method, as described by Zhang et al. (2015b), to explicitly mesh the realistic fault plane parameters. We adopt the fault plane slip model by Simons et al. (2011) with 419 subfaults.
We compare the calculated results both in Japan and northeastern China with GPS observations from the Advanced Rapid Imaging and Analysis Center (ARIA) (http://aria.jpl.nasa.gov/), respectively, as shown in Figs 3(a–a’). Our results are in good agreement with the GPS observations. This huge event also caused coseismic displacement in northeastern China, where coseismic displacement is as much as 2 cm, leading to changes of extensional strain and stress in the E–W direction.
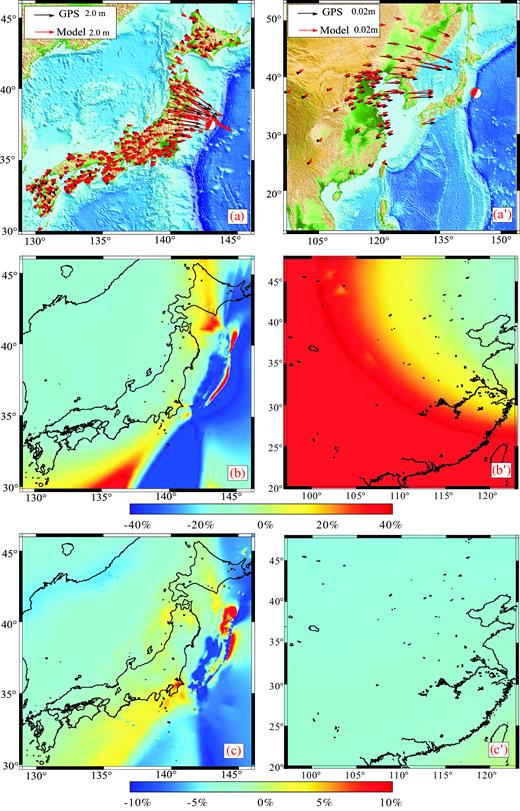
Coseismic displacements due to the occurrence of the 2011 Japan Tōhoku earthquake. (a–a’) Coseismic horizontal displacement by Tōhoku earthquake in Japanese and in northeastern China regions, respectively; (b–b’) Relative error of horizontal coseismic displacement due to without considering the effect of the Earth's ellipticity, heterogeneity and topography in Japanese region and in northeastern China region, respectively; (c–c’) Relative error of horizontal coseismic displacement induced by considering the Earth's topography in Japanese region and in northern China region, respectively. The absolute error is equal to the results obtained with the spherical model subtracted from those obtained with the complex model created in CRUST 1.0 with topography. The relative error is equal to the ratio between the relative error and the result obtained with the spherical model.
To further analyse the influence of the properties and topography of the Earth, we set up two groups of models for comparison. The results exhibit acute topographic undulation and sharp variations along the geological structures. Figs 3(b–b’) shows the relative errors of horizontal coseismic displacement incurred without considering the Earth's ellipticity, heterogeneity and topography. The maximum relative error can reach up to 40 per cent compared with the results of the realistic earth model. In addition, those areas with larger relative error are concentrated on the areas of sharp topographic relief around the Japan Trench, while less than 5 per cent are on Japanese mainland. Instead, the relative error exceeds 40 per cent in most areas with different crust material parameters in northeastern China. Figs 3(c–c’) shows the relative error of horizontal coseismic displacement when only the Earth's topography is considered; the maximum relative error reaches up to 10 per cent in Japan, while no more than 5 per cent in continent China.
5 CONCLUSIONS
Giant earthquakes can produce significant stress change on global scale. Since Lawson & Reid (1908) proposed the elastic rebound theory to explain the occurrence of earthquakes, modern observation networks have provided increasing amount of earthquake-caused deformation, promoting research of coseismic deformation in the Earth's crust. The introduction of the dislocation theory into seismology established the relationship between coseismic deformation and fault dislocation. Around 60 yr later, models by Okada (1985); Wang et al. (2003, 2006), and Sun (1992) are used to calculate coseismic deformation caused by huge earthquakes. There are now many different models, such as the half-space model, 1-D flatten model, and symmetric spherical earth model, to calculate the coseismic effects based on dislocation theory to interpret geodetic observations and assess seismic hazards following mega-earthquakes. However, the realistic Earth is a heterogeneous ellipsoid with topography, 3-D internal heterogenetic structures, and the viscosity structure that varies with time, all these factors could affect coseismic deformation.
In this paper, we focused on the effects of the Earth's curvature, ellipticity, heterogeneity and topography on the coseismic displacement and strain calculations. Our results underscore the important effects of the Earth's curvature, heterogeneity and topography that should be taken into account, especially in the case of mega earthquakes that rupture several hundred kilometres and produce both near and far-field deformation. Among these factors, the Earth's curvature and heterogeneity are most important. The maximum relative error due to the Earth's curvature can reach 4, 30 and 60 per cent when an Earthquake occurs at the Equator, 30°N and 60°N, respectively. On the other hand, taking the 2011 Tōhoku Mw 9.0 Earthquake as example, the effects of the crust material parameters can produce a discrepancy of 30–40 per cent for the coseismic displacement. Comparing with the relative error of the coseismic strain in the Japanese and northern China regions, we emphasize that crustal material parameters contribute significant to the results for northeastern China. The local topography has significant impact on results for Japan, the relative difference of the Earth's topography is about 10 per cent. Meanwhile, the influence of the Earth's ellipticity is relatively small. The effect of the Earth's ellipticity on the surface coseismic deformation is less than 5 per cent when the hypocentre is located at the Equator, and about 30 per cent at the Poles. Our results show the need for accurately addressing coseismic deformation and stress change problems with realistic earth model.
ACKNOWLEDGEMENTS
This research is supported by National Science Foundation of China (41590860, 2016YFC0600504 and 41725017). We acknowledge the variable ETOPO1 by NOAA National Centers for Environmental Information (NCEI), the CRUST1.0 contributed by Gabi Laske et al. (2013) and GyPSuM model developed by Simmons et al. (2010) used in this research. Data in association with this research are available at http://pan.baidu.com/s/1eSBrTbs.




