Comparison of seismic and geodetic strain rates at the margins of the Ordos Plateau, northern China

Middleton, Timothy A; Parsons, Barry; Walker, Richard T

doi:10.1093/gji/ggx446

Summary

Differences between seismic and geodetic strain rates can highlight regions of potential seismic hazard. In China, many of the most devastating historical and recent earthquakes have occurred around the margins of the Ordos Plateau. We construct an earthquake catalogue for the region that covers the 700 yr period from 1315 to 2015, and is thought to be complete for events with M_s > 6. We use Kostrov summations to determine a seismic strain rate tensor for each of the margins of the Ordos Plateau. We also use the latest campaign GPS data to calculate both a continuously varying geodetic strain rate field for the region and individual geodetic strain rate tensors for each of the plateau margins. We then compare our seismic and geodetic strain rate results to identify regions with seismic moment deficits and also calculate expected recurrence intervals from our geodetic moment rates. We find notable seismic strain rate deficits in northern Ningxia (to the west of the Ordos Plateau), in the Hetao and Linhe Grabens (to the north of the plateau), and in the Shanxi Grabens (to the northeast of the plateau). In the Weihe Graben (to the south of the plateau), although there is an overall seismic strain rate excess for the last 700 yr, there is some indication of relative quiescence for the last few centuries. Assuming no aseismic accommodation of deformation, these deficits indicate enhanced potential for large earthquakes in these regions in the future. Either temporal clustering of earthquakes or individual, large-magnitude events with long recurrence intervals could explain these patterns of moment release. Meanwhile, in southern Ningxia (to the southwest of the plateau) we find a seismic strain rate excess, indicating a likely lower level of seismic hazard in this region. In southern Ningxia and the Shanxi Grabens the pattern of strain suggested by the Kostrov summations is consistent with the geodetic strains. In northern Ningxia, the Hetao and Linhe Grabens, and the Weihe Graben—where there are fewer historical earthquakes and sparser GPS station coverage—the seismic and geodetic patterns of strain release are inconsistent.

Asia, Earthquake hazards, Seismicity and tectonics, Continental neotectonics

1 INTRODUCTION

Earthquake hazard in China is severe, and many of the most damaging historical earthquakes in China have occurred around the margins of the Ordos Plateau, including around 19 earthquakes with M_s ≥ 7 (Zhang et al. 2003). The 1556 Huaxian earthquake, which occurred in the Weihe Graben to the south of the Ordos Plateau, is thought to be the deadliest earthquake in history, resulting in the deaths of an estimated 830 000 people (Hou et al. 1998; Yuan & Feng 2010; Feng et al. 2017; Zhou 2016). Other major historical events include: the 1303 Hongdong earthquake on the Huoshan Fault, which killed ≈200 000 people, and the 1739 Yinchuan earthquake on the East Helanshan Fault, which killed ≈50 000 people (Middleton et al. 2016a). In the 20th century, earthquake deaths in China have accounted for more than 50 per cent of the global total (Jordan et al. 2011). Three of the ten deadliest earthquakes since 1900 have occurred in China, and all three had epicentres near the Ordos Plateau: the 1920 Haiyuan, 1976 Tangshan, and 2008 Wenchuan events.

High population densities around the Ordos Plateau make the region particularly susceptible to earthquake disasters. The plateau spans parts of the provinces of Inner Mongolia, Ningxia, Gansu, Hebei, Beijing, Shanxi and Shaanxi, which have a combined population of over 220 million people; and the adjacent North China Plain is one of the most densely populated regions on the planet (see Fig. 1 a; note the logarithmic colour scale). The population density is particularly high at the margins of the Ordos Plateau, immediately adjacent to the main active faults because attractive locations for settlements (in terms of topography and water supply) have been directly controlled by the tectonics.

Figure 1.

(a) Population density map for northern China based on 2015 census data and adjusted to match the 2015 revision of the United Nations World Population Prospects country totals (Columbia University 2015; Doxsey-Whitfield et al. 2015). Colour indicates the number of people per square kilometre on a logarithmic scale. (b) Map of seismic hazard from the Global Seismic Hazard Assessment Program (GSHAP; Zhang et al. 1999). Colours indicate the peak ground acceleration (in ms⁻²) with a 10 per cent exceedance probability in the next 50 yr. (c) SRTM topography in northern China (Farr et al. 2007). Red box shows location of Fig. 2. Inset globe shows the location of these three figures within Asia.

Open in new tab Download slide

The first Chinese seismic hazard maps were produced in the 1950s on the principle that earthquakes of the same magnitude were likely to recur in locations where they had occurred previously (Zhang et al. 1999; Jordan et al. 2011). A second version was published in 1977 and was used to inform national building codes (Zhang et al. 1999; Jordan et al. 2011). The seismic hazard map shown in Fig. 1(b) was constructed as part of the Global Seismic Hazard Assessment Program (GSHAP) and is based on historical earthquake catalogues and previously defined ‘seismic zones’ (Zhang et al. 1999). The map clearly highlights regions of hazard at the margins of the Ordos Plateau, but many of the regions of highest hazard simply correspond to the locations of recent earthquakes, such as the 1920 Haiyuan event and the 1966 Xingtai earthquakes to the east of the plateau. The usefulness of this sort of hazard map, especially in continental regions that are known to have faults with low slip rates and long recurrence intervals, has therefore been questioned (Stein et al. 2012; Stein & Friedrich 2014). For example, Fig. 1(b) does not highlight the Longmenshan as a region of notable hazard, and yet this was the location of the subsequent 2008 Wenchuan earthquake.

An alternative approach to seismic hazard has therefore been to use geodetic measurements to map the current rate of strain accumulation. Assuming no aseismic deformation, regions which show a shortfall in seismic strain compared to geodetic strain are likely to be regions of high seismic risk in the near future, whilst regions with excess seismic strain compared to geodetic strain are likely to be regions of lower seismic risk. However, the length of the earthquake catalogue must be comparable to the recurrence interval of the largest earthquake for reliable seismic strain rates to be estimated. China has arguably the longest and most complete historical earthquake records of anywhere in the world, extending back well over 2000 yr (Lee et al. 1976, 1978; Wang 2004; Liu et al. 2011), making it one of the best possible places to attempt this analysis.

In this study, we use Kostrov’s relation to calculate seismic strain rate tensors for each of the deforming margins of the Ordos Plateau, aiming to assess and update the previous calculations from Wesnousky et al. (1984). We also calculate the magnitudes and azimuths of the principal seismic strain rates, which Wesnousky et al. (1984) did not do. We then compare our results to geodetic strain rates derived from the latest campaign GPS measurements (Zhao et al. 2015) in order to assess the future seismic hazard at the margins of the Ordos block. Finally, we consider our results in relation to Wang et al. (2011), who used an elastic block model with the GPS data from Zhang & Gan (2008) to determine slip rates and seismic moment deficits on major active faults throughout China. We prefer to consider a continuously varying geodetic strain rate field so that the choice of block boundaries does not unduly influence the moment rate for a given seismic zone, though we note that both methodologies assume elastic behaviour of the upper crust.

2 METHODS

2.1 Kostrov summations

Kostrov (1974) showed that the strain rate tensor for N earthquakes that have occurred in a volume V can be calculated from

\begin{equation} \dot{\epsilon }_{ij} = \frac{1}{2 \mu \tau V}\sum _{n = 1}^{N}M_{ij}^{n}, \end{equation}

(1)

where |$\dot{\epsilon }_{ij}$| is the ijth component of the strain rate tensor, μ is the rigidity modulus, τ is the time period of observation, and |$M_{ij}^{n}$| is the ijth component of the seismic moment tensor of the nth earthquake. Wesnousky et al. (1984) used a total catalogue of 19 earthquakes with magnitudes greater than 6.5 from between 1278 and 1984. However, on the basis of population density maps and Gutenberg–Richter statistics, the earthquake catalogues in the Ordos region are thought to be complete for earthquakes with M_s ≥ 6 since 1291 (i.e. soon after the beginning of the Yuan Dynasty in 1271) and M_s ≥ 4.75 since 1484 (Huang et al. 1994). We therefore constructed a catalogue of 54 earthquakes with M_s > 6 for the 700 yr period from 1315 to 2015 based on Lee et al. (1976), Lee et al. (1978), Liu et al. (2011), the China Seismological Bureau (CSB) catalogue (Qin et al. 2002), and the Global Centroid Moment Tensor (GCMT) catalogue (see Data and Resources Section). We also included an additional 34 earthquakes with 5 < M_s ≤ 6, based on the same sources, for which focal mechanisms have already been inferred—but we note that the catalogue is not necessarily complete over this magnitude range. In total, our catalogue includes 88 earthquakes (see Table 1). In addition we note from Gutenberg-Richter statistics, assuming a maximum moment magnitude for the region of M_w 8.0, that ≈90 per cent of the moment release is expected to be in earthquakes of magnitude greater than 6.0. In other words, our incomplete catalogue for magnitudes less than 6.0 will not significantly affect our results.

Table 1.

Open in new tab

Focal parameters for historical earthquakes around the Ordos Plateau.

Year	Month	Day	Lat (°)	Long (°)	M_w^a	M₀^b (Nm)	Eq. ref.	Strike (°)	Dip (°)	Rake (°)	FP ref.	Assigned fault	FP notes
1337	9	8	40.4	115.7	6.5	6.24 × 10¹⁸	Lee et al. (1976)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1352	4	18	35.6	105.3	6.8	1.90 × 10¹⁹	Lee et al. (1976)	130	45	90	Wesnousky et al. (1984)		In literature
1363	7	8	37.6	112.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	50	60	−90	This study	Jiaocheng Fault	Nearest fault
1467	6	18	39.6	112.3	5.5	1.97 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1477	5	13	38.5	106.3	6.5	6.70 × 10¹⁸	Lee et al. (1976)	30	75	−150	Wesnousky et al. (1984)		In literature
1484	2	7	40.5	116.1	6.8	1.76 × 10¹⁹	Liu et al. (2011)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1487	8	19	34.4	108.9	6.3	3.13 × 10¹⁸	Liu et al. (2011)	270	60	−90	This study, Rao et al. (2015)	Lishan Piedmont Fault	Nearest fault
1495	4	10	37.6	105.6	6.3	2.63 × 10¹⁸	Lee et al. (1976)	120	45	45	This study, Liu-Zeng et al. (2015)	Zhongwei-Tongxin Fault	Nearest fault
1501	1	29	34.8	110.1	7.0	3.30 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1502	12	4	39.0	112.6	5.3	9.89 × 10¹⁶	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1514	10	30	38.7	113.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	129	85	18	This study		Nearest instrumental eq
1545	2	x	40.0	114.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	250	65	−135	This study, Li et al. (2015a)	Liulengshan Fault	Nearest fault
1556	1	23	34.5	109.7	7.9	8.32 × 10²⁰^c	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)	Huashan/Weinan Tableland Fault	Zhou (2016)
1561	7	25	37.4	106.0	7.2	6.90 × 10¹⁹	Lee et al. (1976)	145	30	90	Wesnousky et al. (1984)		In literature
1568	5	15	34.4	109.0	6.8	1.80 × 10¹⁹	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)		In literature
1573	1	10	34.4	104.0	6.8	1.48 × 10¹⁹	Lee et al. (1976)	196	57	151	This study, Zheng et al. (2007)	Lintan-Dangchang Fault	Nearest instrumental eq
1580	9	15	39.5	112.3	5.8	5.56 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1581	5	18	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1583	5	18	39.7	113.8	5.5	1.97 × 10¹⁷	Lee et al. (1976)	225	65	−116	This study, Li et al. (2015a)	Hengshan Fault	Nearest fault
1604	10	25	34.2	105.0	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1614	10	23	37.2	112.1	6.0	1.11 × 10¹⁸	Liu et al. (2011)	230	60	−65	Li et al. (2015a)	Jiexiu-Taigu	In literature
1618	5	20	37.0	111.9	6.0	1.11 × 10¹⁸	Liu et al. (2011)	15	90	180	This study	Huoshan Fault	Nearest fault
1618	11	16	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	Liu et al. (2007)	Yuguang Graben Fault	In literature
1622	10	25	36.5	106.3	7.7	3.42 × 10²⁰	Lee et al. (1976)	180	45	90	Wesnousky et al. (1984)		In literature
1624	7	4	35.4	105.9	6.0	1.11 × 10¹⁸	Lee et al. (1976)	160	45	45	This study	Liupanshan Fault	Nearest fault
1626	6	28	39.4	114.2	7.2	8.10 × 10¹⁹	Lee et al. (1976)	220	60	−120	Wesnousky et al. (1984)	Lingqiu Graben Fault	In literature
1627	2	16	37.5	105.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	120	45	45	This study	Zhongwei-Tongxin Fault	Nearest fault
1628	10	7	40.6	114.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1634	1	x	34.0	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1642	6	30	35.0	110.9	6.5	7.30 × 10¹⁸	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1654	7	21	34.3	105.5	7.7	4.27 × 10²⁰	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1658	2	3	39.4	115.7	6.0	1.11 × 10¹⁸	Liu et al. (2011)	45	90	180	This study		Nearest fault
1664	x	x	38.7	112.7	5.5	1.97 × 10¹⁷	Lee et al. (1976)	200	62	−160	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1665	4	16	39.9	116.6	6.5	6.24 × 10¹⁸	Liu et al. (2011)	205	50	160	Liu et al. (2007)		In literature
1673	10	18	40.5	113.5	6.0	1.11 × 10¹⁸	Liu et al. (2011)	235	45	−93	Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	In literature
1673	10	18	40.5	114.1	5.5	1.97 × 10¹⁷	Lee et al. (1976)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1683	11	22	38.7	112.7	7.4	1.42 × 10²⁰	Lee et al. (1976)	200	60	−160	Wesnousky et al. (1984)	Yunzhongshan Fault	In literature
1695	5	18	36.0	111.5	7.2	8.10 × 10¹⁹	Liu et al. (2011)	90	60	30	Wesnousky et al. (1984)		In literature
1704	9	28	34.9	106.8	6.0	1.11 × 10¹⁸	Lee et al. (1976)	140	45	−90	This study		Nearest fault
1709	10	14	37.4	105.3	7.5	1.78 × 10²⁰	Lee et al. (1976)	295	30	30	Wesnousky et al. (1984)		In literature
1718	6	19	35.0	105.2	7.3	8.90 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1720	7	12	40.4	115.5	6.8	1.48 × 10¹⁹	Lee et al. (1976)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1730	9	30	40.0	116.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	30	45	−90	This study		Nearest fault
1739	1	3	38.9	106.5	7.6	2.72 × 10²⁰^d	Lee et al. (1976)	40^d	40^d	−90^d	Wesnousky et al. (1984)	East Helanshan Fault	Middleton et al. (2016a)
1765	9	2	34.8	105.0	7.0	4.00 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1815	10	23	34.8	111.2	7.1	4.20 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1852	5	26	37.5	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	290	30	90	This study		Nearest fault
1881	7	20	33.6	104.6	6.5	6.24 × 10¹⁸	Lee et al. (1976)	120	90	0	This study		Nearest fault
1885	1	14	34.5	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1976)	90	90	0	This study		Nearest fault
1888	11	2	37.1	104.2	6.3	2.63 × 10¹⁸	Lee et al. (1976)	285	30	90	This study		Nearest fault
1898	9	22	39.1	113.0	5.5	1.97 × 10¹⁷	Lee et al. (1976)	230	60	−135	This study, Li et al. (2015a)	Wutaishan Fault	Nearest fault
1911	1	25	39.8	114.5	5.9	7.85 × 10¹⁷	Liu et al. (2011)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1920	12	16	36.5	105.7	8.0	1.20 × 10²¹	Lee et al. (1978)	115	90	0	Wesnousky et al. (1984)		In literature
1920	12	25	35.6	106.3	7.0	3.51 × 10¹⁹	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1920	12	28	35.5	105.5	6.3	2.63 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1921	4	12	35.8	106.2	6.5	6.24 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1929	1	14	40.7	111.3	6.0	1.11 × 10¹⁸	Liu et al. (2011)	70	60	−90	This study	Daqingshan Fault	Nearest fault
1934	1	21	41.0	108.8	6.3	3.13 × 10¹⁸	Liu et al. (2011)	120	60	−90	This study	Seertengshan Fault	Nearest fault
1936	8	1	34.2	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1978)	334	46	38	This study		Nearest instrumental eq
1952	10	8	39.0	112.7	5.5	1.97 × 10¹⁷	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1962	12	7	38.1	106.3	5.5	1.97 × 10¹⁷	Qin et al. (2002)	108	36	144	CSB^e		In literature
1965	1	13	35.0	111.6	5.5	1.97 × 10¹⁷	Qin et al. (2002)	201	65	−158	CSB		In literature
1967	7	28	40.5	115.6	5.4	1.40 × 10¹⁷	Liu et al. (2011)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1967	12	18	36.5	111.2	5.4	1.40 × 10¹⁷	Qin et al. (2002)	355	80	−161	CSB		In literature
1970	12	3	35.9	105.6	5.1	4.95 × 10¹⁶	Qin et al. (2002)	9	74	132	CSB		In literature
1971	6	28	37.9	106.3	5.1	4.95 × 10¹⁶	Qin et al. (2002)	213	63	46	CSB		In literature
1976	4	6	40.2	112.1	6.2	2.21 × 10¹⁸	Liu et al. (2011)	209	75	164	CSB		In literature
1976	9	23	39.9	106.4	6.2	2.21 × 10¹⁸	Qin et al. (2002)	79	68	28	CSB		In literature
1979	6	19	36.83	111.50	5.0	3.51 × 10¹⁶	GCMT^f	278	30	−63	GCMT^f		In literature
1979	8	24	40.83	108.24	5.7	3.94 × 10¹⁷	GCMT	111	44	−65	GCMT		In literature
1981	8	13	40.50	113.40	5.5	1.97 × 10¹⁷	Qin et al. (2002)	183	80	−178	CSB		In literature
1987	1	7	34.23	103.86	5.4	1.40 × 10¹⁷	GCMT	170	65	28	GCMT		In literature
1987	8	10	37.57	105.63	5.3	9.89 × 10¹⁶	GCMT	336	25	−75	GCMT		In literature
1988	1	3	38.13	106.86	5.2	7.00 × 10¹⁶	GCMT	110	57	5	GCMT		In literature
1989	10	18	39.63	113.84	5.4	1.40 × 10¹⁷	GCMT	92	44	−39	GCMT	Hengshan Fault	In literature
1989	10	18	39.77	113.49	5.6	2.79 × 10¹⁷	GCMT	200	75	−175	GCMT	Liulengshan Fault	In literature
1989	10	18	39.83	113.61	5.4	1.40 × 10¹⁷	GCMT	204	76	−176	GCMT	Liulengshan Fault	In literature
1989	10	19	39.94	113.84	6.1	1.57 × 10¹⁸	Li et al. (2015a)	200	44	136	Li et al. (2015a)	Dawang-Tuanbao Fault	In literature
1989	10	19	39.92	113.91	5.9	7.85 × 10¹⁷	Xu et al. (2000)	210	76	−167	Xu et al. (2000)		In literature
1991	3	25	40.10	113.34	5.4	1.40 × 10¹⁷	GCMT	106	82	7	GCMT	Datong Basin Fault	In literature
1996	5	3	40.72	109.69	6.0	1.11 × 10¹⁸	GCMT	308	75	−12	GCMT		In literature
1998	1	10	41.34	114.34	5.7	3.94 × 10¹⁷	GCMT	207	54	135	GCMT		In literature
1999	11	1	39.85	113.74	5.2	7.00 × 10¹⁶	GCMT	122	72	−7	GCMT	Liulengshan Fault	In literature
2000	6	6	37.02	103.91	5.5	1.97 × 10¹⁷	GCMT	96	68	−6	GCMT		In literature
2003	11	13	34.61	104.10	5.1	4.95 × 10¹⁶	GCMT	347	42	53	GCMT		In literature
2013	7	21	34.60	104.31	6.0	1.11 × 10¹⁸	GCMT	196	57	151	GCMT		In literature
2013	7	22	34.65	104.35	5.4	1.40 × 10¹⁷	GCMT	153	37	103	GCMT		In literature
2015	4	15	39.74	106.39	5.5	1.97 × 10¹⁷	GCMT	356	81	−177	GCMT		In literature

Year	Month	Day	Lat (°)	Long (°)	M_w^a	M₀^b (Nm)	Eq. ref.	Strike (°)	Dip (°)	Rake (°)	FP ref.	Assigned fault	FP notes
1337	9	8	40.4	115.7	6.5	6.24 × 10¹⁸	Lee et al. (1976)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1352	4	18	35.6	105.3	6.8	1.90 × 10¹⁹	Lee et al. (1976)	130	45	90	Wesnousky et al. (1984)		In literature
1363	7	8	37.6	112.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	50	60	−90	This study	Jiaocheng Fault	Nearest fault
1467	6	18	39.6	112.3	5.5	1.97 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1477	5	13	38.5	106.3	6.5	6.70 × 10¹⁸	Lee et al. (1976)	30	75	−150	Wesnousky et al. (1984)		In literature
1484	2	7	40.5	116.1	6.8	1.76 × 10¹⁹	Liu et al. (2011)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1487	8	19	34.4	108.9	6.3	3.13 × 10¹⁸	Liu et al. (2011)	270	60	−90	This study, Rao et al. (2015)	Lishan Piedmont Fault	Nearest fault
1495	4	10	37.6	105.6	6.3	2.63 × 10¹⁸	Lee et al. (1976)	120	45	45	This study, Liu-Zeng et al. (2015)	Zhongwei-Tongxin Fault	Nearest fault
1501	1	29	34.8	110.1	7.0	3.30 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1502	12	4	39.0	112.6	5.3	9.89 × 10¹⁶	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1514	10	30	38.7	113.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	129	85	18	This study		Nearest instrumental eq
1545	2	x	40.0	114.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	250	65	−135	This study, Li et al. (2015a)	Liulengshan Fault	Nearest fault
1556	1	23	34.5	109.7	7.9	8.32 × 10²⁰^c	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)	Huashan/Weinan Tableland Fault	Zhou (2016)
1561	7	25	37.4	106.0	7.2	6.90 × 10¹⁹	Lee et al. (1976)	145	30	90	Wesnousky et al. (1984)		In literature
1568	5	15	34.4	109.0	6.8	1.80 × 10¹⁹	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)		In literature
1573	1	10	34.4	104.0	6.8	1.48 × 10¹⁹	Lee et al. (1976)	196	57	151	This study, Zheng et al. (2007)	Lintan-Dangchang Fault	Nearest instrumental eq
1580	9	15	39.5	112.3	5.8	5.56 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1581	5	18	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1583	5	18	39.7	113.8	5.5	1.97 × 10¹⁷	Lee et al. (1976)	225	65	−116	This study, Li et al. (2015a)	Hengshan Fault	Nearest fault
1604	10	25	34.2	105.0	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1614	10	23	37.2	112.1	6.0	1.11 × 10¹⁸	Liu et al. (2011)	230	60	−65	Li et al. (2015a)	Jiexiu-Taigu	In literature
1618	5	20	37.0	111.9	6.0	1.11 × 10¹⁸	Liu et al. (2011)	15	90	180	This study	Huoshan Fault	Nearest fault
1618	11	16	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	Liu et al. (2007)	Yuguang Graben Fault	In literature
1622	10	25	36.5	106.3	7.7	3.42 × 10²⁰	Lee et al. (1976)	180	45	90	Wesnousky et al. (1984)		In literature
1624	7	4	35.4	105.9	6.0	1.11 × 10¹⁸	Lee et al. (1976)	160	45	45	This study	Liupanshan Fault	Nearest fault
1626	6	28	39.4	114.2	7.2	8.10 × 10¹⁹	Lee et al. (1976)	220	60	−120	Wesnousky et al. (1984)	Lingqiu Graben Fault	In literature
1627	2	16	37.5	105.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	120	45	45	This study	Zhongwei-Tongxin Fault	Nearest fault
1628	10	7	40.6	114.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1634	1	x	34.0	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1642	6	30	35.0	110.9	6.5	7.30 × 10¹⁸	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1654	7	21	34.3	105.5	7.7	4.27 × 10²⁰	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1658	2	3	39.4	115.7	6.0	1.11 × 10¹⁸	Liu et al. (2011)	45	90	180	This study		Nearest fault
1664	x	x	38.7	112.7	5.5	1.97 × 10¹⁷	Lee et al. (1976)	200	62	−160	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1665	4	16	39.9	116.6	6.5	6.24 × 10¹⁸	Liu et al. (2011)	205	50	160	Liu et al. (2007)		In literature
1673	10	18	40.5	113.5	6.0	1.11 × 10¹⁸	Liu et al. (2011)	235	45	−93	Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	In literature
1673	10	18	40.5	114.1	5.5	1.97 × 10¹⁷	Lee et al. (1976)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1683	11	22	38.7	112.7	7.4	1.42 × 10²⁰	Lee et al. (1976)	200	60	−160	Wesnousky et al. (1984)	Yunzhongshan Fault	In literature
1695	5	18	36.0	111.5	7.2	8.10 × 10¹⁹	Liu et al. (2011)	90	60	30	Wesnousky et al. (1984)		In literature
1704	9	28	34.9	106.8	6.0	1.11 × 10¹⁸	Lee et al. (1976)	140	45	−90	This study		Nearest fault
1709	10	14	37.4	105.3	7.5	1.78 × 10²⁰	Lee et al. (1976)	295	30	30	Wesnousky et al. (1984)		In literature
1718	6	19	35.0	105.2	7.3	8.90 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1720	7	12	40.4	115.5	6.8	1.48 × 10¹⁹	Lee et al. (1976)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1730	9	30	40.0	116.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	30	45	−90	This study		Nearest fault
1739	1	3	38.9	106.5	7.6	2.72 × 10²⁰^d	Lee et al. (1976)	40^d	40^d	−90^d	Wesnousky et al. (1984)	East Helanshan Fault	Middleton et al. (2016a)
1765	9	2	34.8	105.0	7.0	4.00 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1815	10	23	34.8	111.2	7.1	4.20 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1852	5	26	37.5	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	290	30	90	This study		Nearest fault
1881	7	20	33.6	104.6	6.5	6.24 × 10¹⁸	Lee et al. (1976)	120	90	0	This study		Nearest fault
1885	1	14	34.5	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1976)	90	90	0	This study		Nearest fault
1888	11	2	37.1	104.2	6.3	2.63 × 10¹⁸	Lee et al. (1976)	285	30	90	This study		Nearest fault
1898	9	22	39.1	113.0	5.5	1.97 × 10¹⁷	Lee et al. (1976)	230	60	−135	This study, Li et al. (2015a)	Wutaishan Fault	Nearest fault
1911	1	25	39.8	114.5	5.9	7.85 × 10¹⁷	Liu et al. (2011)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1920	12	16	36.5	105.7	8.0	1.20 × 10²¹	Lee et al. (1978)	115	90	0	Wesnousky et al. (1984)		In literature
1920	12	25	35.6	106.3	7.0	3.51 × 10¹⁹	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1920	12	28	35.5	105.5	6.3	2.63 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1921	4	12	35.8	106.2	6.5	6.24 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1929	1	14	40.7	111.3	6.0	1.11 × 10¹⁸	Liu et al. (2011)	70	60	−90	This study	Daqingshan Fault	Nearest fault
1934	1	21	41.0	108.8	6.3	3.13 × 10¹⁸	Liu et al. (2011)	120	60	−90	This study	Seertengshan Fault	Nearest fault
1936	8	1	34.2	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1978)	334	46	38	This study		Nearest instrumental eq
1952	10	8	39.0	112.7	5.5	1.97 × 10¹⁷	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1962	12	7	38.1	106.3	5.5	1.97 × 10¹⁷	Qin et al. (2002)	108	36	144	CSB^e		In literature
1965	1	13	35.0	111.6	5.5	1.97 × 10¹⁷	Qin et al. (2002)	201	65	−158	CSB		In literature
1967	7	28	40.5	115.6	5.4	1.40 × 10¹⁷	Liu et al. (2011)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1967	12	18	36.5	111.2	5.4	1.40 × 10¹⁷	Qin et al. (2002)	355	80	−161	CSB		In literature
1970	12	3	35.9	105.6	5.1	4.95 × 10¹⁶	Qin et al. (2002)	9	74	132	CSB		In literature
1971	6	28	37.9	106.3	5.1	4.95 × 10¹⁶	Qin et al. (2002)	213	63	46	CSB		In literature
1976	4	6	40.2	112.1	6.2	2.21 × 10¹⁸	Liu et al. (2011)	209	75	164	CSB		In literature
1976	9	23	39.9	106.4	6.2	2.21 × 10¹⁸	Qin et al. (2002)	79	68	28	CSB		In literature
1979	6	19	36.83	111.50	5.0	3.51 × 10¹⁶	GCMT^f	278	30	−63	GCMT^f		In literature
1979	8	24	40.83	108.24	5.7	3.94 × 10¹⁷	GCMT	111	44	−65	GCMT		In literature
1981	8	13	40.50	113.40	5.5	1.97 × 10¹⁷	Qin et al. (2002)	183	80	−178	CSB		In literature
1987	1	7	34.23	103.86	5.4	1.40 × 10¹⁷	GCMT	170	65	28	GCMT		In literature
1987	8	10	37.57	105.63	5.3	9.89 × 10¹⁶	GCMT	336	25	−75	GCMT		In literature
1988	1	3	38.13	106.86	5.2	7.00 × 10¹⁶	GCMT	110	57	5	GCMT		In literature
1989	10	18	39.63	113.84	5.4	1.40 × 10¹⁷	GCMT	92	44	−39	GCMT	Hengshan Fault	In literature
1989	10	18	39.77	113.49	5.6	2.79 × 10¹⁷	GCMT	200	75	−175	GCMT	Liulengshan Fault	In literature
1989	10	18	39.83	113.61	5.4	1.40 × 10¹⁷	GCMT	204	76	−176	GCMT	Liulengshan Fault	In literature
1989	10	19	39.94	113.84	6.1	1.57 × 10¹⁸	Li et al. (2015a)	200	44	136	Li et al. (2015a)	Dawang-Tuanbao Fault	In literature
1989	10	19	39.92	113.91	5.9	7.85 × 10¹⁷	Xu et al. (2000)	210	76	−167	Xu et al. (2000)		In literature
1991	3	25	40.10	113.34	5.4	1.40 × 10¹⁷	GCMT	106	82	7	GCMT	Datong Basin Fault	In literature
1996	5	3	40.72	109.69	6.0	1.11 × 10¹⁸	GCMT	308	75	−12	GCMT		In literature
1998	1	10	41.34	114.34	5.7	3.94 × 10¹⁷	GCMT	207	54	135	GCMT		In literature
1999	11	1	39.85	113.74	5.2	7.00 × 10¹⁶	GCMT	122	72	−7	GCMT	Liulengshan Fault	In literature
2000	6	6	37.02	103.91	5.5	1.97 × 10¹⁷	GCMT	96	68	−6	GCMT		In literature
2003	11	13	34.61	104.10	5.1	4.95 × 10¹⁶	GCMT	347	42	53	GCMT		In literature
2013	7	21	34.60	104.31	6.0	1.11 × 10¹⁸	GCMT	196	57	151	GCMT		In literature
2013	7	22	34.65	104.35	5.4	1.40 × 10¹⁷	GCMT	153	37	103	GCMT		In literature
2015	4	15	39.74	106.39	5.5	1.97 × 10¹⁷	GCMT	356	81	−177	GCMT		In literature

^aMagnitudes for historical earthquakes are estimated from intensities on the New Chinese Intensity Scale using M_s = 0.58 × I₀ + 1.5. M_s is considered equal to M_w for M_s ≤ 8 (Kanamori 1983).

^bM₀ calculated from M_w using M₀ = 10^{|$\frac{3}{2}$| (M_w+6.03)}.

^cSeismic moment and focal parameters for 1556 earthquake re-estimated from Zhou (2016).

^dSeismic moment and focal parameters for 1739 earthquake re-estimated from Middleton et al. (2016a).

^eChina Seismological Bureau Catalogue (Qin et al. 2002).

^fGlobal Centroid Moment Tensor Catalogue.

Table 1.

Open in new tab

Focal parameters for historical earthquakes around the Ordos Plateau.

Year	Month	Day	Lat (°)	Long (°)	M_w^a	M₀^b (Nm)	Eq. ref.	Strike (°)	Dip (°)	Rake (°)	FP ref.	Assigned fault	FP notes
1337	9	8	40.4	115.7	6.5	6.24 × 10¹⁸	Lee et al. (1976)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1352	4	18	35.6	105.3	6.8	1.90 × 10¹⁹	Lee et al. (1976)	130	45	90	Wesnousky et al. (1984)		In literature
1363	7	8	37.6	112.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	50	60	−90	This study	Jiaocheng Fault	Nearest fault
1467	6	18	39.6	112.3	5.5	1.97 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1477	5	13	38.5	106.3	6.5	6.70 × 10¹⁸	Lee et al. (1976)	30	75	−150	Wesnousky et al. (1984)		In literature
1484	2	7	40.5	116.1	6.8	1.76 × 10¹⁹	Liu et al. (2011)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1487	8	19	34.4	108.9	6.3	3.13 × 10¹⁸	Liu et al. (2011)	270	60	−90	This study, Rao et al. (2015)	Lishan Piedmont Fault	Nearest fault
1495	4	10	37.6	105.6	6.3	2.63 × 10¹⁸	Lee et al. (1976)	120	45	45	This study, Liu-Zeng et al. (2015)	Zhongwei-Tongxin Fault	Nearest fault
1501	1	29	34.8	110.1	7.0	3.30 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1502	12	4	39.0	112.6	5.3	9.89 × 10¹⁶	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1514	10	30	38.7	113.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	129	85	18	This study		Nearest instrumental eq
1545	2	x	40.0	114.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	250	65	−135	This study, Li et al. (2015a)	Liulengshan Fault	Nearest fault
1556	1	23	34.5	109.7	7.9	8.32 × 10²⁰^c	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)	Huashan/Weinan Tableland Fault	Zhou (2016)
1561	7	25	37.4	106.0	7.2	6.90 × 10¹⁹	Lee et al. (1976)	145	30	90	Wesnousky et al. (1984)		In literature
1568	5	15	34.4	109.0	6.8	1.80 × 10¹⁹	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)		In literature
1573	1	10	34.4	104.0	6.8	1.48 × 10¹⁹	Lee et al. (1976)	196	57	151	This study, Zheng et al. (2007)	Lintan-Dangchang Fault	Nearest instrumental eq
1580	9	15	39.5	112.3	5.8	5.56 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1581	5	18	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1583	5	18	39.7	113.8	5.5	1.97 × 10¹⁷	Lee et al. (1976)	225	65	−116	This study, Li et al. (2015a)	Hengshan Fault	Nearest fault
1604	10	25	34.2	105.0	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1614	10	23	37.2	112.1	6.0	1.11 × 10¹⁸	Liu et al. (2011)	230	60	−65	Li et al. (2015a)	Jiexiu-Taigu	In literature
1618	5	20	37.0	111.9	6.0	1.11 × 10¹⁸	Liu et al. (2011)	15	90	180	This study	Huoshan Fault	Nearest fault
1618	11	16	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	Liu et al. (2007)	Yuguang Graben Fault	In literature
1622	10	25	36.5	106.3	7.7	3.42 × 10²⁰	Lee et al. (1976)	180	45	90	Wesnousky et al. (1984)		In literature
1624	7	4	35.4	105.9	6.0	1.11 × 10¹⁸	Lee et al. (1976)	160	45	45	This study	Liupanshan Fault	Nearest fault
1626	6	28	39.4	114.2	7.2	8.10 × 10¹⁹	Lee et al. (1976)	220	60	−120	Wesnousky et al. (1984)	Lingqiu Graben Fault	In literature
1627	2	16	37.5	105.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	120	45	45	This study	Zhongwei-Tongxin Fault	Nearest fault
1628	10	7	40.6	114.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1634	1	x	34.0	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1642	6	30	35.0	110.9	6.5	7.30 × 10¹⁸	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1654	7	21	34.3	105.5	7.7	4.27 × 10²⁰	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1658	2	3	39.4	115.7	6.0	1.11 × 10¹⁸	Liu et al. (2011)	45	90	180	This study		Nearest fault
1664	x	x	38.7	112.7	5.5	1.97 × 10¹⁷	Lee et al. (1976)	200	62	−160	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1665	4	16	39.9	116.6	6.5	6.24 × 10¹⁸	Liu et al. (2011)	205	50	160	Liu et al. (2007)		In literature
1673	10	18	40.5	113.5	6.0	1.11 × 10¹⁸	Liu et al. (2011)	235	45	−93	Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	In literature
1673	10	18	40.5	114.1	5.5	1.97 × 10¹⁷	Lee et al. (1976)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1683	11	22	38.7	112.7	7.4	1.42 × 10²⁰	Lee et al. (1976)	200	60	−160	Wesnousky et al. (1984)	Yunzhongshan Fault	In literature
1695	5	18	36.0	111.5	7.2	8.10 × 10¹⁹	Liu et al. (2011)	90	60	30	Wesnousky et al. (1984)		In literature
1704	9	28	34.9	106.8	6.0	1.11 × 10¹⁸	Lee et al. (1976)	140	45	−90	This study		Nearest fault
1709	10	14	37.4	105.3	7.5	1.78 × 10²⁰	Lee et al. (1976)	295	30	30	Wesnousky et al. (1984)		In literature
1718	6	19	35.0	105.2	7.3	8.90 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1720	7	12	40.4	115.5	6.8	1.48 × 10¹⁹	Lee et al. (1976)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1730	9	30	40.0	116.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	30	45	−90	This study		Nearest fault
1739	1	3	38.9	106.5	7.6	2.72 × 10²⁰^d	Lee et al. (1976)	40^d	40^d	−90^d	Wesnousky et al. (1984)	East Helanshan Fault	Middleton et al. (2016a)
1765	9	2	34.8	105.0	7.0	4.00 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1815	10	23	34.8	111.2	7.1	4.20 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1852	5	26	37.5	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	290	30	90	This study		Nearest fault
1881	7	20	33.6	104.6	6.5	6.24 × 10¹⁸	Lee et al. (1976)	120	90	0	This study		Nearest fault
1885	1	14	34.5	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1976)	90	90	0	This study		Nearest fault
1888	11	2	37.1	104.2	6.3	2.63 × 10¹⁸	Lee et al. (1976)	285	30	90	This study		Nearest fault
1898	9	22	39.1	113.0	5.5	1.97 × 10¹⁷	Lee et al. (1976)	230	60	−135	This study, Li et al. (2015a)	Wutaishan Fault	Nearest fault
1911	1	25	39.8	114.5	5.9	7.85 × 10¹⁷	Liu et al. (2011)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1920	12	16	36.5	105.7	8.0	1.20 × 10²¹	Lee et al. (1978)	115	90	0	Wesnousky et al. (1984)		In literature
1920	12	25	35.6	106.3	7.0	3.51 × 10¹⁹	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1920	12	28	35.5	105.5	6.3	2.63 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1921	4	12	35.8	106.2	6.5	6.24 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1929	1	14	40.7	111.3	6.0	1.11 × 10¹⁸	Liu et al. (2011)	70	60	−90	This study	Daqingshan Fault	Nearest fault
1934	1	21	41.0	108.8	6.3	3.13 × 10¹⁸	Liu et al. (2011)	120	60	−90	This study	Seertengshan Fault	Nearest fault
1936	8	1	34.2	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1978)	334	46	38	This study		Nearest instrumental eq
1952	10	8	39.0	112.7	5.5	1.97 × 10¹⁷	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1962	12	7	38.1	106.3	5.5	1.97 × 10¹⁷	Qin et al. (2002)	108	36	144	CSB^e		In literature
1965	1	13	35.0	111.6	5.5	1.97 × 10¹⁷	Qin et al. (2002)	201	65	−158	CSB		In literature
1967	7	28	40.5	115.6	5.4	1.40 × 10¹⁷	Liu et al. (2011)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1967	12	18	36.5	111.2	5.4	1.40 × 10¹⁷	Qin et al. (2002)	355	80	−161	CSB		In literature
1970	12	3	35.9	105.6	5.1	4.95 × 10¹⁶	Qin et al. (2002)	9	74	132	CSB		In literature
1971	6	28	37.9	106.3	5.1	4.95 × 10¹⁶	Qin et al. (2002)	213	63	46	CSB		In literature
1976	4	6	40.2	112.1	6.2	2.21 × 10¹⁸	Liu et al. (2011)	209	75	164	CSB		In literature
1976	9	23	39.9	106.4	6.2	2.21 × 10¹⁸	Qin et al. (2002)	79	68	28	CSB		In literature
1979	6	19	36.83	111.50	5.0	3.51 × 10¹⁶	GCMT^f	278	30	−63	GCMT^f		In literature
1979	8	24	40.83	108.24	5.7	3.94 × 10¹⁷	GCMT	111	44	−65	GCMT		In literature
1981	8	13	40.50	113.40	5.5	1.97 × 10¹⁷	Qin et al. (2002)	183	80	−178	CSB		In literature
1987	1	7	34.23	103.86	5.4	1.40 × 10¹⁷	GCMT	170	65	28	GCMT		In literature
1987	8	10	37.57	105.63	5.3	9.89 × 10¹⁶	GCMT	336	25	−75	GCMT		In literature
1988	1	3	38.13	106.86	5.2	7.00 × 10¹⁶	GCMT	110	57	5	GCMT		In literature
1989	10	18	39.63	113.84	5.4	1.40 × 10¹⁷	GCMT	92	44	−39	GCMT	Hengshan Fault	In literature
1989	10	18	39.77	113.49	5.6	2.79 × 10¹⁷	GCMT	200	75	−175	GCMT	Liulengshan Fault	In literature
1989	10	18	39.83	113.61	5.4	1.40 × 10¹⁷	GCMT	204	76	−176	GCMT	Liulengshan Fault	In literature
1989	10	19	39.94	113.84	6.1	1.57 × 10¹⁸	Li et al. (2015a)	200	44	136	Li et al. (2015a)	Dawang-Tuanbao Fault	In literature
1989	10	19	39.92	113.91	5.9	7.85 × 10¹⁷	Xu et al. (2000)	210	76	−167	Xu et al. (2000)		In literature
1991	3	25	40.10	113.34	5.4	1.40 × 10¹⁷	GCMT	106	82	7	GCMT	Datong Basin Fault	In literature
1996	5	3	40.72	109.69	6.0	1.11 × 10¹⁸	GCMT	308	75	−12	GCMT		In literature
1998	1	10	41.34	114.34	5.7	3.94 × 10¹⁷	GCMT	207	54	135	GCMT		In literature
1999	11	1	39.85	113.74	5.2	7.00 × 10¹⁶	GCMT	122	72	−7	GCMT	Liulengshan Fault	In literature
2000	6	6	37.02	103.91	5.5	1.97 × 10¹⁷	GCMT	96	68	−6	GCMT		In literature
2003	11	13	34.61	104.10	5.1	4.95 × 10¹⁶	GCMT	347	42	53	GCMT		In literature
2013	7	21	34.60	104.31	6.0	1.11 × 10¹⁸	GCMT	196	57	151	GCMT		In literature
2013	7	22	34.65	104.35	5.4	1.40 × 10¹⁷	GCMT	153	37	103	GCMT		In literature
2015	4	15	39.74	106.39	5.5	1.97 × 10¹⁷	GCMT	356	81	−177	GCMT		In literature

Year	Month	Day	Lat (°)	Long (°)	M_w^a	M₀^b (Nm)	Eq. ref.	Strike (°)	Dip (°)	Rake (°)	FP ref.	Assigned fault	FP notes
1337	9	8	40.4	115.7	6.5	6.24 × 10¹⁸	Lee et al. (1976)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1352	4	18	35.6	105.3	6.8	1.90 × 10¹⁹	Lee et al. (1976)	130	45	90	Wesnousky et al. (1984)		In literature
1363	7	8	37.6	112.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	50	60	−90	This study	Jiaocheng Fault	Nearest fault
1467	6	18	39.6	112.3	5.5	1.97 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1477	5	13	38.5	106.3	6.5	6.70 × 10¹⁸	Lee et al. (1976)	30	75	−150	Wesnousky et al. (1984)		In literature
1484	2	7	40.5	116.1	6.8	1.76 × 10¹⁹	Liu et al. (2011)	55	75	−77	This study, Pavlides et al. (1999)	Yanqing Fault	Av. 5 striations
1487	8	19	34.4	108.9	6.3	3.13 × 10¹⁸	Liu et al. (2011)	270	60	−90	This study, Rao et al. (2015)	Lishan Piedmont Fault	Nearest fault
1495	4	10	37.6	105.6	6.3	2.63 × 10¹⁸	Lee et al. (1976)	120	45	45	This study, Liu-Zeng et al. (2015)	Zhongwei-Tongxin Fault	Nearest fault
1501	1	29	34.8	110.1	7.0	3.30 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1502	12	4	39.0	112.6	5.3	9.89 × 10¹⁶	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1514	10	30	38.7	113.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	129	85	18	This study		Nearest instrumental eq
1545	2	x	40.0	114.0	5.3	9.89 × 10¹⁶	Liu et al. (2011)	250	65	−135	This study, Li et al. (2015a)	Liulengshan Fault	Nearest fault
1556	1	23	34.5	109.7	7.9	8.32 × 10²⁰^c	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)	Huashan/Weinan Tableland Fault	Zhou (2016)
1561	7	25	37.4	106.0	7.2	6.90 × 10¹⁹	Lee et al. (1976)	145	30	90	Wesnousky et al. (1984)		In literature
1568	5	15	34.4	109.0	6.8	1.80 × 10¹⁹	Liu et al. (2011)	270	60	−90	Wesnousky et al. (1984)		In literature
1573	1	10	34.4	104.0	6.8	1.48 × 10¹⁹	Lee et al. (1976)	196	57	151	This study, Zheng et al. (2007)	Lintan-Dangchang Fault	Nearest instrumental eq
1580	9	15	39.5	112.3	5.8	5.56 × 10¹⁷	Liu et al. (2011)	20	74	138	This study		Nearest instrumental eq
1581	5	18	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1583	5	18	39.7	113.8	5.5	1.97 × 10¹⁷	Lee et al. (1976)	225	65	−116	This study, Li et al. (2015a)	Hengshan Fault	Nearest fault
1604	10	25	34.2	105.0	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1614	10	23	37.2	112.1	6.0	1.11 × 10¹⁸	Liu et al. (2011)	230	60	−65	Li et al. (2015a)	Jiexiu-Taigu	In literature
1618	5	20	37.0	111.9	6.0	1.11 × 10¹⁸	Liu et al. (2011)	15	90	180	This study	Huoshan Fault	Nearest fault
1618	11	16	39.8	114.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	250	60	−110	Liu et al. (2007)	Yuguang Graben Fault	In literature
1622	10	25	36.5	106.3	7.7	3.42 × 10²⁰	Lee et al. (1976)	180	45	90	Wesnousky et al. (1984)		In literature
1624	7	4	35.4	105.9	6.0	1.11 × 10¹⁸	Lee et al. (1976)	160	45	45	This study	Liupanshan Fault	Nearest fault
1626	6	28	39.4	114.2	7.2	8.10 × 10¹⁹	Lee et al. (1976)	220	60	−120	Wesnousky et al. (1984)	Lingqiu Graben Fault	In literature
1627	2	16	37.5	105.5	6.0	1.11 × 10¹⁸	Lee et al. (1976)	120	45	45	This study	Zhongwei-Tongxin Fault	Nearest fault
1628	10	7	40.6	114.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1634	1	x	34.0	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	334	46	38	This study		Nearest instrumental eq
1642	6	30	35.0	110.9	6.5	7.30 × 10¹⁸	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1654	7	21	34.3	105.5	7.7	4.27 × 10²⁰	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1658	2	3	39.4	115.7	6.0	1.11 × 10¹⁸	Liu et al. (2011)	45	90	180	This study		Nearest fault
1664	x	x	38.7	112.7	5.5	1.97 × 10¹⁷	Lee et al. (1976)	200	62	−160	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1665	4	16	39.9	116.6	6.5	6.24 × 10¹⁸	Liu et al. (2011)	205	50	160	Liu et al. (2007)		In literature
1673	10	18	40.5	113.5	6.0	1.11 × 10¹⁸	Liu et al. (2011)	235	45	−93	Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	In literature
1673	10	18	40.5	114.1	5.5	1.97 × 10¹⁷	Lee et al. (1976)	75	45	−97	This study, Li et al. (2015a)	Yanggao-Tianzhen Graben Fault	Nearest fault
1683	11	22	38.7	112.7	7.4	1.42 × 10²⁰	Lee et al. (1976)	200	60	−160	Wesnousky et al. (1984)	Yunzhongshan Fault	In literature
1695	5	18	36.0	111.5	7.2	8.10 × 10¹⁹	Liu et al. (2011)	90	60	30	Wesnousky et al. (1984)		In literature
1704	9	28	34.9	106.8	6.0	1.11 × 10¹⁸	Lee et al. (1976)	140	45	−90	This study		Nearest fault
1709	10	14	37.4	105.3	7.5	1.78 × 10²⁰	Lee et al. (1976)	295	30	30	Wesnousky et al. (1984)		In literature
1718	6	19	35.0	105.2	7.3	8.90 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1720	7	12	40.4	115.5	6.8	1.48 × 10¹⁹	Lee et al. (1976)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1730	9	30	40.0	116.2	6.5	6.24 × 10¹⁸	Liu et al. (2011)	30	45	−90	This study		Nearest fault
1739	1	3	38.9	106.5	7.6	2.72 × 10²⁰^d	Lee et al. (1976)	40^d	40^d	−90^d	Wesnousky et al. (1984)	East Helanshan Fault	Middleton et al. (2016a)
1765	9	2	34.8	105.0	7.0	4.00 × 10¹⁹	Lee et al. (1976)	105	90	0	Wesnousky et al. (1984)		In literature
1815	10	23	34.8	111.2	7.1	4.20 × 10¹⁹	Liu et al. (2011)	230	60	−90	Wesnousky et al. (1984)		In literature
1852	5	26	37.5	105.2	6.0	1.11 × 10¹⁸	Lee et al. (1976)	290	30	90	This study		Nearest fault
1881	7	20	33.6	104.6	6.5	6.24 × 10¹⁸	Lee et al. (1976)	120	90	0	This study		Nearest fault
1885	1	14	34.5	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1976)	90	90	0	This study		Nearest fault
1888	11	2	37.1	104.2	6.3	2.63 × 10¹⁸	Lee et al. (1976)	285	30	90	This study		Nearest fault
1898	9	22	39.1	113.0	5.5	1.97 × 10¹⁷	Lee et al. (1976)	230	60	−135	This study, Li et al. (2015a)	Wutaishan Fault	Nearest fault
1911	1	25	39.8	114.5	5.9	7.85 × 10¹⁷	Liu et al. (2011)	250	60	−110	This study, Liu et al. (2007)	Yuguang Graben Fault	Nearest fault
1920	12	16	36.5	105.7	8.0	1.20 × 10²¹	Lee et al. (1978)	115	90	0	Wesnousky et al. (1984)		In literature
1920	12	25	35.6	106.3	7.0	3.51 × 10¹⁹	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1920	12	28	35.5	105.5	6.3	2.63 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1921	4	12	35.8	106.2	6.5	6.24 × 10¹⁸	Lee et al. (1978)	160	45	45	This study	Liupanshan Fault	Nearest fault
1929	1	14	40.7	111.3	6.0	1.11 × 10¹⁸	Liu et al. (2011)	70	60	−90	This study	Daqingshan Fault	Nearest fault
1934	1	21	41.0	108.8	6.3	3.13 × 10¹⁸	Liu et al. (2011)	120	60	−90	This study	Seertengshan Fault	Nearest fault
1936	8	1	34.2	105.7	6.0	1.11 × 10¹⁸	Lee et al. (1978)	334	46	38	This study		Nearest instrumental eq
1952	10	8	39.0	112.7	5.5	1.97 × 10¹⁷	Liu et al. (2011)	45	62	−90	This study, Li et al. (2015a)	Yunzhongshan Fault	Nearest fault
1962	12	7	38.1	106.3	5.5	1.97 × 10¹⁷	Qin et al. (2002)	108	36	144	CSB^e		In literature
1965	1	13	35.0	111.6	5.5	1.97 × 10¹⁷	Qin et al. (2002)	201	65	−158	CSB		In literature
1967	7	28	40.5	115.6	5.4	1.40 × 10¹⁷	Liu et al. (2011)	67	69	−81	This study, Pavlides et al. (1999)	Huailai Fault	Av. 3 striations
1967	12	18	36.5	111.2	5.4	1.40 × 10¹⁷	Qin et al. (2002)	355	80	−161	CSB		In literature
1970	12	3	35.9	105.6	5.1	4.95 × 10¹⁶	Qin et al. (2002)	9	74	132	CSB		In literature
1971	6	28	37.9	106.3	5.1	4.95 × 10¹⁶	Qin et al. (2002)	213	63	46	CSB		In literature
1976	4	6	40.2	112.1	6.2	2.21 × 10¹⁸	Liu et al. (2011)	209	75	164	CSB		In literature
1976	9	23	39.9	106.4	6.2	2.21 × 10¹⁸	Qin et al. (2002)	79	68	28	CSB		In literature
1979	6	19	36.83	111.50	5.0	3.51 × 10¹⁶	GCMT^f	278	30	−63	GCMT^f		In literature
1979	8	24	40.83	108.24	5.7	3.94 × 10¹⁷	GCMT	111	44	−65	GCMT		In literature
1981	8	13	40.50	113.40	5.5	1.97 × 10¹⁷	Qin et al. (2002)	183	80	−178	CSB		In literature
1987	1	7	34.23	103.86	5.4	1.40 × 10¹⁷	GCMT	170	65	28	GCMT		In literature
1987	8	10	37.57	105.63	5.3	9.89 × 10¹⁶	GCMT	336	25	−75	GCMT		In literature
1988	1	3	38.13	106.86	5.2	7.00 × 10¹⁶	GCMT	110	57	5	GCMT		In literature
1989	10	18	39.63	113.84	5.4	1.40 × 10¹⁷	GCMT	92	44	−39	GCMT	Hengshan Fault	In literature
1989	10	18	39.77	113.49	5.6	2.79 × 10¹⁷	GCMT	200	75	−175	GCMT	Liulengshan Fault	In literature
1989	10	18	39.83	113.61	5.4	1.40 × 10¹⁷	GCMT	204	76	−176	GCMT	Liulengshan Fault	In literature
1989	10	19	39.94	113.84	6.1	1.57 × 10¹⁸	Li et al. (2015a)	200	44	136	Li et al. (2015a)	Dawang-Tuanbao Fault	In literature
1989	10	19	39.92	113.91	5.9	7.85 × 10¹⁷	Xu et al. (2000)	210	76	−167	Xu et al. (2000)		In literature
1991	3	25	40.10	113.34	5.4	1.40 × 10¹⁷	GCMT	106	82	7	GCMT	Datong Basin Fault	In literature
1996	5	3	40.72	109.69	6.0	1.11 × 10¹⁸	GCMT	308	75	−12	GCMT		In literature
1998	1	10	41.34	114.34	5.7	3.94 × 10¹⁷	GCMT	207	54	135	GCMT		In literature
1999	11	1	39.85	113.74	5.2	7.00 × 10¹⁶	GCMT	122	72	−7	GCMT	Liulengshan Fault	In literature
2000	6	6	37.02	103.91	5.5	1.97 × 10¹⁷	GCMT	96	68	−6	GCMT		In literature
2003	11	13	34.61	104.10	5.1	4.95 × 10¹⁶	GCMT	347	42	53	GCMT		In literature
2013	7	21	34.60	104.31	6.0	1.11 × 10¹⁸	GCMT	196	57	151	GCMT		In literature
2013	7	22	34.65	104.35	5.4	1.40 × 10¹⁷	GCMT	153	37	103	GCMT		In literature
2015	4	15	39.74	106.39	5.5	1.97 × 10¹⁷	GCMT	356	81	−177	GCMT		In literature

^aMagnitudes for historical earthquakes are estimated from intensities on the New Chinese Intensity Scale using M_s = 0.58 × I₀ + 1.5. M_s is considered equal to M_w for M_s ≤ 8 (Kanamori 1983).

^bM₀ calculated from M_w using M₀ = 10^{|$\frac{3}{2}$| (M_w+6.03)}.

^cSeismic moment and focal parameters for 1556 earthquake re-estimated from Zhou (2016).

^dSeismic moment and focal parameters for 1739 earthquake re-estimated from Middleton et al. (2016a).

^eChina Seismological Bureau Catalogue (Qin et al. 2002).

^fGlobal Centroid Moment Tensor Catalogue.

Lee et al. (1976) reported surface wave magnitudes (M_s), calculated from the maximum historically recorded intensities of shaking (I₀) using the empirical relationship M_s = 0.58 × I₀ + 1.5. Lee et al. (1978) also reported surface-wave magnitudes and we assumed that the magnitudes given in the Liu et al. (2011) catalogue were surface-wave magnitudes. For M_s ≤ 8 we can approximate surface-wave magnitude (M_s) as equal to moment magnitude (M_w) (Kanamori 1983) and we therefore calculated seismic moment (M₀) using

\begin{equation} M_{0} = 10^{\frac{3}{2}\left(M_{\text{w}}+6.03\right)}. \end{equation}

(2)

Liu et al. (2011) suggested an error on the magnitudes in their catalogue of ±0.3. This seems reasonable given that a number of other historical catalogues quote magnitudes to the nearest quarter of a magnitude unit. Furthermore, a moment magnitude with an error of ±0.3 equates to a seismic moment that varies by a factor of 2.8 either way. This is similar to Wesnousky et al. (1984), who estimated that the seismic moments in their catalogue were correct to within a factor of 3 either way.

Focal parameters for 49 of these 88 earthquakes were available in the literature (Wesnousky et al. 1984; Xu et al. 2000; Qin et al. 2002; Liu et al. 2007; Li et al. 2015a) or the GCMT catalogue (see Data and Resources Section). For the remaining historical events, we estimated focal parameters from adjacent faults or nearby instrumental earthquakes (see Table 1). For four of the events, we were able to use fault striation measurements from the nearest adjacent fault (Pavlides et al. 1999) to estimate a focal mechanism, assuming that the sense of slip during the earthquake was the same as the Quaternary motion on the nearby fault. In 28 cases, where striations were not present but the earthquake could still reasonably be assigned to the nearest adjacent fault, we used geological strike and dip measurements from the literature, or our own mapped fault traces, and an estimate of the rake based on the known type of faulting (90° for reverse faults; 0° for left-lateral faults; −90° for normal faults; 180° for right-lateral faults; 45° for a combination of reverse and left-lateral faulting etcetera). Again, we assumed that the sense of slip during the earthquake was the same as the Quaternary motion on the nearby fault. In seven instances, we were not confident in assigning the earthquake to the adjacent mapped fault. In these cases, we used the nearest instrumental earthquake as an indicator of the likely focal mechanism. Four of these events were from the southwestern corner of the region and had magnitudes that were similar to the instrumental earthquakes that we compared them to. The other three were from the northern Shanxi Grabens, where the nearby instrumental earthquakes tended to have smaller magnitudes than the historical events (Li et al. 2015a). However, our own recent work in the northern Shanxi Grabens indicated that even short catalogues of much smaller earthquakes were reliable indicators of the pattern, if not the magnitude, of strain release (Middleton et al. 2017).

Focal mechanisms for most of the larger historical events in our catalogue are from Wesnousky et al. (1984), who also used Quaternary fault data, including a number of field studies, to allocate focal parameters. Fault strikes from mapped fault traces are reasonably reliable, but dips and rakes tend to be less well constrained. Hence, Wesnousky et al. (1984) estimated that their focal parameters may be wrong by up to ±15°. A similar level of uncertainty is likely to apply to the focal parameters estimated in this study. However, during our recent work in the northern Shanxi Grabens, we found that uncertainties in dips and rakes of ±15° led to the magnitudes of the principal strain rates varying by up to around 30 per cent, while the azimuths of the principal strain rates only varied by ±8° (Middleton et al. 2017). What this indicates is that uncertainties in our estimated focal parameters have a much smaller influence on our final results than the uncertainties associated with the earthquake magnitudes.

We also updated some of the focal mechanisms in the Wesnousky et al. (1984) catalogue. For example, Wesnousky et al. (1984) assumed that both of their earthquakes in northern Ningxia, the 1477 and 1739 events, had the same mechanism, and used observations of offsets at the Great Wall to determine the fault parameters. We updated the 1739 mechanism on the basis of our own recent study of this event (Middleton et al. 2016a). Similarly, Wesnousky et al. (1984) attributed a predominantly strike-slip mechanism on a southward-dipping fault to the 1556 event and then used the same mechanism for the 1501, 1568, 1642 and 1815 events in the Weihe Graben. However, more recent studies have found fault striations that indicate almost pure normal motion during the 1556 earthquake on a northward-dipping fault (Zhou 2016), so we have updated all of these mechanisms.

Following the divisions used by Wesnousky et al. (1984) we split our calculation into five regions, which we call (from top to bottom and left to right): North Ningxia, South Ningxia, Hetao, Weihe and Shanxi (see Fig. 2). We used these relatively large horizontal extents for our calculations so as to include enough earthquakes for us to be able to apply Kostrov’s relation, and because it is not necessarily the case that all of the accumulating strain is localised on the mapped faults. We used a shear modulus (μ) of 3.3 GPa and a seismogenic thickness (T_s) of 20 km for all calculations. We chose T_s = 20 km as this was the value used by Wesnousky et al. (1984) and because numerous recent studies suggest that earthquake hypocentres in the Ordos region do not typically exceed ≈20 km (Xu et al. 2000; Wang et al. 2013; Cai et al. 2014; Cheng et al. 2014; Li et al. 2015a). (For example, in the catalogue used by Cheng et al. (2014) 91.6 per cent of the earthquakes and 99.9 per cent of the moment release occurred above 20 km.) We used earthquake depths rather than any alternative measures of crustal thickness as our proxy for T_s because it is only the seismogenic portion of the crust that is relevant for Kostrov summations. Then, having obtained the seismic strain rate tensor in each region, we calculated the principal strain rates in order to find the magnitude and azimuth of each of the maximum principal strain rates (see Appendix A). Finally, we determined the value of the parameter ϕ, where |$\tan \left(\phi \right) = \frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}$|⁠, which allows us to quantify the expected pattern of faulting in each region (see Appendix B for details).

Figure 2.

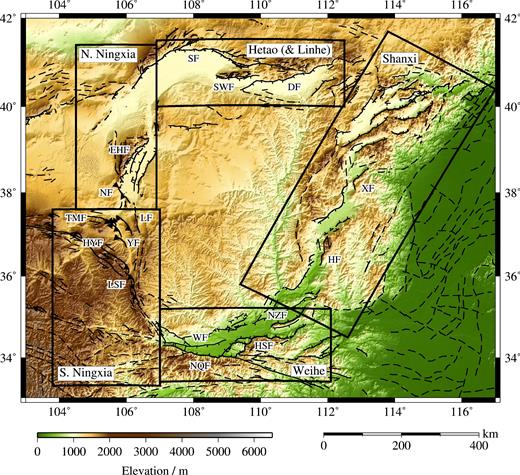
Active faults at the margins of the Ordos Plateau. Black boxes and labels indicate the five regions discussed in this paper. Faults were mapped from satellite imagery (source: http://earth.google.com) and based upon earlier fault maps from Tapponnier & Molnar (1977), Deng et al. (1984), Zhang et al. (1986), The Research Group on Active Fault System around Ordos Massif (1988), Zhang et al. (1990), Xu & Ma (1992), Deng & Liao (1996), Darby & Ritts (2002), Yu (2004), Darby et al. (2005) and Deng et al. (2007). Faults that are inferred or show no evidence of Quaternary activity are marked by dashed lines. Faults are labelled as follows: DF Daqingshan Fault; DFF Danfeng Fault; EHF East Helanshan Fault; HF Huoshan Fault; HSF Huashan Fault; HYF Haiyuan Fault; LF Luoshan Fault; LNF Luonan Fault; LSF Liupanshan Fault; NF Niushoushan Fault; NQF North Qinlingshan Fault; NZF North Zhongtiaoshan Fault; SF Seertengshan Fault; SWF South Wulashan Fault; TMF Tianjinshan-Miboshan Fault; WF Weihe Fault; XF Xizhoushan Fault; YF Yantongshan Fault.

Open in new tab Download slide

We also note here that T_s is inversely proportional in a linear sense to the magnitudes of the seismic strain rates; a smaller seismogenic thickness would result in larger seismic strain rates (and hence smaller seismic moment deficits). However, likely variations in T_s of around ±5 km are not significant enough to affect our overall conclusions.

2.2 Strain rate field from GPS

Numerous GPS studies conducted in the last two decades have provided us with knowledge of the crustal motion in northeast China (Shen et al. 2000; Wang et al. 2001; He et al. 2003; Zhang et al. 2004; Gan et al. 2007; Li et al. 2012; Zhao et al. 2015, 2017). The Crustal Motion Observation Network of China was established in 1998 by the State Seismological Bureau of China (now the China Earthquake Administration) and provides a consistent GPS velocity field over much of China (Liu et al. 2007). The network originally comprised 27 continuous GPS stations and 1056 temporary survey stations, which were occupied in 1999, 2001 and 2004. More recently, the network has been upgraded with 233 new continuous GPS stations and an extra 1000 temporary survey stations, which were visited during field campaigns in 2009, 2011 and 2013 (Li et al. 2012; Zhao et al. 2015). Zhao et al. (2017) drew swath profiles through the GPS data from Zhao et al. (2015) in order to try and estimate slip rates on major active faults around the Ordos Plateau.

We calculated a continuously varying strain rate field from the latest campaign GPS measurements (Zhao et al. 2015), comprising these three occupations, according to the method of Shen et al. (1996) and Floyd et al. (2010). The motivation for considering a continuous strain rate field was that a number (though not all) theories of continental deformation postulate that the whole lithosphere in a deforming region responds to gradients in gravitational potential energy and stresses that are applied at its edges (Bird & Piper 1980; England & McKenzie 1982; Flesch et al. 2001; Calais et al. 2006).

Of the 790 stations in the region of interest (31 to 44°N, and 102 to 120°E), we removed 130 with errors on the northerly or easterly velocities of greater than 0.5 mm a⁻¹ (see Fig. 3a). The majority of these 130 stations are located in the North China Plain, possibly because there are fewer reliably stable monuments in this low-lying, sedimentary terrain. We solved for the easterly and northerly components of velocity and the four horizontal velocity gradients at each GPS site using a least squares inversion, assuming uniform velocity gradients in both the northerly and easterly directions (see Fig. 3b). All GPS sites within a radius r_max were included in each inversion (except for the GPS site at which the calculation was being performed), but they were given a Gaussian weighting (W) according to the square of their distance (r) from the calculation site:

\begin{equation} W = e^{\frac{-r^{2}}{\alpha ^{2}}}, \end{equation}

(3)

where α is a constant that defines the width of the Gaussian smoothing function and determines the horizontal resolution of the continuous model. Following the method of Floyd et al. (2010), we determined a minimum value for r (r_min) by requiring that 75 per cent of GPS sites had at least six GPS sites (the site itself plus its five nearest neighbours) within a radial distance r_min. We obtained r_min = 78 km. Initially, we then set α to have the same value as r_min. We note that a smoothing parameter of 78 km is larger than the typical wavelength of elastic strain accumulation around any one individual fault, but, in this study, we are primarily interested in regional strains. Furthermore, the GPS data is not dense enough to merit a lower value of α. We also investigate the effects of different values of α and r_max below.

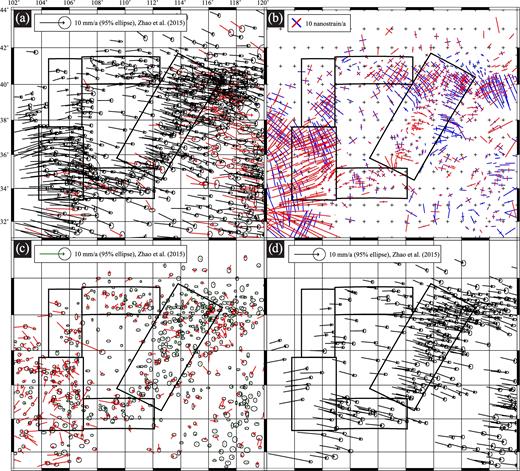
(a) GPS data from Zhao et al. (2015) relative to stable Eurasia. Red vectors indicate stations where northerly or easterly error is ≥ 0.5 mm a−1. Black boxes indicate regions in which Kostrov summations were performed. 790 stations lie within the region shown, of which 660 have errors < 0.5 mm a−1. (b) Strain rate field calculated from GPS at each GPS station, using α = 80 km and rmax = 200 km. Crosses indicate orientation and magnitude of maximum and minimum horizontal strain rate; blue indicates extension and red indicates contraction. (c) Residual vectors obtained when velocities from inversion in (b) are subtracted from the original data in (a). Red vectors indicate stations with residuals ≥ 1 mm a−1. 348 stations have residuals < 1 mm a−1. (d) Remaining 348 vectors from (a) that are used in final strain rate calculation.

Figure 3.

(a) GPS data from Zhao et al. (2015) relative to stable Eurasia. Red vectors indicate stations where northerly or easterly error is ≥ 0.5 mm a⁻¹. Black boxes indicate regions in which Kostrov summations were performed. 790 stations lie within the region shown, of which 660 have errors < 0.5 mm a⁻¹. (b) Strain rate field calculated from GPS at each GPS station, using α = 80 km and r_max = 200 km. Crosses indicate orientation and magnitude of maximum and minimum horizontal strain rate; blue indicates extension and red indicates contraction. (c) Residual vectors obtained when velocities from inversion in (b) are subtracted from the original data in (a). Red vectors indicate stations with residuals ≥ 1 mm a⁻¹. 348 stations have residuals < 1 mm a⁻¹. (d) Remaining 348 vectors from (a) that are used in final strain rate calculation.

Open in new tab Download slide

We then compared the velocities that we obtained from our inversion to the original GPS vectors and calculated a residual at each site (see Fig. 3c). We removed sites with residual velocities greater than 1 mm a⁻¹ (i.e. sites that did not fit a locally smooth field) to leave 348 sites in the region of interest (44 per cent of the original data; 53 per cent of the 660 reliable stations). In other words, we assumed locally homogeneous but regionally varying velocity gradients. For comparison, 500 sites had residuals less than 2 mm a⁻¹ (63 per cent of the original data; 76 per cent of the 660 reliable stations). We then re-calculated the strain rate field on a regular 0.5° grid. If any calculation point did not include at least six GPS stations within a radius of r_max, then no calculation was performed at this site. (See Appendix C for mathematical details of these calculations.)

Finally, in order to compare the GPS results with our Kostrov summations, we also solved for a single set of velocity gradients (and hence a single strain rate tensor) in each Kostrov box. For each of these calculations we selected GPS sites that fell within the relevant Kostrov box from the 660 GPS vectors with errors less than 0.5 mm a⁻¹. These calculations were not weighted by the Gaussian smoothing parameter α, so each GPS site contributed equally to the inversion. Then, having obtained a single geodetic strain rate tensor for each region, we calculated the principal strain rates and the values of the parameter ϕ in the same way as before (see Appendices A and B).

3 RESULTS

3.1 Kostrov summations

Fig. 4(a) shows the results of the Kostrov summations for the Wesnousky et al. (1984) catalogue; Fig. 4(b) shows the results of the Kostrov summations for the earthquake catalogue compiled in this study. The full results of the Kostrov summations are recorded in Table 2.

Figure 4.

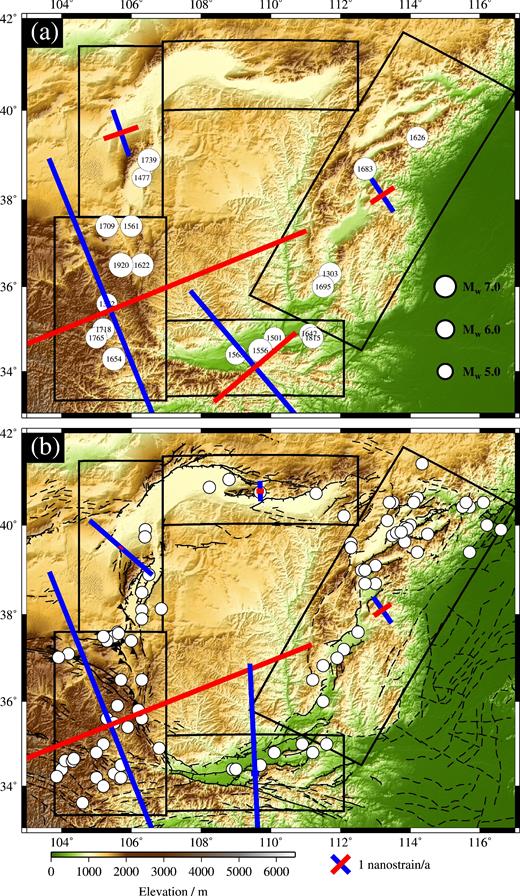
(a) SRTM topography (90 m resolution) of the Ordos Plateau (Farr et al. 2007). Black rectangles indicate Kostrov regions at the margins of the plateau. Historical earthquakes from Wesnousky et al. (1984) are shown as white circles, scaled according to their magnitude and including the year in which they occurred. Crosses indicate orientation and magnitude of maximum and minimum horizontal strain rate from a Kostrov summation in each region using the Wesnousky et al. (1984) earthquake catalogue; blue indicates extension and red indicates contraction. (b) Same as (a), but showing inferred focal mechanisms for our catalogue of historical earthquakes around the margins of the Ordos Plateau (see Table 1). Same earthquake magnitude scale as (a). B marks 1996 Baotou earthquake. Strain rate crosses as in (a), but calculated for our earthquake catalogue. See Table 2 for further details. Note that the scale is exaggerated 10 × for the Kostrov strain rate cross in the Linhe and Hetao Grabens. Faults from Fig. 2 are also shown.

Open in new tab Download slide

Table 2.

Open in new tab

Summary of results from Kostrov summations and GPS around the Ordos Plateau.

Earthquakes	Time	No. eqs	Area	Σ M₀	M₀ rate	\|$\dot{\epsilon }_{1}$\|	\|$\dot{\epsilon }_{2}^{a}$\|	\|$\dot{\epsilon }_{1}$\| az.	\|$\dot{\epsilon }_{1}$\|/\|$\dot{\epsilon }_{2}$\|	ϕ^b	Faulting^c
used	(years)		(km²)	(Nm)	(Nm a⁻¹)	(a⁻¹)	(a⁻¹)	(°)		radians
Earthquake catalogue from Wesnousky et al.* (1984)*
North Ningxia	700	2	86,992	1.66 × 10²⁰	2.37 × 10¹⁷	2.00 × 10⁻⁹	−1.49 × 10⁻⁹	161	−1.34	2.50	SS + normal
South Ningxia	700	8	138,561	2.36 × 10²¹	3.38 × 10¹⁸	1.34 × 10⁻⁸	−1.73 × 10⁻⁸	158	−0.77	2.23	SS + reverse
Hetao	700	0	78,661	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A
Weihe	700	5	93,765	7.61 × 10²⁰	1.09 × 10¹⁸	8.19 × 10⁻⁹	−4.39 × 10⁻⁹	140	−1.87	2.65	SS + normal
Shanxi	700	4	239,349	4.22 × 10²⁰	6.03 × 10¹⁷	1.62 × 10⁻⁹	−1.16 × 10⁻⁹	146	−1.40	2.52	SS + normal
Earthquake catalogue from this study
North Ningxia	700	8	86,992	2.84 × 10²⁰	4.06 × 10¹⁷	3.40 × 10⁻⁹	−8.12 × 10⁻¹¹	131	−41.87	3.12	Normal + SS
South Ningxia	700	30	138,561	2.44 × 10²¹	3.49 × 10¹⁸	1.35 × 10⁻⁸	−1.78 × 10⁻⁸	158	−0.76	2.22	SS + reverse
Hetao	700	5	78,661	7.95 × 10¹⁸	1.14 × 10¹⁶	8.30 × 10⁻¹¹	−3.02 × 10⁻¹¹	178	−2.75	2.79	Normal + SS
Weihe	700	7	93765	9.36 × 10²⁰	1.34 × 10¹⁸	9.03 × 10⁻⁹	3.20 × 10⁻¹⁰	177	28.22	3.18	Normal + normal
Shanxi	700	40	239,349	3.76 × 10²⁰	5.37 × 10¹⁷	1.30 × 10⁻⁹	−8.32 × 10⁻¹⁰	145	−1.56	2.57	SS + normal
GPS-derived strain rates in Kostrov regions
North Ningxia	4	24^d	86,992	6.71 × 10²⁰^e	9.59 × 10¹⁷	6.30 × 10⁻⁹	−8.35 × 10⁻⁹	130	−0.75	2.22	SS + reverse
South Ningxia	4	76^d	138,561	2.05 × 10²¹^e	2.93 × 10¹⁸	4.85 × 10⁻⁹	−1.60 × 10⁻⁸	158	−0.30	1.87	Reverse + SS
Hetao	4	43^d	78,661	3.47 × 10²⁰^e	4.95 × 10¹⁷	2.31 × 10⁻⁹	−4.77 × 10⁻⁹	121	−0.48	2.02	Reverse + SS
Weihe	4	33^d	93,765	3.31 × 10²⁰^e	4.73 × 10¹⁷	3.43 × 10⁻⁹	−3.82 × 10⁻⁹	2	−0.90	2.30	SS + reverse
Shanxi	4	169^d	239,349	3.72 × 10²⁰^e	5.31 × 10¹⁷	1.68 × 10⁻⁹	−1.08 × 10⁻⁹	136	−1.56	2.57	SS + normal

Earthquakes	Time	No. eqs	Area	Σ M₀	M₀ rate	\|$\dot{\epsilon }_{1}$\|	\|$\dot{\epsilon }_{2}^{a}$\|	\|$\dot{\epsilon }_{1}$\| az.	\|$\dot{\epsilon }_{1}$\|/\|$\dot{\epsilon }_{2}$\|	ϕ^b	Faulting^c
used	(years)		(km²)	(Nm)	(Nm a⁻¹)	(a⁻¹)	(a⁻¹)	(°)		radians
Earthquake catalogue from Wesnousky et al.* (1984)*
North Ningxia	700	2	86,992	1.66 × 10²⁰	2.37 × 10¹⁷	2.00 × 10⁻⁹	−1.49 × 10⁻⁹	161	−1.34	2.50	SS + normal
South Ningxia	700	8	138,561	2.36 × 10²¹	3.38 × 10¹⁸	1.34 × 10⁻⁸	−1.73 × 10⁻⁸	158	−0.77	2.23	SS + reverse
Hetao	700	0	78,661	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A
Weihe	700	5	93,765	7.61 × 10²⁰	1.09 × 10¹⁸	8.19 × 10⁻⁹	−4.39 × 10⁻⁹	140	−1.87	2.65	SS + normal
Shanxi	700	4	239,349	4.22 × 10²⁰	6.03 × 10¹⁷	1.62 × 10⁻⁹	−1.16 × 10⁻⁹	146	−1.40	2.52	SS + normal
Earthquake catalogue from this study
North Ningxia	700	8	86,992	2.84 × 10²⁰	4.06 × 10¹⁷	3.40 × 10⁻⁹	−8.12 × 10⁻¹¹	131	−41.87	3.12	Normal + SS
South Ningxia	700	30	138,561	2.44 × 10²¹	3.49 × 10¹⁸	1.35 × 10⁻⁸	−1.78 × 10⁻⁸	158	−0.76	2.22	SS + reverse
Hetao	700	5	78,661	7.95 × 10¹⁸	1.14 × 10¹⁶	8.30 × 10⁻¹¹	−3.02 × 10⁻¹¹	178	−2.75	2.79	Normal + SS
Weihe	700	7	93765	9.36 × 10²⁰	1.34 × 10¹⁸	9.03 × 10⁻⁹	3.20 × 10⁻¹⁰	177	28.22	3.18	Normal + normal
Shanxi	700	40	239,349	3.76 × 10²⁰	5.37 × 10¹⁷	1.30 × 10⁻⁹	−8.32 × 10⁻¹⁰	145	−1.56	2.57	SS + normal
GPS-derived strain rates in Kostrov regions
North Ningxia	4	24^d	86,992	6.71 × 10²⁰^e	9.59 × 10¹⁷	6.30 × 10⁻⁹	−8.35 × 10⁻⁹	130	−0.75	2.22	SS + reverse
South Ningxia	4	76^d	138,561	2.05 × 10²¹^e	2.93 × 10¹⁸	4.85 × 10⁻⁹	−1.60 × 10⁻⁸	158	−0.30	1.87	Reverse + SS
Hetao	4	43^d	78,661	3.47 × 10²⁰^e	4.95 × 10¹⁷	2.31 × 10⁻⁹	−4.77 × 10⁻⁹	121	−0.48	2.02	Reverse + SS
Weihe	4	33^d	93,765	3.31 × 10²⁰^e	4.73 × 10¹⁷	3.43 × 10⁻⁹	−3.82 × 10⁻⁹	2	−0.90	2.30	SS + reverse
Shanxi	4	169^d	239,349	3.72 × 10²⁰^e	5.31 × 10¹⁷	1.68 × 10⁻⁹	−1.08 × 10⁻⁹	136	−1.56	2.57	SS + normal

^aNegative principal strain rate indicates shortening.

^b|$\text{tan}\left(\phi \right) = \frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}$|

^cExpected pattern of faulting depends on exact value of ϕ—see Appendix B.

^dIndicates number of GPS stations in Kostrov region used to solve for best-fitting velocity gradients.

^eExtrapolated over 700 yr for comparison with the Kostrov summations.

Table 2.

Open in new tab

Summary of results from Kostrov summations and GPS around the Ordos Plateau.

Earthquakes	Time	No. eqs	Area	Σ M₀	M₀ rate	\|$\dot{\epsilon }_{1}$\|	\|$\dot{\epsilon }_{2}^{a}$\|	\|$\dot{\epsilon }_{1}$\| az.	\|$\dot{\epsilon }_{1}$\|/\|$\dot{\epsilon }_{2}$\|	ϕ^b	Faulting^c
used	(years)		(km²)	(Nm)	(Nm a⁻¹)	(a⁻¹)	(a⁻¹)	(°)		radians
Earthquake catalogue from Wesnousky et al.* (1984)*
North Ningxia	700	2	86,992	1.66 × 10²⁰	2.37 × 10¹⁷	2.00 × 10⁻⁹	−1.49 × 10⁻⁹	161	−1.34	2.50	SS + normal
South Ningxia	700	8	138,561	2.36 × 10²¹	3.38 × 10¹⁸	1.34 × 10⁻⁸	−1.73 × 10⁻⁸	158	−0.77	2.23	SS + reverse
Hetao	700	0	78,661	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A
Weihe	700	5	93,765	7.61 × 10²⁰	1.09 × 10¹⁸	8.19 × 10⁻⁹	−4.39 × 10⁻⁹	140	−1.87	2.65	SS + normal
Shanxi	700	4	239,349	4.22 × 10²⁰	6.03 × 10¹⁷	1.62 × 10⁻⁹	−1.16 × 10⁻⁹	146	−1.40	2.52	SS + normal
Earthquake catalogue from this study
North Ningxia	700	8	86,992	2.84 × 10²⁰	4.06 × 10¹⁷	3.40 × 10⁻⁹	−8.12 × 10⁻¹¹	131	−41.87	3.12	Normal + SS
South Ningxia	700	30	138,561	2.44 × 10²¹	3.49 × 10¹⁸	1.35 × 10⁻⁸	−1.78 × 10⁻⁸	158	−0.76	2.22	SS + reverse
Hetao	700	5	78,661	7.95 × 10¹⁸	1.14 × 10¹⁶	8.30 × 10⁻¹¹	−3.02 × 10⁻¹¹	178	−2.75	2.79	Normal + SS
Weihe	700	7	93765	9.36 × 10²⁰	1.34 × 10¹⁸	9.03 × 10⁻⁹	3.20 × 10⁻¹⁰	177	28.22	3.18	Normal + normal
Shanxi	700	40	239,349	3.76 × 10²⁰	5.37 × 10¹⁷	1.30 × 10⁻⁹	−8.32 × 10⁻¹⁰	145	−1.56	2.57	SS + normal
GPS-derived strain rates in Kostrov regions
North Ningxia	4	24^d	86,992	6.71 × 10²⁰^e	9.59 × 10¹⁷	6.30 × 10⁻⁹	−8.35 × 10⁻⁹	130	−0.75	2.22	SS + reverse
South Ningxia	4	76^d	138,561	2.05 × 10²¹^e	2.93 × 10¹⁸	4.85 × 10⁻⁹	−1.60 × 10⁻⁸	158	−0.30	1.87	Reverse + SS
Hetao	4	43^d	78,661	3.47 × 10²⁰^e	4.95 × 10¹⁷	2.31 × 10⁻⁹	−4.77 × 10⁻⁹	121	−0.48	2.02	Reverse + SS
Weihe	4	33^d	93,765	3.31 × 10²⁰^e	4.73 × 10¹⁷	3.43 × 10⁻⁹	−3.82 × 10⁻⁹	2	−0.90	2.30	SS + reverse
Shanxi	4	169^d	239,349	3.72 × 10²⁰^e	5.31 × 10¹⁷	1.68 × 10⁻⁹	−1.08 × 10⁻⁹	136	−1.56	2.57	SS + normal

Earthquakes	Time	No. eqs	Area	Σ M₀	M₀ rate	\|$\dot{\epsilon }_{1}$\|	\|$\dot{\epsilon }_{2}^{a}$\|	\|$\dot{\epsilon }_{1}$\| az.	\|$\dot{\epsilon }_{1}$\|/\|$\dot{\epsilon }_{2}$\|	ϕ^b	Faulting^c
used	(years)		(km²)	(Nm)	(Nm a⁻¹)	(a⁻¹)	(a⁻¹)	(°)		radians
Earthquake catalogue from Wesnousky et al.* (1984)*
North Ningxia	700	2	86,992	1.66 × 10²⁰	2.37 × 10¹⁷	2.00 × 10⁻⁹	−1.49 × 10⁻⁹	161	−1.34	2.50	SS + normal
South Ningxia	700	8	138,561	2.36 × 10²¹	3.38 × 10¹⁸	1.34 × 10⁻⁸	−1.73 × 10⁻⁸	158	−0.77	2.23	SS + reverse
Hetao	700	0	78,661	N/A	N/A	N/A	N/A	N/A	N/A	N/A	N/A
Weihe	700	5	93,765	7.61 × 10²⁰	1.09 × 10¹⁸	8.19 × 10⁻⁹	−4.39 × 10⁻⁹	140	−1.87	2.65	SS + normal
Shanxi	700	4	239,349	4.22 × 10²⁰	6.03 × 10¹⁷	1.62 × 10⁻⁹	−1.16 × 10⁻⁹	146	−1.40	2.52	SS + normal
Earthquake catalogue from this study
North Ningxia	700	8	86,992	2.84 × 10²⁰	4.06 × 10¹⁷	3.40 × 10⁻⁹	−8.12 × 10⁻¹¹	131	−41.87	3.12	Normal + SS
South Ningxia	700	30	138,561	2.44 × 10²¹	3.49 × 10¹⁸	1.35 × 10⁻⁸	−1.78 × 10⁻⁸	158	−0.76	2.22	SS + reverse
Hetao	700	5	78,661	7.95 × 10¹⁸	1.14 × 10¹⁶	8.30 × 10⁻¹¹	−3.02 × 10⁻¹¹	178	−2.75	2.79	Normal + SS
Weihe	700	7	93765	9.36 × 10²⁰	1.34 × 10¹⁸	9.03 × 10⁻⁹	3.20 × 10⁻¹⁰	177	28.22	3.18	Normal + normal
Shanxi	700	40	239,349	3.76 × 10²⁰	5.37 × 10¹⁷	1.30 × 10⁻⁹	−8.32 × 10⁻¹⁰	145	−1.56	2.57	SS + normal
GPS-derived strain rates in Kostrov regions
North Ningxia	4	24^d	86,992	6.71 × 10²⁰^e	9.59 × 10¹⁷	6.30 × 10⁻⁹	−8.35 × 10⁻⁹	130	−0.75	2.22	SS + reverse
South Ningxia	4	76^d	138,561	2.05 × 10²¹^e	2.93 × 10¹⁸	4.85 × 10⁻⁹	−1.60 × 10⁻⁸	158	−0.30	1.87	Reverse + SS
Hetao	4	43^d	78,661	3.47 × 10²⁰^e	4.95 × 10¹⁷	2.31 × 10⁻⁹	−4.77 × 10⁻⁹	121	−0.48	2.02	Reverse + SS
Weihe	4	33^d	93,765	3.31 × 10²⁰^e	4.73 × 10¹⁷	3.43 × 10⁻⁹	−3.82 × 10⁻⁹	2	−0.90	2.30	SS + reverse
Shanxi	4	169^d	239,349	3.72 × 10²⁰^e	5.31 × 10¹⁷	1.68 × 10⁻⁹	−1.08 × 10⁻⁹	136	−1.56	2.57	SS + normal

^aNegative principal strain rate indicates shortening.

^b|$\text{tan}\left(\phi \right) = \frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}$|

^cExpected pattern of faulting depends on exact value of ϕ—see Appendix B.

^dIndicates number of GPS stations in Kostrov region used to solve for best-fitting velocity gradients.

^eExtrapolated over 700 yr for comparison with the Kostrov summations.

Our Kostrov summations do not differ significantly from the results of Wesnousky et al. (1984). This is to be expected given that the total seismic moment released by the earthquakes in the Wesnousky et al. (1984) catalogue (M_s ≥ 6.5) constitutes between 58 and 97 per cent (depending on the region) of the seismic moment released by the earthquakes in our catalogue (see Table 2). The magnitudes of the maximum and minimum principal strain rates depend heavily on the parameters assigned to the largest earthquake in each region—particularly the 1739 Yinchuan, the 1920 Haiyuan, the 1556 Huaxian, and the 1303 Hongdong events. (The 1303 earthquake was not included in our catalogue as it occurred just over 700 yr ago, but it was used by Wesnousky et al. (1984)).

Furthermore, the largest uncertainty in the Kostrov summations stems from errors on the magnitude estimates for the historical earthquakes. A moment magnitude with a typical error of ±0.3 (Liu et al. 2011) equates to a seismic moment that varies by a factor of 2.8 either way. In other words, the total moment release (Σ M₀), the moment release rate (M₀ rate), the maximum principal strain rate (⁠|$\dot{\epsilon }_{1}$|⁠) and the minimum principal strain rate (⁠|$\dot{\epsilon }_{2}$|⁠) in Table 2 are all uncertain by up to a factor of ≈3 either way (that is, if the errors are systematic rather than random). In contrast, Wesnousky et al. (1984) suggested typical uncertainties in strike, dip and rake of ±15°, which roughly equate to uncertainties in the azimuths of the maximum and minimum principal strain rates of ±15°. The orientation of the principal strain rates is much better constrained than their magnitude. We also note that our decision to use the same horizontal extents as Wesnousky et al. (1984) means that our strain rates refer to whole regions, parts of which may be deforming very slowly, rather than specific grabens.

The general pattern of strain release is as follows (see Appendix B for the theory associated with interpreting the strain rate results). In northern Ningxia, the deformation appears to be dominated by extension at a strain rate of 3.4 nanostrain a⁻¹ and an azimuth of 131°. This extension could readily be accommodated on the NNE-SSW normal faults in northern Ningxia, particularly on the East Helanshan Fault (see Fig. 2). Meanwhile, Wesnousky et al. (1984) obtained a much larger component of north–south right-lateral strike-slip motion (see Fig. 4a), with the extension occurring at a strain rate of 2.0 nanostrain a⁻¹ and an azimuth of 161°. This difference is also reflected in the ϕ value, which indicates dominant strike-slip faulting with secondary normal faulting for the Wesnousky et al. (1984) summation and dominant normal faulting with secondary strike-slip faulting for our summation. However, 96 per cent of the total moment release is due to the 1739 Yinchuan earthquake, so the result depends very heavily on the parameters used for this event—and we updated the estimate from Wesnousky et al. (1984) on the basis of our own careful field study (Middleton et al. 2016a). We really need a longer catalogue with more large-magnitude events to provide a more accurate summation.

In southern Ningxia, the maximum and minimum principal strain rates are roughly equal in magnitude and opposite in sign, indicating predominantly strike-slip faulting with a small component of contraction. The strain could therefore be taken up on WNW-ESE left-lateral strike-slip faults or NNE-SSW right-lateral strike-slip faults. From the pattern of active faulting, it appears that both types of fault are present: the Haiyuan, Yantongshan and Tianjinshan-Miboshan Faults are all predominantly left-lateral whilst the Luoshan and Niushoushan Faults, which lie approximately at right-angles, are right-lateral (see Fig. 2). In addition, northeast-southwest contraction at a strain rate of 18 nanostrain a⁻¹ and an azimuth of 68° (which corresponds to ≈5 mm a⁻¹ of shortening) is taken up on NNW-SSE striking reverse faults, such as the Liupanshan Fault. The Wesnousky et al. (1984) summation is very similar to our result. Both calculations give ϕ values that suggest dominantly strike-slip faulting with secondary reverse faulting.

North of the Ordos, in the Linhe and Hetao Grabens, the dominant motion is north–south extension at a strain rate of 0.083 nanostrain a⁻¹ and an azimuth of 178°. This motion could be taken up on the Seertengshan, South Wulashan and Daqingshan Faults (see Fig. 2). In addition, there is a small amount of strike-slip motion to be accommodated. This could be achieved by northwest-southeast left-lateral strike-slip faulting on, for example, an extension of the Seertengshan Fault—as occurred in the 1996 Baotou earthquake. Wesnousky et al. (1984) did not have any earthquakes from this region in their catalogue, so we are not able to compare our result with their work. Nonetheless, we note that our seismic strain rate in the northern Ordos is two orders of magnitude smaller than at other margins of the plateau. This difference is much larger than the factor of ≈3 that could arise from errors on the magnitude estimates. Either the strain rate really is much lower in the northern Ordos, or we are missing rare, large-magnitude events from our 700 yr catalogue. For example, the M 7.5 849 earthquake, which would add an additional 2.0 × 10²⁰ Nm to the total moment release—increasing it by more than a factor of 10, has not been included in this summation. Furthermore, palaeoseismological work on the Daqingshan Fault indicates typical recurrence intervals for large earthquakes of more than 2000 yr, so it is plausible that our time window has failed to capture the most important events (Ran et al. 2002, 2003a,b).

In the Weihe Graben, extension occurs at a strain rate of 9 nanostrain a⁻¹ (equivalent to ≈1.8 mm a⁻¹) and an azimuth of 177°, which is consistent with normal-faulting on, for example, the Weihe, North Qinlingshan, Huashan and North Zhongtiaoshan Faults (see Fig. 2). This extension appears to be almost completely biaxial (i.e. matched by vertical thinning rather than any east–west strain). Again, though, 89 per cent of the total moment release is due to the 1556 Huaxian earthquake, so the result depends very heavily on the parameters used for this event. We used recent observations from Zhou (2016) to constrain the focal mechanism for this earthquake, but Wesnousky et al. (1984) used different parameters and obtained a much larger component of strike-slip motion. Again, this difference is reflected in different principal strain rate azimuths (177° compared to 140°) and different ϕ values (3.18 compared to 2.65) for the two summations (see Table 2).

Finally, in the Shanxi Grabens, the predominant motion is strike-slip: either right-lateral strike-slip on faults striking NNE-SSW or left-lateral strike-slip on faults striking WNW-ESE. Given the orientation of faults in the Shanxi Grabens, right-lateral motion is more likely. The Xizhoushan and Huoshan Faults are major right-lateral structures in the Shanxi Grabens, but motion can also be accommodated by oblique slip on the intervening en echelon normal faults (see Fig. 2). There is also good agreement between our summation and the result from Wesnousky et al. (1984); both calculations give ϕ values that suggest dominantly strike-slip faulting with secondary normal faulting.

3.2 Strain rate field from GPS

Fig. 5(a) shows the results of the strain rate calculation for α = 80 km and r_max = 200 km. The results appear to show relatively high strain rates in the interior of the Ordos Plateau. However, these results are due to ‘leakage’ from the deforming margins of the plateau. Figs 5(b)–(d) show that when r_max is reduced, the calculation points in the interior of the plateau do not have enough GPS stations nearby to allow calculation of the velocity gradients and the strain rate. Fig. 6 shows an interpolated map of the second invariant of the geodetic strain rate tensor at each calculation node for α = 80 km and r_max = 200 km. We interpret our GPS-derived strain rate results with the help of the theory outlined in Appendix B. We ignore the interior of the plateau, due to the lack of GPS stations, and instead focus on the pattern of strain release at the margins of the plateau. In most cases, our calculated strain rates are consistent with the velocity differences estimated by Zhao et al. (2017).

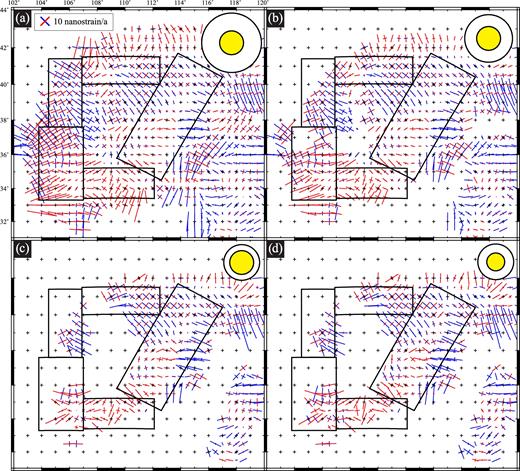
(a) Strain rate field calculated on a regular 0.5° grid from the 348 stations with residuals < 1 mm a−1 (see Fig. 3d). Black boxes indicate Kostrov regions. Crosses indicate orientation and magnitude of maximum and minimum horizontal strain rate; blue indicates extension and red indicates contraction. Yellow circle indicates value of α (radius of circle is 80 km) and white circle indicates value of rmax (radius of circle is 200 km). (b) Same as (a) with α = 80 km and rmax = 160 km. (c) α = 80 km and rmax = 120 km. (d) α = 60 km and rmax = 120 km.

Figure 5.

(a) Strain rate field calculated on a regular 0.5° grid from the 348 stations with residuals < 1 mm a⁻¹ (see Fig. 3d). Black boxes indicate Kostrov regions. Crosses indicate orientation and magnitude of maximum and minimum horizontal strain rate; blue indicates extension and red indicates contraction. Yellow circle indicates value of α (radius of circle is 80 km) and white circle indicates value of r_max (radius of circle is 200 km). (b) Same as (a) with α = 80 km and r_max = 160 km. (c) α = 80 km and r_max = 120 km. (d) α = 60 km and r_max = 120 km.

Open in new tab Download slide

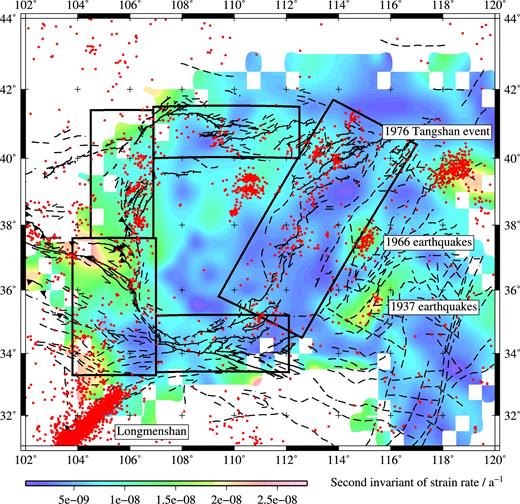
$Second invariant $(\dot{E} = \left(\dot{\epsilon }_{ij}\dot{\epsilon }_{ij}\right)^{\frac{1}{2}})$ of the strain rate field calculated on a regular 0.5° grid with α = 80 km and rmax = 200 km. Black boxes indicate Kostrov regions. Earthquakes of Mw > 2.0 from the International Seismological Centre (ISC) catalogue are shown as red dots (see Data and Resources Section). Faults from Fig. 2 are also shown.$

Figure 6.

Second invariant |$(\dot{E} = \left(\dot{\epsilon }_{ij}\dot{\epsilon }_{ij}\right)^{\frac{1}{2}})$| of the strain rate field calculated on a regular 0.5° grid with α = 80 km and r_max = 200 km. Black boxes indicate Kostrov regions. Earthquakes of M_w > 2.0 from the International Seismological Centre (ISC) catalogue are shown as red dots (see Data and Resources Section). Faults from Fig. 2 are also shown.

Open in new tab Download slide

To the north and west of the northern Ningxia region, on the western side of the Ordos Plateau, there is insufficient GPS data for the strain rate to be reliably resolved (see e.g. Fig. 5c). However, in the southern part of the volume, in the Yinchuan Graben, the predominant strain is consistent with either north–south, right-lateral motion or east–west left-lateral motion (see Fig. 5). Given that most faults in the vicinity are oriented north–south, we assume that the predominant strain is north–south right-lateral motion. In a previous paper about the western Ordos we estimated that, in the Yinchuan Graben, this north–south, right-lateral motion occurs at 3.3 ± 0.5 mm a⁻¹, by fitting an arctangent function through the same GPS data (Middleton et al. 2016b). This is consistent with, though slightly larger than, the estimate of 2.1 ± 1.0 mm a⁻¹ from Zhao et al. (2017), who drew their profile at a different azimuth. In the continuous field, the extensional strain rate is typically very slightly larger than the contractional strain rate indicating a small component of normal motion, although the single strain rate tensor suggests the opposite (see Fig. 7). The azimuth of the maximum principal (extensional) strain rate rotates from ≈120° to ≈160° on moving from north to south, but otherwise the pattern of strain is relatively uniform.

Figure 7.

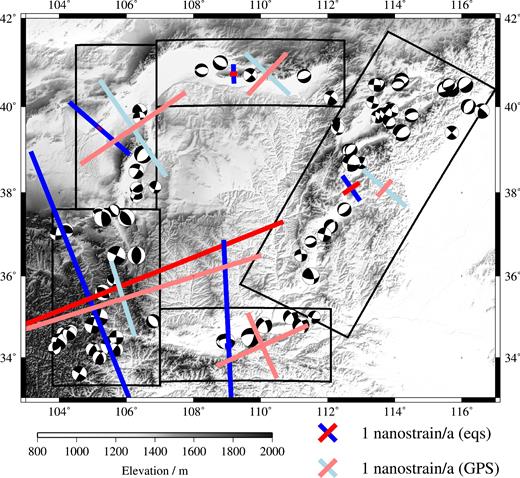
Comparison between Kostrov summations and GPS-derived strain rates. Black boxes indicate Kostrov regions. Brighter coloured crosses indicate orientation and magnitude of maximum and minimum horizontal strain rate from Kostrov summations; paler coloured crosses indicate orientation and magnitude of maximum and minimum horizontal strain rate, calculated from the GPS data within each Kostrov region. Blue indicates extension and red indicates contraction. Note that the scale is exaggerated 10 × for the Kostrov strain rate cross in the Hetao Graben. Inferred focal mechanisms for our catalogue of historical earthquakes around the margins of the Ordos Plateau (see Table 1) are shown in black. The observed mechanisms are consistent with the pattern of faulting expected from the geodetic strain rates in South Ningxia and Shanxi, but not in North Ningxia, Hetao or Weihe (see Table 2).

Open in new tab Download slide

In the southern Ningxia region the predominant strain is approximately east–west contraction, accompanied by approximately north–south extension (see Fig. 5), implying a combination of reverse and strike-slip faulting. The azimuth of the contraction rotates through the region so as to remain roughly perpendicular to the edge of the Tibetan Plateau. The single strain rate tensor for the whole volume indicates that contraction occurs at 16 nanostrain a⁻¹ and an azimuth of 68°, equivalent to a velocity difference across the region of ≈5 mm a⁻¹ (see Fig. 7). This is slightly larger than the estimate from Zhao et al. (2017) of 3.0 ± 1.1 mm a⁻¹, but in agreement with the estimate of 6.0 ± 2.0 mm a⁻¹ (at an azimuth of 75°) from Zhang et al. (2004).

To the north of the Ordos there is a lack of GPS sites in the Linhe Graben (on the western side of the Kostrov volume) and so the strain rate cannot be reliably resolved there (see e.g. Fig. 5c). In the eastern part of the volume, in the Hetao Graben, the predominant GPS-derived strain is east–west left-lateral motion and the typical azimuth of the maximum principal (extensional) strain rate is 135° (see Fig. 5). The single strain rate tensor for the whole volume indicates that northeast–southwest contraction dominates over strike-slip faulting with shortening occurring at 4.8 nanostrain a⁻¹ and an azimuth of 31° (see Fig. 7). This is equivalent to a shortening velocity of ≈0.9 mm a⁻¹, which is also in agreement with the range of 0.4 ± 1.0 mm a⁻¹ from Zhao et al. (2017). However, the apparent predominance of shortening is somewhat surprising given the clear, geomorphological evidence that the adjacent Daqingshan Fault is a normal fault (Ran et al. 2002, 2003a). It is possible that this discrepancy is due to transient post-seismic signals in the GPS from the M 6.0 1996 Baotou earthquake.

In the Weihe Graben, the GPS-derived strain rate field appears to indicate predominantly contraction in a variety of orientations (see Fig. 5). However, the single strain rate tensor shows north–south extension and east–west contraction, implying predominantly strike-slip faulting on northeast-southwest or northwest-southeast planes (see Fig. 7). It is plausible that such motion could be accommodated on the left-lateral Luonan and Danfeng Faults to the southeast of the Weihe Graben (see Fig. 2). However, Zhao et al. (2017) were not able to determine the deformation occurring in the Weihe Graben from their profile through the GPS data. Meanwhile, our catalogue of focal mechanisms and numerous geomorphological studies indicate that it is normal-faulting that predominates within the graben (Hou et al. 1998; Rao et al. 2015; Li et al. 2015b; Du et al. 2017), suggesting an inconsistency between the geology and the geodetic strain rate tensor (see Fig. 7).

In the Shanxi Grabens, on the eastern side of the Ordos, the pattern of strain varies across the region (see Fig. 5). In the northern Shanxi Grabens, the dominant strain is northwest-southeast extension, with varying amounts of northeast-southwest contraction, whilst in the central and southern Shanxi Grabens the rates of strain are notably smaller (see Fig. 6). The single strain rate tensor for the whole volume indicates that extension occurs at 1.7 nanostrain a⁻¹, equivalent to a velocity difference across the region of ≈0.6 mm a⁻¹ (see Fig. 7). This is consistent with the rates quoted by Zhao et al. (2017), although it obscures local variations in extension rate on moving through the different grabens.

In the North China Plain, there are three distinct patches of higher strain rate (see Fig. 6). These appear to correspond to specific seismic events: a pair of earthquakes in 1937 (M 7.6 and 6.8), the 1966 Xingtai series of earthquakes (including events up to M 7.2) and the M_w 7.8 1976 Tangshan earthquake. It is therefore possible that these high strain rates could be due to continuing aftershock sequences or ongoing post-seismic motion. For example, Stein et al. (2009) indicate that aftershock sequences on the continents, particularly on slowly moving faults, can last for decades or sometimes even centuries after the main shock. However, the high strain rates around the 1937 earthquakes are poorly constrained given the GPS coverage (see Fig. 5d).

4 DISCUSSION

4.1 Seismic moment deficits

We now use our individual, GPS-derived strain rate tensors in each Kostrov box (see Table 2) to determine the geodetic moment rate in each region. The geodetic moment rate (⁠|$\dot{M_{0}}$|⁠) is given by (see Appendix D):

\begin{equation} \dot{M_{0}} = \frac{M_{\text{tot}}}{\tau } = 2 \mu V |\dot{\epsilon }_{ij}| \end{equation}

(4)

where M_tot is the total geodetic moment that would be released in the time period τ, μ is the shear modulus, V is the volume of crust under consideration, and |$|\dot{\epsilon }_{ij}|$| is some measure of the magnitude of the geodetic strain rate tensor. We use the largest eigenvalue (in magnitude) of the geodetic strain rate tensor to calculate the geodetic moment rate, assuming that this strain is matched by the strains in the two orthogonal directions such that there is no change in volume. The results are shown in Table 2. We then calculate the moment deficit (total geodetic moment extrapolated over 700 yr minus the total seismic moment over the same time period) for each region. These results are shown in Table 3.

Table 3.

Open in new tab

Moment deficits and geodetic recurrence times.

Region	Seismic M₀ rate	Geodetic M₀ rate	Moment deficit^a	M_w equivalent	per cent seismic	Recurrence time	Recurrence time
	(Nm a⁻¹)	(Nm a⁻¹)	(Nm)		(per cent)	(M_w ≥ 7.0)^b (years)	(M_w ≥ 6.0)^b (years)
North Ningxia	4.06 × 10¹⁷	9.59 × 10¹⁷	3.87 × 10²⁰	7.7	42	224	22
South Ningxia	3.49 × 10¹⁸	2.93 × 10¹⁸	−3.95 × 10²⁰^c	−7.7^c	119	73	7
Hetao	1.14 × 10¹⁶	4.95 × 10¹⁷	3.39 × 10²⁰	7.7	2^d	433	43
Weihe	1.34 × 10¹⁸	4.73 × 10¹⁷	−6.07 × 10²⁰^c	−7.8^c	283	453	45
Shanxi	5.37 × 10¹⁷	5.31 × 10¹⁷	−4.35 × 10¹⁸^c	−6.4^c	101	404	40

Region	Seismic M₀ rate	Geodetic M₀ rate	Moment deficit^a	M_w equivalent	per cent seismic	Recurrence time	Recurrence time
	(Nm a⁻¹)	(Nm a⁻¹)	(Nm)		(per cent)	(M_w ≥ 7.0)^b (years)	(M_w ≥ 6.0)^b (years)
North Ningxia	4.06 × 10¹⁷	9.59 × 10¹⁷	3.87 × 10²⁰	7.7	42	224	22
South Ningxia	3.49 × 10¹⁸	2.93 × 10¹⁸	−3.95 × 10²⁰^c	−7.7^c	119	73	7
Hetao	1.14 × 10¹⁶	4.95 × 10¹⁷	3.39 × 10²⁰	7.7	2^d	433	43
Weihe	1.34 × 10¹⁸	4.73 × 10¹⁷	−6.07 × 10²⁰^c	−7.8^c	283	453	45
Shanxi	5.37 × 10¹⁷	5.31 × 10¹⁷	−4.35 × 10¹⁸^c	−6.4^c	101	404	40

^aGeodetic Σ M₀ minus seismic Σ M₀.

^bAssuming M_max = 1 × 10²¹ Nm (≈ M_w 8).

^cExcess seismic moment.

^d59 per cent when including the 849 Daqingshan earthquake.

Table 3.

Open in new tab

Moment deficits and geodetic recurrence times.

Region	Seismic M₀ rate	Geodetic M₀ rate	Moment deficit^a	M_w equivalent	per cent seismic	Recurrence time	Recurrence time
	(Nm a⁻¹)	(Nm a⁻¹)	(Nm)		(per cent)	(M_w ≥ 7.0)^b (years)	(M_w ≥ 6.0)^b (years)
North Ningxia	4.06 × 10¹⁷	9.59 × 10¹⁷	3.87 × 10²⁰	7.7	42	224	22
South Ningxia	3.49 × 10¹⁸	2.93 × 10¹⁸	−3.95 × 10²⁰^c	−7.7^c	119	73	7
Hetao	1.14 × 10¹⁶	4.95 × 10¹⁷	3.39 × 10²⁰	7.7	2^d	433	43
Weihe	1.34 × 10¹⁸	4.73 × 10¹⁷	−6.07 × 10²⁰^c	−7.8^c	283	453	45
Shanxi	5.37 × 10¹⁷	5.31 × 10¹⁷	−4.35 × 10¹⁸^c	−6.4^c	101	404	40

Region	Seismic M₀ rate	Geodetic M₀ rate	Moment deficit^a	M_w equivalent	per cent seismic	Recurrence time	Recurrence time
	(Nm a⁻¹)	(Nm a⁻¹)	(Nm)		(per cent)	(M_w ≥ 7.0)^b (years)	(M_w ≥ 6.0)^b (years)
North Ningxia	4.06 × 10¹⁷	9.59 × 10¹⁷	3.87 × 10²⁰	7.7	42	224	22
South Ningxia	3.49 × 10¹⁸	2.93 × 10¹⁸	−3.95 × 10²⁰^c	−7.7^c	119	73	7
Hetao	1.14 × 10¹⁶	4.95 × 10¹⁷	3.39 × 10²⁰	7.7	2^d	433	43
Weihe	1.34 × 10¹⁸	4.73 × 10¹⁷	−6.07 × 10²⁰^c	−7.8^c	283	453	45
Shanxi	5.37 × 10¹⁷	5.31 × 10¹⁷	−4.35 × 10¹⁸^c	−6.4^c	101	404	40

^aGeodetic Σ M₀ minus seismic Σ M₀.

^bAssuming M_max = 1 × 10²¹ Nm (≈ M_w 8).

^cExcess seismic moment.

^d59 per cent when including the 849 Daqingshan earthquake.

Fig. 7 shows our individual geodetic and seismic strain rate tensors for each region side by side. Fig. 8 shows a timeline of the earthquakes occurring in each region alongside plots of the moving average of the logarithm of the seismic moment rate. Dotted green lines show the logarithm of the geodetic moment rate, extrapolated back over the last 700 yr. Although the GPS-derived strain rate fields had much better spatial resolution, the Kostrov summations provide us with much better temporal resolution. Fig. 8 allows us to identify periods of time (within each region) when there is a mismatch between the seismic moment rate and the present-day geodetic moment rate (see Section 4.3 for further discussion).

Figure 8.

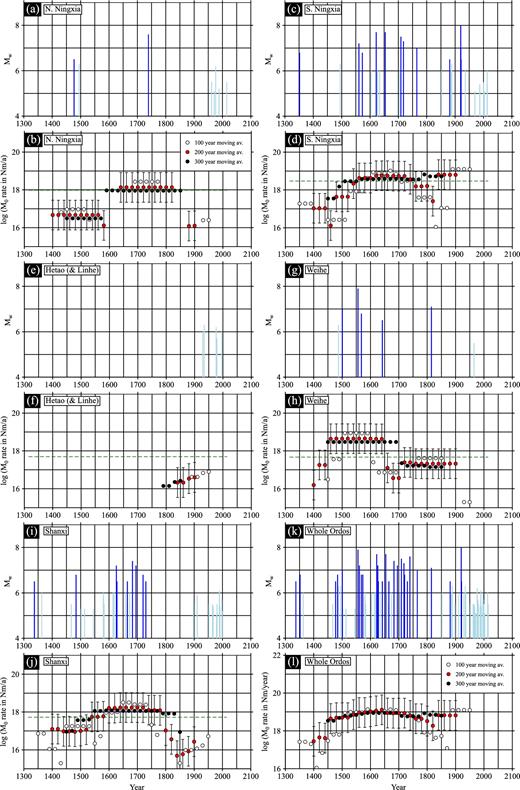
(a) Plot of magnitude (M_w) against time for historical earthquakes with M_w > 5 in northern Ningxia over the last 700 yr. Earthquakes with M_w ≥ 6.0 are shown in darker blue. (b) Moving averages of the log of the seismic moment rate (in Nm a⁻¹) for the last 700 yr, calculated every 20 yr. White dots show 100 yr moving average; red dots show 200 yr moving average; black dots show 300 yr moving average. Error bars, based on the assumption that values of M_w are known to the nearest ± 0.3 magnitude units, are shown for the 200 yr moving average. Dashed green line shows the log of the geodetic M₀ rate, extrapolated over the period from 1315 to 2015. (c) and (d) Equivalent plots for southern Ningxia. (e,f) Equivalent plots for the Hetao and Linhe Grabens. (g,h) Equivalent plots for the Weihe Graben. (i,j) Equivalent plots for the Shanxi Grabens. (k,l) Equivalent plots for all margins of the Ordos Plateau. Note different scale in (l).

Open in new tab Download slide

4.2 Earthquake recurrence times from geodetic strain rates

The recurrence interval (T) for earthquakes of scalar seismic moment ≥M is given by (see Appendix D):

\begin{equation} T(M) = \frac{\beta M_{\text{max}}^{1-\beta }M^{\beta }}{\dot{M_{0}}\left(1-\beta \right)} \end{equation}

(5)

where M_max is the scalar seismic moment of the largest earthquake expected in the region and β is the constant in the Gutenberg-Richter moment-frequency relationship. We use the usual β value of |$\frac{2}{3}$| and a maximum observed scalar seismic moment of 1 × 10²¹ Nm (≈ M_w 8), though the results depend quite significantly on this value of M_max. We calculate recurrence intervals for earthquakes M_w ≥ 7.0 and earthquakes M_w ≥ 6.0 for each region (see Table 3).

4.3 Future seismic hazard

In northern Ningxia, our seismic strain rate tensor indicates almost pure extension, whereas the geodetic strain rate tensor indicates largely north–south right-lateral motion (see Fig. 7). However, the geodetic strain rate tensor is more similar, in pattern though not in magnitude, to the result from Wesnousky et al. (1984), so the difference could be attributed to the focal parameters used for the 1739 earthquake or, potentially, a lack of strike-slip events in our earthquake catalogue. 42 per cent of the geodetic moment is accounted for seismically, leaving a suggested moment deficit of 3.87 × 10²⁰ Nm, equivalent to a single M_w 7.7 earthquake (see Table 3). This is in contrast to Wang et al. (2011), who found a seismic moment excess for this region. However, this discrepancy is likely to be because Wang et al. (2011) significantly overestimated the magnitude of the 1739 earthquake (Middleton et al. 2016a). In addition, we calculate an average geodetic recurrence interval for M_w ≥ 7.0 events of 224 yr (and for M_w ≥ 7.7 events of over 1000 yr), so it is likely that even our 700 yr time period is too short to capture a reliable picture of the seismic moment release. Nonetheless, Figs 8(a) and (b) indicate that, although the results in northern Ningxia are completely dominated by the 1739 event, there is a shortfall in the seismic moment release over the last ≈200 yr. This may indicate an increased seismic hazard, but we note that we could still be a few centuries away from the end of the current earthquake cycle.

In southern Ningxia, the magnitude and azimuth of the seismic and geodetic principal strain rates appear to be reasonably consistent (see Fig. 7). That said, the ϕ values show us that the seismic result indicates strike-slip faulting dominating over reverse faulting, whereas the geodetic result indicates reverse faulting dominating over strike-slip faulting. The seismic moment rate exceeds the geodetic moment rate leading to a moment excess of 3.95 × 10²⁰ Nm, which suggests that southern Ningxia is not likely to be a region of high seismic hazard in the near future. This can also be seen in Fig. 8(d). Wang et al. (2011) did not perform a calculation for the same region, but they found seismic moment excesses on their neighbouring seismic belts.

In the Linhe and Hetao Grabens, there is a large discrepancy between the seismic and geodetic strain rate tensors; the seismic strain rate tensor is nearly two orders of magnitude smaller and rotated by ≈45° (see Fig. 7). Only 2 per cent of the geodetic moment is accounted for seismically, leaving a suggested moment deficit of 3.39 × 10²⁰ Nm, equivalent to a single M_w 7.7 earthquake (see Table 3). The lack of seismic activity can also be clearly seen in Figs 8(e) and (f). Similarly, Wang et al. (2011) identified a seismic moment deficit for the same region, although their deficit was only 2 × 10¹⁸ Nm for the last 100 yr. Extrapolated over 700 yr, this is still an order of magnitude smaller than our deficit. This difference arises because Wang et al. (2011) estimate a seismic moment release of 2.1 × 10¹⁹ Nm for the last 100 yr, whereas we find a much smaller seismic moment release of 7.95 × 10¹⁸ Nm for the whole 700 yr period. However, as discussed in Section 3.1, some of the moment deficit could be accounted for by the M 7.5 849 Daqingshan earthquake. We calculate that the recurrence interval for M_w ≥ 7.0 events is 433 yr, and for M_w ≥ 7.5 events is ≈1400 yr, which is not dissimilar to the ≈2000 yr indicated by palaeoseismology. This leads us to conclude that our earthquake catalogue is missing infrequent but large-magnitude events on this boundary of the plateau, suggesting relatively high levels of seismic hazard over the next few hundred years.

In the Weihe Graben, the seismic moment rate exceeds the geodetic moment rate leading to an apparent moment excess of 6.07 × 10²⁰ Nm, which would suggest that the Weihe Graben is not likely to be a region of high seismic hazard in the near future. However, as noted above, the catalogue in this region is entirely dominated by the 1556 event, and Fig. 8(h) in fact shows that the seismic moment rate has dropped below the geodetic moment rate since around 1650 (though this is within the typical error on the magnitudes of the historical earthquakes). Much like northern Ningxia and the Linhe and Hetao Grabens, it appears that the majority of strain release occurs in infrequent, large-magnitude events–only in the Weihe Graben we are earlier in the seismic cycle.

Finally, Fig. 7 shows good agreement between the seismic and geodetic strain rate tensors in the Shanxi Grabens, though both of these tensors average across the region and obscure the variations within the Kostrov volume (see Section 3.2). The ϕ values show us that both the seismic and geodetic results indicate strike-slip faulting dominating over normal faulting. 101 per cent of the geodetic moment is accounted for seismically, resulting in a small moment excess of 4.35 × 10¹⁸ Nm (see Table 3). Wang et al. (2011) suggested a moment excess for Shanxi, but they combined the Shanxi Grabens with the Weihe Graben in their calculation. However, Fig. 8(j) clearly indicates that there is a lack of recent earthquakes in the Shanxi Grabens. Until around 1750, there is very good agreement between the seismic and geodetic moment rates, and then by 1800 there is a notable seismic strain rate deficit that goes well beyond the error bars due to the uncertainties on the magnitude estimates. Again, this is likely to indicate relatively high levels of seismic hazard in the future. Our estimated geodetic recurrence interval for M_w ≥ 7.0 earthquakes is more than 400 yr, so it is perfectly plausible that an event of this size could happen in the next few centuries. In a previous paper, we found a very similar result when we focussed on just the northern Shanxi Grabens (Middleton et al. 2017).

Lastly, we note that all of our seismic moment deficits should be treated with caution; in many cases our earthquake catalogue spans a time period that is similar to, or sometimes even shorter than, the likely recurrence interval for the largest earthquakes that occur. It is also possible that our moment deficits could be accommodated by fault creep, as is known to be occurring, for example, on the Haiyuan Fault (Jolivet et al. 2012). However, we are not aware of any field evidence to suggest that such aseismic motion is occurring on any of the major faults that bound the Ordos. Furthermore, Xu & Deng (1996), Li et al. (2009), Liu et al. (2011) and Liu & Wang (2012) have suggested, on the basis of palaeoseismology and earthquake records, that earthquakes in northern China might cluster in time and space, with moment release switching between different fault networks over time. Fig. 8(k) appears to attest to such temporal clustering; similarly, Figs 8(h) and (j), for the Weihe and Shanxi Grabens, show rates of seismic moment release that oscillate either side of the projected geodetic moment rate for the last 700 yr. The precise cause of this switching behaviour is unclear, but it could contribute to the present-day moment deficits that we observe. It may also indicate that moment deficits will be accommodated by clusters of smaller earthquakes rather than single large events.

5 CONCLUSIONS

In this study we have performed Kostrov summations for the earthquakes occurring at the margins of the Ordos Plateau over the last 700 yr and compared our results to strain rates derived from the latest campaign GPS measurements. We found notable seismic strain rate deficits in northern Ningxia (especially over the last ≈200 yr), and in the Hetao and Linhe Grabens (over all of the last 700 yr). In the Weihe and Shanxi Grabens, although we found seismic strain rate excesses over the whole of the last 700 yr, we also noted recent deficits over the last ≈365 yr and ≈265 yr, respectively. These deficits indicate enhanced potential for large earthquakes in these regions in the future. In southern Ningxia we found a seismic strain rate excess and no present-day mismatch between seismic and geodetic strain release, indicating a likely lower level of seismic hazard in this region.

6 DATA AND RESOURCES

The GCMT project database was searched using: www.globalcmt.org/CMTsearch.html (last accessed on 8th August 2013).

The International Seismological Centre (ISC) database was searched using: http://www.isc.ac.uk/iscbulletin/search/bulletin/ (last accessed on 15th March 2016).

Most of the figures in this paper were made using the Generic Mapping Tools (Wessel et al. 2013). All other data used in this paper came from published sources listed in the references.

Acknowledgements

This research has been supported by the Natural Environment Research Council (NERC) through a studentship awarded to TAM, the Centre for Observation and Modelling of Earthquakes, Volcanoes and Tectonics (COMET, GA/13/M/031), the Looking inside the Continents from Space (LiCS) large grant (NE/K011006/1), and the NERC/ESRC Earthquakes without Frontiers (EwF) consortium (EwF_NE/J02001X/1_1). We are grateful to: Philip England, John Elliott and Yu Zhou for a number of very useful conversations; and Peizhen Zhang and our colleagues at the China Earthquake Administration (CEA) for their ongoing support. We also wish to thank Philippe Vernant and an anonymous reviewer for their helpful comments on the manuscript.

REFERENCES

Bird

P.

,

Piper

K.

,

1980

.

Plane-stress finite-element models of tectonic flow in southern California

,

Phys. Earth planet. Inter.

,

21,

158

–

175

.

Cai

Y.

,

Wu

J.

,

Fang

L.

,

Wang

W.

,

Huang

J.

,

2014

.

Relocation of the earthquakes in the eastern margin of Ordos block and their tectonic implication in the transition zones of extensional basin

,

Chin. J. Geophys.

,

57

(

4

), 1079–1090 (in Chinese).

Google Scholar

OpenURL Placeholder Text

WorldCat

Calais

E.

,

Dong

L.

,

Wang

M.

,

Shen

Z.

,

Vergnolle

M.

,

2006

.

Continental deformation in Asia from a combined GPS solution

,

Geophys. Res. Lett.

,

33

,

L24319

,

doi:10.1029/2006GL028433

.

Cheng

B.

,

Cheng

S.

,

Zhang

G.

,

Zhao

D.

,

2014

.

Seismic structure of the Helan-Liupan-Ordos western margin tectonic belt in North-Central China and its geodynamic implications

,

J. Asian Earth Sci.

,

87,

141

–

156

.

Columbia University, Center for International Earth Science Information Network

,

2015

.

Gridded Population of the World, Version 4 (GPWv4): Population Density Adjusted to Match 2015 Revision of UN WPP Country Totals

.

Darby

B.

,

Ritts

B.

,

Yue

Y.

,

Meng

Q.

,

2005

.

Did the Altyn Tagh fault extend beyond the Tibetan Plateau?

,

Earth planet. Sci. Lett.

,

240

(

2

),

425

–

435

.

Darby

B.J.

,

Ritts

B.D.

,

2002

.

Mesozoic contractional deformation in the middle of the Asian tectonic collage: the intraplate Western Ordos fold-thrust belt, China

,

Earth planet. Sci. Lett.

,

205

(

1-2

),

13

–

24

.

Deng

Q.

,

Liao

Y.

,

1996

.

Paleoseismology along the range-front fault of Helan Mountains, north central China

,

J. geophys. Res.

,

101,

5873

–

5893

.

Deng

Q.

et al. ,

1984

.

Active faulting and tectonics of the Ningxia-Hui autonomous region, China

,

J. geophys. Res.

,

89,

4427

–

4445

.

Deng

Q.

,

Ran

Y.

,

Yang

X.

,

Min

W.

,

Chu

Q.

,

2007

.

Map of Active Tectonics in China

(in Chinese), Seismological Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Doxsey-Whitfield

E.

,

Macmanus

K.

,

Adamo

S.B.

,

Pistolesi

L.

,

Squires

J.

,

Borkovska

O.

,

Baptista

S.R.

,

2015

.

Taking Advantage of the improved availability of census data: a first look at the gridded population of the world, version 4

,

Pap. Appl. Geogr.

,

1

(

3

),

226

–

234

.

Du

J.

,

Li

D.

,

Wang

Y.

,

Ma

Y.

,

2017

.

Late quaternary activity of the Huashan Piedmont Fault and associated Hazards in the southeastern Weihe Graben, Central China

,

Acta Geol. Sin, (English Edition)

,

91

(

1

),

76

–

92

.

England

P.

,

Bilham

R.

,

2015

.

The Shillong Plateau and the great 1897 Assam earthquake

,

Tectonics

,

34

(

9

),

1792

–

1812

.

England

P.

,

McKenzie

D.

,

1982

.

A thin viscous sheet model for continental deformation

,

Geophys. J. Int.

,

70

(

2

),

295

–

321

.

Farr

T.G.

et al. ,

2007

.

The Shuttle Radar Topography Mission

,

Rev. Geophys.

,

45

(

2

),

1

–

33

.

Feng

X.

,

Ma

J.

,

Zhou

Y.

,

Walker

R.T.

,

Parsons

B.

,

England

P.

,

Rizza

M.A.

,

2017

.

Repeated high stress-drop ruptures on the 1556 Huaxian earthquake normal fault

,

Earth planet. Sci. Lett.

, in

press

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Flesch

L.M.

,

Haines

A.J.

,

Holt

W.E.

,

2001

.

Dynamics of the India-Eurasia collision zone

,

J. geophys. Res.

,

106,

16 435

–

16 460

.

Floyd

M.A.

et al. ,

2010

.

A new velocity field for Greece: Implications for the kinematics and dynamics of the Aegean

,

J. geophys. Res.

,

115

(

B10

),

1

–

25

.

Gan

W.

,

Zhang

P.

,

Shen

Z.-K.

,

Niu

Z.

,

Wang

M.

,

Wan

Y.

,

Zhou

D.

,

Cheng

J.

,

2007

.

Present-day crustal motion within the Tibetan Plateau inferred from GPS measurements

,

J. geophys. Res.

,

112

(

B8

),

1

–

14

.

Gordon

R.G.

,

Houseman

G.A.

,

2015

.

Deformation of Indian Ocean lithosphere: Evidence for a highly nonlinear rheological law

,

J. geophys. Res.

,

120

(

6

),

4434

–

4449

.

He

J.

,

Liu

M.

,

Li

Y.

,

2003

.

Is the Shanxi rift of northern China extending?

,

Geophys. Res. Lett.

,

30

(

23

),

1

–

4

.

Hou

J.

,

Han

M.

,

Chai

B.

,

Han

H.

,

1998

.

Geomorphological observations of active faults in the epicentral region of the Huaxian large earthquake in 1556 in Shaanxi Province, China

,

J. Struct. Geol.

,

20

(

5

),

549

–

557

.

Houseman

G.

,

England

P.

,

1986

.

Finite strain calculations of continental deformation 1. Method and general results for convergent zones

,

J. geophys. Res.

,

91

(

4

),

3651

–

3663

.

Huang

W.

,

Li

W.

,

Cao

X.

,

1994

.

Research on the completeness of earthquake data in the Chinese mainland (I)—North China

,

Acta Seismol. Sin.

,

7

(

3

),

351

–

359

.

Jolivet

R.

et al. ,

2012

.

Shallow creep on the Haiyuan fault (Gansu, China) revealed by SAR interferometry

,

J. geophys. Res.

,

117

(

6

),

1

–

18

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Jordan

T.H.

et al. ,

2011

.

Operational Earthquake Forecasting: State of Knowledge and Guidelines for Utilization

,

Ann. Geophys.

,

54

(

May

),

315

–

391

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Kanamori

H.

,

1983

.

Magnitude scale and quantification of earthquakes

,

Tectonophysics

,

93,

185

–

199

.

Kostrov

V.

,

1974

.

Seismic moment and energy of earthquakes, and seismic flow of rock

,

Izv. Acad. Sci. USSR Phys. Solid Earth

,

1,

23

–

40

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Lee

W. H.K.

,

Wu

F.T.

,

Jacobsen

C.

,

1976

.

A catalog of historical earthquakes in China compiled from recent Chinese publications

,

Bull. seism. Soc. Am.

,

66

(

6

),

2003

–

2016

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Lee

W.H.K.

,

Wu

F.T.

,

Wang

S.C.

,

1978

.

A catalog of instrumentally determined earthquakes in China (magnitude greater than 6) compiled from various sources

,

Bull. seism. Soc. Am.

,

68

(

2

),

383

–

398

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Li

B.

,

Atakan

K.

,

Sørensen

M.B.

,

Havskov

J.

,

2015a

.

Stress pattern of the Shanxi rift system, North China, inferred from the inversion of new focal mechanisms

,

Geophys. J. Int.

,

201

(

2

),

505

–

527

.

Li

D.

,

Du

J.

,

Ma

Y.

,

Xiao

A.

,

2015b

.

Active faults and dip slip rates along the northern margins of the Huashan Mountain and Weinan loess tableland in the southeastern Weihe Graben, central China

,

J. Asian Earth Sci.

,

114,

266

–

278

.

Li

Q.

,

Liu

M.

,

Stein

S.

,

2009

.

Spatiotemporal complexity of continental intraplate seismicity: insights from geodynamic modeling and implications for seismic hazard estimation

,

Bull. seism. Soc. Am.

,

99

(

1

),

52

–

60

.

Li

Q.

,

You

X.

,

Yang

S.

,

Du

R.

,

Qiao

X.

,

Zou

R.

,

Wang

Q.

,

2012

.

A precise velocity field of tectonic deformation in China as inferred from intensive GPS observations

,

Sci. China Earth Sci.

,

55

(

5

),

695

–

698

.

Liu

M.

,

Wang

H.

,

2012

.

Roaming earthquakes in China highlight midcontinental hazards

,

EOS, Trans. Am. geophys. Un.

,

93

(

45

),

453

–

454

.

Liu

M.

,

Yang

Y.

,

Shen

Z.

,

Wang

S.

,

Wang

M.

,

Wan

Y.

,

2007

.

Active tectonics and intracontinental earthquakes in China: The kinematics and geodynamics

, in

Continental Intraplate Earthquakes: Science, Hazard, and Policy Issues

,

vol. 425

, pp.

299

–

318

, eds

Stein

S.

,

Mazzotti

S.

,

Geological Society of America

.

Liu

M.

,

Stein

S.

,

Wang

H.

,

2011

.

2000 years of migrating earthquakes in North China: How earthquakes in midcontinents differ from those at plate boundaries

,

Lithosphere

,

3

(

2

),

128

–

132

.

Liu-Zeng

J.

,

Shao

Y.

,

Klinger

Y.

,

Xie

K.

,

Yuan

D.

,

Lei

Z.

,

2015

.

Variability in magnitude of paleoearthquakes revealed by trenching and historical records, along the Haiyuan Fault, China

,

J. geophys. Res.

,

120

(

12

),

8304

–

8333

.

Middleton

T.A.

,

Walker

R.T.

,

Parsons

B.

,

Lei

Q.

,

Zhou

Y.

,

Ren

Z.

,

2016a

.

A major, intraplate, normal-faulting earthquake: the 1739 Yinchuan event in northern China

,

J. geophys. Res.

,

121

(

1

),

293

–

320

.

Middleton

T.A.

et al. ,

2016b

.

The tectonics of the western Ordos Plateau, Ningxia, China: slip rates on the Luoshan and East Helanshan Faults

,

Tectonics

,

35,

2754

–

2777

.

Middleton

T.A.

,

Elliott

J.R.

,

Rhodes

E.J.

,

Sherlock

S.

,

Walker

R.T.

,

Wang

W.

,

Yu

J.

,

Zhou

Y.

,

2017

.

Extension rates across the northern Shanxi Grabens, China, from Quaternary geology, seismicity and geodesy

,

Geophys. J. Int.

,

209,

535

–

558

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Molnar

P.

,

1979

.

Earthquake recurrence intervals and plate tectonics

,

Bull. seism. Soc. Am.

,

69

(

1

),

115

–

133

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Pavlides

S.B.

,

Zouros

N.C.

,

Fang

Z.

,

Cheng

S.

,

Tranos

M.D.

,

Chatzipetros

A.A.

,

1999

.

Geometry, kinematics and morphotectonics of the Yanqing-Huailai active faults (northern China)

,

Tectonophysics

,

308,

99

–

118

.

Qin

C.

,

Papazachos

C.

,

Papadimitriou

E.

,

2002

.

Velocity field for crustal deformation in China derived from seismic moment tensor summation of earthquakes

,

Tectonophysics

,

359

(

1-2

),

29

–

46

.

Ran

Y.

,

Zhang

P.

,

Hu

B.

,

Guo

W.

,

2002

.

Paleoseismic activity on the Hohhot segment of Daqingshan piedmont fault in the Late Quaternary history

,

Earthq. Res. China

,

18

(

1

), 15–27 (in Chinese).

Google Scholar

OpenURL Placeholder Text

WorldCat

Ran

Y.

,

Zhang

P.

,

Chen

L.

,

2003a

.

Late Quaternary history of paleoseismic activity along the Hohhot Segment of the Daqingshan piedmont fault in Hetao depression zone, North China

,

Ann. Geophys.

,

46

(

October

),

1053

–

1069

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Ran

Y.

,

Zhang

P.

,

Chen

L.

,

2003b

.

Research on the completeness of paleoseismic activity history since Late Quaternary along the Daqingshan piedmont fault in Hetao depression zone, north China

,

Earth Sci. Frontiers

,

10,

207

–

216

(in Chinese

).

Google Scholar

OpenURL Placeholder Text

WorldCat

Rao

G.

,

Lin

A.

,

Yan

B.

,

2015

.

Paleoseismic study on active normal faults in the southeastern Weihe Graben, central China

,

J. Asian Earth Sci.

,

114,

212

–

225

.

Shen

Z.

,

Zhao

C.

,

Yin

A.

,

Li

Y.

,

Jackson

D.D.

,

Fang

P.

,

Dong

D.

,

2000

.

Contemporary crustal deformation in east Asia constrained by Global Positioning System measurements

,

J. geophys. Res.

,

105,

5721

–

5734

.

Shen

Z.-K.

,

Jackson

D.D.

,

Ge

B.X.

,

1996

.

Crustal deformation across and beyond the Los Angeles basin from geodetic measurements

,

J. geophys. Res.

,

101

(

B12

), 27 927–27 957.

Google Scholar

OpenURL Placeholder Text

WorldCat

Stein

S.

,

Friedrich

A.M.

,

2014

.

How much can we clear the crystal ball?

,

Astron. Geophys.

,

55

(

2

),

11

–

17

.

Stein

S.

,

Liu

M.

,

Calais

E.

,

Li

Q.

,

2009

.

Mid-continent earthquakes as a complex system

,

Seism. Res. Lett.

,

80

(

4

),

551

–

553

.

Stein

S.

,

Geller

R.J.

,

Liu

M.

,

2012

.

Why earthquake hazard maps often fail and what to do about it

,

Tectonophysics

,

562-563,

1

–

25

.

Tapponnier

P.

,

Molnar

P.

,

1977

.

Active faulting and tectonics in China

,

J. geophys. Res.

,

82

(

20

),

2905

–

2930

.

The Research Group on Active Fault System around Ordos

Massif

,

1988

.

Active Fault System around Ordos Massif

,

State Seismological Bureau, Seismological Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Wang

H.

,

Liu

M.

,

Cao

J.

,

Shen

X.

,

Zhang

G.

,

2011

.

Slip rates and seismic moment deficits on major active faults in mainland China

,

J. geophys. Res.

,

116

(

B2

),

B02405

,

doi:10.1029/2010JB007821

.

Wang

J.

,

2004

.

Historical earthquake investigation and research in China

,

Ann. Geophys.

,

47

(

June

),

831

–

838

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Wang

J.

,

Zhao

D.

,

Yao

Z.

,

2013

.

Crustal and uppermost mantle structure and seismotectonics of North China Craton

,

Tectonophysics

,

582,

177

–

187

.

Wang

Q.

et al. ,

2001

.

Present-day crustal deformation in China constrained by global positioning system measurements

,

Science

,

294,

574

–

577

.

Wesnousky

S.G.

,

Jones

L.M.

,

Scholz

C.H.

,

Deng

Q.

,

1984

.

Historical seismicity and rates of crustal deformation along the margins of the Ordos block, North China

,

Bull. seism. Soc. Am.

,

74

(

5

),

1767

–

1783

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Wessel

P.

,

Smith

W. H.F.

,

Scharroo

R.

,

Luis

J.

,

Wobbe

F.

,

2013

.

Generic Mapping Tools: Improved Version Released

,

EOS, Trans. Am. geophys. Un.

,

94

(

45

),

409

–

410

.

Xu

X.

,

Deng

Q.

,

1996

.

Nonlinear characteristics of paleoseismicity in China

,

J. geophys. Res.

,

101

(

B3

),

6209

–

6231

.

Xu

X.

,

Ma

X.

,

1992

.

Geodynamics of the Shanxi Rift system, China

,

Tectonophysics

,

208

(

1-3

),

325

–

340

.

Xu

Z.

,

Wang

S.

,

Gao

A.

,

2000

.

Present-day tectonic movement in the northeastern margin of the Qinghai-Xizang (Tibetan) plateau as revealed by earthquake activity

,

Acta Seismol. Sin.

,

13

(

5

),

507

–

515

.

Yu

S.

,

2004

.

A study on characteristics of tectonic block motion and tectonic setting of strong earthquakes in northern part of the Shanxi fault depression zone

,

Acta Seismol. Sin.

,

17

(

4

),

417

–

425

.

Yuan

T.

,

Feng

X.

,

2010

.

The Great 1556 Huaxian Earthquake

,

Seismological Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Zhang

B.

,

Liao

Y.

,

Guo

S.

,

Wallace

R.E.

,

Bucknam

R.C.

,

Hanks

T.C.

,

1986

.

Fault scarps related to the 1739 earthquake and seismicity of the Yinchuan Graben, Ningxia Huizu Zizhiqu, China

,

Bull. seism. Soc. Am.

,

76

(

5

),

1253

–

1287

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Zhang

P.

,

Gan

W.

,

2008

.

Combined model of rigid-block motion with continuous deformation: patterns of present-day deformation in continental China

, in

Investigations into the Tectonics of the Tibetan Plateau.

Geological Society of America Special Paper 444

, pp.

59

–

71

, eds

Burchfiel

B.

,

Wang

E.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Zhang

P.

et al. ,

1990

.

Late Cenozoic tectonic evolution of the Ningxia-Hui Autonomous Region, China

,

Geol. Soc. Am. Bull.

,

102

(

11

),

1484

–

1498

.

Zhang

P.

,

Yang

Z.

,

Gupta

H.K.

,

Bhatia

S.C.

,

Shedlock

K.M.

,

1999

.

Global Seismic Hazard Assessment Program (GSHAP) in continental Asia

,

Ann. Geophys.

,

42

(

December

),

1167

–

1190

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Zhang

P.

,

Deng

Q.

,

Zhang

G.

,

Ma

J.

,

Gan

W.

,

Min

W.

,

Mao

F.

,

Wang

Q.

,

2003

.

Active tectonic blocks and strong earthquakes in the continent of China

,

Sci. China D

,

46

(

October

),

13

–

24

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Zhang

P.

et al. ,

2004

.

Continuous deformation of the Tibetan Plateau from global positioning system data

,

Geology

,

32

(

9

),

809

–

812

.

Zhao

B.

,

Huang

Y.

,

Zhang

C.

,

Wang

W.

,

Tan

K.

,

Du

R.

,

2015

.

Crustal deformation on the Chinese mainland during 1998-2014 based on GPS data

,

Geod. Geodyn.

,

6

(

1

),

7

–

15

.

Zhao

B.

,

Zhang

C.

,

Wang

D.

,

Huang

Y.

,

Tan

K.

,

Du

R.

,

Liu

J.

,

2017

.

Contemporary kinematics of the Ordos block, North China and its adjacent rift systems constrained by dense GPS observations

,

J. Asian Earth Sci.

,

135,

257

–

267

.

Zheng

W.

,

Lei

Z.

,

Yuan

D.

,

He

W.

,

Ge

W.

,

Liu

X.

,

2007

.

Textual research on the historical data of the 1573 AD Minxian earthquake in Gansu Province and discussion on its seismogenic structure

,

Earthq. Res. China

,

23

(

1

), 75–83 (in Chinese).

Google Scholar

OpenURL Placeholder Text

WorldCat

Zhou

Y.

,

2016

.

Investigating past and present continental earthquakes with high-resolution optical imagery

,

DPhil

,

University of Oxford

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

APPENDIX A: KOSTROV SUMMATIONS

The seismic moment tensor encapsulates information about the orientation and magnitude of the faulting in an earthquake and, for a double couple source, is given by

\begin{equation} M_{ij} = M_{0}\left(u_{i}n_{j}+u_{j}n_{i}\right) \end{equation}

(A1)

where |$M_{0} = \mu A \bar{u}$| is the scalar seismic moment (equal to the rigidity modulus times the fault plane area times the average slip) and |$\mathbf {\hat{u}}$| and |$\mathbf {\hat{n}}$| are unit vectors in the direction of slip and the direction of the normal to the fault plane respectively. Kostrov’s relation allows the strain rate tensor to be calculated from a series of seismic moment tensors for N earthquakes that have occurred in a volume V (Kostrov 1974):

\begin{equation} \dot{\epsilon }_{ij} = \frac{1}{2 \mu \tau V}\sum _{n = 1}^{N}M_{ij}^{n}, \end{equation}

(A2)

where |$\dot{\epsilon }_{ij}$| is the ijth component of the strain rate tensor, μ is the rigidity modulus, and τ is the time period of observation. Having obtained the strain rate tensor, we calculated the principal strain rates by solving the following eigenvalue equation:

\begin{equation} \mathbf {\dot{\epsilon }}\mathbf {v} = \lambda \mathbf {v} \end{equation}

(A3)

\begin{equation} \therefore \lambda = \frac{\left(\dot{\epsilon }_{11}+\dot{\epsilon }_{22}\right)\pm \sqrt{\left(\dot{\epsilon }_{11}-\dot{\epsilon }_{22}\right)^{2}+4\dot{\epsilon }_{12}^{2}}}{2}. \end{equation}

(A4)

The (anticlockwise) angle (θ₁) between the principal strain rate axis |$\dot{\epsilon }_{1}$| and the 1-axis was then given by

\begin{equation} \tan \theta _{1} = \frac{\dot{\epsilon }_{1}-\dot{\epsilon }_{11}}{\dot{\epsilon }_{12}}. \end{equation}

(A5)

The azimuth of the principal strain rate axis |$\dot{\epsilon }_{1}$| was 90 ° − θ₁.

APPENDIX B: EXPECTED PATTERN OF FAULTING FROM STRAIN RATES

Fig. B1 illustrates qualitatively how to interpret our strain rate fields. For a more quantitative analysis we followed a similar approach to Houseman & England (1986) and Gordon & Houseman (2015). Considering the horizontal components of the diagonalized strain rate tensor (⁠|$\dot{\epsilon }_{1}$| and |$\dot{\epsilon }_{2}$|⁠), we assumed that |$\dot{\epsilon }_{1}$| is the greater (more positive) principal strain rate. We then defined the angle ϕ according to:

\begin{equation} {}\text{tan}\left(\phi \right) = \frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}. \end{equation}

(B1)

Figure B1.

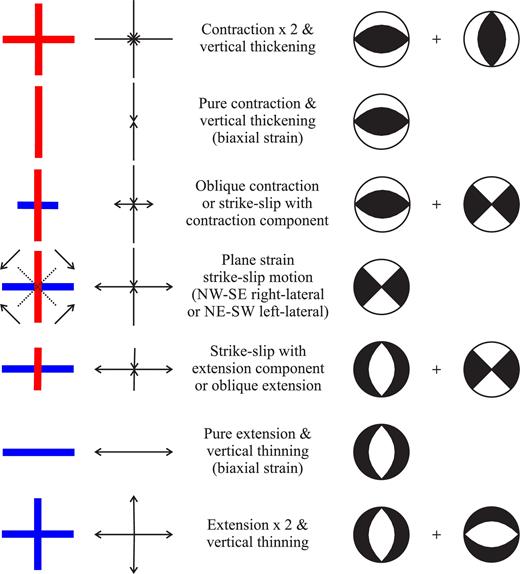
Examples of strain rate crosses to show how they illustrate different patterns of strain. Red bars indicate contractional principal strain rates; blue bars indicate extensional principal strain rates (only horizontal components are shown). Focal mechanisms indicate patterns of faulting that could accommodate the given strain rates. Note that for the strike-slip mechanisms there is an ambiguity between right-lateral motion on northwest-southeast fault planes and left-lateral motion on northeast-southwest fault planes; for the dip-slip mechanisms either nodal plane could be the fault plane.

Open in new tab Download slide

We considered ϕ in the range |$\frac{\pi }{4}$| to |$\frac{5\pi }{4}$| (see Figs B2 and B3). If |$\dot{\epsilon }_{1}$| and |$\dot{\epsilon }_{2}$| are of the same sign, then the strain is taken up on two sets of dip-slip faults. When |$\frac{\pi }{4}<\phi <\frac{\pi }{2}$| we know that |$\frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}>1$|⁠, which can only be true if both |$\dot{\epsilon }_{1}$| and |$\dot{\epsilon }_{2}$| are negative. We therefore have contraction occurring in two orthogonal horizontal directions and we expect reverse faults in two orientations. When |$\pi <\phi <\frac{5\pi }{4}$| we know that |$0<\frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}<1$|⁠, which can only be true if both |$\dot{\epsilon }_{1}$| and |$\dot{\epsilon }_{2}$| are positive. We therefore have extension occurring in two orthogonal horizontal directions and we expect normal faults in two orientations.

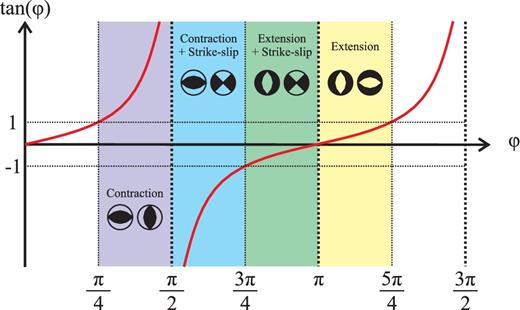
$Plot of tan(ϕ) against ϕ, where $\text{tan}\left(\phi \right) = \frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}$ (red curve). Coloured zones and focal mechanisms indicate the expected styles of faulting in each ϕ range.$

Figure B2.

Plot of tan(ϕ) against ϕ, where |$\text{tan}\left(\phi \right) = \frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}$| (red curve). Coloured zones and focal mechanisms indicate the expected styles of faulting in each ϕ range.

Open in new tab Download slide

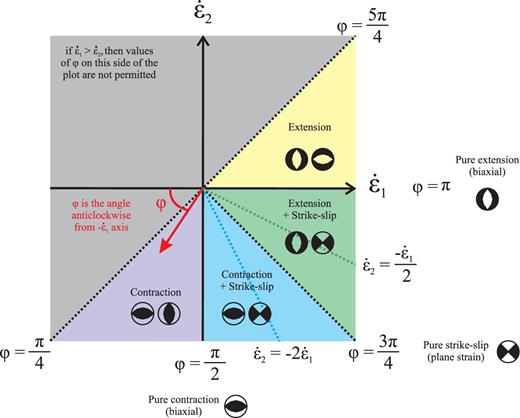
$Phasor diagram in $\dot{\epsilon }_{2}$ against $\dot{\epsilon }_{1}$ space. Again, coloured zones and focal mechanisms indicate the expected styles of faulting in each ϕ range.$

Figure B3.

Phasor diagram in |$\dot{\epsilon }_{2}$| against |$\dot{\epsilon }_{1}$| space. Again, coloured zones and focal mechanisms indicate the expected styles of faulting in each ϕ range.

Open in new tab Download slide

If |$\dot{\epsilon }_{1}$| and |$\dot{\epsilon }_{2}$| are of opposite signs, then the strain is taken up by a combination of dip-slip and strike-slip faulting. When |$\frac{\pi }{2}<\phi <\frac{3\pi }{4}$| we know that |$\frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}<-1$|⁠, which can only be true if |$\dot{\epsilon }_{1}$| is positive and |$\dot{\epsilon }_{2}$| is negative. Furthermore, |$|\dot{\epsilon }_{2}|>|\dot{\epsilon }_{1}|$|⁠. We therefore expect a combination of contraction and strike-slip faulting. The relative importance of dip-slip versus strike-slip faulting can be determined from the exact value of ϕ. Reverse faulting dominates when |$\dot{\epsilon }_{2}<-2\dot{\epsilon }_{1}$|⁠, that is ϕ < (π − tan⁻¹(2)); and strike-slip faulting dominates when |$\dot{\epsilon }_{2}>-2\dot{\epsilon }_{1}$|⁠, that is ϕ > (π − tan⁻¹(2))). When |$\dot{\epsilon }_{2} = -2\dot{\epsilon }_{1}$|⁠, that is ϕ = (π − tan⁻¹(2)), the strain is accommodated by 50 per cent reverse faulting and 50 per cent strike-slip faulting.

Similarly, when |$\frac{3\pi }{4}<\phi <\pi$| we know that |$-1<\frac{\dot{\epsilon }_{2}}{\dot{\epsilon }_{1}}<0$|⁠, which can only be true if |$\dot{\epsilon }_{1}$| is positive and |$\dot{\epsilon }_{2}$| is negative. Furthermore, |$|\dot{\epsilon }_{1}|>|\dot{\epsilon }_{2}|$|⁠. We therefore expect a combination of extension and strike-slip faulting. Normal faulting dominates when |$\dot{\epsilon }_{2}>\frac{-\dot{\epsilon }_{1}}{2}$|⁠, that is |$\phi >(\pi -\text{tan}^{-1}(\frac{1}{2}))$|⁠; and strike-slip faulting dominates when |$\dot{\epsilon }_{2}<\frac{-\dot{\epsilon }_{1}}{2}$|⁠, that is |$\phi <(\pi -\text{tan}^{-1}(\frac{1}{2}))$|⁠. When |$\dot{\epsilon }_{2} = \frac{-\dot{\epsilon }_{1}}{2}$|⁠, that is |$\phi = (\pi -\text{tan}^{-1}(\frac{1}{2}))$|⁠, the strain is accommodated by 50 per cent normal faulting and 50 per cent strike-slip faulting.

APPENDIX C: STRAIN RATE FIELD FROM GPS

We calculated a smoothly varying strain rate field from the GPS data according to the method of Shen et al. (1996) and Floyd et al. (2010). We assumed uniform gradients in the components of horizontal velocity. The method below describes how to calculate the strain rate tensor at an individual point within the region of interest. The same method can be applied whether the calculation points used are the GPS sites themselves or the nodes of a regular grid.

Considering each calculation point in turn, the velocity at a given GPS measurement site is equal to the velocity at the calculation point (which has components U_x and U_y) plus the change in velocity on moving from the calculation point to the GPS site (see Fig. C1). This can be written as:

\begin{equation} V_{x} = U_{x} + \frac{\partial V_{x}}{\partial x}\Delta x + \frac{\partial V_{x}}{\partial y}\Delta y \end{equation}

(C1)

\begin{equation} V_{y} = U_{y} + \frac{\partial V_{y}}{\partial x}\Delta x + \frac{\partial V_{y}}{\partial y}\Delta y. \end{equation}

(C2)

We also know that:

\begin{equation} \dot{\epsilon }_{xx} = \frac{\partial V_{x}}{\partial x} \end{equation}

(C3)

\begin{equation} \dot{\epsilon }_{yy} = \frac{\partial V_{y}}{\partial y} \end{equation}

(C4)

\begin{equation} \dot{\epsilon }_{xy} = \dot{\epsilon }_{yx} = \frac{1}{2}\left(\frac{\partial V_{x}}{\partial y} + \frac{\partial V_{y}}{\partial x}\right) \end{equation}

(C5)

\begin{equation} \dot{\omega }_{xy} = \frac{1}{2}\left(\frac{\partial V_{x}}{\partial y} - \frac{\partial V_{y}}{\partial x}\right) \end{equation}

(C6)

where |$\dot{\omega }_{xy}$| is the rate of rotation about a vertical axis and |$\dot{\epsilon }_{xx}$|⁠, |$\dot{\epsilon }_{xy}$| and |$\dot{\epsilon }_{yy}$| are the horizontal components of the strain rate tensor:

\begin{equation} \mathbf {\dot{\epsilon }} = {\left(\begin{array}{c@{\quad}c}\dot{\epsilon }_{xx} & \dot{\epsilon }_{xy} \\ \dot{\epsilon }_{yx} & \dot{\epsilon }_{yy} \\ \end{array}\right)} \end{equation}

(C7)

and therefore:

\begin{equation} \frac{\partial V_{x}}{\partial y} = \dot{\epsilon }_{xy} + \dot{\omega }_{xy} \end{equation}

(C8)

\begin{equation} \frac{\partial V_{y}}{\partial x} = \dot{\epsilon }_{xy} - \dot{\omega }_{xy}. \end{equation}

(C9)

Substituting eqs (C3), (C4), (C8) and (C9) into eqs (C1) and (C2) we obtain:

\begin{equation} V_{x} = U_{x} + \dot{\epsilon }_{xx}\Delta x + \dot{\epsilon }_{xy}\Delta y + \dot{\omega }_{xy}\Delta y \end{equation}

(C10)

\begin{equation} V_{y} = U_{y} + \dot{\epsilon }_{xy}\Delta x + \dot{\epsilon }_{yy}\Delta y - \dot{\omega }_{xy}\Delta x. \end{equation}

(C11)

Which can be re-written in matrix form as:

\begin{equation} {\left(\begin{array}{c}V_{x} \\ V_{y} \\ \end{array}\right)} = {\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & \Delta x & \Delta y & 0 & \Delta y \\ 0 & 1 & 0 & \Delta x & \Delta y & -\Delta x \\ \end{array}\right)} {\left(\begin{array}{cccccc}U_{x} \\ U_{y} \\ \dot{\epsilon }_{xx} \\ \dot{\epsilon }_{xy} \\ \dot{\epsilon }_{yy} \\ \dot{\omega }_{xy} \\ \end{array}\right)}. \end{equation}

(C12)

This is the same as that obtained by Shen et al. (1996). A similar equation can be written for each GPS site, and so the overall equation is given by

\begin{equation} \mathbf {v} = \mathbf {X}\mathbf {s} \end{equation}

(C13)

where v is a column vector with 2N elements containing the x and y components of velocity at each of the N GPS measurement sites (from 1 to N):

\begin{equation} \mathbf {v} = {\left(\begin{array}{c}V_{x}^{1} \\ V_{y}^{1} \\ \vdots \\ V_{x}^{N} \\ V_{y}^{N} \\ \end{array}\right)}. \end{equation}

(C14)

X is a 2N ×6 matrix and Δx_N and Δy_N are the x and y distances to the Nth GPS measurement site from the calculation point:

\begin{equation} \mathbf {X} = {\left(\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c}1 & 0 & \Delta x_{1} & \Delta y_{1} & 0 & \Delta y_{1} \\ 0 & 1 & 0 & \Delta x_{1} & \Delta y_{1} & -\Delta x_{1} \\ \vdots & \vdots & \vdots & \vdots & \vdots & \vdots \\ 1 & 0 & \Delta x_{N} & \Delta y_{N} & 0 & \Delta y_{N} \\ 0 & 1 & 0 & \Delta x_{N} & \Delta y_{N} & -\Delta x_{N} \\ \end{array}\right)} \end{equation}

(C15)

and s is a column vector containing the various parameters for the calculation point being considered:

\begin{equation} \mathbf {s} = {\left(\begin{array}{c}U_{x} \\ U_{y} \\ \dot{\epsilon }_{xx} \\ \dot{\epsilon }_{xy} \\ \dot{\epsilon }_{yy} \\ \dot{\omega }_{xy} \\ \end{array}\right)}. \end{equation}

(C16)

We solved eq. (C13) by a weighted least squares inversion at each calculation point:

\begin{equation} \mathbf {s} = \left(\mathbf {X}^{T}\mathbf {W}\mathbf {X}\right)^{-1}\mathbf {X}^{T}\mathbf {W}\mathbf {v}, \end{equation}

(C17)

where W is a Gaussian weighting matrix which ensures that GPS sites closer to the calculation point are given greater weighting. The weighting varies with the square of the distance between the calculation point and the GPS site, r, and depends on a scale length α:

\begin{equation} W_{1} = e^{\frac{-r_{1}^{2}}{\alpha ^{2}}}. \end{equation}

(C18)

Higher values of α lead to an increasingly smooth strain rate field, whilst lower values are more sensitive to regional variations. The full weighting matrix consists of only diagonal terms:

\begin{equation} \mathbf {W} = {\left(\begin{array}{ccccc}W_{1} & & & & \\ & W_{1} & & & \\ & & \ddots & & \\ & & & W_{N} & \\ & & & & W_{N} \\ \end{array}\right)}. \end{equation}

(C19)

Figure C1.

U_x and U_y are the x (easterly) and y (northerly) components of velocity at the calculation point under consideration. V_x and V_y are the x and y components of velocity at the GPS measurement site. Δx and Δy are the x and y distances from the calculation point to the GPS measurement site, assuming a spherical Earth.

Open in new tab Download slide

APPENDIX D: CALCULATING EARTHQUAKE RECURRENCE TIMES

This derivation follows the work of Molnar (1979) including the correction suggested by England & Bilham (2015). Re-arranging Kostrov’s relation (Kostrov 1974), we can write:

\begin{equation} \sum _{n = 1}^{N}M_{ij}^{n} = 2 \mu \tau V \dot{\epsilon }_{ij}. \end{equation}

(D1)

Hence the moment rate (⁠|$\dot{M_{0}}$|⁠) is given by

\begin{equation} \dot{M_{0}} = \frac{M_{\text{tot}}}{\tau } = 2 \mu V |\dot{\epsilon }_{ij}|, \end{equation}

(D2)

where M_tot is the total seismic moment released in the time period τ (i.e. the size of the summed moment tensor |$\sum _{n = 1}^{N}M_{ij}^{n}$|⁠), μ is the shear modulus, V is the volume of crust under consideration, and |$|\dot{\epsilon }_{ij}|$| is some measure of the magnitude of the strain rate tensor. The Gutenberg-Richter relationship between frequency and magnitude suggests that the number of earthquakes (N) that we expect to have a scalar seismic moment ≥ M is given by

\begin{equation} N(M) = \alpha M^{-\beta }. \end{equation}

(D3)

The moment density (n, the number of events per unit moment) is therefore given by

\begin{equation} n(M) = -\frac{\text{d}N(M)}{\text{d}M} = \beta \alpha M^{-\beta -1}. \end{equation}

(D4)

The total moment release (M_tot) is found by integrating the moment density times the value of the moment at each increment between the maximum scalar seismic moment (M_max) and zero:

\begin{eqnarray} M_{\text{tot}} &=& \int _{0}^{M_{\text{max}}} M n(M)\text{ d}M = \int _{0}^{M_{\text{max}}} \beta \alpha M^{-\beta } \text{d}M \nonumber\\ &=& \left[\frac{\beta \alpha M^{1-\beta }}{1-\beta }\right]_{0}^{M_{\text{max}}} = \frac{\beta \alpha M_{\text{max}}^{1-\beta }}{1-\beta }. \end{eqnarray}

(D5)

Re-arranging we find:

\begin{equation} \alpha = \frac{M_{\text{tot}}\left(1-\beta \right)}{\beta M_{\text{max}}^{1-\beta }}. \end{equation}

(D6)

Substituting back into eq. (D3):

\begin{equation} N(M) = \frac{M_{\text{tot}}\left(1-\beta \right)}{\beta M_{\text{max}}^{1-\beta }} M^{-\beta }. \end{equation}

(D7)

To convert from the number of events (N) to the rate of events (⁠|$\frac{N}{\tau }$|⁠) we switch M_tot for |$\dot{M_{0}}$| and hence the recurrence interval (T, which is equal to the reciprocal of the rate of events) for earthquakes of scalar seismic moment ≥ M is given by

\begin{equation} T(M) = \frac{\beta M_{\text{max}}^{1-\beta }M^{\beta }}{\dot{M_{0}}\left(1-\beta \right)}. \end{equation}

(D8)

Download all slides

Month:	Total Views:
October 2017	24
November 2017	46
December 2017	171
January 2018	53
February 2018	20
March 2018	18
April 2018	21
May 2018	4
June 2018	8
July 2018	12
August 2018	11
September 2018	6
October 2018	6
November 2018	2
December 2018	15
January 2019	9
February 2019	3
March 2019	14
April 2019	8
May 2019	9
June 2019	4
July 2019	11
August 2019	6
September 2019	7
October 2019	6
November 2019	11
December 2019	10
January 2020	6
February 2020	4
March 2020	10
April 2020	5
May 2020	3
June 2020	14
July 2020	13
August 2020	1
September 2020	2
October 2020	10
November 2020	4
December 2020	3
January 2021	9
February 2021	41
March 2021	24
April 2021	14
May 2021	9
June 2021	13
July 2021	13
August 2021	9
September 2021	2
October 2021	10
November 2021	23
December 2021	27
January 2022	35
February 2022	13
March 2022	25
April 2022	16
May 2022	28
June 2022	44
July 2022	16
August 2022	15
September 2022	58
October 2022	89
November 2022	25
December 2022	65
January 2023	23
February 2023	7
March 2023	10
April 2023	70
May 2023	12
June 2023	9
July 2023	18
August 2023	20
September 2023	17
October 2023	30
November 2023	30
December 2023	38
January 2024	22
February 2024	11
March 2024	17
April 2024	12
May 2024	12
June 2024	9
July 2024	34
August 2024	10
September 2024	13
October 2024	14
November 2024	28
December 2024	15
January 2025	9
February 2025	12
March 2025	32
April 2025	5
May 2025	7

Article Contents

Comparison of seismic and geodetic strain rates at the margins of the Ordos Plateau, northern China

Summary

1 INTRODUCTION

2 METHODS

2.1 Kostrov summations

2.2 Strain rate field from GPS

3 RESULTS

3.1 Kostrov summations

3.2 Strain rate field from GPS

4 DISCUSSION

4.1 Seismic moment deficits

4.2 Earthquake recurrence times from geodetic strain rates

4.3 Future seismic hazard

5 CONCLUSIONS

6 DATA AND RESOURCES

Acknowledgements

REFERENCES

APPENDIX A: KOSTROV SUMMATIONS

APPENDIX B: EXPECTED PATTERN OF FAULTING FROM STRAIN RATES

APPENDIX C: STRAIN RATE FIELD FROM GPS

APPENDIX D: CALCULATING EARTHQUAKE RECURRENCE TIMES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

Article Contents

Comparison of seismic and geodetic strain rates at the margins of the Ordos Plateau, northern China Free

Summary

1 INTRODUCTION

2 METHODS

2.1 Kostrov summations

2.2 Strain rate field from GPS

3 RESULTS

3.1 Kostrov summations

3.2 Strain rate field from GPS

4 DISCUSSION

4.1 Seismic moment deficits

4.2 Earthquake recurrence times from geodetic strain rates

4.3 Future seismic hazard

5 CONCLUSIONS

6 DATA AND RESOURCES

Acknowledgements

REFERENCES

APPENDIX A: KOSTROV SUMMATIONS

APPENDIX B: EXPECTED PATTERN OF FAULTING FROM STRAIN RATES

APPENDIX C: STRAIN RATE FIELD FROM GPS

APPENDIX D: CALCULATING EARTHQUAKE RECURRENCE TIMES

Citations

Views

Altmetric

Email alerts

Astrophysics Data System

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Comparison of seismic and geodetic strain rates at the margins of the Ordos Plateau, northern China