-
PDF
- Split View
-
Views
-
Cite
Cite
K. Kalousová, O. Souček, O. Čadek, Deformation of an elastic shell with variable thickness: a comparison of different methods, Geophysical Journal International, Volume 190, Issue 2, August 2012, Pages 726–744, https://doi.org/10.1111/j.1365-246X.2012.05539.x
Close - Share Icon Share
Summary
Deformation of the outermost parts of single-plate planetary bodies is often modelled in terms of the response of a spherical elastic shell to surface or basal loading. As the thickness of such elastic lithosphere is usually much smaller than the radius of the body, the deformation is commonly approximated by that obtained for a thin elastic shell of uniform thickness. The main advantage of the thin shell approximation is its simplicity—the solution can be expressed analytically if the thickness of the shell is uniform, but even in the case of a thin shell of variable thickness, when the problem must be solved numerically, the computational costs are much lower than in a fully 3-D case. Here we analyse the error of the thin shell approximation by comparing it with the solution obtained for a shell of finite thickness using finite element methods. Special attention is paid to a shell of variable thickness and, in general, to the effect of elastic thickness variations on local deformation. For a shell of uniform thickness with the outer radius corresponding to Mars, we find that the error in radial displacement at low harmonic degrees (ℓ≤ 20) does not exceed 5 per cent for small shell thicknesses (d≤ 50km) and 10 per cent for thick shells (d∼ 250km). Similar accuracy is also found for a shell of variable thickness if the thin shell approximation is used. Our numerical tests indicate that local deformation of a shell is mostly sensitive to the average thickness of the shell in the near zone while the effect of thickness variations in the far zone can be neglected in the first approximation. Consequently, the extremely simple thin shell method, designed for shells of uniform thickness, can be effectively used to obtain a reasonably accurate estimate of deflection even in the case of a shell with varying thickness. Finally, we investigate the deformation of an elastic lithosphere due to viscous flow beneath the shell, and we propose an extension of the concept, recently developed to correct dynamic topography for the effect of an elastic lithosphere, to the case of a shell of variable thickness.
1 Introduction
The topographic load at the surface of a planet or a moon causes pressure variations that must be counterbalanced by static and/or dynamic forces of internal origin. The nature of these forces depends on the rheological properties of the body and, consequently, on its material composition and thermal state. In the absence of seismic data, gravity and topography are often the only observations available to geophysicists that can be used to constrain the deep structure and material properties of solar system bodies.
Topography is usually supported by a combination of three basic physical mechanisms: isostasy, viscous flow driven by density heterogeneity inside the body, and deformation of the uppermost elastic layer in response to surface loading. The analysis of topographic information in conjunction with gravitational data (if available) can indicate which of the mechanisms is dominant and thus helps in understanding the physical state of the body's interior (e.g. McKenzie et al. 2002; Roberts & Zhong 2004; Pauer et al. 2006).
In this paper, we focus on the elastic deformation of an outer shell (elastic lithosphere) of a planetary body due to surface and internal loading. The concept of an elastic lithosphere is based on the assumption that the outer layer behaves as an elastic solid, that is, it can maintain stresses induced by surface deformation over very long timescales. Therefore, the viscosity of this layer has to be sufficiently high for viscous relaxation to be negligible, and simultaneously the stresses have to be small enough not to induce fracturing and low temperature creep. At present, such conditions are likely to be satisfied on some one-plate planets with sufficiently thick upper thermal boundary layers, such as Mars or Mercury, and also on some silicate and icy moons (for discussion of effective elastic thickness, see, e.g. Burov & Diament 1995; Grott & Breuer 2008; Golle et al. 2012).
The response of the elastic lithosphere to surface loading depends on the thickness of the layer and its elastic parameters. Assuming the thickness of the shell to be uniform and small in comparison with the shell radius, Turcotte et al. (1981) derived an analytical expression for the thin shell response. This has found wide applications in planetology and is still one of the basic tools used in studying the internal dynamics of terrestrial bodies and some icy satellites (e.g. Lowry & Zhong 2003; Pauer et al. 2006; Nimmo et al. 2011). On Mars, the formalism developed by Turcotte et al. (1981) has been used not only to evaluate the lithospheric deflection and gravitational signal induced by topographic loads (e.g. Turcotte et al. 2002; McGovern et al. 2002; Belleguic et al. 2005; Beuthe et al. 2012) but also to estimate the possible deformation of the surface due to mantle convection (Zhong 2002; Roberts & Zhong 2004).
The method of Turcotte et al. (1981) is strictly valid only for a thin shell of constant thickness. However, a number of studies dealing with convective cooling of planetary bodies suggest that, at a given time, the elastic lithosphere thickness can show significant lateral variations (e.g. Solomon & Head 1990; Anderson & Smrekar 2006; Grott & Breuer 2010; Orth & Solomatov 2011). A thin shell approximation suitable for this case has been derived by Beuthe (2008) who showed that, under certain assumptions, the problem can be formulated in terms of a coupled system of linear fourth-order partial differential equations. Although the numerical solution of this problem is more demanding than in the case of an elastic shell of uniform thickness, it remains computationally feasible due to the 2-D nature of the thin shell approximation. It should be noted, however, that the accuracy of both approaches is limited and decreases with increasing shell thickness and decreasing wavelength of the load.
In this paper, we compare the thin shell approximations by Turcotte et al. (1981) and Beuthe (2008) with the spectral and finite element calculations obtained for a shell of finite thickness. The goal of this comparison is (i) to evaluate the error of both thin shell approximations, (ii) to assess the effect of shell-thickness variations on local deformation and, possibly, (iii) to provide benchmark results for the community dealing with the flexural response of an elastic lithosphere. In addition, we discuss whether the constant thickness approximation of Turcotte et al. (1981) can be used to estimate the deformation of a shell of variable thickness and whether the approach of Zhong (2002) can be generalized accordingly.
When discussing variations of elastic lithosphere thickness, we must distinguish between the real variations of the lithosphere thickness, existing at a given time and resulting from the instantaneous thermal and stress state of the planet, and the variations that are obtained from analysis of topography and gravity data and that may represent the thickness of the elastic lithosphere in different times in the past (e.g. McGovern et al. 2002). In this paper, we only deal with the former type of the elastic thickness variations and we do not address the problem of ‘frozen-in’ deformation (e.g. Courtney & Beaumont 1983; Albert & Phillips 2000).
The structure of the paper is as follows. In Section 2, we formulate the problem of elastic shell deformation and describe various approaches to its solution (thin shell approximation, spectral method, finite element methods). In Section 3, we discuss the assumptions and estimate the limitations of the thin shell approach. In Section 4, we compare all computational approaches in the case of uniform and variable shell thickness, and we discuss the influence of these variations on local deformation in more detail in Section 5. Section 6 deals with an extension of the approach of Zhong (2002) for a variable lithospheric thickness. All results are summarized and discussed in Section 7.
2 Governing Equations and Methods of Solution
2.1 Formulation of the problem
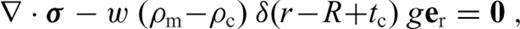
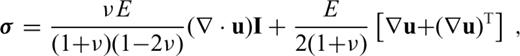
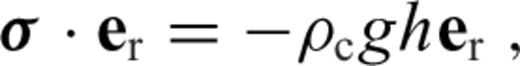
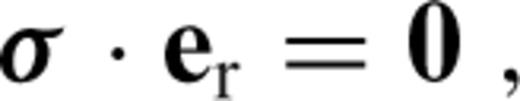
 is the stress tensor, u is the displacement with w denoting its radial component, er is the unit radial vector, g is the gravitational acceleration, δ is the Dirac delta-function, r is the radius, R is the radius of the surface, I is the identity tensor, •T denotes transposition of a matrix, and h is the topographic height.
is the stress tensor, u is the displacement with w denoting its radial component, er is the unit radial vector, g is the gravitational acceleration, δ is the Dirac delta-function, r is the radius, R is the radius of the surface, I is the identity tensor, •T denotes transposition of a matrix, and h is the topographic height.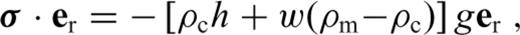
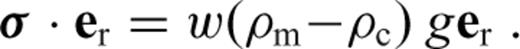
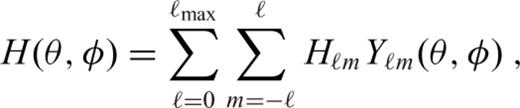
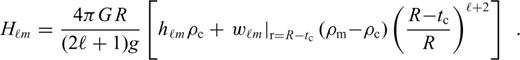
2.2 Thin shell approximation
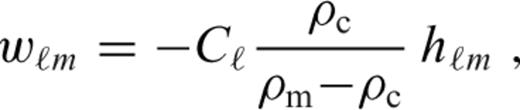
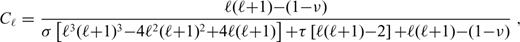
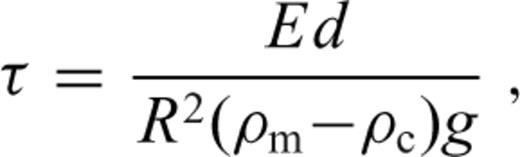
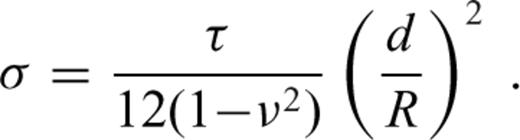
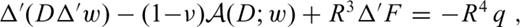
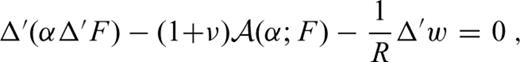
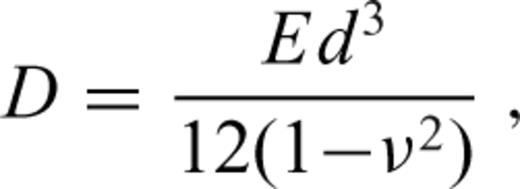
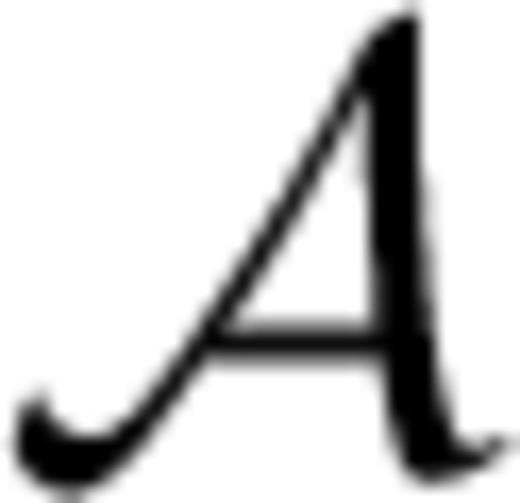 denote surface differential operators defined in spherical coordinates θ and φ as follows:
denote surface differential operators defined in spherical coordinates θ and φ as follows: 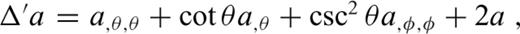
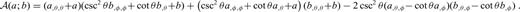
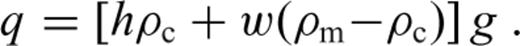
2.3 Spectral solution for a thick shell of constant thickness
If the thickness of the shell does not vary with θ and φ, eqs (1)–(4) can be solved directly in 3-D geometry, that is, without using the thin shell approximation. The radial displacement w then depends not only on lateral coordinates but also on radius r. To solve the eqs (1)–(4), one only needs to slightly modify the spectral methods developed to study the viscoelastic deformation of the Earth (e.g. Sabadini & Vermeersen 2004) or the dynamic geoid (e.g. Hager & Clayton 1989). Here we use the semi-spectral method described by Golle et al. (2012) which has been generalized for compressible materials. The method (hereinafter called SSM) can be used to compute small deformations of a shell of arbitrary thickness with high accuracy and low computational costs. However, the method fails if the thickness of the shell varies laterally or if the material parameters E and ν depend not only on radius but also on θ and φ. The use of a finite element method is then more convenient.
2.4 Finite element solvers
The problem of deformation of an elastic shell of variable thickness was implemented in two numerical finite element software tools—Comsol Multiphysics (version 4.2a, www.comsol.com) and Elmer (http://www.csc.fi/elmer). In both cases, we used standard modules for linear elasticity in axisymmetric geometry, reducing effectively the problem to a 2-D one, which allows for reasonably high spatial resolution. We decided to use two different software tools and thus obtain two independent finite element solutions in order to at least empirically assess and control the error of the finite element approach; the solutions will be referred to as FEM-C and FEM-E for Comsol and Elmer, respectively.
The discrete problem was solved on non-structured triangular meshes, which were first generated in Comsol and then converted to Elmer (using the ElmerGrid tool) to assure the consistency and the comparability of both finite element solutions. As the basis functions we picked triangular second-order Lagrange elements (P2). The typical size of the problem was ∼104 elements corresponding to approximately ∼105 unknowns, allowing the use of direct solvers in both software packages. We performed mesh-refinement resolution testing of both FEM solvers and a fast numerical convergence was obtained even for very coarse initial meshes. This implies that the chosen resolution is fully sufficient.
3 Inherent Limitations of the Thin Shell Approximation
The thin shell approximation is primarily based on the assumption that the displacement is constant across the shell and that σrr is significantly smaller than σθθ and σφφ (for more details, see, e.g. Kraus 1967; Beuthe 2008). Although these assumptions are well satisfied if d≪R and the topographic loads are of wavelength λ≫d, one should always keep in mind that the thin shell solution is only approximate. For example, the estimates of the current elastic lithospheric thickness on Mars range between 100 and 300km (Grott & Breuer 2010), yielding d/R between 0.03 and 0.1 and d/λ between 0.05 and 0.15 (for λ corresponding to the load at harmonic degree 10). These values indicate that the error of the thin shell approximation may not be negligible. In this section and the section that follows, we attempt to quantify the accuracy of the thin shell approximation by comparing it with the solution obtained using a fully 3-D approach.
We consider a shell of constant thickness corresponding in outer radius to Mars (Table 1) deformed by a harmonic load induced by topography hℓ(θ) =AYℓ0(θ), with A = 1000 m. For a given topographic load hℓ and given parameters R, d, E, ν, ρc and ρm (see Table 1), the thin shell solution (TSA-T, Section 2.2) is fully characterized by a single value of the spherical harmonic coefficient wℓ. In contrast, the solution obtained for a shell of finite thickness (SSM, Section 2.3) is a function of radius, wℓ = wℓ(r), and depends also on the depth of the density interface tc. The values of wℓ corresponding to topographic loads at degrees 2–50 computed for different thicknesses of the shell (d =10, 50, 100 and 250km) using the thin shell approximation are shown in Fig. 1. We compare them with the band of values corresponding to the SSM solutions obtained at different radii (r ranging from R−tc to R) and for all admissible values of crustal thickness (tc between 0 and d). The thickness of the band thus gives a rough estimate of the maximum error of the thin shell solution. Note, however, that the error may be even larger because parts of the TSA-T curve lie outside the band of the SSM solutions (Fig. 1 detail).
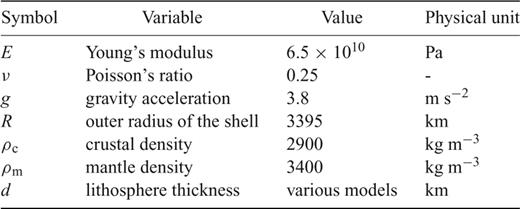
Dependence of radial displacement coefficient wℓ on harmonic degree ℓ of the topographic load for different shell thicknesses, computed using the fully 3-dimensional SSM approach and thin shell approximation TSA-T.
To assess the role of parameter tc, we compare the SSM solutions obtained for two end-member values of tc, namely tc = 0 (denoted by abbreviation BT—‘buoyancy top’) and tc = d (BB—‘buoyancy bottom’). The radial dependence of the SSM solution is then illustrated by plotting the values of coefficient wℓ at the surface (r = R, denoted by DT—‘displacement top’) and at the base of the shell (r = R−d, DB—‘displacement bottom’). In the following, the abbreviation DT-BB refers to the SSM solution obtained at the surface for tc = d, DT-BT is the solution obtained at the surface for tc = 0, and DB-BB denotes the solution at the base of the shell obtained for tc = d.
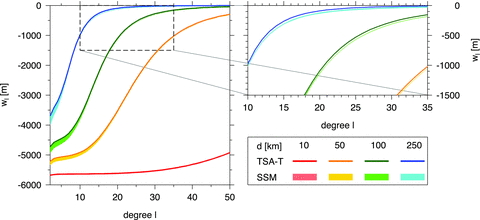
The effect of parameter tc on the radial displacement at the surface is demonstrated in Fig. 2. The absolute value of the difference between the DT-BT and DT-BB solutions monotonically decreases with increasing degree. The rate of the decrease depends on the thickness of the shell, and it is larger for thick shells than for shells of small thickness. This trend can be attributed to the fact that, for a large thickness of the shell, the topography at high degrees is mostly supported by elastic stresses while the buoyancy effect of the density interface becomes negligible. In contrast, the buoyancy is a dominant mechanism maintaining the topographic loads even at high degrees if the thickness of the shell is sufficiently small. The extent of the radial variations in displacement within the shell is illustrated in Fig. 3, where we plot the coefficients wℓ obtained for tc = d computed at the surface (DT-BB) and at the base of the shell (DB-BB). At low degrees, the differences between the two cases are one order of magnitude smaller than in Fig. 2. At high degrees, however, the differences due to variable radius are comparable to or even larger than those due to different values of crustal thickness tc. For further discussion of the accuracy of the thin shell approximation, the reader is referred to, for example, Zhong & Zuber (2000) and Beuthe (2008).
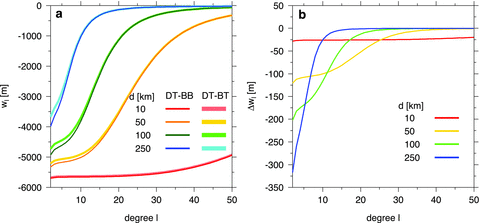
(a) Radial displacement coefficient wℓ at the surface (DT) as a function of harmonic degree ℓ of topographic load computed by SSM for four different shell thicknesses d and two end-member crustal thicknesses, tc = 0 (BT) and tc = d (BB). (b) Difference between the DT-BB and DT-BT solutions.
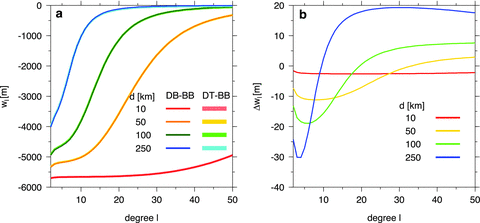
(a) Radial displacement coefficient wℓ as a function of harmonic degree ℓ of topographic load computed by SSM at the base of the shell, r = R−tc (DB), and at the surface, r = R (DT). The results are plotted for four different shell thicknesses d and crustal thickness tc = d (BB). (b) Difference between the DB-BB and DT-BB solutions.
4 Comparison of Different Methods
We now compare different methods designed to compute the deformation of a shell with variable thickness, namely the method proposed by Beuthe (TSA-B, Section 2.2) and the finite element methods (FEM-C, FEM-E) described in Section 2.4. To assess their numerical properties, we first apply them to the elastic shell of constant thickness for which a highly accurate spectral solution (SSM) is available.
4.1 Elastic shell of constant thickness
If the thickness of the elastic shell does not vary laterally, the topographic load at degree ℓ induces deformation which is fully described by radial displacement wℓ at the same degree. This allows the accuracy of the computational methods to be tested in the spectral domain, that is, in the same way as in Section 3. The only inconvenience of this approach is that, in the case of the finite element methods, the harmonic loading function must be first evaluated on a grid, and, after performing the computation, the resultant radial displacement must be expressed in terms of a spherical harmonic function. The transformation from spectral to spatial domain and back produces an additional numerical error, but as we will see, this error is negligible if the grid step is significantly smaller than the wavelength of the spherical harmonic function.
Fig. 4 illustrates the accuracy of different methods (TSA-T, TSA-B, FEM-E and FEM-C) with respect to SSM which is assumed here to have a negligible error (note that the spectral representation in lateral direction is effectively equivalent to a finite-difference scheme of the same order as the spectral cut-off degree, cf.Fornberg 1998). The geometry and material properties of the shells used in testing the accuracy are the same as in Section 3. The quantity Δwℓ, plotted on the vertical axis, is defined as a difference between the radial displacement at degree ℓ obtained by the tested method and the radial displacement computed at the same degree using SSM for tc = 0 at r = R (DT-BT). The shaded area indicates the dispersion of the SSM solution due to its dependence on r and tc (cf.Section 3). It is confined by two curves, Δwℓ = 0 and the curve corresponding to the difference between the SSM solutions obtained for DB-BB (r = R−d, tc = d) and DT-BT (r = R, tc = 0).
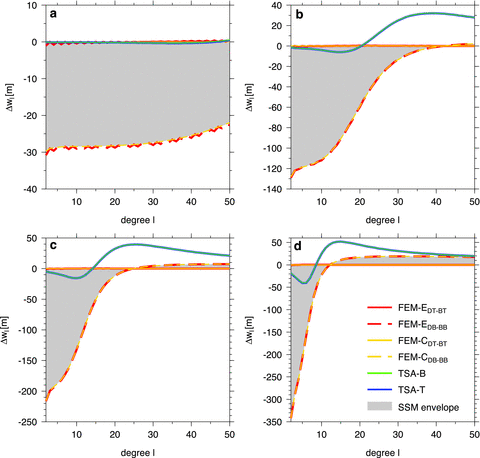
Error of radial displacement coefficient wℓ with respect to the SSM DT-BT solution plotted as a function of harmonic degree ℓ of topographic load. Four different elastic shell thicknesses d are considered: 10km (a), 50km (b), 100km (c) and 250km (d).
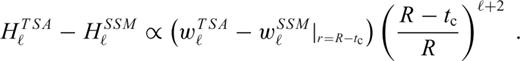
The accuracy of each of the finite element methods (FEM-C, FEM-E) is illustrated in Fig. 4 by the two pairs of curves corresponding to the DT-BT and DB-BB cases. These curves frame the borders of the shaded area, thus confirming the high accuracy of both methods. For small values of d (≤10km), the accuracy of the finite element methods is similar to that of the thin shell methods, but it grows significantly higher for larger values of d. Both finite element methods are comparable in accuracy, but a detailed inspection of the results reveals that FEM-C is slightly more accurate than FEM-E where we are not able to reduce certain minor spurious oscillations in displacement in the case of very thin shells (Fig. 4a). That is why FEM-C will be used as a reference method in the next section, where we deal with a shell of variable thickness for which the semi-spectral method can no longer be used.
4.2 Elastic shell of variable thickness
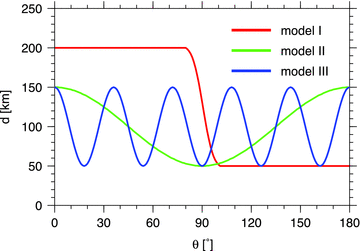
The numerical properties and accuracy of the computational methods are tested on three synthetic models of elastic shells with variable thickness (Fig. 5). The outer radius and material parameters of the shells are the same as in the previous sections (see Table 1). The shells are axisymmetric with thickness d ranging from 50 to 200km in model I and from 50 to 150km in models II and III. Model I consists of two hemispheres of contrasting thicknesses separated by a sharp (but smooth) transition while models II and III exhibit harmonic variations of elastic thickness with a wavelength of 180° and 36°, respectively. Each shell is deformed by the same topographic load as in Section 3 (i.e. harmonic topography with amplitude 1000 m). As the thickness of the shell varies laterally, its response to harmonic loading is more complex than in the case of a shell with uniform thickness: a load of a given degree now induces deformation not only at the same degree but, in general, at all other degrees. That is why we present the resultant radial displacement in the spatial domain, that is, as a function of θ, and not in terms of the spectral coefficients as in previous sections.
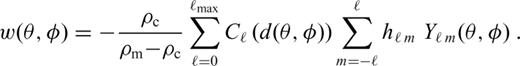
The results obtained for the three model shells described above and for the different loading functions are shown in Figs 6–8. In each figure, rows 1–4 correspond to the loading imposed at degrees 2, 5, 8 and 15, respectively. The panels on the left show the radial displacement w = w(θ) obtained using different computational methods, while the right panels illustrate errors of the individual solutions with respect to the DT-BT solution computed by the reference method (FEM-C). The area in yellow shows the dispersion of the reference FEM-C solution due to its dependence on r and tc. It is bounded by Δw = 0, corresponding to the zero error of the DT-BT solution from one side, and by Δw = wDB-BB−wDT-BT, corresponding to the difference between the DB-BB and DT-BT solutions from the other.
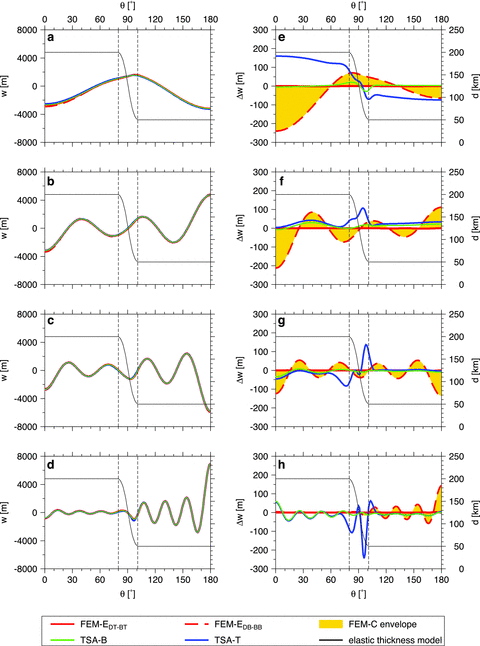
Displacement w (left-hand side) and its absolute error Δw with respect to FEM-C (DT-BT) (right-hand side) as a function of θ for elastic thickness model I. The harmonic loading is imposed at degrees 2 (panels a, e), 5 (b, f), 8 (c, g) and 15 (d, h). The displacement w and error Δw are plotted by colour lines corresponding to different computational methods. The yellow envelope illustrates the dispersion of reference FEM-C method. Elastic thickness model used to calculate w is indicated by the thin black line with a scale plotted on the right.
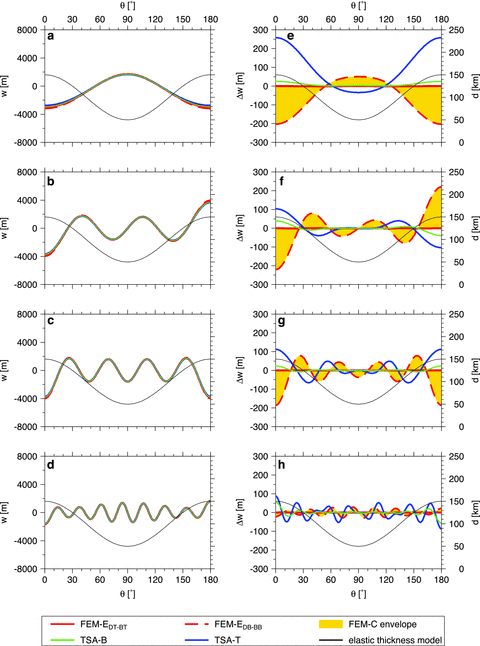
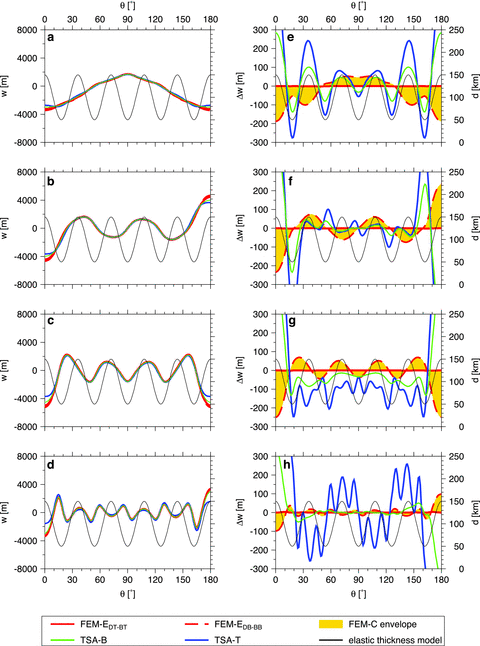
Inspection of the left panels in Figs 6–8 suggests that all of the solutions, including the TSA-T used in local approximation (eq. 20), are rather close to each other, and the differences among them are strikingly small. As could be expected from the tests performed in Section 4.1, there is basically no difference between the FEM-E and FEM-C solutions. This is obvious from the fact that, in the right panels of Figs 6–8, the two red curves corresponding to the FEM-E solutions obtained for the DT-BT (full line) and DB-BB (dashed line) configurations perfectly frame the yellow area corresponding to the FEM-C solutions.
The errors of the TSA-B method (green lines) with respect to FEM-C are of a similar order as the errors obtained for the thin shell approximation in the case of a shell of uniform thickness (cf. Fig. 4). Related to the maximum amplitude of the radial displacement, the error does not exceed a few percent. The relative accuracy is high especially in regions where the thickness of the shell is small, and it deteriorates as the thickness of the shell increases (cf. for example left and right parts of panels in Fig. 6).
The accuracy of the TSA-T method in local approximation (blue lines in Figs 6–8) is rather sensitive to the wavelength of the loading function and the rate of change of shell thickness d with θ. The errors are largest if the wavelength of the load is comparable with or larger than the characteristic length of function d(θ), which is well demonstrated in the top right panels of Figs 6–8 corresponding to degree-2 load. For higher degree loads, the TSA-T solution is almost identical with TSA-B, except for the sharp transitions between the regions of constant thickness in model I (see bottom panel in Fig. 6), or the regions where the local value of d differs significantly from the average value of d in the near field—in polar regions (models II and III) and at local thickness extrema (model III)—see Figs 7 and 8. In general, the estimates of the radial displacement obtained using TSA-T are strikingly accurate. This suggests that the TSA-T method, which is very simple and computationally cheap, can provide a reasonably good, first-order estimate of the radial displacement even for shells with variable thickness, although it was originally designed for uniform thin shells.
5 Effect of Shell Thickness Variations on the Local Deformation
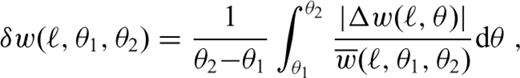

As in the previous section, the absolute error Δw is evaluated with respect to the FEM-C (DT-BT) solution. We note that the expression in the integrand of eq. (21) differs from the usual definition of the relative error (Δw/w) which would diverge in points with zero displacement.
Fig. 9 shows the average relative error δw computed for different regions of model I in dependence on degree ℓ of the loading function. Panels a, b and c show δw obtained from eq. (21) by integrating over the interval (0°, 80°), (100°, 180°) and (80°, 100°), respectively. In the regions where d does not change laterally (Fig. 9, panels a and b, corresponding to d =200km and 50km, respectively), the relative error of TSA-T (blue line) is almost identical to that of TSA-B (green line), except for very low degrees with wavelength larger than or comparable to the size of the domain (∼80°). The relative error of both methods is significantly larger for d =200km than for d =50km (note different scales in panels a and b of Fig. 9). This is comprehensible since the amplitude of the radial displacement w generally decreases with increasing shell thickness, whereas the error Δw of the thin shell approximation increases with increasing d/R. Starting from certain degree (ℓ∼ 10 in Fig. 9a and ∼30 in Fig. 9b) the relative error increases which is associated with the expected deterioration in the accuracy of the thin shell approximation for larger values of d/λ (cf.Section 3).
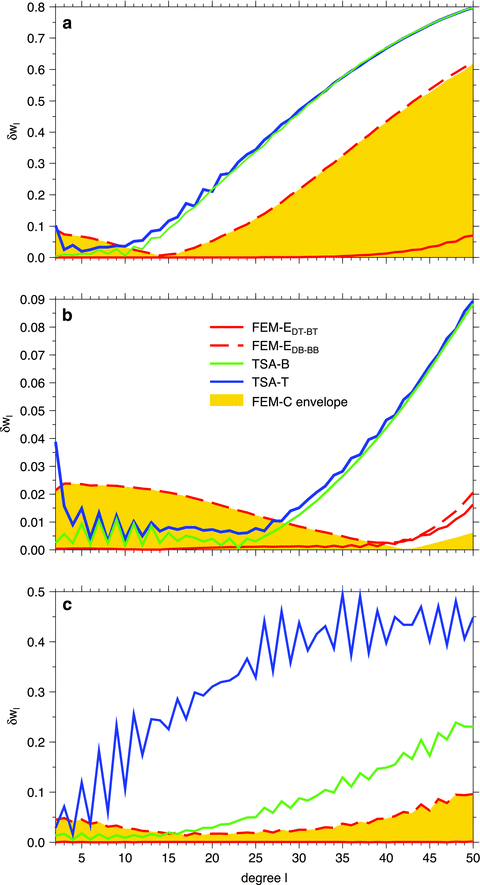
The average relative error δw, eq. (21), as a function of harmonic degree ℓ for different parts of model I. (a) Left part of the model (θ going from 0° to 80°) with elastic thickness d = 200km; (b) right part of the model (100°–180°) with d = 50km; (c) transition region (80°–100°) with d gradually decreasing from 200km to 50km.
Fig. 9(c) shows the relative errors of the methods for the transition region, θ∈ (80°, 100°), in which the shell thickness gradually changes from 200 to 50km. While the errors of TSA-T and TSA-B are basically the same if d is constant (Figs 9a and b), in the region of pronounced thickness variations (Fig. 9c), the TSA-B solution is found to be significantly more accurate than the TSA-T solution, especially for intermediate degrees.
The above results can be generalized as follows: the local deformation of the shell is insensitive to the shell thickness variations if the wavelength of the load is significantly smaller than the characteristic length scale of the thickness variations. This implies that the radial displacement induced by a global load at the point with shell thickness d can be estimated by computing the radial displacement at this point for the shell of uniform thickness d induced by the same load. This approach may provide a reasonable first-order estimate of radial displacement even for very large wavelengths of the load (note that in Fig. 9δw computed for ℓ= 2 never exceeds 10 per cent). However, the accuracy of the above approximation deteriorates in regions where the rate of change of d is large (Fig. 9c) or where the local value of d at the given point does not represent the mean thickness of the shell in its vicinity (e.g. if the point coincides with a local extremum of the shell thickness).
6 Elastic Lithosphere of Variable Thickness in Models of Mantle Flow
So far, we have dealt with an elastic shell deformed due to a topographic load imposed at its surface. Another potentially important source of shell deformation are forces induced by viscous flow in the mantle beneath the elastic lithosphere (Zhong 2002; Roberts & Zhong 2004; Golle et al. 2012).
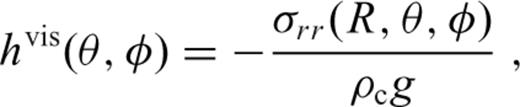
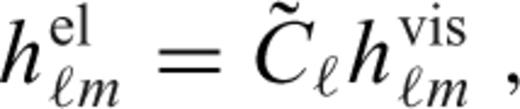
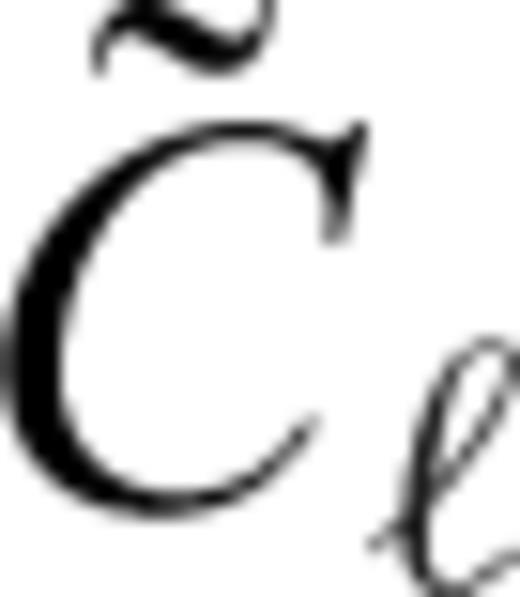 defined as
defined as 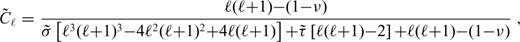
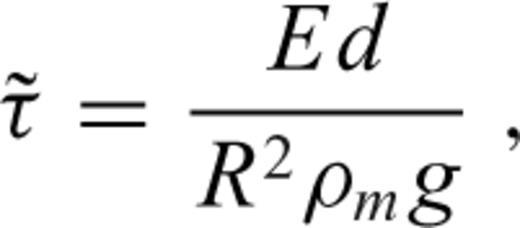
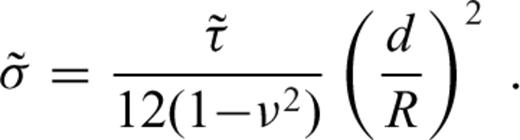
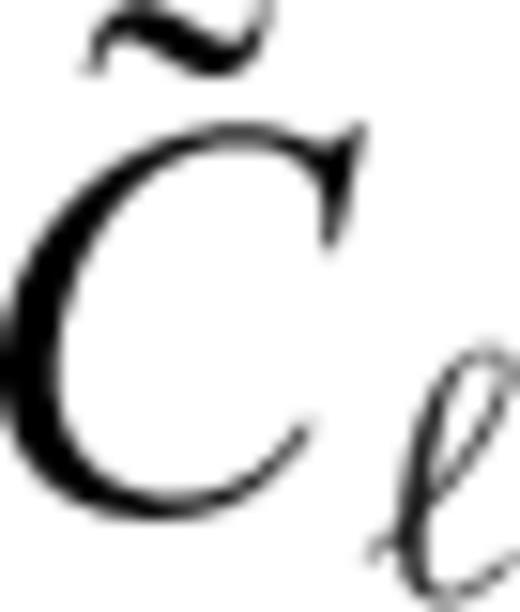 characterizes the flexural response of the elastic shell to a surface radial force Tℓ of degree ℓ normalized with respect to the corresponding isostatic deflection,
characterizes the flexural response of the elastic shell to a surface radial force Tℓ of degree ℓ normalized with respect to the corresponding isostatic deflection, 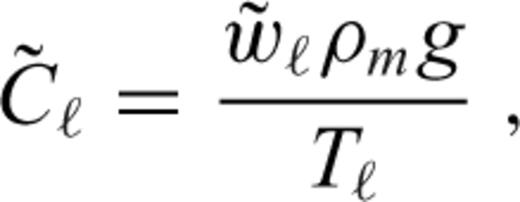
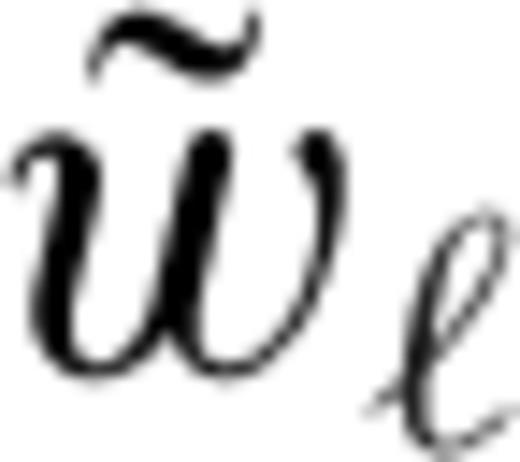 is the spherical harmonic coefficient of the radial displacement induced at the surface of the elastic shell by the same radial force Tℓ (cf. eqs (10)–(12) in Section 2.2). Derivation of eqs eqs (24)–(28) can be found in appendix B.
is the spherical harmonic coefficient of the radial displacement induced at the surface of the elastic shell by the same radial force Tℓ (cf. eqs (10)–(12) in Section 2.2). Derivation of eqs eqs (24)–(28) can be found in appendix B.It should be emphasized, however, that the above formalism is strictly valid only for a thin homogeneous elastic shell with a uniform thickness which is the same as the thickness of the stagnant lid in the viscous model. If this is satisfied, one can indeed prove that a general (not necessarily radial) surface force acting on the bottom boundary of the elastic and viscous shell induces radial deflections hel and hvis, respectively, which are related by eq. (24).
We will now test whether the approach of Zhong (2002) can be generalized to capture also the case with laterally variable lithospheric thickness. Using the finite element solver FEM-C we will investigate the relationship between viscous and elastic deformation for a shell of variable thickness. In particular, we will test whether the dynamic topography obtained for a viscous shell of a given geometry can be corrected for the effect of elasticity in a way analogous to eq. (24), that is, by applying a spectral solver (TSA-B or TSA-T) to an elastic shell of the same geometry. We consider a model of shell thickness variations (thin black lines in Fig. 10) which combines the properties of models I and III used in Section 4.2 by including both long- and intermediate-wavelength features.
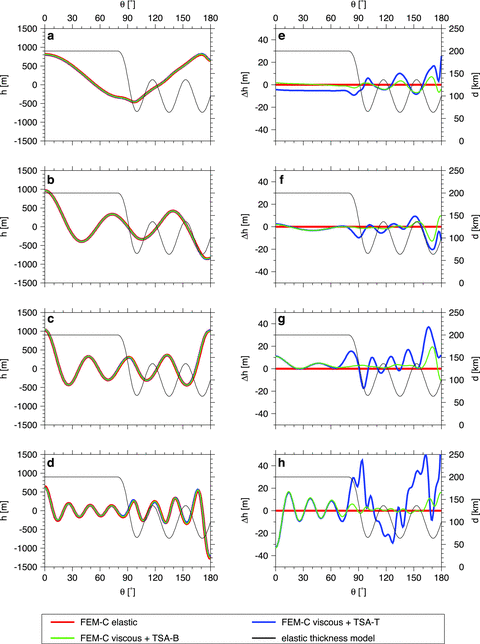
Dynamic topography hel of the elastic shell induced by forces acting at its base (left-hand side) and its absolute error with respect to FEM-C (right-hand side) as a function of θ. The colour lines show the results obtained by different methods. The model of elastic thickness variations is illustrated by the thin black line. Individual rows correspond to loading functions imposed at degree 2 (panels a, e), 5 (b, f), 8 (c, g), and 15 (d, h).
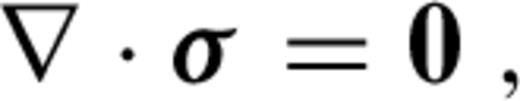
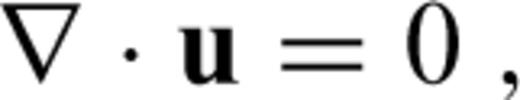
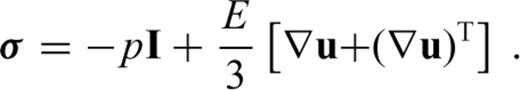
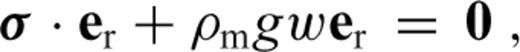
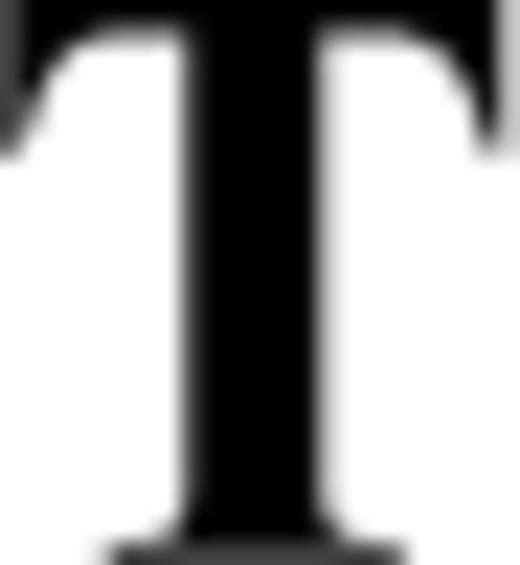 at the bottom surface
at the bottom surface 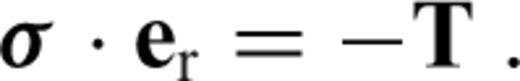
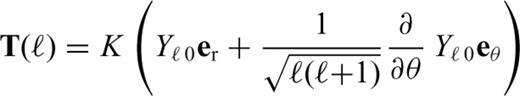
 Pa, is plotted in red in the left panels of Fig. 10. The geometric scaling factor in expression for K is to ensure zero loading at degree one, which otherwise would require special treatment. This solution will be considered as the reference one.
Pa, is plotted in red in the left panels of Fig. 10. The geometric scaling factor in expression for K is to ensure zero loading at degree one, which otherwise would require special treatment. This solution will be considered as the reference one.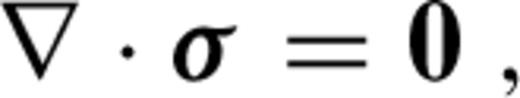
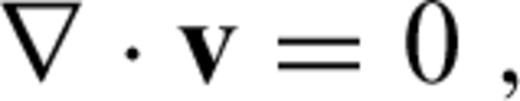
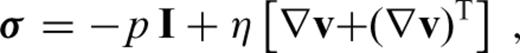
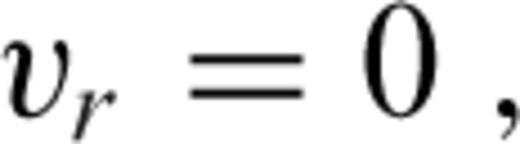
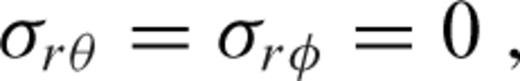
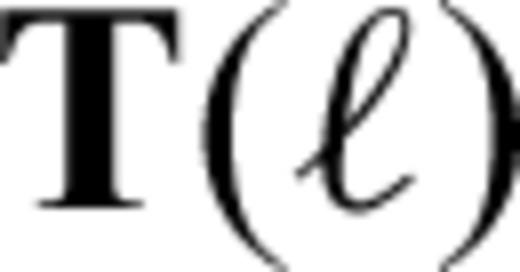 (same as in the first step) at the bottom boundary
(same as in the first step) at the bottom boundary 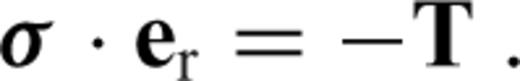
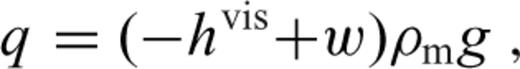
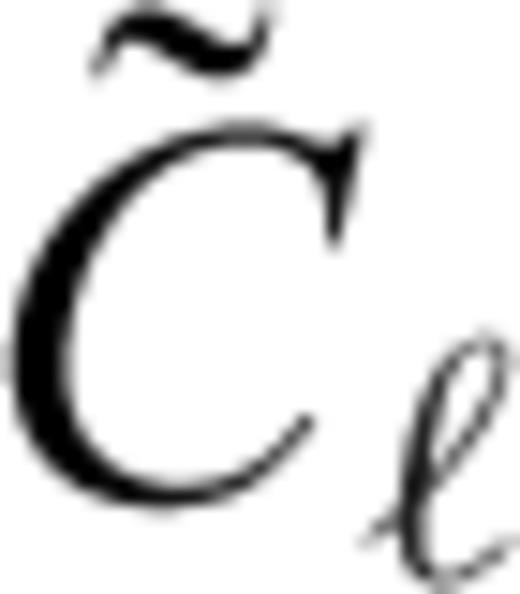 , eq. (25), depending on the local thickness of the shell (cf. eqs 20 and 24)
, eq. (25), depending on the local thickness of the shell (cf. eqs 20 and 24) 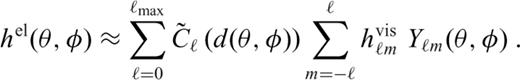
The above results suggest that the method for the elastic correction of a viscous dynamic topography proposed by Zhong (2002) can also be applied to models with a stagnant lid of variable thickness (cf.Zhong et al. 2003). The first-order estimate of the dynamic topography corrected for the elastic lithosphere effect can be obtained using the traditional spectral method developed by Turcotte et al. (1981) and employed also in the work of Zhong (2002). The method must be slightly modified (eq. 42), but its application remains straightforward. A more accurate surface topography can be obtained by solving the equations presented by Beuthe (2008). Owing to the thin shell approximation, the number of unknowns in the equations is not large and the spectral solution is thus less expensive than application of a finite element method to a shell of finite thickness.
7 Concluding Remarks
In this paper, we have analysed the deformation of an elastic spherical shell with variable thickness. We compared two approximate thin shell methods (Turcotte et al. 1981; Beuthe 2008) with methods based on either semi-spectral or finite element discretization of the original problem of finite thickness. For a Mars-like body subject to harmonic loading, we inspected the accuracy of the methods especially at low to intermediate degrees corresponding to the prevailing low-degree character of the observed topography of terrestrial planets (typical linear log–log spectral decay, see, e.g. Turcotte 1987; Čížková 1996; Pauer et al. 2006).
Starting with the case of a shell of uniform thickness, we estimated the inherent inaccuracy of the thin shell methods, arising from both the geometrical and physical assumptions within the thin shell approach. Both thin shell methods coincide in this case, and their errors for low degrees (ℓ≤ 20) do not exceed 5 per cent for small shell thicknesses (d≤50km) and 10 per cent for thick shells (d∼ 250km; see also Figs 1–4).
For a shell of variable thickness, the method of Beuthe (2008) performs with accuracy comparable to the uniform thickness case. When the wavelength of thickness variations is large compared to the wavelength of the load, the errors arise mainly from the thin shell approach—they are confined to regions with high local shell thickness and do not exceed 5–10 per cent (Figs 6 and 7). For models with highly variable thickness, the errors increase but, in general, do not exceed 15 per cent (Figs 6 and 8). It is important to note that this method is essentially 2-D and the solution thus computationally much less demanding than that of the original 3-D problem. Moreover, in the case of a solely normal load, the problem reduces from five to only two coupled partial differential equations, which can be easily solved by the spectral approach outlined in appendix A.
Motivated by the simplicity and good performance of the approach of Turcotte et al. (1981) for shell of uniform thickness, we introduced and investigated also its straightforward extension to the case of variable shell thickness. This approach performs generally more poorly than the approach of Beuthe (2008), especially in regions where the shell thickness varies significantly, but, quite surprisingly, it provides a rather good and computationally very cheap first-order estimate of the resulting displacement (Fig. 9).
Finally, concerning also the force coupling with mantle convection below the shell, we proposed an extension of the concept of Zhong (2002) to the case of a shell of variable thickness. We investigated two methods of spectral correction of a viscous solution to the problem, based on either Beuthe (2008) or Turcotte et al. (1981). The results are again satisfactory with the errors comparable with the case of normal surface loading (Fig. 10).
To sum up, the thin shell methods have proven to be quite reliable and, due to computational effectiveness, very useful tools to estimate the elastic deformation of a spherical shell with variable thickness for general surface and bottom loading. The method of Beuthe (2008) remains very accurate even in regions with high local thickness variability, where the method based on the technique of Turcotte et al. (1981), despite being less accurate, still provides a reasonable estimate and benefits from its tremendous computational simplicity.
Acknowledgments
The authors thank Mikael Beuthe and an anonymous reviewer for their comments and suggestions and Craig Bina for reading the manuscript. The work was supported by Charles University grants GAUK-259099 and SVV-2012-265308, grant No. MSM0021620860 and by the Jindřich Nečas Center for Mathematical Modelling, project LC06052, both financed by the Ministry of Education, Youth and Sports of the Czech Republic.
Appendices
Appendix A: Spectral Solution for A Thin Shell of Variable Thickness
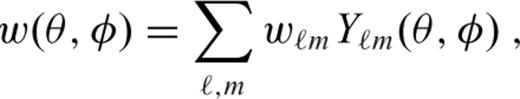
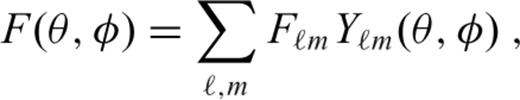

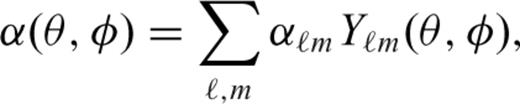
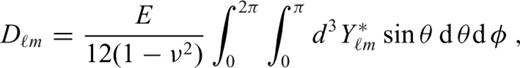
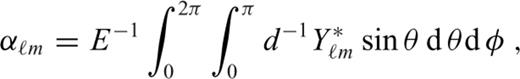
 , eqs (16) and (17), to spherical harmonic functions in expansions (A1), (A2), (A4) and (A5) and then evaluate the products of appropriate spherical harmonic series. Following Beuthe (2008, 2010), we can write
, eqs (16) and (17), to spherical harmonic functions in expansions (A1), (A2), (A4) and (A5) and then evaluate the products of appropriate spherical harmonic series. Following Beuthe (2008, 2010), we can write 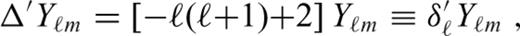
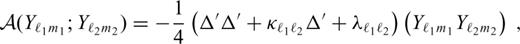
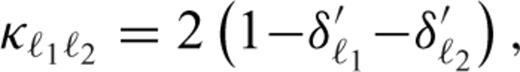
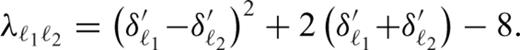
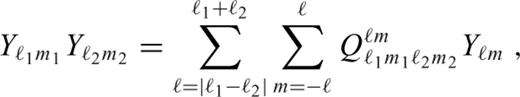
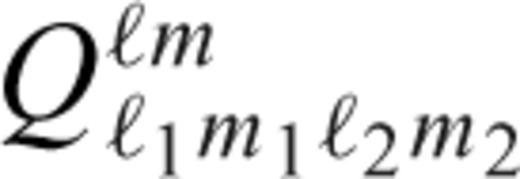 can be rewritten using the Clebsch-Gordan coefficients,
can be rewritten using the Clebsch-Gordan coefficients, 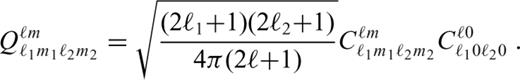
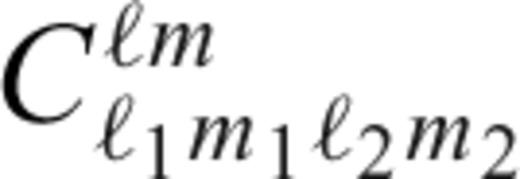 are non-zero only if ℓ, ℓ1 and ℓ2 are non-negative, m = m1+m2, |m|≤ℓ, |m1|≤ℓ1, |m2|≤ℓ2, and |ℓ1−ℓ2|≤ℓ≤ℓ1+ℓ2. Substituting eqs (A1), (A2), (A4) and (A5) in eqs (13) and (14) and applying eqs (A8)–(A12), we obtain
are non-zero only if ℓ, ℓ1 and ℓ2 are non-negative, m = m1+m2, |m|≤ℓ, |m1|≤ℓ1, |m2|≤ℓ2, and |ℓ1−ℓ2|≤ℓ≤ℓ1+ℓ2. Substituting eqs (A1), (A2), (A4) and (A5) in eqs (13) and (14) and applying eqs (A8)–(A12), we obtain 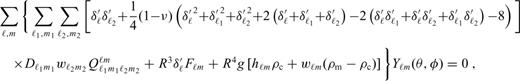
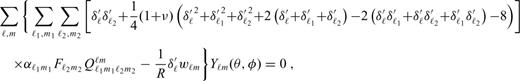
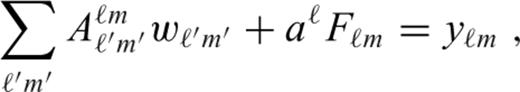
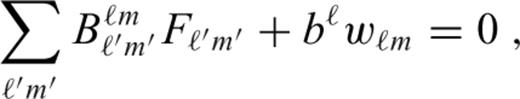
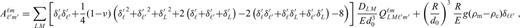
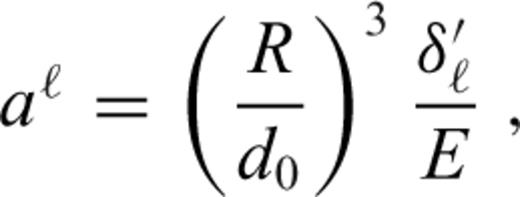
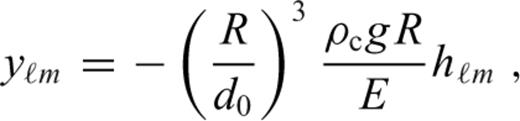
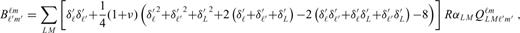
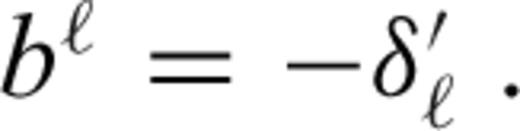
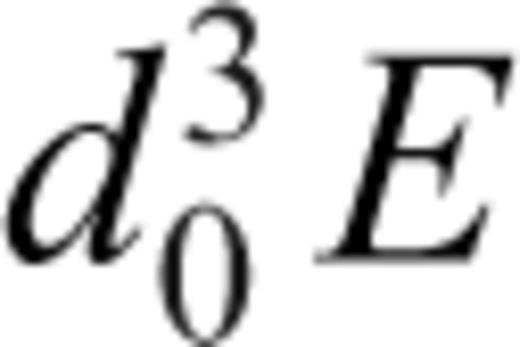 , where d0 is some reference (constant) thickness, and eq. (A15) was multiplied by R. In the axisymmetric geometry, indices m, m1 and m2 are equal to zero, and the total number of unknowns reduces to 2(ℓmax+1). All sums over indices M and m′ in eqs (A16)–(A18) and (A21) vanish, and the Gaunt coefficients
, where d0 is some reference (constant) thickness, and eq. (A15) was multiplied by R. In the axisymmetric geometry, indices m, m1 and m2 are equal to zero, and the total number of unknowns reduces to 2(ℓmax+1). All sums over indices M and m′ in eqs (A16)–(A18) and (A21) vanish, and the Gaunt coefficients 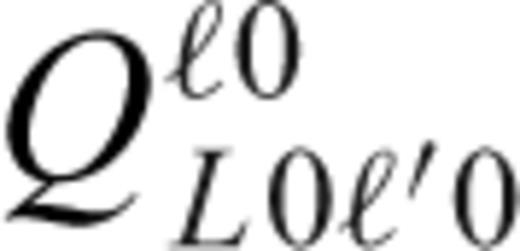 in eqs (A18) and (A21) can easily be evaluated using the analytical formula for the Clebsch-Gordan coefficients with zero m indices (Varshalovich et al. 1988):
in eqs (A18) and (A21) can easily be evaluated using the analytical formula for the Clebsch-Gordan coefficients with zero m indices (Varshalovich et al. 1988): 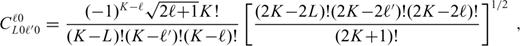
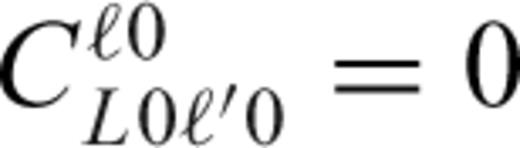 for odd values of 2K.
for odd values of 2K.Appendix B: Derivation of The Flexural Response Coefficient ![graphic]()
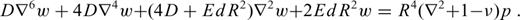
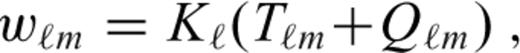
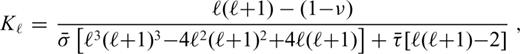
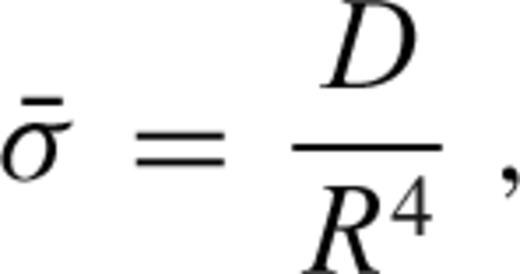
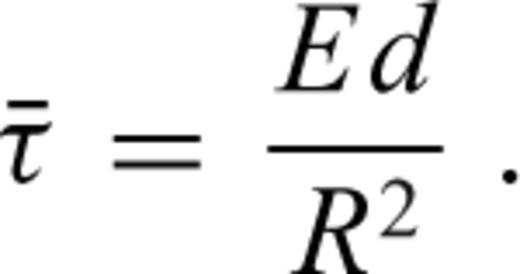
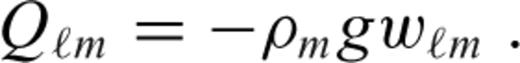
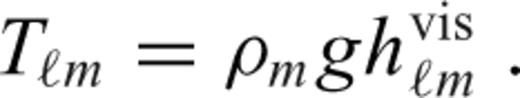
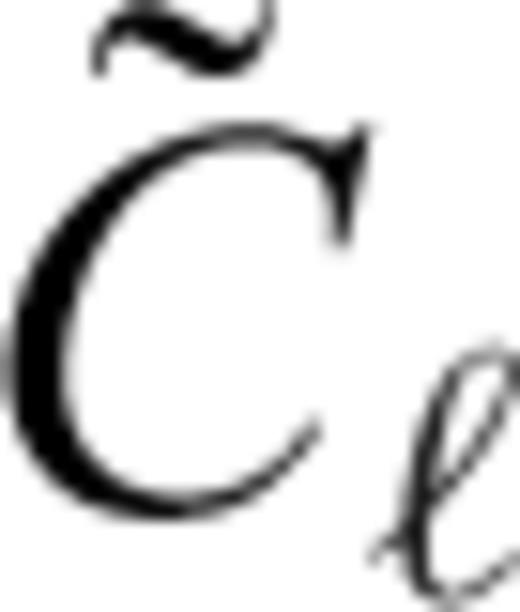 given by eq. (25).
given by eq. (25).References




