-
PDF
- Split View
-
Views
-
Cite
Cite
Andreas Fichtner, Jeannot Trampert, Hessian kernels of seismic data functionals based upon adjoint techniques, Geophysical Journal International, Volume 185, Issue 2, May 2011, Pages 775–798, https://doi.org/10.1111/j.1365-246X.2011.04966.x
Close - Share Icon Share
Summary
We present an extension of the adjoint method that allows us to compute the second derivatives of seismic data functionals with respect to Earth model parameters. This work is intended to serve as a technical prelude to the implementation of Newton-like optimization schemes and the development of quantitative resolution analyses in time-domain full seismic waveform inversion.
The Hessian operator H applied to a model perturbation δm can be expressed in terms of four different wavefields. The forward field u excited by the regular source, the adjoint field u† excited by the adjoint source located at the receiver position, the scattered forward field δu and the scattered adjoint field δu†. The formalism naturally leads to the notion of Hessian kernels, which are the volumetric densities of Hδm. The Hessian kernels appear as the superposition of (1) a first-order influence zone that represents the approximate Hessian, and (2) second-order influence zones that represent second-order scattering.
To aid in the development of physical intuition we provide several examples of Hessian kernels for finite-frequency traveltime measurements on both surface and body waves. As expected, second-order scattering is efficient only when at least one of the model perturbations is located within the first Fresnel zone of the Fréchet kernel. Second-order effects from density heterogeneities are generally negligible in transmission tomography, provided that the Earth model is parameterized in terms of density and seismic wave speeds.
With a realistic full waveform inversion for European upper-mantle structure, we demonstrate that significant differences can exist between the approximate Hessian and the full Hessian—despite the near-optimality of the tomographic model. These differences are largest for the off-diagonal elements, meaning that the approximate Hessian can lead to erroneous inferences concerning parameter trade-offs. The full Hessian, in contrast, allows us to correctly account for the effect of non-linearity on model resolution.
1 Introduction
1.1 Full waveform inversion
Full waveform inversion is a tomographic technique that is based on the numerical simulation of seismic wave propagation. The purely numerical solutions of the wave equation for heterogeneous Earth models provide complete and accurate synthetic seismograms that can be exploited for high-resolution imaging in complex media.
While already initiated in the late 1970s and 1980s (e.g. Bamberger et al. 1977, 1982; Tarantola 1984; Gauthier et al. 1986; Tarantola 1988), full waveform inversion has only recently gained popularity, mainly for two reasons: rapid advances in high-performance computing and our need to reveal the structure of the Earth with increasing detail. Applications of full waveform inversion to real data have now been reported in widely varying contexts, ranging from exploration and engineering problems (e.g. Igel et al. 1996; Operto et al. 2004; Gao et al. 2006; Smithyman et al. 2009) to the imaging of regional- and continental-scale structure (e.g. Dessa et al. 2004; Bleibinhaus et al. 2007, 2009; Chen et al. 2007; Tape et al. 2009, 2010; Fichtner et al. 2009, 2010). Despite the success of full waveform inversion, numerous challenges remain. These include the design of more efficient optimization schemes and the rigorous quantification of model resolution and uncertainties.
1.2 Efficiency of optimization schemes and the Newton method
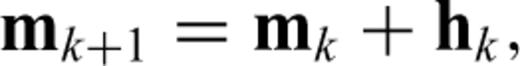
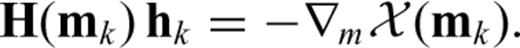
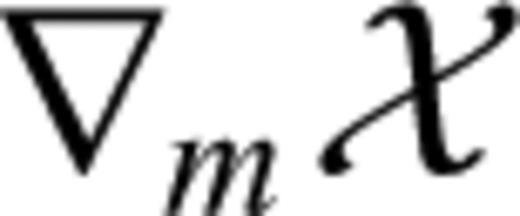 signify the Hessian and the Fréchet derivative of the misfit functional χ with respect to the Earth model. Newton's method converges quadratically provided that the initial model m0 is sufficiently close to the global optimum. It therefore has the potential to reduce the number of iterations needed to reach acceptable solutions. While common practice in non-linear optimization (e.g. Hinze et al. 2009), the feasibility of the Newton method in full waveform inversion has so far only been explored in 1-D synthetic studies (Santosa & Symes 1988; Pratt et al. 1998).
signify the Hessian and the Fréchet derivative of the misfit functional χ with respect to the Earth model. Newton's method converges quadratically provided that the initial model m0 is sufficiently close to the global optimum. It therefore has the potential to reduce the number of iterations needed to reach acceptable solutions. While common practice in non-linear optimization (e.g. Hinze et al. 2009), the feasibility of the Newton method in full waveform inversion has so far only been explored in 1-D synthetic studies (Santosa & Symes 1988; Pratt et al. 1998).1.3 Quantification of resolution
While full waveform inversion is a promising tool, resolution estimates are generally deficient. They are mostly based on synthetic inversions for specific input structures and on the visual inspection of the tomographic images. Synthetic inversions are known to be potentially misleading even in linearized tomographies (Lévêque et al. 1993). Visual inspection is equally inadequate because of the very efficient psychologic trap to mistake the great detail seen in the models as an indicator of comparatively high resolution. In fact, small-scale features may easily appear in full waveform inversion because it hardly requires any explicit regularization—in contrast to classical linearized tomography that is based on the solution of large ill-conditioned linear systems.
Early attempts to analyse—and in fact define—resolution were founded on the equivalence of diffraction tomography and the first iteration of a full waveform inversion (e.g. Devaney 1984; Wu & Toksöz 1987; Mora 1989). However, this equivalence holds only in the impractical case where the misfit χ is equal to the L2 waveform difference  (Fichtner et al. 2008). Furthermore, the analysis of diffraction tomography is feasible only in homogeneous or layered acoustic media.
(Fichtner et al. 2008). Furthermore, the analysis of diffraction tomography is feasible only in homogeneous or layered acoustic media.
Despite being crucial for the interpretation of the tomographic images, methods for the quantification of resolution in realistic applications of full waveform inversion do not exist so far. This absence of a quantitative means to assess the capabilities of full waveform inversion is the source of much scepticism as to whether it is really worth the effort.
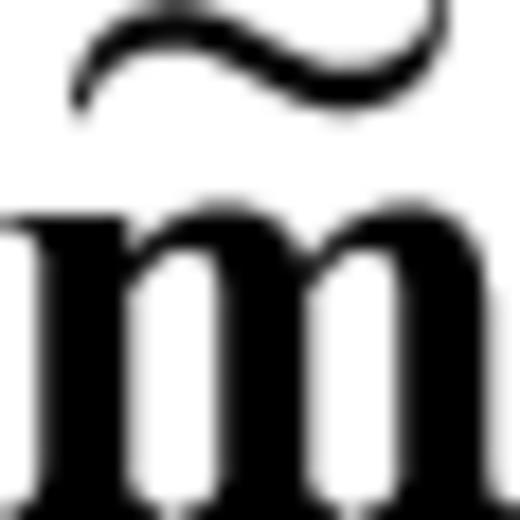 , characterized by
, characterized by 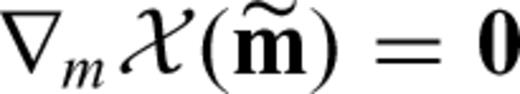 , the Hessian matrix H can be used to infer the resolution of and the trade-offs between model parameters. Approximating χ quadratically around χ yields
, the Hessian matrix H can be used to infer the resolution of and the trade-offs between model parameters. Approximating χ quadratically around χ yields 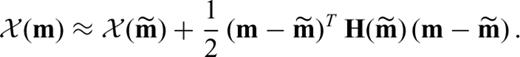
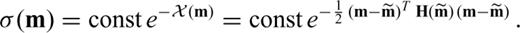
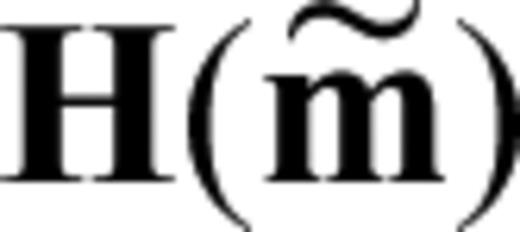 is the inverse posterior covariance matrix in the vicinity of
is the inverse posterior covariance matrix in the vicinity of 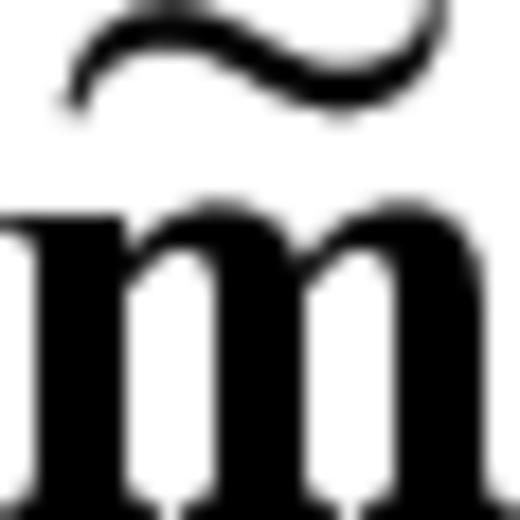 (e.g. Tarantola 2005). It follows that
(e.g. Tarantola 2005). It follows that 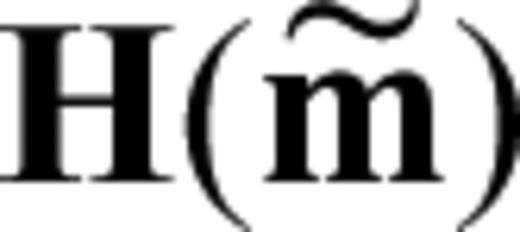 contains all the information on resolution and trade-offs, provided that we are sufficiently close to the global optimum.
contains all the information on resolution and trade-offs, provided that we are sufficiently close to the global optimum.1.4 Objectives and potentials
The key role played by the Hessian in optimization and resolution analysis motivates the development of methods that allow us to compute the second derivatives of χ with optimal efficiency. When a discretized version of the governing equations can be solved explicitly—as in 2-D frequency-domain modelling (Pratt et al. 1998)—the product of H and an arbitrary model vector can be computed conveniently via an extension of the discrete adjoint method. However, in large-scale 3-D applications where the forward problem is solved iteratively in the time domain, the matrix formalism of the discrete adjoint method becomes impractical.
Our prime objective is therefore to generalize the continuous adjoint method to the computation of the Hessian operator H applied to an arbitrary model perturbation δm. This is intended to serve as a technical preparatory step for future developments, and as a means to gain the intuition and experience needed for the meaningful solution of any inverse problem.
The potential of the method developed in the following sections goes far beyond Newton's method and the quantification of uncertainties. It may as well be used for extremal bounds analysis (Meju & Sakkas 2007; Meju 2009; Fichtner 2010), for the determination of optimal step lengths in gradient-based optimization, as a tool to assess second-order effects on seismic data functionals including finite-frequency traveltimes (see Section 4), to study wave propagation through complex media (e.g. Baig & Dahlen 2004), or to design locally independent model parameters as it is classically done in Partitioned Waveform Inversion (Nolet 1990, 2008).
1.5 Which Hessian?
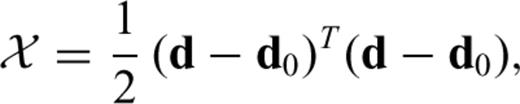
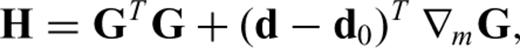
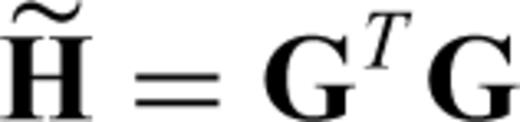
 can differ substantially from H.
can differ substantially from H.The analysis presented in the following paragraphs goes beyond the linear approximation and the assumption of small misfits. It will allow us to compute the exact second derivatives of any data or misfit functional, thus fully accounting for the generally non-linear relation between Earth models and seismic observables. The distinction between linearization and inherent non-linearity will become most apparent in Section 4 where we consider the second derivatives of finite-frequency traveltimes that are commonly considered to be nearly linearly related to Earth structure.
1.6 Outline
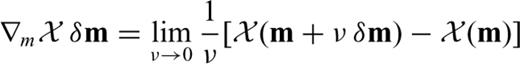
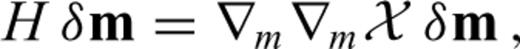
2 The Continuous Adjoint Method for First and Second Derivatives
2.1 First derivatives
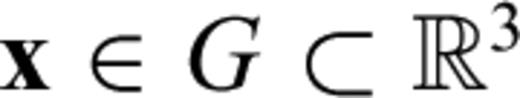 , time t∈T=[t0, t1] and on model parameters
, time t∈T=[t0, t1] and on model parameters 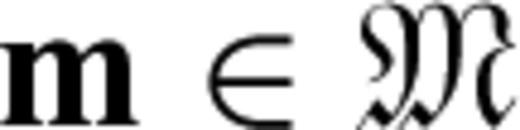
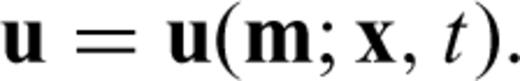
 contains all admissible parameters m(x) =[m(1)(x), m(2)(x), …]. The components m(α)(x) may, for instance, represent the distributions of density ρ, the P velocity vP or the S velocity vS, that is, m(x) =[ρ(x), vP(x), vS(x), …]. The semicolon in eq. (10) indicates that u evolves in space and in time, whereas the model parameters are assumed to be fixed for a given realization of u. The wavefield u is linked via the wave equation, symbolically written as
contains all admissible parameters m(x) =[m(1)(x), m(2)(x), …]. The components m(α)(x) may, for instance, represent the distributions of density ρ, the P velocity vP or the S velocity vS, that is, m(x) =[ρ(x), vP(x), vS(x), …]. The semicolon in eq. (10) indicates that u evolves in space and in time, whereas the model parameters are assumed to be fixed for a given realization of u. The wavefield u is linked via the wave equation, symbolically written as 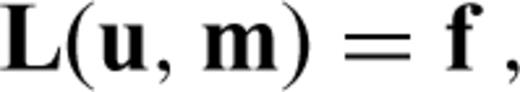
 that we are interested in. The data functional can either play the role of a secondary observable or of a misfit functional that quantifies the discrepancy between observed and calculated waveforms. Without loss of generality we can write
that we are interested in. The data functional can either play the role of a secondary observable or of a misfit functional that quantifies the discrepancy between observed and calculated waveforms. Without loss of generality we can write 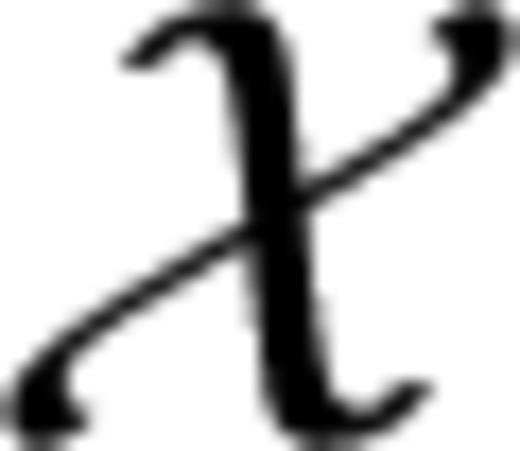 in the form of an integral over time and space, that is,
in the form of an integral over time and space, that is, 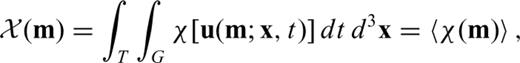
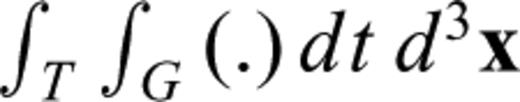 . The derivative of
. The derivative of 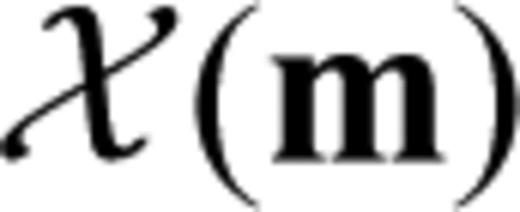 with respect to m in a direction δm follows from the chain rule
with respect to m in a direction δm follows from the chain rule 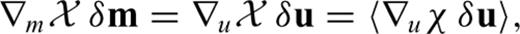
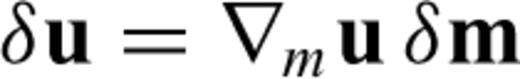
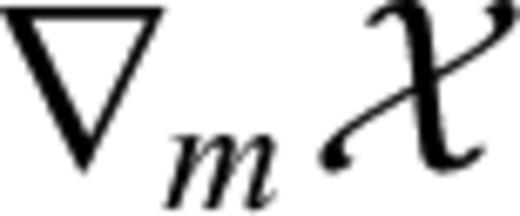 one needs to determine u(m+εδm) for each possible direction δm. This, however, becomes infeasible in the case of numerically expensive forward problems and large model spaces. Consequently, we may not be able to compute
one needs to determine u(m+εδm) for each possible direction δm. This, however, becomes infeasible in the case of numerically expensive forward problems and large model spaces. Consequently, we may not be able to compute 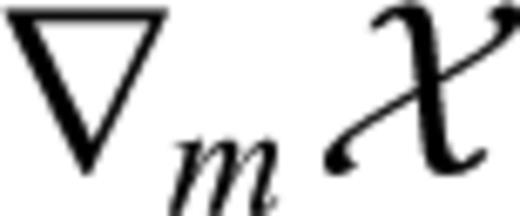 unless we manage to eliminate δu from eq. (13). For this purpose, we differentiate the governing eqs (11) with respect to m. Again invoking the chain rule for differentiation gives
unless we manage to eliminate δu from eq. (13). For this purpose, we differentiate the governing eqs (11) with respect to m. Again invoking the chain rule for differentiation gives 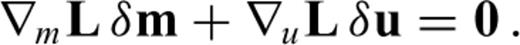
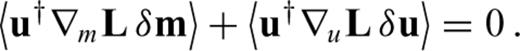
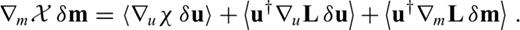
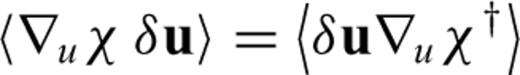
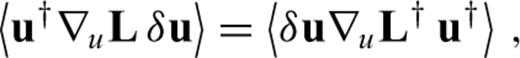
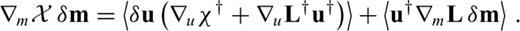
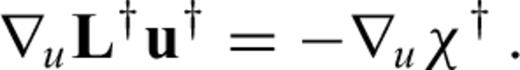
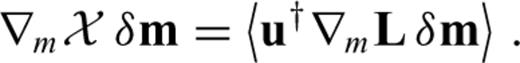
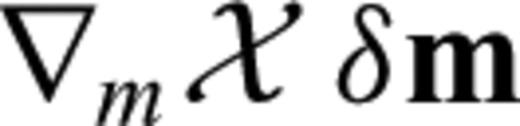 can now be computed for any differentiation direction δm without the explicit knowledge of δu. This advantage comes at the price of having to find the adjoint operator ∇uL† and a solution to the adjoint problem (21). When the operator L is linear in u, it follows that ∇uL(u)u†=L†(u†), and the adjoint eq. (21) can be simplified to
can now be computed for any differentiation direction δm without the explicit knowledge of δu. This advantage comes at the price of having to find the adjoint operator ∇uL† and a solution to the adjoint problem (21). When the operator L is linear in u, it follows that ∇uL(u)u†=L†(u†), and the adjoint eq. (21) can be simplified to 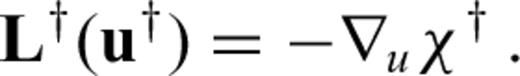
2.1.1 Fréchet kernels
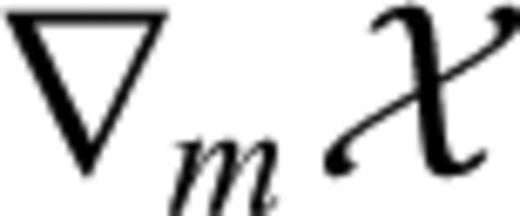
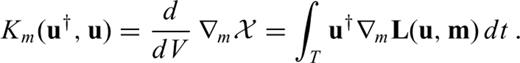
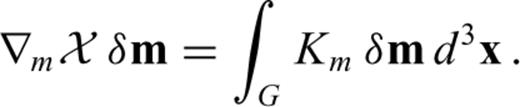
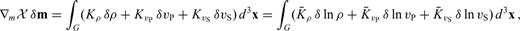
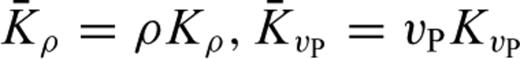 and
and 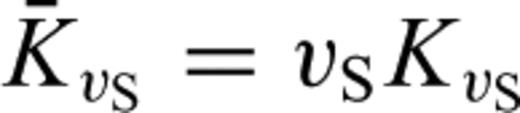 are kernels for relative perturbations. The Fréchet kernels reveal how the data functional
are kernels for relative perturbations. The Fréchet kernels reveal how the data functional 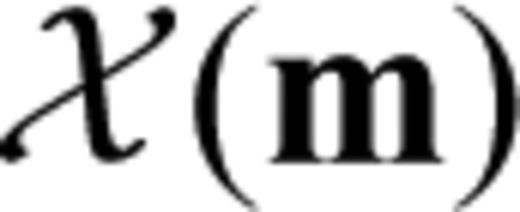 is affected by infinitesimal changes in the model parameters. It is the study of Km for different types of seismic waves and different data functionals that allows us to design efficient inversion schemes and to interpret the results in a physically meaningful way.
is affected by infinitesimal changes in the model parameters. It is the study of Km for different types of seismic waves and different data functionals that allows us to design efficient inversion schemes and to interpret the results in a physically meaningful way.2.1.2 Translation to the discretized model space
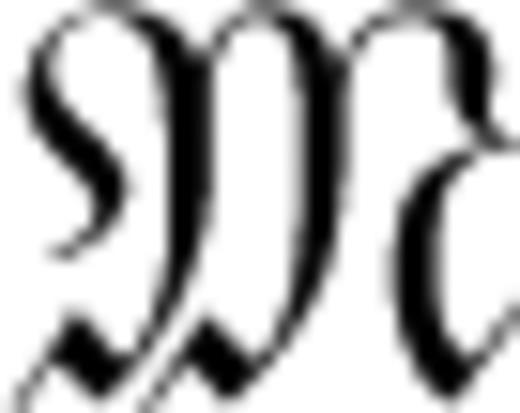 is discretized, meaning that the components m(α) of the space-continuous model m(x) =[m(1)(x), m(2)(x), …] are expressed as a linear combination of N < ∞ basis functions, bi(x)
is discretized, meaning that the components m(α) of the space-continuous model m(x) =[m(1)(x), m(2)(x), …] are expressed as a linear combination of N < ∞ basis functions, bi(x)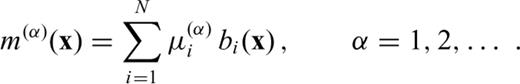
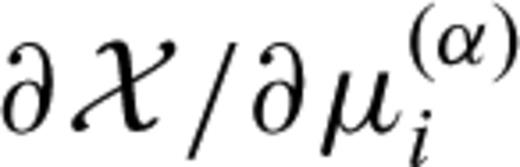 . Using the definition of the classical derivative, we find
. Using the definition of the classical derivative, we find 
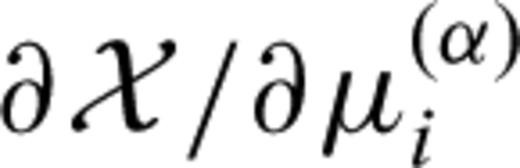 , is given by the projection of the sensitivity kernel
, is given by the projection of the sensitivity kernel 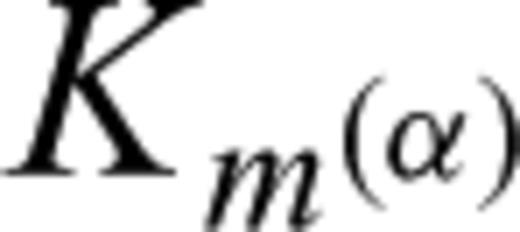 onto the basis function bi.
onto the basis function bi.2.2 Second derivatives

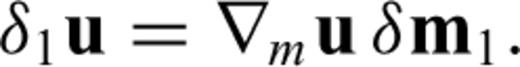
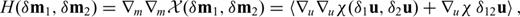
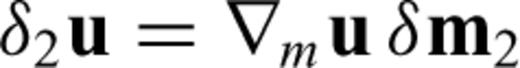
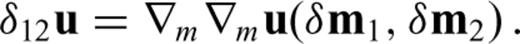
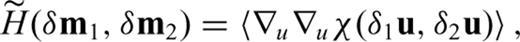
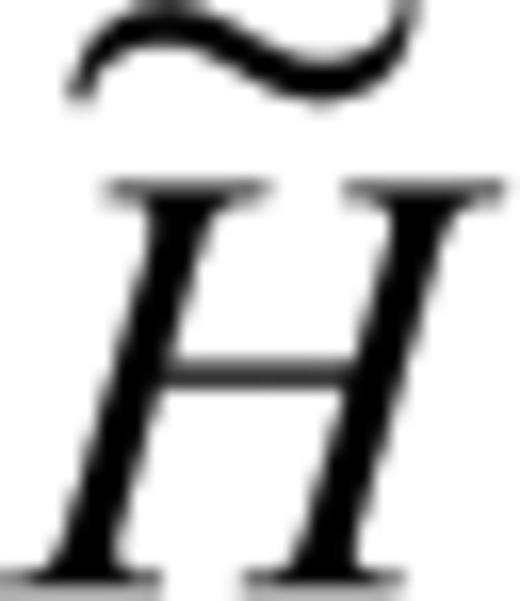 as a computationally less expensive substitute of the full Hessian H.
as a computationally less expensive substitute of the full Hessian H.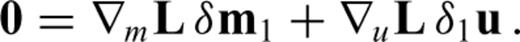
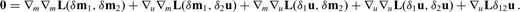
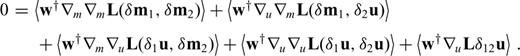
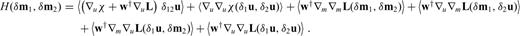
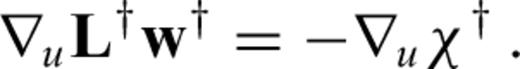

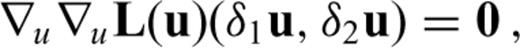
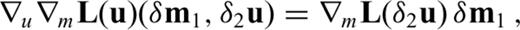

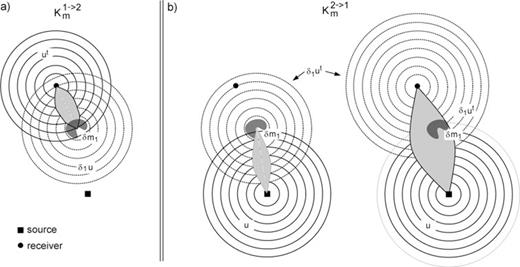
Schematic illustration of the Hessian kernels K1→2m and K2→1m that are related to first- and second-order scattering. (a) Construction of the Hessian kernel K1→2m through the interaction of the the adjoint field u† and the first-order scattered forward field δ1u that is generated when the forward field u impinges on the model perturbation δm1. The Hessian kernel K1→2m, shown as the shaded area, localizes the volume where a perturbation δm2 causes δ1u to generate a second-order scattered field that affects the measurement at the receiver (•). (b) The Hessian kernel K2→1m is the superposition of two influence zones that correspond to the two sources of the differentiated adjoint field δ1u†. The first source, −∇mL†(u†) δm1, excites a scattered field which then generates a secondary influence zone (left panel). A first-order scattered field that originates from within this secondary influence zone can then be scattered again from δm1 and finally affect the measurement at the receiver. The second source of δ1u† is −∇u∇uχ†(δ1u). The corresponding influence zone extends from source to receiver and accounts for the first-order scattering contribution represented by the approximate Hessian  (right panel).
(right panel).
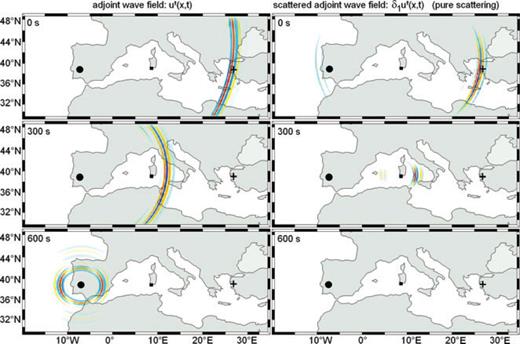
N–S component of the adjoint wavefield u† (left column) and the pure scattering contribution to δ1u† (disregarding the contribution to δ1u† from the change of the adjoint source) plotted at the surface. The adjoint wavefield emanates from the receiver (•) and propagates in reverse time towards the source (+). The adjoint source corresponds to the measurement of a cross-correlation time-shift of the N–S component Love wave at a dominant period of 25 s. The location of the vS perturbation is indicated by ▪. Most of the Love wave energy is scattered forward, that is, in the propagation direction of the adjoint field. The contribution to δ1u† that comes from the perturbation of the adjoint source (see eq. 34 and Section 3.3.2) is not shown to enhance the visibility of the pure scattered wave.
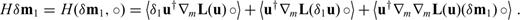
2.2.1 Hessian kernels
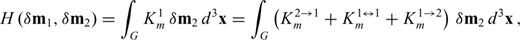
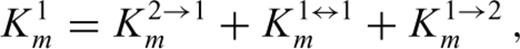
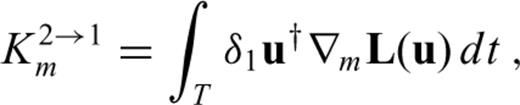
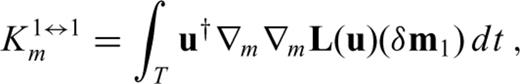
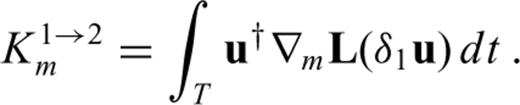
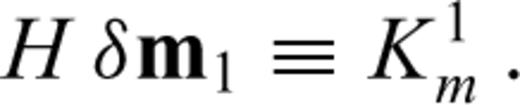

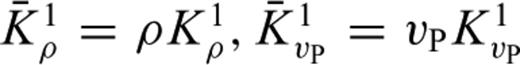 and
and 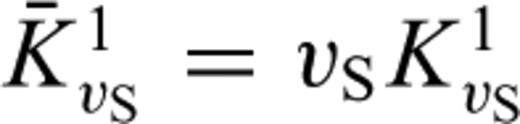 . Unlike Fréchet kernels, Hessian kernels depend on the model perturbation, δm1, either explicitly as in K1↔1m or implicity via δ1u and δ1u†. The comparison of eqs (53) and (55) with eq. (24) reveals that the Hessian kernels K2→1m and K1→2m are closely related to the Fréchet kernel Km. In fact, we find
. Unlike Fréchet kernels, Hessian kernels depend on the model perturbation, δm1, either explicitly as in K1↔1m or implicity via δ1u and δ1u†. The comparison of eqs (53) and (55) with eq. (24) reveals that the Hessian kernels K2→1m and K1→2m are closely related to the Fréchet kernel Km. In fact, we find 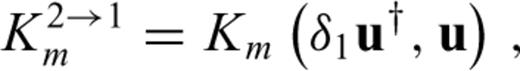
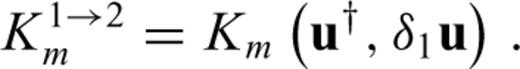
2.2.2 Translation to the discretized model space
 with respect to the discrete model parameters μ(α)i and μ(β)j, that is
with respect to the discrete model parameters μ(α)i and μ(β)j, that is 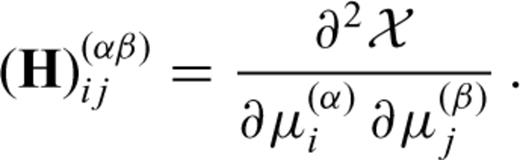
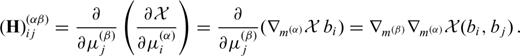
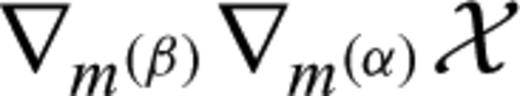 applied to the basis functions bi and bj. It follows that the Hessian kernel K1m for the model perturbation δm1=bi can be interpreted as a continuous representation of the ith row of the Hessian matrix H.
applied to the basis functions bi and bj. It follows that the Hessian kernel K1m for the model perturbation δm1=bi can be interpreted as a continuous representation of the ith row of the Hessian matrix H.The derivation of the adjoint equations in the continuous space followed by the discretization through projection is characteristic for time-domain full waveform inversion. This approach differs from frequency-domain full waveform inversion where the discrete adjoint method is applied to a semi-discrete version of the governing equations. That the continuous and discrete adjoint methods for both first and second derivatives are closely related will be shown in Appendix A.
3 Application to the Seismic Wave Equation
Our developments have so far been general in the sense that the equations do not depend on the particular type of wave equation used to model seismic wave propagation. In the following paragraphs, we will be more specific and apply the adjoint formalism to the 3-D viscoelastic wave equation.
3.1 Governing equations and their adjoints
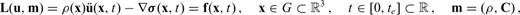
 to its mass density ρ, the stress tensor σ and an external force density f[see Dahlen & Tromp (1998), Kennett (2001) or Aki & Richards (2002) for detailed derivations of eq. 62]. The wave operator L is linear in u. The free surface boundary condition imposes that the normal components of the stress tensor σ vanish at the surface ∂G of the Earth, that is, σn|x∈∂G=0, where n is the unit normal on ∂G. Both the displacement field u and the velocity field
to its mass density ρ, the stress tensor σ and an external force density f[see Dahlen & Tromp (1998), Kennett (2001) or Aki & Richards (2002) for detailed derivations of eq. 62]. The wave operator L is linear in u. The free surface boundary condition imposes that the normal components of the stress tensor σ vanish at the surface ∂G of the Earth, that is, σn|x∈∂G=0, where n is the unit normal on ∂G. Both the displacement field u and the velocity field 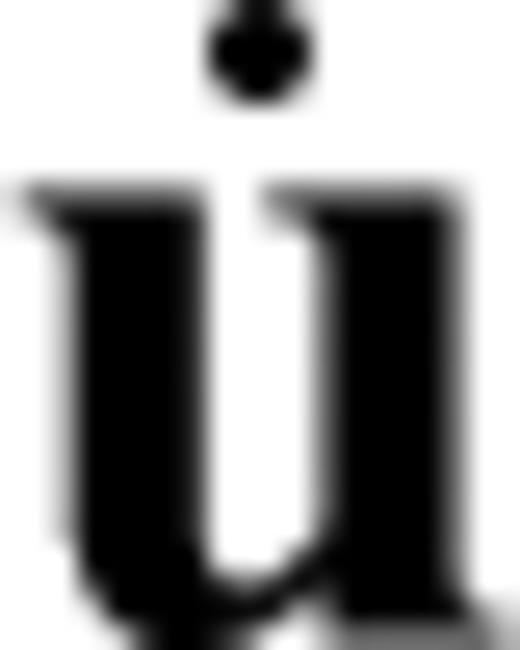 are required to satisfy the initial condition of being equal to zero prior to t= 0:
are required to satisfy the initial condition of being equal to zero prior to t= 0: 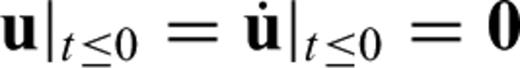 . To obtain a complete set of equations, the stress tensor σ must be related to the displacement field u. For this we assume that σ depends linearly on the history of the strain tensor
. To obtain a complete set of equations, the stress tensor σ must be related to the displacement field u. For this we assume that σ depends linearly on the history of the strain tensor 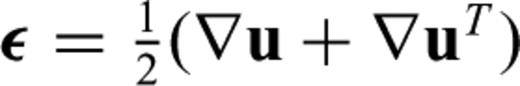
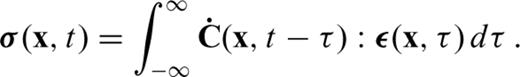
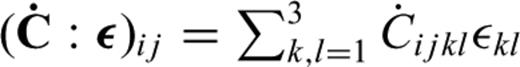 . Eq. (63) defines a linear viscoelastic rheology. The fourth-order tensor C is the elastic tensor. Since the current stress cannot depend on future strain, we require the elastic tensor to be causal: C(t)|t<0=0. The symmetry of ε, the conservation of angular momentum and the relation of C to the internal energy (Aki & Richards 2002) require that the components of C satisfy a set of symmetry relations, Cijkl=Cklij=Cjikl, that reduce the number of independent components to 21. The number of non-zero independent elastic tensor components, or elastic parameters, determines the anisotropic properties of the elastic medium (e.g. Babuška & Cara 1991).
. Eq. (63) defines a linear viscoelastic rheology. The fourth-order tensor C is the elastic tensor. Since the current stress cannot depend on future strain, we require the elastic tensor to be causal: C(t)|t<0=0. The symmetry of ε, the conservation of angular momentum and the relation of C to the internal energy (Aki & Richards 2002) require that the components of C satisfy a set of symmetry relations, Cijkl=Cklij=Cjikl, that reduce the number of independent components to 21. The number of non-zero independent elastic tensor components, or elastic parameters, determines the anisotropic properties of the elastic medium (e.g. Babuška & Cara 1991).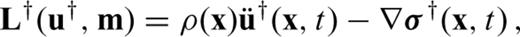
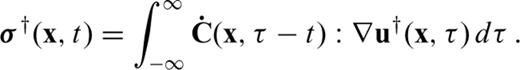
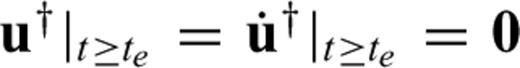 , where te is the time when the observation ends. In non-dissipative media the elastic wave operator L is self-adjoint, meaning that L=L†. The obvious numerical difficulty in solving the adjoint equation is the occurrence of the terminal conditions that require that the adjoint field be zero at time t=te. In practice, this condition can only be met by solving the adjoint equation backwards in time, that is by reversing the time axis from 0 →te to te→ 0. The terminal conditions then act as zero initial conditions, at least in the numerical simulation. Eq. (65) reveals that the adjoint stress tensor σ† at time t depends on future strain from t to te. This results in a growth of elastic energy when the wavefield propagates in the regular time direction from 0 to te. In reversed time, however, the elastic energy decays, so that numerical instabilities do not occur (Tarantola 1988). For efficient strategies to solve the adjoint equation and the time integral that appears in the Fréchet kernels, the reader is referred to Griewank & Walther (2000), Liu & Tromp (2006) or Fichtner et al. (2009).
, where te is the time when the observation ends. In non-dissipative media the elastic wave operator L is self-adjoint, meaning that L=L†. The obvious numerical difficulty in solving the adjoint equation is the occurrence of the terminal conditions that require that the adjoint field be zero at time t=te. In practice, this condition can only be met by solving the adjoint equation backwards in time, that is by reversing the time axis from 0 →te to te→ 0. The terminal conditions then act as zero initial conditions, at least in the numerical simulation. Eq. (65) reveals that the adjoint stress tensor σ† at time t depends on future strain from t to te. This results in a growth of elastic energy when the wavefield propagates in the regular time direction from 0 to te. In reversed time, however, the elastic energy decays, so that numerical instabilities do not occur (Tarantola 1988). For efficient strategies to solve the adjoint equation and the time integral that appears in the Fréchet kernels, the reader is referred to Griewank & Walther (2000), Liu & Tromp (2006) or Fichtner et al. (2009).3.2 First derivatives and Fréchet kernels
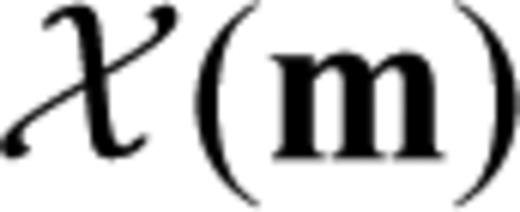 in the direction δm is given by eq. (22) that we repeat here for convenience
in the direction δm is given by eq. (22) that we repeat here for convenience 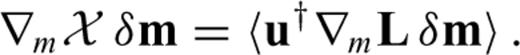
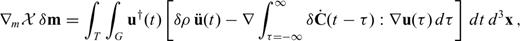
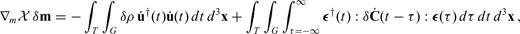
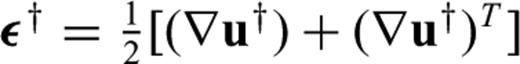 . The Fréchet kernels associated with (68) are
. The Fréchet kernels associated with (68) are 
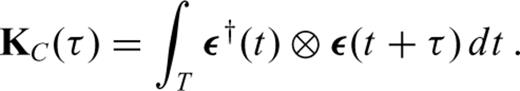
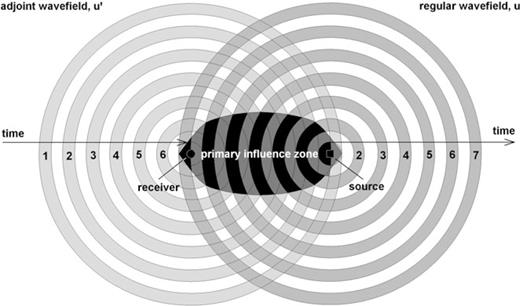
Schematic illustration of the primary influence zone where the regular wavefield u interacts with the adjoint wavefield u†. Numbers are used to mark the regular and adjoint wave fronts at successive points in time. As time goes on, the regular wavefield propagates away from the source while the adjoint wavefield collapses into the receiver. In numerical simulations the adjoint equations are solved backwards in time to satisfy the terminal conditions. On the reverse time axis, the adjoint field propagates away from the receiver, starting at the final observation time. The primary influence zone marks the region where a model perturbation δm generates a first-order scattered wavefield that affects the measurement at the receiver. Perturbations located outside the primary influence zone have no first-order effect on the measurement. The spatial extension of the primary influence zone is proportional to the length of the analysis time window considered in the seismograms.
For most seismic phases, the primary influence zone is a roughly cigar-shaped region connecting the source and the receiver. Its precise geometry depends on many factors including the frequency content, the length of the considered time window, the type of measurement and the reference Earth model, m. Specific examples for common seismic phases and measurements can be found, for instance, in Friederich (1999), Zhou et al. (2004), Yoshizawa & Kennett (2005), Zhao et al. (2005), Liu & Tromp (2006, 2008), Nissen-Meyer et al. (2007), Sieminski et al. (2007a,b) or Zhou (2009).
3.2.1 Perfectly elastic and isotropic medium
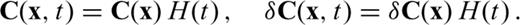
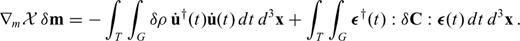

 is composed of three terms
is composed of three terms 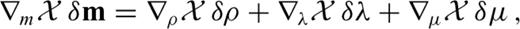
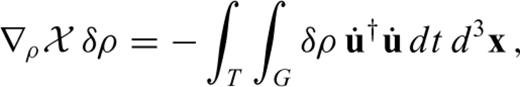
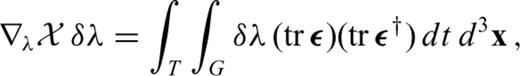
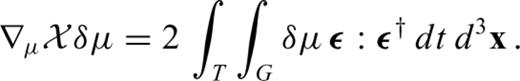
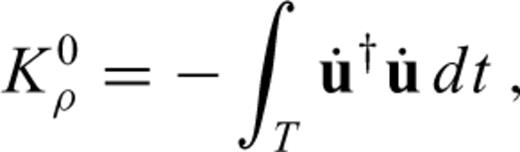

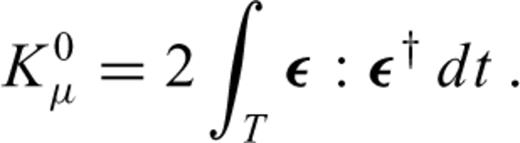
 and the P wave speed
and the P wave speed 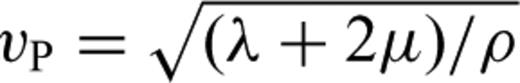

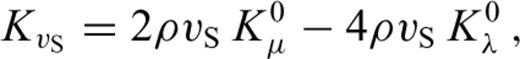
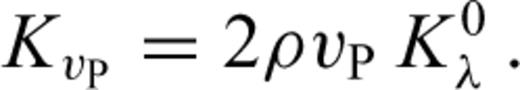
3.3 Second derivatives and Hessian kernels
As we have seen already in Section 2.2.1, the second derivative H(δm1, δm2) can be conveniently expressed in terms of three Hessian kernels, K2→1m, K1→2m and K1↔1m. It follows from eqs (58) and (59) that we can reuse the formulas for Fréchet kernels from Section 3.2 to compute the Hessian kernels K2→1m and K1→2m for specific Earth model parameters. The only difference is the involvement of the scattered adjoint field δ1u† and the scattered forward field δ1u in the kernel calculations.
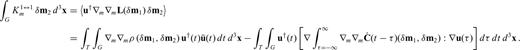
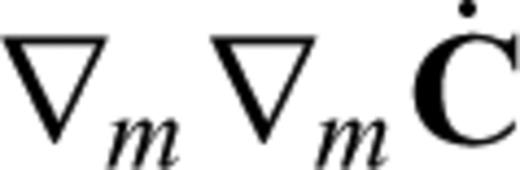 that allow ρ and C to depend on model parameters m other than density and the elastic coefficients themselves. Integrating eq. (78) by parts and writing the resulting expression in terms of the regular and adjoint strain fields, ε and ε†, gives
that allow ρ and C to depend on model parameters m other than density and the elastic coefficients themselves. Integrating eq. (78) by parts and writing the resulting expression in terms of the regular and adjoint strain fields, ε and ε†, gives 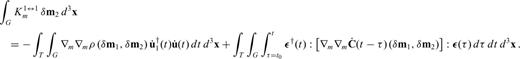
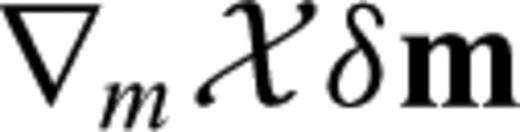 , of general validity. Special cases can be derived by further specifications of the rheology, that is, the elastic tensor components and their time dependence. Again, we consider the perfectly elastic and isotropic case as an example.
, of general validity. Special cases can be derived by further specifications of the rheology, that is, the elastic tensor components and their time dependence. Again, we consider the perfectly elastic and isotropic case as an example.3.3.1 Perfectly elastic and isotropic medium
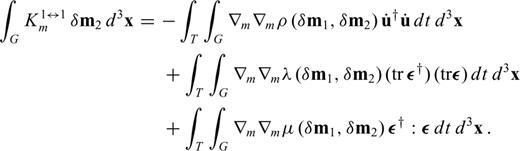
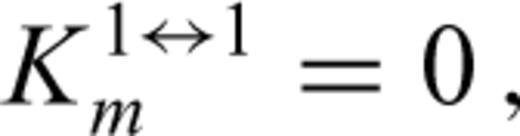
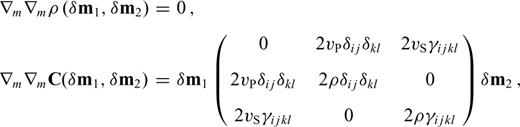
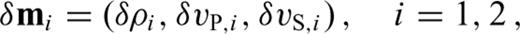
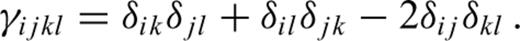
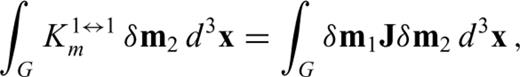
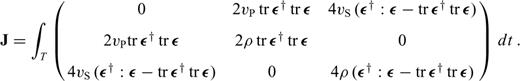
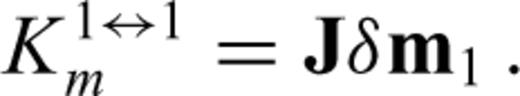
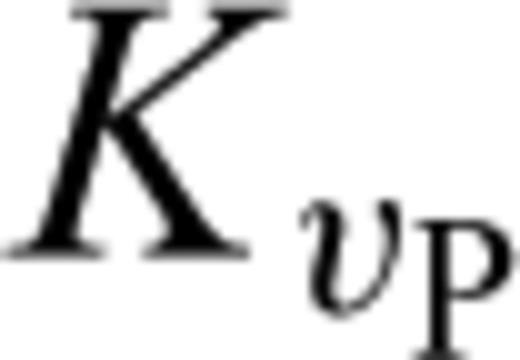 and
and 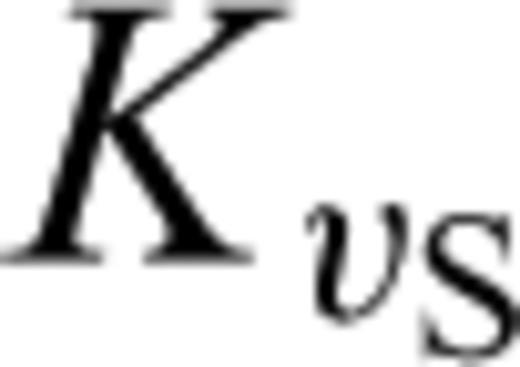 , from paragraph (3.2) reappear in the matrix J. In fact, we may write J in the following form
, from paragraph (3.2) reappear in the matrix J. In fact, we may write J in the following form 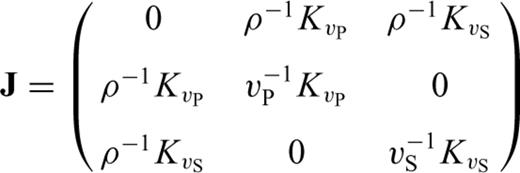
3.3.2 Physical interpretation of the Hessian kernels
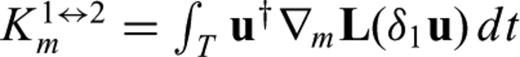 results from the interaction of the adjoint field u† with the first-order scattered field
results from the interaction of the adjoint field u† with the first-order scattered field 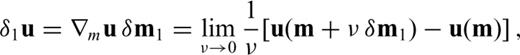
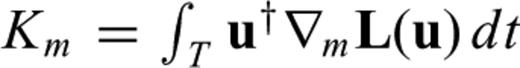 which involves u† and u instead of u† and δ1u. This similarity suggests that the Hessian kernel K1→2m localizes a secondary influence zone where a model perturbation δm2 can cause the first-order scattered field δ1u to generate a second-order scattered field that affects the observation at the receiver. Fig. 2(a) illustrates this process.
which involves u† and u instead of u† and δ1u. This similarity suggests that the Hessian kernel K1→2m localizes a secondary influence zone where a model perturbation δm2 can cause the first-order scattered field δ1u to generate a second-order scattered field that affects the observation at the receiver. Fig. 2(a) illustrates this process.The interpretation of the Hessian kernel  is slightly more involved because the field δ1u† has two sources, as we have seen already in eq. (46).
is slightly more involved because the field δ1u† has two sources, as we have seen already in eq. (46).
One of the two sources, −∇mL†(u†) δm1, excites a scattered adjoint field that is similar to the scattered forward field δ1u but propagates in the opposite direction. The interaction of the scattered adjoint field with the forward field u generates another secondary influence zone that connects the perturbation δm1 to the source. Another perturbation δm2 located within this secondary influence zone causes the forward field u to excite a first-order scattered field δ2u which then interacts with the perturbation δm1 such that the resulting second-order scattered field affects the measurement made at the receiver. This is shown schematically in the left part of Fig. 2(b).
The second source of δ1u† is −∇u∇uχ†(δ1u), which is the derivative of the regular adjoint source. It accounts for the changes of the adjoint source that are due to the perturbation of the forward wavefield u, and it generates an influence zone that extends from the source to the receiver (Fig. 2b, right-hand side). A comparison with eq. (34) reveals that −∇u∇uχ†(δ1u) can be interpreted as the source of the approximate Hessian  which accounts for the first-order scattering contribution to the full Hessian H.
which accounts for the first-order scattering contribution to the full Hessian H.
The complete Hessian kernel K2→1m is thus a superposition of (1) a secondary influence zone that corresponds to second-order scattering, and (2) a primary influence zone that corresponds to the first-order scattering represented by the approximate Hessian.
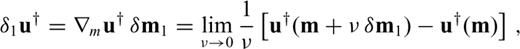
The Hessian kernel  does not appear to have a straightforward intuitive interpretation. It accounts for the non-linearity introduced by the parameterization. Whether
does not appear to have a straightforward intuitive interpretation. It accounts for the non-linearity introduced by the parameterization. Whether  is zero or not, depends strongly on the choice of free parameters, as we have seen already in Section 3.3.1.
is zero or not, depends strongly on the choice of free parameters, as we have seen already in Section 3.3.1.
4 Hessian Kernel Gallery
To bring the previous developments to life, we continue with specific examples of Hessian kernels for a small selection of data functionals and model perturbations. Given the infinite number of seismic data functionals and Earth model parameterizations, our Hessian kernel gallery can naturally not be exhaustive. We nevertheless hope that it provides both physical intuition and a useful illustration of the methodology outlined in Sections 2 and 3.
4.1 Surface wave interaction with point-localized and extended scatterers
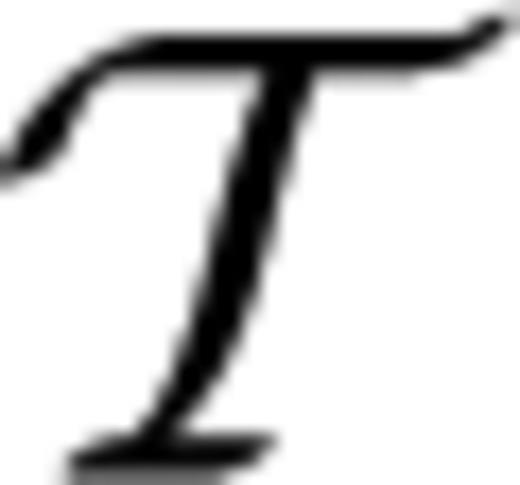 , defined as the global maximum of the correlation function
, defined as the global maximum of the correlation function 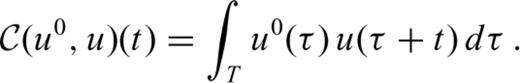
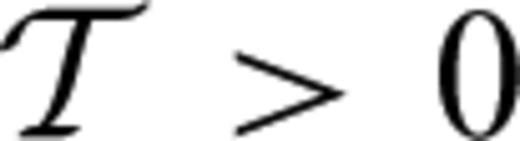 when the synthetic waveform arrives later than the observed waveform, and
when the synthetic waveform arrives later than the observed waveform, and  when the synthetic waveform arrives earlier than the observed waveform. Under the assumption that u0(t) and u(t) are merely shifted in time without being otherwise distorted with respect to each other, the adjoint source corresponding to the data functional
when the synthetic waveform arrives earlier than the observed waveform. Under the assumption that u0(t) and u(t) are merely shifted in time without being otherwise distorted with respect to each other, the adjoint source corresponding to the data functional 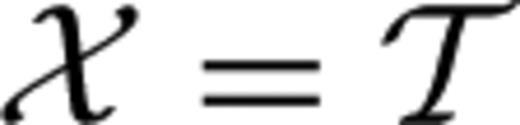 is given by (Luo & Schuster 1991)
is given by (Luo & Schuster 1991) 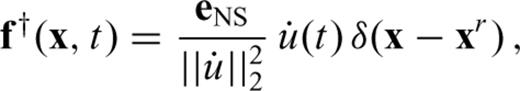
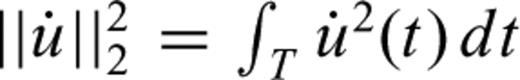 ensures that the resulting Fréchet kernels do not depend on amplitude. Treating observed and synthetic waveforms as time-shifted versions of each other is a simplified but widely used approach because it leads to kernels that are quasi-independent of the actual data. We can thus compute kernels without explicitly measuring a time shift.
ensures that the resulting Fréchet kernels do not depend on amplitude. Treating observed and synthetic waveforms as time-shifted versions of each other is a simplified but widely used approach because it leads to kernels that are quasi-independent of the actual data. We can thus compute kernels without explicitly measuring a time shift.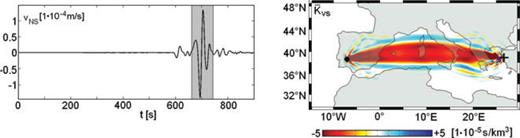
Left-hand side: N–S component synthetic seismogram computed using a spectral-element method (Fichtner & Igel 2008). The time window around the Love wave used to compute Fréchet and Hessian kernels is shaded in grey. The dominant period is 25 s. Right-hand side: Fréchet kernel  for a cross-correlation time-shift measurement on the N–S component Love wave shown to the left-hand side. The source and receiver positions are marked by + and •, respectively.
for a cross-correlation time-shift measurement on the N–S component Love wave shown to the left-hand side. The source and receiver positions are marked by + and •, respectively.
The computation of the Fréchet kernels follows a well-known recipe. First, we solve the forward problem (eqs 62 and 63) to obtain the forward field u that is stored at sufficiently many time steps. Snapshots of u, computed with the help of a spectral-element discretization of the seismic wave equation (Fichtner & Igel 2008), are shown in the left panel of Fig. 4. We then select a time window around the waveform of interest (Fig. 3, left-hand side) and compute the adjoint source given in eq. (92). The adjoint source f† is the right-hand side of the adjoint eq. (21), the solution of which is the adjoint field u†, shown in the left panel of Fig. 5. While the adjoint field propagates in reverse time, the previously stored forward field is loaded and used to compute the Fréchet kernels according to eqs (76) and (77).
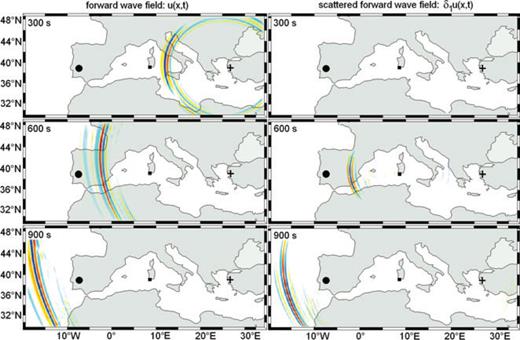
N–S component of the forward wavefield u (left column) and the scattered forward wavefield δ1u plotted at the surface. The source is marked by + and the receiver by • (epicentral distance =25.2°). The location of the vS perturbation is indicated by ▪. The images are dominated by surface waves. Small-amplitude body waves are hardly visible. The vS perturbation acts as a point scatterer (Rayleigh scattering), and most of the Love wave energy is scattered in the forward direction.
The S velocity kernel  corresponding to the cross-correlation time shift measurement on the N–S component Love wave is shown in the right panel of Fig. 3. The kernel is dominated by negative sensitivities within the first Fresnel zone, where a positive vS perturbation leads to earlier-arriving waveforms and to a decrease in the cross-correlation time shift
corresponding to the cross-correlation time shift measurement on the N–S component Love wave is shown in the right panel of Fig. 3. The kernel is dominated by negative sensitivities within the first Fresnel zone, where a positive vS perturbation leads to earlier-arriving waveforms and to a decrease in the cross-correlation time shift  . The width of the first Fresnel zone is proportional to
. The width of the first Fresnel zone is proportional to  , where Td and ℓ denote the dominant period and the length of the ray path between source and receiver, respectively.
, where Td and ℓ denote the dominant period and the length of the ray path between source and receiver, respectively.
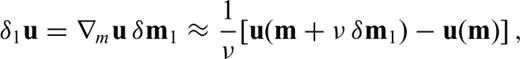
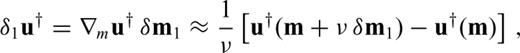
The resulting Hessian kernels  and
and  are shown separately in the top row of Fig. 6. The kernel
are shown separately in the top row of Fig. 6. The kernel  is a superposition of two contributions, labelled F and S. These correspond to the primary influence zone represented by the approximate Hessian (F) and to the secondary influence zone where second-order scattering affects the measurement (See Fig. 2 for a schematic representation). The kernel
is a superposition of two contributions, labelled F and S. These correspond to the primary influence zone represented by the approximate Hessian (F) and to the secondary influence zone where second-order scattering affects the measurement (See Fig. 2 for a schematic representation). The kernel  only extends from the receiver to δvS1. Second-order scattering from δvS1 to an S velocity perturbation within
only extends from the receiver to δvS1. Second-order scattering from δvS1 to an S velocity perturbation within  has an effect on the measurement. The kernel
has an effect on the measurement. The kernel  is restricted to the volume occupied by δvS1. The complete Hessian kernel
is restricted to the volume occupied by δvS1. The complete Hessian kernel  is shown in the bottom row of Fig. 6.
is shown in the bottom row of Fig. 6.
Hessian kernels plotted at the surface of the Earth. The position δvS1 is indicated by ○. Top row: The individual Hessian kernels  and
and  (from left-hand side to right-hand side). The kernel
(from left-hand side to right-hand side). The kernel  has two contributions, labelled F and S. Contribution F represents the primary influence zone that corresponds to the approximate Hessian. Contribution S, encircled by a dotted curve, is a secondary influence zone where second-order scattering affects the measurement. (In Section 5.1, we show how the approximate Hessian can be computed separately.) Bottom row: Composite Hessian kernel
has two contributions, labelled F and S. Contribution F represents the primary influence zone that corresponds to the approximate Hessian. Contribution S, encircled by a dotted curve, is a secondary influence zone where second-order scattering affects the measurement. (In Section 5.1, we show how the approximate Hessian can be computed separately.) Bottom row: Composite Hessian kernel  . The the contribution from second-order scattering is again encircled by a dotted curve and marked with S.
. The the contribution from second-order scattering is again encircled by a dotted curve and marked with S.
An interesting observation is that the sign of  within the secondary influence zones is opposite (positive) to the sign within the primary influence zone (negative) that corresponds to the approximate Hessian. The widths of the secondary influence zones is proportional to
within the secondary influence zones is opposite (positive) to the sign within the primary influence zone (negative) that corresponds to the approximate Hessian. The widths of the secondary influence zones is proportional to  and
and  , where the ℓs→1 and ℓ1→r signify the length of the ray paths from the source to δvS1 and from δvS1 to the receiver, respectively. This explains why the secondary influence zones are slim compared to the primary influence zone (labelled F in Fig. 6) where the width is proportional to
, where the ℓs→1 and ℓ1→r signify the length of the ray paths from the source to δvS1 and from δvS1 to the receiver, respectively. This explains why the secondary influence zones are slim compared to the primary influence zone (labelled F in Fig. 6) where the width is proportional to  .
.
The Hesian kernel K1m shown in Fig. 6 can be interpreted as the continuous representation of the row of the Hessian matrix H that corresponds to the basis function coincident with δvS1. The fully discrete row is obtained by projecting K1m onto the basis functions, according to eq. (61).
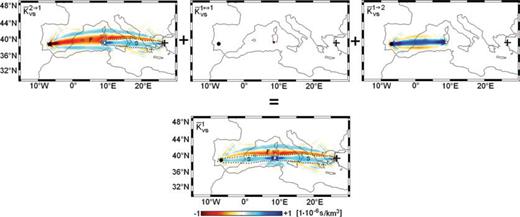
The amplitude of the Hessian kernel  for #x03B4;vS1 located near the centre of the first Fresnel zone is about two orders of magnitude smaller than the amplitude of the Fréchet kernel. This suggests that the single-scattering approximation is well justified in this particular scenario. Locating δvS1 further away from the first Fresnel zone rapidly decreases the amplitude of the corresponding Hessian kernels, as can be seen in Fig. 7. The small second derivatives result from the long propagation distance of the scattered waves that arrive too late to have a significant effect inside the Love wave time window (Fig. 3, left-hand side).
for #x03B4;vS1 located near the centre of the first Fresnel zone is about two orders of magnitude smaller than the amplitude of the Fréchet kernel. This suggests that the single-scattering approximation is well justified in this particular scenario. Locating δvS1 further away from the first Fresnel zone rapidly decreases the amplitude of the corresponding Hessian kernels, as can be seen in Fig. 7. The small second derivatives result from the long propagation distance of the scattered waves that arrive too late to have a significant effect inside the Love wave time window (Fig. 3, left-hand side).
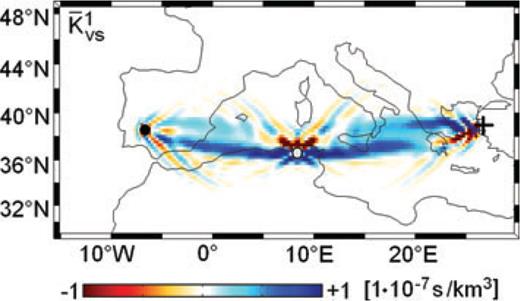
Hessian kernel  corresponding to an S velocity perturbation δvS1 that is located in the outer rim of the Fréchet kernel shown in Fig. 3. The position δvS1 is indicated by ○. The amplitude of
corresponding to an S velocity perturbation δvS1 that is located in the outer rim of the Fréchet kernel shown in Fig. 3. The position δvS1 is indicated by ○. The amplitude of  is one order of magnitude smaller than in Fig. 6 where δvS1 was located near the centre of the first Fresnel zone of the Fréchet kernel.
is one order of magnitude smaller than in Fig. 6 where δvS1 was located near the centre of the first Fresnel zone of the Fréchet kernel.
The recipe for the computation of Hessian kernels is equally applicable when the model perturbation (or basis function) does not effectively act as a point scatterer, as in the previous example. For a spatially extended model perturbation δvS1, such as the one shown in Fig. 8, we are in the Mie scattering regime where the characteristic size of the scatterer is much larger than the dominant period. To calculate the Hessian kernel corresponding to δvS1, we again compute the scattered fields δ1u and δ1u† using the finite-difference approximations from eqs (93) and (94), respectively. The finite-difference step length ν must be sufficiently small to ensure the convergence of the approximation. For the specific perturbation in Fig. 8, we found ν= 1/100 to be appropriate.
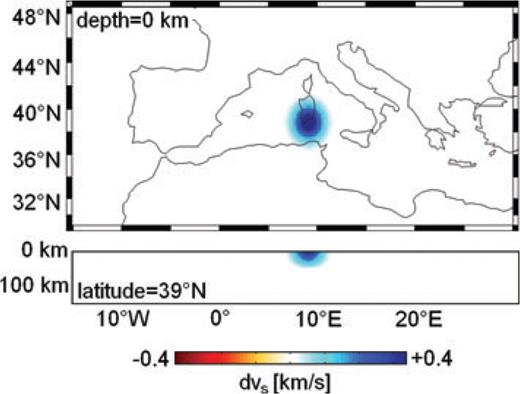
Horizontal (top) and vertical (bottom) slice through the extended vS perturbation used to compute the Hessian kernel  shown in Fig. 9. The maximum perturbation of 0.4 km s−1 near the surface is equal to 10 per cent of the background S velocity.
shown in Fig. 9. The maximum perturbation of 0.4 km s−1 near the surface is equal to 10 per cent of the background S velocity.
Slices through the resulting Hessian kernel  are shown in Fig. 9. As expected for Love waves, the Hessian kernel is largest near the surface and decays rapidly with increasing depth. An interesting observation is the strong asymmetry of the Hessian kernel, as compared to the one computed for an effective point scatterer (Fig. 6). The origin of the asymmetry is difficult to identify on the basis of purely numerical simulations, though we hypothesize that it is related to the non-isotropic radiation pattern of the regular source.
are shown in Fig. 9. As expected for Love waves, the Hessian kernel is largest near the surface and decays rapidly with increasing depth. An interesting observation is the strong asymmetry of the Hessian kernel, as compared to the one computed for an effective point scatterer (Fig. 6). The origin of the asymmetry is difficult to identify on the basis of purely numerical simulations, though we hypothesize that it is related to the non-isotropic radiation pattern of the regular source.
Horizontal (left-hand side) and vertical (right-hand side) slices through the Hessian kernel  that corresponds to the vS perturbation shown in Fig. 8.
that corresponds to the vS perturbation shown in Fig. 8.
4.2 P body waves and the second-order effect of density
The application of the previously described methodology to other types of seismic waves is straightforward and merely requires the choice of different time windows. In the following example, we consider the measurement of a cross-correlation time shift on the vertical component of an 8 s P body wave in the same source–receiver geometry as above. We furthermore extend the analysis to the multiparameter case. The Fréchet kernels for vP, vS and ρ are displayed in Fig. 10(a). As expected, the P wave traveltime is mostly affected by perturbations in vP, whereas variations in vS and ρ have hardly any first-order effect.
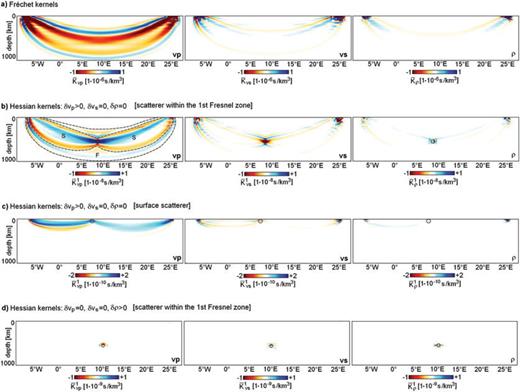
Fréchet and Hessian kernel gallery for the cross-correlation time-shift on the vertical component of an 8 s P wave. The source–receiver geometry is the same as in Fig. 3. (a) Fréchet kernels for vP, vS and ρ (from left-hand side to right-hand side). (b) Hessian kernels  and
and  (from left-hand side to right-hand side) for a vP perturbation δvP1. The position of δvP1 is indicated by ○. In the
(from left-hand side to right-hand side) for a vP perturbation δvP1. The position of δvP1 is indicated by ○. In the  kernel the contributions from the second-order scattering and the approximate Hessian are outlined by dash-dotted curves and labelled S and F, respectively. The amplitudes of
kernel the contributions from the second-order scattering and the approximate Hessian are outlined by dash-dotted curves and labelled S and F, respectively. The amplitudes of  and
and  are small compared to the amplitude of
are small compared to the amplitude of  . (c) The same as in (b) but for a vP perturbation located directly beneath the surface (○). The kernels are comparatively small but different from zero, indicating that second-order scattering from far outside the Fréchet kernel may affect the measurement because the P wave window is sufficiently long (∼15 s). (d) Hessian kernels
. (c) The same as in (b) but for a vP perturbation located directly beneath the surface (○). The kernels are comparatively small but different from zero, indicating that second-order scattering from far outside the Fréchet kernel may affect the measurement because the P wave window is sufficiently long (∼15 s). (d) Hessian kernels  and
and  (from left-hand side to right-hand side) for a density perturbation δρ1. The position of δρ1 is indicated by ○. The kernels are characterized by rapid variations that are localized around the density perturbation. Compared to the Hessian kernels for a vP perturbation in (b), the density Hessian kernels have small amplitudes, indicating that ρ has hardly any second-order effect on the finite-frequency traveltime of P waves.
(from left-hand side to right-hand side) for a density perturbation δρ1. The position of δρ1 is indicated by ○. The kernels are characterized by rapid variations that are localized around the density perturbation. Compared to the Hessian kernels for a vP perturbation in (b), the density Hessian kernels have small amplitudes, indicating that ρ has hardly any second-order effect on the finite-frequency traveltime of P waves.
To study second-order effects on the finite-frequency traveltime of the P wave, we again place a 50 × 50 × 50 km3P velocity perturbation, δvP1, in the centre of the first-order first Fresnel zone of the vP Fréchet kernel  . The dimension of δvP1 is small compared to the wavelength (∼100 km), meaning that we are close to the Rayleigh scattering regime. The corresponding Hessian kernels, shown in Fig. 10b, contain two symmetric lobes that meet at the location of the scatterer. These lobes correspond to the second-order scattering contribution to the Hessian, and are labelled S in the
. The dimension of δvP1 is small compared to the wavelength (∼100 km), meaning that we are close to the Rayleigh scattering regime. The corresponding Hessian kernels, shown in Fig. 10b, contain two symmetric lobes that meet at the location of the scatterer. These lobes correspond to the second-order scattering contribution to the Hessian, and are labelled S in the  kernel. The contribution from the approximate Hessian, labelled F, is clearly visible only in
kernel. The contribution from the approximate Hessian, labelled F, is clearly visible only in  . The Hessian kernels
. The Hessian kernels  and K1ρ are small compared to
and K1ρ are small compared to  . This indicates that second-order scattering from perturbations of different nature, that is, one perturbation in vP and another one in ρ or vS, is rather inefficient.
. This indicates that second-order scattering from perturbations of different nature, that is, one perturbation in vP and another one in ρ or vS, is rather inefficient.
For a scatterer located outside the first Fresnel zone, we observe a similar decrease of the Hessian kernels as for surface waves (see Fig. 7). In the specific case of a vP perturbation near the surface, the corresponding Hessian kernels are around two orders of magnitude smaller than the kernels for δvP1 located in the centre of the Fréchet kernel (Fig. 10c). The fact that scattering from near the surface affects the traveltime measurement at all, can be explained with the finite-frequency content of the P waveform. Doubly-scattered energy from δvP1 and another vP perturbation located within the support of  can still arrive in the measurement window of the P wave that is around 15 s long.
can still arrive in the measurement window of the P wave that is around 15 s long.
The kernels shown in Figs 10(a) and (b) reveal that density perturbations have hardly any effect of the finite-frequency traveltime of P waves through first-order scattering or second-order scattering that also involves a P velocity perturbation. To see whether second-order scattering from two density perturbations can influence the P wave traveltime, we repeat the example from Fig. 10(b), but we replace δvP1 by a density scatterer δρ1. The resulting Hessian kernels, shown in Fig. 10(d), are practically zero, thus indicating that variations in density do not have any significant second-order effect on P wave traveltimes at all.
This observation is closely related to the characteristics of Rayleigh scattering from density perturbations (e.g. Wu & Aki 1985; Tarantola 1986). For δρ1≠ 0 and δvP1=δvS1= 0 most of the energy is scattered in the direction opposite to the propagation direction of the incident wave (Fig. 11). Therefore, the scattered forward field δ1u does not interact with the adjoint field u†, and the partial Hessian kernel K1→2m is close to zero. Similarly, the scattered adjoint field δ1u† propagates in a direction opposite to the adjoint field u†, so that the interaction of δ1u† with the forward field u is not possible. It follows that K2→1m is approximately zero as well. Finally, we have K1↔1m= 0 for pure density perturbations (eq. 88), and the complete Hessian kernel K1m=K2→1m+K1↔1m+K1→2m nearly vanishes.
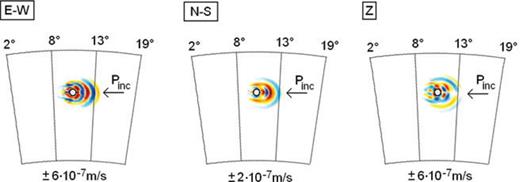
Vertical slices through the E–W (left-hand side), N–S (centre) and Z components of the scattered velocity field  . The snapshots are taken 30 s after the P wave reached the density perturbation δρ1, marked by ○. The direction of the incident P wave is indicated by left-pointing arrows. Clearly visible is the backward scattering associated with δρ1 > 0 and δvS1=δvP1 = 0. Hardly any energy is scattered in the propagation direction of the regular wavefield u.
. The snapshots are taken 30 s after the P wave reached the density perturbation δρ1, marked by ○. The direction of the incident P wave is indicated by left-pointing arrows. Clearly visible is the backward scattering associated with δρ1 > 0 and δvS1=δvP1 = 0. Hardly any energy is scattered in the propagation direction of the regular wavefield u.
5 Full Hessian Versus Approximate Hessian
The approximate Hessian  is commonly used as a computationally less expensive substitute of the full Hessian H, because its computation merely requires first derivatives. To explore the potential differences between
is commonly used as a computationally less expensive substitute of the full Hessian H, because its computation merely requires first derivatives. To explore the potential differences between  and H, we consider—as an example—a realistic 3-D full waveform tomography. As a preparatory step, however, we expand on the computation of approximate Hessian kernels, using the methodology developed in Sections 2 and 3.
and H, we consider—as an example—a realistic 3-D full waveform tomography. As a preparatory step, however, we expand on the computation of approximate Hessian kernels, using the methodology developed in Sections 2 and 3.
5.1 Computing approximate Hessian kernels

 as the solution of the adjoint equation
as the solution of the adjoint equation 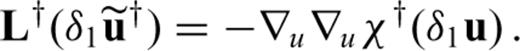
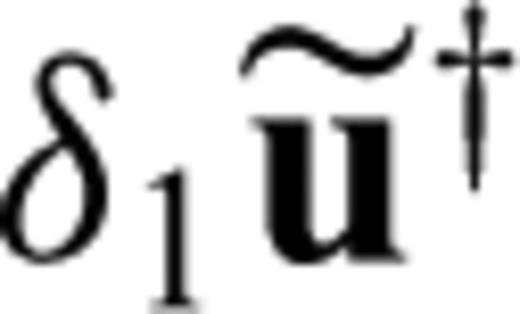 is the contribution to the scattered adjoint field δ1u† that is excited only by the change of the adjoint source. Inserting (96) into (95) yields
is the contribution to the scattered adjoint field δ1u† that is excited only by the change of the adjoint source. Inserting (96) into (95) yields 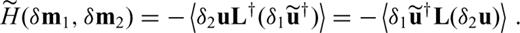
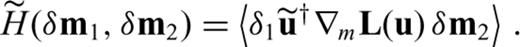
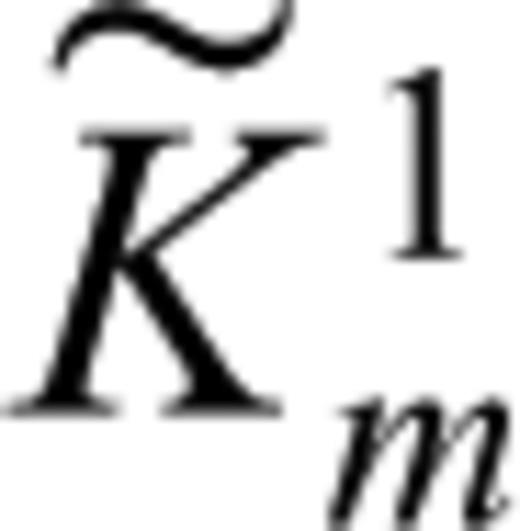 is given by
is given by 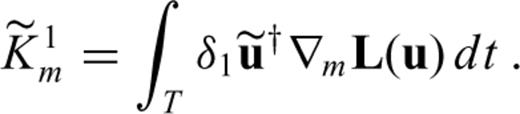
5.2 A realistic example (Influences on our perception of the Iceland plume)
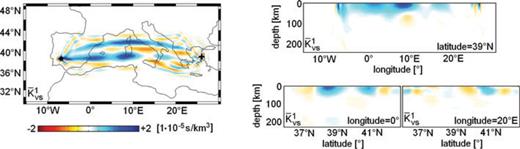
We consider a long-period full waveform tomography for the European upper mantle that is summarized in Fig. 12. The data used in the inversion are three-component seismograms with a dominant period of 100 s, that provide a good coverage of central and northern Europe (Fig. 12, left-hand side). The inversion was based on the measurement of time- and frequency-dependent phase differences (Fichtner et al. 2008). As initial model we used the 3-D mantle structure from S20RTS (Ritsema et al. 1999) combined with the crustal model by Meier et al. (2007a,b). After three conjugate-gradient iterations we obtained the tomographic images that are shown in the centre and right panels of Fig. 12, in the form of perturbations relative to the 1-D model AK135 (Kennett et al. 1995). The achieved waveform fit and the reduction of the initial misfit by nearly 70 per cent indicate that the tomographic model is at least close to optimal.
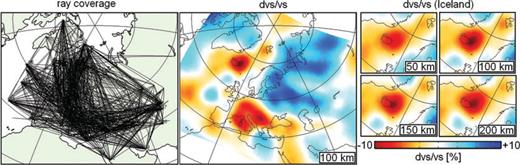
Full waveform tomography for the European upper mantle. Left-hand side: Ray coverage. Centre: Relative S wave speed perturbations at 100 km depth. Right-hand side: Zoom on the Iceland hotspot at various depth levels. The reference model is AK135 (Kennett et al. 1995).
One of the most prominent features in the images is the Iceland plume (Fig. 12, right-hand side) that we choose as our model perturbation δvS1. Horizontal slices through the isolated Iceland plume are shown in the left column of Fig. 13. Then, following the methodology from Sections 2, 3 and 5.1, we compute the corresponding approximate and full Hessian kernels, displayed in the centre and right columns of Fig. 13, respectively.
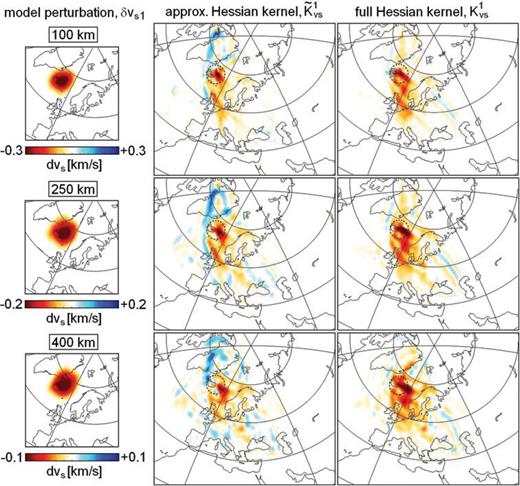
Comparison of approximate and full Hessian kernels. Left-hand side column: Slices through the Iceland plume, which serves as model perturbation δm1= (0, 0, δvS1). Central column: Slices through the approximate Hessian kernel  . The dashed circle indicates the approximate location of the model perturbation. Right-hand side column: Slices through the full Hessian kernel
. The dashed circle indicates the approximate location of the model perturbation. Right-hand side column: Slices through the full Hessian kernel  . The colour scales for the approximate and full Hessian kernels are the same at each depth level.
. The colour scales for the approximate and full Hessian kernels are the same at each depth level.
Each of the kernels can be interpreted as the continuous representation of that row in the (approximate or full) Hessian that is associated with the Iceland plume. The volume occupied by the plume itself, and indicated by dashed circles in Fig. 13, represents the diagonal element. Off-diagonal elements correspond to volumes outside the plume.
Using this terminology, we can say that the diagonal elements of the approximate and full Hessian kernels are nearly identical at depths of around 100 km. This similarity, however, decreases steadily with increasing depth. Large differences in the off-diagonal elements, including opposite signs, are most pronounced beneath Greenland and Central Europe. This indicates that the second-order scattering contribution to the Hessian may not be negligible, even in the vicinity of the optimal model.
The Hessian kernels from Fig. 13 already provide semi-quantitative insight into where and how our image of the Iceland plume is affected by vS structure elsewhere in the upper mantle. While structure beneath southern and eastern Europe has no effect on our perception of the plume ( ), its average vS is dependent on vS beneath northern Europe and parts of Greenland (
), its average vS is dependent on vS beneath northern Europe and parts of Greenland ( ). Based on the quadratic approximation of the misfit functional (eq. 3) we infer that increasing vS in regions where
). Based on the quadratic approximation of the misfit functional (eq. 3) we infer that increasing vS in regions where  can partly be compensated by decreasing vS within the plume volume, and vice versa. Note that the approximate Hessian kernel
can partly be compensated by decreasing vS within the plume volume, and vice versa. Note that the approximate Hessian kernel  would lead us to the erroneous conclusion that a decrease (increase) of vS beneath Greenland combined with a decrease (increase) of the average plume vS would have little effect on the misfit χ.
would lead us to the erroneous conclusion that a decrease (increase) of vS beneath Greenland combined with a decrease (increase) of the average plume vS would have little effect on the misfit χ.
6 Discussion
In the previous sections, we presented an extension of the well-known adjoint method that allows us to compute the second derivatives of seismic data functionals with respect to Earth model parameters. The Hessian applied to a model perturbation, Hδm, can be represented by Hessian kernels that are similar to Fréchet kernels but also involve scattered forward and adjoint fields. This work is intended to serve as a technical prelude for the implementation of Newton's method and the development of quantitative resolution analyses in full waveform inversion. In the following paragraphs, we discuss issues related to computational aspects and to the interpretation of the Hessian kernels.
6.1 Computational requirements and the practical usefulness of Hessian kernels
The computing time required for the calculation of Hessian kernels is twice as long as for Fréchet kernels, because four instead of two wavefield simulations are needed. First, the regular wavefield u has to be modelled and stored at sufficiently many intermediate time steps. The Fréchet kernel Km and the partial Hessian kernel K1↔1m can be computed during the adjoint simulation from the interaction of u and the adjoint field u†. Two additional simulations are then needed for the perturbed regular and adjoint fields, u(m+νδm1) and u†(m+νδm1), that enter the finite-difference approximations for δ1u and δ1u†, respectively (eqs 93 and 94).
The comparatively high numerical costs involved in the computation of Hδm1≡K1m naturally constrain the practical usefulness of the Hessian kernels. The competitiveness of Newton's method in particular will depend critically on the development of efficient algorithms that yield good approximate solutions of Newton's eq. (2) with as few evaluations of Hδm as possible. At least for 1-D full waveform inversion, a full Newton method has already proven efficient (Santosa & Symes 1988; Pratt et al. 1998).
When second derivatives are used for resolution analysis, then we are in a more favourable situation. This is because the Hessian need not be inverted to obtain a quadratic approximation of the misfit functional χ (eq. 3). The second-order expansion of χ about the optimal model already provides invaluable information about resolution and trade-offs. By choosing model perturbations δm to coincide with well-defined geological objects, the Hessian kernel formalism can be used to quantify their effect on the misfit as well as mutual dependencies (Fichtner 2010). Only for a covariance analysis sensu stricto, the inverse Hessian needs to be approximated iteratively.
6.2 Inversion for density?
Our seismically inferred knowledge on density structure is comparatively poor and almost exclusively based on the gravitational effect on long-period free oscillations (Kennett 1998; Ishii & Tromp 2001, 2004; Resovsky & Trampert 2003; Trampert et al. 2004). This is because the sensitivity of traveltime observations to density is practically zero (see for instance Fig. 10a). However, 2-D and 3-D synthetic full waveform inversions suggest that variations in ρ may also be constrained by short-period data where gravity is negligible (Köhn et al. (2010); Y. Capdeville, private communication, 2008). Our hope was therefore that density structure may have a second-order effect on traveltimes. Unfortunately, this does not seem to be the case (Figs 10b and d).
While one may argue that traveltime is not an adequate measurement to detect density variations, the scattering characteristics shown in Fig. 11 suggest that the invisibility of ρ is a more general phenomenon, at least in a transmission tomography setting. Modifications of the measurement will affect the details of the adjoint field. Yet, the scattering direction of the regular and adjoint fields from a pure density perturbation with δvS=δvP= 0 will remain to be opposite to the respective incidence directions. It follows that the second derivatives of any transmission tomography data functional with respect to density are small, provided that the Earth model is parameterized in terms of vP, vS and ρ. Changing the parameterization for instance to m= (κ, μ, ρ), will cause the density derivatives to become alive, though at the expense of substantial trade-offs between the parameters.
6.3 Full Hessian versus approximate Hessian
As we have seen in Section 5, the approximate Hessian  can differ substantially from the full Hessian H, even when the model is close to optimal. The differences include sign changes and are most pronounced in the off-diagonal elements.
can differ substantially from the full Hessian H, even when the model is close to optimal. The differences include sign changes and are most pronounced in the off-diagonal elements.
The explanation for the discrepancy between  and H is contained in eq. (6), and it has two components. (1) The inherent non-linearity of the phase difference measurements and (2) The remaining waveform misfit that is non-zero despite the near-optimality of the model. Both factors appear to be very general because realistic misfits are never zero, and because any measurement has a non-linear contribution. Therefore, we hypothesise that the approximate and full Hessians will be different in other applications as well. This conjecture is supported by the results of Santosa & Symes (1988), who conducted 1-D synthetic waveform inversions.
and H is contained in eq. (6), and it has two components. (1) The inherent non-linearity of the phase difference measurements and (2) The remaining waveform misfit that is non-zero despite the near-optimality of the model. Both factors appear to be very general because realistic misfits are never zero, and because any measurement has a non-linear contribution. Therefore, we hypothesise that the approximate and full Hessians will be different in other applications as well. This conjecture is supported by the results of Santosa & Symes (1988), who conducted 1-D synthetic waveform inversions.
The extent to which the difference between  and H is practically relevant, depends strongly on the particular application. The approximate Hessian is likely to be more efficient when only the diagonal elements are used to pre-condition a descent direction within an iterative optimization scheme. However, in Newton-like methods that include the off-diagonal elements, the full Hessian may effectively lead to faster convergence. To the best of our knowledge, there is so far no experience concerning this issue. A quantitative comparison between conjugate-gradient (e.g. Mora 1987, 1988; Tape et al. 2007; Fichtner et al. 2009), quasi-Newton (e.g. Liu & Nocedal 1989; Pratt et al. 1998; Epanomeritakis et al. 2008; Brossier et al. 2009) and full Newton methods for realistic large-scale problems remains to be done.
and H is practically relevant, depends strongly on the particular application. The approximate Hessian is likely to be more efficient when only the diagonal elements are used to pre-condition a descent direction within an iterative optimization scheme. However, in Newton-like methods that include the off-diagonal elements, the full Hessian may effectively lead to faster convergence. To the best of our knowledge, there is so far no experience concerning this issue. A quantitative comparison between conjugate-gradient (e.g. Mora 1987, 1988; Tape et al. 2007; Fichtner et al. 2009), quasi-Newton (e.g. Liu & Nocedal 1989; Pratt et al. 1998; Epanomeritakis et al. 2008; Brossier et al. 2009) and full Newton methods for realistic large-scale problems remains to be done.
In the context of resolution analysis, the full Hessian should be used because the approximate Hessian can lead to erroneous inferences concerning trade-offs between model parameters, as we have seen in the example from Fig. 13. Only the full Hessian allows us to correctly account for the effect of non-linearity on model resolution.
6.4 Amplitude of traveltime Hessian kernels
Fréchet kernels describe the first-order effect of structure on the measurement. For instance, a positive vP anomaly placed within the first Fresnel zone of the Fréchet kernel in Fig. 10(a) decreases the P wave traveltime shift T because the synthetic P wave arrives earlier. The influence of the second-order effect is less clear because the Hessian kernels contain both strong negative and positive contributions. In any case, the physical relevance of the second-order effect of course needs to be considered relative to both the first-order effect and the unknown contributions of orders three and higher. A comparison of the Fréchet and Hessian kernels shown in Figs 3, 6 and 9 reveals, that the second-order effect on traveltimes can be nearly as large as the first-order effect, provided that the extent of the heterogeneity is sufficiently large. From our experience, however, we know that traveltime is quasi-linearly related to large-scale Earth structure (e.g. Tong et al. 1998). This suggests that the cumulative contribution of all higher-order terms may to some extent compensate for the non-linearity that the second derivatives appear to suggest.
7 Conclusions
We presented an extension of the well-known adjoint method to the computation of the Hessian applied to a model perturbation. The calculations involve the forward wavefield and the adjoint wavefield, as well as their scattered versions. Our approach naturally leads to the concept of Hessian kernels that can be interpreted as the continuous representation of rows (or columns) in the discrete Hessian matrix. The Hessian kernels appear as the superposition of (1) a first-order influence zone that represents the approximate Hessian and (2) second-order influence zones that represent second-order scattering. The Hessian kernels can be represented in terms of Fréchet kernels, which allows for their easy computation using codes with pre-existing adjoint capabilities.
In a series of examples, we examined second-order effects on finite-frequency traveltimes of both surface and body waves. From this we draw the following conclusions: (1) The second-order effect is relevant only when heterogeneities are located within the first Fresnel zone. This is consistent with ray-theory. (2) Second-order scattering that involves heterogeneities of different nature (e.g. vP and vS perturbations) appears to be inefficient, at least for P waves. (3) Second derivatives of any data functional with respect to density are nearly zero, provided that the model is parameterized in terms of density and seismic wave speeds. This result can be explained with the backward-scattering from density perturbations.
Based on a realistic full waveform tomography for European upper-mantle structure, we have shown that significant differences exist between the approximate Hessian and the full Hessian, even in the vicinity of the optimal model. These differences are largest for the off-diagonal elements, and most relevant in resolution and trade-off analysis.
Acknowledgments
First and most of all we would like to thank Theo van Zessen for maintaining the HPC cluster at the Department of Earth Sciences at Utrecht University. Furthermore, we are grateful to Christian Böhm for many vivid discussions on non-linear optimization and the computation of the Hessian for seismic observables. Insightful comments by Brian Kennett, Guust Nolet, Jeroen Ritsema, Qinya Liu, Moritz Bernauer and two anonymous reviewers helped us to improve the manuscript substantially. The numerical simulations presented in this paper were performed on the HPC system HUYGENS, and funded by NCF/NWO under grant SH-161-09.
Appendix
Appendix A: Comparison with the Discrete Adjoint Method
The discrete adjoint method is a special case of the more general continuous adjoint method, applied to physical systems that are governed by algebraic equations. These systems can be either inherently discrete, or they can be the result of a discretization process. In this section, we establish close links between the continuous adjoint method as presented in Section 2 and the discrete adjoint method as it is commonly used for 2-D full waveform tomography in the frequency domain (e.g. Dessa et al. 2004; Bleibinhaus et al. 2007, 2009; Smithyman et al. 2009). Our development is slightly more general than the one presented by Pratt et al. (1998) and Pratt (1999) because it does not rely on a least-squares misfit functional.
1 A First derivatives
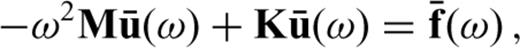
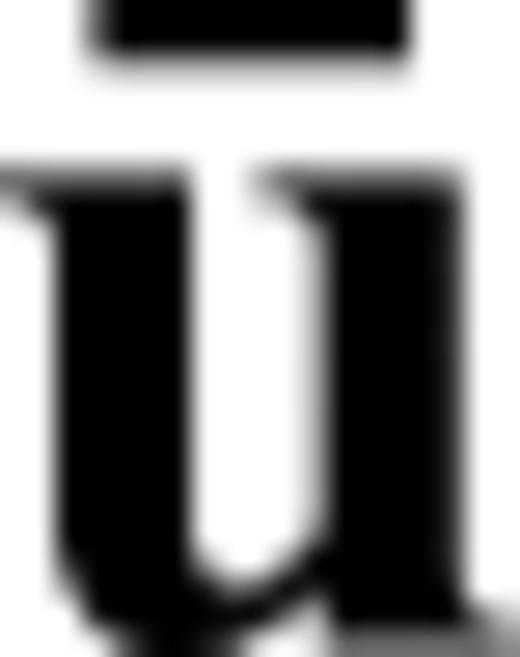 represent the mass matrix, the stiffness matrix and a discrete version of the seismic displacement field. The variables ω and
represent the mass matrix, the stiffness matrix and a discrete version of the seismic displacement field. The variables ω and 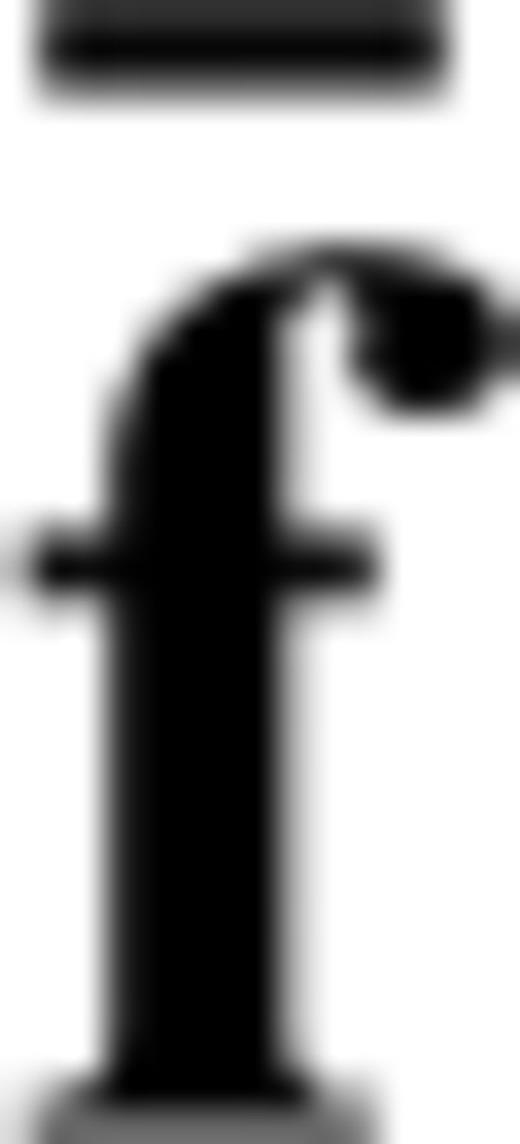 are the angular frequency and the discrete external force density. Defining the impedance matrix L(ω) =−ω2M+K, we can rewrite eq. (A1) in the form of a simple matrix-vector equation
are the angular frequency and the discrete external force density. Defining the impedance matrix L(ω) =−ω2M+K, we can rewrite eq. (A1) in the form of a simple matrix-vector equation 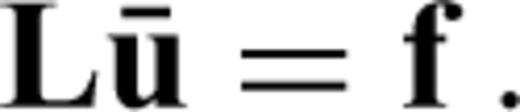
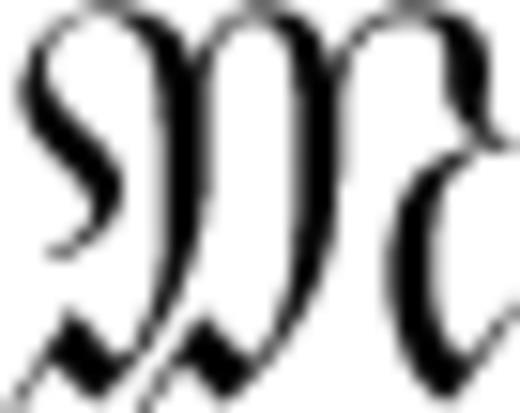 is finite-dimensional, so that any model
is finite-dimensional, so that any model 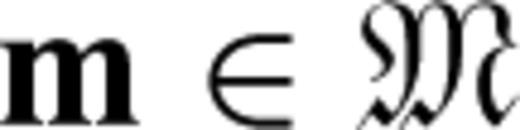 can be written in the form of a vector with n < ∞ components
can be written in the form of a vector with n < ∞ components 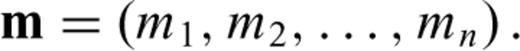
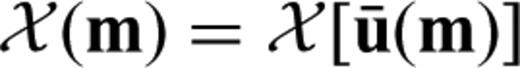 with respect to the model parameters mi
with respect to the model parameters mi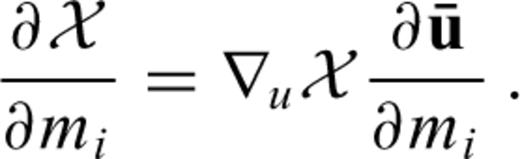
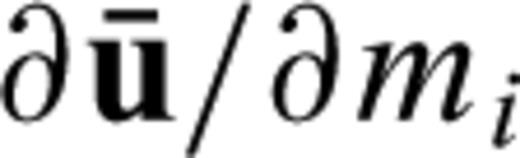 from eq. (A4) we differentiate the discrete wave eq. (A2) with respect to mi
from eq. (A4) we differentiate the discrete wave eq. (A2) with respect to mi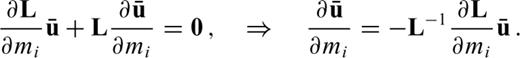
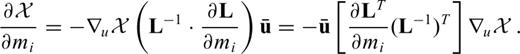
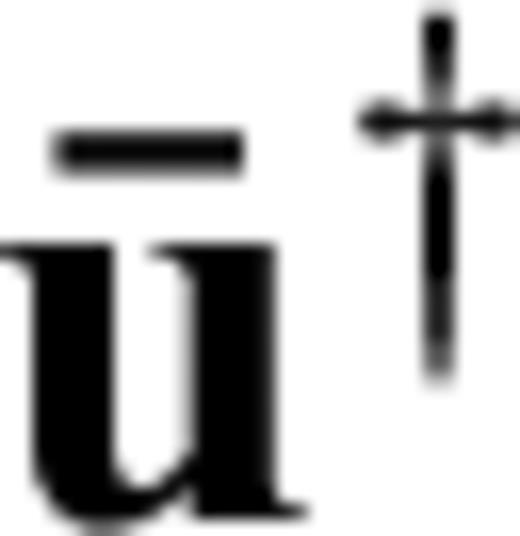 as the solution of the adjoint equation
as the solution of the adjoint equation 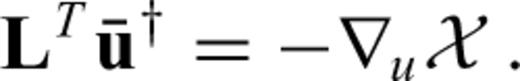
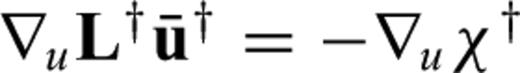 that we found in the continuous case (eq. 21). With the help of the discrete adjoint field
that we found in the continuous case (eq. 21). With the help of the discrete adjoint field 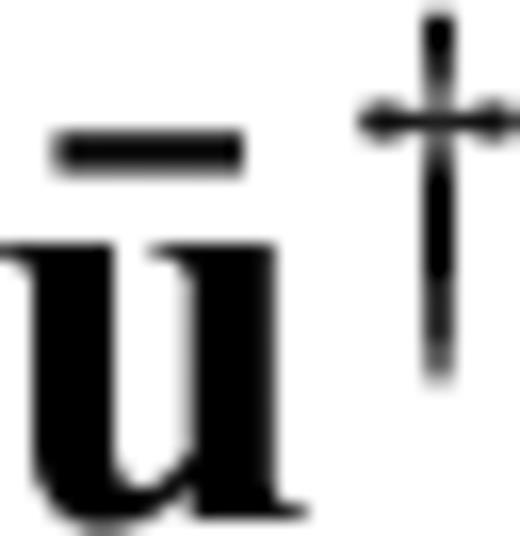 we can now obtain a simple expression for
we can now obtain a simple expression for 
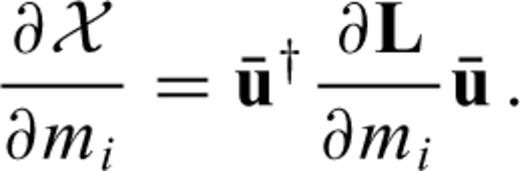
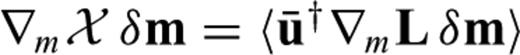 (eq. 22).
(eq. 22).2 A Second derivatives
 , as defined in eq. (A7). Differentiating χ first with respect to mi and then with respect to mj gives
, as defined in eq. (A7). Differentiating χ first with respect to mi and then with respect to mj gives 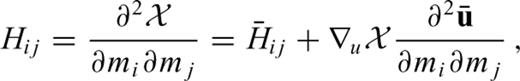
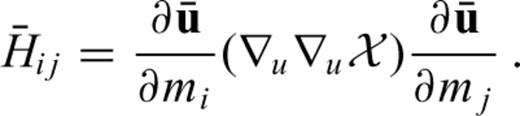
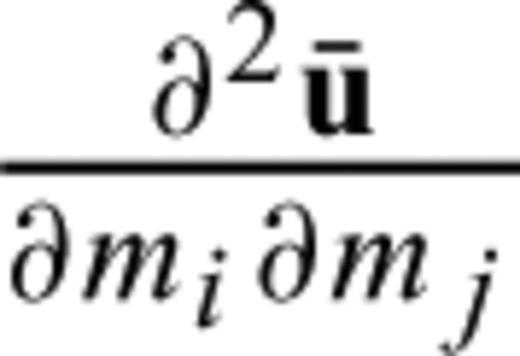 from eq. (A9), we differentiate the forward problem (A2) twice
from eq. (A9), we differentiate the forward problem (A2) twice 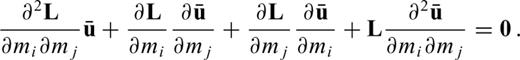
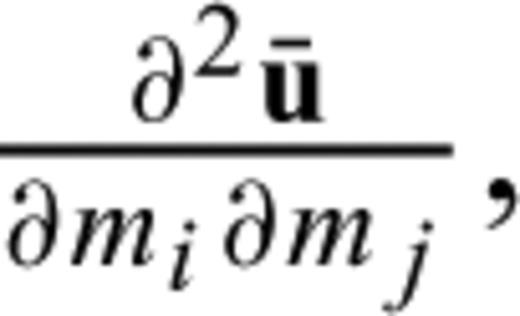 ,
, 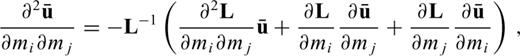
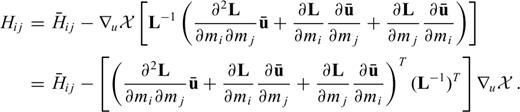
 as the solution of
as the solution of 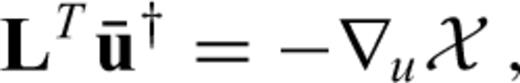
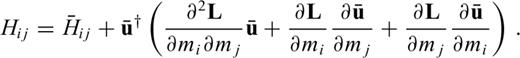
References




