-
PDF
- Split View
-
Views
-
Cite
Cite
Vincent A. van Antwerpen, Wim A. Mulder, Gérard C. Herman, Finite-difference modelling of two-dimensional elastic wave propagation in cracked media, Geophysical Journal International, Volume 149, Issue 1, April 2002, Pages 169–178, https://doi.org/10.1046/j.1365-246X.2002.01632.x
Close - Share Icon Share
Summary
We present a finite-difference modelling technique for 2-D elastic wave propagation in a medium containing a large number of small cracks. The cracks are characterized by an explicit boundary condition. The embedding medium can be heterogeneous. The boundaries of the cracks are not represented in the finite-difference mesh, but the cracks are incorporated as distributed point sources. This enables one to use grid cells that are considerably larger than the crack sizes. We compare our method with an accurate integral representation of the solution and conclude that the finite-difference technique is accurate and computationally fast.
1 Introduction
Modelling wave propagation in media containing inclusions smaller than the wavelength of the probing wavefield is of considerable interest in several areas, for instance, in seismology and in non-destructive evaluation. In seismology, variations in the subsurface of the Earth are present on many scales: from scales much larger than the typical seismic wavelength down to scales that are much smaller. Heterogeneities that are much smaller than the seismic wavelength cannot be distinguished individually using seismic waves, but nevertheless can have a significant effect on the amplitude and phase of the transmitted wavefield. O'Doherty & Anstey (1971) demonstrated this in a classic paper for the case of plane-layered subsurface models.
In the long-wavelength limit, a homogeneous embedding containing small-scale heterogeneities effectively behaves as a homogeneous medium, in which small-scale heterogeneities manifest themselves through apparent anisotropy and/or attenuation and dispersion. Most methods concerning wave propagation in media with embedded inclusions are based on this concept of an effective medium. An excellent overview is given by Hudson & Knopoff (1989).
Alternatively, methods have been developed that focus on the calculation of transmitted wavefields by solving a boundary-value problem. Many of these methods are limited to plane-layered models; see, for instance, Burridge & Chang (1989), who studied pulse propagation through a 1-D multilayered medium. For the scalar case of a large number of cracks embedded in a homogeneous medium, integral-equation techniques have been developed by Muijres et al. (1998).
All methods referred to in the above are not applicable to the case of cracks in the direct vicinity of a boundary or embedded in a heterogeneous medium. Nevertheless, these situations might arise when studying, for instance, wave propagation through a cracked reservoir in a layered-earth model or when investigating the propagation of boundary waves in tunnel walls containing cracks. Finite-difference techniques are well suited for solving wave propagation problems in heterogeneous media. The presence of cracks in this type of method is accounted for by incorporating explicit boundary conditions at the crack location (see, for instance, Coates & Schoenberg 1995; Carcione 1996) or by using zero velocities and small densities in just a few grid points to mimic the crack (Saenger et al. 1999). This implies that each crack boundary has to be incorporated in the finite-difference (FD) mesh, requiring a prohibitive number of grid points in the case of a large number of small-scale cracks.
In a previous paper (Van Baren et al. 2001), an FD technique has been developed for the computation of wave propagation of scalar, 2-D waves in a heterogeneous medium containing a large number of small-scale cracks. Instead of imposing explicit boundary conditions at the crack boundaries, this method accounts for the presence of the cracks by introducing secondary point sources, the strength of which is computed using perturbation theory. In order to represent the point sources properly on a coarse FD grid, an asymptotic method is used, based on the integral representation of the scattered wavefield of a small crack. In the present paper, we extend this method to the more realistic case of scattering of 2-D elastic waves by a compliant crack. The method is based on the asymptotic form of the elastic wavefield scattered by a small compliant crack and the use of the elastic FD operator to this field in order to find the appropriate distribution of the crack over the grid points.
An important assumption upon which our method is based is the fact that interaction between individual cracks is neglected. For higher crack densities, this assumption is no longer valid and higher-order scattering processes have to be taken into account.
2 Representation of the field in terms of secondary sources





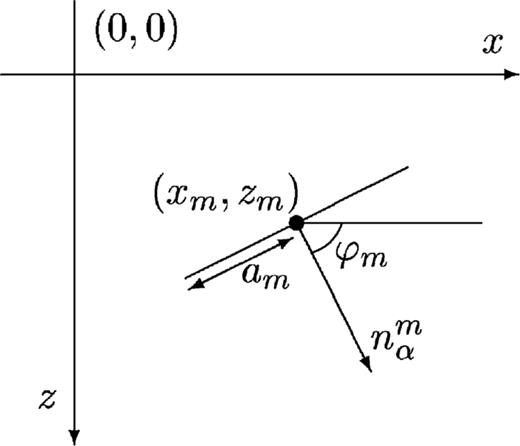
Each crack is represented by a line segment. It can be characterized by the position of its centre, xm= (xm, zm), its half-width am and the angle ϕm with the horizontal. The z-coordinate indicates depth and the x-coordinate refers to the horizontal position. The unit vector normal to the crack is defined as nαm= (cos ϕm, sin ϕm).
 . Later, we transform all of the resulting expressions back to the time domain. From the frequency-domain counterparts of eqs (1) and (2), we can eliminate the stress tensor and obtain
. Later, we transform all of the resulting expressions back to the time domain. From the frequency-domain counterparts of eqs (1) and (2), we can eliminate the stress tensor and obtain 
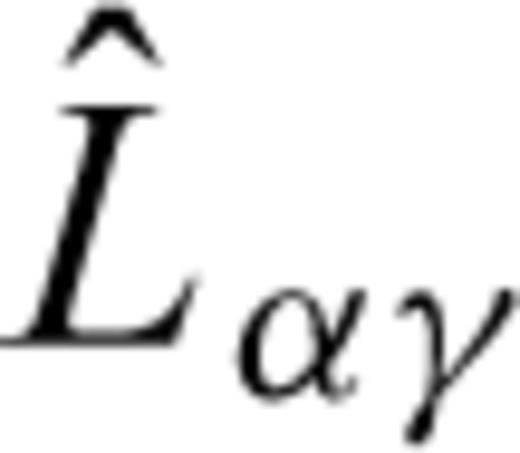 is defined by
is defined by 






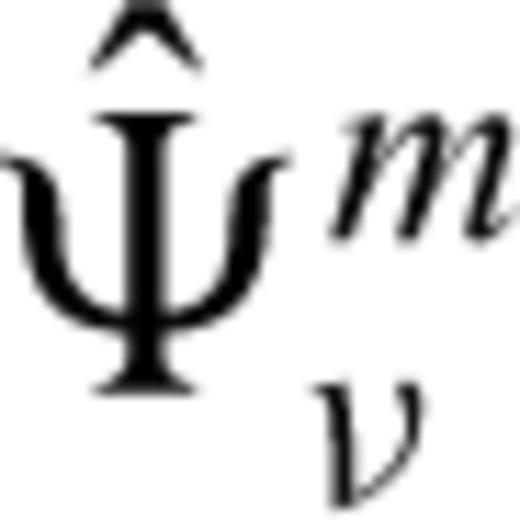 is the particle displacement jump across the mth crack and
is the particle displacement jump across the mth crack and 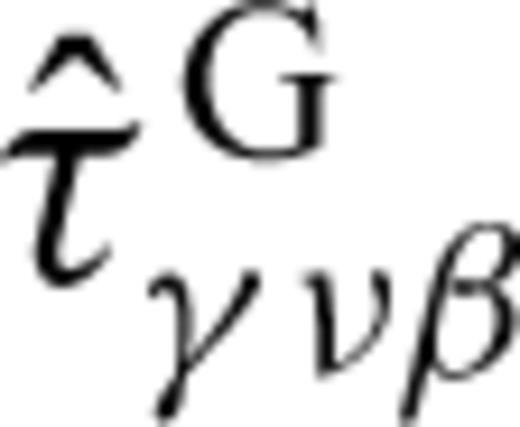 is the Green stress tensor, defined by
is the Green stress tensor, defined by 
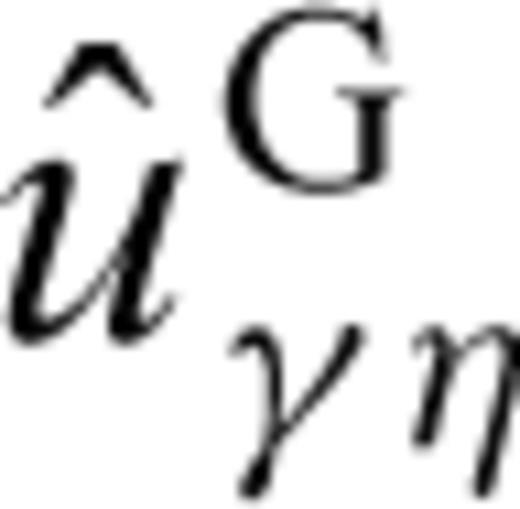 is the elastic Green displacement tensor of the embedding medium. It satisfies the elastodynamic wave equation for a point source, i.e.
is the elastic Green displacement tensor of the embedding medium. It satisfies the elastodynamic wave equation for a point source, i.e. 

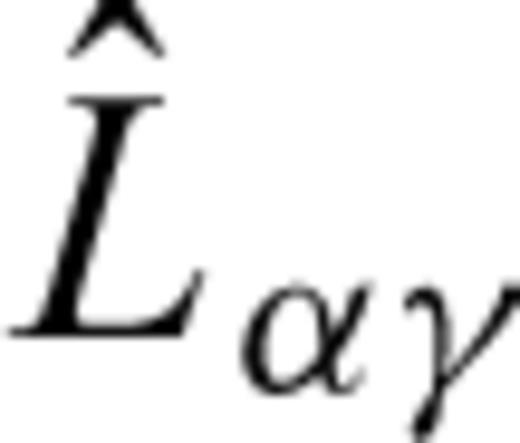 , given by eq. (6), to both sides of eq. (15), yields
, given by eq. (6), to both sides of eq. (15), yields 


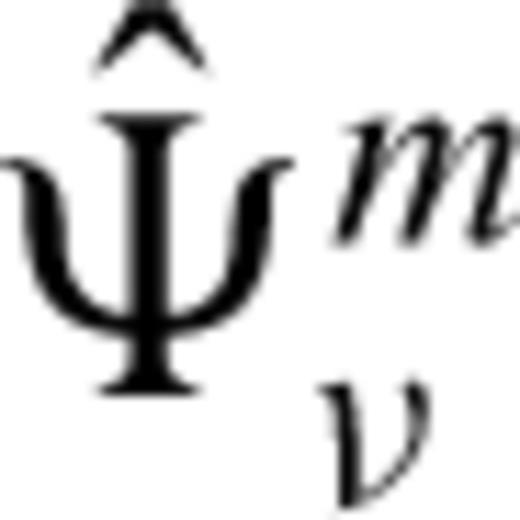 at the cracks, the boundary conditions still have to be imposed. An integral-equation formulation for the source strengths can be obtained from eq. (12), letting the point of observation approach the cracks and applying the boundary condition (4). However, this approach is impractical for heterogeneous media because computing the Green function can be computationally very expensive. Therefore, we approach the problem in a different way by approximating the source strengths
at the cracks, the boundary conditions still have to be imposed. An integral-equation formulation for the source strengths can be obtained from eq. (12), letting the point of observation approach the cracks and applying the boundary condition (4). However, this approach is impractical for heterogeneous media because computing the Green function can be computationally very expensive. Therefore, we approach the problem in a different way by approximating the source strengths 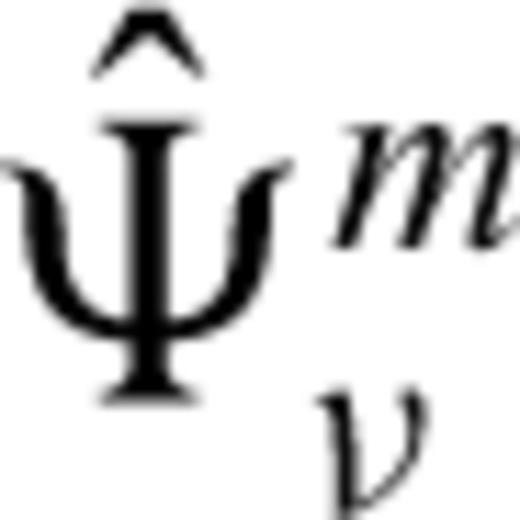 with the aid of perturbation theory and using an FD formulation for computing the solution of eq. (16). Perturbation theory leads to an approximate source strength (Van den Berg 1982) in terms of the stress tensor of the incident field:
with the aid of perturbation theory and using an FD formulation for computing the solution of eq. (16). Perturbation theory leads to an approximate source strength (Van den Berg 1982) in terms of the stress tensor of the incident field: 
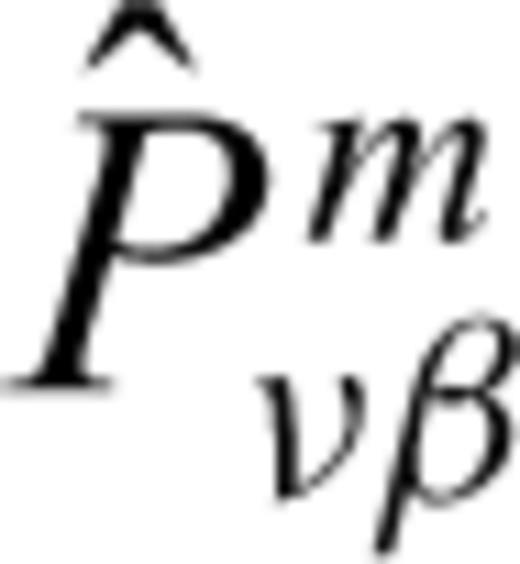 , are given in Appendix A. This approximation is based upon the following assumptions.
, are given in Appendix A. This approximation is based upon the following assumptions.Second- and higher-order scattering effects, i.e. the interactions between the different cracks, are neglected.
The crack size is small compared with the wavelength of the incident wave. This implies that the incident wave is considered to be locally plane at the location of the crack and that the source strength
 can be approximated by the leading-order term in a perturbation series (see also De Hoop 1955a, b). We also neglect variations of the embedding medium in the direct vicinity of the crack.
can be approximated by the leading-order term in a perturbation series (see also De Hoop 1955a, b). We also neglect variations of the embedding medium in the direct vicinity of the crack.
The first assumption is the most restrictive one in our case. In principle, it can be relaxed by taking higher-order terms into account in the Neumann-series expansion of  (see also Muijres et al. 1998). It is not straightforward, however, to discretize these higher-order terms with sufficient accuracy when using the FD scheme.
(see also Muijres et al. 1998). It is not straightforward, however, to discretize these higher-order terms with sufficient accuracy when using the FD scheme.




The scattering problem can now be solved using the FD method. First, the incident field is computed by solving eq. (20) for the (heterogeneous) embedding without accounting for the presence of the cracks; secondly, the (first-order) scattered field is obtained by solving eqs (22) and (23) with a similar technique. In this way, the problem of accounting for the explicit boundary conditions on many small cracks is avoided and replaced by the problem of accounting for the presence of many small point sources on an FD grid. This is discussed in the next section. In order to find a good representation of the dipole point sources occurring on the right-hand side of eq. (22), we need a representation of the wavefield in the direct vicinity of each crack. This is discussed in Appendix B, where expressions are also given for the discrete approximation of the collection of point sources present in sαsc of eq. (23).
3 Finite-difference method





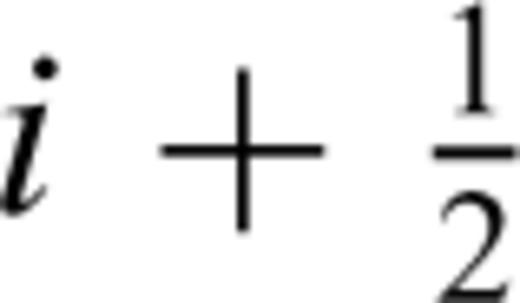 and
and 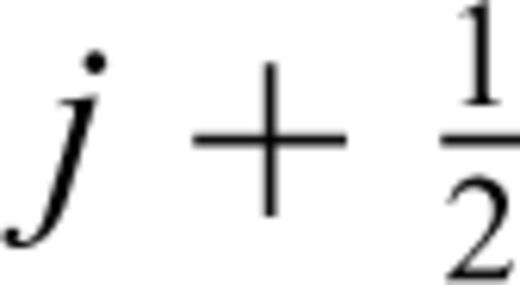 . Time is discretized as tn=t0+nΔt. The quantities ρij, λij and μij are all defined at (xi, zj). Below we will need ρ at (xi+
. Time is discretized as tn=t0+nΔt. The quantities ρij, λij and μij are all defined at (xi, zj). Below we will need ρ at (xi+ Δx, zj). This quantity is denoted by ρ(1)i,j and computed using linear interpolation:
Δx, zj). This quantity is denoted by ρ(1)i,j and computed using linear interpolation: 

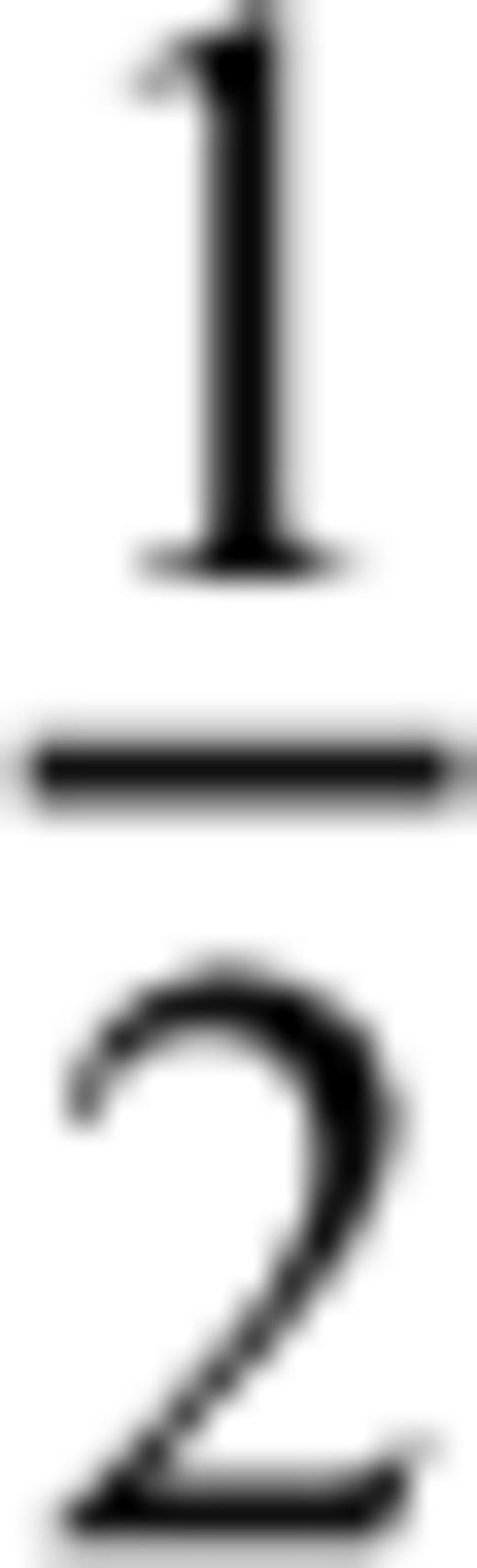 Δz). The quantity μ at the centre of a grid cell
Δz). The quantity μ at the centre of a grid cell 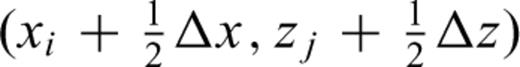 is calculated by bilinear interpolation:
is calculated by bilinear interpolation: 









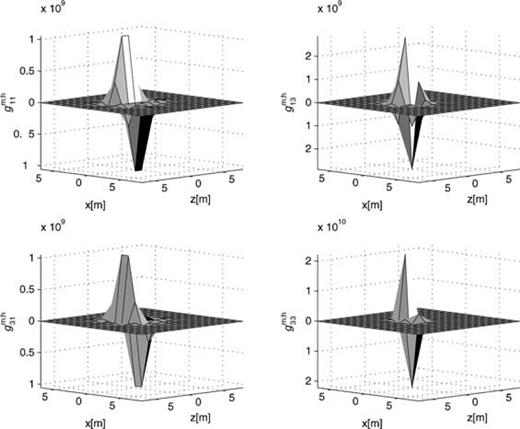
Discrete point-source tensor gανm;h for one crack, computed using the staggered-grid FD operator. The crack is situated in the origin and is oriented along the x-axis. The half-width of the crack, am, is given by am= 0.5 m. The grid spacing is 2 m. The area around the crack, necessary to represent it as a distributed point source, is typically chosen as a square containing 7 × 7 grid cells.
4 Validation of the method
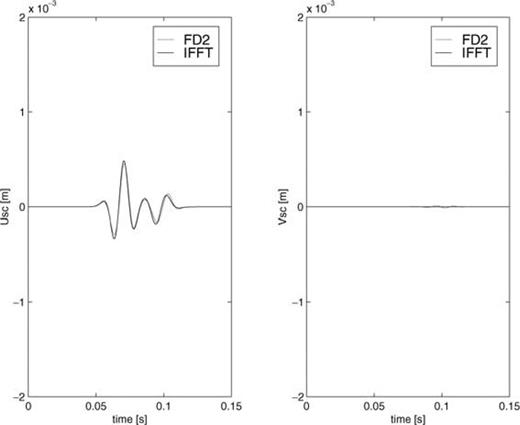
In order to validate our finite-difference method, we apply it to a single crack in a homogeneous embedding and compare its scattered wavefield with the scattered field resulting from a direct evaluation of the integral representation given in eq. (12) and transforming the result to the time domain. The latter method is not based on the discretization of the point-source tensor gανm and therefore is a good validation test to check the accuracy of our method. For this comparison, we use an incident, plane, compressional wave propagating along the vertical axis. The waveform is a Ricker wavelet (second derivative of a Gaussian) with a dominant frequency of 45 Hz, corresponding to ωc≈ 280 rad s−1. The material parameters are chosen as: ρ= 2.3 × 103 kg m−3, λ= 4.0 × 109 N m−2, μ= 5.2 × 109 N m−2, which results in a compressional velocity cp= 2.5 km s−1 and a shear velocity cs= 1.5 km s−1. The compliant crack is situated at the origin (0, 0), parallel to the horizontal axis and has a half-width am= 0.5 m.For this choice of parameters, we have ksam= 0.094 and kpam= 0.057. Therefore, both values are much smaller than 1, which implies that the small-crack approximation is valid. The grid spacings Δx and Δz are both chosen to be equal to 2 m. In Figs 4–6, the horizontal and vertical components of the scattered displacement field in different directions are compared for both methods. The fit obtained is good, indicating that the discretization of the point-source tensor gανm, represented by gανm;h, is accurate. We have found that the discrete representation of the point-source tensor breaks down if the crack itself coincides with a grid point. This is a result of the singular behaviour of the point-source wavefield. For simulations with many cracks, we therefore have to discard cracks very close to grid points. In Fig. 7, we show snapshots of the scattered displacement field around the crack as computed with our method.
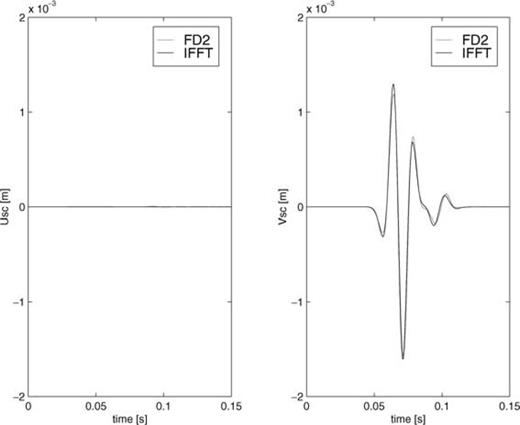
Horizontal and vertical components of the scattered displacement field observed in x= (0, −100). FD refers to our FD method and IR to the accurate integral-representation method. The field is normalized with respect to the incident field.
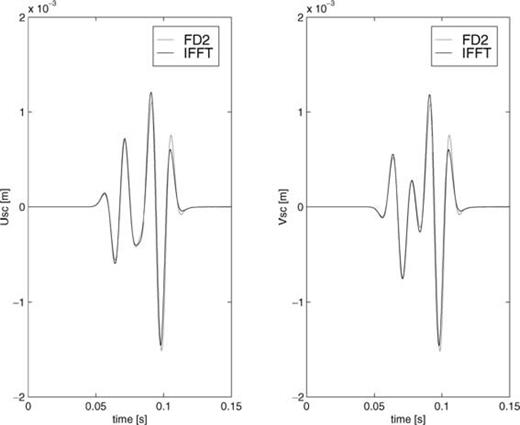
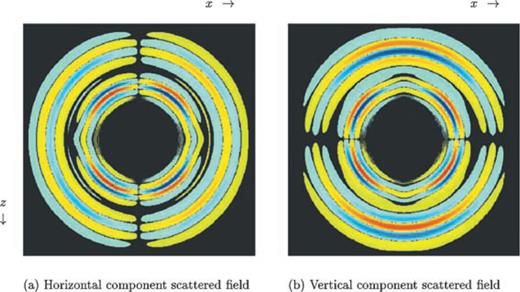
Snapshot of the horizontal and vertical components of the scattered displacement field for a vertically incident compressional wave on a compliant crack. The crack is parallel to the horizontal (x) axis and has a half-width am= 0.5 m.
5 Model study for a cross-well geometry
To illustrate the flexibility of our method, we simulate a cross-well experiment. The model consists of a low-velocity layer, containing 2000 small vertical cracks, situated between two high-velocity layers. The geometry of the experiment is shown in Fig. 8. The seismic source consists of a vertical point force and is situated in the low-velocity layer. In Fig. 9, we show snapshots of the horizontal and vertical components of the incident and scattered field. From the incident-field snapshots, we observe that a significant part of the wavefield is trapped within the low-velocity layer. The snapshots of the scattered field reveal two aspects. First, we see a coherent transmitted part. This is consistent with the concept of effective media (see, for instance, Hudson & Knopoff 1989), where the overall effect of the cracks is accounted for by an effective medium. Secondly, we observe that the backscattered field is much more complex, but nevertheless remains trapped in the low-velocity layer.
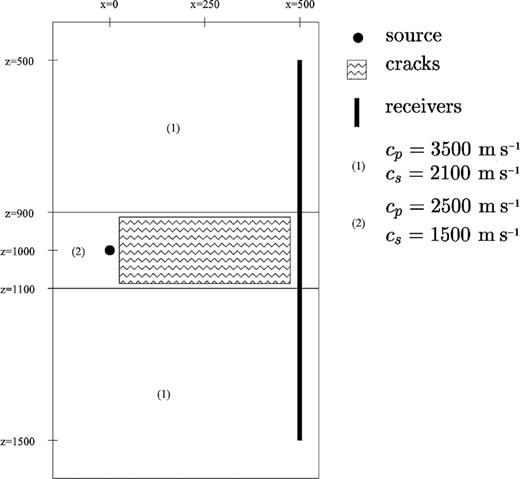
Cross-well geometry used in the example. The middle reservoir layer has a lower velocity than the upper and lower layers and consists of 2000 vertical cracks. The source is situated in the low-velocity layer.
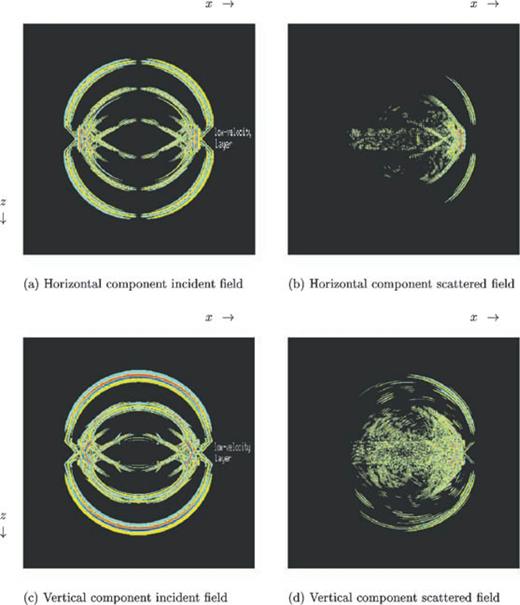
Snapshots of the horizontal and vertical components of the incident displacement field, that would be present in the absence of the cracks, and the displacement field scattered by the cracks. The model is shown in Fig. 8.
6 Discussion and conclusions
We have presented a finite-difference method for computing the scattering of 2-D, elastic waves by many small-scale compliant cracks, characterized by an explicit traction-free boundary condition. We have solved the problem of representing a small crack on an FD grid by deriving a suitable numerical source term. A further approximation of this source term provided a simpler expression that can be factored into a spatial and temporal part. This results in a substantial reduction of computing time, without an appreciable loss of accuracy. The most important limitation is a restriction to first-order scattering, which implies that interaction between cracks is not taken into account. This restriction could be alleviated by taking higher-order terms of the Neumann series into account. This extension, however, is not straightforward since it requires an accurate discretization of the scattered wavefield close to each crack.
We have included examples to validate the method and study the effect of the presence of 2000 small cracks in a low-velocity layer on the transmitted and reflected field. The strength of these effects depends on the number, size and orientation of the cracks.
The extension of the present method to three spatial dimensions is probably straightforward, provided the relevant perturbation expression is used for computing the secondary source strength from the incident field.
Appendix
Appendix A: The source strength in the case of a compliant crack
Without loss of generality, we assume the crack to be located at the origin. The half-width am of the crack is denoted by a. In order to use the results of Van den Berg (1982) directly, we use local coordinates for each crack such that the normal nα, in local coordinates, is given by  . In what follows, local quantities will be indicated with a tilde. At the end, we rotate all quantities back to the global coordinate system. The derivation can be found in more detail in Van den Berg (1982).
. In what follows, local quantities will be indicated with a tilde. At the end, we rotate all quantities back to the global coordinate system. The derivation can be found in more detail in Van den Berg (1982).
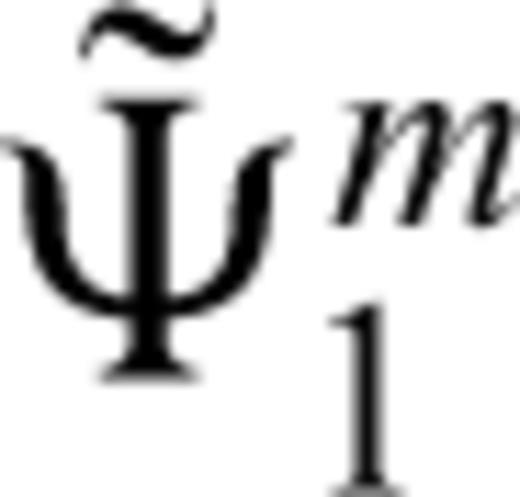 is approximated by a Chebyshev polynomial:
is approximated by a Chebyshev polynomial: 

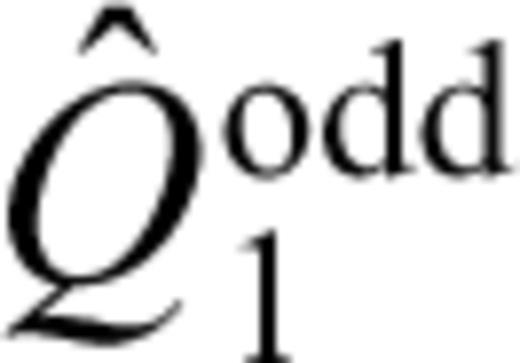 is defined by (see Van den Berg 1982)
is defined by (see Van den Berg 1982) 
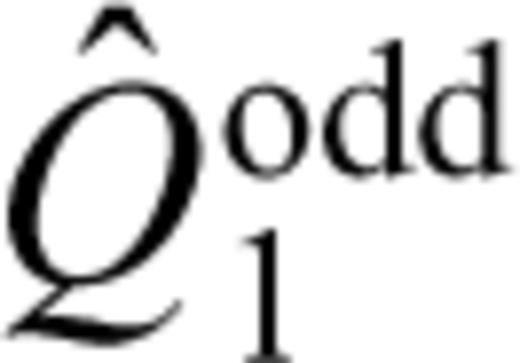 can be calculated using the following series expansions of the Bessel functions (Watson 1944):
can be calculated using the following series expansions of the Bessel functions (Watson 1944): 




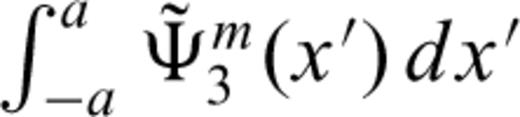 can be found in a similar way. Now,
can be found in a similar way. Now, 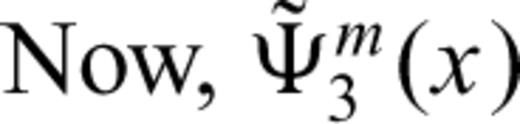 is approximated by a Chebyshev polynomial:
is approximated by a Chebyshev polynomial: 

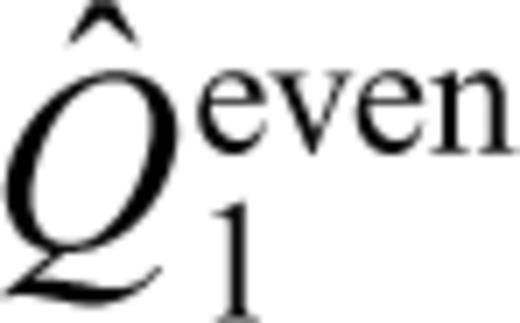 is defined by (see Van den Berg 1982)
is defined by (see Van den Berg 1982) 


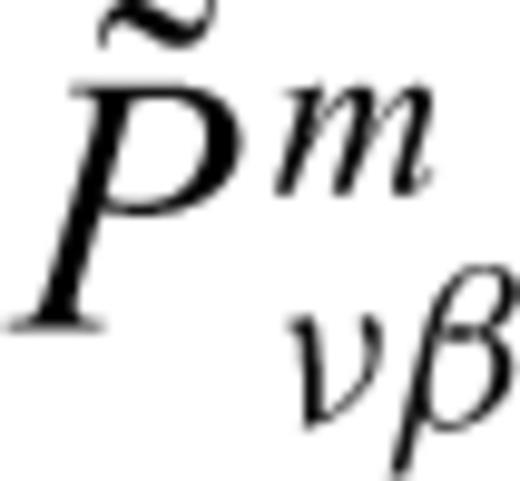 defined by
defined by 


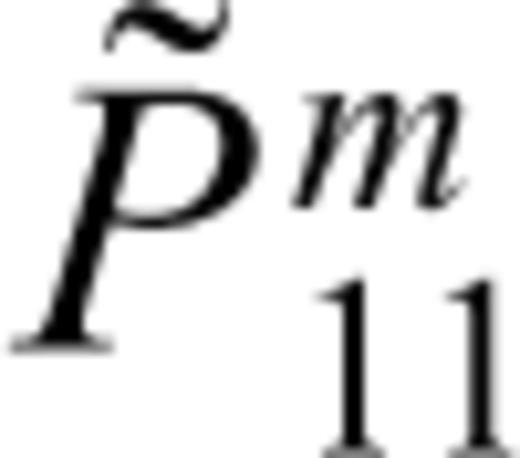 and
and 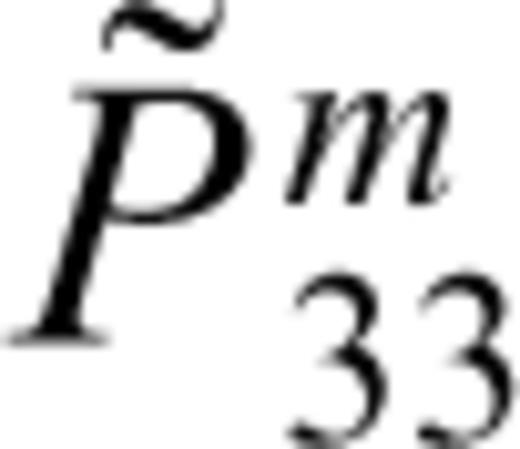 can be expressed as
can be expressed as 
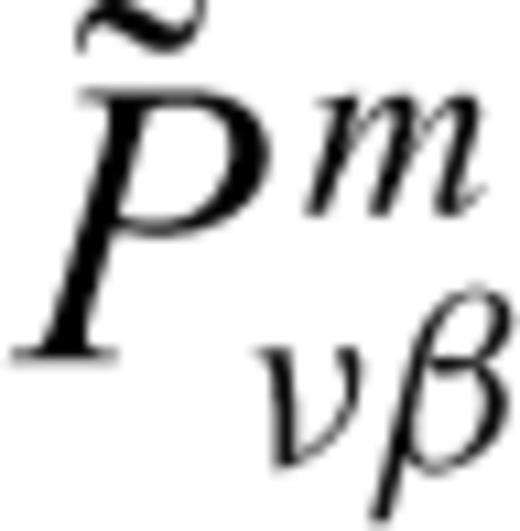 becomes real-valued and frequency-independent. With the aid of the coordinate transformation
becomes real-valued and frequency-independent. With the aid of the coordinate transformation 


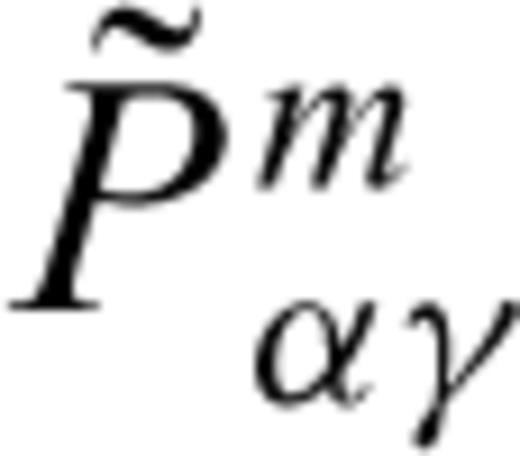 is real-valued and frequency-independent.
is real-valued and frequency-independent.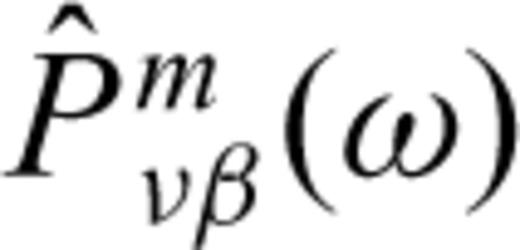 can be neglected for small values of the crack width am, see eqs (A16) and (A17), we can transform eq. (A19) directly to the time domain and obtain
can be neglected for small values of the crack width am, see eqs (A16) and (A17), we can transform eq. (A19) directly to the time domain and obtain 
 given by eq. (A20).
given by eq. (A20).Appendix
Appendix B: Accurate representation of point sources sαsc

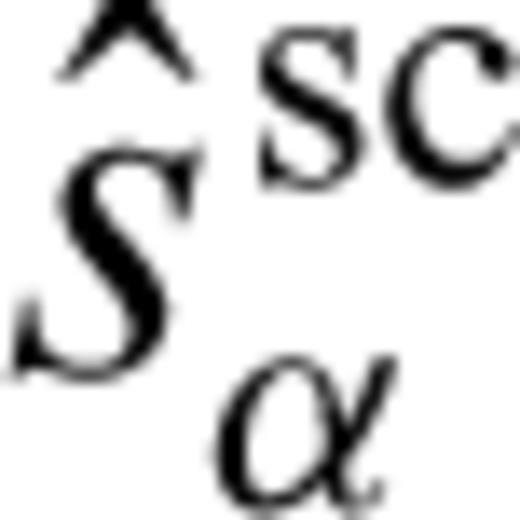 being given by
being given by 
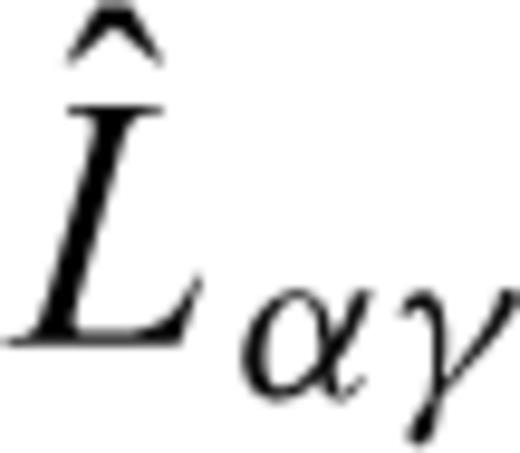 by the operator
by the operator 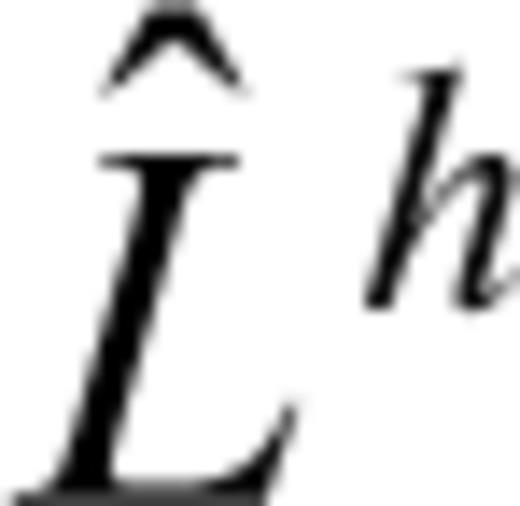 after spatial discretization, which follows from eq. (6) as
after spatial discretization, which follows from eq. (6) as 



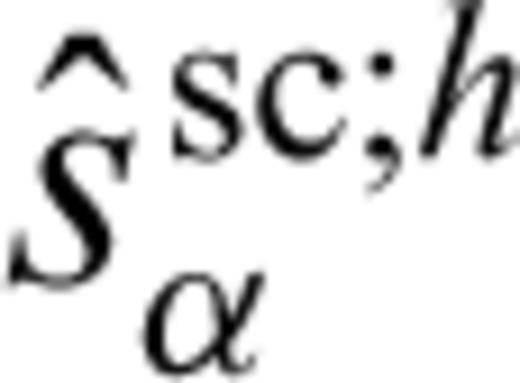 resulting from the single crack by substituting the field
resulting from the single crack by substituting the field 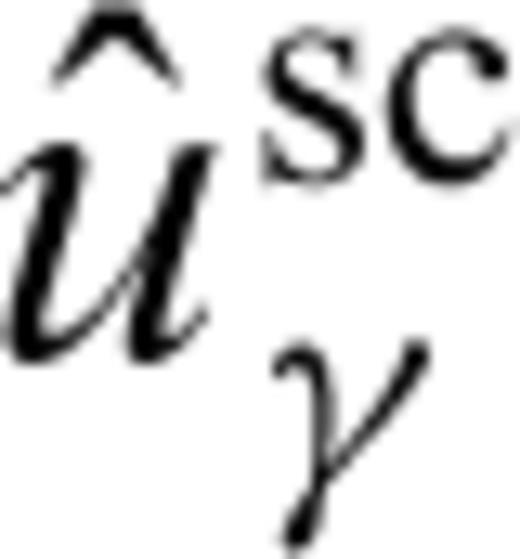 close to the crack in eq. (B6) and evaluating the result.
close to the crack in eq. (B6) and evaluating the result.
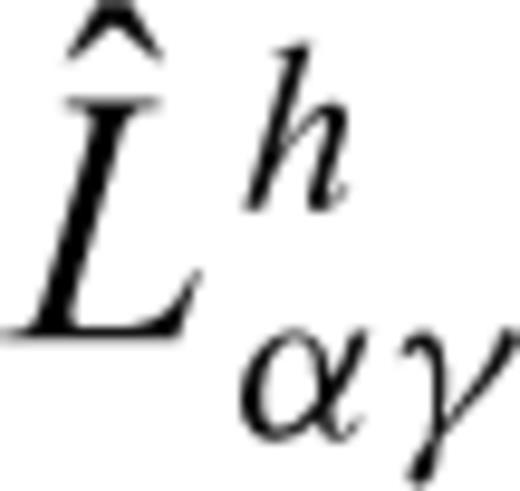 to both sides of eq. (B7),
we obtain
to both sides of eq. (B7),
we obtain 



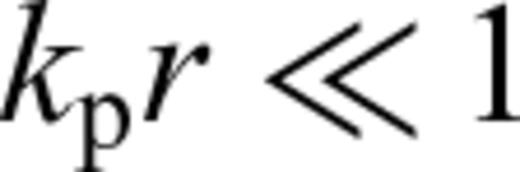 and
and 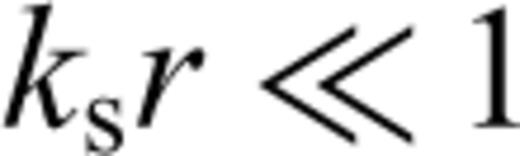 . Therefore, we can employ the leading-order term of the small-argument approximation of the Hankel functions present in
. Therefore, we can employ the leading-order term of the small-argument approximation of the Hankel functions present in 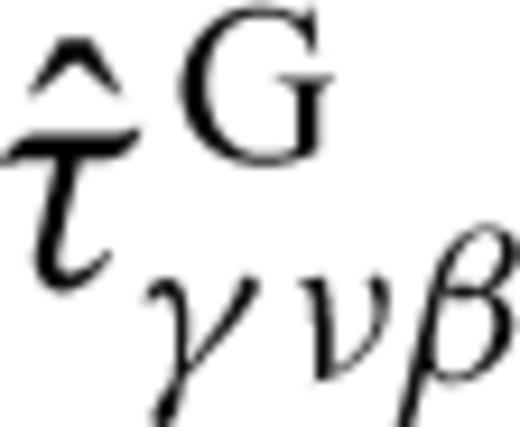 . We obtain
. We obtain 

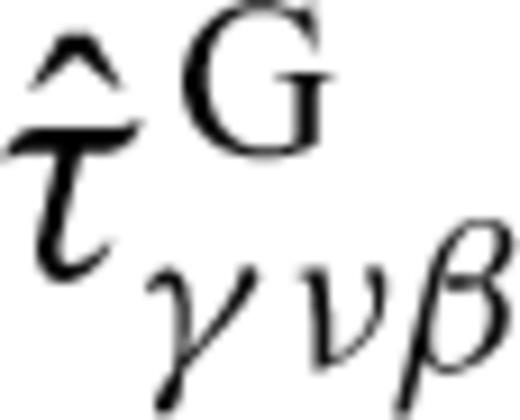 by its approximation close to the crack, given by eq. (B12). Close to the crack, the contribution of the spatial differentiation part (Qαγh) of the operator
by its approximation close to the crack, given by eq. (B12). Close to the crack, the contribution of the spatial differentiation part (Qαγh) of the operator  is the largest owing to the singularity of the Hankel function. Therefore, we replace
is the largest owing to the singularity of the Hankel function. Therefore, we replace 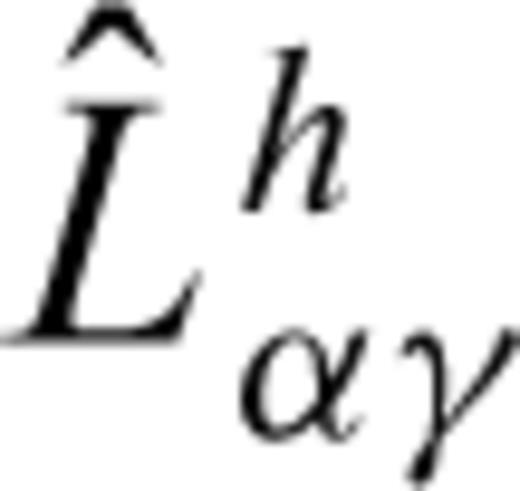 by its dominant spatial differentiation part, Qαγh, and obtain
by its dominant spatial differentiation part, Qαγh, and obtain 
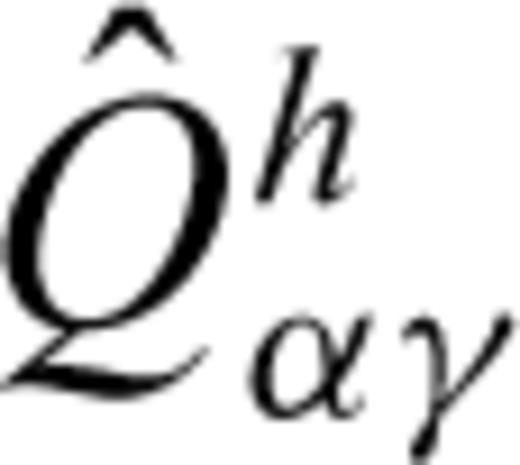 given by eq. (B4). Since the near-field form of the Green tensor is known explicitly, as well as the spatial part of the FD operator, Qαγh, we can compute gανm;h explicitly, by applying Qαγh to
given by eq. (B4). Since the near-field form of the Green tensor is known explicitly, as well as the spatial part of the FD operator, Qαγh, we can compute gανm;h explicitly, by applying Qαγh to 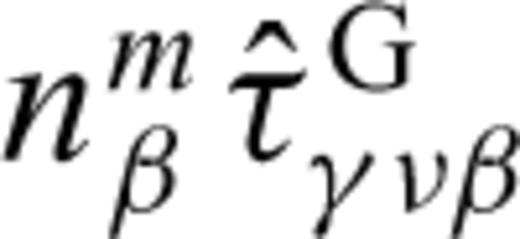 .
.
References




