-
PDF
- Split View
-
Views
-
Cite
Cite
Marco Anzidei, Paolo Baldi, Giuseppe Casula, Alessandro Galvani, Enzo Mantovani, Arianna Pesci, Federica Riguzzi, Enrico Serpelloni, Insights into present‐day crustal motion in the central Mediterranean area from GPS surveys, Geophysical Journal International, Volume 146, Issue 1, July 2001, Pages 98–110, https://doi.org/10.1046/j.0956-540x.2001.01425.x
Close - Share Icon Share
Summary
In this paper we present observations of crustal motion related to a large GPS network located in the central‐western Mediterranean area. Velocities are obtained by the analysis of more than 30 observing sites at which at least three different GPS campaigns were carried out in the time span 1991–1999. The results are presented both in the ITRF96 reference frame and with respect to a Eurasian fixed reference frame. The sites located along the northern African margin, in Sicily and southern Italy show prevalent northeastward movements with a mean velocity of roughly 0.7 cm yr−1. The relatively dense network available in the southern Apennines led us to try a tentative estimate of the average strain rate in this zone, resulting in a maximum extension of 0.021 ± 0.006 × 10−6 yr−1 normal to the chain. In Ionian Greece the two sites located south of the Kephallinia discontinuity (Lefkas and Kastro Ilias) consistently indicate a south to southwestward motion at an average rate of roughly 15 mm yr−1.
1 Introduction
It is widely recognized that the Mediterranean area represents the collision zone between the African/Arabian and Eurasian plates, but the deformation pattern of this region is characterized by a complex space–time distribution of compressional and tensional events, with the opening of relatively large basins such as the Balearic, the Tyrrhenian, the Pannonian and the Aegean ( Fig. 1). This was connected with strong distortion, with lateral migration of several hundred kilometres, of the Palaeocene and Neogene orogenic belts (e.g. Dercourt 1986 ), mainly caused by the indentation of the two African promontories, i.e. Adria and Arabia ( Tapponnier 1997; Mantovani . 1996, 1997a). As a final result of this complex evolution, the Central Mediterranean area is presently comprised of a high number of crustal wedges, moving independently or partially independently with respect to the one another. These wedges have been derived partly from the fragmentation of continental domains such as the Adriatic, the Corsica–Sardinia and the Iblean blocks and partly from the dissection of orogenic belts, decoupled by major tectonic discontinuities, as observed in the Maghrebides, Apennines, Alps, Dinarides and Hellenides.
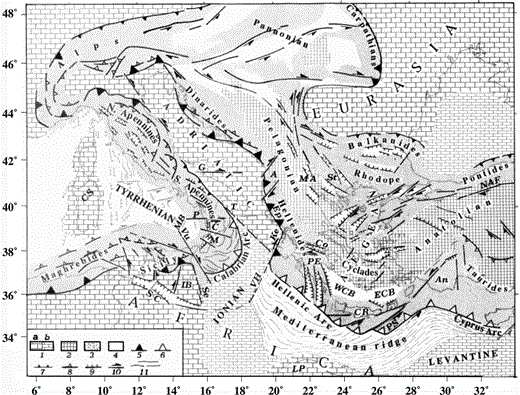
Sketch of the major tectonic lineaments and structural domains in the central Mediterranean region. (1) Continental (a) and oceanic (b) parts of the Africa/Adriatic and Eurasian forelands; (2) Tethyan belt comprised of oceanic remnants and intermediate massifs (Pelagonian, Anatolian and Cyclades arcs); (3) deformation belts developed on the African and Eurasian margins; (4) crustal thinning; (5) active thrust fronts; (6) subduction zones; (7) inactive thrust fronts; (8, 9, 10) compressional, tensional and transcurrent features; (11) main trends of compressional deformation in the Mediterranean Ridge and Calabrian Arc. A: Albania; An: Antalya block; Co: Corinthian trough; C: Crati trough; CR: Crete; CS: Corsica–Sardinia block; ECB: Eastern Cretan basin; Ep: Epirus; G: Gargano fault; Ke: Kefallinia fault; IB: Iblean block; LP: Libyan promontory; M: Messina trough; MA: Macedonia; MB: Marsili basin; NAF: North Anatolian fault; P: Palinuro fault; PE: Peloponnesus; PS: Pliny–Strabo trenches; SC: Sicily Channel; Se: Siracusa escarpment; St: Struma tectonic belt; T: Raranto gulf; VH: Victor Hensen fault; Vu: Vulcano fault; WCB: Western Cretan basin.
Reconstructing the kinematic pattern of such a plate/microplate mosaic is not an easy task. One could try to exploit the large amount of information about strain regimes in the Mediterranean area (e.g. Rebai . 1992 ; Pondrelli . 1995 ; Mantovani . 1997a, 2000) by using it as a constraint in numerical modelling (e.g. Mantovani . 2000 ). However, the results obtained by this kind of approach may be affected by uncertainties, due to unavoidable assumptions and simplifications in the model adopted and to the approximate knowledge of the observed strain field. Some information about the considerable lateral heterogeneity of stress regimes in the study area is given by the available focal mechanisms ( Fig. 2).
Source mechanisms of earthquakes with magnitude M > 5 in the study area: CMT solutions (black and white focal spheres) and body waveform inversion and first‐motion solutions (grey and white symbols). Information on the paper from which focal mechanisms have been taken and a list of data are given by Viti . (2000).
Another important and independent constraint on the kinematic pattern is obtained by geodetic measurements (GPS, VLBI and SLR), which provide information on the motion of a number of points with respect to a common reference frame. Nowadays it is widely accepted that the GPS technique can be successfully used to detect crustal deformation at various scale dimensions, so that permanent GPS arrays are currently used for this purpose all over the world. Due to the low relative velocity of plates in the central Mediterranean area, an accurate estimate of such a parameter would require relatively long observation time spans, which may be reduced by the use of permanent stations. Non‐permanent networks may play an important role in control surveys devoted to geophysical purposes, both at regional and local scales, if few or no permanent stations are available, as may be the case for the Mediterranean area.
A certain number of space geodetic observations have recently been collected at several stations distributed throughout this region. The previous geodetic results were published by Kahle . (1993) for the western Greece area, identifying the Kefallinia fault zone moving at a slip rate of 20 ± 2 mm yr−1.
Successive GPS surveys in the same area ( Kahle . 1993, 1995, 1998; Anzidei . 1996 ; Cocard . 1999 ; Peter . 1998 ) have provided site velocities, relative to a Europe‐fixed reference frame, of 10 mm yr−1, with a general northward motion north of Lefkada island of 35 mm yr−1, with S to SW motion at the tip of the Peloponnesus and of 33 mm yr−1 in Crete. The above velocities define two different kinematic patterns divided by the Kefallinia transform fault. Estimates of geodetic and seismic strains in this area consistently indicate shortening between the Apulian platform and northern Ionian Greece, N–S extension in the Corinth Gulf and dextral shear between the stations located north and south of Lefkada island ( Anzidei . 1997 ; Kahle . 1998 ). The stations located in the Aegean plate show 20–30 mm yr−1 of SW‐oriented motion with respect to Eurasia. GPS ( Oral . 1995 ; Reilinger . 1997 ; Barka & Reilinger 1997; Straub . 1997 ; McClusky . 2000 ) and SLR data ( Noomen . 1996 ; Bianco . 1998 ) in the Anatolian region consistently indicate westward motion of this block with respect to Eurasia, at an average rate of 20–30 mm yr−1.
For the Italian peninsula, the few GPS, SLR and VLBI permanent stations available provide velocities lower than 10 mm yr−1 with respect to Eurasia, with an acceptable agreement among the three different techniques ( Ward 1994; Zarroa . 1994 ; Tomasi 1998; Bianco . 1998 ; Boucher 1998; Riguzzi & Zanutta 1998; Lanotte . 1999 ).
On the basis of SLR observations collected from 1986 to 1993, Bianco . (1998) inferred a lack of deformation in central Europe, assigned CAGL (considered representative of the Sardo‐Corsican block) to the Eurasian domain and LAMP and NOTO to the African plate, while the motion of MATE was recognized as neither purely Euro‐Asiatic nor African.
The central‐western Mediterranean region, and in particular the Italian area and its surroundings, have recently been investigated at both regional and local scales in the frame of two main projects, TYRGEONET ( Anzidei . 1995 ) and GEOMODAP ( Fig. 3). In this paper we describe the results and analysis of the GPS observations collected during several campaigns performed in the time span 1991–1999 by the two networks.
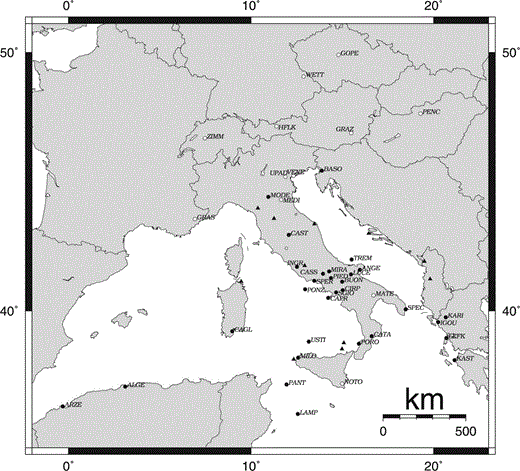
TYRGEONET and GEOMODAP networks. White circles indicate IGS permanent stations, black circles identify the stations used in this analysis, black triangles show other vertices not considered in the present computation.
2 Data analysis
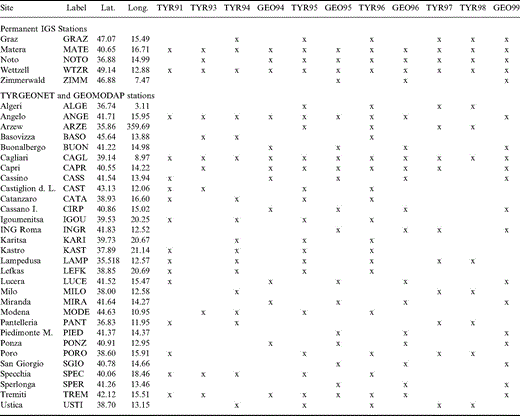
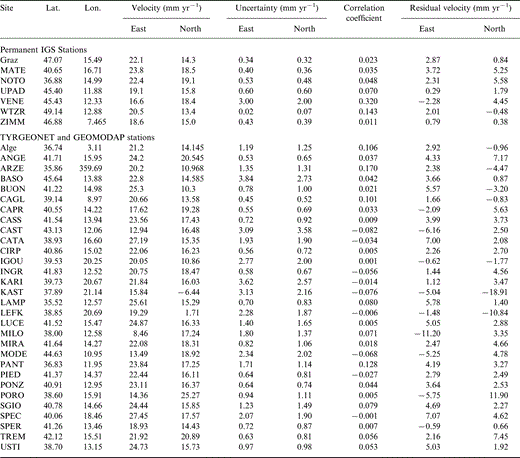
The first GPS measurements date back to 1991 and repeat campaigns were carried out in 1993, 1994, 1995, 1996, 1997, 1998 and 1999, during six to eight days of continuous observations, using dual‐frequency receivers at 30 s sampling rate. Although the whole network consists of more than 50 sites, in this paper we focus our attention on a subnetwork of 35 stations that were occupied simultaneously at least during three different campaigns from 1991 to 1999 ( Table 1). Among them, 30 sites have always been non‐permanent, three became permanent during this time interval (Matera, Noto and Wettzell) and the last two have been permanent since their inclusion in the network (Graz and Zimmerwald).
GPS data processing was performed using the Bernese software version 4.0 ( Rothacher & Mervart 1996). Precise ephemerides, satellite clock corrections, antenna height phase centre variations and other general files provided by CODE (Center of Orbit Determination in Europe) of Bern University were included in the computation. The ambiguity resolution was performed adopting the so‐called wide‐lane technique: first the wide‐lane linear combination is processed, resolving the L5 ambiguities, which are introduced as known in the subsequent run where the L3 linear combination is processed, resolving the narrow‐lane ambiguities. Absolute troposphere delay parameters every 4 hr were estimated for each station, starting from the Saastamoinen standard model.
Each daily session was processed separately, resolving the components of all the independent baselines, which span about 50–1000 km. All the session solutions pertaining to each campaign were adjusted by NETGPS, public‐domain software based on the least‐squares principle that adjusts the baseline Cartesian components and the corresponding covariance matrices pertaining to each observing session, starting from the approximate coordinates of the network sites ( Crespi 1996; Crespi & Riguzzi 1998). The reference frame is defined, including in the computation the ITRF96 coordinates of three or four IGS stations (GRAZ, MATE, NOTO and WTZR) (see Table 1), propagated to the mean epoch of the campaign, together with their uncertainties ( Boucher 1998).
Table 2 shows the mean accuracy of network adjustments in terms of the mean error (mean ellipse semi‐axis computed on the local tangent plane at the 95 per cent confidence level) for each campaign; the mean accuracy increased from 2.8 cm (1991) to few millimetres for the more recent campaigns. This improvement is essentially due to the development of the NAVSTAR‐GPS satellite configuration, the high accuracy of satellite orbit determinations and the progress of the receiver hardware. Moreover, the expansion of the IGS GPS tracking network, which started in Italy in 1994 with Matera (MATE) and improved in the years after NOTO, MEDI, CAGL and UPAD, contributed to improving the global orbit determinations and to the reduction of baseline lengths.
To show the behaviour of some sites better, we computed their temporal trend as time‐series of the station positions with the corresponding rms error, decomposed into the north and east components ( Fig. 4). Fig. 4 also shows the weighted best‐fit straight line for each component. Possible biases may be introduced by the 1991 results; we assume that this fact is due to the poor satellite configuration and orbit information, the short observing time and the reduced external constraints in the adjustment. On the other hand, any eventual residual bias should not change the results, taking into account that these data play a negligible role in the velocity field estimate, due to its low weight.

Time‐series of the north and east components for eight sites of the network; error bars indicate the rms error of each position. The weighted best‐fit straight line for each component is also shown.
Each campaign solution, consisting of the adjusted coordinates and the relative covariance matrices, given in the same reference system was jointly analysed to estimate the velocity field using the QOCA software (Quasi Observation Combination Analysis). This software, developed at the JPL ( Dong . 1998 ; Collier . 1988 ), works under the linear hypothesis at the first order of approximation, thus considering velocities to be constant in time, and solves, with a Kalman Filter approach, for site positions, velocities, network parameters and deformation parameters simultaneously, referring to a specified epoch. In order to introduce external constraints we fix the ITRF96 velocities of the same stations used for definition of the reference frame (GRAZ, MATE, NOTO and WTZR).
The increment of the scalar weighted sum of squared residuals, χ2, from adding new data and the increment in χ2 as the solution is propagated forwards (defined in the general case of Kalman filtering as δχ2) have been used to test the compatibility of different data sets. δχ2 has been used as an indicator of the deviation of the formal uncertainty from the real uncertainty and to rescale the a posteriori uncertainty of each data set ( Dong 1999). Finally, the a posteriori uncertainties of the estimated parameters have been rescaled using the normalized rms error of the final solution ( Dong . 1998 ).
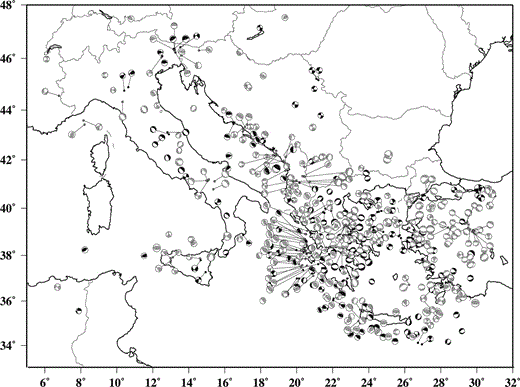
The final ITRF96 velocity solution of the whole network is listed in Table 3 together with the uncertainties and correlation coefficients. A rotation from ITRF96 to a ‘Eurasian fixed’ reference frame has been applied to the velocity field, adopting a rotation rate of 0.22° Ma−1 around a pole located at 48.1°N, 109.0°W ( Qiang . 1999 ); the residual velocities are listed in Table 3 and shown in Fig. 5.
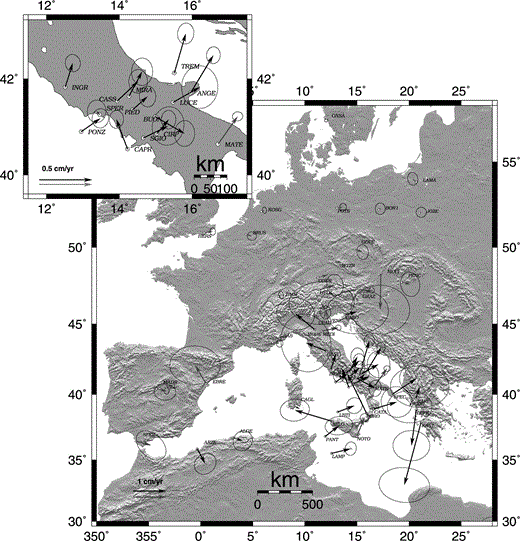
Residual velocities of the TYRGEONET and GEOMODAP stations (black arrows) and IGS stations (grey arrows) computed with respect to a Eurasian fixed reference frame. Error ellipses at 95 per cent confidence level.
It must be stressed that many slightly different Euler vector values have recently been estimated on the basis of geological and seismological data, such as Nuvel1A models (e.g. DeMets . 1994 ), or using space geodetic observations (e.g. Larson et al. 1997; Sillard et al. 1998; Cocard . 1999 ); starting from geodetic coordinates and velocities the result may strongly depend on the selection and the number of sites used in the computation. The model applied in this paper, ITRF96VEL, takes 80 sites to estimate the Euler vector of Eurasia, and adopts statistical criteria to remove unmatched sites in the plates.
Given the velocities and their accuracies of at least three stations, we can estimate the horizontal velocity gradient tensor L ( Malvern 1969) using an inverse problem,

where Δxi and Δyi are the east and north coordinates of the ith station relative to the centroid of the network. The velocities u and v are in the east and north directions, respectively, with the zero subscript denoting the velocity of the centroid. Finally, the four components Lij are the elements of the horizontal velocity gradient tensor L. The eigenvalues and eigenvectors of the strain rate tensor can then be calculated by the formulae in Feigl . (1990) . We applied this approach in the central‐southern Apennines (GEOMODAP network) in order to estimate the average strain rate over the whole area by solving the overdetermined problem for the 12 stations included in the network.
In order to evaluate the pattern of the strain rate in the same area we used a least‐squares inversion over a regular grid, starting from the station velocities and their accuracy, and solving for the velocity components, rotation rate and strain rate components; the method adopted is described in Shen . (1996) .
3 Possible geodynamic implications
The geodetic velocities shown in Fig. 5 may provide significant constraints on the kinematic pattern in terms of rigid block rotation poles and the deformation rate in the central Mediterranean area. However, the main problem is understanding the possible geodynamic meaning of each quantification tentatively carried out. For instance, any determination of a rotation pole is significant only when it may plausibly be assumed that the sites considered belong to the plate involved. On the other hand, the usefulness of strain estimates over large tectonic zones may be doubtful, since one can hardly understand whether the estimated average value relates to a diffuse deformation all over the zone or is instead accommodated in limited tectonic zones, where strain concentrates. Of course, the concept of a ‘large area’ depends on the degree of fracture of the zone considered. This degree is widely recognized to be very high in the central Mediterranean area, particularly with regard to the Apennine–Tyrrhenian system.
In the following we report some reflections on the significant information that, in our opinion, can be derived from the available geodetic data, in the light of the present tectonic knowledge of the study area.
3.1 African block
Four sites are located within the African lithological domain: ARZE, ALGE, LAMP and PANT. However, two of them, ARZE and ALGE, are located on the deformed African margin, i.e. the Maghrebian belt, which could be affected by local deformation. PANT is located within a tectonic zone, the Sicily channel, that has recently undergone (and is probably still undergoing) extension ( Finetti & Del Ben 1986; Reuther 1987). The only site lying in the undeformed African foreland is LAMP, which is, however, located very close to the troughs of the Sicily channel. These uncertainties on whether the above sites can be taken as belonging to the stable African block do not allow any precise interpretation of these data in terms of plate motion. In any case, it is remarkable to note that the trend of the LAMP vector does not confirm the predictions of the Africa–Eurasia kinematic models derived from north Atlantic data (e.g. Dewey . 1989 ; DeMets . 1990, 1994). However, one must be aware that a significant discrimination between different Africa–Eurasia kinematic models would require a longer observation period and, above all, some geodetic points lying well inside the undeformed African domain.
3.2 Sicily and Calabria
As clearly indicated by geological and seismotectonic studies ( Ghisetti & Vezzani 1982; Finetti & Del Ben 1986; Van Dijk & Okkes 1991; Tortorici . 1995 ), this zone has undergone the most intense tectonic activity in the central Mediterranean area during the last 1 Myr. The space–time distribution of the recent deformation indicates considerable crustal fragmentation. The occurrence of extensional tectonics in the Sicily channel implies relative motion between Sicily and Africa. A number of shear zones within the Sicily area ( Fig. 6), associated with neotectonic and seismic activity ( Finetti & Del Ben 1986; Grasso & Ben Avraham 1992; Reuther . 1993 ; Catalano . 1994 ), suggest considerable fragmentation of this African wedge. At least three major blocks, characterized by differential movements, may be recognized: the Ventura, Gela and Iblean, decoupled by the Sciacca and Scicli fault systems ( Fig. 6).
Two major shear zones, the Vulcano and Palinuro fault systems, allow decoupling between the Calabrian sector, escaping southeastwards, and the adjacent regions, i.e. the southern Apennines and Sicily (e.g. Finetti & Del Ben 1986; Van Dijk & Okkes 1991; Tortorici . 1995 ; Mantovani . 1997b ). Furthermore, during the last 1 Myr the Calabrian–Peloritani sector has undergone intense disruption and uplift, with the formation of several troughs, sphenocasms and transverse shear zones ( Ghisetti & Vezzani 1982; Ciaranfi . 1983 ; Sagnotti 1992; Bordoni & Valensise 1998).
The few geodetic vectors presently available in this area only allow some preliminary tentative considerations about the kinematic pattern. The Noto site belongs to the Iblean block, that is, the crustal wedge surrounded by the Siracusa escarpment, the Sicily channel and the Scicli fault system. Numerical modelling of the central‐eastern Mediterranean region ( Mantovani . 2000a ) has shown that the solution that allows one to match the observed strain pattern in the whole study area provides a picture of the kinematics of the Iblean block that is fairly consistent with the Noto vector given in Fig. 5.
The vector of Milo shows an anomalous trend with respect to the general NE trend of the other points in this zone. At present, it is not possible to understand whether this evidence is connected with local deformation or, instead, is representative of the differential kinematics of this sector of the Maghrebian belt with respect to the surrounding zones.
As regards Calabria, the divergence between PORO and CATA could be connected with the extensional deformation in the two major tectonic structures separating the two geodetic sites, i.e. the Mesima graben and the Catanzaro transtensional zone ( Ghisetti & Vezzani 1982; Finetti & Del Ben 1986; Van Dijk & Okkes 1991). A very tentative estimate of the extensional rate implied by the above two vectors provides a value of a few tenths of µstrains per year. However, a unique estimate appears to be insufficient for a significant evaluation of the strain regime in this area.
3.3 Corsica–Sardinia block
The CAGL vector indicates negligible motion of this site with respect to Eurasia. The very low seismicity and recent/present deformation observed in the Corsica–Sardinia continental fragment could imply that the CAGL vector may be taken as representative of the kinematics of the entire block. In this view, the insignificant motion of CAGL is confirmed by the analysis of GPS data collected in Corsica during 1994–1998 within the Alps Project ( Vigny . 1999 ). This evidence, however, does not necessarily imply that Corsica–Sardinia is closely connected with Eurasia.
3.4 Adriatic plate
Seven sites (SPEC, MATE, ANGE, TREM, VENE, UPAD and BASO) are located in the Adriatic lithological domain. The Matera vector is very similar, in terms of both trend and modulus, to those given by the VLBI and SLR techniques ( Ward 1994; Zarroa . 1994 ; Boucher 1998; Tomasi 1998; Bianco . 1998 ). The motion trends of SPEC, ANGE and TREM are consistent with that of MATE. Thus the motion of the southern part of the Adriatic block seems to be fairly well constrained. The kinematics of the northern Adriatic block, however, are poorly constrained, due to the large uncertainties affecting the vectors of BASO, UPAD and VENE. On the other hand, it can be noted that the trends of UPAD and VENE are consistent with the orientation of slip vectors derived from earthquake focal mechanisms and with the geometry of major thrust faults and transcurrent fault systems in the Eastern Alps, i.e. the Adriatic–Eurasia collision boundary ( Anderson & Jackson 1987; Slejko . 1989 ; Castellarin . 1992 ; Mantovani . 1997b ).
3.5 Northern Apennines
Geological, geophysical and palaeomagnetic observations suggest differential kinematics of this orogenic zone with respect to the adjacent Adriatic domain. In particular, post‐Pliocene deformation indicates roughly SW–NE shortening along the outer front of the belt, at the collision boundary with the Adriatic platform, and parallel tensional deformation in the internal side (e.g. Elter . 1975 ; Boccaletti . 1985 ; Castellarin & Vai 1986; Speranza . 1997 ; Montone . 1997 ). Furthermore, several transverse discontinuities have been hypothesized in this area (e.g. Castellarin & Vai 1986), which could allow relative motion between the various sectors of the belt. Neotectonic observations and seismic activity suggest that this kinematic pattern is still active (e.g. Boccaletti . 1985 ; Mantovani . 1997b ).
The velocity vectors of MODE, MEDI and CAST are not very consistent with the kinematics suggested by neotectonic information and also show a very poor internal coherence and large uncertainties, not allowing any significant geodetic constraints on the kinematics of this belt.
3.6 Southern Apennines
In this seismic area the relatively dense GEOMODAP network allows an analysis of local strain. 12 GPS sites located SW–NE across the southern Apennines were repeatedly occupied during four campaigns (1994, 1995, 1996 and 1999), allowing an estimate of the present‐day mean strain rate of the area. Data analysis provides a significant SW–NE extension with a strain rate of (0.021 ± 0.006) × 10−6 yr−1 (at the 1σ level) and a smaller perpendicular compressional component (of the order of 0.01 × 10−6 yr−1) characterized by a large error ( Fig. 7a). The direction of the tensional strain agrees with those deduced from fault plane solutions of earthquakes that occurred during the last century ( Jackson & McKenzie 1988), with seismic strain estimates derived from CMT solutions ( Pondrelli . 1995 ) and historical seismicity ( Selvaggi 1998) and with the results from borehole breakouts ( Montone . 1997 ). With regard to strain rate magnitudes, however, the different techniques suggest rather different values. CMT solutions provide a strain rate of about 0.005 × 10−6 yr−1, while historical seismicity gives values up to 0.06 × 10−6 yr−1. This large variability may be due to the different features of the data sets considered: the time spans of observations (85 yr for CMT, 400 yr for seismicity and 5 yr for GPS), the areas involved, and the number and threshold magnitudes of seismic events.
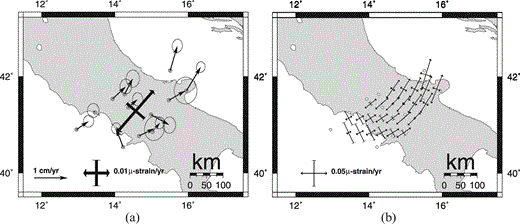
(a) Averaged strain rate estimate in the southern Apennines. Circles indicate geodetic stations and arrows the related velocity vectors with respect to a Eurasian fixed reference frame. (b) Horizontal principal strain rates inverted over a regular grid.
In order to provide information on the strain rate spatial gradient in the southern Apennines, Fig. 7(b) shows the pattern of principal strain rate axes along a roughly E–W belt. There is a progressive transition from dominant N–S compression to NE–SW extension moving from the Tyrrhenian to the Adriatic coast of Italy.
3.7 Greece
The western side of Greece, where the four stations KARI, IGOU, LEFK and KAST are located, corresponds to the collision border of the Aegean–Balkan system with the Adriatic and Ionian structural domains ( Fig. 1). The transition zone between these two domains is marked by the Kephallinia discontinuity, where the Hellenic units overthrust the Adriatic platform. The considerably different resistances that the westward‐drifting Aegean system encounters north and south of the Kephallinia discontinuity, due to the continental character of the Adriatic plate and the oceanic character of the Ionian basin, cause strong lateral variation in the kinematic behaviour of Greece. The northern part, facing the Adriatic, is characterized by low mobility, while the southern part (Peloponnesus) is involved in a relatively fast southwestward escape, at the expense of the Ionian lithosphere along the Hellenic trench (e.g. Underhill 1989; Hatzfeld 1993 ; Mantovani . 1997a ; Peter . 1998 ). The divergence between northern and southern Greece is accommodated by roughly N–S extension in central Greece, mainly in the Corinth Gulf.
The KAST and LEFK vectors indicate a rate of 12–17 mm yr−1 for the southwestward Peloponnesus escape. The IGOU and KARI vectors show poorly consistent trends and are furthermore affected by large uncertainties.
4 Conclusions
Some new constraints may be imposed on the kinematic pattern of the central Mediterranean area from geodetic measurements carried out in the time span 1991–1999.
The sites located in the African domain and southern Italy show a dominant NE to E trend. In particular, a general coherence can be seen between the motions of African sites and those of sites located in the southern Italian zones. This evidence is not consistent with the Nuvel‐1 kinematic model, which provides roughly NNW motion of the margin of Africa Mediterranean ( DeMets . 1994 ). However, the short observation period with respect to the average motion rates of this area and the lack of stations well inside the undeformed African domain do not allow us to estimate the actual geodynamic significance of this result.
The relatively high number of GPS sites in the southern Apennines allowed us to estimate significant NE–SW extension with a strain rate of (0.021 ± 0.006) × 10−6 yr−1 and a smaller, less significant, perpendicular shortening (of the order of 0.01 × 10−6 yr−1).
In Greece the two significant vectors indicate S to SW motion of the Peloponnesus at a rate of roughly 15 mm yr−1.
Acknowledgments
We are grateful to all the Agencies, Universities, technicians and single researchers involved in field surveys. The complete list is reported in Anzidei . (1995) . We also acknowledge C. Noll, product manager of the CDDIS, the CODE data centre of AIUB (Bern) and the GEODAF data archive of the Italian Space Agency (ASI) for providing GPS observations and related files. Thanks are due to Dr Z. K. Shen and Dr D. Dong for discussions on strain rate computation and data elaboration. This work was partially funded by the Italian Space Agency and by EC contract EV5V‐CT94‐0464. The maps were created using the Generic Mapping Tools (GMT) software ( Wessel & Smith 1995).
References





