The coevolution of flower longevity and self-fertilization in hermaphroditic plants

Xu, Kuangyi

doi:10.1111/evo.14303

Abstract

Self-fertilization, prevalent in plants, is typically divided into three modes – prior, competing, and delayed selfing – based on the timing in which it occurs. Flower longevity affects both the opportunity for pollination and the resources allocated for fertility, and thus may influence the selection on different modes of self-fertilization. Additionally, selfing causes fertilization to depend less on pollinators, which may also influence the evolution of flower longevity. Using game-theoretical models, I investigate how inbreeding depression and the pollination environment influences the coevolution of the three modes of self-fertilization with flower longevity. Invasion of prior selfing allows the subsequent evolution of shorter flower longevity, and thus is favored over competing selfing. Prior selfing can also invade even under high inbreeding depression when the pollen deposition rate is low, but is inhibited by a higher level of delayed selfing. In general, the evolution of selfing decreases flower longevity, and reveals asymmetric effects of pollen deposition and removal on flower longevity. This study suggests considering realization of selfing and outcrossing as concrete processes by incorporating flower reproductive strategies (e.g., flower longevity) and pollination ecology (e.g., accrual rate) may offer better understanding of the evolution of mating systems and flower reproductive traits.

Flower longevity, inbreeding, mating systems, plant reproduction, pollination biology, reproductive strategies

The evolution of mating systems, particularly, outcrossing and self-fertilization, constitutes one of the major evolutionary transitions in angiosperms (Stebbins 1974; Barret 2008; Barret 2013). Based on the timing of self-pollination relative to cross-pollination, Lloyd and Schoen (1992) classified self-fertilization into three modes: prior, competing, and delayed selfing. Prior selfing happens when anthers dehisce and stigmas become receptive before anthesis (here defined as the period when a flower is fully functional to allow outcross-pollination to happen), and the two pollinating surfaces are oriented to make contacts. Competing selfing refers to self-fertilization that occurs during anthesis when cross-pollination is happening simultaneously. It can be either autonomous, which does not require pollinators, or pollinator-dependent, which may result from geitonogamy (pollination between flowers within the same individual) or facilitated selfing (Schoen and Lloyd 1992). Delayed selfing happens after opportunities for outcrossing or pollen dispersal have passed, and can be accomplished through mechanisms like corolla abscission, style curvature, reduced herkogamy, or transient self-incompatibility (Goodwillie and Weber 2018).

From a genetic aspect, selfing automatically enjoys the advantage of transmitting 50% more alleles than outcrossing, since it transmits genes through both selfed and outcrossed offspring (Fisher 1941). However, it is opposed by inbreeding depression, which is the fitness reduction in selfed offspring compared to outcrossed offspring, as selfing exposes more recessive deleterious mutations in homozygotes. Classical models have shown that a higher level of competing selfing is favored when inbreeding depression is lower than 0.5, while the condition for prior selfing to invade depends on the outcrossing rate (Lloyd 1979; Lande and Schemske 1985). A more recent model shows that fluctuating pollination visitation rates can select for an intermediate level of prior selfing even under high inbreeding depression (Morgan and Wilson 2005). Unlike the other two types of selfing, delayed selfing can always invade (Lloyd 1979), because it happens after pollination and does not restrict the opportunity for ovules to be outcrossed. Moreover, delayed selfing can provide reproductive assurance when pollinators are lacking. Therefore, it is often regarded as a “best-of-both-worlds” strategy that allows plants to maximize their reproductive fitness (Becerra and Lloyd 1992; Lloyd 1992; Kalisz and Vogler 2003).

However, researchers rarely consider the ecological processes that affect how outcrossing and selfing are implemented and their influences on resource-allocation in floral reproductive strategies. Regarding the ecological aspect, one of the most important factors that affect the reproductive outcome is flower longevity, which has been found to have important effects on mating outcomes (Primack 1985; Sato 2002; Ashman 2004; Roddy et al. 2020). Since the arrival of pollinators is often unpredictable, an outcrossing flower needs to remain open for a certain period to allow the possibility of pollen deposition and removal. Although greater flower longevity can increase pollination opportunities for outcrossing, it imposes a cost because more resources and energy will be spent on the daily maintenance of flowers. Previous models and empirical studies have shown that greater flower longevity is selected for when the rates of pollen deposition and removal are low (Ashman and Schoen 1994; Schoen and Ashman 1995; Ashman 2004). However, these studies focus on predominantly outcrossing populations, and it is not clear how flower longevity interacts with the evolution of mating systems. For example, the evolution of selfing may select for shorter flower longevity because autonomous selfing does not require pollinators and it thus becomes less economical to maintain the flowers for a long period. An extreme case may be cleistogamy, that is, production of non-opening, self-pollinating flowers (Culley and Klooster 2007). On the other hand, decreased flower longevity may allow more energy to be allocated to seed reproduction, which may compensate for the fitness cost of selfing due to inbreeding depression. Indeed, selfing and flower longevity may coevolve with each other. For example, in Leptosiphon jepsonii, a population that evolved a higher level of delayed selfing also shows increased flower longevity (Weber and Goodwillie 2009).

Although the evolution of mating systems has been intensively studied, the effects of floral reproductive strategies and pollination environment are rarely considered (reviewed in Goodwillie et al. 2005, but see Sakai 1995). Therefore, here I use the evolutionary game theory (Maynard Smith 1982) to study the coevolution of flower longevity and the three modes of self-fertilization. In the model, the pollination process is explicitly divided into two aspects: the rate of pollen deposition and ovule fertilization (female fitness accrual rate), and the rate at which pollen is disseminated and enters into the pollen pool to fertilize ovules of other individuals (male fitness accrual rate). The effects of inbreeding depression, and female and male fitness accrual rates on the coevolutionary pattern are investigated.

Model

I assume a hermaphroditic population, where each flower produces equal amounts of pollen and numbers of ovules. Female and male fitness accrual rates are denoted as $g$ and $p$ ⁠. It should be noted that female fitness accrual rate in the model includes both self-pollination (geitonogamy, facilitated selfing and autonomous competing selfing) and outcrossing during anthesis. Throughout the paper, I assume both female and male accrual rates do not change over time.

I assume the amount of pollen is large enough so that the cost of the pollen consumed by self-fertilization can be ignored (i.e., there is no pollen discounting, Porcher and Lande 2005). Figure 1 illustrates how ovules in a flower will be fertilized over time. For prior selfing before anthesis, an individual plant will self-fertilize a proportion

u

of its ovules. During floral anthesis, outcrossing happens at the same time as self-pollination. According to previous classification of modes of self-fertilization, selfing in the anthesis stage can be accomplished through geitonogamy, facilitated self-fertilization and autonomous competing selfing (Lloyd and Schoen 1992), and a proportion of

R

of ovules will be outcrossed out of all fertilized ovules during the stage of anthesis. Following previous empirical evidence (e.g., Harder and Thomson 1989, and refs. in Harder and Wilson 1994) and models (Harder and Wilson 1994; Schoen and Ashman 1996), the proportion of female fitness accrued through outcrossing

G_{T}

in a flower with longevity

T

is modeled as

\begin{matrix} G_{T} (T) = R G_{P} (T) = R (1 - u) (1 - e^{- g T}), \end{matrix}

1

where

G_{P} = (1 - u) (1 - e^{- g T})

is the female fitness accrued during open pollination. The proportion of outcrossing

R

may be regulated through mechanisms like herkogamy or dichogamy. Since there is no pollen discounting, the proportion of pollen disseminated by a flower with longevity

T

is simply

P (T) = 1 - e^{- p T} .

2

I assume flower senescence happens right after the action of delayed selfing. In real populations, this assumption is reasonable for species that perform delayed selfing through flower abscission or wilting (e.g., Sun et al. 2005; Orozco-Ibarrola et al. 2015; for a review, see Goodwillie and Weber 2018). This assumption may not strictly hold for some mechanisms of delayed selfing like transient self-incompatibility or reduced herkogamy, in which the process of delayed selfing may last for several days (Weber and Goodwillie 2009; Duan et al. 2010). However, most of the delayed selfing happens in the late stage of the floral life span, and spans only a relatively short period compared to the whole life span of the flower. Given this assumption, it is easy to see that a higher proportion of delayed selfing will always be favored, since there is no cost. Moreover, many mechanisms of delayed selfing (e.g., flower abscission) may not be able to fertilize all the ovules remaining unfertilized through delayed selfing. Therefore, I assume delayed selfing will only fertilize at most a proportion

l

(⁠

0 \leq l \leq 1

⁠) of the ovules remaining unfertilized.

Figure 1

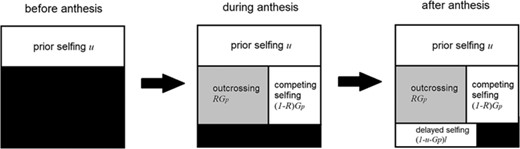
A schematic plot that shows how ovules in a flower will be fertilized. Ovules remaining unfertilized are colored black, and ovules that are selfed and outcrossed are colored white and grey, respectively.

Open in new tab Download slide

In a population dominated by individuals that have a prior selfing rate

u

⁠, an outcrossing proportion

R

and a flower longevity

T

(henceforth I use

{u, R, T}

to denote this combination of strategies), the expected total fitness a single flower will achieve is (Charnov 2020)

\begin{matrix} w = 2 G_{T} + 2 (1 - d) (u + (1 - R) G_{P} + l (1 - u - G_{P})) . \end{matrix}

3

The first term is fitness contributed from outcrossing, and it is

2 G_{T}

because on average, an individual will have

G_{T}

ovules fertilized and its pollen will fertilize

G_{T}

ovules. The second term represents the fitness from self-fertilization, and the three terms in the parenthesis respectively capture the female fitness accrued from prior selfing, selfing during anthesis and delayed selfing. The parameter

d

represents inbreeding depression, defined as the fitness reduction of selfed offspring relative to those produced by outcrossing (Charlesworth and Willis 2009). As in previous game theory models (e.g., Lloyd 1992, Lande and Schemske 1985; Huang and Burd 2019), the model does not consider the evolution of inbreeding depression, so I fix

d

to be a constant parameter.

Suppose there is a rare mutant individual which has a different strategy combination

{u^{'}, R^{'}, T^{'}}

⁠. Therefore, the fitness accrued by a single flower of the mutant individual is

\begin{matrix} w^{'} & = & G_{T}^{'} + \frac{P^{'}}{P} G_{T} + 2 (1 - d) (u^{'} + (1 - R^{'}) G_{P}^{'} \\ + l (1 - u^{'} - G_{P}^{'})), \end{matrix}

4

where

{G_{T}}^{'}

is the female fitness of a single mutant flower accrued through outcrossing, while

P

and

P^{'}

are male fitness accrued by a resident and mutant flower.

G_{T}^{'} + G_{T} P^{'} / P

is the fitness accrued through outcrossing.

For each individual plant, the number of flowers

F

it can produce is constrained by the cost of flower construction and daily maintenance as (Ashman and Schoen 1994)

F = \frac{K}{c (1 + m T)},

5

where

K

in equation (5) is the total reproductive resources available for flower construction and maintenance.

c

is the cost for the construction of a single flower, and

m

is the daily cost of floral maintenance relative to the construction cost. Therefore, the total fitness of the mutant individual relative to the resident after a flower season is

W = \frac{F^{'}}{F} \frac{w^{'}}{w} = \frac{1 + m T}{1 + m T^{'}} \frac{1}{2} (\tilde{G} + \tilde{P}),

6

where

\tilde{G}

and

\tilde{P}

are the relative female and male fitness, given by

\tilde{G} = \frac{G_{T}^{'} + (1 - d) (u^{'} + (1 - R^{'}) G_{P}^{'} + l (1 - u^{'} - G_{P}^{'}))}{G_{T} + (1 - d) (u + (1 - R) G_{P} + l (1 - u - G_{P}))},

7a

\tilde{P} = \frac{\frac{P^{'}}{P} G_{T}^{'} + (1 - d) (u^{'} + (1 - R^{'}) G_{P}^{'} + l (1 - u^{'} - G_{P}^{'}))}{G_{T} + (1 - d) (u + (1 - R) G_{P} + l (1 - u - G_{P}))} .

7b

To find the evolutionarily stable strategy (ESS) (Maynard Smith 1982), I assume the mutant strategy

{u^{'}, R^{'}, T^{'}}

only differs from the resident at one phenotype at a time. Biologically, this assumption means that double mutations are rare and unlikely. It will be shown in the result section that the ESS does not depend on whether or not each phenotype evolves to its ESS before another of the phenotypes evolves. The ESS flower longevity

T^{*}

is found by applying the ESS condition

\frac{\partial W}{\partial T^{'}} |_{\{u^{'}, R^{'}, T^{'}\} = \{u, R, T\}} = 0,

8a

\frac{\partial^{2} W}{\partial {T^{'}}^{2}} |_{\{u^{'}, R^{'}, T^{'}\} = \{u, R, T\}} < 0 .

8b

However, ESS of

u

and

R

cannot be found by this method because

\partial W / \partial u

and

\partial W / \partial R

do not have 0 point (see Supporting Information). Therefore, the ESS of

u

and

R

will be found by invasion analysis (see Results section).

Results

Here, I first show the conditions for the evolution of competing, prior and delayed selfing, and then investigate how selfing influences the evolution of flower longevity. The key results are summarized in Table 1.

Table 1

Open in new tab

Summary of the key model results. $u$ is the proportion of prior selfing, and $R$ is the proportion of outcrossed ovules during anthesis, and $l$ measures the efficacy of delayed selfing. Note that there is no distinguish between prior, competing and delayed selfing when { $u^{*} = 1, R^{*} = 0, T^{*} = 0$ }

inbreeding depression $d < 0.5$	inbreeding depression $d > 0.5$	ESS flower longevity	selfing rate at the ESS state
The ESS is complete prior selfing, non-opening flowers{ $u^{} = 1, R^{} = 0, T^{} = 0$ } (cleistogamy). However, this ESS may not directly invade into an outcrossing population, but { $u = 1, R = 0, T > 0$ } will first invade and then the ESS { $u^{} = 1, R^{} = 0, T^{} = 0$ } can invade into { $u = 1, R = 0, T > 0$ }.	When male fitness accrual rate is low and female fitness accrual rate is high, the ESS is ${u^{} = 1, R^{} = 0, T^{} = 0}$ ⁠, especially when $l$ is small; otherwise, the ESS is outcrossing, open flowers { $u^{} = 0, R^{} = 1, T^{} > 0$ }.	1. A larger $l$ decreases $T^{}$ 2. $T^{}$ is determined more by the male fitness accrual rate 3. When $l$ is large, $T^{*}$ may increase with the female fitness accrual rate.	Selfing rate at the ESS state increases with the male fitness accrual rate, decreases with the female fitness accrual rate

inbreeding depression $d < 0.5$	inbreeding depression $d > 0.5$	ESS flower longevity	selfing rate at the ESS state
The ESS is complete prior selfing, non-opening flowers{ $u^{} = 1, R^{} = 0, T^{} = 0$ } (cleistogamy). However, this ESS may not directly invade into an outcrossing population, but { $u = 1, R = 0, T > 0$ } will first invade and then the ESS { $u^{} = 1, R^{} = 0, T^{} = 0$ } can invade into { $u = 1, R = 0, T > 0$ }.	When male fitness accrual rate is low and female fitness accrual rate is high, the ESS is ${u^{} = 1, R^{} = 0, T^{} = 0}$ ⁠, especially when $l$ is small; otherwise, the ESS is outcrossing, open flowers { $u^{} = 0, R^{} = 1, T^{} > 0$ }.	1. A larger $l$ decreases $T^{}$ 2. $T^{}$ is determined more by the male fitness accrual rate 3. When $l$ is large, $T^{*}$ may increase with the female fitness accrual rate.	Selfing rate at the ESS state increases with the male fitness accrual rate, decreases with the female fitness accrual rate

Table 1

Open in new tab

Summary of the key model results. $u$ is the proportion of prior selfing, and $R$ is the proportion of outcrossed ovules during anthesis, and $l$ measures the efficacy of delayed selfing. Note that there is no distinguish between prior, competing and delayed selfing when { $u^{*} = 1, R^{*} = 0, T^{*} = 0$ }

inbreeding depression $d < 0.5$	inbreeding depression $d > 0.5$	ESS flower longevity	selfing rate at the ESS state
The ESS is complete prior selfing, non-opening flowers{ $u^{} = 1, R^{} = 0, T^{} = 0$ } (cleistogamy). However, this ESS may not directly invade into an outcrossing population, but { $u = 1, R = 0, T > 0$ } will first invade and then the ESS { $u^{} = 1, R^{} = 0, T^{} = 0$ } can invade into { $u = 1, R = 0, T > 0$ }.	When male fitness accrual rate is low and female fitness accrual rate is high, the ESS is ${u^{} = 1, R^{} = 0, T^{} = 0}$ ⁠, especially when $l$ is small; otherwise, the ESS is outcrossing, open flowers { $u^{} = 0, R^{} = 1, T^{} > 0$ }.	1. A larger $l$ decreases $T^{}$ 2. $T^{}$ is determined more by the male fitness accrual rate 3. When $l$ is large, $T^{*}$ may increase with the female fitness accrual rate.	Selfing rate at the ESS state increases with the male fitness accrual rate, decreases with the female fitness accrual rate

inbreeding depression $d < 0.5$	inbreeding depression $d > 0.5$	ESS flower longevity	selfing rate at the ESS state
The ESS is complete prior selfing, non-opening flowers{ $u^{} = 1, R^{} = 0, T^{} = 0$ } (cleistogamy). However, this ESS may not directly invade into an outcrossing population, but { $u = 1, R = 0, T > 0$ } will first invade and then the ESS { $u^{} = 1, R^{} = 0, T^{} = 0$ } can invade into { $u = 1, R = 0, T > 0$ }.	When male fitness accrual rate is low and female fitness accrual rate is high, the ESS is ${u^{} = 1, R^{} = 0, T^{} = 0}$ ⁠, especially when $l$ is small; otherwise, the ESS is outcrossing, open flowers { $u^{} = 0, R^{} = 1, T^{} > 0$ }.	1. A larger $l$ decreases $T^{}$ 2. $T^{}$ is determined more by the male fitness accrual rate 3. When $l$ is large, $T^{*}$ may increase with the female fitness accrual rate.	Selfing rate at the ESS state increases with the male fitness accrual rate, decreases with the female fitness accrual rate

ESS OF OUTCROSSING PROPORTION (⁠ $R$ ⁠) DURING COMPETING SELFING

First, I investigate the ESS state of the outcrossing proportion

R

⁠. When the resident and mutant individuals have the same prior selfing rate and flower longevity (i.e.,

u^{'} = u, T^{'} = T

⁠), but have different outcrossing proportions

R

and

R^{'}

⁠, after some simplification of equation (6), the relative fitness of the mutant individual is

W = 1 + \frac{e^{- g T} (1 - u) (1 - e^{- g T})}{w} (2 d - 1) (R^{'} - R) .

9

Clearly, when inbreeding depression

d < 0.5

⁠,

W

will be greater than 1 if

R^{'} < R

⁠, so a lower outcrossing proportion will always be favored, while when

d > 0.5

⁠, a higher outcrossing proportion will invade. As a result, if the outcrossing proportion

R

can vary from 0 to 1, such as when individuals can completely avoid self-fertilization or outcrossing during anthesis, then the ESS value of

R

is 1 for

d > 0.5

⁠, while 0 for

d < 0.5

⁠.

ESS OF THE PROPORTION OF PRIOR SELFING (⁠ $u$ ⁠)

Next, let us focus on the evolution of the proportion of prior selfing

u

⁠. Since both resident and mutant individuals have the same outcrossing proportion

R

and longevity

T

⁠, the relative fitness of the mutant given in equation (6) becomes

\begin{matrix} W = 1 + \frac{e^{- g t} [(1 - 2 d) R (1 - e^{- g T}) + 2 (1 - d) (1 - l)]}{w} (u^{'} - u) . \end{matrix}

10

When

d < 0.5

⁠, it is clear that

W > 1

when

u^{'} > u

⁠, thus a higher level of prior selfing will be favored and the ESS is

u^{*} = 1 .

Moreover, this invasion condition holds for any value of

R

⁠, which means the evolution of prior selfing does not depend on the level of competing selfing that is already in the population.

Recalling that when $d < 0.5$ ⁠, a higher level of competing selfing $R$ will also invade, it is interesting to note that because the evolution of prior selfing (⁠ $u = 1$ ⁠) will cause all of the ovules to be self-fertilized before anthesis, the evolution of competing selfing will become irrelevant in these cases. When over time this mutant with complete prior selfing dominates the population, a shorter flower longevity (a smaller value of $T$ ⁠) will invade due to its lower maintenance cost. As a result, when $d < 0.5$ ⁠, the ESS strategy will be { $u^{*} = 1, R^{*} = 0, T^{*} = 0$ }. Biologically, it means complete prior selfing with a flower longevity of 0, that is, cleistogamy.

Nevertheless, even under low inbreeding depression (⁠ $d < 0.5$ ⁠), it should be emphasized that a cleistogamous mutant with strategy { $u^{'} = 1, R^{'} = 0, T^{'} = 0$ } will not necessarily invade a predominantly outcrossing population. For example, consider that a cleistogamous mutant arises in a completely outcrossing population with longevity $T$ (where T > 0). Based on equations (6), (7a) and (7b), the relative fitness of the mutant is $W = (1 + m T) (1 - d) / G_{T}$ ⁠. Even under low inbreeding depression (e.g., $d = 0.2$ ⁠), as long as the maintenance cost is small and fitness accrual rate is high enough (e.g., $m = 0.02$ ⁠, $g = 1$ ⁠, $T = 1$ ⁠), the mutant cannot invade as the relative fitness $W < 1$ ⁠. Therefore, evolution toward cleistogamy may often be step-wise. Initially, individuals with a higher level of prior selfing will invade, provided that they have a similar level of flower longevity, which allows the pollen disseminated by the plant to fertilize outcrossing residents; only through pollen dissemination does the mutant enjoy the “transmission advantage” of self-fertilization (Fisher 1941). After individuals with a high prior selfing rate dominates the population, a shorter level of flower longevity can easily invade.

When

d > 0.5

⁠, generally it is not easy to analytically determine whether a higher level of prior selfing

u

will be favored or not. However, invasibility analysis is possible for the special case when delayed selfing is able to fertilize all the remaining ovules, that is,

l = 1

⁠. When

l = 1

⁠, equations (3) and (4) become

w = 2 G_{T} + 2 (1 - d) (1 - G_{T}),

11a

w^{'} = G_{T}^{'} + \frac{P^{'}}{P} G_{T} + 2 (1 - d) (1 - G_{T}^{'}) .

11b

Substituing equations (11a) and (11b) into equation (6), the relative fitness of the mutant becomes

W = 1 + \frac{(1 - 2 d) (1 - e^{- g t}) R}{w} (u^{'} - u) .

12

Therefore, when

d > 0.5

⁠, a lower rate of prior selfing is favored and the ESS is

u^{*} = 0

⁠. Previous model (Lloyd 1979) shows that the condition for a higher level of prior selfing to invade is

d < 1 - R / 2

⁠, so that prior selfing can invade even when inbreeding depression

d > 0.5

⁠. The current results differ from Lloyd's model because the current model incorporates the coevolution of delayed self-fertilization and flower longevity.

In the above analyses, the ESS does not depend on the order of invasion. In other words, the ESS will be the same no matter whether each phenotype evolves to its ESS before another evolves or not. This is because the invasion conditions (equations (9), (10) and (12)) do not depend on the value of the other phenotypes. For example, for the invasion condition of $R$ in equation (9), the term that involves $u$ and $T$ is always positive for all values of $u$ and $T$ ⁠, so whether a larger $R$ will invade only depend on $d$ ⁠.

COEVOLUTION OF FLOWER LONGEVITY WITH SELF-FERTILIZATION

When delayed selfing can fertilize all remaining ovules (⁠ $l = 1$ ⁠)

In the previous section, it has been shown that when $d > 0.5$ and $l = 1$ ⁠, a higher rate of prior and competing selfing cannot invade. In other words, the ESS strategy is $u^{*} = 0, R^{*} = 1$ ⁠, so the phenotypic space { $u, R, T$ } is reduced to a one-dimensional space of longevity $T$ ⁠. Here, I show how delayed selfing can influence the evolution of flower longevity. For the special case when inbreeding depression $d = 1$ ⁠, no selfed seeds can survive to the next generation, so effectively, there is no delayed selfing. Since the population is effectively outcrossing, we return to the previous results obtained by Ashman and Schoen (1994), and as shown in Fig. 2A, the effects of female or male fitness accrual rates on flower longevity are symmetrical, and a higher female or male fitness accrual rate selects for a shorter flower longevity.

Figure 2

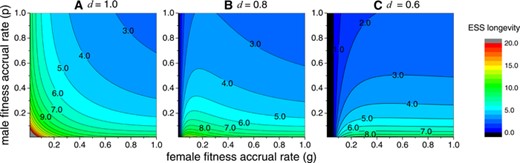
ESS flower longevity under different female and male fitness accrual rates when delayed selfing fertilizes all the remaining ovules (⁠ $l = 1$ ⁠). The three panels (A), (B), and (C), respectively, show results under different levels of inbreeding depression $d = 1, 0.8$ ⁠, and $0.6$ ⁠. The color bar shows different levels of ESS longevity, and $T >$ 20 is colored grey. For all panels, $m = 0.1$ ⁠.

Open in new tab Download slide

When $d < 1$ ⁠, delayed selfing becomes effective. Given the same level of female and male fitness accrual rates, a lower inbreeding depression $d$ always results in a shorter flower longevity, which can be seen by comparing panel (A) with panels (B) and (C) in Fig. 2. This is easy to understand—when inbreeding depression is lower, selfing is more advantageous, and thus an individual is less likely to maintain flowers longer to wait for outcrossing.

Moreover, the incorporation of delayed selfing also changes the effects of the fitness accrual rate on flower longevity. When inbreeding depression is moderately high (⁠ $d = 0.8$ ⁠), a higher female fitness accrual rate may even increase the ESS longevity. In Fig. 2B, for a fixed male fitness accrual rate, ESS flower longevity first increases with female fitness accrual rate $g$ but later decreases when $g$ gets large. Moreover, as inbreeding depression becomes lower (⁠ $d = 0.6$ ⁠) in Fig. 2C, flower longevity generally monotonically increases with female fitness accrual rate $g$ and converges to a certain value. In contrast, flower longevity is more sensitive to the male fitness accrual rate and decreases as the male fitness accrual rate gets larger. It should be noted that in panels (b) and (c), the ESS longevity is $T^{*} = 0$ when the female fitness accrual rate is quite small. In this case, there is no distinction between prior, competing and delayed self-fertilization.

The effect of delayed selfing on reducing flower longevity even under high inbreeding depression (⁠ $d > 0.5$ ⁠) can be explained by performing some analysis on the relative fitness. Suppose a mutant has a shorter flower longevity than the residents (⁠ $T^{'} < T$ ⁠). Certainly, since the residents open their flowers for a longer time, the female and male fitness accrued by the mutant will always be lower than those of the resident, irrespective of whether there is self-fertilization or not. However, compared to the case of no delayed selfing, the relative female and male fitness of the mutant individual will be larger when there is delayed selfing. Moreover, when female fitness accrual rate is high so that only few ovules will remain unfertilized at the time of flower senescence, the beneficial effects from delayed selfing become less prominent since the female fitness $G_{T}$ and $G_{T}^{'}$ is already large. As a result, in Fig. 2, delayed self-fertilization becomes less efficient in lowering ESS flower longevity when the female fitness accrual rate is high.

Delayed selfing and flower longevity co-determine the selfing rate of the flower, here defined as the proportion of self-fertilized seeds out of the total fertilized seeds. When there is delayed selfing, the selfing rate is determined by both flower longevity and the female fitness accrual rate. As shown in Fig. 3, generally, a high selfing rate is found when female fitness accrual rate is low while male fitness accrual rate is high, which corresponds to the condition when delayed selfing results in a short flower longevity in Fig. 2. On the other hand, most ovules will be outcrossed under high female fitness accrual rate and low male fitness accrual rate, and this is the situation when a longer flower life span is favored in Fig. 2. However, selfing rate is more sensitive to the rate of pollen deposition (female fitness accrual rate), rather than the rate of pollen removal (male fitness accrual rate). Moreover, comparing Fig. 3A and B, it can be seen that lower inbreeding depression will increase selfing rate. This is because lower inbreeding depression lowers the ESS flower longevity, so there will be fewer outcrossed ovules.

Figure 3

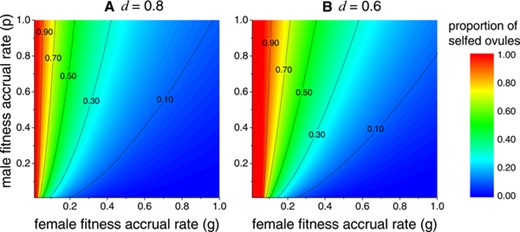
Proportion of selfed ovules under ESS flower longevity at different female and male fitness accrual rates when delayed selfing fertilizes all the remaining ovules (⁠ $l = 1$ ⁠). Panels (A) and (B) respectively show results when inbreeding depression $d = 0.8$ and $0.6$ ⁠. The color bar shows different level of selfing rate, which is the proportion of selfed ovules out of total fertilized ovules. For all panels, $m = 0.1$ ⁠.

Open in new tab Download slide

When delayed selfing cannot fertilize all remaining ovules (⁠ $l < 1$ ⁠)

When delayed selfing cannot fertilize all the remaining ovules (⁠ $l < 1$ ⁠) and $d > 0.5$ ⁠, a higher outcrossing proportion $R$ will always invade (see equations (8a) and (8b)), irrespective of the values of $T$ and $u$ ⁠. Therefore, I can always set $R = 1$ ⁠, so that the phenotypic space of is reduced to two dimensions, that is, $u$ and $T$ ⁠. Equation (9) shows that given a certain value of $T$ ⁠, the ESS prior selfing rate can only be either $u^{*} = 0$ or $u^{*} = 1$ ⁠. Therefore, I can first find the ESS flower longevity conditioned on $u = 0$ based on equation (8), denoted as $T_{u = 0}^{*}$ (the subscription indicates it is conditioned on $u = 0$ ⁠), and then set $T = T_{u = 0}^{*}$ and apply the invasion condition given by equation (9) to see whether a higher prior selfing rate $u$ will invade or not. If a higher $u$ is not favored at $T = T_{u = 0}^{*}$ ⁠, then the ESS strategy is { $u^{*} = 0$ ⁠, $R^{*} = 1, T^{*} = T_{u = 0}^{*}$ }. If a higher $u$ is favored, the ESS strategy is { $u^{*} = 1, R^{*} = 0,$ $T^{*} = 0$ }.

Figure 4 shows ESS flower longevity at different levels of inbreeding depression $d$ and proportions of delayed self-fertilization $l$ ⁠. Generally, { $u^{*} = 1, R^{*} = 0, T^{*} = 0$ } will be the ESS when female fitness accrual rate is low while male fitness accrual rate is high (the black area). In this case, due to rare pollen deposition, outcrossing is inefficient to set seeds. On the other hand, a high selfing rate is more advantageous when pollen removal is frequent because selfing individuals can disseminate more pollen to fertilize outcrossing individuals (i.e., a greater transmission advantage).

Figure 4

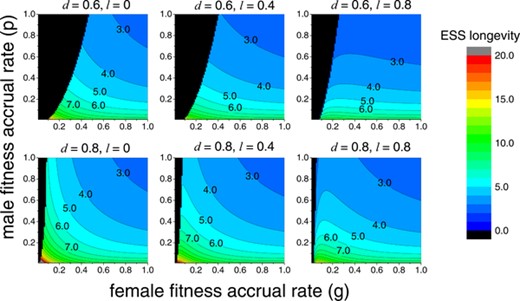
Effects of female and male fitness on ESS flower longevity under coevolution of self-fertilization and flower longevity. The ESS in the black area is ${u^{*} = 1, R^{*} = 0, T^{*} = 0}$ ⁠, and is ${u^{*} = 0, R^{*} = 1, T^{*} > 0}$ in the colored area. Panels show results at different levels of inbreeding depression (⁠ $d = 0.6, 0.8$ ⁠) and delayed selfing rates (⁠ $l = 0, 0.4, 0.8$ ⁠). For all panels, $m = 0.1$ ⁠.

Open in new tab Download slide

To examine the effects of inbreeding depression, by comparing panels with the same value of $l$ ⁠, it can be seen that the strategy { $u^{*} = 1, R^{*} = 0, T^{*} = 0$ } is more likely to be ESS under a lower level of inbreeding depression, since self-fertilization should enjoy more benefits when inbreeding depression is low. Moreover, comparing panels with different values of $l$ ⁠, it can be seen that { $u^{*} = 1, R^{*} = 0, T^{*} = 0$ } is less likely to be an ESS when delayed selfing is able to fertilize a larger proportion of the remaining ovules. Furthermore, within the parameter space in which { $u^{*} = 1, R^{*} = 0, T^{*} = 0$ } is not an ESS (colored area), a higher value of $l$ decreases ESS flower longevity, because a stronger ability of fertilizing ovules through delayed selfing should select for a shorter flower life span spent waiting for outcrossing pollination.

Discussion

How the evolution of different modes of selfing (i.e., prior, competing, and delayed selfing) interacts with floral reproductive strategies and the pollination environment is often poorly understood. This study examines the coevolution of the three modes of self-fertilization with flower longevity, and explores how they are regulated by genetic and ecological factors including inbreeding depression and the rate of pollen deposition and removal. Unlike previous models that separately consider the evolution of different modes of selfing (Lloyd 1979; Morgan and Wilson 2005), the coevolutionary model shows that the evolution of one mode of selfing may prevent the evolution of other modes. When inbreeding depression is low, evolution of prior selfing will replace competing selfing, as the latter requires daily flower maintenance; while when inbreeding depression is high, a higher level of delayed selfing will prevent the evolution of prior selfing. On the other hand, the incorporation of selfing in the model unveils the asymmetric effects of pollen deposition and removal on the evolution of flower longevity, which is not apparent in previous models that assume an outcrossing population (Ashman and Schoen 1994). Specifically, flower longevity is much more sensitive to the rate of pollen removal than to the rate of pollen deposition, and may increase, rather than decrease, with the rate of pollen deposition.

This study also bridges factors that initially seem unrelated. Although the rates of pollen deposition and removal directly affect the evolution of flower longevity, the model shows they can indirectly regulate the evolution of different modes of self-fertilization (Figs. 2 and 4), as well as the selfing rate, which increases with the pollen deposition rate but decreases with the pollen removal rate (Fig. 3). Therefore, it may be valuable to divide the measurements of pollinator visitation rates into the rate of pollen deposition and removal in empirical studies. Similarly, although inbreeding depression directly affects the evolution of selfing, it also indirectly affects flower longevity (Fig. 4).

EVOLUTION OF CLEISTOGAMY

The current model shows that under low inbreeding depression, although both prior and competing selfing are favored, the evolution of prior selfing allows for the later evolution of shorter flower longevity, and finally reach an ESS with complete selfing and 0 flower longevity. Biologically, this ESS state is similar to cleistogamy, that is, the production of permanently closed, self-pollinated flowers. However, it is shown that cleistogamy sometimes cannot directly invade an outcrossing population because of pollen discounting. However, note that pollen discounting in the current model is not due to the consumption of pollen by self-fertilization, but due to short flower longevity.

Cleistogamy has been shown to be present across more than 50 families (Culley and Klooster 2007). Although previous study found cleistogamous flowers appear when pollinators are less frequent (Bennington and McGraw 1995), the current model indicates that cleistogamy is most likely to evolve under a low pollen deposition rate and a high rate of pollen dissemination (Fig. 3). Therefore, a future study that explicitly distinguishes between the two components of pollination may offer better understanding of the evolution of cleistogamy.

The prediction that cleistogamy will be favored under lower inbreeding depression is consistent with the results of previous models (Schoen and Lloyd 1984; Masuda et al. 2001). However, in populations with low inbreeding depression, complete cleistogamy is not common; instead many populations can produce both cleistogamous and open-pollinated flowers (Culley and Klooster 2007; Koontz et al. 2017). This can be due to several factors. First, populations may not be at an evolutionary equilibrium. As discussed previously, cleistogamy often cannot directly invade into an open-pollinated population, but populations will first evolve a higher selfing rate before flower longevity decreases. Second, spatial or temporal variation in pollinator visitation may favor the maintenance of open-pollinated flowers to set more outcrossed seeds and avoid inbreeding depression (Lloyd 1984; Schoen and Lloyd 1984).

COEVOLUTION OF FLOWER LONGEVITY AND SELF-FERTILIZATION

The model predicts that selfing will always decrease flower longevity, which is supported by meta-analysis. Using data from 52 species of annual crucifers, Kunin and Shmida (1997) found outcrossing species generally had a flower life span 25% longer than inbreeding species. Under low inbreeding depression in which outcrossing is favored, it is expected that unavoidable competing selfing due to geitonogamy in self-compatible species would select for shorter-lived flowers (Primack 1985).

The finding that prior self-fertilization can be ESS even under high levels of inbreeding depression when female fitness accrual rate is low may help explain high levels of inbreeding depression in some populations with intermediate or high selfing rates (Husband and Schemske 1996; Winn et al. 2011). A test of this prediction requires more detailed measurements of different modes of self-fertilization, pollination history, flower longevity and inbreeding depression. Moreover, due to the purging of deleterious alleles and thus lower inbreeding depression, prior selfing may finally dominate a population.

Although flower longevity has been frequently studied, there is not much direct evidence regarding how different modes of self-fertilization coevolve with flower longevity. In the annual plant species Leptosiphon jepsonii, individuals usually perform delayed selfing through transient self-incompatibility, in which flowers initially reject self-pollen but become self-compatible 1 or 2 days later. However, Goodwillie and Ness (2005) found variation in the timing of self-compatibility within 17 populations, where some individuals were fully self-compatible at the initial stage of flower anthesis, thus allowing for prior selfing. Moreover, the frequency of these initially self-compatible individuals varied among populations, ranging from 3.2% to 71.0%. Results from the current model suggest that the invasion of early self-compatibility may be associated with the pollination environment leading to a low female fitness accrual rate, or because delayed selfing through transient self-incompatibility does not allow complete reproductive assurance.

The model prediction in Fig. 3 that a higher rate of pollen deposition will inhibit the evolution of prior selfingseems to be supported by previous empirical evidence. A following study by Weber and Goodwillie (2009) simultaneously measured autofertility, pollination visitation rate, and flower longevity in three populations of L. jepsonii with different frequencies of initially self-compatible (ISC) individuals. Consistent with model predictions that prior selfing is favored when the accrual rate is low (Fig. 3), the population with 71% ISC individuals had a low pollinator visiting rate of 0.035 visits per flower per day, a high selfing rate of 0.94, and a short flower longevity of 1.55 days. In another population with a higher visitation rate of 0.78, it had a much lower ISC of only 16% with most individuals were self-compatible in the late stage of anthesis, and also a longer flower life span of 2.51 days, Moreover, as expected from the model prediction (Fig. 2), this population has a much lower selfing rate of 0.31.

LIMITATIONS OF THE MODEL

Obviously, some factors are not incorporated in the current model. For example, it is assumed that the cost of construction of a single flower $c$ is constant irrespective of selfing rate. However, a higher selfing rate is often correlated with changes in floral morphology, such as reduced flower size and increased ovule numbers, referred as the “selfing syndrome” (Sicard and Lenhard 2011). Therefore, the current model may underestimate the advantage of prior selfing as it can save even more reproductive energy for flower construction. The selfing syndrome also suggests that the prior selfing rate $u$ ⁠, outcrossing proportion $R$ ⁠, and delayed selfing rate $l$ may not evolve independently. For example, increase of $u$ (e.g., reduced anther-stigma distance) may inevitably lower $R$ ⁠, which may inhibit the evolution of prior selfing. Complete prior selfing and outcrossing may not be obtained due to constraints in mechanisms or pollination ecology, and the population may finally evolve to an intermediate ESS. In the model, pollen discounting is caused by flower longevity rather than the consumption of pollen by self-fertilization. However, pollen discounting due to selfing should not affect the ESS, since the ESS is either ${u^{*} = 1, R^{*} = 0, T^{*} = 0}$ (no pollen will be dispersed) or ${u^{*} = 0, R^{*} = 1, T^{*} > 0}$ (no prior or competing selfing). Also, it is assumed that delayed selfing will fertilize a constant proportion of unfertilized ovules, $l$ ⁠, irrespective of the absolute number of ovules, which may happen when there is pollen competition. However, if pollen competition is weak, delayed selfing may fertilize a fixed number of ovules (rather than proportion). In this case, $l$ will increase with flower longevity because there will be fewer unfertilized ovules, so I expected larger ESS flower longevity than the current model predicts. Spatial and temporal variation in female and male fitness accrual rates is neglected, and it has been shown that a fluctuating pollination visiting rate can select for a mixed strategy of outcrossing and prior selfing under high inbreeding depression (Morgan and Wilson 2005).

Conclusions

All in all, the current study suggests that the evolution of mating systems may be better understood by considering their coevolution with floral reproductive strategies (e.g., flower longevity in the current study; a negative association between selfing and seed dispersal found in Cheptou and Massol 2009). Specifically, the incorporation of the latter makes the realization of self- and outcrossed- fertilization into a concrete process, which helps to reveal the effects of both genetic (inbreeding depression) and ecological factors (fitness accrual rate) on plant reproduction.

ACKNOWLEDGMENTS

I would like to thank Maria Servedio and Brian Lerch for very useful comments on an earlier draft of this paper.

AUTHOR CONTRIBUTIONS

K.X. conceived of the project, built the model, conducted the analyses, and wrote the manuscripts.

CONFLICT OF INTEREST

The author declares that there is no conflict of interest.

LITERATURE CITED

Ashman

TL

and

DJ

Schoen

.

1994

.

How long should flowers live?

Nature

371

:

788

–

791

.

Google Scholar

Crossref

WorldCat

Ashman

,

T.-L.

, and

D. L.

Schoen

.

1996

. Floral longevity: fitness consequences and resource costs. Pages–

139

in

D. G.

Lloyd

and

S. C. H.

Barrett

, eds.

Floral biology: studies on floral evolution in animal pollinated plants

.

Chapman and Hall

,

New York, NY

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Ashman

,

T. L.

(

2004

). Flower longevity. in

Plant cell death processes

(pp.

349

–

362

).

Academic Press

.

Barrett

,

S. C.

(

2008

).

Major evolutionary transitions in flowering plant reproduction: an overview

.

Barrett

,

S. C.

(

2013

).

The evolution of plant reproductive systems: how often are transitions irreversible?

.

Proc Biol Sci

.

280

: 20130913.

Google Scholar

OpenURL Placeholder Text

WorldCat

Becerra

,

J. X.

, &

D. G.

Lloyd

. (

1992

).

Competition-dependent abscission of self-pollinated flowers of Phormium tenax (Agavaceae): a second action of self-incompatibility at the whole flower level?

Evolution

46

:

458

–

469

.

Bennington

,

C. C.

, &

J. B.

McGraw

. (

1995

).

Natural selection and ecotypic differentiation in Impatiens pallida

.

Ecol. Monogr.

65

:

303

–

324

.

Google Scholar

Crossref

WorldCat

Charlesworth

,

D.

, &

Willis

,

J. H.

(

2009

).

The genetics of inbreeding depression

.

Nature reviews genetics

,

10

(

11

):

783

–

796

.

Charnov

,

E. L.

(

2020

).

The Theory of Sex Allocation

.(MPB-18), Volume

18

(Vol. 113).

Princeton University Press

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

Cheptou

,

P. O.

, &

F.

Massol

. (

2009

).

Pollination fluctuations drive evolutionary syndromes linking dispersal and mating system

.

Am. Nat.

174

:

46

–

55

.

Culley

,

T. M.

, &

M. R.

Klooster

. (

2007

).

The cleistogamous breeding system: a review of its frequency, evolution, and ecology in angiosperms

.

Bot. Rev

,

73

,

1

.

Google Scholar

Crossref

WorldCat

Duan

,

Y. W.

,

A.

Dafni

,

Q. Z.

Hou

,

Y. P.

He

, &

J. Q.

Liu

. (

2010

).

Delayed selfing in an alpine biennial Gentianopsis paludosa (Gentianaceae) in the Qinghai-Tibetan Plateau

.

J. Integr. Plant Biol.

52

:

593

–

599

.

Fisher

,

R. A.

(

1941

).

Average excess and average effect of a gene substitution

.

Ann. Eugen.

11

:

53

–

63

.

Google Scholar

Crossref

WorldCat

Goodwillie

,

C.

,

S.

Kalisz

, &

C. G.

Eckert

. (

2005

).

The evolutionary enigma of mixed mating systems in plants: occurrence, theoretical explanations, and empirical evidence

.

Annu. Rev. Ecol. Evol. Syst.

36

:

47

–

79

.

Google Scholar

Crossref

WorldCat

Goodwillie

,

C.

, &

J. M.

Ness

. (

2005

).

Correlated evolution in floral morphology and the timing of self-compatibility in Leptosiphon jepsonii (Polemoniaceae)

.

Int. J. Plant Sci.

166

:

741

–

751

.

Google Scholar

Crossref

WorldCat

Goodwillie

,

C.

, &

J. J.

Weber

. (

2018

).

The best of both worlds? A review of delayed selfing in flowering plants

.

Am. J. Bot.

105

:

641

–

655

.

Harder

,

L. D.

, &

J. D.

Thomson

. (

1989

).

Evolutionary options for maximizing pollen dispersal of animal-pollinated plants

.

Am. Nat.

133

:

323

–

344

.

Google Scholar

Crossref

WorldCat

Harder

,

L. D.

, &

W. G.

Wilson

. (

1994

).

Floral evolution and male reproductive success: optimal dispensing schedules for pollen dispersal by animal-pollinated plants

.

Evol. Ecol.

8

:

542

–

559

.

Google Scholar

Crossref

WorldCat

Huang

,

Q.

, &

M.

Burd

. (

2019

).

The Effect of Pollen Limitation on the Evolution of Mating System and Seed Size in Hermaphroditic Plants

.

Am. Nat.

193

:

447

–

457

.

Husband

,

B. C.

, &

D. W.

Schemske

. (

1996

).

Evolution of the magnitude and timing of inbreeding depression in plants

.

Evolution

50

:

54

–

70

.

Kalisz

,

S.

, &

D. W.

Vogler

. (

2003

).

Benefits of autonomous selfing under unpredictable pollinator environments

.

Ecology

84

:

2928

–

2942

.

Google Scholar

Crossref

WorldCat

Koontz

,

S. M.

,

C. W.

Weekley

,

S. J.

Haller Crate

, &

E. S.

Menges

. (

2017

).

Patterns of chasmogamy and cleistogamy, a mixed-mating strategy in an endangered perennial

.

AoB Plants

9

: plx059.

Google Scholar

OpenURL Placeholder Text

WorldCat

Kunin

,

W.E.

, and

A.

Shmida

. (

1997

).

Plant reproductive traits as a function of local, regional, and global abundance

.

Conserv. Biol.

11

:

183

–

192

.

Google Scholar

Crossref

WorldCat

Lande

,

R.

, &

D. W.

Schemske

. (

1985

).

The evolution of self-fertilization and inbreeding depression in plants. I. Genetic models

.

Evolution

39

:

24

–

40

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

Lloyd

,

D. G.

(

1979

).

Some reproductive factors affecting the selection of self-fertilization in plants

.

Am. Nat.

113

:

67

–

79

.

Google Scholar

Crossref

WorldCat

Lloyd

,

D. G.

(

1984

).

Variation strategies of plants in heterogeneous environments

.

Biol. J. Linn. Soc.

21

:

357

–

385

.

Google Scholar

Crossref

WorldCat

Lloyd

,

D. G.

, &

D. J.

Schoen

. (

1992

).

Self-and cross-fertilization in plants. I. Functional dimensions

.

Int. J. Plant Sci.

153

:

358

–

369

.

Google Scholar

Crossref

WorldCat

Masuda

,

M.

,

T.

Yahara

, &

M.

Maki

. (

2001

).

An ESS model for the mixed production of cleistogamous and chasmogamous flowers in a facultative cleistogamous plant

.

Evol. Ecol. Res.

3

:

429

–

439

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Maynard Smith

,

J.

(

1982

).

Evolution and the theory of games

.

Cambridge University Press

,

Cambridge

.

Morgan

,

M. T.

, &

W. G.

Wilson

. (

2005

).

Self-fertilization and the escape from pollen limitation in variable pollination environments

.

Evolution

59

:

1143

–

1148

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

Orozco-Ibarrola

,

O. A.

,

P. S.

Flores-Hernandez

,

E.

Victoriano-Romero

,

A. M.

Corona-López

, &

A.

Flores-Palacios

. (

2015

).

Are breeding system and florivory associated with the abundance of Tillandsia species (Bromeliaceae)?

Bot. J. Linn.

177

:

50

–

65

.

Google Scholar

Crossref

WorldCat

Porcher

,

E.

, &

R.

Lande

. (

2005

).

The evolution of self-fertilization and inbreeding depression under pollen discounting and pollen limitation

.

J. Evol. Biol.

18

:

497

–

508

.

Primack

,

R. B.

(

1985

).

Longevity of individual flowers

.

Annu Rev Ecol Evol Syst.

16

:

15

–

37

.

Google Scholar

Crossref

WorldCat

Roddy

,

A. B.

,

C.

Martínez-Perez

,

A. L.

Teixido

,

T. G.

Cornelissen

,

M. E.

Olson

,

R. S.

Oliveira

, &

F. A.

Silveira

. (

2020

).

Towards the flower economics spectrum

.

New Phytol

.

Google Scholar

OpenURL Placeholder Text

WorldCat

Sakai

,

S.

(

1995

).

Evolutionarily stable selfing rates of hermaphroditic plants in competing and delayed selfing modes with allocation to attractive structures

.

Evolution

49

:

557

–

564

.

Sato

,

H.

(

2002

).

The role of autonomous self-pollination in floral longevity in varieties of Impatiens hypophylla (Balsaminaceae)

.

Am. J. Bot.

89

:

263

–

269

.

Schoen

,

D. J.

, &

T. L.

Ashman

. (

1995

).

The evolution of floral longevity: resource allocation to maintenance versus construction of repeated parts in modular organisms

.

Evolution

49

:

131

–

139

.

Schoen

,

D. J.

, &

D. G.

Lloyd

. (

1984

).

The selection of cleistogamy and heteromorphic diaspores

.

Biol. J. Linn. Soc.

23

:

303

–

322

.

Google Scholar

Crossref

WorldCat

Schoen

,

D. J.

, &

D. G.

Lloyd

. (

1992

).

Self-and cross-fertilization in plants. III. Methods for studying modes and functional aspects of self-fertilization

.

Int. J. Plant Sci.

153

:

381

–

393

.

Google Scholar

Crossref

WorldCat

Sicard

,

A.

, and

M.

Lenhard

.

2011

.

The selfing syndrome: a model for studying the genetic and evolutionary basis of morphological adaptation in plants

.

Ann. Bot. (Lond.)

107

:

1433

–

1443

.

Google Scholar

Crossref

WorldCat

Stebbins

,

G.

1974

.

Flowering plants: evolution above the species level

.

Belknap, Cambridge, MA

.

Sun

,

S. G.

,

Guo

,

Y. H.

,

Gituru

,

R. W.

, &

Huang

,

S. Q.

(

2005

).

Corolla wilting facilitates delayed autonomous self-pollination in Pedicularis dunniana (Orobanchaceae)

.

Plant Syst. Evol.

251

:

229

–

237

.

Google Scholar

Crossref

WorldCat

Weber

,

J. J.

, &

Goodwillie

,

C.

(

2009

).

Evolution of the mating system in a partially self-incompatible species: reproductive assurance and pollen limitation in populations that differ in the timing of self-compatibility

.

Int. J. Plant sci

170

:

885

–

893

.

Google Scholar

Crossref

WorldCat

Winn

,

A. A.

,

Elle

,

E.

,

Kalisz

,

S.

,

Cheptou

,

P. O.

,

Eckert

,

C. G.

,

Goodwillie

,

C.

,

Johnston

,

M. O.

,

Moeller

,

D. A.

,

Ree

,

R. H.

,

Sargent

,

R. D.

and

Vallejo-Marín

,

M.

, (

2011

).

Analysis of inbreeding depression in mixed-mating plants provides evidence for selective interference and stable mixed mating

.

Evolution: International Journal of Organic Evolution

,

65

(

12

):

3339

–

3359

.

Associate Editor: P.-O. Cheptou

Handling Editor: A. McAdam

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Month:	Total Views:
December 2022	2
January 2023	4
February 2023	8
March 2023	5
April 2023	6
May 2023	1
June 2023	9
July 2023	11
August 2023	18
September 2023	9
October 2023	10
November 2023	17
December 2023	16
January 2024	17
February 2024	9
March 2024	21
April 2024	10
May 2024	18
June 2024	12
July 2024	9
August 2024	16
September 2024	22
October 2024	11
November 2024	10
December 2024	6
January 2025	9
February 2025	5
March 2025	12
April 2025	5
May 2025	7

Article Contents

The coevolution of flower longevity and self-fertilization in hermaphroditic plants

Abstract

Model

Results

ESS OF OUTCROSSING PROPORTION (⁠ $R$ ⁠) DURING COMPETING SELFING

ESS OF THE PROPORTION OF PRIOR SELFING (⁠ $u$ ⁠)

COEVOLUTION OF FLOWER LONGEVITY WITH SELF-FERTILIZATION

When delayed selfing can fertilize all remaining ovules (⁠ $l = 1$ ⁠)

When delayed selfing cannot fertilize all remaining ovules (⁠ $l < 1$ ⁠)

Discussion

EVOLUTION OF CLEISTOGAMY

COEVOLUTION OF FLOWER LONGEVITY AND SELF-FERTILIZATION

LIMITATIONS OF THE MODEL

Conclusions

ACKNOWLEDGMENTS

AUTHOR CONTRIBUTIONS

CONFLICT OF INTEREST

LITERATURE CITED

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

Article Contents

The coevolution of flower longevity and self-fertilization in hermaphroditic plants

Abstract

Model

Results

ESS OF OUTCROSSING PROPORTION (⁠R⁠) DURING COMPETING SELFING

ESS OF THE PROPORTION OF PRIOR SELFING (⁠u⁠)

COEVOLUTION OF FLOWER LONGEVITY WITH SELF-FERTILIZATION

When delayed selfing can fertilize all remaining ovules (⁠l=1⁠)

When delayed selfing cannot fertilize all remaining ovules (⁠l<1⁠)

Discussion

EVOLUTION OF CLEISTOGAMY

COEVOLUTION OF FLOWER LONGEVITY AND SELF-FERTILIZATION

LIMITATIONS OF THE MODEL

Conclusions

ACKNOWLEDGMENTS

AUTHOR CONTRIBUTIONS

CONFLICT OF INTEREST

LITERATURE CITED

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

ESS OF OUTCROSSING PROPORTION (⁠ $R$ ⁠) DURING COMPETING SELFING

ESS OF THE PROPORTION OF PRIOR SELFING (⁠ $u$ ⁠)

When delayed selfing can fertilize all remaining ovules (⁠ $l = 1$ ⁠)

When delayed selfing cannot fertilize all remaining ovules (⁠ $l < 1$ ⁠)