Consequences of combining sex-specific traits

Abstract

Males and females follow distinct life-history strategies that have co-evolved with several sex-specific traits. Higher investment into parental investment (PI) demands an increased lifespan. Thus, resource allocation toward an efficient immune system is mandatory. In contrast, resources allocated toward secondary sexual signals (ornamentation) may negatively correlate with investment into immunity and ultimately result in a shorter lifespan. Previous studies have addressed how resource allocation toward single sex-specific traits impacts lifetime reproductive success (LRS). However, the trade-offs between diverse sex-specific characteristics and their impact on LRS remain largely unassessed impeding our understanding of life-history evolution. We have designed a theoretical framework (informed by experimental data and evolutionary genetics) that explores the effects of multiple sex-specific traits and assessed how they influence LRS. From the individual sex-specific traits, we inferred the consequences at the population level by evaluating adult sex ratios (ASR). Our theory implies that sex-specific resource allocation toward the assessed traits resulted in a biased ASR. Our model focuses on the impact of PI, ornamentation, and immunity as causal to biased ASR. The framework developed herein can be employed to understand the combined impact of diverse sex-specific traits on the LRS and the eventual population dynamics of particular model systems.

Adult sex ratio, evolutionary game theory, life-history traits, lifetime reproductive success, population dynamics, sexual traits

Males and females are subject to different selection (Klein 2000) resulting in the evolution of divergent life-history strategies maximizing the lifetime reproductive success (LRS). In species with conventional sex roles, females have a higher energy investment per reproductive unit (i.e., parental investment, PI) according to the anisogamy (large female eggs and small male sperm) (Bell 1978). Also, additional investment into offspring upbringing is often a female-specific attribute (Trivers 1972; Dawkins and Carlisle 1976; Clutton-Brock 1988; Wright 1993), and their costly egg production is limited in contrast to the large quantities of small male sperm. These investment differentials and the implied costs explain why usually females are the choosy sex. Female fitness is maximized by egg production, which positively correlates with longevity (Love et al. 2008), whereas increasing mating rates maximizes male fitness as sperm is cheap (Bateman's principle) (Bateman 1948; Trivers 1972; Clutton-Brock 1988). Under this scenario, intrasexual selection is more intense in males (Bateman 1948) resulting in the evolution of their costly secondary sexual characteristics (i.e., ornamentation).

Differentiating how males and females contribute to reproductive success requires the integration of factors that go beyond PI and ornamentation. One crucial factor that influences fitness is the investment into immunity. Under strong selection by parasites (Hamilton et al. 1990), hosts evolved efficient and highly specific immune defense systems that permit the differentiation of self and nonself (Altizer et al. 2003; Boots and Bowers 2004) but are costly to maintain (Sadd and Schmid-Hempel 2009). Males may rather benefit from allocating their resources into secondary sexual characteristics (ornamentation) (Sheldon and Verhulst 1996) and this can potentially result in weaker male immune defense (Zuk and Stoehr 2002). In contrast, prolonged longevity in females imposed by intensified PI can maximize reproductive success; but requires a higher investment into immune defense. Life-history strategies according to Bateman's principle could thus explain the widespread sexual dimorphism in immune defense (Rolff 2002): females typically have a more efficient immune response than males across the animal kingdom (e.g., Schuurs and Verheul 1990; Zuk and McKean 1996; Kurtz et al. 2000; Siva-Jothy 2000).

An intricate link between sexual dimorphism in immunity, ornamentation and PI has been previously suggested (Forbes 2007; Nunn et al. 2008; Roth et al. 2011; Lin et al. 2016). Assessing the interaction of sex-specific traits seems critical to shed light on their contribution to LRS. In addition, theoretical and experimental studies suggest that the interactions of multiple traits when jointly assessed, have the potential to change the population dynamics in an unexpected manner (Moore 1990; Martin 1992; Chapman and Partridge 1996; Pusey et al. 1997; Fleming et al. 2000; Alonzo 2002; Stoehr and Kokko 2006; Kalbe et al. 2009; Alonzo 2010; Kelly and Alonzo 2010; Venkateswaran and Gokhale 2019; Vasconcelos and Rueffler 2020).

We here present our mathematical framework that examined the interaction of multiple (sex-specific) traits for a broad range of species and calculates the LRS of the individuals. Previous models aiming to address the interaction of traits did not include the sex specificity of the assessed traits (Kelly and Alonzo 2010) or they only looked at the impact of one sex-specific trait (e.g., PI) on population sex ratios ignoring interactions with other interlinked sexual or life-history traits (McNamara et al. 2000). Few studies such as the ones by Trivers (2002), Stoehr and Kokko (2006), and Kalbe et al. (2009) address how PI, ornamentation, and immune response, in isolation contribute to the LRS. However they did not consider the combined effect of these traits in both sexes. Moreover, these studies only considered species exhibiting conventional sex roles (competing males and choosing females), but ignore species with higher paternal investment into the upbringing of the offspring. Our theoretical framework aimed to address the so far underrepresented assessment of interactions among sex-specific traits and their population-level consequences. The two significant population-level consequences that emerge from our model are (1) skewed adult sex ratios (ASRs) and (2) different ratios of homozygous and heterozygous individuals between the sexes concerning immune alleles.

Skewed ASR has been observed in wild populations (Darwin 1871; Grant and Grant 2019), severely influencing mate availability and PI (Schacht et al. 2017). However, the causal lifehistory, ecological, and evolutionary processes leading to a skewed ASR remain a black box (Booksmythe et al. 2017). Because ASR can be linked to disease prevalence, sex-specific immune responses have the potential to add to the variation found in ASR (Adimora and Schoenbach 2005; Eberhart-Phillips et al. 2018; Lemaître et al. 2020). Further, the sex-specific PI can skew the ASR (Fisher 1930; Trivers and Willard 1973; Kokko and Jennions 2008). Due to higher survival costs for the more ornamented sex (Clutton-Brock et al. 1985), the sex-specific differences in ornamentation are also known to skew ASR.

In our model, neither did we follow the prediction that PI boosts immunocompetence, nor did we include that ornamentation necessarily decreases immunocompetence, as shown in studies such as Deerenberg et al. (1997) and Lin et al. (2016). Notably, we went beyond the classical assumption typically about sex roles. In animals with conventional sex roles and maternal care, the provisioning of PI that goes beyond the simple production of egg and sperm are attributes of the female sex, while ornamentation is a male-specific trait. However, sex roles have evolved on a gradient, in many species males contribute to paternal investment, with the extreme situation being sex-role reversal (Vincent et al. 1992; Wilson et al. 2003; Roth et al. 2011), with choosy sex and ornamented females (Bernet et al. 1998; Berglund and Rosenqvist 2003). To incorporate the broad range of life-history existing in nature and to overcome the typically made strong assumptions, we used two notational sexes not specified as being male or female.

We aimed for designing a framework in which multiple interlinked traits are studied simultaneously. Notably, we have constructed a holistic framework that captures sex-specific differences in PI, ornamentation, and immune response and presents the consequences of the overall life-history of a specific sex.

Our model loosens the typical assumptions made in life-history theory and provides results that can be generalized across different taxa depending on their sex roles and PI patterns. In our model, we have thus considered the genetic and eco-evolutionary aspects of the sex-specific traits, and most importantly, their combined sex-specific effects while simultaneously including various mating and PI systems.

Model

We amalgamated approaches from standard population genetics and eco-evolutionary processes (Freeman and Herron 2007; Otto and Day 2007; Venkateswaran and Gokhale 2019) (within and between populations) to investigate the interaction dynamics of multiple traits (with sex-specific differences). We first developed a robust method (illustrated in Fig. 1) to study the LRS that arises from immune response, mating competition through ornaments and PI. Later, we used the LRS to investigate the consequences of combining the sex-specific traits that are part of an individual's reproductive lifetime.

Figure 1

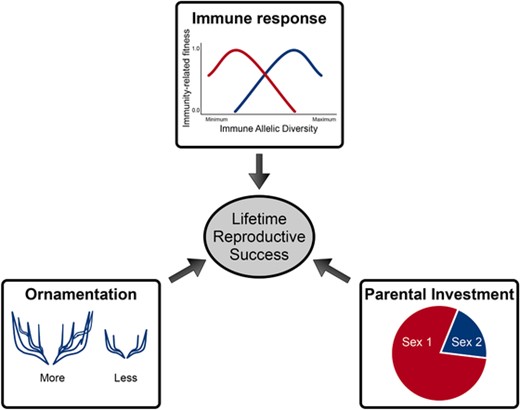
Model representation. Life history and sexual traits affect the lifetime reproductive success. The fitness components from parental investment (PI), immune system, and ornamentation are offspring success, survival of the parent plus offspring, and mating success, respectively. These contribute to an individual's lifetime reproductive success. We assumed that Sex 1 provides more PI than Sex 2. The sex-specific fitness from PI is modeled as frequency dependent because the number of copulations in one sex depends on the availability of the other sex. The individuals of one sex also have different levels of ornamentation, which they use to attract individuals of the other sex as potential mates. The model uses evolutionary game theory that gives frequency-dependent fitnesses of two types of individuals: those with more and those with lower level of ornaments. The individuals also differ in their immune genotypes. Each immune genotype yields a certain immunity-related fitness value that depends on the type and number of different immune alleles. The strength of immune response differs between sexes (sexual immune dimorphism). We modeled the evolution of these immune genotypes using population dynamics. Finally, the fitness obtained from PI, ornamentation, and immune response were used to measure the lifetime reproductive success of an individual.

Open in new tab Download slide

Consider the two sexes in a population, Sex 1 denoted by a filled circle $•$ ⁠, and Sex 2 denoted by a diamond $⋄$ ⁠. We first considered one autosomal immunity locus $A$ having two alleles $A_{1}$ and $A_{2}$ ⁠. The three distinct zygotes genotypes would be $A_{1} A_{1}$ ⁠, $A_{1} A_{2}$ ⁠, and $A_{2} A_{2}$ ⁠. For Sex 1, which throughout this article does major PI, the frequencies of the three genotypes are denoted by $x_{• 1}, x_{• 2}, x_{• 3}$ ⁠. The fitnesses, of the same, are denoted by $W_{• 1}, W_{• 2}$ ⁠, and $W_{• 3}$ ⁠. Similarly, we denote the frequencies and fitnesses for Sex 2. By definition, the frequencies of all individuals in the population sum up to unity. For the initial condition, we assumed the frequencies of Sex 1 and Sex 2 to be 0.5, that is, equal sex ratio; and within a sex, we ensured that we start with equal frequencies of immunity genotypes.

We used standard Mendelian segregation to model the evolution of the different types of individuals in the population. The genotype dynamics follow the segregation pattern (Supporting Information). As with normal Mendelian segregation, we assumed equal sex ratio; half of the offspring are Sex 1 and the other half, Sex 2. Our model considers an infinitely large well-mixed population performing random mating.

LIFETIME REPRODUCTIVE SUCCESS

The LRS of an individual, that is, the overall fitness of an individual, is related to its immunocompetence (the ability to produce a healthy immune response following exposure to a pathogen), the ability to obtain mates, and its offspring success (Stoehr and Kokko 2006; Kalbe et al. 2009; Kelly and Alonzo 2010). Thus, in our model, the sex-specific fitness components resulting from immune response, ornamentation, and parental investment jointly contribute towards the LRS of individuals as shown in Figure 1. Next, we introduce the fitness functions independently starting with immunity.

Immune response

A host's immune allelic diversity helps eliminate a large number of pathogens and disease-causing agents. However, in some cases, having high allelic diversity may reduce efficient immune responses, for example, autoimmune diseases triggered by high major histocompatibility complex (MHC) diversity. Thus, having an optimal number of immune allelic diversity (intermediate diversity) has been shown to be ideal in many systems (Nowak et al. 1992; Milinski 2006; Woelfing et al. 2009). The host's immune allelic diversity can be coarsely split into three parts: low diversity (LD, low efficiency of the immune system), intermediate or optimal diversity (ID, optimal immune efficiency), and high diversity (HD, might reduce the efficiency of the immune system). Recent experimental studies by Roved et al. (2017, 2018), and J. Winternitz and T. Lenz (pers. comm.) show that optimal diversity could differ between the sexes. Based on these ideas, we have different cases that are shown in Figure 2 for one immune locus $A$ with two alleles $A_{1}$ and $A_{2}$ that gives three distinct parent and offspring genotypes $A_{1} A_{1}$ ⁠, $A_{1} A_{2}$ ⁠, and $A_{2} A_{2}$ denoted by $j = {1, 2, 3}$ ⁠. We denote their immune responses by $W_{• j}^{I}$ and $W_{⋄ j}^{I}$ for genotypes $j = {1, 2, 3}$ in the two sexes. In our model, we refer to immune allelic diversity as the number of different immune alleles in the immune loci. Figure 2 shows a schematic representation of the immunity-related fitness versus immune allelic diversity hypotheses. The fitness of three distinct immune genotypes $A_{1} A_{1}$ ⁠, $A_{1} A_{2}$ ⁠, and $A_{2} A_{2}$ positively correlates with the number of different alleles or allelic diversity (Apanius et al. 1997; Eizaguirre et al. 2009). Therefore, genotypes $A_{1} A_{1}$ and $A_{2} A_{2}$ (homozygotes) will have the same fitness value as they both have only one type of allele, but $A_{1} A_{2}$ (heterozygote) that has two different types of alleles will have a higher fitness (heterozygous advantage, and this occurs in both sexes). However, between the sexes, there can be sex-specific differences in host immunity-related fitness versus immune allelic diversity (Roved et al. 2017). We can see this in panels (A) and (C) of Figure 2. Thus, our model accounts for lower, equal, and higher immunity in the sex with higher PI (Sex 1) compared to the other sex (Sex 2). The situation in which Sex 1 can have a higher immune response for a homozygous locus, and lower immune response for a heterozygous locus when compared to Sex 2, and the vice versa, is also taken into account (panel (B) of Fig. 2). In the latter part of the article, we address a realistic nonlinear immune allelic diversity profile, as shown in Figure 3, where there is the negative effect of HD (high immune allelic diversity) (Wegner et al. 2003).

Figure 2

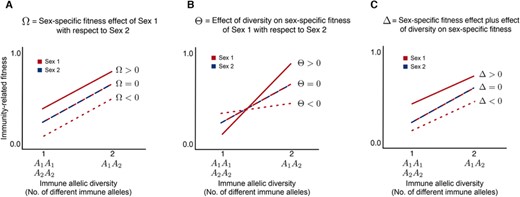
Schematic representation of different scenarios of sex-specific differences in host immunity-related fitness versus immune allelic diversity. We considered three distinct immune genotypes $A_{1} A_{1}$ ⁠, $A_{1} A_{2}$ ⁠, and $A_{2} A_{2}$ that result from mating between individuals having one immune gene locus $A$ with two alleles $A_{1}$ and $A_{2}$ (Mendelian segregation, see Supporting Information). Fitness positively correlates with the number of different alleles or allelic diversity (Apanius et al. 1997; Eizaguirre et al. 2009). So genotypes $A_{1} A_{1}$ and $A_{2} A_{2}$ (homozygotes) will have the same fitness value as they both have only one type of allele. But $A_{1} A_{2}$ (heterozygote), which has two different types of alleles, will have a higher fitness. This is known as heterozygous advantage and occurs within both sexes. However, between the sexes, there can be sex-specific differences (Roved et al. 2017). This is shown in panels (A)–(C). In (A), $Ω > 0$ would imply that Sex 1 will have a higher value of immune response compared to Sex 2 for any given allelic diversity. When $Ω < 0$ ⁠, Sex 1 has a lower values of immune response for any given allelic diversity compared to Sex 2. Another situation is also possible: Sex 1 can have higher immune response for a homozygous locus, and lower immune response for a heterozygous locus when compared to Sex 2. This is shown in (B), where $Θ$ is the difference between the angles of the two lines. In (C), $Δ$ differs from $Ω$ by considering lines that are not parallel to each other, that is, case (C) is a combination of cases (A) and (B). When both sexes have the same immune response patterns, $Ω = Θ = Δ = 0$ ⁠.

Open in new tab Download slide

Figure 3

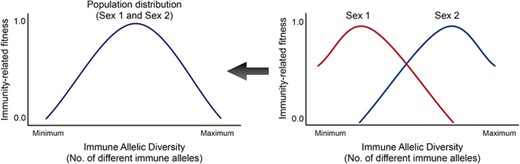
Schematic representation of host immunity-related fitness versus immune allelic diversity. For two immune gene loci $A$ and $B$ each having two alleles $A_{1}$ ⁠, $A_{2}$ and $B_{1}$ ⁠, $B_{2}$ ⁠, there would be 10 distinct zygote genotypes. The population will comprise of individuals with these genotypes. Their immune responses would depend on these genotypes. The probability of immune response might reduce if the individual has too many immunity allele diversity. In the case of MHC, the autoimmune effect of having high MHC allele diversity reduces the probability of immune response (Nowak et al. 1992; Milinski 2006; Woelfing et al. 2009). Thus, there is an optimal allele diversity, which gives the parabolic shape to the curve. Recent studies have shown that males and females can have different optimal diversities (Roved et al. 2017, 2018; Winternitz et al., unpubl. ms.). Plotted here are hypothetical sex-specific optima of immune allelic diversity (Roved et al. 2017). The realized population distribution is what is typically looked at, but in our study we consider sex-specific optima of immune allelic diversity. Some immune genes may follow completely different sex-specific patterns from the one shown here (Roved et al. 2017; De Lisle 2019), and this model can be used for most kinds of immune genes.

Open in new tab Download slide

Our approach can be generalized to any genetic system controlling the immune response or a completely different causal mechanism devoid of the genetic correlation. For example, the effect of nutrients and their impact of the immune system can be captured by a nongenetic model as well (Chandra 1983). Thus, while we focus on the genetic mechanism in the current model, we stress that our framework is independent of the exact mechanism of how the immune response curves develop. Condition of an individual is directly proportional to immune response (resources allocated to self-maintenance, immune defense), which in turn determines survival (Stoehr and Kokko 2006).

Parental investment

Both sexes pay the costs for initial PI, that is, egg and sperm production (Hayward and Gillooly 2011). Besides pregnancy by a single sex, one or both sexes of some species also exhibit external extended parental care, that is, brooding and further parental care provided to the offspring after parturition or hatching (Trivers 1972, 2002; Wade and Shuster 2002; Kokko and Jennions 2003; Alonzo 2010) (Fig. 1). We assume that Sex 1 provides major PI (e.g., male sticklebacks, male pipefish, most female mammals). The fitness from PI will depend on the relative abundance of the other sex and are given by

\begin{matrix} W_{•}^{P} & = & (b^{P} - c_{•}^{P}) \frac{x_{⋄}}{x_{•} + x_{⋄}} \\ W_{⋄}^{P} & = & (b^{P} - c_{⋄}^{P}) \frac{x_{•}}{x_{•} + x_{⋄}} . \end{matrix}

Here,

b^{P}

is the benefit (offspring produced) from PI while

c_{•}^{P}

and

c_{⋄}^{P}

are the costs for PI by Sex 1 and Sex 2, respectively. The frequency of Sex 1 equals

x_{•} = x_{• 1} + x_{• 2} + x_{• 3}

and the frequency of individuals in Sex 2 equals

x_{⋄} = x_{⋄ 1} + x_{⋄ 2} + x_{⋄ 3}

⁠. Because we have assumed that Sex 1 provides maximum PI,

c_{⋄}^{P} < c_{•}^{P} < b^{P}

⁠.

Ornamentation

Mating competitions occur among individuals of the same sex to attract and obtain mates. This competition is exhibited through fights, nuptial gifts, nests, sexual signals, ornament display, and various types of “attractiveness.” We refer to all these as “ornaments.” Ornamentation is a costly signal (Zahavi 1977; Andersson and Simmons 2006; Milinski 2006; Kurtz 2007); but the investment into ornaments is beneficial increasing the chances of acquiring mates (Carranza et al. 1990; Petrie et al. 1991; Berglund et al. 1997; Wong and Candolin 2005).

When one of the sexes participates in mating competition, as shown in Figure 1, two types of individuals of that sex are considered: one type displays more ornaments (⁠

M O

⁠) and the other type displays less ornaments (⁠

L O

⁠). Individuals that win this competition (based on their and their opponents' strategies) are chosen by members of other (choosing) sex. Therefore, the sex that undergoes mating competitions consists of six types of individuals for example,

x_{⋄ j, M O}

and

x_{⋄ j, L O}

where the genotypes are given by

j = {1, 2, 3}

⁠. We here assumed that Sex 2 does the mating competitions (in the latter part of the article, we relax this assumption and allow for Sex 1 to perform both PI and mating competitions). The frequency-dependent fitnesses for Sex 2, from these mating competitions, are denoted as

W_{⋄ M O}^{O}

and

W_{⋄ M O}^{O}

(see Supporting Information for details). We model this interaction as an evolutionary game (Maynard Smith and Price 1973; Maynard Smith 1986; Sigmund and Nowak 1999) described by the following “payoff matrix” (see Supporting Information for details):

\begin{matrix} \begin{matrix} \begin{matrix} M O & L O \end{matrix} \\ \begin{matrix} More ornament or M O \\ Less ornament or L O \end{matrix} (\begin{matrix} \frac{b^{O}}{2} - c_{⋄}^{O} & b^{O} - c_{⋄}^{O} \\ 0 & \frac{b^{O}}{2} \end{matrix}) \end{matrix} . \end{matrix}

Here

b^{O}

is the benefit arising from mating competitions, that is, mating gain and

c_{⋄}^{O}

is the cost that Sex 2 bears attributed to ornament(s). The frequency dependent fitnesses resulting from these interactions are given by

\begin{matrix} W_{⋄ M O}^{O} & = & (\frac{b^{O}}{2} - c_{⋄}^{O}) \frac{x_{⋄, M O}}{x_{⋄, M O} + x_{⋄, L O}} + (b^{O} - c_{⋄}^{O}) \frac{x_{⋄, L O}}{x_{⋄, M O} + x_{⋄, L O}} \\ W_{⋄ L O}^{O} & = & 0 \frac{x_{⋄, M O}}{x_{⋄, M O} + x_{⋄, L O}} + \frac{b^{O}}{2} \frac{x_{⋄, L O}}{x_{⋄, M O} + x_{⋄, L O}}, \end{matrix}

where

x_{⋄, M O} = \sum_{j = 1}^{3} x_{⋄ j, M O}

and

x_{⋄, L O} = \sum_{j = 1}^{3} x_{⋄ j, L O}

⁠.

Having more ornamentation $M O$ is ideal for attracting mates. Taking into account, the condition $c^{O} < \frac{b_{⋄}^{O}}{2}$ in the payoff matrix ensures the dominance of strategy $M O$ (Nowak 2006). When extending this game to a multiple player situation (Gokhale and Traulsen 2014; Chen et al. 2017) many individuals simultaneously participate in mating competition or display secondary sexual ornaments (see Supporting Information). The extension is akin to lekking behavior in which many members of the ornamented sex engage in competitive displays. As seen in equation (3), fitness is standardized within Sex 2 and the genotype frequencies sum to unity. To present our model and its dynamics, we have chosen a system in which the sex with intensified PI (Sex 1) is not involved in mating competitions. However, in nature, we find all sorts of species, such as seahorses, in which the males undergo both higher PI and ornamentation, and our model accounts for such scenarios as well. In the Results section, we have explored both possibilities: (1) the sex with higher PI (Sex 1) is ornamented, and (2) the sex with lower PI (Sex 2) is ornamented.

Overall dynamics

The LRS is a multiplicative effect of the fitness arising from immune response, ornamentation and PI (Stoehr and Kokko 2006; Kelly and Alonzo 2010). Using the LRS values in the Mendelian population dynamics, we can obtain the combined interaction dynamics of the different types of individuals in the population. The population is divided into nine types—the three genotypes (⁠

j

⁠) of Sex 1,

x_{• j}

⁠, and the three genotypes of Sex 2 further split into six according to ornamentation into

x_{⋄ j, M O}

and

x_{⋄ j, L O}

⁠. We refer to them as simply

x_{i}

with

i

as the type of individual. The sum of the frequencies of all the types of individuals in the populations sums up to unity. The LRS, which is the overall fitness of an individual, consists of fitnesses from immunocompetence, mating competition, and PI as (in detail in the Supporting Information):

W_{i} = \{\begin{matrix} \frac{W_{•}^{P}}{1 - W_{• j}^{I}} & if the individual i is a member of Sex 1 \\ \frac{W_{⋄}^{P} . W_{⋄ MO}^{O}}{1 - W_{⋄ j}^{I}} & the individual i is a member of Sex 2 and having more ornamantation \\ \frac{W_{⋄}^{P} . W_{⋄ LO}^{O}}{1 - W_{⋄ j}^{I}} & the individual i is a member of Sex 2 and having less ornamantation . \end{matrix})

The LRS, as shown in equation (4), is multiplicative because we need the fitness terms from both, PI and ornamentation, to calculate an individual's reproductive success. Survival through the reproductive season is crucial for reproductive success. Thus, the survivability term (in the denominator) depends on the immune response (according to this model) over the individual's lifetime as per Stoehr and Kokko (2006) and Kelly and Alonzo (2010) (details and derivation of this equation are given in the Supporting Information). The classical selection equation from population genetics (Crow and Kimura 1970) gives the evolution of the frequency

x_{i}

with average fitness

W_{i}

(Crow and Kimura 1970; Schuster and Sigmund 1983; Hofbauer and Sigmund 1998; Gokhale et al. 2014). The equation can be written as

\dot{x_{i}} = x_{i} (W_{i} - \bar{W}),

where

\bar{W}

is the average population fitness.

Results

LINEAR IMMUNE ALLELIC DIVERSITY PROFILE: SINGLE LOCUS

For one immune locus with two alleles, higher allele diversity induces the specificity of the immune response, as shown in Figure 2. The negative effect of very high diversity was not considered here. Beyond the null model of immune allelic diversity, we included different cases of sexual conflict (Roved et al. 2018). As illustrated in Figure 2, we allowed the possibilities of Sex 1 (the sex undergoing higher PI) to have higher, equal, and lower immunocompetence than Sex 2.

Assuming that none of the sexes were involved in mating competition, the ornamentation game becomes neutral, we can then vary the cost of PI and the immune response curves (as shown in Fig. 2). The resulting equilibrium frequencies are shown in Figure 4. When the cost of PI is zero, and there is no sex-biased difference in immune response, we observed, as expected, that the sex ratio is 1:1. The classical definition of ASR is “number of males:population size” (Ancona et al. 2017). However, in ourmodel, if males provide more PI, they would be Sex 1, and they would be Sex 2 if they do not provide more PI. We thus defined the term ASR as “number of Sex 1:population size”. We ensured that at birth, there is no distortion in the sex ratio (Supporting Information). ASR was calculated after the mature individuals performed mating interactions and PIs (as illustrated in Fig. 5, and plotted in Figs. S1 and S2). The frequency of Sex 1 decreased with increasing PI. However, we still see cases of Sex 1 increasing in frequency under specific scenarios of sexual conflict over the immune allelic diversity (see $Δ > 0$ ⁠, $Ω > 0$ ⁠, or $Θ \neq 0$ in Fig. 4). As discussed in Figure 4, the parameters $Ω$ ⁠, $Δ$ ⁠, and $Θ$ are a measure of the sex difference in the immune response through sexual conflict within the MHC or other immunity-related alleles.

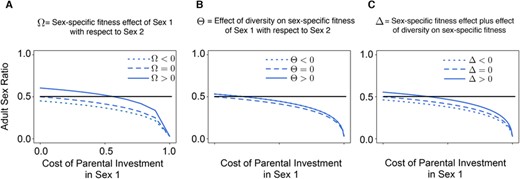
$Adult sex ratio (fraction of Sex 1 in the population) for varying parental investment (PI) and various cases of sexual conflict within immune allelic diversity, as shown in Figure 2. The ornamentation game is neutral, that is, no selection acting on the individuals (details in the Supporting Information). As maintained throughout this study, Sex 1 does maximum PI. Sex 2 does negligible PI. Therefore, its cost is set to zero, that is, c⋄P=0. The black line highlights the even adult sex ratio. (A)–(C) When the cost of PI = 0 and with no sex difference in immune response (Ω=Δ=Θ=0), the obtained adult sex ratio is 1:1. (A) and (C) When PI increased, the frequency of Sex 1 dropped as PI is costly. When Ω>0 and Δ>0, this sex difference in immune response compensates for the cost of PI. Thus, initially, for small cost of PI values, the frequency of Sex 1 was higher than that of Sex 2. However, with increased PI costs, the frequency of Sex 1 became lower than that of Sex 2. The frequency of Sex 1 was the same or lower than that of Sex 2 when Ω=0 and Δ=0 When Ω<0 and Δ<0, frequency of Sex 1 decreased with an increase in PI and it is also always lower than that of Sex 2. (B) Frequency of Sex 1 was lower than Sex 2 for most values of PI cost for most Θ values. Moreover, Θ<0 and Θ>0 gave the same results. The above results highlight the fact that sexual conflict within immune allelic diversity can increase (when Ω>0 and Δ>0 ) or reduce (when Ω<0, δ<0, almost all Θ) the adult sex ratio.$

Figure 4

Adult sex ratio (fraction of Sex 1 in the population) for varying parental investment (PI) and various cases of sexual conflict within immune allelic diversity, as shown in Figure 2. The ornamentation game is neutral, that is, no selection acting on the individuals (details in the Supporting Information). As maintained throughout this study, Sex 1 does maximum PI. Sex 2 does negligible PI. Therefore, its cost is set to zero, that is, $c_{⋄}^{P} = 0$ ⁠. The black line highlights the even adult sex ratio. (A)–(C) When the cost of PI = 0 and with no sex difference in immune response (⁠ $Ω = Δ = Θ = 0$ ⁠), the obtained adult sex ratio is 1:1. (A) and (C) When PI increased, the frequency of Sex 1 dropped as PI is costly. When $Ω > 0$ and $Δ > 0$ ⁠, this sex difference in immune response compensates for the cost of PI. Thus, initially, for small cost of PI values, the frequency of Sex 1 was higher than that of Sex 2. However, with increased PI costs, the frequency of Sex 1 became lower than that of Sex 2. The frequency of Sex 1 was the same or lower than that of Sex 2 when $Ω = 0$ and $Δ = 0$ When $Ω < 0$ and $Δ < 0$ ⁠, frequency of Sex 1 decreased with an increase in PI and it is also always lower than that of Sex 2. (B) Frequency of Sex 1 was lower than Sex 2 for most values of PI cost for most $Θ$ values. Moreover, $Θ < 0$ and $Θ > 0$ gave the same results. The above results highlight the fact that sexual conflict within immune allelic diversity can increase (when $Ω > 0$ and $Δ > 0$ ) or reduce (when $Ω < 0$ ⁠, $δ < 0$ ⁠, almost all $Θ$ ⁠) the adult sex ratio.

Open in new tab Download slide

Figure 5

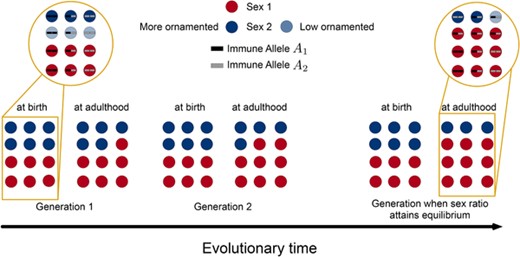
Illustration of the basic results from the model. We assumed that Sex 1 has higher parental investment (PI), and Sex 2 is involved in mating competition. Thus, Sex 2 was split into more ornamentation (⁠ $M O$ ⁠) or less ornamentation (⁠ $L O$ ⁠). The individuals further have diverse immune genotypes. In the first generation, we start with equal numbers of Sex 1 and Sex 2 individuals; with equal number of $M O$ and $L O$ individuals in Sex 2; and an equal amount of $A_{1} A_{1}$ ⁠, $A_{1} A_{2}$ ⁠, and $A_{2} A_{2}$ genotypes. Our goal was to start with all types of individuals having equal frequencies and predict the evolutionary outcome. The recursions ensured that the sex ratio at birth equals 1:1. In continuous time, the fitness components contribute to the LRS. The individuals' overall LRS caused a skew in the adult sex ratio (frequency of all types of adults in a sex determines the adult frequency of a sex, or adult sex ratio of the population). The fitter individuals pass on their traits to the next generations. Over time, we observed the system reaching equilibrium (see Figures S1 and S2). The equilibrium could be biased toward Sex 1 (as shown in this diagram) or Sex 2 depending on their life-history and sexual traits as plotted in Figure 4 (and later, in Fig. 6). Our model further suggested a difference in the number of heterozygous and homozygous individuals (based on their immune allelic diversity). Showed in this figure is a situation with more heterozygous individuals within Sex 1 compared to Sex 2. Also, the vice versa was possible depending on the organism's mating costs, immunity and PI system. A thorough analysis over all these parameters is shown in Figures S3– S5.

Open in new tab Download slide

The parameters represent the effect of allelic diversity on sex-specific fitness of Sex 1 relative to Sex 2. Depending on the sign of $Ω$ ⁠, $Δ$ ⁠, or $Θ$ ⁠, Sex 1 would have a higher, lower or equal value of fitness from immunity compared to Sex 2. The results after including mating competitions are plotted in Figures S3– S5 for a full range of $Ω$ ⁠, $Δ$ ⁠, and $Θ$ ⁠. Figures S3– S5 show how these parameters (⁠ $Ω$ ⁠, $Θ$ ⁠, and $Δ$ ⁠) impacted the adult frequency of the two sexes.

The effect of the full range of cost of ornamentation and PI (on the frequency of Sex 1) was further explored. We observed that under selection, the obtained immunity genotypes deviate from the Hardy-Weinberg equilibrium. Deviation from Hardy-Weinberg equilibrium under selection is not surprising, but over evolutionary time, one sex showed a higher number of heterozygotes compared to the other sex (see Fig. 5). In Figures S3–S5, the ratio between heterozygotes and homozygotes in Sex 1 (compared to Sex 2) is shown. In this setup, the heterozygous immune genotype (⁠ $A_{1} A_{2}$ ⁠) had a higher immune response than the homozygous genotypes $A_{1} A_{1}$ and $A_{2} A_{2}$ (Fig. 3). Thus, an increase in heterozygotes within one sex compared to the other would imply that this sex has a higher average activity of the immune system. A recent study in wild songbird populations, in which the number of heterozygotes and homozygotes, even under selection, turned out to be equal between the sexes (Roved 2019). However, this could be the result of a particular immune response profile, PI and ornamentation costs in that species. Diverse sex-specific immune allelic diversity profiles could determine different ratios of homozygotes and heterozygotes. More empirical studies with various model organisms should shed light on how species show diverse ways of sexual conflict within the immune allelic diversity.

NONLINEAR IMMUNE ALLELIC DIVERSITY PROFILE: MULTIPLE LOCI

For the multiple loci case, as done before for the single locus, we consider both sexes in a population, Sex 1 denoted by a filled circle $•$ ⁠, and Sex 2 denoted by a diamond $⋄$ ⁠. We consider an example of two autosomal immunity loci $A$ and $B$ having two alleles $A_{1}$ ⁠, $A_{2}$ ⁠, and $B_{1}$ ⁠, $B_{2}$ ⁠, respectively. The 10 distinct zygotes genotypes would be $A_{1} B_{1} | A_{1} B_{1}$ ⁠, $A_{1} B_{1} | A_{1} B_{2}$ ⁠, $A_{1} B_{2} | A_{1} B_{2}$ ⁠, $A_{1} B_{1} | A_{2} B_{1}$ ⁠, $A_{1} B_{2} | A_{2} B_{1}$ ⁠, $A_{1} B_{2} | A_{2} B_{2}$ ⁠, $A_{2} B_{1} | A_{2} B_{1}$ ⁠, $A_{2} B_{1} | A_{2} B_{2}$ ⁠, $A_{2} B_{2} | A_{2} B_{2}$ ⁠, and $A_{1} B_{1} | A_{2} B_{2}$ ⁠.

For Sex 1, which as defined throughout this article does major PI), the frequencies of the 10 genotypes are denoted by $x_{• 1}$ ⁠, $x_{• 2}$ ⁠, $x_{• 3}$ ⁠, $x_{• 4}$ ⁠, $x_{• 5}$ ⁠, $x_{• 6}$ ⁠, $x_{• 7}$ ⁠, $x_{• 8}$ ⁠, $x_{• 9}$ ⁠, and $x_{• 10}$ ⁠. The fitnesses, of the same, are denoted by $W_{• 1}, W_{• 2}$ ⁠, $W_{• 3}$ ⁠, $W_{• 4}$ ⁠, $W_{• 5}$ ⁠, $W_{• 6}$ ⁠, $W_{• 7}$ ⁠, $W_{• 8}$ ⁠, $W_{• 9}$ ⁠, and $W_{• 10}$ ⁠. Similarly, we denoted the frequencies and fitnesses for Sex 2. Our model considers an infinitely large well-mixed population undergoing random mating. Also, by definition, the sum of the frequencies of all individuals in the population sums up to unity. We started with an equal sex ratio and equal frequencies of immunity genotypes. The genotype dynamics follow the segregation pattern (see Supporting Information). As with normal Mendelian segregation, at reproduction, we assumed half of the offspring to be Sex 1 and the other half, Sex 2.

In a multiloci scenario, one can include nonlinear density profiles (Nowak et al. 1992; Wegner et al. 2003; Woelfing et al. 2009), as shown in Figure 3. Across species, different sex-specific immune response profiles can be found, depending on the sex-specific selection and phenotypic divergence (Uekert et al. 2006; Love et al. 2008; Oertelt-Prigione 2012). We hypothesize two such scenarios:

the optimal diversity of immune alleles for both sexes is the same, but the immune responses at this optimal diversity differs between the sexes (for instance, females are more prone to acquiring autoimmune diseases; sex hormones such as estrogen, testosterone also affect immune response; Hillgarth and Wingfield 1997; Törnwall et al. 1999; Whitacre 2001), or
the two sexes have different optimal diversity of immune alleles, and the immune response at the same optimal diversity can be identified for both sexes. For instance, as shown in Roved et al. (2017, 2018), males and females have a different optimal diversity, in which males needed a higher allelic diversity to mount a maximum immune response. We considered such a scenario (illustrated in Fig. 3) for the example study we present in the article.

Extending from the one locus scenario, for multiple loci we assumed that only the number of different alleles, that is, the allele diversity produces unequal fitness.

ADULT SEX RATIO IN VARIOUS SPECIES

We chose an immune allelic diversity profile which included a sexual conflict (or sex-specific differences) as displayed in Figure 3. Depending on the model species, one may choose any immune allelic diversity profile with sex-specific differences. We have assumed Sex 1 to contribute higher PI. In some species (e.g., sticklebacks, seahorses) this sex is also involved in mating competitions. In other species (e.g., primates, many birds), that does not contribute higher PI is involved in mating competition. We have considered both these possibilities in our study.

Our results showed that sexual conflict within immune allelic diversity and varying PI might result in ASR bias. The effect of ornamentation plays an essential role in skewing ASRs, as shown in Figure 6. Diverse reproducing species have distinct ornamentation and PI costs. Figure 6 shows the values of ASRs that our model predicted for a range of species. Figure 6A shows the case when Sex 1 performs more PI and ornamentation. In Figure 6B, the gray region shows the case in which both sexes perform equal PI and Sex 2 displays ornamentation. The other regions represent scenarios in which Sex 1 performs more PI, and Sex 2 displays ornamentation. The cases in which both sexes undergo mating competition leading to intrasexual selection, and in which both sexes do not display ornaments, are not shown. The situation in which both sexes display intrasexual mating competitions, for example, would involve an ornamentation game for both Sex 1 and Sex 2 in which addition parameters and complexity can come into play.

Figure 6

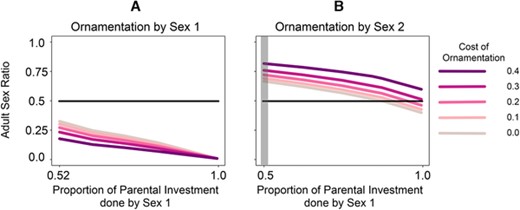
Qualitative difference in the adult sex ratio for diverse range of species with varying parental investment (PI) and ornamentation costs. As defined throughout the article, Sex 1 contributes major PI. For these calculations, we used the sexual conflict Case 4 shown in Figure 3. (A) Species such as sticklebacks in which one sex performs both ornamentation and major PI. We observed that frequency of Sex 1 descended when PI cost increased and even further decreased with a rise of ornamentation cost. (B) The panel highlighted in gray shows bi-PI scenarios. In species where Sex 1 provides most PI and Sex 2 performs elaborate mating competitions, the frequency of Sex 1 reduces with increasing PI. However, this value grows with ascending ornamentation cost in Sex 2. Note that for certain ornamentation and PI values, the adult sex ratios are equal. As shown in previous studies on multiple interactions between traits (Venkateswaran and Gokhale 2019), even in the case where the cost of ornamentation is equal to zero in the mating competition game, the mere presence of that game will deviate the frequency of Sex 2 from a scenario in which there is no ornamentation game.

Open in new tab Download slide

Discussion

Various interacting life history and sexual traits during the reproductive lifespan of an individual determine its LRS (Stoehr and Kokko 2006; Kalbe et al. 2009; Kelly and Alonzo 2010). In this study, we present a framework investigating the eco-evolutionary consequences of the interplay between two or more sex-specific traits. Along with empirical evidence supporting our qualitative predictions, our model showed the emergence of a skewed ASR as a consequence of resource allocation toward different sex-specific traits and their interactions. Our model suggests that the ASR is generally biased against the sex that does higher PI. However, other sex-specific traits have the ability to reverse this skew in ASR, suggesting a trade-off in resource allocation across numerous traits. When one sex allocates substantial resources toward ornamentation and mating competition, the ASR can be skewed toward the sex that contributes PI. Also, sexual immune dimorphism has a sex-specific impact on survival, and thus further strengthens the skew in ASR.

Empirical studies have suggested that the ASR has an impact on sex-specific differences and roles (Liker et al. 2013; Székely et al. 2014; Liker et al. 2015; Henshaw et al. 2019). Our theoretical model predicts that the opposite may also be possible, that is, the combined effect of resource allocation toward numerous sex-specific traits and the implemented sex roles can lead to a biased ASR (Kokko and Jennions 2008; Pipoly et al. 2015). Depending on which sex allocates its resources toward PI, ornamentation and immune response, the bias in ASR can be either toward males or females. A seminal theoretical work by McNamara et al. (2000) that considered parental care, mating opportunities, and sex ratios, modeled a PI game in which a parent could decide to either care or desert its offspring. This study suggested that sex ratio influences parental care. In contrast, we demonstrate that it might be the sex differences in PI that influences ASR. Moreover, previous work focusing on resource allocation toward parental care was studied in isolation from the costs and trade-offs with other essential sex-specific traits. Our model not only includes resource allocation toward other important sex-specific traits (in addition to parental care) but appraises the interactions and trade-offs among them. To this end, we suggest that it is the combination of resource allocation across all these interacting sex-specific traits that causes the identified bias in the ASR. Studying ASR bias is pivotal as it provides essential insights into sex-specific adult mortality. It also determines how many individuals in each sex survive to the next seasons, their mating opportunities, and provides insight into offspring production and fitness (Stenzel et al. 2011). According to Bateman's principle (Bateman 1948), the reproductive success of the sex that performs intrasexual mating competition depends on the number of mating events. In contrast, the sex limited by resource allocation toward PI relies on longevity to increase the number of reproductive events to achieve the same reproductive success as the other sex (Roth et al. 2011). Thus, sex differences in PI, ornamentation, and immunity (Trivers 1972; Hedrick and Temeles 1989; Trivers 2002; Roved et al. 2017) may also give rise to sex-specific differences in longevity (Austad 2006; May 2007). Significantly, sex-specific differences in longevity can manifest into ASR when adults of one sex live longer, which will change their frequency in the population.

Our results suggest that if one parent has higher investment into both PI and ornamentation (e.g., male sticklebacks), the ASR will be biased toward the sex that bears negligible costs for the same traits (e.g., female sticklebacks) (Hagen and Gilbertson 1973), visualized in Figure 6A. This biased ASR implies that resource allocation toward both sexual selection and the upbringing of the offspring is costly and impacts fitness and LRS (Daly 1978).

Such PI caused ASR bias is in strong contrast to the situation when both sexes provide similar levels of PI. For example, many bird species provide high bi-PI while both sexes in free-spawning fish provide equally little investment (Perrone and Zaret 1979; Gross and Sargent 1985; Cockburn 2006). This is presented in the gray-shaded region of Figure 6B. In such cases, when one sex has a higher investment into ornamentation, the ASR will be biased. Our model thus matches the situation that we can find in nature: free-spawning species such as the Atlantic salmon, in which males have elaborate ornaments show highly skewed ASR (7:1 ratio of males to females) (Mobley et al. 2019).

When one sex contributes maximal PI, and the other displays secondary sexual ornaments, ASR is biased toward the sex that invests more in parental care, as shown in the nonshaded regions of Fig. 6B). This could imply that ornamentation is more costly in terms of resource allocation than PI. An enigmatic system that reflects varying degrees of PI and ornamentation are syngnathids, the family of pipefishes, and seahorses with their unique evolution of male pregnancy (Vincent et al. 1992). Here, PI has evolved on a gradient ranging from conventional sex roles to reversed sex roles with several transitions in between (Berglund et al. 1986; Vincent et al. 1992). As a particular example, in Nerophinae, males (Berglund and Rosenqvist 2003) carry the eggs but provide no additional investment. In contrast, Syngnathus have evolved full male pregnancy with a placenta-like system and paternal provisioning of nutrients, oxygen, and immunity (Roth, O., Klein, V., Beemelmanns, A., Scharsack, J. P. & Reusch, T. B. H. Male Pregnancy and Biparental Immune Priming. Am Nat 180, 802–814 (2012). Given the differential PI costs, we would thus expect a decrease in the frequency of S. typhle males compared to N. ophidion males (Berglund and Rosenqvist 2003). Observing sex ratios in syngnathid populations over the mating season and beyond would then help test our model predictions and refine assumptions. However, with increasing ornamentation in females, our model shows that the frequency of males increases because ornaments are costly; for instance, making the bearer more vulnerable to predation.

Our framework calculates the overall fitness (LRS) by considering the sex-specific differences and interactions of several sexual and life-history traits. Studying the combined dynamics of diverse traits highlights the population-level consequences such as skewed ASR (Trivers 2002; Kokko and Jennions 2008). With the aid of more empirical work directed toward investigating sexual immune dimorphism and other sex-specific traits, it will be possible to obtain a more in-depth understanding of sex-specific life history. The question of how sexual dimorphism occurs in the first place is also intriguing. Theoretical studies show how disruptive selection leads to sexual dimorphism. Thus, models that consider tools like adaptive dynamics can be used to show that traits, which go through evolutionary branching, may end up as two sex-specific traits, that is, sexual dimorphism. For instance, recent studies addressed how coevolution of traits and resource competition drive the evolution of sexual dimorphism (Bolnick and Doebeli 2003; Stoehr and Kokko 2006; Vasconcelos and Rueffler 2020); and the work by Vasconcelos and Rueffler (2020) demonstrated that even weak tradeoffs between various traits could result in evolutionary branching that leads to the coexistence of the types.

CHALLENGES AND FUTURE EXTENSIONS

In this study, we have considered large panmictic populations showing deterministic dynamics. It is not possible to perform stability analysis for this model because of an inaccessible generic analytical solution (as explained in Fig. 5). Thus, we plot the numerical solutions in this study. A version of this model that considers finite populations, and therefore, involving stochastic simulations can be a useful future potential extension.

While many sexually reproducing animals are polygamous, species like seahorses are monogamous throughout their lifetime (Vincent and Sadler 1995). The interaction among sex-specific traits would be different between monogamous and polygamous species. For instance, they may not have to bear the costs of attracting mates after one brooding season. Our model can be modified to study the effect of integrating (monogamous and polygamous) mating patterns. Concerning immune genes such as the ones of the MHC, genetically dissimilar individuals mate more often as the evolutionary incentive is to produce optimal MHC diversity offspring (Milinski 2006; Eizaguirre et al. 2009; Kalbe et al. 2009; Woelfing et al. 2009). To this end, mating is not random. Aspects of a model by Kirkpatrick (1982) for two autosomal loci with a female mating preference for a trait that occurs in males is a potential extension of our model. Finally, novel studies as done by Roved et al. (2018) will help inform and distil our theories and understanding further on the complex connections between sex-specific immune profiles and PI.

One of the main aspects of evolution by natural selection is inheritance. In the animal kingdom, offspring usually inherit traits via their parents. Therefore, studies related to sexual selection and sex-specific differences in traits are crucial. We believe our model precisely shows how combining sex-specific variation in traits causing population-level effects directly affects the evolutionary trajectory of a species.

AUTHOR CONTRIBUTIONS

VRV, OR, and CSG designed the project. VRV and CSG developed the model. VRV performed the analyses. All authors wrote the manuscript.

ACKNOWLEDGMENTS

The authors are grateful to Gustavo V. Barroso, Alice Feurtey, Stefano Giamo, Isabel Keller, Hanna Kokko, Tobias L. Lenz, David W. Rogers, Ana Teles, and Jamie Winternitz for the extremely helpful discussions. Funding from the Max Planck Society is graciously acknowledged. OR was supported by funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (MALEPREG: eu-repo/grantAgreement/EC/H2020/755659) and a grant from the German Research Foundation (DFG: 349393951). We also thank the anonymous reviewers for their useful comments.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

LITERATURE CITED

Adimora

A. A.

, and

V. J.

Schoenbach

2005

Social context, sexual networks, and racial disparities in rates of sexually transmitted infections

J. Infect. Dis.

191

S115

–

S122

Month:	Total Views:
December 2022	3
January 2023	6
February 2023	17
March 2023	17
April 2023	27
May 2023	23
June 2023	28
July 2023	30
August 2023	43
September 2023	35
October 2023	47
November 2023	41
December 2023	46
January 2024	44
February 2024	56
March 2024	39
April 2024	37
May 2024	37
June 2024	38
July 2024	42
August 2024	34
September 2024	23
October 2024	15
November 2024	45
December 2024	56
January 2025	31
February 2025	51
March 2025	46
April 2025	31
May 2025	24

Article Contents

Consequences of combining sex-specific traits Open Access

Abstract

Model

LIFETIME REPRODUCTIVE SUCCESS

Immune response

Parental investment

Ornamentation

Overall dynamics

Results

LINEAR IMMUNE ALLELIC DIVERSITY PROFILE: SINGLE LOCUS

NONLINEAR IMMUNE ALLELIC DIVERSITY PROFILE: MULTIPLE LOCI

ADULT SEX RATIO IN VARIOUS SPECIES

Discussion

CHALLENGES AND FUTURE EXTENSIONS

AUTHOR CONTRIBUTIONS

ACKNOWLEDGMENTS

CONFLICT OF INTEREST

LITERATURE CITED

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Consequences of combining sex-specific traits