Here, we correct branch lengths for simulated species trees in Burbrink and Pyron (2011), and discuss the implication of these corrections on gene tree and diversification estimates under different values of the population size parameter, θ (Neμ), and scaled coalescent units. In Burbrink and Pyron (2011), we simulated species trees using the birthdeath.tree function in GEIGER (Harmon et al. 2008), which, given the conditions of our simulations, yielded average branch lengths (edge lengths) generally greater than 1.0. For example, we simulated 100 50-taxon trees in 50 time units under a Yule model with λ (speciation rate) = 0.064, that yields average edge lengths across all trees of 7.52 (standard deviation = 1.14). Unfortunately, we failed to realize that that when simulating gene trees under a clocklike model using different values of θ in the R package “phybase” (Liu 2009), branch lengths are required to be given in terms of mutation units (T) for the species trees, which is equivalent to mutation rate per site per generation across all populations (μ), multiplied by the number of generations (t). Therefore, given our simulated species trees, the average branch lengths in units of time >1 would generally be very large in terms of mutation units. To scale this properly, we here use a standard rate of substitution from mtDNA studies (Brown et al. 1979; Zink et al. 2004; Weir and Schluter 2008), in which rates have been reported to be approximately 2% per million years between taxa (or 1 × 10−8/lineage/year). To simplify these calculations, an organism with a generation time of one year would yield a μ of 1 × 10−8 substitutions/site/year. To scale the branch lengths on the species tree, which are in absolute time units, we make the assumption that the time units are given in millions of years (now equal to generations), which is standard for most chronograms. Therefore, for an organism with one generation per year and the simulated trees now scaled in millions of generations (average = 7.52 × 106), we correct these branch lengths by multiplying all simulated tree edge lengths by 1×10−8. This yields trees with branch lengths in terms of mutational units (T), which is suitable for coalescent simulations in phybase.
To examine the impact of diversification estimation (using Pybus and Harvey's γ, 2000) under different values of θ, we turn our discussion to coalescent units, here defined as T/θ. In Burbrink and Pyron (2011), we discussed absolute values of θ on the improperly scaled species trees, when we should have discussed θ in terms of coalescent units. Using the corrected branch lengths for the 50-taxon species tree, we use the same methods for generating 100 gene trees within each species tree (for 100 species trees) as in Burbrink and Pyron (2011) but using coalescent units ranging from 0.2 to 2.0. We show that the trend is the same as before, in which increasing values of θ (lower coalescent units) yield greater γ-error (Eγ), which represents the difference between the mean gene tree γ (
)and the true value of γ from the species tree (γS): 
. The pattern remains the same for Robinson–Foulds distances (RF; Robinson and Foulds 1981) as well. However, for realistic values with trees properly scaled in mutation units, lower values of θ than those discussed in Burbrink and Pyron (2011) produce greater Eγ and higher RF distances (Fig.1).
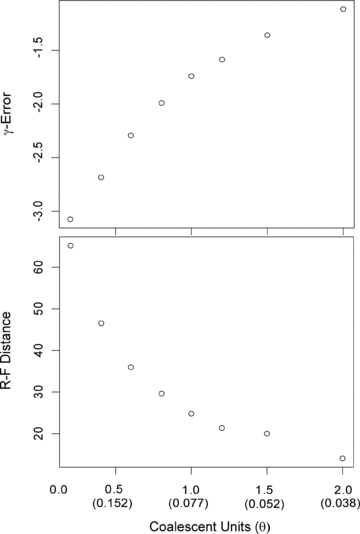
Plots of γ-error and RF distance against coalescent units (θ in parentheses) from 100 simulated species trees with 100 gene trees simulated within each species tree (see text for details).
Previous research has demonstrated that correct topological estimates of species trees become more difficult when individual gene trees are generated with coalescent units below 1.0 (Kubatko and Degnan 2007; Kubatko et al. 2009). Similarly, we also find that estimates of γ become very negatively biased when coalescent units fall below 1.0. For the gene trees here with average mutation units of 0.075, we show that more realistic empirical values of θ approximately 0.06 or greater can mislead conclusions regarding tempos of diversification, suggesting that the group of interest underwent a significant burst of diversification early in their history (γ < –1.64). This is in contrast to unrealistically high values of θ > 1.0 presented in Burbrink and Pyron (2011) as being problematic for estimating tempos of diversification, yet the coalescent units are similar to what we show here. Certainly, values of θ that will yield misleading estimates of γ are relative to branch length. Therefore, lower values of θ than presented here can yield greater γ-error for trees with shorter branch lengths or lower rates of substitution. For instance, if we conducted our simulations with a substitution rate similar to values seen in nuclear genes, 2.2 × 10−9 substitutions/site/generation (Kumar and Subramanian 2002), the trend of increasing Eγ with higher values of θ remains the same as with the mtDNA rates, but a θ of 0.017 (coalescent unit = 1.0) and below yields misleading negative estimates of γ“for most gene trees”(Eγ of –1.95). Therefore, one of the main conclusions in Burbrink and Pyron (2011) was that for most realistic estimates of θ in natural populations, gene trees provide relatively good estimates of γ, despite the disproportionate overestimation of younger node ages. Given our correction to branch length from the species trees described here, this general conclusion may be incorrect. Therefore, standard values of θ estimated in natural populations may yield significantly low values of γ, which would incorrectly suggest that the group of interest diversified in an early burst of speciation. As in Burbrink and Pyron (2011), we strongly suggest that species trees be used when accurate estimates of waiting times between speciation events are required. We thank L. Liu for advice regarding parameterization of phybase and one anonymous reviewer of this erratum.
