-
PDF
- Split View
-
Views
-
Cite
Cite
E. Matene, V. Jacquemet, Fully automated initiation of simulated episodes of atrial arrhythmias, EP Europace, Volume 14, Issue suppl_5, November 2012, Pages v17–v24, https://doi.org/10.1093/europace/eus271
Close - Share Icon Share
Abstract
To develop computational tools for automatically initiating a large number of independent episodes of atrial arrhythmias in electro-anatomical computer models of the atria and therefore facilitating the design of in silico experiments.
A biophysical model of the atria was constructed from segmented medical images of the human atria of a patient with atrial fibrillation (AF). A set of 40 initial conditions were generated based on a priori knowledge about wavefront propagation and the number and location of reentries (1–6 randomly distributed over the atrial epicardium). Simulations were run from each of these initial conditions in three substrates representing different forms of AF dynamics (stable rotors; multiple unstable meandering wavelets; and wavelets broken by repolarization heterogeneities). To demonstrate the applicability of the initiation method for testing clinical of therapeutic interventions, the channel I(Kr) was blocked after 2 s of simulation and its effect on the number of functional reentries was documented. The use of pre-computed initial conditions enabled to successfully generate episodes of simulated AF in each substrate. Blockade of I(Kr) channel prolonged action potential duration, resulting in a reduction of the number of functional reentries. In the substrate with unstable spiral waves, the effect was sufficiently large to terminate AF in about two-thirds of the cases. In the two other substrates, the effect was minor.
These new simulation tools may help investigate in computer models therapeutic interventions in different substrates in order to identify substrate-specific optimal therapy.
Introduction
Atrial fibrillation (AF) is the most common arrhythmia encountered in clinical practice. While not immediately life threatening, AF progressively turns into a chronic disease that provokes severe complications such as palpitations and stroke, leading to more frequent hospitalizations. Unlike ventricular fibrillation, this leaves ample time for diagnosis (signal analysis and identification of the origin of AF) and for the choice of an appropriate therapy.
Biophysical models of atrial anatomy and electrophysiology have been developed to contribute to the understanding of the mechanisms and to the design of diagnosis tools (e.g. signal processing) and therapeutic approaches (e.g. pharmacological or catheter ablation).1 These models provide a computational framework to test hypotheses about the mechanisms of AF therapies by designing and performing the virtual equivalent of clinical studies. Examples of AF therapies investigated using simulation tools include sodium channel blockade,2 catheter or surgical ablation,3–6 anti-tachycardia pacing,7 defibrillation,8,9 and low-energy far-field stimulation.10 The scope of these studies ranges from proof of concept to addressing specific questions about AF termination mechanisms.
In clinical studies, the unavoidable presence of inter-patient variability necessitates careful patient selection, inclusion–exclusion criteria, and adequate statistical analysis. Intra-patient variability, resulting from the differences between successive episodes of atrial arrhythmias in the same patient, is difficult to assess unless the patient is continuously monitored over a long period. In contrast, computer simulations are reproducible. Different therapies can be tested in the same simulated AF episode run again and again. On the other hand, introducing intra- and inter-patient variability in models, which is a crucial step to evaluate the effectiveness of a therapeutic intervention in different conditions, is challenging. Inter-patient variability may be achieved by creating a group of patient-specific geometrical models11,12 and by specifying substrate properties (e.g. conduction velocity and membrane kinetics) corresponding to different types of arrhythmogenic substrates.1,13–18 The present paper focuses on intra-patient variability, i.e. on initiating an ensemble of independent episodes of simulated AF in a model with given substrate properties.
There are typically three ways of generating a set of simulated AF episodes. The first is to apply several initiation protocols, for example, by varying the sites of programmed stimulation or ectopic foci.4,18,19 This physiologically relevant approach is suited for determining the vulnerability of the substrate to AF initiation, but requires the exploration of possibly multidimensional parameter space to find the vulnerability windows and trigger AF. The second approach consists in running a very long AF simulation (up to 10 min), extracting the state of the atrial tissue at regularly distributed time instants (e.g. every 30 s) and running simulations of AF therapy from each of these states.6,7 This method assumes a high sensitivity to initial condition (a pervasive feature of chaos) to ensure the independence of the initial states and therefore does not apply well to organized forms of AF. Additional initial conditions can be generated by adding a random perturbation to the membrane potential field.20,21 In the third, so-called eikonal approach, a set of initial conditions are artificially reconstructed based on a priori knowledge about wavefront propagation (the eikonal equation22) and the number and location of reentries.23 The applicability of this method is limited to the analysis of AF maintenance and termination and gives few insights into AF re-initiation mechanisms. However, it provides a tool for automatically generating an arbitrary large number of independent episodes of simulated AF.24 In addition, the number and location of reentrant circuits (whenever available) can be specified.
This paper demonstrates how the eikonal approach can help in the design of virtual clinical studies by facilitating the estimation of statistical variability among AF episodes in the same substrate and the same patient. The approach is illustrated through the study of the effect of pure potassium channel (IKr) blockade in three different arrhythmogenic substrates in a biophysical model of the human atria.
Methods
Atrial model
The geometry of the atria was reconstructed by segmenting images obtained from a computed tomography scan of a patient with AF and moderate atrial chamber enlargement. Two meshes of the same atrial geometry were created: a full three-dimensional (3D) volumetric mesh and an approximate monolayer mesh (Figure 1).
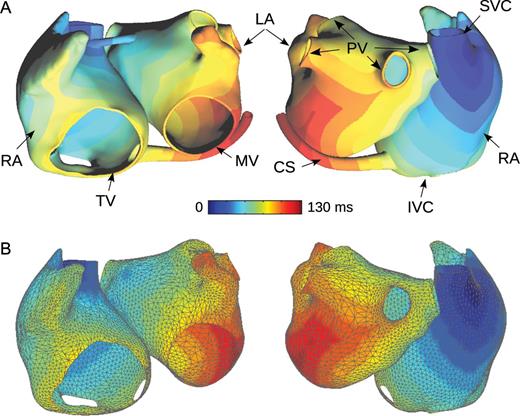
Geometry of a patient-specific atrial model. (A) Full three-dimensional cubic mesh used for running simulations. Activation time simulated during sinus rhythm is colour-coded. (B) Approximate monolayer mesh (triangular mesh) used for designing in silico experiments. Activation times computed in the full three-dimensional model are interpolated in the approximate monolayer mesh and are displayed colour-coded. RA, right atrium; LA, left atrium; PV, pulmonary veins; SVC, superior vena cava; IVC, inferior vena cava; MV, mitral valve; TV, tricuspid valve; CS, coronary sinus.
The full 3D mesh, a cubic grid of 1.04 million nodes and a spatial resolution of 330 μm, includes a fast conduction system (pectinate muscles, terminal crest, and Bachmann's bundle similarly to previous models25–27) as well as rule-based specification of fibre orientation.11,27,28 In the full 3D mesh, the right and the left atria are connected through the septum, the Bachmann's bundle, and the coronary sinus.
The approximate monolayer mesh, a coarse triangular mesh with 5622 nodes and a spatial resolution of 2.1 mm, was derived from the full 3D mesh to represent the mid-myocardial atrial surface. This mesh simplification process involved a combination of the marching cube algorithm, triangulated mesh smoothing, decimation, and remeshing using the software VRMesh (VirtualGrid, Bellevue City, WA, USA) and Matlab (Mathworks, Natick, MA, USA). In contrast to the full 3D mesh, the approximate monolayer mesh does not include 3D structures such as the fast conducting bundles and the coronary sinus, but includes the septum inter-atrial connection (Figure 1).
Since atrial myocardium is thin, data (such as membrane potentials, activation times as in Figure 1B, etc.) can be projected from one mesh onto the other by interpolation/extrapolation.24 This enabled a combined use of the two meshes. The approximate monolayer mesh served to design in silico experiments and create initial conditions (see the next subsections). These initial conditions were then interpolated in the full 3D mesh and simulations were run in the full 3D mesh.
Propagation of the cardiac impulse was simulated in the full 3D mesh in the monodomain framework.29 The ionic current through the cell membrane was described by the Courtemanche et al.30 human atrial cell model. Conduction properties (tissue conductivity) were also adjusted to represent remodelled tissue conditions. Conduction velocities were set to ∼65 cm/s longitudinally (100 cm/s in fast conducting bundles) and 26 cm/s transversally.
The monodomain propagation equation was solved numerically on a cubic grid using finite difference discretization31 and explicit time integration with a time step of 20 μs.
Arrhythmogenic substrates
The membrane kinetics model was modified to reproduce ion channel remodelling.32 Three qualitatively different arrhythmogenic substrates for AF were created.
The first model (‘Kharche’ substrate) had spatially uniform membrane properties and was similar to Kharche et al.16 and Herlin and Jacquemet24 The maximum conductance of the L-type Ca2+ current (ICaL) was reduced by 63%, the transient outward K+ current (Ito) was reduced by 65%, and the inward rectifier K+ current (IK1) was increased by 73%, based on measurements in human chronic AF cells.33,34
In the second, also uniform model (‘Gong’ substrate), dynamical beat-to-beat variations in action potential duration and discordant alternans created a substrate for AF. The current ICaL was increased by 50% and the inward rectifier current IK1 by 200%, as in Gong et al.13
The third model (‘Kneller’ substrate) represented cholinergic AF as proposed by Kneller et al.17 An acetylcholine-dependent K+ current was added17 and ICaL was reduced by 63%, thus considerably decreasing rate adaptation. Spatial variations in acetylcholine concentration were introduced to create intrinsic repolarization gradients.15,17
All three membrane models incorporate the unmodified formulation of the rapid delayed rectifier K+ current (IKr) from the Courtemanche model. To illustrate the potential applications of automated initiation of atrial arrhythmias, IKr channel blockade was simulated (see the section ‘Design of virtual clinical studies’). This intervention was modelled by setting the maximum conductance of the IKr channel to zero.
To assess the electrophysiological properties of each substrate and the effect of IKr channel blockade, simulations were run on a 1D cable with conduction properties similar to those of the atrial model. The time course of the transmembrane potential at the midpoint of the cable was recorded during paced rhythm initiated by intracellular current injection at the extremity of the cable with a cycle length of 500 ms during 10 s. Restitution curves (action potential duration as a function of the preceding diastolic interval) were computed using a premature stimulus applied after steady state was reached (500 ms pacing cycle length). Action potential durations were measured at 95% repolarization.
Creation of initial conditions
In order to set the tissue to a fibrillatory state, the idea is to create initial conditions by positioning spirals on the atrial surface.23 This conceptual description of depolarization wave dynamics is essentially 2D and macroscopic. Accordingly, the approximate monolayer atrial mesh is used for performing this task. The specification of the spatial distribution of reentrant waves may be based on case reports, electrical mapping, a priori knowledge about wave dynamics, or simply based on hypothesized configurations we would like to investigate in silico. Here, 1–6 phase singularities (corresponding to the tip of spirals or functional reentries,35 see Figure 2) were randomly distributed over the atrial surface (on the approximate monolayer mesh). In this case, the initial number of phase singularities is the only input parameter for the initial condition generation algorithm.
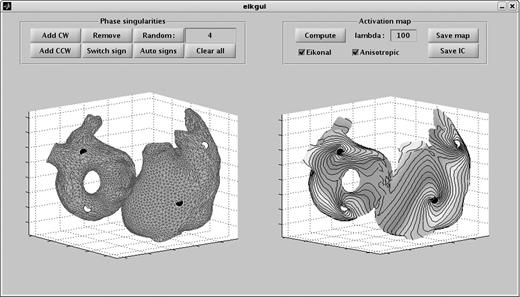
Graphic user interface in Matlab for the design of initial conditions. Black circles represent clockwise (CW) phase singularities and white circles counter-clockwise (CCW) phase singularities. Left panel: manual and random placement of phase singularities on the atrial surface. Right panel: computed activation map used for the creation of the initiation condition.
After the position and direction of rotation of phase singularities are chosen, reentrant activation maps are reconstructed by interpolation using an eikonal-based algorithm described previously.23,24,36 This algorithm assumes that propagation velocity is known at every point of the atrial surface and computes the evolution of wavefronts based on these (possibly anisotropic) propagation velocities. It constitutes an extension of the shortest path algorithm37 that makes it applicable to reentrant activations in a medium with macroscopically heterogeneous anisotropic conduction properties. From this computed activation map, an initial condition is created, i.e. the value of all state variables (membrane potential, ionic concentrations, and channel gate states) at every point in space is specified, assuming that the correspondence between activation time and cell state is the same as in a tissue paced at a cycle length similar to that of the reentry.23 This correspondence is specific to each substrate. In the presence of heterogeneity in membrane kinetics, this correspondence can be made spatially dependent, or an average model can be used over all the tissue for the creation of the initial condition (the latter method was chosen here). Our experience suggests that initial conditions created for a specific substrate may be used for simulations in another substrate (as long as the membrane kinetics model is the same). Here, initial conditions specific to each substrate were generated.
We designed a graphic user interface in Matlab to perform this task interactively (see a snapshot in Figure 2). This interface allows adding, moving, removing phase singularities by mouse click as well as setting and changing their direction of rotation (clockwise or counter-clockwise; see the left panel of Figure 2). Alternatively, distributions of position and direction of rotation or phase singularities can be randomly generated to accelerate the creation of a large number of configurations,24 while ensuring that the phase singularities are not too close to each other (they would annihilate rapidly) and that the directions of rotation are coherent (to avoid adjacent spirals rotating in the same direction24 and to satisfy the topological constraints38). In the case of an odd number of phase singularities, an anatomical reentry around an obstacle (typically a valve) is naturally introduced to guarantee the existence of an activation map compatible with the desired distribution of phase singularities.39,40 Then, the interface allows computing and exporting the activation map and the initial condition for future use in the simulation software. The parameter lambda (see the right panel of Figure 2) is associated with the exit criterion of the eikonal algorithm.24 It controls how much isochrones are ‘bent’ to form spirals. Herlin and Jacquemet24 studied the effect of lambda on spiral patterns. Accordingly, lambda was set to 10 cm.
All these operations can also be performed automatically in a Matlab script to generate a library of initial conditions with different number and location of phase singularities.
Design of virtual clinical studies
The possibility to automatically generate a large number of independent fibrillatory initial conditions facilitates the design of in silico experiments to test hypotheses about diagnostic tools or therapeutic strategies. The ability of control the complexity of the dynamics (as measured by the number of wavelets) opens the way to the analysis of the effect of dynamical complexity on the success of a therapy. This approach is illustrated here through an example of virtual clinical study to test the effect of pure IKr channel blockade on simulated AF, revisiting previous simulation studies in 2D substrates.2,21
The simulation study protocol consisted of the steps illustrated in Figure 3 with m = 3 substrates and n = 40 initial conditions. First, the pro-arrhythmic substrate was specified (see above), including conduction and repolarization properties. Then, 10 initial conditions with 3, 4, 5, and 6 phase singularities (1, 2, 3, and 4 for the Gong substrate since its wavelength is longer; see Figure 4) were automatically created (using the method of the previous subsection), making a total of 40 initial conditions. Simulations were run in the full 3D atrial model from each of the 40 initial conditions for 2 s in the absence of external intervention. Afterwards, the maximum conductance of the IKr channel was abruptly blocked (i.e. was set to zero) over the whole atrial tissue and the simulation was continued for 5 s (see Figure 3). The evolution of the dynamics was assessed by tracking the number of phase singularities. For that purpose, membrane potential maps were projected from the full 3D model onto the approximate monolayer mesh (triangulated surface) and phase singularities were identified on the latter mesh using an algorithm described previously.41 The effect of pharmacological intervention was quantified by documenting the number of phase singularities averaged over the 1 s interval before the intervention and over the 1 s interval before the end of the simulation.
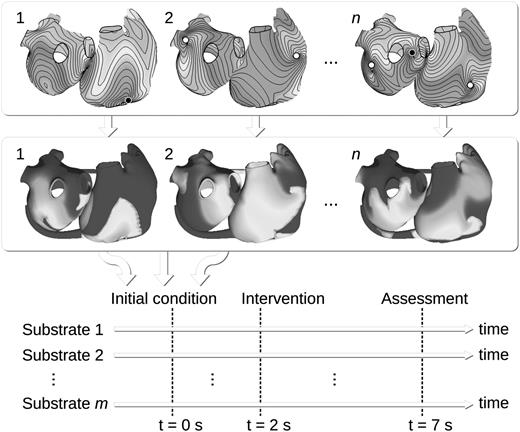
Schematic view illustrating the design of a virtual clinical study. Phase maps are automatically computed (top panel) and n initial conditions are generated (middle panel). Simulations are run for m different sets of substrate properties, starting from each of the n initial conditions. All m × n simulations involve an intervention to be tested (e.g. channel blockade). The outcome is assessed at the end of the simulation.
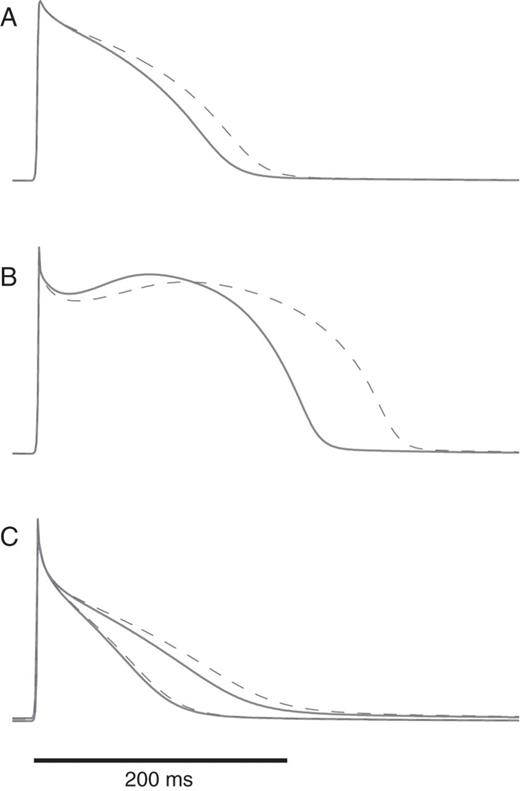
Action potentials in each substrate during paced rhythm at 120 b.p.m. before (solid lines) and after (dashed lines) IKr channel blockade. (A) Kharche substrate; (B) Gong substrate; (C) Kneller substrate; since this substrate is heterogeneous, the action potentials with the shortest and the longest duration are displayed.
Results
Figure 4 shows for each substrate (with and without IKr blockade) the action potentials simulated in a 1D cable paced with a cycle length of 500 ms. As expected, blockade of the outward current IKr prolonged action potential duration, the effect being more pronounced for the Gong substrate. To further illustrate the contrast between the substrates, the corresponding action potential duration restitution curves are displayed in Figure 5.
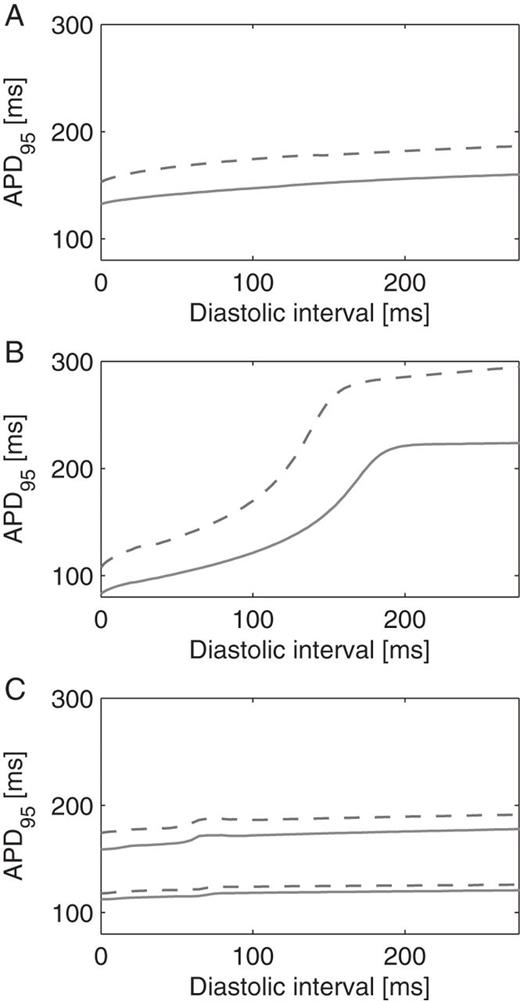
Restitution curves for each substrate before (solid lines) and after (dashed lines) IKr channel blockade. Action potential duration (APD, measured at 95% repolarization) is shown as a function of the diastolic interval. (A) Kharche substrate; (B) Gong substrate; (C) Kneller substrate; since this substrate is heterogeneous, the shortest and longest APDs are displayed.
For each substrate, AF episodes were simulated in the atrial model from initial conditions generated using the eikonal approach. Some of these initial conditions are displayed in Figure 3. With the Kharche and Kneller substrates, AF was maintained for >2 s when the simulation started from any of the 40 initial conditions. With the Gong substrate, 37/40 attempts at initiating AF from these initial conditions were successful. In the three unsuccessful cases, the number of initial spirals was apparently too large for the given tissue size and wave length. These spirals annihilated each other.
In all of the three substrates, simulated AF was observed as multiple wavelets undergoing functional and anatomical reentries. Wavelet dynamics was however different, as illustrated in Figure 6. The Kharche substrate is uniform and with low rate adaptation (flat action potential duration restitution, see Figure 5A). As a result, spiral waves remained stable (e.g. red star in Figure 6A). In contrast, in the Gong substrate (also uniform), steeper restitution (see Figure 5B)-induced dynamical changes in action potential duration (steep dynamical repolarization gradients, e.g. red star in Figure 6B), spiral meandering and wave breaks due to the interplay between depolarization and repolarization waves. Heterogeneities in the Kneller substrate created islands of refractory tissue around which spiral could anchor (e.g. red star in Figure 6C), thus stabilizing the rotors and facilitating AF maintenance. These observations, based on our geometrical model and our AF initiation procedure, are in complete agreement with previous studies using different simulation tools, geometries, and initiation protocols.13,16,17,19,24,27
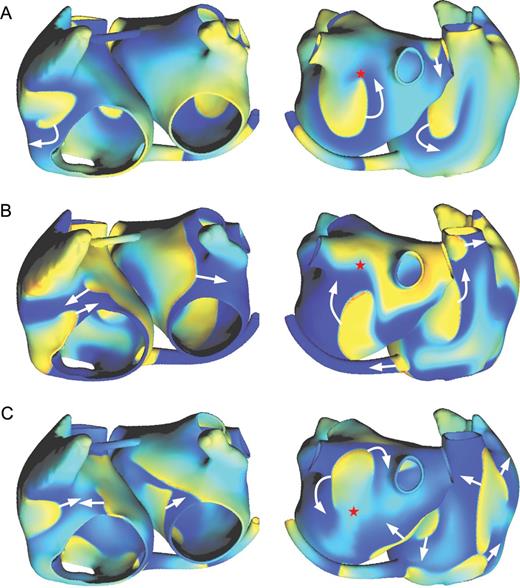
Examples of transmembrane potential maps (left: anterior view; right: posterior view) during simulated atrial fibrillation in three substrates: (A) Kharche substrate; (B) Gong substrate; (C) Kneller substrate. Transmembrane potential is colour-coded, blue corresponding to the resting state and yellow/red to the depolarized state. White arrows represent the direction of depolarization wave propagation. The red stars are referred to in the text.
To illustrate potential applications of automatic simulated AF initiation, AF dynamics was analysed before and after complete IKr channel blockade. Figure 7 reports the average number of phase singularities before and after the intervention for each substrate. The reduction in the number of phase singularities was related to the prolongation of action potential duration (Figures 4 and 5). The effect of IKr channel blockade on the Kneller model was very small, especially in regions with shorter action potentials (where most wave fronts propagate). As a result, the number of phase singularities was not affected. In the Kharche substrate, the prolongation of action potential duration was larger, and therefore the decrease in the number of phase singularities was measurable, although not statistically significant (P=0.1, paired t-test). However, no AF termination was observed (after 5 s). In the Gong substrate, IKr channel blockade lead to AF termination in 63% of the simulations. When AF was still self-maintaining after 5 s, the number of phase singularities was decreased by 37% on an average.
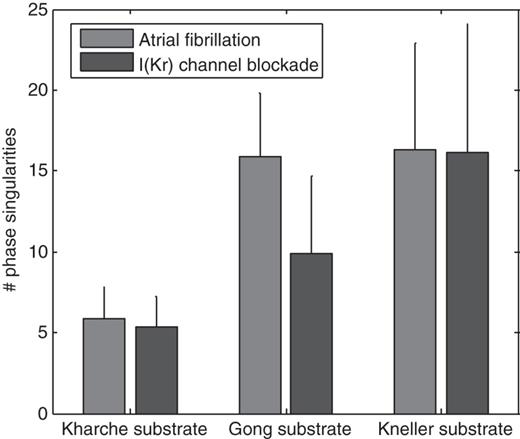
Number of phase singularities during atrial fibrillation before and after I(Kr) channel blockade for the three different substrates. The error bars indicate standard deviations (statistics over 40 simulations; episodes terminated within 5 s by the intervention are excluded).
Discussion
We have developed a computational tool for automatically initiating an arbitrary large number of AF episodes in computer models of the atria. Our approach specifically addresses the issue of how to generate statistical realizations (episodes) of the same process (AF dynamics) in order to facilitate the design and improve the clinical relevance of virtual clinical studies. Only one parameter (the number of initial phase singularities) has to be selected, which greatly decreases the time-consuming need to tune parameters. The graphic user interface further simplifies the procedure and makes the simulation of AF more accessible to students or researchers with little experience in modelling.
The approach was effective at initiating AF in three different types of tissue substrates associated with different forms of AF: a uniform substrate with stable spirals, a substrate leading to wave breaks and transient alternans in action potential duration, and a substrate with intrinsic repolarization heterogeneities. Results obtained in the first substrate confirmed the suitability of our method for organized forms of AF (a situation that has been a source of limitations for other initiation methods7). The number of phase singularities after 2 s of simulation was approximately the same as in the initial condition, as reported previously.24 Results obtained in the second substrate demonstrated that although the eikonal approach fundamentally assumes a periodic activity, the initial conditions generated using that method can successfully initiate more unstable AF dynamics characterized by wave breaks. In this case, the number of phase singularities during the AF episode may not be related to that of the initial condition. In addition, many of the phase singularities were short lived. Therefore, in this substrate, the initial number of phase singularities does not provide a way to control the complexity of AF dynamics. Results obtained in the third substrate show the applicability of the method in the presence of repolarization heterogeneities despite the fact that the eikonal equation ignores repolarization. In this case, phase singularities may move towards regions with intrinsically longer action potential durations17 or towards anatomical obstacles.
In all of these models, the conduction properties were specified in such a way that the wavelength was sufficiently short to enable multiple reentries to coexist.15 Wavelength remains indeed an unavoidable constraint to AF maintenance. When too many phase singularities are incorporated in the initial condition, these wavelets annihilate each other quickly by front–tail interaction. This may provide a way to estimate how many simultaneous wavelets can be sustained in a given substrate.
The idea of creating initial conditions with a given distribution of spiral waves is conceptually based on the hypothesis that AF is maintained by multiple wavelets. Other mechanisms or forms of AF have been proposed. Our approach, with some limitations, may also apply to these situations. If AF is of focal origin, the use of different fibrillatory initial conditions may help simulate independent AF episodes with a focal source at the same location and with the same firing rate. If microstructure plays a role, for instance in the presence of fibrosis, a macroscopically equivalent propagation model could be constructed for the computation of the initial condition, while the full microstructure model would be used for simulating the subsequent evolution. This multiscale approach would facilitate the simulation of micro-reentries. If atrial tissue layers are partially decoupled, slightly different initial conditions may be used in each layer of the 3D model, thus providing insights into 3D reentrant pathways. Our method is, however, limited by thin-walled tissue.24
The example of IKr channel blockade illustrates potential applications. Testing a therapeutic intervention in a model (assessing AF termination or measuring the impact on AF dynamics) can be accelerated by automatically creating a library of initial conditions. These initial conditions do not include any information about the mechanisms that have triggered the AF episode, but this information is usually not available to clinicians when a patient with AF comes to the hospital. By streamlining the design of in silico experiments, our method will facilitate the extension of simulation studies to multiple patient-specific geometries and multiple substrate properties or AF mechanisms.
Conflict of interest: none declared.
Funding
This work was supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Fonds de la Recherche du Québec—Santé (FRQS).



