-
PDF
- Split View
-
Views
-
Cite
Cite
Mark Gersovitz, Jeffrey S. Hammer, The Economical Control of Infectious Diseases, The Economic Journal, Volume 114, Issue 492, January 2004, Pages 1–27, https://doi.org/10.1046/j.0013-0133.2003.0174.x
Close - Share Icon Share
Abstract
The structure of representative agents and decentralisation of the social planner’s problem provide a framework for the economics of infection and associated externalities. Optimal implementation of prevention and therapy depends on: (1) biology including whether infection is person to person or by vectors; (2) whether the infected progress to recovery and susceptibility, immunity, or death; (3) costs of interventions; (4) whether interventions target everyone, the uninfected, the infected, or contacts between the two; (5) individual behaviour leading to two types of externalities. By way of example, if people recover to be susceptible, government subsidies should equally favour prevention and therapy.
The economic approach to infectious diseases is in its infancy, somewhat oddly because many economists have long had the intuition that epidemics and infectious diseases are quintessential manifestations of the principle of an externality, itself a central concept in economics (Gersovitz and Hammer, forthcoming a). Furthermore, epidemiology provides ready‐made dynamic models of disease transmission and economics provides methods of valuing the costs and benefits of health interventions and methods of dynamic optimisation to guide policy. Policy toward infections is of great importance. Yet only recently have economists begun to look at these questions in a formal way.
This paper has two main goals. The overarching goal is to dissect two important externalities involving infectious diseases when there are the options of both prevention and therapy, so that the relative phasing of these two types of interventions is important. To achieve this goal, we need to state the social planner’s or first‐best problem and to compare it to a representative agent’s problem. To avoid compounding the identification of any externalities with problems of myopia, imperfect ability to insure health outcomes, or a disregard for the welfare of future generations, we make assumptions about the behaviour of the representative agent such that these problems do not arise, allowing us to focus exclusively on the externalities that we identify. These assumptions may not always be adequate approximations and a relaxation of these assumptions would lead to further considerations in the design of interventions but we do not deal with these issues in this paper.
The economic literature on infectious diseases has taken as its starting point some special although important concerns. This starting point has influenced modelling strategies in ways that we believe obscures the general structure of private choice and consequent externalities in the process of disease transmission.
One focus of the previous literature has been on vaccinations (Brito et al, 1991; Francis, 1997; Geoffard and Philipson, 1996; Kremer, 1996). It is certainly an important intervention but one that is only possible for a limited number of diseases. Importantly for a modelling strategy, moreover, vaccination is plausibly a discrete decision, to vaccinate or not, and whether it is or not, that is how it has been modelled. Indeed, Francis models vaccination as a discrete choice by identical individuals. With neither an intensive margin (choice of intensity of vaccination) nor an extensive margin (heterogenous individuals), he concludes that vaccination does not exhibit externalities, a result that does not, however, generalise (Gersovitz, 2003).
Philipson (2000 and cited references) and associates and Kremer (1996) have focussed on HIV/AIDS. For this disease prevention is naturally the almost exclusive focus, none of this work analyses therapeutic behaviour, and the transition from infection is to death, rather than to recovered‐and‐susceptible or immune. As we will show, the state that follows infection is important for the analytical tractability of the model, and a fatal disease is not the easiest to analyse. In fact, Geoffard and Philipson (1996) analyse HIV under the assumption that infection raises an individual’s discount rate but does not lead to a diminution in the population; while tractable, such a formulation hardly incorporates the salient feature of this fatal infection. Furthermore, the work of Philipson and his associates formulates prevention as an entirely discrete choice (safe or risky sex). Whether this formulation is realistic for HIV is open to question; regardless, it is clear to us that it ignores the important scope for varying preventive effort that arises for many other diseases which present a virtual continuum of degrees of prevention. Oral‐faecal diseases provide good examples of such a continuum: boil water progressively longer, wash hands on more and more occasions. Kremer (1996) stresses heterogeneous behaviour in the population which leads him to a wide range of interesting conclusions about HIV. For our purposes, however, his assumption that people are not future‐oriented in their risk‐taking behaviour limits the applicability of his model to our question because it confounds myopia with externalities.
In the economics literature on infections, Wiemer (1987) is an exception to the study of one type of intervention in isolation. She models the use of two interventions in the case of schistosomiasis (bilharzia), but under assumptions about costs and benefits that imply that one of the two interventions is used maximally or not at all. Furthermore, she does not model decisions by individuals and the associated externalities of this type of vector‐spread disease. Epidemiologists have also analysed the problem of optimal interventions to control infections, but have not surprisingly ignored many of the issues we investigate.1
Once we have adopted a framework that can achieve our first goal of analysing externalities and infectious diseases, our second goal is to examine a typology of infectious diseases. This typology allows for people to progress from being susceptible to infected (and infectious) to: (1) recovered but again susceptible, or (2) immune, or (3) dead. Furthermore, the typology includes diseases that spread from person to person and those that are spread by intermediate vectors, such as mosquitoes. Finally, the typology allows for the targeting of different interventions at different groups. We show how these different characteristics of the epidemic affect conclusions about how to offset externalities and how the preventive and therapeutic interventions are phased relative to each other.
In fact, we identify two types of externalities: first, infectious people can infect other people who in turn infect others and so on, the source of what we call the pure infection externality. This externality arises if, in choosing their own levels of preventive and therapeutic effort, people do not fully take into account the costs to others who will become infected as a consequence of their being infectious. Second, there is a pure prevention externality that arises because the preventive actions of one individual may directly affect the probability that other people become infected, whether or not the preventive action prevents infection of the individual undertaking it. Typically, the pure prevention externality arises only for diseases that involve a vector and therefore appears only in the last model of the paper. An example is the use of insecticides to kill mosquitoes that carry disease. The person using the insecticide may or may not be bitten and infected but the killing of mosquitoes lessens the probability that others will be bitten and infected, something that the user of the insecticide may disregard. A third type of externality involves pathogen resistance to drugs, both preventive and therapeutic, but we do not examine this potentially important problem.
As is conventional in modelling externalities, the paper begins with the problem of a hypothetical social planner who can directly control all preventive and therapeutic actions, initially in a model of infection from person to person. First, we lay out the accounting for the people who are in different disease statuses and the dynamics that move people from one status to another, the constraints on the optimisation problem. Next, we introduce the objective of decision makers: the maximisation of utility of income net of the costs of the disease in terms of discomfort, fear and economic loss and net of the costs of preventive and therapeutic measures. We then maximise the objective function subject to the constraints, and look at the optimal solution to the social planner’s problem and how it depends on what happens to people who are infected. The next section looks at the decentralised decisions, their deviation from the social planner’s choices, and hence the existence of externalities and the role for public interventions. A penultimate section looks at some of these issues when vectors transmit disease. The paper ends with some concluding remarks.
1. The Social Planner’s Problem
1.1. The Dynamic Constraints
The starting point for the study of optimal policy toward infectious diseases is the classic literature on mathematical epidemiology. It provides the dynamic constraints that condition decisions about infectious diseases. This literature models many diseases, ones transmitted directly from person to person and ones transmitted by vectors (Anderson and May, 1991).
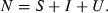
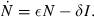
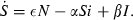
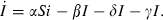
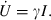
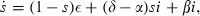
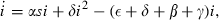
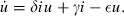
1.2. The Costs and Benefits of Interventions and the Social Planner’s Optimisation
We are now ready to specify the social planner’s objective function. In the total absence of the disease, each person in the society would have a level of income of V0. Because we assume that utility is linear in income, V0 would also be their level of utility.
When the disease exists, however, the social planner likely will be spending resources on prevention and on therapies. Either intervention may be targeted in the sense that only a proportion of the population generates costs associated with the intervention. Let θj, j = a, b be the proportions of the population that generate either preventive or therapeutic costs associated with an infectious disease. We refer to the θj as targeting functions; in general, they depend on s and i. The most natural formulation would be for prevention to be targeted at the susceptible (θa = s) and for therapies to be targeted at the infected (θb = i). Other formulations may, however, be plausible depending on the ability to identify and reach different groups and what makes sense in terms of the disease and the balance of costs and benefits, something considered in more detail in the following sections that deal with special cases. The type of targeting may be a choice variable, but in this paper we will assume that it is a technical given and compare the behaviour of the model under different targeting assumptions.
The government uses two policy interventions, preventive effort of a ≥ 0 units per person at whom prevention is targeted and therapeutic effort of b ≥ 0 units per person at whom therapeutic effort is targeted. The total number of units of these interventions are therefore a θaN and b θbN. The levels of these health inputs per targeted person affect the parameters of the model, α(a) and β(b), γ(b) and δ(b), and thereby determine respectively the rate of new infections and the rates of transition to recovered‐but‐susceptible, immune, and dead. The controls exhibit diminishing marginal products so that: α′ < 0, α′′ > 0, β′ > 0, β′′ < 0, γ′ > 0, γ′′ < 0, and δ′ < 0, δ′′ > 0. This property of our formulation distinguishes it from all the preceding work that we know and it opens the scope for internal solutions to the optimal policy problem and for the analysis of the co‐ordination of multiple interventions phased in a smooth way over the course of an epidemic. We believe that for many if not all diseases there is scope for undertaking additional preventive and therapeutic interventions although they are marginally less and less productive. Interventions are costly; preventive effort costs pa per unit and therapeutic effort costs pb per unit; total costs of the interventions are therefore paaθaN and pbbθbN.

As mentioned, the objective function embodies an assumption of linearity in the value of income net of the costs of illness and expenditures on health interventions. This assumption simplifies many aspects of the subsequent calculations; we introduce concavity into the model via the diminishing returns of health expenditures on the parameters of the dynamics of the epidemic rather than through diminishing marginal utility of income net of all the costs associated with the disease. Without the assumption of linearity, it would be important to specify who pays which costs of the interventions. For instance, the costs of therapies may be deducted only from the incomes of the infected or health insurance may spread these costs across everyone. If each person has a concave utility of consumption net of the total health costs (the costs of prevention, therapies and illness) that each pays, it would be necessary to pay attention to different constraints on the way the social planner can distribute these costs. The social planner’s objective function would be the sum of the concave utilities of the people in different disease statuses; these utilities would depend on the difference between income V0 and the total health costs people pay. Among other simplifications, linearity of the objective function allows us to sidestep the question of the interaction between the epidemic and the health insurance regime, the latter itself a complex topic and one worthy of analysis in future research. Gersovitz and Hammer (forthcoming b) provide numerical results when utility is concave in income net of health expenditures and all the costs of the infection are shared equally in a model of vector‐borne infection.
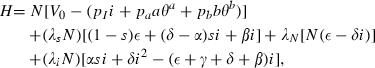
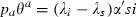
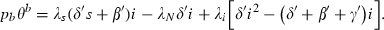
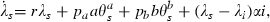
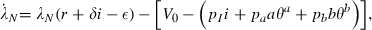
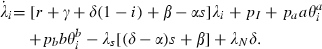
To develop the analysis further we turn to some special cases.
1.3. The Special Case of Susceptible‐Infected‐Susceptible (SIS)
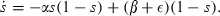
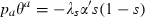
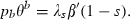
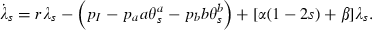
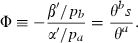
Although the relative emphasis on the two types of policies in terms of their marginal products depends only on the state of the epidemic, it is extremely sensitive to the form of the targeting functions. Table 1 records the eight possible relationships between Φ and s for the combinations of the four formulations of the targeting function for α and the two for β. In case IIA, Φ is relatively high when susceptibles and infecteds are nearly equal and is low for s near either of its extremes, 0 or 1. In this case, prevention efforts are most important when transmission rates are at their maximum because the total (and marginal) costs of prevention do not rise with the level of susceptibles, but the marginal effect of prevention is highest when transmission is fastest. In case IIB, Φ falls monotonically as s rises because costs of prevention rise and those of therapy fall with an increase in susceptibles. In case IIC, Φ rises monotonically as s rises and in case IID, Φ is constant regardless of the value of s, two cases that are less easy to interpret intuitively. The ratios of the marginal products do not translate directly into the ratios of the inputs themselves, perhaps the most direct measure of the relative size of the two efforts. But, there are special cases when the two ratios do move together (see Appendix A for an example) and so Φ helps to understand the possibilities for the co‐movements of the physical inputs during the evolution of an epidemic.
Targeting and the Relative Reliance on Preventive and Therapeutic Policies (Values of Φ of (14))
| . | Values ofθb . | |
|---|---|---|
| I. . | II. . | |
| 1 . | (1 − s) . | |
| Values ofθa | ||
| A. 1 | s | s(1 − s) |
| B. s | 1 | (1 − s) |
| C. (1 − s) | s/(1 − s) | s |
| D. s(1 − s) | 1/(1 − s) | 1 |
| . | Values ofθb . | |
|---|---|---|
| I. . | II. . | |
| 1 . | (1 − s) . | |
| Values ofθa | ||
| A. 1 | s | s(1 − s) |
| B. s | 1 | (1 − s) |
| C. (1 − s) | s/(1 − s) | s |
| D. s(1 − s) | 1/(1 − s) | 1 |
Targeting and the Relative Reliance on Preventive and Therapeutic Policies (Values of Φ of (14))
| . | Values ofθb . | |
|---|---|---|
| I. . | II. . | |
| 1 . | (1 − s) . | |
| Values ofθa | ||
| A. 1 | s | s(1 − s) |
| B. s | 1 | (1 − s) |
| C. (1 − s) | s/(1 − s) | s |
| D. s(1 − s) | 1/(1 − s) | 1 |
| . | Values ofθb . | |
|---|---|---|
| I. . | II. . | |
| 1 . | (1 − s) . | |
| Values ofθa | ||
| A. 1 | s | s(1 − s) |
| B. s | 1 | (1 − s) |
| C. (1 − s) | s/(1 − s) | s |
| D. s(1 − s) | 1/(1 − s) | 1 |
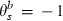 (cases IIA–D of Table 1). Total differentiation of (13a) and (13b), the first‐order conditions, implies:
(cases IIA–D of Table 1). Total differentiation of (13a) and (13b), the first‐order conditions, implies: 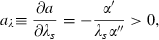
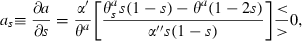
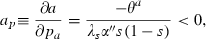
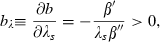
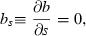
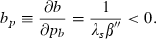
So far we have proceeded on the presumption that the first‐order conditions determine a maximum. In fact, the most generally‐used sufficiency conditions for a maximum do not obtain in this model, but we believe that the way we have characterised the maximisation is, in fact, correct for a very large class of these models. While the problem is concave in the controls because they are subject to diminishing marginal returns, it is not concave in the state because the dynamic equation exhibits increasing marginal returns in the state, a fundamental property of contagion as posited by epidemiologists. Correspondingly, the failure of the sufficiency conditions is not a reflection of the linearity of the instantaneous utility function (the integrand of (9)). Appendix A discusses these issues in more detail.
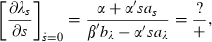
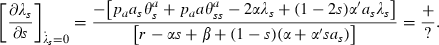
In two cases, IIB with θa = s and IID with θa = s(1 − s), both slopes are positive when the equations of motion are linearised about the steady‐state so long as a variant of the conventional condition that the interest rate at least equals the population growth rate (in the absence of disease) holds, that is r ≥ ε.4 If the slope of the  locus is flatter than that of the
locus is flatter than that of the  locus in s − λs space, there is a unique stable path to the steady state (Figure 1a) because the characteristic equation of the linearised dynamic system has one positive and one negative real root. The variables s and λs move together toward the steady state and b and β move with them so that therapeutic effort increases with more susceptibles. Preventive effort, a, and α move as determined by the relation between a and b as given by Φ, decreasing with the number of susceptibles in IIB and varying with it in IID. If the slope of the
locus in s − λs space, there is a unique stable path to the steady state (Figure 1a) because the characteristic equation of the linearised dynamic system has one positive and one negative real root. The variables s and λs move together toward the steady state and b and β move with them so that therapeutic effort increases with more susceptibles. Preventive effort, a, and α move as determined by the relation between a and b as given by Φ, decreasing with the number of susceptibles in IIB and varying with it in IID. If the slope of the  locus is steeper than that of the
locus is steeper than that of the  locus in s − λs space, however, there is no stable path to the steady state (Figure 1b). In these cases, the model could evolve either to the eradication of the disease, with s = 1, or to the equilibrium without intervention, a = b = 0, or to an intermediate stable equilibrium of the type illustrated in Figure 1a if such exists.5 That such unstable cases exist is consistent with the structure of the model, which should allow the possibility of optimally eradicating the disease or optimally doing nothing in the steady state for some configurations of the phase diagram. We do not pursue these divergent cases here; instead, we restrict the discussion to diseases that are (optimally) neither eradicated nor ignored and in which policy takes the system to an optimal steady state.
locus in s − λs space, however, there is no stable path to the steady state (Figure 1b). In these cases, the model could evolve either to the eradication of the disease, with s = 1, or to the equilibrium without intervention, a = b = 0, or to an intermediate stable equilibrium of the type illustrated in Figure 1a if such exists.5 That such unstable cases exist is consistent with the structure of the model, which should allow the possibility of optimally eradicating the disease or optimally doing nothing in the steady state for some configurations of the phase diagram. We do not pursue these divergent cases here; instead, we restrict the discussion to diseases that are (optimally) neither eradicated nor ignored and in which policy takes the system to an optimal steady state.
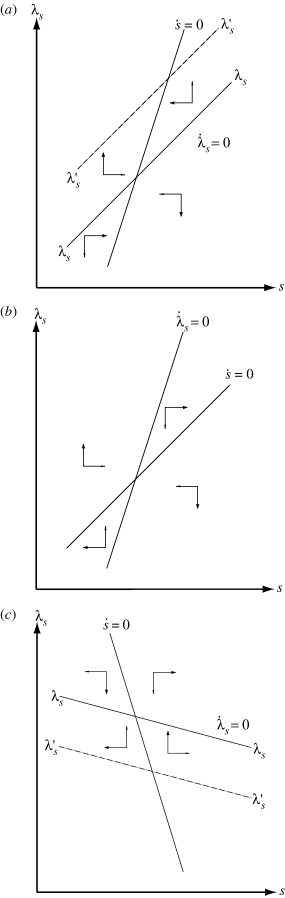
The Phase Diagram for an SIS Disease with Case IIA or D Targetting: (a) A Stable Case, (b) An Unstable Case and (c) A Stable Case
The two remaining cases, IIA with θa = 1 and IIC with θa = 1 − s, are more complex and there are several sub‐cases.6 When the model is linearised about the steady state both slopes may be positive, as in cases IIB and D, and the foregoing analysis obtains. The slope of the  locus may be positive while that of the
locus may be positive while that of the  locus is negative; this case is unstable and we do not discuss it further. Both slopes may be negative; if the
locus is negative; this case is unstable and we do not discuss it further. Both slopes may be negative; if the  locus is less negatively sloped there is a stable saddlepoint (Figure 1c) while the reverse situation is unstable.7
locus is less negatively sloped there is a stable saddlepoint (Figure 1c) while the reverse situation is unstable.7
The parameters of the model are the four prices: pI, pa, pb and r. The parameters pI and r enter (13c) for  but not (12) for
but not (12) for  , nor do they enter the first‐order conditions for a and b. They therefore shift the
, nor do they enter the first‐order conditions for a and b. They therefore shift the  locus but not the
locus but not the  locus. Consider the effect of an increase in pI on s*, the steady‐state number of susceptibles in the two saddlepoint cases. In Figure 1a the
locus. Consider the effect of an increase in pI on s*, the steady‐state number of susceptibles in the two saddlepoint cases. In Figure 1a the  locus shifts up (from λsλs to
locus shifts up (from λsλs to  ) and s* rises; in Figure 1c the
) and s* rises; in Figure 1c the  locus shifts down and s* also rises. Thus in all cases an increase in the direct cost of being infected in terms of pain and suffering increases the steady‐state proportion of the population that is uninfected. The effect on s* of an increase in r is opposite to that of pI. The costs of prevention or therapy are borne immediately while their benefits are received over time. Because an increase in r leads to a diminished weight of the future in decisions, an increase in r leads to an increase in the optimal steady‐state proportion of the population that is infected.
locus shifts down and s* also rises. Thus in all cases an increase in the direct cost of being infected in terms of pain and suffering increases the steady‐state proportion of the population that is uninfected. The effect on s* of an increase in r is opposite to that of pI. The costs of prevention or therapy are borne immediately while their benefits are received over time. Because an increase in r leads to a diminished weight of the future in decisions, an increase in r leads to an increase in the optimal steady‐state proportion of the population that is infected.
The effects of the other two parameters are more complicated, however, because both loci shift. The impact effect (s and λs fixed) of an increase in the price of either preventive or therapeutic interventions is to decrease the amount used via (15c) and (15f) and therefore either a and α or b and β are affected in both equations.
In the case of an increase in pb, the  locus always shifts up regardless of the sign of its slope. The
locus always shifts up regardless of the sign of its slope. The  locus shifts up if its slope is positive and down if its slope is negative. In the case of an equilibrium of the type illustrated in Figure 1a, therefore, the shift in the
locus shifts up if its slope is positive and down if its slope is negative. In the case of an equilibrium of the type illustrated in Figure 1a, therefore, the shift in the  locus tends to lower s* while the shift in the
locus tends to lower s* while the shift in the  locus tends to raise s* and the net outcome is ambiguous even when the algebraic magnitudes of these shifts are taken into account. The rationale for this ambiguity is as follows: The price of a therapeutic intervention, pb, enters the dynamic equation for the co‐state variable in the same way as the cost of being infected, pI. One of the effects of an increase in pb is therefore to raise s, just as an increase in pI does; in effect an increase in the cost of being cured is like an increase in the cost of being infected because every infection induces expenditures on therapeutic inputs. But there is also the fact that it is more expensive to be cured so that it may be desirable to spend less on b and be cured less quickly. That the first effect can dominate is easily seen from the special case when b is fixed at some positive value (perhaps for technological reasons) so that therapeutic effort is not adjusted in response to its price increase. The preventive intervention can still respond, however, as it would to a change in pI and the steady state proportion of the uninfected, s*, is thereby increased. Recall that cases IIB and D of Table 1 must conform to this latter pattern of an ambiguous impact of pb. In contrast, starting from an equilibrium of the type illustrated in Figure 1c, the upward shift of the
locus tends to raise s* and the net outcome is ambiguous even when the algebraic magnitudes of these shifts are taken into account. The rationale for this ambiguity is as follows: The price of a therapeutic intervention, pb, enters the dynamic equation for the co‐state variable in the same way as the cost of being infected, pI. One of the effects of an increase in pb is therefore to raise s, just as an increase in pI does; in effect an increase in the cost of being cured is like an increase in the cost of being infected because every infection induces expenditures on therapeutic inputs. But there is also the fact that it is more expensive to be cured so that it may be desirable to spend less on b and be cured less quickly. That the first effect can dominate is easily seen from the special case when b is fixed at some positive value (perhaps for technological reasons) so that therapeutic effort is not adjusted in response to its price increase. The preventive intervention can still respond, however, as it would to a change in pI and the steady state proportion of the uninfected, s*, is thereby increased. Recall that cases IIB and D of Table 1 must conform to this latter pattern of an ambiguous impact of pb. In contrast, starting from an equilibrium of the type illustrated in Figure 1c, the upward shift of the  locus and the downward shift of the
locus and the downward shift of the  locus work to raise s*.
locus work to raise s*.
 locus also always shifts up regardless of the sign of its slope. When the system is linearised about the steady state, the
locus also always shifts up regardless of the sign of its slope. When the system is linearised about the steady state, the  locus shifts according to the sign of
locus shifts according to the sign of 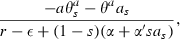
1.4. The Special Case of Susceptible‐Infected‐Dead (SID)
If all people who become infected die, the general model of (10) can be specialised to: U = 0, β = γ = 0, λi = 0. The states are s and i = (1 − s) and the controls are a and b. On the further assumption that being sick is not per se costly, pI = 0. The value of therapeutic measures is to reduce the death rate and thereby gain utility from prolonging a life; formally, the negative valuation of death is embodied in the fact that the dead are not part of N and do not get the utility associated with being alive, V0, net of the expenditures on a and b. To save space, we do not repeat the versions of (11a–d) specialised for this case, but merely comment on the properties of this case that follow from these equations. Furthermore, we discuss only the results for the case in which θb = (1 − s).
The specialised versions of (6) and (11a–d) are independent of N but not of λN and therefore so are the solutions for the optimal interventions, a and b, and for the state of the epidemic, s. The first result implies that the interventions are independent of the scale of the economy. The second result implies that the dimension of the system is three (s, λs and λN) rather than the two of the SIS model. This important difference between the two models arises because the infected die in the SID model which is valued by λN, rather than returning to the susceptible state which is valued at λs, as in the SIS model. Consequently, the SID model is significantly less tractable than the SIS model. The solutions for the SID case are not independent of ε which appears in the specialised versions of (6) and (11d). The multipliers, λs and λN, must be positive under the assumptions about θa, α′ and δ′.
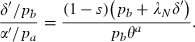
1.5. The Special Case of Susceptible‐Infected‐Uninfectible (SIU)
This case corresponds to β = δ = 0; individuals who are susceptible become infected and then immune. The states are s, i and u = (1 − s − i) and the controls are a and b. The only substantive simplification of the social planner’s problem that we have been able to identify in this case is that the five‐dimensional system of Section 1.2 can be reduced to four because λN does not appear in the dynamic equations for the other variables because people do not die of the disease. We therefore do not present any results for this case except in Section 2.4 on decentralisation.
2. Decentralisation
2.1. The General Problem of Decentralisation
To this point we have discussed the problem of the social planner who directly controls the values of a and b in a model without people who make decisions that affect their own health. The next step is to consider private decisions and their implications for government policy. If people do not take into account the effect on the infection of the general population caused by their ability to infect others if they become infected, they generate a pure infection externality. In our formulation of diseases in which one person directly infects another, the preventive activity of one individual does not, however, affect the probability that other people become infected independently of whether the first person becomes infected, so there is no pure prevention externality. After identifying the externality, we examine how government interventions with subsidies or taxes can decentralise the social planner’s first‐best solution.
In our abstract formulation, governments can subsidise preventive and therapeutic activities, the privately chosen values of a and b. In reality, for some diseases, there will be some inputs that are marketed and some inputs that involve individuals’ non‐marketed and unobservable actions such as avoiding crowded places to varying degrees in the case of tuberculosis prevention or adhering meticulously to drug regimens. When a and b involve such non‐marketed and unobservable actions the subsidy/tax interventions we propose may be infeasible or may have to be targeted only on the marketed components of preventive and therapeutic activities with second‐best implications.
The simplest way to illustrate the pure infection externality and its implications for policy is to assume that private decisions are made by a group of people that we call a household, a construct that we use as the representative decision‐making agent. This construct provides a logically consistent and analytically tractable model to contrast with the model of the social planner: first, the household’s objective function is fully congruent with the social planner’s. Furthermore, the household understands and anticipates how the epidemic will evolve and is fully forward‐looking with regard to its possible future statuses as well as its present situation. Unlike Kremer’s (1996) modelling of individuals’ behaviour which is only oriented to the conditions in the current period, our household takes account in its current decisions of the evolution of the epidemic, its implications for the future risk of infection and its implications for all the household’s descendants. For instance, if the future probability of infection is high it affects the current incentive of the household to make therapeutic expenditures. It is therefore the case that our rationale for government interventions does not depend either on myopia or on a discrepancy between the social planner’s and the representative agents’ valuation of outcomes over the path of the epidemic. Instead, our assumptions isolate the pure externality motivation for government intervention. To the extent that there are deviations from the preceding assumptions on the behaviour of the household, there may be other important reasons for government interventions but they are not the subject of this paper.
As is conventional in the public‐economics treatment of externalities, the only distinction between the social planner and the representative agent is that the household is assumed to be small relative to the population as a whole, in this case so that the proportion of the household in any disease status does not affect the proportion of the population as a whole that is in that status. In particular, this household takes as given the proportion of the population that is infected, which equals the probability, π, that any random contact is with an infected person. Second, the household is assumed to be sufficiently large that it can fulfil the role of a representative agent and therefore that the proportion of the household in each disease status is identical to the corresponding population proportion. Finally, it is this household that takes decisions about the interventions, a and b. Because the instantaneous utility function is linear, there is no sense in which the household is performing any implicit insurance function for its members. A perhaps more realistic but only perhaps (because people do indeed live in households) and less tractable approach would build the private economy up from representative individuals each of whom is in one or another disease status at any one time and taking decisions about either prevention or therapy (or neither if already immune), with regard to their possible future statuses as well as their present situation. For diseases in which people transit from susceptible to infected to dead, the individual’s problem seems tractable, because death is obviously an absorbing state. For individuals who cycle between susceptible and infected, we have not been able to manage a formulation that does not adversely affect the tractability of the model and we leave this task for the future but see no reason why such a formulation should fundamentally alter the nature of the externalities that we identify.
The dynamic equations of this version of the model are the same as in Section 1.1, except that in (3) and (4) the term αSi is replaced by αSπ to denote the exogeneity from the household’s viewpoint of the proportion, π, of the population (in contrast to the proportion, i, of the household) that is infected. There is a consequent change in (6) and (7).
A further change has to be made to the objective function to reflect the possibility of government interventions. If there is an externality, the government may find it optimal to subsidise or tax preventive and/or therapeutic inputs. To allow for these possibilities, we assume that the representative household faces prices of qj = (1 + tj)pj, j = a, b. As is standard in public economics, so that any interventions are revenue neutral in a way that does not have any incentive effects beyond the tj, we assume that the household receives a lump sum payment (possibly negative) of T that it takes as exogenous to its own actions but that in fact equals tapaahθa + tbpbbhθb; a superscript ‘h’ indicates that the variables are evaluated at the household’s values rather than the social planner’s. If this lump sum offset were not part of the package, the household’s welfare would be affected by its experiencing a net loss or gain of income as the government intervenes with taxes or subsidies to offset the externality. The decentralisation results that follow would not obtain as can be seen by following the steps of the proofs without the assumption of revenue neutrality.

2.2. Decentralisation in the SIS Model
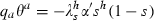
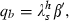
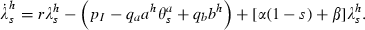
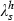 in (13a–b) and (18a–b). It does so with a lump‐sum offset, T, so that any revenues or expenditures from the price interventions also appear in the household’s budget. Because the intervention is only to
in (13a–b) and (18a–b). It does so with a lump‐sum offset, T, so that any revenues or expenditures from the price interventions also appear in the household’s budget. Because the intervention is only to 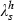 and because of the way
and because of the way 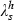 enters (18a–b), a and b activities are affected to the same degree and Φ is unaffected. At the steady state, the intervention is a subsidy (negative tax) at rate t*:
enters (18a–b), a and b activities are affected to the same degree and Φ is unaffected. At the steady state, the intervention is a subsidy (negative tax) at rate t*: 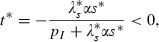
 and s* are the values from the planner’s steady state.8 Furthermore, for any non‐steady‐state s, the government must intervene with a subsidy.9 This finding that the intervention is a subsidy coincides with the intuition that private decisions ignore the benefits to society as a whole from taking preventive and therapeutic measures. Subsidisation is at equal rates because it is equally beneficial in preventing further infection to get a person out of the infected pool as to have prevented the person from getting into it in the first place. These benefits are equally overlooked by the private decision makers. This result contradicts what may be an often‐held presumption that preventive rather than therapeutic efforts are associated with externalities and are the proper domain of public health. In this model, in contrast to the model of vector‐borne diseases in a subsequent section of the paper, preventive activities are pure private goods in that one person’s preventive effort does not affect another person’s risk of infection if the first person does not become infected. Furthermore, the government does not have at its disposal any technology of intervention that private people do not have at theirs. The externality therefore arises only through an individual’s being in the infected pool, either through getting into it without consideration of the risks posed to others or through not getting out of it fast enough for the same reason.
and s* are the values from the planner’s steady state.8 Furthermore, for any non‐steady‐state s, the government must intervene with a subsidy.9 This finding that the intervention is a subsidy coincides with the intuition that private decisions ignore the benefits to society as a whole from taking preventive and therapeutic measures. Subsidisation is at equal rates because it is equally beneficial in preventing further infection to get a person out of the infected pool as to have prevented the person from getting into it in the first place. These benefits are equally overlooked by the private decision makers. This result contradicts what may be an often‐held presumption that preventive rather than therapeutic efforts are associated with externalities and are the proper domain of public health. In this model, in contrast to the model of vector‐borne diseases in a subsequent section of the paper, preventive activities are pure private goods in that one person’s preventive effort does not affect another person’s risk of infection if the first person does not become infected. Furthermore, the government does not have at its disposal any technology of intervention that private people do not have at theirs. The externality therefore arises only through an individual’s being in the infected pool, either through getting into it without consideration of the risks posed to others or through not getting out of it fast enough for the same reason.2.3. Decentralisation in the SID Model
In this case, private decisions are made by a household as given by the Hamiltonian of (17) specialised to the SID model as defined in Section 1.4. As in the SIS model, if the household is to be representative of society as a whole, s must equal sh. Once this substitution is made, the only differences between the equations of the planner’s problem and of the private problem are the qj and an additional term of −αsλs in the equation for  as opposed to the equation for
as opposed to the equation for  .
.
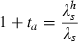
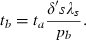
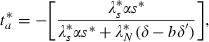
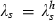 , comparison of the expressions for the change in these two multipliers shows that the change in the former is smaller than the change in the latter.
, comparison of the expressions for the change in these two multipliers shows that the change in the former is smaller than the change in the latter.2.4. Decentralisation in the SIU Model
Decentralisation is harder to analyse in the SIU model than in either the SIS or the SID models. In the SIS and SID models there is only one multiplier equation that differs between the social planner’s and the household’s problems, that associated with the change in s, whereas in the SIU model there are two, associated with the changes in s and in i. We have therefore only been able to characterise the government’s optimal interventions at the steady state.
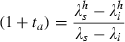
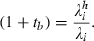
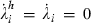 imply that the steady‐state values of the two interventions are equal. Thus, in the steady state, there is an echo of the SIS result that the government’s optimal interventions are at the same rate. A similar intuition applies: At the steady state, either going into the infected pool or not getting out of it imposes a similar externality because either is a permanent (i.e. steady‐state) increase in the size of the infected pool. Furthermore, the fact that (1 + tb)
imply that the steady‐state values of the two interventions are equal. Thus, in the steady state, there is an echo of the SIS result that the government’s optimal interventions are at the same rate. A similar intuition applies: At the steady state, either going into the infected pool or not getting out of it imposes a similar externality because either is a permanent (i.e. steady‐state) increase in the size of the infected pool. Furthermore, the fact that (1 + tb)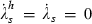 and (1 + ta)
and (1 + ta)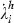
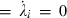 in steady state implies that:
in steady state implies that: 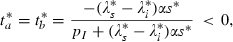
3. Control of a Vector‐borne SIS Disease
Many infectious diseases are transmitted through intermediate hosts, such as mosquitoes, flies, ticks and snails. These hosts must be infected to play their part in the cycle of infection. For instance, in the case of malaria, infected mosquitoes inject people with one stage of the parasite thereby infecting them. Uninfected mosquitoes that bite infected people are in turn infected by a later developmental stage of the parasite in an infected person’s blood, thereby continuing the cycle. Interventions to affect the prevalence of these diseases can take many forms and the package is more complicated than the distinction between prevention and therapy in Sections 1 and 2.
A model of malaria transmission must, therefore, comprise equations for the number of people who are infected (I) and the number of mosquitoes that are infected (Y). For simplicity, we will assume that the total population (of people) is fixed at N, so that there is neither natural growth in the population nor are there deaths associated with malaria. The sum of the number of susceptibles (S) and infecteds equals the whole population, S + I = N, and s, as before, is the proportion of the population that is susceptible. Because we are interested in interventions that affect the total number of mosquitoes (M), we also specify the dynamics of the total mosquito population.12
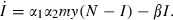
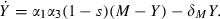
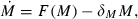
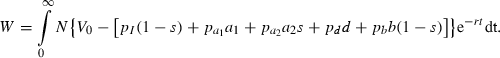
some interventions affect both the probability that an infected person infects an uninfected vector as well as the probability that an infected vector infects an uninfected person, for example, promotion of the wearing of clothes and use of bed nets that lower the chance of bites, summarised by a1, so that α1(a1) with
 ;
;other interventions affect the probability that an uninfected person is infected by an infectious vector but do not prevent uninfected vectors from becoming infected by an infectious person, for example, provision of prophylactic drugs, a2, so that α2(a2) with
 ;
;spraying mosquitoes with insecticides with intensity d, so that δM(d) with
 ;
;provision of drugs that promote recovery, of amount b, so that β(b) with β′ > 0.
Interventions to change the value of α3 affect the probability that an infectious person infects an uninfected vector but do not affect the probability that an infectious vector infects an uninfected person. These interventions are perhaps the least implementable. They might include deterring people from voiding parasites in the case of schistosomiasis, but this type of action has little direct benefit to the infected person and would therefore require monitoring by the government and could not easily be decentralised through taxes and subsidies. Scientific advances provide genuine prospects for genetic engineering of the vector to resist infection, but we leave this type of intervention aside. In the subsequent discussion, α3is therefore treated as a fixed parameter. We also ignore possibilities for changing the form of the relation F(M), for instance through the draining of swamps.
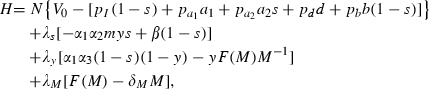
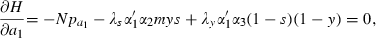
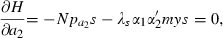
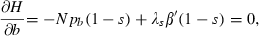
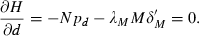
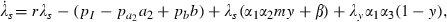
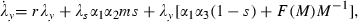
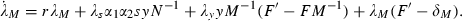
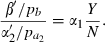
As in the other models, we introduce private decision making by assuming that certain variables are taken as given by a household that is susceptible in the proportion sh. In this case, the total mosquito population (M) and the extent of its infection (y) are exogenous to private decision makers. These assumptions are extreme representations of any actual situation. We are treating insecticidal spraying as a pure public good, an extreme case of a pure prevention externality in which no individual perceives any personal benefit from spraying but society as a whole does. In reality, even at the household level, there is scope for diminishing the population of mosquitoes through insecticidal spraying, but the infiltration of mosquitoes from outside the household’s area of control is much more rapid than if the government is doing co‐ordinated spraying over a large area.
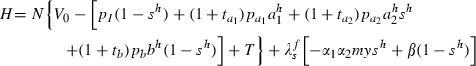
 is the only multiplier and it is associated with the state sh; y and M are exogenous functions of time from the household’s perspective and the government’s expenditure on d is subsumed in T. The first order conditions for this problem are:
is the only multiplier and it is associated with the state sh; y and M are exogenous functions of time from the household’s perspective and the government’s expenditure on d is subsumed in T. The first order conditions for this problem are: 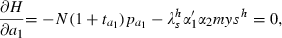
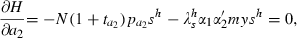
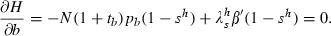
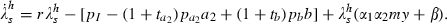
Government intervention to transform the decisions of the household into the dynamics that maximise social welfare requires two types of interventions:
a programme of spraying (d) paid for by the government consistent with (29d); and
a set of price interventions to transform (32a–c) into (29a–c).
Once this complete package is implemented, it is clear from comparison of (29b–c) and (32b–c) that the effect of price interventions for a2 and b is only through the transformation of  into λs. In other words, whatever the price intervention it is applied at equal rates to the prices of these two instruments; this result parallels the equal‐rate result of the SIS model and has the same intuition. Because λy < 0, comparison of (29a) with (32a) shows that a1 is subsidised more (or taxed less) than a2 and b.
into λs. In other words, whatever the price intervention it is applied at equal rates to the prices of these two instruments; this result parallels the equal‐rate result of the SIS model and has the same intuition. Because λy < 0, comparison of (29a) with (32a) shows that a1 is subsidised more (or taxed less) than a2 and b.
4. Conclusions
Our starting point for this paper has been a commonsensical one: mathematical epidemiology provides a parsimonious representation of how infectious diseases spread. Economics suggests an objective function to evaluate the costs of infection and its associated offsetting interventions and especially a role for diminishing returns in the interventions that affect the evolution of the epidemic. All these elements taken together specify the objectives and constraints that determine optimal interventions for public health in a hypothetical socially planned economy. The discrepancy between the social planner’s solution and decentralised decision making defines externalities in the economy, and the scope for subsidy/tax interventions by government to maximise private welfare in the absence of central control of all decisions.
Although we set out a general formulation of this problem for infections that proceed either to recovery and further susceptibility, immunity or death as well as a variant of an infection that depends on vectors, by far the most tractable case is the first, the SIS model. For this type of disease, we looked at the effects of different targeting schemes on the phasing of preventive inputs relative to therapeutic ones, the response of the steady‐state level of susceptibility to the different prices in the model and the role of subsidies in decentralising the social planner’s problem. In this model, the optimal intervention is a subsidy at the same rate to both preventive and therapeutic activities, both in the steady state and during the approach to it, and the result does not depend on the form of targeting. By contrast, the phasing of the two interventions is qualitatively sensitive to the form of targeting. Even so, this model poses difficult technical problems, most especially as regards the sufficient conditions for a welfare‐maximising dynamic policy, something we largely addressed through numerical examples.
With regard to the other models, we provided some results, on the phasing of interventions and on the subsidies and taxes necessary to achieve decentralisation. Targeting is again central to the phasing of interventions. What happens to the infected is critical to the qualitative properties of the tax/subsidy interventions. The SIS model provides an anchor for the discussion of these models and some of the SIS results reappear in one form or another underlining the usefulness of the SIS model as a starting point for the analysis. But these models are all inherently of higher dimension than the SIS model and their properties as a whole are generally more difficult to analyse. Undoubtedly, further progress will depend on more numerical work but again the insights of the SIS model should provide guidance in interpretation; Gersovitz and Hammer (forthcoming b) examine numerically a model of a vector‐borne infection.
Despite the variety of assumptions that we have incorporated into the analysis, there are many alternatives that we have not considered. The basic structure of the model provides scope for analysing many of these alternatives. The assumptions that the representative agent is fully forward looking and cares fully about present and future household members could be modified; deviations from these assumptions would generate additional rationales for government interventions. So would the acquisition of drug resistance by the pathogens. Finally, there may be further economic implications of large‐scale epidemics such as HIV that necessitate a more detailed modelling of the costs of infections as they work their way through the economy as a whole.
Appendix
Appendix: The Second‐Order Conditions for the SIS Model
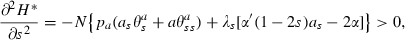
Despite this failure of the commonly‐used sufficiency condition, we believe that the problem of Section 1.3 is well posed and its solution is characterised by the first‐order conditions and the phase diagrams. There are three reasons for our belief.
First, at an intuitive level, the α and β functions may exhibit steeply diminishing returns. In this case, it is hard to see how the solution could be characterised by anything but a conventional optimising approach to a steady‐state level of infection.
Second, consistent with this intuition, the Arrow conditions seem much stronger than are necessary. Zeidan (1984) presents weaker conditions but they are not easy to apply.
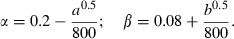
The dynamic equation is the discrete version of (12). In this case, if nothing is done, the equilibrium is an internal one with the steady‐state susceptible fraction of the population being s* = 0.08/0.20 = 0.40 and the corresponding value of W = 6,400. We found the policy rule by iterating on the value function.13 The computation seemed well‐behaved and straightforward, except that there was some slight instability in the values of the controls for the last few values of s at either end of its range. This instability seemed to be associated with the interpolation because it seemed always to be pushed to the end when we added additional points. To save space, Table A.1 shows values of the (endogenous) parameters of the model (α and β) and the value function (W) for ten of the 417 values of the state variable, s, used in the computation. The steady‐state value of s is (approximately) 0.443 and the value of moving there from the no‐intervention steady‐state value of s is the difference between 6,400 and 6,568.
| s . | α . | β . | W . |
|---|---|---|---|
| 0.100 | 0.1846 | 0.0821 | 4,566 |
| 0.200 | 0.1853 | 0.0823 | 5,170 |
| 0.300 | 0.1860 | 0.0825 | 5,833 |
| 0.400 | 0.1868 | 0.0827 | 6,568 |
| 0.443 | 0.1872 | 0.0829 | 6,911 |
| 0.500 | 0.1877 | 0.0830 | 7,394 |
| 0.600 | 0.1888 | 0.0835 | 8,338 |
| 0.700 | 0.1900 | 0.0841 | 9,445 |
| 0.800 | 0.1917 | 0.0852 | 10,801 |
| 0.900 | 0.1941 | 0.0874 | 12,605 |
| s . | α . | β . | W . |
|---|---|---|---|
| 0.100 | 0.1846 | 0.0821 | 4,566 |
| 0.200 | 0.1853 | 0.0823 | 5,170 |
| 0.300 | 0.1860 | 0.0825 | 5,833 |
| 0.400 | 0.1868 | 0.0827 | 6,568 |
| 0.443 | 0.1872 | 0.0829 | 6,911 |
| 0.500 | 0.1877 | 0.0830 | 7,394 |
| 0.600 | 0.1888 | 0.0835 | 8,338 |
| 0.700 | 0.1900 | 0.0841 | 9,445 |
| 0.800 | 0.1917 | 0.0852 | 10,801 |
| 0.900 | 0.1941 | 0.0874 | 12,605 |
| s . | α . | β . | W . |
|---|---|---|---|
| 0.100 | 0.1846 | 0.0821 | 4,566 |
| 0.200 | 0.1853 | 0.0823 | 5,170 |
| 0.300 | 0.1860 | 0.0825 | 5,833 |
| 0.400 | 0.1868 | 0.0827 | 6,568 |
| 0.443 | 0.1872 | 0.0829 | 6,911 |
| 0.500 | 0.1877 | 0.0830 | 7,394 |
| 0.600 | 0.1888 | 0.0835 | 8,338 |
| 0.700 | 0.1900 | 0.0841 | 9,445 |
| 0.800 | 0.1917 | 0.0852 | 10,801 |
| 0.900 | 0.1941 | 0.0874 | 12,605 |
| s . | α . | β . | W . |
|---|---|---|---|
| 0.100 | 0.1846 | 0.0821 | 4,566 |
| 0.200 | 0.1853 | 0.0823 | 5,170 |
| 0.300 | 0.1860 | 0.0825 | 5,833 |
| 0.400 | 0.1868 | 0.0827 | 6,568 |
| 0.443 | 0.1872 | 0.0829 | 6,911 |
| 0.500 | 0.1877 | 0.0830 | 7,394 |
| 0.600 | 0.1888 | 0.0835 | 8,338 |
| 0.700 | 0.1900 | 0.0841 | 9,445 |
| 0.800 | 0.1917 | 0.0852 | 10,801 |
| 0.900 | 0.1941 | 0.0874 | 12,605 |
We increased the four price parameters to indicate the responsiveness of the steady‐state value of s, s*. A 10% increase in pI increases s* by 0.9%. A 10% increase in pa decreases s* by 0.7%. A 10% increase in pb decreases s* by 0.6%. A 10% increase in (1 + r) decreases s* by 3.2%. All the simulations for these comparative steady‐state results as well as other similar sensitivity analysis suggest a well‐behaved problem.
Footnotes
Wickwire (1977) surveys early work and Sethi and Staats (1978), Greenhalgh (1988) and Hocking (1991) are more recent. This literature, however, has several shortcomings. First, the objective function is often poorly specified, with no discounting and a finite horizon. More importantly, marginal costs and benefits are typically assumed constant leading to unrealistic bang‐bang solutions. Usually, there is no discussion of the co‐ordination of multiple interventions. Finally, these models do not incorporate health choices by individuals, and therefore do not discuss externalities and the decentralisation of the optimal policies, a topic we stress.
We assume that each person has the same rate of contacts. Kremer (1996) examines some behavioural aspects of models in which different people have different rates of contact.
While this paper was in the last stage of review, a paper by Goldman and Lightwood (2002) appeared that is the only mathematical discussion of when eradication dominates chronic control of an infection (and vice versa) that we know. Their analysis shows that there can be more than one optimal steady state in a model of the optimal control of infections that is similar to the ones we discuss here and that there can be both stable and unstable optimal steady states. For instance, they provide an example where for high rates of infection the system moves to a steady state with endemic infection while for low levels of infection the system moves toward the (asymptotic) eradication of the infection. They model a somewhat special case where therapy is the only intervention and people recover to be again susceptible. Their analysis should be of pivotal importance to the investigation of this important question in the more complex models we discuss here where we are basically restricting the analysis to the discussion of the properties of a stable endemic optimal steady state and the approach to it on either the assumption that other steady states do not exist or that the system is in the region of attraction to an endemic steady state.
Note that in cases IIB and D the term (α + α′sas) is always positive.
Goldman and Lightwood (2002) demonstrate exactly this possibility of an unstable optimal steady state co‐existing with a stable optimal steady state for their model which only allows for a therapeutic intervention. In this case, if the unstable steady state is perturbed, the system evolves either to the stable steady state of endemic infection or to the eradication of the disease.
In these cases the term (α + α′sas) may be positive or negative and therefore the numerator of (16a) and the denominator of (16b) may be positive or negative. Note, however, that if the denominator of (16b) is negative, so must be the numerator of (16a); it is not possible to have a positively sloped  locus and a negatively sloped
locus and a negatively sloped  locus.
locus.
The results in this sentence follow from the application of such standard references as Kamien and Schwartz (1981, Appendix B). The saddlepoint case is their case IC.
This result follows from multiplying (13c) by (1 + t) and setting it equal to (18c) because both equations equal zero at the steady state.
At s* there is a subsidy, so that  . Now if there were ever a tax corresponding to some lower level of s,
. Now if there were ever a tax corresponding to some lower level of s,  . Between this point and the steady state, there would therefore have to be some intermediate value of s < s* at which
. Between this point and the steady state, there would therefore have to be some intermediate value of s < s* at which  . But at such a point,
. But at such a point,  is increasing faster than λs, compare (18c) with (13c) evaluated at the common values of all variables because the state and costate are equal for the private and public problems at this point where the tax/subsidy equals zero. Consequently,
is increasing faster than λs, compare (18c) with (13c) evaluated at the common values of all variables because the state and costate are equal for the private and public problems at this point where the tax/subsidy equals zero. Consequently,  could never fall relative to λs which would contradict the existence of a steady‐state subsidy. A similar argument holds for s > s* once it is noted that in these situations s is falling (rather than rising) toward the steady state.
could never fall relative to λs which would contradict the existence of a steady‐state subsidy. A similar argument holds for s > s* once it is noted that in these situations s is falling (rather than rising) toward the steady state.
The multipliers for the state N are equal because when there is revenue neutrality, the values of these multipliers are the same in the steady state for the private and social optimisations, as can be seen by setting the equations for the changes in these multipliers (not shown) to zero. Furthermore, the form of these equations for the changes in these multipliers is the same and therefore the entire path of these two multipliers must be the same.
The result follows from multiplying the equation for the change in λs by (1 + ta) and equating it to the equation for the change in  because both changes are zero in the steady state.
because both changes are zero in the steady state.
The dynamic structure of infection in our model, (24) and (25), is an adaptation of the discussion in Anderson and May (1991). As does their basic model, we ignore deaths from malaria and the existence of an animal reservoir of infection on which mosquitoes feed in addition to the human population.
We used a grid of 417 points, with s ranging from 0.005 to 0.985. The density of points was not uniform and was chosen to provide increased accuracy at the limits of the range and around the steady state. We interpolated the value function for intermediate values of s using a cubic spline. We accepted that the value function had converged when the maximum proportional change in the value function at every s in an iteration was less than 0.000001. All calculations were done in double‐precision FORTRAN.
References
Author notes
We thank Edward F. Buffie, Daniel Leonard, Steve Salant and Carl Simon for comments. The findings, interpretations and conclusions in this paper are entirely those of the authors and do not necessarily represent the views of the World Bank, its executive directors or the countries they represent.



