Does Risk of Nest Failure or Adult Predation Influence Hatching Patterns of the Green-Rumped Parrotlet?

Abstract

Resumen

Introduction

Nest predation is the primary cause of breeding failure in most bird species (Lack 1954, Martin 1995). The risk of nest predation may be a critical factor affecting clutch size (Skutch 1985, Lima 1987), developmental rates of nestlings (Ricklefs 1969, Bosque and Bosque 1995), patterns of nest attentiveness (Weathers and Sullivan 1989, Martin and Ghalambor 1999), and patterns of parental effort (Martin 1992, Pease and Grzybowski 1995). Consequently, reproductive strategies that minimize the impact of predation losses on lifetime reproductive success are likely to be strongly favored by natural selection (Martin 1992).

Risk of predation may also affect hatching patterns in birds (Stoleson and Beissinger 1995). Parent birds may adjust the onset of incubation to minimize the risk of loss of their eggs or young to predators or other causes (the Nest Failure Hypothesis), or their own risk of mortality from predators while on the nest or caring for young (the Adult Predation Hypothesis). Risk from both processes has been formally defined in mathematical models that can be used with demographic data to evaluate the optimal onset of incubation (Clark and Wilson 1981, Magrath 1988).

In this paper we examine patterns of risk of total nest failure and predation on adult females in a population of Green-rumped Parrotlets (Forpus passerinus) in Venezuela, based on 5 years of field data from over 900 nesting attempts. We first assess the Nest Failure model to determine whether observed patterns of incubation in parrotlets are consistent with model predictions. Incubation on the first egg should result from higher risks of complete nest failure before the onset of incubation than during the fledging period. We also use a modification of the Adult Predation model to evaluate the effects of risk of predation for adult females on incubation patterns. The Adult Predation model predicts that first-egg incubation results from a higher risk of predation on adult females before, rather than after, the onset of incubation. Below we summarize the important characteristics and components of each model.

The Nest Failure Model

If the probability of total nest failure varies through the course of the nesting cycle, there should be strong selective pressure to minimize the duration of stages at high risk. For example, if nests are more likely to be depredated or damaged by nest competitors when they contain only eggs than when they contain nestlings or both nestlings and eggs, then selection should favor an incubation pattern that minimizes the length of time a nest contains only eggs (the Nest Failure Hypothesis; Hussell 1972, Clark and Wilson 1981). This is achieved by initiating incubation with the first egg and hatching completely asynchronously. Alternatively, if nestlings are more likely to be lost, synchronous hatching will minimize the time that a nest contains nestlings. However, delaying incubation to produce synchronous hatching will also delay the fledging of the first young, making it more likely the nest will fail before any young fledge (Briskie and Sealy 1989). Thus, the optimal degree of asynchrony may represent a tradeoff between a reduced risk of predation of nestlings and increased risk of total brood loss due to delayed fledging when hatching is synchronous, and a reduced risk of predation on eggs and decreased survival of later-hatching chicks when hatching is asynchronous (Stoleson and Beissinger 1995).

Clark and Wilson (1981) developed a model of nest failure to predict the optimal degree of asynchrony in relation to patterns of total nest failure. Their model was based on daily survival probabilities before and after the first hatch. Hussell (1985) modified the model by dividing the nesting cycle into four periods corresponding to the laying (prior to the start of incubation), incubation, nestling, and fledging stages. The expected productivity of a brood, W_m, as a function of the egg on which incubation starts (m) is given by:

$$

(variables for all equations are defined in Table 1). We have used the notation of Magrath (1988) in order to incorporate his later modifications to the model.

Table 1.

Open in new tab

Model parameters for the Nest Failure (NF) and Adult Predation (AP) models

Table 1.

Open in new tab

Model parameters for the Nest Failure (NF) and Adult Predation (AP) models

Hussell (1985) reformulated the model to compare different degrees of asynchrony by calculating the ratio W_m/W_N, the productivity of starting incubation on egg m relative to the productivity of complete synchrony (m = N). Optimal asynchrony occurs when the productivity ratio W_m/W_N is maximized. Hussell demonstrated that when the ratio is calculated, survival probabilities during the incubation and nestling periods cancel out because they do not change with m. Thus, the only relevant parameters affecting the optimal degree of asynchrony are N, t, P₀, and P₃. Clark and Wilson (1981) incorporated the probability of within-brood mortality due to asynchrony into their model by assuming that the last-hatched nestling survives with a reduced probability q. If the penultimate chick is subject to reduced survival as well, the model can be extended with an additional q′ term (Hussell 1985). Hussell also added the term k to the equation, where k is the delay between the laying of egg m and the actual start of incubation, expressed as a fraction of t. However, he demonstrated that optimal synchrony apparently never occurs when k > 0. We therefore have dropped it from our equations. The modified productivity ratio of Hussell (1985) is given by:

$$

These models assume that daily survival probabilities are constant within periods of the nesting cycle, an assumption questioned by Murray (1994).

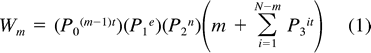
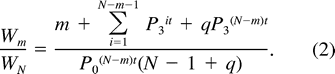
Adult Predation Model

The risk of predation on adult birds tending eggs or nestlings may be even more likely to influence reproductive strategies than would predation on nest contents alone, because an adult risks losing all of its future as well as current reproduction (Charnov and Krebs 1974). Hussell (1972) suggested that if adults are subject to a relatively high risk of predation while incubating, it would be advantageous to minimize the time spent on the nest by delaying the onset of incubation, and thus hatch eggs more synchronously. This may explain why Clark and Wilson (1981) found that most birds hatch their eggs more synchronously than predicted by their Nest Failure model (Magrath 1988). Magrath (1988) formalized this idea in a modification of Hussell's (1985) Nest Failure model by incorporating daily survival probabilities of females for different periods of the nesting cycle (P_Fi). The expected number of fledglings from a nest in which incubation is begun on egg m is given by:

$$

 In effect, Magrath partitioned the survival probabilities P_i from the Nest Failure model into a nest contents component P_Ci and a female survival component P_Fi. The tradeoff between present and future reproduction is incorporated into the model by considering the lifetime reproductive success of a female, estimated here as:

$$

where S_A is the probability of a female surviving from the end of one breeding season to the beginning of the next.

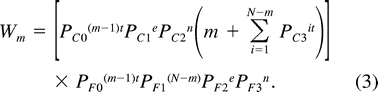
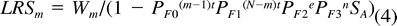
To date, this model has never been evaluated using empirical data. Using a range of hypothetical mortality rates, Magrath (1988) found that the optimal degree of asynchrony involved a tradeoff between present and future reproduction, and varied considerably with survival probabilities during incubation and between breeding attempts.

Methods

Study Site and Species

This study was conducted from May to November, 1989 to 1994, at Hato Masaguaral, a working cattle ranch in the llanos of Guárico, Venezuela (8°34′N, 67°35′W). The habitat is seasonally flooded brushy savanna, pastures, and scattered woodlands (Troth 1979). The Green-rumped Parrotlet is a small (25–35 g) granivorous parrot inhabiting open habitats in northern South America (Forshaw 1989). Clutch size in this species varies greatly (x̄ = 7.0, range 4–10 eggs). Females generally begin incubation on the first egg, and males feed incubating and brooding females, resulting in extreme asynchrony of hatching and fledging (Beissinger and Waltman 1991, Stoleson and Beissinger 1997). The nesting cycle is prolonged for an altricial bird of this size: eggs require 19 to 21 days to hatch, and nestlings fledge 27 to 40 days after hatching.

Parrotlets bred in about 100 nest boxes made of polyvinyl chloride (Beissinger and Bucher 1992). We believe the results presented here have not been biased by the use of artificial nest boxes. During this study, nesting success in 30 natural or semi-natural sites (fence posts made of palm trunks) did not differ significantly (χ²₁ = 3.0, P = 0.13) from nest box success (55% vs. 67%). Because nest boxes were attached to fence posts (Beissinger and Bucher 1992), they were accessible to the same suite of predators as natural nests. Furthermore, for the purposes of testing nest failure models, the relevant data are the relative rates of nest failure during different periods of the nesting cycle, rather than absolute rates. We have no reason to assume that the use of nest boxes affected temporal patterns of predation.

Nest Failure Model

All nest boxes were checked daily prior to and through laying, during hatching, and during fledging to determine exact dates, and at intervals of no more than four days for the rest of the nesting cycle. For calculating rates of nest failure, we excluded nests that failed due to anthropogenic factors, including disturbance and consequences of nest box design, because they are not part of the natural system and would not select for a particular incubation strategy (Bancroft 1985). Nests were considered depredated if all nest contents disappeared. Infanticide (including egg destruction) was common in this population (Beissinger et al. 1998) and determined by the characteristic triangular bite marks on eggs or nestlings made by parrotlet bills. Infanticide has not been considered in prior assessments of the Nest Failure model, but we do so here because it represents an important cause of whole brood loss in this population, and it is an extrinsic mortality factor that may be affected by incubation and hatching patterns.

Because incubation is initiated with the first egg in this species, the interval between the laying of the first egg and the onset of incubation does not exist, and P₀ cannot be estimated directly. For the first assessment of the model, we substituted P₁, the daily probability of survival of the nest contents from the start of incubation to the first hatch, for P₀ in the model (Clark and Wilson 1981, Hussell 1985). The resulting simplified ratio is:

$$

In the parrotlet, the survivorship of last-hatched nestlings varies with brood size. Therefore we calculated the proportional survival rates of penultimately hatched (q′) and last-hatched (q) chicks separately for each brood size, using data from unmanipulated broods where all eggs hatched and at least one young fledged. We included q′ and q in the models only when they differed significantly from the survival rates of earlier-hatched young for that brood size. The model modified to incorporate both rates was:

$$

when N − m > 1. When m = N − 1, then

$$

 Data from 943 nesting attempts were used to calculate the average daily survival probability (DSP) during the incubation (P₁), nestling (P₂), and fledging (P₃) periods using the Mayfield (1975) method, and their standard errors were derived from Johnson's (1979) formula. These data excluded experimental nests in which the duration of hatching or fledging was manipulated (Stoleson and Beissinger 1997). Daily-survival probabilities were compared using the program CONTRAST (Hines and Sauer 1989), using an overall alpha level of 0.10 because these types of tests are prone to Type II errors. For a posteriori comparisons of multiple rates, we divided alpha by the number of comparisons to maintain the overall level of experimentwise error. The mean laying interval t was calculated from 436 nests in which the exact laying dates of first and last eggs were known. To test the assumption that the daily probability of survival was constant within periods of the nesting cycle, we calculated the actual probabilities of survival for each day of the nesting cycle up to 70 days after the laying of the first egg, when n dropped to 10 nests. Within each period (incubation, nestling, and fledging), we used linear regression to estimate DSP as a linear function of nest age. We calculated productivity ratios (W_m/W_N) for values of m from 1 to N for broods of 5, 6, 7, and 8 chicks to determine the optimal degree of hatching asynchrony predicted by the model. We examined several brood sizes because the survival probabilities of last and penultimate chicks vary with offspring number in this species (Beissinger and Waltman 1991, Stoleson and Beissinger 1997).

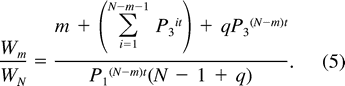
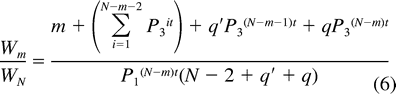
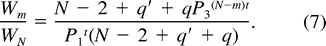
Egg destruction and infanticide commonly occur at unattended parrotlet nests (Beissinger and Waltman 1991, Beissinger et al. 1998). If first-egg incubation functions in part to protect eggs from conspecifics, the substitution of P₁ for P₀ in the Nest Failure model may overestimate the daily survival probability of nest contents prior to the start of incubation. To assess the effect of different values of P₀ on the optimal degree of hatching asynchrony, we calculated productivity ratios for values of m from 1 to N using P₀ values bracketing the value of P₁: (1) P₀ = 1, (2) P₀ = 0.90 × P₁, and (3) P₀ = 0.8418, the daily survival rate of unattended eggs determined from experiments with this population that simulated delayed incubation (Beissinger et al. 1998).

Adult Predation Model

Magrath (1988) examined how the risk of predation on incubating adults affected incubation patterns by modifying Hussell's (1985) equation to include daily survival probabilities of adults (equation 3). Equation 3 excludes the effects of reduced survival for last-hatched chicks (q, q′). We incorporated these terms into the equation as:

$$

 We calculated daily survival probabilities of breeding females for the laying period after the onset of incubation (P_F1), the period from the end of laying until the last hatch (P_F2), and the period from the last hatch until the last fledge (P_F3), using the Mayfield method (Mayfield 1975). Females were considered killed if their nest was depredated or abandoned, and (1) there was evidence of the dead female in the box (e.g., blood, feathers, or body parts), or (2) the female was never resighted subsequently but its mate was seen with a new female. We also conducted analyses with more conservative estimates of female mortality based strictly on known deaths, but results did not differ significantly, therefore those analyses are not presented here.

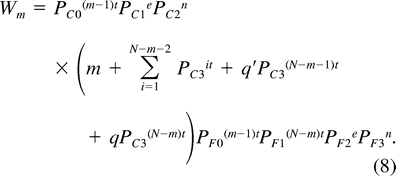
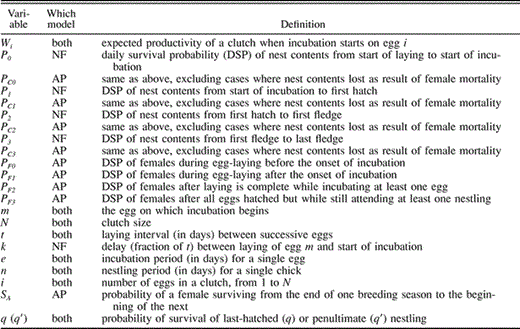
We calculated estimates of P_F1 from records for all nesting attempts initiated from 1989–1994 that did not fail due to human disturbance, and that were not manipulated during laying (n = 673). For P_F2 we used 570 nesting attempts in which a complete clutch was laid and that were not subjected to manipulations before the last egg hatched. For P_F3 we used records of 502 nests that did not fail before their last egg hatched. The daily survival probabilities for nest contents (P_C1) were calculated as described for the Nest Failure model, but excluded nests in which females were lost in addition to the nest contents (Magrath 1988).

As there is no laying period prior to the onset of incubation in this species, we derived an estimate for survivorship during this period (P_F0) from the annual survival rate of females, as calculated using mark-resighting data (0.547; Sandercock et al. 2000). The overall daily probability of survival for females was estimated as the 365th root of the annual survival rate; this value was used for P_F0. The probability of survival from the fledging of a female's last young in one year to the laying of its first egg in the following year (S_A), was calculated as this DSP value raised to the 243rd power (the average number of days between breeding seasons).

We estimated the relative productivity per breeding attempt of different incubation strategies using productivity ratios as in the Nest Failure model. We also estimated the expected lifetime reproductive success of females using different incubation strategies with equation 4. We attempted to assess the sensitivity of parameters in the adult predation/LRS model by determining the effect of a 5% decrease in each parameter on expected LRS for m = 1 and m = 6. For all analyses of the Adult Predation model, we considered only the mean clutch size of 7 eggs.

Results

A total of 386 of 1,001 (38.6%) nesting attempts failed before any young fledged, and an additional 22 nests (2.2%) failed after fledging at least one chick. Most complete failures (72.5%) occurred during incubation for a variety of causes, primarily desertion during laying. Predation was the primary cause of nest failure after hatching. Infanticide, including egg destruction, was uncommon before eggs were hatched, but was an important cause of failure during the nestling and fledging stages. The proportion of losses due to predation and infanticide varied significantly among years (χ²₅ = 29.4, P < 0.001), and ranged from 8.6% to 30.1%. Most documented nest predators were snakes (Boa constrictor, Epichrastes cenchrus, Spilotes pullatus). Nests also were lost to mouse opossums (Marmosa robinsoni), carnivorous ants (unknown species), and rats (Rattus rattus).

Nest Failure Model Parameters

Parrotlet eggs were generally laid at either 24 hr (29.8%) or 48 hr (63.5%) intervals, although occasionally gaps of 3 or more days occurred between successive eggs (6.7% of cases). The mean (±SD) laying interval between eggs (t) at 436 unmanipulated nests was 1.53 ± 0.28 days, and did not vary with clutch size (one-way ANOVA, F_4, 431 = 0.6, P = 0.66). Survival rates for last-hatched, penultimately hatched, and earlier-hatched chicks varied with brood size (Table 2). For all brood sizes, last-hatched chicks had a significantly lower probability of fledging than first through antepenultimately hatched chicks. Penultimately hatched chicks also had reduced survival in broods of 6 and larger.

Table 2.

Open in new tab

Survival rates of parrotlet chicks form unmanipulated nests in which at least one nestling fledged, as a function of brood size and hatching order. Survival rates of early-hatched (first through antepenultimate) chicks from different brood sizes do not differ in their survival rates (χ²₃ = 0.59, P > 0.10), and have been pooled. Where rates of penultimate or last-hatched chicks differed significantly from the rate for earlier-hatched chicks (based on χ² tests with P ≤ 0.05, using program CONTRAST), the relative survival rate (q) is given

Table 2.

Open in new tab

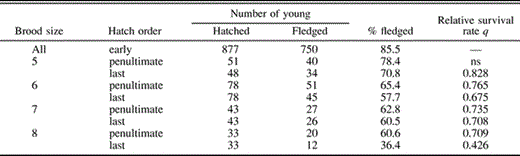
Survival rates of parrotlet chicks form unmanipulated nests in which at least one nestling fledged, as a function of brood size and hatching order. Survival rates of early-hatched (first through antepenultimate) chicks from different brood sizes do not differ in their survival rates (χ²₃ = 0.59, P > 0.10), and have been pooled. Where rates of penultimate or last-hatched chicks differed significantly from the rate for earlier-hatched chicks (based on χ² tests with P ≤ 0.05, using program CONTRAST), the relative survival rate (q) is given

Daily survival probabilities were high throughout the incubation, nestling, and fledging periods (Table 3). The number of nests lost to predation or infanticide varied between 0 and 8 (0–12%) per day (x̄ = 2.57 ± 1.65 nests day⁻¹). The average DSP was significantly higher during the nestling period than either the incubation (χ²₁ = 9.3, P = 0.002) or fledging period (χ²₁ = 6.6, P = 0.01), although the latter two periods did not differ significantly (χ²₁ = 0.4, P = 0.53) from each other. Because periods varied in length, the probability of total nest failure during a particular period was highest during incubation and lowest during fledging (Table 3). The probability of nest failure during an entire breeding cycle was 0.20.

Table 3.

Open in new tab

Daily survival probabilities (DSP) of total nest contents and probabilities of total nest failure for Green-rumped Parrotlet during the incubation, nestling, and fledging periods for the Nest Failure model and the Adult Predation model. DSP values within a model followed by the same letter do not differ significantly (using program CONTRAST, experimentwise α = 0.10)

Table 3.

Open in new tab

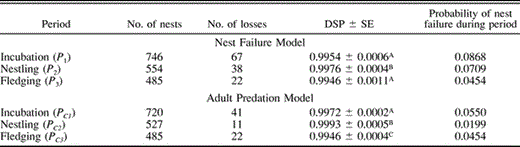
Daily survival probabilities (DSP) of total nest contents and probabilities of total nest failure for Green-rumped Parrotlet during the incubation, nestling, and fledging periods for the Nest Failure model and the Adult Predation model. DSP values within a model followed by the same letter do not differ significantly (using program CONTRAST, experimentwise α = 0.10)

Patterns of daily survival probability varied considerably within and among periods of the nesting cycle (Fig. 1A), partly because the data provided poor resolution to detect patterns with so few losses per day. Fitting the linear equation DSP = A + B × nest age for each period individually provided a somewhat poor fit to the data. Slopes did not differ significantly from 0 in either the incubation (r² = 0.13, P = 0.36), or nestling (r² = 0.04, P = 0.28) periods, but did for the fledging period (r² = 0.66, P < 0.001). Thus, if DSP is assumed to be linear, it was essentially constant within the first two periods. The shape of the cumulative survivorship curve (Fig. 1B) appeared to be relatively linear until the onset of fledging (day 50), and more linear than expected from the calculated DSP values. Nonlinear curves would likely provide a better fit to the fledging period DSP data, but any biological significance of such patterns is unclear.

Figure 1.

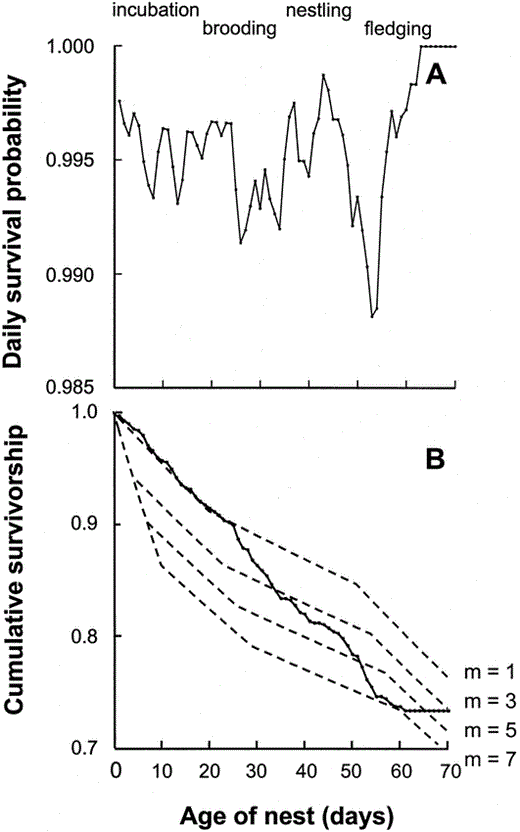
(A) The daily probabilities of survival for parrotlet nests in relation to nest age (days after the first egg), plotted as a 3-day running mean. Brooding varies in duration as a function of clutch size, and represents a transition between incubation and nestling periods. (B) The cumulative probability of survival for parrotlet nests as a function of nest age. Solid line represents the actual cumulative survival probabilities, while dotted lines represent expected values based on m, the egg on which incubation begins, assuming constant rates of survival within periods (from Table 3), using P₀ = 0.9 times P₁

Open in new tabDownload slide

Model Predictions

The optimal degree of hatching asynchrony predicted by productivity ratios was consistent with the observed first-egg incubation (Fig. 2A). When P₀ = P₁, productivity was maximized by initiating incubation on the first egg for all brood sizes, and minimized when incubation was started on the final egg. Productivity ratios, and hence the optimal degree of asynchrony, varied with the initial value used for P₀. When P₀ = 1 (i.e., no likelihood of nest failure before the onset of incubation), productivity was maximized by delaying incubation until the last egg, although productivity varied little among incubation patterns (Fig. 2B). However, when P₀ was less than or equal to P₁ (i.e., nests were as likely or more likely to fail before females initiated incubation as after), productivity was maximized through first-egg incubation. Thus, asynchrony becomes increasingly favored as pre-incubation losses increase relative to the rate of loss after the onset of incubation.

Figure 2.

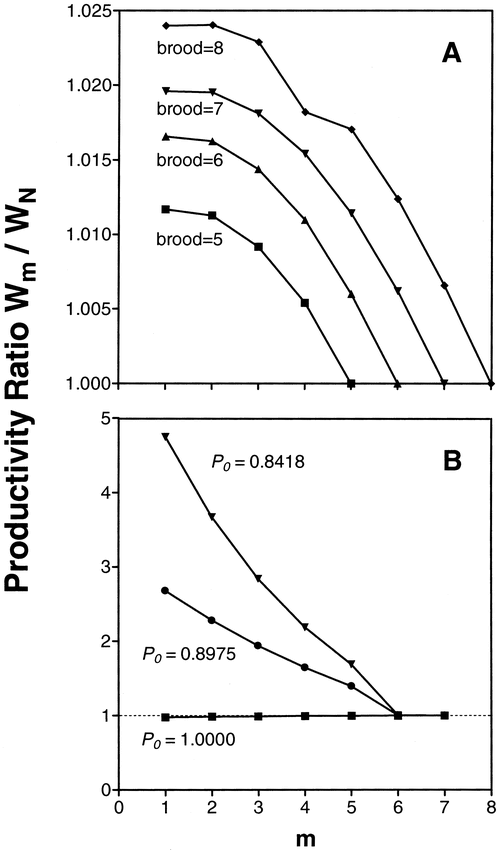
Productivity of asynchronously hatching clutches relative to synchronously hatching clutches (W_m/W_N), as a function of egg on which incubation starts (m) and (A) brood size, with P₀ = P₁ = 0.9954, as calculated from the Nest Failure model; and (B) the daily probability of survival of nests prior to the onset of incubation (P₀) for a clutch of 7. The value P₀ = 0.8418 was derived from field experiments (Beissinger et al. 1998)

Open in new tabDownload slide

Adult Predation Model

The pattern of daily survival of nest contents did not change noticeably when losses associated with female mortality were excluded (Table 3). DSP was highest during the nestling stage and lowest during fledging. The risk of total loss of nest contents was highest during the incubation period and lowest during the nestling period (Table 3).

Daily survival probabilities for breeding females varied little through the course of the nesting cycle (Table 4). Estimated survival rates were slightly but significantly lower during incubation than when caring for nestlings. Females were most likely to die while incubating a full clutch, and least likely to die during laying (Table 4). The probability of mortality for a female during one breeding attempt was 0.091.

Table 4.

Open in new tab

Daily survival probabilities (DSP) and probabilities of mortality for breeding female parrotlets in four periods of the nesting cycle. DSP values followed by the same letter are not significantly different (using program CONTRAST, experimentwise α = 0.10)

Table 4.

Open in new tab

Daily survival probabilities (DSP) and probabilities of mortality for breeding female parrotlets in four periods of the nesting cycle. DSP values followed by the same letter are not significantly different (using program CONTRAST, experimentwise α = 0.10)

Inclusion of female survival in the model made little qualitative difference in productivity ratios (compare Fig. 2B with Fig. 3A). The maximum productivity for broods of 7 young was again dependent on the value used for P_C0, the probability of nest content survival before the onset of incubation (Fig. 3A). When P_C0 = 1, productivity was maximized by beginning incubation on the seventh egg, and decreased with earlier incubation. When P_C0 ≤ P_C1, maximum productivity was achieved with first-egg incubation (Fig. 3A). Similarly, the incubation strategy that maximized lifetime reproductive success was dependent on P_C0, the daily probability of survival for nest contents prior to the onset of incubation (Fig. 3B). When P_C0 was 0.90 times the value of P_C1 or lower, LRS was maximized with first-egg incubation. When P_C0 = 1, LRS was greatest when incubation was delayed until the last egg.

Figure 3.

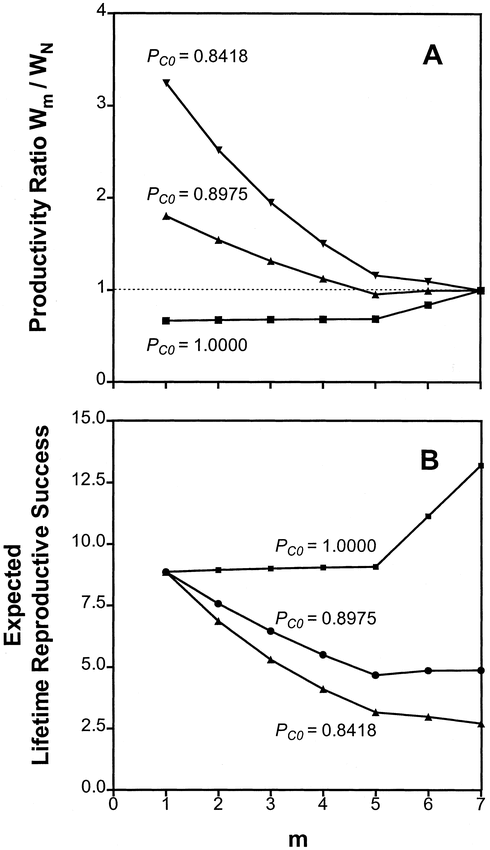
(A) Productivity of asynchronously hatching clutches relative to synchronously hatching clutches (W_m/W_N) as a function of the egg on which incubation starts (m), and the daily probability of survival of nest contents prior to the onset of incubation (P_C0) for clutches of 7, as calculated from the Adult Predation model. (B) Expected lifetime reproductive success of females as a function of the egg on which incubation starts (m), and the daily probability of survival of nest contents prior to the onset of incubation (P_C0) for clutches of 7. The value P_C0 = 0.8418 was derived from field experiments (Beissinger et al. 1998)

Open in new tabDownload slide

Sensitivity Analysis

Sensitivity analysis of the Adult Predation model indicated that the relative effect of some, but not all, parameters varied with m, the egg on which incubation was begun (Table 5). When m = 1, the DSP of females during laying after the onset of incubation (P_F1) had the greatest effect on expected lifetime reproductive success. A 5% decrease in P_F1 produced a 48.9% decrease in expected LRS. Expected LRS also was strongly impacted by the survival probabilities for females during post-laying incubation and during the nestling stage (P_F2 and P_F3), and by the daily survival probability of nest contents during fledging (P_C3). Changes in the values of q, q′, nestling period (n), and average year-to-year survival (S_A) produced only minor changes in LRS (Table 5). Changing either of the DSP values for the period prior to the onset of incubation (P_F0 and P_C0) had no effect on LRS because this period does not exist when incubation begins on the first egg, as indicated by the common end point at m = 1 in Figure 3B.

Table 5.

Open in new tab

Sensitivity of parameters in the Adult Predation model, as indicated by the effect (percent change) of a 5% decrease in each parameter on expected lifetime reproductive success (LRS), when incubation is begun on the first (m = 1) and penultimate (m = 6) of seven eggs. The model used P_C0 = 0.8975 (90% of P_C1). See text for definitions and details of the model

Table 5.

Open in new tab

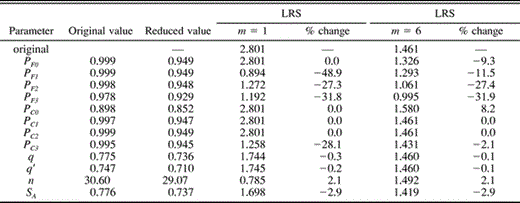
Sensitivity of parameters in the Adult Predation model, as indicated by the effect (percent change) of a 5% decrease in each parameter on expected lifetime reproductive success (LRS), when incubation is begun on the first (m = 1) and penultimate (m = 6) of seven eggs. The model used P_C0 = 0.8975 (90% of P_C1). See text for definitions and details of the model

When m = 6, changes in the DSP during post-laying incubation and fledging stages (P_F2 and P_F3) had the greatest effect on expected lifetime reproductive success (Table 5), although the magnitude of the effects was the same as for when m = 1. A 5% decrease in these parameters produced decreases in expected LRS of 27% and 32%, respectively. The effects of changes in P_F1 and P_C3 were greatly reduced compared to their effects with first-egg incubation because the duration of the post-incubation laying period and the fledging periods are shortened to t = 1.53 days. Changes in P_F0 or P_C0 produced moderate changes in LRS (–9.3% and 8.2%, respectively). The effects of other parameters were approximately the same as with m = 1.

Discussion

Most of our predictions derived from the Nest Failure model were consistent with the first-egg incubation observed in the Green-rumped Parrotlet. However, predictions were dependent on the daily survival probability values used for the period before the onset of incubation. Because the parrotlet begins incubation on the first egg, the daily survival probabilities for the period before the onset of incubation (P₀) used in the Nest Failure model were hypothetical. When P₀ was assumed to be equal to P₁, productivity was maximized with first-egg incubation (Fig. 2A). However, such an assumption probably greatly overestimated P₀, because the presence of an incubating female may serve as an effective deterrent to egg destruction by conspecifics, and perhaps to some predators. Results of experiments in which eggs were placed in unattended nest boxes indicated a daily rate of destruction by conspecifics of 0.158 during the period when most nests were initiated (but no predation; Beissinger et al. 1998). When the corresponding daily survival probability was used for P₀, the model revealed very strong selective pressure for first-egg incubation.

Although incubation patterns in parrots remain poorly known, first-egg incubation appears to be common. For example, this pattern is found in most Amazona parrots (Enkerlin-Hoeflich 1995, Martuscelli 1995), Monk Parakeets (Myiopsitta monachus; Navarro et al. 1992), Thick-billed Parrots (Rhynchopsitta pachyrhyncha; Lanning and Shiflett 1983), and Budgerigars (Melopsittacus undulatus; Wyndham 1981). However, some psittacines initiate incubation after the first egg; these include the Galah (Cacatua roseicapillus; Rowley 1990) and the Little Corella (Cacatua pastinator; Smith 1991). Thus, it appears unlikely that first-egg incubation is phylogenetically fixed. If incubation and hatching patterns reflect differential risk of nest failure or predation on adults, then the semi-asynchronous hatching patterns exhibited by the latter two species suggest two possibilities: (1) they are subject to relatively greater risk of nest failure during fledging than before the onset of incubation, or (2) adult females are subject to a higher risk of predation while incubating than before the onset of incubation. The intermediate patterns of incubation and hatching in these species suggest a tradeoff between opposing selection pressures.

This paper presents the first test of the Nest Failure model in a nonpasserine or a tropical species. Four other published studies have tested the Nest Failure model. Observed degrees of hatching asynchrony were less than predicted for Boat-tailed Grackles (Quiscalus major; Bancroft 1985), Least Flycatchers (Empidonax minimus; Briskie and Sealy 1989), and Yellow Warblers (Dendroica petechia; Hébert and Sealy 1993). For all three of these species, the risk of nest failure was greatest during egg laying prior to the onset of incubation. In contrast, Snow Buntings (Plectrophenax nivalis) were most at risk just prior to fledging, and the model accurately predicted the observed degree of asynchrony across several brood sizes (Hussell 1985).

When risks to breeding female Green-rumped Parrotlets were incorporated into the Nest Failure model, the predictions of the model changed only slightly. This was because female survival varied little among different periods of the nesting cycle. The risk of mortality to females appeared to be relatively uniform whether birds were inside nest boxes during laying and incubation or outside nest boxes during the nestling and fledging stages (Table 4), despite the fact that they have no means to escape predators while inside nest boxes. Any selection pressure resulting from the risk of predation on adults was probably overwhelmed by or in the same direction as the influence of nest failure. The risk of predation on adults is likely to have more influence on incubation patterns when that risk varies significantly during the breeding cycle. For example, in the Pied Flycatcher (Ficedula hypoleuca), female survival was significantly lower while females were particularly active during the nestling and laying periods (Slagsvold and Dale 1996).

These models are a good attempt to quantify the effects of predation pressure on reproductive success and hatching patterns. However, like all models, they do have limitations and weaknesses which suggest productive avenues for future refinements. The models assume a constant risk of nest failure within periods of the nesting cycle (Murray 1994). In this study, however, the daily survival probabilities for nests were variable, and apparently nonlinear in form (Fig. 1). In particular, the DSP dropped drastically soon after hatching, and then generally increased until just prior to fledging. This may be because female parrotlets cease diurnal brooding of nestlings about 7 to 10 days after first hatching, and consequently nestlings suddenly become vulnerable to infanticide throughout much of the day rather than just during the occasional recesses of the female. Thus, the probability of nest survival should be expected to jump from a high value to a much lower one. The general increase in DSP during the nestling period may reflect a decline in the vulnerability of chicks to infanticide with age, although further observations are needed to support this idea. The sudden drop in DSP prior to fledging may be because chicks begin to spend considerable time at the box entrance prior to departure (pers. obs.), making them more susceptible to predation by diurnal predators such as Crane Hawks (Geranospiza caerulescens) and other raptors.

Murray (1994) suggested that a smooth curve was more appropriate than a step function to describe changes in daily survival probabilities between periods of the nesting cycle. If, however, the behavior of parents or chicks directly affects the probability of total nest failure, as in our study, a step-type function may be the most realistic pattern. Such a pattern may not be as clear in the data presented here (Fig. 1A) because of high variation in clutch size in this population, and consequently high variation in the duration of brooding among females.

Both models were affected by changes in P_C0 and P_C3. Most of the values we used for P_C0, the period prior to incubation, were untested assumptions. In addition, it is particularly difficult to differentiate early fledging from losses due to predation. Thus, the models are highly dependent on those rates which are necessarily the hardest to estimate and therefore the least reliable. Good estimates for P_C0 and P_C3 are necessary for the model to produce meaningful results. Both models assumed survival of later-hatched chicks (q′, q) is independent of hatching spreads. However, in many species the occurrence of brood reduction is a function of size asymmetries within a brood rather than of brood size itself (Strehl 1978, Stoleson and Beissinger 1997). Bancroft (1985) demonstrated that when q varies with the degree of asynchrony, the optimal incubation pattern predicted by the model is highly dependent on the absolute and relative values used for q.

Similarly, the duration of brooding by females also may be influenced by the degree of asynchrony. In large broods with extreme size disparities, older chicks may be able to brood their younger nestmates, thus allowing the female to spend less time in the nest (Tarburton and Minot 1987, Magrath 1988). Brooding of nestlings is ignored by the Nest Failure model, which defines the nestling period as beginning with the first hatch. If the presence of a brooding female in the nest affects rates of nest failure, as appears to be the case in the Green-rumped Parrotlet, then a more realistic definition for the incubation period would extend to the termination of brooding. In the Green-rumped Parrotlet, the duration of brooding varies, but generally can continue until about the last hatch. Thus, the definition of P_F2 may be more biologically meaningful than P_C1.

The Adult Predation model was very sensitive to changes in values for female survival after laying (P_F2) and after hatching (P_F3; Table 5). The former parameter is unaffected by changes in incubation pattern, so it affects productivity estimates but not productivity ratios. Both parameters are difficult to estimate because of the problem of differentiating between abandonment and mortality away from the nest (Briskie and Sealy 1989).

Additional factors not considered in these models may play a critical role in determining the optimal degree of asynchrony. For example, delaying incubation may result in reduced viability of first-laid eggs (Stoleson and Beissinger 1999), and thereby offset any benefit derived from higher survival of later-hatched chicks (Stoleson and Beissinger 1997). We have considered infanticide as equivalent to predation as a cause of whole brood loss. However, unlike predation, infanticide frequently results in partial brood loss only. During this study, 48 whole broods were lost to infanticide or egg destruction by conspecifics, but an additional 57 successful broods suffered partial losses from infanticide. We did not include the latter in our calculations, therefore we likely underestimated the losses in productivity associated with infanticide. If incubation patterns affect the probability of infanticide, then partial brood losses may have a powerful influence on the optimal degree of asynchrony. Future refinements of these models should consider the effects of partial brood loss on incubation patterns. Finally, complete asynchrony may spread the peak of nestling food demands (Hussell 1972). Reducing the peak load is unlikely to provide any substantial benefits in energetics (Mock and Schwagmeyer 1990, Siegel et al. 1999), but may reduce the number of trips made by parents, and thus reduce the likelihood of attracting predators to the nest site (Martin and Ghalambor 1999).

In conclusion, patterns of first-egg incubation observed in the Green-rumped Parrotlet are consistent with predictions from the Nest Failure and Adult Predation models when empirically based values are used for rates of failure prior to the onset of incubation (Beissinger et al. 1998). These models may be improved in the future by incorporating non-constant survival rates within single periods of the nesting cycle, the risk of partial brood loss, the duration of brooding by females, and asynchrony-dependent survival rates of later-hatched chicks. Some of these functional relationships may be incorporated into a more complex model by using conditional probabilities. Finally, other factors not included in these models may have profound effects on optimal hatching strategies. In the Green-rumped Parrotlet, the effects of reduced viability of unincubated eggs and partial brood loss due to infanticide are likely to be important factors that constrain reproductive success and influence breeding behavior.

Acknowledgments

We thank M. Apóstol, S. Barreto, K. Brittin, D. Casagrande, J. Clemmons, A. P. Curlee, B. Elderd, D. Gaylor, A. García, J. Gibbs, A. Pacheco, N. Pérez, R. Ramos, S. Spector, E. Steadman, P. Stoleson, S. Tygielski, J. Viñuela, and J. Waltman for field assistance. Tomás Blohm allowed us to live and work on his ranch, and has worked tirelessly to promote conservation in Venezuela. The Smithsonian Institution's Conservation Research Center and Scott Derrickson facilitated visa applications, and Carlos Bosque helped with arrangements in Venezuela. This work was supported by grants from the American Ornithologists' Union, the Frank M. Chapman Fund of the American Museum of Natural History, the National Science Foundation (IBN-9407349 and DEB-9503194), the National Geographic Society, Sigma Xi, the Smithsonian Institution's International Environmental Sciences program in Venezuela, and Yale University. D. J. Hussell helped to clarify nuances of the models. Suggestions by A. Clark, T. W. Clark, C. Brown, D. J. Hussell, B. Sandercock, O. Schmitz, S. Zack, and two anonymous reviewers greatly improved this manuscript.

Literature Cited

Author notes