Role of picture change correction in relativistic density functional theory: an analogy with coupled cluster theory

Author Notes

Abstract

Relativistic density functional theory (RDFT) plays a vital role in electronic structure calculations of heavy-element compounds, where accurate electron density evaluation is essential. We demonstrate that picture change correction (PCC) in RDFT is conceptually analogous to corrections in coupled-cluster theory and that neglecting PCC leads to inconsistencies in electron density evaluation. This work underscores the need to incorporate PCC in RDFT to improve accuracy. Future research should focus on developing computationally efficient schemes to implement PCC without significantly increasing the cost of RDFT calculations.

Graphical Abstract

Open in new tab Download slide

coupled-cluster theory, picture change correction, relativistic density functional theory

Relativistic effects play a significant role in various phenomena, such as the color of gold,^1–3 the melting point of mercury,^1,4 the catalytic activity of heavy metals,^5,6 and the high electromotive force of lead-acid batteries.⁷ Thus, incorporating relativistic effects in quantum chemical calculations is essential, particularly for evaluating molecular properties of heavy-element compounds.

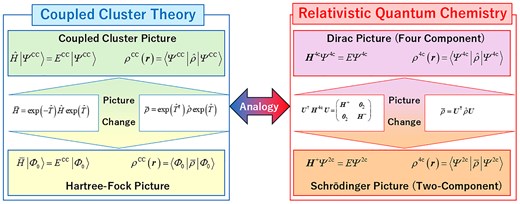
Relativistic quantum chemical calculations are based on one of 2 physical pictures: the Dirac picture and the Schrödinger picture. The former is derived from the Dirac equation, yielding positive- and negative-energy (electronic and positronic) solutions. Since the Dirac Hamiltonian is represented in a 4 × 4 matrix form, relativistic quantum chemical methods in the Dirac picture are known as four-component (4c) relativistic methods. A unitary transformation separates the Dirac Hamiltonian into electronic and positronic components, resulting in a 2 × 2 electronic Hamiltonian. Relativistic quantum chemical methods in the Schrödinger picture, which operate on the unitary-transformed electronic Hamiltonian, are referred to as two-component (2c) relativistic methods.

Our research group has emphasized the importance of the picture change correction (PCC) in relativistic density functional theory (RDFT)⁸ within 2c treatments from the perspectives of the density operator^9,10 and density matrix.^11–13 Furthermore, the corresponding implementations¹⁴ are available in the GAMESS program.¹⁵ Despite the significance of PCC, we are concerned that RDFT calculations without PCC are frequently performed, potentially due to a lack of understanding. Therefore, this Letter clarifies PCC in 2c relativistic treatments by drawing an analogy with PCC in standard coupled-cluster (CC) theory.

First, we briefly summarize the standard CC method, focusing on the evaluation of electron density. The CC wave function is expressed in an exponential form of the cluster operator $\hat{T}$ and reference function Φ₀, typically the Hartree-Fock (HF) wave function.

| Ψ^{CC} ⟩ = \exp (\hat{T}) | Φ_{0} ⟩ = \exp (\sum_{μ} t_{μ} {\hat{τ}}_{μ}) | Φ_{0} ⟩

(1)

Here, $\hat{T}$ includes cluster amplitudes {t_μ} and the excitation operators { ${\hat{τ}}_{μ}$ }, where μ indicates arbitrary excitation levels such as singles (S) { ${\hat{τ}}_{i}^{a}$ }, doubles (D) { ${\hat{τ}}_{i j}^{a b}$ } and triples (T) { ${\hat{τ}}_{i j k}^{a b c}$ }. The excitation operators, truncated at a certain level (e.g. double excitations in the CCSD model), contribute to defining the CC wave function.

The Schrödinger equation for CC theory is given by

\hat{H} | Ψ^{CC} ⟩ = E^{CC} | Ψ^{CC} ⟩

(2)

where $\hat{H}$ is the standard electronic Hamiltonian (or normal-ordered Hamiltonian), for which E^CC is the total energy (or correlation energy) of the CC model. Inserting the CC wave function given in Eq. (1) into Eq. (2), followed by projections onto the reference and excited-state configurations, i.e. Φ₀ and Φ_μ, the energy and amplitude equations are derived:

⟨ Φ_{0} | \hat{H} \exp (\hat{T}) | Φ_{0} ⟩ = E^{CC}

(3)

⟨ Φ_{μ} | \hat{H} \exp (\hat{T}) | Φ_{0} ⟩ = E^{CC} ⟨ Φ_{μ} | \exp (\hat{T}) | Φ_{0} ⟩

(4)

Since the amplitude equations in Eq. (4) includes not only the amplitudes {t_μ} but also the energy E^CC, the set of equations given in Eq. (4) must be solved simultaneously with the energy equation in Eq. (3).

To decouple these equations, the similarity-transformed Hamiltonian $\bar{H}$ is introduced, ensuring a tractable expansion while maintaining accuracy.

\bar{H} = \exp (- \hat{T}) \hat{H} \exp (\hat{T})

(5)

Since the Hamiltonian involves up to 2-electron operators, the expansion of Eq. (5) can be truncated up to the fifth term for any CC models as follows:

\begin{aligned} \bar{H} = \hat{H} & + [\hat{H}, \hat{T}] + \frac{1}{2} [[\hat{H}, \hat{T}], \hat{T}] + \frac{1}{3!} [[[\hat{H}, \hat{T}], \hat{T}], \hat{T}] \\ + \frac{1}{4!} [[[[\hat{H}, \hat{T}], \hat{T}], \hat{T}], \hat{T}] \end{aligned}

(6)

where the bracket means an anticommutator: $[\hat{A}, \hat{B}] =$ $\hat{A} \hat{B} - \hat{B} \hat{A}$ ⁠.

Using the similarity-transformed Hamiltonian, the Schrӧdinger equation of the CC method is described by,

\bar{H} | Φ_{0} ⟩ = E^{CC} | Φ_{0} ⟩

(7)

Note that the quasi-eigen function in Eq. (7) is the HF wave function, not the CC wave function, while the quasi-eigen value is the CC energy. It is natural that replacing $\bar{H}$ with $\hat{H}$ in Eq. (7), the eigen value becomes the HF energy.

The CC electron density is obtained by the expectation value of $\hat{ρ}$ with respect to the CC wave function as follows:

ρ^{CC} (r) = ⟨ Ψ^{CC} | \hat{ρ} | Ψ^{CC} ⟩ = ⟨ Ψ^{CC} | \sum_{i}^{N} δ (r_{i} - r) | Ψ^{CC} ⟩

(8)

where r_i is the electronic coordinate and the summation of the density operator for i runs the electrons from 1 to N, the number of electrons.

When the bra state of the CC wave function is explicitly described, Eq. (8) is rewritten as,

\begin{aligned} ρ^{CC} (r) & = N ⟨ Φ_{0} | \exp ({\hat{T}}^{†}) \hat{ρ} \exp (\hat{T}) | Φ_{0} ⟩ \\ = N ⟨ Φ_{0} | \exp (\sum_{μ} t_{μ} {\hat{τ}}_{μ}^{†}) \hat{ρ} \exp (\sum_{μ} t_{μ} {\hat{τ}}_{μ}) | Φ_{0} ⟩ \end{aligned}

(9)

Here, N is the normalization factor, i.e. $N = 1 /$ $⟨ Φ_{0} | \exp ({\hat{T}}^{†}) \exp (\hat{T}) | Φ_{0} ⟩$ ⁠.

Since the conjugate operator of $\hat{T}$ involves the deexcitation operators ${\hat{τ}}_{μ}^{†}$ ⁠, the expansion of the right-hand side of Eq. (9) is no longer truncated. Therefore, the Lagrange multiplier method is typically employed in order to determine the bra state of CC wave function as follows:

ρ^{CC} (r) = ⟨ Φ_{0} | (1 + \hat{Λ}) \exp (- \hat{T}) \hat{ρ} \exp (\hat{T}) | Φ_{0} ⟩

(10)

Here, the operator $\hat{Λ}$ is defined using the Lagrange multipliers {λ_ν} and the excitation operators.

\hat{Λ} = \sum_{ν} λ_{ν} {\hat{τ}}_{ν}

(11)

The Lagrange multipliers are determined by solving the lambda equation as follows:

⟨ Φ_{0} | (1 + \hat{Λ}) \bar{H} | Φ_{μ} ⟩ = 0

(12)

Let us define a new type of density operator, namely, similarity-transformed density operator $\bar{ρ}$ given by,

\bar{ρ} = (1 + \hat{Λ}) \exp (- \hat{T}) \hat{ρ} \exp (\hat{T}) = N \exp ({\hat{T}}^{†}) \hat{ρ} \exp (\hat{T})

(13)

Adopting $\bar{ρ}$ ⁠, the CC electron density can be obtained using the HF wave function,

ρ^{CC} (r) = ⟨ Φ_{0} | \bar{ρ} | Φ_{0} ⟩

(14)

Both equations evaluating the expectation values of the original and similarity-transformed density operators, $\hat{ρ}$ and $\bar{ρ}$ ⁠, in Eqs. (9) and (14), give the same CC electron density, although the adopted wave functions differ —Ψ^CC and Φ₀, respectively. Thus, the 2 formulations correspond to different pictures for the same property. We might call them the CC and HF pictures, respectively. Notably, even though electron correlation is accounted for in the CC method, evaluating electron density using the density operator $\hat{ρ}$ instead of $\bar{ρ}$ in Eq. (14) results in an electron density at the HF level:

ρ^{HF} (r) = ⟨ Φ_{0} | \hat{ρ} | Φ_{0} ⟩

(15)

We next describe the transformation from the 4c to 2c relativistic theory, focusing on the evaluation of electron density. In the 4c framework, the many-electron relativistic equation is given by

H_{}^{4 c} Ψ_{}^{4 c} = E Ψ_{}^{4 c}

(16)

where Ψ^4c is the 4c wave function, and E is an energy. H^4c is the many-electron relativistic Hamiltonian described by the one-electron Dirac Hamiltonian H^D and the general expression of 4c 2-electron interaction G as follows:

H_{}^{4 c} = \sum_{i} H_{}^{D} (i) + \sum_{i > j} G (i, j)

(17)

The Coulomb interaction, 1/r_ij is frequently adopted as G. In the exact decoupling scheme, H^4c is fully block-diagonalized via a unitary transformation:

U^{†} (i, j, \dots) H_{}^{4 c} U (i, j, \dots) = (\begin{matrix} H_{}^{+} & 0_{2} \\ 0_{2} & H_{}^{-} \end{matrix})

(18)

where H⁺ and H^– are the 2-component electronic and positronic Hamiltonians, respectively. The 2c method employs only the electronic part, H⁺, for calculations. Various approaches have been proposed to obtain H⁺.^16–27 Note that 2 main approaches exist for constructing 2c relativistic Hamiltonians: one employs unitary transformations, as in the infinite-order two-component^16–22 and exact two-component (X2C)^{18,19,23–27} methods; the other uses projection techniques to eliminate small-component contributions, as in the infinite-order regular approximation.^28–30 The present discussion is limited to the former category—2c methods derived via unitary transformation.

The electron density is expressed as the expectation value of the density operator δ with respect to the 4c wavefunction:

ρ^{4 c} (r) = ⟨ Ψ^{4 c} | \hat{ρ} | Ψ^{4 c} ⟩ = ⟨ Ψ^{4 c} | \sum_{i}^{N} δ (r_{i} - r) | Ψ^{4 c} ⟩

(19)

In the exact decoupling scheme, as a consequence of the block-diagonalization of the Hamiltonian, the relationship between 4c and 2c wave functions is given by,

| Ψ^{4 c} ⟩ = U | \begin{matrix} Ψ^{2 c} \\ 0 \end{matrix} ⟩

(20)

Using this equation, the 2c expression of the electron density in Eq. (19) can be rewritten as

ρ^{4 c} (r) = ⟨ Ψ^{2 c} | U^{†} \hat{ρ} U | Ψ^{2 c} ⟩ = ⟨ Ψ^{2 c} | \bar{ρ} | Ψ^{2 c} ⟩

(21)

The picture of density operator changes from $\hat{ρ}$ to $\bar{ρ} (= U^{†} \hat{ρ} U)$ in the 2c transformation. As in the nonrelativistic case, the RDFT adopts the electron density as a fundamental variable. However, if we use the standard density operator $\hat{ρ}$ with the 2c wave function, the electron density is not evaluated correctly:^31–34

ρ^{4 c} (r) \neq ⟨ Ψ^{2 c} | \hat{ρ} | Ψ^{2 c} ⟩

(22)

This is analogous to the case to evaluate the electron density using Eq. (15). Although the similarity-transformed density operator in the middle formula in Eq. (13), i.e. $\bar{ρ} = (1 + \hat{Λ}) \exp (- \hat{T}) \hat{ρ} \exp (\hat{T})$ looks slightly different from the 2c density operator, i.e. $\bar{ρ} (= U^{†} \hat{ρ} U)$ ⁠, the final formula, namely, $\bar{ρ} = N \exp ({\hat{T}}^{†}) \hat{ρ} \exp (\hat{T})$ ⁠, makes clear the analogy.

Here, we provide numerical results illustrating the impact of picture change error on the electron density. Figure 1 shows the radial electron density of a Be-like atom with nuclear charge Z = 80, described using 32s and 23p functions from the universal Gaussian basis sets.³⁵ Calculations were performed using 4 levels of Hamiltonians: nonrelativistic (NR), 2c without and with PCC, and 4c theories.

Fig. 1.

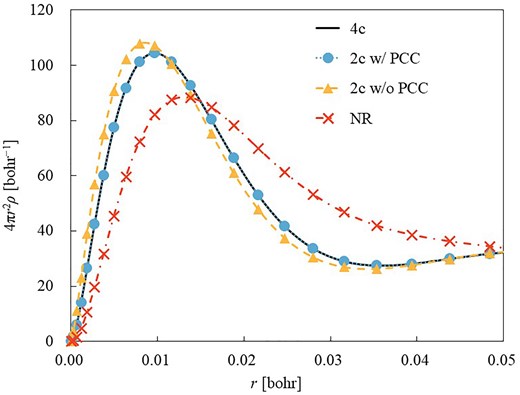
Radial electron density of a Be-like atom with Z = 80 obtained by NR, 2c without and with PCC, and 4c Hamiltonian.

Open in new tab Download slide

A clear difference is observed between the NR and 4c results: the electron density obtained with the 4c Hamiltonian shifts toward the inner region, reflecting the relativistic contraction of inner-shell orbitals. The 2c Hamiltonian with PCC successfully reproduces the 4c results, while the 2c calculation without PCC overestimates the relativistic contraction. The effect of PCC is especially significant in the vicinity of the nucleus. The influence of this density difference on the evaluation of the exchange–correlation energy in RDFT has been discussed in detail in Refs.^8–10

This study highlights the importance of PCC in RDFT and its direct impact on electron density evaluation. By establishing an analogy with CC theory, we have shown that improper handling of the density operator can result in an inaccurate description of electronic properties. The insights gained from this work provide a solid theoretical foundation for improving the accuracy of relativistic quantum chemical calculations and can be applied to various computational methodologies involving heavy elements.

Funding

None declared.

References

Pyykkö

J. P.

Desclaux

Acc. Chem. Res.

1979

276

Month:	Total Views:
April 2025	53
May 2025	64

Article Contents

Role of picture change correction in relativistic density functional theory: an analogy with coupled cluster theory Open Access

Abstract

Funding

References

Author notes

Citations

Views

Altmetric

Email alerts

Related articles in

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

Role of picture change correction in relativistic density functional theory: an analogy with coupled cluster theory