-
PDF
- Split View
-
Views
-
Cite
Cite
Harrison T Reeder, Kyu Ha Lee, Sebastien Haneuse, Characterizing quantile-varying covariate effects under the accelerated failure time model, Biostatistics, Volume 25, Issue 2, April 2024, Pages 449–467, https://doi.org/10.1093/biostatistics/kxac052
Close - Share Icon Share
Summary
An important task in survival analysis is choosing a structure for the relationship between covariates of interest and the time-to-event outcome. For example, the accelerated failure time (AFT) model structures each covariate effect as a constant multiplicative shift in the outcome distribution across all survival quantiles. Though parsimonious, this structure cannot detect or capture effects that differ across quantiles of the distribution, a limitation that is analogous to only permitting proportional hazards in the Cox model. To address this, we propose a general framework for quantile-varying multiplicative effects under the AFT model. Specifically, we embed flexible regression structures within the AFT model and derive a novel formula for interpretable effects on the quantile scale. A regression standardization scheme based on the g-formula is proposed to enable the estimation of both covariate-conditional and marginal effects for an exposure of interest. We implement a user-friendly Bayesian approach for the estimation and quantification of uncertainty while accounting for left truncation and complex censoring. We emphasize the intuitive interpretation of this model through numerical and graphical tools and illustrate its performance through simulation and application to a study of Alzheimer’s disease and dementia.
1. Introduction
Modeling the relationship between a time-to-event outcome |$T$| and a vector of covariates |$\mathbf{ X}$| requires choosing a structure for the covariate effects. The proportional hazards model is by far the most commonly used model, specifying a constant multiplicative effect on the hazard of the outcome, yielding a “hazard ratio.” Though ubiquitous, hazard ratios can be difficult to interpret, and the constant effect across time—that is, the “proportionality” of the hazards—is not always plausible (Hernán, 2010; Uno and others, 2015). As an alternative, the accelerated failure time (AFT) model directly describes shifts in the outcome distribution between populations having different characteristics, via multiplicative effects on event time quantiles (Wei, 1992). Specifically, every survival quantile is multiplied by a constant “acceleration factor,” equivalent to a horizontal stretching or compressing of the survivor function. In other words, the times by which 10|$\%$| of events occur, or 50|$\%$| (i.e., the median survival time), or any other quantile, are shifted by the same multiplicative constant. This common effect across quantiles is the central feature of the AFT model, making it highly interpretable because contrasts of survival quantiles are tangible and often clinically meaningful. Despite the parsimony of a constant multiplicative effect, in some settings, it may be important to allow for more flexible effects across quantiles. For example, consider the study of Alzheimer’s disease (AD) and dementia among older adults. Prospective cohort studies of incident AD and dementia typically enroll subjects and follow them over decades, often subject to left truncation and sometimes complex censoring. Age at AD onset among those with a particular risk factor, for example, may skew earlier than among those without the risk factor. However, because AD is a complex disease that can arise over a long time scale, baseline risk factors may not affect the entire distribution uniformly. For example, a risk factor may not affect the timing of “early-onset” cases, but make “late-onset” cases occur sooner.
Modeling flexibly time-varying hazard ratios is a well-known and commonly used tool under the Cox model, but analogous extensions to flexibly quantile-varying acceleration factors under the AFT model are less well-studied. Some extensions to the AFT include admitting covariates to accommodate “heteroskedasticity” or stratification of the baseline distribution (Hsieh, 2001; Zhou and others, 2017). Recent work by Crowther and others (2022) describes a frequentist spline-based AFT model, with possibly time-varying covariate effects. However, their work considers a less common interpretation of the acceleration factor on the scale of log time, rather than investigating the potential for flexibility on the quantile scale. Separately, Pang and others (2021) consider a frequentist spline-based AFT model using a completely different formulation derived from Prentice and Kalbfleisch (1979), requiring a specialized estimation algorithm and bootstrapping for inference. Neither of these papers explores the Bayesian paradigm or examine the effects of time-dependent covariates that commonly arise in longitudinal studies, for which the resulting relationship varies both over the trajectory of the covariate, and over the survival quantiles.
In this article, we extend the AFT model to allow flexible acceleration factors that vary across quantiles. Our approach builds on a time-varying AFT model first introduced in Cox and Oakes (1984) but seemingly largely overlooked in the literature, and a general framework for flexible covariate effect specification. AFT regression coefficients specified to vary over time can be inverted into quantile-varying acceleration factors, and we develop a regression standardization scheme based on the g-formula to estimate marginal acceleration factors for an exposure. We propose a Bayesian estimation approach using the Stan language, which allows the quantification of uncertainty and increased flexibility. Through simulations, we examine the ability for the proposed flexible AFT effect specification and regression standardization methods to recover true effects in multiple settings and illustrate potential sensitivity to baseline hazard specification.
Finally, we derive new insights into the use of binary time-varying covariates under the AFT model and present novel tools for modeling and visualizing such effects. This further expands the AFT modeling toolkit to cover many extensions commonly used under the Cox model. We motivate these methods with an in-depth analysis of the Religious Orders Study and Memory and Aging Project prospective cohort studies of AD and dementia (Bennett and others, 2018).
2. The AFT model
The standard AFT model with time-invariant effects can be written as a log-linear model of time:
where |$\epsilon$| is a random error term and |$\boldsymbol{\beta}$| is a vector of regression coefficients corresponding with covariates |$\mathbf{ X}$|. We denote the exponentiated error |$T_0 = \exp(\epsilon)$|, representing a hypothetical random variable drawn from the “baseline distribution” having survivor function |$S_0$|. This model structures covariate effects such that the distribution of event times among subjects having covariate pattern |$\mathbf{ x}$|, denoted |$T_{\mathbf{ x}}$|, is directly shifted from the baseline distribution by the transformation
Based on this connection, an equivalent representation of the standard AFT model is given directly via the baseline survivor function |$S_0$| as
The AFT model admits the interpretation of covariate effects as multiplicative shifts of survival quantiles. Defining |$t_{\mathbf{ x}}^{(p)}$| and |$t_{0}^{(p)}$| to be the |$p$|th quantile times under |$\mathbf{ x}$| and baseline, respectively,
Solving for the |$p$|th quantile survival time under |$\mathbf{ x}$| yields
The acceleration factor between two covariate patterns |$\mathbf{ x}$| and |$\mathbf{ x}'$| is then the ratio of |$p$|th quantiles,
Under the standard AFT model, the acceleration factor does not depend on the form of |$S_0$| or the value of |$p$|, characterizing a constant multiplicative covariate effect across the entire distribution.
2.1. AFT model with time-varying components
In the standard AFT model (2.3), the covariate-adjusted survivor function is characterized by the time shift |$t \times \exp(-\mathbf{ X}^{{\mathsf{\scriptscriptstyle T}}}\boldsymbol{\beta})$|. Towards a more flexible AFT model, we replace this time shift with a general increasing function |$V(t\mid\mathbf{ X})$|, yielding the covariate-adjusted survivor function
This formulation, first discussed by Cox and Oakes (1984) in the context of time-varying covariates, reduces to the standard AFT when |$V(t\mid\mathbf{ X}) = t\times\exp(-\mathbf{ X}^{{\mathsf{\scriptscriptstyle T}}}\boldsymbol{\beta})$|, while also admitting other temporal specifications of the relationship between covariates and the outcome distribution. In fact, one interpretation of this |$V$| function is as a transformation linking the distribution of |$T_{\mathbf{ x}}$| under covariates |$\mathbf{ x}$|, and the baseline distribution of |$T_0$|,
Under this model, the |$p$|th quantile survival time for subjects under covariate pattern |$\mathbf{ x}$| is
Now it may no longer be the case that the ratio of |$p$|th quantile survival times between covariate patterns |$\mathbf{ x}$| and |$\mathbf{ x}'$| is a constant factor, but rather a quantile-varying acceleration factor
with notation explicitly capturing the additional potential for dependence on |$p$| and |$S_0$|.
2.1.1. Examples and interpretation
To emphasize both the flexibility and interpretability of this new quantity, Figure 1 shows sample survivor curves and corresponding acceleration factors under simple forms of quantile-varying effect for a single contrast between exposure levels |$X=1$| and |$X=0$|, with baseline |$S_0(t) = \exp(-0.3t)$|. For simplicity, we will interpret the effects at |$p=0.75$| and |$p=0.25$|, that is, the time by which 25|$\%$| and 75|$\%$| of people experience the event, respectively.
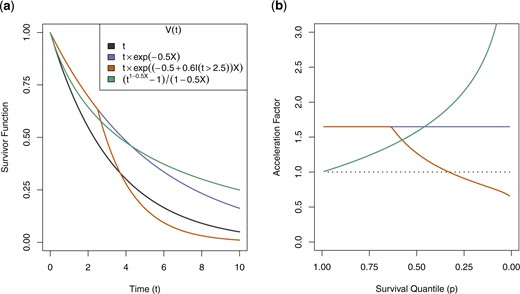
(a) Sample survivor curves. (b) Corresponding, possibly quantile-varying, acceleration factors. Baseline survivor function shown is |$S_0(t) = \exp(-0.3t)$|.
For reference, in each figure the blue curve (second row of the legend) shows a constant acceleration factor of |$\exp(0.5) \approx 1.65$| across quantiles. The green curve (fourth row of the legend) shows a protective effect that is increasingly pronounced among later-onset cases, with |$\xi(0.75\mid 1, 0)=1.25$| and |$\xi(0.25\mid 1, 0)=2$|. In words, the estimated time by which 25|$\%$| of the exposed die is 1.25 times as great as that among the unexposed, but the estimated time by which 75|$\%$| of the exposed die is two times greater than unexposed. Conceptually, this form of protective effect corresponds with delayed onset of all cases among the exposed, but specifically a much longer tail of late-onset cases compared to a standard AFT protective effect.
The orange curve (third row of the legend) shows a more nuanced effect that delays the earliest cases, while also accelerating later-onset cases. Numerically, |$\xi(0.75\mid 1, 0)=1.65$| and |$\xi(0.25\mid 1, 0)=0.9$|, meaning the estimated time by which 25|$\%$| of the exposed die is 1.65 times as great as that among the unexposed, but the estimated time by which 75|$\%$| of the exposed die is only 0.9 times as great as among the unexposed. Conceptually, this form of effect is a “compressing” of the outcome distribution, with earlier events being delayed and later events being accelerated. This is visible in the relative steepness of the survivor curve, with more than 50|$\%$| of all events occurring between times 2 and 4. Furthermore, this represents an effect with “crossing survivor curves,” which despite being common in certain health research domains cannot be modeled by standard proportional hazards or AFT models. In summary, we see that this approach to conceptualizing covariate effects for time-to-event outcomes yields nuanced and interpretable insights beyond what is available from standard proportional hazards or AFT models.
3. Model definition and implementation
The proposed quantile-varying AFT model is purposefully general with respect to the baseline survivor distribution |$S_0$| and the time-varying covariate process |$V$|. In this section, we outline several choices for specifying these model components, weighing tradeoffs between flexibility, stability, and computation. While this modeling framework in principle admits estimation under both frequentist and Bayesian paradigms, we focus on the latter approach and employ a Markov Chain Monte Carlo (MCMC) estimation routine via the No-U-Turn sampler implemented in the Stan language (Carpenter and others, 2017).
3.1. Specification of the covariate process V
Consider a |$d$| length vector of baseline covariates |$\mathbf{ X}$|. For ease of exposition, we focus on an exposure of interest |$X_1$| specified with a flexible regression effect. However, this can readily extend to allow multiple such exposures of interest.
The form of the covariate process |$V$| dictates the potential shapes the quantile-varying acceleration factor for |$X_1$| can take, and requires a balance of flexibility and stability. We focus on spline-based methods, which require a vector of knots |$\boldsymbol{\tau}$| characterizing a set of |$J$| basis functions |$B_1,\dots,B_J$|, and corresponding coefficients |$\boldsymbol{\alpha} = (\alpha_1,\dots,\alpha_J)^{{\mathsf{\scriptscriptstyle T}}}$|. This results in the specification
Note that when |$\boldsymbol{\alpha} = {\mathbf 0}$|, then this reduces to the standard AFT model, allowing straightforward model comparison to assess the flexible effect specification. Then, letting |$B'_j(t\mid \boldsymbol{\tau}) = d B_j(t\mid \boldsymbol{\tau})/dt$|, the derivative of the covariate process used in likelihood computation has the form
One specification inspired by the parametric proportional hazards spline model of Royston and Parmar (2002) and discussed by Crowther and others (2022) is the natural cubic spline basis, which combines cubic polynomial basis functions with a restriction that the ends beyond the lower and upper boundary knots be linear. Natural cubic spline basis functions |$B_k$| and |$B'_k$| are available in statistical software, and our implementation uses a set of numerically stable orthogonalized spline bases, from which the corresponding |$\beta$| and |$\boldsymbol{\alpha}$| are then backtransformed. The resulting |$V$| combines flexibility and stability, with the added advantage of being a smooth function of time.
However, the inverse |$V^{-1}(t\mid\mathbf{ X})$| used in the quantile-varying acceleration factor (2.10) does not have a closed form, and must be computed numerically. Moreover, this specification does not explicitly enforce the constraint that |$V$| be a nondecreasing function, as has been discussed in analogous flexible parametric survival models using restricted cubic splines (Royston and Parmar, 2002; Crowther and others, 2022). However, as has been repeatedly shown with other such methods in the literature, in our application this specification nevertheless performs well.
An alternative that is both computationally simpler and also enforces the proper constraints is specifying |$V$| as a piecewise linear function, yielding a simplified analytical form and closed form inverse. Define |$J + 2$| knots |$0=\tau_{0} < \tau_{1}<\dots<\tau_{J}<\tau_{J+1}=\infty$|, with basis functions |$B_j(t\mid\boldsymbol{\tau}) =t^{-1} (\min\{t,\tau_{j+1}\} - \tau_{j})_{+}$| where |$(z)_{+} = \min\{0,z\}$|. Then, |$V$| simplifies to
with the straightforward derivative |$v(t\mid\mathbf{ X}) = \exp\left\{ -\mathbf{ X}^{{\mathsf{\scriptscriptstyle T}}}\boldsymbol{\beta} - \sum_{j=1}^{J} X_1\alpha_j \mathbb{ I}(\tau_{j} \leq t < \tau_{j+1}) \right\}$|. Computation of the inverse is also straightward and left to Appendix C of the Supplementary material available at Biostatistics online. As above, this reduces to the standard AFT model when |$\boldsymbol{\alpha} = {\mathbf 0}$|.
3.2. Specification of the baseline distribution S0
As with the specification of |$V$|, there are numerous possible choices of baseline distribution characterizing |$S_0$|, both fully parametric and semiparametric. Parametric specifications have several advantages in this setting: they are computationally efficient, well-defined across all quantiles, have tractible inverse survivor functions, and can lead to improved efficiency in smaller samples. Two such parametric specifications are the log-Normal baseline distribution with survivor function defined by |$S_0(t\mid \mu, \sigma) =1 - \Phi(\log t - \mu)/\sigma^2$|, where |$\Phi(\cdot)$| is the standard normal distribution function, and the Weibull baseline distribution defined by |$S_0(t\mid \mu, \sigma) = \exp\left\{ \left[t\times\exp(-\mu)\right]^{\sigma} \right\}$|. Let |$\boldsymbol{\phi} = (\mu,\sigma)^{{\mathsf{\scriptscriptstyle T}}}$| denote the collection of parameters corresponding to the baseline distribution.
Nevertheless, an important benefit of the Bayesian paradigm is the well-established literature on semiparametric AFT survival models with flexible baseline distributions, such as Dirichlet process mixture (DPM) models (Lee and others, 2017) and Polya tree priors (Hanson and others, 2009). Here, we consider a transformed Bernstein polynomial (TBP) prior for |$S_0$| following (Zhou and Hanson, 2018), which defines a parametric centering distribution having survivor function |$S^{*}_{0}(t\mid \boldsymbol{\phi})$| (such as the Weibull or log-Normal defined above), then applies a transformation on the quantile scale using Bernstein polynomial functions to capture a wide array of distributions. Formally, define a vector |$\mathbf{ w}$| of length |$K$| such that |$\sum_{k=1}^K w_k = 1$|, and the Beta(|$a,b$|) distribution function |$G(p \mid a,b) = \Gamma(a+b)[\Gamma(a)\Gamma(b)]^{-1} p^{a-1}(1-p)^{b-1}$|. Then, the baseline survivor function is
Because the domain of |$G$| and the range of |$S^{*}_0$| are both [0,1], this represents a flexible spline transformation of the centering parametric distribution on the scale of survival quantiles. In particular, if |$\mathbf{ w} = (J^{-1},J^{-1},\dots,J^{-1})^{{\mathsf{\scriptscriptstyle T}}}$|, then |$S_0 = S^{*}_0$|, so the TBP specification contains the centering parametric model but can characterize a wide array of survival distribution shapes. An illustration is provided in Appendix F of the Supplementary material available at Biostatistics online. Finally, we place a |$\text{Dirichlet}(\theta)$| prior on |$\mathbf{ w}$| with |$\theta >0$|, where larger values of |$\theta$| correspond to tighter concentration of the elements of |$\mathbf{ w}$| around |$J^{-1}$| and therefore tighter concentration of |$S_0$| around |$S^{*}_0$|.
This specification offers several advantages over other flexible baseline specifications mentioned previously. Importantly, each |$G$| function can be computed recursively, so the overall computation of |$S_0$| is efficient. Moreover, the TBP prior can be sampled using the No-U-Turn algorithm implemented in the Stan language, as described below. By contrast, many other Bayesian nonparametric specifications such as Polya trees and DPM models have discrete parameters that are not admitted in Stan, instead requiring specialized computational methods such as custom MCMC samplers and data augmentation (Hanson and others, 2009; Lee and others, 2017). We believe this is the first such implementation of the TBP prior baseline specification in Stan, allowing us to examine the performance of the specification in a new computational environment.
The main tradeoff with any flexible form for |$S_0$| compared to a fully parametric specification is the increased computational cost, both for the sampler as well as the numerical computation of the inverse function |$S^{-1}_0$| and associated acceleration factors.
3.3. Likelihood
Another important benefit of the Bayesian approach is the ability to seamlessly handle arbitrary censoring and left truncation. Let |$(Y^{l},Y^{u})$| the left and right observed endpoints of a censoring interval around a true event time |$T$|, such that |$Y^{l}\leq T \leq Y^{u}$|. Right censoring corresponds with |$Y^{u} = \infty$|. Define the indicator |$\Delta = \mathbb{ I}(Y^{l} = Y^{u})$| to be a subject observed to experience the event exactly at time |$Y^{l}$|. Finally, let |$L$| represent the possible left-truncation time. Along with the baseline covariates |$\mathbf{ X}$|, denote the observed data for the |$i$|th subject |${\mathcal D}_i = \{y_i^{l},y_i^{u},\delta_i,l_i,\mathbf{ x}_i\}$|.
After specifying |$V$| and |$S_0$|, denote the full set of parameters |$\boldsymbol{\psi} = (\boldsymbol{\beta}^{{\mathsf{\scriptscriptstyle T}}}, \boldsymbol{\alpha}^{{\mathsf{\scriptscriptstyle T}}}, \boldsymbol{\phi}^{{\mathsf{\scriptscriptstyle T}}}, \mathbf{ w}^{{\mathsf{\scriptscriptstyle T}}})^{{\mathsf{\scriptscriptstyle T}}}$|. Then under noninformative censoring, the |$i$|th subject’s likelihood contribution is
where |$f_0$| is the density function corresponding to the baseline distribution. By convention, |$S_0(\infty) = 0$|, so under right censoring this reduces to the standard censored data likelihood.
3.4. Bayesian computation and prior specification
As previously mentioned, we propose Bayesian estimation via the No-U-Turn sampler implemented by the Stan language (Carpenter and others, 2017). In brief, this MCMC algorithm uses gradient information on the log-posterior to generate Markov transitions that efficiently explore the posterior distribution. The implementation can be easily called from R via the rstan package (Stan Development Team, 2020).
To complete the model specification, we consider priors on the parameters |$\boldsymbol{\beta}$|, |$\boldsymbol{\alpha}$|, and |$\boldsymbol{\phi}$|. The No-U-Turn sampler does not require or leverage conjugacy between prior and posterior, so prior distributions can be chosen or adjusted without changing the implementation of the sampler. In the application below, we adopt flat priors for regression parameters |$\boldsymbol{\beta}$| and |$\boldsymbol{\alpha}$|. For parametric distributions, we also adopt a flat prior for the log location parameter |$\log \mu$|, and for the scale parameter a |$\sigma \sim \text{Gamma}(a_{\sigma},b_{\sigma})$| prior. Under the TBP prior, we instead follow previous literature by specifying a multivariate normal prior distribution on |$\log\mu$| and |$\log\sigma$| centered at 0 with covariance |$\Sigma_{\boldsymbol{\phi}}$|. We adopt a |$\mathbf{ w} \sim \text{Dirichlet}(\theta)$| prior for the weights, and a |$\theta \sim \text{Gamma}(a_{\theta},b_{\theta})$| hyperprior on |$\theta$|, regulating the level of flexibility around the parametric centering distribution.
3.5. Model evaluation and comparison
A conceptual benefit of our proposed modeling framework is that the flexible structures naturally encompass simpler models: the standard AFT model is nested within the flexible effect specification of covariate process |$V$|, and a fully parametric baseline is nested within the TBP prior for |$S_0$|. In this section, we propose a model evaluation metric to inform decisions regarding the necessary level of model complexity via the loo package in R (Vehtari and others, 2017).
The expected log pointwise predictive density (ELPD) is a metric for how well a fitted model can predict future out-of-sample data, with larger values meaning better predictive ability. For |$n$| future observations |${\widetilde y}_1,\dots,{\widetilde y}_{n}$|, it is defined via the posterior predictive density |$p({\widetilde y}\mid{\mathcal D})$| as
While typically future out-of-sample data is not available, the ELPD can be estimated by leave-one-out cross-validation by averaging the log posterior predictive distribution for each observed data point of a model fit excluding that data point. This quantity can in turn be estimated efficiently from a single Bayesian model fit via Pareto smoothed importance sampling, which we denote |$\widehat{\text{ELPD}}_{\text{psis-loo}}$| (Vehtari and others, 2017) and has shown improved performance relative to other common Bayesian model criteria, such as Deviance Information Criterion.
Alternatively, in Appendix E of the Supplementary material available at Biostatistics online, we derive a Bayes factor for evidence of a quantile-varying effect against the constant effect encoded when |$\boldsymbol{\alpha}={\mathbf 0}$|.
3.6. Computation of regression standardized acceleration factors
Importantly, under the covariate process |$V$| defined by (3.11), the quantile-varying acceleration factor (2.10) depends on the specified values of all covariates |$\mathbf{ x}$| and |$\mathbf{ x}'$|, not just those that differ. This conditionality on the values of all covariates may be insightful if interest is in assessing effect heterogeneity in subpopulations defined by specific covariate patterns. However, practical interest is often in assessing the effect of an exposure in a population standardized with respect to the other covariates. Therefore, in this section, we propose a regression standardization approach to estimating the quantile-varying acceleration factor for a particular covariate of interest, averaged over the distribution of other covariates. Conceptually, the goal is to first estimate the survivor curves we would observe in the population if everyone was alternately exposed or unexposed, and then back out the quantile-varying acceleration factor that relates the two curves.
For clarity, consider a single binary exposure of interest |$X$|, and vector of additional covariates |$\mathbf{ Z}$|. Then, the marginal ratio of interest is
Following Rothman and others (2021) and Sjölander (2016), define the survivor function for |$X=x$|, standardized to the distribution of |$\mathbf{ Z}$|, as
We then define the corresponding standardized quantile-varying acceleration factor as
where |$[S_{\mathbf{ Z}}]^{-1}(p\mid X=x)$| is the function solving |$S_{\mathbf{ Z}}(t \mid X=x) - p = 0$| for |$t$|. This contrast represents the magnitude of the horizontal shift in the standardized survivor curve |$S_{\mathbf{ Z}}$| between |$X=1$| and |$X=0$|, at each quantile |$p$|.
To estimate and quantify uncertainty for these contrasts, we develop a novel approach based on the Bayesian g-formula (Keil and others, 2018). In brief, for each MCMC draw |$m=1,\dots,M$|, for each |$X=x$| we compute the standardized survivor function
and then form contrast of interest
This may require numerical evaluation of the inverse standardized survivor functions. Estimating posterior mean and credible intervals of |$\xi_{\mathbf{ Z}}$| proceeds using the mean and quantiles of |$\xi^{(1)}_{\mathbf{ Z}},\dots,\xi^{(M)}_{\mathbf{ Z}}$|.
3.7. Simulation study
To examine the operating characteristics of the proposed AFT framework, we performed a simulation study detailed in Appendix B of the Supplementary material available at Biostatistics online that illustrates the performance of quantile-varying acceleration factor estimates across several settings and model specifications. As data-generating mechanisms, we considered true log-Normal baseline hazards having a binary covariate with either constant or quantile-varying effects, and two nuisance covariates.
We fit log-Normal and Weibull parametric models as well as a Weibull-centered TBP prior model, each with either constant, piecewise, or spline effect specifications. This allowed the assessment of performance when the baseline and/or effect were either correctly specified, flexibly approximated, or incorrectly specified. We compared the estimated ELPD metric, the integrated squared error of the baseline hazard |$\int (\widehat{h}_0(t) - h^*_0(t))^2{\rm d}t$|, and the bias, standard error, and coverage probability of the acceleration factors both conditionally and after regression standardization.
With details in the Supplementary material available at Biostatistics online, models with correctly specified effects as well as correctly specified baselines had the best ELPD and least biased, most precise estimates. The next-best performing models were those with TBP prior baselines, which nevertheless exhibited slightly elevated bias and mild undercoverage of the credible intervals especially in the lower quantiles where information loss due to censoring was very high. Models with Weibull parametric baselines performed the poorest across all metrics. We also observed that the TBP prior model implemented in Stan could have trouble initializing in a minority of simulation iterations, which may be due to a combination of finite-difference gradient computations used in the No-U-Turn sampling algorithm with numerical instability that may arise in the computation of the TBP survivor function. This is discussed further in the Supplementary material available at Biostatistics online.
Practically, these results support the use of ELPD model diagnostic criteria to select the final model specification in the data application below, as it was generally concordant with the estimation performance of both the baseline distribution and acceleration factors.
4. Application: cohort study of incident AD and dementia
Motivating the proposed AFT model is the study of adverse cognitive outcomes among older adults, as long timescales and complex disease etiology lend themselves to considering flexible covariate effects on the quantile scale. In this section, we investigate risk factors for AD and dementia in older adults using data collected by the Religious Orders Study and Memory and Aging Project (ROSMAP) cohort studies ongoing since 1994 and 1997, respectively (Bennett and others, 2018). Our analysis focuses on flexible estimation of the association of the genetic marker APOE-|$\epsilon4$| with the timing of AD or dementia onset. Previous analyses of similar cohorts have simply compared incidence rates within age categories to examine whether this marker had differential effects through time (Kukull and others, 2002). So, estimating a quantile-varying acceleration factor for APOE-|$\epsilon4$| is of clinical relevance, while also accounting for other risk factors.
A total of 2694 subjects were enrolled without AD or dementia between ages 65 and 86, and followed until withdrawal or death. Subjects underwent cognitive screening annually to diagnose the onset of AD or dementia, and death status was monitored continuously. Table 1 summarizes a set of baseline binary risk factors collected on the subjects: marital status at baseline, sex, education level, race/ethnicity, and presence of the APOE-|$\epsilon4$| genetic variant. The final analysis data set includes 2335 subjects with complete baseline information. The outcome is defined by the time of diagnosis of AD or dementia, with death treated as a censoring mechanism, yielding a cause-specific analysis. Because we only include subjects with age at least 65, the time scale of analysis is “years since age 65.” Importantly, our analysis accounts for the presence of left truncation (or “delayed entry”) by subjects who enroll after age 65. Though this framework extends to interval censoring, given the short visit intervals relative to the timescale, for this analysis, we defined right-censoring times for AD/dementia onset at the midpoint of the corresponding visit interval.
| . | . | Censored prior . | AD/dementia . | Death . | AD/dementia . |
|---|---|---|---|---|---|
| . | . | to AD/dementia . | and censored . | without . | diagnosis . |
| . | Total . | or death . | prior to death . | AD/dementia . | and death . |
| . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . |
| Total | 2335 (100) | 750 (100) | 123 (100) | 891 (100) | 571 (100) |
| White race/ethnicity | 2178 (93.3) | 687 (91.6) | 100 (81.3) | 849 (95.3) | 542 (94.9) |
| Male sex | 648 (27.8) | 147 (19.6) | 24 (19.5) | 316 (35.5) | 161 (28.2) |
| Married at study entry | 462 (19.8) | 216 (28.8) | 29 (23.6) | 145 (16.3) | 72 (12.6) |
| |$\geq 15$| years of education | 1621 (69.4) | 532 (70.9) | 80 (65) | 609 (68.4) | 400 (70.1) |
| APOE-|$\epsilon4$| genetic variant | 575 (24.6) | 156 (20.8) | 53 (43.1) | 173 (19.4) | 193 (33.8) |
| . | . | Censored prior . | AD/dementia . | Death . | AD/dementia . |
|---|---|---|---|---|---|
| . | . | to AD/dementia . | and censored . | without . | diagnosis . |
| . | Total . | or death . | prior to death . | AD/dementia . | and death . |
| . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . |
| Total | 2335 (100) | 750 (100) | 123 (100) | 891 (100) | 571 (100) |
| White race/ethnicity | 2178 (93.3) | 687 (91.6) | 100 (81.3) | 849 (95.3) | 542 (94.9) |
| Male sex | 648 (27.8) | 147 (19.6) | 24 (19.5) | 316 (35.5) | 161 (28.2) |
| Married at study entry | 462 (19.8) | 216 (28.8) | 29 (23.6) | 145 (16.3) | 72 (12.6) |
| |$\geq 15$| years of education | 1621 (69.4) | 532 (70.9) | 80 (65) | 609 (68.4) | 400 (70.1) |
| APOE-|$\epsilon4$| genetic variant | 575 (24.6) | 156 (20.8) | 53 (43.1) | 173 (19.4) | 193 (33.8) |
| . | . | Censored prior . | AD/dementia . | Death . | AD/dementia . |
|---|---|---|---|---|---|
| . | . | to AD/dementia . | and censored . | without . | diagnosis . |
| . | Total . | or death . | prior to death . | AD/dementia . | and death . |
| . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . |
| Total | 2335 (100) | 750 (100) | 123 (100) | 891 (100) | 571 (100) |
| White race/ethnicity | 2178 (93.3) | 687 (91.6) | 100 (81.3) | 849 (95.3) | 542 (94.9) |
| Male sex | 648 (27.8) | 147 (19.6) | 24 (19.5) | 316 (35.5) | 161 (28.2) |
| Married at study entry | 462 (19.8) | 216 (28.8) | 29 (23.6) | 145 (16.3) | 72 (12.6) |
| |$\geq 15$| years of education | 1621 (69.4) | 532 (70.9) | 80 (65) | 609 (68.4) | 400 (70.1) |
| APOE-|$\epsilon4$| genetic variant | 575 (24.6) | 156 (20.8) | 53 (43.1) | 173 (19.4) | 193 (33.8) |
| . | . | Censored prior . | AD/dementia . | Death . | AD/dementia . |
|---|---|---|---|---|---|
| . | . | to AD/dementia . | and censored . | without . | diagnosis . |
| . | Total . | or death . | prior to death . | AD/dementia . | and death . |
| . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . | (|$\%$|) . |
| Total | 2335 (100) | 750 (100) | 123 (100) | 891 (100) | 571 (100) |
| White race/ethnicity | 2178 (93.3) | 687 (91.6) | 100 (81.3) | 849 (95.3) | 542 (94.9) |
| Male sex | 648 (27.8) | 147 (19.6) | 24 (19.5) | 316 (35.5) | 161 (28.2) |
| Married at study entry | 462 (19.8) | 216 (28.8) | 29 (23.6) | 145 (16.3) | 72 (12.6) |
| |$\geq 15$| years of education | 1621 (69.4) | 532 (70.9) | 80 (65) | 609 (68.4) | 400 (70.1) |
| APOE-|$\epsilon4$| genetic variant | 575 (24.6) | 156 (20.8) | 53 (43.1) | 173 (19.4) | 193 (33.8) |
We compare the fits of standard AFT models with those having piecewise and spline forms for |$V$|, under Weibull and log-Normal baseline specifications as well as a TBP prior baseline with |$K=5$|, centering around the Weibull distribution. We set four break points for the piecewise linear effect at 7.5-year intervals across the follow-up period, and for the spline effect we set two internal knots at quantiles on the log scale. The difference between these specifications is due to the spline being naturally more flexible, allowing it to smooth across knots with irregular spacing, while the piecewise linear model requires break points that span the follow-up period to achieve flexibility. For the parametric scale parameters, we set |$\sigma \sim \text{Gamma}(0.3,0.05)$|, having prior median 1.46|$\%$| and 95|$\%$| central mass between 6e|$-$|5 and 38. For the TBP baseline specification, we set a hyperprior of |$\theta \sim \text{Gamma}(1,1)$|, and consistent with the literature on this model to minimize confounding between the flexibility of |$\boldsymbol{\phi}$| and |$\mathbf{ w}$|, adopted a prior covariance |$\Sigma_{\boldsymbol{\phi}}$| for the Weibull centering parameters equal to the maximum likelihood estimate from a standard Weibull AFT scaled by 10. For each model, we ran three chains each for 2000 adaptation iterations and 10 000 samples, totaling 30 000 samples. After sampling, all potential scale reduction factors were below |$1.01$| and trace plots indicated good mixing. For comparison, we include results from a standard Frequentist Cox proportional hazards model. Additionally, we present Bayesian proportional hazard and proportional odds comparators fit with TBP prior baseline hazards in Appendix A of the Supplementary material available at Biostatistics online.
Table 2 reports the estimates of regression parameters across all AFT specifications, as well as frequentist results from a Cox proportional hazards model. For the AFT models, positive estimates of |$\boldsymbol{\beta}$| correspond with delayed onset of AD or dementia, as do negative estimates for the Cox model. The coefficients estimated for white race/ethnicity, marital status, female sex, and education are stable across all model specifications. Interpreting the Weibull AFT with constant effect of APOE-|$\epsilon 4$|, for example, indicates that being married is associated with a |$\exp(0.1)=1.1$| times greater median time to onset of AD or dementia, with 95|$\%$| credible interval of (1.02–1.2). Flexible effect coefficients of APOE-|$\epsilon 4$| cannot be directly interpreted on the quantile scale, therefore we present graphical tools below.
Regression estimates for time to onset of AD or dementia in the absence of death. AFT results are posterior medians and 95|$\%$| credible intervals for regression parameters. Cox model results are log-hazard ratio estimates and 95|$\%$| confidence intervals
| . | . | AFT Model . | ||
|---|---|---|---|---|
| . | . | . | . | TBP . |
| . | Cox PH . | Log-normal . | Weibull . | (Weibull . |
| . | . | . | . | centered) . |
| White race/ | ||||
| ethnicity, |$\beta_1$| | ||||
| Constant | |$-$|0.28 (|$-$|0.57 to 0.01) | 0.18 (0.03 to 0.31) | 0.08 (|$-$|0.03 to 0.19) | 0.08 (|$-$|0.02 to 0.19) |
| Piecewise linear | 0.18 (0.05 to 0.3) | 0.08 (|$-$|0.02 to 0.17) | 0.07 (|$-$|0.03 to 0.16) | |
| Restricted cubic | 0.15 (0.03 to 0.28) | 0.07 (|$-$|0.02 to 0.16) | 0.07 (|$-$|0.02 to 0.16) | |
| spline | ||||
| Male sex, |$\beta_2$| | ||||
| Constant | 0.06 (|$-$|0.11 to 0.23) | |$-$|0.04 (|$-$|0.13 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.05) | |$-$|0.02 (|$-$|0.08 to 0.04) |
| Piecewise linear | |$-$|0.05 (|$-$|0.12 to 0.03) | |$-$|0.02 (|$-$|0.08 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.03) | |
| Restricted cubic | |$-$|0.04 (|$-$|0.11 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |
| spline | ||||
| Married at study | ||||
| entry, |$\beta_3$| | ||||
| Constant | |$-$|0.26 (|$-$|0.47 to |$-$|0.04) | 0.13 (0.03 to 0.23) | 0.1 (0.02 to 0.19) | 0.1 (0.03 to 0.18) |
| Piecewise linear | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.16) | |
| Restricted cubic | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.15) | |
| spline | ||||
| |$\geq$|15 years of | ||||
| education, |$\beta_4$| | ||||
| Constant | |$-$|0.1 (|$-$|0.26 to 0.07) | 0.07 (|$-$|0.01 to 0.16) | 0.04 (|$-$|0.02 to 0.1) | 0.03 (|$-$|0.03 to 0.1) |
| Piecewise linear | 0.07 (0 to 0.15) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| Restricted cubic | 0.06 (|$-$|0.01 to 0.14) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\beta_5$| | ||||
| Constant | 0.76 (0.61 to 0.92) | |$-$|0.42 (|$-$|0.51 to |$-$|0.34) | |$-$|0.28 (|$-$|0.35 to |$-$|0.22) | |$-$|0.28 (|$-$|0.35 to |$-$|0.21) |
| Piecewise linear | |$-$|0.79 (|$-$|0.95 to |$-$|0.62) | |$-$|0.75 (|$-$|0.92 to |$-$|0.55) | |$-$|0.76 (|$-$|0.94 to |$-$|0.53) | |
| Restricted cubic | |$-$|2.54 (|$-$|2.98 to |$-$|1.95) | |$-$|2.38 (|$-$|3.08 to |$-$|1.23) | |$-$|2.31 (|$-$|3.10 to |$-$|0.93) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_1$| | ||||
| Constant | ||||
| Piecewise linear | 0.86 (0.49 to 1.23) | 0.78 (0.35 to 1.20) | 0.78 (0.28 to 1.24) | |
| Restricted cubic | 1.51 (1.12 to 1.85) | 1.51 (0.77 to 2.01) | 1.49 (0.62 to 2.05) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_2$| | ||||
| Constant | ||||
| Piecewise linear | 0.52 (0.23 to 0.80) | 0.74 (0.39 to 1.06) | 0.8 (0.42 to 1.15) | |
| Restricted cubic | 3.83 (2.73 to 4.47) | 3.63 (1.45 to 4.76) | 3.48 (0.87 to 4.79) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_3$| | ||||
| Constant | ||||
| Piecewise linear | 0.46 (0.11 to 0.81) | 0.97 (0.59 to 1.34) | 1.01 (0.59 to 1.41) | |
| Restricted cubic | 1.07 (0.71 to 1.40) | 1.34 (0.77 to 1.77) | 1.33 (0.67 to 1.81) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_4$| | ||||
| Constant | ||||
| Piecewise linear | |$-$|0.38 (|$-$|1.06 to 0.45) | 0.41 (|$-$|0.23 to 1.20) | 0.39 (|$-$|0.34 to 1.23) | |
| Restricted cubic | ||||
| spline | ||||
| . | . | AFT Model . | ||
|---|---|---|---|---|
| . | . | . | . | TBP . |
| . | Cox PH . | Log-normal . | Weibull . | (Weibull . |
| . | . | . | . | centered) . |
| White race/ | ||||
| ethnicity, |$\beta_1$| | ||||
| Constant | |$-$|0.28 (|$-$|0.57 to 0.01) | 0.18 (0.03 to 0.31) | 0.08 (|$-$|0.03 to 0.19) | 0.08 (|$-$|0.02 to 0.19) |
| Piecewise linear | 0.18 (0.05 to 0.3) | 0.08 (|$-$|0.02 to 0.17) | 0.07 (|$-$|0.03 to 0.16) | |
| Restricted cubic | 0.15 (0.03 to 0.28) | 0.07 (|$-$|0.02 to 0.16) | 0.07 (|$-$|0.02 to 0.16) | |
| spline | ||||
| Male sex, |$\beta_2$| | ||||
| Constant | 0.06 (|$-$|0.11 to 0.23) | |$-$|0.04 (|$-$|0.13 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.05) | |$-$|0.02 (|$-$|0.08 to 0.04) |
| Piecewise linear | |$-$|0.05 (|$-$|0.12 to 0.03) | |$-$|0.02 (|$-$|0.08 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.03) | |
| Restricted cubic | |$-$|0.04 (|$-$|0.11 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |
| spline | ||||
| Married at study | ||||
| entry, |$\beta_3$| | ||||
| Constant | |$-$|0.26 (|$-$|0.47 to |$-$|0.04) | 0.13 (0.03 to 0.23) | 0.1 (0.02 to 0.19) | 0.1 (0.03 to 0.18) |
| Piecewise linear | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.16) | |
| Restricted cubic | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.15) | |
| spline | ||||
| |$\geq$|15 years of | ||||
| education, |$\beta_4$| | ||||
| Constant | |$-$|0.1 (|$-$|0.26 to 0.07) | 0.07 (|$-$|0.01 to 0.16) | 0.04 (|$-$|0.02 to 0.1) | 0.03 (|$-$|0.03 to 0.1) |
| Piecewise linear | 0.07 (0 to 0.15) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| Restricted cubic | 0.06 (|$-$|0.01 to 0.14) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\beta_5$| | ||||
| Constant | 0.76 (0.61 to 0.92) | |$-$|0.42 (|$-$|0.51 to |$-$|0.34) | |$-$|0.28 (|$-$|0.35 to |$-$|0.22) | |$-$|0.28 (|$-$|0.35 to |$-$|0.21) |
| Piecewise linear | |$-$|0.79 (|$-$|0.95 to |$-$|0.62) | |$-$|0.75 (|$-$|0.92 to |$-$|0.55) | |$-$|0.76 (|$-$|0.94 to |$-$|0.53) | |
| Restricted cubic | |$-$|2.54 (|$-$|2.98 to |$-$|1.95) | |$-$|2.38 (|$-$|3.08 to |$-$|1.23) | |$-$|2.31 (|$-$|3.10 to |$-$|0.93) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_1$| | ||||
| Constant | ||||
| Piecewise linear | 0.86 (0.49 to 1.23) | 0.78 (0.35 to 1.20) | 0.78 (0.28 to 1.24) | |
| Restricted cubic | 1.51 (1.12 to 1.85) | 1.51 (0.77 to 2.01) | 1.49 (0.62 to 2.05) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_2$| | ||||
| Constant | ||||
| Piecewise linear | 0.52 (0.23 to 0.80) | 0.74 (0.39 to 1.06) | 0.8 (0.42 to 1.15) | |
| Restricted cubic | 3.83 (2.73 to 4.47) | 3.63 (1.45 to 4.76) | 3.48 (0.87 to 4.79) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_3$| | ||||
| Constant | ||||
| Piecewise linear | 0.46 (0.11 to 0.81) | 0.97 (0.59 to 1.34) | 1.01 (0.59 to 1.41) | |
| Restricted cubic | 1.07 (0.71 to 1.40) | 1.34 (0.77 to 1.77) | 1.33 (0.67 to 1.81) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_4$| | ||||
| Constant | ||||
| Piecewise linear | |$-$|0.38 (|$-$|1.06 to 0.45) | 0.41 (|$-$|0.23 to 1.20) | 0.39 (|$-$|0.34 to 1.23) | |
| Restricted cubic | ||||
| spline | ||||
Regression estimates for time to onset of AD or dementia in the absence of death. AFT results are posterior medians and 95|$\%$| credible intervals for regression parameters. Cox model results are log-hazard ratio estimates and 95|$\%$| confidence intervals
| . | . | AFT Model . | ||
|---|---|---|---|---|
| . | . | . | . | TBP . |
| . | Cox PH . | Log-normal . | Weibull . | (Weibull . |
| . | . | . | . | centered) . |
| White race/ | ||||
| ethnicity, |$\beta_1$| | ||||
| Constant | |$-$|0.28 (|$-$|0.57 to 0.01) | 0.18 (0.03 to 0.31) | 0.08 (|$-$|0.03 to 0.19) | 0.08 (|$-$|0.02 to 0.19) |
| Piecewise linear | 0.18 (0.05 to 0.3) | 0.08 (|$-$|0.02 to 0.17) | 0.07 (|$-$|0.03 to 0.16) | |
| Restricted cubic | 0.15 (0.03 to 0.28) | 0.07 (|$-$|0.02 to 0.16) | 0.07 (|$-$|0.02 to 0.16) | |
| spline | ||||
| Male sex, |$\beta_2$| | ||||
| Constant | 0.06 (|$-$|0.11 to 0.23) | |$-$|0.04 (|$-$|0.13 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.05) | |$-$|0.02 (|$-$|0.08 to 0.04) |
| Piecewise linear | |$-$|0.05 (|$-$|0.12 to 0.03) | |$-$|0.02 (|$-$|0.08 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.03) | |
| Restricted cubic | |$-$|0.04 (|$-$|0.11 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |
| spline | ||||
| Married at study | ||||
| entry, |$\beta_3$| | ||||
| Constant | |$-$|0.26 (|$-$|0.47 to |$-$|0.04) | 0.13 (0.03 to 0.23) | 0.1 (0.02 to 0.19) | 0.1 (0.03 to 0.18) |
| Piecewise linear | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.16) | |
| Restricted cubic | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.15) | |
| spline | ||||
| |$\geq$|15 years of | ||||
| education, |$\beta_4$| | ||||
| Constant | |$-$|0.1 (|$-$|0.26 to 0.07) | 0.07 (|$-$|0.01 to 0.16) | 0.04 (|$-$|0.02 to 0.1) | 0.03 (|$-$|0.03 to 0.1) |
| Piecewise linear | 0.07 (0 to 0.15) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| Restricted cubic | 0.06 (|$-$|0.01 to 0.14) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\beta_5$| | ||||
| Constant | 0.76 (0.61 to 0.92) | |$-$|0.42 (|$-$|0.51 to |$-$|0.34) | |$-$|0.28 (|$-$|0.35 to |$-$|0.22) | |$-$|0.28 (|$-$|0.35 to |$-$|0.21) |
| Piecewise linear | |$-$|0.79 (|$-$|0.95 to |$-$|0.62) | |$-$|0.75 (|$-$|0.92 to |$-$|0.55) | |$-$|0.76 (|$-$|0.94 to |$-$|0.53) | |
| Restricted cubic | |$-$|2.54 (|$-$|2.98 to |$-$|1.95) | |$-$|2.38 (|$-$|3.08 to |$-$|1.23) | |$-$|2.31 (|$-$|3.10 to |$-$|0.93) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_1$| | ||||
| Constant | ||||
| Piecewise linear | 0.86 (0.49 to 1.23) | 0.78 (0.35 to 1.20) | 0.78 (0.28 to 1.24) | |
| Restricted cubic | 1.51 (1.12 to 1.85) | 1.51 (0.77 to 2.01) | 1.49 (0.62 to 2.05) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_2$| | ||||
| Constant | ||||
| Piecewise linear | 0.52 (0.23 to 0.80) | 0.74 (0.39 to 1.06) | 0.8 (0.42 to 1.15) | |
| Restricted cubic | 3.83 (2.73 to 4.47) | 3.63 (1.45 to 4.76) | 3.48 (0.87 to 4.79) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_3$| | ||||
| Constant | ||||
| Piecewise linear | 0.46 (0.11 to 0.81) | 0.97 (0.59 to 1.34) | 1.01 (0.59 to 1.41) | |
| Restricted cubic | 1.07 (0.71 to 1.40) | 1.34 (0.77 to 1.77) | 1.33 (0.67 to 1.81) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_4$| | ||||
| Constant | ||||
| Piecewise linear | |$-$|0.38 (|$-$|1.06 to 0.45) | 0.41 (|$-$|0.23 to 1.20) | 0.39 (|$-$|0.34 to 1.23) | |
| Restricted cubic | ||||
| spline | ||||
| . | . | AFT Model . | ||
|---|---|---|---|---|
| . | . | . | . | TBP . |
| . | Cox PH . | Log-normal . | Weibull . | (Weibull . |
| . | . | . | . | centered) . |
| White race/ | ||||
| ethnicity, |$\beta_1$| | ||||
| Constant | |$-$|0.28 (|$-$|0.57 to 0.01) | 0.18 (0.03 to 0.31) | 0.08 (|$-$|0.03 to 0.19) | 0.08 (|$-$|0.02 to 0.19) |
| Piecewise linear | 0.18 (0.05 to 0.3) | 0.08 (|$-$|0.02 to 0.17) | 0.07 (|$-$|0.03 to 0.16) | |
| Restricted cubic | 0.15 (0.03 to 0.28) | 0.07 (|$-$|0.02 to 0.16) | 0.07 (|$-$|0.02 to 0.16) | |
| spline | ||||
| Male sex, |$\beta_2$| | ||||
| Constant | 0.06 (|$-$|0.11 to 0.23) | |$-$|0.04 (|$-$|0.13 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.05) | |$-$|0.02 (|$-$|0.08 to 0.04) |
| Piecewise linear | |$-$|0.05 (|$-$|0.12 to 0.03) | |$-$|0.02 (|$-$|0.08 to 0.04) | |$-$|0.02 (|$-$|0.08 to 0.03) | |
| Restricted cubic | |$-$|0.04 (|$-$|0.11 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |$-$|0.02 (|$-$|0.07 to 0.03) | |
| spline | ||||
| Married at study | ||||
| entry, |$\beta_3$| | ||||
| Constant | |$-$|0.26 (|$-$|0.47 to |$-$|0.04) | 0.13 (0.03 to 0.23) | 0.1 (0.02 to 0.19) | 0.1 (0.03 to 0.18) |
| Piecewise linear | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.16) | |
| Restricted cubic | 0.13 (0.04 to 0.22) | 0.09 (0.02 to 0.16) | 0.08 (0.02 to 0.15) | |
| spline | ||||
| |$\geq$|15 years of | ||||
| education, |$\beta_4$| | ||||
| Constant | |$-$|0.1 (|$-$|0.26 to 0.07) | 0.07 (|$-$|0.01 to 0.16) | 0.04 (|$-$|0.02 to 0.1) | 0.03 (|$-$|0.03 to 0.1) |
| Piecewise linear | 0.07 (0 to 0.15) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| Restricted cubic | 0.06 (|$-$|0.01 to 0.14) | 0.03 (|$-$|0.02 to 0.09) | 0.03 (|$-$|0.02 to 0.08) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\beta_5$| | ||||
| Constant | 0.76 (0.61 to 0.92) | |$-$|0.42 (|$-$|0.51 to |$-$|0.34) | |$-$|0.28 (|$-$|0.35 to |$-$|0.22) | |$-$|0.28 (|$-$|0.35 to |$-$|0.21) |
| Piecewise linear | |$-$|0.79 (|$-$|0.95 to |$-$|0.62) | |$-$|0.75 (|$-$|0.92 to |$-$|0.55) | |$-$|0.76 (|$-$|0.94 to |$-$|0.53) | |
| Restricted cubic | |$-$|2.54 (|$-$|2.98 to |$-$|1.95) | |$-$|2.38 (|$-$|3.08 to |$-$|1.23) | |$-$|2.31 (|$-$|3.10 to |$-$|0.93) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_1$| | ||||
| Constant | ||||
| Piecewise linear | 0.86 (0.49 to 1.23) | 0.78 (0.35 to 1.20) | 0.78 (0.28 to 1.24) | |
| Restricted cubic | 1.51 (1.12 to 1.85) | 1.51 (0.77 to 2.01) | 1.49 (0.62 to 2.05) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_2$| | ||||
| Constant | ||||
| Piecewise linear | 0.52 (0.23 to 0.80) | 0.74 (0.39 to 1.06) | 0.8 (0.42 to 1.15) | |
| Restricted cubic | 3.83 (2.73 to 4.47) | 3.63 (1.45 to 4.76) | 3.48 (0.87 to 4.79) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_3$| | ||||
| Constant | ||||
| Piecewise linear | 0.46 (0.11 to 0.81) | 0.97 (0.59 to 1.34) | 1.01 (0.59 to 1.41) | |
| Restricted cubic | 1.07 (0.71 to 1.40) | 1.34 (0.77 to 1.77) | 1.33 (0.67 to 1.81) | |
| spline | ||||
| APOE-|$\epsilon4$| genetic | ||||
| variant, |$\alpha_4$| | ||||
| Constant | ||||
| Piecewise linear | |$-$|0.38 (|$-$|1.06 to 0.45) | 0.41 (|$-$|0.23 to 1.20) | 0.39 (|$-$|0.34 to 1.23) | |
| Restricted cubic | ||||
| spline | ||||
The top panel of Table 3 compares estimates of ELPD model criterion for each AFT model. In each case, the spline and piecewise-linear effect specifications outperformed the standard AFT specification. The log-Normal models uniformly underperformed while the Weibull and TBP models performed comparably. To graphically assess the effect of APOE-|$\epsilon 4,$| we report the TBP model and present results for other specifications in Appendix A of the Supplementary material available at Biostatistics online. Results were qualitatively similar for all baseline distributions, with the largest differences in acceleration factor only occurring in the lowest quantiles extrapolated beyond the observed data.
Estimated expected log predictive density (ELPD), multiplied by |$-$|2 to replicate scale of information criteria. Smaller values indicate better model fit
| . | AFT model . | ||
|---|---|---|---|
| . | Log-normal . | Weibull . | TBP (Weibull centered) . |
| AD/dementia onset (death as a censoring mechanism) | |||
| Constant | 5862.0 | 5806.3 | 5800.4 |
| Piecewise linear | 5841.5 | 5788.4 | 5782.2 |
| Restricted cubic spline | 5814.9 | 5780.9 | 5776.8 |
| Death (AD/dementia as a time-varying covariate) | |||
| Constant | 9997.2 | 9666.7 | 9629.8 |
| Piecewise linear | 9919.8 | 9636.7 | 9601.7 |
| Restricted cubic spline | 9884.5 | 9600.9 | 9566.7 |
| . | AFT model . | ||
|---|---|---|---|
| . | Log-normal . | Weibull . | TBP (Weibull centered) . |
| AD/dementia onset (death as a censoring mechanism) | |||
| Constant | 5862.0 | 5806.3 | 5800.4 |
| Piecewise linear | 5841.5 | 5788.4 | 5782.2 |
| Restricted cubic spline | 5814.9 | 5780.9 | 5776.8 |
| Death (AD/dementia as a time-varying covariate) | |||
| Constant | 9997.2 | 9666.7 | 9629.8 |
| Piecewise linear | 9919.8 | 9636.7 | 9601.7 |
| Restricted cubic spline | 9884.5 | 9600.9 | 9566.7 |
Estimated expected log predictive density (ELPD), multiplied by |$-$|2 to replicate scale of information criteria. Smaller values indicate better model fit
| . | AFT model . | ||
|---|---|---|---|
| . | Log-normal . | Weibull . | TBP (Weibull centered) . |
| AD/dementia onset (death as a censoring mechanism) | |||
| Constant | 5862.0 | 5806.3 | 5800.4 |
| Piecewise linear | 5841.5 | 5788.4 | 5782.2 |
| Restricted cubic spline | 5814.9 | 5780.9 | 5776.8 |
| Death (AD/dementia as a time-varying covariate) | |||
| Constant | 9997.2 | 9666.7 | 9629.8 |
| Piecewise linear | 9919.8 | 9636.7 | 9601.7 |
| Restricted cubic spline | 9884.5 | 9600.9 | 9566.7 |
| . | AFT model . | ||
|---|---|---|---|
| . | Log-normal . | Weibull . | TBP (Weibull centered) . |
| AD/dementia onset (death as a censoring mechanism) | |||
| Constant | 5862.0 | 5806.3 | 5800.4 |
| Piecewise linear | 5841.5 | 5788.4 | 5782.2 |
| Restricted cubic spline | 5814.9 | 5780.9 | 5776.8 |
| Death (AD/dementia as a time-varying covariate) | |||
| Constant | 9997.2 | 9666.7 | 9629.8 |
| Piecewise linear | 9919.8 | 9636.7 | 9601.7 |
| Restricted cubic spline | 9884.5 | 9600.9 | 9566.7 |
Figure 2 shows the estimated survivor functions and corresponding quantile-varying acceleration factors for the APOE-|$\epsilon4$| genetic variant, after regression standardization over the distribution of the other baseline covariates. These figures confirm other findings that APOE-|$\epsilon4$| is associated with earlier onset of AD and dementia. However, quantile-varying effects also indicate that the acceleration is strongest among the earliest cases and subsequently diminishes. Both piecewise and spline models estimate that the time by which the first 10|$\%$| of those living with APOE-|$\epsilon4$| develop AD or dementia is earlier than those without the variant by a factor of about 0.5; the median times by which people develop AD or dementia differ by a factor of about 0.75, and the times by which 75|$\%$| develop AD or dementia differ by a factor of about 0.85. Due to censoring of those with advanced age, the acceleration factor at lower quantiles reflects parametric extrapolation beyond the observed distribution, represented in the figure by grey shading. Nevertheless, this finding has clear clinical significance, indicating the particular need to monitor for early-onset AD/dementia at younger ages among those with APOE-|$\epsilon4$|.
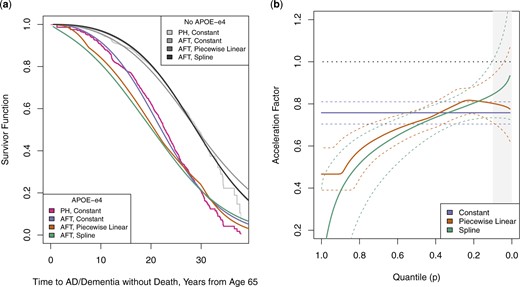
Under a Weibull-centered TBP prior baseline specification: (a) regression standardized survivor function estimates for onset of AD or dementia without death, averaged over other covariates. Regression standardized estimate from Cox proportional hazards model shown for comparison; (b) regression standardized quantile-varying acceleration factor estimates for onset of AD or dementia without death, averaged over other covariates. 95|$\%$| credible intervals represented with dashed lines. Grey shaded region represents area of parametric extrapolation beyond quantiles observed in both groups.
5. Effects of time-varying covariates on the quantile scale
In this section, we extend the proposed AFT model to incorporate binary time-varying covariates and provide graphical tools for effectively interpreting corresponding effects on the quantile scale.
To focus on intuition, consider a single time-varying covariate denoted |$X_1(t)$| with constant regression effect |$\beta_1$|. In particular, let |$X_1(t)$| be a binary-valued step function, such as an indicator for whether a nonterminal event has occurred by time |$t$|. Formally, define |$X_1(t) = \mathbb{ I}(t > t_{X})$|, where |$t_{X}$| is the time at which |$X_1$| changes. To simplify notation, consider a single additional covariate time-invariant covariate |$X_2$|, though the inclusion of multiple additional covariates is straightforward. Embedding these covariates directly in the structure for |$V$| given by (3.11) and setting |$\boldsymbol{\alpha} = {\mathbf 0}$| to denote a constant effect yields
With complete derivation given in Appendix D of the Supplementary material available at Biostatistics online, the acceleration factor at quantile |$p$| between two subjects depends on each person’s value of |$X_2$|, the change time |$t_{X}$| for |$X_1$|, and the baseline distribution |$S_0$|. In particular, for those with |$X_2=x_2$|, the acceleration factor at quantile |$p$| for experiencing |$X_1$| at |$t_X$| versus not experiencing |$X_1$| is
This is a weighted average between 1 and |$\exp(\beta_1)$|, with weight inversely proportional to the duration from |$t_{X}$| to the |$p$|th quantile survival time in the comparison group, |$S_{0}^{-1}(p)\exp(x_2\beta_2)$|. Intuitively, before |$t_{X}$| there is no difference between the individuals, so the acceleration factor is 1, and then after |$t_{X}$| the effect of |$X_1$| starts accumulating, and the acceleration factor increasingly shifts towards |$\exp(\beta_1)$| as |$p$| extends towards 0. Figure 3 illustrates this dynamic.
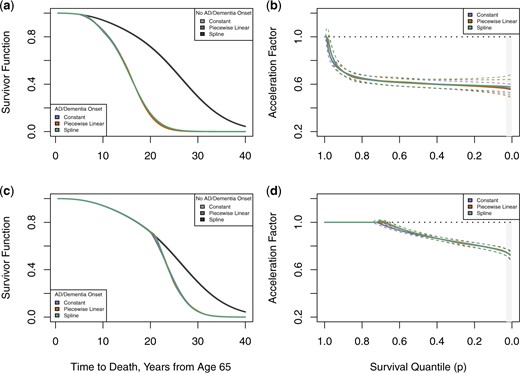
Under a Weibull-centered TBP prior baseline specification: regression standardized survivor function estimates for mortality following onset of AD or dementia at (a) age 70 and (c) age 85, averaged over other covariates; regression standardized survivor function estimates for mortality following onset of AD or dementia at (b) age 70 and (d) age 85, averaged over other covariates. 95|$\%$| credible intervals represented with dashed lines. Grey shaded region represents area of parametric extrapolation beyond quantiles observed in both groups.
Finally, a flexible effect for |$X_1(t)$| can also be specified by adapting the form of (5.22), yielding
Following Haneuse and others (2008), this specification characterizes flexibility in the effect of |$X_1$| over the time scale |$t-t_{X}$| denoting time since the nonterminal event, rather than on the overall time scale of |$t$|, enabling evaluation of the temporal effect of |$X_1$| on its own timescale. Practically, this means that basis functions and knots |$\boldsymbol{\tau}$| must be specified on the corresponding time scale.
5.1. Effect of incident AD and dementia on mortality
To illustrate the AFT framework with a time-varying binary covariate, we perform a secondary analysis of the cohort study to evaluate the association between the onset of AD/dementia and subsequent time to death. We fit models specifying the onset of AD/dementia as a binary time-varying covariate, adjusting for the same time-invariant baseline covariates as in the above analysis (including a constant effect for APOE-|$\epsilon$|4).
For the piecewise linear effect, we set break points at 1, 2, 3, 5, and 10 years after the time of AD onset, and for the spline effect, we set two internal knots at observed quantiles of time from AD onset to death on the log scale. Other settings were as above, though for computation of the acceleration surface described below, we thinned the samples by a factor of 10 to facilitate computation. Table A.1 in Appendix A of the Supplementary material available at Biostatistics online reports estimated model parameters varying baseline survival distribution and effect specification. As before, the estimated baseline covariate coefficients are stable across time-varying effect specifications.
Figures 3(a) and (c) show estimated regression standardized survivor curves under a TBP prior baseline comparing those without AD/dementia onset to those with onset at age 70 and 85, respectively. The curves are identical up until the time of onset, and then once AD/dementia onset occurs mortality increases substantially. The plots indicate similarity between models fit with piecewise and spline effects of AD/dementia onset relative to a constant effect, though the flexible models indicate a small delay in the mortality increase from the time of AD/dementia onset. Corresponding acceleration factors are given in Figures 3(b) and (d), illustrating the trajectory derived in (5.23), where no association exists before the quantile of AD/dementia onset, followed by an increasingly pronounced association after AD/dementia onset.
Plotting acceleration factors for a few AD/dementia onset times of interest may be sufficient in some settings but does not communicate the quantile-varying effect across the entire range of the time-varying covariate. Instead, Figure 4 reports the acceleration factor surface as a contour plot, with the time of AD/dementia onset on the y-axis, the survival quantile on the x-axis, and the color representing the magnitude of the acceleration factor. The two acceleration factor plots in Figure 3 correspond with cross-sections of this surface, by drawing horizontal lines at times 5 and 20 on the y-axis. More generally, looking horizontally across this plot shows the quantile varying acceleration factor corresponding with different times of AD/dementia onset. However, this plot can also be read vertically, to show how the acceleration factor for a particular quantile changes depending on the timing of the time-varying covariate. For example, drawing a vertical line from 0.5 on the x-axis shows the acceleration factor for median survival, varying across times of AD/dementia onset. Therefore, this single plot conveys complex regression effects both as a function of the survival quantile, as well as of the timing of the time-varying covariate.
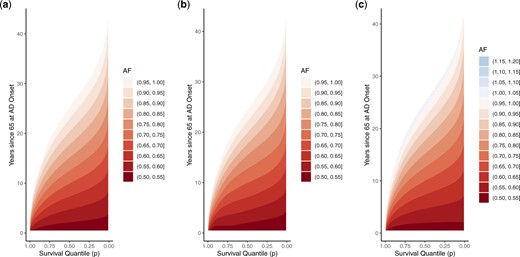
Under a Weibull-centered TBP prior baseline specification, contour plots of regression standardized acceleration factor surface estimates for death following onset of AD/dementia, averaged over other covariates. Time of AD/dementia onset is shown on y-axis, and subsequent survival quantile is shown on x-axis. Color indicates the acceleration factor at the given survival quantile, comparing those with AD/dementia onset at the specified time and those without AD/dementia. Horizontal cross-sections illustrate quantile-varying acceleration factor for AD/dementia onset at a particular time, while vertical cross-sections illustrate acceleration factor at a particular quantile across times of AD/dementia onset. (a) constant effect specification; (b) piecewise linear effect specification; and (c) spline effect specification.
6. Discussion
The AFT model’s specification of multiplicative covariate effects on the quantile scale provides an interpretable and attractive alternative to the standard proportional hazards model. Our proposed extensions to the AFT model enabling quantile-varying acceleration factors, and admitting binary time-varying covariates represent important additions to the standard toolbox for survival analysis. Just as the Cox proportional hazards model benefits from straightforward incorporation of time-varying hazard ratios, the ability to add flexibility to the AFT model regression effects expands the scope of scientific inquiry. Motivated by the study of AD in older adults, we found that the association of the APOE-|$\epsilon4$| gene with AD onset varied substantially across quantiles, with earlier-onset cases accelerated the most and later-onset cases the least.
Moreover, the ability to model, summarize, and communicate the effects of binary time-varying covariates creates new opportunities to examine longitudinal health trajectories. The proposed visualization of these effects as a surface across the covariate timescale and the survival quantiles is particularly valuable, as previous work to incorporate time-varying covariates into AFT models has not focused on communication of effects of time-varying components on the quantile scale (Hanson and others, 2009; Zhou and Hanson, 2018). In our application, this approach illustrated that the association between AD/dementia onset and subsequent mortality varies substantially both across survival quantiles, and depending on the time of AD/dementia onset.
While in principle any increasing choice of |$V$| could be used, our proposed form in (3.11) using an exponential link has the benefit of representing multiplicative effects of the covariates in a direct extension of the AFT model. In theory, one could use other forms of |$V$|, with potentially differing interpretation. For example, one might consider additive forms for |$V$| using monotonically increasing I-splines for the time-varying effect of each covariate, akin to a Generalized Additive Model (Hastie and Tibshirani, 1986). Also, while our focus for clear exposition is on a single quantile-varying effect, in principle additional effects could be specified on other parameters. To address the multiplicity of terms, one might incorporate a prior over the |$\boldsymbol{\alpha}$| parameters that induce shrinkage towards |${\mathbf 0}$|, that is, standard “quantile-invariant” effects.
Finally, our work complements the related literature on censored quantile regression (Portnoy, 2003; Reich and Smith, 2013), which specifies additive effects of covariates on the quantile scale, while our model specifies multiplicative effects on the quantile scale. The biological plausibility or clinical relevance of additive versus multiplicative changes to the survival quantiles depends on the application, so the proposed methodology is a valuable alternative to such methods.
Software
Software in the form of R and Stan code is available at https://github.com/harrisonreeder/aftquantile.
Supplementary material
Supplementary material is available online at http://biostatistics.oxfordjournals.org.
Acknowledgments
We thank the study participants and staff of the Rush Alzheimer’s Disease Center. ROSMAP resources can be requested at https://www.radc.rush.edu.
Conflict of Interest: None declared.
Funding
The Eunice Kennedy Shriver National Institute of Child Health and Human Development (F31HD102159 to H.T.R.); The National Institutes on Aging supported the Religious Orders Study (P30AG010161 and R01AG015819); and the Rush Memory and Aging Project (R01AG017917).


