https://orcid.org/0000-0002-3140-4572
Abstract
Statistical analysis of longitudinal data often involves modeling treatment effects on clinically relevant longitudinal biomarkers since an initial event (the time origin). In some studies including preventive HIV vaccine efficacy trials, some participants have biomarkers measured starting at the time origin, whereas others have biomarkers measured starting later with the time origin unknown. The semiparametric additive time-varying coefficient model is investigated where the effects of some covariates vary nonparametrically with time while the effects of others remain constant. Weighted profile least squares estimators coupled with kernel smoothing are developed. The method uses the expectation maximization approach to deal with the censored time origin. The Kaplan–Meier estimator and other failure time regression models such as the Cox model can be utilized to estimate the distribution and the conditional distribution of left censored event time related to the censored time origin. Asymptotic properties of the parametric and nonparametric estimators and consistent asymptotic variance estimators are derived. A two-stage estimation procedure for choosing weight is proposed to improve estimation efficiency. Numerical simulations are conducted to examine finite sample properties of the proposed estimators. The simulation results show that the theory and methods work well. The efficiency gain of the two-stage estimation procedure depends on the distribution of the longitudinal error processes. The method is applied to analyze data from the Merck 023/HVTN 502 Step HIV vaccine study.
1 Introduction
In preventive HIV vaccine efficacy trials, thousands of HIV uninfected volunteers are randomized to receive vaccine or placebo, and are monitored for HIV infection. Participants diagnosed with HIV infection have various endpoints measured longitudinally starting at the date of diagnosis; these endpoints include viral loads and CD4 cell counts as markers of HIV disease progression and secondary transmission. An objective of such trials is to assess the vaccine effect on the biomarkers, and all previous analyses assessed the biomarkers based on the time from HIV diagnosis (Fitzgerald et al., 2011; Rerks-Ngarm et al., 2013; Janes et al., 2015). However, it is more biologically meaningful to assess whether vaccination modifies the biomarkers over time since actual HIV acquisition. This assessment is challenging because exact times of HIV acquisition are generally unobtainable; rather data are available only on bounds 
and 
between which the true time origin must lie 
, where, as shown in Figure 1, for example, 
is the date of the last antibody (Ab)-based HIV negative diagnostic test result and 
is the date of the first antibody (Ab)-based HIV positive test result. Given details of the HIV testing algorithm described in the application, some participants have 
, at least approximately, such that 
is considered to be directly observed, whereas other participants have 
and 
is unknown. This set-up occurs in other multi-stage longitudinal studies, as depicted in Figure 1.
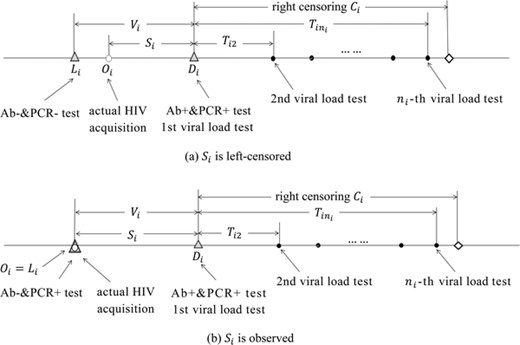
Censored time origin 
in the study of a longitudinal response. Based on the HIV testing algorithm, each infected participant was classified into one of two groups, defined by whether the earliest HIV positive sample was (Ab+, PCR+) or (Ab-, PCR+). (a) For participants with the earliest HIV positive sample (Ab+, PCR+), 
is left censored by 
; (b) For participants with the earliest HIV positive sample (Ab-, PCR+), 
and 
is observed
In Figure 1, for each participant 
, 
is the gap time between the true time origin 
and the time 
when longitudinal markers begin to be measured. The time lapse from 
and 
is 
. For participant i, the longitudinal markers are measured at times 
, where 
is the time between 
and the jth marker measurement, for 
. In the HIV vaccine study, most participants have first measurement time 
at 
; some participants have 
and others have 
. Formally, we write 
and 
such that 
is left censored by 
with censoring indicator 
; 
is observed if 
and 
if 
. The time from 
to the jth sampling time is 
. The time origin is considered censored because 
is left censored.
Semiparametric regression models for longitudinal data have been intensively studied; see Lin and Ying (2001), Hu et al. (2004), Qu and Li (2006), Fan et al. (2007) and Sun et al. (2013), among others. However, to the best of our knowledge, none of these methods address the problem in which the time origin may be censored. In this paper, we study the semiparametric additive model with time-varying effects for longitudinal data with censored time origin. Weighted profile least squares estimators are developed for the unknown parameters as well as for the nonparametric coefficient functions. The expectation maximization approach is utilized to deal with the censored time origin. The proposed method does not assume any specific model for the sampling times, and thus avoids misspecification of the sampling models. The method is applied to investigate the effect of an HIV vaccine on viral load over time since actual HIV acquisition in the Merck 023/HVTN 502 Step study. Asymptotic properties of the parametric and nonparametric estimators and consistent asymptotic variance estimators are derived. Our numerical study shows that the proposed methods work well with satisfying finite sample properties.
The rest of the paper is organized as follows. Section 2 introduces the semiparametric additive model and develops the estimation method. Preliminaries on the data structure and model assumptions are given in Section 2.1. The weighted profile least squares estimators coupled with the kernel smoothing and EM algorithm are developed in Section 2.2. Computational issues about estimation at the boundaries and the weight selection are discussed in Section 2.3. In Section 3, we establish asymptotic properties of the nonparametric and parametric estimators, and in Section 4 study their finite sample performances in simulations. The proposed method is applied to Step trial in Section 5. Concluding remarks are given in Section 6. The proofs of the asymptotic results, additional simulations and data analysis, and the discussions on bandwidth choice are placed in Web Appendices available in the Supporting Information of this article.
2 Profile Weighted Least Squares Estimation through EM Algorithm
2.1 Preliminaries
Suppose that there is a random sample of n participants. For participant i, let 
be the response process and let 
and 
be possibly time-dependent covariates of dimensions 
and 
, respectively, where 
is the time since the actual time origin, and τ is the study duration. We consider the following semiparametric additive time-varying coefficients model
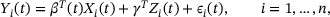
where 
is an unspecified 
vector of smooth regression functions, γ is a 
dimensional vector of parameters, and 
is a mean-zero process. The notation 
represents transpose of a vector or matrix x. Specify the first component of 
as 1 gives a model with a nonparametric baseline response process. The effect of 
is time-varying modeled nonparametrically while the effect of 
is time-independent modeled parametrically.
The observations of 
are taken at time points 
, where 
is the total number of observations from the ith subject. The 
can be written as the sum of two parts 
as shown in Figure 1, where 
is the time from the actual time origin 
participant to left censoring by 
, and 
is the time from the right edge 
of the interval for 
to the jth visit for the ith subject, where visit 1 is at 
. Let 
be the end of follow-up time or censoring time for the ith participant since 
. The censoring time 
is allowed to depend on the covariates 
and 
. The responses for the ith participant can only be observed at the time points before 
since the actual time origin.
The sampling times 
may vary among participants. The number of observations taken from the ith participant by time t is 
, where 
is the indicator function. Let 
be the conditional mean rate of the sampling times for participant i at time t defined by 
, 
. The mean rate function is assumed to only depend on 
, which is the part of the covariates 
that affects the potential sampling times. We denote 
, where 
is an unspecified nonnegative smooth function.
Let 
, 
, 
, 
, 
, 
, 
, where 
is a collection of possible auxiliary variables that are not of interest in the modeling of 
but may be useful in predicting the distribution of 
. For the censored time origin, left-censored data 
and 
are observed. The observed data for participant i can be expressed as 
. The observation is 
if 
and 
if 
, where 
. Although exact times 
may be unobtainable, the values 
, 
and 
at 
are known. Assume that 
are independent identically distributed (iid). The observed data are denoted by 
.
We assume that 
and 
are independent conditional on 
, and that the censoring time 
is noninformative in that 
, 
and 
, 
. Let 
. Assume 
, 
, 
, 
, 
, 
. Assume also that 
and 
are independent conditional on 
, 
, and 
. This assumption implies that, conditional on covariate processes, sampling times are noninformative for the longitudinal response.
2.2 Estimation Procedures
When all 
's are observed, estimation procedure such as in Sun and Wu (2005) and Sun et al. (2013) can be used to analyze model (1). If the unobserved or censored 
's are treated as missing, then 
is not missing at random. The inverse probability weighting of complete-cases method and the augmented inverse probability weighted complete-case method of Robins et al. (1994), which have been successfully adapted in Sun and Gilbert (2012), Sun et al. (2017), Yang et al. (2017) and by many other authors, will not work in this situation. We propose an estimation procedure based on the missing-data principle using the EM-algorithm.
The conditional distribution 
of 
equals 
for 
and 1 for 
. Let 
be the estimated conditional distribution of 
. Let 
. The estimation of model (1) can be based on minimizing the following objective function:
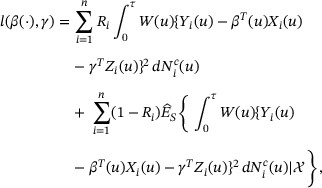
where 
is a nonnegative weight function, and 
is the estimate of the conditional expectation 
, which can be obtained through estimation of 
as we show below.
For ease of presentation, we adopt the notation 
for 
, 
, 
, where 
is a smooth function of 
. The above objective function can be written as
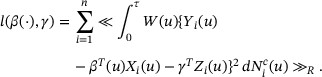
Note that 
, 
and 
are observed. The conditional expectation 
for participant i with 
equals
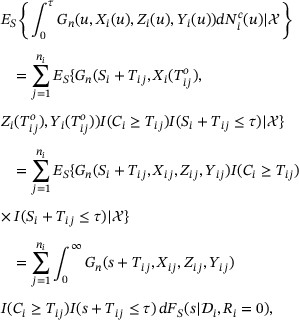
where the last equality holds because 
for 
. Since 
, estimating 
by 
for 
, we have
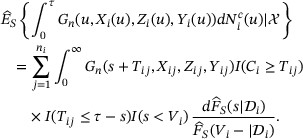
The basic idea of estimating the conditional distribution 
is to transform the data set from left censored to right censored. Assume that 
is bounded by a predetermined constant L. This is reasonable since for the application concerned here 
is less than the time interval between two consecutive testing times that is usually between 3 and 6 months. The distribution of 
based on the left censored data can be estimated by the methods developed for right censored data through the transformation 
. The Kaplan–Meier estimator can be used to estimate distribution of 
when 
is independent of 
. Otherwise, a failure time regression model such as the Cox model can be used to estimate the conditional distribution 
.
Next, we present an estimation procedure that estimates the nonparametric component 
with the kernel smoothing and the parametric component γ with the profile weighted least squares method. Let 
be a symmetric kernel function with compact support. For fixed γ and at time t, we estimate 
by minimizing the following objective function with respect to β:
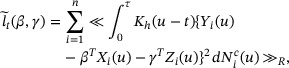
where 
and h is the bandwidth depending on n.
Taking the derivative of 
with respect to β for a fixed γ yields
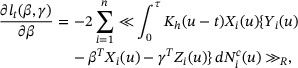
which leads to the following estimating function
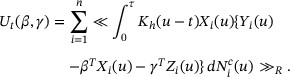
Let 
, and define 
and 
similarly by replacing 
with 
, and 
with 
, respectively. Solving 
for fixed γ and t yields 
, where 
and 
.
Replacing 
by 
in (3) and taking derivative with respect to γ, we obtain the profile estimating function for γ:
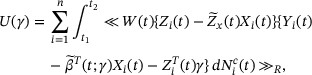
where 
is taken as a subinterval of [0, τ] to avoid boundary problems in the theoretical justifications. In practice, 
can be taken to be very close to [0, τ]. Equation 
can be solved explicitly yielding the weighted profile estimator 
, where
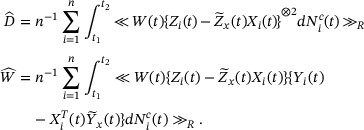
The local profile estimator of 
is given by 
.
2.3 Computational Issues and the Weight Selection
Our estimation procedure uses local smoothing or the local constant method for estimating 
. It is known that the local linear estimation technique, cf. Fan and Gijbels (1996), can improve the performance of estimation at boundaries. For the estimation at the inner points, the local linear and local constant estimators are equivalent, with the same asymptotic distributions. As shown in Fan and Gijbels (1996), the boundary effects from the local constant estimator can be reduced by applying the equivalent kernel of the local linear approach.
Following Fan and Gijbels (1996, sections 2.3.1 and 3.2.2), to reduce the estimation bias for 
at boundary points, for example, 
, we replace 
by the equivalent kernel to the local linear fit modified for the time-varying coefficient model for longitudinal data, defined by 
, where 
. The equivalent kernel 
is a kernel up to a normalizing constant satisfying the finite sample condition 
. This nice feature works to reduce bias for boundary points similar to the symmetrical kernel for interior points. Because it is simple and faster to use the kernel smoothing, we suggest to estimate 
using the equivalent kernel for the boundary time points, while using the standard kernel for the interior time points. Our simulations show that this adjustment works well.
We proposed a weighted profile least squares estimation method coupled with the EM approach for the semiparametric additive time-varying coefficient model for longitudinal data starting from a possibly censored relevant event. The proposed estimators are consistent and asymptotically normal as long as the weight process 
converges in probability to a deterministic function 
. The weight can be selected to improve estimation efficiency, although it is often conveniently taken to be 1. Lin and Carroll (2000) showed that the most efficient estimation of the nonparametric component 
can be achieved by ignoring the within-subject correlation. However, more efficient estimation for the parametric component γ is obtained by using the inverse of true covariance matrix of the longitudinal responses (Lin and Carroll, 2001; Wang et al., 2005). In a simplified situation where the error processes 
are uncorrelated at different times, the optimal weight is inversely proportional to the conditional variance 
of the error process 
(Bickel et al., 1993; Sun et al., 2013; Qi et al., 2017).
We investigated a two-stage estimation procedure for choosing the weight within the framework of the marginal approach that ignores the within-subject correlation. In the first stage, the unit weight function is used to obtain 
and 
. Suppose that 
does not depend on 
, then 
can be consistently estimated by 
≪ 
, where 
is the residual of the first stage estimation. In the second stage, the updated estimators 
and 
are obtained by choosing the weight 
. When 
depends on 
, the optimal weight 
can be estimated using a multivariate kernel estimator (Qi et al., 2017, Web Appendix C). A simulation study is conducted in Section 4.2 to investigate the efficiency of the two-stage estimation procedure.
3 Asymptotic Properties
In this section, we present the asymptotic properties of the proposed estimators. Define 
, 
, and 
, where 
. Let 
and 
. Let γ0 and 
be the true values of γ and 
under model (1), respectively. In addition to the conditional independence assumptions and noninformative censoring assumptions stated in Section 2.1, more regularity conditions are given in Condition A in Web Appendix A.
Ying (1989) showed that the consistency and weak convergence of the Kaplan Meier estimation for the distribution of 
can be extended to the whole line under Condition (A.7). By Lemma 2 presented in Web Appendix B, 
uniformly in 
. Similar asymptotic results hold for 
and 
. It follows that 
and 
converge to 
and 
uniformly in 
, respectively. These results are the basic building blocks for proving the asymptotic results for 
and 
.
Note that 
is the minimizer of 
. In Part (a) of the proof of Theorem 1, we show that 
converges uniformly to a deterministic function of γ that minimizes at 
. The consistency of 
follows by Theorem 5.7 of van der Vaart (1998). By the first-order Taylor expansion of 
at γ0, we have
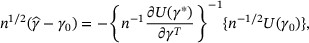
where 
is on the line segment between 
and γ0. To prove the asymptotic normality of 
, it is sufficient to prove that 
converges in probability to a nonsingular matrix, and that 
converges in distribution. The convergence of the information matrix can be obtained by applying Lemma 1 in Web Appendix B. We show in Part (b) of the proof of Theorem 1 that
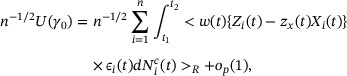
where henceforth we adopt the notation 
.
The asymptotic properties of 
and 
are summarized as Theorems 1 and 2. Theorems 1 and 2 are proved in Web Appendix B assuming that 
and 
are independent conditional on 
and both are independent of 
. Web Appendix C provides an outline of the proofs when the conditional hazard function of 
depends on covariates through the Cox model. This model assumption is for the convenience of theoretical development using the existing large sample results for the Cox model with right censored data (Andersen and Gill, 1982). Web Appendix C also discussed possibility of using other failure time regression models to estimate the conditional distribution of left censored event time.
Theorem 1. Under Condition A, we have
- (a)
as 
; - (b)
as 
, where 
, 
.
The asymptotic variance of 
can be consistently estimated by 
, where
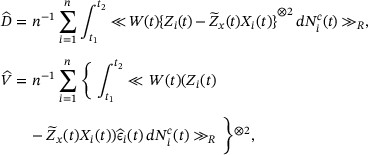
and 
.
Next we present the asymptotic results for 
. First, we introduce a few quantities to be used in the expression of the asymptotic variance of 
. We define 
to be the expected number of sampling points by time t under possibly censored time origin, denoted by 
. Let 
be the natural filtration. Then the intensity 
of 
is given by 
. Hence 
is a 
martingale, with predictable variation process 
.
Theorem 2. Under Condition A, we have
- (a)
converges to 
in probability uniformly in 
as 
; - (b)
For each
, 
as 
, where 
, 
. Here 
, 
.
The covariance matrix of 
can be estimated by 
, where 
. However, consider the approximation
A more refined variance estimation for 
with higher order accuracy can be based on 
, where
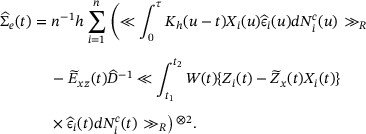
This variance estimator is used in the simulations and in the real data application.
4 Simulation Study
We conduct a numerical study to examine the finite sample performance of the proposed methods. Data are simulated using the following semiparametric additive model 
:
where 
, 
, 
, 
is uniformly distributed on [0,1], and 
is a Bernoulli random variable with 
. The error process 
has a normal distribution with mean 
and variance 1 for participant i where 
follows a standard normal distribution.
For participant i, 
is generated from a uniform distribution on (0,0.8). The left censoring time 
is generated from a uniform distribution on 
with a and b adjusted to yield a desired percentage 
of left censoring for 
. The first sampling point is set as 
, and the rest of the 
's are generated from a Poisson process 
with intensity rate 
, where 
, 
, and 
. Let 
be the responses 
at time points 
following model (16). The right censoring time 
is exponentially distributed with the rate parameter adjusted to give a prespecified percentage 
of right censoring (drop-out or administrative censoring at τ) in the time interval [0, τ], which is the probability of 
. We set 
for the time interval 
. The average number of observations in the interval 
per participant is about 4.7. The Epanechnikov kernel 
, and 
for the estimating function (9). The local constant kernel 
is used for time points in 
while the equivalent kernel to local linear smoothing is applied for the boundary points in 
. For added protection against boundary bias effects, we consider 
as boundary points in the calculation instead of 
.
The performance of the estimator for γ is measured through the bias (Bias), the sample standard error of the estimates (SSE), the estimated standard error of 
(ESE), and the coverage probability (CP) of a 95% confidence interval for γ. The performance of the estimator for the jth component 
on the interval 
is evaluated by the square root of average integrated squared error (RASE) defined by
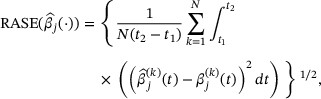
where 
is the kth estimate of 
for 
and N is the number of simulations.
4.1 Simulation Study Using Unit Weight
First, we consider four simulation settings to demonstrate the validity and advantage of the proposed method in handling the censored time origin using unit weight 
. The first three settings show the performances of the proposed estimators with 
, and 50% of left censoring for 
. The fourth setting compares the performances of the proposed estimators with the naive version of the approach that ignores the censored time origin (or 
) by mistreating 
as the measurement times since the actual time origin and 
as the response at 
.
For sample sizes 
, 300, and 500, and bandwidths 
, 0.4, and 0.5, Table 1 shows results based on 500 simulations. The biases of 
are small, and the sample standard errors of 
are close to the estimated standard errors. Both standard errors decrease as the sample size increases, and they decrease with the left censoring percentage 
. The coverage probabilities of 
are close to their 0.95 nominal level. The 
, 
, decrease as sample size increases. The RASEs for 
, 
, also increase as 
increases. The values of SSE and ESE for 
are similar for the three different bandwidth choices. But 
and 
become smaller as bandwidth increases.
Summary statistics for the estimators 
and 
under model (16) with 
left censoring and 30% right censoring. Each entry is based on 500 simulations
 | n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 0% | 200 | 0.3 | 0.0075 | 0.1963 | 0.1886 | 0.938 | 0.3798 | 0.6312 |
| 0.4 | 0.0078 | 0.1958 | 0.1893 | 0.940 | 0.3444 | 0.5742 | ||
| 0.5 | 0.0080 | 0.1952 | 0.1900 | 0.938 | 0.3194 | 0.5370 | ||
| 300 | 0.3 | −0.0030 | 0.1640 | 0.1552 | 0.940 | 0.3076 | 0.5157 | |
| 0.4 | −0.0030 | 0.1637 | 0.1556 | 0.938 | 0.2798 | 0.4688 | ||
| 0.5 | −0.0028 | 0.1636 | 0.1559 | 0.940 | 0.2588 | 0.4359 | ||
| 500 | 0.3 | 0.0002 | 0.1184 | 0.1212 | 0.950 | 0.2370 | 0.4048 | |
| 0.4 | 0.0000 | 0.1181 | 0.1214 | 0.950 | 0.2160 | 0.3738 | ||
| 0.5 | 0.0000 | 0.1181 | 0.1216 | 0.952 | 0.2005 | 0.3571 | ||
| 20% | 200 | 0.3 | 0.0003 | 0.1990 | 0.1891 | 0.930 | 0.3961 | 0.6778 |
| 0.4 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.3559 | 0.6091 | ||
| 0.5 | 0.0005 | 0.1973 | 0.1903 | 0.938 | 0.3295 | 0.5670 | ||
| 300 | 0.3 | −0.0049 | 0.1650 | 0.1554 | 0.926 | 0.3242 | 0.5436 | |
| 0.4 | −0.0048 | 0.1648 | 0.1558 | 0.928 | 0.2928 | 0.4918 | ||
| 0.5 | −0.0046 | 0.1648 | 0.1562 | 0.930 | 0.2713 | 0.4587 | ||
| 500 | 0.3 | 0.0010 | 0.1164 | 0.1212 | 0.958 | 0.2480 | 0.4293 | |
| 0.4 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.2234 | 0.3922 | ||
| 0.5 | 0.0013 | 0.1164 | 0.1217 | 0.960 | 0.2069 | 0.3713 | ||
| 50% | 200 | 0.3 | 0.0013 | 0.2005 | 0.1899 | 0.934 | 0.4474 | 0.7841 |
| 0.4 | 0.0010 | 0.1996 | 0.1911 | 0.936 | 0.3928 | 0.6921 | ||
| 0.5 | 0.0011 | 0.1992 | 0.1917 | 0.936 | 0.3584 | 0.6315 | ||
| 300 | 0.3 | −0.0050 | 0.1663 | 0.1563 | 0.922 | 0.3707 | 0.6415 | |
| 0.4 | −0.0045 | 0.1663 | 0.1571 | 0.926 | 0.3265 | 0.5677 | ||
| 0.5 | −0.0042 | 0.1666 | 0.1575 | 0.926 | 0.2975 | 0.5157 | ||
| 500 | 0.3 | 0.0021 | 0.1170 | 0.1222 | 0.962 | 0.2820 | 0.5166 | |
| 0.4 | 0.0023 | 0.1168 | 0.1226 | 0.964 | 0.2486 | 0.4630 | ||
| 0.5 | 0.0025 | 0.1167 | 0.1228 | 0.960 | 0.2273 | 0.4237 |
| n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 0% | 200 | 0.3 | 0.0075 | 0.1963 | 0.1886 | 0.938 | 0.3798 | 0.6312 |
| 0.4 | 0.0078 | 0.1958 | 0.1893 | 0.940 | 0.3444 | 0.5742 | ||
| 0.5 | 0.0080 | 0.1952 | 0.1900 | 0.938 | 0.3194 | 0.5370 | ||
| 300 | 0.3 | −0.0030 | 0.1640 | 0.1552 | 0.940 | 0.3076 | 0.5157 | |
| 0.4 | −0.0030 | 0.1637 | 0.1556 | 0.938 | 0.2798 | 0.4688 | ||
| 0.5 | −0.0028 | 0.1636 | 0.1559 | 0.940 | 0.2588 | 0.4359 | ||
| 500 | 0.3 | 0.0002 | 0.1184 | 0.1212 | 0.950 | 0.2370 | 0.4048 | |
| 0.4 | 0.0000 | 0.1181 | 0.1214 | 0.950 | 0.2160 | 0.3738 | ||
| 0.5 | 0.0000 | 0.1181 | 0.1216 | 0.952 | 0.2005 | 0.3571 | ||
| 20% | 200 | 0.3 | 0.0003 | 0.1990 | 0.1891 | 0.930 | 0.3961 | 0.6778 |
| 0.4 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.3559 | 0.6091 | ||
| 0.5 | 0.0005 | 0.1973 | 0.1903 | 0.938 | 0.3295 | 0.5670 | ||
| 300 | 0.3 | −0.0049 | 0.1650 | 0.1554 | 0.926 | 0.3242 | 0.5436 | |
| 0.4 | −0.0048 | 0.1648 | 0.1558 | 0.928 | 0.2928 | 0.4918 | ||
| 0.5 | −0.0046 | 0.1648 | 0.1562 | 0.930 | 0.2713 | 0.4587 | ||
| 500 | 0.3 | 0.0010 | 0.1164 | 0.1212 | 0.958 | 0.2480 | 0.4293 | |
| 0.4 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.2234 | 0.3922 | ||
| 0.5 | 0.0013 | 0.1164 | 0.1217 | 0.960 | 0.2069 | 0.3713 | ||
| 50% | 200 | 0.3 | 0.0013 | 0.2005 | 0.1899 | 0.934 | 0.4474 | 0.7841 |
| 0.4 | 0.0010 | 0.1996 | 0.1911 | 0.936 | 0.3928 | 0.6921 | ||
| 0.5 | 0.0011 | 0.1992 | 0.1917 | 0.936 | 0.3584 | 0.6315 | ||
| 300 | 0.3 | −0.0050 | 0.1663 | 0.1563 | 0.922 | 0.3707 | 0.6415 | |
| 0.4 | −0.0045 | 0.1663 | 0.1571 | 0.926 | 0.3265 | 0.5677 | ||
| 0.5 | −0.0042 | 0.1666 | 0.1575 | 0.926 | 0.2975 | 0.5157 | ||
| 500 | 0.3 | 0.0021 | 0.1170 | 0.1222 | 0.962 | 0.2820 | 0.5166 | |
| 0.4 | 0.0023 | 0.1168 | 0.1226 | 0.964 | 0.2486 | 0.4630 | ||
| 0.5 | 0.0025 | 0.1167 | 0.1228 | 0.960 | 0.2273 | 0.4237 |
Summary statistics for the estimators and under model (16) with left censoring and 30% right censoring. Each entry is based on 500 simulations
| n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 0% | 200 | 0.3 | 0.0075 | 0.1963 | 0.1886 | 0.938 | 0.3798 | 0.6312 |
| 0.4 | 0.0078 | 0.1958 | 0.1893 | 0.940 | 0.3444 | 0.5742 | ||
| 0.5 | 0.0080 | 0.1952 | 0.1900 | 0.938 | 0.3194 | 0.5370 | ||
| 300 | 0.3 | −0.0030 | 0.1640 | 0.1552 | 0.940 | 0.3076 | 0.5157 | |
| 0.4 | −0.0030 | 0.1637 | 0.1556 | 0.938 | 0.2798 | 0.4688 | ||
| 0.5 | −0.0028 | 0.1636 | 0.1559 | 0.940 | 0.2588 | 0.4359 | ||
| 500 | 0.3 | 0.0002 | 0.1184 | 0.1212 | 0.950 | 0.2370 | 0.4048 | |
| 0.4 | 0.0000 | 0.1181 | 0.1214 | 0.950 | 0.2160 | 0.3738 | ||
| 0.5 | 0.0000 | 0.1181 | 0.1216 | 0.952 | 0.2005 | 0.3571 | ||
| 20% | 200 | 0.3 | 0.0003 | 0.1990 | 0.1891 | 0.930 | 0.3961 | 0.6778 |
| 0.4 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.3559 | 0.6091 | ||
| 0.5 | 0.0005 | 0.1973 | 0.1903 | 0.938 | 0.3295 | 0.5670 | ||
| 300 | 0.3 | −0.0049 | 0.1650 | 0.1554 | 0.926 | 0.3242 | 0.5436 | |
| 0.4 | −0.0048 | 0.1648 | 0.1558 | 0.928 | 0.2928 | 0.4918 | ||
| 0.5 | −0.0046 | 0.1648 | 0.1562 | 0.930 | 0.2713 | 0.4587 | ||
| 500 | 0.3 | 0.0010 | 0.1164 | 0.1212 | 0.958 | 0.2480 | 0.4293 | |
| 0.4 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.2234 | 0.3922 | ||
| 0.5 | 0.0013 | 0.1164 | 0.1217 | 0.960 | 0.2069 | 0.3713 | ||
| 50% | 200 | 0.3 | 0.0013 | 0.2005 | 0.1899 | 0.934 | 0.4474 | 0.7841 |
| 0.4 | 0.0010 | 0.1996 | 0.1911 | 0.936 | 0.3928 | 0.6921 | ||
| 0.5 | 0.0011 | 0.1992 | 0.1917 | 0.936 | 0.3584 | 0.6315 | ||
| 300 | 0.3 | −0.0050 | 0.1663 | 0.1563 | 0.922 | 0.3707 | 0.6415 | |
| 0.4 | −0.0045 | 0.1663 | 0.1571 | 0.926 | 0.3265 | 0.5677 | ||
| 0.5 | −0.0042 | 0.1666 | 0.1575 | 0.926 | 0.2975 | 0.5157 | ||
| 500 | 0.3 | 0.0021 | 0.1170 | 0.1222 | 0.962 | 0.2820 | 0.5166 | |
| 0.4 | 0.0023 | 0.1168 | 0.1226 | 0.964 | 0.2486 | 0.4630 | ||
| 0.5 | 0.0025 | 0.1167 | 0.1228 | 0.960 | 0.2273 | 0.4237 |
| n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 0% | 200 | 0.3 | 0.0075 | 0.1963 | 0.1886 | 0.938 | 0.3798 | 0.6312 |
| 0.4 | 0.0078 | 0.1958 | 0.1893 | 0.940 | 0.3444 | 0.5742 | ||
| 0.5 | 0.0080 | 0.1952 | 0.1900 | 0.938 | 0.3194 | 0.5370 | ||
| 300 | 0.3 | −0.0030 | 0.1640 | 0.1552 | 0.940 | 0.3076 | 0.5157 | |
| 0.4 | −0.0030 | 0.1637 | 0.1556 | 0.938 | 0.2798 | 0.4688 | ||
| 0.5 | −0.0028 | 0.1636 | 0.1559 | 0.940 | 0.2588 | 0.4359 | ||
| 500 | 0.3 | 0.0002 | 0.1184 | 0.1212 | 0.950 | 0.2370 | 0.4048 | |
| 0.4 | 0.0000 | 0.1181 | 0.1214 | 0.950 | 0.2160 | 0.3738 | ||
| 0.5 | 0.0000 | 0.1181 | 0.1216 | 0.952 | 0.2005 | 0.3571 | ||
| 20% | 200 | 0.3 | 0.0003 | 0.1990 | 0.1891 | 0.930 | 0.3961 | 0.6778 |
| 0.4 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.3559 | 0.6091 | ||
| 0.5 | 0.0005 | 0.1973 | 0.1903 | 0.938 | 0.3295 | 0.5670 | ||
| 300 | 0.3 | −0.0049 | 0.1650 | 0.1554 | 0.926 | 0.3242 | 0.5436 | |
| 0.4 | −0.0048 | 0.1648 | 0.1558 | 0.928 | 0.2928 | 0.4918 | ||
| 0.5 | −0.0046 | 0.1648 | 0.1562 | 0.930 | 0.2713 | 0.4587 | ||
| 500 | 0.3 | 0.0010 | 0.1164 | 0.1212 | 0.958 | 0.2480 | 0.4293 | |
| 0.4 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.2234 | 0.3922 | ||
| 0.5 | 0.0013 | 0.1164 | 0.1217 | 0.960 | 0.2069 | 0.3713 | ||
| 50% | 200 | 0.3 | 0.0013 | 0.2005 | 0.1899 | 0.934 | 0.4474 | 0.7841 |
| 0.4 | 0.0010 | 0.1996 | 0.1911 | 0.936 | 0.3928 | 0.6921 | ||
| 0.5 | 0.0011 | 0.1992 | 0.1917 | 0.936 | 0.3584 | 0.6315 | ||
| 300 | 0.3 | −0.0050 | 0.1663 | 0.1563 | 0.922 | 0.3707 | 0.6415 | |
| 0.4 | −0.0045 | 0.1663 | 0.1571 | 0.926 | 0.3265 | 0.5677 | ||
| 0.5 | −0.0042 | 0.1666 | 0.1575 | 0.926 | 0.2975 | 0.5157 | ||
| 500 | 0.3 | 0.0021 | 0.1170 | 0.1222 | 0.962 | 0.2820 | 0.5166 | |
| 0.4 | 0.0023 | 0.1168 | 0.1226 | 0.964 | 0.2486 | 0.4630 | ||
| 0.5 | 0.0025 | 0.1167 | 0.1228 | 0.960 | 0.2273 | 0.4237 |
Table 2 presents results for estimation of γ and 
with the approach that ignores the censored time origin. It shows that 
, 
, increase dramatically compared to the corresponding results of the proposed estimators in Table 1 that account for the censored time origin. Table 2 also shows that there is little bias in the estimation of the constant effect γ when the censored time origin issue is ignored. Table 3 gives a side-by-side comparison of the proposed estimator for 
versus the approach that misplaces the time origin under 50% left censoring in the presence (
) and absence (
) of right censoring.
Summary statistics of estimation of γ and 
under model (16) with misplaced time origin under 50% left censoring and 30% right censoring. Each entry is based on 500 simulations
 | n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 50% | 200 | 0.3 | −0.0001 | 0.2341 | 0.2231 | 0.932 | 0.5742 | 1.5619 |
| 0.4 | −0.0007 | 0.2339 | 0.2240 | 0.934 | 0.5477 | 1.5296 | ||
| 0.5 | −0.0009 | 0.2336 | 0.2246 | 0.936 | 0.5265 | 1.4946 | ||
| 300 | 0.3 | −0.0055 | 0.2015 | 0.1847 | 0.920 | 0.5355 | 1.5214 | |
| 0.4 | −0.0056 | 0.2014 | 0.1853 | 0.926 | 0.5171 | 1.4991 | ||
| 0.5 | −0.0058 | 0.2018 | 0.1856 | 0.924 | 0.5007 | 1.4689 | ||
| 500 | 0.3 | −0.0013 | 0.1469 | 0.1444 | 0.936 | 0.4809 | 1.4537 | |
| 0.4 | −0.0013 | 0.1467 | 0.1446 | 0.934 | 0.4695 | 1.4396 | ||
| 0.5 | −0.0014 | 0.1465 | 0.1448 | 0.940 | 0.4579 | 1.4168 |
| n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 50% | 200 | 0.3 | −0.0001 | 0.2341 | 0.2231 | 0.932 | 0.5742 | 1.5619 |
| 0.4 | −0.0007 | 0.2339 | 0.2240 | 0.934 | 0.5477 | 1.5296 | ||
| 0.5 | −0.0009 | 0.2336 | 0.2246 | 0.936 | 0.5265 | 1.4946 | ||
| 300 | 0.3 | −0.0055 | 0.2015 | 0.1847 | 0.920 | 0.5355 | 1.5214 | |
| 0.4 | −0.0056 | 0.2014 | 0.1853 | 0.926 | 0.5171 | 1.4991 | ||
| 0.5 | −0.0058 | 0.2018 | 0.1856 | 0.924 | 0.5007 | 1.4689 | ||
| 500 | 0.3 | −0.0013 | 0.1469 | 0.1444 | 0.936 | 0.4809 | 1.4537 | |
| 0.4 | −0.0013 | 0.1467 | 0.1446 | 0.934 | 0.4695 | 1.4396 | ||
| 0.5 | −0.0014 | 0.1465 | 0.1448 | 0.940 | 0.4579 | 1.4168 |
Summary statistics of estimation of γ and under model (16) with misplaced time origin under 50% left censoring and 30% right censoring. Each entry is based on 500 simulations
| n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 50% | 200 | 0.3 | −0.0001 | 0.2341 | 0.2231 | 0.932 | 0.5742 | 1.5619 |
| 0.4 | −0.0007 | 0.2339 | 0.2240 | 0.934 | 0.5477 | 1.5296 | ||
| 0.5 | −0.0009 | 0.2336 | 0.2246 | 0.936 | 0.5265 | 1.4946 | ||
| 300 | 0.3 | −0.0055 | 0.2015 | 0.1847 | 0.920 | 0.5355 | 1.5214 | |
| 0.4 | −0.0056 | 0.2014 | 0.1853 | 0.926 | 0.5171 | 1.4991 | ||
| 0.5 | −0.0058 | 0.2018 | 0.1856 | 0.924 | 0.5007 | 1.4689 | ||
| 500 | 0.3 | −0.0013 | 0.1469 | 0.1444 | 0.936 | 0.4809 | 1.4537 | |
| 0.4 | −0.0013 | 0.1467 | 0.1446 | 0.934 | 0.4695 | 1.4396 | ||
| 0.5 | −0.0014 | 0.1465 | 0.1448 | 0.940 | 0.4579 | 1.4168 |
| n | h | Bias | SSE | ESE | CP | RASE | RASE |
|---|---|---|---|---|---|---|---|---|
| 50% | 200 | 0.3 | −0.0001 | 0.2341 | 0.2231 | 0.932 | 0.5742 | 1.5619 |
| 0.4 | −0.0007 | 0.2339 | 0.2240 | 0.934 | 0.5477 | 1.5296 | ||
| 0.5 | −0.0009 | 0.2336 | 0.2246 | 0.936 | 0.5265 | 1.4946 | ||
| 300 | 0.3 | −0.0055 | 0.2015 | 0.1847 | 0.920 | 0.5355 | 1.5214 | |
| 0.4 | −0.0056 | 0.2014 | 0.1853 | 0.926 | 0.5171 | 1.4991 | ||
| 0.5 | −0.0058 | 0.2018 | 0.1856 | 0.924 | 0.5007 | 1.4689 | ||
| 500 | 0.3 | −0.0013 | 0.1469 | 0.1444 | 0.936 | 0.4809 | 1.4537 | |
| 0.4 | −0.0013 | 0.1467 | 0.1446 | 0.934 | 0.4695 | 1.4396 | ||
| 0.5 | −0.0014 | 0.1465 | 0.1448 | 0.940 | 0.4579 | 1.4168 |
Side-by-side comparison of the proposed estimator for 
under model (16) with the approach that misplaces the time origin under 50% left censoring and 
right censoring. Each entry is based on 500 simulations
RASE( ) | RASE( ) | |||||
|---|---|---|---|---|---|---|
| Proposed | Misplaced | Proposed | Misplaced | |||
 | n | h | method | origin | method | origin |
| 0% | 200 | 0.3 | 0.4078 | 0.5410 | 0.7111 | 1.5325 |
| 0.4 | 0.3557 | 0.5207 | 0.6246 | 1.5081 | ||
| 0.5 | 0.3231 | 0.5033 | 0.5683 | 1.4757 | ||
| 300 | 0.3 | 0.3302 | 0.5084 | 0.5762 | 1.4941 | |
| 0.4 | 0.2903 | 0.4951 | 0.5100 | 1.4791 | ||
| 0.5 | 0.2654 | 0.4818 | 0.4650 | 1.4528 | ||
| 500 | 0.3 | 0.2528 | 0.4686 | 0.4642 | 1.4379 | |
| 0.4 | 0.2230 | 0.4605 | 0.4170 | 1.4294 | ||
| 0.5 | 0.2042 | 0.4505 | 0.3829 | 1.4094 | ||
| 30% | 200 | 0.3 | 0.4474 | 0.5742 | 0.7841 | 1.5619 |
| 0.4 | 0.3928 | 0.5477 | 0.6921 | 1.5296 | ||
| 0.5 | 0.3584 | 0.5265 | 0.6315 | 1.4946 | ||
| 300 | 0.3 | 0.3707 | 0.5355 | 0.6415 | 1.5214 | |
| 0.4 | 0.3265 | 0.5171 | 0.5677 | 1.4991 | ||
| 0.5 | 0.2975 | 0.5007 | 0.5157 | 1.4689 | ||
| 500 | 0.3 | 0.2820 | 0.4809 | 0.5166 | 1.4537 | |
| 0.4 | 0.2486 | 0.4695 | 0.4630 | 1.4396 | ||
| 0.5 | 0.2273 | 0.4579 | 0.4237 | 1.4168 | ||
| RASE() | RASE() | |||||
|---|---|---|---|---|---|---|
| Proposed | Misplaced | Proposed | Misplaced | |||
| n | h | method | origin | method | origin |
| 0% | 200 | 0.3 | 0.4078 | 0.5410 | 0.7111 | 1.5325 |
| 0.4 | 0.3557 | 0.5207 | 0.6246 | 1.5081 | ||
| 0.5 | 0.3231 | 0.5033 | 0.5683 | 1.4757 | ||
| 300 | 0.3 | 0.3302 | 0.5084 | 0.5762 | 1.4941 | |
| 0.4 | 0.2903 | 0.4951 | 0.5100 | 1.4791 | ||
| 0.5 | 0.2654 | 0.4818 | 0.4650 | 1.4528 | ||
| 500 | 0.3 | 0.2528 | 0.4686 | 0.4642 | 1.4379 | |
| 0.4 | 0.2230 | 0.4605 | 0.4170 | 1.4294 | ||
| 0.5 | 0.2042 | 0.4505 | 0.3829 | 1.4094 | ||
| 30% | 200 | 0.3 | 0.4474 | 0.5742 | 0.7841 | 1.5619 |
| 0.4 | 0.3928 | 0.5477 | 0.6921 | 1.5296 | ||
| 0.5 | 0.3584 | 0.5265 | 0.6315 | 1.4946 | ||
| 300 | 0.3 | 0.3707 | 0.5355 | 0.6415 | 1.5214 | |
| 0.4 | 0.3265 | 0.5171 | 0.5677 | 1.4991 | ||
| 0.5 | 0.2975 | 0.5007 | 0.5157 | 1.4689 | ||
| 500 | 0.3 | 0.2820 | 0.4809 | 0.5166 | 1.4537 | |
| 0.4 | 0.2486 | 0.4695 | 0.4630 | 1.4396 | ||
| 0.5 | 0.2273 | 0.4579 | 0.4237 | 1.4168 | ||
Side-by-side comparison of the proposed estimator for under model (16) with the approach that misplaces the time origin under 50% left censoring and right censoring. Each entry is based on 500 simulations
| RASE() | RASE() | |||||
|---|---|---|---|---|---|---|
| Proposed | Misplaced | Proposed | Misplaced | |||
| n | h | method | origin | method | origin |
| 0% | 200 | 0.3 | 0.4078 | 0.5410 | 0.7111 | 1.5325 |
| 0.4 | 0.3557 | 0.5207 | 0.6246 | 1.5081 | ||
| 0.5 | 0.3231 | 0.5033 | 0.5683 | 1.4757 | ||
| 300 | 0.3 | 0.3302 | 0.5084 | 0.5762 | 1.4941 | |
| 0.4 | 0.2903 | 0.4951 | 0.5100 | 1.4791 | ||
| 0.5 | 0.2654 | 0.4818 | 0.4650 | 1.4528 | ||
| 500 | 0.3 | 0.2528 | 0.4686 | 0.4642 | 1.4379 | |
| 0.4 | 0.2230 | 0.4605 | 0.4170 | 1.4294 | ||
| 0.5 | 0.2042 | 0.4505 | 0.3829 | 1.4094 | ||
| 30% | 200 | 0.3 | 0.4474 | 0.5742 | 0.7841 | 1.5619 |
| 0.4 | 0.3928 | 0.5477 | 0.6921 | 1.5296 | ||
| 0.5 | 0.3584 | 0.5265 | 0.6315 | 1.4946 | ||
| 300 | 0.3 | 0.3707 | 0.5355 | 0.6415 | 1.5214 | |
| 0.4 | 0.3265 | 0.5171 | 0.5677 | 1.4991 | ||
| 0.5 | 0.2975 | 0.5007 | 0.5157 | 1.4689 | ||
| 500 | 0.3 | 0.2820 | 0.4809 | 0.5166 | 1.4537 | |
| 0.4 | 0.2486 | 0.4695 | 0.4630 | 1.4396 | ||
| 0.5 | 0.2273 | 0.4579 | 0.4237 | 1.4168 | ||
| RASE() | RASE() | |||||
|---|---|---|---|---|---|---|
| Proposed | Misplaced | Proposed | Misplaced | |||
| n | h | method | origin | method | origin |
| 0% | 200 | 0.3 | 0.4078 | 0.5410 | 0.7111 | 1.5325 |
| 0.4 | 0.3557 | 0.5207 | 0.6246 | 1.5081 | ||
| 0.5 | 0.3231 | 0.5033 | 0.5683 | 1.4757 | ||
| 300 | 0.3 | 0.3302 | 0.5084 | 0.5762 | 1.4941 | |
| 0.4 | 0.2903 | 0.4951 | 0.5100 | 1.4791 | ||
| 0.5 | 0.2654 | 0.4818 | 0.4650 | 1.4528 | ||
| 500 | 0.3 | 0.2528 | 0.4686 | 0.4642 | 1.4379 | |
| 0.4 | 0.2230 | 0.4605 | 0.4170 | 1.4294 | ||
| 0.5 | 0.2042 | 0.4505 | 0.3829 | 1.4094 | ||
| 30% | 200 | 0.3 | 0.4474 | 0.5742 | 0.7841 | 1.5619 |
| 0.4 | 0.3928 | 0.5477 | 0.6921 | 1.5296 | ||
| 0.5 | 0.3584 | 0.5265 | 0.6315 | 1.4946 | ||
| 300 | 0.3 | 0.3707 | 0.5355 | 0.6415 | 1.5214 | |
| 0.4 | 0.3265 | 0.5171 | 0.5677 | 1.4991 | ||
| 0.5 | 0.2975 | 0.5007 | 0.5157 | 1.4689 | ||
| 500 | 0.3 | 0.2820 | 0.4809 | 0.5166 | 1.4537 | |
| 0.4 | 0.2486 | 0.4695 | 0.4630 | 1.4396 | ||
| 0.5 | 0.2273 | 0.4579 | 0.4237 | 1.4168 | ||
Figure 2 shows the average estimates of 
based on 500 simulations under the four simulation settings described above. Figure 2(a)–(c) plots average estimates based on the proposed method corresponding to 0%, 20%, and 50% left censoring for 
, and Figure 2(d) corresponds to the fourth case. Figure 2(a)–(c) shows that the biases are small, thus the estimated curves fit the true curve quite well. In contrast, there are large biases and an obvious time shift in the estimated covariate effect for 
in Figure 2(d).
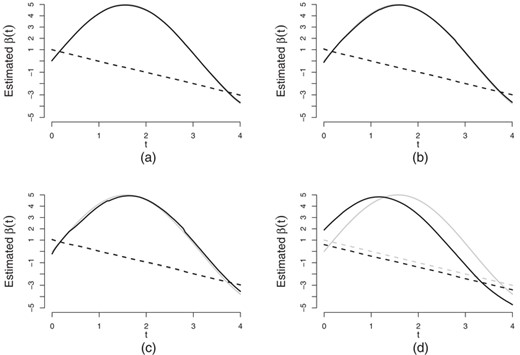
Averages of the estimates for 
and 
for 
, 
and 30% right censoring based on 500 simulations. The solid black lines are for 
and the dashed black lines are for 
. (a)–(c) The biases in the cases of 0%, 20%, and 50% left censoring rate of 
, respectively. (d) The results in the case of misplaced time origin by ignoring 
Figure 3 shows standard errors of 
and 
based on 500 simulations under the four simulation settings. Figure 3(a)–(d) plots results under the four simulation settings. In all four plots, the sample standard error curves are quite close to the estimated standard error curve. In the first three cases, large variations for time near zero are typical for the local linear approach near the boundaries; see page 73 of Fan and Gijbels (1996). The fourth case in Figure 3(d) does not have large variation near zero as the new time zero is shifted from a time point that is of duration 
after the actual time origin for ith subject, 
.
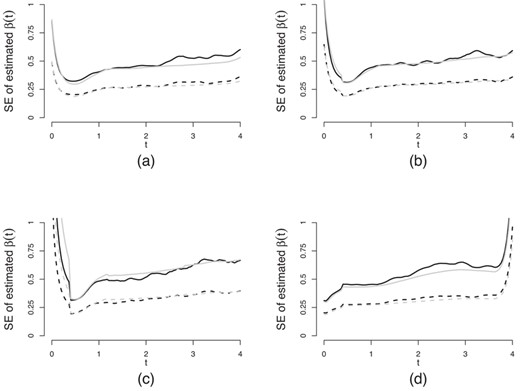
Sample and estimated standard errors of the estimates for 
and 
for 
, 
and 30% right censoring based on 500 simulations. The solid lines are for 
and the dashed lines are for 
. The gray lines are the estimated standard error and the black ones are the sample standard error. (a)–(c) The results in the cases of 0%, 20%, and 50% left censoring rate of 
, respectively. (d) The results in the case of misplaced time origin by ignoring 
Figure 4 shows the coverage probabilities of 95% pointwise confidence intervals for 
and 
for 
based on 500 simulations under the four simulation settings. Figure 4(a)–(c) shows that the proposed estimators have accurate coverage probabilities close to the 0.95 nominal level except for time near zero, while Figure 4(d) shows very poor coverage probabilities for both 
and 
for the approach that ignores the censored time origin.
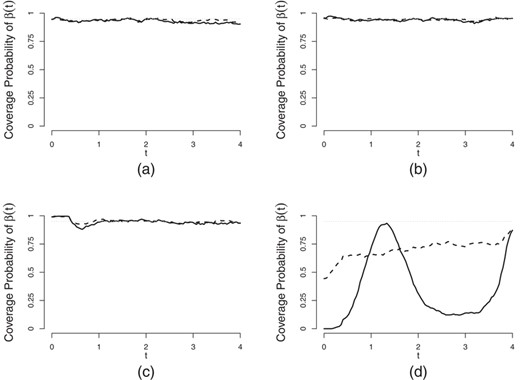
Coverage probabilities of 95% pointwise confidence intervals for 
and 
for 
, 
and 30% right censoring based on 500 simulations. The solid lines are the coverage probabilities for 
and the dashed lines are for 
. (a)–(c) The coverage probabilities of 95% pointwise confidence intervals in the cases of 0%, 20% and 50% left censoring rate of 
, respectively. (d) The results in the case of misplaced time origin by ignoring 
An additional simulation study is conducted in Web Appendix D when the conditional hazard function of 
depends on the baseline covariates through the Cox model. The simulation results presented in Web Tables 1–3 and Web Figures 1–3 show that the theory and methods work well for the Cox model.
4.2 Simulation Study Using the Estimated Weight
A simulation study is conducted to evaluate the efficiency gain of the two-stage estimation procedure. We consider four different error models for 
. In Error Model I, 
is a normal distribution with mean 
and variance 1 conditional on the ith subject, and 
is N(0, 1). In Error Model II, 
has a normal distribution with mean 
and variance of 
conditional on the ith subject, and 
is N(0, 0.52). Error Model III is same as for Error Model II except for 
from N(0, 0.32). In Error Model IV, 
is a Gaussian process with mean 0 and variance 
, and 
and 
are independent for 
. Errors 
and 
for 
are dependent under both Error Models I, II, and III, but independent under Error Models IV. Variance 
of error 
is time-varying under Error Models II–IV, but constant under Error Models I. The second-stage estimator is obtained by using the estimated weight 
where 
is given in Section 2.3.
Define the empirical relative efficiency (Eff) of the weighted estimator 
to 
as 
. The efficiency gain depends on the distribution of error process 
. Table 4 shows the simulation results on performance of the second-stage estimator and its empirical relative efficiency. Overall empirical relative efficiency varies in the range of 1 and 1.35. The amount of the efficiency gain is not observed when variance of 
is constant. The second-stage estimator is most efficient when errors 
at different time points are not correlated. The efficiency gain is less obvious when errors 
are correlated. The simulation study also shows that there is no clear efficiency gain of 
over 
for all error models.
The empirical relative efficiency Eff(γ) of the two-stage estimator using the estimated weight to the estimator using unit weight under model (16) with 20% left censoring and 30% right censoring, n = 200, 300, 500 and 
. Each entry is based on 500 simulations
| Unit Weight | Estimated Weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | Bias | SSE | ESE | CP | Bias | SSE | ESE | CP | Eff(γ) |
| Error Model I | |||||||||
| 200 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.0006 | 0.1984 | 0.1875 | 0.932 | 0.9972 |
| 300 | −0.0048 | 0.1648 | 0.1558 | 0.928 | −0.0050 | 0.1650 | 0.1545 | 0.928 | 0.9988 |
| 500 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.0012 | 0.1162 | 0.1208 | 0.960 | 1.0017 |
| Error Model II | |||||||||
| 200 | 0.0001 | 0.1282 | 0.1263 | 0.952 | 0.0006 | 0.1197 | 0.1143 | 0.940 | 1.0707 |
| 300 | −0.0041 | 0.1070 | 0.1035 | 0.940 | −0.0021 | 0.0992 | 0.0939 | 0.928 | 1.0789 |
| 500 | 0.0000 | 0.0774 | 0.0803 | 0.954 | 0.0009 | 0.0706 | 0.0733 | 0.964 | 1.0959 |
| Error Model III | |||||||||
| 200 | −0.0007 | 0.1066 | 0.1071 | 0.958 | 0.0000 | 0.0918 | 0.0896 | 0.956 | 1.1612 |
| 300 | −0.0036 | 0.0901 | 0.0876 | 0.940 | −0.0013 | 0.0773 | 0.0732 | 0.924 | 1.1665 |
| 500 | −0.0003 | 0.0658 | 0.0679 | 0.956 | 0.0007 | 0.0550 | 0.0570 | 0.964 | 1.1970 |
| Error Model IV | |||||||||
| 200 | −0.0018 | 0.0929 | 0.0954 | 0.954 | −0.0009 | 0.0709 | 0.0715 | 0.950 | 1.3100 |
| 300 | −0.0028 | 0.0794 | 0.0779 | 0.948 | −0.0006 | 0.0602 | 0.0580 | 0.932 | 1.3187 |
| 500 | −0.0009 | 0.0597 | 0.0603 | 0.950 | 0.0003 | 0.0443 | 0.0451 | 0.958 | 1.3481 |
| Unit Weight | Estimated Weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | Bias | SSE | ESE | CP | Bias | SSE | ESE | CP | Eff(γ) |
| Error Model I | |||||||||
| 200 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.0006 | 0.1984 | 0.1875 | 0.932 | 0.9972 |
| 300 | −0.0048 | 0.1648 | 0.1558 | 0.928 | −0.0050 | 0.1650 | 0.1545 | 0.928 | 0.9988 |
| 500 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.0012 | 0.1162 | 0.1208 | 0.960 | 1.0017 |
| Error Model II | |||||||||
| 200 | 0.0001 | 0.1282 | 0.1263 | 0.952 | 0.0006 | 0.1197 | 0.1143 | 0.940 | 1.0707 |
| 300 | −0.0041 | 0.1070 | 0.1035 | 0.940 | −0.0021 | 0.0992 | 0.0939 | 0.928 | 1.0789 |
| 500 | 0.0000 | 0.0774 | 0.0803 | 0.954 | 0.0009 | 0.0706 | 0.0733 | 0.964 | 1.0959 |
| Error Model III | |||||||||
| 200 | −0.0007 | 0.1066 | 0.1071 | 0.958 | 0.0000 | 0.0918 | 0.0896 | 0.956 | 1.1612 |
| 300 | −0.0036 | 0.0901 | 0.0876 | 0.940 | −0.0013 | 0.0773 | 0.0732 | 0.924 | 1.1665 |
| 500 | −0.0003 | 0.0658 | 0.0679 | 0.956 | 0.0007 | 0.0550 | 0.0570 | 0.964 | 1.1970 |
| Error Model IV | |||||||||
| 200 | −0.0018 | 0.0929 | 0.0954 | 0.954 | −0.0009 | 0.0709 | 0.0715 | 0.950 | 1.3100 |
| 300 | −0.0028 | 0.0794 | 0.0779 | 0.948 | −0.0006 | 0.0602 | 0.0580 | 0.932 | 1.3187 |
| 500 | −0.0009 | 0.0597 | 0.0603 | 0.950 | 0.0003 | 0.0443 | 0.0451 | 0.958 | 1.3481 |
The empirical relative efficiency Eff(γ) of the two-stage estimator using the estimated weight to the estimator using unit weight under model (16) with 20% left censoring and 30% right censoring, n = 200, 300, 500 and . Each entry is based on 500 simulations
| Unit Weight | Estimated Weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | Bias | SSE | ESE | CP | Bias | SSE | ESE | CP | Eff(γ) |
| Error Model I | |||||||||
| 200 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.0006 | 0.1984 | 0.1875 | 0.932 | 0.9972 |
| 300 | −0.0048 | 0.1648 | 0.1558 | 0.928 | −0.0050 | 0.1650 | 0.1545 | 0.928 | 0.9988 |
| 500 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.0012 | 0.1162 | 0.1208 | 0.960 | 1.0017 |
| Error Model II | |||||||||
| 200 | 0.0001 | 0.1282 | 0.1263 | 0.952 | 0.0006 | 0.1197 | 0.1143 | 0.940 | 1.0707 |
| 300 | −0.0041 | 0.1070 | 0.1035 | 0.940 | −0.0021 | 0.0992 | 0.0939 | 0.928 | 1.0789 |
| 500 | 0.0000 | 0.0774 | 0.0803 | 0.954 | 0.0009 | 0.0706 | 0.0733 | 0.964 | 1.0959 |
| Error Model III | |||||||||
| 200 | −0.0007 | 0.1066 | 0.1071 | 0.958 | 0.0000 | 0.0918 | 0.0896 | 0.956 | 1.1612 |
| 300 | −0.0036 | 0.0901 | 0.0876 | 0.940 | −0.0013 | 0.0773 | 0.0732 | 0.924 | 1.1665 |
| 500 | −0.0003 | 0.0658 | 0.0679 | 0.956 | 0.0007 | 0.0550 | 0.0570 | 0.964 | 1.1970 |
| Error Model IV | |||||||||
| 200 | −0.0018 | 0.0929 | 0.0954 | 0.954 | −0.0009 | 0.0709 | 0.0715 | 0.950 | 1.3100 |
| 300 | −0.0028 | 0.0794 | 0.0779 | 0.948 | −0.0006 | 0.0602 | 0.0580 | 0.932 | 1.3187 |
| 500 | −0.0009 | 0.0597 | 0.0603 | 0.950 | 0.0003 | 0.0443 | 0.0451 | 0.958 | 1.3481 |
| Unit Weight | Estimated Weight | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| n | Bias | SSE | ESE | CP | Bias | SSE | ESE | CP | Eff(γ) |
| Error Model I | |||||||||
| 200 | 0.0005 | 0.1979 | 0.1899 | 0.932 | 0.0006 | 0.1984 | 0.1875 | 0.932 | 0.9972 |
| 300 | −0.0048 | 0.1648 | 0.1558 | 0.928 | −0.0050 | 0.1650 | 0.1545 | 0.928 | 0.9988 |
| 500 | 0.0013 | 0.1164 | 0.1215 | 0.960 | 0.0012 | 0.1162 | 0.1208 | 0.960 | 1.0017 |
| Error Model II | |||||||||
| 200 | 0.0001 | 0.1282 | 0.1263 | 0.952 | 0.0006 | 0.1197 | 0.1143 | 0.940 | 1.0707 |
| 300 | −0.0041 | 0.1070 | 0.1035 | 0.940 | −0.0021 | 0.0992 | 0.0939 | 0.928 | 1.0789 |
| 500 | 0.0000 | 0.0774 | 0.0803 | 0.954 | 0.0009 | 0.0706 | 0.0733 | 0.964 | 1.0959 |
| Error Model III | |||||||||
| 200 | −0.0007 | 0.1066 | 0.1071 | 0.958 | 0.0000 | 0.0918 | 0.0896 | 0.956 | 1.1612 |
| 300 | −0.0036 | 0.0901 | 0.0876 | 0.940 | −0.0013 | 0.0773 | 0.0732 | 0.924 | 1.1665 |
| 500 | −0.0003 | 0.0658 | 0.0679 | 0.956 | 0.0007 | 0.0550 | 0.0570 | 0.964 | 1.1970 |
| Error Model IV | |||||||||
| 200 | −0.0018 | 0.0929 | 0.0954 | 0.954 | −0.0009 | 0.0709 | 0.0715 | 0.950 | 1.3100 |
| 300 | −0.0028 | 0.0794 | 0.0779 | 0.948 | −0.0006 | 0.0602 | 0.0580 | 0.932 | 1.3187 |
| 500 | −0.0009 | 0.0597 | 0.0603 | 0.950 | 0.0003 | 0.0443 | 0.0451 | 0.958 | 1.3481 |
5 Analysis of Step Study
Step study was a multicenter, double-blind, randomized, placebo-controlled preventive HIV vaccine efficacy trial conducted in North America, the Caribbean, South America, and Australia from 2004 to 2009 (Buchbinder et al., 2008; Fitzgerald et al., 2011; Duerr et al., 2012). A co-primary objective of the study was to determine whether the MRKAd5 HIV gag/pol/nef vaccine, which elicits T cell immune responses to HIV proteins through delivery of the gag, pol, and nef HIV genes to the immune system by the adenovirus type 5 (Ad5) common cold vector, is capable of controlling HIV replication among participants who acquired HIV infection after vaccination. Three thousand HIV-1 negative participants at high risk of HIV infection and with ages between 18 and 45 were enrolled and randomly assigned to receive vaccine or placebo in 1:1 allocation, stratified by sex, study site, and anti-Ad5 neutralizing antibody titer at baseline.
Of the 3000 participants, 174 acquired HIV infection during the trial, 159 of which were male and 15 female. As females comprised only <10% of the sample, we analyze the males only. Study participants received antibody (Ab)-based HIV diagnostic ELISA tests at periodic study visits at Weeks 12, 52, and every six months thereafter through 5 years. Participants with a positive ELISA test had HIV infection confirmed by an antigen-based HIV-specific RNA PCR test. Moreover, for all confirmed HIV infected participants, a “look-back” procedure was applied wherein all earlier available blood samples going back in time were tested for HIV infection using the more sensitive RNA PCR test. The antibody tests used in Step have near-perfect sensitivity to detect HIV infections starting 4 weeks after HIV acquisition, but miss HIV infections before that, whereas the RNA PCR tests have near-perfect sensitivity starting about a week after HIV acquisition. Let 
be the time of the latest negative Ab- test result, 
the first positive Ab+ test result, and 
the actual HIV acquisition time. Based on the HIV testing algorithm, each infected participant was classified into one of two groups, defined by whether the earliest HIV positive sample was (Ab+, PCR+) or (Ab-, PCR+). The (Ab+, PCR+) group has 
such that 
and 
is left censored (Figure 1a), and the (Ab-, PCR+) group has 
and 
such that 
is observed (Figure 1b). The left censoring rate for 
is 70.4%.
At the time of a participant's first antibody-based positive HIV infection diagnosis (
), 18 post-infection visits were scheduled at weeks 0, 1, 2, 8, 12, 26 and every 26 weeks thereafter through week 338. However, the actual dates of visits vary. We define 
as the time from 
to the jth visit for the ith infected participant. At each study visit, HIV viral load 
was measured. A participant is considered censored once he starts antiretroviral therapy (ART), which interferes with the assessment of vaccine effects on viral load and other biomarkers of interest. The censoring time 
is the time from 
to ART initiation, study drop-out, or the end of follow-up, whichever comes first. The right censoring rate of 
was 69.8%.
The data for analysis includes 159 participants (97 vaccine group, 62 placebo group) with 785 visits from HIV infection diagnosis and prior to ART initiation. One hundred and twenty-two participants were in North America or Australia and the rest were in the Caribbean or South America. Information was available on whether the participants were fully adherent to vaccinations and on baseline anti-Ad5 neutralizing antibody titer (Ad5 titer), each of which affect the T cell response to the vaccine and hence could associate with the viral load response. A spaghetti plot of the raw viral load data with one line for each participant by vaccination status and the study region is given in Web Figure 4 in Web Appendix F. We investigate the effect of MRKAd5 HIV-1 gag/pol/nef vaccine versus placebo on longitudinal HIV viral loads among the 159 HIV infected men. With 
, the logarithm (log10) of HIV viral load at time t in years, we analyzed the data with the following model:
where 
is the treatment indicator (
if participant i was assigned vaccine and 0 if placebo), 
is the study site indicator (
if North America or Australia and 0 otherwise), 
is the natural logarithm of baseline Ad5 titer, and 
is the per-protocol indicator (
if participant i was fully adherent to vaccinations and 0 otherwise).
We choose 
years since there are very few observations after 
and 
. The Kaplan–Meier estimator is used to estimate distribution of 
since the covariates in model (18) are not significant with large p-values in fitting the Cox model. Figure 5 shows the plot of the Kaplan–Meier estimator 
. We let 
for 
as the smallest uncensored 
is 0.1397 and the smallest value of 
is 0.0493.
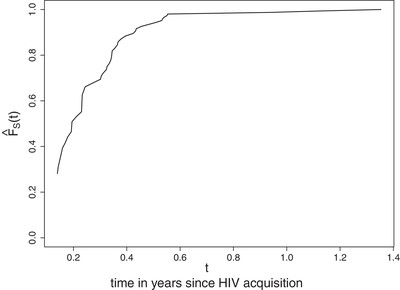
Kaplan–Meier estimator of the distribution function of the time from actual HIV acquisition to the first positive Elisa confirmed by Western Blot or RNA for male HIV infected cases in Step trial
We select bandwidth using the formula 
, where 
. Here 
is the sample variance of 
, for 
and each participant i, and 
is the sample variance of 
. Some discussions on bandwidth choice are given in Web Appendix E. With 
, the bandwidth choice is 
. The estimates of γ1, γ2, and γ3 using unit weight are 0.0241, −0.0127, and −0.0124, with standard error 0.0406, 0.1935, and 0.1573, respectively. The results indicate no significant associations of baseline Ad5 titer, study site, or per-protocol status with the HIV viral load level. The estimates of time-varying effects with 95% pointwise confidence intervals are shown in Figure 6. Figure 6(b) suggests that there is a nonsignificant vaccine effect to reduce viral load after infection. However, the vaccine group tends to have lower viral load than the placebo group and the benefit increases over time.
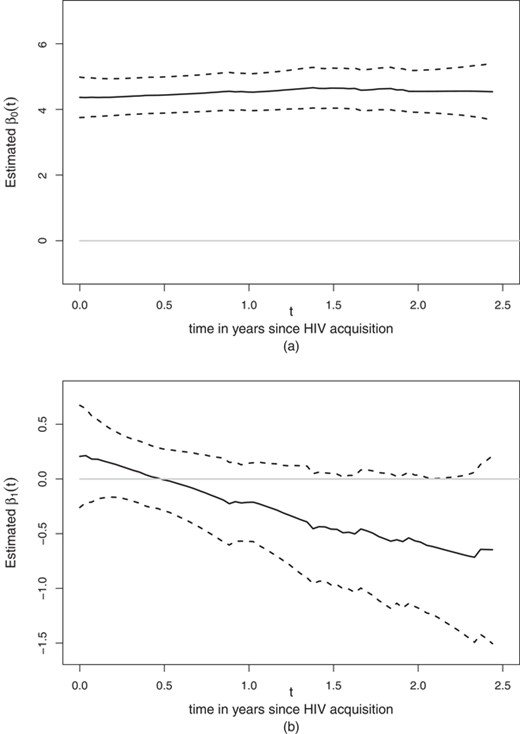
Analysis of HIV viral load level for the male HIV infected cases in Step trial with model (18). (a) The estimate of the intercept 
and its 95% pointwise confidence interval. (b) The estimated effect 
of the vaccine and its 95% pointwise confidence interval. The solid curves are the point estimates and the dashed curves are the confidence intervals
The two-stage estimation procedure with the estimated weight is applied to the analysis of Step study. The results of analysis using the estimated weight are similar and are presented in Web Appendix F.
6 Concluding Remarks
This paper investigated the semiparametric additive time-varying coefficient model for longitudinal data starting from a possibly censored relevant event. The developed method can be applied to assess the HIV vaccine effect on the post HIV infection longitudinal biomarkers such as HIV viral load level since the time of infection. However, the exact time of infection can be censored. The censorship status can be determined by an HIV antibody test followed by a more sensitive antigen-based HIV-specific PCR assay, or by an expanded set of HIV diagnostic assays with varying sensitivity properties (Grebe et al., 2019) and/or sequence diversification molecular clock models (Giorgi et al., 2010; Rossenkhan et al., 2019). The time from HIV acquisition to first HIV antibody positive test is subject to left censoring and its distribution can be estimated based on the Kaplan–Meier estimator or a failure time regression model such as the Cox model. We used the expectation maximization approach to deal with the censored time origin and developed the weighted profile least squares estimation procedure. The nonparametric kernel smoothing method was employed to estimate time-varying covariate effects. We investigated the asymptotic properties of both the parametric and nonparametric estimators and proposed consistent variance estimators.
Our simulation study showed that the proposed estimators work well with small biases and satisfying coverage probabilities for different levels of left censoring and moderate sample sizes while substantial bias was incurred for estimation of time-varying effects when misplacing the time origin by ignoring left censoring. The method was applied to analyze the male HIV infected cases from Step study, suggesting a borderline significant vaccine effect to lower viral load after infection by about a half to three-quarters of a log (base 10) during the period beyond 1.5 years post HIV acquisition. This result should be interpreted with caution given the potential for post-randomization selection bias, which could occur if there are baseline factors not adjusted for in the analysis that predict both viral load and the vaccine effect on HIV acquisition (Shepherd et al., 2006).
As with most statistical modeling, the application of the proposed method should be accompanied by model assessment. Web Figure 5 shows a scatter plot of residuals of the participants with 
for the Step study application. The residual plot is approximately centered around 0 between −2 and 2, which indicates the model fits the data reasonably well. However, it is more desirable to develop formal goodness-of-fit tests to examine the model fitness. The test statistics can be constructed based on certain test processes that are functionals of residual processes. The critical values of the test statistics can be estimated similarly to the technique of Sun et al. (2019). Further work is warranted to understand the empirical and theoretical properties of the tests. Although the development for the censored time origin is based on the semiparametric additive time-varying coefficients model, extensions to the generalized semiparametric regression models of Sun et al. (2013) are possible. The extension can be carried out by applying the EM approach to the expositions of Sun et al. (2013). It would also be interesting to investigate the random mixed-effects model with censored time origin that can be used to estimate subject-specific effects of covariates.
Data Availability Statement
The data that support the findings in this paper are available in the Supporting Information of this article.
Supporting Information
Web Appendices A–F, Tables 1–3, and Figures 1–5 referenced in Sections 2–5 together with the data and computer code are posted online with this paper at the Biometrics website on Wiley Online Library.
Acknowledgments
The authors thank an associate editor and two referees for their valuable comments and suggestions that have greatly improved the paper. This research was partially supported by the National Institutes of Health NIAID [grant number R37 AI054165]. The research of Yanqing Sun was also partially supported by the National Science Foundation [grant numbers DMS-1208978 and DMS-1915829] and the Reassignment of Duties fund provided by the University of North Carolina at Charlotte. We thank the HIV Vaccine Trials Network (HVTN) and Merck for providing the data analyzed in this article. The HVTN is supported through a cooperative agreement with the National Institutes of Health Division of AIDS, grant 5 U01 AI068635. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
