TENET: topological feature-based target characterization in signalling networks

Author Notes

Abstract

Motivation: Target characterization for a biochemical network is a heuristic evaluation process that produces a characterization model that may aid in predicting the suitability of each molecule for drug targeting. These approaches are typically used in drug research to identify novel potential targets using insights from known targets. Traditional approaches that characterize targets based on their molecular characteristics and biological function require extensive experimental study of each protein and are infeasible for evaluating larger networks with poorly understood proteins. Moreover, they fail to exploit network connectivity information which is now available from systems biology methods. Adopting a network-based approach by characterizing targets using network features provides greater insights that complement these traditional techniques. To this end, we present Tenet (Target charactErization using NEtwork Topology), a network-based approach that characterizes known targets in signalling networks using topological features.

Results: Tenet first computes a set of topological features and then leverages a support vector machine-based approach to identify predictive topological features that characterizes known targets. A characterization model is generated and it specifies which topological features are important for discriminating the targets and how these features should be combined to quantify the likelihood of a node being a target. We empirically study the performance of Tenet from a wide variety of aspects, using several signalling networks from BioModels with real-world curated outcomes. Results demonstrate its effectiveness and superiority in comparison to state-of-the-art approaches.

Availability and implementation: Our software is available freely for non-commercial purposes from: https://sites.google.com/site/cosbyntu/softwares/tenet

Contact: [email protected] or [email protected]

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Complex intra- and inter-cellular signalling drives various biological processes, such as growth, proliferation and apoptosis within systems. In systems biology, these molecular interactions are typically modelled as signalling networks (Klamt et al., 2009) that provide a holistic view of the various interactions between different molecular players in the system. As signalling networks become an increasingly acceptable way for representing biological systems, various network-based computational techniques have been developed to analyze these networks with the goal of answering biological needs, such as target characterization (Chua et al., 2014) and target discovery (Yang et al., 2008). In this article, we focus on the target characterization problem for signalling networks.

Target characterization identifies characteristics (e.g. topological features) that distinguishes targets (i.e. nodes) from other nodes in the network. These characteristics can be summarized as models which we refer to as characterization models. Traditionally, targets are characterized based on their molecular characteristics [e.g. structure and binding sites of targets (Maira et al., 2008)] and biological function [e.g. regulation of apoptosis (Yan et al., 2013)]. These traditional approaches focus primarily on the target alone and are oblivious to the presence of other interacting molecules in the system. However, understanding how a target interacts with other molecules in a biological system may provide valuable and holistic insights for superior target characterization. For example, the degree centrality of a target may be leveraged to assess potential toxicity of targets as high degree nodes tend to be involved in essential protein–protein interactions (He et al., 2006) and are potentially toxic as a result. In particular, network-based target characterization techniques can exploit such topological features for superior characterization of targets.

Recently, there have been increasing efforts toward devising network-based target characterization techniques (Hwang et al., 2008; Zhang et al., 2010; McDermott et al., 2012). These methods focus on using topological features to characterize targets of protein–protein interaction (ppi) networks. Specifically, McDermott et al. (2012) performed characterization of targets in protein co-abundancenetworks [The protein co-abundance networks are essentially protein–protein interaction (ppi) networks constructed by identifying highly differentially regulated proteins from proteomics data using specific filters.] using several topological features such as degree centrality. Although this study suggests that multiple topological features can be combined for superior target characterization, it did not explore how these topological features should be combined towards this goal. In contrast, Hwang et al. (2008) concluded that bridging centrality is useful in identifying targets in ppi networks. However, the complexity and diversity of biological networks make target characterization using a single feature challenging as in some networks the chosen feature may perform poorly. Indeed, Chua et al. (2014) showed that bridging centrality performs well in the mapk-pi3k network, but not in the glucose metabolism network. Zhang et al. (2010) proposed the use of machine learning techniques such as support vector machines (svm) and logistic regression for characterizing known targets in a manually curated human ppi network using 15 topological features. In contrast to McDermott et al. (2012), their goal was to identify topological characteristics of drug targets in general, instead of for specific diseases. However, characterizing targets in general assumes that targets of different diseases share similar target characteristics, which may not always be true. Indeed, as we shall see in Section 3, known targets in signalling networks tend to be characterized by different sets of topological features. Consequently, target characterization based on individual disease-specific networks may yield better characterization that is specific to the disease.

A common thread running through the aforementioned target characterization techniques is their focus on ppi networks. Surprisingly, similar systematic study in curated signalling networks has been lacking in the literature. Compared to signalling networks, ppi networks may contain many false-positive ppi in the sense that although these proteins can truly physically bind they may never do so inside cells due to different localization or they are not simultaneously expressed. Furthermore, ppi networks are static. That is, the edges in ppi networks are undirected; there is neither flow of information nor mass between nodes. Hence, they lack of knowledge of the underlying mechanism (i.e. actual signal flow) causing the disease. As network quality directly affects the results of network-based target characterization, the aforementioned limitations of ppi networks may adversely impact the search for superior characteristics of targets. Signalling networks, however, model the dynamic interaction of the biological systems and present an attractive alternative to ppi networks.

In our recent work (Chua et al., 2014), we took the first step to demonstrate how signalling networks can be effectively leveraged to identify topological features that are discriminative of targets using the Wilcoxon test. However, similar to McDermott et al. (2012), this work does not shed any insight on a predictive model to combine these features for identifying potential targets. In this article, we address this limitation by presenting Tenet (Target charactErization using NEtwork Topology), a network-based approach that characterizes known targets in signalling networks using topological features. Specifically, we use an svm-based approach to identify the set of topological features (referred to as predictive topological features) that characterizes known targets and to generate a characterization model using these features. The model specifies which topological features are important for discriminating the targets and how these features should be combined to produce a quantitative score that identifies the likelihood of a node being a target. In particular, Tenet uses feature selection to select predictive topological features and weighted misclassification cost (wmc) to handle svm training issues such as noisy labels and imbalanced data. Our empirical study on four real-world curated signalling networks demonstrates the effectiveness and superiority of Tenet.

2 Materials and methods

2.1 Terminology

A biological signalling network can be modelled as a directed hypergraph $G = (V, E)$ (Klamt et al., 2009) where the nodes V represent molecules (e.g. proteins) and the hyperedges E represent biochemical reactions and processes. A hyperedge connects one node set U to another W, where $U, W \subseteq V$ ⁠. For instance, in the activation of erk, the set U in the hyperedge consists of erk and its kinase, phosphorylated mek whereas W contains the phosphorylated erk (erkpp). Analysis of directed hypergraphs is generally more complex than graphs and many graph algorithms cannot be used directly on hypergraphs. Hence, they are often transformed into graphs containing simple edges for analysis. Methods (e.g. bipartite and substrate graph representation) exist for such transformation (Klamt et al., 2009). In this article, we use the bipartite graph representation as it retains the original information of the hypergraph (Klamt et al., 2009). Signalling networks generally contain characteristics such as feedback and feedforward loops, which are common in complex regulatory control (Kwon et al., 2008). These loops in turn give rise to graph characteristics, such as strongly connected components (scc).

The activity of nodes in the signalling network is generally governed by complex interconnectivity of various nodes in the same network. We refer to a node as a candidate target if when perturbed, it modulates the activity of a specific node (referred to as output node). An output node is a protein that is either involved in some biological processes which may be deregulated, resulting in manifestation of a disease, or be of interest due to its potential role in the disease. For instance, in the mapk-pi3k network (Hatakeyama et al., 2003) that is often implicated in cancer, erkpp can be considered as an output node due to its role in proliferation. Given a signalling network $G = (V, E)$ and an output node $x \in V$ ⁠, let the set of nodes having a path leading to x be denoted as $V_{x} \subseteq V$ ⁠. Then, the set of candidate target nodes in G relevant to x is denoted as $T_{x} \subseteq V_{x}$ ⁠.

Network-based analysis can be applied to signalling networks to study the characteristics and properties of these networks. In this article, we examine a total of 16 topological features that are summarized in Table 1. These features are selected based on their role in measuring relative importance of a node in a signalling network. The formal definitions as well as motivation for selecting these features are given in Chua et al. (2014) (also detailed in Supplementary Material S1.1).

Table 1.

Open in new tab

Topological features

Symbol	Description
θ_u	Degree centrality of node u. The in, out and total degree centralities are denoted as $θ_{in (u)}, θ_{out (u)}$ and $θ_{t o t a l (u)}$ ⁠, respectively
α_u	Eigenvector centrality of node u
β_u	Closeness centrality of node u
γ_u	Eccentricity centrality of node u
δ_u	Betweenness centrality of node u
π_u	Bridging coefficient of node u
ζ_u	Bridging centrality of node u
κ_u	Clustering coefficient of node u. The undirected, in, out, cycle and middleman clustering coefficients are denoted as $κ_{u n d i r (u)}, κ_{i n (u)}, κ_{o u t (u)}, κ_{c y c (u)}$ and $κ_{m i d (u)}$ ⁠, respectively
μ_u	Proximity prestige of node u
ω_u	Target downstream effect of node u

Symbol	Description
θ_u	Degree centrality of node u. The in, out and total degree centralities are denoted as $θ_{in (u)}, θ_{out (u)}$ and $θ_{t o t a l (u)}$ ⁠, respectively
α_u	Eigenvector centrality of node u
β_u	Closeness centrality of node u
γ_u	Eccentricity centrality of node u
δ_u	Betweenness centrality of node u
π_u	Bridging coefficient of node u
ζ_u	Bridging centrality of node u
κ_u	Clustering coefficient of node u. The undirected, in, out, cycle and middleman clustering coefficients are denoted as $κ_{u n d i r (u)}, κ_{i n (u)}, κ_{o u t (u)}, κ_{c y c (u)}$ and $κ_{m i d (u)}$ ⁠, respectively
μ_u	Proximity prestige of node u
ω_u	Target downstream effect of node u

Table 1.

Open in new tab

Topological features

Symbol	Description
θ_u	Degree centrality of node u. The in, out and total degree centralities are denoted as $θ_{in (u)}, θ_{out (u)}$ and $θ_{t o t a l (u)}$ ⁠, respectively
α_u	Eigenvector centrality of node u
β_u	Closeness centrality of node u
γ_u	Eccentricity centrality of node u
δ_u	Betweenness centrality of node u
π_u	Bridging coefficient of node u
ζ_u	Bridging centrality of node u
κ_u	Clustering coefficient of node u. The undirected, in, out, cycle and middleman clustering coefficients are denoted as $κ_{u n d i r (u)}, κ_{i n (u)}, κ_{o u t (u)}, κ_{c y c (u)}$ and $κ_{m i d (u)}$ ⁠, respectively
μ_u	Proximity prestige of node u
ω_u	Target downstream effect of node u

Symbol	Description
θ_u	Degree centrality of node u. The in, out and total degree centralities are denoted as $θ_{in (u)}, θ_{out (u)}$ and $θ_{t o t a l (u)}$ ⁠, respectively
α_u	Eigenvector centrality of node u
β_u	Closeness centrality of node u
γ_u	Eccentricity centrality of node u
δ_u	Betweenness centrality of node u
π_u	Bridging coefficient of node u
ζ_u	Bridging centrality of node u
κ_u	Clustering coefficient of node u. The undirected, in, out, cycle and middleman clustering coefficients are denoted as $κ_{u n d i r (u)}, κ_{i n (u)}, κ_{o u t (u)}, κ_{c y c (u)}$ and $κ_{m i d (u)}$ ⁠, respectively
μ_u	Proximity prestige of node u
ω_u	Target downstream effect of node u

2.2 Topological feature-based target characterization

Intuitively, the goal of topological feature-based target characterization is to use a set of predictive topological features to characterize known targets in a network. Hence, the topological feature-based target characterization problem can be formulated as a supervised learning problem. In a supervised learning problem, a training set ${〈 x_{i}, f (x_{i}) 〉}$ is given where $f (x_{i})$ is the predictor of x_i and the goal is to learn some target function $f : X \to Y$ which can be applied to predict unseen data w. The problem can be subdivided into two categories: regression when the predictor yields a continuous outcome and classification when the outcome is discrete. A regression problem can be converted into a binary classification problem by specifying a threshold h and assigning x_i with f greater than h to one class and the remaining to the other class. We advocate that the topological feature-based target characterization problem is best represented as a regression problem. In this problem, we are interested in finding out how likely one node is a target relative to another node based on a set of predictive topological features. This is different from the target classification problem where we want to find out the class membership of a node. Note that the regression problem can be converted into a classification problem by specifying a threshold h and assigning nodes having target function greater than h to the target class and the rest to the non-target class.

Although we examine 16 topological features, as we shall see later, not all features are relevant to a given signalling network. In fact, incorporating irrelevant features may adversely impact the performance of the prediction model. Hence, it is important to learn a set of predictive topological features that best characterizes targets (referred to as topological feature selection) for a given network. Formally, it is defined as follows.

Definition 1

Given a signalling network

G = (V, E)

and an output node

x \in V

⁠, let

T_{x} \subseteq V

and

X_{all}

denote the set of known targets in G relevant to x, and the set of topological features of G, respectively. Then, the goal of ‘topological feature selection’ is to find a set of ‘predictive topological features’

F \subseteq X_{all}

that maximizes the prediction accuracy for

f (ξ (u, F))

subject to the following conditions:

{\begin{matrix} f (ξ (u, F)) = 1 & when u \in T_{x}, \\ f (ξ (u, F)) = 0 & otherwise . \end{matrix}

(1)

Then the topological feature-based target characterization problem is formally defined as follows.

Definition 2

Given a signalling network $G = (V, E)$ ⁠, an output node

x \in V

⁠, T_x, and

X_{all}

⁠, let

F

denote the set of predictive topological features. Then, for a threshold h, the goal of the‘topological feature-based target characterization problem’ is to identify a set of predictive topological features

F \subseteq X_{all}

using topological feature selection and learn a ‘characterization model’

g (ξ (u, F))

subject to the conditions

{\begin{matrix} g (ξ (u, F)) \in ℜ, \\ g (ξ (u, F)) \geq h & when u \in T_{x}, \\ g (ξ (u, F)) < h & otherwise, \end{matrix}

(2)

that maximizes the target prediction for

g (ξ (u, F))

⁠.

Figure 1 depicts a pictorial overview of the topological feature-based target characterization problem. For example, given the mapk-pi3k signalling network, its associated output node erkpp, the set of known targets in this network and the topological features in Table 1, the goal of this problem is to produce the followings: (i) identify the set of predictive topological features $F = {δ, π, θ_{i n}, θ_{o u t}}$ and (ii) learn a characterization model g(ξ(erkpp, $F))$ ⁠. Note that in Definition 2, there is no need to explicitly specify a threshold h if we are only interested in obtaining the relative rankings of the nodes. The threshold is required if we want to assign class labels (e.g. target class) to the nodes.

Fig. 1.

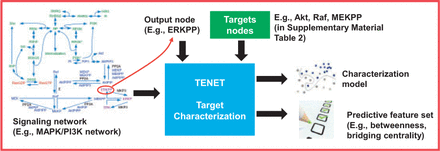
Target characterization problem

Open in new tab Download slide

2.3 svm-based target characterization

We employ support vector classification (svc) to select predictive topological features and support vector regression (svr) to generate the characterization model. The svc and svr are typically formulated as constrained optimization problems and solved using the Lagrangian multiplier method. In general, svm models contain multiple parameters, such as the cost parameter C and parameters related to the kernel function, that affect the learning and performance of the models (Chapelle et al., 2002). We follow the method in Hsu et al. (2003) for training the svm. The feature values are scaled linearly to the range of [0, 1] for each signalling network to avoid features with larger ranges dominating those with smaller ranges. We use stratified (The training data were sampled from the original data such that the ratio of the targets to non-targets is similar to that of the original data.) cross-validation (Supplementary Material S1.3) and grid-search (Hsu et al., 2003) on the training data to identify the best values of the model parameters. Note that cross-validation helps us to avoid the issue of overfitting the data whereas stratification enables us to keep the percentage of targets in the different folds similar to the original dataset. The best parameter is the one that yields the best average prediction accuracy for the cross-validation process. Wherever possible (In our study, we set a lower bound of one target in all our test sets.), we use a 10-fold stratified cross-validation as larger fold numbers reduce pessimistic bias and 10-folds generally give good performances (Kohavi et al., 1995).

Several non-trivial issues, namely, irrelevant or redundant features, noisy labels and imbalanced dataset, need to be addressed in training the svm model for characterizing targets. In particular, we use feature selection to select for appropriate features to be used in the svm model and cost-sensitive learning to handle the issue of noisy labels and imbalanced dataset. We examine three feature selection approaches, namely, backward stepwise elimination (bse) (Marill et al., 1963), Wilcoxon-ROC based elimination (wre) and wre-bse. bse is classifier-aware whereas wre is classifier-independent.wre-bse which performs wre followed by bse is a hybrid approach. Note that compared to classifier-independent methods, classifier-aware methods interact with the classifiers and such interaction can lead to better classification results (Saeys et al., 2007). However, they are typically computationally expensive and run the risk of model-overfitting. Cost sensitive learning is an algorithmic approach that chooses an appropriate strategy specific to the classifier to overcome the bias introduced by imbalanced data and the noise caused by uncertainty in labelling. We use wmc, an approach that proportionates the misclassification cost of the training data according to class. In particular, we use a variable C_i as the cost parameter C:

C_{i} = {\begin{matrix} C^{+} & if y_{i} = + 1 \\ C^{-} & if y_{i} = - 1 \end{matrix}

(3)

subject to the constraints

C^{+} + C^{-} = 1, C^{+} > 0

and

C^{-} > 0

where y_i is the class predictor and C⁺ and C⁻ denote the misclassification cost of the target and non-target classes, respectively.

2.4 The Tenet algorithm

Given a signalling network $G = (V, E)$ ⁠, an output node $x \in V$ ⁠, a known target set $T_{x} \subseteq V$ ⁠, a set of topological features $X_{all}$ and a step-size of the misclassification cost s, Tenet identifies the set of predictive structural features and a characterization model that best characterizes these known targets. Note that $X_{all}$ and s are optional inputs and are set to default values (⁠ $X_{all}$ is set to the 16 topological features given in Table 1 whereas s is set to 0.1.) if they are not given. The known targets T_x can be extracted by following the curation process described in Chua et al. (2014) (Supplementary Material S1.2). The Tenet algorithm comprised three phases, namely, the pruning phase, the feature extraction phase and the model training phase. First, the pruning phase identifies relevant nodes (denoted as V_candidate) that shall be used for training the svm. Then, the feature extraction phase extracts all the topological features (denoted as $X_{all}$ ⁠) of each candidate node and stores them in a $| V_{candidate} | \times | X_{all} |$ matrix H. Finally, in the model training phase, Tenet learns the optimal set of predictive topological features $F$ and the best model parameters of the characterization model $M$ ⁠. We shall now describe these phases in turn. The formal algorithm is given in Supplementary Material S1.4.

2.4.1 Phase 1: Pruning

In this phase, Tenet prunes nodes that do not have paths leading to the output node x. This phase yields a set of potential candidate nodes $V_{candidate} \subset V$ and is used to reduce the subsequent computation. In the pruning process, the given network G is first preprocessed into a bipartite graph and then converted into a directed acyclic graph (dag), a graph with consistent topological ordering, to facilitate indexing of nodes. Note that the node indices shall be used subsequently to perform reachability check to identify the nodes to be pruned. We adopt the method in Engelfiet et al. (1990) for bipartite graph conversion. In order to convert the bipartite graph into its dag representation, we adopt the approach in Tarjan et al. (1972) to identify sccs and replace each scc with a representative node (referred to as meta node). Then, we adopt the indexing approach of Chen et al. (2005) to index the dag. This indexing approach performs depth-first traversal to assign each node v a preorder index (when v is first visited) and a postorder index (when all descendent nodes of v are visited). Finally, an index-based reachability algorithm is used to determine whether there exists a path from each node v to the output node x (denoted as $v \to x$ ⁠). Given a node v and x, let w be the descendent of v that is not in the spanning tree (referred to as non-spanning tree node) and v.preorder and v.postorder denote the preorder and postorder indexes of v, respectively. A path $v \to x$ exists if any of the following conditions are satisfied (Chen et al., 2005):

$v . p r e o r d e r \leq x . p r e o r d e r$ and $v . p o s t o r d e r \geq x . p o s t o r d e r$ .
$w . p r e o r d e r \leq x . p r e o r d e r$ and $w . p o s t o r d e r \geq x . p o s t o r d e r$ .

Note that the pruning step is beneficial in improving execution time for larger sparsely connected networks and for output node that are positioned further upstream. For instance, in the mapk-pi3k network, no nodes are pruned when we select erkpp (downstream) as the output node whereas 17 nodes (47.2%) are pruned when activated Ras (Rasgtp) (upstream) is selected.

2.4.2 Phase 2: Feature extraction

In this phase, for all nodes in V_candidate, Tenet extracts all the topological features in Table 1 for characterizing the known targets.

2.4.3 Phase 3: Model training

Given a matrix of topological feature values H, a target set T_x and a step-size of the misclassification cost s, this phase identifies a set of predictive topological features $F$ and the best parameters for configuring the characterization model $M$ ⁠. First, the misclassification cost of the target class C⁺ is initialized to a default value of 0.5. Then, feature selection is used to obtain the predictive topological feature set $F$ ⁠. We iterate over three different feature selection approaches (bse, wre and wre-bse). Next, the step-size s is used to step through the range of misclassification cost (0–1). In each iteration, the misclassification cost of the target class C⁺ is incremented according to the number of iterations completed, before the svm training is performed to obtain the parameter settings of the characterization model $M$ with the best accuracy.

The bse approach is a well-known greedy approach that progressively removes features from the naïve svm model (built using all topological features) and trains a new best model after each feature removal. The elimination process stops when removal of additional features results in a worse average accuracy of the validation set prediction. In contrast, the wre approach performs two statistical tests, namely, one-tailed Wilcoxon Rank-Sum (referred to as Wilcoxon) and receiver operating characteristics (referred to as roc). The results are used to eliminate features that do not discriminate between targets and non-targets in a significant manner (based on Wilcoxon) and that do not classify targets well (based on roc). Note that we perform two 1-tailed Wilcoxon tests and for each test; P-values smaller than 0.05 are considered significant. Hence, we take the difference of the P-values for both test hypotheses (referred to as P-value difference) and remove features with P-value difference less than 0.9. For the roc analysis, features with auc less than 0.7 (Hosmer Jr et al., 2004) are considered poor performers and are removed. The best characterization model is found by training the svm using the remaining features. The wre-bse approach first performs wre followed by bse.

The worst-case time complexity of Tenet is $O ({(| V | + | E |)}^{2} + O (G (X_{all})) + O (T (\cdot)))$ where $G (X_{all})$ is the worst-case time complexity for extracting the features and $O (T (\cdot))$ is the worst-case time complexity of the feature selection method used. Note that in this article, $G (X_{all}) = O (| V |^{3})$ whereas $O (T (\cdot)) = O (| X_{all} |^{2} \times k \times | V |^{3})$ (for bse) where k is the number of iterations required for the grid-search. Proofs are given in Supplementary Material S1.5.

3 Results and discussion

Tenet is implemented using Java. We shall now present the experiments conducted to study the performance of Tenet and report some of the results here (additional results are given in Supplementary Material). The experiments are performed on a computer system using a 64-bit operating system with 8 gbram and a dual core processor running at 3.60 GHz. We characterize four signalling networks (referred to as individual networks) in BioModels (I₁–I₄ in Table 2) and a combined network that is generated by iteratively performing a union of the nodes and edges in individual networks. The resulting combined network is a graph consisting of four disconnected (The node and edge sets of the individual networks are disjoint.) subgraphs, each representing one individual network. For the combined network, we use each of the signalling network as the test set in turn (C₁–C₄ in Table 2) and examine the effects of generating characterization models from individual networks and from the combined network. Pruning in Tenet is performed on each individual network within the combined network. Supplementary Material S1.3 describes the generation of the training and test data. Note that in all our experiments, we use the linear kernel as it yielded the same accuracy as other kernels but is faster to train (Supplementary Material S1.7.1). We study different variants of Tenet (Table 3) by varying the svm training approach.

Table 2.

Open in new tab

Dataset

Network notation	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Dataset (BioModel ID)	mapk-pi3k (0000000146)	g lucose-stimulated insulin secretion (0000000239)	endomesoderm gene regulatory (0000000235)	glucose metabolism (0000000244)	All networks
Output node(s)	erkpp	atp _{mitochondrial}	Protein_E_Endo16	acetate	{erkpp, atp_{mitochondrial}, Protein_E_Endo16, acetate}
No. of nodes in dataset	36	59	622	47	764	764	764	764
No. of hyperedges in dataset	34	45	778	109	966	966	966	966
No. (%) of targets in dataset	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)	237 (31%)	237 (31%)	237 (31%)	237 (31%)
Cross validation	8-fold	5-fold	10-fold	10-fold	10-fold	10-fold	10-fold	10-fold
Test set	Supplementary Material and Table 5				mapk-pi3k	glucose-stimulated insulin secretion	endomesoderm gene regulatory	glucose metabolism
No. (%) of targets in test set	1 (25%)	1 (10%)	21 (34.4%)	2 (40%)	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)

Network notation	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Dataset (BioModel ID)	mapk-pi3k (0000000146)	g lucose-stimulated insulin secretion (0000000239)	endomesoderm gene regulatory (0000000235)	glucose metabolism (0000000244)	All networks
Output node(s)	erkpp	atp _{mitochondrial}	Protein_E_Endo16	acetate	{erkpp, atp_{mitochondrial}, Protein_E_Endo16, acetate}
No. of nodes in dataset	36	59	622	47	764	764	764	764
No. of hyperedges in dataset	34	45	778	109	966	966	966	966
No. (%) of targets in dataset	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)	237 (31%)	237 (31%)	237 (31%)	237 (31%)
Cross validation	8-fold	5-fold	10-fold	10-fold	10-fold	10-fold	10-fold	10-fold
Test set	Supplementary Material and Table 5				mapk-pi3k	glucose-stimulated insulin secretion	endomesoderm gene regulatory	glucose metabolism
No. (%) of targets in test set	1 (25%)	1 (10%)	21 (34.4%)	2 (40%)	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)

Table 2.

Open in new tab

Dataset

Network notation	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Dataset (BioModel ID)	mapk-pi3k (0000000146)	g lucose-stimulated insulin secretion (0000000239)	endomesoderm gene regulatory (0000000235)	glucose metabolism (0000000244)	All networks
Output node(s)	erkpp	atp _{mitochondrial}	Protein_E_Endo16	acetate	{erkpp, atp_{mitochondrial}, Protein_E_Endo16, acetate}
No. of nodes in dataset	36	59	622	47	764	764	764	764
No. of hyperedges in dataset	34	45	778	109	966	966	966	966
No. (%) of targets in dataset	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)	237 (31%)	237 (31%)	237 (31%)	237 (31%)
Cross validation	8-fold	5-fold	10-fold	10-fold	10-fold	10-fold	10-fold	10-fold
Test set	Supplementary Material and Table 5				mapk-pi3k	glucose-stimulated insulin secretion	endomesoderm gene regulatory	glucose metabolism
No. (%) of targets in test set	1 (25%)	1 (10%)	21 (34.4%)	2 (40%)	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)

Network notation	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Dataset (BioModel ID)	mapk-pi3k (0000000146)	g lucose-stimulated insulin secretion (0000000239)	endomesoderm gene regulatory (0000000235)	glucose metabolism (0000000244)	All networks
Output node(s)	erkpp	atp _{mitochondrial}	Protein_E_Endo16	acetate	{erkpp, atp_{mitochondrial}, Protein_E_Endo16, acetate}
No. of nodes in dataset	36	59	622	47	764	764	764	764
No. of hyperedges in dataset	34	45	778	109	966	966	966	966
No. (%) of targets in dataset	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)	237 (31%)	237 (31%)	237 (31%)	237 (31%)
Cross validation	8-fold	5-fold	10-fold	10-fold	10-fold	10-fold	10-fold	10-fold
Test set	Supplementary Material and Table 5				mapk-pi3k	glucose-stimulated insulin secretion	endomesoderm gene regulatory	glucose metabolism
No. (%) of targets in test set	1 (25%)	1 (10%)	21 (34.4%)	2 (40%)	9 (25%)	6 (10.2%)	206 (33.1%)	16 (34%)

Table 3.

Open in new tab

Tenet variant and wmc weight ratios used in experiment

$\sqrt$ indicates the approach(es) used in the variant.

3.1 Performance metrics

We evaluate the performance of Tenet based on prediction accuracy [The accuracy for the validation and test sets are denoted as $ϕ_{X} (val)$ and $ϕ_{X} (test)$ ⁠, respectively, where X indicates the method used for training the svm model. Average prediction accuracy is denoted as $\bar{ϕ}$ ] (⁠ $ϕ$ ⁠), sensitivity (tpr), specificity (tnr) and precision (ppv) of the generated characterization models using the same training and test set. The definitions are as follows: $ϕ$ = $\frac{tp + tn}{tp + tn + fp + fn}$ ⁠, tpr= $\frac{tp}{tp + fn}$ ⁠, tnr= $\frac{tn}{fp + tn}$ and ppv= $\frac{tp}{tp + fp}$ where $tp, tn, fp$ and $fn$ denote true positive, true negative, false positive and false negative prediction, respectively. Note that ppv is set to 0 when the classifier did not make any positive prediction. We include an additional metric feature reduction factor (frf) to compare the performance of the feature selection methods. Formally, frf = 1− $\frac{| F |}{X_{all}}$ where $X_{all}$ is the entire set of features considered in the study. The performance of different characterization models is compared using an integrated performance score (This score can be modified according to the needs of the application.) $P = \sum_{m \in M} v {al}_{m}$ where $M = {\bar{ϕ} (val), ϕ (test),$ TPR, TNR, PPV} and val_m is the value of metric m. Note that a larger score indicates better performance.

3.2 Feature selection

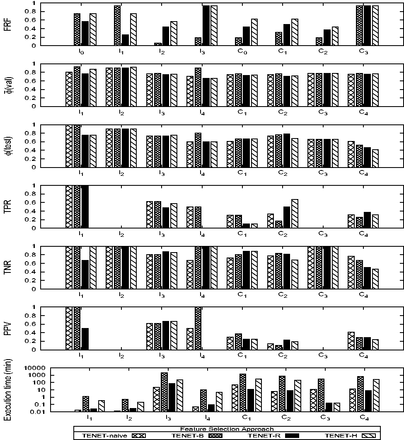
First, we examine the performance of different feature selection approaches (Tenet-b, Tenet-r and Tenet-h) and compare it with Tenet-naïve for different signalling networks. Note that in this set of experiments, we study the effect of the feature selection approaches in isolation. The effect of incorporating wmc into the svm shall be investigated later. Table 4 reports the predictive feature sets for each network using different approaches. In total, 24 experiments were conducted as there are three feature selection methods and eight networks (I₁–I₄ and C₁–C₄). Amongst these 24 experiments, 25% of the predictive feature sets consist of only one feature whereas the remaining had multiple features (ranging from 4 to 15 features). This supports our previous observation (Chua et al., 2014) that multiple features result in better prediction of known targets. Observe that in Table 4, bridging centrality is not always in the predictive feature set (e.g. I₂). Figure 2 plots the performances of different feature selection approaches. We can make several observations. First, no single approach performs consistently well on all performance metrics. In fact, network topology plays an important role in feature selection. For instance, I₄ has extremely high density of edges (ratio of edges to nodes) compared to other networks. The connectivity features of such networks become less informative and other features such as target downstream effect become more important. Hence, the most appropriate feature selection approach is dependent on the signalling network. However, we note that for larger sized networks, a larger number of features are informative (regardless of feature selection approach). This is perhaps because larger networks provide greater richness of context and diversity of structure in the sub-networks. As network sizes are growing and network analysis demands applicability to larger networks, future methods might benefit particularly from the use of multiple features. Second, feature selection generally led to an improvement in prediction accuracy (87.5% for validation dataset and 50% in test dataset) over the naïve approach. An exception is C₄ in which feature selection resulted in poorer performance. In C₄, the characterization model is generated using I₁, I₂ and I₃ as training data whereas I₄ is used as the test data. The characteristics of the known targets in the training data may be quite different from that of the test data. Indeed, from Table 4, we observe that bridging coefficient π is included in the predictive topological feature set of C₄, but not in I₄. Including redundant features may lead to poorer performance. Third, the models generally have high specificity due to imbalanced dataset. Fourth, Tenet-r has the best runtime performance, followed by Tenet-h and Tenet-b. The poorer performance of Tenet-b is due to the interaction of the feature selection approach with the classifier (classifier-aware approach) which is different from Tenet-r where the feature selection approach is a wrapper layer that sits on top of the classifier. Finally, the size of the networks used for training affects the runtime performance. In general, larger size networks require longer runtime. In the Supplementary Material S1.7.6, we report Tenet’s performance on the human cancer signalling network containing more than 2500 nodes.

Fig. 2.

Performance of different feature selection approaches

Open in new tab Download slide

Table 4.

Open in new tab

Features selected by various feature selection approaches

Data	Tenet-b	Tenet-r	Tenet-h
I₁	δ, π, θ_in, θ_out	δ, ζ, β, ϑ, θ_out, μ, κ_undir	δ, ζ, β, ϑ
I₂	θ_in	δ, π, β, κ_undir, κ_cyc, α, θ_in, κ_in, μ, κ_mid, θ_out, θ_total	π, β, κ_cyc, κ_undir
I₃	δ, ζ, π, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, κ_out, θ_out, ω, θ_total, κ_undir	δ, ζ, ϑ, α, κ_mid, θ_out, θ_total, ω, κ_undir	δ, ζ, ϑ, α, θ_out, θ_total, κ_undir
I₄	ζ, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, ω, κ_out, θ_out, θ_total, κ_undir	ω	ω
C₁	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, μ, ω, κ_undir	δ, ζ, π, β, ϑ, α, κ_mid, κ_undir, θ_out	ζ, π, ϑ, α, θ_out, κ_undir
C₂	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, κ_undir	δ, ζ, α, κ_mid, θ_out, ω, θ_total, κ_undir	δ, ζ, α, κ_mid, ω, κ_undir
C₃	θ_in	ζ	ζ
C₄	ζ, π, β, κ_cyc, ϑ, α, κ_in, θ_in, ω, κ_out, θ_out, θ_total, κ_undir	δ, ζ, π, ϑ, α, κ_mid, θ_out, ω, θ_total, κ_undir	ζ, π, ϑ, α, κ_undir, ω, θ_out, θ_total, κ_mid

Data	Tenet-b	Tenet-r	Tenet-h
I₁	δ, π, θ_in, θ_out	δ, ζ, β, ϑ, θ_out, μ, κ_undir	δ, ζ, β, ϑ
I₂	θ_in	δ, π, β, κ_undir, κ_cyc, α, θ_in, κ_in, μ, κ_mid, θ_out, θ_total	π, β, κ_cyc, κ_undir
I₃	δ, ζ, π, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, κ_out, θ_out, ω, θ_total, κ_undir	δ, ζ, ϑ, α, κ_mid, θ_out, θ_total, ω, κ_undir	δ, ζ, ϑ, α, θ_out, θ_total, κ_undir
I₄	ζ, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, ω, κ_out, θ_out, θ_total, κ_undir	ω	ω
C₁	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, μ, ω, κ_undir	δ, ζ, π, β, ϑ, α, κ_mid, κ_undir, θ_out	ζ, π, ϑ, α, θ_out, κ_undir
C₂	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, κ_undir	δ, ζ, α, κ_mid, θ_out, ω, θ_total, κ_undir	δ, ζ, α, κ_mid, ω, κ_undir
C₃	θ_in	ζ	ζ
C₄	ζ, π, β, κ_cyc, ϑ, α, κ_in, θ_in, ω, κ_out, θ_out, θ_total, κ_undir	δ, ζ, π, ϑ, α, κ_mid, θ_out, ω, θ_total, κ_undir	ζ, π, ϑ, α, κ_undir, ω, θ_out, θ_total, κ_mid

Table 4.

Open in new tab

Features selected by various feature selection approaches

Data	Tenet-b	Tenet-r	Tenet-h
I₁	δ, π, θ_in, θ_out	δ, ζ, β, ϑ, θ_out, μ, κ_undir	δ, ζ, β, ϑ
I₂	θ_in	δ, π, β, κ_undir, κ_cyc, α, θ_in, κ_in, μ, κ_mid, θ_out, θ_total	π, β, κ_cyc, κ_undir
I₃	δ, ζ, π, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, κ_out, θ_out, ω, θ_total, κ_undir	δ, ζ, ϑ, α, κ_mid, θ_out, θ_total, ω, κ_undir	δ, ζ, ϑ, α, θ_out, θ_total, κ_undir
I₄	ζ, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, ω, κ_out, θ_out, θ_total, κ_undir	ω	ω
C₁	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, μ, ω, κ_undir	δ, ζ, π, β, ϑ, α, κ_mid, κ_undir, θ_out	ζ, π, ϑ, α, θ_out, κ_undir
C₂	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, κ_undir	δ, ζ, α, κ_mid, θ_out, ω, θ_total, κ_undir	δ, ζ, α, κ_mid, ω, κ_undir
C₃	θ_in	ζ	ζ
C₄	ζ, π, β, κ_cyc, ϑ, α, κ_in, θ_in, ω, κ_out, θ_out, θ_total, κ_undir	δ, ζ, π, ϑ, α, κ_mid, θ_out, ω, θ_total, κ_undir	ζ, π, ϑ, α, κ_undir, ω, θ_out, θ_total, κ_mid

Data	Tenet-b	Tenet-r	Tenet-h
I₁	δ, π, θ_in, θ_out	δ, ζ, β, ϑ, θ_out, μ, κ_undir	δ, ζ, β, ϑ
I₂	θ_in	δ, π, β, κ_undir, κ_cyc, α, θ_in, κ_in, μ, κ_mid, θ_out, θ_total	π, β, κ_cyc, κ_undir
I₃	δ, ζ, π, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, κ_out, θ_out, ω, θ_total, κ_undir	δ, ζ, ϑ, α, κ_mid, θ_out, θ_total, ω, κ_undir	δ, ζ, ϑ, α, θ_out, θ_total, κ_undir
I₄	ζ, β, κ_cyc, ϑ, α, κ_in, κ_mid, μ, ω, κ_out, θ_out, θ_total, κ_undir	ω	ω
C₁	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, μ, ω, κ_undir	δ, ζ, π, β, ϑ, α, κ_mid, κ_undir, θ_out	ζ, π, ϑ, α, θ_out, κ_undir
C₂	δ, ζ, π, β, κ_cyc, ϑ, α, θ_in, κ_mid, θ_out, κ_undir	δ, ζ, α, κ_mid, θ_out, ω, θ_total, κ_undir	δ, ζ, α, κ_mid, ω, κ_undir
C₃	θ_in	ζ	ζ
C₄	ζ, π, β, κ_cyc, ϑ, α, κ_in, θ_in, ω, κ_out, θ_out, θ_total, κ_undir	δ, ζ, π, ϑ, α, κ_mid, θ_out, ω, θ_total, κ_undir	ζ, π, ϑ, α, κ_undir, ω, θ_out, θ_total, κ_mid

3.3 Effect of varying wmc

Intuitively, when we vary the wmc, we expect that as the target misclassification cost C⁺ increases, the prediction accuracy, sensitivity, specificity and precision would display a negative skewed, increasing, decreasing and positive skewed distribution, respectively. This is because a large C⁺ eventually results in a model that is likely biased towards classifying data as targets. We noted the following when the wmc was varied. First, amongst the individual networks, only I₃ (Fig. 3) displays the expected trends. This could be due to the extreme small target size (1 or 2) in the test set that resulted in extreme fluctuations in the performance metrics and deviation from the expected trends. Hence, the target size of the test set can have significant impact on the observed results. Second, the performance of the combined networks C₁, C₂ and C₄ (Supplementary Material S1.7.2) resembles that of I₃, possibly due to the large size of I₃ dominating over other networks used for training. This implies large training networks can have undue influence on the characterization model. Third, sensitivity generally improves whereas specificity generally deteriorates when the target misclassification cost is set higher than the non-target misclassification cost (⁠ $C^{+} > C^{-}$ ⁠). The choice of an appropriate model depends on the application. Fourth, the prediction accuracy tends to display a skewed distribution where accuracy initially increases (or remains constant) with increasing C⁺, and then decreases with increasing C⁺. Fifth, individual networks and combined networks behave differently. In individual networks, prediction accuracy, sensitivity and precision generally improve when C⁺ is set larger than C⁻. However, in combined networks, sensitivity improves whereas other performance criteria deteriorate when C⁺ is set larger than C⁻. Hence, there is no single universal best value of C⁺ and the choice of C⁺ depends on the network.

Fig. 3.

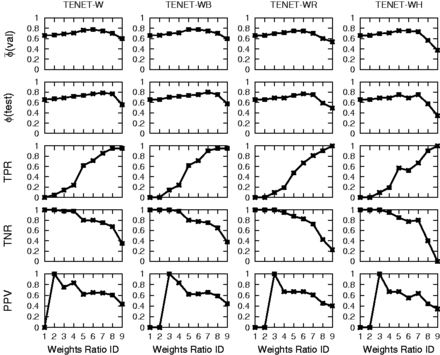
Performance of Tenet variants incorporating feature selection approach and wmc for the endomesoderm gene regulatory network

Open in new tab Download slide

3.4 Best Tenet variant

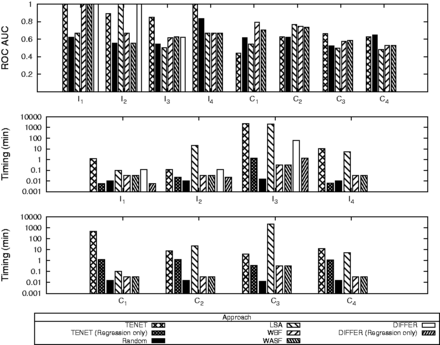
We identify the best Tenet variant (Table 5) using the integrated performance score $P$ ⁠. We note the following. First, the best Tenet variant is network dependent. Second, variants incorporating both wmc and feature selection generally perform well. Specifically, setting C⁺ greater than C⁻ led to better results. Third, Tenet variants based on individual networks (I₁ to I₄) outperform that based on combined networks (C₁–C₄). The poorer performance of the combined networks may be due to insufficient number of training networks, inappropriate or insufficient features used for training or that signalling networks by nature have distinct characteristics and it is just not possible to have a generalized model. Finally, the predictive topological features differ across networks (Tables 4 and 5). Hence, as we mentioned in Section 1, a single set of predictive topological features may not effectively characterize known targets in all signalling networks. When we compare the results with that in our previous work, we note that the set of predictive topological features is different from the discriminative topological features (dtf) identified in Chua et al. (2014) although there was an overlap of at least 50% of the features (We consider only I₁ to I₃ and exclude I₄ from this comparison as no dtf was found at P-value less than 0.05). The difference is due to the different approach used to identify the features. The characterization models (We use svm with wmc and wre to generate the characterization models.) generated by these dtfs also yielded poorer average roc (0.873) than that generated using Tenet (0.913) (Approach Differ in Fig. 4).

Table 5.

Open in new tab

Summary of best Tenet variant for different networks

	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Best approaches	Tenet-b^a, Tenet-wb (C⁺ = 0.1, 0.2, 0.3, 0.4)	Tenet-wh (C⁺ = 0.9^a)	Tenet-wb (C⁺ = 0.7^a)	Tenet-wb (C⁺ = 0.2, 0.3, 0.4, 0.6, 0.8^a)	Tenet-wh (C⁺ = 0.6^a)	Tenet-r^a	Tenet-wr (C⁺ = 0.8^a), Tenet-wh (C⁺ = 0.8)	Tenet-naïve^a
$P$	4.935	4.109	3.86	4.9	3.08	3.022	3.268	2.917
$\bar{ϕ} (val)$ [ $Δ \bar{ϕ} (val)$ ]	0.935 [0.16]	0.82 [−0.087]	0.747 [−0.02]	0.9 [0.268]	0.734 [−0.013]	0.711 [−0.052]	0.561 [−0.274]	0.757 [0]
$ϕ (test)$ [ $Δ ϕ (test)$ ]	1 [0]	0.9 [0]	0.803 [0.088]	1 [0.667]	0.694 [0.136]	0.78 [0.070]	0.724 [0.097]	0.609 [0]
tpr [Δtpr]	1 [0]	1 [ $\infty^{b}$ ]	0.905 [0.462]	1 [1]	0.4 [0.333]	0.5 [0.502]	0.602 [ $\infty^{b}$ ]	0.313 [0]
tnr [Δtnr]	1 [0]	0.889 [−0.111]	0.75 [−0.063]	1 [0.499]	0.808 [0.105]	0.811 [0.048]	0.788 [−0.212]	0.767 [0]
ppv [Δppv]	1 [0]	0.5 [ $\infty^{b}$ ]	0.655 [0.058]	1 [1]	0.444 [0.48]	0.231 [0.615]	0.593 [ $\infty^{b}$ ]	0.471 [0]

	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Best approaches	Tenet-b^a, Tenet-wb (C⁺ = 0.1, 0.2, 0.3, 0.4)	Tenet-wh (C⁺ = 0.9^a)	Tenet-wb (C⁺ = 0.7^a)	Tenet-wb (C⁺ = 0.2, 0.3, 0.4, 0.6, 0.8^a)	Tenet-wh (C⁺ = 0.6^a)	Tenet-r^a	Tenet-wr (C⁺ = 0.8^a), Tenet-wh (C⁺ = 0.8)	Tenet-naïve^a
$P$	4.935	4.109	3.86	4.9	3.08	3.022	3.268	2.917
$\bar{ϕ} (val)$ [ $Δ \bar{ϕ} (val)$ ]	0.935 [0.16]	0.82 [−0.087]	0.747 [−0.02]	0.9 [0.268]	0.734 [−0.013]	0.711 [−0.052]	0.561 [−0.274]	0.757 [0]
$ϕ (test)$ [ $Δ ϕ (test)$ ]	1 [0]	0.9 [0]	0.803 [0.088]	1 [0.667]	0.694 [0.136]	0.78 [0.070]	0.724 [0.097]	0.609 [0]
tpr [Δtpr]	1 [0]	1 [ $\infty^{b}$ ]	0.905 [0.462]	1 [1]	0.4 [0.333]	0.5 [0.502]	0.602 [ $\infty^{b}$ ]	0.313 [0]
tnr [Δtnr]	1 [0]	0.889 [−0.111]	0.75 [−0.063]	1 [0.499]	0.808 [0.105]	0.811 [0.048]	0.788 [−0.212]	0.767 [0]
ppv [Δppv]	1 [0]	0.5 [ $\infty^{b}$ ]	0.655 [0.058]	1 [1]	0.444 [0.48]	0.231 [0.615]	0.593 [ $\infty^{b}$ ]	0.471 [0]

Note: C⁺ values are provided in bracket besides approaches using wmc. $Δ_{x} = \frac{x_{best} - x_{naïve}}{x_{naïve}}$ where x_best and $x_{naïve}$ are the values of performance metric x of the best Tenet variant and Tenet-naïve, respectively.

^aBest models selected for generating the characterization model.

^bInstances where $x_{naïve} = 0$ ⁠.

Table 5.

Open in new tab

Summary of best Tenet variant for different networks

	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Best approaches	Tenet-b^a, Tenet-wb (C⁺ = 0.1, 0.2, 0.3, 0.4)	Tenet-wh (C⁺ = 0.9^a)	Tenet-wb (C⁺ = 0.7^a)	Tenet-wb (C⁺ = 0.2, 0.3, 0.4, 0.6, 0.8^a)	Tenet-wh (C⁺ = 0.6^a)	Tenet-r^a	Tenet-wr (C⁺ = 0.8^a), Tenet-wh (C⁺ = 0.8)	Tenet-naïve^a
$P$	4.935	4.109	3.86	4.9	3.08	3.022	3.268	2.917
$\bar{ϕ} (val)$ [ $Δ \bar{ϕ} (val)$ ]	0.935 [0.16]	0.82 [−0.087]	0.747 [−0.02]	0.9 [0.268]	0.734 [−0.013]	0.711 [−0.052]	0.561 [−0.274]	0.757 [0]
$ϕ (test)$ [ $Δ ϕ (test)$ ]	1 [0]	0.9 [0]	0.803 [0.088]	1 [0.667]	0.694 [0.136]	0.78 [0.070]	0.724 [0.097]	0.609 [0]
tpr [Δtpr]	1 [0]	1 [ $\infty^{b}$ ]	0.905 [0.462]	1 [1]	0.4 [0.333]	0.5 [0.502]	0.602 [ $\infty^{b}$ ]	0.313 [0]
tnr [Δtnr]	1 [0]	0.889 [−0.111]	0.75 [−0.063]	1 [0.499]	0.808 [0.105]	0.811 [0.048]	0.788 [−0.212]	0.767 [0]
ppv [Δppv]	1 [0]	0.5 [ $\infty^{b}$ ]	0.655 [0.058]	1 [1]	0.444 [0.48]	0.231 [0.615]	0.593 [ $\infty^{b}$ ]	0.471 [0]

	I₁	I₂	I₃	I₄	C₁	C₂	C₃	C₄
Best approaches	Tenet-b^a, Tenet-wb (C⁺ = 0.1, 0.2, 0.3, 0.4)	Tenet-wh (C⁺ = 0.9^a)	Tenet-wb (C⁺ = 0.7^a)	Tenet-wb (C⁺ = 0.2, 0.3, 0.4, 0.6, 0.8^a)	Tenet-wh (C⁺ = 0.6^a)	Tenet-r^a	Tenet-wr (C⁺ = 0.8^a), Tenet-wh (C⁺ = 0.8)	Tenet-naïve^a
$P$	4.935	4.109	3.86	4.9	3.08	3.022	3.268	2.917
$\bar{ϕ} (val)$ [ $Δ \bar{ϕ} (val)$ ]	0.935 [0.16]	0.82 [−0.087]	0.747 [−0.02]	0.9 [0.268]	0.734 [−0.013]	0.711 [−0.052]	0.561 [−0.274]	0.757 [0]
$ϕ (test)$ [ $Δ ϕ (test)$ ]	1 [0]	0.9 [0]	0.803 [0.088]	1 [0.667]	0.694 [0.136]	0.78 [0.070]	0.724 [0.097]	0.609 [0]
tpr [Δtpr]	1 [0]	1 [ $\infty^{b}$ ]	0.905 [0.462]	1 [1]	0.4 [0.333]	0.5 [0.502]	0.602 [ $\infty^{b}$ ]	0.313 [0]
tnr [Δtnr]	1 [0]	0.889 [−0.111]	0.75 [−0.063]	1 [0.499]	0.808 [0.105]	0.811 [0.048]	0.788 [−0.212]	0.767 [0]
ppv [Δppv]	1 [0]	0.5 [ $\infty^{b}$ ]	0.655 [0.058]	1 [1]	0.444 [0.48]	0.231 [0.615]	0.593 [ $\infty^{b}$ ]	0.471 [0]

^aBest models selected for generating the characterization model.

^bInstances where $x_{naïve} = 0$ ⁠.

Fig. 4.

Performance of different prioritization approaches

Open in new tab Download slide

3.5 Comparison with state-of-the-art approaches

Recall that state-of-the-art techniques such as McDermott et al. (2012), Zhang et al. (2010) and Hwang et al. (2008) focus on ppi networks instead of signalling networks. To the best of our knowledge, there does not exist any target characterization technique for signalling networks. However, one way to investigate the performance of Tenet is to examine how well the characterization model generated by it prioritizes known targets. Intuitively, target prioritization aims to rank the nodes according to their potential of being a target based on some importance measures (e.g. gene expression level; Chen et al., 2011). A more detailed exposure to the target prioritization problem as well as how Tenet is used to prioritize known targets is given in Supplementary Material S1.6.

For our study, we compare Tenet with several network-aware target prioritization approaches, namely, random prioritization, lsa (Gustafson et al., 1996) and NetworkPrioritizer (Kacprowski et al., 2013). Comparison with network-unaware techniques as well as ppi network-based techniques is reported in the Supplementary Material S1.7.3 and Supplementary Data, respectively.

In random prioritization, the nodes were randomly assigned a rank in the range [1– $| V |$ ] where $| V |$ is the number of nodes in the network and we assume that no ranking ties are present. lsa was performed using Copasi (Sahle et al., 2006) with the following configuration: {task=sensitivities; subtask=time series; function=all variables of the model; and variable=all parameter values}. We consider both Weighted Borda Fuse (wbf) and Weighted AddScore Fuse (wasf) in NetworkPrioritizer and consider all features provided. Note that uniform weights were used for rank aggregation as we do not have prior knowledge of the best weights or features to consider. For Tenet, we use the characterization model to generate prioritization ranks of known targets. Specifically, we apply the svm models to obtain these ranks. The svm type is set to ϵ-svr [In ϵ-svr, the error function is an ϵ-insensitive loss function and error smaller than ϵ is ignored (Chang et al., 2011).] with default ϵ value (1 × 10⁻³) and the svm parameters are set according to the best models for each network (Table 5 and Supplementary Material S1.7). Note that the nodes are ranked in decreasing order of the regression score and higher ranked nodes are more likely to be targets.

The experimental results reveal that the normalized ranks (The normalized rank of a node u for a particular approach x is defined as $Ψ_{norm (x) : u} = \frac{Ψ_{x : u}}{ma x_{i \in V} (Ψ_{x} : i)}$ ⁠.) of a given node vary widely using different approaches (Supplementary Material S1.7.5). Hence, an approach that performs better for one particular network can perform poorly in another. We further perform roc analysis based on the rankings of the nodes in the test set for each network. From Figure 4, we observe that Tenet outperforms other approaches in terms of the quality of the prioritization results, particularly for individual networks, and is comparable in terms of runtime performance when svm training is performed offline [Tenet (Regression only)].

4 Conclusions

We propose Tenet, an svm-based approach that characterizes known targets in signalling networks using topological features by identifying a set of predictive topological features and using them to generate a characterization model. Tenet uses feature selection to remove redundant features, thereby improving prediction accuracy of the characterization models and wmc to improve other performance criteria (e.g. sensitivity). Our empirical study reveals that the characterization models generated by Tenet outperform state-of-the-art approaches in prioritizing signalling and ppi networks. In summary, the contribution of this work is a machine learning-based framework that affords flexibility in characterizing signalling networks of different sizes and with different number of known targets. Although Tenet is evaluated on a small (Manual target curation, a time-intensive process, is needed to identify known targets of signalling networks for validating our experimental results.) number of signalling networks, it can easily incorporate additional signalling networks without any modification to the framework. As part of future work, we intend to explore how the characterization models learnt by Tenet can be leveraged for target prioritization of signalling networks with unknown targets.

Funding

This work was supported in part by a Singapore MOE AcRF Tier 1 Grant RGC 1/13 to SSB and by a Duke-NUS block grant to LTK.

Conflict of Interest: none declared.

References

Chang

C.-C.

et al. . (

2011

)

Libsvm: a library for support vector machines

ACM Trans. Intell. Syst. Technol.

Month:	Total Views:
November 2016	3
December 2016	3
February 2017	9
March 2017	9
May 2017	5
June 2017	5
July 2017	5
August 2017	5
September 2017	3
October 2017	6
November 2017	5
December 2017	13
January 2018	17
February 2018	16
March 2018	25
April 2018	35
May 2018	29
June 2018	21
July 2018	20
August 2018	18
September 2018	11
October 2018	9
November 2018	32
December 2018	13
January 2019	7
February 2019	19
March 2019	21
April 2019	28
May 2019	25
June 2019	18
July 2019	16
August 2019	20
September 2019	24
October 2019	19
November 2019	15
December 2019	18
January 2020	17
February 2020	6
March 2020	15
April 2020	7

Article Contents

TENET: topological feature-based target characterization in signalling networks Free

Abstract

1 Introduction

2 Materials and methods

2.1 Terminology

2.2 Topological feature-based target characterization

2.3 svm-based target characterization

2.4 The Tenet algorithm

2.4.1 Phase 1: Pruning

2.4.2 Phase 2: Feature extraction

2.4.3 Phase 3: Model training

3 Results and discussion

3.1 Performance metrics

3.2 Feature selection

3.3 Effect of varying wmc

3.4 Best Tenet variant

3.5 Comparison with state-of-the-art approaches

4 Conclusions

Funding

References

Author notes

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

Looking for your next opportunity?

This Feature Is Available To Subscribers Only

TENET: topological feature-based target characterization in signalling networks