Fast-SL: an efficient algorithm to identify synthetic lethal sets in metabolic networks

Author Notes

Abstract

Motivation: Synthetic lethal sets are sets of reactions/genes where only the simultaneous removal of all reactions/genes in the set abolishes growth of an organism. Previous approaches to identify synthetic lethal genes in genome-scale metabolic networks have built on the framework of flux balance analysis (FBA), extending it either to exhaustively analyze all possible combinations of genes or formulate the problem as a bi-level mixed integer linear programming (MILP) problem. We here propose an algorithm, Fast-SL, which surmounts the computational complexity of previous approaches by iteratively reducing the search space for synthetic lethals, resulting in a substantial reduction in running time, even for higher order synthetic lethals.

Results: We performed synthetic reaction and gene lethality analysis, using Fast-SL, for genome-scale metabolic networks of Escherichia coli, Salmonella enterica Typhimurium and Mycobacterium tuberculosis. Fast-SL also rigorously identifies synthetic lethal gene deletions, uncovering synthetic lethal triplets that were not reported previously. We confirm that the triple lethal gene sets obtained for the three organisms have a precise match with the results obtained through exhaustive enumeration of lethals performed on a computer cluster. We also parallelized our algorithm, enabling the identification of synthetic lethal gene quadruplets for all three organisms in under 6 h. Overall, Fast-SL enables an efficient enumeration of higher order synthetic lethals in metabolic networks, which may help uncover previously unknown genetic interactions and combinatorial drug targets.

Availability and implementation: The MATLAB implementation of the algorithm, compatible with COBRA toolbox v2.0, is available at https://github.com/RamanLab/FastSL

Contact: [email protected]

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

In the recent years, genome-scale metabolic networks have been reconstructed for many organisms (Edwards and Palsson, 2000; Jamshidi and Palsson, 2007; Kim etal., 2011; Thiele etal., 2005, 2011). These networks have been studied using tools such as flux balance analysis (FBA) (Kauffman et al., 2003; Varma and Palsson, 1994), for the identification of drug targets (Jamshidi and Palsson, 2007; Thiele etal., 2011), targets for metabolic engineering (Alper etal., 2005) and to understand the robustness of organisms through systematic experimental evaluation of gene knockouts (Deutscher etal., 2006; Kuepfer etal., 2005). Another important aspect of analyzing these reconstructed metabolic networks is the identification of combinations of genes, which when simultaneously deleted, abolish growth in silico (Deutscher etal., 2006; Harrison etal., 2007; Henry etal., 2009; Suthers etal., 2009; Güell et al., 2014). These sets, termed ‘synthetic lethals’, reveal complex interactions in metabolic networks. Synthetic lethals have been analyzed in the past for prediction of novel genetic interactions and analyzing the extent of robustness of biological networks (Raghunathan etal., 2009). Prediction of phenotypic behavior on genetic perturbations has also been studied in many reconstructions (Fang etal., 2010; Plata etal., 2010; Sigurdsson etal., 2012; Thiele et al., 2005; Wodke etal., 2013) for model validation.

FBA has been proven to accurately predict phenotypes following various genetic perturbations (Edwards and Palsson, 2000; Famili etal., 2003); previous reports also suggest that FBA can reliably predict synthetic lethal genes in metabolic networks of organisms such as Saccharomyces cerevisiae (Harrison etal., 2007). The identification of synthetic lethal genes in metabolic networks also finds application in combinatorial therapy, as combinatorial deletion strategies are more difficult for the organism to resist (Hartman etal., 2014; Navid, 2011; Zimmermann et al., 2007). Since the systematic evaluation of these targets in vivo is challenging, computational approaches have been of great interest to overcome this difficulty (Pinney etal., 2007).

Exhaustive enumeration of synthetic lethals of higher orders was previously performed by parallelizing the deletions on a cluster of computers (Deutscher etal., 2006; Henry etal., 2009). However, exhaustive enumeration is computationally very expensive, and even prohibitive, in case of larger metabolic networks. Another algorithm for identifying synthetic lethal reactions and genes is ‘SL Finder’, published by Maranas and co-workers (Suthers etal., 2009). SL Finder elegantly poses the identification of synthetic lethals as a bi-level Mixed Integer Linear Programming (MILP) problem; the algorithm has been applied for the identification of synthetic lethal doublets and triplets in Escherichiacoli.

Reaction essentiality has been previously inferred using elementary modes and minimal cut sets (Behre etal., 2008). Even though there are efficient algorithms to analyze minimal cut sets in a metabolic network, the MILP formulation is fundamentally NP-hard (Acuña etal., 2009) and is prohibitive in case of large networks. Other methods also suggest ways for reduction of metabolic networks and alternate formulations to enumerate minimal cut sets for the identification of synthetic lethal sets (Chindelevitch etal., 2014; von Kamp and Klamt, 2014).

We here propose an alternative algorithm, Fast-SL, which circumvents the computational complexity of both exhaustive enumeration and bi-level MILP, through an iterative reduction of the search space for higher order synthetic lethal sets. We also present an efficient method to rigorously identify lethal gene sets, identifying upto quadruple lethal gene sets that were not previously identified. Fast-SL formulation for gene deletions also compares favorably with logical transformation of model (LTM) approach (Zhang etal., 2015), which transforms the stoichiometric matrix such that lethal gene deletion sets can be identified by merely identifying lethal reaction sets applying the Fast-SL algorithm on the transformed matrix (using the pre-print of an earlier version of this paper available at arXiv.org). Fast-SL provides a rapid way to gain insights into the genetic robustness of organisms by identifying synthetic lethal sets even up to the order of four.

2 Methods

2.1 Overview

FBA involves the formulation of a Linear Programming (LP) problem, whose objective function typically is to maximize flux through the biomass reaction (v_bio), subject to the constraints obtained from the stoichiometry of the metabolic network (represented by the stoichiometric matrix S). FBA has also been used to simulate the effects of the removal of one or more genes/reactions from a metabolic network. The phenotype obtained as a result of gene/reaction deletion is classified as a lethal phenotype, if the maximum growth-rate obtained by FBA is less than a specified cut-off, typically 1% of the in silico maximum wild-type growth rate (Deutscher etal., 2008), denoted as v_co. We here propose an alternative algorithm to identify synthetic lethals, using an iterative approach that greatly reduces the search space for the synthetic lethals. The standard FBA formulation to identify effects of reaction deletions is as given below:

max . v_{b i o}

(1)

s . t .

Σ_{j} s_{i j} v_{j} = 0 \forall i \in M, \forall j \in J

(2)

L B_{j} \leq v_{j} \leq U B_{j} \forall j \in J

(3)

v_{d} = 0 d \in D \subset J

(4)

Here,

J represents the set of all reactions in the metabolic model

M represents the set of all metabolites in the metabolic model

D represents the set of reactions whose fluxes are set to zero (for deletion)

v_j represents the flux through the j^th reaction

v _bio represents the flux through the biomass reaction

s_ij represents the corresponding element in the stoichiometric matrix S

LB_j and UB_j represent the lower and upper bounds of the fluxes through the j^th reaction respectively

The maximum v_bio obtained here, using Equations (1)–(3), for the wild-type strain, is designated as $v_{b i o, W T}$ ⁠. Further details on the FBA formulation, such as the substrate uptake fluxes and the upper and lower bounds are given in Supplementary File S1.

2.2 Fast-SL algorithm

The objective of Fast-SL is to enumerate combinations of reactions, which when deleted, abolish growth. We achieve this by a combination of pruning the search space and exhaustively iterating through the remaining combinations. We successively compute: (i) J_sl, the set of single lethal reactions, (ii) J_dl (⁠

J_{d l} \subset J^{2}

⁠), the set of synthetic lethal reaction pairs, and (iii)

J_{t l} \subset J^{3}

⁠, the set of synthetic lethal reaction triplets. Initially, we use FBA to compute a flux distribution, corresponding to maximum growth rate, while minimizing the sum of absolute values of the fluxes, i.e. the

ℓ_{1}

-norm of the flux vector. We hereafter denote this flux distribution as the ‘minimum norm’ solution of the FBA LP problem. We denote the set of reactions that carry a non-zero flux in this minimum norm solution as J_nz. Below, we outline the minimum norm FBA formulation, corresponding to maximum wild-type growth rate obtained earlier (⁠

v_{b i o, W T}

⁠):

min . Σ_{j} | v_{j} |

(5)

s . t .

v_{b i o} = v_{b i o, W T}

(6)

Σ_{j} s_{i j} v_{j} = 0 \forall i \in M, \forall j \in J

(7)

L B_{j} \leq v_{j} \leq U B_{j} \forall j \in J

(8)

2.2.1 Identifying single lethal reactions (J_sl)

If a reaction is essential (single lethal) in a given environment, constraining its flux to zero results in the abolishment of biomass flux. We argue that the set of all such single lethal reactions, J_sl, is completely contained in J_nz. Conversely, $J - J_{n z}$ does not contain any of the single lethal reactions, which are essential for growth in the medium under consideration. This is because, if it is possible to identify a flux distribution that admits maximum biomass flux (as enforced by the constraint in the Equation (6)), and at the same time zero flux through certain reactions (⁠ $D \subset J - J_{n z}$ ⁠), obviously, those reactions cannot be essential for the growth of the organism. This can also be understood in light of the FBA formulation given by Equations (1)–(4): the constraint in Equation (4) for the reactions in the set $D \subset J - J_{n z}$ will not have any impact on the biomass flux (setting v_d = 0 for reactions already carrying zero flux in the minimum norm solution will not affect the solution to FBA). Hence, for the lethality analyses of order one, we look only in the set of reactions with non-zero fluxes, J_nz. We therefore compute single lethal reactions (J_sl) by performing exhaustive single reaction deletions only in J_nz, instead of J.

2.2.2 Identifying double lethal reactions (J_dl)

We posit that for every pair in the set J_dl, at least one of the reactions will be in J_nz. Consider any pair of reactions i and $j \in J$ ⁠. Only two types of such pairs exist:

i and $j \notin J_{n z}$
at least one of i or $j \in J_{n z}$

For pairs of type (i):

Suppose, both reactions of a pair do not belong to J_nz. This implies that both have zero flux through them under the minimum norm formulation and hence deleting them simultaneously does not produce a lethal phenotype and consequently, they do not form a lethal reaction pair. Our algorithm identifies and eliminates such pairs for consideration and hence reduces the search space substantially. Table 2 illustrates the savings obtained in terms of the number of LPs solved in comparison to exhaustive enumeration.

For pairs of type (ii):

For all the other reaction pair combinations (i.e. at least one reaction of a pair $\in J_{n z} - J_{s l}$ ⁠), we first obtain the minimum norm solution after removing a reaction, say, $i \in J_{n z} - J_{s l}$ ⁠, and obtain the set of non-zero fluxes $J_{n z, i}$ ⁠. It is important to note that, under this deletion, the $v_{b i o, W T}$ of Equation (6) will be replaced by the corresponding maximum flux through the biomass reaction after removing the i^th reaction, $v_{b i o, i}$ ⁠. This is because removal of the i^th reaction may not always result in the same maximum value of the wild-type biomass flux, $v_{b i o, W T}$ ⁠, as it was obtained prior to the deletion and constraining so may result in an infeasible solution. Therefore, the RHS in Equation (6) is the maximum biomass obtainable under the deletion of reaction i, denoted as $v_{b i o, i}$ and not $v_{b i o, W T}$ ⁠. Similar to Fast-SL for single lethal reactions, we restrict our search space for potential synthetic double lethal deletions to the set $J_{n z, i} - J_{s l}$ ⁠. Under this configuration, as the reaction i is already removed, a synthetic lethal reaction $j \in J_{n z, i} - J_{s l}$ ⁠, would actually correspond to a lethal reaction pair ${i, j}$ ⁠.

Algorithm 1 shows the Fast-SL implementation to identify lethal single and double reaction deletions as explained above. We illustrate the application of Fast-SL to identify single and double lethal reactions in the E.coli iAF1260 model, as well as the algorithm for identifying lethal reaction triplets, in Supplementary File S1. The algorithm can be further extended to quadruplets and higher orders using a similar approach.

Algorithm 1: Algorithm to identify single and double lethal reaction sets.

Input: SBML model of an organism

Output: Set of single lethal reactions J_sl

Set of double lethal reactions J_dl

Do FBA to obtain the maximum biomass flux for wild-type, $v_{b i o, W T}$

Do FBA to obtain minimum norm solution corresponding to $v_{b i o, W T}$

Identify set of reactions J_nz, having non-zero fluxes

Set $0.01 * v_{b i o, W T}$ as the cut-off for lethality, v_co

for each reaction $i \in J_{n z}$ do

Set the upper and lower bounds of v_i to zero

Do FBA to maximise growth rate, $v_{b i o, i}$

if $v_{b i o, i} \leq v_{c o}$ then

Add i to the set J_sl

endif

Reset bounds on v_i

end for

for each reaction $i \in J_{n z} - J_{s l}$ do

Set the upper and lower bounds of v_i to zero

Do FBA to obtain minimum norm solution corresponding to $v_{b i o, i}$

Identify set of reactions $J_{n z, i}$ ⁠, having non-zero fluxes

for each reaction $j \in J_{n z, i} - J_{s l}$ do

Set the upper and lower bounds of v_j to zero

Do FBA to maximise growth rate $v_{b i o, i j}$

if $v_{b i o, i j} \leq v_{c o}$ then

Add ${i, j}$ to the set J_dl

endif

Reset the bounds on v_j

endfor

Reset bounds on v_i

end for

2.3 Fast-SL algorithm for gene deletions

The synthetic lethal gene deletions can be obtained using a similar approach to that of Fast-SL for lethal reaction deletions by additionally considering the Gene–Protein–Reaction (GPR) associations in the model. As these associations are often ‘many-to-many’, it is non-trivial to identify all the lethal gene sets from lethal reaction sets of the same order. To account for this complexity, Fast-SL groups the reactions based on their GPR associations. Each time a reaction is deleted, other associated reactions are also removed, based on the underlying GPR rules. The lethal reaction sets obtained using this method are then analyzed for lethal gene deletions up to the order of four. Further details on the gene deletion algorithm are available in Supplementary File S1.

We implemented Fast-SL for both reaction and gene deletions in MATLAB (R2013b, The Mathworks Inc.), interfacing with COBRA Toolbox v2.0 (Schellenberger etal., 2011).

2.4 Parallel Fast-SL algorithm

To further improve the time profile of the Fast-SL algorithm, we have developed a parallel version of our algorithm to identify both synthetic lethal reaction and gene sets, which enables us to even identify synthetic lethal quadruplets, within a few hours. Unlike the exhaustive enumeration algorithm, the Fast-SL algorithm by itself is not embarrassingly parallel. However, the enumeration of a particular order of synthetic lethals can be easily parallelized. For example, in the case of single lethal reactions, once the minimized $ℓ_{1}$ -norm solution is identified, the subsequent LPs to be solved for identifying J_sl can be evaluated in parallel. A similar strategy can be applied to first identify the potential synthetic lethal sets (reaction sets with non-zero fluxes, obtained using the $ℓ_{1}$ -norm solution) at each stage of a particular order and then perform the deletions in parallel to further reduce the time taken to identify synthetic lethal reaction and gene sets. This parallelization scheme ensures a superior utilization of computing resources available.

3 Results

We performed gene and reaction deletions up to the order of four using Fast-SL for the genome-scale metabolic networks of E.coliiAF1260 (Feist etal., 2007) and two important pathogenic organisms, Salmonellaenterica Typhimurium LT2 STM_v1.0 (Thiele etal., 2011) and Mycobacterium tuberculosis iNJ661 (Jamshidi and Palsson, 2007).

3.1 Fast-SL massively prunes the search space for synthetic lethal reactions

The Fast-SL formulation eliminates large sections of the search space for synthetic lethals, as described earlier, resulting in a massive speed-up over exhaustive search. Fast-SL formulation results in more than a 4000-fold reduction in the search space for synthetic lethal triplets in E.coli; for a smaller model such as that of M.tuberculosis with 1028 reactions, the reduction is over 300-fold.

In order to appreciate the speed-up offered by Fast-SL, consider the E.coliiAF1260 model that has 2 382 reactions. For aerobic growth under minimal glucose conditions, the maximum wild-type growth rate as obtained by FBA, $v_{b i o, W T}$ ⁠, is 0.9290 mmol gDW^–1 h^–¹. The minimum norm formulation, given by Equations (5)–(8), results in a flux vector having 406 reactions with non-zero fluxes, and the same growth rate, $v_{b i o, W T}$ ⁠. The set J_nz comprises of these 406 reactions. As mentioned earlier, Fast-SL analyzes the effect of deletion of reactions in J_nz to identify lethal reaction sets: we identified 278 single lethal reactions (J_sl) after solving only 379 LP problems instead of 2 051. Extending this formulation, Fast-SL identified 1.56 million reaction pairs whose deletion would not result in a lethal phenotype and solved only 6 084 LPs to identify lethal reaction pairs. We have identified 96 synthetic lethal reaction pairs and 247 synthetic lethal reaction triplets in E.coli, which match exactly with the results obtained through exhaustive enumeration of lethal reaction sets and also the MCSEnumerator Algorithm (von Kamp and Klamt, 2014).

Table 1 illustrates the comparison between the MCSEnumerator and the Fast-SL for the E.coli model, using workstation with a 2.4 GHz Intel Xeon E5645 processor with six cores available for computation, it takes approximately 9.3 h for the Fast-SL algorithm to compute the synthetic lethal quadruplets, J_ql. While, it has been reported that the MCSEnumerator method takes approximately 18.5 h using two 3.07 GHz Xeon X5650 processors with 12 cores available for the computation of J_ql.

Table 1.

Open in new tab

Comparison of the time taken for Fast-SL and MCSEnumerator algorithms for the E.coli iAF1260 model

Order of SLs	No. of SLs	CPU time taken for MCSEnumerator (using 12 cores)	CPU time taken for Fast-SL Algorithm (using 6 cores)
Single	278	11 s	2.8 s
Double	96	39.1 s	17.2 s
Triple	247	16.8 min	8.5 min
Quadruple	402	18.5 h	9.3 h

Order of SLs	No. of SLs	CPU time taken for MCSEnumerator (using 12 cores)	CPU time taken for Fast-SL Algorithm (using 6 cores)
Single	278	11 s	2.8 s
Double	96	39.1 s	17.2 s
Triple	247	16.8 min	8.5 min
Quadruple	402	18.5 h	9.3 h

Notes: The times reported are for a workstation with a 2.4 GHz Intel Xeon E5645 processor with 16 GB DDR3 RAM running Windows 8.1 using the IBM CPLEX v12.5.1 solver

Table 1.

Open in new tab

Comparison of the time taken for Fast-SL and MCSEnumerator algorithms for the E.coli iAF1260 model

Order of SLs	No. of SLs	CPU time taken for MCSEnumerator (using 12 cores)	CPU time taken for Fast-SL Algorithm (using 6 cores)
Single	278	11 s	2.8 s
Double	96	39.1 s	17.2 s
Triple	247	16.8 min	8.5 min
Quadruple	402	18.5 h	9.3 h

Order of SLs	No. of SLs	CPU time taken for MCSEnumerator (using 12 cores)	CPU time taken for Fast-SL Algorithm (using 6 cores)
Single	278	11 s	2.8 s
Double	96	39.1 s	17.2 s
Triple	247	16.8 min	8.5 min
Quadruple	402	18.5 h	9.3 h

Notes: The times reported are for a workstation with a 2.4 GHz Intel Xeon E5645 processor with 16 GB DDR3 RAM running Windows 8.1 using the IBM CPLEX v12.5.1 solver

It has been reported that the SL Finder algorithm (Suthers etal., 2009) is able to enumerate all synthetic lethal triple reaction sets in $\approx 6.75$ days, on a 3 GHz processor. We have been unable to perform a systematic comparison owing to the difference in platforms (General Algebraic Modelling System (GAMS) versus MATLAB), as well as processors used. However, we note that the savings obtained through a pruning of reaction space and the fact that we solve only a large number of small LPs instead of a bi-level MILP, render Fast-SL as a powerful alternative for metabolic networks of any size.

Table 2 enumerates the number of LPs solved by the proposed algorithm as compared to the exhaustive enumeration for all three organisms. For each of the three models under consideration, Fast-SL provides a significant reduction in the search-space for the enumeration of synthetic lethal reaction sets. A complete listing of lethal reaction sets for all three organisms is available in Supplementary File S2.

Table 2.

Open in new tab

Summary of reaction deletions for the three organisms under consideration

	E.coli	S.Typhimurium	M. tuberculosis
Model Name	iAF1260	STM_v1.0	iNJ661
Medium	M9/glc	M9/glc	Middlebrook 7H9
Number of reactions, $\| J \|$	2382	2546	$1028$
Number of exchange and diffusion reactions^a	331	378	86
Number of reactions in J_nz	406	484	414

Single lethal reactions J_sl

Exhaustive LPs^b	2051	2168	939
LPs solved by Fast-SL	379	456	399
Number of single lethal reactions	278	329	309

Lethal reaction pairs J_dl

Exhaustive LPs solved	$1.57 \times 10^{6}$	$1.69 \times 10^{6}$	$2.00 \times 10^{5}$
LPs solved by Fast-SL	$6084$	$9803$	$5058$
Number of lethal reaction pairs	96	152	75

Lethal reaction triplets J_tl

Exhaustive LPs solved	$9.27 \times 10^{8}$	$1.04 \times 10^{9}$	$4.21 \times 10^{7}$
LPs solved by Fast-SL	223 469	$460 142$	$177 000$
Number of lethal reaction triplets	247	275	140

Lethal reaction quadruplets J_ql

Exhaustive LPs	$4.10 \times 10^{11}$	$4.75 \times 10^{11}$	$6.63 \times 10^{9}$
LPs solved by Fast-SL	$1.43 \times 10^{7}$	$3.01 \times 10^{7}$	$1.19 \times 10^{7}$
Number of lethal reaction quadruplets	402	1008	463

	E.coli	S.Typhimurium	M. tuberculosis
Model Name	iAF1260	STM_v1.0	iNJ661
Medium	M9/glc	M9/glc	Middlebrook 7H9
Number of reactions, $\| J \|$	2382	2546	$1028$
Number of exchange and diffusion reactions^a	331	378	86
Number of reactions in J_nz	406	484	414

Single lethal reactions J_sl

Exhaustive LPs^b	2051	2168	939
LPs solved by Fast-SL	379	456	399
Number of single lethal reactions	278	329	309

Lethal reaction pairs J_dl

Exhaustive LPs solved	$1.57 \times 10^{6}$	$1.69 \times 10^{6}$	$2.00 \times 10^{5}$
LPs solved by Fast-SL	$6084$	$9803$	$5058$
Number of lethal reaction pairs	96	152	75

Lethal reaction triplets J_tl

Exhaustive LPs solved	$9.27 \times 10^{8}$	$1.04 \times 10^{9}$	$4.21 \times 10^{7}$
LPs solved by Fast-SL	223 469	$460 142$	$177 000$
Number of lethal reaction triplets	247	275	140

Lethal reaction quadruplets J_ql

Exhaustive LPs	$4.10 \times 10^{11}$	$4.75 \times 10^{11}$	$6.63 \times 10^{9}$
LPs solved by Fast-SL	$1.43 \times 10^{7}$	$3.01 \times 10^{7}$	$1.19 \times 10^{7}$
Number of lethal reaction quadruplets	402	1008	463

^aGenerally not considered for lethality analyses

^bExcluding exchange reactions

Table 2.

Open in new tab

Summary of reaction deletions for the three organisms under consideration

	E.coli	S.Typhimurium	M. tuberculosis
Model Name	iAF1260	STM_v1.0	iNJ661
Medium	M9/glc	M9/glc	Middlebrook 7H9
Number of reactions, $\| J \|$	2382	2546	$1028$
Number of exchange and diffusion reactions^a	331	378	86
Number of reactions in J_nz	406	484	414

Single lethal reactions J_sl

Exhaustive LPs^b	2051	2168	939
LPs solved by Fast-SL	379	456	399
Number of single lethal reactions	278	329	309

Lethal reaction pairs J_dl

Exhaustive LPs solved	$1.57 \times 10^{6}$	$1.69 \times 10^{6}$	$2.00 \times 10^{5}$
LPs solved by Fast-SL	$6084$	$9803$	$5058$
Number of lethal reaction pairs	96	152	75

Lethal reaction triplets J_tl

Exhaustive LPs solved	$9.27 \times 10^{8}$	$1.04 \times 10^{9}$	$4.21 \times 10^{7}$
LPs solved by Fast-SL	223 469	$460 142$	$177 000$
Number of lethal reaction triplets	247	275	140

Lethal reaction quadruplets J_ql

Exhaustive LPs	$4.10 \times 10^{11}$	$4.75 \times 10^{11}$	$6.63 \times 10^{9}$
LPs solved by Fast-SL	$1.43 \times 10^{7}$	$3.01 \times 10^{7}$	$1.19 \times 10^{7}$
Number of lethal reaction quadruplets	402	1008	463

	E.coli	S.Typhimurium	M. tuberculosis
Model Name	iAF1260	STM_v1.0	iNJ661
Medium	M9/glc	M9/glc	Middlebrook 7H9
Number of reactions, $\| J \|$	2382	2546	$1028$
Number of exchange and diffusion reactions^a	331	378	86
Number of reactions in J_nz	406	484	414

Single lethal reactions J_sl

Exhaustive LPs^b	2051	2168	939
LPs solved by Fast-SL	379	456	399
Number of single lethal reactions	278	329	309

Lethal reaction pairs J_dl

Exhaustive LPs solved	$1.57 \times 10^{6}$	$1.69 \times 10^{6}$	$2.00 \times 10^{5}$
LPs solved by Fast-SL	$6084$	$9803$	$5058$
Number of lethal reaction pairs	96	152	75

Lethal reaction triplets J_tl

Exhaustive LPs solved	$9.27 \times 10^{8}$	$1.04 \times 10^{9}$	$4.21 \times 10^{7}$
LPs solved by Fast-SL	223 469	$460 142$	$177 000$
Number of lethal reaction triplets	247	275	140

Lethal reaction quadruplets J_ql

Exhaustive LPs	$4.10 \times 10^{11}$	$4.75 \times 10^{11}$	$6.63 \times 10^{9}$
LPs solved by Fast-SL	$1.43 \times 10^{7}$	$3.01 \times 10^{7}$	$1.19 \times 10^{7}$
Number of lethal reaction quadruplets	402	1008	463

^aGenerally not considered for lethality analyses

^bExcluding exchange reactions

3.2 Fast-SL rigorously identifies synthetic lethal genes

Fast-SL carefully considers the GPR associations to rigorously identify synthetic lethal gene deletions up to order four for the organisms. Table 3 shows the number of lethal gene deletions identified for the organisms under consideration. We corroborated these results by performing exhaustive triple gene deletions on a computer cluster with 1000 nodes for all three organisms and we found an exact match.

Table 3.

Open in new tab

Summary of gene deletions for the three organisms under consideration

	E.coli	S.Typhimurium	M.tuberculosis
Model name	iAF1260	STM_v1.0	iNJ661
Number of genes	1260	1270	661

Single lethal genes

Exhaustive LPs	1260	1270	661
LPs solved by Fast-SL	389	464	355
Number of single lethal genes	188	201	188

Lethal gene pairs

Exhaustive LPs	574 056	570 846	111 628
LPs solved Fast-SL	$3644$	3202	2470
Number of lethal gene pairs	69	87	49

Lethal gene triplets

Exhaustive LPs	$2.04 \times 10^{8}$	$2.03 \times 10^{8}$	$1.75 \times 10^{7}$
Number of processors used	896	896	448
Equivalent serial time	$\approx 689$ days	$\approx 944$ days	$\approx 19$ days
LPs solved by Fast-SL	$109 180$	97 641	55 967
Time taken for Fast-SL	321 s	329 s	145 s
Number of lethal gene triplets	285	175	333

Lethal gene quadruplets

Exhaustive LPs	$5.47 \times 10^{10}$	$5.41 \times 10^{10}$	$2.06 \times 10^{9}$
LPs solved by Fast-SL	$2.54 \times 10^{6}$	$2.32 \times 10^{6}$	$9.39 \times 10^{5}$
Time taken for Fast-SL	1.91 h	2.35 h	0.89 h
Number of lethal gene quadruplets	376	445	1804

	E.coli	S.Typhimurium	M.tuberculosis
Model name	iAF1260	STM_v1.0	iNJ661
Number of genes	1260	1270	661

Single lethal genes

Exhaustive LPs	1260	1270	661
LPs solved by Fast-SL	389	464	355
Number of single lethal genes	188	201	188

Lethal gene pairs

Exhaustive LPs	574 056	570 846	111 628
LPs solved Fast-SL	$3644$	3202	2470
Number of lethal gene pairs	69	87	49

Lethal gene triplets

Exhaustive LPs	$2.04 \times 10^{8}$	$2.03 \times 10^{8}$	$1.75 \times 10^{7}$
Number of processors used	896	896	448
Equivalent serial time	$\approx 689$ days	$\approx 944$ days	$\approx 19$ days
LPs solved by Fast-SL	$109 180$	97 641	55 967
Time taken for Fast-SL	321 s	329 s	145 s
Number of lethal gene triplets	285	175	333

Lethal gene quadruplets

Exhaustive LPs	$5.47 \times 10^{10}$	$5.41 \times 10^{10}$	$2.06 \times 10^{9}$
LPs solved by Fast-SL	$2.54 \times 10^{6}$	$2.32 \times 10^{6}$	$9.39 \times 10^{5}$
Time taken for Fast-SL	1.91 h	2.35 h	0.89 h
Number of lethal gene quadruplets	376	445	1804

Table 3.

Open in new tab

Summary of gene deletions for the three organisms under consideration

	E.coli	S.Typhimurium	M.tuberculosis
Model name	iAF1260	STM_v1.0	iNJ661
Number of genes	1260	1270	661

Single lethal genes

Exhaustive LPs	1260	1270	661
LPs solved by Fast-SL	389	464	355
Number of single lethal genes	188	201	188

Lethal gene pairs

Exhaustive LPs	574 056	570 846	111 628
LPs solved Fast-SL	$3644$	3202	2470
Number of lethal gene pairs	69	87	49

Lethal gene triplets

Exhaustive LPs	$2.04 \times 10^{8}$	$2.03 \times 10^{8}$	$1.75 \times 10^{7}$
Number of processors used	896	896	448
Equivalent serial time	$\approx 689$ days	$\approx 944$ days	$\approx 19$ days
LPs solved by Fast-SL	$109 180$	97 641	55 967
Time taken for Fast-SL	321 s	329 s	145 s
Number of lethal gene triplets	285	175	333

Lethal gene quadruplets

Exhaustive LPs	$5.47 \times 10^{10}$	$5.41 \times 10^{10}$	$2.06 \times 10^{9}$
LPs solved by Fast-SL	$2.54 \times 10^{6}$	$2.32 \times 10^{6}$	$9.39 \times 10^{5}$
Time taken for Fast-SL	1.91 h	2.35 h	0.89 h
Number of lethal gene quadruplets	376	445	1804

	E.coli	S.Typhimurium	M.tuberculosis
Model name	iAF1260	STM_v1.0	iNJ661
Number of genes	1260	1270	661

Single lethal genes

Exhaustive LPs	1260	1270	661
LPs solved by Fast-SL	389	464	355
Number of single lethal genes	188	201	188

Lethal gene pairs

Exhaustive LPs	574 056	570 846	111 628
LPs solved Fast-SL	$3644$	3202	2470
Number of lethal gene pairs	69	87	49

Lethal gene triplets

Exhaustive LPs	$2.04 \times 10^{8}$	$2.03 \times 10^{8}$	$1.75 \times 10^{7}$
Number of processors used	896	896	448
Equivalent serial time	$\approx 689$ days	$\approx 944$ days	$\approx 19$ days
LPs solved by Fast-SL	$109 180$	97 641	55 967
Time taken for Fast-SL	321 s	329 s	145 s
Number of lethal gene triplets	285	175	333

Lethal gene quadruplets

Exhaustive LPs	$5.47 \times 10^{10}$	$5.41 \times 10^{10}$	$2.06 \times 10^{9}$
LPs solved by Fast-SL	$2.54 \times 10^{6}$	$2.32 \times 10^{6}$	$9.39 \times 10^{5}$
Time taken for Fast-SL	1.91 h	2.35 h	0.89 h
Number of lethal gene quadruplets	376	445	1804

Fast-SL identified 285 lethal gene triplets under minimal glucose conditions in the E.coliiAF1260 model. The SL Finder algorithm (Suthers etal., 2009) identified only 158 lethal gene triplets (in the same model under the same medium conditions). We thus identified 127 new lethal gene triplets in E.coli using Fast-SL. Perhaps, these triplets were not identified by SL Finder owing to the complexity in defining the binary variable for gene deletions using the bi-level MILP formulation. To accommodate the gene–reaction associations, the SL Finder approach introduces new binary variables (corresponding to genes) and imposes additional constraints on them (corresponding to gene–reaction rules). This introduction of new variables and constraints would increase the problem size significantly depending upon the number of genes present in the model as well as the gene-reaction rules, which may add to the difficulty in identification of all the lethal gene sets using the SL Finder approach.

Among the newly identified triplets using Fast-SL, 121 belong to central carbon metabolism, four triplets belong to amino acid synthesis and the rest are involved in metal-ion transport reactions. More information on these 127 gene triplets obtained can be found in Supplementary File S3. Using the parallel Fast-SL algorithm we were able to identify lethal gene quadruple sets for all the three organisms in less than 6 h. A complete listing of lethal gene sets for all three organisms is available in Supplementary File S4.

3.3 Missing biomass precursors in lethal gene deletions

To further demonstrate why certain deletions are lethal for the organism’s survival, we identified the missing precursor metabolites for the synthetic lethal gene sets in E.coli using the method available from the COBRA Toolbox (Schellenberger etal., 2011). Under the FBA formulation, failure of an organism to produce any of the biomass precursors results in a zero growth-rate. Figure 1 summarizes our findings for the given biomass configuration in (Feist etal., 2007). The biomass of E.coli comprises amino acids, cofactors, inorganic ions, lipids, lipopolysaccharides (LPS), metabolites required for maintenance (ATP), murein and nucleic acids. From the lethal single and double gene deletion sets obtained using Fast-SL, we identified that they predominantly involve non-production of essential metabolites such as tetrahydrofolates, Coenzyme A and S-Adenosyl methionine. Interestingly, more than 30% of the deletions in synthetic lethal triplets and quadruplets primarily affect mechanisms involved in ATP production required for maintenance. In 48 of the quadruple lethal gene sets, we observed that the organism is unable to produce more than 70% of the biomass precursors under consideration, belonging to all metabolite groups except the inorganic ions (as their exchanges are unaffected under these deletions). These observations reiterate the robustness of cellular metabolism and at the same time, the central and critical role played by co-factors and ATP.

Fig. 1

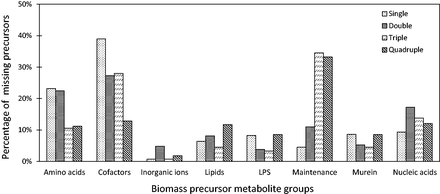
Missing biomass precursors under lethal gene deletions in Escherichia coli . The biomass constituents are classified into eight different groups as given in the model, namely, amino acids, cofactors, inorganic ions, lipids, lipopolysaccharides (LPS), metabolites required for maintenance (ATP), murein and nucleic acids. The figure illustrates the percentage of missing biomass precursors under single, double, triple and quadruple lethal gene deletions

Open in new tab Download slide

It is important to note that approximately 14% of all lethal deletions (up to order four) result in a non-zero, but severely hampered, growth rate (here it is less than 1% of the maximum wild-type growth rate, $v_{b i o, W T}$ ⁠) and therefore do not have any missing precursors under the optimal FBA configuration.

4 Discussion

In this study, we describe a new algorithm to rapidly identify synthetic lethal reaction/gene sets in genome-scale metabolic networks. The identification of synthetic lethals in organisms can be used to understand complex genetic interactions between genes and identify drug targets for combinatorial therapy (Kim etal., 2011; Lee et al., 2009; Sigurdsson etal., 2012). We build on the popular framework of FBA, extending it to identify synthetic lethals; our algorithm exploits the structure of the metabolic network better than previous algorithms, to eliminate combinations of reactions/genes that are guaranteed not to produce a lethal phenotype under the conditions considered.

Importantly, our algorithm also identifies synthetic lethal gene sets rigorously, by carefully considering the GPR associations in the metabolic model. Fast-SL therefore manages to identify 127 new lethal gene triplets in E.coli, which were not identified by a previous study (Suthers etal., 2009) (indicated in Supplementary File S3). Further, we confirmed that our algorithm does not miss out on any synthetic lethal gene sets, by cross-checking with an exhaustive analysis of triple gene deletions on a computer cluster. Our algorithm for finding synthetic lethal gene sets also outperforms the LTM method (Zhang etal., 2015) which increases the problem size in the case of E.coli from 1668 × 2382 to 5372 × 7287. For the same model, our approach avoids this transformation and consequently solves far fewer LPs, thereby computing the lethal sets in much less time.

Fast-SL utilizes the flux corresponding to $ℓ_{1}$ -norm minimization, which can be easily formulated as an LP. It is important to note that there may be multiple J_nz sets corresponding to the minimum sum of absolute values of fluxes (i.e. minimized $ℓ_{1}$ -norm solution) and these J_nz sets may also vary in terms of their sizes. It does not matter which J_nz set one may begin the algorithm with, because in all the J_nz sets, the arguments that J_sl is completely contained in J_nz and at least one of i or j of a lethal pair (i, j) belongs to J_nz and so on, always hold true. However, smaller the size of the set J_nz in each step, faster the algorithm would be. More importantly, minimization of the $ℓ_{1}$ -norm of the flux vector may not always converge to the sparsest possible solution, which is often denoted as the $ℓ_{0}$ -norm solution. Here, it is also important to note that Fast-SL does not require the sparsest solution to work; a reasonably sparse solution already achieves a significant search space reduction, while circumventing the complexity of the $ℓ_{0}$ -norm MILP formulation.

Our work does have its limitations. As with any other metabolic network analysis technique, our method suffers from any inadequacies present in the model. Nevertheless, our algorithm can identify a list of lethal (and non-lethal) phenotypes, which can be used to refine the metabolic model, based on disagreements with experimental results. Further, the synthetic lethals predicted by our algorithm are valid only in a particular environment/growth medium; it is however straightforward to identify lethal sets for other environments, by altering the constraints suitably.

In sum, we see three main contributions of our method. First, Fast-SL achieves a massive reduction in the search space and obviates the need for performing an exhaustive analysis of combinatorial gene/reaction deletions. This can facilitate the identification of combinatorial drug targets in organisms, even up to the order of four, which was previously nearly intractable (Navid, 2011). Second, Fast-SL also compares favorably with the MCSEnumerator algorithm, eliminating the need to solve complex MILPs. Finally, Fast-SL also rigorously identifies lethal gene sets, uncovering lethal gene sets not previously identified by other algorithms. Overall, Fast-SL enables a rapid evaluation of combinatorial gene and reaction deletions in genome-scale metabolic networks, which may help identify previously unknown genetic interactions and combinatorial drug targets.

Acknowledgements

The authors thank Dr. Rupesh Nasre and Aarthi Ravikrishnan for useful discussions and critical reading of the manuscript. The use of the high-performance computing facility HPCE at IIT Madras is also gratefully acknowledged. The authors also thank three anonymous reviewers for a critical reading of the manuscript and valuable suggestions.

Funding

K.R. acknowledges funding from IIT Madras and the grant BT/PR4949/BRB/10/1048/2012 from the Department of Biotechnology, Government of India.

Conflict of Interest: none declared.

References

Acuña

et al. . (

2009

Modes and cuts in metabolic networks: complexity and algorithms

Biosystems

–

Month:	Total Views:
November 2016	6
December 2016	4
January 2017	12
February 2017	21
March 2017	29
April 2017	14
May 2017	26
June 2017	25
July 2017	22
August 2017	28
September 2017	24
October 2017	23
November 2017	12
December 2017	43
January 2018	48
February 2018	34
March 2018	50
April 2018	55
May 2018	40
June 2018	51
July 2018	48
August 2018	41
September 2018	23
October 2018	29
November 2018	47
December 2018	23
January 2019	22
February 2019	31
March 2019	64
April 2019	58
May 2019	43
June 2019	43
July 2019	39
August 2019	59
September 2019	36
October 2019	28
November 2019	40
December 2019	31
January 2020	40
February 2020	26

Article Contents

Fast-SL: an efficient algorithm to identify synthetic lethal sets in metabolic networks Free

Abstract

1 Introduction

2 Methods

2.1 Overview

2.2 Fast-SL algorithm

2.2.1 Identifying single lethal reactions (Jsl)

2.2.2 Identifying double lethal reactions (Jdl)

2.3 Fast-SL algorithm for gene deletions

2.4 Parallel Fast-SL algorithm

3 Results

3.1 Fast-SL massively prunes the search space for synthetic lethal reactions

3.2 Fast-SL rigorously identifies synthetic lethal genes

3.3 Missing biomass precursors in lethal gene deletions

4 Discussion

Acknowledgements

Funding

References

Author notes

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

Looking for your next opportunity?

This Feature Is Available To Subscribers Only

Fast-SL: an efficient algorithm to identify synthetic lethal sets in metabolic networks

2.2.1 Identifying single lethal reactions (J_sl)

2.2.2 Identifying double lethal reactions (J_dl)