Assembling short reads from jumping libraries with large insert sizes

Author Notes

Abstract

Motivation: Advances in Next-Generation Sequencing technologies and sample preparation recently enabled generation of high-quality jumping libraries that have a potential to significantly improve short read assemblies. However, assembly algorithms have to catch up with experimental innovations to benefit from them and to produce high-quality assemblies.

Results: We present a new algorithm that extends recently described exSPAnder universal repeat resolution approach to enable its applications to several challenging data types, including jumping libraries generated by the recently developed Illumina Nextera Mate Pair protocol. We demonstrate that, with these improvements, bacterial genomes often can be assembled in a few contigs using only a single Nextera Mate Pair library of short reads.

Availability and implementation: Described algorithms are implemented in C++ as a part of SPAdes genome assembler, which is freely available at bioinf.spbau.ru/en/spades.

Contact: [email protected]

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

In an article titled ‘De novo fragment assembly with short mate-paired reads: Does the read length matter?’, Chaisson etal. (2009) argued that availability of paired reads with long and accurate insert sizes (rather than the increase in the read length) is the most important factor for improving the quality of short read assemblies. However, while paired reads with long insert sizes have been extensively used in many assembly projects, robust generation of read-pairs with accurate insert sizes proved to be difficult and have only been achieved recently.

The recently emerged sample preparation technologies open new opportunities for genome assembly from short reads. For example, Illumina Nextera Mate Pair protocol generates long inserts (3 kb and longer) that feature rather tight insert size distribution and small rate of non-circularized fragments that result in read-pairs with abnormal distances. As discussed in Chaisson etal. (2009), such read-pair libraries may enable assemblies approaching the quality of assemblies from long reads of length equal to the insert size. Moreover, they can potentially substitute the existing assembly approaches based on a combination of short paired-end libraries (with insert size less than 1 kb) and long jumping libraries (with insert sizes typically longer than 1 kb) by a pipeline based on a single Nextera Mate Pair library.

However, even though the popular assembly algorithms perform well with the previously proposed approaches to sample preparation, they have not kept up with recent experimental innovations. To catch up, bioinfomaticians either need to design novel tools for every technology improvement or to develop a universal assembler that can be easily modified to support new data types. For example, Ray (Boisvert etal., 2010) and SPAdes (Bankevich etal., 2012) [with the recently implemented exSPAnder (Prjibelski etal., 2014) algorithm] use similar approach to repeat resolution that can be adapted for new types of sequencing data. However, the recently proposed Nextera Mate Pair libraries present new computational challenges that go beyond the algorithmic framework of both Ray and SPAdes. In this work, we describe several algorithmic advances to exSPAnder that allows one to efficiently utilize jumping libraries and to perform assembly using only high-quality Nextera Mate Pair libraries.

The exSPAnder algorithm (Prjibelski etal., 2014) is based on the path extension framework that was proposed by the authors of the Ray assembler (Boisvert etal., 2010) and later implemented in the Telescoper (Bresler etal., 2012) and PERGA (Zhu etal., 2014) assemblers. Given a path P in the assembly graph (Bankevich etal., 2012; Prjibelski etal., 2014), exSPAnder iteratively attempts to grow it by choosing one of its extension edges (all edges starting at the terminal vertex of the path P). The assembly graph is defined as simplified de Bruijn graph (Pevzner etal., 2001) of k-mers in reads after removal of bulges, tips and chimeric edges.

To extend a path P, exSPAnder computes the scoring function ${Score}_{P} (e)$ for each extension edge e using read-pairs with one read mapping to P and another read mapping to e (further referred to as (P, e)-connecting read-pairs). Afterward, exSPAnder decides whether to select the top-scoring extension edge or to stop growing P. It iteratively repeats the path extension procedure starting with single-edge paths until every edge in the assembly graph is covered by at least one path and no path can be extended further. To generate equivalent contigs on both strands, exSPAnder is implemented as a bidirectional approach that can extend a path in both directions.

While the scoring function ${Score}_{P} (e)$ described in Prjibelski etal. (2014) works well with short libraries, it appears to be rather inefficient when using jumping libraries. The key limitation of the previously defined scoring function is that it analyses only (P, e)-connecting read-pairs (where e is an extension edge of path P) and ignores read-pairs that connect path P with other edges. When an edge e is short and the variations in the insert sizes are large, there is a danger that no (P, e)-connecting read-pairs exist and thus $Score (P, e) = 0$ even if e is the correct extension edge (Fig. 1). Thus, the decision rule may stop extending path P or even select an incorrect extension edge. Additionally, the approach described in Prjibelski etal. (2014) is inapplicable for scaffolding procedure, since it is unable to jump over coverage gaps. In this article, we extend the exSPAnder approach to scaffolding. This extension is important since scaffolding with jumping libraries may dramatically improve the assembly quality.

Fig. 1.

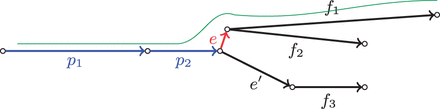
An example of the assembly graph with path $P = (p_{1}, p_{2})$ (blue) and its correct short extension edge e (red). In this case, there may be no (P, e)-connecting read-pairs, but there may be $(P, f_{1})$ -connecting read-pairs since the correct genomic path includes the path (p₁, p₂, e, f₁), which is shown in green above the graph

Open in new tab Download slide

We describe several algorithms that address these bottlenecks based on the following idea. Consider a set of extension paths $E$ [rather than extension edges as in Prjibelski etal. (2014)] that contain all sufficiently long paths (longer than the insert size) starting from the extension edges of the path P. Once the set $E$ is constructed, we choose the best-scoring path E in $E$ and extend path P by the first edge of E. Our analysis has shown that such conservative extension (by the first edge of the best-scoring extension path rather than by the entire path) provides more accurate assemblies. To perform scaffolding procedure, we allow extension paths to ‘jump’ over coverage gaps in the assembly graph.

This intuitive approach, while appealing, is often impractical since the assembly graph is usually tangled, resulting in a prohibitively large number of extension paths. To reduce the running time, we have implemented the new algorithm based on the observation that, instead of the exhaustive search through the set of all extension paths, one can significantly prune this set using single reads and paired-end libraries (if available).

We demonstrate that the new algorithm enables assemblies of nearly complete genomes from a single Nextera Mate Pair library. We also show that SPAdes, coupled with the improved exSPAnder algorithm, outperforms other popular assemblers, such as ABySS (Simpson etal., 2009), IDBA-UD (Peng etal., 2012), Ray (Boisvert etal., 2010), SOAPdenovo (Li etal., 2010) and Velvet (Zerbino and Birney, 2008) on various types of datasets.

2 Methods

2.1 The exSPAnder framework

2.1.1 Rectangles

exSPAnder utilizes the concept of the rectangle graph introduced by Bankevich et al. (2012) and further developed in (Vyahhi etal., 2012). Let e and $e'$ be edges in the assembly graph (see (Bankevich etal., 2012) for the construction of the assembly graph) separated by a known distance D and $(r, r')$ be a read-pair, such that read r maps to e at position x₀ and read $r'$ maps to $e'$ at position y₀ (Fig. 2a). We note that while D is not known a priori, exSPAnder only considers edges that are connected by a previously constructed path, which unambiguously defines distance D.

(a) A read-pair (r,r′) mapping to edges e and e′ in the assembly graph at positions x0 and y0, respectively. (b) Read-pair (r,r′) is represented as a point (x0, y0) in the rectangle (e,e′). (c) Since the insert size varies, most read-pairs correspond to the points scattered within the confidence strip in the rectangle (e,e′). (d) An example of a composite rectangle formed by paths P=(p1,p2,p3) and E=(e1,e2,e3), which consists of nine simple rectangles. Note that the confidence strip crosses only five out of nine simple rectangles. The points outside the confidence strip appear in eight out of nine simple rectangles and represent read-pairs with abnormal insert sizes

Fig. 2.

(a) A read-pair $(r, r')$ mapping to edges e and $e'$ in the assembly graph at positions x₀ and y₀, respectively. (b) Read-pair $(r, r')$ is represented as a point (x₀, y₀) in the rectangle $(e, e')$ ⁠. (c) Since the insert size varies, most read-pairs correspond to the points scattered within the confidence strip in the rectangle $(e, e')$ ⁠. (d) An example of a composite rectangle formed by paths $P = (p_{1}, p_{2}, p_{3})$ and $E = (e_{1}, e_{2}, e_{3})$ ⁠, which consists of nine simple rectangles. Note that the confidence strip crosses only five out of nine simple rectangles. The points outside the confidence strip appear in eight out of nine simple rectangles and represent read-pairs with abnormal insert sizes

Open in new tab Download slide

Figure 2b shows the read-pair

(r, r')

represented as a point (x₀, y₀) within the rectangle formed by the edges e and

e'

⁠. We further refer to this rectangle simply as

(e, e')

⁠. Because of variations in the insert sizes, real read-pairs connecting edges e and

e'

typically correspond to the points that are scattered in the confidence strip—a strip between the

45 °

lines

y = x - d_{min}

and

y = x - d_{max}

within the rectangle

(e, e')

(Fig. 2c), where

\begin{matrix} d_{min} = D - I_{min} + ReadLength, \\ d_{max} = D - I_{max} + ReadLength. \end{matrix}

Here, $[I_{min}, I_{max}]$ is the confidence interval of the insert size distribution defined as the smallest insert size interval that contains at least 80% of read-pairs. Since reads may have variable lengths (e.g. after quality trimming or error correction), we set ReadLength as the maximal read length across all reads in the current library.

2.1.2 The decision rule

The decision rule relies on the scoring function that will be described in the next section. To extend a path P, we score all extension edges $e_{1}, \dots, e_{n}$ and select e_i as a correct extension if the following conditions are met:

${Score}_{P} (e_{i}) > C \cdot {Score}_{P} (e_{j})$ for all $j \neq i$
${Score}_{P} (e_{i}) > Θ$

Here, C and Θ are the exSPAnder parameters described in (Prjibelski etal., 2014). If no extension edge meets these conditions, the algorithm stops growing path P.

In the case of multiple read-pair libraries, we process them in the order of increasing insert sizes until a certain library provides an extension edge satisfying the decision rule. We stop growing path P if no library provides an extension edge satisfying this rule. Processing libraries in a step-by-step fashion (rather than incorporating all libraries at once) has proven to result in more accurate and continuous assemblies.

2.2 Scoring function

Given a path

P = (p_{1}, p_{2}, \dots, p_{n})

and its extension path

E = (e_{1}, e_{2}, \dots, e_{m})

⁠, the composite rectangle for paths P and E is formed by

n \cdot m

simple rectangles (p_i, e_j) (Fig. 2d). The distance D_ij between a pair of edges p_i and e_j according to the paths P and E is equal to

D_{i j} = \sum_{k = i}^{n} L ength (p_{k}) + \sum_{l = 1}^{j - 1} L ength (e_{l}) .

We define the following variables [see Prjibelski etal. (2014) for more details]:

${Expected}_{D_{i j}} (p_{i}, e_{j})$ ⁠: the expected number of (p_i, e_j)-connecting read-pairs;
${Observed}_{D_{i j}} (p_{i}, e_{j})$ ⁠: the observed number of (p_i, e_j)-connecting read-pairs.

To filter out rectangles filled by chimeric read-pairs, we use the support function

{Support}_{D_{i j}} (p_{i}, e_{j}) = {\begin{array}{l} 1, & {Density}_{D_{i j}} (p_{i}, e_{j}) > Ψ \\ 0, & otherwise \end{array}

where the density value is defined as

{Density}_{D_{i j}} (p_{i}, e_{j}) = \frac{{Observed}_{D_{i j}} (p_{i}, e_{j})}{{Expected}_{D_{i j}} (p_{i}, e_{j})} .

Thus, exSPAnder ignores rectangles with a density lower than a pre-defined threshold $Ψ$ ⁠.

While this approach worked well for short libraries, our benchmarking revealed that it deteriorates for long jumping libraries that typically have a higher rate of read-pairs with abnormal insert sizes (referred to as chimeric read-pairs).

We thus define a new support function that evaluates whether a simple rectangle (p_i, e_j) within the composite rectangle (P, E) can be considered as trusted and used for calculating the scoring function:

{Support}_{D_{i j}} (p_{i}, e_{j}) = {\begin{array}{l} 1, & {Observed}_{D_{i j}} (p_{i}, e_{j}) > η \\ 0, & otherwise \end{array}

where η is a user-controlled parameter with very conservative default value η = 30.

While it is not clear how to select optimal η, our analysis of the distribution of the number of chimeric points within all rectangles across a wide range of bacterial genomes revealed that hardly any rectangles contain more than 30 chimeric points. We note that by setting the parameter η, one essentially ignores the contribution from small rectangles containing less than η points. While it may appear that we unfairly ignore small rectangles, our benchmarking revealed that this approach actually improves the assembly quality. Moreover, the users can change the parameter η in the case of assembly projects with unusually low or high coverage.

When the extension path contains a single edge e, exSPAnder uses the following path-edge scoring function:

{Score}_{P} (e) = \frac{\sum_{i = 1}^{n} S {upport}_{D_{i}} (p_{i}, e) \cdot {Expected}_{D_{i}} (p_{i}, e)}{\sum_{i = 1}^{n} E {xpected}_{D_{i}} (p_{i}, e)} .

In this article, we generalize this path-edge scoring function to a path–path scoring function as follows:

\begin{matrix} {Score}_{P} (E) = \frac{\sum_{i = 1}^{n} \sum_{j = 1}^{m} S {upport}_{D_{i j}} (p_{i}, e_{j}) \cdot {Expected}_{D_{i j}} (p_{i}, e_{j})}{\sum_{i = 1}^{n} \sum_{j = 1}^{m} E {xpected}_{D_{i j}} (p_{i}, e_{j})} . \end{matrix}

Given a confidence interval $[I_{min}, I_{max}]$ of the insert size distribution, we call a path long if its length exceeds $I_{\max}$ and short otherwise. The algorithm that we describe below limits attention to the long extension paths $(e_{1}, e_{2}, \dots, e_{m})$ whose prefix $(e_{1}, e_{2}, \dots, e_{m - 1})$ is short. Given a path P, for each extension edge e_i of P, we construct a set of extension paths $E$ ⁠. A top-scored path E in $E$ is called a representative path for edge e (Fig. 3a). The score of the extension edge e is now defined as the score of its representative path, i.e. ${Score}_{P} (e) = {Score}_{P} (E)$ ⁠.

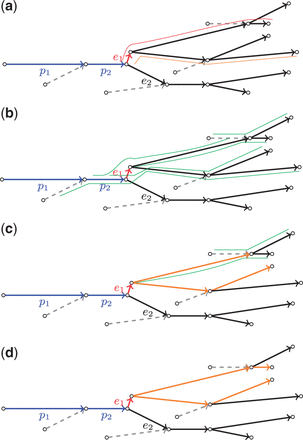
(a) An example of path P in the assembly graph (shown in blue) and its extension edges e1 and e2. The representative path for e1 is shown in red above the graph, whereas another extension path for e1 (with lower score) is shown in orange. (b–d) A step-by-step example of the work of ExtensionSearch algorithm for constructing extension paths (marked orange) for edge e1 using the pre-constructed paths from the set S (shown as five green paths in the top figure). At each step, the ExtensionSearch algorithm grows an extension path E (that is shorter than Imax) using only E-consistent extension edges (with respect to S)

Fig. 3.

(a) An example of path P in the assembly graph (shown in blue) and its extension edges e₁ and e₂. The representative path for e₁ is shown in red above the graph, whereas another extension path for e₁ (with lower score) is shown in orange. (b–d) A step-by-step example of the work of ExtensionSearch algorithm for constructing extension paths (marked orange) for edge e₁ using the pre-constructed paths from the set $S$ (shown as five green paths in the top figure). At each step, the ExtensionSearch algorithm grows an extension path E (that is shorter than I_max) using only E-consistent extension edges (with respect to $S$ ⁠)

Open in new tab Download slide

The new approach to define ${Score}_{P} (e)$ can be applied to the libraries with both short and long insert sizes. While the resulting improvements are significant for long insert sizes, they appear to be minor for the libraries with small insert sizes. Thus, in the default exSPAnder mode, the new scoring function is used only for the jumping libraries.

2.3 Constructing extension paths

In the case of long libraries, the Depth-First Search (DFS) algorithm for exploring all paths and selecting representative paths becomes rather slow, e.g. the number of extension paths can reach millions even for a bacterial genome. To decrease the number of extension paths, we developed the ExtensionSearch algorithm that uses a set of pre-constructed paths $S$ that are generated by the previous exSPAnder algorithm (Prjibelski etal., 2014) using single reads and short paired-end libraries if they are available.

We use the notation Suffix(E, l) [and Prefix(E, l)] to refer to a path formed by the last (first) l edges of a path E. For a path E and a set of pre-constructed paths $S$ ⁠, we say that an extension edge e of path E is E-consistent (with respect to $S$ ⁠) if $S$ contains a path $E'$ ⁠, such that $Suffix (E + e, l) = Prefix (E', l)$ for some l > 0. Instead of extending a path E by all its extension edges (like in the DFS algorithm), ExtensionSearch uses the following heuristics to construct extension paths:

Extend a path E only by E-consistent extension edges;
Extend only paths that are shorter than I_max.

As the result, we obtain a set of extension paths that ‘comply’ with the set of pre-constructed paths $S$ with length at least I_max (Fig. 3b–d).

ExtensionSearch greatly reduces the number of the extension paths when compared with the DFS algorithm. However, in the tangled regions of the assembly graph with many bulges (corresponding to variations in repeats) and loops (corresponding to tandem duplications), the number of paths is still high (Fig. 4). For example, each bulge potentially doubles the number of extension paths explored by the exSPAnder algorithm (e.g. ExtensionSearch can select either of edges e₁ and e₂ in Fig. 4a). Each loop potentially multiples the number of extension paths by the (unknown) multiplicity of the loop (i.e. the number of times the loop traverses the edge e₂ in Fig. 4b). In the ExtensionSearch, we focus only on simple bulges (Fig. 4a) and simple loops (Fig. 4b) since they represent the majority of all cases that may trigger the increase in the running time of the algorithm.

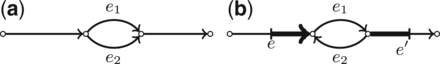
An example of a simple bulge (a) and simple loop (b) consisting of edges e1 and e2. A simple bulge (loop) is formed by two parallel (anti-parallel) edges between two vertices. Regions used for calculating the local coverage in the vicinity of the loop are marked with bold segments

Fig. 4.

An example of a simple bulge (a) and simple loop (b) consisting of edges e₁ and e₂. A simple bulge (loop) is formed by two parallel (anti-parallel) edges between two vertices. Regions used for calculating the local coverage in the vicinity of the loop are marked with bold segments

Open in new tab Download slide

To limit the explosion of the extension paths, we add the following constrains to the ExtensionSearch algorithm:

For each bulge formed by two edges, only the top-scoring edge is used as an extension edge.
Each simple loop is traversed as a fixed number of times equal to the estimated multiplicity of the loop. The loop multiplicity is estimated as the closest integer to $C_{loop} / C_{local}$ ⁠, where C_loop is the average read coverage of the loop edges, and C_local is the read coverage in the vicinity of the loop, i.e. the average read coverage of the last ReadLength nucleotides of edge e and first ReadLength nucleotides of edge $e'$ (Fig. 4b).

Our benchmarking has demonstrated that the described modifications reduce the running time by an order of magnitude.

2.4 Scaffolding

2.4.1 Jumping over the coverage gaps

Existing genome assemblers are often complemented by scaffolding tools such as Bambus (Pop etal., 2004), Opera (Gao etal., 2011), SCARPA (Donmez and Brudno, 2013), SOPRA (Dayarian etal., 2010) and SSPACE (Boetzer etal., 2011) to improve the contiguity of the resulting assemblies. However, most of these scaffolding tools work with contigs rather than the assembly graphs and none of them uses the rectangle framework that exSPAnder utilizes. We thus added a rectangle-based scaffolder to exSPAnder and evaluated its performance.

Jumping from an out-tip to an in-tip. A coverage gap typically creates a pair of tips in the assembly graph [see Bankevich etal. (2012) for details] formed by an out-tip (an edge that ends in a vertex with out-degree 0) and an in-tip (an edge that starts in a vertex with in-degree 0). We further refer to these tips as paired tips. Since coverage gaps are usually short, read-pairs from the jumping libraries often span them. Below we describe how ExtensionSearch finds pairs of tips and uses them for scaffolding.

Let E be an extension path for a path P, such that E ends with an out-tip e and $Length (E) < I_{max}$ (Fig. 5a). To further extend path E, we search for an in-tip paired with e by considering a set of P-supported edges, i.e. all edges $e'$ that have $(P, e')$ -connecting read-pairs. Since the set of P-supported edges typically contains many false short edges (due to high rate of chimeric read-pairs in the jumping libraries), we filter out all P-supported edges shorter than a certain threshold (default value is $500 bp$ ⁠).

Fig. 5.

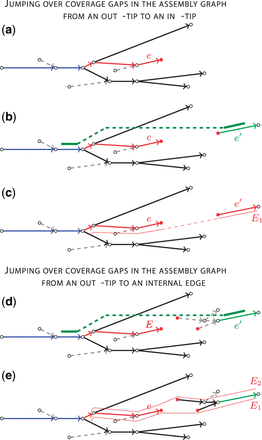
Jumping over coverage gaps in the assembly graph from an out-tip to an in-tip: (a) an extension path E (marked red) ending with an out-tip e; (b) the only P-supported edge $e'$ is an in-tip (marked green); (c) the path E is extended by an edge $e'$ with a gap (red line). Jumping over coverage gaps in the assembly graph from an out-tip to an internal edge: (d) the only P-supported edge $e'$ is not an in-tip (marked green) and (e) paths E₁ and E₂ that start with in-tips and contain P-supported edge $e'$ ⁠, both paths are considered as possible extensions for E (shown by red lines)

Open in new tab Download slide

Figure 5b presents a simple example when there is only one P-supported edge $e'$ and this edge is an in-tip. We then consider e and $e'$ as paired tips and extend the path E by edge $e'$ with a gap (Fig. 5c). Since the size of a gap is difficult to estimate using a jumping library with large insert size variation, we assign a fixed length to each gap (100 bp by default). Once we extended the path E with an edge, we continue growing E using ExtensionSearch until its length exceeds I_max.

Jumping from an out-tip to an internal edge. A more difficult (and more common) case is illustrated in Figure 5d, where there exists only one P-supported edge $e'$ and this edge is not an in-tip. Such situations arise when the in-tip paired with e is either not P-supported or is shorter than $500 bp$ (and thus ignored). To grow the path E in such cases, we consider all in-tips in the assembly graph and extend them further using ExtensionSearch limiting the path length to $I_{max} - Length (E)$ ⁠. Afterward, we select only paths that contain edge $e'$ and use them as potential extensions for E (Fig. 5e).

When assembling real datasets, we often encounter several P-supported edges longer than $500 bp$ ⁠. In this case, we apply the strategy described above, i.e. extend the paths starting from every in-tip and choose paths containing at least one P-supported edge. If some of the extension paths remain shorter than I_max, we continue growing them with the ExtensionSearch algorithm.

However, growing paths from every in-tip can be extremely time-consuming, especially for single-cell datasets that often contain thousands of coverage gaps. To address this issue, we implement the described approach the other way around: instead of starting a path from every in-tip, we start growing paths from P-supported edges in the reverse direction and select only those that reach an in-tip. Since the number of long P-supported edges is typically much smaller than the number of all in-tips in the assembly graph in the case of single-cell assemblies, this implementation greatly reduces the running time of exSPAnder.

2.4.2 Jumping over complex subgraphs

Even after applying the described heuristics for run-time reduction, there are cases when the number of extension paths remains huge. Such cases are often associated with complex subgraphs of the assembly graph (typically formed by short repeats with high multiplicities). To keep the running time under control, exSPAnder stops growing a path if the number of its extension paths exceeds a threshold. The threshold is automatically calculated based on the number of edges in the assembly graph (e.g. the threshold value is set to 50 for graphs with > 10 000 edges).

A better approach is to use jumping libraries and to ‘jump over’ complex subgraphs in the assembly graph (instead of generating all extension paths traversing these complex subgraphs). If the ‘size’ of a complex subgraph is smaller than the insert size, a path P may start on ‘one side’ of this subgraph and be connected with edges on the ‘other side’ of this subgraph, thus allowing us to jump over the entire subgraph and to continue growing P. The question is how to identify such complex subgraphs and jump over them.

To jump over complex subgraphs, we first identify a path P with unusually large number of extension paths. Afterward, we find all P-supported edges and order them using the rule: an edge $e'$ follows an edge e if $e'$ can be reached by ExtensionSearch within a certain distance starting from e. If all P-supported edges can be ordered into a single list, we extend path P by the first edge in this list (with a gap).

3 Results

To evaluate how availability of Nextera Mate Pair libraries affects the quality of assembly, we assembled several bacterial genomes using multicell datasets provided by Illumina (Nextera Mate Pair libraries only). In this article, we describe benchmarking (using seven different assemblers and three scaffolders) on Meiothermusruberstr.21T (Tindall etal., 2010) Nextera Mate Pair library and additionally, on Escherichiacolist.K12subst.MG1655 (Blattner etal., 1997) single-cell dataset that contains both a short paired-end library and a long jumping library. Results for other Nextera Mate Pair libraries are presented in the Supplementary Material.

Since the assemblers we used for comparison were not designed for assembling Nextera Mate Pair libraries, we have conducted additional optimization and selected the optimal k-mer sizes (with respect to N50) to ensure fair benchmarking with these assemblers. We ran ABySS 1.3.6 (Simpson etal., 2009), Ray 2.0.0 (Boisvert etal., 2010), SOAPdenovo 2.0.4 (Li etal., 2010), Velvet 1.2.10 (Zerbino and Birney, 2008) and Velvet-SC (Chitsaz etal., 2011) (based on Velvet 0.7.62, released on March 11, 2011) with the k-mer sizes 59, 57, 71, 99 and 105, respectively. Iterative de Bruijn graph assemblers IDBA-UD 1.1.1 (Peng etal., 2012), SPAdes 3.0.0 (with the previous version of exSPAnder (Prjibelski etal., 2014)] and SPAdes 3.5.0 (that implements the new algorithm described in this article) were run with the default parameters. In addition to scaffolds, we also provide information about contigs generated by SPAdes 3.5 (referred to as SPAdes 3.5 ctg). We have also included results for such popular scaffolders as Opera 2.0 (Gao etal., 2011), SCARPA 0.241 (Donmez and Brudno, 2013) and SSPACE 3.0 (Boetzer etal., 2011). To perform a fair comparison, we ran all scaffolders on the contigs that were assembled by SPAdes 3.5.0 using all data as single-end reads (discarding read-pair information).

The resulting assemblies were evaluated with QUAST 2.3 (Gurevich etal., 2013) using standard metrics: NGA50 (NG50 corrected for assembly errors), the total number of scaffolds in the assembly, the size of the largest scaffold, the number of misassemblies, the fraction of genome covered and the number of uncalled bases (N) in the assembly.

Table 1 benchmarks various assemblers on M.ruber Nextera Mate Pair library (mean insert size 3.6 kb). Some of the assemblers used in the comparison produce rather inaccurate assemblies (e.g. 95 misassemblies for Ray and 244 misassemblies for SOAPdenovo). Also, some assemblers generate very large number of unspecified symbols N (ABySS, Ray, SOAPdenovo and Velvet). Interestingly, most assemblers showed rather unstable behavior with Nextera Mate Pair libraries with exception of IDBA-UD and SPAdes (originally developed as single-cell assemblers). SPAdes + exSPAnder assembles an almost complete M.ruber genome with less than 0.03% of unspecified nucleotides and the largest scaffold capturing more than 93% of the genome.

Table 1.

Open in new tab

Comparison of the assemblies for the M.ruber str. 21T (Tindall et al., 2010) (genome size 3.1 Mb) Nextera Mate Pair library

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
ABySS	59	61	100	162	4	99.4	599
IDBA-UD	—	55	139	168	7	99.1	16
Opera	—	111	44	272	18	99.2	115
Ray	57	7	373	45	95	84.2	1834
SCARPA	—	129	61	389	1	99.2	1
SOAPdenovo	71	1	1449	411	244	92.8	36 360
SSPACE	—	305	14	757	6	99.4	26
Velvet	99	1716	11	3011	4	99.7	541
Velvet-SC	105	4	1099	21	18	98.3	0
SPAdes 3.0	—	1701	6	2879	3	99.9	37
SPAdes 3.5 ctg	—	1716	6	1716	2	99.9	0
SPAdes 3.5	—	2892	5	2893	2	99.9	23

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
ABySS	59	61	100	162	4	99.4	599
IDBA-UD	—	55	139	168	7	99.1	16
Opera	—	111	44	272	18	99.2	115
Ray	57	7	373	45	95	84.2	1834
SCARPA	—	129	61	389	1	99.2	1
SOAPdenovo	71	1	1449	411	244	92.8	36 360
SSPACE	—	305	14	757	6	99.4	26
Velvet	99	1716	11	3011	4	99.7	541
Velvet-SC	105	4	1099	21	18	98.3	0
SPAdes 3.0	—	1701	6	2879	3	99.9	37
SPAdes 3.5 ctg	—	1716	6	1716	2	99.9	0
SPAdes 3.5	—	2892	5	2893	2	99.9	23

Each assembly is represented by scaffolds if not indicated otherwise (marked with ctg). K, the k-mer size; NGA50, in kb; no., the total number of contigs/scaffolds longer than 500 bp; largest, for the length of the longest contig/scaffold assembled (in kb); no. mis is the number of misassemblies; GF, the percentage of genome mapped; No. N’s, the number of unspecified nucleotides per 100 kb. In each column, the best values are indicated in bold. Assemblies with very poor quality (e.g. low genome fraction, small NG50, relatively large number of misassemblies) are shown in gray and are ignored when selecting the best values for each metric. All metrics were computed using only contigs/scaffolds longer than 500 bp.

Table 1.

Open in new tab

Comparison of the assemblies for the M.ruber str. 21T (Tindall et al., 2010) (genome size 3.1 Mb) Nextera Mate Pair library

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
ABySS	59	61	100	162	4	99.4	599
IDBA-UD	—	55	139	168	7	99.1	16
Opera	—	111	44	272	18	99.2	115
Ray	57	7	373	45	95	84.2	1834
SCARPA	—	129	61	389	1	99.2	1
SOAPdenovo	71	1	1449	411	244	92.8	36 360
SSPACE	—	305	14	757	6	99.4	26
Velvet	99	1716	11	3011	4	99.7	541
Velvet-SC	105	4	1099	21	18	98.3	0
SPAdes 3.0	—	1701	6	2879	3	99.9	37
SPAdes 3.5 ctg	—	1716	6	1716	2	99.9	0
SPAdes 3.5	—	2892	5	2893	2	99.9	23

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
ABySS	59	61	100	162	4	99.4	599
IDBA-UD	—	55	139	168	7	99.1	16
Opera	—	111	44	272	18	99.2	115
Ray	57	7	373	45	95	84.2	1834
SCARPA	—	129	61	389	1	99.2	1
SOAPdenovo	71	1	1449	411	244	92.8	36 360
SSPACE	—	305	14	757	6	99.4	26
Velvet	99	1716	11	3011	4	99.7	541
Velvet-SC	105	4	1099	21	18	98.3	0
SPAdes 3.0	—	1701	6	2879	3	99.9	37
SPAdes 3.5 ctg	—	1716	6	1716	2	99.9	0
SPAdes 3.5	—	2892	5	2893	2	99.9	23

SPAdes generates similar high-quality assemblies on all Nextera Mate Pair libraries (see Supplementary Material) and often results in assemblies of very few contigs with the quality that approaches the quality of the assemblies from long Pacific Biosciences reads (Chin etal., 2013). Thus, Nextera Mate Pair libraries provide a valuable low-cost trade-off when compared with the assemblies that use Pacific Biosciences reads.

In Table 2, we also present a comparison between selected tools on E.coli single-cell dataset with paired-end and jumping libraries. In addition, we ran ALLPATHS-LG (Gnerre etal., 2011) (build 47561, released on September 15, 2013) with the default parameters using both libraries together. As Table 2 indicates SPAdes (both versions 3.0 and 3.5) and IDBA-UD outperform other tools on this dataset. However, when using both libraries together, SPAdes generates more accurate and continuous assemblies comparing to IDBA-UD and at the same time captures the largest genome fraction.

Table 2.

Open in new tab

Comparison of the assemblies for the E.coli st. K12 subst. MG1655 (Blattner et al., 1997) (genome size 4.7 Mb) single-cell dataset with paired-end and jumping libraries

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
Only paired-end library
ABySS	47	87	186	199	9	90.5	111
IDBA-UD	—	105	482	265	7	95.0	0
Opera	—	67	513	202	4	94.6	7
Ray	55	49	422	198	23	90.3	1475
SCARPA	—	84	486	209	3	94.8	6
SOAPdenovo	71	16	728	150	7	78.2	17
SSPACE	—	66	534	209	2	94.6	0
Velvet	81	22	128	178	3	62.3	10
Velvet-SC	55	21	634	135	4	92.7	0
SPAdes 3.0	—	117	453	285	3	94.9	0
SPAdes 3.5 ctg	—	117	459	285	4	94.9	0
SPAdes 3.5	—	121	452	285	4	94.9	2
Both paired-end and jumping libraries
ABySS	47	87	186	199	9	90.5	111
ALLPATHS-LG	—	1	483	132	23	50.7	3801
IDBA-UD	—	105	557	416	16	95.0	0
Opera	—	71	388	202	28	94.6	359
Ray	55	95	361	281	28	92.7	427
SCARPA	—	132	413	630	29	94.8	505
SOAPdenovo	71	16	673	150	63	78.3	743
SSPACE	—	123	402	488	21	94.7	478
Velvet	81	24	145	178	17	67.5	330
Velvet-SC	55	—	1617	1	0	29.4	0
SPAdes 3.0	—	357	404	1551	11	95.6	108
SPAdes 3.5 ctg	—	319	414	653	10	95.6	0
SPAdes 3.5	—	356	392	693	10	95.6	36

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
Only paired-end library
ABySS	47	87	186	199	9	90.5	111
IDBA-UD	—	105	482	265	7	95.0	0
Opera	—	67	513	202	4	94.6	7
Ray	55	49	422	198	23	90.3	1475
SCARPA	—	84	486	209	3	94.8	6
SOAPdenovo	71	16	728	150	7	78.2	17
SSPACE	—	66	534	209	2	94.6	0
Velvet	81	22	128	178	3	62.3	10
Velvet-SC	55	21	634	135	4	92.7	0
SPAdes 3.0	—	117	453	285	3	94.9	0
SPAdes 3.5 ctg	—	117	459	285	4	94.9	0
SPAdes 3.5	—	121	452	285	4	94.9	2
Both paired-end and jumping libraries
ABySS	47	87	186	199	9	90.5	111
ALLPATHS-LG	—	1	483	132	23	50.7	3801
IDBA-UD	—	105	557	416	16	95.0	0
Opera	—	71	388	202	28	94.6	359
Ray	55	95	361	281	28	92.7	427
SCARPA	—	132	413	630	29	94.8	505
SOAPdenovo	71	16	673	150	63	78.3	743
SSPACE	—	123	402	488	21	94.7	478
Velvet	81	24	145	178	17	67.5	330
Velvet-SC	55	—	1617	1	0	29.4	0
SPAdes 3.0	—	357	404	1551	11	95.6	108
SPAdes 3.5 ctg	—	319	414	653	10	95.6	0
SPAdes 3.5	—	356	392	693	10	95.6	36

Each assembly is represented by scaffolds if not indicated otherwise (marked with ctg). K, the k-mer size; NGA50, in kb; no., the total number of contigs/scaffolds longer than 500 bp; largest stands for the length of the longest contig/scaffold assembled (in kb); no. mis, the number of misassemblies; GF, the percentage of genome mapped; no. N’s, the number of unspecified nucleotides per 100 kb. In each column, the best values are indicated in bold. Assemblies with very poor quality (e.g. low genome fraction, small NG50, relatively large number of misassemblies) are shown in gray and are ignored when selecting the best values for each metric. All metrics were computed using only contigs/scaffolds longer than 500 bp.

Table 2.

Open in new tab

Comparison of the assemblies for the E.coli st. K12 subst. MG1655 (Blattner et al., 1997) (genome size 4.7 Mb) single-cell dataset with paired-end and jumping libraries

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
Only paired-end library
ABySS	47	87	186	199	9	90.5	111
IDBA-UD	—	105	482	265	7	95.0	0
Opera	—	67	513	202	4	94.6	7
Ray	55	49	422	198	23	90.3	1475
SCARPA	—	84	486	209	3	94.8	6
SOAPdenovo	71	16	728	150	7	78.2	17
SSPACE	—	66	534	209	2	94.6	0
Velvet	81	22	128	178	3	62.3	10
Velvet-SC	55	21	634	135	4	92.7	0
SPAdes 3.0	—	117	453	285	3	94.9	0
SPAdes 3.5 ctg	—	117	459	285	4	94.9	0
SPAdes 3.5	—	121	452	285	4	94.9	2
Both paired-end and jumping libraries
ABySS	47	87	186	199	9	90.5	111
ALLPATHS-LG	—	1	483	132	23	50.7	3801
IDBA-UD	—	105	557	416	16	95.0	0
Opera	—	71	388	202	28	94.6	359
Ray	55	95	361	281	28	92.7	427
SCARPA	—	132	413	630	29	94.8	505
SOAPdenovo	71	16	673	150	63	78.3	743
SSPACE	—	123	402	488	21	94.7	478
Velvet	81	24	145	178	17	67.5	330
Velvet-SC	55	—	1617	1	0	29.4	0
SPAdes 3.0	—	357	404	1551	11	95.6	108
SPAdes 3.5 ctg	—	319	414	653	10	95.6	0
SPAdes 3.5	—	356	392	693	10	95.6	36

Assembler	K	NGA50	No.	Largest	No. mis	GF	No. N’s
Only paired-end library
ABySS	47	87	186	199	9	90.5	111
IDBA-UD	—	105	482	265	7	95.0	0
Opera	—	67	513	202	4	94.6	7
Ray	55	49	422	198	23	90.3	1475
SCARPA	—	84	486	209	3	94.8	6
SOAPdenovo	71	16	728	150	7	78.2	17
SSPACE	—	66	534	209	2	94.6	0
Velvet	81	22	128	178	3	62.3	10
Velvet-SC	55	21	634	135	4	92.7	0
SPAdes 3.0	—	117	453	285	3	94.9	0
SPAdes 3.5 ctg	—	117	459	285	4	94.9	0
SPAdes 3.5	—	121	452	285	4	94.9	2
Both paired-end and jumping libraries
ABySS	47	87	186	199	9	90.5	111
ALLPATHS-LG	—	1	483	132	23	50.7	3801
IDBA-UD	—	105	557	416	16	95.0	0
Opera	—	71	388	202	28	94.6	359
Ray	55	95	361	281	28	92.7	427
SCARPA	—	132	413	630	29	94.8	505
SOAPdenovo	71	16	673	150	63	78.3	743
SSPACE	—	123	402	488	21	94.7	478
Velvet	81	24	145	178	17	67.5	330
Velvet-SC	55	—	1617	1	0	29.4	0
SPAdes 3.0	—	357	404	1551	11	95.6	108
SPAdes 3.5 ctg	—	319	414	653	10	95.6	0
SPAdes 3.5	—	356	392	693	10	95.6	36

Each assembly is represented by scaffolds if not indicated otherwise (marked with ctg). K, the k-mer size; NGA50, in kb; no., the total number of contigs/scaffolds longer than 500 bp; largest stands for the length of the longest contig/scaffold assembled (in kb); no. mis, the number of misassemblies; GF, the percentage of genome mapped; no. N’s, the number of unspecified nucleotides per 100 kb. In each column, the best values are indicated in bold. Assemblies with very poor quality (e.g. low genome fraction, small NG50, relatively large number of misassemblies) are shown in gray and are ignored when selecting the best values for each metric. All metrics were computed using only contigs/scaffolds longer than 500 bp.

Acknowledgement

We would like to thank Ilya Chorny from Illumina for providing various datasets for Nextera Mate Pair libraries, which are now available at Illumina BaseSpace public repository (https://basespace.illumina.com).

Funding

This study was supported by the Russian Science Foundation [14-50-00069].

Conflict of Interest: none declared.

References

Bankevich

et al. . (

2012

)

SPAdes: a new genome assembly algorithm and its applications to single-cell sequencing

J. Comput. Biol.

455

–

477

Month:	Total Views:
November 2016	1
December 2016	2
January 2017	11
February 2017	21
March 2017	14
April 2017	25
May 2017	19
June 2017	11
July 2017	15
August 2017	10
September 2017	9
October 2017	10
November 2017	5
December 2017	26
January 2018	20
February 2018	36
March 2018	44
April 2018	38
May 2018	69
June 2018	64
July 2018	59
August 2018	35
September 2018	40
October 2018	44
November 2018	51
December 2018	24
January 2019	24
February 2019	31
March 2019	40
April 2019	41
May 2019	22
June 2019	25
July 2019	38
August 2019	27
September 2019	38
October 2019	20
November 2019	19
December 2019	38
January 2020	40
February 2020	29

Article Contents

Assembling short reads from jumping libraries with large insert sizes Free

Abstract

1 Introduction

2 Methods

2.1 The exSPAnder framework

2.1.1 Rectangles

2.1.2 The decision rule

2.2 Scoring function

2.3 Constructing extension paths

2.4 Scaffolding

2.4.1 Jumping over the coverage gaps

2.4.2 Jumping over complex subgraphs

3 Results

Acknowledgement

Funding

References

Author notes

Supplementary data

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

Looking for your next opportunity?

This Feature Is Available To Subscribers Only

Assembling short reads from jumping libraries with large insert sizes