-
PDF
- Split View
-
Views
-
Cite
Cite
Hui Yu, KangKang Li, WenMin Dong, ShuangHong Song, Chen Gao, JianYu Shi, Attention-based cross domain graph neural network for prediction of drug–drug interactions, Briefings in Bioinformatics, Volume 24, Issue 4, July 2023, bbad155, https://doi.org/10.1093/bib/bbad155
Close - Share Icon Share
Abstract
Drug–drug interactions (DDI) may lead to adverse reactions in human body and accurate prediction of DDI can mitigate the medical risk. Currently, most of computer-aided DDI prediction methods construct models based on drug-associated features or DDI network, ignoring the potential information contained in drug-related biological entities such as targets and genes. Besides, existing DDI network-based models could not make effective predictions for drugs without any known DDI records. To address the above limitations, we propose an attention-based cross domain graph neural network (ACDGNN) for DDI prediction, which considers the drug-related different entities and propagate information through cross domain operation. Different from the existing methods, ACDGNN not only considers rich information contained in drug-related biomedical entities in biological heterogeneous network, but also adopts cross-domain transformation to eliminate heterogeneity between different types of entities. ACDGNN can be used in the prediction of DDIs in both transductive and inductive setting. By conducting experiments on real-world dataset, we compare the performance of ACDGNN with several state-of-the-art methods. The experimental results show that ACDGNN can effectively predict DDIs and outperform the comparison models.
INTRODUCTION
Co-administration of two or more drugs is common in therapeutic treatment but it may lead to unexpectedly adverse reactions in human body due to pharmacokinetic or pharmacodynamical behavior. The interaction between two or more drugs is termed as drug–drug interaction (DDI), which may induce unexpected side effects and even life-threatening risks [1, 2]. To identify DDIs, traditional methods usually use experimental testings (in vitro) and clinical trials, but they have the disadvantages of costliness, low-efficiency and time-consuming. Thanks to the rapid development of artificial intelligence, computer-aided DDI prediction methods (in silico) with the advantage of cheap, effective and fast are employed, which have be gained many concerns from both academy and industry recently [3, 4].
A series of machine learning models have been proposed for DDI prediction, among which models based on drug-self features are the simplest and direct way. For instance, Ryu et al. [5] proposed a deep neural network model, which directly utilized drug structure information to generate drug structural features and constructed a deep neural network to predict potential DDI. Fokoue et al. [6] constructed various drug similarity features based on kinds of drug-related information and adopted logistic regression to predict possible DDIs. Rohani et al. [7] calculated multiple drug similarities and Gaussian interaction curves of drug pairs, then neural network was exploited to perform DDI prediction. Through combining various drug-related data (e.g. pharmacology-related features and drug description information), Shen et al. [8] exploited neural networks to learn drug feature representation and the full connection layer was used to predict DDIs. In addition to directly utilizing drug-self features, drug-related networks can also be used to construct prediction models. For example, Yu et al. [9] developed a Drug-drug interactions via semi-nonnegative matrix factorization (DDINMF) method that utilized semi-nonnegative matrix factorization to predict enhancive and degressive DDIs. Shi et al. [10] explored rich structural information between drugs in DDI network and proposed balance regularized semi-nonnegative matrix factorization [11] to predict DDIs in cold start scenarios. Wang et al. [12] developed Graph of Graphs Neural Network (GoGNN) model, which extracted features from both molecular graphs and DDI networks in hierarchical style and adopted dual-attention mechanism to differentiate the importance of neighbor information. Zhang et al. [13] proposed a sparse feature learning ensemble method with linear neighborhood regularization (SFLLN) model that combines sparse feature learning ensemble method with linear neighborhood regularization for DDI prediction. Chen et al. [14] proposed a multi-scale feature fusion deep learning model named Multi-scale feature fusion for drug-drug interaction prediction (MUFFIN), which can jointly learn the drug representation based on both the drug-self structure information and the Knowledge Graph (KG) with rich biomedical information. He et al. [15] developed a graph neural network (GNN)-based multi-type feature fusion model for DDI prediction, which can effectively integrate three kinds of drug-related information, including drug molecular graph, Simplified Molecular-Input Line-Entry System (SMILES) sequences and topological information in DDI network.
However, above methods neglect rich knowledge contained in biomedical entities related to drugs, such as proteins, genes and targets. In fact, other entities related to drugs also contain rich information [16–19], which can reflect the property of drugs to some extent. There is likely interaction between drugs that act on same protein [20]. For instance, both cyclosporine and cimetidine can act on CYP3A4 enzyme, in which cyclosporine is metabolized by CYP3A4 enzyme, and cimetidine can inhibit the activity of CYP3A4 enzyme. Combined use of these two drugs will increase the blood concentration of cyclosporine and cause toxicity [21]. Therefore, it is necessary to consider information contained in other types of drug-related entities. Moreover, existing network based models could not make effective predictions for drugs without any known DDI records, as they can not extract effective information from DDI network for these drugs.
To tackle the above limitations, in this paper, we propose an end-to-end attention-based cross domain graph neural network (ACDGNN) model, which fully considers drug’s neighbor information from different entity domains and comprehensively considers the feature information and structure information of drugs. Thus, ACDGNN can learn representative embeddings of drugs and make prediction for drugs without any DDIs. Through combining with attention mechanism, ACDGNN works on drug-related heterogeneous networks by information passing mechanism between different entity domains to effectively extract the information of neighborhood entities (drug-related entities). We conducted extensive experiments on real-world dataset under three different kinds of data split strategies. And the results demonstrate that ACDGNN outperforms comparison methods in both transductive and inductive setting.
Compared to previous works, ACDGNN has the following contributions.
(i) ACDGNN takes drug-related biomedical entities into consideration and extracts more comprehensive semantic information of drugs from heterogeneous biomedical network.
(ii) Considering the inherent heterogeneity between different entities, ACDGNN adopts cross-domain transformation to eliminate heterogeneity and could learn more expressive embeddings for DDI prediction.
(iii) ACDGNN can eliminate the heterogeneity between different types of entities and effectively predict DDIs in transductive and inductive scenarios.
METHOD
Prediction task and framework
Given a heterogeneous network which contains multiple types of domain entities by |$\mathcal{G}(\mathcal{V},\mathcal{E},\mathcal{F},\Phi )$|, where |$\mathcal{V}$| describes the set of all the entities in the network, and |$\mathcal{E}=\{(v_{i},v_{j})|v_{i},v_{j} \in \mathcal{V}\}$| represents the set of links in |$\mathcal{G}$|. The features of all the nodes are denoted by matrix |$\mathcal{F}\in \mathbb{R}^{N\times f}$|, where |$N$| represents the number of nodes in the heterogeneous network and |$f$| is the dimension of the features. There are multiple types of entities in the heterogeneous network, such as drugs, diseases and genes, and these entities belong to different entity domains. Here, we denote the set of entity domain’s label as |$\mathcal{O}$|, and each vertex |$v \in \mathcal{V}$| belongs to one of the entity domains, denoted by |$\Phi (v):\mathcal{V}\rightarrow \mathcal{O}$|, where |$\Phi $| is the mapping function from |$\mathcal{V}$| to |$\mathcal{O}$|. The set of all the drugs in heterogeneous network |$\mathcal{G}$| is denoted by |$\mathcal{D}$|, |$\mathcal{D}\subset \mathcal{V}$| and |$\mathcal{R}$| denotes the set of DDI types. The set of known DDIs is described by |$\mathcal{T}=\{(d_{i},d_{j},r)|d_{i},d_{j}\in \mathcal{D},r\in \mathcal{R}\}$|, where the triplet |$(d_{i},d_{j},r)$| indicates there exists an interaction of type |$r$| between drug |$d_{i}$| and |$d_{j}$|.
In this paper, the main task is to predict the specific type of DDI between drugs. More precisely, given drugs |$d_{i},d_{j}\in \mathcal{D}$|, we aim to predict whether there exists a DDI of type |$r\in \mathcal{R}$|, i.e. to determine how likely a triplet |$(d_{i},d_{j},r)$| belongs to |$\mathcal{T}$|.
The overall framework of ACDGNN is illustrated in Figure 1. It is an end-to-end learning model, and we will present detailed description in the following sections.
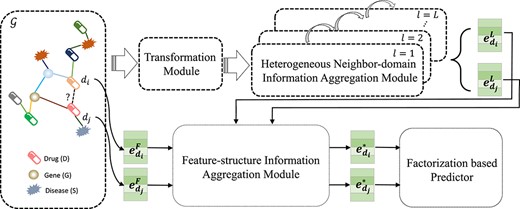
The overall framework of ACDGNN. The input of ACDGNN is a heterogeneous network |$\mathcal{G}$| on the left, in which different shapes represent different entities and the color of the edge represents the corresponding relation. In transformation module, cross-domain transformation is performed on all entities to reduce the heterogeneity. Then, in order to obtain network structure embedding, heterogeneous neighbor-domain information aggregation module takes the transformed information of different entities as input and propagate the information from neighbors via attention mechanism. The initial feature and network structure embedding of entities (drugs as the example in this figure) are aggregated in a weighted way in feature-structure information aggregation module and combining the outputs of the heterogeneous neighbor-domain information aggregation module to generate the final embedding of entities, which will be fed into the factorization based predictor for DDI prediction.
Input module and transformation module
As is shown in Figure 1, the input of ACDGNN is a heterogeneous network |$\mathcal{G}$|, which contains inter-domain links (e.g. drug–protein interaction) and intra-domain links (e.g. protein–protein interactions). To acquire the initial features of drugs in the network, inspired by Ryu et al. [5], structural similarity feature of each drug is calculated based on chemical fingerprints. Then, principal component analysis (PCA) is applied to filter the possible noise and reduces the dimension. For entities of other types, we initialize their embeddings using KG method Translating Embeddings (TransE) [17].
ACDGNN captures higher order neighbor information via multi-layer information propagation mechanism. It is worth noting that different types of nodes belong to different domains in heterogeneous network, simply using GNN-based methods to capture network structure information cannot capture the heterogeneity. To solve this problem, inspired by the practice of Hong et al. [22], cross-domain transformation is applied to the neighbors in different domains. Take drug |$d\in \mathcal{D}$| as an example, we denote the embedding at |$l^{th}$| layer of node |$d$| as |$\boldsymbol{e}_{d}^{l}$|, where |$l$| is the number of layers in heterogeneous neighbor-domain information aggregation module. For |$d$|’s neighboring nodes, ACDGNN adopts specific transformation matrix for cross-domain transformation, which maps the embeddings of neighboring nodes to a low-dimensional vector space same as |$d$|. Let |$N_{d}^{o}$| be the set of neighbors of |$d$| and each neighbor belong to a domain |$o\in \mathcal{O}$|. For simplicity, here, linear transformation is adopted to realize the mapping of entities in different domains:
where |$h\in N_{d}^{o}$|, |$\Phi (d)$| and |$\Phi (h)$| are the domain’s label that |$d$| and |$h$| belong to, respectively. |$\boldsymbol{W}_{\Phi (h)\Phi (d)}^{l}$| is the transformation matrix at |$l^{th}$| layer which maps entity |$h$| in domain |$\Phi (h)$| to domain |$\Phi (d)$| and also is a learnable parameter matrix. Different transformation matrix |$\boldsymbol{W}_{\Phi (h)\Phi (d)}^{l}$| distinguishes different domains and the projected entity embedding |$\boldsymbol{e}_{h}^{l,\Phi (d)}$| sits in the vector space of domain |$\Phi (d)$|.
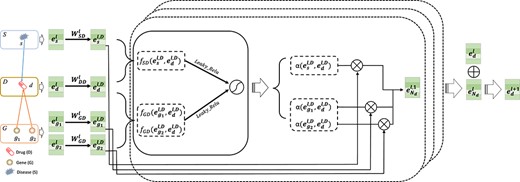
Transformation module and heterogeneous neighbor-domain information aggregation module. Taking drug entity |$d$| as an example, which has neighbors in gene domain (|$g_{1}$| and |$g_{2}$|) and disease domain (|$s$|), we first apply domain transformation on its neighbors with transformation module. Then, we calculate attention coefficient |$\alpha $| by using the transformed embedding and aggregate information from neighbors with |$\alpha $| to obtain embedding of |$d$| at layer |$l$|, |$\boldsymbol{e}_{N_{d}}^{l}$|. The |${(l+1)}^{th}$| layer embedding |$\boldsymbol{e}_{d}^{l+1}$| of |$d$| is obtained by aggregating |$\boldsymbol{e}_{d}^{l}$| and |$\boldsymbol{e}_{N_{d}}^{l}$|.
Heterogeneous neighbor-domain information aggregation module
To extract the structural information of entities, we design heterogeneous neighbor-domain information aggregation module to process the transformed entity embeddings, as is illustrated in Figure 2. In this module, we apply attention mechanism to differentiate the importance of neighbor nodes. For neighbor node |$h\in N_{d}^{o}$|, the attention coefficient is computed in the form as:
where |$f(\boldsymbol{e}_{h}^{l,\Phi (d)},\boldsymbol{e}_{d}^{l,\Phi (d)})$| is the attention coefficient of |$h$| to |$d$|, which can be implemented in many ways [17, 23]. Here, we adopt the computation form used in Graph Attention Network (GAT) [24]:
where the attention coefficient at |$l^{th}$| layer is parameterized by vector |$\boldsymbol{a}^{l}$|, which can be adaptively updated in training.
To stabilize the learning process of our model and improve the generalizability, multi-head attention mechanism is employed to extract neighbor’s information [25, 26]. Specifically, |$K$| independent attention heads execute the computation of Eq. 2, then the neighbors’ information are aggregated in the form as:
where |$\alpha _{k}(\boldsymbol{e}_{h}^{l,\Phi (d)},\boldsymbol{e}_{d}^{l,\Phi (d)})$| are attention coefficients computed by the |$k^{th}$| attention head.
At last, we apply non-linear transformation to aggregate the information of entity |$d$| and its neighbors’ information, the embedding of entity |$d$| at |${(l+1)}^{th}$| layer is computed as the following:
where |$\boldsymbol{W}_{l+1}$| and |$\boldsymbol{b}_{l+1}$| are learnable parameters.
Feature-structure information aggregation module
The original features of entities are considered in the process of neighborhood information aggregation, however, there exist the following problems: (1) In heterogeneous networks, some nodes have few neighbors, as a consequence, the learned embeddings based on the network structure are not expressive enough. For instance, in the dataset used in this paper, there are 130 drugs that have neighbors <10. (2) Even for entities with many neighbors, the learned embeddings cannot distinguish the importance of initial features and structural embeddings [27]. Therefore, in this module, the initial feature and structural embedding of entities are aggregated weightedly.
Given an entity |$d\in \mathcal{V}$|, the initial feature of |$d$| is denoted by |$\boldsymbol{e}_{d}^{F}$| and the structural embedding at the final layer |$L^{th}$| in the heterogeneous neighbor-domain information aggregation module is represented by |$\boldsymbol{e}_{d}^{L}$|. These two kinds of information are aggregated in a weighted fashion as the following:
where |$(\boldsymbol{e}_{d}^{L})^{^{\prime}}=\boldsymbol{W}_{s}\boldsymbol{e}_{d}^{L}$| and |$(\boldsymbol{e}_{d}^{F})^{^{\prime}}=\boldsymbol{W}_{f}\boldsymbol{e}_{d}^{F}$|, similar to transformation module, |$\boldsymbol{e}_{d}^{L}$| and |$\boldsymbol{e}_{d}^{F}$| are transformed into the same representation space by learnable parameters |$\boldsymbol{W}_{s}$| and |$\boldsymbol{W}_{f}$|. |$\alpha _{s}$| is the weight coefficient of structural embedding, which is calculated by the following process (|$\alpha _{f}$| is calculated in similar way):
where |$\overrightarrow{\boldsymbol{a}}$| is a learnable parameter vector in attention mechanism.
In order to preserve the original feature’s information and structural information, we concatenate them with the aggregated embedding |$\boldsymbol{e}_{d}^{A}$|. Ultimately, the final embedding of entity is obtained by the following formula:
where |$\boldsymbol{e}_{d}^{F}$| is the initial feature of entity |$d$|, |$\boldsymbol{e}_{d}^{L}$| and |$\boldsymbol{e}_{d}^{A}$| are obtained from Eqs 5 and 6, respectively.
DDI prediction
For now, the embeddings of all the nodes in heterogeneous network are obtained and these embeddings will be exploited to predict DDI. Recall the prediction task mentioned before: given triplet |$(d_{i},d_{j},r)$|, where |$d_{i},d_{j}\in \mathcal{D}, r\in \mathcal{R}$|, ACDGNN aims at predicting the ground-truth label of |$(d_{i},d_{j},r)$|, where |$1$| for positive and |$0$| for negative. In this paper, we adopt the tensor factorization-based decoder for DDI prediction, which is firstly introduced by Mariana et al. [16], the formula is defined as
where |$\sigma $| is sigmoid function, which maps the calculated scores to [0, 1]. |$\boldsymbol{M}_{r}$| is the parameter matrix specific to relation |$r$|, |$\boldsymbol{R}$| is the parameter matrix shared by all relations. |$(\boldsymbol{e}_{d_{j}}^{*})^{T}$| is the transpose of |$\boldsymbol{e}_{d_{j}}^{*}$|.
We assign different labels to positive and negative samples, 1 for positive and 0 for negative. To optimize the parameters of our model, cross-entropy loss is adopted, which has the following form:
where |$\mathcal{T_{+}}$| and |$\mathcal{T_{-}}$| are the set of positive and negative samples, respectively. And the negative samples are generated by randomly replacing one entity in positive samples. |$y$| indicates the labels of samples.
Theoretically, the embeddings obtained through the optimization of Eq. 10 can reflect interaction pattern of drugs. To explicitly model this idea, we add another constraint term in the loss. Specifically, a Jaccard similarity matrix is calculated based on interaction matrix corresponding to known DDIs. And PCA is applied to the Jaccard similarity matrix. The following loss is calculated:
where |$\mathcal{D_{T}}$| is the set of drugs in training set. |$\boldsymbol{s}_{d_{i}}$| represents the feature of |$d_{i}$| in Jaccard similarity matrix. |$\boldsymbol{W}_{a}$| is feature transformation matrix, which aims at translating drug features to the vector space that aggregated feature belongs to.
With the optimization of Eq. 11, the learned embeddings can capture the interaction behavior of drugs, which could improve the prediction performance. The final loss of ACDGNN comprises the basic loss and constraint loss:
where |$\lambda $| is weighting factor.
The pseudocode of ACDGNN is presented in the Supplementary Material and the source code and data are available at https://github.com/KangsLi/ACDGNN.
EXPERIMENT
Dataset
To construct the heterogeneous network with different entities of drugs, we adopt the dataset collected by Yu et al. [17], which integrates the Hetionet dataset [28] and dataset collected by Ryu et al. [5]. In the end, we obtain 34 124 nodes out of 10 types (e.g. gene, disease, pathway, molecular function, etc.) with 1 882 571 edges from 24 relation types. Due to the pages’ limitation, the detailed statistics of the experimental dataset is presented in the Supplementary Material.
Setup
We use random search for hyper-parameters fine-tuning and determine the optimal values based on the overall prediction performance on validation set. The details are described in section 3.5. In the training process, the model was trained on minibatches of 1024 DDI tuples by using the Adam optimizer with learning rate |$5e-4$|. To avoid overfitting, dropout is applied in the output of attention mechanism and heterogeneous neighbor-domain information aggregation module. The hyper-parameter |$\lambda $| is set to |$3e-3$|. ACDGNN is used for multi-typed DDI prediction and we select five metrics: accuracy (ACC), area under the receiver operating characteristic (AUC), area under the precision-recall curve (AUPR), F1 and KAPPA as the evaluation criteria.
It is worth noting that in the heterogeneous neighbor-domain information aggregation module, for drug entities, we do not consider their neighbor of drugs, namely we ignoring the link between drugs. The reason behind that is the information aggregation can be performed in a consistent way without the need of considering whether drugs have known DDIs or not. Under this setting, we can split the experimental dataset with different policy in the following experiments.
Baselines
We compare ACDGNN with the following baselines:
(i) SSI-DDI [29]: Considers the molecular graph structure of drugs and extract each node hidden features as substructures with multi-layer GAT. Then the interactions between these substructures are computed to predict DDI types.
(ii) MHCADDI [30]: Drug are also regarded as a molecular graph, combined with co-attention mechanism to calculate the power between atoms, and then learn the embedding representation of the drug entity to make prediction.
(iii) DeepDDI [5]: It uses chemical substructure similarity of the drugs as input and predicts the interaction type through a deep neural network.
(iv) SumGNN [17]: Extract subgraphs on a heterogeneous network and employs the attention mechanism to encode the subgraph and subsequently predict multi-type DDIs.
(v) KGNN [31]: Designed an end-to-end framework which can capture drug and its potential neighborhoods by mining their associated relations in knowledge graph to resolve the DDI prediction.
(vi) DDIMDL [32]: Develops a multi-modal deep learning model for DDI prediction. It obtains multiple drug similarities based on different drug-related attributes and employs deep neural networks to make DDI prediction.
(vii) LaGAT [33]: A link-aware graph attention method for DDI prediction, which is able to generate different attention pathways for drug entities based on different drug pair links.
(viii) GoGNN [12]: A model that leverages the dual attention mechanism in the view of graph of graphs to capture the information from both entity graphs and entity interaction graph hierarchically.
(ix) SFLLN [13]: Proposed a sparse feature learning ensemble method that integrate four drug features and extarct drug–drug relations with linear neighborhood regularization.
Result analysis
In this section, we show the performance of different comparison methods. The experimental dataset is randomly split into training, validation and test set with a ratio 6:2:2 based on DDI tuples. For each DDI tuple, a negative sample is generated as discussed in section 2.5. They were generated before training to ensure that all the comparison methods are trained on the same data. To be specific, we ensure train/validation/test set contain samples from all classes (termed as partition policy 1). The dataset is randomly divided for 10 times, and the final comparison results are the average of best for each time. The comparison results are shown in Table 1, in which bold text denotes the best and underlined text represents suboptimal one among all compared models. From Table 1, we can find that ACDGNN achieves the best performance in DDI prediction under the partition policy 1, which accurately predicts the correct DDIs.
| Methods . | ACC . | AUC . | AUPR . | F1 . | Precision . | Recall . | KAPPA . |
|---|---|---|---|---|---|---|---|
| ACDGNN | 96.71 | 98.81 | 98.35 | 94.11 | 95.64 | 93.74 | 92.23 |
| SSI-DDI | 93.42 | 97.79 | 97.41 | 93.42 | 94.35 | 91.78 | 86.85 |
| MHCADDI | 79.54 | 87.28 | 84.79 | 79.39 | 76.71 | 81.29 | 59.09 |
| SumGNN | 87.81 | 94.17 | 93.67 | 87.67 | 88.24 | 86.61 | 75.36 |
| KGNN | 85.16 | 90.86 | 89.57 | 77.62 | 83.58 | 77.34 | 72.12 |
| DDIMDL | 83.07 | 87.53 | 85.68 | 79.95 | 84.69 | 80.34 | 56.12 |
| DeepDDI | 78.06 | 84.72 | 82.07 | 77.71 | 81.26 | 78.41 | 56.12 |
| LaGAT | 91.85 | 96.64 | 95.36 | 91.87 | 89.68 | 89.38 | 81.45 |
| GoGNN | 86.78 | 92.38 | 91.16 | 86.58 | 85.42 | 80.69 | 73.56 |
| SFLLN | 82.79 | 86.48 | 83.69 | 79.86 | 83.47 | 79.66 | 55.27 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | Precision . | Recall . | KAPPA . |
|---|---|---|---|---|---|---|---|
| ACDGNN | 96.71 | 98.81 | 98.35 | 94.11 | 95.64 | 93.74 | 92.23 |
| SSI-DDI | 93.42 | 97.79 | 97.41 | 93.42 | 94.35 | 91.78 | 86.85 |
| MHCADDI | 79.54 | 87.28 | 84.79 | 79.39 | 76.71 | 81.29 | 59.09 |
| SumGNN | 87.81 | 94.17 | 93.67 | 87.67 | 88.24 | 86.61 | 75.36 |
| KGNN | 85.16 | 90.86 | 89.57 | 77.62 | 83.58 | 77.34 | 72.12 |
| DDIMDL | 83.07 | 87.53 | 85.68 | 79.95 | 84.69 | 80.34 | 56.12 |
| DeepDDI | 78.06 | 84.72 | 82.07 | 77.71 | 81.26 | 78.41 | 56.12 |
| LaGAT | 91.85 | 96.64 | 95.36 | 91.87 | 89.68 | 89.38 | 81.45 |
| GoGNN | 86.78 | 92.38 | 91.16 | 86.58 | 85.42 | 80.69 | 73.56 |
| SFLLN | 82.79 | 86.48 | 83.69 | 79.86 | 83.47 | 79.66 | 55.27 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | Precision . | Recall . | KAPPA . |
|---|---|---|---|---|---|---|---|
| ACDGNN | 96.71 | 98.81 | 98.35 | 94.11 | 95.64 | 93.74 | 92.23 |
| SSI-DDI | 93.42 | 97.79 | 97.41 | 93.42 | 94.35 | 91.78 | 86.85 |
| MHCADDI | 79.54 | 87.28 | 84.79 | 79.39 | 76.71 | 81.29 | 59.09 |
| SumGNN | 87.81 | 94.17 | 93.67 | 87.67 | 88.24 | 86.61 | 75.36 |
| KGNN | 85.16 | 90.86 | 89.57 | 77.62 | 83.58 | 77.34 | 72.12 |
| DDIMDL | 83.07 | 87.53 | 85.68 | 79.95 | 84.69 | 80.34 | 56.12 |
| DeepDDI | 78.06 | 84.72 | 82.07 | 77.71 | 81.26 | 78.41 | 56.12 |
| LaGAT | 91.85 | 96.64 | 95.36 | 91.87 | 89.68 | 89.38 | 81.45 |
| GoGNN | 86.78 | 92.38 | 91.16 | 86.58 | 85.42 | 80.69 | 73.56 |
| SFLLN | 82.79 | 86.48 | 83.69 | 79.86 | 83.47 | 79.66 | 55.27 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | Precision . | Recall . | KAPPA . |
|---|---|---|---|---|---|---|---|
| ACDGNN | 96.71 | 98.81 | 98.35 | 94.11 | 95.64 | 93.74 | 92.23 |
| SSI-DDI | 93.42 | 97.79 | 97.41 | 93.42 | 94.35 | 91.78 | 86.85 |
| MHCADDI | 79.54 | 87.28 | 84.79 | 79.39 | 76.71 | 81.29 | 59.09 |
| SumGNN | 87.81 | 94.17 | 93.67 | 87.67 | 88.24 | 86.61 | 75.36 |
| KGNN | 85.16 | 90.86 | 89.57 | 77.62 | 83.58 | 77.34 | 72.12 |
| DDIMDL | 83.07 | 87.53 | 85.68 | 79.95 | 84.69 | 80.34 | 56.12 |
| DeepDDI | 78.06 | 84.72 | 82.07 | 77.71 | 81.26 | 78.41 | 56.12 |
| LaGAT | 91.85 | 96.64 | 95.36 | 91.87 | 89.68 | 89.38 | 81.45 |
| GoGNN | 86.78 | 92.38 | 91.16 | 86.58 | 85.42 | 80.69 | 73.56 |
| SFLLN | 82.79 | 86.48 | 83.69 | 79.86 | 83.47 | 79.66 | 55.27 |
Till now, we have presented the results of experiments in transductive scenario, i.e., the drugs in test set were also included in the training set (partition policy 1). Next, in order to evaluate our method’s performance in inductive setting, which means new drugs that not included in the training set (also termed as cold start problem), we split the dataset on basis of the drugs instead of DDIs. It is more practical than transductive scenario. In order to evaluate the ability of ACDGNN for predicting the DDIs in inductive setting, here, we define the isolated drug represents the drug who has no any links in DDI network but has known links with other entities, such as gene, disease and so on. We divide the dataset according to the following two strategies: (1) Splitting all drugs as the training/validation/test set and ensure that in each validation/test triplet, one drug is from the training set and the other drug is from the validation/test set (the partition policy is recorded as 2). (2) Similarly, divide the data into training/validation/test set and ensure that the drugs in each validation/test triplet are both not appeared in the training set (the partition policy is marked as 3). The comparison results are shown in Tables 2 and 3, respectively. It can be seen that the prediction results of models under 2 and 3 scenarios are inferior to those of under 1. Accoring to results in Tables 2 and 3, it could be concluded that without prior knowledge about the isolated drugs, the performances of all models for 2 and 3 decrease, especially in 3. The experimental results also demonstrate that ACDGNN outperforms all other state-of-the-art methods in inductive DDI prediction, which illustrates the effectiveness of our model again.
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 |
| SSI-DDI | 73.81 | 81.57 | 81.95 | 73.50 | 47.61 |
| MHCADDI | 71.80 | 78.89 | 77.25 | 71.73 | 43.61 |
| DeepDDI | 66.48 | 72.49 | 71.79 | 66.44 | 32.96 |
| DDIMDL | 67.16 | 72.87 | 72.36 | 67.58 | 34.82 |
| SumGNN | 67.70 | 81.51 | 81.81 | 65.75 | 35.40 |
| LaGAT | 71.89 | 80.98 | 81.86 | 69.56 | 40.82 |
| GoGNN | 61.27 | 67.04 | 65.19 | 62.35 | 29.28 |
| SFLLN | 63.49 | 69.83 | 68.74 | 65.85 | 31.38 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 |
| SSI-DDI | 73.81 | 81.57 | 81.95 | 73.50 | 47.61 |
| MHCADDI | 71.80 | 78.89 | 77.25 | 71.73 | 43.61 |
| DeepDDI | 66.48 | 72.49 | 71.79 | 66.44 | 32.96 |
| DDIMDL | 67.16 | 72.87 | 72.36 | 67.58 | 34.82 |
| SumGNN | 67.70 | 81.51 | 81.81 | 65.75 | 35.40 |
| LaGAT | 71.89 | 80.98 | 81.86 | 69.56 | 40.82 |
| GoGNN | 61.27 | 67.04 | 65.19 | 62.35 | 29.28 |
| SFLLN | 63.49 | 69.83 | 68.74 | 65.85 | 31.38 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 |
| SSI-DDI | 73.81 | 81.57 | 81.95 | 73.50 | 47.61 |
| MHCADDI | 71.80 | 78.89 | 77.25 | 71.73 | 43.61 |
| DeepDDI | 66.48 | 72.49 | 71.79 | 66.44 | 32.96 |
| DDIMDL | 67.16 | 72.87 | 72.36 | 67.58 | 34.82 |
| SumGNN | 67.70 | 81.51 | 81.81 | 65.75 | 35.40 |
| LaGAT | 71.89 | 80.98 | 81.86 | 69.56 | 40.82 |
| GoGNN | 61.27 | 67.04 | 65.19 | 62.35 | 29.28 |
| SFLLN | 63.49 | 69.83 | 68.74 | 65.85 | 31.38 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 |
| SSI-DDI | 73.81 | 81.57 | 81.95 | 73.50 | 47.61 |
| MHCADDI | 71.80 | 78.89 | 77.25 | 71.73 | 43.61 |
| DeepDDI | 66.48 | 72.49 | 71.79 | 66.44 | 32.96 |
| DDIMDL | 67.16 | 72.87 | 72.36 | 67.58 | 34.82 |
| SumGNN | 67.70 | 81.51 | 81.81 | 65.75 | 35.40 |
| LaGAT | 71.89 | 80.98 | 81.86 | 69.56 | 40.82 |
| GoGNN | 61.27 | 67.04 | 65.19 | 62.35 | 29.28 |
| SFLLN | 63.49 | 69.83 | 68.74 | 65.85 | 31.38 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 |
| SSI-DDI | 65.30 | 69.08 | 68.26 | 63.85 | 30.61 |
| MHCADDI | 66.16 | 68.14 | 67.11 | 64.12 | 32.32 |
| DeepDDI | 59.26 | 63.20 | 63.21 | 58.50 | 18.54 |
| DDIMDL | 61.24 | 64.49 | 64.16 | 60.33 | 23.69 |
| SumGNN | 58.00 | 64.90 | 63.65 | 55.50 | 15.99 |
| LaGAT | 63.22 | 66.93 | 66.38 | 60.75 | 25.47 |
| GoGNN | 55.46 | 60.56 | 61.65 | 53.64 | 14.76 |
| SFLLN | 56.35 | 61.37 | 62.48 | 53.87 | 15.21 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 |
| SSI-DDI | 65.30 | 69.08 | 68.26 | 63.85 | 30.61 |
| MHCADDI | 66.16 | 68.14 | 67.11 | 64.12 | 32.32 |
| DeepDDI | 59.26 | 63.20 | 63.21 | 58.50 | 18.54 |
| DDIMDL | 61.24 | 64.49 | 64.16 | 60.33 | 23.69 |
| SumGNN | 58.00 | 64.90 | 63.65 | 55.50 | 15.99 |
| LaGAT | 63.22 | 66.93 | 66.38 | 60.75 | 25.47 |
| GoGNN | 55.46 | 60.56 | 61.65 | 53.64 | 14.76 |
| SFLLN | 56.35 | 61.37 | 62.48 | 53.87 | 15.21 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 |
| SSI-DDI | 65.30 | 69.08 | 68.26 | 63.85 | 30.61 |
| MHCADDI | 66.16 | 68.14 | 67.11 | 64.12 | 32.32 |
| DeepDDI | 59.26 | 63.20 | 63.21 | 58.50 | 18.54 |
| DDIMDL | 61.24 | 64.49 | 64.16 | 60.33 | 23.69 |
| SumGNN | 58.00 | 64.90 | 63.65 | 55.50 | 15.99 |
| LaGAT | 63.22 | 66.93 | 66.38 | 60.75 | 25.47 |
| GoGNN | 55.46 | 60.56 | 61.65 | 53.64 | 14.76 |
| SFLLN | 56.35 | 61.37 | 62.48 | 53.87 | 15.21 |
| Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . |
|---|---|---|---|---|---|
| ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 |
| SSI-DDI | 65.30 | 69.08 | 68.26 | 63.85 | 30.61 |
| MHCADDI | 66.16 | 68.14 | 67.11 | 64.12 | 32.32 |
| DeepDDI | 59.26 | 63.20 | 63.21 | 58.50 | 18.54 |
| DDIMDL | 61.24 | 64.49 | 64.16 | 60.33 | 23.69 |
| SumGNN | 58.00 | 64.90 | 63.65 | 55.50 | 15.99 |
| LaGAT | 63.22 | 66.93 | 66.38 | 60.75 | 25.47 |
| GoGNN | 55.46 | 60.56 | 61.65 | 53.64 | 14.76 |
| SFLLN | 56.35 | 61.37 | 62.48 | 53.87 | 15.21 |
Parameter analysis
In this section, we will analyze the impact of the key parameters in ACDGNN, including the entities’ embedding dimension |$f$|, the number of information propagation layers |$l$| in the heterogeneous neighbor-domain information aggregation module and the number of heads |$K$| in the multi-head attention mechanism.
Firstly, we analyze the impact of |$f$| on the prediction performance of ACDGNN under the three data partition polices. In our experiment, we empirically set the hyper-parameters |$l$| and |$K$| both to 2, and take |$f$| as the independent variable while the various performance metrics as the dependent variables for parameter analysis. The results are shown in Figure 3 1(a), 2(a) and 3(a). We can find that under the three data partition strategies, the model achieves the best performance when |$f$| is 64, 64 and 16, respectively. After reaching the optimal dimension, the performance of the model tends to decline with the increase of |$f$|. The possible reason is that introduceing too many parameters may lead to overfitting of the model, which reduces its generalization ability.
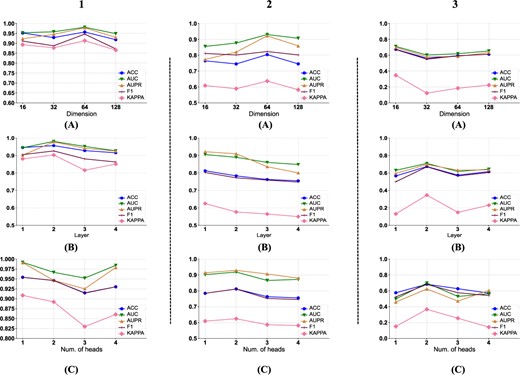
Parameter analysis of ACDGNN. Subplots on row (A) presents the impact of embedding dimension on model performance under three data split policies. Subplots on row (B) and (C) illustrates effect of information propagation layers and number of attention heads on model performance, respectively.
Then we analyze the impact of |$l$| on the prediction performance under the three data partition polices. In this part, we select the optimal |$f$| under each data partition strategy as 64, 64, 16 respectively. The results are shown in Figure 3 1(b), 2(b) and 3(b). It can be seen that the optimal |$l$| is 2, 1 and 2 respectively under the three data partition strategies, which indicates that in heterogeneous networks, directly connected neighbors and the skip-connection neighbors are help to the prediction of DDI [34], while considering higher-order |$(>2)$| neighbor’s information may introduce additional noise, thus reducing the prediction performance of the model.
Finally, we analyze the effect of |$K$| under three partition polices. Here, the optimal |$f$| and |$l$| under policy 1 are set to 64 and 2 respectively, while under policy 2, they are set to 64 and 1, and under the policy 3, be set as 16 and 2. The experimental results are shown in Figure 3 1(c), 2(c) and 3(c). It can be seen that under the three data partition strategies, the optimal |$K$| is 1, 2 and 2 respectively. For the policies 2 and 3, due to the drugs in test set that unseen in the training phase, compared with partition policy 1, the representation learning process cannot be carried out very well. Therefore, the introduction of too many attention heads |$(>2)$| may also lead to overfitting of the model. This phenomenon is similar to hyper-parameter |$f$| and |$l$|.
Ablation study
To study whether the components of ACDGNN have an effect on the final performance, we conduct the following ablation studies. First, we verify the effectiveness of the transformation module. We remove it and directly take the embedding of the entity itself as the input of the heterogeneous neighbor-domain information aggregation module at each layer, which is represented by ACDGNN w/o CDT (cross domain transformation). Secondly, we check the effectiveness of the feature-structure information aggregation module of Eq. 6. We also remove it and the embedding representation used by this model is composed of the feature information and structure information of drugs. Due to constraint loss (Eq. 12) depending on this module, so it will not be added in the final loss, that is, the final training loss of this model is |$L_{base}$|, which is represented by ACDGNN w/o FSIA (feature structure information aggregation). Besides, to evalute the contributions of drug-related biomedical entities to model performance, we removed gene nodes and target nodes from network |$\mathcal{G}$| and the corresponding models are presented ACDGNN w/o Gene and ACDGNN w/o Target.
The comparison results are shown in Table 4. It can be found that under the partition strategies 1 and 2, considering the transformation module and the feature-structure information aggregation module at the same time can effectively improve the prediction performance, which is about 2% higher than the second on average. However, under partition strategy 3, considering the transformation module does not seem to significantly improve the generalization performance, while slightly decrease under some metrics (such as ACC, F1 and KAPPA). The possible reason is that the transformation module introduces more parameters when aggregating the neighborhood information, resulting in overfitting. Moreover, we can find that the removal of gene nodes and target nodes lead to significant performance drop, as the model could not extract comprehensive drug interaction information with absence of certain entities and thus produces sub-optimal nodes’ representations.
| . | Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . | |
|---|---|---|---|---|---|---|---|
| 1 | ACDGNN | 96.71 | 98.81 | 98.35 | 94.41 | 92.23 | |
| ACDGNN w/o FSIA | 93.79 | 94.14 | 90.99 | 91.37 | 82.58 | ||
| ACDGNN w/o CDT | 88.74 | 92.37 | 95.41 | 88.61 | 79.49 | ||
| ACDGNN w/o Gene | 92.58 | 93.73 | 93.81 | 89.57 | 81.63 | ||
| ACDGNN w/o Target | 92.36 | 92.96 | 93.15 | 88.86 | 80.86 | ||
| 2 | ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 | |
| ACDGNN w/o FSIA | 78.02 | 85.32 | 93.46 | 77.89 | 56.18 | ||
| ACDGNN w/o CDT | 74.82 | 84.21 | 92.13 | 74.78 | 49.64 | ||
| ACDGNN w/o Gene | 77.68 | 84.29 | 92.35 | 75.76 | 54.79 | ||
| ACDGNN w/o Target | 77.24 | 83.97 | 91.86 | 75.13 | 54.28 | ||
| 3 | ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 | |
| ACDGNN w/o FSIA | 65.92 | 64.59 | 59.17 | 65.77 | 31.84 | ||
| ACDGNN w/o CDT | 69.00 | 68.60 | 60.45 | 68.18 | 38.00 | ||
| ACDGNN w/o Gene | 64.93 | 63.75 | 58.64 | 64.61 | 30.49 | ||
| ACDGNN w/o Target | 64.25 | 63.18 | 57.96 | 63.81 | 29.67 | ||
| . | Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . | |
|---|---|---|---|---|---|---|---|
| 1 | ACDGNN | 96.71 | 98.81 | 98.35 | 94.41 | 92.23 | |
| ACDGNN w/o FSIA | 93.79 | 94.14 | 90.99 | 91.37 | 82.58 | ||
| ACDGNN w/o CDT | 88.74 | 92.37 | 95.41 | 88.61 | 79.49 | ||
| ACDGNN w/o Gene | 92.58 | 93.73 | 93.81 | 89.57 | 81.63 | ||
| ACDGNN w/o Target | 92.36 | 92.96 | 93.15 | 88.86 | 80.86 | ||
| 2 | ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 | |
| ACDGNN w/o FSIA | 78.02 | 85.32 | 93.46 | 77.89 | 56.18 | ||
| ACDGNN w/o CDT | 74.82 | 84.21 | 92.13 | 74.78 | 49.64 | ||
| ACDGNN w/o Gene | 77.68 | 84.29 | 92.35 | 75.76 | 54.79 | ||
| ACDGNN w/o Target | 77.24 | 83.97 | 91.86 | 75.13 | 54.28 | ||
| 3 | ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 | |
| ACDGNN w/o FSIA | 65.92 | 64.59 | 59.17 | 65.77 | 31.84 | ||
| ACDGNN w/o CDT | 69.00 | 68.60 | 60.45 | 68.18 | 38.00 | ||
| ACDGNN w/o Gene | 64.93 | 63.75 | 58.64 | 64.61 | 30.49 | ||
| ACDGNN w/o Target | 64.25 | 63.18 | 57.96 | 63.81 | 29.67 | ||
| . | Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . | |
|---|---|---|---|---|---|---|---|
| 1 | ACDGNN | 96.71 | 98.81 | 98.35 | 94.41 | 92.23 | |
| ACDGNN w/o FSIA | 93.79 | 94.14 | 90.99 | 91.37 | 82.58 | ||
| ACDGNN w/o CDT | 88.74 | 92.37 | 95.41 | 88.61 | 79.49 | ||
| ACDGNN w/o Gene | 92.58 | 93.73 | 93.81 | 89.57 | 81.63 | ||
| ACDGNN w/o Target | 92.36 | 92.96 | 93.15 | 88.86 | 80.86 | ||
| 2 | ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 | |
| ACDGNN w/o FSIA | 78.02 | 85.32 | 93.46 | 77.89 | 56.18 | ||
| ACDGNN w/o CDT | 74.82 | 84.21 | 92.13 | 74.78 | 49.64 | ||
| ACDGNN w/o Gene | 77.68 | 84.29 | 92.35 | 75.76 | 54.79 | ||
| ACDGNN w/o Target | 77.24 | 83.97 | 91.86 | 75.13 | 54.28 | ||
| 3 | ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 | |
| ACDGNN w/o FSIA | 65.92 | 64.59 | 59.17 | 65.77 | 31.84 | ||
| ACDGNN w/o CDT | 69.00 | 68.60 | 60.45 | 68.18 | 38.00 | ||
| ACDGNN w/o Gene | 64.93 | 63.75 | 58.64 | 64.61 | 30.49 | ||
| ACDGNN w/o Target | 64.25 | 63.18 | 57.96 | 63.81 | 29.67 | ||
| . | Methods . | ACC . | AUC . | AUPR . | F1 . | KAPPA . | |
|---|---|---|---|---|---|---|---|
| 1 | ACDGNN | 96.71 | 98.81 | 98.35 | 94.41 | 92.23 | |
| ACDGNN w/o FSIA | 93.79 | 94.14 | 90.99 | 91.37 | 82.58 | ||
| ACDGNN w/o CDT | 88.74 | 92.37 | 95.41 | 88.61 | 79.49 | ||
| ACDGNN w/o Gene | 92.58 | 93.73 | 93.81 | 89.57 | 81.63 | ||
| ACDGNN w/o Target | 92.36 | 92.96 | 93.15 | 88.86 | 80.86 | ||
| 2 | ACDGNN | 81.44 | 91.88 | 93.28 | 80.86 | 62.89 | |
| ACDGNN w/o FSIA | 78.02 | 85.32 | 93.46 | 77.89 | 56.18 | ||
| ACDGNN w/o CDT | 74.82 | 84.21 | 92.13 | 74.78 | 49.64 | ||
| ACDGNN w/o Gene | 77.68 | 84.29 | 92.35 | 75.76 | 54.79 | ||
| ACDGNN w/o Target | 77.24 | 83.97 | 91.86 | 75.13 | 54.28 | ||
| 3 | ACDGNN | 67.29 | 70.94 | 69.65 | 67.00 | 34.57 | |
| ACDGNN w/o FSIA | 65.92 | 64.59 | 59.17 | 65.77 | 31.84 | ||
| ACDGNN w/o CDT | 69.00 | 68.60 | 60.45 | 68.18 | 38.00 | ||
| ACDGNN w/o Gene | 64.93 | 63.75 | 58.64 | 64.61 | 30.49 | ||
| ACDGNN w/o Target | 64.25 | 63.18 | 57.96 | 63.81 | 29.67 | ||
To summarize, the introduction of cross domain transformation and feature-structure information aggregation module can improve the DDI prediction performance. On the one hand, it can capture the information of neighbors in different domains through appropriate domain transformation; on the other hand, by weighted aggregation of feature information and structure information, ACDGNN can distinguish the importance of them. In addition, the constraint loss forces the embedding learned by ACDGNN to be consistent with the drug interaction behavior, therefore, a more representative embedding representation can be learned, leading to improvement of the final prediction performance. Besides, comprehensive use of information in drug-related entities is of great benefit to the prediction of DDI.
Case study
We conduct case studies to investigate the usefulness of ACDGNN in practice. Here, we use all the known DDI triples in our dataset to train the prediction model, and then make predictions for the remaining drug pairs. We construct a ranked list of (drug |$i$|, drug |$j$|, DDI type |$r$|) triples, in which the triples are ranked by predicted probability scores. A higher prediction score between two drugs suggests that they have a higher probability of an interaction occurrence. We investigate the 20 highest ranked predictions in the list. For these 20 drug pairs, we apply DrugBank (https://go.drugbank.com/interax/multi_search) and Drug Interactions Checker tool provided by Drugs.com (https://www.drugs.com/) to find the evidence support for them and collect the descriptions about their interactions.
Fifteen DDI events can be confirmed among these 20 events (only top five are shown in Table 5 due to the pages’ limitation), the complete results are listed in the Supplementary Material. As shown in Table 5, the interaction between Diazepam and Chromium is predicted to cause the event #72, and means Diazepam may decrease the excretion rate of Chromium which could result in a higher serum level. Studies have shown that chromium functions as an active component of glucose tolerance factor (GTF). This factor facilitates binding of insulin to the cell and promotes the uptake of glucose [35]. Meanwhile, diazepam alone was found to inhibit insulin secretion [36], which supports the predictions of our model. The interaction between Buprenorphine and Imidafenacin is predicted to cause the event #49, means the risk or severity of adverse effects can be increased when Imidafenacin is combined with Butylscopolamine. It has been reported that Butylscopolamine binds to muscarinic M3 receptors in the gastrointestinal tract [37]. Similarly, Imidafenacin binds to and antagonizes muscarinic M1 and M3 receptors with high affinity [38]. The results indicate that our proposed ACDGNN model is effective in predicting novel DDIs. Other five DDIs deserve to be confirmed by further experiments. In addition, we also found that a certain drug may be closely related to a certain DDI event. For example, 4 of the top 20 predictions related to event #47 (the metabolism decrease) are related to Barnidipine. More attention should be paid on ‘Barnidipine’.
| Drug A . | Drug B . | Evidence source . | Description . |
|---|---|---|---|
| Diazepam | Selenium | Drugbank tool | Diazepam may decrease the excretion rate of Selenium which could result in a higher serum level. |
| Diazepam | Chromium | Drugbank tool | Diazepam may decrease the excretion rate of Chromium which could result in a higher serum level. |
| Imidafenacin | Butylscopolamine | Drugbank tool | The risk or severity of adverse effects can be increased when Imidafenacin is combined with Butylscopolamine. |
| Buprenorphine | Palonosetron | Drugbank tool | Palonosetron may increase the central nervous system depressant (CNS depressant) activities of Buprenorphine. |
| Methscopolamine | Toloxatone | N.A. | N.A. |
| Drug A . | Drug B . | Evidence source . | Description . |
|---|---|---|---|
| Diazepam | Selenium | Drugbank tool | Diazepam may decrease the excretion rate of Selenium which could result in a higher serum level. |
| Diazepam | Chromium | Drugbank tool | Diazepam may decrease the excretion rate of Chromium which could result in a higher serum level. |
| Imidafenacin | Butylscopolamine | Drugbank tool | The risk or severity of adverse effects can be increased when Imidafenacin is combined with Butylscopolamine. |
| Buprenorphine | Palonosetron | Drugbank tool | Palonosetron may increase the central nervous system depressant (CNS depressant) activities of Buprenorphine. |
| Methscopolamine | Toloxatone | N.A. | N.A. |
N.A.: The evidence of the given DDI is not available till now.
| Drug A . | Drug B . | Evidence source . | Description . |
|---|---|---|---|
| Diazepam | Selenium | Drugbank tool | Diazepam may decrease the excretion rate of Selenium which could result in a higher serum level. |
| Diazepam | Chromium | Drugbank tool | Diazepam may decrease the excretion rate of Chromium which could result in a higher serum level. |
| Imidafenacin | Butylscopolamine | Drugbank tool | The risk or severity of adverse effects can be increased when Imidafenacin is combined with Butylscopolamine. |
| Buprenorphine | Palonosetron | Drugbank tool | Palonosetron may increase the central nervous system depressant (CNS depressant) activities of Buprenorphine. |
| Methscopolamine | Toloxatone | N.A. | N.A. |
| Drug A . | Drug B . | Evidence source . | Description . |
|---|---|---|---|
| Diazepam | Selenium | Drugbank tool | Diazepam may decrease the excretion rate of Selenium which could result in a higher serum level. |
| Diazepam | Chromium | Drugbank tool | Diazepam may decrease the excretion rate of Chromium which could result in a higher serum level. |
| Imidafenacin | Butylscopolamine | Drugbank tool | The risk or severity of adverse effects can be increased when Imidafenacin is combined with Butylscopolamine. |
| Buprenorphine | Palonosetron | Drugbank tool | Palonosetron may increase the central nervous system depressant (CNS depressant) activities of Buprenorphine. |
| Methscopolamine | Toloxatone | N.A. | N.A. |
N.A.: The evidence of the given DDI is not available till now.
CONCLUSION
In this paper, we propose a new method ACDGNN: attention-based cross domain graph neural network. ACDGNN acts on heterogeneous networks and learns the embedding representation of drug entities by aggregating neighborhood information for multi-typed DDI prediction. ACDGNN is consisted by five modules: the input module takes a heterogeneous network as input, which contains many types of nodes and edges; the transformation module is used to map the information from neighbors to a homogeneous low-dimensional embedding space; the heterogeneous neighbor-domain information aggregation module exploits the multi-head attention mechanism to aggregate the neighborhood information; the feature-structure information aggregation module combines the entity’s attributes and the network structure information in the way of weighted aggregation to obtain the final embedding representation of the entity; the final decomposition based predictor uses the embedding of drug pairs and interaction types to make prediction. The proposed approach is compared with several state-of-the-art baselines using real-life datasets. The experimental results show that the proposed model achieves competitive prediction performance. In addition, we also performed ablation analysis and case study to verify the effectiveness of the method.
An Attention-based cross domain graph neural network model for DDI prediction is proposed in this paper.
ACDGNN considers other types of drug-related entities and propagate information through cross domain operation for learning informative representation of drugs.
ACDGNN can eliminate the heterogeneity between different types of entities and effectively predict DDIs in transductive and inductive scenarios.
FUNDING
This work was supported by National Nature Science Foundation of China (Grant No. 61872297), Shaanxi Provincial Key Research & Development Program, China (Grand No. 2023-YBSF-114), CAAI-Huawei MindSpore Open Fund (Grant No. CAAIXSJLJJ-2022-035A) and the Fundamental Research Funds for the Central Universities (Grand No. SY20210003). Thanks for the Center for High Performance Computation, Northwestern Polytechnical University to provide computation resource.
Author Biographies
Hui Yu received his master’s and PhD degrees from Northwestern Polytechnical University, Xi’an, China, where he works currently as an associate professor. He has published >50 papers in peer reviewed journals and conferences. His research interests include bioinformatics, machine learning and data mining.
KangKang Li is currently pursuing his Master’s degree in the School of Computer Science at Northwestern Polytechnical University, Xi’an, China. He received his bachelor’s degree in software engineering from Chongqing University, Chongqing, China. He is interested in graph representation learning and applications.
WenMin Dong received his master’s degrees from Northwestern Polytechnical University, Xi’an, China. He received his bachelor’s degree in Computer Science and Technology from Anhui jianzhu university, Hefei, China. He is interested in machine learning and data mining.
Shuanghong Song has received her PhD degree from Northwestern Polytechnical University, Xi’an, China. She works currently as an associate professor in Shaanxi Normal University. She has published about 30 papers in peer reviewed journals and conferences. Her research interests includes Pharmacology of Traditional Chinese medicine’ Cphytochemistry and osteoporosis.
Chen Gao has received his master’s degree from Northwestern Polytechnical University in 2014, Xi’an, China. Then he works currently as an Senior engineer in Xi’an high-tech Research Institute. He has published >30 papers in peer reviewed journals and conference. His research interests include system simulation, artificial intelligence and data mining.
Jian-Yu Shi received his master’s and PhD degrees from Northwestern Polytechnical University, Xi’an, China, where he is currently working as a professor. He was selected as the Postdoctoral Fellow in the first round of the Hong Kong Scholars Program in 2011 and worked in the University of Hong Kong during 2012–2014. He has published 40+ peer-reviewed papers and has >10 years research experience in AI in drug discovery. His research interests include matrix factorization, graph neural network, drug.drug interaction, drug combination and precision medicine.


