Search
Close
Search
Advanced Search
Search Menu
AI Discovery Assistant

Abstract

Motivation

Effective computational methods to predict drug–protein interactions (DPIs) are vital for drug discovery in reducing the time and cost of drug development. Recent DPI prediction methods mainly exploit graph data composed of multiple kinds of connections among drugs and proteins. Each node in the graph usually has topological structures with multiple scales formed by its first-order neighbors and multi-order neighbors. However, most of the previous methods do not consider the topological structures of multi-order neighbors. In addition, deep integration of the multi-modality similarities of drugs and proteins is also a challenging task.

Results

We propose a model called ALDPI to adaptively learn the multi-scale topologies and multi-modality similarities with various significance levels. We first construct a drug–protein heterogeneous graph, which is composed of the interactions and the similarities with multiple modalities among drugs and proteins. An adaptive graph learning module is then designed to learn important kinds of connections in heterogeneous graph and generate new topology graphs. A module based on graph convolutional autoencoders is established to learn multiple representations, which imply the node attributes and multiple-scale topologies composed of one-order and multi-order neighbors, respectively. We also design an attention mechanism at neighbor topology level to distinguish the importance of these representations. Finally, since each similarity modality has its specific features, we construct a multi-layer convolutional neural network-based module to learn and fuse multi-modality features to obtain the attribute representation of each drug–protein node pair. Comprehensive experimental results show ALDPI’s superior performance over six state-of-the-art methods. The results of recall rates of top-ranked candidates and case studies on five drugs further demonstrate the ability of ALDPI to discover potential drug-related protein candidates.

Contact

[email protected]

drug–protein interaction prediction, drug—protein heterogeneous graph, multi-scale neighbor topologies, multi-modality similarities, neighbor topology-level attention

1 Introduction

Predicting drug–protein interactions (DPIs) is an important step in drug discovery and repositioning [1–3]. Accurately and effectively identifying the interactions between drugs and targets can facilitate the drug development process and reduce the required time and cost [4, 5]. Computational prediction of novel DPI candidates may screen potential candidates for biologists to discover the true DPIs using experiments [6].

Early methods, including ligand-based and molecular docking, have been proposed to predict DPIs. Ligand-based approaches compare similarities between candidate ligand and the known ligands of a target protein, and then estimate the possibility that the candidate ligand binds to the protein [7, 8]. Docking simulation methods utilize the 3D structure of the protein and dynamically simulate them to assess the affinity of the interaction between drug molecules and proteins [9, 10]. However, these methods are severely limited by the unknown 3D structure and ligand information of most proteins [11–13].

Recent studies have shown that machine learning methods are more effective and achieve better performance in predicting DPI [14, 15]. These methods can be divided into four main categories namely: biological characteristic-based, similarity-based, network-based and deep learning-based. In the biological characteristic-based methods, Ding et al. [16] extracted the characteristics of drugs and proteins from drug molecular fingerprints and protein amino acid sequences. They then applied a support vector machine (SVM) model to predict DPIs. Chu et al. [17] introduced multi-label learning and community detection to the task and used random forest for prediction. Two methods [18, 19] fed the drug structures and protein sequences into a rotation forest-based model to evaluate the DPI tendency. Similarity-based methods are proposed based on the assumptions that if drug |$r$| interacts with protein |$p$|⁠, then (i) drug |$r$| is likely to interact with proteins that are similar to |$p$|⁠, (2) protein |$p$| is likely to interact with drugs that are similar to |$r$| and (iii) drugs similar to |$r$| are likely to interact with proteins similar to |$p$|⁠. Ezzat et al. [20] used chemical structure similarities of drugs and sequence similarities of proteins and DPIs to establish a matrix factorization framework. They also proposed weighted |$k$| nearest known neighbors as a preprocessing step to estimate the interaction possibility of unknown cases. Several methods combine drug similarity and protein similarity and predict novel interaction candidates by SVM, principal component analysis (PCA), Gaussian kernel model and matrix factorization [21–24]. They used only one type of drug similarity and protein similarity. However, the types of similarities were diverse. Olayan et al. [25] and Xuan et al. [26] integrated multiple similarities between drugs and proteins and applied random forest and gradient boosting decision trees to obtain drug–protein interaction scores, respectively. DTI-CDF (cascade deep forest) [27] also extracted hybrid similarity features of drugs and proteins and predicted them using a cascade deep forest model. Because the topology of heterogeneous networks may also assist in DPI prediction, network-based methods have gained wider attention. Bleakly et al. [28] and Mei et al. [29] established a common bipartite local model for prediction. Luo et al. [30] first constructed a drug–protein heterogeneous network based on several types of drug- and protein-associated connections. They then applied singular value decomposition to learn feature vectors containing topological information of nodes and predicted novel DPIs. However, the models mentioned above are shallow prediction models, which are unable to learn deep features from related data and capture potential connections in the network.

Deep learning techniques have proven to be powerful predictors in many fields. Recently, deep learning-based methods have been used to predict DPIs. Lee et al. [31] constructed deep neural network (DNN) model to capture the local residue patterns of proteins participating in DPIs. Specifically, they performed convolution operations on different lengths of sequences to capture local features. Wang et al. [32] utilized PCA to learn drug- and protein-related feature matrices and predicted by the long short-term memory model. They ignored important similarity information. Sun et al. [33] combined similarities data and preserved the consistency of the features and functions of drugs. Several other methods integrated multiple similarities between drugs and proteins and predict novel interactions by convolutional neural network (CNN), fully connected autoencoder and gated recurrent unit (GRU) models [34–36]. In addition, graph neural network-based methods also consider topological information and node features in graph. Sun et al. [37] developed a prediction model based on graph convolution and generative adversarial network using a single type of drug and protein similarity. Zhao et al. [38] first constructed a heterogeneous network using drug-protein pairs as nodes. They then learned node features using graph convolutional networks and predicted DPI using DNNs. Although the above works have made crucial efforts in DPI prediction, there are still some spaces that can be improved.

In this study, we propose a model called ALDPI to predict novel drug–protein interactions. The model learns the topological representation in a drug–protein heterogeneous graph and integrates the multi-modality similarities of drugs and proteins. The main contributions of our model are described as follows:

  • We calculated multi-modality similarities of drugs and proteins based on different source data, and these similarities reflect how similar two drugs (two proteins) are from different views. We then utilized interactions between drugs and proteins and multi-modality similarities of drugs and proteins to construct the drug–protein heterogeneous graph.

  • To deeply integrate the multi-order neighbor topology information of nodes in the graph, we propose an adaptive topology graph learning module. The module softly selects the weights of the different connected edges to generate multiple new topology graphs.

  • A module based on graph convolution autoencoder is constructed to learn the multiple topology representations of nodes based on different order neighbor topologies. Since these topology representations have different importance for DPI prediction, we further establish a neighbor topology-level attention mechanism to discriminate the importance and obtain an enhanced topology representation of node.

  • We designed a multi-layer CNN-based strategy to deeply integrate the multi-modality similarities of drugs and proteins. The specific modality attribute learning module learns specific features from different modality similarities, and these features are integrated by the convolution layer to form the attribute representation of the node pair. The results of the evaluation metrices show that our model is superior to the six state-of-the-art methods, and the case studies prove the ability of ALDPI to predict potential drug–protein interactions.

2 Materials and method

2.1 Overview of ALDPI

We propose a novel deep learning model called ALDPI that combines multi-order neighbor topologies and multi-modality similarities of drugs and proteins for DPI prediction. The pipeline of the ALDPI method is shown in Figures 1 and 2. First, we construct the drug–protein heterogeneous graph based on drug- and protein-related interactions and multiple types of similarities (Figure 1). Then, the topology representations of nodes and the attribute representations of drug–protein node pairs are learned, respectively (Figure 2A and B). Finally, we combine these two representations to estimate the interaction score of a pair of drug and protein (Figure 2C).

2.2 Dataset

The dataset from Luo et al. [30] contains 708 drugs extracted from the DrugBank database [39], 1512 proteins from the Human Protein Reference Database (HPRD) [40] and 5603 diseases from the Comparative Toxicogenomics Database (CTD) [41]. We collect the latest drug–protein interaction (DPI) data from DrugBank to update the dataset. We remove drugs and proteins without DPIs and diseases that are not associated to drugs and proteins. There are 570 drugs, 467 proteins and 5420 diseases. The latest dataset provides corresponding 2816 DPIs and 7016 drug–drug interactions (DDIs) from DrugBank, 1452 protein-protein interactions (PPIs) from HPRD, 178 477 drug-disease associations and 544 437 protein-disease associations from CTD. In addition, the chemical structure similarity of drugs is the Tanimoto coefficient of the product-graphs of their chemical structures, and the sequence similarity of the proteins is calculated using Smith-Waterman score based on their amino acid sequences.

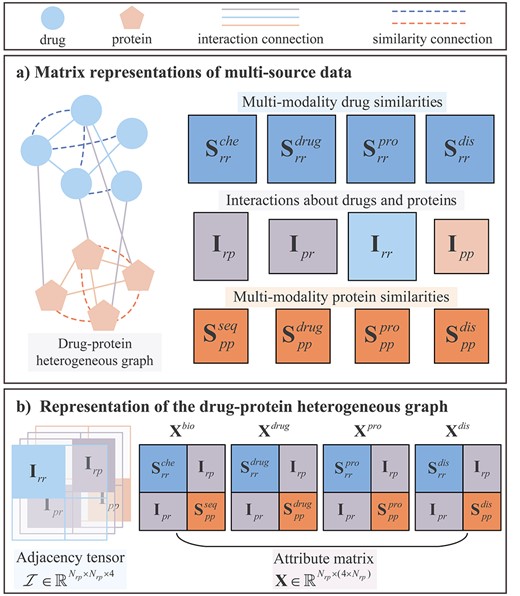
Matrix representations of multi-source data and construction of the drug–protein heterogeneous graph. (A) matrix representations of multi-source data including multi-modality similarities and interactions about drugs and proteins. (B) adjacency relationship and attribute representations of drug–protein heterogeneous graph.
Figure 1

Matrix representations of multi-source data and construction of the drug–protein heterogeneous graph. (A) matrix representations of multi-source data including multi-modality similarities and interactions about drugs and proteins. (B) adjacency relationship and attribute representations of drug–protein heterogeneous graph.

Open in new tabDownload slide

2.3 Matrix representation of multi-source data and heterogeneous graph construction

2.3.1 Matrix representation of interactions and associations

Suppose there are |$N_r$| drug nodes, denoted as |$V_R= \{r_1,r_2,\ldots ,r_{N_r} \}$|⁠, |$N_p$| protein nodes, denoted as |$V_P= \{p_1,p_2,\ldots ,p_{N_p} \}$| and |$N_d$| disease nodes, denoted as |$V_D= \{d_1,d_2,\ldots ,d_{N_d} \}$|⁠. We defined interaction matrix |$\bf{I}$| and association matrix |$\bf{A}$| according to the connection relationships (interaction or association).

The interaction matrix |$\bf{I}$| is defined:
(1)
where |$({\textrm{{I}}}_{rp})_{ij}=1$| means there is an observed interaction between drug node |$r_i$| and protein node |$p_j$|⁠, and |$({\textrm{{I}}}_{rp})_{ij}=0$| indicates unknown or non-existing interaction between |$r_i$| and |$p_j$|⁠. |$\textbf{I}_{rr}$| (⁠|$\textbf{I}_{pp}$|⁠) records the interactions between |$N_r$| drugs (⁠|$N_p$| proteins). |$({\textrm{{I}}}_{rr})_{ij}=1$| (⁠|$({\textrm{{I}}}_{pp})_{ij}=1$|⁠) if the interaction between the |$i$|th drug node (protein node) and the |$j$|th drug node (protein node) has been observed, |$({\textrm{{I}}}_{rr})_{ij}=0$| (⁠|$({\textrm{{I}}}_{pp})_{ij}=0$|⁠) otherwise.
The association matrix |$\bf{A}$| is defined:
(2)
where |$\textbf{A}_{rd}$| and |$\textbf{A}_{pd}$| are defined to assist the prediction of drug–protein interactions because the therapeutic effects of drugs on diseases reflect their affinity for disease-related proteins. |$({\textrm{{A}}}_{rd})_{ij}=1$| (⁠|$({\textrm{{A}}}_{pd})_{ij}=1$|⁠) indicates that the drug node |$r_i$| (protein node |$p_i$|⁠) is associated with the disease node |$d_j$|⁠, |$({\textrm{{A}}}_{rd})_{ij}=0$| (⁠|$({\textrm{{A}}}_{pd})_{ij}=0$|⁠) otherwise.

2.3.2 Matrix representation of multi-modality similarities

Owing to different drug-related data, we may obtain multi-modality similarity matrices of drugs, which are defined as
(3)
where |$\textbf{S}_{rr}^{che}$| is calculated based on drug chemical structures using the Tanimoto coefficient [42] and provided by [30]. Based on the drugs interacting with each drug and the associated diseases of each drug, we calculated drug functional similarity based on DDIs |$\textbf{S}_{rr}^{drug}$| and one based on drug indications |$\textbf{S}_{rr}^{dis}$| using the cosine similarity. |$({\textrm{{S}}}_{rr}^{pro})_{ij}$| is calculated via the drug-target interaction vector of |$r_i$| and that of |$r_j$| by the Gaussian interaction profile (GIP) kernel similarity [23]. The value range of |$({\textrm{{S}}}_{rr})_{ij}$| is |$[0,1]$|⁠, and a large value indicates higher similarities between the two drugs.
Similarly, the multi-modality similarity matrices of proteins are defined as
(4)
where the initial protein sequence similarity matrix |$\textbf{S}_{pp}^{seq}$| is obtained from [30]. It records the protein sequence-based similarity score calculated by the Smith-Waterman algorithm [43] and is normalized by min-max normalization. We calculate the cosine similarity between any two row vectors in |$\textbf{I}_{pp}$| (⁠|$\textbf{A}_{pd}$|⁠) to obtain |$\textbf{S}_{pp}^{pro}$| (⁠|$\textbf{S}_{pp}^{dis}$|⁠). We define the transpose matrix of |$\textbf{I}_{rp}$| as a protein-drug interaction (PDI) matrix |$\textbf{I}_{pr}$|⁠, and obtain |$\textbf{S}_{pp}^{drug}$| by utilizing the GIP kernel similarity [23] for |$\textbf{I}_{pr}$|⁠.

2.3.3 Construction of drug–protein heterogeneous graph

To fully utilize the drug- and protein-related interactions and multi-modal similarities, we constructed a drug–protein heterogeneous graph |$\rm{G}=(\mathcal{I},\textbf{X})$| and set the total number of drug nodes and protein nodes to |$N_{rp}$| (⁠|$N_{rp}=N_r+N_p$|⁠). As shown in Figure 1B, four types of interactions between drugs and proteins are represented by the adjacency tensor |$\mathcal{I}\in \mathbb{R}^{{N_{rp}}\times{N_{rp}}\times 4}$|⁠,
(5)
where ‘;’ denotes the stack operation from top to bottom. |$\left [\textbf{I}_{rr};\textbf{I}_{rp};\textbf{I}_{pr};\textbf{I}_{pp}\right ]$| applied the matrix extension operations to form |$\left [\textbf{I}_{rr}^{^{\prime}};\textbf{I}_{rp}^{^{\prime}};\textbf{I}_{pr}^{^{\prime}};\textbf{I}_{pp}^{^{\prime}}\right ]$|⁠. Take |$\textbf{I}_{rr}\in \mathbb{R}^{N_r\times N_r}$| for an example, we first fix |$\textbf{I}_{rr}$| as the upper-left part of the drug–drug interaction extension matrix, and pad 0 to the rest to obtain |$\textbf{I}_{rr}^{^{\prime}}\in \mathbb{R}^{N_{rp}\times N_{rp}}$|⁠. We also have a concatenate attribute matrix |$\textbf{X}\in \mathbb{R}^{N_{rp}\times N_f}$| meaning that the |$N_f$|-dimensional feature is given for each drug node or protein node in |$\rm{G}$|⁠. The attribute matrix contains the interactions between drugs and proteins and the multi-model similarities of drugs and proteins. According to the source of similarity, we divide multi-modality similarities into four categories: biological characteristics-based, drug-based, protein-based and indication-based. These specific attribute matrices |$\textbf{X}^{bio}$|⁠, |$\textbf{X}^{drug}$|⁠, |$\textbf{X}^{pro}$|⁠, |$\textbf{X}^{dis}\in \mathbb{R}^{N_{rp}\times N_{rp}}$| are constructed based on these similarities and drug–protein interactions, respectively. They are represented as follows,
(6)
These attribute matrices are concatenated to obtain |$\textbf{X}\in \mathbb{R}^{N_{rp}\times N_{f}}$| (Figure 1B),
(7)
where |$N_f=4\times N_{rp}$| and |$\lVert $| denotes the concatenation operation from beginning to end.
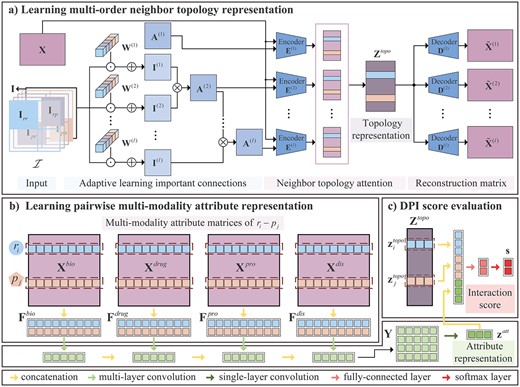
The pipeline of the proposed ALDPI method for DPI prediction. Given drug $r_i$ and protein $p_j$, two types of representations are learned by (A) topology representation learning module based on convolution operations, graph convolutional autoencoder and neighbor topology-level attention and (B) attribute representation learning module consist of CNN. Finally, (C) topology and attribute representation are integrated to estimate the interaction score of $r_i-p_j$.
Figure 2

The pipeline of the proposed ALDPI method for DPI prediction. Given drug |$r_i$| and protein |$p_j$|⁠, two types of representations are learned by (A) topology representation learning module based on convolution operations, graph convolutional autoencoder and neighbor topology-level attention and (B) attribute representation learning module consist of CNN. Finally, (C) topology and attribute representation are integrated to estimate the interaction score of |$r_i-p_j$|⁠.

Open in new tabDownload slide

2.4 Capturing graph topology and learning node feature

Facing the drug–protein heterogeneous graph, we establish a topology graph learning module to adaptively adjust weight of connections and obtain the multiple topology graphs. Then different topology representations of node are learned by graph convolutional autoencoders, and they contribute differently to the prediction of DPI. Therefore, N-attention (neighbor topology-level attention) is proposed to measure the attention weight of each representation.

2.4.1 Adaptive neighbor-based topology graph learning

Previous work applied random walks to connect from the start node to neighbor nodes and captured the topology information of the graph. They also gave the same weight to all connections in the graph. Indeed, the interaction connections between different nodes in |$\rm{G}$| may have various contributions to the evaluation of DPI scores, we propose an adaptive graph learning module. The adjacency tensor |$\mathcal{I}$| is fed to the convolution layer with |$1\times 1$| filter to softly select the weights of different interactions. The filters are represented as |$\textbf{W}^{({l})}\in \mathbb{R}^{1\times 1\times n_{{filter}}}$| where |$l$| denotes the layer of |$1\times 1$| convolution, |$1$| is the width and length of the filters, and |$n_{filter}$| is the number of filters. The output |$\textbf{I}^{(l)}$| of |$l$|th |$1\times 1$| convolution layer is
(8)
where |$\textrm{w}_{{i}}^{({l})}$| is the value of |$\textbf{W}^{({l})}$| that fed in a |$softmax$| layer and |$\odot $| is the Hadamard product with broadcast mechanism. |$\textbf{I}_{{i}}^{^{\prime}}$| is the |$i$|th matrix of the adjacency tensor |$\mathcal{I}$|⁠, such as, |$\textbf{I}_{1}^{^{\prime}}=\textbf{I}_{{rr}}^{^{\prime}}$| and |$\textbf{I}_{2}^{^{\prime}}=\textbf{I}_{{rp}}^{^{\prime}}$|⁠. Specifically, |$\textbf{I}^{(l)}$| can be represented as follows,
(9)
|$\textbf{I}^{(l)}\in \mathbb{R}^{N_{rp}\times{N_{rp}}}$| is the softly chosen interaction matrix from |$\mathcal{I}$|⁠, which contains four types of interaction connections between drug nodes and protein nodes. In addition, each node may be connected to itself, and we add self-connection in |$\textbf{I}^{(l)}$|⁠. Equation (9) becomes as follows,
(10)
where |$\textbf{I}\in \mathbb{R}^{N_{rp}\times{N_{rp}}}$| is the identify matrix.
For each drug node in |$\textrm{G}$|⁠, it usually has multi-scale topologies. For example, its first-order neighbor topology contains directly connected nodes, and the |$l$|th-order neighbor topology may be learned by the composition of |$[\textbf{I}^{(1)},\textbf{I}^{(2)},\ldots ,\textbf{I}^{(l)}]$|⁠. We use the second-order neighbor topology as an example to explain the composition strategy. Given |$\textbf{I}^{(1)}$| and |$\textbf{I}^{(2)}$|⁠, we perform matrix multiplication of them and then normalize the product by Laplace for numerical stability,
(11)
where |$\textbf{A}^{(2)}$| is the second-order topology graph and |$\textbf{D}$| is the degree matrix of the product |$\textbf{I}^{(1)}\textbf{I}^{(2)}$|⁠. Similarly, we can obtain the following |$l$|th-order neighbor topology graph |$\textbf{A}^{(l)}$|⁠,
(12)
In particularly, we stipulate that |$\textbf{A}^{(1)}=\textbf{D}^{-\frac{1}{2}}(\textbf{I}_{{rr}}^{^{\prime}}+\textbf{I}_{{rp}}^{^{\prime}}+\textbf{I}_{{pr}}^{^{\prime}}+\textbf{I}_{{pp}}^{^{\prime}}+\textbf{I})\textbf{D}^{-\frac{1}{2}}$|⁠.

2.4.2 Neighbor topology encoding by graph convolutional autoencoder

To learn topological representations of drug and protein nodes, the adaptive neighbor-based topology graph |$\textbf{A}^{(l)}$| and concatenate attribute matrix |$\textbf{X}$| are integrated by graph convolutional autoencoders. The representations capture topology information formed by neighbor topologies of different orders and contain attribute information of drugs and proteins.

Encoder. The |$\textbf{A}^{(l)}$| and |$\textbf{X}$| are fed into the graph convolutional encoder, and the |$e$|th layer embedding output |$\textbf{Z}_{E(e)}^{(l)}$| can be represented as follows,
(13)
where |$\textbf{W}_{E(e)}^{(l)}$| is the weight matrix of the |$e$|th layer in the encoder module, |$\sigma (\cdot )$| is the Leaky ReLU activation function in equation (13) and the initial |$\textbf{Z}_{E(0)}^{(l)}=\textbf{X}$|⁠. We denote the last layer output embedding as |$\textbf{Z}^{(l)}\in \mathbb{R}^{N_{rp}\times N_{k}}$|⁠, where |$N_k$| is the dimension of node embedding.
Decoder. The graph convolutional decoder module projects |$\textbf{Z}^{(l)}$| back to the original space to obtain the optimal node embeddings. Given |$\textbf{Z}_{D(d)}^{(l)}$| as the input of the decoder module, the decoding process can be defined as follows,
(14)
where |$\textbf{W}_{D(d)}^{(l)}$| is the weight matrix of the |$d$|th decoder layer, |$\textbf{Z}_{D(d)}^{(l)}$| represents output of the |$d$|th layer. |$\sigma (\cdot )$| is the Leaky ReLU activation function in equation (14) and the initial |$\textbf{Z}_{D(0)}^{(l)}=\textbf{Z}^{(l)}$|⁠. The final output of decoder module is the reconstruction matrix of |$\textbf{X}$|⁠, which is denoted as |$\tilde{\textbf{X}}^{{(l)}}$|⁠.
Attention mechanism of neighbor topology. In addition, different-order neighbor topology graphs may contain different topological structure information. The independent |$l$| graph convolutional encoder modules are applied to the neighbor topology graph set |$[\textbf{A}^{(1)},\textbf{A}^{(2)},\ldots ,\textbf{A}^{(l)}]$|⁠, and we can obtain the topology representation set |$[\textbf{Z}^{(1)},\textbf{Z}^{(2)},\ldots ,\textbf{Z}^{(l)}]$|⁠. Different representations may have various contributions to DPI prediction, we establish a neighbor topology-level attention mechanism (N-attention) to distinguish their importance. We use the topology vector |$\textbf{z}_{{i}}^{({k})}$| of |$i$|th node in |$\textbf{Z}^{({k})} (1\leq k\leq l)$| as an example to explain it. The attention weight of |$\textbf{z}_{{i}}^{({k})}$| is defined as follows,
(15)
where |$\textbf{W}_{N}$| and |$\textbf{b}_{N}$| are the weight matrix and bias vector, respectively, |$\textbf{h}_{N}$| is the weight vector that captures multiple order contexts and |$\sigma (\cdot )$| is the Tanh activation function in Equation (15). The normalized attention score is obtained as follows,
(16)
Similarly, we can obtain the other attention scores |$[{\beta }_{i}^{(1)},{\beta }_{i}^{(2)},\ldots ,{\beta }_{i}^{(l)}]$| of the |$i$|th node. The large attention score indicates the importance of the corresponding topology vector. For all nodes in |$\textrm{G}$|⁠, their attention score vectors are defined as |$[{\boldsymbol{\beta }}^{(1)},{\boldsymbol{\beta }}^{(2)},\ldots ,{\boldsymbol{\beta }}^{(l)}]$|⁠. The attention enhanced topology representation matrix is obtained as follows,
(17)
where |$diag({\boldsymbol{\beta }}^{(k)})$| denotes diagonal matrix of score vector |${\boldsymbol{\beta }}^{(k)}$|⁠.
Optimization of autoencoder. The learning process of the graph convolutional autoencoders is to minimize the loss function
(18)
where |$\tilde{\textbf{X}}^{{(m)}}$| is the decoded reconstruction matrix with topology matrix |$\textbf{A}^{{(m)}}$| and topology representation matrix |$\textbf{Z}^{{topo}}$| as input and |$ \left \| \cdot \right \|_{F}$| is the Frobenius norm of a matrix.

2.5 Learning multi-modality attribute representation

The graph convolutional autoencoder modules concatenate |$\textbf{X}^{bio}$|⁠, |$\textbf{X}^{drug}$|⁠, |$\textbf{X}^{pro}$| and |$\textbf{X}^{dis}$| as input features and completely integrate multi-modal similarities. To learn the features of each modality similarity and distinguish their contributions, we establish a selective multi-modality attribute learning model.

2.5.1 Constructing attribute matrix of drug–protein node pair

As shown in Figure 2B, |$\textbf{x}_{i}^{bio}$| and |$\textbf{x}_{j}^{bio}$| denote the attribute vectors of |$r_i$| and |$p_j$| in |$\textbf{X}^{bio}$|⁠. Then they are concatenated column-wise to obtain the attribute matrix |$\textbf{F}^{bio}$| of the |$r_i-p_j$| pair, which is defined as follows,
(19)
Similarly, we may obtain |$\textbf{F}^{drug}$|⁠, |$\textbf{F}^{pro}$| and |$\textbf{F}^{dis}$|⁠.

2.5.2 Pairwise attribute feature learning

The pairwise attribute feature learning module is constructed based on a CNN, which contains the specific modality attribute learning part and the fusion part.

Specific modality attribute learning. To learn specific representations of attribute matrices which formed by different modal similarities, the specific learning module applies independent two convolution-max pooling layers to |$\textbf{F}^{bio}$|⁠, |$\textbf{F}^{drug}$|⁠, |$\textbf{F}^{pro}$| and |$\textbf{F}^{dis}$|⁠. We use |$\textbf{F}^{bio}$| as an example to describe the process in datil. To learn marginal information, we first pad zeros around |$\textbf{F}^{bio}$|⁠, and then fed it into the first convolution-max pooling layer to obtain the output |$\textbf{Y}_{first}^{bio}$| as follows,
(20)
where * denotes convolution operation, |$\textbf{W}_{first}^{bio}$| and |$\textbf{b}_{first}^{bio}$| denote filter and bias vector of the first convolution layer. |$\sigma (\cdot )$| is the ReLU activation function in equation (20), and |$max()$| represents the max pooling layer which may further select more representative features. Let |$\textbf{Y}_{second}^{bio}$| represent the output feature map of the second convolution-max pooling layer. Similarly, we can obtain specific feature map set |$[\textbf{Y}_{second}^{bio},\textbf{Y}_{second}^{drug},\textbf{Y}_{second}^{pro},\textbf{Y}_{second}^{dis}\in \mathbb{R}^{n_w\times n_l \times n_{channel}}]$|⁠, where |$n_w$|⁠, |$n_l$| and |$n_{channel}$| are the width, length and the number of channels of each map, respectively. It is worth noting that the multi-layer convolutions applied to different modality attribute matrices are independent.
Fusion. The four feature maps are concatenated column-wise to form |$\textbf{Y}$|⁠,
(21)
Applying convolution layer in which the width of filters |$\textbf{W}_{select}$| is equal to |$4\times{n_{w}}$| to |$\textbf{Y}$|⁠, we can adaptively extract and select important features from each specific feature map. The attribute representation |$\textbf{Z}^{att}$| of |$r_i-p_j$| after the second max pooling layer is flattened as a |$\textbf{z}^{att}$|⁠.

2.5.3 The final representation of pairwise drug–protein

Given the learned topology representation matrix |$\textbf{Z}^{topo}$|⁠, we obtain the topology vectors |$\textbf{z}_{i}^{topo}$| of the drug node |$r_i$| and |$\textbf{z}_{j}^{topo}$| of the protein node |$p_j$|⁠. The final representation |$\textbf{z}$| of pairwise drug–protein is formed by concatenating |$\textbf{z}_{i}^{topo}$|⁠, |$\textbf{z}_{j}^{topo}$| and |$\textbf{z}^{att}$|⁠,
(22)

2.6 Interaction score evaluation and optimization

2.6.1 drug–protein interaction prediction

The |$\textbf{z}$| is fused by a fully connected layer and a |$softmax$| layer to obtain the evaluation interaction score of pairwise |$r_i-p_j$| as,
(23)
where |$\textbf{W}$| and |$\textbf{b}$| are the weight matrix and bias vector, respectively. |$\textbf{s}=\left [\textrm{s}_0,\textrm{s}_1\right ]$| where |$\textrm{s}_1$| and |$\textrm{s}_0$| are the predicted scores that |$r_i-p_j$| has or has no interactions.

2.6.2 Loss function and optimization

The loss function is the cross-entropy loss between the ground truth distribution of DPI and the prediction score |$\textbf{s}$| is defined as,
(24)
where |$\textrm{T}$| is a set of training samples, |$\textrm{y}_{label}$| represents the actual interaction case between drug and protein. If the interaction between the drug and protein is known, |$\textrm{y}_{label}=1$|⁠, otherwise |$\textrm{y}_{label}=0$|⁠.

3 Results and discussion

3.1 Performance evaluation

To facilitate the comparison between the proposed method and other methods, we performed 10-fold cross-validation (CV) for each experiment. The 2816 known DPIs (positive samples) are divided into ten subsets. In each fold CV, the training set contains nine positive subsets and the same number of randomly selected unknown drug–protein interaction pairs, while the remaining one positive subset and the remaining unknown drug–protein interaction pairs are used for testing. Moreover, during each fold CV, the drug similarity matrix |$\textbf{S}_{rr}^{pro}$| and protein similarity matrix |$\textbf{S}_{pp}^{drug}$| are recalculated according to the drug–protein interactions in the training set.

Evaluation measures include the area under receiver operating characteristic (ROC) curve (AUC) [44], the area under the precision-recall (PR) curve (AUPR) [45] since there are imbalanced data distributions, top |$k$| recall rates and Wilcoxon test. For each fold of each predictive method, we calculated the following metrics,
(1)
 
(2)
where |$\textrm{TP}$| is true positive, |$\textrm{FP}$| is false positive, |$\textrm{TN}$| is true negative and |$\textrm{FN}$| is false negative. Based on these metrics, we draw ROC curve and PR curve and calculate their AUC and AUPR. Since biologists usually select the top-ranked predicted candidates for further validation by wet-lab experiments, we use the recall rates of the top |$k (k=30,60,\ldots ,240)$| candidate drug–protein pairs as another performance indicator. We also apply the Wilcoxon test apply to determine whether the proposed method’s improvement is significant.
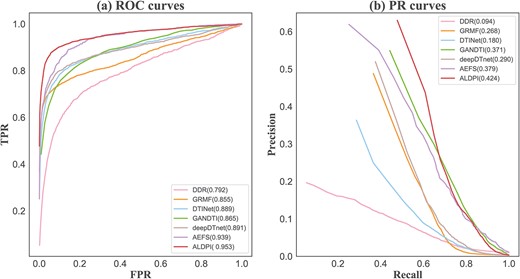
The comparison of the ALDPI with other six state-of-the-art methods in AUC and AUPR. (A) ROC curves of different DPI prediction methods. (B) PR curves of different DPI prediction methods.
Figure 3

The comparison of the ALDPI with other six state-of-the-art methods in AUC and AUPR. (A) ROC curves of different DPI prediction methods. (B) PR curves of different DPI prediction methods.

Open in new tabDownload slide

3.2 Implementation and parameter settings

Our method ALDPI is implemented by Python on an Nvidia GeForce GTX 2080Ti graphic card with 11G graphic memory. In the adaptive topology graph learning module, the layer of |$1\times 1$| convolution is set 3. For the graph convolutional autoencoder-based module, the number of encoding layers and decoding layers is 2, the dimensions of node embedding are 1024 and 256 after the first encoder layer and the second encoder layer, respectively. In the multi-layer CNNs, the filter size of the former two layers is |$3\times 5$|⁠, and the filters size of the last layer is |$4\times 5$|⁠. The learning rates of the graph convolutional autoencoder-based module and CNN are set as 0.001 and 0.0001, respectively.

3.3 Comparison with other methods

Six state-of-the-art methods in comparison include AEFS [33], deepDTnet [35], GANDTI [37], DTINet [30], GRMF [20] and DDR [25]. For fair comparison, the hyperparameters in comparison model are set by the recommended range of the corresponding literature. (⁠|$\lambda _{1}=0.001$|⁠, |$\lambda _{2}=0.01$|⁠, |$\lambda _{e}=2$|⁠, |$\lambda _{d}=2$| for AEFS; |$\alpha =0.8$|⁠, |$lr=0.001$| for deepDTnet; |$l=512$|⁠, |$k=256$|⁠, |$lr=0.005$| for GANDTI; |$r=0.8$|⁠, |$n=10$| for DTINet; |$\eta =0.5$|⁠, |$\lambda _{d}=0.1, \lambda _{t}=0.1, \lambda _{l}=2$| for GRMF; |$n=600$|⁠, |$k=5$| for DDR.)

Figure 3 shows the average ROC and PR curves of ALDPI and other comparison methods for all the 570 drugs. ALDPI achieved the highest average AUC of 0.953, which is superior than 1.4|$\%$| by AEFS, 6.2|$\%$| by deepDTnet, 6.4|$\%$| by DTINet, 8.8|$\%$| by GANDTI, 9.8|$\%$| by GRMF and 16.1|$\%$| by DDR (Figure 3A). In terms of average AUPR over all the drugs, the best performance of 0.424 was obtained by ALDPI, which is, respectively, 4.5, 5.3, 13.4, 15.6, 24.4 and 33.0|$\%$| higher than that of AEFS, GANDTI, deepDTnet, GRMF, DTINet and DDR (Figure 3B). In addition, we also draw the ROC and PR curves of ALDPI for each fold CV, and then calculate their AUCs and AUPRs, respectively (Supplementary Figure 1). We also performed experimental comparison on the two golden datasets, including Luo’s dataset [30] and Yamanishi’s dataset [49]. The average AUCs and AUPRs of ALDPI and the compared methods are listed in Supplementary Tables 1, 2 and 3. We observed that ALDPI still achieved higher AUCs and AUPRs than other methods over Luo’s dataset and Yamanishi’s dataset, which indicates that ALDPI has good generality over various datasets.

Recall rates of all method under different top $k$.
Figure 4

Recall rates of all method under different top |$k$|⁠.

Open in new tabDownload slide

In order to evaluate the impact of the training set on the prediction performance, we use the datasets containing different ratios of known DTIs and unknown drug–protein interaction pairs to train ALDPI. In 10-fold CV, we divide 2816 known DPIs into 10 subsets and take 9 of them as the training set. We add different ratios of known DPIs and unknown drug–protein interaction pairs to the training set, and the experimental results are shown in Supplementary Table 4. The results show that when the ratio of the known DPIs to unknown drug–protein interaction pairs in the training set is 1:1, ALDPI achieved the best prediction performance (AUC =0.953, AUPR = 0.424). When the ratio is 1:5, ALDPI obtained the second-best performance, and AUC and AUPR decreased by 0.3|$\%$| and 1.0|$\%$|⁠, respectively. When the ratio is 1:10, 1:20, 1:30 and 1:40, the AUC decreased by 1.8, 2.0, 2.4 and 4.5|$\%$| respectively, and the AUPR decreased by 2.6, 3.6, 2.9 and 6.8|$\%,$| respectively. The lowest AUC and AUPR of ALDPI are 0.904 and 0.337, respectively, when the ratio is 1:50. In summary, the performance of our model gradually decreased when the number of unknown drug–protein interaction pairs increased. Therefore, we choose a training set with a ratio of 1:1 to train ALDPI.

Our method ALDPI achieved the best performance in both AUC and AUPR, and the AEFS achieved the second-best AUC and AUPR.ALDPI based on the graph convolutional autoencoder and CNN could deeply integrate drug and protein-related multi-modal similarity features. AEFS encodes the features of drugs and proteins and preserves the consistency of the chemical properties and functions of drugs. Fully connected autoencoder-based deepDTnet and generative adversarial networks based GANDTI also learn deep features to predict DPI, and they also achieved good results (deepDTnet’AUC = 0.891, GANDTI’AUPR = 0.371). The AUC of DTINet was higher than that of GRMF, but its AUPR was lower 8.8|$\%$| than GRMF. DDR performed much worse than other methods, one possible reason is that it neglected the attribute information of drugs and proteins. Our finding is that the deep representation of features learned based on deep learning frameworks contributes to improving performance compared to shallow prediction models. In addition, our method ALDPI also capture multi-order topological structure of heterogeneous graph. The machine learning-based DTINet and GRMF extracted topological properties and their performance is higher DDR. The results shows that the learning topology structure information of graph is vital for the promoting prediction.

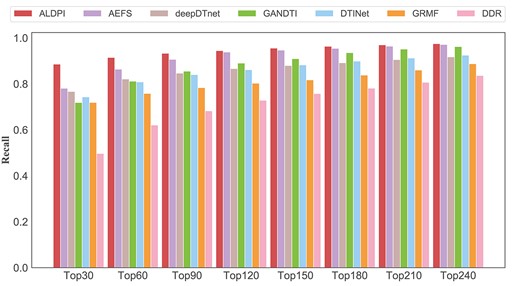
Figure 4 shows the top-k recall rates of all methods. The higher the recall rate, the more drug-related proteins could be correctly identified. Under different threshold k, ALDPI outperformed other methods and ranked 88.6% in the top 30, 91.5% in the top 60 and 93.3% in the top 90. AEFS achieved the second-best performance, with recall rates of 78.1, 86.4 and 90.7% in the top 30, 60 and 90. In the top 120–240, the recall rate of AEFS was close to that of ALDPI. The recall rates of deepDTnet and DTINet are almost the same, the GANDTI’ recall rates were lower than those in the top 30 and 60 and higher than those after the top 90. The performances of GRMF and DDR are not as good as the above methods. The recall rates of the former model in the top 30, 60 and 90 are 71.9, 75.8 and 78.4%, respectively, and those of the latter model are 49.7, 62.1 and 68.3%, respectively. In addition, we used the Wilcoxon test to evaluate whether ALDPI’s performance was better than the comparison method. The statistical results given in Table 1 indicates that the performance of ALDPI is significantly better than other methods (⁠|${P}$| value < 0.05).

Table 1
Open in new tab

Comparion between ALDPI and other methods based on AUCs and AUPRs with the paired Wilcoxon test

AEFSdeepDTnetGANDTIDTINetGRMFDDR
|${P}$| value based on AUC5.2408e-162.0531e-232.0342e-053.6250e-036.7494e-041.9779e-03
|${P}$| value based on AUPR1.7719e-033.2424e-704.7648e-794.3421e-195.5668e-282.5750e-09
AEFSdeepDTnetGANDTIDTINetGRMFDDR
|${P}$| value based on AUC5.2408e-162.0531e-232.0342e-053.6250e-036.7494e-041.9779e-03
|${P}$| value based on AUPR1.7719e-033.2424e-704.7648e-794.3421e-195.5668e-282.5750e-09
Table 1
Open in new tab

Comparion between ALDPI and other methods based on AUCs and AUPRs with the paired Wilcoxon test

AEFSdeepDTnetGANDTIDTINetGRMFDDR
|${P}$| value based on AUC5.2408e-162.0531e-232.0342e-053.6250e-036.7494e-041.9779e-03
|${P}$| value based on AUPR1.7719e-033.2424e-704.7648e-794.3421e-195.5668e-282.5750e-09
AEFSdeepDTnetGANDTIDTINetGRMFDDR
|${P}$| value based on AUC5.2408e-162.0531e-232.0342e-053.6250e-036.7494e-041.9779e-03
|${P}$| value based on AUPR1.7719e-033.2424e-704.7648e-794.3421e-195.5668e-282.5750e-09
Table 2
Open in new tab

The top 10 candidate target proteins of five drugs

Enflurane
RankGeneEvidenceRankGeneEvidence
1GABRA3DrugBank6GABRG2DrugBank
2GABRB2DrugBank7GABRDDrugBank
3GABRB3DrugBank8GABRA1DrugBank
4GABRG3DrugBank9KCNQ5DrugBank
5GABRA4DrugBank10GABRG1DrugBank
Aripiprazole
RankGeneEvidenceRankGeneEvidence
1HTR1BDrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2ADRA2CDrugBank,DrugCentral7ADRA2BDrugBank,DrugCentral
3HTR6DrugBank,DrugCentral8HTR1DDrugBank,DrugCentral
4HTR1ADrugBank,DrugCentral9OPRD1DrugBank
5ADRA2ADrugBank,DrugCentral10CHRM2DrugBank,DrugCentral
Amoxapine
RankGeneEvidenceRankGeneEvidence
1ADRA1ADrugBank6GABRG3DrugBank
2HTR2CDrugBank7ADRA1BDrugBank
3HTR1BDrugBank8HMGCRUnconfirmed
4CHRM3DrugBank,DrugCentral9CHRM1DrugBank,DrugCentral
5GABRB3DrugBank10DRD1DrugBank,DrugCentral
Amitriptyline
RankGeneEvidenceRankGeneEvidence
1CHRM1DrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral7CHRM5DrugBank,DrugCentral
3ADRA1DDrugBank,DrugCentral8SLC6A2DrugBank,DrugCentral,ChEMBL
4HTR1DDrugBank9ADRA1ADrugBank,DrugCentral
5ADRA1BDrugBank10HTR7DrugBank,DrugCentral
Paroxetine
RankGeneEvidenceRankGeneEvidence
1ADRA2BDrugBank6CHRM1DrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral,ChEMBL7HTR1DDrugBank
3CHRM5DrugBank,DrugCentral8DRD2DrugBank
4HTR1FDrugBank9ADRA1ADrugBank
5HTR1BDrugBank10ADRA2ADrugBank
Enflurane
RankGeneEvidenceRankGeneEvidence
1GABRA3DrugBank6GABRG2DrugBank
2GABRB2DrugBank7GABRDDrugBank
3GABRB3DrugBank8GABRA1DrugBank
4GABRG3DrugBank9KCNQ5DrugBank
5GABRA4DrugBank10GABRG1DrugBank
Aripiprazole
RankGeneEvidenceRankGeneEvidence
1HTR1BDrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2ADRA2CDrugBank,DrugCentral7ADRA2BDrugBank,DrugCentral
3HTR6DrugBank,DrugCentral8HTR1DDrugBank,DrugCentral
4HTR1ADrugBank,DrugCentral9OPRD1DrugBank
5ADRA2ADrugBank,DrugCentral10CHRM2DrugBank,DrugCentral
Amoxapine
RankGeneEvidenceRankGeneEvidence
1ADRA1ADrugBank6GABRG3DrugBank
2HTR2CDrugBank7ADRA1BDrugBank
3HTR1BDrugBank8HMGCRUnconfirmed
4CHRM3DrugBank,DrugCentral9CHRM1DrugBank,DrugCentral
5GABRB3DrugBank10DRD1DrugBank,DrugCentral
Amitriptyline
RankGeneEvidenceRankGeneEvidence
1CHRM1DrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral7CHRM5DrugBank,DrugCentral
3ADRA1DDrugBank,DrugCentral8SLC6A2DrugBank,DrugCentral,ChEMBL
4HTR1DDrugBank9ADRA1ADrugBank,DrugCentral
5ADRA1BDrugBank10HTR7DrugBank,DrugCentral
Paroxetine
RankGeneEvidenceRankGeneEvidence
1ADRA2BDrugBank6CHRM1DrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral,ChEMBL7HTR1DDrugBank
3CHRM5DrugBank,DrugCentral8DRD2DrugBank
4HTR1FDrugBank9ADRA1ADrugBank
5HTR1BDrugBank10ADRA2ADrugBank
Table 2
Open in new tab

The top 10 candidate target proteins of five drugs

Enflurane
RankGeneEvidenceRankGeneEvidence
1GABRA3DrugBank6GABRG2DrugBank
2GABRB2DrugBank7GABRDDrugBank
3GABRB3DrugBank8GABRA1DrugBank
4GABRG3DrugBank9KCNQ5DrugBank
5GABRA4DrugBank10GABRG1DrugBank
Aripiprazole
RankGeneEvidenceRankGeneEvidence
1HTR1BDrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2ADRA2CDrugBank,DrugCentral7ADRA2BDrugBank,DrugCentral
3HTR6DrugBank,DrugCentral8HTR1DDrugBank,DrugCentral
4HTR1ADrugBank,DrugCentral9OPRD1DrugBank
5ADRA2ADrugBank,DrugCentral10CHRM2DrugBank,DrugCentral
Amoxapine
RankGeneEvidenceRankGeneEvidence
1ADRA1ADrugBank6GABRG3DrugBank
2HTR2CDrugBank7ADRA1BDrugBank
3HTR1BDrugBank8HMGCRUnconfirmed
4CHRM3DrugBank,DrugCentral9CHRM1DrugBank,DrugCentral
5GABRB3DrugBank10DRD1DrugBank,DrugCentral
Amitriptyline
RankGeneEvidenceRankGeneEvidence
1CHRM1DrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral7CHRM5DrugBank,DrugCentral
3ADRA1DDrugBank,DrugCentral8SLC6A2DrugBank,DrugCentral,ChEMBL
4HTR1DDrugBank9ADRA1ADrugBank,DrugCentral
5ADRA1BDrugBank10HTR7DrugBank,DrugCentral
Paroxetine
RankGeneEvidenceRankGeneEvidence
1ADRA2BDrugBank6CHRM1DrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral,ChEMBL7HTR1DDrugBank
3CHRM5DrugBank,DrugCentral8DRD2DrugBank
4HTR1FDrugBank9ADRA1ADrugBank
5HTR1BDrugBank10ADRA2ADrugBank
Enflurane
RankGeneEvidenceRankGeneEvidence
1GABRA3DrugBank6GABRG2DrugBank
2GABRB2DrugBank7GABRDDrugBank
3GABRB3DrugBank8GABRA1DrugBank
4GABRG3DrugBank9KCNQ5DrugBank
5GABRA4DrugBank10GABRG1DrugBank
Aripiprazole
RankGeneEvidenceRankGeneEvidence
1HTR1BDrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2ADRA2CDrugBank,DrugCentral7ADRA2BDrugBank,DrugCentral
3HTR6DrugBank,DrugCentral8HTR1DDrugBank,DrugCentral
4HTR1ADrugBank,DrugCentral9OPRD1DrugBank
5ADRA2ADrugBank,DrugCentral10CHRM2DrugBank,DrugCentral
Amoxapine
RankGeneEvidenceRankGeneEvidence
1ADRA1ADrugBank6GABRG3DrugBank
2HTR2CDrugBank7ADRA1BDrugBank
3HTR1BDrugBank8HMGCRUnconfirmed
4CHRM3DrugBank,DrugCentral9CHRM1DrugBank,DrugCentral
5GABRB3DrugBank10DRD1DrugBank,DrugCentral
Amitriptyline
RankGeneEvidenceRankGeneEvidence
1CHRM1DrugBank,DrugCentral6HTR2CDrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral7CHRM5DrugBank,DrugCentral
3ADRA1DDrugBank,DrugCentral8SLC6A2DrugBank,DrugCentral,ChEMBL
4HTR1DDrugBank9ADRA1ADrugBank,DrugCentral
5ADRA1BDrugBank10HTR7DrugBank,DrugCentral
Paroxetine
RankGeneEvidenceRankGeneEvidence
1ADRA2BDrugBank6CHRM1DrugBank,DrugCentral
2HTR1ADrugBank,DrugCentral,ChEMBL7HTR1DDrugBank
3CHRM5DrugBank,DrugCentral8DRD2DrugBank
4HTR1FDrugBank9ADRA1ADrugBank
5HTR1BDrugBank10ADRA2ADrugBank
Table 3
Open in new tab

Top 15 of predicted drug–protein pair candidates

RankDrug IDDrug nameProtein IDGeneEvidence
1DB06710MethyltestosteroneP04150NR3C1DrugCentral
2DB00624TestosteroneP04150NR3C1DrugCentral
3DB00700EplerenoneP04150NR3C1DrugCentral,ChEMBL
4DB00603Medroxyprogesterone AcetateP04150NR3C1DrugCentral,ChEMBL
5DB00990ExemestaneP04150NR3C1Literature [48]
6DB04839Cyproterone AcetateP04150NR3C1DrugCentral
7DB00408LoxapineP25100ADRA1DDrugCentral,ChEMBL
8DB00679ThioridazineP25100ADRA1DDrugCentral
9DB00910ParicalcitolP04150NR3C1Unconfirmed
10DB00334OlanzapineP08912CHRM5DrugCentral
11DB00652PentazocineP41143OPRD1DrugCentral
12DB00187EsmololP07550ADRB2DrugCentral,ChEMBL
13DB00247MethysergideP28221HTR1DDrugCentral
14DB00334OlanzapineP25100ADRA1DDrugCentral
15DB00458ImipramineP08913ADRA2ADrugCentral,ChEMBL
RankDrug IDDrug nameProtein IDGeneEvidence
1DB06710MethyltestosteroneP04150NR3C1DrugCentral
2DB00624TestosteroneP04150NR3C1DrugCentral
3DB00700EplerenoneP04150NR3C1DrugCentral,ChEMBL
4DB00603Medroxyprogesterone AcetateP04150NR3C1DrugCentral,ChEMBL
5DB00990ExemestaneP04150NR3C1Literature [48]
6DB04839Cyproterone AcetateP04150NR3C1DrugCentral
7DB00408LoxapineP25100ADRA1DDrugCentral,ChEMBL
8DB00679ThioridazineP25100ADRA1DDrugCentral
9DB00910ParicalcitolP04150NR3C1Unconfirmed
10DB00334OlanzapineP08912CHRM5DrugCentral
11DB00652PentazocineP41143OPRD1DrugCentral
12DB00187EsmololP07550ADRB2DrugCentral,ChEMBL
13DB00247MethysergideP28221HTR1DDrugCentral
14DB00334OlanzapineP25100ADRA1DDrugCentral
15DB00458ImipramineP08913ADRA2ADrugCentral,ChEMBL
Table 3
Open in new tab

Top 15 of predicted drug–protein pair candidates

RankDrug IDDrug nameProtein IDGeneEvidence
1DB06710MethyltestosteroneP04150NR3C1DrugCentral
2DB00624TestosteroneP04150NR3C1DrugCentral
3DB00700EplerenoneP04150NR3C1DrugCentral,ChEMBL
4DB00603Medroxyprogesterone AcetateP04150NR3C1DrugCentral,ChEMBL
5DB00990ExemestaneP04150NR3C1Literature [48]
6DB04839Cyproterone AcetateP04150NR3C1DrugCentral
7DB00408LoxapineP25100ADRA1DDrugCentral,ChEMBL
8DB00679ThioridazineP25100ADRA1DDrugCentral
9DB00910ParicalcitolP04150NR3C1Unconfirmed
10DB00334OlanzapineP08912CHRM5DrugCentral
11DB00652PentazocineP41143OPRD1DrugCentral
12DB00187EsmololP07550ADRB2DrugCentral,ChEMBL
13DB00247MethysergideP28221HTR1DDrugCentral
14DB00334OlanzapineP25100ADRA1DDrugCentral
15DB00458ImipramineP08913ADRA2ADrugCentral,ChEMBL
RankDrug IDDrug nameProtein IDGeneEvidence
1DB06710MethyltestosteroneP04150NR3C1DrugCentral
2DB00624TestosteroneP04150NR3C1DrugCentral
3DB00700EplerenoneP04150NR3C1DrugCentral,ChEMBL
4DB00603Medroxyprogesterone AcetateP04150NR3C1DrugCentral,ChEMBL
5DB00990ExemestaneP04150NR3C1Literature [48]
6DB04839Cyproterone AcetateP04150NR3C1DrugCentral
7DB00408LoxapineP25100ADRA1DDrugCentral,ChEMBL
8DB00679ThioridazineP25100ADRA1DDrugCentral
9DB00910ParicalcitolP04150NR3C1Unconfirmed
10DB00334OlanzapineP08912CHRM5DrugCentral
11DB00652PentazocineP41143OPRD1DrugCentral
12DB00187EsmololP07550ADRB2DrugCentral,ChEMBL
13DB00247MethysergideP28221HTR1DDrugCentral
14DB00334OlanzapineP25100ADRA1DDrugCentral
15DB00458ImipramineP08913ADRA2ADrugCentral,ChEMBL

3.4 Case studies

To demonstrate the ability of ALDPI to discover potential DPIs, we applied case studies for five drugs, namely Enflurane, Aripiprazole, Amoxapine, Amitriptyline and Paroxetine. The top 10 protein candidates for each drug are collected, with 50 candidates in total (Table 2).

First, the DrugBank [39] is a web-enabled database containing comprehensive drug data covering drug function, drug targets and so on. The DrugCentral [46] is also an online public database that provides up-to-date drug information, such as the interactions between drugs and proteins. The ChEMBL database [47] records bioactive drug-like small molecule data, which are abstracted and curated from the primary scientific literature. As shown in Table 2, 49 candidates were inferred from the DrugBank database. DrugCentral and ChEMBL contain 23 and 2 candidate proteins, respectively. It indicated that these candidate proteins are indeed interacted with the corresponding drugs.

Next, Table 3 lists the 15 drug–protein pair candidates with the highest predicted interaction scores to further verify the utility of ALDPI. The Drug Central verified 10 drug–protein pair candidates, and the ChEMBL recorded two candidates. These drugs have been confirmed to affect the corresponding proteins in humans.

In addition to the DPIs in humans confirmed by the database, several candidates were supported by literatures or experiments on animals. DrugCentral and ChEMBL verified the interactions between loxapine and ADRA1D, imipramine and ADRA2A in rattus norvegicus, and esmolol and ADRB2 in cavia porcellus. These evidences also laid the foundation for exploration of interactions in humans. In a recent study, Wang et al. [48] selected exemestane for functional validation and drug availability to treat glucocorticoid resistance. Overall, these cases further demonstrated the capability of our model is able to discover the potential candidate DPIs.

3.5 Prediction of novel drug–protein interactions

Our proposed model ALDPI is used to predict protein candidates, which are related with the drugs. All of the known DPIs are applied to train ALDPI. The top 30 ranked protein candidates and corresponding interaction scores for each drug predicted by our model are listed in Supplementary Table 5. Supplementary Table 5 may assist biologists in discovering novel drug-related proteins in wet-lab experiments.

4 Conclusion

In this study, we proposed a method ALDPI to predict candidate drug–protein interactions. The drug–protein heterogeneous graph was constructed to benefit extracting the multi-order neighbor topology structures. The proposed adaptive graph learning module can transform the heterogeneous graph into multiple new graphs with different neighbor topologies. The graph convolutional autoencoders were applied to learn the representation of nodes based on the different-order neighbor topology. The topology representation-level attention mechanism was established to assign higher weights to the more informative topological representations. The multi-layer CNN-based module was designed to learn the attribute features of different modality similarities and selectively fuse these features. Evaluated using 10-fold CV, ALDPI outperformed the state-of-the-art methods under the evaluation measures of AUC, AUPR, top-k recall values and Wilcoxon test. The case studies further proved that our model has the ability to predict novel drug–protein interactions. In conclusion, the experimental results demonstrated that ALDPI is a reliable tool for biologists to screen candidate DPIs.

Key Points

  • A drug–protein heterogeneous graph is constructed, which benefits the extraction and representation of neighbor topology information and multi-modelity similarity attributes of nodes.

  • The new topology graphs obtained by the established graph learning module contain the multi-order neighbor topologies and reveal the potential connections between nodes.

  • A newly neighbor topology-level attention mechanism is proposed to discriminate the importance of multiple topology representations of nodes, which are learned by graph convolutional autoencoders based on different order neighbor topology graphs.

  • A novel strategy based on multi-layer CNNs is designed to learn the specific features corresponding to different modality similarities and then deeply integrate these features.

Funding

The work was supported by the Natural Science Foundation of China (61972135, 62172143); Natural Science Foundation of Heilongjiang Province (LH2019A029); China Postdoctoral Science Foundation (2019M650069, 2020M670939); Heilongjiang Postdoctoral Scientific Research Staring Foundation (BHLQ18104); Fundamental Research Foundation of Universities in Heilongjiang Province for Technology Innovation (KJCX201805); Innovation Talents Project of Harbin Science and Technology Bureau (2017RAQXJ094); Fundamental Research Foundation of Universities in Heilongjiang Province for Youth Innovation Team (RCYJTD201805); and the Foundation of Graduate Innovative Research (YJSCX2021-077HLJU).

Kaimiao Hu is studying for his master’s degree in the School of Computer Science and Technology at Heilongjiang University, Harbin, China. Her research interests include complex network analysis and deep learning.

Hui Cui, PhD (The University of Sydney), is a lecturer at Department of Computer Science and Information Technology, La Trobe University, Melbourne, Australia. Her research interests lie in data-driven and computerized models for biomedical and health informatics.

Tiangang Zhang, PhD (The University of Tokyo), is an associate professor of the School of Mathematical Science, Heilongjiang University, Harbin, China. His current research interests include complex network analysis and computational fluid dynamics.

Chang Sun is a PhD candidate in the College of Computer Science, Nankai University, Tianjin China. His current research interests include bioinformatics and deep learning.

Ping Xuan, PhD (Harbin Institute of Technology), is a professor at the School of Computer Science and Technology, Heilongjiang University, Harbin, China. Her current research interests include complex network analysis, deep learning and medical image analysis.

References

1.

Hao
 
M
,
Bryant
 
SH
,
Wang
 
Y
.
Open-source chemogenomic data-driven algorithms for predicting drug-target interactions
.
Brief Bioinform
 
2019
;
20
(
4
):
1465
–
74
.

Google Scholar

Crossref
Search ADS
PubMed

 
2.

Chen
 
X
,
Yan
 
CC
,
Zhang
 
X
, et al.  
Drug-target interaction prediction: databases, web servers and computational models
.
Brief Bioinform
 
2016
;
17
(
4
):
696
–
712
.

Google Scholar

Crossref
Search ADS
PubMed

 
3.

Zhao
 
Q
,
Yu
 
H
,
Ji
 
M
, et al.  
Computational model development of drug-target interaction prediction: a review
.
Curr Protein Pept Sci
 
2019
;
20
(
6
):
492
–
4
.

Google Scholar

Crossref
Search ADS
PubMed

 
4.

Zheng
 
S
,
Li
 
Y
,
Chen
 
S
, et al.  
Predicting drug-protein interaction using quasi-visual question answering system
.
Nature Machine Intelligence
 
2020
;
2
(
2
):
134
–
40
.

Google Scholar

Crossref
Search ADS

 
5.

Lin
 
X
,
Li
 
X
,
Lin
 
X
.
A review on applications of computational methods in drug screening and design
.
Molecules
 
2020
;
25
(
6
):
1375
.

Google Scholar

Crossref
Search ADS

 
6.

Hu
 
SS
,
Zhang
 
C
,
Chen
 
P
, et al.  
Predicting drug-target interactions from drug structure and protein sequence using novel convolutional neural networks
.
BMC bioinformatics
 
2019
;
20
(
25
):
1
–
12
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
7.

Keiser
 
MJ
,
Roth
 
BL
,
Armbruster
 
BN
, et al.  
Relating protein pharmacology by ligand chemistry
.
Nat Biotechnol
 
2007
;
25
(
2
):
197
–
206
.

Google Scholar

Crossref
Search ADS
PubMed

 
8.

Keiser
 
MJ
,
Setola
 
V
,
Irwin
 
JJ
, et al.  
Predicting new molecular targets for known drugs
.
Nature
 
2009
;
462
(
7270
):
175
–
81
.

Google Scholar

Crossref
Search ADS
PubMed

 
9.

Cheng
 
AC
,
Coleman
 
RG
,
Smyth
 
KT
, et al.  
Structure-based maximal affinity model predicts small-molecule druggability
.
Nat Biotechnol
 
2007
;
25
(
1
):
71
–
5
.

Google Scholar

Crossref
Search ADS
PubMed

 
10.

Morris
 
GM
,
Huey
 
R
,
Lindstrom
 
W
, et al.  
AutoDock4 and AutoDockTools4: automated docking with selective receptor flexibility
.
J Comput Chem
 
2009
;
30
(
16
):
2785
–
91
.

Google Scholar

Crossref
Search ADS
PubMed

 
11.

Wang
 
K
,
Zhou
 
R
,
Li
 
Y
, et al.  
DeepDTAF: a deep learning method to predict protein-ligand binding affinity
.
Brief Bioinform
 
2021
;
1
–
15
.

Google Scholar

OpenURL Placeholder Text

 
12.

Sachdev
 
K
,
Gupta
 
MK
.
A comprehensive review of feature based methods for drug target interaction prediction
.
J Biomed Inform
 
2019
;
93
:
103159
.

Google Scholar

Crossref
Search ADS
PubMed

 
13.

Weng
 
Y
,
Lin
 
C
,
Zeng
 
X
, et al.  
Drug target interaction prediction using multi-task learning and co-attention
.
IEEE International Conference on Bioinformatics and Biomedicine (BIBM)
 
2019
;
528
–
33
.

Google Scholar

OpenURL Placeholder Text

 
14.

Bagherian
 
M
,
Sabeti
 
E
,
Wang
 
K
, et al.  
Machine learning approaches and databases for prediction of drug-target interaction: a survey paper
.
Brief Bioinform
 
2021
;
22
(
1
):
247
–
69
.

Google Scholar

Crossref
Search ADS
PubMed

 
15.

Wang
 
R
,
Li
 
S
,
Wong
 
MH
, et al.  
Drug-protein-disease association prediction and drug repositioning based on tensor decomposition
.
IEEE International Conference on Bioinformatics and Biomedicine (BIBM)
 
2018
;
305
–
12
.

Google Scholar

OpenURL Placeholder Text

 
16.

Ding
 
Y
,
Tang
 
J
,
Guo
 
F
.
Identification of drug-target interactions via multiple information integration
.
Inform Sci
 
2017
;
418
:
546
–
60
.

Google Scholar

OpenURL Placeholder Text

 
17.

Chu
 
Y
,
Shan
 
X
,
Chen
 
T
, et al.  
DTI-MLCD: predicting drug-target interactions using multi-label learning with community detection method
.
Brief Bioinform
 
2021
;
22
(
3
):
1
–
15
.

Google Scholar

Crossref
Search ADS
PubMed

 
18.

Wang
 
L
,
You
 
ZH
,
Chen
 
X
, et al.  
Rfdt: a rotation forest-based predictor for predicting drug-target interactions using drug structure and protein sequence information
.
Curr Protein Pept Sci
 
2018
;
19
(
5
):
445
–
54
.

Google Scholar

Crossref
Search ADS
PubMed

 
19.

Li
 
Y
,
Huang
 
YA
,
You
 
ZH
, et al.  
Drug-target interaction prediction based on drug fingerprint information and protein sequence
.
Molecules
 
2019
;
24
(
16
):
2999
.

Google Scholar

Crossref
Search ADS

 
20.

Ezzat
 
A
,
Zhao
 
P
,
Wu
 
M
, et al.  
Drug-target interaction prediction with graph regularized matrix factorization
.
IEEE/ACM Trans Comput Biol Bioinform
 
2016
;
14
(
3
):
646
–
56
.

Google Scholar

Crossref
Search ADS
PubMed

 
21.

Bleakley
 
K
,
Yamanishi
 
Y
.
Supervised prediction of drug-target interactions using bipartite local models
.
Bioinformatics
 
2009
;
25
(
18
):
2397
–
403
.

Google Scholar

Crossref
Search ADS
PubMed

 
22.

Peng
 
L
,
Liao
 
B
,
Zhu
 
W
, et al.  
Predicting drug-target interactions with multi-information fusion
.
IEEE J Biomed Health Inform
 
2015
;
21
(
2
):
561
–
72
.

Google Scholar

Crossref
Search ADS
PubMed

 
23.

Van Laarhoven
 
T
,
Nabuurs
 
SB
,
Marchiori
 
E
.
Gaussian interaction profile kernels for predicting drug-target interaction
.
Bioinformatics
 
2011
;
27
(
21
):
3036
–
43
.

Google Scholar

Crossref
Search ADS
PubMed

 
24.

Liu
 
Y
,
Wu
 
M
,
Miao
 
C
, et al.  
Neighborhood regularized logistic matrix factorization for drug-target interaction prediction
.
PLoS Comput Biol
 
2016
;
12
(
2
):
1
–
26
.

Google Scholar

OpenURL Placeholder Text

 
25.

Olayan
 
RS
,
Ashoor
 
H
,
Bajic
 
VB
.
DDR: efficient computational method to predict drug-target interactions using graph mining and machine learning approaches
.
Bioinformatics
 
2018
;
34
(
7
):
1164
–
73
.

Google Scholar

Crossref
Search ADS
PubMed

 
26.

Xuan
 
P
,
Chen
 
B
,
Zhang
 
T
, et al.  
Prediction of drug-target interactions based on network representation learning and ensemble learning
.
IEEE/ACM Trans Comput Biol Bioinform
 
2020
;
1
–
12
.

Google Scholar

OpenURL Placeholder Text

 
27.

Chu
 
Y
,
Kaushik
 
AC
,
Wang
 
X
, et al.  
DTI-CDF: a cascade deep forest model towards the prediction of drug-target interactions based on hybrid features
.
Brief Bioinform
 
2021
;
22
(
1
):
451
–
62
.

Google Scholar

Crossref
Search ADS
PubMed

 
28.

Bleakley
 
K
,
Yamanishi
 
Y
.
Supervised prediction of drug-target interactions using bipartite local models
.
Bioinformatics
 
2009
;
25
(
18
):
2397
–
403
.

Google Scholar

Crossref
Search ADS
PubMed

 
29.

Mei
 
JP
,
Kwoh
 
CK
,
Yang
 
P
, et al.  
Drug-target interaction prediction by learning from local information and neighbors
.
Bioinformatics
 
2013
;
29
(
2
):
238
–
45
.

Google Scholar

Crossref
Search ADS
PubMed

 
30.

Luo
 
Y
,
Zhao
 
X
,
Zhou
 
J
, et al.  
A network integration approach for drug-target interaction prediction and computational drug repositioning from heterogeneous information
.
Nat Commun
 
2017
;
8
(
1
):
1
–
13
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
31.

Lee
 
I
,
Keum
 
J
,
Nam
 
H
.
DeepConv-DTI: prediction of drug-target interactions via deep learning with convolution on protein sequences
.
PLoS Comput Biol
 
2019
;
1
–
21
.

Google Scholar

OpenURL Placeholder Text

 
32.

Wang
 
YB
,
You
 
ZH
,
Yang
 
S
, et al.  
A deep learning-based method for drug-target interaction prediction based on long short-term memory neural network
.
BMC Med Inform Decis Mak
 
2020
;
20
(
2
):
1
–
9
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
33.

Sun
 
C
,
Cao
 
Y
,
Wei
 
JM
, et al.  
Autoencoder-based drug-target interaction prediction by preserving the consistency of chemical properties and functions of drugs
.
Bioinformatics
 
2021
;
1
–
9
.

Google Scholar

OpenURL Placeholder Text

 
34.

Zhao
 
Y
,
Zheng
 
K
,
Guan
 
B
, et al.  
DLDTI: a learning-based framework for drug-target interaction identification using neural networks and network representation
.
J Transl Med
 
2020
;
18
(
1
):
1
–
15
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
35.

Zeng
 
X
,
Zhu
 
S
,
Lu
 
W
, et al.  
Target identification among known drugs by deep learning from heterogeneous networks
.
Chem Sci
 
2020
;
11
(
7
):
1775
–
97
.

Google Scholar

Crossref
Search ADS
PubMed

 
36.

Xuan
 
P
,
Zhang
 
Y
,
Cui
 
H
, et al.  
Integrating multi-scale neighbouring topologies and cross-modal similarities for drug-protein interaction prediction
.
Brief Bioinform
 
2021
;
22
(
5
):
1
–
8
.

Google Scholar

Crossref
Search ADS
PubMed

 
37.

Sun
 
C
,
Xuan
 
P
,
Zhang
 
T
, et al.  
Graph convolutional autoencoder and generative adversarial network-based method for predicting drug-target interactions
.
IEEE/ACM Trans Comput Biol Bioinform
 
2020
;
1
–
11
.

Google Scholar

OpenURL Placeholder Text

 
38.

Zhao
 
T
,
Hu
 
Y
,
Valsdottir
 
LR
, et al.  
Identifying drug-target interactions based on graph convolutional network and deep neural network
.
Brief Bioinform
 
2021
;
22
(
2
):
2141
–
50
.

Google Scholar

Crossref
Search ADS
PubMed

 
39.

Wishart
 
DS
,
Feunang
 
YD
,
Guo
 
AC
, et al.  
DrugBank 5.0: a major update to the DrugBank database for 2018
.
Nucleic Acids Res
 
2018
;
46
(
D1
):
D1074
–
82
.

Google Scholar

Crossref
Search ADS
PubMed

 
40.

Keshava Prasad
 
TS
,
Goel
 
R
,
Kandasamy
 
K
, et al.  
Human protein reference database-2009 update
.
Nucleic Acids Res
 
2009
;
37
(
suppl_1
):
D767
–
72
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
41.

Davis
 
AP
,
Grondin
 
CJ
,
Johnson
 
RJ
, et al.  
Comparative toxicogenomics database (CTD): update 2021
.
Nucleic Acids Res
 
2021
;
49
(
D1
):
D1138
–
43
.

Google Scholar

Crossref
Search ADS
PubMed

 
42.

Iorio
 
F
,
Bosotti
 
R
,
Scacheri
 
E
, et al.  
Discovery of drug mode of action and drug repositioning from transcriptional responses
.
Proc Natl Acad Sci
 
2010
;
107
(
33
):
14621
–
6
.

Google Scholar

Crossref
Search ADS
PubMed

 
43.

Wang
 
W
,
Yang
 
S
,
Zhang
 
X
, et al.  
Drug repositioning by integrating target information through a heterogeneous network model
.
Bioinformatics
 
2014
;
30
(
20
):
2923
–
30
.

Google Scholar

Crossref
Search ADS
PubMed

 
44.

Hajian-Tilaki
 
K
.
Receiver operating characteristic (ROC) curve analysis for medical diagnostic test evaluation
.
Caspian J Intern Med
 
2013
;
4
(
2
):
627
–
30
.

Google Scholar

PubMed
OpenURL Placeholder Text

 
45.

Saito
 
T
,
Rehmsmeier
 
M
.
The precision-recall plot is more informative than the ROC plot when evaluating binary classifiers on imbalanced datasets
.
PLoS One
 
2015
;
10
(
3
):
1
–
21
.

Google Scholar

Crossref
Search ADS

 
46.

Avram
 
S
,
Bologa
 
CG
,
Holmes
 
J
, et al.  
DrugCentral 2021 supports drug discovery and repositioning
.
Nucleic Acids Res
 
2021
;
49
(
D1
):
D1160
–
9
.

Google Scholar

Crossref
Search ADS
PubMed

 
47.

Mendez
 
D
,
Gaulton
 
A
,
Bento
 
AP
, et al.  
ChEMBL: towards direct deposition of bioassay data
.
Nucleic Acids Res
 
2019
;
47
(
D1
):
D930
–
40
.

Google Scholar

Crossref
Search ADS
PubMed

 
48.

Wang
 
AL
,
Panganiban
 
R
,
Qiu
 
W
, et al.  
Drug repurposing to treat glucocorticoid resistance in asthma
.
Journal of Personalized Medicine
 
2021
;
11
(
3
):
175
–
88
.

Google Scholar

Crossref
Search ADS
PubMed

 
49.

Yamanishi
 
Y
, et al.  
Prediction of drug target interaction networks from the integration of chemical and genomic spaces
.
Bioinformatics
 
2008
;
24
(
13
):
232
–
40
.

Google Scholar

Crossref
Search ADS

 
© The Author(s) 2022. Published by Oxford University Press. All rights reserved. For Permissions, please email: [email protected]
This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)
Issue Section:
Problem solving protocol
Download all slides
  • Supplementary data

    • Supplementary data

    Supplemental_Figure_1_bbab606 - docx file
    Supplemental_File_1_bbab606 - docx file
    Supplemental_Table_1_bbab606 - docx file
    Supplemental_Table_2_bbab606 - docx file
    Supplemental_Table_3_bbab606 - docx file
    Supplemental_Table_4_bbab606 - docx file
    Supplemental_Table_5_bbab606 - xlsx file