A deep learning method for repurposing antiviral drugs against new viruses via multi-view nonnegative matrix factorization and its application to SARS-CoV-2

Su, Xiaorui; Hu, Lun; You, Zhuhong; Hu, Pengwei; Wang, Lei; Zhao, Bowei

doi:10.1093/bib/bbab526

Abstract

The outbreak of COVID-19 caused by SARS-coronavirus (CoV)-2 has made millions of deaths since 2019. Although a variety of computational methods have been proposed to repurpose drugs for treating SARS-CoV-2 infections, it is still a challenging task for new viruses, as there are no verified virus-drug associations (VDAs) between them and existing drugs. To efficiently solve the cold-start problem posed by new viruses, a novel constrained multi-view nonnegative matrix factorization (CMNMF) model is designed by jointly utilizing multiple sources of biological information. With the CMNMF model, the similarities of drugs and viruses can be preserved from their own perspectives when they are projected onto a unified latent feature space. Based on the CMNMF model, we propose a deep learning method, namely VDA-DLCMNMF, for repurposing drugs against new viruses. VDA-DLCMNMF first initializes the node representations of drugs and viruses with their corresponding latent feature vectors to avoid a random initialization and then applies graph convolutional network to optimize their representations. Given an arbitrary drug, its probability of being associated with a new virus is computed according to their representations. To evaluate the performance of VDA-DLCMNMF, we have conducted a series of experiments on three VDA datasets created for SARS-CoV-2. Experimental results demonstrate that the promising prediction accuracy of VDA-DLCMNMF. Moreover, incorporating the CMNMF model into deep learning gains new insight into the drug repurposing for SARS-CoV-2, as the results of molecular docking experiments reveal that four antiviral drugs identified by VDA-DLCMNMF have the potential ability to treat SARS-CoV-2 infections.

SARS-CoV-2, drug repositioning, constrained multi-view nonnegative matrix factorization, deep learning, graph convolutional network

1 Introduction

Coronaviruses (CoVs) have become a major public health concern due to two severe CoV outbreaks at the beginning of 21st century, including severe acute respiratory syndrome-associated coronavirus (SARS-CoV) in 2002 [4] and Middle East respiratory syndrome-associated coronavirus (MERS-CoV) in 2012 [8]. Unfortunately, the coronavirus disease 2019 (COVID-19) caused by a new enveloped RNA |$\beta $|-CoV [55], named SARS-CoV-2, has produced a global pandemic since December 2019 [72] with tens of millions of infected people and millions of death. At present, there are still no proven effective drugs for SARS-CoV-2, despite increasing efforts made by pharmaceutical companies in drug development [15].

Due to the ability of significantly accelerating the drug development process, reducing overall costs and avoiding risks [31], drug repositioning is believed as a promising and efficient computational way to discover new indications of approved drugs. Hence, in order to response the urgent demand for effectively treating SARS-CoV-2 infections, a variety of drug repositioning methods have been recently proposed and they are broadly classified into two categories including structure-based and network-based methods [9]. Among them, structure-based methods target to identify chemical compounds that may act on SARS-CoV-2 by using molecular docking [49], whereas network-based ones predict novel virus-drug associations (VDAs), which associate SARS-CoV-2 to approved drugs, from a given VDA network. Though promising, structure-based methods suffer from the disadvantage of being time-consuming when searching for an effective compound against SARS-CoV-2 [1]. It is for this reason that we focus our study on network-based methods. However, for new viruses, such as SARS-CoV-2, without any known VDAs, predicting their potential drugs would certainly result in a well-known cold-start problem, which inhibits the development of accurate network-based methods to repurpose approved drugs [46].

To address this problem, network-based methods often integrate the biological knowledge of viruses into VDA networks, thus alleviating the influence exerted by the lack of VDAs involving new viruses [18]. In particular, IRNMFVDA [58] first constructs a VDA matrix based on VDAs, a drug similarity matrix and a virus similarity matrix. An indicator matrix is then used to determine the most likely drugs for SARS-CoV-2 with nonnegative matrix factorization (NMF). Similar to IRNMFVDA, SCPMF [40] also combines VDAs and the similarity information of drugs and viruses to generate a heterogeneous network and then identifies novel VDAs related to SARS-CoV-2 by utilizing similarity constrained probabilistic NMF. In addition to these NMF-based models, there are also several attempts made from an alternative view. For example, VDA-KATZ [70] considers the identification of novel VDAs as a problem of counting the number of connection paths between viruses and drugs in a heterogeneous network and applies a network-based association prediction model to infer possible drugs associated with SARS-CoV-2. Inspired by the link prediction works of layer attention graph convolution network (GCN)[66] and multi-view GCN [11], SANE [56] designs an attentive network embedding model by considering the sequence information of drugs and viruses as node attributes and potential drugs against COVID-19 can be identified with an attention-based pre-depth-first-search strategy. VDA-RWR [47] incorporates VDAs with the similarity information of drugs and viruses and then applies a random walk with restart method to estimate the probability of antiviral drugs against SARS-CoV-2.

Hence, the development of network-based methods has been inspired by the increasing coverage of genomic data [33], which gains new insights into the patterns characterizing already known VDAs to identify the missing ones. As mentioned above, state-of-the-art network-based methods rely on the perception that similar viruses are possibly be treated by the same drug. To this end, they construct a VDA matrix for a given VDA network and refine it by additionally considering the similarity information of drugs and viruses. However, such refinement fails to capture the structural and genomic forces that govern VDA networks if without placing further constraints to strengthen the perception of interest [17]. Taking NMF-based methods as an example, they adopt traditional NMF models to project viruses and drugs into a low-rank latent feature space (LFS), where not all similarity information of viruses and drugs are consistently preserved when compared with those in their original feature space [32]. Moreover, according to the results presented in Section of Ablation study, we note that the similarity between viruses and drugs, which is impossible to exist in reality, is observed from the visualization of their latent features obtained with NMF. With such noisy information, NMF-based methods assign a larger prediction score to virus-drug pairs that share more similar partners including not only drugs but also viruses and are prone to identify more false-positive VDAs by confusing the perception about how new viruses are associated with drugs. Our results suggest that the fundamental reason for the failure of network-based methods is the lack of such a constraint that accounts for the enhancement and consistency of our perception during refinement.

Figure 1

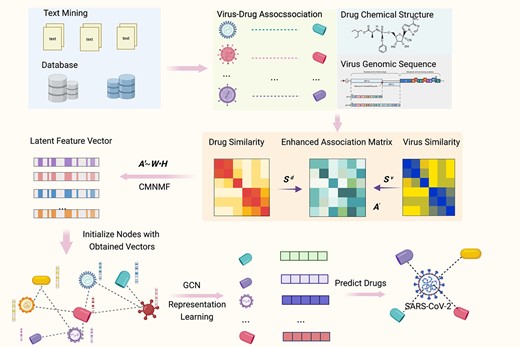
An illustration of the complete procedure of VDA-DLCMNMF.

Open in new tab Download slide

In this work, we propose a novel constrained multi-view nonnegative matrix factorization (CMNMF) model to ensure that, for drugs and viruses, their respective similarity information in a low-rank LFS are consistent with those in their original feature space by generating few noisy information. To do so, two similarity matrices are first constructed for drugs and viruses by using chemical structures and genome sequences respectively. Combining them with the VDA matrix, we further obtain an enhanced association matrix, each element of which indicates the association strength between corresponding drug and virus from a more comprehensive perspective. Modified from traditional NMF, CMNMF formulates additional constraints on these three matrices. In doing so, the optimization procedure of CMNMF is targeted toward to preserving the similarity information of drugs and viruses in LFS as much as possible. By taking the latent feature vectors of drugs and viruses as their initial node representations, we apply a graph convolutional network with attention-based neighbor sampling to optimize the representation of drugs and viruses in a given VDA network and then develop a deep learning method, namely VDA-DLCMNMF, for predicting potential drugs that can be used to treat infections caused by new viruses. The major contributions of this work are summarized as follows.

|$\bullet $| Regarding network-based drug repurposing methods, our experimental results suggest that the fundamental reason for their failure is the lack of such a constraint that accounts for the enhancement and consistency of the intuitive perception about the potential drugs that new viruses are more likely to associate with.
|$\bullet $| A novel CMNMF model is proposed to ensure that the respective similarity information of viruses and drugs are preserved when projected from their own feature spaces onto a unified LFS by generating few noisy information. To avoid random initialization, we take the latent feature vectors of viruses and drugs as their initial node representations and then develop a deep learning method, namely VDA-DLCMNMF, to precisely prioritize known drugs for new viruses.
|$\bullet $| Experimental results on three VDA datasets with different size demonstrate the promising performance of VDA-DLCMNMF in repurposing antiviral drugs against SARS-CoV-2 in terms of several metrics. Besides, the results of molecular docking experiments reveal that incorporating CMNMF into deep learning gains new insight into the drug repurposing for SARS-CoV-2, as four novel drugs identified by our method are proved to have the potential ability to bind with important functional receptors of SARS-CoV-2.

The rest of this article is organized as follows. The section of Materials and Methods first describes the VDA datasets used in the experiments and then presents the details of VDA-DLCMNMF. Comparing VDA-DLCMNMF with several state-of-the-art models, we give the experimental results in the section of Experiments, following which we end the article with a in-depth discussion and a conclusion.

2 Materials and Methods

As shown in Figure 1, VDA-DLCMNMF is composed of three steps, including enhanced VDA matrix construction, LFS extraction with CMNMF and GCN-based drug repurposing. Before presenting the details of VDA-DLCMNMF, we describe the VDA datasets used in our experiments.

Figure 2

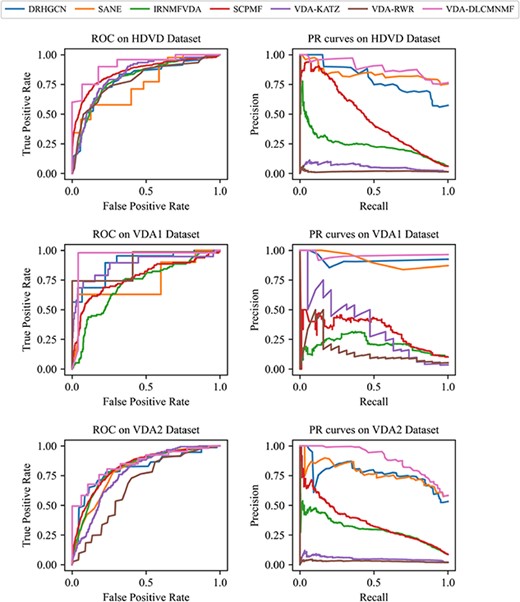
ROC and AUPR curves obtained by VDA-DLCMNMF and other competing methods on three datasets based on 5-fold CV.

Open in new tab Download slide

2.1 VDA datasets

To evaluate the performance of VDA-DLCMNMF, three datasets with different sizes are collected for discovering potential drugs against SARS-CoV-2, and they are denoted as HDVD, VDA1 and VDA2, respectively. The statistics of these three datasets are shown in Table 1.

Table 1

Open in new tab

The statistics of three datasets used in the experiments

Datasets	Viruses	Drugs	VDAs
HDVD	34	219	455
VDA1	11	78	96
VDA2	69	128	770

Table 1

Open in new tab

The statistics of three datasets used in the experiments

Datasets	Viruses	Drugs	VDAs
HDVD	34	219	455
VDA1	11	78	96
VDA2	69	128	770

HDVD [40] is a database for experimentally supported human drug-virus associations, built by assembling a significant number of experimentally validated drug–virus interaction entries from relevant literatures with text mining technology. HDVD includes 34 viruses, 219 drugs and 455 confirmed human drug–virus interactions.

VDA1 dataset is constructed based on the 96 known VDAs between 11 viruses similar to SARS-CoV-2, such as SARS-CoV [4], MERS-CoV [8] and influenza A viruses [10] and 78 small molecular drugs. These interactions are collected from the DrugBank [63], NCBI [50] and PubMed [5] datasets.

VDA2 dataset is collected from the DrugVirus.info database [2], which provides various experimentally validated VDA-related resources. After removing the viruses with incomplete genome sequences, VDAs contain totally 770 VDAs between 69 viruses and 128 drugs.

2.2 Enhanced VDA matrix construction

As mentioned before, the main idea of drug repurposing for new viruses follows the perception that similar viruses are more likely to be treated by the same drugs. In this step of VDA-DLCMNMF, we target to construct an enhanced VDA matrix by seamlessly considering both VDAs and the biological knowledge of drugs and viruses. To this end, we first construct two similarity matrices based on chemical structures of drugs and genomic sequences of viruses and then design a new association measure to obtain the enhanced VDA matrix.

In addition, it is supposed to illustrate the notations used throughout this paper before introducing VDA-DLCMNMF in detail. The vector is denoted by lowercase boldface letters (e.g. |$\textbf{{v}} \in \mathbb{R}^{{d}}$|⁠), matrix is denoted by uppercase boldface letters (e.g. |$\textbf{{X}} \in \mathbb{R}^{{m}\times{n}}$|⁠). Then, we denote the set by |$\mathcal{D(\cdot )}$|⁠, hyperparameter by uppercase letters (e.g. |${T}$|⁠) and scalars by lowercase letters (e.g. |${d}$|⁠, |${k}$|⁠).

The similarity matrix of drugs is denoted as |$\textbf{{S}}^{\textbf{{d}}}\in \mathbb{R}^{{n}_{d}\times{n}_{d}}$|⁠, where |${n}_{d}$| is the number of drugs, and it is constructed on the chemical structures, including atom, bond, branch, closed-loop and break specifications, obtained from simplified molecular input line entry system (SMILES) [62]. As one of the most commonly used database for molecular structures [60], SMILES has been widely used in calculating the similarity of drugs from the structural perspective. We download the SMILES database from DrugBank [63] with version 5.1.8 and use Babel chemistry toolbox [45] with version 2.3.1 to convert SMILES strings into molecular access system (MACCS) chemical fingerprints, each bit of which indicates the existence of a particular substructure in the compound. Given the MACCS fingerprints of all drugs, the Tanimoto index [67] is adopted to the measure the fingerprint-based molecular similarity between pairwise drugs. Assuming that |$d_i$| and |$d_j$| are two drugs and their MACCS fragment bit-strings sets are |$\mathcal{D}({i})$| and |$\mathcal{D}({j}),$| respectively, |$\textbf{{S}}^{\textbf{{d}}}_{{i}{j}}$| is the similarity between |$d_i$| and |$d_j$| in |$\textbf{{S}}^{\textbf{{d}}}$| and its value can be computed with (1).

$$\begin{align}& \textbf{{S}}^{\textbf{{d}}}_{{i}{j}} = {\frac{\mathcal{D}({i}) \cap \mathcal{D}({j})}{\mathcal{D}({i}) \cup \mathcal{D}({j})}} \end{align}$$

(1)

Regarding the similarity of viruses, the genomic sequences of viruses are used and they can be downloaded from the NCBI [50]. Let |$\textbf{{S}}^{\textbf{{v}}}\in \mathbb{R}^{{n}_{v}\times{n}_{v}}$|⁠, where |${n}_{v}$| denotes the number of viruses, be the similarity matrix of viruses. For each element of |$\textbf{{S}}^{\textbf{{v}}}$|⁠, its value can be obtained by using a sequence alignment software MAFFT [24].

A VDA network is a bipartite graph, where edges are only existed between viruses and their associated drugs. A |${n}_{d}\times{n}_{v}$| matrix, denoted as |$\textbf{{A}}$|⁠, is introduced to represent the topological structure of a given VDA network. For an arbitrary element, say |$\textbf{{A}}_{{i},{j}}$|⁠, its value is 1 if |$d_i$| and |$v_j$| are associated and 0 otherwise. The purpose of this step is to construct an enhanced association matrix, i.e. |$\textbf{{A}}^{^{\prime}}$|⁠, by integrating |$\textbf{{S}}^{\textbf{{d}}}$|⁠, |$\textbf{{S}}^{\textbf{{v}}}$| and |$\textbf{{A}}$|⁠. With |$\textbf{{A}}^{^{\prime}}$|⁠, we are able to ensure that (i) similar viruses are more likely to be associated with the same drugs and (ii) similar drugs are more likely to be associated with the same viruses. Obviously, the former one is of particular significance to repurpose drugs for new viruses. |$\textbf{{A}}^{^{\prime}}$| can be obtained with (2).

$$\begin{align}& \textbf{{A}}^{^{\prime}} = \textbf{{S}}^{\textbf{{d}}}\textbf{{A}}\textbf{{S}}^{\textbf{{v}}} \end{align}$$

(2)

According to the above formula, it is possible that the values of elements in |$\textbf{{A}}^{^{\prime}}$| are much larger than those in |$\textbf{{S}}^{\textbf{{v}}}$| and |$\textbf{{S}}^{\textbf{{d}}}$|⁠. Hence, we adopt a min-max normalization to each row of |$\textbf{{A}}^{^{\prime}}$|⁠, thus constraining the values within a range |$[0,1]$|⁠. For each element of |$\textbf{{A}}^{^{\prime}}$|⁠, its value is given by (3).

$$\begin{align}& \textbf{{A}}^{^{\prime}}_{{i},{j}} = \frac{\textbf{{A}}^{^{\prime}}_{{i},{j}} - min(\textbf{{A}}^{^{\prime}}_{{i},:})}{max(\textbf{{A}}^{^{\prime}}_{{i},:}) - min(\textbf{{A}}^{^{\prime}}_{{i},:})}, \end{align}$$

(3)

where |$\textbf{{A}}^{^{\prime}}_{{i},:}$| is the |${i}$|-th row of |$\textbf{{A}}^{^{\prime}}$| and |$max(\textbf{{A}}^{^{\prime}}_{{i},:}) $| and |$min(\textbf{{A}}^{^{\prime}}_{{i},:})$| return the maximum and minimum values respectively in |$\textbf{{A}}^{^{\prime}}_{{i},:}$|⁠.

2.3 The CMNMF model

Regarding the task of drug repurposing for new viruses, the failure of existing network-based methods is due to their incapability of capturing the structural and genomic forces that play an important role in determining VDAs. To overcome this problem, we propose the CMNMF model and present its details as below.

Assuming that |${k}$| is the dimension of LFS, we define two matrices, i.e. |$\textbf{{W}}\in \mathbb{R}^{{k}\times{n}_{{d}}}$| and |$\textbf{{H}}\in \mathbb{R}^{{k}\times{n}_{{v}}}$|⁠, to denote the respective projection results of drugs and viruses in the LFS. Regarding the product of |$\textbf{{W}}$| and |$\textbf{{H}}$|⁠, CMNMF uses it to approximate |$\textbf{{A}}^{^{\prime}}$| rather than |$\textbf{{A}}$|⁠, which is commonly used by existing network-based methods. Thus, |$\textbf{{W}}$| and |$\textbf{{H}}$| are derived by using (4). In doing so, our perception about new viruses can be further enhanced.

$$\begin{align}& \textbf{{A}}^{^{\prime}} \approx \textbf{{W}}^{\textbf{{T}}}\textbf{{H}} \end{align}$$

(4)

In order to preserve the similarity information of drugs and viruses presented in their respective feature spaces, additional constraints are introduced by CMNMF from different views as given by (5) and (6), where |$\textbf{{w}}_{\textbf{{i}}} = \textbf{{W}}_{\textbf{{i},:}}$| is the latent feature vector of drug |$d_i$|⁠, |$\textbf{{h}}_{\textbf{{j}}} = \textbf{{H}}_{\textbf{{j},:}}$| is the latent feature vector of virus |$v_j$|⁠, and |$|| \cdot ||_{F}$| is the Frobenius norm.

$$\begin{align}& \sum_{i=1}^{{n}_{{d}}} \sum_{m=1}^{{n}_{d}} \textbf{{S}}^{{d}}_{{i},{m}} {|| \textbf{{w}}_{\textbf{{i}}} - \textbf{{w}}_{\textbf{{m}}} ||}_F^{2} \end{align}$$

(5)

$$\begin{align}& \sum_{j=1}^{{n}_{{v}}} \sum_{n=1}^{{n}_{{v}}} \textbf{{S}}^{{v}}_{{j},{n}} {|| \textbf{{h}}_{\textbf{{j}}} - \textbf{{h}}_{\textbf{{n}}} ||}_F^{2} \end{align}$$

(6)

With (5) and (6), the optimization of |$\textbf{{W}}$| and |$\textbf{{H}}$| is driven not only by |$\textbf{{A}}^{^{\prime}}$| but also by |$\textbf{{S}}^{{d}}$| and |$\textbf{{S}}^{{v}}$|⁠. A theoretical analysis is provided to verify the rationality behind these two constraints. Taking (5) as an example, since |$\textbf{{S}}^{{d}}_{{i},{m}}$| is a constant, the minimization of (5) can be achieved if the value of |${|| \textbf{{w}}_{\textbf{{i}}} - \textbf{{w}}_{\textbf{{m}}} ||}_F^{2}$| is small enough. In this regard, the latent feature vectors of drugs tend to gather together in the LFS. Moreover, if two drugs, i.e. |$d_i$| and |$d_m$|⁠, are similar, they certainly have a larger value of |$\textbf{{S}}^{{d}}_{{i},{m}}$|⁠, and thus |${|| \textbf{{w}}_{\textbf{{i}}} - \textbf{{w}}_{\textbf{{m}}} ||}_F^{2}$| should be smaller than others in order to minimize (5). In other words, the latent feature vectors of two drugs are much closer in the LFS if they are more similar. Given the above analysis, it is believed that the introduction of (5) and (6) allows CMNMF to preserve the similarity information of drugs and viruses in the LFS with only few noisy information generated.

The complete objective function of CMNMF is defined as

$$\begin{align}& \begin{aligned} \mathcal{J}(\textbf{{W}},\textbf{{H}})=& \frac{1}{2} \sum_{i=1}^{{n}_{{d}}} \sum_{j=1}^{{n}_{{v}}} (\textbf{{A}}^{^{\prime}}_{{i},{j}} - {\textbf{{w}}_{\textbf{{i}}}}^{T}\textbf{{h}}_{\textbf{{j}}})^{2}\\ &+\frac{\alpha}{2}\sum_{i=1}^{{n}_{{d}}} \sum_{m=1}^{{n}_{d}} \textbf{{S}}^{{d}}_{{i},{m}}{|| \textbf{{w}}_{\textbf{{i}}} - \textbf{{w}}_{\textbf{{m}}} ||}_F^{2}\\ &+\frac{\beta}{2}\sum_{j=1}^{{n}_{{v}}} \sum_{n=1}^{{n}_{v}} \textbf{{S}}^{{v}}_{{j},{n}} {|| \textbf{{h}}_{\textbf{{j}}} - \textbf{{h}}_{\textbf{{n}}} ||}_F^{2} \\ &+\frac{\lambda_{W}}{2}||\textbf{{W}}||_{F}^{2} + \frac{\lambda_{H}}{2}||\textbf{{H}}||_{F}^{2}\\ & s.t. \textbf{{W}} \ge 0, \textbf{{H}} \ge 0, \end{aligned} \end{align}$$

(7)

where |$\alpha $|⁠, |$\beta $|⁠, |$\lambda _{W}$| and |$\lambda _{H}$| are the regularization coefficients. The purpose of CMNMF is to find |$\textbf{{W}}$| and |$\textbf{{H}}$| that minimize |$\mathcal{J}(\textbf{{W}},\textbf{{H}})$|⁠. Here, a stochastic gradient decent method is adopted to solve this minimization problem. In particular, we first eliminate the inequality constraints by introducing Lagrange multipliers and obtain |$\mathcal{L}(\textbf{{W}},\textbf{{H}})$| as follows.

$$\begin{align}& \begin{aligned} \mathcal{L}(\textbf{{W}},\textbf{{H}})=&\frac{1}{2} Tr(\textbf{{A}}^{^{\prime}} \textbf{{A}}^{^{\prime}{T}})-Tr(\textbf{{W}}^{{T}}\textbf{{H}}\textbf{{A}}^{^{\prime}{T}})\\ &+\frac{1}{2}Tr(\textbf{{W}}^{{T}}\textbf{{H}}\textbf{{H}}^{{T}}\textbf{{W}})+\frac{\alpha}{2} Tr(\textbf{{W}}\textbf{{Q}}_{{d}}\textbf{{W}}^{{T}})\\ &+\frac{\beta}{2} Tr(\textbf{{H}}\textbf{{Q}}_{v}\textbf{{H}}^{{T}})+\frac{\lambda_{W}}{2} Tr(\textbf{{W}}\textbf{{W}}^{{T}})+\frac{\lambda_{H}}{2} Tr(\textbf{{H}}\textbf{{H}}^{{T}})\\ &+Tr(\varPhi \textbf{{W}}^{{T}})+Tr(\varPsi \textbf{{H}}^{{T}}). \end{aligned} \end{align}$$

(8)

In (8), |$Tr(\cdot )$| represents the matrix trace, |$\varPhi = [\phi _{ik}]$| and |$\varPsi = [\psi _{jk}]$| are the Lagrange multipliers for the inequalities of (7), i.e. |$\textbf{{w}}_{\textbf{{ik}}}\ge 0$| and |$\textbf{{h}}_{\textbf{{jk}}}\ge 0$|⁠, respectively, |$\textbf{{Q}}_{\textbf{{d}}}$| and |$\textbf{{Q}}_{\textbf{{v}}}$| are the Laplacian similarity matrices of |$\textbf{{S}}^{{d}}$| and |$\textbf{{S}}^{{v}}$|⁠, respectively. After that, we solve the minimization problem of |$\mathcal{L}(\textbf{{W}},\textbf{{H}})$| by using its the Karush–Kuhn–Tucker conditions and obtain the update rules of |$\textbf{{W}}$| and |$\textbf{{H}}$| as follows.

$$\begin{align}& \textbf{{w}}_{\textbf{{ik}}}^{^{\prime}} \leftarrow \textbf{{w}}_{\textbf{{ik}}} \frac{(\textbf{{H}}\textbf{{A}}^{^{\prime}})_{ik}-(\alpha \textbf{{W}}\textbf{{Q}}_{\textbf{{d}}})_{ik}}{(\textbf{{H}}\textbf{{H}}^{{T}}\textbf{{W}})_{ik} + (\lambda_{W}\textbf{{W}})_{ik}} \end{align}$$

(9)

$$\begin{align}& \textbf{{h}}_{\textbf{{jk}}}^{^{\prime}} \leftarrow \textbf{{h}}_{\textbf{{jk}}} \frac{(\textbf{{W}}\textbf{{A}}^{^{\prime}})_{jk}- (\alpha \textbf{{H}}\textbf{{Q}}_{\textbf{{v}}})_{jk}}{(\textbf{{W}}\textbf{{W}}^{{T}}\textbf{{H}})_{jk} + (\lambda_{H}\textbf{{H}})_{jk}} \end{align}$$

(10)

An iterative procedure is applied by VDA-DLCMNMF to obtain the optimum results of |$\textbf{{W}}$| and |$\textbf{{H}}$| until a convergence is reached.

2.4 GCN-based drug repurposing

Without loss of generality, we still use |$\textbf{{W}}$| and |$\textbf{{H}}$| to denote their optimum results in terms of minimizing (8) and give the details of how VDA-DLCMNMF repurposes drugs for new viruses.

Compared with traditional network representation learning algorithms, such as DeepWalk [48] and Node2Vec [14], GNN has the advantage of processing and integrating node features [51]. As a specific type of GNN, spatial-based GCN [28, 68] receives much attention due to its high efficiency and flexibility in dealing with the heterogeneous information of input. Thus, VDA-DLCMNMF adopts it to learn the node representations of viruses and drugs in a given VDA network and then uses them to predict potential associations for new viruses.

When incorporating GCN into VDA-DLCMNMF, we adopt the attention-based strategy in neighborhood sampling for giving an accurate learning. To do so, the attention coefficients for all VDAs are first calculated, and then they are used to weight VDAs with the softmax function. Given a drug |$d_{i}$| and a virus |$v_{j}$|⁠, |$e_{ij}$| and |$\alpha _{ij}$| are defined as its attention coefficient and weight, respectively, and their definitions are given as follows.

$$\begin{align}& e_{ij} = \mathcal{A}(\textbf{{w}}_{\textbf{{i}}}, \textbf{{h}}_{\textbf{{j}}}) \end{align}$$

(11)

$$\begin{align}& \alpha_{ij} = softmax_{j}(e_{ij}) = \frac{exp(e_{ij})}{\sum_{p\in{\mathcal{N}({i})}}exp(e_{ip})} \end{align}$$

(12)

In (11), |$\mathcal{A}:\mathbb{R}^{{k}}\times \mathbb{R}^{{k}}\rightarrow \mathbb{R}$| is a shared attentional mechanism. |$\mathcal{N}({i})$| in (12) denotes the set of all VDAs involving |$d_i$|⁠. For the sake of convenience, the attention weights for all pairs of |$d_i$| and |$v_j$| can be represented with a matrix |$\textbf{{W}}^{\textbf{{a}}} \in \mathbb{R}^{{n}_{d}\times{n}_{v}}$|⁠, which can be explicitly calculated with (13).

$$\begin{align}& \textbf{{W}}^{\textbf{{a}}} = softmax((\textbf{{W}}^{\textbf{{T}}}\textbf{{H}})\times \textbf{{A}}) \end{align}$$

(13)

A heuristic neighborhood sampling strategy is adopted by VDA-DLCMNMF to improve the efficiency of training a GCN. Taking |$d_i$|⁠, or |$v_j$|⁠, as an example, we select the top |$T$| viruses, or drugs, to compose |${\mathcal{T}}(d_i)$|⁠, or |${\mathcal{T}}(v_j)$|⁠, in the descending order of attention weights in |$\textbf{{W}}^{\textbf{{a}}}$|⁠. Since |$\textbf{{W}}^{\textbf{{a}}}$| is already determined before training, this process is only applied once. The representations of drugs and viruses are then updated iteratively by using |${\mathcal{T}}(d_i)$| and |${\mathcal{T}}(v_j),$| respectively, rather than the whole VDA network, thus reducing the training time.

Here, |$d_i$| is taken as an example to illustrate the process of learning its representation. Let |$\textbf{{r}}_{{\mathcal{T}}(d_i)}^{({l})}$| and |$\textbf{{r}}_{d_i}^{({l})}$| denote the neighbor information of |$d_i$| and the representation of |$d_i$| respectively at the |${l}$|-th layer in the GCN, their definitions are

$$\begin{align}& \textbf{{r}}_{{\mathcal{T}}(d_i)}^{({l})}= \sum_{v_j \in{\mathcal{T}}(d_i)} \textbf{{W}}^{\textbf{{a}}}_{{i},{j}}\textbf{{r}}_{v_j}^{({l}-1)} \end{align}$$

(14)

$$\begin{align}& \textbf{{r}}_{d_i}^{({l})} = \sigma (\textbf{{W}}^{({l})} \cdot CONCAT(\textbf{{r}}_{d_i}^{({l-1})}, \textbf{{r}}_{{\mathcal{T}}(d_i)}^{(l)}), \end{align}$$

(15)

where |$\textbf{{W}}^{({l})}$| is the weight matrix of the |$l$|-th layer, |$CONCAT(\cdot )$| is the concatenation function applied to learn the neighbor information from |${T}(d_i)$|⁠, and |$\sigma (\cdot )$| is the sigmoid activation function. Regarding the initialization of |$\textbf{{r}}_{d_{i}}$|⁠, we have |$\textbf{{r}}_{\textbf{d}_{i}}^{\textbf{({0})}} = \textbf{{w}}_{\textbf{{i}}}$| to avoid a random initialization. Similarly, we can also obtain |$\textbf{{r}}_{v_j}$| for an arbitrary virus |$v_j$|⁠.

Assuming that there are total |${L}$| layers in the GCN, for a new virus |$v_j$|⁠, its probability of being associated with a drug |$d_{i}$| is computed by multiplying their final representations as given by (16). The activation function allows the result of |${s}_{ij}$| fall into the range |$[0,1]$|⁠.

$$\begin{align}& {s}_{ij} = \sigma(\textbf{{r}}_{d_i}^{({L})} \cdot \textbf{{r}}_{v_j}^{{(L)}}) \end{align}$$

(16)

2.5 Complexity analysis

At each epoch, |$\textbf{{W}}$|⁠, |$\textbf{{H}}$|⁠,|$\textbf{{W}}^{a}$| and |$\textbf{{r}}^{(L)}$| are updated according to Equations (9), (10) and (13)–(15). The update of |$\textbf{{W}}$| and |$\textbf{{H}}$| takes time |${O}{({k} {n}_{{d}} {k} {n}_{{v}} )}$|⁠. The time required to calculate |$\textbf{{W}}^{a}$| is |${O}{({n}_{{d}} {k} {n}_{{v}})}$|⁠. After calculating the attention weight matrix, we select the top |${T}$| neighborhoods for each node in VDA network, which takes time |${O}{(2{n}_{{d}}T{n}_{{v}})}$|⁠. The computation of |$\textbf{{r}}^{(L)}$| has the time complexity |${O}{({T}^{{L}})}$|⁠. Hence, the time used for one iteration is |${O}{(({k} + {k}^{2} + 2{T}){n}_{{d}}{n}_{{v}} + {T}^{{L}})}$|⁠. In this study, we normally have |${T} \ll{n}_{{d}}, {n}_{{v}}, {k}$| and |${L} = 2$|⁠. As a result, the time complexity can be further simplified to |${O}({k}^{2}{n}_{{d}}{n}_{{v}})$|⁠. Assuming that the number of epochs is |${E}$|⁠, the overall time complexity is |${O}({E}{k}^{2}{n}_{{d}}{n}_{{v}})$|⁠.

3 Results

3.1 Evaluation metrics and experimental settings

Five-fold cross-validation (CV) is used to evaluate the performance of VDA-DLCMNMF. We perform the 5-fold CVs by alternatively selecting one fold as the test set and the rest as the training set. The negative samples are selected on each fold to ensure that no unseen node is generated in negative dataset. In other words, negative samples are selected by paring up drugs and viruses whose associations are not found in each fold. To do so, we first obtain the complementary set of VDAs in each fold, then randomly select the negative samples with the same size of positive samples from the complementary set so as to compose the negative dataset. As a result, positive and negative samples are balanced in each fold.

Additionally, five evaluation metrics, including accuracy (Acc.), sensitivity (Sen.), specificity (Spe.) AUC and AUPR, are adopted to measure the performance. Definitions of the first three metrics are given as

$$\begin{align}& Acc. = \frac{TP+TN}{TP+TN+FP+FN} \end{align}$$

(17)

$$\begin{align}& Sen. = \frac{TP}{TP+FN} \end{align}$$

(18)

$$\begin{align}& Spe. = \frac{TN}{TN+FP}, \end{align}$$

(19)

where |$TP$|⁠, |$FP$|⁠, |$TN$| and |$FN$| denote the numbers of true positive, false positive, true negative and false negative associations, respectively. AUC is the area under the receiver operating characteristic (ROC) curve, which can be plotted by true positive rate and false positive rate. AUPR is the area under the precision-recall curve, which can be plotted by precision and recall (Sen.).

In the experiments, VDA-DLCMNMF is compared with five state-of-the-art network-based drug repositioning methods, including DRHGCN [35], SANE [56], IRNMFVDA [58], SCPMF [40], VDA-RWR [47] and VDA-KATZ [70]. Among them, DRHGCN is a general drug repurposing method by introducing a layer attention mechanism to combine the embeddings of drugs and viruses from multiple graph convolution layers, SANE addresses the cold-start problem by introducing an LSTM unit to learn initial representations for drug and virus from drug chemical structure and virus genomic sequence, while the other three methods are specifically proposed for discovering potential antiviral drugs for SARS-CoV-2 as mentioned in the section of Introduction. All the experiments are performed on the working machine equipped with Intel Core I7 2.6GHz and 16GB RAM.

Regarding the parameters involved in VDA-DLCMNMF, an in-depth analysis of parameter sensitivity is performed to determine their optimal values with grid search. We determine their optimal values by using the method of control variates, which alternatively update each parameter. In specific, we vary the values of |$\alpha $|⁠, |$\beta $|⁠, |$\lambda _{W}$| and |$\lambda _{H}$| from 0 to 1 at a step size of 0.001. Given the constraints that |$\alpha = \beta $| and |$\lambda _{W} = \lambda _{H}$|⁠, we conduct several trials with different combinations of parameter values and select the one with the best performance as the final values of these parameters. In addition, regarding the parameters used in GCN, we select the layer |${L} = 2$| and |${T} = 4$|⁠. For the other competing methods, their parameters are assigned with the values recommended in relevant literature. The parameter settings for all the five methods are presented in Table 2.

Table 2

Open in new tab

Parameter settings used by VDA-DLCMNMF and four competing state-of-the-art methods

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

Table 2

Open in new tab

Parameter settings used by VDA-DLCMNMF and four competing state-of-the-art methods

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

3.2 Performance comparison of different methods

The detailed results of 5-fold CV are shown in Table 3. To visually compare the performance of all five methods, we also plot their ROC curves and PR curves in Figure 2.

Table 3

Open in new tab

Experimental results of 5-fold CV

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRHGCN	0.7713	0.7689	0.7791	0.7713	0.7845	0.7298	0.7299	0.7841	0.8085	0.8271	0.7029	0.7030	0.7689	0.8177	0.7449
SANE	0.8352	0.8103	0.8580	0.8944	0.8598	0.7705	0.7489	0.7834	0.8080	0.8379	0.8019	0.7008	0.7307	0.8018	0.7553
IRNMFVDA	0.3856	0.7314	0.3631	0.8037	0.2156	0.6227	0.4852	0.6834	0.7102	0.2005	0.5317	0.6496	0.5205	0.8147	0.2971
SCPMF	0.7661	0.4693	0.7854	0.8549	0.4783	0.7150	0.4403	0.7464	0.7543	0.3684	0.7660	0.3969	0.8012	0.8293	0.3517
VDA-KATZ	0.5777	0.6995	0.5762	0.8253	0.0698	0.6691	0.6976	0.6684	0.8803	0.3380	0.7119	0.5441	0.7152	0.7743	0.0583
VDA-RWR	0.6550	0.7400	0.6700	0.7875	0.0218	0.8278	0.4824	0.7831	0.8582	0.1383	0.6613	0.5022	0.6643	0.6675	0.0322
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRHGCN	0.7713	0.7689	0.7791	0.7713	0.7845	0.7298	0.7299	0.7841	0.8085	0.8271	0.7029	0.7030	0.7689	0.8177	0.7449
SANE	0.8352	0.8103	0.8580	0.8944	0.8598	0.7705	0.7489	0.7834	0.8080	0.8379	0.8019	0.7008	0.7307	0.8018	0.7553
IRNMFVDA	0.3856	0.7314	0.3631	0.8037	0.2156	0.6227	0.4852	0.6834	0.7102	0.2005	0.5317	0.6496	0.5205	0.8147	0.2971
SCPMF	0.7661	0.4693	0.7854	0.8549	0.4783	0.7150	0.4403	0.7464	0.7543	0.3684	0.7660	0.3969	0.8012	0.8293	0.3517
VDA-KATZ	0.5777	0.6995	0.5762	0.8253	0.0698	0.6691	0.6976	0.6684	0.8803	0.3380	0.7119	0.5441	0.7152	0.7743	0.0583
VDA-RWR	0.6550	0.7400	0.6700	0.7875	0.0218	0.8278	0.4824	0.7831	0.8582	0.1383	0.6613	0.5022	0.6643	0.6675	0.0322
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Best results are bolded.

Table 3

Open in new tab

Experimental results of 5-fold CV

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRHGCN	0.7713	0.7689	0.7791	0.7713	0.7845	0.7298	0.7299	0.7841	0.8085	0.8271	0.7029	0.7030	0.7689	0.8177	0.7449
SANE	0.8352	0.8103	0.8580	0.8944	0.8598	0.7705	0.7489	0.7834	0.8080	0.8379	0.8019	0.7008	0.7307	0.8018	0.7553
IRNMFVDA	0.3856	0.7314	0.3631	0.8037	0.2156	0.6227	0.4852	0.6834	0.7102	0.2005	0.5317	0.6496	0.5205	0.8147	0.2971
SCPMF	0.7661	0.4693	0.7854	0.8549	0.4783	0.7150	0.4403	0.7464	0.7543	0.3684	0.7660	0.3969	0.8012	0.8293	0.3517
VDA-KATZ	0.5777	0.6995	0.5762	0.8253	0.0698	0.6691	0.6976	0.6684	0.8803	0.3380	0.7119	0.5441	0.7152	0.7743	0.0583
VDA-RWR	0.6550	0.7400	0.6700	0.7875	0.0218	0.8278	0.4824	0.7831	0.8582	0.1383	0.6613	0.5022	0.6643	0.6675	0.0322
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRHGCN	0.7713	0.7689	0.7791	0.7713	0.7845	0.7298	0.7299	0.7841	0.8085	0.8271	0.7029	0.7030	0.7689	0.8177	0.7449
SANE	0.8352	0.8103	0.8580	0.8944	0.8598	0.7705	0.7489	0.7834	0.8080	0.8379	0.8019	0.7008	0.7307	0.8018	0.7553
IRNMFVDA	0.3856	0.7314	0.3631	0.8037	0.2156	0.6227	0.4852	0.6834	0.7102	0.2005	0.5317	0.6496	0.5205	0.8147	0.2971
SCPMF	0.7661	0.4693	0.7854	0.8549	0.4783	0.7150	0.4403	0.7464	0.7543	0.3684	0.7660	0.3969	0.8012	0.8293	0.3517
VDA-KATZ	0.5777	0.6995	0.5762	0.8253	0.0698	0.6691	0.6976	0.6684	0.8803	0.3380	0.7119	0.5441	0.7152	0.7743	0.0583
VDA-RWR	0.6550	0.7400	0.6700	0.7875	0.0218	0.8278	0.4824	0.7831	0.8582	0.1383	0.6613	0.5022	0.6643	0.6675	0.0322
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Best results are bolded.

Figure 3

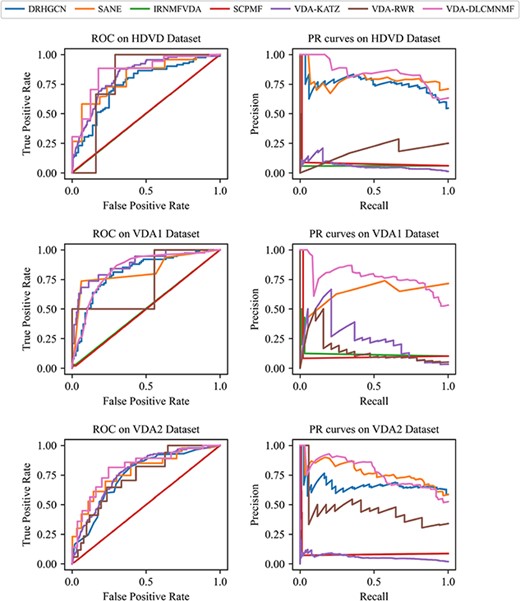
ROC and AUPR curves obtained by VDA-DLCMNMF and other competing methods on three datasets for de novo test.

Open in new tab Download slide

For the performance of two NMF-based methods, we note that SCPMF performs better than IRNMFVDA across all three datasets, as the scores of Acc. obtained by SCPMF are better by 38.05%, 9.23% and 23.43% than those of IRNMFVDA on HDVD, VDA1 and VDA2, respectively. Besides, for IRNMFVDA, its fluctuation in Acc. is more intensive, as the standard deviation of Acc. yielded by IRNMFVDA is 0.098 larger than the others. The reasons attributable for the unsatisfactory performance of IRNMFVDA are 2-fold. First, the indicator matrix used by IRNMFVDA is constructed based on a VDA matrix and the attribute matrices of drugs and viruses and a simple concatenation of these three matrices makes the indicator matrix sparser. Taking HDVD as an example, the VDA network of HDVD is the sparsest when compared with those of the other two datasets and the worst performance of IRNMFVDA is observed on it. Second, when applied to different datasets, the generalization ability of IRNMFVDA is poor due to the lack of a proper normalization process.

Regarding VDA-KATZ and VDA-RWR, although both of them are network-based methods, they perform quite differently when predicting novel VDAs in the experiments. In particular, the best performance of VDA-KATZ is achieved in the 5-fold CV of VDA2, which could be an indicator that VDA-KATZ prefers dense VDA networks. The main reason for that phenomenon is ascribed to the motivation of VDA-KATZ, which is to utilize network paths to predict potential associations. In doing so, KDA-KATZ tends to yield a better performance for dense VDA networks with more network paths. Compared with VDA-KATZ, VDA-RWR is not always better than VDA-KATZ across all datasets. Among the results in Table 3, it is observed that for the VDA1 dataset, VDA-RWR performs the best among all methods except VDA-DLCMNMF in terms of Acc., whereas for the other two datasets, its performance in terms of Acc. is just fair. The main reason why VDA-RWR yields the second best score of Acc. on the VDA1 dataset is that VDA-RWR has a strong ability in learning the topological characteristics from small VDA networks. However, its worse performance obtained on HDVD and VDA2 demonstrates that its learning ability is constrained by the sparsity of VDA networks, which heavily affects the effectiveness of random walk from different perspectives. In particular, when dealing with sparse VDA networks, viruses and drugs with less degrees are difficult to be visited by the random walk of VDA-RWR, as their topological information is not sufficient. On the other hand, for dense VDA networks, more associations are involved during random walk, but the existence of false-positive associations could decrease the accuracy of VDA-RWR. Moreover, both VDA-KATZ and VDA-RWR achieve the low AUPR value with only 0.1554 and 0.0641 on average, which indicates that they are easily misled by false positive samples, especially when compared with those deep learning-based methods, including DRHGCN, SANE and VDA-CMNMF.

Regrading two deep learning-based methods DRHGCN and SANE, both of them have relatively stable performances among all metrics, which is mainly because of the attention mechanism adopted in them. Though both DRHGCN and SANE are constructed based on GCN, SANE performs better than DRHGCN across all three datasets, as the scores of Acc. obtained by SANE are better by 6.39%, 4.07% and 9.9% than those of DRHGCN on three datasets, respectively. The reason for this is that the information contained in SANE is not only the network topology but also the drug/virus attribute feature learned by LSTM from drug chemical structure/virus genomic sequence. On the other hand, though DRHGCN performs as not well as SANE, it still achieves the better performance than the other baselines, which further demonstrate that robustness of deep learning-based methods.

Among all drug repurposing methods compared in the experiments, VDA-DLCMNMF yields a bigger margin in terms of Acc., AUC and AUPR across all datasets, as it achieves the best performance on HDVD, VDA1 and VDA2. There are also several points worth further commentary. First, compared with NMF-based methods, VDA-DLCMNMF adopts the CMNMF model to preserve the similarity information of drugs and diseases when projecting them onto a unified LFS and thus yields a promising performance in drug repurposing. Second, the generalization ability of VDA-DLCMNMF is further improved by learning the network spatial structure with attention-based layer aggregation, and it is also for this reason that VDA-DLCMNMF yields the largest scores of Acc. and AUC in all cases. In summary, it is believed that VDA-DLCMNMF is a useful tool to discover novel VDAs.

3.3 De novo VDA prediction

To assess the capability of VDA-DLCMNMF in predicting potential indications for new drugs, we choose the drug pair with chemical similarity over 0.7 to conduct a de novo test. For each of this kind of drug pairs, we randomly select a drug and remove all VDAs related to it in turn as the test samples and other existing associations are used as training sample. The random selection procedure has been repeated for 50 times and the ROC and PR curves obtained by each prediction model are depicted in Figure 3.

Figure 4

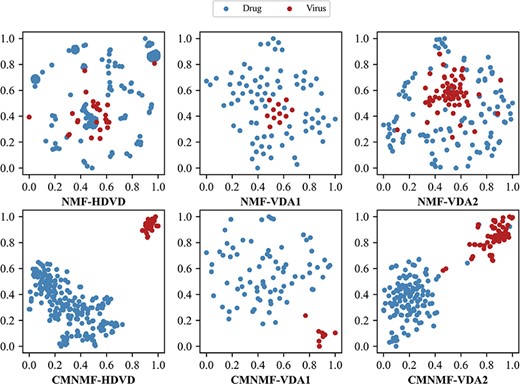
The latent feature vectors of drugs and viruses obtained by NMF and CMNMF are visualized in a 2D space by t-SNE.

Open in new tab Download slide

First of all, according to the ROC and PR curves, we note that the overall performance of VDA-DLCMNMF is better than the other competing prediction models, as its average AUC and AUPR scores are the largest across all the three datasets. In this regard, we reason that VDA-DLCMNMF is more robust toward the bias resulted from the existence of redundancy drugs. Second, regarding the NMF-based models, i.e. IRNMFVDA and SCPMF, their ROC and PR curves indicate that their performances in the de novo test are much worse than those in the 5-fold CV. Hence, the performance of NMF-based models is heavily dependent on the similarity of drugs, which is an important information source for them to learn latent vectors. Lastly, the deep learning-based models, including DRHGCN and SANE, are less affected by the removal of redundant drugs, as they do not need the similarity information of drugs to perform their tasks.

3.4 Ablation study

To better demonstrate the advantage of VDA-DLCMNMF in drug repurposing, an in-depth ablation study has been conducted with extensive experiments. To do so, we first design four variants of VDA-DLCMNMF and evaluate their performance on the datasets of HDVD, VDA1 and VDA2. A detailed description about these variants are listed as below, and the difference between them and VDA-DLCMNMF are also discussed.

|$\bullet $|NMF is designed without considering any constraints. The input of NMF is only the VDA network, and the latent vectors of drugs and viruses are used as their final representations. Given a pair of drug and disease, their probability of being associated is computed with (16).
|$\bullet $|CMNMF is used alone to discover novel VDAs. Similar to NMF, the latent vectors of drugs and viruses learned from CMNMF are explicitly used to compute the probability with (16).
|$\bullet $||${\textbf{GCN}}_{{random}}$| is a variant of the last part of VDA-DLCMNMF, which selects neighbor receptive field in a random manner.
|$\bullet $|GCN is the last part of VDA-DLCMNMF. In the ablation study, the representation of drugs and viruses are randomly initialized for GCN.
|$\bullet $|NMF-GCN is implemented by combining NMF and GCN. The main difference between NMF-GCN and VDA-DLCMNMF lies in the initial representation of drugs and viruses for GCN, as NMF-GCN and VDA-DLCMNMF use the latent feature vectors learned by NMF and CMNMF, respectively.

Experimental results of the variants of VDA-DLCMNMF are shown in Table 4. As mentioned before, the CMNMF model is adopted by VDA-DLCMNMF to obtain the reliable initial representations of drugs and viruses. Compared with NMF, CMNMF integrates |$S_d$| and |$S_v$| into |$A$|⁠, thus obtaining an enhanced association matrix, i.e. |$\textbf{{A}}^{^{\prime}}$|⁠. To demonstrate the advantage and effectiveness of CMNMF, we first compare the performance of CMNMF with that of NMF on all the three datasets. As indicated by Table 4, it is seen that in terms of Acc., CMNMF perform better by 3.75%, 9.37% and 0.94% than NMF for the datasets of HDVD, VDA1 and VDA2, respectively. This could be a strong indicator that the latent vectors obtained by CMNMF are capable of retaining the characteristics of drugs and viruses from the perspectives of network topology and biological knowledge and hence they are able to improve the prediction accuracy of VDA-DLCMNMF.

Table 4

Open in new tab

Experimental results of ablation study

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
NMF	0.7810	0.7802	0.7824	0.7811	0.8268	0.7395	0.6974	0.7672	0.7400	0.8522	0.7680	0.7558	0.7765	0.7680	0.8063
CMNMF	0.8185	0.8154	0.8220	0.8185	0.8694	0.8332	0.8442	0.8295	0.8334	0.9059	0.7774	0.7309	0.7955	0.7849	0.8388
\|$\textrm{GCN}_{random}$\|	0.7081	0.8201	0.6318	0.7965	0.7157	0.6250	0.6767	0.5833	0.5967	0.5670	0.7000	0.6423	0.7422	0.7769	0.7573
GCN	0.7516	0.6669	0.7761	0.8034	0.7761	0.6547	0.6137	0.7204	0.7606	0.7204	0.7558	0.7658	0.7656	0.8191	0.7657
NMF-GCN	0.8000	0.8656	0.7541	0.8979	0.8532	0.8500	0.8667	0.9095	0.9133	0.9333	0.7290	0.7343	0.7278	0.8018	0.7852
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
NMF	0.7810	0.7802	0.7824	0.7811	0.8268	0.7395	0.6974	0.7672	0.7400	0.8522	0.7680	0.7558	0.7765	0.7680	0.8063
CMNMF	0.8185	0.8154	0.8220	0.8185	0.8694	0.8332	0.8442	0.8295	0.8334	0.9059	0.7774	0.7309	0.7955	0.7849	0.8388
\|$\textrm{GCN}_{random}$\|	0.7081	0.8201	0.6318	0.7965	0.7157	0.6250	0.6767	0.5833	0.5967	0.5670	0.7000	0.6423	0.7422	0.7769	0.7573
GCN	0.7516	0.6669	0.7761	0.8034	0.7761	0.6547	0.6137	0.7204	0.7606	0.7204	0.7558	0.7658	0.7656	0.8191	0.7657
NMF-GCN	0.8000	0.8656	0.7541	0.8979	0.8532	0.8500	0.8667	0.9095	0.9133	0.9333	0.7290	0.7343	0.7278	0.8018	0.7852
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Best results are bolded.

Table 4

Open in new tab

Experimental results of ablation study

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
NMF	0.7810	0.7802	0.7824	0.7811	0.8268	0.7395	0.6974	0.7672	0.7400	0.8522	0.7680	0.7558	0.7765	0.7680	0.8063
CMNMF	0.8185	0.8154	0.8220	0.8185	0.8694	0.8332	0.8442	0.8295	0.8334	0.9059	0.7774	0.7309	0.7955	0.7849	0.8388
\|$\textrm{GCN}_{random}$\|	0.7081	0.8201	0.6318	0.7965	0.7157	0.6250	0.6767	0.5833	0.5967	0.5670	0.7000	0.6423	0.7422	0.7769	0.7573
GCN	0.7516	0.6669	0.7761	0.8034	0.7761	0.6547	0.6137	0.7204	0.7606	0.7204	0.7558	0.7658	0.7656	0.8191	0.7657
NMF-GCN	0.8000	0.8656	0.7541	0.8979	0.8532	0.8500	0.8667	0.9095	0.9133	0.9333	0.7290	0.7343	0.7278	0.8018	0.7852
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Methods\ Datasets	HDVD					VDA1					VDA2
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
NMF	0.7810	0.7802	0.7824	0.7811	0.8268	0.7395	0.6974	0.7672	0.7400	0.8522	0.7680	0.7558	0.7765	0.7680	0.8063
CMNMF	0.8185	0.8154	0.8220	0.8185	0.8694	0.8332	0.8442	0.8295	0.8334	0.9059	0.7774	0.7309	0.7955	0.7849	0.8388
\|$\textrm{GCN}_{random}$\|	0.7081	0.8201	0.6318	0.7965	0.7157	0.6250	0.6767	0.5833	0.5967	0.5670	0.7000	0.6423	0.7422	0.7769	0.7573
GCN	0.7516	0.6669	0.7761	0.8034	0.7761	0.6547	0.6137	0.7204	0.7606	0.7204	0.7558	0.7658	0.7656	0.8191	0.7657
NMF-GCN	0.8000	0.8656	0.7541	0.8979	0.8532	0.8500	0.8667	0.9095	0.9133	0.9333	0.7290	0.7343	0.7278	0.8018	0.7852
VDA-DLCMNMF	0.8649	0.8625	0.9118	0.9299	0.9097	0.9000	0.9667	0.9333	0.9250	0.9715	0.7849	0.7688	0.8361	0.8631	0.8770

Best results are bolded.

In addition to the quantitative analysis, we visualize the latent vectors of drugs and viruses in a 2D space by t-SNE [59] and expect that the advantage of CMNMF can be better appreciated. According to Figure 4, it is observed that CMNMF is able to clearly distinguish drugs and viruses while introducing only few noisy information. In other words, the latent feature vectors obtained by CMNMF are more representative than those obtained by NMF. Moreover, we also note from Table 4 and Figure 4 that CMNMF contributes more in improving the accuracy of VDA-DLCMNMF on VDA1 than on the other two datasets, and the reasons are 2-fold. First, among all datasets, VDA1 is the smallest one with only 96 VDAs, and such a small VDA network is more sensitive to the quality of latent feature vectors of drugs and viruses. Second, comparing the distributions of latent vectors in 2D space, we note that the latent vectors obtained by NMF from VDA1 are uniformly distributed and they are not separated into different clusters as CMNMF do. In this regard, the rationality behind the proposal of CMNMF can be verified.

Due to the advantage of CMNMF, VDA-DLCMNMF performs better than both NMF-GCN, GCN|$_{random}$| and GCN, which further indicates that initializing the representation of drugs and viruses with their latent feature vectors obtained by CMNMF provides a more effective way for VDA-DLCMNMF to discover novel VDAs. It is noted that regrading GCN|$_{random}$|⁠, its performance in terms of Acc. is the worst among all competing models for each dataset. This could be a strong indicator that for GCN without attention mechanism, its performance is prone to be influenced by the noisy in VDA networks. However, the performance of GCN is still not as good as NMF-GCN, even if when it adopts attention mechanism, a conclusion thus be made that GCN is not applicable to predict isolated nodes in a given network, such as new viruses in VDA network, due to the random initialization of node representation. On the other hand, according to the performance of VDA-DLCMNMF and NMF-GCN, the accuracy of GCN can be improved by integrating with either CMNMF or NMF, which is able to solve the cold-start problem for isolated nodes. Additionally, the performance of CMNMF and NMF is also improved with the integration of GCN that strengthens the learning ability in terms of network representation. Therefore, concerning the respective advantages of CMNMF and GCN, it is the integration of them that leads to the promising performance of VDA-DLCMNMF in drug repurposing.

3.5 Application to drug repositioning of diseases

In order to prove the robustness of the DLCMNMF, we implement it on two golden standard datasets, including Fdataset [13] and Cdataset [37], for drug repurposing of diseases. We then compare the performance of CMNMF with two cutting-edge methods DRRS [36] and BNNR [65] on two datasets, respectively. In this section, 5-fold CV is used to evaluate the performance of DLCMNMF and two baselines, and all parameters are the same as their original works. The results are shown in Table 5.

Table 5

Open in new tab

Experimental results of case study on drug repositioning of diseases

Methods\ Datasets	Fdataset					Cdataset
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRRS	0.8314	0.5241	0.8374	0.9093	0.3512	0.8345	0.5249	0.8378	0.9093	0.3489
BNNR	0.9576	0.3637	0.9638	0.9280	0.5634	0.9632	0.4236	0.9683	0.9407	0.6566
DLCMNMF	0.8541	0.9501	0.7965	0.9297	0.9090	0.8432	0.9058	0.7737	0.9501	0.9266

Methods\ Datasets	Fdataset					Cdataset
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRRS	0.8314	0.5241	0.8374	0.9093	0.3512	0.8345	0.5249	0.8378	0.9093	0.3489
BNNR	0.9576	0.3637	0.9638	0.9280	0.5634	0.9632	0.4236	0.9683	0.9407	0.6566
DLCMNMF	0.8541	0.9501	0.7965	0.9297	0.9090	0.8432	0.9058	0.7737	0.9501	0.9266

Best results are bolded.

Table 5

Open in new tab

Experimental results of case study on drug repositioning of diseases

Methods\ Datasets	Fdataset					Cdataset
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRRS	0.8314	0.5241	0.8374	0.9093	0.3512	0.8345	0.5249	0.8378	0.9093	0.3489
BNNR	0.9576	0.3637	0.9638	0.9280	0.5634	0.9632	0.4236	0.9683	0.9407	0.6566
DLCMNMF	0.8541	0.9501	0.7965	0.9297	0.9090	0.8432	0.9058	0.7737	0.9501	0.9266

Methods\ Datasets	Fdataset					Cdataset
	Acc.	Sen.	Spe.	AUC	AUPR	Acc.	Sen.	Spe.	AUC	AUPR
DRRS	0.8314	0.5241	0.8374	0.9093	0.3512	0.8345	0.5249	0.8378	0.9093	0.3489
BNNR	0.9576	0.3637	0.9638	0.9280	0.5634	0.9632	0.4236	0.9683	0.9407	0.6566
DLCMNMF	0.8541	0.9501	0.7965	0.9297	0.9090	0.8432	0.9058	0.7737	0.9501	0.9266

Best results are bolded.

Although both of DRRS and BNNR are trained on the same heterogeneous drug-disease networks, BNNR performs better than DRRS across all evaluation metrics expect Sen., and the main reason for that phenomenon is that BNNR specifically designs a relaxed penalty function to process noisy entries [65]. Regarding the performance of VDA-DLCMNMF, we note that VDA-DLCMNMF performs better by 0.17% and 35.46%, 0.94% and 27% than BNNR in terms of AUC and AUPR on Fdataset and Cdataset, respectively. Since BNNR demonstrates its ability in distinguishing negative samples as indicated by Spe., it also yields the best performance in terms of Acc.. However, for the task of drug repurposing, we are more concerned with the ability of discovering precise drug-disease associations. In this regard, VDA-DLCMNMF is preferred over BNNR, as the Sen. scores obtained by VDA -DLCMNMF are almost 60% and 48% larger than those of BNNR on FDataset and CDataset, respectively. In other words, the prediction accuracy of VDA-DLCMNMF in terms of Sen. AUC and AUPR could be a strong indicator that VDA-DLCMNMF is better in distinguishing between true positive samples and false negative samples when compared with DRRS and BNNR. Hence, we have reason to believe that VDA-DLCMNMF is also promising tool for the task of drug repurposing.

3.6 Identifying potential drugs for SARS-CoV-2

Taking SARS-CoV-2 as an example, we apply VDA-DLCMNMF to discover potential drugs that can be used to treat SARS-CoV-2 from the datasets of HDVD, VDA1 and VDA2. Specifically, for each VDA network of these datasets, we first apply VDA-DLCMNMF to obtain the probability of being associated with SARS-CoV-2 representation for each drug with (16) and then select the top 10 drugs in ascending order of probability for giving a detailed analysis. The results are shown in Table 6.

Table 6

Open in new tab

The predicted top 10 drugs associated with SARS-CoV-2 on three datasets

Datasets	Rank	Drug name	Evidence	Rank	Drug name	Evidence
HDVD	1	Remdesivir	PMID:32020029	6	Chloroquine	PMID:32074550
	2	Tenofovir	–	7	Rimantadine	PMID:31133031; PMID:15288617
	3	EIDD-2801	[53]	8	Equilin	PMID:27169275; PMID:32194980
	4	Dactinomycin	PMID:1335030; PMID:32194980	9	Camostat	PMID:22496216
	5	Ribavirin	PMID:22555152	10	Berberine	–
VDA1	1	Remdesivir	PMID:32020029	6	Indinavir	PMID:15144898
	2	Cobicistat	–	7	Camostat	PMID:22496216
	3	Mycophenolic acid	PMID:5799033	8	Tenofovir	–
	4	Ribavirin	PMID:22555152	9	FK506	–
	5	Chloroquine	PMID:32074550	10	Zanamivir	PMID:15200845
VDA2	1	Chlorpromazine	PMID:8811199	6	Quinacrine	PMID:23301007
	2	Chloroquine	PMID:32074550	7	Tenofovir	–
	3	Gemcitabine	PMID:24841273	8	Indomethacin	PMID:5284360
	4	Ribavirin	PMID:22555152	9	Camostat	PMID:22496216
	5	Favipiravir	[44]	10	Zanamivir	PMID:15200845

Datasets	Rank	Drug name	Evidence	Rank	Drug name	Evidence
HDVD	1	Remdesivir	PMID:32020029	6	Chloroquine	PMID:32074550
	2	Tenofovir	–	7	Rimantadine	PMID:31133031; PMID:15288617
	3	EIDD-2801	[53]	8	Equilin	PMID:27169275; PMID:32194980
	4	Dactinomycin	PMID:1335030; PMID:32194980	9	Camostat	PMID:22496216
	5	Ribavirin	PMID:22555152	10	Berberine	–
VDA1	1	Remdesivir	PMID:32020029	6	Indinavir	PMID:15144898
	2	Cobicistat	–	7	Camostat	PMID:22496216
	3	Mycophenolic acid	PMID:5799033	8	Tenofovir	–
	4	Ribavirin	PMID:22555152	9	FK506	–
	5	Chloroquine	PMID:32074550	10	Zanamivir	PMID:15200845
VDA2	1	Chlorpromazine	PMID:8811199	6	Quinacrine	PMID:23301007
	2	Chloroquine	PMID:32074550	7	Tenofovir	–
	3	Gemcitabine	PMID:24841273	8	Indomethacin	PMID:5284360
	4	Ribavirin	PMID:22555152	9	Camostat	PMID:22496216
	5	Favipiravir	[44]	10	Zanamivir	PMID:15200845

Table 6

Open in new tab

The predicted top 10 drugs associated with SARS-CoV-2 on three datasets

Datasets	Rank	Drug name	Evidence	Rank	Drug name	Evidence
HDVD	1	Remdesivir	PMID:32020029	6	Chloroquine	PMID:32074550
	2	Tenofovir	–	7	Rimantadine	PMID:31133031; PMID:15288617
	3	EIDD-2801	[53]	8	Equilin	PMID:27169275; PMID:32194980
	4	Dactinomycin	PMID:1335030; PMID:32194980	9	Camostat	PMID:22496216
	5	Ribavirin	PMID:22555152	10	Berberine	–
VDA1	1	Remdesivir	PMID:32020029	6	Indinavir	PMID:15144898
	2	Cobicistat	–	7	Camostat	PMID:22496216
	3	Mycophenolic acid	PMID:5799033	8	Tenofovir	–
	4	Ribavirin	PMID:22555152	9	FK506	–
	5	Chloroquine	PMID:32074550	10	Zanamivir	PMID:15200845
VDA2	1	Chlorpromazine	PMID:8811199	6	Quinacrine	PMID:23301007
	2	Chloroquine	PMID:32074550	7	Tenofovir	–
	3	Gemcitabine	PMID:24841273	8	Indomethacin	PMID:5284360
	4	Ribavirin	PMID:22555152	9	Camostat	PMID:22496216
	5	Favipiravir	[44]	10	Zanamivir	PMID:15200845

Datasets	Rank	Drug name	Evidence	Rank	Drug name	Evidence
HDVD	1	Remdesivir	PMID:32020029	6	Chloroquine	PMID:32074550
	2	Tenofovir	–	7	Rimantadine	PMID:31133031; PMID:15288617
	3	EIDD-2801	[53]	8	Equilin	PMID:27169275; PMID:32194980
	4	Dactinomycin	PMID:1335030; PMID:32194980	9	Camostat	PMID:22496216
	5	Ribavirin	PMID:22555152	10	Berberine	–
VDA1	1	Remdesivir	PMID:32020029	6	Indinavir	PMID:15144898
	2	Cobicistat	–	7	Camostat	PMID:22496216
	3	Mycophenolic acid	PMID:5799033	8	Tenofovir	–
	4	Ribavirin	PMID:22555152	9	FK506	–
	5	Chloroquine	PMID:32074550	10	Zanamivir	PMID:15200845
VDA2	1	Chlorpromazine	PMID:8811199	6	Quinacrine	PMID:23301007
	2	Chloroquine	PMID:32074550	7	Tenofovir	–
	3	Gemcitabine	PMID:24841273	8	Indomethacin	PMID:5284360
	4	Ribavirin	PMID:22555152	9	Camostat	PMID:22496216
	5	Favipiravir	[44]	10	Zanamivir	PMID:15200845

We note that 8, 7 and 9 out of the Top 10 drugs discovered in HDVD, VDA1 and VDA2, respectively, have been validated by recent publications. Among these validated drugs, Remdesivir obtains the largest probability scores in both HDVD and VDA1, and it has been recently recognized as a promising antiviral drug against a wide array of RNA viruses infection in cultured cells, mice and nonhuman primate models [39, 61]. As an adenosine analogue, Remdesivir incorporates into nascent viral RNA chains, thus resulting in the pre-mature termination. Moreover, Remdesivir is able to inhibit the viral infection of Vero-E6 cells by clinically isolating SARS-CoV-2 in an in vitro assay [61]. In the dataset of VDA2, chlorpromazine is predicted as the most likely drug for the treatment of SARS-CoV-2, and it is widely used to study virus entry by clathrin-mediated endocytosis of several viruses, including West Nile virus and influenza virus [6]. Since SARS-CoV also utilizes the clathrin-mediated endocytosis pathway for entry into host cell [6], it is possible for chlorpromazine to act similarly on MERS-CoV and SARS-CoV as a potential broad-spectrum CoV inhibitor.

It can also be observed from Table 6 that three drugs, including ribavirin, chloroquine and camostat, are found among the Top 10 drugs in all the three datasets. In particular, ribavirin is an approved antiviral drug to inhibit the production of Inosine-5|$^{^{\prime}}$|-monophosphate dehydrogenase, which interacts with the viral protein nsp14 [64]. It is for this reason that ribavirin has been recommended in the clinical practice for SARS-CoV-2 pneumonia diagnosis and Treatment Plan Edition 5-Revised [27]. As a traditional drug for the treatment of malaria, chloroquine phosphate is shown to have apparent efficacy and acceptable safety against COVID-19 associated pneumonia based on multi-center clinical trials conducted in China [12]. In addition to the ability of increasing the endosomal PH required for virus/cell fusion, Chloroquine is capable of interfering with the glycosylation of cellular receptors of SARS-CoV [29]. As a result, chloroquine is recommended in the next version of the Guidelines for the Prevention, Diagnosis, and Treatment of COVID-19 pneumonia, which is issued by the National Health Commission of the People’s Republic of China for the treatment of COVID-19 infection for larger populations in future [12]. Known as one of commercial serine protease inhibitors, Camostat partially blocks the infection of SARS-CoV [20]. Moreover, when used together with cathepsin inhibitor EST, it can effectively prevent both cell entry and the multistep growth of SARS-CoV in human Calu-3 airway epithelial cells [25, 71].

In summary, the above analysis demonstrates the promising performance of VDA-DLCMNMF in discovering potential drugs for SARS-CoV-2, as most of the Top 10 drugs predicted by VDA-DLCMNMF are found to be effective when used to treat SARS-CoV-2 according to a careful literature review. Moreover, such a high accuracy could be also a strong indicator that VDA-DLCMNMF is able to precisely discover potential drugs for a new virus.

3.7 Molecular docking experiment

To further explain the reliability of VDA-DLCMNMF, we have conducted structure-based molecular docking experiments [42] to all the drugs listed in Table 6. For each drug, we compute its intermolecular binding ability with SARS-CoV-2 spike protein or human angiotensin-converting enzyme 2 (ACE2), which are important functional receptors for SARS and other CoVs [19, 34].

Specifically, we first download the structures of SARS-CoV-2 spike receptor-binding domain bound with ACES (PDB ID: 6M0J) from RCSB Protein Data Bank [3], and the chemical structures of drugs are obtained from the DrugBank in the PDB format. After that, the PDB data of drugs are converted into pdbqt files by AutoDockTools [41]. For each drug, its pdbqt file is considered as the input of AutoDock software, with which we are able to complete the molecular docking experiment by taking the spike protein and ACE2 as receptors and each drug as a ligand of interest. The experimental results of molecular docking on all the 20 drugs in Table 6 are shown in Table 7, where the binding energies of these drugs are recorded. When using AutoDock to conduct molecular docking experiments, one should note that the binding energy is the binding free energy. For an arbitrary drug, the lower its binding energy is, the stronger its binding ability is.

Table 7

Open in new tab

Binding energies between predicted drugs and the SARS-CoV-2 spike protein/ACE2

Drug name	Binding energy (kcal/mol)	Drug name	Binding energy (kcal/mol)
Berberine	\|$-7.39$\|	Camostat	\|$-7.43$\|
Chloroquine	\|$-6.40$\|	Chlorpromazine	\|$-6.82$\|
Cobicistat	\|$-7.93$\|	Dactinomycin	\|$-2.29$\|
EIDD-2801	\|$-5.45$\|	Equilin	\|$-7.68$\|
Favipiravir	\|$-4.24$\|	FK506	\|$-9.72$\|
Gemcitabine	\|$-4.89$\|	Indinavir	\|$-8.95$\|
Indomethacin	\|$-6.43$\|	Mycophenolic acid	\|$-5.60$\|
Quinacrine	\|$-6.50$\|	Remdesivir	\|$-7.25$\|
Ribavirin	\|$-6.87$\|	Rlmantadine	\|$-6.67$\|
Tenofovir	\|$-6.44$\|	Zanamivir	\|$-5.80$\|

Drug name	Binding energy (kcal/mol)	Drug name	Binding energy (kcal/mol)
Berberine	\|$-7.39$\|	Camostat	\|$-7.43$\|
Chloroquine	\|$-6.40$\|	Chlorpromazine	\|$-6.82$\|
Cobicistat	\|$-7.93$\|	Dactinomycin	\|$-2.29$\|
EIDD-2801	\|$-5.45$\|	Equilin	\|$-7.68$\|
Favipiravir	\|$-4.24$\|	FK506	\|$-9.72$\|
Gemcitabine	\|$-4.89$\|	Indinavir	\|$-8.95$\|
Indomethacin	\|$-6.43$\|	Mycophenolic acid	\|$-5.60$\|
Quinacrine	\|$-6.50$\|	Remdesivir	\|$-7.25$\|
Ribavirin	\|$-6.87$\|	Rlmantadine	\|$-6.67$\|
Tenofovir	\|$-6.44$\|	Zanamivir	\|$-5.80$\|

Table 7

Open in new tab

Binding energies between predicted drugs and the SARS-CoV-2 spike protein/ACE2

Drug name	Binding energy (kcal/mol)	Drug name	Binding energy (kcal/mol)
Berberine	\|$-7.39$\|	Camostat	\|$-7.43$\|
Chloroquine	\|$-6.40$\|	Chlorpromazine	\|$-6.82$\|
Cobicistat	\|$-7.93$\|	Dactinomycin	\|$-2.29$\|
EIDD-2801	\|$-5.45$\|	Equilin	\|$-7.68$\|
Favipiravir	\|$-4.24$\|	FK506	\|$-9.72$\|
Gemcitabine	\|$-4.89$\|	Indinavir	\|$-8.95$\|
Indomethacin	\|$-6.43$\|	Mycophenolic acid	\|$-5.60$\|
Quinacrine	\|$-6.50$\|	Remdesivir	\|$-7.25$\|
Ribavirin	\|$-6.87$\|	Rlmantadine	\|$-6.67$\|
Tenofovir	\|$-6.44$\|	Zanamivir	\|$-5.80$\|

Drug name	Binding energy (kcal/mol)	Drug name	Binding energy (kcal/mol)
Berberine	\|$-7.39$\|	Camostat	\|$-7.43$\|
Chloroquine	\|$-6.40$\|	Chlorpromazine	\|$-6.82$\|
Cobicistat	\|$-7.93$\|	Dactinomycin	\|$-2.29$\|
EIDD-2801	\|$-5.45$\|	Equilin	\|$-7.68$\|
Favipiravir	\|$-4.24$\|	FK506	\|$-9.72$\|
Gemcitabine	\|$-4.89$\|	Indinavir	\|$-8.95$\|
Indomethacin	\|$-6.43$\|	Mycophenolic acid	\|$-5.60$\|
Quinacrine	\|$-6.50$\|	Remdesivir	\|$-7.25$\|
Ribavirin	\|$-6.87$\|	Rlmantadine	\|$-6.67$\|
Tenofovir	\|$-6.44$\|	Zanamivir	\|$-5.80$\|

We note that for Remdesivir, its binding energy with SARS-CoV-2 spike protein/ACE2 is |$-7.39$| kcal/mol while that for Chlorpromazine is |$-6.82$| kcal/mol. For ribavirin, chloroquine and camostat that are listed among the Top 10 drugs in all datasets, their binding energies are |$-6.87$| kcal/mol, |$-6.40$| kcal/mol and |$-7.43$| kcal/mol, respectively. Overall, the binding energies of these five drugs are positioned at a relatively lower level as indicated by Table 7. This finding further validates the eligibility of these drugs in treating SARS-CoV-2.

According to the Table 6, there are a total of four drugs, including tenofovir [26], Berberine [16], cobicistat [30] and FK506 [52], yet to be validated, as there is no evidence to confirm their effort for the treatment of SARS-CoV-2. Hence, we have also conducted molecular docking experiments for these four drugs and presented their binding sites in Figure 5, where the green and cyan parts denote the structures of ACE2 and SARS-CoV-2 spike protein, respectively. It is observed from Table 7 that the binding synergies of these four drugs are even lower than several validated drugs, such as favipiravir, gemcitabine and dactinomycin, thus indicating a strong association they have with SARS-CoV-2. Moreover, particular attention is given to cobicistat and FK506, which obtain lower binding energies when compared with ribavirin and camostat. In particular, FK506 has the lowest binding energy with SARS-CoV-2 spike protein/ACE2 among all the 20 drugs. Overall, we reason that the associations of these four drugs are possibly existed, but missed by laboratory experiments, and thus they are likely to have therapeutic effects against SARS-CoV-2. It also should be noted that molecular docking do not necessarily prove that the drug can treat SARS-CoV-2, the results obtained by molecular docking just provide a therapeutic possibility. Accurate results require in-depth follow-up experimental verifications.

Figure 5

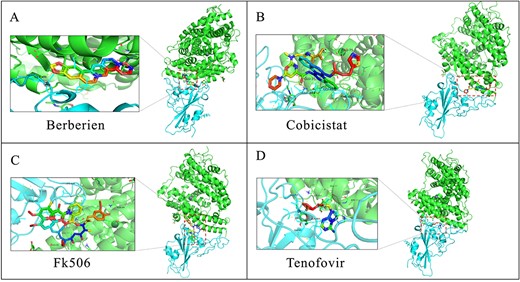
Molecular docking results for Berberine, cobicistat, FK506 and Tenofovir bound with SARS-CoV-2 spike protein/ACE2.

Open in new tab Download slide

4 Discussion and Conclusion

To facilitate the development of antiviral drugs against new diseases, we propose a novel deep learning-based method, namely VDA-DLCMNMF, for drug repurposing with CMNMF and apply it to discover novel drugs that are more likely to treat SARS-CoV-2. Regarding the drug repurposing for new viruses, the major difficulty lying in here is that there are no known associations between new viruses and existing drugs; hence, it is of great significance to effectively solve the cold-start problem. To this end, we first construct an enhanced association matrix by integrating VDAs, chemical structures of drugs and genomic sequences of viruses. After that, the CMNMF model is designed to address the cold-start problem by precisely constructing the latent feature vectors of drugs and viruses in a unified LFS from the structural and genomic perspectives. VDA-DLCMNMF then adopts a GCN with attention-based neighbor sampling to learn the representations of drugs and viruses, which are initialized with their latent feature vectors at beginning. The probability of a drug being associated with a new virus can thus be computed based on their final representations. Extensive experiments have been conducted to evaluate the performance of VDA-DLCMNMF, and their results demonstrate the superior accuracy of VDA-DLCMNMF on three datasets created for SARS-CoV-2 when comparing it with several state-of-the-art drug repurposing methods. Moreover, for each dataset, most of the top 10 drugs predicted by VDA-DLCMNMF are validated by literature review. Even for those without any evidence, the results of molecular docking, to some extent, indicate their potential ability in treating SARS-CoV-2.

There are several reasons to explain the success of VDA-DLCMNMF in drug repurposing for SARS-CoV-2. First of all, the selection of proper biological knowledge of drugs and viruses, as well as how to process them, provides a solid basis for the following steps of VDA-DLCMNMF. Obviously, it is impossible for existing drug repurposing methods to discover novel VDAs of new viruses if without any other source of information about viruses, especially in an effort to discover potential drugs for new viruses. To this end, we make use of the chemical structures of drugs and the genomic sequences of viruses, and integrate them into a given VDA network for the purpose of constructing an enhanced association matrix. With such a matrix, we are able to strengthen our perception about the formation of VDAs involving new viruses, which is that similar viruses are more likely to be associated with the same drugs. Moreover, as indicated by [38], it is the integration with the biological knowledge of drugs and viruses that offers us an alternative view to improve the quality of VDA networks.

Second, our experimental results reveal that the fundamental reason accounting for the failure of existing network-based models is the lack of such an ability that precisely captures the characteristics of drugs and viruses, which are used to govern VDA networks respectively from the structural and genomic perspectives. Besides, the cold-start problem introduced by new viruses can also be addressed by properly capturing the characteristics of new viruses. In this regard, we develop the CMNMF model modified from traditional NMF. For the CMNMF model, its main purpose is to reconstruct the enhanced association matrix, rather than the original VDA matrix, by using the latent features of drugs and viruses. Moreover, additional constraints are defined from different views, thus ensuring that the similarity information of drugs and viruses are completely projected onto a unified LFS. An extra benefit of doing so is to avoid the noisy information generated after projection, such as the unexpected similarity between drugs and viruses. According to experimental results, the CMNMF model plays a critical role in contributing to the promising performance of CMNMF.

Last, but not least, VDA-DLCMNMF takes advantage of the powerful representation ability of GCN to learn the representations of drugs and viruses from a given VDA matrix. There are three points worth noting: (i) since GCN only accepts the adjacency matrix as input, we could not be able to apply the enhanced association matrix to GCN; (ii) instead of randomly initializing the representation of drugs and viruses, we use their latent feature vectors obtained with CMNMF to complete the initialization task; (iii) to accelerate the training of GCN, we adopt a heuristic neighborhood sampling strategy, which updates the representation of a virus, or a drug, by only using a part of viruses, or drugs, with high quality as indicated by their attention weights; and (iv) VDA-DLCMNMF integrates an attention mechanism into GCN, thus enhancing the information granularity by combining the latent features of drugs and viruses with the topological feature of VDA network.

Though experimental results indicate that VDA-DLCMNMF is a promising tool for repurposing drugs for new viruses, there is still room for further improvement. Specifically, we would like to adapt different solutions, such as variational inference [21, 54] and reparameterization techniques [43], to address the CMNMF model in a more efficient manner. Furthermore, as our future work, we are interested in exploring the possibility of using more biological knowledge, such as intracellular gene regulatory networks [7], drug–drug interactions [69] and drug–disease interactions [57], to construct complex heterogeneous networks and also using higher-order structures [22, 23] to enrich the representations of drugs and viruses.

Key Points

An enhance association matrix is designed by integrating chemical structures of drugs and the genomic sequences of viruses into a given VDA network, thus strengthening our perception about the potential drugs that new viruses are more likely to associate with.
We propose a novel CMNMF model to address the cold-start problem related to new viruses by reconstructing the enhance association matrix with the constraints from different views. The similarity information of drugs and viruses can thus be completely projected onto a unified latent feature space.
We develop a drug repositioning model, namely VDA-DLCMNMF, to identify potential drugs for new viruses with GCN. The latent feature vectors learned from CMNMF are used as the initial representations of drugs and viruses. VDA-DLCMNMF also adopts an attention-based neighbor sampling strategy to train GCN for drug repurposing.
Experimental results on three VDA datasets demonstrate the promising performance of VDA-DLCMNMF in repurposing antiviral drugs against SARS-CoV-2. Four novel drugs identified by our method are proved to have the potential ability to bind with important functional receptors of SARS-CoV-2.

5 Data availability

The dataset and source code can be freely downloaded from https://github.com/Blair1213/DLMNMF.

6 Author contributions statement

X.S., L.H. and L.W. conceived the experiments; X.S. and L.H. conducted the experiments; Z.Y. and B.Z. analyzed the results.

Acknowledgments

The authors would like to thank colleagues and the anonymous reviewers who have provided valuable feedback to help improve the paper.

Funding

This work was supported in part by the Natural Science Foundation of Xinjiang Uygur Autonomous Region (2021D01D05), in part by the Pioneer Hundred Talents Program of Chinese Academy of Sciences, in part by the National Natural Science Foundation of China (62172355), in part by the Awardee of the NSFC Excellent Young Scholars Program (61722212), in part by the Science and Technology Innovation 2030-New Generation Artificial Intelligence Major Project (2018AAA0100100) and the Tianshan youth-Excellent Youth (2019Q029).

Xiaorui Su is a doctoral student in Xinjiang Technical Institute of Physics and Chemistry, Chinese Academy of Science, Urumqi, China. Her research interests include machine learning, network representation learning, computational biology and bioinformatics.

Lun Hu, PhD, is a professor in Xinjiang Technical Institute of Physics & Chemistry, Chinese Academy of Science, Urumqi, China. His research interests include machine learning, big data analysis and its applications in bioinformatics.

Zhuhong You, PhD, is a professor in School of Computer Science, Northwestern Polytechnical University, Xi’an, China. His research interests include neural networks, intelligent information processing, sparse representation and its applications in bioinformatics.

Pengwei Hu, PhD, is a professor in Xinjiang Technical Institute of Physics & Chemistry, Chinese Academy of Science, Urumqi, China. His research interests include machine learning, big data analysis and its applications in bioinformatics.

Lei Wang, PhD, is a professor in Big Data and Intelligent Computing Research Center, Guangxi Academy of Science, Nanning, China. His research interests include data mining, pattern recognition, machine learning, deep learning, computational biology and bioinformatics.

Bowei Zhao now is a doctoral student in Xinjiang Technical Institute of Physics and Chemistry, Chinese Academy of Science, Urumqi, China. His research interests include machine learning, complex networks analysis, graph neural network and their applications in bioinformatics.

References

1.

Alonso

H

,

Bliznyuk

AA

,

Gready

JE

.

Combining docking and molecular dynamic simulations in drug design

.

Med Res Rev

2006

;

26

(

5

):

531

–

68

.

2.

Petter

I

,

Andersen

AI

,

Lysvand

H

, et al.

Discovery and development of safe-in-man broad-spectrum antiviral agents

.

Int J Infect Dis

2020

;

93

:

268

–

76

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

3.

Berman

HM

,

Westbrook

J

,

Feng

Z

, et al.

The protein data bank

.

Nucleic Acids Res

2000

;

28

(

1

):

235

–

42

.

4.

Bosch

BJ

,

Martina

BEE

,

Van Der Zee

R

, et al. (eds).

Severe acute respiratory syndrome coronavirus (SARS-CoV) infection inhibition using spike protein heptad repeat-derived peptides

.

Proc Natl Acad Sci USA

2004

;

101

(

22

):

8455

–

60

.

5.

Canese

K

,

Weis

S

.

PubMed: the bibliographic database

.

NCBI Handbook

2013

;

2

:

1

.

Google Scholar

OpenURL Placeholder Text

WorldCat

6.

Chamoun-Emanuelli

AM

,

Pecheur

EI

,

Simeon

RL

, et al.

Phenothiazines inhibit hepatitis c virus entry, likely by increasing the fluidity of cholesterol-rich membranes

.

Antimicrob Agents Chemother

2013

;

57

(

6

):

2571

–

81

.

7.

Cheng

J

,

Zhang

J

,

Zhongdao

W

, et al.

Inferring microenvironmental regulation of gene expression from single-cell RNA sequencing data using scMLnet with an application to COVID-19

.

Brief Bioinform

2021

;

22

(

2

):

988

–

1005

.

8.

De Groot

RJ

,

Baker

SC

,

Baric

RS

, et al.

Commentary: middle east respiratory syndrome coronavirus (MERS-CoV): announcement of the coronavirus study group

.

J Virol

2013

;

87

(

14

):

7790

–

2

.

9.

Dotolo

S

,

Marabotti

A

,

Facchiano

A

, et al.

A review on drug repurposing applicable to COVID-19

.

Brief Bioinform

2020

;

1

–

16

.

Google Scholar

OpenURL Placeholder Text

WorldCat

10.

Fraser

C

,

Donnelly

CA

,

Cauchemez

S

, et al.

Pandemic potential of a strain of influenza a (h1n1): early findings

.

Science

2009

;

324

(

5934

):

1557

–

61

.

11.

Haitao

F

,

Huang

F

,

Liu

X

, et al.

MVGCN: data integration through multi-view graph convolutional network for predicting links in biomedical bipartite networks

.

Bioinformatics

2021

. https://doi.org/10.1093/bioinformatics/btab651.

Google Scholar

OpenURL Placeholder Text

WorldCat

12.

Gao

J

,

Tian

Z

,

Yang

X

.

Breakthrough: chloroquine phosphate has shown apparent efficacy in treatment of COVID-19 associated pneumonia in clinical studies

.

Biosci Trends

2020

;

14

(

1

):

1

–

11

.

13.

Gottlieb

A

,

Stein

GY

,

Ruppin

E

, et al.

PREDICT: a method for inferring novel drug indications with application to personalized medicine

.

Mol Syst Biol

2011

;

7

(

1

):

496

.

14.

Grover

A

,

Leskovec

J

.

node2vec: scalable feature learning for networks

. In:

Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining

. San Francisco California USA: ACM Digital Library,

2016

,

855

–

64

.

15.

Guan

W-j

,

Zheng-yi Ni

YH

,

Liang

W-h

, et al.

Clinical characteristics of coronavirus disease 2019 in China

.

N Engl J Med

2020

;

382

(

18

):

1708

–

20

.

16.

Hahn

FE

,

Ciak

J

.

Berberine

. In:

Mechanism of Action of Antimicrobial and Antitumor Agents

.

Springer

,

1975

,

577

–

84

.

17.

He

T

,

Bai

L

,

Y-S

.

Vicinal vertex allocation for matrix factorization in networks

.

IEEE Trans Cybernet

2021

;1–14.

Google Scholar

OpenURL Placeholder Text

WorldCat

18.

He

T

,

Liu

Y

,

Ko

TH

, et al.

Contextual correlation preserving multiview featured graph clustering

.

IEEE Trans Cybernet

2019

;

50

(

10

):

4318

–

31

.

Google Scholar

Crossref

WorldCat

19.

Hoffmann

M

,

Kleine-Weber

H

,

Krüger

N

, et al.

The novel coronavirus 2019 (2019-nCoV) uses the SARS-coronavirus receptor ACE2 and the cellular protease TMPRSS2 for entry into target cells

.

BioRxiv

2020

.

Google Scholar

OpenURL Placeholder Text

WorldCat

20.

Hoffmann

M

,

Kleine-Weber

H

,

Schroeder

S

, et al.

SARS-CoV-2 cell entry depends on ACE2 and TMPRSS2 and is blocked by a clinically proven protease inhibitor

.

Cell

2020

;

181

(

2

):

271

–

80

.

21.

Lun

H

,

Chan

KCC

,

Yuan

X

, et al.

A variational Bayesian framework for cluster analysis in a complex network

.

IEEE Trans Knowl Data Eng

2020

;

32

(

11

):

2115

–

28

.

Google Scholar

OpenURL Placeholder Text

WorldCat

22.

Hu

L

,

Pan

X

,

Yan

H

, et al.

Exploiting higher-order patterns for community detection in attributed graphs

.

Integr Comput-Aided Eng

2021

;

28

:

1

–

12

.

Preprint

.

Google Scholar

Crossref

WorldCat

23.

Lun

H

,

Zhang

J

,

Pan

X

, et al.

HiSCF: leveraging higher-order structures for clustering analysis in biological networks

.

Bioinformatics

2021

;

37

(

4

):

542

–

50

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

24.

Katoh

K

,

Standley

DM

.

Mafft multiple sequence alignment software version 7: improvements in performance and usability

.

Mol Biol Evol

2013

;

30

(

4

):

772

–

80

.

25.

Kawase

M

,

Shirato

K

,

van der Hoek

L

, et al.

Simultaneous treatment of human bronchial epithelial cells with serine and cysteine protease inhibitors prevents severe acute respiratory syndrome coronavirus entry

.

J Virol

2012

;

86

(

12

):

6537

–

45

.

26.

Kearney

BP

,

Flaherty

JF

,

Shah

J

.

Tenofovir disoproxil fumarate

.

Clin Pharmacokinet

2004

;

43

(

9

):

595

–

612

.

27.

Khalili

JS

,

Zhu

H

,

Mak

NSA

, et al.

Novel coronavirus treatment with ribavirin: groundwork for an evaluation concerning COVID-19

.

J Med Virol

2020

;

92

(

7

):

740

–

6

.

28.

Kipf

TN

,

Welling

M

.

Semi-supervised classification with graph convolutional networks

.

2016

.

Preprint arXiv:1609.02907

.

29.

Ledford

H

.

Chloroquine hype is derailing the search for coronavirus treatments

.

Nature

2020

;

580

(

7805

):

573

–

4

.

30.

Lepist

E-I

,

Phan

TK

,

Roy

A

, et al.

Cobicistat boosts the intestinal absorption of transport substrates, including HIV protease inhibitors and GS-7340, in vitro

.

Antimicrob Agents Chemother

2012

;

56

(

10

):

5409

–

13

.

31.

Li

J

,

Zheng

S

,

Chen

B

, et al.

A survey of current trends in computational drug repositioning

.

Brief Bioinform

2016

;

17

(

1

):

2

–

12

.

32.

Li

L

,

Gao

Z

,

Wang

Y-T

, et al.

SCMFMDA: predicting microRNA-disease associations based on similarity constrained matrix factorization

.

PLoS Comput Biol

2021

;

17

(

7

):

e1009165

.

33.

Li

M

,

Zhang

W

.

PHIAF: prediction of phage-host interactions with GAN-based data augmentation and sequence-based feature fusion

.

Brief Bioinform

2021

. https://doi.org/10.1093/bib/bbab348.

Google Scholar

OpenURL Placeholder Text

WorldCat

34.

Li

W

,

Moore

MJ

,

Vasilieva

N

, et al.

Angiotensin-converting enzyme 2 is a functional receptor for the SARS coronavirus

.

Nature

2003

;

426

(

6965

):

450

–

4

.

35.

Lijun

C

,

Lu

C

,

Xu

J

, et al.

Drug repositioning based on the heterogeneous information fusion graph convolutional network

.

Brief Bioinform

2021

;

22

(6):bbab319.

Google Scholar

OpenURL Placeholder Text

WorldCat

36.

Luo

H

,

Li

M

,

Wang

S

, et al.

Computational drug repositioning using low-rank matrix approximation and randomized algorithms

.

Bioinformatics

2018

;

34

(

11

):

1904

–

12

.

37.

Luo

H

,

Wang

J

,

Li

M

, et al.

Drug repositioning based on comprehensive similarity measures and bi-random walk algorithm

.

Bioinformatics

2016

;

32

(

17

):

2664

–

71

.

38.

Lv

H

,

Shi

L

,

Berkenpas

JW

, et al.

Application of artificial intelligence and machine learning for COVID-19 drug discovery and vaccine design

.

Brief Bioinform

2021

;

22

(6):bbab320.

Google Scholar

OpenURL Placeholder Text

WorldCat

39.

Malin

JJ

,

Suárez

I

,

Priesner

V

, et al.

Remdesivir against COVID-19 and other viral diseases

.

Clin Microbiol Rev

2020

;

34

(

1

):

e00162

–

20

.

40.

Meng

Y

,

Jin

M

,

Tang

X

, et al.

Drug repositioning based on similarity constrained probabilistic matrix factorization: COVID-19 as a case study

.

Appl Soft Comput

2021

;

103

:

107135

.

41.

Morris

GM

,

Huey

R

,

Lindstrom

W

, et al.

Autodock4 and autodocktools4: automated docking with selective receptor flexibility

.

J Comput Chem

2009

;

30

(

16

):

2785

–

91

.

42.

Morris

GM

,

Lim-Wilby

M

.

Molecular docking

. In:

Molecular Modeling of Proteins

.

Springer

,

2008

,

365

–

82

.

43.

Mostafa

H

,

Wang

X

.

Parameter efficient training of deep convolutional neural networks by dynamic sparse reparameterization

. In:

International Conference on Machine Learning

.

PMLR

,

2019

,

4646

–

55

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

44.

Naydenova

K

,

Muir

KW

,

Wu

L-F

, et al.

Structure of the SARS-CoV-2 RNA-dependent RNA polymerase in the presence of favipiravir-RTP

.

Proc Natl Acad Sci USA

2021

;

118

(

7

).

Google Scholar

OpenURL Placeholder Text

WorldCat

45.

O’Boyle

NM

,

Banck

M

,

James

CA

, et al.

Open Babel: an open chemical toolbox

.

J Chem

2011

;

3

(

1

):

1

–

14

.

Google Scholar

OpenURL Placeholder Text

WorldCat

46.

Pang

J

,

Huang

Y

,

Xie

Z

, et al.

Collaborative city digital twin for the COVID-19 pandemic: a federated learning solution

.

Tsinghua Sci Technol

2021

;

26

(

5

):

759

–

71

.

Google Scholar

Crossref

WorldCat

47.

Peng

L

,

Shen

L

,

Junlin

X

, et al.

Prioritizing antiviral drugs against SARS-CoV-2 by integrating viral complete genome sequences and drug chemical structures

.

Sci Rep

2021

;

11

(

1

):

1

–

11

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

48.

Perozzi

B

,

Al-Rfou

R

,

Skiena

S

.

DeepWalk: online learning of social representations

. In:

Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining

. New York USA: ACM Digital Library,

2014

,

701

–

10

.

49.

Pinzi

L

,

Rastelli

G

.

Molecular docking: shifting paradigms in drug discovery

.

Int J Mol Sci

2019

;

20

(

18

):4331.

Google Scholar

OpenURL Placeholder Text

WorldCat

50.

Sayers

EW

,

Beck

J

,

Bolton

EE

, et al.

Database resources of the national center for biotechnology information

.

Nucleic Acids Res

2021

;

49

(

D1

):

D10

.

51.

Scarselli

F

,

Gori

M

,

Tsoi

AC

, et al.

The graph neural network model

.

IEEE Trans Neural Netw

2008

;

20

(

1

):

61

–

80

.

52.

Schreiber

SL

,

Crabtree

GR

.

The mechanism of action of cyclosporin A and FK506

.

Immunol Today

1992

;

13

(

4

):

136

–

42

.

53.

Sheahan

TP

,

Sims

AC

,

Zhou

S

, et al.

An orally bioavailable broad-spectrum antiviral inhibits SARS-CoV-2 and multiple endemic, epidemic and bat coronavirus

.

Biorxiv

2020

.

Google Scholar

OpenURL Placeholder Text

WorldCat

54.

Shen

X

,

Yi

B

,

Liu

H

, et al.

Deep variational matrix factorization with knowledge embedding for recommendation system

. In:

IEEE Transactions on Knowledge and Data Engineering

. IEEE Xplore,

2019

.

55.

Sohrabi

C

,

Alsafi

Z

,

O’neill

N

, et al.

World health organization declares global emergency: a review of the 2019 novel coronavirus (COVID-19)

.

Int J Surg

2020

;

76

:

71

–

6

.

56.

Xiaorui

S

,

You

Z

,

Wang

L

, et al.

SANE: a sequence combined attentive network embedding model for COVID-19 drug repositioning

.

Appl Soft Comput

2021

;

111

:107831.

Google Scholar

OpenURL Placeholder Text

WorldCat

57.

Xiaorui

S

,

You

Z

,

Yi

H

.

Prediction of LncRNA-disease associations based on network representation learning

. In:

2020 IEEE International Conference on Bioinformatics and Biomedicine (BIBM)

.

IEEE

,

2020

,

1805

–

12

.

Google Scholar

Google Preview

OpenURL Placeholder Text

WorldCat

58.

Tang

X

,

Cai

L

,

Meng

Y

, et al.

Indicator regularized non-negative matrix factorization method-based drug repurposing for COVID-19

.

Front Immunol

2021

;

11

:

3824

.

Google Scholar

OpenURL Placeholder Text

WorldCat

59.

Van der Maaten

L

,

Hinton

G

.

Visualizing data using t-SNE

.

J Mach Learn Res

2008

;

9

(

11

):

2579

–

605

.

Google Scholar

OpenURL Placeholder Text

WorldCat

60.

Vidal

D

,

Thormann

M

,

Pons

M

.

Lingo, an efficient holographic text based method to calculate biophysical properties and intermolecular similarities

.

J Chem Inf Model

2005

;

45

(

2

):

386

–

93

.

61.

Wang

M

,

Cao

R

,

Zhang

L

, et al.

Remdesivir and chloroquine effectively inhibit the recently emerged novel coronavirus (2019-nCoV) in vitro

.

Cell Res

2020

;

30

(

3

):

3

.

Google Scholar

PubMed

OpenURL Placeholder Text

WorldCat

62.

Weininger

D

.

Smiles, a chemical language and information system. 1. Introduction to methodology and encoding rules

.

J Chem Inf Comput Sci

1988

;

28

(

1

):

31

–

6

.

Google Scholar

Crossref

WorldCat

63.

Wishart

DS

,

Feunang

YD

,

Guo

AC

, et al.

Drugbank 5.0: a major update to the DrugBank database for 2018

.

Nucleic Acids Res

2018

;

46

(

D1

):

D1074

–

82

.

64.

Wittine

K

,

Babić

MS

,

Makuc

D

, et al.

Novel 1, 2, 4-triazole and imidazole derivatives of l-ascorbic and imino-ascorbic acid: synthesis, anti-HCV and antitumor activity evaluations

.

Bioorg Med Chem

2012

;

20

(

11

):

3675

–

85

.

65.

Yang

M

,

Luo

H

,

Li

Y

, et al.

Drug repositioning based on bounded nuclear norm regularization

.

Bioinformatics

2019

;

35

(

14

):

i455

–

63

.

66.

Yu

Z

,

Huang

F

,

Zhao

X

, et al.

Predicting drug–disease associations through layer attention graph convolutional network

.

Brief Bioinform

2021

;

22

(

4

):

bbaa243

.

67.

Zeng

X

,

Zhu

S

,

Weiqiang

L

, et al.

Target identification among known drugs by deep learning from heterogeneous networks

.

Chem Sci

2020

;

11

(

7

):

1775

–

97

.

68.

Zhang

S

,

Tong

H

,

Jiejun

X

, et al.

Graph convolutional networks: a comprehensive review

.

Comput Social Netw

2019

;

6

(

1

):

1

–

23

.

Google Scholar

Crossref

WorldCat

69.

Zhang

T

,

Leng

J

,

Liu

Y

.

Deep learning for drug–drug interaction extraction from the literature: a review

.

Brief Bioinform

2020

;

21

(

5

):

1609

–

27

.

70.

Zhou

L

,

Wang

J

,

Liu

G

, et al.

Probing antiviral drugs against SARS-CoV-2 through virus-drug association prediction based on the KATZ method

.

Genomics

2020

;

112

(

6

):

4427

–

34

.

71.

Zhou

Y

,

Vedantham

P

,

Lu

K

, et al.

Protease inhibitors targeting coronavirus and filovirus entry

.

Antiviral Res

2015

;

116

:

76

–

84

.

72.

Zhu

N

,

Zhang

D

,

Wang

W

, et al.

A novel coronavirus from patients with pneumonia in China, 2019

.

N Engl J Med

2020

;

382

:727–33.

Google Scholar

OpenURL Placeholder Text

WorldCat

This article is published and distributed under the terms of the Oxford University Press, Standard Journals Publication Model (https://dbpia.nl.go.kr/journals/pages/open_access/funder_policies/chorus/standard_publication_model)

Download all slides

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

Methods\ Datasets	HDVD	VDA1	VDA2
IRNMFVDA	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|	\|$\alpha = \beta = 0.8, \lambda _1 = \lambda _2 = 0.1$\|
SCPMF	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|	\|$\lambda _{W} = \lambda _{H} = 1, \lambda _{1} = \lambda _{2} = 0.1$\|
VDA-KATZ	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5,$\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|	\|$\beta = 0.04, w = 0.9, \gamma _{v} = \gamma _{d} = 2.5 $\|
VDA-RWR	\|$r = 0.5, \mu = 0.7, \alpha = 0.7 $\|	\|$r = 0.7, \mu = 0.9, \alpha = 0.5 $\|	\|$r = 0.5, \mu = 0.9, \alpha = 0.9 $\|
VDA-DLCMNMF	\|$\alpha = \beta = 0.003, \lambda _{W} = \lambda _{H} = 0.005$\|	\|$\alpha = \beta = 0.005, \lambda _{W} = \lambda _{H} = 0.1$\|	\|$\alpha = \beta = 0.002, \lambda _{W} = \lambda _{H} = 0.1$\|

Month:	Total Views:
December 2021	50
January 2022	176
February 2022	25
March 2022	38
April 2022	25
May 2022	33
June 2022	13
July 2022	30
August 2022	24
September 2022	22
October 2022	19
November 2022	21
December 2022	17
January 2023	26
February 2023	15
March 2023	17
April 2023	17
May 2023	9
June 2023	38
July 2023	29
August 2023	16
September 2023	16
October 2023	15
November 2023	13
December 2023	21
January 2024	82
February 2024	74
March 2024	91
April 2024	81
May 2024	72
June 2024	54
July 2024	55
August 2024	55
September 2024	57
October 2024	57
November 2024	51
December 2024	37
January 2025	39
February 2025	35
March 2025	63
April 2025	46
May 2025	20

Article Contents

A deep learning method for repurposing antiviral drugs against new viruses via multi-view nonnegative matrix factorization and its application to SARS-CoV-2

Abstract

1 Introduction

2 Materials and Methods

2.1 VDA datasets

2.2 Enhanced VDA matrix construction

2.3 The CMNMF model

2.4 GCN-based drug repurposing

2.5 Complexity analysis

3 Results

3.1 Evaluation metrics and experimental settings

3.2 Performance comparison of different methods

3.3 De novo VDA prediction

3.4 Ablation study

3.5 Application to drug repositioning of diseases

3.6 Identifying potential drugs for SARS-CoV-2

3.7 Molecular docking experiment

4 Discussion and Conclusion

5 Data availability

6 Author contributions statement

Acknowledgments

Funding

References

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

Article Contents

A deep learning method for repurposing antiviral drugs against new viruses via multi-view nonnegative matrix factorization and its application to SARS-CoV-2 Free

Abstract

1 Introduction

2 Materials and Methods

2.1 VDA datasets

2.2 Enhanced VDA matrix construction

2.3 The CMNMF model

2.4 GCN-based drug repurposing

2.5 Complexity analysis

3 Results

3.1 Evaluation metrics and experimental settings

3.2 Performance comparison of different methods

3.3 De novo VDA prediction

3.4 Ablation study

3.5 Application to drug repositioning of diseases

3.6 Identifying potential drugs for SARS-CoV-2

3.7 Molecular docking experiment

4 Discussion and Conclusion

5 Data availability

6 Author contributions statement

Acknowledgments

Funding

References

Citations

Views

Altmetric

Email alerts

Citing articles via

Latest

Most Read

Most Cited

This Feature Is Available To Subscribers Only

A deep learning method for repurposing antiviral drugs against new viruses via multi-view nonnegative matrix factorization and its application to SARS-CoV-2